Равновеликие фигуры

Цели урока: Повторить тему «Площадь параллелограмма». Вывести формулу площади треугольник, ввести понятие равновеликих фигур. Решение задач по теме «Площади равновеликих фигур».

Ход урока

I. Повторение.

1) Устно по готовому чертежу вывести формулу площади параллелограмма.

2) Какова зависимость между сторонами параллелограмма и высотами, опущенными на них?

(по готовому чертежу)

зависимость обратно пропорциональная.

3) Найти вторую высоту (по готовому чертежу)

4) Найти площадь параллелограмма по готовому чертежу.

Решение:

5) Сравните площади параллелограммов S1, S2, S3

. (Они имеют равные площади, у всех основание a и высота h).

Определение: Фигуры, имеющие равные площади, называются равновеликими.

II. Решение задач.

1) Доказать, что всякая прямая, проходящая через точку пересечения диагоналей, делит его на 2 равновеликие части.

Решение:

2) В параллелограмме ABCD CF и CE высоты. Доказать, что AD ∙ CF = AB ∙ CE.

 

3) Дана трапеция с основаниями a и 4a. Можно ли через одну из её вершин провести прямые, разбивающие трапецию на 5 равновеликих треугольников?

 

Решение: Можно. Все треугольники равновеликие.

4) Доказать, что если на стороне параллелограмма взять точку A и соединить её с вершинами, то площадь получившегося треугольника ABC равна половине площади параллелограмма.

Решение:

5) Торт имеет форму параллелограмма. Малыш и Карлсон делят его так: Малыш указывает на поверхности торта точку, а Карлсон по прямой, проходящей через эту точку, разрезает торт на 2 куска и один из кусков забирает себе. Каждый хочет получить кусок побольше. Где Малыш должен поставить точку?

Решение: В точке пересечения диагоналей.

6) На диагонали прямоугольника выбрали точку и провели через неё прямые, параллельные сторонам прямоугольника. По разные стороны образовались 2 прямоугольника. Сравните их площади.

 

Решение:

III. Изучение темы «Площадь треугольника»

начать с задачи:

«Найти площадь треугольника, у которого основание a, а высота h».

 

 

Ребята, используя понятие равновеликих фигур, доказывают теорему.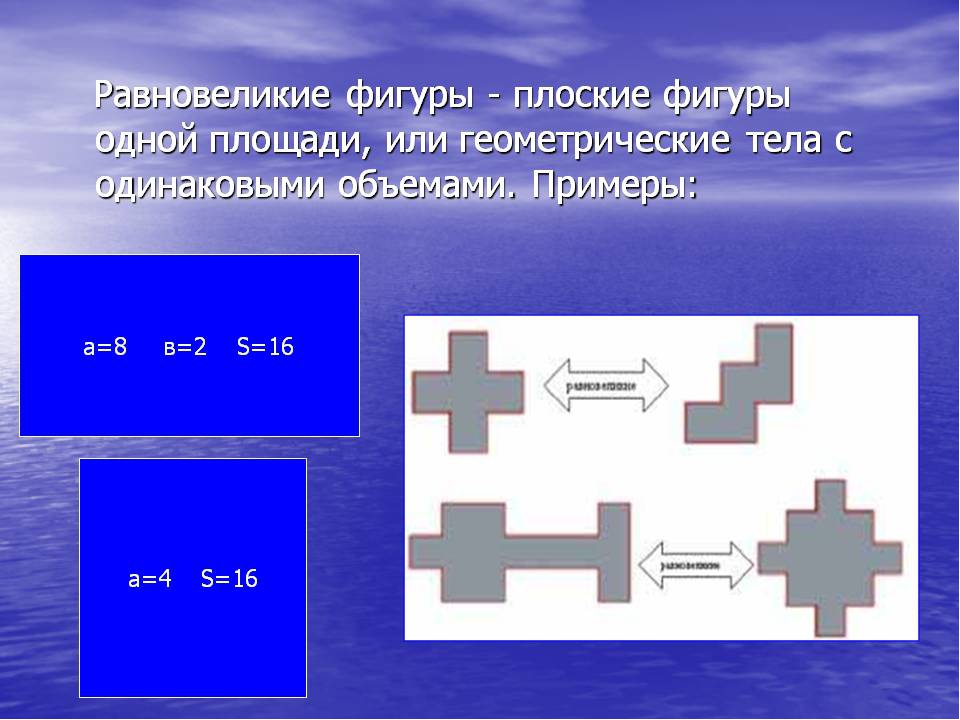

Достроим треугольник до параллелограмма.

Площадь треугольника равна половине площади параллелограмма.

Задание: Начертите равновеликие треугольники. 

Используется модель (из бумаги вырезаны 3 цветных треугольника и склеены у оснований).

Упражнение №474. «Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой».

У треугольников одинаковые основания a и одна и та же высота h. Треугольники имеют одинаковую площадь

Вывод: Фигуры, имеющие равные площади, называются равновеликими.

Вопросы к классу:

1. Равновелики ли равные фигуры?
2. Сформулируйте обратное утверждение. Верно ли оно?
3. Верно ли:
   а) Равносторонние треугольники равновелики?
   б) Равносторонние треугольники с равными сторонами равновелики?
   в) Квадраты с равными сторонами равновелики?
   г) Докажите, что параллелограммы, образованные при пересечении двух полос одинаковой ширины под разными углами наклона друг к другу, равновелики. Найдите параллелограмм наименьшей площади, образующийся при пересечении двух полос одинаковой ширины. (Показать на модели: полоски одинаковой ширины)

IV. Шаг вперёд!

На доске написаны задания по выбору:

1. «Разрежьте треугольник двумя прямыми линиями так, чтобы можно было из частей сложить прямоугольник».

Решение:

 

2. «Разрежьте прямоугольник по прямой линии на 2 части, из которых можно сложить прямоугольный треугольник».

Решение:

3) В прямоугольнике проведена диагональ. В одном из получившихся треугольников проведена медиана. Найдите соотношения между площадями фигур .

Решение:

 

Ответ:

3.

Из олимпиадных задач:

«В четырёхугольнике ABCD точка E- середина AB, соединена с вершиной D, а F – середина CD, с вершиной B. Доказать, что площадь четырёхугольника EBFD в 2 раза меньше площади четырёхугольника ABCD.

Решение: провести диагональ BD.

Упражнение №475.

«Начертите треугольник ABC. Через вершину В проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади».

Использовать теорему Фалеса (разделить АC на 3 равные части).

V. Задача дня.

Для неё отвела крайнюю правую часть доски, на которой пишу задачу сегодняшнего дня. Ребята могут решать её, а могут и не решать. На уроке данную задачу мы сегодня не решаем. Просто те, кому они интересны, могут списать её, решить её дома или в перемену. Обычно уже в перемену многие ребята начинают решать задачу, если решили, то показывают решение, и я фиксирую это в специальной таблице.

На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача).

«В параллелограмме вырезан параллелограмм. Разделите оставшуюся часть на 2 равновеликие фигуры».

Решение: Секущая AB проходит через точку пересечения диагоналей параллелограммов O и O1.

Дополнительные задачи (из олимпиадных задач):

1) «В трапеции ABCD (AD || BC) вершины A и B соединены с точкой M – серединой стороны CD. Площадь треугольника ABM равна m. Найти площадь трапеции ABCD».

Решение:

Треугольники ABM и AMK – равновеликие фигуры, т.к. AM – медиана.

S_∆ABK = 2m, ∆BCM = ∆MDK, S_ABCD = S_∆ABK = 2m.

Ответ: S_ABCD = 2m.

2) «В трапеции ABCD (AD || BC) диагонали пересекаются в точке O. Доказать, что треугольники AOB и COD равновеликие».

Решение:

S_∆BCD = S_∆ABC, т.к. у них общее основание BC и одинаковая высота.

3) Сторона АВ произвольного треугольника АВС продолжена за вершину В так, что ВР = АВ, сторону АС за вершину А так, что АМ = СА, сторону ВС за вершину С так, что КС = ВС. Во сколько раз площадь треугольника РМК больше площади треугольника АВС?

Решение:

В треугольнике

МВС: МА = АС, значит, площадь треугольника ВАМ равна площади треугольника АВС. В треугольнике АРМ: ВР = АВ, значит, площадь треугольника ВАМ равна площади треугольника АВР. В треугольнике АРС: АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК: ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК: ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,

Ответ: Площадь треугольника МРК в 7 раз больше площади треугольника АВС.

4) Сцепленные параллелограммы.

2 параллелограмма расположены так, как показано на рисунке: они имеют общую вершину и ещё по одной вершине у каждого из параллелограммов лежит на сторонах другого параллелограмма. Доказать, что площади параллелограммов равны.

Решение:

 и , значит,

Список использованной литературы:

1. Учебник «Геометрия 7-9» (авторы Л. С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев (Москва, «Просвещение», 2003).
2. Олимпиадные задачи разных лет, в частности из учебного пособия «Лучшие задачи математических олимпиад» (составитель А.А. Корзняков, Пермь, «Книжный мир», 1996).
3. Подборка задач, накопленных за много лет работы.

Приложение.

Какие фигуры называют разными. Равновеликие фигуры

Цель: формирование понятия “равные фигуры”.

• сформировать способность к фиксированию понятия “равные фигуры”, к фиксированию умения нахождения равных фигур;
• развивать математическую речь, геометрическое мышление; тренировать мыслительные операции;
• совершенствовать навыка счета в пределах 9;
• воспитывать в учащихся дисциплинированность, умение совместной деятельности.

Ход урока

1. Организационный момент

Вступительное слово учителя.

Пираты — это морские разбойники, главной их цель всегда была поиск клада. Мы будем добрыми пиратами и отправимся в морское путешествие на поиски нашего клада. Мне в руки попала старинная пиратская карта.

Она очень запутанная, на ней отмечено множество островов, чтобы запутать искателей, но нужно попасть на остров, на котором спрятаны сокровища. Чтобы его найти, нам нужно будет преодолеть множество препятствий. Вы готовы? Тогда в путь.

Путешествовать мы будем на корабле.

Отправляемся на первый остров.

2. Устные счет

Итак, следуя нашей карте, мы оказались на острове под названием “Устный счет”. И чтобы двинуться дальше, нам необходимо выполнить задания:

Назови соседей чисел: 3, 6, 8;

Заполни пропуски:

7,….,….,….,…, 12

10,…,…., 7,….,…,….,…., 2

Реши пример по числовому отрезку.

3. Актуализация знаний

Следующий остров, встретившийся нам на пути, это “Геометрический остров”. Он таит в себе свои тайны и загадки, которые нам необходимо раскрыть!

Ребята нужно вспомнить и нарисовать все известные нам геометрические фигуры. (Круг, квадрат, ромб, овал, прямоугольник)

Посмотрите на рисунок, какие фигуры изображены?

По каким признакам можно разбить все фигуры на группы? (Цвет, форма, размер) . Назови эти группы.

4. Ознакомление с новым материалом

Мы удачно справились с заданием и можем отправиться на следующий остров. На третьем острове я нашла тайные послания для нас с вами. У каждого на парте есть конверт. Давайте откроем их и посмотрим, какое на этот раз испытание нас ждёт. (В каждом конверте находятся большой и маленький зеленый квадрат, большой и маленький синий треугольник, большой и маленький желтый прямоугольник, два красных круга одинакового размера)

Ребята, вспомним, по каким признакам делятся все фигуры? (Цвет, форма, размер)

Задание: разбейте по парам фигуры, находящиеся в конверте, так, чтобы менялся только один признак – размер.

Смогли ли вы разбить все предметы по парам? (Нет)

Почему? (Потому что два круга одинаковы по размеру, цвету и форме)

Докажите, что эти фигуры одинаковы. (Наложением)

Давайте подумаем, как можно такие фигуры назвать? (Из предложенных вариантов учитель выбирает понятие “равные фигуры”)

Итак, ребята, тема нашего урока “Равные фигуры”. (Тема фиксируется на доске)

Давайте поближе познакомимся с ними. Для этого нам нужно отправиться на следующий остров, который так и называется: “Равные фигуры”.

Прибыв на остров, я сразу заметила на песке различные фигуры, зарисовала их, так как волна могла в любой момент их смыть.

Посмотрите на доску, вот эти фигуры:

Если среди них равные? (Дети сначала определяют визуально равные фигуры, затем к доске вызывается ученик)

Как мы узнаем, действительно эти фигуры равны или нет? (Путем наложения одной фигуры на другую). Выполняется практическое действие.

Итак, какие же фигуры мы можем назвать равными? (Равными фигурами являются те, которые совпадают при наложении).

Определим, какие признаки у равных фигур должны совпадать.

Под темой урока на доске фиксируется краткая запись рассуждений детей.

(Равные фигуры всегда одинаковой формы и одинакового размера, а цвет может различаться)

Как вы считаете, 1 и 2 фигуры – равные?

Как мы это проверим? (Ученики совмещают фигуры и убеждаются, что они равны)

А как вы думаете, 2 и 3 фигуры равны? (Выполняется аналогичная работа)

Ребята, а 1 и 3 фигура равны?

Почему? (Они обе равны фигуре 2, значит, равны друг другу)

Давайте проверим наложением.

Ребята делают вывод, учитель кратко фиксирует на доске 1=2 и 2=3, то 1=3 (Если первая фигура равна второй, а вторая третьей, то первая фигура равна третьей)

У меня возникла проблема, а если я не могу наложить фигуры, например, они нарисованы в тетради, как проверить, равны они или нет? (Можно посчитать по клеткам)

Отправляемся на следующий остров.

5. Первичное закрепление

Работа с учебником.

1) Стр. 36 №1. Найди равные фигуры и раскрась их одинаковым цветом. Работа выполняется по вариантам:

1 вариант — №1 а)

2 вариант — №1 б)

Ребята, и с этим заданием вы справились, но продолжить наше путешествие мы не можем, корабль наткнулся на риф, нам необходимо его снова собрать. Потому что по карте последний остров именно тот, который нам нужен!

2) Стр. 36 №2.

6. Повторение пройденного

Вы сегодня были храбры и не боялись сложных испытаний, которые встречались нам на островах. И в награду за это вы можете стать учителями-капитанами корабля. Но быть капитаном не просто, вам нужно многое знать и уметь, поэтому постарайтесь справиться со следующими заданиями:

1) Учащимся предлагается стать учителем: придумать задание к рисунку, проконтролировать выполнение, оценить.

2) Раздаются карточки. Нужно найти все ошибки. Взаимопроверка по парам.

8=8 4+3=8 8-2>8-3

7>4 3+1

3

7. Итог урока, рефлексия

Мы прибыли на последний остров, а вот и клад! Наш путь оказался не напрасным, ведь нам в награду достались такие сокровища!

Ребята, как вы понимаете фразу “Знания — наше богатство”?

Перед вами на столе два смайлика — грустный и веселый. Если у вас хорошее настроение, приклейте к кораблю желтый веселый смайлик, если плохое — красный.

Мы с вами теперь опытные путешественники и кладоискатели, и в следующий раз нас будут ждать новые приключения! Спасибо за работу на уроке!

В повседневной жизни нас с вами окружают множество различных предметов. Часть из них имеют одинаковые размеры и одинаковую форму. Например, две одинаковые простыни или два одинаковых куска мыла, две одинаковых монеты и т.д.

В геометрии фигуры, имеющие одинаковые размеры и форму, называются равными фигурами . На рисунке ниже изображены две фигуры А1 и А2. Чтобы установить равенство этих фигур, нам необходимо одну из них скопировать на кальку. А затем передвигать кальку и совместить копию одной фигуры с другой фигурой.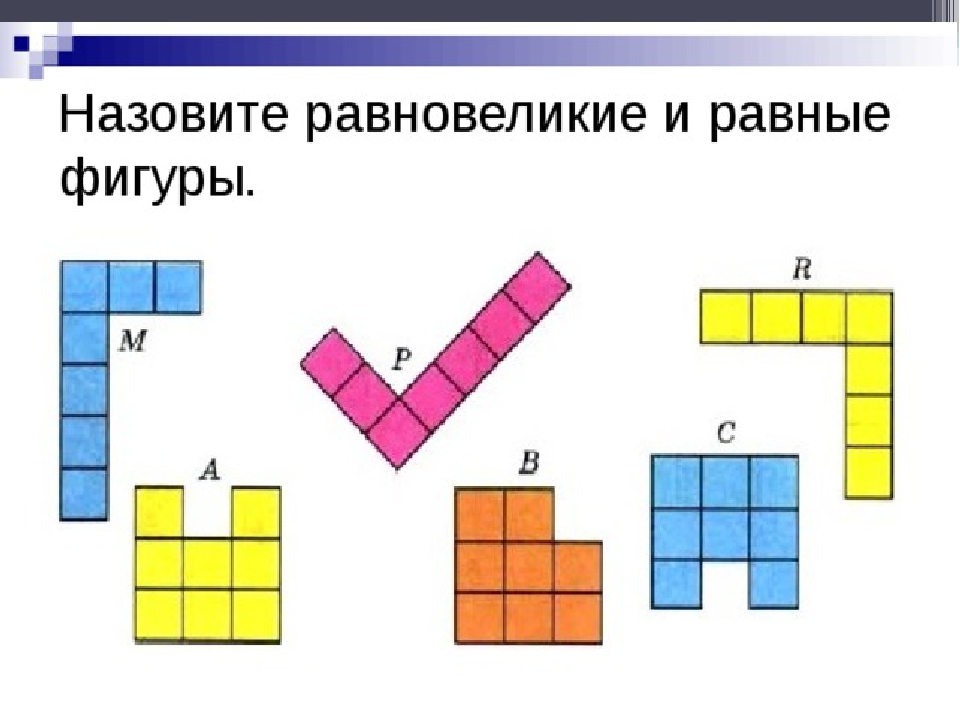 Если они совместятся, то это означает, что эти фигуры являются одинаковыми фигурами. При это записывают А1=А2 используя обычный знак равенства.

Определение равенства двух геометрических фигур

Мы можем представить, что на вторую фигуру накладывали первую фигуру, а не её копию на кальке. Поэтому в дальнейшем будем говорить о наложении самой фигуры, а не её копии, на другую фигуру. Исходя из всего вышесказанного можно сформулировать определение равенства двух геометрических фигур .

Две геометрические фигуры называются равными, если их можно совместить наложением одной фигуры на другую. В геометрии для некоторых геометрических фигур (например, треугольники) сформулированы специальные признаки, при выполнении которых можно говорить о том, что фигуры равны.

какой угол называется развернутым? Какие фигуры называются равными? Обьясните как сравнить два отрезка? какая точка называется

серединой отрезка?

Какой луч называется биссектрисой угла?

что такое градусная мера угла?

Какая фигура называется треугольником?Какие треугольники называются равными?Какой отрезок называют медианой треугольника?Какой отрезок называют

биссектрисой треугольника?Какой отрезок называют высотой треугольника?Какой треугольник называется равнобедренным?Какой треугольник называется равносторонним?Что такое окружность? Определение радиуса, диаметра, хорды.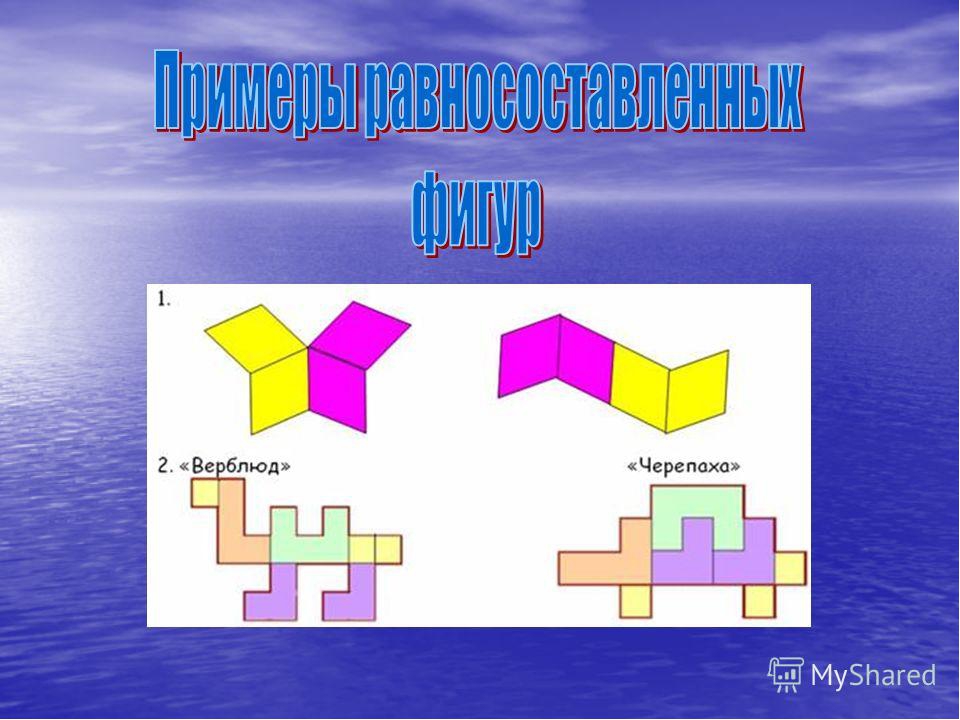 Дайте определение параллельных прямых.Какой угол называется внешним углом треугольника?Какой треугольник называется остроугольным, какой треугольник называется тупоугольным, какой прямоугольным. Как называются стороны прямоугольного треугольника?Свойство двух прямых, параллельных третьей.Теорема о прямой, пересекающей одну из параллельных прямых.Свойство двух прямых перпендикулярных к третьей

Какая фигура называется ломаной? Что такое звенья вершины и длина ломаной?

Объясните какая ломанная называется многоугольником. Что такое вершины, стороны, периметр и диагонали многоугольника? Какой многоугольник называется выпуклым?
Объясните какие углы называются выпуклыми углами многоугольника. Выведите формулу для вычисления суммы углов выпуклого n-угольника. Докажите, что сумма внешних углов выпуклого многоугольника. ВЗЯТЫХ по одному прикаждой вершине, равна 360 градусов.
Чему равна сумма углов выпукого четырехугольника?

1)Какая фигура называется четырехугольником?

2)Что такое вершины,углы стороны диагонали периметр четырехугольника?
3)Какие углы стороны четырехугольник называется выпуклым?
4)чему равна сумма углов выпуклого четырехугольника?
5)какой четырех угольник называется выпуклым?
6)какой четырех угольник называют параллелограмм?
7)какими свойствами обладает параллелограмм?
8)назовите признаки параллелограмма.
9)сформулируйте свойства прямоугольника.
10)какой четырехугольник называется квадратом?
11)сформулируйте свойства ромба.
12)какой четырехугольник называется ромбом?
13)какой четырехугольник называется прямоугольником?
14)какими свойствами обладает квадрат? ответьте пожалуйста кратко…

Геометрия Атанасян 7,8,9 класс «Вопросы ответы на вопросы для повторения к главе 2 к учебнику геометрии 7-9 класс атанасян Объясните, какая фигура

называется треугольником.
2. Что такое периметр треугольника?
3. Какие треугольники называются равными?
4. Что такое теорема и доказательство теоремы?
5. Объясните, какой отрезок называется перпендикуляром, проведённым из данной точки к данной прямой.
6. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?
7. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник?
8. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?
9. Какой треугольник называется равнобедренным?
10. Как называются стороны равнобедренного треугольника?
11. Какой треугольник называется равносторонним?
12. Сформулируйте свойство углов при основании равнобедренного треугольника.
13. Сформулируйте теорему о биссектрисе равнобедренного треугольника.
14. Сформулируйте первый признак равенства треугольников.
15. Сформулируйте второй признак равенства треугольников.
16. Сформулируйте третий признак равенства треугольников.
17. Дайте определение окружности.
18. Что такое центр окружности?
19. Что называется радиусом окружности?
20. Что называется диаметром окружности?
21. Что называется хордой окружности?

Одним из основных понятий в геометрии является фигура. Под этим термином подразумевается множество точек на плоскости, ограниченное конечным числом линий. Некоторые фигуры могут рассматриваться как равные, что тесно связано с понятием движения. Геометрические фигуры могут рассматриваться не изолированно, а в том или ином соотношении друг с другом – их взаимное расположение, соприкосновение и прилегание, положение «между», «внутри», соотношение, выраженное в понятиях «больше», «меньше», «равно». Геометрия изучает инвариантные свойства фигур, т.е. те, которые остаются неизменными при тех или иных геометрических преобразованиях. Такое преобразование пространства, при котором остается неизменным расстояние между точками, составляющими ту или иную фигуру, называется движением.Движение может выступать в разных вариантах: параллельный перенос, тождественное преобразование, поворот вокруг оси, симметрия относительно прямой или плоскости, центральная, поворотная, переносная симметрия.

Движение и равные фигуры

Если возможно такое движение, которое приведет к совмещению одной фигуры с другой, такие фигуры называют равными (конгруэнтными). Две фигуры, равные третьей, равны и между собою – такое утверждение было сформулировано еще Евклидом, основоположником геометрии.Понятие конгруэнтных фигур может быть объяснено и более простым языком: равными называются такие фигуры, которые полностью совпадут при наложении их друг на друга.Это достаточно легко определить, если фигуры даны в виде неких предметов, которыми можно манипулировать – например, вырезаны из бумаги, поэтому в школе на уроках нередко прибегают к такому способу объяснения данного понятия. Но две фигуры, начерченные на плоскости, нельзя физически наложить друг на друга. В данном случае доказательством равенства фигур выступает доказательство равенства всех элементов, составляющих эти фигуры: длина отрезков, размер углов, диаметр и радиус, если речь идет об окружности.

Равновеликие и равносоставленные фигуры

С равными фигурами не следует смешивать равновеликие и равносоставленные фигуры – при всей близости данных понятий.
Равновеликими называются такие фигуры, которые имеют равную площадь, если это фигуры на плоскости, или равный объем, если речь идет о трехмерны телах. Совпадение всех элементов, составляющих данные фигуры, не является обязательным. Равные фигуры будут равновеликими всегда, но не всякие равновеликие фигуры можно назвать равными.Понятие равносоставленности чаще всего применяют к многоугольникам. Оно подразумевает, что многоугольники можно разбить на одинаковое количество соответственно равных фигур. Равносоставленные многоугольники всегда являются равновеликими.

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели урока: Повторить тему «Площадь параллелограмма». Вывести формулу площади треугольник, ввести понятие равновеликих фигур. Решение задач по теме «Площади равновеликих фигур».

Ход урока

I. Повторение.

1) Устно по готовому чертежу вывести формулу площади параллелограмма.

2) Какова зависимость между сторонами параллелограмма и высотами, опущенными на них?

(по готовому чертежу)

зависимость обратно пропорциональная.

3) Найти вторую высоту (по готовому чертежу)

4) Найти площадь параллелограмма по готовому чертежу.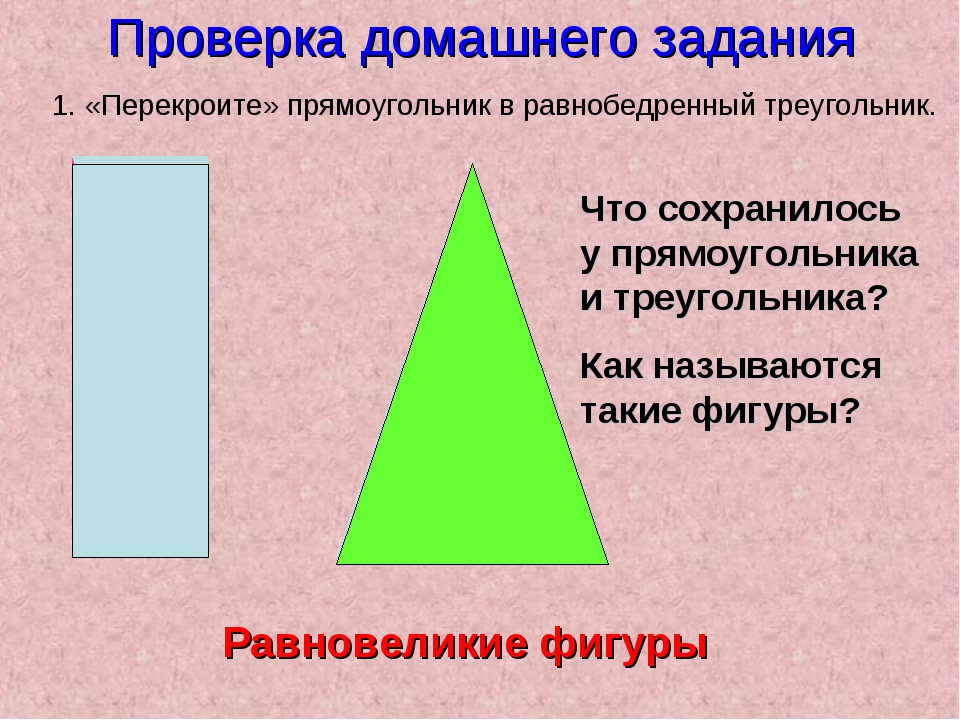

Решение:

5) Сравните площади параллелограммов S1, S2, S3 . (Они имеют равные площади, у всех основание a и высота h).

Определение: Фигуры, имеющие равные площади, называются равновеликими.

II. Решение задач.

1) Доказать, что всякая прямая, проходящая через точку пересечения диагоналей, делит его на 2 равновеликие части.

Решение:

2) В параллелограмме ABCD CF и CE высоты. Доказать, что AD ∙ CF = AB ∙ CE.

3) Дана трапеция с основаниями a и 4a. Можно ли через одну из её вершин провести прямые, разбивающие трапецию на 5 равновеликих треугольников?

Решение: Можно. Все треугольники равновеликие.

4) Доказать, что если на стороне параллелограмма взять точку A и соединить её с вершинами, то площадь получившегося треугольника ABC равна половине площади параллелограмма.

Решение:

5) Торт имеет форму параллелограмма. Малыш и Карлсон делят его так: Малыш указывает на поверхности торта точку, а Карлсон по прямой, проходящей через эту точку, разрезает торт на 2 куска и один из кусков забирает себе. Каждый хочет получить кусок побольше. Где Малыш должен поставить точку?

Решение: В точке пересечения диагоналей.

6) На диагонали прямоугольника выбрали точку и провели через неё прямые, параллельные сторонам прямоугольника. По разные стороны образовались 2 прямоугольника. Сравните их площади.

Решение:

III. Изучение темы «Площадь треугольника»

начать с задачи:

«Найти площадь треугольника, у которого основание a, а высота h».

Ребята, используя понятие равновеликих фигур, доказывают теорему.

Достроим треугольник до параллелограмма.

Площадь треугольника равна половине площади параллелограмма.

Задание: Начертите равновеликие треугольники.

Используется модель (из бумаги вырезаны 3 цветных треугольника и склеены у оснований).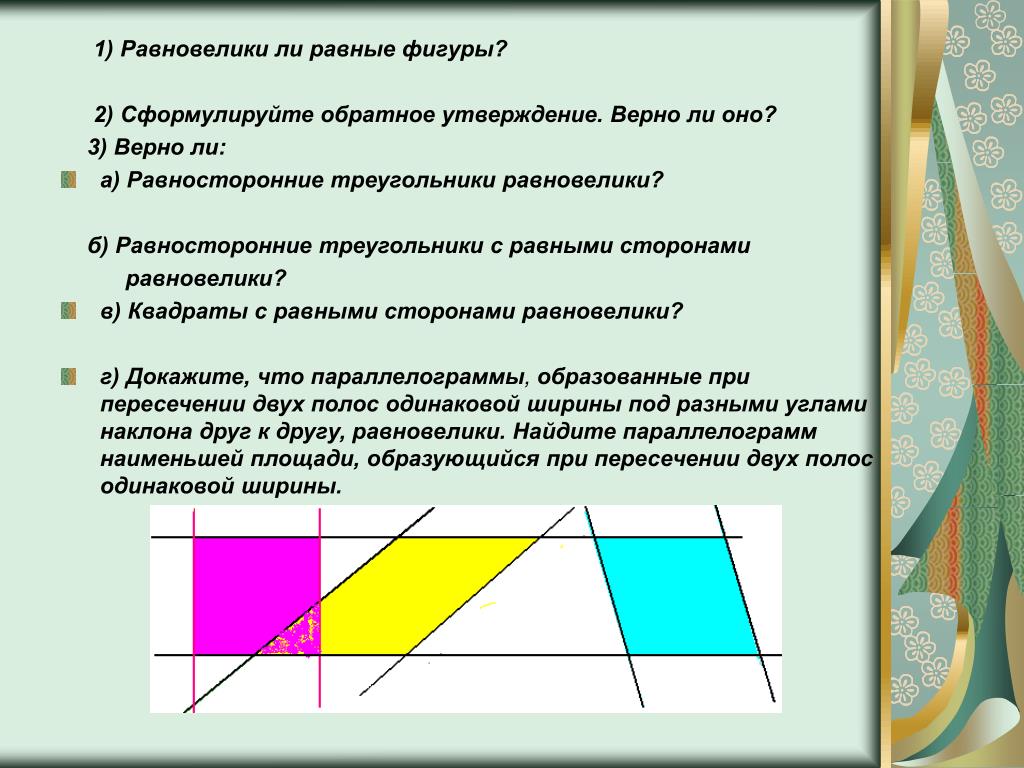

Упражнение №474. «Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой».

У треугольников одинаковые основания a и одна и та же высота h. Треугольники имеют одинаковую площадь

Вывод: Фигуры, имеющие равные площади, называются равновеликими.

Вопросы к классу:

1. Равновелики ли равные фигуры?
2. Сформулируйте обратное утверждение. Верно ли оно?
3. Верно ли:
   а) Равносторонние треугольники равновелики?
   б) Равносторонние треугольники с равными сторонами равновелики?
   в) Квадраты с равными сторонами равновелики?
   г) Докажите, что параллелограммы, образованные при пересечении двух полос одинаковой ширины под разными углами наклона друг к другу, равновелики. Найдите параллелограмм наименьшей площади, образующийся при пересечении двух полос одинаковой ширины. (Показать на модели: полоски одинаковой ширины)

IV. Шаг вперёд!

На доске написаны задания по выбору:

1. «Разрежьте треугольник двумя прямыми линиями так, чтобы можно было из частей сложить прямоугольник».

Решение:

2. «Разрежьте прямоугольник по прямой линии на 2 части, из которых можно сложить прямоугольный треугольник».

Решение:

3) В прямоугольнике проведена диагональ. В одном из получившихся треугольников проведена медиана. Найдите соотношения между площадями фигур .

Решение:

Ответ:

3. Из олимпиадных задач:

«В четырёхугольнике ABCD точка E- середина AB, соединена с вершиной D, а F – середина CD, с вершиной B. Доказать, что площадь четырёхугольника EBFD в 2 раза меньше площади четырёхугольника ABCD.

Решение: провести диагональ BD.

Упражнение №475.

«Начертите треугольник ABC. Через вершину В проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади».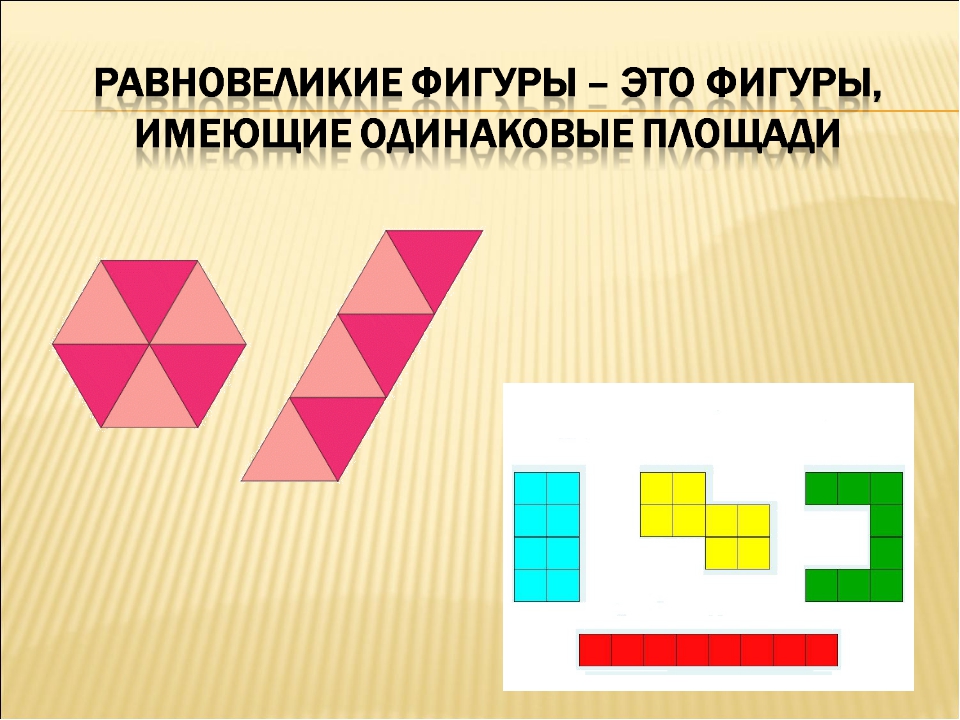

Использовать теорему Фалеса (разделить АC на 3 равные части).

V. Задача дня.

Для неё отвела крайнюю правую часть доски, на которой пишу задачу сегодняшнего дня. Ребята могут решать её, а могут и не решать. На уроке данную задачу мы сегодня не решаем. Просто те, кому они интересны, могут списать её, решить её дома или в перемену. Обычно уже в перемену многие ребята начинают решать задачу, если решили, то показывают решение, и я фиксирую это в специальной таблице. На следующем уроке к этой задаче обязательно возвращаемся, уделяя её решению небольшую часть урока (а на доске может быть записана новая задача).

«В параллелограмме вырезан параллелограмм. Разделите оставшуюся часть на 2 равновеликие фигуры».

Решение: Секущая AB проходит через точку пересечения диагоналей параллелограммов O и O1.

Дополнительные задачи (из олимпиадных задач):

1) «В трапеции ABCD (AD || BC) вершины A и B соединены с точкой M – серединой стороны CD. Площадь треугольника ABM равна m. Найти площадь трапеции ABCD».

Решение:

Треугольники ABM и AMK – равновеликие фигуры, т.к. AM – медиана.
S ∆ABK = 2m, ∆BCM = ∆MDK, S ABCD = S ∆ABK = 2m.

Ответ: S ABCD = 2m.

2) «В трапеции ABCD (AD || BC) диагонали пересекаются в точке O. Доказать, что треугольники AOB и COD равновеликие».

Решение:

S ∆BCD = S ∆ABC , т.к. у них общее основание BC и одинаковая высота .

3) Сторона АВ произвольного треугольника АВС продолжена за вершину В так, что ВР = АВ, сторону АС за вершину А так, что АМ = СА, сторону ВС за вершину С так, что КС = ВС. Во сколько раз площадь треугольника РМК больше площади треугольника АВС?

Решение:

В треугольнике МВС : МА = АС, значит, площадь треугольника ВАМ равна площади треугольника АВС. В треугольнике АРМ : ВР = АВ, значит, площадь треугольника ВАМ равна площади треугольника АВР. В треугольнике АРС : АВ = ВР, значит, площадь треугольника ВАС равна площади треугольника ВРС. В треугольнике ВРК : ВС = СК, значит, площадь треугольника ВРС равна площади треугольника РКС. В треугольнике АВК : ВС = СК, значит, площадь треугольника ВАС равна площади треугольника АСК. В треугольнике МСК: МА = АС, значит, площадь треугольника КАМ равна площади треугольника АСК. Получаем 7 равновеликих треугольников. Значит,

Ответ: Площадь треугольника МРК в 7 раз больше площади треугольника АВС.

4) Сцепленные параллелограммы.

2 параллелограмма расположены так, как показано на рисунке: они имеют общую вершину и ещё по одной вершине у каждого из параллелограммов лежит на сторонах другого параллелограмма. Доказать, что площади параллелограммов равны.

Решение:

и , значит,

Список использованной литературы :

1. Учебник «Геометрия 7-9» (авторы Л. С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев (Москва, «Просвещение», 2003).
2. Олимпиадные задачи разных лет, в частности из учебного пособия «Лучшие задачи математических олимпиад» (составитель А.А. Корзняков, Пермь, «Книжный мир», 1996).
3. Подборка задач, накопленных за много лет работы.

Рекомендуем также

Площадь. Равновеликие фигуры [Love Soft]

Равновеликие фигуры — плоские фигуры с одинаковыми площадями или геометрические тела с одинаковыми объемами.

Разрезанием на части и перекладыванием их можно любой многоугольник превратить в равновеликий ему квадрат.

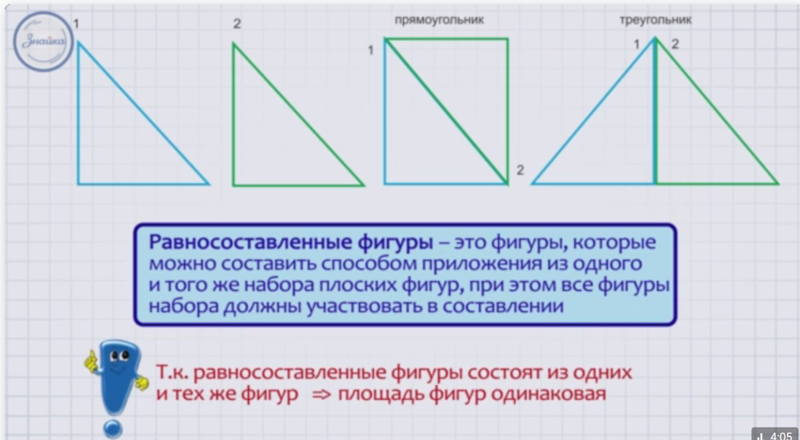
Это следствие из теоремы Больяй — Гервина: равносоставленные фигуры являются равновеликими, а равновеликие многоугольники являются равносоставленными.

Понятие равносоставленности лежит в основе «метода разбиения», применяемого для вычисления площадей многоугольников: параллелограмм «разрезанием и перекладыванием» сводят к прямоугольнику, треугольник — к параллелограмму, трапецию — к треугольнику.

Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.

Достроим треугольник до прямоугольника. Площадь треугольника равна половине площади прямоугольника.

Проведем через середину боковой стороны трапеции прямую, параллельную второй боковой стороне. Площадь трапеции равна площади полученного параллелограмма.

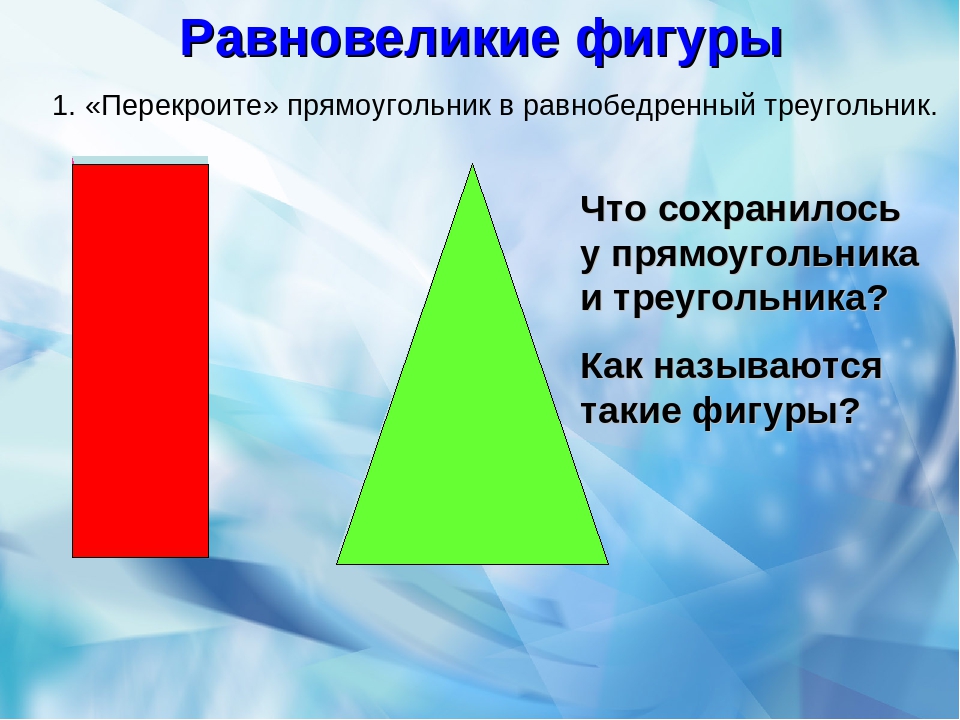
Перекраивание трапеции в равносоставленный треугольник:

видео — Площадь трапеции. Сведение к площади треугольника

Подробнее

Пло­щадь тра­пе­ции с ос­но­ва­ни­я­ми длин a и b и дли­ной вы­со­ты h рав­на S=(a+b)/2•h. Убе­дить­ся в этом мож­но вос­поль­зо­вав­шись фор­му­лой для вы­чис­ле­ния пло­ща­ди тре­уголь­ни­ка. Для это­го необ­хо­ди­мо разре­зать тра­пе­цию на та­кие ча­сти, из ко­то­рых мож­но со­ста­вить треугольник.

Разре­жем тра­пе­цию вдоль ли­нии, со­еди­ня­ю­щей вер­ши­ну с се­ре­ди­ной проти­во­по­лож­ной бо­ко­вой сто­ро­ны. По­вер­нём от­ре­зан­ный тре­уголь­ник до того момен­та, ко­гда оба ос­но­ва­ния тра­пе­ции ока­жут­ся на од­ной прямой. Убедитесь, что две ча­сти бо­ко­вой сто­ро­ны при этом ля­гут на од­ну прямую, то есть, получится дей­стви­тель­но тре­уголь­ник.

Одна из сторон получив­ше­го­ся тре­уголь­ни­ка име­ет дли­ну, рав­ную сум­ме длин оснований трапе­ции, а дли­на вы­со­ты тре­уголь­ни­ка, про­ве­дён­ной к этой стороне, сов­пада­ет с вы­со­той тра­пе­ции.

Один из способов подсчё­та пло­ща­ди тре­уголь­ни­ка со­сто­ит в на­хож­де­нии половины произве­дения дли­ны сто­ро­ны на дли­ну вы­со­ты, опу­щен­ную на эту сторону. При­ме­нение это­го спо­со­ба и да­ёт при­выч­ную фор­му­лу площа­ди трапеции.

Модель мож­но сде­лать из доски толщиной около 10 мм. Для удобства демон­стра­ции две ча­сти, на которые она разрезает­ся, удобно со­еди­нять между собой при по­мо­щи маг­ни­тов.

Равносоставленность

Равновеликие многогранники не всегда являются равносоставленными. Так, например, куб и равновеликий ему правильный тетраэдр не являются равносоставленными — так называемая теорема Дена.

Вопросы

• Квадраты с равными сторонами равновелики?

• Равносторонние треугольники с равными сторонами равновелики?

• Равносторонние треугольники равновелики?

Задачи

Задача A

Доказать, что всякая прямая, проходящая через точку пересечения диагоналей параллелограмма, делит его на 2 равновеликие части.

Доказательство.

Задача B — Про торт и бесстыдную птичку

Решается на основании задачи A.

У бабушки было два внука, которые должны были приехать на выходные погостить. Она, как любая добропорядочная бабушка, приготовила для них торт. И поставила его на подоконник. Но пока он там стоял, над домом бабушки пролетала бесстыдная птичка. И так получилось, что она справила свою нужду аккурат на краешек торта. Бабушка увидав это не упала духом и решила, что этот кусочек она просто вырежет (см рисунок). Бабушка была очень справедливая, внуков любила одинаково, и к своей работе относилась трепетно. Помогите бабушке разделить весь оставшийся торт на две совершенно одинаковые по площади части.

Бабушка имеет идеальный глазомер, она легко способна находить на глаз середины и пересечения любых отрезков. И у бабушки есть замечательный нож, которым она умеет лихо отрезать куски торта по любой намеченной прямой.

Решение.

Задание

Начертите равновеликие треугольники.

Решение.

Задача

Доказать, что медиана делит треугольник на два равновеликих треугольника.

Решение.

У треугольников одинаковые основания и одна и та же высота. Поэтому треугольники имеют одинаковую площадь.

Следствие. Диагонали параллелограмма разбивают его на четыре равновеликих треугольника.

Задача

Доказать, что медианы треугольника разбивают его на шесть равновеликих треугольников.

Решение.

Рассмотреть попарно эти шесть треугольников. У них одинаковые основания и одна и та же высота. Поэтому попарно треугольники имеют одинаковую площадь. В силу транзитивности все 6 треугольников равновелики.

Задача

Начертите треугольник ABC. Через вершину B проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади.

Решение.

Подсказка: Используйте теорему Фалеса: (разделите АC на 3 равные части).

У треугольников одинаковые основания и одна и та же высота. Поэтому треугольники имеют одинаковую площадь.

Задача

Постройте полукруг, равновеликий данному кругу.

Постройте круг, равновеликий данному полукругу.

Задача

Доказать, что круг на рисунке разбит на 9 равновеликих частей

Решение

Но капитан словно бы и не заметил нашего недоверия. Он положил чертёж на бочку и стал объяснять. — Перед вами круг с двумя взаимно перпендикулярными диаметрами. Каждый диаметр разделён на три равные части, а каждая из этих трёх равных частей, в свою очередь, представляет собой диаметр малого круга. Как видите, таких малых кругов в большом круге пять, и они совершенно одинаковы

Известно, что если диаметр круга уменьшить, допустим, в три раза, то площадь круга уменьшится при этом в трижды три раза.

Отсюда следует, что площадь каждого из пяти малых кругов в девять раз меньше большого. Ведь три в квадрате равно девяти ( 3 * 3 = 9 ) !

Капитан перевёл дух и продолжал:

— Остаётся вычислить, чему равна площадь каждой из четырёх заштрихованных частей, заключённых между малыми кругами.

— Ну, это просто! — сейчас же выскочил я.- Если площадь большого круга принять за 9/9, то площадь всех пяти малых кругов составит 5/9, а на оставшиеся четыре части придётся 4/9. И части эти, само собой, тоже конгруэнтны.

— Отсюда ясно,- подытожил Пи,- что площадь каждой из заштрихованных частей также составляет 1/9 часть площади большого круга. Вот и выходит, что площадь большого круга разделена на девять равновеликих частей.

Задача

Найти площадь четвертой части

Решение

Подсказка. Нужно соединить точку внутри четырехугольника с его вершинами.

После этого существующие отрезки станут медианами треугольников. Как известно, медиана делит площадь треугольника пополам.

Отсюда уравнения:

И легко получаем c+d = 32+16-20 = 28

Вывод — квадрат на рисунке можно заменить на любой четырехугольник.

mat/geom/area.txt · Последние изменения: 2016/01/18 00:22 — kc

геометрия — Как соотносятся множества равновеликих и равносоставленных фигур?

Это довольно тонкий вопрос. Здесь важно то, какое определение берётся за основу.

Прежде всего, есть классический результат: теорема Бойяи — Гервина. Она утверждает, что для многоугольников, разрезаемых на многоугольники, условие совпадения площадей является необходимым и достаточным для того, чтобы при разрезании на конечное число частей один многоугольник можно было превратить в другой.

Аналогичное утверждение для трёхмерного пространства уже неверно, то есть для многогранников, разрезаемых на конечное число многогранников, это не так. Это так называемая «Третья проблема Гильберта». Она была решена отрицательно в начале XX века Максом Дэном, который показал, что тетраэдр и куб равного объёма нельзя превратить друг в друга таким путём.

Теперь вернёмся к случаю плоскости. Допустим, у нас есть круг и квадрат одинаковой площади. Мы хотим их разрезать на «хорошие» части с помощью ножниц. Здесь можно ставить вопрос об уточнении того, какие части называются «хорошими», но пусть это будут фигуры многоугольного типа, граница которых может состоять из отрезков и дуг окружностей. Тогда можно доказать, что равносоставленность не имеет места, сравнивая длины «выпуклых» и «вогнутых» участков.

Заметим, что при разрезаниях «классического» типа граничные точки фигур могут принадлежать сразу двум фигурам, соединяемым вместе. Но что будет, если этого не допускать, но при этом разрешить разбиение на любые части — какой угодно «формы»?

Рассмотрим такое определение. {50}$%. Однако обязательное условие состоит в том, что число частей разбиения является конечным.

Для аналогичного понятия в трёхмерном пространстве давно были известны ещё более парадоксальные случаи разбиения фигур, но этого вопроса я сейчас касаться не буду.

отвечен 3 Май ’13 21:37

Измерение площади и объёма — презентация онлайн

1. Измерение площади и объёма

Элементы параллелепипеда:
• грани
• рёбра
• вершины
Площадь полной поверхности:
S=2ab+2bc+2ac=2(ab+bc+ac)
Обьём параллелепипеда:
V=abc
c
b
a
Площадь полной поверхности куба.
4см
4см
S = a .a= a²
Sn.к.=6а2
S = 6*42 =96(cм2)
Ответ: 96 см2
Запиши в тетрадь:
Определение 1.
Фигуры, имеющие равные площади,
называются равновеликими.
Определение 2.
Фигуры, составленные из одинакового
набора фигур, называются
равносоставленными.
Определение 3.
Равные фигуры – это фигуры, равные по
размерам и имеющие одинаковую форму.

5. Задание 1. Укажите равновеликие фигуры.

6. Задание 2. Являются ли данные фигуры равновеликими? Почему?

7. Задание 3.Являются ли данные фигуры равновеликими? Почему?

Задание 4.Найти равносоставленные,
равные
.
и равновеликие фигуры
Разрезанием на части и перекладыванием фигур можно
любой многоугольник превратить в равновеликий ему
квадрат.
Понятие равносоставленности лежит в основе «метода
разбиения», применяемого для вычисления площадей
многоугольников: параллелограмм «разрезанием и
перекладыванием» сводят к прямоугольнику, треугольник — к
прямоугольнику, трапецию — к треугольнику.

10. Подумай…и ответь «да» или «нет»

Верно ли, что равносоставленные фигуры всегда
равновелики?
Верно ли, что равновеликие фигуры всегда
равносоставленные?
Может ли 2 равносоставленных треугольника
иметь разные площади?

11.

Свойства объёма • Объёмные тела, составленные из
одинаковых частей, имеют одинаковый
объём
• В отличие от многоугольников, два
многогранника, имеющие одинаковый объём,
не всегда можно разделить на одинаковые
части
• Если, не меняя формы плоской фигуры,
увеличить её размеры в n раз, то её площадь
увеличится в n* n раз.

12. Самостоятельная работа

1 вариант (девочки)
1) Дано:
прямоугольный
параллелепипед
а=8см
в=5см
с=3см
Найти: Sп, Vп
2) Дано:
куб
а=8см
Найти: Sк, Vк
2 вариант (мальчики)
1) Дано:
прямоугольный
параллелепипед
а=3см
в=11см
с=5см
Найти: Sп, Vп
2) Дано:
куб
а=6см
Найти: Sк, Vк

Какие фигуры называют равными равновеликими. Две геометрические фигуры называются равными, если их можно совместить

Фигуры называют равными, если совпадает их форма и размеры. Из этого определения следует, например, что если заданные прямоугольник и квадрат имеют равные площади, то они всё-равно не становятся равными фигурами, так как это разные фигуры по форме. Или, два круга однозначно имеют одну и туже форму, но если их радиусы различны, то это тоже не равные фигуры, так как не совпадают их размеры. Равными фигурами являются, например, два отрезка одинаковой длины, два круга с одинаковым радиусом, два прямоугольника с попарно равными сторонами (короткая сторона одного прямоугольника равна короткой стороне другого, длинная сторона одного прямоугольника равна длинной стороне другого).

На глаз бывает трудно определить, равны ли фигуры, имеющие одинаковую форму. Поэтому для определения равенства простых фигур их измеряют (с помощью линейки, циркуля). У отрезков длину, у кругов радиус, у прямоугольников длину и ширину, у квадратов только одну любую сторону. Тут следует отметить, что не все фигуры можно сравнивать. Нельзя, например, определить равенство прямых, т. к. любая прямая бесконечна и, следовательно, все прямые, можно сказать, равны между собой. То же самое касается лучей. Хотя у них есть начало, но нет конца.

Если же мы имеем дело со сложными (произвольными) фигурами, то бывает даже сложно определить, имеют ли они одинаковую форму. Ведь фигуры могут быть перевернуты в пространстве. Посмотрите на рисунок ниже. Трудно сказать, одинаковые ли это по форме фигуры или нет.

Таким образом, нужно иметь надежный принцип сравнения фигур. Он таков: равные фигуры при наложении друг на друга совпадают .

Чтобы сравнить две изображенные фигуры наложением, на одну из них накладывают кальку (прозрачную бумагу) и копируют (срисовывают) на нее форму фигуры. Копию на кальке пытаются наложить на вторую фигуру так, чтобы фигуры совпали. Если это удастся, то заданные фигуры равные. Если нет, то фигуры не равные. При наложении кальку можно поворачивать как угодно, а также переворачивать.

Если можно вырезать сами фигуры (или они представляют собой отдельные плоские объекты, а не нарисованы) то калька не нужна.

При изучении геометрических фигур можно заметить множество их особенностей, связанных с равенством их частей. Так, если сложить круг вдоль диаметра, то две его половинки окажутся равными (они совпадут наложением). Если разрезать прямоугольник по диагонали, то получится два прямоугольных треугольника. Если один из них повернуть на 180 градусов по часовой или против часовой стрелки, то он совпадет со вторым. То есть диагональ разбивает прямоугольник на две равные части.

«Цилиндром называется тело» — Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Цилиндр, осевое сечение, которого-квадрат называется равносторонним. Проект «Математика в профессии «Повар, кондитер». Задача № 3. Цилиндры. Высотой цилиндра называется расстояние между плоскостями оснований. Высота цилиндра 8 м, радиус основания 5 м. Цилиндр пересечен плоскостью так, что в сечении получился квадрат.

«Площади фигур геометрия» — Равные фигуры имеют равные площади. в). чему будет равна площадь фигуры составленной из фигур А и Г. Фигуры разбиты на квадраты со стороной 1см. Равные фигуры б). Площадь параллелограмма. Фигуры имеющие равные площади называются равновеликими. Площади различных фигур. Единицы измерения площадей. Площадь треугольника.

«Площади фигур» — Площадь треугольника. Площадь плоской фигуры – неотрицательное число. Пусть S – площадь треугольника АВС. Решение: Теорема: Площадь параллелограмма. Решение. Площадь квадрата со стороной 1 равна 1. Задача. Разрезания и складывания. Равные многоугольники имеют равные площади. Четвертое свойство: Теорема доказана.

«Построение геометрических фигур» — Методы изображения и построения пространственных фигур на плоскости. Построения на проекционном чертеже. П4: Построить (найти) точку пересечения данных прямой и окружности. Требования – искомая фигура (совокупность фигур) с указанными свойствами. Алгебраический метод. Этапы решения задач на построение.

«Геометрическая прогрессия» — 1073741823 > 3000000, значит купец проиграл! Геометрическая прогрессия. Бесконечная сумма оказалась равна вполне конечной величине – высоте треугольника. Свойство геометрической прогрессии: Решение задачи: b1 = 1, q =2, n =30. Bn = b1· qn – 1 – формула n-го члена прогрессии.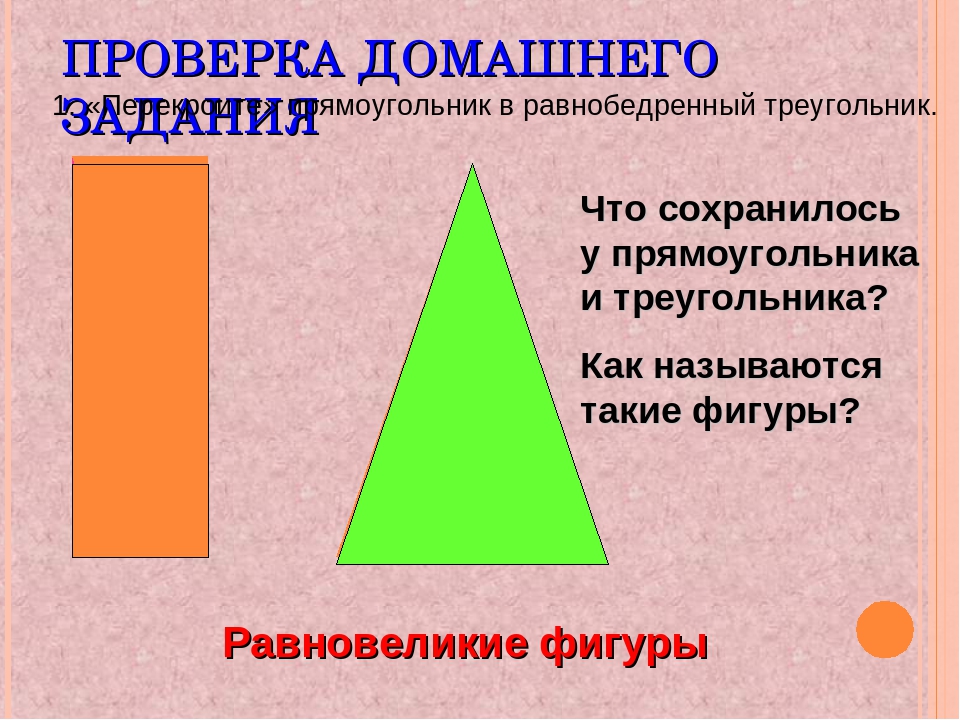 Формула суммы бесконечной убывающей геометрической прогрессии:

«Подобие фигур» — Растения. Геометрия. Подобие нас окружает. Игрушки. Подобие в нашей жизни. Вот некоторые примеры из нашей жизни. Если изменить (увеличить или уменьшить) все размеры плоской фигуры в одно и то же число раз (отношение подобия), то старая и новая фигуры называются подобными. Использовались материалы Интернета.

Фигуры, которые совпадают при наложении называются РАВНЫМИ. Две геометрические фигуры называются равными, если их можно совместить при наложении

9. объясните, как сравнить два отрезка и как сравнить 2 угла. Один отрезок накладываешь на другой чтобы конец первого совместился с концом второго, если при этом другие два конца не совместились значит отрезки не равны, если совместились то равны. Чтобы сравнить 2 отрезка нужно сравнить их длины, чтобы сравнить 2 угла надо сравнить их градусную меру, Два угла называются равными, если их можно совместить наложением. Чтобы установить, равны есть два неразвернутых углы или нет, необходимо совместить сторону одного угла со стороной вторым таким образом, чтобы две другие стороны оказались по одну сторону от совмещенных сторон . Наложить один угол на другой угол таким образом, чтобы у них совпали вершины и по одной стороне, а две другие оказались по одну сторону от совместившихся сторон. Если вторая сторона одного угла совместиться со второй стороной другого угла, то данные углы равны. (Наложи углы так чтобы сторона одного совместилась со стороной др., а две др. оказались по одну сторон от совместившихся сторон. если две др стороны совместятся то углы полностью совместятся а значит они равны.)

10.Какая точка называется серединой отрезка? Середина отрезка-это точка, которая делит данный отрезок на две равные части. Точка делящая отрезок пополам называется серединой отрезка.

11. Биссектрисой (от лат. bi- «двойное» и sectio «разрезание») угла называется луч, выходящий из вершины угла и проходящий через его внутреннюю область, который образует с его сторонами два равных угла. Или луч исходящий из вершины угла и делящий его на два равных угла называют биссектрисой угла.

12. Как производится измерение отрезков. Измерить отрезок, соизмеримый с единицей – это значит узнать, сколько раз в нем содержится единица или какая-нибудь доля единицы. Измерение отрезка осуществляется посредством сравнения его с некоторым отрезком, принятым за единицу. Измерять длину отрезка можно с помощью линейки или измерительной ленты. Нужно наложить один отрезок на другой,который мы приняли за единицу измерения, чтобы их концы совместились.

? 13. Как связаны между собой длины отрезков AB и CD, если: а) отрезки AB и CD равны; б) отрезок AB меньше отрезка CD?

А) длины отрезков AB и CD равны. Б) длина отрезка АВ меньше длины отрезка CD.

14. Точка C делит отрезок AB на два отрезка. Как связаны между собой длины отрезков AB, AC и CB? Длина отрезка АВ равна сумме длин отрезков AC и CB. Чтобы найти длину отрезка AB надо сложить длины отрезков AC и CB.

15. Что такое градус? Что показывает градусная мера угла? Углы измеряют в разных единицах измерениях. Это могут быть градусы, радианы. Чаще всего углы измеряют в градусах. (Не следует путать этот градус с мерой измерения температуры, где также используется слово «градус) . Измерение углов основано на сравнении их с углом, принятым за единицу измерения. Обычно за единицу измерения углов принимают градус — угол, равный 1/180 части развернутого угла. Градус — единица измерения плоских углов в геометрии.(В качестве единицы измерения геометрических углов принят градус – часть развернутого угла.) .

Градусная мера угла показывает, сколько раз градус и его части — минута и секунда — укладываются в данном угле, то есть градусная мера — величина, отражающая количество градусов, минут и секунд между сторонами угла.

16. Какая часть градуса называется минутой, а какая – секундой? 1/60 часть градуса называется минутой, а 1/60 часть минуты — секундой. Минуты обозначают знаком «′», а секунды — знаком «″»

? 17.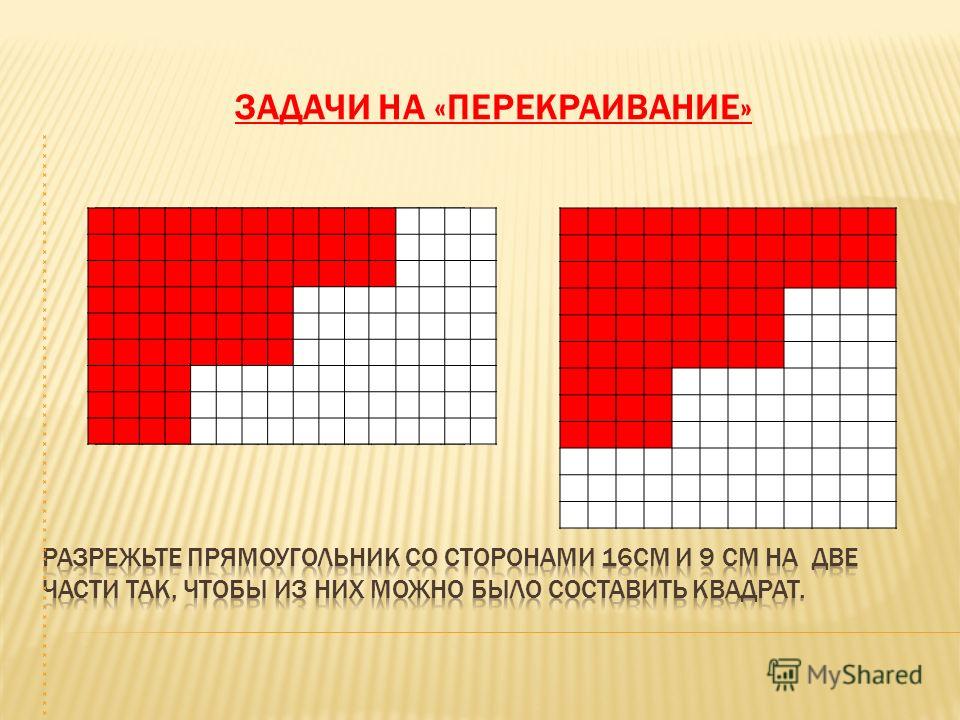 Как связаны между собой градусные меры двух углов, если: а) эти углы равны; б) один угол меньше другого? а) градусная мера углов одинакова. б) Градусная мера одного угла меньше градусной меры второго угла.

18. Луч OC делит угол AOB на два угла. Как связаны между собой градусные меры углов AOB, AOC иCOB? Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.Градусная мера угла AOB равна сумме градусных мер его частей AOC иCOB.

Одним из основных понятий в геометрии является фигура. Под этим термином подразумевается множество точек на плоскости, ограниченное конечным числом линий. Некоторые фигуры могут рассматриваться как равные, что тесно связано с понятием движения. Геометрические фигуры могут рассматриваться не изолированно, а в том или ином соотношении друг с другом – их взаимное расположение, соприкосновение и прилегание, положение «между», «внутри», соотношение, выраженное в понятиях «больше», «меньше», «равно». Геометрия изучает инвариантные свойства фигур, т.е. те, которые остаются неизменными при тех или иных геометрических преобразованиях. Такое преобразование пространства, при котором остается неизменным расстояние между точками, составляющими ту или иную фигуру, называется движением.Движение может выступать в разных вариантах: параллельный перенос, тождественное преобразование, поворот вокруг оси, симметрия относительно прямой или плоскости, центральная, поворотная, переносная симметрия.

Движение и равные фигуры

Если возможно такое движение, которое приведет к совмещению одной фигуры с другой, такие фигуры называют равными (конгруэнтными). Две фигуры, равные третьей, равны и между собою – такое утверждение было сформулировано еще Евклидом, основоположником геометрии.Понятие конгруэнтных фигур может быть объяснено и более простым языком: равными называются такие фигуры, которые полностью совпадут при наложении их друг на друга.Это достаточно легко определить, если фигуры даны в виде неких предметов, которыми можно манипулировать – например, вырезаны из бумаги, поэтому в школе на уроках нередко прибегают к такому способу объяснения данного понятия. Но две фигуры, начерченные на плоскости, нельзя физически наложить друг на друга. В данном случае доказательством равенства фигур выступает доказательство равенства всех элементов, составляющих эти фигуры: длина отрезков, размер углов, диаметр и радиус, если речь идет об окружности.

Равновеликие и равносоставленные фигуры

С равными фигурами не следует смешивать равновеликие и равносоставленные фигуры – при всей близости данных понятий.
Равновеликими называются такие фигуры, которые имеют равную площадь, если это фигуры на плоскости, или равный объем, если речь идет о трехмерны телах. Совпадение всех элементов, составляющих данные фигуры, не является обязательным. Равные фигуры будут равновеликими всегда, но не всякие равновеликие фигуры можно назвать равными.Понятие равносоставленности чаще всего применяют к многоугольникам. Оно подразумевает, что многоугольники можно разбить на одинаковое количество соответственно равных фигур. Равносоставленные многоугольники всегда являются равновеликими.

Цель: формирование понятия “равные фигуры”.

• сформировать способность к фиксированию понятия “равные фигуры”, к фиксированию умения нахождения равных фигур;
• развивать математическую речь, геометрическое мышление; тренировать мыслительные операции;
• совершенствовать навыка счета в пределах 9;
• воспитывать в учащихся дисциплинированность, умение совместной деятельности.

Ход урока

1. Организационный момент

Вступительное слово учителя.

Пираты — это морские разбойники, главной их цель всегда была поиск клада. Мы будем добрыми пиратами и отправимся в морское путешествие на поиски нашего клада. Мне в руки попала старинная пиратская карта.

Она очень запутанная, на ней отмечено множество островов, чтобы запутать искателей, но нужно попасть на остров, на котором спрятаны сокровища. Чтобы его найти, нам нужно будет преодолеть множество препятствий. Вы готовы? Тогда в путь.

Путешествовать мы будем на корабле.

Отправляемся на первый остров.

2. Устные счет

Итак, следуя нашей карте, мы оказались на острове под названием “Устный счет”. И чтобы двинуться дальше, нам необходимо выполнить задания:

Назови соседей чисел: 3, 6, 8;

Заполни пропуски:

7,….,….,….,…, 12

10,…,…., 7,….,…,….,…., 2

Реши пример по числовому отрезку.

3. Актуализация знаний

Следующий остров, встретившийся нам на пути, это “Геометрический остров”. Он таит в себе свои тайны и загадки, которые нам необходимо раскрыть!

Ребята нужно вспомнить и нарисовать все известные нам геометрические фигуры. (Круг, квадрат, ромб, овал, прямоугольник)

Посмотрите на рисунок, какие фигуры изображены?

По каким признакам можно разбить все фигуры на группы? (Цвет, форма, размер) . Назови эти группы.

4. Ознакомление с новым материалом

Мы удачно справились с заданием и можем отправиться на следующий остров. На третьем острове я нашла тайные послания для нас с вами. У каждого на парте есть конверт. Давайте откроем их и посмотрим, какое на этот раз испытание нас ждёт. (В каждом конверте находятся большой и маленький зеленый квадрат, большой и маленький синий треугольник, большой и маленький желтый прямоугольник, два красных круга одинакового размера)

Ребята, вспомним, по каким признакам делятся все фигуры? (Цвет, форма, размер)

Задание: разбейте по парам фигуры, находящиеся в конверте, так, чтобы менялся только один признак – размер.

Смогли ли вы разбить все предметы по парам? (Нет)

Почему? (Потому что два круга одинаковы по размеру, цвету и форме)

Докажите, что эти фигуры одинаковы. (Наложением)

Давайте подумаем, как можно такие фигуры назвать? (Из предложенных вариантов учитель выбирает понятие “равные фигуры”)

Итак, ребята, тема нашего урока “Равные фигуры”. (Тема фиксируется на доске)

Давайте поближе познакомимся с ними. Для этого нам нужно отправиться на следующий остров, который так и называется: “Равные фигуры”.

Прибыв на остров, я сразу заметила на песке различные фигуры, зарисовала их, так как волна могла в любой момент их смыть.

Посмотрите на доску, вот эти фигуры:

Если среди них равные? (Дети сначала определяют визуально равные фигуры, затем к доске вызывается ученик)

Как мы узнаем, действительно эти фигуры равны или нет? (Путем наложения одной фигуры на другую). Выполняется практическое действие.

Итак, какие же фигуры мы можем назвать равными? (Равными фигурами являются те, которые совпадают при наложении).

Определим, какие признаки у равных фигур должны совпадать.

Под темой урока на доске фиксируется краткая запись рассуждений детей.

(Равные фигуры всегда одинаковой формы и одинакового размера, а цвет может различаться)

Как вы считаете, 1 и 2 фигуры – равные?

Как мы это проверим? (Ученики совмещают фигуры и убеждаются, что они равны)

А как вы думаете, 2 и 3 фигуры равны? (Выполняется аналогичная работа)

Ребята, а 1 и 3 фигура равны?

Почему? (Они обе равны фигуре 2, значит, равны друг другу)

Давайте проверим наложением.

Ребята делают вывод, учитель кратко фиксирует на доске 1=2 и 2=3, то 1=3 (Если первая фигура равна второй, а вторая третьей, то первая фигура равна третьей)

У меня возникла проблема, а если я не могу наложить фигуры, например, они нарисованы в тетради, как проверить, равны они или нет? (Можно посчитать по клеткам)

Отправляемся на следующий остров.

5. Первичное закрепление

Работа с учебником.

1) Стр. 36 №1. Найди равные фигуры и раскрась их одинаковым цветом. Работа выполняется по вариантам:

1 вариант — №1 а)

2 вариант — №1 б)

Ребята, и с этим заданием вы справились, но продолжить наше путешествие мы не можем, корабль наткнулся на риф, нам необходимо его снова собрать. Потому что по карте последний остров именно тот, который нам нужен!

2) Стр. 36 №2.

6. Повторение пройденного

Вы сегодня были храбры и не боялись сложных испытаний, которые встречались нам на островах. И в награду за это вы можете стать учителями-капитанами корабля. Но быть капитаном не просто, вам нужно многое знать и уметь, поэтому постарайтесь справиться со следующими заданиями:

1) Учащимся предлагается стать учителем: придумать задание к рисунку, проконтролировать выполнение, оценить.

2) Раздаются карточки. Нужно найти все ошибки. Взаимопроверка по парам.

8=8 4+3=8 8-2>8-3

7>4 3+1

3

7. Итог урока, рефлексия

Мы прибыли на последний остров, а вот и клад! Наш путь оказался не напрасным, ведь нам в награду достались такие сокровища!

Ребята, как вы понимаете фразу “Знания — наше богатство”?

Перед вами на столе два смайлика — грустный и веселый. Если у вас хорошее настроение, приклейте к кораблю желтый веселый смайлик, если плохое — красный.

Мы с вами теперь опытные путешественники и кладоискатели, и в следующий раз нас будут ждать новые приключения! Спасибо за работу на уроке!

Равновеликие многоугольники

Два многоугольника называются равновеликими, если их площади равны

Примером равновеликих многоугольников могут служить любые равные многоугольники. Обратное утверждение, конечно, неверно: равновеликие многоугольники могут быть не равными. Также примером равновеликих многоугольников являются равносоставленные многоугольники.

Задача деления площадей фигур с помощью прямых, пересекающих их, и превращения одной фигуры в другую путем разрезания и пересоставления их частей возникла еще в древности из потребностей практики, землемерия и архитектуры. В сохранившемся на арабском языке сочинении Евклида «О делении фигур» рассматривается вопрос о том, как можно с помощью прямой линии, проходящей через данную точку, разделить пополам или в некотором отношении площадь данного многоугольника.

Проблема деления площадей особенно интересовала математиков эпохи Возрождения. Одной из самых простых и удобных для измерения площадей фигур является квадрат. Поэтому издавна появилось стремление превращать любую фигуру в равновеликий квадрат. Евклид, например, ставит и решает задачу о построении квадрата, равновеликого данному многоугольнику.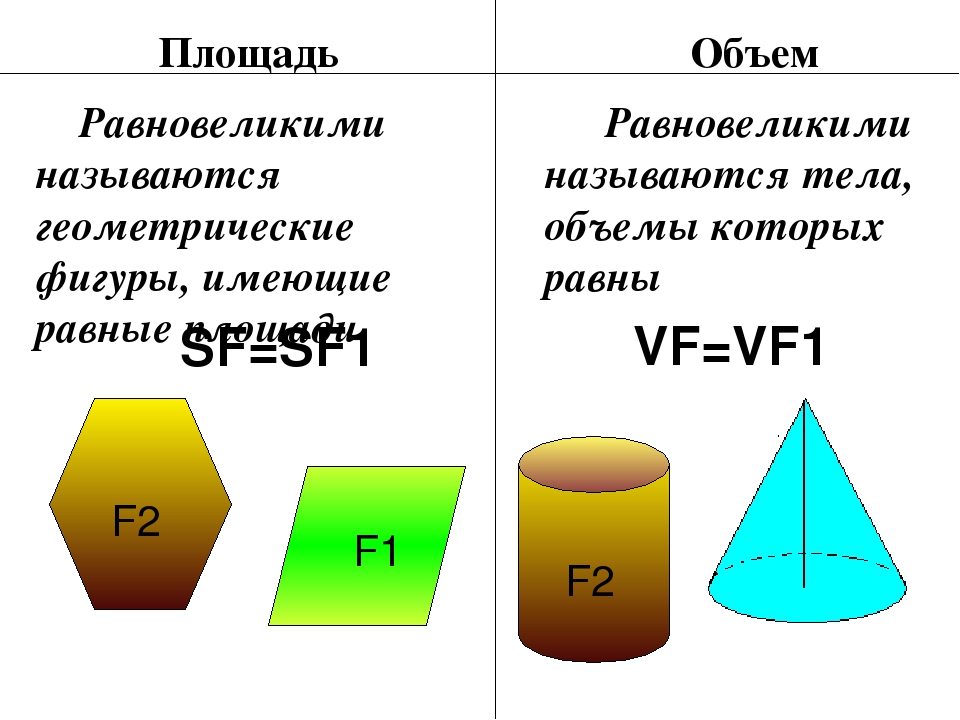

Задачи преобразования равновеликих фигур занимали умы ученых 19 века и поныне интересуют математиков.

Рассмотрим несколько типов задач:

Практические задачи (задачи на «разрезание»):

Задача № 1:

Разделить данный треугольник на три равновеликих треугольника прямыми, выходящими из одной вершины.

Решение

Разделим сторону АС на три равных отрезка (AD, DN, NC). Проведем через вершину B три прямые, проходящие через точки D, N. Образуются три треугольника: ABD, DBN, NBC.

Полученные треугольники являются равновеликими, так как имеют общую высоту и равные стороны, к которым эта высота проведена.

Предлагаем задачи для самостоятельного решения.

Задача № 2:

Вырежьте из бумаги два равных прямоугольника, у каждого из которых одна сторона вдвое больше другой. Один из них разрежьте на 2 части так, чтобы из них можно было составить прямоугольный треугольник. Другой разрежьте на 3 части так, чтобы из них можно было составить квадрат.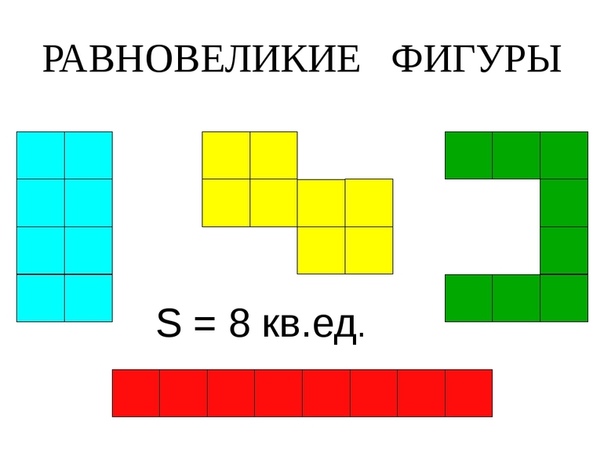

Задача № 3:

Постройте прямоугольный треугольник и покажите, как его разрезать на части так, чтобы из них можно было сложить прямоугольник, равновеликий данному треугольнику.

Задача № 4:

Постройте треугольник, не являющийся прямоугольным. Покажите, как его разрезать на три части так, чтобы из них можно было сложить прямоугольник с тем же основанием, равновеликий данному треугольнику.

Задача № 5:

Нарисуйте на клетчатой бумаге два разных прямоугольных треугольника, у которых площади:

1) равны двум клеткам

2) равны трем клеткам

3) равны 4,5 клеткам

Задача № 6:

Нарисуйте на клетчатой бумаге квадрат, площадь которого равна 2, 4, 5, 8, 9, 10, 16, 17, 18, 20, 25, 26 клеткам.

Задача № 7:

Превратить треугольник в равновеликий ему параллелограмм.

Задача № 8:

Превратить параллелограмм в равновеликий ему треугольник.

Задача № 9:

Постройте квадрат, площадь которого в два раза больше пощади данного квадрата.

Задача № 10:

Вырежьте из бумаги два равных прямоугольных треугольника и составьте из них:

1) равнобедренный треугольник

2) прямоугольник

3) параллелограмм, не являющийся прямоугольником

Объясните, почему площади всех полученных фигур равны между собой.

Задача № 11:

Данный прямоугольник разделить на 4 равновеликие части прямыми, выходящими из одной вершины.

Задача № 12:

Данный параллелограмм разделить на 4 равновеликие части прямыми, выходящими из одной вершины.

Задача № 13:

Данный параллелограмм разделить на 3 равновеликие части прямыми, выходящими из одной вершины.

Задачи на построение:

Задача № 1: Дан треугольник ABC. Найдите геометрическое место точек P, для которых треугольники APB и ABC равновелики.

Решение:

Поскольку равновеликие треугольники APB и ABC имеют общее основание AB, то равны их высоты, проведенные из вершин соответственно C и P. Значит, геометрическое место точек Р совпадает с геометрическим местом точек, удаленных от прямой АВ на расстояние, равное высоте CH треугольника АВС, а это, как известно, — две параллельные прямые, удаленные от прямой АВ на расстояние, равное CH.

Предлагаем задачи для самостоятельного решения.

Задача № 2:

Дан треугольник ABC. Найдите геометрическое место точек P, для которых треугольники APB и APC равновелики.

Задача № 3:

Дан треугольник ABC. Найдите геометрическое место точек P, для которых треугольники APB, APC и BPC равновелики.

Подсказка:

Задачи на доказательство:

Задача № 1:

Точка O лежит на прямой, содержащей диагональ AC параллелограмма ABCD. Докажите, что площади треугольников AOB и AOD равны.

Решение

Выполним дополнительное построение: ВМ, DN – высоты. Затем рассмотрим прямоугольные треугольники AND и СМВ. Т. к. сторона AD равна стороне BC (по свойству параллелограмма), а угол DAC равен углу BCA (накрест лежащие углы при параллельных прямых AD ,BC и секущей AC), то треугольник AND будет равен треугольнику СМВ. Из равенства треугольников следует равенство соответствующих сторон BM=DN. Значит, площадь треугольника AOB будет равна площади треугольника AOD, так как эти треугольники имеют общую сторону АО и равные высоты, проведенные к этой стороне.

Предлагаем задачи для самостоятельного решения.

Задача № 2:

Докажите, что медианы разбивают треугольник на шесть равновеликих треугольников.

Задача № 3:

Отрезок, соединяющий середины двух противоположных сторон выпуклого четырёхугольника, разделил его на два четырёхугольника, имеющих равные площади. Докажите, что эти стороны параллельны.

Задача № 4:

Докажите, что треугольники ABC и DHF равновелики, если угол A равен углу D и AB: DH = DF : AC.

Задача №5:

В треугольнике АВС проведены медианы АМ и ВК, которые пересекаются в точке О. Докажите, что треугольники АОК и ВОМ равновелики. Попробуйте дать два различных доказательства.

Задача №6:

Трапеция равновелика треугольнику, образованному продолжениями её боковых сторон и меньшим основанием. Докажите, что отношение длин оснований этой трапеции равно.

Задача №7:

Диагонали трапеции АВСD с основаниями АВ и СD пересекаются в точке О. Докажите, что треугольники АОD и ВОС имеют равные площади.

Похожие фигурки

Говорят, что две фигуры похожий если они одинаковой формы. Говоря более математическим языком, две фигуры подобны, если их соответствующие углы равны конгруэнтный , а отношения длин их соответствующих сторон равны.

Это обычное отношение называется масштаб .

Символ ∼ используется для обозначения сходства.

Пример 1:

На рисунке ниже пятиугольник А Б С Д Е ∼ пятиугольник В Вт Икс Д Z .

(Обратите внимание, что порядок, в котором вы пишете вершины, имеет значение; например, пятиугольник А Б С Д Е является нет похоже на пятиугольник В Z Д Икс Вт . )

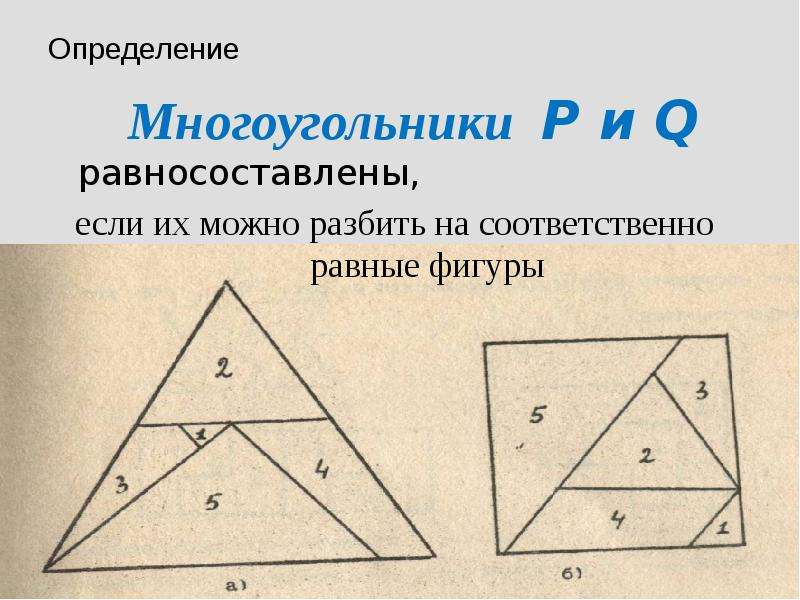Пример 2:

Два цилиндра похожи. Найдите масштабный коэффициент и радиус второго цилиндра.

Высота цилиндра справа 1 3 высота цилиндра слева.Итак, масштабный коэффициент 1 3 .

Чтобы получить радиус меньшего цилиндра, разделите 1,8 от 3 .

1,8 ÷ 3 знак равно 0,6

Значит, радиус меньшего цилиндра 0,6 см.

Заметим, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью вращения , размышления , переводы , и расширения .

Пример 3:

На рисунке выше шестиугольник А 1 Б 1 С 1 Д 1 Е 1 Ф 1 переворачивается горизонтально, чтобы получить А 2 Б 2 С 2 Д 2 Е 2 Ф 2 .

Затем шестиугольник А 2 Б 2 С 2 Д 2 Е 2 Ф 2 переводится как получить А 3 Б 3 С 3 Д 3 Е 3 Ф 3 .

Шестиугольник А 3 Б 3 С 3 Д 3 Е 3 Ф 3 расширяется на масштабный коэффициент 1 2 получить А 4 Б 4 С 4 Д 4 Е 4 Ф .

Обратите внимание, что

А 1 Б 1 С 1 Д 1 Е 1 Ф 1 ∼ А 2 Б 2 С 2 Д 2 Е 2 Ф 2 ∼ А 3 Б 3 С 3 Д 3 Е 3 Ф 3 ∼ А 4 Б 4 С 4 Д 4 Е 4 Ф 4 .

То есть все четыре шестиугольника подобны. (На самом деле, первые три конгруэнтны.)

Пример 4:

Рассмотрим пятиугольник п Вопрос р С Т на координатной плоскости.

Ротация на 180 ° о происхождении отводит пятиугольник к п ‘ Вопрос ‘ р ‘ С ‘ Т ‘ .

Теперь расширение относительно начала координат с помощью масштабного коэффициента 2 берет пятиугольник п ‘ Вопрос ‘ р ‘ С ‘ Т ‘ к п ‘ ‘ Вопрос ‘ ‘ р ‘ ‘ С ‘ ‘ Т ‘ ‘ .

Обратите внимание, что п Вопрос р С Т ∼ п ‘ Вопрос ‘ р ‘ С ‘ Т ‘ ∼ п ‘ ‘ Вопрос ‘ ‘ р ‘ ‘ С ‘ ‘ Т ‘ ‘ .То есть все три пятиугольника подобны. (И первые два совпадают.)

Иллюстративная математика

Комментарий IM

Цель задания — помочь учащимся перейти от неформального представления о конгруэнтности как «одинакового размера, одинаковой формы», которое они учат в начальной школе, и приступить к разработке определения конгруэнтности в терминах жестких трансформаций. Задание также можно использовать, чтобы проиллюстрировать важность разработки общих математических определений (МН 6).Обратите внимание, что термин «конгруэнтность» в задании не используется; его следует ввести в конце обсуждения как слово, которое мы используем для более точного определения «того же размера, той же формы».

Понятие эквивалентности является глубоким в математике, и в первом классе учащиеся начинают исследовать, что означает равенство двух чисел (1.OA.D.7). Но что означает, что две геометрические фигуры «одинаковы»? В первом классе учащиеся начинают изучать, что означает, что две одномерные фигуры имеют одинаковую длину (1.MD.A), в третьем классе учащиеся изучают, что означает, что две двумерные фигуры имеют одинаковую площадь (3.MD.C), а в пятом классе изучают, что означает, что два трехмерных объекта имеют одинаковую площадь. тот же объем (5.MD.C). Таким образом, к концу начальной школы у учащихся появляется представление о том, что понятие «одинаковости» имеет нюансы в геометрическом контексте. Они также говорят о том, что означает, что две фигуры имеют одинаковую форму, а на повседневном языке мы говорим, что два прямоугольника имеют «одинаковую форму». Но что означает, что две фигуры имеют «одинаковую форму и размер»? Если два прямоугольника имеют одинаковую площадь, имеют ли они одинаковый размер и форму? Без более точного определения того, что мы подразумеваем под одинаковым размером, одинаковой формой, мы не можем сказать да или нет.

Общее определение конгруэнтности гласит, что два многоугольника конгруэнтны, если существует соответствие между вершинами и соответствующие стороны имеют одинаковую длину и соответствующие углы имеют одинаковую меру. Это хорошо, если говорить о конгруэнтности фигур с изогнутыми сторонами. Определение конгруэнтности в терминах жестких преобразований охватывает все виды фигур, и мы можем показать, что из него следует традиционное определение многоугольников.Поскольку жесткие преобразования, применяемые к фигуре, представляют собой просто формализацию идеи взять эту фигуру и переместить ее, не растягивая и не ломая ее, это определение также имеет то преимущество, что формализует интуитивное представление о том, что означает, что две фигуры являются двумя фигурами. одинакового размера и одинаковой формы: если вы можете наложить одно на другое, чтобы не было промежутков или наложений, то они имеют одинаковый размер и одинаковую форму.

При правильном использовании это задание может инициировать разговор, который приведет от понятия одинакового размера и формы в начальной школе к более формальному определению конгруэнтности в средней школе в терминах жестких движений. Для ответа на первый вопрос учащиеся должны иметь доступ к различным инструментам, включая кальку или прозрачные пленки, ножницы, ленту, линейки, транспортиры и т. д. в группах класс может обсудить достоинства и недостатки различных возможных определений. Учителя должны ожидать, что учащиеся подойдут к этому как минимум тремя разными способами:

• Аргументы, основанные на внешнем виде фигуры: они выглядят так, будто имеют одинаковый размер и форму.Если учащиеся предлагают такой подход, учитель может спросить, означает ли это, что любые два прямоугольника соответствуют требованиям, поскольку в каком-то смысле они выглядят одинаково. То же самое можно спросить об окружностях или эллипсах и других непрямолинейных фигурах. Это может помочь установить, что похожести недостаточно.
• Аргументы, основанные на измерениях. Учащиеся могут измерить длины сторон и углы, и если соответствующие стороны и углы имеют одинаковые размеры, они могут сделать вывод, что две фигуры имеют одинаковый размер и форму. Учитель может спросить учащихся, как бы они применили этот подход к фигурам с изогнутыми сторонами, как в наборе C. Это может подтолкнуть учащихся к поиску более общего определения.
• Аргументы, основанные на наложении одной фигуры на другую и проверке их точного совпадения. Это может стать основой для определения конгруэнтности в терминах жестких движений.

Набор С поднимает очень важный вопрос о природе конгруэнтности. Если две фигуры являются зеркальными отображениями, считается ли это, что они имеют одинаковый размер и форму или нет? (По соглашению, математическое сообщество согласилось, что это так, но могло быть принято другое решение.) Набор D поднимает другой вопрос: если фигура состоит из нескольких «частей», можем ли мы двигать их каждую по отдельности или мы должны двигать их вместе? (Опять же, мы согласны с тем, что при определении конгруэнтности фигуру следует рассматривать как единое целое.)

После обсуждения возможных определений понятия «одинаковый размер, одинаковая форма» учащимся, которые уже знакомы с жесткими преобразованиями, можно дать формальное определение:

Две фигуры A и B конгруэнтны, если одна из них является образом другой при выполнении последовательности жестких преобразований.

Если учащиеся еще не были ознакомлены с жесткими преобразованиями, задание можно использовать для мотивации их учебы. Что значит «переместить одну фигуру поверх другой так, чтобы они точно выстроились в линию»? Геометрия в старших классах движется в направлении уточнения этих представлений о конгруэнтности («одинаковая форма»), что приводит к тщательному изучению перемещений, отражений и вращений. Например, несколько важных вех в геометрии средней школы включают использование этих преобразований для определения конгруэнтности двух треугольников на основе информации об их сторонах и углах.В этом смысле это задание является началом перехода, в котором учащиеся могут прийти к пониманию того, что понятие эквивалентности геометрических фигур является тонким и глубоким.

Решение

а. Для множества A эти две фигуры представляют собой прямоугольники с отрезанными противоположными вершинами. Кажется, что они имеют одинаковый размер и одинаковую форму. Мы можем измерить длины сторон и углы двух фигур. Если мы начнем с верхней левой вершины для синей формы и с крайней левой вершины для желтой фигуры, двигаясь по часовой стрелке, длины сторон и измерения углов окажутся одинаковыми.

Мы также можем попытаться выровнять их с помощью поворотов, отражений и перемещений: верхняя левая вершина синей фигуры может быть перемещена, чтобы совпасть с крайней левой вершиной желтой фигуры. Затем мы можем вращать синюю фигуру против часовой стрелки вокруг этой общей вершины, пока она не ляжет точно поверх желтой фигуры (со сторонами и вершинами, совпадающими).

Эти две фигуры кажутся одинакового размера и одинаковой формы.

Для набора B приблизительный размер и форма двух фигурок одинаковы, но на глаз (без измерения) трудно сказать однозначно.⠀ При более внимательном рассмотрении заметна разница в углах. Нижняя левая вершина зеленой фигуры приблизительно равна прямому углу, в то время как ни один из углов желтой фигуры не близок к прямому углу. Итак, эти две формы различны.

Мы также можем попытаться выровнять их с помощью поворотов, отражений и перемещений: кончик желтой молнии можно совместить с кончиком зеленой молнии путем перемещения. Затем мы можем вращаться вокруг этой общей вершины и обнаружить, что, хотя они и имеют примерно одинаковую форму, они никогда не совпадают идеально, то есть либо некоторые вершины, либо некоторые стороны не совпадают.

Эти две фигуры не кажутся одинаковыми по размеру и форме.

Для набора C эти две фигуры определенно выглядят так, как будто они имеют одинаковый размер и форму: они выглядят как два одинаковых флага, развевающихся на ветру, и отличаются только цветом. Прямые стороны этих фигур имеют одинаковую длину. Измерить изогнутые стороны непросто, поэтому измерение нам здесь не поможет.

Мы также можем попытаться выровнять их с помощью поворотов, отражений и переводов: мы не можем перевести и повернуть красную фигуру, чтобы она совпадала с синей, потому что четыре угла двух фигур не идентичны (для двух пар углов, сделанных в вершинах острые, а для двух других эти углы тупые). Чтобы совместить две фигуры, мы можем переместить верхнюю правую вершину красной фигуры так, чтобы она совпадала с верхней правой вершиной синей фигуры. Затем мы можем вращать красную фигуру вокруг этой общей вершины до тех пор, пока она не разделит общее (прямое) ребро с синей фигурой. Отражение вокруг линии, содержащей это ребро, сопоставит все части (углы и стороны) с синей фигурой.

Эти две фигуры кажутся одинакового размера и одинаковой формы.

Для набора D каждое изображение представляет собой пару треугольников, и эти треугольники выглядят так, как будто они имеют одинаковый размер и одинаковую форму.Длины сторон треугольников одинаковы, а все углы кажутся равными 60 градусам, поэтому все треугольники равносторонние. Каждый из первой пары треугольников имеет тот же размер и ту же форму, что и каждый из второй пары треугольников. Однако треугольники не «склеены» одинаково.

Мы также можем попытаться выровнять их с помощью поворотов, отражений и переводов: мы можем перемещать и вращать каждый из отдельных треугольников в синей паре, чтобы он совпадал с одним из треугольников из фиолетовой пары. Однако это требует различных переводов и отражений для каждого треугольника.

Эти две фигуры не кажутся одинаковыми по размеру и форме.

В наборе E эти фигурки кажутся одинаковой формы, но, возможно, разного размера — трудно сказать без измерения. Тщательное измерение длин сторон как бы подтверждает это, и при попытке наложить одну на другую они не совпадают.

Эти две фигуры не кажутся одинаковыми по размеру и форме.€

б. Две фигуры имеют одинаковый размер и одинаковую форму, если одну можно переместить, не растягивая и не разрывая, чтобы точка за точкой совпала с другой. Говоря более формально, две фигуры конгруэнтны, если одна из них является образом другой в результате последовательности жестких преобразований.

Конгруэнтность, равенство и сходство | Encyclopedia.com

---

Что значит сказать, что один квадрат «равен» другому? Вероятно, кажется разумным сказать, что два квадрата равны, если они имеют стороны одинаковой длины. Если площади двух квадратов равны, то и стороны у них будут одинаковой длины. Но хотя «равные площади означают равные стороны» верно для квадратов, это , а не верно для большинства геометрических фигур.

Рассмотрим прямоугольники, показанные ниже. Площади A, B и D равны 2 квадратным единицам, но неразумно говорить, что прямоугольник A «равен» прямоугольнику D, хотя их площади равны.

В геометрии есть специальный математический язык для описания некоторых из этих взаимосвязей.Если прямоугольник B переместить, повернуть на бок (вращение) и сдвинуть (перемещение), он точно впишется в прямоугольник A.

Две геометрические фигуры называются конгруэнтными , если они имеют одинаковый размер и одинаковую форму. Две конгруэнтные фигуры можно заставить точно совпадать. Прямоугольник A конгруэнтен прямоугольнику B. В математической записи это записывается как A ≅ B.

Посмотрите на два многоугольника ниже. Они конгруэнтны? Можно ли сдвинуть (переместить) один из многоугольников, повернуть (повернуть) и перевернуть (отразить) так, чтобы он точно поместился над другим? Ответ положительный, и, следовательно, эти две формы конгруэнтны. Их соответствующие или совпадающие углы конгруэнтны, как и их соответствующие стороны.

два	Connogrent If:
сегменты линии	мера их длины одинаково
Круги	У них есть конгруэнтные радиусы
углов	они имеют одинаковую меру (градусы)
Многоугольники	их соответствующие части (стороны и углы) конгруэнтны

сам по себе), симметричный (поскольку A ≅ B означает, что B ≅ A) и транзитивный (поскольку A ≅ B≅ F означает, что A ≅ F).

Когда создается точная копия формы, в результате получаются конгруэнтные формы. Иногда вместо точной копии изготавливается масштабная модель или чертеж меньшего или большего размера, чем оригинал. Чертежи, копии фотографий, миниатюры, увеличенные изображения — все это примеры отношений, несколько отличных от конгруэнтности.

Посмотрите на рисунок, на котором изображены прямоугольник A и прямоугольник C. Стороны прямоугольника A имеют размеры 1 на 2 единицы. Стороны прямоугольника C имеют размеры 2 на 4 единицы.Соответствующие углы двух прямоугольников равны. Прямоугольник A можно увеличить, чтобы он выглядел как прямоугольник C, или C можно было уменьшить, чтобы он выглядел как A.

Математический термин для уменьшения или увеличения фигуры — расширение. Стороны этих двух прямоугольников пропорциональны: 1:2 = 2:4. Когда одну фигуру можно превратить в другую путем расширения, эти две фигуры подобны.

Две геометрические фигуры называются подобными , если они имеют одинаковую форму, так что их соответствующие стороны пропорциональны.Две одинаковые фигуры могут быть разного размера, но всегда имеют одинаковую форму.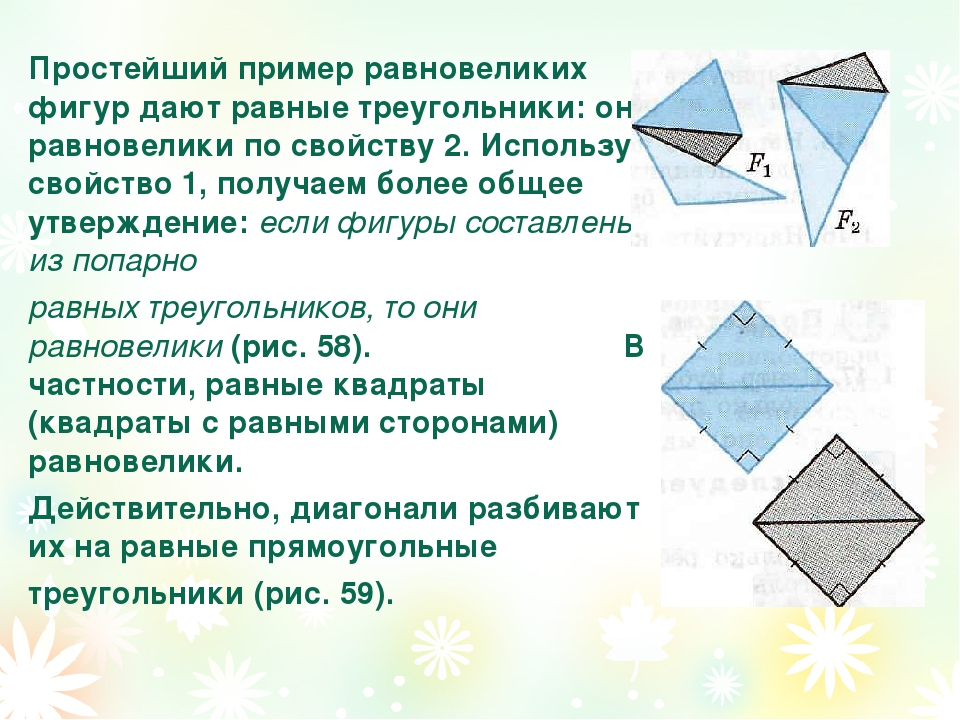

Прямоугольник A подобен прямоугольнику C. В математической записи это записывается как A ≈ C. Две конгруэнтные фигуры также всегда будут подобны друг другу, поэтому A ≈ B.

Посмотрите еще раз на прямоугольники. Независимо от того, как прямоугольник D расширяется, перемещается, поворачивается или отражается, он не может иметь ту же форму, что и A или C. Таким образом, D не конгруэнтен и не похож ни на какой другой прямоугольник на этом рисунке.

см. также Копировальный аппарат.

Люсия Маккей

Библиография

Конкл, Гейл С. Формы и восприятие: интуитивный подход к геометрии. Бостон: Prindle, Weber, & Schmidt, Inc., 1974.

%PDF-1.4 % 115 0 объект > внешняя ссылка эндообъекта 115 264 0000000044 00000 н 0000006361 00000 н 0000006414 00000 н 0000007670 00000 н 0000091919 00000 н 0000092707 00000 н 0000092776 00000 н 0000093113 00000 н 0000093215 00000 н 0000093302 00000 н 0000093632 00000 н 0000093725 00000 н 0000096021 00000 н 0000096074 00000 н 0000096630 00000 н 0000096717 00000 н 0000096777 00000 н 0000097990 00000 н 0000099788 00000 н 0000155434 00000 н 0000156759 00000 н 0000157982 00000 н 0000159797 00000 н 0000214206 00000 н 0000214544 00000 н 0000214638 00000 н 0000240493 00000 н 0000252861 00000 н 0000255925 00000 н 0000257624 00000 н 0000258004 00000 н 0000258311 00000 н 0000258363 00000 н 0000259336 00000 н 0000259391 00000 н 0000259464 00000 н 0000259493 00000 н 0000259845 00000 н 0000260833 00000 н 0000260903 00000 н 0000261283 00000 н 0000261338 00000 н 0000261411 00000 н 0000261762 00000 н 0000261803 00000 н 0000266704 00000 н 0000266745 00000 н 0000271597 00000 н 0000272814 00000 н 0000274628 00000 н 0000288415 00000 н 0000289628 00000 н 0000289936 00000 н 00002

00000 н 00002 00000 н 00002

00000 н 00002

00000 н 00002 00000 н 00002
00000 н 00002
00000 н 0000291025 00000 н 0000291154 00000 н 0000291291 00000 н 0000291445 00000 н 0000291574 00000 н 0000291711 00000 н 0000291865 00000 н 0000291994 00000 н 0000292131 00000 н 0000292285 00000 н 0000292414 00000 н 0000292550 00000 н 0000292704 00000 н 0000292946 00000 н 0000293099 00000 н 0000293252 00000 н 0000293405 00000 н 0000293558 00000 н 0000293714 00000 н 0000293870 00000 н 0000294023 00000 н 0000294177 00000 н 0000294419 00000 н 0000294570 00000 н 0000294722 00000 н 0000294874 00000 н 0000295019 00000 н 0000295167 00000 н 0000295321 00000 н 0000295472 00000 н 0000295626 00000 н 0000295869 00000 н 0000296022 00000 н 0000296180 00000 н 0000296333 00000 н 0000296486 00000 н 0000296642 00000 н 0000296795 00000 н 0000296949 00000 н 0000297078 00000 н 0000297207 00000 н 0000297361 00000 н 0000297490 00000 н 0000297627 00000 н 0000297781 00000 н 0000297995 00000 н 0000298153 00000 н 0000298309 00000 н 0000298460 00000 н 0000298616 00000 н 0000298767 00000 н 0000298919 00000 н 0000299073 00000 н 0000299202 00000 н 0000299339 00000 н 0000299493 00000 н 0000299711 00000 н 0000299864 00000 н 0000300017 00000 н 0000300169 00000 н 0000300323 00000 н 0000300480 00000 н 0000300633 00000 н 0000300787 00000 н 0000300916 00000 н 0000301040 00000 н 0000301194 00000 н 0000301342 00000 н 0000301495 00000 н 0000301648 00000 н 0000301802 00000 н 0000301931 00000 н 0000302063 00000 н 0000302217 00000 н 0000302365 00000 н 0000302517 00000 н 0000302669 00000 н 0000302823 00000 н 0000302990 00000 н 0000303143 00000 н 0000303275 00000 н 0000303412 00000 н 0000303566 00000 н 0000303695 00000 н 0000303827 00000 н 0000303981 00000 н 0000304110 00000 н 0000304264 00000 н 0000304393 00000 н 0000304518 00000 н 0000304672 00000 н 0000304896 00000 н 0000305049 00000 н 0000305207 00000 н 0000305359 00000 н 0000305510 00000 н 0000305664 00000 н 0000305815 00000 н 0000305973 00000 н 0000306140 00000 н 0000306291 00000 н 0000306443 00000 н 0000306595 00000 н 0000306749 00000 н 0000306878 00000 н 0000307010 00000 н 0000307164 00000 н 0000307293 00000 н 0000307425 00000 н 0000307579 00000 н 0000307708 00000 н 0000307845 00000 н 0000307999 00000 н 0000308211 00000 н 0000308368 00000 н 0000308524 00000 н 0000308681 00000 н 0000308838 00000 н 0000308990 00000 н 0000309144 00000 н 0000309363 00000 н 0000309516 00000 н 0000309674 00000 н 0000309832 00000 н 0000309984 00000 н 0000310135 00000 н 0000310287 00000 н 0000310441 00000 н 0000310570 00000 н 0000310700 00000 н 0000310854 00000 н 0000310983 00000 н 0000311115 00000 н 0000311269 00000 н 0000311398 00000 н 0000311550 00000 н 0000311704 00000 н 0000311833 00000 н 0000311963 00000 н 0000312117 00000 н 0000312246 00000 н 0000312371 00000 н 0000312525 00000 н 0000312654 00000 н 0000312784 00000 н 0000312938 00000 н 0000313067 00000 н 0000313195 00000 н 0000313349 00000 н 0000313554 00000 н 0000313707 00000 н 0000313852 00000 н 0000314002 00000 н 0000314158 00000 н 0000314303 00000 н 0000314344 00000 н 0000354168 00000 н 0000354209 00000 н 0000355895 00000 н 0000355936 00000 н 0000374402 00000 н 0000374915 00000 н 0000375231 00000 н 0000375776 00000 н 0000376092 00000 н 0000377306 00000 н 0000377405 00000 н 0000378734 00000 н 0000379951 00000 н 0000382062 00000 н 0000437489 00000 н 0000438705 00000 н 0000440817 00000 н 0000494691 00000 н 0000495910 00000 н 0000498025 00000 н 0000556696 00000 н 0000557913 00000 н 0000560025 00000 н 0000586792 00000 н 0000588115 00000 н 0000588164 00000 н 0000588245 00000 н 0000588317 00000 н 0000588382 00000 н 0000588447 00000 н 0000588520 00000 н 0000588877 00000 н 00005

00000 н 0000590975 00000 н 0000591030 00000 н 0000591103 00000 н 0000591461 00000 н 0000595568 00000 н 0000595667 00000 н 0000595725 00000 н 0000595815 00000 н 0000595865 00000 н 0000595914 00000 н 0000595972 00000 н 0000596037 00000 н 0000596110 00000 н 0000596473 00000 н 0000005636 00000 н трейлер ] /Info 109 0 R /Prev 1138145 /Size 379 /Root 116 0 R >> startxref 0 %%EOF 378 0 объект > ручей xROHQٙmvյ-,LRI!1 %(Ky\XDoG%}ͼ

Результаты подсчета точек для 60 срезов сферы одинакового размера (1 + 1 см).

..

Контекст 1

… начнем с результатов подсчета очков для моделей одинакового размера (1 + 1 см) (рис. 6). Напомним, что мы усредняем результаты по 60 срезам в каждой трехмерной модели. Как правило, для N tot (общее количество точек, включая точки в пустотах) от 100 до 2500 и p от 0,1 до 0,9 метод подсчета точек является точным в этом тесте. Это означает, что средние измеренные пропорции синих сфер (цветные точки, рис. 6) равны …

Контекст 2

… (1 + 1 см) модели (рис. 6). Напомним, что мы усредняем результаты по 60 срезам в каждой трехмерной модели. Как правило, для N tot (общее количество точек, включая точки в пустотах) от 100 до 2500 и p от 0,1 до 0,9 метод подсчета точек является точным в этом тесте. Это означает, что средние измеренные пропорции синих сфер (цветные точки, рис. 6) очень близки к истинной объемной пропорции в моделях (штриховые линии на верхней панели рис. 6 или линии «нулевой ошибки» на других панелях). Средние абсолютные ошибки варьируются от положительных до отрицательных и всегда находятся в пределах 1% или 0,01 (положительных или отрицательных) для отдельных моделей (средняя панель рис. 6), а средняя относительная ошибка составляет …

Контекст 3

… для N tot (общее количество точек, включая пустые) от 100 до 2500 и p от 0,1 до 0,9 метод подсчета точек является точным в этом тесте. Это означает, что средние измеренные пропорции синих сфер (цветные точки, рис. 6) очень близки к истинной объемной пропорции в моделях (штриховые линии на верхней панели рис.6 или строки «ноль ошибок» на других панелях). Средние абсолютные ошибки варьируются от положительных до отрицательных и всегда находятся в пределах 1% или 0,01 (положительных или отрицательных) для отдельных моделей (средняя панель рис. 6), а средняя относительная ошибка всех моделей вместе взятых (p = 0,1-0,9) составляет ~0,0%, т. е. систематическая погрешность отсутствует (нижняя панель рис. 6). …

Контекст 4

… пропорции синих сфер (цветные точки, рис. 6) очень близки к истинным объемным пропорциям в моделях (штриховые линии на верхней панели рис.6 или строки «ноль ошибок» на других панелях). Средние абсолютные ошибки варьируются от положительных до отрицательных и всегда находятся в пределах 1% или 0,01 (положительных или отрицательных) для отдельных моделей (средняя панель рис. 6), а средняя относительная ошибка всех моделей вместе взятых (p = 0,1-0,9) составляет ~0,0%, т. е. систематическая погрешность отсутствует (нижняя панель рис. 6). Исключением является модель p = 0,01, где результаты очень изменчивы в относительном выражении, но подсчет нескольких тысяч точек, вероятно, даст точные значения …

Контекст 5

… панель на рис. 6 или строки «нулевой ошибки» на других панелях). Средние абсолютные ошибки варьируются от положительных до отрицательных и всегда находятся в пределах 1% или 0,01 (положительных или отрицательных) для отдельных моделей (средняя панель рис. 6), а средняя относительная ошибка всех моделей вместе взятых (p = 0,1-0,9) составляет ~0,0%, т. е. систематическая погрешность отсутствует (нижняя панель рис. 6). Исключением является модель p = 0,01, где результаты очень изменчивы в относительном выражении, но подсчет нескольких тысяч точек, вероятно, даст точные значения …

Контекст 6

… любые эффекты нарезки, как описано ниже. Как и ожидалось, общая точность улучшается при увеличении N tot. Для компонента с p = 0,5 в модели 1 + 1 см стандартное отклонение лучше 5% абсолютного (10% относительного) получается для N tot = 225 точек и стандартного отклонения ~1,5% абсолютного (~0,5% относительного). ) получается при N tot = 2500 точек (рис. 6). Для моделей 1 + 2 см и 1 + 3 см общая точность также улучшается при подсчете большего количества точек (рис.7). Однако стандартные отклонения остаются высокими для моделей с синими сферами радиусами 5 и 10 см даже при N tot = 2500 точек (рис. 7). …

Контекст 7

. .. теперь сравните абсолютное стандартное отклонение, полученное при подсчете множества точек на одном срезе моделей, которое является ошибкой подсчета (рис. 8, слева), с абсолютным стандартное отклонение, полученное при подсчете одной точки на каждом из 60 срезов (рис. 8, справа), что является нашей общей точностью на рисунках 6 и 7….

Контекст 8

… правильная пропорция компонента в среднем, т. е. они оба точны без каких-либо исправлений, если количество точек или линий (т. е. объектов, пересекаемых линиями) велико достаточно (рис. 6, 7, 9, 10). Это справедливо как для моделей одинакового, так и неравного размера. Подсчет точек точен даже при низких значениях N для моделей со сферами одинакового размера (рис. 6). Бывают ситуации, когда точность подсчета точек и подсчетов линий снижается из-за малых отсчетов или большой разницы в размерах компонентов).Тем не менее, основная проблема заключается в определении значения N, которое обеспечит необходимую точность, необходимую для ответа на изучаемый научный вопрос, что также потребует достаточно высокого . ..

Многоугольники – объяснение и примеры

Вы слышали о многоугольнике? Ну, вокруг нас полигона! Большинство распространенных форм, которые вы видите или изучаете каждый день, представляют собой многоугольники. Вы видите, что стена прямоугольной формы представляет собой многоугольник.

Игральная кость, имеющая квадратную форму, вид спереди представляет собой многоугольник.Кусок пиццы имеет треугольную форму, следовательно, многоугольник.

В этой статье вы узнаете:

• Что такое многоугольники и как они выглядят.
• Различные типы многоугольников.

Что такое многоугольник?

В математике многоугольник — это замкнутая двумерная фигура, состоящая из отрезков прямых, но не кривых. Термин «полигон» происходит от греческого слова «поли-», означающего «много», и «-гон», означающего «углы».

Наиболее распространенными примерами многоугольников являются треугольник, прямоугольник и квадрат. Проще говоря, многоугольники — это простые фигуры или формы, состоящие только из отрезков линий.

Примечание: Окружности, трехмерные объекты, любые формы, содержащие кривые, и любые незамкнутые формы не являются многоугольниками.

Многоугольники были известны людям с древних времен. греки изучали невыпуклый правильный многоугольник в 7 ^ом веке до н.э. на кратере Аристофана. Томас Брэдвардин был первым известным человеком, изучавшим невыпуклые многоугольники в 14 ^-м -м веке.Концепция полигонов была обобщена в 1952 году Джеффри Колином.

Теперь, когда вы поняли, что такое многоугольник, давайте рассмотрим различные многоугольники и то, как они выглядят.

Типы многоугольников

в зависимости от сторон и углов, многоугольники классифицируются на различных типов, а именно,

1. Regular Polygon
2. Нерегулярный полигон
3. Выпуклый полигон
4. вогнутый многоугольник

Обычный полигон

Правильный многоугольник — это многоугольник, у которого все внутренние углы равны, а также все стороны равны. Существуют различные типы правильных многоугольников.

Это:

• Треугольник : Равносторонний треугольник – это правильный многоугольник с тремя равными сторонами и тремя равными углами.
• Четырехугольник. Четырехугольник – это правильный многоугольник с четырьмя углами и четырьмя сторонами. Примеры четырехугольников:

а. Квадрат : Четырехугольник, у которого 4 стороны равны и четыре угла равны 90 градусов каждый.

б. Прямоугольник:

c. Параллелограмм : Противоположные стороны параллельны, противоположные стороны равны по длине, противоположные углы равны

d. Воздушный змей : две пары смежных сторон имеют одинаковую длину; форма имеет ось симметрии.

эл. Ромб : Особый тип параллелограмма, в котором все четыре стороны имеют одинаковую длину, как у квадрата, сплющенного по бокам.

• Пятиугольник : Многоугольник с 5 равными сторонами и углом
• Шестиугольник: Правильный многоугольник с 6 равными сторонами и 6 равными углами.
• Семиугольник: Правильный многоугольник с 7 равными сторонами и 7 одинаковыми углами.
• Восьмиугольник: Восьмиугольник имеет 8 равных сторон и 8 равных углов. Лучший пример восьмиугольника из реальной жизни — дорожный знак «СТОП».
• Нонагон: Имеет 9 равных сторон и 9 одинаковых углов.
• Hendecagon: Имеет 11 равных сторон и 11 равных углов.
• Додекагон: правильный многоугольник с 12 равными сторонами и 12 одинаковыми углами
• Трискайдекагон: Имеет 13 равных сторон и 13 одинаковых углов.
• Tetrakaidecagon : Имеет 14 равных сторон и 14 одинаковых углов.
• Пятиугольник: Пятиугольник — это правильный многоугольник с 15 равными сторонами и 15 одинаковыми углами.
• Hexakaidecagon : имеет 16 сторон и углов.
• Семиугольник : Имеет 17 сторон и углов.
• Octakaidecagon: Имеет 18 сторон и углов
• Enneadecagon: 19 сторон и 19 углов.
• Икосагон: Имеет равные стороны и 20 равных углов
• Гексагон: Имеет 100 равных сторон и 100 равных углов.
• Чилиагон: Имеет 1000 сторон
• Мириагон: 10000 сторон.
• Мегагон: Один миллион сторон.
• n-угольник : Имеет n- равных сторон.

Неправильный многоугольник

Неправильный многоугольник — это многоугольник с разной мерой углов и длин сторон.

Примеры неправильных многоугольников:

Выпуклый многоугольник

Это тип многоугольника, все внутренние углы которого строго меньше 180 градусов. Вершина выпуклого многоугольника всегда направлена ​​наружу от центра фигуры.

Вогнутый многоугольник

Если один или несколько внутренних углов многоугольника больше 180 градусов, он называется вогнутым многоугольником. Вогнутый многоугольник может иметь как минимум четыре стороны — вершина указывает внутрь многоугольника.

Ниже приведены несколько мнемоник, помогающих запомнить названия некоторых многоугольников:

• Квадроцикл имеет 4 колеса и, следовательно, четырехугольник.
• Вашингтон, округ Колумбия, в США имеет 5 сторон (Пентагон).
• A H гребешок имеет 6 сторон ( H эксагон).
• S 7-гранный эптагон ( S четный).
• У осьминога 8 щупалец (восьмиугольник).
• Термины N onagon и N ine оба начинаются с буквы N.
• A Decagon имеет 10 сторон, точно так же, как десятичная точка D имеет 10 цифр.

Применение многоугольников в реальной жизни

Понимание форм важно в геометрии. Формы имеют широкое применение в реальных приложениях.

Например:

• Плитки, по которым вы ходите, имеют квадратную форму, что означает, что они многоугольники.
• Ферма здания или моста, стены здания и т.д., являются примерами многоугольников. Фермы имеют треугольную форму, а стены прямоугольной формы.
• Прямоугольная часть стула, на котором вы сидите, является примером многоугольника.
• Прямоугольный экран вашего ноутбука, телевизора или мобильного телефона является примером многоугольника.
• Примером многоугольника является прямоугольное футбольное поле или игровая площадка.
• Бермудский треугольник, который имеет треугольную форму, представляет собой многоугольник.
• Египетские пирамиды также являются примером многоугольника (треугольника)
• Звездообразные фигуры являются примером многоугольника.
• Дорожные знаки также являются примером полигонов.

Пример

У Джона есть прямоугольный лист бумаги. Он хочет разрезать бумагу так, чтобы получить еще два многоугольника (кроме прямоугольника) того же размера и формы. Предложите возможные пути.

Решение

Существует два возможных способа разрезать прямоугольный лист бумаги таким образом, чтобы он получил еще два многоугольника (отличных от прямоугольника) одинакового размера и формы:

1. Он может разрезать прямоугольный лист лист бумаги ровно от центра по вертикали, чтобы получились два квадрата одинакового размера и формы.
2. Он может разрезать прямоугольный лист бумаги по диагонали, чтобы получить два треугольника одинакового размера и формы.

 

 

Открытые учебники | Сиявула

Математика

Наука

• • Читать онлайн

  • Учебники

    • Английский

      • Класс 7А

      • Класс 7Б

      • Класс 7 (объединенные А и В)

    • Африкаанс

      • Граад 7А

      • Граад 7Б

      • Graad 7 (A en B saam)

  • Пособия для учителей

• • Читать онлайн

  • Учебники

    • Английский

      • Класс 8А

      • Класс 8Б

      • Класс 8 (объединенные A и B)

    • Африкаанс

      • Граад 8А

      • Граад 8Б

      • Graad 8 (A en B saam)

  • Пособия для учителей

• • Читать онлайн

  • Учебники

    • Английский

      • Класс 9А

      • Класс 9Б

      • Класс 9 (объединенные А и В)

    • Африкаанс

      • Граад 9А

      • Граад 9Б

      • Graad 9 (A en B saam)

  • Пособия для учителей

• • Читать онлайн

  • Учебники

    • Английский

      • Класс 4А

      • Класс 4Б

      • Класс 4 (объединенные А и В)

    • Африкаанс

      • Граад 4А

      • Граад 4Б

      • Graad 4 (A en B saam)

  • Пособия для учителей

• • Читать онлайн

  • Учебники

    • Английский

      • Класс 5А

      • Класс 5Б

      • Класс 5 (объединенные А и В)

    • Африкаанс

      • Граад 5А

      • Граад 5Б

      • Graad 5 (A en B saam)

  • Пособия для учителей

• • Читать онлайн

  • Учебники

    • Английский

      • Класс 6А

      • Класс 6Б

      • Класс 6 (объединенные А и В)

    • Африкаанс

      • Граад 6А

      • Граад 6Б

      • Graad 6 (A en B saam)

  • Пособия для учителей

Лицензирование нашей книги

Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:

CC-BY-ND (фирменные версии)

Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.

Узнайте здесь больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.

CC-BY (версии без торговой марки)

Эти небрендированные версии одного и того же контента доступны для совместного использования, адаптации, преобразования, изменения или дальнейшего развития любым способом, при единственном требовании — отдать должное Сиявуле.