Различные способы решения систем уравнений (подготовка к ГИА)
1) Цели урока:
Образовательные:
- Закрепить, углубить, обобщить знания и умения решения систем уравнений, используя способы: алгебраического сложения, подстановки, графический, замены переменной.
- Познакомить с решением симметрических систем уравнений.
b. Развивающие:
- Умение находить и анализировать наиболее рациональные способы решения систем уравнения.
- Формировать навыки коллективной и самостоятельной работы.
- Развитие мыслительных и творческих способностей учащихся через умение действовать в нестандартной ситуации.
с. Воспитывающие:
- Способность выработке обобщать изучаемые факты.
- Прививать у учеников интерес к предмету через решение систем уравнений различными способами.
- Формировать умение четко и ясно излагать свои мысли и грамотно выполнять
математические задачи.

2) Проверка домашнего задания (на экране (Презентация. Слайд 2) записаны системы уравнений и ответы).
(При необходимости показать решение системы d на доске.)
1) Что называется решением системы уравнений с двумя переменными.
2) Какие способы решения систем уравнений вы использовали в домашней работе?
3) А какие еще способы вы знаете?
3) Устно:
На дом вам было задано повторить из курса геометрии:
- Уравнение окружности
- Что называется графиком уравнения с двумя переменными
– Так что же называется графиком уравнения с двумя переменными?
Слайд 3:
4) Презентация:
Учитель:
Двое учащихся по желанию получили творческие задания, используя дополнительную литературу, нашли материал, подобрали систему и сделали презентации.
- Решение систем уравнений графическим способом.

- Решение симметрических систем уравнений.
На предыдущих уроках мы рассматривали решение систем уравнений методом замены переменных. Общего правила выбора замены переменных не существует, однако можно выделить два вида систем уравнений, когда есть разумная замена переменных:
- Симметрические системы уравнений, которые сейчас рассмотрим в презентации.
- Системы уравнений, одно из которых однородное – рассмотрим на следующих уроках при подготовке к ГИА.
У каждого учащегося лежит на парте:
- распечатка презентации,
- домашнее задание.
5) Домашнее задание: (прокомментировать)
6) Работа с классом:
Учащийся решает у доски, остальные решают в тетрадях.
Ответ: (1;2), (1;-2).
7) Самостоятельная работа:
Приложение 2.
8) Итоги урока:
Оценки.
- Какие способы решения систем уравнений использовали на уроке?
- С каким видом систем уравнений познакомились на уроке?
- Какой способ решения систем уравнения применяется при их решении?
Историческая справка:
Все способы решения систем уравнения знали давно, но точной даты не известно. Хотя в книге Ньютона “Всеобщая арифметика” эти способы имеются.
Открытый урок по теме «Решение систем уравнений различными способами»
Цели урока:
- Систематизация знаний, умений и навыков при решении систем уравнений различными способами.
- Развитие: вычислительных навыков устного и письменного счета, умений применять знания на практике в новых условиях, межпредметных связей с историей, астрономией и информатикой.
- Воспитание интереса к предмету, патриотизма, чувства прекрасного, гордости за свою страну, самостоятельности и умения работать в заданном темпе.

- Развитие слухового и слухо-зрительного восприятия. Формирование математически грамотной речи учащихся.
Тип урока: урок обобщения и систематизации знаний, умений и навыков.
Словарь: средневековый ученый, Николай Коперник, российский ученый, Константин Эдуардович Циолковский, Галактика, Солнце, способ подстановки, способ сложения, выразить одну переменную через другую.
Ход урока
I. Организационный момент.
План урока
- Организационный момент.
- Устная работа.
- Самостоятельная работа.
- Физминутка.
- Выполнение упражнений.
- Домашнее задание.
- Итог урока.
Сегодня у нас с вами необычный урок. Мы с вами очередной раз совершим виртуальное путешествие. Мы отправимся с вами в путешествие по необъятным просторам космического пространства. Как вы думаете, почему я выбрала такое путешествие? (потому что скоро 12 апреля – День космонавтики). Совершенно верно.
Как вы думаете, почему я выбрала такое путешествие? (потому что скоро 12 апреля – День космонавтики). Совершенно верно.
II. Устная работа.
Перед началом нашего путешествия необходимо размяться и ответить на несколько вопросов. (Приложение 1, Слайд 2)
- Какие способы решения систем уравнений вы знаете?
- Является ли пара чисел (2; — 1) решением системы уравнений?
- Выразите одну переменную через другую.
1) х + у = 2;
2) х – 2у = 4.
Молодцы!
III. Самостоятельная работа.
Решить систему уравнений: (Приложение 1, Слайд 3)
IV. Физминутка.
Прежде чем вы приступите к работе надо выполнить физминутку.
V. Выполнение упражнений.
Учащиеся работают в программе PowerPoint. (Приложение 1)
Итак, мы отправляемся.
Впервые человек начал задумываться о космосе очень давно. Еще в XV веке средневековый ученый Коперник обратил свой взор в небо. (Приложение 1, Слайд 4)
Российский ученый Циолковский мечтал о полетах людей в космос и даже придумывал эскизы ракет.
Мечту Константина Эдуардовича Циолковского воплотил в реальность советский конструктор космических ракет Сергей Павлович Королев. (Приложение 1, Слайд 6)
А полетел в космос первый в мире советский космонавт Юрий Алексеевич Гагарин (Приложение 1, Слайд 7)
Вот и мы с вами совершим сегодня путешествие в практически неизведанные дали космического пространства.
Для того чтобы перемещаться по необъятным просторам космоса нам необходимо определять координаты нашего местонахождения.
В космосе есть своя определенная система координат, но сегодня мы воспользуемся координатами, полученными при решении систем уравнений двумя способами: способом подстановки и способом сложения.
Ну, что? Приступим к решению?
1. Решить систему уравнений способом подстановки:
(Приложение 1, Слайд 8).Ответ: (– 2; 5).
Выберите правильный ответ. (Приложение 1, Слайд 12).
Молодцы! Мы определили координаты расположения одной из многочисленных галактик. Это наша Галактика в которой мы живем. (Приложение 1, Слайд 15).
Кто прочитает, что это за галактика?
2. Решить систему уравнений способом сложения или вычитания: (Приложение 1, Слайд 9).
Ответ: (1; 2).
Выберите правильный ответ. (Приложение 1, Слайд 13).
Хорошо! А сейчас мимо нас пролетает комета с данными координатами (комета Галлея).
Прочитайте, что это за комета? (Приложение 1, Слайд 16).
3. Решить систему уравнений любым удобным способом: (Приложение 1, Слайд 10).
1 способ (подстановки)
Ответ: (3; – 2).
2 способ (сложения)
Ответ: (3; – 2).
Выберите правильный ответ. (Приложение 1, Слайд 14).
Молодцы! А теперь мы оказались возле звезды по имени Солнце.
Кто прочитает, что это за звезда? (Приложение 1, Слайд17).
VI. Домашнее задание.
1. Решить систему уравнений любым удобным способом: (Приложение 1, Слайд 11).
1 способ (подстановки).
Ответ: (6; – 1).
2 способ (сложения).
Ответ: (6; – 1).
VII. Итог урока.
Различные способы решения систем уравнений
Различные
способы решения систем двух линейных уравненийс двумя переменными
Учитель математики: Узденова Л. П.
П.
Тип урока: систематизации и обобщения изученного.
Класс: 7. Дата урока: 20.05.17 г.
Цель урока:
• Обработка и закрепление умений и навыков решения систем линейных уравнений;
• Показать рациональность применения
для конкретной системы;
. Развивать коммуникативные навыки;
. Формировать навыки самоконтроля, познавательного интереса к предмету.
Ход урока
«Когда человек не знает, к какой пристани он держит путь, для него ни один ветер не будет попутным»
Сенека
Организационный момент (2 мин.)
Минутка психологического настроя на урок:
Совет ученику: На уроке тебе пригодятся
активность, большое внимание,
твои знания и умения.
Прояви на уроке старание!
Актуализация знаний (10 мин.)
Учитель: Мы с вами продолжаем заниматься решением систем двух линейных
уравнений с двумя переменными различными способами.
• Что означает решить систему уравнений?
. Сколько решений может иметь система уравнений?
. Что является графиком линейной функции?
• Система состоит из двух линейных уравнений. А каким может быть взаимное расположение двух прямых на плоскости?
• Сколько общих точек имеют прямые в каждом из этих случаев?
• Сколько решений может иметь система в зависимости от взаимного расположения прямых на плоскости?
Учащиеся называют способы решения, на доске появляется следующие записи:
• способ сложения;
• способ подстановки;
• графический способ;
Практическое применение всех способов решения:
Для решения систем линейных уравнений нам известно три способа решения.
Предлагаю применить каждый из этих способов для решения следующей
системы
У доски решают заданную систему своим способом, который определен с
помощью жеребьевки.
Подведем итог нашей работы.
Понравилось ли вам решать систему предложенным вам способом?
Какой из данных методов наиболее оптимален для данной системы уравнений?
Во всех ли случаях решения мы получили одинаковый ответ?
Почему это произошло?
Практическая работа по выбору рационального способа
решения системы линейных уравнений.
Нельзя хвалить один способ и использовать его при решении всех
систем уравнений, а другой считать ненужным, неправильным. Если математики придумали столько различных способов решения, и все они до сих пор применяются на практике, то можно сделать вывод, что для любой системы найдется наиболее рациональный способ. Наша с вами задача научиться делать этот выбор Предлагается вашему вниманию пять систем, вам необходимо для каждой из них определить рациональный способ решения и обосновать свой выбор.
Учащиеся у доски решают ту систему, которая им досталась в результате
жеребьевки.
Остальные обучающиеся работают на местах.
Подведение итогов урока.
Какой же вывод можно вынести из проделанной работы?
Хочется надеяться, что теперь прежде чем решать систему своим любимым
Способом, задумаетесь: “ А может быть другой метод решения более удобен,
рационален в данной ситуации?”
Домашнее задание: подобрать по две системы линейных уравнений на каждый способ решения.
Этапы урока | Задачи этапа | Деятельность учителя | Деятельность учащихся | УУД |
1. Организационный момент | Создать благоприятный психологический настрой на работу | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.
| Включаются в деловой ритм урока.
| Личностные: самоопределение. Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. |
2. Актуализация | Актуализация опорных знаний и способов действий. | Работа по кругу. (Внешний, внутренний круги) 1 вариант встает во внутренний круг, 2 вариант встает во внешний круг напротив друг друга. Повторяем алгоритмы решения систем уравнений методом подстановки и методом алгебраического сложения. 1 вопрос: назовите этапы метода подстановки. Поворачиваемся налево и перемещаемся на 6 человек, разворачиваемся и отвечаем на 2 вопрос 2 вопрос: Назовите этапы метода алгебраического сложения, если имеются противоположные коэффициенты Поворачиваемся налево и перемещаемся на 3 человека, разворачиваемся и отвечаем на 3 вопрос 3 вопрос: Назовите этапы метода алгебраического сложения, если нет противоположных коэффициентов После этого рассаживаемся за парты | Учащиеся передвигаются и повторяют известные им алгоритмы. | Коммуникативные: развитие устной научной речи, умение слушать и говорить. Познавательные: анализ и разделение алгоритма на два случая (2 и 3 вопрос). |
3.Целеполагание и мотивация | Обеспечение мотивации учения детьми, принятие ими целей урока. | На доске записаны две системы линейных уравнений. К доске выходят 4 человека и пробуют решить системы двумя способами. Ответить на вопрос: Какую систему, каким способом легче решить? Где будет более рациональное решение? Какая цель нашего урока сегодня? | Решают системы
Делают вывод: Когда удобнее использовать методы решения систем уравнений
Цель урока: Решение систем уравнений разными способами, находить удобный способ решения. | Регулятивные: целеполагание. Коммуникативные: постановка вопросов. Познавательные: самостоятельное выделение-формулирование цели урока. |
4. Закрепление | Выявление пробелов изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу. |
| Учащиеся работают в тетради индивидуально. По одному человеку выходят к доске. | Регулятивные: контроль, оценка, коррекция. Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия.
|
5. Организация контроля | Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков. | Самостоятельная работа в парах Одна работа на двоих. Необходимо рационально распределить задания друг с другом, чтобы успеть выполнить работу. 1 вариант
2 вариант
10 минут на выполнение работы. После окончания выполнения учащиеся меняются работами с соседней партой и осуществляют проверку работы одноклассников. Оценивается выполнение работы и как оценивается работа одноклассников. | Самостоятельное решение в тетради.
Взаимоконтроль работы | Регулятивные: контроль, коррекция, самоконтроль и оценка одноклассника. Личностные: самоопределение, развитие доверия к своему партнеру Коммуникативные: управление поведением партнера, контроль, коррекция, оценка действий партнера. |
6. Подведение итогов урока. | Дать качественную оценку работы класса и отдельных учащихся | -Чему сегодня научились на уроке? — Что понравилось на уроке? —Оценить отдельных учащихся | Правильно выбирать способ решения систем уравнений. | Регулятивные: оценка-осознание уровня и качества усвоения; контроль |
7. Информация о домашнем задании | Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания. | №697, 698 решать различными способами |
|
|
8. Рефлексия | Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе. | Перед уходом с урока на листе ватмана (лист рефлексии) нарисовать смайлик Если все было на уроке понятно, то улыбающийся, если остались непонятые вопросы, то нет. |
| Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли и эмоции; Познавательные: рефлексия. |
Как новый алгоритм преодолевает ограничение скорости решения линейных уравнений
Сантош Вемпала и Ричард Пенг из Технологического института Джорджии, придумали новый, более быстрый способ решения некоторых систем линейных уравнений, «рабочую лошадку современных вычислений». Используя случайность, новый алгоритм предлагает принципиально новый — и более быстрый — способ выполнения одного из самых простых вычислений в математике и информатике.
Учащиеся начальной школы на уроках математики, вероятно, сталкиваются с учителями, которые предостерегают их от простого угадывания ответа при решении задачи. Но новое доказательство показывает, что на самом деле правильное предположение иногда бывает лучшим способом решения систем линейных уравнений (одно из фундаментальных вычислений в математике).
Но новое доказательство показывает, что на самом деле правильное предположение иногда бывает лучшим способом решения систем линейных уравнений (одно из фундаментальных вычислений в математике).
В результате это доказательство устанавливает первый метод, способный превзойти то, что ранее было жёстким ограничением скорости решения некоторых задач этих типов.
«Это одна из самых фундаментальных вычислительных задач, — сказал Марк Гисбрехт из Университета Ватерлоо. — Теперь у нас есть доказательство того, что мы можем вычислять быстрее».
Новый метод, предложенный Ричардом Пенгом и Сантошем Вемпала из Технологического института Джорджии, был опубликован в июле и представлен в январе на ежегодном симпозиуме ACM-SIAM по дискретным алгоритмам, где он получил награду за лучшую работу.
Линейные системы включают в себя два или более уравнений с переменными, которые показывают различные способы отношения между элементами. Системы «линейны», так как единственная допустимая степень в точности равна 1, а графики решений уравнений образуют плоскости.
Типичный пример линейной системы — также, вероятно, знакомый студентам-математикам — включает в себя скотный двор, заполненный курами и свиньями. Сколько там кур и свиней, если известно, что имеется 10 голов и 30 ног? По мере изучения алгебры студенты знакомятся с определённой процедурой решения этой задачи: записать систему из двух алгебраических уравнений и решить её.
Однако линейные системы способны на большее, чем просто подсчёт кур и свиней. Они возникают во многих практических ситуациях. Например, строительство более прочного моста или более незаметного самолёта может включать решение систем с миллионами взаимозависимых линейных уравнений. С более фундаментальной точки зрения, линейные системы возникают во многих основных задачах оптимизации в информатике, которые включают в себя поиск наилучших значений для набора переменных в рамках системы ограничений. Если мы сможем быстрее решать линейные системы, то мы также сможем быстрее решать и эти задачи.
«Линейные системы — рабочая лошадка современных вычислений», — считает Вемпала.
В новом доказательстве найден более быстрый способ решения большого класса линейных систем, обходя один из основных методов, обычно используемых в этом процессе. Этот метод, называемый матричным умножением, ранее установил жёсткое ограничение скорости вычисления линейных систем. Он по-прежнему используется в данной работе, но в дополнительной роли. Авторы связывают его с новым подходом, который, по сути, является формой обученного гадания.
«Вы можете угадать свой путь к решениям», — сказал Пенг. И ни один учитель не рассердится на вас за это.
Математика скотного двора
Чтобы получить представление о линейных системах и способах их решения, давайте вернёмся на скотный двор, но представим, что теперь это больше похоже на зверинец: куры, однорогие носороги и двурогие козы. Вы делаете быстрый подсчёт и определяете, что имеется 12 голов, 38 ног и 10 рогов. Можете ли вы выяснить, сколько там животных каждого вида?
Чтобы продолжить, назначьте переменную каждому виду животных (c — для кур, r — для носорогов, g — для коз) и напишите уравнение для каждого признака. Числа, или коэффициенты, перед каждой переменной отражают количественную характеристику признака, которым обладает каждое животное.
Числа, или коэффициенты, перед каждой переменной отражают количественную характеристику признака, которым обладает каждое животное.
Теперь у вас есть три уравнения и три неизвестных.
Один из способов их решения — это преобразовать одно уравнение, выразив одну переменную через две другие. Например, 0c + 1r + 2g = 10 превращается в r = 10 – 2g. Подставьте это выражение вместо r в два других уравнения и продолжите эту процедуру, пока все переменные не будут определены в терминах всего одной переменной, для которой можно найти точное решение. Затем вы можете повторить этот процесс, используя найденную переменную, чтобы найти решение для следующей переменной.
Ещё один, более сложный, способ поиска решения — создать матрицу, элементами которой служат коэффициенты уравнений. Три уравнения превращаются в эту матрицу.
Далее неизвестное количество кур, носорогов и коз мы представляем другой матрицей.
Наконец, мы представляем наблюдаемое количество голов, ног и рогов третьей матрицей.
Мы можем объединить эти три матрицы в единую линейную систему, где первая матрица, умноженная на матрицу с переменными элементами, равна третьей матрице — в этот момент мы можем найти решение для второй матрицы с помощью линейной алгебры.
При преобразовании уравнений или использовании матричного подхода, в конечном счёте, для решения задачи выполняется одно и то же общее количество вычислительных шагов. Это число равно количеству переменных системы в кубе (n3). В этом случае у нас три переменных, так что решение занимает 33 = 27 вычислительных шагов. Если бы у нас было четыре вида животных и четыре уравнения, для решения задачи потребовалось бы 43 = 64 шага.
За последние 50 лет исследователи нашли способы более эффективного выполнения этой процедуры. Часто можно применять более короткие пути — способы повторного использования или комбинирования операций, которые позволяют решать линейные системы за меньшее количество шагов.
Сантош Вемпала и Ричард ПенгВ конечном счёте всё сводится к тому, что решение любой линейной системы можно свести к матричному умножению, которое на данный момент, по крайней мере теоретически, можно выполнить за n2,37286 шагов.
В различных технических применениях требуется решать линейные системы еще быстрее — потенциально за n2 шагов. Мы используем матричное умножение, потому что это лучший доступный инструмент, но это не означает, что своего открытия не ожидает ещё лучший инструмент.
«Нет никаких причин для того, чтобы эта проблема решения линейных систем зависела от улучшений матричного умножения», — сообщил Вемпала.
Угадывание решений
Для понимания нового и усовершенствованного инструмента нужно помнить о другом устоявшемся методе решения линейных систем. Это интуитивный способ, к которому можно обратиться, впервые столкнувшись со стаей кур, грохотом носорогов и перевозкой коз, собранных вместе: угадайте значения всех переменных, подставьте их в уравнения, проверьте, как далека от истины эта догадка, и угадайте снова.
К этому «итеративному подходу» часто прибегают инженеры и учёные. Это хорошо работает для многих практических задач, потому что эксперты, как правило, не гадают вслепую, что сокращает количество итеративных догадок, которые они должны сделать, прежде чем найти решение.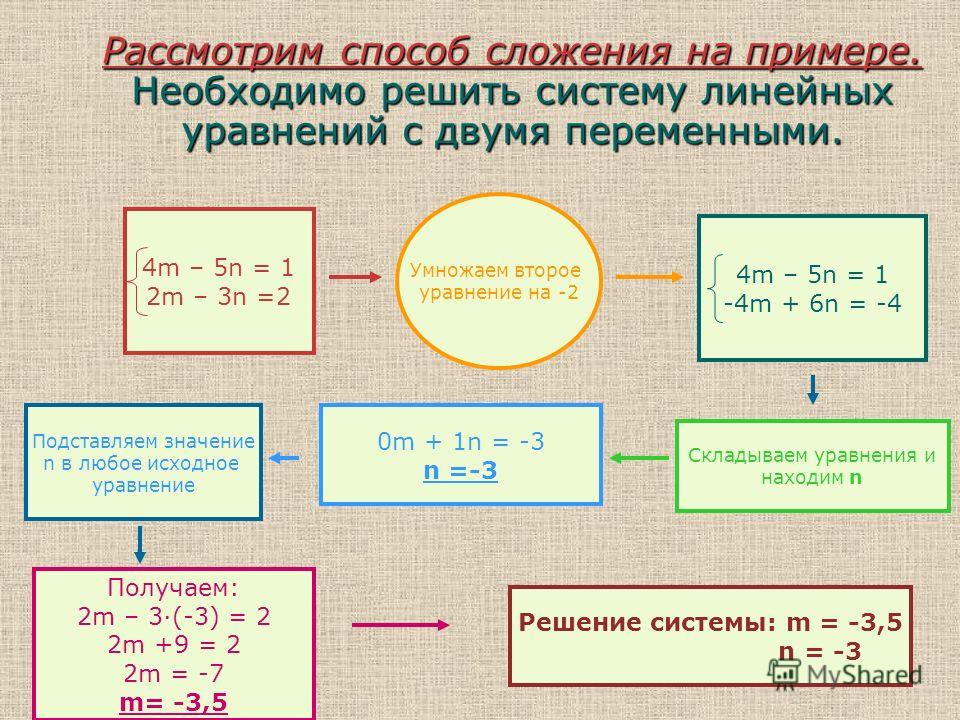
«При решении реальных научных вычислительных задач люди проявляют очень хорошую интуицию, относительно того, какими должны быть ответы», — сказал Пенг.
Итеративные методы полезны в конкретных случаях, когда интуиция может оказать некоторую поддержку. Они также полезны в более общем случае, когда линейная система, которую вы пытаетесь решить, имеет большое количество переменных, коэффициенты при которых равны нулю.
Эта особенность присутствует — и полезна — в примере со скотным двором, где самый простой признак, используемый при решении, — рога. Почему? Поскольку у цыплят нет рогов, член в уравнении, соответствующий цыплятам, исчезает, и задача с тремя видами животных сводится к задаче фактически для двух переменных. Убрав рога из расчётов, вы можете с помощью полученной информации быстро решить уравнения для ног и голов.
В более сложных линейных системах этот тип отношений, в котором не все признаки относятся ко всем переменным, может быть широко распространён. В системе могут быть миллионы переменных и миллионы уравнений, но каждое уравнение может включать только небольшое количество общих переменных. Линейные системы такого типа называются «разреженными», что отражает тот факт, что большинство переменных входит в большинство уравнений с нулевыми коэффициентами. Такая ситуация часто возникает в реальных линейных системах. И именно в таких системах итеративные методы могут превосходить матричное умножение.
В системе могут быть миллионы переменных и миллионы уравнений, но каждое уравнение может включать только небольшое количество общих переменных. Линейные системы такого типа называются «разреженными», что отражает тот факт, что большинство переменных входит в большинство уравнений с нулевыми коэффициентами. Такая ситуация часто возникает в реальных линейных системах. И именно в таких системах итеративные методы могут превосходить матричное умножение.
«Это работает только в случае достаточно разреженных матриц», — сказал Уильямс.
Но до этой новой работы никому не удавалось доказать, что итеративные методы всегда быстрее матричного умножения для всех разреженных линейных систем.
Согласованная случайность
В новом методе Пенга и Вемпала используется усовершенствованная версия стратегии итеративных догадок: вместо того чтобы делать только одну догадку, их алгоритм делает много догадок параллельно. Такой подход ускоряет поиск, точно так же и вы быстрее найдёте драгоценный камень в лесу, если поиском занято много людей одновременно.
«Именно параллелизм отвечает за волшебство», — отметил Гисбрехт.
Может показаться очевидной польза сортировки нескольких одновременных догадок, но это усложняет работу стратегии. Эффективность нового алгоритма во многом зависит от умения делать первоначальные догадки, порождающие итеративный процесс, и разумно объединять плоды параллельных догадок в один окончательный ответ.
Если вернуться к примеру скотного двора, алгоритм может сделать три первоначальных догадки, где каждая догадка — это матрица 3 на 1, определяющая количество кур, носорогов и коз. Алгоритм проверяет, насколько далека от истины каждая догадка, а затем делает новые догадки, продолжая параллельные потоки догадок.
Ключ к конечному успеху алгоритма заключается в том, что три первоначальные догадки он делает случайным образом. Случайность может показаться не очень хорошей основой для догадок, но как универсальный метод она имеет свои преимущества, особенно при решении огромных задач. А именно благодаря случайности вы не будете непроизвольно смещать свой поиск в сторону одной части задачи, потенциально пренебрегая областью, в которой находится фактическое решение.
«Я должен убедиться, что все мои догадки достаточно случайны, чтобы охватывать все возможные комбинации, — сказал Пенг. — Это ужасный способ делать догадки, который в конечном счёте становится предпочтительным методом, поскольку задача становится очень большой».
Большая часть сложной технической работы в статье Пенга и Вемпала включает в себя доказательство того, что различные нити случайных догадок также работают сообща, включая любую конкретную догадку, которая на самом деле является решением задачи.
«Существует согласованная случайность», — сказал Вемпала.
Это означает, что случайные догадки не только учитывают точные значения самих догадок, но и охватывают все потенциальные догадки, лежащие между ними. Это похоже на ситуацию, когда два человека ведут поиск в лесу и просматривают не только землю перед собой, но и всю линию видимости между ними.
«Также покрыта вся область между двумя [догадками]», — сказал Вемпала.
Эта функция поиска гарантирует, что алгоритм где-то обнаружит решение. Но сама по себе она не определяет, что такое решение в действительности. Для этого — чтобы фактически взять решение в свои руки — Пенг и Вемпала должны доказать кое-что ещё.
Но сама по себе она не определяет, что такое решение в действительности. Для этого — чтобы фактически взять решение в свои руки — Пенг и Вемпала должны доказать кое-что ещё.
Алгоритм отслеживает свои случайные догадки, как записи в матрице. Поиск решения среди записей в матрице становится вопросом матричного умножения, что, конечно, является препятствием, которое они намеревались обойти. Но и здесь они пользуются преимуществами случайности, которую использовали для заполнения записей в матрице.
Поскольку записи в матрице случайны и между ними осуществляется координация, сама матрица приобретает определённые симметрии. Эти симметрии делают возможным применение сокращённых способов вычислений. Как и в случае с любым высокосимметричным объектом, достаточно знать, как выглядит одна его часть, чтобы восстановить его целиком.
В результате алгоритм Пенга и Вемпала может найти решение для такой матрице быстрее, чем для матрицы с тем же числом элементов, но без полезных симметрий. Симметрии матрицы также дают ещё одно важное преимущество: они помогают гарантировать, что догадки (в отношении значений переменных) никогда не вырастут настолько большими, что станут громоздкими, с точки зрения алгоритмической эффективности.
Симметрии матрицы также дают ещё одно важное преимущество: они помогают гарантировать, что догадки (в отношении значений переменных) никогда не вырастут настолько большими, что станут громоздкими, с точки зрения алгоритмической эффективности.
По теме:
Mathematicians Discover the Perfect Way to Multiply
On Your Mark, Get Set, Multiply
A New Approach to Multiplication Opens the Door to Better Quantum Computers
«Нам пришлось контролировать, насколько велико появляющееся число, когда мы делаем эту догадку и координацию», — сказал Пенг.
Пенг и Вемпала доказывают, что их алгоритм может найти решение любой разреженной линейной системы за n2,332 шагов. Этот результат превосходит показатель степени для лучшего алгоритма матричного умножения (n2,37286) примерно на четыре сотых. Это небольшое улучшение матричного умножения в ближайшее время не будет иметь значения для практических применений, но как доказательство правильности концепции оно представляет собой целую пропасть: оно показывает, что есть качественно лучший способ решения линейных систем.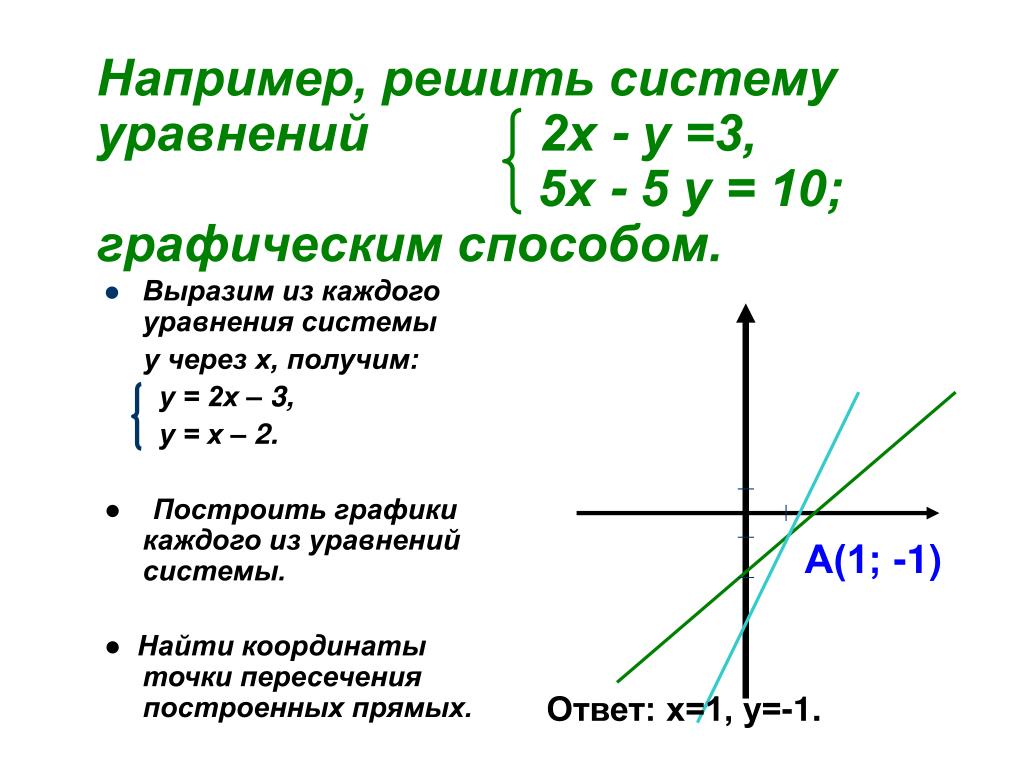
«С философской точки зрения, мы раньше не знали, есть ли способ вычислений, более быстрый, чем матричное умножение», — сказал Вемпала. Но теперь мы знаем.
А если вам хочется подтянуть свои знания алгоритмов или математики — то будем рады видеть вас в числе наших студентов на курсах «Алгоритмы и структуры данных» и «Математика для Data Science». Возможно, именно вы создадите алгоритм, который поставит новый рекорд скорости вычислений.
Узнайте, как прокачаться в других специальностях или освоить их с нуля:
Другие профессии и курсыПРОФЕССИИ
КУРСЫ
ФИО | Манякова Вера Алексеевна | ||||||||||||||
Место работы | МБОУ СОШ № 82 | ||||||||||||||
Должность | Учитель математики | ||||||||||||||
Предмет | Математика | ||||||||||||||
Класс | 9 | ||||||||||||||
Базовый учебник | А. | ||||||||||||||
Название урока | Методы решения систем уравнений с двумя переменными | ||||||||||||||
Тип урока | Урок обобщения и систематизации знаний | ||||||||||||||
Образовательная среда урока | Компьютер, проектор, учебники по математике, раздаточный материал, мел, доска, электронная презентация, выполненная в программе Power Point. | ||||||||||||||
Формы работы учащихся | Фронтальная, индивидуальная. | ||||||||||||||
Цель урока | Предметные | Личностные | Метапредметные результаты | ||||||||||||
Знать: алгоритм решения систем уравнений: графическим способом; способом подстановки; способом сложения. Уметь: решать системы уравнений второй степени различными способами. Применять: полученные знания для решения систем уравнений различных уровней сложности. | определять личностный смысл деятельности; осуществлять выбор в соответствии с задачей деятельности. | Познавательные УУД: определять способы решения и обосновывать свое мнение; анализировать задачу, ситуацию; Регулятивные УУД: выполнять самопроверку и самооценку выполнения учебного задания; умение планировать и осуществлять деятельность, направленную на решение проблем различного характера. Коммуникативные УУД: предлагать и обосновывать своё мнение. | |||||||||||||
Задачи урока: Образовательные — обобщение, систематизация и углубление знаний учащихся по изучаемой теме, формирование умений применять разные способы решения систем уравнений; Воспитательные — развитие творческих способностей учеников, привитие интереса к изучаемому предмету; Развивающие — формирование навыков самостоятельной деятельности, выработка внимания. | |||||||||||||||
Этапы урока | Деятельность учителя | Деятельность ученика | Формируемые УУД | ||||||||||||
Организационный (2мин) | Приветствие учащихся. Проверка учителем готовности класса к уроку; организация внимания. — Здравствуйте, садитесь! Начинаем наш урок. Сдайте пожалуйста тетради с домашней работой. | Слушают учителя, настраиваются на работу, проверяют готовность к уроку. | Умение слушать и вступать в диалог. Умение выделять нравственный аспект поведения. | ||||||||||||
Актуализация знаний, (10 мин) | Вступительное слово учителя. Вспомним, чем мы занимались на прошлом уроке? | Отвечают на вопрос. | Познавательные: применение предметных знаний; выполнение учебных заданий. Регулятивные: выделение и осознание того, что уже пройдено; умение распознавать на слух вопросы и отвечать на них. Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог. | ||||||||||||
Индивидуальное задание | Для решения следующего индивидуального задания, необходимы двое учащихся. Задание: Решить систему равнений — 1) методом подстановки; 2) методом сложения используя формулы сокращённого умножения. | Решают у доски. | |||||||||||||
Актуализация знаний. | Ребята, давайте вспомним: А) Что называется решением системы уравнений? Б) Что значит решить систему уравнений? В) Дайте понятие равносильности двух систем уравнений? Г) Какие методы решения систем уравнений вы знаете: | Отвечают у доски А) Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство. Б) Решить систему уравнений – значит найти все её решения или доказать, что решений нет. В) Две системы уравнений называются равносильными, если они имеют одни и те же решения, или если обе системы не имеют решений. Г) Графический метод, подстановки, алгебраического сложения, введения новой переменной. | Познавательные: структурирование знаний, выбор способов решения задач, анализ объектов и синтез. Регулятивные: умение проговаривать последовательность действий на уроке, Коммуникативные: развитие умения слушать и вступать в диалог, задавать вопросы. Личностные: осуществлять выбор в соответствии с задачей деятельности. | ||||||||||||
1) Попробуем определить, какой из этих способов лучше применить в каждом из следующих заданий: — Какой недостаток имеет графический метод решения систем уравнений. 2) Рассмотрим вторую систему: Какой метод решения вы бы предложили. 3) Рассмотрим следующую систему уравнений: Какой из методов позволяет упростить данную систему? . 4) Сколько решений может иметь система уравнений? . . | 1) в данном случае лучше применить графический способ, т.к. первое уравнение задаёт окружность с центром (-1; 2) и радиусом r=3. Графиком второго уравнения являются два луча, исходящие из точки (-1; -1). Данная система имеет 3 решения (-1; -1), (-4; 2) и (2;2). — Этот метод ненадёжен, т.к. не всегда даёт точные ответы; поэтому полученные значения нужно проверять. 2) в данном случае лучше применить метод подстановки. Из второго уравнения выражаем и подставив в первое уравнение, дорешиваем систему. 3) Методом алгебраического сложения получим , выберем одно из этих уравнений, например 2, получим систему: . А дальше решаем способом подстановки. 4) Прямая и окружность могут иметь две точки пересечения, одну или ни одной. Парабола и прямая могут иметь 2 общие точки, одну или ни одной. Гипербола и прямая пересекаются в 2 точках, в 1 или ни одной. | ||||||||||||||
Самостоятельная работа (12 мин) | Выполним самостоятельную работу. Условия заданий – на листочках, возьмите их, впишите фамилию. Первые пять заданий – с выбором ответа, шестое задание – практическая работа. Задания оцениваются в баллах.
Закончили. Возьмите карандаши и проверьте вашу работу. Если ответ верный, ставим «плюс», не верный- ставим» — минус». Подсчитайте количество полученных баллов и оцените себя в соответствии со шкалой перевода баллов в отметки. 10 баллов – «5» 8-9 баллов – «4» 5-7 баллов – «3» Поднимите руки, у кого получилось 8-10 баллов. Молодцы. Отложите работу. | Выполняют письменное задание в готовых бланках. Учащиеся проверяют свой результат, выставляют отметку. | Познавательные: применение предметных знаний, выбор способов решения задач. Регулятивные: анализировать и оценивать результат работы; Личностные: самооценка. | ||||||||||||
Физкультминутка (1 мин) | А сейчас немного отдохнём и выполним гимнастику для глаз. | Делают гимнастику. | |||||||||||||
Проверка индивидуального задания. (4 мин) | Задание: Решить систему равнений — 1) методом подстановки; 2) методом сложения. | 1 ученик – Я решала методом подстановки. Получив биквадратное уравнение, применила метод введения новой переменной. 2 ученик — Я решал эту систему с помощью формул сокращенного умножения. Применив метод сложения разбил систему на две более лёгкие системы. | Познавательные УУД: определение способа решения и обоснование своего мнения; Регулятивные УУД: умение планировать и осуществлять деятельность, направленную на решение задачи. Коммуникативные УУД: предлагать и обосновывать своё мнение. | ||||||||||||
Работа с листами подготовки к ОГЭ (8 мин) | А теперь разберем несколько заданий из 2 части сборника Лысенко. Открываем стр. 275, №163. Как будем решать данную систему. А дорешаете эту систему вы дома. Открываем стр. 306, №507.Решим задачу. А дорешаете вы её дома. Если успеем. Открываем стр. 276, №179. Решим систему уравнений. | Разбирают задания вместе с классом. Делают пометки. Введём новые переменные Получим: Решая его, получим значения для m и n, и произведём обратную замену… Пусть первый раствор имеет концентрацию m %, а второй раствор n %. Тогда получим систему… Данную систему решаем с помощью формул сокращенного умножения (разности квадратов). | Познавательные: уметь решать примеры по выбранному правилу; ставить, формулировать и решать проблемы. Регулятивные: умение проговаривать последовательность действий на уроке, Коммуникативные: умение слушать, обращаться с вопросом к учителю и сверстнику. Личностные: навыки сотрудничества в разных ситуациях, самооценка. | ||||||||||||
Домашнее задание | Дорешать номера №163, 507, 179 и решить №139, 141, 162 из сборника Лысенко. | Записывают домашнее задание. | Личностные: готовность и способность к саморазвитию; самооценка. | ||||||||||||
Рефлексия. Подведение итогов урока (1мин) | На что был направлен наш урок? | 1) Урок был ориентирован на отработку навыков решения систем уравнения различными методами. 2) Разобрали задания из ОГЭ. | Познавательные: Выделение и формулирование познавательной цели, рефлексия способов и условий действия. Анализ и синтез объектов. Регулятивные: Оценка-осознание уровня и качества усвоения. Коммуникативные: Умение с достаточной полнотой и точностью выражать свои мысли. Личностные: Ценностно-смысловая ориентация | ||||||||||||
Как решить систему уравнений в Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют.
 Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A. - Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
- Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
=МОБР(массив)Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
- Выполняется запуск Мастера функций.
 Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK». - Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
- Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.

- Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
=МУМНОЖ(Массив1;Массив2)Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
- В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
- Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B.
 После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter. - После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.
Урок: Обратная матрица в Excel
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. 2+4*x-132
2+4*x-132
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
 В нем следует нажать на кнопку «OK».
В нем следует нажать на кнопку «OK».Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Урок: Подбор параметра в Excel
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».

- Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
- Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
=МОПРЕД(массив)Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
- Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД».
 После этого жмем на кнопку «OK».
После этого жмем на кнопку «OK». - Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
- Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
- Аналогичным образом производим подсчет определителей для остальных трех таблиц.
- На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.

- Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
14x1+2x2+8x3=110
7x1-3x2+5x3=32
5x1+x2-2x3=17
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B.
 Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами. - Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
=B8:E8-$B$7:$E$7*(B8/$B$7)Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.

- После этого копируем полученную строку и вставляем её в строчку ниже.
- Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
- Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
- В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
=B13:E13-$B$12:$E$12*(C13/$C$12)После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь следует выполнить обратную прогонку по методу Гаусса.
 Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:=B17:E17/D17Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
- Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
=(B16:E16-B21:E21*D16)/C16Жмем привычное уже нам сочетание клавиш для применения формулы массива.
- Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
=(B15:E15-B20:E20*C15-B21:E21*D15)/B15Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений.
 Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТРешение систем уравнений: какой метод использовать?
Системы уравнений — это несколько уравнений, у которых есть общее решение. Студенты сталкиваются с этими системами уравнений, когда есть несколько «неизвестных» или переменных, которые им еще не были заданы. Когда это происходит, цель студентов — использовать полученную информацию в уравнениях для решения всех переменных.
Студенты сталкиваются с этими системами уравнений, когда есть несколько «неизвестных» или переменных, которые им еще не были заданы. Когда это происходит, цель студентов — использовать полученную информацию в уравнениях для решения всех переменных.
Для решения систем уравнений студентам полезно иметь базовые знания простых алгебраических уравнений, переменных и построения графиков линейных уравнений.
Как решить систему уравнений?
Для решения систем уравнений используются три метода: построение графиков, подстановка и исключение.
Чтобы решить систему путем построения графиков, вы просто графите данные уравнения и найдете точки, где они все пересекаются. Координата этой точки даст вам значения переменных, которые вы решаете. Это наиболее эффективно, когда уравнения уже записаны в форме пересечения наклона.
Следующий метод — подстановка. Подстановку лучше всего использовать, когда одно из уравнений выражается в терминах одной из переменных, например y = 2x + 4, но уравнениями всегда можно манипулировать. Первым шагом в этом методе является решение одного из уравнений для одной переменной. Как только выражение для переменной найдено, замените или вставьте выражение в другое уравнение, в котором исходная переменная должна была найти числовое значение следующей переменной. Последний шаг — заменить числовое значение, которое было найдено, на соответствующую переменную в исходном уравнении.
Подстановку лучше всего использовать, когда одно из уравнений выражается в терминах одной из переменных, например y = 2x + 4, но уравнениями всегда можно манипулировать. Первым шагом в этом методе является решение одного из уравнений для одной переменной. Как только выражение для переменной найдено, замените или вставьте выражение в другое уравнение, в котором исходная переменная должна была найти числовое значение следующей переменной. Последний шаг — заменить числовое значение, которое было найдено, на соответствующую переменную в исходном уравнении.
Третий метод — устранение. Исключение — это сложение уравнений вместе, чтобы создать уравнение только с одной переменной. Это может быть сделано только в том случае, если коэффициенты одной переменной в обоих уравнениях противоположны и будут уравновешивать друг друга после сложения. Исключение лучше всего использовать, когда это уже происходит в уравнениях, но уравнениями также можно манипулировать для создания общих коэффициентов путем умножения или деления уравнений на определенное число. Следующим шагом будет использование созданного нами уравнения, чтобы найти значение переменной, а затем вставить это значение обратно в исходное уравнение, чтобы найти оставшуюся переменную.
Следующим шагом будет использование созданного нами уравнения, чтобы найти значение переменной, а затем вставить это значение обратно в исходное уравнение, чтобы найти оставшуюся переменную.
Вот пример задачи, в которой необходимо решить систему уравнений:
Логан ответил на 0,8 вопросов по математике столько же, сколько вопросов на испанском, и ответил на 5 вопросов на английском больше, чем на испанском. Если Логан ответил всего на 33 вопроса, на сколько математических вопросов ответил Логан?
Как решить эту проблему?
Первый шаг — составить уравнения из словесной задачи.Для этого мы должны присвоить переменные каждой неизвестной части проблемы. Переменные x, y и z будут представлять количество вопросов по математике, испанскому и английскому языкам, на которые Логан ответил соответственно.
Поскольку Логан ответил в 0,8 раза больше математических вопросов, чем на испанских, уравнение для представления этого будет 0,8y = x. Второе уравнение будет z = y + 5, чтобы представить, как Логан ответил на пять вопросов на английском языке больше, чем на испанском. Окончательное уравнение будет x + y + z = 33, чтобы представить, как Логан ответил в общей сложности на 33 вопроса.
Второе уравнение будет z = y + 5, чтобы представить, как Логан ответил на пять вопросов на английском языке больше, чем на испанском. Окончательное уравнение будет x + y + z = 33, чтобы представить, как Логан ответил в общей сложности на 33 вопроса.
Если вернуться к исходному вопросу, то цель этой задачи — выяснить, на сколько математических вопросов ответил Логан. Поскольку первое уравнение, которое мы нашли, было 0.8y = x, мы можем видеть, что нам нужна только переменная y, чтобы найти значение x или количество математических вопросов, на которые были даны ответы. Поскольку два уравнения уже решены с использованием двух переменных, 0,8y = x и z = y + 5, подстановка будет наиболее эффективным методом. Чтобы использовать этот метод, мы бы заменили эти уравнения на переменные x и y третьего уравнения, которое дало бы нам (0.8у) + у + (у + 5) = 33.
Следующим шагом будет решение этого уравнения для переменной y, комбинируя подобные термины: 2,8y = 28, что даст нам y = 10 или 10 ответов на испанские вопросы. Теперь, когда мы нашли значение переменной y, мы можем снова подставить его в уравнение 0.8y = x, чтобы найти значение x. Подставив y на его значение 10, мы получим 0,8 (10) = x, что даст нам значение 8 для x.
Теперь, когда мы нашли значение переменной y, мы можем снова подставить его в уравнение 0.8y = x, чтобы найти значение x. Подставив y на его значение 10, мы получим 0,8 (10) = x, что даст нам значение 8 для x.
Какой ответ?
Логан ответил на 8 математических вопросов.
Какие концепции мы использовали?
Для решения этой примерной задачи мы использовали несколько различных математических концепций. Первым, что мы использовали, было как писать уравнения из текстовых задач. Благодаря нашему пониманию проблемы мы смогли присвоить каждому неизвестному аспекту проблемы переменную, а затем создать уравнения, основанные на их взаимосвязях в задаче, которые мы затем распознали бы как систему уравнений.
Вторая концепция, которую мы использовали, — решение системы.Уравнения не были записаны в форме пересечения наклона, поэтому построение графиков не было бы эффективным методом. Не было переменных, которые были бы противоположны друг другу, поэтому мы также исключили метод исключения. Признав замещение как лучший метод для использования, мы смогли эффективно использовать наши математические навыки для решения неизвестных переменных в системе уравнений.
Не было переменных, которые были бы противоположны друг другу, поэтому мы также исключили метод исключения. Признав замещение как лучший метод для использования, мы смогли эффективно использовать наши математические навыки для решения неизвестных переменных в системе уравнений.
Если это то, что вы хотите для своего ребенка — начать легко!
Позвоните сейчас (303) 502-8345 и узнайте больше!
Где у вашего ребенка математические навыки?
Топ-3 метода решения систем уравнений [Видео]
Привет, ребята! Добро пожаловать в этот видеоролик, посвященный сравнению различных методов решения системы уравнений.
Если вы помните, система уравнений — это когда у вас есть более одного уравнения с неизвестными переменными в данной задаче. Итак, чтобы решить эту проблему, вам необходимо найти значения всех переменных в каждом уравнении.
Это можно сделать тремя разными способами: методом подстановки, методом исключения и с использованием расширенной матрицы.
В этом видео я предполагаю, что вы уже знаете, как выполнять каждый метод, поэтому я хочу потратить много времени на объяснение не того, как их выполнять, а, скорее, когда использовать каждый метод.
Сначала я устно расскажу вам, когда использовать каждый метод, затем я напишу три разных примера, и мы вместе решим, какой метод наиболее эффективен для каждой системы.
Когда использовать метод подстановки
Вы должны использовать метод подстановки, когда одна из переменных в одном из ваших уравнений уже изолирована (ее коэффициент равен 1).
Когда использовать метод исключения
Вы должны использовать метод исключения, когда одни и те же переменные во всех уравнениях имеют один и тот же коэффициент или когда они имеют один и тот же, но отрицательный коэффициент.
Когда использовать расширенную матрицу
Вы должны использовать расширенную матрицу, когда методы замены и исключения либо непрактичны, либо вообще невозможны.
Теперь давайте посмотрим на три разные системы и воспользуемся тем, что мы только что узнали, чтобы подумать, какой метод наиболее полезен для каждой системы.
ПРИМЕР СИСТЕМЫ № 1
\ (5x — 58y = -883 \)
\ (- 5x + 2y = -13 \)
ПРИМЕР СИСТЕМЫ № 2
\ (9x + 4y = 65 \)
\ (x — 18y = -2 \)
ПРИМЕР СИСТЕМЫ № 3
\ (2x + 7y — 3z = 47 \)
\ (x — 4y + 8z = -33 \)
\ (7x + 2y + 10z = 11 \)
Итак, мы пройдемся по каждой системе, решим, какой метод будет наиболее эффективным, а затем решим с помощью этого метода.
Пример метода исключения
Хорошо, давайте посмотрим на это первое уравнение.
\ (5x — 58y = -883 \)
\ (- 5x + 2y = -13 \)
Теперь, вспоминая объяснение, которое я дал, когда использовать каждый метод, обратите внимание на то, что я сказал об исключении : «Вам следует использовать метод исключения, когда одни и те же переменные во всех уравнениях имеют один и тот же коэффициент или когда у них один и тот же, но отрицательный коэффициент».
Что ж, именно это верно в случае этой конкретной системы.Итак, давайте решим эту систему, используя исключение .
\ (- 56y = -896 \)
\ (y = 16 \)
Теперь мы вставляем нашу переменную y обратно в одно из исходных уравнений. Я воткну его в первую.
\ (5x — 58 (16) = -883 \)
\ (5x — 928 = -883 \)
\ (5x = 45 \)
\ (x = 9 \)
Отлично, поэтому мы Я решил эту систему с помощью исключения, потому что у наших двух переменных был одинаковый коэффициент или когда у них был одинаковый, но отрицательный коэффициент (как в нашем случае).
Пример метода замены
Перейдем к системе №2.
\ (9x + 4y = 65 \)
\ (x — 18y = -2 \)
Хорошо, давайте снова вспомним, что было сказано в нашем объяснении, когда использовать каждый метод. Вспомните, что было сказано о подстановке: «Вы должны использовать метод подстановки, когда одна из переменных в одном из ваших уравнений уже изолирована».
Ну так обстоит дело с этой системой. Наша переменная \ (x \) во втором уравнении имеет коэффициент 1.Итак, давайте решим эту систему с помощью подстановки.
\ (9 (18y — 2) + 4y = 65 \)
\ (162y — 18 + 4y = 65 \)
\ (166y = 83 \)
\ (y = \ frac {1} {2} \)
\ (x = 18 (\ frac {1} {2}) — 2 \)
\ (x = 7 \)
Это было очень просто решить с помощью подстановки. Помните, что означающее, которое поможет вам узнать, когда его использовать, — это то, если в одном из уравнений есть переменная, которая уже изолирована.
Пример расширенной матрицы
Давайте посмотрим на нашу последнюю систему, систему №3.
\ (2x + 7y — 3z = 47 \)
\ (x — 4y + 8z = -33 \)
\ (7x + 2y + 10z = 11 \)
Помните, что мы говорили о том, когда использовать расширенную матрицу. Что ж, сейчас хорошее время. Использование исключения или замены в этом отношении потребует гораздо больше работы, чем использование расширенной матрицы.
Итак, давайте настроим нашу матрицу и решим.
\ (\ begin {bmatrix} \ left. \ Begin {matrix} 2 & 7 & -3 \\ 1 & -4 & 8 \\ 7 & 2 & 10 \ end {matrix} \ right | & \ begin {matrix} 47 \\ -33 \\ 11 \ end {matrix} \ end {bmatrix} \)
\ (R_ {1} \ leftrightarrow R_ {2} \)
\ (\ begin {bmatrix} \ left.\ begin {matrix} 1 & -4 & 8 \\ 2 & 7 & -3 \\ 7 & 2 & 10 \ end {matrix} \ right | & \ begin {matrix} -33 \\ 47 \\ 11 \ end {matrix} \ end {bmatrix} \)
\ (\ begin {matrix} \\ -2R_ {1} + R_ {2} = R_ {2 } \\ -7R_ {1} + R_ {3} = R_ {3} \ end {matrix} \ begin {bmatrix} \ left. \ Begin {matrix} 1 & -4 & 8 \\ 0 & 15 & -19 \\ 0 & 30 & -46 \ end {matrix} \ right | & \ begin {matrix} -33 \\ 113 \\ 242 \ end {matrix} \ end {bmatrix} \)
\ (\ begin {matrix} \\ \ frac {R_ {2}} {15} = R_ {2} \\ \ end {matrix} \ begin {bmatrix} \ left.\ begin {matrix} 1 & -4 & 8 \\ 0 & 1 & \ frac {-19} {15} \\ 0 & 30 & -46 \ end {matrix} \ right | & \ begin {matrix} -33 \\ \ frac {113} {15} \\ 242 \ end {matrix} \ end {bmatrix} \)
\ (\ begin {matrix} 4R_ {2} + R_ {1} = R_ {1} \\ \\ -30R_ {2} + R_ {3} = R_ {3} \ end {matrix} \ begin {bmatrix} \ left.\ Begin {matrix} 1 & 0 & \ frac {44} { 15} \\ 0 & 1 & \ frac {-19} {15} \\ 0 & 0 & -8 \ end {matrix} \ right | & \ begin {matrix} \ frac {-43} {15} \\ \ frac {113 } {15} \\ 16 \ end {matrix} \ end {bmatrix} \)
\ (\ begin {matrix} \\ \\ \ frac {R_ {3}} {- 8} = R_ {3} \ end {матрица} \ begin {bmatrix} \ left.\ begin {matrix} 1 & 0 & \ frac {44} {15} \\ 0 & 1 & \ frac {-19} {15} \\ 0 & 0 & 1 \ end {matrix} \ right | & \ begin {matrix} \ frac {-43} {15} \\ \ frac {113} {15} \\ -2 \ end {matrix} \ end {bmatrix} \)
\ (\ begin {matrix} — \ frac {44} {15} R_ {3} + R_ {1} = R_ {1} \\ \ frac {19} {15} R_ {3} + R_ {2} = R_ {2} \\ \ end {matrix} \ begin {bmatrix} \ left. \ begin {matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {matrix} \ right | & \ begin {matrix} 3 \\ 5 \\ — 2 \ end {matrix} \ end {bmatrix} \ begin {bmatrix} x \\ y \\ z \ end {bmatrix} \)
\ (x = 3 \), \ (y = 5 \), \ (z = -2 \)
Надеюсь, что это видео по сравнению методов решения систем было для вас полезным.
Увидимся в следующий раз!
5.3: Решить системы уравнений методом исключения
Навыки для развития
К концу этого раздела вы сможете:
- Решите систему уравнений методом исключения
- Решите приложения систем уравнений методом исключения
- Выберите наиболее удобный метод решения системы линейных уравнений
Примечание
Прежде чем вы начнете, пройдите тест на готовность.
- Упростим −5 (6−3a).
Если вы пропустили эту проблему, просмотрите [ссылка] . - Решите уравнение \ (\ frac {1} {3} x + \ frac {5} {8} = \ frac {31} {24} \).
Если вы пропустили эту проблему, просмотрите [ссылка] .
Мы решили системы линейных уравнений с помощью построения графиков и подстановки. Построение графиков хорошо работает, когда переменные коэффициенты малы, а решение имеет целочисленные значения. Подстановка хорошо работает, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.
Третий метод решения систем линейных уравнений называется методом исключения. Когда мы решили систему с помощью подстановки, мы начали с двух уравнений и двух переменных и свели ее к одному уравнению с одной переменной. То же самое мы сделаем и с методом исключения, но у нас будет другой способ добиться этого.
Метод исключения основан на добавочном свойстве равенства. Свойство сложения равенства говорит, что когда вы добавляете одинаковую величину к обеим сторонам уравнения, вы все равно получаете равенство.Мы расширим свойство сложения равенства, чтобы сказать, что когда вы добавляете равные количества к обеим сторонам уравнения, результаты равны.
Для любых выражений a , b , c и d ,
\ [\ begin {array} {lc} \ text {if} & a = b \\ \ text {and} & c = d \\ \ text {then} & a + c = b + d \ end {array} \]
Чтобы решить систему уравнений методом исключения, мы начнем с обоих уравнений в стандартной форме. Затем мы решаем, какую переменную будет легче всего устранить.Как мы решаем? Мы хотим, чтобы коэффициенты одной переменной были противоположными, чтобы мы могли сложить уравнения и исключить эту переменную.
Затем мы решаем, какую переменную будет легче всего устранить.Как мы решаем? Мы хотим, чтобы коэффициенты одной переменной были противоположными, чтобы мы могли сложить уравнения и исключить эту переменную.
Обратите внимание, как это работает, когда мы складываем эти два уравнения вместе:
\ [\ begin {array} {l} 3x + y = 5 \\ \ underline {2x-y = 0} \\ 5x \ quad \ quad = 5 \ end {array} \]
и складываются с нулем, и мы получаем одно уравнение с одной переменной.
Попробуем еще:
\ [\ left \ {\ begin {array} {l} {x + 4 y = 2} \\ {2 x + 5 y = -2} \ end {array} \ right.\]
На этот раз мы не видим переменную, которую можно было бы немедленно удалить, если мы добавим уравнения.
Но если мы умножим первое уравнение на −2, мы сделаем коэффициенты при x противоположными. Мы должны умножить каждый член в обеих частях уравнения на −2.
Теперь мы видим, что коэффициенты членов x противоположны, поэтому x будут исключены, когда мы сложим эти два уравнения.
Сами сложите уравнения — результат должен быть −3 y = −6.И это кажется несложным, не так ли? Вот как бы это выглядело.
Сделаем еще один:
\ [\ left \ {\ begin {array} {l} {4 x-3 y = 10} \\ {3 x + 5 y = -7} \ end {array} \ right. \]
Не похоже, чтобы коэффициенты одной переменной были противоположными, умножая одно из уравнений на константу, если только мы не используем дроби. Поэтому вместо этого нам придется умножить оба уравнения на константу.
Мы можем сделать коэффициенты x противоположными, если умножим первое уравнение на 3, а второе на −4, так что мы получим 12 x и −12 x .
Это дает нам эти два новых уравнения:
Когда мы складываем эти уравнения,
\ [\ [\ left \ {\ begin {array} {r} {12 x-9 y = 30} \\ {\ underline {-12 x-20 y = 28}} \\\ end {array} \ вправо. \\\ quad \ qquad {-29 y = 58} \] \]
\\\ quad \ qquad {-29 y = 58} \] \]
, исключаются значения x , и остается −29 y = 58.
Как только мы получаем уравнение с одной переменной, мы его решаем.Затем мы подставляем это значение в одно из исходных уравнений, чтобы найти оставшуюся переменную. И, как всегда, мы проверяем наш ответ, чтобы убедиться, что он является решением обоих исходных уравнений.
Теперь мы увидим, как использовать исключение для решения той же системы уравнений, которую мы решили с помощью построения графиков и подстановки.
Упражнение \ (\ PageIndex {2} \)
Решите систему устранением. \ (\ left \ {\ begin {array} {l} {3 x + y = 5} \\ {2 x-3 y = 7} \ end {array} \ right. \)
- Ответ
(2, -1)
Упражнение \ (\ PageIndex {3} \)
Решите систему устранением.\ (\ left \ {\ begin {array} {l} {4 x + y = -5} \\ {-2 x-2 y = -2} \ end {array} \ right. \)
\)
- Ответ
(-2,3)
Шаги перечислены ниже для удобства.
КАК РЕШИТЬ СИСТЕМУ УРАВНЕНИЙ ПУТЕМ ИСКЛЮЧЕНИЯ.
- Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробными, очистите их.
- Сделайте коэффициенты одной переменной противоположными.
- Решите, какую переменную исключить.
- Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположными.
- Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Найдите оставшуюся переменную.
- Подставьте решение из шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений .

Сначала мы рассмотрим пример, в котором мы можем сразу исключить одну переменную.
Упражнение \ (\ PageIndex {4} \)
Решите систему устранением. \ (\ left \ {\ begin {array} {l} {x + y = 10} \\ {x-y = 12} \ end {array} \ right. \)
- Ответ
Упражнение \ (\ PageIndex {5} \)
Решите систему устранением. \ (\ left \ {\ begin {array} {l} {2 x + y = 5} \\ {x-y = 4} \ end {array} \ right. \)
- Ответ
(3, -1)
Упражнение \ (\ PageIndex {6} \)
Решите систему устранением.\ (\ left \ {\ begin {array} {l} {x + y = 3} \\ {-2 x-y = -1} \ end {array} \ right. \)
- Ответ
(-2,5)
В упражнении \ (\ PageIndex {7} \) мы сможем сделать коэффициенты одной переменной противоположными, умножив одно уравнение на константу.
Упражнение \ (\ PageIndex {7} \)
Решите систему устранением. \ (\ left \ {\ begin {array} {l} {3 x-2 y = -2} \\ {5 x-6 y = 10} \ end {array} \ right. \)
- Ответ
Упражнение \ (\ PageIndex {8} \)
Решите систему устранением.\ (\ left \ {\ begin {array} {l} {4 x-3 y = 1} \\ {5 x-9 y = -4} \ end {array} \ right. \)
- Ответ
(1,1)
Упражнение \ (\ PageIndex {9} \)
Решите систему методом исключения. \ (\ Left \ {\ begin {array} {l} {3 x + 2 y = 2} \\ {6 x + 5 y = 8} \ end {array} \ right. \ )
- Ответ
(-2,4)
Теперь мы рассмотрим пример, в котором нам нужно умножить оба уравнения на константы, чтобы сделать коэффициенты одной переменной противоположными.
Упражнение \ (\ PageIndex {10} \)
Решите систему устранением.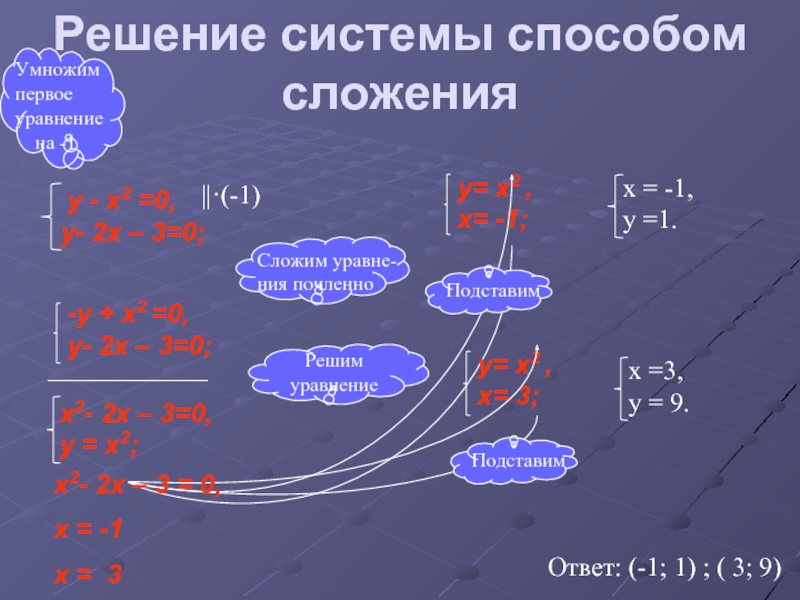 \ (\ left \ {\ begin {array} {l} {4 x-3 y = 9} \\ {7 x + 2 y = -6} \ end {array} \ right. \)
\ (\ left \ {\ begin {array} {l} {4 x-3 y = 9} \\ {7 x + 2 y = -6} \ end {array} \ right. \)
- Ответ
В этом примере мы не можем умножить одно уравнение на любую константу, чтобы получить противоположные коэффициенты. Поэтому мы стратегически умножим оба уравнения на константу, чтобы получить противоположности.
Упражнение \ (\ PageIndex {11} \)
Решите систему устранением.\ (\ left \ {\ begin {array} {l} {3 x-4 y = -9} \\ {5 x + 3 y = 14} \ end {array} \ right. \)
- Ответ
(1,3)
Упражнение \ (\ PageIndex {12} \)
Решите систему устранением. \ (\ left \ {\ begin {array} {l} {7 x + 8 y = 4} \\ {3 x-5 y = 27} \ end {array} \ right. \)
- Ответ
(4, −3)
Когда система уравнений содержит дроби, мы сначала очистим дроби, умножив каждое уравнение на его ЖК-дисплей.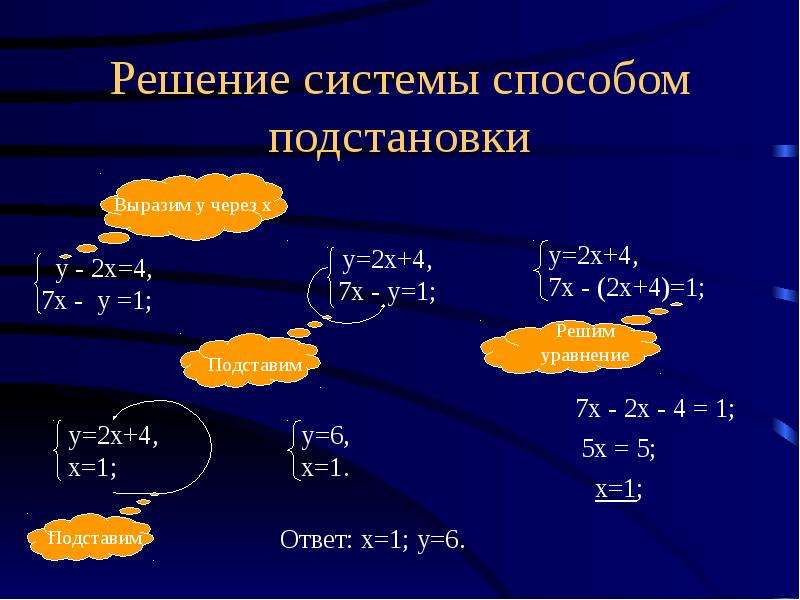
Упражнение \ (\ PageIndex {13} \)
Решите систему устранением. \ (\ left \ {\ begin {array} {l} {x + \ frac {1} {2} y = 6} \\ {\ frac {3} {2} x + \ frac {2} {3} y = \ frac {17} {2}} \ end {array} \ right. \)
- Ответ
В этом примере в обоих уравнениях есть дроби. Нашим первым шагом будет умножение каждого уравнения на его ЖК-дисплей, чтобы очистить дроби.
Упражнение \ (\ PageIndex {14} \)
Решите систему устранением.\ (\ left \ {\ begin {array} {l} {\ frac {1} {3} x- \ frac {1} {2} y = 1} \\ {\ frac {3} {4} xy = \ frac {5} {2}} \ end {array} \ right. \)
- Ответ
(6,2)
Упражнение \ (\ PageIndex {15} \)
Решите систему устранением. \ (\ left \ {\ begin {array} {l} {x + \ frac {3} {5} y = — \ frac {1} {5}} \\ {- \ frac {1} {2} x- \ frac {2} {3} y = \ frac {5} {6}} \ end {array} \ right. \)
\)
- Ответ
(1, −2)
В разделе «Решение систем уравнений с помощью построения графиков» мы увидели, что не все системы линейных уравнений имеют единственную упорядоченную пару в качестве решения.Когда два уравнения действительно представляли собой одну и ту же линию, решений было бесконечно много. Мы назвали это последовательной системой. Когда два уравнения описывали параллельные линии, решения не было. Мы назвали это несовместимой системой.
Упражнение \ (\ PageIndex {16} \)
Решите систему методом исключения. \ (\ Left \ {\ begin {array} {l} {3 x + 4 y = 12} \\ {y = 3- \ frac {3} {4} x} \ end { array} \ right. \)
- Ответ
\ (\ begin {array} {ll} & \ left \ {\ begin {align} 3 x + 4 y & = 12 \\ y & = 3- \ frac {3} {4} x \ end {выровнено} \правильно.\\\\\ text {Запишите второе уравнение в стандартной форме.} & \ left \ {\ begin {array} {l} {3 x + 4 y = 12} \\ {\ frac {3} {4} x + y = 3} \ end {array} \ right.
 \\ \\ \ text {Очистите дроби, умножив второе уравнение на 4.} & \ left \ {\ begin {align} 3 x + 4 y & = 12 \ \ 4 \ left (\ frac {3} {4} x + y \ right) & = 4 (3) \ end {align} \ right. \\\\ \ text {Упростить.} & \ left \ {\ begin {array} {l} {3 x + 4 y = 12} \\ {3 x + 4 y = 12} \ end {array} \ right . \\\\ \ text {Чтобы исключить переменную, мы умножаем второе уравнение на -1.} & \ left \ {\ begin {array} {c} {3 x + 4 y = 12} \\ \ underline {- 3 x-4 y = -12} \ end {array} \ right.\\ & \ qquad \ qquad \ quad 0 = 0 \\ \ text {Упростить и добавить.} \ end {array} \)
\\ \\ \ text {Очистите дроби, умножив второе уравнение на 4.} & \ left \ {\ begin {align} 3 x + 4 y & = 12 \ \ 4 \ left (\ frac {3} {4} x + y \ right) & = 4 (3) \ end {align} \ right. \\\\ \ text {Упростить.} & \ left \ {\ begin {array} {l} {3 x + 4 y = 12} \\ {3 x + 4 y = 12} \ end {array} \ right . \\\\ \ text {Чтобы исключить переменную, мы умножаем второе уравнение на -1.} & \ left \ {\ begin {array} {c} {3 x + 4 y = 12} \\ \ underline {- 3 x-4 y = -12} \ end {array} \ right.\\ & \ qquad \ qquad \ quad 0 = 0 \\ \ text {Упростить и добавить.} \ end {array} \)Это верное заявление. Уравнения непротиворечивы, но зависимы. Их графики будут одной линией. У системы бесконечно много решений.
Заметили ли вы, что после того, как мы очистили дроби во втором уравнении, эти два уравнения совпадают? Это означает, что у нас есть совпадающие линии.
Упражнение \ (\ PageIndex {17} \)
Решите систему устранением.\ (\ left \ {\ begin {array} {l} {5 x-3 y = 15} \\ {y = -5 + \ frac {5} {3} x} \ end {array} \ right. \ )
\ )
- Ответ
бесконечно много решений
Упражнение \ (\ PageIndex {18} \)
Решите систему устранением. \ (\ left \ {\ begin {array} {l} {x + 2 y = 6} \\ {y = — \ frac {1} {2} x + 3} \ end {array} \ right. \)
- Ответ
бесконечно много решений
Упражнение \ (\ PageIndex {19} \)
Решите систему устранением.\ (\ left \ {\ begin {array} {l} {- 6 x + 15 y = 10} \\ {2 x-5 y = -5} \ end {array} \ right. \)
- Ответ
\ (\ begin {array} {ll} \ text {Уравнения в стандартной форме.} & \ Left \ {\ begin {align} -6 x + 15 y & = 10 \\ 2 x-5 y & = -5 \ end {align} \ right. \\\\ \ text {Умножьте второе уравнение на 3, чтобы исключить переменную.} & \ Left \ {\ begin {array} {l} {- 6 x + 15 y = 10} \\ {3 (2 x-5 y) = 3 (-5)} \ end {array} \ right. \\\\ \ text {Упростить и добавить.
 } & \ Left \ {\ begin {align} {-6 x + 15 y = 10} \\ \ underline {6 x-15 y = -15} \ end {align} \ right.\\ & \ qquad \ qquad \ quad0 \ neq 5 \ end {array} \)
} & \ Left \ {\ begin {align} {-6 x + 15 y = 10} \\ \ underline {6 x-15 y = -15} \ end {align} \ right.\\ & \ qquad \ qquad \ quad0 \ neq 5 \ end {array} \)Это утверждение неверно. Уравнения несовместимы, поэтому их графики будут параллельными линиями.
В системе нет решения.
Упражнение \ (\ PageIndex {20} \)
Решите систему устранением. \ (\ left \ {\ begin {array} {l} {- 3 x + 2 y = 8} \\ {9 x-6 y = 13} \ end {array} \ right. \)
- Ответ
нет решения
Упражнение \ (\ PageIndex {21} \)
Решите систему устранением.\ (\ left \ {\ begin {array} {l} {7 x-3 y = -2} \\ {-14 x + 6 y = 8} \ end {array} \ right. \)
- Ответ
нет решения
Некоторые прикладные задачи переводятся непосредственно в уравнения стандартной формы, поэтому мы будем использовать метод исключения для их решения. Как и прежде, мы используем нашу стратегию решения проблем, чтобы оставаться сосредоточенными и организованными.
Как и прежде, мы используем нашу стратегию решения проблем, чтобы оставаться сосредоточенными и организованными.
Упражнение \ (\ PageIndex {22} \)
Сумма двух чисел равна 39.Их разница — 9. Найдите числа.
- Ответ
\ (\ begin {array} {ll} \ textbf {Шаг 1. Прочтите} \ text {проблема} & \\ \ textbf {Шаг 2. Определите} \ text {то, что мы ищем.} & \ Text { Мы ищем два числа.} \\\ textbf {Шаг 3. Имя} \ text {то, что мы ищем.} & \ Text {Пусть n = первое число.} \\ & \ text {m = второе number} \\\ textbf {Шаг 4. Переведите} \ text {в систему уравнений.} & \\ & \ text {Сумма двух чисел равна 39.} \\ & n + m = 39 \\ & \ text {Их разница составляет 9.} \\ & n − m = 9 \\ \\ \ text {Система:} & \ left \ {\ begin {array } {l} {n + m = 39} \\ {nm = 9} \ end {array} \ right. \\\\ \ textbf {Шаг 5. Решите} \ text {систему уравнений. } & \\ \ text {Чтобы решить систему уравнений, используйте} \\ \ text {исключение. Уравнения имеют стандартную} \\ \ text {форму, а коэффициенты m являются} & \\ \ text {противоположными.
 Добавить.} & \ Left \ {\ begin {array} {l} {n + m = 39} \\ \ underline {n-m = 9} \ end {array} \ right. \\ & \ quad 2n \ qquad = 48 \\ \\\ text {Решить для n.} & n = 24 \\ \\ \ text {Замените n = 24 одним из исходных} & n + m = 39 \\ \ text {уравнения и решите форму.} & 24 + m = 39 \\ & m = 15 \\ \ textbf {Шаг 6. Отметьте} \ text {ответ.} & \ text {Поскольку 24 + 15 = 39 и 24−15 = 9, ответы проверяются.} \\ \ textbf {Шаг 7. Ответ} \ text {вопрос.} & \ text {Числа 24 и 15.} \ end {array} \)
Добавить.} & \ Left \ {\ begin {array} {l} {n + m = 39} \\ \ underline {n-m = 9} \ end {array} \ right. \\ & \ quad 2n \ qquad = 48 \\ \\\ text {Решить для n.} & n = 24 \\ \\ \ text {Замените n = 24 одним из исходных} & n + m = 39 \\ \ text {уравнения и решите форму.} & 24 + m = 39 \\ & m = 15 \\ \ textbf {Шаг 6. Отметьте} \ text {ответ.} & \ text {Поскольку 24 + 15 = 39 и 24−15 = 9, ответы проверяются.} \\ \ textbf {Шаг 7. Ответ} \ text {вопрос.} & \ text {Числа 24 и 15.} \ end {array} \)
Упражнение \ (\ PageIndex {23} \)
Сумма двух чисел равна 42. Их разность равна 8. Найдите числа.
- Ответ
Цифры 25 и 17.
Упражнение \ (\ PageIndex {24} \)
Сумма двух чисел равна −15. Их разница -35. Найдите числа.
- Ответ
Числа −25 и 10.
Упражнение \ (\ PageIndex {25} \)
Джо каждый день останавливается в ресторане, где подают гамбургеры, по дороге на работу.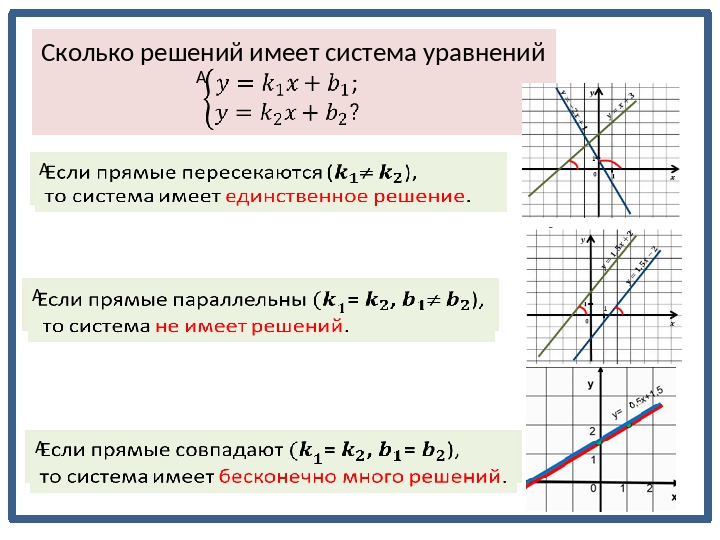 В понедельник он заказал средний картофель фри и два небольших газированных напитка, в которых в общей сложности было 620 калорий.Во вторник у него было два заказа среднего картофеля фри и одна небольшая газировка, в общей сложности 820 калорий. Сколько калорий в одной порции среднего картофеля фри? Сколько калорий в одной маленькой газировке?
В понедельник он заказал средний картофель фри и два небольших газированных напитка, в которых в общей сложности было 620 калорий.Во вторник у него было два заказа среднего картофеля фри и одна небольшая газировка, в общей сложности 820 калорий. Сколько калорий в одной порции среднего картофеля фри? Сколько калорий в одной маленькой газировке?
- Ответ
Упражнение \ (\ PageIndex {26} \)
Малик останавливается в продуктовом магазине, чтобы купить пакет подгузников и 2 банки смеси. В общей сложности он тратит 37 долларов. На следующей неделе он останавливается и покупает 2 пакета подгузников и 5 банок смеси на общую сумму 87 долларов.Сколько стоит сумка с подгузниками? Сколько можно смеси?
- Ответ
Пакет с подгузниками стоит 11 долларов, а банка молочной смеси — 13 долларов.
Упражнение \ (\ PageIndex {27} \)
Чтобы получить ежедневное количество фруктов в течение дня, Саша съела банан и 8 ягод клубники в среду, получив 145 калорий. В следующую среду она съела два банана и 5 ягод клубники, получив в общей сложности 235 калорий для фруктов.Сколько калорий в банане? Сколько калорий в клубнике?
В следующую среду она съела два банана и 5 ягод клубники, получив в общей сложности 235 калорий для фруктов.Сколько калорий в банане? Сколько калорий в клубнике?
- Ответ
Банан содержит 105 калорий, а клубника — 5 калорий.
Когда вам придется решать систему линейных уравнений в более позднем математическом классе, вам обычно не говорят, какой метод использовать. Вам нужно будет принять это решение самостоятельно. Так что вы захотите выбрать самый простой метод, который сводит к минимуму ваши шансы на ошибку.
Упражнение \ (\ PageIndex {28} \)
Для каждой системы линейных уравнений решите, что удобнее будет решить заменой или исключением. Поясните свой ответ.
- \ (\ left \ {\ begin {array} {l} {3 x + 8 y = 40} \\ {7 x-4 y = -32} \ end {array} \ right. \)
- \ (\ left \ {\ begin {array} {l} {5 x + 6 y = 12} \\ {y = \ frac {2} {3} x-1} \ end {array} \ right.
 \ )
\ )
- Ответ
1. \ (\ left \ {\ begin {array} {l} {3 x + 8 y = 40} \\ {7 x-4 y = -32} \ end {array} \ right.\)
Поскольку оба уравнения имеют стандартную форму, использование исключения будет наиболее удобным.
2. \ (\ left \ {\ begin {array} {l} {5 x + 6 y = 12} \\ {y = \ frac {2} {3} x-1} \ end {array} \ right . \)
Поскольку одно уравнение уже решено относительно и , использование подстановки будет наиболее удобным.
Упражнение \ (\ PageIndex {29} \)
Решите для каждой системы линейных уравнений, что удобнее решить: заменой или исключением.Поясните свой ответ.
- \ (\ left \ {\ begin {array} {l} {4 x-5 y = -32} \\ {3 x + 2 y = -1} \ end {array} \ right. \)
- \ (\ left \ {\ begin {array} {l} {x = 2 y-1} \\ {3 x-5 y = -7} \ end {array} \ right. \)
- Ответ
- Поскольку оба уравнения имеют стандартную форму, использование исключения будет наиболее удобным.

- Поскольку одно уравнение относительно xx уже решено, использование подстановки будет наиболее удобным.
- Поскольку оба уравнения имеют стандартную форму, использование исключения будет наиболее удобным.
Упражнение \ (\ PageIndex {30} \)
Решите для каждой системы линейных уравнений, что удобнее решить: заменой или исключением.Поясните свой ответ.
- \ (\ left \ {\ begin {array} {l} {y = 2 x-1} \\ {3 x-4 y = -6} \ end {array} \ right. \)
- \ (\ left \ {\ begin {array} {l} {6 x-2 y = 12} \\ {3 x + 7 y = -13} \ end {array} \ right. \)
- Ответ
- Поскольку одно уравнение для yy уже решено, использование подстановки будет наиболее удобным;
- Поскольку оба уравнения имеют стандартную форму, использование исключения будет наиболее удобным.
Примечание
Получите доступ к этим онлайн-ресурсам, чтобы получить дополнительные инструкции и попрактиковаться в решении систем линейных уравнений методом исключения.
- Решение системы уравнений методом исключения
- Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробными, очистите их.
- Сделайте коэффициенты одной переменной противоположными.
- Решите, какую переменную исключить.
- Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположными.
- Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Найдите оставшуюся переменную.
- Подставьте решение из шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений .

Практика ведет к совершенству
Решите систему уравнений методом исключения
В следующих упражнениях решите системы уравнений методом исключения.
Упражнение \ (\ PageIndex {1} \)
\ (\ left \ {\ begin {array} {l} {5 x + 2 y = 2} \\ {-3 x-y = 0} \ end {array} \ right. \)
Упражнение \ (\ PageIndex {2} \)
\ (\ left \ {\ begin {array} {l} {- 3 x + y = -9} \\ {x-2 y = -12} \ end {array} \ right. \)
- Ответ
\ ((6,9) \)
Упражнение \ (\ PageIndex {3} \)
\ (\ left \ {\ begin {array} {l} {6 x-5 y = -1} \\ {2 x + y = 13} \ end {array} \ right. \)
Упражнение \ (\ PageIndex {4} \)
\ (\ left \ {\ begin {array} {l} {3 x-y = -7} \\ {4 x + 2 y = -6} \ end {array} \ right.\)
- Ответ
\ ((- 2,1) \)
Упражнение \ (\ PageIndex {5} \)
\ (\ left \ {\ begin {array} {l} {x + y = -1} \\ {x-y = -5} \ end {array} \ right. \)
\)
Упражнение \ (\ PageIndex {6} \)
\ (\ left \ {\ begin {array} {l} {x + y = -8} \\ {x-y = -6} \ end {array} \ right. \)
- Ответ
\ ((- 7, -1) \)
Упражнение \ (\ PageIndex {7} \)
\ (\ left \ {\ begin {array} {l} {3 x-2 y = 1} \\ {-x + 2 y = 9} \ end {array} \ right.\)
Упражнение \ (\ PageIndex {8} \)
\ (\ left \ {\ begin {array} {l} {- 7 x + 6 y = -10} \\ {x-6 y = 22} \ end {array} \ right. \)
- Ответ
\ ((- 2, -4) \)
Упражнение \ (\ PageIndex {9} \)
\ (\ left \ {\ begin {array} {l} {3 x + 2 y = -3} \\ {-x-2 y = -19} \ end {array} \ right. \)
Упражнение \ (\ PageIndex {10} \)
\ (\ left \ {\ begin {array} {l} {5 x + 2 y = 1} \\ {-5 x-4 y = -7} \ end {array} \ right.\)
- Ответ
\ ((- 1,3) \)
Упражнение \ (\ PageIndex {11} \)
\ (\ left \ {\ begin {array} {l} {6 x + 4 y = -4} \\ {-6 x-5 y = 8} \ end {array} \ right. \)
\)
Упражнение \ (\ PageIndex {12} \)
\ (\ left \ {\ begin {array} {l} {3 x-4 y = -11} \\ {x-2 y = -5} \ end {array} \ right. \)
- Ответ
\ ((- 1,2) \)
Упражнение \ (\ PageIndex {13} \)
\ (\ left \ {\ begin {array} {l} {5 x-7 y = 29} \\ {x + 3 y = -3} \ end {array} \ right.\)
Упражнение \ (\ PageIndex {14} \)
\ (\ left \ {\ begin {array} {l} {6 x-5 y = -75} \\ {-x-2 y = -13} \ end {array} \ right. \)
- Ответ
\ ((- 5,9) \)
Упражнение \ (\ PageIndex {15} \)
\ (\ left \ {\ begin {array} {l} {- x + 4 y = 8} \\ {3 x + 5 y = 10} \ end {array} \ right. \)
Упражнение \ (\ PageIndex {16} \)
\ (\ left \ {\ begin {array} {l} {2 x-5 y = 7} \\ {3 x-y = 17} \ end {array} \ right.\)
- Ответ
\ ((6,1) \)
Упражнение \ (\ PageIndex {17} \)
\ (\ left \ {\ begin {array} {l} {5 x-3 y = -1} \\ {2 x-y = 2} \ end {array} \ right. \)
\)
Упражнение \ (\ PageIndex {18} \)
\ (\ left \ {\ begin {array} {l} {7 x + y = -4} \\ {13 x + 3 y = 4} \ end {array} \ right. \)
- Ответ
\ ((- 2,10) \)
Упражнение \ (\ PageIndex {19} \)
\ (\ left \ {\ begin {array} {l} {- 3 x + 5 y = -13} \\ {2 x + y = -26} \ end {array} \ right.\)
Упражнение \ (\ PageIndex {20} \)
\ (\ left \ {\ begin {array} {l} {3 x-5 y = -9} \\ {5 x + 2 y = 16} \ end {array} \ right. \)
- Ответ
\ ((2,3) \)
Упражнение \ (\ PageIndex {21} \)
\ (\ left \ {\ begin {array} {l} {4 x-3 y = 3} \\ {2 x + 5 y = -31} \ end {array} \ right. \)
Упражнение \ (\ PageIndex {22} \)
\ (\ left \ {\ begin {array} {l} {4 x + 7 y = 14} \\ {-2 x + 3 y = 32} \ end {array} \ right.\)
- Ответ
\ ((- 7,6) \)
Упражнение \ (\ PageIndex {23} \)
\ (\ left \ {\ begin {array} {l} {5 x + 2 y = 21} \\ {7 x-4 y = 9} \ end {array} \ right. \)
\)
Упражнение \ (\ PageIndex {24} \)
\ (\ left \ {\ begin {array} {l} {3 x + 8 y = -3} \\ {2 x + 5 y = -3} \ end {array} \ right. \)
- Ответ
\ ((- 9,3) \)
Упражнение \ (\ PageIndex {25} \)
\ (\ left \ {\ begin {array} {l} {11 x + 9 y = -5} \\ {7 x + 5 y = -1} \ end {array} \ right.\)
Упражнение \ (\ PageIndex {26} \)
\ (\ left \ {\ begin {array} {l} {3 x + 8 y = 67} \\ {5 x + 3 y = 60} \ end {array} \ right. \)
Ответ
\ ((9,5) \)
Упражнение \ (\ PageIndex {27} \)
\ (\ left \ {\ begin {array} {l} {2 x + 9 y = -4} \\ {3 x + 13 y = -7} \ end {array} \ right. \)
Упражнение \ (\ PageIndex {28} \)
\ (\ left \ {\ begin {array} {l} {\ frac {1} {3} xy = -3} \\ {x + \ frac {5} {2} y = 2} \ end {array} \правильно.\)
- Ответ
\ ((- 3,2) \)
Упражнение \ (\ PageIndex {29} \)
\ (\ left \ {\ begin {array} {l} {x + \ frac {1} {2} y = \ frac {3} {2}} \\ {\ frac {1} {5} x- \ frac {1} {5} y = 3} \ end {array} \ right. \)
\)
Упражнение \ (\ PageIndex {30} \)
\ (\ left \ {\ begin {array} {l} {x + \ frac {1} {3} y = -1} \\ {\ frac {1} {2} x- \ frac {1} {3 } y = -2} \ end {array} \ right. \)
- Ответ
\ ((- 2,3) \)
Упражнение \ (\ PageIndex {31} \)
\ (\ left \ {\ begin {array} {l} {\ frac {1} {3} xy = -3} \\ {\ frac {2} {3} x + \ frac {5} {2} y = 3} \ end {array} \ right.\)
Упражнение \ (\ PageIndex {32} \)
\ (\ left \ {\ begin {array} {l} {2 x + y = 3} \\ {6 x + 3 y = 9} \ end {array} \ right. \)
- Ответ
бесконечно много решений
Упражнение \ (\ PageIndex {33} \)
\ (\ left \ {\ begin {array} {l} {x-4 y = -1} \\ {-3 x + 12 y = 3} \ end {array} \ right. \)
Упражнение \ (\ PageIndex {34} \)
\ (\ left \ {\ begin {array} {l} {- 3 x-y = 8} \\ {6 x + 2 y = -16} \ end {array} \ right. \)
\)
- Ответ
бесконечно много решений
Упражнение \ (\ PageIndex {35} \)
\ (\ left \ {\ begin {array} {l} {4 x + 3 y = 2} \\ {20 x + 15 y = 10} \ end {array} \ right. \)
Упражнение \ (\ PageIndex {36} \)
\ (\ left \ {\ begin {array} {l} {3 x + 2 y = 6} \\ {-6 x-4 y = -12} \ end {array} \ right. \)
- Ответ
бесконечно много решений
Упражнение \ (\ PageIndex {37} \)
\ (\ left \ {\ begin {array} {l} {5 x-8 y = 12} \\ {10 x-16 y = 20} \ end {array} \ right.\)
Упражнение \ (\ PageIndex {38} \)
\ (\ left \ {\ begin {array} {l} {- 11 x + 12 y = 60} \\ {-22 x + 24 y = 90} \ end {array} \ right. \)
- Ответ
непоследовательно, нет решения
Упражнение \ (\ PageIndex {39} \)
\ (\ left \ {\ begin {array} {l} {7 x-9 y = 16} \\ {-21 x + 27 y = -24} \ end {array} \ right. \)
\)
Упражнение \ (\ PageIndex {40} \)
\ (\ left \ {\ begin {array} {l} {5 x-3 y = 15} \\ {y = \ frac {5} {3} x-2} \ end {array} \ right.\)
- Ответ
непоследовательно, нет решения
Упражнение \ (\ PageIndex {41} \)
\ (\ left \ {\ begin {array} {l} {2 x + 4 y = 7} \\ {y = — \ frac {1} {2} x-4} \ end {array} \ right. \)
Решить приложения систем уравнений методом исключения
В следующих упражнениях переведите в систему уравнений и решите.
Упражнение \ (\ PageIndex {42} \)
Сумма двух чисел равна 65.Их разница составляет 25. Найдите числа.
- Ответ
Цифры 20 и 45.
Упражнение \ (\ PageIndex {43} \)
Сумма двух чисел равна 37. Их разница равна 9. Найдите числа.
Упражнение \ (\ PageIndex {44} \)
Сумма двух чисел равна −27. Их разница -59. Найдите числа.
Их разница -59. Найдите числа.
- Ответ
Цифры 16 и −43.
Упражнение \ (\ PageIndex {45} \)
Сумма двух чисел равна -45. Их разница -89. Найдите числа.
Упражнение \ (\ PageIndex {46} \)
Андреа покупает новые рубашки и свитера. Она может купить 3 рубашки и 2 свитера за 114 долларов или 2 рубашки и 4 свитера за 164 доллара. Сколько стоит рубашка? Сколько стоит свитер?
- Ответ
Рубашка стоит 16 долларов, а свитер — 33 доллара.
Упражнение \ (\ PageIndex {47} \)
Питер покупает канцелярские товары. Он может купить 3 пакета бумаги и 4 степлера за 40 долларов, или он может купить 5 пакетов бумаги и 6 степлеров за 62 доллара. Сколько стоит пачка бумаги? Сколько стоит степлер?
Упражнение \ (\ PageIndex {48} \)
Общее количество натрия в 2 хот-догах и 3 стаканах творога составляет 4720 мг. Общее количество натрия в 5 хот-догах и 2 стаканах творога составляет 6300 мг.Сколько натрия в хот-доге? Сколько натрия в стакане творога?
Общее количество натрия в 5 хот-догах и 2 стаканах творога составляет 6300 мг.Сколько натрия в хот-доге? Сколько натрия в стакане творога?
- Ответ
В хот-доге 860 мг. В стакане творога 1000 мг.
Упражнение \ (\ PageIndex {49} \)
Общее количество калорий в 2 хот-догах и 3 чашках творога составляет 960 калорий. Общее количество калорий в 5 хот-догах и 2 стаканах творога составляет 1190 калорий. Сколько калорий в хот-доге? Сколько калорий в стакане творога?
Выберите наиболее удобный метод решения системы линейных уравнений
В следующих упражнениях решите, что будет удобнее решить систему уравнений путем замены или исключения.
Упражнение \ (\ PageIndex {50} \)
- \ (\ left \ {\ begin {array} {l} {8 x-15 y = -32} \\ {6 x + 3 y = -5} \ end {array} \ right. \)
- \ (\ left \ {\ begin {array} {l} {x = 4 y-3} \\ {4 x-2 y = -6} \ end {array} \ right.
 \)
\)
- Ответ
- ликвидация
- замена
Упражнение \ (\ PageIndex {51} \)
- \ (\ left \ {\ begin {array} {l} {y = 7 x-5} \\ {3 x-2 y = 16} \ end {array} \ right.\)
- \ (\ left \ {\ begin {array} {l} {12 x-5 y = -42} \\ {3 x + 7 y = -15} \ end {array} \ right. \)
Упражнение \ (\ PageIndex {52} \)
- \ (\ left \ {\ begin {array} {l} {y = 4 x + 9} \\ {5 x-2 y = -21} \ end {array} \ right. \)
- \ (\ left \ {\ begin {array} {l} {9 x-4 y = 24} \\ {3 x + 5 y = -14} \ end {array} \ right. \)
- Ответ
- замена
- ликвидация
Упражнение \ (\ PageIndex {53} \)
- \ (\ left \ {\ begin {array} {l} {14 x-15 y = -30} \\ {7 x + 2 y = 10} \ end {array} \ right.\)
- \ (\ left \ {\ begin {array} {l} {x = 9 y-11} \\ {2 x-7 y = -27} \ end {array} \ right.
 \)
\)
Повседневная математика
Упражнение \ (\ PageIndex {54} \)
Норрис может греб на 3 мили против течения за то же время, за которое он гребет на 5 миль вниз по течению. Решите систему. \ (\ left \ {\ begin {array} {l} {r-c = 3} \\ {r + c = 5} \ end {array} \ right. \)
- для r, его скорость гребли в стоячей воде.
- Затем решите относительно c, скорость течения реки.
- Ответ
- г = 4
- с = 1
Упражнение \ (\ PageIndex {55} \)
Джози хочет приготовить 10 фунтов смеси для троп из орехов и изюма, и она хочет, чтобы общая стоимость смеси для троп составила 54 доллара. Орехи стоят 6 долларов за фунт, а изюм — 3 доллара за фунт. Решите систему \ (\ left \ {\ begin {array} {l} {n + r = 10} \\ {6 n + 3 r = 54} \ end {array} \ right. \), Чтобы найти n, количество фунтов орехов и rr, количество фунтов изюма, которое она должна использовать.
Письменные упражнения
Упражнение \ (\ PageIndex {56} \)
Решите систему
\ (\ left \ {\ begin {array} {l} {x + y = 10} \\ {5 x + 8 y = 56} \ end {array} \ right. \)
- путем замены
- , построив график
- Какой метод вы предпочитаете? Почему?
- Ответ
- (8, 2)
3. Ответы будут разными.
Упражнение \ (\ PageIndex {57} \)
Решите систему \ (\ left \ {\ begin {array} {l} {x + y = -12} \\ {y = 4- \ frac {1} {2} x} \ end {array} \ right .\)
- путем замены
- , построив график
- Какой метод вы предпочитаете? Почему?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Метод исключения для решения линейных систем (Алгебра 1, Системы линейных уравнений и неравенств) — Mathplanet
Другой способ решения линейной системы — использовать метод исключения.В методе исключения вы либо складываете, либо вычитаете уравнения, чтобы получить уравнение с одной переменной.
Когда коэффициенты одной переменной противоположны, вы добавляете уравнения, чтобы исключить переменную, а когда коэффициенты одной переменной равны, вы вычитаете уравнения, чтобы исключить переменную.
Пример
$$ \ begin {matrix} 3y + 2x = 6 \\ 5y-2x = 10 \ end {matrix} $$
Мы можем исключить переменную \ (x \), добавив два уравнения.
$$ 3y + 2x = 6 $$
$$ \ underline {+ \: 5y-2x = 10} $$
$$ = 8лет \: \: \: \: \; \; \; \; = 16 $$
$$ \ begin {matrix} \: \: \: y \: \: \: \: \: \; \; \; \; \; = 2 \ end {matrix} $$
Теперь значение \ (y \) можно подставить в любое из исходных уравнений, чтобы найти значение \ (x \)
.
$$ 3y + 2x = 6 $$
$$ 3 \ cdot {\ color {зеленый} 2} + 2x = 6 $$
$$ 6 + 2x = 6 $$
$$ x = 0 $$
Решение линейной системы: \ ((0, 2) \).
Чтобы избежать ошибок, перед началом исключения убедитесь, что все одинаковые термины и знаки равенства находятся в одних и тех же столбцах.
Если у вас нет уравнений, в которых вы можете исключить переменную путем сложения или вычитания, вы можете непосредственно начать с умножения одного или обоих уравнений на константу, чтобы получить эквивалентную линейную систему, в которой вы можете исключить одну из переменных путем сложения. или вычитание.
Пример
$$ \ begin {matrix} 3x + y = 9 \\ 5x + 4y = 22 \ end {matrix} $$
Начните с умножения первого уравнения на \ (- 4 \) так, чтобы коэффициенты \ (y \) были противоположны
$$ \ begin {matrix} \ color {green} {- 4} \ cdot (3x + y) = \ color {green} {- 4} \ cdot 9 \\ 5x + 4y = 22 \ end {matrix} $ $
$$ \ Rightarrow $$
$$ — 12x-4y = -36 $$
$$ \ underline {+ 5x + 4y = 22} $$
$$ = — 7x \: \: \: \: \: \: \: \: \: \: = -14 $$
$$ \ begin {matrix} \: \: \; \: \: x \: \: \: \: \: \: \: \: \: \: \: = 2 \ end {matrix} $$
Подставьте \ (x \) в любое из исходных уравнений, чтобы получить значение \ (y \)
$$ 3x + y = 9 $$
$$ 3 \ cdot {\ color {зеленый} 2} + y = 9 $$
$$ 6 + y = 9 $$
$$ y = 3 $$
Решение линейной системы: \ ((2, 3) \)
Видеоурок
Решите следующую линейную систему, используя метод исключения
$$ \ begin {matrix} 2y — 4x = 2 \\ y = -x + 4 \ end {matrix} $$
youtube.com/embed/dZ8RDsuez7g?fs=1&hl=sv_SE&rel=0″ allowfullscreen=»»/>
Системы уравнений в SAT Math: Подготовка к алгебре и практика
Конечно, вы хорошо разбирались в уравнениях с одной переменной, и теперь они не проблема, но что вы делаете, когда вам предлагают сразу несколько уравнений и несколько переменных? Это то, что мы называем «системами уравнений», и, к счастью для нас, это чрезвычайно предсказуемые типы проблем с множеством методов их решения.В зависимости от того, как вам больше всего нравится работать, вы можете выбрать свое собственное приключение, когда дело доходит до задач системы уравнений.
Но прежде чем вы выберете метод, который лучше всего подходит вам (или конкретной проблеме), давайте рассмотрим все возможные варианты, которые у вас есть, а также типы вопросов, которые вы увидите в день тестирования. Эти вопросы всегда будут появляться один или два раза в любом заданном тесте, поэтому лучше понять все стратегии, которые есть в вашем распоряжении.
Это будет ваш полный справочник по вопросам системы уравнений — что это такое, какие существуют различные способы их решения и как вы увидите их на SAT.
Что такое системы уравнений?
Системы уравнений — это набор из двух (или более) уравнений, которые имеют две (или более) переменные. Уравнения полагаются друг на друга и могут быть решены только с информацией, которую предоставляет каждое.
Большую часть времени на тесте SAT вы будете видеть систему уравнений, которая включает два уравнения и две переменные, но, конечно же, нет ничего необычного в том, что вы увидите три уравнения и / или три переменные в любом количестве комбинаций. .
Системы уравнений также можно решить множеством способов. Как всегда с SAT, то, как вы решите свои проблемы, в основном зависит от того, как вы предпочитаете работать, а также от того, сколько времени у вас есть, чтобы посвятить проблеме.
Три метода решения задачи системы уравнений:
# 1 : построение графика
# 2 : подстановка
# 3 : вычитание
Давайте рассмотрим каждый метод и увидим их в действии на примере той же системы уравнений.
Для нашего примера допустим, что наша заданная система уравнений:
$$ 2y + 3x = 38 $$
$$ y — 2x = 12 $$
Метод решения 1: построение графиков
Будет только одно решение для системы уравнений, и это одно решение будет пересечением двух линий. Чтобы построить график наших уравнений, мы должны сначала преобразовать каждое уравнение в форму с угловым пересечением. Если вы знакомы с линиями и уклонами, вы знаете, что форма пересечения откоса выглядит так:
долл. США y = mx + b
долл. СШАИтак, давайте представим наши два уравнения в форме пересечения наклона.
$ 2y + 3x = 38 $
$ 2y = -3x + 38 $
$ y = {-3/2} x + 19
$и
$ y — 2x = 12 $
$ y = 2x + 12 $
Теперь давайте изобразим каждое уравнение на графике, чтобы найти точки пересечения.
После того, как мы изобразили наше уравнение, мы увидим, что пересечение находится в (2, 16).
Итак, наши окончательные результаты: $ x = 2 $ и $ y = 16 $
.Метод решения 2: Замена
Чтобы решить нашу систему уравнений с помощью подстановки, мы должны выделить одну переменную в одном из уравнений, а затем использовать эту найденную переменную для второго уравнения , чтобы найти оставшуюся переменную.
Например, у нас есть два уравнения,
$ 2y + 3x = 38 $
$ y — 2x = 12 $
Итак, давайте выберем только одно из уравнений, а затем выделим одну из переменных.
В этом случае давайте выберем второе уравнение и выделим наше значение $ y $.
$ y — 2x = 12 $
$ y = 2x + 12 $
Затем мы должны подставить найденную переменную во второе уравнение. (В данном случае, поскольку мы использовали второе уравнение для выделения нашего $ y $, нам нужно вставить это значение $ y $ в первое уравнение .)
$ 2y + 3x = 38 $
$ 2 (2x + 12) + 3x = 38 $
$ 4x + 24 + 3x = 38 $
$ 24 + 7x = 38 $
$ 7x = 14 $
долл. США x = 2
США x = 2
И, наконец, вы можете найти числовое значение для вашей первой переменной ($ y $), подставив числовое значение для вашей второй переменной ($ x $) в любое уравнение.
$ 2y + 3x = 38 $
$ 2y + 3 (2) = 38 $
$ 2y + 6 = 38 $
$ 2y = 32 $
$ y = 16 $
или
$ y — 2x = 12 $
$ г — 2 (2) = 12 $
$ г — 4 = 12 $
$ y = 16 $
В любом случае, вы нашли значение ваших $ x $ и $ y $.
Опять же, $ x = 2 $ и $ y = 16 $
Метод решения 3: вычитание
В качестве последнего метода решения систем уравнений вы можете полностью вычесть одну из переменных, чтобы найти значение второй переменной. Мы делаем это, вычитая одно уравнение целиком из другого полного уравнения.
Обратите внимание, что вы можете сделать это только в том случае, если рассматриваемые переменные (та, которую вы хотите исключить) точно такие же, как . Если они НЕ совпадают, тогда мы должны сначала умножить все уравнение на необходимое количество, чтобы получилось из одинаковых.
Если они НЕ совпадают, тогда мы должны сначала умножить все уравнение на необходимое количество, чтобы получилось из одинаковых.
В случае наших двух уравнений ни одна из наших переменных не равна.
$ 2y + 3x = 38 $
$ y — 2x = 12 $
В этом случае давайте решим вычесть наши значения $ y $ и отменить их. Это означает, что мы должны сначала сделать их равными , умножив наше второе уравнение на 2, чтобы оба значения $ y $ совпали.
$ 2y + 3x = 38 $
$ y — 2x = 12 $
Становится:
$ 2y + 3x = 38 $ (Это первое уравнение остается неизменным)
и
$ 2 (y — 2x = 12) $ => $ 2y — 4x = 24 $ (Все уравнение умножается на 2)
И теперь мы можем сократить наши значения $ y $, вычтя все второе уравнение из первого.
$ 2y + 3x = 38 $
–
$ 2y — 4x = 24 $
———————
$ 3x — -4x = 14 $
$ 7x = 14 $
долл. США x = 2
долл. США
СШАТеперь, когда мы выделили наше значение $ x $, мы можем подставить его в любое из наших двух уравнений, чтобы найти значение $ y $.
$ 2y + 3x = 38 $
$ 2y + 3 (2) = 38 $
$ 2y + 6 = 38 $
$ 2y = 32 $
$ y = 16 $
или
$ y — 2x = 12 $
$ г — 2 (2) = 12 $
$ г — 4 = 12 $
$ y = 16 $
Наши окончательные результаты снова равны $ x = 2 $ и $ y = 16 $.
Хотя есть много способов решить ваши проблемы, не позволяйте этим знаниям ошеломить вас; с практикой вы найдете для себя лучший метод решения.
Независимо от того, какой метод мы используем для решения наших проблем, система уравнений будет иметь либо одно решение, — то есть, каждая переменная будет иметь числовое значение — без решения, либо бесконечные решения .
Чтобы система уравнений имела бесконечное решение , каждая система фактически идентична. Это означает, что это та же линия и .
Это означает, что это та же линия и .
Чтобы система уравнений имела без решение , значения $ x $ будут равны, если для значений $ y $ установлено значение 1 (что означает, что обе переменные — $ x $ и $ y $ — будет равно).Причина, по которой это правда, заключается в том, что в результате получатся две параллельные линии, так как линии будут иметь одинаковый наклон. У системы нет решения, потому что две линии никогда не встретятся и, следовательно, не имеют точки пересечения.
Например,
Поскольку наша система не будет иметь решения, когда и наши значения $ y $, и наши значения $ x $ равны , это означает, что не будет решения, в котором мы удалили бы обе наши переменные путем их отмены.
В этом случае наиболее целесообразным решением данной проблемы будет вычитание.Почему? Мы можем видеть это, потому что два значения $ x $ ($ 2x $ и $ 4x $) кратны друг другу, поэтому мы можем легко перемножить одно уравнение, чтобы уравнять их.
$ 2x — 5лет = 8 $
$ 4x + ky = 17 $
Теперь давайте умножим верхнее уравнение, чтобы сравнять наши значения $ x $. Итак, системная пара,
$ 2 (2x — 5лет = 8) $
$ 4x + ky = 17 $
Становится,
$ 4x — 10 лет = 16) 9000 $ 3
–
$ 4x + ky = 17 $
———————-
$ -10лет — ky = -1 $
Чтобы НЕТ решения, наши два значения $ y $ должны уравновеситься до нуля.Итак, давайте установим наши два значения $ y $ равными друг другу:
$ -10y — ky = 0 $
$ -ки = 10лет $
$ k = -10 $
Наше значение $ k $ должно быть -10, чтобы наша система уравнений не имела решения.
Наш окончательный ответ — A , -10.
[Примечание: не попадайтесь на удочку ответа +10! Вы все еще вычитаете свою систему уравнений, поэтому внимательно следите за своими отрицаниями.]
Кроме того, не беспокойтесь об этом, если вас расстраивает или сбивает с толку попытка решить, какой из трех методов решения «лучше всего» подходит для конкретной проблемы! Вы почти всегда сможете решить свои задачи по системе уравнений, независимо от того, какой метод вы выберете.
Например, вы могли бы также выбрать график этого вопроса. Если бы вы это сделали, вам сначала нужно было бы преобразовать каждое уравнение в форму пересечения наклона:
$ 2x — 5лет = 8 $
$ 4x + ky = 17 $
$ 2x — 5лет = 8 $
$ -5y = -2x + 8 $
$ y = 2/5 (x) + 8 $
и
$ 4x + ky = 17 $
$ ky = -4x + 17 $
$ y = {-4 / k} (x) + 17 $
Теперь мы знаем, что система уравнений не будет иметь решения только тогда, когда каждая переменная уравновесится до нуля, поэтому давайте приравняем наши две переменные $ x $, чтобы найти $ k $.
$ 2/5 (x) = {-4 / k} (x)
долларов США$ 2/5 = {-4} / тыс. $
{2k} долл. США / 5 = -4
долл. США$ 2k = -20 $
$ k = -10 $
Опять же, наше значение $ k $ равно -10.
Наш окончательный ответ — A , -10.
Как видите, никогда не существует «лучшего» метода решения вопроса с системой уравнений, только метод решения, который вам больше всего нравится.
Все дороги ведут в Рим, поэтому не беспокойтесь, пытаясь найти «правильный» метод решения проблем вашей системы.
Типичные вопросы по системам уравнений
Большинство вопросов о системе уравнений в SAT сообщают вам, что это система уравнений, за счет явного использования слов «системы уравнений» в самом вопросе.
(мы рассмотрим, как решить этот вопрос позже в руководстве)
Другие задачи просто представят вам несколько уравнений с общими переменными и попросят вас найти значение одной из переменных или даже комбинацию переменных (например, значение $ x + y $ или $ x — y $).
(мы рассмотрим, как решить этот вопрос позже в руководстве)
И, наконец, последний тип вопроса о системе уравнений попросит вас найти числовое значение переменной, для которой НЕТ решения, как в предыдущем примере.
Готовы выйти за рамки простого чтения о SAT? Тогда вам понравится бесплатная пятидневная пробная версия для нашей программы SAT Complete Prep . Разработанная и написанная экспертами PrepScholar SAT , наша программа SAT адаптируется к вашему уровню навыков по более чем 40 вспомогательным навыкам, чтобы вы могли сосредоточить свое обучение на том, что принесет вам наибольший прирост баллов.
Разработанная и написанная экспертами PrepScholar SAT , наша программа SAT адаптируется к вашему уровню навыков по более чем 40 вспомогательным навыкам, чтобы вы могли сосредоточить свое обучение на том, что принесет вам наибольший прирост баллов.
Нажмите на кнопку ниже, чтобы попробовать!
Стратегии решения вопросов по системам уравнений
Все вопросы по системам уравнений можно решить с помощью тех же методов, которые мы описали выше, но есть дополнительные стратегии, которые вы можете использовать для наиболее точного и целесообразного решения ваших вопросов.
# 1: Для начала найдите переменную, которая уже является наиболее изолированной
Конечная цель — найти значения всех переменных, но мы можем сделать это, только найдя для начала одну переменную.Самый простой способ решить эту одну переменную — выделить (или исключить) переменную, которая имеет наименьшее количество коэффициентов или, по-видимому, является наиболее изолированной.
Например,
$ 5x — 3 года = -13 $
$ 2x + y = 19 $
Если мы используем подстановку, нам проще всего сначала выделить значение $ y $ во втором уравнении. Это уже самая изолированная переменная, поскольку у нее нет коэффициентов, и поэтому нам не придется иметь дело с дробями, как только мы заменим ее значение в первом уравнении.
Если, с другой стороны, мы использовали вычитание, все равно лучше нацелить и исключить наши значения $ y $. Почему? Потому что у нас есть $ 3y $ и $ y $, что означает, что нам нужно только умножить второе уравнение на 3, чтобы сопоставить наши значения $ y $. Если бы мы поставили цель и исключили наши значения $ x $, нам пришлось бы умножить обоих уравнения — первое на 2, а второе на 5, чтобы наши значения $ x $ совпадали.
Хотя вы всегда можете найти свои решения, независимо от того, какие переменные вы решите изолировать или исключить, всегда приятно сэкономить время, энергию и нервы (не говоря уже о том, чтобы избежать возможных ошибок), выбрав в первую очередь простые решения.
# 2: Практикуйте все три метода решения, чтобы определить, какой из них наиболее удобен для вас
Лучший способ решить, какая система решения уравнений подходит вам, , лучше всего — это попрактиковаться в нескольких задачах (хотя это поможет вашей гибкости, если вы научитесь использовать все доступные методы решения , даже если один или два подходит вам лучше, чем другие).
Когда вы проверяете себя по системным вопросам, постарайтесь решить каждый из них, используя более одного метода, чтобы увидеть, какой из них наиболее удобен для вас лично.
# 3: Используйте вычитание для вопросов, требующих поиска более чем одной переменной
В большинстве вопросов, касающихся систем уравнений с множественными переменными, вам будет предложено найти $ x + y $ или $ x — y $, которые почти всегда легче всего найти с помощью метода вычитания.
Также наиболее полезно использовать метод вычитания, когда у нас есть три или более переменных, особенно, когда это комбинация нескольких переменных И трех или более переменных.
Мы увидим этот вид проблемы в действии в следующем разделе.
Готовы взяться за решение системных проблем и проверить свои стратегии?
Проверьте свои знания
Теперь давайте проверим ваши знания системы уравнений на реальных математических вопросах SAT.
Ответы: 300, E, 12
Объяснение ответа:
1. Как мы обрисовали в общих чертах в нашем разделе стратегии, почти всегда легче всего найти значение нескольких переменных, используя метод вычитания (хотя, опять же, это не метод , а только метод ).
Мы, , несколько ограничены, так как у нас есть три переменные и только два уравнения. Почему это важно? Что ж, мы можем найти индивидуальные значения для каждой переменной, если у нас есть то же количество уравнений, что и у нас есть переменные, но в данном случае это не так. Это означает, что нам нужно использовать решение, которое даст нам $ x + y $, поскольку мы не можем найти значение $ x $ или $ y $ в одиночку.
Итак, воспользуемся вычитанием.
Для этого мы должны вычесть аналогичные переменные, и, к счастью для нас, оба уравнения имеют одно значение $ x + y $.Это означает, что мы можем изолировать нашу переменную $ z $.
$ x + y + 3z = 600 $
$ x + y + z = 400 $
Итак, давайте вычтем их.
$ x + y + 3z = 600 $
–
$ x + y + z = 400 $
————————-
$ 2z = 200 $
$ z = 100 $
Теперь, когда у нас есть значение $ z $, мы можем заменить его в любом из уравнений, чтобы найти значение $ x + y $.
Поскольку всегда проще всего использовать наиболее изолированную переменную (меньше математики для нас!), Позвольте нам подставить наше второе уравнение для нашего значения $ z $.
$ x + y + z = 400 $
$ x + y + 100 = 400 $
$ x + y = 300 $
Наш окончательный ответ для значения $ x + y $ — 300.
Обратите внимание, однако, что если вы предпочитаете использовать замену, вы определенно можете это сделать.
Поскольку мы пытаемся найти $ x + y $, давайте выделим его как желаемую переменную в одном из наших уравнений.
$ x + y + 3z = 600 $
$ x + y + z = 400 $
Давайте воспользуемся нашим первым уравнением.
$ x + y + 3z = 600 $
$ x + y = 600 — 3z $
А теперь мы можем подставить наше значение $ x + y $ во второе уравнение.
$ x + y + z = 400 $
$ (600 — 3z) + z = 400 $
600 $ — 2z = 400 9000 $ 3
$ -2z = -200 $
$ z = 100 $
Теперь, когда мы нашли наше значение для $ z $, мы можем подставить его в любое уравнение, чтобы найти числовое значение для нашего $ x + y $.
Воспользуемся для этого вторым уравнением.Почему второе? Потому что каждое значение уже является наиболее изолированным и с ним легче всего работать, но каждый вопрос будет работать в любом случае.
$ x + y + z = 400 $
$ x + y + 100 = 400 $
$ x + y = 300 $
И снова наш окончательный ответ: $ x + y = 300 $
Как видите, вам подойдет любой метод — все зависит от того, как вы любите работать.
2. Опять же, хотя и не способ решения нашей проблемы , только , проще всего использовать вычитание, когда у нас есть три или более переменных в наших уравнениях или мы пытаемся найти комбинацию переменных (в данном случае значение $ y + z $).В данном случае у нас есть и то, и другое, поэтому давайте воспользуемся вычитанием.
$ 3x + 2y + 2z = 19 $
$ 3x + y + z = 14 $
Наши значения $ x $ идентичны, поэтому давайте просто вычтем второе уравнение из первого.
$ 3x + 2y + 2z = 19 $
–
$ 3x + y + z = 14 $
—————————
$ y + z = 5 $
Наш окончательный ответ: E , $ y + z = 5 $
.3. В этом случае давайте воспользуемся методом подстановки, чтобы выделить одно из наших значений и вставить его в одно из других уравнений нашей системы.
Уравнения, которые нам даны:
$ x = 3v
$$ v = 4t
долларов США$ x =
pt $ $ v $ уже изолирован, поэтому давайте вернем его в наше первое уравнение.
$ v = 4t
долларов США$ x = 3v
$$ x = 3 (4т) 9000 $ 3
$ х = 12т $
Теперь нам также сказали, что $ x = pt $, поэтому мы можем приравнять эти два выражения.
$ х = 12т $
$ x =
pt $$ 12t =
pt $Поскольку 12 и $ p $ действуют как коэффициенты (числа перед переменной) для $ t $, мы можем видеть, что они равны.
Это означает, что $ p = 12 $
Наш окончательный ответ — 12.
Вы сделали это! Воздушные шары и конфетти для вас!
На вынос
Как видите, системы уравнений — одни из самых универсальных проблем, когда дело доходит до методов их решения (хотя сами проблемы не так уж и разнообразны). Хотя вы можете решить многие задачи на тесте SAT разными способами, большинство из них не так гибко, поэтому будьте уверены, что у вас есть много вариантов, как действовать в вопросах по системе уравнений.
После того, как вы попрактикуетесь и познакомитесь с этими типами вопросов, вы найдете для себя лучший метод — ваши сильные стороны и время — для прохождения теста. И довольно скоро вы сможете задавать вопросы по системам уравнений разными способами, с завязанными глазами и руками за спиной (хотя, честно говоря, никто не знает, зачем вам это нужно).
И довольно скоро вы сможете задавать вопросы по системам уравнений разными способами, с завязанными глазами и руками за спиной (хотя, честно говоря, никто не знает, зачем вам это нужно).
Что дальше?
Вы говорите, что системы — это совсем несложно? Вы говорите, что готовы к математическим задачам? Что ж, вам повезло! У нас больше руководств по математике, чем вы можете представить, и все они охватывают важные аспекты математической секции SAT.Линии и углы, многоугольники, целые числа, соотношения … любая тема, которую вам нужно освежить, находится у вас под рукой, поэтому максимально используйте свое время и энергию и нацельтесь на любую из ваших известных проблемных областей до дня теста.
Хотите знать самые ценные стратегии для решения математических задач SAT? Ознакомьтесь с нашими руководствами по добавлению ответов и добавлению чисел, которые помогут уточнить подавляющее большинство ваших вопросов по SAT математике.
Хотите получить наивысший балл? Не ищите ничего, кроме нашего руководства по получению отличных 800 баллов по математике SAT, написанного отличником.
Хотите улучшить свой SAT на 160 баллов?
Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой SAT на 160 или более баллов.
Наша программа полностью онлайн, и она адаптирует то, что вы изучаете, к вашим сильным и слабым сторонам. Если вам понравилось это руководство по математической стратегии, вам понравится наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по индивидуальным навыкам, чтобы вы могли учиться наиболее эффективно.Мы также дадим вам пошаговую программу, которой нужно следовать, чтобы вы никогда не запутались, что изучать дальше.
Воспользуйтесь нашей 5-дневной бесплатной пробной версией:
15 Системы уравнений Действия для вашего класса
Если бы система уравнений была человеком, он, вероятно, был бы моим заклятым врагом. Я изо всех сил пытался найти способы, чтобы студенты понимали, что представляет собой система уравнений, а затем чтобы они решали, используя разные методы.В первый год обучения этому я помню, как просто пытался научить своих учеников из лаборатории математики одному способу, чтобы они «пережили» конец модульного теста. Блин, как бы мне хотелось вернуть этих студентов и получить второй шанс научить их системам уравнений. Теперь у меня не только есть больше трюков для обучения студентов решению систем уравнений, я также нашел так много забавных заданий по системам уравнений, которые помогают студентам по-настоящему понять, как решать с помощью различных стратегий. Итак, ознакомьтесь с этими 15 упражнениями по системам уравнений, которые помогут студентам понять и попрактиковаться в поиске решения двух линейных уравнений.
Я изо всех сил пытался найти способы, чтобы студенты понимали, что представляет собой система уравнений, а затем чтобы они решали, используя разные методы.В первый год обучения этому я помню, как просто пытался научить своих учеников из лаборатории математики одному способу, чтобы они «пережили» конец модульного теста. Блин, как бы мне хотелось вернуть этих студентов и получить второй шанс научить их системам уравнений. Теперь у меня не только есть больше трюков для обучения студентов решению систем уравнений, я также нашел так много забавных заданий по системам уравнений, которые помогают студентам по-настоящему понять, как решать с помощью различных стратегий. Итак, ознакомьтесь с этими 15 упражнениями по системам уравнений, которые помогут студентам понять и попрактиковаться в поиске решения двух линейных уравнений.
Я считаю, что студентам действительно важно понимать, что они делают, решая систему уравнений. Им нужно не просто совершать движения, но и уметь по-разному видеть систему уравнений. В этом посте я составил список заданий, которые помогут вашим ученикам попрактиковаться в решении систем уравнений различными методами. Эти действия сосредоточены на решении систем уравнений путем замены или исключения .Идеи для действий по решению систем уравнений с построением графиков см. В этом посте.
В этом посте я составил список заданий, которые помогут вашим ученикам попрактиковаться в решении систем уравнений различными методами. Эти действия сосредоточены на решении систем уравнений путем замены или исключения .Идеи для действий по решению систем уравнений с построением графиков см. В этом посте.
Список
Лабиринт системы уравнений
Обзорная игра для всего класса
Поместите его в форму перехвата склона Халява
Раскраска
Карты задач
Думайте, выбирайте, переворачивайте, проверяйте
Загадочные сундуки
Oreo Activity
Быстрая проверка
Alien Search and Shade
Проблемы с изображением
Задания
Манга High Online Practice-Elimination
Онлайн-практика Game-Замена
Трехступенчатая математика на входе и выходе Бургер и другие задачи с тремя действиями
Погрузимся в
В этом посте мы рассмотрим некоторые упражнения и то, как они могут работать в вашем классе. В системах уравнений много движущихся частей, поэтому у нас есть много дел, на которые стоит обратить внимание. Некоторые из них будут работать, чтобы представить тему, а другие лучше подходят для практики. Помните, что вы можете использовать любое из этих упражнений, чтобы просмотреть системы уравнений позже в этом году.
В системах уравнений много движущихся частей, поэтому у нас есть много дел, на которые стоит обратить внимание. Некоторые из них будут работать, чтобы представить тему, а другие лучше подходят для практики. Помните, что вы можете использовать любое из этих упражнений, чтобы просмотреть системы уравнений позже в этом году.
— основной продукт в моем классе, и мы делаем их почти каждый день. Каждый раз, когда мы делаем перерыв на несколько дней или пару недель в лабиринтах, ученики испытывают такое облегчение, когда мы снова начинаем их делать. Они уверены, что делают лабиринты, потому что они не такие устрашающие.
В этом наборе из 3 лабиринтов учащиеся решают системы уравнений различными способами. В нем есть один лабиринт для замены, один для исключения и один смешанный. Эти лабиринты занимают немного больше времени, чем некоторые другие лабиринты, потому что на решение проблем уходит больше времени. Поэтому, планируя использовать эти лабиринты, имейте в виду, что они займут много времени.
В дополнение к этим лабиринтам, есть набор из 3 лабиринтов, который фокусируется только на решении систем уравнений методом исключения, и еще один набор из 3 лабиринтов, который фокусируется на решении систем уравнений путем подстановки.
Хотите еще больше бесплатных эксклюзивных лабиринтов? Когда вы присоединитесь к клубу «Лабиринт месяца», вы получите бесплатный лабиринт по математическим концепциям в средней школе, который будет отправляться вам на почту каждый месяц.
Да! Зарегистрируйся в клубе «Лабиринт месяца»!
Не могу дождаться встречи с вами там!
Мне нравится проверять юнит-тесты, играя в игры с обзором всего класса. Одна из моих любимых игр — Knockout. Вы воспроизводите его на проекторе, и он работает как со Smartboard, так и без него. Студенты выбирают персонажа на доске, и появляется вопрос.Моя любимая особенность этой игры — это то, что все ученики отвечают на все вопросы. Иногда мне кажется, что, когда вы играете в игру с обзором, некоторые ученики соскакивают с крючка, но в этой игре этого не происходит. Чтобы узнать больше о нокауте, прочтите этот пост.
Чтобы узнать больше о нокауте, прочтите этот пост.
В этой игре на выбывание по системе уравнений есть различные типы вопросов, в том числе просьба к учащимся преобразовать уравнение в форму пересечения наклона и решить, используя замену, исключение и построение графиков. Студентам нравится эта игра, и они действительно заканчивают свою работу, играя в нее.
Похоже, моим ученикам нужно много попрактиковаться в приведении уравнений в форму пересечения наклона. Я чувствую, что мы практикуем этот навык круглый год, и каждый раз, когда мы это делаем, мы получаем все больше и больше от них. Это бесплатная страница для студентов, чтобы просто попрактиковаться в изменении уравнения на форму пересечения уклона. Это хороший способ попрактиковаться в корректировке линейного уравнения в форме пересечения наклона при решении с заменой. Если он находится в форме пересечения наклона, то решить его будет очень легко.
Раскраски увлекают учащихся и дают им передышку. В этой системе уравнений раскраска фактическая раскраска учеников минимальна. Достаточно просто дать им перерыв, не снимая на картинке раскраски всего учебного периода. Выполняя это задание, учащиеся отрабатывают решение с использованием замены или исключения. Я считаю, что с этой темой студентам нужно много практики, и решение каждой задачи требует времени. Когда дело доходит до уравнений, важно предлагать учащимся различные типы задач.Им недостаточно понимать концепцию, они также должны уметь решать новые ситуации. Этот набор задач даст им изрядное количество повторений.
В этой системе уравнений раскраска фактическая раскраска учеников минимальна. Достаточно просто дать им перерыв, не снимая на картинке раскраски всего учебного периода. Выполняя это задание, учащиеся отрабатывают решение с использованием замены или исключения. Я считаю, что с этой темой студентам нужно много практики, и решение каждой задачи требует времени. Когда дело доходит до уравнений, важно предлагать учащимся различные типы задач.Им недостаточно понимать концепцию, они также должны уметь решать новые ситуации. Этот набор задач даст им изрядное количество повторений.
Этот набор карточек задач системы уравнений содержит графики, подстановки и количество решений задач. Вопросы несложные. Это дает студентам дополнительную практику для оттачивания вновь обретенных навыков. Карточки маленькие, и ученики могут заполнять их с партнером или в небольшой группе.
Мне нравится использовать этот набор карточек с заданиями в целевой игре.Вы можете узнать больше о целевой игре здесь. По сути, это игра, в которой учащиеся решают задачи и могут бросить мяч в цель. Это идеальное сочетание работы и развлечений. Или ознакомьтесь с другими идеями о том, как использовать карточки с заданиями в классе средней школы.
По сути, это игра, в которой учащиеся решают задачи и могут бросить мяч в цель. Это идеальное сочетание работы и развлечений. Или ознакомьтесь с другими идеями о том, как использовать карточки с заданиями в классе средней школы.
Это упражнение с самопроверкой отлично подходит в качестве центра или для быстрых финишеров. Студентам предлагается система уравнений и решение. Они должны оценить, верное решение или нет. Если это правильно, они отмечают это скрепкой.Закончив работу над проблемой, учащиеся могут перевернуть страницу, чтобы убедиться, что они были правы, и мгновенно дать им обратную связь по поводу своего обучения.
Эти проблемы могут быть решены заменой или удалением. Если вы дадите учащимся графики, они также смогут попрактиковаться в построении графиков. Это полезное практическое задание, которое помогает учащимся найти несколько правильных вариантов ответа, а не традиционный формат множественного выбора. Вашим ученикам понравится сложность этого задания.
Ким Хью в «Математических сказках из источника» использует загадочные коробки, чтобы знакомить свой класс с системами уравнений. Это состоит в том, чтобы дать студентам коробку с задачей и монетами внутри. Учащиеся работают в группах, чтобы попытаться разгадать «загадку». Проблема не является невыполнимой, но ученики должны глубоко копнуть, чтобы использовать то, что они знают, для ее решения. Мне нравятся такие виды открытий, потому что они дают детям возможность продемонстрировать свои навыки установки на рост.Хотя я еще не использовал этот подход, это интересный способ начать эту единицу обучения.
На днях один студент спросил, когда системы уравнений будут уместны в их жизни. — легкомысленно спросила она, как будто ничто из того, что мы когда-либо изучаем по математике, не имеет значения в ее жизни. Что ж, я продолжил говорить ей, что системы уравнений были одним из самых важных математических понятий, о которых она когда-либо узнавала.
Несколько дней спустя я напомнил ей об этом разговоре, когда мы использовали Oreos для исследования решения систем уравнений.Это упражнение от Math Made Possible помогает учащимся определить вес одной пластины на основе другой предоставленной информации. Это отличный пример того, как люди выясняют или решают различные проблемы с помощью систем уравнений. В качестве бонуса я принес настоящие Орео. Каждый раз, когда вы можете связать задачи, которые решают ученики, со съедобными угощениями, ученики внезапно начинают считать математику очень актуальной!
Как учителя, мы всегда ищем быстрые способы проверить, понимают ли учащиеся.Что ж, эта быстрая проверка от Scaffolded Math and Science работает отлично. Это пустой шаблон, в который можно добавить любую систему уравнений. Это делает его удобным, потому что вы можете добавить именно тот тип задачи, который вам нужен. У него две проблемы на странице, и я распечатываю эти две на странице, поэтому у меня четыре проблемы на странице. У меня ученики решают по две задачи. Конечно, это зависит от того, сколько у нас времени. Часто я не вижу, чтобы в конце урока у каждого ребенка было достаточно времени, чтобы быстро выполнить все задачи.
У меня ученики решают по две задачи. Конечно, это зависит от того, сколько у нас времени. Часто я не вижу, чтобы в конце урока у каждого ребенка было достаточно времени, чтобы быстро выполнить все задачи.
Это задание «Поиск пришельцев и тени» от Hoppe Ninja Math отлично подходит для выполнения домашних заданий. В нем 9 задач, и ученики решают задачу и одинаково заштриховывают все квадраты с этим ответом. В конце концов, они раскроют картинку со всеми затенениями. Они также получат много практики в увлекательной игровой форме.
В этом задании нет ключа для ответа, поэтому вам придется заполнить его самостоятельно, если вы хотите получить ключ для ответа. Когда я делаю это, я обычно бросаю вызов своим классам на первом уроке и смотрю, сможет ли кто-нибудь из них обыграть меня и при этом быть точным.Это добавляет немного дружеского соревнования.
Mash-up Math предлагает множество задач с изображениями, которые визуально представляют системы уравнений. Я люблю использовать их как разминку после лабиринта или как задачу быстрого финишера. Некоторые из них легче, чем другие, и они также дают детям отличную практику с мысленной математикой. Их применение безгранично. Сначала некоторые из моих учеников хотели бросить довольно быстро, но после того, как они сделали несколько, они, похоже, действительно получили удовольствие и приняли вызов.К тому же им нравятся картинки в этих загадках.
Некоторые из них легче, чем другие, и они также дают детям отличную практику с мысленной математикой. Их применение безгранично. Сначала некоторые из моих учеников хотели бросить довольно быстро, но после того, как они сделали несколько, они, похоже, действительно получили удовольствие и приняли вызов.К тому же им нравятся картинки в этих загадках.
Иногда я просто хочу, чтобы мои ученики много практиковались. Я обнаружил, что когда я даю им лист и говорю, идите, они могут быть ошеломлены. Вот почему я создал карточную игру «Выбери карточную игру». Я беру лист с сайта вроде того, что здесь, и мои дети достают свои доски. Затем мы начинаем играть в карточную игру по выбору. Это игра в стиле Price is Right, которую я разбираю здесь шаг за шагом. Обычно после каждого вопроса ученики выбирают карту из моей огромной колоды карт, и та, у которой самая высокая карта, получает наибольшее количество очков.Детям это нравится, и это помогает им мотивировать, когда они решают практические задачи.
Эта ссылка приведет вас к набору из 12 бесплатных рабочих листов, которые включают построение графиков, замену и исключение. Кроме того, проблемы переходят от простых к более сложным. У него даже есть системы, в которых у вас есть более двух уравнений для дополнительной задачи.
Когда ученики из Manga High играют в эту игру, они попрактиковались в решении систем уравнений с исключением. Во время игры учащиеся получают бесплатные подсказки и бесплатное решение.Кроме того, вопросы задают нечто большее, чем просто решение проблемы. Студенты также должны ответить на вопросы о том, что происходит в системе уравнений. Эта игра веселая и увлекательная. Он отлично подходит для быстрых финишеров. Им нравится, что они делают то, чего не делают другие ученики. В конце концов, вы можете попросить учащихся сказать вам свои баллы, чтобы они несли ответственность.
Эта игра с системами уравнений от Math Games дает студентам возможность попрактиковаться с заменами. Во время игры учащиеся сразу же узнают, как у них дела. На выполнение этих задач требуется время, и каждый может выполнять их в своем собственном темпе. Когда ученики заканчивают вопрос, он говорит им, правы они или нет, но не говорит им, почему их ответ неправильный. В игре сказано, что это решение с заменой, но я считаю, что многие вопросы лучше подходят для исключения. Это означает, что учащиеся могут взглянуть на каждую систему уравнений и решить, какой метод лучше подходит для решения задачи.
Во время игры учащиеся сразу же узнают, как у них дела. На выполнение этих задач требуется время, и каждый может выполнять их в своем собственном темпе. Когда ученики заканчивают вопрос, он говорит им, правы они или нет, но не говорит им, почему их ответ неправильный. В игре сказано, что это решение с заменой, но я считаю, что многие вопросы лучше подходят для исключения. Это означает, что учащиеся могут взглянуть на каждую систему уравнений и решить, какой метод лучше подходит для решения задачи.
Как только учащиеся приобретут навыки решения систем уравнений, они смогут применить это на практике. Вы можете найти множество проблем из реальной жизни по этой теме. Одна, что мне действительно нравится, — это задача из трех актов, связанная с рестораном In-N-Out. Это очень популярное место, где можно поесть среди учеников младших классов в нашем районе.
Здесь вы можете найти больше задач 3 Act, чтобы студенты применяли свои новые навыки для решения реальных задач, на случай, если гамбургеры вам не по вкусу. Вы можете выбрать один о билетах в Диснейленд или другой о спуске воды в туалете. Я вижу привлекательность для восьмиклассников по обеим этим темам. Замечательно наблюдать, как студенты работают и борются с такими проблемами. У них появляется шанс не просто найти быстрый и легкий ответ. Это укрепляет их мышцы настойчивости, и в то же время они получают возможность увидеть математику в реальном мире.
Вы можете выбрать один о билетах в Диснейленд или другой о спуске воды в туалете. Я вижу привлекательность для восьмиклассников по обеим этим темам. Замечательно наблюдать, как студенты работают и борются с такими проблемами. У них появляется шанс не просто найти быстрый и легкий ответ. Это укрепляет их мышцы настойчивости, и в то же время они получают возможность увидеть математику в реальном мире.
Попробуй одно
Система уравнений может казаться похожей на гамбургер размером 100 x 100 в In-N-Out, потому что у него так много слоев.Не думайте, что вы должны все делать. Просто попробуйте что-то новое и посмотрите, как ваши ученики на это отреагируют. Вы можете увеличивать вовлеченность по одному занятию за раз и, в свою очередь, увеличивать удержание учащимися концепции. Удачи тебе и не забывай получать удовольствие от обучения математике.
Большое спасибо за чтение! До скорого.
Связанные5.1 — Решение систем уравнений
5. 1 — Решение систем уравнений
1 — Решение систем уравненийДо этого момента мы имели дело только с одним уравнением за раз.Теперь будем работать с более чем переменной и более чем одним уравнением. Это так называемые системы уравнений. При ответе на систему уравнений вам нужно указать значение для каждой переменной.
Решение систем линейных уравнений
Когда мы закончим рассмотрение двух глав, посвященных решению систем уравнений, их будет шесть. способы, которые мы можем использовать для решения системы линейных уравнений
- Графически
- Постройте оба уравнения и найдите точку пересечения.
- Неточно вручную.
- Полезно при использовании техники.
- Больше подходит для нелинейных систем.
- Сначала необходимо решить уравнение для y.
- Замена
- Решите одно уравнение для одной переменной, а затем подставьте его в другое уравнение.
- Лучшая алгебраическая техника для нелинейных систем.

- Хорошо работает, когда переменная может быть легко решена, имеет коэффициент, равный единице.
- Работает лучше, когда дроби и корни не используются.
- Добавление / исключение
- Умножьте одно или несколько уравнений на константу, а затем сложите два уравнения. чтобы исключить одну переменную.
- Хорошо подходит для линейной системы, когда нет переменной с коэффициентом, равным единице.
- Хорошо работает для систем уравнений 2×2 (2 уравнения с 2 переменными), но становится утомительно и трудоемко для больших систем.
- Исключение Гаусса / Исключение Гаусса Джордана
- Использует элементарные операции для создания эквивалентных уравнений.
- Работает для неквадратных систем линейных уравнений.
- Построен на концепции исключения сложения, но вместо получения новых уравнений старое уравнение заменяется эквивалентным уравнением.
- При применении с матрицами из главы 6, вероятно, самый быстрый способ решить большую
система линейных уравнений от руки.
 Безусловно, любимый метод инструктора.
Безусловно, любимый метод инструктора. - Правило Крамера
- Использует определители матрицы, чтобы найти решение.
- Работает только для квадратных систем линейных уравнений, в которых определитель матрица коэффициентов не равна нулю.
- Подходит для компьютера или калькулятора, где есть определяющая программа.
- Медленно вручную.
- Медленно на калькуляторе без программы, так как каждый определитель должен быть введен вручную.
- Может использоваться, когда вам нужно найти только одну из переменных.
- Матричная алгебра / Матрица инверсии
- Использует обратную матрицу для поиска решения.
- Работает только для квадратных систем линейных уравнений, в которых определитель матрица коэффициентов не равна нулю.
- Подходит для компьютера или калькулятора, где есть функция, обратная матрице.
- Медленно вручную.
- Быстрые действия на калькуляторе.

- Вернет десятичные ответы, но вы можете использовать дробную клавишу, чтобы преобразовать их в целые числа.
Замена
Метод подстановки работает как с нелинейными, так и с линейными уравнениями.
- Решите одно из уравнений относительно одной из переменных.
- Подставьте это выражение вместо переменной в другом уравнении.
- Решите уравнение для оставшейся переменной
- Выполните обратную замену значения переменной, чтобы найти другую переменную.
- Чек
Процесс обратной подстановки включает в себя получение значения переменной, найденной на шаге 3, и подставив его обратно в выражение, полученное на шаге 1 (или исходную задачу), чтобы найти оставшаяся переменная.
Важно, чтобы при решении системы уравнений были указаны обе переменные. Общий
ошибка студентов состоит в том, что они находят одну переменную и останавливаются на ней. Вы должны указать ценность для всех
переменные.
Было бы неплохо проверить свой ответ в обоих уравнениях, но, вероятно, достаточно, чтобы проверить в уравнении вы не изолировали переменную на первом этапе. То есть, если вы решили для y в первое уравнение на шаге 1, используйте второе уравнение, чтобы проверить ответ.
Графический подход
Графический подход хорошо работает с графическим калькулятором, но не точен вручную (действительно эти точки пересекаются на 1/6 или 1/7?), если только график не попадает точно на линии сетки.
- Решите каждое уравнение относительно y. Это может включать плюс и минус, если есть член y 2 . Если ты не построение графиков с помощью калькулятора или компьютера, вы можете пропустить этот шаг.
- Изобразите каждое уравнение.
- Найдите точки пересечения.
- Проверить!
Важно проверить свои ответы, чтобы убедиться, что вы прочитали точку пересечения правильно.
Иногда калькулятор не может указать точку пересечения с помощью команды пересечения.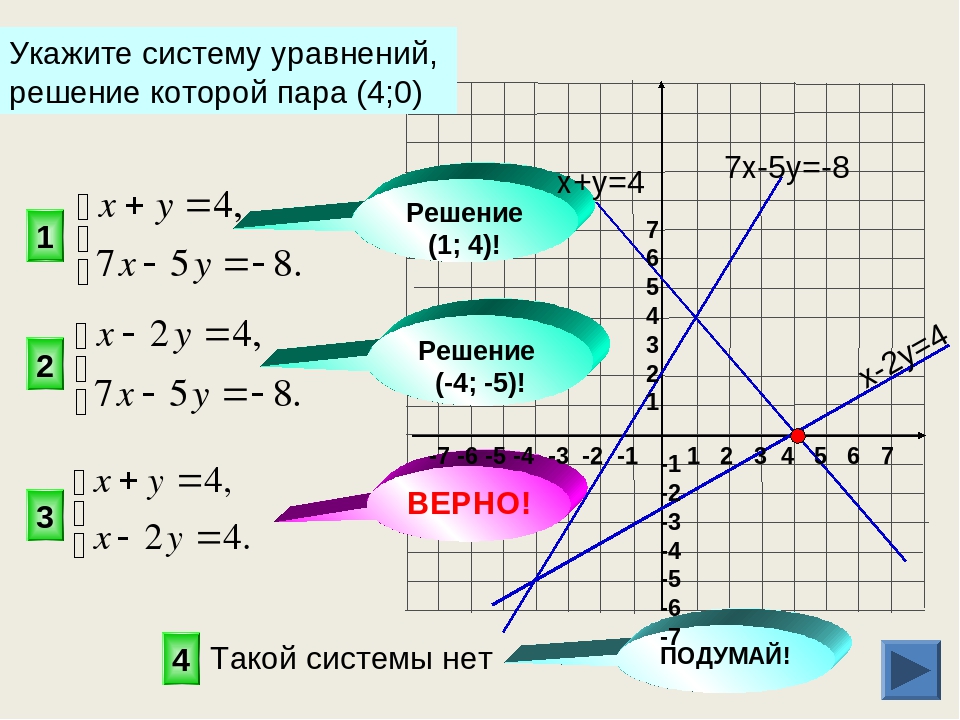




 Повторяют вместе с разными людьми, и поэтому идет объективное повторение материала. Кроме того они сами говорят и слушают одноклассника.
Повторяют вместе с разными людьми, и поэтому идет объективное повторение материала. Кроме того они сами говорят и слушают одноклассника.




 Г. Мордкович, П.В. Семенов. – Алгебра. 9 класс. Учебник и задачник для учащихся общеобразоватльных учреждний. – 16-е изд., доп. – М.: Мнемозина, 2013.
Г. Мордкович, П.В. Семенов. – Алгебра. 9 класс. Учебник и задачник для учащихся общеобразоватльных учреждний. – 16-е изд., доп. – М.: Мнемозина, 2013.









 Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
 После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
 После этого жмем на кнопку «OK».
После этого жмем на кнопку «OK».
 Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
 Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива: Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения. \ Begin {matrix} 1 & 0 & \ frac {44} { 15} \\ 0 & 1 & \ frac {-19} {15} \\ 0 & 0 & -8 \ end {matrix} \ right | & \ begin {matrix} \ frac {-43} {15} \\ \ frac {113 } {15} \\ 16 \ end {matrix} \ end {bmatrix} \)
\ Begin {matrix} 1 & 0 & \ frac {44} { 15} \\ 0 & 1 & \ frac {-19} {15} \\ 0 & 0 & -8 \ end {matrix} \ right | & \ begin {matrix} \ frac {-43} {15} \\ \ frac {113 } {15} \\ 16 \ end {matrix} \ end {bmatrix} \) 
 \\ \\ \ text {Очистите дроби, умножив второе уравнение на 4.} & \ left \ {\ begin {align} 3 x + 4 y & = 12 \ \ 4 \ left (\ frac {3} {4} x + y \ right) & = 4 (3) \ end {align} \ right. \\\\ \ text {Упростить.} & \ left \ {\ begin {array} {l} {3 x + 4 y = 12} \\ {3 x + 4 y = 12} \ end {array} \ right . \\\\ \ text {Чтобы исключить переменную, мы умножаем второе уравнение на -1.} & \ left \ {\ begin {array} {c} {3 x + 4 y = 12} \\ \ underline {- 3 x-4 y = -12} \ end {array} \ right.\\ & \ qquad \ qquad \ quad 0 = 0 \\ \ text {Упростить и добавить.} \ end {array} \)
\\ \\ \ text {Очистите дроби, умножив второе уравнение на 4.} & \ left \ {\ begin {align} 3 x + 4 y & = 12 \ \ 4 \ left (\ frac {3} {4} x + y \ right) & = 4 (3) \ end {align} \ right. \\\\ \ text {Упростить.} & \ left \ {\ begin {array} {l} {3 x + 4 y = 12} \\ {3 x + 4 y = 12} \ end {array} \ right . \\\\ \ text {Чтобы исключить переменную, мы умножаем второе уравнение на -1.} & \ left \ {\ begin {array} {c} {3 x + 4 y = 12} \\ \ underline {- 3 x-4 y = -12} \ end {array} \ right.\\ & \ qquad \ qquad \ quad 0 = 0 \\ \ text {Упростить и добавить.} \ end {array} \) } & \ Left \ {\ begin {align} {-6 x + 15 y = 10} \\ \ underline {6 x-15 y = -15} \ end {align} \ right.\\ & \ qquad \ qquad \ quad0 \ neq 5 \ end {array} \)
} & \ Left \ {\ begin {align} {-6 x + 15 y = 10} \\ \ underline {6 x-15 y = -15} \ end {align} \ right.\\ & \ qquad \ qquad \ quad0 \ neq 5 \ end {array} \) Добавить.} & \ Left \ {\ begin {array} {l} {n + m = 39} \\ \ underline {n-m = 9} \ end {array} \ right. \\ & \ quad 2n \ qquad = 48 \\ \\\ text {Решить для n.} & n = 24 \\ \\ \ text {Замените n = 24 одним из исходных} & n + m = 39 \\ \ text {уравнения и решите форму.} & 24 + m = 39 \\ & m = 15 \\ \ textbf {Шаг 6. Отметьте} \ text {ответ.} & \ text {Поскольку 24 + 15 = 39 и 24−15 = 9, ответы проверяются.} \\ \ textbf {Шаг 7. Ответ} \ text {вопрос.} & \ text {Числа 24 и 15.} \ end {array} \)
Добавить.} & \ Left \ {\ begin {array} {l} {n + m = 39} \\ \ underline {n-m = 9} \ end {array} \ right. \\ & \ quad 2n \ qquad = 48 \\ \\\ text {Решить для n.} & n = 24 \\ \\ \ text {Замените n = 24 одним из исходных} & n + m = 39 \\ \ text {уравнения и решите форму.} & 24 + m = 39 \\ & m = 15 \\ \ textbf {Шаг 6. Отметьте} \ text {ответ.} & \ text {Поскольку 24 + 15 = 39 и 24−15 = 9, ответы проверяются.} \\ \ textbf {Шаг 7. Ответ} \ text {вопрос.} & \ text {Числа 24 и 15.} \ end {array} \) \ )
\ )

 \)
\)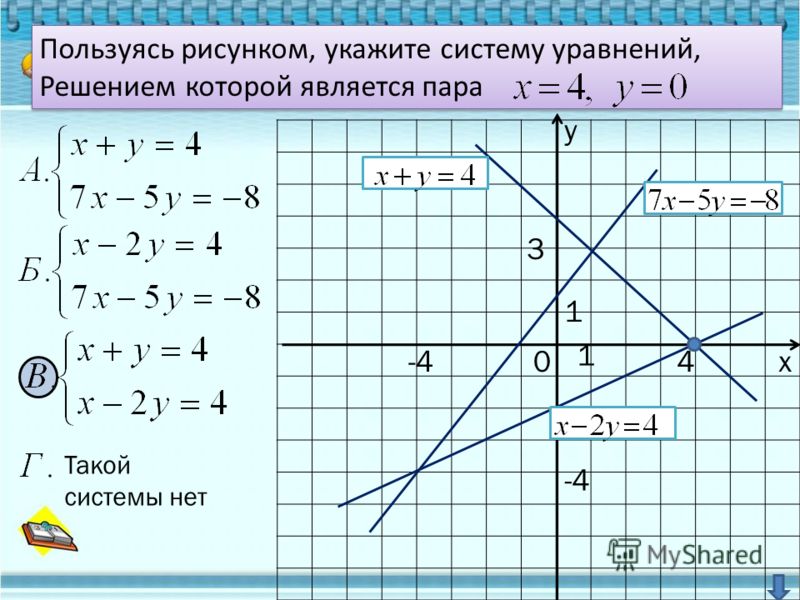 \)
\)
 Безусловно, любимый метод инструктора.
Безусловно, любимый метод инструктора.