«Методы решения систем уравнений». Факультатив по математике
При планировании внеклассной работы, ставлю перед собой цель: вызвать интерес учащихся к предмету. Факультативы способствуют развитию математического кругозора, творческих способностей учащегося, привитию навыков самостоятельной работы и тем самым повышению качества математической подготовки учащегося.
Данный факультатив провела в 9 классе после изучения темы, как повторительно-обобщающий, позволяющий не только обобщить и закрепить полученные знания. На это занятие приглашены 10 участников 7 класса, в котором я работаю (из них 2 содокладчика).
Тема: “Методы решения систем уравнений”.Тип урока – пресс-конференция.
Цели:
- поиск различных способов и методов решения систем уравнений, умение выступать перед аудиторией с подготовленными сообщениями.
- стимулирование творческого мышления нестандартными методами.
- обобщение и систематизация знаний учащихся по данной теме, приучать работе со справочной и дополнительной литературой.
- развитие математического мышления, взаимовыручки, взаимопомощи, умению вести культурную дискуссию, правильной математической речи.
- воспитание чувства ответственности.
Оборудование: плакаты, таблицы, схема, карточки — смотри Приложение 1
Председатель: учитель
Экспертная группа: учитель, родитель, ученик.
Повестка (план конференции):
- Сообщение 1. Из истории решения систем уравнения /Оглоблина О./ 9 класс
- Сообщение 2. Решение систем методом подстановки /Хохлов Д./ 9 класс
- Сообщение 3. Системы симметричных уравнений /Троянова К./ 9 класс
- Сообщение 4. Системы линейных уравнений с параметрами /Заблоцкий Н./ 7 класс
- Сообщение 5. Геометрические приемы решения систем уравнений /Кравец В./ 9 класс
- Сообщение 6. Метод Крамера или метод определителей /Трифонова Е./ 9 класс
Решение (Заключение)
Творческая работа – выпуск стенгазеты “Вести с конференции”
1 сообщение
Из истории решения систем уравнений.
Издавна применялось исключение неизвестных из линейных уравнений. В XVII — XVIII в.в. приемы исключения разрабатывали Ферма, Ньютон, Лейбниц, Эйлер, Безу, Лагранж (портреты находятся на стенде в кабинете).
В современной записи система двух линейных уравнений с двумя неизвестными имеет вид:
Решение этой системы выражается формулами
Благодаря методу координат, созданному в XVII в. Ферма и Декартом, стало возможным решать системы уравнений графически.
В древневавилонских текстах, написанных в III – II тысячелетиях до н.э., содержится немало задач, решаемых с помощью составления систем уравнений, в которые входят и уравнения второй степени. Например, Задача № 20. Площади двух своих квадратов я сложил: 25. Сторона второго квадрата равна стороны первого и еще 5. Соответствующая система уравнений в современной записи имеет вид:
Для решения системы (1) вавилонский автор возводит во втором уравнении у в квадрат, получаем у2 = х2 + х + 25,
подставив, получаем 1х2 + 6 х = , решая уравнение, находим х, затем у.
Диофант, который не имел обозначений для многих неизвестных, прилагал немало усилий для выбора неизвестного таким образом, чтобы свести решение системы к решению одного уравнения.
Задача 21. “Найти два натуральных числа, зная, что их сумма = 20, а сумма их квадратов 208”.
Задачу так же решали составлением системы уравнений,
но решал Диофант, выбирая в качестве неизвестного половину разности искомых чисел, т.е.
Далее
x2 + y2 = (z + 10)2 + (10 – z)2 = 2z2 + 200, а по условию =208
2z2 + 200 = 208
z = ± 2 z = — 2- не уд. услов. задачи
поэтому, если z = 2 x = 12, а у = 8.
2 сообщение
Решение систем методом подстановки.
С системами уравнений мы познакомились в курсе алгебры 7-го класса, но это были системы специального вида – системы двух линейных уравнений с двумя переменными
Алгоритм, который был выработан в 7 классе, вполне пригоден для решения систем любых двух уравнений с двумя переменными х и у.
- Выразить у через х из одного уравнения системы.
- Подставить полученное выражение вместо у в другое уравнение системы.
- Решить полученное уравнение относительно х.
- Подставить поочередно каждый из найденных на 3 шаге корней уравнения вместо х в выражение у через х, полученное на первом шаге.
- Записать ответ в виде пар значений (х;у).
Покажу как работает этот метод при решении более сложных систем. /Кравец В./
х2 – ху – 2у2 = 0
решим полученное уравнение относительно х
Д = у2 — 4•1 (- 2у2) = 9у2 , = 3 | y |
3 сообщение
Решение систем симметрических уравнений.
1)
Существует универсальный метод решения: вводится подстановка
Преобразуем первое уравнение системы, прибавив к обеим частям ху
х2 + ху + ху + у2 = 4 + ху
х2 + 2ху + у2 = 4 + ху
( х + у)2 = 4 + ху
Получим систему
Применим универсальную подстановку
Рассмотрим решение еще одной системы
( х + у)5 = х5 + 5х4у + 10х3у2 + 10х2у3 + 5ху4 + у5 = ( х5 + у5) + 5ху (х3 + у3) + 10х2у2(х + у)
х3 + у3 = ( х + у)3 – 3ху ( х + у), используем формулу (2)
55 = 275 + 5z • 53 – 15z2 •5 + 10z2 + 5 / : 25
53 = 11 + 25z – 3z2 + 2z2, z2
Д = 169, z1 = 19 z2 = 6
4 докладчик
Системы линейных уравнений с параметром
Напомню на примерах три случая:
а) когда коэффициенты при х и у не пропорциональны
б) когда коэффициенты все пропорциональны
в) коэффициенты при х пропорциональны коэффициентам при у, но не пропорциональны свободным членам.
Эти знания необходимы при решении следующих заданий:
*Определите все значения параметра а, при которых система уравнений
Решение
5 сообщение
Геометрический прием решения систем уравнений
Решение
По теореме обратной теореме Пифагора, из уравнения х2 + у2 =32 , числа х и у являются катетами АBD ( D – прямой) с гипотенузой АВ = 3.
Рассматривая второе уравнение у2 + z2 = 16, построим BDC, где у и z – катеты, а ВС = 4 – гипотенуза.
Третье уравнение y2 = xz подсказывает, что число у есть среднее пропорциональное чисел х и z.
По теореме обратной теореме о пропорциональных отрезках АВС = 900
АС = ( х + z ) = = 5,
Тогда AB2 = AD • AC, 9 = х • 5, х =
BC2 = DC • AC, 16 = z • 5, z =
BD2 = y2 = x • z =·
BD = = y.
Такой прием дает потерю корней, легко убедиться,
что х = ± 9/5; у = ± 12/5; z = ± 16/5.
Для данной системы задания могут быть и другие.
Например, чему равно значение выражения
ху + уz ; х + у + z; х + у; х + z;
6 сообщение
Метод Крамера
Система вида
называется системой двух линейных уравнений с
двумя неизвестными, где а
Одним из основных методов решения данной системы является метод Крамера или метод определителей. По коэффициентам данной системы составляем три определителя: (главный), х – определитель неизвестного х; у – определитель неизвестного у.
* Решить систему
*Найдите все значения параметра b, при которых система имеет единственное решение
Творческая работа по карточкам взаимотренажера “Рисуем координатами”.
Решите системы и постройте фигуру по координатам.
Конференция закончилась. Я верю, что у вас появилось желание попробовать свои силы в решении систем. Возьмите задания и приступайте к творческой работе.
А теперь наступило время оформить следующий выпуск математический газеты “Вести с конференции”.
Список литературы
1. Г.И. Глейзер “История математики в школе”
2. И.Я. Депман “За страницами учебника алгебры”
3. М.Л. Галицкий А.М.Гольдман “Сборник задач по алгебре 8-9”
4. А.Г. Мордкович “Алгебра 9”. “Алгебра 7”
5. Ю.Н. Макарычев “Алгебра 9”. “Алгебра 7”
Приложение
urok.1sept.ru
Различные способы решения уравнений и систем линейных уравнений
Различные способы решения уравнений и систем линейных уравнений
Бедевко И.А. 11Муниципальное бюджетное общеобразовательное учреждение средняя школа №30
Караева Д.А. 11Муниципальное бюджетное общеобразовательное учреждение средняя школа №30
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Уже третий год я занимаюсь очень интересным делом – исследовательской работой. В этот раз я выбрала не менее познавательную тему, чем предыдущие. «Различные способы решения уравнений и систем линейных уравнений». В прошлом году у меня была похожая тема о нестандартных задачах, с которыми мы так часто встречаемся на олимпиадах и ,к сожалению, теряемся. Она дала мне большой опыт и много новых знаний. Такой же результат у меня и с новой работой этого года.
Я решила остановиться именно на уравнениях, потому что они занимают ведущее место в школьном курсе алгебры. На их изучение отводится времени больше, чем на любую другую тему. Сила теории уравнений в том, что она не только имеет теоритическое значение, но и служит целям, с которыми мы встречаемся на практике. Большинство задач о количественных отношениях сводится к решению различных видов уравнений. Изучая способы их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т.д.) Но конечно главное в изучении уравнений, как и в любых других темах, – это самостоятельная и очень усердная работа.
Главная цель – поиск наиболее оптимальных способов решения систем уравнений, которые помогают нам углубляться в тему, закреплять, расширять наши теоритические знания, но приступая к ней, понадобится немало общематематических представлений, понятий, умений.
История уравнений
В далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, еще не было ни монет, ни кошельков. Но были кучи, а также горшки, корзины, которые успешно заменяли тайники-хранилища, вмещающих неизвестное количество предметов. Они использовались даже в древних задачах: «Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37…», — поучал во II тысячелетии до новой эры египетский писец Ахмес. В математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы очень даже успешно справлялись с такими задачами. Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном источнике не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями: «Смотри!», «Делай так!», «Ты правильно нашел». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений. Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого трактата – «Китаб аль-джебер валь- мукабала» («Книга о восстановлении и противопоставлении») – со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
Сама алгебра как искусство решать уравнения зародилась очень давно в связи с потребностью практики, в результате поиска решениий однотипных задач. Самые ранние дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были известны приёмы решения линейных уравнений.
Под влиянием исследований молодого французского математика Э.Галуа (1811-1832) в дальнейшем развитии, особенно в двадцатом веке, алгебра все более определялась как наука об общих алгебраических операциях (действиях). Значение современной алгебры выходит далеко за приделы учения об уравнениях. Алгебра широко применяется в любом разделе математики, в естествознании и техники, при этом неразрывно связана с уравнениями.
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Оказывается, квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя совершенную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и например, полные квадратные уравнения. Они появились у вавилонян в связи с землемерной практикой.
Правило решения уравнений, изложено в вавилонских текстах и совпадает по существу с современным, однако не известно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без способов их решения.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
Зачатки алгебраического мышления находят и в египетских папирусах.
Например в папирусе Ахмеса (первый математик) есть специальный раздел «Вычисление кучи». Так же как и в Вавилоне под словом «куча» подразумевается неизвестная величина.
Квадратные уравнения у Аль-Хорезми.
В алгебраическом трактате Аль-Хорезми (учёного математика азиатского происхождения) дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корням», т. е. a= bx.
2) «Квадраты равны числу», т. е. a = c.
3) «Корни равны числу», т. е. ax = c.
4) «Квадраты и числа равны корням», т. е. a + c = bx.
5) «Квадраты и корни равны числу», т. е. a + bx = c.
6) «Корни и числа равны квадратам», т. е. bx + c = a.
Пример.
«Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения + 21 =10x).
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножь 5 само на себя, от произведения отними21, останется 4. Извлеки корень из 4, получишь 2. отними 2 от 5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат Аль-Хорезми является первой дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
СВОЙСТВА КОЭФФИЦИЕНТОВ КВАДРАТНОГО УРАВНЕНИЯ.
Если а+ b+c= 0, то =1, =.
Пример. Рассмотрим уравнение +4х – 5= 0.
а+b+c= 1+4+(-5)= 0, следовательно, =1, = =-5. Значит корнями этого уравнения являются 1 и –5.
Выполним проверку через дискриминант:
D= – 4ас= 16 – 4∙1∙(–5)= 36.
= = = – 5.
= = = 1.
Ответ: (-5;1)
Если b= а+c, то = –1, = .
Пример. Рассмотрим уравнение 2+8х +6 = 0.
а+c=2+6=8, значит = –1, == -3. Значит корнями этого уравнения являются –1 и –3. Проверим это с помощью нахождения дискриминанта:
D= – 4ас=64 – 4∙2∙6= 16.
= = = = –3.
= = = -1.
Ответ: (-3;-1)
СПОСОБ ПЕРЕБРОСКИ.
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат. Если а±b+c≠0, то используется прием переброски:
2 – 11х+5=0
– 11х+10= 0
Далее легко найти корни по теореме Виета:
+ = -p; = 10; =q
=10; =5
Но корни уравнения необходимо поделить на 2, тогда корни равны 5 и 0,5.
Ответ: 5; 0,5.
ЗАКОНОМЕРНОСТЬ КОЭФФИЦИЕНТОВ.
Иногда встречаются квадратные уравнения с большими коэффициентами. В этом случае полезно использовать их закономерность:
1) Если в уравнении a+ bx + c = 0 коэффициент b равен (+1), а коэффициент с численно равен коэффициенту а, т.е. a + (+1)∙ х+ а= 0, то его корни равны: = –а; = — – .
Пример. Рассмотрим уравнение 6 +37х +6 = 0.
37=+1, следовательно = -6; = — –.
Ответ: (-6; -)
2)Если в уравнении a – bx + c = 0 коэффициент b равен (+ 1),а коэффициент с численно равен коэффициенту а, т.е. a – (+1)∙ х+ а= 0, то его корни равны = а; = –.
Пример. Рассмотрим уравнение 15 –226х +15 = 0.
+1=226 и 15=15,значит = 15; = — –.
Ответ: (15; — )
Если в уравнении a+ bx + c = 0 коэффициент b равен ( – 1), а коэффициент с численно равен коэффициенту а, т.е. a – (-1)∙ х- а= 0, то его корни равны = –а; =–.
Пример. Рассмотрим уравнение 17 +288х – 17 = 0.
+1=228, а=с=17, значит = -17; = .
Ответ: (-17; )
Если в квадратном уравнении a+ bx + c = 0 коэффициент b равен ( – 1), а коэффициент с численно равен коэффициенту а, имея вид a + (-1)∙ х- а= 0, то его корни равны = а; = .
Пример. Рассмотрим уравнение 10 –99 х – 10 = 0.
-1=99 и коэффициент а=с, следовательно, =10; = -0,2
Ответ: (10; -0,2)
Кубическое уравнение.
Кубическое уравнение – это уравнение третьей степени вида:
a + b + cx + d = 0 .
Известные формулы Кардано для решения уравнений этого типа очень сложны и почти не применяются на практике. Поэтому я рекомендую другой путь решения уравнений третьей степени.
1) Сначала путём подбора надо найти один из корней уравнения. Кубические уравнения всегда имеют по крайней мере один корень, причем целый корень кубического уравнения с целыми коэффициентами является делителем свободного члена d. Коэффициенты этих уравнений обычно подобраны так, что искомый корень лежит среди небольших целых чисел: 0, ± 1, ± 2, ± 3. Поэтому мы будем искать корень среди этих чисел и проверять его путём подстановки в уравнение. Вероятность успешного нахождения корня при таком подходе очень высока. Предположим, что этот корень x1 .
2) Второй этап решения – это деление многочлена a + b + cx + d на двучлен (x –x1). Согласно теореме Безу (Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами, при этом если старший коэффициент равен 1, то все рациональные корни — целые) это деление без остатка возможно, и мы получим в результате многочлен второй степени, который надо приравнять к нулю. Решая полученное квадратное уравнение, мы найдём оставшиеся два корня, если они есть.
Пример . Решить уравнение: – 3 – 13x + 15 = 0 .
Найдём первый корень подбором чисел: 0, ± 1, ± 2, ± 3 и подставим в уравнение. В результате находим, =1.
Тогда делим левую часть этого уравнения на двучлен x – 1, и получаем:
Теперь, решим квадратное уравнение: – 2x – 15 = 0
D= – 4ас=4+60=64
= = =-3
= = = 5
Ответ: (-3;1;5;)
Задачи на уравнения:
Числитель дроби на 1 меньше знаменателя. Если увеличить числитель дроби на 5, а знаменатель на 3, то дробь увеличится на . Найти дробь.
Решение: Пусть х- числитель дроби, а (х+1) – знаменатель, тогда дробь имеет вид:
; после увеличения: =.
Составим и решим уравнение:
+ =
+ — = 0 2(х+1)(х+4)
2х(х+4) + (х+1)(х+4) – 2(х+5)(х+1) = 0
2+ 8х + + 4х + х + 4 – (2х +10)(х+1) = 0
2+ 8х + + 4х + х + 4 – 2 – 2х – 10х – 10 = 0
+ х – 6 = 0
D= – 4ас=1+4(-6)=25
= = = -3
= = = 2
Следовательно: знаменатель равен х+1= 2+1=3, а числитель равен 2.
Ответ: .
Задача из ОГЭ на составление уравнений:
Первый велосипедист выехал из посёлка по шоссе со скоростью 21 км/ч. Через час после него со скоростью 15 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 9 часов после этого догнал первого.
Решение: Пусть х км/ч – скорость третьего велосипедиста.
Составим и решим уравнение:
— =9, где х-21 и х-15 – скорости сближения.
Избавимся от знаменателя:
х-15(2*21) – 15(х-21) = 9(х-15)(х-21)
42х -630-15х+315=9-324х+2835
42х -630-15х+315-9+324х-2835=0
-9+351х-3150=0
-39х+350=0
D= – 4ас=1521-1400=121
= = = 14-этот корень не подходит условию
= = = 25
Ответ: 25 км/ч.
Решение систем линейных уравнений.
Для того, чтобы решить систему уравнений, состоящую из двух или более уравнений, я рассмотрела несколько методов.
Метод Крамера.
Приведём пример:
x+2y+z=-1
3x-y-z=-1
-2x+2y+3z=5
1)Составим первоначальную матрицу из коэффициентов при неизвестных и обозначим её :
1 2 1 2) Заменим первый столбец матрицы числами после знака равно:
3 -1 -1 1 2 1
-2 2 3 x= 3 -1 -1
-2 2 3
3) Сделаем тоже самое со вторым и третьим столбцом:
1 -1 1 1 2 -1
3 -1 -1 z= 3 -1 -1
-2 5 3 -2 2 5
4) Найдём определитель (дискриминант) для каждой матрицы:
1. -3+4+6-(2-2+18)=7-18+-11
2. 3-10-2-(-5+2-6)=-9+9=0
3. -3+15-2-(2-9-5)=10+12=22
4. -5-6+4-(-2-2+30)=-7+16=11
x= 0, y=22, z=-33, = -11
5)Далее найдём корни по формулам:
==0 == -2 == 3
Ответ: 0; -2; 3
Метод Гаусса(метод треугольника)
x+2y+z=-1
3x-y-z=-1
-2x+2y+3z=5
Оставляем первое уравнение без изменений и умножим его на то число, чтобы при сложении х уничтожился во втором. Т.е. второе уравнение после сложения уже записываем без х.
Далее, умножаем и первое, и второе уравнение на -2, чтобы и в третьем уравнении избавиться от х.
И наконец умножаем третье уравнение на -7, тем самым избавляясь при сложении от у.
x+2y+z=-1 (-3) (-2)
-7y-4z=2 (-2)
-2y+z=7
Получаем треугольник:
х+2у+ z=-1 И методом подстановки находим все корни : z=3
-7у-4z=2 -7у=2+12, у= -2
-15z=-45 х=-1+4-3=0
Ответ: 0; -2; 3
Метод Гаусса(метод прямоугольников)
х+2у+3z=5
4х+5у+6z=8
7х+8у=2
Составим матрицу и приведём её к единичной:
1 2 3 5 1 0 0 х
4 5 6 8 0 1 0 у
7 8 0 2 0 0 1 z
Первую троку оставляем без изменений; во второй строке первый коэффициент равен 0, а остальные два найдём с помощью метода прямоугольников:
Вместе с разрешающим элементом(1 в первой строке) и коэффициентом, который нам надо найти, составляем прямоугольник и вычитаем его диагонали: 1*5-2*4=-3.
Затем, составляем прямоугольник со вторым коэффициентом во второй строке(а первый равен 0) и так со всеми оставшимся числами.
1 2 3 5 1 2 3 5
0 -3 -6 -12 4 5 6 8
0 -6 -21 -33 7 8 0 2
Для того, чтобы упростить вычисления, сократим последние 2 строки на -3 и продолжим вычисление:
Теперь разрешающим элементов является 1 во второй строке.
1 2 3 5 1 0 -1 -3 Сократим и здесь третью строку на
0 1 2 4 0 1 2 4 (-3)
0 2 7 11 0 0 3 3
Получим новую матрицу с разрешающим элементом 1 в третьей строке:
1 0 -1 -3 1 0 0 -2
0 1 2 4 0 1 0 2
0 0 1 1 0 0 1 1
Крайние числа в последней матрице и есть корни уравнения:
х=-2; у=2; z=1
Ответ: -2; 2; 1
Заключение
Я исследовала различные методы для решения уравнений и систем линейных уравнений, чтобы развивать потребность у старшеклассников в нахождении рациональных способов их решения.
Обобщая нестандартные методы решения систем линейных уравнений, работа может быть рекомендована как учащимся школы, так и студентам первого курса.
Я постараюсь продолжить работу над этой темой дальше, чтобы находить и совершенствовать навыки интересных, нестандартных и оптимальных способов решения.
Список использованной литературы:
1)https://ru.wikipedia.org/wiki/Галуа,_Эварист
2)http://sar18021977.ucoz.ru/load/issledovatelskaja_rabota_uchenicy_8_kl_quot_istorija_vozniknovenija_i_razvitija_uravnenij_quot/1-1-0-1
3)http://textarchive.ru/c-2865846.html
4)http://wiki.iteach.ru/index.php/История_возникновения_уравнений_(работа_учащихся_в_проекте_Равновесие)
5) А. Н. Бекаревич «Уравнения в школьном курсе математики» Минск. 1968 г., 99 стр.
6) В. С. Гиренович «Математика в школе» № 3 Виды самостоятельных работ. 1998 г.
Просмотров работы: 200
school-science.ru
Понятие системы уравнений. |
|||||
|
|||||
Свойства систем уравнений: |
|||||
Линейные системы уравнений с двумя неизвестными: |
|||||
|
Линейные системы уравнений с двумя переменными — это система вида: |
|||||
|
Прямые — графики уравнений системы пересекаются в одной точке. Система имеет единственное решение: |
|||||
| Прямые — графики уравнений системы — параллельны. Система не имеет решений. | |||||
|
Прямые — графики уравнений системы совпадают. Система имеет бесконечно много решений: | |||||
dpva.ru
Различные способы решения систем уравнений (подготовка к ГИА)
1) Цели урока:
Образовательные:
- Закрепить, углубить, обобщить знания и умения решения систем уравнений, используя способы: алгебраического сложения, подстановки, графический, замены переменной.
- Познакомить с решением симметрических систем уравнений.
b. Развивающие:
- Умение находить и анализировать наиболее рациональные способы решения систем уравнения.
- Формировать навыки коллективной и самостоятельной работы.
- Развитие мыслительных и творческих способностей учащихся через умение действовать в нестандартной ситуации.
с. Воспитывающие:
- Способность выработке обобщать изучаемые факты.
- Прививать у учеников интерес к предмету через решение систем уравнений различными способами.
- Формировать умение четко и ясно излагать свои мысли и грамотно выполнять математические задачи.
2) Проверка домашнего задания (на экране (Презентация. Слайд 2) записаны системы уравнений и ответы).
(При необходимости показать решение системы d на доске.)
1) Что называется решением системы уравнений с двумя переменными.
2) Какие способы решения систем уравнений вы использовали в домашней работе?
3) А какие еще способы вы знаете?
3) Устно:
На дом вам было задано повторить из курса геометрии:
- Уравнение окружности
- Что называется графиком уравнения с двумя переменными
– Так что же называется графиком уравнения с двумя переменными?
Слайд 3:
4) Презентация:
Учитель:
Двое учащихся по желанию получили творческие задания, используя дополнительную литературу, нашли материал, подобрали систему и сделали презентации.
- Решение систем уравнений графическим способом.
- Решение симметрических систем уравнений.
На предыдущих уроках мы рассматривали решение систем уравнений методом замены переменных. Общего правила выбора замены переменных не существует, однако можно выделить два вида систем уравнений, когда есть разумная замена переменных:
- Симметрические системы уравнений, которые сейчас рассмотрим в презентации.
- Системы уравнений, одно из которых однородное – рассмотрим на следующих уроках при подготовке к ГИА.
У каждого учащегося лежит на парте:
- распечатка презентации,
- домашнее задание.
5) Домашнее задание: (прокомментировать)
Приложение 1.
6) Работа с классом:
Учащийся решает у доски, остальные решают в тетрадях.
Ответ: (1;2), (1;-2).
7) Самостоятельная работа:
Приложение 2.
8) Итоги урока:
Оценки.
- Какие способы решения систем уравнений использовали на уроке?
- С каким видом систем уравнений познакомились на уроке?
- Какой способ решения систем уравнения применяется при их решении?
Историческая справка:
Все способы решения систем уравнения знали давно, но точной даты не известно. Хотя в книге Ньютона “Всеобщая арифметика” эти способы имеются.
urok.1sept.ru
§ 3. Системы линейных уравнений
Литература: (1, с. 18-34; 2, с. 82-100; 3, с. 286-275)
Основные понятия
Системой линейных уравнений называется совокупность рассматриваемых совместно нескольких линейных уравнений.
В системе может быть любое число уравнений с любым числом неизвестных.
Решением системы уравнений называется совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, то есть обращающая их в тождества.
Система, имеющая решение, называется совместной, в противном случае – несовместной.
Для решения системы применяют различные методы.
Решение систем
 линейных уравнений с
линейных уравнений с неизвестными
неизвестными
Пусть  (число уравнений равно числу неизвестных).
(число уравнений равно числу неизвестных).
Метод Крамера
Рассмотрим решение системы трёх линейных уравнений с тремя неизвестными:
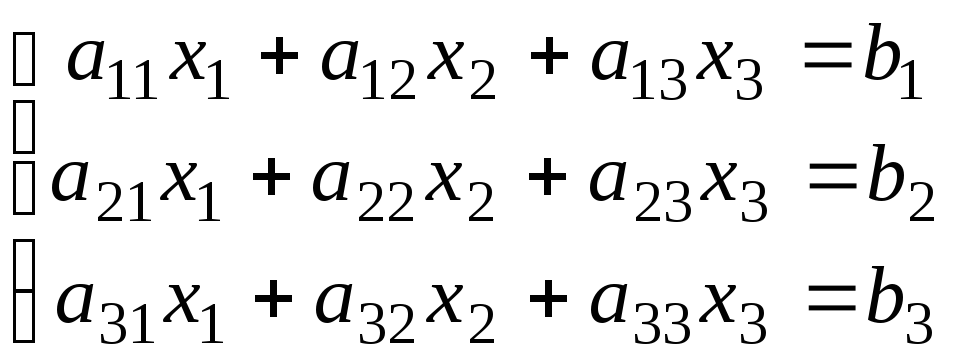 (7)
(7)
Для нахождения
неизвестных  применим формулу Крамера:
применим формулу Крамера:
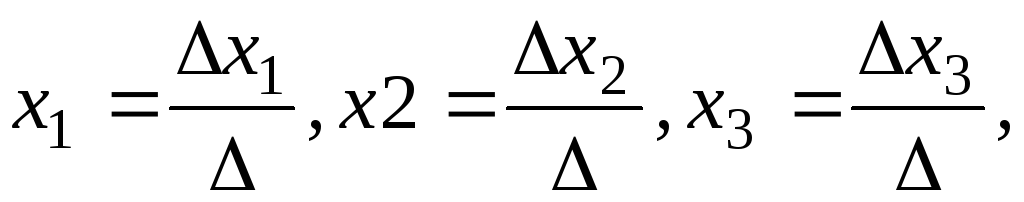 (8)
(8)
где  — определитель системы, элементы которого
есть коэффициенты при неизвестных:
— определитель системы, элементы которого
есть коэффициенты при неизвестных:
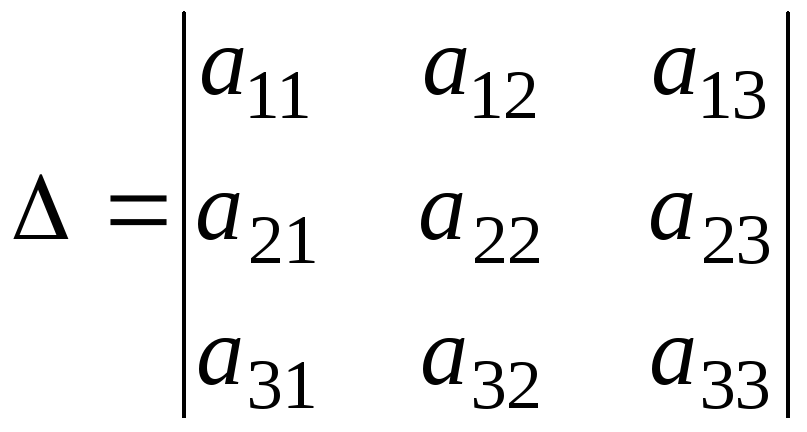 .
.
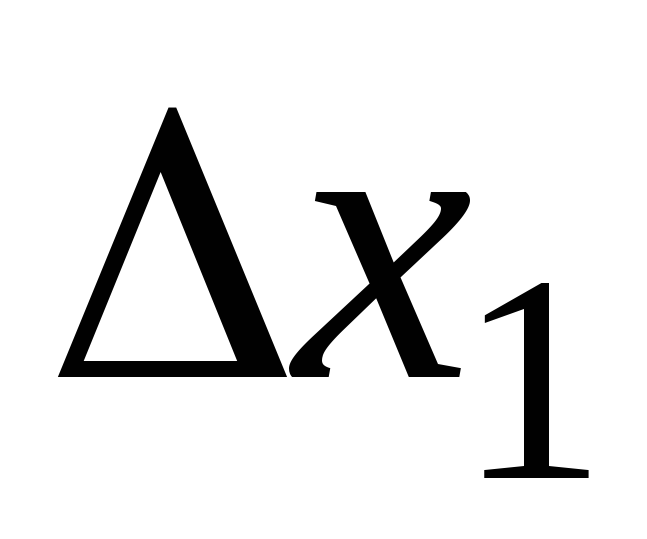 получается путём
замены первого столбца определителя
получается путём
замены первого столбца определителя  столбцом свободных членов:
столбцом свободных членов:
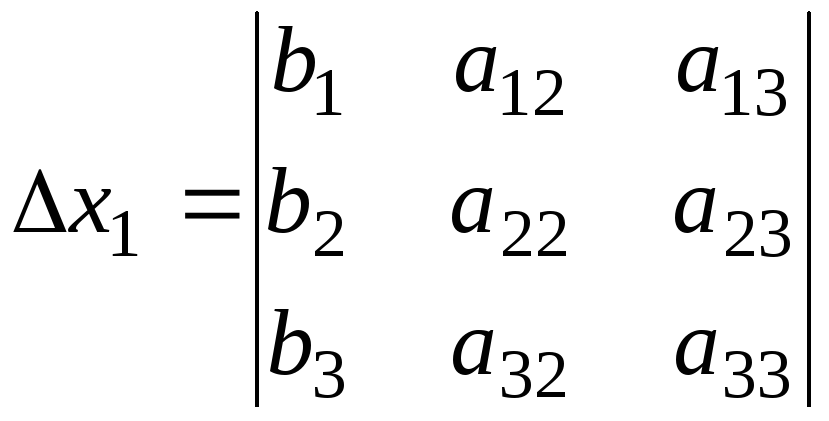 .
.
Аналогично:
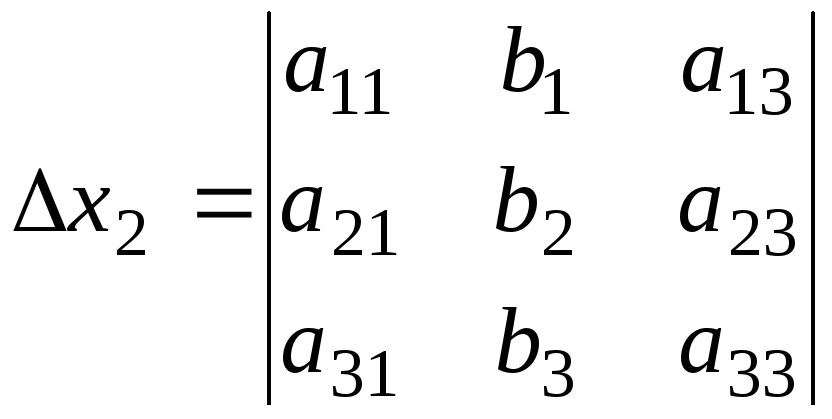 ;
;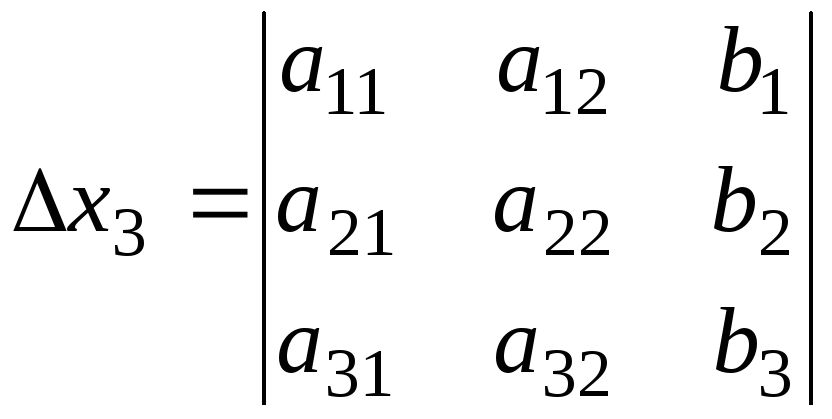 .
.
Пример 1. Решить систему по формуле Крамера:
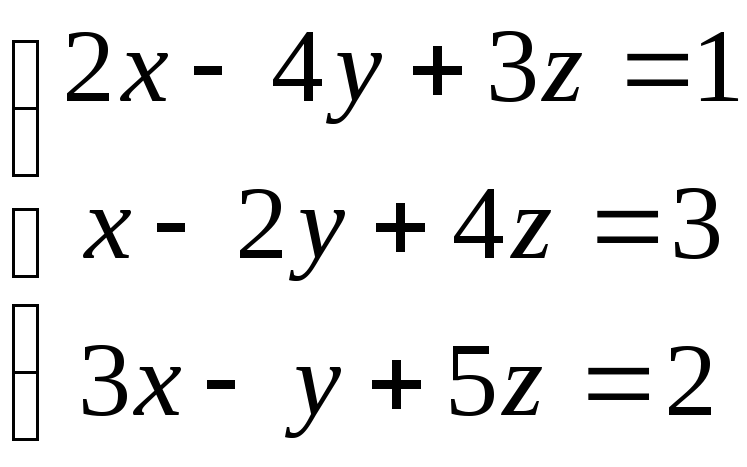 .
.
Решение: Воспользуемся формулами (8):
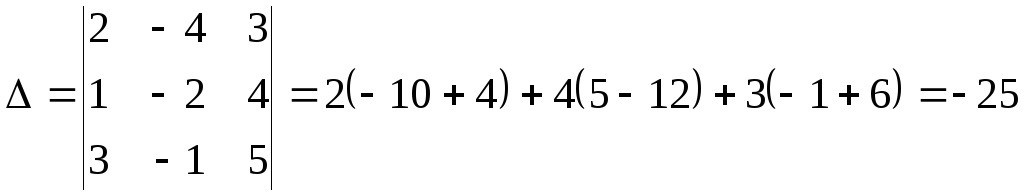 ;
;
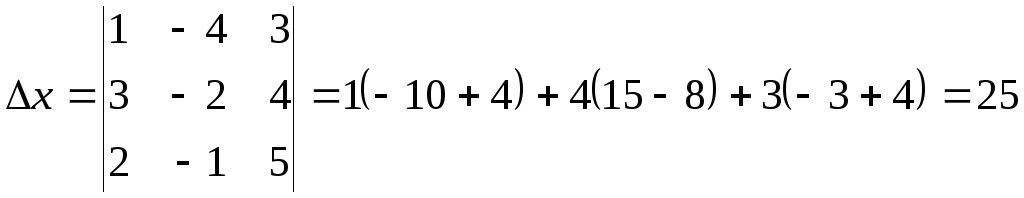 ;
;
 ;
;
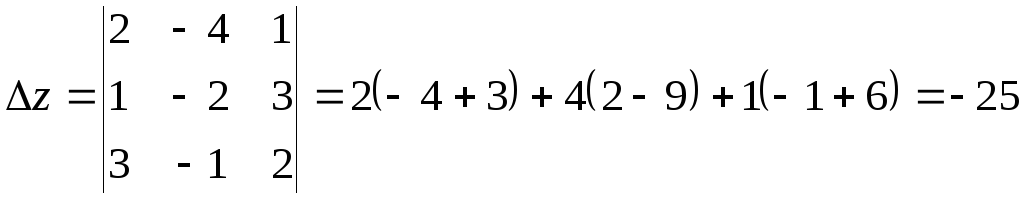 ;
;
Тогда
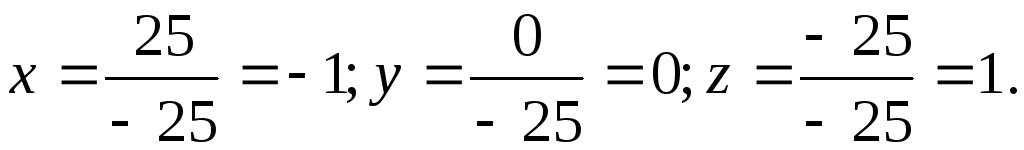
Ответ:  .
.
Для любой системы 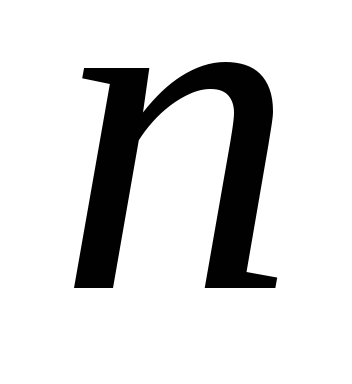 линейных уравнений с
линейных уравнений с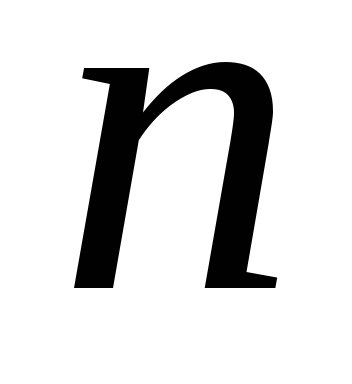 неизвестными можно утверждать:
неизвестными можно утверждать:
Если определить системы
 ,
то система имеет единственное решение,
которое может быть найдено по формулам
Крамера.
,
то система имеет единственное решение,
которое может быть найдено по формулам
Крамера.Если
 ,
то правило Крамера неприменимо. В этом
случае система может иметь бесчисленное
множество решений, если
,
то правило Крамера неприменимо. В этом
случае система может иметь бесчисленное
множество решений, если или не иметь их, если хотя бы один из
определителей
или не иметь их, если хотя бы один из
определителей не равен нулю.
не равен нулю.
Матричный способ решения
Рассмотрим решение системы (7) трёх линейных уравнений с тремя неизвестными матричным способом.
Используя правила
умножения матриц, данную систему
уравнений можно записать в виде: 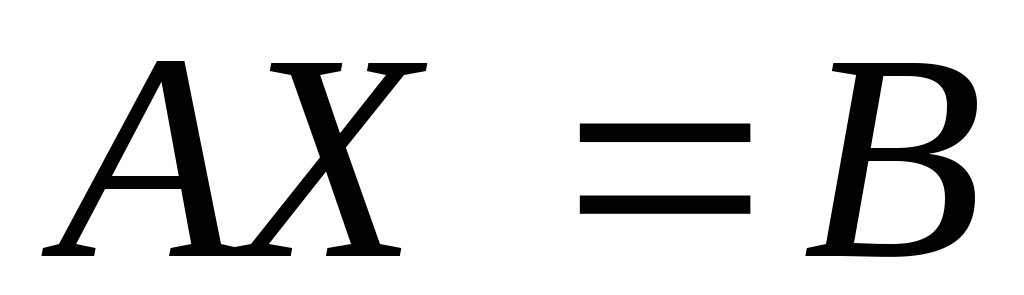 ,
где
,
где
 .
.
Пусть матрица  невырожденная, т.е.
невырожденная, т.е. .
Умножая обе части матричного уравнения
слева на матрицу
.
Умножая обе части матричного уравнения
слева на матрицу ,
обратную матрице
,
обратную матрице ,
получим:
,
получим: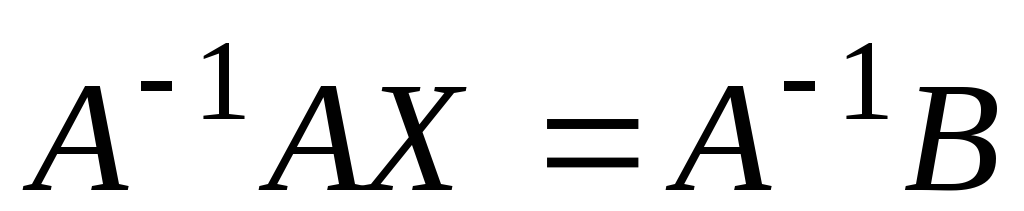 .
.
Учитывая, что 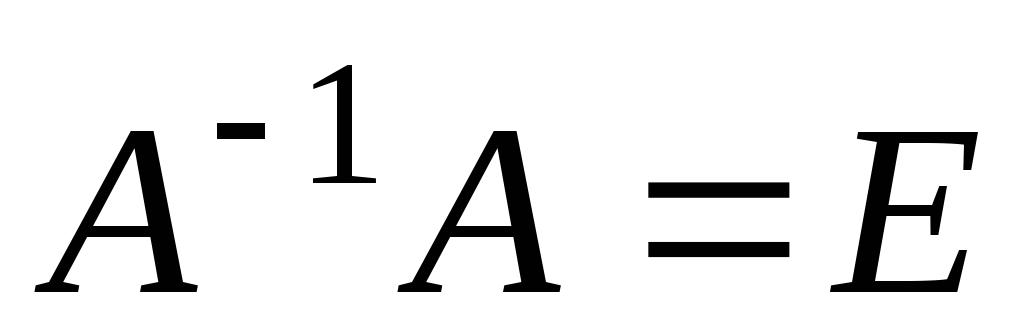 ,
имеем
,
имеем
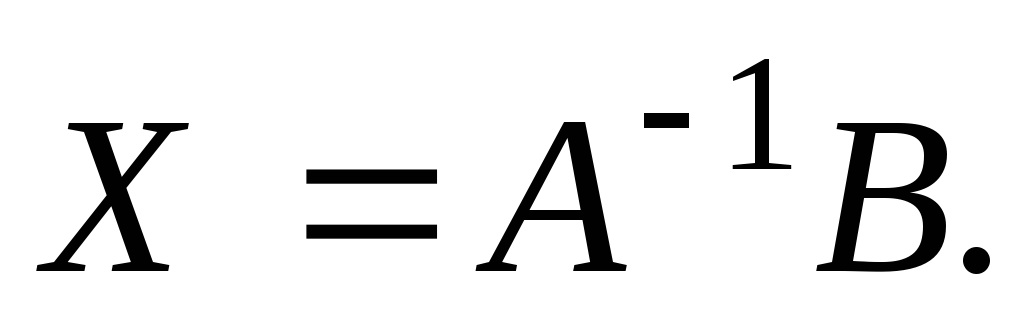 (9)
(9)
Пример 2. Решить систему матричным способом:
 .
.
Решение: Введём матрицы:
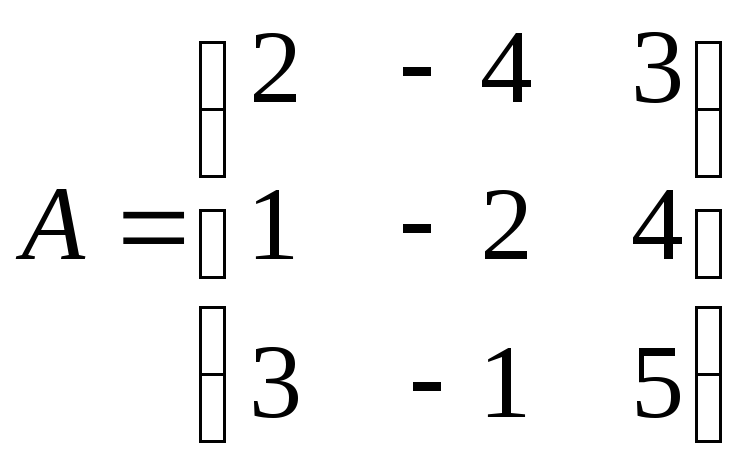 —
из коэффициентов при неизвестных;
—
из коэффициентов при неизвестных;
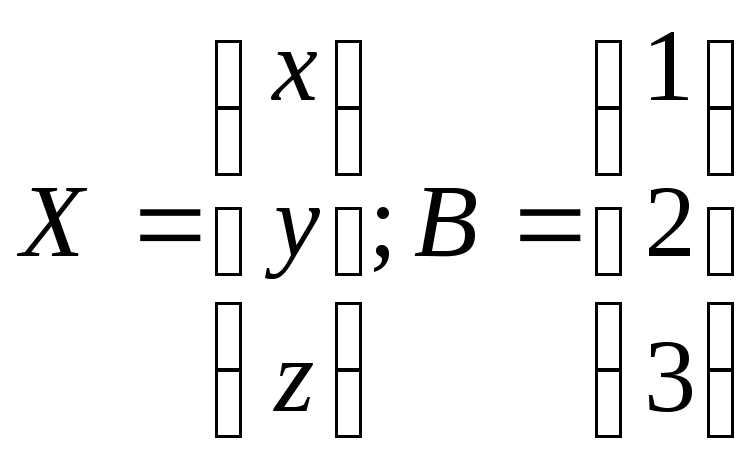 —
столбец свободных членов.
—
столбец свободных членов.
Тогда систему можно записать матричным уравнением: .
Воспользуемся
формулой (9). Найдём обратную матрицу 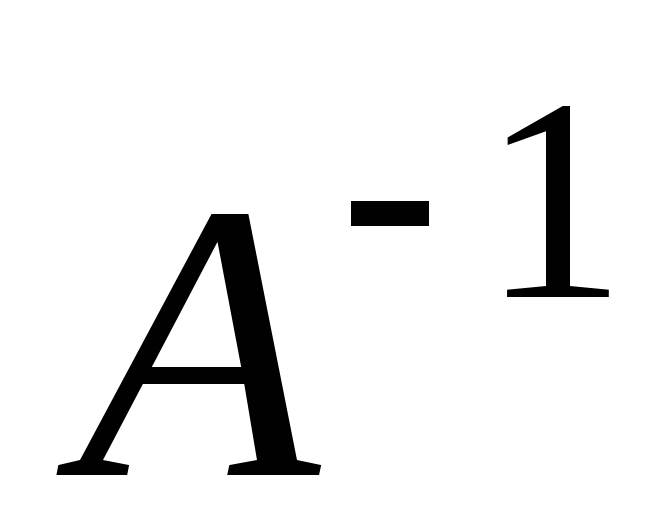 по формуле (6):
по формуле (6):
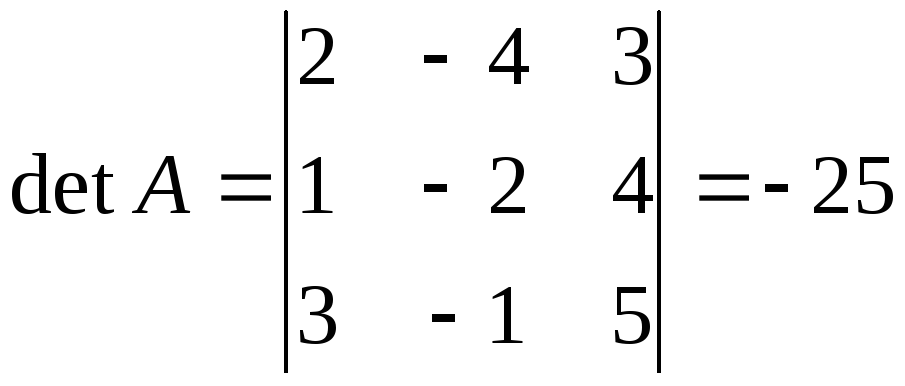 ;
;
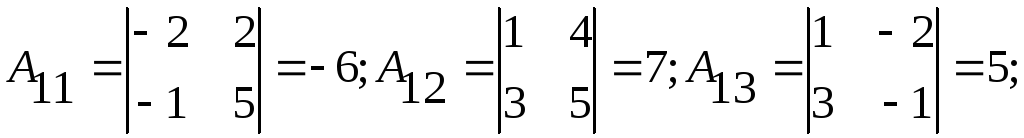
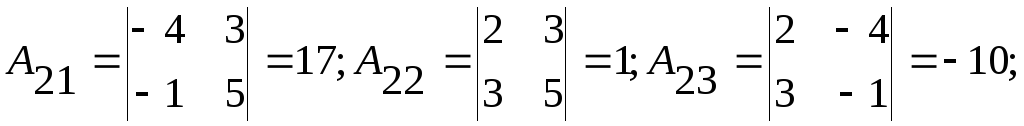
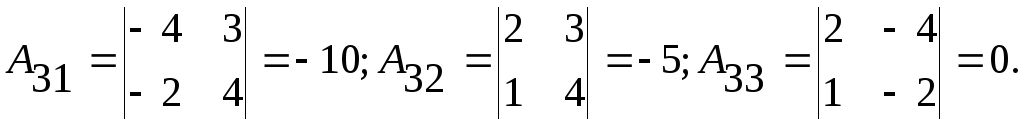
Тогда
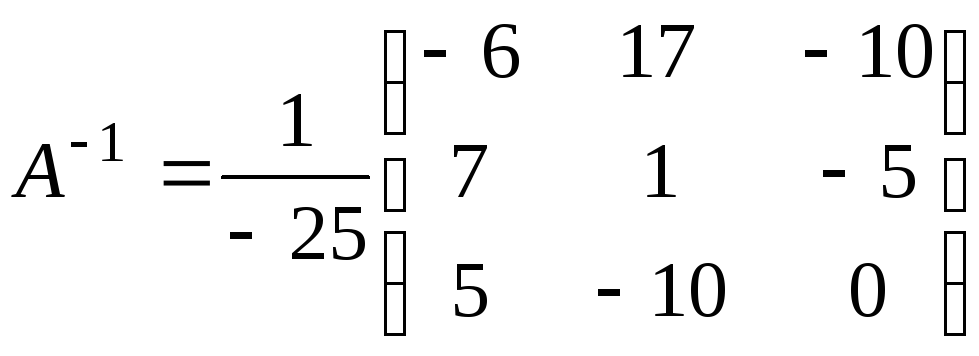 .
.
Следовательно,
 Получили:
Получили:
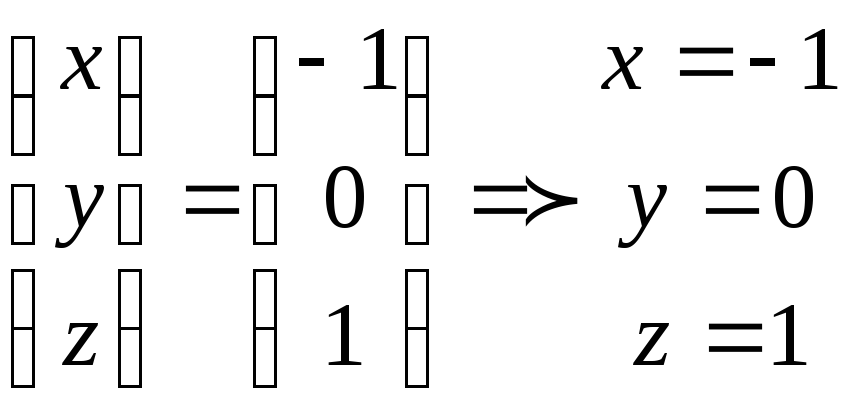 .
.
Ответ: 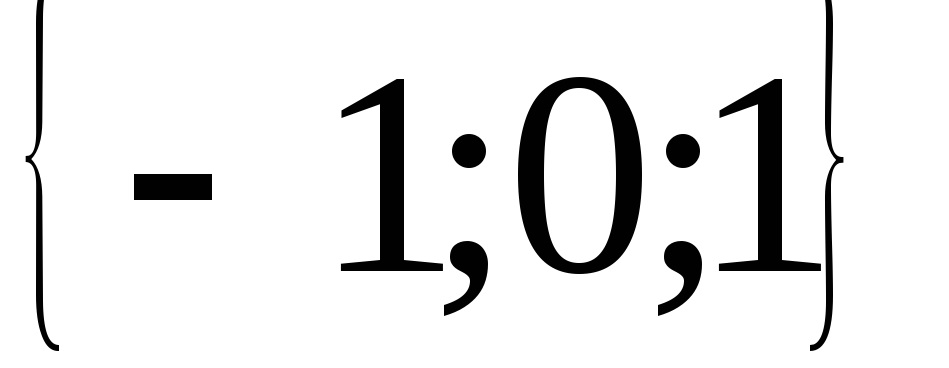 .
.
Метод последовательного исключения неизвестных (метод Гаусса)
Основная идея применяемого метода заключается в последовательном исключении неизвестных. Поясним смысл этого метода на системе трёх уравнений с тремя неизвестными:
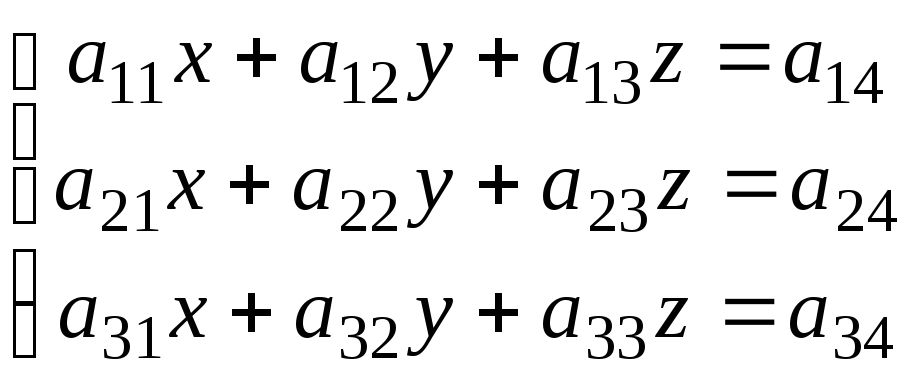 .
. 
Допустим, что 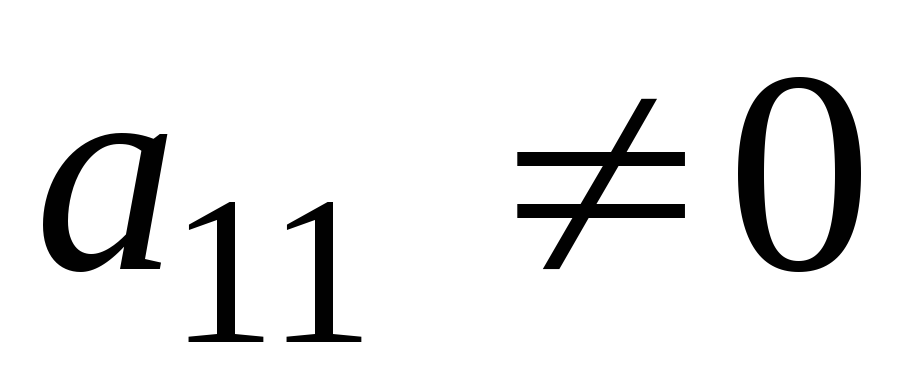 (если
(если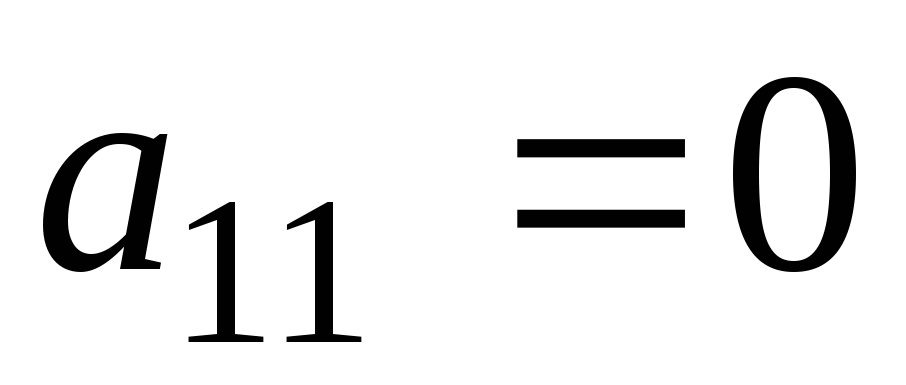 ,
то изменим порядок уравнений, выбрав
первым уравнением то, в котором коэффициент
при
,
то изменим порядок уравнений, выбрав
первым уравнением то, в котором коэффициент
при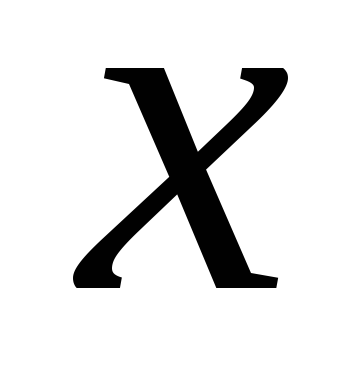 не равен нулю).
не равен нулю).
Первый шаг: а) делим
уравнение  на
на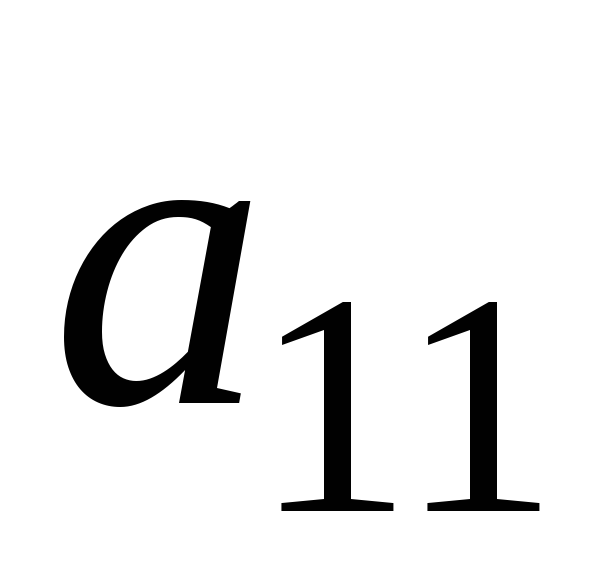 ;
б) умножаем полученное уравнение на
;
б) умножаем полученное уравнение на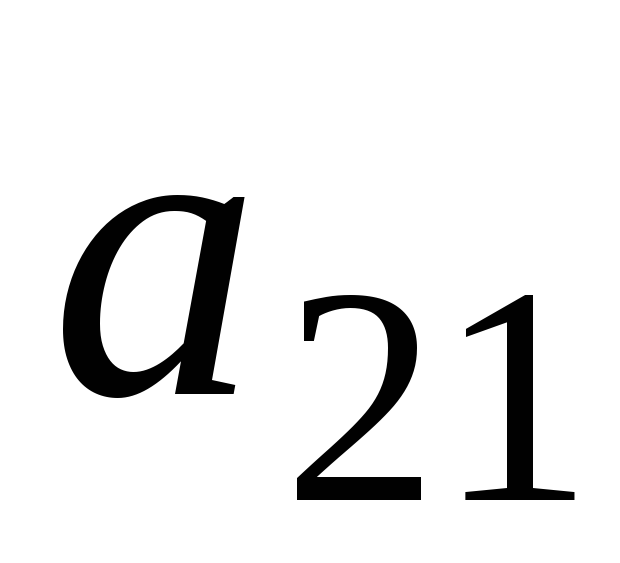 и вычитаем из
и вычитаем из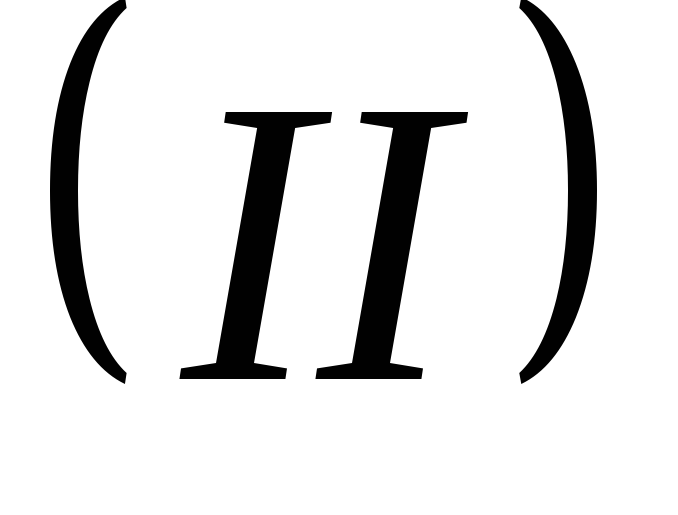 ;
в) затем полученное умножаем на
;
в) затем полученное умножаем на и вычитаем из
и вычитаем из .
В результате первого шага будем иметь
систему:
.
В результате первого шага будем иметь
систему:


причём
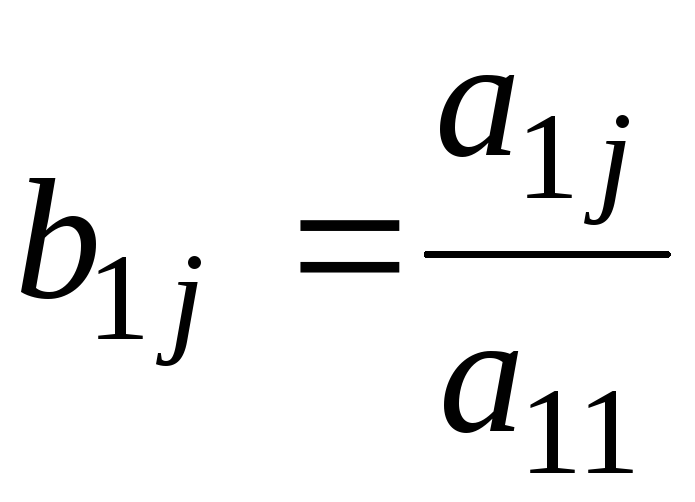
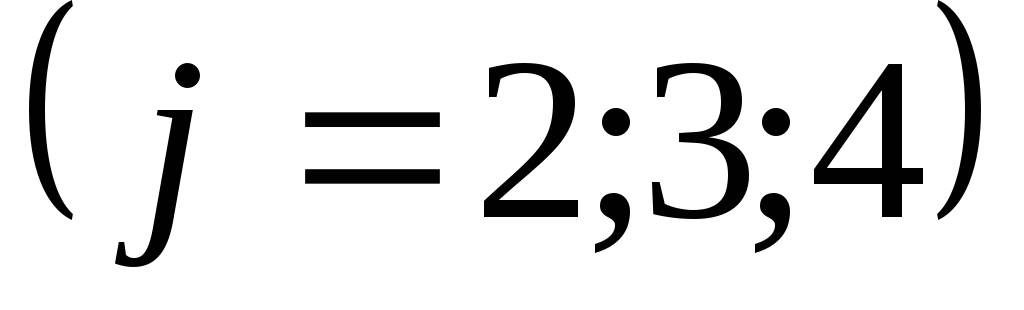 ,
,
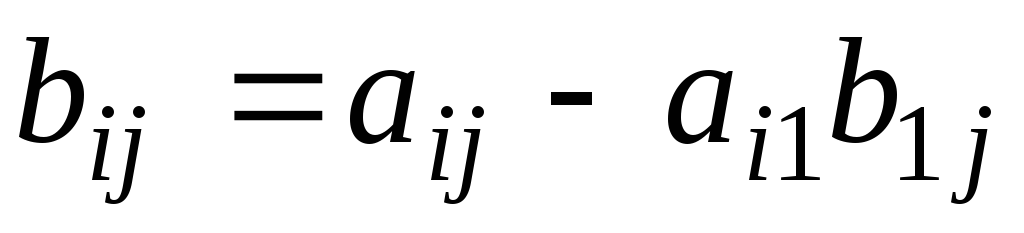
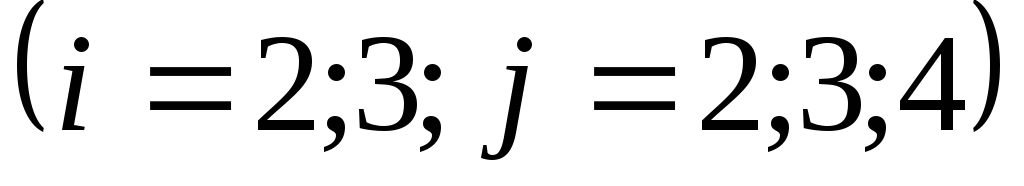
Второй шаг: поступаем
с уравнением 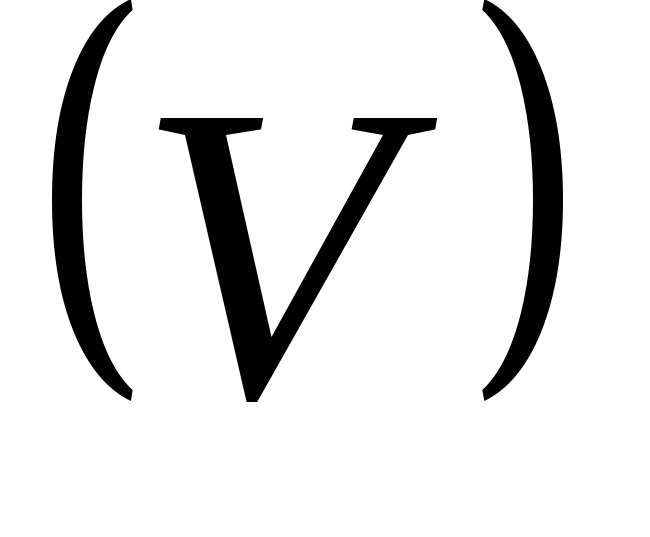 и
и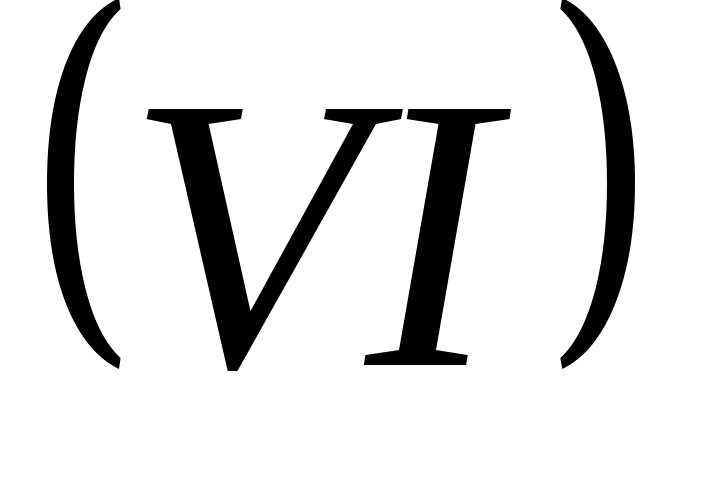 точно так же, как с уравнениями
точно так же, как с уравнениями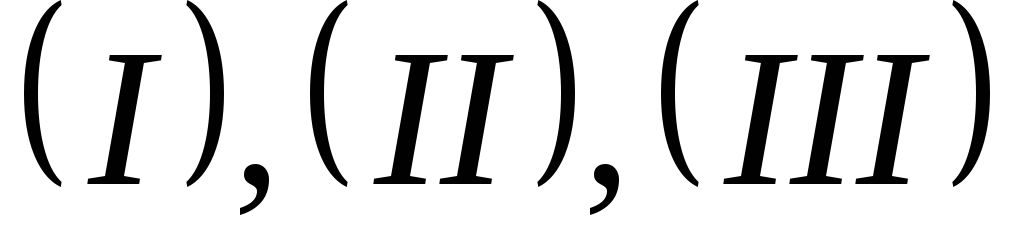 .
.
В итоге исходная система преобразуется к так называемому ступенчатому виду:

Из преобразованной системы все неизвестные определяются последовательно без труда.
Замечание. Практически удобнее приводить к ступенчатому виду не саму систему уравнений, а матрицу из коэффициентов, при неизвестных, и свободных членов.
Пример 3. Решить методом Гаусса систему:
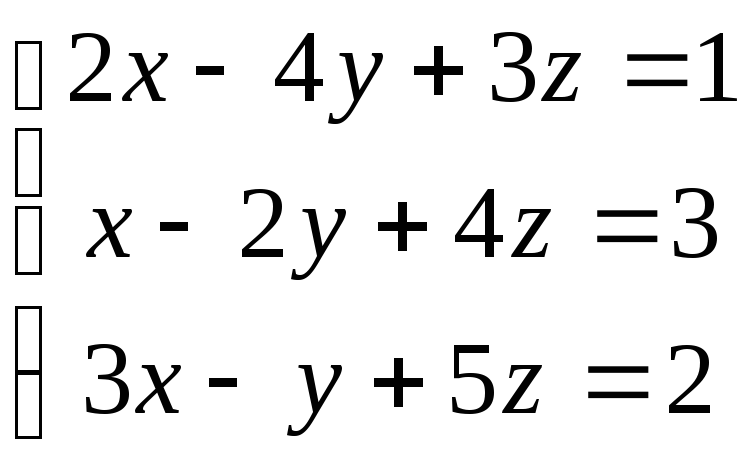 .
.
Переход от одной матрицы к другой будем записывать при помощи знака эквивалентности ~.
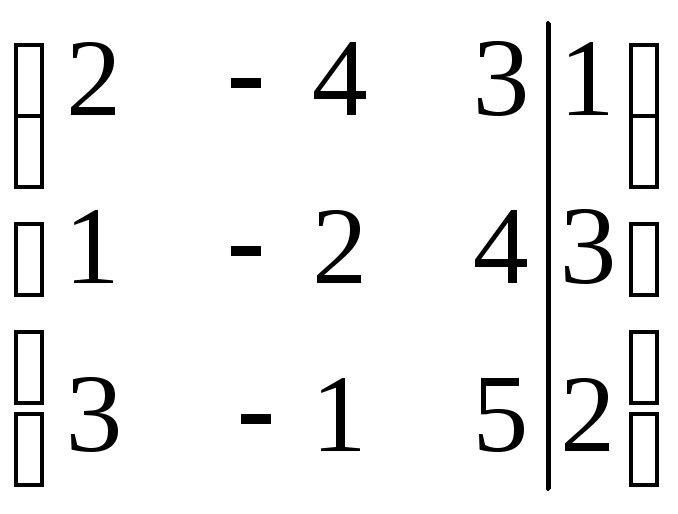 ~
~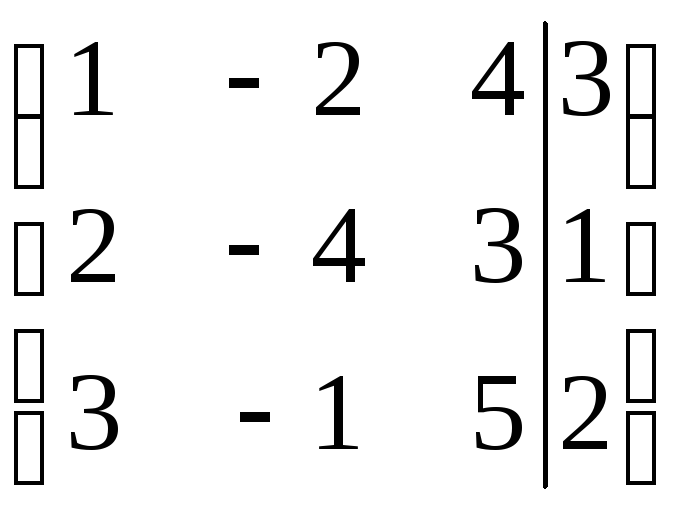 ~
~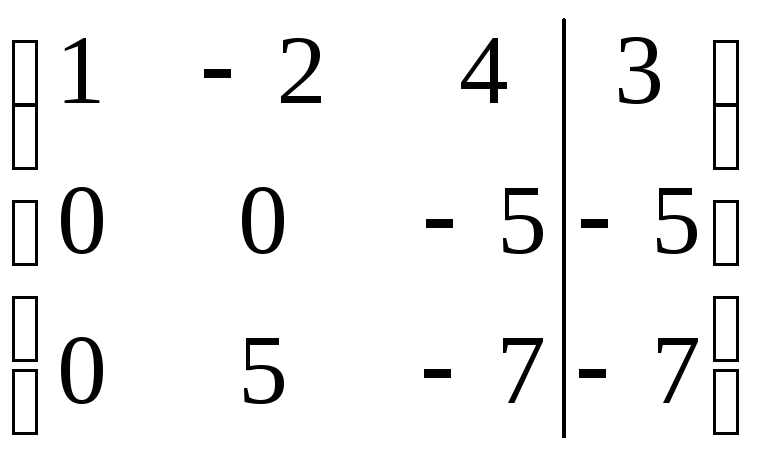 ~
~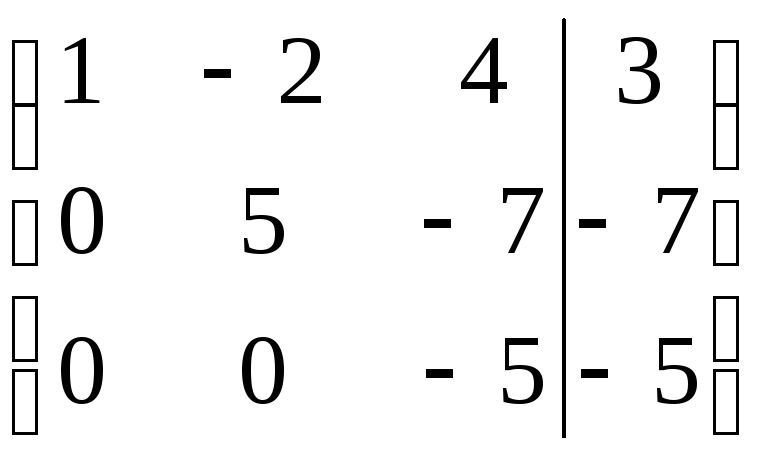 ~
~
~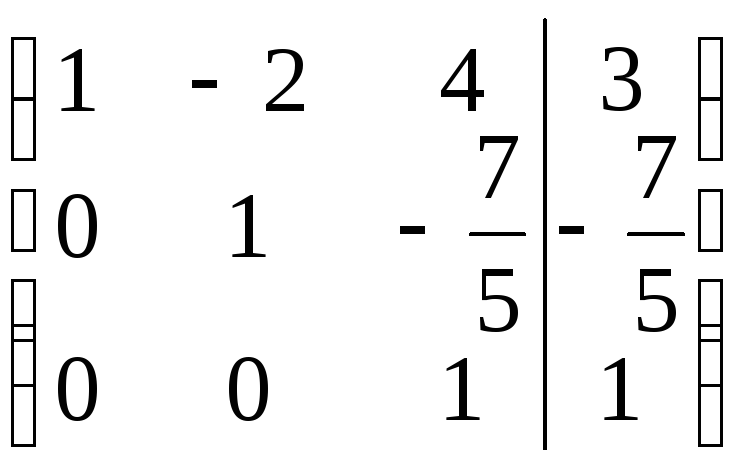 .
.
По полученной матрице выписываем преобразованную систему:
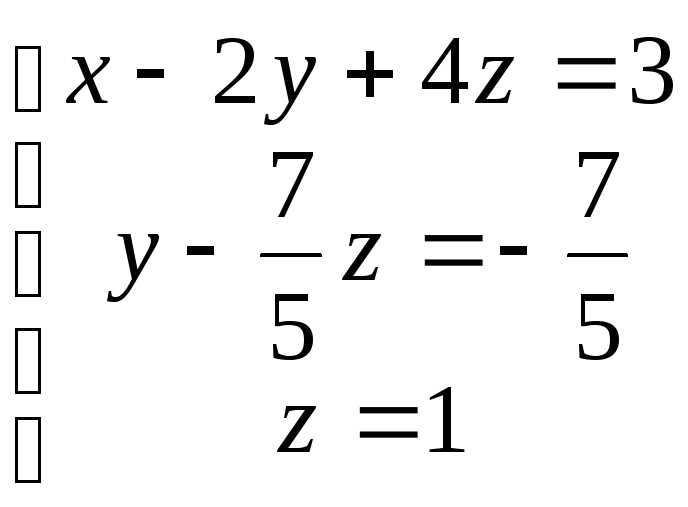 .
.
Тогда

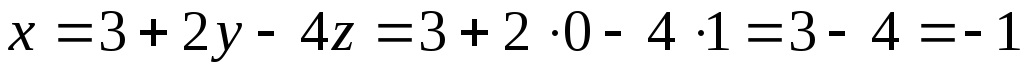
Ответ:  .
.
Замечание: Если
система имеет единственное решение, то
ступенчатая система приводится к
треугольной, то есть к такой, в которой
последнее уравнение будет содержать
одно неизвестное. В случае неопределённой
системы, то есть такой, в которой число
неизвестных больше числа линейно
независимых уравнений, треугольной
системы не будет, так как последнее
уравнение будет содержать более одного
неизвестного (система имеет бесчисленное
множество решений). Когда же система
несовместна, то, после приведения её к
ступенчатому виду, она будет содержать
хотя бы одно  значение вида
значение вида ,
то есть уравнение, в котором все
неизвестные имеют нулевые коэффициенты,
а правая часть отлична от нуля (система
решений не имеет). Метод Гаусса применим
к произвольной системе линейных уравнений
(при любых
,
то есть уравнение, в котором все
неизвестные имеют нулевые коэффициенты,
а правая часть отлична от нуля (система
решений не имеет). Метод Гаусса применим
к произвольной системе линейных уравнений
(при любых и
и ).
).
Теорема существования решения системы линейных уравнений
При решении системы линейных уравнений методом гаусса ответ на вопрос, совместна или несовместна данная система может быть дан лишь в конце вычислений. Однако часто бывает важно решить вопрос о совместности или несовместности системы уравнений, не находя самих решений. Ответ на этот вопрос даёт следующая теорема Кронекера-Капелли.
Пусть дана система 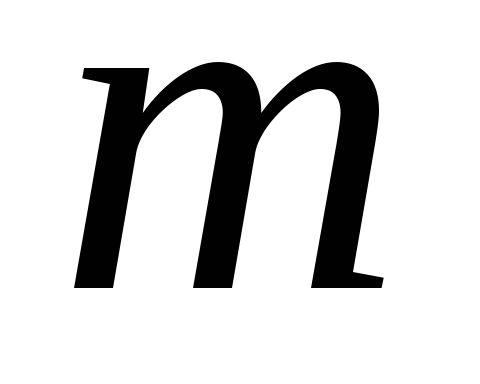 линейных уравнений с
линейных уравнений с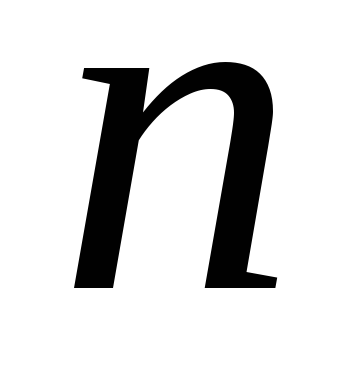 неизвестными:
неизвестными:
 (10)
(10)
Для того, чтобы система (10) была совместной, необходимо и достаточно чтобы ранг матрицы системы
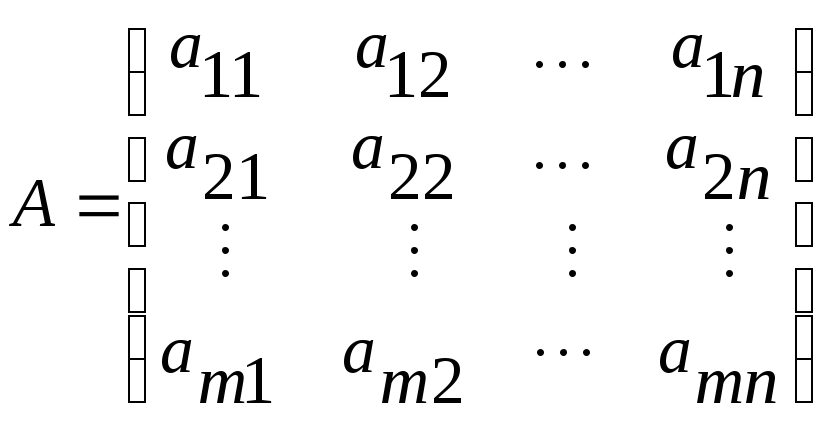 .
.
был равен рангу её расширенной матрицы
 .
.
Причём, если 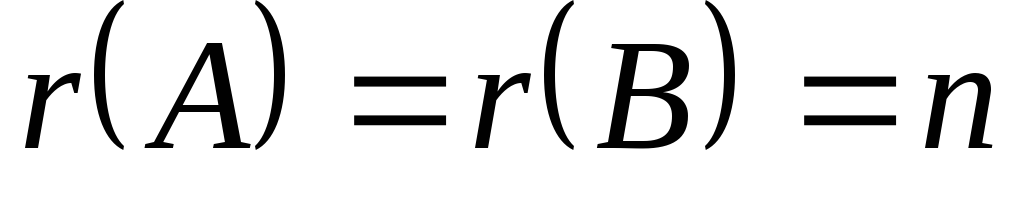 ,
то система (10) имеет единственное решение;
если же
,
то система (10) имеет единственное решение;
если же ,
то система имеет бесчисленное множество
решений.
,
то система имеет бесчисленное множество
решений.
Линейная, однородная система
 уравнений с
уравнений с неизвестными
неизвестными
Рассмотрим однородную систему (все свободные члены равны нулю) линейных уравнений:
 .
.
Эта система всегда
совместна, так как она имеет нулевое
решение  .
.
В следующей теореме даны условия, при которых система имеет также решения, отличные от нулевого.
Терема. Для того,
чтобы однородная система линейчатых
уравнений имела нулевое решение,
необходимо и достаточно, чтобы её
определитель  был равен нулю:
был равен нулю:
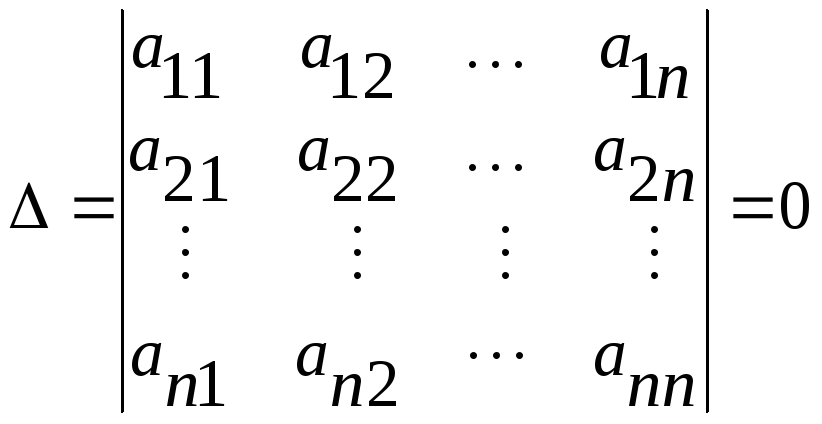 .
.
Таким образом,
если 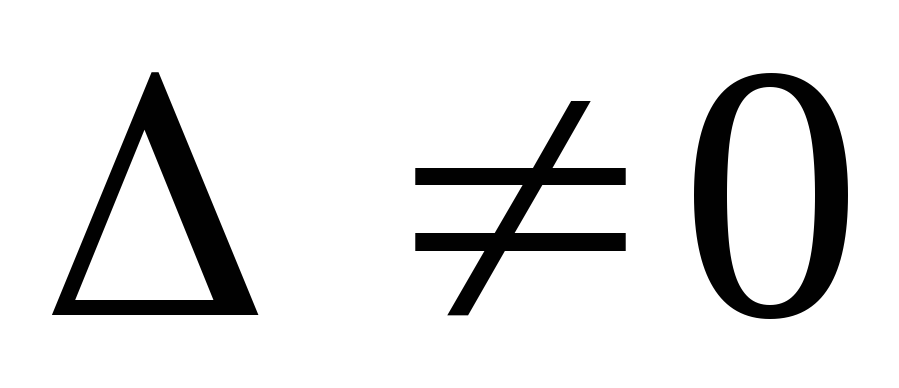 ,
то решение
,
то решение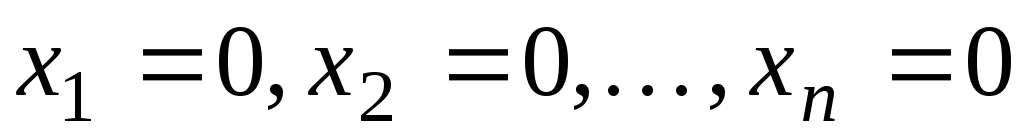 — единственное. Если
— единственное. Если ,
то существует бесконечноё множество
других ненулевых решений. Укажем один
из способов отыскания решений для
однородной системы трёх линейных
уравнений с тремя неизвестными в случае
,
то существует бесконечноё множество
других ненулевых решений. Укажем один
из способов отыскания решений для
однородной системы трёх линейных
уравнений с тремя неизвестными в случае .
.
Можно доказать,
что если 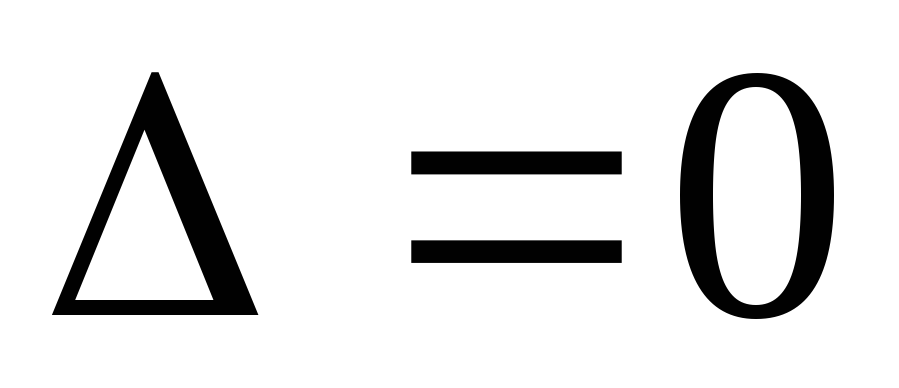 ,
а первое и второе уравнения непропорциональны
(линейно независимы), то третье уравнение
есть следствие первых двух. Решение
однородной системы трёх уравнений с
тремя неизвестными сводится к решению
двух уравнений с тремя неизвестными.
Появляется так называемое свободное
неизвестное, которому можно придавать
произвольные значения.
,
а первое и второе уравнения непропорциональны
(линейно независимы), то третье уравнение
есть следствие первых двух. Решение
однородной системы трёх уравнений с
тремя неизвестными сводится к решению
двух уравнений с тремя неизвестными.
Появляется так называемое свободное
неизвестное, которому можно придавать
произвольные значения.
Пример 4. Найти все решения системы:
 .
.
Решение. Определитель этой системы
 .
.
Поэтому система имеет нулевые решения. Можно заметить, что первые два уравнения, например, непропорциональны, следовательно, они линейно независимые. Третье является следствием первых двух (получается, если к первому уравнению прибавить удвоенное второе). Отбросив его, получим систему двух уравнений с тремя неизвестными:
 .
.
Полагая, например, 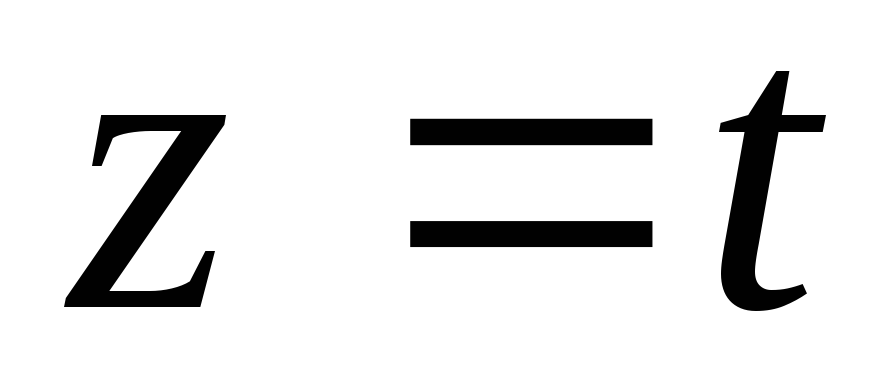 ,
получим
,
получим
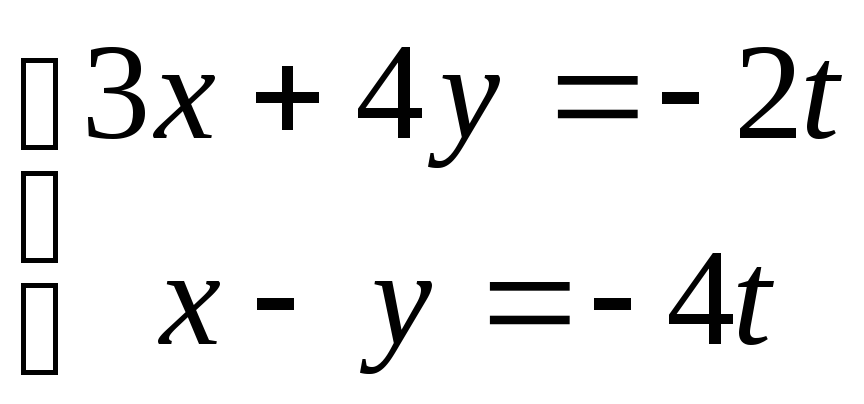 .
.
Решая систему двух
линейных уравнений, выразим 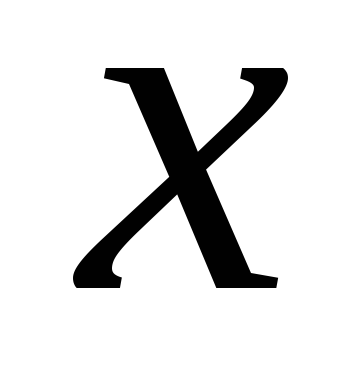 ичерез
ичерез :
: .
Следовательно, решение системы можно
записать в виде:
.
Следовательно, решение системы можно
записать в виде: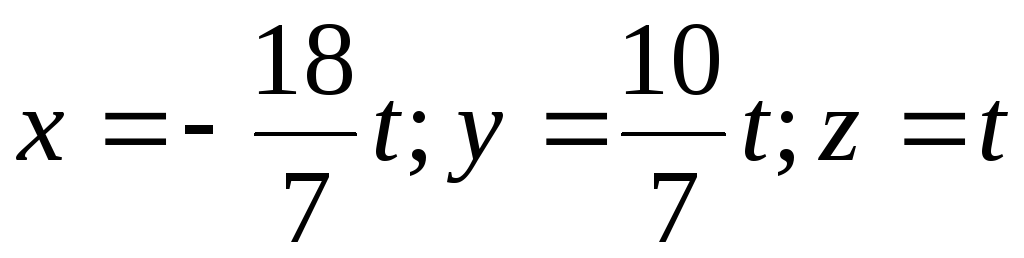 ,
где
,
где — произвольное число.
— произвольное число.
Пример 5. Найти все решения системы:
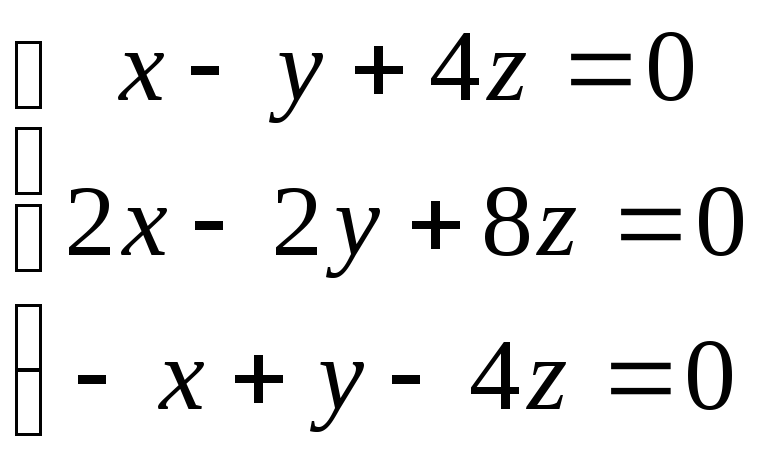 .
.
Решение. Нетрудно
видеть, что в данной системе только одно
независимое уравнение (два других ему
пропорциональны). Система из трёх
уравнений с тремя неизвестными свелась
к одному уравнению с тремя неизвестными.
Появляются два свободных неизвестных.
Найдя, например, из первого уравнения 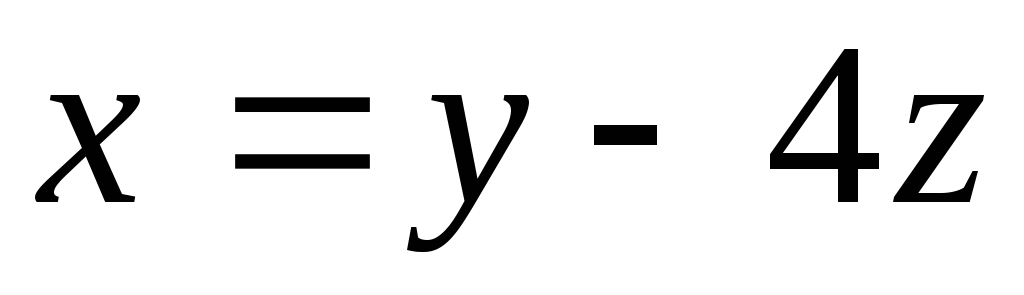 при произвольных
при произвольных и
и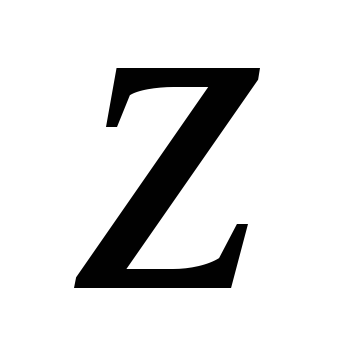 ,
получим решения данной системы. Общих
вид решения можно записать
,
получим решения данной системы. Общих
вид решения можно записать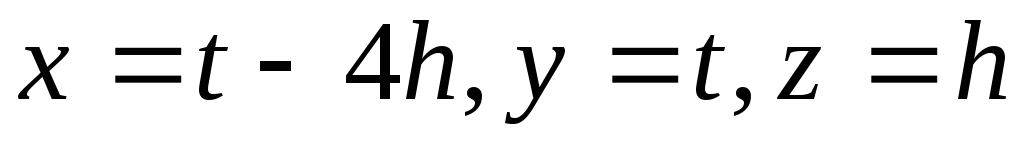 ,
где
,
где и
и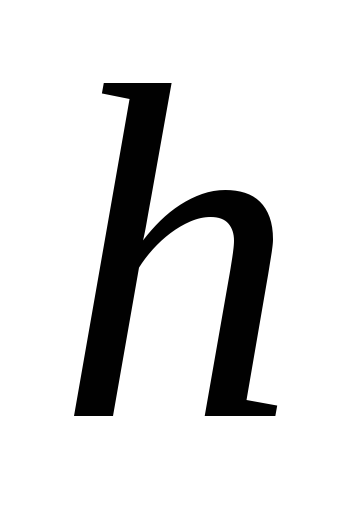 — произвольные числа.
— произвольные числа.
Вопросы для самопроверки
Сформулируйте
правило Крамера для решения системы 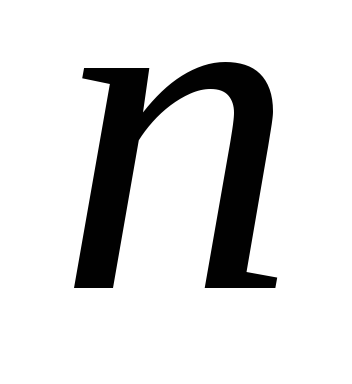 линейных уравнений с
линейных уравнений с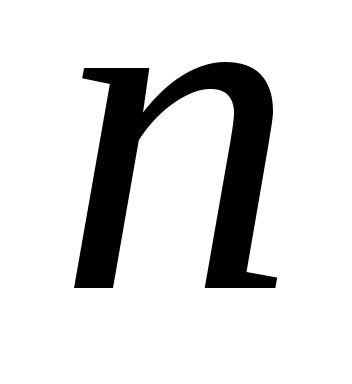 неизвестными.
неизвестными.
В чём сущность матричного способа решения систем?
В чём заключается метод Гаусса решения системы линейных уравнений?
Сформулируйте теорему Кронекера-Капелли.
Сформулируйте необходимое и достаточноё условие существования ненулевых решений однородной системы линейных уравнений.
Примеры для самостоятельного решения
Найдите все решения систем:
1.  ; 2.
; 2. ;
;
3. 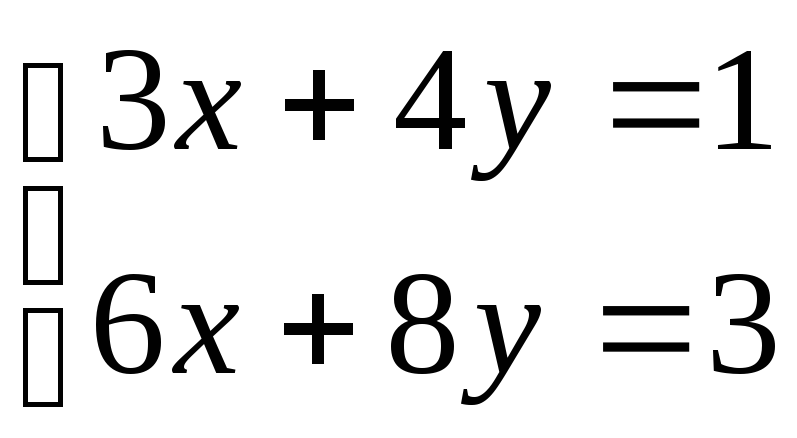 ; 4.
; 4. ;
;
5.  ; 6.
; 6.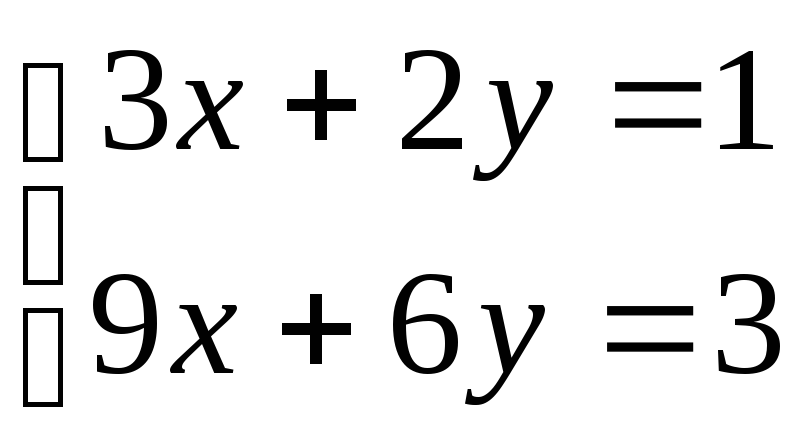 ;
;
7.  ; 8.
; 8.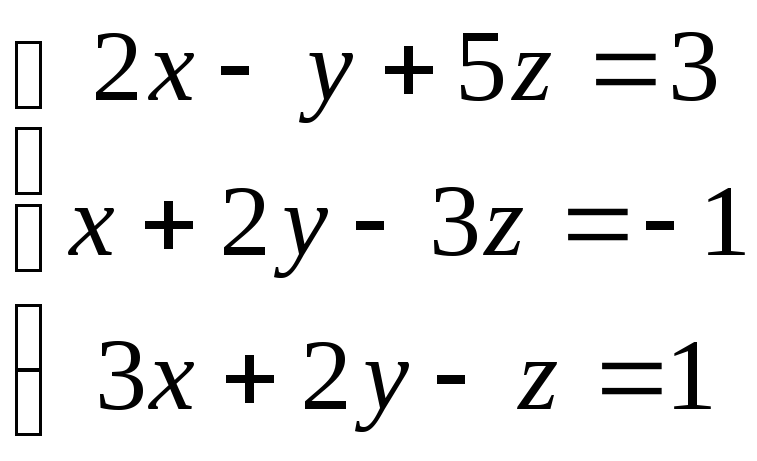 ;
;
9.  ; 10.
; 10. ;
;
11. 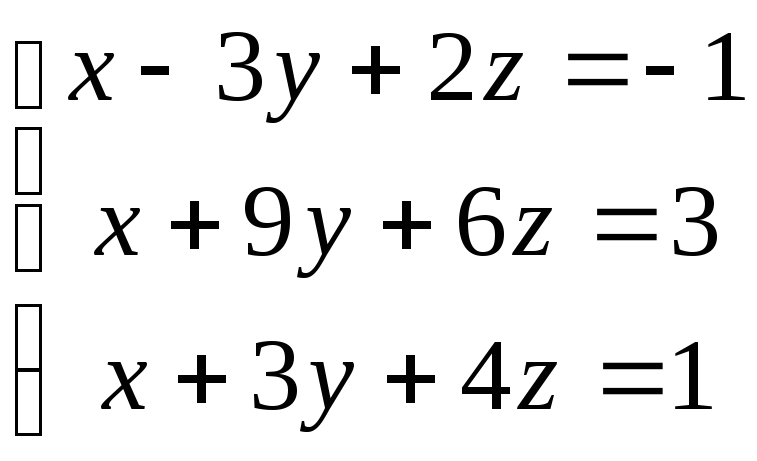 ; 12.
; 12. ;
;
13. 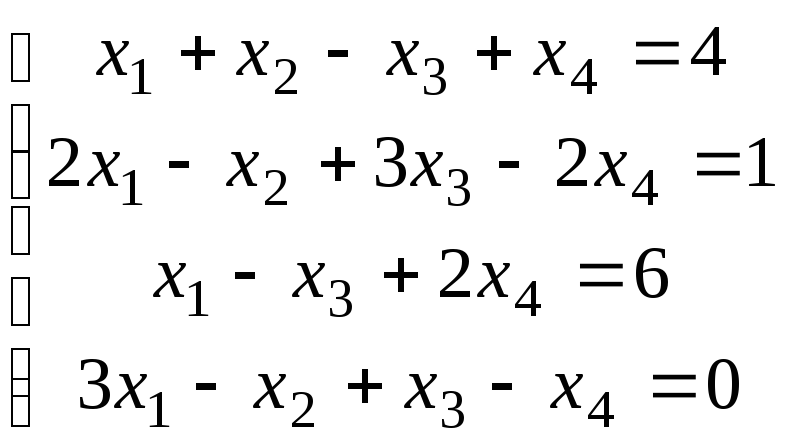 ;
14.
;
14. 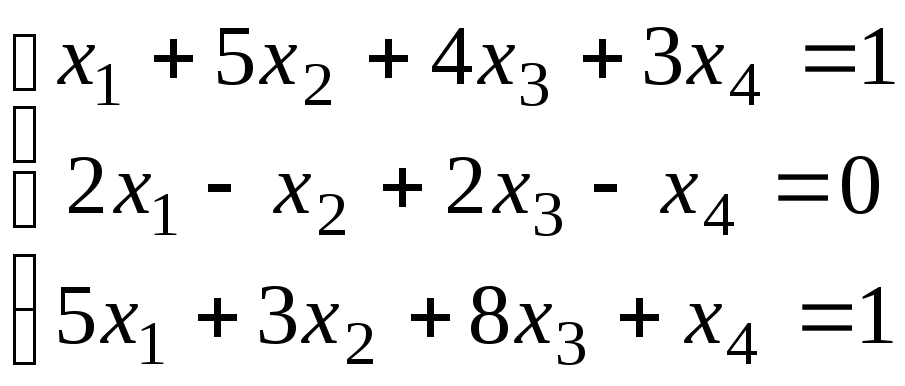 ;
;
15.  .
.
Определите, при
каких значениях  и
и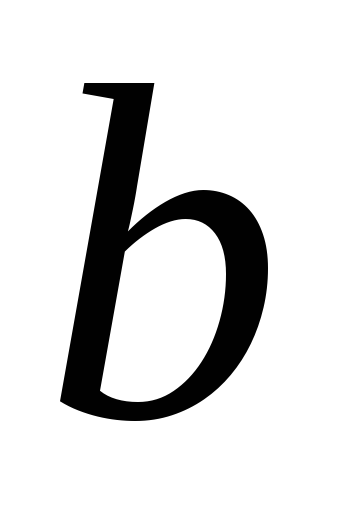 система уравнений
система уравнений
а) имеет единственное решение;
б) не имеет решения;
в) имеет бесконечно много решений.
16.  ; 17.
; 17. ;
;
Найти все решения следующих однородных систем:
18.  ; 19.
; 19.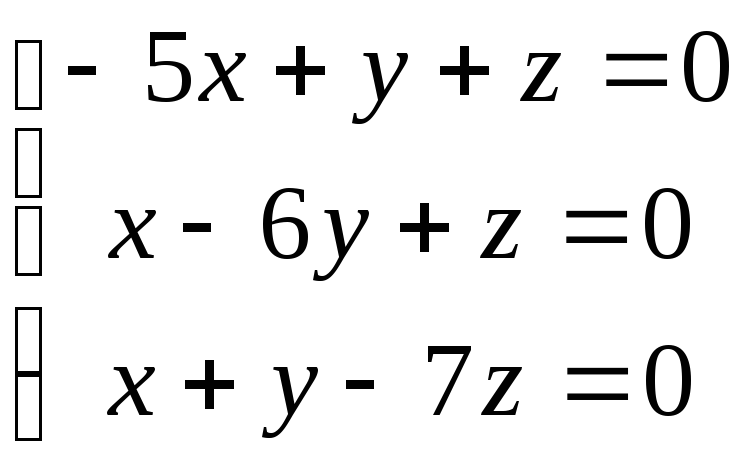 ;
;
20.  ; 21.
; 21.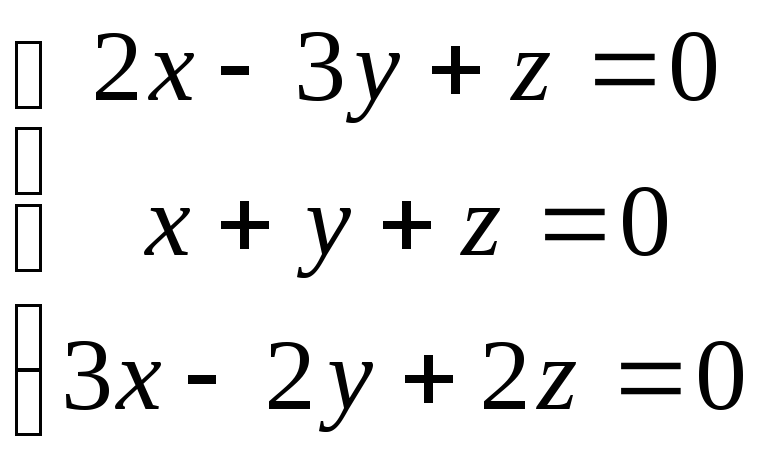 ;
;
22.  ; 23.
; 23.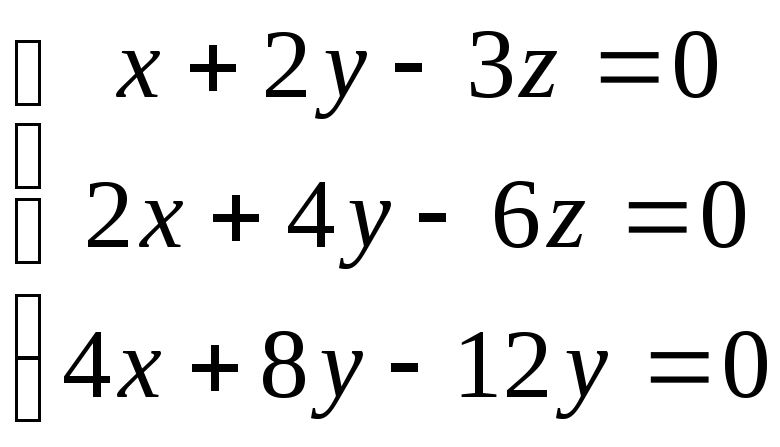 ;
;
Ответы к примерам
1. 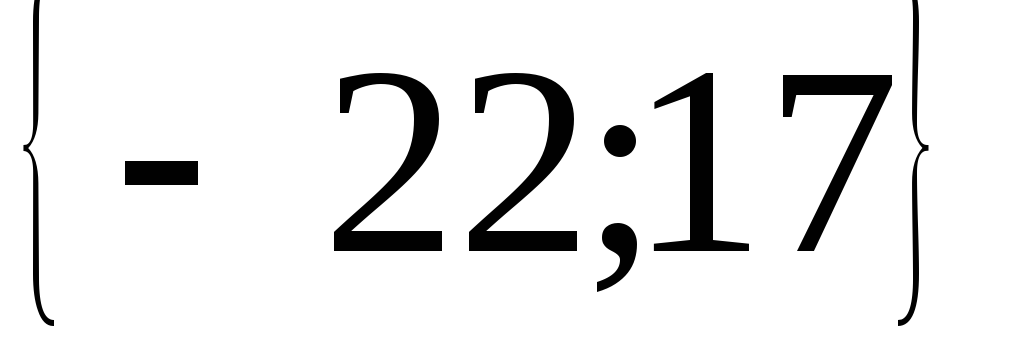 ; 2.
; 2. ; 3.
Ǿ; 4. Ǿ;
; 3.
Ǿ; 4. Ǿ;
5. 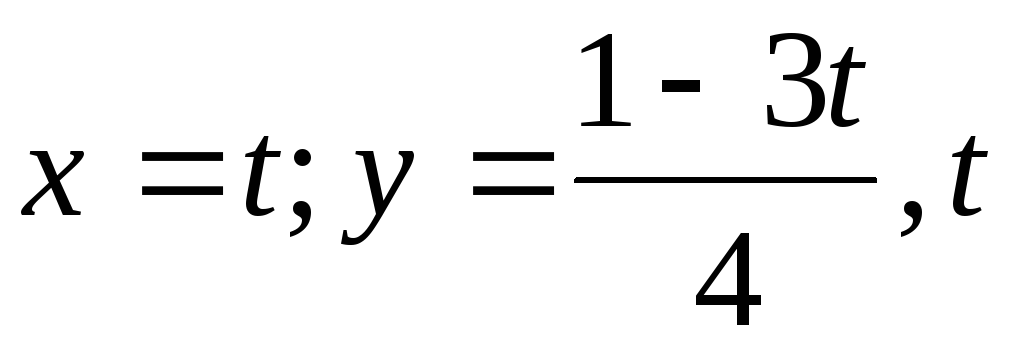 — произвольное число.
— произвольное число.
6.  ,
где
,
где — произвольное число.
— произвольное число.
7. 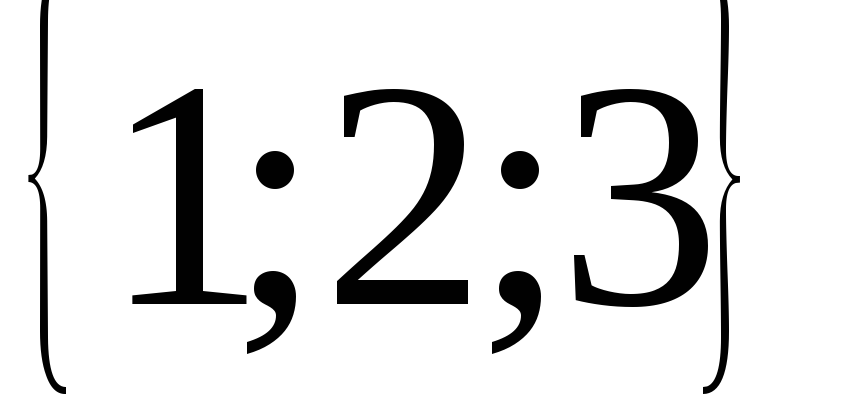 ; 8.
; 8.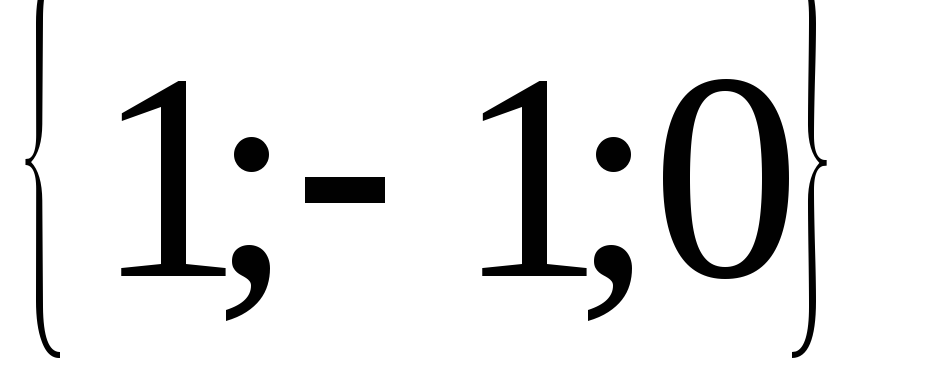 ; 9.
Ǿ; 10. Ǿ;
; 9.
Ǿ; 10. Ǿ;
11. 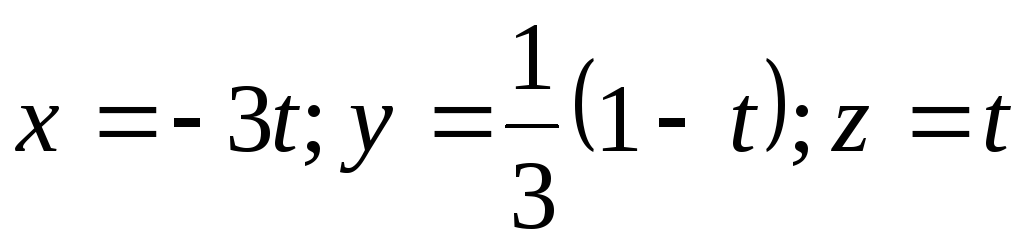 ,
где
,
где — произвольное число.
— произвольное число.
12. 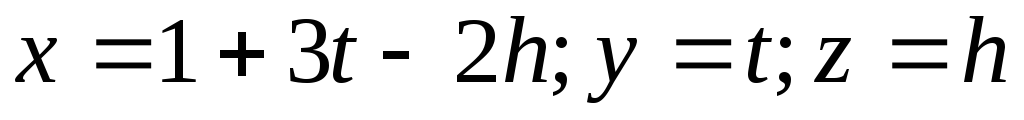 ,
где
,
где и
и — произвольные числа.
— произвольные числа.
13. 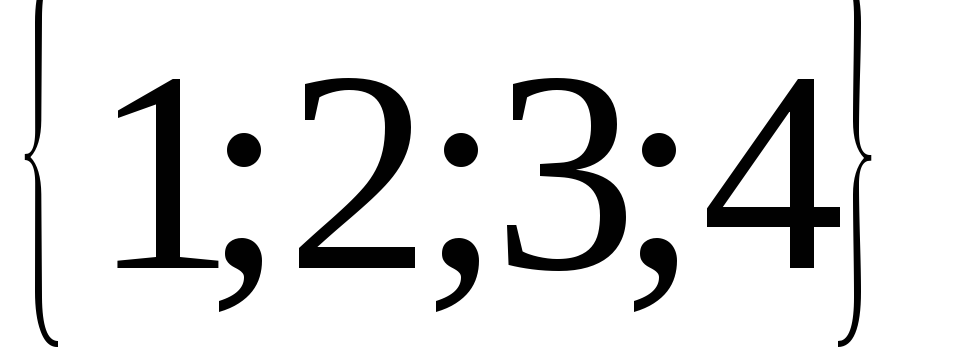 ; 14.
; 14. где
где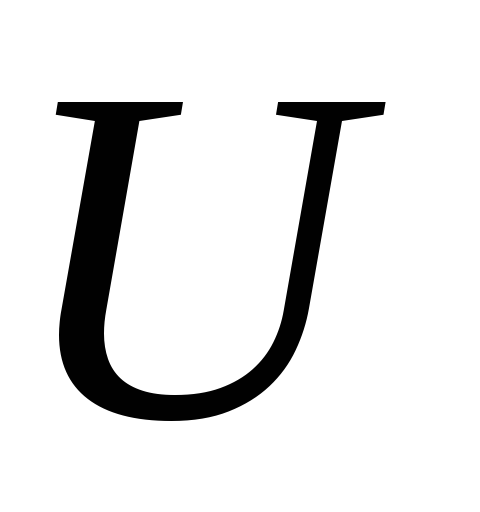 и
и — произвольные числа.
— произвольные числа.
15. Ǿ; 16. а)  ;
б)
;
б)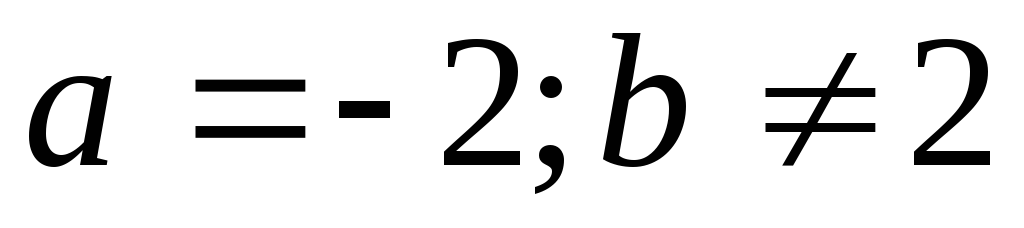 ;
в)
;
в)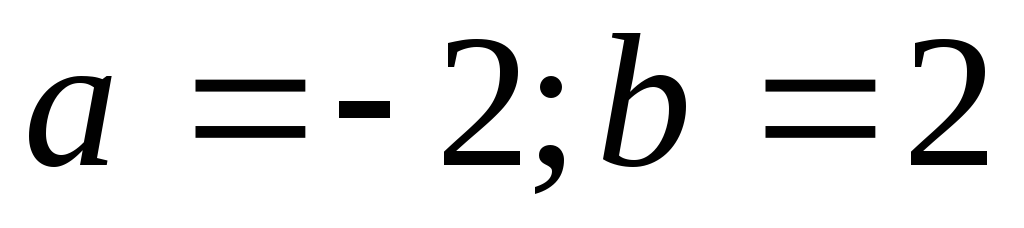 .
.
17. а) 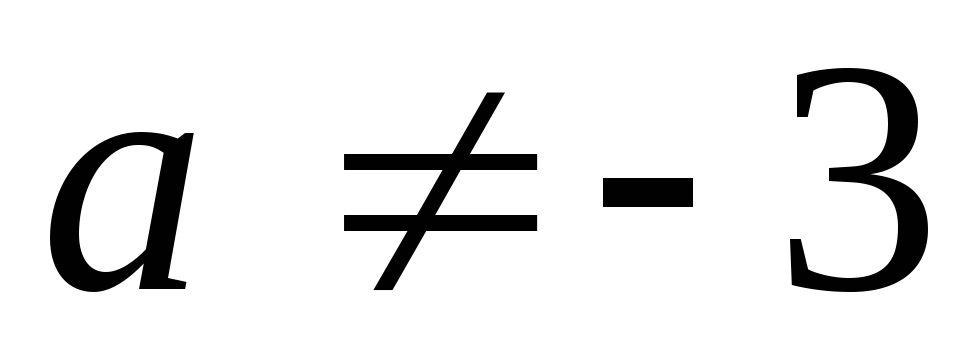 ;
б)
;
б)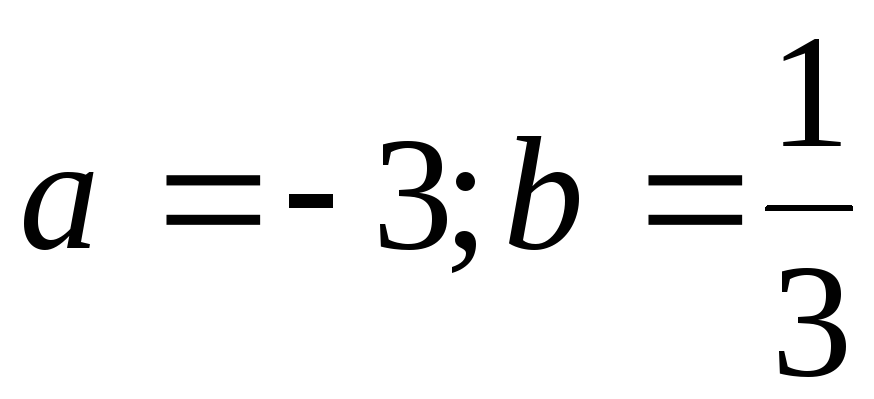 ;
в)
;
в)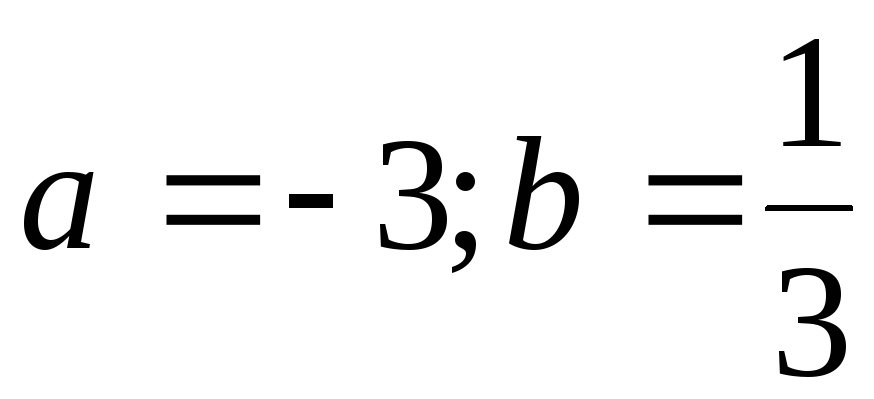 ;
;
18. 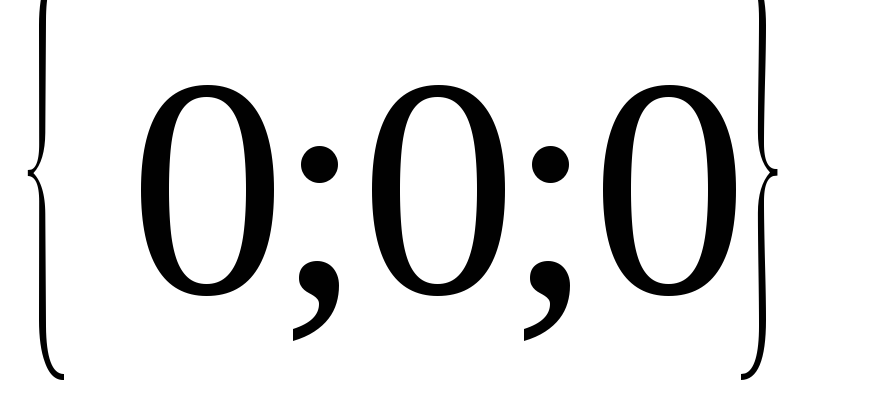 ; 19.
; 19.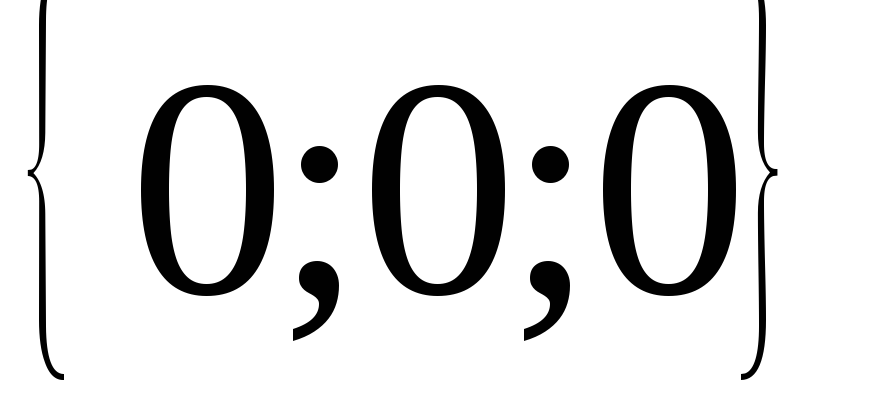 ; 20.
; 20.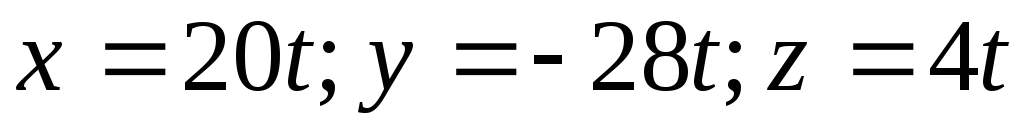 ,
где
,
где — произвольное число.
— произвольное число.
21. 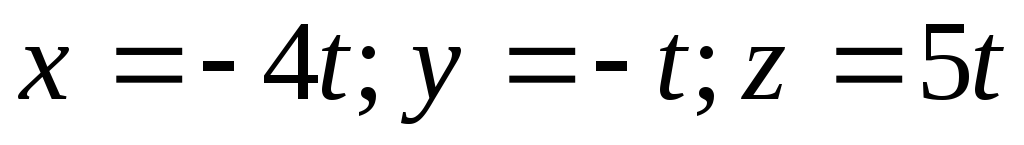 ,
где
,
где — произвольное число.
— произвольное число.
22.  ,
где
,
где — произвольное число.
— произвольное число.
23.  ,
где
,
где и
и — произвольные числа.
— произвольные числа.
studfile.net
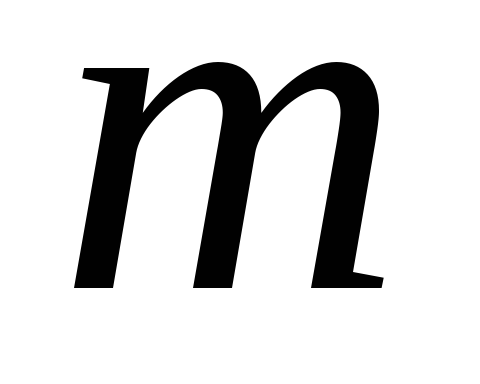 линейных уравнений с
линейных уравнений с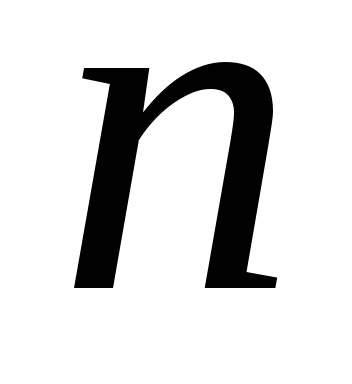 неизвестными
неизвестными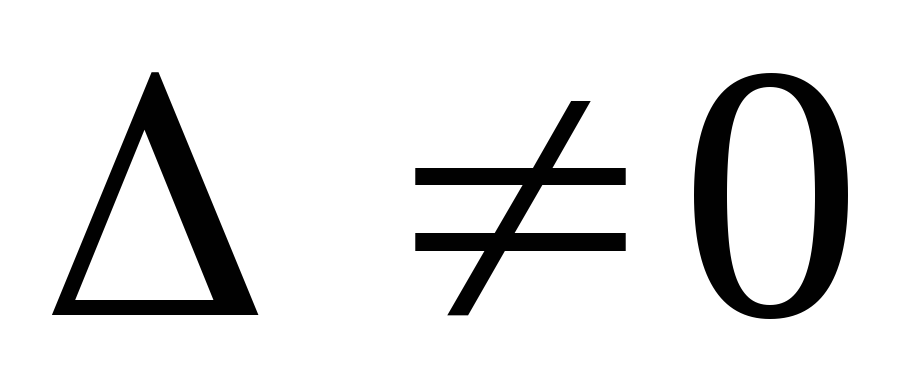 ,
то система имеет единственное решение,
которое может быть найдено по формулам
Крамера.
,
то система имеет единственное решение,
которое может быть найдено по формулам
Крамера.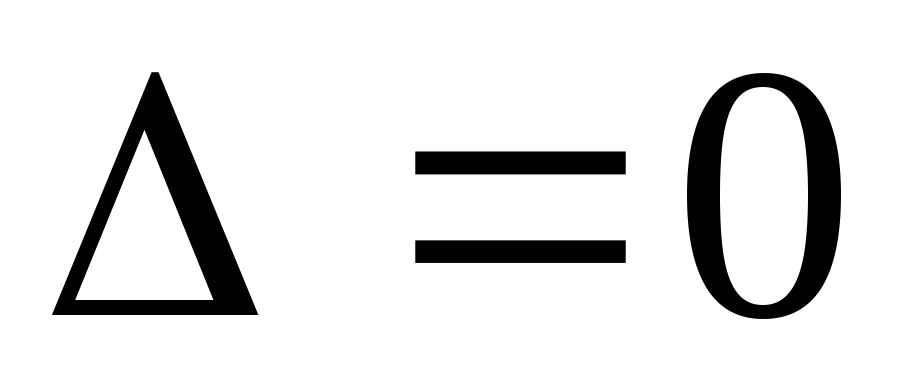 ,
то правило Крамера неприменимо. В этом
случае система может иметь бесчисленное
множество решений, если
,
то правило Крамера неприменимо. В этом
случае система может иметь бесчисленное
множество решений, если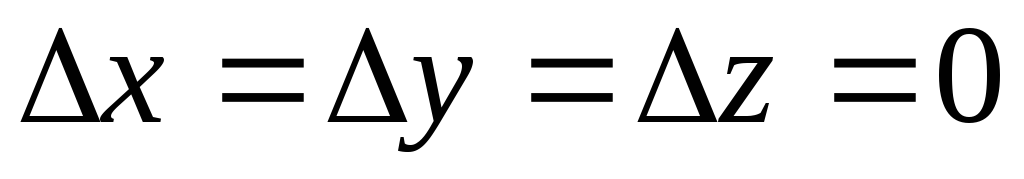 или не иметь их, если хотя бы один из
определителей
или не иметь их, если хотя бы один из
определителей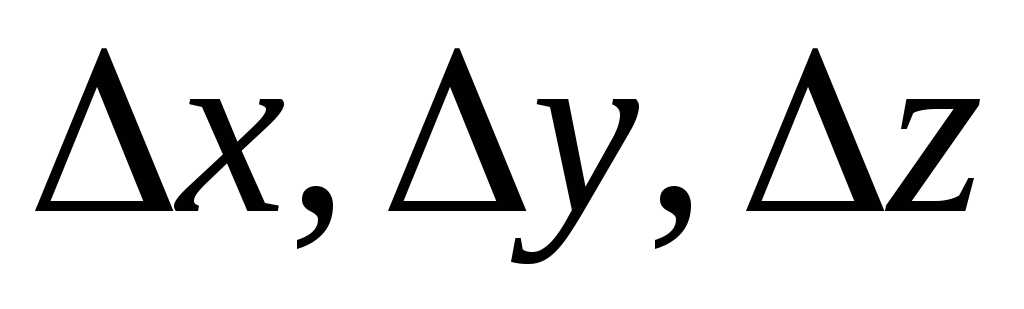 не равен нулю.
не равен нулю. уравнений с
уравнений с неизвестными
неизвестными