Фибоначчиева система счисления — Википедия
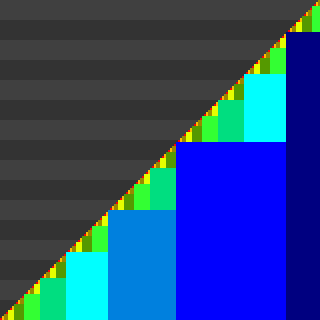
Фибоначчиева система счисления — смешанная система счисления для целых чисел на основе чисел Фибоначчи F2=1, F3=2, F4=3, F5=5, F6=8 и т. д.
 | ||
| Число | Запись в | Код Фибоначчи |
|---|---|---|
| 0 | 0……0 | |
| F2=1 | 1 | 11 |
| F3=2 | 10 | 011 |
| F4=3 | 100 | 0011 |
| 4 | 101 | |
| F5=5 | 1000 | 00011 |
| 6 | 1001 | 10011 |
| 7 | 1010 | 01011 |
| F6=8 | 10000 | 000011 |
| … | ||
| Fn − 1 | 101010… | …0101011 |
| Fn | 10……00 | 00……011 |
| Fn + 1 | 10……01 | 10……011 |
Любое неотрицательное целое число a{\displaystyle a} можно единственным образом представить последовательностью битов …εk…ε4ε3ε2 (εk∈{0,1}{\displaystyle \varepsilon _{k}\in \{0,1\}}) так, что a=∑kεkFk{\displaystyle a=\sum _{k}\varepsilon _{k}F_{k}}, причём последовательность {ε k} содержит лишь конечное число единиц, и не имеет пар соседних единиц: ∀k≥2:(εk=1)⇒(εk+1=0){\displaystyle \forall k\geq 2:(\varepsilon _{k}=1)\Rightarrow (\varepsilon _{k+1}=0)}. За исключением последнего свойства, данное представление аналогично двоичной системе счисления.
Обоснование[править | править код]
В основе лежит теорема Цекендорфа[1] — любое неотрицательное целое число единственным образом представимо в виде суммы некоторого набора чисел Фибоначчи с индексами больше единицы, не содержащего пар соседних чисел Фибоначчи.
Доказательство существования легко провести по индукции. Любое целое число a≥1{\displaystyle a\geq 1} попадёт в промежуток между двумя соседними числами Фибоначчи, то есть для некоторого n≥2{\displaystyle n\geq 2} верно неравенство: Fn≤a<Fn+1{\displaystyle F_{n}\leq a<F_{n+1}}. Таким образом, a=Fn+a′{\displaystyle a=F_{n}+a’}, где a′=a−Fn < Fn−1{\displaystyle a’=a-F_{n}\ <\ F_{n-1}}, так что разложение числа a′{\displaystyle a’} уже не будет содержать слагаемого Fn−1{\displaystyle F_{n-1}}.
Использование[править | править код]
Юпана[править | править код]

Предполагают, что некоторые разновидности юпаны (абака инков) использовали фибоначчиеву систему счисления, чтобы минимизировать необходимое для вычислений число зёрен[2].
В теории информации[править | править код]
На основе фибоначчиевой системы счисления строится код (кодирование) Фибоначчи — универсальный код для натуральных чисел (1, 2, 3…), использующий последовательности битов. Поскольку комбинация 11 запрещена в фибоначчиевой системе счисления, её можно использовать как маркер конца записи.
Для составления кода Фибоначчи по записи числа в фибоначчиевой системе счисления следует переписать цифры в обратном порядке (так, что старшая единица оказывается последним символом) и приписать в конце ещё раз 1 (см. таблицу). То есть, кодовая последовательность имеет вид:
- ε2ε3…εn1,
где n — номер самого старшего разряда с единицей.
Арифметика[править | править код]
Сложение чисел в позиционных системах счисления выполняется с использованием переноса, позволяющего устранять последствия переполнения разряда. Например, в двоичной системе: 01 + 01 = 02 = 10.
В фибоначчиевой системе счисления дело обстоит сложнее:
- Во-первых, вес старших разрядов не является кратным весу разряда, из которого требуется перенос. При сложении двух единиц в одном разряде требуется перенос не только влево, но и вправо: 0200 = 1001. При переносе в отсутствующие разряды ε1 и ε0 следует помнить, что F1=1=F2 и F0=0.
- Во-вторых, требуется избавляться от соседних единиц: 011 = 100. Правило для раскрытия двоек является следствием этого равенства: 0200 = 0100 + 0011 = 0111 = 1001.
| Число | Представление через степени φ{\displaystyle \varphi } |
|---|---|
| 1 | 1 |
| 2 | 10,01 |
| 3 | 100,01 |
| 4 | 101,01 |
| 5 | 1000,1001 |
| 6 | 1010,0001 |
| 7 | 10000,0001 |
| 8 | 10001,0001 |
| 9 | 10010,0101 |
| 10 | 10100,0101 |
| 11 | 10101,0101 |
| 12 | 100000,101001 |
| 13 | 100010,001001 |
| 14 | 100100,001001 |
Похожее устройство имеет позиционная система счисления с иррациональным основанием, равным золотому сечению φ=(1+5)/2{\displaystyle \varphi =(1+{\sqrt {5}})/2}.
Любое вещественное число x из отрезка [0,1] допускает разложение в ряд через отрицательные степени золотого сечения:
- x=∑k=−1−∞εkφk,εk∈{0,1}{\displaystyle x=\sum _{k=-1}^{-\infty }\varepsilon _{k}\varphi ^{k},\qquad \varepsilon _{k}\in \{0,1\}}
где {εk}{\displaystyle \left\{\varepsilon _{k}\right\}} обладает тем же свойством отсутствия соседних единиц. Коэффициенты находятся последовательным сравнением x с φ−1{\displaystyle \varphi ^{-1}} — золотым сечением отрезка [0,1], вычитанием φ−1{\displaystyle \varphi ^{-1}} (если εk=1{\displaystyle \varepsilon _{k}=1}) и умножением на φ{\displaystyle \varphi }. Из этого нетрудно видеть, что любое неотрицательное вещественное число допускает разложение:
- a=∑k=N−1−∞εkφk,{\displaystyle a=\sum _{k=N-1}^{-\infty }\varepsilon _{k}\varphi ^{k}\,,}
где N таково, что a<φN{\displaystyle a<\varphi ^{N}}. Разумеется, следует считать, что εk=0{\displaystyle \varepsilon _{k}=0} для всех k⩾N{\displaystyle k\geqslant N}.
Эти формулы полностью аналогичны формулам для обычных позиционных систем с целыми основаниями. Оказывается, что любое неотрицательное целое число (и, более общо, всякий неотрицательный элемент кольца Z+φZ{\displaystyle {\mathbb {Z} }+\varphi {\mathbb {Z} }}) имеет представление лишь с конечным количеством единиц, то есть в виде конечной суммы неповторяющихся степеней золотого сечения.[3]
Аналогия между числами Фибоначчи и степенями золотого сечения основана на одинаковой форме тождеств:
- Fk=Fk−1+Fk−2{\displaystyle F_{k}=F_{k-1}+F_{k-2}}
- φk=φk−1+φk−2{\displaystyle \varphi ^{k}=\varphi ^{k-1}+\varphi ^{k-2}}
позволяющих устранение соседних единиц. Прямой связи между представлением натуральных чисел в системе золотого сечения и в фибоначчиевой не имеется.
Правила сложения аналогичны показанным выше с той поправкой, что перенос в сторону младших разрядов распространяется без ограничения. В данной системе счисления можно производить и умножение.
Для целых чисел a=∑kεkFk {\displaystyle a=\sum _{k}\varepsilon _{k}F_{k}\ } и b=∑lζlFl {\displaystyle b=\sum _{l}\zeta _{l}F_{l}\ } можно определить «умножение»[4]
- a∘b=∑k,lεkζlFk+l,{\displaystyle a\circ b=\sum _{k,l}\varepsilon _{k}\zeta _{l}F_{k+l},}
которое аналогично умножению чисел в двоичной системе счисления.
Разумеется, данная операция не является настоящим умножением чисел, и выражается формулой:[5]
- a∘b=3ab−a⌊(b+1)φ−2⌋−b⌊(a+1)φ−2⌋,{\displaystyle a\circ b=3ab-a\lfloor (b+1)\varphi ^{-2}\rfloor -b\lfloor (a+1)\varphi ^{-2}\rfloor ,}
где ⌊⋅⌋{\displaystyle \lfloor \cdot \rfloor } — целая часть, φ=1+52{\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}} — золотое сечение.
Эта операция обладает ассоциативностью, на что впервые обратил внимание Дональд Кнут[6]. Следует отметить, что другое «произведение» ∑k,lεkζlFk+l−2,{\displaystyle \sum _{k,l}\varepsilon _{k}\zeta _{l}F_{k+l-2},} отличающееся лишь сдвигом на два разряда, уже не является ассоциативным.
ru.wikipedia.org
Код Фибоначчи Википедия
Фибоначчиева система счисления — смешанная система счисления для целых чисел на основе чисел Фибоначчи F2=1, F3=2, F4=3, F5=5, F6=8 и т. д.
 | ||
| Число | Запись в | Фибоначчи |
|---|---|---|
| 0 | 0……0 | |
| F2=1 | 1 | 11 |
| F3=2 | 10 | 011 |
| F4=3 | 100 | 0011 |
| 4 | 101 | 1011 |
| F5=5 | 1000 | 00011 |
| 6 | 1001 | 10011 |
| 7 | 1010 | 01011 |
| F6=8 | 10000 | 000011 |
| … | ||
| Fn − 1 | 101010… | …0101011 |
| Fn | 10……00 | 00……011 |
| Fn + 1 | 10……01 | 10……011 |
Представление натуральных чисел[ | ]
Любое неотрицательное целое число a{\displaystyle a} можно единственным образом представить последовательностью битов …εk…ε4ε3ε2 (εk∈{0,1}{\displaystyle \varepsilon _{k}\in \{0,1\}}) так, что a=∑kεkFk{\displaystyle a=\sum _{k}\varepsilon _{k}F_{k}}, причём последовательность {εk} содержит лишь конечное число единиц, и не имеет пар соседних единиц: ∀k≥2:(εk=1)⇒(εk+1=0){\displaystyle \forall k\geq 2:(\varepsilon _{k}=1)\Rightarrow (\varepsilon _{k+1}=0)}. За исключением последнего свойства, данное представление аналогично двоичной системе счисления.
Обоснование[ | ]
В основе лежит теорема Цекендорфа[1] — любое неотрицательное целое число единственным образом представимо в виде суммы некоторого набора чисел Фибоначчи с индекс
ru-wiki.ru
Фибоначчи — Википедия
Леона́рдо Пиза́нский (лат. Leonardus Pisanus, итал. Leonardo Pisano, около 1170 года, Пиза — около 1250 года, там же) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи.
Отец Фибоначчи по торговым делам часто бывал в Алжире, и Леонардо изучал там математику у арабских учителей. Позже Фибоначчи посетил Египет, Сирию, Византию, Сицилию. Он ознакомился с достижениями античных и индийских математиков в арабском переводе. На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки. Труд Леонардо Фибоначчи «Книга абака» способствовал распространению в Европе позиционной системы счисления, более удобной для вычислений, чем римская нотация; в этой книге были подробно исследованы возможности применения индийских цифр, ранее остававшиеся неясными, и даны примеры решения практических задач, в частности, связанных с торговым делом[1]. Позиционная система приобрела в Европе популярность в эпоху Возрождения[2].
Леонардо Пизанский никогда не называл себя Фибоначчи; этот псевдоним был дан ему позднее, предположительно Гийомом Либри (Guglielmo Libri Carucci dalla Sommaja) в 1838 году. Слово Fibonacci — сокращение от двух слов «filius Bonacci», появившихся на обложке «Книги абака»; они могли означать либо «сын Боначчо», либо, если интерпретировать слово Боначчи как фамилию, «сын Боначчи». Согласно третьей версии, само слово Боначчи нужно тоже понимать как прозвище, означавшее «удачливый». Сам он обычно подписывался Боначчи; иногда он использовал также имя Леонардо Биголло — слово bigollo на тосканском наречии значило «странник», а также «бездельник»[3][4].
Фибоначчи родился в итальянском городе Пиза, предположительно в 1170-е годы (в некоторых источниках стоит 1180 год). Его отец, Гильермо, был торговцем. В 1192 году он был назначен представлять пизанскую торговую колонию в Северной Африке и часто бывал в Беджаи, Алжир. По желанию отца, который хотел, чтобы Леонардо стал хорошим торговцем, он переехал в Алжир и изучал там математику (искусство вычислений) у арабских учителей. Позже Фибоначчи посетил Египет, Сирию, Византию, Сицилию[5].
В 1200 году Леонардо вернулся в Пизу и принялся за написание своего первого труда «Книги абака»[5]. В то время в Европе о позиционной системе счисления и арабских цифрах знали очень немногие. В своей книге Фибоначчи всячески поддерживал индийские приёмы вычисления и методы[6]. По словам историка математики А. П. Юшкевича, «„Книга абака“ резко возвышается над европейской арифметико-алгебраической литературой XII—XIV веков разнообразием и силой методов, богатством задач, доказательностью изложения… Последующие математики широко черпали из неё как задачи, так и приёмы их решения». По первой книге многие поколения европейских математиков изучали индийскую позиционную систему счисления[6].
Книга заинтересовала императора Фридриха II и его придворных, среди которых был астролог Микаель Скотус (Michael Scotus), философ Теодорус Физикус (Theodorus Physicus) и Доминикус Хиспанус (Dominicus Hispanus). Последний предложил, чтобы Леонардо пригласили ко двору в одно из посещений императором Пизы около 1225 года, где ему задавал задачи Иоган Палермский, ещё один придворный философ Фридриха II. Некоторые из этих задач появились в последующих работах Фибоначчи
Несколько лет Фибоначчи жил при дворе императора. К этому времени относится его работа «Книга квадратов», написанная в 1225 году. Книга посвящена диофантовым уравнениям второй степени и ставит Фибоначчи в один ряд с такими учёными, развивавшими теорию чисел, как Диофант и Ферма[7]. Единственное упоминание о Фибоначчи после 1228 года относится к 1240 году, когда ему в Пизанской республике была назначена пенсия за заслуги перед городом[4].
Прижизненных портретов Фибоначчи не сохранилось, а существующие являются современными представлениями о нём. Леонардо Пизанский не оставил практически никаких автобиографических сведений; единственным[9] исключением является второй абзац «Книги абака», где Фибоначчи излагает причины, побудившие его написать книгу:
Когда отцу моему была назначена должность таможенного чиновника, заведовавшего в Беджайе делами стекавшихся к нему пизанских торговцев, он в отрочестве моём призвал меня к себе и предложил несколько дней учиться счётному искусству, сулившему немало удобств и выгод для моего будущего. Наученный благодаря мастерству учителей основам индийского счёта, я приобрёл большую любовь к этому искусству и заодно узнал, что кое-что об этом предмете известно среди египтян, сирийцев, греков, сицилийцев и провансальцев, развивших свои методы. Позже, во время торговых путешествий по всем этим краям, я посвятил много труда подробному изучению их методов и, кроме того, овладел искусством научного спора. Однако по сравнению с методом индийцев все построения этих людей, включая подход алгорисмиков и учение Пифагора, кажутся почти заблуждениями, а потому я решил, изучив как можно внимательнее индийский метод, изложить его в пятнадцати главах настолько понятно, насколько смогу, с добавлениями от собственного разума и с кое-какими полезными примечаниями из геометрии Евклида, вставленными по ходу сочинения. Дабы пытливый читатель мог изучить индийский счёт наиболее вдумчивым образом, я сопроводил почти каждое утверждение убедительным доказательством; рассчитываю, что латинский народ отныне не будет лишён самых точных сведений об искусстве вычислений. Если же, паче чаяния, я пропустил что-то более или менее важное, а может быть, необходимое, то молю о прощении, ибо нет среди людей никого, кто был бы безгрешен или обладал способностью всё предвидеть.
Оригинальный текст (лат.)
Cum genitor meus a patria publicus scriba in duana bugee pro pisanis mercatoribus ad eam confluentibus constitutus preesset, me in pueritia mea ad se venire faciens, inspecta utilitate et commoditate futura, ibi me studio abbaci per aliquot dies stare voluit et doceri. Vbi ex mirabili magisterio in arte per novem figuras indorum introductus, scientia artis in tantum mihi pre ceteris placuit, et intellexi ad illam quod quicquid studebatur ex ea apud egyptum, syriam, greciam, siliciam, et provinciam cum suis variis modis, ad que loca negotiationis causa postea peragravi per multum studium et disputationis didici conflictum. Sed hoc totum etiam, et algorismum atque artem pictagore quasi errorem computavi respectu modi indorum. Quare, amplectens strictius ipsum modum indorum et attentius studems in eo, ex proprio sensu quedam addens et quedem etiam ex subtilitatibus euclidis geometrice artis apponens, summam huius libri, quam intelligibilius potui, in quindecim capitulis distinctam componere laboravi, fere omnia que inserui certa probatione ostendens, ut extra perfecto pre ceteris modo hanc scientiam appetentes instruantur, et gens latina de cetero, sicut hactenus, absque illa minime inveniatur. Si quid forte minus aut plus iusto vel necessario intermisi, mihi deprecor indulgeatur, cum nemo sit qui vitio careat et in omnibus undique sit circumspectus.
Однако точный смысл этого абзаца нельзя считать полностью известным, потому что его текст, как и весь латинский текст книги, дошёл до нас с ошибками, внесёнными переписчиками.[10][11]

Значительную часть усвоенных им знаний он изложил в своей «Книге абака» (Liber abaci, 1202 год; до наших дней сохранилась только дополненная рукопись 1228 года)[2]. Эта книга состоит из 15 глав и содержит почти все арифметические и алгебраические сведения того времени, изложенные с исключительной полнотой и глубиной. Первые пять глав книги посвящены арифметике целых чисел на основе десятичной нумерации. В VI и VII главе Леонардо излагает действия над обыкновенными дробями. В VIII—X главах изложены приёмы решения задач коммерческой арифметики, основанные на пропорциях. В XI главе рассмотрены задачи на смешение. В XII главе приводятся задачи на суммирование рядов — арифметической и геометрической прогрессий, ряда квадратов и, впервые в истории математики, возвратного ряда, приводящего к последовательности так называемых чисел Фибоначчи. В XIII главе излагается правило двух ложных положений и ряд других задач, приводимых к линейным уравнениям. В XIV главе Леонардо на числовых примерах разъясняет способы приближённого извлечения квадратного и кубического корней. Наконец, в XV главе собран ряд задач на применение теоремы Пифагора и большое число примеров на квадратные уравнения. Леонардо впервые в Европе использовал отрицательные числа, которые рассматривал как долг[6]. Книга посвящена Микаелю Скотусу[4].
Другая книга Фибоначчи, «Практика геометрии» (Practica geometriae, 1220 год), состоит из семи частей и содержит разнообразные теоремы с доказательствами, относящиеся к измерительным методам. Наряду с классическими результатами Фибоначчи приводит свои собственные — например, первое доказательство того, что три медианы треугольника пересекаются в одной точке (Архимеду этот факт был известен, но если его доказательство и существовало, до нас оно не дошло). Среди землемерных приёмов, которым посвящён последний раздел книги, — использование определённым образом размеченного квадрата для определения расстояний и высот. Для определения числа π{\displaystyle \pi } Фибоначчи использует периметры вписанного и описанного 96-угольника, что приводит его к значению 3,1418{\displaystyle 3,1418}[6]. Книга была посвящена Доминикусу Хиспанусу[4]. В 1915 году Р. С. Арчибальд занимался восстановлением утерянной работы Евклида о делении фигур, базируясь на «Практике геометрии» Фибоначчи и французском переводе арабской версии[10].
В трактате «Цветок» (Flos, 1225 год) Фибоначчи исследовал кубическое уравнение x3+2×2+10x=20{\displaystyle x^{3}+2x^{2}+10x=20}, предложенное ему Иоанном Палермским на математическом состязании при дворе императора Фридриха II[6]. Сам Иоанн Палермский почти наверняка заимствовал это уравнение из трактата Омара Хайяма «О доказательствах задач алгебры», где оно приводится как пример одного из видов в классификации кубических уравнений. Леонардо Пизанский исследовал это уравнение, показав, что его корень не может быть рациональным или же иметь вид одной из квадратичных иррациональностей, встречающихся в X книге Начал Евклида, а затем нашёл приближённое значение корня в шестидесятеричных дробях, равное 1;22,07,42,33,04,40[7], не указывая, однако, способа своего решения[4].
«Книга квадратов» (Liber quadratorum, 1225 год) содержит ряд задач на решение неопределённых квадратных уравнений. Фибоначчи работал над поиском чисел, которые, будучи добавленными к квадратному числу, вновь дадут квадратное число. Он отметил, что числа x2+y2{\displaystyle x^{2}+y^{2}} и x2−y2{\displaystyle x^{2}-y^{2}} не могут быть квадратными одновременно[7], а также использовал для поиска квадратных чисел формулу x2+(2x+1)=(x+1)2{\displaystyle x^{2}+(2x+1)=(x+1)^{2}}[4]. В одной из задач книги, также первоначально предложенной Иоанном Палермским, требовалось найти рациональное квадратное число, которое, будучи увеличено или уменьшено на 5, вновь даёт рациональные квадратные числа[6].
Среди не дошедших до нас произведений Фибоначчи трактат Di minor guisa по коммерческой арифметике, а также комментарии к книге X «Начал» Евклида[4].
Оставаясь верным математическим турнирам, основную роль в своих книгах Фибоначчи отводит задачам, их решениям и комментариям. Задачи на турниры предлагал как сам Фибоначчи, так и его соперник, придворный философ Фридриха II Иоган Палермский[8]. Задачи Фибоначчи, как и их аналоги, продолжали использовать в различных математических учебниках несколько столетий. Их можно встретить в «Сумме арифметики» Пачиоли (1494), в «Приятных и занимательных задачах» Баше де Мизириака (1612), в «Арифметике» Магницкого (1703), в «Алгебре» Эйлера (1768)[2].
Задача о размножении кроликов[править | править код]
В место, огороженное со всех сторон стеной, поместили пару кроликов, природа которых такова, что любая пара кроликов производит на свет другую пару каждый месяц, начиная со второго месяца своего существования. Сколько пар кроликов будет через год? (Ответ: 233 пары). Для поиска ответа используется рекуррентная числовая последовательность 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, … (по ней составлена последовательность A000045 в OEIS; отличие в том, что вторая последовательность начинается с нуля и единицы, а не с единицы и двойки), в которой каждое последующее число равно сумме двух предыдущих; ответом, в соответствии с условиями задачи, является тринадцатый член (завершение каждого месяца — это перескок к следующему члену последовательности; текущий член последовательности перед началом опыта — это первый; всего месяцев двенадцать). В честь учёного она носит название чисел Фибоначчи. Числа Фибоначчи нашли своё применение во многих областях математики. Одним из важных свойств последовательности является тот факт, что предел отношения an+1{\displaystyle a_{n+1}} к an{\displaystyle a_{n}} равен золотому сечению[2]. Наглядно формирование последовательности можно показать следующим образом:
1: 1 + 1 = 2 2: 1 + 2 = 3 3: 2 + 3 = 5 4: 3 + 5 = 8 5: 5 + 8 = 13 6: 8 + 13 = 21 7: 13 + 21 = 34 8: 21 + 34 = 55 9: 34 + 55 = 89 ... и т. д.
Задачи о гирях[править | править код]
Задача о выборе наилучшей системы гирь для взвешивания на рычажных весах[12][13] впервые была сформулирована именно Фибоначчи. Леонардо Пизанский предлагает два варианта задачи:
- Простой вариант: требуется найти пять гирь, с помощью которых можно найти все веса меньше 30, при этом гири можно класть только на одну чашу весов (Ответ: 1, 2, 4, 8, 16). Решение строится в двоичной системе счисления[2].
- Сложный вариант: требуется найти наименьшее число гирь, с помощью которого можно взвесить все веса меньше заданного (Ответ: 1, 3, 9, 27, 81,…). Решение строится в системе счисления по основанию три[2] и в общем случае представляет собой последовательность A000244 в OEIS.
Задачи по теории чисел[править | править код]
Кроме задачи о кроликах, Фибоначчи предлагал ряд других задач по теории чисел[10]:
- Найти число, которое делится на 7 и даёт в остатке единицу при делении на 2, 3, 4, 5 и 6; (Ответ: 301)
- Найти число, произведение которого с семёркой даёт остатки 1, 2, 3, 4, 5 при делении на 2, 3, 4, 5, 6, соответственно;
- Найти квадратное число (то есть число, равное квадрату целого числа), которое при увеличении или уменьшении на 5 давало бы квадратное число.
Некоторые другие задачи[править | править код]
- Найти число, 19/20 которого равно квадрату самого числа. (Ответ: 19/20)[2].
- Сплав из 30 весовых частей состоит из трёх металлов: первый металл достоинством по три монеты на одну часть, второй металл по две монеты на одну часть, а у третьего металла каждые две части стоят по одной монете; стоимость всего сплава 30 монет. Сколько частей каждого металла содержит сплав? (Ответ: 3 части первого металла, 5 частей второго металла, 22 части третьего). В таких терминах Фибоначчи переформулировал известную задачу о птицах, в которой были использованы те же самые числа (30 птиц трёх разных видов стоят 30 монет, по заданным ценам найти количество птиц каждого вида)[6].
- «Шуточная задача о семи старухах», которые шли в Рим, и у каждой было по семь мулов, на каждом из которых по семь мешков, в каждом из которых по семь хлебов, в каждом из которых по семь ножей, каждый из которых в семи ножнах. Нужно найти общее число предметов. Эта задача обошла много стран, первое известное упоминание о ней было ещё в Древнем Египте в папирусе Ахмеса. (Ответ: 137 256)[2][6].
 Памятник Фибоначчи в Пизе
Памятник Фибоначчи в ПизеВ XIX веке в Пизе был поставлен памятник учёному. Ранее статуя стояла в Giardino Scotto, а после того, как в 1978 году Франк Джонсон нарисовал портрет Фибоначчи с этой статуи, она была перенесена на кладбище Кампосанто, расположенном в Пизе на Пьяцца деи Мираколи.
Именем Фибоначчи названы улицы в Пизе (Lungarno Fibonacci) и во Флоренции (Via Fibonacci). Кроме того, имя Фибоначчи носит ассоциация Fibonacci Association[14] и издаваемый ею научный журнал Fibonacci Quarterly[15], посвящённые числам Фибоначчи, проект Евросоюза в сфере образования[16], а также другие программы[10].
При покровительстве императора Леонардо Пизанский написал несколько книг[3][4][8]:
- «Книга абака» (Liber abaci), 1202 год, дополнена в 1228 году;
- «Практика геометрии» (Practica geometriae), 1220 год;
- «Цветок» (Flos) 1225 год;
- «Книга квадратов» (Liber quadratorum), 1225 год;
- Di minor guisa, утеряно;
- Комментарии к книге X «Начал» Евклида, утеряно;
- Письмо Теодорусу, 1225 год.
- ↑ N. Ambrosetti. L’eredità arabo-islamica nelle scienze e nelle arti del calcolo dell’Europa. — LED Edizioni Universitarie, 2008. — С. 220—221.
- ↑ 1 2 3 4 5 6 7 8 Карпушина Н. «Liber abaci» Леонардо Фибоначчи, Математика в школе, № 4, 2008.
- ↑ 1 2 A brief biographical sketch of Fibonacci, his life, times and mathematical achievements.
- ↑ 1 2 3 4 5 6 7 8 9 Leonardo Pisano Fibonacci
- ↑ 1 2 R.Knott, D.A.Quinney and PASS Maths The life and numbers of Fibonacci
- ↑ 1 2 3 4 5 6 7 8 История математики: в 3 т. / под редакцией А. П. Юшкевича. — М.: Наука, 1970. — Т. I: С древнейших времён до начала Нового времени. — С. 260—267.
- ↑ 1 2 3 4 Frances Carney Gies Leonardo Pisano//Энциклопедия Британника
- ↑ 1 2 3 Яглом И. М. Итальянский купец Леонардо Фибоначчи и его кролики. // Квант, 1984. № 7. С. 15-17
- ↑ [1] Treccani, l’Enciclopedia Italiana: Fibonacci, Leonardo (detto Leonardo Pisano)
- ↑ 1 2 3 4 EIGHT HUNDRED YEARS YOUNG// A. F. HORADAM
- ↑ RICHARD E.GRIMM//THE AUTOBIOGRAPHY OF LEONARDO PISANO
- ↑ А. П. Стахов. Две знаменитые задачи Фибоначчи http://www.goldenmuseum.com/1001TwoProblems_rus.html Архивная копия от 16 декабря 2010 на Wayback Machine
- ↑ Леонардо Пизано Фибоначчи http://www.xfibo.ru/fibonachi/leonardo-pisano-fibonacci.htm Архивная копия от 8 апреля 2014 на Wayback Machine
- ↑ The Fibonacci Association Архивировано 8 июня 2007 года.
- ↑ Fibonacci Quarterly
- ↑ Fibonacci Project
- Щетников А. И. К реконструкции итерационного метода решения кубических уравнений в средневековой математике. Труды третьих Колмогоровских чтений. Ярославль: Изд-во ЯГПУ, 2005, с. 332—340.
- Glushkov S. On approximation methods of Leonardo Fibonacci. Historia Mathematica, 3, 1976, p. 291—296.
- Sigler, L. E. Fibonacci’s Liber Abaci, Leonardo Pisano’s Book of Calculations» Springer. New York, 2002, ISBN 0-387-40737-5.
ru.wikipedia.org
Кодирование Фибоначчи | Портал информатики для гиков
Кодирование Фибоначчи кодирует целое число в двоичное число с использованием представления числа Фибоначчи. Идея основана на теореме Цекендорфа, которая гласит, что каждое положительное целое число может быть записано однозначно в виде суммы различных несмежных чисел Фибоначчи (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 141, …… ..).
Кодовое слово Фибоначчи для конкретного целого числа — это в точности целочисленное представление Цекендорфа с обратным порядком его цифр и добавлением дополнительной «1» в конце. Дополнительная 1 добавляется для обозначения конца кода (обратите внимание, что код никогда не содержит двух последовательных единиц в соответствии с теоремой Цекендорфа . Представление использует числа Фибоначчи, начинающиеся с 1 (2-го числа Фибоначчи). Таким образом, используемые числа Фибоначчи 1, 2 , 3, 5, 8, 13, 21, 34, 55, 89, 141, …….
Учитывая число n, выведите его код Фибоначчи.
Примеры:
Input: n = 1 Output: 11 1 is first Fibonacci number in this representation and an extra 1 is appended at the end. Input: n = 11 Output: 001011 11 is sum of 8 and 3. The last 1 represents extra 1 that is always added. A 1 before it represents 8. The third 1 (from beginning) represents 3.
Мы настоятельно рекомендуем вам свернуть браузер и попробовать это в первую очередь.
Следующий алгоритм принимает целое число в качестве входных данных и генерирует строку, в которой хранится кодировка Фибоначчи.
Найти наибольшее число Фибоначчи f, меньшее или равное n. Скажи, что это я номер в серии Фибоначчи. Длина кодового слова для n будет i + 3 символа (один для дополнительного 1 добавляется в конце, один, потому что я индекс, и один для ‘/ 0’). Предполагая, что ряд Фибоначчи хранится:
Fibonacci code word for 143 is 01010101011
иллюстрация
Область применения:
Обработка и сжатие данных — представление данных (которые могут быть текстом, изображением, видео…) таким образом, чтобы пространство, необходимое для хранения или передачи данных, было меньше размера входных данных. Статистические методы используют коды переменной длины, причем более короткие коды назначаются символам или группе символов, которые имеют более высокую вероятность появления. Если коды должны использоваться по шумному каналу связи, их устойчивость к вставке битов, удалению и к переворотам битов имеет большое значение.
Подробнее о приложении читайте здесь .
Эта статья предоставлена Яшем Варяни . Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по обсуждаемой теме
Рекомендуемые посты:
Кодирование Фибоначчи
0.00 (0%) 0 votes
espressocode.top
Числа Фибоначчи – ключ к разгадке кода Вселенной? :: SYL.ru
Более восьмисот лет назад в Италии, в городе Пизе, жил человек, вплотную приблизившийся к разгадке тайны создания всего сущего. Звали его Леонардо Фибоначчи. Провидению было угодно сподобить его на нахождение последовательности чисел, описывающих код Создателя, общий для земной и космической природы. На вид этот набор цифр кажется немудреным, но чем больше человечество его изучает, тем больше удивляется глубине этого открытия. Название этого ряда – числа Фибоначчи.

Что такое ряд Фибоначчи
Числа Фибоначчи представляют собой ряд чисел, каждое из которых равно двум предыдущим, просуммированным между собой. Вторая цифра равна первой, это единица. Третья — двойка, сумма двух первых. Третья – пятерка, то есть два плюс три. И так до бесконечности. На протяжении многих столетий эта последовательность изумляет математиков, физиков, астрономов, астрологов, художников, биологов, и представителей многих других профессий. Общность законов развития организмов, растений, галактик, а также наши представления о прекрасном описываются, как выясняется при их глубоком изучении, закономерностями, выражением которых стали числа Фибоначчи.
Числа Фибоначчи и спираль
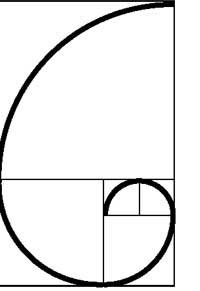
Графическое изображение чисел Фибоначчи представляет собой спираль, которую часто можно наблюдать в естественных организмах. Мало того, ее можно видеть и на небе, галактики расширяются точно так же, как и воронки водоворотов, а улитки закручены по тем же математическим законам, что и ряды семян подсолнуха. Пары человеческих хромосом содержат информацию о его генотипе. Из них восьмая, тринадцатая и двадцать первая несут в себе наследственные болезни. Каждая из этих цифр – число Фибоначчи. Философы утверждают, что развитие человечества происходит по спирали. Этому есть математическое подтверждение, и касается оно не только цивилизационных изменений. Даже обычная еловая шишка растет так же. В общности самых простых и очень сложных процессов, происходящих во вселенной, видится некий общий код, выраженный в ясной и безупречной цифровой форме. Числа Фибоначчи в природе подтверждают гениальное открытие великого математика.
Числа Фибоначчи и искусство

Наше чувство прекрасного кажется субъективным. В самом деле, вкусы разнятся, как и характеры. Но есть и нечто общее в мировосприятии всех людей. Давным-давно, еще до того, как были открыты числа Фибоначчи, художники и архитекторы интуитивно вывели формулу «золотого сечения». Смысл его в том, что любая композиция делится на два отрезка, меньший из которых относится к большему, как тот – к их суммарной длине. Если эта пропорция не соблюдена, то монумент получится невыразительным, а здание уродливым. Интересно, что пропорционально сложенный человек своей фигурой демонстрирует «золотое сечение». То же можно сказать и о каждом красивом лице. Музыкальные произведения некоторых композиторов, например Шопена, также содержат в себе гармонию, которую математически выражают числа Фибоначчи. Учитывая все это, можно предположить существование объективной красоты и совершенства. Получается, что пушкинский Сальери, выверяя гармонию алгеброй, поступал, в общем-то, правильно, хотя никакие расчеты не в силах заменить истинной гениальности. Как говорят в таких случаях математики, это необходимое, но не достаточное условие.
www.syl.ru
Кодирование Фибоначчи — это… Что такое Кодирование Фибоначчи?
Фибоначчиева система счисления — смешанная система счисления для целых чисел на основе чисел Фибоначчи F2=1, F3=2, F4=3, F5=5, F6=8 и т.д.
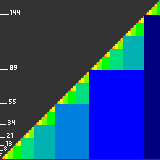 | ||
| Число | Запись в ФСС | Код Фибоначчи |
|---|---|---|
| 0 | 0……0 | |
| F2=1 | 1 | 11 |
| F3=2 | 10 | 011 |
| F4=3 | 100 | 0011 |
| 4 | 101 | 1011 |
| F5=5 | 1000 | 00011 |
| 6 | 1001 | 10011 |
| 7 | 1010 | 01011 |
| F6=8 | 10000 | 000011 |
| … | ||
| Fn-1 | 101010… | …0101011 |
| Fn | 10……00 | 00……011 |
| Fn+1 | 10……01 | 10……011 |
Представление натуральных чисел
Любому неотрицательному целому числу 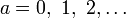 можно единственным образом представить через последовательность битов …εk…ε4ε3ε2:
можно единственным образом представить через последовательность битов …εk…ε4ε3ε2: 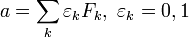 , причём последовательность {εk} содержит лишь конечное число единиц, и не имеет пар соседних единиц:
, причём последовательность {εk} содержит лишь конечное число единиц, и не имеет пар соседних единиц: 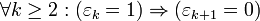 . За исключением последнего свойства, данное представление аналогично двоичной системе счисления.
. За исключением последнего свойства, данное представление аналогично двоичной системе счисления.
Обоснование
В основе лежит теорема Цеккендорфа — любое неотрицательное целое число представимо в виде суммы некоторого набора чисел Фибоначчи, не содержащего пары соседних чисел Фибоначчи. Причём представление такое единственно.
Доказательство существования легко провести по индукции. Любое целое число 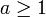 попадёт в промежуток между двумя соседними числами Фибоначчи, то есть для некоторого
попадёт в промежуток между двумя соседними числами Фибоначчи, то есть для некоторого 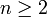 верно неравенство:
верно неравенство: 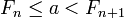 . Таким образом, a = Fn + a‘, где
. Таким образом, a = Fn + a‘, где 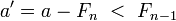 , так что разложение числа a‘ уже не будет содержать слагаемого Fn − 1.
, так что разложение числа a‘ уже не будет содержать слагаемого Fn − 1.
Использование в теории информации
На основе фибоначчиевой системы счисления строится код (кодирование) Фибоначчи — универсальный код для натуральных чисел (1, 2, 3…), использующий последовательности битов. Поскольку комбинация 11 запрещена в Фибоначчиевой системы счисления, её можно использовать как маркер конца записи. Для составления кода Фибоначчи по записи числа в фибоначчиевой системе счисления следует переписать цифры в обратном порядке (так, что старшая единица оказывается последним символом) и приписать в конце ещё раз 1 (см. таблицу). То есть, кодовая последовательность имеет вид:
- ε2ε3…εn1,
где n — номер самого старшего разряда с единицей.
Арифметика
При сложении чисел в позиционных системах счисления приходится выполнять перенос, то есть устранять последствия переполнения разряда. Например, в двоичной системе: 01 + 01 = 02 = 10. В фибоначчиевой системе дело обстоит намного сложнее. Во-первых, вес старших разрядов не является кратным весу разряда, из которого требуется перенос. При сложении двух единиц в одном разряде требуется перенос не только вправо, но и влево: 0200 = 1001. При переносе в отсутствующие разряды ε1 и ε0 следует помнить, что F1=1=F2 и F0=0. Во-вторых, требуется избавляться от соседних единиц: 011 = 100. Правило для раскрытия двоек является следствием этого равенства: 0200 = 0100 + 0011 = 0111 = 1001.
Обобщение на действительные числа
Похожее устройство имеет позиционная система счисления для действительных чисел, основанием которой служит золотое сечение 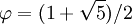 — иррациональное число. Оказывается, что любое действительное число x из отрезка [0,1] допускает разложение в ряд через отрицательные степени золотого сечения:
— иррациональное число. Оказывается, что любое действительное число x из отрезка [0,1] допускает разложение в ряд через отрицательные степени золотого сечения:
где {εk} обладает тем же свойством отсутствия соседних единиц. Коэффициенты находятся последовательным сравнением x с 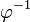 — золотым сечением отрезка [0,1], вычитанием
— золотым сечением отрезка [0,1], вычитанием 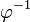 (если εk=1) и умножением на
(если εk=1) и умножением на 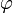 . Из этого нетрудно видеть, что любое неотрицательное действительное число допускает разложение:
. Из этого нетрудно видеть, что любое неотрицательное действительное число допускает разложение:
где N таково, что 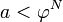 . Разумеется, следует считать что
. Разумеется, следует считать что 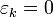 для всех
для всех 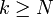 .
.
| Число | Представление через степени 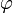 |
|---|---|
| 1 | 1, |
| 2 | 10,01 |
| 3 | 100,01 |
| 4 | 101,01 |
| 5 | 1000,1001 |
| 6 | 1010,0001 |
| 7 | 10000,0001 |
| 8 | 10001,0001 |
| 9 | 10010,0101 |
| 10 | 10100,0101 |
| 11 | 10101,0101 |
| 12 | 100000,101001 |
| 13 | 100010,001001 |
| 14 | 100100,001001 |
Эти формулы полностью аналогичны формулам для обычных позиционных систем с целыми основаниями. Оказывается, что любое неотрицательное целое число (и, более общо, всякий неотрицательный элемент кольца 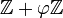 ) имеет представление лишь с конечным количеством единиц, то есть в виде конечной суммы неповторяющихся степеней золотого сечения.[1]
) имеет представление лишь с конечным количеством единиц, то есть в виде конечной суммы неповторяющихся степеней золотого сечения.[1]
Аналогия между числами Фибоначчи и степенями золотого сечения основана на одинаковой форме тождеств:
позволяющих устранение соседних единиц. Прямой связи между представлением натуральных чисел в системе золотого сечения и в фибоначчиевой не имеется.
Правила сложения аналогичны показанным выше с той поправкой, что перенос в сторону младших разрядов распространяется без ограничения. В данной системе счисления можно производить и умножение.
Фибоначчиево «произведение»
Для целых чисел 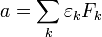 и
и 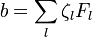 можно определить «произведение»[2]
можно определить «произведение»[2]
 ,
,
формула для которого аналогична формуле умножения двоичных чисел.
Разумеется, данная операция не является настоящим умножением чисел, и выражается[3] формулой:
![a\circ b = 3 a b - a [\varphi^{-2}(b+1)] - b [\varphi^{-2}(a+1)]\ ,](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) где […] — целая часть.
где […] — целая часть.
Эта операция обладает ассоциативностью. Впервые на ассоциативность этой операции обратил внимание Дональд Кнут[4]. Следует отметить, что другое «произведение» 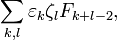 отличающееся лишь сдвигом на два разряда, уже не будет ассоциативно.
отличающееся лишь сдвигом на два разряда, уже не будет ассоциативно.
Источники
Wikimedia Foundation. 2010.
dic.academic.ru
Код Фибоначчи — это… Что такое Код Фибоначчи?
Фибоначчиева система счисления — смешанная система счисления для целых чисел на основе чисел Фибоначчи F2=1, F3=2, F4=3, F5=5, F6=8 и т.д.
| Число | Запись в ФСС | Код Фибоначчи |
|---|---|---|
| 0 | 0……0 | |
| F2=1 | 1 | 11 |
| F3=2 | 10 | 011 |
| F4=3 | 100 | 0011 |
| 4 | 101 | 1011 |
| F5=5 | 1000 | 00011 |
| 6 | 1001 | 10011 |
| 7 | 1010 | 01011 |
| F6=8 | 10000 | 000011 |
| … | ||
| Fn-1 | 101010… | …0101011 |
| Fn | 10……00 | 00……011 |
| Fn+1 | 10……01 | 10……011 |
Представление натуральных чисел
Любому неотрицательному целому числу можно единственным образом представить через последовательность битов …εk…ε4ε3ε2: , причём последовательность {εk} содержит лишь конечное число единиц, и не имеет пар соседних единиц: . За исключением последнего свойства, данное представление аналогично двоичной системе счисления.
Обоснование
В основе лежит теорема Цеккендорфа — любое неотрицательное целое число представимо в виде суммы некоторого набора чисел Фибоначчи, не содержащего пары соседних чисел Фибоначчи. Причём представление такое единственно.
Доказательство существования легко провести по индукции. Любое целое число попадёт в промежуток между двумя соседними числами Фибоначчи, то есть для некоторого верно неравенство: . Таким образом, a = Fn + a‘, где , так что разложение числа a‘ уже не будет содержать слагаемого Fn − 1.
Использование в теории информации
На основе фибоначчиевой системы счисления строится код (кодирование) Фибоначчи — универсальный код для натуральных чисел (1, 2, 3…), использующий последовательности битов. Поскольку комбинация 11 запрещена в Фибоначчиевой системы счисления, её можно использовать как маркер конца записи. Для составления кода Фибоначчи по записи числа в фибоначчиевой системе счисления следует переписать цифры в обратном порядке (так, что старшая единица оказывается последним символом) и приписать в конце ещё раз 1 (см. таблицу). То есть, кодовая последовательность имеет вид:
- ε2ε3…εn1,
где n — номер самого старшего разряда с единицей.
Арифметика
При сложении чисел в позиционных системах счисления приходится выполнять перенос, то есть устранять последствия переполнения разряда. Например, в двоичной системе: 01 + 01 = 02 = 10. В фибоначчиевой системе дело обстоит намного сложнее. Во-первых, вес старших разрядов не является кратным весу разряда, из которого требуется перенос. При сложении двух единиц в одном разряде требуется перенос не только вправо, но и влево: 0200 = 1001. При переносе в отсутствующие разряды ε1 и ε0 следует помнить, что F1=1=F2 и F0=0. Во-вторых, требуется избавляться от соседних единиц: 011 = 100. Правило для раскрытия двоек является следствием этого равенства: 0200 = 0100 + 0011 = 0111 = 1001.
Обобщение на действительные числа
Похожее устройство имеет позиционная система счисления для действительных чисел, основанием которой служит золотое сечение — иррациональное число. Оказывается, что любое действительное число x из отрезка [0,1] допускает разложение в ряд через отрицательные степени золотого сечения:
где {εk} обладает тем же свойством отсутствия соседних единиц. Коэффициенты находятся последовательным сравнением x с — золотым сечением отрезка [0,1], вычитанием (если εk=1) и умножением на . Из этого нетрудно видеть, что любое неотрицательное действительное число допускает разложение:
где N таково, что . Разумеется, следует считать что для всех .
| Число | Представление через степени |
|---|---|
| 1 | 1, |
| 2 | 10,01 |
| 3 | 100,01 |
| 4 | 101,01 |
| 5 | 1000,1001 |
| 6 | 1010,0001 |
| 7 | 10000,0001 |
| 8 | 10001,0001 |
| 9 | 10010,0101 |
| 10 | 10100,0101 |
| 11 | 10101,0101 |
| 12 | 100000,101001 |
| 13 | 100010,001001 |
| 14 | 100100,001001 |
Эти формулы полностью аналогичны формулам для обычных позиционных систем с целыми основаниями. Оказывается, что любое неотрицательное целое число (и, более общо, всякий неотрицательный элемент кольца ) имеет представление лишь с конечным количеством единиц, то есть в виде конечной суммы неповторяющихся степеней золотого сечения.[1]
Аналогия между числами Фибоначчи и степенями золотого сечения основана на одинаковой форме тождеств:
позволяющих устранение соседних единиц. Прямой связи между представлением натуральных чисел в системе золотого сечения и в фибоначчиевой не имеется.
Правила сложения аналогичны показанным выше с той поправкой, что перенос в сторону младших разрядов распространяется без ограничения. В данной системе счисления можно производить и умножение.
Фибоначчиево «произведение»
Для целых чисел и можно определить «произведение»[2]
- ,
формула для которого аналогична формуле умножения двоичных чисел.
Разумеется, данная операция не является настоящим умножением чисел, и выражается[3] формулой:
- где […] — целая часть.
Эта операция обладает ассоциативностью. Впервые на ассоциативность этой операции обратил внимание Дональд Кнут[4]. Следует отметить, что другое «произведение» отличающееся лишь сдвигом на два разряда, уже не будет ассоциативно.
Источники
Wikimedia Foundation. 2010.
partners.academic.ru
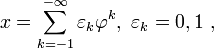
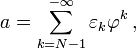
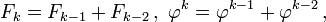
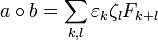 ,
,![a\circ b = 3 a b - a [\varphi^{-2}(b+1)] - b [\varphi^{-2}(a+1)]\ ,](/800/600/https/dic.academic.ru/pictures/wiki/files/48/08c1b4cbe18e534a0bfa7f377219722d.png) где […] — целая часть.
где […] — целая часть.