| 1. | Произведение бинома и переменной (обыкн. дроби) | 1 вид — рецептивный | лёгкое | 2 Б. | Решение уравнения. |
| 2. | Произведение биномов (целые числа) | лёгкое | 2 Б. | Решение уравнения. | |
| 3. | Произведение трёх множителей (десятичные дроби) | 1 вид — рецептивный | лёгкое | 3 Б. | Решение уравнения. |
| 4. | Произведение трёх множителей (обыкновенные дроби и смешанные числа) | 2 вид — интерпретация | среднее | 4 Б. | Решение уравнения. |
| 5. | Уравнение, общий множитель (целые числа) | 1 вид — рецептивный | среднее | 4 Б. | Решение уравнения. |
| 6. | Дробь (разность квадратов) | 2 вид — интерпретация | среднее | 3 Б. | Сокращение дроби. |
| 7. | Разность квадратов (целые числа) | 2 вид — интерпретация | среднее | 3 Б. | Вычисление значения выражения. |
План-конспект урока по алгебре (7 класс) по теме: «Разложение многочлена на множители способом группировки.»
Учитель математики Пестрова Е.А.
Тема: Разложение многочлена на множители способом группировки.
Цели урока:
- деятельность учащихся по самостоятельному выводу алгоритма разложения многочлена на множители способом группировки
- продолжить работу по формированию у каждого учащегося личной потребности в последовательной деятельности, связанной с “открытием” нового правила, развитию творческих способностей учащихся;
- продолжить работу по формированию ответственности учащихся за свою деятельность на уроке, умений самостоятельно добывать знания, овладению способами и критериями самоконтроля и самооценки.
Тип урока: изучение нового, проблемный.
Методы обучения: проблемный, частично-поисковый.
Форма организации учебной деятельности: групповая, фронтальная, индивидуальная.
Оборудование: компьютер, проектор
Ход урока
I. Мотивационно-ориентировочная часть
1. Актуализация опорных знаний.
Устная работа (тест)
(Эта часть урока сопровождается материалами презентации.) Вынести за скобки общий множитель:
1) 6m+9n
2) –ax +ay
3) a2 –a b
4) 8m2n – 4mn3
5) (a +b) – x (a +b)
Когда мы выносим общий множитель за скобки, мы представляем многочлен в виде произведения множителей. Для чего это может быть нужно?
Решите уравнение:
1) 5 x (x+1) =0 , x=0 или x=-1.
2) 6x – 3×2 =0 , 3x(2-x) =0 , x=0 или x=2.
2. Мотивирование необходимости разложения многочлена на множители.
(Эта часть урока сопровождается материалами презентации.)
Решите уравнение: x2 +3x +6 +2x =0
Создается проблемная ситуация: задача знакома на первый взгляд, но не решается. Мы знаем, что удобно решать уравнение, в правой части которого 0, раскладывая его левую часть
Значит, этот способ разложения на множители не подходит
Есть ли общий множитель у всех слагаемых?
Постановка учебной задачи: научиться раскладывать многочлен на множители другим способом.
II. Операционно-исполнительная часть.
(Эта часть урока сопровождается материалами презентации.)
1. Рассмотрим многочлен 5x +5y +m x +my.
Есть ли общий множитель у всех слагаемых?
Применим “метод пристального взгляда”. Что вы увидели?
Давайте объединим их в группы. — Каким законом сложения воспользуемся?
( 5x +5y ) +(m x +my)
Что можно сделать с общим множителем в каждой группе?
Каким законом умножения воспользуемся? 5 (x +y) +m (x +y)
Сколько сейчас получилось слагаемых?
Что интересного заметили в получившемся выражении?
Вынесем его за скобки.
(x +y) (5 +m)
Что мы получили?
Значит, многочлен представили в виде произведения. Каким способом?
Поэтому этот способ называется способом группировки.
2. А сейчас ученики, сидящие за первой партой каждого ряда, составят алгоритм разложения многочлена на множители.
(Эта часть урока сопровождается материалами презентации.)
В это время проводится беседа с остальными:
Нельзя ли этот же многочлен разложить на множители, группируя слагаемые иначе? Какие законы сложения и умножения будем использовать?
Фронтальная работа с пооперационным контролем:
(5x +5y) + (m x +my) = x (5 +m) + y (5 +m) =(x +y) (5 +m)
Какой получился результат?
3) Заслушиваются составленные варианты алгоритмов. (Эта часть урока сопровождается материалами презентации). Дискуссия, коррекция. Тем самым создается модель алгоритма, ее анализ, уточнение.
Окончательный вариант звучит так:
а) выполнить группировку слагаемых, имеющих общий множитель;
в) отдельно в каждой группе найти общий множитель и вынести его за скобки;
с) в получившемся выражении найти общий множитель и вынести его за скобки.
Этот алгоритм поможет учащимся в дальнейшей работе на этом и последующих уроках.
4) Отработка правила. (Эта часть урока сопровождается материалами презентации.)
Работая с алгоритмом, учащиеся действуют поэтапно, отдавая себе отчет, что надо сделать и почему. Происходит осознание нового правила, его осмысление и запоминание.
а) Фронтальная работа с пооперационным контролем.
Разложить на множители
а х+ ау — х — у
ав-8а-бх+8х
x 2 m- x2n + y2 m- y2n
б) Дифференцированные задания по уровням. (Раздаточный материал из презентации распечатывается и ученикам кладется на парту.)
Ситуация выбора в процессе выполнения самостоятельной работы. Учащиеся могут выбрать один из предложенных вариантов, который кажется им соответствующим их уровню знаний, то есть вырабатывается навык самооценки.
А. Задания нормативного уровня.
1) 7а-7в+ аn – b n
2) x y+ 2y+2x+4
3) y2a-y2b+x2 a- x2b
Б. Задания компетентного уровня
1) x y+ 2y-2x-4
2) 2сх – су – 6х + 3у
3) х2 +x y+ xy2+y3
С. Задания творческого уровня
1) x4 +x3y- xy3-y4
2) ху2 – ву2 – ах + ав + у2 — а
3) х2 – 5х + 6
На обратной стороне карточки приведены решения. Каждый ученик выполняет самостоятельно выбранные задания, а затем подвергает пооперационному контролю. Отметки по итогам самостоятельной работы на первом уроке выставляются по желанию.
На первом уроке – “открытие” правила. Отработка будет в дальнейшем.
III. Подведение итогов.
Какая задача состояла перед нами в начале урока? Можно ли считать, что мы ее решили?
(Эта часть урока сопровождается материалами презентации.)
Вернемся к нашему уравнению:
x2+3x+6+2x=0
x(x+3) +2(3+x) =0
(x+3) (x+2) =0
Ответ: х=-3 или х=-2.
А теперь придумайте уравнение, для решения которого нужно применить изученный способ. Решите его.
IV. Домашнее задание
(Раздаточный материал.)
1) Найти значение выражения х2у – у + ху2 – х при х=4, у=0,25
Решить уравнения:
а) у3 – 2у2 + у – 2 =0
б) х2 + х3 = х3 + х4
1) Вычислить 2,7 *6,2 – 9,3 *1,2 + 6,2 * 9,3 – 1,2 *2,7
2) Решить уравнения:
а) х3 – 8х2 + 3х – 24 = 0,
б) у2 – 2у = 3у – 6
» Разложение на множители многочленов»

 Технологическая карта урока
Технологическая карта урока
Тема: Разложение многочлена на множители
Мордкович А.Г, П.В, Семёнова 7 класс, учебник для общеобразовательных учреждений. –М.: Мнемозина, 2012
Цель урока: повторение и систематизация материала по теме: «Разложение многочлена на множители», закрепление умения и навыков в применении различных способов разложения на множители
Основные понятия: формулы сокращённого умножения, разложение многочлена на множители, способ группировки, вынесение множителя за скобки, рациональное вычисление.
Формы работы учащихся: Фронтальная, парная, индивидуальная
Личностные: Ученик получит возможность научиться ясно, точно и грамотно излагать свои мысли; получит возможность для формирования компетентности в общении.
Метапредметные : Ученик повторит, закрепит умения и навыки разложения многочлена на множители; осуществлять самоконтроль, взаимоконтроль в процессе достижения результата.
Предметные: получит возможность углубить и развить умение раскладывать многочлен на множители разными способами
Организация деятельности учащихся на уроке:
учебники по математике, раздаточный материал (карточки с дополнительным заданием, карточки с домашним заданием)
Этапы урока
Деятельность учителя
Деятельность учащегося
1.Организационный момент
Установочная беседа
Дома:№ 33.42б), г)
Слушают учителя, (психологический настрой)
Записывают домашнее задание.
2)Актуализация знаний
Подводит учащихся к цели урока Я предлагаю работать над темой:
« Разложение на множители многочлена различными способами»
Значит, как вы думаете, на уроке какая цель стоит перед нами?»
Слушают учителя и стараются формулировать цель урока
Формулируют цель: «Повторить способы разложения на множители многочлена и пытаться работать над применение данных способов при разложении на множители многочленов
3 а)
Устная работа.
3б) Ответьте на вопрос:
1. )х2-2ху – у2 =( х-у)2
2)х2+ху + у2=( х+у)2
3. )3х-9х=3х(х-3)
4.)х(а+с)-2(а+с)=(а+с)(х+2)
а)6 · 0,31 – 0,31 · 3 .
б) 3 · 8,5 – 1,5 · 3 .
квадрата или куба
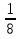
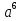 ;
; 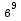 ;
;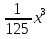 ;
; 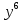 ;
; 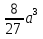
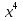 ; 81
; 81
а) 64 – 81
– 81
б) 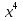 + 6
+ 6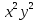 +9
+9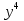
в) 8+ 27
Задает вопрос: « Что значит разложить многочлен на множители?» если учащиеся затрудняются в помощь им таблица из Приложения №1
Предлагает учащимся составить таблицу на магнитной доске: «Способы разложения на множители многочлена»
( Приложение №2)
Учащиеся отвечают устно на вопрос учителя .
( Разложить многочлен на множители это значит представить его в виде произведения более простых многочленов)
Один ученик у доски, а все остальные помогают с места составляет таблицу способы разложения на множители.
4) Повторение теоретического материала
(Практическая работа)
Предлагает ученикам повторить: ( Приложение №1)
а) Характеристику каждого приема.
б) Разложения на множители многочлена, предложив на карточках соединить линиями соответствующие части в определениях.
в) Формулы сокращенного умножения
г) Записывать на доске соответствующие формулы
Учащиеся по раздаточному материалу
Выполняют задание предложенное учителем
Один ученик у доски записывает соответствующие формулы
5) Закрепление материала
1) Математическая эстафета по рядам (Приложение №3) работа в группах. Одновременно подумать над вопросом: « Для чего нужно уметь разлагать на множители многочлены?»
2) Решить уравнение:
а) 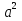 — 81 = 0
— 81 = 0
б) 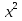 + 14 х + 49 = 0
+ 14 х + 49 = 0
3) № 33.42 а) в)
Учащиеся передают каждой парте задание, проверяя выполнение предыдущей пары
Учащиеся у доски выполняют предложенные задания
6) Самостоятельная работа
Учитель предлагает задание каждой паре, проверка по ключу предложенному учащимся(Приложение №4,№5)
№ п/п
Разложение на множители
Ответ
Буква
1.
2.
3.
4.
5.
6.
7.
32х – 8а
4х² +36х³
15с (а+b) + 8(a+b)
4ac+4ad – b(c + d)
ax– 3x+4a – 12
25-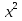
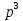 — 27
— 27
8(4х–а)
4х² (1+ 9х)
(a+b)(15c + 8)
(c + d)(4a – b)
(a– 3)(x + 4)
( 5-х)(5+х)
(р-3)( 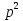 +3р +9)
+3р +9)
м
о
л
о
д
ц
ы
4х² (1+9х)
(a– 3)(x + 4)
23с(а+b)
(c+d)(4a–b)
(a+b)(15c+8)
о
д
а
о
л
8(4х–а)
( 5-х)(5+х)
(р-3) ( 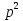 +3р +9)
+3р +9)
24(x-a)
м
Ц
Ы
К
Учащиеся выполняют самостоятельную работу и оценивают себя
Итог и выставление оценок.
Учитель задает вопросы: Какие способы разложения на множители вы знаете? Перечислите.
Какие формулы сокращенного умножения мы используем при разложении на множители многочлены.
Учитель выставляют оценки.
Учащиеся отвечают на вопросы учителя.
Выставляют оценку за урок.
Рефлексия
Ответьте на вопросы:
Довольны ли вы своей работой на уроке?
На каком этапе урока?
Чувствовали вы себя успешными?
Какие затруднения испытывали?
Отвечают на вопросы учителя.
План-конспект урока по алгебре (7 класс) на тему: Разложение многочлена на множители способом группировки
Тема: «Разложение многочлена на множители способом группировки»
Дата: 5.03.09
Цели:
- Образовательная: создание условий для развития у учащихся учебно-познавательной компетентности на основе темы «Разложение многочлена на множители способом группировки»;
- Развивающая: создание условий для развития памяти, внимания, логического мышления, математической зоркости;
- Воспитательная: формировать у учащихся коммуникативные компетенции, а именно: развитие у учащихся устной и письменной математической речи, навыки работы в группе.
Тип урока: вторичное закрепление.
Методы: беседа, метод самостоятельной работы.
Формы работы: фронтальная, индивидуальная, работа в группах, коллективная.
Оборудование: учебник под ред. Ю. Н.Макарычева Алгебра-7, индивидуальные задания, компьютер, доска.
План урока.
1 этап. Мотивационно — ориентировочный:
- ОНУ
- Актуализация опорных знаний.
2.1) Графический тест теоретического характера.
2.2) Задание «Стрела».
2 этап. Операционно – исполнительский:
- «Картинная галерея».
- Самостоятельная работа.
- Дифференцированная работа в группах.
- Выполнение упражнений*
3 этап. Рефлексивно – оценочный:
- Постановка д.з.
- Рефлексия
- Подведение итогов урока.
Ход урока
I этап. Мотивационно – ориентировочный.
- ОНУ.
Здравствуйте, ребята и уважаемые гости. Сегодня у нас урок закрепления материала по теме «Разложение многочлена на множители способом группировки». В тетрадях запишем число и тему урока.
На прошлом уроке мы учились раскладывать многочлен на множители способом группировки. Сегодня мы с вами будем продолжать отрабатывать эти навыки.
Перед вами маршрутные листы. Давайте начнем их заполнять: подпишем и выберем из предложенных смайликов тот, который соответствует вашему настроению на начало урока.
- Актуализация опорных знаний
2.1) Графический тест теоретического характера.
«∆» — да; «-» — нет.
Верно ли утверждение, определение, свойство?
- Одночленом называют сумму числовых и буквенных множителей.
- Буквенный множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
- Целое выражение, которое содержит произведение чисел и букв, называют одночленом.
- Сумма показателей степеней всех букв, входящих в одночлен, называется степенью одночлена.
- Одинаковые или отличающиеся друг от друга только коэффициентами члены, называются подобными членами.
- Алгебраическая сумма нескольких одночленов называется одночленом.
- В результате умножения многочлена на одночлен получается одночлен.
- В результате умножения одночлена на многочлен получается многочлен.
- Многочлен, в котором отсутствуют подобные члены и каждый из них одночлен стандартного вида, называется многочленом стандартного вида.
- Чтобы раскрыть скобки, перед которыми стоит знак «+», скобки надо опустить, сохранив знак каждого члена, который заключен в скобки.
- Когда раскрываем скобки, перед которыми стоит знак «-», скобки опускаем, и знаки членов, которые были заключены в скобки, меняют на противоположные.
Проверка: — -∆∆∆ — — ∆∆∆∆
Выставите себе оценки:
«5» — нет ошибок
«4» — две ошибки
«3» — четыре ошибки
«2» — более четырех ошибок.
- Задание «Стрела»
I вариант.
3х2 + 12ух +3у + 12х3 = + (3х2+3у) = + 3(х2+у) =
II вариант.
3х2 + 12ух +3у + 12х3 = + (3х2+12х3) = +3х2(1+4х)=
II этап. Операционно – исполнительский.
- «Картинная галерея».
На доске портреты ученых – математиков. Возле каждого портрета подписаны числовые выражения. Я читаю предложения. Ваша задача: выполнить действия и по полученным ответам догадаться, о каком ученом шла речь в моем тексте.
Архимед | Пифагор | Евклид | Декарт | Галуа |
(a2-c)(d2+c-b) | (c2-d)(a+c-b) | (a+c)(d2+b2-b) | (d2-b)(a+c-b2) | (a-b)(c2+d2-1) |
- ac2 – ad + c3 – cd – bc2 +bd = …
- ac2 + ad2 – bc2 – bd2 + b – a = …
- ad2 + cd2 – ab + ab2 – cb + cb2 = …
- Этот античный ученый побеждал на Олимпийских играх и впервые открыл математическую теорию музыки. Пифагор.
- Ученый, который несмотря на свою молодость, успел сделать много открытий в математике, но, к сожалению, был убит на дуэли в 21 год. Галуа.
- Его любимая фраза – «Что и требовалось доказать». Евклид.
- Самостоятельная работа.
Проверим, как вы можете применять метод группировки самостоятельно.
У каждого карточка с заданием. Решения проводим в тетрадях. Ответы вносим в учетную карточку.
Самостоятельная работа содержит три уровня сложности: «на 3», «на 4» и «на 5».
I вариант | II вариант | |
Группа А | ||
| 1) x(a – b) + y(a – b) | |
| 2) a(x + c) – b(x + c) | |
| 3) 2(x – 7) – y(7 – x) | |
| 4) x – p + (p – x)c | |
| 5) 5(b – 4) + x(4 – b) | |
Группа В | ||
| 1) 2c(x + y) + p(x + y) | |
| 2) c(x – 8) + (8 – x) | |
| 3) ax – ay + bx – by | |
| 4) 2x + ac + cx +2a | |
| 5). 5(b – 4) + [(4 – b) | |
Группа С | ||
| 1) (x – 3) – y(x – 3) | |
| 2) 5(b – 4) +x(4 – b) | |
| 3) 5a + 5y +pa +py | |
| 4) 2x + 7y + 14 +xy | |
| 5) ay – 12bx +3ax – 4by | |
ОТВЕТЫ
Группа А I вариант (b+c)(a+p) (x – y)(a – b) (b – 5)(3 + a) (n – m)(y – 1) (2a+b)(1+a) | Группа B I вариант (a+b)(3a – m) (a – 5)(x – 1) (a+b)(x + c) (a+b)(4+y) (3a-b)(1+a) | Группа C I вариант (c+8)(1 — c) (a – 3)(2+ b) (a – c)(3 + x) (6+y)(x+7) (2x – 3)(x2+2x) |
Группа А II вариант (a — b)(x+y) (x +c)(a – b) (x – 7)(2 + y) (x – p)(1 – c) (b — 4)(5-x) | Группа B II вариант (x+y)(2c+p) (x – 8)(c – 1) (x – y)(a + b) (x+a)(2+c) (1+c)(3c – a) | Группа C II вариант (x – 3)(1 – y) (b – 4)(5 – x) (a+y)(5 + p) (7 + x)(y +2) (3x – y)(a – 4b) |
- Дифференцированная работа в группах
Те, кто решил 4 и 5 заданий, верно, решают задания карточки №1; те, кто решил 3 и менее заданий, верно, вам будут задания карточки №2.
Карточка №1 Карточка №2
- Разложите на множители: №711 учебника стр. 142
А) bx + 6b – xc – 6c
Б) 4c2 – 64d4
В) -18а2 + 12а – 2
2. Решите уравнение:
х3 – 4х2 – 16х +64 = 0.
- Выполнение упражнений*
III этап. Рефлексивно – оценочный.
- Постановка д.з.
№790(а,б), №792, №795(а)*
- Рефлексия.
Итак, наш урок подошел к концу. Сегодня мы продолжили использовать способ группировки для разложения многочлена на множители.
- Давайте еще раз вспомним, как же разложить многочлен на множители способом группировки?
- Все ли вам было понятно?
- С каким настроением вы уходите с урока вы покажите с помощью выбора смайлика.
- Подведение итогов урока.
Оцените свою деятельность на уроке в своих маршрутных листах.
Благодарю вас за урок, мне было интересно с вами работать. Урок окончен!
Презентация к уроку по алгебре (7 класс) по теме: Презентация «Разложение многочлена на множители с помощью комбинации различных приемов»
Слайд 1
Разложение многочлена на множители с помощью комбинации различных приемов Никитина Т.Н., учитель математики МОУ ВСОШ № 2Слайд 2
Цели : 1. Систематизировать, расширить и углубить знания, умения применять различные способы разложения многочлена на множители и их комбинации. 2. Способствовать развитию наблюдательности, умения анализировать, сравнивать, делать выводы.
Слайд 3
Задание 1. Соединить линиями соответствующие части определения: Разложение многочлена на множители — это Представление многочлена в виде суммы двух или нескольких многочленов Представление многочлена в виде произведения двух или нескольких одночленов Представление многочлена в виде произведения двух или нескольких многочленов
Слайд 4
Задание 2. Закончите определение Представление многочлена в виде произведения одночлена и многочлена называется …. Вынесением общего множителя за скобки
Слайд 5
Задание 3. Восстановить порядок выполнения действий при разложении многочлена на множители способом группировки. Чтобы разложить многочлен на множители способом группировки, нужно Вынести в каждой группе общий множитель (в виде многочлена) за скобки Сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель Вынести в каждой группе общий множитель в виде одночлена за скобки 1 2 3
Слайд 6
Задание 4. Отметить знаком «+» верные выражения а) а 2 + в 2 — 2ав = ( а – в ) 2 б) m 2 + 2mn – n 2 = ( m – n) 2 в) 2pt – p 2 – t 2 = ( p – t ) 2 г) 2cd + c 2 + d 2 = ( c + d ) 2 + +
Слайд 7
Вынесение общего множителя за скобки Формулы сокращенного умножения Способ группировки 20х 3 у 2 + 4 х 2 у в(а + 5 ) – с ( а + 5 ) 15а 3 в + 3а 2 в 3 2у ( х – 5 ) + х ( х – 5 ) а 4 – в 4 27 в 3 + а 6 х 2 + 6х + 9 49 m – 25 n 2вх – 3ау – 6ву + ах а + ав – 5а – 5в 2 а n -5 bn – 10 bn + am 3 a + 3 ab – 7 a – 7 b Метод разложения на множители
Слайд 8
1 ряд 2 ряд 3 ряд 3a + 12b 16a 2 + 8ab + b 2 10a + 15c 2a + 2b + a 2 + ab 3m – 3n + mn –n 2 4a 2 – 9b 2 9a 2 – 16b 2 5a – 25b 6xy – ab – 2bx -3ay 7a 2 b – 14ab 2 + 7ab 4a 2 – 3ab + a – ag + 3bg –g 4a 2 + 28 ab + 49 b 2 m 2 + mn – m – mg – ng + g 9a 2 – 30ab + 25b 2 b(a + c) + 2a + 2c 4a 2 – 4ab +b 2 2(a 2 + 3bc) +a(3b+4c) 5a 3 c– 20acb – 10ac 2(3a 2 + bc) + a(3a 2 + bc) 144a 2 — 25b 2 х 2 – 3 x – 5x + 15 25a 2 + 70ab + 49b 2 9a 3 b – 18ab 2 – 9ab 9a 2 – 6ac + c 2
Слайд 9
Ответы 1 ряд 2 ряд 3 ряд 3(а + 4в) (4а + в) 2 5(2а + 3с) (2 + а)(а + в) (3 + n)(m – n) (2а – 3в)(2а + 3в) (3а – 4в)(3а + 4в) 5(а -5в) (3у – в)(2х – а) 7ав(а – 2в + 1) (а – g) (а – 3в +1) (2а + 4в) 2 ( m –g)(m + n – 1) (3а – 5в) 2 (а + с)(в + 2) ( 2а – в) 2 (2а + 3в)(а + 2с) 5ас(а 2 – 4в – 2) (2 + а)( 3a 2 + bc ) (12а – 5в)(12а + 5в) (х – 3)(х – 5) (5а + 7в) 2 9ав(а 2 – 2в – 1) (3а — с) 2
Слайд 10
1. Вынести общий множитель за скобку (если он есть). 2. Попробовать разложить многочлен на множители по формулам сокращенного умножения. 3. Попытаться применить способ группировки (если предыдущие способы не привели к цели).
Слайд 11
Вынесение общего множителя за скобку Из каждого слагаемого, входящего в многочлен, выносится некоторый одночлен, входящий в качестве множителя во все слагаемые. Таким общим множителем может быть не только одночлен, но и многочлен.
Слайд 12
Группировка Бывает, что члены многочлена не имеют общего множителя, но после заключения нескольких членов в скобки (на основе переместительного и сочетательного законов сложения) удается выделить общий множитель, являющийся многочленом.
Слайд 13
Применение формул сокращенного умножения Группа из двух, трех (или более) слагаемых, которая обращает выражение, входящее в одну из формул сокращенного умножения, заменяется произведением многочленов.
Слайд 14
Задание 4. Разложить многочлен на множители и указать, какие приемы использовались при этом Пример 1. 36а 6 в 3 – 96а 4 в 4 + 64 а 2 в 5 . Пример 2. а 2 + 2ав + в 2 – с 2 . Пример 3. у 3 — 3у 2 + 6у – 8. (у – 2)(у 2 – у + 4). (а + в – с)(а + в +с). 4а 2 в 3 (3а 2 – 4в) 2
План-конспект урока по алгебре (7 класс) по теме: Урок «Разложение многочлена на множители»
ФИО учителя : Титова Ирина Григорьевна
МБОУ СОШ №288 территориального образования : г. Заозерск. Мурманская область
Тема урока :Разложение многочлена на множители с помощью комбинации
различных приемов
Класс: 7, уровень базовый.
Тип урока: «открытие нового знания»
Цели урока:
— показать применение различных способов для разложения на множители многочлена
— повторить способы разложения на множители и закрепить их знание в ходе упражнений
— вырабатывать навыки и умения учащихся в применении формул сокращенного умножения.
— развивать логическое мышление учащихся и интерес к предмету.
Планируемые результаты:
1)личностные: Использование различных приемов проверки правильности выполнения
задания (опора на изученные правила, алгоритм выполнения арифметических действий).
2)метапредметные : Регулятивные- обнаружение и формулирование учебной проблемы с
учителем.
Познавательные- делать предположения об информации, которая нужна для решения
предметной учебной задачи.
Коммуникативные- уметь оформлять свои мысли в устной и письменной речи с учетом
речевых ситуаций.
Форма контроля : Индивидуальная, коллективная работа.Самостоятельная работа.
Ход урока:
1)Повторение:
Задание №1(на доске (или слайд) список алгебраических выражений, которые учащиеся должны рассмотреть):
(1) 4а2в(1+3а)
(2) (х-3)(х2+3х+9)
(3) 27х6у3-72х4у4+48х2у5
(4) (6а+1)2
(5) (8а-вс)(8а+вс)
(6) х2-у2+а2+2ха
(7) а2+10а+25-в2
(8)х(х-5)(15+2х)
(9) а4+4в4
(10) -4а2+40ав-100в2
Распределите данные выражения на группы и объясните по какому признаку
проведено распределение.(Учащиеся сначала выделили две группы. В первую вошли
выражения 1,2,4,5,8, поскольку в каждом из них есть двучлен, выступающий в качестве
отдельного множителя. Во вторую группу все остальные множители, ведь ни в одном из
них не встречались «умножение друг на друга скобки».Некоторые обучающиеся отметили,
что во второй группе есть и двучлены (9),и трехчлены (3,10) ,и четырехчленны (6,7).
После анализа формулируется цель урока: « Разложение на множители с помощью
комбинирования различных способов» (многочлены из второй группы).
Задание №2 (устно), (запись на доске или слайд) 🙁 х-у)2 =х2-2ху + у2.
Задание №2 .Найти ошибку:
1.( х-у)2 =х2-2ху — у2 ;
2.( х-у)2 =х2-ху + у2;
3.( х-у)2 =х-2ху + у ;
4. ( х-у)2 =х2+2ху — у2;
5.( х-у)2 =х2-2ху + у.
Задание №3 (устно) Найдите верные формулы, которые записаны в непривычном порядке
и содержащие ошибку ,исправьте ошибочную запись:
1.а2+в2-2ав=(а-в)2
2.х2+2ху-у2=(х-у)2
3.2рв-р2-в2=(р-в)2
4.2вс +с2+в2=(с+в)2.
Какие способы разложения на множители мы вспомнили?
Какие еще способы разложения на множители мы изучали?
(запись на доске) :ас+ вс= а(в+с) .Приведите пример.
ас+вс-ар-вр= (ас+вс) +(-ар-вр)=с(а+в)-р(а+в)=(а+в)(с-р)
Задание №4.
Провести классификацию данных многочленов по способу разложения на множители
(на доске (или слайд) список алгебраических выражений, которые учащиеся должны
классифицировать):
Методы разложения на множители.
Вынесение общего множителя за скобки | Формулы сокращенного умножения | Способ группировки |
20х3у2 + 4 х2у | a4 – b8 | 2bx – 3ay -6by + ax |
b(a + 5) – c(a +5) | 27b3 +a6 | a2 + ab – 5a – 5b |
15a3b + 3a2b3 | x2+6x +9 | 2an -5bm-10bn + am |
2y(x -5) +x(x – 5) | 49m4 — 25n2 | 3a2 + 3ab -7a -7b |
С остальными учащимися даем характеристику каждому перечисленному приему.
Новый материал:
Задание №5.
Преобразуйте выражения 3,10,6,7 (письменно).№3 и№6-работа вместе с учителем,
№10 и №7-самостоятельно.
№3. 27х6у3-72х4у4+48х2у5
С какого способа следует начать? (ответ : вынесение общего множителя)
3х2у3(9х4-24х2у+16у2).
Что можно сказать о выражении стоящем в скобках? (ответ: квадрат разности)
3х2у3 (3х-4у)2. (№10 -самостоятельно.)
№6 . х2-у2+а2+2ха
Начнем ли мы в этом задании с вынесения общего множителя за скобки? (ответ:
Нет общего множителя, нужно попробовать группировку)
Попытка может быть такой : (х2-у2 )+ (а2+2ха)= (х-у)(х+у) +а (а+2х), тогда возникает вопрос что
делать дальше?
Сделаем другую группировку: (х2 +2ха) + (-у2+а2)=х(х+2а) +(а-у)(а+у),опять возникает вопрос что
делать дальше.
Может использовать другой способ разложения или использовали не все варианты
группировки? Слагаемые можно объединять не только парами, но и по три слагаемых.
Какие три слагаемых можно объединить? (ответ: слагаемые, в которых есть множители
х,а и ха).
(х2 +а2+2ха) -у2=(х+а)2-у2=(х+а-у)(х+а+у),(каждый этап комментируется учителем и
обучающимися).
Справились ли мы с поставленной задачей? (ответ: разложили на множители). Совокупность различных приемов разложения на множители позволяет легко и изящно производить арифметические вычисления, решать уравнения вида ах2 + вх + с = 0 (а0) – такие уравнения называются квадратными, мы начнем изучать в 8-м классе, решать задачи на делимость, доказывать тождества.
Задание №6
Решить уравнения:
а) х2 – 15х + 56 = 0
Решение.
х2 – 7х – 8х + 56 = 0,
(х2 – 7х) – (8х – 56) =0,
х(х – 7) – 8(х – 7) = 0,
(х – 7)(х – 8) = 0,
х=7, х=8
б) х2 + 10х + 21 = 0
Решение.
х2 + 10х + 25 – 4 = 0
(х + 5)2 – 4 = 0
(х + 5 -2)(х +5 +2) = 0
(х +3)(х + 7) = 0
х = -3, х = -7.
При разложении многочлена на множители мы увидели полный квадрат и таким образом применили еще один прием разложения на множители: метод выделения полного квадрата.
Рефлексия:
Задание № 7. Разложить многочлен на множители: учебник А.Г.Мордковича «Алгебра 7 № 34.1(а,в),
34.2(а,в),34.8(а,в),34.9(а,в)
Мы убедились, что на практике при решении примеров часто приходится использовать комбинацию различных приемов. Каков план их последовательного применения?
Ответ:
1.Вынести общий множитель за скобку (если он есть).
2.Попробовать разложить многочлен на множители по формулам сокращенного умножения.
3.Попытаться применить способ группировки (если предыдущие способы не привели к цели).
Задание № 8. Самостоятельная работа
Разложить на множители, используя различные способы.
Вариант 1 | Вариант 2 |
5а3 – 125ав2 | 63ав3 – 7а2в |
а2 – 2ав + в2 – ас + вс | m2 + 6mn + 9n2 – m – 3n |
(с – а)(с + а) – в(в – 2а) | (в – c)(в + c) – а(а + 2c) |
х2 – 3х + 2 | х2 + 4х + 3 |
х4 + 5х2 + 9 | х4 + 3х2 + 4 |
Самостоятельная работа проверяется на уроке .
Оценить работу учащихся и ориентировать в домашнем задании
Домашнее задание
- Если вы получили оценку “2” или “3” – № 34.6 (а, в), 34.4, 34.3.
- “4” – № 34.12 -3415.
- “5”– № 34.16-34.20.