Разложение многочленов на множители. Способ группировки

Вспомним, что многочлен – это сумма одночленов, а одночлен – это произведение степеней и чисел. Если у многочлена есть общий член, то мы выносили его за скобки, таким образом раскладывали многочлен на множители. Это был первый метод разложения многочлена на множители.

Но у многочлена может и не быть общего множителя, в таком случае мы будем искать его только у группы членов. Таким образом, мы разбиваем многочлен на группы и в каждой группе выносим общий множитель. Далее возможно, что у всех групп образуется общий      множитель, и мы сможем его вынести.

Пример 1:

.

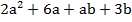Очевидно, что общего множителя у данного многочлена нет. Значит, нам нужно его разбить на группы таким образом, чтобы в каждой группе был общий множитель, и кроме того постараться разбить так, чтобы после вынесения общих множителей в группах образовался общий множитель для всех групп.

Сгруппируем первый со вторым и третий с четвертым:

.

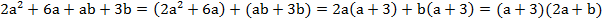Обратим внимание на тот факт, что группы можно объединять по-разному, но лучше группировать те члены, где очевидно есть общий множитель.

Рассмотрим первый пример с другой стороны, сгруппируем первый член с третьим, а второй с четвертым:

.

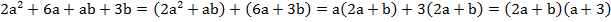Видим, что при таком варианте группировки выражение получается такое же, как и в первом случае.

Пример 2:

;

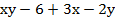сгруппируем первый с четвертым и второй с третьим:

;

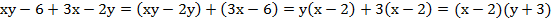
в данном примере также можно проверить, есть ли другие варианты группировки, например, сгруппировать первый член с третьим и второй с четвертым.

При выборе групп следует обратить внимание на такой момент. После выбора первой группы нужно проверить, есть ли общий множитель во второй группе, и если его нет, то группировать нужно иначе.

Пример 3:

.

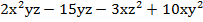Сгруппируем крайние члены между собой, а средние между собой:

.

 

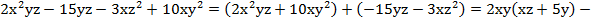
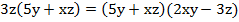Рассмотрим вычислительные задачи.

Пример 4 – разложить на множители и вычислить:

; , .

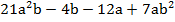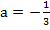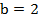Сгруппируем первый член с последним, а средние между собой:

.

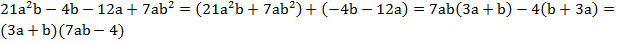Подставим значения переменных:

.

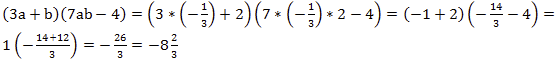Пример 5:

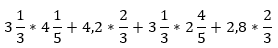
В данном случае выполнять вычисления напрямую будет достаточно долго и сложно, поэтому попробуем разложить выражение на множители способом группировки. Объединим первый член с третьим, а второй с четвертым:

.

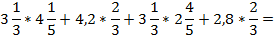
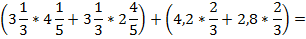
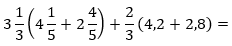
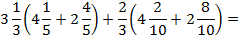
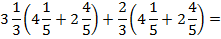
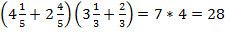
Вывод: на данном уроке мы рассмотрели второй метод разложения многочлена на множители – метод группировки. Мы решили много примеров, простых и более сложных, и вычислительные задачи, чтобы наработать технику выполнения данной операции.

 

Список литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. – М.: Просвещение, 2010.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. – М.: ВЕНТАНА-ГРАФ.
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал E -science.ru (Источник).
2. Школьный помощник (Источник).

 

Домашнее задание

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7, № 848 (а-г), с. 216.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7, № 849, с. 216.
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7, № 346, с. 127.

interneturok.ru

«Разложение многочлена на множители» (7-й класс)

Цели:

• систематизировать, расширить и углубить знания, умения учащихся применять различные способы разложения многочлена на множители;
• способствовать развитию наблюдательности, умения анализировать, сравнивать, делать выводы;
• побуждать учеников к самоконтролю, взаимоконтролю, вызвать у них потребность в обосновании своих высказываний.

Оборудование: экран, магнитная доска, набор карточек для сбора задания 2 на магнитной доске, карточки с заданием теста.

Этап 1. Повторение

Задание 1. В парах выполняется задание теста

Тест

1. Разложение многочлена на множители – это:

А) представление многочлена в виде суммы двух или нескольких многочленов;

Б) представление многочлена в виде произведения двух или нескольких одночленов;

В) представление многочлена в виде произведения двух или нескольких многочленов.

2. Завершить утверждение.

Представление многочлена в виде произведения одночлена и многочлена называется вынесением общего множителя за скобки.

3. Восстановить порядок выполнения действий при разложении многочлена на множители способом группировки.

Чтобы разложить многочлен на множители способом группировки, нужно:

А) вынести в каждой группе общий множитель (в виде многочлена) за скобки;

Б) сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель;

В) вынести в каждой группе общий множитель в виде одночлена за скобки.

4. Отметить знаком плюс верные выражения.

а) а² + в² – 2ав = ( а – в)²;

б) m² + 2mn – n² = (m – n)²;

в) 2pt – p² – t² = (p – t)²;

г) 2cd + c² + d² = (c + d)².

Проверка итогов работы осуществляется с помощью экрана. (Слайд 2. Презентация)

Задание 2. На магнитной доске двое учеников выполняют задание

Провести классификацию данных многочленов по способу разложения на множители.

Метод разложения на множители.

Вынесение общего множителя за скобки	Формулы сокращенного умножения	Способ группировки
20х3у2 + 4 х2у	a4 – b8	2bx – 3ay -6by + ax
b(a + 5) – c(a +5)	27b3 +a6	a2 + ab – 5a – 5b
15a3b + 3a2b3	x2+6x +9	2an -5bm-10bn + am
2y(x -5) +x(x – 5)	49m4 — 25n2	3a2 + 3ab -7a -7b

С остальными учащимися даем характеристику каждому перечисленному приему, демонстрируя на экране.

Вынесение общего множителя (слайд 3)

Из каждого слагаемого, входящего в многочлен, выносится некоторый одночлен, входящий в качестве множителя во все слагаемые.

Таким общим множителем может быть не только одночлен, но и многочлен.

Группировка (слайд 4)

Бывает, что члены многочлена не имеют общего множителя, но после заключения нескольких членов в скобки (на основе переместительного и сочетательного законов сложения) удается выделить общий множитель, являющийся многочленом.

Применение формул сокращенного умножения (слайд 5)

Группа из двух, трех (или более) слагаемых, которая обращает выражение, входящее в одну из формул сокращенного умножения, заменяется произведением многочленов.

Задание 3. “Математическая эстафета”

Работа по командам. На последней парте каждого ряда находится листок с 8 заданиями (по два задания на каждую парту). Ученики, получившие листок, выполняют первые два задания и передают листок впереди сидящим ребятам. Работа считается оконченной, когда учитель получает три листка с выполненными 8 заданиями. Побеждает та команда, в которой раньше решат 8 примеров.

Проверка итогов работы осуществляется с помощью экрана (слайд 6).

Задания:

1 ряд	2 ряд	3 ряд
3a + 12b	16a2 + 8ab + b2	10a + 15c
2a + 2b + a2 + ab	3m – 3n + mn –n2	4a2 – 9b2
9a2 – 16b2	5a – 25b	6xy – ab – 2bx -3ay
7a2b – 14ab2 + 7ab	4a2 – 3ab + a – ag + 3bg –g	4a2 + 28 ab + 49 b2
m2 + mn – m – mg – ng + g	9a2 – 30ab + 25b2	b(a + c) + 2a + 2c
4a2 – 4ab +b2	2(a2 + 3bc) +a(3b+4c)	5a3c– 20acb – 10ac
2(3a2 + bc) + a(4b + 3c)	144a2 — 25b2	х2 – 3x – 5x + 15
25a2 + 70ab + 49b2	9a3b – 18ab2 – 9ab	9a2 – 6ac + c2

Этап 2

На практике при решении примеров часто приходится использовать комбинацию различных приемов. Поэтому, чтобы решать такие примеры сегодня, мы попытаемся выработать план их последовательного применения. Здесь нужны не только знания, но и опыт.

Задание 4. Разложить многочлен на множители и указать, какие приемы использовались при этом

Пример 1. 36а⁶в³ – 96а⁴в⁴ + 64 а²в⁵.

Решение. 36а⁶в³ – 96а⁴в⁴ + 64 а²в⁵ = 4а²в³(9а⁴ – 24а²в + 16в²) = 4а²в³(3а² – 4в)²

Комбинировали два приема:

— вынесение общего множителя за скобки;

— использование формул сокращенного умножения.

Пример 2. а² + 2ав + в² – с².

Решение. а² + 2ав + в² – с² = (а² + 2ав + в²) – с² = (а +в)² – с² = (а + в – с)(а +в +с).

Комбинировали два приема:

— группировку;

— использование формул сокращенного умножения.

Пример 3. у³ — 3у² + 6у – 8.

Решение. у³ — 3у² + 6у – 8 = (у³ – 8) - (3у² – 6у) = (у – 2)(у² + 2у + 4) – 3у(у – 2) = (у – 2)(у² – у + 4).

Комбинировали три приема:

— группировку;

— использование формул сокращенного умножения.

— вынесение общего множителя за скобки.

Эти примеры показывают, что при разложении многочлена на множители полезно соблюдать следующий порядок (слайд 7).

1. Вынести общий множитель за скобку (если он есть).
2. Попробовать разложить многочлен на множители по формулам сокращенного умножения.
3. Попытаться применить способ группировки (если предыдущие способы не привели к цели).

Задание 5

Совокупность различных приемов разложения на множители позволяет легко и изящно производить арифметические вычисления, решать уравнения вида ах² + вх + с = 0 (а0) – такие уравнения называются квадратными, мы начнем изучать в 8-м классе, решать задачи на делимость, доказывать тождества.

1. Решить уравнения:

1. Решить уравнения:

а) х² – 15х + 56 = 0

Решение.

х² – 7х – 8х + 56 = 0,

(х² – 7х) – (8х – 56) =0,

Х(х – 7) – 8(х – 7) = 0,

(Х – 7)(х – 8) = 0,

Х=7, х=8

б) х² + 10х + 21 = 0

Решение.

х² + 10х + 25 – 4 = 0

(х + 5)² – 4 = 0

(х + 5 -2)(х +5 +2) = 0

(х +3)(х + 7) = 0

х = -3, х = -7.

При разложении многочлена на множители мы увидели полный квадрат и таким образом применили еще один прием разложения на множители: метод выделения полного квадрата.

Этап 3

Задание 6. Самостоятельная работа

Разложить на множители, используя различные способы.

Вариант 1	Вариант 2
5а3 – 125ав2	63ав3 – 7а2в
а2 – 2ав + в2 – ас + вс	m2 + 6mn + 9n2 – m – 3n
(с – а)(с + а) – в(в – 2а)	(в – c)(в + c) – а(а + 2c)
х2 – 3х + 2	х2 + 4х + 3
х4 + 5х2 + 9	х4 + 3х2 + 4

Самостоятельная работа проверяется на уроке с помощью экран (слайд 9).

Подведение итогов урока

Провести фронтальный обзор основных этапов урока; отметить, что, кроме трех основных приемов разложения на множители: вынесения общего множителя за скобки, группировки, использование формул сокращенного умножения, познакомились еще с двумя способами: методом выделения полного квадрата, предварительным преобразованием; оценить работу учащихся и ориентировать в домашнем задании (слайд 10).

Домашнее задание

1. Если вы получили оценку “2” или “3” –  № 998 (а, в), 1002, 1004.
2. “4” – № 1083 (а, в), 1085 (а-в),1090 (а).
3. “5”–  № 1083 (а, в), 1085 (а-в),1090 (а), 1089 (а, в).

urok.1sept.ru

Решение задач и уравнений на тему «Разложение многочленов на множители».

План-конспект открытого урока по теме: «Разложение многочленов на множители» 7 класс

Дорогу осилит идущий,

а математику мыслящий.

Тема урока: «Решение задач и уравнений на тему «Разложение многочленов на множители»

Цель урока. Показать значимость формул сокращенного умножения при решении задач и уравнений.

Задачи урока:

1. образовательные: повторить формулы сокращенного умножения; научить применять формулы сокращенного умножения при решении задач и уравнений; проверить знания учащихся путем тестирования;

2. развивающие: развивать интерес к предмету, познавательную активность, пробудить способность к саморазвитию;

3. воспитательные: воспитывать любовь к Матери.

Тип урока. Урок-практикум.

Оборудование. Карточки, портрет С.В.Ковалевской, доклад «Биография С.В. Ковалевской», стенд «Мама – основа семьи»

Структура урока

I Оргмомент (1 мин)

II Проверка домашнего задания (2 мин)

III Повторение теоретической части (4 мин)+ карточная работа

IV Устная работа (5 мин)

V Решение задач (работа в тетрадях)(12 мин)

VI Физкультминутка (2 мин)

VII Разминка ума (3 мин)

VIII Решение уравнений (4 мин)

IX Тестирование (4 мин)

X Доклад «Биография С.В.Ковалевской» (4 мин)

XI Обобщение (2 мин)

XII Подведение итогов (2 мин)

Ход урока

I Оргмомент (Знакомство с целями и задачи урока)

II Проверка домашнего задания (просмотр работ)

Разложить на множители:

№395 (2) 1-(х²-2ху+у²)=1-(х-у)²=(1-х+у)(1+х-у)

№396 (2) a²-b²-a-b=(a-b)(a+b-1)

№408 (2) 6(a+b)+(a+b)²=(a+b)(6+a+b)

№409 (2) (a+2)²-(a+2)(2-a)=(a+2)(a+2-2+a)=2a(a+2)

Индивидуально: №405 (2,4)

III Повторение теоретической части + карточная работа

1. Сформулируйте формулы сокращенного умножения

1. (a + b)² = a² + 2ab + b²

2. (a − b)² = a² − 2ab + b²
3. a² − b² = (a + b)(a − b)

4. (a − b)³ = a³ − 3a²b + 3ab² − b³

5. (a + b)³ = a³ + 3a²b + 3ab² + b³

6. a³ + b³ = (a + b)(a² − ab + b²)

7. a³ − b³ = (a − b)(a² + ab + b²)

2. Перечислите алгоритм разложения многочлена на множители:

   1. Вынести общий множитель за скобки, если он имеется;

   2. Попробовать разложить многочлен на множители по формулам сокращенного умножения

   3. Попытаться применять способ группировки (если предыдущие способы не привели к цели)

Карточка №1 (среднему ученику)

1. Разложите на множители

3у²-27=3(у-3)(у+3)

2(a-b)+(a-b)²=(a-b)(2+a-b)

x²-6x+9=(x-3)²

2. Решите уравнение

х²-25=0; x₁=5, x₂=-5.

х³-4х=0; x₁=0, x₂=2, x₃=-2

Карточка №2 (слабому ученику)

3. Разложите на множители

4-а²=(2-a)(2+a)

(x+y)²-(x+y)=(x+y)(x+y-1)

x²-25=(x-5)(x+5)

4. Решите уравнение

х²-1=0, x₁=-1, x₂=1.

x(x+1)=0, x₁=0, x₂=-1.

IV Устная работа

Учитель: Ребята! Кто больше всех на свете хочет, чтобы вы были здоровы, счастливы, умны, удачливы? Кто больше всех радуется успехами ребенка?

Да, Мама! Мама – это самое дорогое богатство у ребенка. Любите своих Мам, берегите их, радуйте своими успехами.

1. Разложите на множители

1. 2у²-18=2(у-3)(у+3)

2. 4(х-у)+3(х-у)²=(х-у)(4+3х-3у)

3. 2х²-12х+18=2(х-3)²

2. Решите уравнение:

1. х²-16=0

(х-4)(х+4)=0

х₁=4, х₂=-4

Ответ. 4; -4.

2. х²-8х+16=0

(х-4)²=0

(х-4)(х-4)=0

х₁=4, х₂=4

Ответ. 4.

3. х⁴=4х²

х⁴-4х²=0

х²(х²-4)=0

х²(х-2)(х+2)=0

х₁=0, х₂=2, х₃=-2

Ответ. 0; 2; -2.

V Решение задач (работа в тетрадях)

Я тетрадь свою открою

И наклонно положу.

Я, друзья, от вас не скрою,

Ручку я вот так держу!

Сяду прямо, не согнусь,

За работу я берусь.

Записываем в тетрадях число, «классная работа», тему «Решение задач и уравнений»

№418. Ширина прямоугольника меньше стороны квадрата на 12 м, а длина этого прямоугольника больше стороны того же квадрата на 12 м. сравнить площади прямоугольника и квадрата.

Решение.

S_кв=a², S_np=ab

х м – сторона квадрата,

(х-12) м – ширина прямоугольника,

(х+12) м – длина прямоугольника

S_кв=х² м²,

S_np=(х-12)(х+12)=х²-144 м²

S_кв> S_np

Ответ. S_кв> S_np

№419 Скорость пассажирского поезда равно 60 км/ч, а товарного – 40 км/ч. Найти расстояние между двумя пунктами, если пассажирский поезд проходит это расстояние на 2 ч быстрее, чем товарный.

Решение.

х км – расстояние между двумя пунктами;

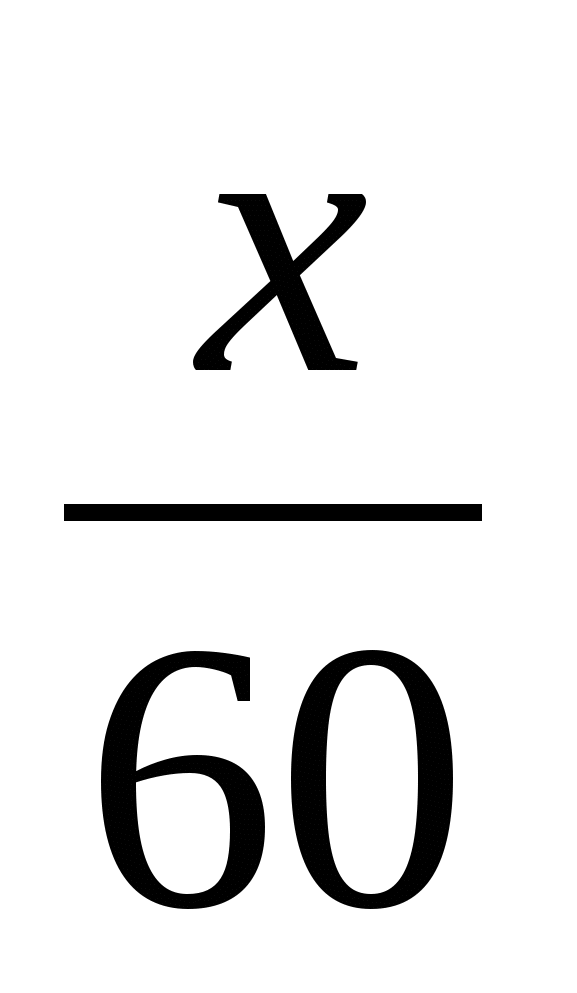ч – время движения пассажирского поезда;

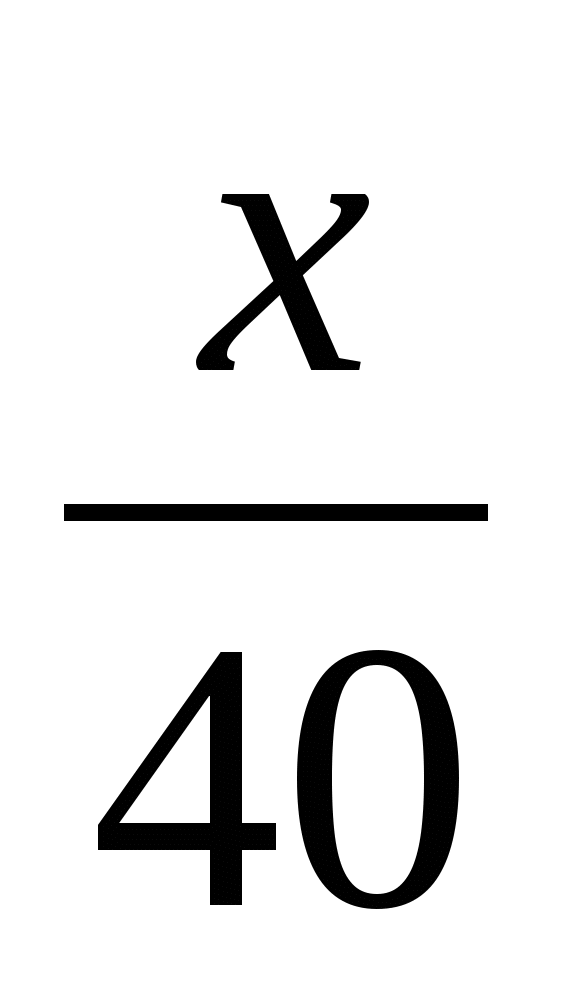ч – время движения товарного поезда.

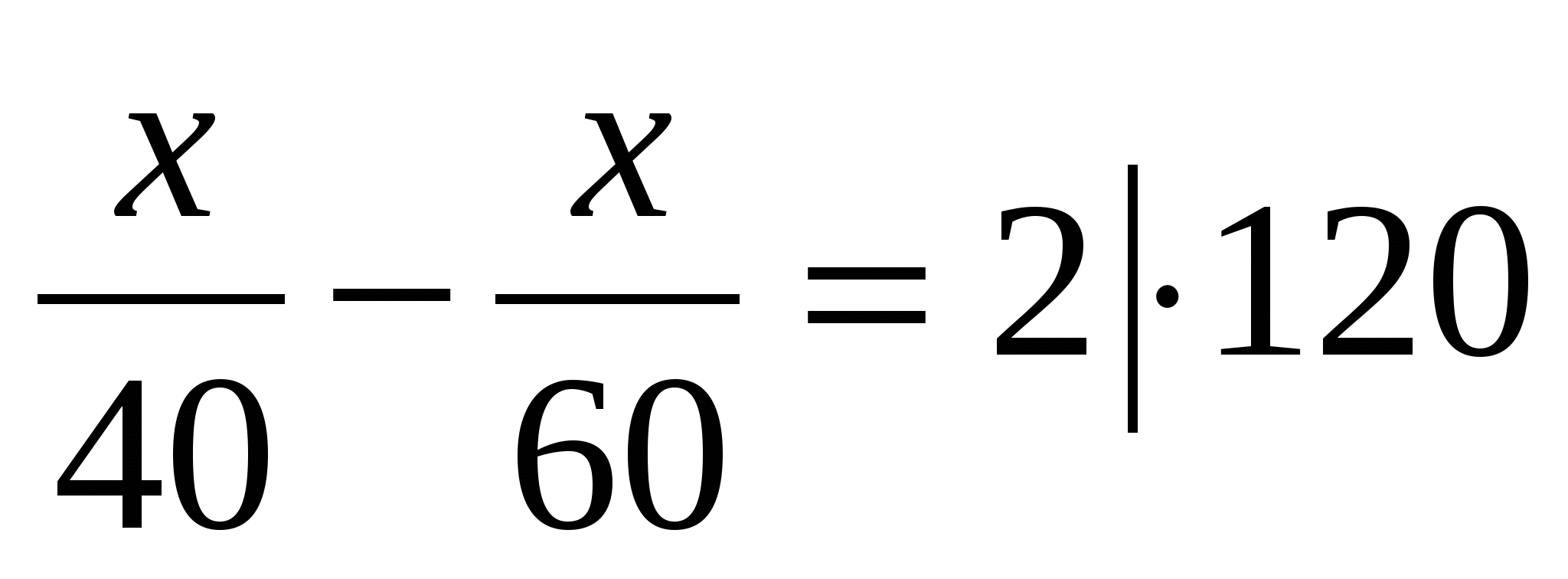
3х-2х=240,

х=240.

240 км – расстояние между двумя пунктами.

Ответ. 240.

Учитель: Ребята! Если вы были бы машинистами, что бы вам посоветовала

Мама?

Ученик: Не отвлекаться, быть бодрым.

VI Физкультминутка

VII Разминка ума

Мама посчитала, что если дать детям по четыре конфеты, то три конфеты останутся лишними. А чтобы дать по пять конфет, двух конфет не хватает. Сколько было детей у мамы?

Решение.

Пусть у мамы было х детей. Тогда

4х+3=5х-2, х=5.

Ответ. 5 детей.

VIII Решение уравнений

№417 (I вариант-1, II вариант – 3)

1. 1. (3х-1)²-(3х-2)²=0

(3х-1-3х+2)(3х-1+3х-2)=0

1(6х-3)=0

,

6х-3=0,

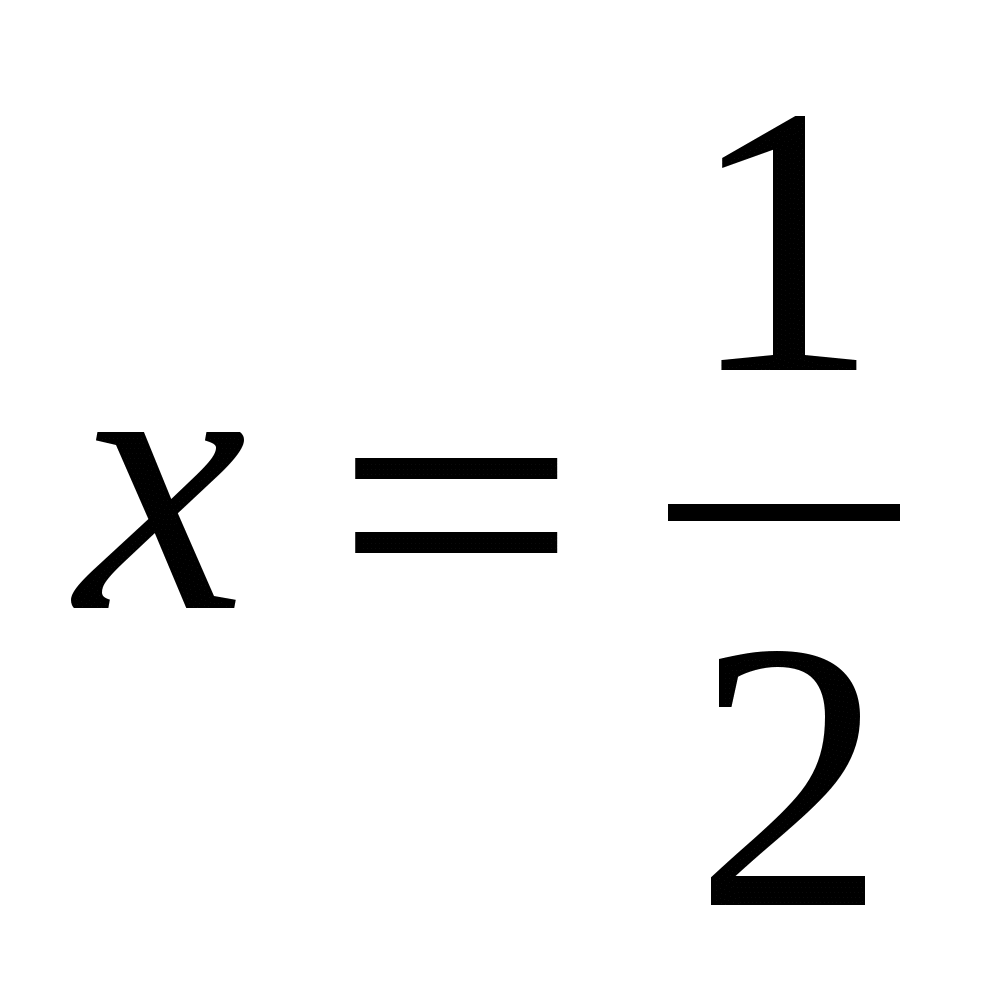
Ответ.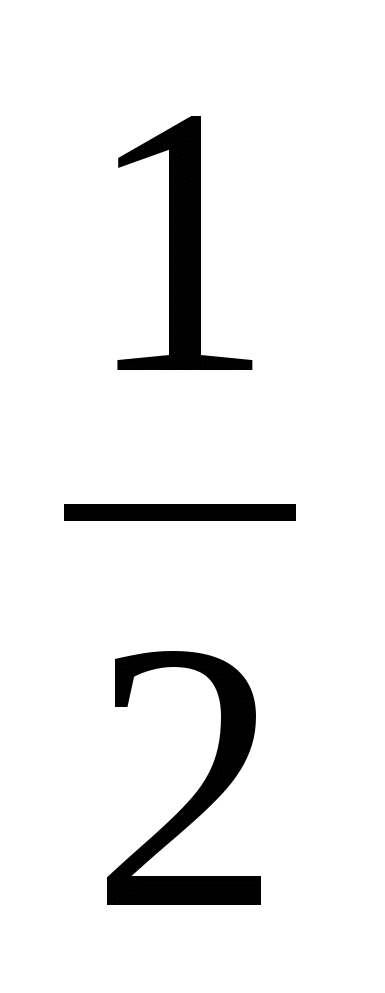

3) (х+3)(х+7)-(х+4)²=0

х²+7х+3х+21-х²-8х-16=0

2х+5=0

х=-2,5

Ответ. -2,5

5)(3х+2)(3х-2)-(3х-4)²=28

9х²-4-9х²+24х-16=28 кто быстрее? Из двух вариантов.

24х=48

х=2.

Ответ. х=2

IX Тестирование

Вариант 1.

1. 1. Разложите на множители многочлен 18х²у⁴-6ху³, вынося за скобки (-2ху³).

1. -2ху³(-9ху-3)

2. -2ху³(9ху+6)

3. -2ху³(-9ху+3)

4. -2ху³(6-9ху)

1. 1. Представьте в виде произведения выражение 2c(b—a)-d(a—b)

1. (a-b)(2c-d)

2. (b-a)(2c+d)

3. (b-a)(2c-d)

4. (a-b)(2c+d)

1. 1. Разложите на множители многочлен 18mn²-27nm²-3n²

1. -3n(3m-n)²

2. -3n(3m+n)²

3. 3n(3m-n)²

4. 3n(6n-9m)²

1. 1. Представьте в виде произведения многочлен 15x²+4c-6x-10cx

1. (3x-2c)(5x+2)

2. (5x-2)(2c-3x)

3. (3x-2c)(5x-2)

4. (3x+2c)(2-5x)

1. 5. Решите уравнение 8y³-50y=0

1)

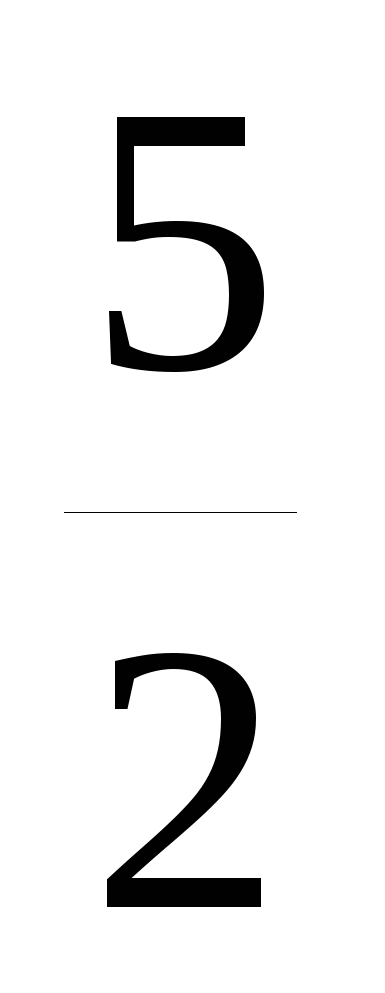
2)

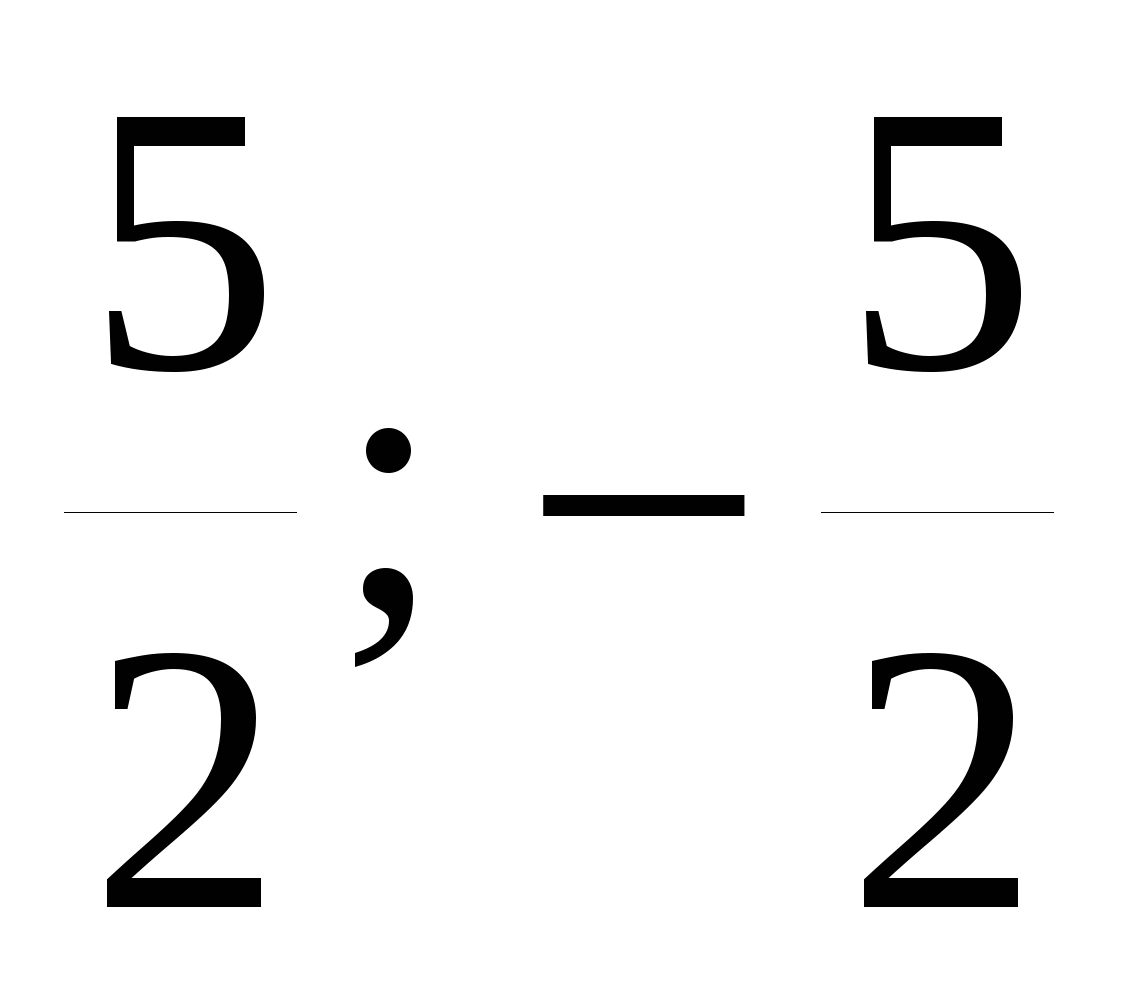
3)

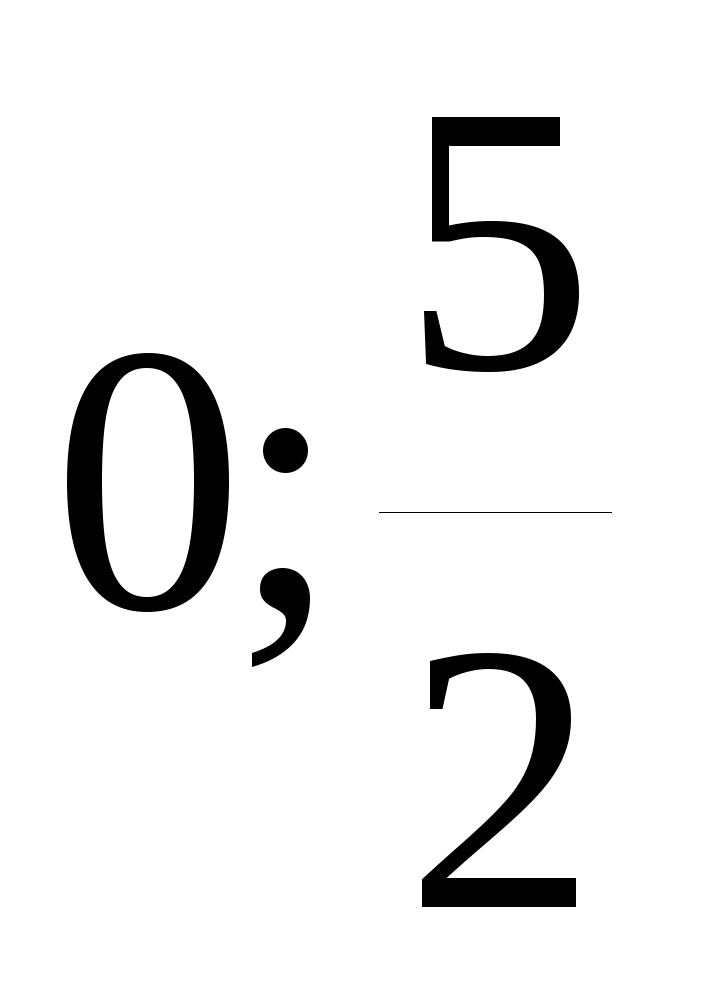
4)

Вариант 2.

1. Разложите на множители многочлен 15a³b-3a²b², вынося за скобки (-3a²b).

   1. -3a²b(b-5a)

   2. -3a²b(-5a-b)

   3. -3a²b(5a-b)

   4. -3a²b(-5a+3b)

2. Представьте в виде произведения выражение a(x—y)-2b(y—x)

   1. (x-y)(a-2b)

   2. (y-x)(a-2b)

   3. (x-y)(a+2b)

   4. (y-x)(a+2b)

3. Разложите на множители многочлен 2m³-12m²n+18mn²

   1. 2(m-3)²n²

   2. 2m(3m-n)²

   3. 2m(m-3n)²

   4. -2m(m-3n)²

4. Представьте в виде произведения многочлен 4n²-15a-6an+10n

   1. (4n-3a)(n+2)

   2. (3a+4n)(n-2)

   3. (3a-2n)(2n+5)

   4. (2n-3a)(2n+5)

5. Решите уравнение 4x⁴-9x²=0

1)

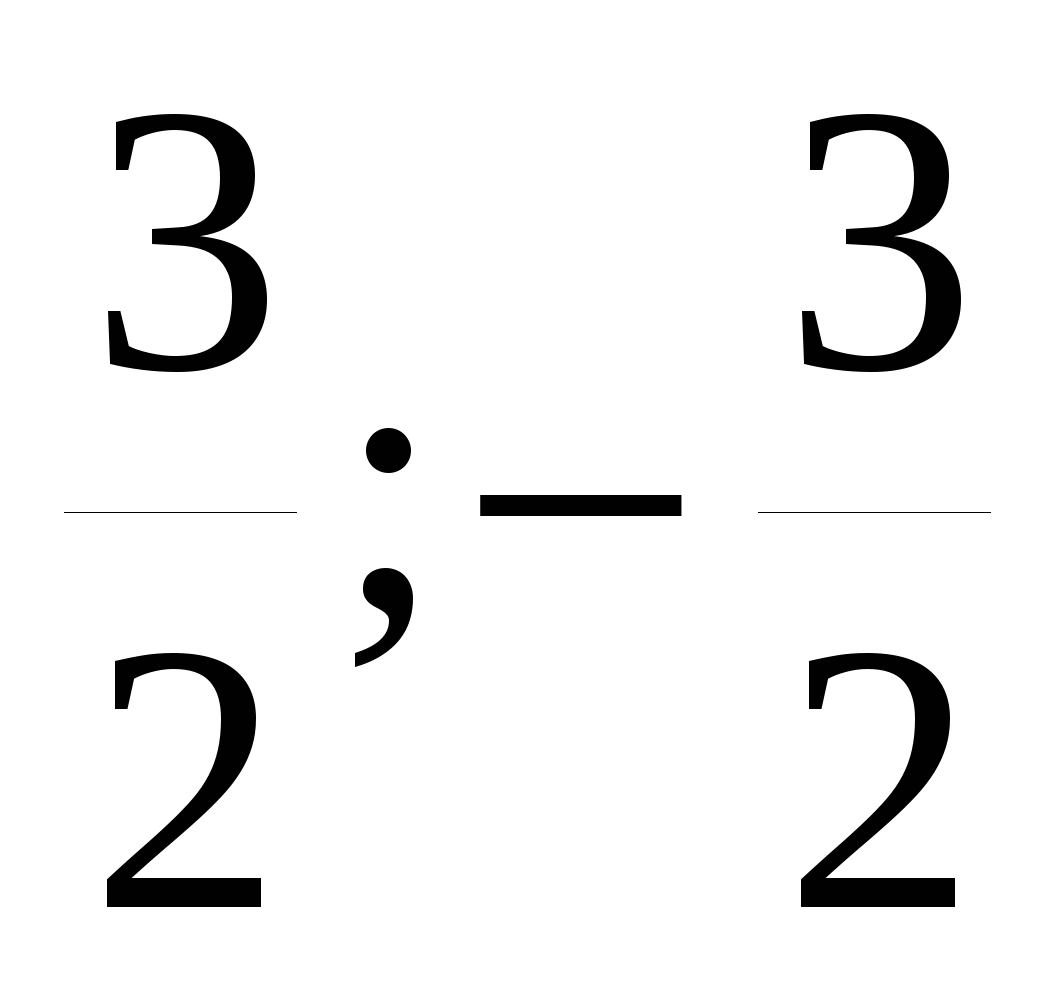
2)

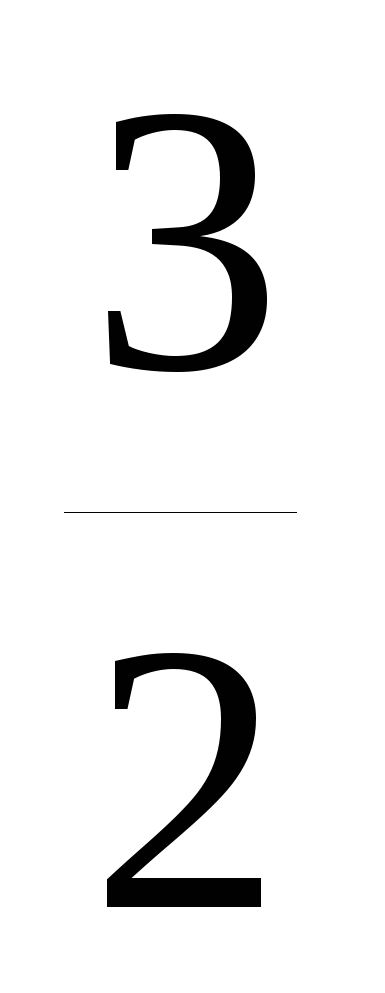
3)

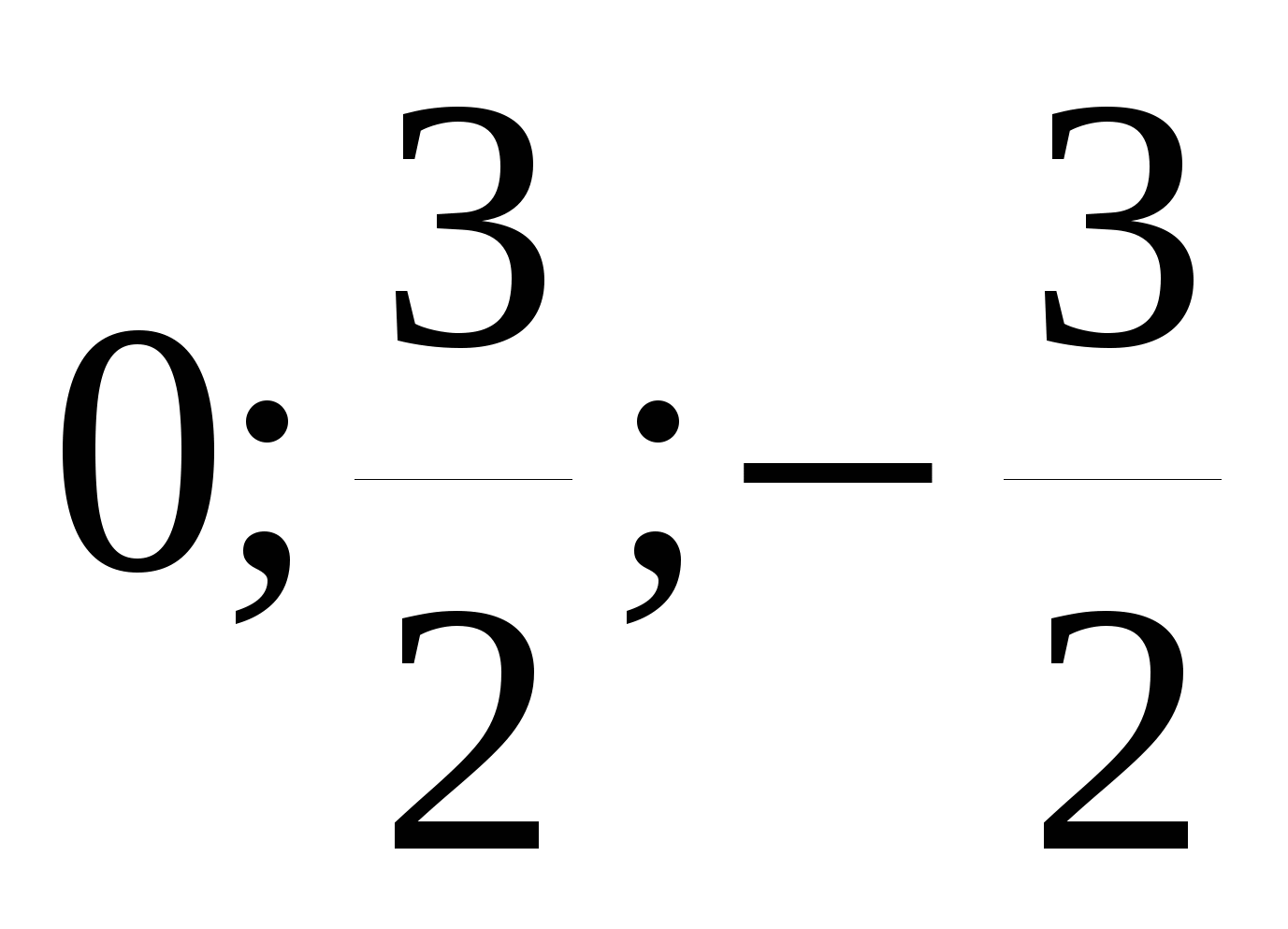
4)

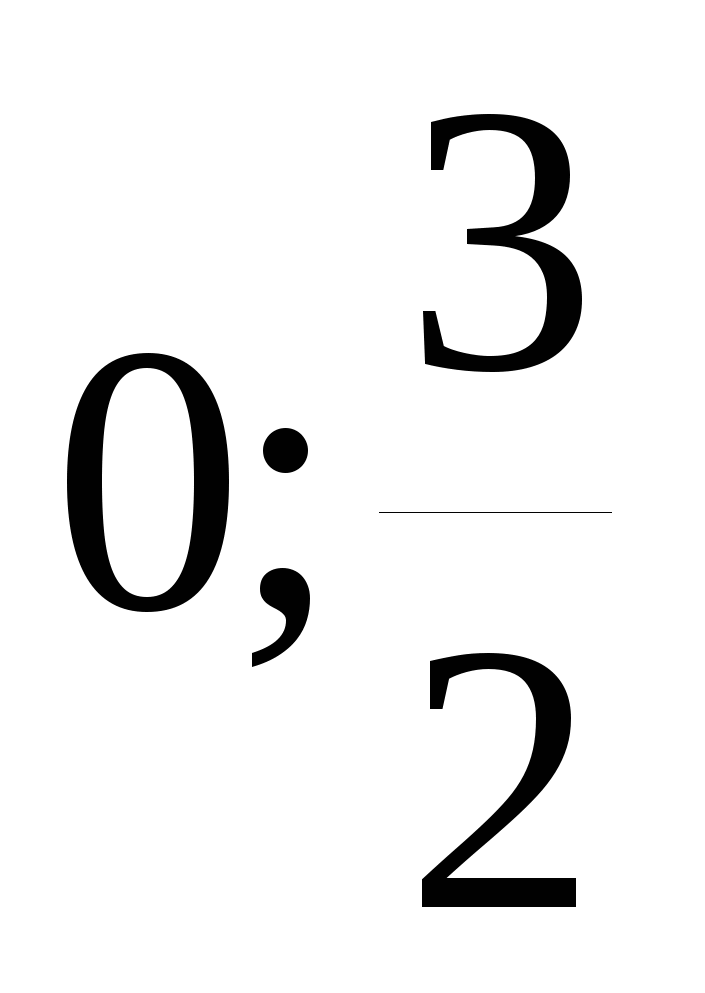
X Доклад «Биография С.В.Ковалевской» (читает ученик)

XI Обобщение

XII Подведение итогов.

Ребята, на данном уроке мы решали задачи и уравнения с использованием формул сокращенного умножения, применяли алгоритм разложения многочленов на множители при выполнении некоторых заданий.

Сегодня вы еще больше убедились как важно знать формулы сокращенного умножения, они нам нужны будут и на выпускных экзаменах.

.

Стихотворение о Маме (читает учитель)

Мама, очень-очень

Я тебя люблю!

Так люблю, что ночью

В темноте не сплю

Вглядываюсь в темень,

Зорьку тороплю.

Мамочка родная, я тебя люблю!

Ребята, пусть эти слова ваши Мамы будут слышать не только сейчас, когда она нужна вам, но и тогда, когда Мама будет нуждаться в вашем внимании и заботе.

Домашнее задание. №417 (2;4), №420, №426 (индивидуально)

infourok.ru

Примеры разложения многочленов на множители

1. Примеры с решением квадратного уравнения

Пример 1.1

Разложить многочлен на множители:
x⁴ + x³ – 6x².

Решение

Выносим x² за скобки:
.
Решаем квадратное уравнение x² + x – 6 = 0:
.
Корни уравнения:
,   .

Отсюда получаем разложение многочлена на множители:
.

Ответ

.

Пример 1.2

Разложить на множители многочлен третьей степени:
x³ + 6x² + 9x.

Решение

Выносим x за скобки:
.
Решаем квадратное уравнение x² + 6x + 9 = 0:
Его дискриминант:   .
Поскольку дискриминант равен нулю, то корни уравнения кратные: ;
.

Отсюда получаем разложение многочлена на множители:
.

Ответ

.

Пример 1.3

Разложить на множители многочлен пятой степени:
x⁵ – 2x⁴ + 10x³.

Решение

Выносим x³ за скобки:
.
Решаем квадратное уравнение x² – 2x + 10 = 0.
Его дискриминант:   .
Поскольку дискриминант меньше нуля, то корни уравнения комплексные: ;
,   .

Разложение многочлена на множители имеет вид:
.

Если нас интересует разложение на множители с действительными коэффициентами, то:
.

Ответ

.

Примеры разложения многочленов на множители с помощью формул

Примеры с биквадратными многочленами

Пример 2.1

Разложить биквадратный многочлен на множители:
x⁴ +x² – 20.

Решение

Применим формулы:
a² + 2ab + b² = (a + b)²;
a² – b² = (a – b)(a + b).

;
.

Ответ

.

Пример 2.2

Разложить на множители многочлен, сводящийся к биквадратному:
x⁸ +x⁴ + 1.

Решение

Применим формулы:
a² + 2ab + b² = (a + b)²;
a² – b² = (a – b)(a + b):

;

;
.

Ответ

.

Пример 2.3 с возвратным многочленом

Разложить на множители возвратный многочлен:
.

Решение

Возвратный многочлен имеет нечетную степень. Поэтому он имеет корень x = –1. Делим многочлен на x – (–1) = x + 1. В результате получаем:
.
Делаем подстановку:
,   ;
;


;
.

Ответ

.

Примеры разложения многочленов на множители с целыми корнями

Пример 3.1

Разложить многочлен на множители:
.

Решение

Предположим, что уравнение

имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x). То есть целый корень может быть одним из чисел:
–6, –3, –2, –1, 1, 2, 3, 6.
Подставляем поочередно эти значения:
(–6)³ – 6·(–6)² + 11·(–6) – 6 = –504;
(–3)³ – 6·(–3)² + 11·(–3) – 6 = –120;
(–2)³ – 6·(–2)² + 11·(–2) – 6 = –60;
(–1)³ – 6·(–1)² + 11·(–1) – 6 = –24;
1³ – 6·1² + 11·1 – 6 = 0;
2³ – 6·2² + 11·2 – 6 = 0;
3³ – 6·3² + 11·3 – 6 = 0;
6³ – 6·6² + 11·6 – 6 = 60.

Итак, мы нашли три корня:
x₁ = 1, x₂ = 2, x₃ = 3.
Поскольку исходный многочлен – третьей степени, то он имеет не более трех корней. Поскольку мы нашли три корня, то они простые. Тогда
.

Ответ

.

Пример 3.2

Разложить многочлен на множители:
.

Решение

Предположим, что уравнение

имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
–2, –1, 1, 2.
Подставляем поочередно эти значения:
(–2)⁴ + 2·(–2)³ + 3·(–2)³ + 4·(–2) + 2 = 6;
(–1)⁴ + 2·(–1)³ + 3·(–1)³ + 4·(–1) + 2 = 0;
1⁴ + 2·1³ + 3·1³ + 4·1 + 2 = 12;
2⁴ + 2·2³ + 3·2³ + 4·2 + 2 = 54.

Итак, мы нашли один корень:
x₁ = –1.
Делим многочлен на x – x₁ = x – (–1) = x + 1:

Тогда,
.

Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.

Итак, мы нашли еще один корень x₂ = –1. Можно было бы, как и в предыдущем случае, разделить многочлен     на   , но мы сгруппируем члены:
.

Поскольку уравнение x ² + 2 = 0 не имеет действительных корней, то разложение многочлена на множители имеет вид:
.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 18-06-2015

1cov-edu.ru

Конспект урока «Разложение многочленов на множители с помощью формул»

Петухова Татьяна Дионисовна, учитель математики и информатики МАОУ Винзилинской СОШ им. Г. С. Ковальчука

Тема урока: «Разложение многочлена на множители с помощью формул» ¹

Класс: 7

Место и роль урока в изучаемой теме.

Данный урок входит в систему уроков по теме «Разложение многочленов на множители». Это краткосрочный проект. Учащиеся в процессе работы открывают новый способ разложения многочленов на множители. Результатом работы учащихся – формула, позволяющая разложить многочлен вида 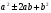на множители.

Тип урока: комбинированный

Цели урока:

• Вывод формулы — формулы разложения многочлена на множители;

• Обучение распознаванию способов разложения на множители, необходимых для решения каждого конкретного примера;

• Создание условий для того, чтобы учащиеся убедились, что они сами открыли несколько универсальных способов разложения многочленов на множители.

Формы обучения: коллективная; групповая.

Ход урока

Структурные элементы

Время

Дидактика

Деятельность

учителя

учащиеся

1. Организационный момент

Менее 1 мин

Слова Рене Декарта «Мало иметь хороший ум, главное- хорошо его применять»

Приветствие.

Ребята, предлагаю слова великого французского философа и математика Рене Декарта принять как добрый совет, которому вы будете следовать на сегодняшнем уроке, да и вообще по жизни в целом. Итак, открываем тетради.

Приветствуют учителя.

2. Подготовительный. Постановка проблемы. Целеполагание

15 мин.

Многочлены

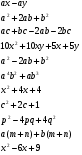
Кластер

Вынесение общего множителя за скобки

Способ группировки

?

Способы разложения многочленов на множители

Веер целей:

• Повторить знакомые способы разложения многочленов на множители;

• Узнать, как раскладываются многочлены на множители способом группировки

• Научиться выносить общий множитель за скобки

• Открыть новые способы разложения на множители

Знакомит с замыслом проекта, мотивирует учащихся. Помогает в постановке цели.

Напомните, пожалуйста, тему, которую мы изучаем.

Я выписала различные алгебраические выражения. Проклассифицируйте их по способам разложения.

Какую форму работы выберем?

Группам предлагается рассказать о результатах классификации

Предлагается для первой и второй групп многочленов показать решения

Предлагается поставить цель урока или выбрать утверждение из предложенного веера, которое относится к сегодняшнему уроку

Разложение многочленов на множители

Учащиеся объединяются в четверки и приступают к работе. Каждое выражение записано на отдельной карточке и ученики просто раскладывают их по группам

Каждая группа рассказывает о результатах классификации.

Заполняется кластер.

https://cloud.mail.ru/public/5CqS/9y4gKvN7T

Показываются решения на доске.

Формулируется проблема: учащиеся говорят, что для остальных групп способы необходимо найти

Работают с веером целей:

+

—

—

+

3. Планирование деятельности по реализации проекта

2 мин.

Инструктаж.

Конверт № 1 (выдается каждой группе)

Конверт А (выдается в зависимости от выбранной подсказки поэтапно)

Конверт Б

Конверт В

Конверт Г

Предлагаю начать с разложения на множители многочлена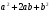

Если группа испытывает трудности в планировании поиска, вы можете воспользоваться подсказками из конверта № 1

При дальнейших затруднениях можно получить дальнейшие подсказки (поэтапно) из конвертов с буквой, под которой стоит выбранная вами подсказка.

Работа в группах продолжается. Распределение деятельности между участниками проекта

4. Подготовка продукта

13 мин.

Конверт № 1

Выберите наиболее понравившуюся подсказку:

А – воспользуйтесь фигурами из конверта, чтобы построить модель;

Б – подставьте вместо букв числа, найдите значение выражения и попробуйте выдвинуть гипотезу;

В – из четырех фигур в конверте сложите одну;

Г – представьте 2ab в виде суммы двух слагаемых

Для выступления группы, выбравшей подсказку А или В

https://cloud.mail.ru/public/DNHT/DTpT5pGAE

Наблюдает, советует, косвенно руководит деятельностью, консультирует подготовку к презентации

2А – сложите из фигур квадрат

3А – найдите площадь получившегося квадрата двумя способами

4А – чему равна сторона получившегося квадрата? Площадь квадрата через сторону?

2Б – выразите значения через выбранные числа

3Б – запишите значения выражения в виде квадрата чисел

4Б – как это число записать через выбранные?

2В – чему равна сторона получившегося квадрата?

3В – чему равна площадь квадрата? Как её ещё можно найти?

2Г – 2ab = ab + ab

3Г — воспользуйтесь способом группировки

Анализируют информацию, выполняют задания, готовят материал и выступающего к защите

5. Представление, отчет

12 мин.

Упражнение «Думающий колпак»

поможет учащимся сосредоточить внимание на собственном слухе и процессе слушания, а также способствует развитию памяти. Оно также снимает напряжение в мышцах головы. В этом упражнении большим и указательным пальцами мягко оттягивают назад и прижимают, массируя, раковины ушей. Массаж начинают сверху и идут вниз вдоль «свернутых» частей ушной раковины вплоть до мочек ушей. Держите голову прямо, чтобы подбородку было удобно. Упражнение повторяют трижды

Слушает, задает вопросы в роли рядового участника, оценивает усилия учащихся, результаты решения проблемы, качество отчета.

Представление результатов деятельности группы: каждая группа рассказывает о ходе своей работы, воспользовались ли подсказками, сколько подсказок открыли

6. Рефлексия. Постановка домашнего задания

 2 мин

Кластер

Вынесение общего множителя за скобки

Способ группировки

?

Способы разложения многочленов на множители

Притча.

Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»

Какой же результат мы получили?

Что запишем в пустующий сектор?

Вы не только открыли этот способ разложения на множители. Одна из групп предложила представить одночлен 2ab в виде суммы ab + ab. Обратите, пожалуйста, внимание на этот момент, так как это тоже способ, используемый при разложении многочленов на множители

Но вопросы остались. Например, как можно разложить на множители многочлен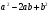? Предлагаю дома подумать над этим вопросом.

Послушайте притчу. Ребята! Давайте мы попробуем с вами оценить каждый свою работу за урок.

Кто работал так, как первый человек?

Кто работал добросовестно? Кто принимал участие в строительстве храма?

Мы вывели формулу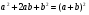

Сочли необходимым продолжить открытие способов разложения многочленов на множители

Поднимают руку

1 ^{При разработке проекта урока использован конспект урока учителя математики ГБОУ школы № 572 г. Москвы Л. К. Быковой «Разложение на множители с помощью формул». Газета «Математика» № 9/2003}

infourok.ru

Конспект по алгебре по теме «Разложение многочлена на множители»

Краткосрочный план

7.1В Многочлены

Школа: КГУ «Средняя школа №4»

Дата:

ФИО учителя: Дроган Мария Васильевна

класс: 7

Участвовали:

Не участвовали:

Тема урока

Разложение многочлена на множители (1 урок)

Цели обучения, достигаемые на этом уроке (Ссылка на учебный план)

7.2.1.12

раскладывать алгебраические выражения на множители вынесением общего множителя за скобки и способом группировки

Цель урока

— знать способы разложения алгебраических выражений на множители;

— раскладывать алгебраические выражения на множители вынесением общего множителя за скобки и способом группировки.

Критерии оценивания

Все:

— знают способ разложения алгебраических выражений на множители вынесением общего множителя за скобки;

— знают способ разложения алгебраических выражений на множители способом группировки

— раскладывают алгебраические выражения на множители вынесением общего множителя за скобки и способом группировки

Большинство:

— решают уравнения, используя способ разложения алгебраических выражений на множители

Некоторые:

— раскладывают многочлен на множители вынесением общего множителя за скобки и способом группировки при решении задач.

Уровень мыслительных навыков

знание, понимание, применение, анализ

Языковые задачи

Учащиеся будут:

приводить обоснование выполнения умножение одночлена на многочлен и умножение многочленов

— объяснять способ разложения многочлена на множители вынесением общего множителя за скобки;

— объяснять способ разложения многочлена на множители способом группировки

Предметная лексика и терминология:

одночлен;

степень одночлена;

коэффициент одночлена;

— многочлен;

— подобные члены

Серия полезных фраз для диалога/письма

… раскрыть скобки и привести подобные члены;

чтобы умножить многочлен на одночлен нужно … ;

чтобы умножить многочлен на многочлен нужно … .

Воспитание ценностей

Сотрудничество, уважение, взаимопомощь, ответственность, культура поведения при работе в группе

Межпредметная связь

геометрия, топология

Предыдущие знания

Одночлен, преобразования алгебраических выражений, действия с многочленами

Ход урока

Запланированные этапы урока

Виды упражнений, запланированных на урок:

Ресурсы

Начало урока

Психологический настрой.

2 мин

Индивидуальная работа

4 мин

Самопроверка

Организационный момент.

Давайте наш урок начнем с пожелания друг другу добра. Я желаю тебе добра, ты желаешь мне добра, мы желаем друг другу добра. Если будет трудно — я тебе помогу. Я рада, что у нас отличное настроение. Надеюсь, что урок пройдет интересно и увлекательно.

«Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта – это путь самый горький».

Конфуций.

На нашем уроке мы будем использовать все пути к знаниям. Девизом урока станет высказывание «Дорогу осилит идущий, а математику мыслящий»

Для каждого — лист успешности, с помощью которого учащиеся в течении всего урока оценивают свои успехи на уроке (ставят баллы)

Лист успешности:

Ф.И.

Графический тест

Задание 1:

Задание 2:

Задание 3:

В конце урока учащиеся сдают листы успешности и тетради. После проверки классной работы учитель добавляет баллы от себя за решения и актуальность записей.

Прежде чем приступить к изучению нового материала, проверим домашнее задание (14.8). Учащиеся комментируют с места решения заданий, если допущены ошибки, корректируют.

Графический тест теоретического материала.

Для того чтобы вспомнить теорию, мы проведем графический тест

Верно ли утверждение, определение, свойство?

1. Одночленом называют сумму числовых и буквенных множителей.

2. Буквенный множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.

3. Целое выражение, которое содержит произведение чисел и букв, называют одночленом.

4. Сумма показателей степеней всех букв входящих в одночлен называемый степенью одночлена.

5. Одинаковые или отличающиеся друг от друга только коэффициентами, называют подобными членами.

6. Алгебраическая сумма нескольких одночленов называется одночленом.

7. В результате умножения многочлена на одночлен получается одночлен.

8. В результате умножения одночлена на многочлен получается многочлен.

9. Многочлен, в котором отсутствуют подобные члены и каждый из них одночлен стандартного вида называется многочленом стандартного вида.

10. Чтобы раскрыть скобки, перед которыми стоит знак “+”, скобки надо опустить, сохранив знак каждого члена, который был заключен в скобки.

11. Когда раскрываем скобки, перед которыми стоит знак “-”, скобки опускаем, и знаки членов, которые были заключены в скобки, меняют на противоположные

Формативное оценивание:

Самопроверка по образцу на слайде: —+++—++++

Метод «Сигналы рукой»

Я понимаю __________ и могу объяснить (большой палец руки направлен вверх)

Я все еще не понимаю _________ (большой палец руки направлен в сторону)

Я не совсем уверен в _______________(помахать рукой)

Обратная связь:

В каком из заданий допущены ошибки?

(Слайд 2)

(Слайд 3)

(Слайд 4)

(Слайд 5)

(Слайд 6)

Середина урока

Фронтальная работа.

Работа в парах

Дифференциация по темпу

5 минут

Работа в группах

Уровневая дифференциация

5 минут

Дифференциация по уровню сложности заданий

9 минут

3 минуты

Дифференциация по уровню сложности заданий

10 минут

На последних уроках мы говорили о преобразованиях выражений.

— С какими преобразованиями мы работали на последнем уроке?

( раскрытие скобок)

-Чтобы раскрыть скобки и привести подобные надо…?

— Какие приемы (правила) мы при этом использовали?

(-умножение одночлена на многочлен

-умножение многочлена на многочлен)

-Чтобы умножить многочлен на одночлен нужно….

-Чтобы умножить многочлен на многочлен нужно ….

Для подготовки к изучению новой темы я провожу:

У вас на столах лежат карточки, на которых написаны выражения. Составьте из них верные равенства (найдите пары равных выражений). Можно делать вспомогательные записи в тетрадях.

Задание 1: «Найти соответствие»

Цель: знать правила умножения одночлена на многочлен и многочлена на многочлен.

Критерий оценивания:

учащийся умеет выполнять умножение одночлена на двучлен;

учащийся умеет выполнять умножение одночлена на трехчлен;

учащийся умеет выполнять умножение двучлена на двучлен;

учащийся умеет выполнять умножение трехчлена на трехчлен.

Уровень навыков мышления: знание

1. 3а + 3b = 3(a +b)

2. xy – x²y = xy(x – y)

3. 14mn²-49 mn³-35 mn⁴= 7mn² (2 — 7n-5n²)

4. ху – 6 +3х – 2у = (х-2)(у+3)

5. 2ax + 2ay + 3bx + 3by = (2a + 3b)(x + y)

6. x² + 4x – y² + 6y – 5 = (x + y – 1)(x – y + 5)

Проверяем получившиеся равенства.

Дескриптор: учащийся понимает правило умножения одночлена на многочлен и умеет его применять

Формативное оценивание: Проставляем баллы в оценочный лист.

Метод «Сигналы рукой»

Я понимаю __________ и могу объяснить (большой палец руки направлен вверх)

Я все еще не понимаю _________ (большой палец руки направлен в сторону)

Я не совсем уверен в _______________(помахать рукой)

Обратная связь:

Какие ошибки допустили при выполнении этого задания?

Что нужно повторить, чтобы этих ошибок больше не допускать?

Организую затруднения в индивидуальной деятельности.

На интерактивной доске выписаны получившиеся равенства. По какому принципу вы можете сгруппировать полученные равенства?

Учащиеся разбивают получившиеся равенства на три группы.

1 группа: умножение одночлена на многочлен

2 группа: умножение многочлена на многочлен

Можно ли поменять местами левую и правую части этих равенств?

         Да.

Учащиеся на доске меняют местами части равенств.

Как называются выражения, записанные в левом столбике?

         Многочлены.

А в правом?

         Произведение многочленов.

Как мы можем назвать действие, которое надо выполнить, чтобы перейти от многочлена к произведению многочленов?

         Разложение многочлена на множители.

Запишите в тетрадях тему урока «Разложение многочлена на множители».

Совместная постановка целей

Что значит разложить многочлен на множители?

       Преобразовать многочлен в произведение двух или нескольких многочленов.

Обучающиеся распределяются по группам:

А –легкие задания,

В — задания средней сложности,

С- задания сложного уровня .

Существует целый ряд приемов для разложения многочленов на множители. Начнем с вынесения за скобки общего множителя.

Задание 2:

Группа А составляет алгоритм вынесения общего множителя за скобки.

1. 3а + 3b = 3(a +b)

2.xy – x²y = xy(x – y)

3. 14mn²-49 mn³-35 mn⁴= 7mn² (2 — 7n-5n²)

Каждая группа составляет алгоритм вынесения общего множителя за скобки и представляют на ватмане.

Вынесение общего множителя за скобки

Алгоритм нахождения общего множителя нескольких одночленов

• Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, — он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).

• Найти переменные, которые входят в каждый член многочлена и выбрать для каждой из них наименьший (из имеющихся) показатель степени.

• Произведение коэффициента и переменной, найденного на первом и втором шагах, является общим множителем, который целесообразно вынести за скобки.

Обратная связь:

«Две звезды, одно пожелание»

Каждая группа оценивает алгоритм выступающей группы.

Группа В составляет алгоритм способа группировки:

1. ху – 6 +3х – 2у = (х-2)(у+3)

2. 2ax + 2ay + 3bx + 3by = (2a + 3b)(x + y)

3. x² + 4x – y² + 6y – 5 = (x + y – 1)(x – y + 5)

Способ группировки:

Алгоритм разложения многочлена на множители способом группировки.

1. Сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель

2. Вынести в каждой группе общий множитель в виде одночлена за скобки

3. Вынести в каждой группе общий множитель (в виде многочлена) за скобки.

Группа С составляет алгоритм 2х способов разложения алгебраических выражений на множители.

Группы представляют способы разложения. Оформляют на плакате в виде кластера.

Обратная связь:

«Две звезды, одно пожелание»

Давайте еще раз перечислим приемы, с помощью которых можно разложить многочлен на множители

Вынесение общего множителя за скобки

Способ группировки.

Задание 3:

Цель: 7.2.1.12 раскладывать алгебраические выражения на множители вынесением общего множителя за скобки и способом группировки.

Критерий оценивания:

раскладывает алгебраические выражения на множители вынесением общего множителя за скобки и способом группировки.

Уровень навыков мышления: понимание

«Угадай слово»

1 группа (уровень А)

2 группа

(уровень В)

5p² + 10p О

12p²y + 9 py – 6 py O

9xy + 3x²y² Т

2y(x -5) +x(x – 5) T

20х³у² + 4 х²у Л

2an -5bm-10bn + am Л

15a³b + 3a²b³ Я

-27а³b+18a²b² Я

27а³b+18a²b² И

35a²+7a²b²+5b+b³ И

a² + ab – 5a – 5b П

2bx – 3ay -6by + ax П

14(m-n)+x(m-n) Г

3x²-x+3xy-y-3xz+z Г

3группа

(уровень С)

b(a + 5) – c(a +5) О

mr²+nr²+mr-sr²+nr-sr Т

ax²+by²+ay²+bx²+cx²+cy² Л

a³b²— 3а³b + 5а²b² — 15а²b Я

3z²-z+3zr-r-3zk+k И

(0,09х-0,81y)y-(0,81x-7,29y)x П

z+k)y-(k-z)x+(3k-2z)xy-(-2z+3k) Г

1 группа:

3ху(3+ху)

5p(p+2)

(a-5)(a+b)

5p(p+2)

4x²y(5xy+1)

5p(p+2)

(m-n)(14+x)

9a²b(3a+2b)

3a²b(5a+b²)

2 группа:

(x-5)(2y+x)

3py(4p+1)

(x-3y)(2b+a)

3py(4p+1)

(a-5b)(2n+m)

3py(4p+1)

(3x-1)(x+y-z)

(5+b²)(7a²+b)

-9a²b(3a-2b)

3 группа:

r(r+1)(m+n-s)

NGG

(a+5)(b-c)

0,09(x-9y)(y-9x)

(a+5)(b-c)

(x²+y²)(a+b+c)

(a+5)(b-c)

(k- z)(y-x)+(3k-2z)(xy-1)

(3z-1)(z+r-k)

a²b(b-3)(a+5)

Выполняют задание и получают слово.На столах у учащихся приготовлены листы ответов и задания в виде таблиц.

Топология

Дескриптор:

учащийся:

—применяет алгоритм спосба вынесения общего множителя за скобки;

— применяет алгоритм способа группировки. Формативное оценивание:

Самопроверка по ключевому слову на слайде. Проставляем баллы в оценочный лист.

Метод «Сигналы рукой»

Я понимаю __________ и могу объяснить (большой палец руки направлен вверх)

Я все еще не понимаю _________ (большой палец руки направлен в сторону)

Я не совсем уверен в _______________(помахать рукой)

Обратная связь:

— Учащиеся, справившиеся с заданиями корректирует ошибки.

— Какие задания вызвали затруднеия?

— Какой из способов вам показался наиболее сложнее?

Физминутка

Цель: снять физическое утомление, обеспечить переключение вида деятельности и повысить умственную работоспособность учащихся;

Повысить интерес к предмету через дополнительную информацию.

Действие учителя: координирование действий ученика

У вас на столах находятся бумажные ленты, разделенные по ширине пополам пунктирной линией. Давайте склеим из них кольца. Но не как попало, а так, чтобы белая сторона ленты была склеена с цветной. Перед склейкой перекрутите ленту один раз. Получилось знаменитое в математике бумажное кольцо. У него есть даже особое название – лист Мебиуса. А теперь разрежьте ножницами склеенную ленту посередине, вдоль пунктирной линии. Как вы думаете, что получится? Конечно, если бы мы не перекрутили ленту перед склейкой, все было бы просто: из одного широкого кольца получилось бы два узких. А что сейчас?

– Вот какие неожиданные вещи происходят с простой бумажной полоской, если склеить из нее лист Мебиуса. У этого листа масса удивительных свойств.

Лист Мебиуса – один из объектов области математики под названием топология (по-другому “геометрия положения”). Удивительные свойства листа Мебиуса – он имеет один край, одну сторону, – не связаны с его положением в пространстве, с понятиями расстояния, угла и тем не менее имеют вполне геометрический характер. Изучением таких свойств занимается топология. Оказывается, свойства такого типа, несмотря на кажущуюся их непривычность, связаны как раз с наиболее абстрактными математическими дисциплинами, именно с алгеброй и теорией функций. В топологии изучаются свойства фигур и тел, которые не меняются при их непрерывных деформациях (как если бы они были сделаны из резины).

Работа по учебнику

дифференциация по уровню сложности задания.

Группа (А)

Цель: применять способ вынесения общего множителя за скобки при разложении многочлена.

Критерий оценивания: применяют способ вынесения общего множителя за скобки при разложении многочлена.

Уровень навыков мышления: применение

№15.1

Дескриптор: применяет способ вынесения общего множителя за скобки при разложении многочлена.

Группа (В)- решение уравнений

Цель: применять разложение многочлена на множители при решении уравнений.

Критерий оценивания:

решают уравнения, используя способ разложения алгебраических выражений на множители

Уровень навыков мышления: анализ

№ 15.8

Дескриптор:

учащийся решает уравнения , используя способ разложения алгебраических выражений на множители

Группа (С)- самостоятельно

Цель:

решать задачи, применяя способы разложения многочлена на множители

Критерий оценивания: учащийся решает задачи на применение разложения многочлена на множители

Уровень навыков мышления: синтез

Предложи решение задачи:

Длину прямоугольника уменьшили на 4 см и получили квадрат, площадь которого меньше площади прямоугольника на 12см². Найдите площадь прямоугольника.

Дескриптор:

— учащийся составляют краткое условие задачи ;

— учащийся применяет способы разложения на множители при решении задачи.

Формативное оценивание:

Самопроверка по ответам на слайде.

Проставляем баллы в оценочный лист.

Метод «Сигналы рукой»

Обратная связь:

Учитель – ученик, корректировка знаний.

Группа Джиггсо .Рассчитываются по номерам в новые группы(1,2 -1 группа; 3,4— 2 группа; 5,6-3 группа) и проводят взаимообучение.

(Слайд 7)

(Слайд 8)

(Видео)

Конец урока

1 минута

Подсчитывают баллы по листу оценивания и выбирают домашнее по количеству набранных баллов.

Домашнее задание дифференцированное:

Уровень А — № 15.4 примеры стр. 107

Уровень В — № 15.10 уравнения стр.108

Уровень С — Составь задачу на использование разложения многочлена на множители одним из способов по дополнительным источникам.

Обратная связь:

Есть ли вопросы по домашнему заданию?

(Слайд 9)

1 минута

Рефлексия: «Светофор — смайлики»

— Задания на уроке трудные, многое не понял

— некоторые задания на уроке вызвали затруднения

-урок понятен, можно двигаться дальше

(Слайд 10)

Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими?

Оценивание – как Вы планируете проверять уровень усвоения материала учащимися?

Охрана здоровья и соблюдение техники безопасности

Парная работа по темпу, уровневая дифференциация учащихся по группам; домашнее задание – по уровню сложности.

Формативное оценивание и обратная связь, взаимопроверка, самопроверка по заданным дескрипторам. Методы и приемы: индивидуальная работа, парная работа, групповая работа.

Физминутка – смена вида деятельности.

ТБ при работе с ножницами

Рефлексия по уроку

Была ли реальной и доступной цель урока или учебные цели?

Все ли учащиесы достигли цели обучения? Если ученики еще не достигли цели, как вы думаете, почему? Правильно проводилась дифференциация на уроке?

Эффективно ли использовали вы время во время этапов урока? Были ли отклонения от плана урока, и почему?

Используйте данный раздел урока для рефлексии. Ответьте на вопросы, которые имеют важное значение в этом столбце.

Итоговая оценка

Какие две вещи прошли действительно хорошо (принимайте в расчет, как преподавание, так и учение)?

1:

2:

Какие две вещи могли бы улучшить Ваш урок (принимайте в расчет, как преподавание, так и учение)?

1:

2:

Что нового я узнал из этого урока о своем классе или об отдельных учениках, что я мог бы использовать при планировании следующего урока?

infourok.ru

Урок по алгебре на тему «Разложение многочлена на множители с помощью комбинации различных приемов»

ФИО учителя :Титова Ирина Григорьевна

МБОУ СОШ №288 территориального образования : г. Заозерск. Мурманская область

Тема урока :Разложение многочлена на множители с помощью комбинации

различных приемов

Класс: 7, уровень базовый.

Тип урока: «открытие нового знания»

Цели урока:

— показать применение различных способов для разложения на множители многочлена

— повторить способы разложения на множители и закрепить их знание в ходе упражнений

— вырабатывать навыки и умения учащихся в применении формул сокращенного умножения.

— развивать логическое мышление учащихся и интерес к предмету.

Планируемые результаты:

1)личностные:Использование различных приемов проверки правильности выполнения

задания (опора на изученные правила, алгоритм выполнения арифметических действий).

2)метапредметные : Регулятивные- обнаружение и формулирование учебной проблемы с

учителем.

Познавательные- делать предположения об информации, которая нужна для решения

предметной учебной задачи.

Коммуникативные- уметь оформлять свои мысли в устной и письменной речи с учетом

речевых ситуаций.

Форма контроля : Индивидуальная, коллективная работа.Самостоятельная работа.

Ход урока:

1)Повторение:

Задание №1(на доске (или слайд) список алгебраических выражений, которые учащиеся должны рассмотреть):

(1) 4а²в(1+3а)

(2) (х-3)(х²+3х+9)

(3) 27х⁶у³-72х⁴у⁴+48х²у⁵

(4) (6а+1)²

(5) (8а-вс)(8а+вс)

(6) х²-у²+а²+2ха

(7) а²+10а+25-в²

(8)х(х-5)(15+2х)

(9) а⁴+4в⁴

(10) -4а²+40ав-100в²

Распределите данные выражения на группы и объясните по какому признаку

проведено распределение.(Учащиеся сначала выделили две группы. В первую вошли

выражения 1,2,4,5,8, поскольку в каждом из них есть двучлен, выступающий в качестве

отдельного множителя. Во вторую группу все остальные множители, ведь ни в одном из

них не встречались «умножение друг на друга скобки».Некоторые обучающиеся отметили,

что во второй группе есть и двучлены (9),и трехчлены (3,10) ,и четырехчленны (6,7).

После анализа формулируется цель урока: « Разложение на множители с помощью

комбинирования различных способов» (многочлены из второй группы).

Задание №2 (устно), (запись на доске или слайд) 🙁 х-у)² =х²-2ху + у².

Задание №2 .Найти ошибку:

1.( х-у)² =х²-2ху — у² ;

2.( х-у)² =х²-ху + у²;

3.( х-у)² =х-2ху + у ;

4. ( х-у)² =х²+2ху — у²;

5.( х-у)² =х²-2ху + у.

Задание №3 (устно) Найдите верные формулы, которые записаны в непривычном порядке

и содержащие ошибку ,исправьте ошибочную запись:

1.а²+в²-2ав=(а-в)²

2.х²+2ху-у²=(х-у)²

3.2рв-р²-в²=(р-в)²

4.2вс +с²+в²=(с+в)².

Какие способы разложения на множители мы вспомнили?

Какие еще способы разложения на множители мы изучали?

(запись на доске) :ас+ вс= а(в+с) .Приведите пример.

ас+вс-ар-вр= (ас+вс) +(-ар-вр)=с(а+в)-р(а+в)=(а+в)(с-р)

Задание №4.

Провести классификацию данных многочленов по способу разложения на множители

(на доске (или слайд) список алгебраических выражений, которые учащиеся должны

классифицировать):

Методы разложения на множители.

Вынесение общего множителя за скобки	Формулы сокращенного умножения	Способ группировки
20х3у2 + 4 х2у	a4 – b8	2bx – 3ay -6by + ax
b(a + 5) – c(a +5)	27b3 +a6	a2 + ab – 5a – 5b
15a3b + 3a2b3	x2+6x +9	2an -5bm-10bn + am
2y(x -5) +x(x – 5)	49m4 — 25n2	3a2 + 3ab -7a -7b

С остальными учащимися даем характеристику каждому перечисленному приему.

Новый материал:

Задание №5.

Преобразуйте выражения 3,10,6,7 (письменно).№3 и№6-работа вместе с учителем,

№10 и №7-самостоятельно.

№3. 27х⁶у³-72х⁴у⁴+48х²у⁵

С какого способа следует начать?(ответ : вынесение общего множителя)

3х²у³(9х⁴-24х²у+16у²).

Что можно сказать о выражении стоящем в скобках?(ответ: квадрат разности)

3х²у³ (3х-4у)². (№10 -самостоятельно.)

№6 . х²-у²+а²+2ха

Начнем ли мы в этом задании с вынесения общего множителя за скобки? (ответ:

Нет общего множителя, нужно попробовать группировку)

Попытка может быть такой : (х²-у² )+ (а²+2ха)= (х-у)(х+у) +а (а+2х), тогда возникает вопрос что

делать дальше?

Сделаем другую группировку: (х² +2ха) + (-у²+а²)=х(х+2а) +(а-у)(а+у),опять возникает вопрос что

делать дальше.

Может использовать другой способ разложения или использовали не все варианты

группировки? Слагаемые можно объединять не только парами, но и по три слагаемых.

Какие три слагаемых можно объединить? (ответ: слагаемые, в которых есть множители

х,а и ха).

(х² +а²+2ха) -у²=(х+а)²-у²=(х+а-у)(х+а+у),(каждый этап комментируется учителем и

обучающимися).

Справились ли мы с поставленной задачей? (ответ: разложили на множители). Совокупность различных приемов разложения на множители позволяет легко и изящно производить арифметические вычисления, решать уравнения вида ах² + вх + с = 0 (а0) – такие уравнения называются квадратными, мы начнем изучать в 8-м классе, решать задачи на делимость, доказывать тождества.

Задание №6

Решить уравнения:

а) х² – 15х + 56 = 0

Решение.

х² – 7х – 8х + 56 = 0,

(х² – 7х) – (8х – 56) =0,

х(х – 7) – 8(х – 7) = 0,

(х – 7)(х – 8) = 0,

х=7, х=8

б) х² + 10х + 21 = 0

Решение.

х² + 10х + 25 – 4 = 0

(х + 5)² – 4 = 0

(х + 5 -2)(х +5 +2) = 0

(х +3)(х + 7) = 0

х = -3, х = -7.

При разложении многочлена на множители мы увидели полный квадрат и таким образом применили еще один прием разложения на множители: метод выделения полного квадрата.

Рефлексия:

Задание № 7. Разложить многочлен на множители: учебник А.Г.Мордковича «Алгебра 7 № 34.1(а,в),

34.2(а,в),34.8(а,в),34.9(а,в)

Мы убедились, что на практике при решении примеров часто приходится использовать комбинацию различных приемов. Каков план их последовательного применения?

Ответ:

1.Вынести общий множитель за скобку (если он есть).

2.Попробовать разложить многочлен на множители по формулам сокращенного умножения.

3.Попытаться применить способ группировки (если предыдущие способы не привели к цели).

Задание № 8. Самостоятельная работа

Разложить на множители, используя различные способы.

Вариант 1	Вариант 2
5а3 – 125ав2	63ав3 – 7а2в
а2 – 2ав + в2 – ас + вс	m2 + 6mn + 9n2 – m – 3n
(с – а)(с + а) – в(в – 2а)	(в – c)(в + c) – а(а + 2c)
х2 – 3х + 2	х2 + 4х + 3
х4 + 5х2 + 9	х4 + 3х2 + 4

Самостоятельная работа проверяется на уроке .

Оценить работу учащихся и ориентировать в домашнем задании

infourok.ru