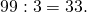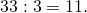Разложение составных чисел на простые множители
Составное число всегда можно единственным способом представить как произведение нескольких простых чисел. При арифметических действиях с обыкновенными дробями, если у них разные знаменатели в одном числовом выражении, необходимо привести дроби к сопоставимому виду.
Чтобы произвести такие действия (преобразовать дроби в равновеликие с одинаковыми знаменателями), нужно иметь систему (правило и форму записи) разложения составных чисел на простые множители.
Определение. Разложить число на простые множители — значит записать число в виде произведения простых чисел.
- Правило. Чтобы разложить число на простые множители, надо:
- — записать его слева от вертикальной черты;
- — справа от черты записать первый делитель числа — самое маленькое число из таблицы простых чисел, на которое данное число делится без остатка;
- — в следующей строке слева под числом записать делимое первого этапа, которое является частным от деления данного числа на записанный справа на одной строке с ним делитель;
- — справа найти (как и первый делитель) наименьшее простое число, на которое делимое первого этапа делится без остатка, это число будет вторым делителем числа;
- — слева записать делимое второго этапа, которое есть частное от деления предыдущей строки делимого на ее же делитель;
- — для делимого второго этапа также найти делитель из наименьшего числа простых чисел, записать его на той же строке справа н т. д., пока в делимом последнего этапа не будет стоять 1;
- — делители, стоящие справа от черты, записать множителями данного числа.
Перемножив между собой множители, стоящие справа от черты, мы получаем исходное число.
12 376 = 2 * 2 * 2 * 7 * 13 * 17;
1 421 = 7 * 7 * 29;
8 = 2 * 2 * 2.
Внимание! Делители справа у составных чисел увеличиваются слева направо. При разложении на множители простых чисел справа от черты стоит одно число (один делитель) — заданное число, а слева от черты стоят заданное число и число 1.
Запись опубликована в рубрике Математика с метками множитель, разложение, числа. Добавьте в закладки постоянную ссылку.
shkolo.ru
Разложение числа на простые множители онлайн
Любое натуральное число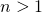 можно представить в виде произведения простых чисел. Это представление называется разложением числа
можно представить в виде произведения простых чисел. Это представление называется разложением числа 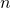 на простые множители.
на простые множители.Натуральное число 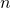 называется делителем целого числа
называется делителем целого числа 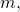
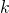 верно равенство
верно равенство 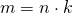 . В этом случае говорят, что
. В этом случае говорят, что 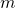 делится на
делится на 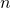 или что число
или что число 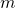 кратно числу
кратно числу 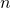 .
.Простым числом
называют натуральное число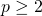 , делящееся только на себя и на единицу. Составным числом называют число, имеющее больше двух различных делителей (любое натуральное число
, делящееся только на себя и на единицу. Составным числом называют число, имеющее больше двух различных делителей (любое натуральное число 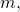 не равное
не равное 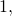 имеет как минимум два делителя:
имеет как минимум два делителя: 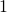 и
и 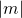 ). Например, числа
). Например, числа 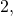
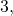
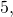
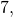
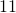 – простые, а числа
– простые, а числа 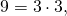
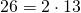 – составные. Основная теорема арифметики. Любое натуральное число
– составные. Основная теорема арифметики. Любое натуральное число 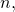 большее единицы, можно разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования сомножителей.
большее единицы, можно разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования сомножителей. Данная программа раскладывает число в произведение простых множителей онлайн. Разложить число на множители онлайн с её помощью очень просто.
Как разложить число на множители?
В школе на уроках математики разложение числа на множители обычно записывают столбиком (в две колонки). Делается это так: в левую колонку выписываем исходное число, затем
- Берём самое маленькое простое число — 2 и по признакам делимости или обычным делением проверяем, делится ли исходное число на 2.
- Если делится, то в правую колонку выписываем 2. Далее делим исходное число на 2 и записываем результат в левую колонку под исходным числом.
- Если не делится, то берём следующее простое число — 3.
Повторяем эти шаги, при этом работаем уже с последним числом в левой колонке и с текущим простым числом. Разложение заканчивается, когда в левой колонке будет записано число 1.
Чтобы лучше понять алгоритм, разберём несколько примеров.
Пример. Разложить на множители число 84.Решение. Записываем число 84 в левую колонку:
Берём первое простое число — два и проверяем, делится ли 84 на 2. Так как 84 оканчивается на 4, а 4 делится на 2, то и 84 делится на 2 по признаку делимости. Записываем 2 в правую колонку. 84:2 = 42, число 42 записываем в левую колонку. Получили вот что:
Теперь работаем уже с числом 42. Число 42 делится на 2, поэтому записываем 2 в правую колонку, 42:2 = 21, число 21 записываем в левую колонку.
Число 21 на 2 не делится, поэтому проверяем его делимость на следующее простое число — 3. Число 21 делится на 3, 21:3 = 7. Записали 3 в правую колонку, 7 — в левую. Получили
Число 7 — простое число, поэтому в правой колонке записываем 7, в левую пишем 1. В итоге получили:
Всё, число разложено!
В результате в правой колонке оказались записаны все простые множители числа 84. То есть 84=2∙2∙3∙7.
О калькуляторе
Программа раскладывает числа на множители методом перебора делителей. Для вычислений используется длинная арифметика, поэтому раскладывать можно даже большие числа. Однако если число простое или имеет большие простые делители, разложение его на множители происходит очень медленно.
umath.ru
Разложение чисел на простые множители
Онлайн-калькулятор «Разложение числа на простые множители» позволит вам разложить любое составное число на простые множители. Для этого вам нужно ввести число в поле и нажать кнопку «Вычислить». Особенностью данного калькулятора является то, что он не просто выдаст ответ, но и представит подробное решение. С помощью нашего калькулятора Вы сможете быстро получить результат, а подробное решение поможет вам разобраться, как был произведен расчет.
Введите число:
Вычислить
Все натуральные числа можно разделить на две группы чисел: простые и составные.
Простое число – это число, которые имеют только два делителя (единица и само это число), т.е. делится без остатка только на единицу и на само себя. Принято считать, что единица (1) не является простым числом. Пример простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 и т.д. Простых чисел бесконечное множество, ниже в таблице представлены простые числа до 1000.
Составное число – это число, которые имеют более двух делителей. Любое составное число может быть представлено в виде произведенения простых чисел, например: 84 = 2 · 2 ·3 ·7.
Таблица простых чисел до 1000
| 2 | 3 | 5 | 7 | 11 | 13 |
| 17 | 19 | 23 | 29 | 31 | 37 |
| 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 |
| 97 | 101 | 103 | 107 | 109 | 113 |
| 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 |
| 191 | 193 | 197 | 199 | 211 | 223 |
| 227 | 229 | 233 | 239 | 241 | 251 |
| 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 |
| 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 |
| 401 | 409 | 419 | 421 | 431 | 433 |
| 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 |
| 509 | 521 | 523 | 541 | 547 | 557 |
| 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 |
| 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 |
| 709 | 719 | 727 | 733 | 739 | 743 |
| 751 | 757 | 761 | 769 | 773 | 787 |
| 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 |
| 877 | 881 | 883 | 887 | 907 | 911 |
| 919 | 929 | 937 | 941 | 947 | 953 |
| 967 | 971 | 977 | 983 | 991 | 997 |
calc.by
«Как разложить число на простые множители?» – Яндекс.Знатоки
Чтобы разложить число на множители, для начала следует убедиться, что число раскладывается на множители. Например, результатом разложения числа 17 станет число 17, так как оно является простым.
Самая большая проблема связана именно с распознаванием простого числа: когда оно уже точно не делится. И ещё хочу маленько рассказать о признаках делимости, без которых вам, как правило, не удастся разложить число на множители
Например, возьмём число 308490.
Легко заметить, что это число — чётное, то есть делится на 2. Тогда
308490 = 2*154245
2 — простое число. Поэтому работаем с 154245.
Это нечётное число, на 2 оно точно не делится. Но оно заканчивается на 5, так что явно делится на 5. И тогда
308490 = 2*5*30849 (Вообще-то, вместо того, чтобы делить по отдельности на 2 и на 5, можно разделить сразу на 10, но моя цель — показать признаки делимости)
Теперь рассмотрим 30849. Оно не чётное, и не заканчивается на 5, так что попробуем разделить его на 3.
Признак делимости числа на 3: число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.
В нашем случае, если 3+0+8+4+9 делится на 3, то и 30849 делится на 3. И, действительно,
3+0+8+4+9 = 24
24 делится на 3, тогда
308490 = 2*3*5*10283
10283. На 2 и 5 оно не делится, на 3, если посмотреть, тоже. Если оно не делится на 2, то не делится и на 4, 6, 8, 10, 12 и др., если не делится на 3, то не делится и на 9, 15, 18, 21 и т.д.
И самое маленькое число, насчёт которого мы не можем быть уверены: 7.
Признак делимости на 7: Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7.
Чтобы проще было воспринимать, давайте посмотрим на нашем числе:
10283 делится на 7, если 1028 — 2*3 делится на 7.
1028 — 2*3 = 1022. Не понятно.
1022 делится на 7, если 102 — 2*2 делится на 7.
102 — 2*2 = 98.
98 делится на 7, потому что 98 = 2*49 = 2*7*7 (это я только что разложил 98 на множители, к вашему вопросу)
Таким образом, и 10283 делится на 7. Тогда
308490 = 2*3*5*7*1469
Попытаемся сделать что-нибудь с 1469. Первые десять чисел в качестве делителей отпадают сразу. Попробуем взять 11.
Признак делимости на 11: число делится на 11 тогда и только тогда, когда сумма его чётных по номеру цифр равна сумме нечётных, или отличается от неё на 11.
В нашем случае, 1+6 должно быть равно 4+9, или отличаться от неё на 11. Но это условие не выполняется, поэтому 1469 не делится на 11.
1469 также не делится на 12, но нельзя быть уверенным, что оно не делится на 13.
Признак делимости на 13: Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверенным числом единиц, кратно 13.
То есть, 1469 делится на 13, если 146 + 9*4 делится на 13
146 + 9*4 = 182
182 делится на 13, если 18 + 2*4 делится на 13
18 + 2*4 = 26.
26 делится на 13. Значит, и 1469 делится на 13. Тогда
308490 = 2*3*5*7*13*113
113 — простое число. Это можно доказать следующим образом:
113 точно не делится ни на одно число меньше 17. Тогда самый большой делитель этого числа должен быть меньше, чем 113 : 16 и больше, чем 16. 113 : 16 это 7 с небольшим остатком. 7 < 16, следовательно, 113 не имеет делителей, то есть является простым числом.
Результат нашего разложения:
308490 = 2*3*5*7*13*113
Извините за длинный текст, может быть за лишнюю информацию. Надеюсь, то что я написал было хоть чуть-чуть понятно и вам поможет)
yandex.ru
Простые и составные числа. Разложение на простые множители
Простым числом называется такое число, которое имеет только два делителя – единицу и само это число. Например, число 11 можно без остатка разделить только на 1 и на 11, значит это число простое.
 Составным числом называется такое число, которое имеет более двух делителей.
Составным числом называется такое число, которое имеет более двух делителей.
Число 24 можно разделить на 1, на 2, на 3, на 4, на 6, на 8 и на 12, следовательно, это число составное.
Среди натуральных чисел есть одно, которое не относится ни к простым, ни к составным числам, так как оно имеет всего один делитель. Это число 1.
Разложение на множители
При сокращении дробей полезно представлять числа в виде произведений простых множителей. Возьмём, например число 210. Сначала его представим так:
210 = 21 · 10
Но числа 21 и 10 составные. Каждое из них можно представить в виде произведений: 10 = 5 · 2; 21 = 7 · 3. Отсюда получаем:
210 = 5 · 2 · 7 · 3
Теперь в произведении 5 · 2 · 7 · 3 все множители являются простыми числами. Таким образом задача выполнена: число 210 разложено на простые множители.
Это же число можно было бы разложить на простые множители другими способами:
210 = 30 · 7 = 3 · 10 · 7 = 3 · 2 · 5 · 7
210 = 70 · 3 = 7 · 10 · 3 = 7 · 2 · 5 · 7
Получились те же самые простые множители, только записанные в другом порядке возрастания:
210 = 2 · 3 · 5 · 7
Произведение 2 · 3 · 5 · 7 называют разложением числа 210 на простые множители.
 Любое составное число можно разложить на простые множители. Мы можем использовать разные способы разложения, но результат будет одинаковый: разложение будет одно и то же, если не учитывать порядка расположения множителей.
Любое составное число можно разложить на простые множители. Мы можем использовать разные способы разложения, но результат будет одинаковый: разложение будет одно и то же, если не учитывать порядка расположения множителей.
При разложении чисел на простые множители используются признаки делимости чисел. Разложим на простые множители число 504. Число делится на 2. Значит, 2 есть один из простых множителей числа 504. Число 2 пишем справа от знака равенства, а частное 252 под числом 504. Далее 252 делим на 2, получаем 126 и так продолжаем до тех пор, пока последующее число можно разделить на 2. 63 не можем разделить на 2, делим на 3, получаем 21, далее 21 делим на 3, получаем 7, а 7 можем разделить только на 7.
504 = 2 · 2 · 2 · 3 · 3 · 7
252
126
63
21
7
1
Разложение на множители помогает сократить дроби и привести их к общему знаменателю, извлечь корень, ведь чем меньше числа, тем проще оперировать ими.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Разложение числа на простые множители
Вам также может пригодиться калькулятор разложения чисел на простые множители.
Основная теорема арифметики гласит:
Любое натуральное число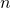 , большее единицы, можно разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования сомножителей.
, большее единицы, можно разложить в произведение простых чисел, причём это разложение единственно с точностью до порядка следования сомножителей.Как разложить число на множители?
Вот последовательность действий при разложении числа на простые множители:
- Берём самое маленькое простое число — 2 и по признакам делимости или обычным делением проверяем, делится ли наше число на 2.
- Если делится, то выписываем 2 в столбец с простыми множителями и делим наше число на 2 (получаем новое число). Далее снова проверяем, делится ли новое число на 2.
- Если не делится, то переходим к следующему простому числу — 3.
Эти три шага выполняются до тех пор, пока наше число не окажется равным 1.
Далее рассмотрим несколько примеров.
Разложить на простые множители число 54
- Число 54 делится на 2. Выписываем 2 в правый столбик.
 Записываем 27 в левый столбец.
Записываем 27 в левый столбец. - 27 не делится на 2, зато делится на 3. Выписываем 3 в правый столбик.
 Число 9 записываем в левую колонку.
Число 9 записываем в левую колонку. - 9 делится на 3. Снова выписываем 3 в правый столбик.
 В левый выписываем 3.
В левый выписываем 3. - Число 3 делится на 3,
 В правый столбик выписываем 3, в левый — 1. Разложение закончено.
В правый столбик выписываем 3, в левый — 1. Разложение закончено.
Разложить на простые множители число 65
- Число 65 не делится на 2 (так как оно оканчивается на нечётное число 5).
- 65 не делится на 3 (сумма цифр равна 11, а 11 не делится на 3).
- Зато 65 делится на 5. Выписываем число 5 в правую колонку.
 Теперь проверять мы будем уже число 13.
Теперь проверять мы будем уже число 13. - Число 13 — простое, его можно разделить только на 13. Выписываем в правую колонку 13, в левую — 1. Наше разложение закончено.
Разложить на простые множители число 99
- Число 99 не делится на 2, зато делится на 3.

- 33 также делится на 3.

- Число 11 — простое, поэтому разложение завершено.
Разложить на простые множители число 162
Разложить на простые множители число 1500
umath.ru
Разложение числа на простые множители
Данный калькулятор поможет разложить число на простые множители. Напомним, что основная теорема арифметики гласит, что любое целое число большее единицы можно разложить на простые множители. Т. е. представить как произведение множителей, в качестве которых выступают простые числа.
Простое число — число, которые имеют только два делителя — единицу и само себя.
Например, число 5 простое, так как делится без остатка только на 1 и на 5. А число 33 не простое, так как делится на 1, на 3 и на 11.
Разложение числа на простые множители
Пример разложения числа на простые множители
-

Шаг 1
Разложим на простые множители число 84. На листе проведем вертикальную линию и слева напишем наше число 82. Начнем перебирать простые числа, начиная с 2 и искать первое, на которое можно без остатка разделить 84. Первое же число 2 нам подходит, так как 84 делится на 2 без остатка и получается 42. Запишем справа от черты напротив 84 наш делитель 2, а под 84 полученный результат от деления — 42.
- Теперь поступим так же с числом 42. Понятно, что 42 делится на 2, поэтому справа пишем 2, а под числом 42 результат деления — 21.

Шаг 2
- Число 21 не делится на 2. Значит берем следующее простое число 3. На 3 число 21 делится — пишем справа 3, а под 21 результат деления 7.

Шаг 3
- Число 7 делится только на себя и на 1 — оно простое. Пишем справа 7, а слева под семеркой 1. На этом разложение на простые множители числа 84 закончено. Мы получили, что 84 состоит из произведения множителей 2, 2, 3, 7 — они у нас записаны справа от вертикальной черты.

Шаг 4
В итоге получаем: 84 = 2 • 2 • 3 • 7. Мы разложили число на простые множители.
Ваша оценка
[Оценок: 8 Средняя: 4.1]Разложить число на простые множители онлайн Автор admin средний рейтинг 4.1/5 — 8 рейтинги пользователей
calculat.ru
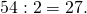 Записываем 27 в левый столбец.
Записываем 27 в левый столбец.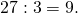 Число 9 записываем в левую колонку.
Число 9 записываем в левую колонку.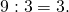 В левый выписываем 3.
В левый выписываем 3.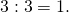 В правый столбик выписываем 3, в левый — 1. Разложение закончено.
В правый столбик выписываем 3, в левый — 1. Разложение закончено.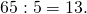 Теперь проверять мы будем уже число 13.
Теперь проверять мы будем уже число 13.