Разложение на множители | YouClever
Для чего нужно раскладывать многочлен на множители?
Чтобы облегчить себе жизнь! После того как ты сделаешь это, выражение станет намного проще и ты сможешь с ним «разобраться»! Ты как бы делишь одну большую и сложную проблему, на несколько маленьких и простых и потом разбираешься с каждой маленькой проблемой по отдельности.
Как это сделать?
Прочитай эту статью и у тебя не останется вопросов по этой теме. Сначала мы разберем что означают все «сложные» слова, потом объясним все пять ВОЛШЕБНЫХ способов разложения многочлена на множители. И затем разберем на примерах как это делать.
Let’s dive right in… (Поехали!)
Одночлены
– это могут быть числа, переменные, произведения чисел и переменных, а так же переменные в степени (если забыл, что такое степень, посмотри тему «Степень и ее свойства»)
Например:
- \(4;\)
- \(x;\)
- \(4x;\)
- \(4{{x}^{2}};\)
- \(4{{x}^{2}}y;\)
Все это — одночлены. Видишь у них нет знаков «+» или «-«, как бы нет других членов…
СОДЕРЖНИЕ СТАТЬИ
Многочлен
— это выражение, состоящее из суммы (или разности) нескольких одночленов различного вида:
- \(\displaystyle 4{{x}^{2}}+9x\)
- \(\displaystyle 2{{x}^{3}}-16{{x}^{2}}+4x\)
- \(\displaystyle 8x\cdot 4{{y}^{2}}-12+4{{x}^{2}}y-3{{y}^{2}}\cdot {{x}^{4}}+6-5{{y}^{2}}{{x}^{4}}\).
Что такое множители?
Так, ну давай по порядку. Как не трудно догадаться, слово «множитель» происходит от слова «умножать».
Возьмем, например, число \(12\), разложить его на множители означает расписать его в виде «умножения» или, как принято говорить в математике «произведения» множителей. Так \(12\) мы можем получить, умножив \(2\) на \(6\), а \(6\), в свою очередь, можно представить как произведение \(2\) и \(3\).
Чтоб было более наглядно, обратимся к картинке:

На картинке мы видим пошаговое разложение на множители, те которые подчеркнуты – это множители, которые дальше разложить уже нельзя, т.е. их нельзя уже представить в виде произведения (можно конечно представить каждое из них как единица, умноженная на само число, но это нам ничего не дает).
Я обещал, что картинка все разъяснит, ну разве из нее не понятно, что, \(12=2\cdot 6\), а \(6=2\cdot 3\)? Вот и я говорю, что элементарно!
Иными словами, \(2\cdot 2\cdot 3=12\). Тут \(2\), еще раз \(2\) и \(3\) – это и есть множители, на которые мы раскладываем.
Зачем нужно раскладывать многочлен на множители?
Это самый главный вопрос. Я уже говорил — чтобы облегчить тебе жизнь. Раскладывая многочлен на множители, ты упрощаешь выражение! Ты как бы делишь одну большую и сложную проблему, на несколько маленьких и простых и потом разбираешься с каждой маленькой проблемой по отдельности.
А теперь «официальное» определение.
Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. При этом каждый множитель может быть как многочленом, так и одночленом.
Длячего нужно знать все пять способов?
Потому что нет универсального способа, подходящего для всех многочленов.
Давай посмотрим на каждый из них…
5 способов разложения многочлена на множители
1. Вынесение общего множителя за скобки
\(\displaystyle ac+bc=c(a+b)\)
2. Использование формул сокращенного умножения.
\(\begin{array}{l}\left[ 1 \right]\ \ \ \ {{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\\\left[ 2 \right]\ \ \ \ {{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\\\left[ 3 \right]\ \ \ \ {{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)\\\left[ 4 \right]\ \ \ \ {{\left( a+b \right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\\\left[ 5 \right]\ \ \ \ {{\left( a-b \right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\\\left[ 6 \right]\ \ \ \ {{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\\\left[ 7 \right]\ \ \ \ {{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\end{array}\)
3. Метод группировки.
Применяется если преобразование не очевидно.
Здесь, например, можно переставить второй член на другое место:

\({{x}^{3}}-5{{x}^{2}}y-3xy+15{{y}^{2}}\)
группируем члены парами, получаем:
\(({{x}^{3}}-5{{x}^{2}}y)-(3xy-15{{y}^{2}})\)
\({{x}^{2}}(x-5y)-3y(x-5y)\)
\(({{x}^{2}}-3y)(x-5y)\)
4. Метод выделения полного квадрата.
Можно преобразовать многочлен и привести к виду разности квадратов, например и применить формулу сокращенного умножения
\({{x}^{4}}-4{{x}^{2}}-1=\underbrace{{{x}^{4}}-2\cdot 2\cdot {{x}^{2}}+4}_{\text{ }{{\left( {{x}^{2}}-2 \right)}^{2}}}-4-1={{\left( {{x}^{2}}-2 \right)}^{2}}-5=\left( {{x}^{2}}-2+\sqrt{5} \right)\left( {{x}^{2}}-2-\sqrt{5} \right)\)
5. Разложение квадратного трехчлена на множители.
Квадратный трехчлен – многочлен вида
\(a{{x}^{2}}+bx+c=0\)
Теорема. Если квадратное уравнение \(a{{x}^{2}}+bx+c=0\) имеет корни \({{x}_{1}},\text{ }{{x}_{2}}\), то его можно записать в виде:
\(a{{x}^{2}}+bx+c=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)\).
А теперь подробнее о каждом из 5-ти способов разложения на множители
1. Вынесение общего множителя за скобки
Это один из самых элементарных способов упростить выражение. Для применения этого метода давай вспомним распределительный закон умножения относительно сложения (не пугайся этих слов, ты обязательно знаешь этот закон, просто мог забыть его название).
Закон гласит: чтобы сумму двух чисел умножить на третье число, нужно каждое слагаемое умножить на это число и полученные результаты сложить, иначе говоря, \(a\left( b\text{ }+\text{ }c \right)\text{ }=\text{ }ab\text{ }+\text{ }ac\).
Так же можно проделать и обратную операцию, \(ab\text{ }+\text{ }ac\text{ }=\text{ }a\left( b\text{ }+\text{ }c \right)\), вот именно эта обратная операция нас и интересует. Как видно из образца, общий множитель а, можно вынести за скобку.
Подобную операцию можно проделывать как с переменными, такими как \(x\) и \(y\), например, так и с числами: \(6\text{ }+\text{ }8\text{ }=\text{ }2\left( 3\text{ }+\text{ }4 \right)\).
Да, это слишком элементарный пример, так же, как и приведенный ранее пример, с разложением числа \(12\), ведь все знают, что числа \(6\), \(8\) и \(12\) делятся на \(2\), а как быть, если вам досталось выражение посложнее:
\(3xy+123y\)?
Как узнать на что, например, делится число \(123\), неет, с калькулятором-то любой сможет, а без него слабо? А для этого существуют признаки делимости, эти признаки действительно стоит знать, они помогут быстро понять, можно ли вынести за скобку общий множитель.
Признаки делимости
Запомнить их не так сложно, скорее всего, большинство из них и так тебе были знакомы, а что-то будет новым полезным открытием, подробнее в таблице:
| Делится на | Признак делимости числа на данный делитель |
| 2 | Оканчивается одной из цифр: 0, 2, 4, 6, 8 |
| 3 | Сумма цифр делится на 3 |
| 5 | Последняя цифра 5 или 0 |
| 7 | Разность между числом десятков и удвоенной цифрой единиц делится на семь |
| 9 | Сумма цифр делится на 9 |
| 10 | Последняя цифра – ноль |
| 11 | Разность между суммой цифр, стоящих на нечетных местах, и суммой цифр, стоящих на четных местах, делится на 11 |
Примечание: В таблице не хватает признака делимости на 4. Если две последние цифры делятся на 4, то и всё число делится на 4.
Ну как тебе табличка? Советую ее запомнить!
Что ж, вернемся к выражению \(3xy+123y\), может вынести за скобку \(y\) да и хватит с него? Нет, у математиков принято упрощать, так по полной, выносить ВСЕ что выносится!
И так, с игреком все понятно, а что с числовой частью выражения? Оба числа нечетные, так что на \(2\) разделить не удастся,
Можно воспользоваться признаком делимости на \(3\), сумма цифр \(1\), \(2\) и \(3\), из которых состоит число \(123\), равна \(6\), а \(6\) делится на \(3\), значит и \(123\) делится на \(3\).
Зная это, можно смело делить в столбик, в результате деления \(123\) на \(3\) получаем \(41\) (признаки делимости пригодились!). Таким образом, число \(3\) мы можем вынести за скобку, так же, как y и в результате имеем:
\(3xy\text{ }+\text{ }123y\text{ }=\text{ }3y\cdot \left( x\text{ }+\text{ }41 \right)\).
Чтоб удостовериться, что разложили все верно, можно проверить разложение, умножением!
Также общий множитель можно выносить и в степенных выражениях. Вот тут, например, \(2{{x}^{3}}-16{{x}^{2}}+4x\), видишь общий множитель?
У всех членов этого выражения есть иксы – выносим, все делятся на \(2\) – снова выносим, смотрим что получилось: \(2{{x}^{3}}-16{{x}^{2}}+4x=2x({{x}^{2}}-8x+2)\).
2. Формулы сокращенного умножения
Формулы сокращенного умножения уже упоминались в теории, если ты с трудом помнишь что это, то тебе стоит освежить их в памяти «Формулы сокращенного умножения».
Ну, а если ты считаешь себя очень умным и тебе лень читать такую тучу информации, то просто читай дальше, глянь на формулы и сразу берись за примеры.
Суть этого разложения в том, что бы заметить в имеющемся перед тобой выражении какую-то определенную формулу, применить ее и получить, таким образом, произведение чего-то и чего-то, вот и все разложение. Дальше приведены формулы:
\(\begin{array}{l}\left[ 1 \right]\ \ \ \ {{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}\\\left[ 2 \right]\ \ \ \ {{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\\\left[ 3 \right]\ \ \ \ {{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)\\\left[ 4 \right]\ \ \ \ {{\left( a+b \right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}\\\left[ 5 \right]\ \ \ \ {{\left( a-b \right)}^{3}}={{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}}\\\left[ 6 \right]\ \ \ \ {{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\\\left[ 7 \right]\ \ \ \ {{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\end{array}\)
А теперь попробуй, разложи на множители следующие выражения, используя приведенные выше формулы:
- \(16{{b}^{2}}-8b+1\)
- \(-42c+9{{c}^{2}}+49\)
- \({{\left( 5\text{a} \right)}^{2}}-3\)
- \(\frac{\left( 4\text{a}+2\text{b} \right)\cdot \left( 4\text{a}-2\text{b} \right)}{16{{\text{a}}^{2}}+4{{\text{b}}^{2}}-16\text{ab}}\)
- \({{\left( 3\text{a} \right)}^{3}}-1\)
- \({{a}^{4}}-12{{a}^{3}}+48{{a}^{2}}-64a;\)
А вот что должно было получиться:
- \({{\left( 4\text{b}-1 \right)}^{2}}\)
- \({{\left( 3\text{c}-7 \right)}^{2}}\)
- \(\left( 5\text{a}-\sqrt{3} \right)\cdot \left( 5\text{a}+\sqrt{3} \right)\)
- \(\frac{\left( 2\text{a}+\text{b} \right)}{\left( 2\text{a}-\text{b} \right)}\)
- \(\left( 3\text{a}-1 \right)\left( 9{{\text{a}}^{2}}+3\text{a}+1 \right)\)
- \({{a}^{4}}-12{{a}^{3}}+48{{a}^{2}}-64a=a\cdot {{(a-4)}^{3}}\)
Как ты успел заметить, эти формулы – весьма действенный способ разложения на множители, он подходит не всегда, но может очень пригодиться!
3. Группировка или метод группировки
А вот тебе еще примерчик:
\({{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}\)
ну и что с ним делать будешь? Вроде бы и на \(3\) что-то делится и на \(5\), а что-то на \(x\) и на \(y\)
\(y\)Но все вместе на что-то одно не разделишь, ну нет тут общего множителя, как не ищи, что, так и оставить, не раскладывая на множители?
Тут надо смекалку проявить, а имя этой смекалке – группировка!
Применяется она как раз, когда общие делители есть не у всех членов. Для группировки необходимо найти группки слагаемых, имеющих общие делители и переставить их так, чтобы из каждой группы можно было получить один и тот же множитель.
Переставлять местами конечно не обязательно, но это дает наглядность, для наглядности же можно взять отдельные части выражения в скобки, их ставить не запрещается сколько угодно, главное со знаками не напутать.
Не очень понятно все это? Объясню на примере:
В многочлене \({{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}\) ставим член – \(3xy\) после члена – \(5x2y\) получаем \({{x}^{3}}-5{{x}^{2}}y-3xy+15{{y}^{2}}\)
\({{x}^{3}}-5{{x}^{2}}y-3xy+15{{y}^{2}}\)группируем первые два члена вместе в отдельной скобке и так же группируем третий и четвертый члены, вынеся за скобку знак «минус», получаем: \(({{x}^{3}}-5{{x}^{2}}y)-(3xy-15{{y}^{2}})\)
А теперь смотрим по отдельности на каждую из двух «кучек», на которые мы разбили выражение скобками.
Хитрость в том, чтоб разбить на такие кучки, из которых можно будет вынести максимально большой множитель, либо, как в этом примере, постараться сгруппировать члены так, чтобы после вынесения из кучек множителей за скобку у нас внутри скобок оставались одинаковые выражения.
Из обеих скобок выносим за скобки общие множители членов, из первой скобки \({{x}^{2}}\), а из второй \(3y\), получаем: \({{x}^{2}}(x-5y)-3y(x-5y)\)
Но это же не разложение!
После разложения должно остаться только умножение, а пока у нас многочлен просто поделен на две части…
НО! Этот многочлен имеет общий множитель. Это \((x-5y)\)
\((x-5y)\)за скобку и получаем финальное произведение \(({{x}^{2}}-3y)(x-5y)\)
Бинго! Как видишь, тут уже произведение и вне скобок нет ни сложения, ни вычитания, разложение завершено, т.к. вынести за скобки нам больше нечего.
Может показаться чудом, что после вынесения множителей за скобки у нас в скобках остались одинаковые выражения \((x-5y)\), которые опять же мы и вынесли за скобку.
И вовсе это не чудо, дело в том, что примеры в учебниках и в ЕГЭ специально сделаны так, что большинство выражений в заданиях на упрощение или разложение на множители при правильном к ним подходе легко упрощаются и резко схлопываются как зонтик при нажатии на кнопку, вот и ищи в каждом выражении ту самую кнопку.
Что-то я отвлекся, что у нас там с упрощением? Замысловатый многочлен принял более простой вид: \({{x}^{3}}-3xy-5{{x}^{2}}y+15{{y}^{2}}=({{x}^{2}}-3y)(x-5y)\).
Согласись, уже не такой громоздкий, как был?
4. Выделение полного квадрата.
Иногда для применения формул сокращенного умножения (повтори тему «Формулы сокращенного умножения») необходимо преобразовать имеющийся многочлен, представив одно из его слагаемых в виде суммы или разности двух членов.
В каком случае приходится это делать, узнаешь из примера:
Многочлен \({{x}^{2}}-4x+2\) в таком виде не может быть разложен при помощи формул сокращенного умножения, поэтому его необходимо преобразовать. Возможно, поначалу тебе будет не очевидно какой член на какие разбивать, но со временем ты научишься сразу видеть формулы сокращенного умножения, даже если они не присутствуют не целиком, и будете довольно быстро определять, чего здесь не хватает до полной формулы, а пока – учись, студент, точнее школьник.
Для полной формулы квадрата разности здесь нужно \(4\) вместо \(2\). Представим третий член \(2\) как разность \(4-2\), получим: \({{x}^{2}}-4x+4-2=({{x}^{2}}-4x+4)-2\) К выражению в скобках можно применить формулу квадрата разности (не путать с разностью квадратов!!!), имеем: \({{\left( x-2 \right)}^{2}}-2\), к данному выражению можно применить формулу разности квадратов (не путать с квадратом разности!!!), представив \(2\), как \(\sqrt{2}\), получим: \((x-2-\sqrt{2})(x-2+\sqrt{2})\).
Не всегда разложенное на множители выражение выглядит проще и меньше, чем было до разложения, но в таком виде оно становится более подвижным, в том плане, что можно не париться про смену знаков и прочую математическую ерунду. Ну а вот тебе для самостоятельного решения, следующие выражения нужно разложить на множители.
Примеры:
- \(25{{m}^{2}}-49{{n}^{2}};\)
- \({{b}^{2}}-{{(a+1)}^{2}};\)
- \({{(x-y)}^{2}}-{{(x+y+1)}^{2}};\)
- \({{x}^{2}}+2{x}-3\)
- \({{x}^{2}}+6x+5;\)
Ответы:
1. \(25{{m}^{2}}-49{{n}^{2}}=(5m-7n)\cdot (5m+7n)\)
2. \({{b}^{2}}-{{(a+1)}^{2}}=(b-a-1)\cdot (b+a+1)\)
3. \(\begin{array}{l}{{(x-y)}^{2}}-{{(x+y+1)}^{2}}=\ (x-y-x-y-1)\cdot (x-y+x+y+1)\\=-(2y+1)\cdot (2x+1)\end{array}\)
4. \({{x}^{2}}+2{x}-3=(x+3)\cdot (x-1)\)
5. \(\displaystyle {{x}^{2}}+6x+5={{x}^{2}}+6x+9-4={{(x+3)}^{2}}-{{2}^{2}}=\)
\(\displaystyle=(x+3-2)\cdot (x+3+2)=(x+1)\cdot (x+5)\)
5. Разложение квадратного трехчлена на множители
О разложении квадратного трехчлена на множители смотри далее в примерах разложения.
Примеры 5 методов разложения многочлена на множители
1. Вынесение общего множителя за скобки. Примеры.
Помнишь, что такое распределительный закон? Это такое правило: \(ac+bc=c\left( a+b \right)\)
Пример:
Разложить многочлен на множители \(10{{x}^{4}}-15{{x}^{3}}\).
Решение:
\(10{{x}^{4}}-15{{x}^{3}}=2\cdot \underline{5\cdot {{x}^{3}}}\cdot {x}-3\cdot \underline{5\cdot {{x}^{3}}}=5{{x}^{3}}\left( 2{x}-3 \right)\).
Еще пример:
Разложи на множители \(12{{y}^{3}}-2y\).
Решение:
\(12{{y}^{3}}-2y=6\cdot \underline{2\cdot y}\cdot {{y}^{2}}-\underline{2\cdot y}\).
Если слагаемое целиком выносится за скобки, в скобках вместо него остается единица!
\(12{{y}^{3}}-2y=6\cdot \underline{2\cdot y}\cdot {{y}^{2}}-\underline{2\cdot y}=2y\left( 6{{y}^{2}}-1 \right)\).
2. Формулы сокращенного умножения. Примеры.
Чаще всего используем формулы разность квадратов, разность кубов и сумма кубов. Помнишь эти формулы? Если нет, срочно повтори тему «Формулы сокращенного умножения»!
Пример:
Разложите на множители выражение \({{x}^{3}}-8{{y}^{6}}\).
Решение:
В этом выражении несложно узнать разность кубов:
\(\displaystyle \begin{array}{l}{{x}^{3}}-8{{y}^{6}}={{x}^{3}}-{{\left( 2{{y}^{2}} \right)}^{3}}=\left( x-2{{y}^{2}} \right)\left( {{x}^{2}}+x\cdot 2{{y}^{2}}+{{\left( 2{{y}^{2}} \right)}^{2}} \right)=\\=\left( x-2{{y}^{2}} \right)\left( {{x}^{2}}+2x{{y}^{2}}+4{{y}^{4}} \right)\end{array}\)
Пример:
Разложите на множители многочлен \({{x}^{4}}-1\).
Решение:
\(\displaystyle \begin{array}{l}{{x}^{4}}-1={{\left( {{x}^{2}} \right)}^{2}}-{{1}^{2}}=\left( {{x}^{2}}-1 \right)\left( {{x}^{2}}+1 \right)=\\=\left( {{x}^{2}}-{{1}^{2}} \right)\left( {{x}^{2}}+1 \right)=\left( x+1 \right)\left( x-1 \right)\left( {{x}^{2}}+1 \right).\end{array}\)
3. Метод группировки. Примеры
Иногда можно поменять слагаемые местами таким образом, чтобы из каждой пары соседних слагаемых можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен превратится в произведение.
Пример:
Разложите на множители многочлен \(2{{x}^{3}}+{{x}^{2}}y-6xy-3{{y}^{2}}\).
Решение:
Сгруппируем слагаемые следующим образом:
\(2{{x}^{3}}+{{x}^{2}}y-6xy-3{{y}^{2}}=(2{{x}^{3}}+{{x}^{2}}y)-(6xy+3{{y}^{2}})\).
В первой группе вынесем за скобку общий множитель \({{x}^{2}}\), а во второй − \(3y\):
\((2{{x}^{3}}+{{x}^{2}}y)-(6xy+3{{y}^{2}})={{x}^{2}}(2x+y)-3y(2x+y)\).
Теперь общий множитель \(\left( 2x+y \right)\) также можно вынести за скобки:
\({{x}^{2}}(2x+y)-3y(2x+y)=(2x+y)({{x}^{2}}-3y)\).
4. Метод выделения полного квадрата. Примеры.
Если многочлен удастся представить в виде разности квадратов двух выражений, останется только применить формулу сокращенного умножения (разность квадратов).
Пример:
Разложите на множители многочлен \({{x}^{2}}+6{x}-7\).
Решение: Пример:
\begin{array}{*{35}{l}}
{{x}^{2}}+6{x}-7=\underbrace{{{x}^{2}}+2\cdot 3\cdot x+9}_{квадрат\ суммы\ {{\left( x+3 \right)}^{2}}}-9-7={{\left( x+3 \right)}^{2}}-16= \\
=\left( x+3+4 \right)\left( x+3-4 \right)=\left( x+7 \right)\left( x-1 \right) \\
\end{array}
Разложите на множители многочлен \({{x}^{4}}-4{{x}^{2}}-1\).
Решение:
\begin{array}{*{35}{l}}
{{x}^{4}}-4{{x}^{2}}-1=\underbrace{{{x}^{4}}-2\cdot 2\cdot {{x}^{2}}+4}_{квадрат\ разности{{\left( {{x}^{2}}-2 \right)}^{2}}}-4-1={{\left( {{x}^{2}}-2 \right)}^{2}}-5= \\
=\left( {{x}^{2}}-2+\sqrt{5} \right)\left( {{x}^{2}}-2-\sqrt{5} \right) \\
\end{array}
5. Разложение квадратного трехчлена на множители. Пример.
Квадратный трехчлен – многочлен вида \(a{{x}^{2}}+bx+c=0\), где \(x\) – неизвестное, \(a\), \(b\), \(c\) – некоторые числа, причем \(a\ne 0\).
Значения переменной \(x\), которые обращают квадратный трехчлен в ноль, называются корнями трехчлена. Следовательно, корни трехчлена – это корни квадратного уравнения \(a{{x}^{2}}+bx+c=0\).
Если не помнишь, как находить эти корни, читай тему «Квадратные уравнения».
Теорема.
| Если квадратное уравнение \(a{{x}^{2}}+bx+c=0\) имеет корни \({{x}_{1}},\text{ }{{x}_{2}}\), то его можно записать в виде: \(a{{x}^{2}}+bx+c=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)\). |
Пример:
Разложим на множители квадратный трехчлен: \(2{{x}^{2}}+5x-3\).
Сначала решим квадратное уравнение:Теперь можно записать разложение данного квадратного трехчлена на множители:
\(\begin{array}{l}2{{x}^{2}}+5x-3=0.\\{{x}_{1,2}}=\frac{-5\pm \sqrt{{{5}^{2}}-4\cdot 2\cdot \left( -3 \right)}}{2\cdot 2}=\frac{-5\pm \sqrt{25+24}}{4}=\frac{-5\pm 7}{4};\\{{x}_{1}}=\frac{1}{2};\text{ }{{x}_{2}}=-3.\end{array}\)
\(2{{x}^{2}}+5x-3=2\left( x-\frac{1}{2} \right)\left( x+3 \right)\).
Теперь твое мнение…
Мы расписали подробно как и для чего раскладывать многочлен на множители.
Мы привели массу примеров как это делать на практике, указали на подводные камни, дали решения…
А что скажешь ты?
Как тебе эта статья? Ты пользуешься этими приемами? Понимаешь их суть?
Пиши в комментриях и… готовься к экзамену!
Пока что он самый важный в твоей жизни.
Удачи.
youclever.org
Множитель. Разложение на множители
Множитель – один из компонентов умножения.
Пример: В выражении \(7ab(x-y)(3+m)\) всего \(5\) множителей: \(7\), \(a\), \(b\), \((x-y)\) и \((3+m)\).
Разложить на множители – значит представить выражение в виде произведения множителей.
Примеры:
\(6x^2+5x=x(6x+5)\)
\(36c-c^3=c(36-c^2 )=c(6-c)(6+c)\)
\(12=3 \cdot 4=3 \cdot 2 \cdot 2\)
Такое разложение — штука полезная, она помогает сокращать дроби, решать уравнения методом расщепления и многое другое.
Примеры:
Важно! Разложить на множители можно далеко не любое выражение. Например, выражение \(3am-6c +x\) не раскладывается в принципе.
Замечание: \(3am-6c +x=3(am-2c)+x\) – не является разложением на множители, так как есть стоящее отдельно прибавление икса.
Основные способы разложения на множители
-
Вынесение общего множителя за скобки
Пример: \(2am+8m=2m(a+4)\)
Важно! В математике принято выносить за скобку все общие множители. Поэтому разложение \(2am+8m=2(am+4m)\) или \(2am+8m=m(2a+8)\) считается неполным. -
Группировка
Смысл метода в том, что мы:
— группируем члены выражения, заключая их в скобки\(3ax+9x+8a+24=(3ax+9x)+(8a+24)=…\)
— после чего выносим из получившихся скобок общие множители\(…=3x(a+3)+8(a+3)=…\)
— а теперь все выражение как бы заключаем в общую скобку и выносим из нее одинаковые скобки, полученные ранее (выделены красным):
\(…=(3x\)\((a+3)\)\(+8\)\((a+3)\)\()=\)\((a+3)\)\((3x+8)\)
Важно! Члены исходного выражения должны быть сгруппированы на первом шаге таким образом, чтобы после вынесения общих множителей на втором шаге, остались одинаковые скобки. Иначе невозможно будет выполнить третий шаг. В этом состоит основная трудность применения данного метода. Но с опытом вы научитесь видеть как именно надо группировать члены выражения:
Пример: \(5x-3x^2-15+x^3=x^3-3x^2+5x-15=(x^3-3x^2 )+(5x-15)=\)
\(=x^2 (x-3)+5(x-3)=(x^2 (x-3)+5(x-3))=(x-3)(x^2+5)\) -
Использование формул сокращенного умножения
Примеры:
\(x^2+4x+4=x^2+2·2·x+2^2=(x+2)^2=(x+2)(x+2)\)
\(25x^2-9=(5x)^2-3^2=(5x-3)(5x+3)\)
\(25+16x^2-40x=16x^2-40x+25=(4x)^2-2·4x·5+5^2=(4x-5)^2\)
Чтобы уверенно использовать этот способ, естественно, надо назубок знать все формулы сокращённого умножения. И поверьте, они вам еще встретятся в самых разных заданиях. Так что не поленитесь и выучите их. -
Разложение квадратного трёхчлена:
Пример. Разложить на множители \(2x^2-11x+12\)
Трехчлен вида \(ax^2+bx+c\) можно представить в виде \(a(x-x_1 )(x-x_2 )\) , где \(x_1\) и \(x_2\)- корни квадратного уравнения \(ax^2+bx+c=0\).
Решение: Решим квадратное уравнение \(2x^2-11x+12=0\)
\(x_1=1,5;\) \(x_2=4\)
Значит, \(2x^2-11x+12=2(x-1,5)(x-4)\)
Ответ: \(2(x-1,5)(x-4)\)
Матхак! Разложение на множители — это действие, обратное раскрытию скобок. Поэтому правильность любого разложения всегда можно проверить, раскрыв скобки получившегося выражения и приведя подобные слагаемые. Если в результате мы вернемся к исходному – значит разложение проведено верно.
\(2(x-1,5)(x-4)=(2x-3)(x-4)=2x(x-4)-3(x-4)=2x^2-8x-3x+12=2x^2-11x+12\)
Выражение совпадает с исходным, значит разложили правильно.
Смотрите также:
Разложение на множители методом деления многочленов «уголком»
cos-cos.ru
Разложение квадратного трехчлена на множители с помощью теоремы Виета — решения.егэцентр.рф
Разложение квадратного трехчлена на множители может пригодится при решении неравенств из задачи С3 или задачи с параметром С5. Так же многие текстовые задачи B13 решатся значительно быстрее, если вы владеете теоремой Виета.
Эту теорему, конечно, можно рассматривать с позиций 8-го класса, в котором она впервые проходится. Но наша задача — хорошо подготовиться к ЕГЭ и научиться решать задания экзамена максимально эффективно. Поэтому в этом уроке рассмотрен подход немного отличный от школьного.
Формулу корней уравнения по теореме Виета знают (или хотя бы видели) многие:
$$x_1+x_2 = -\frac{b}{a}, \quad x_1 · x_2 = \frac{c}{a},$$
где `a, b` и `c` — коэффициенты квадратного трехчлена `ax^2+bx+c`.
Чтобы научиться легко пользоваться теоремой, давайте поймем, откуда она берется (так будет реально легче запомнить).
Пусть перед нами есть уравнение `ax^2+ bx+ с = 0`. Для дальнейшего удобства разделим его на `a` получим `x^2+\frac{b}{a} x + \frac{c}{a} = 0`. Такое уравнение называется приведенным квадратным уравнением.
Важная мысль урока: любой квадратный многочлен, у которого есть корни, можно разложить на скобки. Предположим, что наш можно представить в виде `x^2+\frac{b}{a} x + \frac{c}{a} = (x + k)(x+l)`, где `k` и `l` — некоторые константы.
Посмотрим, как раскроются скобки:
$$(x + k)(x+l) = x^2 + kx+ lx+kl = x^2 +(k+l)x+kl.$$
Таким образом, `k+l = \frac{b}{a}, kl = \frac{c}{a}`.
Это немного отличается от классической трактовки теоремы Виета — в ней мы ищем корни уравнения. Я же предлагаю искать слагаемые для разложения на скобки — так не нужно помнить про минус из формулы (имеется в виду `x_1+x_2 = -\frac{b}{a}`). Достаточно подобрать два таких числа, сумма которых равна среднему коэффициенту, а произведение — свободному члену.
Если нам нужно решение именно уравнения, то оно очевидно: корни `x=-k`или `x=-l` (так как в этих случаях одна из скобок занулится, значит, будет равно нулю и все выражение).
На примере покажу алгоритм, как раскладывать квадратный многочлен на скобки.
Пример первый. Алгоритм разложения квадратного трехчлена на множители
Путь у нас есть квадртаный трехчлен `x^2+5x+4`.
Он приведенный (коэффициент у `x^2` равен единице). Корни у него есть. (Для верности можно прикинуть дискриминант и убедиться, что он больше нуля.)
Дальнейшие шаги (их нужно выучить, выполнив все тренировочные задания):
- Выполнить следующую запись: $$x^2+5x+4=(x \ldots)(x \ldots).$$ Вместо точек оставьте свободное место, туда будем дописывать подходящие числа и знаки.
- Рассмотреть все возможные варианты, как можно разложить число `4` на произведение двух чисел. Получим пары «кандидатов» на корни уравнения: `2, 2` и `1, 4`.
- Прикинуть, из какой пары можно получить средний коэффициент. Очевидно, что это `1, 4`.
- Записать $$x^2+5x+4=(x \quad 4)(x \quad 1)$$.
- Следующий этап — расставить знаки перед вставленными числами.
Как понять и навсегда запомнить, какие знаки должны быть перед числами в скобках? Попробуйте раскрыть их (скобки). Коэффициент перед `x` в первой степени будет `(± 4 ± 1)` (пока что знаков мы не знаем — нужно выбрать), и он должен равняться `5`. Очевидно, что здесь будут два плюса $$x^2+5x+4=(x + 4)(x + 1)$$.
Выполните эту операцию несколько раз (привет, тренировочные задания!) и больше проблем с этим не будет никогда.
Если нужно решить уравнение `x^2+5x+4`, то теперь его решение не составит труда. Его корни: `-4, -1`.
Пример второй. Разложение на множители квадратного трехчлена с коэффициентами различных знаков
Пусть нам нужно решить уравнение `x^2-x-2=0`. Навскидку дискриминант положительный.
Идем по алгоритму.
- $$x^2-x-2=(x \ldots ) (x \ldots).$$
- Разложение двойки на целые множители есть только одно: `2 · 1`.
- Пропускаем пункт — выбирать не из чего.
- $$x^2-x-2=(x \quad 2) (x \quad 1).$$
- Произведение наших чисел отрицательное (`-2` — свободный член), значит, одно из них будет отрицательное, а другое — положительное.
Поскольку их сумма равна `-1` (коэффициент при `x`), то отрицательным будет `2` (интуитивное объяснение — двойка большее из двух чисел, оно сильнее «перетянет» в отрицательную сторону). Получим $$x^2-x-2=(x — 2) (x + 1).$$
Третий пример. Разложение квадратного трехчлена на множители
Уравнение `x^2+5x -84 = 0`.
- $$x+ 5x-84=(x \ldots ) (x \ldots).$$
- Разложение 84 на целые множители: `4· 21, 6· 14, 12· 7, 2·42`.
- Поскольку нам нужно, чтобы разница (или сумма) чисел равнялась 5, то нам подойдет пара `7, 12`.
- $$x+ 5x-84=(x\quad 12) (x \quad 7).$$
- $$x+ 5x-84=(x + 12) (x — 7).$$
Надеюсь, разложение этого квадратного трехчлена на скобки понятно.
Если нужно решение уравнения, то вот оно: `12, -7`.
Задания для тренировки
Предлагаю вашему вниманию несколько примеров, которые легко решаются с помощью теоремы Виета. (Примеры взяты из журнала «Математика», 2002.)
- `x^2+x-2=0`
- `x^2-x-2=0`
- `x^2+x-6=0`
- `x^2-x-6=0`
- `x^2+x-12=0`
- `x^2-x-12=0`
- `x^2+x-20=0`
- `x^2-x-20=0`
- `x^2+x-42=0`
- `x^2-x-42=0`
- `x^2+x-56=0`
- `x^2-x-56=0`
- `x^2+x-72=0`
- `x^2-x-72=0`
- `x^2+x-110=0`
- `x^2-x-110=0`
- `x^2+x-420=0`
- `x^2-x-420=0`
Спустя пару лет после написания статьи появился сборник из 150 заданий для разложения квадратного многочлена по теореме Виета.
Ставьте лайки и задавайте вопросы в комментариях!
xn--e1aajtm3cwc.xn--c1adb6aplz9c.xn--p1ai
Разложение на множители разности степеней
Частично использовать разложение на множители разность степеней мы уже умеем — при изучении темы «Разность квадратов» и «Разность кубов» мы научились представлять как произведение разность выражений, которые можно представить как квадраты или как кубы некоторых выражений или чисел.
Формулы сокращенного умножения
По формулам сокращенного умножения:
разность квадратов можно представить как произведение разности двух чисел или выражений на их сумму
Разность кубов можно представить как произведение разности двух чисел на неполный квадрат суммы
Переход к разности выражений в 4 степени
Опираясь на формулу разности квадратов, попробуем разложить на множители выражение $a^4-b^4$
Вспомним, как возводится степень в степень — для этого основание остается прежним, а показатели перемножаются, т. е ${(a^n)}^m=a^{n*m}$
Тогда можно представить:
$a^4={{(a}^2)}^2$
$b^4={{(b}^2)}^2$
Значит, наше выражение можно представить, как $a^4-b^4={{(a}^2)}^2$-${{(b}^2)}^2$
Далее можно заметить, что теперь многочлен представляет собой разность квадратов одночленов $a^2$ и $b^2$ .Разложим многочлен на множители как произведение разности одночленов на их сумму
Теперь в первой скобке мы вновь получили разность чисел, значит вновь можно разложить на множители как произведение разности двух чисел или выражений на их сумму: $a^2-b^2=\left(a-b\right)(a+b)$.
Исходное выражение принимает вид
Теперь вычислим произведение второй и третьей скобок используя правило произведения многочленов, — умножим каждый член первого многочлена на каждый член второго многочлена и сложим результат. Для этого сначала первый член первого многочлена — $a$ — умножим на первый и второй член второго (на $a^2$ и $b^2$),т.е. получим $a\cdot a^2+a\cdot b^2$, затем второй член первого многочлена -$b$- умножим на первый и второй члены второго многочлена (на $a^2$ и $b^2$),т.е. получим $b\cdot a^2 + b\cdot b^2$ и составим сумму получившихся выражений
$\left(a+b\right)\left(a^2+b^2\right)=a\cdot a^2+a\cdot b^2+ b \cdot a^2 + b\cdot b^2 = a^3+ab^2+a^2b+b^3$
Запишем разность одночленов 4 степени с учетом вычисленного произведения:
$a^4-b^4={{(a}^2)}^2$-${{(b}^2)}^2={(a}^2-b^2)(a^2+b^2)$=$\ \left(a-b\right)(a+b)(a^2+b^2)\ $=
Переход к разности выражений в 6 степени
Опираясь на формулу разности квадратов попробуем разложить на множители выражение $a^6-b^6$
Вспомним, как возводится степень в степень — для этого основание остается прежним, а показатели перемножаются, т. е ${(a^n)}^m=a^{n\cdot m}$
Тогда можно представить:
$a^6={{(a}^3)}^2$
$b^6={{(b}^3)}^2$
Значит, наше выражение можно представить, как $a^6-b^6={{(a}^3)}^2-{{(b}^3)}^2$
Далее можно заметить, что теперь многочлен представляет собой разность квадратов одночленов $a^2$ и $b^2$ .Разложим многочлен на множители как произведение разности одночленов на их сумму
В первой скобке мы получили разность кубов одночленов, во второй сумму кубов одночленов, теперь вновь можно разложить на множители разность кубов одночленов как произведение разности двух чисел на неполный квадрат суммы $a^3-b^3=\left(a-b\right)(a^2+ab+b^2)$
Исходное выражение принимает вид
$a^6-b^6={(a}^3-b^3)\left(a^3+b^3\right)=\left(a-b\right)(a^2+ab+b^2)(a^3+b^3)$
Вычислим произведение второй и третье скобок используя правило произведения многочленов, — умножим каждый член первого многочлена на каждый член второго многочлена и сложим результат.
$(a^2+ab+b^2)(a^3+b^3)=a^5+a^4b+a^3b^2+a^2b^3+ab^4+b^5$
Запишем разность одночленов 6 степени с учетом вычисленного произведения:
$a^6-b^6={(a}^3-b^3)\left(a^3+b^3\right)=\left(a-b\right)(a^2+ab+b^2)(a^3+b^3)=(a-b)(a^5+a^4b+a^3b^2+a^2b^3+ab^4+b^5)$
Разложение на множители разности степеней
Проанализируем формулы разности кубов, разности $4$ степеней, разности $6$ степеней
Мы видим, что в каждом из данных разложений присутствует некоторая аналогия, обобщая которую получим:
Пример 1
Разложить на множители ${32x}^{10}-{243y}^{15}$
Решение: Сначала представим каждый одночлен как некоторый одночлен в 5 степени:
\[{32x}^{10}={(2x^2)}^5\]\[{243y}^{15}={(3y^3)}^5\]Используем формулу разности степеней
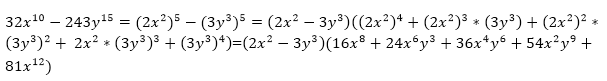
Рисунок 1.
spravochnick.ru
Разложение многочлена на множители: вынесение за скобки, способ группировки, делением
Тестирование онлайн
Разложение многочлена на множители
Представление многочлена в виде произведения нескольких многочленов (или одночленов)
Например,
Вынесение общего множителя за скобки
Необходимо проанализировать каждый член многочлена, найти общую часть (если такая имеется). Например, в выражении каждый член имеет y. Переменную y можно вынести за скобки.
Переменные, входящие в каждый член многочлена выносят за скобки в степенях с наименьшим показателем, который встречается. В примере встречается y2, y5 и y4. Выносим за скобки y2.
Что останется от каждого члена после вынесения общего множителя за скобки? Что записать в скобках? Необходимо каждый член разделить на общий множитель, который выносим за скобки. Например, при вынесении y2 за скобки в нашем примере
Если числовые коэффициенты каждого члена многочлена имеют наибольший общий делитель, то его тоже можно вынести за скобки. В нашем примере НОД(18; 30; 6)=6
Если за скобки выносят множитель «-1» (еще говорят «выносят минус»), то в скобках знак каждого слагаемого меняется на противоположный
Общим множителем могут быть и многочлены. Например, для выражения общим множителем является многочлен
Выносим за скобки, получим
Всегда можно проверить верно ли выполнено вынесение общего множителя за скобки. Для этого необходимо выполнить умножение общего множителя на многочлен в скобках и проверить, что полученное выражение полностью совпадает с первоначальным.
Способ группировки
Если члены многочлена не имеют общего множителя, то следует попытаться разложить его методом группировки.
Для этого надо объединить в группы те члены, которые имеют общие множители, и вынести за скобки общий множитель каждой группы. После этого может оказаться общий множитель многочлен у получившихся групп, который выносят за скобки.
Группировать члены многочлена можно по-разному. Не при всякой группировке удастся разложить многочлен на множители.
Разложение многочлена иногда невозможно известными методами. Тогда разложить многочлен возможно, отыскав один корень и разделив многочлен на многочлен.
Корень многочлена P(x) — это такое число c при котором P(c)=0. Например,
Если многочлен с целыми коэффициентами имеет корни, то их следует искать среди чисел , где m — целый делитель a0, а k — натуральный делитель an
Например,
Если хотя бы один корень найден, остается разделить многочлен на выражение x-c, где c — это корень уравнения.
Например,
fizmat.by
Раздожение квадратного трехчлена на множители
Разложение квадратного трехчлена на линейные множители можно выполнить, используя следующую теорему.
Теорема
(О разложении квадратного трёхчлена на множители)
1) Если квадратное уравнение
имеет два корня x1 и x2, квадратный трёхчлен ax²+bx+c можно разложить на множители по формуле
2) Если уравнение имеет один корень x1, квадратный трёхчлен можно представить в виде
3) Если уравнение не имеет корней, то квадратный трёхчлен ax²+bx+c в действительных числах не раскладывается на множители.
Примеры разложения квадратного трёхчлена на линейные множители.
Чтобы разложить квадратный трёхчлен на множители, надо решить квадратное уравнение
Подставляем a=2, x1=3, x2= -1/2 в формулу
Получаем
Удобно внести 2 во вторые скобки. Для этого 2 умножим на каждое слагаемое в этих скобках:
Таким образом,
Квадратный трехчлен раскладываем на множители по формуле
Чтобы внести множитель в скобки, представим его как квадрат (чтобы воспользоваться свойством степеней a²b²=(ab)²): 9=3².
Корни квадратного уравнения можно найти через дискриминант (или дискриминант, делённый на 4), по теореме, обратной теореме Виета или используя формулы особых случаев.
Разложить квадратный трёхчлен на множители можно, не прибегая к помощи теоремы о разложении квадратного трёхчлена на множители. Для этого слагаемое с bx представляют в виде суммы или разности двух слагаемых и используют способ группировки.
Например,
Выбирайте для себя тот способ, который нравится лично вам, в котором вы чувствуете себя наиболее уверенно и не допускаете ошибок.
Разложение квадратного трёхчлена на линейные множители в алгебре используется для сокращения дробей, при решении уравнений и неравенств, при построении графиков и т.д.
www.algebraclass.ru