Разложение квадратного трехчлена на множители
Разложение квадратного трехчлена
на множители
Если квадратный трехчлен имеет хотя бы один корень, то его можно разложить на множители. Для этого следует воспользоваться формулой
ax2 + bx + c = a(x – x1)(x – x2)
Иногда эту формулу формулируют в более понятном виде в виде утверждения:
если m и n – корни квадратного уравнения ax2 + bx + c = 0, то
ax2 + bx + c = a(x – m)(x – n)
Из данного утверждения следует алгоритм разложения квадратного трехчлена на множители:
-
найти корни квадратного трехчлена m и n, т.е. решить уравнение
-
записать выражение a(x – m)(x – n)
Решать уравнение можно любым способом (для этого чаще всего используют формулу корней).
Например, нужно разложить на множители квадратный трехчлен x2 + 5x – 6.
Решая уравнение x2 + 5x – 6 = 0, получим корни m = 1 и n = – 6. Следовательно,
x2 + 5x – 6 = (х – 1)(х + 6).
Онлайн калькулятор
для разложения квадратного трехчлена
на множители
Для получения объяснения того, как тот или иной квадратный трехчлен раскладывается на множители, вы можете воспользоваться формой вверху страницы. Просто введите квадратный трехчлен и нажмите кнопку «Разложить на множители».
mathonline.um-razum.ru
Разложение квадратного трёхчлена на множители. Видеоурок. Алгебра 8 Класс
Итак вернёмся к квадратному уравнению 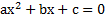 , где
, где 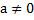 .
.
То, что стоит у нас в левой части, называется квадратным трёхчленом.
Справедлива теорема: Если 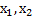 – корни квадратного трёхчлена, то справедливо тождество
– корни квадратного трёхчлена, то справедливо тождество
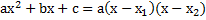
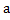 – старший коэффициент,
– старший коэффициент, 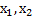 – корни уравнения.
– корни уравнения.Итак, мы имеем квадратное уравнение – квадратный трёхчлен, где корни квадратного уравнения также называются корнями квадратного трёхчлена. Поэтому если мы имеем корни квадратного трёхчлена, то этот трёхчлен раскладывается на линейные множители.
Доказательство:
Доказательство данного факта выполняется с помощью теоремы Виета, рассмотренной нами в предыдущих уроках.
Давайте вспомним, о чём говорит нам теорема Виета:
Если 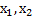 – корни квадратного трёхчлена, у которого
– корни квадратного трёхчлена, у которого 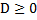
 .
.Из данной теоремы вытекает следующее утверждение, что 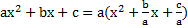 .
.
Мы видим, что, по теореме Виета, 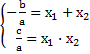 , т. е., подставив данные значения в формулу выше, мы получаем следующее выражение
, т. е., подставив данные значения в формулу выше, мы получаем следующее выражение

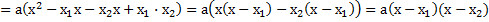 ,
,
что и требовалось доказать.
Вспомним, что мы доказали теорему, что если 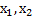 – корни квадратного трёхчлена, то справедливо разложение
– корни квадратного трёхчлена, то справедливо разложение 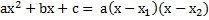 .
.
Теперь давайте вспомним пример квадратного уравнения 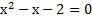 , к которому с помощью теоремы Виета мы подбирали корни
, к которому с помощью теоремы Виета мы подбирали корни 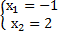 . Из этого факта мы можем получить следующее равенство благодаря доказанной теореме:
. Из этого факта мы можем получить следующее равенство благодаря доказанной теореме:
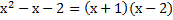
Теперь давайте проверим правильность данного факта простым раскрытием скобок:
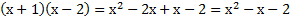
Видим, что на множители мы разложили верно, и любой трёхчлен, если он имеет корни, может быть разложен по данной теореме на линейные множители по формуле 
Однако давайте проверим, для любого ли уравнения возможно такое разложение на множители:
Возьмём, к примеру, уравнение 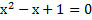 . Для начала проверим знак дискриминанта
. Для начала проверим знак дискриминанта
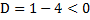 , а мы помним, что для выполнения выученной нами теоремы D должен быть больше 0, поэтому в данном случае разложение на множители по изученной теореме невозможно.
, а мы помним, что для выполнения выученной нами теоремы D должен быть больше 0, поэтому в данном случае разложение на множители по изученной теореме невозможно.
Поэтому сформулируем новую теорему: если квадратный трёхчлен не имеет корней, то его нельзя разложить на линейные множители.
Итак, мы рассмотрели теорему Виета, возможность разложения квадратного трёхчлена на линейные множители, и теперь решим несколько задач.
Задача №1
В данной группе мы будем по факту решать задачу, обратную к поставленной. У нас было уравнение, и мы находили его корни, раскладывая на множители. Здесь мы будем действовать наоборот. Допустим, у нас есть корни квадратного уравнения 
Обратная задача такова: составьте квадратное уравнение, чтобы 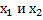 были его корнями.
были его корнями.
Для решения данной задачи существует 2 способа.
Способ 1
Поскольку  – корни уравнения, то
– корни уравнения, то 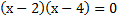 – это квадратное уравнение, корнями которого являются заданные числа. Теперь раскроем скобки и проверим:
– это квадратное уравнение, корнями которого являются заданные числа. Теперь раскроем скобки и проверим: 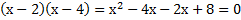
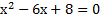
Это был первый способ, по которому мы создали квадратное уравнение с заданными корнями, в котором нет каких-либо других корней, поскольку любое квадратное уравнение имеет не более двух корней.
Способ 2
Данный способ предполагает использование обратной теоремы Виета.
Если  – корни уравнения, то они удовлетворяют условию, что
– корни уравнения, то они удовлетворяют условию, что 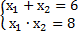 .
.
Для приведённого квадратного уравнения 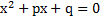 ,
, 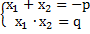 , т. е. в данном случае
, т. е. в данном случае 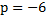 , а
, а 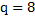 .
.
Таким образом, мы создали квадратное уравнение, которое имеет заданные корни.
Задача №2
Необходимо сократить дробь 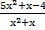 .
.
Мы имеем трёхчлен в числителе и трёхчлен в знаменателе, причём трёхчлены могут как раскладываться, так и не раскладываться на множители. Если же и числитель, и знаменатель раскладываются на множители, то среди них могут оказаться равные множители, которые можно сократить.
В первую очередь необходимо разложить на множители числитель 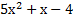 .
.
Вначале необходимо проверить, можно ли разложить данное уравнении на множители, найдём дискриминант  . Поскольку
. Поскольку 
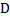 зависит от произведения
зависит от произведения 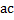 (
(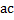 должно быть меньше 0), в данном примере
должно быть меньше 0), в данном примере 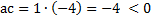 , т. е. заданное уравнение имеет корни.
, т. е. заданное уравнение имеет корни.Дальше разложим трёхчлен на множители 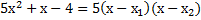 , т. е. для решения нам необходимы корни
, т. е. для решения нам необходимы корни 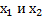 , для этого нам необходимо решить соответствующее квадратное уравнение:
, для этого нам необходимо решить соответствующее квадратное уравнение:

Для решения используем теорему Виета:
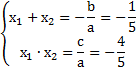
В данном случае, поскольку мы имеем дело с корнями, то просто подобрать корни будет довольно сложно. Но мы видим, что коэффициенты уравновешены, т. е. если предположить, что 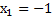 , и подставить это значение в уравнение, то получается следующая система:
, и подставить это значение в уравнение, то получается следующая система: 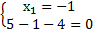 , т. е. 5-5=0. Таким образом, мы подобрали один из корней данного квадратного уравнения.
, т. е. 5-5=0. Таким образом, мы подобрали один из корней данного квадратного уравнения.
Второй корень мы будем искать методом подставления уже известного 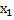 в систему уравнений, к примеру,
в систему уравнений, к примеру, 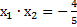 , т.е.
, т.е. 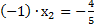 .
.
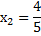
Таким образом, мы нашли оба корня квадратного уравнения и можем подставить их значения в исходное уравнение, чтобы разложить его на множители:
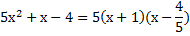
Вспомним изначальную задачу, нам необходимо было сократить дробь 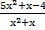 .
.
Попробуем решить поставленную задачу, подставив вместо числителя 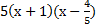 .
.
 , необходимо не забыть, что при этом знаменатель не может равняться 0, т. е.
, необходимо не забыть, что при этом знаменатель не может равняться 0, т. е. 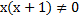 ,
, 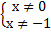 .
.
Если данные условия будут выполняться, то мы сократили исходную дробь до вида 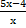 .
.
Задача №3 (задача с параметром)
При каких значениях параметра сумма корней квадратного уравнения
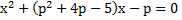 равна 0?
равна 0?
Если корни данного уравнения существуют, то 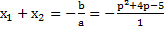 , вопрос: когда
, вопрос: когда  .
.
Для того чтобы найти значения p, нам необходимо решить следующее уравнение
 . Однако не забудьте, что записать необходимые значения p мы можем не просто после решения данного уравнения, поскольку они должны как минимум существовать, это значит, что должно выполняться неравенство
. Однако не забудьте, что записать необходимые значения p мы можем не просто после решения данного уравнения, поскольку они должны как минимум существовать, это значит, что должно выполняться неравенство 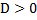 .
.
Попробуем сразу подобрать первый корень уравнения  по теореме Виета:
по теореме Виета:
 , отсюда видно, что
, отсюда видно, что 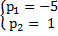 , для того чтобы проверить правильность корней, проверяем их по теореме Виета:
, для того чтобы проверить правильность корней, проверяем их по теореме Виета: 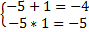 . Мы определили, что
. Мы определили, что 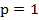 или
или 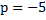 , поэтому эти цифры становятся для нас подозрительными, т. е. теми, что могут удовлетворять нашему условию.
, поэтому эти цифры становятся для нас подозрительными, т. е. теми, что могут удовлетворять нашему условию.
Проверим, что 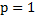 подходит для нас, поскольку
подходит для нас, поскольку 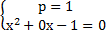 , такая система может существовать, поэтому из второго уравнения получаем следующее:
, такая система может существовать, поэтому из второго уравнения получаем следующее: 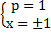 .
.
Таким же образом проверим 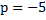 :
: 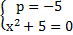 , где мы сразу видим, что
, где мы сразу видим, что 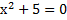 не имеет корней, таким образом даём ответ на поставленный вопрос: При значении параметра
не имеет корней, таким образом даём ответ на поставленный вопрос: При значении параметра 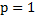 , сумма корней квадратного уравнения равна 0.
, сумма корней квадратного уравнения равна 0.
Итак, мы вспомнили теорему Виета и рассмотрели тему «Разложение квадратного трёхчлена на линейные множители» с её помощью, а также выяснили, что следующее применение теоремы Виета это вычисление всех выражений, которые зависят от суммы и произведения корней.
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Вся элементарная математика (Источник).
- Портал Естественных Наук (Источник).
- Интернет-портал аКак? (Источник).
Домашнее задание
- Разложите квадратные трёхчлены на множители: а)
 ; б)
; б)  ; в)
; в)  .
. - Сократите дроби: а)
 ; б)
; б)  ; в)
; в)  ;
; - №534, №538, №543 Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
interneturok.ru
Разложение многочлена на множители по модулю
Этот калькулятор находит все неразлагаемые множители многочлена одной переменной по модулю p, используя алгоритм Элвина Берлекампа. Описание алгоритма следует за калькулятором.

Разложение многочлена на множители методом Берлекампа
Входной многочлен
save Сохранить share Поделиться extension Виджет
Разложение многочлена на множители методом Берлекампа
Алгоритм представленный тут — это краткая компиляция алгоритма, описанного в Искусстве программирования Дональда Кнута .
Входные данные
- u(x) — многочлен степени n, n>=2
- p — модуль, простое число
Подготовка
- Убедиться, что входной полином монический, если нет — разделить все коэффициенты на старший коэффициент un
- Проверить, что полином свободен от квадратов используя Разложение многочлена в конечном поле свободное от квадратов
- Для каждого свободного от квадратов множителя степени 2 и выше — прогнать следующий алгоритм
Алгоритм
- Найти матрицу Q (n * n ), где n — степень многочлена по следующему алгоритму:
- Инициализировать вектор A (a0, a1 … an-1) = 1,0…0
- Инициализировать первую строку матрицы Q (q0,0, q0,1 … q0,n-1) = 0,0…0
- Цикл по i = 1..n-1 выполнить:
- Цикл по k = 1..n-1 выполнить:
- Установить t = an-1
- Цикл по j = n-1 .. 0 выполнить:
- aj=aj-1-t*uj, подразумевается, что a-1 = 0
- Установить значения строки i матрицы Q из вектора A
- Вычесть 1 из элемента qi,i матрицы Q
- Цикл по k = 1..n-1 выполнить:
- Найти v[1] … v[r] линейно независимые векторы, такие что v[1] Q = v[2] Q = … v[r] Q = (0,0…0)
- Установить все элементы n-размерного вектора C в -1 : c0 = c1 = .. = cn-1 = -1
- Установить r = 0
- Цикл по k = 0 … n-1 выполнить:
- Цикл по j = 0 … n-1 выполнить:
- Если qk,j ≠ 0 и cj<0
- Установить a = qk,j
- Умножить столбец j матрицы Q на -1/a
- Добавить к оставшимся столбцам (i ≠ j) столбец j умноженный на qk,i
- иначе (Если qk,j=0 или cj >= 0)
- Установить r = r + 1
- Установить каждый элемент i нового n-размерного вектора v[r] в одно из следующих значений:
- ak,s, если найден такой s-элемент вектора C, такой, что cs = i
- 1, если i = k
- 0 — в противном случае
- Если qk,j ≠ 0 и cj<0
- Цикл по j = 0 … n-1 выполнить:
- Найти r множителей полинома u(x), используя векторы v[2] … v[r]
- Найти все wi = gcd(u(x),v[2]-s) ≠ 1 для каждого s = 0 … p
- Если количество w < r выполнить:
- Цикл по j=3 … r до тех пор пока w < r
- Заменить wi множителями, найденными алгоритмом Евклида: gcd(v[j]-s,wi) ≠ 1 для каждого s = 0 … p
planetcalc.ru
Схема (метод) Горнера. Примеры. Разложение многочлена на множители
РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ ПО СХЕМЕ ГОРНЕРА
5x5 — 2x4 — 25x3 + 10x2 + 20x — 8
Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа -8 являются ±1, ±2, ±4, ±8. Начнем их подставлять по-очереди:
1: 5 — 2 — 25 + 10 + 20 — 8 = 0 ⇒ число 1 является корнем многочлена
Мы нашли 1 из корней многочлена. Корнем многочлена является 1, а значит исходный многочлен должен делиться на x — 1. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 1. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:
| Во вторую ячейку второй строки запишем число 5, просто перенеся его из соответствующей ячейки первой строки. | |
| 1 ∙ 5 — 2 = 3 | |
| 1 ∙ 3 — 25 = -22 | |
| 1 ∙ (-22) + 10 = -12 | |
| 1 ∙ (-12) + 20 = 8 | |
| 1 ∙ 8 — 8 = 0 |
Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.
Таким образом мы исходный многочлен разложили на множители:
5x5 — 2x4 — 25x3 + 10x2 + 20x — 8 = (x — 1)(5x4 + 3x3 — 22x2 — 12x + 8)
Но это еще не конец. Можно попробовать разложить таким же способом многочлен 5x4 + 3x3 — 22x2 — 12x + 8.
Опять ищем корень среди делителей свободного члена. Делителями числа 8 являются ±1, ±2, ±4, ±8.
1: 5 + 3 — 22 — 12 + 8 = -18 ⇒ число 1 не является корнем многочлена
-1: 5 — 3 — 22 + 12 + 8 = 0 ⇒ число -1 является корнем многочлена
Напишем найденный корень в нашу схему Горнера и начнем заполнять пустые ячейки:
| Во вторую ячейку третьей строки запишем число 5, просто перенеся его из соответствующей ячейки второй строки. | |||||||||||||||||||||
| -1 ∙ 5 + 3 = -2 | |||||||||||||||||||||
| -1 ∙ (-2) — 22 = -20 | |||||||||||||||||||||
| -1 ∙ (-20) — 12 = 8 | |||||||||||||||||||||
| -1 ∙ 8 + 8 = 0 |
Таким образом мы исходный многочлен разложили на множители:
5x5 — 2x4 — 25x3 + 10x2 + 20x — 8 = (x — 1)(x + 1)(5x3 — 2x2 — 20x + 8)
Теперь найдем корень многочлена 5x3 — 2x2 — 20x + 8. Делителями числа 8 являются ±1, ±2, ±4, ±8.
1: 5 — 2 — 20 + 8 = -9 ⇒ число 1 не является корнем многочлена
-1: -5 — 2 + 20 + 8 = 29 ⇒ число -1 не является корнем многочлена
2: 5 ∙ 8 — 2 ∙ 4 — 20 ∙ 2 + 8 = 0 ⇒ число 2 является корнем многочлена
| Во вторую ячейку четвертой строки запишем число 5, просто перенеся его из соответствующей ячейки третьей строки. | ||||||||||||||||||||||||||||
| 2 ∙ 5 — 8 = 8 | ||||||||||||||||||||||||||||
| 2 ∙ 8 — 20 = -4 | ||||||||||||||||||||||||||||
| 2 ∙ (-4) + 8 = 0 |
Таким образом мы исходный многочлен разложили на множители:
5x5 — 2x4 — 25x3 + 10x2 + 20x — 8 = (x — 1)(x + 1)(x — 2)(5x2 + 8x — 4)
Многочлен 5x2 + 8x — 4 тоже можно разложить на множители. Для этого можно решить квадратное уравнение через дискриминант, а можно поискать корень среди делителей числа -4. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -2
| Во вторую ячейку четвертой строки запишем число 5, просто перенеся его из соответствующей ячейки третьей строки. | |||||||||||||||||||||||||||||||||||
| -2 ∙ 5 + 8 = -2 | |||||||||||||||||||||||||||||||||||
| -2 ∙ (-2) — 4 = 0 |
Таким образом мы исходный многочлен разложили на линейные множители:
5x5 — 2x4 — 25x3 + 10x2 + 20x — 8 = (x — 1)(x + 1)(x — 2)(x + 2)(5x — 2)
А корнями многочлена являются:
x = ±1; ±2; 0.4
tutata.ru
8.2.5. Разложение квадратного трехчлена на линейные множители
Квадратный трехчлен ax2+bx+c можно разложить на линейные множители по формуле:
ax2+bx+c=a (x-x1)(x-x2), где x1, x2 — корни квадратного уравнения ax2+bx+c=0.
Разложить квадратный трехчлен на линейные множители:
Пример 1). 2x2-7x-15.
Решение. Найдем корни квадратного уравнения: 2x2-7x-15=0.
a=2; b=-7; c=-15. Это общий случай для полного квадратного уравнения. Находим дискриминант D.
D=b2-4ac=(-7)2-4∙2∙(-15)=49+120=169=132>0; 2 действительных корня.
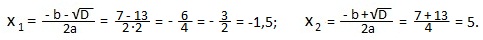
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
2x2-7x-15=2 (х+1,5)(х-5)=(2х+3)(х-5). Мы представили данный трехчлен 2x2-7x-15 в виде произведения двучленов 2х+3 и х-5.
Ответ: 2x2-7x-15=(2х+3)(х-5).
Пример 2). 3x2+2x-8.
Решение. Найдем корни квадратного уравнения:
3x2+2x-8=0.
a=3; b=2; c=-8. Это частный случай для полного квадратного уравнения с четным вторым коэффициентом (b=2). Находим дискриминант D1.
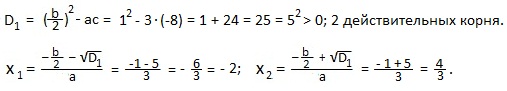
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
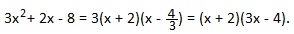
Мы представили трехчлен 3x2+2x-8 в виде произведения двучленов х+2 и 3х-4.
Ответ: 3x2+2x-8=(х+2)(3х-4).
Пример 3). 5x2-3x-2.
Решение. Найдем корни квадратного уравнения:
5x2-3x-2=0.
a=5; b=-3; c=-2. Это частный случай для полного квадратного уравнения с выполненным условием: a+b+c=0 (5-3-2=0). В таких случаях первый корень всегда равен единице, а второй корень равен частному от деления свободного члена на первый коэффициент:
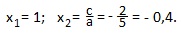
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
5x2-3x-2=5 (х-1)(х+0,4)=(х-1)(5х+2). Мы представили трехчлен 5x2-3x-2 в виде произведения двучленов х-1 и 5х+2.
Ответ: 5x2-3x-2=(х-1)(5х+2).
Пример 4). 6x2+x-5.
Решение. Найдем корни квадратного уравнения:
6x2+x-5=0.
a=6; b=1; c=-5. Это частный случай для полного квадратного уравнения с выполненным условием: a-b+c=0 (6-1-5=0). В таких случаях первый корень всегда равен минус единице, а второй корень равен минус частному от деления свободного члена на первый коэффициент:

Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
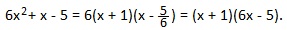
Мы представили трехчлен 6x2+x-5 в виде произведения двучленов х+1 и 6х-5.
Ответ: 6x2+x-5=(х+1)(6х-5).
Пример 5). x2-13x+12.
Решение. Найдем корни приведенного квадратного уравнения:
x2-13x+12=0. Проверим, можно ли применить теорему Виета. Для этого найдем дискриминант и убедимся, что он является полным квадратом целого числа.
a=1; b=-13; c=12. Находим дискриминант D.
D=b2-4ac=132-4∙1∙12=169-48=121=112.
Применим теорему Виета: сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, а произведение корней должно быть равно свободному члену:
x1+x2=13; x1∙x2=12. Очевидно, что x1=1; x2=12.
Применим формулу: ax2+bx+c=a (x-x1)(x-x2).
x2-13x+12=(х-1)(х-12).
Ответ: x2-13x+12=(х-1)(х-12).
Пример 6). x2-4x-6.
Решение. Найдем корни приведенного квадратного уравнения:
x2-4x-6=0.
a=1; b=-4; c=-6. Второй коэффициент — четное число. Находим дискриминант D1.
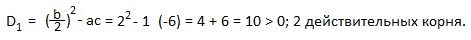
Дискриминант не является полным квадратом целого числа, поэтому, теорема Виета нам не поможет, и мы найдем корни по формулам для четного второго коэффициента:
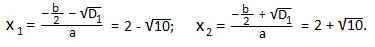
Применим формулу: ax2+bx+c=a (x-x1)(x-x2) и запишем ответ:
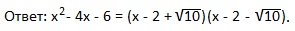
Друзья, для того, чтобы разложить квадратные трехчлены на множители, мы решали каждое квадратное уравнение рациональным способом. Все эти способы мы рассмотрели ранее в теме: «Решение полных квадратных уравнений».
www.mathematics-repetition.com
Разложение многочлена на множители. Теорема Безу и схема Горнера
Разложение многочлена на множители. Теорема Безу и схема Горнера
При решении уравнений и неравенств нередко возникает необходимость разложить на множители многочлен, степень которого равна трем или выше. В этой статье мы рассмотрим, каким образом это сделать проще всего.
Как обычно, обратимся за помощью к теории.
Теорема Безу утверждает, что остаток от деления многочлена  на двучлен
на двучлен  равен
равен  .
.
Но для нас важна не сама теорема, а следствие из нее:
Если число  является корнем многочлена
является корнем многочлена  , то многочлен
, то многочлен  делится без остатка на двучлен
делится без остатка на двучлен  .
.
Перед нами стоит задача каким-то способом найти хотя бы один корень многочлена, потом разделить многочлен на  , где
, где  — корень многочлена. В результате мы получаем многочлен, степень которого на единицу меньше, чем степень исходного. А потом при необходимости можно повторить процесс.
— корень многочлена. В результате мы получаем многочлен, степень которого на единицу меньше, чем степень исходного. А потом при необходимости можно повторить процесс.
Эта задача распадается на две: как найти корень многочлена , и как разделить многочлен на двучлен.
Остановимся подробнее на этих моментах.
1. Как найти корень многочлена.
Сначала проверяем, являются ли числа 1 и -1 корнями многочлена.
Здесь нам помогут такие факты:
Если сумма всех коэффициентов многочлена равна нулю, то число  является корнем многочлена.
является корнем многочлена.
Например, в многочлене  сумма коэффициентов равна нулю:
сумма коэффициентов равна нулю:  . Легко проверить, что
. Легко проверить, что  является корнем многочлена.
является корнем многочлена.
Если сумма коэффициентов многочлена при четных степенях  равна сумме коэффициентов при нечетных степенях, то число
равна сумме коэффициентов при нечетных степенях, то число  является корнем многочлена. Свободный член считается коэффициентом при четной степени, поскольку
является корнем многочлена. Свободный член считается коэффициентом при четной степени, поскольку  , а
, а  — четное число.
— четное число.
Например, в многочлене  сумма коэффициентов при четных степенях
сумма коэффициентов при четных степенях  :
:  , и сумма коэффициентов при нечетных степенях
, и сумма коэффициентов при нечетных степенях  :
:  . Легко проверить, что
. Легко проверить, что  является корнем многочлена.
является корнем многочлена.
Если ни 1, ни -1 не являются корнями многочлена, то двигаемся дальше.
Для приведенного многочлена степени  (то есть многочлена, в котором старший коэффициент — коэффициент при
(то есть многочлена, в котором старший коэффициент — коэффициент при  — равен единице) справедлива формула Виета:
— равен единице) справедлива формула Виета:
 , где
, где  — корни многочлена
— корни многочлена  .
.
Есть ещё  формул Виета, касающихся остальных коэффициентов многочлена, но нас интересует именно эта.
формул Виета, касающихся остальных коэффициентов многочлена, но нас интересует именно эта.
Из этой формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также является целым числом.
Исходя из этого, нам надо разложить свободный член многочлена на множители, и последовательно, от меньшего к большему, проверять, какой из множителей является корнем многочлена.
Рассмотрим, например, многочлен 
Делители свободного члена:  ;
;  ;
;  ;
; 
Сумма всех коэффициентов многочлена равна  , следовательно, число 1 не является корнем многочлена.
, следовательно, число 1 не является корнем многочлена.
Сумма коэффициентов при четных степенях  :
: 
Сумма коэффициентов при нечетных степенях  :
: 
 , следовательно, число -1 также не является корнем многочлена.
, следовательно, число -1 также не является корнем многочлена.
Проверим, является ли число 2 корнем многочлена:  , следовательно, число 2 является корнем многочлена. Значит, по теореме Безу, многочлен
, следовательно, число 2 является корнем многочлена. Значит, по теореме Безу, многочлен  делится без остатка на двучлен
делится без остатка на двучлен  .
.
2. Как разделить многочлен на двучлен.
Многочлен можно разделить на двучлен столбиком.
Разделим многочлен  на двучлен
на двучлен  столбиком:
столбиком:

Есть и другой способ деления многочлена на двучлен — схема Горнера.

Посмотрите это видео, чтобы понять, как делить многочлен на двучлен столбиком, и с помощью схемы Горнера.
Замечу, что если при делении столбиком какая-то степень неизвестного в исходном многочлене отсутствует, на её месте пишем 0 — так же, как при составлении таблицы для схемы Горнера.
Итак, если нам нужно разделить многочлен  на двучлен
на двучлен  и в результате деления мы получаем многочлен
и в результате деления мы получаем многочлен  , то коэффициенты многочлена
, то коэффициенты многочлена  мы можем найти по схеме Горнера:
мы можем найти по схеме Горнера:

Мы также можем использовать схему Горнера для того, чтобы проверить, является ли данное число корнем многочлена: если число  является корнем многочлена
является корнем многочлена  , то остаток от деления многочлена на
, то остаток от деления многочлена на  равен нулю, то есть в последнем столбце второй строки схемы Горнера мы получаем 0.
равен нулю, то есть в последнем столбце второй строки схемы Горнера мы получаем 0.
Используя схему Горнера, мы «убиваем двух зайцев»: одновременно проверяем, является ли число  корнем многочлена
корнем многочлена  и делим этот многочлен на двучлен
и делим этот многочлен на двучлен  .
.
Пример. Решить уравнение:

1. Выпишем делители свободного члена, и будем искать корни многочлена среди делителей свободного члена.
Делители числа 24: 
2. Проверим, является ли число 1 корнем многочлена.
Сумма коэффициентов многочлена  , следовательно, число 1 является корнем многочлена.
, следовательно, число 1 является корнем многочлена.
3. Разделим исходный многочлен на двучлен  с помощью схемы Горнера.
с помощью схемы Горнера.
А) Выпишем в первую строку таблицы коэффициенты исходного многочлена.

Так как член, содержащий  отсутствует, в том столбце таблицы, в котором должен стоять коэффициент при
отсутствует, в том столбце таблицы, в котором должен стоять коэффициент при  пишем 0. Слева пишем найденный корень: число 1.
пишем 0. Слева пишем найденный корень: число 1.
Б) Заполняем первую строку таблицы.

В последнем столбце, как и ожидалось, мы получили ноль, мы разделили исходный многочлен на двучлен  без остатка. Коэффициенты многочлена, получившегося в результате деления изображены синим цветом во второй строке таблицы:
без остатка. Коэффициенты многочлена, получившегося в результате деления изображены синим цветом во второй строке таблицы:

Будем делить дальше. Нам нужно найти корни многочлена  . Корни также ищем среди делителей свободного члена, то есть теперь уже числа -24.
. Корни также ищем среди делителей свободного члена, то есть теперь уже числа -24.
Легко проверить, что числа 1 и -1 не являются корнями многочлена 
В) Продолжим таблицу. Проверим, является ли число 2 корнем многочлена  :
:

Так степень многочлена, который получается в результате деления на единицу меньше степени исходного многочлена, следовательно и количество коэффициентов и количество столбцов на единицу меньше.
В последнем столбце мы получили -40 — число, не равное нулю, следовательно, многочлен  делится на двучлен
делится на двучлен  с остатком, и число 2 не является корнем многочлена.
с остатком, и число 2 не является корнем многочлена.
Идем дальше.
В) Проверим, является ли число -2 корнем многочлена  . Так как предыдущая попытка оказалась неудачной, чтобы не было путаницы с коэффициентами, я сотру строку, соответствующую этой попытке:
. Так как предыдущая попытка оказалась неудачной, чтобы не было путаницы с коэффициентами, я сотру строку, соответствующую этой попытке:

Отлично! В остатке мы получили ноль, следовательно, многочлен  разделился на двучлен
разделился на двучлен  без остатка, следовательно, число -2 является корнем многочлена. Коэффициенты многочлена, который получается в результате деления многочлена
без остатка, следовательно, число -2 является корнем многочлена. Коэффициенты многочлена, который получается в результате деления многочлена  на двучлен
на двучлен  в таблице изображены зеленым цветом.
в таблице изображены зеленым цветом.

В результате деления мы получили квадратный трехчлен  , корни которого легко находятся по теореме Виета:
, корни которого легко находятся по теореме Виета: 
Итак, корни исходного уравнения  :
:
{ }
}
Ответ: { }
}
И.В. Фельдман, репетитор по математике.
ege-ok.ru
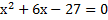 ; б)
; б) 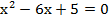 ; в)
; в) 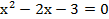 .
. ; б)
; б) 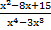 ; в)
; в) 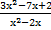 ;
;