Уравнение — Википедия

Первое печатное появление знака равенства в книге Роберта Рекорда в 1557 году (записано уравнение 14x + 15 = 71)

Уравне́ние — равенство вида

f(x1,x2…)=g(x1,x2…){\displaystyle f\left(x_{1},x_{2}\dots \right)=g\left(x_{1},x_{2}\dots \right)},

где чаще всего в качестве f,g{\displaystyle f,g} выступают числовые функции, хотя на практике встречаются и более сложные случаи — например, уравнения для вектор-функций, функциональные уравнения и другие.

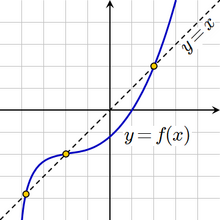Иллюстрация графического метода нахождения корней уравнения x = f(x)

Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.).

Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными».

Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения.

Про корни говорят, что они удовлетворяют данному уравнению.

Решить уравнение означает найти множество всех его решений (корней) или доказать, что корней нет.

Равносильные уравнения[править | править код]

Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней.

Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому.

Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения.

Третье важное свойство задаётся теоремой: если функции f,g{\displaystyle f,g} заданы над областью целостности, то уравнение

f(x)⋅g(x)=0{\displaystyle f(x)\cdot g(x)=0}

эквивалентно совокупности уравнений

f(x)=0,g(x)=0{\displaystyle f(x)=0,\qquad g(x)=0}.

Это означает, что все корни первого уравнения являются корнями одного из двух других уравнений, и позволяет находить корни первого уравнения в два приёма, решая каждый раз более простые уравнения.

Основные свойства[править | править код]

С алгебраическими выражениями, входящими в уравнения, можно выполнять операции, которые не меняют его корней, в частности:

1. в любой части уравнения можно раскрыть скобки;
2. в любой части уравнения можно привести подобные слагаемые;
3. любой член уравнения можно перенести из одной части в другую, заменив его знак на противоположный;
4. к обеим частям уравнения можно прибавить одно и то же выражение;
5. из обеих частей уравнения можно вычесть одно и то же выражение;
6. обе части уравнения можно умножать или делить на одно и то же число, отличное от нуля.

Уравнения, которые являются результатом этих операций, являются эквивалентными начальному уравнению. Однако для свойств 4 и 5 существует ограничение: в случае прибавления к обеим частям уравнения одного и того же выражения (или в случае вычитания из обеих частей уравнения одного и того же выражения), содержащего неизвестное и теряющего смысл при неизвестном, принимающем значения корней данного уравнения, получится уравнение, неэквивалентное исходному (начальному). Но если к обеим частям уравнения прибавить одно и то же выражение (или из обеих частей уравнения вычесть одно и то же выражение), содержащее неизвестное и теряющее смысл лишь при значениях неизвестного, не являющихся корнями данного уравнения, то получится уравнение, эквивалентное начальному.

Умножение или деление обеих частей уравнения на выражение, содержащее неизвестное, может привести, соответственно, к появлению посторонних корней или к потере корней.

Возведение обеих частей уравнения в квадрат может привести к появлению посторонних корней.

Следствие уравнения и посторонние корни[править | править код]

Уравнение

F(x)=G(x){\displaystyle F\left(x\right)=G\left(x\right)}

называется следствием уравнения

f(x)=g(x){\displaystyle f\left(x\right)=g\left(x\right)},

если все корни второго уравнения являются корнями первого. Первое уравнение может иметь дополнительные корни, которые для второго уравнения называются посторонними. Посторонние корни могут появиться при преобразованиях, необходимых для нахождения корней уравнений. Для того чтобы их обнаружить, необходимо проверить корень подстановкой в исходное уравнение. Если при подстановке уравнение становится тождеством, то корень настоящий, если нет — посторонний.

Пример[править | править код]

Уравнение 2×2−1=x{\displaystyle {\sqrt {2x^{2}-1}}=x} при возведении обеих частей в квадрат даёт уравнение 2×2−1=x2{\displaystyle 2x^{2}-1=x^{2}}, или x2=1{\displaystyle x^{2}=1}. Оба уравнения являются следствием исходного. Последнее из них легко решить; оно имеет два корня x=1{\displaystyle x=1} и x=−1{\displaystyle x=-1}.

При подстановке первого корня в исходное уравнение образуется тождество 1=1{\displaystyle {\sqrt {1}}=1}. При подстановке другого корня получается неправильное утверждение 1=−1{\displaystyle {\sqrt {1}}=-1}. Таким образом, второй корень нужно отбросить как посторонний.

Различают алгебраические уравнения, уравнения с параметрами, трансцендентные, функциональные, дифференциальные и другие виды уравнений.

Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ существования и количества корней в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней.

К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения не выше четвёртой степени: линейное, квадратное, кубическое уравнения и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней.

Уравнения, в которые входят трансцендентные функции, называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны.

В общем случае, когда аналитического решения найти не удаётся, применяют вычислительные (численные) методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения.

Алгебраические уравнения[править | править код]

Алгебраическим уравнением называется уравнение вида

P(x1,x2,…,xn)=0,{\displaystyle P\left(x_{1},x_{2},\ldots ,x_{n}\right)=0,}

где P{\displaystyle P} — многочлен от переменных x1,…,xn{\displaystyle x_{1},\ldots ,x_{n}}, которые называются неизвестными.

Коэффициенты многочлена P{\displaystyle P} обычно берутся из некоторого поля F{\displaystyle F}, и тогда уравнение P(x1,x2,…,xn)=0{\displaystyle P\left(x_{1},x_{2},\ldots ,x_{n}\right)=0} называется алгебраическим уравнением над полем F{\displaystyle F}. Степенью алгебраического уравнения называют степень многочлена P{\displaystyle P}.

Например, уравнение

y4+xy2+y2z5+x3−xy2+3×2−sin⁡1=0{\displaystyle y^{4}+{\frac {xy}{2}}+y^{2}z^{5}+x^{3}-xy^{2}+{\sqrt {3}}x^{2}-\sin {1}=0}

является алгебраическим уравнением седьмой степени от трёх переменных (с тремя неизвестными) над полем вещественных чисел.

Линейные уравнения[править | править код]

• в общей форме: a1x1+a2x2+⋯+anxn+b=0{\displaystyle a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}+b=0}
• в канонической форме: a1x1+a2x2+⋯+anxn=b{\displaystyle a_{1}x_{1}+a_{2}x_{2}+\dots +a_{n}x_{n}=b}

Квадратные уравнения[править | править код]

ax2+bx+c=0,a≠0{\displaystyle ax^{2}+bx+c=0,\quad a\neq 0}

где x{\displaystyle x} — свободная переменная, a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c} — коэффициенты, причём a≠0{\displaystyle a\neq 0}.

Выражение ax2+bx+c{\displaystyle ax^{2}+bx+c} называют квадратным трёхчленом. Корень такого уравнения (корень квадратного трёхчлена) — это значение переменной x{\displaystyle x}, обращающее квадратный трёхчлен в нуль, то есть значение, обращающее квадратное уравнение в тождество. Коэффициенты квадратного уравнения имеют собственные названия: коэффициент a{\displaystyle a} называют первым или старшим, коэффициент b{\displaystyle b} называют вторым или коэффициентом при x{\displaystyle x}, c{\displaystyle c} называется свободным членом этого уравнения. Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент a{\displaystyle a}: x2+px+q=0{\displaystyle x^{2}+px+q=0}, где p=ba{\displaystyle p={\frac {b}{a}}}, а q=ca{\displaystyle q={\frac {c}{a}}}. Полным квадратным уравнением называют такое, все коэффициенты которого отличны от нуля. Неполным квадратным уравнением называется такое, в котором хотя бы один из коэффициентов кроме старшего (либо второй коэффициент, либо свободный член) равен нулю.

Для нахождения корней квадратного уравнения ax2+bx+c=0{\displaystyle ax^{2}+bx+c=0} в общем случае следует пользоваться приводимым ниже алгоритмом:

Графиком квадратичной функции f(x)=ax2+bx+c{\displaystyle f\left(x\right)=ax^{2}+bx+c} в прямоугольных координатах является парабола. Она пересекает ось абсцисс в точках, соответствующих корням квадратного уравнения f(x)=0{\displaystyle f\left(x\right)=0}.

Кубические уравнения[править | править код]

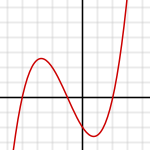График кубической функции

ax3+bx2+cx+d=0,a≠0{\displaystyle ax^{3}+bx^{2}+cx+d=0,\quad a\neq 0}

Для графического анализа кубического уравнения в прямоугольных координатах используется кубическая парабола.

Любое кубическое уравнение канонического вида можно привести к более простому виду

y3+py+q=0{\displaystyle y^{3}+py+q=0},

поделив его на a{\displaystyle a} и подставив в него замену x=y−b3a{\displaystyle x=y-{\tfrac {b}{3a}}}. При этом коэффициенты будут равны:

q=2b327a3−bc3a2+da=2b3−9abc+27a2d27a3{\displaystyle q={\frac {2b^{3}}{27a^{3}}}-{\frac {bc}{3a^{2}}}+{\frac {d}{a}}={\frac {2b^{3}-9abc+27a^{2}d}{27a^{3}}}},

p=ca−b23a2=3ac−b23a2{\displaystyle p={\frac {c}{a}}-{\frac {b^{2}}{3a^{2}}}={\frac {3ac-b^{2}}{3a^{2}}}}.

Уравнение четвёртой степени[править | править код]

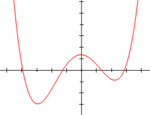
f(x)=ax4+bx3+cx2+dx+e=0,a≠0.{\displaystyle f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0.}

Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).

Так как f(x){\displaystyle f\left(x\right)} является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если a>0{\displaystyle a>0}, то функция возрастает до плюс бесконечности с обеих сторон, и следовательно, имеет глобальный минимум. Аналогично, если a<0{\displaystyle a<0}, то функция убывает до минус бесконечности с обеих сторон, и следовательно, имеет глобальный максимум.

Системы линейных алгебраических уравнений[править | править код]

Система уравнений вида:

{a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2…am1x1+am2x2+⋯+amnxn=bm{\displaystyle {\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\dots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\dots +a_{2n}x_{n}=b_{2}\\\dots \\a_{m1}x_{1}+a_{m2}x_{2}+\dots +a_{mn}x_{n}=b_{m}\\\end{cases}}}

(1)

Здесь m{\displaystyle m} — количество уравнений, а n{\displaystyle n} — количество неизвестных. x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[1].

Система называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной. Система называется квадратной, если число m уравнений равно числу n неизвестных. Решение системы — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему обращает все её уравнения в тождества. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Уравнения с параметрами[править | править код]

Уравнением с параметрами называется математическое уравнение, внешний вид и решение которого зависит от значений одного или нескольких параметров. Решить уравнение с параметром означает:

1. Найти все системы значений параметров, при которых данное уравнение имеет решение.
2. Найти все решения для каждой найденной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.

Уравнения с параметром могут быть как линейными, так и нелинейными.

Пример линейного уравнения с параметром:

ax+1=4,{\displaystyle a\,x+1=4,}

Пример нелинейного уравнения с параметром:

logx2a+37−x=5,{\displaystyle {\mbox{log}}_{x^{2}}{\frac {a+3}{7-x}}=5,}

где x{\displaystyle x} — независимая переменная, a{\displaystyle a} — параметр.

Трансцендентные уравнения[править | править код]

Трансцендентным уравнением называется уравнение, не являющееся алгебраическим. Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические функции, например:

• cos⁡x=x{\displaystyle \cos x=x}
• lg⁡x=x−5{\displaystyle \lg x=x-5}
• 2x=lg⁡x+x5+40{\displaystyle 2^{x}=\lg x+x^{5}+40}

Более строгое определение таково: трансцендентное уравнение — это уравнение вида f(x)=g(x){\displaystyle f\left(x\right)=g\left(x\right)}, где функции f{\displaystyle f} и g{\displaystyle g} являются аналитическими функциями, и по крайней мере одна из них не является алгебраической.

Функциональные уравнения[править | править код]

Функциональным уравнением называется уравнение, выражающее связь между значением функции (или функций) в одной точке с её значениями в других точках. Многие свойства функций можно определить, исследуя функциональные уравнения, которым эти функции удовлетворяют. Термин «функциональное уравнение» обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них. Например:

• функциональному уравнению

f(s)=2sπs−1sin⁡(πs2)Γ(1−s)f(1−s){\displaystyle f\left(s\right)=2^{s}\pi ^{s-1}\sin \left({\frac {\pi s}{2}}\right)\Gamma \left(1-s\right)f\left(1-s\right)}

где Γ(z){\displaystyle \Gamma (z)} — гамма-функция Эйлера, удовлетворяет дзета-функция Римана ζ.

• Следующим трём уравнениям удовлетворяет гамма-функция; она является единственным решением этой системы трёх уравнений:

f(x)=f(x+1)x{\displaystyle f\left(x\right)={f\left(x+1\right) \over x}}

f(y)f(y+12)=π22y−1f(2y){\displaystyle f\left(y\right)f\left(y+{\frac {1}{2}}\right)={\frac {\sqrt {\pi }}{2^{2y-1}}}f\left(2y\right)}

f(z)f(1−z)=πsin⁡(πz){\displaystyle f\left(z\right)f\left(1-z\right)={\pi \over \sin \left(\pi z\right)}} (формула дополнения Эйлера).

• Функциональное уравнение

f(az+bcz+d)=(cz+d)kf(z){\displaystyle f\left({az+b \over cz+d}\right)=\left(cz+d\right)^{k}f\left(z\right)}

где a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c}, d{\displaystyle d} являются целыми числами, удовлетворяющими равенству ad−bc=1{\displaystyle ad-bc=1}, то есть |abcd|=1{\displaystyle {\begin{vmatrix}a&b\\c&d\end{vmatrix}}=1}, определяет f{\displaystyle f} как модулярную форму порядка k.

Дифференциальные уравнения[править | править код]

Дифференциальным уравнением называется уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестн

ru.wikipedia.org

Уравнение и его корни

Цели:  Познакомить учащихся с понятиями:  уравнение, корни уравнения, решение уравнений. Научить отличать линейные уравнения от остальных уравнений.

Задачи:  Изучить основные определения по теме.  Научиться выбирать корни уравнения из предложенных чисел. Показать уравнения, у которых более 1 корня. Вспомнить решение простейших уравнений.

Ход урока:

Учитель делит учащихся  на 3 группы. (При ответе на вопросы для групп учитель сам назначает того, кто будет отвечать.)

Организационный момент.

Вступительное слово учителя: про уравнения, методы решения уравнений в 2-5 классе, о способах  решения   уравнений в 6 классе( что измениться).

ЗАДАНИЕ 1:

На основе теоретических сведений из 2-6 классов учащимся предлагается в группах сформулировать понятие «уравнение». Для этого каждой группе выдаются  таблички со словами :  равенство, верное, выражение, содержащее,  равно, Х, знаки действий, неизвестное.   Учащиеся должны продолжить фразу: «УРАВНЕНИЕ ЭТО-…», используя предложенные им слова (  несколько слов лишние).

Группа, которая раньше справиться с заданием озвучивает свой вариант ответа. Далее свои ответы озвучивают другие группы.  Учитель анализирует ответы и говорит правильный.

ЗАДАНИЕ 2:

На основе определения учащимся предлагается выбрать из предложенных выражений те, которые являются  уравнениями  и из букв правильных ответов составить слово ( корень).

Примеры.

Группа которая первой справилась с заданием озвучивает  правильный ответ, объясняя принцип выбора

( наличие неизвестного, равенство).

Учитель  обращает внимание  на разнообразие уравнений и  акцентирует внимание учащихся  на уравнения под буквами: О, Р, Е и вводит понятие линейного уравнения.

Слово «корень» имеет непосредственное отношение к уравнениям. Сейчас мы разберемся какое.

ЗАДАНИЕ 3:  

Подберите число, которое превращает данное уравнение в верное числовое равенство.

Каждой группе выдаётся одно уравнение ( список всех уравнений на доске), список чисел на доске ( экране).

Уравнения для групп:

2х + 5 = 3 ( х+1)         4 х² = 8х      3х – 5х = 2( х+4 )

Числа :  -2,  -1,  1,  2.

Учитель подводит итоги и вводит определение корня уравнения.  Затем  речь идет о количестве корней в уравнении.  Учитель говорит о том, что корней в уравнении может быть различное количество. Затем предлагает учащимся сыграть в игру.

Учащиеся называют любое число ( до 7), а  учитель пишет уравнение в котором именно столько корней, сколько назвали.

Например:   2:   (х+3)(2-х)=0    4:  ( 2х+3)(х-7)(х+5)х=0

При этом учитель подводит к  уравнениям, в которых нет корней или любое число является корнем уравнения и пишет примеры таких уравнений.

ЗАДАНИЕ 4:

Придумайте уравнение, в котором 3 корня. Каждая группа обсуждает и пишет своё уравнение  на доске.

Учитель вводит понятие «решить уравнение», ссылаясь на предыдущие примеры.

ЗАДАНИЕ 5:

Решите уравнения. (Устный счет)

На доске ( экране ) список уравнений. Учащимся предлагается решить  представленные уравнения

Уравнения.

Проверка  полученных знаний:

ЗАДАНИЕ 6:

Группам предлагается выбрать  верное высказывание:

1.  Любое равенство называется уравнением.

2.  Любое  уравнение имеет хотя бы один корень.

3.  Существуют уравнения, у которых нет корней.

4.  Существует уравнение,  корнем которого являются числа 2 и 3.

5.  Алгебраическое выражение, содержащее неизвестное, называется уравнением.

6.  Решить уравнение – это значит найти все его корни.

7.  Уравнение 5(х+3)= 2х+3х  -называется линейным.

Правильные ответы : 3,4,7

Учитель анализирует ответы и обращает внимание на  высказывания, в  определении правильности которых были допущены ошибки.   

Подведение итогов урока и домашнее задание.

videouroki.net

Урок по алгебре на тему «Уравнение и его корни» (7 класс)

Урок №2

Тема урока: Уравнение и его корни

Цель урока: ознакомление учащихся с равносильными уравнениями; формирование знаний учащихся об основных свойствах уравнений и умений решать уравнения, используя эти свойства, развитие логики, воображения, умение анализировать, развитие чувства товарищества, взаимопомощи, воспитание любви к предмету.

Тип урока: комбинированный.

Средства обучения: классная доска, обучающая таблица, карточки с заданиями для групп, учебник « Алгебра 7 класс» Ю.Н. Макарычев, Н.Г. Миндюк и др.

Ход урока

I. Проверка домашнего задания

1. Проверить выполнение домашнего задания и ответить на вопросы, возникшие у учащихся при его выполнении.

2. Фронтальный опрос

1)Что такое уравнение?

Что называется корнем уравнения?

Что означает решить уравнение?

2) Для каждого из уравнений подобрать корень из данных чисел:

а) 2х+4=6 б) х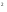-4=0 в) (х+1)(4+х)=0 г) 2(х-1)=х+4

Числа: 6; 2; 1; -1; -2; -4.

3)Составьте уравнение, корнем которого является число 8

4) Выберите правильный ответ.

Уравнение х+5=5:

1. 1. 1. 1. имеет множество корней;

         2. не имеет корней;

         3. имеет только один корень.

Уравнение х+3=х:

а) имеет множество корней;

б) не имеет корней;

в) имеет только один корень 5) Найдите числа, которые нужно записать в квадратики, чтобы получилось верное равенство. 5 + □ = 13, 5 — □=13, 5 * □ = 15, 13 = □ — 5,
20 : □ = 5, 5 = □ : 20, 3 * □ – 5 = 10, 15 – 2 * □ = 5,
II. Восприятие и осознание нового материала. Рассмотрим два уравнения: х+5=7 и х-1=1 .Решением каждого из этих уравнений есть число 2 (х=2).Такие уравнения называются равносильными. Два уравнения называются равносильными, если они имеют одинаковые решения. Равносильными считаются и уравнения, не имеющие корней, например х+5=х и х-8=х. Вопрос классу : являются ли равносильными уравнения: а) х – 3= 0 и 3х =9; б) 0х = 3 и х+6=х? Какие из уравнений равносильны уравнению 3х=15: а) 6х=30; б)9х=45; в)3х-15=0; г)3х-1=14; д)3х+15=20; е)3х+15=18?

Чтобы решать более сложные уравнения, следует научиться заменять их более простыми уравнениями и равносильными данным.

Например, используя распределительное свойство умножения а(в+с)=ав+ас, можно утверждать, что значения выражений 5х+3х и 8х при любом значении х равны. Следовательно, равносильны такие уравнения: 5х+3х=10 и 8х=10.Другимим словами, если раскрыть скобки и привести подобные слагаемые в любой части уравнения, то получим уравнение равносильное данному.

Кроме того, если к обеим частям верного равенства прибавить одно и тоже число, то получится верное равенство. Например, если к обеим частям уравнения 3х=12-2х прибавить 2х, то получим уравнение 3х+2х=12 равносильное данному. Это все равно, что перенести члены уравнения из одной части в другую, при этом изменивши знак.

Мы также знаем, что если обе части числового равенства умножить или разделить на одно и тоже, отличное от нуля, число, то получим верное равенство. Поэтому, если обе части уравнения умножить или разделить на одно и то же , отличное от нуля, число, то получим уравнение равносильное данному.

Например, -3х+7=5, умножим обе части на (-1), получим 3х-7=-5. Эти уравнения имеют одни и те же корни.

Таким образом, всегда справедливы такие свойства уравнений.

Учащиеся находят свойства в учебнике и зачитывают вслух.

Основные свойства уравнений :

1. В любой части уравнения можно привести подобные
слагаемые или раскрыть скобки, если они есть.

2.Любой член уравнения можно переносить из одной части уравнения в другую, изменивши его знак на противоположный. 3.Обе части уравнения можно умножать и делить на одно и то же число, отличное от нуля. Рассмотреть решение следующих уравнений с объяснением учителя: 3(х-1)=12; 2х-3=3х+2; 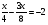. III. Закрепление и осознание знаний учащихся

1)Являются ли равносильными уравнения: а) 2х+5=10 и 2х=10; б)6-х=5 и х=11; 6х-1=2х+3 и 4х=4(ответ объяснить)

3)Решение уравнений с использованием основных свойств уравнений. Решить №129(2 столбик), №131 с комментариями у доски.

4)Работа в группах. Группы составлены таким образом, чтобы в каждой группе был ученик с высоким уровнем учебных достижений. Задание для групп одинаковое. Решить уравнение

А) х+3=3х-4

Б) 5(х-1)=2х-3

В)(х+3)-(х-1)=4х

Г)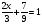

Д) 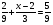(дополнительное задание для группы, которая справится быстрее всех).

Проверка решений у доски. Один представитель из группы показывает решение одного уравнения. Оцениваются руководители групп. Остальные, если считает руководитель.

IV. Домашнее задание: Решить №121, №122 (задания для обязательного выполнения), №239 (дополнительно по желанию).

V. Итог урока.

Какие уравнения называются равносильными?

Приведите примеры равносильных уравнений.

Сформулируйте основные свойства уравнений.

Составьте уравнение равносильное уравнению 10х=30.

infourok.ru

Целое уравнение и его корни

Определение:

Целым уравнением с одной переменной называется уравнение, левая и правая части которого — целые выражения.

Отличие целого уравнения от дробно-рационального заключается в том, что областью определения целого уравнения является множество всех действительных чисел. То есть аргумент может принимать любые значения.

Среди уравнений найдем те, которые являются целыми уравнениями с одной переменной.

Целыми будут следующие уравнения.

Каждое из этих уравнений можно преобразовать.

Первое уравнение:

Во втором уравнении:

В третьем уравнении:

Определение:

Степень многочлена P(x) называют степенью уравнения P(x)=0.

Степень первого уравнения  P(x)=3, степень второго уравнения P(x)=4, степень третьего уравнения P(x)=4.

Рассмотрим пример: определить степень уравнений.

1.                 

2.                  

3.                 

4.                   

Любое уравнение 1 — й степени можно привести к виду  - это линейное уравнение, и оно имеет не более одного корня.

Уравнение 2 — й степени можно привести к виду  - это квадратное уравнение и оно имеет не более двух корней.

Уравнение 3 — й степени можно записать в виде , оно имеет не более трёх корней.

Уравнения 4 — й степени можно представить в виде , оно имеет не более четырёх корней.

Любое целое уравнение n - й степени можно представить в таком виде , оно имеет не более n корней.

Причём, во всех этих случаях, a≠0.

Пример.

Решить уравнение:

Данное уравнение имеет три корня.

Рассмотрим пример: решить уравнение.

Так как для него трудно найти способ решения, будем работать с исходной записью. Введём замену.

Получим новое уравнение, решим его:

При решении этого уравнения мы применили способ введения новой переменной. С помощью этого способа легко решать уравнения вида . Такие уравнения имеют специальное название — «биквадратные уравнения».

Алгоритм решения биквадратного уравнения:

1.                Ввести новую переменную .

2.                Решить уравнение , полученное после подстановки новой переменной.

3.                Выполняю обратную подстановку .

4.                Найти корни исходного биквадратного уравнения.

Пример.

Решить уравнение:

Приведем его к биквадратному уравнению:

Введём новую переменную и выполним подстановку:

videouroki.net

Презентация к уроку по алгебре (7 класс) на тему: Презентация по теме: «Уравнение и его корни» к учебнику Г.К. Муравина, 7 класс

Слайд 1

Методическая разработка Соловьевой Е.В. МБОУ СОШ №1, с.Вольно-Надеждинское , Приморского края . Алгебра 7 класс У равнение и его корни

Слайд 2

На нижней полке в 4 раза больше книг, чем на верхней. х 4х – 15 Если с нижней полки переставить на верхнюю 15 книг…, 4х х + 15 то книг станет поровну: 4х – 15 = х + 15 Равенства, содержащие переменную, называют уравнениями с одной переменной или уравнениями с одним неизвестным Задача. На нижней полке в 4 раза больше книг, чем на верхней. Если с нижней полки переставить на верхнюю 15 книг, то книг станет поровну. Сколько книг на верхней полке? Уравнение с одной переменной Сколько переменных содержит данное уравнение? переменной. — уравнение с одной

Слайд 3

Решение уравнения Задача. На нижней полке в 4 раза больше книг, чем на верхней. Если с нижней полки переставить на верхнюю 15 книг, то книг станет поровну. Сколько книг на верхней полке? 4х – 15 = х + 15 Свойства уравнений: Слагаемое можно переносить из одной части уравнения в другую, изменив его знак на противоположный. 4х = + 15 – 15 х + 15 – х л евая правая

Слайд 4

Решение уравнения Задача. На нижней полке в 4 раза больше книг, чем на верхней. Если с нижней полки переставить на верхнюю 15 книг, то книг станет поровну. Сколько книг на верхней полке? 4х – 15 = х + 15 Свойства уравнений: Слагаемое можно переносить из одной части уравнения в другую, изменив его знак на противоположный. л евая правая 4х – x = 15 + 15 3 х = 30 :3 О бе части уравнения можно умножить или разделить на одно и то же число, отличное от нуля, получится уравнение равносильное данному. х = 10 Ответ: 10 книг . Проверка: х=10, то 4 10 – 15 = 10 + 15, 25=25 – верно 10 – корень уравнения. Корнем уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство Сколько корней имеет данное уравнение?

Слайд 5

0 = 0 – верно 8 — корень уравнения. 0 = 0 – верно 5 — корень уравнения. 0 = 0 – верно 4 — корень уравнения. х = 5, то ( 5 – 4)( 5 – 5)( 5 – 8) = 0, 0 1 -4 -1 0 Уравнение с одной переменной ( х – 4) ( х –5) ( х – 8)=0 Проверка: х = 4, то ( 4 – 4)( 4 – 5)( 4 – 8) = 0, х = 8, то ( 8 – 4)( 8 – 5)( 8 – 8) = 0, 4 -3 3 0 – это уравнение имеет три корня х = 4, х = 5, х = 8 Ответ : 4 5 8 ; ; . Существуют уравнения, которые имеют более одного корня.

Слайд 6

( х –5) ( х – 8) + 5 Уравнение с одной переменной ( х – 4) ( х –5) ( х – 8)=0 Решим уравнение : Ответ : ( х – 4) = 0 или = 0 или = 0 х – 4 х –5 х – 8 л евая правая х – 4 = 0 + 4 л евая правая 4 х – 5 = 0 5 л евая правая х – 8 = 0 + 8 8 4 5 8 ; ; . Произведение равно нулю, если хотя бы один из множителей равен нулю. Решите уравнение: (5х+60)(-42х+13)=0

Слайд 7

х Уравнение с одной переменной Ответ: Решите уравнение: х + 2 = х = х х + 2 л евая правая х + 2 = х 2 Решение: 0 х = 2 | :0 – на нуль делить нельзя решений нет решений нет . Решить уравнение – значит найти все его корни или доказать, что корней нет

Слайд 8

Уравнения, имеющие одни и те же корни, называют равносильными. Уравнение с одной переменной Найдите корни уравнения х 2 = 9 . Найдите корни уравнения (х-3)(х+3)=0. Ответ: 3, -3. Ответ: 3, -3. Сравните полученные корни. х 2 = 9 и (х-3)(х+3)=0 – равносильные уравнения. Уравнения, не имеющие корней, также считают равносильными.

Слайд 9

2 – корень уравнения. х -2 – не является корнем уравнения. (-2 ) , х = -2, то (-2) х Уравнение с одной переменной № 112 (а ) Какие из чисел -2, 2, -5, 0, 3 являются корнями уравнения х 2 =10-3х ? 2 = 10 — 3 х 4 = 16 – неверно 2 , х = 2, то 2 х 2 = 10 — 3 4 = 4 – верно … Ответ: 2, -5 . Кл: №116, №121, №120 Д / З: правила, № 111, №117

Слайд 10

Интернет-ресурсы http ://www.mathvaz.ru — досье школьного учителя математики.

nsportal.ru

Открытый урок по алгебре в 7 классе «Уравнение и его корни»

Открытый урок по алгебре в 7 классе коррекционной школы для учащихся

с ограниченными возможностями здоровья

Тема урока: Уравнение и его корни

Цель урока

образовательная : Познакомить учащихся с понятиями:  уравнение, корни уравнения, решение уравнений. Научить отличать линейные уравнения от остальных уравнений.

коррекционная: Развивать последовательность мышлении, учить выделять из общего частное

воспитательная: Воспитывать трудолюбие, активность в работе, потребность в труде

Задачи: Изучить основные определения по теме.  Научиться выбирать корни уравнения из предложенных чисел. Показать уравнения, у которых более 1 корня. Вспомнить решение простейших уравнений.

Метод обучения: объяснение, устные и письменные упражнения, иллюстрация

Форма контроля: проверка домашнего задания в консультативной форме, опрос по парам

Оборудование: раздаточный материал, таблицы

Тип урока: изучение нового материала.

                                                Ход урока:

1.Организационный момент

   Отчет дежурного о готовности класса на урок.

2.Актуализация прежних знаний.

Решить уравнение: 7а=1,4.

x+1,8=5,9

51,2-x=10,2

Решить задачу:

а) Какое число меньше 3,6 в 4 раза?

б) Периметр квадрата равен 4,8 м. Найдите его сторону.

В) Площадь прямоугольника 9,6 кв.см, длина – 1.2 см. Найдите ширину прямоугольника.

3. Изучение нового материала

Класс делится на 6 групп (по рядам и вариантам).

Задание 1:

На основе теоретических сведений из 2-6 классов учащимся предлагается в группах сформулировать понятие «уравнение». Для этого каждой группе выдаются  таблички со словами :  равенство, верное, выражение, содержащее,  равно, Х, знаки действий, неизвестное.   Учащиеся должны продолжить фразу: «УРАВНЕНИЕ ЭТО-…», используя предложенные им слова (  несколько слов лишние).

Группа, которая раньше справиться с заданием озвучивает свой вариант ответа. Далее свои ответы озвучивают другие группы.  Учитель анализирует ответы и говорит правильный.

Задание 2:

На основе определения учащимся предлагается выбрать из предложенных выражений те, которые являются  уравнениями  и из букв правильных ответов составить слово ( корень).

М) 8а-3 К) 3а=15 Е) 7а-6=0

Р) 2x+1=8 Ь) 1,6-а=0,8

О) x+7=18 Н) 1,5x=6

Д) а+в

Примеры.

Группа которая первой справилась с заданием озвучивает  правильный ответ, объясняя принцип выбора

( наличие неизвестного, равенство).

Учитель  обращает внимание  на разнообразие уравнений и  акцентирует внимание учащихся  на уравнения под буквами: О, Р, Е и вводит понятие линейного уравнения.

Слово «корень» имеет непосредственное отношение к уравнениям. Сейчас мы разберемся какое.

Задание 3:  

Подберите число, которое превращает данное уравнение в верное числовое равенство.

Каждой группе выдаётся одно уравнение ( список всех уравнений на доске), список чисел на доске ( экране).

Уравнения для групп:

2х + 5 = 3 ( х+1)         4 х² = 8х      3х – 5х = 2( х+4 )

Числа :  -2,  -1,  1,  2.

Учитель подводит итоги и вводит определение корня уравнения.  Затем  речь идет о количестве корней в уравнении.  Учитель говорит о том, что корней в уравнении может быть различное количество. Затем предлагает учащимся сыграть в игру.

Учащиеся называют любое число ( до 7), а  учитель пишет уравнение в котором именно столько корней, сколько назвали.

Например:   2:   (х+3)(2-х)=0    4:  ( 2х+3)(х-7)(х+5)х=0

При этом учитель подводит к  уравнениям, в которых нет корней или любое число является корнем уравнения и пишет примеры таких уравнений.

Физминутка на общее развитие организма детей /конечностей и туловища/ 
«Петрушка». Исходное положение: руки опущены, расслаблены. Одновременно хаотичным

встряхиванием рук и ног достичь расслабления мышц до чувств тепла и покраснение ладоней. 

«Потягивание кошечки».

Задание 4: Придумайте уравнение, в котором 3 корня.

Каждая группа обсуждает и пишет своё уравнение  на доске.

Учитель вводит понятие «решить уравнение», ссылаясь на предыдущие примеры.

Задание 5:

Группам предлагается выбрать  верное высказывание:

1.  Любое равенство называется уравнением.

2.  Любое  уравнение имеет хотя бы один корень.

3.  Существуют уравнения, у которых нет корней.

4.  Существует уравнение,  корнем которого являются числа 2 и 3.

5.  Алгебраическое выражение, содержащее неизвестное, называется уравнением.

6.  Решить уравнение – это значит найти все его корни.

7.  Уравнение 5(х+3)= 2х+3х  -называется линейным.

Правильные ответы : 3,4,7

Учитель анализирует ответы и обращает внимание на  высказывания, в  определении правильности которых были допущены ошибки.   

4.Физминутка для глаз

Крепко зажмурить глаза на 3-5 секунд, а затем открыть их на такое же время. Повторять 6-8 раз. 
Быстро моргать в течение 10-12 секунд, открыть глаза , отдыхать 10-12 секунд. Повторять 3 раза. 
Исходное положение: сидя, закрыть веки, массировать их с помощью ладоней.

5. Самостоятельная работа. 

Замените:

а) уравнение 0,3x=-4 равносильным уравнением с целым коэффициентом.

б) уравнение 5x-4=21 равносильным уравнением вида ax=b где a и b некоторые числа

Первые три

учащихся справившиеся с заданием получают оценку.

6. Задание на дом: 

П.6 выучить определения №112, 117 Придумать и решить два линейных уравнения.

8. Итог урока.

 Выставляются оценки за самостоятельную работу и активность на уроке

infourok.ru