Formuly_sokrashchennogo_umnozhenija_shpargalka

Формулы сокращенного умножения

Разность квадратов: ;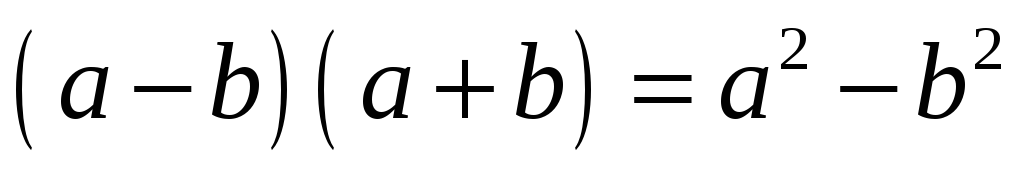

Квадрат суммы: ;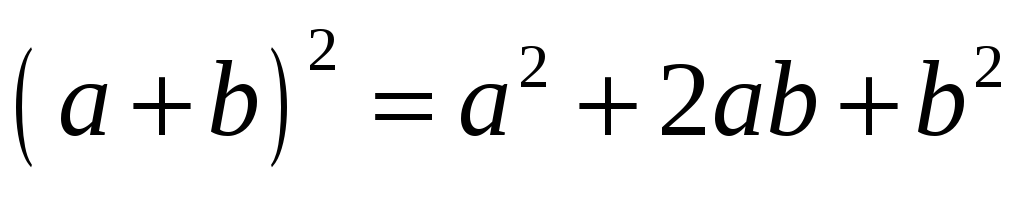

Квадрат разности: ;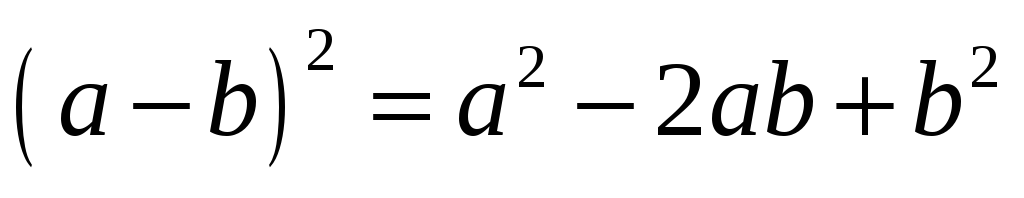

Сумма кубов: ;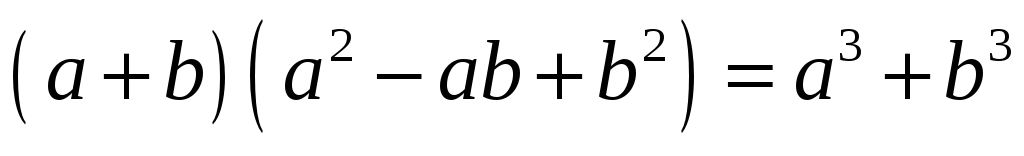

Разность кубов: ;

Куб суммы: ;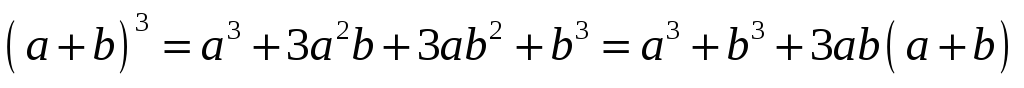

Куб разности: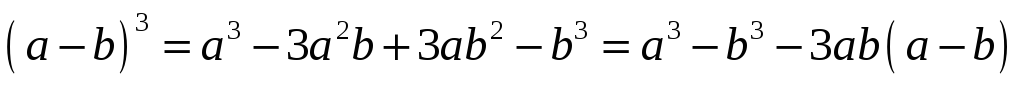

;

Квадрат трехчлена: .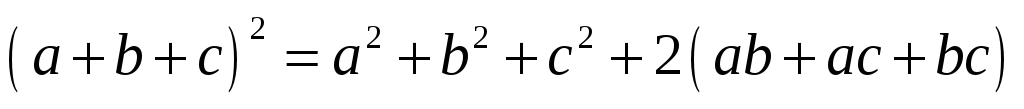

Замечание: Формулы в прямом прочтении дают сокращенное умножение многочленов или возведение их в степень. В обратном прочтении – разложение многочлена на множители.

Формула разложения квадратного трехчлена на множители

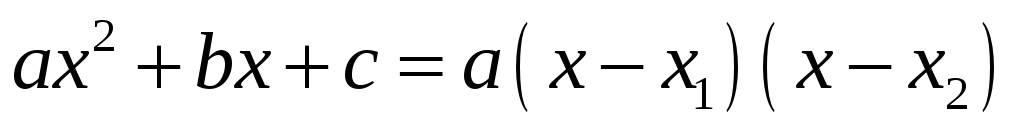
Следует помнить, что квадратный многочлен можно разложить на множители, если у него есть действительные корни, т. е. 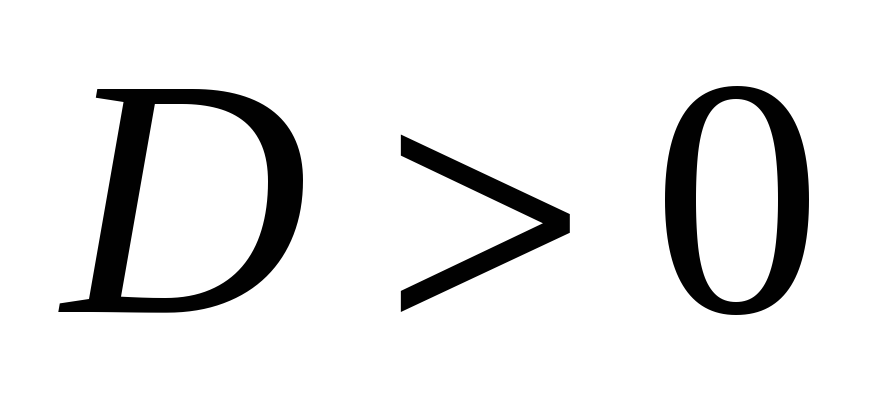. При этом надо обратить особое внимание, что если , то формула будет иметь вид:

,

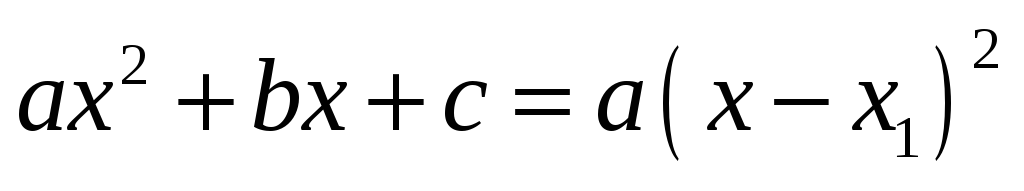
и Вы скорее всего не заметили формулу полного квадрата двучлена (квадрат суммы или квадрат разности).

Стоит так же помнить, что если 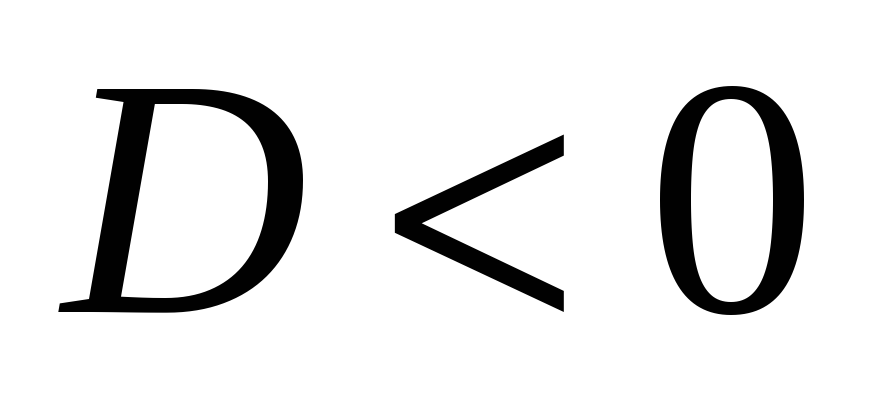, то квадратный трехчлен на множители не раскладывается. Так, например, не стоит пытаться разложить на множители неполный квадрат суммы или разности (второй множитель формул суммы и разности кубов): .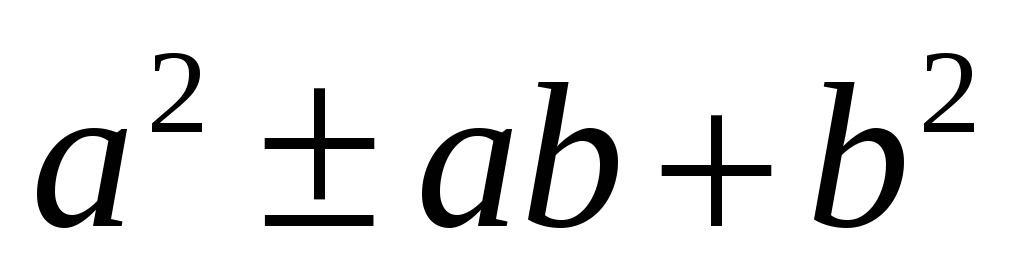

Формулы корней квадратного уравнения

Общий вид квадратного уравнения: .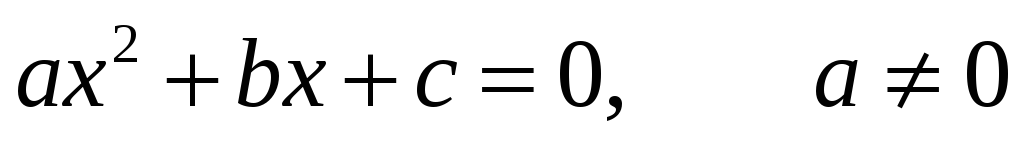

Дискриминант квадратного уравнения: .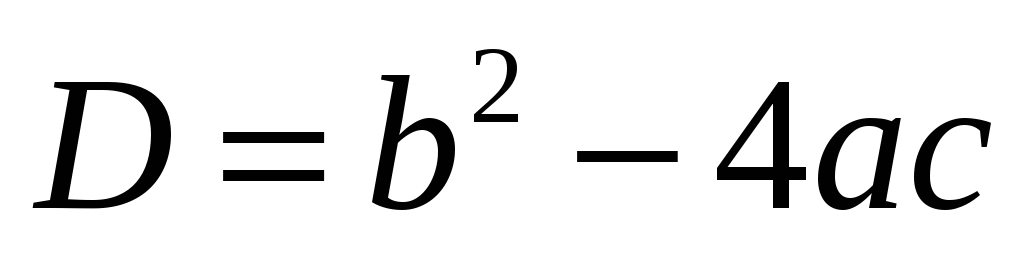

Если

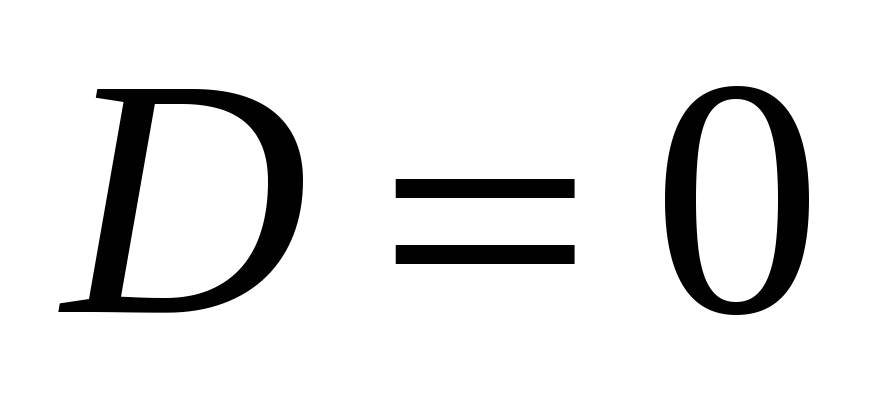, то квадратное уравнение действительных корней не имеет.

Если , то квадратное уравнение имеет одни действительный корень кратности два, который находится по формуле: .

Если 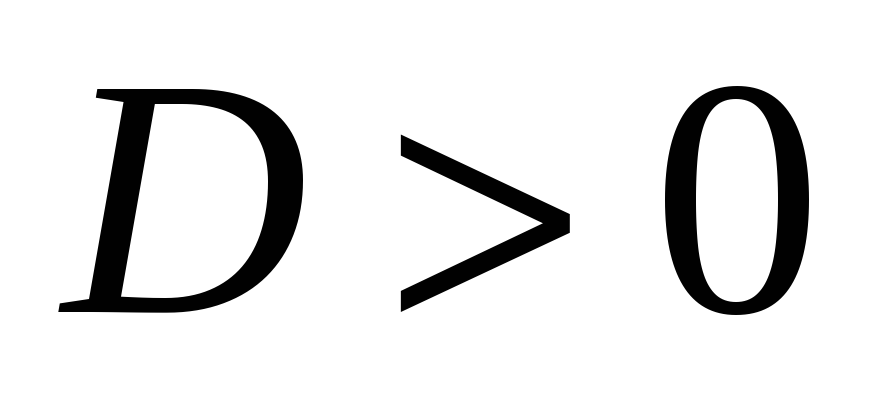, то квадратное уравнение имеет два действительных корня, которые находятся по формулам: .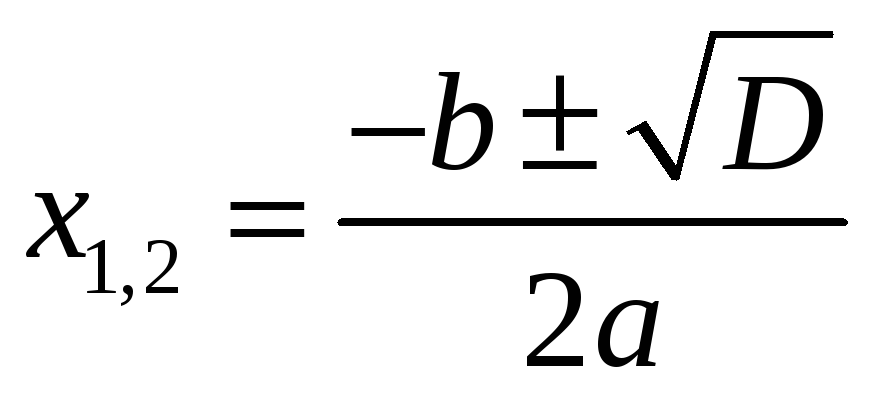

Формулы корней квадратного уравнения с четным вторым коэффициентом.

Общий вид уравнения: .

Дискриминант: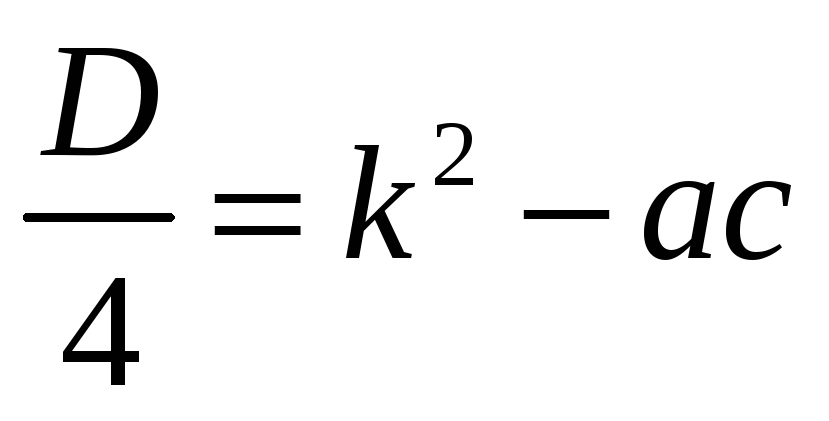

.

Условия существования корней прежние, т. е. .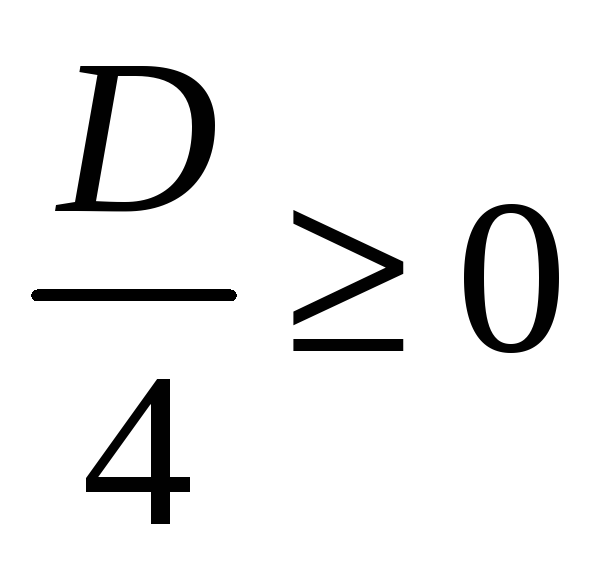

Корни: .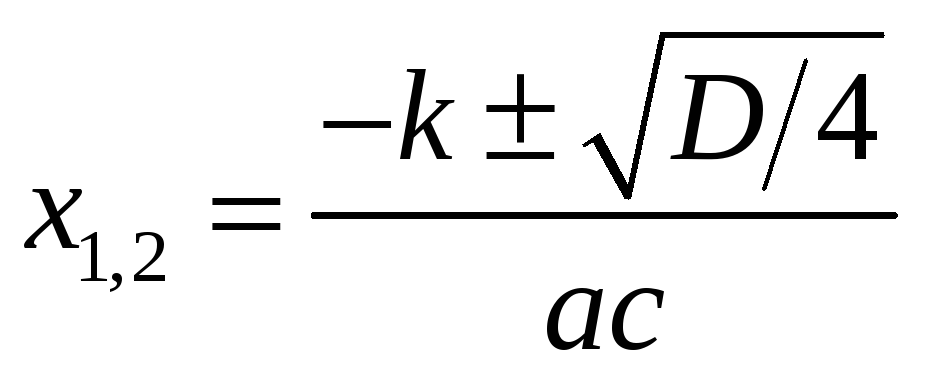

Теорема Виета.

Квадратное уравнение называется приведенным, если его старший коэффициент равен 1. Любое квадратное уравнение можно привести, разделив обе его части на старший коэффициент.

Общий вид приведенного квадратного уравнения: .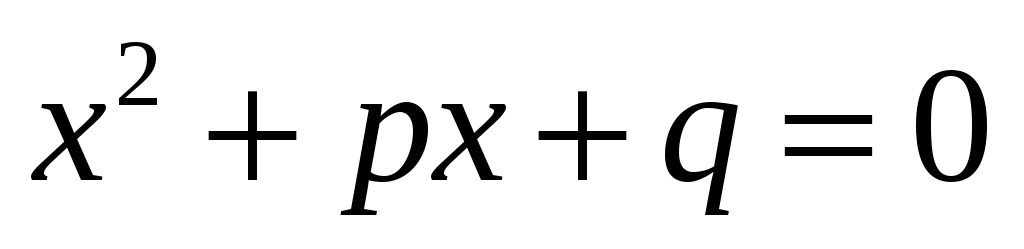

Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение равно свободному члену.

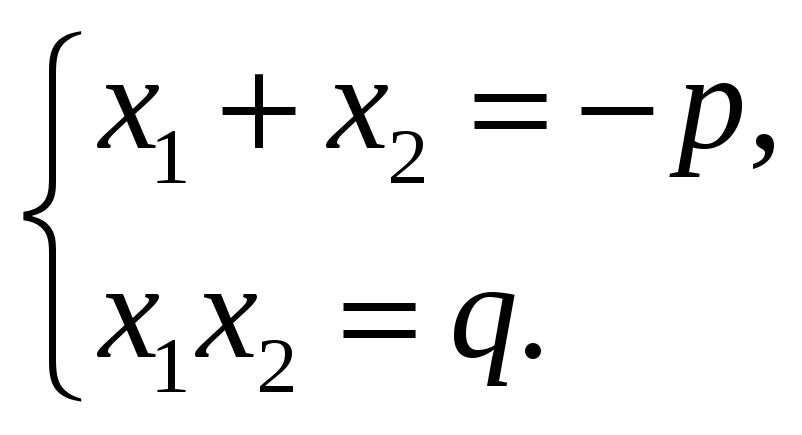
Верна и обратная теорема.

studfile.net

Как разложить на множители квадратный трехчлен: примеры применения формулы

Разложение многочленов для получения произведения иногда кажется запутанным. Но это не так сложно, если разобраться в процессе пошагово. В статье подробно рассказано, как разложить на множители квадратный трехчлен.

Понятие и определение

Многим непонятно, как разложить на множители квадратный трехчлен, и для чего это делается. Сначала может показаться, что это бесполезное занятие. Но в математике ничего не делается просто так. Преобразование нужно для упрощения выражения и удобства вычисления.

Многочлен, имеющий вид – ax²+bx+c, называется квадратным трехчленом. Слагаемое «a» должно быть отрицательным или положительным. На практике это выражение называется квадратным уравнением. Поэтому иногда говорят и по-другому: как разложить квадратное уравнение.

Интересно! Квадратным многочлен называют из-за самой его большой степени – квадрата. А трехчленом из-за 3-х составных слагаемых.

Некоторые другие виды многочленов:

• линейный двучлен (6x+8),
• кубический четырехчлен (x³+4x²-2x+9).

Разложение квадратного трехчлена на множители

Сначала выражение приравнивается к нулю, затем нужно найти значения корней x1 и x2. Корней может не быть, может быть один или два корня. Наличие корней определяется по дискриминанту. Его формулу надо знать наизусть: D=b²-4ac.

Если результат D получается отрицательный, корней нет. Если положительный – корня два. Если в результате получился ноль – корень один. Корни тоже высчитываются по формуле.

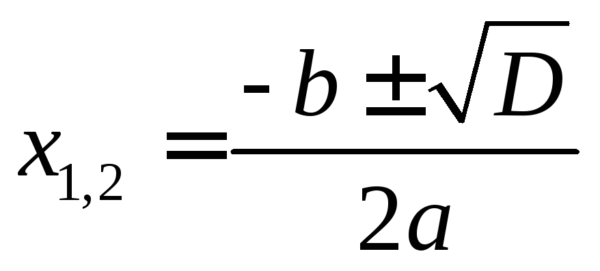
Если при вычислении дискриминанта получается ноль, можно применять любую из формул. На практике формула просто сокращается: -b / 2a.

Формулы для разных значений дискриминанта различаются.

Если D положительный:

Если D равен нулю:

a(x-x1)2

Если выражение отрицательное, считать ничего не нужно.

Это интересно! Как найти и чему будет равна длина окружности

Онлайн калькуляторы

В интернете есть онлайн калькулятор. С его помощью можно выполнить разложение на множители. На некоторых ресурсах предоставляется возможность посмотреть решение пошагово. Такие сервисы помогают лучше понять тему, но нужно постараться хорошо вникнуть.

Если тема понятна, рекомендуется использовать онлайн калькулятор для проверки решения.

Полезное видео: Разложение квадратного трехчлена на множители

Примеры

Предлагаем просмотреть простые примеры, как разложить квадратное уравнение на множители.

Пример 1

Здесь наглядно показано, что в результате получится два x, потому что D положительный. Их и нужно подставить в формулу. Если корни получились отрицательные, знак в формуле меняется на противоположный.

Нам известна формула разложения квадратного трехчлена на множители: a(x-x1)(x-x2). Ставим значения в скобки: (x+3)(x+2/3). Перед слагаемым в степени нет числа. Это значит, что там единица, она опускается.

Это интересно! Как раскрыть модуль действительного числа и что это такое

Пример 2

Этот пример наглядно показывает, как решать уравнение, имеющее один корень.

Подставляем получившееся значение:

9(x-1/3)2.

Пример 3

Дано: 5x²+3x+7

Сначала вычислим дискриминант, как в предыдущих случаях.

5x²+3x+7=0

D=b²-4ac

D=9-4*5*7=9-140= -131.

Дискриминант отрицательный, значит, корней нет.

После получения результата стоит раскрыть скобки и проверить результат. Должен появиться исходный трехчлен.

Альтернативный способ решения

Некоторые люди так и не смогли подружиться с дискриминантом. Можно еще одним способом произвести разложение квадратного трехчлена на множители. Для удобства способ показан на примере.

Дано: x²+3x-10

Мы знаем, что должны получиться 2 скобки: (_)(_). Когда выражение имеет такой вид: x²+bx+c, в начале каждой скобки ставим x: (x_)(x_). Оставшиеся два числа – произведение, дающее «c», т. е. в этом случае -10. Узнать, какие это числа, можно только методом подбора. Подставленные числа должны соответствовать оставшемуся слагаемому.

Это интересно! Уроки математики: умножение на ноль главное правило

К примеру, перемножение следующих чисел дает -10:

• -1, 10,
• -10, 1,
• -5, 2,
• -2, 5.

Далее выполняем подбор и смотрим, чтобы получилось выражение, которое было сначала:

1. (x-1)(x+10) = x2+10x-x-10 = x2+9x-10. Нет.
2. (x-10)(x+1) = x2+x-10x-10 = x2-9x-10. Нет.
3. (x-5)(x+2) = x2+2x-5x-10 = x2-3x-10. Нет.
4. (x-2)(x+5) = x2+5x-2x-10 = x2+3x-10. Подходит.

Значит, преобразование выражения x2+3x-10 выглядит так: (x-2)(x+5).

Важно! Стоит внимательно следить за тем, чтобы не перепутать знаки.

Разложение сложного трехчлена

Если «a» больше единицы, начинаются сложности. Но все не так трудно, как кажется.

Чтобы выполнить разложение на множители, нужно сначала посмотреть, возможно ли что-нибудь вынести за скобку.

Например, дано выражение: 3x²+9x-30. Здесь выносится за скобку число 3:

3(x²+3x-10). В результате получается уже известный трехчлен. Ответ выглядит так: 3(x-2)(x+5)

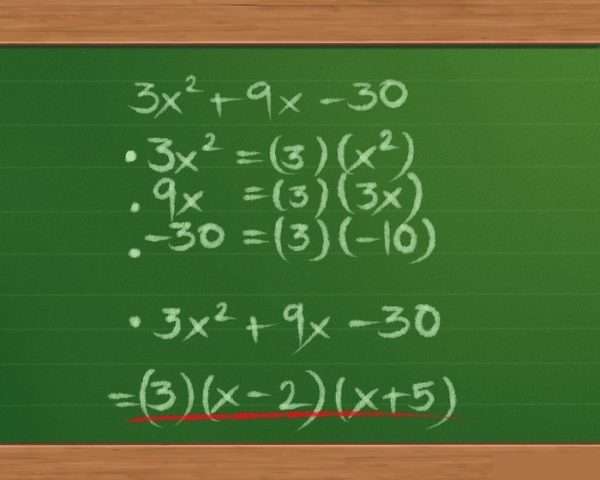
Как раскладывать, если слагаемое, которое находится в квадрате отрицательное? В данном случае за скобку выносится число -1. К примеру: -x²-10x-8. После выражение будет выглядеть так:

(-1)(x2+6x+9)

Схема мало отличается от предыдущей. Есть лишь несколько новых моментов. Допустим, дано выражение: 2x²+7x+3. Ответ также записывается в 2-х скобках, которые нужно заполнить (_)(_). Во 2-ю скобку записывается x, а в 1-ю то, что осталось. Это выглядит так: (2x_)(x_). В остальном повторяется предыдущая схема.

Число 3 дают числа:

• -1, -3,
• -3, -1,
• 3, 1,
• 1, 3.

Решаем уравнения, подставляя данные числа. Подходит последний вариант. Значит, преобразование выражения 2x²+7x+3 выглядит так: (2x+1)(x+3).

Это интересно! Считаем правильно: как находить процент от суммы и числа

Другие случаи

Преобразовать выражение получится не всегда. При втором способе решение уравнения не потребуется. Но возможность преобразования слагаемых в произведение проверяется только через дискриминант.

Стоит потренироваться решать квадратные уравнения, чтобы при использовании формул не возникало трудностей.

Полезное видео: разложение трехчлена на множители

Вывод

Пользоваться можно любым способом. Но лучше оба отработать до автоматизма. Также научиться хорошо решать квадратные уравнения и раскладывать многочлены на множители нужно тем, кто собирается связать свою жизнь с математикой. На этом строятся все следующие математические темы.

tvercult.ru

Моделирование в электроэнергетике — Разложение на множители алгебраического многочлена степени n

Разложение на множители алгебраического многочлена степени n

Любой алгебраический многочлен степени n может быть представлен в виде произведения n-линейных множителей вида  и постоянного числа, которое является коэффициентов многочлена при старшей ступени х, т.е.

где — являются корнями многочлена.

Корнем многочлена  называют число  (действительное или комплексное), обращающее многочлен в нуль. Корнями многочлена могут быть как действительные корни, так и комплексно-сопряженные корни, тогда многочлен может быть представлен в следующем виде:

Рассмотрим методы разложения многочленов степени «n» в произведение множителей первой и второй степени.

Способ №1. Метод неопределенных коэффициентов.

Коэффициенты такого преобразованного выражения определяются методом неопределенных коэффициентов. Суть метода сводится к тому, что заранее известен вид множителей, на которые разлагается данный многочлен. При использовании метода неопределённых коэффициентов справедливы следующие утверждения:

П.1. Два многочлена тождественно равны в случае, если равны их коэффициенты при одинаковых степенях х.

П.2. Любой многочлен третьей степени разлагается в произведение линейного и квадратного множителей.

П.3. Любой многочлен четвертой степени разлагается на произведение двух многочленов второй степени.

Пример 1.1. Необходимо разложить на множители кубическое выражение:

П.1. В соответствии с принятыми утверждениями для кубического выражения справедливо тождественное равенство:

П.2. Правая часть выражения может быть представлена в виде слагаемых следующим образом:

П.3. Составляем систему уравнений из условия равенства коэффициентов при соответствующих степенях кубического выражения.

Данная система уравнений может быть решена методом подбора коэффициентов (если простая академическая задача) или использованы методы решения нелинейных систем уравнений. Решая данную систему уравнений, получим, что неопределённые коэффициенты определяются следующим образом:

; ; ; 

Таким образом, исходное выражение раскладывается на множители в следующем виде:

Данный метод может использоваться как при аналитических выкладках, так и при компьютерном программировании для автоматизации процесса поиска корня уравнения.

Способ №2. 

Формулы Виета

Формулы Виета — это формулы, связывающие коэффициенты алгебраических уравнений степени n и его корни. Данные формулы были неявно представлены в работах французского математика Франсуа Виета (1540 — 1603). В связи с тем, что Виет рассматривал только положительные вещественные корни, поэтому у него не было возможности записать эти формулы в общем явном виде.

Для любого алгебраического многочлена степени n, который имеет n-действительных корней,

справедливы следующие соотношения, которые связывают корни многочлена с его коэффициентами:

Формулами Виета удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням.

Пример 2.1. Рассмотрим, как связаны корни многочлена с его коэффициентами на примере кубического уравнения

В соответствии с формулами Виета взаимосвязь  корней многочлена с его коэффициентами имеет следующий вид:

Аналогичные соотношения можно составить для любого полинома степени n.

 

Способ №3. Разложение квадратного уравнения на множители с рациональными корнями

Из последней формулы Виета следует, что корни многочлена являются делителями его свободного члена и старшего коэффициента. В связи с этим, если в условии задачи задан многочлен степени n c целыми коэффициентами

то данный многочлен имеет рациональный корень  (несократимая дробь), где p — делитель свободного члена  , а q – делитель старшего коэффициента . В таком случае многочлен степени n можно представить в виде (теорема Безу):

 Многочлен , степень которого на 1 меньше степени начального многочлена, определяется делением многочлена степени n двучлен   , например, с помощью схемы Горнера или самым простым способом — «столбиком».

Пример 3.1. Необходимо разложить многочлен на множители

П.1. В связи с тем, что коэффициент при старшем слагаемом равен единицы, то рациональные корни данного многочлена являются делителями свободного члена выражения, т.е. могут быть целыми числами .  Подставляем каждое из представленных чисел в исходное выражение найдем, что корень представленного многочлена равен .

Выполним деление исходного многочлена на двучлен:

Воспользуемся схемой Горнера

В верхней строке выставляются коэффициенты исходного многочлена, при этом первая ячейка верхней строки остается пустой.

В первой ячейке второй строки записывается найденный корень (в рассматриваемом примере  записывается число «2»), а следующие значения в ячейках вычисляются определенным образом и они являются коэффициентами многочлена, который получится в результате деления многочлена на двучлен. Неизвестные коэффициенты определяются следующим образом:

Во вторую ячейку второй строки переносится значение из соответствующей ячейки первой строки (в рассматриваемом примере записывается число «1»).

В третью ячейку второй строки записывается значение произведения первой ячейки на вторую ячейку второй строки плюс значение из третьей ячейки первой строки (в рассматриваемом примере  2 ∙1 -5 = -3).

В четвертую ячейку второй строки записывается значение произведения первой ячейки на третью ячейку второй строки плюс значение из четвертой ячейки первой строки (в рассматриваемом примере 2 ∙ (-3) +7 = 1).

И  так далее. Последняя ячейка второй строки является остатком деления многочлена на двучлен. В случае если деление происходит на корень уравнения, то остаток должен быть равен «0».

Таким образом, исходный многочлен раскладывается на множители:

П.2. Далее раскладывается на множители многочлен третьей степени (кубическое выражение).

Способ №4. Использование формул сокращенного умножения

Формулы сокращенного умножения применяют для упрощения вычислений, а также разложение многочленов на множители. Формулы сокращенного умножения позволяют упростить решение отдельных задач.

Формулы, используемые для разложения на множители

Формулы, используемые для разложения на слагаемые

Деление формул на две группы выполнено условно для удобства запоминания, а любые равенства справедливы как при чтении их слева направо, так и справа налево. 

Пример 4.1. Необходимо разложить многочлен на множители

П.1. Воспользуемся формулой сокращенного умножения для разности квадратов и преобразуем исходное выражение к следующему виду:

П.2. Далее решаются квадратные уравнения и исходный многочлен раскладывается на множители.

Пример 4.2. Необходимо разложить многочлен четвертой степени на множители

П.1. Воспользуемся формулой сокращенного умножения для разности квадратов и преобразуем исходное выражение к следующему виду:

П.2. Далее решаются квадратные уравнения и исходный многочлен раскладывается на множители.

 

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

simenergy.ru

Разложение многочленов на множители

Разложение многочленов на множители – это тождественное преобразование, в результате которого многочлен преобразуется в произведение нескольких сомножителей – многочленов или одночленов.

Существует несколько способов разложения многочленов на множители.

Способ 1. Вынесение общего множителя за скобку.

Это преобразование основывается на распределительном законе умножения: ac + bc = c(a + b). Суть преобразования заключается в том, чтобы выделить в двух рассматриваемых компонентах общий множитель и «вынести» его за скобки.

Пример.

Разложим на множители многочлен 28х³ – 35х⁴.

Решение.

1. Находим у элементов 28х³ и 35х⁴ общий делитель. Для 28 и 35 это будет 7; для х³ и х⁴ – х³. Иными словами, наш общий множитель 7х³ .

2. Каждый из элементов представляем в виде произведения множителей, один из которых
7х³ : 28х³ – 35х⁴ = 7х³ ∙ 4 – 7х³ ∙ 5х.

3. Выносим за скобки общий множитель
7х³ : 28х³ – 35х⁴ = 7х³ ∙ 4 – 7х³ ∙ 5х = 7х³(4 – 5х).

Способ 2. Использование формул сокращенного умножения. «Мастерство» владением этим способом состоит в том, чтобы заметить в выражении одну из формул сокращенного умножения.

Пример.

Разложим на множители многочлен х⁶ – 1.

Решение.

1. К данному выражению мы можем применить формулу разности квадратов. Для этого представим х⁶ как (х³)², а 1 как 1², т.е. 1. Выражение примет вид:
(х³)² – 1 = (х³ + 1) ∙ (х³ – 1).

2. К полученному выражению мы можем применить формулу суммы и разности кубов:
(х³ + 1) ∙ (х³ – 1) = (х + 1) ∙ (х² – х + 1) ∙ (х – 1) ∙ (х² + х + 1).

Итак,
х⁶ – 1 = (х³)² – 1 = (х³ + 1) ∙ (х³ – 1) = (х + 1) ∙ (х² – х + 1) ∙ (х – 1) ∙ (х² + х + 1).

Способ 3. Группировка. Способ группировки заключается в объединение компонентов многочлена таким образом, чтобы над ними было легко совершать действия (сложение, вычитание, вынесение общего множителя).

Пример.

Разложим на множители многочлен х³ – 3х² + 5х – 15.

Решение.

1. Сгруппируем компоненты таким образом: 1-ый со 2-ым, а 3-ий с 4-ым
(х³ – 3х²) + (5х – 15).

2. В получившемся выражении вынесем общие множители за скобки: х² в первом случае и 5 – во втором.
(х³ – 3х²) + (5х – 15) = х²(х – 3) + 5(х – 3).

3. Выносим за скобки общий множитель х – 3 и получаем:
х²(х – 3) + 5(х – 3) = (х – 3)( х² + 5).

Итак,
х³ – 3х² + 5х – 15 = (х³ – 3х²) + (5х – 15) = х²(х – 3) + 5(х – 3) = (х – 3) ∙ ( х² + 5).

Закрепим материал.

Пример.

Разложить на множители многочлен a² – 7ab + 12b².

Решение.

1. Представим одночлен 7ab в виде суммы 3ab + 4ab. Выражение примет вид:
a² – (3ab + 4ab) + 12b².

Раскроем скобки и получим:
a² – 3ab – 4ab + 12b².

2. Сгруппируем компоненты многочлена таким образом: 1-ый со 2-ым и 3-ий с 4-ым. Получим:
(a² – 3ab) – (4ab – 12b²).

3. Вынесем за скобки общие множители:
(a² – 3ab) – (4ab – 12b²) = а(а – 3b) – 4b(а – 3b).

4. Вынесем за скобки общий множитель (а – 3b):
а(а – 3b) – 4b(а – 3b) = (а – 3 b) ∙ (а – 4b).

Итак,
a² – 7ab + 12b² =
= a² – (3ab + 4ab) + 12b² =
= a² – 3ab – 4ab + 12b² =
= (a² – 3ab) – (4ab – 12b²) =
= а(а – 3b) – 4b(а – 3b) =
= (а – 3 b) ∙ (а – 4b).

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Многочлены. Разложение многочлена на множители: способы, примеры :: SYL.ru

Понятия «многочлен» и «разложение многочлена на множители» по алгебре встречаются очень часто, ведь их необходимо знать, чтобы с легкостью производить вычисления c большими многозначными числами. В этой статье будет описано несколько способов разложения. Все они достаточно просты в применении, стоит лишь правильно подобрать нужный в каждом конкретном случае.

Понятие многочлена

Многочлен является суммой одночленов, то есть выражений, содержащих только операцию умножения.

Например, 2 * x * y – это одночлен, а вот 2 * x * y + 25 — многочлен, который состоит из 2 одночленов: 2 * x * y и 25. Такие многочлены называет двучленами.

Иногда для удобства решения примеров с многозначными значениями выражение необходимо преобразовать, например, разложить на некоторое количество множителей, то есть чисел или выражений, между которыми производится действие умножения. Есть ряд способов разложения многочлена на множители. Стоит рассмотреть их начиная с самого примитивного, который применяют еще в начальных классах.

Группировка (запись в общем виде)

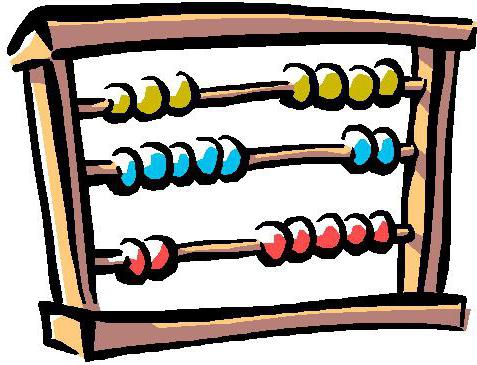
Формула разложения многочлена на множители способом группировки в общем виде выглядит таким образом:

ac + bd + bc + ad = (ac + bc) + (ad + bd)

Необходимо сгруппировать одночлены так, чтобы в каждой группе появился общий множитель. В первой скобке это множитель с, а во второй – d. Это нужно сделать для того, чтобы затем вынести его за скобку, тем самым упростив вычисления.

Алгоритм разложения на конкретном примере

Простейший пример разложения многочлена на множители способом группировки приведен ниже:

10ас + 14bc – 25a — 35b = (10ас – 25а) + (14bc — 35b)

В первую скобку нужно взять слагаемые с множителем а, который и будет общим, а во вторую – со множителем b. Обратите внимание на знаки + и – в готовом выражении. Мы ставим перед одночленом тот знак, который был в начальном выражении. То есть нужно работать не с выражением 25а, а с выражением -25. Знак минус как бы «приклеить» к стоящему за ним выражению и всегда учитывать его при вычислениях.

На следующем шаге нужно вынести множитель, который является общим, за скобку. Именно для этого и делается группировка. Вынести за скобку – значит выписать перед скобкой (опуская знак умножения) все те множители, которые с точностью повторяются во всех слагаемых, которые находятся в скобке. Если в скобке не 2, а 3 слагаемых и больше, общий множитель должен содержаться в каждом из них, иначе его нельзя вынести за скобку.

В нашем случае — только по 2 слагаемых в скобках. Общий множитель сразу виден. В первой скобке – это а, во второй – b. Здесь нужно обратить внимание на цифровые коэффициенты. В первой скобке оба коэффициента (10 и 25) кратны 5. Это значит, что можно вынести за скобку не только а, но и 5а. Перед скобкой выписать 5а, а затем каждое из слагаемых в скобках поделить на общий множитель, который был вынесен, и также записать частное в скобках, не забывая о знаках + и — Со второй скобкой поступить также, вынести 7b, так как и 14 и 35 кратно 7.

Итак:

10ас + 14bc – 25a — 35b = (10ас – 25а) + (14bc — 35b) = 5а(2c — 5) + 7b(2c – 5).

Получилось 2 слагаемых: 5а(2c — 5) и 7b(2c – 5). Каждое из них содержит общий множитель (все выражение в скобках здесь совпадает, значит, является общим множителем): 2с – 5. Его тоже нужно вынести за скобку, то есть во второй скобке остаются слагаемые 5а и 7b:

5а(2c — 5) + 7b(2c – 5) = (2c – 5)*(5а + 7b).

Итак, полное выражение:

10ас + 14bc – 25a — 35b = (10ас – 25а) + (14bc — 35b) = 5а(2c — 5) + 7b(2c – 5) = (2c – 5)*(5а + 7b).

Таким образом, многочлен 10ас + 14bc – 25a — 35b раскладываается на 2 множителя: (2c – 5) и (5а + 7b). Знак умножения между ними при записи можно опускать

Иногда встречаются выражения такого типа: 5а² + 50а³ , здесь можно вынести за скобку не только а или 5а, а даже 5а². Всегда нужно стараться вынести максимально большой общий множитель за скобку. В нашем случае, если разделить каждое слагаемое на общий множитель, то получается:

5а² / 5а² = 1; 50а³ / 5а² = 10а (при вычислении частного нескольких степеней с равными основаниями основание сохраняется, а показатель степени вычитается). Таким образом, в скобке остается единица (ни в коем случае не забывайте писать единицу, если выносите за скобку целиком одно из слагаемых) и частное от деления: 10а. Получается, что:

5а² + 50а³ = 5а² (1 + 10а)

Формулы квадратов

Для удобства вычислений были выведены несколько формул. Они называются формулами сокращенного умножения и используются довольно часто. Эти формулы помогают разложить на множители многочлены, содержащие степени. Это еще один действенный способ разложения на множители. Итак, вот они:

• a² + 2ab + b² = (a + b)² — формула, получившая название «квадрат суммы», так как в результате разложения в квадрат берется сумма чисел, заключенная в скобки, то есть значение этой суммы умножается само на себя 2 раза, а значит, является множителем.
• a² + 2ab — b² = (a — b)^{2 —} формула квадрата разности, она аналогична предыдущей. В результате получается разность, заключенная в скобки, содержащаяся в квадратной степени.
• a² — b² = (a + b)(а — b) — это формула разности квадратов, так как изначально многочлен состоит из 2 квадратов чисел или выражений, между которыми производится вычитание. Пожалуй, из трех названных она используется чаще всего.

Примеры на вычисления по формулам квадратов

Вычисления по ним производятся достаточно просто. Например:

1. 25x² + 20xy + 4y² — используем формулу «квадрат суммы».
2. 25x² являетсяквадратом выражения 5х. 20ху — удвоенное произведение 2*(5х*2у), а 4y² — это квадрат 2у.
3. Таким образом, 25x² + 20xy + 4y² = (5x+ 2у)² = (5x+ 2у)(5x+ 2у). Данный многочлен раскладывается на 2 множителя (множители одинаковые, поэтому записывается в виде выражения с квадратной степенью).

Действия по формуле квадрата разности производятся аналогично этим. Остается формула разность квадратов. Примеры на эту формулу очень легко определить и найти среди других выражений. Например:

• 25а² — 400 = (5а — 20)(5а + 20). Так как 25а² = (5а)², а 400 = 20²
• 36х² — 25у² = (6х — 5у) (6х + 5у). Так как 36х² = (6х)², а 25у² = (5у²)
• с² — 169b² = (с — 13b)(c + 13b). Так как 169b² = (13b)²

Важно, чтобы каждое из слагаемых являлось квадратом какого-либо выражения. Тогда этот многочлен подлежит разложению на множители по формуле разности квадратов. Для этого не обязательно, чтобы над числом стояла именно вторая степень. Встречаются многочлены, содежащие большие степени, но все равно подходящие к этим формулам.

a⁸+10a⁴+25 = (a⁴)² + 2*a⁴*5 + 5² = (a⁴+5)²

В данном примере а⁸можно представить как (a⁴)², то есть квадрат некого выражения. 25 — это 5², а 10а⁴ — это удвоенное произведение слагаемых 2*a⁴*5. То есть данное выражение, несмотря на наличие степеней с большими показателями, можно разложить на 2 множителя, чтобы в последствии работать с ними.

Формулы кубов

Такие же формулы существуют для разложения на множители многочленов, содержащих кубы. Они немного посложнее тех, что с квадратами:

• a³ + b³ = (а + b)(a² — ab + b²) — эту формулу называют суммой кубов, так как в начальном виде многочлен представляет собой сумму двух выражений или чисел, заключенных в куб.
• a³ — b³ = (а — b)(a² + ab + b²) — формула, идентичная предыдущей, обозначена как разность кубов.
• a³ + 3a²b + 3ab²+ b³ = (a + b)^{3 —} куб суммы, в результате вычислений получается сумма чисел или выражений, заключенная в скобки и умноженная сама на себя 3 раза, то есть находящаяся в кубе
• a³ — 3a²b + 3ab² — b³ = (a — b)³ — формула, составленная по аналогии предыдущей с изменением лишь некоторых знаков математических операций (плюс и минус), имеет название «куб разности».

Последние две формулы практически не испольуются с целью разложения многочлена на множители, так как они сложны, и достаточно редко встречаются многочлены, полностью соответствующие именно такому строению, чтобы их можно было разложить по этим формулам. Но их все равно нужно знать, так как они потребуются при действиях в обратном направлении — при раскрытии скобок.

Примеры на формулы кубов

Рассмотрим пример: 64a³ − 8b³ = (4a)³ − (2b)³ = (4a − 2b)((4a)² + 4a*2b + (2b)²) = (4a−2b)(16a² + 8ab + 4b²).

Здесь взяты достаточно простые числа, поэтому сразу можно увидеть, что 64а³ — это (4а)³, а 8b³ — это (2b)³. Таким образом, этот многочлен раскладывается по формуле разность кубов на 2 множителя. Действия по формуле суммы кубов производятся по аналогии.

Важно понимать, что далеко не все многочлены подлежат разложению хотя бы одним из способов. Но есть такие выражения, которые содержат большие степени, чем квадрат или куб, но их также можно разложить по формуам сокращенного умножения. Например: x¹² + 125y³=(x⁴)³+(5y)³=(x⁴+5y)*((x⁴)² − x⁴*5y+(5y)²)=(x⁴ + 5y)(x⁸ − 5x⁴y + 25y²).

В этом примере содержится аж 12 степень. Но даже его возможно разложить на множители по формуле суммы кубов. Для этого нужно представить х¹² как (x⁴)³ , то есть как куб какого-либо выражения. Теперь в формулу вместо а нужно подставлять именно его. Ну а выражение 125у³ — это куб 5у. Далее следует составить произведение по формуле и произвести вычисления.

На первых порах или в случае возникших сомнений, вы всегда можете произвести проверку обратным умножением. Вам нужно лишь раскрыть скобки в получившемся выражении и выполнить действия с подобными слагаемыми. Этот метод относится ко всем перечисленным способам сокращения: как к работе с общим множителем и группировке, так и к действиям по формулам кубов и квадратных степеней.

www.syl.ru

Как разложить квадратный трёхчлен на множители?

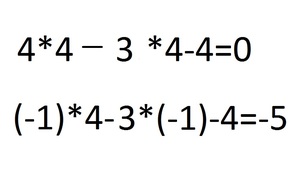
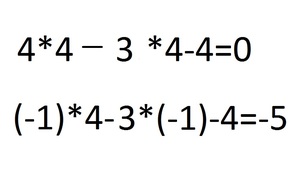Мир погружён в огромное количество чисел. Любые исчисления происходят с их помощью.

Люди учат цифры для того, чтобы в дальнейшей жизни не попадаться на обман. Необходимо уделять огромное количество времени, чтобы быть образованным и рассчитать собственный бюджет.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Математика — это точная наука, которая играет большую роль в жизни. В школе дети изучают цифры, а после, действия над ними.

Действия над числами бывают совершенно разными: умножение, разложение, добавление и прочие. Помимо простых формул, в изучении математики используют и более сложные действия. Существует огромное количество формул, по которым узнают любые значения.

Это интересно: разность векторов, определение разности.

В школе, как только появляется алгебра, в жизнь школьника добавляются формулы упрощения. Бывают уравнения, когда неизвестных числа два, но найти простым способом не получится. Трёхчлен — соединение трёх одночленов, с помощью простого метода отнимания и добавления. Трёхчлен решается с помощью теоремы Виета и дискриминанта.

Формула разложения квадратного трёхчлена на множители

Существуют два правильных и простых решения примера:

• дискриминант;
• теорема Виета.

Квадратный трёхчлен имеет неизвестный в квадрате, а также число без квадрата. Первый вариант для решения задачи использует формулу Виета. Это простая формула, если цифры, что стоят перед неизвестным, будут минимальным значением.

Для других уравнений, где число стоит перед неизвестным, уравнение необходимо решать через дискриминант. Это более сложное решение, но используют дискриминант намного чаще, нежели теорему Виета.

Изначально, для нахождения всех переменных уравнения необходимо возвести пример к 0. Решение примера можно будет проверить и узнать правильно ли подстроены числа.

Это интересно: умножение на 0 — правило для любого числа.

Дискриминант

1. Необходимо приравнять уравнение к 0.

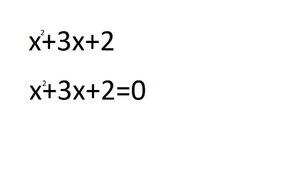
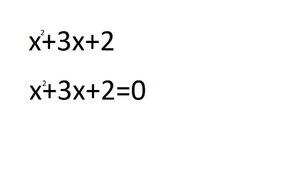
2. Каждое число перед х будет названо числами a, b, c. Так как перед первым квадратным х нет числа, то оно приравнивается к 1.

3. Теперь решение уравнения начинается через дискриминант:

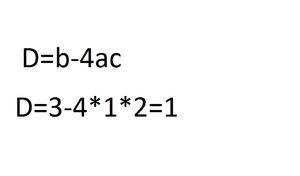
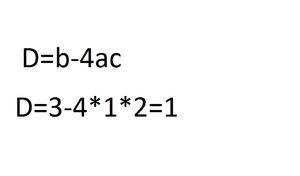
4. Теперь нашли дискриминант и находим два х. Разница заключается в том, что в одном случае перед b будет стоять плюс, а в другом минус:

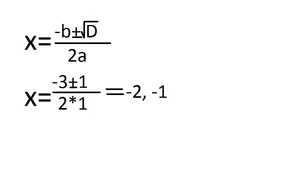
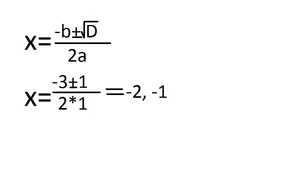
5. По решению два числа получилось -2 и -1. Подставляем под первоначальное уравнение:

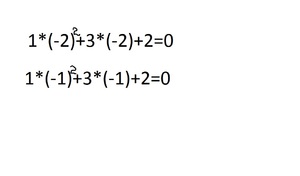
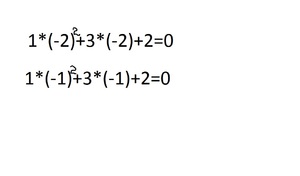
6. В этом примере получилось два правильных варианта. Если оба решения подходят, то каждое из них является истинным.

Через дискриминант решают и более сложные уравнение. Но если само значение дискриминанта будет меньше 0, то пример неправильный. Дискриминант при поиске всегда под корнем, а отрицательное значение не может находиться в корне.

Это интересно: признак перпендикулярности прямой и плоскости, теория и практика.

Теорема Виета

Применяется для решения лёгких задач, где перед первым х не стоит число, то есть a=1. Если вариант совпадает, то расчёт проводят через теорему Виета.

Для решения любого трёхчлена необходимо возвести уравнение к 0. Первые шаги у дискриминанта и теоремы Виета не отличаются.

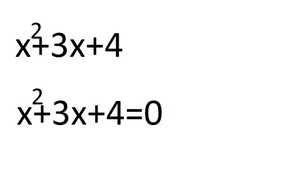
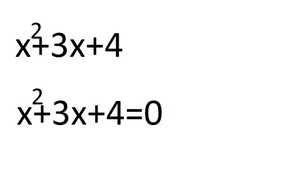
2. Теперь между двумя способами начинаются отличия. Теорема Виета использует не только «сухой» расчёт, но и логику и интуицию. Каждое число имеет свою букву a, b, c. Теорема использует сумму и произведение двух чисел.

Запомните! Число b всегда при добавлении стоит с противоположным знаком, а число с остаётся неизменным!

Подставляя значения данные в примере, получаем:

Это интересно: что такое разность в математике?

3. Методом логики подставляем наиболее подходящие цифры. Рассмотрим все варианты решения:

1. Цифры 1 и 2. При добавлении получаем 3, но если умножить, то не получится 4. Не подходит.
2. Значение 2 и -2. При умножении будет -4, но при добавлении получается 0. Не подходит.
3. Цифры 4 и -1. Так как в умножении стоит отрицательное значение, значит, одно из чисел будет с минусом. При добавлении и умножении подходит. Правильный вариант.

4. Остаётся только проверить, раскладывая числа, и посмотреть правильность подобранного варианта.

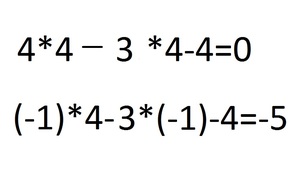
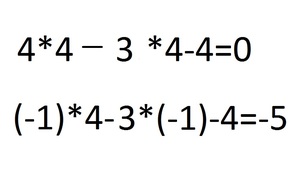
5. Благодаря онлайн-проверке мы узнали, что -1 не подходит по условию примера, а значит является неправильным решением.

При добавлении отрицательного значения в примере, необходимо цифру заносить в скобки.

В математике всегда будут простые задачи и сложные. Сама наука включает в себя разнообразие задач, теорем и формул. Если понимать и правильно применять знания, то любые сложности с вычислениями будут пустяковыми.

Математика не нуждается в постоянном запоминании. Нужно научится понимать решение и выучить несколько формул. Постепенно, по логическим выводам, можно решать похожие задачи, уравнения. Такая наука может с первого взгляда показаться очень тяжёлой, но если окунутся в мир чисел и задач, то взгляд резко изменится в лучшую сторону.

Технические специальности всегда остаются самыми востребованными в мире. Сейчас, в мире современных технологий, математика стала незаменимым атрибутом любой сферы. Нужно всегда помнить о полезных свойствах математики.

Разложение трёхчлена с помощью скобки

Кроме решения привычными способами, существует ещё один — разложение на скобки. Используют с применением формулы Виета.

1. Приравниваем уравнение к 0.

ax ² + bx+ c= 0

2. Корни уравнения остаются такими же, но вместо нуля теперь используют формулы разложения на скобки.

ax ² + bx+ c = a ( x – x 1 ) ( x – x 2 )

3. Пример уравнения.

2 x ² – 4 x – 6 = 2 ( x + 1 ) ( x – 3 )

4. Решение х=-1, х=3

obrazovanie.guru

Конспект «Разложение на множители» — УчительPRO

Разложение на множители

---

---

Очень часто числитель и знаменатель дроби представляют собой алгебраические выражения, которые сначала нужно разложить на множители, а потом, обнаружив среди них одинаковые, разделить на них и числитель, и знаменатель, то есть сократить дробь. Заданиям разложить многочлен на множители посвящена целая глава учебника по алгебре в 7-м классе. Разложение на множители можно осуществить 3 способами, а также комбинацией этих способов.

 1. Применение формул сокращенного умножения

Как известно, чтобы умножить многочлен на многочлен, нужно каждое слагаемое одного многочлена умножить на каждое слагаемое другого многочлена и полученные произведения сложить.  Есть, как минимум, 7 (семь) часто встречающихся случаев умножения многочленов, которые вошли в понятие «Формулы сокращенного умножения». Например, 

Таблица 1. Разложение на множители 1-м способом

---

---

2. Вынесение общего множителя за скобку

Этот способ основан на применении распределительного закона умножения. Например,

Каждое слагаемое исходного выражения мы делим на множитель, который выносим, и получаем при этом выражение в скобках (то есть в скобках остаётся результат деления того, что было, на то, что выносим). Прежде всего нужно правильно определить множитель, который надо вынести за скобку.

Общим множителем может быть и многочлен в скобках:

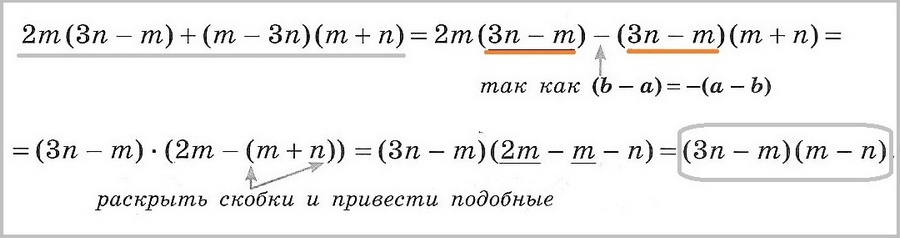
При выполнении задания «разложите на множители» надо быть особенно внимательным со знаками при вынесении общего множителя за скобки. Чтобы поменять знак у каждого слагаемого в скобке (b — a), вынесем за скобку общий множитель -1, при этом каждое слагаемое в скобке разделится на -1: (b — a) = — (a — b).

В том случае если выражение в скобках возводится в квадрат (или в любую чётную степень), то числа внутри скобок можно менять местами совершенно свободно, так как вынесенные за скобки минусы при умножении всё равно превратятся в плюс:  (b — a)² = (a — b)², (b — a)⁴ = (a — b)⁴ и так далее…

---

---

3. Способ группировки

Иногда общий множитель имеется не у всех слагаемых в выражении, а только у некоторых. Тогда можно попробовать сгруппировать слагаемые в скобки так, чтобы из каждой можно было какой-то множитель вынести. Способ группировки — это двойное вынесение общих множителей за скобки.

---

---

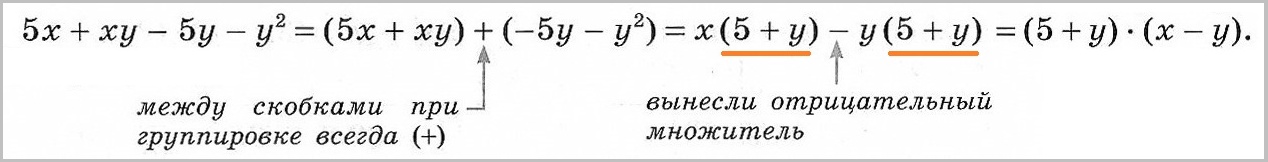
4. Использование сразу нескольких способов

Иногда нужно применить не один, а несколько способов разложения многочлена на множители сразу.

---

Это конспект по теме «Разложение на множители». Выберите дальнейшие действия:

uchitel.pro