Формула расчета длины окружности
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.
Определение длины окружности
Формула расчёта длинны окружности
Произвести расчёт окружности можно по следующей формуле:
L = πD = 2πr
r – радиус окружности
D – диаметр окружности
L – длина окружности
π – 3.14
Пример нахождения длинны окружности
Задача:
Вычислить длину окружности, имеющей радиус 10 сантиметров.
Формула для вычисления дины окружности имеет вид:
L = πD = 2πr
где L – длина окружности, π – 3,14, r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в
1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).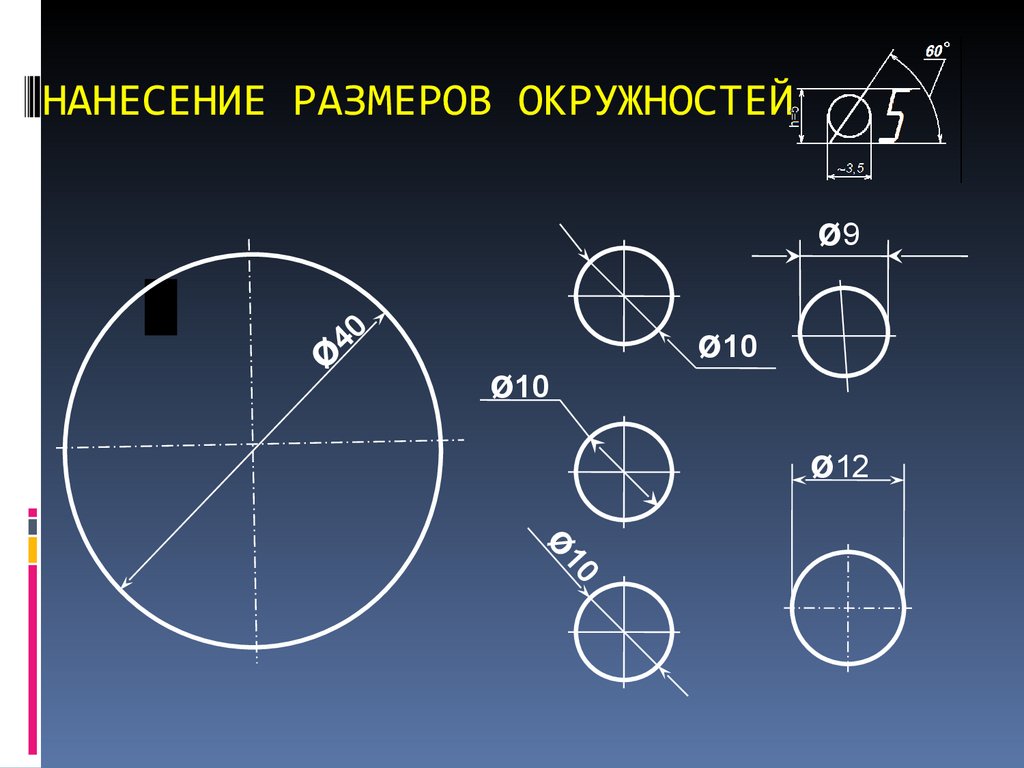
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Длина окружности — формула, как ее найти
Обновлено 22 июля 2021 Просмотров: 143 738 Автор: Дмитрий Петров- Что такое окружность
- Длина окружности через диаметр
- Формула длины окружности
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня у нас очередная математическая тема. Ее проходят в 6-м классе. Называется она – ДЛИНА ОКРУЖНОСТИ.
Эта важная величина для решения многих задачек. В том числе и во время Единого госэкзамена.
Так что наша статья будет крайне полезна школьникам-выпускникам. А для всех остальных это хороший повод освежить свои знания.
Что такое окружность
Но для начала напомним, что называют окружностью.
Окружность – это кривая замкнутая линия, которая состоит из множества точек. И эти точки находятся на одном расстоянии от центра окружности.
Определение несколько «тяжеловатое», но это официальная формулировка, которая также приводится в школьных учебниках. Графически все выглядит гораздо проще.
Вот пример окружности, у которой все точки на кривой «С» равноудалены от центра «О».
Кстати, расстояние от центра до границы окружности называется радиус и обозначается он буквой «R».
А отрезок, который соединяет две точки на окружности и проходит через ее центр – это диаметр «D». И, как всем известно, диаметр – это два сложенных радиуса (D = 2R).
Интересный факт! Точка тоже является в некотором роде окружностью. В математике ее называют «окружностью нулевого радиуса».
А чтобы начертить правильную окружность, нужно воспользоваться специальным прибором – циркулем. Им же можно нарисовать и окружность нужного радиуса.
Длина окружности через диаметр
Зачем мы так подробно рассказали о самой окружности, ее радиусе и диаметре? Все просто – без них не обойтись при расчете длины окружности.
Эту зависимость заметили еще в Древнем Египте. Тогдашние математики были весьма продвинуты в различных инженерных расчетах. Достаточно вспомнить, насколько надежно построены пирамиды. Им более 5 тысяч лет, а кажется, что простоят еще столько же и даже больше.
Так вот, египтяне определили, что соотношение длины окружности и ее диаметра – величина постоянная.
Другими словами, если взять совершенно разные по размерам окружности, а потом поделить их длины на их же диаметры, то получится одно и то же число.
У египтян это было число 3. Но впоследствии было получено более точное значение, которое равно 22/7 или 3 целых и 1/7.
Так появилась математическая постоянная «ПИ». Сейчас это один из столпов науки, с помощью которого решаются многие задачи.
Кстати, само название «пи» происходит от греческого слова «περιφέρεια», что как раз переводится как окружность. А «περίμετρος» — это диаметр.
Этими обозначениями и воспользовался математик Леонард Эйлер, когда в 1737 году представил научному сообществу число «пи», обозначив его изначально буквой выше упомянутых слов.
И сейчас уже каждый школьник знает, что число «пи» равно 3,14. Это значение взято за базовое, хотя на самом деле в нем бесконечное количество знаков после запятой.
Формула длины окружности
Ну а теперь главный вывод из этого исторического экскурса. Согласно вычислениям еще древнеегипетских ученых, формула длины окружности выглядит так:
Но чаще всего эту формулу принято писать без знаков умножения:
Формула эта единственная. И других возможностей рассчитать длину окружности — нет. Хотя ее можно представить, как диаметр умноженный на ПИ, но это уже банальность.
Вот и все, что мы хотели рассказать по этой теме, а более подробно смотрите в приведенном видеоролике:
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Как найти длину окружности? Ответ на webmath.
 ru
ruОстались вопросы?
Каким образом можно вычислить длину окружности при условии, что площадь круга (S) является известной величиной?
Площадь круга (S) рассчитывается путем умножения числа Пи на длину его радиуса (R), возведенную в квадратную степень (S = ПR²). Из указанного равенства можно выразить радиус:
R² = S/ П
Если избавиться от квадратной степени, то получится:
R = √(S/П)
Длина окружности (L) рассчитывается путем умножения числа Пи на длину радиуса, и последующего умножения на два полученного в результате числа:
L = 2ПR
Если R = √(S/П), то L = 2П*√(S/П)
Каким образом можно найти длину окружности, диаметр которой составляет 2 см?
Длина окружности (L) представляет собой число, которое получено в результате умножения числа Пи на диаметр данной окружности:
L = П*D
В конкретном случае:
L = 3,14*2 = 6,28 см.
Ответ: Длина окружности с диаметром 2 см составляет 6,28 см.
Дан квадрат, вокруг которого описана окружность. Ее длина составляет 12 Пи см. Как можно найти длину окружности, вписанной в этот же квадрат?
Известно, что длина окружности (L) рассчитывается путем умножения на два произведения числа Пи и длины ее радиуса (R). Формула выглядит так:
2ПиR
Из данной формулы можно выразить радиус
R = 12пи/2пи = 6 см
Радиус окружности, описанной около квадрата, равен 6 см.
Теперь можно вычислить сторону квадрата, вокруг которого описана данная окружность. Ее длина составляет R корней из 2:
а = 6 корней из 2.
Рассчитываем длину малого радиуса (r), который равен половине длины стороны квадрата:
r = а/2 = 6 корней из 2/2 = 3 корней из 2.
Длина окружности, вписанной в квадрат, рассчитывается по той же формуле:
L = 6 корней из 2 Пи.
Каким образом можно вычислить длину окружности, а также найти ее площадь, при условии, что радиус этой окружности равен 30 см?
Радиус окружности, равный 30 см, обозначается как R.
Площадь окружности можно найти, умножив число Пи на квадрат длины ее радиуса:
S = πR²
Подставим в формулу известные величины:
S = π*30² = 900π см. кв.
Длина окружности обозначается как С и рассчитывается путем умножения на 2 произведения числа Пи и ее радиуса:
C = 2πR
Снова подставляем в формулу величины, которые известны:
C = 2π*30 = 60π см
Ответ: Площадь окружности равна 900π см², а ее длина составляет 60π см.
Дана окружность, в которую вписан правильный треугольник. Его площадь составляет 12√3 см кв. Как можно вычислить длину окружности в данном случае?
По условию задачи известно, что треугольник является правильным, что
означает равенство всех его трех сторон. 2 * √3 ÷ 4
2 * √3 ÷ 4
Зная площадь, мы получаем возможность вычислить длину стороны а. Она будет равна ± √48. Учитывая то, что сторона не может быть отрицательной величиной, можно говорить о том, что сторона а равна √48.
После того как длина стороны стала известна, можно приступить к вычислению площади описанной и вписанной окружности. Для этого не достает еще одного элемента – длины радиуса.
Радиус описанной окружности (R) равен длине стороны треугольника, разделенной на √3:
R = √48 ÷ √3 = 4 см.
Радиус вписанной окружности (r) можно получить, разделив на 2 радиус описанной окружности:
r = 4/2 = 2 см.
Вычисленные длины радиусов вписанной и описанной окружностей позволяют определить ее длину ℓ, которая равна произведению числа Пи и радиуса окружности, умноженному на 2:
ℓ = 2πR
В нашем случае длина описанной окружности рассчитывается как:
ℓ= 2πR = 2π4 = 8π
Длина вписанной окружности будет составлять:
ℓ= 2πR = 2π2 = 4π
Известно, что радиус окружности равен 12 см. Как вычислить ее площадь и
длину при Пи=3,14?
Как вычислить ее площадь и
длину при Пи=3,14?
В условии задачи говорится о том, что радиус окружности R равен 12 см. Ее длина может быть вычислена посредством умножения на 2 произведения длины радиуса и числа Пи:
C=2πR
Известно, что число Пи – это константа, равная 3,14. Тогда длина окружности (С)высчитывается следующим образом:
C=2*3*12=72 см
Площадь окружности можно найти, умножив число Пи на длину ее радиуса, возведенную в квадратную степень:
S=πR²=3,14*12²=3,14*144=452,16 см кв.
Как можно вычислить радиус окружности и ее диаметр, если известно, что ее длина составляет 20 Пи см?
По условию задачи длина окружности равна 20 Пи см. Зная формулу, по которой вычисляется длина окружности, можно записать следующее равенство:
2Пи = 2ПиR
Можно сократить Пи в обеих частях записанного равенства, в результате чего получится, что:
2R = 20
Теперь высчитаем, чему равна длина радиуса окружности:
R = 20/2 = 10 см.
Длина диаметра равна длине радиуса, умноженной на 2:
D = R*2 = 10*2 = 20 cм.
Длина дуги окружности составляет 6Пи см, при этом ее градусная мера равна 120 градусов. Каким образом можно вычислить радиус окружности?
Полная градусная мера любой окружности равна 360 градусов. В случае, описанном в задании, градусная мера окружности составляет 120 градусов, что равно 1/3 части 360 градусов. Это позволяет сделать вывод о том, что длина окружности (L) может быть рассчитана следующим образом:
L = 6Пи * 3 = 18Пи
Формула, по которой вычисляется длина окружности, выглядит так:
L =2пR
Из данной формулы можно выразить радиус (R):
R = L/2Пи
В заданном случае длина радиуса будет равна:
18Пи/2Пи = 9 см.
Как на радиус окружности повлияет увеличение ее длины на 9,42 см?
Обозначим прежнюю длину окружности как L, а новую – как L₁. Тогда можно
записать следующее равенство:
Тогда можно
записать следующее равенство:
L₁ — L = 9,42 см
Прежний радиус окружности примем за R, а новый ее радиус, который получится в результате увеличения длины, обозначим как R₁. Для того чтобы вычислить ее значение, следует сначала записать формулу, по которой вычисляется прежняя длина данной окружности:
L = 2πR
Тогда формула для вычисления новой длины окружности будет иметь такой вид:
L + 9,42 = 2πR₁
Отнимем от новой длины старую, и в итоге получим:
2πR₁ — 2πR = 9,42 см.
Перенесем 2Пи из левой части равенства в правую:
R₁ — R = 9,42 : 2π = 1,5 см.
Ответ: В результате увеличения длины окружности на 9,42 см ее радиус станет больше на 1,5 см.
Как можно вычислить радиус окружности, вписанной в правильный треугольник, зная то, что площадь данного треугольника превышает площадь окружности на 27√3-9π?
Радиус окружности, которая вписана в правильный треугольник, обозначим r. Ее площадь (S) является произведением числа Пи и квадрата ее радиуса:
Ее площадь (S) является произведением числа Пи и квадрата ее радиуса:
S = πr²
В случае треугольника, все стороны которого одинаковы, радиус вписанной в него окружности равен третьей части высоты, являющейся также и медианой.
Площадь правильного треугольника рассчитывается так:
Sтр = (1/2)*(2r/tg30)*3r = (1/2)*(2r√3)*3r = 3√3r².
Согласно условию задачи 3√3r² = πr² + 27√3 — 9π.
Перенесем πr² из левой части равенства в правую, изменив его знак на противоположный:
3√3r² — πr² = 27√3 — 9π
Вынесем в правой части равенства r² за скобки. То же самое сделаем с числом 9 в левой части равенства:
r²(3√3 — π) = 9(3√3 — π)
Сокращаем в обеих частях одинаковый множитель (3√3 — π) и получаем:
r² = 9
Таким образом, радиус окружности равен корню квадратному из 9:
r =3 см.
Дано две окружности, радиус одной из которых пятикратно превышает радиус
другой. Каким образом вычислить радиус каждой из этих окружностей, если
известно, что диаметр второй из окружностей на 240 мм меньше, чем диаметр
первой?
Каким образом вычислить радиус каждой из этих окружностей, если
известно, что диаметр второй из окружностей на 240 мм меньше, чем диаметр
первой?
Обозначим радиус второй окружности буквой х. В данном случае радиус первой окружности нужно обозначить как 5х. Известно, что разница между длинами диаметров двух окружностей равна 240 мм. На основании этого можно составить следующее равенство:
5х-х=240:2, что равно 4х=120
Теперь можно найти значение х:
х=120:4=30 мм.
Таким образом, радиус второй окружности равен 30 мм. Это позволяет вычислить радиус первой окружности, который в 5 раз больше радиуса второй из них:
30*5=150 мм.
Как можно высчитать радиус окружности, когда известна ее градусная мера и длина дуги?
Длина дуги обозначена как L. В качестве обозначения ее градусной меры
используется α. Через R обозначена длина радиуса данной окружности. Формула расчета длины дуги выглядит так:
Формула расчета длины дуги выглядит так:
L = πR · α / 180°
Это же равенство может быть переписано следующим образом:
πR · α = L · 180°
Отсюда выведем радиус:
R = L · 180° / (π·α).
Как высчитать радиус окружности, длина дуги которой составляет 3,14 см, а ее градусная мера равна 18 градусам?
Длина окружности (L) равна произведению числа Пи и радиуса, которое умножено на 2:
L = 2Пиr
Согласно заданию, длина дуги равна 3,14, что равно значению константы Пи.
Дуга способна поместиться в длине окружности 2 пи r/пи =2 r раз
Подставив в равенство значения, которые известны, мы получим:
360:18=20 раз
Длина окружности будет равна:
3,14*20=20Пи
2Пиr = 20Пи
Сократим 2Пи в каждой из частей равенства и получим, что:
r=10 см.
Площадь круга составляет 169Пи см. Чему равна длина окружности в данном
случае?
Чему равна длина окружности в данном
случае?
Для решения поставленной задачи следует записать формулу расчета площади круга:
S=πr2
Эта величина указана в задании, и составляет 169Пи. Это значит, что:
πr2 = 169π
Можно сократить одинаковый множитель Пи в обеих частях равенства:
r2= 169
r = √169 = 13 см.
Длина окружности обозначена С. Она считается по следующей формуле:
С = 2πr
Длина радиуса уже известна, и ее можно подставить в формулу расчета длины окружности:
С = 2* π*13 = 26π см.
В окружность вписан квадрат площадью 36 дм кв. Чему в этом случае будет равна площадь круга и длина окружности?
Известно, что площадь круга представляет собой величину, равную длине
стороны этого квадрата, возведенной во вторую степень Sкв = а². Это
значит, что в данном случае а² = 36 дм.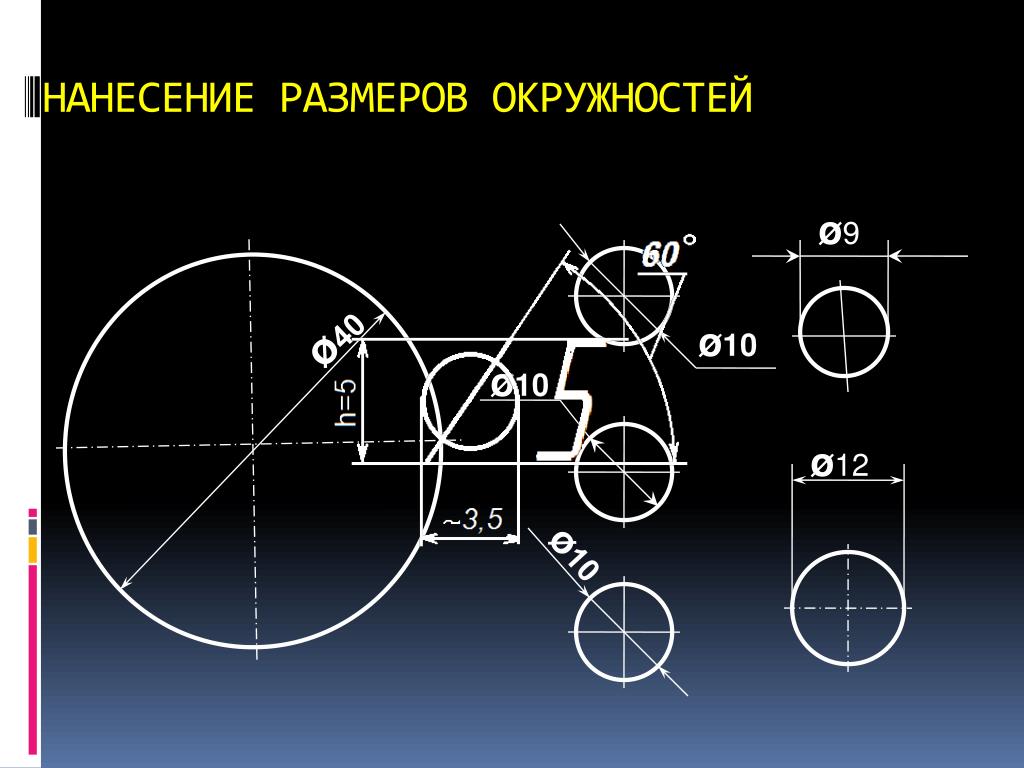 Для того чтобы найти значение а,
нужно извлечь квадратный корень из 36:
Для того чтобы найти значение а,
нужно извлечь квадратный корень из 36:
а = √36 = 6 дм.
Длина диагонали (d) квадрата считается по приведенной ниже формуле:
d = a√2 = 6√2 дм.
Радиус (R)окружности, которая описана около квадрата, равен половине длины ее диагонали:
R = d/2 = 3√2 дм.
Площадь круга можно посчитать, умножив число Пи на квадрат его радиуса:
S = πR² = π · (3√2)² = 18π дм. кв.
Длина окружности рассчитывается посредством умножения на два числа Пи, после чего полученное число умножается на длину радиуса окружности:
C = 2πR = 2π · 3√2 = 6√2π дм.
Длина окружности составляет 3,5 дм. Диаметр второй окружности равен 5/7 ее диаметра. Как вычислить длину второй окружности?
Ниже записана формула, которая используется для того, чтобы рассчитать длину окружности:
С = Пи*d,
где Пи – это константа, равная 3,14, а d – это диаметр окружности.
Отношение длины первой окружности к длине второй окружности равно отношению их диаметров:
C/C1 = d/d1
d1 = 5/7 d
В условии сказано, что длина первой окружности С = 3,5 дм. Таким образом:
C1 = 5/7 *C = 5/7 * 3,5 = 2,5 дм.
Длина радиуса окружности составляет 14 см. Какова будет ее длина при условии, что П=22/7?
Для того чтобы узнать длину окружности (C), следует воспользоваться формулой, предназначенной для ее расчета. Она выглядит так:
C = П*R*2
Если подставить в эту формулу величины, которые даны по условию задачи, то получим:
22/7*14*2=22/7*28/1=88 см.
Ответ: Длина окружности равна 88 см.
Какой будет длина окружности при условии, что ее половина составляет 25,5 см?
Длина окружности равна длине ее половины, умноженной на 2. Это значит, что в данном случае нужно умножить число 25,5, обозначающее половину длины окружности, на 2:
25,5*2 = 51 см.
Круг имеет площадь Пи м кв. Какова будет длина окружности данного круга?
Для вычисления длины окружности необходимо число Пи умножить на два и умножить на длину его радиуса (2πR). Для данной задачи это будет выглядеть следующим образом:
2π · 3√2 = 6√2π дм.
Для того чтобы посчитать площадь круга, необходимо умножить число Пи на радиус, взятый в квадрат (S = πR²). По условию задачи площадь круга равна Пи м кв. Это значит, что:
πR² = π
Из данного равенства можно выразить R
R — √π/π = 1
Зная длину радиуса, можно переходить к вычислению длины окружности (С):
C = 2πR = 2π x 1 = 2π
Ответ: Длина окружности равна 2π.
Какова формула длины окружности, при условии, что длина ее радиуса составляет R?
С целью вычисления длины окружности (С) используется приведенная ниже формула:
C=2πR
Ее составляющими является постоянное число Пи и радиус окружности (R),
длину которой необходимо вычислить.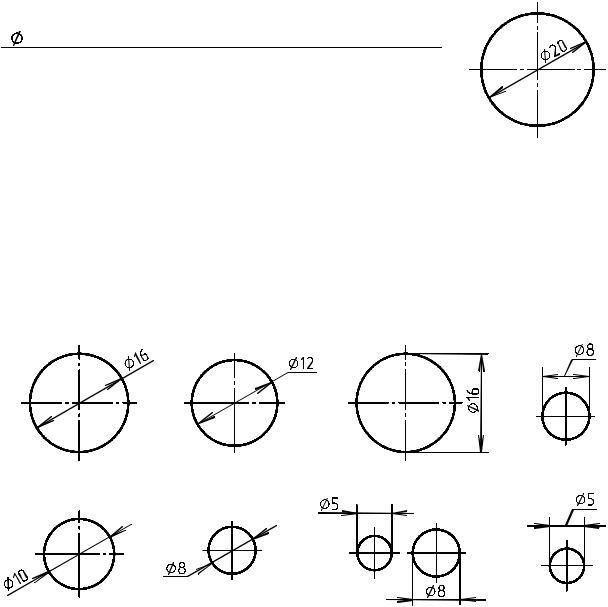
Какова формула расчета длины окружности, диаметр которой составляет 15 см?
Если длина диаметра окружности является известной величиной, то его нужно умножить на постоянное число Пи, равное 3,14, для того чтобы найти длину этой окружности. Формула выглядит так:
С = πD
В условии говорится, что диаметр окружности равен 15 см:
С = 3,14 * 15 = 47,1 cм.
Ответ: Длина окружности равна 47,1 см.
В результате деления длины окружности на величину ее диаметра получается число, приблизительно равное 22/7. Каким образом можно высчитать длину окружности с диаметром 10 см?
Для расчета длины окружности (С) нужно знать длину ее радиуса (R) или диаметра (d). Тогда могут быть использованы следующие формулы:
C = 2πR или C = πd
По условию задания d = 10 см, а π = 22/7. Тогда длина окружности будет равна:
C = πd = (22/7) * 10 = 220/7 ≈ 31,4 см.
В каком виде представлены формулы, которые используются для вычисления площади круга и длины окружности (через диаметр и через радиус)?
В случае, если длина диаметра (d) или длина радиуса (R) окружности известны, то эти величины можно использовать для нахождения длины окружности. При этом следует воспользоваться одной из формул:
С=πd или С=2πR.
Эти величины также помогут вычислить площадь круга. Формулы выглядят следующим образом:
S=πr² или S=π(d\2)².
Можно ли вычислить длину диаметра окружности, если известна только ее длина?
Нужно записать формулу расчета длины окружности, для того чтобы понять, существует ли взаимосвязь между этой величиной и диаметром окружности:
L = π·d
Очевидно, что длина окружности является результатом умножения числа Пи на длину ее диаметра.
Если длина окружности известна, то ее можно использовать для определения
диаметра (d). Это можно сделать следующим образом:
Это можно сделать следующим образом:
d = L/π.
Во сколько раз длина окружности превышает ее диаметр, и в каком виде представлена формула ее расчета через диаметр?
Длину окружности (С) можно рассчитать через диаметр (d), если воспользоваться нижеприведенной формулой:
С = π*d
Это формула демонстрирует, что длина окружности больше длины ее диаметра в π раз. Именно отношение длины окружности к величине ее диаметра и является числом π.
Какова формула вычисления отношения длины окружности к величине, означающей ее диаметр?
Число π представляет собой константу, которая получается в результате деления длины окружности (С) на ее диаметр (d). В виде формулы это выглядит так:
π = С/d
Площадь круга составляет 185 см кв. Как вычислить 30% от длины окружности при заданных исходных?
Располагая информацией о том, что площадь круга равна произведению числа Пи и квадрата ее радиуса (S=πr²), можно через нее выразить радиус:
r² = S/π = 185/π
Избавляемся от квадратной степени:
r = √(185/π) см.
Следующим шагом в решении задачи станет вычисление длины окружности, которая находится путем умножения на 2 числа Пи и радиуса окружности:
С=2πr= C=2π√(185/π) = 2√(185π) см.
На последнем этапе находим 30%. Принимаем всю длину окружности за 100%:
2√(185π) — 100%
х — 30%
Тогда х можно найти следующим образом:
х=(30*2√(185π))/100 = 0,6√(185π) см.
Как выглядят формулы определения длины окружности через радиус и через диаметр? В какое количество раз длина диаметра окружности меньше ее длины?
Существует две формулы, которые предназначены для расчета длины окружности (С). Они отличаются друг от друга тем, что элементом одной из них является радиус (r), а другой – диаметр (D):
C=2Пr и C=ПD.
Для того чтобы понять, во сколько раз длина окружности превышает длину ее диаметра, нужно произвести деление этих величин:
С/D
В результате получается число Пи, которое является постоянным и имеет
значение примерно 3,14.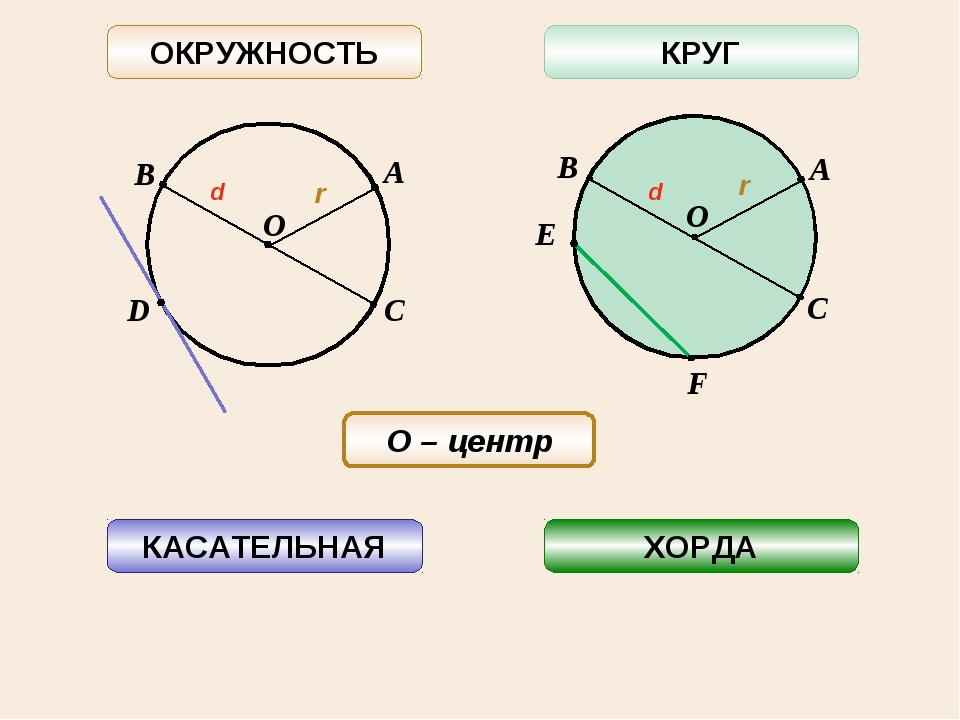
Длина окружности, обозначаемая как L, может быть вычислена при условии, что известен ее диаметр (D). При этом следует воспользоваться формулой L = Пи*D. Можно ли использовать данную формулу с целью вычисления длины диаметра окружности, длина которой составляет 126 м. (число Пи считать равным 3)?
Формула расчета длины окружности (С) через диаметр (D) выглядит так:
С = Пи*D
Исходя из условий задания, это равенство может быть записано в следующем виде:
126=3*D
Отсюда можно выразить диаметр:
D=126:3=42 м.
Длина окружности и площадь круга • Математика • Онлайн-конвертеры единиц измерения
Определения и формулы
В геометрии окружностью называется совокупность точек на плоскости, которые находятся на одном расстоянии от точки, называемой центром окружности. Иными словами, окружность — это геометрическое место точек, находящихся в одной плоскости и равноудаленных от точки, называемой центром. Расстояние между любой точкой окружности до центра этой окружности называется радиусом. Мы привыкли видеть окружность в форме круглой линии или круга. Однако так окружность выглядит только в евклидовой геометрии. В некоторых метрических пространствах, например, в чебышевском или манхэттенском пространстве окружности выглядят скорее квадратными.
Расстояние между любой точкой окружности до центра этой окружности называется радиусом. Мы привыкли видеть окружность в форме круглой линии или круга. Однако так окружность выглядит только в евклидовой геометрии. В некоторых метрических пространствах, например, в чебышевском или манхэттенском пространстве окружности выглядят скорее квадратными.
Диаметр круга — это наибольший отрезок, соединяющий две точки на окружности. Или, точнее, это отрезок, соединяющий две точки окружности и проходящий через ее центр. Диаметр окружности равен ее удвоенному радиусу. Любой диаметр разделяет окружность, а точнее, круг, на две равные половины.
Говоря точным языком, окружность — это линия или замкнутая кривая, которая окружает часть плоскости, называемую кругом.
Длина окружности
Длина C окружности — это длина замкнутой плоской кривой, ограничивающей круг, то есть это расстояние, равное длине границы круга. Она измеряется в единицах длины. Если разделить длину любой окружности на ее диаметр D, получится число 3. 14159265359… Это число — одна из самых важных констант в математике, которое обозначается греческой буквой пи (π):
14159265359… Это число — одна из самых важных констант в математике, которое обозначается греческой буквой пи (π):
где R — радиус окружности. Если решить это уравнение для длины окружности, мы получим формулу, которая всем нам знакома с детства:
Математическая константа π широко используется в многих формулах в математике, технике, архитектуре и строительстве. Несмотря на то, что число π известно с древних времен, греческой буквой пи его стали обозначать совсем недавно — с середины XVIII века. π — иррациональное и трансцендентное число. Это означает, что его нельзя точно представить в виде простой дроби и оно не является корнем любого многочлена с рациональными коэффициентами. Есть много чисел, которые являются иррациональными, но не являются трансцендентными. Например, √2 — иррациональное, но не трансцендентное число, так как оно является корнем уравнения x² — 2 = 0. Интересно отметить, что поскольку точное значение π определить невозможно, значит невозможно найти и точное значение длины окружности или площади любого круга.
Площадь круга
Поскольку TranslatorsCafe.com — сайт для переводчиков, в том числе с английского языка, вначале отметим, что в английском языке площадь круга не совсем корректно называется area of a circle, что буквально означает «площадь окружности», то есть площадь кривой линии (окружность — это кривая!), а, как известно, у линии не может быть площади. Но ничего, так уж сложилось и англоговорящие люди привыкли к этой неточности.
Итак, площадь A круга, то есть части плоскости, лежащей внутри окружности радиуса R, равна произведению числа π на квадрат радиуса:
Во многих других языках, в том числе и в русском, такой путаницы в терминах «круг» и «окружность» нет. Впрочем, она есть в других терминах. Площадь круга можно также описать как число единичных квадратов, которые покрывают круг, лежащий внутри окружности.
Окружности в архитектуре
Окружность — весьма совершенная форма, потому что каждая точка окружности находится на одном и том же расстоянии от ее центра. Как и другие совершенные формы, окружность часто используют архитекторы. Круг и окружность широко применяются в архитектуре, и это при том, что круглые здания строить труднее, чем здания прямоугольной формы. Поэтому для постройки круглых зданий всегда была нужна особая мотивация. Возможно, что самая серьезная мотивация была религиозной. Окружности и сферы можно найти практически в любой культуре, религии или системе верований в качестве магических знаков или символов. Многие культовые здания и сооружения являются окружностями в плане — например, буддийские ступы в форме полусферы или Стоунхендж.
Как и другие совершенные формы, окружность часто используют архитекторы. Круг и окружность широко применяются в архитектуре, и это при том, что круглые здания строить труднее, чем здания прямоугольной формы. Поэтому для постройки круглых зданий всегда была нужна особая мотивация. Возможно, что самая серьезная мотивация была религиозной. Окружности и сферы можно найти практически в любой культуре, религии или системе верований в качестве магических знаков или символов. Многие культовые здания и сооружения являются окружностями в плане — например, буддийские ступы в форме полусферы или Стоунхендж.
Тысячи лет люди наблюдали Солнце и Луну, и первые строители использовали их форму в конструкциях жилищ и поселений, потому что ведь на земле легко было разметить окружность — все, что для этого требовалось — это веревка из кожи или другого материала, да пара колышков.
Среди наиболее известных деталей собора Парижской Богоматери — три огромных окна-розетки с витражами. На фотографии показана западная роза над главным порталом собора
Северное окно-розетка с витражом в парижском Нотр-Даме
Архитекторы считают окружность и сферу самыми совершенными из всех геометрических форм. Покрытия зданий в форме верхней части сферы, то есть купола, широко применяются в архитектуре и бывают различных форм и размеров. Они могут быть полусферическими или заостренной на вершине формы, или с конусным верхом, который можно увидеть в исламской архитектуре. Они могут иметь совершенную сферическую форму, как римские и византийские купола или могут плавно заостряться на вершине, и тогда купол становится похожим на луковицу, как в православных храмах или в архитектурных стилях Великих Моголов.
Покрытия зданий в форме верхней части сферы, то есть купола, широко применяются в архитектуре и бывают различных форм и размеров. Они могут быть полусферическими или заостренной на вершине формы, или с конусным верхом, который можно увидеть в исламской архитектуре. Они могут иметь совершенную сферическую форму, как римские и византийские купола или могут плавно заостряться на вершине, и тогда купол становится похожим на луковицу, как в православных храмах или в архитектурных стилях Великих Моголов.
Позолоченный купол Исаакиевского собора в Сант-Петербурге имеет почти полусферическую форму
Тадж-Махал в индийском городе Агре — знаменитый пример архитектуры стиля моголов с пятью луковичными куполами
Сферические купола часто используются в архитектуре индуистских храмов, как например, в этом беломраморном индуистском храме Шри Сварминараян Мандир в канадском городе Торонто
Полукруглые арки известны со второго тысячелетия до нашей эры. Древнеримские архитекторы систематически использовали их в своих сооружениях. На снимке показан арочный мост Турнель над р. Сеной в Париже
На снимке показан арочный мост Турнель над р. Сеной в Париже
Окружность в технике
Невозможно представить себе технику без колес и других деталей в форме окружности. Некоторые из них (например, шасси самолетов и колеса автомобилей) хорошо видны. Другие спрятаны в компьютерах, стиральных и посудомоечных машинах, холодильниках, турбинах и другом оборудовании.
Сферические радиопрозрачные купола антенн часто используются для защиты механизмов поворота антенн и электронного оборудования радиолокационных станций
Люки в космических кораблях, такие как этот люк в спускаемом аппарате корабля Союз ТМА-А, часто делаются круглой формы, так как такая конструкция без углов позволяет сильно уменьшить механические напряжения, а также облегчает их герметизацию
В машинном отделении в музее Тауэрского моста в Лондоне можно увидеть старые работающие механизмы подъема моста
Сколько колес можно насчитать на этой фотографии, сделанной на первом этаже Музея науки и техники в Лондоне?
Окружности в сельском хозяйстве
Пролетая над пустынями, в которых ничего не растет, мы часто видим зеленые круги.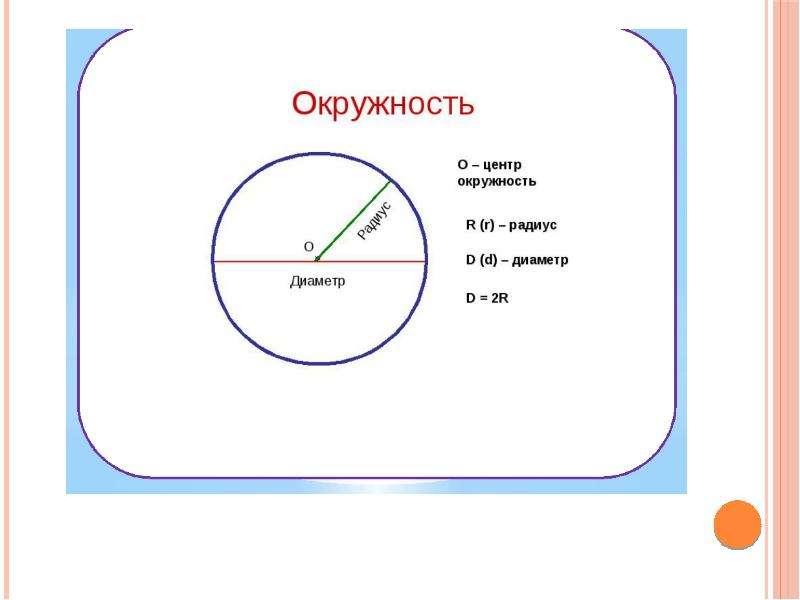 Это поля, которые имеют такую форму из-за того, что фермеры используют системы кругового орошения с центральной осью, вокруг которой вращается оросительное устройство.
Это поля, которые имеют такую форму из-за того, что фермеры используют системы кругового орошения с центральной осью, вокруг которой вращается оросительное устройство.
Круглые поля с системами кругового орошения в пустыне Мохаве в штате Невада можно наблюдать, пролетая из Торонто в Сан-Франциско; радиус окружности обычно равен ¼ мили или 400 м, длина окружности 2,5 км, а площадь такого поля составляет 125 акров или чуть более 50 гектаров
Автор статьи: Анатолий Золотков
%d0%b4%d0%bb%d0%b8%d0%bd%d0%b0%20%d0%be%d0%ba%d1%80%d1%83%d0%b6%d0%bd%d0%be%d1%81%d1%82%d0%b8 — со всех языков на все языки
Все языкиРусскийАнглийскийИспанский────────Айнский языкАканАлбанскийАлтайскийАрабскийАрагонскийАрмянскийАрумынскийАстурийскийАфрикаансБагобоБаскскийБашкирскийБелорусскийБолгарскийБурятскийВаллийскийВарайскийВенгерскийВепсскийВерхнелужицкийВьетнамскийГаитянскийГреческийГрузинскийГуараниГэльскийДатскийДолганскийДревнерусский языкИвритИдишИнгушскийИндонезийскийИнупиакИрландскийИсландскийИтальянскийЙорубаКазахскийКарачаевскийКаталанскийКвеньяКечуаКиргизскийКитайскийКлингонскийКомиКомиКорейскийКриКрымскотатарскийКумыкскийКурдскийКхмерскийЛатинскийЛатышскийЛингалаЛитовскийЛюксембургскийМайяМакедонскийМалайскийМаньчжурскийМаориМарийскийМикенскийМокшанскийМонгольскийНауатльНемецкийНидерландскийНогайскийНорвежскийОрокскийОсетинскийОсманскийПалиПапьяментоПенджабскийПерсидскийПольскийПортугальскийРумынский, МолдавскийСанскритСеверносаамскийСербскийСефардскийСилезскийСловацкийСловенскийСуахилиТагальскийТаджикскийТайскийТатарскийТвиТибетскийТофаларскийТувинскийТурецкийТуркменскийУдмуртскийУзбекскийУйгурскийУкраинскийУрдуУрумскийФарерскийФинскийФранцузскийХиндиХорватскийЦерковнославянский (Старославянский)ЧеркесскийЧерокиЧеченскийЧешскийЧувашскийШайенскогоШведскийШорскийШумерскийЭвенкийскийЭльзасскийЭрзянскийЭсперантоЭстонскийЮпийскийЯкутскийЯпонский
Все языкиРусскийАнглийскийИспанский────────АймараАйнский языкАлбанскийАлтайскийАрабскийАрмянскийАфрикаансБаскскийБашкирскийБелорусскийБолгарскийВенгерскийВепсскийВодскийВьетнамскийГаитянскийГалисийскийГреческийГрузинскийДатскийДревнерусский языкИвритИдишИжорскийИнгушскийИндонезийскийИрландскийИсландскийИтальянскийЙорубаКазахскийКарачаевскийКаталанскийКвеньяКечуаКитайскийКлингонскийКорейскийКрымскотатарскийКумыкскийКурдскийКхмерскийЛатинскийЛатышскийЛингалаЛитовскийЛожбанМайяМакедонскийМалайскийМальтийскийМаориМарийскийМокшанскийМонгольскийНемецкийНидерландскийНорвежскийОсетинскийПалиПапьяментоПенджабскийПерсидскийПольскийПортугальскийПуштуРумынский, МолдавскийСербскийСловацкийСловенскийСуахилиТагальскийТаджикскийТайскийТамильскийТатарскийТурецкийТуркменскийУдмуртскийУзбекскийУйгурскийУкраинскийУрдуУрумскийФарерскийФинскийФранцузскийХиндиХорватскийЦерковнославянский (Старославянский)ЧаморроЧерокиЧеченскийЧешскийЧувашскийШведскийШорскийЭвенкийскийЭльзасскийЭрзянскийЭсперантоЭстонскийЯкутскийЯпонский
Как обозначается длина окружности в физике.
 Как найти длину окружности: через диаметр и радиус
Как найти длину окружности: через диаметр и радиусИ в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S — в данном случае Допустим, в задаче она равна 30 кв.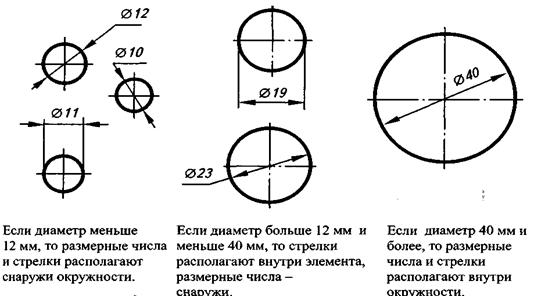 м. Получаем:
м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность .
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
- (·)O — называется центром окружности.
- Отрезок, который соединяет центр и любую точку окружности, называется радиусом окружности . Радиус окружности обозначается буквой «R ». На рисунке выше — это отрезок «OA ».
- Отрезок, который соединяет
две точки окружности и проходит через её центр, называется диаметром окружности .
Диаметр окружности обозначается буквой «D ». На рисунке выше — это отрезок «BC ».
На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение «D = 2R ».

Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым
для всех окружностей и обозначается греческой буквой π («Пи»).
π
≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π
,
округленное до разряда сотых
π
≈ 3,14…
Теперь, зная, что такое число π , мы можем записать формулу длины окружности.
Запомните!
Длина окружности — это произведение числа π и диаметра окружности.
Длина окружности обозначается буквой «С
» (читается как «Це»).
C = π
D
C = 2π
R , так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Условие задачи:
Определите диаметр окружности, если её длина равна 56,52 дм. (π ≈ 3,14 ).
Выразим из формулы длины окружности диаметр.
C = π
D
D = С / π
D = 56,52 / 3,14 = 18
дм
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки «A
» и «B
». Эти точки делят окружность
на две части, каждую из которых называют дугой .
Это синяя дуга «AB
» и черная дуга «AB
». Точки «A
» и «B
» называют концами дуг .
Точки «A
» и «B
» называют концами дуг .
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Нас окружает множество предметов. И многие из них имеют круглую форму. Она задана им для удобного использования. Взять, например, колесо. Если бы оно было изготовлено в форме квадрата, то как бы катилось по дороге?
Для того чтобы изготовить предмет круглой формы, нужно знать, как выглядит формула длины окружности через диаметр. Для этого сначала определим, что же представляет собой это понятие.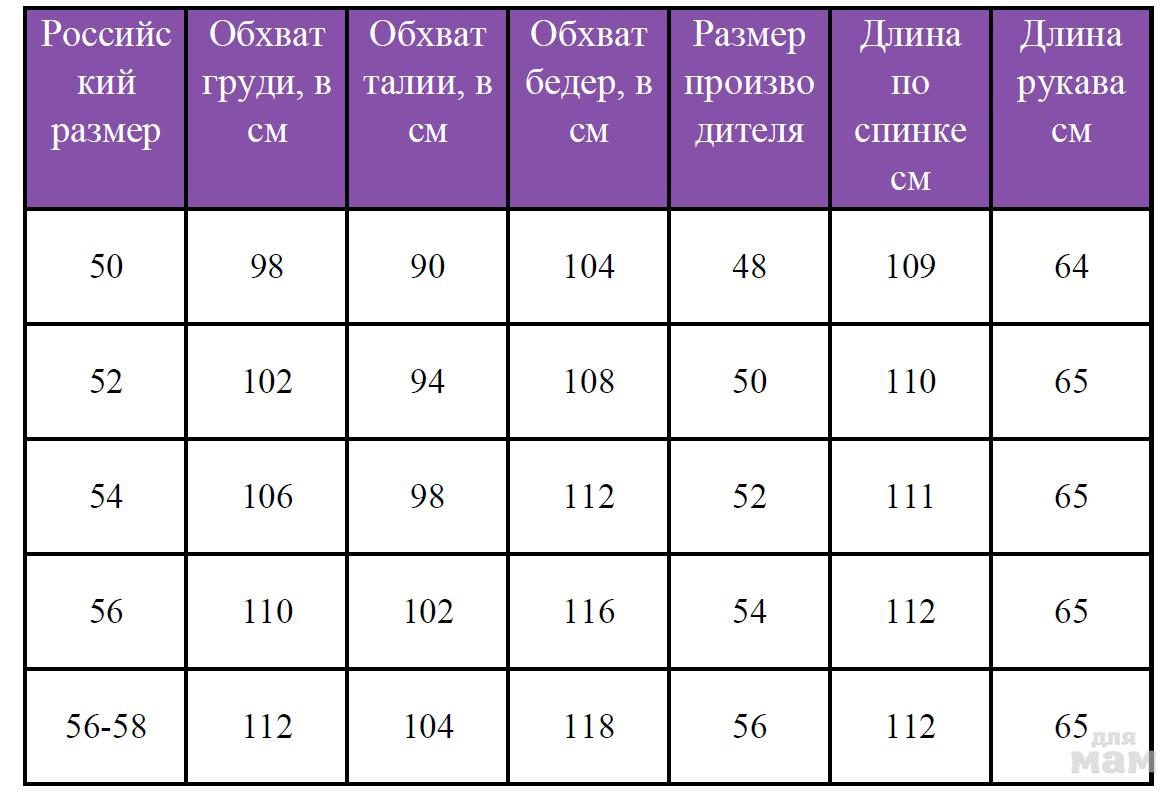
Круг и окружность
Окружностью является множество точек, которые размещены на равном расстоянии от основной точки — центра. Это расстояние называется радиусом.
Расстояние между двумя точками на данной линии называется хордой. Помимо того, если хорда проходит через основную точку (центр), тогда она называется диаметром.
А теперь рассмотрим, что такое круг. Совокупность всех точек, которые находятся внутри очертания, называется кругом.
Что такое длина окружности?
После того как мы рассмотрели все определения, мы можем высчитывать диаметр окружности. Формула будет рассмотрена немного позже.
Для начала мы попробуем измерить длину очертания стакана. Для этого мы обмотаем его ниткой, затем ее измерим линейкой и узнаем приблизительную длину воображаемой линии вокруг стакана. Потому что размер зависит от правильного измерения предмета, а данный способ не является надежным. Но тем не менее сделать точные измерения вполне возможно.
Для этого опять вспомним о колесе. Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.
Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.
Если внимательно проследить за этими изменениями, то увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И данное число является постоянным. Дальше рассмотрим, как определяется диаметр окружности: формула для этого применится в примере ниже. И рассмотрим ее, следуя шаг за шагом.
Формула окружности через диаметр
Поскольку длина очертания пропорциональна к радиусу, то и соответственно пропорциональна диаметру. Поэтому ее длину мы условно означим буквой C, диаметр — d. Поскольку соотношение длины очертания и диаметра — постоянное число, то его можно определить.
Проделав все подсчеты, мы определим число, которое приблизительно равно 3,1415… По той причине, что при подсчетах конкретное число не получилось, то обозначим его буквой π . Этот значок нам пригодится для того, чтобы была выведена формула длины окружности через диаметр.
Проведем воображаемую линию через центральную точку и измерим расстояние между двумя крайними. Это и будет диаметр. Если будем знать диаметр окружности, формула для определения длины ее самой будет выглядеть так: C = d * π .
Если мы будем определять длину разных очертаний, то если известен их диаметр, формула будет применена одна и та же. Поскольку знак π — это приблизительное исчисление, то и было решено умножать диаметр на 3,14 (число, округленное до сотых).
Как вычислить диаметр: формула
На этот раз попробуем с помощью данной формулы вычислить другие величины, помимо длины очертания. Чтобы вычислить диаметр по длине окружности, формула используется та же. Только для этого ее длину делим на π . Это будет выглядеть так d = C / π .
Рассмотрим, как эта формула действует на практике. К примеру, нам известна длина очертания колодца, следует вычислить его диаметр. Измерить его невозможно, поскольку из-за погодных условий нет доступа к нему. А задача у нас — изготовить крышку. Что будем делать в таком случае?
А задача у нас — изготовить крышку. Что будем делать в таком случае?
Нужно воспользоваться формулой. Возьмем длину очертания колодца — к примеру, 600 см. В формулу ставим конкретное число, а именно С = 600 / 3,14. В результате мы получим приблизительно 191 см. Округлим результат до 200 см. Затем с помощью циркуля рисуем круглую линию с радиусом в 100 см.
Поскольку очертание с большим диаметром нужно чертить соответствующим циркулем, то такой инструмент можно изготовить самому. Для этого возьмем рейку нужной длины и на каждом конце вбиваем по гвоздю. Устанавливаем один гвоздь в заготовку и слегка его вбиваем, для того чтобы он не сдвинулся с намеченного места. А с помощью второго чертим линию. Приспособление очень простое и удобное.
Современные технологии позволяют для вычисления длины очертания использовать онлайн-калькулятор. Для этого нужно всего лишь ввести диаметр окружности. Формула будет применена автоматически. Так же можно вычислять длину окружности с помощью радиуса. Кроме того, если вы знаете длину окружности, онлайн-калькулятор вычисляет радиус и диаметр с помощью данной формулы.
Кроме того, если вы знаете длину окружности, онлайн-калькулятор вычисляет радиус и диаметр с помощью данной формулы.
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни.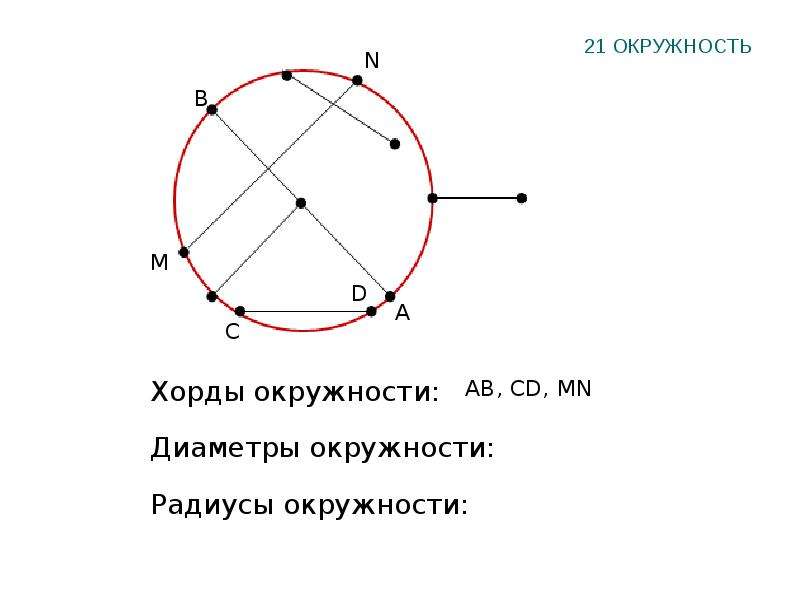 Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.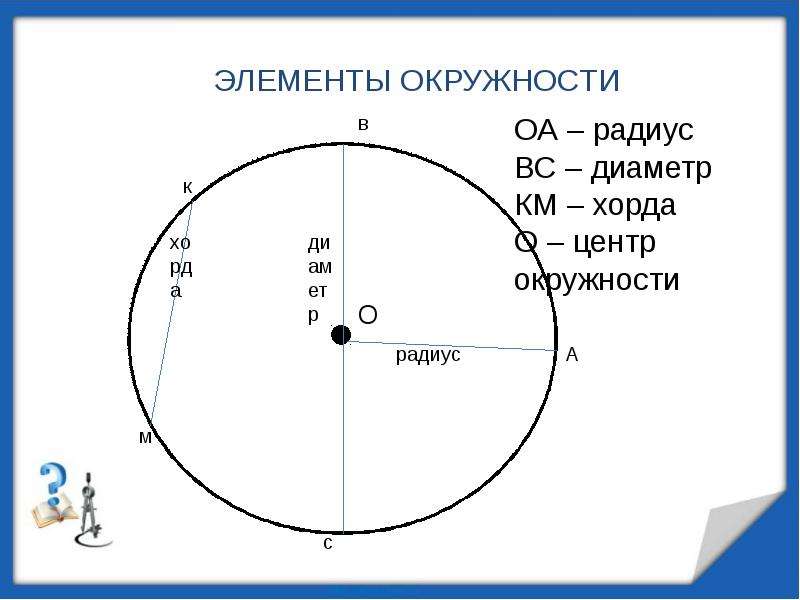
Как определить размер кольца — как измерить палец для колечка? Таблица диаметров
Нет никаких сложностей в том, чтобы выбрать кольцо для себя. Вы просто приходите в любой ювелирный магазин и просите специалиста измерить ваш палец и подобрать подходящий размер кольца. Но как быть, когда украшение выбирается в подарок? Как определить размер кольца на палец и не рассекретить план? Задать вопрос «в лоб» – не вариант, а о способах самостоятельно узнать размер знают далеко не все. Но не переживайте – в этой статье мы расскажем о нескольких отличных способах снятия мерок. Выбирайте подходящий и уже во всеоружии отправляйтесь за подарком!
Что такое размер пальца?
Начнём с изучения матчасти: что такое размер пальца и зачем его нужно знать? Возьмите любое своё кольцо; проведите воображаемую линию от одного его края до другого – проще говоря, измерьте диаметр. Для большей точности все замеры проводятся в миллиметрах. Получившийся результат и есть нужный вам параметр. Зная эти цифры, вы с лёгкостью подберёте подходящий подарок и рассчитаете размер.
Зная эти цифры, вы с лёгкостью подберёте подходящий подарок и рассчитаете размер.
Как правило, шаг градации в размерах составляет 0,5 мм – в ювелирных магазинах вы увидите размеры 16, затем 16,5, затем 17 и так далее. Теперь, когда мы разобрались в терминологии и технических нюансах, поговорим о том, как узнать размер кольца.
Как узнать размер пальца для кольца?
Поскольку вариант с походом в ювелирный и консультацией специалиста здесь не подходит, мы расскажем о нескольких тайных способах снятия мерок. Каждый из них достаточно хорош и точен – мы постарались всё проверить сами. Итак, как определяют размер кольца настоящие сыщики?
Способ первый: при помощи нитки
Начнём с того, как определить свой размер кольца по окружности пальца. При достаточной сноровке, рассчитать размер пальца для кольца можно дома с помощью нитки.
Определяем размер кольца при помощи ниткиЕсли вы хотите узнать размер безымянного пальца под обручальное кольцо, незаметно для невесты (например, пока она спит) оберните нитку вокруг её пальца и пометьте точку, где концы нити соединяются.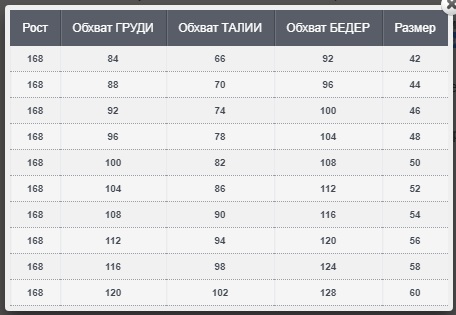 Точно так же вам придётся мерить обхват сустава. Затем распрямите нитку и измерьте расстояние между точками соприкосновения. Среднее значение двух получившихся цифр разделите на 3,14. Готово!
Точно так же вам придётся мерить обхват сустава. Затем распрямите нитку и измерьте расстояние между точками соприкосновения. Среднее значение двух получившихся цифр разделите на 3,14. Готово!
Теперь вы знаете нужный диаметр (он же размер) кольца. А за счёт того, что вы смогли замерить толщину пальца и сустав одновременно, украшение не будет ни жать, ни болтаться. Как видите, узнать размер пальца для кольца можно в домашних условиях.
Способ второй: при помощи ручки и бумаги
Этот способ гораздо проще первого, поскольку не требует тайных «операций» вокруг чужих пальцев — мы узнаем размер кольца по диаметру другого. Возьмите у человека, которому вы готовите подарок, любое кольцо. Положите его на бумагу и обведите украшение по внутреннему периметру. Диаметр получившегося круга и будет размером кольца. Но будьте внимательны – для замеров нужно брать кольцо с того пальца, на который вы в будущем наденете подарок, ведь у всех пальцев разные обхваты.
Способ третий: при помощи друзей
Как узнавать размер пальца, если вы слишком боитесь быть рассекреченным? Очень легко – спросите друзей.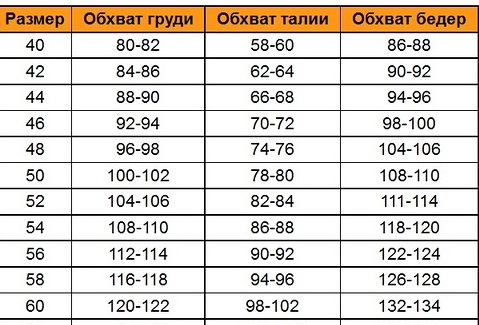 Самый сложный этап в этом способе – найти друга, который гарантированно сохранит ваш план в тайне. Дальше – проще: либо друг уже знает размер и просто сообщает его вам, либо он спокойно, не вызывая подозрений, узнаёт его и таким образом помогает вам с выбором подарка. Скажите другу спасибо — ведь он помог вам понять размер без кольца!
Самый сложный этап в этом способе – найти друга, который гарантированно сохранит ваш план в тайне. Дальше – проще: либо друг уже знает размер и просто сообщает его вам, либо он спокойно, не вызывая подозрений, узнаёт его и таким образом помогает вам с выбором подарка. Скажите другу спасибо — ведь он помог вам понять размер без кольца!
Способ четвёртый: по имеющемуся кольцу
Для самых отважных расскажем, как по имеющемуся кольцу определить размер колечка. Стоит отметить, что этот способ — самый точный, но и самый рискованный. Если вы на 100% уверены, что «объект» не заметит пропажу одного из своих украшений — смело в бой! На один день превратитесь в наглого воришку и украдите у человека какое-нибудь кольцо. Отправляйтесь с украшением к ювелиру — тот измерит диаметр кольца и скажет, какого оно размера. Не забудьте вернуть украденное на место!
Лайфхак: определяем размер по своим пальцам
Способ подойдёт для тех, кто не знает, как незаметно подобрать кольцо девушке, не зная размера безымянного пальца. Этим секретным методом часто пользуются парни, собирающиеся сделать предложение своей любимой. Попросите у неё одно из колец, «просто примерить». Наденьте украшение на палец и запомните место, где кольцо сидело удобнее всего. Пока память свежа, бегите к ювелиру и просите его измерить диаметр отмеченного места. Готово, вы великолепны!
Этим секретным методом часто пользуются парни, собирающиеся сделать предложение своей любимой. Попросите у неё одно из колец, «просто примерить». Наденьте украшение на палец и запомните место, где кольцо сидело удобнее всего. Пока память свежа, бегите к ювелиру и просите его измерить диаметр отмеченного места. Готово, вы великолепны!
Имейте в виду, что в среднем, самый маленький размер женских колец — 14-й, а самый большой — 22-й. Поэтому если ваше значение вдруг получилось сильно меньше или больше, возможно, вы где-то допустили промах — постарайтесь высчитать нужный диаметр ещё раз.
Дополнительные рекомендации
При измерении пальцев важно помнить несколько важных нюансов.
Во-первых, для наиболее точных результатов идеально мерить палец трижды: утром, днём и вечером. В зависимости от времени суток руки могут отекать или опухать, поэтому нужно подобрать кольцо, которое не будет жать даже при опухших пальцах. Не стоит замерять пальцы в жаркие дни или после активных занятий спортом. Снимите мерки несколько раз и в разные дни – если хотя бы два значения похожи друг на друга, значит, вы нашли точный размер.
Снимите мерки несколько раз и в разные дни – если хотя бы два значения похожи друг на друга, значит, вы нашли точный размер.
Во-вторых, важно знать толщину подарочного кольца. Если оно будет тонким (до 7мм), полученное при замерах значение округляйте до ближайшего. Например, если при измерениях у вас получилось значение 15,8, то нужным размером станет 16-й. Если же кольцо будет толще 7мм, стоит сделать запас в размере, равный 0,5мм. При том же значении в 15,8 лучше будет выбрать размер 16,5.
Бонус – таблица определения размеров ювелирных колец по длине окружности пальца
Если вы хотите заказать кольцо заграницей, вам очень пригодится сетка размеров колец. Обратите внимание — все измерения указаны не в сантиметрах (см), а в миллиметрах (мм). Одним из указанных способов измерьте окружность пальца и соотнесите результат с одним из пунктов этой таблицы:
Таблица размеров ювелирных колецНа этом всё. Надеемся, наши советы были для вас полезны, и вы не прогадаете с размером подарочного кольца. Желаем удачи в этом ответственном деле!
Желаем удачи в этом ответственном деле!
Автор: Александра Циклаури
Диаметр круга — Формула, Примеры
В круге диаметр — это линия, проходящая через центр и пересекающаяся с окружностью на каждом конце. Он в два раза больше радиуса окружности.
Каков диаметр круга?
Диаметром окружности называется любой отрезок прямой линии, проходящий через центр окружности и концы которого лежат на окружности окружности. Диаметр также известен как самая длинная хорда окружности.
Определение диаметра
Диаметр определяется как удвоенная длина радиуса окружности. Радиус измеряется от центра круга до одной конечной точки круга, тогда как расстояние диаметра измеряется от одного конца круга до точки на другом конце круга, проходящей через центр. Диаметр обозначается буквой D. На окружности окружности бесконечное число точек, это означает, что окружность имеет бесконечное число диаметров, и каждый диаметр окружности имеет одинаковую длину.
Обратите внимание на следующий рисунок, на котором синей линией показан диаметр круга. Желтая линия от центра до одной конечной точки круга — это радиус, а внешняя граница, отмеченная черной пунктирной кривой, — это окружность круга.
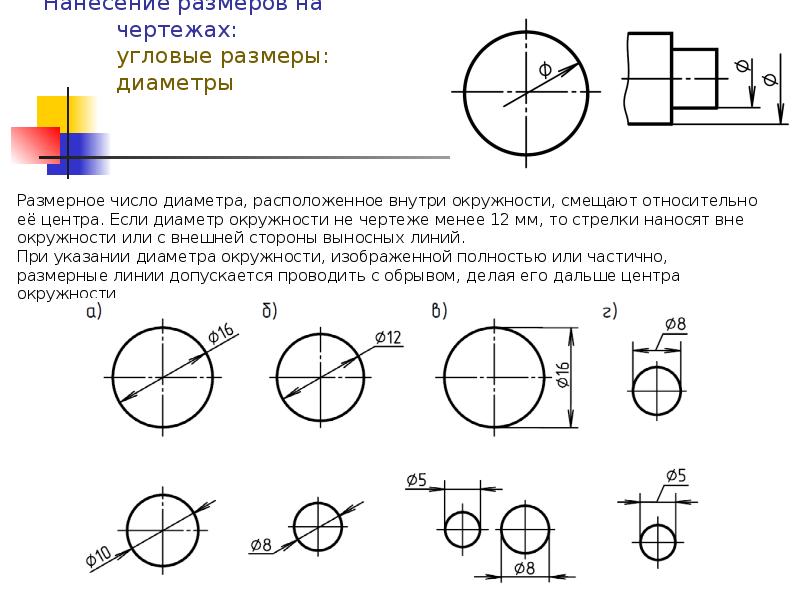
Обозначение диаметра
Φ — это символ, который используется в технике для обозначения диаметра. Этот символ обычно используется в технических спецификациях и чертежах. Φ25 мм означает, что диаметр круга составляет 25 мм.
Диаметр окружности Формула
Все мы знаем, что диаметр является частью круга. Давайте разберемся с некоторыми терминами, прежде чем мы узнаем формулу диаметра круга.
- Радиус (r) — это длина отрезка от центра окружности до конечной точки окружности.
- Окружность (C) относится к замкнутой границе круга. Он также известен как периметр круга.Мы можем вывести формулу диаметра из длины окружности и радиуса окружности.

Диаметр круга по окружности
Мы можем легко вывести формулу диаметра из длины окружности. Формула длины окружности: C = πd; здесь, C = длина окружности, d = диаметр окружности, π = константа (3.141)
Формула диаметра с использованием длины окружности: Диаметр = Длина окружности ÷ π
Диаметр круга с использованием радиуса
Радиус — это длина отрезка от центра окружности до конечной точки окружности, а диаметр — это удвоенная длина радиуса окружности.Используя это определение, формула для диаметра выглядит так: D = радиус × 2,
.Формула диаметра с использованием площади круга
Мы можем вывести формулу диаметра круга, используя формулу площади круга, которая равна площади = π(Радиус) 2 . Следовательно, формула диаметра круга с использованием площади D = 2 √ Площадь / π.
Как рассчитать диаметр круга?
Диаметр круга можно рассчитать, если задан радиус или длина окружности.
Попробуем найти диаметр по приведенным выше формулам на практическом примере. Обратите внимание на приведенный ниже пример.
Пример: Джек начертил круг радиусом 3 единицы. Каков диаметр круга?
Решение:
Дано: Радиус окружности = 3 единицы
Диаметр круга = 2 × радиус
= 2 × 3 = 6 единиц.
Следовательно, диаметр круга равен 6 единицам.
☛Статьи, относящиеся к диаметру окружности
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о диаметре круга и связанных с ним темах.
Часто задаваемые вопросы о Diameter
Что такое диаметр?
Диаметр — это прямая линия, проходящая через центр окружности и делящая окружность на две части. Это самая длинная хорда круга, которая пересекает окружность на каждом конце.
Какой символ используется для обозначения диаметра?
В технике для обозначения диаметра используется символ ⌀. Его часто называют «фи». Этот символ фи используется для описания диаметра круглого сечения.Например, «⌀20» означает, что диаметр круга составляет 20 единиц измерения.
Его часто называют «фи». Этот символ фи используется для описания диаметра круглого сечения.Например, «⌀20» означает, что диаметр круга составляет 20 единиц измерения.
Что такое радиус и диаметр?
Радиус и диаметр круга являются двумя важными частями круга, которые взаимозависимы друг от друга. Радиус круга — это отрезок, который начинается от центра круга и заканчивается на окружности круга. Это половина длины диаметра круга, т. Е. Радиус = диаметр / 2. Диаметр окружности — это отрезок, проходящий через центр окружности и имеющий две точки на окружности.Это в два раза больше длины радиуса окружности, т. е. диаметр = 2 × радиус.
Как рассчитать диаметр?
Диаметр круга можно рассчитать по заданным параметрам. Если заданы такие параметры, как радиус, окружность или площадь, мы можем напрямую использовать следующие формулы.
- Диаметр = длина окружности ÷ π (если указана длина окружности)
- Диаметр = 2 × радиус (если указан радиус)
- Диаметр = 2√[Площадь/π] (если дана площадь)
Пример диаметра?
Если вы посмотрите на колесо цикла, шипы проходят от одного конца к другому через центр. Мы можем связать это с диаметром круга, поскольку диаметр — это отрезок, который начинается с одного конца круга и заканчивается на другом конце круга, проходящем через центр.
Мы можем связать это с диаметром круга, поскольку диаметр — это отрезок, который начинается с одного конца круга и заканчивается на другом конце круга, проходящем через центр.
Как найти диаметр по окружности?
Если длина окружности известна, то мы можем легко найти значение диаметра, подставив значения в формулу: Диаметр = C ÷ π; где «C» — длина окружности, а π — константа, значение которой равно 3,14.
Как найти площадь круга по диаметру?
Площадь круга рассчитывается по формуле: πr 2 . Если задан диаметр, мы можем найти радиус, разделив значение диаметра на 2. Получив радиус, мы можем подставить его значение в формулу: πr 2 , чтобы получить площадь круга, или непосредственно применить формула площади с диаметром, A = π(d/2) 2 = πd 2 /4
Для чего нужен калькулятор отношения диаметра к окружности?
Калькулятор отношения диаметра к окружности — это онлайн-инструмент, используемый для определения значения длины окружности. В калькуляторе диаметра окружности введите размер диаметра и получите значение окружности в течение нескольких секунд. Вы также можете попробовать калькулятор диаметра для прямых расчетов.
В калькуляторе диаметра окружности введите размер диаметра и получите значение окружности в течение нескольких секунд. Вы также можете попробовать калькулятор диаметра для прямых расчетов.
Какова формула диаметра круга, если известен радиус круга?
Если радиус окружности дан в единицах «r», то легко определить диаметр окружности по формуле. С определением радиуса мы знаем, что это половина диаметра, следовательно, формула диаметра = 2r.
Как называется половина диаметра круга?
Диаметр круга — это отрезок линии от одного конца круга до другого конца круга, проходящий через центр круга. Принимая во внимание, что радиус круга — это длина отрезка линии от центра круга до точки на окружности круга. Следовательно, радиус равен половине диаметра окружности.
Как диаметр связан с радиусом окружности?
Радиус круга равен половине диаметра.Отношение между радиусом и диаметром можно математически выразить формулой: Диаметр = 2 × радиус.
Является ли диаметр половиной радиуса?
Нет, диаметр не равен половине радиуса; это вдвое больше радиуса окружности. Он представлен формулой: Диаметр = 2 × Радиус.
Окружности, начало координат, радиус, диаметр, окружность, пи, сектор, касательная
Определение: Окружность — это простая фигура, состоящая из тех точек на плоскости, которые находятся на заданном расстоянии от данной точки — центра.
Происхождение : центр круга
Радиус : расстояние от центра круга до любой его точки.
Диаметр : наибольшее расстояние от одного конца круга до другого. Диаметр = 2 × радиус (d = 2r).
Окружность : расстояние по окружности.
Длина окружности $= \pi \x диаметр$.
Длина окружности $= \pi \times d = 2 \times \pi \times r$
$\pi$ — pi : число равное 3.141592.. . или $\приблизительно \frac{22}{7}$, то есть $\frac{\text{длина окружности}}{\text{диаметр}}$ любой окружности.
. или $\приблизительно \frac{22}{7}$, то есть $\frac{\text{длина окружности}}{\text{диаметр}}$ любой окружности.
Дуга : изогнутая линия, являющаяся частью окружности круга.
Дуга окружности измеряется в градусах или радианах — например: 90° или $\frac{\pi}{2}$ — четверть окружности,
180° или $\pi$ — половина окружности круг.
Дуга меньше 360° (или $2\pi$), потому что это вся окружность.
Хорда : отрезок линии внутри круга, который касается 2 точек на круге.2$
Уголки
Центральный уголок
Если длина дуги равна $\theta$ градусам или радианам, то измерение центрального угла также равно $\theta$ (градусы или радианы).
Если вы знаете длину дуги (в дюймах, ярдах, футах, сантиметрах, метрах…), вы можете найти измерение соответствующего центрального угла ($\theta$) по формуле:
$\theta = 360 \cdot \frac{l}{P} = \frac{360 \cdot l}{2 \cdot \pi \cdot r} = \frac{180 \cdot l}{\pi \cdot r} $
$l$ — длина дуги. \circ$
\circ$
Углы между двумя секущими
Случай 1: две секущие пересекают внутри окружности.
Когда две секущие пересекаются внутри круга, размер каждого образовавшегося угла равен половине суммы дуг.На рисунке дуга AB равна 60°, а дуга CD равна 50°.
Таким образом, углы 1 и 2 равны ½(60° + 50°) = 55°
Случай 2: две секущие пересекают вне окружности.
Измерение образовавшегося угла равно половине разности дуг.2)\фракция{\тета}{360}$
Основная информация о кругах (Геометрия, Круги) — Mathplanet
Окружность – это все точки одной плоскости, находящиеся на одинаковом расстоянии от центральной точки. Окружность состоит только из точек на границе. Вы можете думать о круге как обруче. Это только точки на границе, которые являются кругом. Точки внутри обруча не являются частью круга и называются внутренними точками.
Расстояние между серединой и границей круга называется радиусом. Отрезок, концы которого лежат на окружности и проходят через ее середину, называется диаметром. Диаметр в два раза больше радиуса. Отрезок, концы которого лежат на окружности, но не проходят через середину, называется хордой.
Отрезок, концы которого лежат на окружности и проходят через ее середину, называется диаметром. Диаметр в два раза больше радиуса. Отрезок, концы которого лежат на окружности, но не проходят через середину, называется хордой.
Расстояние по окружности называется окружностью C и может быть определено либо с помощью радиуса r, либо с помощью диаметра d:
$$C=2\pi r$$
$$C=\pi d$$
Круг равен 360°.Вы можете разделить круг на более мелкие части. Часть окружности называется дугой, а дуга называется в соответствии с ее углом. Дуги делятся на малые дуги (0° < v < 180°), большие дуги (180° < v < 360°) и полуокружности (v = 180°).
Длина дуги l определяется путем подстановки градусной меры дуги v и длины окружности всего круга C в следующую формулу:
$$l=C\cdot\frac{v}{360}$$
Когда диаметры пересекаются в центре окружности, они образуют центральные углы.Например, когда вы разрезаете торт, вы начинаете резать кусочки с середины.
Пример
Как и в торте выше, мы делим наш круг на 8 частей с одинаковым углом. Длина окружности равна 20 единицам длины. Определить длину дуги каждой детали.
Сначала нам нужно найти угол для каждой части, так как мы знаем, что полный круг равен 360°, мы можем легко сказать, что каждая часть имеет угол 360/8=45°. Подставляем эти значения в нашу формулу длины дуг:
$$l=C\cdot\frac{v}{360}$$
$$l=20\cdot \frac{45}{360}=2.5$$
Следовательно, длина наших дуг составляет 2,5 единицы длины. Мы могли бы еще проще сказать это, просто погрузив окружность на количество частей одинакового размера: 20/8 = 2,5
.Видеоурок
Какой будет угол дуги окружности, если мы разделим цикл на 12 частей одинакового размера
бесплатных печатных шаблонов кругов — большие и маленькие трафареты
Я думаю, что сегодня я взволнован больше, чем когда впервые представил свои шаблоны в форме сердца в блоге.
Сегодня у меня есть масса различных БЕСПЛАТНЫХ шаблонов кругов для печати , которые вы можете распечатать!
Что в них такого классного, так это то, что у них безграничный потенциал.
Я чувствую, что мне нужны круглые формы для проектов примерно раз в месяц.
Я уже использовал их примерно в 7 различных поделках и могу придумать около 100 других способов их использования.
Бесплатные шаблоны кругов для печати
Я решил сделать свои собственные круги разного размера, потому что я часто ловлю себя на том, что беру случайные круглые предметы, такие как кружка или пластиковая крышка, которые служат шаблоном для поделок.
Теперь я могу просто взять шаблон точного размера, который мне нужен, вместо того, чтобы копаться в поисках самодельного шаблона круга!
Эти формы можно бесплатно скачать и распечатать.
Просто убедитесь, что вы установили PIN-код одного из изображений на этой странице (используя красную кнопку Pinterest вверху страницы) в качестве напоминания о том, где вы нашли эти круглые формы!
Они понадобятся вам снова и снова!
Очень большая круглая форма для вырезания
Иногда вам просто нужен очень большой шаблон круга.
Этот 7-дюймовый вырезанный лист печатается на полноразмерном листе бумаги.
Просто нажмите на изображение, чтобы загрузить его в формате PDF и сохранить на свой компьютер:
Шаблон большого круга (диаметр 7 дюймов)
(щелкните изображение, чтобы загрузить)
2 больших круга на одной странице
Если в вашем проекте требуется круглая форма немного меньшего размера, этот второй набор состоит из двух больших шаблонов, которые распечатываются на одной странице.Они 5″ в диаметре.
Два больших круга на одной странице (диаметр 5 дюймов)
(щелкните изображение, чтобы загрузить)
Трафареты для средних кругов
Если у вас есть проект, который требует многократного повторения нескольких одинаковых узоров, вот целая страница кругов среднего размера.
Этот загружаемый файл содержит два 4-дюймовых круга на любой случай, когда вам понадобится шаблон круглой трассировки.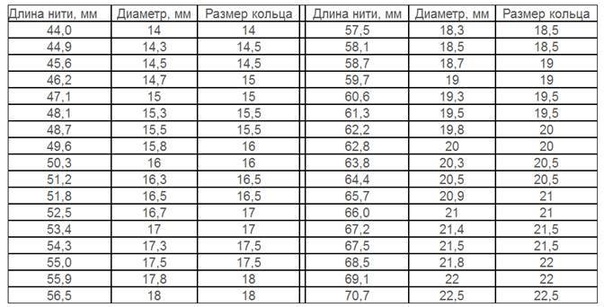
Печатные средние круги диаметром 4 дюйма
(нажмите на картинку для загрузки)
Шесть маленьких кругов на одной странице
Вот набор из 6 трехдюймовых круглых контуров малого и среднего размера.
Мы с детьми снова и снова использовали эти формы для создания забавных поделок и этикеток. Применение действительно безгранично!
6 круглых контуров (диаметр 3″)
(нажмите на картинку для загрузки)
Крошечные контуры кругов — точки для печати
Пожалуй, это моя любимая распечатка из всех.
Набор из 12 крошечных кружочков диаметром 2 дюйма, которые можно распечатать.
Моя подруга, Сайра, заметила, что они идеально подходят для любого проекта, где требуется горошек или большие кусочки конфетти.
Я думаю, они идеально подойдут для Новогодней ночи или даже для пиньяты. Я их люблю!
Я их люблю!
2-дюймовые контуры кругов для печати (диаметр 2 дюйма)
(щелкните изображение, чтобы загрузить)
Различные круги – четыре разных размера на одной странице
Наконец, у меня есть один лист бумаги, содержащий круги четырех разных размеров.
Иногда я не знаю точно, какой размер мне нужен, прежде чем начать проект. Этот лист идеально подходит для этого.
Они указаны в дюймах, чтобы вы могли легко найти нужный размер.
Шаблоны кругов 4″, 3″, 2″ и 1″
(щелкните изображение, чтобы загрузить)
Проекты для круглых трафаретов — горошек, круглые этикетки, конфетти
Вот как я использовал эти шаблоны кругов или думаю, что смогу использовать их в ближайшем будущем:
- Используйте маленькие кружки для любого проекта , требующего горошек
- Используйте маленькие круги для фона плаката в стиле конфетти
- Используйте средние круги для этикеток для банок или этикеток для классной доски любого типа
- Используйте большие круглые формы в качестве трафаретов для вырезания круглых картинок для альбомов
- Простое вырезание, обведение или рисование Спокойное времяпрепровождение для малышей
- Симпатичный круглый баннер для дня рождения
- В качестве основы для милого новогоднего украшения ручной работы
- Распечатайте стопку кругов среднего размера 3″ или 4″ и u используйте их вместо блокнотов
- Уникальные подарочные ярлыки на день рождения или Рождество
- Контур для украшения торта в качестве ориентира для нанесения посыпки или цветного сахара
- Выкройка кругов для рукоделия или шитья
- Распечатайте их на цветном картоне, чтобы создать цветные большие или маленькие точки – мгновенные красные, желтые, розово-зеленые, синие, фиолетовые, оранжевые или черные круги! Так много применений для самых разных проектов.
 А еще лучше распечатайте эти шаблоны на ЗОЛОТОМ картоне, чтобы создать великолепные украшения.
А еще лучше распечатайте эти шаблоны на ЗОЛОТОМ картоне, чтобы создать великолепные украшения.
Существует ООООООООООООООО многих способов использования этих трафаретов кругов для печати. Для чего вы будете их использовать?
Нужны другие бесплатные формы для печати?
Вот еще несколько вырезов, которые могут вам понравиться:
Еще от WhatMommyDoes
Диаметр вписанной окружности — Engineer-Educators.com
Диаметр вписанной окружности – это расстояние по окружности, вписанной внешним бордюром (или краем) проезжей части с круговым движением.Как показано на рис. 6-1, это сумма диаметра центрального острова (включая перрон, если он есть) и удвоенного диаметра проезжей части. Диаметр вписанной окружности определяется рядом конструктивных задач. Дизайнеру часто приходится экспериментировать с различными диаметрами, прежде чем определить оптимальный размер в данном месте.
На кольцевых развязках с одной полосой размер вписанной окружности в значительной степени зависит от требований к повороту конструкции транспортного средства. Диаметр должен быть достаточно большим, чтобы вместить проектируемое транспортное средство, сохраняя при этом достаточную кривизну прогиба, чтобы обеспечить безопасную скорость движения для небольших транспортных средств.Однако ширина проезжей части, ширина въезда и выезда, радиусы въезда и выезда, а также углы въезда и съезда также играют важную роль в размещении расчетного транспортного средства и обеспечении отклонения. Тщательный выбор этих геометрических элементов может позволить использовать меньший диаметр вписанной окружности в ограниченных местах. Как правило, диаметр вписанной окружности должен составлять не менее 30 м (100 футов) для размещения транспортного средства конструкции WB-15 (WB-50). Кольцевые развязки меньшего размера можно использовать на некоторых перекрестках местных улиц или коллекторных улиц, где расчетным транспортным средством может быть автобус или грузовой автомобиль.
Диаметр должен быть достаточно большим, чтобы вместить проектируемое транспортное средство, сохраняя при этом достаточную кривизну прогиба, чтобы обеспечить безопасную скорость движения для небольших транспортных средств.Однако ширина проезжей части, ширина въезда и выезда, радиусы въезда и выезда, а также углы въезда и съезда также играют важную роль в размещении расчетного транспортного средства и обеспечении отклонения. Тщательный выбор этих геометрических элементов может позволить использовать меньший диаметр вписанной окружности в ограниченных местах. Как правило, диаметр вписанной окружности должен составлять не менее 30 м (100 футов) для размещения транспортного средства конструкции WB-15 (WB-50). Кольцевые развязки меньшего размера можно использовать на некоторых перекрестках местных улиц или коллекторных улиц, где расчетным транспортным средством может быть автобус или грузовой автомобиль.
На кольцевых развязках с двумя полосами размещение расчетного транспортного средства обычно не является ограничением. Размер кольцевой развязки обычно определяется либо необходимостью достижения прогиба, либо необходимостью согласования въездов и выездов по окружности с разумными радиусами въезда и выезда между ними. Как правило, диаметр вписанной окружности двухполосной кольцевой развязки должен составлять не менее 45 м (150 футов).
Размер кольцевой развязки обычно определяется либо необходимостью достижения прогиба, либо необходимостью согласования въездов и выездов по окружности с разумными радиусами въезда и выезда между ними. Как правило, диаметр вписанной окружности двухполосной кольцевой развязки должен составлять не менее 45 м (150 футов).
В общем, меньшие вписанные диаметры лучше для общей безопасности, поскольку они помогают поддерживать более низкие скорости.Однако в высокоскоростных средах проектирование геометрии захода на посадку является более важным, чем в низкоскоростных средах. Большие вписанные диаметры обычно позволяют обеспечить лучшую геометрию подхода, что приводит к снижению скорости подхода транспортных средств. Большие вписанные диаметры также уменьшают угол, образованный между путями въезда и движения транспортных средств, тем самым снижая относительную скорость между этими транспортными средствами и приводя к уменьшению частоты столкновений при въезде и движении (2). Следовательно, для кольцевых развязок в высокоскоростных средах могут потребоваться диаметры, которые несколько больше, чем рекомендуемые для низкоскоростных сред. Однако очень большие диаметры (более 60 м [200 футов]), как правило, не следует использовать, потому что они будут иметь высокие скорости движения и больше аварий с большей серьезностью. На рис. 6-19 представлены рекомендуемые диапазоны диаметров вписанных окружностей для различных участков.
Однако очень большие диаметры (более 60 м [200 футов]), как правило, не следует использовать, потому что они будут иметь высокие скорости движения и больше аварий с большей серьезностью. На рис. 6-19 представлены рекомендуемые диапазоны диаметров вписанных окружностей для различных участков.
Сколько градусов в окружности?
Любишь геометрию? Мы делаем! Мы хотели сделать Чудо дня об особой форме, но не могли решить, какую фигуру использовать.Однако чем больше мы думали об этом, тем больше мы возвращались к той же форме. Что это было? Круг, конечно!
Что вам больше всего нравится в кругах? Нам нравятся их идеально круглые формы. У них нет тех заостренных концов, которые вы найдете на квадратах и треугольниках.
Некоторые из наших любимых вещей имеют форму кругов. Например, наш любимый десерт — пирог — имеет форму круга. Как и наша любимая игрушка: хула-хуп. Какие еще предметы в форме круга вы видите или используете каждый день?
Какие еще предметы в форме круга вы видите или используете каждый день?
Учителя геометрии определяют окружность как набор точек на плоскости, находящихся на одинаковом расстоянии от центральной точки.Это означает, что круги плоские. Когда вы изучаете круги, вы узнаете, что у каждого круга есть радиус, диаметр, длина окружности и площадь.
Радиус круга — это расстояние от его центра до края. Диаметр круга — это расстояние поперек круга в его самом широком месте. Диаметр круга всегда ровно в два раза больше его радиуса.
Периметр круга — расстояние вокруг его края — называется его окружностью. Чтобы вычислить длину окружности, нужно знать ее радиус.
Формула длины окружности: 2πr, где r — радиус окружности, а π — число пи (приблизительно 3,141592). Поскольку диаметр круга в два раза больше радиуса, вы также можете представить формулу длины окружности как πd, где d — диаметр круга.
Площадь круга измеряется количеством квадратных единиц внутри круга. Еще раз, вам нужно знать радиус. Формула площади круга: πr 2 . 2 в формуле — это показатель степени, что означает, что вы умножаете радиус сам на себя. Таким образом, вместо формулы площади круга можно было бы написать πrr.
Еще раз, вам нужно знать радиус. Формула площади круга: πr 2 . 2 в формуле — это показатель степени, что означает, что вы умножаете радиус сам на себя. Таким образом, вместо формулы площади круга можно было бы написать πrr.
Одна интересная вещь о кругах, которую знают все учителя геометрии, заключается в том, что если вы знаете один из этих фактов — радиус, диаметр, длину окружности или площадь — вы можете вычислить все остальные значения! Например, если вы знаете радиус круга, вы можете вычислить его диаметр, длину окружности и площадь.
Еще один интересный аспект кругов заключается в том, что каждый круг можно разделить на 360 единиц, называемых градусами.Итак, если вы совершите полный круг, вы повернетесь на 360 градусов. Если вы просто повернетесь наполовину — полукругом — вы повернетесь на 180 градусов.
Так почему же 360 градусов вместо чего-то попроще, например, 100 градусов? Математики считают, что виноваты древние вавилоняне. Около 2400 г.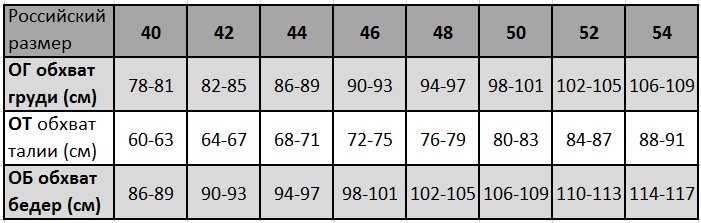 до н.э. они заметили круговое движение Земли вокруг Солнца. Они также подсчитали, что для завершения этой круговой орбиты потребовалось около 360 дней.
до н.э. они заметили круговое движение Земли вокруг Солнца. Они также подсчитали, что для завершения этой круговой орбиты потребовалось около 360 дней.
Поэтому круговой путь решили разделить на 360 градусов.Таким образом, они могли легко отслеживать прохождение каждого дня по круговому календарю. Так что если вы запутались в геометрии с количеством градусов в окружности, виноваты вавилоняне!
(PDF) Обнаружение инвариантных по размеру кругов
1. Сечения откликов операций свертки на изображения идеальных кругов (без добавления шума).
2. Выходные массивы для зашумленных тестовых изображений.
3. Позиционная точность определения центра круга при наличии
аддитивного шума.
4. Ширина пика отклика и окружающий его «пьедестал»
фона для определенного уровня шума.
В экспериментах использовались следующие операции свертки:
•ориентационное кольцо,
•логарифмически радиальное фазово-кодированное кольцо,
•логарифмически радиальное фазово-кодированное кольцо ориентации и
•масштабное ядро инвариантности, K
rs 0 (0,1).
Представлены результаты применения операций свертки
, описанных выше, к изображению размером 128 ×
128 пикселей, содержащему круг радиусом R16 пикселей.
Интенсивность фона была установлена на ноль, а
пикселей внутри круга были установлены на 255. Изображение было
реальным, чтобы предотвратить эффекты недостаточного или переполнения с
добавленным шумом. Операторы были оконными в радиусе с
минимумом R
min
8 пикселей и максимумом R
max
,
24 пикселя, окно было нулем вне этого диапазона и
единицей между
мин.
и
мин.
.
5.1. Пик отклика при отсутствии шума
Каждый из операторов свертки применялся к изображению
, содержащему круг радиусом 16 пикселей, но
не содержащему добавленного шума. Поперечное сечение результирующего пика
на выходе для каждой из сверток показано на
рис. 4.
Кольцо ориентации дает ширину пика (полная ширина
на половине высоты) 22 пикселя.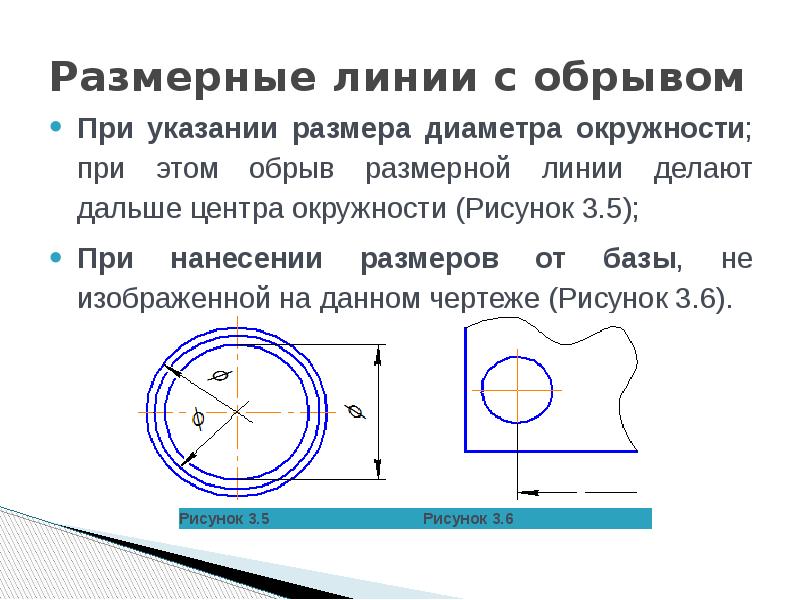 что примерно соответствует ширине кольца оператора (R
что примерно соответствует ширине кольца оператора (R
max
–
R
min
).Кольцо с фазовым кодированием дает более узкий пик
, чем пик кольца ориентации, 9 пикселей (полная ширина на половине высоты
). Это связано с когерентной интеграцией
(конструктивная и деструктивная интеграция) кодирования фазы
. Включение ориентации в фазовое кодирование
оказывает относительно небольшое влияние на ширину пика отклика
. Ядро инвариантности генерирует пик шириной немного на
больше, размером 13 пикселей (полная ширина на половине высоты).
5.2. Обнаружение круга в шуме
Изображение идеального круга использовалось для анализа эффективности операций свертки для обнаружения круга в присутствии шума
(рис. 5). Белый гауссовский шум
с нулевым средним значением был добавлен для изменения отношения сигнал-шум в изображении круга
. Одну возможную меру отношения сигнал-шум в
этом контексте можно найти, взяв отношение энергии
отклика детекторного фильтра в центре объекта из-за
идеального бесшумного круга с центром на xc;ysxc
ÿ
2, и среднее квадратичное значение
отклика фильтра на шум только в этом положении,
E\{ynxc
jj
2\}. Отношение сигнал/шум обнаружения (SNR) составляет
Отношение сигнал/шум обнаружения (SNR) составляет
, определяемое как [17]: 21
Это SNR дает меру того, как пик выходного сигнала
выделяется над основанием фонового шума, но страдает
недостатком, заключающимся в том, что разные методы обнаружения будут
давать разные SNR для данной добавленной дисперсии шума.
Это затрудняет процесс сравнения, например,
точности обнаружения центра объекта как функции ОСШ.Поэтому мы сообщаем о точности позиционного обнаружения
как функции добавленной дисперсии шума.
Если для окружности с центром в x
c
положение пика
ответа на выходе фильтра обнаружения измеряется (в конкретном испытании
) как x
p
, мы
производительность фильтров можно получить более глубокое представление о характеристиках фильтров, оценив среднюю радиальную
ошибку в обнаруженном положении по ряду испытаний: 0:5
() 22
Аналогичную процедуру можно использовать для оценки дисперсии
с
2
r (или стандартного отклонения,
с
обнаруженной средней ошибки 90 в 3)
позиции по ряду испытаний. Если распределение
Если распределение
обнаруженных положений относительно правильного центра является приблизительно
гауссовым (для любого конкретного значения шума изображения), мы
ожидаем, что средняя ошибка в обнаруженном положении будет
близко к распределению Рэлея. В этом случае стандартное
отклонение средней ошибки положения,
с
r, и средняя
ошибка положения, r, будут примерно равны [18].
Величина аддитивного шума варьировалась в диапазоне от
с
2
n3:102 до
с
2
n3:106.Было измерено положение пика на выходе
каждого оператора свертки и записана ошибка
между ним и ожидаемым центром окружности. Был выполнен анализ методом Монте-Карло
с 50 попытками на
эксперимента (500 попыток на эксперимент для ядра инвариантности
), и были записаны ошибки в обнаруженном положении.
Средняя ошибка определения положения для каждого из
T.
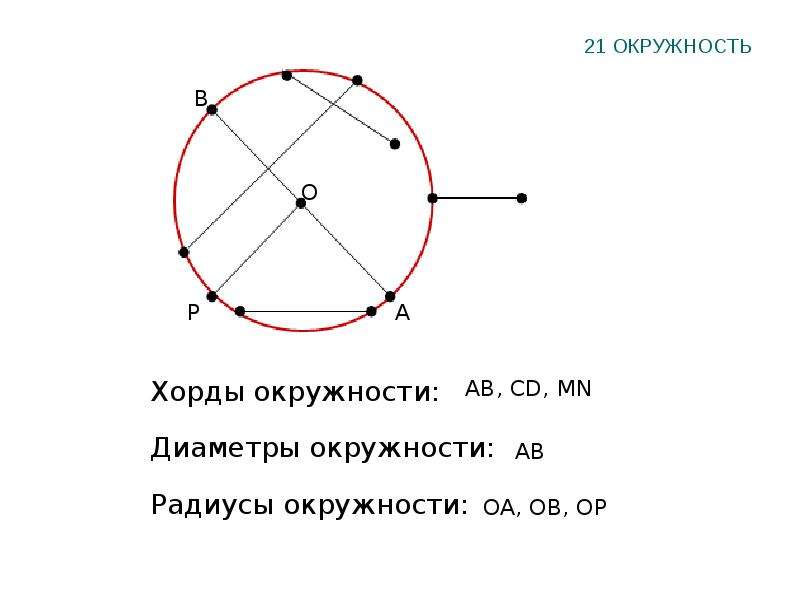

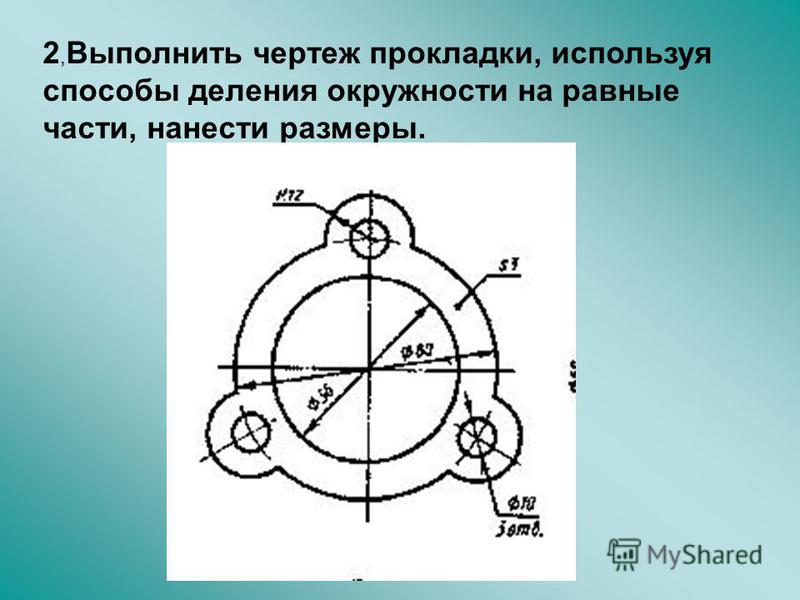 А еще лучше распечатайте эти шаблоны на ЗОЛОТОМ картоне, чтобы создать великолепные украшения.
А еще лучше распечатайте эти шаблоны на ЗОЛОТОМ картоне, чтобы создать великолепные украшения.