Доказательство теоремы Фалеса (8 класс)
1. Теорема Фалеса
Демонстрационный материал8 класс
2. Фалес Милетский
Древнегреческий философ, родоначальник античнойи вообще европейской философии и науки, основатель
милетской школы.
Сочинения Фалеса не сохранились, однако Аристотель
называет его первым ионийским философом.
Важнейшей заслугой Фалеса в области математики
считается перенесение им из Египта в Грецию первых
начал теоретической элементарной геометрии:
• Вертикальные углы равны.
• Углы при основании равнобедренного треугольника равны.
• Треугольник определяется стороной и прилежащими к ней двумя углами.
• Диаметр делит круг на две равные части.
Фалесу приписывается решение двух геометрических задач практического
характера: определения расстояния корабля на море от Милетской гавани и
определения высоты пирамиды по длине её тени.
3. Задача
Через середину М стороны АВ треугольника АВС проведена прямая,параллельная стороне AС.

Докажите, что BN = NC.
Решение
B
Через точку С проведем СD || AB
AM = MB – по условию
3
AM = СD
(AMDC – параллелограмм)
M 1
N
2 D
ВMN =
4
A
MВ = CD
1 = 2
3 = 4
C
CDN
BN = NC
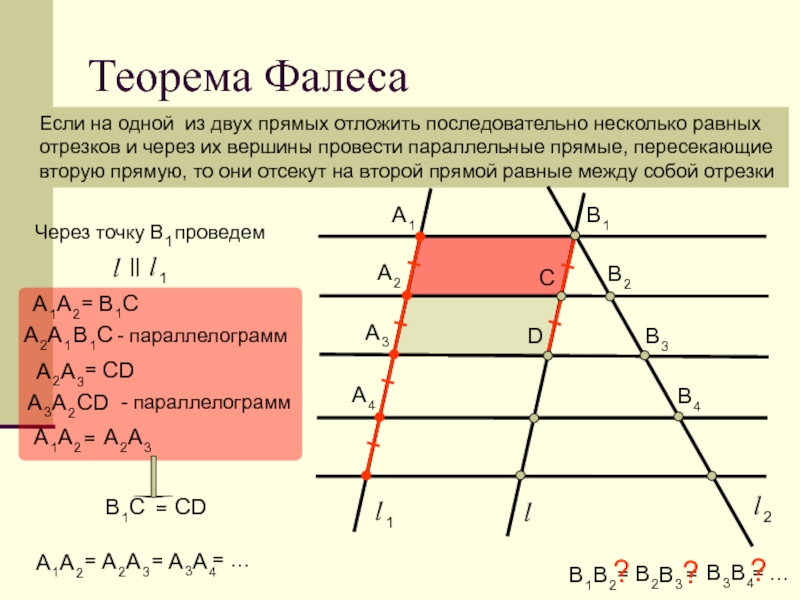
4. Теорема Фалеса
Если на одной из двух прямых отложить последовательно несколько равныхотрезков и через их вершины провести параллельные прямые, пересекающие
вторую прямую, то они отсекут на второй прямой равные между собой отрезки
A1
A2
A3
A4
l1
A 1A 2 = A 2A 3 = A 3A 4= …
B1
B2
B3
B4
l2
=…
= В 2В 3?
= В 3В 4?
В 1В 2?
5. Теорема Фалеса
Если на одной из двух прямых отложить последовательно несколько равныхотрезков и через их вершины провести параллельные прямые, пересекающие
вторую прямую, то они отсекут на второй прямой равные между собой отрезки
A1
Через точку В 1 проведем
l
||
l1
A 1A 2 = B 1C
A 2A 1 B 1C — параллелограмм
A 2A 3 = СD
A 3A 2 CD — параллелограмм
B1
A2
A3
С
D
A4
B2
B3
B4
A 1 A 2 = A 2A 3
В 1С = СD
A 1A 2 = A 2A 3 = A 3A 4= …
l1
l
l2
=…
= В 2В 3?
= В 3В 4?
В 1В 2?
6.
 Теорема Фалеса Если на одной из двух прямых отложить последовательно несколько равных
Теорема Фалеса Если на одной из двух прямых отложить последовательно несколько равныхотрезков и через их вершины провести параллельные прямые, пересекающие
вторую прямую, то они отсекут на второй прямой равные между собой отрезки
A1
В треугольнике В1DВ 3
В 1С = СD
A2
CB2 || DB3
A3
В 1В 2= В 2В 3
B1
С
D
A4
A 1A 2 = A 2A 3 = A 3A 4= …
B3
B4
Аналогично можно
доказать
В 2В 3= В 3В 4
B2
l1
Закрыть
l
l2
=…
= В 2В 3?
= В 3В 4?
В 1В 2?
Презентация «Теорема Фалеса» — геометрия, презентации
материалов
Содержание слайдов
Номер слайда 1
Теорема Фалеса Евклид (300г.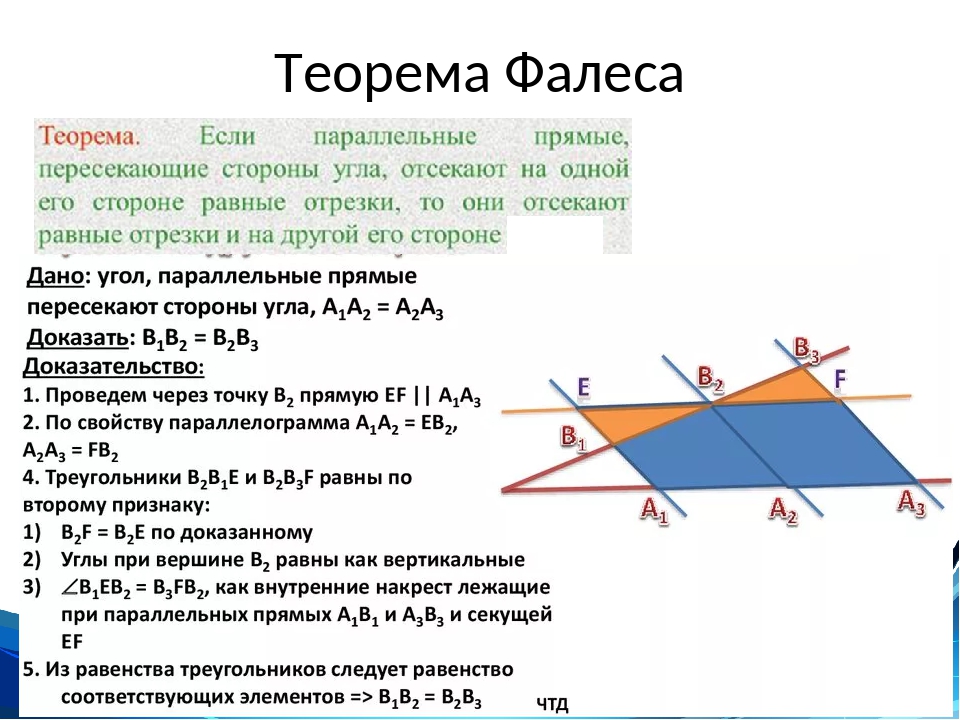 до н.э.) счёл эту задачу неразрешимой, при этом ранее Фалес (600г. до н.э.) наоборот решил её как частность в своей теореме. ЦЕЛЬ УРОКА: Доказать теорему Фалеса. Научиться применять её при решении задач.
до н.э.) счёл эту задачу неразрешимой, при этом ранее Фалес (600г. до н.э.) наоборот решил её как частность в своей теореме. ЦЕЛЬ УРОКА: Доказать теорему Фалеса. Научиться применять её при решении задач.
Теорема (теорема Фалеса). Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону угла, то на другой стороне угла отложатся равные отрезки. Дано: АВ = ВС, АА1 1 ВВ1 1 СС1 Доказать: A1 B1 = B1 C1. Доказательство. Проведем AK∥A1 C1, BM∥A1 C1, тогда AK∥BM. 2) ∆ABK=∆BCM по 2-му признаку (AB=BC по условию, ∠BAK=∠CBM и ∠ABK=∠BCM), значит AK=BM.3) Т.к. четырехугольники AA1 B1 K и BB1 C1 M — параллелограммы (их противоположные стороны параллельны), то A1 B1 = AK, B1 C1 = BM. Значит, A1 B1 = B1 C1. ЧТД.
2) ∆ABK=∆BCM по 2-му признаку (AB=BC по условию, ∠BAK=∠CBM и ∠ABK=∠BCM), значит AK=BM.3) Т.к. четырехугольники AA1 B1 K и BB1 C1 M — параллелограммы (их противоположные стороны параллельны), то A1 B1 = AK, B1 C1 = BM. Значит, A1 B1 = B1 C1. ЧТД.
Номер слайда 3
Замечания:1. Отложенных равных отрезков может быть два, три и более. 2. Теорема Фалеса справедлива не только для сторон угла, но и для произвольных прямых.
Номер слайда 4Теорема (обратная теореме Фалеса).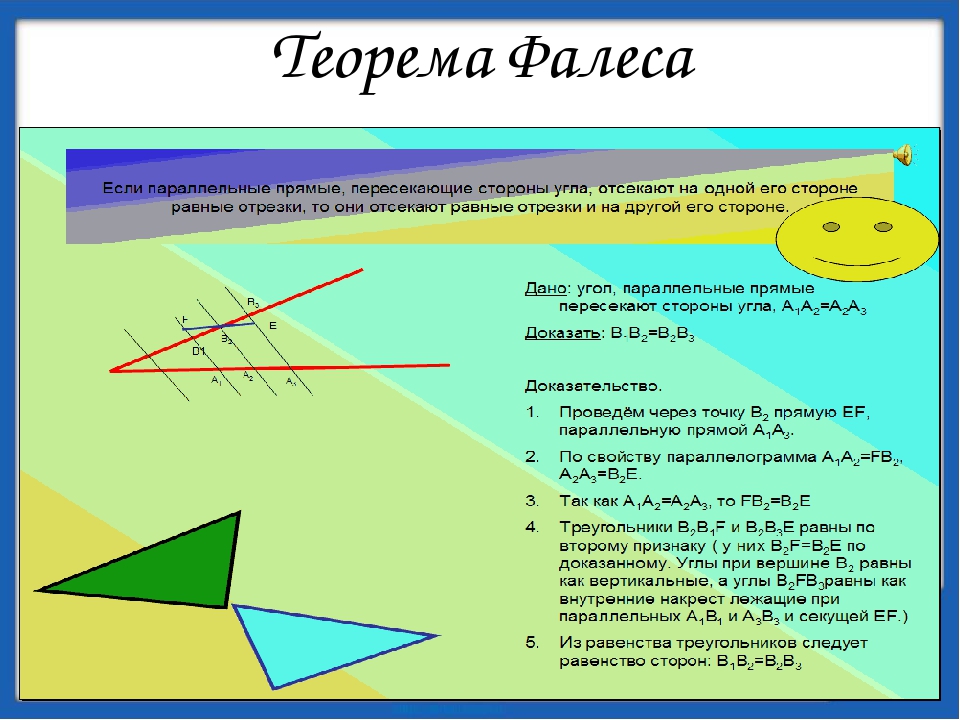 Если на сторонах угла от его вершины отложить равные отрезки (AB = BC, AB1 = B1 C1), то прямые, проходящие через их концы, будут параллельны (BB1 ∥ СС1).
Если на сторонах угла от его вершины отложить равные отрезки (AB = BC, AB1 = B1 C1), то прямые, проходящие через их концы, будут параллельны (BB1 ∥ СС1).
Номер слайда 5
Алгоритм деления отрезка на равные части: Построить отрезок. Построить луч, исходящий из одного из концов отрезка. С помощью циркуля отложить на луче необходимое количество отрезков равной длины. Провести прямую через последнюю точку на луче и другой конец отрезка. Провести прямые, проходящие через оставшиеся точки на луче, параллельные прямой, построенной в предыдущем пункте.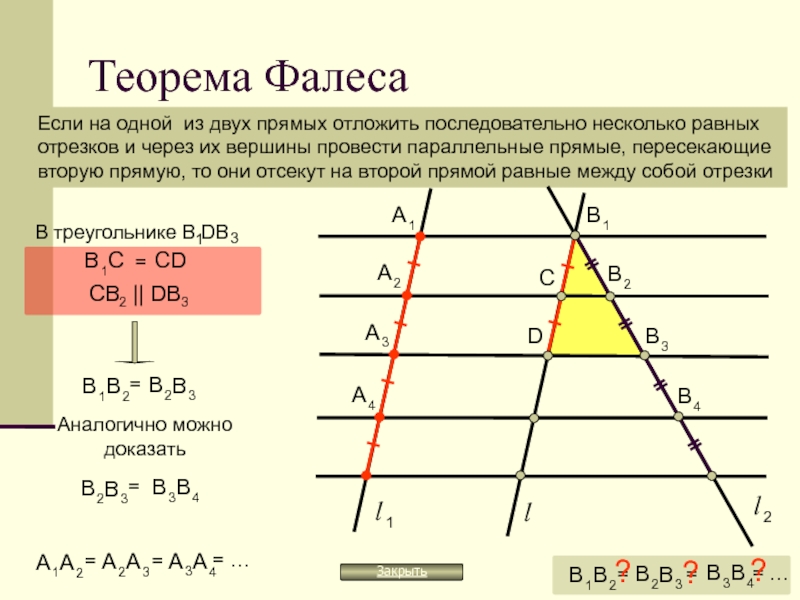
Номер слайда 6
Задача на готовом чертеже. ABCEF4512 EF║AC. Найти: РАВС
Номер слайда 7
Физкультминутка
Номер слайда 8
Номер слайда 9
Домашнее задание. Гл. 1 §7 № 97
Гл. 1 §7 № 97
Обобщенная теорема Фалеса — ГЕОМЕТРИЯ — Уроки для 8 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
Урок № 25
Тема. Обобщенная теорема Фалеса
Цель: сформировать у учащихся понятие о отношение отрезков, пропорциональные отрезки; сформировать осознанное понимание учащимися содержания теоремы о пропорциональных отрезках (обобщение теоремы Фалеса) и идеи ее доведения, а также возможность записи теоремы в виде двух разных равенств. Формировать у учащихся умения:
· воспроизводить содержание изученных на уроке утверждений;
· находить на рисунке пропорциональные отрезки;
· записывать равенство отношений пропорциональных отрезков по условию задачи для нахождения неизвестных длин отрезков;
· использовать теорему о пропорциональных отрезка для решения задачи на построение четвертого пропорционального отрезка.
Тип урока: усвоение новых знаний.
Наглядность и оборудование: конспект «Теорема Фалеса».
Ход урока
I. Организационный этап
· ориентировочный план изучения раздела;
· количество учебных часов, которое отведено для его изучения;
· примерное содержание материала;
· основные требования к знаниям и умениям учащихся;
· примерное содержание заданий, которые будут вынесены на контроль.
(Эту информацию можно поместить на стенде «Справочно-информационный уголок» в кабинете математики. С целью экономии времени предложить учащимся для самостоятельного ознакомления во внеурочное время).
II. Проверка домашнего задания
Если на предыдущем уроке было предложено ученикам дома решения задач контрольной работы или коррекционную работу и т. п.), то правильность выполнения этой работы учитель проверяет, собрав тетради на проверку (для оценивания).
п.), то правильность выполнения этой работы учитель проверяет, собрав тетради на проверку (для оценивания).
III. Формулировка цели и задач урока
Для понимания учащимися логики изучения материала и с целью создания мотивации учебной деятельности учащихся на уроке предлагаем им выполнить практическую работу.
Практическая работа
1. Выполните изображение произвольного отрезка АВ. С помощью циркуля и линейки разделите отрезок АВ на две части в отношении 2 : 3. (Точку деления обозначьте буквой С). (Замечание: во время выполнения построения используем теорему Фалеса и алгоритм решения задачи на деление данного отрезка на п равных частей.)
2. Измерьте длины всех отрезков ( АВ , АС , СВ , AY , АХ , XY), образовавшихся на рисунке 1.
3. Вычислите значение частиц: АС : ВС ; АС : АВ ; AY : XY; AY : АХ. Сравните полученные числа. Что вы заметили? Можете ли вы объяснить полученные результаты?
@ Выполняя построения, соответствующие условию задачи 1, ученики получают конфигурацию, подобную той, что изображена на рис. 1.
1.
После выполнения измерений и вычислений в соответствии с условиями заданий 2 и 3 ученики должны заметить, что, независимо от длины отрезка АВ и градусной меры угла ХАВ и несмотря на неточность измерений, среди полученных значений долей длин образованных отрезков есть равные числа, существование которых ученики не могут объяснить. Учитель предлагает учащимся сравнить рис.1 с рисунком теореме Фалеса и найти одинаковые и отличительные черты. После этого ученики должны заметить, что, несмотря на определенное сходство (параллельные прямые пересекают стороны угла), случай на рис. 1 не полностью соответствует условию теоремы Фалеса. Таким образом формулируется проблема. Существует необходимость обобщения теоремы Фалеса для случая, когда параллельные прямые пересекают стороны угла, отхватывая на одной из сторон произвольные отрезки, а также выражение зависимости между полученными отрезками в алгебраической форме. Решения поставленной проблемы является основой целью этого урока.
IV. Актуализация опорных знаний
Актуализация опорных знаний
Для успешного усвоения учащимися содержания понятий «отношение отрезков», «пропорциональные отрезки», содержания теоремы о пропорциональных отрезках (обобщение теоремы Фалеса) и идеи ее доведения, а также понимание учащимися возможности записи теоремы в виде двух равенств ученикам следует активизировать знания и умения относительно определения и свойства пропорции; содержания теоремы Фалеса.
Выполнение устных упражнений
1. Среди записей: , ab, a : b, а — b, а + b выбрать те, которые можно назвать отношением чисел а и b . Что может показывать это отношение?
2. Как называется запись ? Как называются числа а , b , с, d в этой записи?
3. Известно, что равенство является правильной. Какие из предложенных ниже равенств являются правильными? Почему?
а) ad = bс; b) ; в) ; г) ; д) .
4. а) АК : KB = 2 : 3 (рис. 2). Найдите: АК : АВ; ВК : АК; ВК : АВ;
б) ВК : АВ = m : n. Найдите АК : ВК; АК : АВ.
Найдите АК : ВК; АК : АВ.
5. Найдите NH (рис. 3), если АВ = 10.
V. Усвоение знаний
План изучения нового материала
1. Представление о содержании понятий «отношение отрезков»; «пропорциональные отрезки».
2. Теорема о пропорциональных отрезках (формулировка и идея доказательства).
3. Построение четвертого пропорционального отрезка.
@ Как показывает опыт, трудности восприятия содержания, а отсюда применение обобщенной теоремы Фалеса, возникают потому, что ученики не понимают смысла понятия «пропорциональные отрезки». Следовательно, изучение нового материала следует начинать с формирования сознательного понимания учащимися понятия пропорциональных отрезков с последующим закреплением его содержания на примерах.
За такого способа изучения материала формулировку теоремы о пропорциональных отрезках является простым обобщением результатов практической работы, поэтому, прежде чем формулировать утверждение теоремы, учитель может предложить учащимся самостоятельно составить обобщенное утверждение (исходя из равенств, которые учащиеся получили во время выполнения практической работы). Учителю следует подчеркнуть, что выполнена построение не является доказательством утверждения (это лишь иллюстрация теоремы). Ученики должны понимать, что составленное утверждение должно быть доказанным. Поскольку строгое математическое доказательство обобщенной теоремы Фалеса является достаточно сложным для учащихся 8 класса, то предоставляется только идея доказательства утверждения теоремы о пропорциональных отрезках со ссылкой на доказанную ранее теорему Фалеса. Заметим, что, в отличие от традиционного учебника, в новом учебнике формулируется и доказывается утверждение для отрезков, которые последовательно расположены на каждой из сторон угла (за такого подхода к формулировке теоремы ссылки на теорему Фалеса становится более понятным).
Учителю следует подчеркнуть, что выполнена построение не является доказательством утверждения (это лишь иллюстрация теоремы). Ученики должны понимать, что составленное утверждение должно быть доказанным. Поскольку строгое математическое доказательство обобщенной теоремы Фалеса является достаточно сложным для учащихся 8 класса, то предоставляется только идея доказательства утверждения теоремы о пропорциональных отрезках со ссылкой на доказанную ранее теорему Фалеса. Заметим, что, в отличие от традиционного учебника, в новом учебнике формулируется и доказывается утверждение для отрезков, которые последовательно расположены на каждой из сторон угла (за такого подхода к формулировке теоремы ссылки на теорему Фалеса становится более понятным).
Что касается пропорциональности отрезков, которые имеют общий конец в вершине угла, то в новом учебнике довольно оригинально доказан этот факт через применение к ранее доказанного утверждения одного из свойств пропорции.
После обработки понятие пропорциональных отрезков и формулировки и доказательства теоремы о пропорциональных отрезках желательно на примерах закрепить путем составления соответствующих пропорций за готовыми рисунками понимание учащимися содержания теоремы.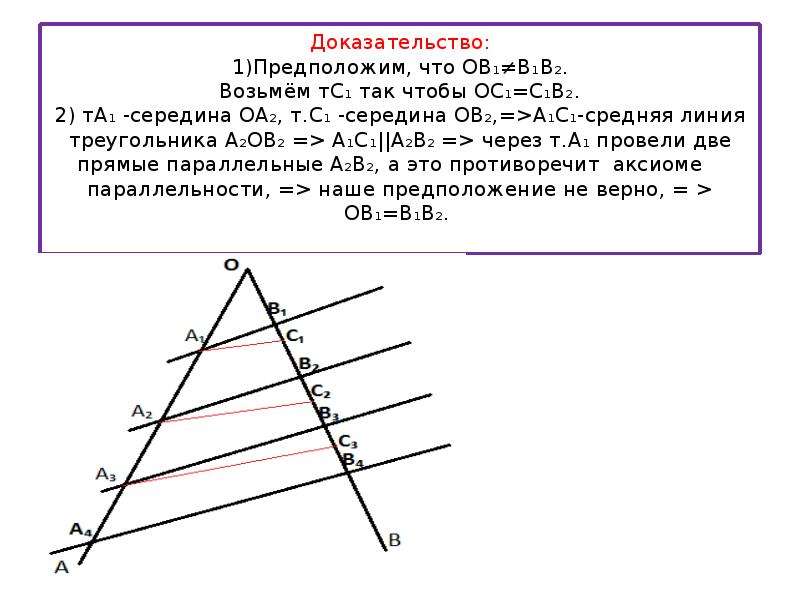
Если учащиеся хорошо усвоили теоретический материал, а также демонстрируют понимание содержания теорем и умение применять его на примерах, можно на этом уроке изучить схему решения базовой задачи на построение четвертого пропорционального отрезка.
VI. Закрепление знаний, формирование первоначальных умений
Выполнение письменных упражнений
1. Определите, есть отрезки длиной а и b пропорциональны отрезкам с и d , если:
а) а = 8 см, b = 24 см, с = 7 см, d = 12 см;
б) а = 9 см, b = 14 см, с = 7 см, d = 18 см.
2. По данным рисунка 4 найдите х, если а || b.
3. Прямая KM параллельна стороне АС треугольника ABC (рис. 5). Найдите отрезок MС , если АК = 2 см, KB = 6 см, ВМ = 9 см.
4. Прямая MN параллельна основаниям трапеции ABCD (рис. 6). Найдите сторону CD, если AM : AB = 4 : 5, CN = 3 см.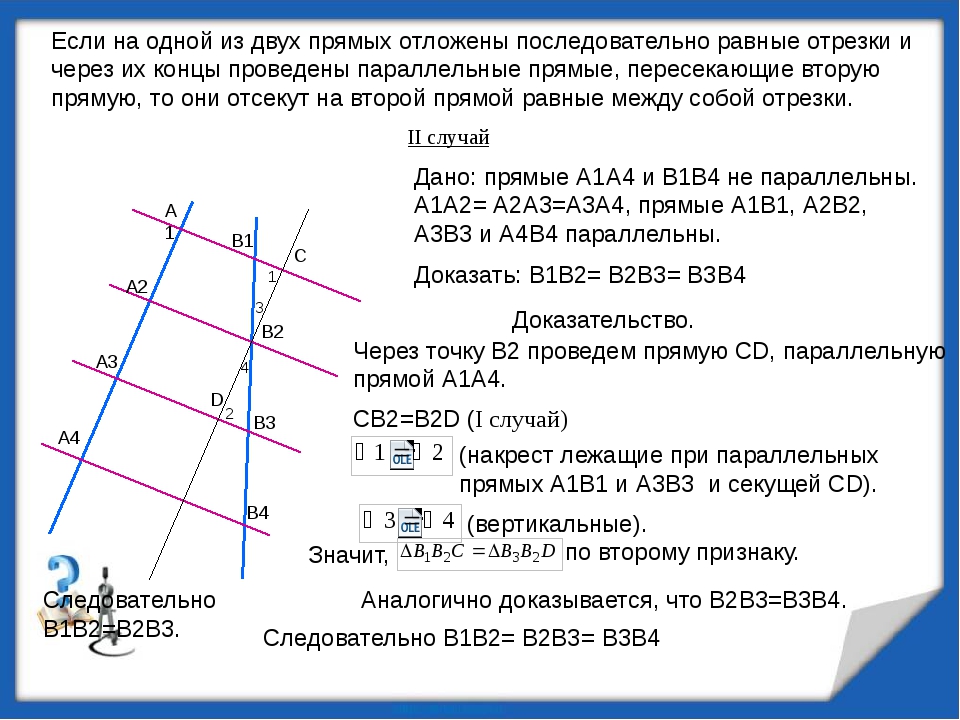
5. Даны отрезки а , b , с. Постройте отрезки: 1) ; 2) .
6. На рис. 7 BE : ЕА = 4 : 6, BD : DC = 6 : 7. Найдите отношение СК : КЕ .
VII. Итоги урока
На каком из приведенных рисунков допущена ошибка в изображении параллельных прямых а и b ?
VIII. Домашнее задание
Изучить теоретический материал.
Решить задачи.
- 1. По данным рисунка 8 найдите х, если а || b.
- 2.
2. Прямая KM параллельна стороне АС треугольника ABC (рис. 5). Найдите отрезок МС, если АК : KB = 2 : 3, ВС = 10 см.
3. Прямая MN параллельна основаниям трапеции ABCD (рис. 6). Найдите сторону АВ , если AM : ND = 3 : 2, CN = 2 см, АМ = 9 см.
4*. Даны отрезки а , b , c. Постройте отрезки: а) ; б) .
МАТЕМАТИКА В ШКОЛЕ 448 — Геометрия-8. Т
Тема 1. Многоугольники
Тема 2. Теорема о сумме углов выпуклого n-угольника
Тема 3. Выпуклые многоугольники (формулы)
Тема 4. Свойства и признаки параллелограмма Знать все свойства параллелограмма на русском языке, доказать любые два. Доказательства смотрите ниже.
Тема 5-1. Свойство противоположных сторон параллелограмма
Тема 5-2. Свойство противоположных углов параллелограмма
Тема 5-3. Свойство диагоналей параллелограмма
Тема 5-4. Свойство углов параллелограмма, прилежащих к одной стороне
Тема 6-1. Признак параллелограмма по равенству двух пар противоположных сторон Знать все ПРИЗНАКИ параллелограмма на русском языке, доказать любые два. Доказательства смотрите ниже
Тема 6-2. Признак параллелограмма по равенству противоположных углов
Тема 6-3. Признак параллелограмма по диагоналям, которые точкой пересечения делятся пополам
Признак параллелограмма по диагоналям, которые точкой пересечения делятся пополам
Тема 6-4. Признак параллелограмма по сумме углов, прилежащих к каждой из дух смежных сторон
Тема 6-5. Признак параллелограмма по равенству и параллельности одной пары сторон
Тема 7-1. Трапеция. Виды трапеций
Тема 7-2. Свойства и признаки равнобедренной трапеции Знать все СВОЙСТВА и ПРИЗНАКИ трапеции на русском языке, доказать одну (любую) теорему. Доказательства смотрите ниже
Тема 7-3. Свойство углов равнобедренной трапеции
Тема 7-4. Свойство диагоналей равнобедренной трапеции
Тема 7-5. Признак равнобедренной трапеции по равенству углов при основании
Тема 7-6. Признак равнобедренной трапеции по равенству диагоналей
Тема 9-1. Свойства и признаки прямоугольника Знать все СВОЙСТВА и ПРИЗНАК прямоугольника на русском языке, доказать одну (любую) теорему. Доказательства смотрите ниже
Тема 9-2. Свойство диагоналей прямоугольника
Свойство диагоналей прямоугольника
Тема 9-3. Признак прямоугольника (по равенству диагоналей)
Тема 10. Свойства и признаки ромба Знать все СВОЙСТВА и ПРИЗНАКИ ромба на русском языке, доказать один признак и одно свойство ромба. Доказательства смотрите ниже
Тема 11-1. Первое свойство ромба
Тема 11-2. Второе свойство ромба
Тема 11-3. Первый признак ромба
Тема 11-4. Второй признак ромба
Тема 12. Свойства и признаки квадрата Знать все СВОЙСТВА и ПРИЗНАКИ квадрата на русском языке
Тема 13. Классификация четырехугольников
Тема 15. Теорема Фалеса Ответить формулировки теоремы на внеурочке, доказательство по желанию.
Урок геометрии по теме «Теорема Пифагора». 8-й класс
Цель: создание условий для усвоения учащимися теоремы Пифагора, включение их в процесс поиска формулировок и доказательств, формирование навыка применения теоремы Пифагора при решении задач
Тип урока: Урок изучения и первичного закрепления новых знаний
Формы работы учащихся: фронтальная, групповая, индивидуальная
Необходимое техническое оборудование: компьютер, проектор, экран, колонки
Таблица 1.
Таблица 2.
| № | Этап урока | Название используемых ЭОР | Деятельность учителя | Деятельность ученика | Время |
| 1 | Организационный момент | Приветствие учащихся, создание рабочей обстановки | Приветствие учителя | 1 | |
| 2 | Проверка домашнего задания | Какие трудности возникли при выполнении домашнего задания? Выяснение причин невыполнения задание. | Два ученика у доски объясняют по готовым чертежам решение задач №16 и №17 (§46) из домашнего задания | 3 | |
| 3 | Актуализация опорных знаний | Какие треугольники называются
подобными? Сформулируйте признаки подобия треугольников? Определение прямоугольного треугольника? Элементы прямоугольного треугольника? Свойство острых углов прямоугольного треугольника? Попробуйте самостоятельно сформулировать Признаки подобия прямоугольных треугольников? Докажите, что высота опущенная на гипотенузу разбивает прямоугольный треугольник на два подобных треугольника? Как вычислить площадь прямоугольного треугольника? Решение задач: 1. 2. Гипотенуза прямоугольного треугольника 6см, высота опущенная из вершины прямого угла равна 2см. Чему равна площадь? 3. У прямоугольного треугольника катет равен 8см, и гипотенуза 10см. Найдите площадь. |
Учащиеся отвечают на поставленные
вопросы. Один ученик у доски выполняет доказательство? Остальные учащиеся выполняют запись в тетрадь Устно решают предложенные задачи |
7 | |
| 4 | Мотивация учебно-познавательной деятельности | При решении третьей задачи у нас
возникла проблема, которую мы пока не можем решить.
Решить данную задачу нам поможет знаменитая теорема Пифагора, о которой Иоган Кеплер сказал: “Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора” Краткая справка о жизни и деятельности Пифагора |
3 | ||
| 5 | Изучение нового материала | Ресурс №1
Пропорциональные отрезки в прямоугольном треугольнике (N 185665) (фрагменты 1-2) |
Внимание на экран Вопросы : Сформулируйте теорему Пифагора? Математическая запись теоремы На чем основано доказательство теоремы? Назовите подобные треугольники. Какие соотношения сторон подобных треугольников? Как получить искомое соотношение? |
Просматривают ЭОР Отвечают на вопросы учителя Записывают теорему и ее доказательство в тетрадь |
|
| Ресурс №2 Теорема Пифагора. И3 Слайд презентации Ресурс №3 Пифагоровы тройки. И4 |
Запишите теорему и ее доказательство в
тетрадь. Существует более 500 различных доказательств данной теоремы. Рассмотрим еще одно доказательство. С теоремой Пифагора связано открытие Пифагором несоизмеримых отрезков. (Рассказ учителя о несоизмеримых отрезках, и построении отрезков длины √2, √3, √5 и т.д.) Пифагор нашел способ отыскания соизмеримых сторон прямоугольного
треугольника. |
Просматривают ЭОР Выполняют построение в тетради Записывают определение несоизмеримых отрезков Просматривают ЭОР, делают записи в тетрадь |
10 | ||
| 6 | Физкультминутка | Комплекс упражнений для глаз. Упражнение выполняются сидя или стоя, отвернувшись от экрана, при ритмичном дыхании. Закрыть глаза, не напрягая глазные мышцы, на счёт 1-4, широко раскрыть глаза и посмотреть вдаль на счёт 1-6. Повторить 4-5 раз. |
Выполняют гимнастику для глаз | 1 | |
| 7 | Решение задач с применением теоремы Пифагора | Объясняет решение задачи: В
прямоугольном треугольнике с углом 600 вписан ромб со
стороной 6см так, что угол 600 общий и все вершины лежат на
сторонах треугольника. |
Слушают объяснения записывают решение в тетрадь | 6 | |
| 8 | Работа в группах | Слайд Презентации | Группам из четырех человек даются
карточки с заданиями и табло с ответами
На экране компьютера карта Древнего мира Если соединить города, где родился, набирался опыта и жил Пифагор, отрезками, то получиться прямоугольный треугольник |
Каждый ученик решает свою задачу и ставит свою карточку на свое место. В результате в группах получается – карта Средиземноморья. | 4 |
| 9 | Самостоятельная работа | Ресурс №4 Самостоятельная работа по
теме «Теорема Пифагора» |
Организует самостоятельную работу по
карточкам. (материал ЭОР) (материал ЭОР) |
Выполняют самостоятельную работу | 7 |
| 10 | Историческая справка о теореме Пифагора | Ресурс №5 мультфильм о т.Пифагора,Весёлый приключенческий телесериал «Головастики» телеканала»Карусель» (серия 3) |
Внимательно просмотрите мультфильм. Найдите ошибку диктора. Как вы думаете, почему он допустил эту ошибку? | 2 | |
| 11 | Итоги урока | Подводит итоги урока.
— Какие открытия мы совершили сегодня на уроке? Чему научились? У прямоугольного треугольника катет равен 8см, и гипотенуза 10см. Найдите площадь Объявляет оценки за урок. Комментирует домашнее задание §49 Теорема Пифагора, исторические сведения, №6, 7, 8 Дополнительно найти другие доказательства теоремы Пифагора |
Отвечают на поставленные вопросы
Записывают задание в дневник |
2 |
Технологическая карта урока геометрия «Теорема Пифагора», 8 класс
Технологическая карта урока
ФИО: Попова Мария Владимровна
Предмет: геометрия
Тема: «Теорема Пифагора»
Тип урока: изучение и первичное закрепление новых знаний и способов деятельности
Участники: обучающиеся 8 класса
Цели: Развивающие:
Создать условия, в которых учащиеся могли бы самостоятельно планировать и анализировать собственные действия, находить выход из любой ситуации, реально оценивать свои возможности и знания.
Воспитательные:
Воспитывать познавательный интерес к предмету, любовь к поисковым решениям, культуру поведения при фронтальной, групповой и индивидуальной работе.
Образовательные:
1) ознакомить и обеспечить овладение учащимися основными алгоритмическими приемами при нахождении сторон прямоугольного треугольника при помощи теоремы Пифагора
2) показать практическое применение теоремы Пифагора в жизни.
3) способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления.
Планируемый результат обучения, в том числе и формирование УУД: Предметные:
Понимать, что такое «теорема Пифагора». Знать, как найти неизвестную сторону прямоугольного треугольника при помощи теоремы Пифагора.
Личностные:
Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные :работа над понятием информация-знание
Познавательные УУД: умение ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
Коммуникативные УУД: умение оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.
Регулятивные УУД: умение определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.
Личностные УУД: способность к самооценке на основе критерия успешности учебной деятельности.
Основные понятия: Теорема Пифагора
Межпредметные связи: математика
Ресурсы: — Учебник для общеобразовательных учреждений : «Геометрия 7-9 класс» А. В. Погорелов.
— презентация к уроку
— карточки для рефлексии
Этапы урока | Деятельность учителя Содержание учебного материала | Деятельность учащихся | Формирование УУД |
Организационный момент | Приветствие, проверка готовности к уроку | Проверяют готовность своего рабочего места | |
2. знаний | Вопросы по пройденному материалу. 1.Какой треугольник называется прямоугольным? 2.Как называются стороны прямоугольного треугольника? 3. Сформулировать определение косинуса острого угла в прямоугольном треугольнике. | Учащиеся отвечают на вопросы учителя. | Коммуникативные: Умение с достаточной полнотой и точностью выражать свои мысли Позновательные: Уметь отличать новое от уже известного с помощью учителя |
2. Постановка проблемы. Определение цели. | Создание проблемной ситуации. Предлагается задача. Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты? Слушает высказывания учащихся. Анализирует и корректирует. Учитель организует диалог, направленный на формулирование проблемы: как найти неизвестную сторону в прямоугольном треугольнике, если известны две другие стороны | Анализируют задачу, делают чертёж, возникает вопрос как найти гипотенузу? Предлагают свои версии решения задачи. Отвечают на вопросы учителя Ученики проговаривают проблему. «Как найти гипотенузу по двум катетам» Записывают проблему в тетрадь. | Регулятивные: Уметь проговаривать алгоритм действий; уметь определять и формулировать цель на уроке с помощью учителя; Познавательные: Самостоятельное выделение и формулирование познавательной цели; Позновательные: Выдвижение гипотез и их обоснование |
3.Изучение новых знаний | Учитель организует практическую работу. Раздает разноцветные фигуры по группам (прямоугольные треугольники со сторонами a,b, c) Вопросы к практической работе. 1.Установите связь между гипотенузой и катетами, пользуясь моделями фигур 2.Можно ли увидеть закономерность между длинами катетов и гипотенузы? Учитель выслушивает ответы у каждой группы и задает вопросы.
Зависимость, которую мы с вами установили, в геометрии называют теоремой Пифагора. Учитель совместно с учащимися формулируют цель урока. А теперь попытаемся доказать теорему Пифагора. Теорема Пифагора выражает зависимость между гипотенузой и катетами прямоугольного треугольника. Учитель предлагает найти и прочитать в учебнике формулировку теоремы Пифагора (стр. 92 §63). | Учащиеся работают в группах. Анализируют, работают с фигурами. Ученики предлагают свои версии разрешения проблемы. Делают вывод. Проговаривают. Записывают в тетради число и тему урока, Находят и читают в учебнике теорему Пифагора Работа по учебнику. Учащиеся самостоятельно записывают доказательство в тетрадь. | Позновательные: Умение самостоятельно определять и высказывать свои гипотезы с целью выделения признаков Преобразование модели с целью выявления общих законов Построение логической цепи рассуждений Формулирование познавательной цели Построение логической цепи рассуждений Установление причинно-следственных связей |
З. Первичное закрепление полученных знаний | Решение задач: 1.Найдите гипотенузу прямоугольного треугольника по данным катетам: а=5,в=6. 2.В прямоугольном треугольнике найдите катет в, если с=13,а=12. Проверка решения. Решим задачу стр. 101 № 2 по учебнику. | Работают возле доски, записывают решение в тетрадь. Работа возле доски. Учащиеся записывают формулу в тетрадь. Учащиеся применяют полученные знания и записывают решения в тетрадь | Познавательные: Выбор наиболее эффективных способов решения задачи в зависимости от конкретных условий Коммуникативные: Умение работать возле доски, при необходимости получить помощь товарищей |
4.Решение задач на применение теоремы. | Организует решение задач по учебнику. Задача № 2 стр. 101 на доске и в тетради. Боковая сторона равнобедренного треугольника равна 17 см, а основание равно 16 см. Найти высоту, проведенную к основанию. Организует обсуждение полученных результатов | Анализируют задачу, при необходимости общаются с учителем. Решение записывают в тетрадях. 1 ученик решает у доски и проговаривает алгоритм решения. | Умение самостоятельно применять теорему Пифагора |
5.Физкульт пауза. | Учитель включает музыку | Ученики выполняют упражнения | Контроль за своим физическим состоянием |
6.Информация о домашнем задании | 1.Выучить формулировку и доказательство теоремы Пифагора (стр. 92 §63). 2. Найдите ещё одно доказательство теоремы Пифагора Стр. 101 №3 | Записывают домашнее задание в дневниках | Планирование своей домашней работы |
7.Обобщение и систематизация знаний | Организует работув парах по вариантам. 1 вариант: а) Катеты прямоугольного треугольника равны 12 см и 5 см. Найти гипотенузу этого треугольника. б) Гипотенуза прямоугольного треугольника равна 5 см, а один из катетов 3 см. 2 вариант: а) Катеты прямоугольного треугольника равны 6 см и 8 см. Найти гипотенузу этого треугольника. б) Гипотенуза прямоугольного треугольника равна 13 см, а один из катетов 12 см. Организует проверку. | Решение в парах, самопроверка в парах | Познавательные: выбор наиболее эффективных способов решения задачи в зависимости от конкретных условий в парах; |
8. Подведение итогов учебного занятия | Подведём итог нашей работы на уроке. — Вспомним, какую цель мы с вами ставили? — Достигли цели? | Отвечают на вопросы учителя. | Выделение и осознание учащимися того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения |
9.Рефлексия учебной деятельности | Организует рефлексию и самооценку учениками собственной учебной деятельности предлагаются следующие фразы: «Сегодня на уроке я повторил…» «Сегодня на уроке я узнал…» «Сегодня на уроке я научился…» «Было интересно…» | Продолжают фразы. Самооценивание | Познавательные: Способность к самооценке на основе критерия успешности учебной деятельности; Коммуникативные: Уметь критически относится к себе и к своим знаниям |
Дополнительные главы геометрии. 8 класс: О курсе
Курс ориентирован на слушателей, владеющих школьной программой 8 класса по геометрии. Учащиеся познакомятся с яркими геометрическими сюжетами, систематизируют теоретические знания, научатся решать задачи повышенной сложности.
Учащиеся познакомятся с яркими геометрическими сюжетами, систематизируют теоретические знания, научатся решать задачи повышенной сложности.
Курс поможет школьникам не только на уроках геометрии в школе, но и позволит успешнее выступать на олимпиадах, а учителям математики — лучше понять аспекты теории и задачные акценты, примыкающие к школьной программе и характерные для математических олимпиад, использовать задачную базу курса на занятиях в школе.
Курс состоит из 13 обязательных и 6 лекционных модулей, 49 видеолекций с конспектами, 270 обязательных упражнений и факультативных задач для самостоятельного решения.
Учебные модули
|
— Вписанные углы |
— Луночки Гиппократа |
Внутри каждого модуля есть:
— видео с кратким конспектом, где обсуждается теория и разбираются примеры решения задач,
— упражнения с автоматической проверкой, позволяющие понять, как усвоена теория,
— задачи для самостоятельного решения, которые не учитываются в прогрессе и не идут в зачет по модулю, но позволяют качественно повысить свой уровень.
В каждом разделе есть ответы на популярные вопросы, где можно уточнить свое понимание теории или условия задачи, но нельзя получить подсказки по решению.
По итогам обучения выдается электронный сертификат. Для его получения необходим зачет по всем учебным модулям, кроме лекционных. Условие получения зачета по модулю — успешное выполнение не менее 70% упражнений. Сертификаты могут учитываться при отборе на очные программы по направлению «Наука».
Сертификаты могут учитываться при отборе на очные программы по направлению «Наука».
Если ученик не успеет получить зачет по отдельным модулям, то он не сможет получить сертификат, но сможет возобновить обучение, когда курс стартует в следующий раз. При этом выполнять пройденные модули заново не потребуется (но может быть предложено, если соответствующие учебные материалы обновятся).
В следующий раз курс будет открыт осенью 2020 года.
Математика для 8-го класса: теоремы о треугольниках и доказательства в геометрии — видео и уроки
Каждый видеоурок длится около пяти минут и предназначен для того, чтобы помочь 8-классникам запомнить теоремы о треугольниках и их доказательства, которые вы представили в классе. Веселые и беззаботные видеоролики исследуют постулаты, доказательства и теоремы треугольников с использованием углов, гипотенуз и сторон и показывают учащимся, как применять их для решения геометрических задач. Вы можете использовать викторины с несколькими вариантами ответов, чтобы увидеть, где у учащихся могут возникнуть вопросы, а экзамен по главе может проверить, что они запомнили из этой главы.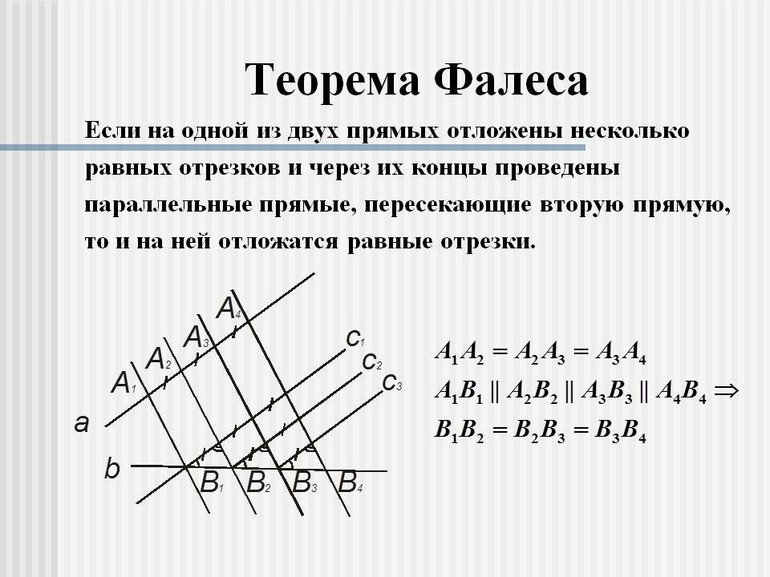
| Урок | Цель |
|---|---|
| Применение подобных треугольников | Учащиеся изучают способы решения приложений подобных треугольников. |
| Постулаты о сходстве треугольников: SAS, ASA и SSS | Учащиеся рассматривают примеры постулатов SAS, ASA и SSS, чтобы найти соответствие двух треугольников. |
| Доказательства конгруэнтности: соответствующие части конгруэнтных треугольников | Преподаватели предлагают задачи, в которых учащиеся применяют соответствующие части доказательства конгруэнтных треугольников. |
| Обратное утверждение: объяснение и пример | Учащиеся узнают, что для использования обратного утверждения в качестве основания в любом доказательстве оно должно сначала быть истинным. |
| Преобразования подобия в соответствующих фигурах | На этом уроке учащиеся определяют, подобны ли две заданные фигуры, используя определение подобия в терминах преобразований подобия. |
| Доказательство соотношений в фигурах с использованием конгруэнтности и подобия | На уроке учащиеся применяют конгруэнтность и подобие треугольников для доказательства соотношений в геометрических фигурах. |
| Попрактиковаться в доказательстве отношений | Учащиеся имеют возможность попрактиковаться в решении задач, подтверждающих отношения. |
| Теорема AAS (угол-угол-сторона): доказательство и примеры | Учащиеся узнают, что утверждает теорема угол-угол-сторона и как ее доказать. |
| Теорема HA (угол гипотенузы): доказательство, объяснение и примеры | Преподаватели объясняют теорему об угле гипотенузы. |
| Теорема HL (каттер гипотенузы): определение, доказательство и примеры | На этом уроке учащиеся собирают информацию о теореме катета гипотенузы. |
| Теорема о биссектрисе перпендикуляра: доказательство и пример | Учащиеся изучают теорему о биссектрисе отрезка, рассматривая пример биссектрисы данного отрезка. |
| Теорема о биссектрисе угла: доказательство и пример | Урок основан на предыдущем уроке и использует биссектрису заданного угла для доказательства теоремы о биссектрисе. |
| Конгруэнтность прямоугольных треугольников: определение теорем LA и LL | Учащиеся изучают теоремы LA и LL. |
| Конгруэнтность равнобедренных треугольников: доказательство теоремы | Учащиеся узнают, что когда углы при основании равнобедренного треугольника конгруэнтны, углы, противоположные этим сторонам, также конгруэнтны. |
Фалес и Пифагор: ранний вклад в геометрию — видео и стенограмма урока
Фалес
Фалес родом из Милета в Малой Азии и был греком. Он родился около 624 г. до н.э. и умер около 547 г. до н.э. Да, это было давно, но он внес значительный вклад в геометрию.Фактически, некоторые считают его первым математиком. Посетив Египет, он смог рассчитать высоту пирамиды. Ему приписывают пять заметных вкладов в область геометрии, один из которых назван в его честь.
Во-первых, диаметр круга делит круг пополам или делит его пополам. Во-вторых, углы при основании равнобедренного треугольника равны друг другу. В-третьих, когда у вас есть две пересекающиеся прямые линии, противоположные или вертикальные углы равны друг другу.Четвертый важный вклад гласит, что когда два треугольника имеют два равных угла и одну равную сторону, то они конгруэнтны или равны друг другу. Пятая называется теоремой Фалеса. Он гласит, что угол, вписанный или проведенный внутри полукруга или полукруга, будет прямым углом. Эти пять вкладов приписываются Фалесу, потому что он предоставил первое письменное доказательство этих теорем. Теперь поговорим о Пифагоре.
Пифагор
Пифагор родился около 569 г. до н.э. в Греции и жил где-то около 500-475 г. до н.э.В то время как Фалеса называли первым математиком, Пифагора называли первым чистым математиком. Неудивительно, поскольку Фалес действительно давал Пифагору совет о том, как он может развивать свои математические знания.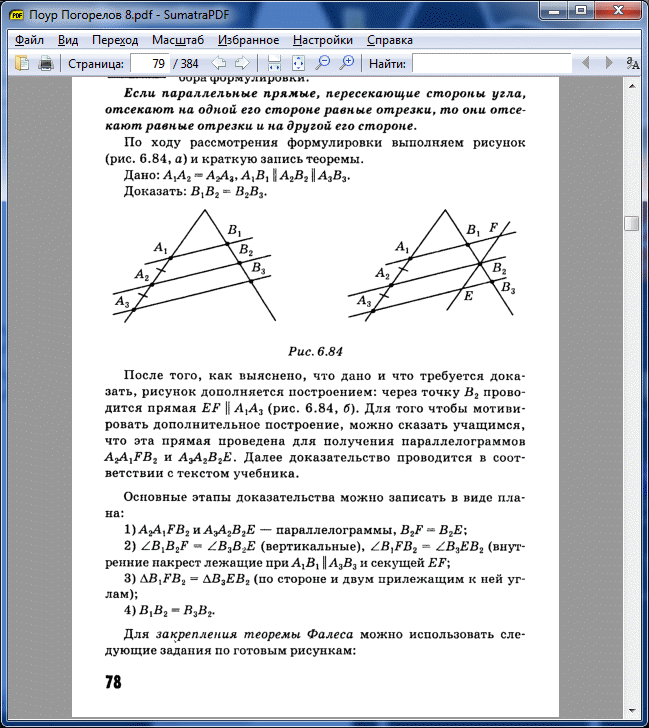 Пифагор также внес большой вклад в изучение геометрии, и ему приписывают следующие четыре учения.
Пифагор также внес большой вклад в изучение геометрии, и ему приписывают следующие четыре учения.
Во-первых, три угла треугольника в сумме дают два прямых угла или 180 градусов. Второй назван в его честь. Это называется теоремой Пифагора, которая говорит нам, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов двух других сторон.В-третьих, это использование и построение различных фигур и форм для решения уравнений. В-четвертых, Пифагор понял и смог построить тетраэдр, куб и октаэдр. Пифагору приписывают эти учения, потому что он, как и Фалес, предоставил первое письменное доказательство этого.
Сегодня
Сейчас мы говорили и о Фалесе, и о Пифагоре. Какое из их учений вы используете чаще всего? Вы можете сказать, что это теорема Пифагора, а если углубиться глубже, то можно сказать, что это теорема Фалеса.Или это может быть их другой вклад. Что бы вы ни выбрали, вы можете видеть, что все их вклады все еще используются сегодня, и современные математики иногда используют их учения для доказательства еще большего количества теорем.
Итоги урока
Чему мы научились? Мы узнали, что и Фалес, и Пифагор — греки. Сроки их жизни пересекались, и Фалес фактически консультировал Пифагора в его математических поисках большего количества знаний. Оба внесли большой вклад в изучение геометрии.Фалесу приписывают учение о том, что диаметр делит окружность пополам, углы при основании равнобедренного треугольника равны, противоположные или вертикальные углы двух пересекающихся прямых равны, два треугольника равны, если они имеют два угла и одну прямую, которые являются то же самое, и что угол, проведенный внутри полукруга, будет прямым углом. Это последнее учение также известно как теорема Фалеса.
Пифагору приписывают учение о том, что сумма углов треугольника составляет 180 градусов или два прямых угла; квадрат гипотенузы прямоугольного треугольника равен сумме квадратов двух других сторон; построение фигур и фигур можно использовать для решения уравнений; и построение тетраэдра, куба и октаэдра.
Результаты обучения
После завершения этого урока вы должны быть в состоянии:
- Обобщать предысторию Фалеса и Пифагора
- Объясните математические понятия, которые приписывают созданию
Теоремы о кругах
Несколько интересных фактов об углах и окружностях.
Вписанный угол
Прежде всего, определение:
Вписанный угол : угол, образованный точками, лежащими на окружности окружности.
A и C — «конечные точки»
B — «вершина»
Поиграй с этим здесь:
Когда вы перемещаете точку «B», что происходит с углом?
Теоремы о вписанном угле
Вписанный угол а° составляет половину центрального угла 2а°
(Называется Угол в центре теоремы )
И (с фиксированными конечными точками) …
… угол a° равен всегда один и тот же ,
независимо от того, где он находится на одной дуге между конечными точками:
Угол a° равен тому же .
(называется теорема о углах, опирающихся на одну и ту же дугу)
Пример: Каков размер Angle POQ? (О — центр круга)
Угол POQ = 2 × Угол PRQ = 2 × 62° = 124°
Пример: Каков размер Angle CBX?
Угол ADB = 32° также равен углу ACB.
И угол ACB также равен углу XCB.
Значит, в треугольнике BXC угол BXC = 85°, а угол XCB = 32°
Теперь используйте углы треугольника, добавленные к 180 °:
Угол CBX + Угол BXC + Угол XCB = 180°
Угол CBX + 85° + 32° = 180°
Угол CBX = 63°
Угол полуокружности (теорема Фалеса)
Угол , вписанный в окружность диаметром , всегда прямой:
(Конечными точками являются концы диаметра круга,
точка вершины может быть где угодно на окружности.)
Почему? Потому что: Вписанный угол 90° составляет половину центрального угла 180° (с использованием приведенной выше теоремы об угле в центре) |
Еще одна веская причина, почему это работает
Мы также можем повернуть фигуру на 180°, чтобы получился прямоугольник!
Это это прямоугольник, потому что все стороны параллельны, а обе диагонали равны.
Итак, все его внутренние углы прямые (90°).
Итак, поехали! Независимо от того, , где , этот угол равен
по окружности, всегда равен 90°
Пример: Каков размер угла BAC?
Теорема об угле в полуокружности говорит нам, что угол ACB = 90°
Теперь используйте углы треугольника, добавленные к 180 °, чтобы найти угол BAC:
.Угол ВАС + 55° + 90° = 180°
Угол ВАС = 35°
Нахождение центра круга
Мы можем использовать эту идею, чтобы найти центр круга:
- начертите прямой угол из любого места на окружности круга, затем нарисуйте диаметр в том месте, где две ножки касаются круга
- сделайте это снова, но с другим диаметром
Там, где пересекаются диаметры, находится центр!
Рисование круга
Когда мы знаем две противоположные точки на окружности, мы можем нарисовать эту окружность.
Вставьте несколько булавок или гвоздей в эти точки и используйте строительный угольник, например:
Циклический четырехугольник
«Циклический» четырехугольник имеет каждую вершину на окружности: | |
В циклическом четырехугольнике противоположных углов составляют 180° :
|
Пример: Каков размер угла WXY?
Противоположные углы вписанного четырехугольника в сумме дают 180°
Угол WZY + Угол WXY = 180°
69° + угол WXY = 180°
Угол WXY = 111°
Угол касательнойКасательная линия касается окружности только в одной точке. Всегда образует прямой угол с радиусом окружности. |
Доказательство теоремы Пифагора Евклида – Написание антологии
Евклидово доказательство теоремы Пифагора
Кэтрин Лоу ’18
MATH-386: Математический семинар
Статья Кэтрин представляет собой очень подробное изложение евклидовского доказательства теоремы Пифагора. Это доказательство не часто встречается за пределами курса геометрии для бакалавров. Кэтрин взялась за доказательство без предварительной работы по геометрии. Она работала, чтобы понять материал, а затем представила его логически и математически. Ее объяснения показывают полное понимание математических понятий, они подробны и ясны. Она использует сложные и утонченные математические рассуждения. Она правильно использует терминологию и обозначения во всей своей статье (в которой много обозначений). Ее статья является самостоятельным, математически простым для понимания (для тех, у кого есть опыт чтения доказательств) и логическим продолжением евклидовского доказательства теоремы Пифагора.
Это доказательство не часто встречается за пределами курса геометрии для бакалавров. Кэтрин взялась за доказательство без предварительной работы по геометрии. Она работала, чтобы понять материал, а затем представила его логически и математически. Ее объяснения показывают полное понимание математических понятий, они подробны и ясны. Она использует сложные и утонченные математические рассуждения. Она правильно использует терминологию и обозначения во всей своей статье (в которой много обозначений). Ее статья является самостоятельным, математически простым для понимания (для тех, у кого есть опыт чтения доказательств) и логическим продолжением евклидовского доказательства теоремы Пифагора.
– Венди Вебер
1. Аннотация
В этой статье делается попытка доказать важную теорему из «Элементов» Евклида: доказательство Евклида теоремы Пифагора. Статья начинается с введения в «Элементы» и их истории. Далее в статье устанавливаются некоторые основополагающие принципы доказательств Евклида: определения, постулаты и общие понятия. Затем он перечисляет и объясняет некоторые из более ранних утверждений, которые необходимы для завершения более поздних доказательств.Затем доказывается предложение I.47, теорема Пифагора, за которым следует предложение I.48, обратное ему.
Затем он перечисляет и объясняет некоторые из более ранних утверждений, которые необходимы для завершения более поздних доказательств.Затем доказывается предложение I.47, теорема Пифагора, за которым следует предложение I.48, обратное ему.
Одна из величайших работ по математике — «Начала» Евклида; Автор Уильям Данэм утверждает, что из всех когда-либо написанных книг «только Библия подверглась более тщательному изучению» (30). Элементы содержали 465 предложений в 13 книгах, охватывающих темы как геометрии, так и теории чисел. Следует отметить, что большинство теорем изначально не были работой Евклида, но он собрал работы других и представил их «ясно, организованно, логично» (Dunham 31).Одним из таких утверждений было доказательство Евклидом теоремы Пифагора. Евклид не был первым, кто доказал это, но этот постулат, в отличие от многих других, был полностью его собственной работой. Были опубликованы сотни доказательств теоремы Пифагора (Колпас), но доказательство Евклида было уникальным как по своему подходу, так и по своей организации, как и остальные «Элементы». Написанные в 300 г. до н.э., «Начала» Евклида остаются, пожалуй, самым важным текстом по математике.
Написанные в 300 г. до н.э., «Начала» Евклида остаются, пожалуй, самым важным текстом по математике.
Евклид начал «Элементы» с 23 определений.Он определил такие вещи, как линия, прямой угол и параллельные линии: «Параллельные прямые линии — это прямые линии, которые, находясь в одной плоскости и производясь бесконечно в обоих направлениях, не пересекаются друг с другом ни в одном направлении» (Данхем 33). . Обратите внимание, что Евклид определял параллельные прямые как линии, которые никогда не пересекаются, а не равноудаленные от них везде, как это часто делается.
Отсюда Евклид ввел пять постулатов. Это были самоочевидные утверждения, построенные на определениях; их не нужно было доказывать, и они принимались как данность.Постулат 1 гласил: «[Возможно] провести прямую линию из любой точки в любую точку» (Данхем 34). Другим важным постулатом, использованным в его доказательстве теоремы Пифагора, был постулат 4: «Все прямые углы равны друг другу» (Данхем 35). Для любого, кто изучал геометрию, эти утверждения неоспоримы, что и имел в виду Евклид.
Для любого, кто изучал геометрию, эти утверждения неоспоримы, что и имел в виду Евклид.
Рисунок 1: Постулат 5
Самым противоречивым аспектом «Элементов» Евклида был постулат 5. В нем говорилось: «Если прямая линия, падающая на две прямые, образует внутренние углы с одной и той же стороны меньше двух прямых, то две прямые, если их провести бесконечно, пересекутся на та сторона, на которой углы меньше двух прямых» (Данэм 35).Другими словами, если α + β меньше двух прямых углов, прямые AB и CD пересекаются в некоторой точке (рис. 1). Этот постулат был гораздо сложнее и менее очевиден, чем предыдущие; многие математики считали, что на самом деле это была теорема, и ее не следует принимать за истину. Евклид, понимая это мнение, избегал использования постулата 5 в своих предложениях. Он вообще не использовал его в первых 28 предложениях.
Следуя постулатам, Евклид ввел пять общих понятий. Как и постулаты, это были признанные факты, которые не требовалось доказывать; однако общие понятия носили «более общий характер, не специфичный для геометрии», в отличие от постулатов (Dunham 36). Общее понятие 1 было эквивалентом транзитивного свойства сложения: «Вещи, которые равны одной и той же вещи, также равны друг другу» (Dunham 36). Общее понятие 2 гласило: «Если равные прибавляются к равным, все становится равным» (Dunham 36). С алгебраической точки зрения, если a = b, то a + c = b + c.
Общее понятие 1 было эквивалентом транзитивного свойства сложения: «Вещи, которые равны одной и той же вещи, также равны друг другу» (Dunham 36). Общее понятие 2 гласило: «Если равные прибавляются к равным, все становится равным» (Dunham 36). С алгебраической точки зрения, если a = b, то a + c = b + c.
Чтобы доказать теорему Пифагора, Евклид использовал выводы из своих более ранних доказательств. Мы рассмотрим предложения, необходимые для доказательства этой и других теорем.
- Рисунок 2: Предложение I.4
- Рисунок 3: Предложения I.13 и I.14
Предложение I.4 доказало конгруэнтность двух треугольников; это широко известно как теорема сторона-угол-сторона, или SAS. Евклид доказал, что «если у двух треугольников две стороны и угол между ними равны соответственно двум сторонам и углу между ними другого, то такие треугольники конгруэнтны во всех отношениях» (Данхем 39). На рисунке 2, если AC = DF, AB = DE и ∠CAB = ∠FDE, то эти два треугольника конгруэнтны. Это означает, что не только оставшиеся стороны и углы равны, но и два треугольника имеют одинаковую площадь.
На рисунке 2, если AC = DF, AB = DE и ∠CAB = ∠FDE, то эти два треугольника конгруэнтны. Это означает, что не только оставшиеся стороны и углы равны, но и два треугольника имеют одинаковую площадь.
В предложении I.8 Евклид доказал еще одну теорему сравнения. Если у двух треугольников все три стороны одного треугольника равны всем трем сторонам другого треугольника, то такие треугольники равны. Это называется теоремой сторона-сторона-сторона, или SSS.
Евклид показал, как построить прямую, перпендикулярную другой прямой в предложении I.11. Он показал, что эту прямую можно провести из точки на прямой или из точки, не лежащей на прямой. Это предложение было одним из многих конструктивных доказательств. Предложение I.14 рассматривается, когда линия прямая. В I.13 Евклид показал, что если линия CBD на рисунке 3 прямая, то сумма углов ∠CBA и ∠ABD составляет два прямых угла.
Рисунок 4: Предложение I.16
Предложение I.14 противоположно этому: если ∠CBA и ∠ABD в сумме дают два прямых угла, то линия CBD является прямой линией. Предложение I.16 гласит: «В любом треугольнике, если одна из сторон произведена, внешний угол больше любого из внутренних и противоположных углов» (Данэм 41). То есть на рисунке 4 ∠DCA больше, чем ∠CBA или ∠BAC. Чтобы доказать это, Евклид разделил пополам отрезок AC линией BF, где BE = EF. Затем он нарисовал отрезок FC. Поскольку AE = EC по делению пополам, BE = EF по построению и ∠1 = ∠2 (поскольку вертикальные углы равны), мы видим, что ∆AEB и ∆CEF конгруэнтны по SAS, постулат I.4.Ясно, что ∠DCA больше, чем ∠FCE, а поскольку ∠FCE = ∠BAE, ∠DCA больше внутреннего угла ∠BAC. Аналогичным образом Евклид показал, что ∠DCA также больше внутреннего угла ∠CBA.
Предложение I.16 гласит: «В любом треугольнике, если одна из сторон произведена, внешний угол больше любого из внутренних и противоположных углов» (Данэм 41). То есть на рисунке 4 ∠DCA больше, чем ∠CBA или ∠BAC. Чтобы доказать это, Евклид разделил пополам отрезок AC линией BF, где BE = EF. Затем он нарисовал отрезок FC. Поскольку AE = EC по делению пополам, BE = EF по построению и ∠1 = ∠2 (поскольку вертикальные углы равны), мы видим, что ∆AEB и ∆CEF конгруэнтны по SAS, постулат I.4.Ясно, что ∠DCA больше, чем ∠FCE, а поскольку ∠FCE = ∠BAE, ∠DCA больше внутреннего угла ∠BAC. Аналогичным образом Евклид показал, что ∠DCA также больше внутреннего угла ∠CBA.
В предложении I.27 Евклид доказал, что «если прямая, падающая на две прямые, делает противоположные углы равными друг другу, прямые будут параллельны» (Данхем 44). Учитывая, что углы 1 и 2 на рис. 5 равны, он предположил, что прямые AB и CD пересекаются в точке G, и искал противоречие.В треугольнике, согласно предложению I.16, внешний угол ∠2 больше любого внутреннего угла. Однако, поскольку ∠1 = ∠2, имеем противоречие. Следовательно, прямые AB и CD никогда не пересекаются и по определению параллельны.
Однако, поскольку ∠1 = ∠2, имеем противоречие. Следовательно, прямые AB и CD никогда не пересекаются и по определению параллельны.
Рисунок 5: Предложение I.27
Другое доказательство конструкции было дано в предложении I.31. Здесь Евклид показал, как построить прямую, параллельную данной прямой, через точку, не принадлежащую данной прямой.
Рисунок 6: Предложение I.32
Предложение I.32 — хорошо известный факт геометрии: три внутренних угла любого треугольника в сумме дают два прямых угла. На рисунке 6 Евклид построил линию CE, параллельную линии BA. Следовательно, ∠1 равно ∠4, а ∠2 равно ∠5, как показано в предложении I.29. Итак, сумма внутренних углов ΔABC составила: ∠1 + ∠2 + ∠3 = ∠4 + ∠5 + ∠3 = 2 прямых угла.
Это уравнение верно, потому что прямая BCD — прямая, равная двум прямым углам по Предложению I.14 (Данхэм 46).
В предложении I.41 Евклид доказал эквивалент уравнения A = ½bh для площади треугольника. Он показал, что если треугольник и параллелограмм имеют общее основание и лежат между одними и теми же параллельными прямыми (то есть имеют одинаковую высоту), то площадь параллелограмма вдвое больше площади треугольника. На рисунке 7 треугольник и параллелограмм делят отрезок базовой линии AB и попадают между параллельными прямыми AB и CD. Согласно предложению I.41, площадь треугольника равна половине площади параллелограмма.
На рисунке 7 треугольник и параллелограмм делят отрезок базовой линии AB и попадают между параллельными прямыми AB и CD. Согласно предложению I.41, площадь треугольника равна половине площади параллелограмма.
Рисунок 7: Предложение I.41
Последней теоремой, необходимой Евклиду для доказательства теоремы Пифагора, было предложение I.46. Здесь он показал, как построить квадрат из заданного отрезка. Следующим предложением было его доказательство теоремы Пифагора.
5. Предложение I.47Теорема: В прямоугольных треугольниках квадрат стороны, опирающейся на прямой угол, равен квадратам сторон, образующих прямой угол (Данэм 48).
В отличие от типичного алгебраического понимания теоремы Пифагора как a² + b² = c², Евклид построил фактические квадраты BCED, ABFG и ACKH из сторон прямоугольного треугольника ΔABC, используя предложение I.46 (рис. 8). Эта форма стала называться «ветряной мельницей», когда доказательство Евклида стало популярным. Евклид стремился доказать, что площадь BCED равна сумме соответствующих площадей ABFG и ACKH.
Евклид стремился доказать, что площадь BCED равна сумме соответствующих площадей ABFG и ACKH.
- Рисунок 8: «Ветряная мельница»
- Рисунок 9: Треугольники ΔABD и ΔFBC
Евклид использовал предложение I.31, чтобы провести линию AL через A параллельно линии BD. Отсюда Евклид стремился доказать, что площадь квадрата ABFG равна площади прямоугольника BDLM, а площадь квадрата ACKH равна площади прямоугольника CELM. Чтобы показать, что отрезки CA и AG лежат на одной прямой, Евклид отметил, что ∠BAC был прямым углом по гипотезе, а ∠GAB был прямым углом по построению квадрата. Таким образом, два угла в сумме дают два прямых угла; по предложению I.14 прямая CG — прямая.
Используя постулат 1, Евклид провел отрезки AD и FC, образовав треугольники ΔABD и ΔFBC (рис. 9). Поскольку они являются сторонами одного квадрата, AB по построению равен FB. Аналогично, BD = BC. Мы видим, что: ∠ABD = ∠ABC + ∠CBD = ∠ABC + (прямой угол)
Аналогично, ∠FBC = ∠ABC + ∠FBA = ∠ABC + (прямой угол)
Следовательно, по постулату 4, который утверждает, что все прямые углы равны: ∠ABD = ∠ABC + (прямой угол) = ∠FBC
По предложению I. 4, доказывающему теорему сторона-угол-сторона, ΔABD и ΔFBC конгруэнтны, поскольку AB = FB, BD = BC и ∠ABD = ∠FBC.Используя предложение I.41, Евклид заметил, что площадь ΔABD и прямоугольника BDLM имеют общий отрезок базовой линии BD и лежат между параллельными прямыми BD и AL. Таким образом, площадь (прямоугольник BDLM) = 2 площади (ΔABD)
4, доказывающему теорему сторона-угол-сторона, ΔABD и ΔFBC конгруэнтны, поскольку AB = FB, BD = BC и ∠ABD = ∠FBC.Используя предложение I.41, Евклид заметил, что площадь ΔABD и прямоугольника BDLM имеют общий отрезок базовой линии BD и лежат между параллельными прямыми BD и AL. Таким образом, площадь (прямоугольник BDLM) = 2 площади (ΔABD)
Точно так же ΔFBC и квадрат ABFG имеют общий отрезок базовой линии BF и попадают между параллельными прямыми BF и CG, поскольку мы показали, что CG действительно является прямой линией. Итак, Площадь (квадрат ABFG) = 2 Площадь (ΔFBC)
Мы уже показали, что ΔABD и ΔFBC конгруэнтны по SAS, поэтому мы можем заключить: Площадь (прямоугольник BDLM) = 2 Площадь (ΔABD) = 2 Площадь (ΔFBC) = Площадь (квадрат ABFG)
Следовательно, площадь (прямоугольник BDLM) = площадь (квадрат ABFG)
Рисунок 10: Треугольники ΔACE и ΔKCB
Евклид наполовину закончил свое доказательство.Затем он использовал аналогичный метод, чтобы показать, что площадь квадрата ACKH равна площади прямоугольника CELM. Отрезки AE и BK он провел так, чтобы получились треугольники ΔACE и ΔKCB (рис. 10). Поскольку ∠BAC — прямой угол по условию, а ∠CAH — прямой по построению, ∠BAH в сумме составляет два прямых угла, и по предложению I.14 прямая BAH — прямая.
Отрезки AE и BK он провел так, чтобы получились треугольники ΔACE и ΔKCB (рис. 10). Поскольку ∠BAC — прямой угол по условию, а ∠CAH — прямой по построению, ∠BAH в сумме составляет два прямых угла, и по предложению I.14 прямая BAH — прямая.
Затем Евклид показал, что ΔACE конгруэнтно ΔKCB. Стороны AC и CK — две стороны одного квадрата, поэтому их длины равны. Точно так же BC и CE равны.Затем он доказал, что ∠KCB = ∠ACE: ∠KCB = ∠BCA + ∠ACK = ∠BCA + (прямой угол). Кроме того, ∠ACE = ∠BCA + ∠BCE = ∠BCA + (прямой угол). Следовательно, ∠KCB = ∠BCA + (прямой угол) = ∠ACE
Поскольку ΔACE и ΔKCB имеют две стороны и их внутренние углы равны, ΔACE конгруэнтно ΔKCB по SAS.
Возвращаясь к предложению I.41, Евклид заметил, что ΔACE и прямоугольник CELM имеют общее основание CE и попадают между параллельными прямыми CE и AL. Таким образом, Площадь (прямоугольник CELM) = 2 Площадь (ΔACE)
Кроме того, ΔKCB и квадрат ACKH имеют общее основание CK и попадают между параллельными прямыми CK и BH, поскольку мы уже доказали, что линия BH является прямой линией.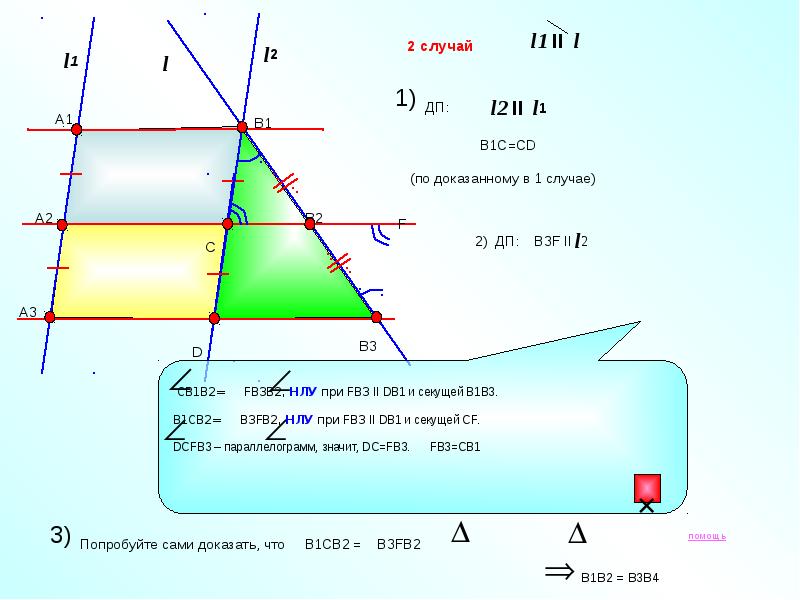 Таким образом, Площадь (квадрат ACKH) = 2 Площадь (ΔKCB)
Таким образом, Площадь (квадрат ACKH) = 2 Площадь (ΔKCB)
Поскольку ΔKCB и ΔACE конгруэнтны, их площади равны: Площадь (прямоугольник CELM) = 2 Площадь (ΔACE) = 2 Площадь (ΔKCB) = Площадь (квадрат ACKH)
Следовательно, площадь (прямоугольник CELM) = площадь (квадрат ACKH)
Наконец, поскольку площадь (квадрат BCED) = площадь (прямоугольник BDLM) + площадь (прямоугольник CELM)
По построениюимеем: Площадь (квадрат BCED) = Площадь (прямоугольник BDLM) + Площадь (прямоугольник CELM) = Площадь (квадрат ABFG) + Площадь (квадрат ACKH)
Итак, мы видим, что площадь квадрата на стороне, противоположной прямому углу, равна сумме площадей квадратов на двух других сторонах.Доказательство Евклида завершено.
6. Предложение I.48Хотя теорема Пифагора хорошо известна, немногие знакомы с доказательством ее обратной. Евклид немедленно последовал за предложением I.47 с доказательством обратной теоремы Пифагора в I.48.
Рисунок 11: Предложение I. 48
48
Теорема: Если в треугольнике квадрат одной из сторон равен квадратам двух оставшихся сторон треугольника, то угол между оставшимися двумя сторонами треугольника прямой.
Из этой гипотезы Евклид построил ΔABC, приняв BC² = AB² + AC² (рис. 11). Затем он показал, что угол ∠BAC прямой. Он провел отрезок AE перпендикулярно AC, используя Предложение I.11. Затем он построил AD = AB и соединил D с C отрезком CD. Теперь у него было два треугольника: ΔBAC и ΔDAC.
Треугольники имеют общую сторону AC, и AD = AB по построению. Поскольку отрезки AC и AE перпендикулярны, угол ∠DAC должен быть прямым. По теореме Пифагора CD² = AD² + AC²
Замена AD = AB, CD² = AD² + AC² = AB² + AC²
Из нашей гипотезы CD² = AB² + AC² = BC²
Поскольку CD² = BC², CD должен быть равен BC.Поскольку все три стороны равны по длине, ΔBAC и ΔDAC конгруэнтны по SSS, предложение I.8. Но если они конгруэнтны, то ∠DAC = ∠BAC, поэтому угол ∠BAC должен быть прямым. Таким образом, обратная теорема Пифагора доказана.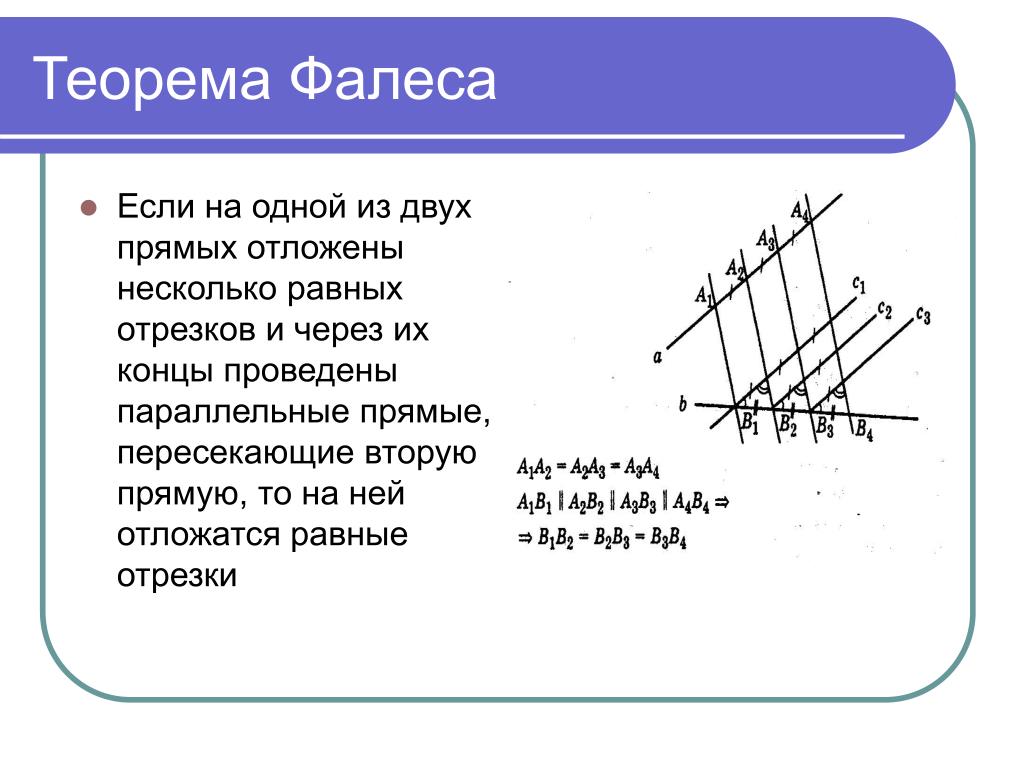
Доказательство Евклидом теоремы Пифагора — лишь одно из 465 доказательств, включенных в «Элементы». В отличие от многих других доказательств в его книге, этот метод, скорее всего, был его собственной работой. Его доказательство уникально по своей организации, оно использует только определения, постулаты и предложения, истинность которых он уже доказал.Доказательство Евклида использует геометрический подход, а не алгебраический; обычно теорема Пифагора рассматривается в терминах a² + b² = c², а не в виде реальных квадратов. Другие предложения в «Элементах» содержат тот же уровень организации, ясности и изобретательности, что и предложения I.47 и I.48. «Начала» Евклида — математический шедевр, вполне заслуживающий внимания.
Процитировано работ
Данэм, Уильям. «Доказательство Евклида теоремы Пифагора». Путешествие через гениев: великие теоремы математики.Нью-Йорк: Wiley Science Editions, 1990. 27–60. Распечатать.
Колпас, Сид Дж. «Математическое сокровище: доказательство теоремы Пифагора Джеймса А. Гарфилда». Математическая ассоциация Америки.
Математическая ассоциация Америки, 2016. Интернет. 9 апреля 2017 г.
Теорема о центральном угле. В геометрии центральный угол опирается… | by Wojciech Wieczorek
В геометрии центральный угол, опирающийся на дугу, в два раза больше любого вписанного угла той же дуги.
Если бы ваш учитель математики начал урок с вопроса о ваших ассоциациях с теоремой о центральном угле, вы бы ответили, говоря о теореме Фалеса? Если да, то ответ будет: «Да, но только на одну треть.Это потому, что дуга, на которую можно опираться вписанным углом, может иметь полуокружность, большую или малую длину. Полукруг известен как теорема Фалеса. И мы начнем сначала с его объяснения; но непосредственно перед началом, для удобства чтения, давайте ознакомимся с определениями, которые будут использоваться.
Вершина: точка пересечения двух линий (в нашем случае).
Диаметр: Любой отрезок прямой линии, проходящий через центр окружности и концы которого лежат на этой окружности.Существует бесконечное количество возможностей для его рисования.
Хорда: отрезок прямой линии, соединяющий любые две точки на окружности, где диаметр является самым длинным.
Дуга: часть окружности круга.
Центральный угол: угол в центре круга между двумя радиусами.
Вписанный угол: угол вершины окружности между ее хордами.
Угол, образуемый дугой: Вершина, концы хорд которой охватывают данную дугу.
Когда диаметр проходит через центр окружности, то центральный угол, образуемый дугой полуокружности, равен просто 180° , без сомнения. И, если теория верна, любой вписанный угол, концы хорд которого лежат в соответствующих концах этого диаметра, должен быть вдвое меньше — 90° . Таким образом, у нас получился бы прямоугольный треугольник, где диаметр — это гипотенуза.
Таким образом, у нас получился бы прямоугольный треугольник, где диаметр — это гипотенуза.
Обозначим концы диаметра как A и A’, их углы как α и α’, и вершину этого вписанного угла, ß , как B. Соединив их, мы получили треугольник. Более того, это будет прямоугольный треугольник, так как вписанный угол прямой; с диаметром, являющимся его гипотенузой.
Это выглядит так:
Готовы? Устойчивый? Идти! Чтобы доказать эту чрезвычайно полезную теорему.
Геометрическое доказательство для удобства
Обратите внимание, что отрезки от центра O окружности до вершин являются ее радиусами. И они делят треугольник AA’B на два других, но не на любые треугольники.Они должны быть равнобедренными, потому что у каждого две равные стороны, равные радиусу нашей окружности.
При этом оба угла между сторонами радиуса и 3-м коленом должны быть равны; следовательно, ß=α+α’.
А мы знаем, что сумма углов треугольника равна 180° . Сложив все треугольники AA’B , мы получим:
Итак, действительно угол ß прямой.
qed
Доказательство Пифагора для небольшого развлечения
Первоначально я назвал этот раздел «Доказательство Пифагора», но мне так понравилось его писать, что пришлось обозначить дополнительное «для небольшого развлечения». здесь.
Считаем, что вписанный угол ∠ABA’, вдвое меньше центрального угла, прямой. Если это так, то должна выполняться теорема Пифагора.
Не беспокойтесь об угле θ ; это будет объяснено через секунду, но сначала давайте применим формулу, чтобы показать то, что мы пытаемся доказать, а именно:
Это θ — это просто угол, на который линия наклонена от начала координат. Вот и все.
Вот и все.
Имея его, мы могли разложить нашу линию на составляющие по оси.И с небольшой помощью тригонометрии мы смогли их вычислить: компонент, записанных таким образом, известны как полярные координаты.
Вернемся к самому доказательству. Нам нужно разложить стороны по прямому углу на x, y -компонент, а затем по теореме Пифагора соединить обе их длины.
Длина AB :
Обратите внимание, что компонент x- представляет собой сложение r и r ⋅ cosθ .В то время как и состоят из одного значения.
Длина A’B :
Здесь стоит упомянуть длину x-компоненты, в отличие от той же ранее, заставляющей нас вычесть из r r ⋅ cosθ .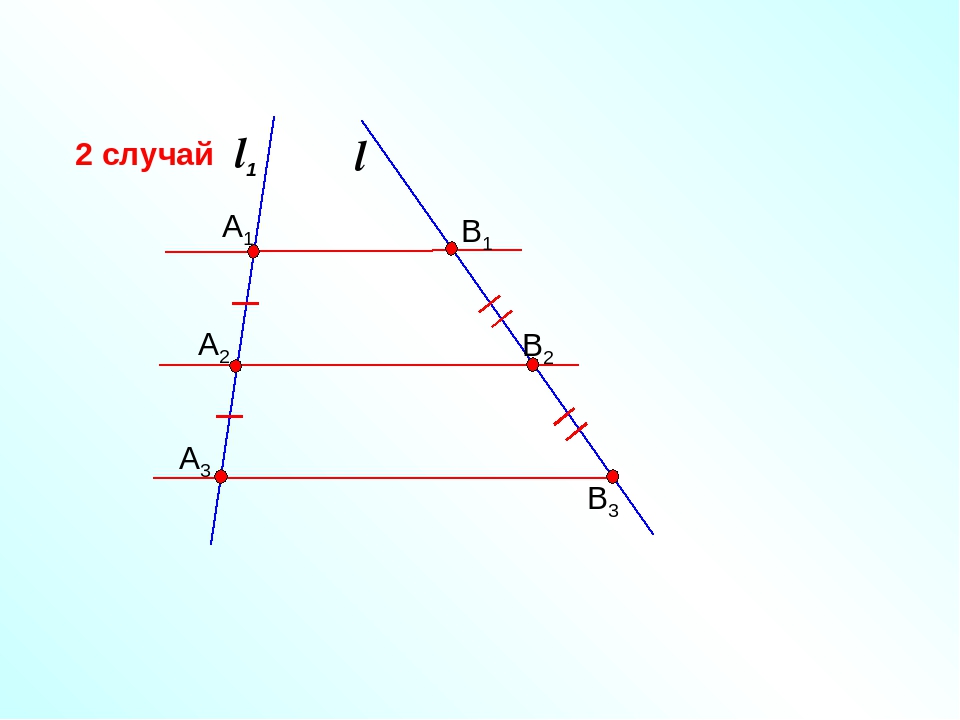 Также посмотрите и сравните y-компоненты: они равны. Что, если подумать об этом, не должно быть сюрпризом.
Также посмотрите и сравните y-компоненты: они равны. Что, если подумать об этом, не должно быть сюрпризом.
Теперь мы можем вернуться к нашей исходной формуле, подставить эти значения и проверить, равны ли ее стороны или нет.
Как видно, все правильно — так и будет.
q.e.d
Что отличает большой (и малый) случай от случая Фалеса, так это тот факт, что теперь радиусы не образуют диаметр. Эти радиусы создают больший центральный угол, чем 180° . Это означает, что, если теорема все еще верна, любой вписанный угол, меньший в два раза, больше, чем 90° .
Это выглядит так:
Геометрическое доказательство
Для доказательства этого (и следующего) случая необходимы три вещи.Два из них нам уже известны: Отрезки от центра окружности до каждой вершины — это радиусы. И они делят нашу фигуру на два равнобедренных треугольника. Но какой третий?
И они делят нашу фигуру на два равнобедренных треугольника. Но какой третий?
Если «скопировать» OB, и повернуть вокруг перпендикулярной оси, отметив противоположную точку на окружности как B’ , то получится диаметр.
Теперь, проведя по одной дополнительной хорде от B’ к каждому A и A’ , мы могли бы разделить всю эту задачу на две, скажем, левую и правую.Где оба могут быть исследованы по теореме Фалеса, потому что BB’ — это диаметр, центральный угол равен 180° , а вписанный угол ∠BAB’ и ∠BA’B’ равен 90° . Конечно, ABB’ , A’BB’ — прямоугольные треугольники.
Левый выглядит так:
Найдя угол ∠AOB’ , мы узнаем, какова левая часть центрального угла. Что это может быть? Угол ∠BAB’ равен 90° , но так как его верхняя часть равна α , то нижняя часть должна быть 90°-α , а угол ∠AB’O должен быть таким же ! Итак, суммируя углы нижнего треугольника, получаем:
Что это может быть? Угол ∠BAB’ равен 90° , но так как его верхняя часть равна α , то нижняя часть должна быть 90°-α , а угол ∠AB’O должен быть таким же ! Итак, суммируя углы нижнего треугольника, получаем:
Таким образом, левая часть центрального угла действительно в два раза больше α.
Разложенная правая часть выглядит так:
И делаем все так же, как и с левой частью, получаем:
Значит, действительно, центральный угол в два раза больше любого вписанного, опирающегося на ту же дугу.
ч.д.д
Последний случай, когда центральный угол меньше 180° . Все шаги идентичны основному случаю. Но сначала давайте посмотрим, как это выглядит:
Геометрическое доказательство
Что мы делаем, так это предоставляем диаметр BB’ , который снова разделит нашу задачу на левую и правую части.
Левый:
Угол ∠BAB’ равен 90° , а его верхняя часть α . Таким образом, нижняя часть должна быть 90°-α. Угол ∠AB’O должен быть точно таким же. Таким образом, сумма углов нижнего треугольника:
После применения ситуация следующая:
Правый:
И в последний раз вписанный угол ∠BA’B’ равен 90 ° . Поскольку его верхняя часть равна α’ , нижняя должна быть равна 90°-α’ .Также угол ∠A’B’O имеет такой же размер. Суммируя углы нижнего треугольника, мы получаем:
, что дает:
Итак, в этом случае теорема о центральном угле также работает.
qed
Геометрия — 1206310 | CPALMS.org
Угол ВВЕРХ: Игрок 1:В этом интерактивном учебном пособии в стиле ретро-видеоигры изучите процессы построения для построения биссектрисы угла, копирования угла и построения линии, параллельной заданной линии, через точку, не лежащую на этой линии, с помощью различных инструментов.
ПРИМЕЧАНИЕ. В этом учебном пособии используется как построение биссектрисы угла, так и построение для копирования угла в качестве возможности расширения, чтобы также построить линию, параллельную заданной линии, через точку, не находящуюся на линии. Учащиеся также учатся определять соответствующие углы, образующиеся при пересечении секущей параллельных прямых, и обнаруживают с помощью Geogebra, что эти углы равны.
Тип: Оригинальное учебное пособие для учащихся
Круглогодичные школьные дебаты: выявление ошибочных рассуждений — часть вторая: Это вторая часть серии из двух частей. Научитесь выявлять ошибочные рассуждения в этой серии интерактивных руководств. Вы узнаете, что некоторые эксперты говорят о круглогодичных школах, какие исследования были проведены по поводу их эффективности и какие аргументы можно привести за и против круглогодичного обучения. Затем вы прочитаете речь в пользу круглогодичных школ и определите ошибочные рассуждения в аргументе, в частности использование поспешных обобщений.
Научитесь выявлять ошибочные рассуждения в этой серии интерактивных руководств. Вы узнаете, что некоторые эксперты говорят о круглогодичных школах, какие исследования были проведены по поводу их эффективности и какие аргументы можно привести за и против круглогодичного обучения. Затем вы прочитаете речь в пользу круглогодичных школ и определите ошибочные рассуждения в аргументе, в частности использование поспешных обобщений.
Обязательно завершите первую часть перед второй! Нажмите ЗДЕСЬ , чтобы запустить первую часть.
Тип: Оригинальное учебное пособие для учащихся
Вымпел компании Challenge: вписанные круги треугольников: Узнайте, как легко Кэти создает круговой логотип с надписью на шаблоне треугольного вымпела своей компании. Если она выполнит задание первой, она выиграет бонус в размере 1000 долларов США! Следуйте этому интерактивному руководству.
Если она выполнит задание первой, она выиграет бонус в размере 1000 долларов США! Следуйте этому интерактивному руководству.
Тип: Оригинальное учебное пособие для учащихся
Круглогодичные школьные дебаты: выявление ошибочных рассуждений — часть первая:Научитесь выявлять ошибочные рассуждения в этом интерактивном учебном пособии по английскому языку, состоящем из двух частей. Вы узнаете, что некоторые эксперты говорят о круглогодичных школах, какие исследования были проведены по поводу их эффективности и какие аргументы можно привести за и против круглогодичного обучения.Затем вы прочитаете речь в пользу круглогодичных школ и определите ошибочные рассуждения в аргументе, в частности использование поспешных обобщений.
Обязательно завершите обе части этой серии! Нажмите ЗДЕСЬ , чтобы открыть вторую часть.
Тип: Оригинальное учебное пособие для учащихся
Встретить меня на полпути:Спланируйте экспедицию на байдарке, научившись выполнять основные геометрические построения, включая копирование сегмента, построение биссектрисы сегмента, построение перпендикулярной биссектрисы сегмента и построение перпендикулярных сегментов с помощью различных инструментов в этом интерактивном учебном пособии.
Тип: Оригинальное учебное пособие для учащихся
Оценка аргумента – Часть четвертая: Инаугурационная речь Джона Кеннеди: Изучите инаугурационную речь президента Джона Ф. Кеннеди в этом интерактивном руководстве. Вы изучите аргумент Кеннеди, основное утверждение, более мелкие утверждения, причины и доказательства.
Кеннеди в этом интерактивном руководстве. Вы изучите аргумент Кеннеди, основное утверждение, более мелкие утверждения, причины и доказательства.
В четвертой части вы будете использовать то, что вы узнали из этой серии, чтобы оценить общую аргументацию Кеннеди.
Обязательно завершите предыдущие части этой серии перед тем, как приступить к части 4.
- Нажмите ЗДЕСЬ , чтобы запустить первую часть.
- Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
- Нажмите ЗДЕСЬ , чтобы запустить третью часть.
Тип: оригинальное учебное пособие для учащихся
Человек не на своем месте: Узнайте, как построить вписанный квадрат в круг и почему в этом интерактивном руководстве используются определенные конструкции.
Тип: Оригинальное учебное пособие для учащихся
Оценка аргумента – Часть третья: Инаугурационная речь Джона Кеннеди:Изучите инаугурационную речь президента Джона Ф. Кеннеди в этом интерактивном руководстве. Вы изучите аргумент Кеннеди, основное утверждение, более мелкие утверждения, причины и доказательства.К концу этой серии из четырех частей вы должны быть в состоянии оценить его общую аргументацию.
В третьей части вы прочтете больше о речи Кеннеди и определите меньшее утверждение в этом разделе его речи. Вы также оцените соответствие этого меньшего утверждения основному утверждению и оцените причины и доказательства Кеннеди.
Обязательно выполните все четыре части этой серии!
- Нажмите ЗДЕСЬ , чтобы запустить первую часть.

- Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
- Нажмите ЗДЕСЬ , чтобы запустить четвертую часть.
Тип: оригинальное учебное пособие для учащихся
Где эта вышка сотовой связи?:Найдите расположение и зону покрытия вышек сотовой связи, чтобы определить центр и радиус круга по его уравнению, используя стратегию заполнения квадрата в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Проектирование с помощью шестиугольников: Узнайте, как построить вписанный правильный шестиугольник и равносторонний треугольник в окружность в этом интерактивном учебном пособии.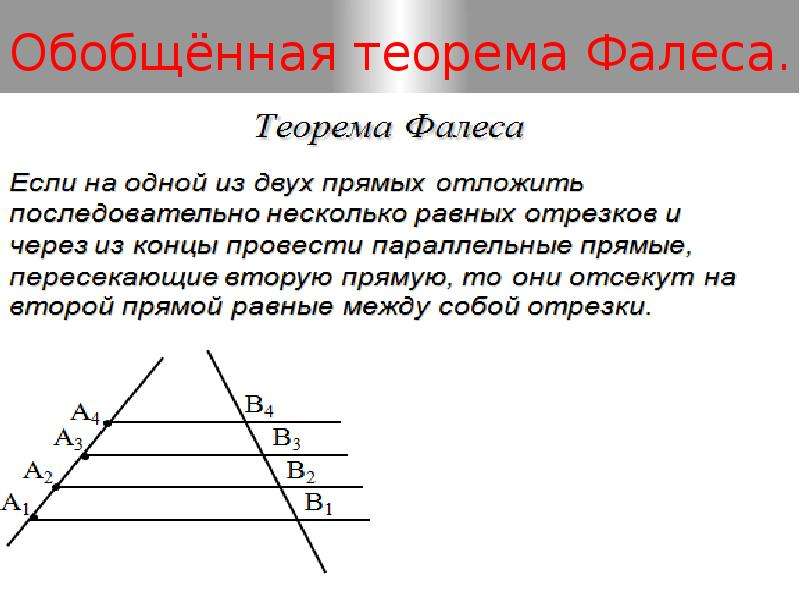
Тип: Оригинальное учебное пособие для учащихся
Как новый:Узнайте, как описать окружность вокруг треугольника в этом интерактивном руководстве по конструкциям.Возьмите циркуль, линейку, карандаш и бумагу, чтобы следовать!
Тип: Оригинальное учебное пособие для учащихся
Высокотехнологичные качели:В этом интерактивном учебном пособии вы узнаете, как найти точку на направленном отрезке, которая делит его в заданном отношении.
Тип: Оригинальное учебное пособие для учащихся
Круг вверх!: Узнайте, как написать уравнение окружности, используя теорему Пифагора , зная ее центр и радиус, используя пошаговые инструкции в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Готов к взлету! — Часть вторая:Это вторая часть серии руководств, состоящей из двух частей.В этом интерактивном учебном пособии вы потренируетесь определять цель говорящего, используя речь пионера авиации Амелии Эрхарт. Вы изучите использование ею риторических призывов, включая этос, логос, пафос и кайрос. Наконец, вы оцените эффективность использования Эрхартом риторических призывов.
Обязательно сначала выполните первую часть. Щелкните здесь, чтобы запустить ЧАСТЬ ПЕРВУЮ.
Тип: Оригинальное учебное пособие для учащихся
Готов к взлету! — Первая часть: Это первая часть серии руководств, состоящей из двух частей. В этом интерактивном учебном пособии вы потренируетесь определять цель говорящего, используя речь пионера авиации Амелии Эрхарт. Вы изучите использование ею риторических призывов, включая этос, логос, пафос и кайрос. Наконец, вы оцените эффективность использования Эрхартом риторических призывов.
В этом интерактивном учебном пособии вы потренируетесь определять цель говорящего, используя речь пионера авиации Амелии Эрхарт. Вы изучите использование ею риторических призывов, включая этос, логос, пафос и кайрос. Наконец, вы оцените эффективность использования Эрхартом риторических призывов.
Щелкните здесь, чтобы запустить ЧАСТЬ ВТОРАЯ .
Тип: Оригинальное учебное пособие для учащихся
Описательное письмо: Глаза в небе (часть 4 из 4): Попрактикуйтесь в написании различных аспектов описательного эссе об ученых, использующих дроны для исследования ледников в Перу.Этот интерактивный учебник является четвертой частью серии из четырех частей. В этом заключительном уроке вы узнаете об элементах основного абзаца. Вы также создадите основной абзац с подтверждающими доказательствами. Наконец, вы узнаете об элементах заключения и потренируетесь в создании «подарка».
Вы также создадите основной абзац с подтверждающими доказательствами. Наконец, вы узнаете об элементах заключения и потренируетесь в создании «подарка».
Это руководство является четвертой частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Описательное письмо: Глаза в небе (часть 3 из 4): Узнайте, как написать введение для описательного эссе в этом интерактивном руководстве.Этот учебник является третьей частью серии из четырех частей. В предыдущих уроках этой серии учащиеся проанализировали информационный текст и видео об ученых, использующих дроны для исследования ледников в Перу. Студенты также определили центральную идею и важные детали текста и написали эффективное резюме. В третьей части вы узнаете, как написать введение для описательного эссе об исследованиях ученых.
В третьей части вы узнаете, как написать введение для описательного эссе об исследованиях ученых.
Это руководство является третьей частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Чертежи строительства:С помощью этого интерактивного учебного пособия вы научитесь строить биссектрису отрезка прямой с помощью линейки и циркуля.
Тип: Оригинальное учебное пособие для учащихся
Сравнение митоза и мейоза: Сравните и сопоставьте митоз и мейоз в этом интерактивном руководстве. Вы также свяжете их с процессами полового и бесполого размножения и их последствиями для генетической изменчивости.
Вы также свяжете их с процессами полового и бесполого размножения и их последствиями для генетической изменчивости.
Тип: Оригинальное учебное пособие для учащихся
Кусочки ниндзя Нэнси:Узнайте, как определить форму поперечного сечения, созданного пересечением секущей плоскости с пирамидой или призмой, в этом интерактивном учебном пособии на тему ниндзя.
Тип: Оригинальное учебное пособие для учащихся
Вокруг света с прямоугольными треугольниками: В этом интерактивном учебном пособии вы узнаете, как использовать тригонометрические соотношения для определения высоты известных памятников и решить задачу из реальной жизни.
Тип: Оригинальное учебное пособие для учащихся
Доказательство теорем о треугольниках:Используйте свойства, постулаты и теоремы, чтобы доказать теорему о треугольнике.В этом интерактивном уроке вы также узнаете, как доказать, что линия, параллельная одной стороне треугольника, пропорционально делит две другие стороны.
Тип: Оригинальное учебное пособие для учащихся
Рак: мутировавшие клетки вышли из-под контроля!: Изучите взаимосвязь между мутациями, клеточным циклом и неконтролируемым ростом клеток, который может привести к раку, с помощью этого интерактивного руководства.
Тип: Оригинальное учебное пособие для учащихся
Банковский выстрел:В этом задании учащимся предлагается использовать сходство для решения задачи в контексте, который будет знаком многим, хотя большинство учащихся привыкли использовать интуицию, а не геометрические рассуждения, для подготовки кадра.
Тип: Задача решения проблем
Они похожи?: В этой задаче учащимся дается изображение двух треугольников, которые кажутся подобными, но сходство которых нельзя доказать без дополнительной информации. Попросите учащихся предоставить последовательность преобразований подобия, которая отображает один треугольник в другой, используя определение подобия в терминах преобразований подобия.
Попросите учащихся предоставить последовательность преобразований подобия, которая отображает один треугольник в другой, используя определение подобия в терминах преобразований подобия.
Тип: Задача решения проблем
Рулон туалетной бумаги:Целью этого задания является привлечение учащихся к геометрическому моделированию и, в частности, к выводу алгебраических взаимосвязей между переменными, вытекающими из геометрических ограничений.
Тип: Задача решения проблем
Монеты по кругу: Используя таблицу диаметров монет разного достоинства, учащихся просят определить, сколько монет помещается вокруг центральной монеты.
Тип: Задача решения проблем
Проблема с маяком:В этой задаче учащимся предлагается смоделировать явления на поверхности земли, исследуя видимость лампы маяка с лодки.
Тип: Задача решения проблем
Солнечное затмение: Это задание на решение задач побуждает учащихся исследовать, почему солнечные затмения случаются редко, путем изучения радиуса Солнца и самого дальнего расстояния между Луной и Землей.
Тип: Задача решения проблем
Чудо средней точки:Это задание на решение проблемы дает учащимся возможность доказать факт о четырехугольниках: если мы соединим середины произвольного четырехугольника, чтобы образовать новый четырехугольник, то новый четырехугольник будет параллелограммом, даже если первоначальный четырехугольник таковым не был.
Тип: Задача решения проблем
От горы Уитни до Долины Смерти: Это задание вовлекает учащихся в открытое задание по моделированию, в котором используется подобие прямоугольных треугольников.
Тип: Задача решения проблем
Кратчайший отрезок линии от точки P до линии L:Это базовое задание по геометрии, предназначенное для того, чтобы помочь учащимся развить некоторые основные геометрические свойства, которые на первый взгляд могут показаться довольно очевидными.В этом случае основное свойство, о котором идет речь, состоит в том, что кратчайший путь от точки к линии встречается с линией под прямым углом, что имеет решающее значение для многих дальнейших разработок предмета.
Тип: Задача решения проблем
Семь кругов III: Это дает возможность смоделировать конкретную ситуацию с помощью математики. После того, как репрезентативная картина ситуации, описанной в задаче, будет нарисована (преподаватель может дать здесь указания по мере необходимости), решение задачи требует понимания определения функции синуса.
После того, как репрезентативная картина ситуации, описанной в задаче, будет нарисована (преподаватель может дать здесь указания по мере необходимости), решение задачи требует понимания определения функции синуса.
Тип: Задача решения проблем
Расширение линии:В этом задании учащимся предлагается сделать выводы о линии после того, как она была увеличена в 2 раза.
Тип: Задача решения проблем
Бег по дорожке II: Цель этого задания — смоделировать знакомый объект, олимпийскую трассу, используя геометрические фигуры. Расчеты периметров этих фигур объясняют ступенчатый старт бегунов в беге на 400 метров.
Расчеты периметров этих фигур объясняют ступенчатый старт бегунов в беге на 400 метров.
Тип: Задача решения проблем
Бег по дорожке I:В этой задаче геометрия применяется к 400-метровой дорожке, чтобы найти ее периметр.
Тип: Задача решения проблем
Скрепка: В этом задании типографская сетка служит фоном для стандартной скрепки.Метрическая шкала измерений нарисована поперек нижней части сетки, а скрепка проходит в обоих направлениях немного за пределы сетки. Ученикам дают примерную длину скрепки и определяют количество одинаковых скрепок, сделанных из проволоки заданной длины.
Ученикам дают примерную длину скрепки и определяют количество одинаковых скрепок, сделанных из проволоки заданной длины.
Тип: Задача решения проблем
Рожок мороженого:В этом задании учащиеся сделают набросок бумажной обертки от рожка для мороженого, с помощью этого наброска выведут формулу площади поверхности обертки и оценят максимальное количество оберток, которые можно вырезать из прямоугольного листа бумаги. .
Тип: Задача решения проблем
Насколько толстая банка газировки? (Вариант I): В этом задании на решение задач учащиеся должны найти площадь поверхности банки из-под газировки, вычислить, сколько кубических сантиметров алюминия она содержит, и оценить ее толщину.
Тип: Задача решения проблем
Сколько листьев на дереве? (Версия 2):Это задача математического моделирования, направленная на разумную оценку чего-то, что слишком велико для точного подсчета, а именно количества листьев на дереве.
Тип: Задача решения проблем
Сколько листьев на дереве?: Это задача математического моделирования, направленная на разумную оценку чего-то, что слишком велико для точного подсчета, а именно количества листьев на дереве.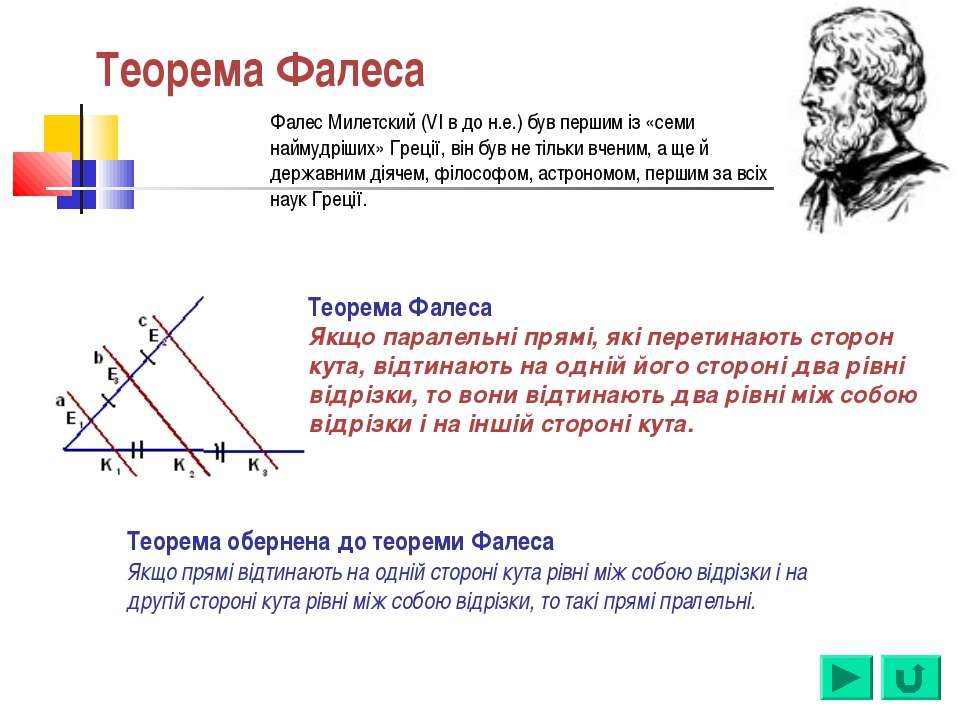
Тип: Задача решения проблем
Сколько клеток в теле человека?:В этом задании по решению проблем учащимся предлагается применить понятия массы, объема и плотности в контексте реального мира, чтобы определить, сколько клеток содержится в организме человека.
Тип: Задача решения проблем
Глобальная система позиционирования II: Отражая современность используемых технологий, это сложная задача по геометрическому моделированию, в которой учащиеся с нуля открывают для себя геометрические принципы, лежащие в основе программного обеспечения, используемого системами GPS.
Тип: Задача решения проблем
Архимед и королевская корона:В этом задании на решение задач используется сказка об Архимеде и короне царя Сиракуз, чтобы определить объем и массу золота и серебра.
Тип: Задача решения проблем
Склоны и круги:Цель этого задания — познакомить учащихся с алгебраическим подходом к хорошо известному результату классической геометрии, а именно к тому, что точка X лежит на окружности диаметра AB, если угол ?AXB прямой
Тип: Задача решения проблем
Единичные квадраты и треугольники: В этом задании на решение задач учащимся предлагается найти площадь треугольника, используя единичные квадраты и отрезки.
Тип: Задача решения проблем
Треугольники, вписанные в окружность:Это задание на решение проблем побуждает учащихся использовать идеи о линейных функциях, чтобы определить, когда определенные углы являются прямыми углами.
Тип: Задача решения проблем
Прием у доктора: Целью задания является анализ правдоподобного сценария реальной жизни с использованием геометрической модели. Задача требует знания формул объема для цилиндров и конусов, некоторых геометрических рассуждений, связанных с подобными треугольниками, а также уделяет внимание разумным приближениям и поддержанию разумного уровня точности во всем.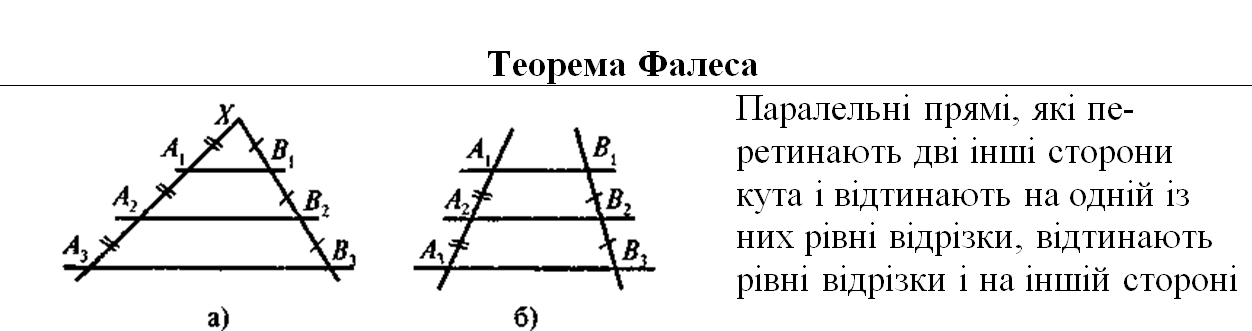
Тип: Задача решения проблем
Почему АСА работает?:В этом задании на решение задач учащимся предлагается показать отражение одного треугольника в другом треугольнике.
Тип: Задача решения проблем
Когда SSA работает для определения конгруэнтности треугольников?: В этой задаче мы рассматривали SSA.Критерии соответствия треугольника, SSS, SAS, ASA, требуют трех частей информации. Интересно, однако, что не всех трех частей информации о сторонах и углах достаточно, чтобы определить треугольник с точностью до конгруэнтности.
Тип: Задача решения проблем
Семь кругов II:Эта задача обеспечивает конкретную геометрическую постановку для изучения жестких преобразований плоскости.
Тип: Задача решения проблем
Середины сторон параллелограмма: Это довольно прямое задание, направленное на то, чтобы учащиеся использовали ранее полученные результаты для изучения новых фактов о параллелограммах, а не для получения их из первых принципов.
Тип: Задача решения проблем
Вписывание квадрата в круг:Это задание дает учащимся возможность применить теоремы о конгруэнтности треугольников в явном, интересном контексте.
Тип: Задача решения проблем
Вписывание шестиугольника в окружность:В этом задании на решение задач учащимся предлагается вписать равносторонние треугольники и правильные шестиугольники в круг с помощью циркуля и линейки.
Тип: Задача решения проблем
Почему SAS работает?: В этом задании на решение задач учащимся предлагается объяснить, почему данные треугольники равны, и построить отражения точек.
Тип: Задача решения проблем
Отражения и равносторонние треугольники II:Это задание дает учащимся возможность увидеть влияние отражений на явный объект и увидеть, что отражения не всегда коммутируют.
Тип: Задача решения проблем
Отражения и равносторонние треугольники:Это задание является одним из серии заданий, использующих жесткие преобразования плоскости для изучения симметрии классов треугольников, при этом особое внимание в этом задании уделяется классу равносторонних треугольников
Тип: Задача решения проблем
Отраженные треугольники: В этом задании учащимся предлагается с помощью линейки и циркуля построить линию, через которую отражается треугольник.
Тип: Задача решения проблем
Центральная часть:Целью этого задания является использование геометрических и алгебраических рассуждений для моделирования реального сценария. В частности, учащиеся в нескольких местах (явно или неявно) должны рассуждать о том, когда делать приближения разумно и когда округлять, когда использовать равенство или равенство.неравенства и выбор единиц измерения для работы (например, мм против см).
Тип: Задача решения проблем
Теннисные мячи в банке: Эта задача основана на выводе формулы объема сферы. Если сфера радиуса 1 заключена в цилиндр радиуса 1 и высоты 2, то объем, не занимаемый сферой, равен объему «двухвершинного конуса» с вершиной в центре сферы и основаниями, равными к основаниям цилиндра
Если сфера радиуса 1 заключена в цилиндр радиуса 1 и высоты 2, то объем, не занимаемый сферой, равен объему «двухвершинного конуса» с вершиной в центре сферы и основаниями, равными к основаниям цилиндра
Тип: Задача решения проблем
Два колеса и ремень:В этом задании сочетаются два навыка: использование отношения между касательным сегментом к окружности и радиусом, касающимся этого касательного сегмента, и вычисление длин дуг окружности с учетом радиусов и центральных углов.
Тип: Задача решения проблем
Прямоугольные треугольники, вписанные в окружности I: Это задание дает хорошую возможность использовать равнобедренные треугольники и их свойства, чтобы показать интересный и важный результат о треугольниках, вписанных в окружность: тот факт, что эти треугольники всегда прямоугольные, часто называют теоремой Фалеса.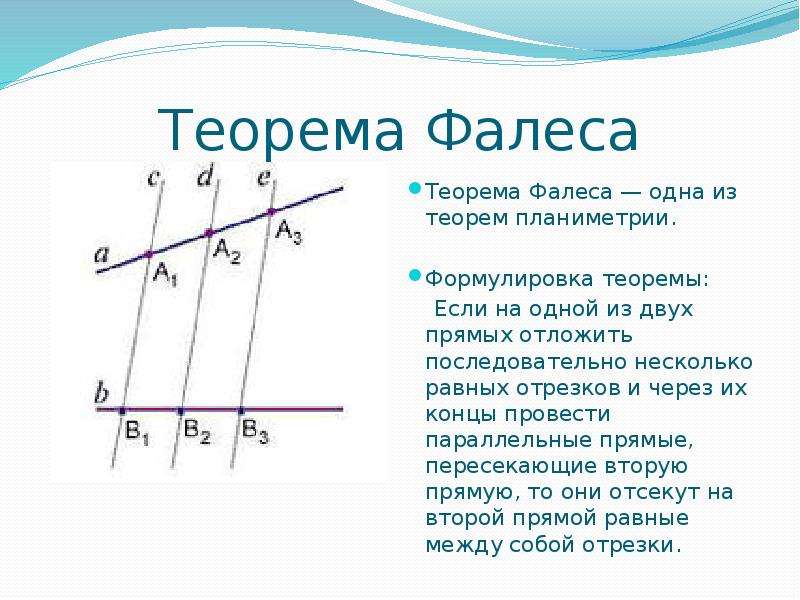
Тип: Задача решения проблем
Размещение пожарного гидранта:В этом задании на решение задач учащимся предлагается разместить пожарный гидрант на равном расстоянии от трех заданных точек.
Тип: Задача решения проблем
Почему SSS работает?:Эта конкретная задача по решению проблем демонстрирует соответствие между двумя треугольниками, демонстрируя перемещение, отражение и вращение.
Тип: Задача решения проблем
Построение рисунка плитки путем отражения восьмиугольников: В этом задании отражения применяются к правильному восьмиугольнику, чтобы построить шаблон из четырех восьмиугольников, охватывающих четырехугольник: основное внимание в задании уделяется использованию свойств отражений для вывода о том, что четырехугольник на самом деле является квадратом.
Тип: Задача решения проблем
Построение рисунка плитки путем отражения шестиугольников:В этом задании отражения применяются к правильному шестиугольнику, чтобы построить шаблон из шести шестиугольников, заключающих в себе седьмой: основное внимание в задании уделяется использованию свойств отражений для получения этого шаблона из семи шестиугольников.
Тип: Задача решения проблем
Разделение угла пополам: В этом задании на решение учащимся предлагается разделить заданный угол пополам.
Тип: Задача решения проблем
Конгруэнтны ли треугольники?:Цель этого задания в первую очередь ориентирована на оценивание: учащимся предлагается продемонстрировать знания о том, как определять конгруэнтность треугольников.
Тип: Задача решения проблем
Расположение склада:В этом задании на решение задач учащимся предлагается разместить склад (точку) на равном расстоянии от трех дорог (линий).
Тип: Задача решения проблем
Вписывание треугольника в окружность: Эта задача знакомит с центром описанной окружности треугольника и показывает, как его можно использовать для вписания треугольника в окружность.
Тип: Задача решения проблем
Центр окружности треугольника:Эта задача показывает, что все три серединных перпендикуляра сторон треугольника пересекаются в одной точке, используя характеристику биссектрисы отрезка как множества точек, равноудаленных от двух концов отрезка.
Тип: Задача решения проблем
Касательные линии и радиус окружности: В этом задании на решение задач учащимся предлагается найти точку пересечения перпендикуляра отрезка из центра окружности и касательной.
Тип: Задача решения проблем
Семь кругов I:Это задание предназначено для моделирования конкретной ситуации с геометрией. Размещение семи монет в виде круга — это конкретный и забавный эксперимент, который приводит к подлинному математическому вопросу: дает ли физическая модель с монетами понимание того, что происходит с семью кругами на плоскости?
Тип: Задача решения проблем
Установка разбрызгивателей: Эта задача моделирования включает в себя несколько различных типов геометрических знаний и решение задач: нахождение площадей секторов окружностей, использование тригонометрических соотношений для решения прямоугольных треугольников и разложение сложной фигуры, включающей несколько дуг окружности, на части, площади которых можно найти.
Тип: Задача решения проблем
Пренебрегая кривизной Земли:В этом задании геометрические понятия, а именно свойства касательных окружностей и прямоугольных треугольников, применяются в ситуации моделирования. Ключевым геометрическим моментом в этой задаче является признание того, что линия обзора от вершины горы к горизонту касается земли.Затем мы можем использовать прямоугольный треугольник, в котором одна сторона касается окружности, а другая сторона является радиусом окружности, чтобы исследовать эту ситуацию.
Тип: Задача решения проблем
Разделение пополам угла и середины отрезков: Эта задача обеспечивает построение биссектрисы угла путем сведения ее к биссектрисе угла с нахождением середины отрезка. Стоит соблюдать симметрию — как для нахождения середины, так и для биссектрисы цель состоит в том, чтобы разрезать объект на две равные части.
Стоит соблюдать симметрию — как для нахождения середины, так и для биссектрисы цель состоит в том, чтобы разрезать объект на две равные части.
Тип: Задача решения проблем
Вписывая окружность в треугольник II:Это задание на решение проблемы фокусируется на замечательном факте, который вытекает из построения вписанной окружности в треугольник: все биссектрисы трех углов треугольника ABC пересекаются в одной точке.
Тип: Задача решения проблем
Регулярные замощения плоскости: В этом задании исследуются способы покрытия плоскости правильными многоугольниками в очень строгом порядке, называемом правильной мозаикой. Эти мозаики изучаются здесь с помощью алгебры, которая входит в картину через формулу измерения внутренних углов правильного многоугольника (которую, следовательно, следует ввести или повторить перед началом задачи). Цель задания — с помощью алгебры понять, какие замощения плоскости правильными многоугольниками возможны.
Эти мозаики изучаются здесь с помощью алгебры, которая входит в картину через формулу измерения внутренних углов правильного многоугольника (которую, следовательно, следует ввести или повторить перед началом задачи). Цель задания — с помощью алгебры понять, какие замощения плоскости правильными многоугольниками возможны.
Тип: Задача решения проблем
Нахождение равных треугольников:В этом учебном пособии учащиеся будут использовать постулаты SSS, ASA, SAS и AAS для нахождения конгруэнтных треугольников
Тип: Учебник
Использование SSS в доказательстве: В этом руководстве обсуждается разница между теоремой и аксиомой.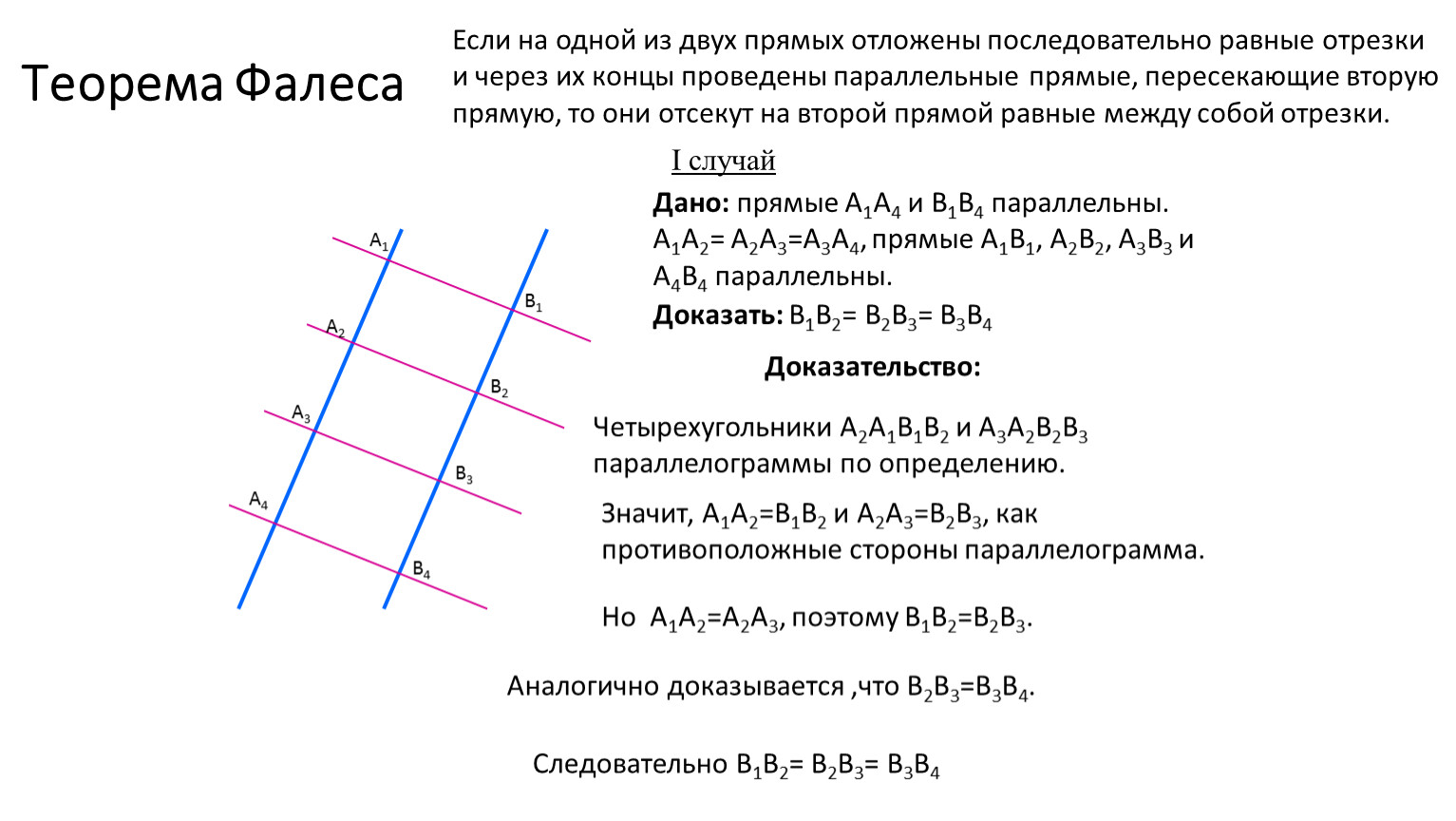 Он также показывает, как использовать SSS в доказательстве.
Он также показывает, как использовать SSS в доказательстве.
Тип: Учебник
Постулаты конгруэнтности треугольников:В этом руководстве обсуждаются постулаты SSS, SAS, ASA и AAS для конгруэнтных треугольников. Это также показывает, что AAA подходит только для сходства, а SSA не годится ни для того, ни для другого.
Тип: Учебник
Конгруэнтные треугольники и SSS: В этом видео учащиеся узнают о конгруэнтных треугольниках и постулате «Сторона-Сторона-Сторона».
Тип: Учебник
Линия отражения:С помощью интерактивного инструмента учащимся показано, как отразить отрезок прямой.Перед просмотром этого видео учащиеся должны иметь представление об уклоне и средней точке.
Тип: Учебник
Линия отражения:В этом уроке используется средняя точка двух линий, чтобы найти линию отражения.
Тип: Учебник
Очки после ротации: Учащиеся увидят, что происходит, когда фигуру поворачивают вокруг начала координат на -270 градусов. Перед просмотром этого видео рекомендуется иметь представление о прямоугольных треугольниках.
Перед просмотром этого видео рекомендуется иметь представление о прямоугольных треугольниках.
Тип: Учебник
Параллельные прямые, секущие и треугольники:В этом учебном пособии учащимся показаны восемь углов, образованных при пересечении двух параллельных прямых поперечной линией.Также в этом видео есть обзор треугольников.
Тип: Учебник
Язык геометрии: Прежде чем изучать какую-либо новую концепцию, важно, чтобы учащиеся выучили и использовали общий язык и последовательно обозначали концепции.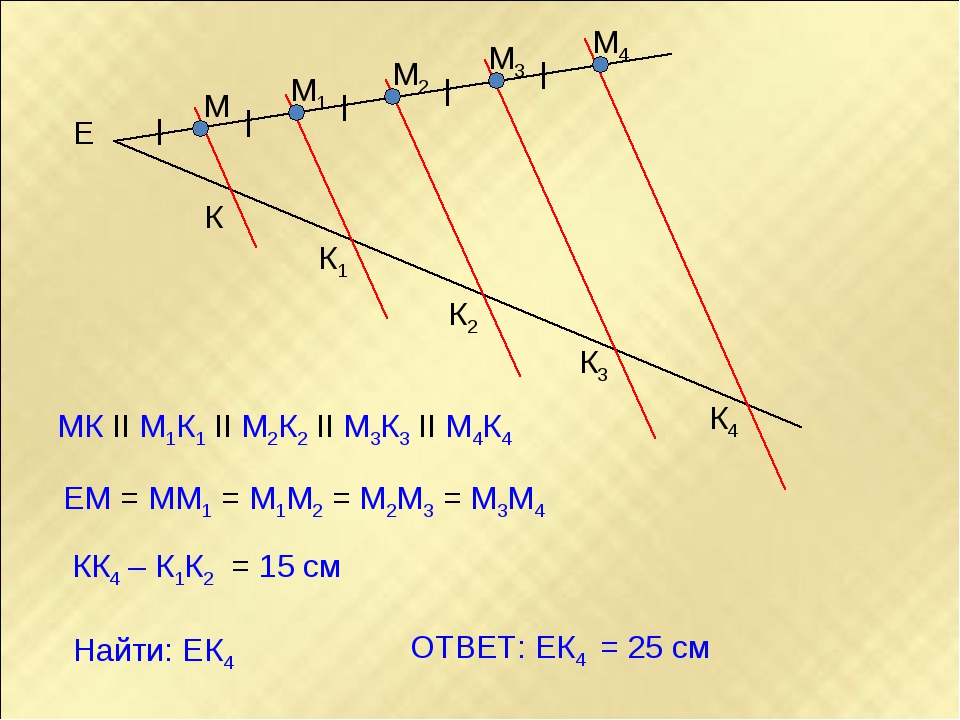 Этот учебник знакомит учащихся с точкой, линией и плоскостью.
Этот учебник знакомит учащихся с точкой, линией и плоскостью.
Тип: Учебник
Доказательство равенства вертикальных углов:В этом уроке учащиеся доказывают, что вертикальные углы равны. Перед просмотром этого видео учащиеся должны иметь представление о дополнительных ракурсах.
Тип: Учебник
Нахождение меры вертикальных углов: Студенты будут использовать алгебру, чтобы найти меру вертикальных углов или углов, противоположных друг другу, когда две линии пересекаются. Перед просмотром этого видео учащиеся должны иметь представление о дополнительных и дополнительных ракурсах.
Перед просмотром этого видео учащиеся должны иметь представление о дополнительных и дополнительных ракурсах.
Тип: Учебник
Введение в вертикальные углы:В этом учебном пособии учащиеся будут использовать свои знания о дополнительных, смежных и вертикальных углах для решения задач, связанных с пересечением двух прямых.
Тип: Учебник
Использование тригонометрии для поиска недостающей информации: Этот учебник покажет учащимся, как использовать тригонометрию для поиска недостающей информации в прямоугольных треугольниках.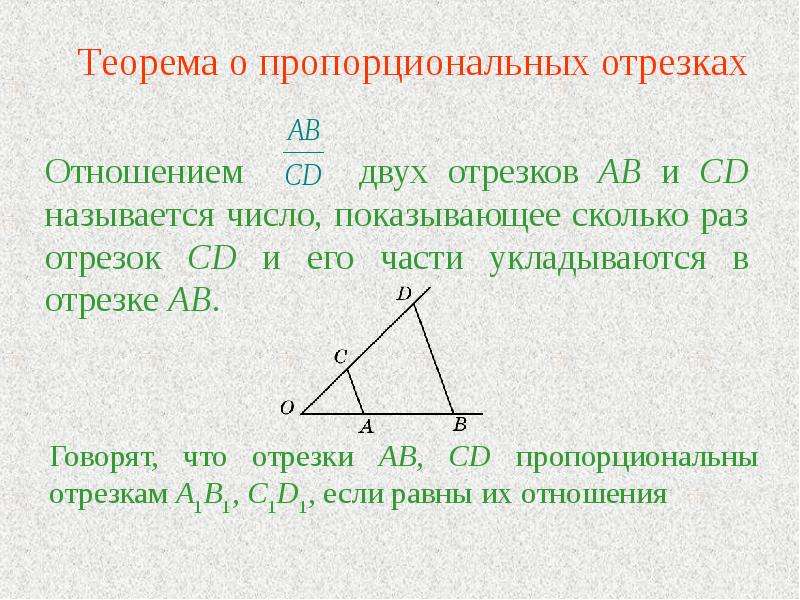 В этом видео показаны рабочие примеры использования тригонометрических соотношений для поиска недостающей информации и оценки других тригонометрических соотношений.
В этом видео показаны рабочие примеры использования тригонометрических соотношений для поиска недостающей информации и оценки других тригонометрических соотношений.
Тип: Учебник
Базовая тригонометрия:Этот туториал дает введение в тригонометрию.В этом ресурсе обсуждаются три основные функции тригонометрии: синус, косинус и тангенс.
Тип: Учебник
Параллельные линии: Параллельные прямые имеют одинаковый наклон и не имеют общих точек. Однако не всегда очевидно, описывают ли два уравнения параллельные прямые или одну и ту же прямую.
Однако не всегда очевидно, описывают ли два уравнения параллельные прямые или одну и ту же прямую.
Тип: Учебник
Перпендикулярные линии:Перпендикулярные линии имеют наклоны, которые являются отрицательными обратными величинами друг к другу, но почему?
Тип: Учебник
Снаряд под углом:В этом видео обсуждается, как вычислить горизонтальное смещение снаряда, запущенного под углом.
Тип: Учебник
Обратная теорема Пифагора
Мы предполагаем, что вы знакомы с теоремой Пифагора.
Обратная теорема Пифагора:
Если квадрат длины наибольшей стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
То есть в ΔABC, если c2=a2+b2, то ∠C — прямоугольный треугольник, ΔPQR — прямой угол.
Мы можем доказать это от противного.
Предположим, что c2=a2+b2 в ΔABC и треугольник , а не прямоугольный.
Теперь рассмотрим другой треугольник ΔPQR. Мы строим ΔPQR так, чтобы PR=a, QR=b и ∠R — прямой угол.
По теореме Пифагора (PQ)2=a2+b2.
Но мы знаем, что a2+b2=c2 и a2+b2=c2 и c=AB.
Итак, (PQ)2=a2+b2=(AB)2.
То есть (PQ)2=(AB)2.
Поскольку PQ и AB являются длинами сторон, мы можем извлечь положительные квадратные корни.
PQ=AB
То есть все три стороны ΔPQR конгруэнтны трем сторонам ΔABC. Таким образом, два треугольника конгруэнтны по свойству конгруэнтности стороны-стороны-стороны.
Поскольку ΔABC конгруэнтна ΔPQR, а ΔPQR — прямоугольный треугольник, ΔABC также должен быть прямоугольным.
Пример 1:
Проверить, является ли треугольник со сторонами 6 см, 10 см и 8 см прямоугольным.
Проверить, является ли квадрат длины самой длинной стороны суммой квадратов двух других сторон.
(10)2=?(8)2+(6)2 100=?64+36 100=100
Примените обратную теорему Пифагора.
Поскольку квадрат длины наибольшей стороны равен сумме квадратов двух других сторон, по теореме, обратной теореме Пифагора, треугольник является прямоугольным.
Следствие теоремы делит треугольники на остроугольные, прямоугольные и тупоугольные.
В треугольнике со сторонами a, b и c, где c — длина наибольшей стороны,
если c2
если c2>a2+b2, то треугольник тупоугольный.
Пример 2:
Проверить, является ли треугольник со сторонами 5, 7 и 9 единиц остроугольным, прямоугольным или тупоугольным.
 Катеты прямоугольного треугольника 8см и 7см. Найдите площадь.
Катеты прямоугольного треугольника 8см и 7см. Найдите площадь.
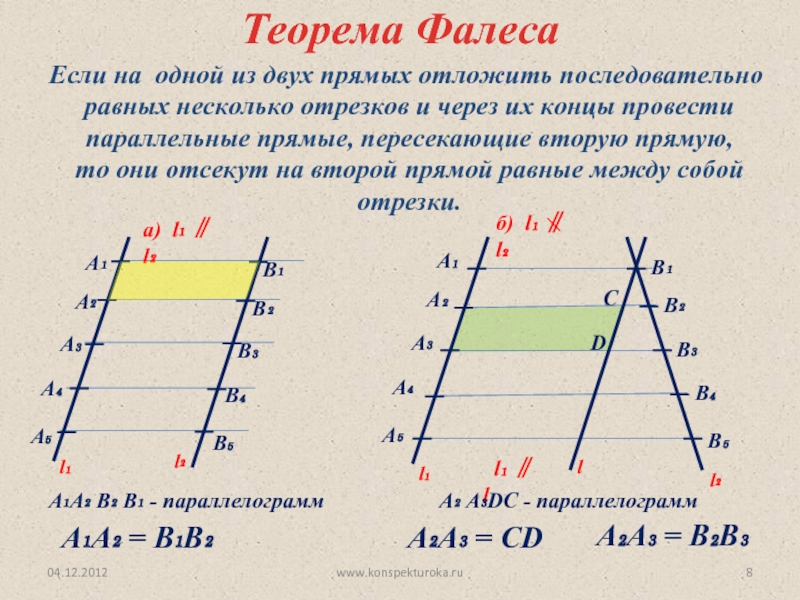 ЭОР Пифагоровы тройки.
ЭОР Пифагоровы тройки. Найдите стороны треугольника.
Найдите стороны треугольника.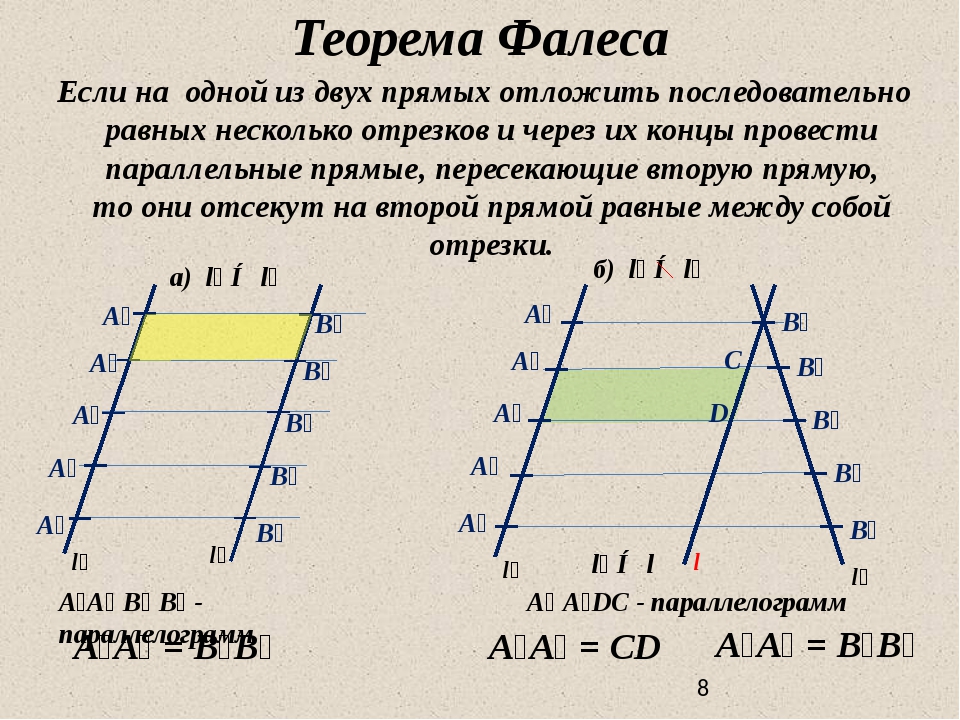
 Актуализация
Актуализация


 Записать формулы на доске.
Записать формулы на доске.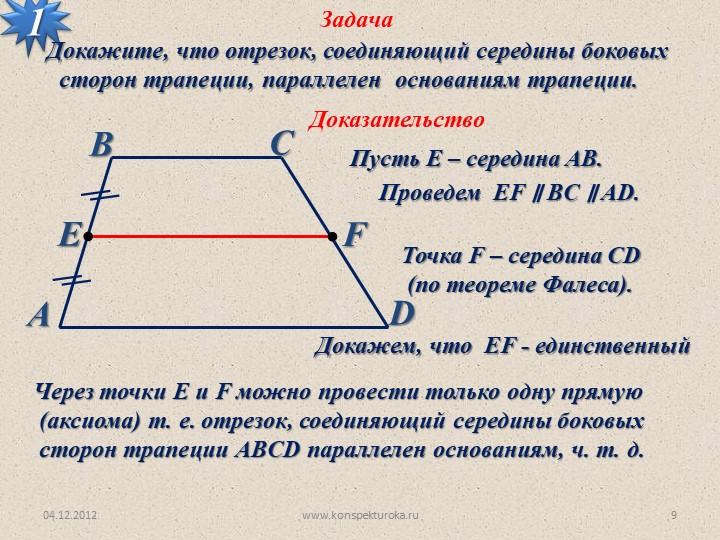
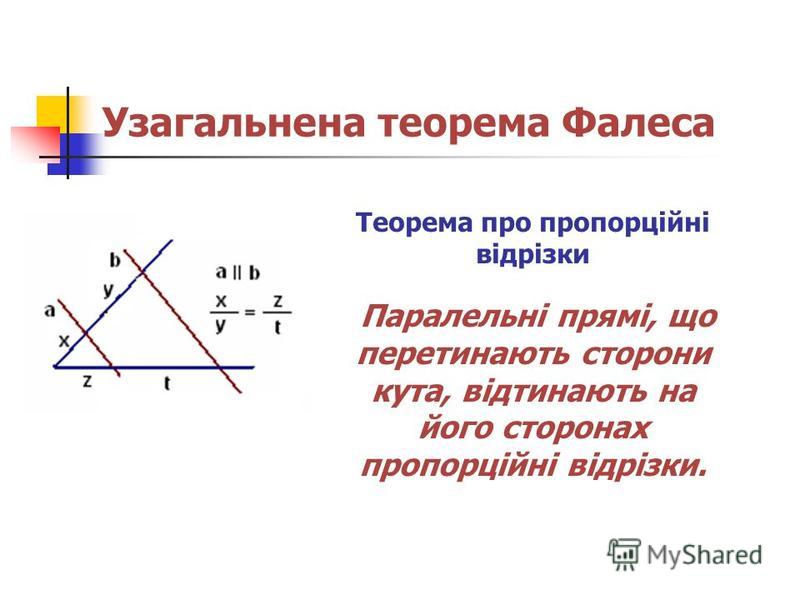
 Движения
Движения