Чем отличается окружность от круга
На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.
Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.
Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.

Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.
Выводы TheDifference.ru
- Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
- Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.
thedifference.ru
Чем отличается окружность от круга
На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.
Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности.

Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность.
Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.
Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга.
Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность.
Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии.
Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга.
Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.
Разница между кругом и окружностью заключается в следующем:
- Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой.
- Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.
imgist.ru
Что такое окружность и круг, в чем их отличия и примеры данных фигур из жизни
Школьная пора для большинства взрослых людей ассоциируется с беззаботным детством. Конечно, многие неохотно посещают школу, но только там они могут получить базовые знания, которые впоследствии пригодятся им в жизни. Одним из таких является вопрос о том, что такое окружность и круг. Спутать данные понятия достаточно просто, ведь слова являются однокоренными. Но разница между ними не настолько большая, как может показаться неопытному ребенку. Дети данную тему любят по причине ее простоты.
Что такое окружность?

Окружность — это замкнутая линия, каждая точка которой равно удалена от центральной. Самым ярким примером окружности является обруч, который представляет собой замкнутое тело. Собственно, и говорить особо об окружности не приходится. В вопросе о том, что такое окружность и круг, значительно интереснее вторая его часть.
Что такое круг?

Представьте, что вы решили разукрасить нарисованную выше окружность. Для этого можно выбрать любые краски: синие, желтые или зеленые — кому что ближе по душе. И вот вы начали заполнять пустоту чем-то. После того как это было закончено, у нас получилась фигура, которая называется кругом. По сути, круг — это часть поверхности, очерченная окружностью.
У круга есть несколько важных параметров, часть из которых также характерна и для окружности. Первый — это радиус. Им называется расстояние между центральной точкой круга (ну или окружности) и самой окружностью, что создает границы кругу. Вторая важная характеристика, которая неоднократно используется в школьных задачах — это диаметр (то есть расстояние между противоположными точками окружности).
Ну и наконец, третья характеристика, присущая кругу — это площадь. Данное свойство специфичное только для него, окружность не имеет площади в силу того, что у нее нет ничего внутри, а центр, в отличие от круга, скорее воображаемый, чем настоящий. В самом же круге можно установить четкий центр, через который провести ряд линий, которые делят его на сектора.
Примеры круга в реальной жизни
На самом деле возможных предметов, которые можно назвать разновидностью круга, достаточно. Например, если посмотреть на колесо машины прямо, то вот вам пример готового круга. Да, он необязательно должен быть заполнен однотонно, вполне возможны различные узоры внутри него. Второй пример круга — это солнце. Конечно, на него посмотреть будет тяжело, но оно на небе выглядит, как маленький кружочек.
Да, сама звезда Солнце — это не круг, она имеет еще и объем. Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.
Отличия окружности от круга

Значит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга. Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.
Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность — это граница круга. Вот чем отличается окружность от круга.
Что такое сектор?
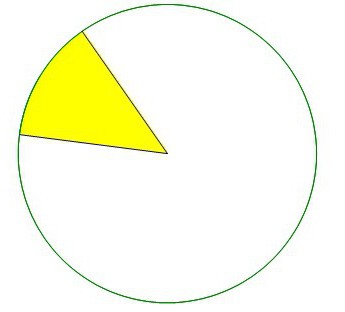
Сектор — это участок круга, который образуется двумя проведенными по нему радиусами. Чтобы понять это определение, нужно просто вспомнить пиццу. Когда ее разрезают на равные кусочки, все они и являются секторами круга, который представлен в виде такого вкусного блюда. При этом совершенно необязательно секторы должны быть равны. Они могут быть разной величины. Например, если отрезать половину пиццы, то она также будет сектором этого круга.
Предмет, отображаемый этим понятием, может иметь только круг. Окружность (радиус тоже можно провести, конечно, но после этого она станет кругом) не имеет площади, поэтому и сектор выделить не получится.
Выводы
Да, тема о круге и окружности (что это такое) очень проста для понимания. Но вообще все то, что касается этих геометрических фигур, является самым сложным для изучения. Школьнику нужно быть готовым к тому, что круг — фигура капризная. Но, как говорится, тяжело в учении — легко в бою. Да, геометрия — наука сложная. Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.
fb.ru
В чем отличие круга от окружности
Библиографическое описание:
В чем отличие круга от окружности // Молодой ученый. 2016. №28. URL https://moluch.ru/archive/132/55020/ (дата обращения: 22.12.2019).
По пути в школу, в спортивную секцию или же просто идя на встречу с друзьями, ребенок видит множество круглых предметов. Не всегда мы определяем для себя название того или иного предмета. Согласитесь, что мы часто видим различные круглые вещи. Однако школьнику, у которого есть геометрия, важно знать один момент: круг и окружность отличается. В этой статье мы приведем примеры окружности и круга, чтобы вы научились различать два этих понятия.
Окружность – это довольно простое понятие. Запомните, что окружностью является замкнутая линия, каждая точка которой находится на одинаковом расстоянии от центра. Более понятным примером окружности является всем известный предмет. Какой?.. Если вдруг забудете, что же такое окружность, представьте обруч, ведь он наглядный пример окружности. Этот метод запоминания называется ассоциативным, он намного эффективнее, нежели обычное «зазубривание».
Итак, с окружностью разобрались, переходим к понятию «круг». Круг – это геометрическая фигура, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Круг, в отличие от окружности, обладает пространством внутри. Следовательно, мы можем говорить о наличии у круга площади. Площадь круга — численная характеристика фигуры, показывающая размер этой фигуры в квадратных единицах. Стандартное обозначение площади — буква S. Чтобы найти площадь круга, нужно знать несколько математических определений. Во-первых, вы должны иметь представление о числе Пи (π). Что же такое этот загадочный знак? π — математическая константа, которая выражает отношение длины окружности к ее диаметру. Этот постоянный показатель равен примерно 3,14. Для нахождения площади круга также необходимо знать, что такое радиус — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности (или поверхности сферы), а также длина этого отрезка. Получаем формулу площади круга: S=πr2
Подытожим! Для нахождения площади круга вам нужно, во-первых, отличать круг от окружности (помните про ассоциативный метод запоминания), во-вторых, знать формулу нахождения площади круга (и все понятия, связанные с формулой) и, в-третьих, искренне интересоваться математикой. Вместе с myalfaschool.ru вы можете заниматься математикой онлайн не выходя из дома, а также «Альфа-школа» гарантирует только самые увлекательные математические задания. Мы ждем вас!
Основные термины (генерируются автоматически): окружность, круг, площадь круга, нахождение площади круга.
Похожие статьи
Урок математики: «Площадь круга. Длина окружности. Цилиндр.»
Цель урока: формирование представлений о геометрических телах: шар, конус, цилиндр и их элементы. Научить различать в окружающем мире предметы, имеющие форму изучаемых фигур. Тип урока: урок «открытия» нового знания.
Урок математики: «Окружность и круг» | Статья в журнале…
Цель: формирование представлений у обучающихся о понятиях окружности и круга; формирование умения строить окружность с помощью циркуля по заданному радиусу и диаметру. Тип урока: урок «открытия» нового знания.
Вычисление площадей фигур, изображенных на клетчатой бумаге
При подготовке к основному государственному экзамену я встретился с заданиями, в которых требуется вычислить площадь фигуры, изображенной на клетчатом листе бумаги. Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой трапецию…
Применение теоремы Паппа-Гульдена | Статья в журнале…
…полукруга, круга, четверти круга, сегмента круга (объем тела вращения фигура, лежащей в плоскости целиком по одну строну от оси вращения, равен
площадь сечения, тело вращения, произведение длины окружности, площадь основания, площадь, объем тел вращения…
Развитие творческого мышления учащихся при изучении понятий…
Почему люки круглые? Окружности и круг в архитектуре. Шар, сфера и их элементы. Типы правильных многогранников.
Нахождение площади поверхности призмы. Конструирование разных видов призм. Почему люки круглые? Окружности и круг в архитектуре.
Обобщение одной из основных задач аналитической геометрии
3) числа вершин», «Исследование влияния радиуса окружности на длину окружности и площадь круга».
Нахождение площади поверхности прямоугольного параллелепипеда, куба. Параллельность прямых.Перпендикулярность прямых.
Окружность, эллипс, гипербола, парабола.
Рис. 2. Фокальная окружность. Найдем , если точка расположена вне круга: тогда уравнение геометрического места точек
Если же точка расположена внутри круга, то: (2). Для описания данного геометрического места точек необходимо отдельно рассмотреть следующие случаи
Окружность и круг. Центр и радиус окружности. Хорда и диаметр…
Основа модели берется окружность круга и строится вокруг нее вписанный и описанный многогранники. Путем анализа определяем конкретный вид геометрической фигуры и синтезируем их, как комплексный вид чертежа модели в трех плоскостях.
Коэффициент формы как геометрическая характеристика
стороны которых касаются вписанной окружности, в том числе: правильные многоугольники, ромбы и треугольники; нижнюю границу значений Кf для всего множества четырехугольников образуют прямоугольники (рисунок 3).
Золотой треугольник
Найти расстояние между центрами этих окружностей. Найти радиусы вневписанных окружностей золотого треугольника. Найти расстояния между скрещивающимися ребрами золотой пирамиды (Золотая пирамида, пирамида у которой каждая грань – золотой треугольник).
Чем отличается окружность от круга |
На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.
Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.
Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.
Station20.ru определил, что разница между кругом и окружностью заключается в следующем:
Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.
station20.ru
Разница между Кругом и Эллипсом | Разница Между
Ключевое отличие: Круг и Эллипс имеют замкнутые изогнутые формы. В круге все точки одинаково далеки от центра, что не относится к эллипсу; в эллипсе все точки находятся на разных расстояниях от центра.
Математически круг является основной формой в области геометрии и ее определения: круг — это форма, в которой все точки находятся на одинаковом расстоянии от его центра. Он назван его центром. Некоторыми реальными примерами круга являются колеса, тарелка и (поверхность) монеты.
Слово ‘цирк’Происходит от греческого термина‘Киркос’, Который является метатезисом гомеровского греческого и означает‘обруч‘ или же ‘кольцо». Круг был известен еще до записи истории. Солнце и Луна являются естественными примерами круга, в то время как даже короткий стебель, дующий на ветру, образует форму круга в песке. Принцип круга был применен при формировании колес и механизмов доисторическим человеком. Сейчас, в современную эпоху, существует множество разновидностей механизмов, основанных на форме круга. Изучение круга и его развитие применимо в областях математики, геометрии, астрономии и исчисления.
В терминологии круга используются следующие термины:
дуга: любая связанная часть круга.
Центр: точка на равном расстоянии от точек на окружности.
Радиусотрезок, соединяющий центр круга с любой точкой на самом круге; или длина такого отрезка, равная половине диаметра.
Диаметротрезок, конечные точки которого лежат на окружности и который проходит через центр; или длина такого отрезка, который является наибольшим расстоянием между любыми двумя точками на окружности. Это особый случай аккорда, а именно самого длинного аккорда, и он вдвое больше радиуса.
длина окружностие: длина одной цепи по кругу.
Аккорд: отрезок, конечные точки которого лежат на окружности.
касательный: копланарная прямая, которая касается круга в одной точке.
Semicirclе: область, ограниченная диаметром, и дуга, лежащая между конечными точками диаметра. Это частный случай кругового сегмента, а именно самого большого.
Круговой сектор: область, ограниченная двумя радиусами и дуга, лежащая между радиусами.
Математически эллипс является распространенной формой в области математики. Его определение гласит: изогнутая линия, образующая замкнутый контур, где сумма расстояний от двух точек (фокусов) до каждой точки на линии постоянна. Реальные примеры эллипса: обруч, стакан воды и простая тарелка для обеда, когда они наклонены, чтобы смотреть под углом.
Аполлоний Пергский дал название «эллипс» в своей конике, которая подчеркивает связь кривой с применением областей. Это кривая на плоскости, которая окружает две точки фокусировки, так что прямая линия, проведенная из одной из точек фокусировки в любую точку кривой, а затем обратно в другую точку фокусировки, имеет одинаковую длину для каждой точки кривой. Его форма представлена его эксцентриситетом, который произвольно близок к 1. Изучение эллипса и его свойств широко применимы в области физики, астрономии и техники. Орбиты планет с Солнцем в одной из фокусных точек, лун, вращающихся вокруг планет, и другие системы, имеющие два астрономических тела, являются общими примерами эллиптических траекторий. Форма планет и звезд часто хорошо описывается эллипсоидами. Эллипс также считается самой простой фигурой Лиссажу, образованной, когда горизонтальные и вертикальные движения являются синусоидами с одинаковой частотой.
Термины, используемые в основном в терминологии эллипса:
фокус: Расстояние от центра, и выражается в терминах большого и малого радиусов.
эксцентричность: Эксцентриситет эллипса (обычно обозначаемый как e или ε) выражается в терминах с использованием коэффициента уплощения.
директриса: это линия, параллельная малой оси, с которой связан каждый фокус.
Латус прямой кишки: Хорды эллипса, которые перпендикулярны большой оси и проходят через один из ее фокусов, называются широчайшей прямой кишкой эллипса.
Большая / Малая осьСамый длинный и самый короткий диаметры эллипса. Длина большой оси равна сумме двух линий генератора.
Полу мажор / Полу минор оси: Расстояние от центра до самой дальней и ближайшей точки на эллипсе. Половина большой / малой оси.
Аккорды: Середины набора параллельных аккордов эллипса коллинеарны.
Длина окружности: он связан с длиной большой полуоси и эксцентриситетом и является неотъемлемой частью эллипса.
Сравнение между Кругом и Эллипсом:
Круг | Эллипс | |
Определения | Круг — это круглая плоская фигура, граница которой (окружность) состоит из точек, равноудаленных от неподвижной точки (центра). | Эллипс представляет собой правильную овальную форму, отслеживаемую точкой, движущейся в плоскости, так что сумма его расстояний от двух других точек (фокусов) является постоянной, или он получается, когда конус разрезается наклонной плоскостью, что не пересекать базу. |
вариации | Круги не различаются по форме; они остаются той же форм |
ru.natapa.org
|
Частное учреждение профессионального образования «Юридический полицейский колледж» Реферат по математике на тему: «Круг, окружность, шар, сфера их отличия»
Выполнила: Студентка группа 18ПД Бабина В.А
Проверил: Щербаков К.В.
Тула – 2018 В обычной жизни нам приходится замечать множество предметов, которые по своей форме напоминают окружности и круги, но редко кто задумывается о том, чем окружность отличается от круга и что у них общего. Окружность– это замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Окружностью называют линию, которая ограничивает круг. Правильную окружность можно изобразить с помощью циркуля. Ножку с иголкой нужно установить в задуманную точку, и тогда ножка с карандашиком начертит замкнутую линию. Эта линия разделяет плоскость на две части: внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, т. к. плоскость в общем понимании не имеет границ. Для отличия, можно заштриховать внутреннюю область. Часть, которая осталась внутри, называется кругом. Окружность имеет центр — это начальная точка нарисованная циркулем. Если задуманная точка лежит на окружности, это означает, что она ей принадлежит. Можно обозначить дуги окружности, ими будут любые 2 точки, ограничивающие окружность, т. е. любые две точки A и B окружности разбивают ее на две части; каждая из этих частей и называется дугой. Если провести линию через эти точки, то получим хорду. А хорда, проходящая через центр окружности, имеет название диаметра. Если же от центра провести линии к точке на окружности, то получится радиус окружности. Круг– является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Пространство, закрепленное границей, включая центр круга принадлежит кругу. Если провести линию от одной точки на границе круга до другой через центр, то такое расстояние будет называться диаметром круга. Если от центра круга провести прямую линию до любой отметки на его границе, то это расстояние называется радиус. Два радиуса, равноудалённые от центра круга, будут соответствовать его диаметру. Следовательно, диаметр в два раза больше радиуса. Если от одной точки круга провести хорду, то хорда и соответствующая ей дуга будет образовывать сегмент круга. Окружность и круг имеют общий радиус и диаметр. Отличие окружности и круга Окружность, как любая линия имеет длину, а круг, как любая геометрическая фигура имеет площадь. Круг имеет площадь, но её нет у окружности. Круг содержит центр окружности, а окружность, содержит сам круг. Без окружности не было бы круга, но она существует самостоятельно. Окружность проводит границу круга снаружи, а круг – внутренняя часть окружности. И круг, и окружность имеют одинаковый центр. Пример: Таким образом, круг является некоторым участком плоскости, а окружность — всего лишь граница этого участка. Чтобы лучше понять это, представьте себе кольцо (я возьму что-нибудь круглое и съедобное, например, бублик). Это и будет нашей окружностью. Бублик имеет дырочку. Дырочка к бублику не относится, дырочку от бублика съесть нельзя, а вот сам бублик можно кушать. Понимаете? Всё, что лежит внутри окружности, к самой окружности не относится (за исключением окружности с нулевым радиусом). Теперь мысленно вставим в бублик круглую булочку, так, чтобы булочка идеально вписалась в бублик (чтобы не было зазоров и проч.). Булочка и бублик образуют круг. Бублик будет границей этого круга, частью круга (бублик принадлежит кругу, а так как за бублик мы взяли окружность, то окружность принадлежит кругу). И булочку, и бублик можно съесть. Пример с бубликом и булочкой является самым наглядным примером, который при желании можно повторить дома, хотя здесь достаточно всё представить мысленно.
Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью).
В повседневной жизни мы редко говорим сфера, чаще шар или шарик. И не все понимают какая разница между этими двумя геометрическими понятиями. Наверное можно сказать, что сфера это внешняя оболочка шара. Воздушный шарик, например, на самом деле не шар, а сфера. При условии, конечно, его абсолютной «круглости». Как я понимаю, то у шара абсолютно все точки поверхности равноудалены от его центра, а у сфер это условие не является обязательным.
Пример: Апельсин, футбольный мяч, арбуз, похожи на шар. Из всех тел заданного объёма шар имеет наименьшую поверхность. Поверхность шара называют сферой. Расстояние от точек сферы до её центра называется радиусом сферы и обычно обозначается R. Радиусом также называется любой отрезок, соединяющий точку сферы с её центром.
Читайте также: Рекомендуемые страницы: Поиск по сайту |
Поиск по сайту: |
poisk-ru.ru