Элементарные функции — Википедия

Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций^[1]:

Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.

Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.

Рассматривая функции комплексного переменного, Лиувилль определил элементарные функции несколько шире. Элементарная функция y(x){\displaystyle y(x)} переменной x{\displaystyle x} — аналитическая функция, которая может быть представлена как алгебраическая функция y(x)=ϕ(x,z1,…,zr),{\displaystyle y(x)=\phi (x,z_{1},…,z_{r}),} причём:

• z1{\displaystyle z_{1}} является логарифмом или экспонентой от некоторой алгебраической функции g1(x),{\displaystyle g_{1}(x),}
• z2{\displaystyle z_{2}} является логарифмом или экспонентой от некоторой алгебраической функции g2(x,z1),{\displaystyle g_{2}(x,z_{1}),}

…

• zr{\displaystyle z_{r}} является логарифмом или экспонентой от некоторой алгебраической функции gr(x,z1,…,zr−1).{\displaystyle g_{r}(x,z_{1},…,z_{r-1}).}

Например, y(x)=sin⁡(x){\displaystyle y(x)=\sin(x)} — элементарная функция в этом смысле, поскольку она является алгебраической функцией от показательной функции eix:{\displaystyle e^{ix}:}

sin⁡(x)=(eix)2−12ieix.{\displaystyle \sin(x)={\frac {(e^{ix})^{2}-1}{2ie^{ix}}}.}

Вообще, с помощью указанного тождества все тригонометрические и обратные тригонометрические функции можно выразить через логарифмы, экспоненты, арифметические действия, а также операцию взятия квадратного корня. Разумеется, при этом будет использована мнимая единица i=−1.{\displaystyle i={\sqrt {-1}}.}

Функция y(x)=eex{\displaystyle y(x)=e^{e^{x}}} тоже является элементарной, поскольку её можно представить в виде:

y(x)=ϕ(x,z1,z2),{\displaystyle y(x)=\phi (x,z_{1},z_{2}),} где z1=ex, z2=ez1, ϕ(x,z1,z2)=z2.{\displaystyle z_{1}=e^{x},\ z_{2}=e^{z_{1}},\ \phi (x,z_{1},z_{2})=z_{2}.}

Не ограничивая общности рассмотрения, можно считать функции z1,…,zr{\displaystyle z_{1},\dots ,z_{r}} алгебраически независимыми. Это означает, что алгебраическое соотношение ψ(x,z1,…,zr)=0{\displaystyle \psi (x,z_{1},…,z_{r})=0} может выполняться для всех x{\displaystyle x}, только если коэффициенты полинома ψ(x,z1,…,zr){\displaystyle \psi (x,z_{1},…,z_{r})} равны нулю.

Дифференцирование элементарных функций[править | править код]

Производная элементарной функции всегда является элементарной функцией и может быть найдена за конечное число действий. Именно, по правилу дифференцирования сложной функции

y′(x)=ddxϕ(x,z1,…,zr)=∂ϕ∂x+∑i=1r∂ϕ∂zidzidx,{\displaystyle y'(x)={\frac {d}{dx}}\phi (x,z_{1},\dots ,z_{r})={\frac {\partial \phi }{\partial x}}+\sum \limits _{i=1}^{r}{\frac {\partial \phi }{\partial z_{i}}}{\frac {dz_{i}}{dx}},}

где z1′(z){\displaystyle z_{1}'(z)} равно или g1′/g1{\displaystyle g_{1}’/g_{1}} или z1g1′{\displaystyle z_{1}g_{1}’} в зависимости от того, логарифм ли z1{\displaystyle z_{1}} или экспонента и т. д. На практике удобно использовать таблицу производных.

Интегрирование элементарных функций[править | править код]

Интеграл элементарной функции не всегда сам является элементарной функцией. Наиболее распространённые функции, интегралы которых найдены, собраны в таблице интегралов. В общем случае проблема интегрирования элементарных функций решается алгоритмом Риша, основанном на теореме Лиувилля:

Теорема Лиувилля. Если интеграл от элементарной функции y=ϕ(x,z1,…zr){\displaystyle y=\phi (x,z_{1},\dots z_{r})} сам является элементарной функцией, то он представим в виде

∫ϕ(x,z1(x),…,zr(x))dx=∑iAiln⁡(ψi(x,z1,…zr))+ψ0(x,z1,…,zr)+C,{\displaystyle \int \phi (x,z_{1}(x),\dots ,z_{r}(x))\,dx=\sum \limits _{i}A_{i}\ln(\psi _{i}(x,z_{1},\dots z_{r}))+\psi _{0}(x,z_{1},\dots ,z_{r})+C,}

где Ai{\displaystyle A_{i}} — некоторые комплексные числа, а ψi{\displaystyle \psi _{i}} — алгебраические функции своих аргументов.

Доказательство этой теоремы Лиувилль основал на следующем принципе. Если интеграл от y{\displaystyle y} берётся в элементарных функциях, то верно

∫ϕ(x,z1(x),…zr(x))dx=ψ(x,z1(x),…zs(x))+const{\displaystyle \int \phi (x,z_{1}(x),\dots z_{r}(x))\,dx=\psi (x,z_{1}(x),\dots z_{s}(x))+\operatorname {const} }

где ψ{\displaystyle \psi } — алгебраическая функция, zr+1{\displaystyle z_{r+1}} — логарифм или экспонента алгебраической функции x,z1,…zr{\displaystyle x,z_{1},\dots z_{r}} и т. д. Функции z1,…zs{\displaystyle z_{1},\dots z_{s}} являются алгебраически независимыми и удовлетворяют некоторой системе дифференциальных уравнений вида

z1′=ρ1(x,z1,…,zs),…{\displaystyle z_{1}’=\rho _{1}(x,z_{1},\dots ,z_{s}),\dots }

где ρi{\displaystyle \rho _{i}} — алгебраические функции своих аргументов. Если z1=z1(x,C),…{\displaystyle z_{1}=z_{1}(x,C),\dots } — семейство решений этой системы, то

∫ϕ(x,z1(x,C),…)dx=ψ(x,z1(x,C),…zs(x,C))+const{\displaystyle \int \phi (x,z_{1}(x,C),\dots )\,dx=\psi (x,z_{1}(x,C),\dots z_{s}(x,C))+\operatorname {const} }

откуда

ψ(x,z1(x),…)=ψ(x,z1(x,C),…zs(x,C))+f(C){\displaystyle \psi (x,z_{1}(x),\dots )=\psi (x,z_{1}(x,C),\dots z_{s}(x,C))+f(C)}

Для некоторых классов интегралов эта теорема позволяет весьма просто исследовать разрешимость в элементарных функциях задачи об интегрировании.

Интегрирование функций вида p(x)eq(x){\displaystyle p(x)e^{q(x)}}[править | править код]

Следствие теоремы Лиувилля (См. Ритт, с. 47 и сл.). Если интеграл

∫p(x)eq(x)dx,{\displaystyle \int p(x)e^{q(x)}\,dx,}

где p,q{\displaystyle p,q} — полиномы, берётся в элементарных функциях, то

∫p(x)eq(x)dx=r(x)eq(x){\displaystyle \int p(x)e^{q(x)}\,dx=r(x)e^{q(x)}},

где r(x){\displaystyle r(x)} — тоже некоторый полином, удовлетворяющий дифференциальному уравнению

r′+q′(x)r=p(x){\displaystyle r’+q'(x)r=p(x)}

Пример. В частности, интеграл

∫ex2dx{\displaystyle \int e^{x^{2}}\,dx}

не берётся, поскольку подстановка

r=Axn+…(A≠0){\displaystyle r=Ax^{n}+\dots \quad (A\not =0)}

в уравнение

r′+2xr=1{\displaystyle r’+2xr=1}

даёт A=0{\displaystyle A=0}. Интеграл же

∫xex2dx{\displaystyle \int xe^{x^{2}}\,dx}

берётся, поскольку

r′+2xr=x{\displaystyle r’+2xr=x}

имеет решение r=1/2{\displaystyle r=1/2}. При этом, конечно,

∫xex2dx=ex22+const{\displaystyle \int xe^{x^{2}}\,dx={\frac {e^{x^{2}}}{2}}+\operatorname {const} }

Доказательство следствия. В силу теоремы Лиувилля

∫p(x)eq(x)dx=ψ0(x,eq(x))+∑Ailn⁡ψi(x,eq(x))+const{\displaystyle \int p(x)e^{q(x)}\,dx=\psi _{0}(x,e^{q(x)})+\sum A_{i}\ln \psi _{i}(x,e^{q(x)})+\operatorname {const} }

Тогда в силу принципа Лиувилля при произвольной константе C{\displaystyle C} верно

∫p(x)Ceq(x)dx=ψ0(x,Ceq(x))+∑Ailn⁡ψi(x,Ceq(x))+f(C){\displaystyle \int p(x)Ce^{q(x)}\,dx=\psi _{0}(x,Ce^{q(x)})+\sum A_{i}\ln \psi _{i}(x,Ce^{q(x)})+f(C)}

Дифференцируя по C{\displaystyle C} и полагая C=1{\displaystyle C=1}, видим, что интеграл выражается алгебраически через x,eq(x){\displaystyle x,e^{q(x)}}, то есть

∫p(x)eq(x)dx=ψ(x,eq(x)).{\displaystyle \int p(x)e^{q(x)}\,dx=\psi (x,e^{q(x)}).}

Опять применяя принцип Лиувилля, имеем

Cψ(x,eq(x))=ψ(x,Ceq(x))+f(C).{\displaystyle C\psi (x,e^{q(x)})=\psi (x,Ce^{q(x)})+f(C).}

Дифференцируя по C{\displaystyle C} и полагая C=1{\displaystyle C=1}, имеем

ψ(x,z)=z∂ψ(x,z)∂z+B(B=const){\displaystyle \psi (x,z)=z{\frac {\partial \psi (x,z)}{\partial z}}+B\quad (B=\operatorname {const} )}

при z=eq(x){\displaystyle z=e^{q(x)}}, а следовательно, в силу алгебраической независимости x,eq(x){\displaystyle x,e^{q(x)}}, при всех x,z{\displaystyle x,z}. Поэтому

ψ(x,z)=−B+zr(x),{\displaystyle \psi (x,z)=-B+zr(x),}

где r{\displaystyle r} — некоторая алгебраическая функция x{\displaystyle x}. Таким образом,

∫p(x)eq(x)dx=r(x)eq(x)+const,{\displaystyle \int p(x)e^{q(x)}\,dx=r(x)e^{q(x)}+\operatorname {const} ,}

Коль скоро сам интеграл заведомо является целой функцией x{\displaystyle x}, то r{\displaystyle r} — полином. Следствие доказано.

Интегрирование алгебраических функций[править | править код]

Наиболее сложным оказался вопрос об интегрировании в элементарных функциях функций алгебраических, то есть о взятии абелевых интегралов, которому посвящены обширные исследования Вейерштрасса, Пташицкого^[2] и Риша^[3].

Теорема Лиувилля является основой для создания алгоритмов символьного интегрирования элементарных функций, реализуемых, напр., в Maple.

См. также: Список интегралов элементарных функций

Теория Лиувилля не распространяется на вычисление пределов. Неизвестно, существует ли алгоритм, который по заданной элементарной формулой последовательности даёт ответ, имеет ли она предел или нет. Например, открыт вопрос о том, сходится ли последовательность 1n3sin⁡n{\displaystyle {\frac {1}{n^{3}\sin n}}}.^[4]

1. ↑ Элементарная математика, 1976, с. 113—114..
2. ↑ Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. Art. 2 B 2 (W. Wirtinger, 1901 г.)
3. ↑ Дэвенпорт Дж. Интегрирование алгебраических функций. Гл. 4. М., «Мир», 1985
4. ↑ Q&A

Степенная функция — Википедия

Материал из Википедии — свободной энциклопедии

Степенна́я фу́нкция — функция y=xa{\displaystyle y=x^{a}}, где a{\displaystyle a} (показатель степени) — некоторое вещественное число^[1]. К степенным часто относят и функцию вида y=kxa{\displaystyle y=kx^{a}}, где k — некоторый (ненулевой) коэффициент^[2]. Существует также комплексное обобщение степенной функции. На практике показатель степени почти всегда является целым или рациональным числом.

Область определения[править | править код]

Если показатель степени — целое число, то можно рассматривать степенную функцию на всей числовой прямой (кроме, возможно, нуля). В общем случае степенная функция определена при x>0{\displaystyle x>0}. Если a>0{\displaystyle a>0}, то функция определена также и при x=0{\displaystyle x=0}, иначе ноль является её особой точкой.

Рациональный показатель степени[править | править код]

Пример: из третьего закона Кеплера вытекает, что период T обращения планеты вокруг Солнца связан с большой полуосью A её орбиты соотношением: T=kA3/2{\displaystyle T=kA^{3/2}} (полукубическая парабола).

Свойства[править | править код]

См. также: Возведение в степень

Степенная функция комплексного переменного z в общем виде определяется формулой^[3]:

y=zc=ec⋅Ln⁡(z){\displaystyle y=z^{c}=e^{c\cdot \operatorname {Ln} (z)}}

Здесь показатель степени c — некоторое комплексное число. Значение функции, соответствующее главному значению логарифма, называется главным значением степени. Например, значение ii{\displaystyle i^{i}} равно e−(4k+1)π2,{\displaystyle e^{-(4k+1){\frac {\pi }{2}}},} где k — произвольное целое, а его главное значение есть eiln⁡(i)=e−π2.{\displaystyle e^{i\ln(i)}=e^{-{\frac {\pi }{2}}}.}

Комплексная степенная функция обладает значительными отличиями от своего вещественного аналога. В силу многозначности комплексного логарифма она, вообще говоря, также имеет бесконечно много значений. Однако два практически важных случая рассматриваются отдельно.

1. При натуральном показателе степени функция y=zn{\displaystyle y=z^{n}} однозначна и n-листна^[4].
2. Если показатель степени — положительное рациональное число, то есть (несократимая) дробь pq{\displaystyle {\frac {p}{q}}}, то у функции будет q различных значений^[3].

ТИП (функция ТИП) — Служба поддержки Office

В этой статье описаны синтаксис формулы и использование функции ТИП в Microsoft Excel.

Описание

Возвращает тип значения. Функция ТИП используется, когда результаты вычисления другой функции зависят от типа значения в конкретной ячейке.

Синтаксис

ТИП(значение)

Аргументы функции ТИП описаны ниже.

• Значение    Обязательный. Любое значение Microsoft Excel, например число, текст, логическое значение и т. д.

Тип значения	Функция ТИП возвращает
Число	1
Текст	2
Логическое значение	4
Значение ошибки	16
Массив	64

Замечания

• Функция ТИП особенно удобна, когда используются такие функции, как АРГУМЕНТ и ВВОД, которые допускают данные различных типов. Функция ТИП позволяет выяснить, какой тип данных был возвращен функцией.

• С помощью функции ТИП нельзя определить, содержится ли в ячейке формула. Эта функция только определяет тип результирующего (отображаемого) значения. Если аргумент «значение» является ссылкой на ячейку, содержащую формулу, функция ТИП возвращает тип результата вычисления формулы.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
Климов
Формула	Описание	Результат
=ТИП(A2)	Возвращает тип значения в ячейке A2. Текстовый тип обозначается цифрой 2.	2
=ТИП(«г-н «&A2)	Возвращает тип значения «г-н Климов», которое является текстовым.	2
=ТИП(2+A2)	Возвращает тип формулы в ячейке C6 со значением 16 — тип сообщения об ошибке #ЗНАЧ!. Сообщение об ошибке #ЗНАЧ! отображено в ячейке C7.	16
=(2+A2)	Значение ошибки, возвращаемое формулой =(2+A2), которая используется в ячейке C2.	#ЗНАЧ!
=ТИП({1;2:3;4})	Возвращает тип массива констант — 64.	64

Производственная функция

Производственная функция – зависимость объемов производства от количества и качества имеющихся производственных факторов, выраженная с помощью математической модели. Производственная функция дает возможность выявить оптимальный размер издержек, необходимых для производства некоторой порции товаров. При этом функция всегда предназначается для конкретной технологии – интеграция новых разработок влечет необходимость пересмотра зависимости.

 

Производственная функция: общий вид и свойства

 

Для производственных функций характерны следующие свойства:

 

• Повышение объемов выпуска за счет одного производственного фактора всегда предельно (пример – в одном помещении может работать ограниченное число специалистов).

 

• Производственные факторы бывают взаимозаменяемыми (человеческие ресурсы заменяются роботами) и взаимодополняемыми (работники нуждаются в инструментах и станках).

 

В общем виде производственная функция выглядит так:

 

Q = f (K, M, L, T, N),

 

где под К понимается капитал (имеющиеся станки), L – человеческие ресурсы, M – траты на сырье и полуфабрикаты, Т – применяемые в производстве технологии, N – предпринимательский талант. Q – объем производства, который зависит от всех вышеперечисленных переменных.

 

Производственная функция: виды

 

Особой популярностью пользуются два вида производственных функций: двухфакторная модель и функция Кобба-Дугласа.

 

Двухфакторная модель рассматривает зависимость объемов выпуска от таких факторов, как издержки на труд и капитал. Соответственно, функция имеет сокращенный вид:

 

Q = f (L, K)

 

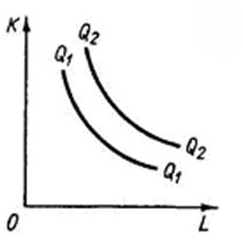
Для анализа с помощью этого метода часто используются изокванты – прямые, соединяющие все возможные точки сочетаний факторов, позволяющих производить конкретный объем продукции. В результате график, по оси абсцисс которого указываются затраты на труд, по оси ординат – капитал, превращается в

карту изоквант, являющуюся графическим выражением производственной двухфакторной модели.

 

Карта обладает такими свойствами:

 

• Чем дальше изокванта располагается от нулевой точки, тем больше объем выпуска.

 

• Если изокванта имеет нисходящий вид, значит, уменьшение использования капитала вызовет повышение издержек на оплату труда при необходимости сохранить объемы выпуска прежними.

 

• Форма изокванты зависит от возможности заменить капитал дополнительной единицей труда. Количество капитала, необходимое для замещения дополнительной единицы труда, носит название предельная норма замещения.

 

Функция Кобба-Дугласа предполагает зависимость объема производства от тех же факторов – капитала и затрат на труд. Однако формула имеет несколько иной вид:

 

Y = AKaLb

 

где а, b – это постоянные значения (константы). Если сумма констант равна единице, говорят о постоянном эффекте масштаба. Важно отметить, что постоянные а и b могут принимать только положительные значения.

                                                                                             

Формула Кобба-Дугласа может корректироваться при необходимости учесть дополнительные факторы. Например, если нужно включить в расчет земельные ресурсы, добавляется одна переменная N и одна константа y. Формула обретает вид:

 

Y = AKaLbNy

 

Нестандартные изокванты

 

Изокванты могут иметь нестандартные конфигурации:

 

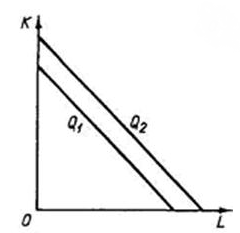
• При совершенной взаимозаменяемости ресурсов. Тогда объем может быть получен за счет использования лишь одного фактора: труда или капитала.

 

 

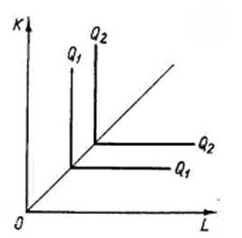
• При фиксированной структуре. Для выпуска требуемого объема продукции необходимо задействовать оба ресурса, притом в фиксированных пропорциях.

 

 

• При возможности действовать несколькими методами.

 

 

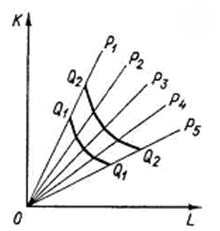
По мере движения от P1 к P5 предельная норма замещения снижается. Подобные карты изоквант активно используются при линейном программировании.

 

• При несовершенной замещаемости. Предполагается, что замена одного фактора другим возможна в некоторых пределах, однако, полное замещение недопустимо (либо нецелесообразно в экономическом плане).