2.2. Решение систем трех линейных уравнений с тремя неизвестными
Для системы 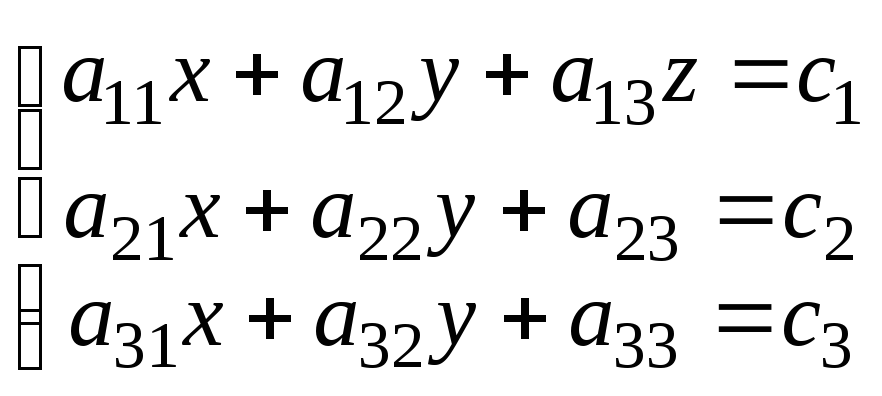 составляем
главный определитель
составляем
главный определитель
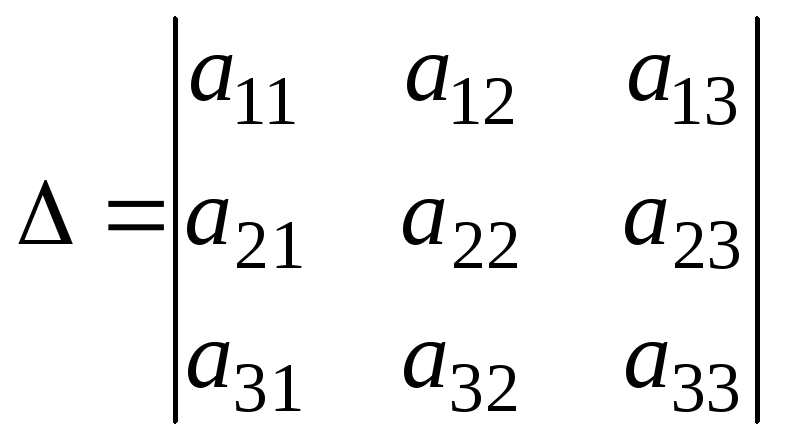 и вычисляем его.
и вычисляем его.
Затем составляем дополнительные определители

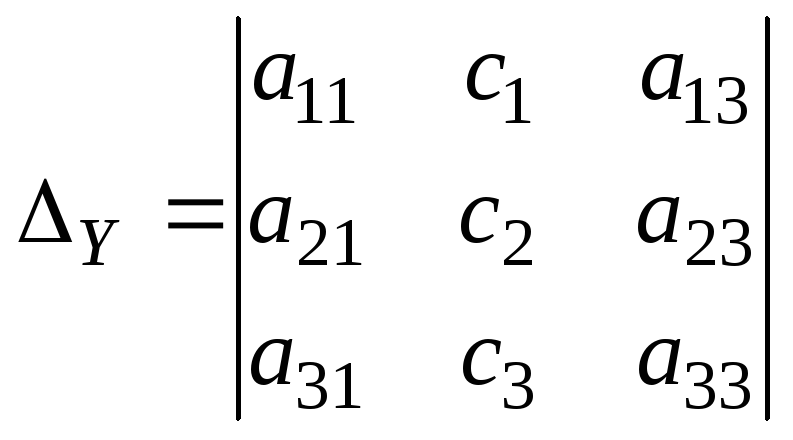

и вычисляем их.
По правилу Крамера решение системы находят по формулам
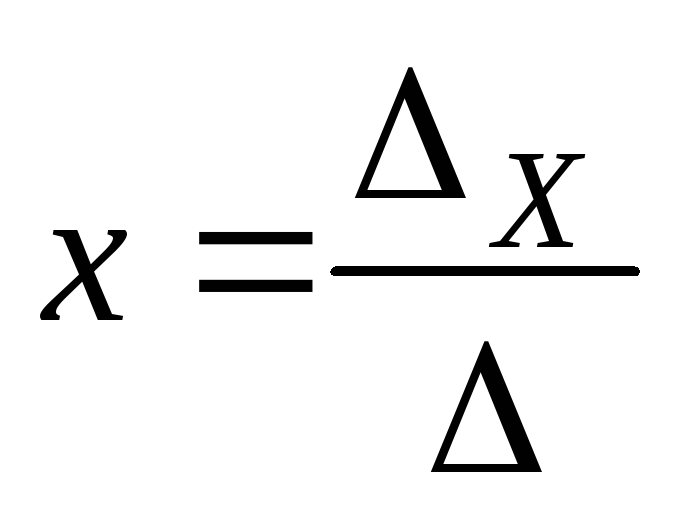
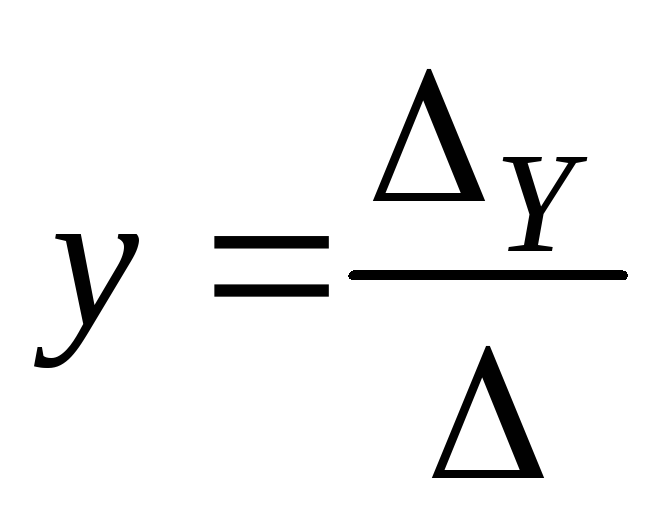 ;
; 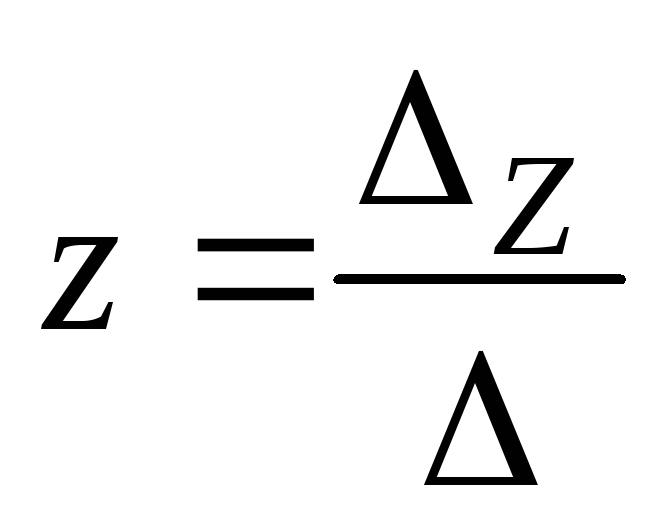 ,если
,если 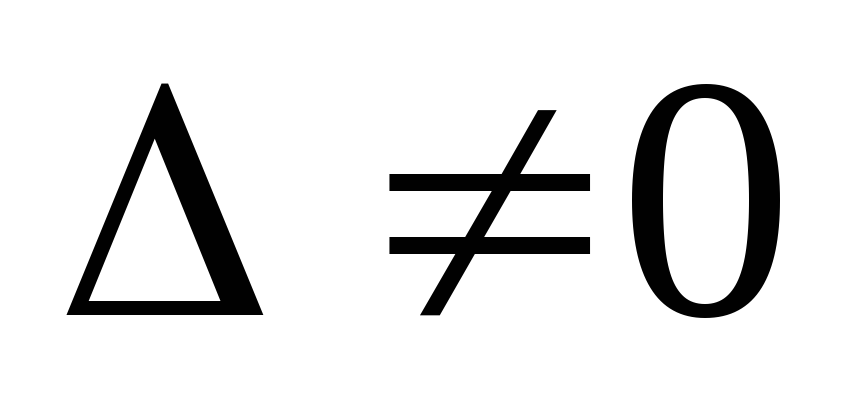
Примеры:
1) 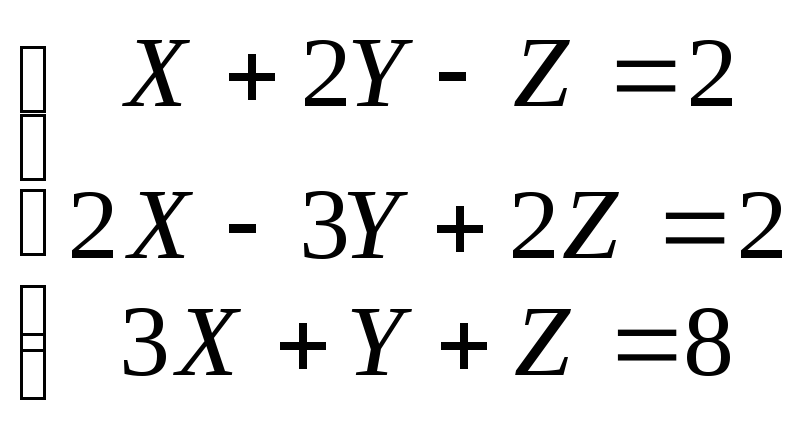
Вычислим:
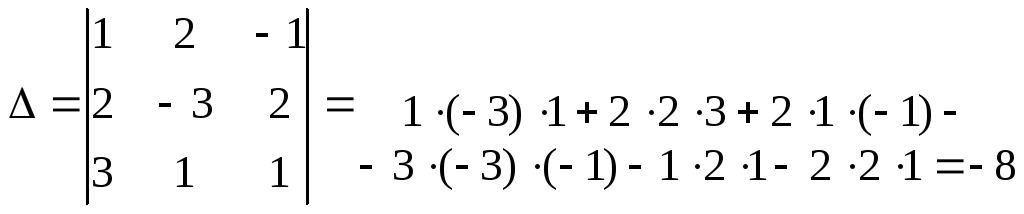

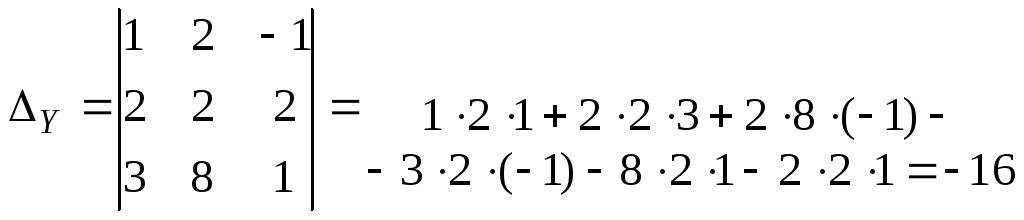
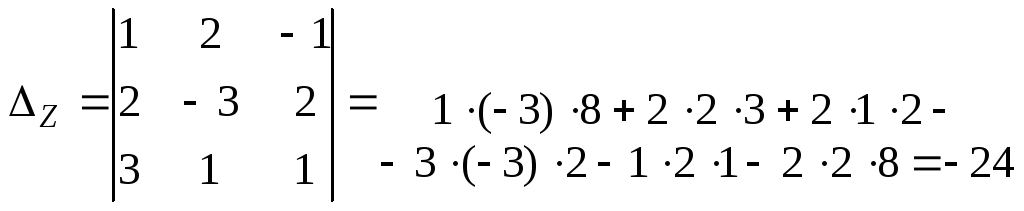
По формулам Крамера находим:
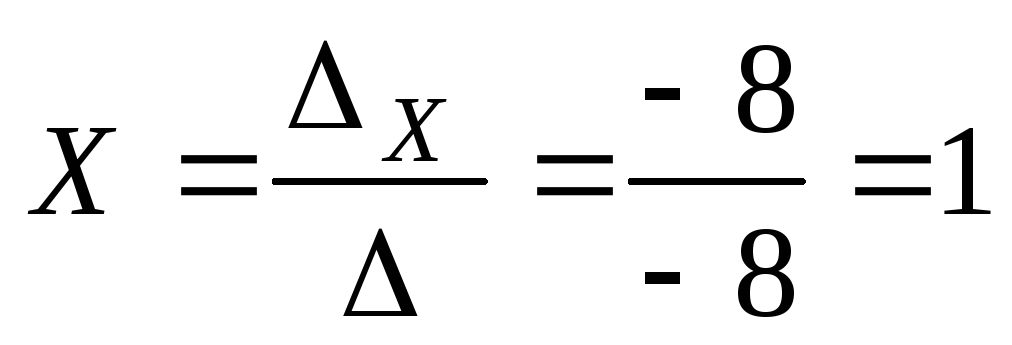
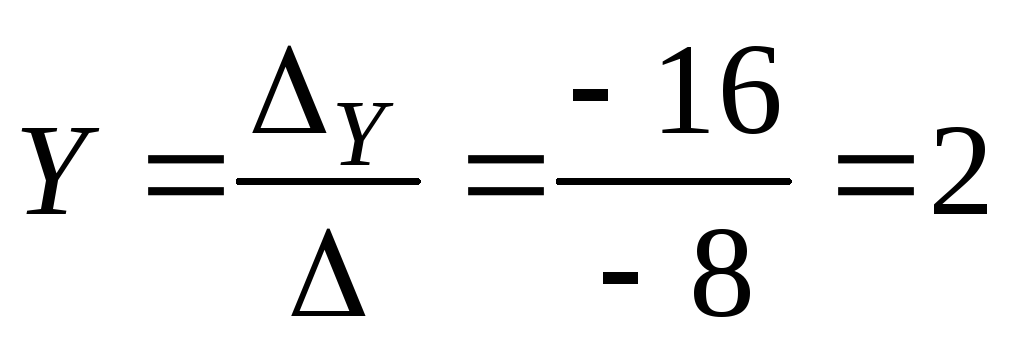
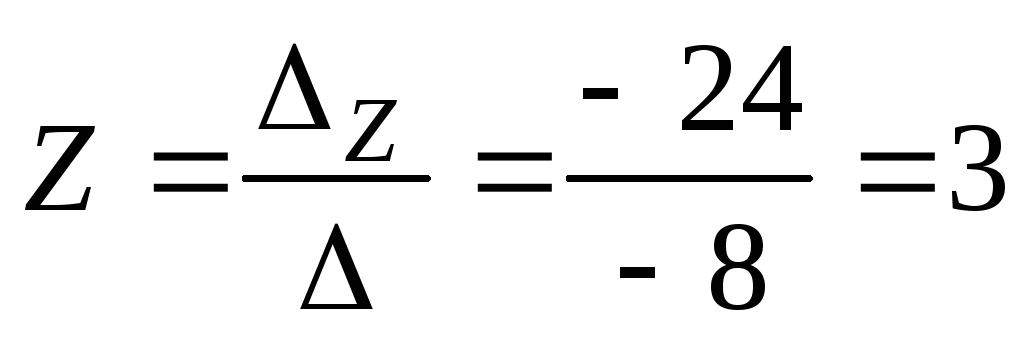
Ответ: (1; 2; 3)
2) 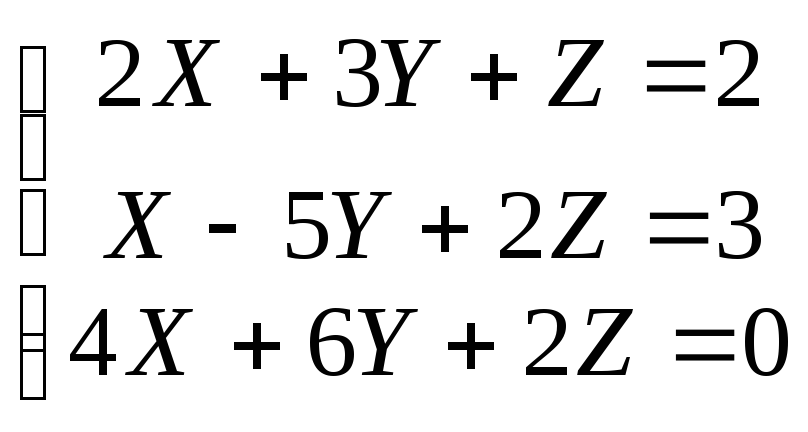
Вычислим:
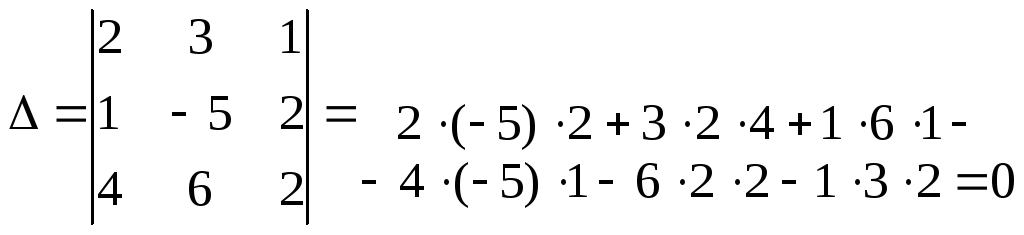
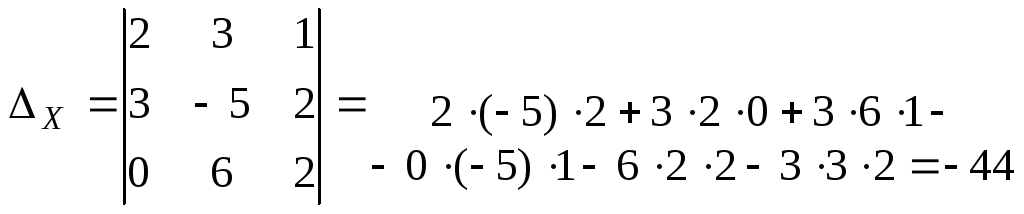
Так как главный
определитель 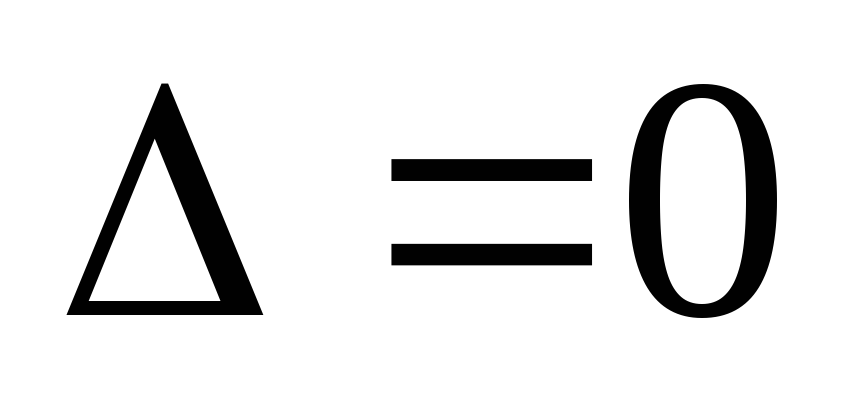 ,
а хотя бы один дополнительный не равен
нулю (в нашем случае
,
а хотя бы один дополнительный не равен
нулю (в нашем случае 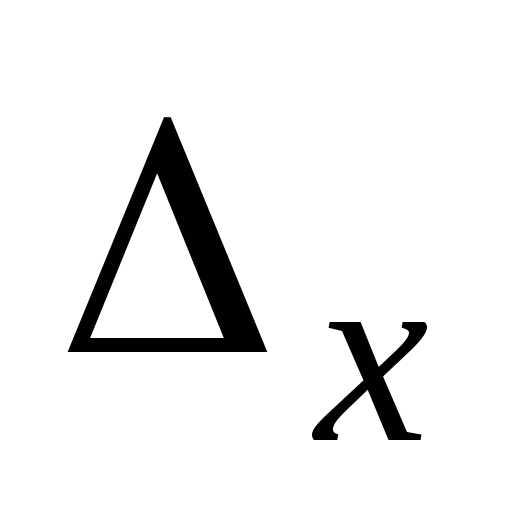
3) 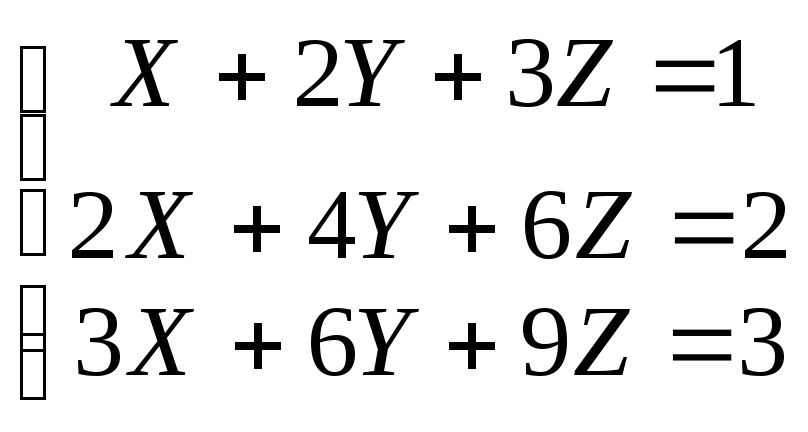
Вычислим:
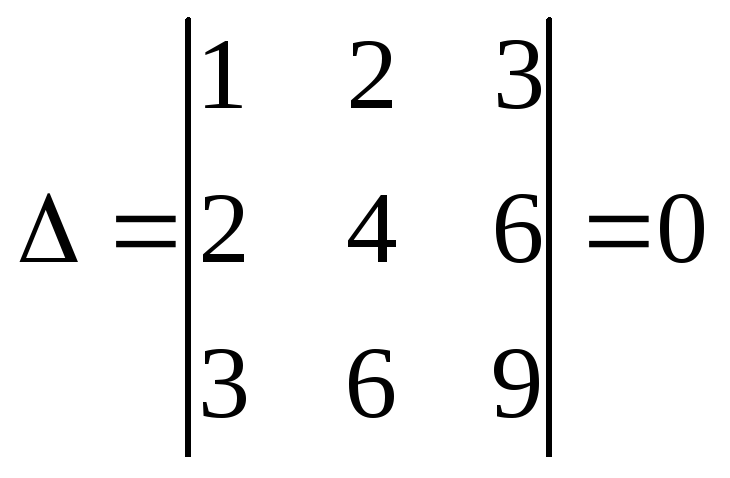
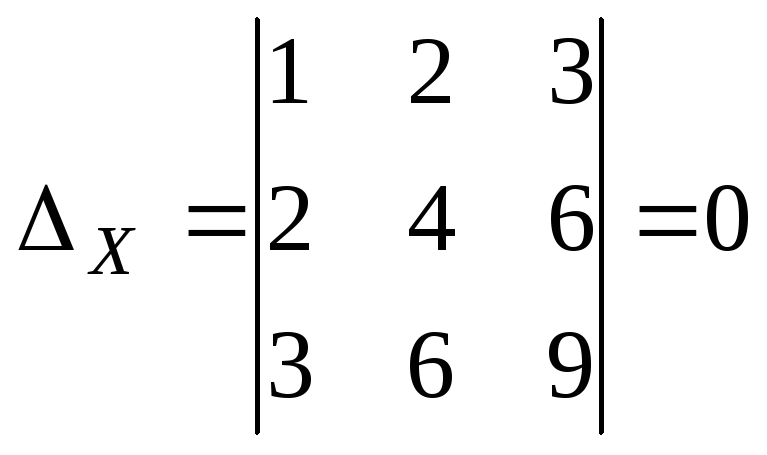
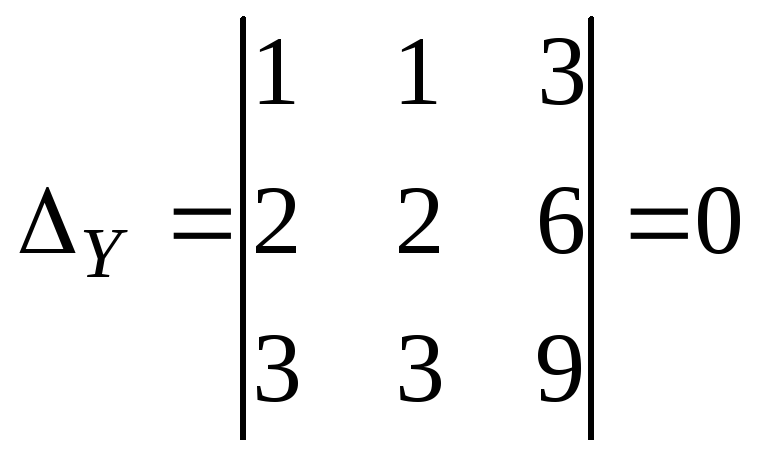
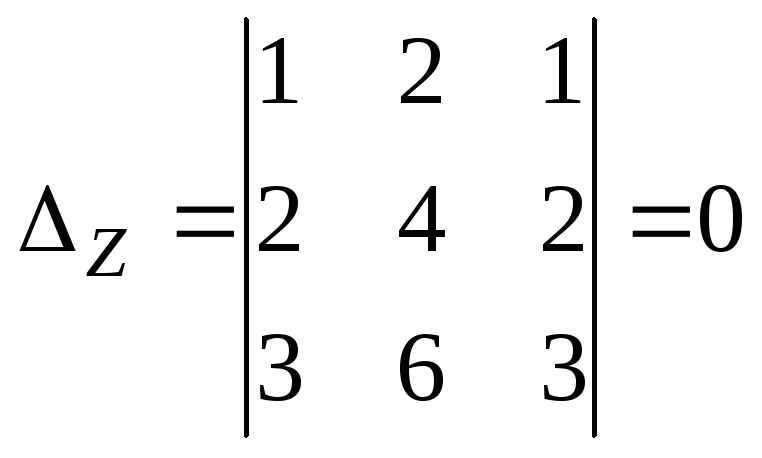
Так как все
определители равны нулю, то система
имеет бесконечное множество решений,
которое можно найти так 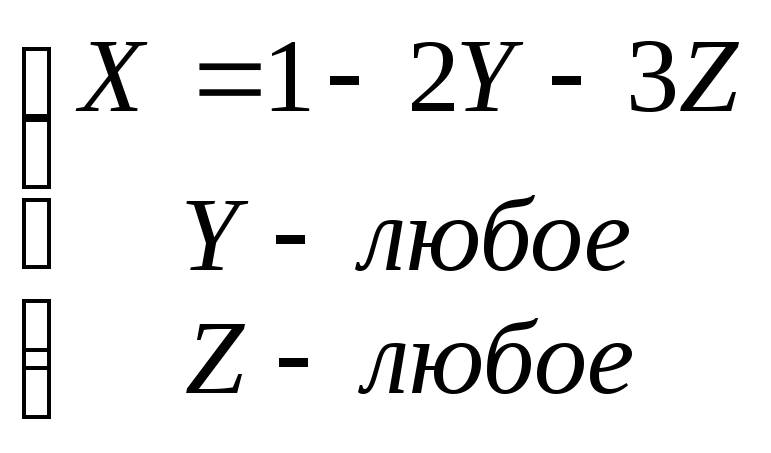
Решите самостоятельно системы:
а) 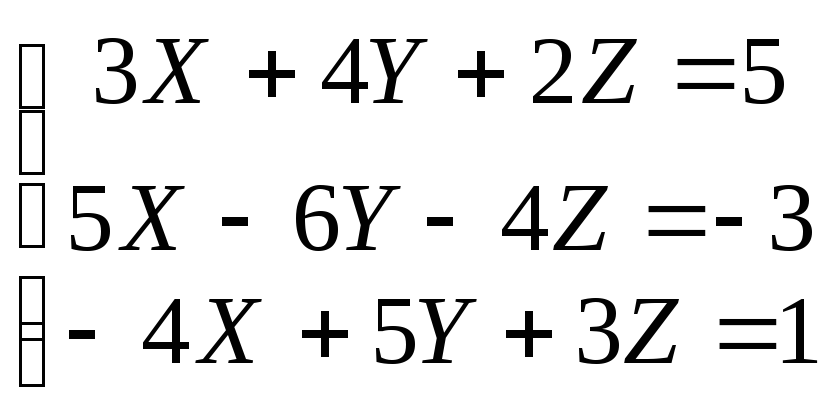

Ответ: а) ( 1; 2; 5 )
б)  ;
; ;
;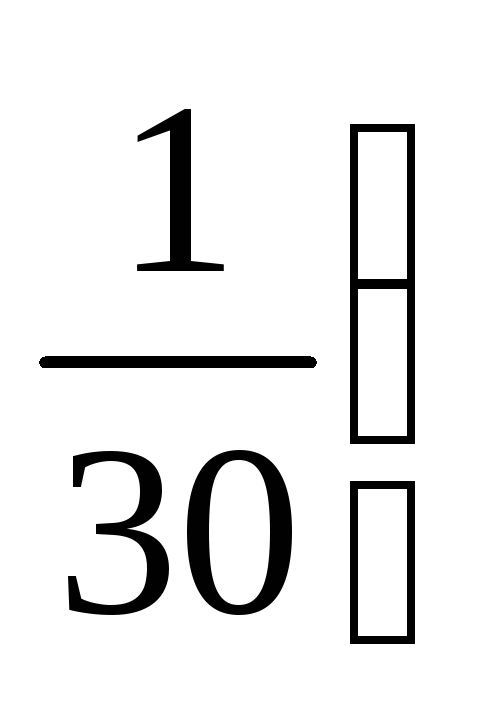
Практическое занятие № 3 на тему:
Скалярное произведение двух векторов и его приложение
1. Если дан  и
и ,
то скалярное произведение находим по
формуле:
,
то скалярное произведение находим по
формуле: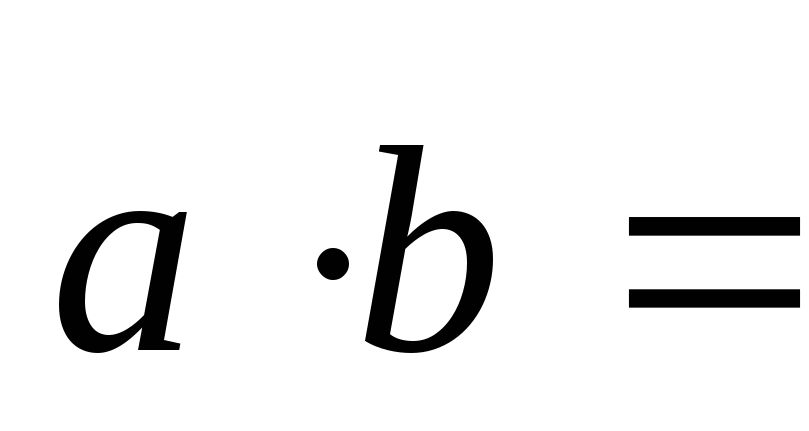
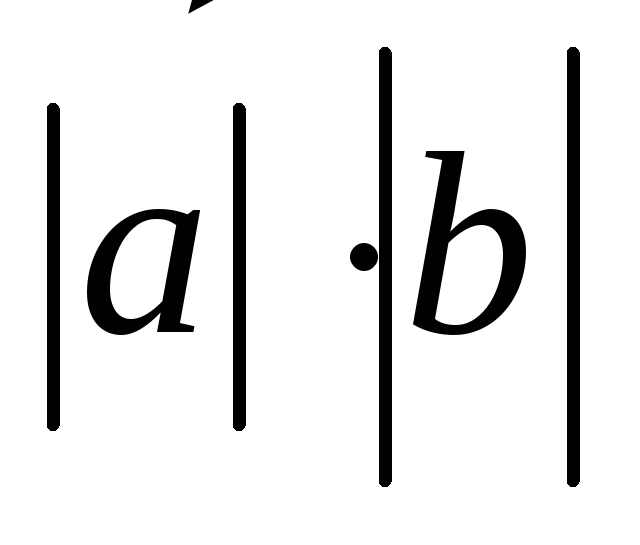 ∙
∙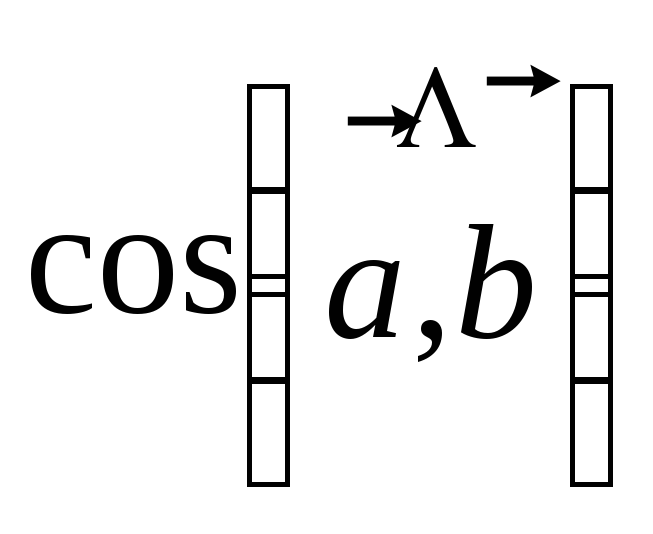
2.Если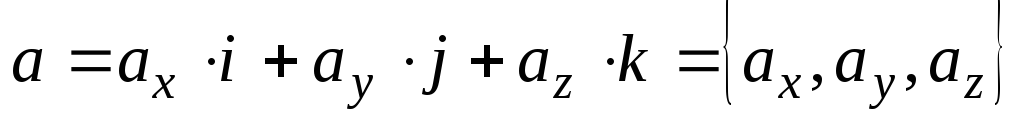
 ,
то скалярное произведение этих двух
векторов находим по формуле
,
то скалярное произведение этих двух
векторов находим по формуле 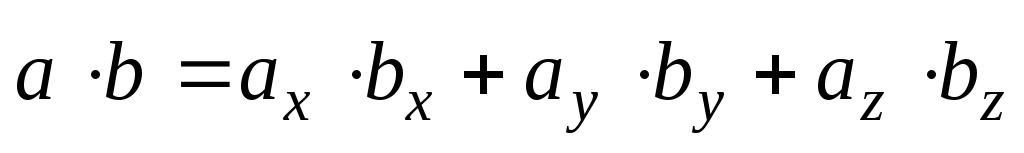
Примеры:
1. Даны два вектора 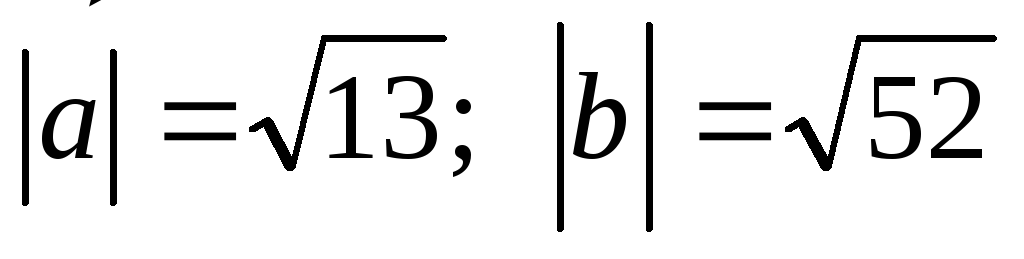 и
и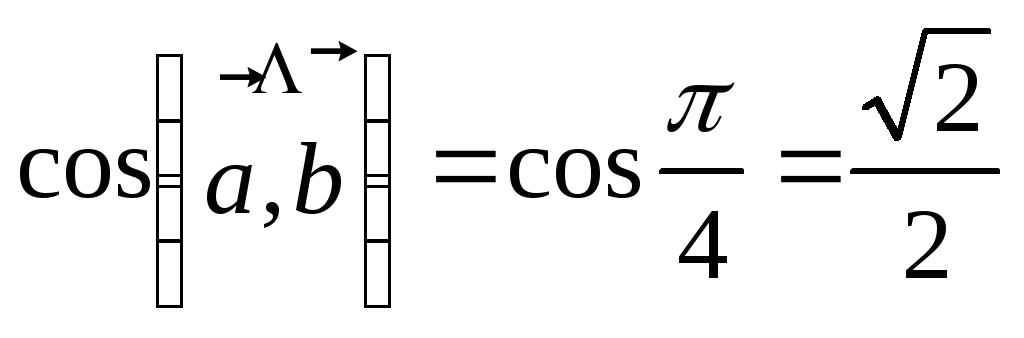
Их скалярное произведение находим так:
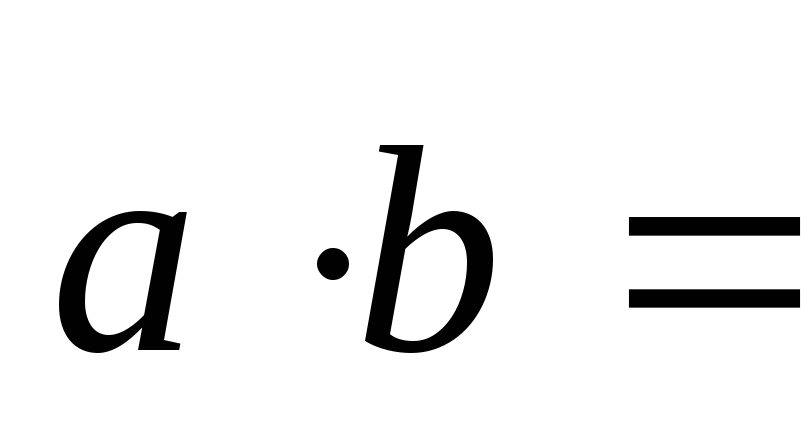
 .
.
2. Даны два вектора:
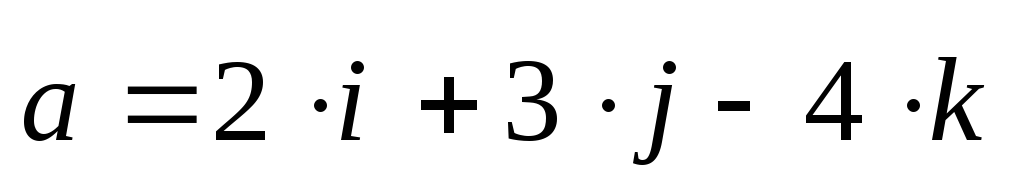 ={2;3;–4}
={2;3;–4} 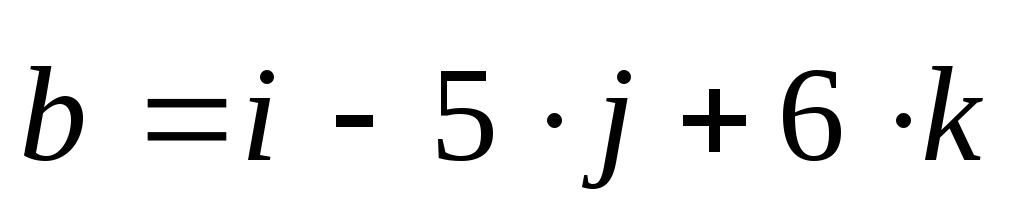 ={1;
–5; 6}
={1;
–5; 6}
скалярное произведение находят так:
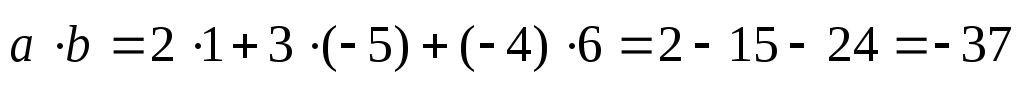
3. ,
, 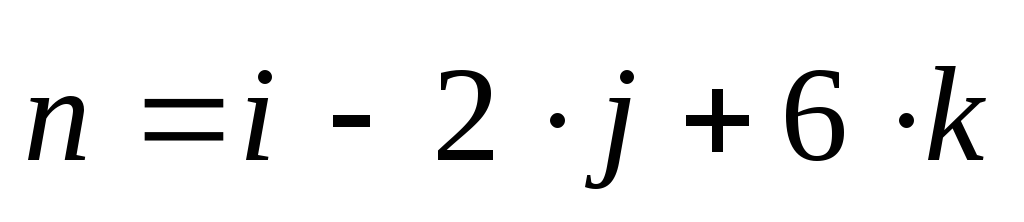

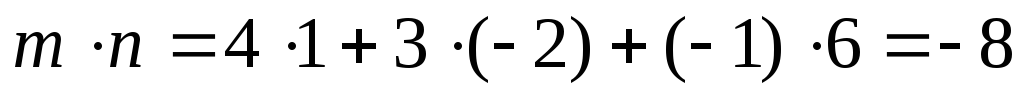
3.1 Нахождение работы постоянной силы на прямолинейном участке пути
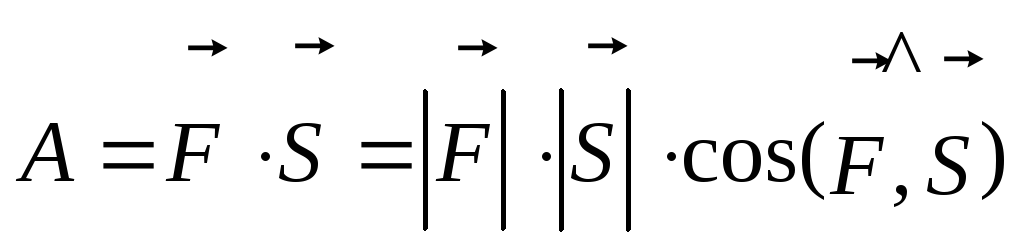
Примеры:
1) Под действием силы в 15Н тело переместилось по прямой на 2 метра. Угол между силой и направлением перемещения =60
Дано: 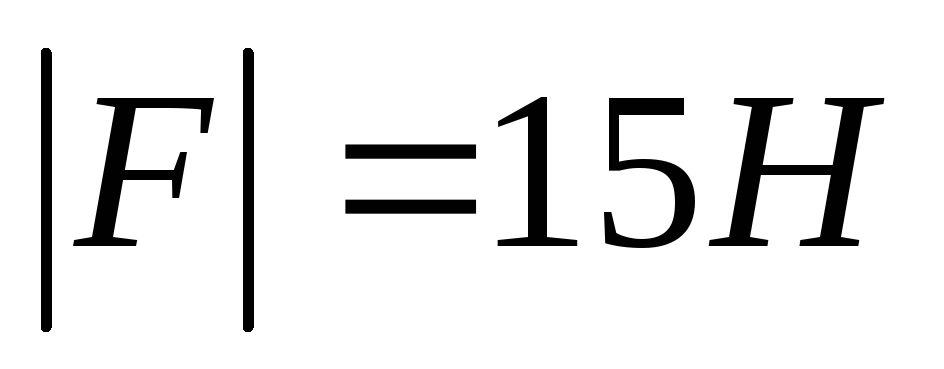

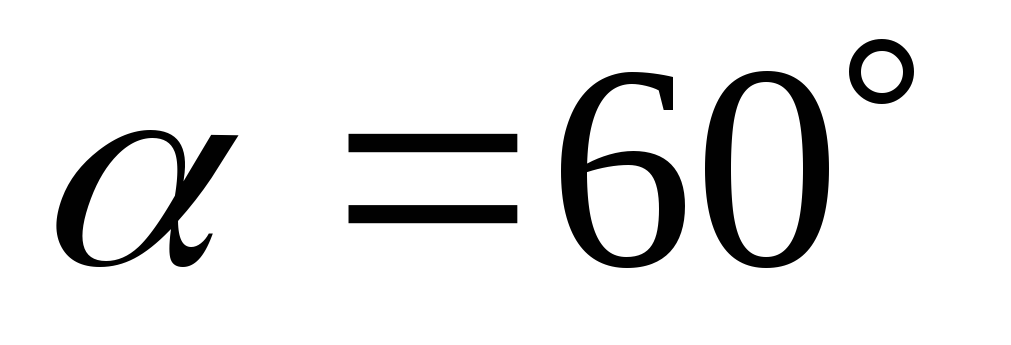
Решение: 
2) Дано: 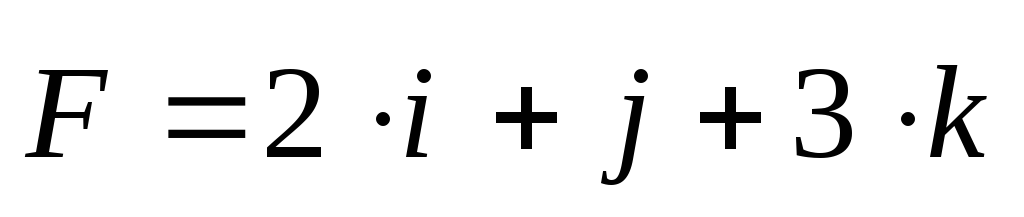
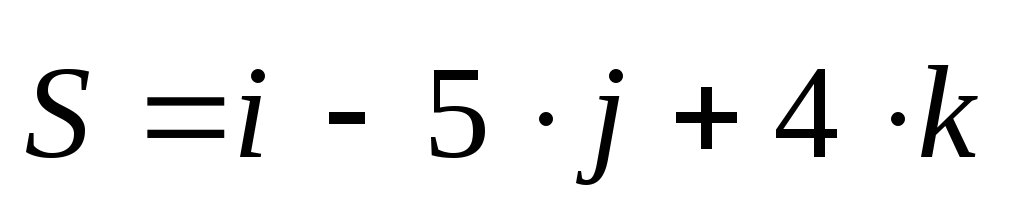
Найти А.
Решение: 
3) Из точки М(1; 2; 3) в точку N(5; 4; 6) переместилось тело под действием силы 60Н. Угол между направлением силы и вектором перемещения =450. Вычислить работу, совершаемую этой силой.
Решение: находим
вектор перемещения 
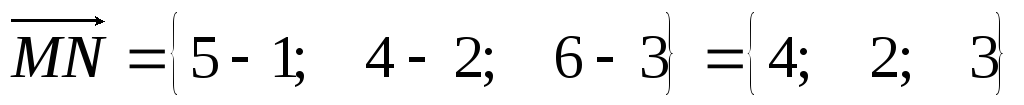
Находим модуль вектора перемещения:

По формуле  находим работу:
находим работу:
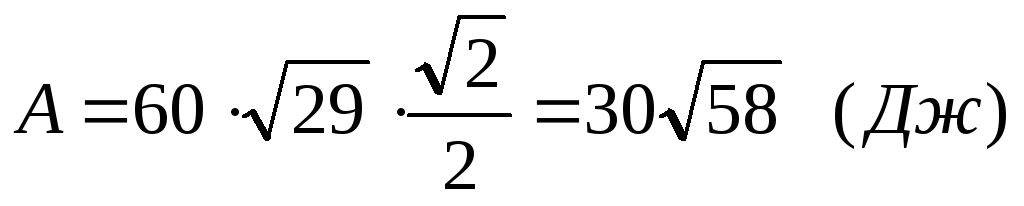
3.2 Определение ортогональности двух векторов
Два вектора
ортогональны, если 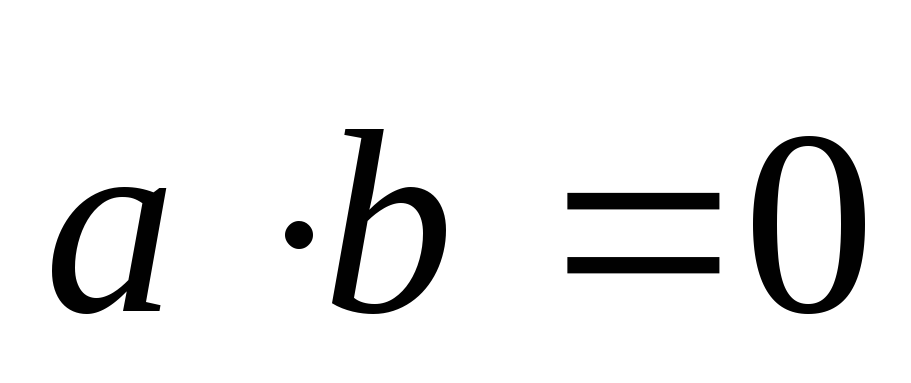 ,
то есть
,
то есть
 так как
так как 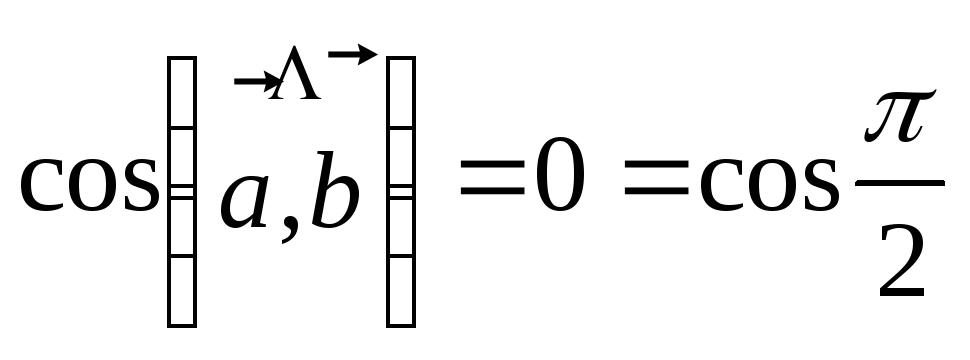
Примеры:
1) 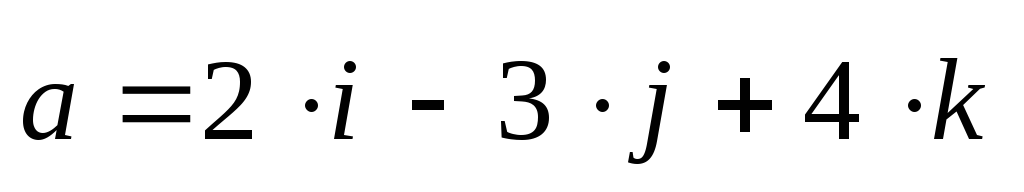
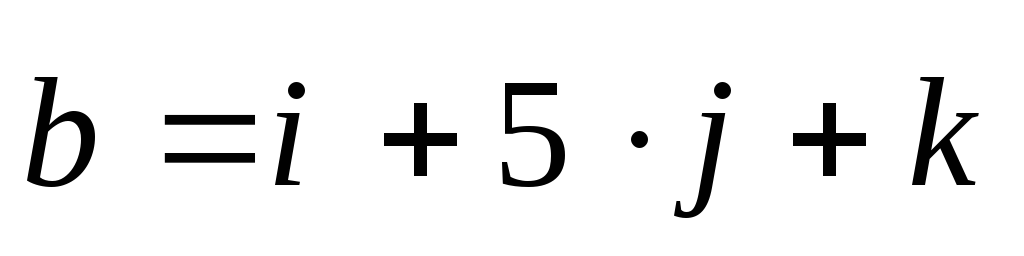


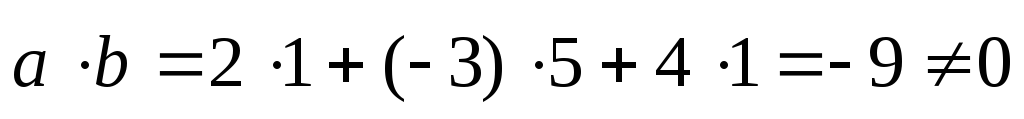 –не ортогональны
–не ортогональны



 –ортогональны
–ортогональны
3) Определить, при
каком
векторы 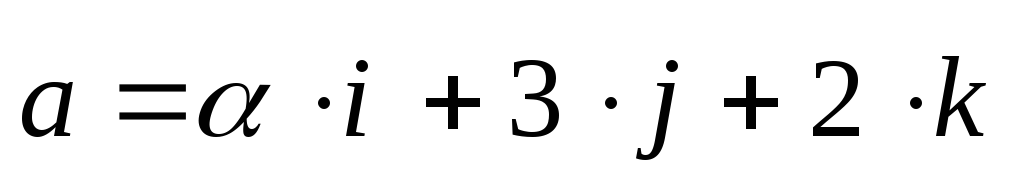 и
и  взаимно-ортогональны.
взаимно-ортогональны.
Так как  ,
то
,
то 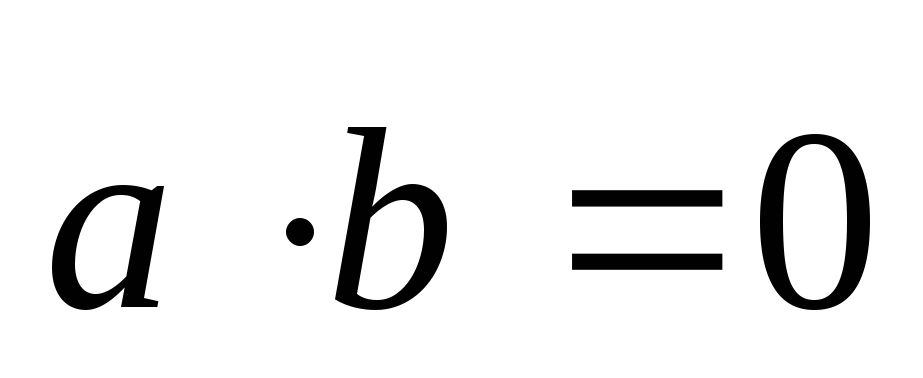 ,
значит
,
значит



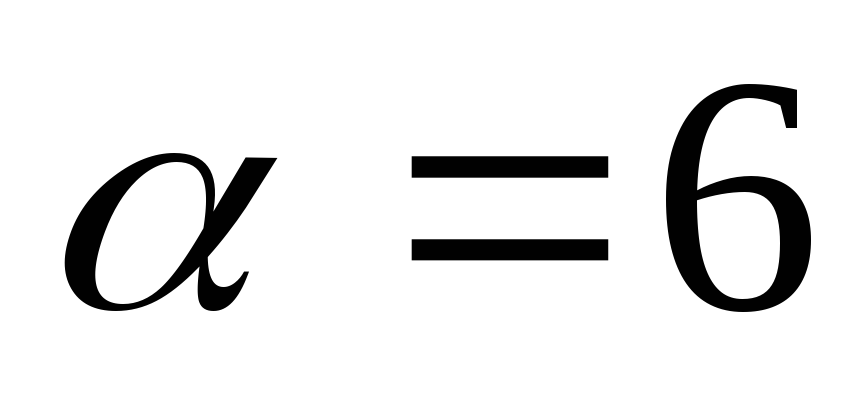
Решите самостоятельно:
а) 
 .
Найти их скалярное произведение.
.
Найти их скалярное произведение.
б) Вычислить, какую
работу производит сила 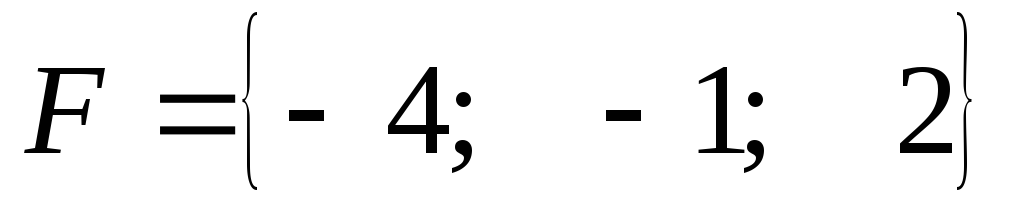 ,
если точка ее приложения, двигаясь
прямолинейно, переместилась из точки
M
(5; -6; 1) в точку N
(1; -2; 3)
,
если точка ее приложения, двигаясь
прямолинейно, переместилась из точки
M
(5; -6; 1) в точку N
(1; -2; 3)
в) Определить,
ортогональны ли вектора 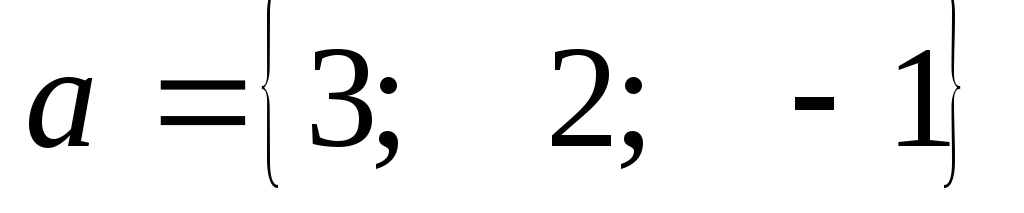 и
и

Ответы: а) 1 б) 16 в) да
3.3.Нахождение угла между векторами
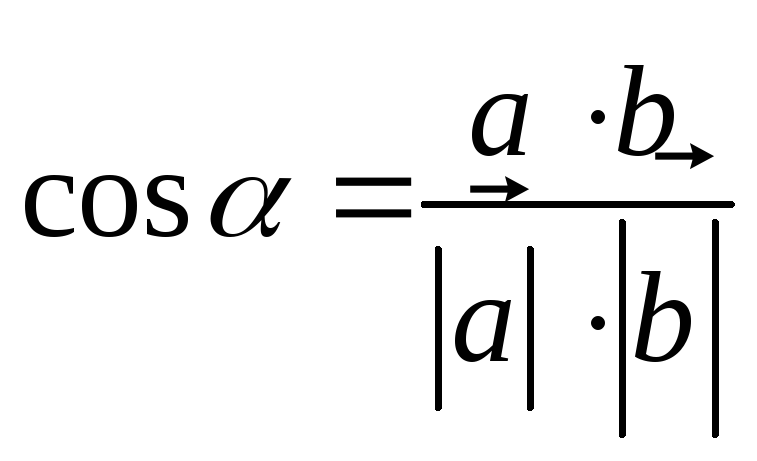
Примеры:
1) 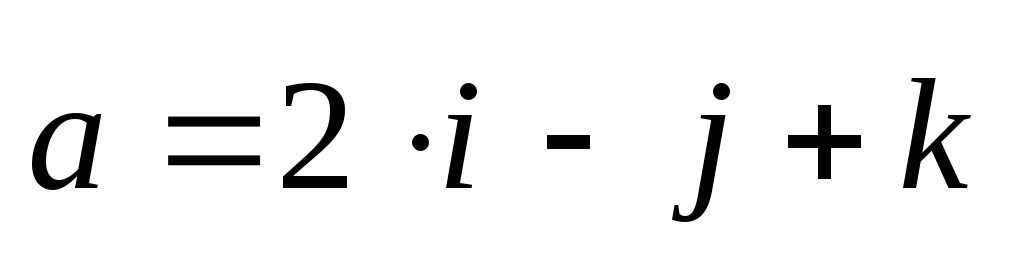
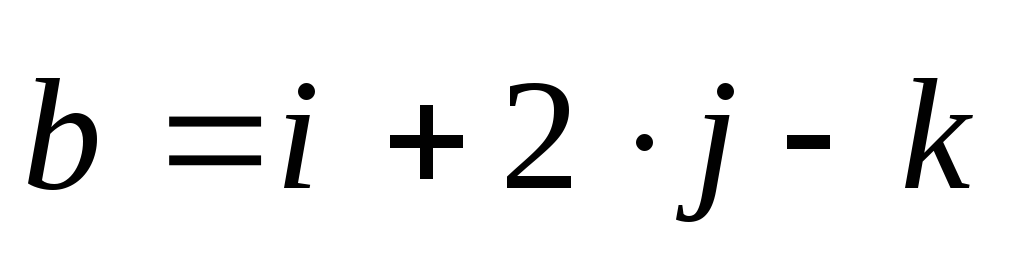 .
Найти
.
Найти  .
.
Решение:
Находим 
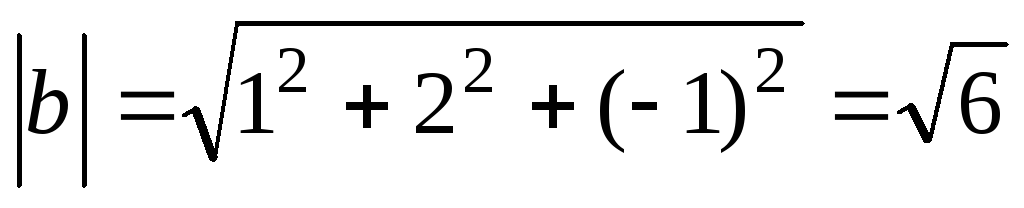
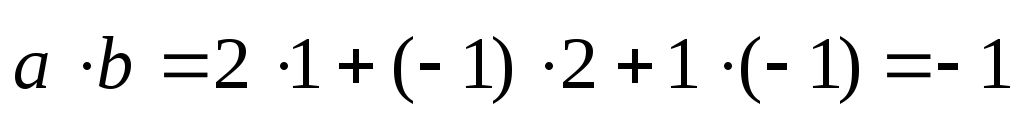
подставляем в формулу:
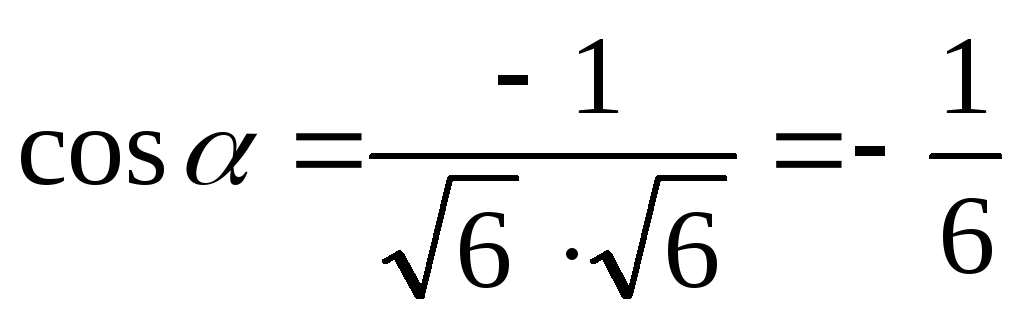
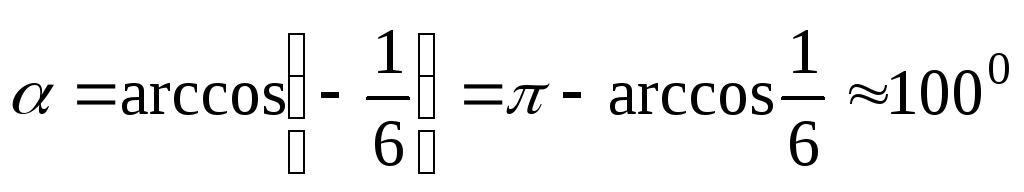 .
.
1). Даны вершины треугольника А(3; 2; –3), В(5; 1; –1), С(1; –2; 1). Найти угол при вершине А.
Решение:
Находим 
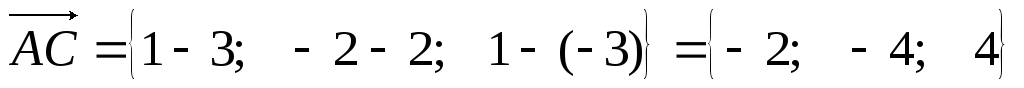
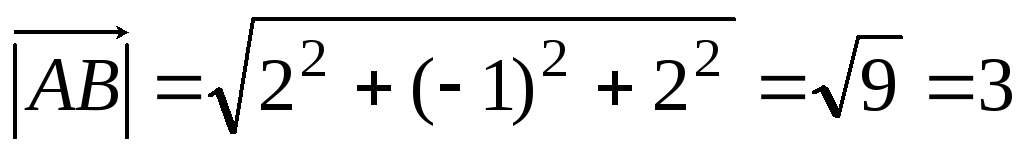

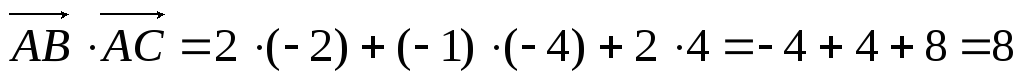
Подставим в формулу: 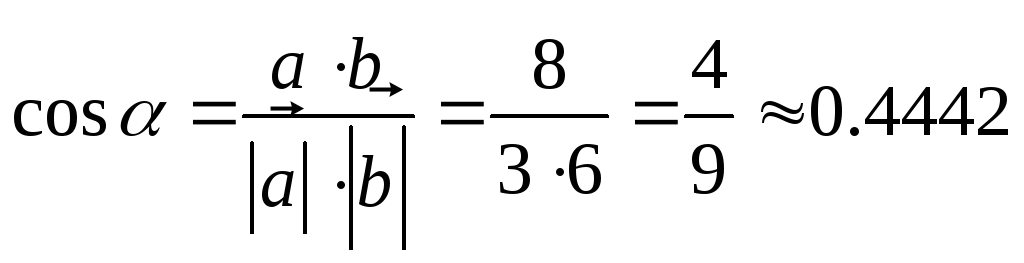

Решите самостоятельно:
Даны вершины треугольника А(3; 5; -2), В(5; 7; -1), С(4; 3; 0). Определить внутренний угол при вершине А.
Ответ: 90о
Практическое занятие № 4 на тему:
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ И ЕГО ПРИЛОЖЕНИЕ.
Формула для нахождения векторного произведения двух векторов:
Примеры:
1) Найти модуль векторного произведения:
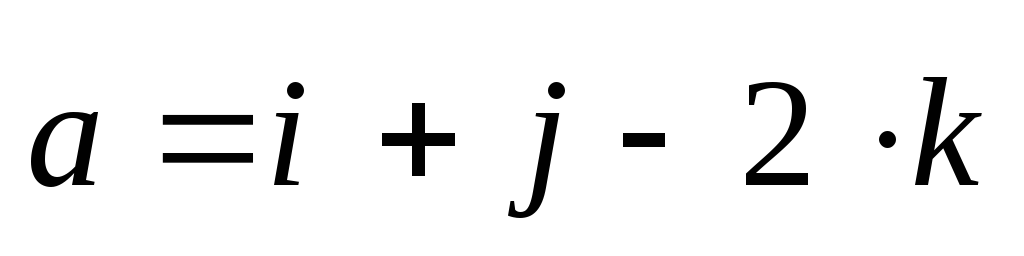

Решение:
Составим определитель и вычислим его (по правилу Саррюса или по теореме о разложении определителя по элементам первой строки).
1-ый способ: по правилу Саррюса
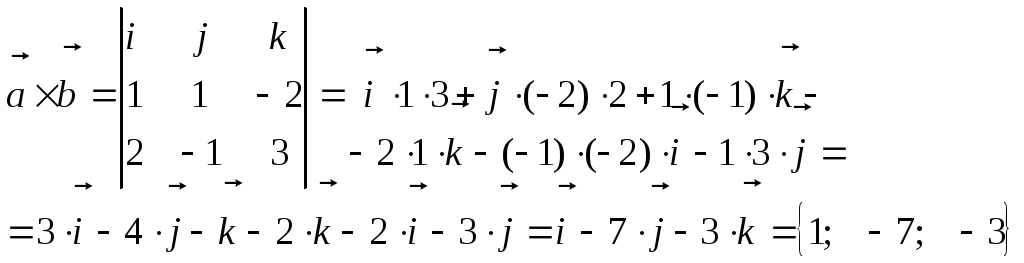
2-й способ: разложим определитель по элементам первой строки.
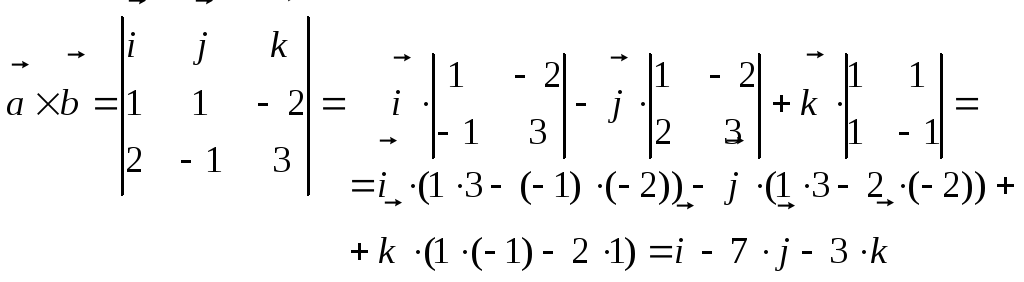
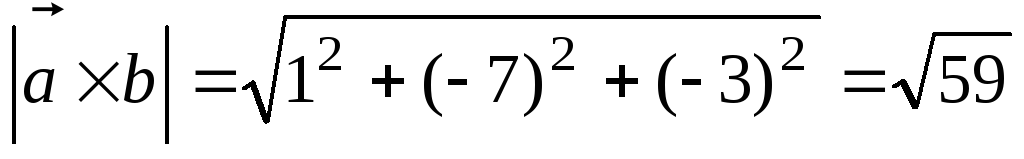
2) Найти модуль векторного произведения:

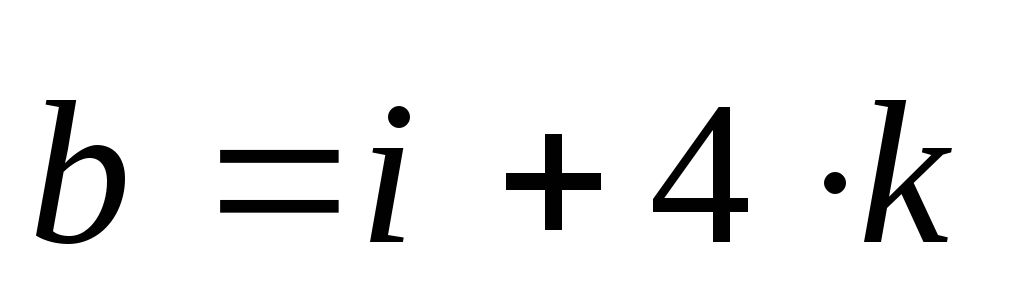
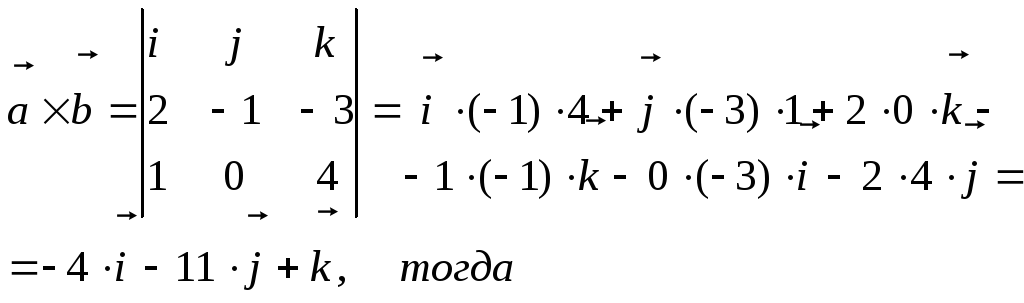
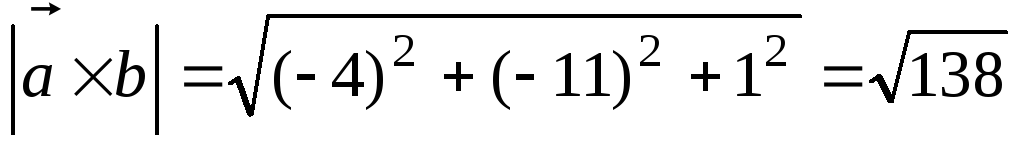
4.1. ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПАРАЛЛЕЛОГРАММА, ПОСТРОЕННОГО НА ДВУХ ВЕКТОРАХ.
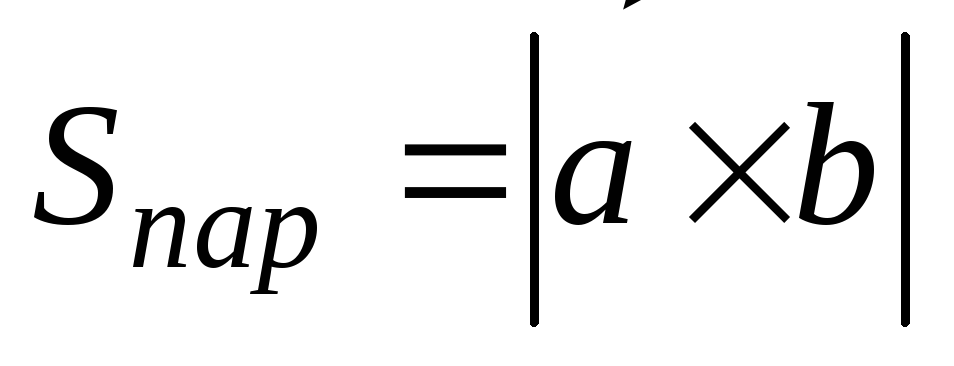
Примеры:
1) Вычислить площадь параллелограмма, построенного на векторах
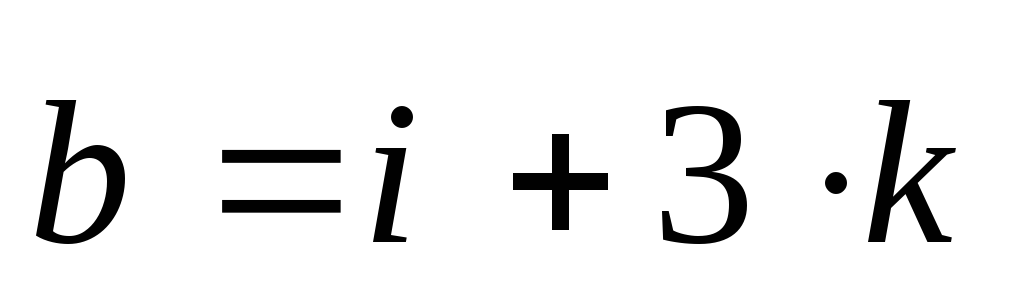
Решение.

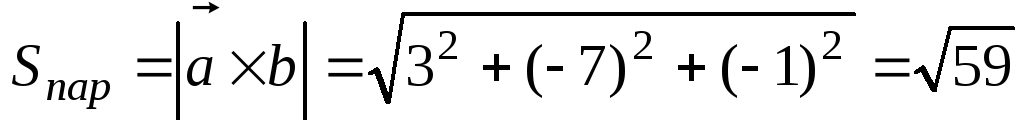
2). Найти векторное произведение и его модуль
Ответ: 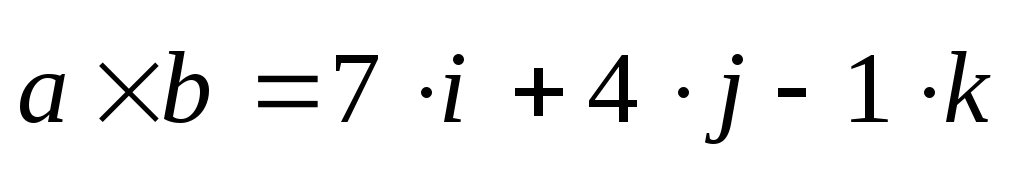
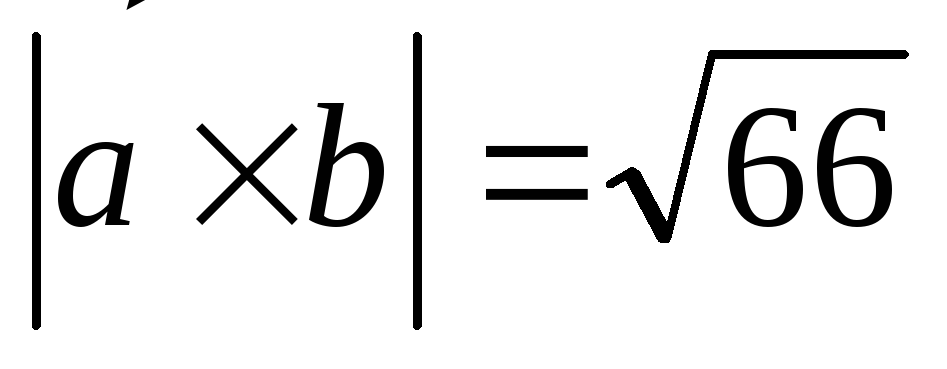
4.2. ВЫЧИСЛЕНИЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА

Пример: даны вершины треугольника А(1; 0; -1), В(1; 2; 0), С(3; -1; 1). Вычислить площадь треугольника.
Решение:
Сначала найдем координаты двух векторов, выходящих из одной вершины.

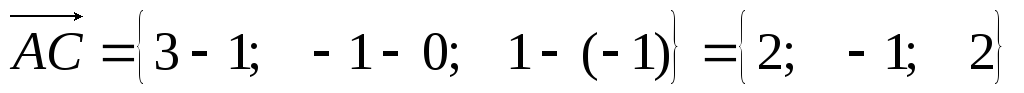
Найдем их векторное произведение

найдем 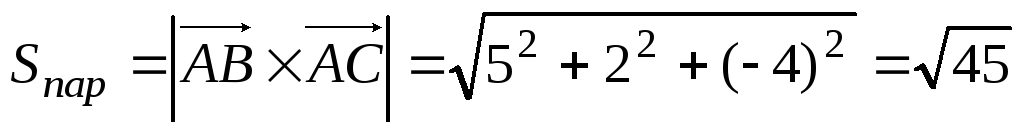
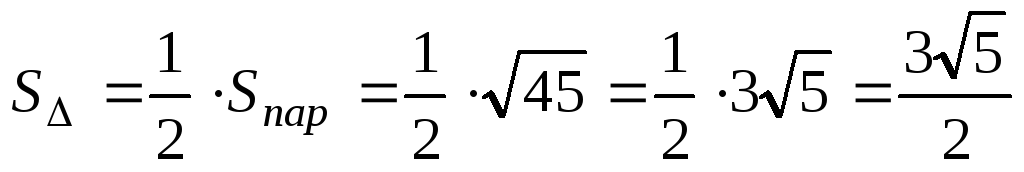
4.3. ОПРЕДЕЛЕНИЕ КОЛЛИНЕАРНОСТИ ДВУХ ВЕКТОРОВ
Если вектора 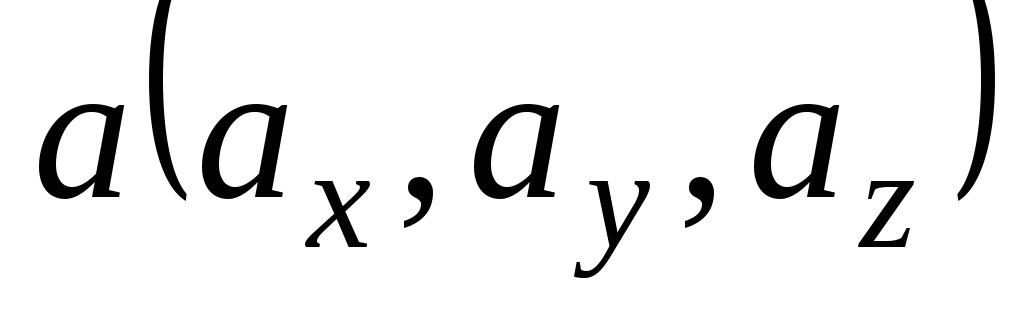 и
и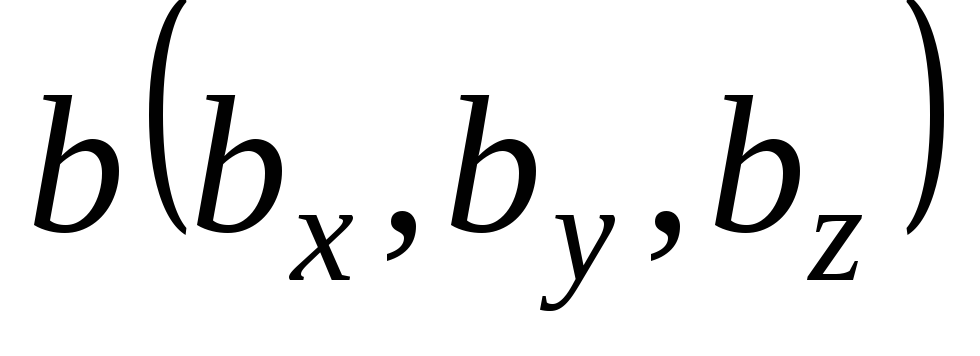 коллинеарны, то
коллинеарны, то
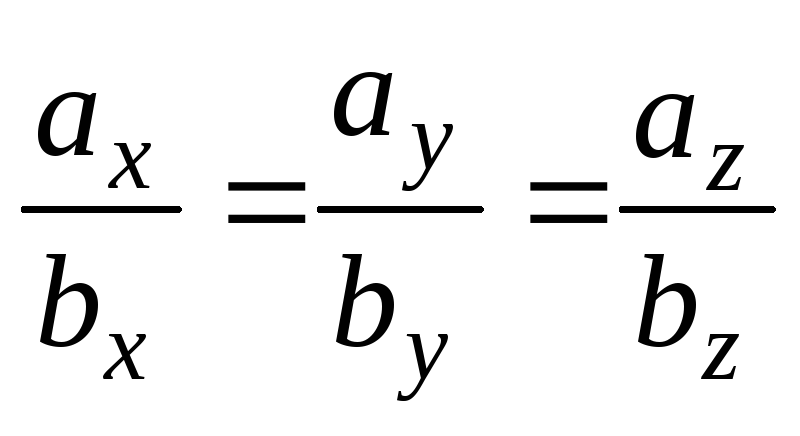 , т. е. координаты
векторов должны быть пропорциональны.
, т. е. координаты
векторов должны быть пропорциональны.
Примеры:
а) Даны вектора:: 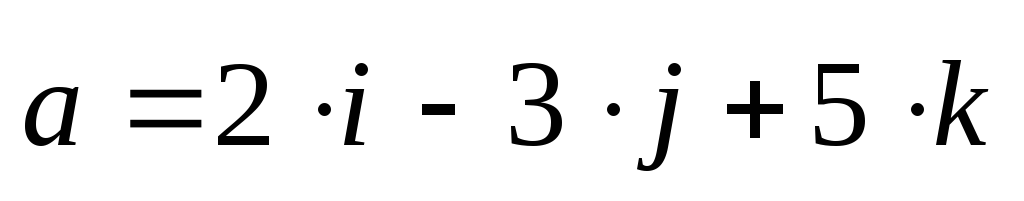 ,
,  .
.
Они коллинеарны
потому, что 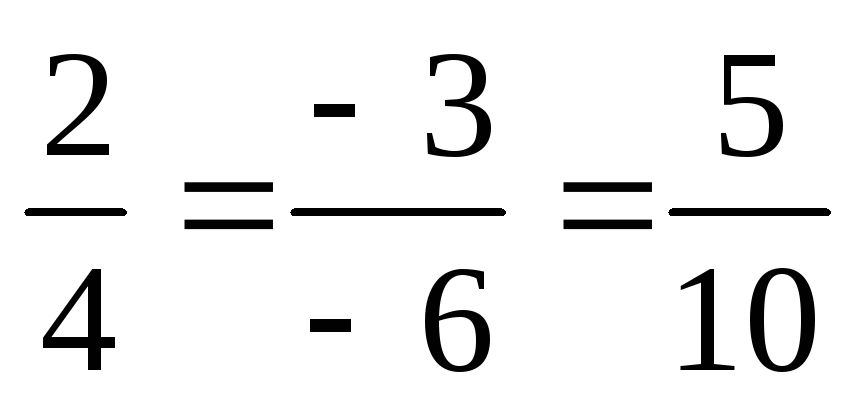 и
и
после сокращения
каждой дроби получается соотношение 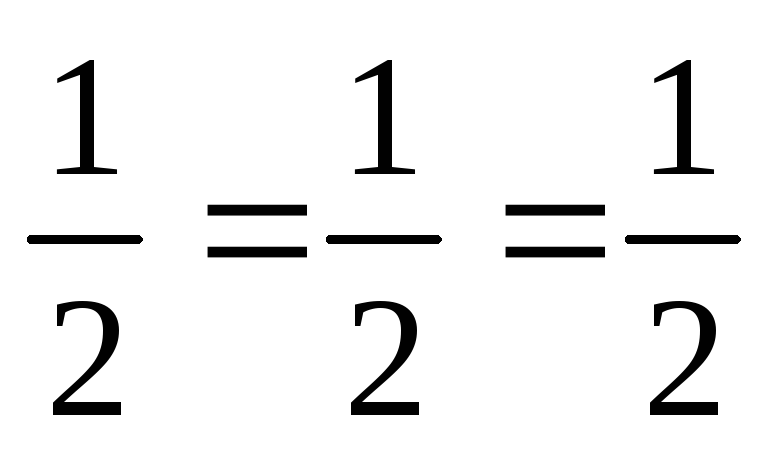
б) Даны вектора: 
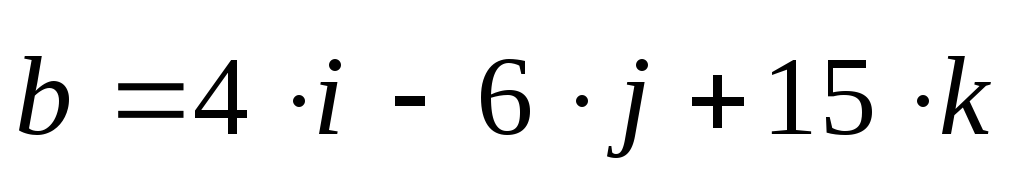 .
.
Они не коллинеарны,
потому, что 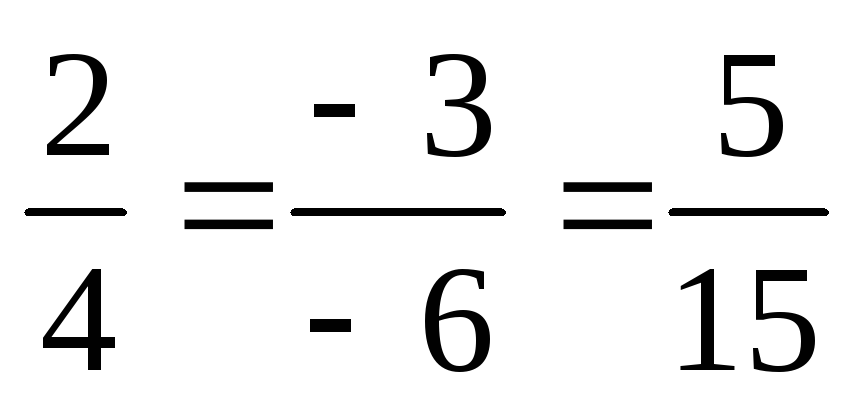 или
или 
Решите самостоятельно:
а) При каких
значениях m
и n
вектора 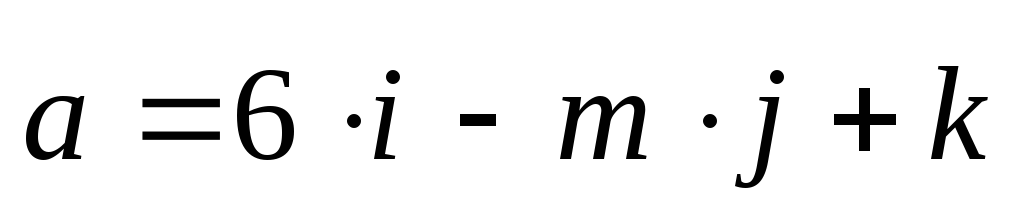 коллинеарны?
коллинеарны?

Ответ: 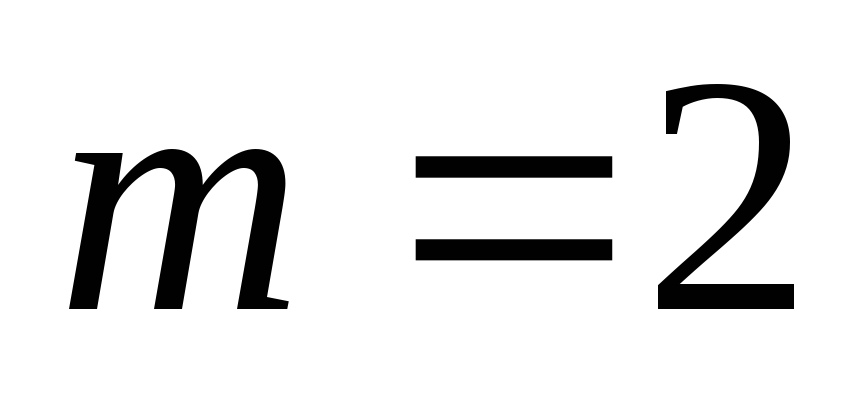 ;
; 
б) Найти векторное
произведение и его модуль 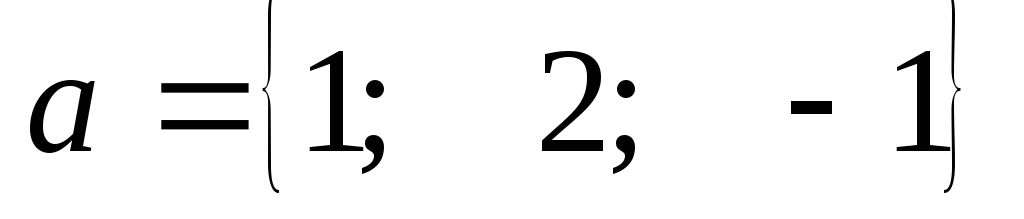 ,
, 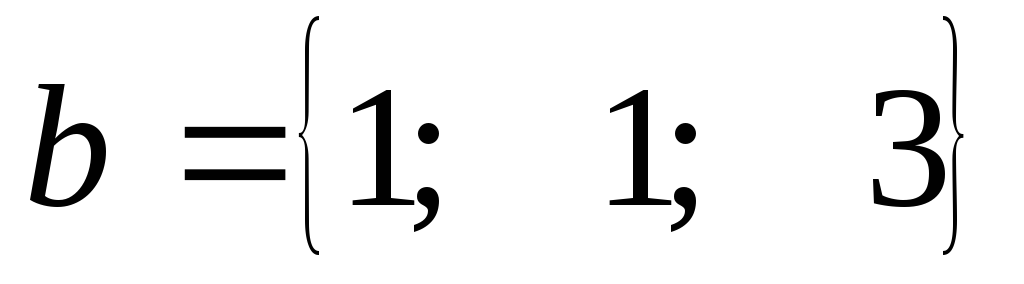 .
.
Ответ: 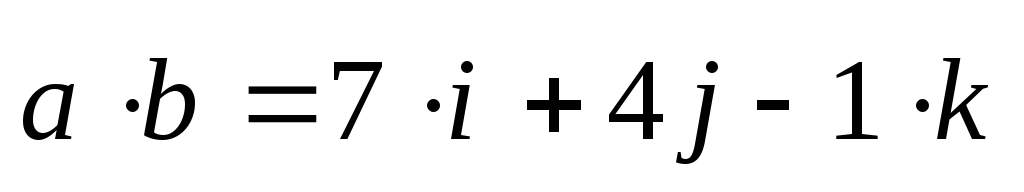 ,
, .
.
Практическое занятие № 5 на тему:
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
Примеры:
Задача № 1. Найти
уравнение прямой, проходящей через
точку А(-2; 3) параллельно прямой 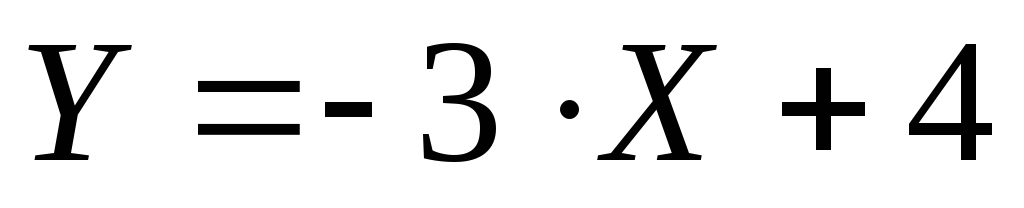
Решение:
1. Найдем угловой
коэффициент прямой 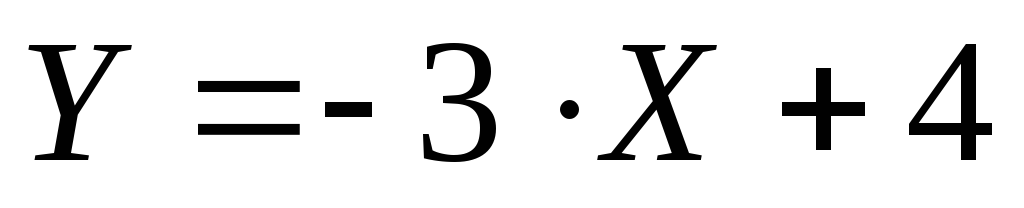 .
.
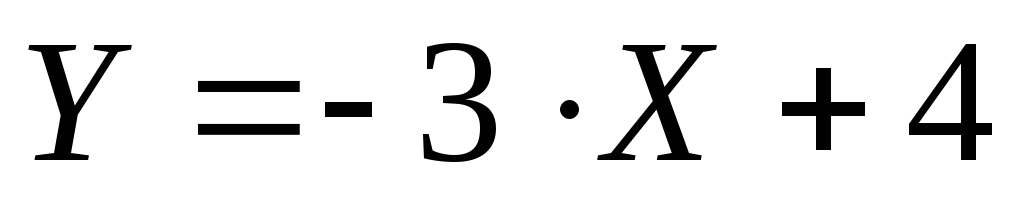 — это уравнение
прямой с угловым коэффициентом и
начальной ординатой (
— это уравнение
прямой с угловым коэффициентом и
начальной ординатой (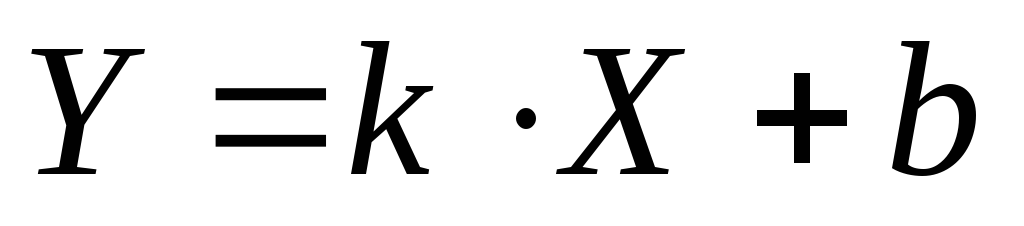 ).
Поэтому
).
Поэтому 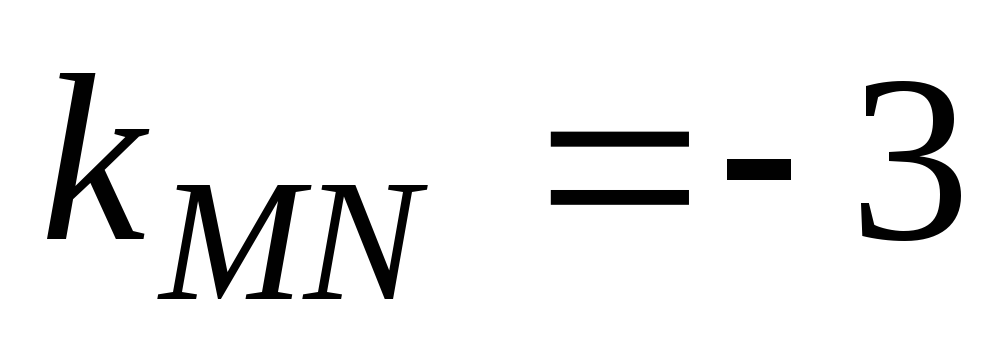 .
.
2. Так как прямые
MN
и АС
параллельны, то их угловые коэффициенты
равны, т.е. 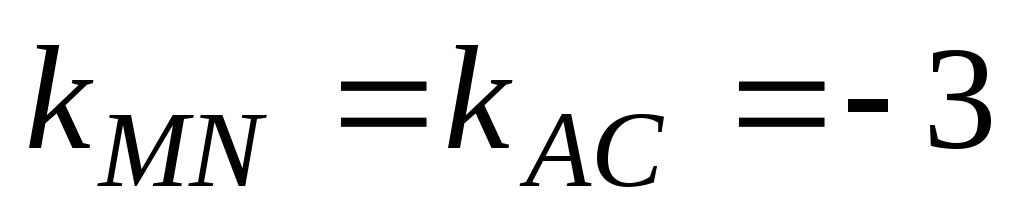 .
.
3. Для нахождения уравнения прямой АС воспользуемся уравнением прямой, проходящей через точку с данным угловым коэффициентом:
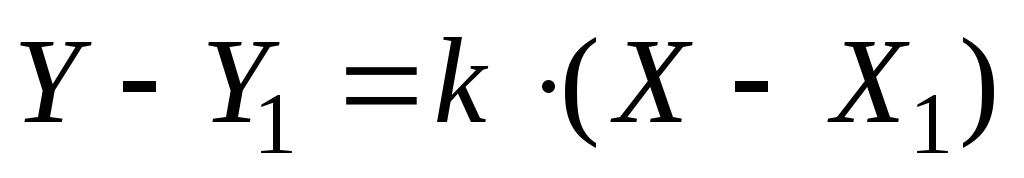 .
В эту формулу вместо
.
В эту формулу вместо  и
и  подставим координаты точки А(-2; 3), вместо
подставим координаты точки А(-2; 3), вместо 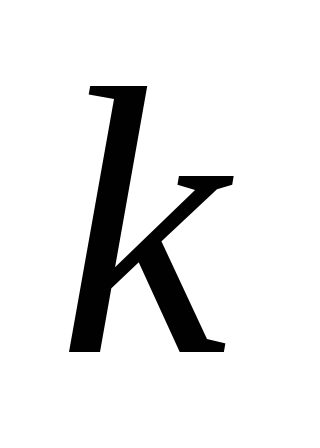 подставим
– 3. В результате подстановки получим:
подставим
– 3. В результате подстановки получим:
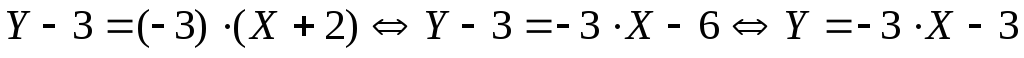
Ответ: 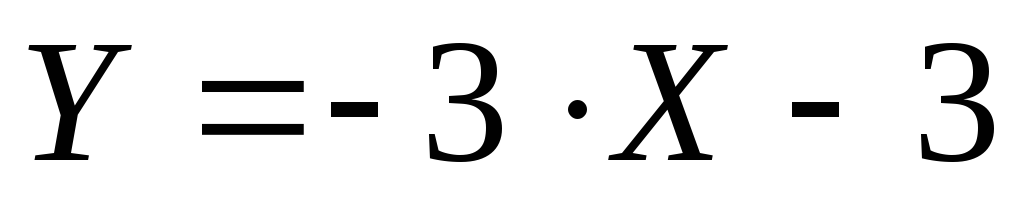
Задача №2. Найти
уравнение прямой, проходящей через
точку К(1; –2)
параллельно прямой 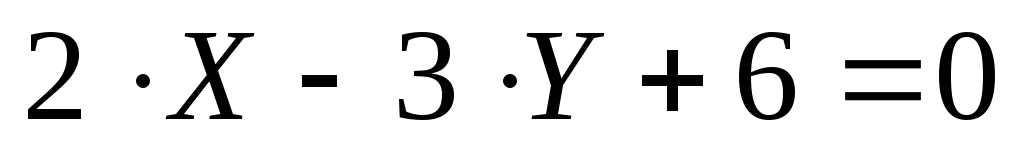 .
.
Решение:
1. Найдем угловой
коэффициент прямой 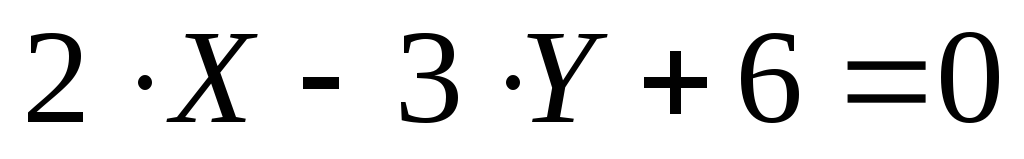 .
.
 —
это общее уравнение прямой, которое в
общем виде задается формулой
—
это общее уравнение прямой, которое в
общем виде задается формулой 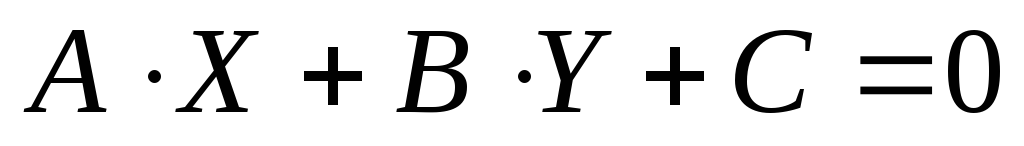 .
Сравнивая уравнения
.
Сравнивая уравнения 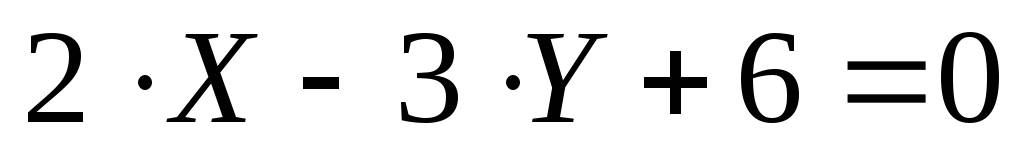 и
и  находим, что А
= 2, В = –3. Угловой
коэффициент прямой, заданной уравнением
находим, что А
= 2, В = –3. Угловой
коэффициент прямой, заданной уравнением  ,
находится по формуле
,
находится по формуле 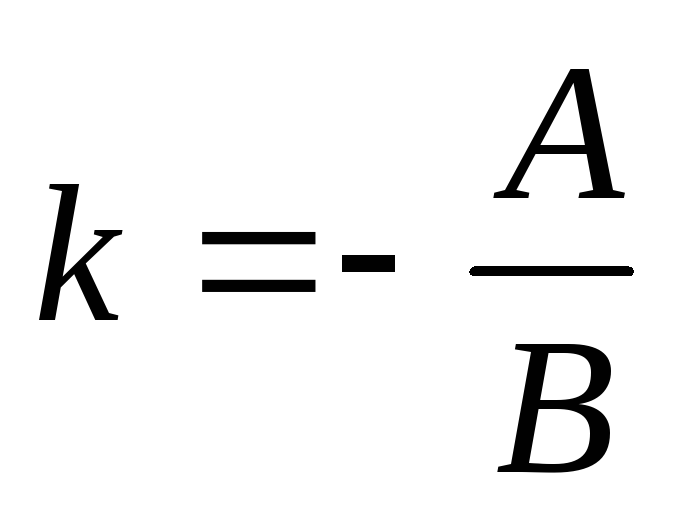 .
Подставив в эту формулу А = 2 и В = –3,
получим угловой коэффициент прямой MN.
Итак,
.
Подставив в эту формулу А = 2 и В = –3,
получим угловой коэффициент прямой MN.
Итак, 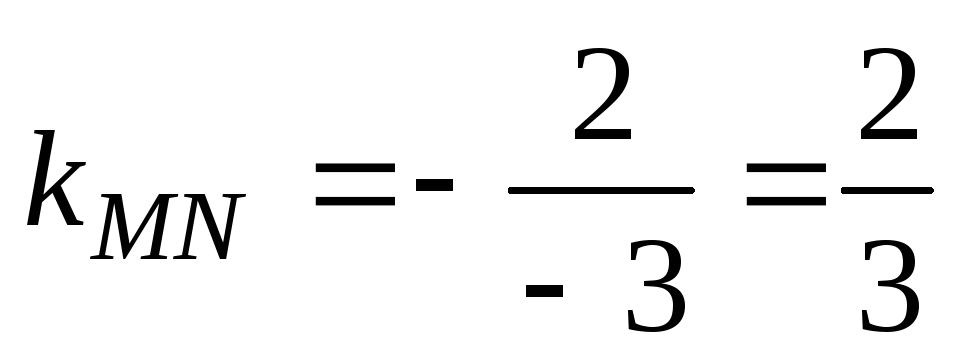 .
.
2. Так как прямые
MN
и КС параллельны, то их угловые коэффициенты
равны: 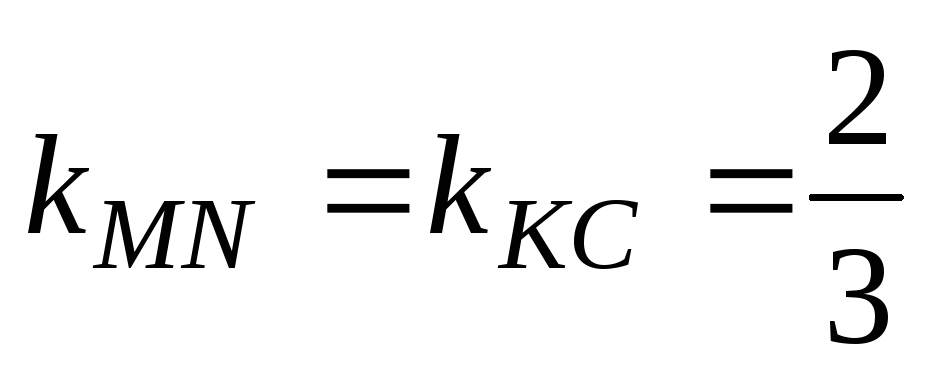 .
.
3. Для нахождения
уравнения прямой КС воспользуемся
формулой уравнения прямой, проходящей
через точку с данным угловым коэффициентом  .
В эту формулу вместо
.
В эту формулу вместо 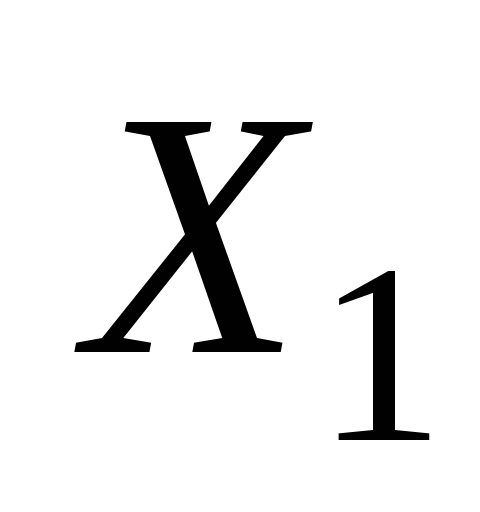 и
и  подставим координаты точки К(–2; 3),
вместо
подставим координаты точки К(–2; 3),
вместо 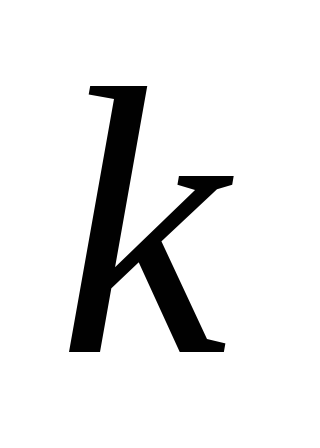 подставим
подставим 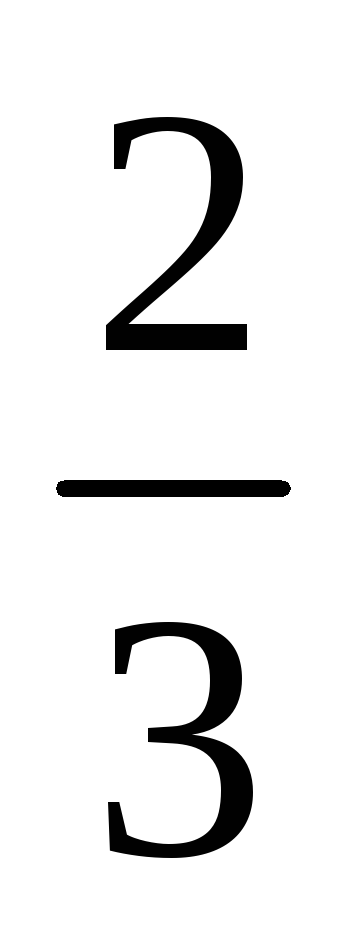 .
В результате подстановки получим:
.
В результате подстановки получим: 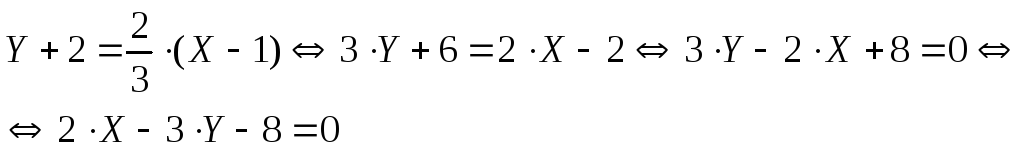
Ответ: 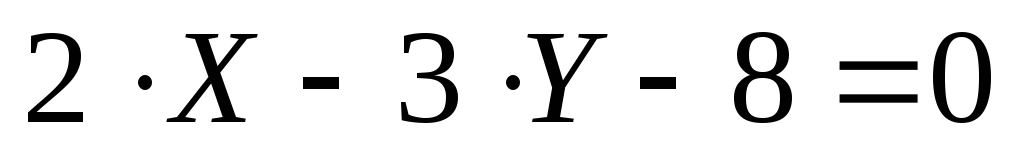
Задача № 3. Найти
уравнение прямой, проходящей через
точку К(–1; –3) перпендикулярно прямой 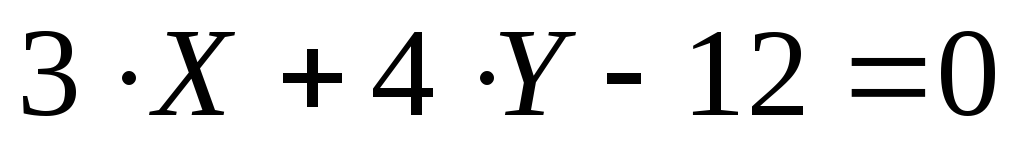 .
.
Решение:
1. 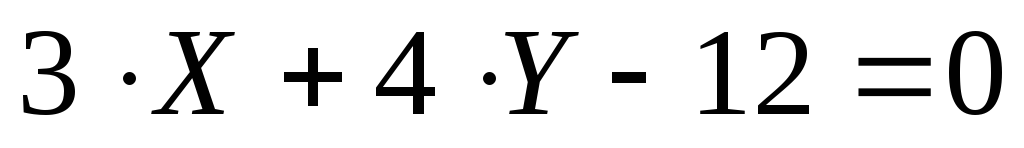 – это общее уравнение прямой, которое
в общем виде задается формулой
– это общее уравнение прямой, которое
в общем виде задается формулой 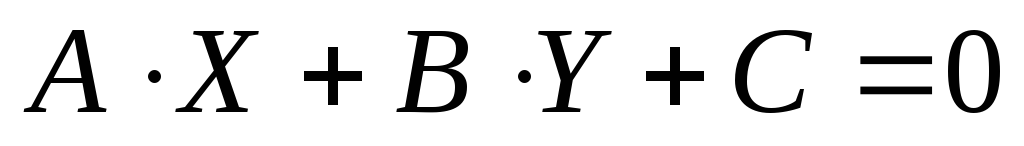 .
.
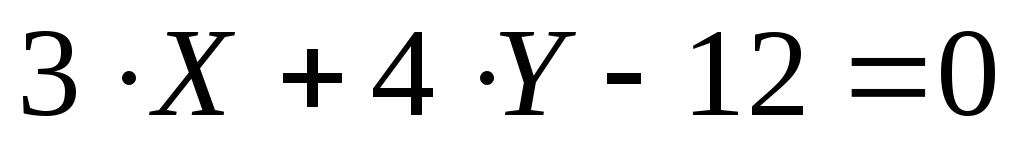 и
и  находим, что А
= 3, В = 4.
находим, что А
= 3, В = 4.
Угловой коэффициент
прямой, заданной уравнением 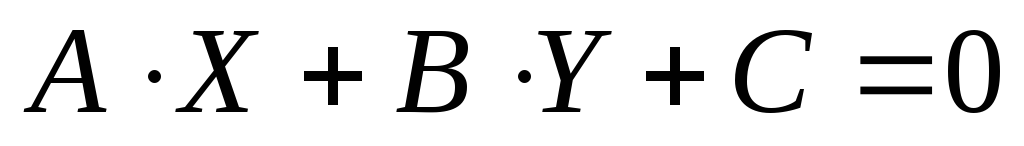 ,
находится по формуле:
,
находится по формуле:  .
Подставив в эту формулу А
= 3 и В = 4, получим
угловой коэффициент прямой MN:
.
Подставив в эту формулу А
= 3 и В = 4, получим
угловой коэффициент прямой MN: 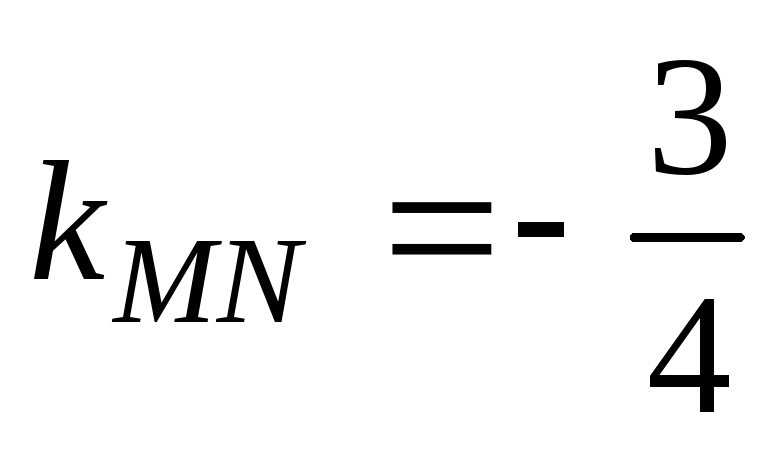 .
.
2. Так как прямые MN и КD перпендикулярны, то их угловые коэффициенты обратно пропорциональны и противоположны по знаку:
 .
.
3. Для нахождения уравнения прямой КD воспользуемся формулой уравнения прямой, проходящей через точку с данным угловым коэффициентом
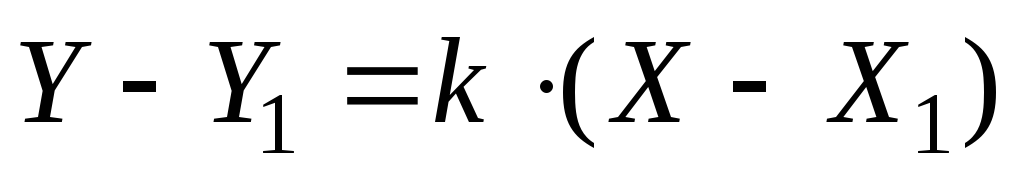 .
В эту формулу вместо
.
В эту формулу вместо 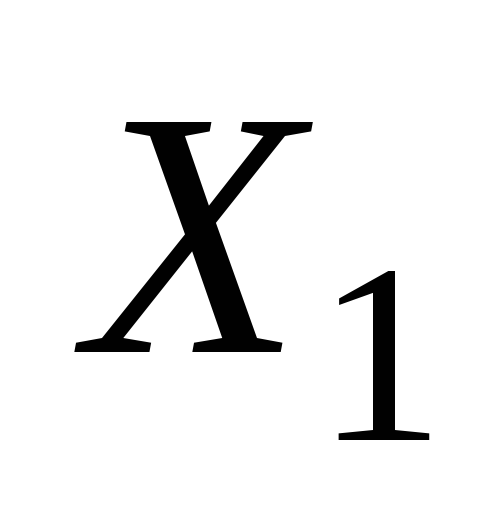 и
и  подставим координаты точки К(–1;
–3), вместо
подставим координаты точки К(–1;
–3), вместо 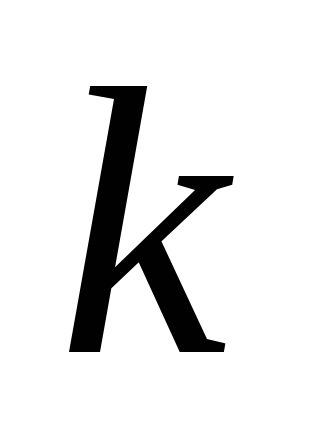 подставим
подставим 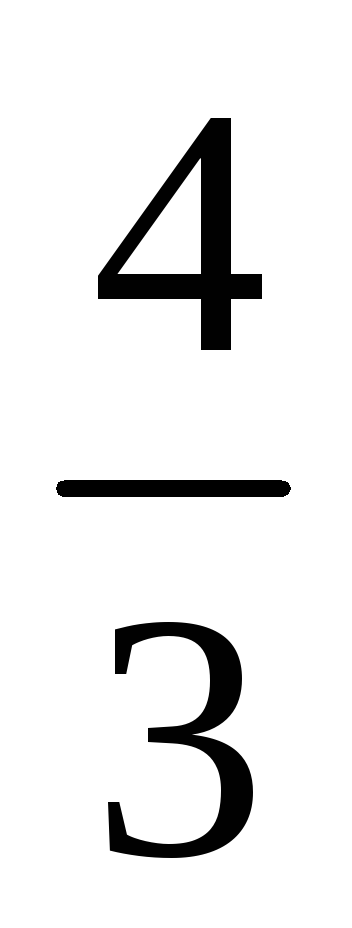 .
В результате подстановки получим:
.
В результате подстановки получим: 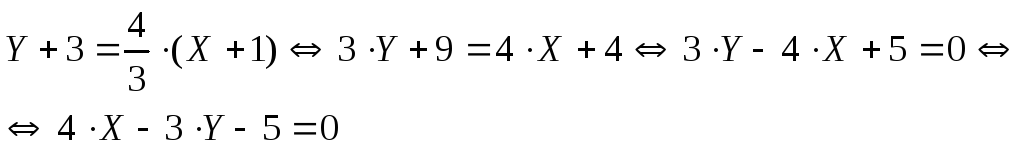
Ответ: 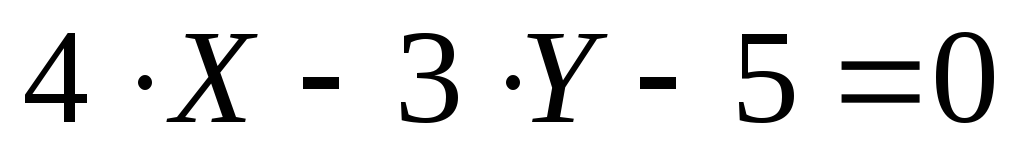
Решите самостоятельно:
1. Найти уравнение
прямой, проходящей через точку К(–4; 1)
параллельно прямой 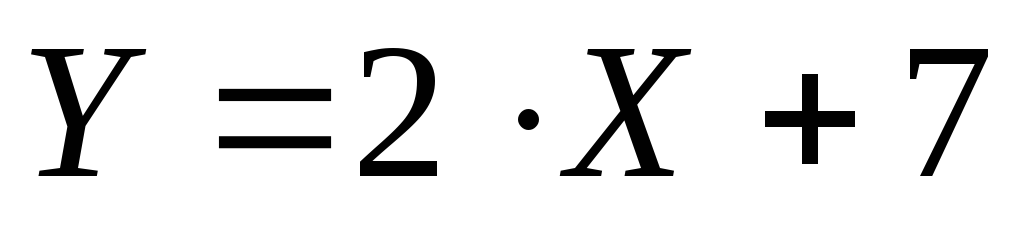 .
.
Ответ: 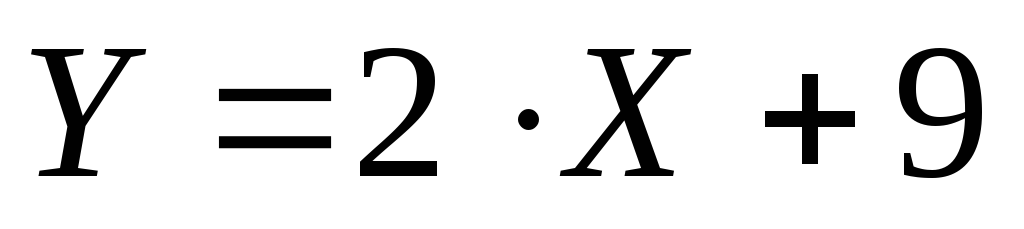 .
.
2. Найти уравнение
прямой, проходящей через точку К(5; –2)
параллельно прямой 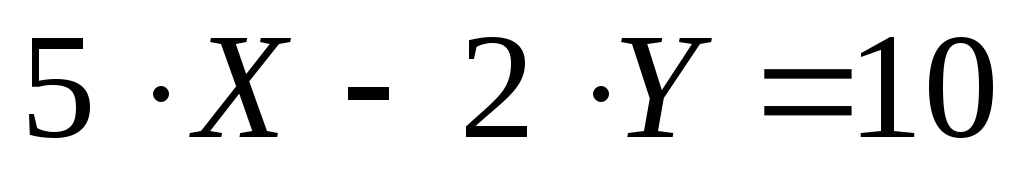 .
.
Ответ: .
3. Найти уравнение прямой, проходящей через точку К(–2; –6) перпендикулярно прямой .
Ответ:  .
.
4. Найти уравнение
прямой, проходящей через точку К(7; –2)
перпендикулярно прямой  .
.
Ответ: 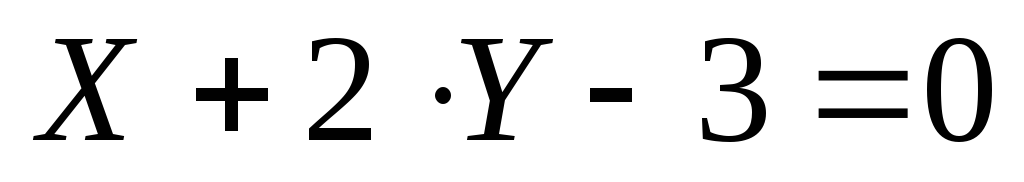 .
.
5. Найти уравнение
перпендикуляра, опущенного из точки
К(–6; 7) на прямую 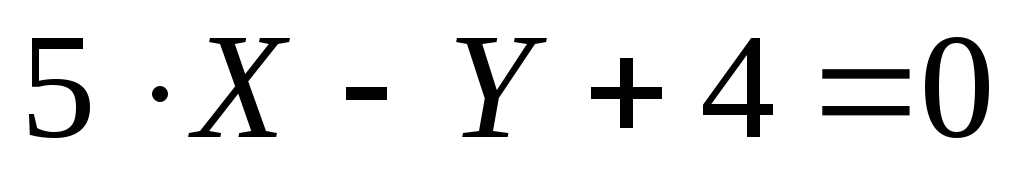 .
.
Ответ: 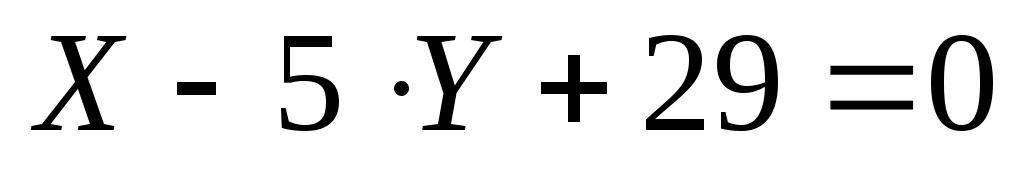 .
.
Практическое занятие № 6 на тему:
studfile.net
15) Решение систем трёх линейных уравнений с тремя неизвестными с помощью определителей третьего порядка
Системы трёх линейных уравнений с тремя неизвестными имеют вид:
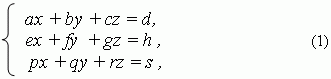
где a, b, c, d, e, f, g, h, p, q, r, s – заданные числа; x, y, z – неизвестные. Числа a, b, c, e, f, g, p, q, r – коэффициенты при неизвестных; d, h, s – свободные члены. Решение этой системы может быть найдено теми же двумя основными методами, рассмотренными выше: подстановки и сложения или вычитания. Мы же рассмотрим здесь подробно только метод Крамера.
Во-первых, введём понятие определителя третьего порядка. Выражение

называется определителем третьего порядка.
Запоминать это выражение не нужно, так как его легко получить, если переписать таблицу (2), добавив справа первые два столбца. Тогда оно вычисляется путём перемножения чисел, расположенных на диагоналях, идущих от a, b, c – направо ( со знаком « + » ) и от c, a, b – налево ( со знаком « – » ), и затем суммированием этих произведений:
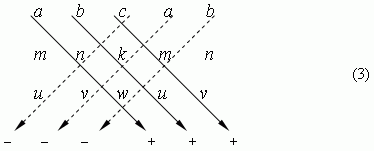
Используя определитель третьего порядка (2), можно получить решение системы уравнений (1) в виде:
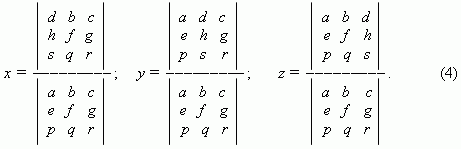
16) Числовая функция и способы её задания
17) Свойства функции (область определения и значения)
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
18) Свойства функции (Монотонность функции.)
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
19) Свойства функции (Четность (нечетность), переодичность)
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.
Периодическость функции.
Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
studfile.net
Система 3-х уравнений первой степени с 3-мя неизвестными
Пусть мы имеем систему
 Аналогично
уравнением с двумя неизвестными. Находим
определители
Аналогично
уравнением с двумя неизвестными. Находим
определители 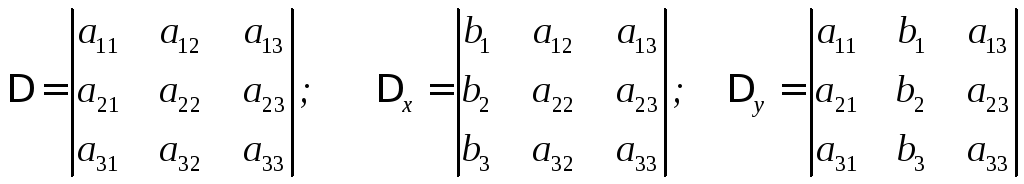
Аналогично
этому находим  .
.
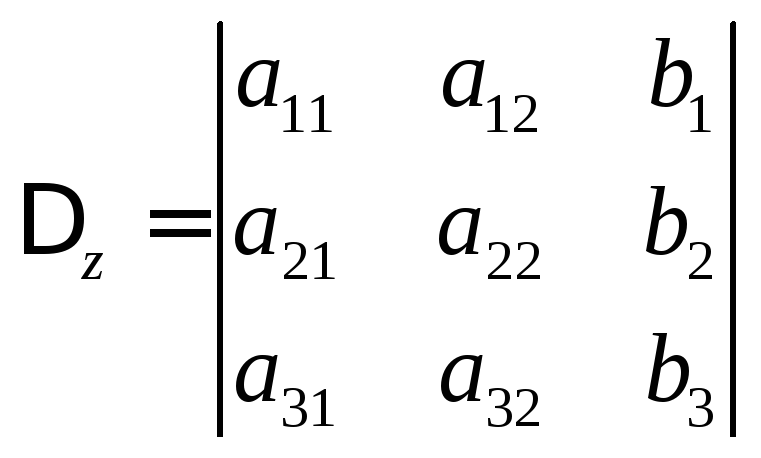 После
этого находим x,
y,
z
по формулам Крамера. Считая
После
этого находим x,
y,
z
по формулам Крамера. Считая 
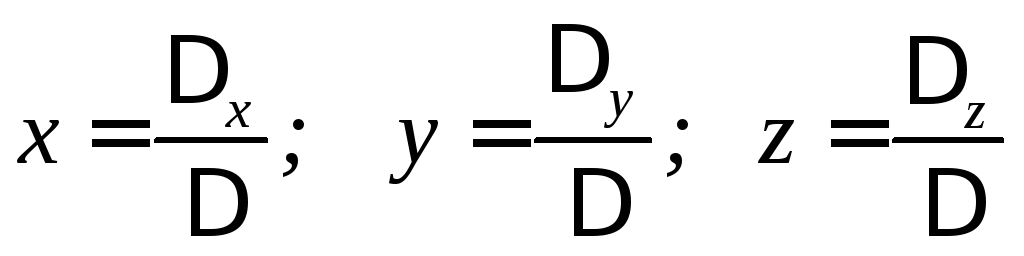 .
.
Аналогичные формулы имеют место для систем уравнений с большим числом неизвестных.
Пример
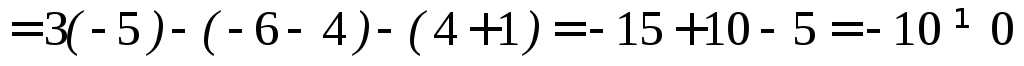
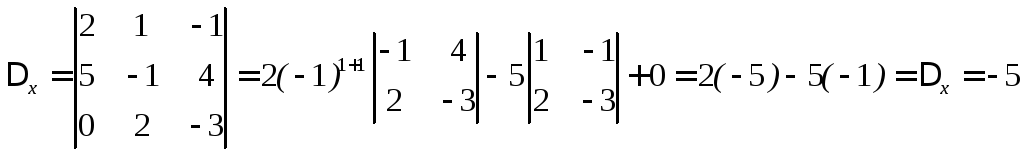
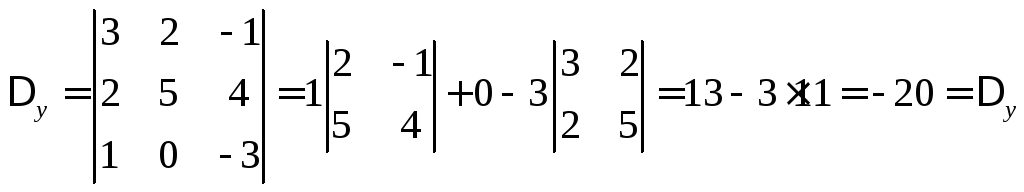

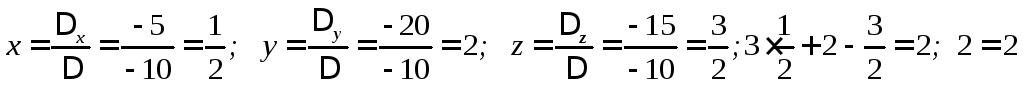 .
.
Еще
пример 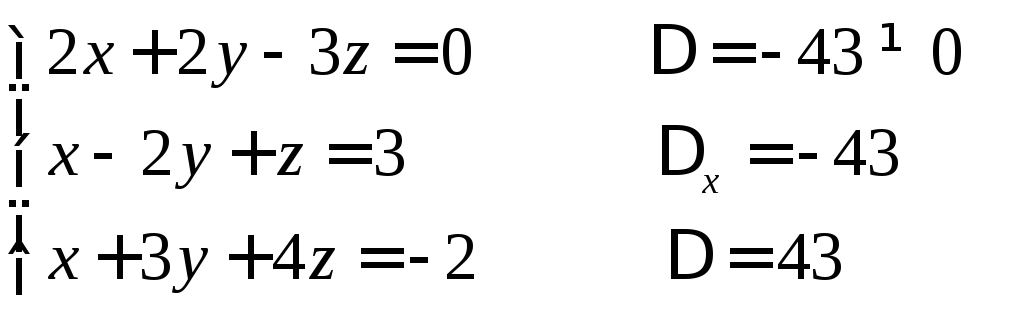

Однородная система 3-х уравнений с 3-мя неизвестными
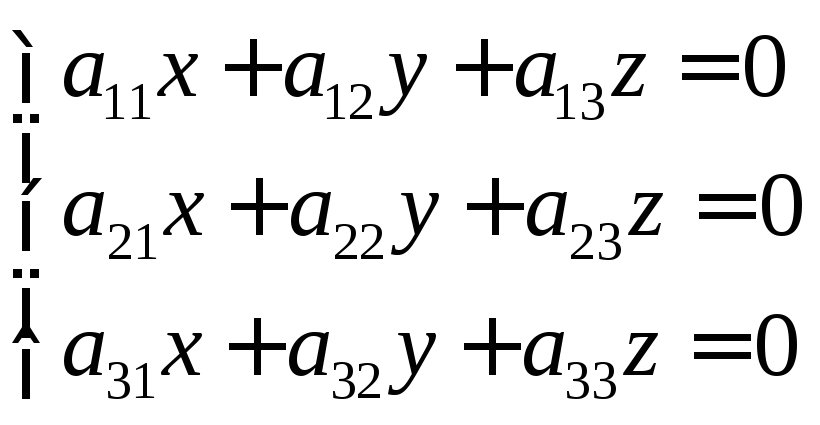 В
этом случае
В
этом случае 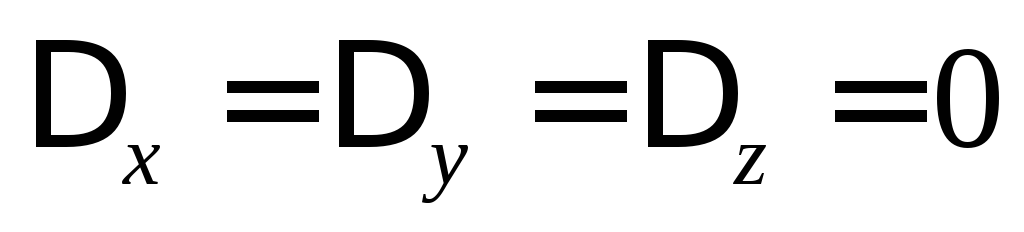 .
.
1)
И при этом 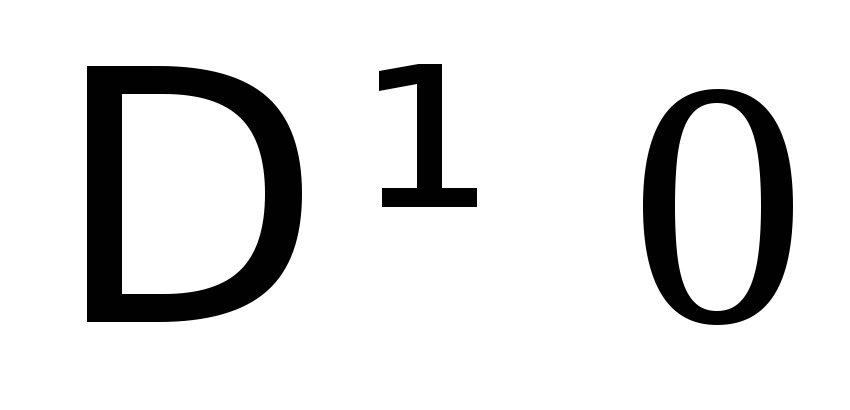 система имеет единственное решение
система имеет единственное решение 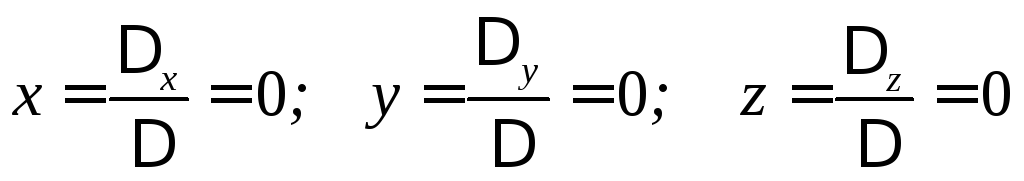
2)
Если  система имеет множество решений.
Аналогично решается система 4-х
уравнений с 4-мя неизвестными.
система имеет множество решений.
Аналогично решается система 4-х
уравнений с 4-мя неизвестными.
Системы линейных уравнений и матрицы
Понятие о матрицах
Совокупность чисел, расположенных в виде прямоугольной таблицы называют матрицей.
Например, матрица обозначается или двумя вертикальными линиями или скобками. Числа, составляющие таблицу мы будем называть элементами матрицы. В матрице различают строки (количество их обозначают обычно «m») и столбцы их число обозначают буквой «n». Если m ≠ n, то такая матрица называется прямоугольной, а при n = m ее называют квадратной.
Например 
Здесь
m
= n.
При изучении матриц для удобства числа
заменяют буквенными обозначениями 
У этой матрицы «m» строк и «n» Каждый элемент матрицы aij. Здесь первый индекс обозначает номер строки (i = 1,2, ….. m), а второй индекс обозначает номер столбца (j = 1, 2, ….n).
Если
мы рассмотрим другую матрицу В  ,
то каждый элемент этой матрицы будет
bij.
Две матрицы называются равными, если
они имеют одинаковые размеры и равны
их элементы, стоящие на одинаковых
местах (aij = bij)
и записывают так А = В.
,
то каждый элемент этой матрицы будет
bij.
Две матрицы называются равными, если
они имеют одинаковые размеры и равны
их элементы, стоящие на одинаковых
местах (aij = bij)
и записывают так А = В.
Число строк называют порядком матрицы.
Матрица
размером 1 x
n
называют строкой. Р = ( 1 -4 0 2
-1), а размером m
x
1 – столбцом 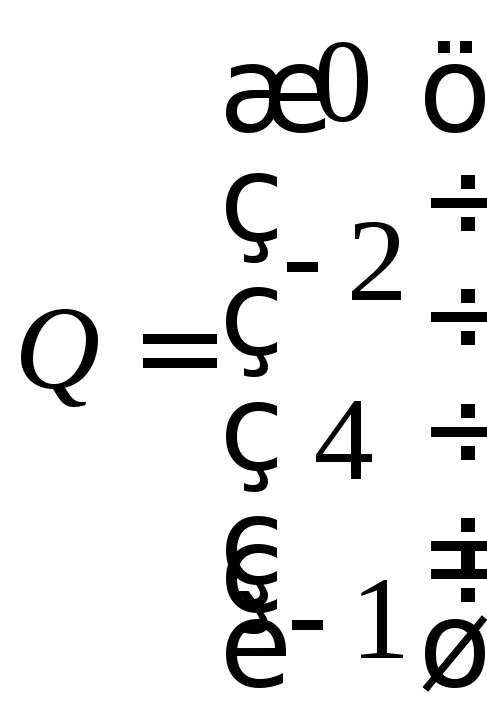 .
.
Сложение матриц и умножение их на число
Пусть
мы имеем две матрицы А и В одного и того
же размера. Суммой их будет новая матрица
С = А + В, в которой сij = aij + bij .
Можно произвести и вычитание матриц С
= А – В, тогда сij = aij – bij.
При умножении матрицы А на произвольное
число α
получаем новую матрицу С = α
А, где cij = αaij
.
Можно произвести и вычитание матриц С
= А – В, тогда сij = aij – bij.
При умножении матрицы А на произвольное
число α
получаем новую матрицу С = α
А, где cij = αaij
 .
Матрица О, целиком состоящая из нулей
называется нулевой, и для нее А + О = А.
Отметим свойства матриц. Для матриц А,
В, и С одинакового размера А + В = В + А, (А
+ В) + С = А + (В + С), α
(А + В) = αА
+ αВ,
(α
+ β)
А= (α
+ β)
А = αА
+ βА
.
Матрица О, целиком состоящая из нулей
называется нулевой, и для нее А + О = А.
Отметим свойства матриц. Для матриц А,
В, и С одинакового размера А + В = В + А, (А
+ В) + С = А + (В + С), α
(А + В) = αА
+ αВ,
(α
+ β)
А= (α
+ β)
А = αА
+ βА
Транспонирование матриц
Операция
над матрицей А, при которой ее строки
становятся столбцами с теми же номерами,
а столбцы – строками, называется
транспонированием и обозначается  .
.
Например  ,
то
,
то 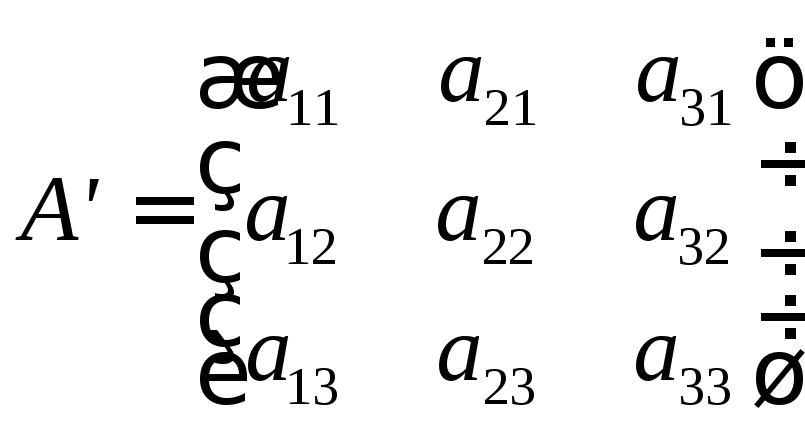
Операция
транспонирования обладает следующими
свойствами: 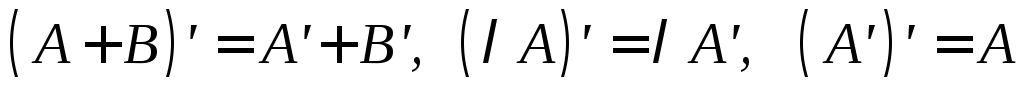
Диагональ а11 а22 ….аnn квадратичной матрицы называется главной диагональю матрицы, у которой все элементы, не стоящие на главной диагонали, равны нулю, называется диагональной
Матрица
S
называется симметрической,
если она не меняется при транспонировании,
т.е.  .
У симметрической матрицы элементы,
симметричные относительно главной
диагонали, равны.
.
У симметрической матрицы элементы,
симметричные относительно главной
диагонали, равны.
Матрица
К называется кососимметрической,
если при транспонировании она меняет
свой знак, т.е. 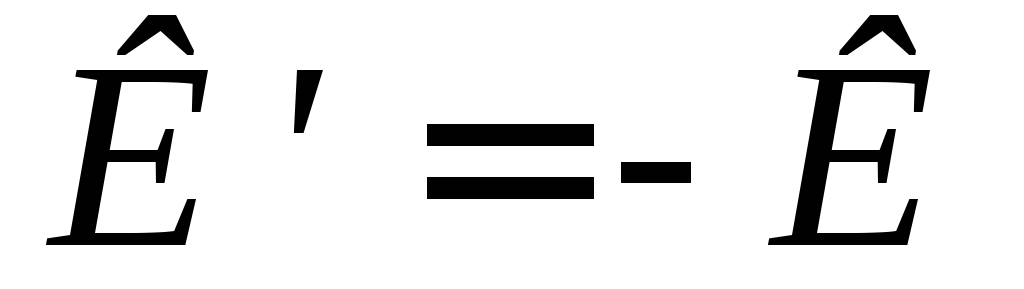 .
У кососимметрической матрицы на главной
диагонали стоят нули, а элементы,
симметричные относительно этой диагонали,
отличаются только знаком.
.
У кососимметрической матрицы на главной
диагонали стоят нули, а элементы,
симметричные относительно этой диагонали,
отличаются только знаком.
Например 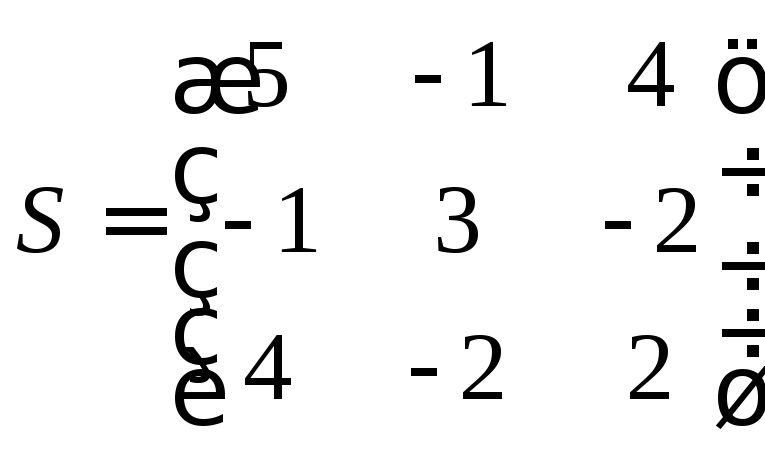 тогда
тогда .
.
У кососимметрической матрицы

Квадратная
матрица, у которой элементы, составляющие
главную диагональ, равны единице, а
остальные равны нулю называется единичной
матрицей 
studfile.net
Решение системы трех уравнений первой степени с тремя неизвестными
Для решения системы уравнений вида
существуют общие формулы для нахождения x, y, z. Поскольку в развернутом виде формулы очень громоздки, принято обозначать их через введение понятия определителя или детерминанта третьего порядка, как
Тогда решение уравнений можно представить в виде
т.е. каждое из неизвестных равно дроби, знаменатель которой есть определитель, составленный из коэффициентов при неизвестных, а числитель получается из этого определителя заменой коэффициентов при соответствующем неизвестном на свободные члены.
Решение системы сводится к трем случаям
Определитель, стоящий в знаменателе формул (составленный из коэффициентов при неизвестных) не равен нулю
тогда система уравнений имеет единственное решение соответствующее формулам вышеОпределитель, стоящий в знаменателе формул (составленный из коэффициентов при неизвестных) равен нулю, но ни один из определителей в числителе не равен нулю
тогда система уравнений не имеет решений, потому что уравнения друг другу противоречат
- Определитель, стоящий в знаменателе формул (составленный из коэффициентов при неизвестных) равен нулю, определители в числителе также равны нулю
тогда система уравнений имеет бесчисленное множество решений, потому что одно из уравнений есть следствие двух других
Калькулятор:

Решение системы трех уравнений первой степени с тремя неизвестными
Точность вычисленияЗнаков после запятой: 2
save Сохранить share Поделиться extension Виджет
planetcalc.ru