Калькулятор квадратных уравнений — решение квадратных уравнений онлайн
Этот калькулятор квадратных формул работает как решить квадратное уравнение решатель квадратных уравнений, который помогает решить квадратное уравнение заданное квадратное уравнение с помощью формулы квадратного уравнения.
Что ж, прежде чем узнать об этом калькулятор квадратных уравнений квадратных уравнений, давайте начнем с некоторых основ!
Что такое квадратичная формула?Квадратичная формула считается одним из самых эффективных инструментов математики. Эта формула является решение квадратного уравнения полиномиального уравнения второй степени. Стандартная форма квадратного уравнения упоминается ниже:
ax1 bx c = 0
Куда;
- ‘A’ – квадратичный коэффициент
- «X» – неизвестное
- ‘B’ – линейный коэффициент
- “C” – постоянная
Решение этого уравнения называется корнем уравнения.
Итак, решение квадратного уравнения квадратных уравнений онлайн имеет не более двух корней, поэтому решение квадратных уравнений в конечном итоге означает нахождение корней (квадратного уравнения).
Наш калькулятор квадратных формул также использует ту же формулу для [решения квадратного уравнения].
Есть три возможности получить корни (квадратного уравнения), но помните, что эти возможности зависят от значения Дискриминанта.
- Если b2 – 4ac = 0, то будет только один корень
- Если b2 – 4ac> 0, то будет только два действительных корня
- Если b2 – 4ac <0, то будет два комплексных корня
Коэффициенты квадратного уравнения:
Также важно отметить, что числа, то есть a, b и c, считаются коэффициентами уравнения и не могут быть «0». Все они действительные числа, не зависящие от x. Если A = 0, то уравнение называется не квадратичным, а линейным.
Если B² <4AC, то определитель Δ будет отрицательным, как решать квадратные уравнения уравнение это уравнение не имеет действительных корней.
Наш квадратичный калькулятор также может вам помочь, если вы можете записать уравнение в такой форме:
ax2 bx c = 0
Калькулятор квадратной формулы:Этот калькулятор квадратных уравнений квадратной формулы представляет собой инструмент, который помогает решить квадратное уравнение квадратное уравнение, используя квадратную формулу или завершив метод квадратов. Вам просто нужно сформировать уравнение, метод вычисления и ввести параметры уравнения; этот решатель квадратной формулы лучше всего подойдет вам!
Вам просто нужно сформировать уравнение, метод вычисления и ввести параметры уравнения; этот решатель квадратной формулы лучше всего подойдет вам!
Не волнуйтесь; этот решатель решение квадратного уравнения квадратных уравнений онлайн довольно прост в использовании и имеет продуманный и удобный интерфейс!
Входы:Форма уравнения:
Вы должны выбрать форму уравнения; это форма, в соответствии с которой вы должны ввести значения в обозначенные поля нашего калькулятора квадратичных функций.
В этом калькулятор квадратных уравнений используется следующая форма:
- Ax2 Bx C = 0 (стандартная форма)
- A (x – H) 2 K = 0 (форма вершины)
- A (x-x₁) (x-x₂) = 0 (Факторная форма)
Наш калькулятор квадратных уравнений квадратного уравнения позволяет вам решить квадратное уравнение квадратное уравнение, используя формулу корней квадратного уравнения и завершив метод квадратов.
Если вы выбрали форму Ax2 Bx C = 0, вам необходимо ввести значения A, B и C
Если вы выбрали форму A (x – H) 2 K = 0, то вам необходимо ввести значения A, H и K
Если вы выбрали форму A (x-x₁) (x-x₂) = 0, вам необходимо ввести значения A, x1 и x2
Вывод:После того, как решить квадратное уравнение указанные выше значения, наш решатель (квадратного уравнения) покажет следующее:
Показать корни:Этот калькулятор квадратного корня показывает корень или корни вашего данного уравнения.
Покажите упрощение:Калькулятор шаг за шагом упростит данное уравнение.
Показать дискриминант:Если вы решите решение квадратных уравнений онлайн с помощью формулы квадратичного, то наш калькулятор квадратичного дискриминанта покажет дискриминант
Покажите квадратичный график:Этот калькулятор квадратичных графиков показывает вам полный квадратичный график для данного уравнения!
Как решать квадратные уравнения?Когда дело доходит до решения квадратных уравнений, квадратная формула используется для выполнения вычислений. 2x. Говорят, что «b» является коэффициентом, который появляется при умножении линейного члена x, а коэффициент «c» считается постоянным.
2x. Говорят, что «b» является коэффициентом, который появляется при умножении линейного члена x, а коэффициент «c» считается постоянным.
как решать квадратные уравнения следующего выражения x2 3x 1?
В этом случае a = 1 (это коэффициент умножения на квадратный член x2), b = 3b = 3 (коэффициент, умноженный на линейный член x) и c = 1 (константа).
Какие сейчас коэффициенты, если у вас есть следующее выражение: 5/4 3/4 x 1/2 x2
В этом случае a = 1/2 (это коэффициент умножения на квадратичный член x2), b = 3/4 (коэффициент, умноженный на линейный член x) и c = 5/4 (константа).
Пример №3:Какие коэффициенты, если у вас есть следующее выражение: -3 1/2
В этом случае a = 0, поскольку данное выражение не содержит квадратичного члена x2. Итак, это не считается квадратичным выражением.
Подставьте коэффициенты, которые вы нашли в формуле (шаг 2):
Формула:\ [x = \ dfrac {-b \ pm \ sqrt {b ^ 2 – 4ac}} {2a} \]
Теперь вам нужно заменить значения коэффициентов a, b и c. 2 – 4 (-3) (1)}} {2 (-3)} \]
2 – 4 (-3) (1)}} {2 (-3)} \]
После того, как вы подставили значения a, b и c, вы должны упростить значения в уравнении. Из предыдущего примера у вас есть:
\ [x = \ dfrac {-2 \ pm \ sqrt {4 – 12}} {(- 6)} \]
\ [x = \ dfrac {-2 \ pm \ sqrt {-8}} {(- 6)} \]
Загляните внутрь квадратного корня (шаг 4):Если значение положительное, то уравнение имеет два действительных корня. Если значение равно 0, то существует только один действительный корень, а если значение внутри квадратного корня отрицательное, то будет два комплексных корня. В предыдущем примере у вас есть -8 внутри квадратного корня, что означает, что у вас есть два сложных решения (как показано ниже):
\ [x = \ dfrac {-2 \ pm \ sqrt {4 – 12}} {(- 6)} \]
\ [x = \ dfrac {-2 \ pm \ sqrt {-8}} {(- 6)} \]
\ [x = \ dfrac {-2 \ pm \ sqrt {8} \, i} {(- 6)} \]
К счастью, вы узнали, как решать квадратные уравнения (вручную). 2 – 4ac}} {2a} \]
2 – 4ac}} {2a} \]
Имейте в виду, поскольку b2 – 4ac <0, квадратный корень из определителя будет мнимым значением. Отсюда:
Re (x) = -B / 2A
Im (x) = ± (√Δ) / 2A
Решение квадратного уравнения методом построения графиков:Итак, из графика параболы узнайте вершину, ось симметрии, точку пересечения по оси y, точку пересечения с x.
Задача имеет два решения, и они демонстрируют точки пересечения уравнения, которые являются точкой пересечения с осью x (это точка, в которой ось x пересекается кривой. При этом составляется график данного уравнения x2 3x – 4 = 0, можно рассматривать как решить квадратное уравнение:
Вершина:Это демонстрация пика. Итак, вершина (квадратного уравнения) указывает точку пика параболы. Если парабола открывается вверх, то говорят, что вершина – это самая высокая точка, а если парабола открывается вниз, то вершина называется самой низкой точкой.
Ось симметрии:Ось симметрии делит параболу на две равные половины; он всегда проходит через вершину параболы.
Корни также называют пересечением по оси x. Он расположен ниже оси x или выше оси x на графике. Поэтому для определения корня квадратичной функции положим y = 0
Y-перехват:Каждая парабола имеет точку пересечения с осью y, и говорят, что это точка, в которой функция пересекает ось y. Это вычисляется путем установки переменной x в уравнении на 0.
Итак, давайте начнем решать графически,
Сначала возьмем уравнение f (x) = 2×2 – 4x-1 или Y = 2×2 – 4x-1.
Здесь a = 2, b = -4 и c = -1.
Если «a» имеет положительное значение, то помните, что парабола открывается вверх на графике. Сначала вам нужно найти вершину x:
х = (- Ь) / 2а
х = (- (- 4)) / 2 (2)
х = 1
Теперь вам нужно найти вершину Y:
Вы должны подставить значение x в уравнение 2×2 – 4x-1
у = 2 (1) 2-4 (1) -1
у = 2 – 4 – 1
у = 3
Итак, у вас есть ось симметрии: x = 1
Теперь вам нужно найти точку пересечения по оси x, используя формулу корней квадратного уравнения:
\ [x = \ dfrac {- (- 4) \ pm \ sqrt {(- 4) ^ 2 – 4 (2) (- 1)}} {2 (2)} \]
\ [x = \ dfrac {4 \ pm \ sqrt {16 8}} {4} \]
\ [x = \ dfrac {4 \ pm \ sqrt {24}} {4} \]
\ [x = \ dfrac {4 \ pm 4. 2 – 4 (-1) (1)}} {2 (-1)} \]
2 – 4 (-1) (1)}} {2 (-1)} \]
\ [x = \ dfrac {-2 \ pm \ sqrt {8}} {-2} \]
х1 = – 0,414214
х2 = 2,414214
Теперь найдите y-точку пересечения:
х2 2х 1 = 0
(0) 2 2 (0) 1 = 0
y-intercept = 1, теперь вам нужно нанести значения на график!
Для чего используется квадратичная формула?Квадратичная формула – это хорошо известная формула, которая встречается повсюду в математике. Он часто учитывается при решении всевозможных геометрических задач, таких как:
- Увеличение площади
- Учитывая фиксированный периметр
- Многочисленные проблемы с Word
Есть много людей, которые задаются вопросом, есть ли какая-либо связь между этой формулой (квадратным уравнением) и методом завершения квадрата. Проще говоря, вы получите квадратную формулу, просто решив решение квадратных уравнений онлайн, заполнив квадрат. Это в точности та же идея, которая вытекает из известной всем нам формулы квадратичных уравнений!
Важность квадратного уравнения в реальной жизни:Будучи студентом, вас могут принимать во внимание по различным вопросам математики. Кроме того, студенты обычно используют это уравнение в таких предметах, как решать квадратные уравнения инженерия и физика. Есть и другие профессии, которые используют (квадратные уравнения):
Кроме того, студенты обычно используют это уравнение в таких предметах, как решать квадратные уравнения инженерия и физика. Есть и другие профессии, которые используют (квадратные уравнения):
- Военные и правоохранительные органы – (для определения траектории ракет, выпущенных артиллерией)
- Инженеры – (относится к гражданскому строительству)
- Уравнение движения (как на игровой площадке, так и в игровых ситуациях, оно описывает траекторию полета мяча и определяет высоту брошенного мяча)
- Наука (Астрономы – описывают орбиту планет, солнечных систем и галактик)
- Сферы сельского хозяйства (оптимальное расположение границ для производства самого большого поля)
- Проще говоря, вам просто нужно заполнить квадрат ax2 bx c = 0, чтобы получить формулу корней
- квадратного уравнения
- Вам следует разделить обе части уравнения на «а», чтобы коэффициент при x2 был равен 1.
 2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня.
2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня.Как узнать, имеет ли квадратное уравнение одно решить квадратное уравнение онлайн, два или нет?
Это помогает определить, сколько существует решений (квадратного уравнения). Если дискриминант положительный, говорят, что есть 2 корня. Если он равен нулю, значит есть только 1 корень. Если дискриминант отрицательный, то говорят, что корней 0.
Other Languages: Quadratic Formula Calculator, Løs Andengradsligning, Quadratische Gleichungen Lösen, Kinci Dereceden Denklem Çözücü, Rozwiązywanie Równań Kwadratowych, Kalkulator Persamaan Kuadrat, Risolvere Equazioni Di Secondo Grado, Résoudre Une Équation Du Second Degré, Equazioni Di Secondo Grado, Resolver Ecuaciones De Segundo Grado, Toisen Asteen Yhtälön Ratkaisu, Řešení Kvadratické Rovnice, 二次方程式の解, حل المعادلات التربيعية, 이차방정식 계산기
Математика для блондинок: Квадратное уравнение решение онлайн
Не легкая сегодня жизнь у учащихся. Для её облегчения предлагаю вашему вниманию калькуляторы уравнений: квадратное уравнение решение онлайн. Надеюсь, этот калькулятор поможет вам в решении квадратных уравнений. Продавцам оценок без разницы, а вот учителя требуют ещё и определение квадратного уравнения знать. Вот оно на картинке.
Для её облегчения предлагаю вашему вниманию калькуляторы уравнений: квадратное уравнение решение онлайн. Надеюсь, этот калькулятор поможет вам в решении квадратных уравнений. Продавцам оценок без разницы, а вот учителя требуют ещё и определение квадратного уравнения знать. Вот оно на картинке.
Распечатайте картинку, повесьте её на стену и каждый вечер читайте на ночь вместо молитвы. Подобные ежедневные упражнения очень здорово помогают превращать запор мысли в понос слов. Последнее предложение я вычеркнул специально. Детям его знать ещё рано, а взрослым оно не нужно вообще. Лично я тем математикам, которые выдают комплексные решения, платил бы комплексную зарплату: действительная часть равна минимальной зарплате, а в комплексной части зарплаты можно обещать всё, что угодно. Хоть Царство Небесное. Естественно, не здесь и сейчас, а где-то там и после смерти. Ведь мертвые никогда не требуют выполнения обещаний.Но вернемся к нашим уравнениям. Квадратное уравнение является уравнением второго порядка.
 У квадратного уравнения есть своя формула, которую вы можете видеть на картинке. Если подходить к написанному на картинке с позиции тупой бюрократической функции, то икс не является корнем квадратного уравнения. Это переменная. Корнями квадратного уравнения являются определенные числовые значения переменной икс. При подстановке корней в квадратное уравнение оно должно превращаться в верное равенство. У квадратного уравнения может быть два корня (разные числа, возведенные в квадрат, могут давать одинаковый результат; знаки плюс и минус делают числа разными), один корень или квадратное уравнение может вообще не иметь корней. Последние уравнения, не имеющие корней, я бы назвал «плохое квадратное уравнение». Правильно составленное квадратное уравнение всегда должно иметь решение. Здесь мы упираемся в очень неудобный и интересный вопрос: откуда берутся квадратные уравнения и зачем они нужны? Уравнения ради решений — это маразм или дрессировка обезьян (воспитание тупых бюрократических функций, пригодных для использования в любых бюрократических системах).
У квадратного уравнения есть своя формула, которую вы можете видеть на картинке. Если подходить к написанному на картинке с позиции тупой бюрократической функции, то икс не является корнем квадратного уравнения. Это переменная. Корнями квадратного уравнения являются определенные числовые значения переменной икс. При подстановке корней в квадратное уравнение оно должно превращаться в верное равенство. У квадратного уравнения может быть два корня (разные числа, возведенные в квадрат, могут давать одинаковый результат; знаки плюс и минус делают числа разными), один корень или квадратное уравнение может вообще не иметь корней. Последние уравнения, не имеющие корней, я бы назвал «плохое квадратное уравнение». Правильно составленное квадратное уравнение всегда должно иметь решение. Здесь мы упираемся в очень неудобный и интересный вопрос: откуда берутся квадратные уравнения и зачем они нужны? Уравнения ради решений — это маразм или дрессировка обезьян (воспитание тупых бюрократических функций, пригодных для использования в любых бюрократических системах). Уравнения как математический инструмент? Тогда где и как этот инструмент применяется? Квадратное уравнение, взятое с потолка (как это обычно делается для учебников), может не иметь решений. Ведь на правильность составления нас уравнения проверять не учат. Тупо пишем квадратное уравнение в учебник, тупо берем из учебника и решаем.
Уравнения как математический инструмент? Тогда где и как этот инструмент применяется? Квадратное уравнение, взятое с потолка (как это обычно делается для учебников), может не иметь решений. Ведь на правильность составления нас уравнения проверять не учат. Тупо пишем квадратное уравнение в учебник, тупо берем из учебника и решаем.Дискриминант квадратного уравнения применяется для нахождения его корней. Дискриминант равен квадрату второго коэффициента минус четыре произведения первого коэффициента и свободного члена уравнения. Если дискриминант больше нуля, тогда уравнение имеет два корня. Если дискриминант равен нулю (дискриминант 0), тогда квадратное уравнение имеет всего один корень. Если дискриминант меньше нуля, тогда уравнение не имеет корней — это уравнение взял с потолка какой-то неук.
Теперь рекомендую вашему вниманию специальные калькуляторы для решения квадратный уравнений онлайн с подробным решением:
— дается подробное решение с формулой дискриминанта, с графиком уравнения и анализом вершин кривой. — пример подробного решения уравнения на этом калькуляторе вы можете видеть на картинке ниже.
— пример подробного решения уравнения на этом калькуляторе вы можете видеть на картинке ниже. Решение квадратных уравнений — презентация онлайн
1. Решение квадратных уравнений
2. Что вы можете сказать об это уравнении ?
2х2+5=0
Что вы можете сказать об это
уравнении ?
2
2х +5=0
2
4х -5х=0
2
х
– 3х – 4 = 03. Что вы можете сказать об это уравнении ?
2х2+5=0
Что вы можете сказать об это
уравнении ?
4
5х +
2
7х -33
=04. Тест «Виды квадратных уравнений»
ФФ. И.
И.
х4 + 5х2 +3 = 0
6х2 + 9 = 0
х2 – 3х = 0
-х2 + 2х +4 = 0
3х + 6х2 + 7 =0
Полное
Неполное
Приведенное
Биквадратное
Общий бал5. Тест «Виды квадратных уравнений»
ФФ.И.
х4 + 5х2 +3 = 0
Полное
+
6х2 + 9 = 0
3х + 6х2 + 7 =0
+
+
Приведенное
+
+
+
х2 – 3х = 0
-х2 + 2х +4 = 0
Неполное
+
Биквадратное
+
Общий бал6. Этапы решения квадратного уравнения
• Определять вид уравнения.
• Определять коэффициенты квадратного
уравнения.
• Вычислять дискриминант, определять
количество корней
• Вычислять корни уравнения по формуле.7. Заполни таблицу
ФФ.И.
x2+ 6x + 8 =0
2×2+ 3x — 2 =0
-x2+ 7x + 18 =0
а
b
c
D=b²-4ac8. Заполни таблицу
ФФ.И.
x2+ 6x + 8 =0
2×2+ 3x — 2 =0
-x2+ 7x + 18 =0
а
b
1 6
2 3
-1 7
c
D=b²-4ac
8
-2
18
4
25
9
2
5
39.
 Отметьте пункт, который вызвал наибольшие затруднения 1.Определять вид уравнения
Отметьте пункт, который вызвал наибольшие затруднения 1.Определять вид уравнения
2.Определять коэффициенты квадратного
уравнения
3.Вычислять дискриминант, определять
количество корней
4.Вычислять корни уравнения по формуле10. Заполни таблицу
Ф.И.
Нет
Знаю
формулы для
решения
уравнений
Понимаю, как
решать
уравнения.
Умею решать
квадратные
уравнения.
Не очень
хорошо
Хорошо
Отлично,
без ошибокРешение высшей математики онлайн
‹— Назад В разделе «Решение квадратных уравнений с вещественными коэффициентами» мы видели, что в поле комплексных чисел любой квадратный трехчлен с вещественными коэффициентами имеет корни, этих корней два, если дискриминант отличен от нуля, и один в противном случае. Теперь, когда мы имеем возможность извлекать корни из комплексных чисел, мы можем найти корни квадратного трехчлена с комплексными коэффициентами, то есть решить уравнение где , , — комплексные числа, .
Выполняя те же действия, что и в разделе «Решение квадратных уравнений с вещественными коэффициентами», приходим к уравнению
Обозначив , , получим уравнение , где . Такое уравнение мы умеем решать. В результате получатся два корня, если , и один, если . Так как тогда и только тогда, когда дискриминант равен нулю, то количество корней определяется тем же условием: равен дискриминант нулю или нет. Кроме того, заметим, что если , то и . Поэтому корни уравнения можно записать в виде(17.16)
где означает одно из решений (любое!) уравнения . Отметим, что формулы (17.5) также можно записать в виде (17.
Оказывается, что в поле комплексных чисел корни всегда существуют не только у квадратного трехчлена, но и у любого многочлена.
Теорема 17.1 Любой многочлен ненулевой степени с коэффициентами из поля комплексных чисел имеет в этом поле хотя бы один корень.
Данная теорема по традиции называется основной теоремой алгебры. Доказательство ее достаточно сложное и поэтому здесь оно не приводится.Интересно выяснить, сколько корней имеет многочлен степени . Мы уже знаем, что если , то корень один, если , то, как учили в школе, корней два. Кроме того, мы уже выяснили, что многочлен имеет ровно различных корней, если .
Теорема 17.2 Для любого многочлена ненулевой степени в поле комплексных чисел справедливо разложение на множители:(17.  17)
17)
Доказательство пропускаем. Читатель может найти его в [5].
Очевидно, что в указанном разложении числа , ,…, являются корнями многочлена и других корней у него быть не может. Однако среди чисел могут быть и одинаковые. Поэтому корней может быть меньше, чем . Число одинаковых скобок в разложении (17.17) называется кратностью соответствующего корня. Например, если
то — корень кратности 2, и — корни кратности 1 или, иначе, простые корни.Из предыдущей теоремы легко получить теорему, дающую ответ на вопрос о числе корней многочлена.
Теорема 17.3 В поле комплексных чисел любой многочлен ненулевой степени имеет ровно корней, если каждый корень считать столько раз, какова его кратность.По вопросу практического нахождения корней стоит отметить следующее. Для нахождения корней многочленов третьей и четвертой степеней существуют формулы, позволяющие выразить корни многочлена через его коэффициенты.
 Для многочлена третьей степени — это формула Кардано. Нахождение корней многочлена четвертой степени сводится к нахождению корней многочлена третьей степени методом, принадлежащим Феррари. Для многочленов выше четвертой степени доказано, что их корни нельзя выразить через их коэффициенты с помощью радикалов.
Для многочлена третьей степени — это формула Кардано. Нахождение корней многочлена четвертой степени сводится к нахождению корней многочлена третьей степени методом, принадлежащим Феррари. Для многочленов выше четвертой степени доказано, что их корни нельзя выразить через их коэффициенты с помощью радикалов.Однако, даже для многочленов третьей и четвертой степени, как правило, корни находят без использования указанных выше формул, так как те дают очень громоздкие выражения. Обычно корни находят приближенно, с помощью различных вычислительных алгоритмов (см. главу 9).
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
3x 1 2 решение.
 Решение уравнений с двумя переменными
Решение уравнений с двумя переменнымидля решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач.
 C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами.
C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.Как решать уравнения?
В этом разделе мы вспомним (или изучим – уж кому как) самые элементарные уравнения. Итак, что такое уравнение? Говоря человеческим языком, это какое-то математическое выражение, где есть знак равенства и неизвестное.
 Которое, обычно, обозначается буквой «х» . Решить уравнение — это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное тождество. Напомню, что тождество – это выражение, которое не вызывает сомнения даже у человека, абсолютно не отягощенного математическими знаниями. Типа 2=2, 0=0, ab=ab и т.д. Так как решать уравнения? Давайте разберёмся.
Которое, обычно, обозначается буквой «х» . Решить уравнение — это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное тождество. Напомню, что тождество – это выражение, которое не вызывает сомнения даже у человека, абсолютно не отягощенного математическими знаниями. Типа 2=2, 0=0, ab=ab и т.д. Так как решать уравнения? Давайте разберёмся.Уравнения бывают всякие (вот удивил, да?). Но всё их бесконечное многообразие можно разбить всего на четыре типа.
4. Все остальные.)
Всех остальных, разумеется, больше всего, да…) Сюда входят и кубические, и показательные, и логарифмические, и тригонометрические и всякие другие. С ними мы в соответствующих разделах плотно поработаем.
Сразу скажу, что иногда и уравнения первых трёх типов так накрутят, что и не узнаешь их… Ничего. Мы научимся их разматывать.
И зачем нам эти четыре типа? А затем, что линейные уравнения решаются одним способом, квадратные другим, дробные рациональные — третьим, а остальные не решаются вовсе! Ну, не то, чтобы уж совсем никак не решаются, это я зря математику обидел.
 ) Просто для них существуют свои специальные приёмы и методы.
) Просто для них существуют свои специальные приёмы и методы.Но для любых (повторяю — для любых! ) уравнений есть надёжная и безотказная основа для решения. Работает везде и всегда. Эта основа — Звучит страшно, но штука очень простая. И очень (очень!) важная.
Собственно, решение уравнения и состоит из этих самых преобразований. На 99%. Ответ на вопрос: «Как решать уравнения? » лежит, как раз, в этих преобразованиях. Намёк понятен?)
Тождественные преобразования уравнений.
В любых уравнениях для нахождения неизвестного надо преобразовать и упростить исходный пример. Причем так, чтобы при смене внешнего вида суть уравнения не менялась. Такие преобразования называются тождественными или равносильными.
Отмечу, что эти преобразования относятся именно к уравнениям. В математике ещё имеются тождественные преобразования выражений. Это другая тема.
Сейчас мы с вами повторим все-все-все базовые тождественные преобразования уравнений.

Базовые потому, что их можно применять к любым уравнениям – линейным, квадратным, дробным, тригонометрическим, показательным, логарифмическим и т.д. и т.п.
Первое тождественное преобразование: к обеим частям любого уравнения можно прибавить (отнять) любое (но одно и то же!) число или выражение (в том числе и выражение с неизвестным!). Суть уравнения от этого не меняется.
Вы, между прочим, постоянно пользовались этим преобразованием, только думали, что переносите какие-то слагаемые из одной части уравнения в другую со сменой знака. Типа:
Дело знакомое, переносим двойку вправо, и получаем:
На самом деле вы отняли от обеих частей уравнения двойку. Результат получается тот же самый:
х+2 — 2 = 3 — 2
Перенос слагаемых влево-вправо со сменой знака есть просто сокращённый вариант первого тождественного преобразования. И зачем нам такие глубокие познания? – спросите вы.
 В уравнениях низачем. Переносите, ради бога. Только знак не забывайте менять. А вот в неравенствах привычка к переносу может и в тупик поставить….
В уравнениях низачем. Переносите, ради бога. Только знак не забывайте менять. А вот в неравенствах привычка к переносу может и в тупик поставить….Второе тождественное преобразование : обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение. Здесь уже появляется понятное ограничение: на ноль умножать глупо, а делить и вовсе нельзя. Это преобразование вы используете, когда решаете что-нибудь крутое, типа
Понятное дело, х = 2. А вот как вы его нашли? Подбором? Или просто озарило? Чтобы не подбирать и не ждать озарения, нужно понять, что вы просто поделили обе части уравнения на 5. При делении левой части (5х) пятёрка сократилась, остался чистый икс. Чего нам и требовалось. А при делении правой части (10) на пять, получилась, знамо дело, двойка.
Вот и всё.
Забавно, но эти два (всего два!) тождественных преобразования лежат в основе решения всех уравнений математики. Во как! Имеет смысл посмотреть на примерах, что и как, правда?)
Примеры тождественных преобразований уравнений.
 Основные проблемы.
Основные проблемы.Начнём с первого тождественного преобразования. Перенос влево-вправо.
Пример для младшеньких.)
Допустим, надо решить вот такое уравнение:
3-2х=5-3х
Вспоминаем заклинание: «с иксами — влево, без иксов — вправо!» Это заклинание — инструкция по применению первого тождественного преобразования.) Какое выражение с иксом у нас справа? 3х ? Ответ неверный! Справа у нас — 3х ! Минус три икс! Стало быть, при переносе влево, знак поменяется на плюс. Получится:
3-2х+3х=5
Так, иксы собрали в кучку. Займёмся числами. Слева стоит тройка. С каким знаком? Ответ «с никаким» не принимается!) Перед тройкой, действительно, ничего не нарисовано. А это значит, что перед тройкой стоит плюс. Так уж математики договорились. Ничего не написано, значит, плюс. Следовательно, в правую часть тройка перенесётся с минусом. Получим:
-2х+3х=5-3
Остались сущие пустяки.
 Слева — привести подобные, справа — посчитать. Сразу получается ответ:
Слева — привести подобные, справа — посчитать. Сразу получается ответ:В этом примере хватило одного тождественного преобразования. Второе не понадобилось. Ну и ладно.)
Пример для старшеньких.)
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Предлагаемый вашему вниманию бесплатный калькулятор располагает богатым арсеналом возможностей для математических вычислений. Он позволяет использовать онлайн калькулятор в различных сферах деятельности: образовательной , профессиональной и коммерческой . Конечно, применение калькулятора онлайн особенно популярно у студентов и школьников , он значительно облегчает им выполнение самых разных расчётов.
Вместе с тем калькулятор может стать полезным инструментом в некоторых направлениях бизнеса и для людей разных профессий.
 Безусловно, необходимость применения калькулятора в бизнесе или трудовой деятельности определяется прежде всего видом самой деятельности. Если бизнес и профессия связаны с постоянными расчётами и вычислениями, то стоит опробовать электронный калькулятор и оценить степень его полезности для конкретного дела.
Безусловно, необходимость применения калькулятора в бизнесе или трудовой деятельности определяется прежде всего видом самой деятельности. Если бизнес и профессия связаны с постоянными расчётами и вычислениями, то стоит опробовать электронный калькулятор и оценить степень его полезности для конкретного дела.Данный онлайн калькулятор может
- Корректно выполнять стандартные математические функции, записанные одной строкой типа — 12*3-(7/2) и может обрабатывать числа больше, чемсчитаем огромные числа в онлайн калькулятореМы даже не знаем, как такое число назвать правильно (тут 34 знака и это совсем не предел ).
- Кроме тангенса , косинуса , синуса и других стандартных функций — калькулятор поддерживает операции по расчёту арктангенса , арккотангенса и прочих.
- Доступны в арсенале логарифмы , факториалы и другие интересные функции
- Данный онлайн калькулятор умеет строить графики !!!
Для построения графиков, сервис использует специальную кнопку (график серый нарисован) или буквенное представление этой функции (Plot).
 Чтобы построить график в онлайн калькуляторе, достаточно записать функцию: plot(tan(x)),x=-360..360 .
Чтобы построить график в онлайн калькуляторе, достаточно записать функцию: plot(tan(x)),x=-360..360 .Мы взяли самый простой график для тангенса, и после запятой указали диапазон переменной X от -360 до 360.
Построить можно абсолютно любую функцию, с любым количеством переменных, например такую: plot(cos(x)/3z, x=-180..360,z=4) или ещё более сложную, какую сможете придумать. Обращаем внимание на поведение переменной X — указан промежуток от и до с помощью двух точек.
Единственный минус (хотя трудно назвать это минусом) этого онлайн калькулятора это то, что он не умеет строить сферы и другие объёмные фигуры — только плоскость.
Как работать с Математическим калькулятором
1. Дисплей (экран калькулятора) отображает введенное выражение и результат его расчёта обычными символами, как мы пишем на бумаге. Это поле предназначено просто для просмотра текущей операции. Запись отображается на дисплее по мере набора математического выражения в строке ввода.

2. Поле ввода выражения предназначено для записи выражения, которое нужно вычислить. Здесь следует отметить, что математические символы, используемые в компьютерных программах, не всегда совпадают с теми, которые обычно мы применяем на бумаге. В обзоре каждой функции калькулятора вы найдёте правильное обозначение конкретной операции и примеры расчётов в калькуляторе. На этой странице ниже приводится перечень всех возможных операций в калькуляторе, также с указанием их правильного написания.
3. Панель инструментов — это кнопки калькулятора, которые заменяют ручной ввод математических символов, обозначающих соответствующую операцию. Некоторые кнопки калькулятора (дополнительные функции, конвертер величин, решение матриц и уравнений, графики) дополняют панель задач новыми полями, где вводятся данные для конкретного расчёта. Поле «History» содержит примеры написания математических выражений, а также ваши шесть последних записей.
Обратите внимание, при нажатии кнопок вызова дополнительных функций, конвертера величин, решения матриц и уравнений, построения графиков вся панель калькулятора смещается вверх, закрывая часть дисплея.
 Заполните необходимые поля и нажмите клавишу «I» (на рисунке выделена красным цветом), чтобы увидеть дисплей в полный размер.
Заполните необходимые поля и нажмите клавишу «I» (на рисунке выделена красным цветом), чтобы увидеть дисплей в полный размер.4. Цифровая клавиатура содержит цифры и знаки арифметических действий. Кнопка «С» удаляет всю запись в поле ввода выражения. Чтобы удалять символы по одному, нужно использовать стрелочку справа от строки ввода.
Старайтесь всегда закрывать скобки в конце выражения. Для большинства операций это некритично, калькулятор online рассчитает всё верно. Однако, в некоторых случаях возможны ошибки. Например, при возведении в дробную степень незакрытые скобки приведут к тому, что знаменатель дроби в показателе степени уйдет в знаменатель основания. На дисплее закрывающая скобка обозначена бледно-серым цветом, её нужно закрыть, когда запись закончена.
Назначение сервиса .Клавиша Символ Операция pi pi Постоянная pi е е Число Эйлера % % Процент () () Открыть/Закрыть скобки , , Запятая sin sin(?) Синус угла cos cos(?) Косинус tan tan(y) Тангенс sinh sinh() Гиперболический синус cosh cosh() Гиперболический косинус tanh tanh() Гиперболический тангенс sin -1 asin() Обратный синус cos -1 acos() Обратный косинус tan -1 atan() Обратный тангенс sinh -1 asinh() Обратный гиперболический синус cosh -1 acosh() Обратный гиперболический косинус tanh -1 atanh() Обратный гиперболический тангенс x 2 ^2 Возведение в квадрат х 3 ^3 Возведение в куб x y ^ Возведение в степень 10 x 10^() Возведение в степень по основанию 10 e x exp() Возведение в степень числа Эйлера vx sqrt(x) Квадратный корень 3 vx sqrt3(x) Корень 3-ей степени y vx sqrt(x,y) Извлечение корня log 2 x log2(x) Двоичный логарифм log log(x) Десятичный логарифм ln ln(x) Натуральный логарифм log y x log(x,y) Логарифм I / II Сворачивание/Вызов дополнительных функций Unit Конвертер величин Matrix Матрицы Solve Уравнения и системы уравнений Построение графиков Дополнительные функции (вызов клавишей II) mod mod Деление с остатком ! ! Факториал i / j i / j Мнимая единица Re Re() Выделение целой действительной части Im Im() Исключение действительной части |x| abs() Модуль числа Arg arg() Аргумент функции nCr ncr() Биноминальный коэффициент gcd gcd() НОД lcm lcm() НОК sum sum() Суммарное значение всех решений fac factorize() Разложение на простые множители diff diff() Дифференцирование Deg Градусы Rad Радианы  Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).
Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач). Инструкция . Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.
где А, В, С — задаваемые матрицы, Х — искомая матрица. Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A -1 . Если задано выражение A·X — B = C , то необходимо, сначала сложить матрицы C + B , и находить решение для выражения A·X = D , где D = C + B (). Если задано выражение A*X = B 2 , то предварительно матрицу B надо возвести в квадрат . Рекомендуется также ознакомиться с основными действиями над матрицами .Пример №1 . Задание . Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1:Умножаем обе части этого равенства слева на A -1 и справа на B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1
Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1Обратная матрица A -1:
Найдем обратную матрицу B -1 .
Транспонированная матрица B T:
Обратная матрица B -1:
Матрицу X ищем по формуле: X = A -1 ·C·B -1
Ответ:Пример №2 . Задание. Решить матричное уравнение
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.Пример №3 . Задание. Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим справа обе части уравнения на A -1: X·A·A -1 = B·A -1 , откуда находим, что X = B·A -1
Найдем обратную матрицу A -1 .
Транспонированная матрица A T:
Обратная матрица A -1:
Матрицу X ищем по формуле: X = B·A -1
Ответ: >Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет.
 Умение решать их совершенно необходимо.
Умение решать их совершенно необходимо.Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение.
 А именно:
А именно:- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении.
 Например:
Например:- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0.
 Вывод:
Вывод:- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x
2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Как решать квадратные уравнения. Калькулятор онлайн
Квадратное уравнение – решается просто! *Далее в тексте «КУ». Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:
Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше. Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.

Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах. Приступим! Содержание статьи:
Квадратное уравнение – это уравнение вида:
где коэффициенты a, b и с произвольные числа, при чём a≠0.
В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:
1. Имеют два корня.
2. *Имеют только один корень.
3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней
Как вычисляются корни? Просто!
Вычисляем дискриминант. Под этим «страшным» словом лежит вполне простая формула:
Формулы корней имеют следующий вид:
*Эти формулы нужно знать наизусть.

Можно сразу записывать и решать:
Пример:
1. Если D > 0, то уравнение имеет два корня.
2. Если D = 0, то уравнение имеет один корень.
3. Если D
Давайте рассмотрим уравнение:
По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти. Всё правильно, так и есть, но…
Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:
х 1 = 3 х 2 = 3
Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.
Теперь следующий пример:
Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.
Вот и весь процесс решения.
Квадратичная функция.
Здесь показано, как решение выглядит геометрически.
 Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).
Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).Это функция вида:
где х и у — переменные
a, b, с – заданные числа, при чём a ≠ 0
Графиком является парабола:
То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть статью у Инны Фельдман.
Рассмотрим примеры:
Пример 1: Решить 2x 2 +8 x –192=0
а=2 b=8 c= –192
D = b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600
Ответ: х 1 = 8 х 2 = –12
*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.
Пример 2: Решить x 2 –22 x+121 = 0
а=1 b=–22 c=121
D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0
Получили, что х 1 = 11 и х 2 = 11
В ответе допустимо записать х = 11.

Ответ: х = 11
Пример 3: Решить x 2 –8x+72 = 0
а=1 b= –8 c=72
D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224
Дискриминант отрицательный, решения в действительных числах нет.
Ответ: решения нет
Дискриминант отрицательный. Решение есть!
Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.
Понятие комплексного числа.
Немного теории.
Комплексным числом z называется число вида
z = a + bi
где a и b – действительные числа, i – так называемая мнимая единица.
a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение.
Мнимая единица равна корню из минус единицы:
Теперь рассмотрим уравнение:
Получили два сопряжённых корня.

Неполное квадратное уравнение.
Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.
Случай 1. Коэффициент b = 0.
Уравнение приобретает вид:
Преобразуем:
Пример:
4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2
Случай 2. Коэффициент с = 0.
Уравнение приобретает вид:
Преобразуем, раскладываем на множители:
*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.
Пример:
9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0
x 1 = 0 x 2 = 5
Случай 3. Коэффициенты b = 0 и c = 0.
Здесь понятно, что решением уравнения всегда будет х = 0.
Полезные свойства и закономерности коэффициентов.
Есть свойства, которые позволяют решить уравнения с большими коэффициентами.
а x 2 + bx + c =0 выполняется равенство
a + b + с = 0, то
— если для коэффициентов уравнения а x 2 + bx + c =0 выполняется равенство
a + с = b , то
Данные свойства помогают решить определённого вида уравнения.

Пример 1: 5001 x 2 –4995 x – 6=0
Сумма коэффициентов равна 5001+(– 4995)+(– 6) = 0, значит
Пример 2: 2501 x 2 +2507 x +6=0
Выполняется равенство a + с = b , значит
Закономерности коэффициентов.
1. Если в уравнении ax 2 + bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны
аx 2 + (а 2 +1)∙х+ а= 0 = > х 1 = –а х 2 = –1/a.
Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.
х 1 = –6 х 2 = –1/6.
2. Если в уравнении ax 2 – bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны
аx 2 – (а 2 +1)∙х+ а= 0 = > х 1 = а х 2 = 1/a.
Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.
х 1 = 15 х 2 = 1/15.
3. Если в уравнении ax 2 + bx – c = 0 коэффициент «b» равен (a 2 – 1), а коэффициент «c» численно равен коэффициенту «a» , то его корни равны
аx 2 + (а 2 –1)∙х – а= 0 = > х 1 = – а х 2 = 1/a.

Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.
х 1 = – 17 х 2 = 1/17.
4. Если в уравнении ax 2 – bx – c = 0 коэффициент «b» равен (а 2 – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны
аx 2 – (а 2 –1)∙х – а= 0 = > х 1 = а х 2 = – 1/a.
Пример. Рассмотрим уравнение 10х 2 – 99х –10 = 0.
х 1 = 10 х 2 = – 1/10
Теорема Виета.
Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.
45 = 1∙45 45 = 3∙15 45 = 5∙9.
В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.
Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.

СПОСОБ ПЕРЕБРОСКИ
При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Если а ± b+c ≠ 0, то используется прием переброски, например:
2х 2 – 11х+ 5 = 0 (1) => х 2 – 11х+ 10 = 0 (2)
По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1
Полученные корни уравнения необходимо разделить на 2 (так как от х 2 «перебрасывали» двойку), получим
х 1 = 5 х 2 = 0,5.
Каково обоснование? Посмотрите что происходит.
Дискриминанты уравнений (1) и (2) равны:
Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х 2:
У второго (изменённого) корни получаются в 2 раза больше.

Потому результат и делим на 2.
*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.
Ответ: х 1 = 5 х 2 = 0,5
Кв. ур-ие и ЕГЭ.
О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).
Что стоит отметить!
1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:
15+ 9x 2 — 45x = 0 или 15х+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.
Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).
2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
— это уравнение вида ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда — это просто число D = b 2 − 4ac.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают.
 Взгляните на примеры — и сами все поймете:
Взгляните на примеры — и сами все поймете:Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты.
 Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
Решить квадратные уравнения:
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3.
 \\ \end{align}\]
\\ \end{align}\]Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется, если b = 0 или c = 0, т.
 е. коэффициент при переменной x или свободный элемент равен нулю.
е. коэффициент при переменной x или свободный элемент равен нулю.Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c/a)
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0.
Решение неполных квадратных уравнений.
Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства.
 Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Смотрите также:
Квадратное уравнение имеет вид ax 2 + bx + c = 0.
Неполными квадратными уравнениями являются уравнения трех видов:
- ax 2 + bx = 0, когда коэффициент c = 0.

- ax 2 + c = 0, когда коэффициент b = 0.
- ax 2 = 0, когда и b и с равны 0.
Коэффициент же a по определению квадратного уравнения не может быть равен нулю.
Неполные квадратные уравнения решаются проще, чем полные квадратные. Способы решения различаются в зависимости от вида неполного квадратного уравнения.
Проще всего решаются уравнения вида ax 2 = 0. Если a по определению квадратного уравнения не может быть равно нулю, то очевидно, что нулю может быть равен только x 2 , а значит, и сам x. У уравнений такого вида всегда есть один корень, он равен 0.
Неполные квадратные уравнения. Решение неполных квадратных уравнений
Например:
–3x 2 = 0
x 2 = 0/–3
x 2 = 0
x = √0
x = 0Уравнения вида ax 2 + c = 0 преобразуются к виду ax 2 = –c и решаются аналогично предыдущему. Однако корней здесь либо два, либо не одного.
ax 2 + c = 0
ax 2 = –c
x 2 = –c/a
x = √(–c/a)Здесь если подкоренное выражение отрицательно, то корней у уравнения нет.
 Если положительно, то корней будет два: √(–c/a) и –√(–c/a). Пример решения подобного уравнения:
Если положительно, то корней будет два: √(–c/a) и –√(–c/a). Пример решения подобного уравнения:4x 2 – 16 = 0
4x 2 = 16
x 2 = 16 / 4
x 2 = 4
x = √4
x 1 = 2; x 2 = –2Неполные квадратные уравнения вида ax 2 + bx = 0 решается вынесением общего множителя за скобку. В данном случае им является x. Получается уравнение x(ax + b) = 0. Это уравнение имеет два корня: либо x = 0, либо ax + b = 0. Решая второе уравнение получаем x = –b/a. Таким образом, уравнения вида ax 2 + bx = 0 имеют два корня: x 1 = 0, x 2 = –b/a. Пример решения такого уравнения:
3x 2 – 10x = 0
x(3x – 10) = 0
x 1 = 0; x 2 = 10/3 = 3,(33)Нахождение корней квадратного уравнения 8 класс
Формула
Корни квадратного уравнения ax 2 + bx + c = 0 можно найти по
формуле: , где — дискриминантквадратного уравнения.
Возможны три правила:
Правило 1
1. D > 0.8.2.1. Решение неполных квадратных уравнений
Тогда уравнение имеет 2 различных корня:
Пример
2x 2 + 7x — 4 = 0;a = 2, b = 7, c = -4.

D = 7 2 — 4 2 (- 4) = 81 > 0,
x 1 = -7 — ? 81 2 2 = — 4;
x 2 = -7 + ? 81 2 2 = 1 2 .
Правило 2
2. D = 0. Тогда уравнение имеет единственный корень.Пример
x 2 — 4x + 4 = 0.D = (-4) 2 — 4 1 4 = 0, x = — -4 2 1 = 2.
Заметим, что x 2 — 4x + 4 = 0 x = 2.
Правило 3
3. DПример
3x 2 — x + 7 = 0.D = (-1) 2 — 4 3 7 = -83
С четным вторым коэффициентом
Правило, формулы
Если b = 2k, то корни уравнения ax + 2kx + c = 0 находятся по формуле:Пример 1
1. x + 18x + 32 = 0.a = 1; b = 18 => k = b 2 = 9; c = 32.
D 1 = D 4 = (18 2 ) 2 — 1 32 = 49 > 0, значит уравнение имеет 2 корня:
x 1 = -9 -? 49 1 = -16, x 2 = -9 + 7 = -2.
Пример 2
2. 3x 2 + 2x + 1 = 0.a = 3; b 2 = 1; c = 1.

D 1 = D 4 = 1 2 — 1 3 = -2
Пример 3
3. 196x 2 + 28x + 1 = 0.a = 196; b 2 = -14; c = 1.
D 1 = D 4 = (- 14) 2 — 196 = 0, значит уравнение имеет один корень.
x = 14 196 = 1 14 .
Формулы сокращенного умножения
Формулы сокращенного умножения.
— Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.
— Применение формул сокращенного умножения при решении примеров.
Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения.
Решение квадратных уравнений
Формулы сокращенного умножения нужно знать наизусть .
Пусть а, b R. Тогда:
1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a + b) 2 = a 2 + 2ab + b 2
2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a — b) 2 = a 2 — 2ab + b 2
3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
a 2 — b 2 = (a -b) (a+b)
4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.

a 3 + b 3 = (a + b) (a 2 — ab + b 2)
7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.
Применение формул сокращенного умножения при решении примеров.
Пример 1.
Вычислить
а) Используя формулу квадрата суммы двух выражений, имеем
(40+1) 2 = 40 2 + 2 · 40 · 1 + 1 2 = 1600 + 80 + 1 = 1681
б) Используя формулу квадрата разности двух выражений, получим
98 2 = (100 – 2) 2 = 100 2 — 2 · 100 · 2 + 2 2 = 10000 – 400 + 4 = 9604
Пример 2.
Вычислить
Используя формулу разности квадратов двух выражений, получим
Пример 3.
Упростить выражение
(х — у) 2 + (х + у) 2
Воспользуемся формулами квадрата суммы и квадрата разности двух выражений
(х — у) 2 + (х + у) 2 = х 2 — 2ху + у 2 + х 2 + 2ху + у 2 = 2х 2 + 2у 2
Формулы сокращенного умножения в одной таблице:
(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)1.
 Выделение полного квадрата. Формулы корней квадратного уравнения.
Выделение полного квадрата. Формулы корней квадратного уравнения.
2.Примеры решения квадратных уравнений.
3.Решение неполных квадратных уравнений.
4.Разложение квадратного трехчлена на сомножители.Более простым способом. Для этого вынесите z за скобки. Вы получите : z(аz + b) = 0. Множители можно расписать: z=0 и аz + b = 0, так как оба могут давать в результате ноль. В записи аz + b = 0 перенесем второй вправо с другим знаком. Отсюда получаем z1 = 0 и z2 = -b/а. Это и есть корни исходного .
Если же имеется неполное уравнение вида аz² + с = 0, в данном случае находятся простым переносом свободного члена в правую часть уравнения. Также поменяйте при этом его знак. Получится запись аz² = -с. Выразите z² = -с/а. Возьмите корень и запишите два решения — положительное и отрицательное значение корня квадратного.
Обратите внимание
При наличии в уравнении дробных коэффициентов помножьте все уравнение на соответствующий множитель так, чтобы избавиться от дробей.
 2 — 4*a*c. Значение D может быть больше, меньше или равно нулю. Если D больше или меньше нуля, то корня будет два, если D=0, то остается всего один корень, более точно можно сказать, что D в этом случае имеет два равнозначных корня. Подставьте известные коэффициенты a, b, c в формулу и вычислите значение.
2 — 4*a*c. Значение D может быть больше, меньше или равно нулю. Если D больше или меньше нуля, то корня будет два, если D=0, то остается всего один корень, более точно можно сказать, что D в этом случае имеет два равнозначных корня. Подставьте известные коэффициенты a, b, c в формулу и вычислите значение.После того как вы нашли дискриминант, для нахождения х воспользуйтесь формулами: x(1) = (- b+sqrt{D})/2*a; x(2) = (- b-sqrt{D})/2*a, где sqrt — это функция, означающая извлечение квадратного корня из данного числа. Посчитав эти выражения, вы найдете два корня вашего уравнения, после чего уравнение считается решенным.
Если D меньше нуля, то он все равно имеет корни. В школе данный раздел практически не изучается. Студенты вузов должны знать о том, что появляется отрицательное число под корнем. От него избавляются выделяя мнимую часть, то есть -1 под корнем всегда равно мнимому элементу «i», который умножается на корень с таким же положительным числом. К примеру, если D=sqrt{-20}, после преобразования получается D=sqrt{20}*i.
 После этого преобразования, решение уравнения сводится к такому же нахождению корней, как было описано выше.
После этого преобразования, решение уравнения сводится к такому же нахождению корней, как было описано выше.Теорема Виета заключается в подборе значений x(1) и x(2). Используется два тождественных уравнения: x(1) + x(2)= -b; x(1)*x(2)=с. Причем очень важным моментом является знак перед коэффициентом b, помните, что этот знак противоположен тому, который стоит в уравнении. С первого взгляда кажется, что посчитать x(1) и x(2) очень просто, но при решении вы столкнетесь с тем, что числа придется именно подбирать.
Элементы решения квадратных уравнений
По правилам математики некоторые можно разложить на множители: (a+x(1))*(b-x(2))=0, если вам посредством формул математики удалось преобразовать подобным образом данное квадратное уравнение, то смело записывайте ответ. x(1) и x(2) будут равны рядом стоящим коэффициентам в скобках, но с противоположным знаком.Также не стоит забывать про неполные квадратные уравнения. У вас может отсутствовать какое-то из слагаемых, если это так, то все его коэффициенты просто равны нулю.
 2 или x ничего не стоит, то коэффициенты а и b равны 1.
2 или x ничего не стоит, то коэффициенты а и b равны 1.В современном обществе умение производить действия с уравнениями, содержащими переменную, возведённую в квадрат, может пригодиться во многих областях деятельности и широко применяется на практике в научных и технических разработках. Свидетельством тому может служить конструирование морских и речных судов, самолётов и ракет. При помощи подобных расчётов определяют траектории перемещения самых разных тел, в том числе и космических объектов. Примеры с решением квадратных уравнений находят применение не только в экономическом прогнозировании, при проектировании и строительстве зданий, но и в самых обычных житейских обстоятельствах. Они могут понадобиться в туристических походах, на спортивных состязаниях, в магазинах при совершении покупок и в других весьма распространённых ситуациях.
Разобьём выражение на составляющие множители
Степень уравнения определяется максимальным значением степени у переменной, которую содержит данное выражение.
 В случае, если она равна 2, то подобное уравнение как раз и называется квадратным.
В случае, если она равна 2, то подобное уравнение как раз и называется квадратным.Если изъясняться языком формул, то указанные выражения, как бы они ни выглядели, всегда можно привести к виду, когда левая часть выражения состоит из трёх слагаемых. Среди них: ax 2 (то есть переменная, возведённая в квадрат со своим коэффициентом), bx (неизвестное без квадрата со своим коэффициентом) и c (свободная составляющая, то есть обычное число). Всё это в правой части приравнивается 0. В случае, когда у подобного многочлена отсутствует одно из его составляющих слагаемых, за исключением ax 2 , оно называется неполным квадратным уравнением. Примеры с решением таких задач, значение переменных в которых найти несложно, следует рассмотреть в первую очередь.
Если выражение на вид выглядит таким образом, что слагаемых у выражения в правой части два, точнее ax 2 и bx, легче всего отыскать х вынесением переменной за скобки. Теперь наше уравнение будет выглядеть так: x(ax+b). Далее становится очевидно, что или х=0, или задача сводится к нахождению переменной из следующего выражения: ax+b=0.
 Указанное продиктовано одним из свойств умножения. Правило гласит, что произведение двух множителей даёт в результате 0, только если один из них равен нулю.
Указанное продиктовано одним из свойств умножения. Правило гласит, что произведение двух множителей даёт в результате 0, только если один из них равен нулю.Пример
x=0 или 8х — 3 = 0
В результате получаем два корня уравнения: 0 и 0,375.
Уравнения такого рода могут описывать перемещение тел под действием силы тяжести, начавших движение из определённой точки, принятой за начало координат. Здесь математическая запись принимает следующую форму: y = v 0 t + gt 2 /2. Подставив необходимые значения, приравняв правую часть 0 и найдя возможные неизвестные, можно узнать время, проходящее с момента подъёма тела до момента его падения, а также многие другие величины. Но об этом мы поговорим позднее.
Разложение выражения на множители
Описанное выше правило даёт возможность решать указанные задачи и в более сложных случаях. Рассмотрим примеры с решением квадратных уравнений такого типа.
X 2 — 33x + 200 = 0
Этот квадратный трёхчлен является полным.
 Для начала преобразуем выражение и разложим его на множители. Их получается два: (x-8) и (x-25) = 0. В результате имеем два корня 8 и 25.
Для начала преобразуем выражение и разложим его на множители. Их получается два: (x-8) и (x-25) = 0. В результате имеем два корня 8 и 25.Примеры с решением квадратных уравнений в 9 классе позволяют данным методом находить переменную в выражениях не только второго, но даже третьего и четвёртого порядков.
Например: 2x 3 + 2x 2 — 18x — 18 = 0. При разложении правой части на множители с переменной, их получается три, то есть (x+1),(x-3) и (x+3).
В результате становится очевидно, что данное уравнение имеет три корня: -3; -1; 3.
Извлечение квадратного корня
Другим случаем неполного уравнения второго порядка является выражение, на языке букв представленное таким образом, что правая часть строится из составляющих ax 2 и c. Здесь для получения значения переменной свободный член переносится в правую сторону, а после этого из обеих частей равенства извлекается квадратный корень. Следует обратить внимание, что и в данном случае корней уравнения обычно бывает два. Исключением могут служить лишь только равенства, вообще не содержащие слагаемое с, где переменная равна нулю, а также варианты выражений, когда правая часть оказывается отрицательной.
 В последнем случае решений вообще не существует, так как указанные выше действия невозможно производить с корнями. Примеры решений квадратных уравнений такого типа необходимо рассмотреть.
В последнем случае решений вообще не существует, так как указанные выше действия невозможно производить с корнями. Примеры решений квадратных уравнений такого типа необходимо рассмотреть.В данном случае корнями уравнения окажутся числа -4 и 4.
Вычисление пощади земельного участка
Потребность в подобного рода вычислениях появилась в глубокой древности, ведь развитие математики во многом в те далёкие времена было обусловлено необходимостью определять с наибольшей точностью площади и периметры земельных участков.
Примеры с решением квадратных уравнений, составленных на основе задач такого рода, следует рассмотреть и нам.
Итак, допустим имеется прямоугольный участок земли, длина которого на 16 метров больше, чем ширина. Следует найти длину, ширину и периметр участка, если известно, что его площадь равна 612 м 2 .
Приступая к делу, сначала составим необходимое уравнение. Обозначим за х ширину участка, тогда его длина окажется (х+16). Из написанного следует, что площадь определяется выражением х(х+16), что, согласно условию нашей задачи, составляет 612.
 Это значит, что х(х+16) = 612.
Это значит, что х(х+16) = 612.Решение полных квадратных уравнений, а данное выражение является именно таковым, не может производиться прежним способом. Почему? Хотя левая часть его по-прежнему содержит два множителя, произведение их совсем не равно 0, поэтому здесь применяются другие методы.
Дискриминант
Прежде всего произведём необходимые преобразования, тогда внешний вид данного выражения будет выглядеть таким образом: x 2 + 16x — 612 = 0. Это значит, мы получили выражение в форме, соответствующей указанному ранее стандарту, где a=1, b=16, c=-612.
Это может стать примером решения квадратных уравнений через дискриминант. Здесь необходимые расчёты производятся по схеме: D = b 2 — 4ac. Данная вспомогательная величина не просто даёт возможность найти искомые величины в уравнении второго порядка, она определяет количество возможных вариантов. В случае, если D>0, их два; при D=0 существует один корень. В случае, если D
О корнях и их формуле
В нашем случае дискриминант равен: 256 — 4(-612) = 2704.
 Это говорит о том, что ответ у нашей задачи существует. Если знать, к , решение квадратных уравнений нужно продолжать с применением ниже приведённой формулы. Она позволяет вычислить корни.
Это говорит о том, что ответ у нашей задачи существует. Если знать, к , решение квадратных уравнений нужно продолжать с применением ниже приведённой формулы. Она позволяет вычислить корни.Это значит, что в представленном случае: x 1 =18, x 2 =-34. Второй вариант в данной дилемме не может являться решением, потому что размеры земельного участка не могут измеряться в отрицательных величинах, значит х (то есть ширина участка) равна 18 м. Отсюда вычисляем длину: 18+16=34, и периметр 2(34+18)=104(м 2).
Примеры и задачи
Продолжаем изучение квадратных уравнений. Примеры и подробное решение нескольких из них будут приведены далее.
1) 15x 2 + 20x + 5 = 12x 2 + 27x + 1
Перенесём всё в левую часть равенства, сделаем преобразование, то есть получим вид уравнения, который принято именовать стандартным, и приравняем его нулю.
15x 2 + 20x + 5 — 12x 2 — 27x — 1 = 0
Сложив подобные, определим дискриминант: D = 49 — 48 = 1. Значит у нашего уравнения будет два корня.
 Вычислим их согласно приведённой выше формуле, а это значит, что первый из них буде равен 4/3, а второй 1.
Вычислим их согласно приведённой выше формуле, а это значит, что первый из них буде равен 4/3, а второй 1.2) Теперь раскроем загадки другого рода.
Выясним, есть ли вообще здесь корни x 2 — 4x + 5 = 1? Для получения исчерпывающего ответа приведём многочлен к соответствующему привычному виду и вычислим дискриминант. В указанном примере решение квадратного уравнения производить не обязательно, ведь суть задачи заключается совсем не в этом. В данном случае D = 16 — 20 = -4, а значит, корней действительно нет.
Теорема Виета
Квадратные уравнения удобно решать через указанные выше формулы и дискриминант, когда из значения последнего извлекается квадратный корень. Но это бывает не всегда. Однако способов для получения значений переменных в данном случае существует множество. Пример: решения квадратных уравнений по теореме Виета. Она названа в честь который жил в XVI веке во Франции и сделал блестящую карьеру благодаря своему математическому таланту и связям при дворе.
 Портрет его можно увидеть в статье.
Портрет его можно увидеть в статье.Закономерность, которую заметил прославленный француз, заключалась в следующем. Он доказал, что корни уравнения в сумме численно равны -p=b/a, а их произведение соответствует q=c/a.
Теперь рассмотрим конкретные задачи.
3x 2 + 21x — 54 = 0
Для простоты преобразуем выражение:
x 2 + 7x — 18 = 0
Воспользуемся теоремой Виета, это даст нам следующее: сумма корней равна -7, а их произведение -18. Отсюда получим, что корнями уравнения являются числа -9 и 2. Сделав проверку, убедимся, что эти значения переменных действительно подходят в выражение.
График и уравнение параболы
Понятия квадратичная функция и квадратные уравнения тесно связаны. Примеры подобного уже были приведены ранее. Теперь рассмотрим некоторые математические загадки немного подробнее. Любое уравнение описываемого типа можно представить наглядно. Подобная зависимость, нарисованная в виде графика, называется параболой. Различные её виды представлены на рисунке ниже.

Любая парабола имеет вершину, то есть точку, из которой выходят её ветви. В случае если a>0, они уходят высоко в бесконечность, а когда a
Наглядные изображения функций помогают решать любые уравнения, в том числе и квадратные. Этот метод называется графическим. А значением переменной х является координата абсцисс в точках, где происходит пересечение линии графика с 0x. Координаты вершины можно узнать по только что приведённой формуле x 0 = -b/2a. И, подставив полученное значение в изначальное уравнение функции, можно узнать y 0 , то есть вторую координату вершины параболы, принадлежащую оси ординат.
Пересечение ветвей параболы с осью абсцисс
Примеров с решением квадратных уравнений очень много, но существуют и общие закономерности. Рассмотрим их. Понятно, что пересечение графика с осью 0x при a>0 возможно только если у 0 принимает отрицательные значения. А для a0. В противном случае D
По графику параболы можно определить и корни. Верно также обратное.
 То есть если получить наглядное изображение квадратичной функции нелегко, можно приравнять правую часть выражения к 0 и решить полученное уравнение. А зная точки пересечения с осью 0x, легче построить график.
То есть если получить наглядное изображение квадратичной функции нелегко, можно приравнять правую часть выражения к 0 и решить полученное уравнение. А зная точки пересечения с осью 0x, легче построить график.Из истории
С помощью уравнений, содержащих переменную, возведённую в квадрат, в старину не только делали математические расчёты и определяли площади геометрических фигур. Подобные вычисления древним были нужны для грандиозных открытий в области физики и астрономии, а также для составления астрологических прогнозов.
Как предполагают современные деятели науки, одними из первых решением квадратных уравнений занялись жители Вавилона. Произошло это за четыре столетия до наступления нашей эры. Разумеется, их вычисления в корне отличались от ныне принятых и оказывались гораздо примитивней. К примеру, месопотамские математики понятия не имели о существовании отрицательных чисел. Незнакомы им были также другие тонкости из тех, которые знает любой школьник современности.

Возможно, ещё раньше учёных Вавилона решением квадратных уравнений занялся мудрец из Индии Баудхаяма. Произошло это примерно за восемь столетий до наступления эры Христа. Правда, уравнения второго порядка, способы решения которых он привёл, были самыми наипростейшими. Кроме него, подобными вопросами интересовались в старину и китайские математики. В Европе квадратные уравнения начали решать лишь в начале XIII столетия, но зато позднее их использовали в своих работах такие великие учёные, как Ньютон, Декарт и многие другие.
Неполные квадратные уравнения представляют собой частный случай равенств второго порядка. Необходимо уметь решать эти уравнения, поскольку они часто встречаются не только в математических, но и в физических задачах. Методам их решения посвящена эта статья.
Квадратные уравнения: полные и неполные
Перед тем как разбирать способы решения неполных квадратных уравнений, следует рассмотреть, что они собой представляют.
На рисунке ниже изображен общий вид равенств второго порядка, которые так называются из-за максимального значения степени переменной (она равна 2), содержащейся в них.

Где a, b и c — числа (коэффициенты). Неполное уравнение получается тогда, когда один из этих коэффициентов становится равным нулю (за исключением числа a, поскольку если оно занулится, то уравнение перестанет быть квадратным). Поскольку остается всего три возможные комбинации нулевых коэффициентов, то выделяют следующие типы неполных равенств второго порядка:
- Только b=0. Тогда уравнение преобразуется к виду a*x 2 + c = 0. Оно называется чистым или простым неполным равенством квадратного типа.
- Только c=0. Тогда получаем вид: a*x 2 + b*x = 0. Оно получило название смешенного неполного уравнения квадратного.
- Наконец, если b=0 и c=0, то мы имеем выражение a*x 2 =0.
Последний вид неполного уравнения не рассматривается ни в одном математическом курсе, поскольку его решение является очевидным и единственно возможным: x=0.
Можно ли решать неполные уравнения с помощью формулы с дискриминантом?
Да, можно, поскольку этот способ является универсальным для любых выражений второго порядка.
 Однако неполные уравнения квадратные в 8 классе школы уже встречаются, и изучаться они начинают раньше, чем полные равенства этого типа, для которых уже приводится формула с дискриминантом. Кроме того, рассматриваемый вид равенств является достаточно простым, чтобы применять к ним универсальные формулы и производить ряд ненужных вычислений.
Однако неполные уравнения квадратные в 8 классе школы уже встречаются, и изучаться они начинают раньше, чем полные равенства этого типа, для которых уже приводится формула с дискриминантом. Кроме того, рассматриваемый вид равенств является достаточно простым, чтобы применять к ним универсальные формулы и производить ряд ненужных вычислений.Рассмотрим простые и понятные способы решения неполных уравнений второго порядка.
Решение простого неполного уравнения
Схема его решения в общем случае представлена на рисунке ниже.
Объясним подробнее каждый отмеченный на ней шаг. Первым делом необходимо привести уравнение к виду, указанному в начале этой схемы. Условие задачи может быть так составлено, что исходное равенство будет содержать больше двух слагаемых. Все их необходимо упростить (умножить, сложить и вычесть) до вида чистого неполного равенства.
После этого свободный член c переносится в правую часть равенства и делится на коэффициент a. Для получения неизвестных x остается взять квадратный корень из отношения -c/a, при этом нужно не забывать и учитывать, что он может быть, как со знаком минус, так и с положительным знаком.

Что следует из представленной на рисунке формулы? Во-первых, корней чистого неполного квадратного равенства всегда 2-а, при этом по модулю они оба равны, а по знаку отличаются. Во-вторых, если числа c и a имеют один знак, то корни x будут мнимыми, если c и a разного знака, тогда получаются два действительных решения.
Для решения квадратного уравнения, у которого c=0, следует проделать такой же первый шаг, как и в случае определения корней чистого неполного равенства, то есть привести его к виду с двумя слагаемыми: одно из них должно содержать x 2 , а другое x. Затем, следует применить метод факторизации, то есть разложить левую часть равенства на множители. В отличие от полного уравнения это сделать очень просто, поскольку один из множителей всегда будет иксом. Сказанное выше можно записать в виде формулы:
Это равенство имеет решение, если каждый его множитель является нулем. Результат вычисления корней представлен на рисунке ниже.
Таким образом, корни этого типа неполного уравнения всегда будут действительными числами, причем один из них равен нулю.
 Знак второго корня определяется отношением ненулевых коэффициентов b/a.
Знак второго корня определяется отношением ненулевых коэффициентов b/a.Примеры математических задач
Теперь приведем наглядные примеры квадратных неполных уравнений с решением.
Пример 1. Найдите корни равенства 135-(2x + 3) (2x — 3) = 0. Раскрываем скобки, получаем: 135-4*x 2 +9=0. Заметим, что члены, содержащие x в первой степени, сократились. Выполняя перенос свободных членов в правую часть и деление их на -4, получаем: x 2 = 36. Откуда следуют два корня: 6 и -6.
Пример 2. 23*(x 2 -2)=34*x-46. Как и в первом случае, раскрываем скобки и переносим все слагаемые в левую часть. Имеем: 23*x 2 -46-34*x+46=0. Теперь сокращаем свободные члены и разлагаем сумму на множители, получаем: x*(23*x-34)=0. Откуда следует, что x=0 и x = 34/23≈1,47826.
Решение примеров показало, что алгоритм нахождения корней любого вида неполного уравнения второго порядка является достаточно простым, поэтому нет никакого смысла запоминать представленные на рисунках выше формулы.

Пример физической задачи
Многие школьники слышали от своего учителя физики о том, что Галилео Галилей в XVII веке проводил эксперименты по вычислению ускорения свободного падения, сбрасывая различные тела с башни в Пизе. Многим это покажется любопытным, но не существует ни одного исторического свидетельства, что такие эксперименты ученый действительно проводил. Однако в том же XVII веке их выполнил другой итальянец.
Джованни Риччоли — астроном и иезуит, который смог действительно вычислить ускорение падения свободного, сбрасывая глиняные шары с высоты башни Азинелли, находящейся в городе Болонье. Риччоли получил значение ускорения равное 9,6 м/с 2 (современная величина равна 9,81 м/с 2). Зная это число, необходимо определить, сколько времени глиняный шар падал на землю, учитывая, что высота башни равна 97,6 метра.
Для решения задачи необходимо вспомнить, что путь при равноускоренном движении выражается формулой: l=v 0 *t+g*t 2 /2. Поскольку в момент, когда Риччоли отпускал шар, скорость последнего была равна нулю, то член v 0 *t = 0.
 Тогда мы приходим к уравнению: 97,6 = 9,6*t 2 /2. Откуда получаем, что t = 4,51 секунды (отрицательный корень был сознательно отброшен).
Тогда мы приходим к уравнению: 97,6 = 9,6*t 2 /2. Откуда получаем, что t = 4,51 секунды (отрицательный корень был сознательно отброшен).Дискриминантный калькулятор
Калькулятор дискриминанта — это онлайн-инструмент, который предоставляет значение дискриминанта для заданных коэффициентов в квадратном уравнении. Онлайн-калькулятор дискриминанта STUDYQUERIES делает вычисления быстрее и проще, отображая значение за доли секунды.
Как пользоваться дискриминантным калькулятором?Чтобы использовать калькулятор дискриминанта, выполните следующие действия:
- Шаг 1: Введите значения коэффициентов, такие как «a», «b» и «c», в соответствующие поля.
- Шаг 2: Теперь нажмите «Рассчитать», чтобы увидеть результат.
- Шаг 3: Значение дискриминанта отображается в поле вывода
Дискриминантный калькулятор
Что такое дискриминант?Квадратичная формула: $$ x = \ frac {-b \ pm \ sqrt {b ^ 2-4ac}} {2a} $$
Его можно найти, используя формулу корней квадратного уравнения для определения дискриминантной функции.
Дискриминантный калькулятор Он представлен как b²-4ac, а дискриминант может быть нулевым, положительным или отрицательным. Это указывает на то, не будет ли решения, одного решения или двух решений.
Он представлен как b²-4ac, а дискриминант может быть нулевым, положительным или отрицательным. Это указывает на то, не будет ли решения, одного решения или двух решений.Обратите внимание на следующие характеристики формулы дискриминантной алгебры:
- Нулевой дискриминант указывает, что существуют повторяющиеся вещественные числа решения квадратичной;
- В случае отрицательного дискриминанта ни одно из решений не является действительным;
- У квадратного уравнения есть два различных решения, которые являются действительными числами для положительного дискриминанта.2-4ac <0 $$
Здесь,
a, b, c = действительные числа
a ≠ 0
дискриминант = отрицательный
Если радикал отрицательный, значение под ним будет отрицательным. Нет реальных решений для нахождения квадратного корня из отрицательного числа, потому что вы не можете использовать действительные числа.
 Однако можно использовать и мнимые числа. Тогда у вас будет два сложных решения: одно путем сложения мнимого квадратного корня, а другое — путем его вычитания.2-4ac> 0 \ as \ a \ perfect \ square \ as \ well $$
Однако можно использовать и мнимые числа. Тогда у вас будет два сложных решения: одно путем сложения мнимого квадратного корня, а другое — путем его вычитания.2-4ac> 0 \ as \ a \ perfect \ square \ as \ well $$ Здесь,
a, b, c = действительные числа
a ≠ 0
дискриминант = положительный и полный квадрат
Следовательно, корни квадратного уравнения не равны, действительны и рациональны.
Что нужно помнить при использовании квадратичной формулы- Совершенно важно, чтобы уравнение было составлено правильно, чтобы прийти к решению.
- Убедитесь, что 2a и квадратный корень из целого числа (b² — 4ac) помещены в знаменатель.2 — 4ac $$ Он определяет количество и тип решений квадратного уравнения. Если дискриминант положительный, есть 2 реальных решения. Если он равен 0, существует 1 реальное повторяющееся решение. Если дискриминант отрицательный, есть 2 комплексных решения (но нет реальных решений).
 Дискриминант также может рассказать нам о поведении графика квадратичной функции. Часто задаваемые вопросы
Дискриминант также может рассказать нам о поведении графика квадратичной функции. Часто задаваемые вопросы Когда дискриминант равен нулю, сколько чисел решения будет у квадратного уравнения?
Дискриминант или определитель квадратного уравнения — это компонент квадратного корня квадратной формулы b²-4ac.Дискриминант должен быть равен нулю, чтобы решение было единственным. Если дискриминант меньше нуля, решение не может быть найдено. В том случае, если оно больше нуля, может быть два реальных решения уравнения.
Каковы различные формы квадратного уравнения?
Три основных формы квадратного уравнения —
- Стандартная форма
- Факторная форма
- Форма вершины.
Стандартная форма квадратного уравнения представлена как y = ax² + bx + c, а дискриминант квадратного уравнения в данном случае равен b² — 4ac.Факторная форма квадратного уравнения представлена как y = (ax + c) (bx + d).
 Вершинная форма квадратного уравнения представлена как y = a (x + b) ² + c.
Вершинная форма квадратного уравнения представлена как y = a (x + b) ² + c.Следует отметить, что числа a, b и c.
Какое значение имеют квадратные уравнения?
Квадратные уравнения используются в нашей повседневной жизни по-разному, включая вычисление площадей, определение прибыли от продукта и вычисление скорости объекта. В квадратном уравнении будет по крайней мере одна квадратная переменная, представленная в виде ax² + bx + c = 0, где x — переменная, ‘a’ ‘b’ ‘c’ — константы, а ‘a’ не равняются нулю.Дискриминантную квадратичную функцию можно использовать для нахождения решения уравнения.
Что означает дискриминант 0?
Это означает, что у вас есть 0 под квадратным корнем в квадратной формуле, если дискриминант равен 0. 0 — это квадратный корень из нуля. Когда это происходит, плюсовые и минусовые части квадратной формулы просто исчезают. Остается одно решение.
Что такое дискриминант 3x²- 10x = — 2?
Здесь a = 3, b = -10 и c = 2.
 Подставляем значения. Следовательно, дискриминант равен 76.
Подставляем значения. Следовательно, дискриминант равен 76.Что такое дискриминант в математике?
Дискриминант в математике — параметр объекта или системы, вычисляемый для помощи в их классификации или решении. В случае квадратного уравнения ax² + bx + c = 0 дискриминант равен b² — 4ac; для кубического уравнения x³ + ax² + bx + c = 0 дискриминант равен a²b² + 18abc — 4b³ — 4a³c — 27c².
Сообщение навигации
Дискриминантный калькулятор— Дискриминантный калькулятор Oniine
Дискриминантное выражение b 2 — 4ac используется при вычислении квадратных уравнений.Дискриминантная формула также используется для определения природы корней уравнения.
Что такое дискриминантный калькулятор?
«Калькулятор дискриминанта Cuemath» — это онлайн-инструмент, который помогает в вычислении значения дискриминанта полиномиального уравнения. Онлайн-калькулятор дискриминанта Cuemath поможет вам рассчитать значение дискриминанта за несколько секунд.

Как пользоваться калькулятором дискриминанта?
Чтобы найти значение дискриминанта, выполните следующие действия.
- Шаг 1: Введите значения a, b и c из уравнения (ax 2 + bx + c = 0) в указанные поля ввода.
- Шаг 2: Нажмите кнопку «Рассчитать» , чтобы найти значение дискриминанта.
- Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести другие значения.
Как найти дискриминантный калькулятор?
Дискриминат — это математическая величина, полученная из коэффициентов полиномиального уравнения, которая в дальнейшем используется для определения природы корней, независимо от того, являются ли корни уравнения действительными, равными или мнимыми.Дискриминант уравнения вида ax 2 + bx + c = 0 вычисляется по приведенной ниже формуле:
Здесь D — значение дискриминанта.

Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенный пример:Каким должно быть значение дискриминанта (D) в уравнении 2x 2 — x + 8?
Решение:D = b 2 — 4ac
(-1) 2 — 64 = 0
1–64
Следовательно, D = — 63
Таким образом, дискриминант равен -63 уравнения 2x 2 — x + 8
Аналогичным образом можно найти дикриминант
.- 5x 2 + 2x + 5 = 0
- 2x 2 -7x + 3 = 0
Квадратные уравнения: Резюме
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.
 е. вы, вероятно, разговариваете по мобильному телефону). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, разговариваете по мобильному телефону). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.Раздел 2-7: Квадратные уравнения: сводка
В предыдущих двух разделах мы довольно много говорили о решении квадратных уравнений.Здесь возникает логичный вопрос: какой метод мы должны использовать для решения данного квадратного уравнения? К сожалению, ответ зависит от обстоятельств.
Если ваш инструктор указал метод, который следует использовать, то это, конечно, тот метод, который вам следует использовать. Однако, если ваш инструктор НЕ указал метод, который следует использовать, нам придется принять решение самостоятельно.
 Вот общий набор рекомендаций, которые может помочь при определении того, какой метод использовать.
Вот общий набор рекомендаций, которые может помочь при определении того, какой метод использовать.- Это явно проблема свойства квадратного корня? Другими словами, состоит ли уравнение ТОЛЬКО из квадрата и константы.Если это так, то, вероятно, проще всего использовать свойство квадратного корня.
- Это фактор? Если так, то, вероятно, это лучший вариант. Обратите внимание, что вам не следует тратить много времени на то, чтобы определить, учитывается ли квадратное уравнение. Взгляните на уравнение, и если вы можете быстро определить, что в нем учитывается, то согласитесь с этим. Если вы не можете быстро определить, что это за факторы, не беспокойтесь об этом.
- Если вы достигли этого момента, значит, вы определили, что уравнение имеет неправильную форму для свойства квадратного корня и не учитывает множители (или что вы не можете быстро увидеть, что оно множится).Итак, на данный момент единственным реальным вариантом является квадратная формула.

Как только вы решите достаточное количество квадратных уравнений, приведенный выше набор рекомендаций станет для вас почти второй натурой, и вы обнаружите, что проходите их почти не задумываясь.
Также обратите внимание, что нигде в наборе руководящих указаний не было завершение упомянутого квадрата. Причина в том, что это долгий метод, который может ошибаться, если вы торопитесь.Квадратичная формула также всегда будет работать, и ее использование намного короче. В общем, вы должны использовать квадрат только в том случае, если ваш инструктор потребовал, чтобы вы его использовали.
В качестве метода решения завершение квадрата всегда должно быть вашим последним выбором. Однако это не означает, что это не важный метод. Мы увидим, как завершение квадратного процесса возникает в нескольких разделах следующих глав. Интересно, что когда мы увидим этот процесс в следующих разделах, мы не будем решать уравнения! Этот процесс очень полезен во многих ситуациях, решение которых — только одно.
 2} + bx + c = 0 \]
2} + bx + c = 0 \]мы получим один из следующих трех возможных наборов решений.
- Два реальных различных ( т. Е. не равных) решений.
- Двойной корень. Вспомните, это возникает, когда мы можем разложить уравнение на полный квадрат.
- Два комплексных решения.
Это ЕДИНСТВЕННЫЕ возможности для решения квадратных уравнений в стандартной форме. Однако обратите внимание, что если мы начнем с рационального выражения в уравнении, мы можем получить разные наборы решений, потому что нам может потребоваться избежать одного из возможных решений, чтобы не получить деление на ноль ошибок.2} — 4ac> 0 \). В этом случае мы будем извлекать квадратный корень из положительного числа, поэтому квадратный корень будет действительным числом. Следовательно, числитель в формуле корней квадратного уравнения будет — \ (b \) плюс или минус действительное число. Это означает, что в числителе будут два разных действительных числа.
 2} — 4ac = 0 \).2} — 4 \ left ({49} \ right) \ left ({81} \ right) = 0 \]
2} — 4ac = 0 \).2} — 4 \ left ({49} \ right) \ left ({81} \ right) = 0 \]В этом случае мы получим двойной корень, поскольку дискриминант равен нулю. Вот она,
\ [x = — \ frac {9} {7} \]Нахождение дискриминанта квадратного уравнения с помощью TI-84 Plus C Silver Edition.
Управление настройками файлов cookie
Вы можете управлять своими предпочтениями в отношении того, как мы используем файлы cookie для сбора и использования информации, пока вы находитесь на веб-сайтах TI, изменяя статус этих категорий.
Категория Описание Разрешить Аналитические и рабочие файлы cookie Эти файлы cookie, включая файлы cookie из Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI и видеть, как посетители перемещаются по нашим сайтам. Это помогает нам улучшить работу сайтов TI (например, облегчая вам поиск информации на сайте). 
Рекламные и маркетинговые файлы cookie Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах. Мы также можем передавать эту информацию третьим лицам для этих целей.Эти файлы cookie помогают нам адаптировать рекламные объявления в соответствии с вашими интересами, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы. Функциональные файлы cookie Эти файлы cookie помогают идентифицировать вас и хранить ваши действия и информацию об учетной записи, чтобы предоставлять расширенные функциональные возможности, в том числе более персонализированный и релевантный опыт на наших сайтах.
 Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно.
Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно.Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно.
Файлы cookie социальных сетей Эти файлы cookie позволяют идентифицировать пользователей и контент, подключенный к онлайн-социальным сетям, таким как Facebook, Twitter и другим платформам социальных сетей, и помогают TI улучшить охват социальных сетей. Строго необходимо Эти файлы cookie необходимы для работы сайтов TI или для выполнения ваших запросов (например, для отслеживания того, какие товары вы поместили в корзину на TI.com, для доступа к защищенным областям сайта TI или для управления настроенными вами настройки файлов cookie). Всегда на связи Решите квадратное уравнение через квадратную формулу
Быстрый! Мне нужна помощь с: Выберите пункт справки по математике.
 ..Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, AreaConversion, VolumeConversion, FindConversion, Massage анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основ , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители GCF многочлены, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Экспоненты, Образцы, Упрощение, Упрощение, Методы Правые треугольники, Ветер, рисунок
..Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, AreaConversion, VolumeConversion, FindConversion, Massage анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основ , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители GCF многочлены, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Экспоненты, Образцы, Упрощение, Упрощение, Методы Правые треугольники, Ветер, рисунокДискриминант — Центр академической поддержки
Что такое дискриминант квадратичной функции и для чего он используется?
Дискриминант квадратичной функции — это значение, определяемое значениями a, b, и c функции.
 Это значение скажет нам, сколько решений будет у квадратичной. Это также позволяет нам проделать некоторую работу по упрощению квадратной формулы, прежде чем мы начнем решать.
Это значение скажет нам, сколько решений будет у квадратичной. Это также позволяет нам проделать некоторую работу по упрощению квадратной формулы, прежде чем мы начнем решать.Наша стандартная формула для квадратичной функции:
y = ax 2 + bx + c
Дискриминант — это то же самое, что и часть квадратной формулы, стоящая под корнем (квадратный корень). Вот общая формула дискриминанта.
b 2 -4 ac
Интерпретация дискриминанта
Дискриминантная формула получается из радикала в квадратной формуле.Наши правила о квадратных корнях гласят, что мы не можем иметь отрицательные числа под корнем, если мы не хотим работать с мнимым числом i . Нам не нужно будет использовать мнимые числа для работы с дискриминантом.
Значение дискриминанта говорит вам, имеет ли квадратичный 2 решения, 1 решение или нет реальных решений.
· Если b 2 — 4 ac упрощается до положительного числа, тогда квадратичная функция имеет 2 решения.

· Если b 2 — 4 ac упрощается до 0, то квадратичная функция имеет 1 решение.
· Если b 2 — 4 ac упрощается до отрицательного числа, то квадратичная функция не имеет действительных решений.
Квадратичная функция, имеющая 2 решения, дважды пересечет ось x .
Квадратичная функция, имеющая 1 решение, будет касаться оси x своей вершиной.
Квадратичная функция, не имеющая реальных решений, не будет пересекать ось x .
Например,
Используйте дискриминант, чтобы определить, сколько решений будет у квадратичной. Затем используйте формулу корней квадратного уравнения, чтобы найти эти решения.
2 x 2 + 5 x + 3 = 0
· Шаг 1. Найдите свои значения для a , b, и c
o Наша общая формула квадратичного уравнения: ax 2 + bx + c = 0.

§ Это означает, что a = 2, b = 5 и c = 3
§ Убедитесь, что одна часть уравнения равна нулю.Обычно это можно сделать путем сложения или вычитания
· Шаг 2. Вставьте свои значения для a , b и c в дискриминантную формулу и упростите результат
o Дискриминантная формула: b 2 — 4 ac
5 2 — 4 (2) (3)
25–24
1
· Шаг 3: Интерпретируйте результаты.
o Если результат положительный, имеем 2 реальных решения
o Если результат равен нулю, мы имеем 1 реальное решение
o Если результат отрицательный, у нас нет реальных решений (2 мнимых решения)
§ Наш результат — 1, что является положительным числом.Это означает, что у нас будет 2 решения.
· Шаг 4. Подставьте значения a, b, и c в формулу корней квадратного уравнения, чтобы найти решения уравнения.

Практические задачи
Воспользуйтесь дискриминантом, чтобы определить, сколько реальных решений будет иметь каждая квадратичная функция, а затем воспользуйтесь формулой корней квадратного уравнения, чтобы найти любые существующие решения.
1. 5 x 2 + 16 x — 84 = 0 2.3 x 2 — 41 x + 110 = 0
3. -2 x 2 + 8 x — 5 = 0 4. 18 x 2 — 45 x — 50 = 0
5. 3 x 2 — 44 x = -96 6.5 x 2 — 47 x = 156
Что дискриминант говорит вам о графике?
Дискриминант показывает и тип и количество решений графа . Если b 2 — 4ac> 0, график имеет два реальных решения. Если b 2 — 4ac = 0, график имеет одно реальное решение.
 Если b 2 — 4ac <0, график имеет два мнимых решения.
Если b 2 — 4ac <0, график имеет два мнимых решения.Щелкните, чтобы увидеть полный ответ
Аналогично, что вам может сказать дискриминант?
Дискриминант сообщает нам следующую информацию о квадратном уравнении: является ли решение действительным или мнимым числом. Если решение рациональное или иррациональное. Если решение — одно уникальное число или два разных числа.
Во-вторых, почему дискриминант важен? Дискриминант квадратного уравнения является важным , потому что он сообщает нам количество и тип решений.Эта информация полезна, потому что она служит двойной проверкой при решении квадратных уравнений любым из четырех методов (факторизация, завершение квадрата, использование квадратных корней и использование формулы квадратного уравнения).
Из этого, как узнать, есть ли у графа отрицательный дискриминант?
Если , дискриминант отрицательный , это означает, что корни квадратичной функции не являются действительными числами.

 2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня.
2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня. Для её облегчения предлагаю вашему вниманию калькуляторы уравнений: квадратное уравнение решение онлайн. Надеюсь, этот калькулятор поможет вам в решении квадратных уравнений. Продавцам оценок без разницы, а вот учителя требуют ещё и определение квадратного уравнения знать. Вот оно на картинке.
Для её облегчения предлагаю вашему вниманию калькуляторы уравнений: квадратное уравнение решение онлайн. Надеюсь, этот калькулятор поможет вам в решении квадратных уравнений. Продавцам оценок без разницы, а вот учителя требуют ещё и определение квадратного уравнения знать. Вот оно на картинке.  У квадратного уравнения есть своя формула, которую вы можете видеть на картинке. Если подходить к написанному на картинке с позиции тупой бюрократической функции, то икс не является корнем квадратного уравнения. Это переменная. Корнями квадратного уравнения являются определенные числовые значения переменной икс. При подстановке корней в квадратное уравнение оно должно превращаться в верное равенство. У квадратного уравнения может быть два корня (разные числа, возведенные в квадрат, могут давать одинаковый результат; знаки плюс и минус делают числа разными), один корень или квадратное уравнение может вообще не иметь корней. Последние уравнения, не имеющие корней, я бы назвал «плохое квадратное уравнение». Правильно составленное квадратное уравнение всегда должно иметь решение. Здесь мы упираемся в очень неудобный и интересный вопрос: откуда берутся квадратные уравнения и зачем они нужны? Уравнения ради решений — это маразм или дрессировка обезьян (воспитание тупых бюрократических функций, пригодных для использования в любых бюрократических системах).
У квадратного уравнения есть своя формула, которую вы можете видеть на картинке. Если подходить к написанному на картинке с позиции тупой бюрократической функции, то икс не является корнем квадратного уравнения. Это переменная. Корнями квадратного уравнения являются определенные числовые значения переменной икс. При подстановке корней в квадратное уравнение оно должно превращаться в верное равенство. У квадратного уравнения может быть два корня (разные числа, возведенные в квадрат, могут давать одинаковый результат; знаки плюс и минус делают числа разными), один корень или квадратное уравнение может вообще не иметь корней. Последние уравнения, не имеющие корней, я бы назвал «плохое квадратное уравнение». Правильно составленное квадратное уравнение всегда должно иметь решение. Здесь мы упираемся в очень неудобный и интересный вопрос: откуда берутся квадратные уравнения и зачем они нужны? Уравнения ради решений — это маразм или дрессировка обезьян (воспитание тупых бюрократических функций, пригодных для использования в любых бюрократических системах). Уравнения как математический инструмент? Тогда где и как этот инструмент применяется? Квадратное уравнение, взятое с потолка (как это обычно делается для учебников), может не иметь решений. Ведь на правильность составления нас уравнения проверять не учат. Тупо пишем квадратное уравнение в учебник, тупо берем из учебника и решаем.
Уравнения как математический инструмент? Тогда где и как этот инструмент применяется? Квадратное уравнение, взятое с потолка (как это обычно делается для учебников), может не иметь решений. Ведь на правильность составления нас уравнения проверять не учат. Тупо пишем квадратное уравнение в учебник, тупо берем из учебника и решаем. — пример подробного решения уравнения на этом калькуляторе вы можете видеть на картинке ниже.
— пример подробного решения уравнения на этом калькуляторе вы можете видеть на картинке ниже.  И.
И. Отметьте пункт, который вызвал наибольшие затруднения 1.Определять вид уравнения
Отметьте пункт, который вызвал наибольшие затруднения 1.Определять вид уравнения

 17)
17) Для многочлена третьей степени — это формула Кардано. Нахождение корней многочлена четвертой степени сводится к нахождению корней многочлена третьей степени методом, принадлежащим Феррари. Для многочленов выше четвертой степени доказано, что их корни нельзя выразить через их коэффициенты с помощью радикалов.
Для многочлена третьей степени — это формула Кардано. Нахождение корней многочлена четвертой степени сводится к нахождению корней многочлена третьей степени методом, принадлежащим Феррари. Для многочленов выше четвертой степени доказано, что их корни нельзя выразить через их коэффициенты с помощью радикалов. Решение уравнений с двумя переменными
Решение уравнений с двумя переменными C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами.
C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами. Которое, обычно, обозначается буквой «х» . Решить уравнение — это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное тождество. Напомню, что тождество – это выражение, которое не вызывает сомнения даже у человека, абсолютно не отягощенного математическими знаниями. Типа 2=2, 0=0, ab=ab и т.д. Так как решать уравнения? Давайте разберёмся.
Которое, обычно, обозначается буквой «х» . Решить уравнение — это найти такие значения икса, которые при подстановке в исходное выражение, дадут нам верное тождество. Напомню, что тождество – это выражение, которое не вызывает сомнения даже у человека, абсолютно не отягощенного математическими знаниями. Типа 2=2, 0=0, ab=ab и т.д. Так как решать уравнения? Давайте разберёмся. ) Просто для них существуют свои специальные приёмы и методы.
) Просто для них существуют свои специальные приёмы и методы.
 В уравнениях низачем. Переносите, ради бога. Только знак не забывайте менять. А вот в неравенствах привычка к переносу может и в тупик поставить….
В уравнениях низачем. Переносите, ради бога. Только знак не забывайте менять. А вот в неравенствах привычка к переносу может и в тупик поставить…. Основные проблемы.
Основные проблемы. Слева — привести подобные, справа — посчитать. Сразу получается ответ:
Слева — привести подобные, справа — посчитать. Сразу получается ответ: Безусловно, необходимость применения калькулятора в бизнесе или трудовой деятельности определяется прежде всего видом самой деятельности. Если бизнес и профессия связаны с постоянными расчётами и вычислениями, то стоит опробовать электронный калькулятор и оценить степень его полезности для конкретного дела.
Безусловно, необходимость применения калькулятора в бизнесе или трудовой деятельности определяется прежде всего видом самой деятельности. Если бизнес и профессия связаны с постоянными расчётами и вычислениями, то стоит опробовать электронный калькулятор и оценить степень его полезности для конкретного дела. Чтобы построить график в онлайн калькуляторе, достаточно записать функцию: plot(tan(x)),x=-360..360 .
Чтобы построить график в онлайн калькуляторе, достаточно записать функцию: plot(tan(x)),x=-360..360 .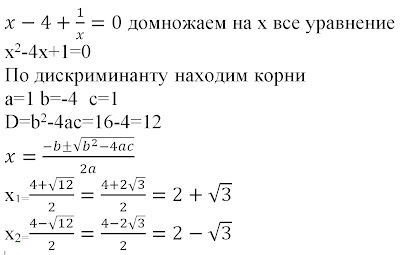
 Заполните необходимые поля и нажмите клавишу «I» (на рисунке выделена красным цветом), чтобы увидеть дисплей в полный размер.
Заполните необходимые поля и нажмите клавишу «I» (на рисунке выделена красным цветом), чтобы увидеть дисплей в полный размер. Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).
Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).  Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1
Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1 Умение решать их совершенно необходимо.
Умение решать их совершенно необходимо. А именно:
А именно:

 Например:
Например: Вывод:
Вывод:


 Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).
Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).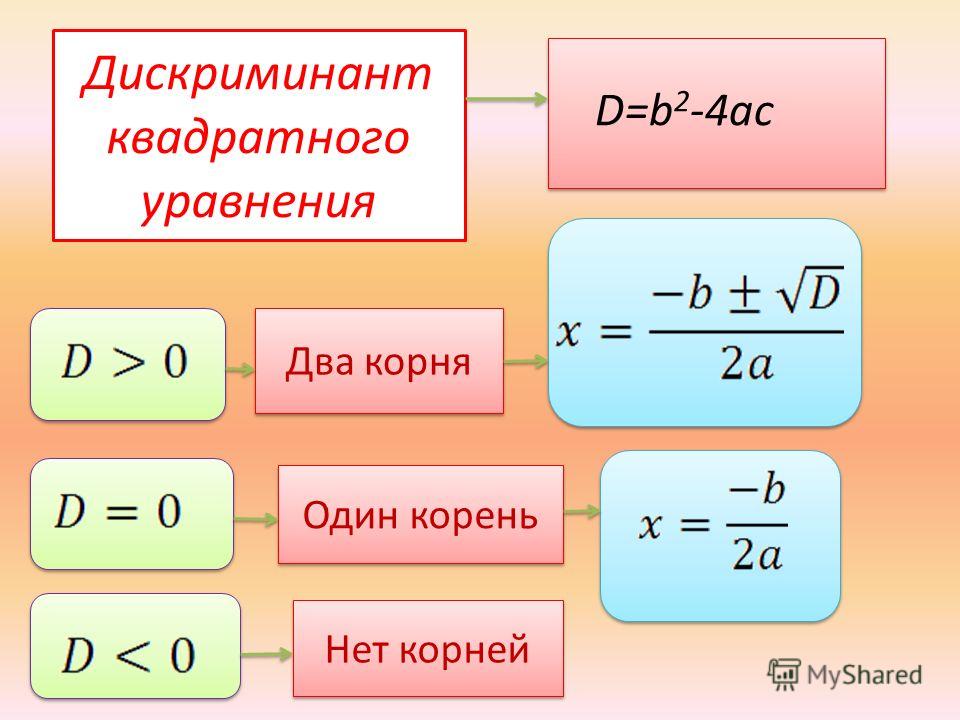






 Взгляните на примеры — и сами все поймете:
Взгляните на примеры — и сами все поймете: Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много. \\ \end{align}\]
\\ \end{align}\] е. коэффициент при переменной x или свободный элемент равен нулю.
е. коэффициент при переменной x или свободный элемент равен нулю. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
 Если положительно, то корней будет два: √(–c/a) и –√(–c/a). Пример решения подобного уравнения:
Если положительно, то корней будет два: √(–c/a) и –√(–c/a). Пример решения подобного уравнения:



 Выделение полного квадрата. Формулы корней квадратного уравнения.
Выделение полного квадрата. Формулы корней квадратного уравнения. 2 — 4*a*c. Значение D может быть больше, меньше или равно нулю. Если D больше или меньше нуля, то корня будет два, если D=0, то остается всего один корень, более точно можно сказать, что D в этом случае имеет два равнозначных корня. Подставьте известные коэффициенты a, b, c в формулу и вычислите значение.
2 — 4*a*c. Значение D может быть больше, меньше или равно нулю. Если D больше или меньше нуля, то корня будет два, если D=0, то остается всего один корень, более точно можно сказать, что D в этом случае имеет два равнозначных корня. Подставьте известные коэффициенты a, b, c в формулу и вычислите значение. После этого преобразования, решение уравнения сводится к такому же нахождению корней, как было описано выше.
После этого преобразования, решение уравнения сводится к такому же нахождению корней, как было описано выше. 2 или x ничего не стоит, то коэффициенты а и b равны 1.
2 или x ничего не стоит, то коэффициенты а и b равны 1. В случае, если она равна 2, то подобное уравнение как раз и называется квадратным.
В случае, если она равна 2, то подобное уравнение как раз и называется квадратным. Указанное продиктовано одним из свойств умножения. Правило гласит, что произведение двух множителей даёт в результате 0, только если один из них равен нулю.
Указанное продиктовано одним из свойств умножения. Правило гласит, что произведение двух множителей даёт в результате 0, только если один из них равен нулю. Для начала преобразуем выражение и разложим его на множители. Их получается два: (x-8) и (x-25) = 0. В результате имеем два корня 8 и 25.
Для начала преобразуем выражение и разложим его на множители. Их получается два: (x-8) и (x-25) = 0. В результате имеем два корня 8 и 25. В последнем случае решений вообще не существует, так как указанные выше действия невозможно производить с корнями. Примеры решений квадратных уравнений такого типа необходимо рассмотреть.
В последнем случае решений вообще не существует, так как указанные выше действия невозможно производить с корнями. Примеры решений квадратных уравнений такого типа необходимо рассмотреть. Это значит, что х(х+16) = 612.
Это значит, что х(х+16) = 612. Это говорит о том, что ответ у нашей задачи существует. Если знать, к , решение квадратных уравнений нужно продолжать с применением ниже приведённой формулы. Она позволяет вычислить корни.
Это говорит о том, что ответ у нашей задачи существует. Если знать, к , решение квадратных уравнений нужно продолжать с применением ниже приведённой формулы. Она позволяет вычислить корни. Вычислим их согласно приведённой выше формуле, а это значит, что первый из них буде равен 4/3, а второй 1.
Вычислим их согласно приведённой выше формуле, а это значит, что первый из них буде равен 4/3, а второй 1. Портрет его можно увидеть в статье.
Портрет его можно увидеть в статье.
 То есть если получить наглядное изображение квадратичной функции нелегко, можно приравнять правую часть выражения к 0 и решить полученное уравнение. А зная точки пересечения с осью 0x, легче построить график.
То есть если получить наглядное изображение квадратичной функции нелегко, можно приравнять правую часть выражения к 0 и решить полученное уравнение. А зная точки пересечения с осью 0x, легче построить график.

 Однако неполные уравнения квадратные в 8 классе школы уже встречаются, и изучаться они начинают раньше, чем полные равенства этого типа, для которых уже приводится формула с дискриминантом. Кроме того, рассматриваемый вид равенств является достаточно простым, чтобы применять к ним универсальные формулы и производить ряд ненужных вычислений.
Однако неполные уравнения квадратные в 8 классе школы уже встречаются, и изучаться они начинают раньше, чем полные равенства этого типа, для которых уже приводится формула с дискриминантом. Кроме того, рассматриваемый вид равенств является достаточно простым, чтобы применять к ним универсальные формулы и производить ряд ненужных вычислений.
 Знак второго корня определяется отношением ненулевых коэффициентов b/a.
Знак второго корня определяется отношением ненулевых коэффициентов b/a.
 Тогда мы приходим к уравнению: 97,6 = 9,6*t 2 /2. Откуда получаем, что t = 4,51 секунды (отрицательный корень был сознательно отброшен).
Тогда мы приходим к уравнению: 97,6 = 9,6*t 2 /2. Откуда получаем, что t = 4,51 секунды (отрицательный корень был сознательно отброшен). Он представлен как b²-4ac, а дискриминант может быть нулевым, положительным или отрицательным. Это указывает на то, не будет ли решения, одного решения или двух решений.
Он представлен как b²-4ac, а дискриминант может быть нулевым, положительным или отрицательным. Это указывает на то, не будет ли решения, одного решения или двух решений. Однако можно использовать и мнимые числа. Тогда у вас будет два сложных решения: одно путем сложения мнимого квадратного корня, а другое — путем его вычитания.2-4ac> 0 \ as \ a \ perfect \ square \ as \ well $$
Однако можно использовать и мнимые числа. Тогда у вас будет два сложных решения: одно путем сложения мнимого квадратного корня, а другое — путем его вычитания.2-4ac> 0 \ as \ a \ perfect \ square \ as \ well $$  Дискриминант также может рассказать нам о поведении графика квадратичной функции. Часто задаваемые вопросы
Дискриминант также может рассказать нам о поведении графика квадратичной функции. Часто задаваемые вопросы  Вершинная форма квадратного уравнения представлена как y = a (x + b) ² + c.
Вершинная форма квадратного уравнения представлена как y = a (x + b) ² + c. Подставляем значения. Следовательно, дискриминант равен 76.
Подставляем значения. Следовательно, дискриминант равен 76.

 е. вы, вероятно, разговариваете по мобильному телефону). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, разговариваете по мобильному телефону). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. Вот общий набор рекомендаций, которые может помочь при определении того, какой метод использовать.
Вот общий набор рекомендаций, которые может помочь при определении того, какой метод использовать.
 2} + bx + c = 0 \]
2} + bx + c = 0 \] 2} — 4ac = 0 \).2} — 4 \ left ({49} \ right) \ left ({81} \ right) = 0 \]
2} — 4ac = 0 \).2} — 4 \ left ({49} \ right) \ left ({81} \ right) = 0 \]
 Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно.
Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. ..Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, AreaConversion, VolumeConversion, FindConversion, Massage анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основ , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители GCF многочлены, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Экспоненты, Образцы, Упрощение, Упрощение, Методы Правые треугольники, Ветер, рисунок
..Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, AreaConversion, VolumeConversion, FindConversion, Massage анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основ , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители GCF многочлены, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Экспоненты, Образцы, Упрощение, Упрощение, Методы Правые треугольники, Ветер, рисунок Это значение скажет нам, сколько решений будет у квадратичной. Это также позволяет нам проделать некоторую работу по упрощению квадратной формулы, прежде чем мы начнем решать.
Это значение скажет нам, сколько решений будет у квадратичной. Это также позволяет нам проделать некоторую работу по упрощению квадратной формулы, прежде чем мы начнем решать.


 Если b 2 — 4ac <0, график имеет два мнимых решения.
Если b 2 — 4ac <0, график имеет два мнимых решения.