Функциональное уравнение — Википедия
Функциональное уравнение — уравнение, выражающее связь между значением функции в одной точке с её значениями в других точках. Многие свойства функций можно определить, исследуя функциональные уравнения, которым эти функции удовлетворяют. Термин «функциональное уравнение» обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них.
Функциональному уравнению:
- f(s)=2sπs−1sin(πs2)Γ(1−s)f(1−s){\displaystyle f(s)=2^{s}\pi ^{s-1}\sin \left({\frac {\pi s}{2}}\right)\Gamma (1-s)f(1-s)},
где Γ(z){\displaystyle \Gamma (z)} — гамма-функция Эйлера, удовлетворяет дзета-функция Римана ζ{\displaystyle \zeta }.
Гамма-функция является единственным решением этой системы трёх уравнений:
- f(x)=f(x+1)x{\displaystyle f(x)={f(x+1) \over x}}
- f(y)f(y+12)=π22y−1f(2y){\displaystyle f(y)f\left(y+{\frac {1}{2}}\right)={\frac {\sqrt {\pi }}{2^{2y-1}}}f(2y)}
- f(z)f(1−z)=πsin(πz){\displaystyle f(z)f(1-z)={\pi \over \sin(\pi z)}} (формула дополнения Эйлера)
Функциональное уравнение:
- f(az+bcz+d)=(cz+d)kf(z){\displaystyle f\left({az+b \over cz+d}\right)=(cz+d)^{k}f(z)},
где a,b,c,d{\displaystyle a,b,c,d} являются целыми числами, удовлетворяющими равенству ad−bc=1{\displaystyle ad-bc=1}, то есть:
- |abcd|=1{\displaystyle {\begin{vmatrix}a&b\\c&d\end{vmatrix}}\,=1},
определяет f{\displaystyle f} как модулярную форму порядка k{\displaystyle k}.
Функциональные уравнения Коши:
Функциональные уравнения Коши приводятся друг к другу. Так, уравнение f(x1x2)=f(x1)f(x2){\displaystyle f(x_{1}x_{2})=f(x_{1})f(x_{2})} приводится к уравнению g(y1+y2)=g(y1)+g(y2){\displaystyle g(y_{1}+y_{2})=g(y_{1})+g(y_{2})} после замены g(y)=log|f(expy)|{\displaystyle g(y)=\log \left|f(\exp y)\right|} (для этого, естественно, нужно, чтобы f(x){\displaystyle f(x)} не была тождественным нулём). В классе непрерывных функций и в классе монотонных функций приведённые решения — единственные, если не считать вырожденное решение f(x)≡0{\displaystyle f(x)\equiv 0}. Однако в более широких классах функций возможны весьма экзотические решения, см. статью «Базис Гамеля».
Другие:
- f(x+y)+f(x−y)=2[f(x)+f(y)]{\displaystyle f(x+y)+f(x-y)=2[f(x)+f(y)]} — квадратичное уравнение или тождество параллелограмма, удовлетворяет f(x)=kx2{\displaystyle f(x)=kx^{2}},
- f(x+y2)=f(x)+f(y)2{\displaystyle f\left({\frac {x+y}{2}}\right)={\frac {f(x)+f(y)}{2}}} — уравнение Йенсена, удовлетворяют все линейные функции f(x)=ax+b{\displaystyle f(x)=ax+b},
- f(x+y)f(x−y)=f(x)2{\displaystyle f(x+y)f(x-y)=f(x)^{2}} — уравнение Лобачевского (версия уравнения Йенсена), удовлетворяет f(x)=acx{\displaystyle f(x)=ac^{x}},
- f(x+y)+f(x−y)=2[f(x)f(y)]{\displaystyle f(x+y)+f(x-y)=2[f(x)f(y)]} — уравнение Даламбера,
- f(h(x))=f(x)+1{\displaystyle f(h(x))=f(x)+1} — уравнение Абеля[en],
- f(h(x))=cf(x){\displaystyle f(h(x))=cf(x)} — уравнение Шрёдера[en], решением является функция Кёнигса, связанная с функцией h(x){\displaystyle \textstyle h(x)}.
Частным видом функциональных уравнений является рекуррентное соотношение, содержащее неизвестную функцию от целых чисел и оператор сдвига.
Линейные рекуррентные соотношения:
- a(n)=∑i=1,kci⋅a(n−i){\displaystyle a(n)=\sum _{i=1,k}c_{i}\cdot a(n-i)}
(где c1,c2,…,ck{\displaystyle c_{1},c_{2},\dots ,c_{k}} — константы, не зависящие от n{\displaystyle n}) имеют теорию, аналогом которой является теория линейных дифференциальных уравнений. Например, для линейного рекуррентного соотношения:
- a(n)=3a(n−1)+4a(n−2){\displaystyle a(n)=3a(n-1)+4a(n-2)},
достаточно найти два линейно независимых решения, все остальные решения будут их линейными комбинациями.
Чтобы найти эти решения, надо подставить в рекуррентное соотношение пробную функцию a(n)=λn{\displaystyle a(n)=\lambda ^{n}} с неопределённым параметром λ{\displaystyle \lambda } и попробовать найти те λ{\displaystyle \lambda }, при которых будет удовлетворяться данное рекуррентное соотношение. Для приведённого примера получим квадратное уравнение λ2=3λ+4{\displaystyle \lambda ^{2}=3\lambda +4} с двумя различными корнями λ=−1{\displaystyle \lambda =-1} и λ=4;{\displaystyle \lambda =4;} поэтому общим решением для данного рекуррентного соотношения будет формула a(n)=d14n+d2(−1)n{\displaystyle a(n)=d_{1}4^{n}+d_{2}(-1)^{n}} (константы d1{\displaystyle d_{1}} и d2{\displaystyle d_{2}} подбираются так, чтобы при n=1{\displaystyle n=1} и n=2{\displaystyle n=2} формула давала нужные значения для величин a(1){\displaystyle a(1)} и a(2){\displaystyle a(2)}). В случае кратных корней многочлена дополнительными пробными решениями служат функции nλn,{\displaystyle n\lambda ^{n},} n2λn{\displaystyle n^{2}\lambda ^{n}} и так далее.
Одним из широко известных рекуррентных соотношений является a(n)=a(n−1)+a(n−2){\displaystyle a(n)=a(n-1)+a(n-2)}, определяющее последовательность Фибоначчи.
Существуют некоторые общие методы решения функциональных уравнений.
В частности, полезным может оказаться применение понятия об инволюции, то есть, использование свойств функций, для которых f(f(x))=x{\displaystyle f(f(x))=x}; простейшие инволюции:
- f(x)=−x{\displaystyle f(x)=-x}, f(x)=1x{\displaystyle f(x)={\frac {1}{x}}}, f(x)=11−x+1{\displaystyle f(x)={\frac {1}{1-x}}+1}, f(x)=1−x{\displaystyle f(x)=1-x}.
Например, для решения уравнения:
- f2(x+y)=f2(x)+f2(y){\displaystyle f^{2}(x+y)=f^{2}(x)+f^{2}(y)}
для всех x,y∈R{\displaystyle x,y\in \mathbb {R} } и f:R→R{\displaystyle f:\mathbb {R} \to R}, положим x=y=0{\displaystyle x=y=0}: f2(0)=f2(0)+f2(0){\displaystyle f^{2}(0)=f^{2}(0)+f^{2}(0)}. Тогда f2(0)=0{\displaystyle f^{2}(0)=0} и f(0)=0{\displaystyle f(0)=0}. Далее, положив y=−x{\displaystyle y=-x}:
- f2(x−x)=f2(x)+f2(−x){\displaystyle f^{2}(x-x)=f^{2}(x)+f^{2}(-x)}
- f2(0)=f2(x)+f2(−x){\displaystyle f^{2}(0)=f^{2}(x)+f^{2}(-x)}
- 0=f2(x)+f2(−x){\displaystyle 0=f^{2}(x)+f^{2}(-x)}
Квадрат вещественного числа неотрицателен, и сумма неотрицательных чисел равна нулю тогда и только тогда когда оба числа равны 0. Значит f2(x)=0{\displaystyle f^{2}(x)=0} для всех x{\displaystyle x} и f(x)≡0{\displaystyle f(x)\equiv 0} является единственным решением этого уравнения.
- Головинский И. А. Ранняя история аналитических итераций и функциональных уравнений. // Историко-математические исследования. М.: Наука, вып. XXV, 1980, с. 25-51.
- Kuczma M. On the functional equation φn(x) = g(x). Ann. Polon. Math. 11 (1961) 161—175.
- Kuczma M. An introduction to the theory of functional equations and inequalities. Warszawa — Kraków — Katowice: Polish Scientific Publishers & Silesian University, 1985.
- Лихтарников Л. М. Элементарное введение в функциональные уравнения. СПб.: Лань, 1997.
Функциональные уравнения
Мы с наслаждением познаем математику… Она восхищает нас, как цветок лотоса.
К числу наиболее сложных задач школьной математики относятся задачи, связанные с решением функциональных уравнений. В настоящей статье приводятся определение и методы решения таких уравнений, а также рассматриваются примеры решения соответствующих задач.
Основные понятия и свойства
Функциональные уравнения являются уравнениями повышенной сложности и записываются в общем виде следующим образом:
(1)
и
, (2)
где . При решении функциональных уравнений (1) и (2), как правило, необходимо использовать следующие теоремы.
Теорема 1. Если функция возрастает на отрезке , то на этом отрезке уравнение (1) будет равносильно уравнению .
Теорема 2. Если функция убывает на отрезке и при этом нечетное, то на этом отрезке уравнение (1) будет равносильно уравнению .
Отметим, что в этом случае функциональное уравнение (1) будет иметь не более одного корня. Это утверждение вытекает из того факта, что уравнение (1) равносильно уравнению , левая часть которой представляет собой возрастающую функцию, а правая часть – убывающую функцию. Известно, что в таком случае, если уравнение имеет корень, то этот корень будет единственным.
Необходимо заметить, если функция на отрезке убывает и при этом четное число, то в таком случае для решения уравнений вида (1) необходимо привлекать другие методы
Теорема 3. Если функция возрастает (или убывает) на всей области определения переменной в уравнении (2), то уравнение будет равносильно уравнению .
Доказательство приведенных выше теорем приводится во втором учебном пособии из списка рекомендованной литературы.
Решение функциональных уравнений
Пример 1. Решить уравнение . (3)
Решение. Из уравнения (3) следует, что . Введем в рассмотрение функцию . Тогда уравнение (3) принимает вид функционального уравнения . Поскольку функция на области определения является возрастающей, то согласно теореме 1 уравнение (3) будет равносильно уравнению . Решая квадратное уравнение , получаем . Следовательно, уравнение (3) имеет корень .
Ответ: .
Пример 2. Решить уравнение . (4)
Решение. Поскольку областью допустимых значений переменной в уравнении (4) являются , то из данного уравнения получаем функциональное уравнение
. (5)
Так как функция является возрастающей на области определения, то уравнение (5) равносильно уравнениям или . Решая уравнение , получаем и .
Ответ: , .
Пример 3. Решить уравнение . (6)
Решение. Перепишем уравнение (6) в виде функционального уравнения . Так как функция возрастает на всей числовой оси , то уравнение будет равносильно уравнениям или .
Первый корень уравнения легко найти подбором. Этим корнем является .
Так как , то для поиска остальных корней уравнения (6) рассмотрим квадратное уравнение . Отсюда получаем и .
Ответ: , , .
При решении следующего функционального уравнения нельзя использовать теорему 2, поэтому здесь применяется другой метод.
Пример 4. Решить уравнение . (7)
Решение. Если обозначить , то из уравнения (7) получим систему уравнений
(8)
Отсюда следует, что и . Если оба уравнения системы (8) возвести в квадрат, а затем из первого уравнения вычесть второе, то получим .
Рассмотрим два случая.
1. Пусть , тогда или . Квадратное уравнение имеет единственный положительный корень .
2. Пусть . Тогда , где . После возведения в квадрат обеих частей данного уравнения получаем уравнение , корнями которого являются и .
Ответ: , , .
Пример 5. Решить уравнение . (9)
Решение. Уравнение (9) равносильно функциональному уравнению
. (10)
Так как функция является возрастающей на всей числовой оси , то уравнение (10) равносильно уравнению . Первый корень уравнения находим подбором, т.е. .
Поскольку и , то уравнение (9) других корней не имеет.
Ответ: .
Пример 6. Решить систему уравнений (11)
Решение. Введем в рассмотрение функцию . В таком случае из системы (11) получаем совокупность двух уравнений и , т.е. здесь имеем функциональное уравнение .
Так как для функции выполняется условие теоремы 1, то уравнение равносильно уравнению , т.е. для решения заданной системы уравнений необходимо рассмотреть уравнения или , где .Корень уравнения находим подбором. Так как и , то является единственным корнем кубического уравнения. Так как и , то .
Поскольку система уравнений (11) является симметрической (относительно вхождения переменных и ) и найденный корень является единственным, то .
Ответ: , .
Пример 7. Решить систему уравнений
(12)
Решение. Введем в рассмотрение функцию , где . В таком случае система уравнений (12) принимает вид
Из данной системы уравнений вытекает функциональное уравнение вида . Так как функция является убывающей и выполняется условие теоремы 2, то уравнение равносильно уравнению , т.е. или .
Так как функция возрастает на области определения, то уравнение имеет не более одного корня. Этот единственный корень нетрудно найти подбором.
Однако в систему уравнений (12) все переменные входят симметрично и известно, что является единственным корнем этой системы уравнений,
поэтому и .
Ответ: , , .
Пример 8. Решить уравнение . (13)
Решение. Так как уравнение (13) равносильно уравнению , (14)
то положим и представим уравнение (14) в виде функционального уравнения (2), в котором , и .
Поскольку функция является возрастающей на положительной полуоси , то при решении уравнения можно воспользоваться теоремой 3. Согласно этой теореме уравнение (2) равносильно уравнению , т.е. решение уравнения (14) сводится к решению уравнения . Отсюда получаем .
Ответ: .
Пример 9. Решить систему уравнений (15)
Решение. Первое уравнение системы (15) принимает вид функционального уравнения . Так как функция всегда является возрастающей, то из уравнения получаем . В таком случае из второго уравнения системы (15) следует .
Ответ: , , , .
Для более глубокого изучения методов решения задач, связанных с решением функциональных уравнений, можно использовать учебные пособия из списка рекомендуемой литературы.
Рекомендуемая литература
1. Супрун В.П. Математика для старшеклассников: задачи повышенной сложности. – М.: КД «Либроком» / URSS, 2017. – 200 с.
2. Супрун В.П. Математика для старшеклассников: нестандартные методы решения задач. – М.: КД «Либроком» / URSS, 2017. – 296 с.
Остались вопросы?
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Функциональное уравнение Коши — Википедия
Функциональное уравнение Коши для функции f:R→R{\displaystyle f:\mathbb {R} \to \mathbb {R} } имеет вид
- f(x+y)=f(x)+f(y){\displaystyle f(x+y)=f(x)+f(y)}.
Функцию, удовлетворяющую этому уравнению, называют аддитивной. Этот термин применяется для произвольных функций, не только над R{\displaystyle \mathbb {R} }.
Уравнение Коши является одним из старейших и наиболее простых функциональных уравнений, однако его решение в вещественных числах является достаточно сложным. В рациональных числах может быть доказано с использованием элементарной математики, что существует единственное семейство решений вида f(x)=cx{\displaystyle f(x)=cx}, где c — произвольная константа. Это семейство решений является одним из решений и на множестве вещественных чисел. Дополнительные ограничения, накладываемые на f{\displaystyle f}, могут исключать возможность существования других решений. Например, линейные функции f(x)=cx{\displaystyle f(x)=cx} оказываются единственно возможными решениями, если:
С другой стороны, если нет никаких дополнительных ограничений на f{\displaystyle f}, то существует бесконечно много других функций, которые удовлетворяют уравнению (см. статью «Базис Гамеля»). Это было доказано в 1905 году Георгом Гамелем с использованием базиса Гамеля, а значит и аксиомы выбора. Обобщение Третьей проблемы Гильберта на случай многомерных пространств использует это уравнение.
Другие формы функционального уравнения Коши[править | править код]
Следующие функциональные уравнения эквивалентны аддитивному уравнению Коши f(x+y)=f(x)+f(y){\displaystyle f\left(x+y\right)=f\left(x\right)+f\left(y\right)}:
Вырожденным решением этих уравнений является функция f(x)=0{\displaystyle f\left(x\right)=0}.
Докажем, что за знак функции можно выносить рациональные числа. Возьмём n∈N{\displaystyle n\in \mathbb {N} }:
- f(nx)=f(x+x+⋯+x)=f(x)+f(x)+⋯+f(x)=nf(x){\displaystyle f(nx)=f(x+x+\cdots +x)=f(x)+f(x)+\cdots +f(x)=nf(x)},
- f(xn)=nf(x/n)n=f(x)n{\displaystyle f\left({\frac {x}{n}}\right)={\frac {nf(x/n)}{n}}={\frac {f(x)}{n}}}.
Теперь положим x=y=0{\displaystyle x=y=0} и y=−x{\displaystyle y=-x}:
- f(0)=f(0)+f(0)⇒f(0)=0{\displaystyle f(0)=f(0)+f(0)\Rightarrow f(0)=0},
- f(0)=f(x)+f(−x)⇒f(−x)=−f(x){\displaystyle f(0)=f(x)+f(-x)\Rightarrow f(-x)=-f(x)}.
Собрав всё вместе, получим:
- ∀a∈Q,x∈R:f(ax)=af(x){\displaystyle \forall a\in \mathbb {Q} ,x\in \mathbb {R} :f(ax)=af(x)}.
Положив x=1{\displaystyle x=1} и обозначив c=f(1){\displaystyle c=f\left(1\right)}, мы имеем единственное семейство решений f(x)=cx{\displaystyle f(x)=cx} над Q{\displaystyle \mathbb {Q} }.
Доказательство существования нелинейных решений не конструктивно и основано на аксиоме выбора. С её помощью доказывается существование базиса Гамеля в любом векторном пространстве, в том числе бесконечномерном.
Рассмотрим R{\displaystyle \mathbb {R} } как векторное пространство над полем Q{\displaystyle \mathbb {Q} }: в нём есть базис Гамеля. Возьмём коэффициент перед некоторым базисным вектором α{\displaystyle \alpha } в разложении числа x{\displaystyle x} по базису — это и будет значение f(x){\displaystyle f(x)}. Полученная функция принимает рациональные значения (как коэффициент при разложении над Q{\displaystyle \mathbb {Q} }) и не равна тождественно нулю (f(α)=1{\displaystyle f(\alpha )=1}), а потому не может быть линейна. Нетрудно понять, что она аддитивна, то есть удовлетворяет уравнению Коши.
В общем случае пусть {rα}{\displaystyle \{r_{\alpha }\}} — базис Гамеля множества действительных чисел R{\displaystyle \mathbb {R} } над полем рациональных чисел Q{\displaystyle \mathbb {Q} }. Тогда для каждого вещественного x{\displaystyle x} существует разложение по базису Гамеля x=kα1rα1+⋯+kαnrαn{\displaystyle x=k_{\alpha _{1}}r_{\alpha _{1}}+\cdots +k_{\alpha _{n}}r_{\alpha _{n}}} (где ki∈Q{\displaystyle k_{i}\in \mathbb {Q} }), причём такое разложение единственно с точностью до порядка членов разложения и членов с нулевыми множителями. Для аддитивной функции f(x){\displaystyle f(x)} должно быть выполнено условие f(x)=kα1fα1+⋯+kαnfαn{\displaystyle f(x)=k_{\alpha _{1}}f_{\alpha _{1}}+\cdots +k_{\alpha _{n}}f_{\alpha _{n}}}, где fαn=f(rαn){\displaystyle f_{\alpha _{n}}=f(r_{\alpha _{n}})} будут фиксированными вещественными числами (за знак аддитивной функции можно выносить рациональные множители, см. предыдущий раздел). Очевидно, что функция f(x){\displaystyle f(x)}, заданная с помощью этого соотношения, при любом выборе вспомогательных чисел fαn{\displaystyle f_{\alpha _{n}}} удовлетворяет аддитивному уравнению Коши f(x+y)=f(x)+f(y){\displaystyle f(x+y)=f(x)+f(y)}. Однако только в том случае, когда fαn≡c⋅rαn{\displaystyle f_{\alpha _{n}}\equiv c\cdot r_{\alpha _{n}}}, где c{\displaystyle c} это произвольное вещественное число, рассматриваемая функция оказывается линейной функцией.
Сейчас мы докажем, что всякое нелинейное решение должно быть достаточно необычной функцией — его график y=f(x){\displaystyle y=f(x)} должен быть всюду плотен в R2{\displaystyle \mathbb {R} ^{2}}. Это означает, что любой, сколь угодно малый круг на плоскости содержит по крайней мере одну точку этого графика. Из этого легко выводятся другие свойства, такие как разрывность в любой точке, немонотонность и неограниченность на любом интервале.
Мы можем, поделив функцию на c=f(1){\displaystyle c=f(1)}, считать, что ∀a∈Q:f(a)=a{\displaystyle \forall a\in \mathbb {Q} :f(a)=a}. (Если f(1)=0{\displaystyle f(1)=0}, то ∀a∈Q:f(a)=0{\displaystyle \forall a\in \mathbb {Q} :f(a)=0}, и рассуждения, приводимые ниже, сохраняют свою силу с минимальными изменениями, если предположить, что найдётся точка α∈R{\displaystyle \alpha \in \mathbb {R} }, для которой f(α)≠0{\displaystyle f(\alpha )\neq 0}.) Если функция f(x){\displaystyle f(x)} не линейна, то f(α)≠α{\displaystyle f(\alpha )\neq \alpha } для некоторого α∈R{\displaystyle \alpha \in \mathbb {R} }: положим f(α)=α+δ,δ≠0{\displaystyle f(\alpha )=\alpha +\delta ,\delta \neq 0}. Покажем теперь, как найти точку графика в произвольном круге с центром в точке (x,y){\displaystyle (x,y)}, радиуса r{\displaystyle r}, где x,y,r∈Q,r>0,x≠y{\displaystyle x,y,r\in \mathbb {Q} ,r>0,x\neq y}. Ясно, что этого достаточно для плотности графика y=f(x){\displaystyle y=f(x)} всюду в R2{\displaystyle \mathbb {R} ^{2}}.
Положим β=y−xδ{\displaystyle \beta ={\frac {y-x}{\delta }}} и выберем рациональное число b≠0{\displaystyle b\neq 0}, близкое к β{\displaystyle \beta }, таким образом, чтобы:
- |β−b|<r3|δ|{\displaystyle \left|\beta -b\right|<{\frac {r}{3\left|\delta \right|}}}
Затем выберем рациональное число a{\displaystyle a}, близкое к α{\displaystyle \alpha }, так, чтобы:
- |α−a|<r3|b|{\displaystyle \left|\alpha -a\right|<{\frac {r}{3\left|b\right|}}}
Теперь возьмем X=x+b(α−a){\displaystyle X=x+b(\alpha -a)} и, используя функциональное уравнение, получим:
- Y=f(X)=f(x+b(α−a)){\displaystyle Y=f(X)=f(x+b(\alpha -a))}
- =x+bf(α)−bf(a){\displaystyle =x+bf(\alpha )-bf(a)}
- =y−δβ+bf(α)−bf(a){\displaystyle =y-\delta \beta +bf(\alpha )-bf(a)}
- =y−δβ+b(α+δ)−ba{\displaystyle =y-\delta \beta +b(\alpha +\delta )-ba}
- =y+b(α−a)−δ(β−b){\displaystyle =y+b(\alpha -a)-\delta (\beta -b)}
Но тогда (Y−y)2+(X−x)2=(b(α−a)−δ(β−b))2+(b(α−a))2⩽(r3+r3)2+(r3)2<r2{\displaystyle (Y-y)^{2}+(X-x)^{2}=(b(\alpha -a)-\delta (\beta -b))^{2}+(b(\alpha -a))^{2}\leqslant \left({\frac {r}{3}}+{\frac {r}{3}}\right)^{2}+\left({\frac {r}{3}}\right)^{2}<r^{2}}, то есть точка (X,Y){\displaystyle (X,Y)} оказалась внутри круга.
Также можно показать[1], что когда аддитивная функция f(x){\displaystyle f(x)} не является линейной, она будет разрывной в любой точке вещественной оси, а также не сохраняет знак, не ограничена ни сверху, ни снизу, не монотонна, не интегрируема и не измерима на любом сколь угодно малом интервале, заполняя, в соответствии с доказанным выше утверждением о плотности графика y=f(x){\displaystyle y=f(x)} всюду на плоскости R2{\displaystyle \mathbb {R} ^{2}}, на любом сколь угодно малом интервале своими значениями всю числовую ось (−∞,+∞){\displaystyle \left(-\infty ,+\infty \right)} плотным образом.
Функциональные уравнения
Общепризнано, что решение задач является важнейшим средством формирования у школьников системы основных математических знаний, умений и навыков, ведущей формой учебной деятельности учащихся в процессе учения математики, является одним из основных средств их математического развития.
Ориентируя школьников на поиски красивых, изящных решений математических задач, учитель тем самым способствует эстетическому воспитанию учащихся и повышению их математической культуры. И всё же главная цель задач — развить творческое и математическое мышление учащихся, заинтересовать их математикой, привести к “открытию” математических фактов.
Достичь этой цели с помощью одних стандартных задач невозможно. Необходимы задачи, направленные на воспитание у учащихся устойчивого интереса к изучению математики, творческого отношения к учебной деятельности математического характера. Необходимы специальные упражнения для обучения школьников способам самостоятельной деятельности, для овладения ими методами научного познания реальной действительности и приемами умственной деятельности, которыми пользуются ученые-математики, решая ту или иную задачу.
В данной статье речь идет о функциональных уравнениях, о методах их решения. Функциональным уравнением называется соотношение, выражающее определённое свойство, которым обладает некоторый класс функций (некоторая функция).
Простейшими примерами функциональных уравнений могут служить : f(x) =f(- x) – уравнение чётности, f(x+Т) = f(x) – уравнение периодичности и др.
Функция f(x) называется решением данного функционального уравнения, если она удовлетворяет ему при всех значениях аргумента в области её определения.
Например, функции f(x) = ax2,f(x)=sin2x, где aR, являются частными решениями приведённых соответственно выше уравнений, в чём убедимся подстановкой ах2= а (-х)2.
Решить функциональное уравнение – значит установить, имеет ли оно решения, и найти их, если они имеются.
Приведем примеры решения функциональных уравнений методом подстановки. Этот метод заключается в том, что, применяя вместо х (или у) различные подстановки и комбинируя полученные уравнения с исходным, получаем (обычно путём исключения) алгебраическое уравнение относительно искомой функции.
Пример 1.
1) Пусть
2) Подставим в исходное уравнение, получим
3)Заменим z на получим или после преобразований в правой части уравнения:
4)Итак, получили два уравнения:
5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением, получим:
Пример 2. 2
1)Заменим в уравнении на , получим 2 .
2) Умножим обе части исходного уравнения 2 на (-2) и сложим с уравнением 2 ,
получим:
.
Пример 3.
- Пусть тогда уравнение принимает вид:.
- Заменим в уравнении на , получим .
- Умножим уравнение на (-2) и сложим с уравнением , получим Таким образом,
Пример 4.
1) Заменим в уравнение на , .
2)Умножим уравнение на и вычтем из уравнения ,получим —
, где
Пример 5. ,
1)Заменим в уравнении на получим .
2)Выразим из исходного уравнения , получим
или .
3)Подставим в уравнение , получим .
Выполним преобразования
Пример 6. .
- Заменим на , получим
- Умножим обе части уравнения на и вычтем из уравнения
получим
Пример 7.
1)Пусть , тогда уравнение принимает вид:
2)Пусть тогда исходноеуравнение принимает вид:
3)Умножим обе части уравнения из п.1 на 2, а обе части уравнения из п.2 на (-3) и почленно сложим получившиеся уравнения:
Пример 8.
1) Заменим на , получим или .
2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:
получаем :
Литература
- Кострикина Н.П. “Задачи повышенной трудности в курсе алгебры 7-9 классов” — М: “Просвещение”, 1991г.
- Смышляев В.К.. Практикум по решению задач школьной математики. – М: “Просвещение”, 1978г.
§ 6. Применение элементов математического анализа к решению функциональных уравнений п. 6.1. Предельный переход
Идею предельного перехода проиллюстрируем на следующих примерах.
Пример 17. Решить в классе непрерывных функций уравнение
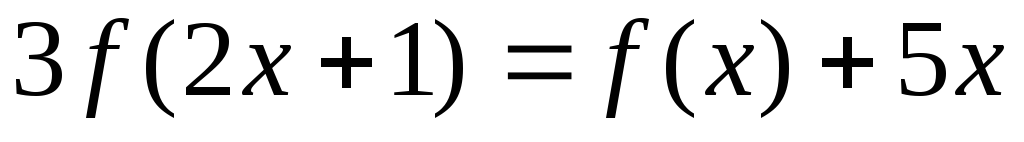 (6.1)
(6.1)
где х  R.
R.
Решение. Заменив
х на 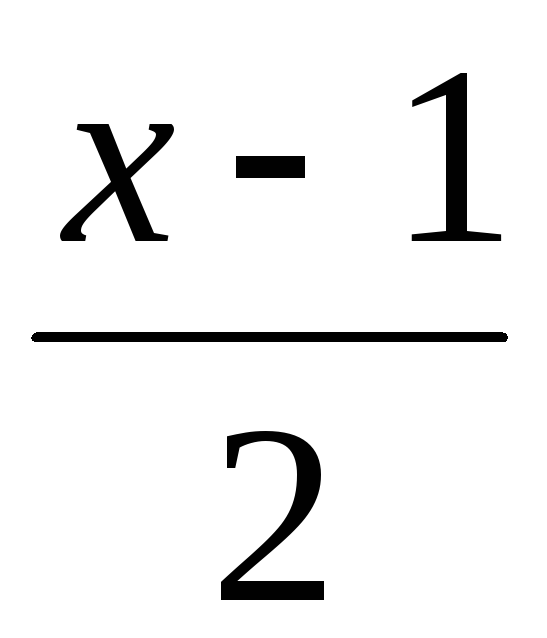 ,
получим
,
получим
 (6.2)
(6.2)
Используя ту же замену, из уравнения (6.2) последовательно получим
 ,
,
 ,
,
……………………………………..
Методом математической индукции можно доказать, что
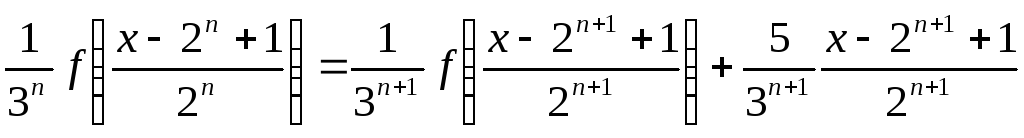 (6.3)
(6.3)
Сложив все уравнения, начиная с (6.2), получим
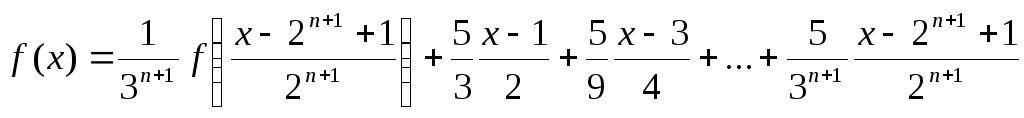 (6.4)
(6.4)
Так как функция f(х) непрерывна, то при любом фиксированном х
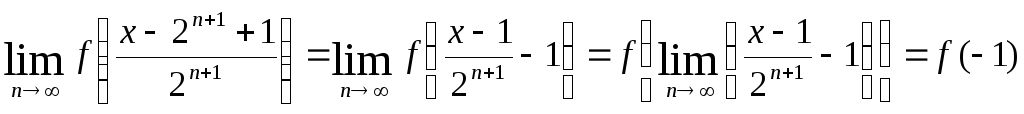
Здесь 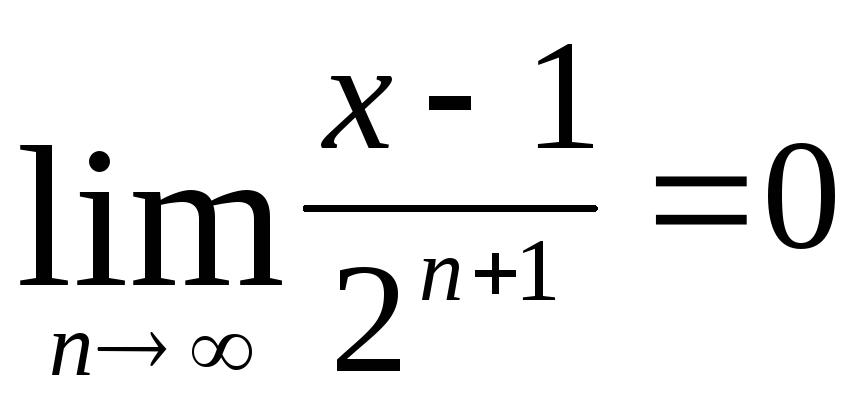 .
Из (6.1)
.
Из (6.1)  .
Тогда
.
Тогда
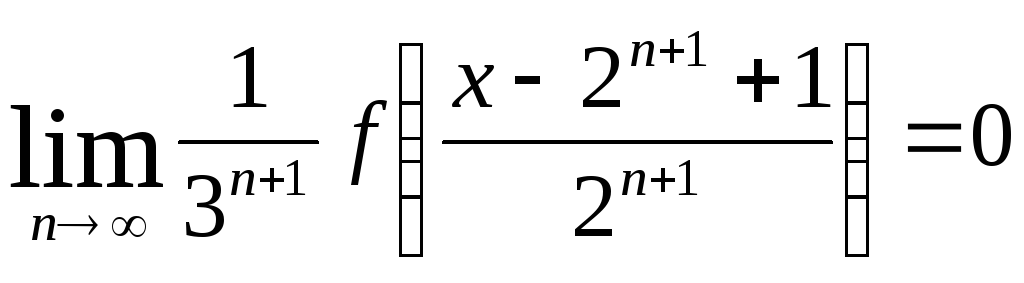
Левая часть равенства (6.4) не зависит от n, поэтому существует ее предел при n → ∞. Переходя к пределу в равенстве (6.4), при n → ∞ имеем
 (6.5)
(6.5)
Правая часть (6.5) является суммой трех бесконечно убывающих прогрессий

Итак,  ,
что и подтверждается проверкой.
,
что и подтверждается проверкой.
Пример
18. Функция f: R→R непрерывна в точке 0 и для любого x  R
выполнено равенство
R
выполнено равенство
2f(2x) = f(x)+x.
Найти все такие f.
Решение. Пусть функция f удовлетворяет условию. Тогда

Тривиальная проверка показывает, что функция x/3 действительно является искомой.
Пример 19. Доказать, что уравнение
 ,
,  (6.6)
(6.6)
не имеет непрерывных решений.
Решение. Допустим, что существует непрерывное решение функционального уравнения (6.6). Подставим в исходное уравнения вместо x выражение
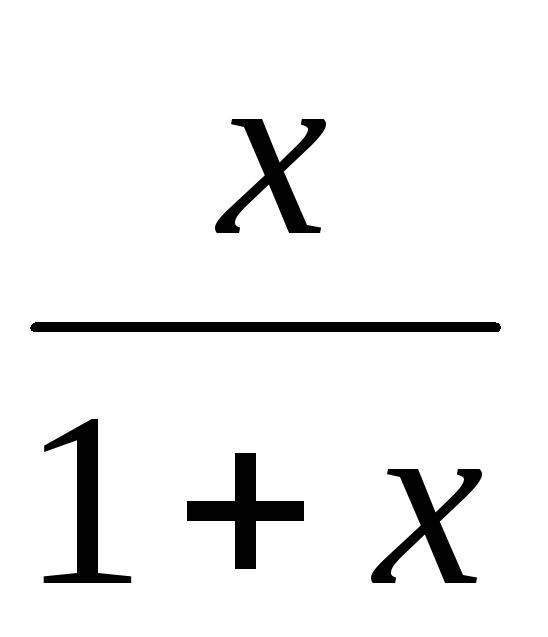
ведь если x ≥ 0, то и

получим:
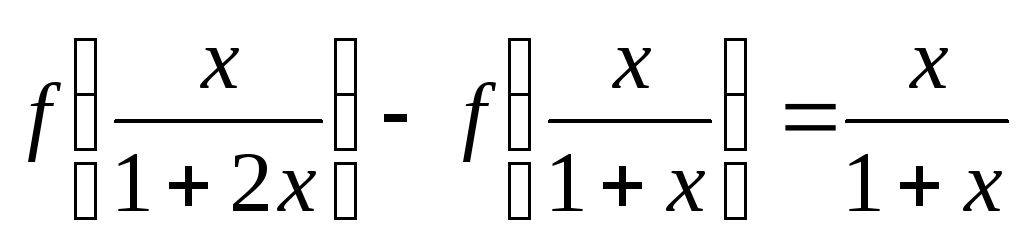 (6.7)
(6.7)
Теперь сделаем такую же замену

в соотношении (6.7):
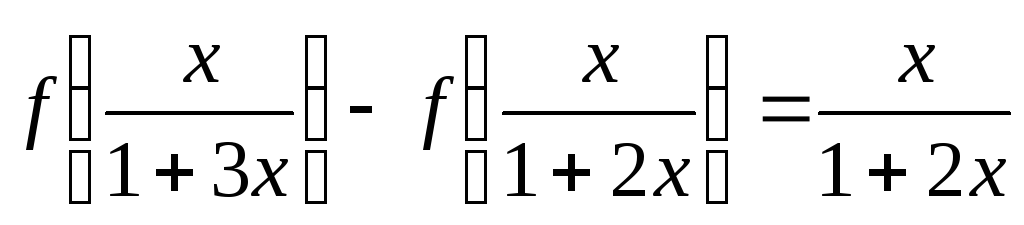 (6.8)
(6.8)
Описанную операцию проделаем ещё несколько pаз. На n-ом шаге имеем:
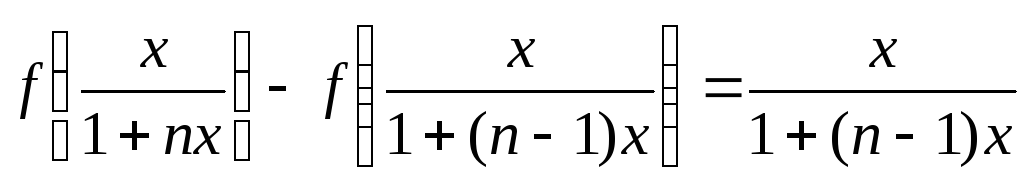
Сложим все получившиеся выражения, начиная с (6.6) (всего будет n выражений), и приведем подобные слагаемые:
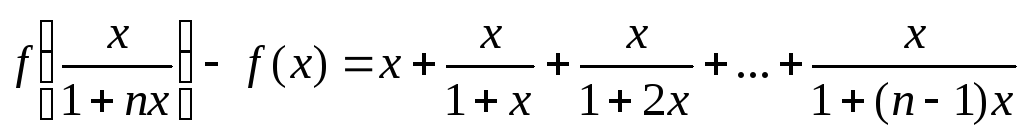 (6.9)
(6.9)
Равенство (6.9) верно для любого натурального n. Зафиксируем x, а n устремим к ∞. Ввиду непрерывности f(x) в точке x = 0, находим
 (6.10)
(6.10)
где
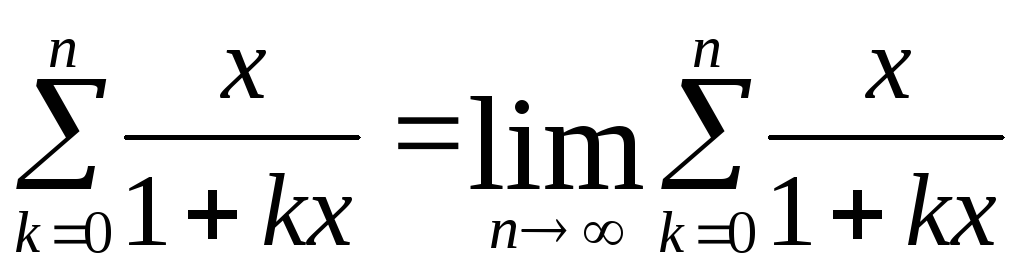
В левой части (6.10) при конкретном (фиксированном) x стоит некоторая константа, т.е. при данном x ряд в правой части (6.10) сходится к этой константе. Мы же покажем, что этот ряд расходится для любого значения x > 0, таким образом, придём к противоречию.
Для любого натурального k и x > 0 верно неравенство

так что
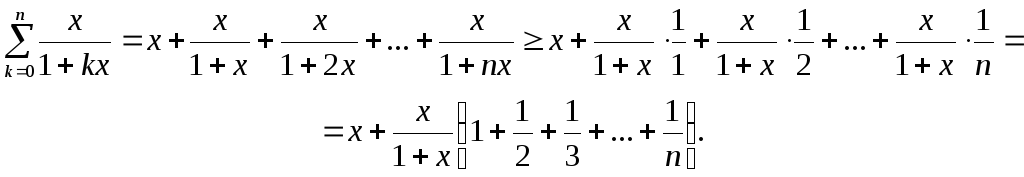
Гармонический ряд
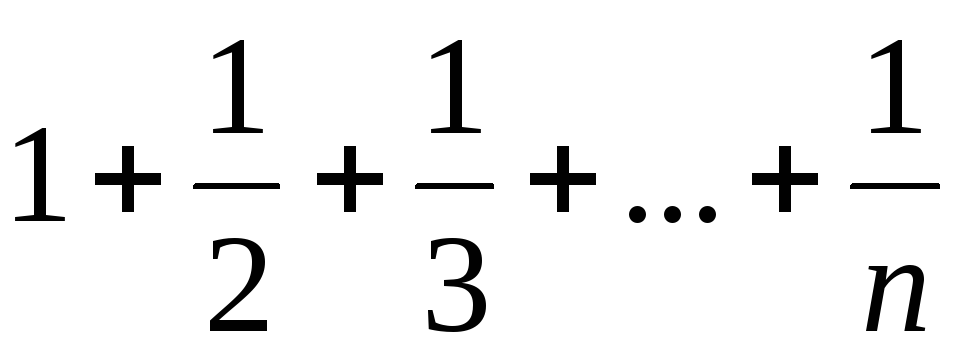
неограниченно возрастает при увеличении n (известный факт), следовательно,
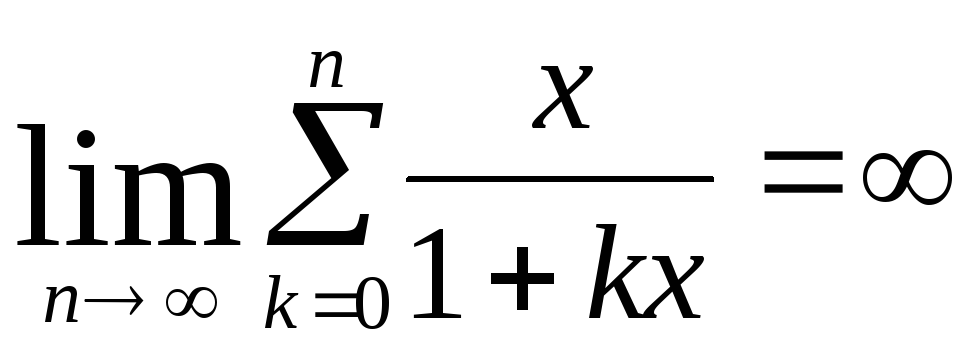
расходится к ∞. Что и требовалось доказать.
Пример 20. Найти f(x), ограниченную на любом конечном интервале, удовлетворяющую функциональному уравнению:

Решение. x = 0  f(0)
= 0;
f(0)
= 0;

…………………………………………

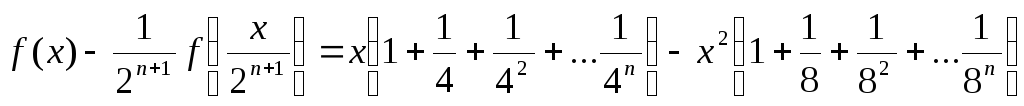
переходя к lim при x → ∞ используя непрерывность f(x) и f(0) = 0 получаем, что
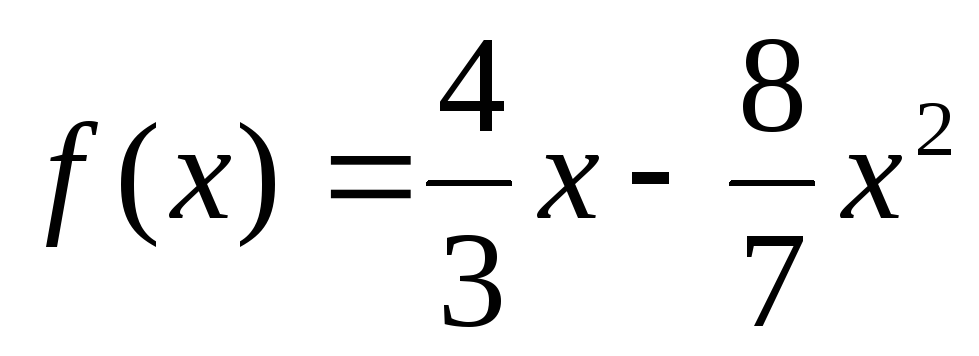 .
.
Пример 21. Решить функциональное уравнение
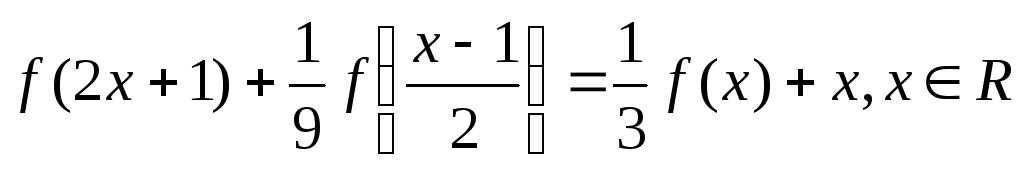 (6.11)
(6.11)
в классе непрерывных функций.
Решение. Выполнив замену 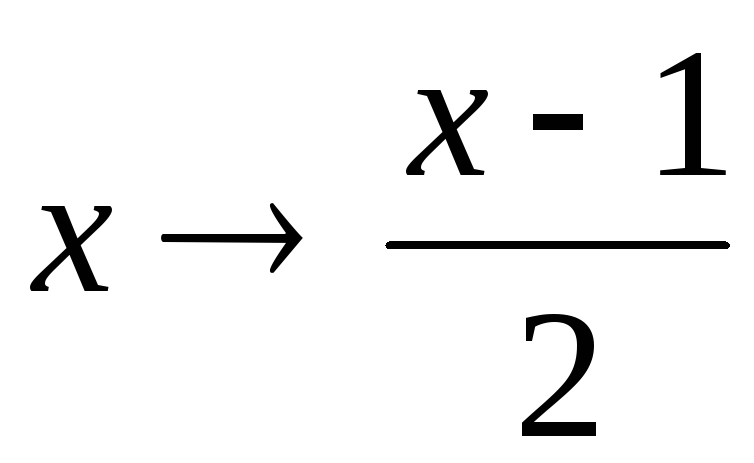 ,
получим
,
получим
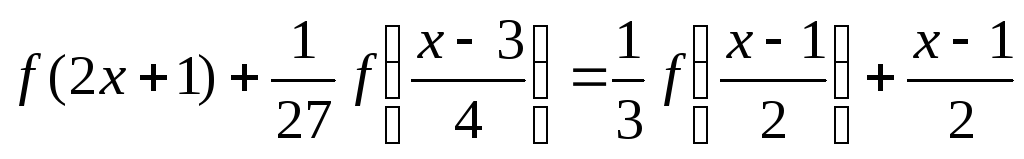 (6.12)
(6.12)
Складывая
(6.11) с уравнением (6.12), умноженным на 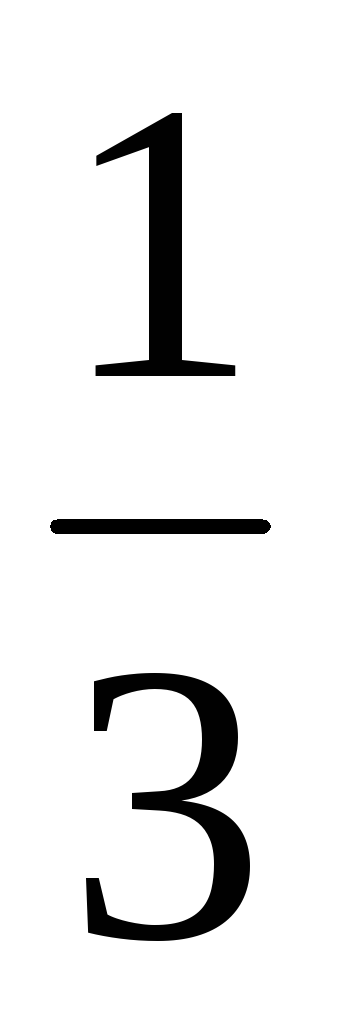 ,
получим
,
получим
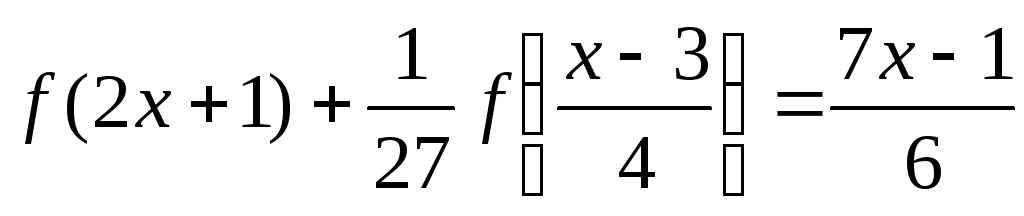
Это
уравнение решается аналогично уравнению
(6.1). Найдем подстановку, переводящую  в
в .
Для этого положим
.
Для этого положим  .
Отсюда
.
Отсюда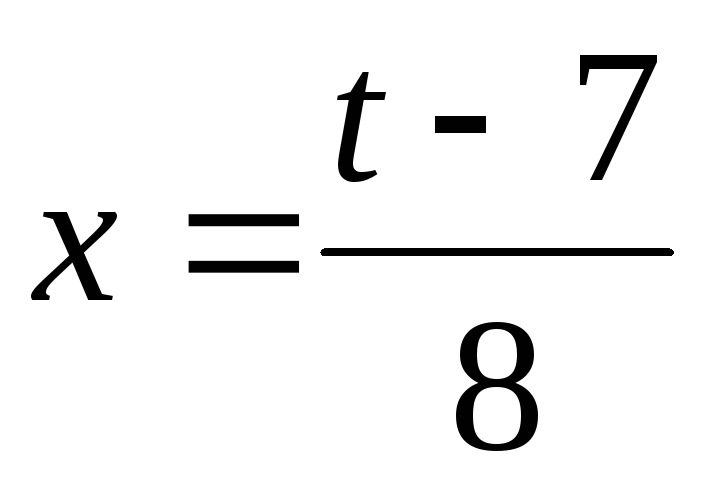 .
Выполнивn
раз подстановку
.
Выполнивn
раз подстановку  ,
получим систему уравнений, из которой
находим
,
получим систему уравнений, из которой
находим
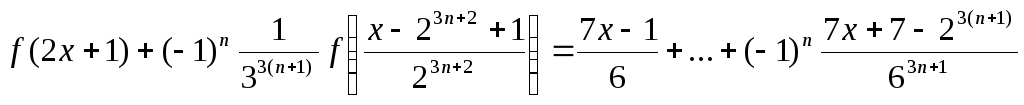
Отсюда при n → ∞
 ,
или
,
или  ,
,
что и подтверждается проверкой.
\
П. 6.2. Дифференцирование
В некоторых случаях для нахождения решения функционального уравнения целесообразно продифференцировать обе части уравнения, если, конечно, производная существует. В результате получим функциональное уравнение, которое содержит и производную неизвестной функции. Решим это уравнение относительно производной. Тогда неизвестная функция является одной из первообразных для найденной производной. Этот метод уже применялся при решении уравнения Коши в классе дифференцируемых функций.
Пример 22. Найти в классе функций, имеющих непрерывные производные, решение уравнения
f(3x+2)
= 3f(x), x  R. (6.13)
R. (6.13)
Решение. Попытки решить уравнение методом предельного перехода не приводят к желаемому результату. Левая и правая части (6.13) являются функциями от х. Они равны, следовательно, равны их производные по х. Продифференцируем (6.13) и после сокращения получим
f′(3x+2) = 3f′(x)
Это
уравнение уже можно решить методом
предельного перехода. Выполнив подстановку 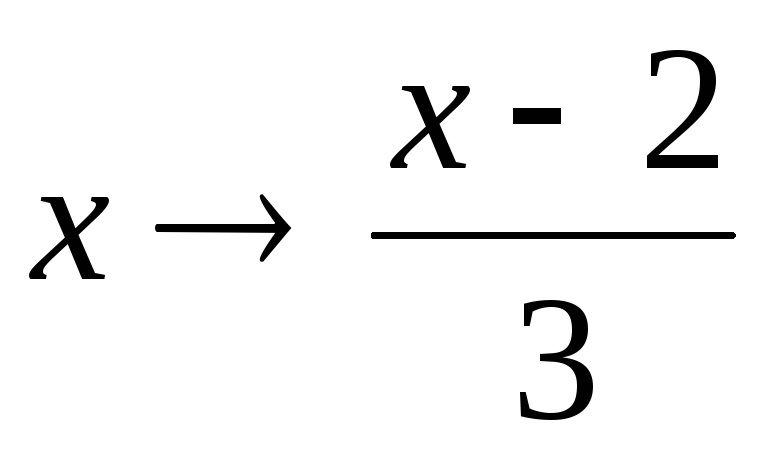 ,
получим цепочку равенств
,
получим цепочку равенств

Ввиду
непрерывности  ,
при n
→ ∞, имеем
,
при n
→ ∞, имеем
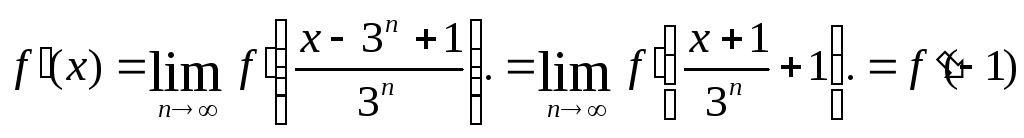
Итак,  = k, где
k ===
= k, где
k ===  .
Первообразная функция f(х)
== kx + b.
Подставив в (6.13) х = –1, получим f(—1)
= 0.
Кроме того, f(–1)
= – k + b,
т. е. k
= b.
.
Первообразная функция f(х)
== kx + b.
Подставив в (6.13) х = –1, получим f(—1)
= 0.
Кроме того, f(–1)
= – k + b,
т. е. k
= b.
Легко проверить, что f (х) = k (х + 1) удовлетворяет условию при произвольном k.
Пример 23. Найти все действительные дифференцируемые функции, удовлетворяющие функциональному уравнению
 (6.14)
(6.14)
Решение. Пусть f удовлетворяет данному уравнению. Тогда

т.е. f(0)[1+f 2(x)] = 0, и, следовательно, f(0) = 0.
После преобразований имеем
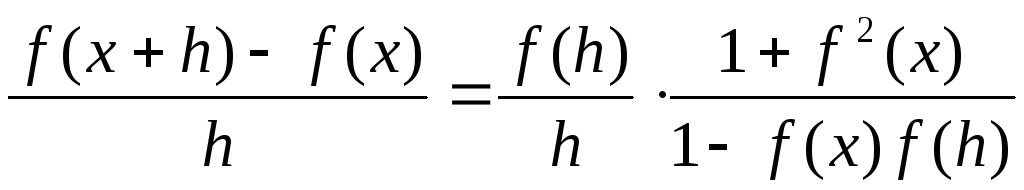 ,
(6.15)
,
(6.15)
откуда, с учётом
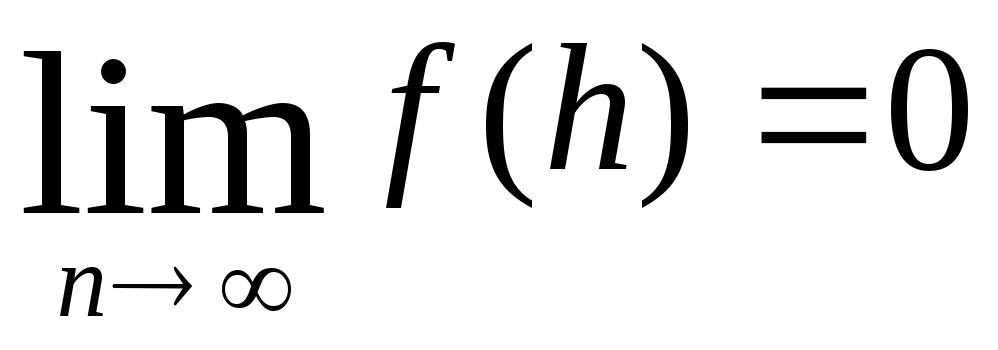
следует, что
f(x) = C (1+f 2(x)), (6.16)
где C = f′(0). Значит,
 ,
,
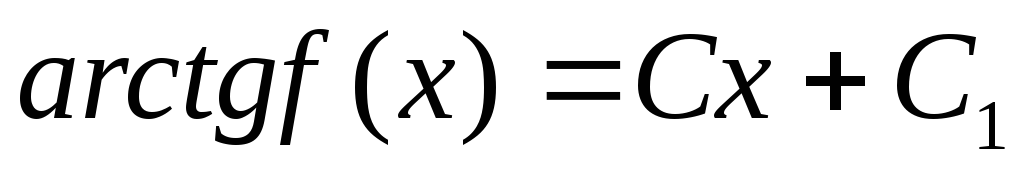
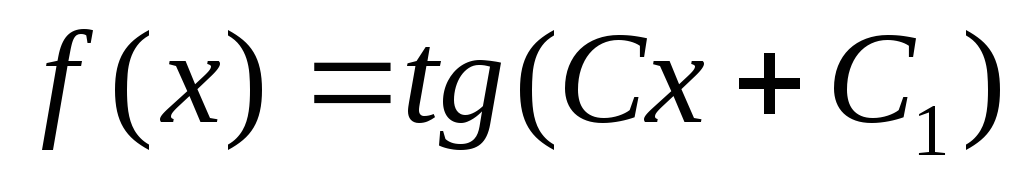
Условие f(0) = 0 означает, что C1 = 0, т.е. f(x) = tg Cx. Очевидно, все функции вида tg Cx подходят под условие задачи.
Пример 24. Найти функцию f(x), удовлетворяющую уравнению
f′(x)
+xf (-x) = ax x  R, a = const.
R, a = const.
Решение. f′(-x)-xf(x) = —ax. Введём новые функции
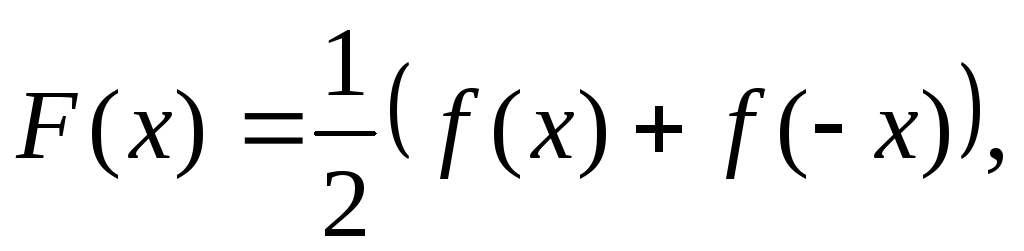
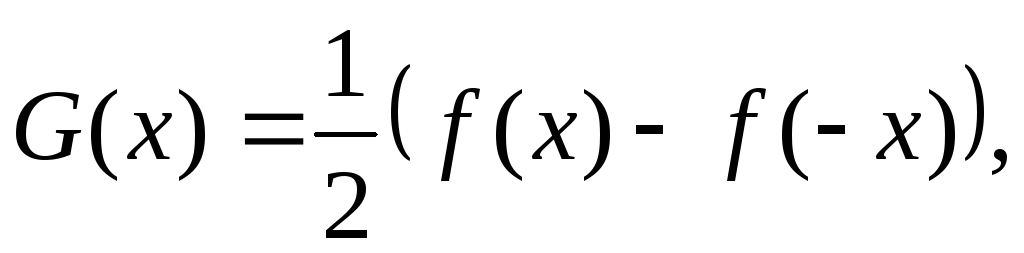
Ясно, что функция F(x) — чётная, а G(x) — нечётная функции, причём f(x) = F(x)+G(x). Получим уравнение относительно новых функций F(x) и G(x):
G′(x)-xG(x) = 0, F′(x) +xF(x) = ax,
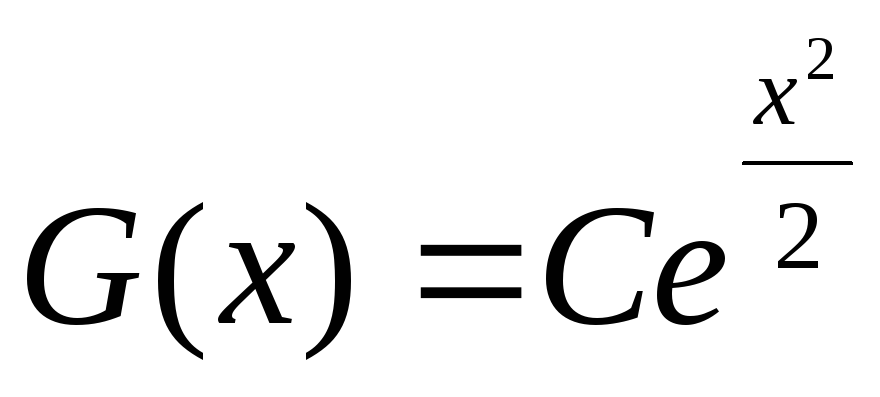
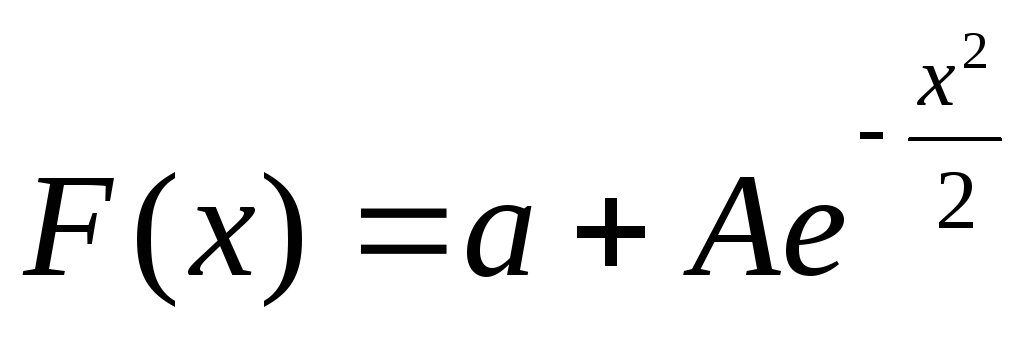
Так как G(-x) = —G(x), то G(x) ≡ 0 и

Непосредственной проверкой убеждаемся в том, что при любых числах a, A функция f(x) является решением исходного уравнения.
4 Методы, основанные на монотонности функций
При
решении уравнений типа  в ряде случаев весьма эффективным
является метод, который использует
монотонность функций
в ряде случаев весьма эффективным
является метод, который использует
монотонность функций 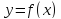 и
и .
Если функция
.
Если функция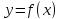 непрерывна и возрастает (убывает) на
отрезке
непрерывна и возрастает (убывает) на
отрезке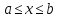 ,
а функция
,
а функция непрерывна и убывает (возрастает) на
этом же отрезке, то уравнение
непрерывна и убывает (возрастает) на
этом же отрезке, то уравнение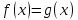 на отрезке
на отрезке может иметь не более одного корня.
может иметь не более одного корня.
Напомним,
что функция  называетсявозрастающей (или убывающей)
на отрезке
называетсявозрастающей (или убывающей)
на отрезке 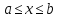 ,
если для любых
,
если для любых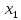 ,
,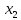 ,
удовлетворяющих неравенствам
,
удовлетворяющих неравенствам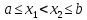 ,
выполняется неравенство
,
выполняется неравенство (соответственно,
(соответственно, ).
Если функция
).
Если функция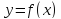 является на отрезке
является на отрезке возрастающей или убывающей, то она
называется монотонной на этом отрезке.
возрастающей или убывающей, то она
называется монотонной на этом отрезке.
В
этой связи при решении уравнения  необходимо иследовать функции
необходимо иследовать функции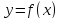 и
и на монотонность, и если одна из этих
функций на отрезке
на монотонность, и если одна из этих
функций на отрезке убывает, а другая функция – возрастает,
то необходимо или попытаться подбором
найти единственный корень уравнения,
или показать, что такого корня не
существует. Если, например, функция
убывает, а другая функция – возрастает,
то необходимо или попытаться подбором
найти единственный корень уравнения,
или показать, что такого корня не
существует. Если, например, функция возрастает, а
возрастает, а убывает для
убывает для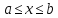 и при этом
и при этом ,
то корней уравнения
,
то корней уравнения среди
среди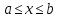 нет. Особенно такой метод эффективен в
том случае, когда обе части уравнения
нет. Особенно такой метод эффективен в
том случае, когда обе части уравнения представляют собой весьма «неудобные»
для совместного исследования функции.
представляют собой весьма «неудобные»
для совместного исследования функции.
Кроме
того, если функция 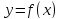 является монотонной на отрезке
является монотонной на отрезке и уравнение
и уравнение (где с – некоторая константа) имеет на
этом отрезке корень, то этот корень
единственный.
(где с – некоторая константа) имеет на
этом отрезке корень, то этот корень
единственный.
Задачи и решение
Пример 4.1. Решить уравнение
 .
(4.1)
.
(4.1)
Решение. Областью
допустимых значений уравнения (4.1)
являются  .
Рассмотрим функции
.
Рассмотрим функции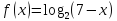 и
и .
Известно , что функция
.
Известно , что функция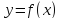 для
для являются убывающей, а функция
являются убывающей, а функция – возрастающей. В этой связи уравнения(4.1)
может иметь только один корень, т.е.
– возрастающей. В этой связи уравнения(4.1)
может иметь только один корень, т.е. ,
который легко находиться подбором.
,
который легко находиться подбором.
Ответ: 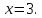
Пример 4.2. Решить уравнение
 (4.2)
(4.2)
Решение.
Введем новую переменную 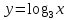 .
Тогда
.
Тогда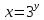 ,
,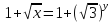 и уравнения (4.2) принимает вид
и уравнения (4.2) принимает вид
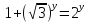 (4.3)
(4.3)
Уравнение
(4.3) имеет очевидной корень  .
Покажем, что других корней нет. Для этого
разделим обе части уравнения (4.3) на
.
Покажем, что других корней нет. Для этого
разделим обе части уравнения (4.3) на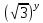 ,
тогда
,
тогда
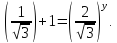 (4.4)
(4.4)
Так
как  ,
а
,
а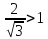 ,
то левая часть уравнения (4.4) является
убывающей функцией, а первая часть –
возрастающей функцией. Поэтому уравнения
(4.4) если имеет корень, так только один.
Ранее было установлено, что
,
то левая часть уравнения (4.4) является
убывающей функцией, а первая часть –
возрастающей функцией. Поэтому уравнения
(4.4) если имеет корень, так только один.
Ранее было установлено, что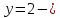 корень
уравнения (4.3). Следовательно, этот корень
единственный.
корень
уравнения (4.3). Следовательно, этот корень
единственный.
Таким
образом, имеем  .
Тогда единственный корнем уравнения
(4.2) является
.
Тогда единственный корнем уравнения
(4.2) является .
.
Пример 4.3. Решить уравнение
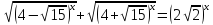 (4.5)
(4.5)
Решение. Разделим обе части уравнения (4.5) на 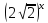 ,
тогда
,
тогда
 (4.6)
(4.6)
Подбором
нетрудно установить, что  является корнем уравнения (4.6). покажем,
что других корней это уравнение не
имеет.
является корнем уравнения (4.6). покажем,
что других корней это уравнение не
имеет.
Обозначим 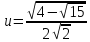 и
и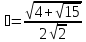 .
Очевидно, что
.
Очевидно, что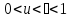 .
Следовательно, каждая из функций
.
Следовательно, каждая из функций и
и является убывающей и при этом
является убывающей и при этом .
.
Если 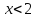 ,
то
,
то ,
,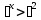 и
и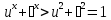 .
.
Если  ,
то
,
то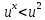 ,
, и
и .
.
Следовательно,
среди  или
или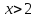 корней уравнения (4.6) нет.
корней уравнения (4.6) нет.
Ответ: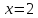
5 Методы решения функциональных уравнений
К числу наиболее сложных задач на вступительных конкурсных экзаменах по математике относятся задачи, решение которых сводится к рассмотрению функциональных уравнений вида
 (5.1)
(5.1)
или
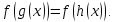 (5.2)
(5.2)
где  некоторые
функции и
некоторые
функции и
Методы решения функциональных уравнений (5.1), (5.2) основаны на использовании следующих теорем.
Теорема
5.1. Корни
уравнения 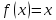 являются
корнями уравнения (5.1).
являются
корнями уравнения (5.1).
Доказательство. Пусть  – корень уравнения
– корень уравнения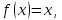 т.е.
т.е.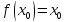 .
Тогда
справедливы равенства
.
Тогда
справедливы равенства
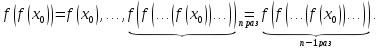
Отсюда следует, что

т.е.  является корнем уравнения (5.1).
является корнем уравнения (5.1).
Теорема
5.2. Если 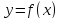 — возрастающая функция на отрезке
— возрастающая функция на отрезке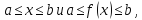 то
на данном отрезке уравнения (5.1) и
то
на данном отрезке уравнения (5.1) и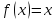 равносильны.
равносильны.
Доказательство. Пусть  является корнем уравнения (5.1), т.е.
является корнем уравнения (5.1), т.е.  .
Предположим, что
.
Предположим, что  не является корнем уравнения
не является корнем уравнения ,
т.е.
,
т.е. .
Не нарушая общности рассуждений, будем
считать, что
.
Не нарушая общности рассуждений, будем
считать, что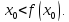 Тогда в силу возрастания функции
Тогда в силу возрастания функции
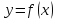 справедливы
неравенства
справедливы
неравенства
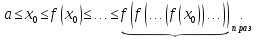
Так
как 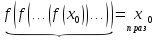 ,
то из приведенных выше неравенств
следует
,
то из приведенных выше неравенств
следует .
Таким образом, получили ложное неравенство.
А это означает, что
.
Таким образом, получили ложное неравенство.
А это означает, что .
.
Отсюда и из теоремы 5.1 следует справедливость теоремы 5.2.
Следствие
1. Если
функция 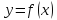 возрастает для любогоx,
то уравнения (5.1) и f(x)=x равносильны.
возрастает для любогоx,
то уравнения (5.1) и f(x)=x равносильны.
Следствие 2. Если функция y=f(x) возрастает на своей области определения, то уравнения (5.1) и f(x)=x равносильны.
Более
сложным является решение уравнения
(5.1) в том случае, когда на некотором
отрезке  функция
функция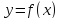 является убывающей.
является убывающей.
В данном случае имеют место аналогии теоремы 5.2 и двух следствий только при условии, что в уравнении (5.1) число n нечетное.
Теорема
5.3. Если y=f(x)
– убывающая функция на отрезке 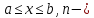 нечетное
и
нечетное
и то на данном отрезке уравнения (5.1) иf(x)=x равносильны.
то на данном отрезке уравнения (5.1) иf(x)=x равносильны.
Доказательство. Пусть 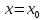 является корнем уравнения (5.1), т.е.
является корнем уравнения (5.1), т.е. 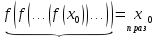
Предположим,
что  не является корнем уравнения
не является корнем уравнения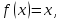 т.е.
т.е. .
Не нарушая общности рассуждений, будем
считать, что
.
Не нарушая общности рассуждений, будем
считать, что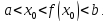 Тогда в силу убывания функции
Тогда в силу убывания функции на отрезке
на отрезке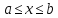 получаем неравенства
получаем неравенства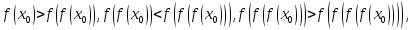 и
т.д.
и
т.д.
Так
как  нечетное, то
нечетное, то .
.
Поскольку  ,
то из последнего неравенства получаем
,
то из последнего неравенства получаем
Так
как 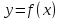 – убывающая функция, то
– убывающая функция, то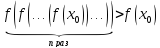 ,
т.е.
,
т.е. .
Получили противоречие тому, что по
предположению
.
Получили противоречие тому, что по
предположению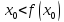 .
Следовательно
.
Следовательно
Отсюда, с учетом теоремы 5.1, следует справедливость теоремы 5.3.
Следствие 3. Если функция y=f(x) убывает для любого x и n – нечетное, то уравнения (5.1) и f(x)=x равносильны.
Следствие 4. Если функция y=f(x) убывает на своей области определения и n – нечетное, то уравнения (5.1) и f(x)=x равносильны.
Так
как в рассмотренных выше случаях функция 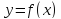 является убывающей, то уравнение
является убывающей, то уравнение может иметь только один корень. Поскольку
уравнение (5.1) с убывающей функцией
может иметь только один корень. Поскольку
уравнение (5.1) с убывающей функцией и нечетнымn равносильно
уравнению
и нечетнымn равносильно
уравнению 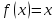 ,
то уравнение (5.1) также имеет более одного
корня.
,
то уравнение (5.1) также имеет более одного
корня.
Если
в уравнении (5.1)  — убывающая функция, аn – четное,
то в общем случае уравнения (5.1) и
— убывающая функция, аn – четное,
то в общем случае уравнения (5.1) и 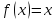 не являются равносильными. Например,
уравнение
не являются равносильными. Например,
уравнение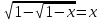 имеет три корня
имеет три корня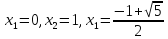 и только третий корень удовлетворяет
уравнению
и только третий корень удовлетворяет
уравнению
В данном случае для поиска корней уравнения (5.1) необходимо проводить дополнительные исследования.
Теорема
5.4. Если  – возрастающая (или убывающая) функция
на области допустимых значений уравнения
(5.2), то уравнения (5.2) и
– возрастающая (или убывающая) функция
на области допустимых значений уравнения
(5.2), то уравнения (5.2) и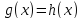 равносильны.
равносильны.
Доказательство. 1)
Пусть 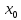 — корень уравнения (5.2), т.е.
— корень уравнения (5.2), т.е. Предположим, что
Предположим, что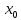 не
является корнем уравнения
не
является корнем уравнения т.е.
т.е. .
Не нарушая общности рассуждений, будем
считать, что
.
Не нарушая общности рассуждений, будем
считать, что Отсюда в зависимости от того, какой
является функцияy=f(x) на
области допустимых значений уравнения
(5.2) возрастающей или убывающей, получаем
неравенство
Отсюда в зависимости от того, какой
является функцияy=f(x) на
области допустимых значений уравнения
(5.2) возрастающей или убывающей, получаем
неравенство  соответственно. В каждом из двух случаем
имеем ложное неравенство. Значит,
соответственно. В каждом из двух случаем
имеем ложное неравенство. Значит,
2)
Пусть 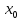 — корень уравнения
— корень уравнения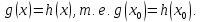 Отсюда следует
Отсюда следует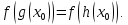
Следствие
5. Если 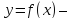 возрастающая (или убывающая) функция
на области значений
возрастающая (или убывающая) функция
на области значений то уравнения (5.2) и
то уравнения (5.2) и равносильны.
равносильны.
Также
следует отметить, что при решении
функционального уравнения (5.2) необходимо
внимательно рассматривать случай, когда
функция  является четной.
является четной.
Теорема
5.5. Если
четная функция 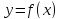 определена на отрезке
определена на отрезке и возрастает (или убывает) при
и возрастает (или убывает) при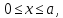 то на данном отрезке уравнение (5.2)
равносильно совокупности уравнений
то на данном отрезке уравнение (5.2)
равносильно совокупности уравнений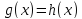 и
и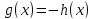 при условии, что
при условии, что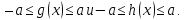
Доказательство проводится
по аналогии с доказательством предыдущей
теоремы. При этом используется четность
функции 
Анализ
функции 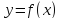 на монотонность удобно осуществлять с
помощью производной: если функция
на монотонность удобно осуществлять с
помощью производной: если функция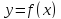 дифференцируема на отрезке
дифференцируема на отрезке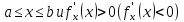 ,
то функция
,
то функция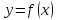 является возрастающей (убывающей) на
данном отрезке.
является возрастающей (убывающей) на
данном отрезке.
Задачи и решения
Пример 5.1. Решить уравнение
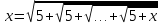 (5.3)
(5.3)
где
квадратный корень берется n раз
(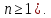
Решение. Из
условия задачи следует, что 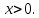 Пусть
Пусть тогда уравнение (5.3) принимает вид
функционального уравнения (5.1).
тогда уравнение (5.3) принимает вид
функционального уравнения (5.1).
Так
как при 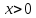 функция
функция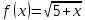 возрастает и
возрастает и то уравнение (5.3) равносильно уравнению
то уравнение (5.3) равносильно уравнению ,
т.е.
,
т.е.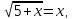 положительным решением которого является
положительным решением которого является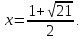
Ответ: 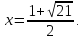
Пример 5.2. Решить уравнение
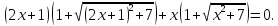 (5.4)
(5.4)
Решение. Перепишем исходное уравнение (5.4) в виде функционального уравнения типа (5.2), т.е.
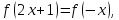 (5.5)
(5.5)
где 
Поскольку 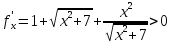 для любого значенияx, то
функция y=f(x) является
возрастающей на всей числовой оси
для любого значенияx, то
функция y=f(x) является
возрастающей на всей числовой оси 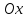 . Следовательно,
вместо функционального уравнения (5.5)
можно рассматривать равносильное ему
уравнение
. Следовательно,
вместо функционального уравнения (5.5)
можно рассматривать равносильное ему
уравнение 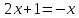 ,
для которого
,
для которого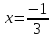 является решением.
является решением.
Ответ: 
Пример 5.3. Решить уравнение
 (5.6)
(5.6)
Решение. Преобразуем уравнение (5.6) следующим образом:


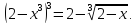
Отсюда получаем уравнение
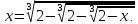 (5.7)
(5.7)
Пусть  тогда уравнение (5.7) принимает вид
тогда уравнение (5.7) принимает вид
 (5.8)
(5.8)
Так
как функция 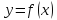 является убывающей на всей числовой
осиOx, то
(согласно Следствию 3) уравнение (5.8)
равносильно уравнению
является убывающей на всей числовой
осиOx, то
(согласно Следствию 3) уравнение (5.8)
равносильно уравнению  т.е. уравнение (5.7) равносильно уравнению
т.е. уравнение (5.7) равносильно уравнению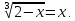 Отсюда следует уравнение
Отсюда следует уравнение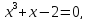 которое имеет единственный действительный
корень
которое имеет единственный действительный
корень .
.
Ответ: 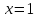 .
.
Пример 5.3. Решить уравнение
 (5.9)
(5.9)
Решение. Поскольку 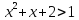 при всехx,
то областью допустимых значений уравнения
(5.9) является множество всех действительных
чисел.
при всехx,
то областью допустимых значений уравнения
(5.9) является множество всех действительных
чисел.
Положив  увидим, что заданное уравнение (5.9)
принимает вид
увидим, что заданное уравнение (5.9)
принимает вид где
где Так как их
Так как их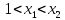 следует, что
следует, что

то
функция  является возрастающей на области
значений функций
является возрастающей на области
значений функций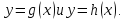 В этой связи уравнение (5.9) равносильно
уравнению
В этой связи уравнение (5.9) равносильно
уравнению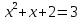 и,
следовательно, имеет два корня
и,
следовательно, имеет два корня
Ответ: 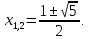
Функциональные уравнения Википедия
Функциональное уравнение — уравнение, выражающее связь между значением функции в одной точке с её значениями в других точках. Многие свойства функций можно определить, исследуя функциональные уравнения, которым эти функции удовлетворяют. Термин «функциональное уравнение» обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них.
Примеры[ | ]
Функциональному уравнению:
- f(s)=2sπs−1sin(πs2)Γ(1−s)f(1−s){\displaystyle f(s)=2^{s}\pi ^{s-1}\sin \left({\frac {\pi s}{2}}\right)\Gamma (1-s)f(1-s)},
где Γ(z){\displaystyle \Gamma (z)} — гамма-функция Эйлера, удовлетворяет дзета-функция Римана ζ{\displaystyle \zeta }.
Гамма-функция является единственным решением этой системы трёх уравнений:
- f(x)=f(x+1)x{\displaystyle f(x)={f(x+1) \over x}}
- f(y)f(y+12)=π22y−1f(2y){\displaystyle f(y)f\left(y+{\frac {1}{2}}\right)={\frac {\sqrt {\pi }}{2^{2y-1}}}f(2y)}
- f(z)f(1−z)=πsin(πz){\displaystyle f(z)f(1-z)={\pi \over \sin(\pi z)}} (формула дополнения Эйлера)
Функциональное уравнение:
- f(az+bcz+d)=(cz+d)kf(z){\displaystyle f\left({az+b \over cz+d}\right)=(cz+d)^{k}f(z)},
где a,b,c,d{\displaystyle a,b,c,d} являются целыми числами, удовлетворяющими равенству