Движение по окружности — Физика
Лекция №5
Движение по окружности.
Криволинейное движение – движение, траекторией которого является кривая линия. Вектор скорости в любой точке направлен по касательной к траектории. Любой участок криволинейного движения приближённо можно представить в виде дуги окружности.
Движение тела по окружности является частным случаем криволинейного движения. Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения. Это движение с переменным ускорением.
Вектор скорости всегда направлен по касательной к окружности. Величина скорости постоянная, направление скорости всё время меняется.
Ускорение при движении по окружности называют центростремительным. Оно всегда, в каждой точке, направлено к центру окружности. Центростремительное ускорение не меняет модуля скорости, но изменяет направление скорости.

Наряду с вектором перемещения удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах.

Линейное и угловое Δφ перемещения при движении тела по окружности.
Длина дуги связана с углом поворота соотношением Δl = RΔφ.
Δl — длина дуги
R — радиус окружности
Δφ — угловое перемещение
При малых углах поворота Δl ≈ Δs.
Δs — модуль линейного перемещения тела
Величины, характеризующие движение по окружности с постоянной по модулю скоростью.
Число полных оборотов за время t. Обозначается N.N=t/T или N=tν
Период обращения Т – время одного полного оборота (время, за которое тело совершает один полный оботот, т.е. поворачивается на угол 2π. Единица измерения — секунда [с].
T=t/N T=1/ν 
Частота v (греческая буква «ню») – число полных оборотов за 1 с. Единица измерения герц [Гц]
ν=N/t ν=1/T
Линейная скорость υ показывает, какой путь проходит тела за 1 секунду.

Угловой скоростью ω тела в данной точке круговой траектории называют предел (при Δt → 0) отношения малого углового перемещения Δφ к малому промежутку времени Δt:

Угловая скорость измеряется в рад/с.
Угловая скорость показывает на какой угол поворачивается тело за 1 секунду.

Связь между модулем линейной скорости υ и угловой скоростью ω:
υ = ωR
Центростремительное ускорение:

Модуль центростремительного ускорения связан с линейной υ и угловой ω скоростями соотношениями:

Движение тела по окружности можно описывать с помощью двух координат x и y.
Скорость тела в каждый момент можно разложить на две составляющие Vx и Vy
Задача №1
Колесо совершает за одну минуту:
а) 30 оборотов;
б) 1500 оборотов.
Определите его период.
а) T = 60 с/30 = 2 с;
б) T = 60 с/1500 = 0,04 с.
Задача №2
Частота вращения воздушного винта самолета 25 Гц. За какое время винт совершает 3000 оборотов.

Задача №3
Период вращения Земли вокруг своей оси равен 1 сут. Определите частоту ее вращения.

Задача №4
Колесо радиуса 0,5 м прокатилось 100 м. Определите угловое перемещение колеса.

Задача №5
Определите угловую скорость вала, вращающегося:
а) с периодом 10 с;
б) с частотой 30 Гц.

Задача №6
Колесо велосипеда имеет радиус 25 см. Определите линейную скорость точек обода колеса, если оно вращается с частотой 4 Гц.

Задача №7
Точильный круг радиусом 10 см делает один оборот за 0,2 с. Найдите скорость точек, наиболее удаленных от оси вращения.
multiurok.ru
Урок физики «Равномерное движение по окружности», 10 класс, ФГОС
10 класс Раздел «Кинематика»
Урок №
Тема урока: Равномерное движение по окружности
Цель урока: ознакомить учащихся с равномерным движением по окружности и физическими величинами, характеризующими это движение
Задачи урока: Образовательная — сформировать у учащихся представления о характеристиках равномерного движения по окружности.
Развивающие: формировать умение определять вид движения тела; сравнивать, анализировать, обобщать данные о движении тела; умение
формировать умения использовать основные понятия, формулы и физические законы движения тела при движении по окружности;
развивать физическое мышление учащихся через практическую деятельность.
Воспитывающие: потребность познания окружающего мира, любознательность, внимательность и трудолюбие.
Планируемые результаты: Предметные: знать — определения и формулы периода, частоты, линейной и угловой скорости, центростремительного ускорения; уметь — применять формулы кинематики криволинейного движения при решении задач.
Личностные: формирование умений управлять своей учебной деятельностью, формирование интереса к физике при анализе явлений формирование мотивации постановкой познавательных задач.
Метапредметные: применять знания законов движения по окружности в повседневной жизни.
Тип урока: изучение нового материала
Ход урока
1.ОРГАНИЗАЦИОННЫЙ МОМЕНТПроверка наличия домашнего задания.
2. АКТУАЛИЗАЦИЯ ЗНАНИЙ А) и Б) выполняем одновременно.
А) В начале занятия давайте проведем физическую разминку в виде физического футбола по темам: «Равноускоренное прямолинейное движение. Свободное падение». Первый учащийся задаёт вопрос по теме и говорит кому направляет этот пас. Второй отвечает. Задает свой вопрос и т.д.
Б) написать формулы на доске по теме свободное падение. Дополнительный вопрос. С какого этажа дома упал предмет без начальной скорости, если он находился в полете 2 с?
3.ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Криволинейное движение в природе и технике более распространено, чем прямолинейное. Примеры: движение лыжника с горки на горку, движение человека на карусели, движение стержня ручки во время письма, движение частей станка при обработки детали(шлифование), полет волейбольного мяча после удара и тому подобное.
Любое криволинейное движение можно представить как последовательность движений по дугам окружностей различных радиусов.
Рассмотрим частный случай криволинейного движения — движение по окружности, которое в окружающем мире распространено: движение стрелки часов, движение искусственных спутники Земли, зубчатые колесики в велосипеде; движение автомобиля и поезда на выпуклых мостах.
Движение по окружности – это вращательное движение.
Демонстрация. Шарик на нити.
Вращательным движением тела называется такое движение, при котором все точки описывают окружности, центры которых находятся на одной прямой, называемой осью вращения.
Нарисуем окружность укажем в некоторых точках направление вектора мгновенной скорости.

Мгновенная скорость тела, движущегося по окружности, направлена по касательной к ней в этой точке.
Наблюдая движение брызг грязи из-под колес автомобиля, что буксует мы в этом можем убедиться.
(см. рис учебника). По касательной также разлетаются раскаленные частицы металла отрываются от стального резца, если коснуться им поверхности вращающегося точильного камня.
Величина | обозначение | Единица измерения | Формула |
Период | Т | с | Т=t/n; T=2πr/v |
Частота | υ | Гц | υ =n/t=1/Т |
Линейная скорость | v | м/с | v=2πr/T=ωr; v=Δl/Δt |
Угловая скорость | ω | рад/с | ω=v/r=2π/T= Δφ/Δt |
Ускорение | а | м/с2 | a=v2/r= ω2r |
Мы будем изучать движение точки по окружности с постоянной по модулю скоростью. Его называют равномерным движением по окружности.
Составим таблицу характеристик этого движения. Учащиеся по очереди выходят заполнять таблицу, руководствуясь учебником.
Скорость точки, движущейся по окружности, называют линейной скоростью.
Линейная скорость v — это физическая величина, характеризующая криволинейное движение и равна отношению пути Δl, пройденного телом по криволинейной траектории за малый промежуток времени Δt, к величине этого промежутка
Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за который тело совершает один полный оборот.
Период вращения Т — это физическая величина, равная времени одного полного оборота.
Единица периода вращения в СИ — секунда ([Т] = с).
Частота вращения — это физическая величина, численно равна числу полных оборотов за единицу времени.
Угловая скорость — это физическая величина, равная отношению угла поворота радиуса, проведенного к телу от центра круга, по которому движется тело, к промежутку времени, в течение которого этот поворот осуществлялся.
Основная задача механики для равномерного движения по окружности состоит так же в определении положения тела в любой момент времени.
Поскольку движение по кругу происходит в одной плоскости, то для описания движения можно воспользоваться двухмерной системой координат. Если связать точку начала координат с центром круга, по которому движется тело, а начальное положение тела соединить с точкой пересечения окружности и оси Ох, то координаты х и можно вычислить по формулам: х=Rсоsφ; y=Rsinφ.
Поскольку угол φ меняется с течением времени по закону φ = ωt, то уравнение координаты для равномерного движения по окружности имеет следующий вид: х=Rсоs ωt;y=Rsin ωt.
ЗАКРЕПЛЕНИЕ. РЕШЕНИЕ ЗАДАЧ У ДОСКИ. Вызываю 3 ученика.
1. Кабинка карусели движется по окружности радиусом 24 м. Период его вращения равен 30с. Чему равна скорость движения кабинки?
Дано:
R=24м
Т=30с v=2πR/T v=2*π*24м /30с=48 π /30м/с=5 м/с
v-? Ответ: 5 м/с
Вопрос к классу
Чему равен период вращения часовой стрелки часов? минутной? секундной?
Тм=1ч=3600с;
Тс=1мин=60с;
Тч=12ч=12*3600с=43200с.
2. Во сколько раз скорость конца минутной стрелки башенных часов Биг-Бен в Лондоне больше скорости конца минутной стрелки наручных часов, если длина стрелки башенных часов — 4,2 м, а длина стрелки наручных часов — 1,5 см?
Справка. Часы на башне Биг-Бен в Лондоне до настоящего времени являются самыми большими в мире. Диаметр циферблата – 7 метров. Длина стрелок – 2,7 и 4,2 метра. Часовой механизм считается эталоном надежности, общий вес его составляет 5 тонн.
Дано:
Rб=4,2м Тмб = Тмр =1ч=3600с v=2πr/T
Rр=1,5 см = 1,5*10-2 м vб/ vб =(2*π*4,2м / 3600с/)*(3600с/2*π*1,5*10-2 м )=280 раз
vб/ vб -? Ответ: 280 раз
3.Напишите уравнение движения материальной точки, движущейся по дуге радиусом 5 м с угловой скоростью π/4 рад/с. Какими будут координаты точки через 3 с после начала отсчета времени?
Дано:
R=5м х=Rсоs ωt; y=Rsin ωt
ω= π/4 рад/с
х(t)-? х=5соs π/4t; y=5sin π/4t
y (t)-?
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ. РАБОТА ПО КАРТОЧКЕ.
Детская карусель за одну минуту совершает 4 оборота. Найти период и частоту, с которой она вращается.
Дано:
N=4об
T=1мин 60с Т=t/N T=60с/4=15с υ=N/t υ=4/60=1/15=0.067Гц
T-?
υ -? Ответ: 15 с,15 Гц
РЕФЛЕКСИЯ
Что нового узнали? Сложно ли использовать формулы при решении задач?
ДОМАШНЕЕ ЗАДАНИЕ
1. Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский Физика 10 –М.: Просвещение, 2017.
§ 15,16 читать, учить определения, формулы. Выполнить с.61 А1-А4.
2.Проект в виде буклета «Равномерное движение по окружности» (по желанию)
xn--j1ahfl.xn--p1ai
Урок 4. равномерное движение точки по окружности — Физика — 10 класс
Физика, 10 класс
Урок 04.Равномерное движение точки по окружности
Перечень вопросов, рассматриваемых на уроке:
- Равномерное движение точки по окружности и его характеристики.
- Центростремительное ускорение.
Глоссарий по теме
Криволинейное движение – это движение по дугам окружностей разных радиусов.
Ускорение – это векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло, при ∆t → 0

Равномерное движение точки по окружности — движение точки с постоянной по модулю скоростью (ν = const) по траектории, представляющей собой окружность.
Ключевые слова
Криволинейное движение; движение по окружности; скорость; радиус кривизны; изменение скорости; центростремительное ускорение.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56
Марон Е.А., Марон А.Е. Сборник качественных задач по физике. М., Просвещение, 2006
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22
Открытые электронные ресурсы:
http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm
Теоретический материал для самостоятельного изучения
1. Мы уже знакомы с равноускоренным движением. Как же меняются скорость и ускорение при криволинейном движении? Сегодня рассмотрим равномерное движение по окружности, узнаем, что такое центростремительное ускорение.
Если траектория движения тела прямая линия, то движение прямолинейное; если траектория кривая линия – криволинейное движение. Напомним, что траектория – это линия, вдоль которой двигалось тело.
При изучении равноускоренного движения мы заметили, что в некоторых случаях тело движется по прямой, например свободное падение тел, а в некоторых по кривой – тело, брошенное под углом к горизонту.
Рассмотрим движение тела, брошенного под углом к горизонту. Траекторией является парабола.
Возьмем разные точки на линии и нарисуем векторы скорости  . Вектор скорости направлен по касательной, а ускорение свободного падения направлен вниз.
. Вектор скорости направлен по касательной, а ускорение свободного падения направлен вниз.
Векторы  и
и  не лежат на одной прямой, угол между ними не равен нулю.
не лежат на одной прямой, угол между ними не равен нулю.
Это естественно, так как, если ускорение образует угол со скоростью, то изменение скорости направлено не так, как скорость. Это приводит к изменению направления скорости. Изменение скорости  направлено как ускорение. Скорость через некоторый промежуток времени образует некоторый угол с
направлено как ускорение. Скорость через некоторый промежуток времени образует некоторый угол с  Итак, сформулируем первый вывод: если угол между векторами скорости и ускорения не равен нулю, то движение будет криволинейным.
Итак, сформулируем первый вывод: если угол между векторами скорости и ускорения не равен нулю, то движение будет криволинейным.
2.Может ли быть движение одновременно равномерным и криволинейным? Да, например, движение по окружности.
Равномерное движение точки по окружности — это движение точки с постоянной по модулю скоростью (v = const) по траектории, представляющей собой окружность. Но, скорость – это векторная величина, а для векторной величины одинаково важны и модуль, и направление. Т.к. при движении по окружности скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Если есть изменение скорости (точнее её направления), значит, есть ускорение

Сформулируем второй важный вывод: любое криволинейное движение является движением с ускорением, потому что меняется направление вектора скорости.
Решим задачу: найдем ускорение тела, равномерно движущегося по окружности.
Рассмотрим равномерное движение тела по окружности с центром в точке О. В какой-то момент времени, скорость тела в точке А была .
.
Модули скоростей равны:

но вектора скоростей  не равны.
не равны.

Поэтому построим вектор  для тела, движущегося по окружности. Перенесем вектор
для тела, движущегося по окружности. Перенесем вектор  в начало вектора
в начало вектора и найдем разность векторов.
и найдем разность векторов.

 направлен в сторону
направлен в сторону .
.
Вспомним, что вектор направлен по касательной, а касательная перпендикулярна радиусу окружности. Проведем радиусы к обеим точкам и обозначим угол между ними через ?.
направлен по касательной, а касательная перпендикулярна радиусу окружности. Проведем радиусы к обеим точкам и обозначим угол между ними через ?.
Что можно сказать об угле между векторами  ? Он равен малому углу, как углы с взаимно перпендикулярными сторонами.
? Он равен малому углу, как углы с взаимно перпендикулярными сторонами.
Рассмотрим равнобедренный треугольник со сторонами  ,
,  . Углы у основания равны.
. Углы у основания равны.
Если угол φ стремится к нулю, то углы у основания совпадут и станут равными 900

Вектор  будет перпендикулярен вектору
будет перпендикулярен вектору  в пределе, а значит вектор ускорения
в пределе, а значит вектор ускорения  тоже перпендикулярен
тоже перпендикулярен  т.е направлен по радиусу к центру окружности. Поэтому часто его называют центростремительным ускорением
т.е направлен по радиусу к центру окружности. Поэтому часто его называют центростремительным ускорением
Теперь следующая задача: как найти модуль вектора ускорения. Давайте рассмотрим два треугольника: треугольник, образованный векторами  и треугольник, образованный радиусами и хордой. У этих треугольников углы при вершинах равны, они равнобедренные. Треугольники подобны и, следовательно, выполняются соотношения подобия.
и треугольник, образованный радиусами и хордой. У этих треугольников углы при вершинах равны, они равнобедренные. Треугольники подобны и, следовательно, выполняются соотношения подобия.


Промежуток времени мал, поэтому очень мал и угол при вершине, в пределе он стремится к нулю. Тогда можно сказать, что длина хорды s равна длине дуги АВ при

Длина дуги АВ это путь, пройденный точкой от А до В,
тогда запишем:

Умножим на и получим:
и получим:

В левой части мы получили отношение изменения скорости за некоторый промежуток времени к этому промежутку времени т.е. ускорение:

Равномерное движение точки по окружности является движением с переменным ускорением и переменной скоростью. Модули скорости и ускорения остаются постоянными


- Криволинейное движение — это движение по дугам окружностей разных радиусов.

А если меняется радиус, то меняется и центростремительное ускорение. Чем меньше радиус, тем больше ускорение при одинаковой скорости.
Всегда при равномерном криволинейном движении вектор ускорения перпендикулярен вектору скорости, поэтому центростремительное ускорение иногда называют нормальным ускорением, от слова нормаль, т.е. перпендикуляр.
Основные выводы:
— движение криволинейное, так как траекторией является окружность;
— движение равномерное, так как модуль скорости не меняется;
— вектор скорости направлен по касательной к окружности;
-вектор ускорения направлен к центру окружности;
— модуль центростремительного ускорения равен: 
Примеры и разбор решения заданий
1. Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
При движении по окружности линейная скорость и центростремительное ускорение связаны соотношением 
где R = 50 м; υ=  км/ч = 10 м/с.
км/ч = 10 м/с.
Тогда ac = (10 м/с)2 / 50 м = 2 м/с2.
Ответ: 2 м/с2
2. Две материальные точки движутся по окружностям радиусами R1 = 10 см и R2 = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?
Дано:
R1 =10см = 0,10 м
R2 = 30см = 0,30 м

Найти — 
Задано два объекта:
1) материальная точка, которая движется по окружности R1;
2) материальная точка, которая движется по окружности R2.
При движении по окружности центростремительное ускорение и линейная скорость связаны соотношением

Для тела 1 уравнение (1) примет вид:

для тела 2:

Тогда

Центростремительное ускорение тела (2) меньше  ускорения тела (1) в 3 раза.
ускорения тела (1) в 3 раза.
resh.edu.ru
Движение по кругу. Готовимся к олимпиадам, 10 класс
В предлагаемых задачах тела движутся одновременно: одно прямолинейно, другое – по кругу. Все задачи – комбинированные.
Задача 1. Маленький шарик влетает со скоростью  см/с в малое отверстие в стенке полого цилиндра, вращающегося вокруг своей оси. Радиус
см/с в малое отверстие в стенке полого цилиндра, вращающегося вокруг своей оси. Радиус  см цилиндра много больше толщины его стенок. Скорость шарика перпендикулярна оси цилиндра. Какой должна быть минимальная угловая скорость вращения цилиндра
см цилиндра много больше толщины его стенок. Скорость шарика перпендикулярна оси цилиндра. Какой должна быть минимальная угловая скорость вращения цилиндра  для того, чтобы шарик вылетел наружу, не испытав соударений? Ответ выразите в рад/с, округлив до целых. Силу тяжести не учитывайте.
для того, чтобы шарик вылетел наружу, не испытав соударений? Ответ выразите в рад/с, округлив до целых. Силу тяжести не учитывайте.

К задаче 1
Решение.
Чтобы шарик мог вылететь из цилиндра, нyжно, чтобы к моменту, когда он пролетит расстояние  , отверстие цилиндра оказалось бы в той же точке, что и шарик. Таким образом, угол, на который должен повернуться цилиндр, равен
, отверстие цилиндра оказалось бы в той же точке, что и шарик. Таким образом, угол, на который должен повернуться цилиндр, равен  где
где  — произвольное натуральное число.
— произвольное натуральное число.
Время, за которое шарик пройдёт расстояние  , равно
, равно  Поэтому угловая скорость вращения цилиндра должна быть равна
Поэтому угловая скорость вращения цилиндра должна быть равна
![Rendered by QuickLaTeX.com \[\omega=\frac{\varphi}{t}=\frac{\pi+2\pi\cdot n}{\frac{2R}{\upsilon}}=\frac{(2n+1)\cdot\pi\cdot\upsilon}{2R}.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-500135fee067a2b2958cbe813668a0a0_l3.png)
Таким образом, минимальная угловая скорость вращения цилиндра, при которой шарик может беспрепятственно из него вылететь, равна
![Rendered by QuickLaTeX.com \[\omega_{min}=\frac{\pi\cdot\upsilon}{2R}=3.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c1448588f8c9c56c589ea40d768b6dcd_l3.png)
Ответ: 3 рад/с.
Задача 2. Кузьма бежал по кругу с постоянной скоростью. В точке  он встретил Матвея, который бежал с постоянным ускорением по диаметру
он встретил Матвея, который бежал с постоянным ускорением по диаметру  Скорость Матвея в момент встречи была равна скорости Кузьмы. Кузьма, не изменяя скорости, пробежал полкруга и встретился с Матвеем в точке
Скорость Матвея в момент встречи была равна скорости Кузьмы. Кузьма, не изменяя скорости, пробежал полкруга и встретился с Матвеем в точке  куда тот как раз успел добежать. Определите отношение модуля ускорения Кузьмы к модулю ускорения Матвея. Ответ округлить до десятых.
куда тот как раз успел добежать. Определите отношение модуля ускорения Кузьмы к модулю ускорения Матвея. Ответ округлить до десятых.

К задаче 2
Решение.
Пусть скорость Кузьмы (синяя стрелка)  ускорение Матвея
ускорение Матвея  радиус окружности
радиус окружности  время между встречами
время между встречами  Кузьма преодолел расстояние
Кузьма преодолел расстояние
![Rendered by QuickLaTeX.com \[\upsilon\cdot t=\pi\cdot R,\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-03175730e560953ca45c6eef6af6bfeb_l3.png)
а Матвей
![Rendered by QuickLaTeX.com \[\upsilon\cdot t+\frac{a\cdot t^2}{2}=2R.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a4ed611a4d3573943e673dbbefaca29d_l3.png)
Исключая время, получим
![Rendered by QuickLaTeX.com \[\pi\cdot R+\frac{a\cdot\pi^2\cdot R^2}{2\upsilon^2}=2R,\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1f706a05178a224d12b368d1d6459229_l3.png)
откуда ускорение Матвея равно
![Rendered by QuickLaTeX.com \[a=\frac{2(2-\pi)\cdot\upsilon^2}{\pi^2\cdot R}<0,\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-74716f509b0abaf1f996a3f0994d06fd_l3.png)
то есть Матвей двигался равнозамедленно.
При этом ускорение Кузьмы (нормальное) равно  Тогда искомое отношение есть
Тогда искомое отношение есть
![Rendered by QuickLaTeX.com \[\frac{\pi^2}{2(2-\pi)}\approx4,3.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-68b450680eb0f3ca75e25ff50a3aba89_l3.png)
Ответ: 4,3.
Задача 3. Школьник Василий посмотрел на электронной карте координаты своего дома и выяснил, что они равны  с.ш. и
с.ш. и  в.д. После этого он задался вопросом: с какой скоростью движется его дом относительно земной оси? Ответ выразить в м/с. округлив до целых. Считать, что радиус Земли равен
в.д. После этого он задался вопросом: с какой скоростью движется его дом относительно земной оси? Ответ выразить в м/с. округлив до целых. Считать, что радиус Земли равен  км, а один оборот вокруг своей оси она совершает за
км, а один оборот вокруг своей оси она совершает за  ч.
ч. 
Решение.
Дом Василия движется по окружности радиуса  где
где  — широта местности.
— широта местности.

К задаче 3
Угловая скорость вращения Земли
![Rendered by QuickLaTeX.com \[\omega=\frac{2\pi}{T}.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-aa8bcfcf3bba2202ddc1c361f3a9f84a_l3.png)
Скорость дома относительно земной оси равна
![Rendered by QuickLaTeX.com \[\upsilon=\omega\cdot r=\frac{2\pi}{T}R\cdot\cos\alpha=329.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-eb38a1175e4f8d810eb32d7fa44fd5a9_l3.png)
Ответ: 329 м/с.
Задача 4. Стартуя из точки  спортсмен движется равноускоренно до точки
спортсмен движется равноускоренно до точки  после которой модуль скорости спортсмена остается постоянным вплоть до точки
после которой модуль скорости спортсмена остается постоянным вплоть до точки 

К задаче 4
Во сколько раз время, затраченное спортсменом на участок  больше, чем на участок
больше, чем на участок  если модуль ускорения на обоих участках одинаков? Траектория
если модуль ускорения на обоих участках одинаков? Траектория  — полуокружность. Ответ округлить до целых.
— полуокружность. Ответ округлить до целых.
Решение.
Начальная скорость  спортсмена равна 0, поэтому в точке
спортсмена равна 0, поэтому в точке  спортсмен будет иметь скорость
спортсмен будет иметь скорость  которая будет постоянна по величине вплоть до точки
которая будет постоянна по величине вплоть до точки  В этом соотношении
В этом соотношении  — его ускорение,
— его ускорение,  — время движения из точки
— время движения из точки  в точку
в точку 
Поскольку участок  представляет собой полуокружность, то на ее преодоление спортсмен затратит время
представляет собой полуокружность, то на ее преодоление спортсмен затратит время  где
где  — период обращения.
— период обращения.
При движении по окружности  где
где  — угловая скорость. Выходит, что
— угловая скорость. Выходит, что  следовательно,
следовательно,  \\
\\
При движении по окружности с постоянной скоростью ускорение  становится центростремительным, то есть
становится центростремительным, то есть  откуда
откуда  следовательно,
следовательно, 
Итак,  и
и  откуда
откуда 
Ответ: 3.
Задача 5. Тело брошено со скоростью  м/с под углом
м/с под углом  к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения и в точке наивысшего подъема тела над поверхностью земли. Ответы выразить в метрах, округлив до десятых. Ускорение свободного падения принять равным
к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения и в точке наивысшего подъема тела над поверхностью земли. Ответы выразить в метрах, округлив до десятых. Ускорение свободного падения принять равным  м/с
м/с
Решение.
Радиус кривизны траектории есть отношение квадрата скорости тела к нормальному ускорению тела.
Найдём нормальные ускорения в начальный момент и в наивысшей точке. Они равны 
Скорости тела в интересующие нас моменты  (так как горизонтальная составляющая не меняется) и
(так как горизонтальная составляющая не меняется) и 
Таким образом радиусы кривизны составят
![Rendered by QuickLaTeX.com \[R_1=\frac{\upsilon^2}{g\cdot\cos\alpha}=14,4.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9ef638483052396f76ca520506f63209_l3.png)
и
![Rendered by QuickLaTeX.com \[R_2=\frac{\upsilon^2\cdot\cos^2\alpha}{g}=5,1.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ea5e17433b9f370526e4789abe5adbaa_l3.png)
Ответ: 14,4 м и 5,1 м.
easy-physic.ru
Движение тела по криволинейной траектории. Движение по окружности. Характеристики вращательного движения. Центростремительное ускорение
Для начала определимся, какие принципиальные отличия есть у криволинейного движения (рис. 1) относительно прямолинейного и к чему эти отличия приводят.

Рис. 1. Траектория криволинейного движения
Поговорим о том, как удобно описывать движение тела при криволинейном движении.
Можно разбить движение на отдельные участки, на каждом из которых движение можно считать прямолинейным (рис. 2).
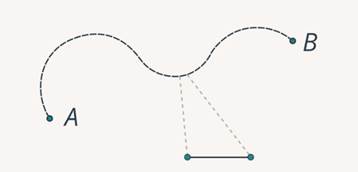
Рис. 2. Разбиение криволинейного движения на участки прямолинейного движения
А дальше на каждом из этих участков мы можем пользоваться законами прямолинейного движения, которые мы уже знаем. В принципе, такой подход возможен.
Однако более удобным является следующий подход. Мы представим это движение как совокупность нескольких движений по дугам окружностей (рис. 3). Обратите внимание, что таких разбиений меньше, чем в предыдущем случае, кроме того, движение по окружности является криволинейным. К тому же примеры движения по окружности в природе встречается очень часто. Из этого можно сделать вывод:
Для того чтобы описывать криволинейное движение, нужно научиться описывать движение по окружности, а потом произвольное движение представлять в виде совокупностей движений по дугам окружностей.

Рис. 3. Разбиение криволинейного движения на движения по дугам окружностей
Итак, начнем изучение криволинейного движения с изучения равномерного движения по окружности. Давайте разберемся, каковы принципиальные отличия криволинейного движения от прямолинейного. Для начала вспомним, что в девятом классе мы изучили тот факт, что скорость тела при движении по окружности направлена по касательной к траектории (рис. 4). Кстати, этот факт вы можете пронаблюдать на опыте, если посмотрите, как движутся искры при использовании точильного камня.

Рис. 4. Направление скорости при движении по окружности
Рассмотрим движение тела по дуге окружности (рис. 5).
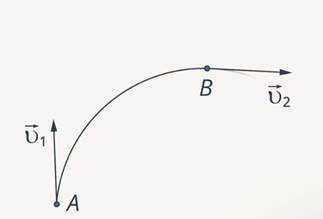
Рис. 5. Скорость тела при движении по окружности
Обратите внимание, что в данном случае модуль скорости тела в точке  равен модулю скорости тела в точке
равен модулю скорости тела в точке  :
:

Однако вектор  не равен вектору
не равен вектору  . Итак, у нас появляется вектор разности скоростей (рис. 6):
. Итак, у нас появляется вектор разности скоростей (рис. 6):

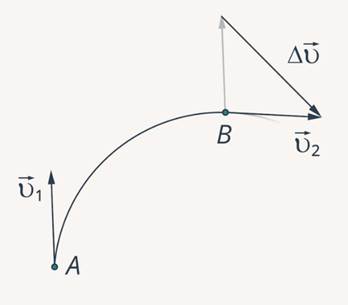
Рис. 6. Вектор разности скоростей
Причем изменение скорости произошло через некоторое время  . Таким образом, мы получаем знакомую комбинацию:
. Таким образом, мы получаем знакомую комбинацию:

Это не что иное, как изменение скорости за промежуток времени, или ускорение тела. Можно сделать очень важный вывод:
Движение по криволинейной траектории является ускоренным. Природа этого ускорения – непрерывное изменение направление вектора скорости.
Еще раз отметим, что, даже если говорится, что тело равномерно движется по окружности, имеется в виду, что модуль скорости тела не изменяется. Однако такое движение всегда является ускоренным, поскольку изменяется направление скорости.
В девятом классе вы изучали, чему равно такое ускорение и как оно направлено (рис. 7). Центростремительное ускорение 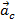 всегда направлено к центру окружности, по которой движется тело.
всегда направлено к центру окружности, по которой движется тело.
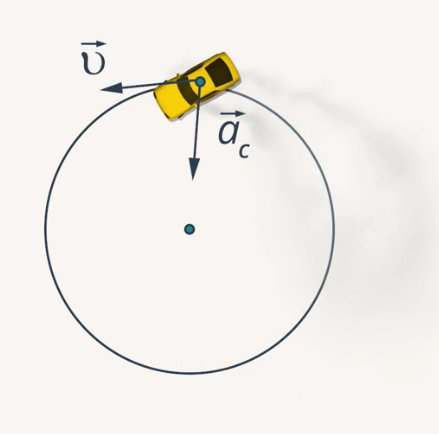
Рис. 7. Центростремительное ускорение
Модуль центростремительного ускорения может быть рассчитан по формуле:

Переходим к описанию равномерного движения тела по окружности. Договоримся, что скорость  , которой вы пользовались по время описания поступательного движения, теперь будет называться линейной скоростью. И под линейной скоростью мы будем понимать мгновенную скорость в точке траектории вращающегося тела.
, которой вы пользовались по время описания поступательного движения, теперь будет называться линейной скоростью. И под линейной скоростью мы будем понимать мгновенную скорость в точке траектории вращающегося тела.

Рис. 8. Движение точек диска
Рассмотрим диск, который для определенности вращается по часовой стрелке. На его радиусе отметим две точки  и
и  (рис. 8). Рассмотрим их движение. За некоторое время
(рис. 8). Рассмотрим их движение. За некоторое время  эти точки переместятся по дугам окружности и станут точками
эти точки переместятся по дугам окружности и станут точками  и
и  . Очевидно, что точка
. Очевидно, что точка  совершила большее перемещение, чем точка
совершила большее перемещение, чем точка  . Из этого можно сделать вывод, что чем дальше от оси вращения находится точка, тем с большей линейной скоростью она движется
. Из этого можно сделать вывод, что чем дальше от оси вращения находится точка, тем с большей линейной скоростью она движется 
Однако если внимательно посмотреть на точки  и
и  , можно сказать, что неизменным остался угол
, можно сказать, что неизменным остался угол  , на который они повернулись относительно оси вращения
, на который они повернулись относительно оси вращения  . Именно угловые характеристики мы и будем использовать для описания движения по окружности. Отметим, что для описания движения по окружности можно использовать угловые характеристики.
. Именно угловые характеристики мы и будем использовать для описания движения по окружности. Отметим, что для описания движения по окружности можно использовать угловые характеристики.
Начнем рассмотрение движения по окружности с самого простого случая – равномерного движения по окружности. Напомним, что равномерным поступательным движением называется движение, при котором за любые равные промежутки времени тело совершает одинаковые перемещения. По аналогии можно дать определение равномерного движения по окружности.
Равномерным движением по окружности называется движение, при котором за любые равные промежутки времени тело поворачивается на одинаковые углы.
Аналогично понятию линейной скорости вводится понятие угловой скорости.
Угловой скоростью равномерного движения ( называется физическая величина, равная отношению угла, на который повернулось тело, ко времени, за которое произошел этот поворот.
называется физическая величина, равная отношению угла, на который повернулось тело, ко времени, за которое произошел этот поворот.
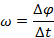
В физике чаще всего используется радианная мера угла. Например, угол в  равен
равен 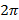 радиан. Измеряется угловая скорость в радианах в секунду:
радиан. Измеряется угловая скорость в радианах в секунду:

Найдем связь между угловой скоростью вращения точки и линейной скоростью этой точки.

Рис. 9. Связь между угловой и линейной скоростью
Точка  проходит при вращении дугу длиной
проходит при вращении дугу длиной  , поворачиваясь при этом на угол
, поворачиваясь при этом на угол  . Из определения радианной меры угла можно записать:
. Из определения радианной меры угла можно записать:

Разделим левую и правую части равенства на промежуток времени  , за который было совершено перемещение, затем воспользуемся определением угловой и линейной скоростей:
, за который было совершено перемещение, затем воспользуемся определением угловой и линейной скоростей:


Обратим внимание, что чем дальше точка находится от оси вращения, тем выше ее линейная скорость. А точки, расположенные на самой оси вращения, неподвижны. Примером этого может служить карусель: чем ближе вы находитесь к центру карусели, тем легче вам на ней удержаться.
Такая зависимость линейной и угловой скоростей используется в геостационарных спутниках (спутники, которые всегда находятся над одной и той же точкой земной поверхности). Благодаря таким спутникам мы имеем возможность получать телевизионные сигналы.
Вспомним, что ранее мы вводили понятия периода и частоты вращения.
Период вращения – время одного полного оборота. Период вращения обозначается буквой 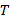 и измеряется в секундах в СИ:
и измеряется в секундах в СИ:

Частота вращения – физическая величина, равная количеству оборотов, которое тело совершает за единицу времени.
Частота обозначается буквой  и измеряется в обратных секундах:
и измеряется в обратных секундах:

Они связаны соотношением:
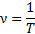
Существует связь между угловой скоростью и частотой вращения тела. Если вспомнить, что полный оборот равен 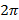 , легко увидеть, что угловая скорость:
, легко увидеть, что угловая скорость:

Подставляя эти выражения в зависимость между угловой и линейной скоростью, можно получить зависимость линейной скорости от периода или частоты:

Запишем также связь между центростремительным ускорением и этими величинами:

Таким образом, мы знаем связь между всеми характеристиками равномерного движения по окружности.
Подытожим. На этом уроке мы начали описывать криволинейное движение. Мы поняли, каким образом можно связать криволинейное движение с движением по окружности. Движение по окружности всегда является ускоренным, а наличие ускорения обуславливает тот факт, что скорость всегда меняет свое направление. Такое ускорение называется центростремительным. Наконец, мы вспомнили некоторые характеристики движения по окружности (линейную скорость, угловую скорость, период и частоту вращения) и нашли соотношения между ними.
Список литературы
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
- А.П. Рымкевич. Физика. Задачник 10-11. – М.: Дрофа, 2006.
- О.Я. Савченко. Задачи по физике. – М.: Наука, 1988.
- А.В. Перышкин, В.В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Аyp.ru (Источник).
- Википедия (Источник).
Домашнее задание
Решив задачи к данному уроку, вы сможете подготовиться к вопросам 1 ГИА и вопросам А1, А2 ЕГЭ.
- Задачи 92, 94, 98, 106, 110 – сб. задач А.П. Рымкевич, изд. 10
- Вычислите угловую скорость движения минутной, секундной и часовой стрелок часов. Вычислите центростремительное ускорение, действующее на кончики этих стрелок, если радиус каждой из них равен одному метру.
interneturok.ru
План-конспект урока по физике «Равномерное движение по окружности» (10 класс)
Тема: Равномерное движение тела по окружности. Период и частота обращения. Угловая скорость.
Цель: обучающая — познакомить учащихся с понятием «криволинейное движение», физическими величинами, которые характеризуют это движение;
развивающая – научить учащихся использовать свои знания для решения соответствующих задач, формировать умения объяснять процессы, которые происходят при равномерном движении тела по окружности, развивать память, познавательный интерес;
воспитательная – воспитывать внимание, чувство ответственности во время самостоятельной работы, формировать жизненные компетентности учащихся.
Оборудование: фотографии для демонстрации направления скорости во время движения по окружности, проигрыватель дисков, вентилятор, которые работают на разных частотах вращения.
Тип урока: урок изучения нового материала.
Демонстрации: направление линейной скорости во время движения по окружности.
План урока.
1. Организационный этап. (1 мин.)
2. Сообщение темы, цели и задач урока. (2 мин.)
3. Актуализация опорных знаний. (5 мин.)
4. Изучение нового материала. (21 мин.)
5. Закрепление. (12 мин.)
6. Подведение итогов урока. (3 мин.)
7. Домашнее задание. (1 мин.)
Ход урока.
1. Организационный этап.
Приветствие. Организация рабочих мест.
2. Сообщение темы, цели и задач урока.
Учитель сообщает тему и цели урока.
3. Актуализация опорных знаний.
3.1. Ответы на вопросы
— При свободном падении движение тела…
А) Равномерное. Б) Неравномерное. В) Равноускоренное.
Г) Равнозамедленное. Д) Среди ответов правильного нет.
— Ускорение свободного падения направлено…
А) вертикально вверх при движении тела вверх.
Б) Вертикально вниз при падении тела вниз.
В) Всегда вертикально вниз.
Г) Всегда вертикально вверх.
Д) Среди ответов правильного нет.
— Шарик падает на землю. Если сопротивление воздуха отсутствует, то скорость шарика…
А )Увеличивается. Б) Уменьшается. В) Остается постоянной.
Г) Сначала увеличивается, потом уменьшается.
Д) Среди ответов правильного нет.
— Тело бросили вертикально вверх. Если сопротивление воздуха отсутствует,
то ускорение тела…
А) В верхней точке равняется нулю.
Б) В верхней точке изменяет направление.
В) Увеличивается при падении на землю.
Г) Уменьшается при падении на землю.
Д) Одинаково на протяжении всего полета.
3.2. Решение задач.
Задача 1.
Шарик бросили вертикально вверх. Какие из представленных графиков отвечают движению этого шарика? Сопротивление воздуха отсутствует. h – высота шарика над землей, v и a – модули скорости и ускорения соответственно…
h v v a
t t t t
А) а; Б)б; В)в; Г)г; Д) среди ответов А-Г правильного нет.
Задача 2.
Шарик упал на горизонтальную поверхность и, ударившись, подпрыгнул на ту же высоту. Какие из приведенных графиков соответствуют движению этого шарика? Сопротивление воздуха отсутствует. h – высота шарика над землей, v и a – модули скорости и ускорения соответственно…
h v v a
t t t t
А) а; Б)б; В)в; Г)г; Д) среди ответов А-Г правильного нет.
4. Изучение нового материала.
4.1. Равномерное движение материальной точки окружности. Линейная скорость.
Движение тела по окружности является частным случаем криволинейного движения.
Движение, при котором материальная точка движется по окружности с постоянной скоростью, называют равномерным движением по окружности.
Допустим, что материальная точка движется равномерно по окружности и в момент t1 находится в положении А (рис. 1), а в момент t2 точка заняла положение В. Радиус, проведенный из центра окружности к материальной точке, за это время описал угол φ, который называют угловым перемещением.
Угловое перемещение в международной системе единиц выражают в радианах.
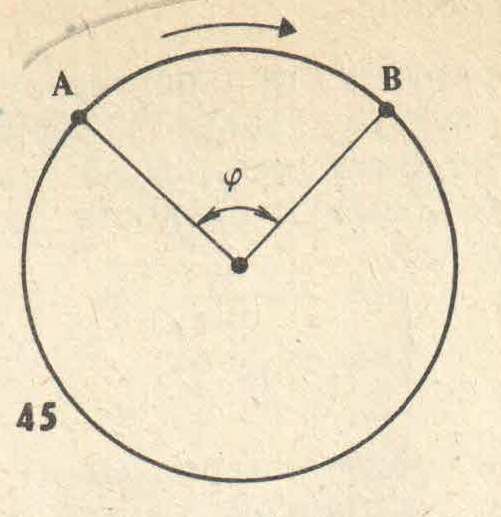
Рисунок 1.
Радиан – центральный угол между двумя радиусами окружности, длина дуги между двумя радиусами окружности. Т.е. наряду с вектором перемещения Δl удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах (рис 2). Длина дуги связана с углом поворота соотношением
Δl = R Δφ.При малых углах поворота Δl ≈ Δs.
Рисунок 2.Допустим что материальная точка равномерно движется по окружности радиусом R (рис. 1). Так как движение точки равномерное, то модуль скорости постоянен. Например, за очень малое время точка переместилась из положения А1 в положение В1 (на рис. 3 для наглядности перемещение А1 В1 показано увеличенным).
Тогда по общему определению скорости линейная скорость на участке направлена вдоль хорды А1 В1. так как хорда при уменьшении промежутка времени все более приближается к дуге, то вектор скорости в середине участка А1 В1 (в точке С) направлен по касательной к дуге.
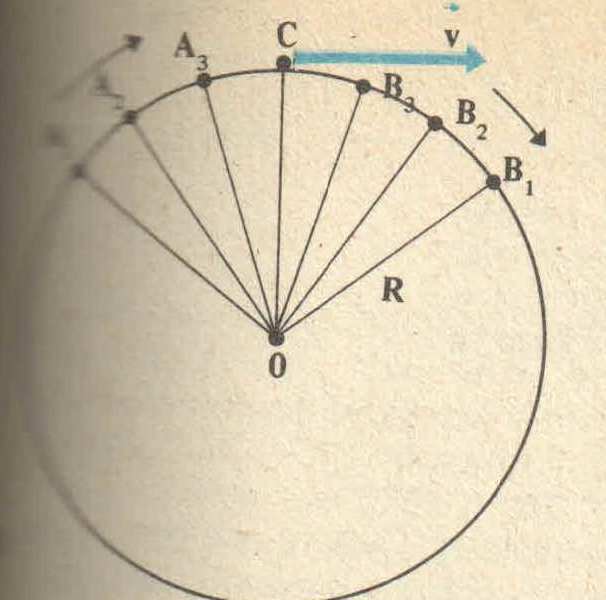
Рисунок 3.
Следовательно, и мгновенная скорость в любой другой точке окружности направлена по касательной. В этом можно убедиться, если прижать к вращательному точильному камню конец стального прутка. Раскаленные частицы, отрывающиеся от камня и летящие с той скоростью, которой они обладали в момент отрыва, будут видны в виде искр.
Направление вылета искр всегда совпадает с касательной к окружности в той точке, где пруток касается камня, по касательной окружности движутся и брызги от колес буксующего автомобиля (рис 4). Таким образом, линейная скорость тела, движущегося по окружности, оставаясь постоянной по модулю, непрерывно изменяется по направлению и в любой точке направлена по касательной к траектории.
Так как модуль линейной скорости постоянен, то его можно определить по формуле . За один оборот () тело пройдет расстояние, равное длине окружности: s = 2πR, или , учтя, что Т = , 2πR.
Найдем отношение линейной скорости к угловой:
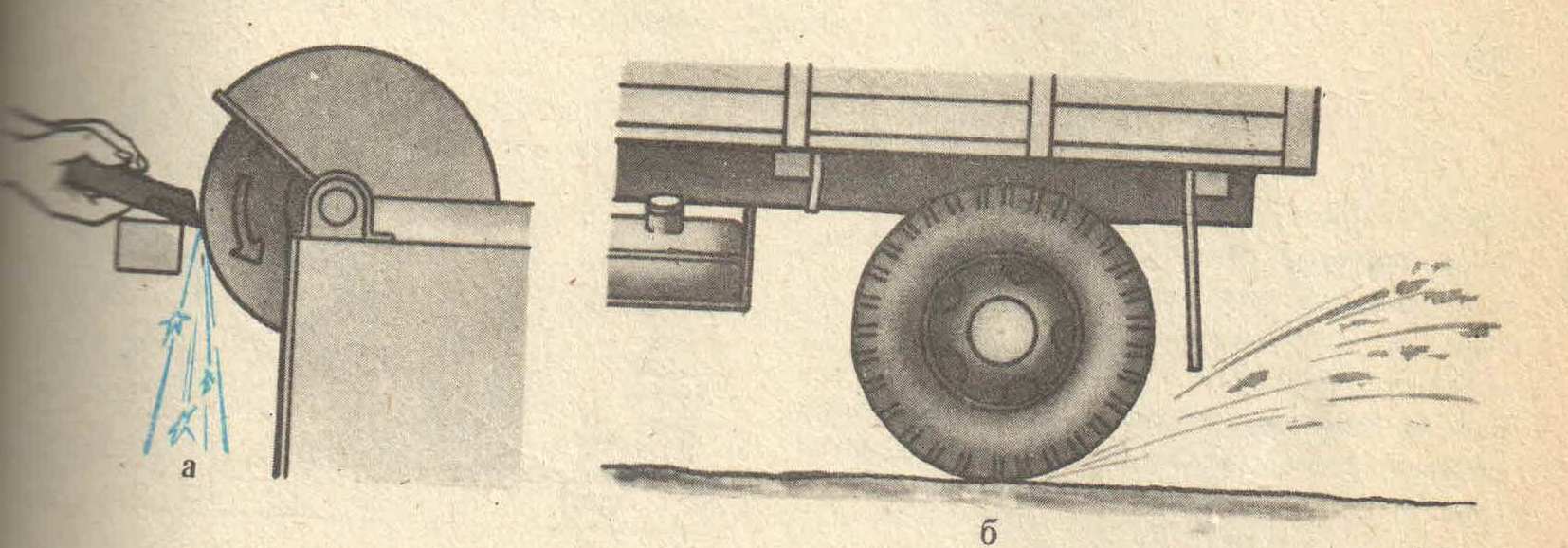 Рисунок 4.
Рисунок 4.
= R.
Таким образом,
v =wRw =
4.2. Угловая скорость.
Угловой скоростью ω тела в данной точке круговой траектории называют отношение углового перемещения Δφ к промежутку времени Δt, в течение которого это перемещение произошло.
ω=∆φ/∆t
Угловая скорость измеряется в рад/с. За единицу угловой скорости в Международной системе единиц принята скорость такого равномерного движения тела по окружности, при котором в каждую секунду совершается угловое перемещение в 1 радиан. Эта единица угловой скорости называется радиан в секунду и обозначается 1 рад/с.
Связь между модулем линейной скорости υ и угловой скоростью ω:
v = ωR.При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора .
4.3. Ускорение при равномерном движении тела по окружности.
При равномерном движении тела по окружности его линейная скорость, оставаясь постоянной по модулю, непрерывно изменяется по направлению. Но изменение скорости по направлению свидетельствует о том, что при равномерном движении тела по окружности есть ускорение, которое и является причиной непрерывного изменения направления скорости. Это ускорение получило название центростремительное.
По определению ускорение характеризует быстроту изменения скорости и равно отношению изменения скорости к промежуточному времени, за которое это изменение произошло, а его направление совпадает с направлением вектора изменения скорости
= , или в скалярной форме =
Как найти центростремительное ускорение? Допустим, что тело, равномерно движущееся по окружности, в момент времени находилось в точке А (рис.5), а через очень малый промежуток времени переместилось в очень близко расположенную точку В (на рисунке расстояние АВ для наглядности показано увеличенным). Скорость в точке А обозначим A, а в точке В В. Модули скорости в точках А и В одинаковы. Для того, чтобы найти изменение скорости за времявычесть (по правилу треугольника) из вектора В вектор А.
∆ = В — А
Векторы скоростей и в точках A и B направлены по касательным к окружности в этих точках. Модули скоростей одинаковы υA = υB = υ.
Из подобия треугольников OAB и BCD (рис. 5) следует:
=
а = == ;
Таким образом, при равномерном движении тела (материальной точки) по окружности ускорение в любой точке траектории перпендикулярно скорости движения и направлено к центру окружности. Модуль его равен частному от деления квадрата линейной скорости на радиус вращения.
Итак, равномерное движение тела по окружности является движением с ускорением. Модуль ускорения
а =
направлено по радиусу к центру окружности. Его называют центростремительным ускорением. Модуль центростремительного ускорения связан с линейной υ и угловой ω скоростями соотношениями:
а = = R
При изменении положения тела на окружности изменяется направление скорости и ускорения. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем.
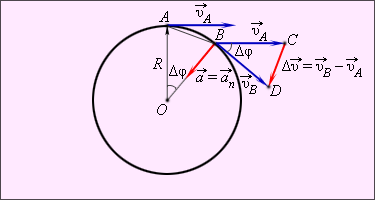
Рисунок 5.
4.4. Частота и период обращения.
Частотой обращения называют число оборотов материальной точки вокруг центра обращения за секунду. Частоту обращения принято обозначать греческой буквой v(ню):
V =
Рисунок 6. Рисунок 7.
где — число оборотов, совершенных за время . За единицу частоты в международной системе единиц 1 оборот в секунду. Его сокращенное обозначение – 1 с -1.
Периодом обращения называется время, в течение которого совершается один оборот точки по окружности. Период обозначают буквой Т:
Т =За единицу периода в международной системе единиц принята секунда — 1 с. Нетрудно заметить, что период и частота – величины взаимно обратные:
Т =5. Закрепление.
5.1. Решение задач.
Задача 1.
Определите модуль скорости и центростремительного ускорения точек земной поверхности на экваторе. Радиус Земли принять равным 6400 км.
Дано:
R = 6400 км = 6,4 . 106 м;
Т = 24 ч = 8,64 . 104 с
Найти:
V — ?
ацс — ?
Решение:
Точки земной поверхности на экваторе движутся по окружности радиуса R , поэтому модуль их скорости
R = .
V = . 102 ≈ 4,65 . 102 = 465 м/с
Центростремительное ускорение можно найти:
ацс =
ацс = = = . 10-2 = 3,4 . 10-2 = 0,034 м/с
Ответ:= 465 м/с; ацс = 0,034 м/с
Задача 2.
Велосипедист движется по закруглению дороги радиусом 100 м со скоростью 10 м/с . С каким ускорением он проходит закругление?
Дано:
R = 100 м;
V = 10 м/с;
Найти:
ацс = ?
Решение:
Велосипедист движется равномерно по дуге окружности радиуса R, поэтому возникает центростремительное ускорение, которое можно определить по формуле:
ацс = ; ацс = = = 1 м/с.
Ответ: ацс = 1 м/с.
Задача 3.
Каков радиус кривизны закругления дороги, если по ней автомобиль движется с центростремительным ускорением 2 м/с2 при скорости 72 км/ч?
Дано:
ацс = 2 м/с2
= 72 км/ч = 20 м/с
Найти:
R = ?
Решение:
Из формулы центростремительного ускорения опредилим радиус кривизны закругления дороги:
ацс = → R = R = [].
R = = = 200 м
Ответ: R = 200 м.
6. Подведение итогов урока.
Открытый микрофон.
«На уроке я узнал (а) о… Особенно интересным было… Не понятным осталось…»
7. Домашнее задание
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский. Физика, 10 класс, М., «Просвещение», 2016. Читать § 16-17 (с.57-62).
Решить задачи 1,2 (с.63).
infourok.ru
Равномерное движение по окружности. Видеоурок. Физика 11 Класс
На этом уроке мы рассмотрим криволинейное движение, а именно равномерное движение тела по окружности. Вспомним величины, которые характеризуют вращательное движение. Также решим несколько задач из сборника для подготовки к единому государственному экзамену различной сложности по данной теме, которые позволят вам увидеть, как применять на практике изученный материал
В уравнения кинематики равномерного движения по окружности входят следующие понятия:
1. T (период) – время одного полного оборота.
2.  – частота обращения.
– частота обращения.
Частота и период – обратно пропорциональные величины:
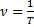
3. R – радиус окружности, по которому движется тело
4.  – линейная скорость (скорость вдоль траектории). Так как за время, равное периоду, тело проходит путь, равный длине окружности, то:
– линейная скорость (скорость вдоль траектории). Так как за время, равное периоду, тело проходит путь, равный длине окружности, то:

5.  – угловая скорость. Она равна отношению угла поворота за все время периода ко времени одного полного оборота.
– угловая скорость. Она равна отношению угла поворота за все время периода ко времени одного полного оборота.

Линейная скорость связана с угловой следующим соотношением:

6. Если происходит равномерное движение по окружности, то это не означает, что оно не имеет ускорения. Скорость по величине не меняется, но по направлению скорость меняется все время. Поэтому нормальное ускорение, которое характеризует быстроту изменения направления скорости, в данном случае называется центростремительным (направлено к центру окружности) и вычисляется по следующим формулам:
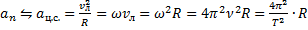
Найти линейную скорость точки при движении по окружности радиусом 1 м при угловой скорости  . Варианты ответа: 1.
. Варианты ответа: 1. 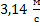 ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  .
.
Дано:  ;
; 
Найти: 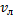
Решение
Линейная скорость находится по следующей формуле:

Ответ: 3.  .
.
Найти период вращения вала при частоте 60 оборотов в минуту. Варианты ответа: 1.  ; 2.
; 2. 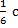 ; 3.
; 3.  ; 4.
; 4. 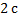 .
.
Дано: 
Найти: 
Решение
Частота равна 60 оборотов в минуту, а минута – это 60 секунд, следовательно, за 60 секунд выполняется 60 оборотов, а за одну секунду выполняется один оборот. Одна секунда и есть искомый период вращения.


Ответ: 3.  .
.
Длина минутной стрелки часов в 1,5 раза больше длины часовой стрелки. Во сколько раз скорость конца минутной стрелки больше скорости конца часовой? Варианты ответа: 1. 12; 2. 18; 3. 24; 4. 36.
Дано: 
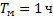 ;
; 
Найти: 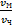
Решение
Скорость при движении по окружности вычисляется по формуле:

Следовательно:

Ответ: 2. 18.
Найти радиус вращающегося колеса, если известно, что линейная скорость точки, лежащей на ободе, в 4 раза больше линейной скорости точки, лежащей на 0,9 м ближе к оси колеса.
Дано:  ;
;  (см. Рис. 1)
(см. Рис. 1)
Найти: R
Решение
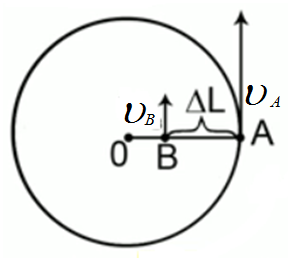
Рис. 1. Иллюстрация к задаче
На рисунке 1 изображено колесо. Точка A лежит на ободе, точка B ближе к оси колеса на 
При вращении колеса общей кинематической величиной для всех точек является угловая скорость (все точки двигаются с одной и той же угловой скоростью).
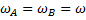
Следовательно, линейная скорость точки A равна:
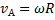
Линейная скорость точки B равна:
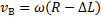
Поэтому, если:

то:
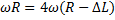
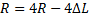
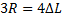
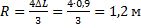
Ответ: 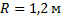 .
.
Найти скорость и ускорение Исаакиевского собора, обусловленные вращением Земли.
Дано: 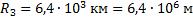 – радиус Земли; Исаакиевский собор находится в Санкт-Петербурге, который находится на
– радиус Земли; Исаакиевский собор находится в Санкт-Петербурге, который находится на 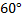 северной широты
северной широты 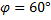 ;
; 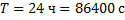 – время обращения Земли вокруг своей оси (см. Рис. 2).
– время обращения Земли вокруг своей оси (см. Рис. 2).
Найти: 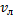 ;
; 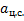
Решение

Рис. 2. Иллюстрация к задаче
Исаакиевский собор вместе с Землей совершает движение по окружности, радиус которой равен:
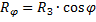
Следовательно, скорость Исаакиевского собора будет равна отношению длины этой окружности к периоду:
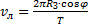
Подставим в это выражение известные значения:
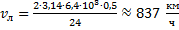
Центростремительное ускорение вычисляется по формуле:
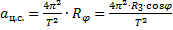
Подставим в это выражение известные значения:
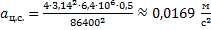
Ответ: 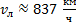 ;
; 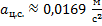 .
.
Список литературы
- Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10. – М.: Просвещение, 2008.
- А.П. Рымкевич. Физика. Задачник 10–11. – М.: Дрофа, 2006.
- О.Я. Савченко. Задачи по физике. – М.: Наука, 1988.
- А.В. Перышкин, В.В. Крауклис. Курс физики. Т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.
- Орлов В.А., Демидова М.Ю., Никифоров Г.Г., Ханнанов Н.К. Оптимальный банк заданий для подготовки к ЕГЭ. Единый государственный экзамен 2015. Физика. Учебное пособие. – М.: Интеллект-Центр, 2015
Домашнее задание
- Упражнение 5 (1,2) стр. 52 – Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский. Физика 10 (см. список рекомендованной литературы)
- Автомобиль движется по дороге со скоростью 72 км/час. Определите, с какой скоростью относительно Земли движется ось его колеса, его нижняя и верхняя точки.
- Период вращения лопастей ветряной мельницы равен 5 с. Определите число оборотов лопастей за 1 ч.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал eduspb.com (Источник).
- Интернет-портал Abramova.vitut.ru (Источник).
- Интернет-портал Bambookes.ru (Источник).
interneturok.ru