Решение задач онлайн

Решение Ваших математических задач в онлайн режиме. Бесплатная версия программы предоставляет Вам только ответы. Если вы хотите увидеть полное решение, Вы должны зарегистрироваться для бесплатной полной пробной версии.

Основы математики

Онлайн программа решения математических задач предлагает Вам решение в режиме онлайн задач с дробями, корнями, метрическими преобразованиями.
Вы можете найти площадь и объем прямоугольника, окружности, треугольника, трапеции, куба, цилиндра, конуса, пирамиды, шара.
Вы можете упростить, найти значение, объединять и умножать выражения.

Онлайн программа решения задач курса предварительной алгебры (геометрии)

Вы можете решать все задачи с основного раздела математики а также координатных задач, простых уравнений, неравенств, упрощать выражения.
Вы можете подсчитывать выражения, объединить выражения и умножать / делить выражения.

Онлайн программа решения задач по алгебре

Мы рекомендуем Вам зарегистрироваться для этой онлайн программы.
Решите Ваши задачи (уравнения, неравенства, радикалы, построение графиков, решение полиномов) в онлайн режиме.
Если Ваша домашняя работа включает в себя математические уравнения, неравенства, функции, многочлены, матрицы, значит регистрация для тестовой версии — это правильный выбор.

Онлайн программа решения задач по тригонометрии

Находит значения всех типов выражений (синус, косинус, тангенс, котангенс, секанс, косеканс), уравнений, неравенств.
Строит графики тригонометрических функций.
Тригонометрия прямоугольного треугольника.

Онлайн программа решения задач курса предварительной алгебры

Включает в себя все вышеперечисленное функции плюс нахождение пределов (LIM), сумм, матриц.

Онлайн программа решения задач курса высшей математики

Решение задач c определенными, неопределенными интегралами.

Онлайн программа решения статистических задач

Решайте задач с нахождением вероятности, комбинаторные задачи. Статистические задачи — найти среднее (арифметическое, геометрическое, квадратическое) значение, распределение, нормальное распределение, т-распределение.
Онлайн программа успешно проводит тестирование статистических гипотез

www.math10.com

Уроки по геометрии в режиме онлайн

Геометрия – наука, без которой невозможно представить себе современный мир и общество. Она оказала огромное влияние на развитие человечества, и переоценить роль этой науки поистине сложно. К сожалению, у многих возникают проблемы с изучением геометрии, которая изобилует сложными темами с большим количеством формул и правил. Без помощи опытных педагогов самостоятельное изучение и уж тем более подготовка к экзамену по геометрии будет очень трудной и малоэффективной.

Но что же делать, если в школе на уроке тему усвоить не удалось, а на дополнительные занятия с помощью репетитора или на посещение отдельных факультативных занятий нет ни времени, ни денег? Такие ситуации, к сожалению, нередки, а значит, нужно браться за поиски других методов. Наш образовательный портал поможет решить проблему! В этом помогут видеоуроки по геометрии. Зайдите в раздел видео «Геометрия» и приступайте к изучению. Видеоуроки и ролики с лекциями представляют крайне эффективный метод усвоения информации.

На страницах портала находятся материалы по школьным темам с 7 по 11 класс:

Программа 7 класса включает уроки геометрии онлайн по таким темам, как измерение отрезков и углов (их сравнение), лучи и угол (смежные и вертикальные), перпендикулярные прямые и т.д. Множество видеоуроков посвящено решениям геометрических задач по темам «Параллельные прямые и сумма углов треугольника», «Построение» и т.д. Эти материалы позволят подготовиться к экзамену по геометрии наиболее тщательно.

Видеоуроки по программе 8 класса посвящены повторению темы «Треугольники», раскрывают понятие четырехугольников, помогают в решении сложных задач и объясняют их применение в доказательстве теорем. Стоит отметить, что все конспекты уроков по геометрии представлены на нашем сайте абсолютно бесплатно.

Материалы за 9 класс также представляют собой бесплатные конспекты уроков по геометрии. Такие темы, как «Метод координат», «Координаты вектора», «Сложение и вычитание векторов», «Умножение вектора на число в координатах», а также множество других подробно описываются в формате видео. Видеоуроки по геометрии за 10 класс средней общеобразовательной школы посвящены таким темам, как «Предмет стереометрии, ее аксиомы, следствия из них», «Решение задач по стереометрии», «Параллельность прямых и плоскостей, их свойства». Описание этих тем сопровождается решением соответствующих задач.

Поскольку, помимо обязательных для изучения тем, которые входят в стандартный учебник по геометрии, бесплатные видеоматериалы образовательного портала InternetUrok.ru содержат немало дополнительных уроков, у каждого пользователя есть возможность значительно повысить уровень своих знаний. Этот метод изучения геометрии имеет ряд преимуществ. Это, прежде всего, большая экономия времени: ведь ознакомление с материалами учебника по геометрии в режиме онлайн протекает гораздо быстрее. Кроме того, количество видеолекций постоянно растет: ведь современный мир видеоуроков непрерывно развивается, в нем появляется множество новых материалов. Также стоит отметить, что запись видеоуроков осуществляется настолько качественно, что их использование в учебе рекомендуют сами преподаватели.

Просмотр учебного видео дополняет уроки в школе. Заходите на наш сайт и просматривайте уроки геометрии бесплатно и на высокой скорости – эффективность такого метода обучения доказана уже давно. Наш сайт предлагает вам сборник видеоуроков с примерами экзаменационных задач по геометрии, а это значит, что с его помощью подготовка к экзамену по геометрии может проходить бесплатно и гораздо быстрее, нежели при использовании традиционных печатных учебников. Отметим, что сегодня почти любая школа использует формат видео, чтобы сделать уроки максимально информативными и полезными для учеников.

interneturok.ru

Осваиваем простые приемы решения геометрических задач

Идея I

Если в четырехугольнике суммы противоположных углов равны 180°, то вокруг этого четырехугольника можно описать окружность.

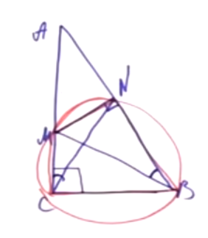
Задача. Дан прямоугольный треугольник ABC. На катете АС выбрана произвольная точка М. Из точки М опущен перпендикуляр MN на гипотенузу. Докажите, что углы MCN и MBN равны.

Решение. Угол MNB — прямой. По условию, треугольник ABC прямоугольный, значит, есть еще один прямой угол. Обратим внимание на четырехугольник MNBC: в нем есть два противолежащих прямых угла, их сумма равна 180°. Следовательно, вокруг четырехугольника MNBC можно описать окружность. Углы, равенство которых нужно доказать, опираются на одну дугу MN и являются вписанными. Два вписанных угла опираются на одну и ту же дугу, значит, они равны.

Геометрия. 7 класс

Учебник предназначен для изучения геометрии в 7 классе общеобразовательных организаций. В нем предусмотрена уровневая дифференциация, позволяющая формировать у школьников познавательный интерес к математике.

Купить

Идея II

Если известен угол треугольника, можно найти угол между биссектрисами, обращенными в сторону этого угла.

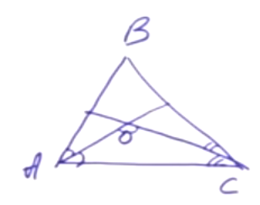
Задача. Дан треугольник ABC. Проведены биссектрисы углов A и С, они пересекаются в точке O. Найдите угол AOC (т.е. есть угол между биссектрисами).

Решение. Известно, что ∠ABC = ∠В. Эту задачу легко решить с помощью теоремы суммы углов треугольников. ∠A + ∠C = 180° – ∠B. Суммы половинок углов А и С равны 90° – ½ ∠B. Тогда ∠AOC = 90° + ½ ∠B.

Совмещение идей I и II

Некоторые задачи находятся как бы на пересечении нескольких идей решения.

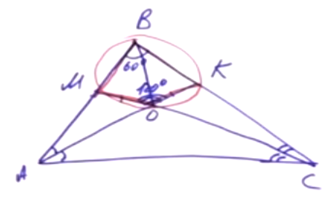
Задача. Дан треугольник ABC. Известно, что угол В равен 60°. Проведены биссектрисы углов: АК и СМ, они пересекаются в точке О. Докажите, что отрезок ОМ равен отрезку ОК.

Решение. Найдем угол АОС по формуле 90° + ½ ∠B. ∠В = 120°. Обращаем внимание на четырехугольник МВКО. В нем сумма противоположных углов равна 180°, значит, вокруг него можно описать окружность. О — точка пересечения биссектрис треугольника АВС. Следовательно, луч ВО делит угол АВС пополам. ∠МВО = ∠ОВК. Данные углы являются вписанными, значит, равны и дуги, на которые они опираются. Дуга МО равна дуге ОК. Известно, что равные дуги стягивают равные хорды. Хорда ОМ равна хорде ОК.

Идея III

Если из двух точек, лежащих в одной полуплоскости, отрезок между двумя другими точками виден под одним и тем же углом, то эти 4 точки лежат на одной окружности.

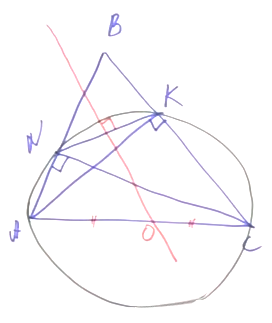
Задача. Дан остроугольный треугольник АВС. Проведены две высоты: АК и СN. Докажите, что серединный перпендикуляр отрезка NK пересекает отрезок АС в середине (точка О является серединой отрезка АС).

Решение. ∠ANC = ∠AKC. Мы можем нарисовать окружность вокруг четырехугольника ANKC. Отрезок NK является в этой окружности хордой, а АС — диаметром, поскольку он виден из точек N и K под прямым углом. Серединный перпендикуляр проведен к хорде, он содержит диаметр окружности. Два диаметра пересекаются в центре окружности. О — это центр окружности. АО и ОС — это диаметры. Следовательно, АО = ОС.

Читайте также:

Идея IV

Если в треугольнике продлить медиану и построить параллелограмм, можно извлечь много дополнительных данных для решения задачи.

Задача. Дан треугольник АВС и его медиана ВМ. Известно, что ВМ в два раза меньше стороны АВ. Докажите, что угол МВС равен сумме ∠А + ∠С.

Решение. Воспользуемся построением параллелограмма. Проведем МК. BM = ½ ВК. Следовательно, АВ = ВК. В этом случае треугольник АВК является равнобедренным. В равнобедренном треугольнике углы при основании равны, значит, ∠ВАК = ∠ВКА. ∠КАМ = ∠С. ∠АКВ = ∠СВК. Из этого мы получаем необходимое равенство.

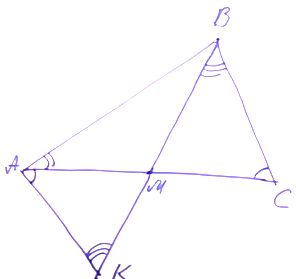
Совмещение идей III и IV

Задача. Дан треугольник АВС, в котором проведена медиана ВМ. На медиане ВМ выбрана точка К так, что ∠ВАС = ∠АКМ. Докажите, что ∠ АСВ = ∠МКС.

Решение. Продлим медиану на ее длину и получим точку N. BM = MN. ABCN — параллелограмм. ∠BAC = ∠ACN. Из точек К и С, лежащих по одну сторону от прямой, видим отрезок AN под одним и тем же углом. Вокруг четырехугольника AKCN описываем окружность. Поскольку ABCN — параллелограмм, ∠NAC = ∠BCA. Но углы NAC и NKC являются вписанными, опирающимися на одну дугу. Следовательно, ∠NAC = ∠NKC. Так мы доказали, что ∠МКС = ∠МСВ.

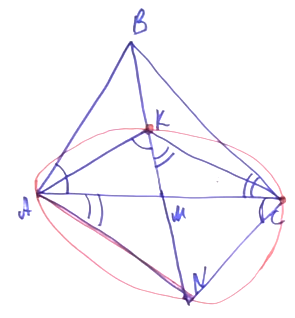
Геометрия. 8 класс. Рабочая тетрадь № 1

Рабочая тетрадь содержит различные виды заданий на усвоение и закрепление нового материала, задания развивающего характера, дополнительные задания, которые позволяют проводить дифференцированное обучение.

Купить

Идея V

Если в прямоугольном треугольнике АВС проведена медиана из вершины прямого угла, то медиана СМ будет равняться половине гипотенузы АВ. То есть СМ = АМ = МВ.

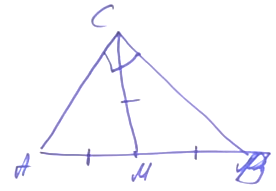
Задача. Дан треугольник АВС. На внешние стороны построены два прямоугольных треугольника: ADB и BEC. Докажите что отрезок DE, соединяющий вершины прямых улов, не больше полпериметра треугольника АВС.

Решение. Проведем медианы через точки M и N (середины сторон АВ и ВС). Соединим точки, образовав четырехугольник DENM. Звено ломаной DE не превосходит сумму длин отрезков DM + MN + NE. DE ≤ DM + MN + NE = ½ АВ + ½ АС + ½ ВС. Следовательно, DE ≤ ½ Р_авс

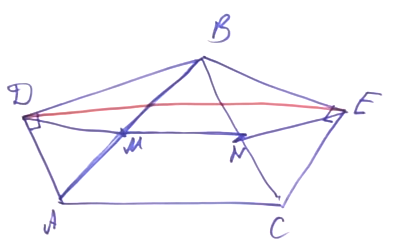
Факт, обратный данному. Если в треугольнике АВС медиана СМ равна половине стороны АВ, значит, АСВ = 90°. Т.е. если в треугольнике медиана равна половине стороны, к которой она проведена, то этот треугольник является прямоугольным. Рассмотрим эту идею, продемонстрировав также, как только с помощью линейки можно решить задачу на построение перпендикуляра к данной прямой.

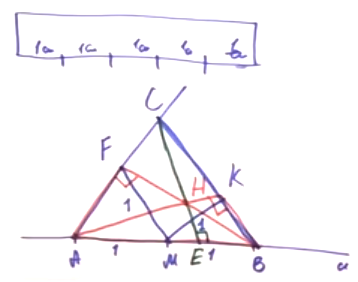
Возьмем линейку с ценой деления 1 см. Отложим отрезки: точки А, М и В, так, что АМ = МВ = 1 см. Развернув линейку, поставим точку F (MF = 1 см) и точку К (МК = 1 см). С помощью линейки соединим A и F, B и K и продлим прямые до пересечения в точке С. На рисунке виден треугольник АFВ. FM в нем медиана, равняющаяся половинке стороны. Следовательно, угол F — прямой. Таким же свойством обладает треугольник АКВ. В треугольнике АСВ отрезки АК и ВF являются высотами. Значит, точка H в пересечении высот является центром треугольника. Если соединить СН и продлить в СЕ, это тоже будет высота треугольника АВС. Следовательно, СЕ перпендикулярно АВ. Так, только с помощью линейки мы провели прямую, перпендикулярную данной.

В  учебниках авторства Мерзляка А.Г., Полонского В.Б. и Якира М.С. образцовые задачи, демонстрирующие ту или иную идею решения, выделены и обозначены изображением ключа. 

#ADVERTISING_INSERT#

rosuchebnik.ru

Математика онлайн

В сервис по мере возможности добавляются новые калькуляторы, а существующие постоянно совершенствуются. Если вам не удалось найти нужный вам калькулятор, которым может быть решена математическая задача, или у вас есть предложения по усовершенствованию уже существующего калькулятора, то сообщите об этом на электронную почту [email protected]

Преимущества нашего сервиса:

• Не требует регистрации.
  Для пользования Math34.biz не требуется регистрации на сайте. Математика онлайн может решаться уже сейчас, без лишней траты времени на заполнение почтовых ящиков и других личных данных.
• Бесплатный. Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.
• Подробное решение. На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом был получен ответ.
• Высокая скорость получения ответа. Математика онлайн решается в сервисе Math34.biz всего за несколько секунд.
• Точность расчета. В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает 100% точность в решение математических задач онлайн. Также у сервиса не может быть опечаток, а последовательность действий всегда четкая и интуитивно понятная.
• Наличие примеров решения задач. Еще до того, как вы введете данные, вы можете посмотреть, как онлайн сервис решает математические задачи на конкретных примерах. Примеры находятся справа от кнопки «Решение». Выберете пример из выпадающего списка и нажмите кнопку «Решение» и вы увидите, как выглядит ответ задачи по математике.
• Удобный интерфейс. Каждый оценит по достоинству удобство пользования сайтом. Удобное меню позволяет быстро переключаться между задачами.

Как пользоваться сервисом?

Решение математики онлайн — это простой и удобный способ справиться с математическими задачами, которые на первый взгляд кажутся непростыми или сверить самостоятельное решение. Пользование сервисом Math34.biz удобное и понятное любому пользователю, попадающему на сайт первый раз. Слева находится меню с названием математических задач, которые можно решить в нашем сервисе: пределы, производная, интегралы, алгебраические уравнения, дифференциальные уравнения, неравенства и многое дрогое. Выберете необходимую вам задачу. Нажав на нее, вы попадете в калькулятор решения с полями, в которые необходимо ввести данные вашей задачи. Заполняете поля и нажимаете кнопку «Решение» — за считанные секунды ответ готов. Чтобы у вас не возникло трудностей с вводом вашей математической задачи, в сервисе предусмотрен раздел Функции и константы https://Math34.biz/functions. В нем вы можете просмотреть как различные константы, элементарные, тригонометрические и гиперболические функции вводятся на сайте.

С нами математика онлайн решается просто и легко. Используйте Math34.biz для решения любых математических задач.

Неравенства. Тождества

math24.biz

решение 📝 задач онлайн и письменно

В областях математики, требующих хорошо развитого пространственного воображения, а именно такой дисциплиной является начертательная геометрия, решение задач онлайн зачастую может стать единственным выходом для студентов гуманитарного склада ума.

Хотя, простыми расчетами на бытовом уровне все мы пользуемся в повседневной жизни, сложные математические и тем более геометрические задачи, а также умение правильно чертить пригодятся в будущем только узким специалистам.

Если добавить к сказанному сложность создания чертежей, которых требует решение задач по инженерной графике и «начерталке», становится понятно: для большинства студентов намного более целесообразным оказывается заказать решение задач по математике, инженерной графике и начертательной геометрии. Решение задач можно получить в режиме онлайн.

Заполнение короткой формы непосредственно на сайте займет меньше минуты, как только вы это сделаете – ваша заявка на решение задач (начертательная геометрия), онлайн поддержки во время экзамена или письменной контрольной, написание курсовой или выполнение чертежей автоматически будет разослано всем специалистам нужного профиля.

Уже через небольшой промежуток времени перед вами окажется несколько предложений от опытных специалистов-практиков, способных выполнить поставленную задачу. За вами останется окончательный выбор исполнителя для решения задач по инженерной графике или онлайн решения задач по начертательной геометрии (по условиям сотрудничества, срокам сдачи, ценам).

Большинство пользователей нашего сайта предпочитают заказать инженерную графику (чертежи) и последующую помощь на экзамене (онлайн решение задач по начертательной геометрии) у одного и того же специалиста. Это оправданно, поскольку стиль выполнения заданий в обоих случаях одинаков, а это лишний раз дает понять преподавателю, что работу и дома, и в аудитории выполнял один человек.

Если вам нужна помощь в такой сложной дисциплине, как начертательная геометрия, закажите решение задач онлайн. В заявку также можно включить:

·         выполнение чертежей, эпюров в карандаше или в компьютерных программах

·         исправление чертежей и эпюров

·         решение задач в Паскаль

·         полное решение всей методички и т.д.

Возможно, вы захотите не только заказать начертательную геометрию и инженерную графику. Сайт «ВсёСдал!» — это виртуальное сообщество действующих специалистов во всех областях науки и учебных дисциплинах. 

vsesdal.com

Решение задач онлайн 📝 на заказ без посредников.

Решение задач на заказ – простой и действенный способ сдачи проверочных работ в университете.

Задачи – это неотъемлемая часть всех технических и естественных дисциплин. Все разделы физики, химии, биологии, подразделы высшей математики и экономики – все это требует знания определенных формул, а также навыков и умений решения задач разных типов и сложности.

Чтобы научиться решать задачи, вам потребуется, как минимум, несколько дней. Они уйдут на то, чтобы как следует разобраться в теме, хорошо выучить все необходимые формулы, проработать разные способы решения задач каждого типа, а также дать информации как следует «устаканиться» в голове. Если у вас есть время и желание учиться в течение всего семестра, и вы можете позволить себе неспешно осваивать решение задач, вам очень повезло. Всем остальным мы предлагаем заказать решение задач на нашем сайте.

Большинство современных студентов занято всем на свете, но только не учебой. Это понятно: студенческие годы – самое веселое и беззаботное время. После школы перед молодыми людьми открывается огромный и интересный мир, в который они погружаются с головой. Учебе в их жизни почти не остается места. Так было во все времена. Однако сейчас вести беззаботную студенческую жизнь стало намного легче. Ведь есть интернет, где при необходимости можно заказать срочное решение задач по физике, химии, высшей математике, информатике или другим предметам.

Заказать решение задач

Решение задач за деньги – это простой, быстрый и эффективный способ сдать контрольную или лабораторную работу, зачет или экзамен. Если вы решили заказать решение задач, первое, что вам нужно – найти место, где это можно сделать. Выбрать из множества одинаковых предложений сайт, где решают задачи действительно качественно может быть непросто. Но мы можем сказать с уверенностью: если вы зашли на сайт Vsesdal.com, вы попали по адресу.

Почему именно у нас лучше всего оформить решение задач на заказ?

Низкие цены. Вы будете общаться напрямую с исполнителем, безо всякого посредничества. А значит, вам не придется ничего переплачивать. Решение задач за деньги на нашем сайте стоит в среднем в 2-3 раза меньше, чем на других ресурсах.

Удобный сервис. Чтобы заказать решение задач, нужно всего лишь опубликовать проект на нашем сайте и выбрать исполнителя из числа откликнувшихся. Вы всегда сможете напрямую обсудить с исполнителем детали работы: стоимость, сроки выполнения, способы решение задач (если, к примеру, ваш преподаватель в университете требует от вас решения определенным способом) и т.п.

Высококлассные специалисты. Каждый исполнитель, зарегистрированный на нашем сайте, является дипломированным специалистом в своей области. Вы всегда можете посмотреть анкету исполнителя, прочитать там информацию о нем, ознакомиться с отзывами, оставленными предыдущими заказчиками. Доверьте решение контрольных работ настоящему профессионалу.

Гарантия на все работы. Если вдруг вы недовольны исполнителем, которому доверили платное решение задач, если он не справился с порученным ему заданием – мы возвращаем вам 100% оплаченной суммы.

Срочное решение задач

Решение задач за деньги может быть выполнено в кратчайшие сроки. Это вам нужно будет обговорить лично с исполнителем. Срочное решение задач имеет смысл заказывать в том случае, если в ближайшие дни у вас контрольная, экзамен или зачет, а времени на подготовку уже практически не осталось.

Обращаясь к нам с просьбой выполнить решение задач на заказ, вы избавляете себя от многих проблем, связанных с учебой.

Пока наши исполнители выполняют для вас решение задач на заказ, вы можете вести свой привычный образ жизни, проводить время в компании хороших людей, готовиться к Новому году или наслаждаться весенним солнышком.

На нашем сайте вы можете оформить заказ на совершенно любую работу, будь то курсовая или диплом, лабораторная или отчет по практике, доклад или чертеж. Можете даже заказать бизнес план: на нашем сайте всегда найдется исполнитель, готовый выполнить ваш заказ.

Кроме того, мы можем оказать вам онлайн помощь по физике, математике или любому другому предмету прямо во время экзамена.

vsesdal.com