Презентация к уроку (алгебра, 10 класс) по теме: РЕШЕНИЕ ДРОБНО-РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ.10 КЛАСС.
ИСАКОВА СИРЕНЬ ХИКАМУТДИНОВНА
Учитель математики высшей категории
МБОУ «Средняя общеобразовательная школа №8»ЕМР
ТЕМА: «РЕШЕНИЕ ДРОБНО-РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ»
Цель: формирование системы по решению дробно-рациональных неравенств методом интервалов.
Литература:
- Никольский С.М., Алгебра и начала анализа: учебник для 10 класса общеобразовательных учреждений, М., «Просвещение», 2007
- Колмогоров А.Н., Алгебра и начала анализа: учебник для 10-11 класса общеобразовательных учреждений, М., «Просвещение», 2006
- Н.В. Александрова, «Математические термины», «Высшая школа», 1978
- Макарычев Ю.Н., Алгебра 8 класс: учебник для школ и классов с углубленным изучением математики, М., «Мнемозина», 2006
Материалы: обобщающие таблицы, компьютер, проектор.
Ход урока:
- Организационный момент.
Сообщение темы, цели урока.
- Актуализация.
Слайд 2, слайд 3
Какое неравенство называется рациональным?
( Неравенство, левая и правая части которого есть рациональные выражения относительно х, называют рациональным неравенством с неизвестным x)
Что значит решить неравенство?
(Решить неравенство – значит найти все его решения или показать, что их нет)
Какого вида неравенства решают методом интервалов?
(, , , , где и — целые выражения с одним неизвестным)
Метод интервалов?
(Метод интервалов – метод решения неравенств с одной переменной, который позволяет решать любые неравенства одна часть которых – нуль, а другая является произведением или частным функций, не меняющих знак на известном промежутке)
Слайд 4
- Вводная беседа.
3.1 Разбор метода интервалов на примере функции которая является произведением линейных множителей.
Слайд 5
Нули функции:
или или
3.2 Ознакомление с алгоритмом применения метода интервалов.
Слайд 6
Алгоритм применения метода интервалов
- Ввести функцию
- Указать область определения функции
- Найти нули функции
- Отметить на координатной прямой нули функции и область определения, учитывая строгость неравенства
- Выяснить знак функции на каждом промежутке подсчетом или рассуждением
- Записать ответ
- Закрепление
4.1 Слайд 7
- ,
.
Ответ:
4.2 Слайд 8
Ответ: .
4.3 Слайд 9
Ответ:
4.4 Слайд 10
Ответ:
4.5 Слайд 11
Слайд 12
— корень четной кратности
Для решения таких неравенств обычно применяют общий метод интервалов. Это метод решения неравенств с одной переменной, который позволяет решать неравенства, имеющие в произведении или в дроби одинаковые двучлены.
Итак, если корень повторяется четное число раз, то при переходе через него знак дроби (произведения) не меняется.
Ответ:
4.6 Слайд 13
— корень нечётной кратности
— корень чётной кратности
— корень нечётной кратности
Ответ:
4.7 Слайд 14
— корень чётной кратности
— корень чётной кратности
— корень нечётной кратности
Ответ:
- Итог урока.
Неравенства какого вида называются дробно-рациональными?
Каким методом можно решать дробно-рациональные неравенства?
В чем заключается суть метода интервалов?
В каких случаях применяется общий метод интервалов?
- Домашнее задание.
№ 2.87 (б,е), №2.91 (г), №2.92 (е)
(Никольский С.М., Алгебра и начала анализа: учебник для 10 класса общеобразовательных учреждений, М., «Просвещение», 2007)
Методическая разработка по алгебре (10 класс) по теме: Решение неравенств методом интервалов
МБОУ « СОШ п. Новопушкинское» Энгельсского района
Учитель: Харитонова Т.Е.
Предмет: алгебра и начала анализа
Класс» 10, общеобразовательный.
Учебник: « Алгебра и начала анализа 10-11» под ред. А.Н. Колмогорова
Тема: Решение неравенств методом интервалов
Тип урока: урок закрепления и совершенствования знаний
Цели урока:
- совершенствовать навыки применения метода интервалов при решении неравенств;
- показать учащимся возможность применения метода интервалов при решении неравенств различной сложности;
- развитие навыков логического мышления, умения анализировать, преодолевать трудности при решении математических задач, навыков самоконтроля, умения пользоваться опорными знаниями для их применения в новой ситуации;
- формирование навыков культуры общения, самостоятельности;
- воспитывать ответственное отношение к учебному труду.
Ход урока
- Организационный момент
Предварительная организация класса, психологический настрой учащихся.
2.Постановка целей урока ( фронтальная работа с классом)
Задание: Найти область определения функции y = .
Что требуется найти.
Что называется областью определения функции?
При каком условии данная функция сушествует?
Таким образом задача сводится к шерению неравенства
Умеем мы решать такие неравенства? Как? Рассмотреть различные варианты ответов учащихся. Остановить внимание на применении метода интервалов. Значит наша задача сегодня продолжить применение метода интервалов при решении неравенств различной сложности.
3.Проверка домашнего задания, воспроизведение коррекции знаний. У доски работают 3 учащихся.
Задание: Решить неравенство.
а) х2(3-х)(х+2)>0
б)
в) (х-4) │5-3х│
С остальными учащимися выполнить устные упражнения.
Цель: Вспомнить алгоритм решения неравенств методом интервалов и применить их при решении следующих упражнений.
1 Назовите нули функции
а) f(х)= (х+3)(х-2)
б) f(х)=х2(х-8)
в) f(х)=(х-3)(х+1)(2-х)
г) f(х)=(7-х)(х-4)2
2. Выберите те неравенства при решении которых можно встретить соседние интервалы с одинаковыми знаками. Что заметили? (в корнях четной степени смена занака не произошла) В дальнейшем мы проверим подтвердиться ли это наблюдение при решении других неравенств.
3. Решить неравенства. х3≤ х (учащиеся предлагают применить метод интервалов. Устно по заготовленному на доске рисунку находят решение данного неравенства
(-∞; -1]U[0; 1]
А я предлагаю такое решение
х3≤ х ,
х2≤1
х2-1≤0
(х-1)(х+1)≤0, х=1 х=-1
+ — + х
-1 1
Ответ: [-1;1]
Что не так? Предложить учащимся сами найти причину по которой получили разные решения. Чаще всего учащиеся замечают, что при сокращении теряется одно из решений х=0. В этом случае напомнить что х может быть любым числом как положительным, так и отрицательным. И неравенство х2 ≤1 не эквивалентно неравенству х2 ≤ х. Таким образом метод сокращения в данной случае не подходит. Давайте проверим в каких случаях можно пользоваться сокращением. Рассмотреть решение примера из домашнео задания ) х2(3-х)(х+2)>0
Таким образом и этот вопрос требует подтверждения, поэтому переходим к следующему заданию.
4. Самостоятельная работа исследовательского характера. Работа по группам. В процессе решения учаещиеся полученные результаты записывают в таблицу. Предусмотрено самопроверка и оценивание работы каждой группой.
Задание для первой группы
Нервенство | Область определения | Нули функции. Схема и знаки. | Ответ |
(х2+2)(3-х)2(7-х)(х+5)3≥0 | |||
Задание для второй группы.
(2-х)(11+х)3(7-х)4(3-х)6≥0 | |||
Х-4
5-3Х≠0 х≠ 4
Урок алгебры в 10 классе по теме
Урок алгебры в 10 классе по теме «Решение неравенств методом интервалов».
Цели урока:
Образовательные:
проконтролировать знания учащихся по усвоению алгоритма решения неравенств методом интервалов;
выработать умения и навыки по их самостоятельному применению при решении упражнений по образцу, в сходной, измененной ситуации.
Повторить основные приемы преобразования и решения рациональных и дробно-рациональных неравенств методом интервалов, акцентировать внимание учащихся на поиске и прогнозировании ошибок.
Развивающие:
продолжить развитие умения решать более сложные неравенства;
обеспечить развитие математической речи, самооценки, умение работать во времени.
Воспитательные:
создать условия для развития коммуникативных навыков;
умения работать в парах; побуждать учащихся к самоанализу своей деятельности,умения выслушивать ответы одноклассников.
Оборудование:
Дидактические материалы: презентация к уроку, плакаты –шаги схемы “Обобщенный метод интервалов решения неравенств ”; карточки для творческой работы в парах, для самостоятельной работы и для тестирования.
Ход урока
1. Организация начала урока. (1 мин.)
– Здравствуйте, ребята. Запишите число и тему урока “Метод интервалов решения неравенств”. Почти все неравенства школьного курса можно решить методом интервалов. Сегодня мы ответим на вопросы : Какие неравенства мы можем решать методом интервалов? Какие преобразования необходимо сделать , чтобы привести неравенство к виду неравенства , решаемого методом интервалов. И составим схему обобщенного метода интервалов решения неравенств.
Познакомьтесь с планом урока.
План урока
Проверка домашнего задания.
Беседа. Обобщение теоретических знаний и составление схемы обобщенного метода интервалов.
Применение знаний. Индивидуальная работа и работа в парах.
Применение метода интервалов при решении задач.
Самостоятельная работа.
Итог урока. Рефлексия.
Домашнее задание.
2. Проверка выполнения домашнего задания. (5 мин.)
На экран выносятся решения неравенств с ошибками.(Приложение 1). Учащимся предлагается сверить свою работу с записью на экране и найти ошибку. Вызванный ученик аргументированно объясняет решение, затем отвечает следующий. По готовым ответам к домашним заданиям исправить свои ошибки.( Приложение 2).
3. Беседа . Обобщенный метод интервалов решения неравенств.( 7 мин)
На доске выписаны несколько неравенств : 1. (х-8)(х+1)(х-2)>0
2. (6-х)(9+х)(х-3)<0
3. (х-5)²(х+4)³х<0
4. >0
5. х²+2х-15<0
6. (2х+1)(3х-6)(х-5)<0
Вопросы: 1.В чем заключается метод интервалов решения неравенств? Какого вида неравенства решают этим методом?
+2. На примере неравенства (1) расскажите , как решают неравенства методом интервалов.
3. На примере остальных неравенств расскажите , какие преобразования необходимо сделать, чтобы привести левую часть неравенств к виду (х-х1)(х-х2)(х-х3)…(х-хп) ?
4. На примере неравенства (3) расскажите план решения неравенств с учетом кратности корней. Ответ сопровождается составлением схемы обобщенного метода интервалов решения неравенств на магнитной доске.
1 шаг. Приравнять левую часть неравенства к нулю и решить уравнение.
2 шаг. Отметить на числовой прямой корни уравнения
3 шаг. В правом крайнем интервале поставить знак «+» , а дальше пользуясь свойством чередования, расставить знаки в остальных интервалах, меняя знак при переходе через корень нечетной степени, и сохранить знак при переходе через корень четной степени.
4 шаг. Записать ответ в соответствии со знаком неравенства.
4. Парная работа. ( 6 мин)
1 задание( творческое). Составить неравенство по готовой картинке и предупредить возможные ошибки.
( Приложение 3).
По мере готовности пары выходят к доске .
2 задание . Решить тест. (Приложение4) Взаимопроверка по готовым ответам. Правильные ответы проектируются на экран.
(Приложение 5)
5.Применение метода интервалов.( 10 мин).
1.Решить задачу. Длина прямоугольника на 3 см больше ширины. Какую длину должен иметь прямоугольник, чтобы его площадь была меньше 28 см²?
Решение:
Пусть длина прямоугольника х см ,х>0, тогда его ширина (х-3)см. S=х(х-3) см²
Зная, что S<28 см² , составим и решим неравенство:
х(х-3)<28
х²-3х-28<0 х²-3х-28=0
(х+4)(х-7)<0 х1+х2=3
+ — + х1*х2=-28 , х1=-4 х2=7
────о───о────›
-4 7
Выбираем промежуток (-4;7) и учитывая условия х>0 и х-3>0, получаем (3;7).
Значит, длина прямоугольника должна быть больше 3 , но меньше 7.
2.Найти область определения функции у=.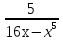
Решение:
16х-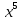 >0
>0
х(16-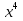 )>0
)>0
х(4-х²)(4+х²)>0
х(2-х)(2+х)(4+х²)>0 Выражение 4+х²>0 при любых значениях х
х(х-2)(х+2)<0
Х1=0 Х2=2 Х3=-2
— + — +
────о──────о──────о───────›
-2 0 2
Ответ: D(y)=(-∞;-2)(0;2)
6. Самостоятельная работа. ( 12 мин) (Приложение 6)
7.Итог урока. Прокомментировать оценки учащихся.( 2 мин)
8. Рефлексия. Заполнить табличку. ( 2 мин)
1. Сегодня на уроке было интересно ___________________________________
2. Сегодня на уроке я научился _______________________________________
3. Сегодня на уроке мне показалось важным ___________________________
8. Домашнее задание. № 2.77(е), 2.78 (в,г,д)
Приложение 1. Проверка домашнего задания.
№ 2.71 (в) №2.67 (з)
(х+3)(х+4)²(х+5)³<0 (х²+3х)(х²-16)>0
Х1=-3 Х2=-4 Х3=-5 Х(Х+3)(Х-4)(Х+4)>0
— + — + Х1=0 Х2=3 Х3=4 Х4=-4
────о─────о─────о─────› + — + — +
-5 -4 -3 ─────о────о────о────о──────›
(-∞;-5)U(-4;-3) -4 0 3 4
(-∞;-4)U(0;3)U(4;+
№2.76 (в) №2.77(г)
>1 <0
-1>0 (х+2)²(х+1)(х-3)>0
>0 Х1=-2 Х2=-1 Х3=3
>0 Х1=2 Х2=-1 + + — +
+ — + ────о────о────о──────›
───о────о─────› -2 -1 3
-1 2 (-∞;-2)U(-2;-1)U(3;+∞)
(-∞;-1)U(2;+∞ )
Приложение 2. Правильные ответы .
№2.71 (в) (-5;-4)U(-4;-3)
№2.67(з) (-∞;-4)U(-3;0)U(4;+∞)
№2.76(в) (-∞;-1)U(4;+∞)
№2.77(г) (-1;3)
Приложение 3.
1 пара
Составьте неравенство по картинке . Выделены промежутки-ответы. Предупредите о возможных ошибках.
+ + — +
─────о────о───
о───›-1 0 4
(-∞;-1)U(-1;0)U(4;+∞)
2 пара
Составьте неравенство по картинке . Выделены промежутки-ответы. Предупредите о возможных ошибках.
+ — + — +
───о───о───о───о───›
-2 -1 5 7
(-2;-1)U(5;7)
3 пара
Составьте неравенство по картинке . Выделены промежутки-ответы. Предупредите о возможных ошибках.
+ — — +
─────о────о────о─────›
-5 -4,5 3
(-∞;-5)U(3;+∞)
4 пара
Составьте неравенство по картинке . Выделены промежутки-ответы. Предупредите о возможных ошибках.
+ — + +
─────о─────о─────о─────────›
-6 1 8
(-6;1)
Приложение 4 Т Е С Т
Вариант 1
Метод интервалов решения неравенств.
Выберите один правильный по вашему мнению ответ и впишите в бланк ответов . Бланк расположен под тестом.
1.Укажите наибольшее целое число, принадлежащее промежутку (-7; -1,8)
А -1
В -7
С -2
2.Какой из промежутков является решением неравенства х-5>0 ?
А (5;+∞)
В (-5;5)
С (-∞;5)
3.Найдите корни уравнения (х-1)(Х-2)(х+3)=0
А 1;2;3
В 1;2;-3
С -1;-2;-3
4.Решением какого неравенства является промежуток (-3;2)?
А (х+3)(х+2)<0
В (х+3)(х-2)<0
С (х-3)(х+2)>0
5.Решите неравенство х16
А (-∞;4)
В (-4;4)С (4;+∞)
Бланк ответов .
№ задания
1 задание
2задание
3 задание
4 задание
5 задание
Ваш ответ
За каждый правильный ответ- 1 балл.
Количество баллов:_______
Т Е С Т
Вариант 2
Метод интервалов решения неравенств.
Выберите один правильный по вашему мнению ответ и впишите в бланк ответов . Бланк расположен под тестом.
1.Укажите наименьшее целое число, принадлежащее промежутку (-5,3; 2)
А -5
В 2
С -4
2.Какой из промежутков является решением неравенства х+5>0 ?
А (-5;5)
В (-5;+∞)
С (-∞;5)
3.Найдите корни уравнения (х+1)(Х-2)(х-3)=0
А 1;2;3
В -1;2;3
С -1;-2;-3
4.Решением какого неравенства является промежуток (-2;3)?
А (х+3)(х+2)<0
В (х+3)(х-2)>0
С (х-3)(х+2)<0
5.Решите неравенство х16
А (-∞;-4)U(4;+∞)
В (-4;4)
С (4;+∞)
Бланк ответов .
№ задания
1 задание
2задание
3 задание
4 задание
5 задание
Ваш ответ
За каждый правильный ответ- 1 балл.
Количество баллов:_______
Приложение 5. Проверка теста.
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Вариант 1
С
А
В
В
В
Вариант 2
А
В
В
С
А
Приложение 6. Самостоятельная работа.
Вариант А1 Вариант А2
1.Решите неравенство: 1. Решите неравенство:
а)(х+2)(х-3)(х+1)>0 а) (х-2)(х+3)(х-1)<0
б) х(4-х)(х-2)>0 б)(3-х)(х+2)х>0
в) (х-1)²(х-4)³(х+5)<0 в) (х+4)²(х-5)(х+3)³<0
2.Найти область определения 2.Найти область определения
функции у= функции у=
Метод интервалов решения неравенств
Просмотр содержимого документа
«Метод интервалов решения неравенств»
Метод интервалов решения неравенств.
Цели: совершенствовать навыки применения метода интервалов при решении неравенств различной сложности; учить работать самостоятельно, находить и исправлять ошибки; готовиться к ЕГЭ.
Ход урока
I. Орг. момент.
II. Проверка домашнего задания.
1) Три человека оформляют решение на доске.
2) Остальные работают с учителем.
Математический диктант.
1. Представьте в виде многочлена квадрат разности 2а и 8.
2. Вычислите 5!
3. Разложите на множители 4а*а-16х*х.
4. Решите неравенство: (х-5)(1-х)0
5. Решите неравенство: (х+4)(х+4)(х-3)
Выполняется самопроверка мат. диктанта, взаимопроверка домашнего задания.
III. Решение упражнений.
№ 2.72 (д, ж) Один человек у доски с полным комментарием, остальные в тетрадях.
№ 2.72 (е, з) Два человека на доске, остальные в тетрадях. Взаимопроверка.
IV. Подготовка к ЕГЭ.




V. Итоги урока.
Ответить на вопросы обучающихся. Выставить оценки за урок.
VI. Домашнее задание.
№ 2.70.
Урок по теме «Решение неравенств методом интервалов»
Тема урока: «Решение неравенств методом интервалов»
Цели урока:
Образовательная:
— создать условия для повторения и обобщения знаний учащихся по теме «Решение неравенств методом интервалов»;
— активизировать работу учащихся по применению знаний и умений к решению задач,
— подготовка к ОГЭ.
Развивающая:
— содействовать развитию познавательного интереса к предмету;
— развитие навыков логического мышления, умения анализировать, преодолевать трудности при решении математических задач,
— развитие навыков самоконтроля, умения пользоваться опорными знаниями для их применения в новой ситуации;
Воспитательная:
— воспитывать ответственное отношение к изучению математики, трудолюбие, взаимопомощь, волю и настойчивость в достижении поставленной цели.
— Тип урока: комбинированный
Методы обучения: объяснительно-иллюстративный, практический, частично-поисковый.
Формы обучения: индивидуальная, фронтальная, групповая
Технология: личностно-ориентированная.
Оборудование урока: компьютер, проектор, презентация, интерактивная доска, диагностические карты, памятки.
Ход урока:
I. Оргмомент:
Цель: обеспечение нормальной обстановки для работы, психологическая подготовка учащихся к предстоящему уроку.
(Учащимся сообщается тема урока и цели, подчеркивается актуальность повторения данной темы для подготовки к ОГЭ). Вступительное слово учителя: – Здравствуйте, ребята! Перед нами сегодня стоит задача: повторить метод интервалов для решения неравенств.
Девиз сегодняшнего урока: “Нельзя изучать математику глядя на то, как это делает сосед”. Только свой труд в изучении математики может принести результаты. Однажды я прочла высказывание : «Получать готовую информацию и запоминать ее может компьютер, а человек должен думать».
Наши знания должны работать и дать положительный результат на экзамене. Сегодня каждый из вас проведет диагностику своих знаний по данной теме, для этого у каждого диагностические карты, в которых вы оцените свои знания и возможности по каждому из разделов. Ознакомьтесь, пожалуйста, с листами учёта знаний.
Права и обязанности:
— если желаешь высказывать свою мысль, то подними руку
— когда кто-то говорит, все слушают и не перебивают;
— сдерживаться от оценивания и резких высказываний в адрес других учеников
Ответы учащихся фиксируются в лист учёта знаний учащихся:
Ф.И учащегося____________________________________________________
Права и обязанности:— если желаешь высказывать свою мысль, то подними руку
— когда кто-то говорит, все слушают и не перебивают;
— сдерживаться от оценивания и резких высказываний в адрес других учеников
Критерии оценок: «5»- нет ошибок, «4» — одна ошибка, «3» — две ошибки, «2» — более двух
II. Проверка домашнего задания
Цель: выяснить, какие затруднения возникли у учащихся при выполнении домашнего задания, дать возможность исправить эти ошибки самостоятельно каждому
Учитель: (Учащиеся обмениваются тетрадями и проводят взаимопроверку домашних заданий в парах по ответам на слайде презентации). Выставляют оценки в «Листы учёта знаний».
II Математический диктант
Цель: актуализировать и систематизировать знания учащихся
Учитель: Читает вопросы( учащиеся записывают ответы в тетрадь). Один из учащихся пишет с обратной стороны доски
Вопросы:
Запишите формулу для вычисления дискриминанта квадратного уравнения.
Сколько корней может иметь квадратное уравнение?
Записать формулы корней квадратного уравнения при условии, что дискриминант больше 0.
Когда ветви параболы направлены вниз, а когда – вверх?
Что называется нулями функции?
Запишите промежутки: а) от 0 до 5, включая 0 и не включая 5;
б) промежуток от 3 до 9, не включая 3 и включая 9.
III Теоретическая разминка «Найди ошибку»
Цель: Самостоятельное нахождение и исправление ошибок
Учитель:
Вам предстоит найти ошибку в каждом из неравенств и исправить её
(Учащиеся проверяют по ответам на слайде презентации). Выставляют оценки в «Листы учёта знаний».
IV Самостоятельная работа
Цель: актуализировать и систематизировать знания учащихся
V. Реши ОГЭ
Цель: Применение предметных ЗУНов в условиях решения учебных задач повышенной сложности
Вариант 1.
Решите методом интервалов неравенства:
а)(4x-4)(x+5) ≥ 0
б) 9x2-3x-2 ≤ 0
Вариант 2.
Решите методом интервалов неравенства:
а) (2x-7)(x+6)≤ 0
б) 4x2-4x-3 ≥ 0
Учащиеся выполняют самостоятельную работу и сверяют свои ответы с ответами на слайде презентации.
Ответы:
1 вариант: а) (-∞;-5];[1;+∞)
б) [-1/3;2/3]
2 вариант: а) [-6;3,5]
б) (-∞;-0,5];[1,5;+∞)
VI Домашнее задание
Цель: формирование саморегуляции и анализ
Ваше домашнее задание нескольких уровней. Каждый выбирает уровень себе по силам.
Начальный уровень
Решить неравенство методом интервалов
1) (х + 4)(х – 2) > 0
2) х2 +3х + 2 ≤ 0
3) (х – 5)/(х + 6) < 0
4) (х + 1)(х – 3) >0
5) х2 – 3х – 4 ≤ 0
6) (х – 7)/(х +8) < 0
Средний уровень
Решить неравенство методом интервалов
1) х2 — 7х + 12 ≤ 0
2) (х + 9)(х – 3) < 0
3) х (9 + х)(х – 11) > 0
4) (х + 4)(6 – х)(х – 12) ≥0
5) (х + 8)/(х — 5) >0
6) (х – 7)/(х + 4) > 0
Достаточный уровень
Решить неравенство методом интервалов
1) (х – 3)(х +6)/(х + 4) ≥ 0
2) (х + 4)2(х + 2)(х – 3) ≤ 0
3) (9 – х2)(4х2 + 1) > 0
4) (8 – 4х)/(х + 3) ≥ 0
5) (16 – х2)(3х2 + 2) ≤ 0
6) (х + 3)/(9 — 2х) ≤ 0
«Рефлексия».
Цель: сравнить предвари тельные цели и реально достигнутые результаты.
Прошу всех подсчитать баллы, заработанные на уроке.
Учащиеся по диагностическим картам подсчитывают баллы, заработанные на уроке. Выставляются оценки за урок.
Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:
сегодня я узнал…было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
Конспект урока «Решение неравенств методом интервалов»
Филиал МОУ «новомичуринская СОШ №3» «Денисовская ООШ»
«Решение неравенств
методом интервалов»
Учитель математики: Груздева С.Ю.
Тема урока: Решение неравенств методом интервалов
Цель урока:
акцентировать внимание учащихся на поиске и прогнозировании ошибок.
Развивающая: развитие логического мышления, памяти, внимания; выработка математической зоркости и критичности мышления.
Воспитательная: воспитание трудолюбия, интереса к предмету, умения внимательно выслушивать ответы одноклассников.
Этапы урока:
Ι. Организационный момент.
(формулируется тема урока, сообщается цель урока, план урока)
ΙΙ. Устная работа.( 8 минут)
Назовите целые числа, входящие в промежуток (-1;5].
Сколько натуральных чисел принадлежит этому промежутку?
Решите неравенство:
а) -5х>20
б) (х+1)(х-3)<0
в) 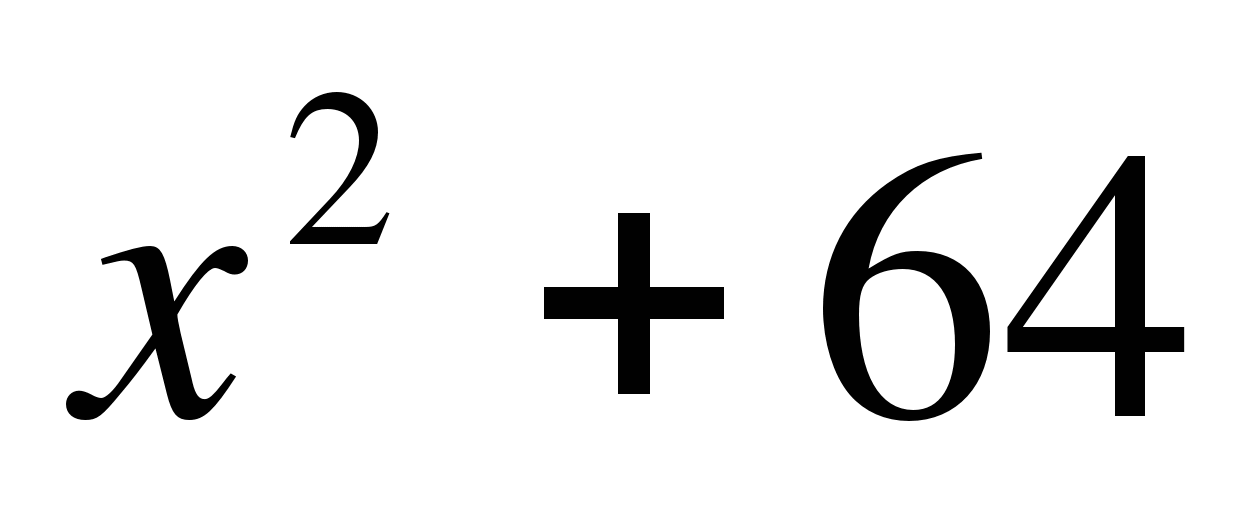 <0
<0
г) 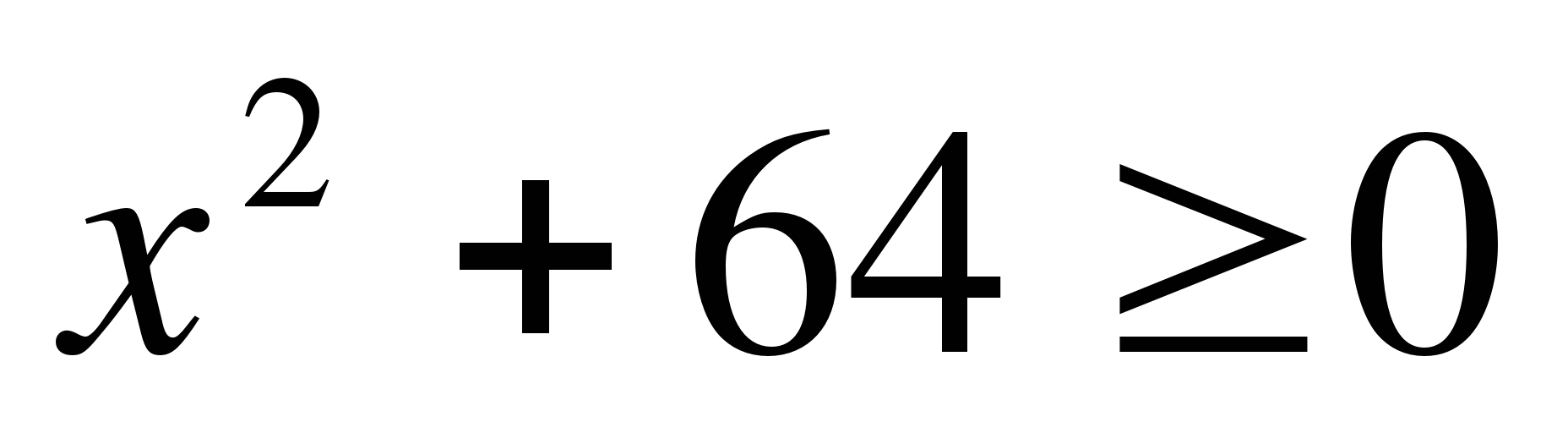
д) 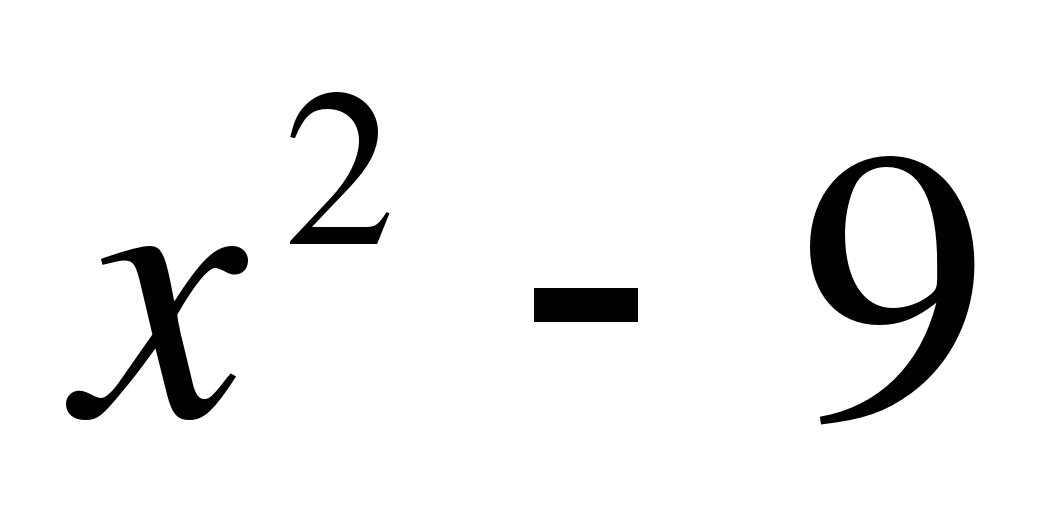 <0
<0
е) 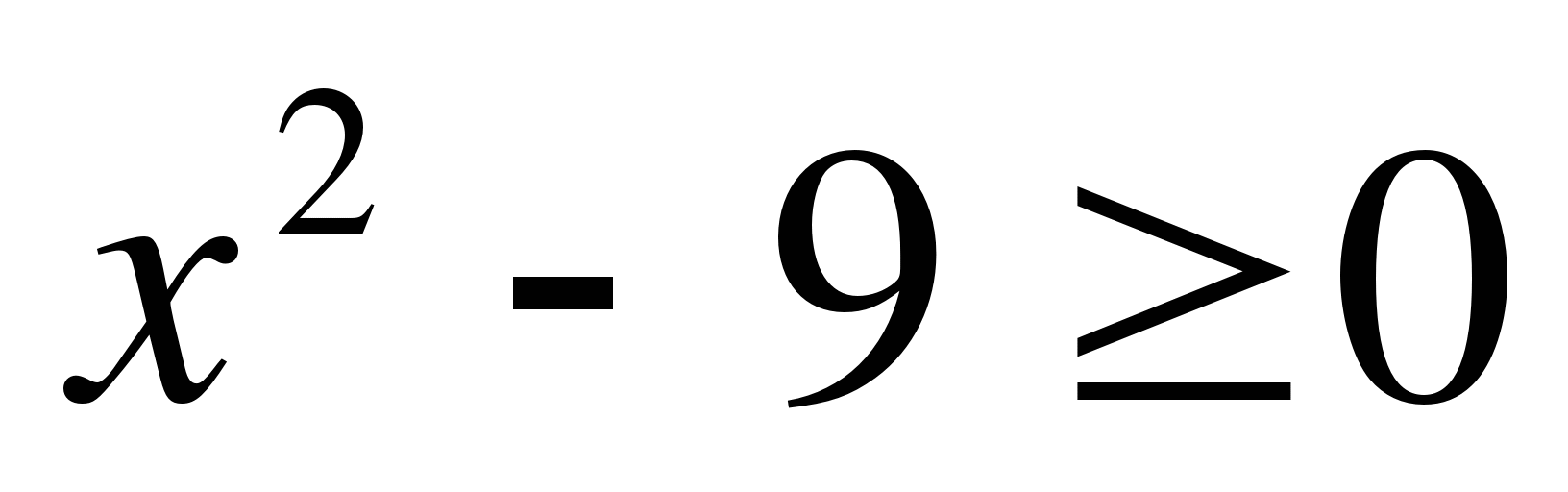
ж) 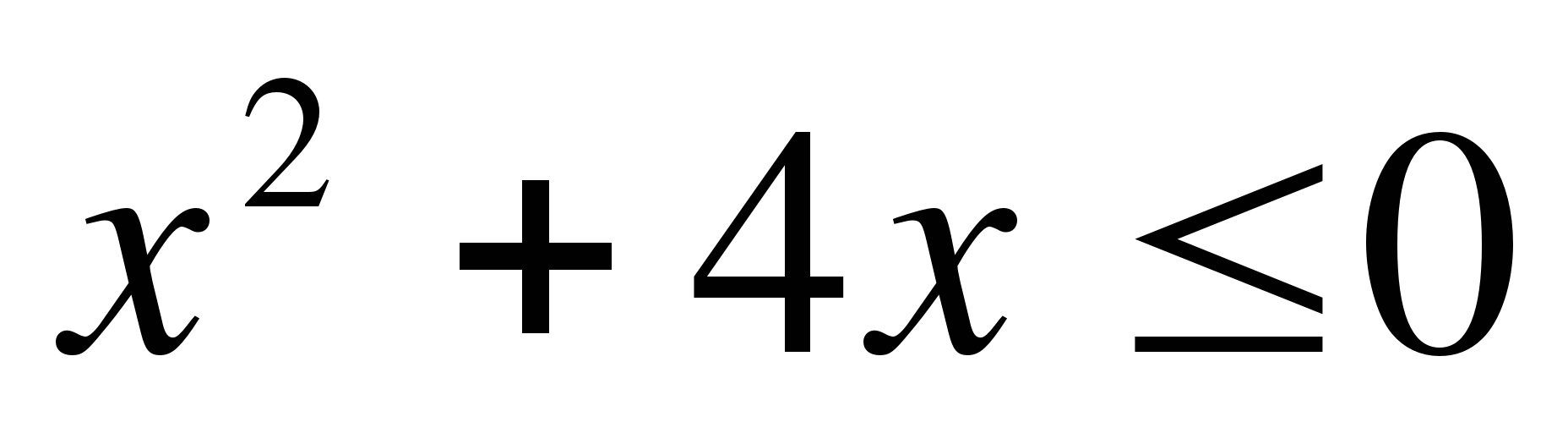
з) 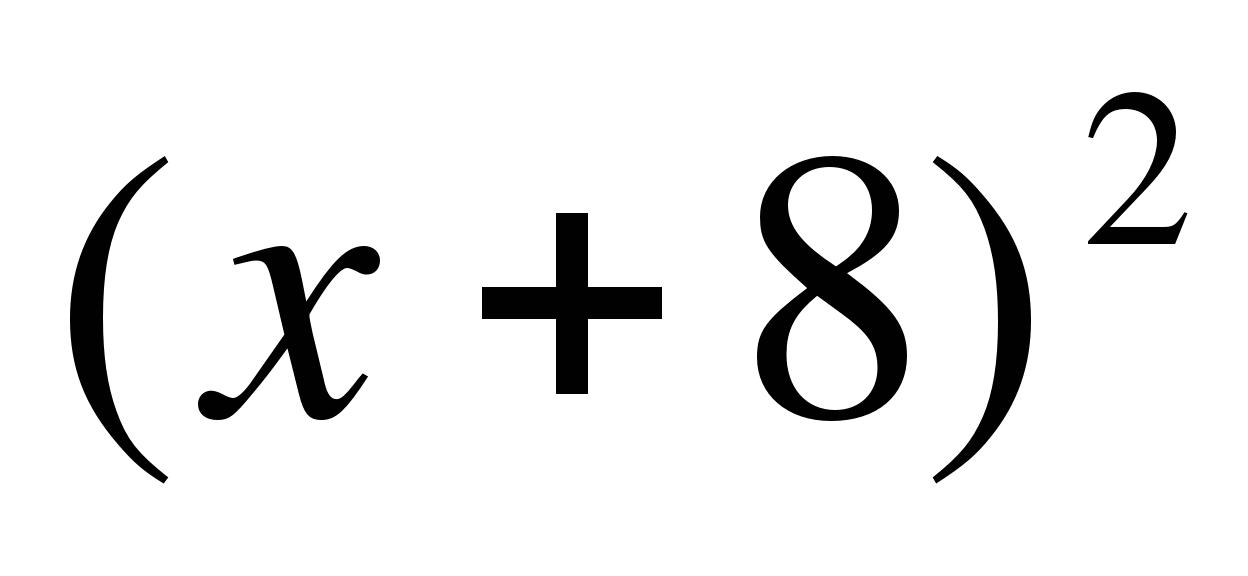 >0
>0
и) 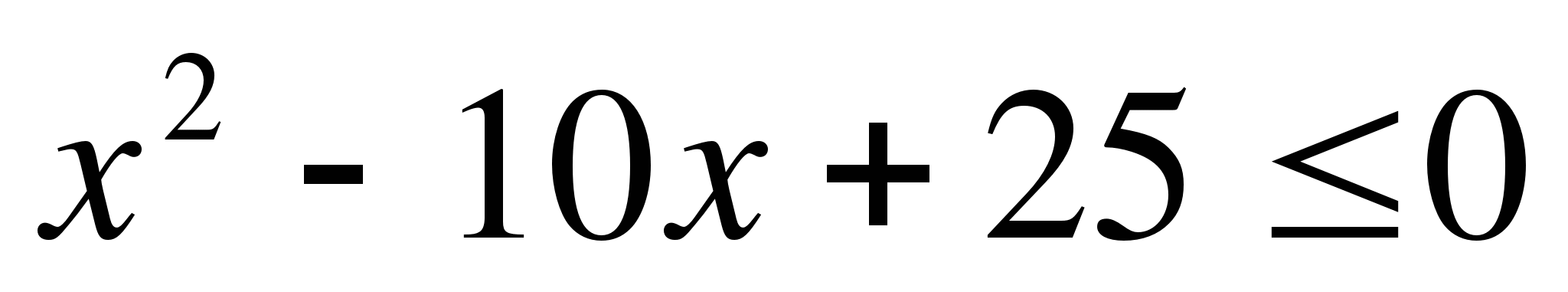
3) Определите знак выражения 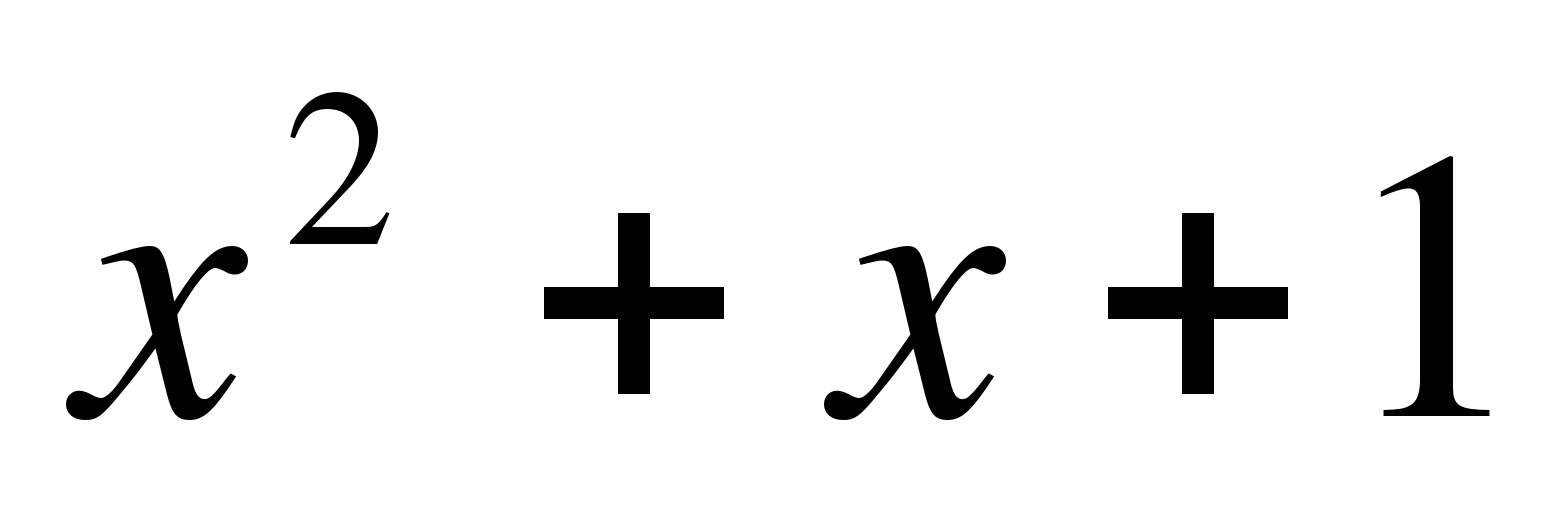
4) Найдите ошибку в решении неравенства
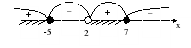
5) Найдите ошибку в решении неравенства
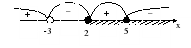
6) Найдите ошибку в решении неравенства
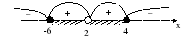
7) Равносильны ли неравенства:
а) (2x+5)(3-2x)<0 и 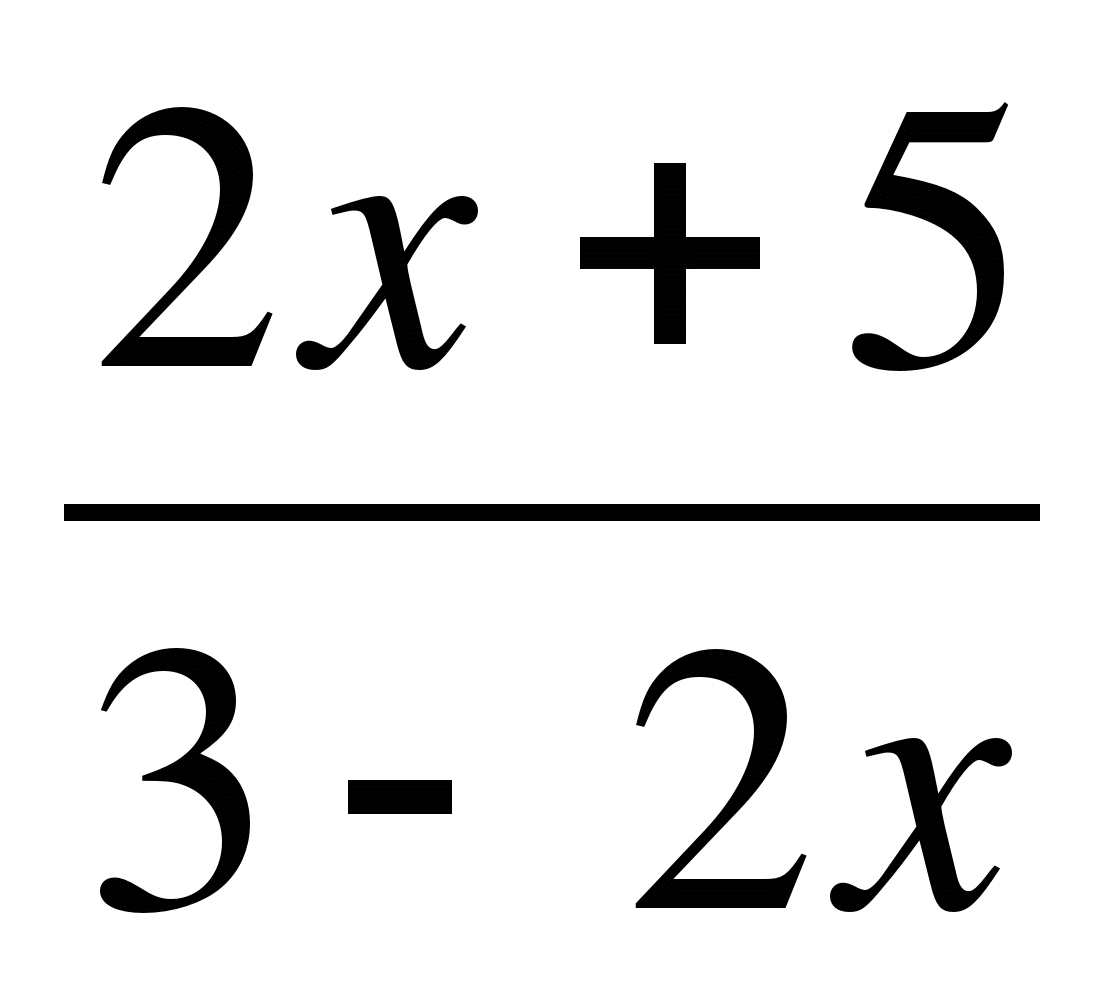 <0
<0
б) и
ΙΙΙ. Тренажёр. (7 минут)
< 82
–2x > 0
2
7–x > 0
2
–3x > –6
2
-2х < -8
3
4x > 1
3
12x > 4
3
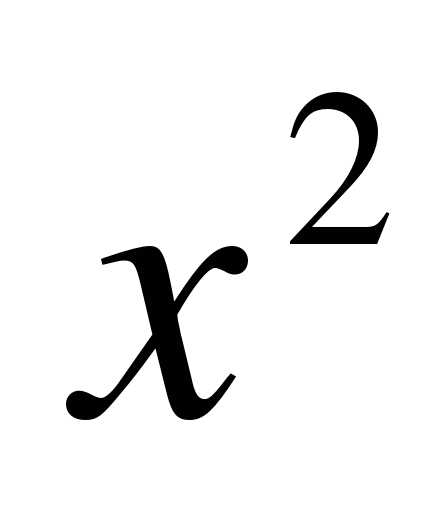 >25
>25
3
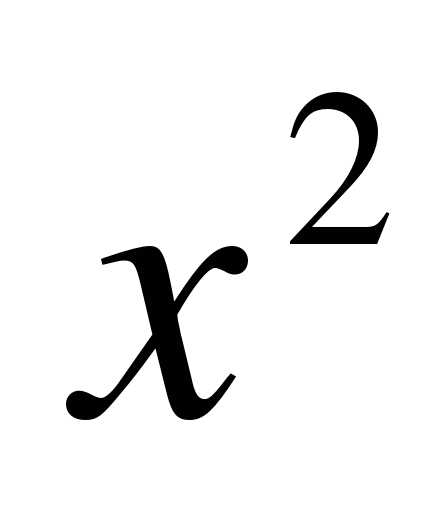 < 36
< 36
4
– 4x > 1
4
– 12x > 4
4
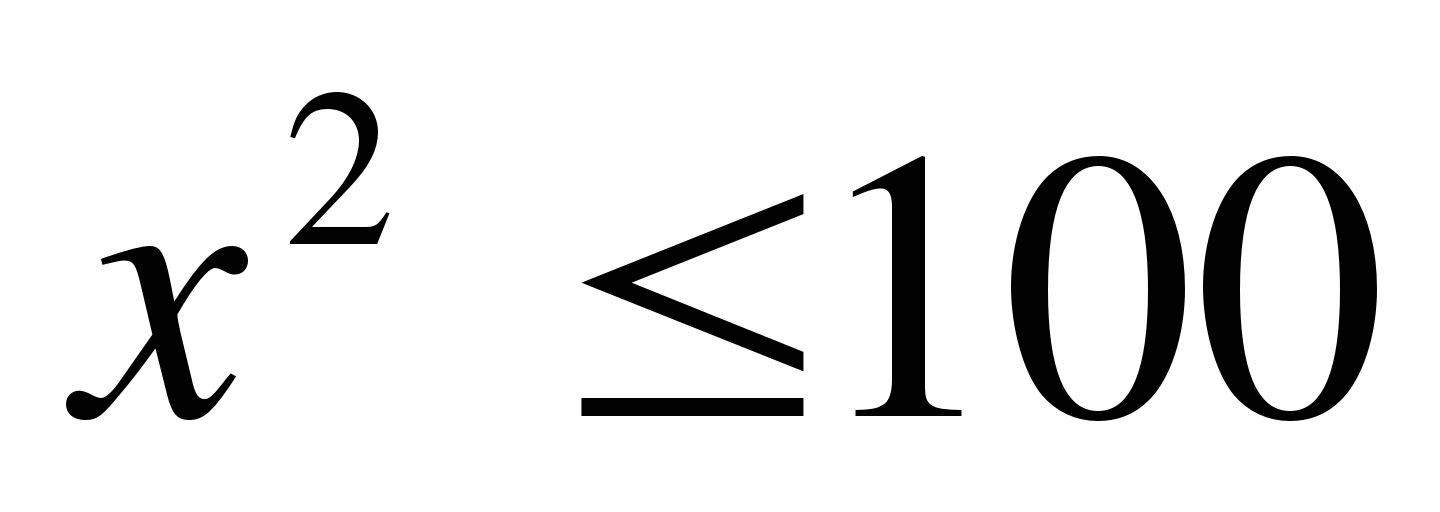
4
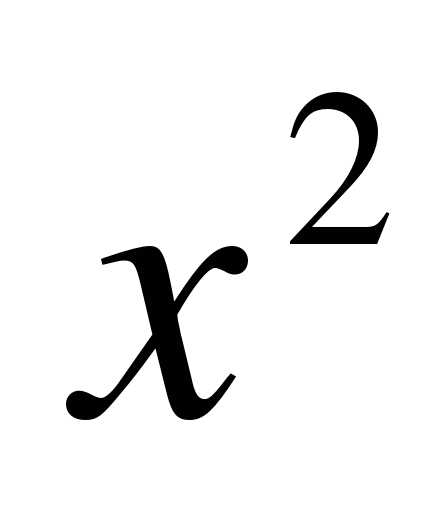 > 81
> 81
5
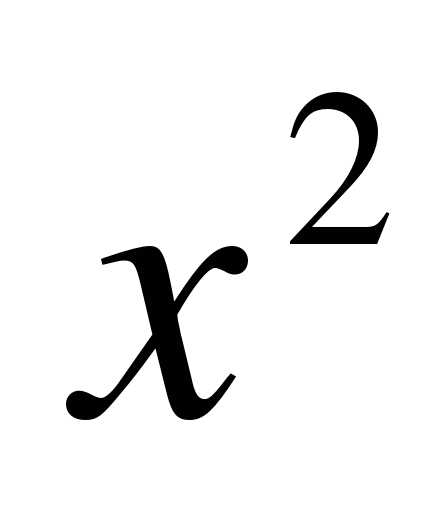 > 4
> 4
5
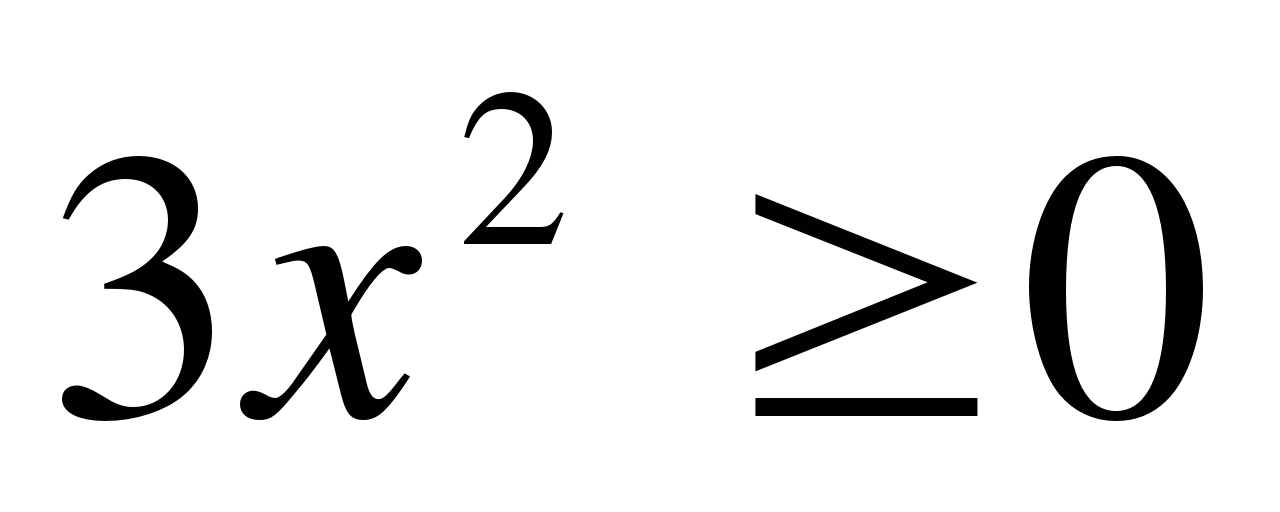
5
x(x+4) < 0
5
x(x+5) > 0
6
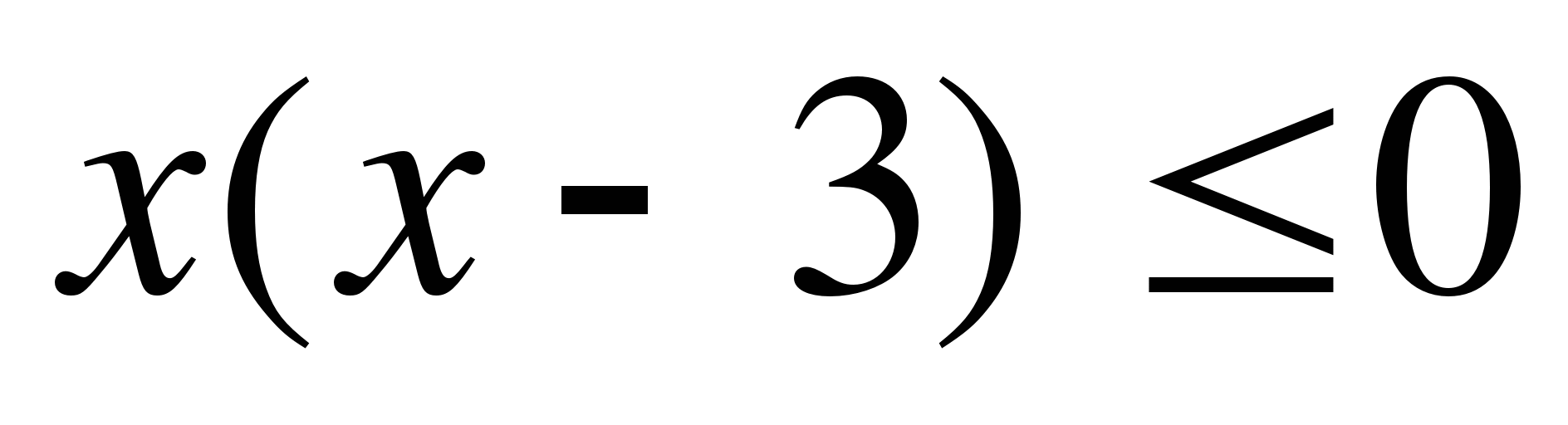
6
– x < 0
6
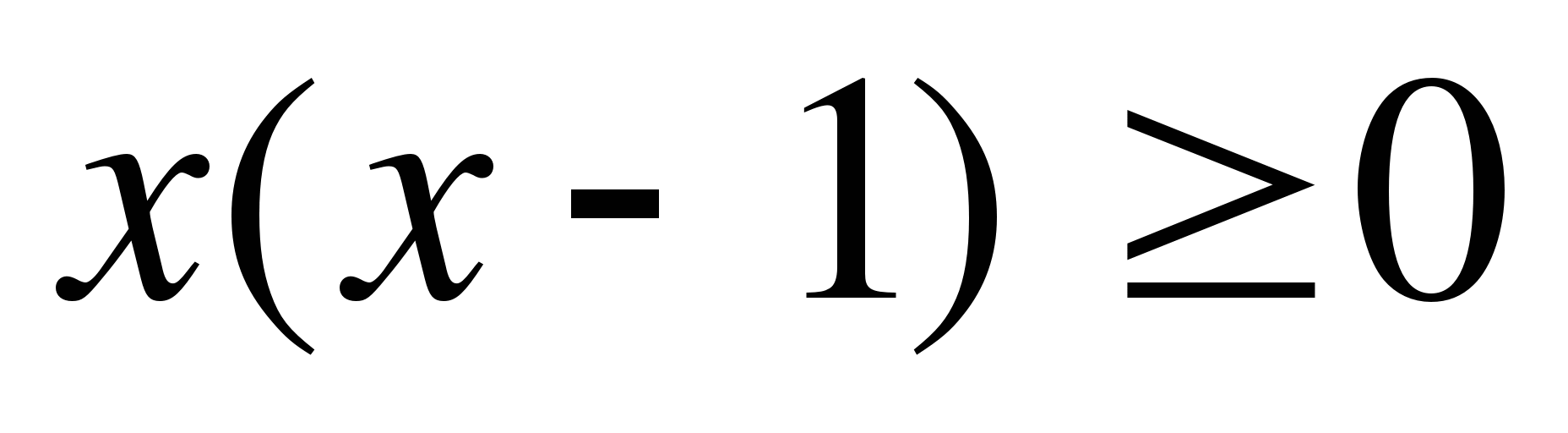
6
x(x-3) 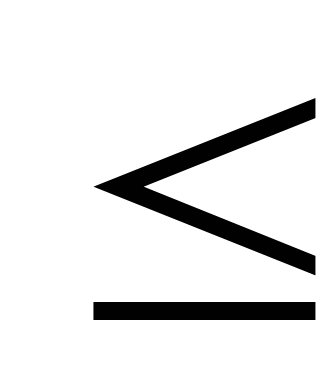 0
0
7
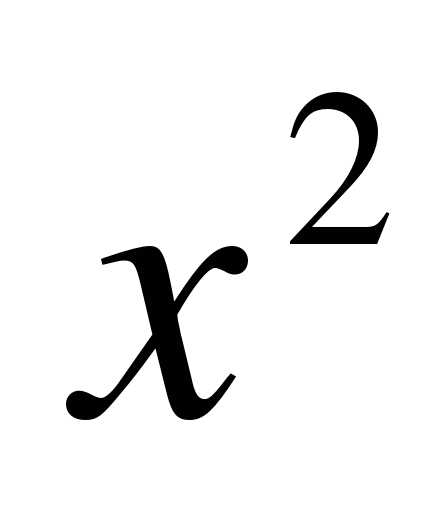 < 0
< 0
7
(x –3)(x+2) < 0
7
2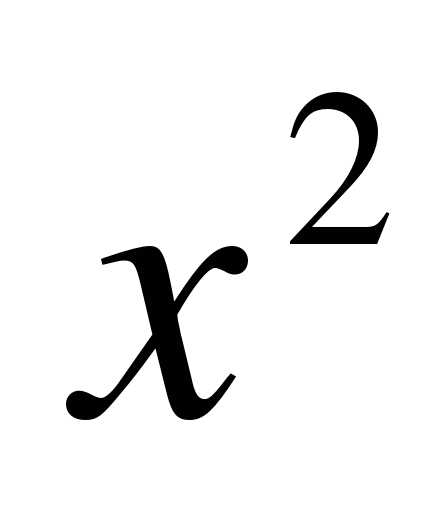 > 0
> 0
7
5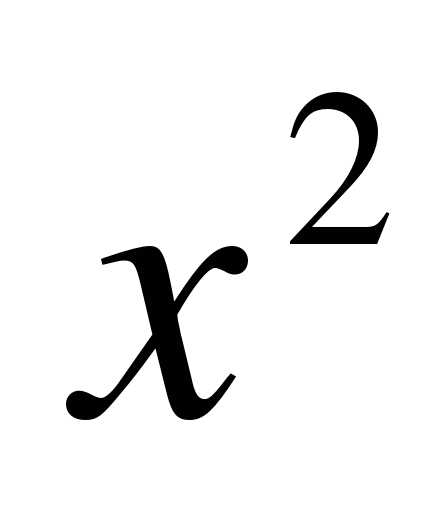 > 0
> 0
8
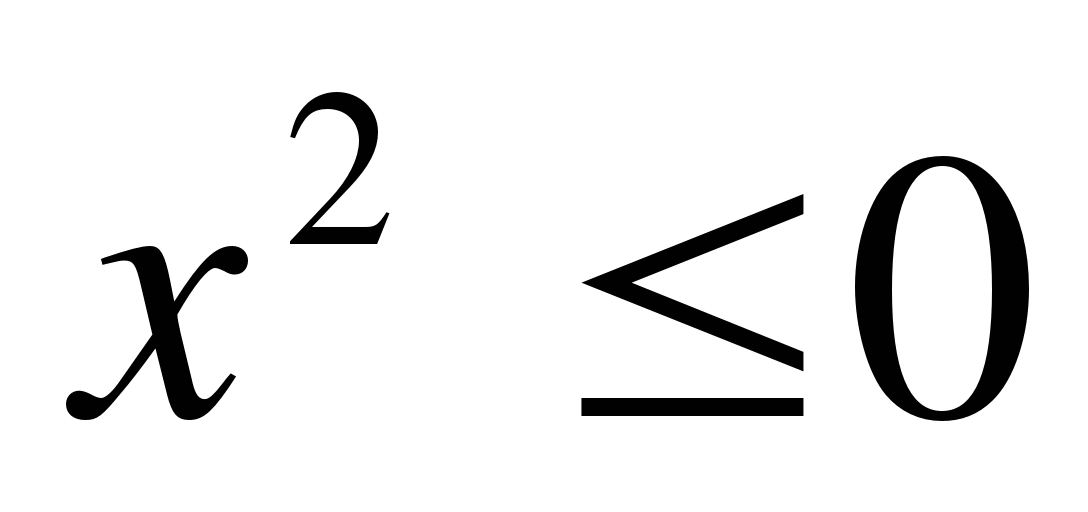
8
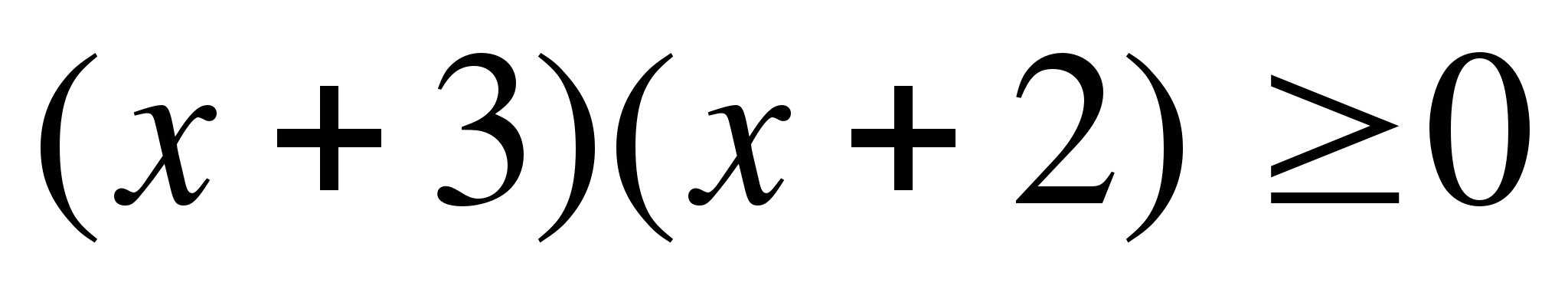
8
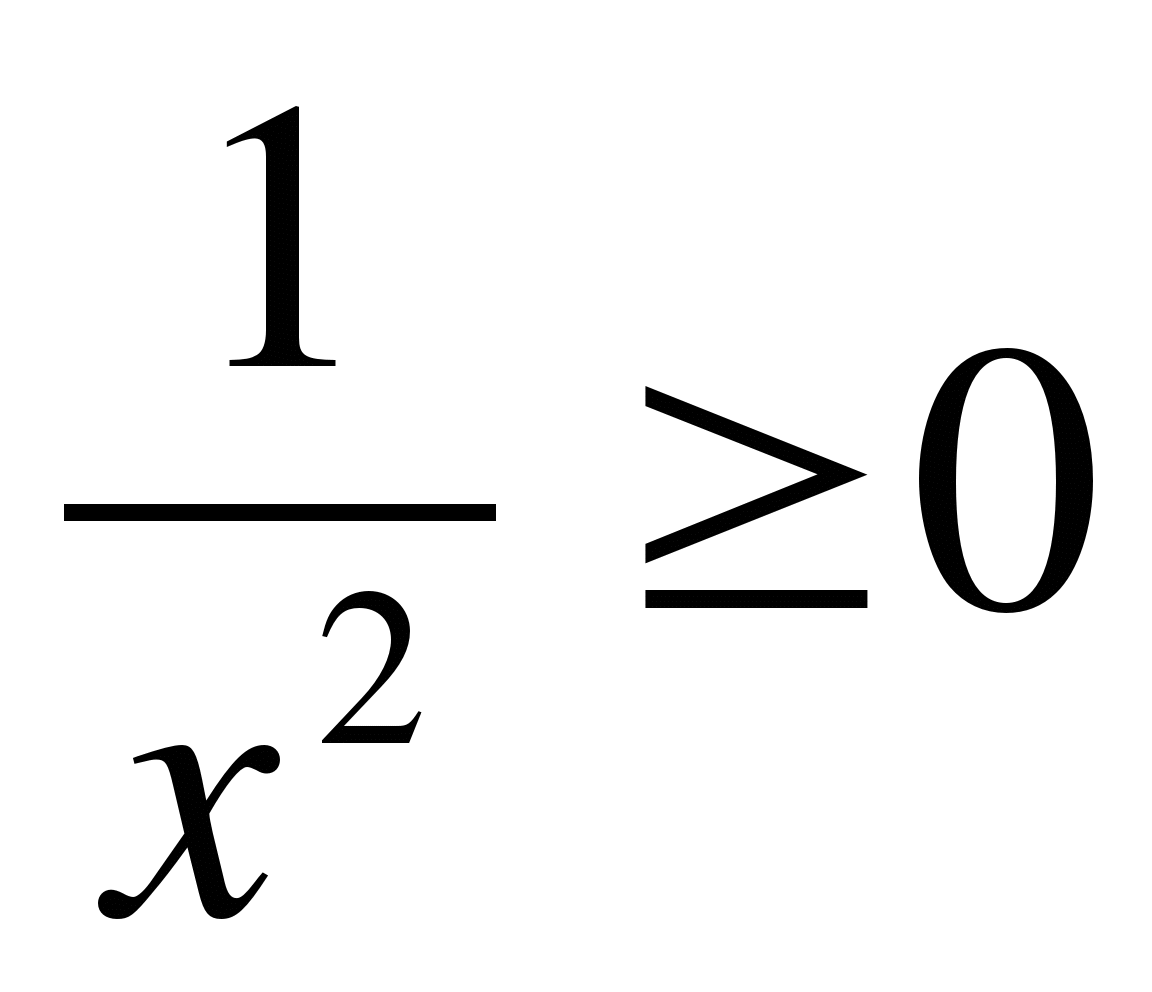
8
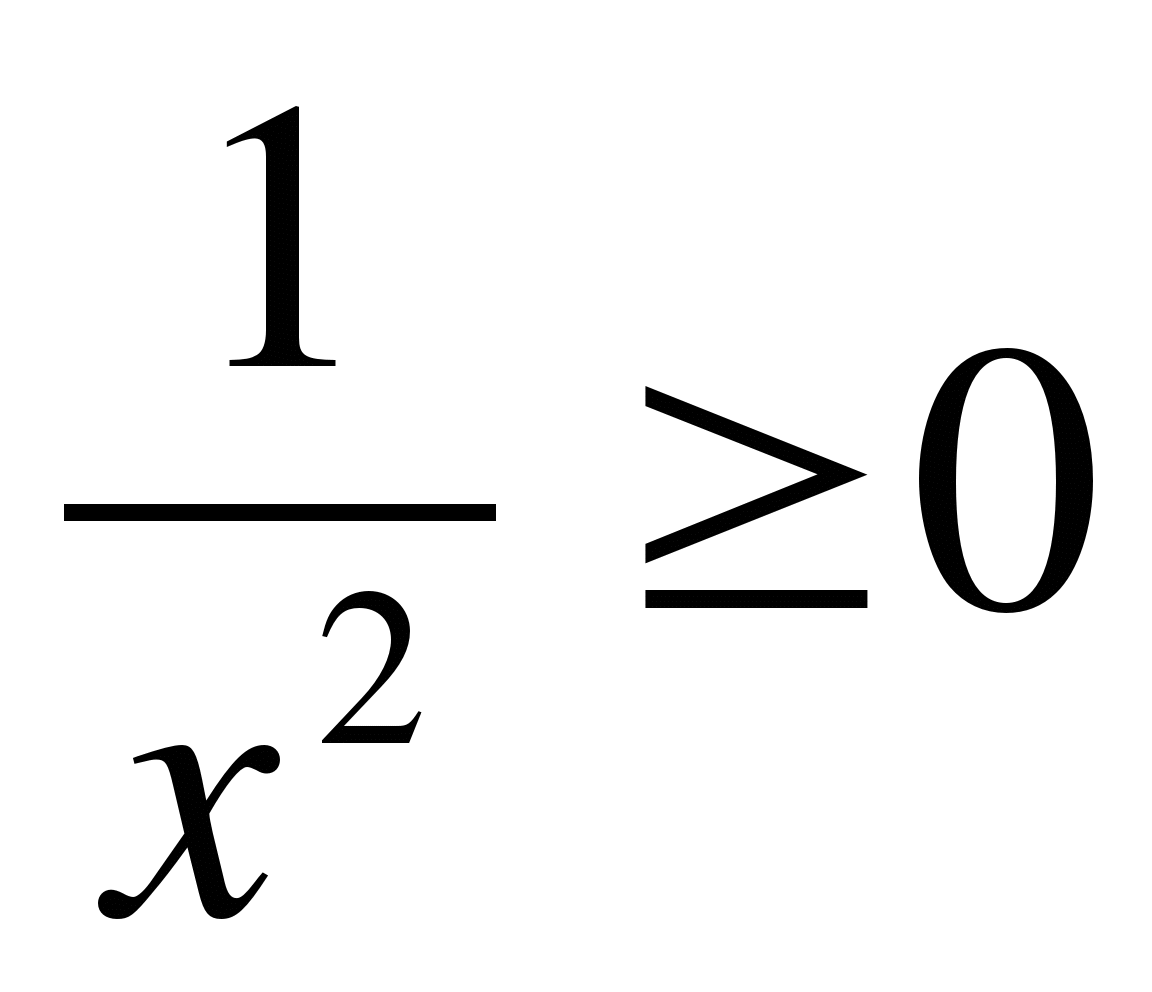
9
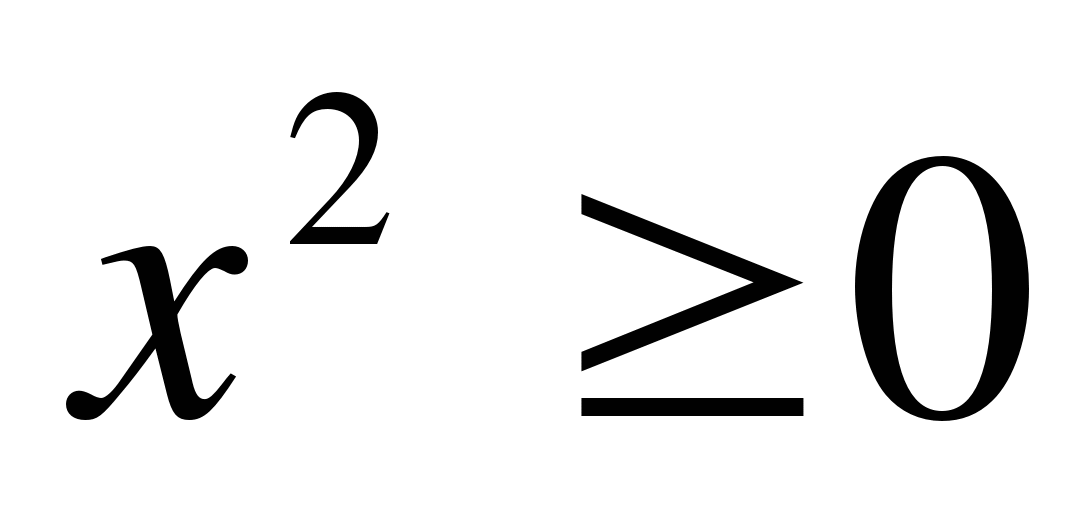
9
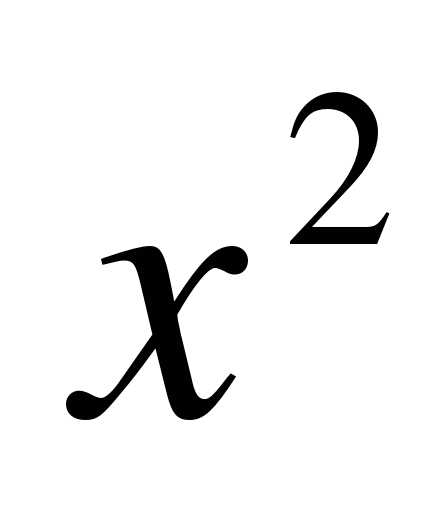 > 9
> 9
9
(x –5)(x-6) > 0
9
(x-2)(x-5) > 0
10
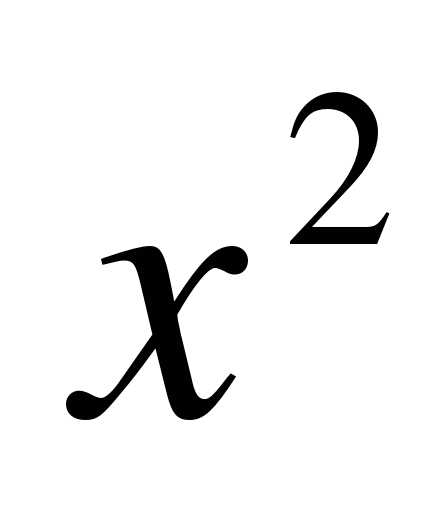 > 0
> 0
10
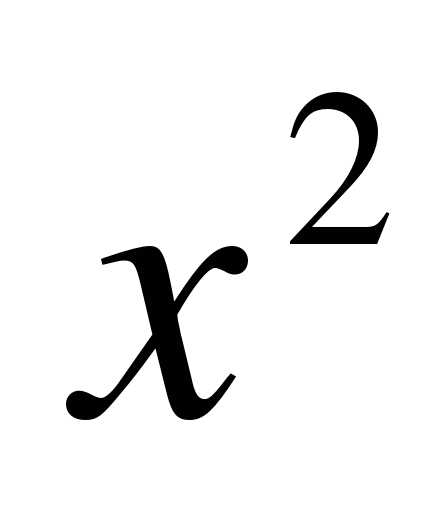 > – 9
> – 9
10
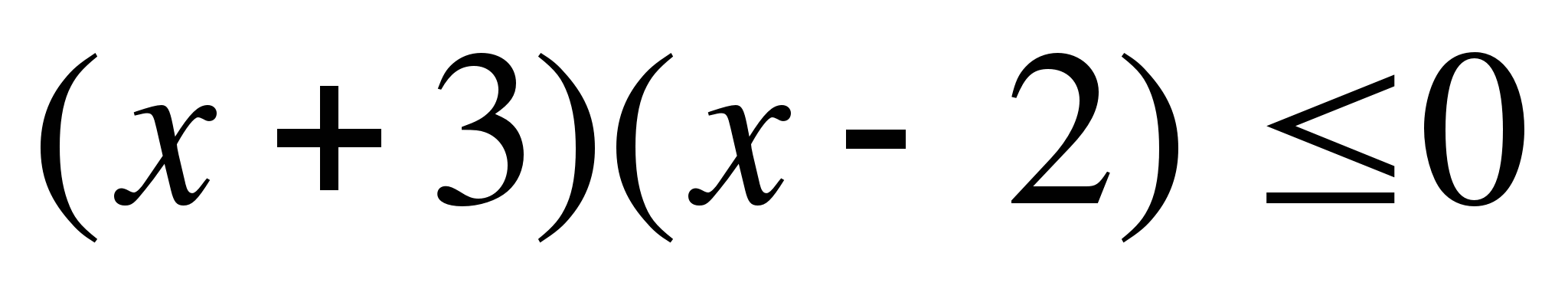
10
(x+1)(x-4) 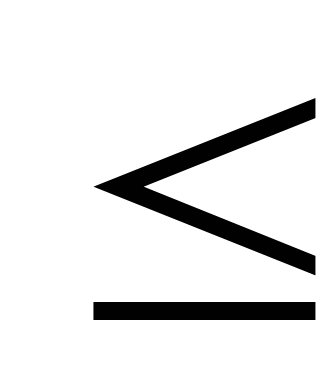 0
0
11
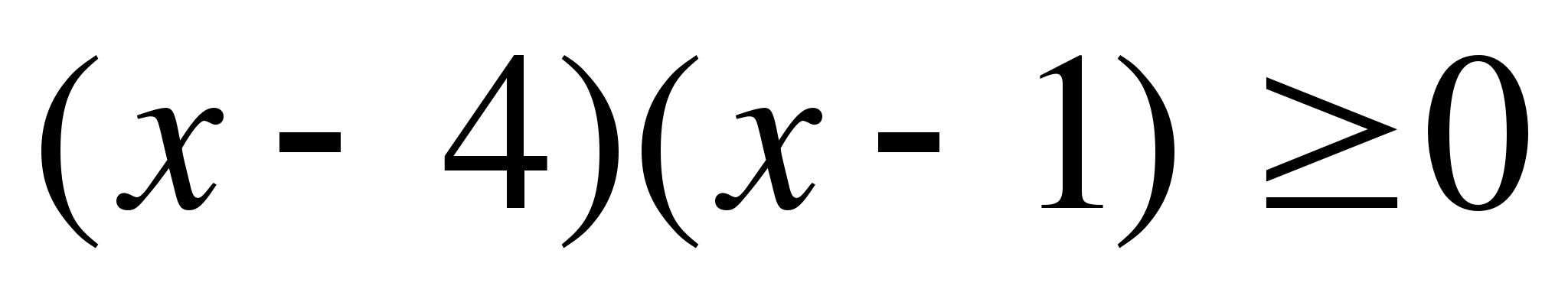
11
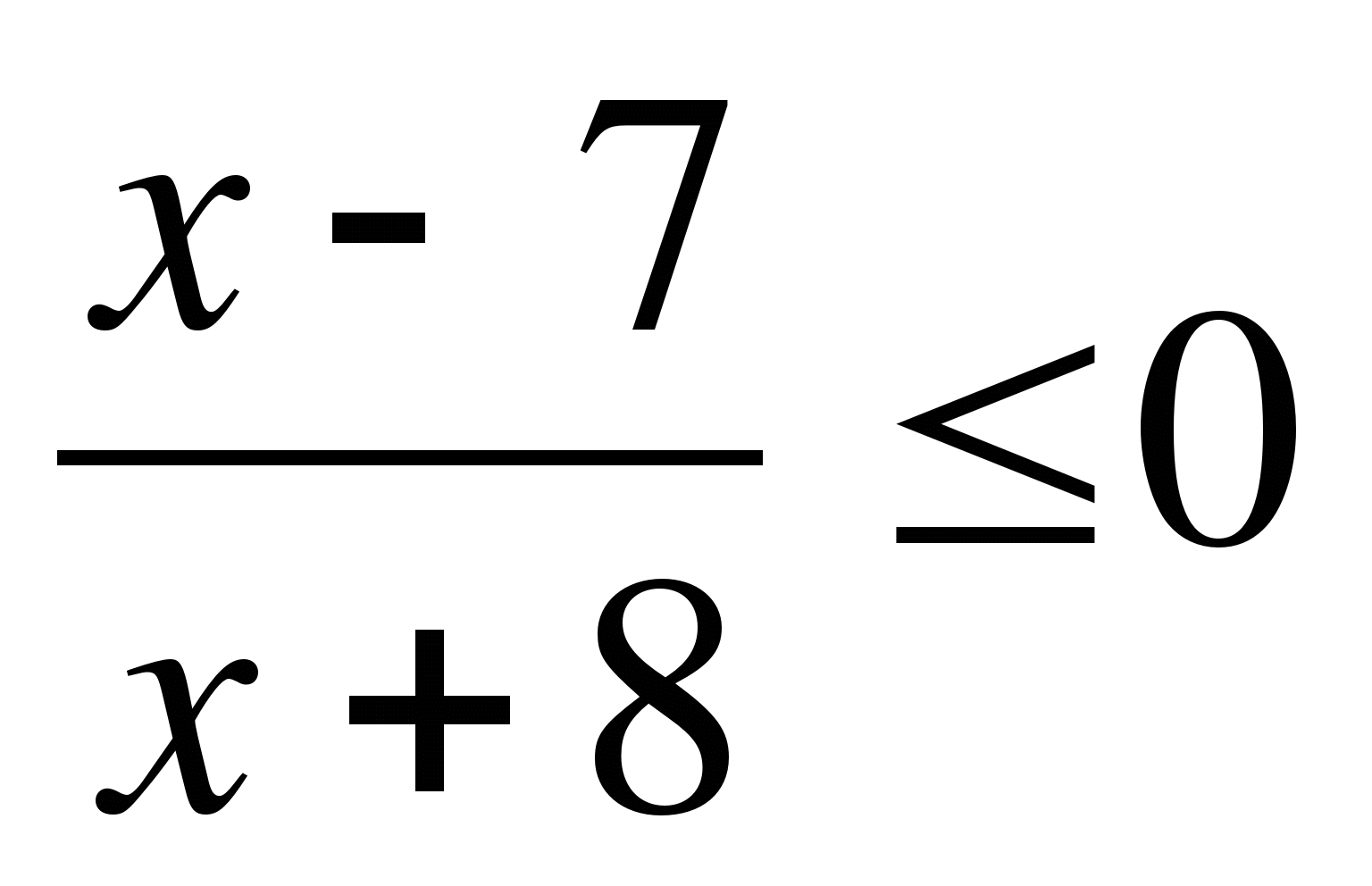
11
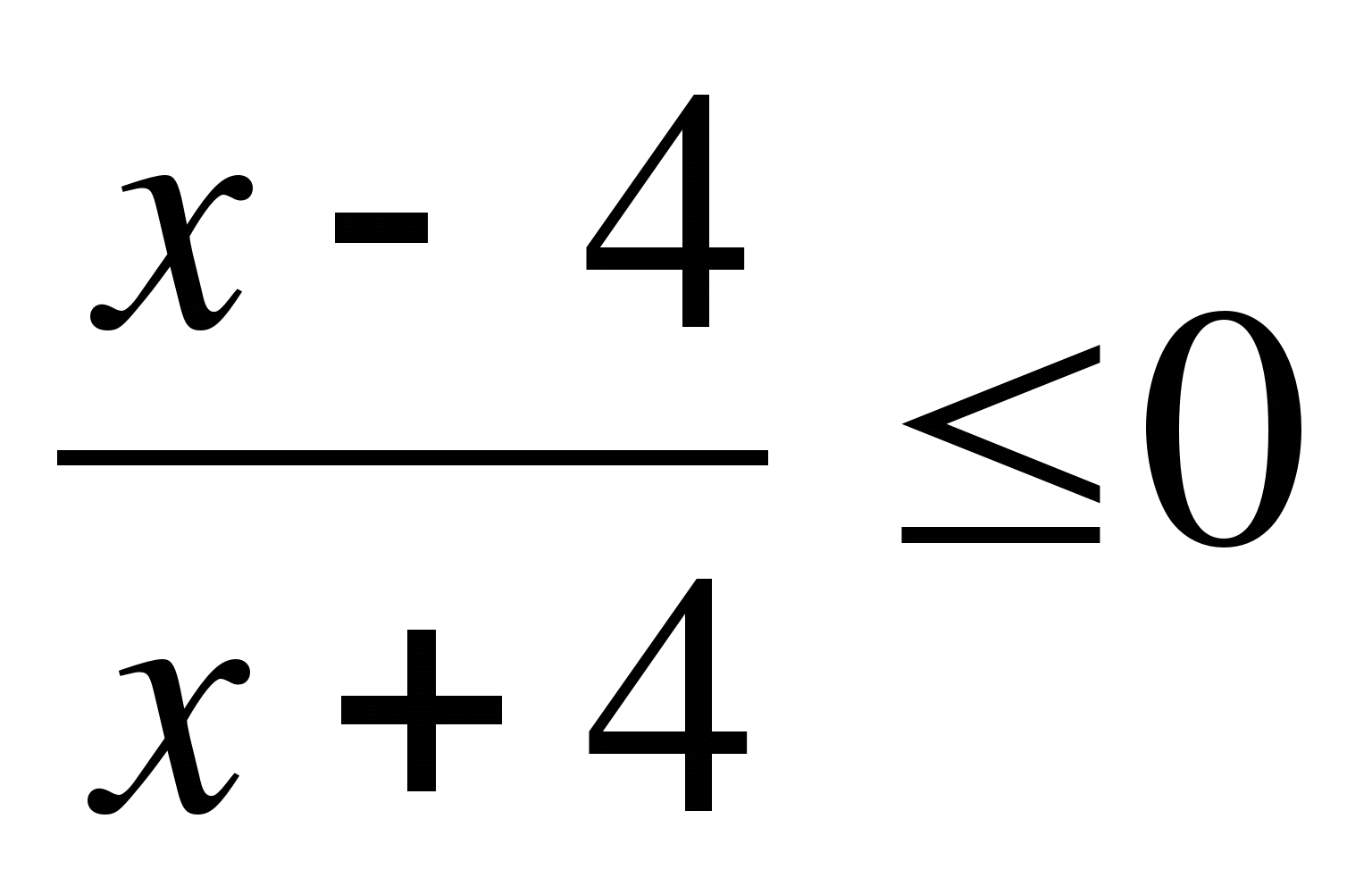
11
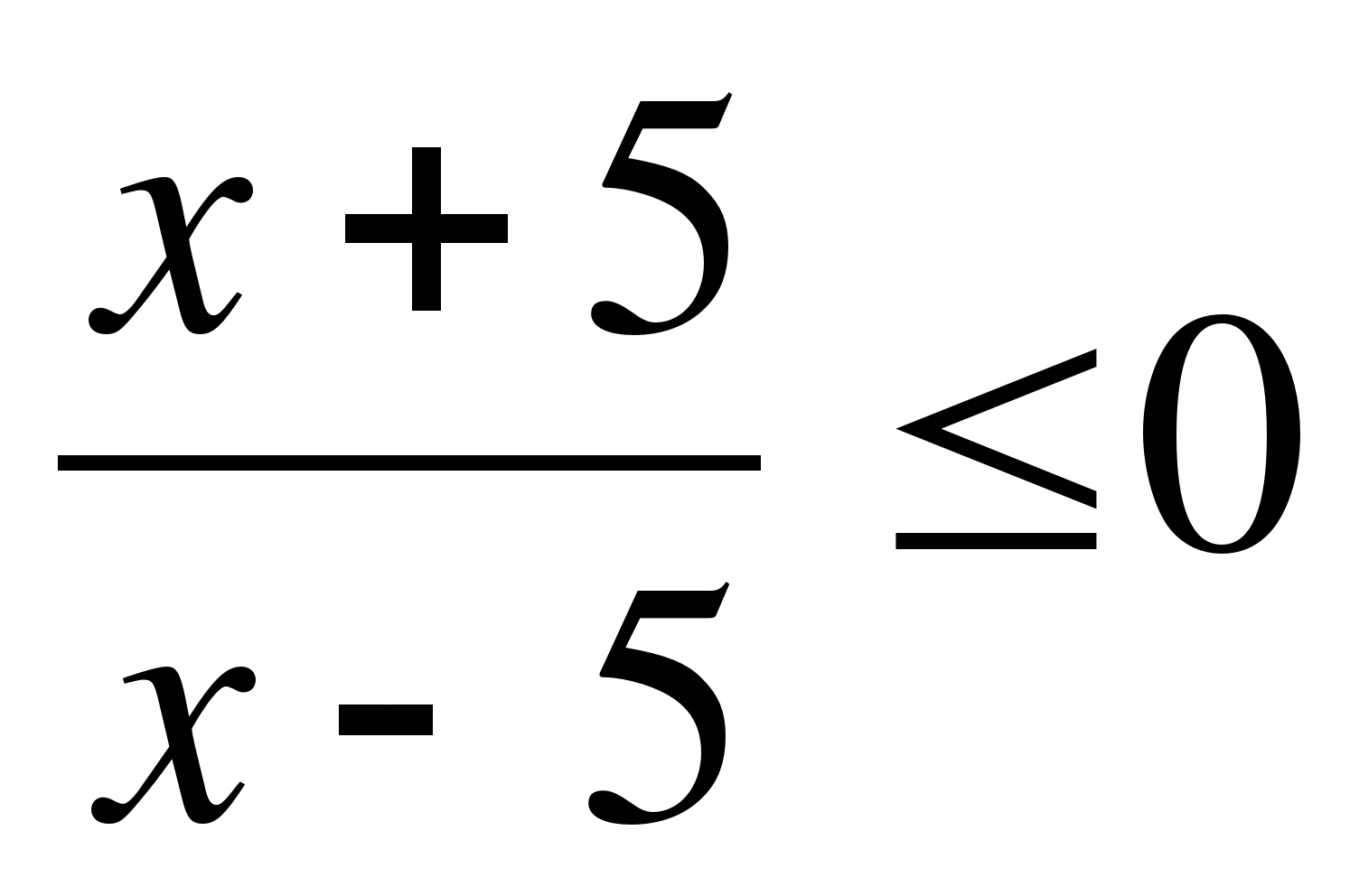
12
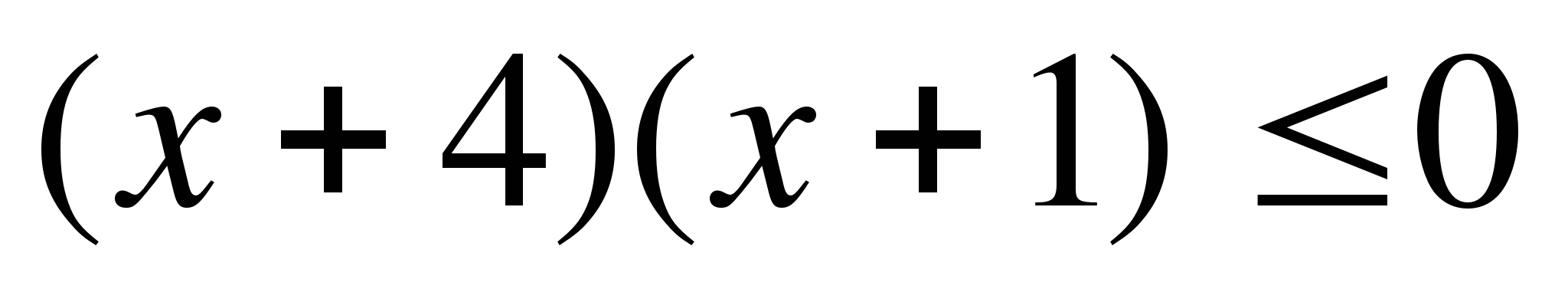
12
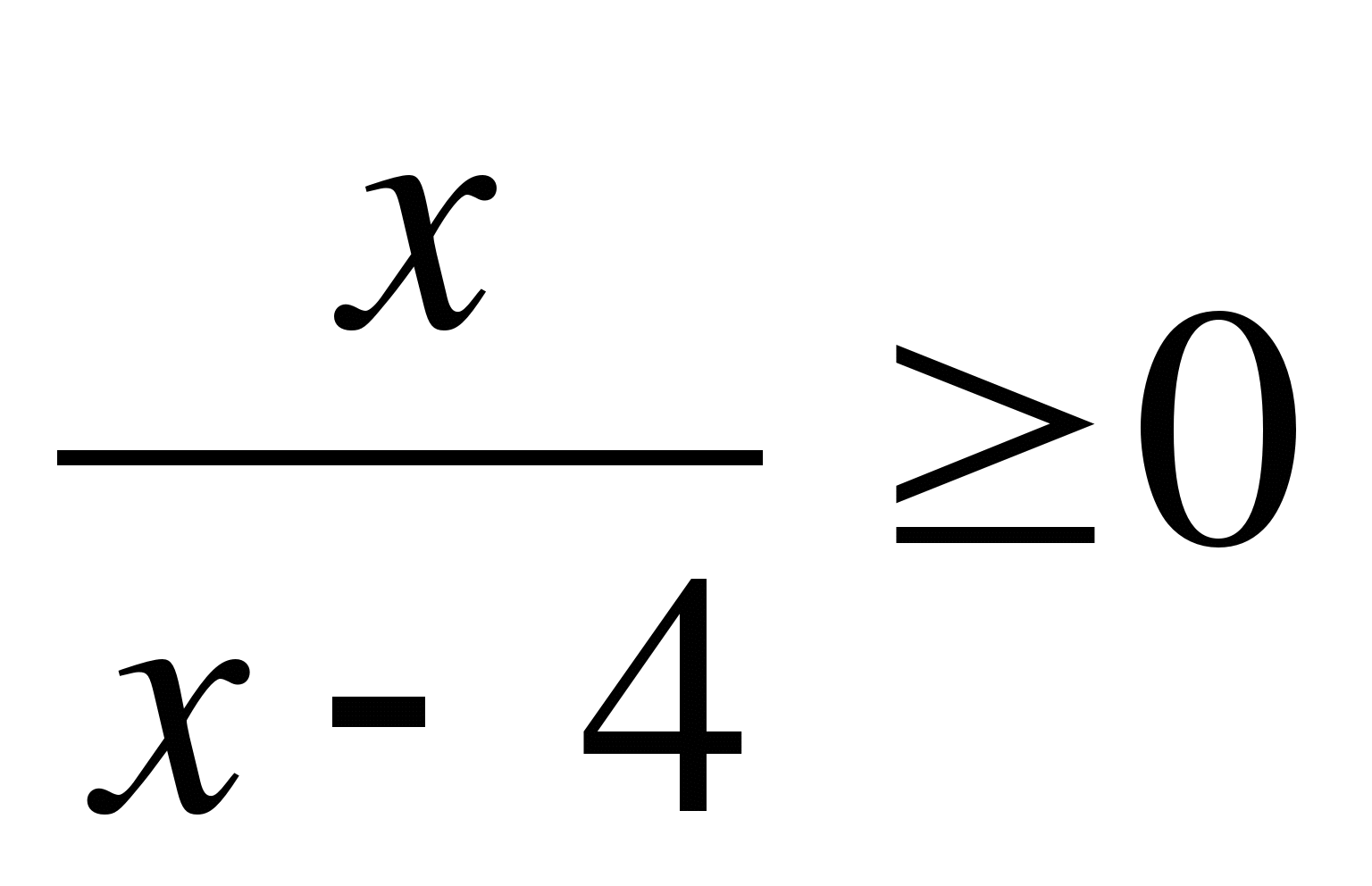
12
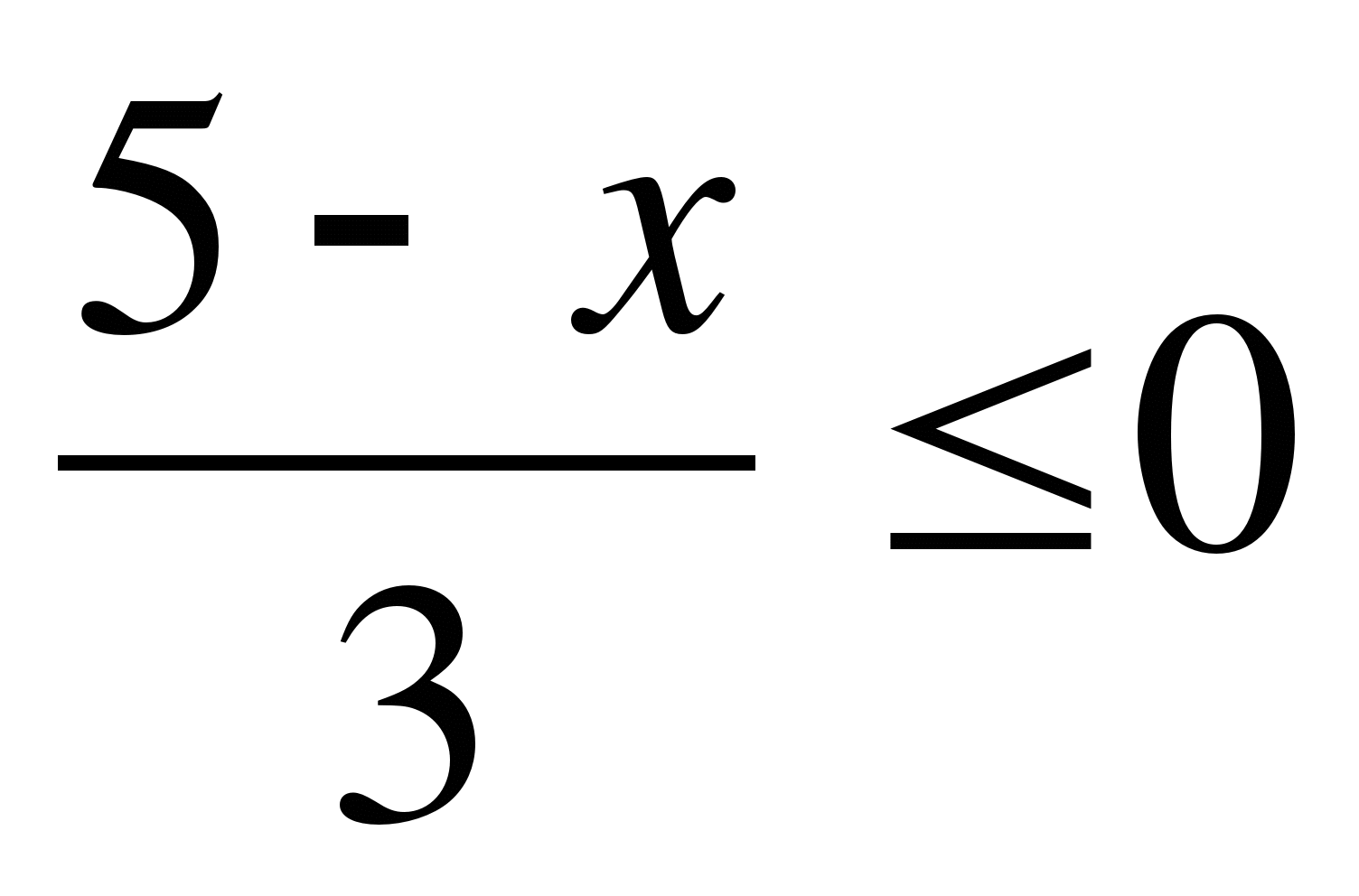
12
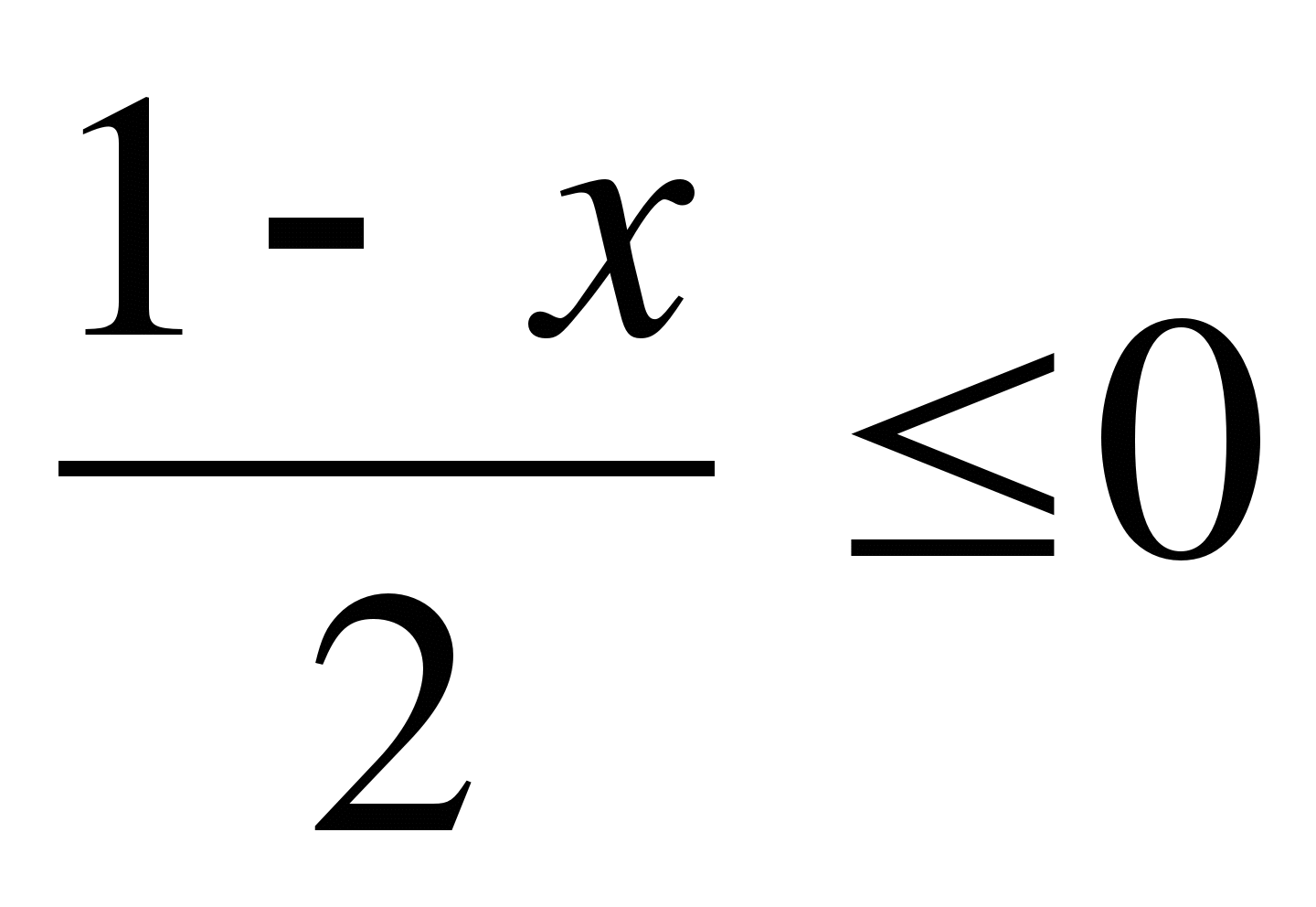
13
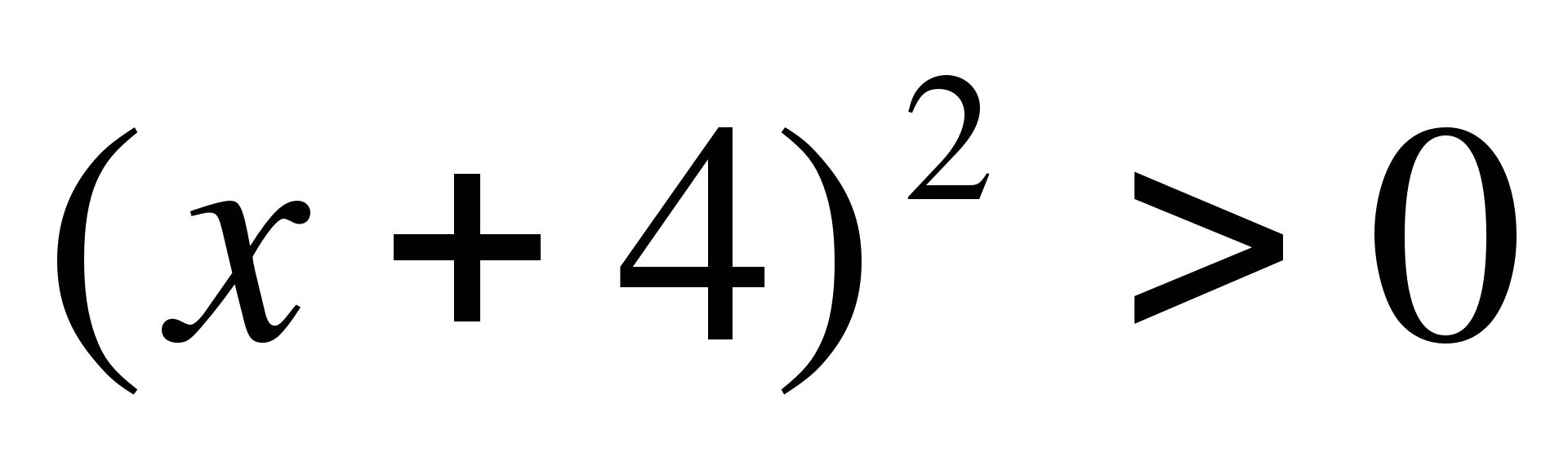
13
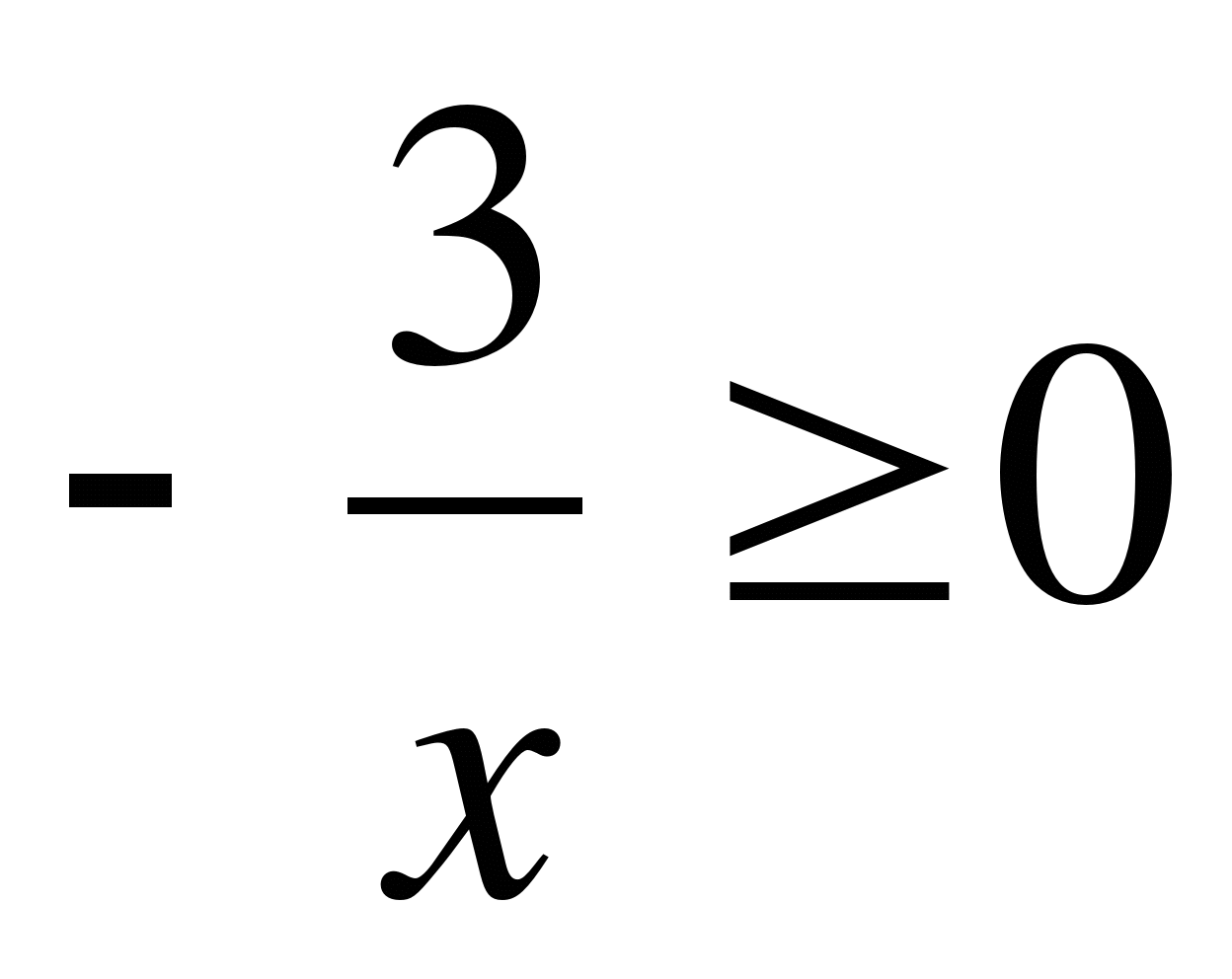
13
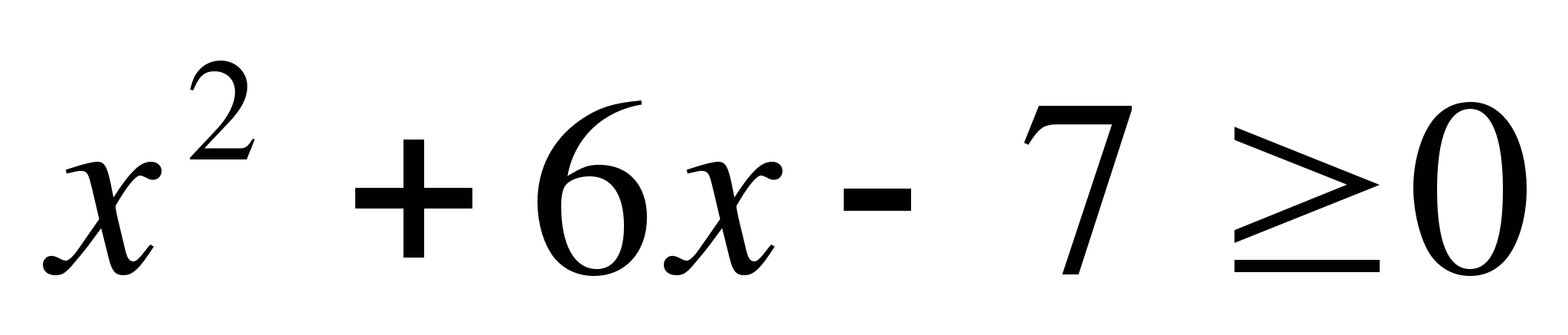
13
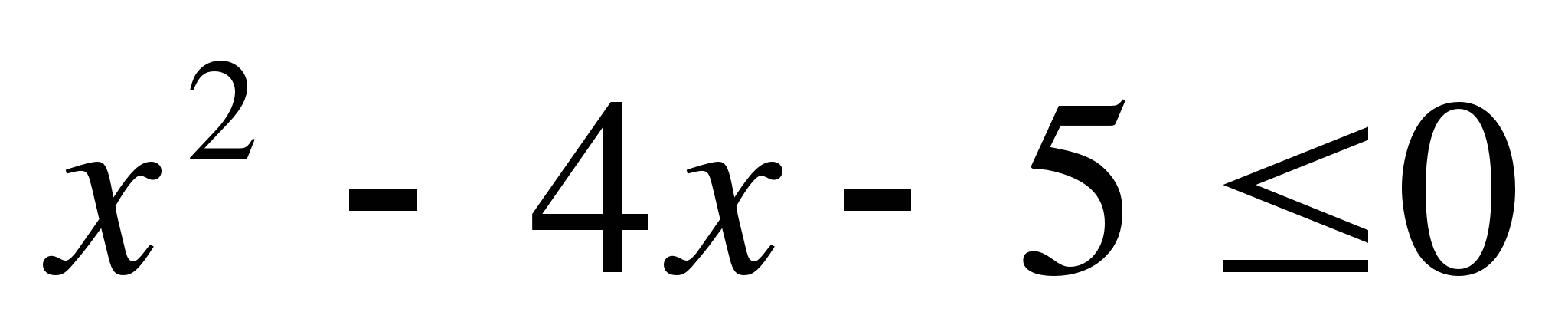
14
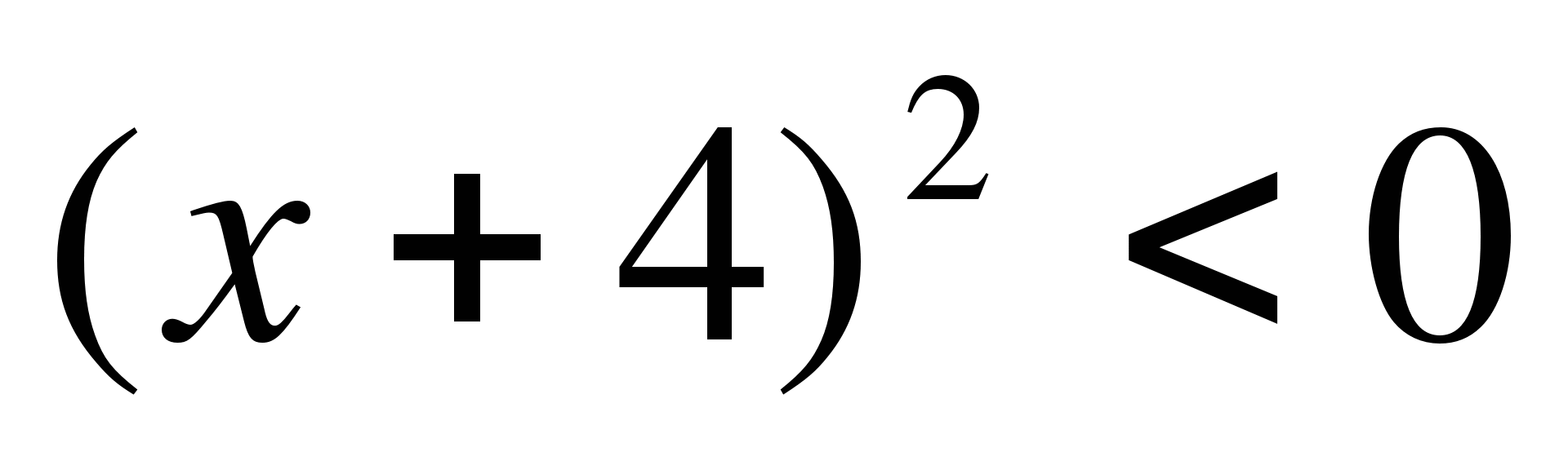
14
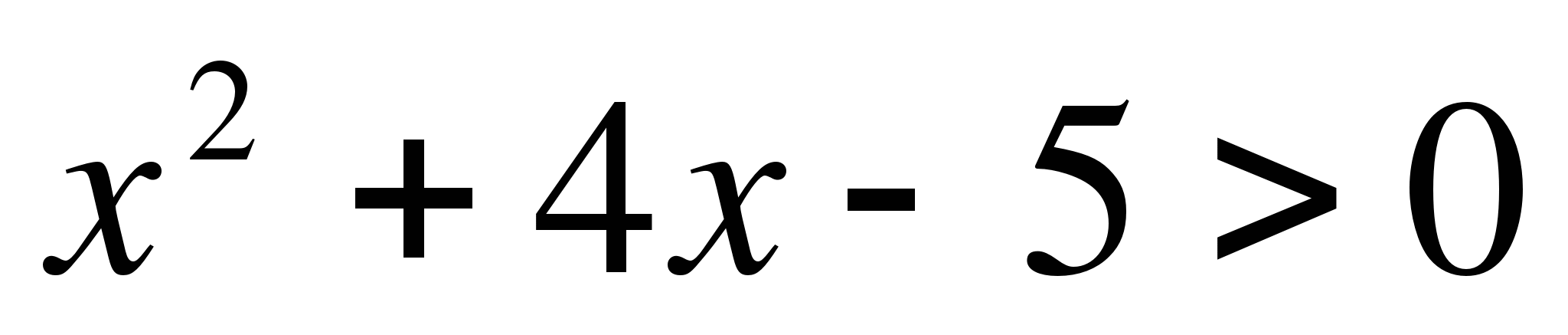
14
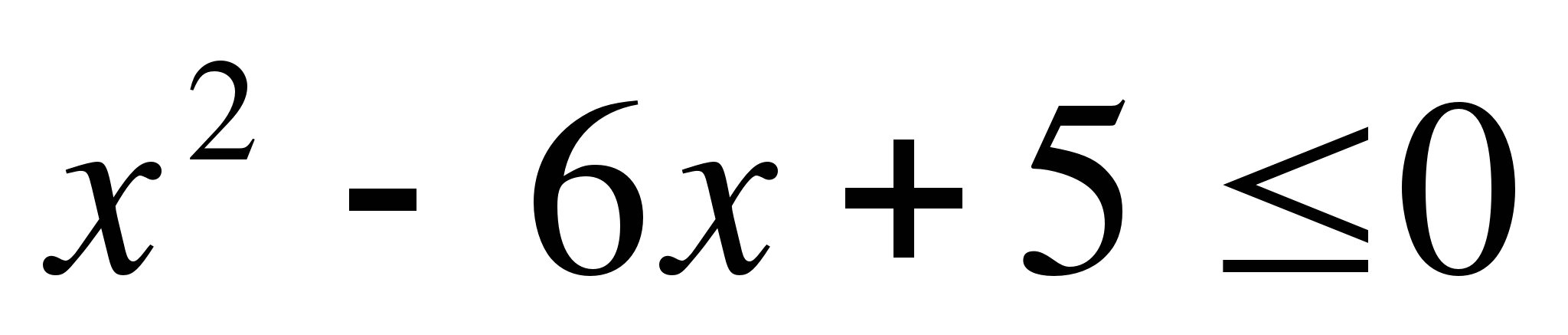
14
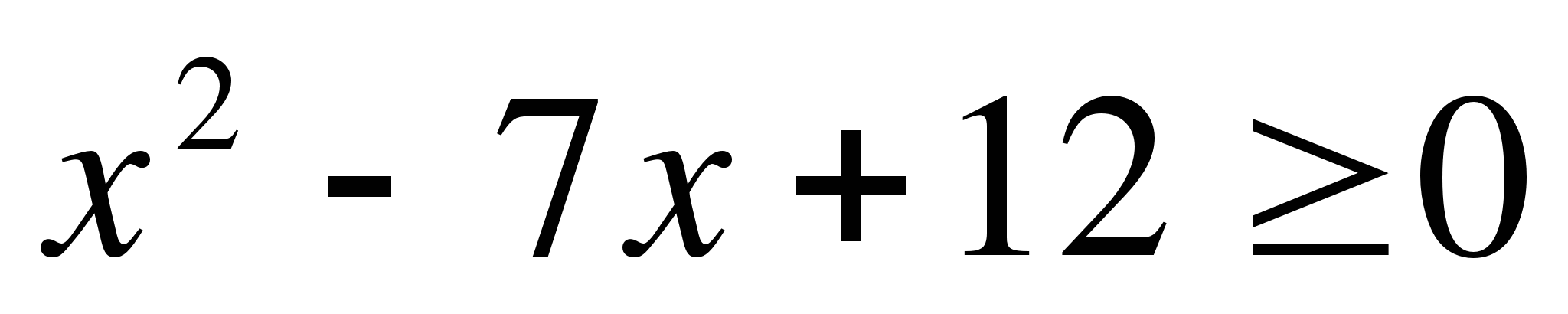
15
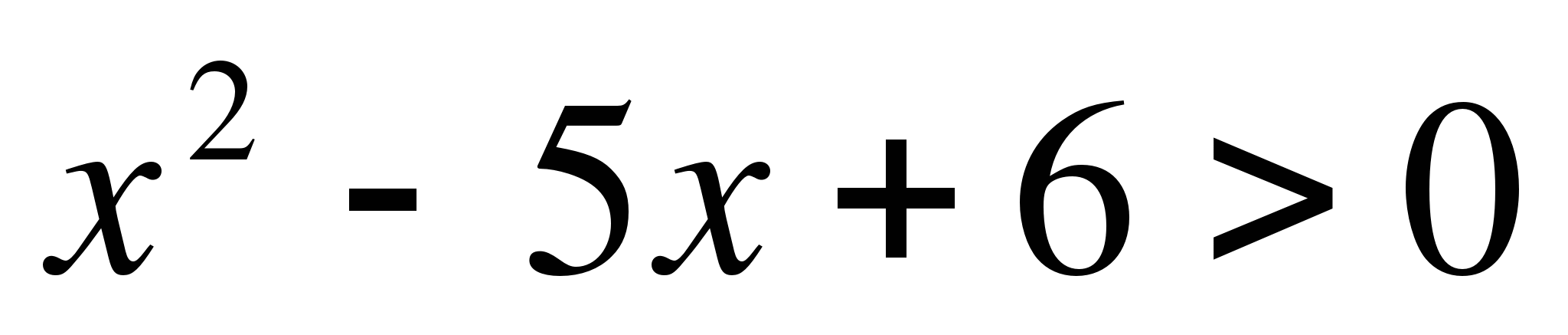
15
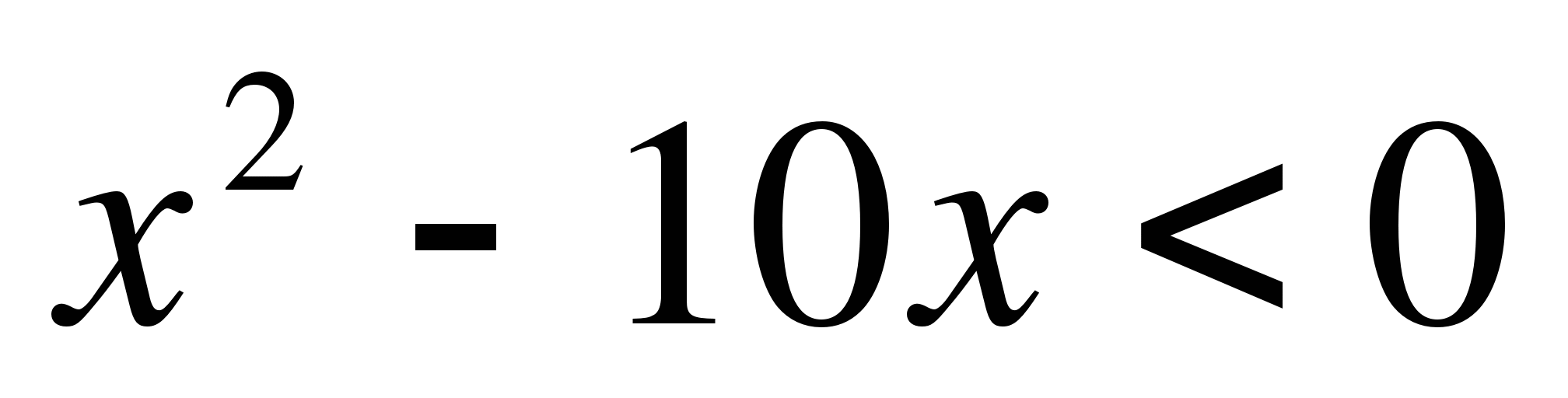
15
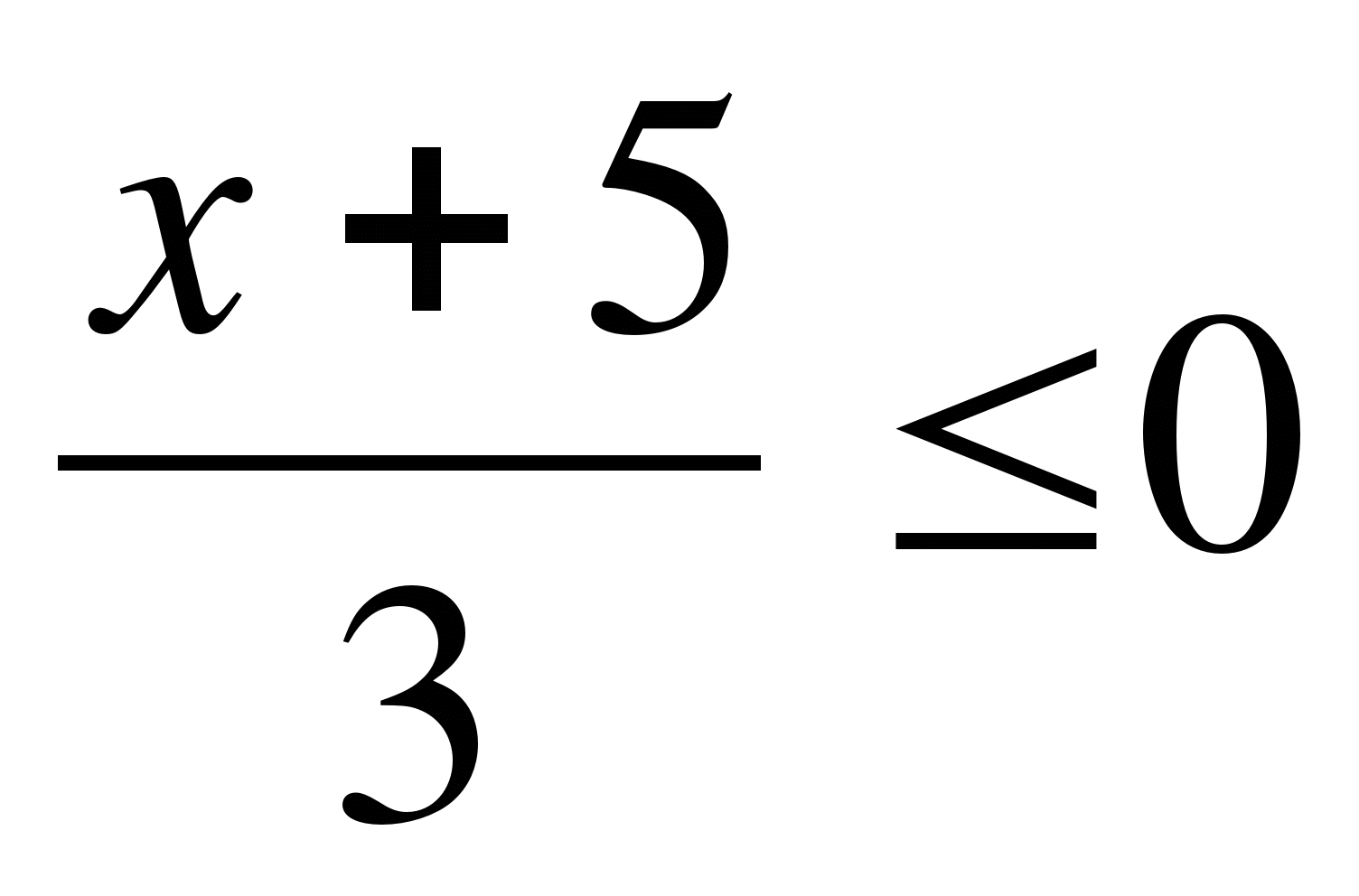
15
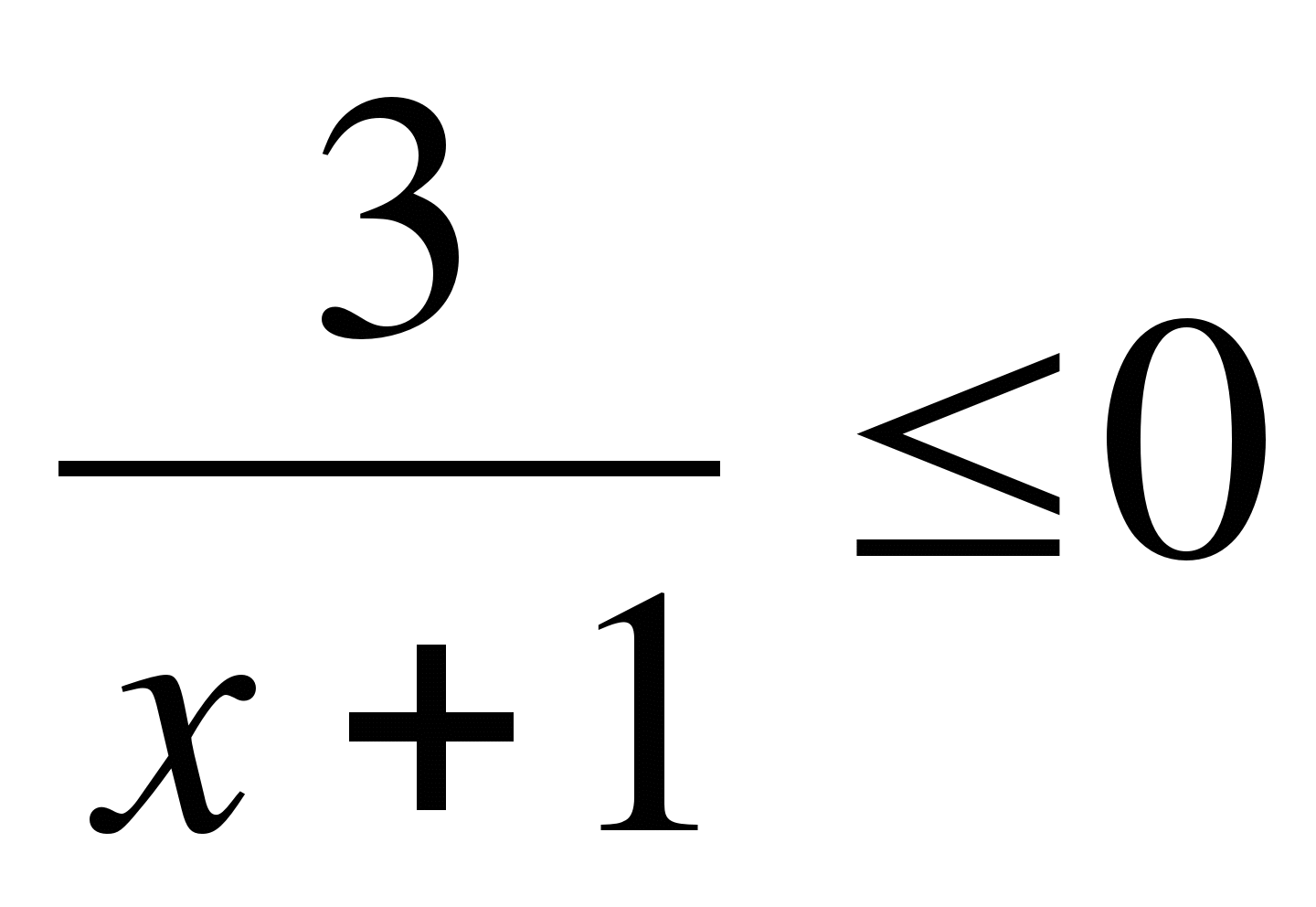
16
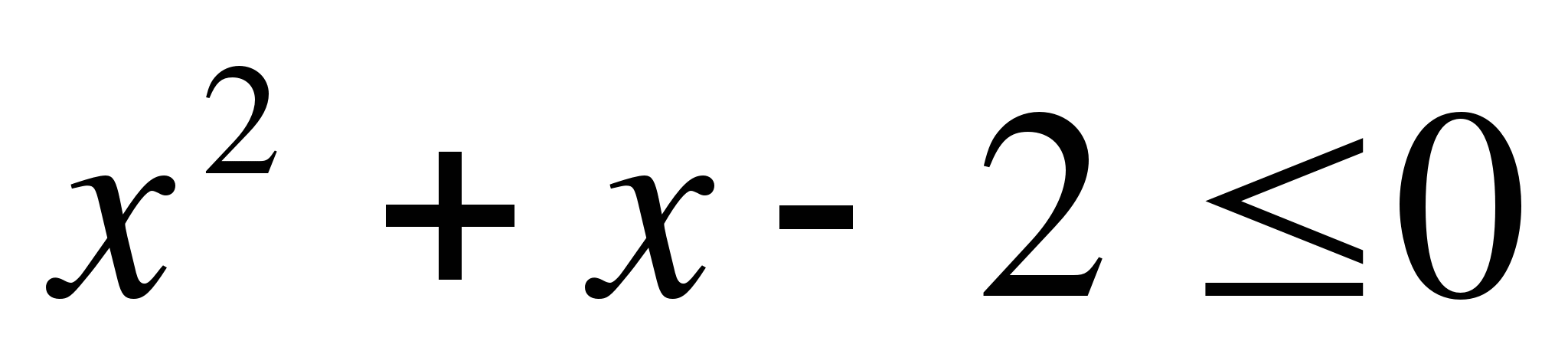
16
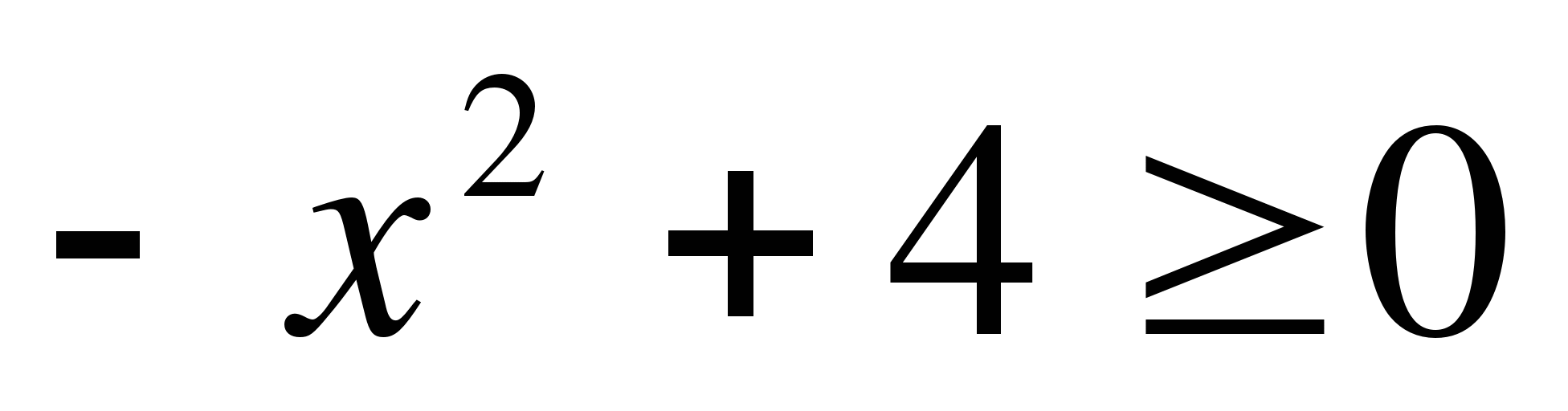
16
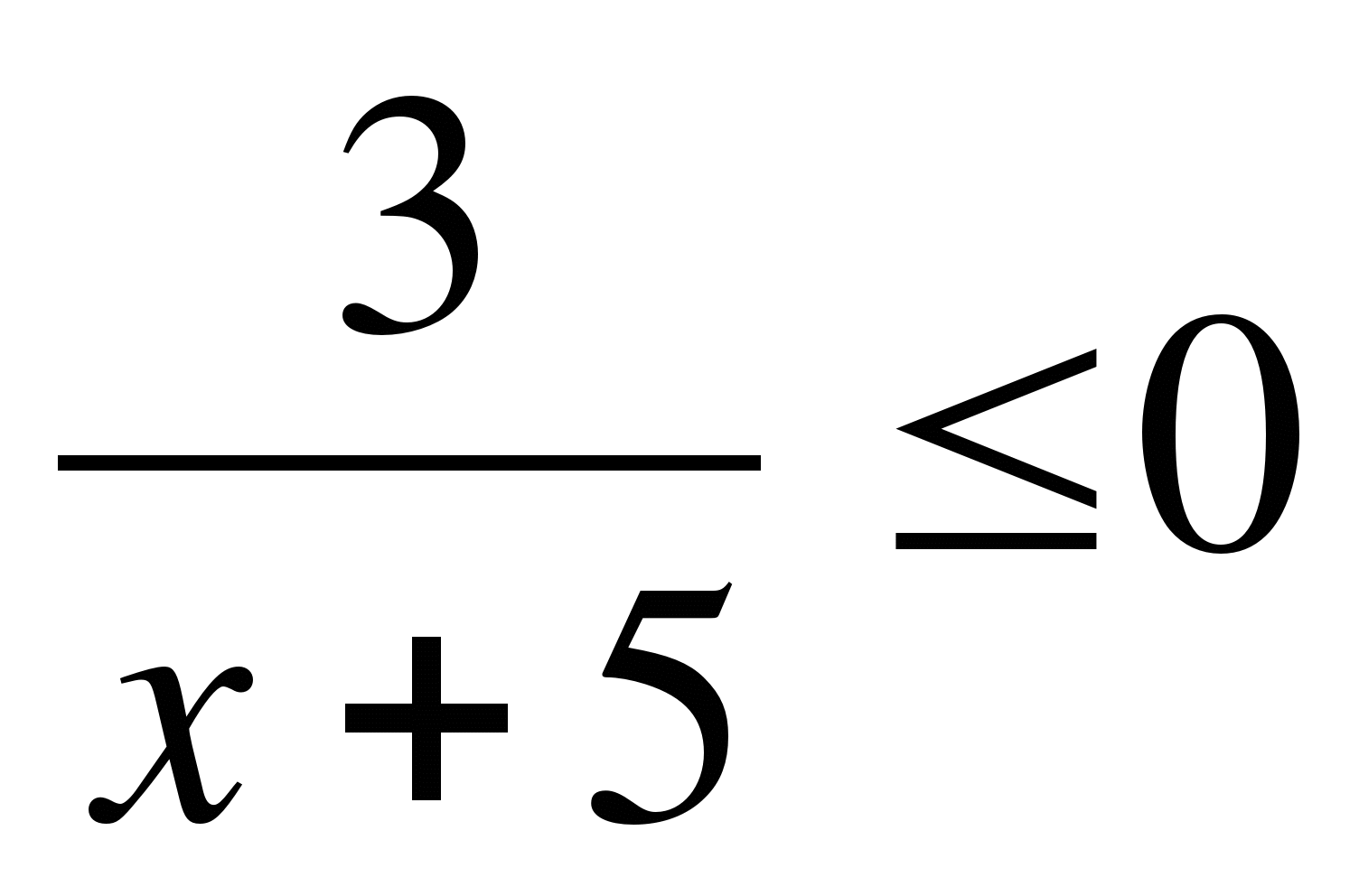
16
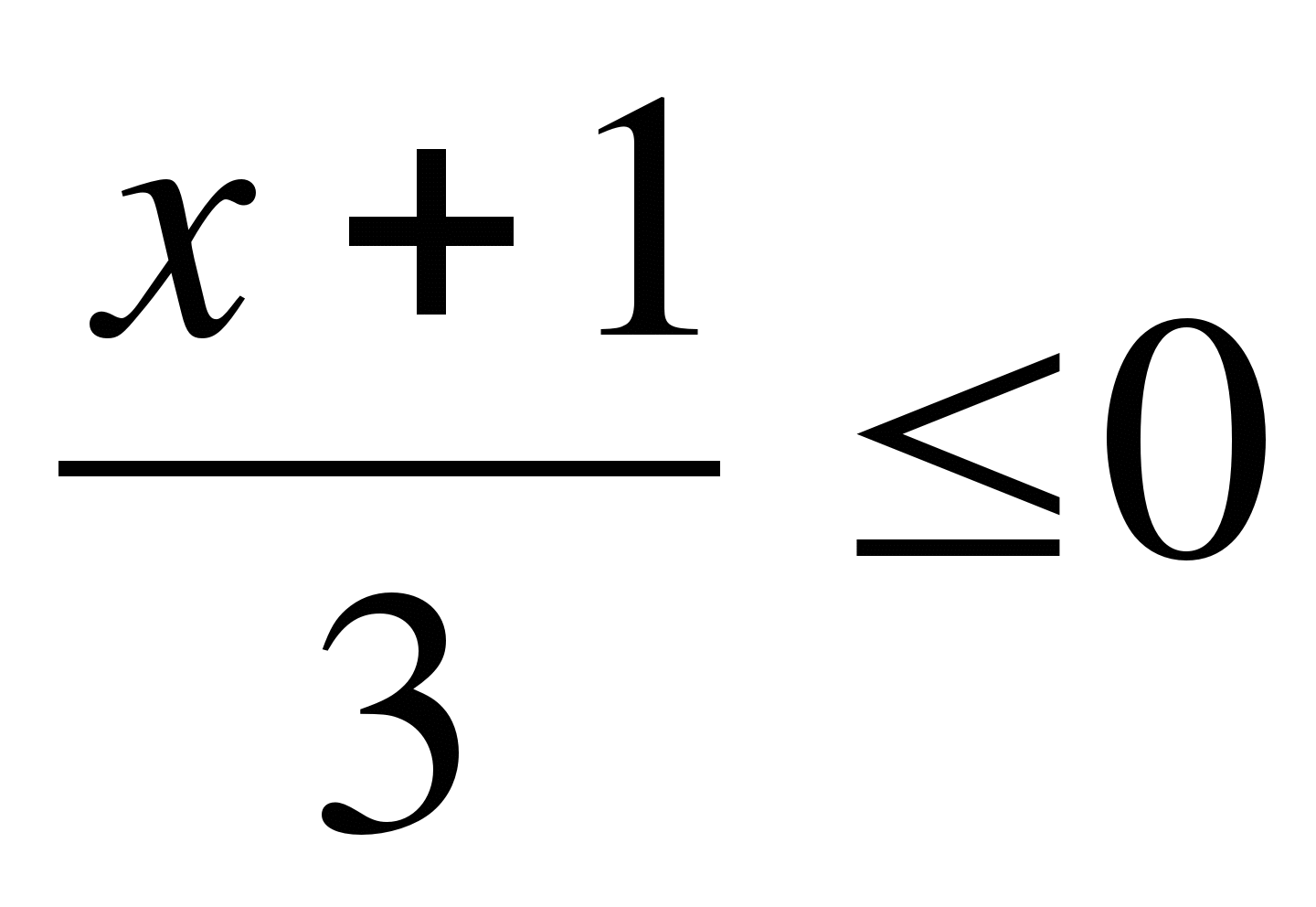
17
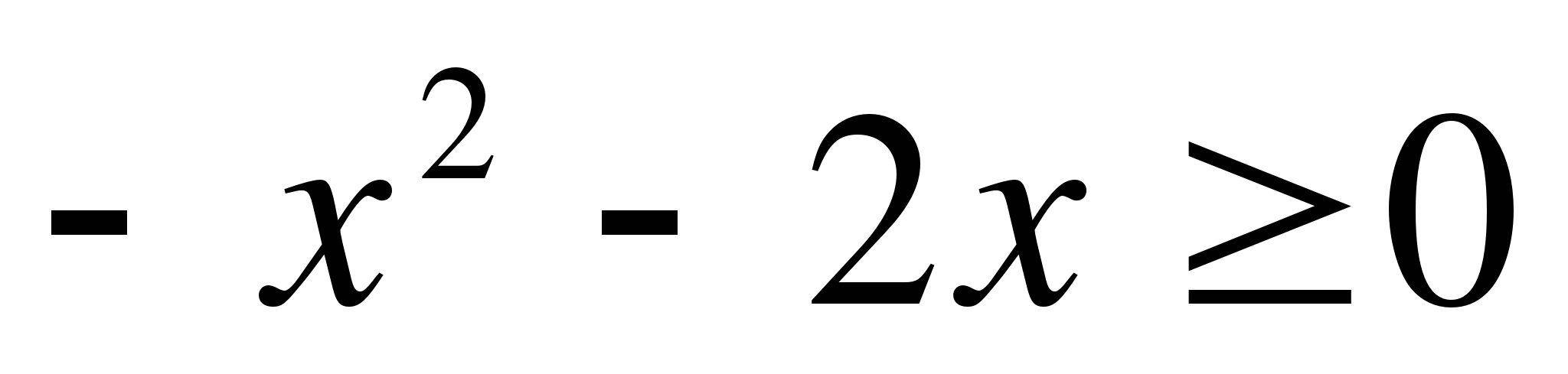
17
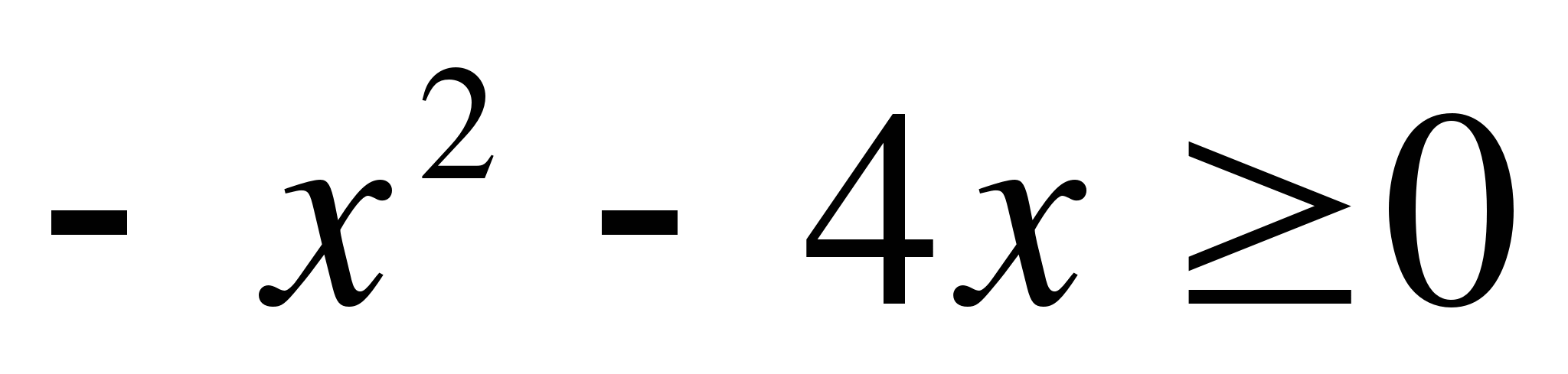
17
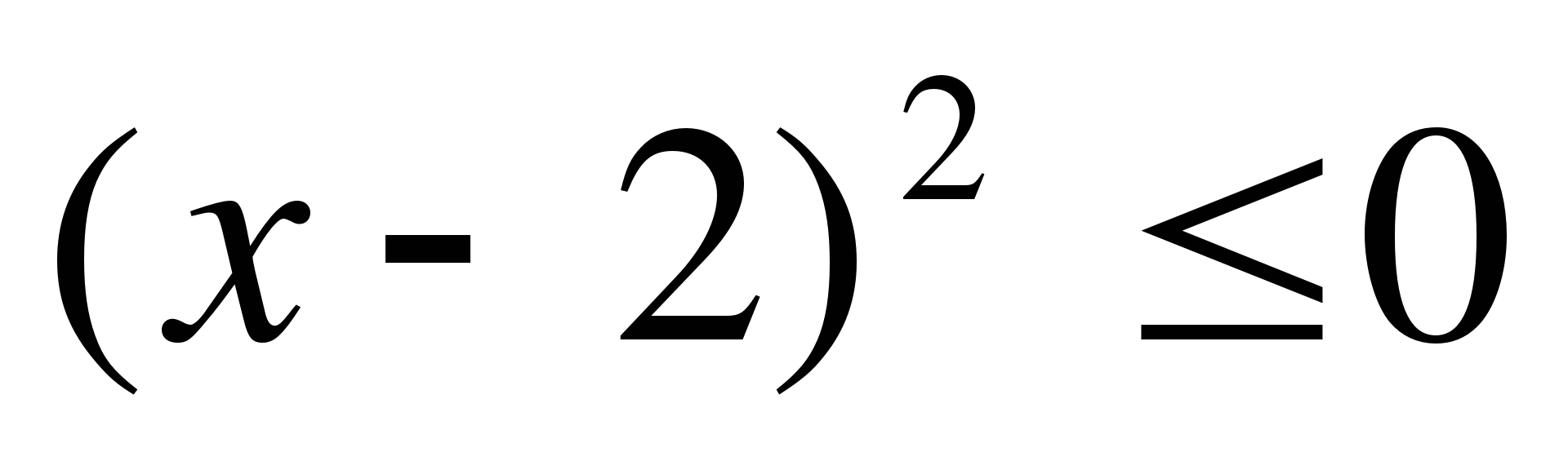
17
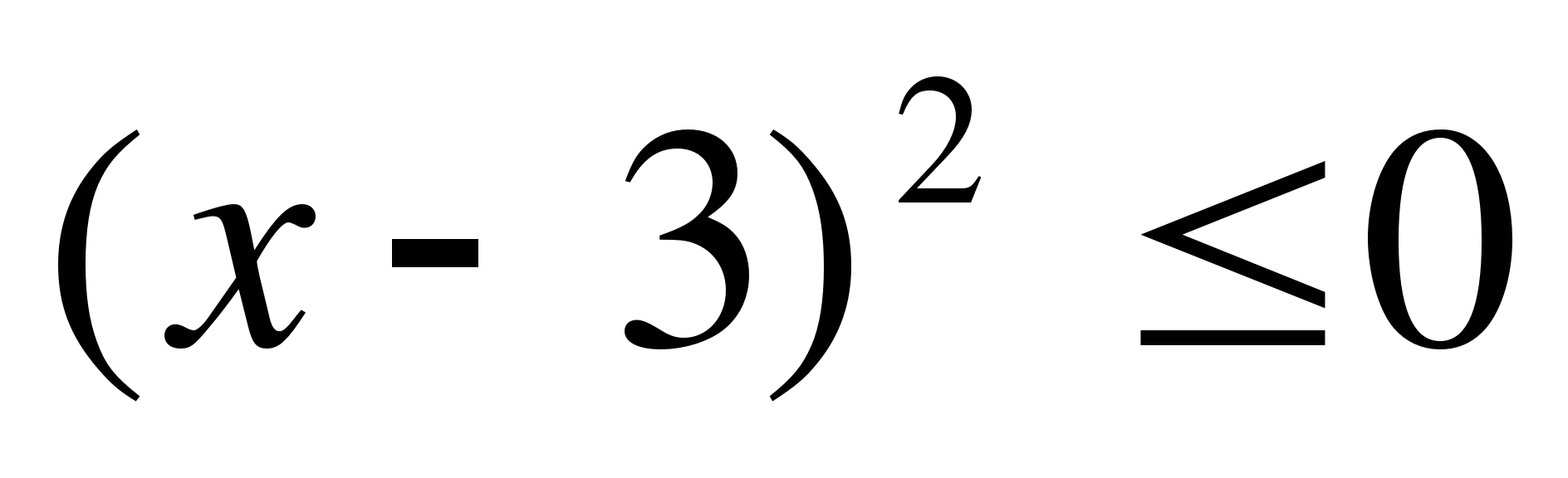
18
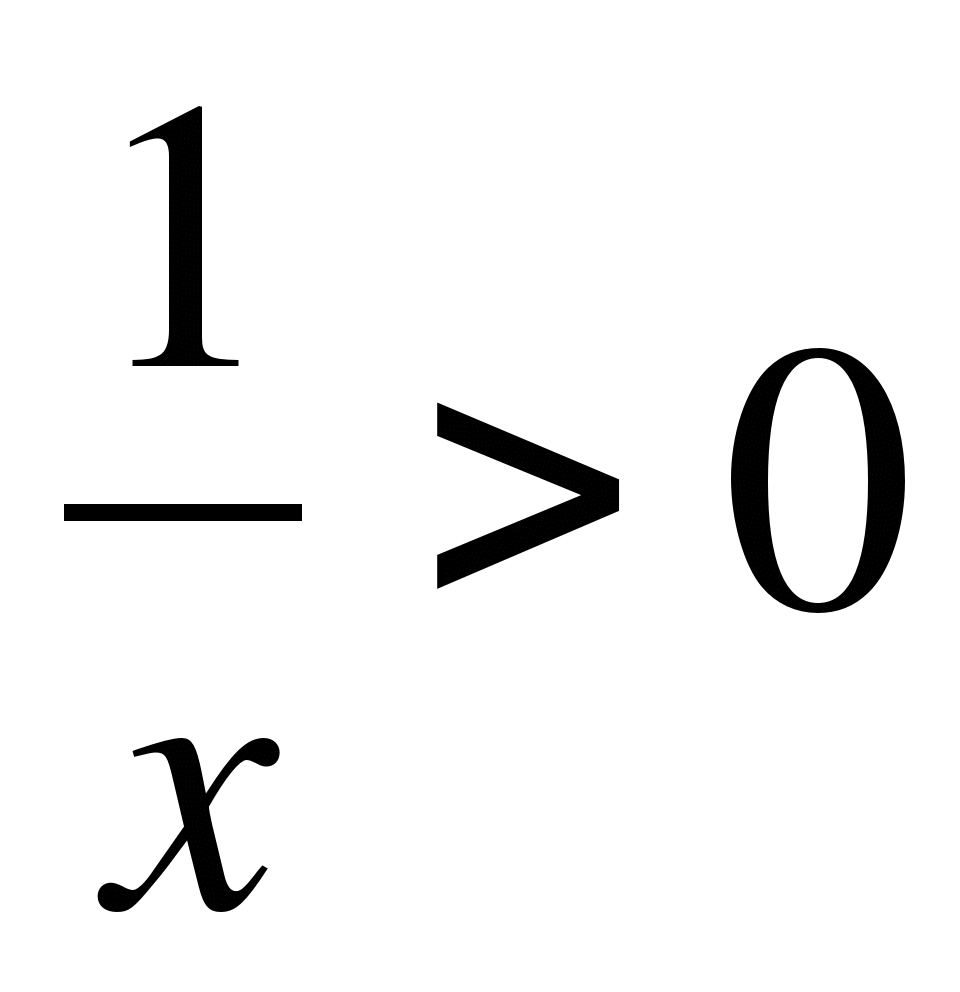
18
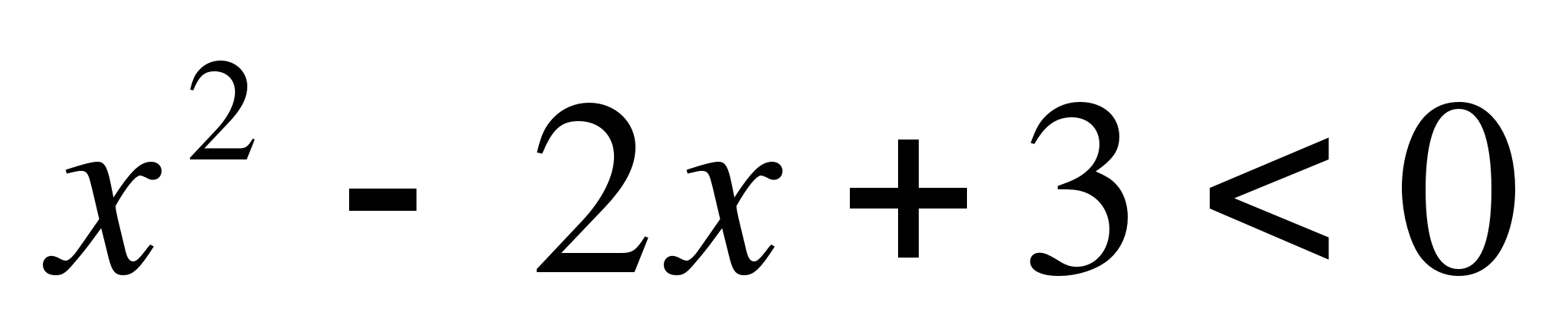
18
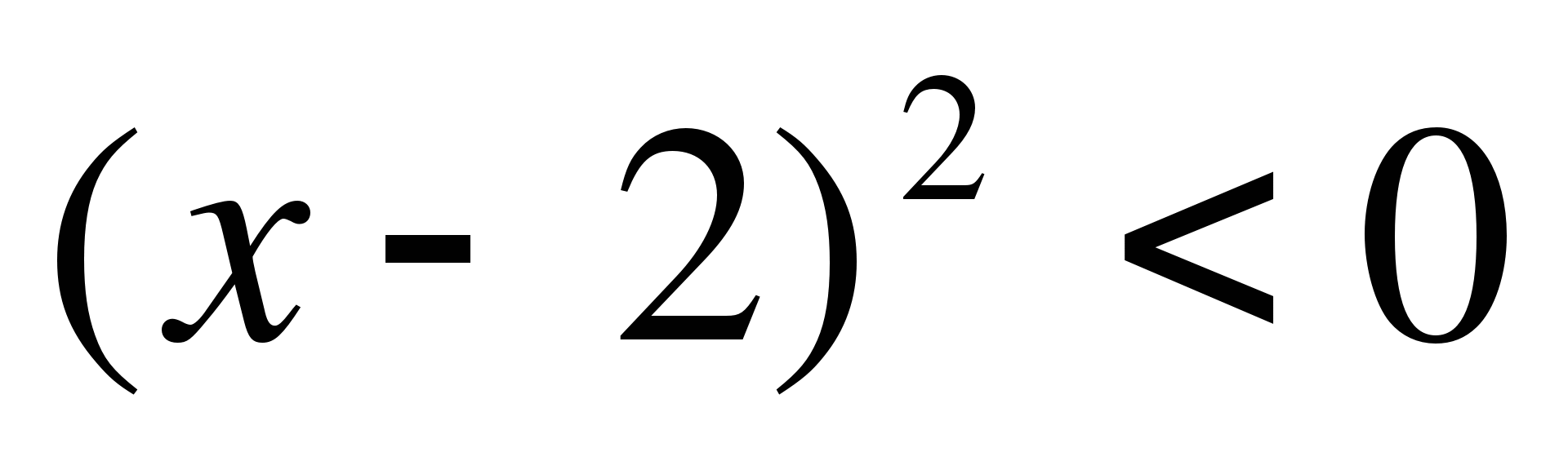
18
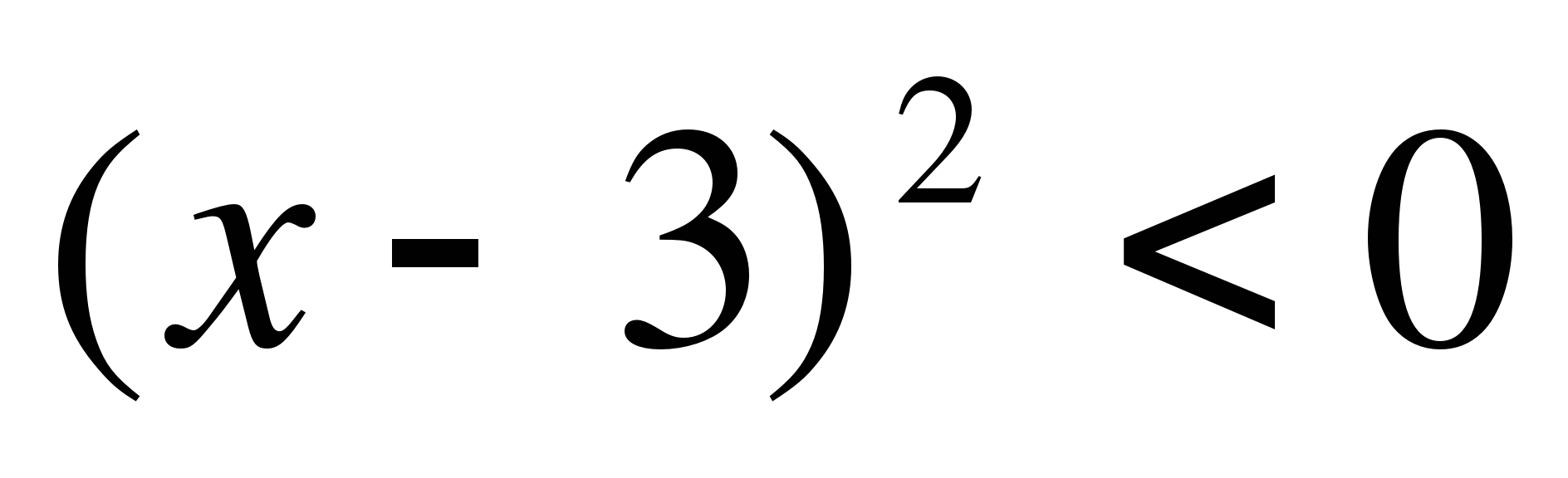
19
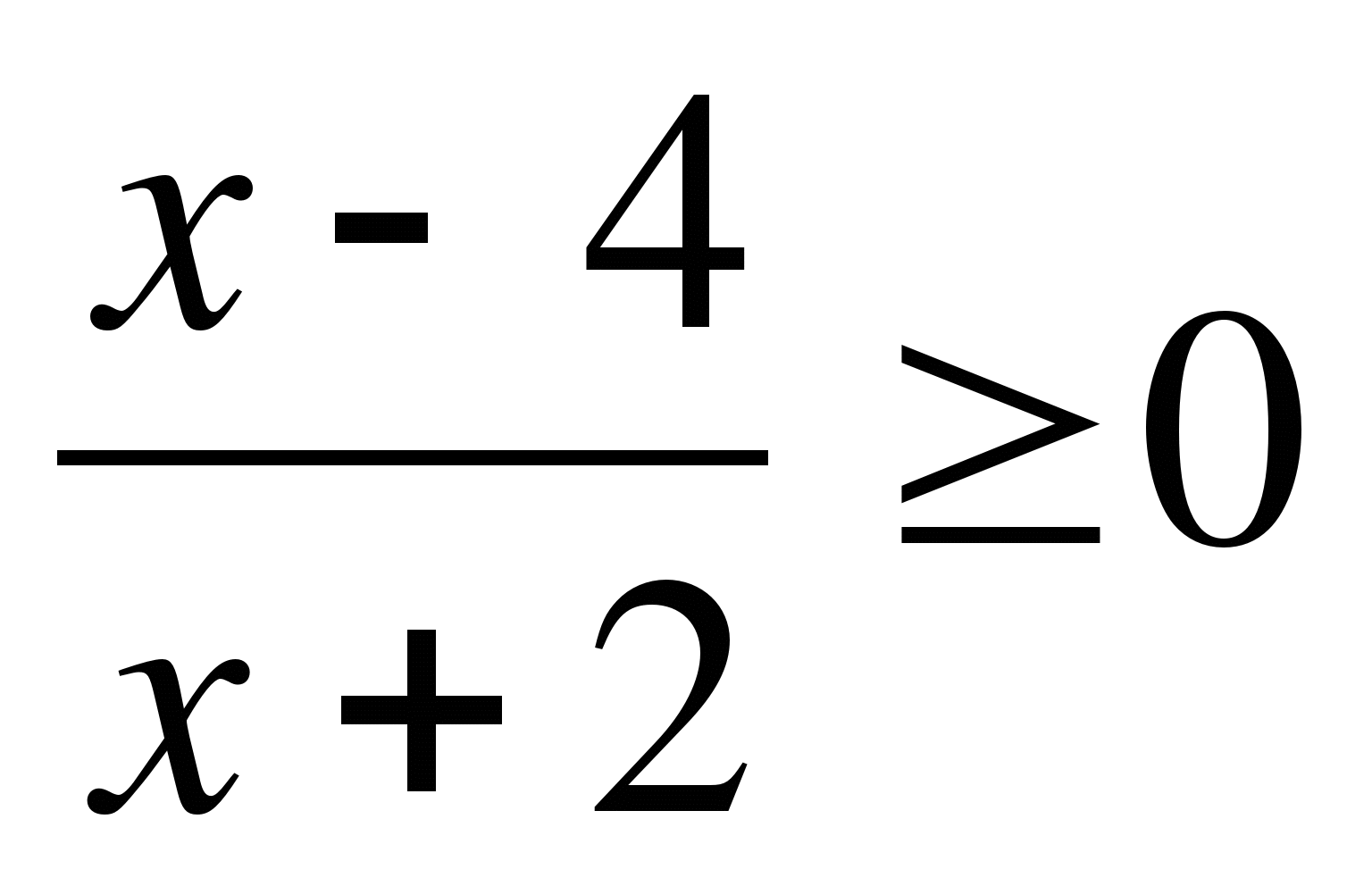
19
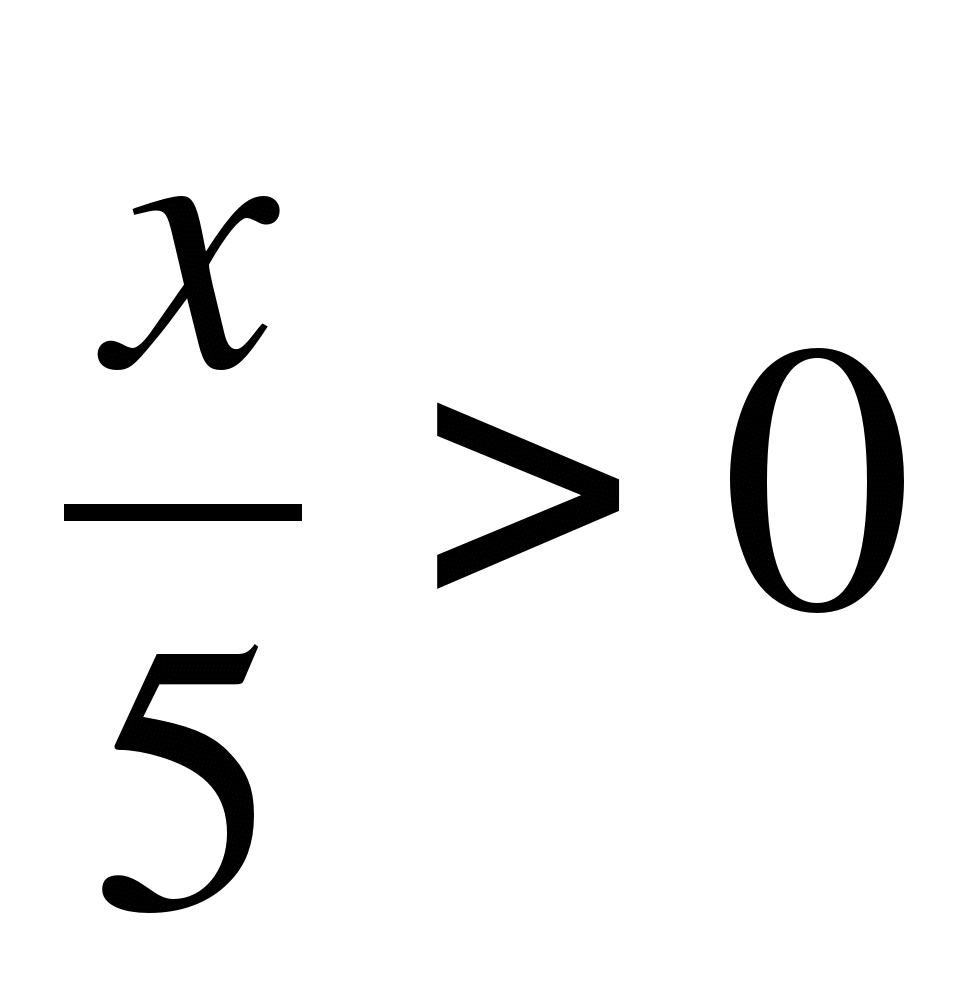
19
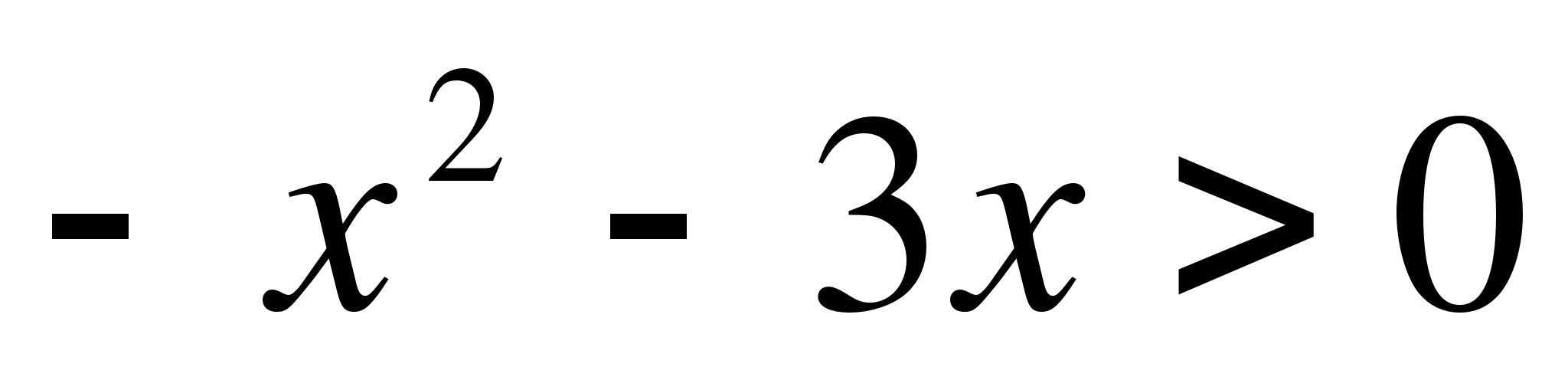
19
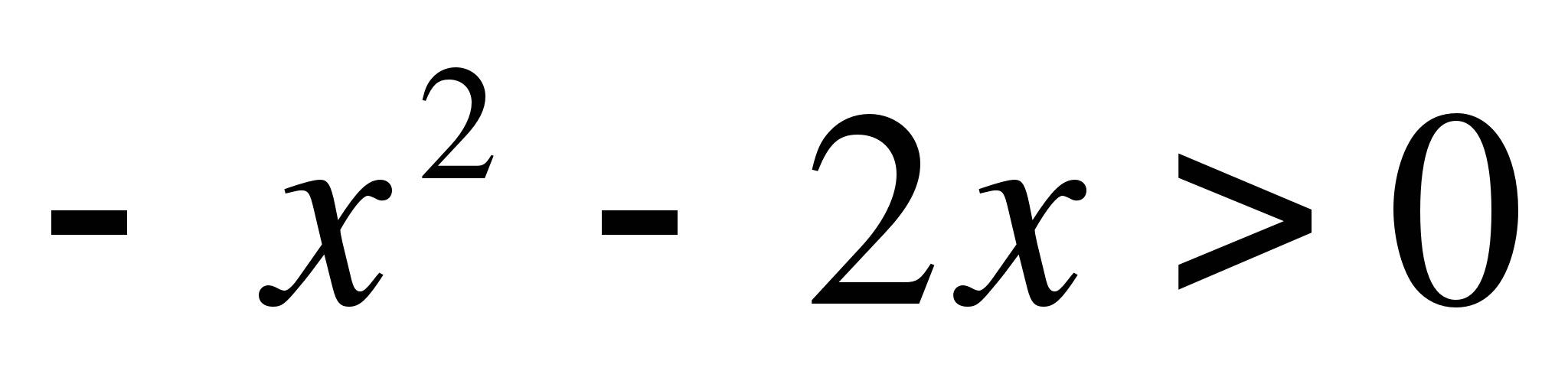
20
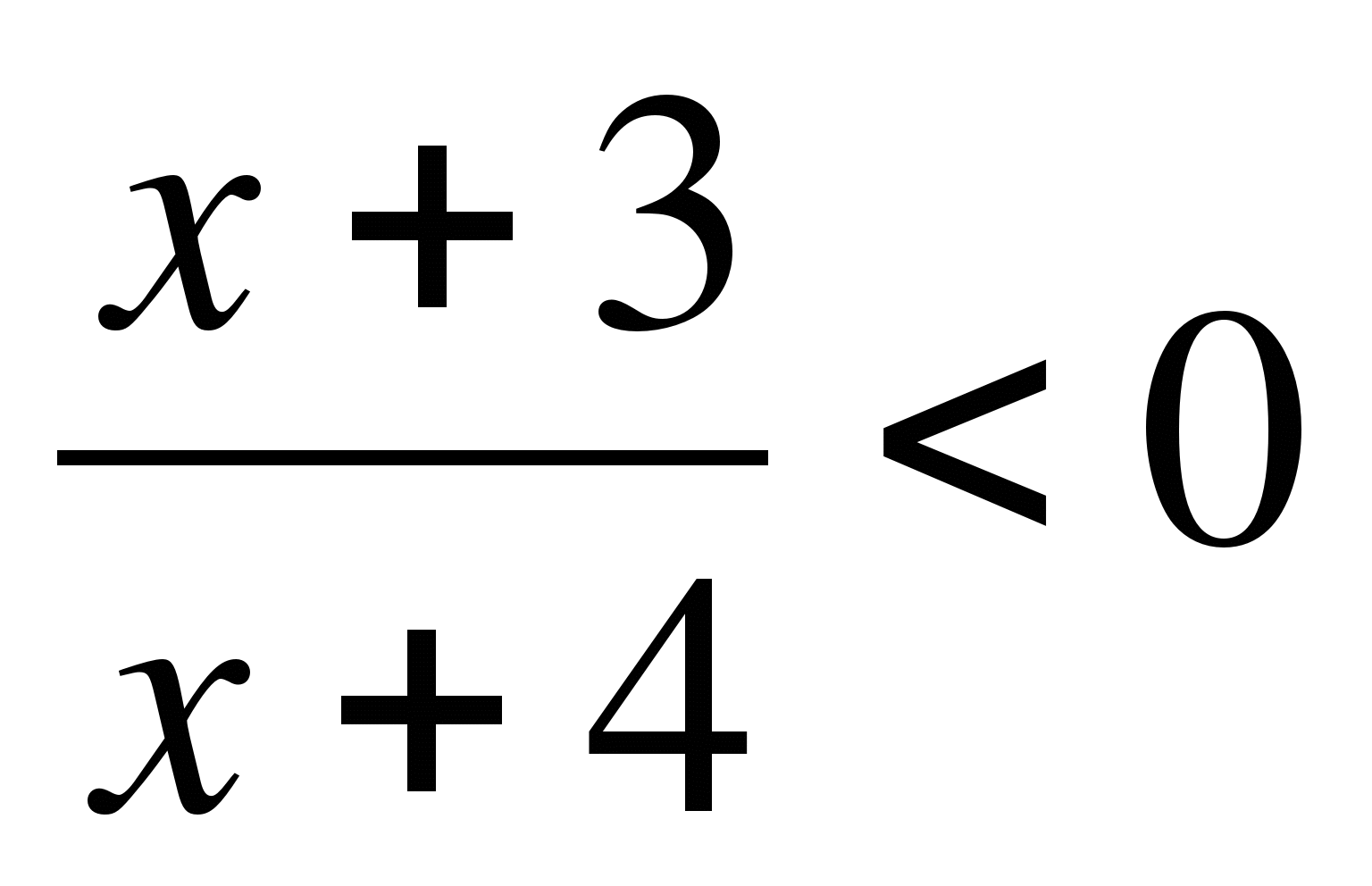
20
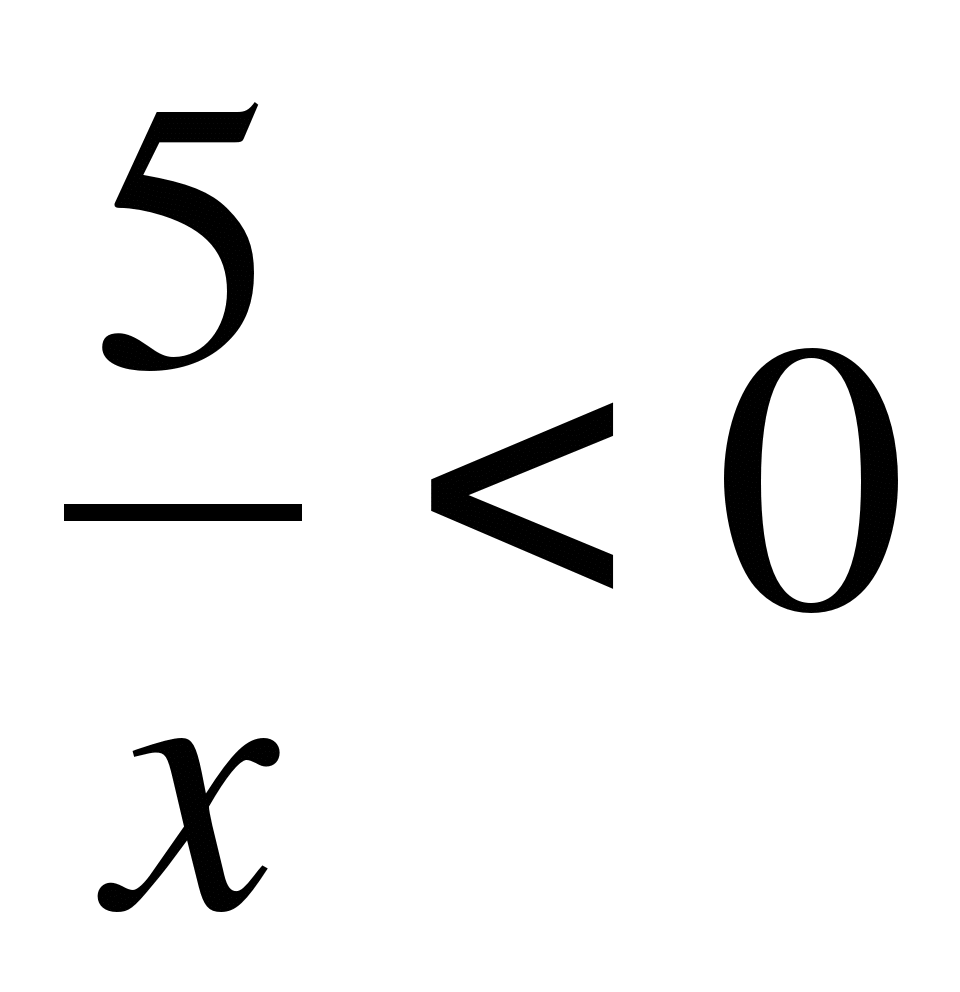
20
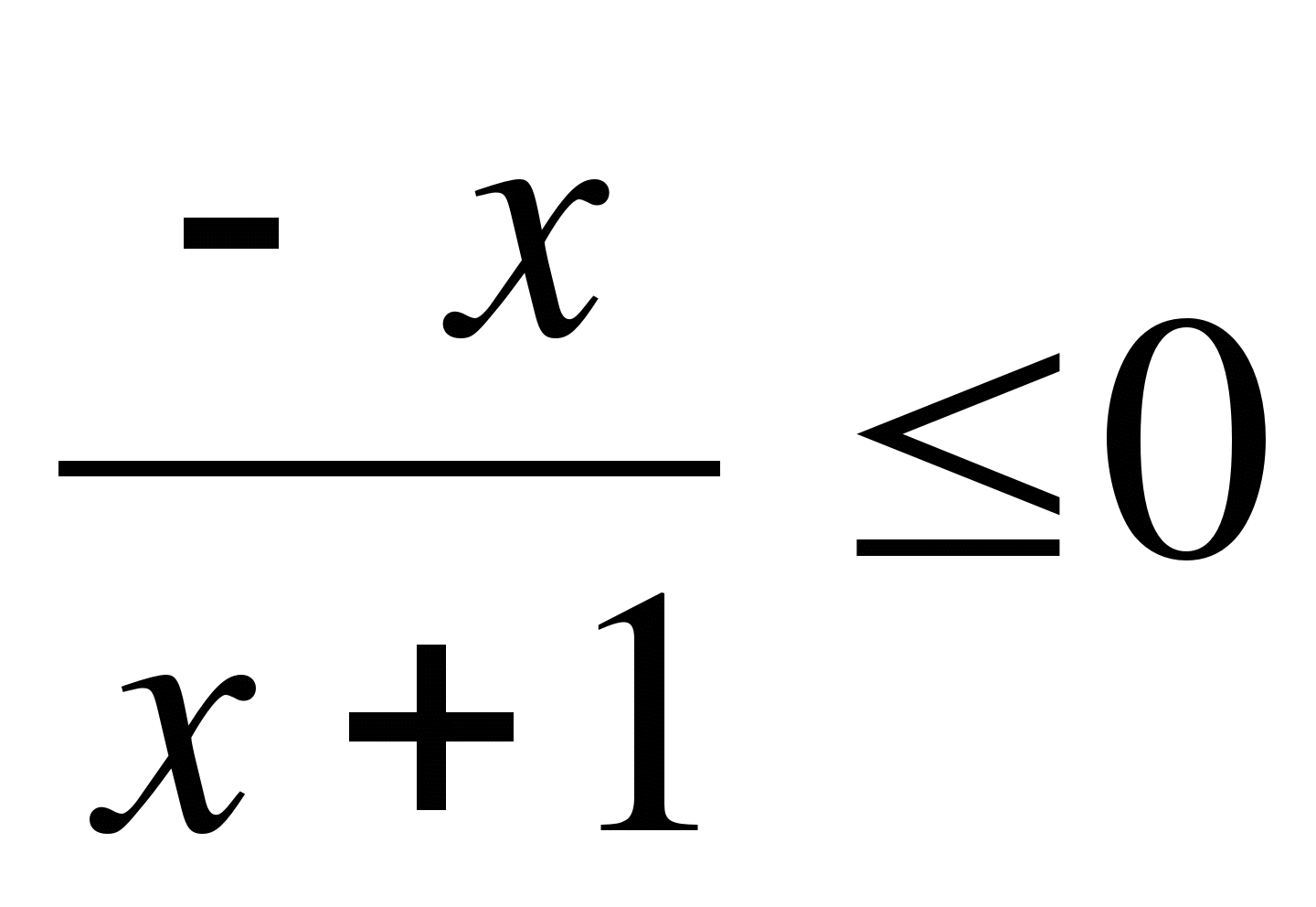
20
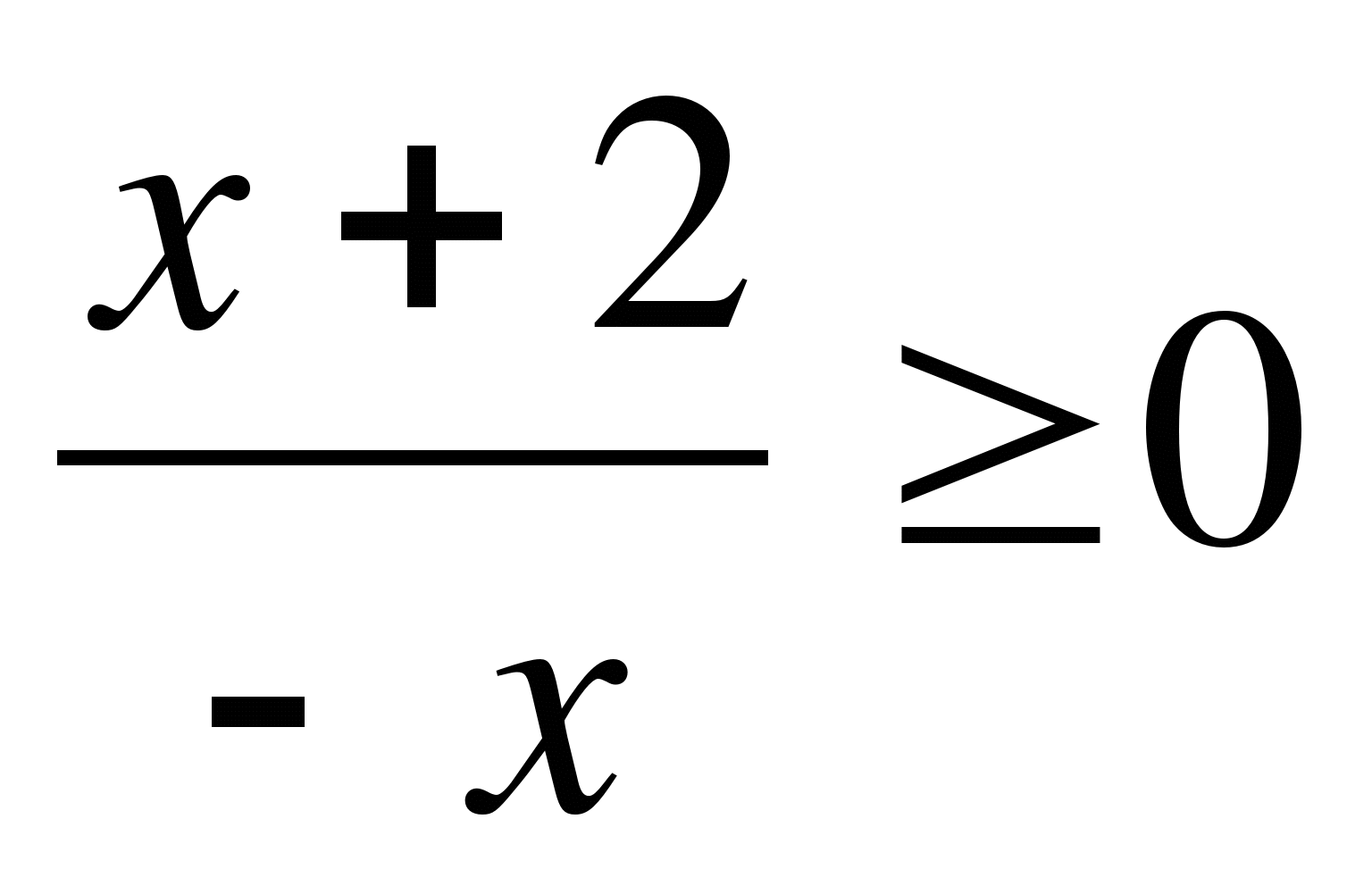
Ответы к заданиям тренажёра.
4
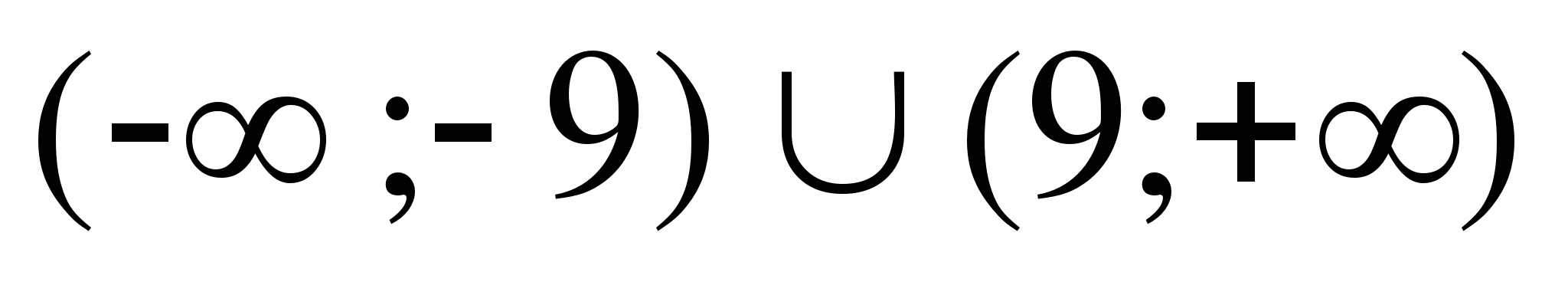
5
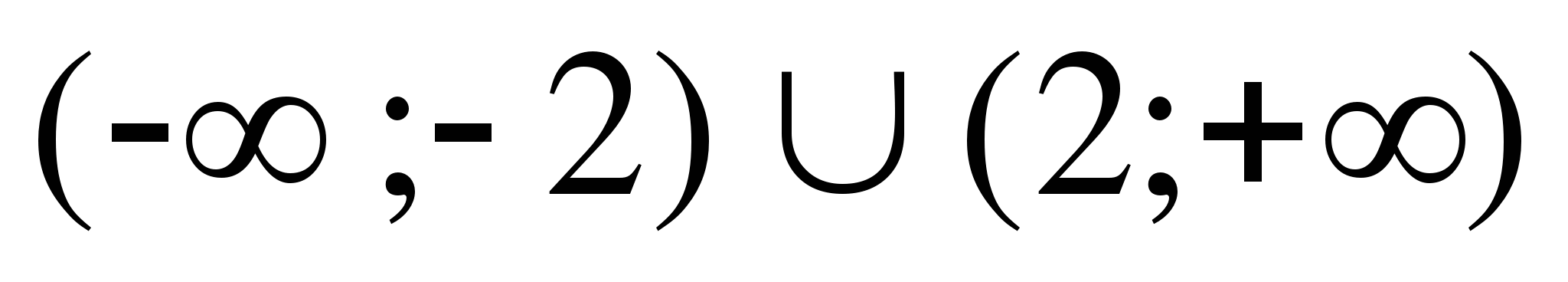
5
R
5
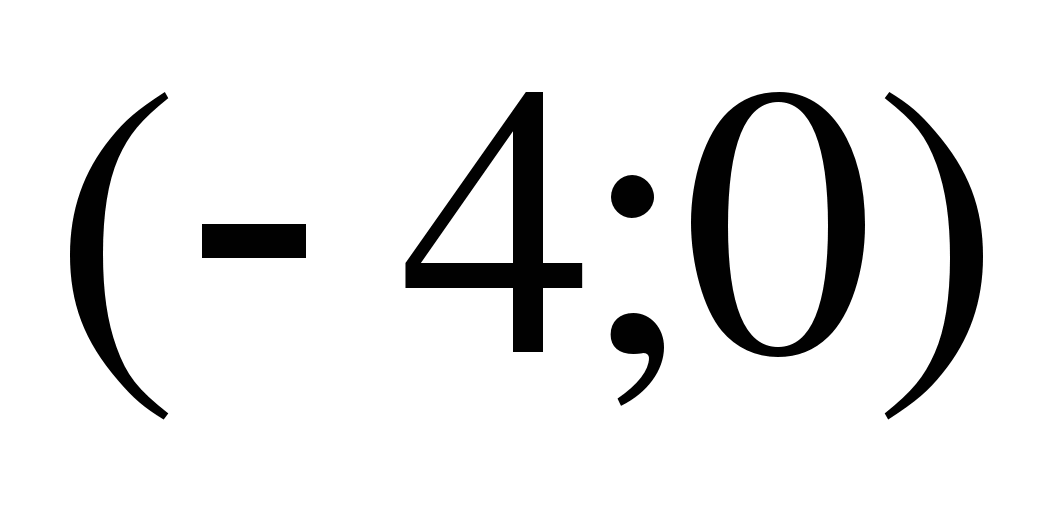
5
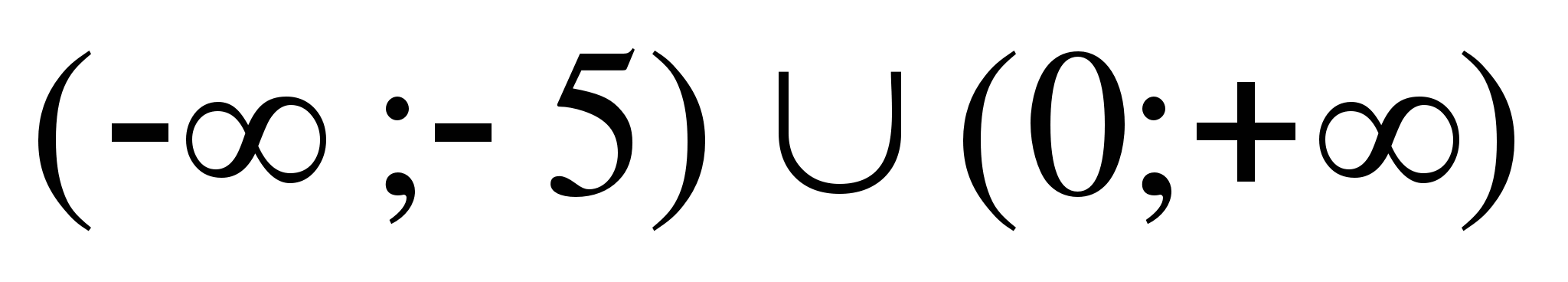
6
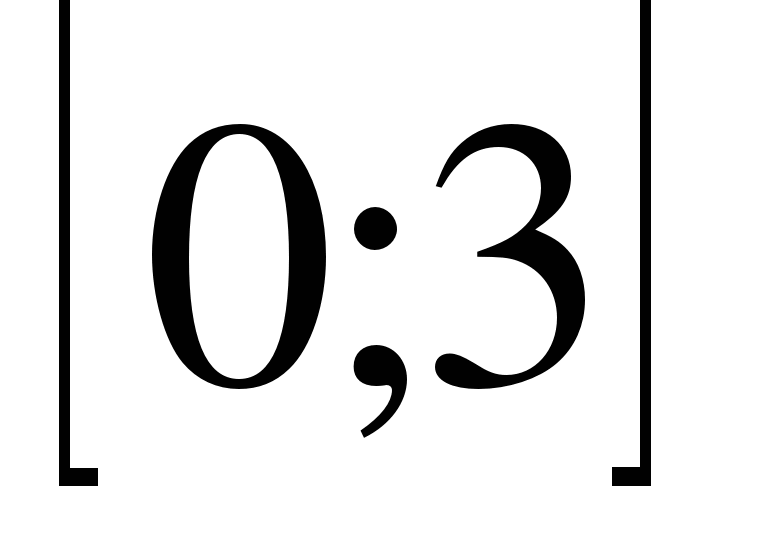
6
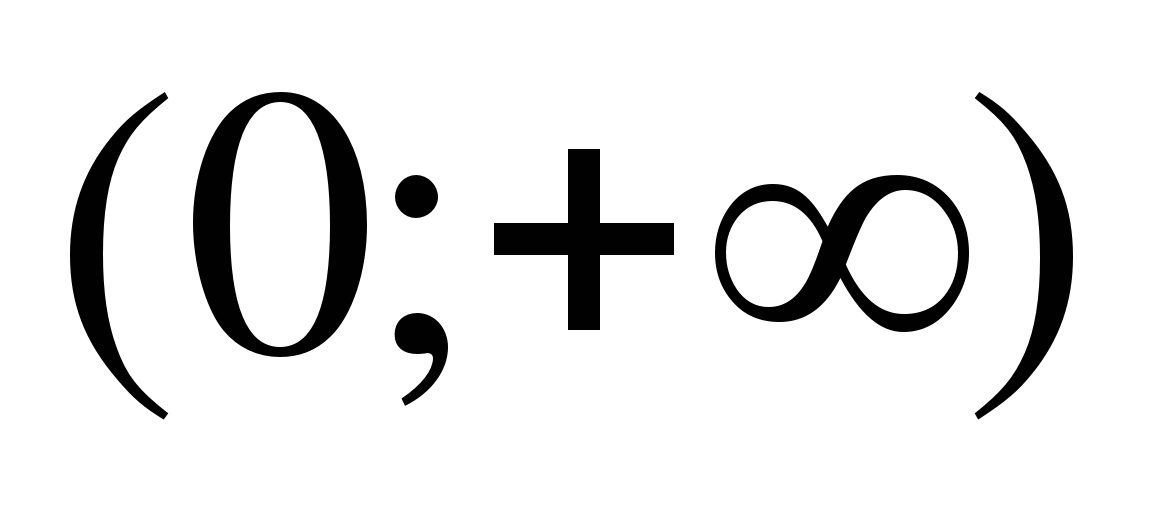

6
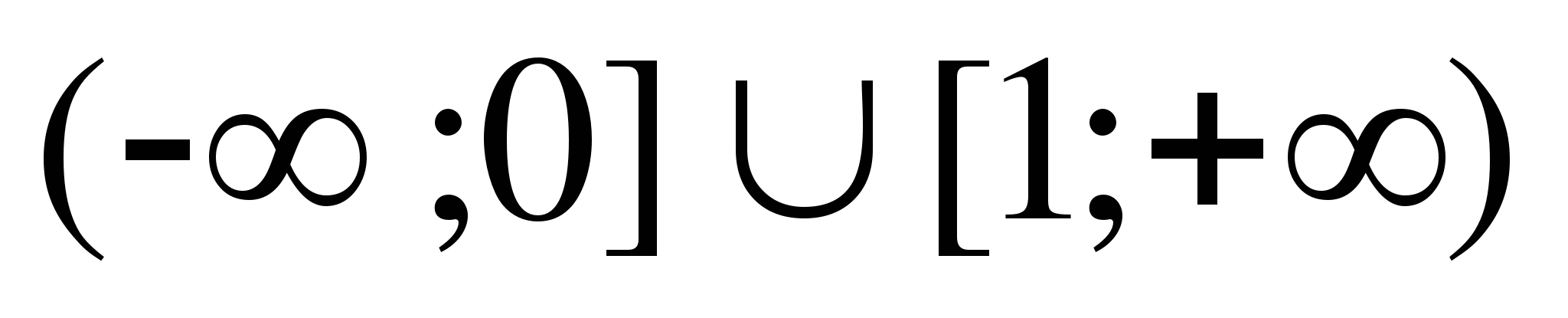
6
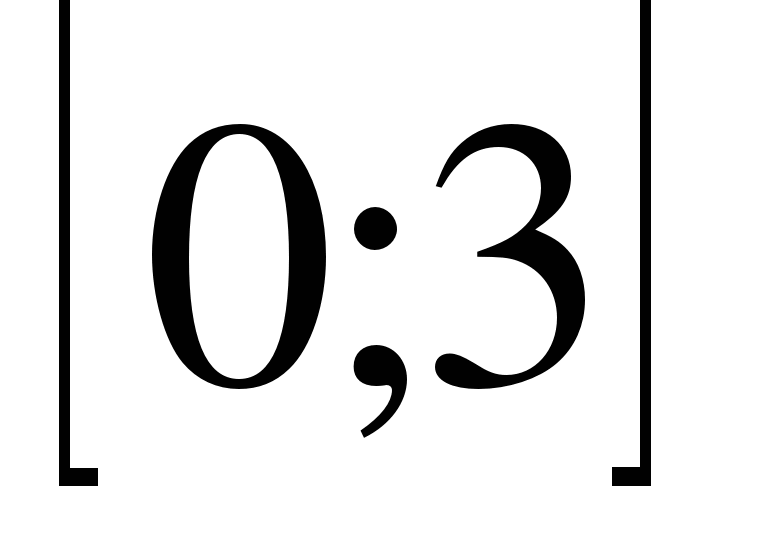
7
нет решений
7
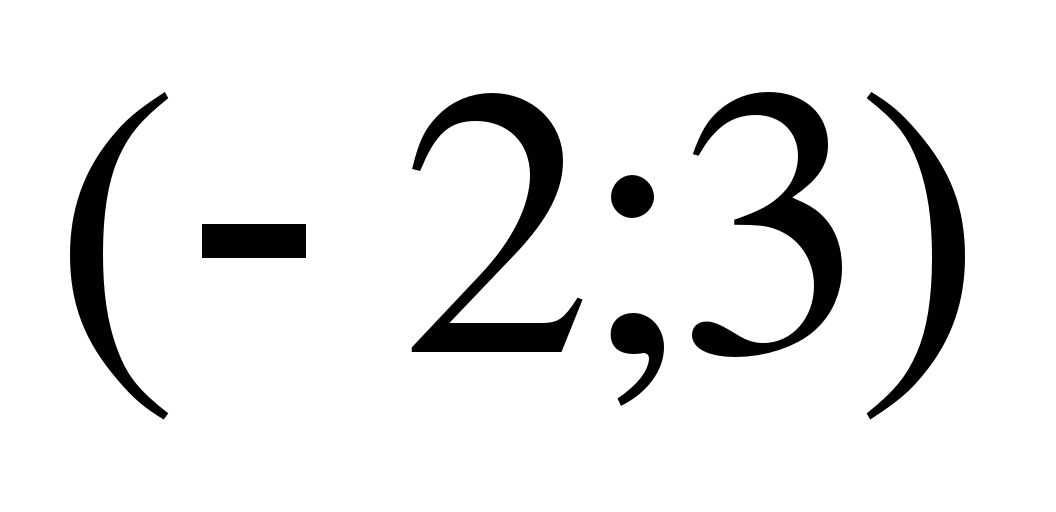
7
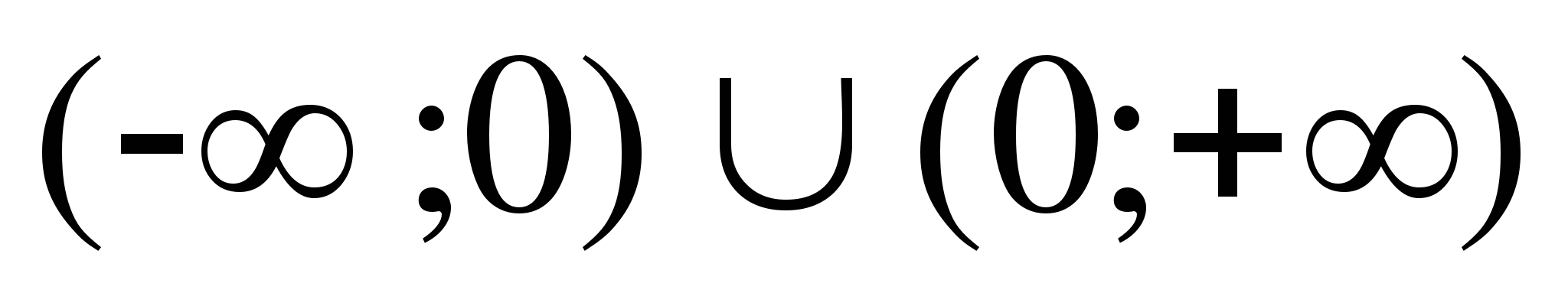
7
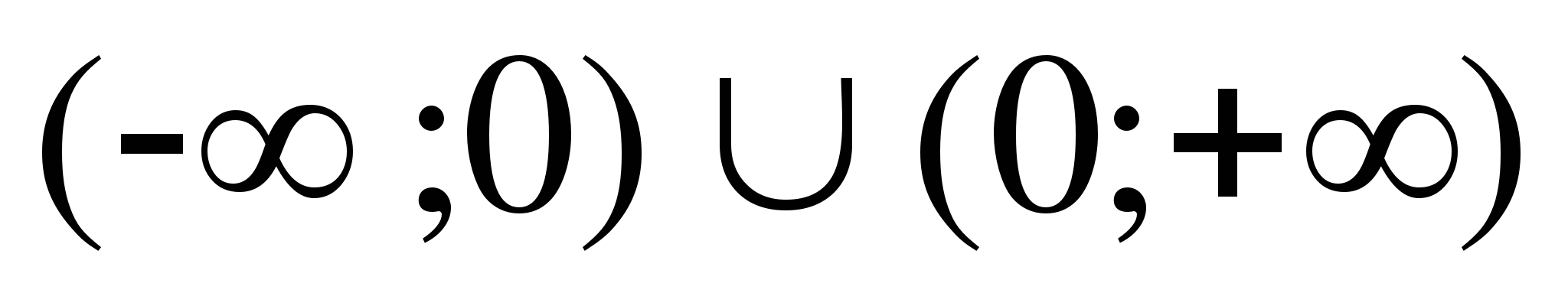
8
0
8
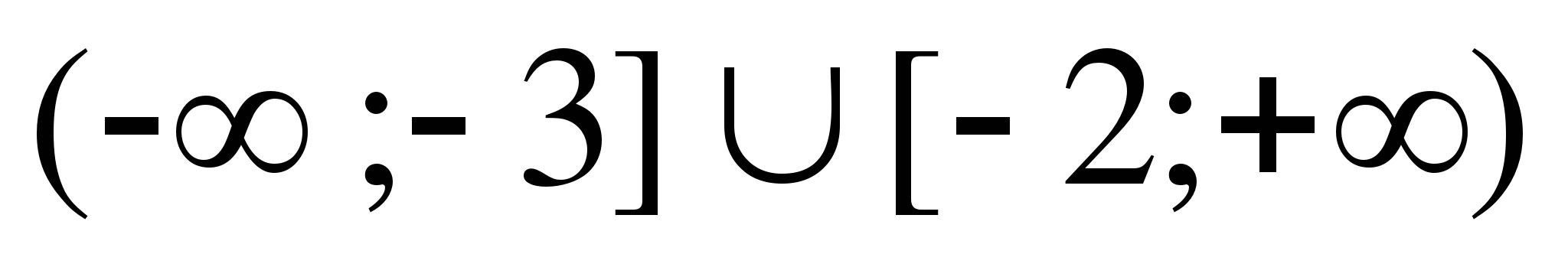
8
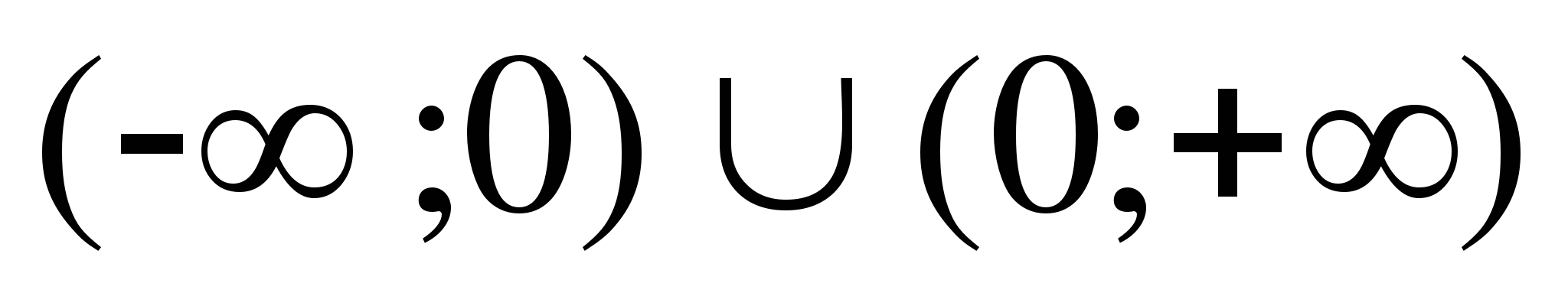
8
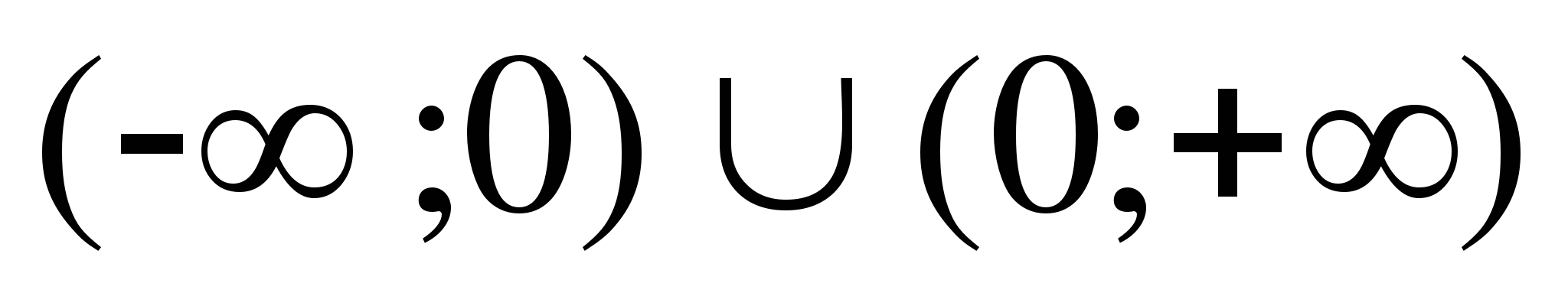
9
R
9
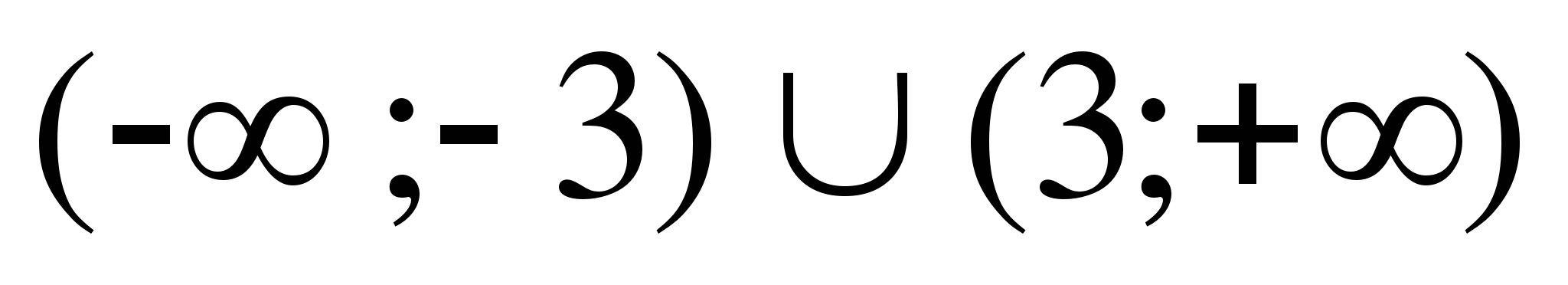
9

9
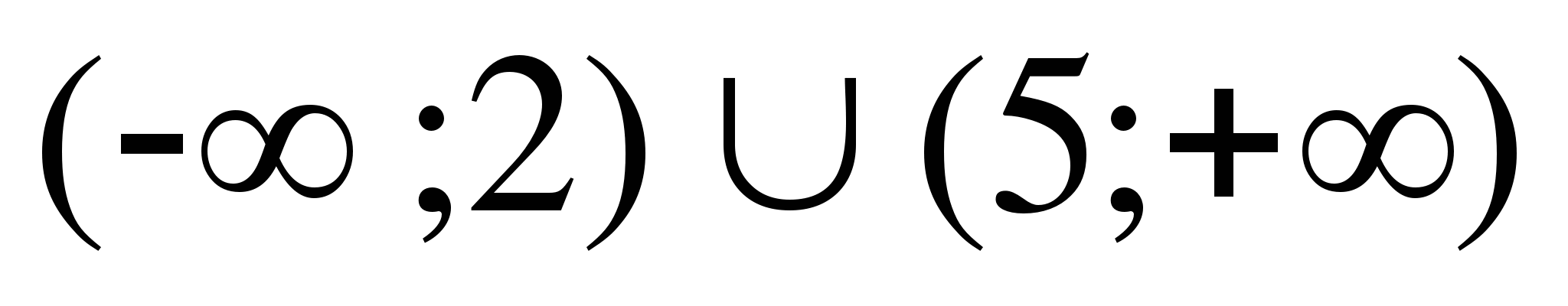
10
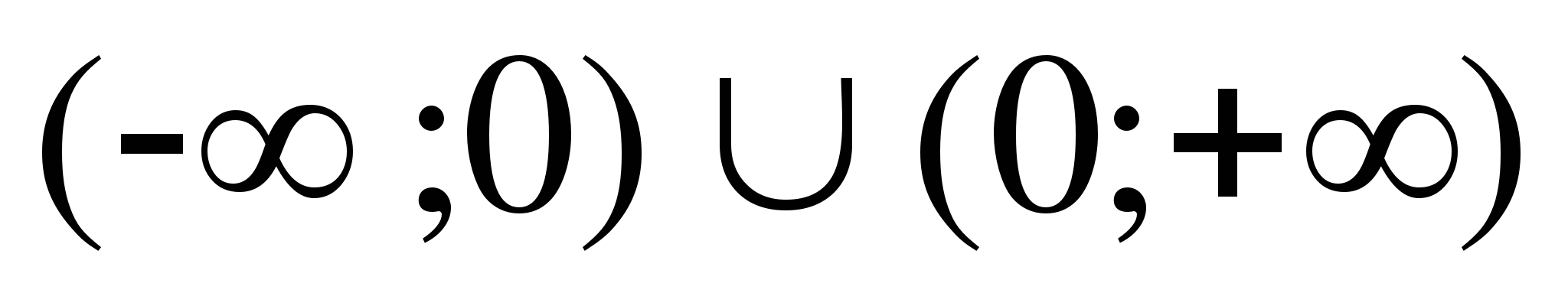
10
R
10
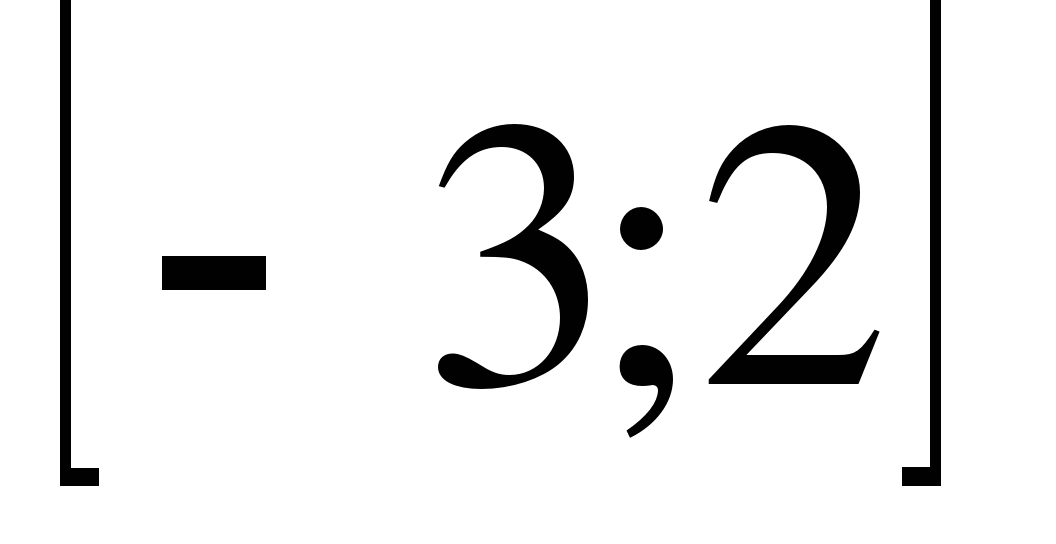
10
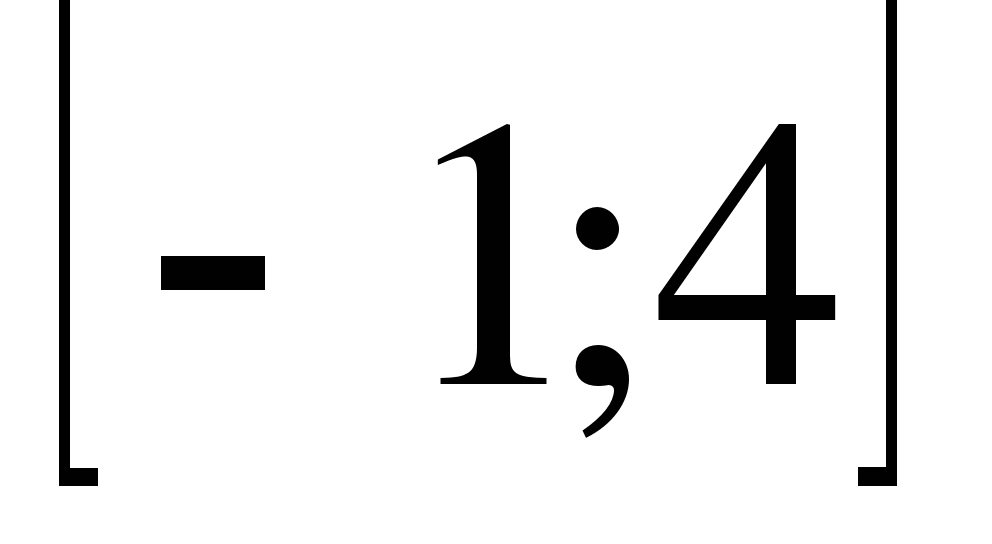
11
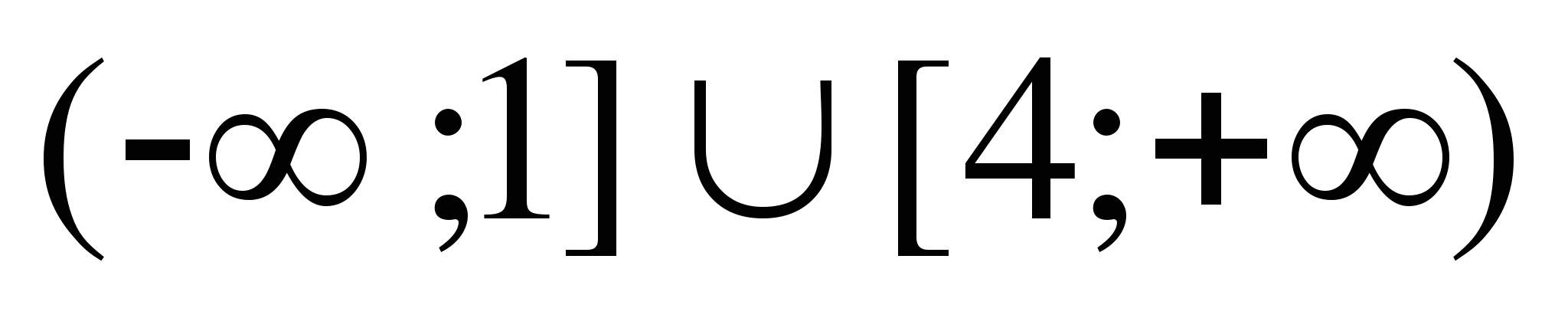
11
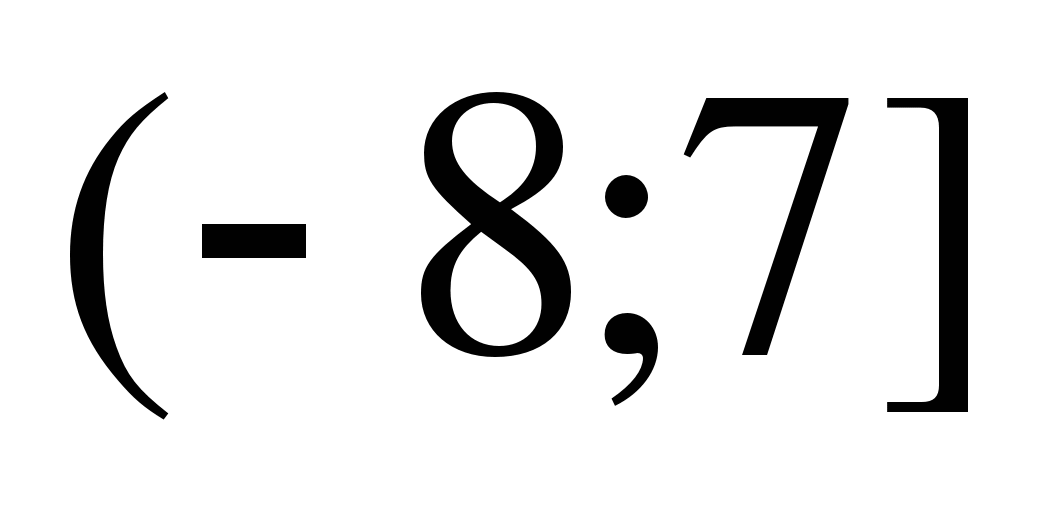
11
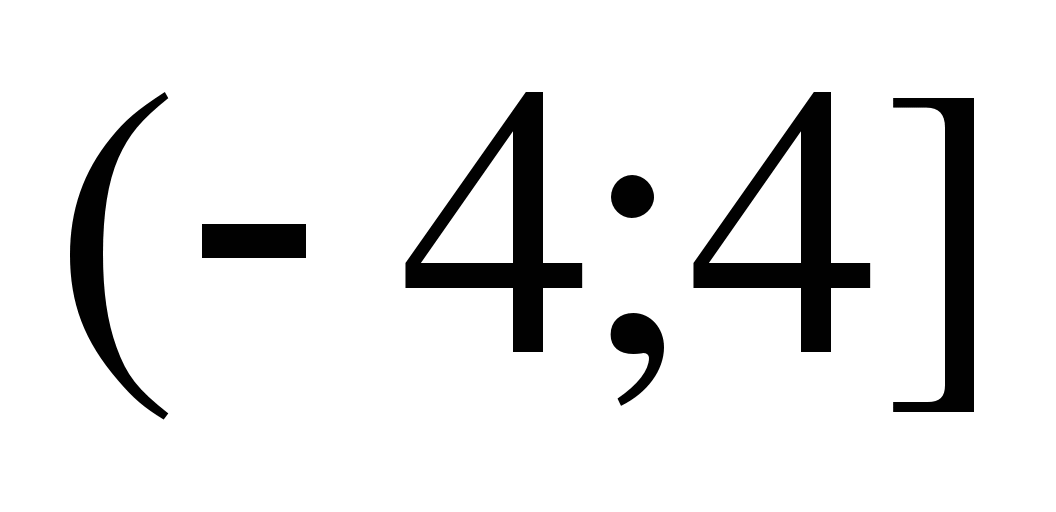
11
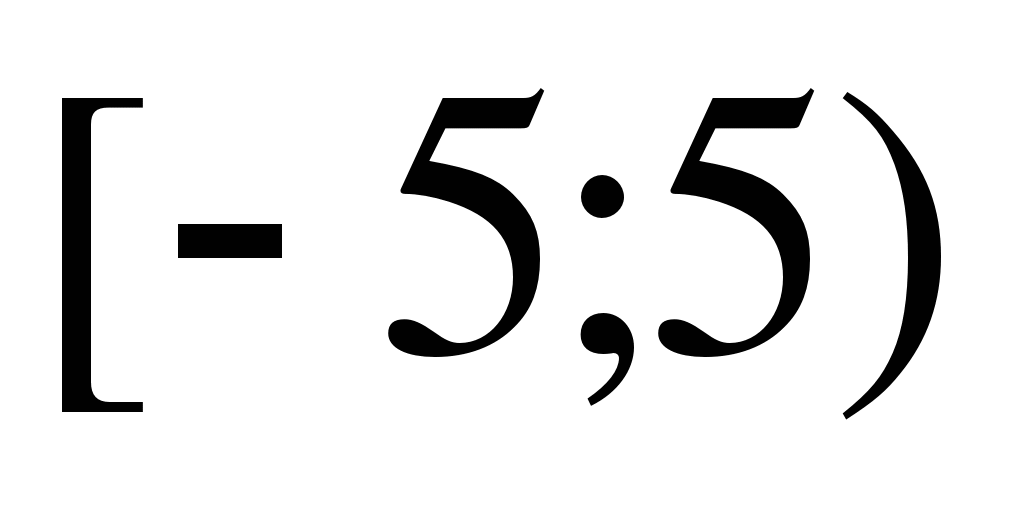
12
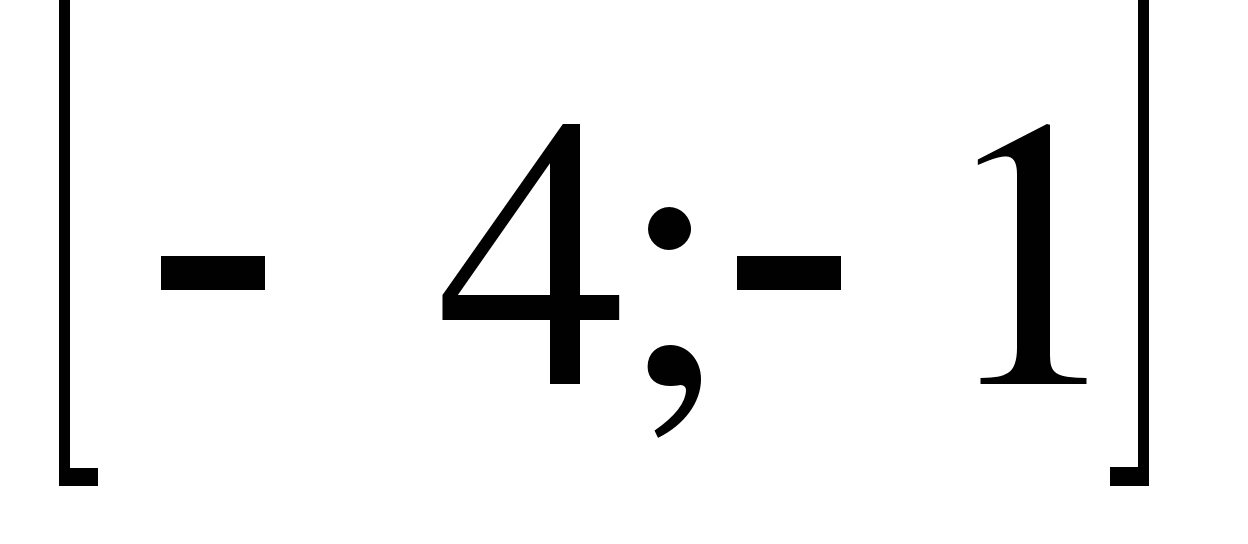
12
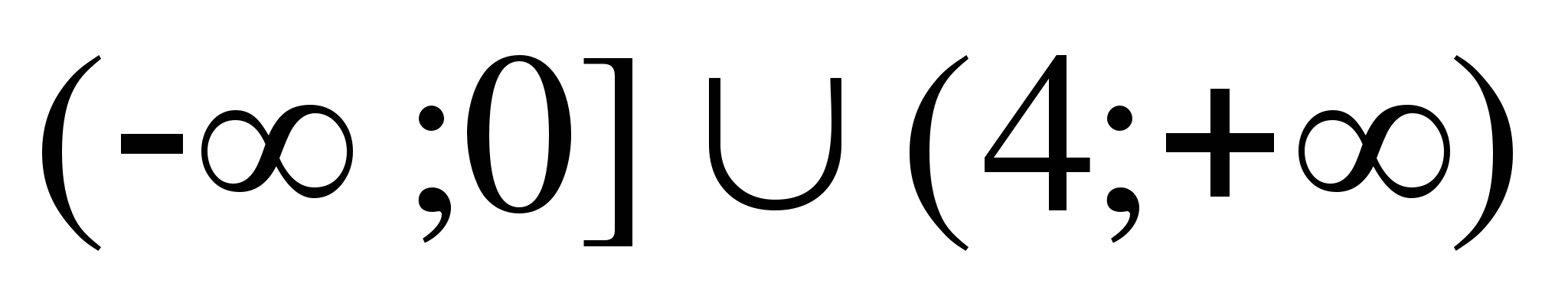
12
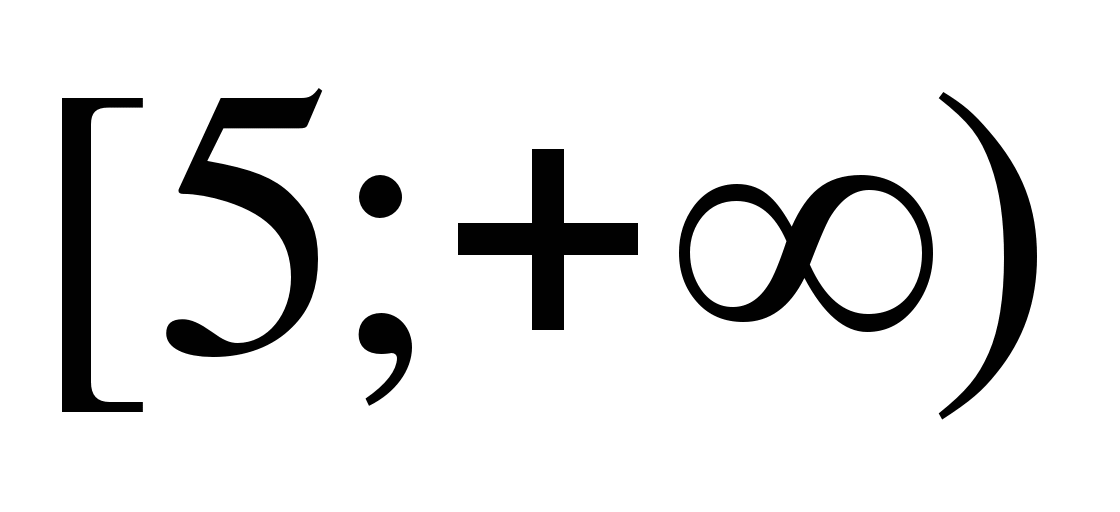
12
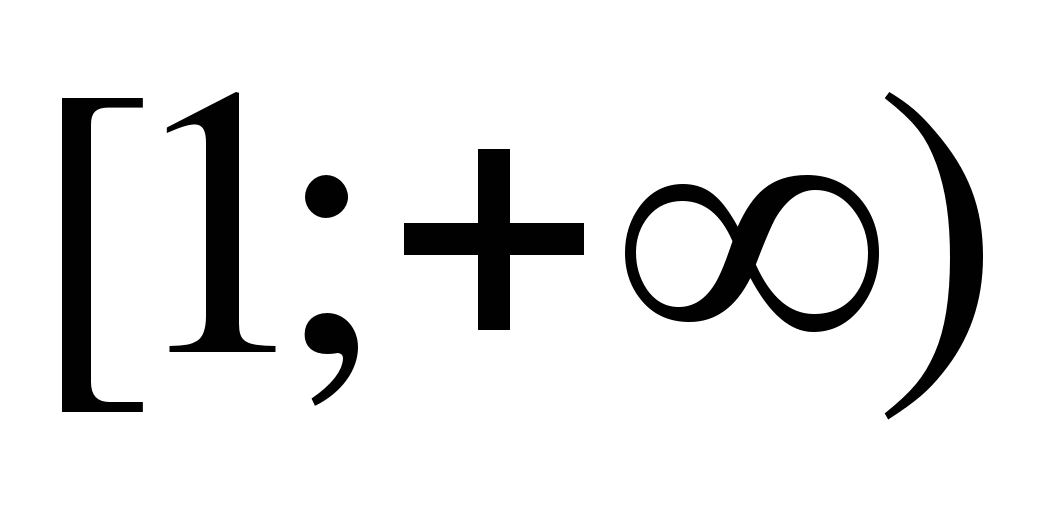
13
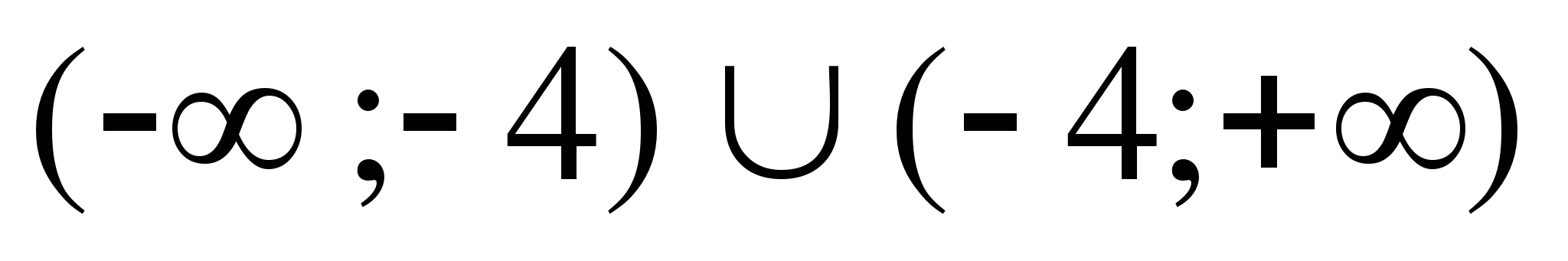
13
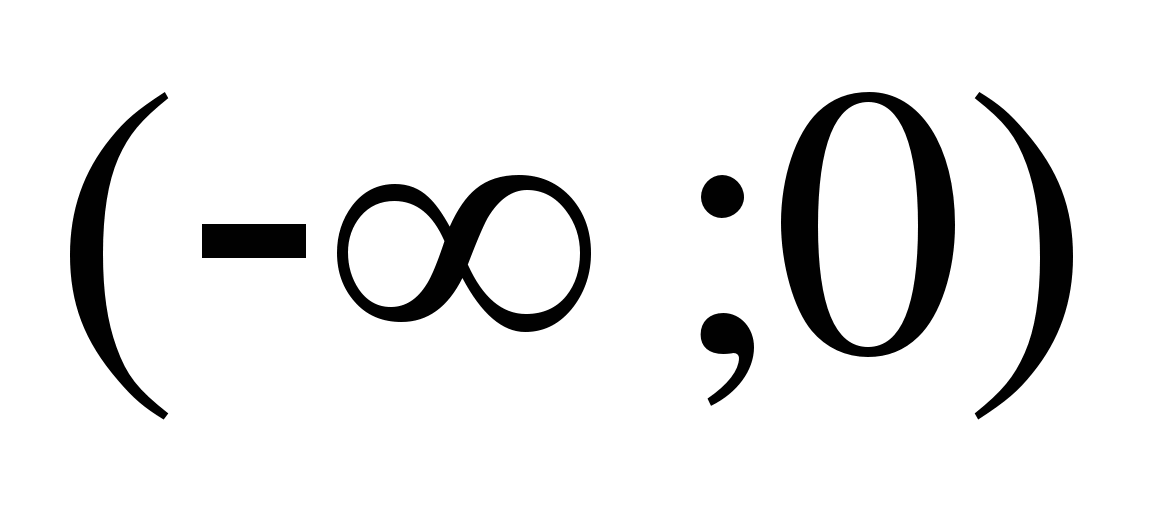
13
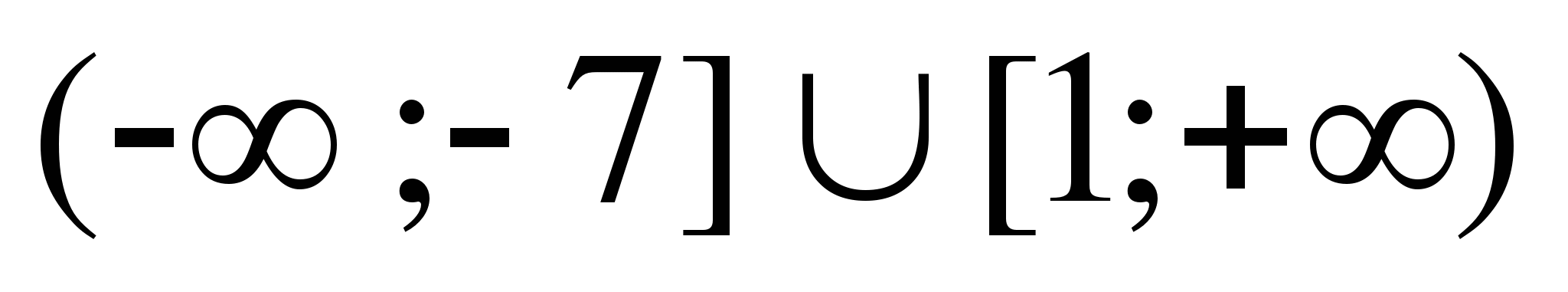
13
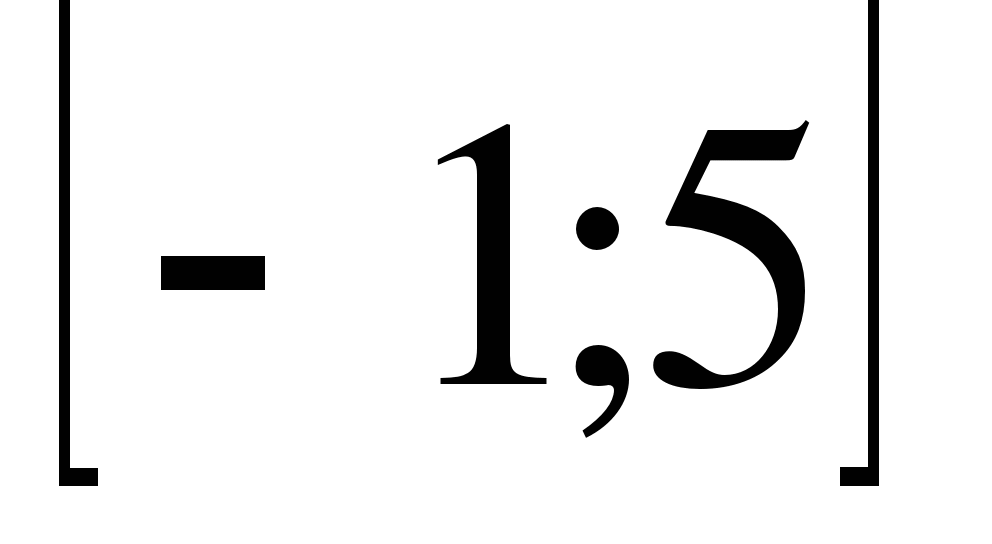
14
нет решений
14
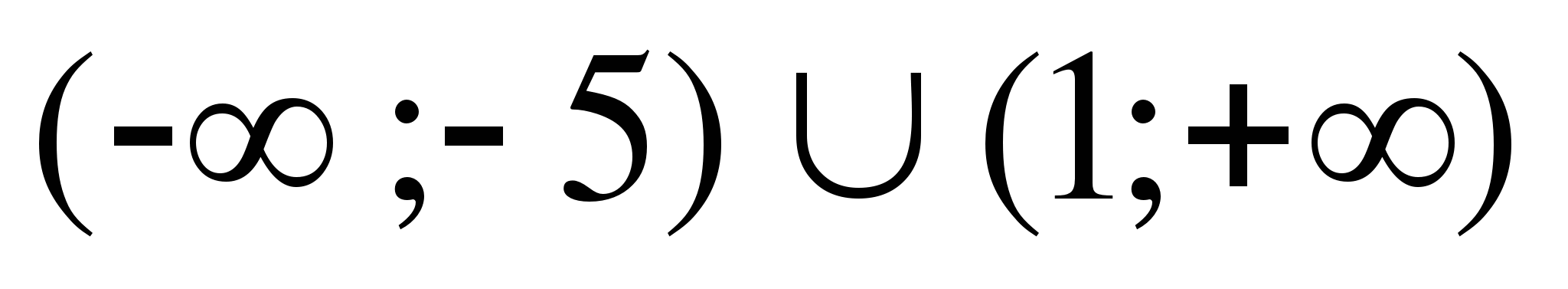
14
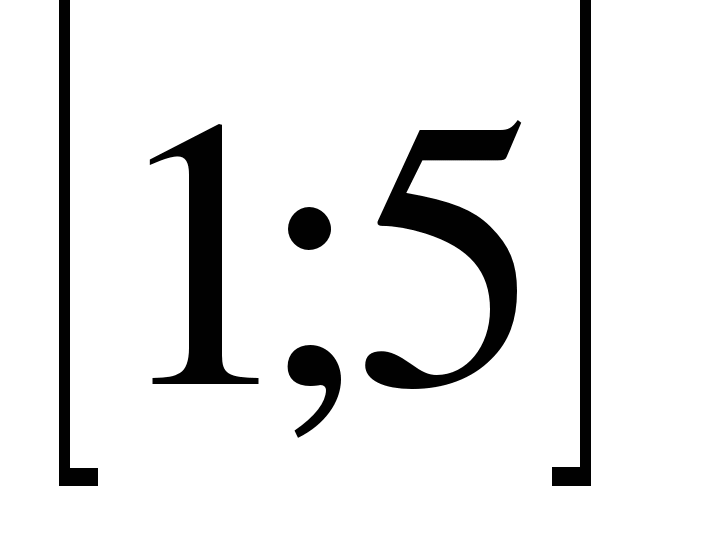
14
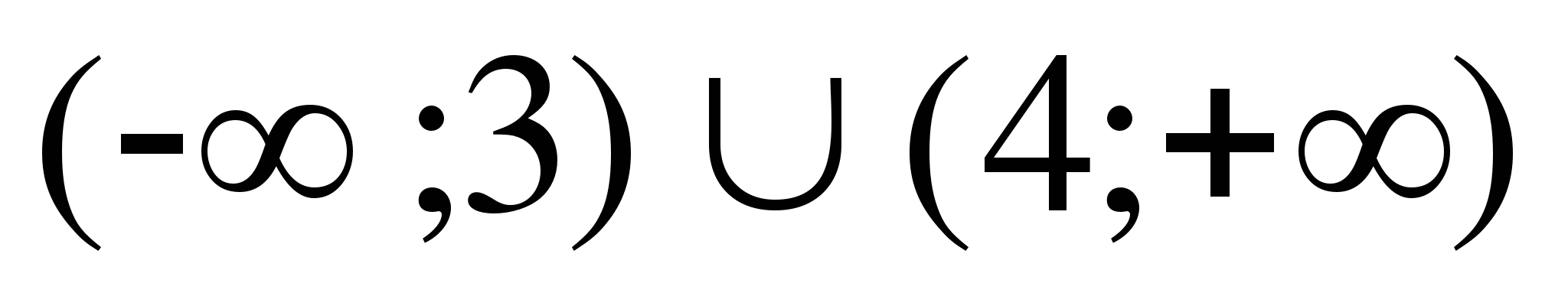
15
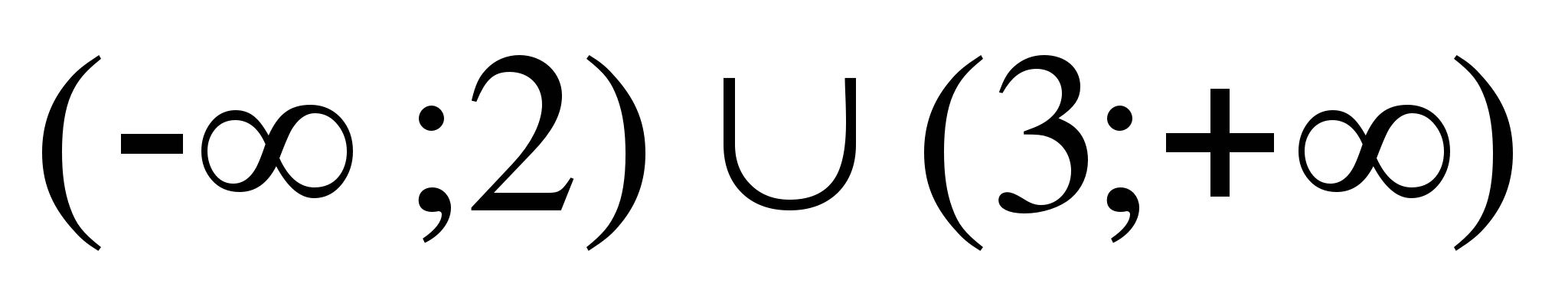
15
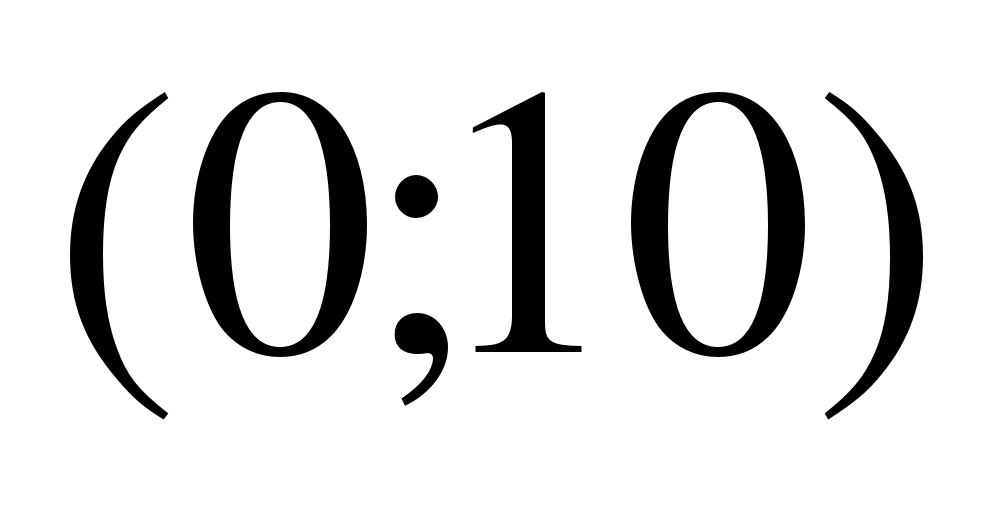
15
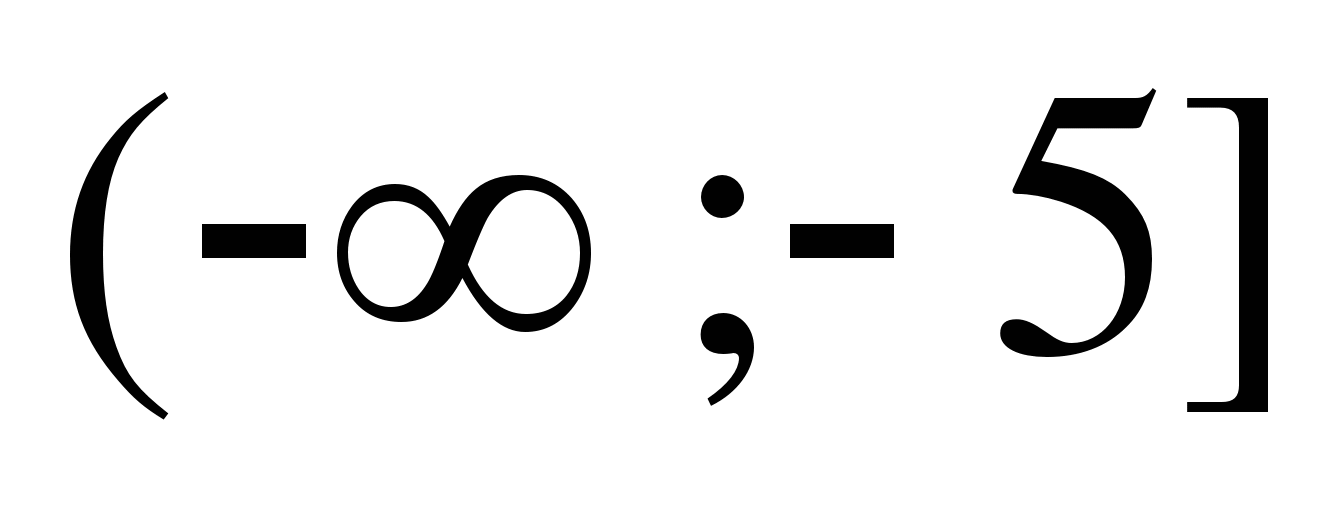
15
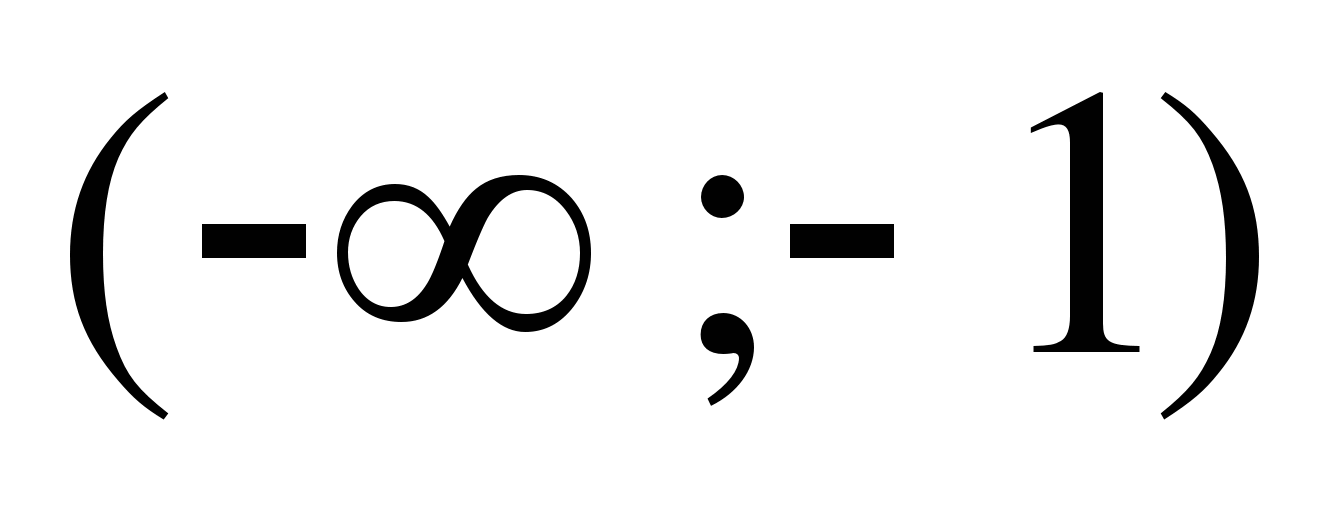
16
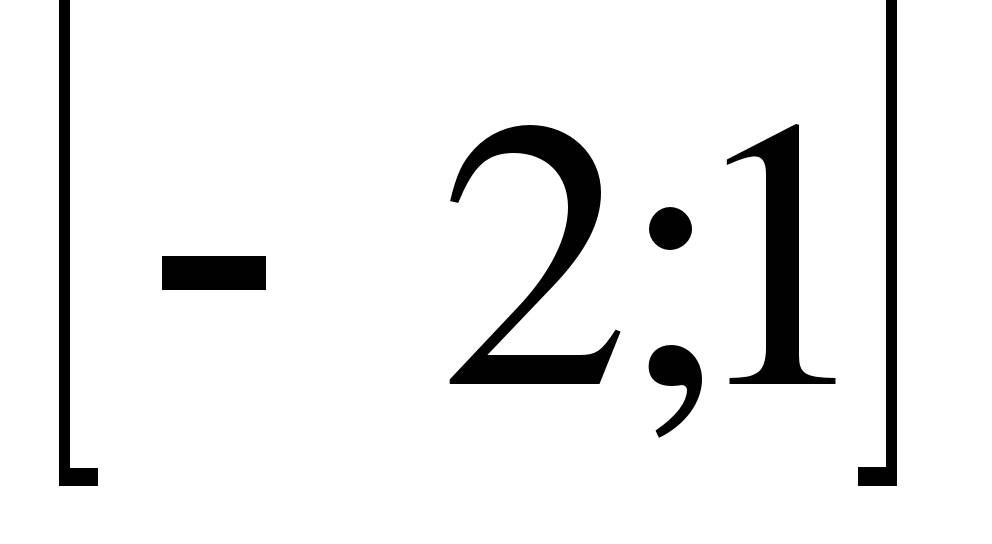
16
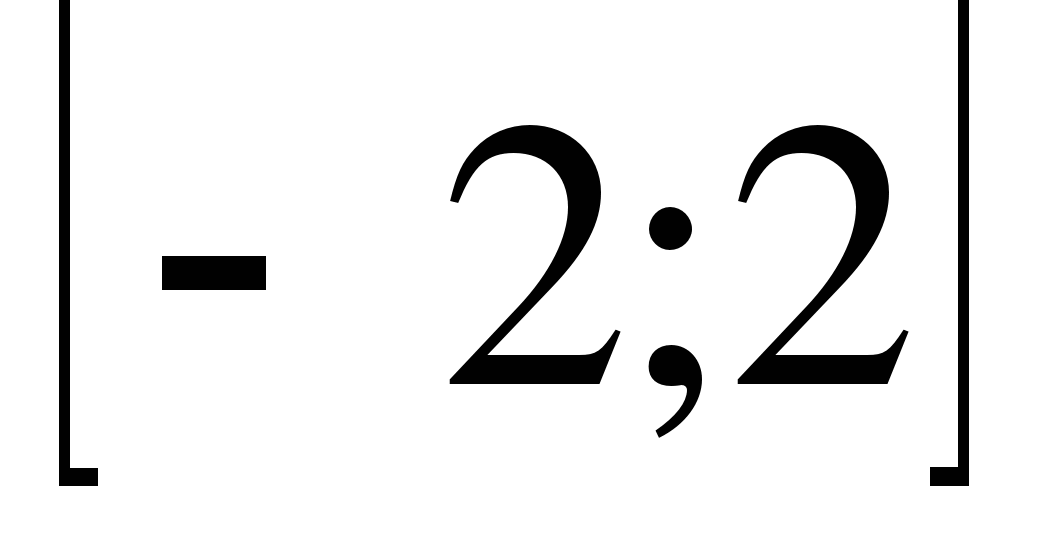
16
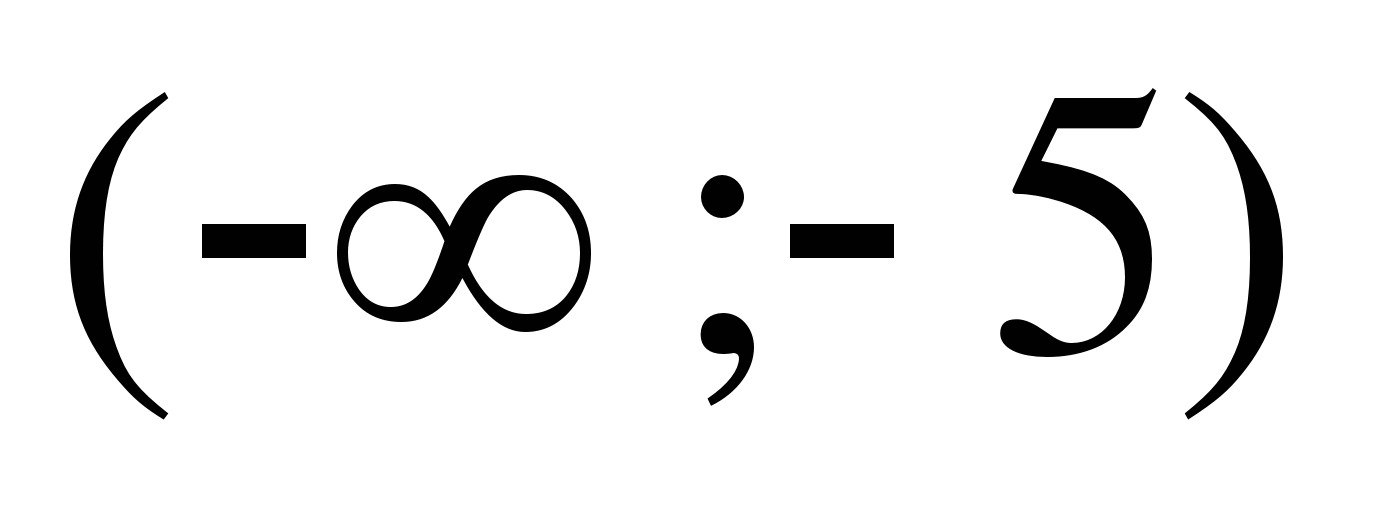
16
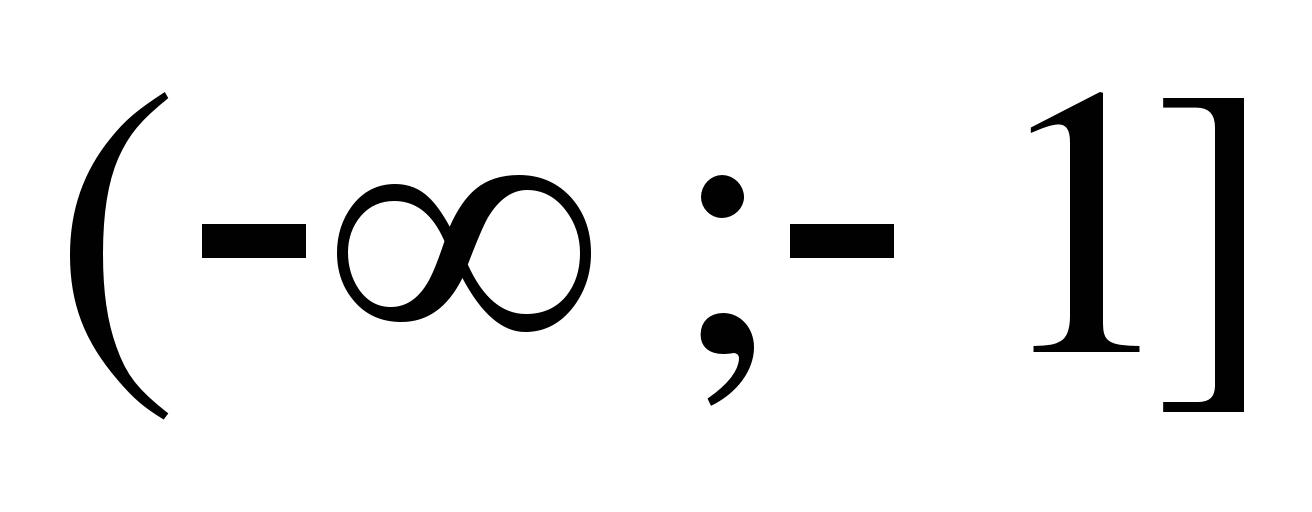
17
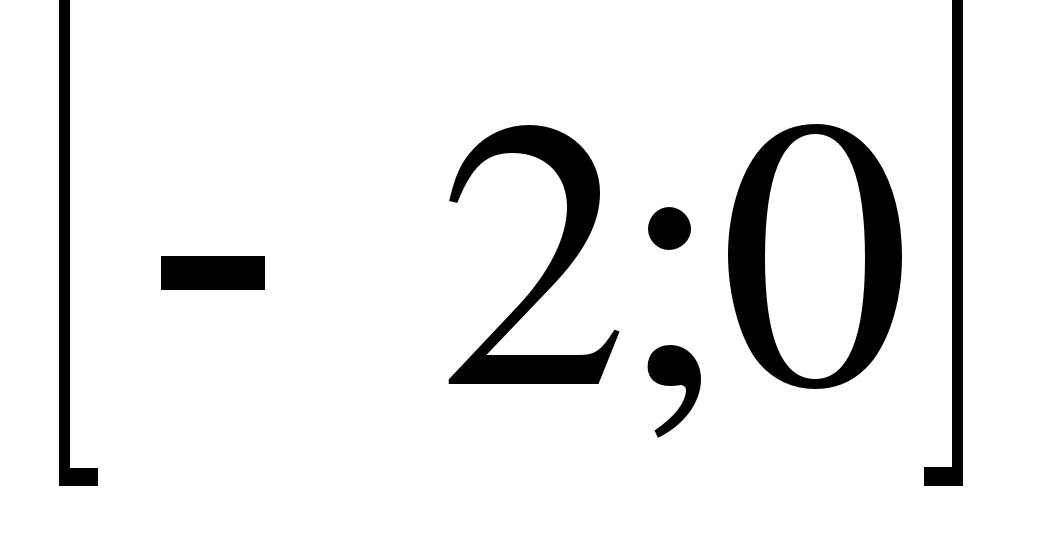
17
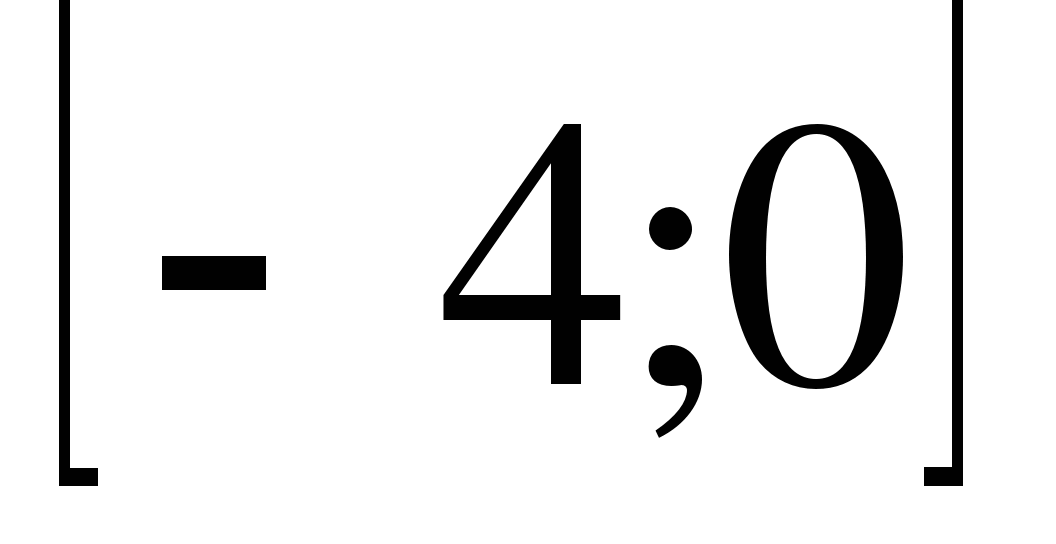
17
2
17
3
18
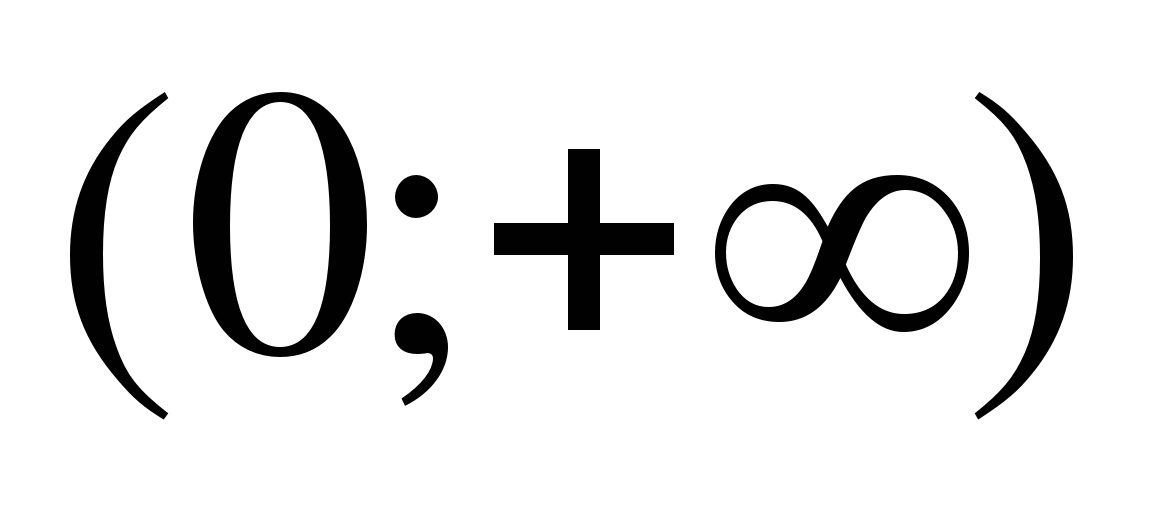
18
нет решений
18
нет решений
18
нет решений
19
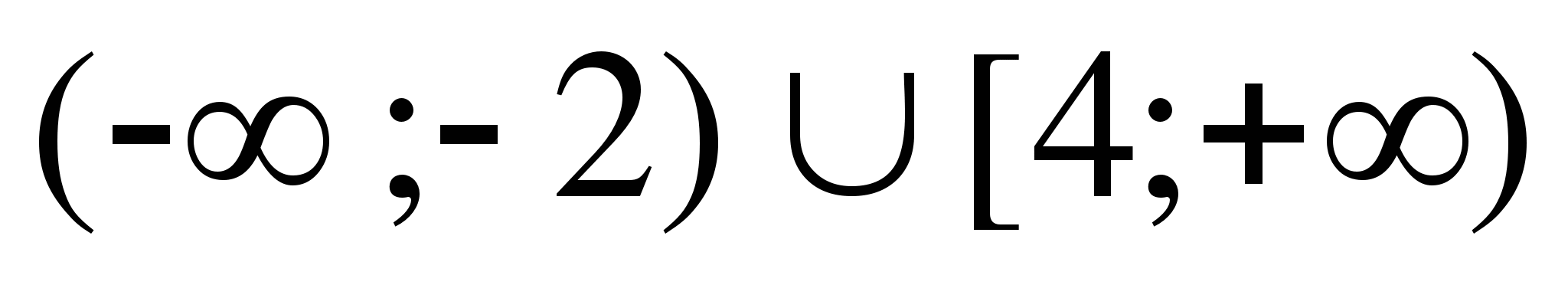
19
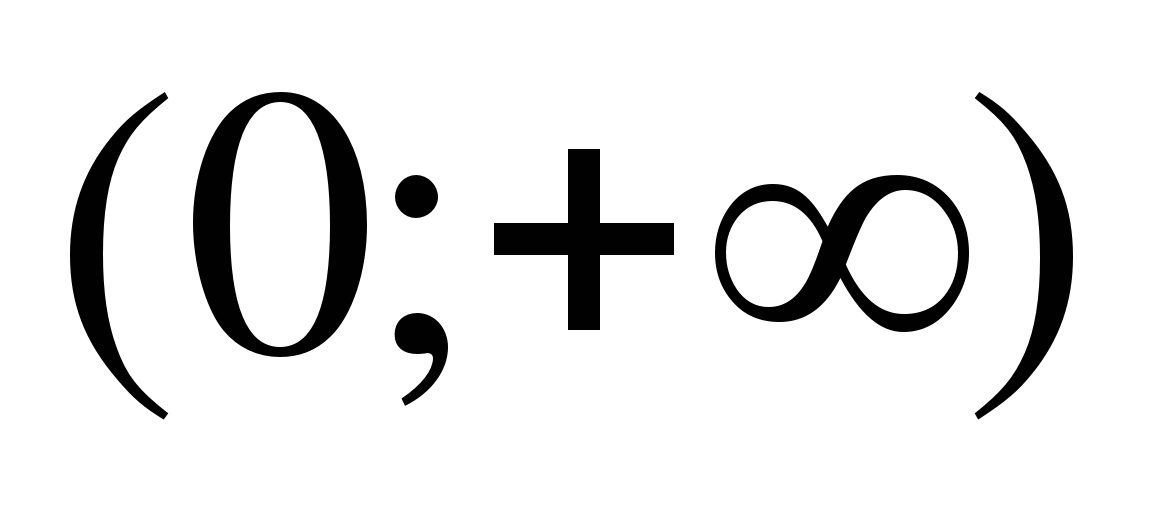
19
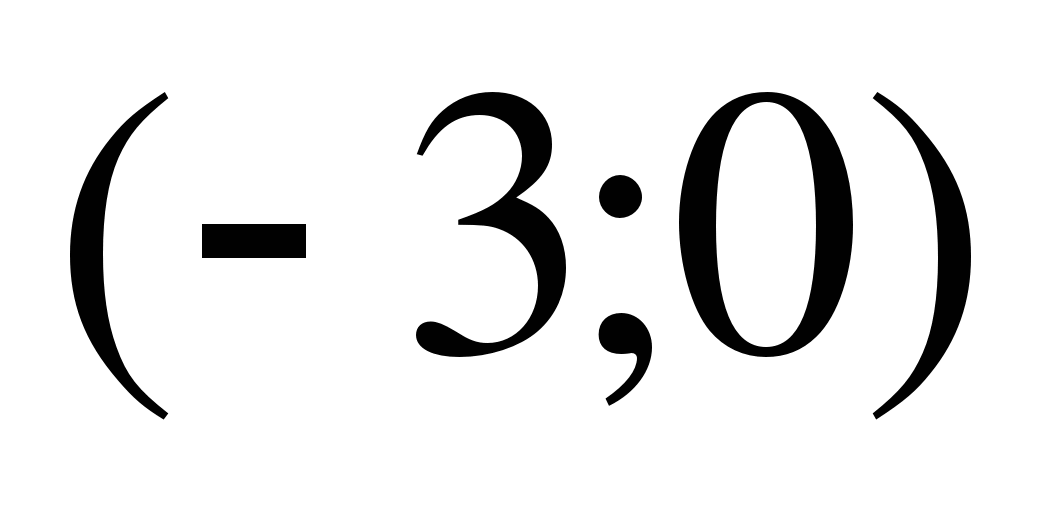
19
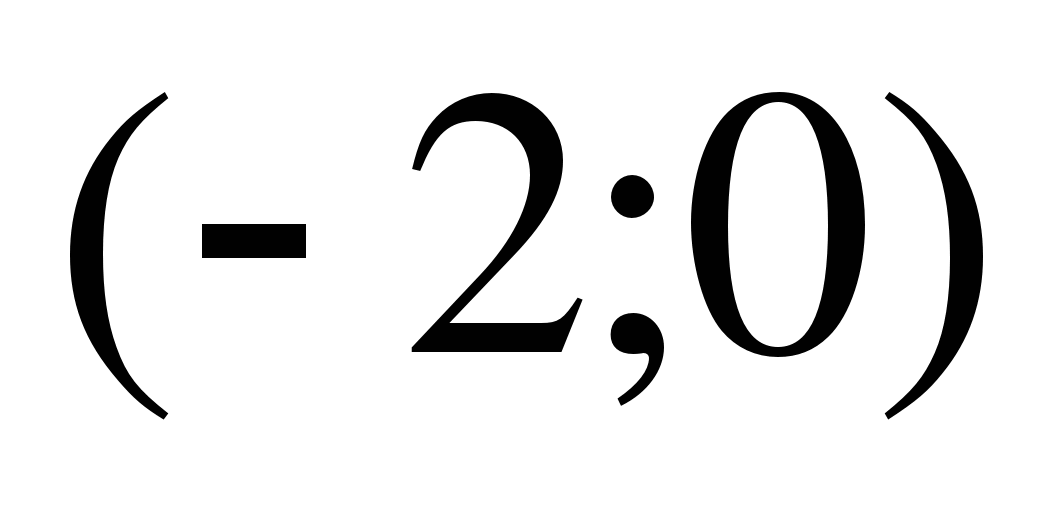
20
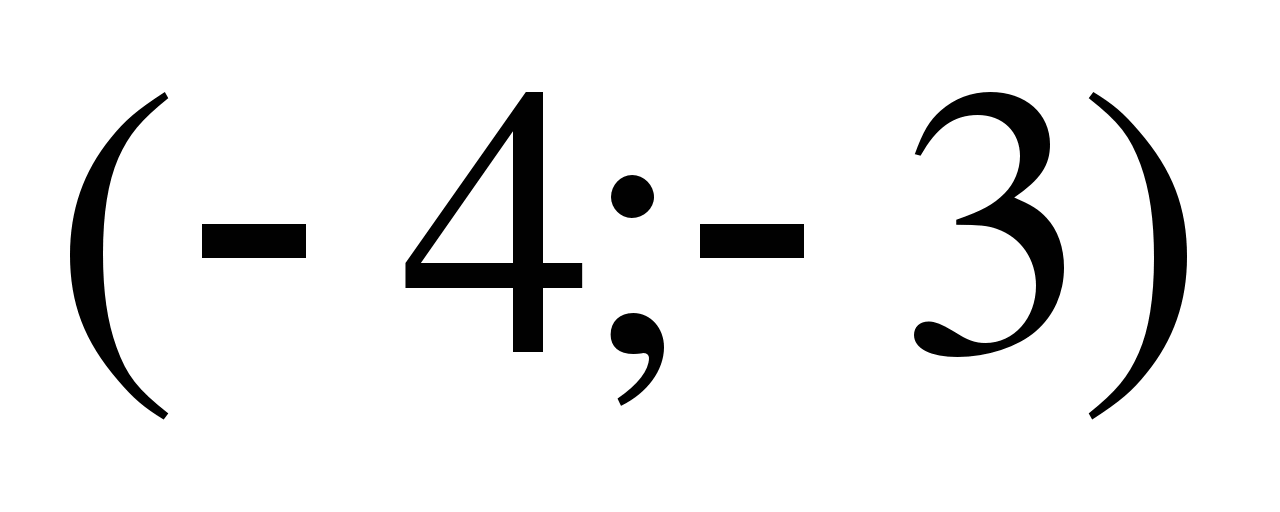
20
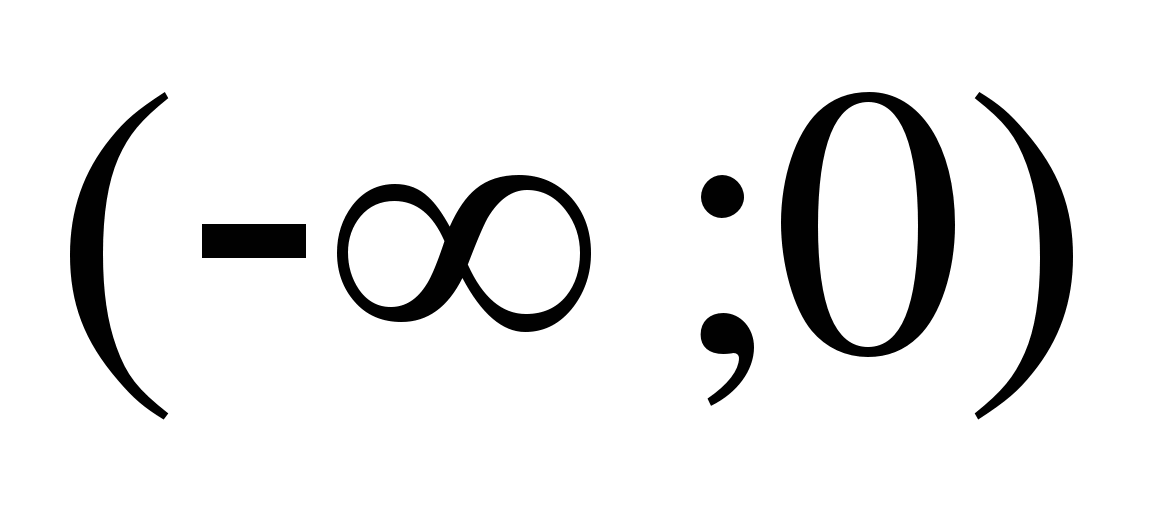
20
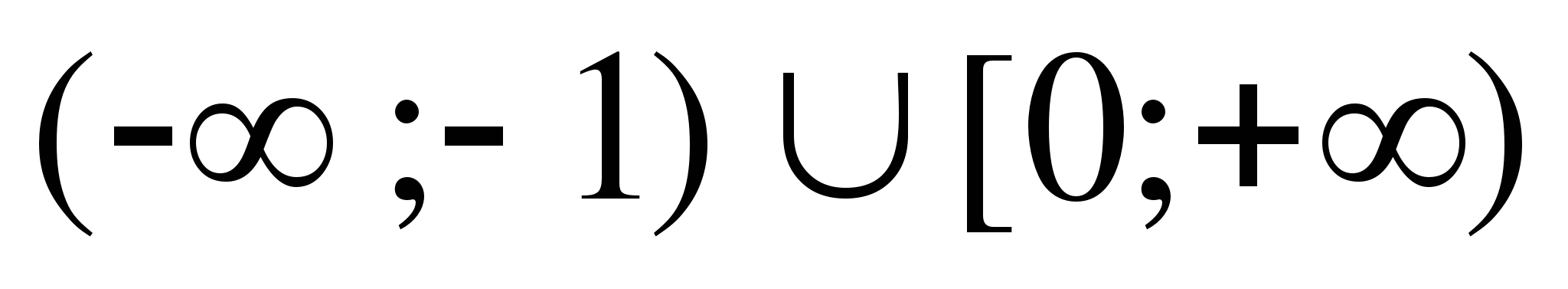
20
[-2;0)
По вариантам на время ученики выполняют задания, не переписывая условия на свои листочки. По окончании времени по сигналу учителя «Стоп» ученики заканчивают работу, сверяют свои ответы с ответами, записанными заранее на обратной стороне доски, после чего сдают свои листы ответов для проверки учителем.
Нормы выставления оценок за тренажёр: «2» 0 – 4
«3» 5 — 10
«4» 11 – 14
«5» 15 – 20.
Во время работы класса по тренажеру трое учеников у доски перерешивают задания №4, 5, 6 из устной работы.
ΙV. Письменная работа.
(Параллельно выполняется на доске и в тетрадях)
№1. Решите неравенство:
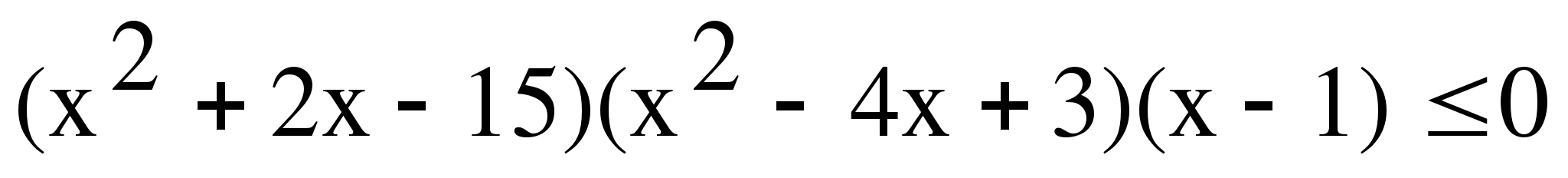
№2. Решите неравенство:
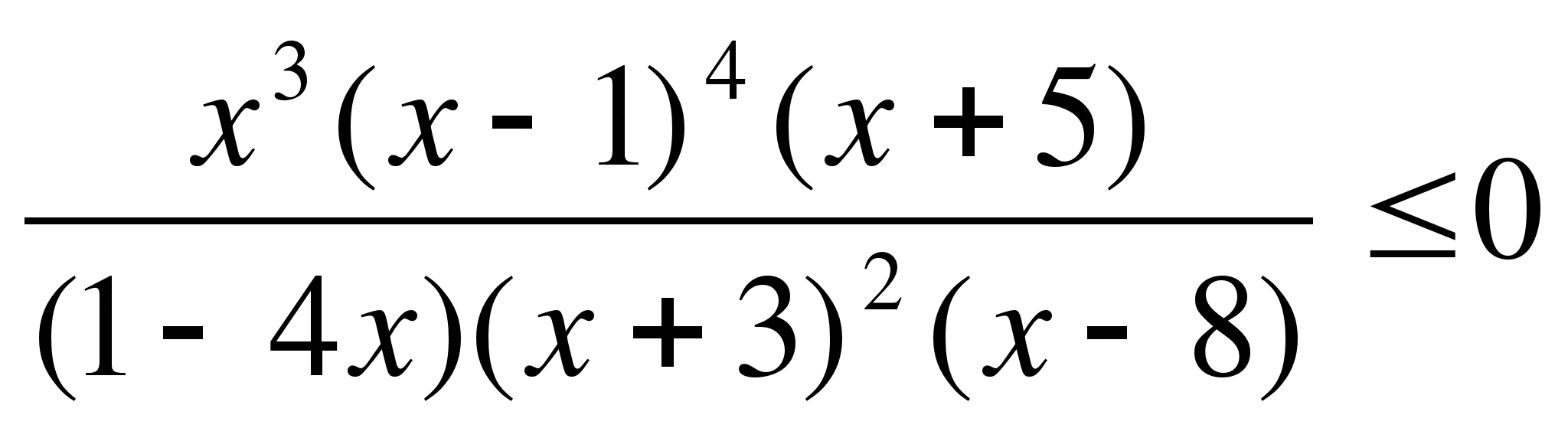
№3. Найдите область определения функции:
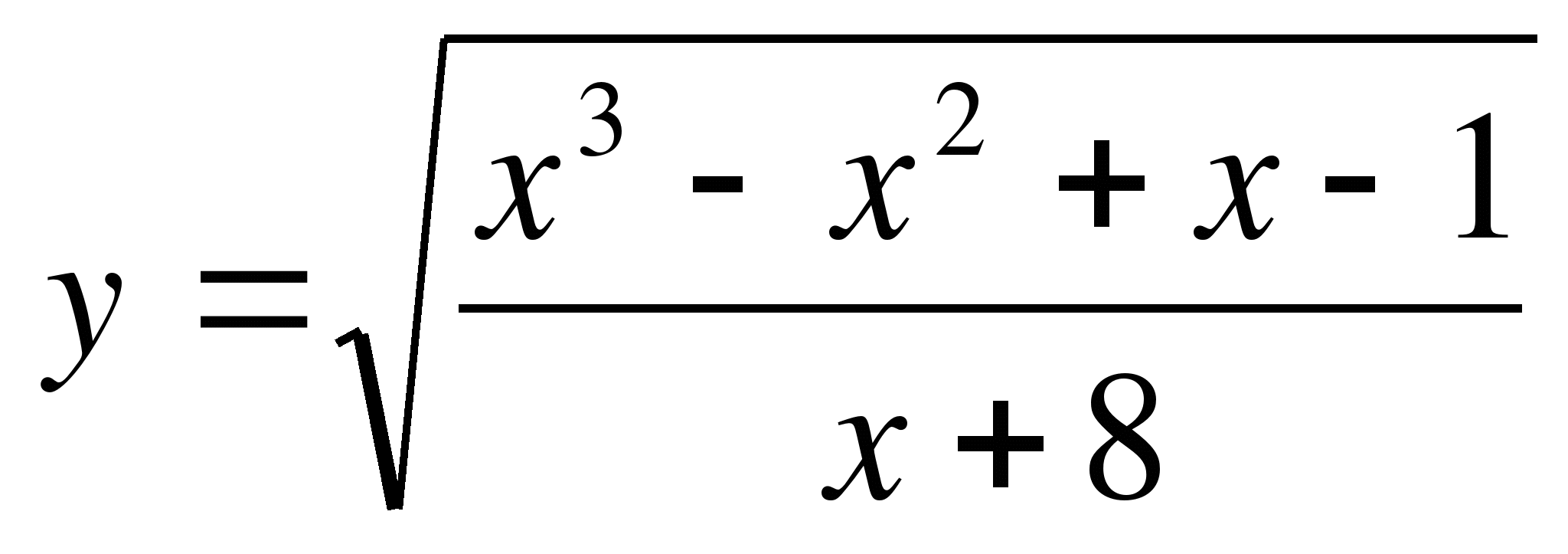
№4. Найдите область определения функции:
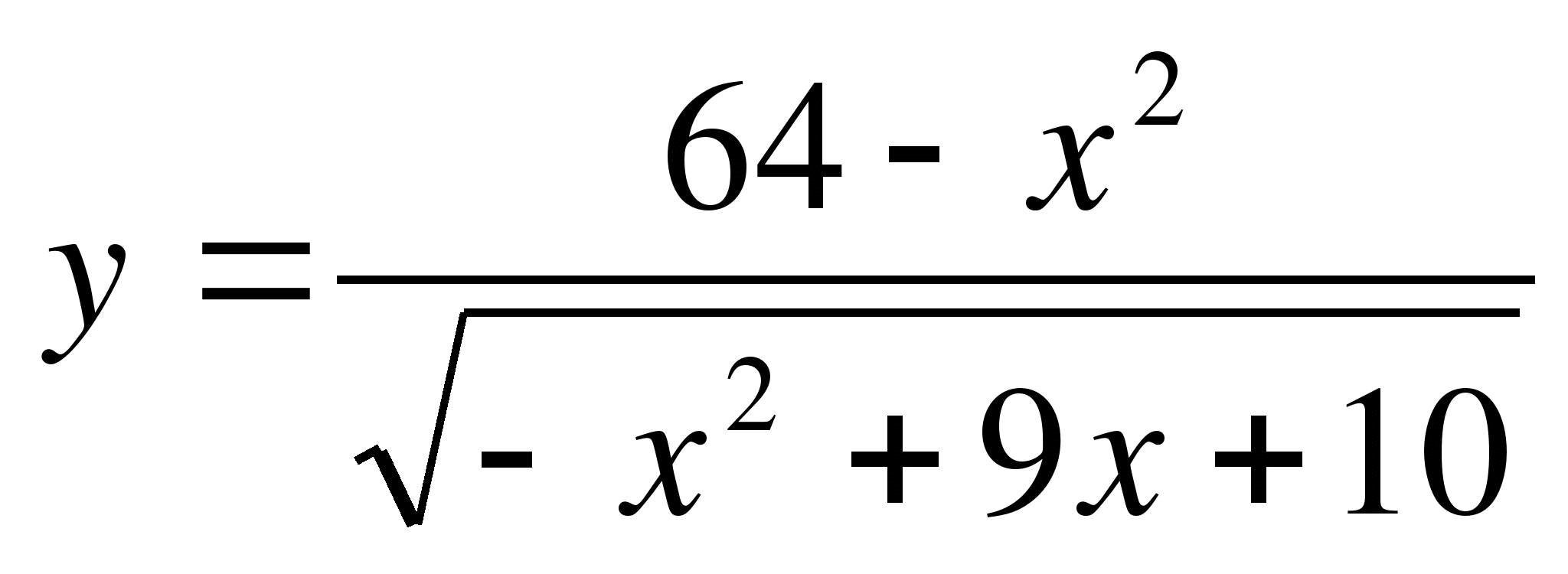
№5. Найдите целое решение неравенства:
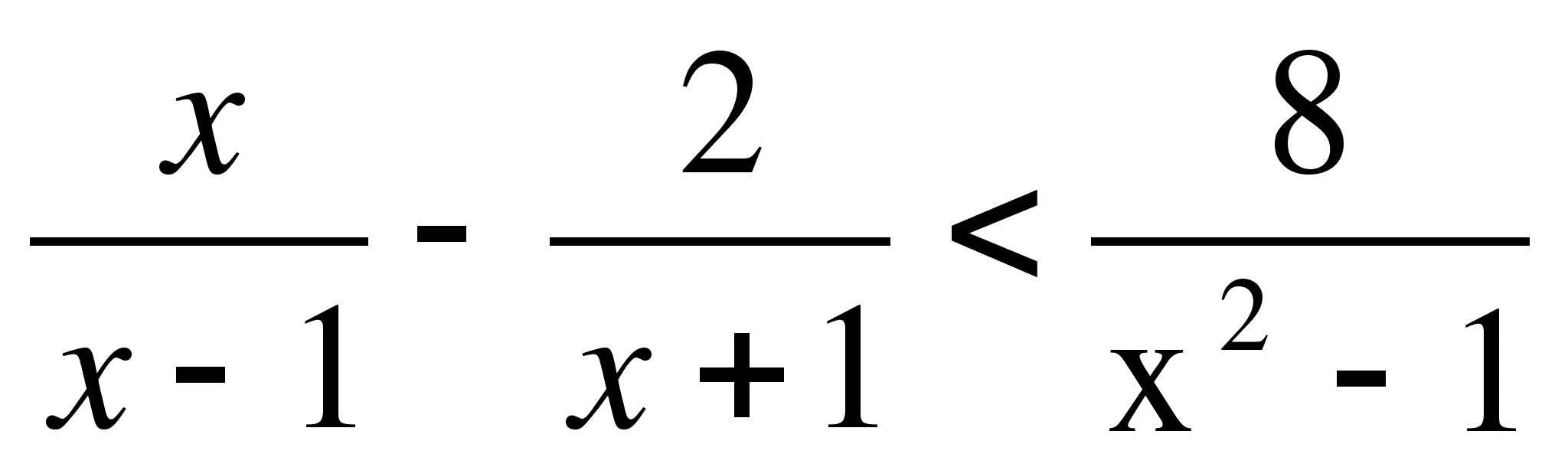
№6. Решите неравенство:
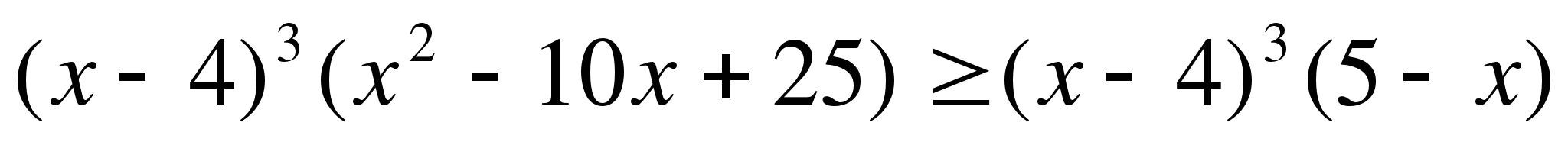
V. Рефлексия.
1) Перечислите основные трудности, которые вы испытывали во время урока.
2) Что вам наиболее удалось, какие задания были выполнены наиболее успешно?
3) Откройте учебник [Ш] и запишите номер и пункт задания по этой теме, которое
вызывает трудности. Их разберём на дополнительном уроке.
VΙ. Домашнее задание.
Учебник [Ш]: №555(3), №560(2), №591.
VΙΙ. Подведение итогов урока, выставление оценок.
(За урок каждый ученик получает оценку, учитывая устную работу, оценку за
тренажёр, письменную работу.)
Конспект урока алгебры в 10 классе «Решение тригонометрических неравенств методом интервалов»
Тема: «Решение тригонометрических неравенств методом интервалов»
Цель урока:
Повторить ранее изученный теоретический материал, обобщить метод интервалов на решение тригонометрических неравенств.
Сформировать навыки решения тригонометрических неравенств.
Учить детей обобщать, анализировать, делать выводы.
Тип урока: урок ознакомления с новым материалом
Оборудование урока: ноутбук, мультимедийный проектор, интерактивная доска.
Ход урока
Сообщение темы, цели и задач урока. Мотивация учебной деятельности.
Подготовка к изучению нового материала че¬рез повторение и актуализацию опорных знаний.
(Учащиеся решают устно задания, предложенные в виде слайдовой презентации)
Решить уравнение: (слайд №1)
1) sin x = ; 4) cos x = 1; 7) sin x = √3; 10) tg x = -1;
2) cos x = — 0,3; 5) sin x = -1; 8) cos x = -1; 11) sin x = 0;
3) tg x = √3; 6) cos x = 0; 9) sin x = 1; 12) ctg x = — 0,5.
Найти наименьший положительный период функции: (слайд №2)
f(x) = cos 3x; ( T1= )
f(x) = 3 sin ; (T1= 5 )
f(x) = sin cos 2x; (T1= 4 )
f(x) = sin 3x + 4cos 4x; (T1= 2 )
f(x) = . (T1= 6 )
c) Решите неравенство: (слайд №3, слайд№4) 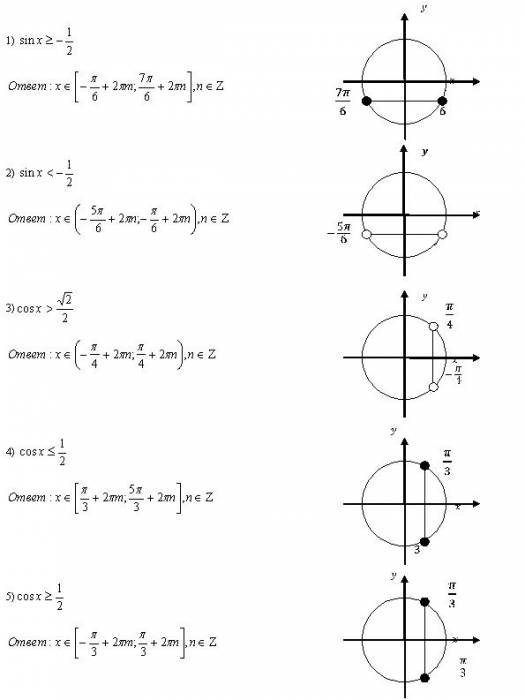
Ознакомление с новым материалом
Одним из основных методов решения более сложных тригонометрических неравенств является метод интервалов. Метод интервалов при решении тригонометрических неравенств применяется на промежутке [0; T┤), где T – общий период всех тригонометрических функций, входящих в неравенство. Решение неравенства, полученное на промежутке [0; T┤), периодически продолжают на всю числовую ось. (Слайд № 5) 


Итак, мы решили тригонометрические неравенства методом интервалов, который ещё называют обобщённым методом интервалов.
3.Первичное осмысление и закрепление связей и отношений в объектах изучения
Учащимся класса дается одно неравенство, которое они решают самостоятельно. После чего решение данного неравенства проецируется на экран, что позволяет учащимся проверить правильность своего решения, если есть ошибки, то исправить их. Такой способ закрепления изученного материала способствует более осознанному усвоению нового материала. (Слайд № 8)


Литература:
Мордкович А.Г., Семенов П.В. Алгебра иначала анализа. 10 класс. (профильный уровень). М.: Мнемозина, 2008.
Рязановский А.Р. 500 срособов и методов решения задач по математике для школьников и поступающих в вузы. М.: Дрофа,2001.
Тимофеев Г.Н. Математика для поступающих в вузы: Учебное пособие. Йошкар-Ола, 2002.