Урок 42. линейные уравнения и неравенства с двумя переменными — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №42. Линейные уравнения и неравенства с двумя переменными
Перечень вопросов, рассматриваемых в теме:
- Решение уравнений, неравенств, систем уравнений и систем неравенств с двумя переменными;
- Изображение в координатной плоскости множества решений уравнений, неравенств, систем уравнений, систем неравенств;
- Нахождение площади получившейся фигуры.
Глоссарий по теме
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными, где a, b и c — некоторые числа (a ≠ 0 , b ≠0), а, х и у — переменные.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
– М.: Просвещение, 2014.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. Учебник: Алгебра 9 кл с углубленным изучением математики Мнемозина, 2014.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Историческая справка
Уравнения, а также системы уравнений имеют давнюю историю. Нам известно, что уже в Древнем Вавилоне и Индии повседневные задачи, связанные с земляными работами или планированием военных расходов, а также астрономическими наблюдениями решались с помощью уравнений и их систем.
В то время еще не существовало привычного нам формального языка математики. Вавилоняне, также, как и индусы не использовали в своих трактатах привычные нам «икс» и «игрек».
Вместе с тем, если перевести в привычный нам вид те уравнения, которые умели решать в Древнем Вавилоне, то мы увидим: . И в древнем индийском манускрипте «Ариабхаттиам», датируемом 499 годом нашей эры, также встречаются задачи, решаемые с помощью квадратных уравнений. Индийские мудрецы (слово ученый тоже еще не существовало) уже не ограничивались решением конкретных житейских задач, но и работали над решением квадратного уравнения в общем виде.
Привычный нам вид уравнения обретают только в конце шестнадцатого века, благодаря трудам Франсу Виета (1540 – 1603 гг.). Именно он, помимо прочих своих научных достижений обладает и неофициальным титулом «создатель алгебры». Поскольку разработал и активно внедрял символический язык алгебры – те самые, привычные нам «иксы и игреки».
Актуализация знаний
1. Найдите уравнения, которые являются линейными.
Найдите уравнения, которые являются линейными.
4х + 5у = 10; ; у = 7х +4
Ответ: 4х + 5у = 10; у = 7х +4
Сегодня на уроке мы вспомним что такое линейные уравнения и неравенства с двумя переменными; системы линейный уравнений и неравенств, а также научимся изображать множество на плоскости, задаваемое линейным уравнением и неравенством.
- Линейные уравнения с двумя переменными.
Уравнение вида ах + by +с =0, где а,b,с – некоторые числа, называется линейным уравнением с двумя переменными х и у.
Решением уравнения ах + by +с =0, где а,b,с – некоторые числа, называется пара значений обращающая уравнение в верное числовое равенство.
Если одновременно а и b, то уравнение ах + by +с =0 является уравнением некоторой прямой. Для построения прямой достаточно найти две точки этой прямой.
Пример
Построить график уравнения 2х+у =1
у = -2х + 1
Если х=0, то у=1;
Если х=2, то у=-3.
На координатной плоскости отметим точки с координатами (0;1) и (2;-3). Через две точки на плоскости проведем прямую. Полученная прямая является геометрической моделью уравнения 2х+у =1.
Через две точки на плоскости проведем прямую. Полученная прямая является геометрической моделью уравнения 2х+у =1.
- Линейные неравенства с двумя переменными.
Линейным неравенством с двумя переменными называется неравенство вида ах + bу + с < 0 или ах + bу + с > 0, где х и у – переменные, а, b, c – некоторые числа.
Решением неравенства с двумя переменными называется пара значений переменных, обращающая его в верное равенство.
Является ли пара (2;1) решением неравенства 5х + 2у > 4 . Является, тк при подстановке в него вместо х числа 2, а вместо у числа 1 получается верное равенство 10 + 2 > 4.
Если каждое решение неравенства с двумя переменными изобразить точкой в координатной плоскости, то получится график этого неравенства. Он является некоторой фигурой.
Пример
Найти множество точек координатной плоскости, удовлетворяющих неравенству 3х – 2у +6 > 0.
- Уравнение 3х – 2у +6 = 0 является уравнением прямой, проходящей через точки(- 2; 0) и (0; 3).

- Пусть точка М1(х1,у1) лежит в заштрихованной полуплоскости (ниже прямой 3х – 2у +6 = 0, аМ2(х1,у2)лежит на прямой 3х – 2у +6 = 0. Тогда 2у2 – 3х1 – 6 = 0, а 2у1 – 3х1 – 6 < 0, т.к. у1< у2
Изобразим множество точек координатной плоскости, удовлетворяющих неравенству 3х – 2у +6 > 0 штриховкой (рис. 1)
Рисунок 1 – решение неравенства 3х – 2у +6 > 0
Если в линейном неравенстве с двумя переменными знак неравенства заменить знаком равенства, то получится линейное уравнение ах + by +с =0, графиком которого является прямая при условии, что и . Прямая разбивает плоскость на две полуплоскости. Одна из них является графиком неравенства ах + bу + с < 0, а другая – графиком неравенства ах + bу + с > 0
Чтобы решить неравенство ах + bу + c < 0 или aх + bу + c > 0, достаточно взять какую-нибудь точку М1(х1; у1), не лежащую на прямой aх + bу + c = 0, и определить знак числа aх1 + bу1 + c.
Пример
Изобразите в координатной плоскости множества решений неравенства 2х + 3у < 6
Начертим график уравнения 2х + 3у = 6.
Пара (0;0) является решением неравенства 2х + 3у < 6, и принадлежит нижней полуплоскости, значит графиком неравенства 2х + 3у < 6 является нижняя полуплоскость (рис. 2).
Рисунок 2 – решение неравенства 2х + 3у < 6
- Система линейных уравнений с двумя переменными.
Система вида , где а,b,с,d,e,f – некоторые числа, называется линейной системой с двумя переменными х и у.
Пара значений переменных, обращающая каждое уравнение системы уравнений с двумя переменными в верное равенство называют решением системы.
Решить систему – значит найти множество ее решений.
Пример
Решите систему:
Каждое решение уравнения с двумя переменными представляет координаты некоторой его точки его графика. Каждое решение системы есть координаты общих точек графиков уравнений системы. Построим графики этих уравнений и найдем координаты точки пересечения (рис.3).
Построим графики этих уравнений и найдем координаты точки пересечения (рис.3).
Рисунок 3 – решение системы
Система имеет единственное решение: x = 4 , y = 4 .
- Система линейных неравенств с двумя переменными.
Системой линейных неравенств с двумя переменными называется такая система неравенств, которая в своем составе имеет два и более линейных неравенств с двумя переменными.
Рассмотрим систему линейных неравенств с двумя переменными на примере:
- Построим прямые х – у = 2 и х + 3у = 6
- Пара (4;1) является решением как первого, так и второго неравенства, те является общим решением неравенств системы. Такую пару чисел называют решением системы неравенств с двумя переменными. Множество общих решений неравенств есть множество решений системы (пересечение множеств решений неравенств, составляющих систему).
Множество решение системы изображается двойной штриховкой. (плоской угол) (рис. 4).
Рисунок 4 – решение системы
Примеры и разбор решения заданий тренировочного модуля
Пример 1
Изобразите в координатной плоскости множества решений неравенства 3х – 2у + 6 0.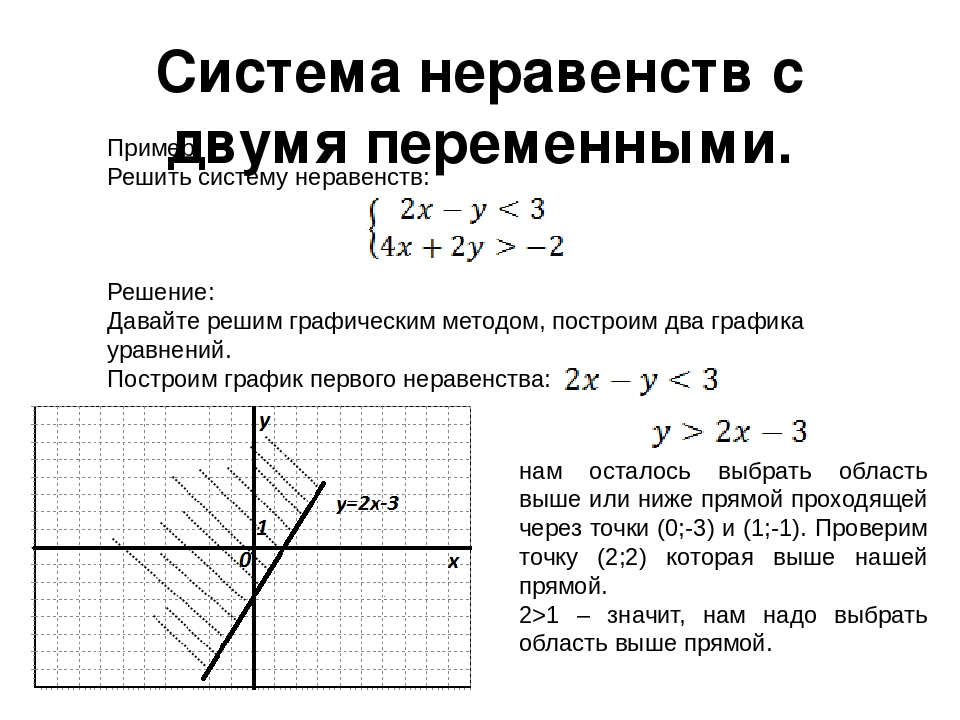
- Начертим график уравнения 3х – 2у + 6 = 0
- Отметим в какой-нибудь полуплоскости, например, точку (1;2).
Пара (1;2) не является решением неравенства и принадлежит нижней полуплоскости, значит графиком неравенства является верхняя полуплоскость вместе с прямой 3х – 2у + 6 = 0. 9 (рис. 5)
Рисунок 5 – решение неравенства
Пример 2
Изобразим на координатной плоскости множество решений системы
Построим прямые х + у = 3 и 4х – 5у = 20.
Множество решений первого неравенства показано горизонтальной штриховкой, а множество решений второго неравенства – вертикальной штриховкой. Двойная штриховка – множество решений системы. Система задает плоский угол (рис. 6)
Рисунок 6 – решение системы
Если к системе добавить еще одно неравенство
, то получится система трех неравенств с двумя переменными
Этой системой задается треугольник (рис. 7)
Рисунок 7 – решение системы
Точка О принадлежит , левая часть неравенства положительна, и поэтому множество его решений – объединение множеств .
Уравнения и неравенства с двумя переменными. Примеры решения
Дата публикации: .
Урок и презентация на тему: «Уравнения и неравенства с двумя переменными»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать: Уравнения и неравенства с двумя переменными (PPTX)
Ребята, мы разобрались с уравнениями и неравенствами с одной переменной. Теперь давайте перейдем к более общему и сложному случаю — к уравнениям и неравенствам с двумя переменными.
 2=0$ имеет всего одно решение $х=-2$ и $у=-4$. Поскольку, сумма двух не отрицательных чисел может равняться нулю, когда они одновременно равны нулю. В данном примере мы получили всего одно решение.
2=0$ имеет всего одно решение $х=-2$ и $у=-4$. Поскольку, сумма двух не отрицательных чисел может равняться нулю, когда они одновременно равны нулю. В данном примере мы получили всего одно решение.Если дано целое рациональное уравнение с несколькими переменными и целочисленными коэффициентами, и также требуется найти целые (или рациональные) решения данного уравнения, то принято говорить, что задано диофантово уравнение.
Диофантовы уравнения решаются довольно трудно, и не всегда сразу можно придумать ходы решения. Часто помогает теория делимости целых чисел. Также отмечу, что современные методы программирования позволяют решать многие уравнения на компьютерах, используя так называемые численные методы.
Пример.
Найти целочисленные решения уравнения: $5x+4y=17$.
Решение.
В общем случае мы могли бы на декартовой системе координат изобразить прямую и получить множество всех решений, но нам требуется найти только целочисленные решения.
Воспользуемся известными предложениями теории делимости целых чисел.
Приведем наше уравнение к виду: $y=\frac{17-5x}{4}$.
Целое число $17-5х$ должно делиться без остатка на 4.
При делении на 4 возможны четыре случая:
а) остаток от деления на 4 равен нулю, то есть $х=4k$.
б) остаток от деления на 4 равен единице, то есть $х=4k+1$.
в) остаток от деления на 4 равен двум, то есть $х=4k+2$.
г) остаток от деления на 4 равен трем, то есть $х=4k+3$, где k — целое число.
Рассмотрим каждый случай отдельно:
а) Если $х=4k$, то $17-5x=17-20k$ не делится нацело на 4, т.к. каждый член разности должен делиться на 4, а число 17 не делится на 4.
б) Если $х=4k+1$, то $17-5x=17-20k-5=12-20k$ делится нацело на 4.
в) Если $х=4k+2$, то $17-5x=17-20k-10=7-20k$ не делится на 4.
г) Если $х=4k+3$, то $17-5x=17-20k-15=2-20k$ не делится на 4.
Среди всех возможных вариантов нам подошел лишь один вариант: $х=4k+1$.
Найдем y: $y=\frac{17-5x}{4}=\frac{17-20k-5}{4}=3-5k.$
Целым решением нашего уравнения является любая пара чисел $(4k+1;3-5k)$,
где k – любое целое число. 2=13$.
2=13$.
Решение.
Воспользуемся формулой разности квадратов: $(4x-2y)(4x+2y)=13$.
Мы получили произведение двух чисел в левой части уравнения. Заметим, что в правой части уравнения получилось простое число, которое делится только на себя и единицу по модулю.
Число 13 получается лишь в четырех случаях при произведении двух чисел:
а) Первый сомножитель равен 1, второй сомножитель равен 13.
б) Первый сомножитель равен 13, второй сомножитель равен 1.
в) Первый сомножитель равен -1, второй сомножитель равен -13.
г) Первый сомножитель равен -13, второй сомножитель равен -1.
Значит, нам надо решить совокупность 4 систем.
а)$\begin {cases} 4x-2y=1, \\ 4x+2y=13 \end {cases}$.
б)$\begin {cases} 4x-2y=13, \\ 4x+2y=1 \end {cases}$.
в)$\begin {cases} 4x-2y=-1, \\ 4x+2y=-13 \end {cases}$.
г) $\begin {cases} 4x-2y=-13, \\ 4x+2y=-1 \end {cases}$.
Решением каждой системы является пара чисел: а) $(1,75;3)$; б) $(1,75;-3)$;
в) $(-1,75;-3)$; г) $(-1,75;3)$.
Получается, что в данном примере целочисленных решений нет, но суть метода решения должна быть ясна.
Ответ: целочисленных решений нет.
Неравенства
Неравенства вида $p(x;y)>0$, $p(x;y)Решением неравенства $p(x;y)>0$ называют всякую пару чисел, которые удовлетворяют данному неравенству (неравенство превращается в верное числовое неравенство). Решения неравенств с двумя переменными также проще изображать на графиках в декартовой системе координат. Рассмотрим несколько примеров.
Пример.
Решить неравенство: $2x+5y>7$.
Решение.
Для начала выразим у через х: $y>\frac{7-2x}{5}$.
Построим прямую $y=\frac{7-2x}{5}$. Множество всех решений неравенства расположено, либо выше, либо ниже данной прямой.
Можно подставить любую пару чисел и проверить: выполнилось неравенство или нет. Если неравенство выполнилось, то мы выбираем в качестве решения ту область, которой принадлежат эти пара чисел, если не выполнилось, то выбираем противоположную область. 2-6x+2, \\ y≤x+5 \end {cases}$.
2-6x+2, \\ y≤x+5 \end {cases}$.
Неравенства с двумя переменными
Рассмотрим неравенство:
Определение:
Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство.
Тогда пара значений (2; -1) является решением данного неравенства, но это не единственное решение.
Пример.
Проверить, является ли пара чисел (-2; 3) решением неравенств.
Подставим пару этих значений в каждое неравенство и проверим, обратятся ли они в верные числовые неравенства:
Получили, что в первом и во втором случаях — верное неравенство, а в третьем — пара чисел (-2; 3) не является решением данного неравенства.
Пример.
Найти два каких-нибудь решения неравенства:
Очевидно,
что х может быть любым числом.
Например:
Среди множества решений данного неравенства будут пары чисел: (5; 17) и (-3; 8).
Так как неравенство с двумя переменными имеет множество решений, то их сложно перечислить. Увидеть множество решений неравенства с двумя переменными позволяет график.
Изобразим на координатной плоскости множество точек, заданных неравенством:
Построим график уравнения:
Графиком является прямая и для её построения достаточно двух точек:
Возьмём на прямой некоторую точку М с координатами (). Если мы возьмём точку К выше прямой, видно, что её абсцисса = , а вот ордината > . Тогда получаем, что координаты точки К не удовлетворяют неравенству. Если же взять точку, расположенную ниже прямой, с абсциссой = , то видно, что её ордината будем < . Тогда координаты этой точки будут удовлетворять неравенству:
Получили
множество точек находящихся ниже.
Изобразим на координатной плоскости множество точек, заданных неравенством:
Изобразим график уравнения:
Возьмём на графике некоторую точку М с координатами (). Если мы возьмём точку К выше графика, то видно, что её абсцисса = , а вот ордината > . Тогда получаем, что координаты точки удовлетворяют неравенству. Если же взять точку N, расположенную ниже графика, с абсциссой = , то видно, что её ордината будем < . Тогда координаты этой точки будут не удовлетворять неравенство:
Выберем нужное нам множество. Получаем:
Изобразим на координатной плоскости множество точек, заданных неравенством:
Изобразим график:
Взяв любую точку внутри окружности, можно увидеть, что её координаты удовлетворяют неравенству. Координаты точек, находящихся вне окружности не удовлетворяют неравенству.
Вернёмся к неравенству, решением будет являться множество точек находящихся внутри окружности и принадлежащих ей:
Изобразим на координатной плоскости множество точек, заданных неравенством:
Это
уравнение обратной пропорциональности, графиком является гипербола. Составим
таблицу значений:
Составим
таблицу значений:
Отметим полученные точки на координатной плоскости и изобразим график:
Линии графика разделили координатную плоскость на три области. Координаты точек из области А будут удовлетворять неравенству. Координаты точек из области B не удовлетворяют неравенству. И если точка принадлежит области С, то точки этой области будут удовлетворять неравенству.
Множеством решений неравенства будут — А и С, включая линии графика.
Примеры решения уравнения, неравенства и системы неравенств с двумя переменными, содержащие знак модуля
Уравнения, неравенства и системы неравенств с двумя переменными, содержащие знак модуля
Примеры с решениями
Пример №319.Найти множество точек координатной плоскости , координаты которых удовлетворяют уравнению:
Решение:
а) Запишем уравнение в виде
Это уравнение имеет единственное решение т. е. данному уравнению удовлетворяют координаты только одной точки
е. данному уравнению удовлетворяют координаты только одной точки
б) Уравнение равносильно совокупности уравнений и Искомое множество состоит из всех точек, принадлежащих биссектрисам I и III, а также II и IV координатных углов (рис. 26.11).
в) Уравнение равносильно совокупности двух систем:
Первой из них удовлетворяют точки, принадлежащие биссектрисе II координатного угла, второй системе — точки, принадлежащие биссектрисе III координатного угла (рис. 26.12).
г) Запишем уравнение в виде
Это уравнение окружности с центром в точке и радиусом 1 (рис. 26.13).
Пример №320.Изобразить на координатной плоскости фигуру , координаты точек которой удовлетворяют системе неравенств
и найти площадь этой фигуры.
Решение:
Построим графики функций и (рис. 26.14).
Решив систему уравнений
находим общую точку этих графиков, лежащую в I квадранте (рис. 26.14). Аналогично, решив систему уравнений
26.14). Аналогично, решив систему уравнений
находим общую точку графиков функций и лежащую во II квадранте.
Неравенству (1) удовлетворяют все точки координатной плоскости, расположенные выше графика функции а неравенству (2) — все точки координатной плоскости, лежащие ниже графика функции
Следовательно, системе (1), (2) удовлетворяют все точки, лежащие внутри прямоугольника полученного при пересечении графиков функций и Так как то
Пример №321.Найти все такие пары целых чисел которые удовлетворяют системе неравенств
Решение:
Запишем данную систему в следующем виде:
Так как то из неравенств (3) и (4) следует, что
Целыми числами, удовлетворяющими неравенству (5), являются лишь 0 и 1, поэтому система (3), (4) может иметь целые решения только при и .
1) Если , то система (3), (4) примет вид
Второму из этих неравенств удовлетворяют целые числа 0, 1 и 2. Проверка показывает, что первому неравенству удовлетворяют
Проверка показывает, что первому неравенству удовлетворяют
лишь 0 и 2. Следовательно, пары чисел и образуют решения исходной системы неравенств.
2) Если то система (3), (4) приводится к виду
Второму неравенству системы (6) удовлетворяет единственное целое число которое является также и решением первого неравенства.
Ответ.
Пример №322.Изобразить на координатной плоскости фигуру , координаты точек которой определяются неравенством
и найти площадь фигуры .
Решение:
1) Рассмотрим сначала случай Тогда неравенство (7) примет вид
Если то неравенство (8) можно записать так:
Множество точек, удовлетворяющих условиям — это треугольник образованный прямой (рис. 26.15) и координатными полуосями
Если то неравенство (8) примет вид
а множество точек таких, что — это треугольник симметричный треугольнику относительно оси
Аналогично рассматриваются случаи и которым соответствуют треугольники и симметричные соответственно треугольникам и относительно оси .
Таким образом, фигура, определяемая неравенством (8), представляет собой квадрат с центром в точке и вершинами
Заметим, что симметрия фигуры относительно координатных осей следует из того, что наряду с точкой этой фигуре принадлежат точки так как Площадь этой фигуры равна
2) Рассмотрим теперь неравенство (7). Так как фигуру , определяемую неравенством (7), можно получить из фигуры , заданной неравенством (8), с помощью параллельного переноса (сдвига на вектор то — квадрат (рис. 26.16) с центром в точке и вершинами
Площадь фигуры , как и фигуры , равна .
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Решение задач по математике
Возможно вам будут полезны эти страницы:
Решение систем неравенств с двумя переменными, алгебра ,9 класс
Предмет: | алгебра | |||||
Дата: 4. | ФИО учителя: Харченко Татьяна Викторовна | |||||
Класс: 9-Б | Кол-во присутствующих:17 | Кол-во отсутствующих:2 | ||||
Тема урока | Решение систем неравенств с двумя переменными | |||||
Цели обучения данного урока | -уметь решать системы неравенств с двумя переменными | |||||
Предполагаемый результат | Все учащиеся смогут:
| |||||
Большинство учащихся смогут: решать системы нелинейных неравенств с двумя переменными, содержащими квадратичную функцию и окружность, гиперболу и окружность, окружности с разными центрами, гиперболу, параболу и прямые. | ||||||
Некоторые учащиеся смогут: решать системынелинейных неравенств с двумя переменными с модулем, находитьобщее решение системы нелинейных уравнений с двумя переменными с модулем | ||||||
Языковая цель | Развитие навыков: построения графиков линейной, квадратичной, дробно-рациональной функций и окружности, нахождения решений систем неравенств с двумя переменными Основные термины и словосочетания:
Полиязычие:перевод терминовна казахский и английский языки; Используемый язык для диалога/письма на уроке: побуждающий диалог Вопросы для обсуждения:
| |||||
Ценности | — умение работать в команде; -умение ставить правильно проблемный вопрос; -умение анализировать и обобщать. | |||||
Предшествующие знания | Линейная функция и ее график, квадратичная функция и ее график, дробно-рациональная функция и ее график, уравнение окружности, точки пересечения графиков функций, решение неравенств с двумя переменными. | |||||
План | ||||||
Планируемое время | Запланированная деятельность | Ресурсы | ||||
Начало урока (10/) | I. Стадия вызова 1. Организационный момент. Создание положительного эмоционального настроя. Видеоролик «Что происходит в мире за 1 минуту». Исходя из просмотренного видеоролика, учитель предлагает попробовать следовать девиз «Сделай за минуту» и выполнить часть заданий урока в течение 1 минуты. 2.Анаграмма.(улучшение внимания). Из данного слова нужно составить как можно больше слов. Каждую букву разрешается использовать столько раз, сколько она встречается в слове. Тот, кто назовет больше всех слов – победит. На выполнение задания дается 1минуты. (слово – 1 балл, если из 3-5 букв, 2 балла- если из 5-8 букв, 3 балла- из 9 букв) Из слова «Математика» нужно составить как можно больше слов. Каждую букву разрешается использовать столько раз, сколько она встречается в слове, т.е. буквы «а» -три раза, «м», «т»-два раза, а остальные по одному. Возможные варианты ответов: актикт кит мак мат так там тик | тема мама такт тата аким | метка атака катет макет матка тетка мамка | аммиак татами | ||
Из 8-ми букв | ||||||
тематика | ||||||
Из 9-ти букв | ||||||
математик | ||||||
Высокий уровень мышления- из 6-9 букв
Средний уровень мышления- из 4-5 букв
Низкий уровень мышления – только из 3 букв
3. Выход на тему. Прием Мозговой штурм.(1 мин)
Выход на тему. Прием Мозговой штурм.(1 мин)
А) Какие темы мы изучили в 1 четверти и в каком порядке?
Б) Как вы думаете, какой может быть тема нашего урока, если она новая для вас и изучается после темы «Решение неравенств с двумя переменными»?
Б) Буквенно-картинный трехъязычный ребус позволит правильно произнести и записать тему урока (1 мин)
neravenstv
өзгермелі
Дескрипторы:
отгадывают изображения предметов
применяют правила по разгадыванию ребуса
переводят слова на русский язык
записывают предполагаемый ответ
ПК, интерактивная доска, видеоролик
(https://www.youtube.com/watch?v=q8QMa6PWk7w)
4.Актуализация жизненного опыта. Целеполагание.(1 мин)
Зная тему урока, сформулируйте цель нашего урока.
Предполагаемый ответ: научиться решать системы нелинейных неравенств с двумя переменными
4.Кроссенс. Девять картинок связаны одной центральной, расположите их в определенном порядке так, чтобы получился тематический последовательный круг. Объясните ваш выбор.
5. Собери пазл.Каждой группе предлагается пазл «Структурно-логическая таблица по теме: «Неравенства с двумя переменными». Участники команды за 1 минуту должны собрать пазл, который будет верным помощником при изучении новой темы. По истечении 1 минуты команда, закончившая первой, получает право зачитать на свое усмотрение любой из 3 пропущенных вопросов — пазлов и дать ответ на него. Если отвечающий не смог дать ответ, то члены команды вправе ему помочь. Далее отвечает команда, закончившая сбор пазла второй и третьей и т.д. Группа экспертов фиксирует результаты.Дескрипторы:
– собирают целое из частей
– вписывают недостающие термины
–записывают предполагаемый ответ
1. Вставьте пропущенное слово: «Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство
Вставьте пропущенное слово: «Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство
в … числовое неравенство».
2.Задайте неравенством с двумя переменными множество точек, расположенных вне круга с центром в точке(3;-2) и радиусом, равным 5.
3.Решение какого неравенство изображено на графике?
Ответы:
1. Верное
2.
3.
1.Какое неравенство задаёт множество точек круга, включая линию окружности, с центром в точке (-2;6) и радиусом, равным 3?
2. Графиком линейного уравнения с двумя переменными является ….
3.Решение какого неравенство изображено на графике?
Ответы:
1.
2.прямая
3.у
(Ф) После каждого этапа учащиеся отмечают результат своей работы
Я хорошо справился с заданиямиЯ не все понял при выполнении упражнении
Я ничего не понял, надо включаться в работу
Тест 19 эл учебник
Основная часть (20-25 минут)
II. Осмысление
Осмысление
1. Объяснение нового материала (10 мин)
Видеоурок «Системы неравенств с двумя переменными».
2.(Г) Первичное осмысление изученного.
ЗнаниеАналогия. Вспомните алгоритм решения систем неравенств с одной переменной и составьте алгоритм решения систем неравенств с двумя переменными
Заполните таблицу
1.Решить каждое неравенство отдельно2.Найти пересечение решений неравенств 3.Записать общий ответ
Первичная проверка понимания
ДА-НЕТ-ка
Верно ли, что
1.Если обе части неравенства умножить или разделить на одно и то же отрицательное число, то получится равносильное неравенство?
2.Если из одной части неравенства в другую перенести слагаемое с противоположным знаком, то получится верное неравенство?
3.Если к обеим частям неравенства прибавить
( отнять) одно и то же число( выражение) , то получится верное неравенство?
4. Решить систему неравенств с двумя переменными-значит найти множество пар чисел, обращающих каждое неравенство в неверное.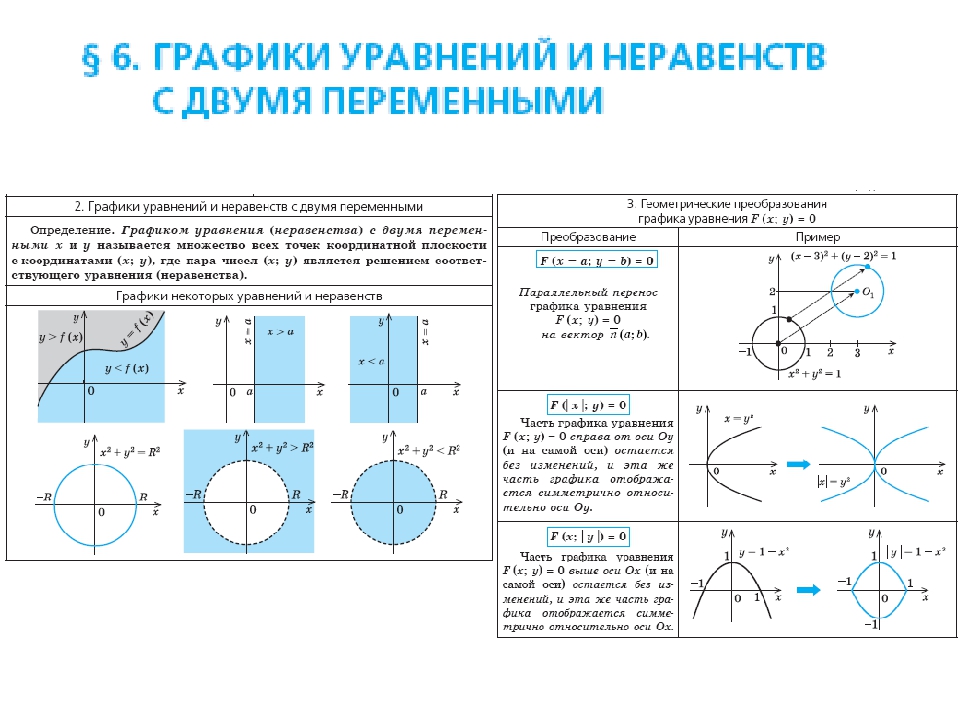
5. Решением системы неравенств является пересечение решений неравенств, входящих в систему.
Нет
Да
Да
Нет
Да
Применение новых знаний
Решите системы неравенств
«5 баллов»-
«4 балла»-
«3 балла»-
Анализ
«ТАНК» – развитие навыков аргументации
Т – тезис (Я считаю, что….)
А – аргументация (Так, как…)
Н – наглядность (Например,….)
К – кольцевание (Таким образом,….)
Математическая модель
Дескрипторы:
условие краткое к задаче-1 балл
математическая модель- 3 балла.
Составление системы неравенств и ее решение 3 балла
Ответ 1 балл.
Сотовая связь действует в радиусе 10 км- 30 км от станции. Нанесите на карту города область, в которой всегда будет работать связь, если станция имеет координаты (5,10)
Синтез
Найди ошибку
1.
Для решения каких проблем можно применять системы неравенств с двумя переменными
Оценка.
Метод «Дуэт». Найдите соответствие между системой неравенств и ее решением (5 мин)
2.3.
4.
5.
А)
В)
С)
D)
E)
Сверка с образцом.
Правильные ответы:
1-Е (2 балла), 2- D (1 балл), 3-А (2 балла), 4-С (3 балла),5-В ( 2 балла)
Итого- 10 баллов. Правильный ответ-1 балл
4. (Формативное оценивание).
Оцените свою работу на уроке с помощью фразеологизмов, приклеив стикеры
светлая голова
каша в голове
ни в зуб ногой
Проанализируйте уровень приобретенных знаний на данном этапе.
«светлая голова» – мне все ясно, я удовлетворен своей работой, могу применять в работе;
«каша в голове» – необходимо еще поработать над собой, чтобы до конца разобрать в материале, но сделаю это самостоятельно;
«ни в зуб ногой» – мне многие моменты не ясны, необходима консультация
III. Подведение итогов.
Подведение итогов.
Рефлексия.
ин)
Стадия рефлексии и оценки.
1. Итог урока.
0-6 баллов- «2»
7-10 баллов- «3»
11-15 баллов-«4»
16-20 баллов- «5»
Рефлексия содержания учебного материала
«Чемодан, мясорубка, корзина»
Чемодан– всё, что пригодится в дальнейшем
Мясорубка– информацию переработаю
Корзина – всё выброшу
Дома: параграф 7, № 117(б,г,д), № 119(б,г)
Творческое задание. Сферы применения неравенств с двумя переменными.
Дополнительная информацияДифференциация – Как вы планируете помогать учащимся? Какие задания вы планируете давать более способным ученикам?
Наблюдения
Были ли цели обучения/урока достижимыми?
Чему сегодня научились учащиеся?
Какой была атмосфера обучения?
Успешными ли были действия по дифференциации между учащимися?
Придерживался ли я временного графика? Какие отступления от плана я сделал и почему?
Итоговое оценивание
Назовите два наиболее успешных момента (как преподавания, так и обучения)
Назовите два момента, которые бы способствовали улучшению урока (как преподавания, так и обучения)
Что нового я узнал о классе и его отдельных учащихся, и как это отразится на проведении моего следующего урока?
Раздел долгосрочного плана: Уравнения, неравенства с двумя переменными и их системы (17 ч) | Школа: | ||||||
Дата: | ФИО учителя: | ||||||
Класс:9 | Количество присутствующих: |
| отсутствующих: | ||||
Тема урок | Неравенства с двумя переменными | ||||||
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | 9. | ||||||
Цели урока | • Вывести алгоритм решения неравенств с двумя переменными; • Научиться находить решения неравенств с двумя переменными. | ||||||
Критерии оценивания | Знание и понимание: осуществят подготовку к пониманию материала через повторение графиков, рассмотрят графический способ решения неравенств. Применение: выполнят решение задач | ||||||
Языковые цели
| Лексика и терминология, специфичная для предмета: — линейное/квадратное/дробное уравнение; — переменная/ось(и)/масштаб/кривая; — пересечение/точка пересечения; — таблица значений/множество точек; — заменить/преобразовать; — построить график/прямую/кривую; — нанести точки на график; — изобразить кривую; — уравнение окружности; Полезные выражения для диалогов и письма: —
оси Оx и Оy представляют собой …. — точки на этой прямой/кривой… — таким образом, прямая представляет собой….; — оси координат x и y положительные или отрицательные; — координаты записываются в виде упорядоченных пар….; — корни уравнения являются точками пересечения….; | ||||||
Привитие ценностей | обучение на протяжении всей жизни: отбор информации по теме урока, установление соответствий между понятиями и примерами сотрудничество: работа с партнером, интерактивная лекция прозрачность: проверка выполненных работ с обратной связью учителя, тем самым итоги работы прозрачны и обобщены. | ||||||
Межпредметные связи |
| ||||||
Навыки использования ИКТ |
| ||||||
Предварительные знания
| Понятие
линейного, квадратного и дробного уравнений и построение графиков. | ||||||
Ход урока | |||||||
Запланированные этапы урока | Запланированная деятельность на уроке | Ресурсы | |||||
Начало урока. 2 мин
| 1. Организационный момент. Проверить готовность учащихся к уроку. Сформулировать тему и цели урока.
| Презентация к уроку.
| |||||
Середина урока
4 мин
16 мин
16 мин
| 2. 1. Какие неравенства называются неравенствами с двумя переменными? 2. Что называется решением неравенства с двумя переменными? 3. Что называется множеством решения неравенства? 4. Объясните правило пробной точки? 5. Дайте определение линейному неравенству с двумя переменными? 3. Стартер
4. Решение задач в группах Использование (применение) правил в новых ситуациях. Самопроверка в группе с правильными ответами на доске. Разобрать ошибки вместе с учащимися. Обратная связь учителя по работе ученика. 5. Самостоятельное решение задач. Практика решения задач. Развитие критического мышления: анализ, синтез, оценка. 1. Изобразите на координатной плоскости множество точек, задаваемое неравенством , если: a) b) 2. a) b) c) d) Дескриптор: · Приводит неравенство к стандартному виду; · Строит чертеж; · Находит множество точек; | Презентация к уроку
Приложение 1
Презентация
Макрычев Н.Г. Алгебра 9.
Приложение 2
| |||||
Конец урока 2 мин
| Побуждение учеников оценивать свою деятельность
| Презентация | |||||
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? | Здоровье и соблюдение техники безопасности | |||||
Работа
с партнером подразумевает консультирование. Предполагаю развитие навыков высокого порядка через отбор информации, установление соответствий примера и понятий. | ФО по целям обучения. · отработка понимания изученных определений · практика решения задач | Смена деятельности Групповая посадка детей. Техника безопасности.
| |||||
Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? | Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. | ||||||
1. | |||||||
| Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?
Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках? + | ||||||
Презентация «Неравенства с двумя переменными» 2часть (гипербола)
библиотека
материалов
Содержание слайдов
Номер слайда 1
Неравенства с двумя переменными (гипербола) Учитель математики Попова Н. В. МАОУ СОШ № 48, г. Тюмень
В. МАОУ СОШ № 48, г. Тюмень
Номер слайда 2
Общая схема решения ху > к, если к > 0 часть плоскости, расположенная выше гиперболы у =к/х в 1 четверти и ниже гиперболы в 3 четверти. гиперболу изображают пунктирной линией
Номер слайда 3
Общая схема решения ху 0 часть плоскости, расположенная между ветками гиперболы у =к/х. Гиперболу изображают пунктирной линией
Гиперболу изображают пунктирной линией
Номер слайда 4
Общая схема решения ху
Номер слайда 5
Общая схема решения ху > к, если к
Номер слайда 6
В классе: № 488(б), № 497(в), №498(в) Домашнее задание: п21, п22 прочитать примеры, № 488(а), №497(а), №498(а)
Номер слайда 7
№497(в) Пересечение полуплоскости, расположенной ниже прямой у = 2х – 1 и полуплоскости ниже прямой у = х — 3.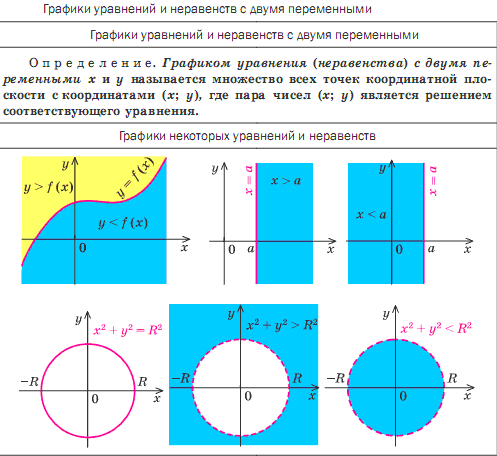 Прямые — пунктирные линии.
Прямые — пунктирные линии.
Номер слайда 8
№498(в) Пересечение полуплоскости, расположенной правее прямой х = — 2 и полуплоскости ниже прямой у = 3.
Номер слайда 9
№500(а) Пересечение части плоскости, расположенной выше параболы у = хІ, и полуплоскости ниже прямой у = 4),.
Номер слайда 10
№500(б) Пересечение части плоскости, расположенной внутри окружности хІ + уІ = 4 и полуплоскости ниже прямой у=х.
Номер слайда 11
Общая схема решения хІ + уІ ≥ аІ, часть плоскости, расположенная за окружностью хІ + уІ = аІ.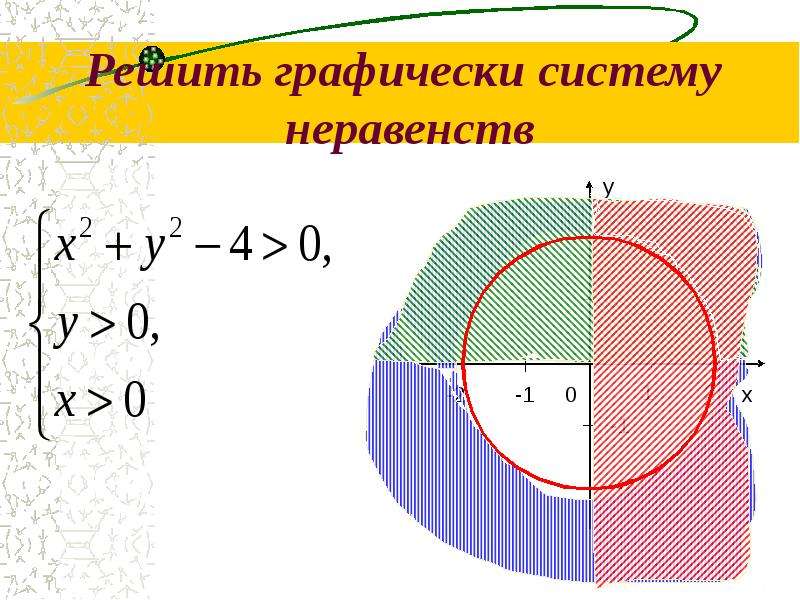 окружность изображают сплошной линией
окружность изображают сплошной линией
3.8: Линейные неравенства (две переменные)
Решения линейных неравенств
Мы знаем, что линейное уравнение с двумя переменными имеет бесконечно много упорядоченных парных решений, которые на графике образуют линию. С другой стороны, линейное неравенство с двумя переменными имеет набор решений, состоящий из области, определяющей половину плоскости.
| Линейное уравнение | Линейное неравенство |
|---|---|
| \ (y = \ frac {3} {2} x + 3 \) | \ (у \ leq \ frac {3} {2} x + 3 \) |
Рисунок \ (\ PageIndex {1} \) | Рисунок \ (\ PageIndex {2} \) |
Для неравенства линия определяет одну границу заштрихованной области. Это означает, что любая упорядоченная пара, находящаяся в заштрихованной области, включая граничную линию, будет удовлетворять неравенству. Чтобы убедиться в этом, выберите несколько контрольных точек и подставьте их в неравенство.
Это означает, что любая упорядоченная пара, находящаяся в заштрихованной области, включая граничную линию, будет удовлетворять неравенству. Чтобы убедиться в этом, выберите несколько контрольных точек и подставьте их в неравенство.
| \ (\ color {Cerulean} {Test \: point} \) | \ (у \ leq \ frac {3} {2} x + 3 \) |
| \ ((0,0) \) | \ (\ begin {align} 0 & \ leq \ frac {3} {2} (0) +3 \\ 0 & \ leq 3 \ quad \ color {Cerulean} {\ checkmark} \ end {align} \) |
| \ ((2,1) \) | \ (\ begin {align} 1 & \ leq \ frac {3} {2} (2) +3 \\ 1 & \ leq 3 + 3 \\ 1 & \ leq 6 \ quad \ color {Cerulean} {\ checkmark} \ конец {выровнен} \) |
| \ ((- 2, -1) \) | \ (\ begin {align} -1 & \ leq \ frac {3} {2} (- 2) +3 \\ -1 & \ leq -3 + 3 \\ -1 & \ leq 0 \ quad \ color {Cerulean} {\ checkmark} \ end {align} \) |
Кроме того, мы можем видеть, что упорядоченные пары за пределами заштрихованной области не решают линейное неравенство.
\ (\ begin {array} {c | c} {\ underline {\ color {Cerulean} {Test \: point}}} & {\ underline {y \ leq \ frac {3} {2} x + 3} } \\ {(- 2,3)} & {3 \ leq \ frac {3} {2} (- 2) +3} \\ {} & {3 \ leq -3 + 3} \\ {} & {3 \ leq 0 \ quad \ color {red} {x}} \ end {array} \)
График решения, установленного для линейного неравенства, всегда является областью. Однако граница не всегда может быть включена в этот набор. В предыдущем примере линия была частью набора решений из-за части «или равно» во включительном неравенстве \ (≤ \).Если у нас есть строгое неравенство \ (<\), мы бы использовали пунктирную линию, чтобы указать, что эти точки не включены в набор решений.
| Неисключительная граница | Включая Граница |
|---|---|
| \ (y <\ frac {3} {2} x + 3 \) | \ (у \ leq \ frac {3} {2} x + 3 \) |
Рисунок \ (\ PageIndex {3} \) | Рисунок \ (\ PageIndex {4} \) |
Рассмотрим точку \ ((0, 3) \) на границе; эта упорядоченная пара удовлетворяет линейному уравнению. Часть инклюзивного неравенства «или равно» делает его частью набора решений.
Часть инклюзивного неравенства «или равно» делает его частью набора решений.
\ (\ begin {array} {c | c} {\ underline {y <\ frac {3} {2} x + 3}} & {\ underline {y \ leq \ frac {3} {2} x + 3}} \\ {3 <\ frac {3} {2} (0) +3} & {3 \ leq \ frac {3} {2} (0) +3} \\ {3 <0 + 3} & {3 \ leq 0 + 3} \\ {3 <3 \ quad \ color {red} {x}} & {3 \ leq 3 \ quad \ color {Cerulean} {\ checkmark}} \ end {array} \ )
До сих пор мы видели примеры неравенства «меньше». Теперь рассмотрим следующие графы с такой же границей:
| Больше, чем (вверху) | Меньше (ниже) |
|---|---|
| \ (y \ geq \ frac {3} {2} x + 3 \) | \ (у \ leq \ frac {3} {2} x + 3 \) |
Рисунок \ (\ PageIndex {5} \) | Рисунок \ (\ PageIndex {6} \) |
Учитывая приведенные выше графики, чего можно ожидать, если мы будем использовать начало координат \ ((0, 0) \) в качестве контрольной точки?
\ (\ begin {array} {c | c} {\ underline {y \ geq \ frac {3} {2} x + 3}} & {\ underline {y \ leq \ frac {3} {2} x +3}} \\ {0 \ geq \ frac {3} {2} (0) +3} и {0 \ leq \ frac {3} {2} (0) +3} \\ {0 \ geq 0 +3} & {0 \ leq0 + 3} \\ {0 \ geq 3 \ quad \ color {red} {x}} & {0 \ leq 3 \ quad \ color {Cerulean} {\ checkmark}} \ end { массив} \)
Упражнение \ (\ PageIndex {1} \)
Какая из упорядоченных пар \ ((- 2, −1), (0, 0), (−2, 8), (2, 1), \) и \ ((4, 2) \) решает неравенство \ (y> — \ frac {1} {2} x + 2 \)?
- Ответ
\ ((- 2, 8) \) и \ ((4, 2) \)
Графические решения линейных неравенств
Решения линейных неравенств представляют собой заштрихованную полуплоскость, ограниченную сплошной или пунктирной линией.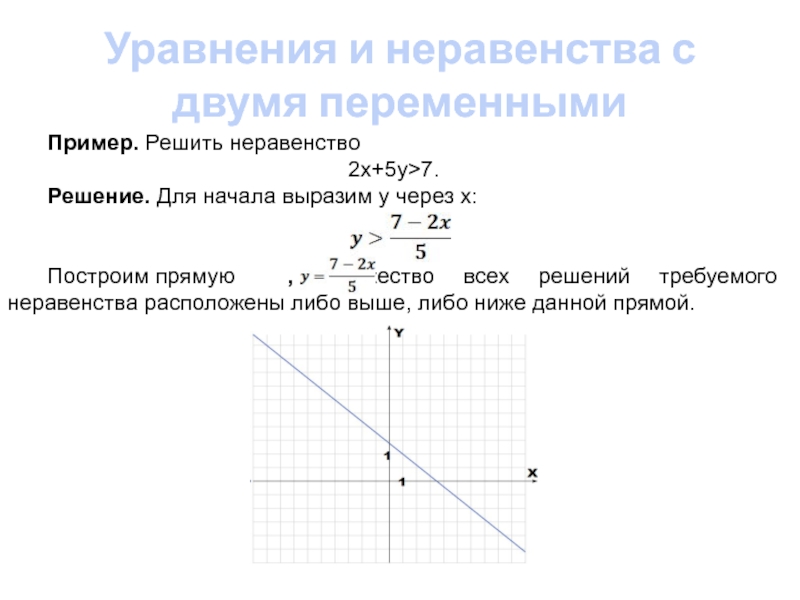 Эта граница либо входит в решение, либо нет, в зависимости от заданного неравенства. Если нам дано строгое неравенство, мы используем пунктирную линию, чтобы указать, что граница не включена. Если нам дано инклюзивное неравенство, мы используем сплошную линию, чтобы указать, что оно включено. Шаги для построения графика набора решений для неравенства с двумя переменными описаны в следующем примере.
Эта граница либо входит в решение, либо нет, в зависимости от заданного неравенства. Если нам дано строгое неравенство, мы используем пунктирную линию, чтобы указать, что граница не включена. Если нам дано инклюзивное неравенство, мы используем сплошную линию, чтобы указать, что оно включено. Шаги для построения графика набора решений для неравенства с двумя переменными описаны в следующем примере.
Пример \ (\ PageIndex {1} \)
График набора решений:
\ (у> −3x + 1 \).
Решение :
Шаг 1 : Постройте граничную линию. В этом случае изобразите пунктирную линию \ (y = −3x + 1 \) из-за строгого неравенства. При осмотре мы видим, что наклон равен \ (m = −3 = — \ frac {3} {1} = \ frac {rise} {run} \), а точка пересечения \ (y \) — \ ((0 , 1) \).
Рисунок \ (\ PageIndex {7} \)
Шаг 2 : Проверьте точку , а не на границе. Обычная контрольная точка — начало координат \ ((0, 0) \).Контрольная точка помогает нам определить, какую половину плоскости затенить.
Обычная контрольная точка — начало координат \ ((0, 0) \).Контрольная точка помогает нам определить, какую половину плоскости затенить.
\ (\ begin {array} {c | c} {\ underline {\ color {Cerulean} {Test \: point}}} & {\ underline {y> -3x + 1}} \\ {(0,0 )} & {0> -3 (0) +1} \\ {} & {0> 1 \ quad \ color {red} {x}} \ end {array} \)
Шаг 3 : Закрасьте область, содержащую растворы. Поскольку контрольная точка \ ((0, 0) \) не была решением, она не лежит в области, содержащей все упорядоченные парные решения. Поэтому заштрихуйте половину плоскости, на которой нет этой контрольной точки.В этом случае заштрихуйте линию выше границы.
Ответ :
Рисунок \ (\ PageIndex {8} \)
Рассмотрим проблему затенения выше или ниже граничной линии, когда неравенство имеет форму пересечения уклона. Если \ (y> mx + b \), то заштрихуйте над линией. Если \ (y
Пример \ (\ PageIndex {2} \)
График набора решений:
\ (2x − 5y≥ − 10 \).
Решение :
Здесь граница определяется линией \ (2x − 5y = −10 \). Поскольку неравенство носит инклюзивный характер, обозначим границу сплошной линией. В этом случае нарисуйте граничную линию, используя точки пересечения.
Рисунок \ (\ PageIndex {9} \)
Затем проверьте точку; это помогает решить, какую область затенять.
\ (\ begin {array} {c | c} {\ underline {\ color {Cerulean} {Test \: point}}} & {\ underline {2x-5y \ geq -10}} \\ {(0, 0)} & {2 (0) -5 (0) \ geq -10} \\ {} & {0 \ geq -10 \ quad \ color {Cerulean} {\ checkmark}} \ end {array} \)
Так как контрольная точка находится в наборе решений, заштрихуйте половину плоскости, которая ее содержит.
Ответ :
Рисунок \ (\ PageIndex {10} \)
В этом примере обратите внимание, что набор решений состоит из всех упорядоченных пар ниже граничной линии. Это может показаться нелогичным из-за исходного \ (≥ \) в неравенстве. Это показывает, что лучше всего проверить точку. Решите для \ (y \), и вы увидите, что затенение правильное.
В форме пересечения откоса вы можете видеть, что область под линией границы должна быть заштрихована.Альтернативный подход состоит в том, чтобы сначала выразить границу в форме пересечения наклона, нанести ее на график, а затем заштриховать соответствующую область.
Пример \ (\ PageIndex {3} \)
График набора решений:
\ (у <2 \).
Решение :
Сначала изобразите граничную линию \ (y = 2 \) пунктирной линией из-за строгого неравенства.
Рисунок \ (\ PageIndex {11} \)
Теперь проверьте точку.
\ (\ begin {array} {c | c} {\ underline {\ color {Cerulean} {Test \: point}}} & {\ underline {y <2}} \\ {(0,0)} & {0 <2 \ quad \ color {Cerulean} {\ checkmark}} \ end {array} \)
В этом случае закрасьте область, содержащую тестовую точку.
Ответ :
Рисунок \ (\ PageIndex {12} \)
Упражнение \ (\ PageIndex {2} \)
График набора решений:
\ (5x − y≤10 \).
- Ответ
Рисунок \ (\ PageIndex {13} \)
графов линейных неравенств — элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Проверить решения неравенства с двумя переменными
- Распознать связь между решениями неравенства и его графиком
- График линейных неравенств
Проверка решения неравенства по двум переменным
Мы научились решать неравенства по одной переменной. Теперь мы рассмотрим неравенства по двум переменным. Неравенства по двум переменным имеют множество приложений. Например, если вы управляете бизнесом, вы хотите, чтобы ваш доход превышал ваши расходы, чтобы ваш бизнес приносил прибыль.
Теперь мы рассмотрим неравенства по двум переменным. Неравенства по двум переменным имеют множество приложений. Например, если вы управляете бизнесом, вы хотите, чтобы ваш доход превышал ваши расходы, чтобы ваш бизнес приносил прибыль.
Линейное неравенство
Линейное неравенство — это неравенство, которое можно записать в одной из следующих форм:
, где оба не равны нулю.
Вы помните, что у неравенства с одной переменной было много решений? Решение неравенства — любое число больше 3.Мы показали это на числовой строке, закрасив числовую строку справа от 3 и поставив открывающую скобку на 3. См. (Рисунок).
Точно так же неравенства с двумя переменными имеют множество решений. Любая упорядоченная пара, которая делает неравенство истинным, когда мы подставляем значения, является решением неравенства.
Решение линейного неравенства
Упорядоченная пара — это решение линейного неравенства, если неравенство истинно, когда мы подставляем значения x и y .
Решение
- ⓐ
- ⓑ
- ⓒ
- ⓓ
- ⓔ
ⓐ да ⓑ да ⓒ да ⓓ да ⓔ нет
ⓐ да ⓑ да ⓒ нет ⓓ нет ⓔ да
Распознать связь между решениями неравенства и его графиком
Теперь посмотрим, как решения неравенства соотносятся с его графом.
Давайте снова подумаем о числовой прямой на (Рисунок).Точка разделяла эту числовую линию на две части. С одной стороны от 3 все числа меньше 3. С другой стороны от 3 все числа больше 3. См. (Рисунок).
Решение для — это заштрихованная часть числовой прямой справа от.
Точно так же линия разделяет плоскость на две области. По одну сторону от линии есть точки с. По другую сторону линии находятся точки с. Мы называем линию пограничной линией.
Граница
Линия с уравнением — это граница, отделяющая область where от области where.
Для неравенства в одной переменной конечная точка отображается в круглых скобках или скобках в зависимости от того, включено ли в решение или нет:
Аналогичным образом, для неравенства по двум переменным граничная линия показана сплошной или пунктирной линией, чтобы указать, включена ли эта линия в решение. Это кратко показано на (Рисунок)
Это кратко показано на (Рисунок)
Граничная линия не включена в решение. | Граничная линия включена в решение. |
| Граничная линия пунктирная. | Граничная линия сплошная. |
Теперь давайте посмотрим на то, что мы обнаружили на (Рисунок). Мы начнем с построения линии, а затем нанесем пять протестированных точек. См. (Рисунок).
На (рис.) Мы обнаружили, что некоторые точки были решениями неравенства, а некоторые — нет.
Какие из нанесенных нами точек являются решениями неравенства? Точки и являются решениями неравенства.Обратите внимание, что они оба находятся по одну сторону от ограничивающей линии.
Две точки и находятся по другую сторону границы, и они не являются решениями неравенства. По этим двум точкам.
В чем суть? Потому что точка — это решение уравнения. Итак, дело в граничной линии.
Итак, дело в граничной линии.
Давайте возьмем другую точку слева от граничной линии и проверим, является ли она решением неравенства. Точка явно выглядит слева от ограничивающей линии, не так ли? Это решение неравенства?
Любая точка, которую вы выбираете слева от граничной линии, является решением неравенства.Все точки слева — решения.
Точно так же все точки на правой стороне граничной линии, на стороне с и, не являются решениями. См. (Рисунок).
График неравенства показан на (Рисунок) ниже. Линия делит плоскость на две области. Затененной стороной показаны решения неравенства.
Точки на граничной линии не являются решениями неравенства, поэтому сама линия не является частью решения. Мы показываем это, делая линию пунктирной, а не сплошной.
График неравенства.Показана граничная линия. Напишите неравенство, показанное на графике.
Запишите неравенство, показанное на графике с линией границы.
Запишите неравенство, показанное на графике с линией границы.
Показана граничная линия. Напишите неравенство, показанное на графике.
Запишите неравенство, показанное заштрихованной областью на графике с линией границы.
Запишите неравенство, показанное заштрихованной областью на графике с линией границы.
Упражнения по разделам
Письменные упражнения
Лестер считает, что решение любого неравенства со знаком> — это область над линией, а решение любого неравенства со знаком <- это область под линией. Лестер прав? Объясните, почему да или почему нет.
Объясните, почему на некоторых графиках линейных неравенств граничная линия сплошная, а на других пунктирная.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Глава 4 Упражнения на повторение
Прямоугольная система координат
Точки графика в прямоугольной системе координат
В следующих упражнениях нанесите каждую точку в прямоугольную систему координат.
Определить точки на графике
В следующих упражнениях назовите упорядоченную пару каждой точки, показанной в прямоугольной системе координат.
Проверка решений уравнения с двумя переменными
Какие упорядоченные пары являются решениями заданных уравнений в следующих упражнениях?
Заполните таблицу решений линейного уравнения с двумя переменными
В следующих упражнениях заполните таблицу, чтобы найти решения каждого линейного уравнения.
Найти решения линейного уравнения с двумя переменными
В следующих упражнениях найдите три решения каждого линейного уравнения.
Построение графиков линейных уравнений
Распознавать связь между решениями уравнения и его графика
В следующих упражнениях для каждой упорядоченной пары определите:
- ⓐ Является ли упорядоченная пара решением уравнения?
- ⓑ Находится ли точка на линии?
ⓐ да; да ⓑ да; нет
Построение линейного уравнения по точкам
В следующих упражнениях построите график путем нанесения точек.
График Вертикальные и горизонтальные линии
В следующих упражнениях нанесите на график каждое уравнение.
В следующих упражнениях нарисуйте каждую пару уравнений в одной прямоугольной системе координат.
и
Графики с пересечениями
Определение пересечений x и y на графике
В следующих упражнениях найдите точки перехвата x и y .
Найдите точки пересечения x и y из уравнения прямой
В следующих упражнениях найдите точки пересечения каждого уравнения.
Построение линии с помощью точек пересечения
В следующих упражнениях построите график с использованием точек пересечения.
Уклон прямой
Используйте географические доски для моделирования уклона
В следующих упражнениях найдите уклон, смоделированный на каждой геодлане.
В следующих упражнениях моделируйте каждый уклон. Нарисуйте картинку, чтобы показать свои результаты.
Используется, чтобы найти наклон прямой по ее графику
В следующих упражнениях найдите наклон каждой показанной линии.
Найдите наклон горизонтальной и вертикальной линий
В следующих упражнениях найдите наклон каждой линии.
Используйте формулу наклона, чтобы найти наклон линии между двумя точками
В следующих упражнениях используйте формулу наклона, чтобы найти наклон линии между каждой парой точек.
Построение линии с заданной точкой и наклоном
В следующих упражнениях нарисуйте каждую линию с заданной точкой и наклоном.
;
x — перехват;
y — перехват 1;
Решите наклонные приложения
В следующих упражнениях решите эти приложения для уклонов.
Крыша, изображенная ниже, имеет высоту 10 футов и высоту 15 футов. Какой у нее уклон?
Горная дорога поднимается на 50 футов для бега на 500 футов. Какой у нее уклон?
Форма пересечения уравнения прямой
Распознайте связь между графиком и формой наклона-пересечения уравнения прямой
В следующих упражнениях используйте график, чтобы найти наклон и точку пересечения y каждой линии. Сравните значения с уравнением.
Сравните значения с уравнением.
Определить наклон и точку пересечения оси Y по уравнению прямой
В следующих упражнениях определите наклон и пересечение y каждой линии.
Построение линии по ее наклону и пересечению
В следующих упражнениях нарисуйте линию каждого уравнения, используя ее наклон и точку пересечения y .
В следующих упражнениях определите наиболее удобный метод построения графика каждой линии.
График и интерпретация углов наклона и пересечения
Кэтрин — частный повар. Уравнение моделирует связь между ее недельными затратами, C , в долларах, и количеством обедов, m , которые она обслуживает.
- ⓐ Найдите стоимость Кэтрин за неделю, когда она не обслуживает гостей.
- ⓑ Найдите стоимость за неделю, когда она приготовит 14 блюд.
- ⓒ Интерпретируйте наклон и C -перехват уравнения.
- ⓓ Изобразите уравнение.
Марджори преподает фортепиано. Уравнение моделирует соотношение между ее недельной прибылью, P , в долларах, и количеством уроков, которые она преподает студентам, s .
- ⓐ Найдите прибыль Марджори за неделю, когда она не учит студентов.
- ⓑ Найдите прибыль за неделю, когда она проведет 20 уроков для студентов.
- ⓒ Интерпретируйте наклон и P — перехват уравнения.
- ⓓ Изобразите уравнение.
ⓐ — 250 ⓑ 450 ⓒ Наклон 35 означает, что еженедельная прибыль Марджори в размере P увеличивается на 35 фунтов стерлингов за каждый дополнительный урок учащегося, который она преподает. Перехват P означает, что, когда количество уроков равно 0, Марджори теряет 250 фунтов стерлингов. Ⓓ
Перехват P означает, что, когда количество уроков равно 0, Марджори теряет 250 фунтов стерлингов. Ⓓ
Использование уклонов для определения параллельных линий
В следующих упражнениях используйте наклоны и точки пересечения по оси Y, чтобы определить, параллельны ли линии.
Использование уклонов для определения перпендикулярных линий
В следующих упражнениях используйте наклоны и точки пересечения по оси Y, чтобы определить, перпендикулярны ли линии.
Найдите уравнение прямой
Найдите уравнение прямой с учетом наклона и точки пересечения y -пересечение
В следующих упражнениях найдите уравнение прямой с заданным наклоном и точкой пересечения по оси Y.Запишите уравнение в форме угла наклона и точки пересечения.
В следующих упражнениях найдите уравнение линии, показанной на каждом графике. Запишите уравнение в форме угла наклона и точки пересечения.
Найдите уравнение прямой с учетом наклона и точки
В следующих упражнениях найдите уравнение прямой с заданным уклоном, содержащей заданную точку. Запишите уравнение в форме угла наклона и точки пересечения.
, пункт
Горизонтальная строка, содержащая
Найти уравнение прямой по двум точкам
В следующих упражнениях найдите уравнение прямой, содержащей заданные точки. Запишите уравнение в форме угла наклона и точки пересечения.
и
и.
Найти уравнение прямой, параллельной данной прямой
В следующих упражнениях найдите уравнение прямой, параллельной данной прямой и содержащей данную точку. Запишите уравнение в форме угла наклона и точки пересечения.
Запишите уравнение в форме угла наклона и точки пересечения.
линия, точка
линия, точка
Найти уравнение прямой, перпендикулярной заданной
В следующих упражнениях найдите уравнение прямой, перпендикулярной данной прямой и содержащей данную точку. Запишите уравнение в форме угла наклона и точки пересечения.
линия, точка
линия, точка
График линейных неравенств
Проверка решения неравенства по двум переменным
В следующих упражнениях определите, является ли каждая упорядоченная пара решением заданного неравенства.
ⓐ да ⓑ нет ⓒ да ⓓ да ⓔ нет
Распознать связь между решениями неравенства и его графиком
В следующих упражнениях запишите неравенство, показанное заштрихованной областью.
Запишите неравенство, показанное на графике с линией границы.
Запишите неравенство, показанное на графике с линией границы.
Запишите неравенство, показанное заштрихованной областью на графике с линией границы.
Запишите неравенство, показанное заштрихованной областью на графике с линией границы.
График линейных неравенств
В следующих упражнениях нанесите на график каждое линейное неравенство.
Изобразите линейное неравенство.
Изобразите линейное неравенство.
Изобразите линейное неравенство.
Изобразите линейное неравенство.
Изобразите линейное неравенство.
Изобразите линейное неравенство.
Графические системы линейных неравенств
Чтобы построить линейный
неравенство
в двух переменных (скажем,
Икс
и
у
), сначала получите
у
один на одной стороне. Затем рассмотрим соответствующее уравнение, полученное заменой знака неравенства на знак равенства. График этого уравнения представляет собой линию.
Затем рассмотрим соответствующее уравнение, полученное заменой знака неравенства на знак равенства. График этого уравнения представляет собой линию.
Если неравенство строгое ( < или > ), начертите штриховой линией.Если неравенство не строгое ( ≤ или ≥ ), начертите сплошной линией.
Наконец, выберите одну точку, которая не находится ни на одной строке ( ( 0 , 0 ) обычно самый простой) и решите, удовлетворяют ли эти координаты неравенству или нет. Если это так, заштрихуйте полуплоскость, содержащую эту точку. Если нет, закройте другую полуплоскость.
Аналогичным образом изобразите каждое из неравенств в системе.Решение система неравенств — область пересечения всех решений в системе.
Пример 1:
Решите систему неравенств, построив графики:
у ≤ Икс — 2 у > — 3 Икс + 5
Сначала изобразим неравенство
у
≤
Икс
—
2
. Связанное уравнение
у
знак равно
Икс
—
2
.
Связанное уравнение
у
знак равно
Икс
—
2
.
Поскольку неравенство ≤ , не строгий, граница сплошная.
Постройте прямую линию.
Рассмотрим точку, которая не находится на линии — скажем, ( 0 , 0 ) — и подставляем в неравенство у ≤ Икс — 2 .
0 ≤ 0 — 2 0 ≤ — 2
Это неправда.Итак, решение не содержит точки ( 0 , 0 ) . Заштрихуйте нижнюю половину линии.
Аналогичным образом нарисуйте пунктирную линию для соответствующего уравнения второго неравенства
у
>
—
3
Икс
+
5
которое имеет строгое неравенство. Смысл
(
0
,
0
)
не удовлетворяет неравенству, поэтому заштрихуйте половину, не содержащую точки
(
0
,
0
)
.
Смысл
(
0
,
0
)
не удовлетворяет неравенству, поэтому заштрихуйте половину, не содержащую точки
(
0
,
0
)
.
Решение системы неравенств — это область пересечения решений двух неравенств.
Пример 2:
Решите систему неравенств, построив графики:
2 Икс + 3 у ≥ 12 8 Икс — 4 у > 1 Икс < 4
Перепишем первые два неравенства с у один на одной стороне.
3 у ≥ — 2 Икс + 12 у ≥ — 2 3 Икс + 4 — 4 у > — 8 Икс + 1 у < 2 Икс - 1 4
Теперь изобразим неравенство
у
≥
—
2
3
Икс
+
4
. Связанное уравнение
у
знак равно
—
2
3
Икс
+
4
.
Связанное уравнение
у
знак равно
—
2
3
Икс
+
4
.
Поскольку неравенство ≥ , не строгий, граница сплошная.
Постройте прямую линию.
Рассмотрим точку, которая не находится на линии — скажем, ( 0 , 0 ) — и подставляем в неравенство.
0 ≥ — 2 3 ( 0 ) + 4 0 ≥ 4
Это неправда.Итак, решение не содержит точки ( 0 , 0 ) . Заштрихуйте верхнюю половину линии.
Аналогичным образом проведем пунктирную линию соответствующего уравнения второго неравенства
у <
2
Икс
-
1
4
которое имеет строгое неравенство. Смысл
(
0
,
0
)
не удовлетворяет неравенству, поэтому заштрихуйте половину, не содержащую точки
(
0
,
0
)
.
Смысл
(
0
,
0
)
не удовлетворяет неравенству, поэтому заштрихуйте половину, не содержащую точки
(
0
,
0
)
.
Нарисуйте пунктирную вертикальную линию Икс знак равно 4 которое является родственным уравнением третьего неравенства.
Здесь точка ( 0 , 0 ) удовлетворяет неравенству, поэтому заштрихуйте половину, содержащую точку.
Решение системы неравенств — это область пересечения решений трех неравенств.
4.1 Линейные неравенства двух переменных — алгебра колледжа для управленческих наук
Линейное уравнение с двумя переменными — это уравнение типа, которое иногда записывается без обозначения функции как. Напомним, что график этого уравнения представляет собой линию, образованную всеми точками, удовлетворяющими уравнению.
Линейное неравенство с двумя переменными аналогично, но содержит неравенство. Некоторые примеры:
Линейные неравенства также могут быть записаны с обеими переменными на одной стороне уравнения, например
Решением линейного неравенства будут все точки, удовлетворяющие неравенству.Обратите внимание, что линия делит координатную плоскость на две половины; на одной половине, а на другой. Набор решений для линейного неравенства будет полуплоскостью, и, чтобы показать набор решений, мы заштриховываем часть координатной плоскости, где точки лежат в наборе решений.
- При необходимости перепишите линейное неравенство в форме, удобной для построения графиков, например в форме пересечения наклона.
- Изобразите соответствующее линейное уравнение.
- Для строгого неравенства (<или>) нарисуйте пунктирную линию, чтобы показать, что точки на линии не являются частью решения
- Для неравенства, содержащего знак равенства (или), нарисуйте сплошную линию, чтобы показать, что точки на линии являются частью решения.

- Выберите контрольную точку, а не на линии. (0,0) или (0,1) самые простые!
- Подставляем контрольную точку в неравенство
- Если неравенство верно в контрольной точке, заштрихуйте полуплоскость со стороны, включая контрольную точку
- Если неравенство не соответствует действительности в контрольной точке, закрасьте полуплоскость на той стороне, которая не включает контрольную точку.
а. Изобразите график решения для
Поскольку это строгое неравенство, мы построим график в виде пунктирной линии.
Теперь выбираем контрольную точку не на прямой, например (0,0).
Подставляя (0,0) в неравенство, получаем
Это верное утверждение, поэтому мы закрасим ту сторону плоскости, которая включает (0,0).
г. Изобразите график решения для
Это не написано в форме, которую мы привыкли использовать для построения графиков, поэтому мы могли бы сначала решить ее.
Поскольку это неравенство включает в себя знак равенства, мы будем строить график в виде сплошной линии.
Теперь выбираем тестовую точку не на линии. (0,0) — удобный выбор. Подставляя (0,0) в неравенство, получаем
НЕТ!
Поскольку это ложное утверждение, мы закрашиваем половину плоскости, которая не включает (0,0).
Изобразите график решения
Системы линейных неравенствВ главе о системах уравнений мы искали решения системы линейных уравнений — точку, которая удовлетворяла бы всем уравнениям в системе.Аналогичным образом мы можем рассматривать систему линейных неравенств. Решением системы линейных неравенств является множество точек, удовлетворяющих всем неравенствам в системе.
С помощью одного линейного неравенства мы можем показать множество решений графически. Аналогичным образом с помощью системы линейных неравенств мы показываем множество решений графически. Мы находим его, ища, где перекрываются области, обозначенные отдельными линейными неравенствами.
Построить график решения системы линейных неравенств
Мы можем смотреть на графики каждого из неравенств, но лучший способ — изобразить наборы решений на одних и тех же осях, чтобы увидеть решение системы неравенств как область, в которой они пересекаются.Вы можете стереть покрытые части только один раз, чтобы показать набор решений.
С технологией есть несколько калькуляторов, которые построят график линейных неравенств. Desmos может сделать это, если вы введете или. Для систем вы можете поместить их в одну строку со вторым в скобках, и это будет отображать только набор решений системы. В приведенном выше примере это {}.
Построить график решения системы линейных неравенств
Следующий вопрос похож на проблему, которую мы решили с помощью систем в главе о системах.
Компания производит базовую и премиальную версии своего продукта. Базовая версия требует 20 минут сборки и 15 минут покраски. Премиум-версия требует 30 минут сборки и 30 минут покраски. Если в компании есть штат на 3900 минут сборки и 3300 минут покраски каждую неделю. Сколько единиц товара можно производить в пределах их штата?
Премиум-версия требует 30 минут сборки и 30 минут покраски. Если в компании есть штат на 3900 минут сборки и 3300 минут покраски каждую неделю. Сколько единиц товара можно производить в пределах их штата?
Обратите внимание, что эта проблема отличается от вопроса, который мы задали в первом разделе, поскольку мы больше не озабочены полным использованием персонала, нас интересует только то, что возможно.Как и раньше, мы определим b : количество произведенных базовых продуктов, p : количество произведенных премиальных продуктов.
Так же, как мы создавали уравнения в первом разделе, теперь мы можем создавать неравенства, поскольку мы знаем, что часы, используемые в производстве, должны быть меньше или равны доступным часам. Это приводит к двум неравенствам:
Построение этих неравенств дает нам набор решений.
Поскольку рассматривать отрицательное количество элементов неразумно, мы можем дополнительно ограничить решения первым квадрантом. Это также можно представить, добавив неравенства.
Это также можно представить, добавив неравенства.
В наборе решений мы видим решение системы уравнений, решенных в предыдущем разделе: 120 базовых продуктов и 50 продуктов премиум-класса. Набор решений показывает, что, если компания не желает полностью использовать персонал, существует множество других возможных комбинаций продуктов, которые они могут производить.
Методы, которые мы использовали выше, являются ключевыми в области математики, называемой линейным программированием, которая широко используется в бизнесе.В следующем разделе мы рассмотрим линейное программирование.
Алгебра 1: линейные неравенства в одной и двух переменных: лучи и полуплоскости: алгебра I: TI Math Nspired
Управление настройками файлов cookie
Вы можете управлять своими предпочтениями относительно того, как мы используем файлы cookie для сбора и использования информации, пока вы находитесь на веб-сайтах TI, изменяя статус этих категорий.
| Категория | Описание | Разрешить |
|---|---|---|
| Аналитические и рабочие файлы cookie | Эти файлы cookie, включая файлы cookie из Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI и видеть, как посетители перемещаются по нашим сайтам.Это помогает нам улучшить работу сайтов TI (например, облегчая вам поиск информации на сайте). | |
| Рекламные и маркетинговые файлы cookie | Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами.Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах. Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламные объявления в соответствии с вашими интересами, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы. | |
| Функциональные файлы cookie | Эти файлы cookie помогают идентифицировать вас и хранить ваши действия и информацию об учетной записи, чтобы предоставлять расширенные функциональные возможности, включая более персонализированный и релевантный опыт на наших сайтах.Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. Если вы не разрешите использование этих файлов cookie, некоторые или все функции и услуги сайта могут работать некорректно. | |
| Файлы cookie социальных сетей | Эти файлы cookie позволяют идентифицировать пользователей и контент, подключенный к онлайн-социальным сетям, таким как Facebook, Twitter и другим платформам социальных сетей, и помогают TI улучшить охват социальных сетей. | |
| Строго необходимо | Эти файлы cookie необходимы для работы сайтов TI или для выполнения ваших запросов (например, для отслеживания того, какие товары вы поместили в корзину на TI. com, для доступа к защищенным областям сайта TI или для управления настроенными вами настройки файлов cookie). com, для доступа к защищенным областям сайта TI или для управления настроенными вами настройки файлов cookie). | Всегда на связи |
Уравнения и неравенства с двумя переменными — SAS
Выдайте каждому студенту входной билет (M-8-2-3_Entrance Ticket.док). Учащиеся моделируют выбор, записывая три уравнения и три неравенства. Дайте достаточно времени для завершения. Обсудите значение переменных; попросите учащихся определить переменную и объяснить роль переменной в уравнении / неравенстве. Попросите учащихся объяснить обоснованность своих уравнений / неравенств.
Действие 1: Меню
Отобразить следующий пример меню:
Товар . | Цена |
Сэндвич | |
Чашка супа | 2 доллара. |
Салат Брошенный | $ 3,55 |
Рулон | |
Фонтанный напиток | $ 1,25 |
Молоко | |
Брауни | $ 1,95 |
«Как мы узнаем, сколько стоит один бутерброд, если мы знаем, что два бутерброда стоят 7 долларов.30? Давайте возьмем s , чтобы обозначить стоимость одного бутерброда. Мы могли бы написать следующее уравнение и решить для s :
2 с = 7,30
с = 3,65
Один бутерброд стоит 3,65 доллара ».
«Сколько стоит одна упаковка молока, если мы знаем, что четыре упаковки молока за вычетом стоимости одного брошенного салата равны 4,25 доллара?» Пусть м — стоимость одной упаковки молока и т — стоимость брошенного салата.Мы могли бы написать следующее уравнение и решить для м :
4 м — t = 4,25 м представляет 1 пакет молока; т представляет собой подброшенный салат
4 м — 3,55 = 4,25 Замените значение т , указанное в меню.
4 м = 4,25 + 3,55 Добавьте 3,55 с обеих сторон.
4 м = 7.80 Выполните операцию.
м = 1,95 Разделить обе стороны на 4.
Одна упаковка молока стоит 1,95 доллара ».
«Иногда мы не знаем стоимость того или другого товара, но нам сообщают количество каждого товара и общую сумму. Например, мы можем знать, что стоимость 5 булочек и 3 бутербродов равна 15 долларам США. Мы бы записали уравнение как 5 r + 3 s = 15.”
Например, мы можем знать, что стоимость 5 булочек и 3 бутербродов равна 15 долларам США. Мы бы записали уравнение как 5 r + 3 s = 15.”
“ Какое решение или упорядоченная пара ( r , s ) сделают это уравнение верным? Другими словами, какие значения, замененные на r и s , сделают уравнение истинным? »
Предложите учащимся обсудить возможности. Некоторые возможности
r = 1,05; с = 3,25 или (1,05, 3,25)
«Подставляя обратно в уравнение, получаем
5 (1.05) + 3 (3,25) = 15
15 = 15
«Таким образом, стоимость ролла и сэндвича может составить 1,05 и 3,25 доллара соответственно».
«Если мы определим значение для одной переменной, мы сможем решить уравнение для другой переменной, поэтому, если мы догадались, что r = 1,05, то мы можем заменить r и решить для s :
5 r + 3 с = 15
5 (1. 05) + 3 с = 15 Замещающее значение r .
05) + 3 с = 15 Замещающее значение r .
5,25 + 3 с = 15 Выполните операцию.
3 с = 15 — 5,25 Вычтите 5,25 с каждой стороны.
3 с = 9,75 Выполнить операцию.
с = 3,25 Разделите каждую сторону на 3. ”
Эту процедуру можно использовать для поиска решений уравнения с двумя переменными.Проведите студентов через процесс поиска еще трех решений и обсудите идею бесконечного множества решений.
Некоторые другие решения включают:
«Давайте заменим 2,25 доллара на s и решим r :
5 r + 3 с = 15
5 r + 3 (2,25) = 15 Подставляем значение с .
5 r + 6,75 = 15 Выполнить операцию.
5 r = 15 — 6,75 Вычтем 6,75 с обеих сторон.
5 r = 8,25 Выполнить операцию.
r = 1,65 Разделить каждую сторону на 5.
Таким образом. . .
r = 1,65; с = 2,25, решение (1,65, 2,25) ».
«Давайте подставим 1 доллар.35 для r и решите для s :
5 r + 3 с = 15
5 (1,35) + 3 с = 15 Подставляем значение на .
6,75 + 3 с = 15 Выполнить операцию.
3 с = 15 — 6,75 Вычтем 6,75 с обеих сторон.
3 с = 8,25 Выполните операцию.
с = 2,75 Разделить каждую сторону на 3.
Таким образом. . .
r = 1,35; с = 2,75, решение (1,35, 2,75) ».
«Давайте заменим 3,85 доллара на s и решим r :
5 r + 3 с = 15
5 r + 3 (3.85) = 15 Подставляем значение с ,
5 r + 11,55 = 15 Выполнить операцию.
5 r = 15 — 11,55 Вычтем по 11,55 с обеих сторон.
5 r = 3,45 Выполнить операцию.
r = 0,69 Разделим каждую сторону на 5.
Таким образом. . .
r = 0.69; с = 3,85, решение (0,69, 3,86) ».
«Мы также можем изучить решения неравенства с помощью меню».
«Предположим, мы знаем, что стоимость четырех пакетов молока и трех бутербродов меньше или равна $ 15,50. Как мы могли написать этот сценарий, используя неравенство? Как мы могли найти возможные решения? »
«Мы можем записать неравенство как…»
«Чтобы найти возможные решения, мы будем использовать тот же процесс, что и раньше. Давайте заменим значение одной из переменных, а затем решим другую переменную «.
Давайте заменим значение одной из переменных, а затем решим другую переменную «.
«Мы попробуем оценить стоимость бутерброда в 3,50 доллара США и заменим это значение на s :»
«Возможное решение (1,25, 3,50). Другими словами, пакет молока должен стоить 1,25 доллара или меньше 1,25 доллара, И сэндвич должен стоить 3,50 доллара или меньше 3,50 доллара, чтобы общая сумма была меньше или равной 15,50 долларов. Решение этого типа проблем происходит в повседневной жизни, когда люди определяют, достаточно ли у них денег для покупки блюд из меню.”
Попросите учащихся найти еще три решения этого неравенства. Затем попросите их написать еще два неравенства из меню и найти четыре решения. Проведите в классе обсуждение, в котором рассматриваются уравнения, неравенства, переменные, подставляемые значения и их взаимосвязь.
Переписывание уравнений и неравенств в форме пересечения наклона
«Мы рассмотрели несколько уравнений с разными буквенными переменными. Давайте рассмотрим некоторые уравнения с двумя конкретными переменными, x и y, , и рассмотрим форму уравнения с пересечением наклона и пересечения . Форма уравнения с пересечением наклона определяется как линейное уравнение в форме y = mx + b , где значение m представляет наклон или постоянную скорость изменения, а значение b представляет y — перехват или отправная точка ». (Примечание: это краткое определение предполагает, что учащиеся уже знакомы с формой пересечения наклона и терминами «наклон» и
Давайте рассмотрим некоторые уравнения с двумя конкретными переменными, x и y, , и рассмотрим форму уравнения с пересечением наклона и пересечения . Форма уравнения с пересечением наклона определяется как линейное уравнение в форме y = mx + b , где значение m представляет наклон или постоянную скорость изменения, а значение b представляет y — перехват или отправная точка ». (Примечание: это краткое определение предполагает, что учащиеся уже знакомы с формой пересечения наклона и терминами «наклон» и
« y -перехват.«Если это не так, то здесь следует провести более подробное обсуждение.»
«Рассмотрим уравнение 4 x + y = 15. Записано ли это уравнение в форме углового пересечения?» (№)
«Это уравнение не записывается в форме пересечения наклона. Уравнение в форме пересечения угла наклона решается для y . Другими словами, y изолированы. Почему мы можем захотеть преобразовать это уравнение, чтобы оно было записано в форме пересечения наклона? » (Уравнения, записанные в форме пересечения наклона, легко показывают нам ценную информацию, а именно наклон и пересечение y графика или задачи.)
Почему мы можем захотеть преобразовать это уравнение, чтобы оно было записано в форме пересечения наклона? » (Уравнения, записанные в форме пересечения наклона, легко показывают нам ценную информацию, а именно наклон и пересечение y графика или задачи.)
«Чтобы определить наклон и пересечение y предыдущего уравнения, мы преобразуем его так, чтобы оно было записано в форме пересечения наклона. Для этого мы должны решить уравнение для y . Мы можем сделать это, вычтя 4 x с каждой стороны. Этот процесс дает нам:
y = -4 x + 15 форма пересечения наклона ».
«Теперь, когда уравнение имеет форму пересечения наклона, мы можем легко определить наклон и точку пересечения y .Какой наклон? » ( — 4) «Что такое перехват y ?» (15)
«Давайте запишем еще одно уравнение в форме пересечения наклона:
.
5 x + 3 y = 15
3 y = -5 x + 15 Вычтите 5 x с каждой стороны.
Разделите каждую сторону на 3.”
«Иногда у нас есть линейные неравенства по двум переменным, x и y . Точно так же, как нам выгодно преобразовать такие уравнения в форму пересечения наклона, мы также можем решить эти типы неравенств для y . Рассмотрим неравенство -2 x + y <12. ”
«Что мы можем сделать, чтобы изменить это неравенство так, чтобы и были изолированы?» (прибавьте 2 раза с обеих сторон.)
«Добавив 2 x к обеим сторонам, мы получим y <2 x + 12».
«Давайте посмотрим на еще один:
.-3 x + 18 y ≥ 6
18 y ≥ 3 x + 6 Добавьте 3 x с обеих сторон.
y ≥ 3/18 x + 6/18 Разделите обе стороны на 18.
y ≥ 1/6 x + 1/3 Уменьшить все дроби.”
Задание 2: Игра на память
Перед началом урока вырежьте карты памяти (M-8-2-3_Memory Cards.docx) и положите их в конверт. Подготовьте достаточно конвертов, чтобы ученики могли играть парами или небольшими группами, и распределите их соответственно. Попросите учащихся положить каждую карту лицом вниз и перемешать их так, чтобы расположение конкретных карт было неизвестно. Студенты должны по очереди переворачивать две карточки. Если перевернутые карточки показывают эквивалентные уравнения или неравенства, учащийся выигрывает эту пару.Если карточки не совпадают, ученик переворачивает их, и игра продолжается со следующим учеником в группе. Игра заканчивается, когда все карты совпадают. Побеждает ученик с наибольшим количеством пар.
Построение графиков линейных уравнений и неравенств с двумя переменными
«Теперь мы построим график некоторых линейных уравнений и неравенств с двумя переменными. Вы изобразили линейные уравнения и неравенства для одной переменной в Уроке 1 этого модуля, используя числовую линию.В двух переменных мы строим графики уравнений и неравенств на координатной плоскости ».
Вы изобразили линейные уравнения и неравенства для одной переменной в Уроке 1 этого модуля, используя числовую линию.В двух переменных мы строим графики уравнений и неравенств на координатной плоскости ».
«Рассмотрим уравнение y — 5 x = −10. Ранее мы обсуждали преимущества переписывания уравнений в форме пересечения наклона. Это также упрощает построение графиков этих уравнений ».
«Давайте сначала решим для y :
y — 5 x = -10 Решите относительно y , если уравнение еще не указано в форме пересечения наклона.
y = 5 x — 10 Добавьте 5 x с каждой стороны ».
«Теперь, когда уравнение имеет форму пересечения наклона, как мы можем изобразить соответствующую линию на координатной плоскости?» (Сначала постройте точку пересечения y в точке (0, −10). Затем подсчитайте «пять, более одного» от точки к точке.) (Примечание: здесь предполагается, что у учащихся были нарисованные линии раньше. Если нет , потребуется дальнейшее обсуждение.)
Затем подсчитайте «пять, более одного» от точки к точке.) (Примечание: здесь предполагается, что у учащихся были нарисованные линии раньше. Если нет , потребуется дальнейшее обсуждение.)
Продемонстрируйте линейный график для студентов.
«Помните, что график линии показывает все наборы упорядоченных пар ( x, y ), которые удовлетворяют уравнению».
«Теперь посмотрим, что происходит с аналогичным неравенством: y — 5 x <−10. Для устранения неравенства используйте те же операции, что и инструменты.
y — 5 x <-10 Решите относительно y .
y <5 x — 10 Добавьте 5 x с каждой стороны.”
y — 5 x ≤ -10 “Решите относительно y .
y ≤ 5 x — 10 Добавьте 5 x с каждой стороны ».
y — 5 x > -10 “Решить для y.
y > 5 x -10 Добавьте 5 x с каждой стороны.”
y — 5 x ≥ -10 “Решите относительно y .
y ≥ 5 x — 10 Добавьте 5 x с каждой стороны ».
«Как и график линейного уравнения, график линейного неравенства должен отображать все наборы упорядоченных пар ( x, y ), которые удовлетворяют неравенству».
Попросите студентов записать три упорядоченные пары, удовлетворяющие неравенству.Когда ученики сделают это, попросите их написать на доске свои заказанные пары. После того, как все примеры решений будут записаны на доске, нанесите соответствующие точки на большой координатной сетке, чтобы студенты могли их увидеть.
«Что вы заметили на графике этого неравенства? Все ли упорядоченные пары выстраиваются в линию, как на графике уравнения? » (Нет. Неравенство имеет гораздо больше решений, чем уравнение.)
«Как видите, график линейного неравенства состоит не только из линии.Вместо этого, когда мы строим график линейного неравенства, мы фактически строим граничную линию и полуплоскость упорядоченных пар. Граничная линия — это линия, которую мы бы изобразили, если бы неравенство было на самом деле уравнением (или что происходит, когда мы заменяем символ неравенства знаком равенства). Полуплоскость относится к половине координатной плоскости, на которой находятся решения неравенства. Эта половина будет либо выше, либо ниже ограничительной линии. Заштриховываем полуплоскость, в которой находятся решения нашего неравенства.Давайте возьмем для примера наше неравенство ».
«Сначала нарисуем граничную линию».
Нарисуйте линию y = 5x — 10 на координатной плоскости, чтобы студенты могли видеть.
«Иногда граница будет сплошной, а иногда пунктирной или пунктирной. Это зависит от того, включены ли упорядоченные пары граничной линии в набор решений неравенства. Какими способами мы могли бы определить, включены ли упорядоченные пары на граничной линии в решение, установленное для неравенства? » (Студенты могут предложить проверить упорядоченную пару от граничной линии, подставив эти значения x и y в неравенство.Они должны обнаружить, что в этом случае граничная линия IS включает в график . Приведите их к выводу, что простой способ узнать это заключается в том, что используемый символ неравенства больше, чем символ OR EQUAL TO.)
«Поскольку в нашем неравенстве используется символ« больше или равно », линия границы включается в график и должна оставаться сплошной. Теперь нам нужно определить подходящую полуплоскость для затенения. Это будет либо «выше», либо «ниже» линии.Как определить, какую полуплоскость заштриховать? » (Студенты могут предложить проверить упорядоченную пару из любой полуплоскости и посмотреть, какая из них имеет значения x и y , которые удовлетворяют неравенству. Приведите их к обнаружению, что если контрольная точка правильно удовлетворяет неравенству, полуплоскость содержащая эту контрольную точку, включается в график неравенства и должна быть заштрихована.)
Это будет либо «выше», либо «ниже» линии.Как определить, какую полуплоскость заштриховать? » (Студенты могут предложить проверить упорядоченную пару из любой полуплоскости и посмотреть, какая из них имеет значения x и y , которые удовлетворяют неравенству. Приведите их к обнаружению, что если контрольная точка правильно удовлетворяет неравенству, полуплоскость содержащая эту контрольную точку, включается в график неравенства и должна быть заштрихована.)
Заштрихуйте полуплоскость на координатной сетке, чтобы учащиеся могли ее увидеть.
«Итак, чтобы построить график линейного неравенства с двумя переменными, мы выполняем следующие три шага:
- 1. Изобразите его как уравнение и выберите пунктирную линию для <или> и сплошную линию для ≤ или ≥.
- 2. Выберите контрольную точку (упорядоченную пару) и подставьте ее в исходное неравенство.

- 3. Заштрихуйте полуплоскость, содержащую точку, если точка действительно является решением.Если точка не является решением, закрасьте вторую половину плоскости ».
Посмотрите на следующие дополнительные примеры с классом:
Двухшаговые линейные неравенства по двум переменным
«Давайте рассмотрим еще пару примеров:
.2 y + 6 x ≤ -6
2 y ≤ -6 x — 6 Выделите член y , вычтя 6 x с каждой стороны.
y ≤ -3 x — 3 Разделите каждый член в обеих частях уравнения на 2. »
«Чтобы изобразить неравенство, нам нужно сначала заменить неравенство знаком равенства и изобразить его как уравнение.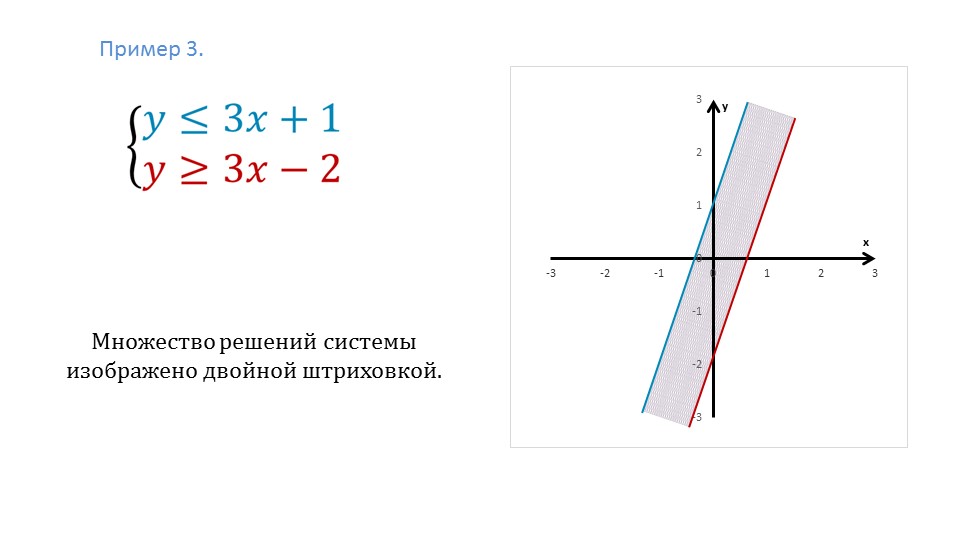 Мы замечаем, что неравенство ≤, поэтому наша линия будет сплошной. Мы будем использовать контрольную точку (0, 0), чтобы определить, какую полуплоскость затенить. Обратите внимание, что подойдет любая контрольная точка. Точка (0, 0) приводит к ложному утверждению, поэтому мы закрасим полуплоскость, которая не содержит точки (0, 0).”
Мы замечаем, что неравенство ≤, поэтому наша линия будет сплошной. Мы будем использовать контрольную точку (0, 0), чтобы определить, какую полуплоскость затенить. Обратите внимание, что подойдет любая контрольная точка. Точка (0, 0) приводит к ложному утверждению, поэтому мы закрасим полуплоскость, которая не содержит точки (0, 0).”
«Наш следующий пример уникален, потому что в нем есть дробь для уклона:
−7x + 14y> 28
14y> 7x + 28 Изолируйте член y , добавив 7 x с каждой стороны.
Разделите каждый член в обеих частях уравнения на 14. ”
«Чтобы изобразить неравенство, нам нужно сначала заменить неравенство знаком равенства и изобразить его как уравнение.Мы замечаем, что неравенство>, поэтому наша линия будет пунктирной. Мы будем использовать ту же контрольную точку (0, 0), чтобы определить, какую полуплоскость затенять. Точка (0, 0) приводит к ложному утверждению, поэтому мы закрасим полуплоскость, которая не содержит точки (0, 0) ».
Точка (0, 0) приводит к ложному утверждению, поэтому мы закрасим полуплоскость, которая не содержит точки (0, 0) ».
Задание 3: Построение графиков линейных неравенств
Распределить графические неравенства (M-8-2-3_Graphing Inequalities.docx и M-8-2-3_Graphing Inequalities KEY.docx). Попросите студентов заполнить его.Обходите комнату, пока ученики работают, чтобы ответить на вопросы и убедиться, что все ученики находятся на правильном пути.
Добавочный номер:
- Кратко обсудим построение графиков системы линейных неравенств. Это включает построение графиков двух неравенств на одной и той же координатной плоскости. Решение системы — это то, где области решения каждого отдельного неравенства перекрываются. Предоставьте учащимся рабочий лист системных расширений (M-8-2-3_Systems Extension.docx и M-8-2-3_Systems Extension KEY.docx) . Этот рабочий лист представляет четыре примера построения графика линейной системы неравенств с двумя переменными.
 Это естественное продолжение этого урока, и его также можно использовать в качестве повторения.
Это естественное продолжение этого урока, и его также можно использовать в качестве повторения.
2.3 Построение графиков двумерных неравенств — промежуточная алгебра
Цели обучения
- Определите и выполните шаги для построения графика линейного неравенства с двумя переменными
- Определите, входит ли упорядоченная пара в набор решений линейного неравенства
- Определите и выполните шаги для построения графика системы линейных неравенств с двумя переменными
- Определите, входит ли упорядоченная пара в набор решений системы линейных неравенств
Знаете ли вы, что при совершении покупок в Интернете вы используете линейное неравенство? Когда вы используете опцию для просмотра товаров в определенном ценовом диапазоне, вы просите поисковую систему использовать линейное неравенство на основе цены.По сути, вы говорите «покажите мне все товары на продажу от 50 до 100 долларов», что можно записать как \ ({50} \ le {p} \ le {100} \), где \ (p \) — это цена. В этом разделе вы примените все, что вы знаете о построении графиков линейных уравнений, для построения графиков линейных неравенств.
В этом разделе вы примените все, что вы знаете о построении графиков линейных уравнений, для построения графиков линейных неравенств.
Как перейти от алгебраической формы неравенства, например \ (y> 3x + 1 \), к графику этого неравенства? Построить график неравенства довольно просто, если вы выполните несколько шагов.
Графическое изображение неравенств
Чтобы построить график неравенства:
- Постройте соответствующую граничную линию.
- Замените знак \ (\ lt, \; \; \ gt, \; \; \ le, \; \; \) или \ (\ ge \) в неравенстве на =, чтобы найти уравнение граничной линии .
- Найдите хотя бы одну упорядоченную пару по обе стороны от граничной линии и подставьте эти значения \ ((x, y) \) в неравенство. Заштрихуйте область, содержащую упорядоченные пары, которые делают неравенство истинным.
- Если в неравенстве используется знак \ (\ le \; \; \) или \ (\ ge \), то точки на граничной линии являются решениями , поэтому для рисования граничной линии следует использовать сплошную линию.

- Если в неравенстве используется знак \ (\ lt \; \; \) или \ (\ gt \), то точки на граничной линии являются решениями , а не , поэтому вы должны использовать пунктирную линию для граничной линии.
Построим график неравенства \ (x + 4y \ leq4 \).
Чтобы построить граничную линию, найдите по крайней мере два значения, лежащих на линии \ (x + 4y = 4 \). Вы можете выбрать любое значение для \ (x \), а затем найти соответствующее значение \ (y \), или наоборот. Иногда проще всего использовать перехватчики \ (x \) и \ (y \) — сначала подставляя 0 вместо \ (x \) и находя значение \ (y \), а затем подставляя 0 вместо \ ( y \) и находим \ (x \).
Постройте точки \ ((0,1) \) и \ ((4,0) \) и проведите через эти две точки линию границы. Линия сплошная, потому что \ (\ le \) означает «меньше или равно », поэтому все упорядоченные пары вдоль линии включены в набор решений.
Следующий шаг — найти область, содержащую решения. Это выше или ниже границы? Чтобы определить область, в которой выполняется неравенство, вы можете протестировать пару упорядоченных пар, по одной с каждой стороны граничной линии.
Если вы замените \ ((- 1,3) \) на \ (x + 4y \ leq4 \):
\ (\ begin {array} {r} -1 + 4 \ left (3 \ right) \ leq4 \\ — 1 + 12 \ leq4 \\ 11 \ leq4 \ end {array} \)
Это ложное утверждение, поскольку 11 не меньше или равно 4. Сторона, содержащая \ ((- 1,3) \), должна быть закрашена , а не .
С другой стороны, если вы замените \ ((2,0) \) на \ (x + 4y \ leq4 \):
\ (\ begin {array} {r} 2 + 4 \ left (0 \ right) \ leq4 \\ 2 + 0 \ leq4 \\ 2 \ leq4 \ end {array} \)
Это правда! Область, которая включает \ ((2,0) \), должна быть заштрихована, так как это область решений.
И вот он: график множества решений для \ (x + 4y \ leq4 \).
Графическое изображение линейных неравенств с двумя переменными
Пример
Изобразите неравенство \ (2y \ gt 4x-6 \).
Показать решение
Найдите две точки, которые удовлетворяют уравнению \ (2y = 4x-6 \), чтобы создать граничную линию. Когда \ (x = 0 \), мы имеем \ (2y = -6 \), поэтому одна точка на прямой — это \ ((0, -3) \). Мы также могли бы использовать пересечение оси Y, но это дает дробную часть, которую труднее изобразить.Когда \ (x = 2 \), мы имеем \ (2y = 8-6 \), поэтому другая точка на прямой — это \ ((2,1) \).
Мы также могли бы использовать пересечение оси Y, но это дает дробную часть, которую труднее изобразить.Когда \ (x = 2 \), мы имеем \ (2y = 8-6 \), поэтому другая точка на прямой — это \ ((2,1) \).
Постройте точки и нанесите линию на график. Линия пунктирна, потому что в неравенстве стоит знак>, а не \ (\ ge \), и поэтому точки на линии являются , а не решениями неравенства.
\ (\ Displaystyle у = 2х-3 \)
Найдите упорядоченную пару по обе стороны от ограничивающей линии. Вставьте значения x и y в неравенство
\ (2y> 4x-6 \) и посмотрите, какая упорядоченная пара приводит к истинному утверждению.
Поскольку \ (2 (1)> 4 (-3) -6 \) эквивалентно \ (2> -20 \), точка \ ((- 3,1) \) приводит к истинному утверждению. Область, которая включает \ ((- 3,1) \), должна быть заштрихована.
Поскольку \ (2 (1)> 4 (4) -6 \) эквивалентно \ (2> 10 \), точка \ ((4,1) \) приводит к ложному утверждению. Область, которая включает \ ((4,1) \), должна быть закрашена , а не .
Ответ
График неравенства \ (2y> 4x-6 \):
Небольшое замечание о проблемах, описанных выше: точка \ ((0,0) \) — отличный выбор для проверки, какую сторону линии затенять, поскольку для этого требуется очень мало вычислений.Если ваша граничная линия проходит через начало координат, вы не можете использовать \ ((0,0) \), но другие хорошие варианты включают \ ((0,1) \) или \ ((1,0) \).
Множественные неравенства
Чтобы создать систему неравенств, вам нужно построить график двух или более неравенств вместе. Давайте использовать \ (2y> 4x-6 \) и \ (x + 4y \ le 4 \), поскольку мы уже изобразили каждый из них в предыдущих примерах.
Мы видели, что решением неравенства \ (2y> 4x-6 \) было множество всех точек над линией, показанных красным на графике ниже.Мы также видели, что решением \ (x + 4y \ le 4 \) было множество всех точек ниже синей линии на другом графике. Обратите внимание, что первая граница пунктирная, а вторая — сплошная.
Объединение двух недавних примеров: решение для \ (2y> 4x-6 \) — это область над пунктирной красной линией, а решение для \ (x + 4y \ le4 \) — это область ниже сплошной синей линии. линия.
Чтобы найти решения, удовлетворяющие обоим неравенствам, нам нужен набор всех точек, которые одновременно находятся над пунктирной красной линией и ниже сплошной синей линии.Нам нужна перекрывающаяся область, которая была закрашена синим и красным, как показано на графике ниже.
Решением системы неравенств является перекрывающаяся область, заштрихованная как красным, так и синим цветом на графике слева. На правом графике область решения — это та, которая содержит контрольную точку \ ((0,0) \).
Решение системы двух неравенств также можно найти, построив график двух линий и выбрав контрольные точки в каждой из четырех областей. На правом графике выше область решения обозначена зеленым цветом. Контрольная точка в \ ((0,0) \) находится в области решения: она удовлетворяет обоим неравенствам, потому что \ (0> 0-6 \) и \ (0 + 0 \ le 4 \).
На правом графике выше область решения обозначена зеленым цветом. Контрольная точка в \ ((0,0) \) находится в области решения: она удовлетворяет обоим неравенствам, потому что \ (0> 0-6 \) и \ (0 + 0 \ le 4 \).
Пример
Изобразите решение системы двух неравенств: \ (2x-y> -8 \) и \ (x + 3y \ ge-8 \). Граничные линии показаны на графике ниже.
Показать решение
Для этой задачи мы попробуем четыре разных тестовых точки: по одной в каждом регионе.
Контрольная точка: \ ((- 10,0) \)
| \ (\ begin {align *} 2x-y &> — 8 \\ 2 (-10) — (0) &> — 8 \\ — 20 &> — 8 \ end {align *} \) | \ (\ begin {align *} x + 3y & \ ge-8 \\ (- 10) +3 (0) & \ ge-8 \\ — 10 & \ ge-8 \ end {align *} \) |
Оба утверждения неверны.
Контрольная точка: \ ((0, -5) \)
| \ (\ begin {align *} 2x-y &> — 8 \\ 2 (0) — (- 5) &> — 8 \\ 5 &> — 8 \ end {align *} \) | \ (\ begin {align *} x + 3y & \ ge-8 \\ (0) +3 (-5) & \ ge-8 \\ — 15 & \ ge-8 \ end {align *} \) |
Первое утверждение верно, а второе — ложно.
Контрольная точка: \ ((0,0) \)
| \ (\ begin {align *} 2x-y &> — 8 \\ 2 (0) — (0) &> — 8 \\ 0 &> — 8 \ end {align *} \) | \ (\ begin {align *} x + 3y & \ ge-8 \\ (0) +3 (0) & \ ge-8 \\ 0 & \ ge-8 \ end {align *} \) |
Оба утверждения верны.
Контрольная точка: \ ((0,10) \)
| \ (\ begin {align *} 2x-y &> — 8 \\ 2 (0) — (10) &> — 8 \\ — 10 &> — 8 \ end {align *} \) | \ (\ begin {align *} x + 3y & \ ge-8 \\ (0) +3 (10) & \ ge-8 \\ 30 & \ ge-8 \ end {align *} \) |
Первое утверждение неверно, но второе верно.
Ответ
Единственной контрольной точкой, удовлетворяющей обоим неравенствам, была \ ((0,0) \), поэтому эта область должна быть закрашена. Область решения — та, которая находится справа.
Сводка
Когда неравенства изображаются на координатной плоскости, решения располагаются в области координатной плоскости, которая представлена заштрихованной областью на плоскости.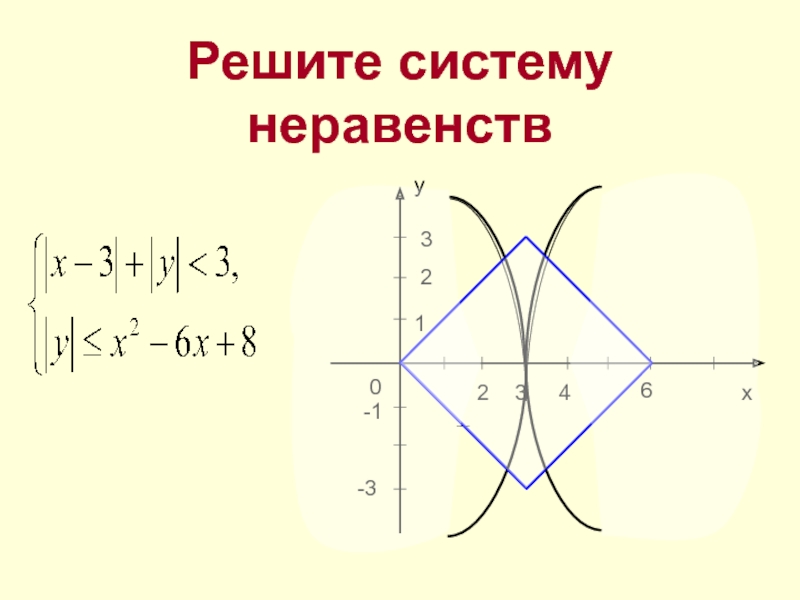

 11.18
11.18
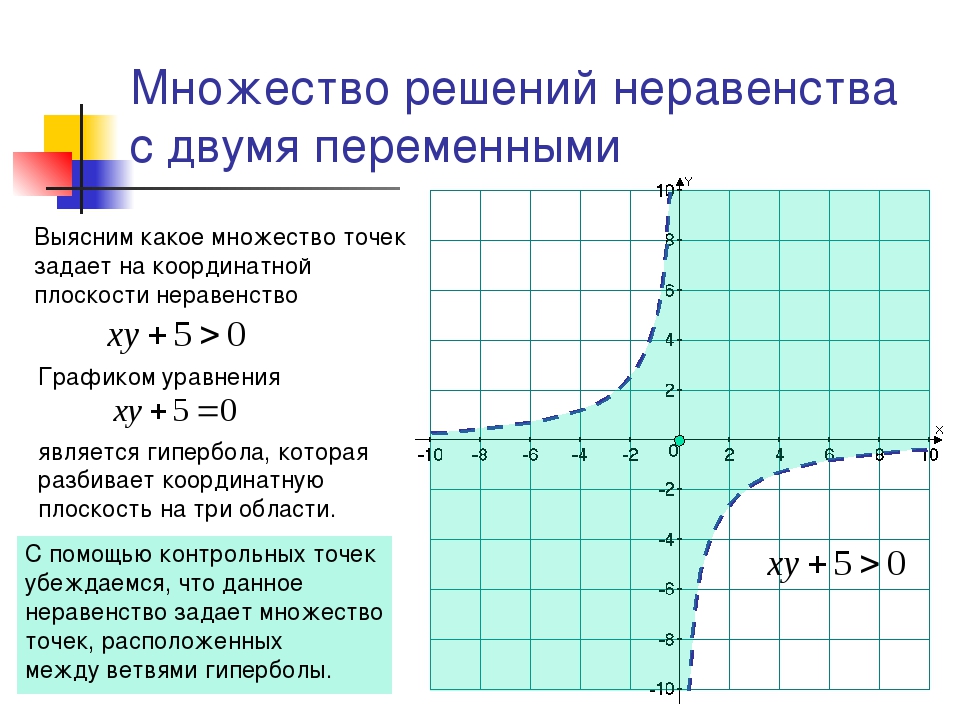

 2.2.3 решать
неравенства с двумя переменными;
2.2.3 решать
неравенства с двумя переменными; ;
;
 Актуализация
знаний.
Актуализация
знаний. 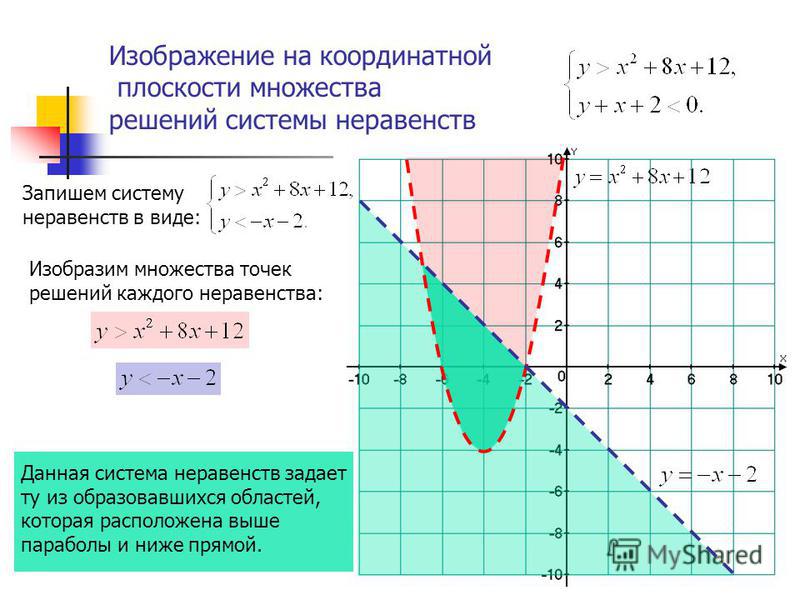 Изобразите на координатной плоскости множество
точек, задаваемое неравенством:
Изобразите на координатной плоскости множество
точек, задаваемое неравенством:


 25
25
 Это естественное продолжение этого урока, и его также можно использовать в качестве повторения.
Это естественное продолжение этого урока, и его также можно использовать в качестве повторения.