Смешанные числа. Сложение и вычитание
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Смешанные числа: определения, примеры
Смешанное число — это число, состоящее из натурального числа и обыкновенной дроби. Пишут в виде n
Где n — целая часть, — дробная часть.
Смешанное число равно сумме своей целой и дробной части. То есть
Примеры смешанных чисел
Каждое такое смешанное число содержит целую и дробную части.
Чтобы точно определять, какая именно перед вами дробь, запомните:
- Дробь виданазывается правильной дробью. В ней числитель всегда меньше знаменателя.
- Дробь виданазывается неправильной. В таких дробях числитель больше знаменателя или равен ему.
- Дробь виданазывается смешанной дробью/смешанным числом. Такая дробь состоит из целой части (натуральное число) и дробной части.

Смешанные числа можно складывать, вычитать, умножать и делить. Давайте узнаем, как именно это делать.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Сложение смешанных чисел
Всего мы рассмотрим три типа сложения со смешанными числами. В каждом подпункте приведено необходимое правило и примеры выполнения решений.
Сложение смешанного числа и натурального числа
Первое правило сложения смешанных чисел Чтобы сложить смешанное число и натуральное число, прибавьте натурально число к целой части смешанного числа, а дробную часть оставьте нетронутой. |
Представим первое правило в виде буквенных выражений.
Выполним сложение смешанного числа и натурального числа d.
Известно, что любое смешанное число равное сумме целой и дробной частей.
Это значит, что
Тогда
Рассмотрим примеры сложения смешанных чисел с натуральными числами.
Пример 1. Выполните сложение смешанного числа и натурального числа 18.
Как решаем:
Записываем выражение
Согласно правилу, прибавляем к натуральному числу целую часть смешанного числа:
Дробная часть записывается без изменений:
Решаем:
Ответ:
Пример 2. Выполните сложение смешанного числа и натурального числа 10.
Как решаем:
Записываем выражение:
Согласно правилу, прибавляем к натуральному числу целую часть смешанного числа:
Дробная часть записывается без изменений:
Решаем:
Ответ:
Пример 3. Выполните сложение смешанного числа и натурального числа 2.
Как решаем:
Записываем выражение:
Согласно правилу, прибавляем к натуральному числу целую часть смешанного числа:
Дробная часть записывается без изменений:
Решаем:
Ответ:
Сложение смешанного числа со смешанным числом
Второе правило сложения смешанных чисел Чтобы сложить смешанное число с другим смешанным числом, сложите сначала целые части этих чисел, а затем — дробные части. |
Представим правило в виде буквенных выражений.
Выполним сложение смешанного числа и смешанного числа
Следуя правилу, запишем выражение в виде:
Рассмотрим примеры сложения смешанных чисел.
Пример 1. Сложите смешанное число и смешанное число
Как решаем:
Записываем выражение:
Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части:
Решаем: складываем целые части 2 + 7 = 9.
Чтобы выполнить сложение дробных частей, воспользуемся правилом сложения дробей с разными знаменателями: приведем дроби к наименьшему общему знаменателю и выполним сложение.
Наименьшее общее кратное — 15.
Если в результате сложения получилась сократимая дробь, сокращайте, не задумываясь: сокращаем на
Ответ:
Пример 2. Сложите смешанное число и смешанное число
Как решаем:
Записываем выражение:
Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части:
Решаем: складываем целые части 13 + 2 = 15.
Складываем дробные части
Наименьшее общее кратное 12 и 20 равно 60.
Сокращаем дробь на 2 =
Ответ:
Таким же образом можно складывать три, четыре и больше натуральных чисел. Не забывайте сокращать дроби и выделять целые части из неправильных дробей.
Сложение смешанного числа и правильной дроби
Третье правило сложения смешанных чисел 1 Чтобы выполнить сложение смешанного числа и правильной дроби, прибавьте к дроби дробную часть смешанного числа, а целую часть оставьте без изменений. |
Представим правило в виде буквенного выражения.
Если нам нужно сложить смешанное число и правильную дробь , то запишем следующее выражение:
Рассмотрим примеры сложения смешанных чисел с обыкновенными дробями.
Пример 1. Выполните сложение обыкновенной дроби и смешанного числа 5
Как решаем:
Записываем выражение:
Согласно правилу, складываем дробь с дробной частью смешанного числа:
Складываем дроби
Наименьшее общее кратное 5 и 20 равно 5.
Ответ:
Пример 2. Выполните сложение правильной дроби и смешанного числа
Как решаем:
Записываем выражение:
Следуя правилу, складываем дробь с дробной частью смешанного числа:
Складываем дроби
Наименьшее общее кратное 4 и 2 равно 2.
Ответ:
Чтобы выполнить сложение смешанного числа и неправильной обыкновенной дроби, выделите целую часть из неправильной дроби и выполните сложение смешанных чисел.
Пример 3: выполните сложение и
Выделим целую часть из неправильной дроби:
Теперь можем выполнить сложение двух смешанных чисел:
Вычисляем:
Наименьшее общее кратное 5 и 2 = 10
Выделим целую часть:
Ответ:
Вычитание смешанных чисел
Рассмотрим три типа вычитания со смешанными числами. В каждом подпункте вы найдете правила и решение примеров с разбором.
Вычитание одного смешанного числа из другого
Первое правило вычитания смешанных чисел Любое смешанное число можно представить в виде суммы целой и дробной части. |
Это значит, что
Исходя из значения дробных частей, вычитание можно выполнять тремя способами.
Если дробная часть уменьшаемого больше дробной части вычитаемого , то выполняем вычитание целой части вычитаемого из целой части уменьшаемого, затем выполняем вычитание дробных частей. Вот так:
Пример. Выполните вычитание
Как решаем:
Чтобы решить пример, нужно выяснить, какая из дробных частей больше:
или
Чтобы сравнить две дроби, приведем их к наименьшему общему знаменателю.
Наименьшее общее кратное 4 и 8 — 16
По правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, чей числитель больше.
Это значит, что
Следуя правилу, выполняем вычитание.
Вычитаем дробные части
НОК = 8
Ответ:
Второе правило вычитания смешанных чисел Если дробные части смешанных чисел равны. То есть , то их разность равна нулю. |
В этом случае разность смешанных чисел равна разности целых частей этих чисел. Вот так:
Пример. Выполните вычитание:
Как решаем:
Дробные части смешанных чисел равны. Это значит, что
Следуя правилу, выполним вычитание:
Ответ:
Третье правило вычитания смешанных чисел Если дробная часть уменьшаемого меньше дробной части вычитаемого , то вычитание выполняется вот так |
Пример. Найдите значение разности смешанных чисел и
Как решаем:
Запишем выражение
Сначала выясним, как из дробных частей больше. Для этого приведем их к НОЗ.
Для этого приведем их к НОЗ.
НОК 5 и 15 = 5
Следуя правилу, решаем:
Выполним вычитание дроби из натурального числа:
Ответ:
Вычитание смешанного числа из натурального числа
Четвертое правило вычитания смешанных чисел Чтобы из целого числа вычесть смешанное число, сначала отнимите от натурального числа целую часть смешанного числа, а затем отнимите от этой разности дробную часть смешанного числа. |
Представим правило в виде буквенного выражения:
Пример. Отнимите от натурального числа 15 смешанное число
Как решаем:
Запишем выражение:
Следуя правилу, выполним вычитание целой части смешанного числа из натурального числа:
Ответ:
Вычитание дроби из целого числа
Пятое правило вычитания смешанных чисел Чтобы вычесть обыкновенную дробь из целого числа, нужно это число представить в виде дроби. |
Пример. Отнимите от целого числа 6 обыкновенную дробь
Как решаем:
Запишем выражение
Представим натуральное число 6 в виде дроби
Тогда
Ответ:
Умножение смешанных чисел
Давайте разберемся как выполнять умножение в примерах, где есть смешанные числа
Умножение смешанного числа на смешанное число
Первое правило умножения смешанных чисел Чтобы умножить одно смешанное число на другое, нужно перевести обы смешанных числа в неправильные дроби, а затем выполнить умножение по правилу умножения дробей |
Пример. Выполните умножение смешанного числа и
Как решаем:
Запишем выражение
Следуя правилу, переведем смешанные числа в неправильные дроби.
Выполним умножение:
Из полученной неправильной дроби выделяем целую часть
Ответ:
Умножение смешанного числа на обыкновенную дробь
Второе правило умножения смешанных чисел Чтобы выполнить умножение смешанного числа и обыкновенной дроби, представьте смешанное число в виде неправильной дроби и выполните умножение дробей. |
Пример. Умножьте смешанное число на обыкновенную дробь
Как решаем:
Запишем выражение
Представим смешанное число в виде неправильной дроби.
Выполним умножение дробей
Выделим из полученной неправильной дроби целую часть
Ответ:
Умножение целого числа на дробь
Третье правило умножения смешанных чисел Чтобы умножить целое число на дробь, просто умножьте это число на числитель дроби. |
Пример. Выполните умножение числа 7 на обыкновенную дробь
Как решаем:
Запишем выражение:
Выделим из получившейся неправильной дроби целую часть
Ответ:
Деление смешанных чисел
Вы уже рассмотрели три типа арифметических действий со смешанными числами. Осталось разобраться, как выполнять деление в примерах, где есть смешанные числа. Давай научимся это делать.
Давай научимся это делать.
Деление смешанного числа на смешанное число
Первое правило деления смешанных чисел Чтобы разделить одно смешанное число на другое, переведите оба числа в неправильные дроби и выполните деление, следуя правилу деления дробей. |
Пример. Найдите результат деления смешанного числа на смешанное число
Как решаем:
Запишем выражение:
Следуя правилу, переведем оба смешанных числа в неправильные дроби.
Пользуясь правилом деления дробей, находим частное:
Ответ:
Деление смешанного числа на целое число
Второе правило деления смешанных чисел Чтобы разделить смешанное число на целое число, переведите смешанное число в неправильную дробь и выполните деление. |
Пример. Разделите смешанное число на натуральное число 15
Как решаем:
Запишем выражение
Следуя правилу, переведем смешанное число в неправильную дробь
Выполним деление
Ответ:
Деление целого числа на смешанное число
Третье правило деления смешанных чисел Чтобы разделить целое число на смешанное число, переведите смешанное число в неправильную дробь и выполните деление. |
Пример. Выполните деление натурального числа 30 на смешанное число
Запишем выражение
Представим смешанное число в виде неправильной дроби
Выполним деление
Выделим из полученной неправильной дроби целую часть
Ответ:
Деление смешанного числа на обыкновенную дробь
Четвертое правило деления смешанных чисел Чтобы разделить смешанное число на обыкновенную дробь, представьте смешанное число в виде неправильной дроби и выполните деление. |
Пример. Разделите смешанное число на обыкновенную дробь
Как решаем:
Запишем выражение
Представим смешанное число в виде неправильной дроби
Выполним деление, следуя правилу деления дробей:
Ответ:
Смешанные числа
В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.
Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.
Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.
Сложение целого числа и правильной дробиВстречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь . Чтобы решить этот пример, нужно число 2 представить в виде дроби . Затем сложить дроби с разными знаменателями:
А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: , а конец так: . Различие в том, что в первом случае число 2 и дробь соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что это свёрнутая форма записи смешанного числа, а — развёрнутая.
Когда перед нами смешанное число вида , мы должны понимать, что знак сложения опущен.
Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Значит значение выражения равно
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
Пример 2. Найти значение выражения
Представим число 3 в виде дроби . Затем сложим дроби с разными знаменателями:
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
Пример 3. Найти значение выражения
Можно записать вместе число 2 и дробь , но этот ответ не будет окончательным, поскольку в дроби можно выделить целую часть.
Поэтому в данном примере сначала нужно выделить целую часть в дроби . Пять вторых это две целых и одна вторая:
Теперь в главном выражении вместо дроби запишем смешанное число
Получили новое выражение . В этом выражении смешанное число запишем в развёрнутом виде:
В этом выражении смешанное число запишем в развёрнутом виде:
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
Теперь свернём полученное смешанное число:
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:
Сложение смешанных чисел
Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
Получили . Теперь в главном выражении заменяем дробные части на полученную дробь
Теперь в главном выражении заменяем дробные части на полученную дробь
Теперь свернем полученное смешанное число:
Таким образом, значение выражения равно . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Пример 2. Найти значение выражения
Запишем смешанные числа в развёрнутом виде:
Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
Теперь вычислим дробные части:
Получили смешанное число . Теперь в главном выражении заменяем выражение в скобках на полученное смешанное число
Теперь в главном выражении заменяем выражение в скобках на полученное смешанное число
Получили выражение . В данном случае число 8 надо прибавить к целой части смешанного числа . Для этого смешанное число можно временно развернуть, чтобы было понятнее, что с чем складывать:
Сложим целые части. Получаем 9
Сворачиваем готовый ответ:
Таким образом, значение выражения равно .
Полное решение этого примера выглядит следующим образом:
Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Пример 3. Найти значение выражения
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:
Сложение целого и смешанного числа
Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
Здесь смешанная дробь была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ .
Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
Пример 2. Найти значение выражения
В этом примере, как и в предыдущем, нужно сложить целые части:
Осталось свернуть целую и дробную части, но дело в том, что дробная часть представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
Вычитание дроби из целого числа
Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби , и выполнить вычитание дробей с разными знаменателями:
Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:
Пример 2. Найти значение выражения .
Найти значение выражения .
Представим число 2 в виде дроби , и выполним вычитание дробей с разными знаменателями:
Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:
Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения , не приводя на бумаге никаких вычислений.
Представим, что число 3 это три пиццы:
Нужно вычесть из них . Мы помним, что треть выглядит следующим образом:
Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть
Получилось (две целых и две трети пиццы).
Чтобы убедиться в правильности решения, можно найти значение выражения обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
Пример 3. Найти значение выражения
Представим число 3 в виде дроби . Затем выполним вычитание дробей с разными знаменателями:
Затем выполним вычитание дробей с разными знаменателями:
Вычитание смешанного числа из целого числа
Теперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения .
Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число перевести в неправильную дробь. После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:
Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:
Пример 2. Найти значение выражения
Представим 6 в виде дроби , а смешанное число , в виде неправильной дроби. После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:
Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.
Этот процесс легко поддаётся воображению.
К примеру, если нужно быстро найти значение выражения , то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)
Тогда от той пиццы, от которой отрезали останется пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.
Вычитание смешанных чисел
Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения:
Чтобы решить этот пример, нужно смешанные числа и перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
Если от трёх целых пицц вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:
Пример 2. Найти значение выражения
Найти значение выражения
Переводим смешанные числа и в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение целого числа на дробь
Чтобы целое число умножить на дробь, достаточно умножить это целое число на числитель дроби, а знаменатель оставить без изменения.
Например, умножим число 5 на дробь . Чтобы решить этот пример, нужно число 5 умножить на числитель дроби , а знаменатель оставить без изменения:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:
Пример 2. Найти значение выражения
Найти значение выражения
Умножим число 3 на числитель дроби
В ответе получилась неправильная дробь , но мы выделили её целую часть и получили 2.
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:
Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
Пример 3. Найти значение выражения
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
Пример 4. Найти значение выражения
Умножим число 3 на числитель дроби
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Пример 1. Найти значение выражения
Переведём смешанное число в неправильную дробь. После перевода это число превратится в дробь . Затем можно будет умножить эту дробь на
После перевода это число превратится в дробь . Затем можно будет умножить эту дробь на
Допустим, имеются одна целая и половина пиццы:
Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:
Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:
Поэтому значение выражения было равно 1
Умножение смешанных чисел
Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить и . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
Теперь разберемся со смешанным множителем . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще раза.
Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще раза.
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
Но ещё осталось взять от изначальной целой пиццы и половины, ведь множителем было смешанное число . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:
Деление целого числа на дробь
Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Например, разделим число 3 на дробь . Здесь число 3 — это делимое, а дробь — делитель.
Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 3 на дробь
Допустим, имеются три целые пиццы:
Если мы зададим вопрос «cколько раз (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
Поэтому значение выражения равно 6.
Пример 2. Найти значение выражения
Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь
Допустим, имеются две целые пиццы:
Зададим вопрос «Сколько раз пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби . После выделения целой части в этой дроби получим
Теперь поставим вопрос так: «Сколько раз (одна целая и половина пиццы) содержится в двух пиццах?».
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Тогда каждый кусок будет третью от этого количества:
Поэтому значение выражения равно
Пример 3. Найти значение выражения
Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 5 на
Дробь это 2 целых и . Проще говоря, две целые и четверть пиццы:
А выражение определяет сколько раз содержится в пяти целых пиццах. Ответом было смешанное число .
То есть пиццы содержится в пяти целых пиццах раза.
Давайте нащупаем в пяти пиццах два раза по
Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой от , которые не вместились. Двумя девятыми они являются по той причине, что в пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
Поэтому значение выражения равно
Деление дроби на целое число
Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Пример 1. Разделим дробь на число 2
Чтобы разделить дробь на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь
Пусть имеется половина пиццы:
Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Чтобы решить этот пример, нужно дробь умножить на число, обратное числу 2. Обратное числу 2 это дробь
Пример 3. Найти значение выражения
Умножаем первую дробь на число, обратное числу 3. Обратное числу 3 это дробь
Деление целого числа на смешанное число
Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на .
Чтобы решить этот пример, нужно делитель перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
Затем умножить число 2 на дробь, обратную делителю.
Переведём делитель в неправильную дробь, получим . Затем умножим 2 на дробь, обратную дроби . Обратная для дроби это дробь
Допустим, имеются две целые пиццы:
Зададим вопрос «Сколько раз (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переводим делитель в неправильную дробь, получаем . Теперь умножаем число 5 на дробь, обратную дроби . Обратная для дроби это дробь
Теперь умножаем число 5 на дробь, обратную дроби . Обратная для дроби это дробь
Сначала мы получили ответ , затем сократили эту дробь на 5, и получили , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ
Деление смешанного числа на целое число
Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим на 2. Чтобы решить этот пример, нужно делимое перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число в неправильную дробь, получим .
Теперь умножаем на число, обратное числу 2. Обратное числу 2 это дробь
Допустим, имеется одна целая и половина пиццы:
Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:
Для этого сначала разделим на две части целую пиццу:
Затем разделим поровну на две части и половину:
Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:
Поэтому значение выражения равно
Пример 2. Найти значение выражения
Переведём делимое в неправильную дробь, получим . Теперь умножаем на число, обратное числу 4. Обратное числу 4 это дробь .
Деление смешанных чисел
Чтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.
Пример 1. Найти значение выражения
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
Как решать дальше мы уже знаем. Первую дробь нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь .
Дорешаем данный пример до конца:
Допустим, имеются две целые и половина пиццы:
Если зададим вопрос «Сколько раз (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
Пример 2. Найти значение выражения
Найти значение выражения
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь
Сначала мы получили дробь. Эту дробь мы сократили на 9. В результате получили дробь , но такой ответ нас тоже не устроил и мы выделили в дроби целую часть. В результате получили окончательный ответ .
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Урок 72.
 сложение смешанных дробей — Математика — 5 класс
сложение смешанных дробей — Математика — 5 классМатематика
5 класс
Урок № 72
Сложение смешанных дробей
Перечень рассматриваемых вопросов:
– сложение смешанной дроби с целым числом;
– сложение смешанной дроби с правильной дробью;
– сложение смешанных дробей с общим знаменателем;
– сложение смешанных дробей с разными знаменателями;
– преобразование неправильных дробей в смешанное число.
Тезаурус
Смешанная дробь – сумма натурального числа и правильной дроби, записанная без знака плюс.
Целая часть смешанной дроби – натуральное число в смешанной дроби.
Дробная часть смешанной дроби – правильная дробь в смешанной дроби.
Переместительное свойство сложения – от перестановки слагаемых местами сумма не меняется.
Сочетательное свойство сложения – чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.
Порядок убывания – расположение элементов от большего к меньшему.
Порядок возрастания – расположение элементов от меньшего к большему.
Обязательная литература
1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Ранее мы говорили, что смешанная дробь – это сумма натурального числа и правильной дроби. При сложении смешанных дробей используют законы сложения. Рассмотрим это на примере:
Каждую смешанную дробь представим, как сумму целой и дробной части.
Вспомним переместительное свойство сложения – от перестановки слагаемых местами сумма не меняется. Перегруппируем слагаемые. Запишем сначала сумму целых частей, а затем сумму дробных частей. Сложим отдельно целые и дробные части обеих дробей. Полученную сумму запишем смешанной дробью, то есть уберём знак плюс между натуральным числом и правильной дробью.
Для удобства будем считать, что у каждого натурального числа есть дробная часть, равная нулю, а у каждой правильной дроби есть целая часть, равная нулю. С учётом этого складывать натуральные числа и правильные дроби со смешанными дробями можно по тому же правилу.
Например:
Проведём те же преобразования, что и в предыдущем примере: отдельно сложим целые и дробные части обоих чисел. Запишем сумму целой и дробной части в виде смешанной дроби, т. е. без знака плюс.
Рассмотрим пример, в котором к смешанной дроби прибавляют простую дробь.
Отдельно складываем целые части и дробные части. Сумму натурального числа и дроби записываем смешанным числом, т. е. без знака плюс.
е. без знака плюс.
При сложении двух смешанных дробей сумма дробных частей может оказаться неправильной дробью. Посмотрим на примере, как действовать в таком случае.
Сумма дробных частей получилась равной семи пятым. Преобразуем неправильную дробь в смешанную. Семь пятых – это одна целая и две пятых. С учётом этого сумма данных смешанных чисел равна четырём целым и двум пятым.
Если необходимо сложить смешанные дроби, дробные части которых имеют разные знаменатели, то сначала нужно привести дробные части к общему знаменателю, а потом выполнить сложение.
Общий знаменатель дробных частей равен пятнадцати. Сумма будет равна семи целым тринадцати пятнадцатым. Обратите внимание на запись решения данного примера. Здесь уже нет промежуточных вычислений сумм целых и дробных частей. Записывать эти вычисления не нужно, достаточно понимать последовательность своих действий.
Рассмотрим ещё одно выражение:
В этом выражении у обоих слагаемых есть и целая, и дробная части. Дробные части имеют различные знаменатели. Приводим дробные части к общему знаменателю. Отдельно складываем целые и дробные части, не записывая это подробно. Сумма дробных частей оказалась равной сорока трём тридцатым, это неправильная дробь. Преобразуем её в смешанную дробь. Сорок три тридцатых – это одна целая тринадцать тридцатых. Выполним сложение семи и одной целой тринадцати тридцатых. Получим восемь целых тринадцать тридцатых.
Дробные части имеют различные знаменатели. Приводим дробные части к общему знаменателю. Отдельно складываем целые и дробные части, не записывая это подробно. Сумма дробных частей оказалась равной сорока трём тридцатым, это неправильная дробь. Преобразуем её в смешанную дробь. Сорок три тридцатых – это одна целая тринадцать тридцатых. Выполним сложение семи и одной целой тринадцати тридцатых. Получим восемь целых тринадцать тридцатых.
Вычислим:
При решении этого выражения можно выполнить действия по порядку: сначала найти суммы в скобках, затем сложить полученные суммы.
В этом случае нам придётся приводить дроби к общему знаменателю. Выполним это решение:
Можно решить это выражение другим способом, вспомнив сочетательный и переместительные свойства сложения:
Во втором случае решение получилось короче, нам не пришлось приводить дроби к общему знаменателю.
Сегодня мы рассмотрели сложение смешанных дробей с натуральными числами, правильными дробями и смешанными дробями. Во всех этих случаях мы действовали по одному правилу: отдельно складывали целые и дробные части слагаемых, а затем складывали полученные результаты.
Во всех этих случаях мы действовали по одному правилу: отдельно складывали целые и дробные части слагаемых, а затем складывали полученные результаты.
Тренировочные задания
№ 1. Выберите выражения, в решении которых допущены ошибки или решение не доведено до верного ответа:
В первом выражении приведено полное, верное решение: отдельно сложены целые и дробные части смешанных дробей. Дробные части приведены к общему знаменателю. Сумма дробных частей оказалась неправильной дробью, эта дробь правильно преобразована в смешанную дробь. Сложение натурального числа и смешанной дроби выполнено верно.
Во втором выражении при сложении дробных частей, правильно приведённых к общему знаменателю, также получилась неправильная дробь, верно произведено сокращение этой неправильной дроби, но она не преобразована в смешанную дробь. В ответе получилось число, дробная часть которого является неправильной дробью. Это неверная запись ответа, хотя вычисления произведены правильно.
В третьем выражении неправильно выполнено сложение дробных частей. Дроби не приводятся к общему знаменателю, складывается числитель с числителем, знаменатель со знаменателем, что не является верным нахождением суммы двух дробей. В ответе получилась сократимая дробь, которая сокращена верно.
Ответ: ошибки допущены во 2 и 3 выражениях.
№ 2. Вычислите периметр прямоугольного участка земли, если его ширина м, а длина на м больше.
Периметр прямоугольника – это сумма длин всех его сторон. Так как у прямоугольника противоположные стороны попарно равны, достаточно знать длину и ширину прямоугольника. Ширина известна, она равна м, а о длине сказано, что она на м больше. Найдём длину прямоугольника, для этого к ширине прибавим м.
(м) – длина прямоугольника.
При сложении мы привели дробные части к общему знаменателю, сложили их, преобразовали получившуюся неправильную дробь в смешанную дробь и сложили её с суммой целых частей.
Теперь найдём периметр прямоугольника. Сложим длины четырёх его сторон:
Сложим длины четырёх его сторон:
(м) – периметр прямоугольника
Заметим, что промежуточные вычисления – отдельное сложение целых и дробных частей – записывать не обязательно.
Смешанная дробь. Действия со смешанными дробями
Смешанной называют дробь, имеющую целую и дробную части.
Записываются они как \(a\)\(\frac{m}{n}\), где – \(a\) целое число,\(\frac{m}{n}\) — правильная дробь.
Например: \(2\)\(\frac{3}{5}\) здесь \(2\) – целая часть, \(\frac{3}{5}\) – дробная часть (правильная дробь).
\(17\)\(\frac{17}{18}\) здесь \(17\) – целая часть, \(\frac{17}{18}\) – дробная часть (правильная дробь).
Фактически такие дроби представляют собой сумму целого числа и дроби, то есть между целой и дробной частью стоит знак «плюс» (а не «умножить»).
Например: \(2\frac{3}{5}=2+\frac{3}{5}\)
Это не нужно заучивать, просто поймите суть. Вдумайтесь, что на практике означает, например, запись: «на складе осталось \(2\)\(\frac{3}{5}\) мешка муки»? Что на складе лежит два полных мешка и еще один заполненный на \(\frac{3}{5}\). Где здесь место умножению? Очевидно ведь, что это два плюс еще \(\frac{3}{5}\) мешка муки! Понимать этот момент очень важно, потому что здесь допускается огромное количество ошибок при вычислениях со смешанными дробями (см. ниже).
Вдумайтесь, что на практике означает, например, запись: «на складе осталось \(2\)\(\frac{3}{5}\) мешка муки»? Что на складе лежит два полных мешка и еще один заполненный на \(\frac{3}{5}\). Где здесь место умножению? Очевидно ведь, что это два плюс еще \(\frac{3}{5}\) мешка муки! Понимать этот момент очень важно, потому что здесь допускается огромное количество ошибок при вычислениях со смешанными дробями (см. ниже).
Превращение смешанной дроби в неправильную
Чтобы преобразовать смешанную дробь в неправильную нужно целую часть умножить на знаменатель дробной и прибавить к результату числитель — получиться числитель неправильной дроби. Знаменатель при этом не меняется. То есть,
\(a\)\(\frac{m}{n}\)\(=\)\(\frac{a·n + m}{n}\).
Например, при преобразовании \(2\)\(\frac{3}{5}\) получим \(\frac{2·5 + 3}{5}=\frac{13}{5}\).
Почему вычисление производиться именно так? Все дело в плюсе, стоящем между целой и дробной частью (см. выше). На самом деле, полное преобразование выглядит вот так:
выше). На самом деле, полное преобразование выглядит вот так:
Но расписывать все так подробно слишком долго, да и незачем, проще сразу получать ответ, пользуясь формулой выше.
Превращение неправильной дроби в смешанную
Чтобы преобразовать неправильную дробь в смешанную, в ней нужно выделить целую часть.
Чтобы этого добиться, мы задаем себе вопрос – сколько раз знаменатель целиком «помещается» в числителе?
Например, пусть нам нужно представить как смешанную дробь \(\frac{13}{5}\). Сколько раз пятерка «помещается» в тринадцати? Два раза. Третий раз уже «не влезет». Значит, целая часть будет равна двойке, а дробная – остатку, то есть \(\frac{3}{5}\). Оформляем: \(\frac{13}{5}\)\(=\)\(\frac{10 + 3}{5}\)\(=\)\(\frac{10}{5}\)\(+\)\(\frac{3}{5}\)\(=2+\)\(\frac{3}{5}\)\(=2\)\(\frac{3}{5}\). Вот еще примеры с верным преобразованием:
\(\frac{37}{11}\)\(=\)\(\frac{33 + 4}{11}\)\(=\)\(\frac{33}{11}\)\(+\)\(\frac{4}{11}\)\(=3+\)\(\frac{4}{11}\)\(=3\)\(\frac{4}{11}\)
\(\frac{26}{3}\)\(=\)\(\frac{24 + 2}{3}\)\(=\)\(\frac{24}{3}\)\(+\)\(\frac{2}{3}\)\(=8+\)\(\frac{2}{3}\)\(=8\)\(\frac{2}{3}\)
А вот пример неправильного выделения целой части:
\(\frac{7}{2}\)\(=\)\(\frac{4 + 3}{2}\)\(=\)\(\frac{4}{2}\)\(+\)\(\frac{3}{2}\)\(=2+\)\(\frac{3}{2}\)\(=2\)\(\frac{3}{2}\)
В чем ошибка? В том, что дробная часть должна быть правильной дробью. А здесь не так — значит целая часть выделена не полностью. Действительно, ведь двойка в семерке нацело помещается три раза, а не два. Поэтому верным будет вот такое выделение:
А здесь не так — значит целая часть выделена не полностью. Действительно, ведь двойка в семерке нацело помещается три раза, а не два. Поэтому верным будет вот такое выделение:
\(\frac{7}{2}\)\(=\)\(\frac{6 + 1}{2}\)\(=\)\(\frac{6}{2}\)\(+\)\(\frac{1}{2}\)\(=3+\)\(\frac{1}{2}\)\(=3\)\(\frac{1}{2}\)
Превращение смешанной дроби в десятичную
Чтобы преобразовать смешанную дробь в десятичную, нужно в дробной части поделить числитель на знаменатель, после чего сложить результат с целой частью.
Например: \(2\)\(\frac{3}{5}\)\(=2+\)\(\frac{3}{5}\)\(=2+0,6=2,6\)
\(7\)\(\frac{11}{25}\)\(=7+\)\(\frac{11}{25}\)\(=7+0,44=7,44\)
Отсюда вывод:
Смешанная дробь – обычное число, причем целая часть представляет собой то, что будет стоять до запятой, а дробная – после.
Наиболее частые ошибки при работе со смешанной дробью
Главной причиной большинства ошибок является забывание описанного выше момента – между целой и дробной частью стоит «плюс», а не «умножить».
Пример: Вычислить \(2\)\(\frac{3}{5}\)\(:\)\(\frac{1}{5}\)
Ошибочное решение: \(2\)\(\frac{3}{5}\)\(:\)\(\frac{1}{5}\)\(=2\)\(\frac{3}{5}\)\(·\)\(\frac{5}{1}\)\(=2\)\(\frac{3 · 5}{5 · 1}\)\(=2·3=6\)
Правильное решение: \(2\)\(\frac{3}{5}\)\(:\)\(\frac{1}{5}\)\(=(2+\)\(\frac{3}{5}\)\():\)\(\frac{1}{5}\)\(=\)\(\frac{2·5+3}{5}\)\(:\)\(\frac{1}{5}\)\(=\)\(\frac{13}{5}\)\(·\)\(\frac{5}{1}\)\(=\)\(\frac{13 · 5}{5 · 1}\)\(=13\)
Пример: Вычислить \(3\)\(\frac{1}{5}\)\(·1\)\(\frac{1}{4}\)
Ошибочное решение: \(3\)\(\frac{1}{5}\)\(·1\)\(\frac{1}{4}\)\(=3·\)\(\frac{1}{5}\)\(·1·\)\(\frac{1}{4}\)\(=\)\(\frac{3}{5}\)\(·\)\(\frac{1}{4}\)\(=\)\(\frac{3 · 1}{5 · 4}\)\(=\)\(\frac{3}{20}\)
Правильное решение: \(3\)\(\frac{1}{5}\)\(·1\)\(\frac{1}{4}\)\(=(3+\)\(\frac{1}{5}\)\()·(1+\)\(\frac{1}{4}\)\()=\)\(\frac{3·5 + 1}{5}\)\(·\)\(\frac{1·4 + 1}{4}\)\(=\)\(\frac{16}{5}\)\(·\)\(\frac{5}{4}\)\(=\)\(\frac{16 · 5}{5 · 4}\)\(=4\)
Из того, что целая и дробная части соединены знаком плюс следует еще один вывод:
Если перед смешанной дробью стоит знак минус, то он стоит и перед целой частью, и перед дробной.

Например: \(-7\) \(\frac{5}{9}\)\(=-(7+\) \(\frac{5}{9}\)\()=-7-\) \(\frac{5}{9}\).
Это важно помнить при вычитании смешанных дробей.
Пример. Вычислить \(4\)\(\frac{3}{5}\)\(-2\)\(\frac{1}{5}\).
Решение: \(4\)\(\frac{3}{5}\)\(-2\)\(\frac{1}{5}\)\(=(4+\)\(\frac{3}{5}\)\()-(2+\)\(\frac{1}{5}\)\()=4+\)\(\frac{3}{5}\)\(-2-\)\(\frac{1}{5}\)\(=4-2+\)\(\frac{3}{5}\)\(-\)\(\frac{1}{5}\)\(=2+\)\(\frac{3-1}{5}\)\(=2+\)\(\frac{2}{5}\)\(=2\)\(\frac{2}{5}\).
Вообще вычитание (сложение) смешанных дробей удобно проводить в два этапа: сначала отдельно вычесть (сложить) целые части, а затем – дробные.
Смотрите также:
Дроби (шпаргалка)
Сложение смешанных дробей. Дроби в виде смешанного числа.
Давайте сначала вспомним пройденные темы. Повторение – мать учения, кто не повторил, тот забыл.
- Дробь как термин будет обозначает тип деления, который рассматривается как часть целого и указывает на разделение целого на равные доли или части, где знаменатель показывает, на сколько частей мы разделили, а числитель – сколько взяли частей от этого целого.

- Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Вспомнили? Двигаемся дальше.
Смешанная дробь состоит из целого и дробного числа. Например, \(2\frac{2}{7}\) — смешанная дробь, в которой \(2\) – целое число, а \(\frac{2}{7}\)- дробь.
Как сложить две смешанные дроби?
Существуют два способа.
Первый способ.
- Переводим в неправильные дроби.
- Приводим к общему знаменателю, пользуясь основным свойством дробей.
- Складываем полученные дроби.
- Исходную новую дробь переводим в правильную:
Второй способ.
- Отдельно складываем дробную и целую части соответственно.

- Исходную новую дробь переводим в правильную:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Чувашский государственный педагогический институт им. И.Я.Яковлева
И.Я.Яковлева
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов по русскому языку. Люблю свой предмет и своих учеников. Мне всегда интересно показать своим ученикам что-то новое и интересное в своём предмете, помогать сделать трудное легким, непонятное понятным и научить искать информацию в огромном «море знаний». Всегда радуют успехи учеников, которые получают высокие баллы на ОГЭ и ЕГЭ.
Люблю свой предмет и своих учеников. Мне всегда интересно показать своим ученикам что-то новое и интересное в своём предмете, помогать сделать трудное легким, непонятное понятным и научить искать информацию в огромном «море знаний». Всегда радуют успехи учеников, которые получают высокие баллы на ОГЭ и ЕГЭ.
Репетитор по математике
Симферопольский государственный университет им. Фрунзе, Таврический национальный университет им Вернадского
Фрунзе, Таврический национальный университет им Вернадского
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 4-11 классов. Готовлю к ОГЭ и ЕГЭ.
С удовольствием окажу помощь школьникам в овладении английским языком, в повышении уровня языковой компетенции. На наших занятиях мы будем использовать упражнения на формирование 4 основных навыков при изучении любого иностранного языка: на формирование навыков чтения, говорения, письма и аудирования, а также будем использовать приемы мнемотехники и скорочтения для достижения большей продуктивности.
Готовлю к ОГЭ и ЕГЭ.
С удовольствием окажу помощь школьникам в овладении английским языком, в повышении уровня языковой компетенции. На наших занятиях мы будем использовать упражнения на формирование 4 основных навыков при изучении любого иностранного языка: на формирование навыков чтения, говорения, письма и аудирования, а также будем использовать приемы мнемотехники и скорочтения для достижения большей продуктивности.
Репетитор по математике
Омский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Использую классическую методику преподавания. Мои ученики получают высокие балы по ОГЭ. Индивидуально подхожу к объяснению материала, выбираю доступные способы обучения, использую приемы соответственно возрасту и интересам ребенка. Добиваюсь полного понимания изучаемого материала. Прививаю и поддерживаю интерес детей к предмету.
Использую классическую методику преподавания. Мои ученики получают высокие балы по ОГЭ. Индивидуально подхожу к объяснению материала, выбираю доступные способы обучения, использую приемы соответственно возрасту и интересам ребенка. Добиваюсь полного понимания изучаемого материала. Прививаю и поддерживаю интерес детей к предмету.
Похожие статьи
Сложение и вычитание обыкновенных дробей. Приведение дробей к одному знаменателю. Понятие о НОК
- Сложение и вычитание дробей с одинаковыми знаменателями
- Сложение и вычитание дробей с разными знаменателями
- Понятие о НОК
- Приведение дробей к одному знаменателю
- Как сложить целое число и дробь
1Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,
Пример 1:
Пример 2:
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
2Сложение и вычитание дробей с разными знаменателями.

Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи. Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
3Наименьшее общее кратное (НОК)
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.

- Перемножить все числа в произведении, это и будет НОК.
Например, найдем НОК чисел 28 и 21:
4Приведение дробей к одному знаменателю
Вернемся к сложению дробей с разными знаменателями.
Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители. Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.
5Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например:
Если мы складываем целое число и смешанную дробь, мы прибавляем это число к целой части дроби, например:
Тренажер 1
Сложение и вычитание дробей с одинаковыми знаменателями.

Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
В этом тесте проверяется умение складывать дроби с одинаковыми знаменателями. При этом нужно соблюдать два правила:
При этом нужно соблюдать два правила:
- Если в результате получается неправильная дробь, нужно перевести ее в смешанное число.
- Если дробь можно сократить, обязательно сократите ее, иначе будет засчитан неправильный ответ.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- С ответом
- С отметкой о просмотре
Тренажер 2
Сложение и вычитание дробей с разными знаменателями.

Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
Тест поможет проверить, как вы умеете складывать дроби с разными знаменателями. Перед тем, как сложить дроби, необходимо привести их к одинаковому знаменателю. Записывая результат, соблюдаем два правила:
Перед тем, как сложить дроби, необходимо привести их к одинаковому знаменателю. Записывая результат, соблюдаем два правила:
- Если в результате сложения получается неправильная дробь, нужно перевести ее в смешанное число.
- Если дробь можно сократить, обязательно сократите ее, иначе будет засчитан неправильный ответ.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- С ответом
- С отметкой о просмотре
Шаг 14.
 Смешанные числа | Репетитор по Математике
Смешанные числа | Репетитор по МатематикеВ предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.
Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.
Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.
Содержание урока
Сложение целого числа и правильной дробиКакой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
То есть опустить знак сложения:
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
Теперь свернём полученное смешанное число:
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:
Сложение смешанных чиселДля начала запишем смешанные числа в развёрнутом виде:
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
Теперь свернем полученное смешанное число:
Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Вы уже понимаете, что откуда взялось.
Запишем смешанные числа в развёрнутом виде:
Сгруппируем целые и дробные части по отдельности:
Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
Теперь вычислим дробные части:
Сложим целые части. Получаем 9
Сворачиваем готовый ответ:
Полное решение этого примера выглядит следующим образом:
Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:
Сложение целого и смешанного числаПопробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
В этом примере, как и в предыдущем, нужно сложить целые части:
Вычитание дроби из целого числаЕсли имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:
Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:
Представим, что число 3 это три пиццы:
Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть
Вычитание смешанного числа из целого числаЕсли из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:
Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.
Этот процесс легко поддаётся воображению.
Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.
Вычитание смешанных чиселЕсли от трёх целых пицц вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:
К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение целого числа на дробьЛюбое целое число можно умножить на дробь. Для этого достаточно умножить это число на числитель дроби.
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:
Получился бы тот же результат. Выглядело бы это следующим образом:
Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Допустим, имеются одна целая и половина пиццы:
Умножение смешанных чиселПопробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:
Если в ответе получится неправильная дробь, выделим в ней целую часть:
Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Допустим, имеются три целые пиццы:
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
Допустим, имеются две целые пиццы:
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
Деление дроби на целое числоЧтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Пусть имеется половина пиццы:
Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
Деление целого числа на смешанное числоДопустим, имеются две целые пиццы:
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
Деление смешанного числа на целое числоЧтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Допустим, имеется одна целая и половина пиццы:
Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:
Затем разделим поровну на две части и половину:
Деление смешанных чиселЧтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.
То есть умножить первую дробь на дробь, обратную второй.
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
Дорешаем данный пример до конца:
Допустим, имеются две целые и половина пиццы:
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
Дробей — сложение и вычитание смешанных чисел
Как Как вы помните, смешанное число состоит из целого числа и дробной части. Любое смешанное число также можно записать как неправильную дробь, в которой числитель больше знаменателя, как показано в следующем примере:
Пример 1
Добавить смешанный чисел, складываем сначала целые числа, а затем дроби.
Если сумма
дробь — неправильная дробь, тогда мы меняем ее на смешанное число.
Вот пример. Сумма целых чисел 3 и 1 равна 4. Дроби 2/5
и 3/5, сложите до 5/5, или 1. Добавьте 1 к 4, чтобы получить ответ, который равен 5.
Добавьте 1 к 4, чтобы получить ответ, который равен 5.
Пример 2
Если знаменатели дробей различны, то сначала найдите эквивалентные дроби с общий знаменатель перед сложением.Например, добавим 4 1/3 к 3 2/5. Используя изученные нами методы, вы можете найти наименьший общий знаменатель из 15. Ответ 7/15.
Вычитание смешанные числа очень похожи на их добавление. Но что происходит, когда дробное часть вычитаемого числа больше дробной части числа, из которого вы вычитаете?
Вот пример: вычтем 3 3/5 из 4 1/3.Сначала вы найдете ЖК-дисплей; вот 15.
4 1/3 — 3 3/5 4 15/5 — 3 15/9 | Написать
обе дроби как эквивалентные дроби со знаминателем 15. |
3 + 1 5/15 — 3 9/15 3 + 20/15 — 3 9/15 | С вы пытаетесь вычесть большую дробь из меньшей, вам нужно чтобы «позаимствовать» единицу из целого числа 4, измените его на 15/15 и добавить его к дроби. |
3 20/15 — 3 9/15 15/11 | Сейчас задача становится 3 20/15 минус 3 9/15, и ответ — 11/15. |
назад наверх
Сложение и вычитание смешанных дробей
Смешанная дробь — это целое число
и объединенная дробь:
| | |
| 1 3 4 | |
| (одна и три четверти) |
Чтобы упростить их сложение и вычитание, просто сначала преобразуйте в неправильные дроби:
У неправильной дроби верхнее число
больше или равно
нижнее число:
| | |
| 7 4 | |
| (семь четвертей или семь четвертей) |
Вы видите, что 1 3 4 совпадает с 7 4 ?
Другими словами, «одна и три четверти» — это то же самое, что «семь четвертей».
(Вы можете прочитать, как преобразовать из или в смешанные дроби)
Добавление смешанных фракций
Для добавления смешанных фракций:
Как это:Пример: что такое 2
3 4 + 3 1 2 ?Преобразовать в неправильные дроби:
2 3 4 знак равно 11 4
3 1 2 знак равно 7 2
Общий знаменатель 4:
11 4 остается как 11 4
7 2 становится 14 4
(путем умножения верха и низа на 2)
Теперь добавьте:
11 4 + 14 4 знак равно 25 4
Преобразовать обратно в смешанные дроби:
25 4 = 6 1 4
Когда вы набираетесь опыта, вы можете делать это быстрее, как в этом примере:
Пример: Что такое 3
5 8 +1 3 4Преобразуйте их в неправильные дроби:
3 5 8 знак равно 29 8
1 3 4 знак равно 7 4
Сделайте тот же знаменатель: 7 4 становится 14 8 (путем умножения верха и низа на 2)
И добавить:
29 8 + 14 8 знак равно 43 8 = 5 3 8
Вычитание смешанных дробей
Следуйте тому же методу, но вместо прибавления вычтите:
Пример: что такое 15
3 4 — 8 5 6 ?Преобразовать в неправильные дроби:
15 3 4 знак равно 63 4
8 5 6 знак равно 53 6
Общий знаменатель 12:
63 4 становится 189 12
53 6 становится 106 12
Теперь вычесть:
189 12 — 106 12 знак равно 83 12
Преобразовать обратно в смешанные дроби:
83 12 = 6 11 12
935, 1414, 1415, 1416, 936, 1417, 3585, 3586, 3587
Как складывать дроби и смешанные дроби
Дроби являются частью повседневной жизни. Их используют во всех сферах, от статистики до кулинарии. От оценки количества осадков до определения времени — они являются мерой различных величин, связанных с любым измеряемым веществом.
Их используют во всех сферах, от статистики до кулинарии. От оценки количества осадков до определения времени — они являются мерой различных величин, связанных с любым измеряемым веществом.
Проще говоря, дроби являются частью поровну разделенного сегмента. В более точных математических терминах дробь используется для представления равных частей коллекции.
Например, давайте представим, что мальчик ест 3/4 часть торта. Это означает, что торт делится на четыре равные части, и мальчик съедает три части или порции торта.
Как представлены дроби
Дробь обычно представлена двумя числами, разделенными линией. Число, которое написано над линией, называется числителем. Знаменатель — это число под чертой. Знаменатель используется для представления общего количества равных частей коллекции. Числитель используется для представления частей или частей коллекции.
Смешанные фракции
Смешанную дробь также иногда называют смешанным числом.Смешанная дробь состоит из двух частей: целой части и дробной части, т. Е. 3 1/4.
Е. 3 1/4.
Неправильная дробь образуется, если число в знаменателе меньше числа в числителе, то есть 3/4.
Обычно неправильную дробь переводят в смешанную. Например, 23/4 — неправильная дробь. При преобразовании в смешанную фракцию получается 5 ¾.
Шаги для преобразования неправильной фракции в смешанную фракцию
- Возьмите числитель дроби (число над чертой) на и разделите его на знаменатель неправильной дроби (число под чертой).
- Знаменатель считается делителем, а числитель — делимым.
- Частное деления, выполненного на «этапе 1», записывается как целочисленная часть смешанной дроби.
- Запишите делитель в качестве знаменателя, а остаток в качестве числителя смешанной дроби
Пример
Перевести 9/4 в смешанные фракции. Вы можете преобразовать неправильную дробь 9/4 в смешанную, выполнив следующие действия.
- Числитель здесь 9, а знаменатель 4. Итак, разделив 9 на 4
- После деления 9 на 4 получается 2 в качестве частного.

- При делении 9 на 4 в качестве остатка получается 1.
Полученная смешанная дробь будет 2 ¼.
Шаги для преобразования смешанной фракции в неправильную фракцию
- Умножьте знаменатель на целое число, затем сложите полученный результат с числителем.
- Запишите ответ, полученный на шаге 1, в числитель дроби.Знаменатель оставьте неизменным.
Пример
Давайте рассмотрим смешанную дробь, 2 ¾, и преобразуем ее в неправильную дробь. Чтобы разбить его, знаменатель смешанной дроби равен 4, а числитель — 3. Целая числовая часть смешанной дроби равна 2. Выполнение следующих шагов:
- Умножьте знаменатель 4 на целое число 2. Получится 8. Затем к 8 добавьте числитель 3.
- Запишите 11 в числитель дроби.Оставьте тот же знаменатель. В результате получается неправильная дробь 11/4.
Добавление фракции и смешанной фракции
Сложение дробей со смешанными дробями — это, по сути, нахождение суммы обеих дробей. Шаги, чтобы найти добавление смешанной фракции к фракции, обсуждаются ниже:
Шаги, чтобы найти добавление смешанной фракции к фракции, обсуждаются ниже:
- Преобразование смешанных фракций в неправильную дробь.
- Проверьте знаменатели дроби и найдите НОК (наименьшее общее кратное).
- Разделите результат НОК на знаменатель каждой дроби и умножьте числитель на частное.
- Сложите сумму произведения и поместите НОК в знаменатель.
[(Числитель дроби 1 * (НОК / знаменатель дроби 1)] + [Числитель дроби 2 * (НОК / знаменатель дроби 2)] / НОК
Пример
Нахождение суммы ¼ + 3 ½. Вы можете сложить две дроби, ¼ и 3 ½, выполнив следующие действия:
- Есть только одна смешанная дробь из двух операндов, равных 3 ½.После преобразования 3 ½ в неправильную дробь результат становится 7/2.
- Знаменатели двух дробей — 2 и 4. НОК 2 и 4 равны 4.
- Результат НОК: 4. Разделите НОК со знаменателем ¼, так что 4 разделится на знаменатель 4. Результатом будет 1, которую вы умножите на числитель, 1, в результате получится сумма 1.

Аналогично, тот же шаг нужно выполнить во второй дроби. Сумма будет равна 14. Наконец, вы можете сложить сумму произведения и поместить НОК в знаменатель.
- ([Числитель дроби 1 * (НОК / знаменатель дроби 1)] + [Числитель дроби 2 * (НОК / знаменатель дроби 2)]) / НОК
- = ([1 * (4/4)] + [7 * (4/2)]) / 4
- = (1 + 14) / 4 = 15/4
После сложения результат будет 15/4, что является неправильной дробью. Однако его можно было преобразовать в смешанную фракцию. Действия по преобразованию неправильной фракции в смешанные описаны выше.
Заключение
Дроби очень важны не только для математики, но и в нашей повседневной жизни.Вычисление с использованием дробей требуется практически во всех областях, поэтому понимание того, как преобразовывать смешанные и неправильные дроби, сэкономит ваше время и поможет обеспечить точность результатов.
Оставьте первый комментарий ниже.
Сложение и вычитание смешанных чисел — Предалгебра
Цели обучения
К концу этого раздела вы сможете:
- Модель сложения смешанных чисел с общим знаменателем
- Сложить смешанные числа с общим знаменателем
- Модель вычитания смешанных чисел
- Вычесть смешанные числа с общим знаменателем
- Сложить и вычесть смешанные числа с разными знаменателями
Прежде чем начать, пройдите тест на готовность.
- Нарисуйте рисунок к модели
Если вы пропустили эту проблему, просмотрите (рисунок). - Изменить на смешанный номер.
Если вы пропустили эту проблему, просмотрите (рисунок). - Заменить дробь на неправильную.
Если вы пропустили эту проблему, просмотрите (рисунок).
Модель сложения смешанных чисел с общим знаменателем
До сих пор мы складывали и вычитали правильные и неправильные дроби, но не смешанные числа. Давайте начнем с размышления о сложении смешанных чисел с использованием денег.
Если у Рона есть доллар и четверть, у него есть доллары.
Если у Дона есть доллары и четверть, то у него есть доллары.
Что, если Рон и Дон сложат свои деньги? У них будут доллары и четвертаки. Они складывают доллары и складывают четвертинки. Это делает доллары. Поскольку две четверти — это полдоллара, у них будет полтора доллара, или доллар.
*** QuickLaTeX не может составить формулу:
\ begin {array} {} \\ \\ \\ \ phantom {\ rule {0. 6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +2 \ frac {1} {4} \ hfill \\ \ text {________} \ hfill \\ \\ \\ \ phantom {\ rule {0.8em} {0ex}} 3 \ frac {2} {4} = 3 \ frac {1} {2} \ hfill \ end {array}
*** Сообщение об ошибке:
В преамбуле выравнивания вставлен пропущенный #.
начальный текст: $ \ begin {array} {}
Отсутствует $ вставлен.
начальный текст: ... \\ \ phantom {\ rule {0.6em} {0ex}} 1 \ frac {1} {4}
Extra}, или забытый $.
начальный текст: ... \\ \ phantom {\ rule {0.6em} {0ex}} 1 \ frac {1} {4}
Отсутствует} вставлено.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Extra}, или забытый $.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Отсутствует} вставлено.начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Extra}, или забытый $.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Отсутствует} вставлено.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Extra}, или забытый $.
6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +2 \ frac {1} {4} \ hfill \\ \ text {________} \ hfill \\ \\ \\ \ phantom {\ rule {0.8em} {0ex}} 3 \ frac {2} {4} = 3 \ frac {1} {2} \ hfill \ end {array}
*** Сообщение об ошибке:
В преамбуле выравнивания вставлен пропущенный #.
начальный текст: $ \ begin {array} {}
Отсутствует $ вставлен.
начальный текст: ... \\ \ phantom {\ rule {0.6em} {0ex}} 1 \ frac {1} {4}
Extra}, или забытый $.
начальный текст: ... \\ \ phantom {\ rule {0.6em} {0ex}} 1 \ frac {1} {4}
Отсутствует} вставлено.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Extra}, или забытый $.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Отсутствует} вставлено.начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Extra}, или забытый $.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Отсутствует} вставлено.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Extra}, или забытый $. начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Отсутствует} вставлено.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Отсутствует} вставлено.
Когда вы складывали доллары, а затем четверти, вы складывали целые числа, а затем складывали дроби.
Мы можем использовать круги с дробями для моделирования этого же примера:
Выполнение упражнения по манипуляции с математикой «Сложение / вычитание смешанных чисел» поможет вам лучше понять, как складывать и вычитать смешанные числа.
Модель и укажите сумму.
Решение
Мы будем использовать круги с дробями, целые круги для целых чисел и кусочки для дробей.
Это то же самое, что и целое. Итак,
Используйте модель, чтобы добавить следующее.Нарисуйте картинку, чтобы проиллюстрировать вашу модель.
5
Используйте модель, чтобы добавить следующее. Нарисуйте картинку, чтобы проиллюстрировать вашу модель.
5
Смоделируйте и дайте сумму смешанным числом.
и дайте сумму как смешанное число. Нарисуйте картинку, чтобы проиллюстрировать вашу модель.
и дайте сумму как смешанное число.Нарисуйте картинку, чтобы проиллюстрировать вашу модель.
Сложить смешанные числа
Моделирование с помощью дробных кругов помогает проиллюстрировать процесс сложения смешанных чисел: мы складываем целые числа и складываем дроби, а затем, если возможно, упрощаем результат.
Сложите смешанные числа с общим знаменателем.
Шаг 1. Сложите целые числа.
Шаг 2. Сложите дроби.
Шаг 3. По возможности упростите.
Найдите сумму:
Найдите сумму:
В (рисунок) сумма дробей была правильной дробью. Теперь мы рассмотрим пример, в котором сумма является неправильной дробью.
Найдите сумму:
Найдите сумму:
Найдите сумму:
Альтернативный метод сложения смешанных чисел — преобразовать смешанные числа в неправильные дроби, а затем сложить неправильные дроби. Этот метод обычно пишется горизонтально.
Этот метод обычно пишется горизонтально.
Сложите путем преобразования смешанных чисел в неправильные дроби:
Решение
Поскольку задача была задана в смешанной числовой форме, мы запишем сумму в виде смешанного числа.
Найдите сумму, преобразовав смешанные числа в неправильные дроби:
Найдите сумму, преобразовав смешанные числа в неправильные дроби:
(рисунок) сравнивает два метода сложения на примере выражения.Какой способ ты предпочитаешь?
*** QuickLaTeX не может составить формулу:
\ begin {array} {} \\ \\ \ hfill \ phantom {\ rule {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill \ frac {+6 \ frac {4 } {5}} {\ phantom {\ rule {0.6em} {0ex}} 9 \ frac {6} {5}} \ hfill \\ \ hfill 9+ \ frac {6} {5} \ hfill \\ \ hfill 9 + 1 \ frac {1} {5} \ hfill \\ \ hfill 10 \ frac {1} {5} \ hfill \ end {array}
*** Сообщение об ошибке:
В преамбуле выравнивания вставлен пропущенный #.начальный текст: $ \ begin {array} {}
Отсутствует $ вставлен.
начальный текст: ... ill \ phantom {\ rule {0.8em} {0ex}} 3 \ frac {2} {5}
Extra}, или забытый $.
начальный текст: ... ill \ phantom {\ rule {0.8em} {0ex}} 3 \ frac {2} {5}
Отсутствует} вставлено.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: . .. le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Extra}, или забытый $.начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
.. le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Extra}, или забытый $.начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
*** QuickLaTeX не может составить формулу:
\ begin {array} {} \\ \ hfill 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill \ frac {17} {5} + \ frac {34} {5} \ hfill \\ \ hfill \ frac {51} {5} \ hfill \\ \ hfill 10 \ frac {1} {5} \ hfill \ end {array}
*** Сообщение об ошибке:
В преамбуле выравнивания вставлен пропущенный #.начальный текст: $ \ begin {array} {}
Отсутствует $ вставлен.
начальный текст: $ \ begin {array} {} \\ \ hfill 3 \ frac {2} {5}
Extra}, или забытый $. начальный текст: $ \ begin {array} {} \\ \ hfill 3 \ frac {2} {5}
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Extra}, или забытый $.начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
начальный текст: $ \ begin {array} {} \\ \ hfill 3 \ frac {2} {5}
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Extra}, или забытый $.начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Модель вычитания смешанных чисел
Давайте снова подумаем о пицце, чтобы смоделировать вычитание смешанных чисел с общим знаменателем.Предположим, вы только что испекли целую пиццу и хотите отдать половину пиццы своему брату. Что нужно сделать с пиццей, чтобы дать ему половину? Вы должны разрезать его как минимум на две части. Тогда вы можете отдать ему половину.
Что нужно сделать с пиццей, чтобы дать ему половину? Вы должны разрезать его как минимум на две части. Тогда вы можете отдать ему половину.
Мы будем использовать дробные круги (пицца!), Чтобы визуализировать процесс.
Начни с одного целого.
Алгебраически вы бы написали:
Используйте модель, чтобы вычесть:
Решение
Используйте модель, чтобы вычесть:
Используйте модель, чтобы вычесть:
Что, если мы начнем с нескольких целых? Давайте разберемся.
Используйте модель, чтобы вычесть:
Решение
Используйте модель, чтобы вычесть:
Используйте модель, чтобы вычесть:
В следующем примере мы вычтем более одного целого.
Используйте модель, чтобы вычесть:
Решение
Используйте модель, чтобы вычесть:
Используйте модель, чтобы вычесть:
Что если вы начнете со смешанного числа и вам нужно вычесть дробь? Подумайте об этой ситуации: вам нужно положить три четверти в счетчик парковки, но у вас есть только счет и одна четверть. Что ты мог сделать? Вы можете поменять долларовую купюру на четверть. Стоимость четвертаков такая же, как и одна долларовая купюра, но четверти более полезны для счетчика парковки. Теперь вместо счета и одной четверти у вас есть четвертаки, и вы можете положить четверти в счетчик.
Что ты мог сделать? Вы можете поменять долларовую купюру на четверть. Стоимость четвертаков такая же, как и одна долларовая купюра, но четверти более полезны для счетчика парковки. Теперь вместо счета и одной четверти у вас есть четвертаки, и вы можете положить четверти в счетчик.
Моделирует то, что происходит, когда мы вычитаем дробь из смешанного числа. Мы вычли три четверти из одного доллара и одной четверти.
Мы также можем смоделировать это, используя дробные круги, так же, как мы это делали для сложения смешанных чисел.
Используйте модель, чтобы вычесть:
Используйте модель для вычитания. Нарисуйте картинку, чтобы проиллюстрировать вашу модель.
Используйте модель для вычитания. Нарисуйте картинку, чтобы проиллюстрировать вашу модель.
Вычесть смешанные числа с общим знаменателем
Теперь вычтем смешанные числа без использования модели. Но это может помочь представить себе модель, когда вы читаете шаги.
Но это может помочь представить себе модель, когда вы читаете шаги.
Вычтите смешанные числа с общими знаменателями.
- Перепишите задачу вертикально.
- Сравните две дроби.
- Если верхняя фракция больше нижней, переходите к шагу 3.
- Если нет, в верхнем смешанном числе возьмите одно целое и прибавьте его к дробной части, получив смешанное число с неправильной дробью.
- Вычтите дроби.
- Вычтите целые числа.
- Упростите, если возможно.
Найди отличия:
Решение
Поскольку задача была задана со смешанными числами, мы оставляем результат как смешанные числа.
Найди отличия:
Найди отличия:
Так же, как мы делали со сложением, мы могли вычитать смешанные числа, сначала преобразовывая их в неправильные дроби. Мы должны записать ответ в той форме, в которой он был дан, поэтому, если нам дадут смешанные числа для вычитания, мы запишем ответ как смешанное число.
Вычтите смешанные числа с общим знаменателем как неправильные дроби.
Шаг 1. Перепишите смешанные числа как неправильные дроби.
Шаг 2. Вычтите числители.
Шаг 3. Запишите ответ в виде смешанного числа, по возможности упростив дробную часть.
Найдите разницу, преобразовав смешанные числа в неправильные дроби:
Найдите разницу, преобразовав смешанные числа в неправильные дроби:
Сложение и вычитание смешанных чисел с разными знаменателями
Чтобы сложить или вычесть смешанные числа с разными знаменателями, мы сначала преобразуем дроби в эквивалентные дроби с помощью ЖК-дисплея.Затем мы можем выполнить все шаги, которые мы использовали выше для сложения или вычитания дробей с одинаковыми знаменателями.
Добавить:
Решение
Поскольку знаменатели разные, мы перепишем дроби как эквивалентные дроби с ЖК-дисплеем. Затем мы добавим и упростим.
Затем мы добавим и упростим.
Мы записываем ответ в виде смешанного числа, потому что в задаче нам были даны смешанные числа.
Добавить:
Добавить:
Вычесть:
Решение
Поскольку знаменатели дробей различны, мы перепишем их как эквивалентные дроби с ЖК-дисплеем. Получив такую форму, мы вычтем.Но сначала нам нужно будет занять.
Нам выдали смешанные числа, поэтому мы оставляем ответ смешанным числом.
Найди отличия:
Найди отличия:
Вычесть:
Решение
Мы видим, что ответ будет отрицательным, так как мы вычитаем из. Как правило, когда мы знаем, что ответ будет отрицательным, легче вычесть с неправильными дробями, чем со смешанными числами.
Вычесть:
Вычесть:
Ключевые концепции
- Сложите смешанные числа с общим знаменателем.

- Сложите целые числа.
- Сложите дроби.
- Упростите, если возможно.
- Вычтите смешанные числа с общими знаменателями.
- Перепишите задачу вертикально.
- Сравните две дроби.
Если верхняя дробь больше нижней дроби, переходите к шагу 3.
Если нет, в верхнем смешанном числе возьмите одно целое и добавьте его к дробной части, получив смешанное число с неправильной дробью. - Вычтите дроби.
- Вычтите целые числа.
- Упростите, если возможно.
- Вычтите смешанные числа с общим знаменателем как неправильные дроби.
- Перепишите смешанные числа как неправильные дроби.
- Вычтите числители.
- Запишите ответ в виде смешанного числа, по возможности упростив дробную часть.
Практика ведет к совершенству
Модель сложения смешанных номеров
В следующих упражнениях используйте модель, чтобы найти сумму. Нарисуйте картинку, чтобы проиллюстрировать вашу модель.
Нарисуйте картинку, чтобы проиллюстрировать вашу модель.
Сложить смешанные числа с общим знаменателем
В следующих упражнениях добавьте.
Модель вычитания смешанных чисел
В следующих упражнениях используйте модель, чтобы найти разницу. Нарисуйте картинку, чтобы проиллюстрировать вашу модель.
Вычесть смешанные числа с общим знаменателем
Найдите разницу в следующих упражнениях.
Сложение и вычитание смешанных чисел с разными знаменателями
В следующих упражнениях запишите сумму или разницу в виде смешанного числа в упрощенной форме.
Смешанная практика
В следующих упражнениях выполните указанную операцию и запишите результат в виде смешанного числа в упрощенной форме.
Письменные упражнения
Нарисуйте диаграмму и используйте ее, чтобы объяснить, как сложить
Эдгару придется заплатить за проезд, чтобы доехать до города.
ⓐ Объясните, как он может внести сдачу в счет перед тем, как уйти, чтобы у него была точная сумма, которая ему нужна.
ⓑ Чем ситуация Эдгара похожа на то, как вы вычитаете
Сложите дважды, сначала оставив их как смешанные числа, а затем переписав как неправильные дроби. Какой метод вы предпочитаете и почему?
Вычтите дважды, сначала оставив их как смешанные числа, а затем переписав как неправильные дроби. Какой метод вы предпочитаете и почему?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
Что такое сложение смешанных чисел?
Добавление смешанных чиселДробь, состоящая из целого числа и дробной части, называется смешанным числом.
Неправильные дроби, дроби больше единицы, записанные в виде целого числа и правильной дроби, называются смешанными числами.
Сложение смешанных чисел с одинаковыми знаменателями
В одной корзине 2 4 ⁄ 5 кг яблок, а в другой — 3 3 ⁄ 5 кг яблок.Сколько всего яблок в обеих корзинах?
Здесь, чтобы найти количество яблок в обеих корзинах, мы складываем смешанные числа 2 4 ⁄ 5 и 3 3 ⁄ 5 . Знаменатели обеих дробных частей одинаковы. Итак, чтобы сложить смешанные числа с одинаковыми знаменателями, мы складываем целые части вместе и дробные части вместе, а затем объединяем сумму двух, как показано ниже:
Складываем целую часть с целой частью и дробную часть с дробной частью.
Если сумма дробных частей является неправильным числом, преобразуйте ее в смешанное число.
Соедините сумму целых чисел и дробей.
Таким образом, имеется 6 2 ⁄ 5 кг яблок.
Что мы сделали:
2 4 ⁄ 5 + 3 3 ⁄ 5 = 2 + 3 + 4 ⁄ 5 + 3 ⁄ 5
= 5 + 7 ⁄ 5
= 5 + 1 2 ⁄ 5
= 6 2 ⁄ 5
Сложение смешанных чисел с разными знаменателями
Теперь давайте рассмотрим пример, чтобы понять сложение смешанных чисел с разными знаменателями.
У Сьюзан 1 4 ⁄ 7 литров апельсинового сока. У Кита 2 2 ⁄ 5 литров апельсинового сока. Сколько у них апельсинового сока?
Здесь, чтобы найти ответ, нам нужно сложить смешанные числа 1 4 ⁄ 7 и 2 2 ⁄ 5 . Здесь знаменатели обеих дробных частей разные.
Для сложения смешанных чисел используйте любой из следующих методов:
Метод 1 :
- Сложите отдельно целые числа и отдельно сложите непохожие дроби.

Добавить 1 4 ⁄ 7 + 2 2 ⁄ 5 | |
Сложение целых чисел | Сложение Отличие дробей |
| 1 + 2 = 3 | 4 ⁄ 7 + 2 ⁄ 5 LCM 7 и 5 равно 35. Следовательно, 4 ⁄ 7 = 4 ⁄ 7 911 511 911⁄52 5 = 20 ⁄ 35 и 2 ⁄ 5 = 2 ⁄ 5 x 7 ⁄ 7 = 14 ⁄54 35119 359 4 ⁄ 7 + 2 ⁄ 5 = 20 ⁄ 35 + 14 ⁄ 35 = 34 ⁄ 35 |
3 + 34 ⁄ 35 = 3 34 ⁄ 35
Метод 2 :
1 4 ⁄ 7 = 11 ⁄ 7 и 2 2 ⁄ 5 = 12 ⁄ 5
1 4 ⁄ 7 + 2 2 ⁄ 5 = 11 ⁄ 7 + 12 ⁄ 5
Следовательно,
НОК 7 и 5 = 35
Итак,
11 ⁄ 7 = 11 ⁄ 7 x 5 ⁄ 5 = 55 ⁄ 35
и
12 ⁄ 5 = 12 ⁄ 5 x 7 ⁄ 7 = 84 ⁄ 35
Следовательно,
11 ⁄ 7 + 12 ⁄ 5 = 55 ⁄ 35 + 84 ⁄ 35
= 139 ⁄ 35
139 ⁄ 35 = 3 34 ⁄ 35
Сложение и вычитание смешанных чисел
Сложение и вычитание смешанного числа очень похоже на сложение и вычитание правильных дробей. Большая разница в том, что в смеси есть целые числа.
Большая разница в том, что в смеси есть целые числа.
(5 + 3) + ()
Шаг 2 : Теперь мы сложим целые числа и сложим дроби.
5 + 3 = 8
Для сложения дробей нам потребуются общие знаменатели.
Теперь, когда у нас есть общие знаменатели, мы можем сложить числители и оставить знаменатель прежним.
Шаг 3 : Запишите ответ на обе части в виде смешанного числа:
2.) Мы проделаем те же шаги в этом примере с одним небольшим изменением в конце.Шаг 1 : Отделите целое число от дробной части каждого числа.
2 + 6 +
Шаг 2 : Сложите целые числа, а затем сложите дроби.
2 + 6 = 8
Опять же, нам нужно будет получить общие знаменатели, чтобы мы могли складывать дроби.
Знаменатель второй дроби уже равен 10, поэтому мы готовы сложить.
В этом примере ответом на дробную часть является неправильная дробь. Измените его на смешанное число, чтобы его можно было добавить к целой числовой части задачи.
Измените его на смешанное число, чтобы его можно было добавить к целой числовой части задачи.
Шаг 3 : Добавьте целочисленный ответ к дробному ответу.
Следовательно,
Шаги для вычитания смешанных чисел очень похожи на шаги для сложения смешанных чисел. Однако прежде чем работать с целым числом и дробью, вы должны получить общие знаменатели и убедиться, что вам не нужно брать взаймы.Мы рассмотрим этот пример, в котором вам не нужно брать взаймы, а в следующем примере вам нужно будет заимствовать, чтобы вы могли увидеть и то, и другое.
3.) Шаг 1 : Найдите общие знаменатели.Можем вычесть без займов. Итак, мы готовы продолжить.
Шаг 2 : Вычтите целые числа и вычтите дроби.
8 — 2 = 6
Шаг 3 : Запишите ответ в виде смешанного числа.
4.) Шаг 1 : Получите общие знаменатели и определите, нужно ли вам заимствовать. В этом примере у нас есть Это пример, в котором нам нужно заимствовать 1 из 7. Однако имейте в виду, что 1 на самом деле
Однако имейте в виду, что 1 на самом деле
Итак
Шаг 2 : Вычтите целые числа и дроби .
Новая задача:
6 — 3 = 3
Шаг 3 : Запишите ответ в виде смешанного числа.
Существуют и другие методы, например использование неправильных дробей, но если вам нужен смешанный ответ, это может стать трудным.Цифры могут быть очень большими, что облегчает совершение ошибок.
Сложение дробей с целыми числами
Сложение дробей с целыми числами по сути то же самое, что преобразование смешанного числа в неправильную дробь (просто помните, как правильно складывать целые числа).
Действительно, предположим, что мы хотим сложить целое число $$$ {m} $$$ и дробь $$$ \ frac {{n}} {{q}} $$$.
Если $$$ \ frac {{n}} {{q}} $$$ — правильная дробь, то $$$ {m} \ frac {{n}} {{q}} $$$ — смешанное число а задача — преобразовать смешанное число в неправильную дробь.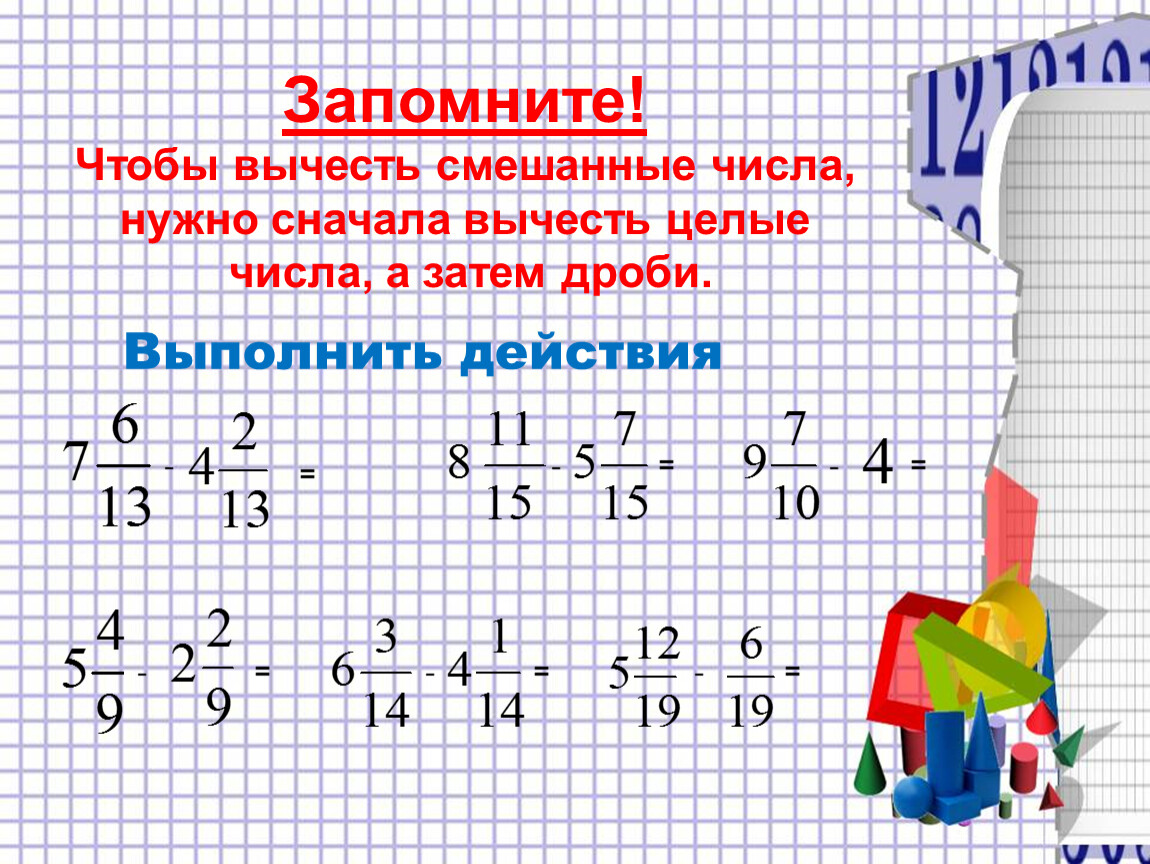
Если $$$ \ frac {{n}} {{q}} $$$ — неправильная дробь, это мало что меняет.
Известно, что целое число $$$ {m} $$$ можно представить в виде дроби $$$ \ frac {{m}} {{1}} $$$.
Теперь $$$ {m} + \ frac {{n}} {{q}} = \ frac {{m}} {{1}} + \ frac {{n}} {{q}} = \ frac {{{m} {q}}} {{q}} + \ frac {{n}} {{q}} = \ frac {{{m} {q} + {n}}} {{q }} $$$.
Формула для сложения дробей с целыми числами : $$$ {\ color {green} {{{m} + \ frac {{n}} {{q}} = \ frac {{{m} {q}) + {n}}} {{q}}}}} $$$.
Пример 1. Найдите $$$ {3} + \ frac {{6}} {{7}} $$$.
Решим пошагово:
$$$ {3} + \ frac {{6}} {{7}} = \ frac {{3}} {{1}} + \ frac {{ 6}} {{7}} = \ frac {{{3} \ cdot {\ color {red} {{{7}}}}}} {{{1} \ cdot {\ color {red} {{{ 7}}}}}} + \ frac {{6}} {{7}} = \ frac {{21}} {{7}} + \ frac {{6}} {{7}} = \ frac { {27}} {{7}} $$$.
Если вам нужно смешанное число, преобразуйте $$$ \ frac {{27}} {{7}} $$$ в смешанное число: $$$ \ frac {{27}} {{7}} = {3 } \ frac {{6}} {{7}} $$$ (обратите внимание, что это то же самое, что и $$$ {3} + \ frac {{6}} {{7}} $$$).
Ответ : $$$ \ frac {{27}} {{7}} = {3} \ frac {{6}} {{7}} $$$.
Следующий пример.
Пример 2. Найдите $$$ — {9} + \ frac {{13}} {{8}} $$$.
Воспользуемся прямой формулой:
$$$ — {9} + \ frac {{13}} {{8}} = \ frac {{- {9} \ cdot {8} + {13}}} { {8}} = \ frac {{- {72} + {13}}} {{8}} = — \ frac {{59}} {{8}} $$$.
При необходимости преобразовать в смешанное число: $$$ — \ frac {{59}} {{8}} = — {7} \ frac {{3}} {{8}} $$$
Ответ : $$$ — \ frac {{59}} {{8}} = — {7} \ frac {{3}} {{8}} $$$.
Следующий пример.
Пример 3. Найдите $$$ — \ frac {{9}} {{4}} + {\ left (- {3} \ right)} $$$.
$$$ — \ frac {{9}} {{4}} + {\ left (- {3} \ right)} = — \ frac {{9}} {{4}} + {\ left ( — \ frac {{{3} \ cdot {\ color {red} {{{4}}}}}} {{{1} \ cdot {\ color {red} {{{4}}}}}} \ right)} = — \ frac {{9}} {{4}} + {\ left (- \ frac {{12}} {{4}} \ right)} = \ frac {{- {9} + { \ left (- {12} \ right)}}} {{4}} = \ frac {{- {9} — {12}}} {{4}} = — \ frac {{21}} {{4 }} $$$.
При необходимости преобразовать в смешанную дробь: $$$ — \ frac {{21}} {{4}} = — {5} \ frac {{1}} {{4}} $$$.
Ответ : $$$ — \ frac {{21}} {{4}} = — {5} \ frac {{1}} {{4}} $$$.
А теперь пора попрактиковаться.
Упражнение 1. Найдите $$$ {2} + \ frac {{6}} {{7}} $$$.
Ответ : $$$ \ frac {{20}} {{7}} = {2} \ frac {{6}} {{7}} $$$.
Следующее упражнение.
Упражнение 2. Найдите $$$ {9} + {\ left (- \ frac {{29}} {{5}} \ right)} $$$.
Ответ : $$$ \ frac {{16}} {{5}} = {3} \ frac {{1}} {{5}} $$$.
Следующее упражнение.
Упражнение 3. Найдите $$$ — {5} + \ frac {{99}} {{8}} $$$.
Ответ : $$$ \ frac {{59}} {{8}} = {7} \ frac {{3}} {{8}} $$$.
.


 Вот так:
Вот так:







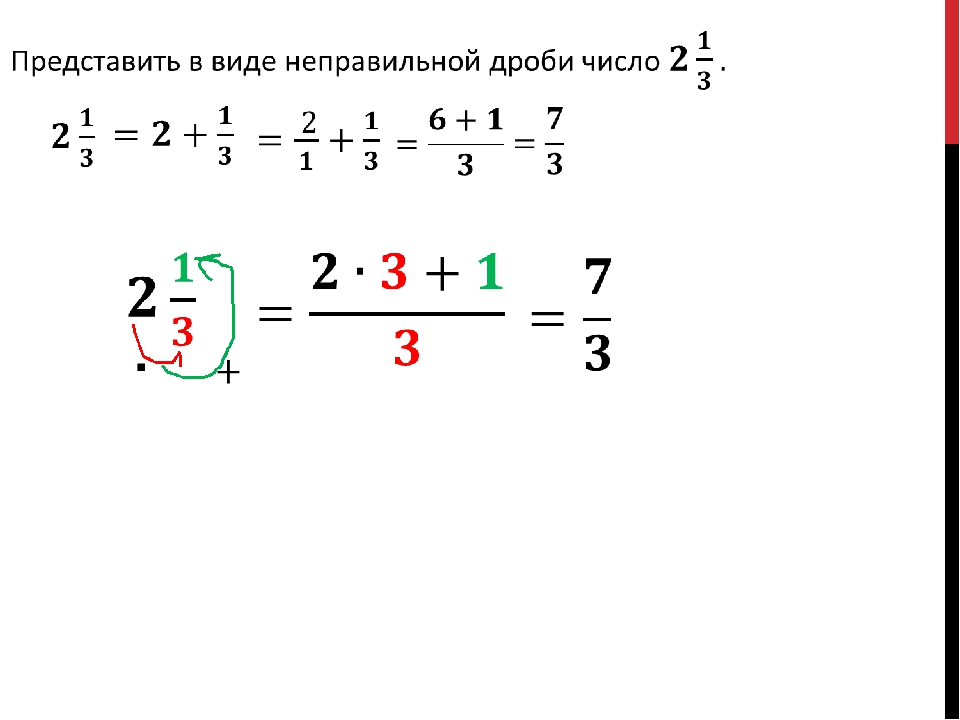 6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +2 \ frac {1} {4} \ hfill \\ \ text {________} \ hfill \\ \\ \\ \ phantom {\ rule {0.8em} {0ex}} 3 \ frac {2} {4} = 3 \ frac {1} {2} \ hfill \ end {array}
*** Сообщение об ошибке:
В преамбуле выравнивания вставлен пропущенный #.
начальный текст: $ \ begin {array} {}
Отсутствует $ вставлен.
начальный текст: ... \\ \ phantom {\ rule {0.6em} {0ex}} 1 \ frac {1} {4}
Extra}, или забытый $.
начальный текст: ... \\ \ phantom {\ rule {0.6em} {0ex}} 1 \ frac {1} {4}
Отсутствует} вставлено.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Extra}, или забытый $.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Отсутствует} вставлено.начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Extra}, или забытый $.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Отсутствует} вставлено.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Extra}, или забытый $.
6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +2 \ frac {1} {4} \ hfill \\ \ text {________} \ hfill \\ \\ \\ \ phantom {\ rule {0.8em} {0ex}} 3 \ frac {2} {4} = 3 \ frac {1} {2} \ hfill \ end {array}
*** Сообщение об ошибке:
В преамбуле выравнивания вставлен пропущенный #.
начальный текст: $ \ begin {array} {}
Отсутствует $ вставлен.
начальный текст: ... \\ \ phantom {\ rule {0.6em} {0ex}} 1 \ frac {1} {4}
Extra}, или забытый $.
начальный текст: ... \\ \ phantom {\ rule {0.6em} {0ex}} 1 \ frac {1} {4}
Отсутствует} вставлено.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Extra}, или забытый $.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Отсутствует} вставлено.начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Extra}, или забытый $.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Отсутствует} вставлено.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Extra}, или забытый $. начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Отсутствует} вставлено.
начальный текст: ... m {\ rule {0.6em} {0ex}} 1 \ frac {1} {4} \ hfill \\ +
Отсутствует} вставлено.
 .. le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Extra}, или забытый $.начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
.. le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Extra}, или забытый $.начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: ... le {0.8em} {0ex}} 3 \ frac {2} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
 начальный текст: $ \ begin {array} {} \\ \ hfill 3 \ frac {2} {5}
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Extra}, или забытый $.начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
начальный текст: $ \ begin {array} {} \\ \ hfill 3 \ frac {2} {5}
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Extra}, или забытый $.начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Extra}, или забытый $.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill
Отсутствует} вставлено.
начальный текст: ... l 3 \ frac {2} {5} +6 \ frac {4} {5} \ hfill \\ \ hfill

