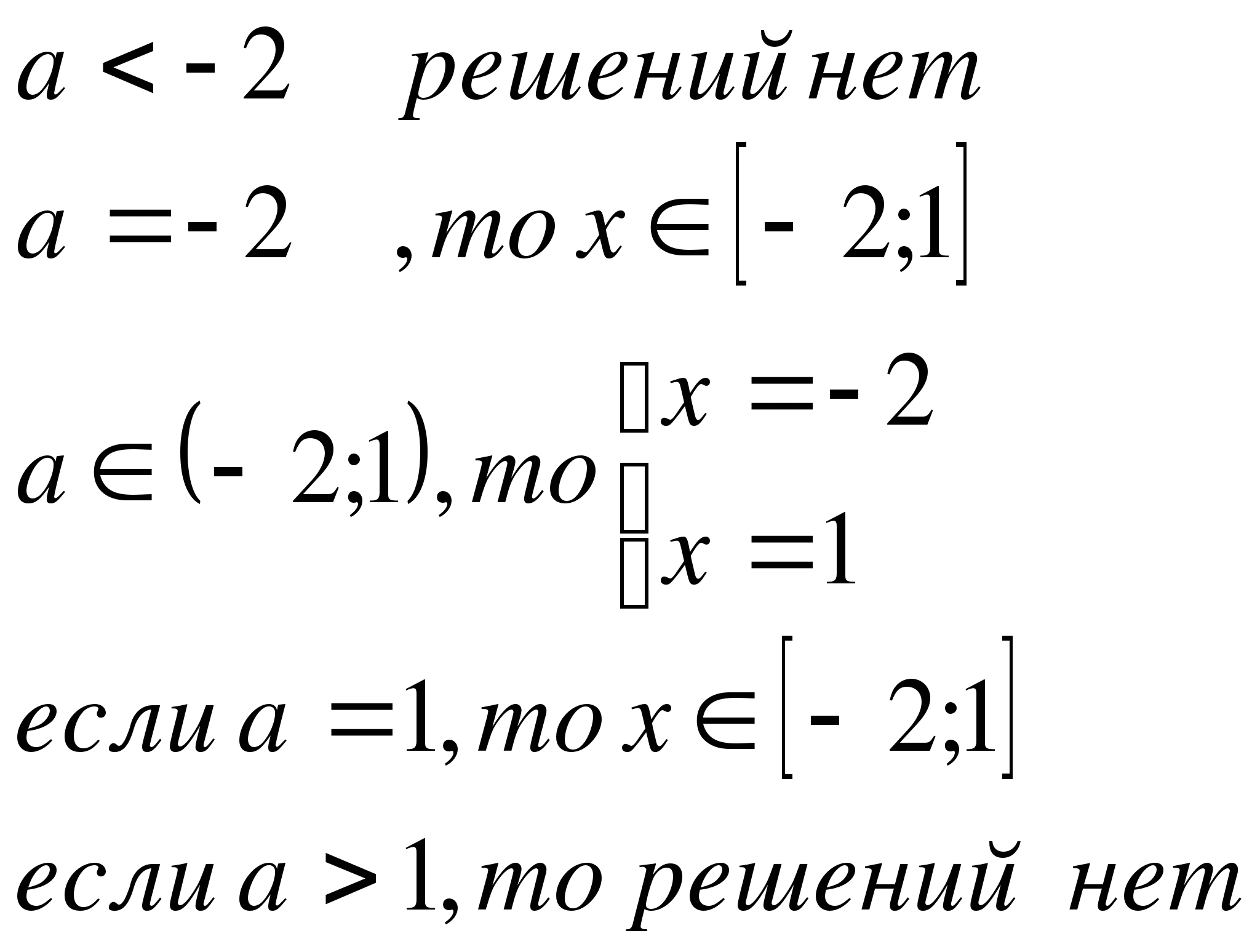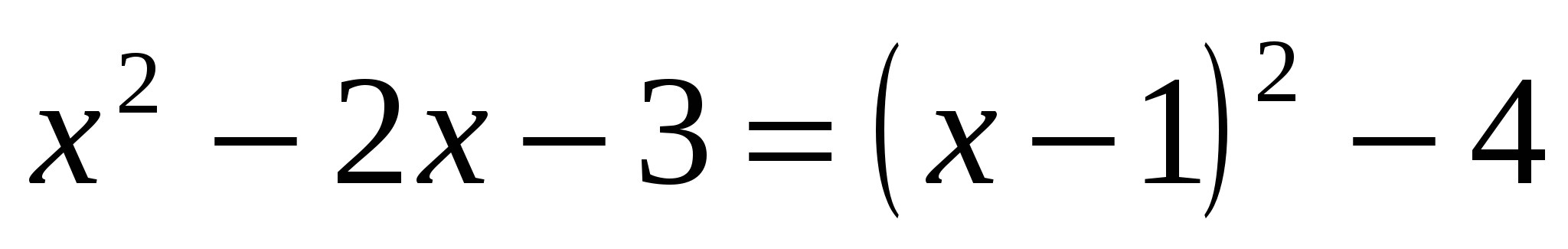Графическое решение неравенства с параметром и модулем
Здесь будет применен прием домножения на сопряженное выражение, и применен графический способ решения данного неравенства.
Задача. Найдите все значения параметра  , при которых неравенство выполняется на отрезке
, при которых неравенство выполняется на отрезке ![Rendered by QuickLaTeX.com x \in [-1;0]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5596c98e35d8ae71d6b730807dc0fcfc_l3.png) :
:
![Rendered by QuickLaTeX.com \[\mid x+a^2 \mid \leqslant \mid a+x^2 \mid\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-fea1e7568ff0ac785d55e2ac87651e5c_l3.png)
Перепишем:
![Rendered by QuickLaTeX.com \[\mid x+a^2 \mid - \mid a+x^2 \mid\leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0149441abd0360e8ba0ede1eed4e51e4_l3.png)
Применим прием «борьбы» с разностью двух положительных выражений: домножим на сопряженное выражение. Тогда неравенство будет записано:
![Rendered by QuickLaTeX.com \[(x+a^2 - a-x^2)( x+a^2 +a+x^2)\leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a47cc58f909d0b802b0b4cf4e5d08882_l3.png)
![Rendered by QuickLaTeX.com \[(x- a-(x^2- a^2))( x+a^2 +a+x^2)\leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-870f9050e10b00337b4d8c3446564943_l3.png)
Общий множитель в первой скобке выносим, а во второй – увидим и выделим полные квадраты:
![Rendered by QuickLaTeX.com \[(x- a)(1-x- a)( a^2 +a+\frac{1}{4}+x^2+x+\frac{1}{4}-\frac{2}{4})\leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-41ab5c653aeefcbbd64cf3f809f921fb_l3.png)
![Rendered by QuickLaTeX.com \[(x- a)(1-x- a) \left( \left(a+\frac{1}{2}\right)^2+\left(x+\frac{1}{2}\right)^2-\left(\frac{\sqrt{2}}{2}\right)^2\right)\leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-60a4226c3eaffc92ae45635077333ed2_l3.png)
Если теперь ввести систему координат  , то в ней можно построить три объекта:
, то в ней можно построить три объекта:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{a= x}\\{ a=1-x}\\{\left(a+\frac{1}{2}\right)^2+\left(x+\frac{1}{2}\right)^2=\left(\frac{\sqrt{2}}{2}\right)^2}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d4c8796054ec3c2715a6ab15ac93e762_l3.png)
То есть две пересекающиеся прямые и окружность. Строим:

Рисунок 1. Построение линий
Теперь возьмем произвольную точку, например, с координатами  и подставим ее координаты в неравенство. Видим, что все множители положительны и неравенство не выполняется. Оно не будет выполняться во всей области, но как только мы пересечем какую-либо ее границу, то попадем в область, где неравенство выполняется. Поэтому закрасим такие области в шахматном порядке:
и подставим ее координаты в неравенство. Видим, что все множители положительны и неравенство не выполняется. Оно не будет выполняться во всей области, но как только мы пересечем какую-либо ее границу, то попадем в область, где неравенство выполняется. Поэтому закрасим такие области в шахматном порядке:

Рисунок 2. Обозначение областей, где неравенство выполняется.
Теперь коричневыми вертикалями отграничим область ![Rendered by QuickLaTeX.com x \in [-1;0]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5596c98e35d8ae71d6b730807dc0fcfc_l3.png) , и посмотрим, при каких
, и посмотрим, при каких  неравенство выполняется.
неравенство выполняется.

Рисунок 3. Ярким зеленым цветом и желтой полоской обозначаем решение неравенства на заданном отрезке
Очевидно, что это 
 . А координату «верхушки» окружности найдем как разность радиуса и координаты центра:
. А координату «верхушки» окружности найдем как разность радиуса и координаты центра: .
.
Ответ: ![Rendered by QuickLaTeX.com a \in \{-1\} \cup [\frac{\sqrt{2}}{2}-\frac{1}{2};1]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-992c325000cfd264564cbf2d9f09de9d_l3.png) .
.
easy-physic.ru
Неравенства с модулем, содержащие параметр
Неравенства с модулем, содержащие параметр
Ниже предлагаются задачи, которые могут помочь учителю подготовить учащихся 9–11 классов к решению уравнений и неравенств с модулем, содержащих параметр. Понимание задач значительно облегчается, если учащиеся овладеют навыками построения графиков функций с модулем.
I.Вспомогательные задачи.
1.Построить графики функций
а) б) в) г) д) е) ж)
2.Построить график функции .
3.Определить число корней уравнения при всех значениях a. Ответ. а) Если а < 0, то решений нет; б) если а = 0, то уравнение имеет два решения; в) если 0 < а < 4, то четыре решения; г) если а = 4, то три решения; д) если a > 4, то решений два.
4.Определить число корней уравнения при всех значениях a.
Ответ. а) Если а < 0, то решений нет; б) если а = 0, то уравнение имеет два решения; в) если 0 < а < 3, то четыре решения; г) если а = 3, то три решения; д) если a > 3, то решений два.
5.Решить неравенство при всех значениях параметра а. Ответ. а) нет решений при a < 0; б) при a = 0; в) при а > 0.
6.Найти все значения а, при которых корни уравнения заключены между числами –2 и 4.
Решение. График функции – парабола, ветви которой направлены вверх. Значения параметра находятся из системы неравенств .
Ответ. 1 < a < 7.
7.Найти все значения а, при которых уравнение имеет два корня, один из которых меньше числа 2, а другой больше 3.
Решение. Если а
Ответ.
8.Найти все значения a, при которых корни уравнения больше 1.
Ответ.
9.Найти все значения a, при которых неравенство выполняется для любого
Решение.
График функции – парабола, ветви которой направлены вверх. Значения параметра находятся из системы неравенств .
Ответ.
II.Основные задачи.
Задача 1 (ЕГЭ). Найдите все значения a, при каждом из которых наименьшее значение функции больше, чем
Решение.
1.Функция f имеет вид
а) при или , её график состоит из двух частей параболы с ветвями, направленными вверх, и осью симметрии ;
б) при её график представляет часть параболы с ветвями, направленными вниз.
2.Если 3-2а принадлежит отрезку , то наименьшее значение функция может принимать только на концах отрезка, то есть при х = 1 или х = 5 (см. рис. 1 и 2).
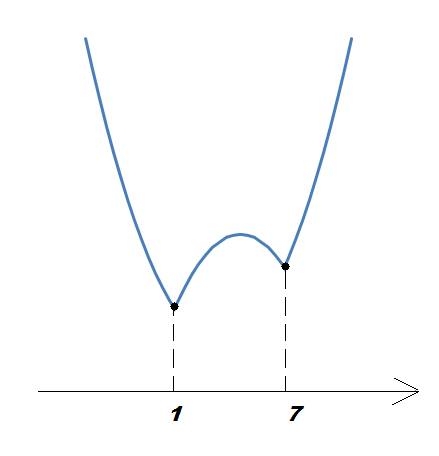
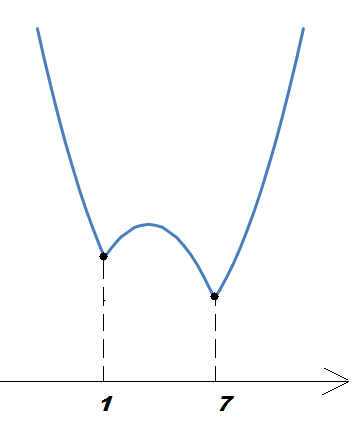
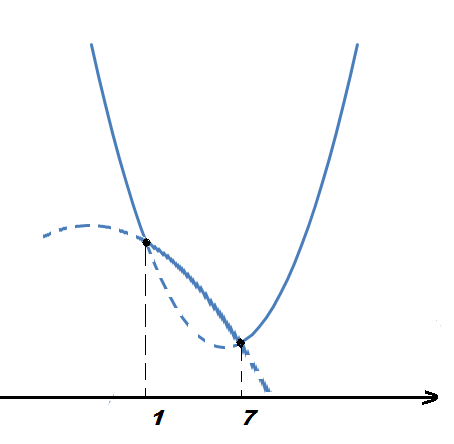
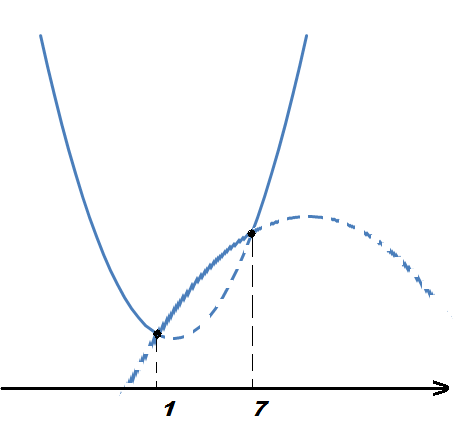
Рис.1 Рис.2 Рис.3 Рис.4
Если, то наименьшее значение функция может принимать ещё и в точке
(см. рис.3 и 4).
3.Таким образом, наименьшее значение функции f больше тогда и только тогда, когда выполняются системы неравенств
а)
б)
Объединяя решения обеих систем, получим
Ответ.
Более наглядным и, как нам представляется, доступным для учащихся является способ, связанный с построением касательной к графику функции, не содержащей параметр. Такой график занимает на координатной плоскости фиксированное положение, что значительно облегчает решение неравенства. Рассмотрим аналогичную задачу.
Задача 2 (ЕГЭ). Найдите все значения a, при каждом из которых наименьшее значение функции больше 1.
Решение. Сформулируем задачу иначе: найдите все значения а, при каждом из которых все точки графика функции лежат выше точек графика функции
Функция при или имеет вид , её график состоит из двух частей параболы с ветвями, направленными вверх, и осью симметрии .
При функция её графиком является часть параболы с ветвями, направленными вниз.
График линейной функции при каждом значении а представляет собой прямую, проходящую через точку Р(0;1) (см. рис.5). При этом прямая имеет с графиком функции общие точки (от одной до четырёх), если занимает в I-III четвертях положение между прямой, проходящей через точку М(1;0) (она выделена синим цветом) и касательной к левой ветви параболы (выделена красным цветом). Примером такой прямой служит прямая зелёного цвета. При этом часть графика функции
Уравнение прямой синего цвета можно найти по формуле прямой, проходящей через две точки Получим
Уравнение касательной получим, решая систему уравнений Заметим, что касание происходит при значит Также можно учесть, что при этом уравнение имеет единственное решение, а значит его дискриминант должен быть равен 0: Значение не удовлетворяет условию, так как при этом что больше 1.
Ответ.
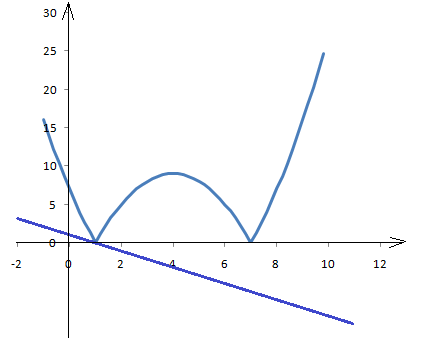 Рис.5
Рис.5
infourok.ru
| 1. | Линейное уравнение с параметром | 2 вид — интерпретация | лёгкое | 4 Б. | |
| 2. | Уравнение с модулем и параметром | 2 вид — интерпретация | лёгкое | 7 Б. | Решение уравнения с модулем и параметром. |
| 3. | Показательное уравнение с параметром | 2 вид — интерпретация | лёгкое | 2 Б. | Нахождение параметра. |
| 4. | Неравенство с модулем и параметром | 2 вид — интерпретация | лёгкое | 7 Б. | Решение неравенства с модулем и параметром. |
| 5. | Линейное уравнение с двумя параметрами | 2 вид — интерпретация | среднее | 8 Б. | Решение линейного уравнения с двумя параметрами. |
| 6. | Квадратичная функция с параметром | 2 вид — интерпретация | среднее | 2 Б. | Нахождение параметра. |
| 7. | Линейное неравенство с параметром | 2 вид — интерпретация | среднее | 6 Б. | Решение линейного неравенства с параметром. |
| 8. | Квадратичное неравенство с параметром | 2 вид — интерпретация | среднее | 7 Б. | Решение квадратичного неравенства с параметром. |
| 9. | Неравенство n-ой степени с параметром | 2 вид — интерпретация | среднее | 3 Б. | Неравенство с параметром. Чётная степень. |
| 10. | Линейное уравнение с параметром (с разложением на множители) | 2 вид — интерпретация | среднее | 3 Б. | Предлагается решить линейное уравнение с параметром (с разложением на множители) или выражения при неизвестном в левой части, или выражения в правой части. |
| 11. | Наименьшее целочисленное значение параметра | 3 вид — анализ | сложное | 3 Б. | Определяется наименьшее целочисленное значение параметра, при котором уравнение имеет два корня. |
| 12. | Логарифмическое неравенство с параметром | 3 вид — анализ | сложное | 4 Б. | Предлагается решить логарифмическое неравенство с параметром. Параметр находится в основании логарифма. |
| 13. | Показательное уравнение с параметром | 3 вид — анализ | сложное | 4 Б. | Определяется значение параметра, при котором показательное уравнение не имеет корней. Само уравнение не решается. |
www.yaklass.ru
Решение уравнений и неравенств с модулем ( из опыта работы).
Решение уравнений и неравенств с модулем
(Из опыта работы Кирьяновой Т.Ф. учителя математики
МБОУ СОШ № 9 г. Пушкино.).
В средней общеобразовательной школе (6 – 9 кл) тема «Решение уравнений и неравенств с модулем» не выделена отдельно. Поэтому на протяжении всех четырёх лет надо отводить уроки для последовательного рассмотрения основных способов решений таких уравнений и неравенств. Тогда в 10 – 11 классах освободиться время для нестандартных методов решений многих задач содержащих модуль.
Определение модуля даётся в 6 классе и поэтому уже в шестом классе можно вывести первые свойства.
1. 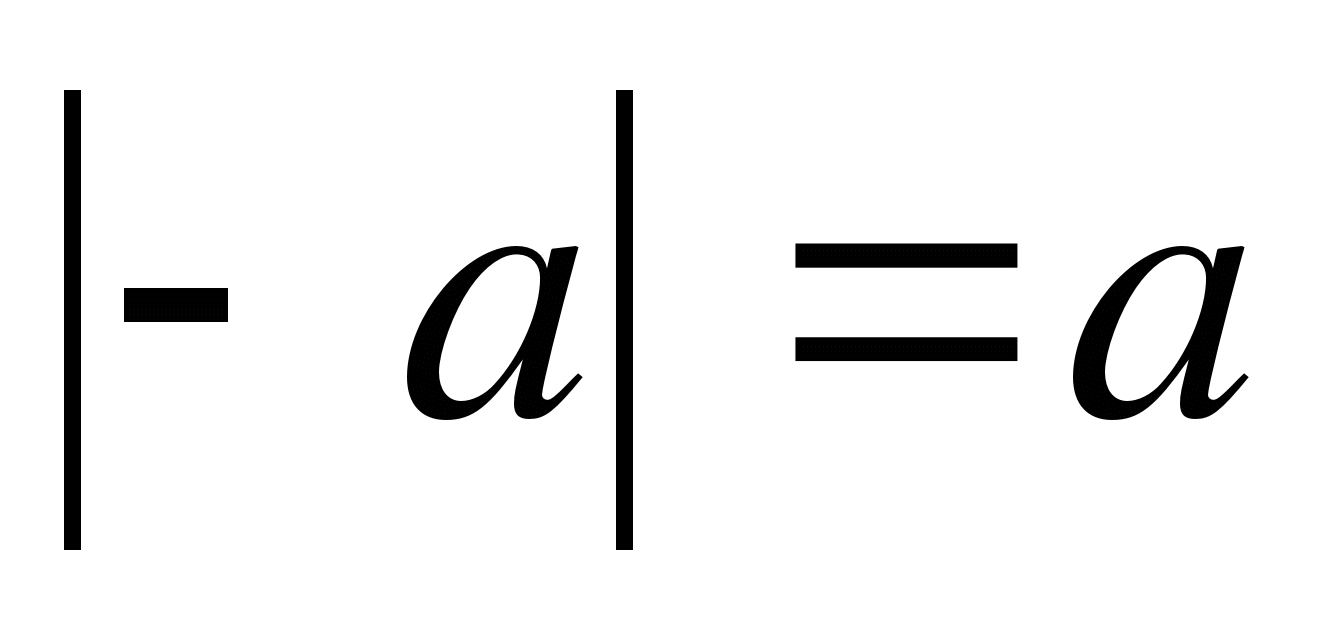
2. 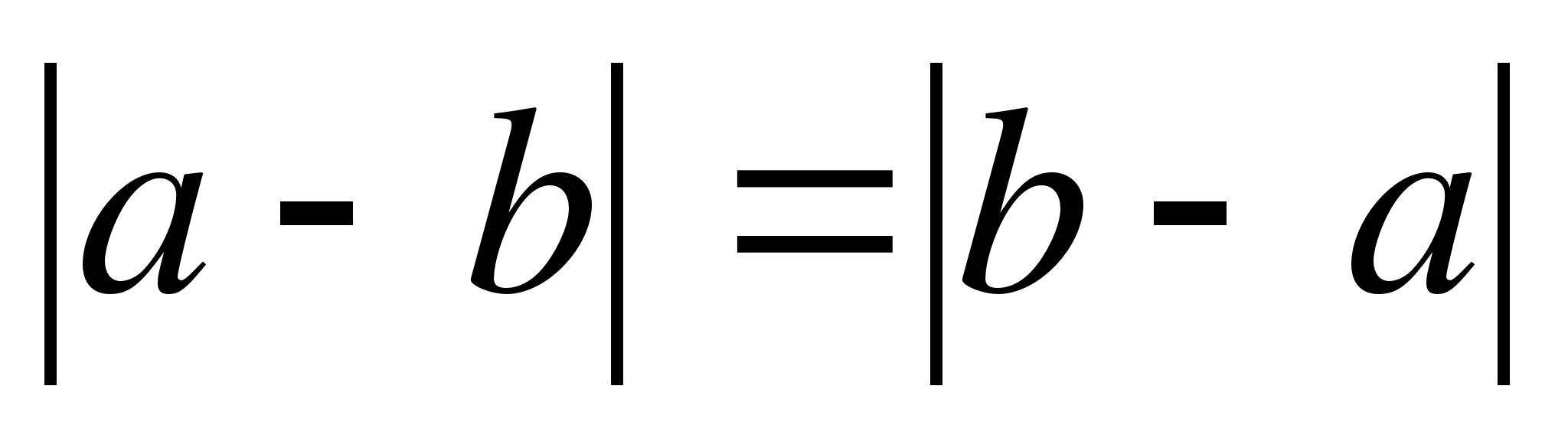
3. 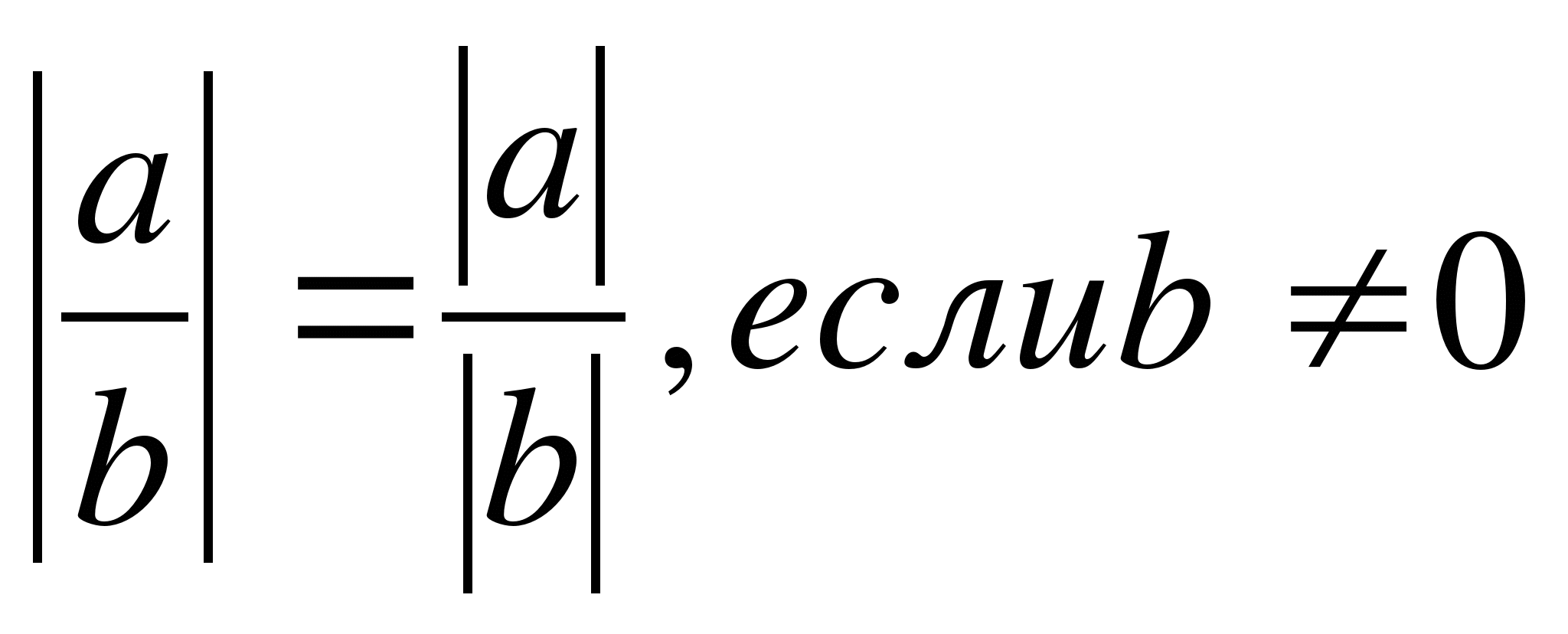
4. 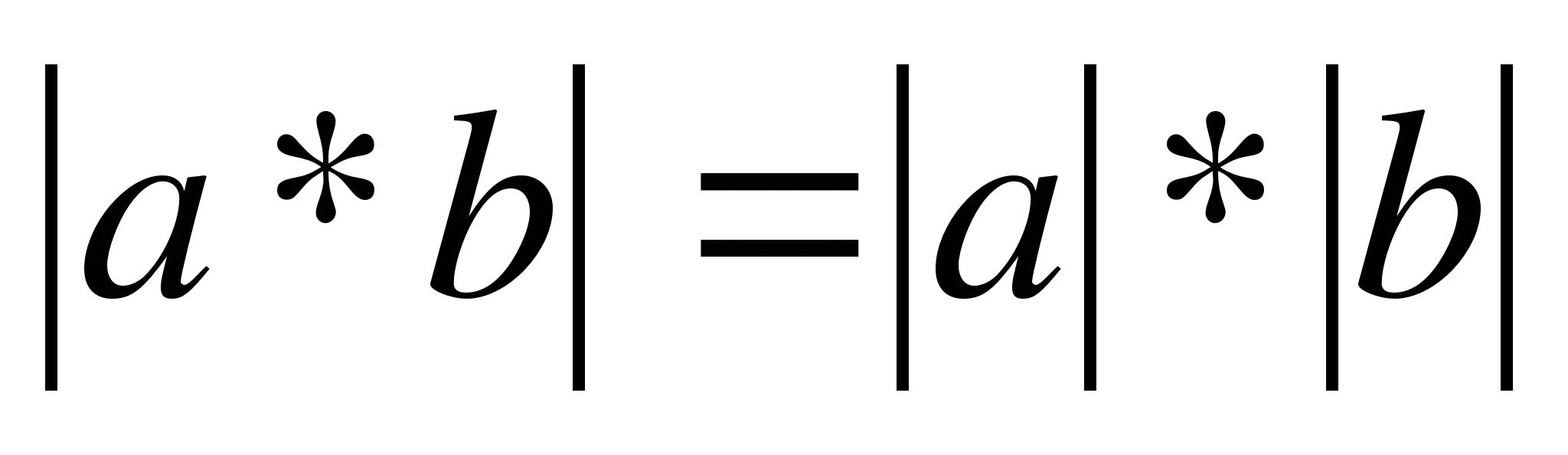
И выделить время для решений простейших уравнений:
1. 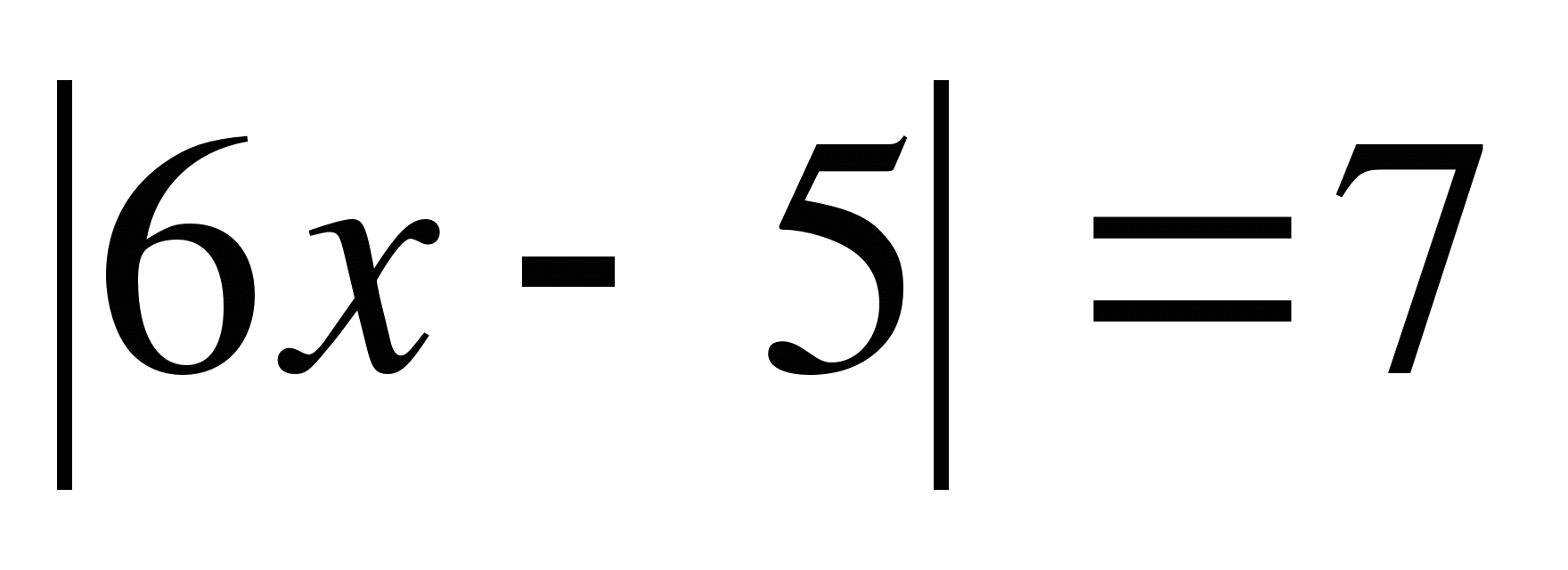 3.
3. 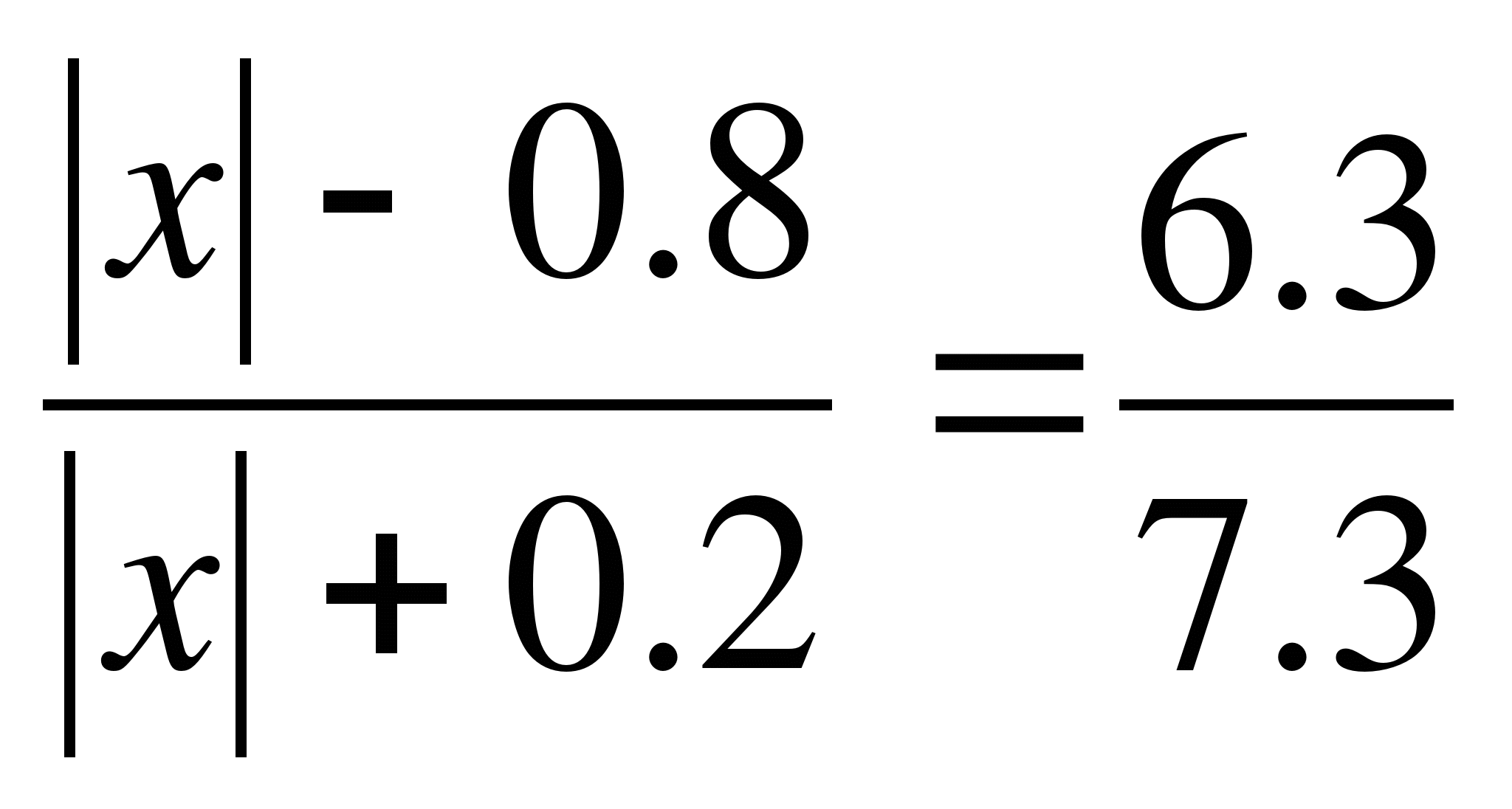
2.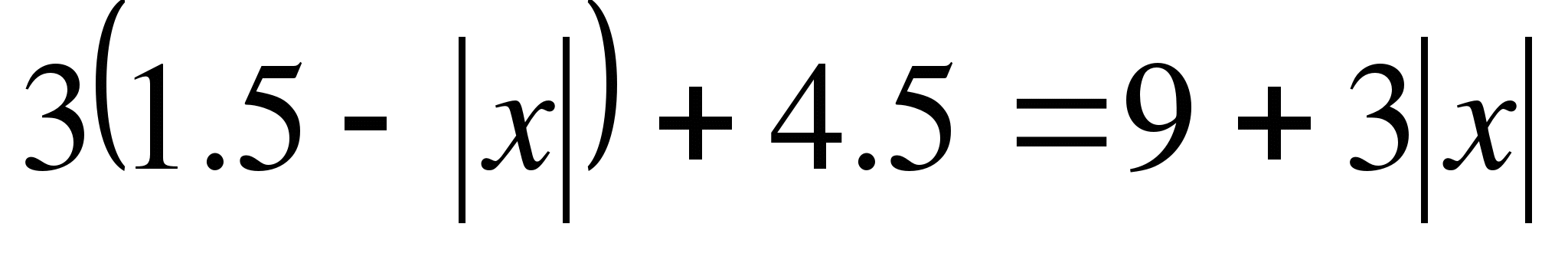 4. при каких значениях p уравнение
4. при каких значениях p уравнение
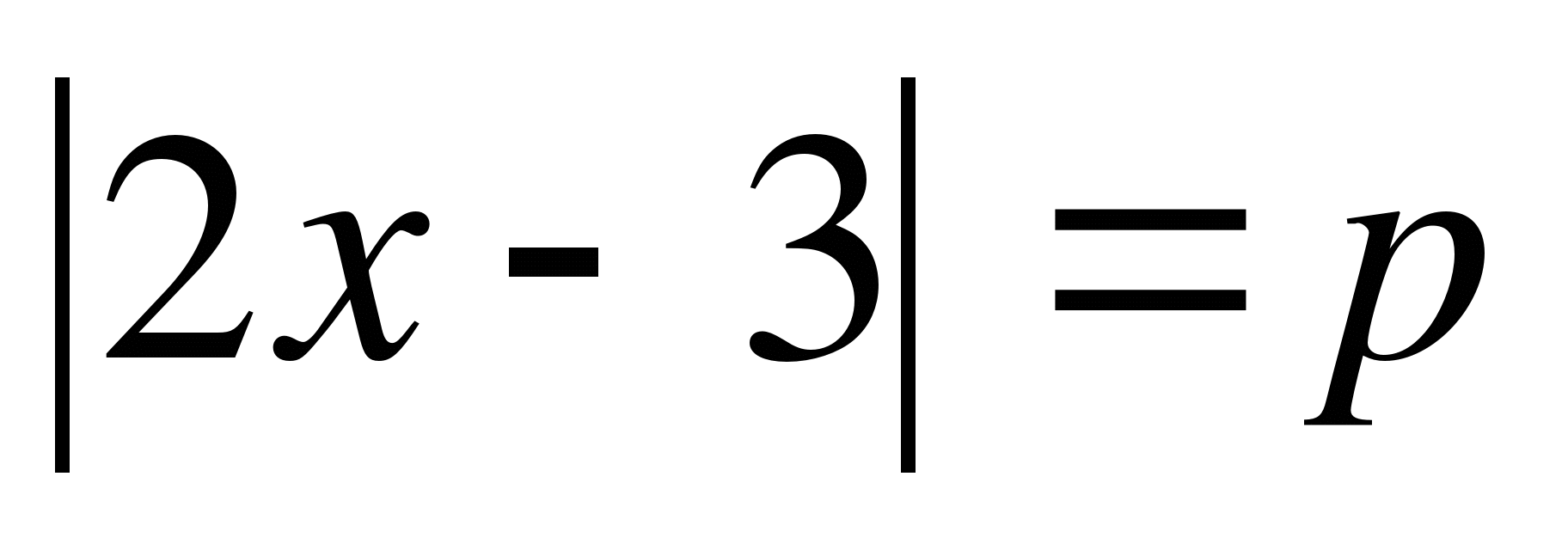
В 8 классе, после прохождения тем: «квадратные и дробные рациональные уравнения», увеличивается разнообразие уравнений, решение которых основывается на правилах которые конечно же обосновываются)
1.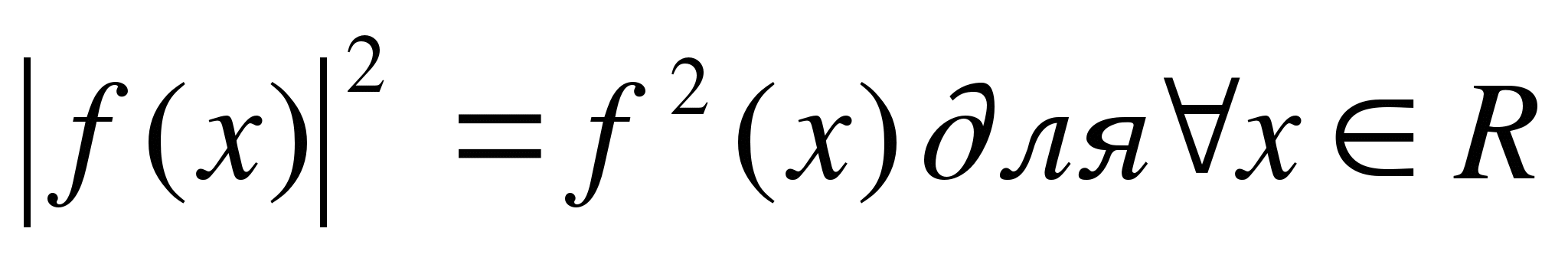
2.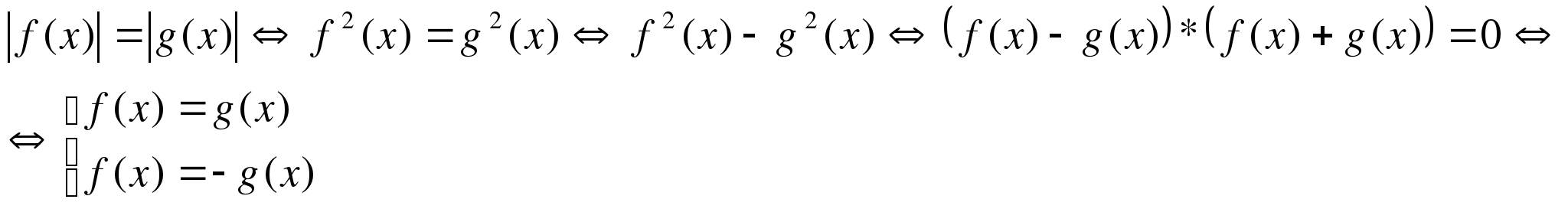
3. 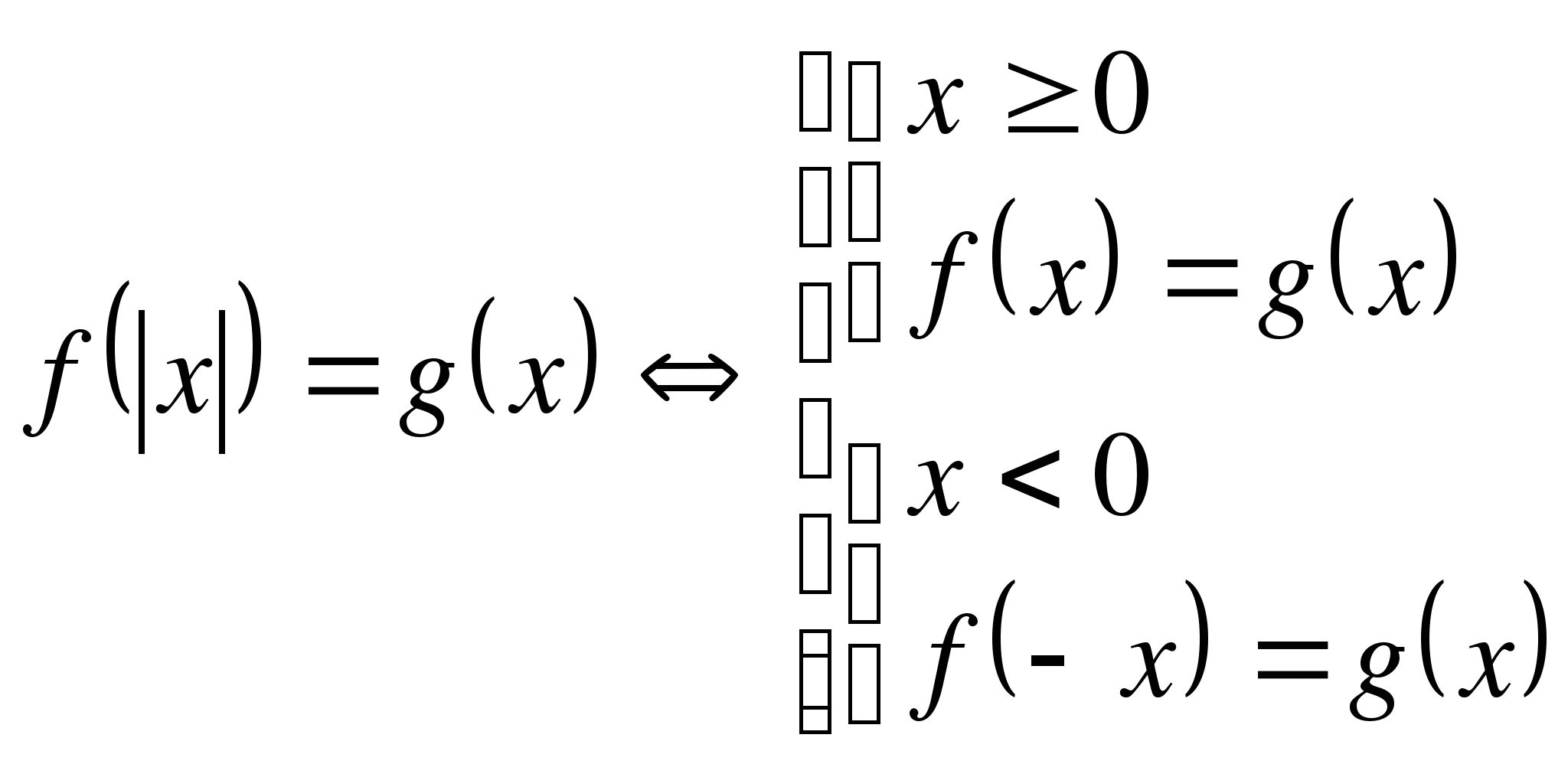
Например. а) 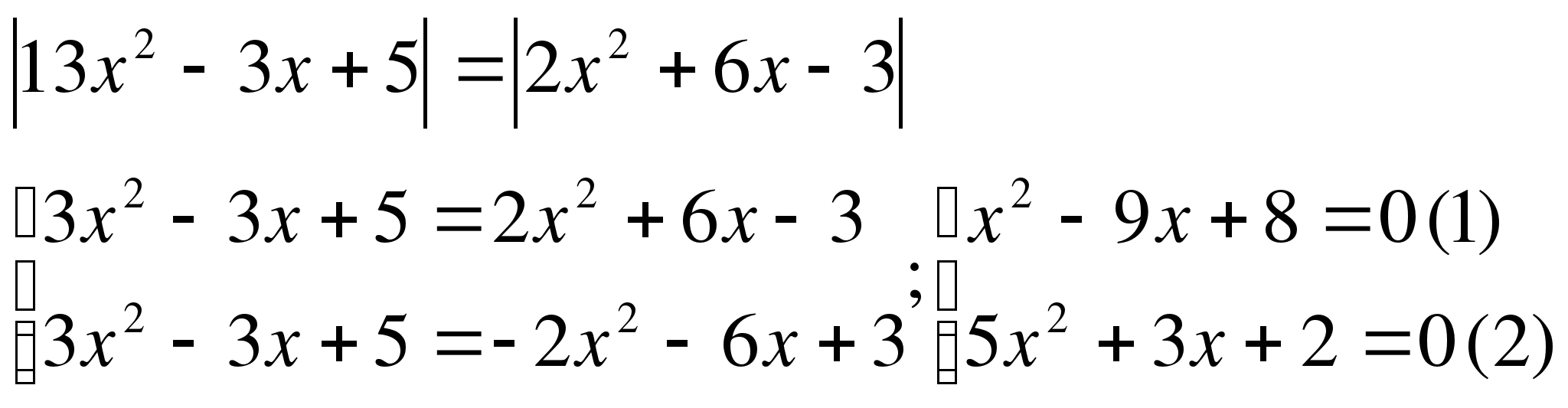
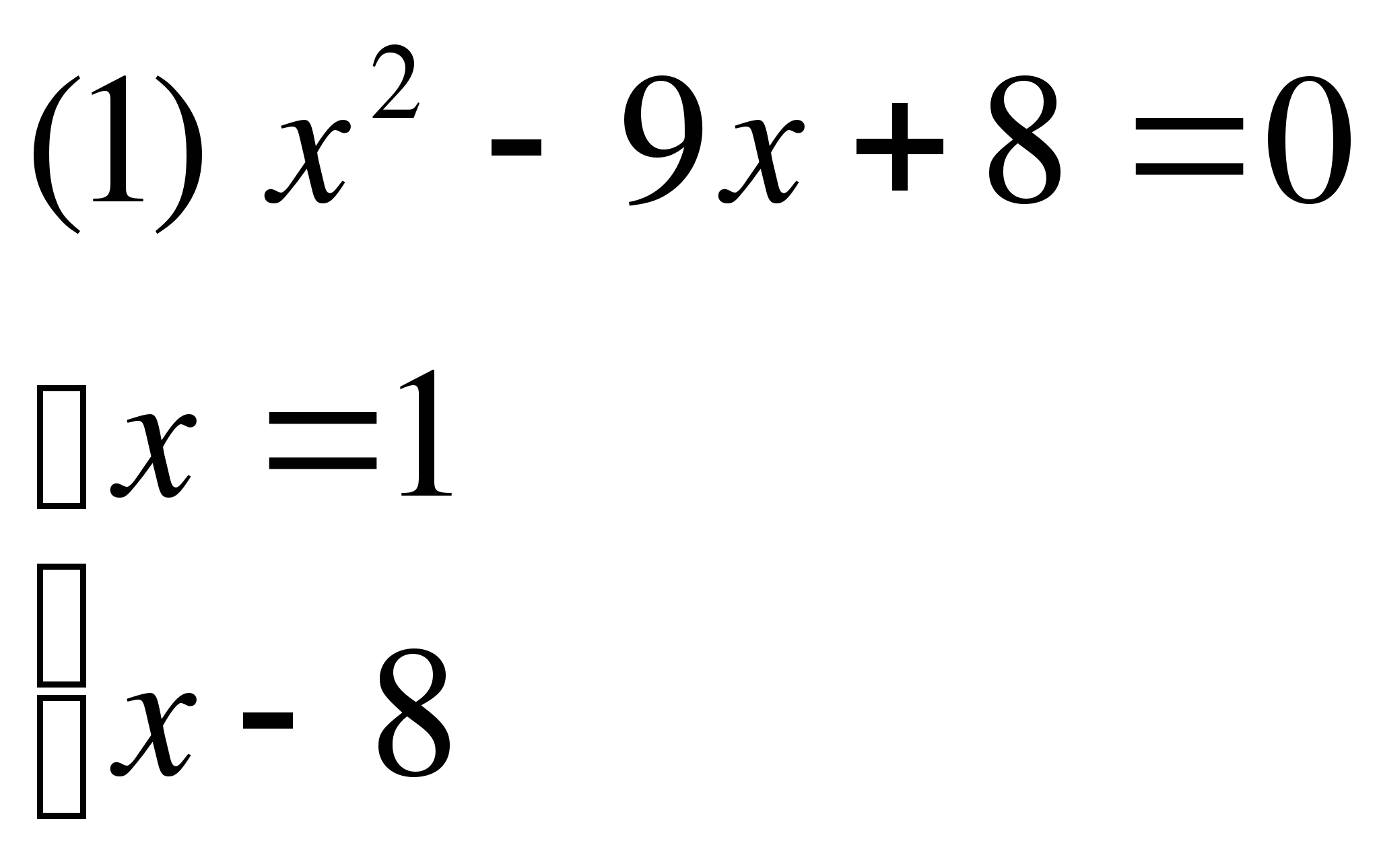
 Следовательно
Следовательно 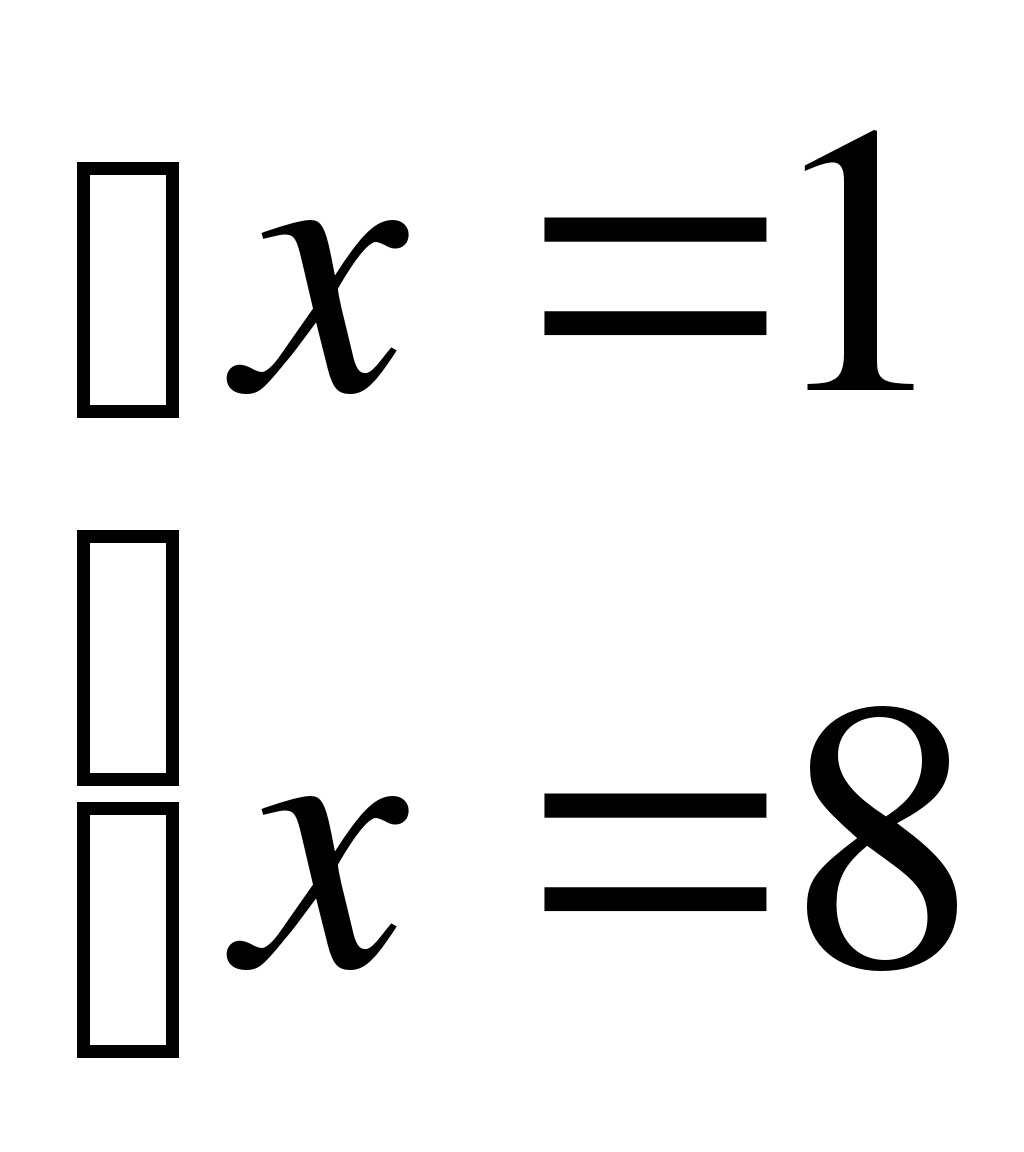 Ответ:1;8.
Ответ:1;8.
б) 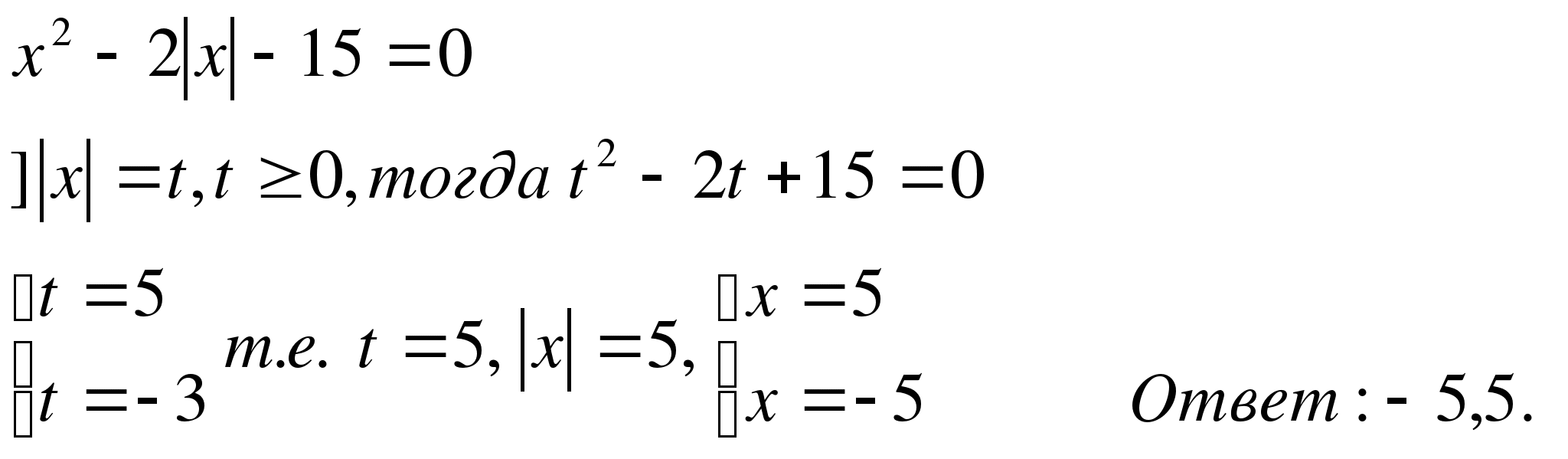
в) 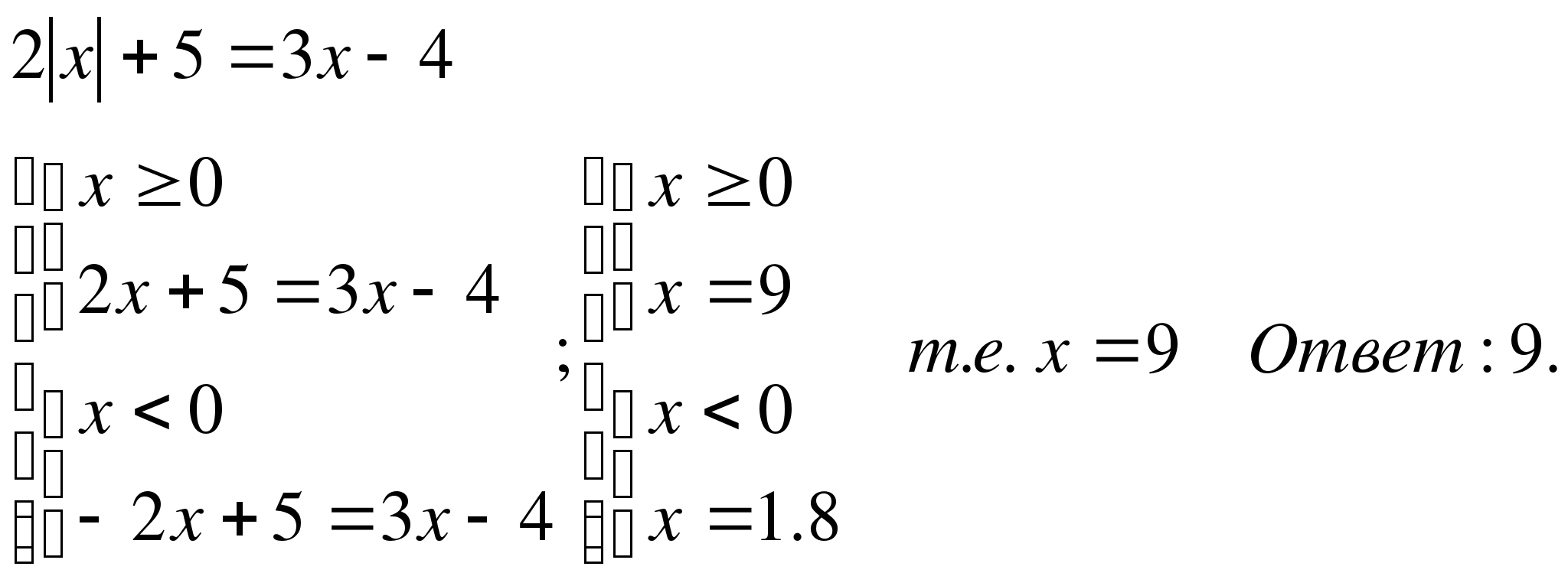

После изучения темы: «Неравенство с одной переменной и их системы» следует вывести следующие соотношения:
1. 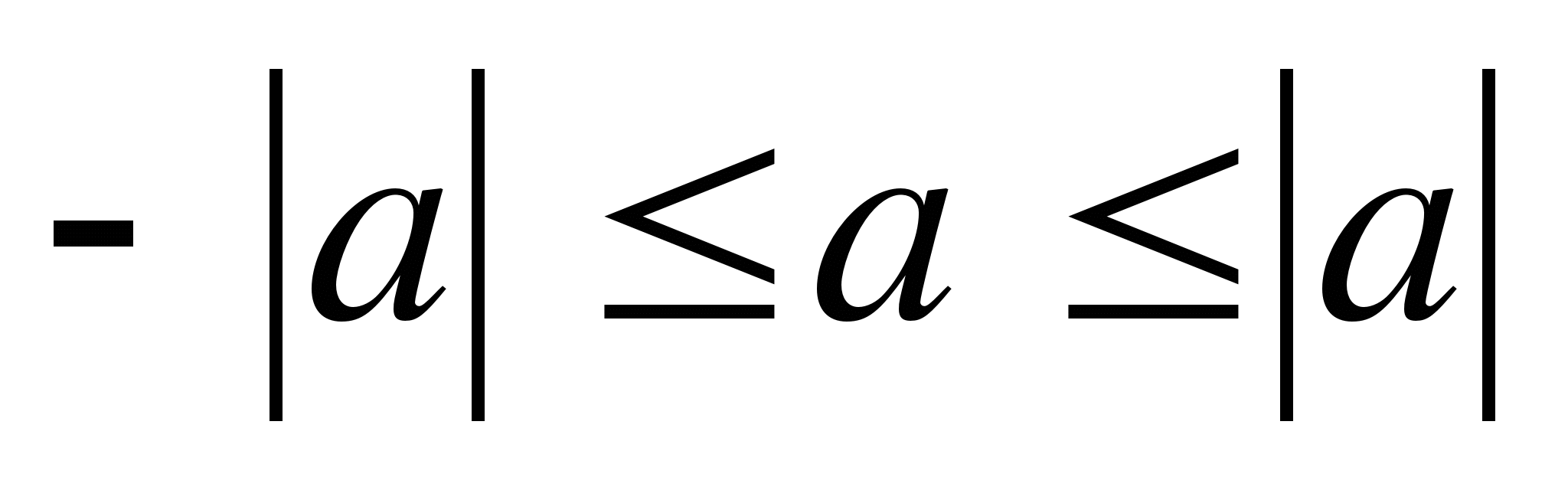
2. 
3. 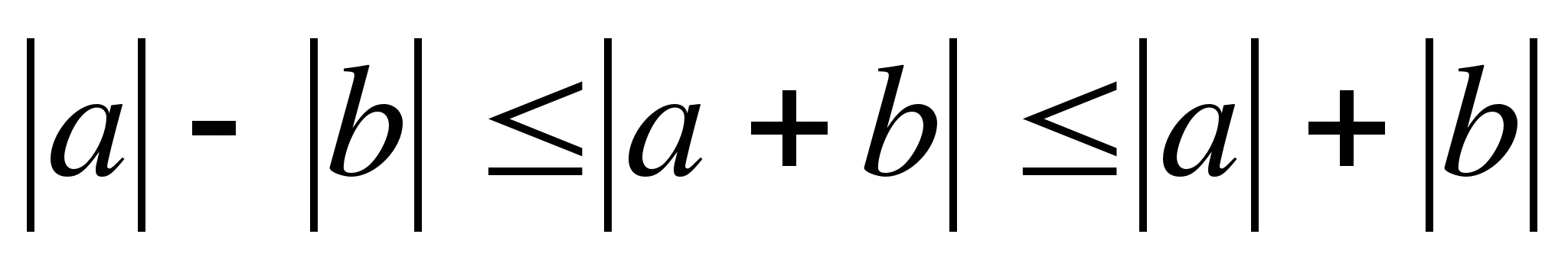
4. 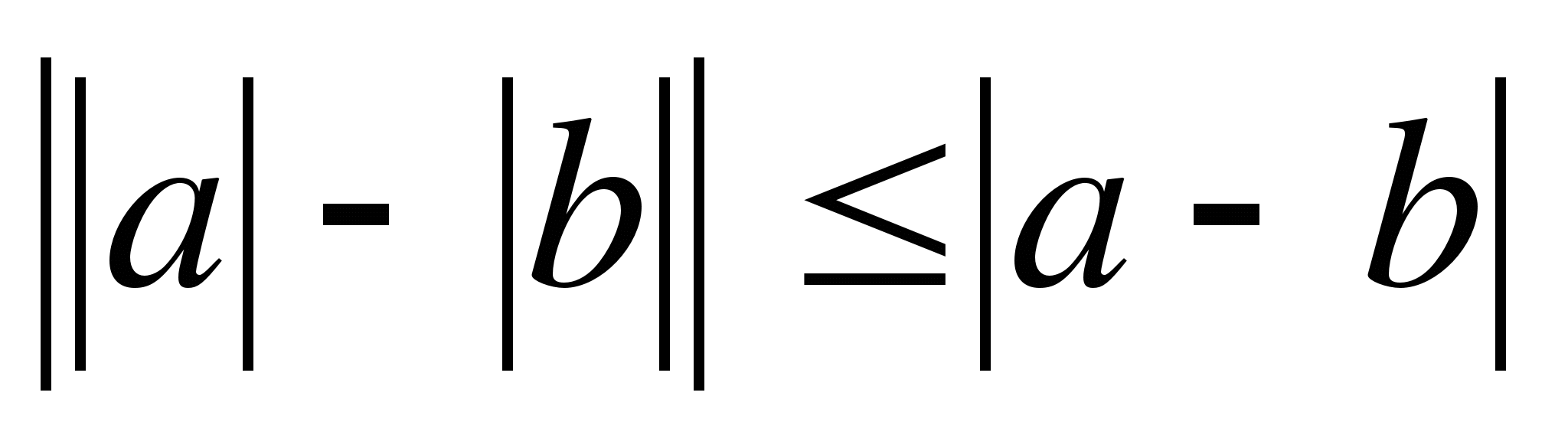
5. 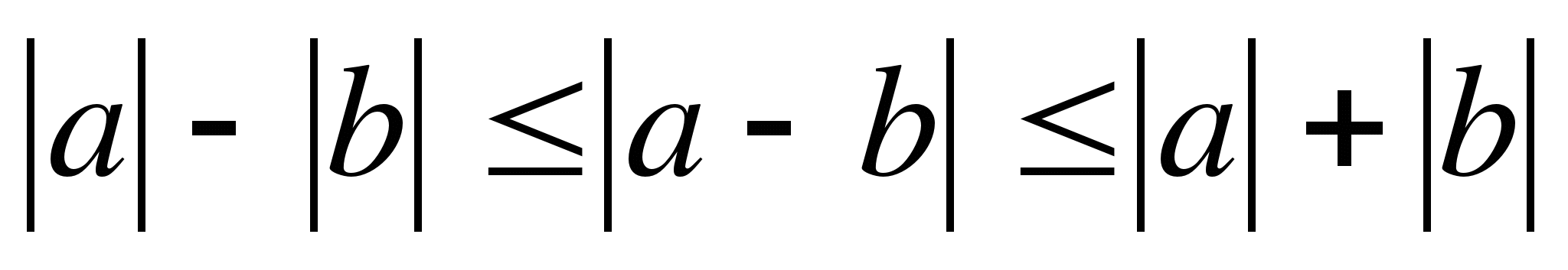
6. 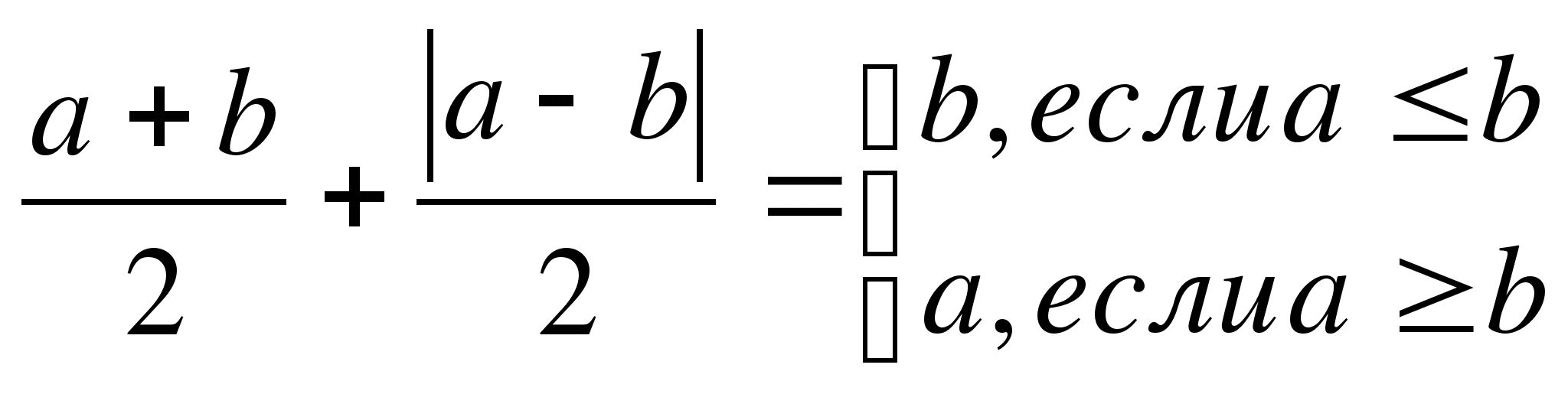
7. 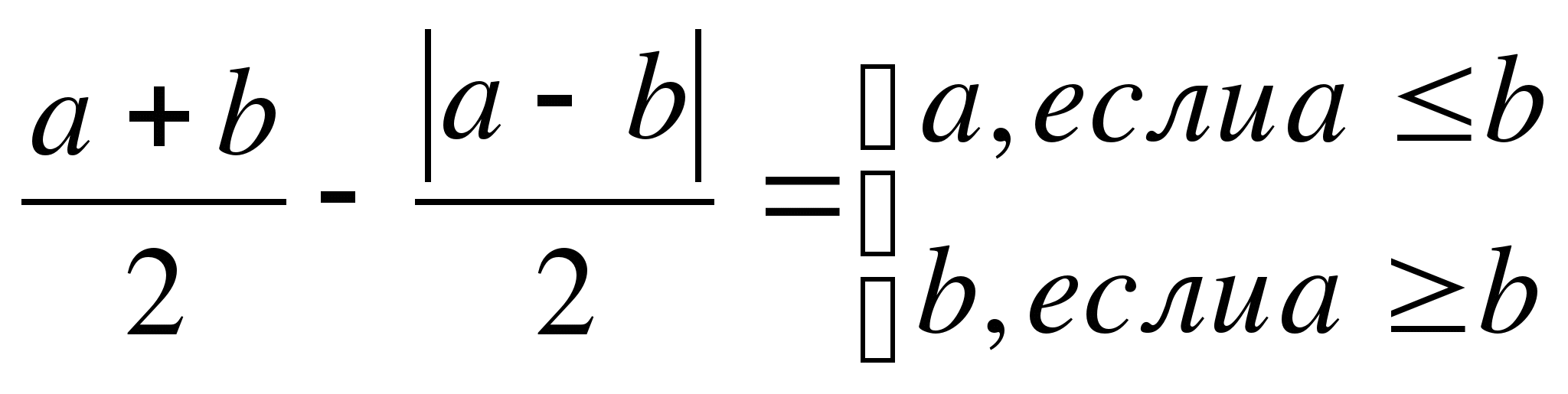
8. 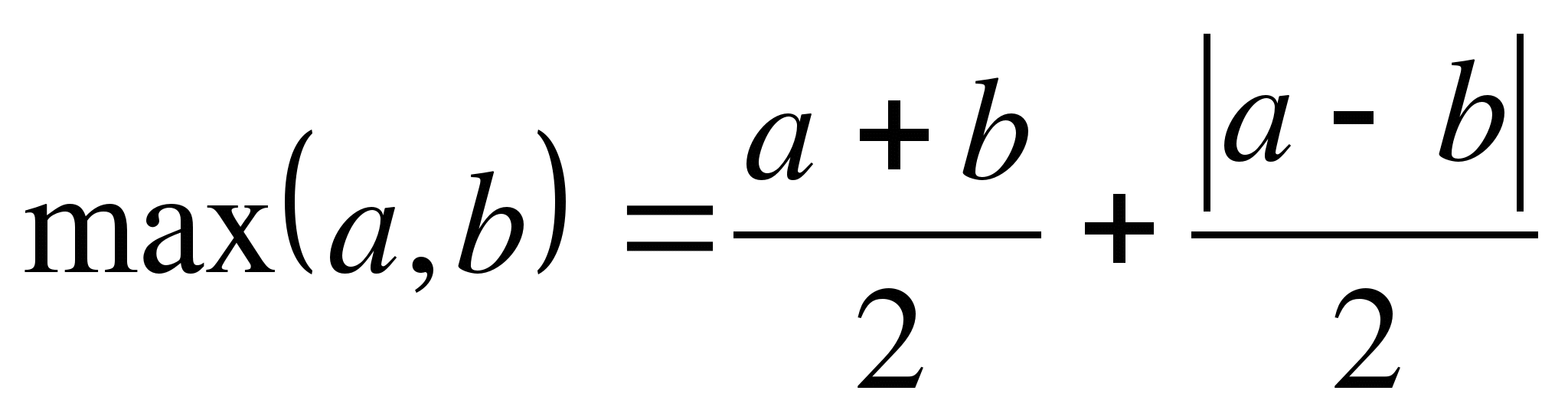
9. 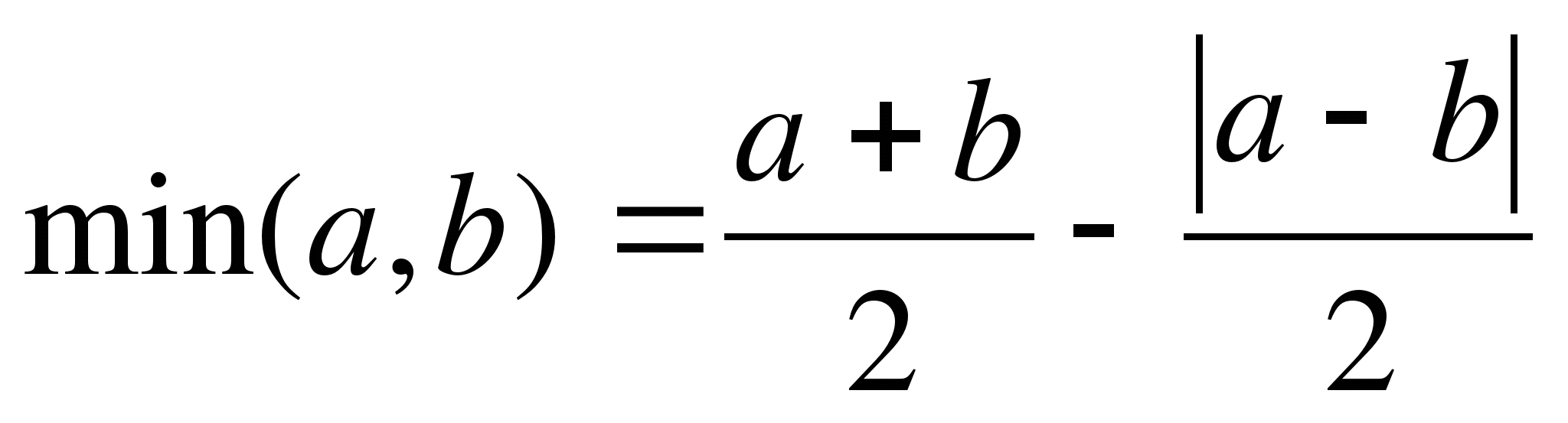
Доказательство этих соотношений очень хорошо приведены у В. П. Моденова «Математика»
Далее надо рассмотреть схемы решений следующих уравнений и неравенств:
1) 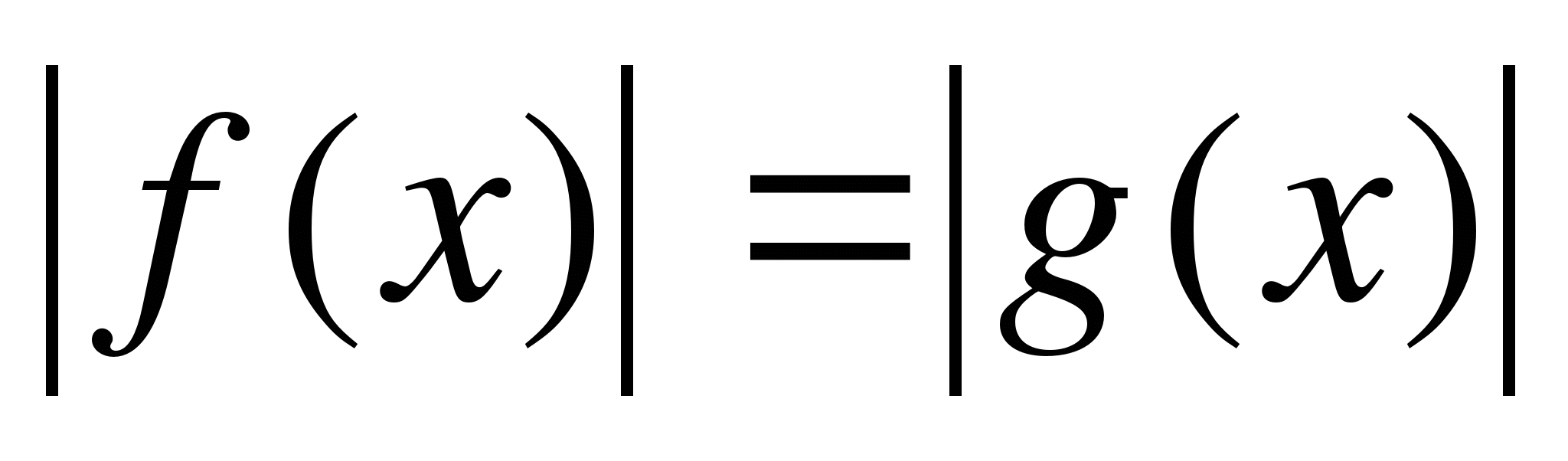
1 способ 2 способ
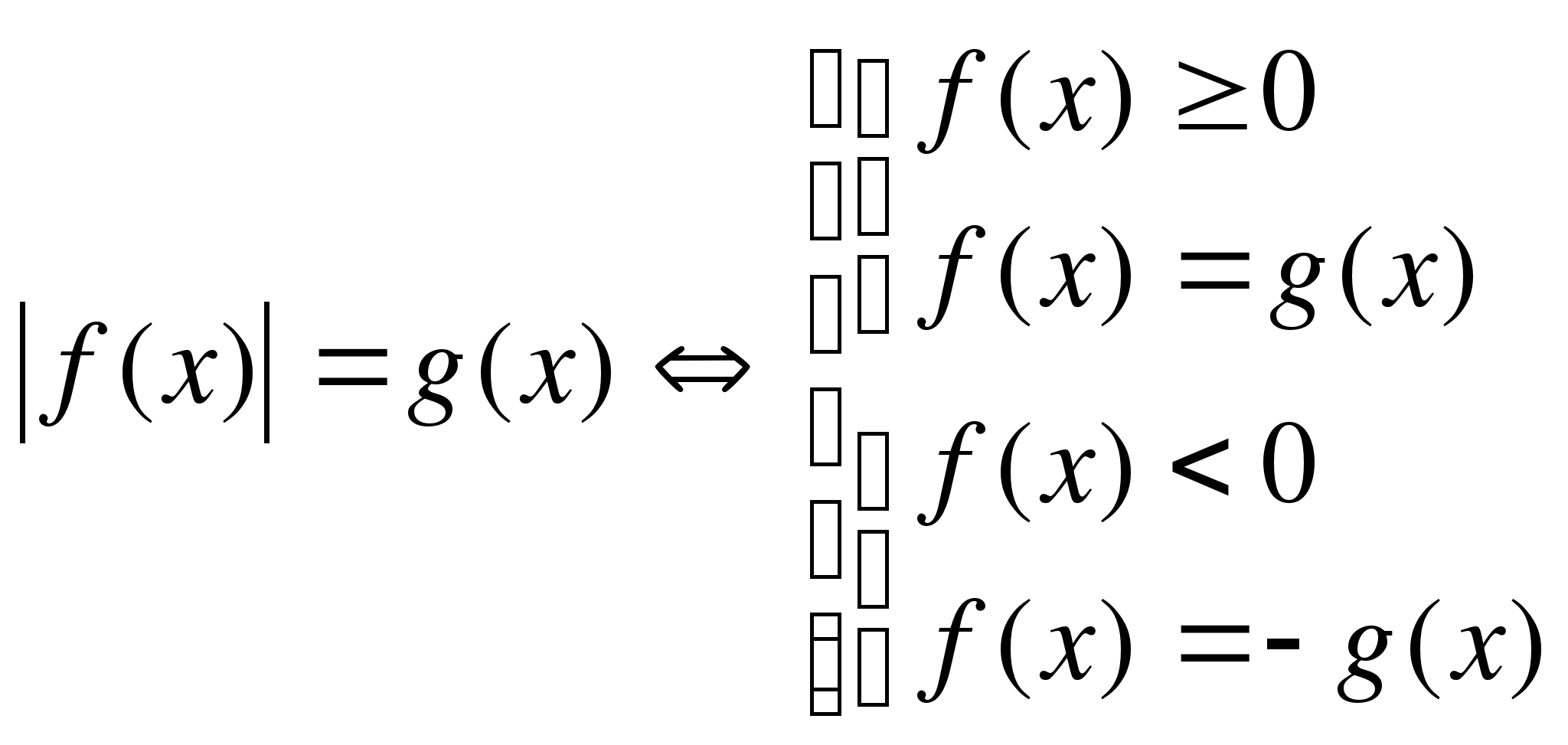
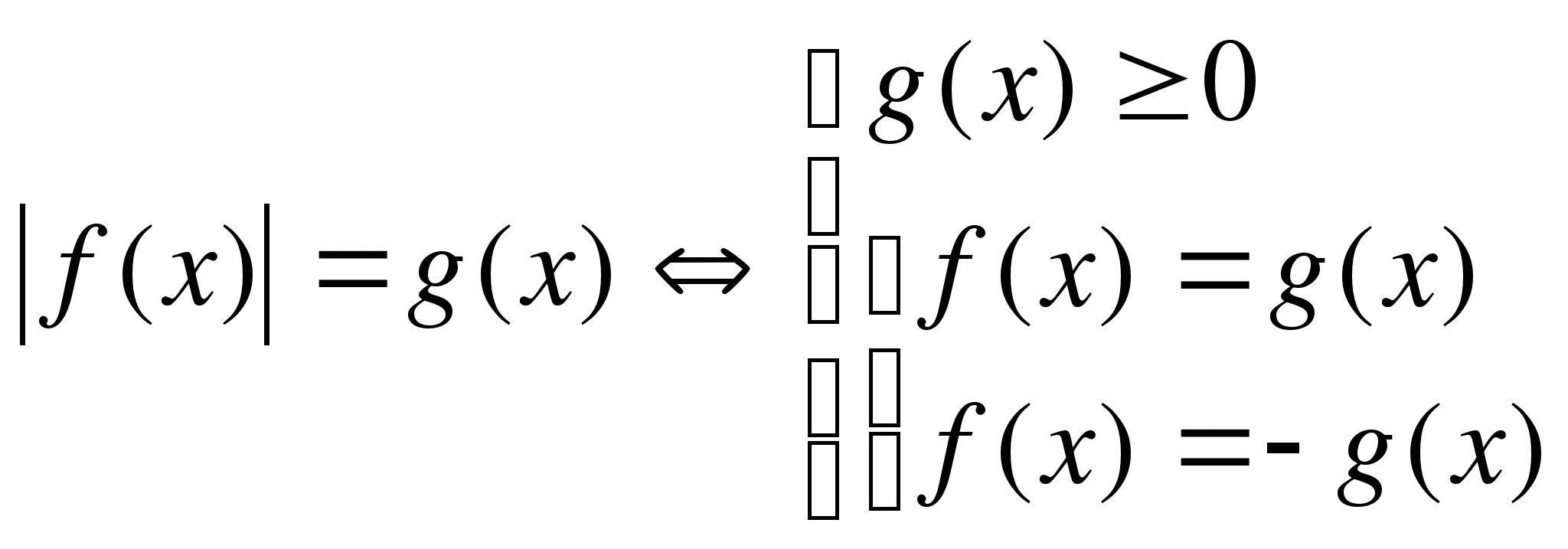
Второй способ хорош тем, что не надо сравнивать f(x) с нулём
Например, 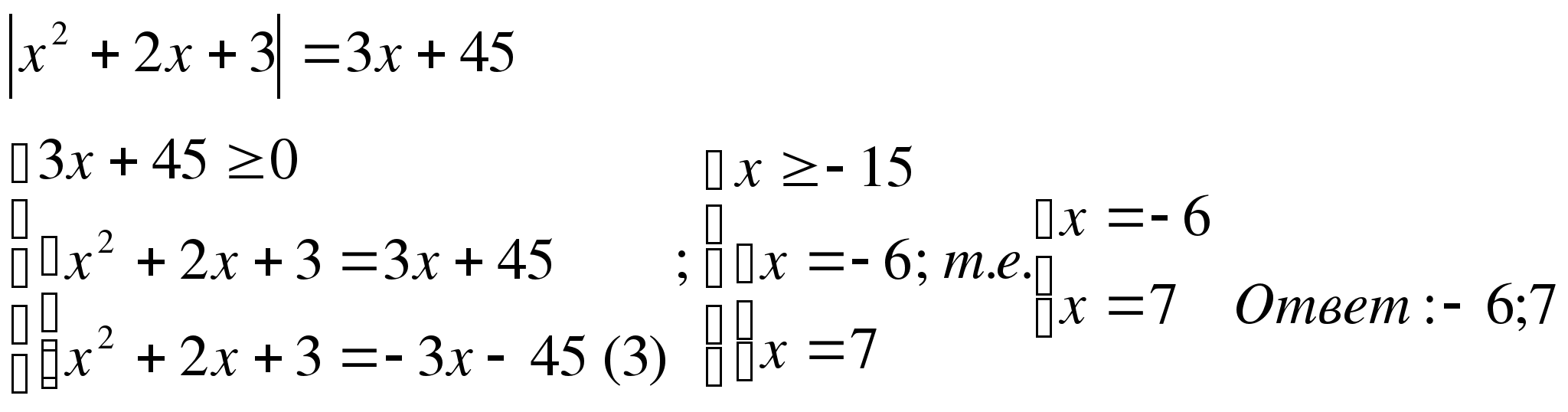
(3) 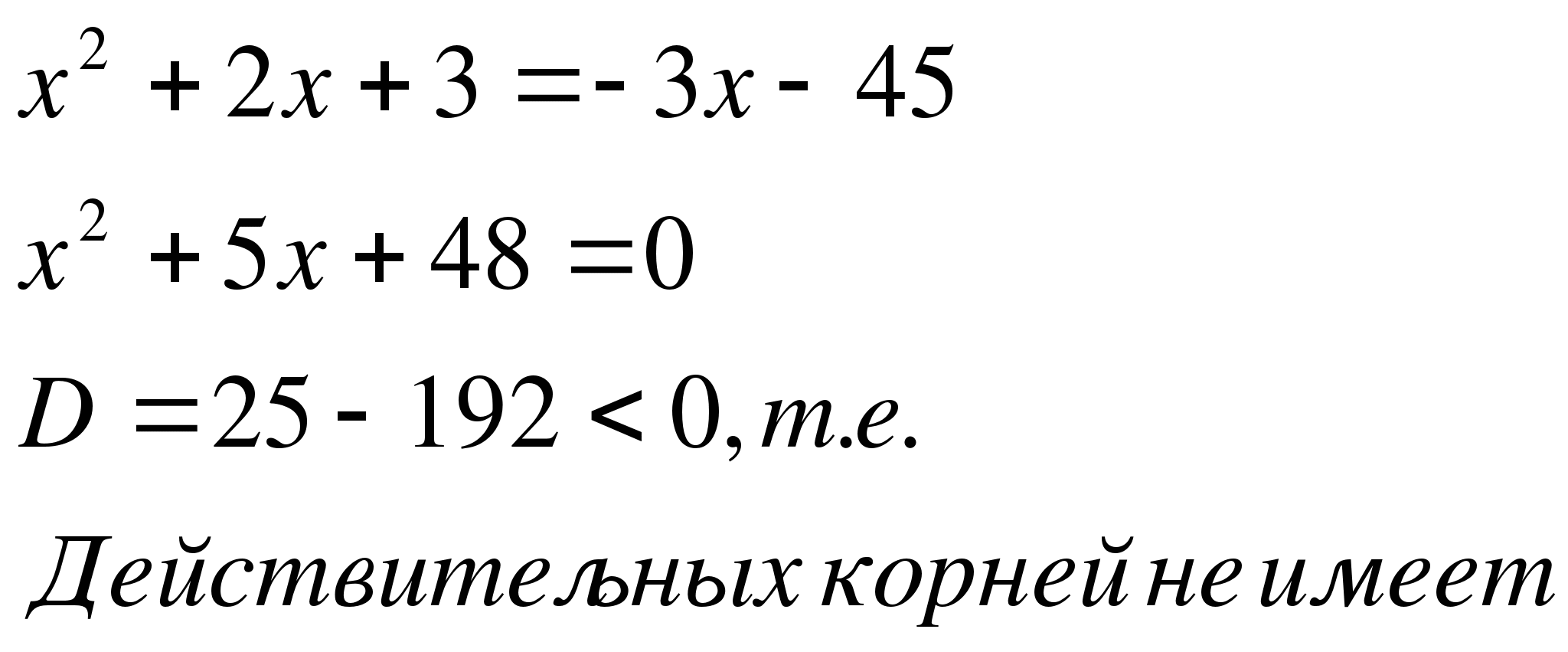
2) 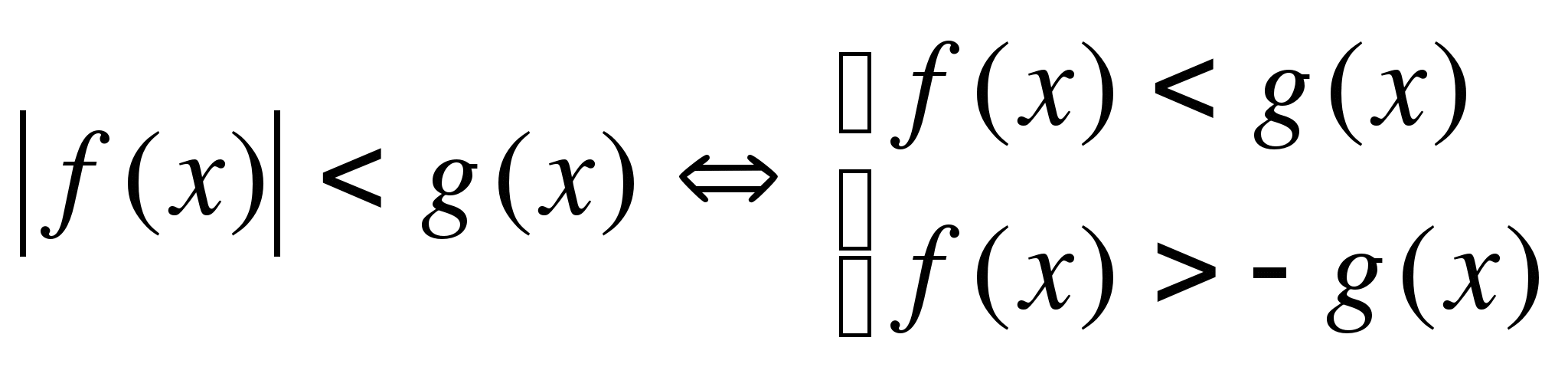
3) 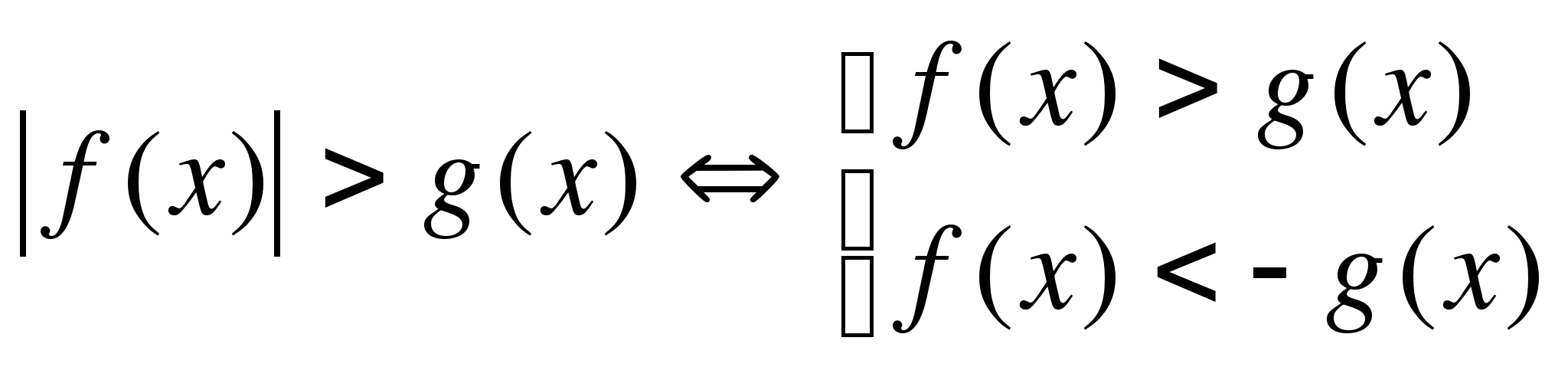
4) 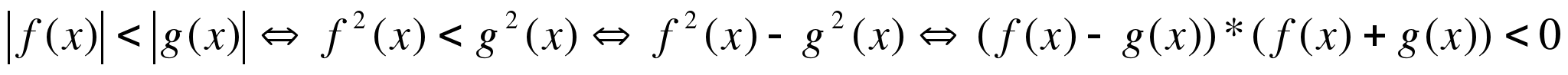
5) 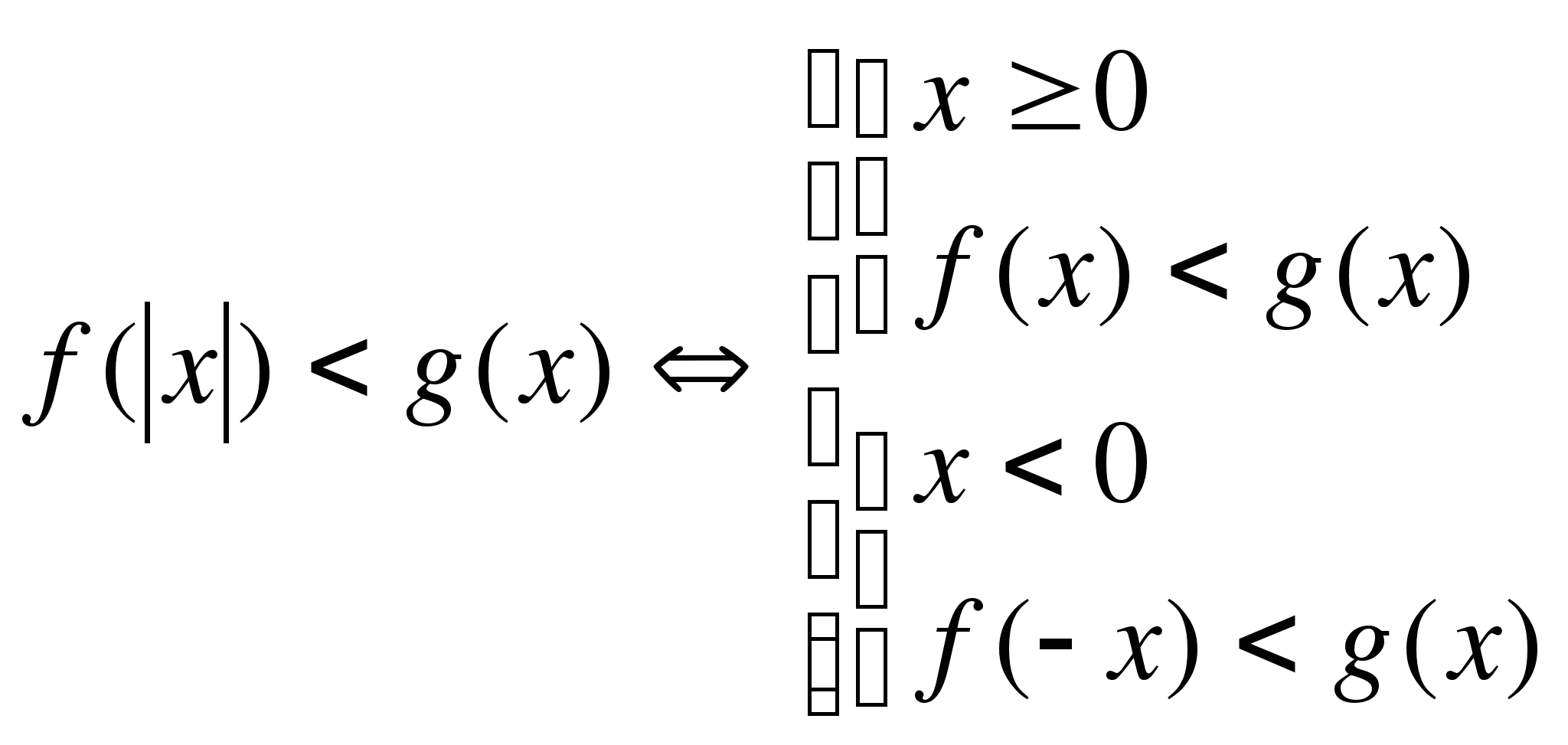
Все эти схемы надо отрабатывать на занятиях, которые не являются сложными. Так как, на первых уроках, самое главное это – теория.
а) 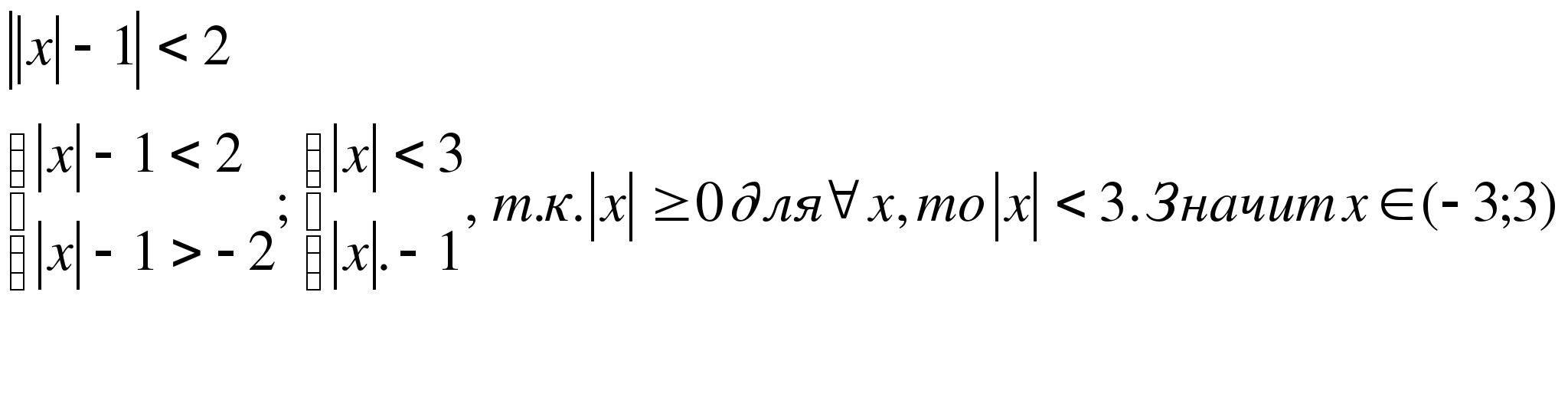
Ответ: 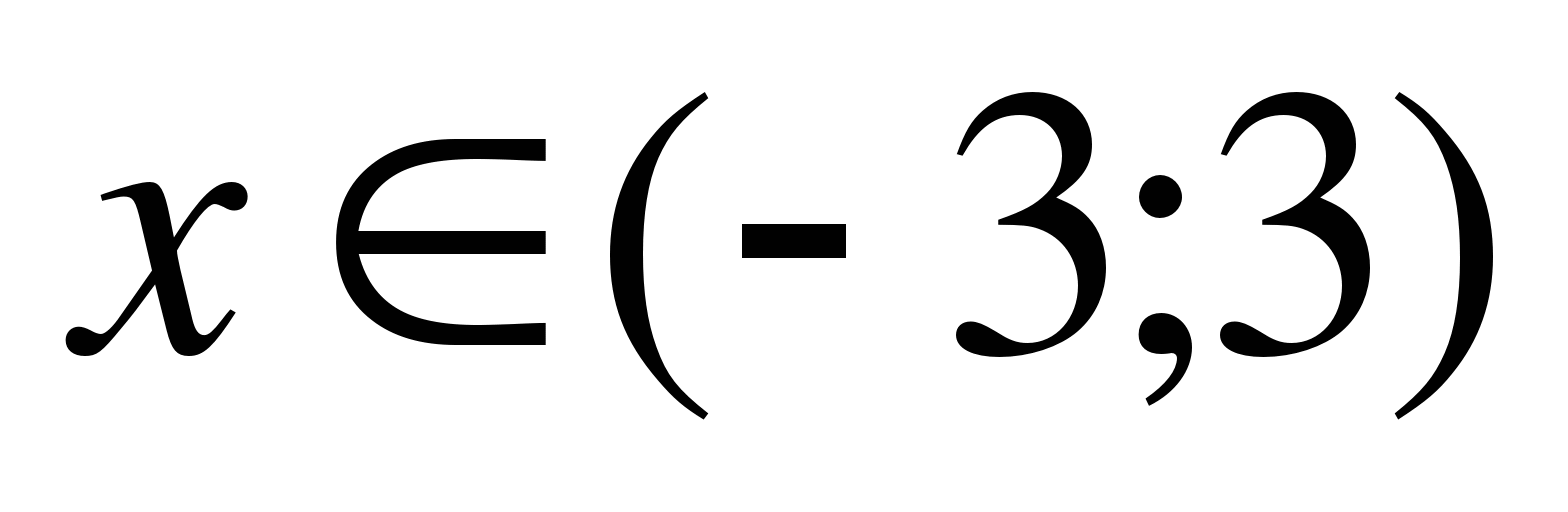
б) 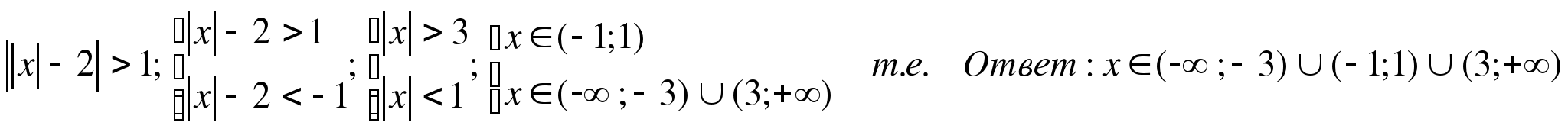
в) 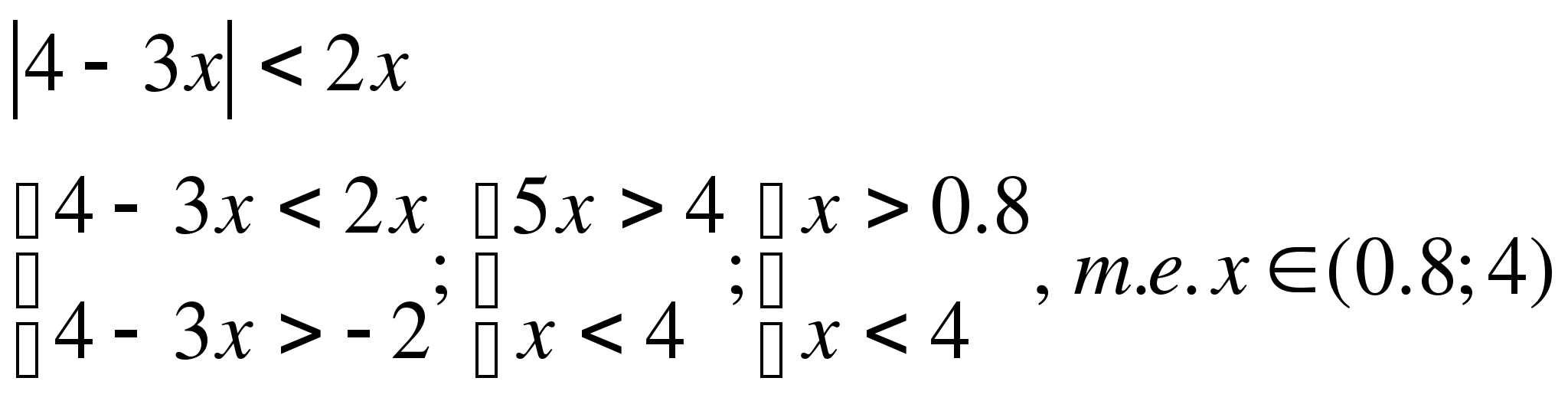
Ответ: 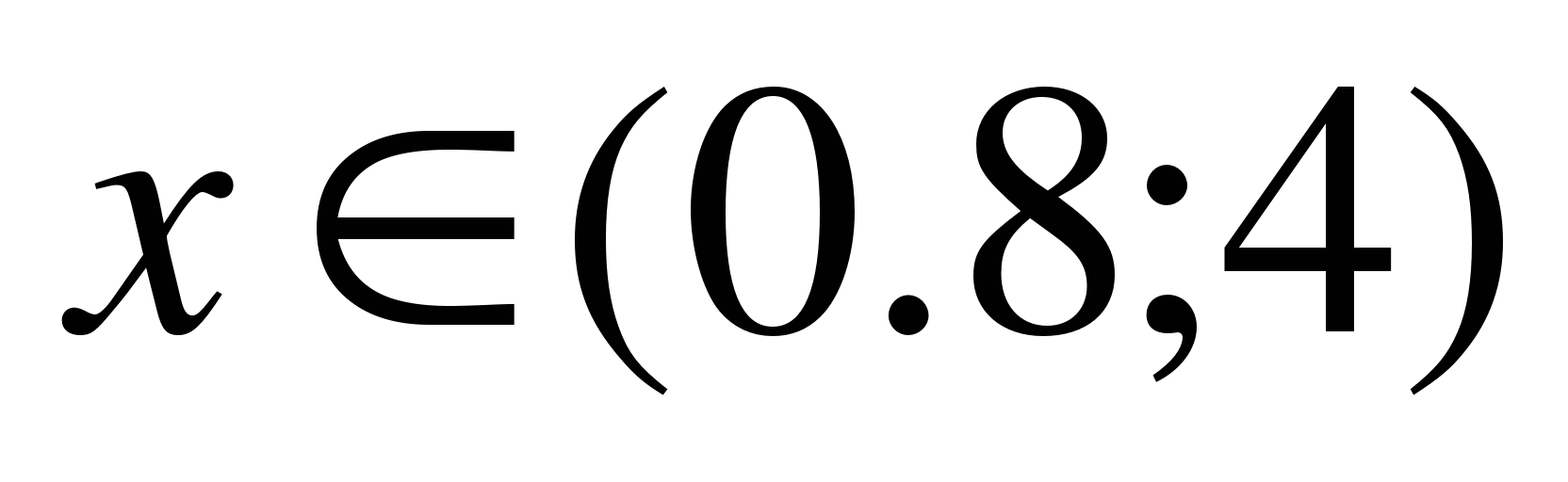
г) 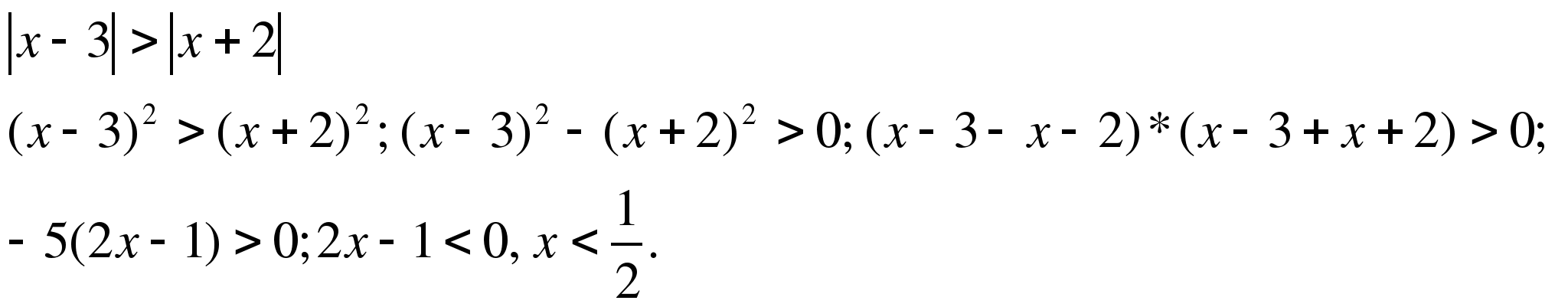
Ответ: 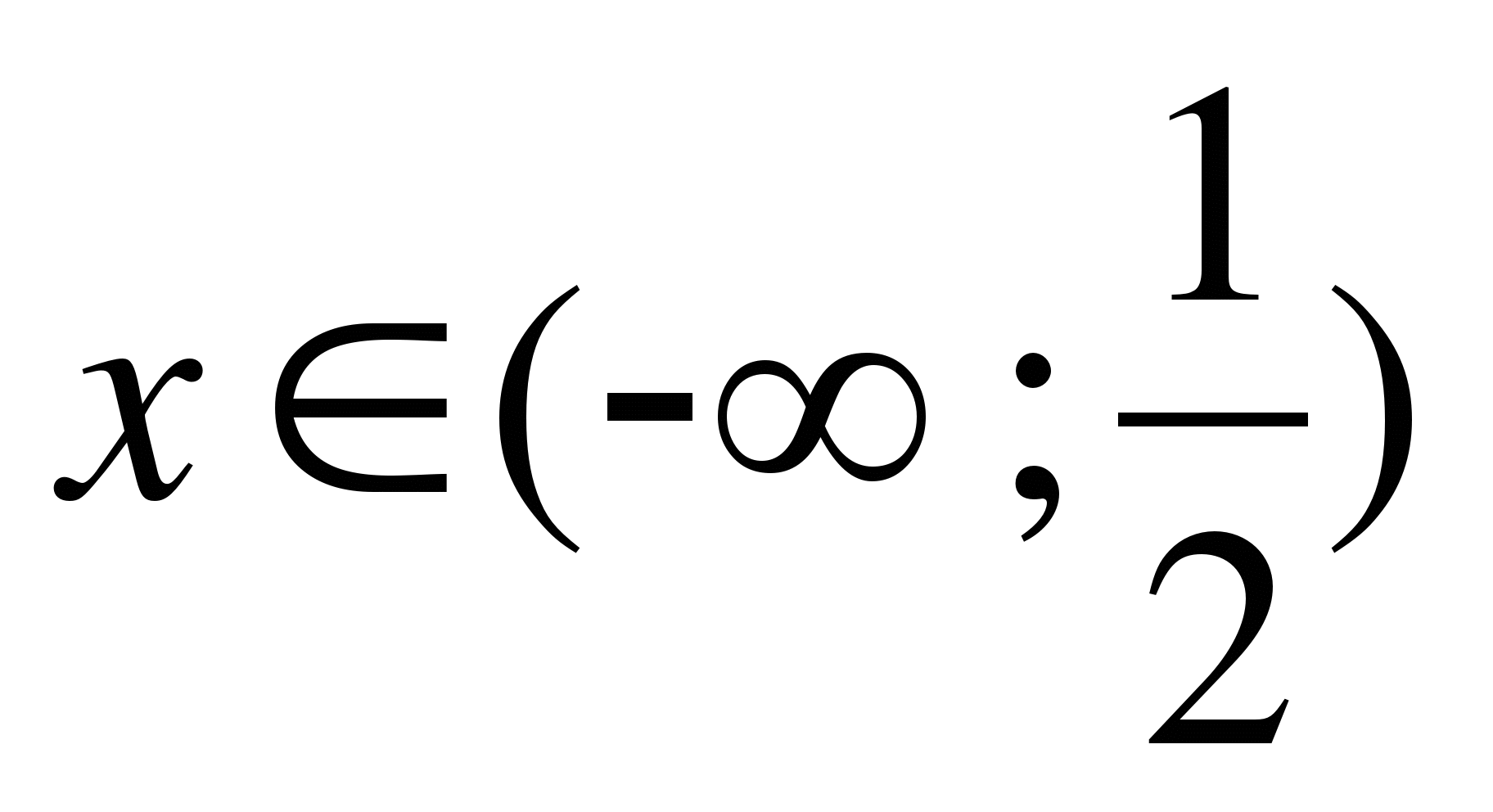
В девятом классе, после изучения квадратных неравенств, все предыдущие схемы просто надо разнообразить. А вот после «Метода интервалов» остаётся рассмотреть решение уравнений и неравенств содержащих более одного модуля
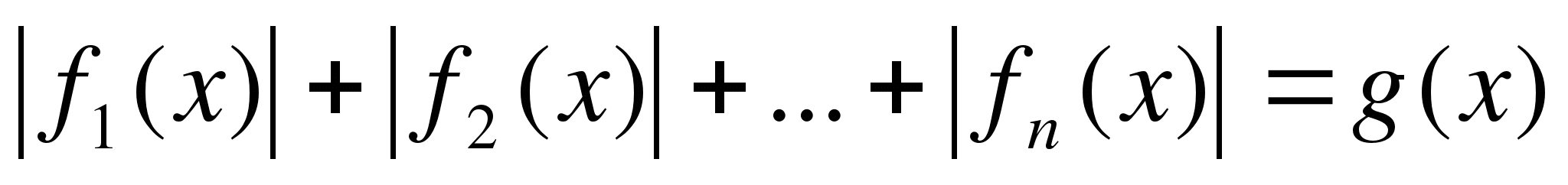
Находят О.Д.З. исходного уравнения
Определяют точки разрыва и нули функции

На каждом из промежутков, на которые найденные точки разбивают О.Д.З, исходное уравнение заменяется равносильным, не содержащим знаков абсолютной величины (это возможно в силу того, что функции на этих промежутках знакопостоянны).
1. 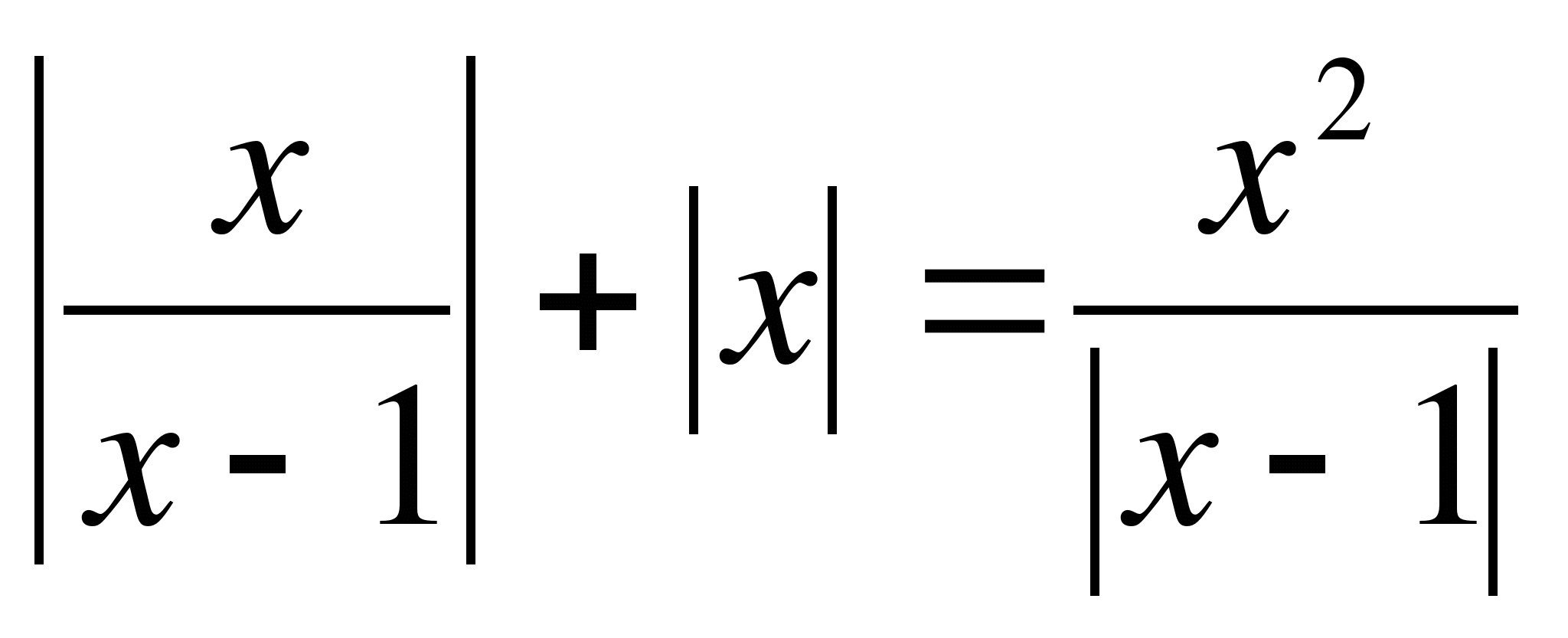
1) О.Д.З. 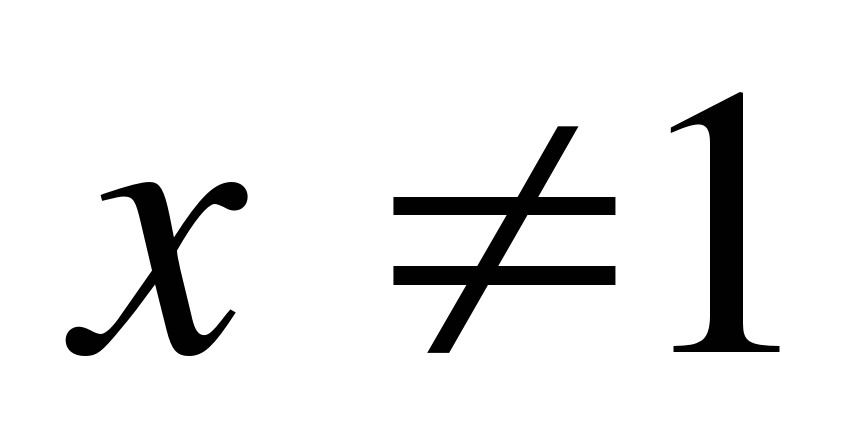
2) Нули модуля: x=0
3)




 x
x
х + 0 — 1 +
х-1
x — + +
x-1 — — +
Тогда исходное уравнение равносильно совокупности систем:
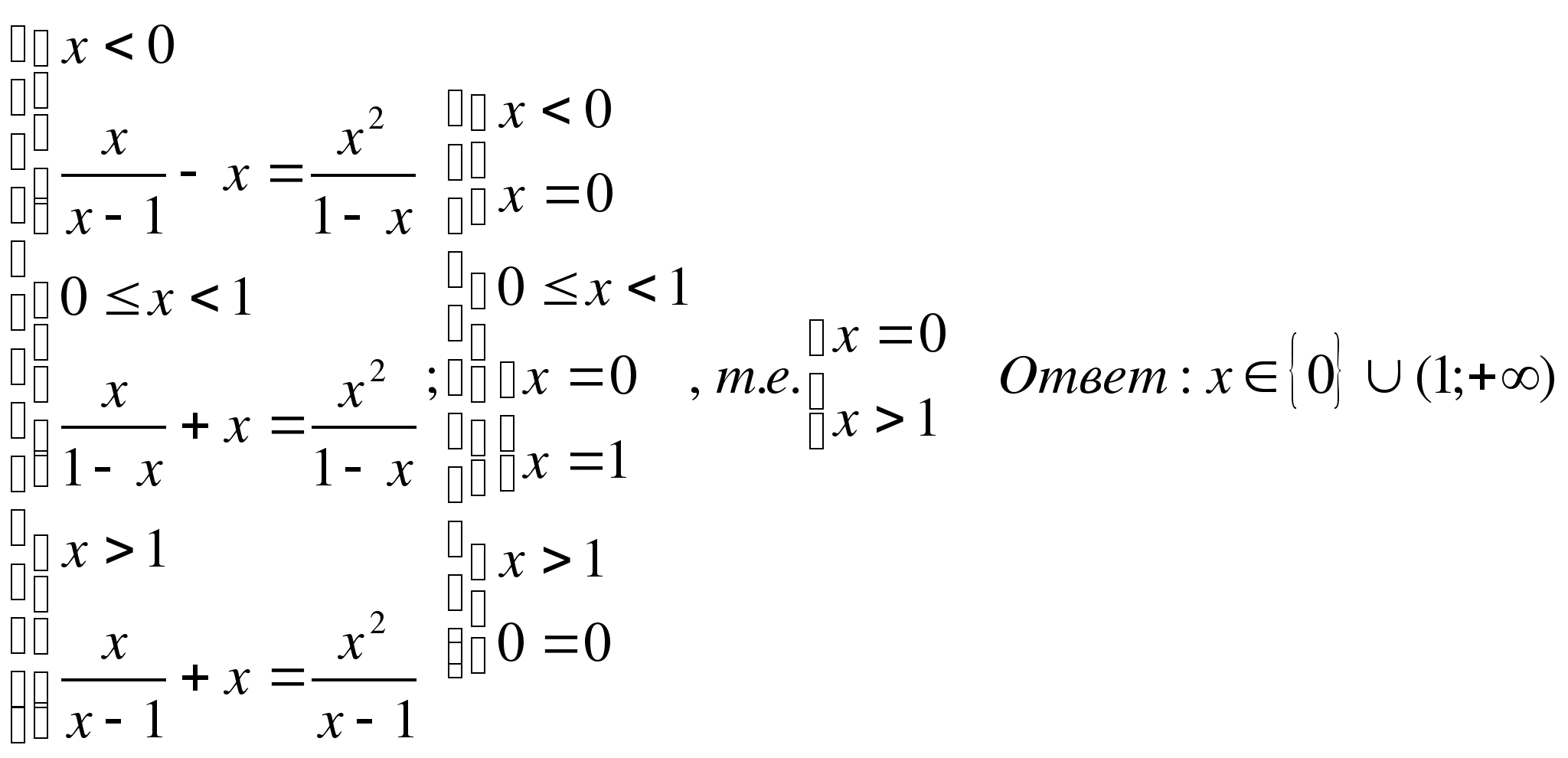
2. 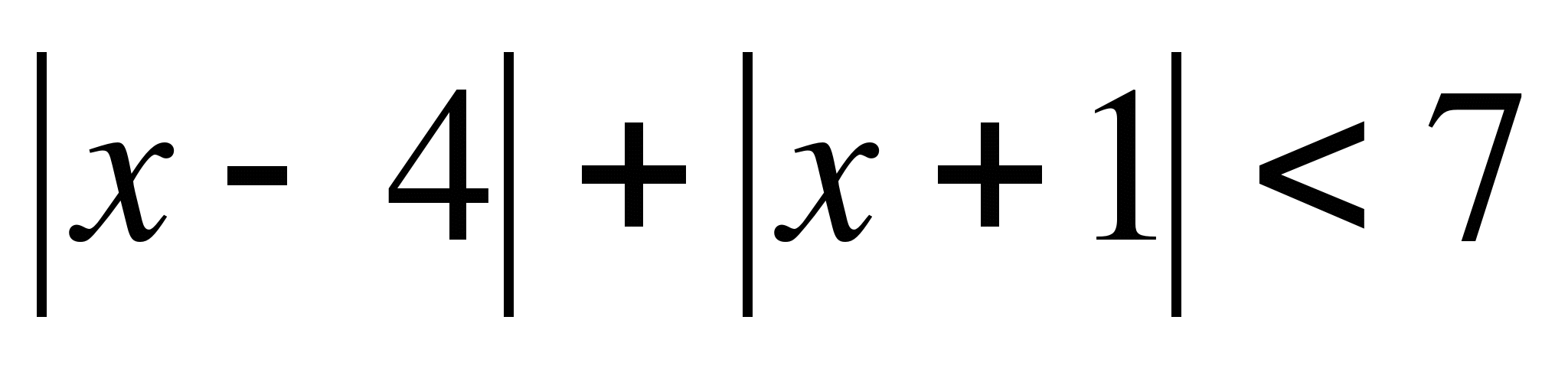
1. О.Д.З. 
2. Нули модуля: 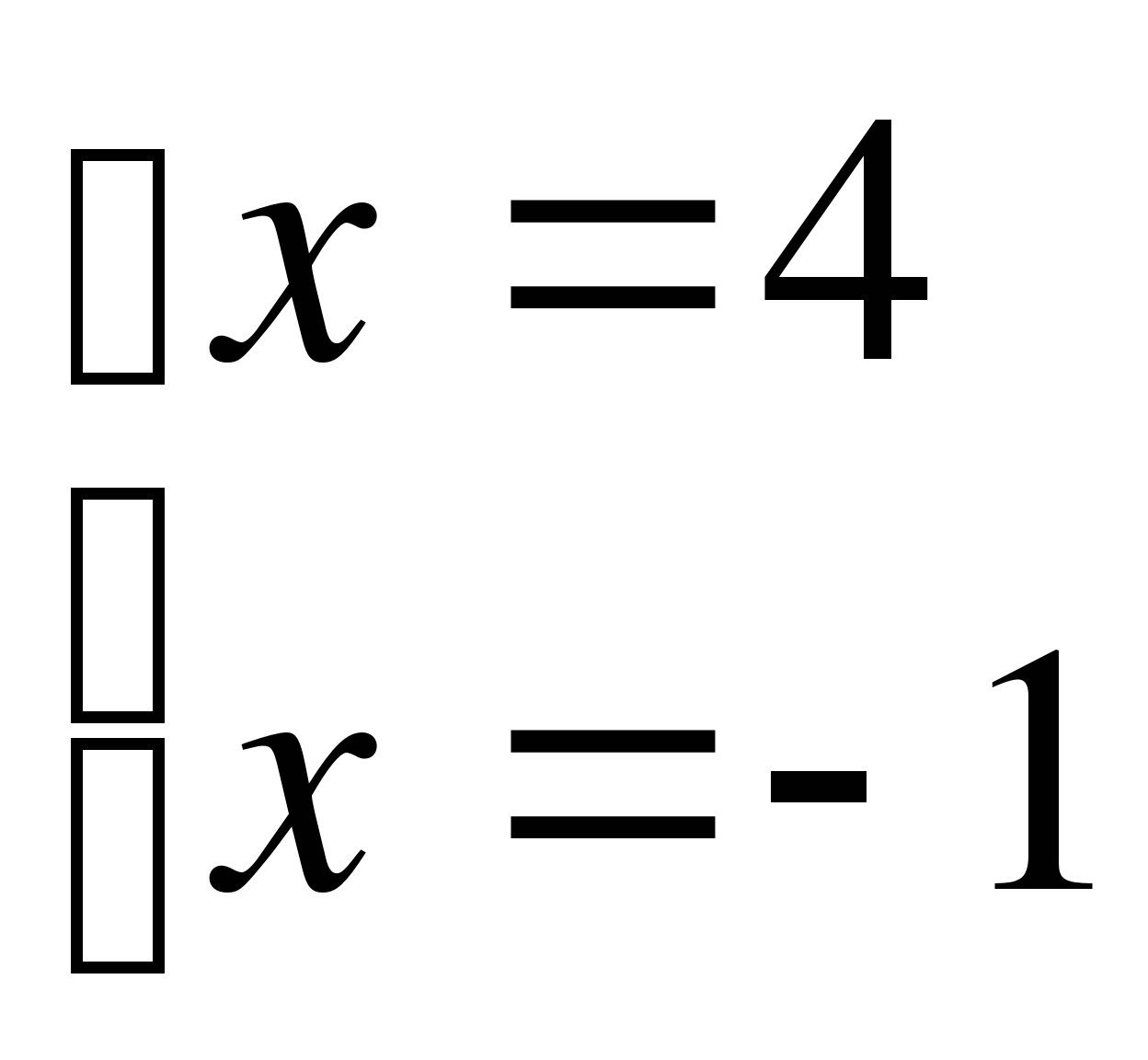
3.



 -1 4 x
-1 4 x
x-4 — — +

x+1 — + +

Тогда данное неравенство равносильно совокупности систем неравенств:
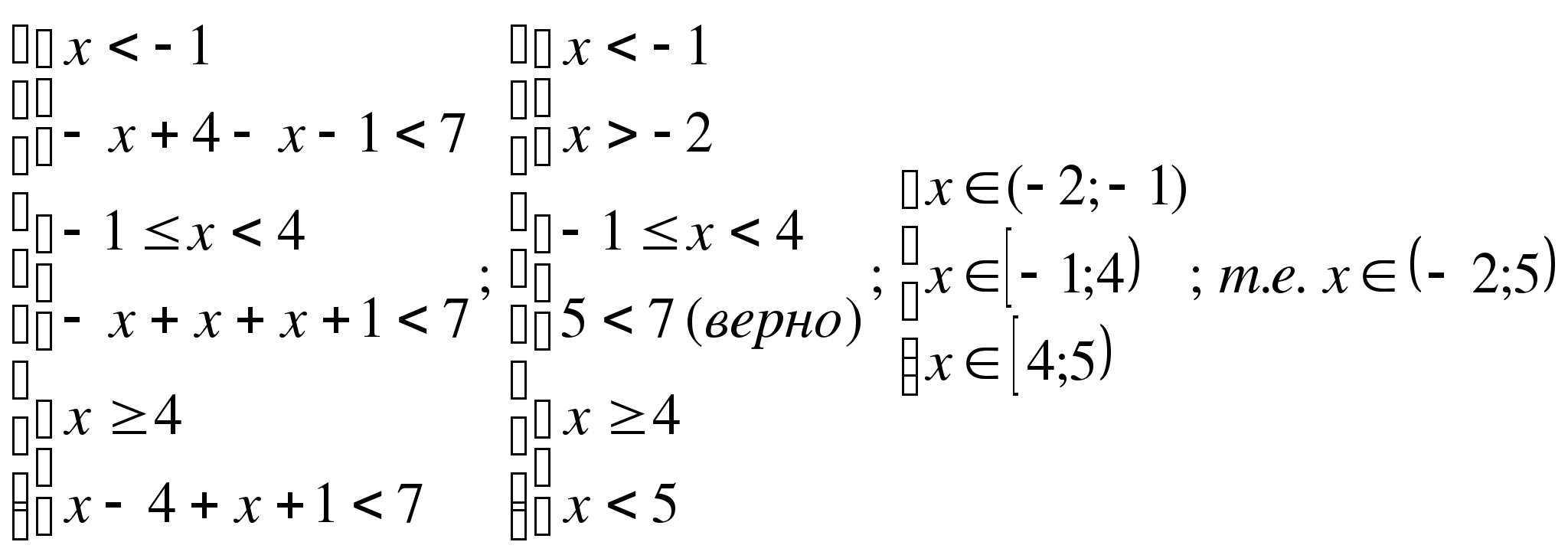
Ответ: 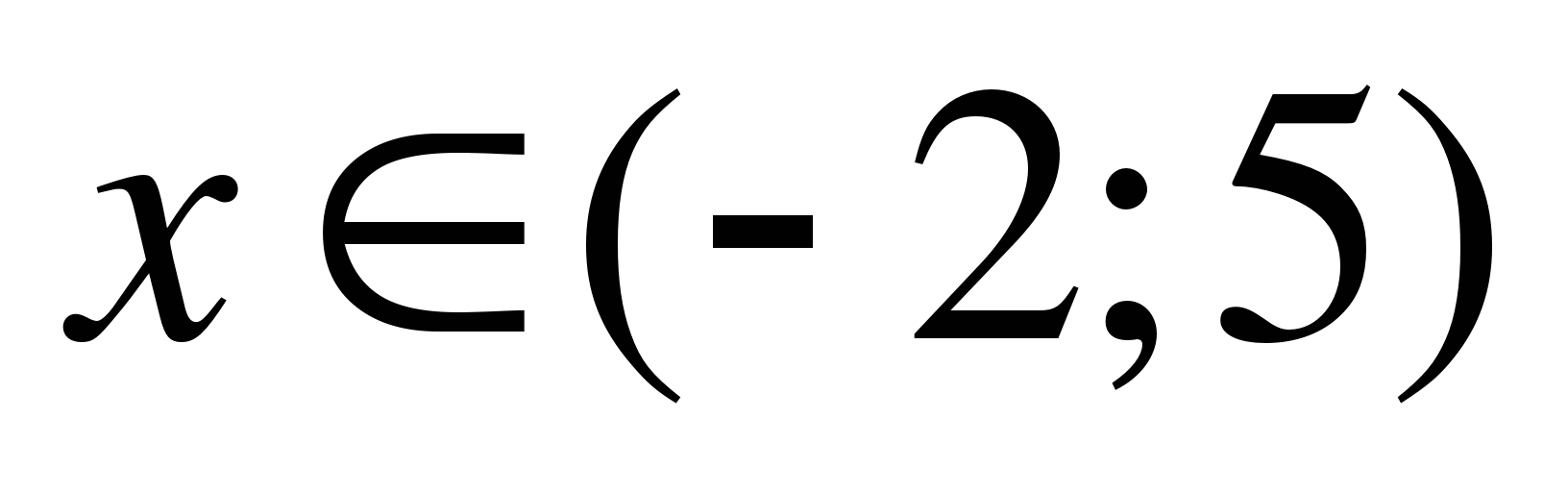
В конце 9 класса следует оставить время для разбора некоторых способов решения уравнений и неравенств с параметром. Учащиеся уже знакомы с графиком функции 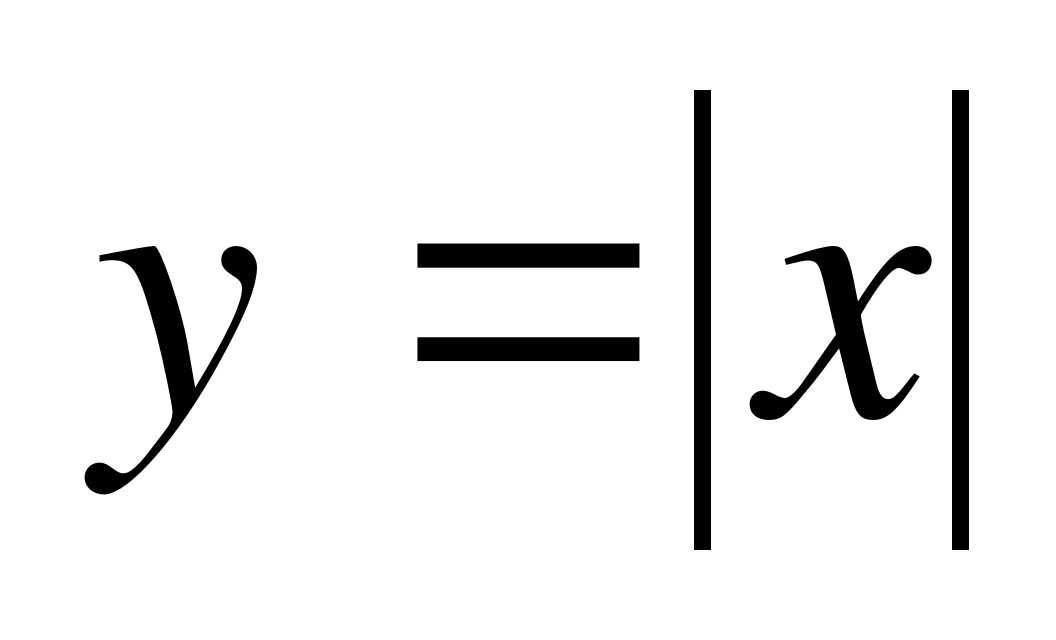 и построением графиков с помощью преобразований. Полезно выполнить построение графиков с модулями, симметрией. Рассмотреть графики неравенств.
и построением графиков с помощью преобразований. Полезно выполнить построение графиков с модулями, симметрией. Рассмотреть графики неравенств.
1. 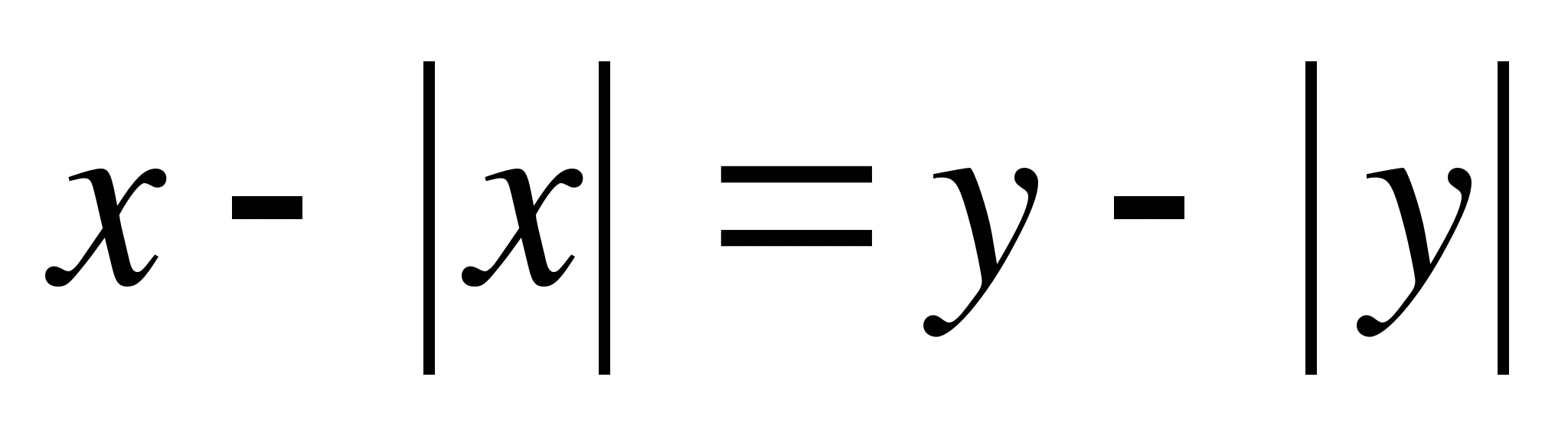
Рассмотрим все случаи раскрытия модулей. Чтобы долго не выписывать, можно записывать формулы прямо в соответствующих координатных четвертях.
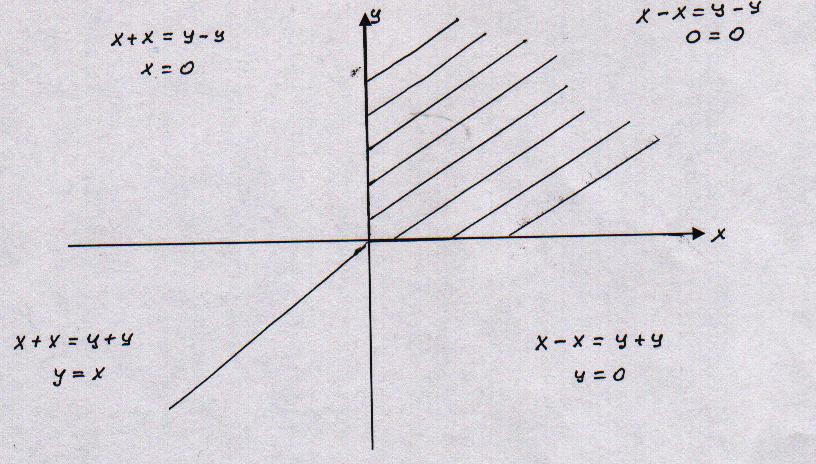

3. 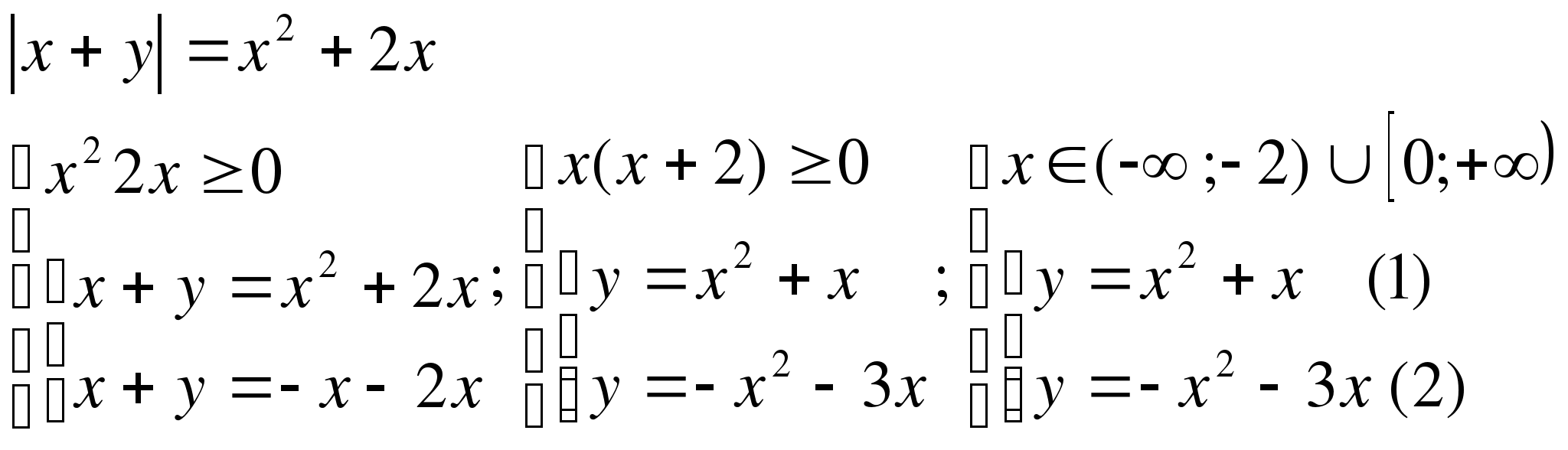
Строим графики двух парабол и берём у каждой ту часть, где 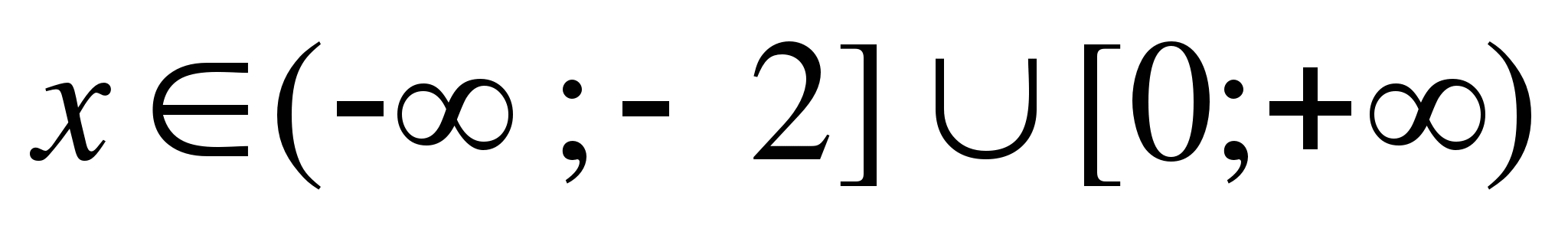
(1) 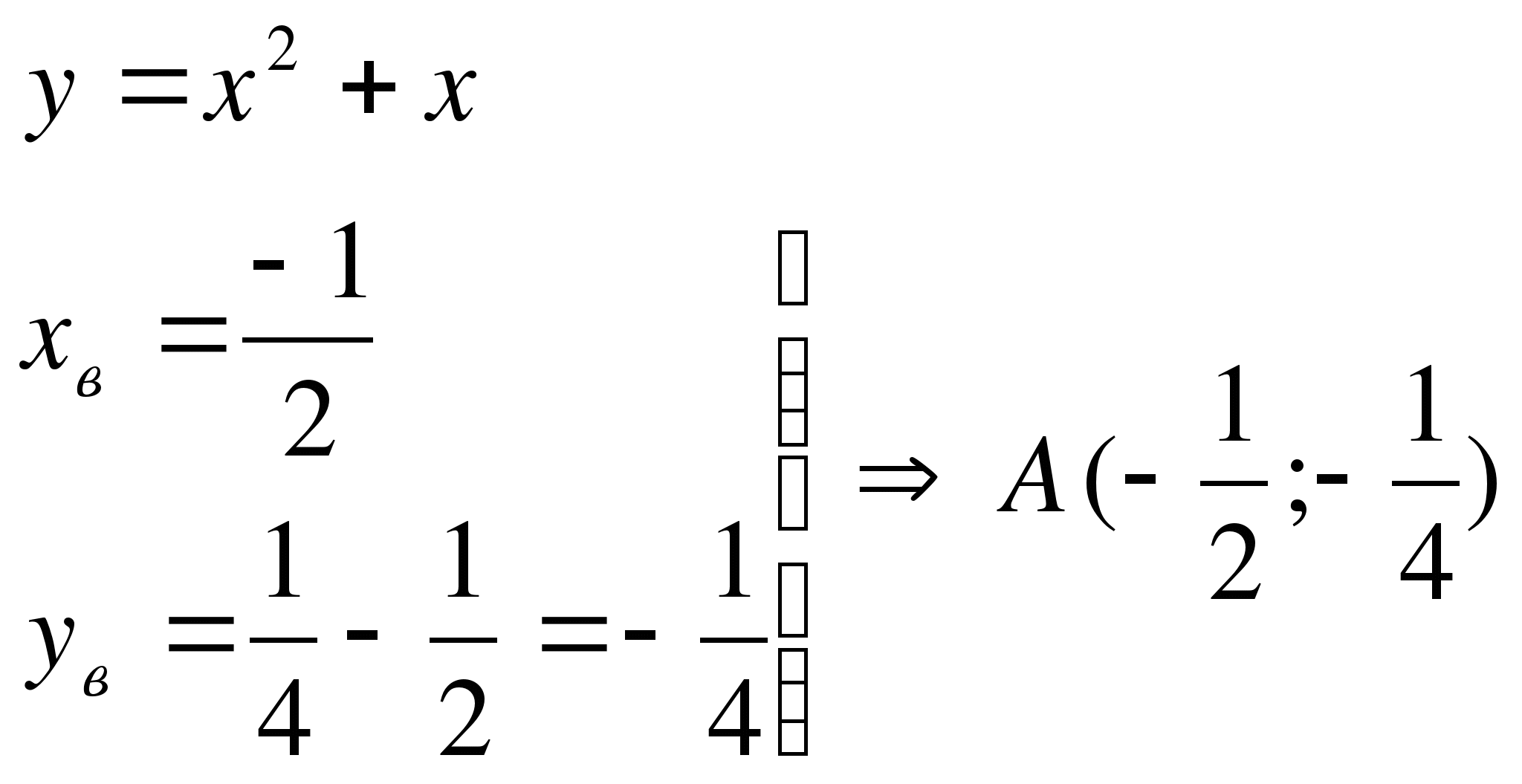 (2)
(2)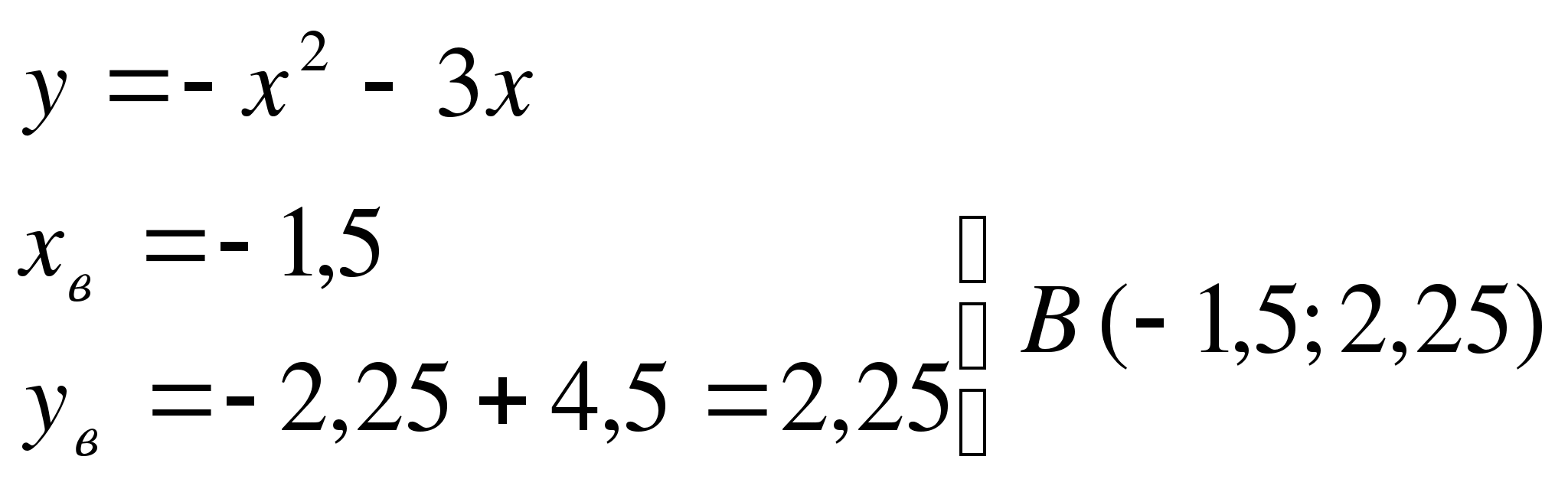
Ось симметрии задаётся уравнением 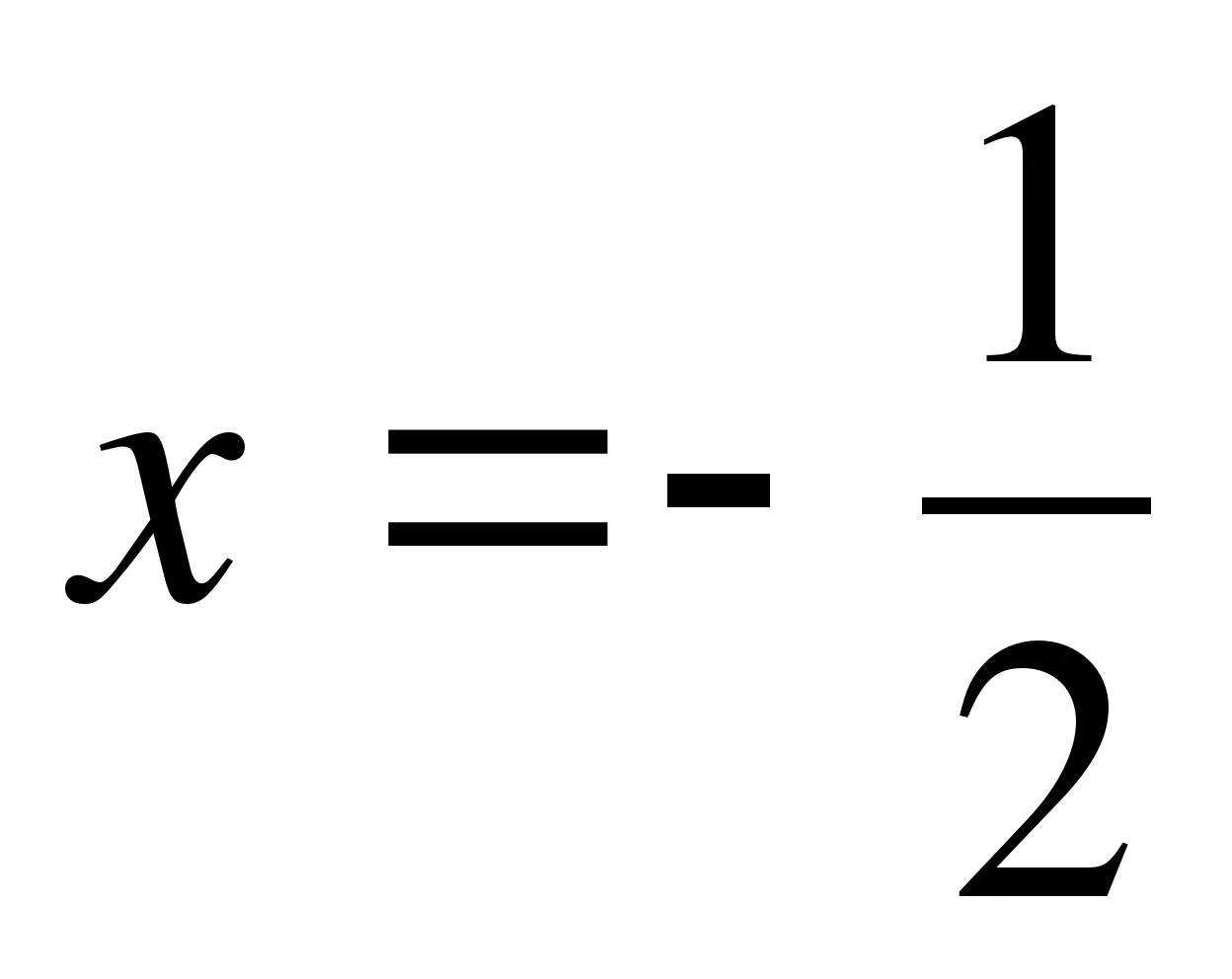 Ось симметрии задаётся уравнением
Ось симметрии задаётся уравнением 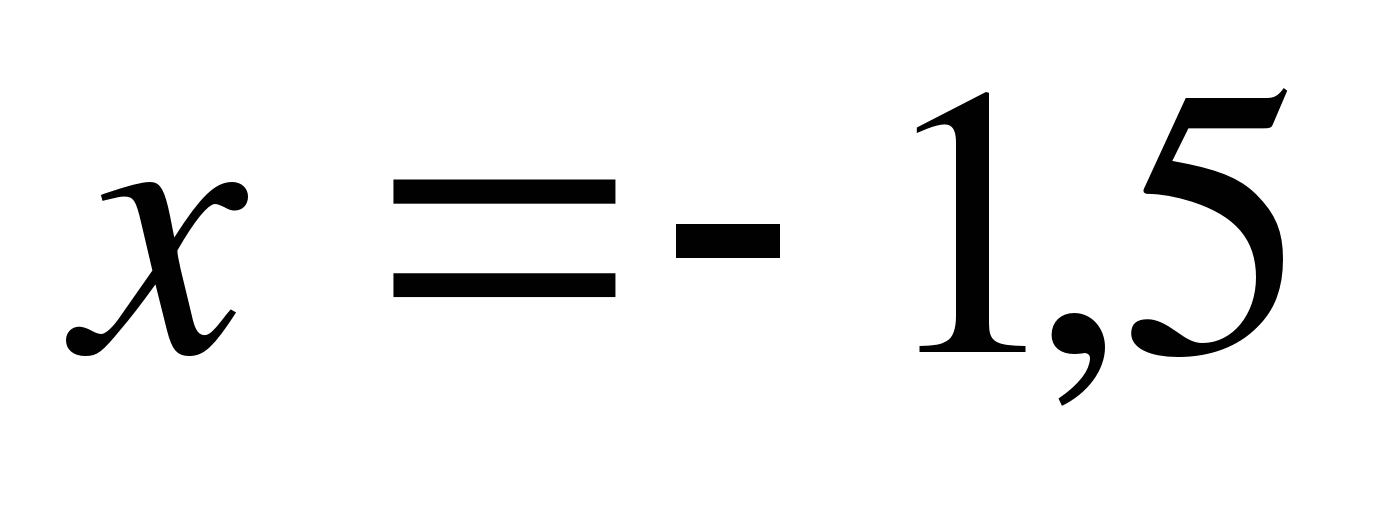
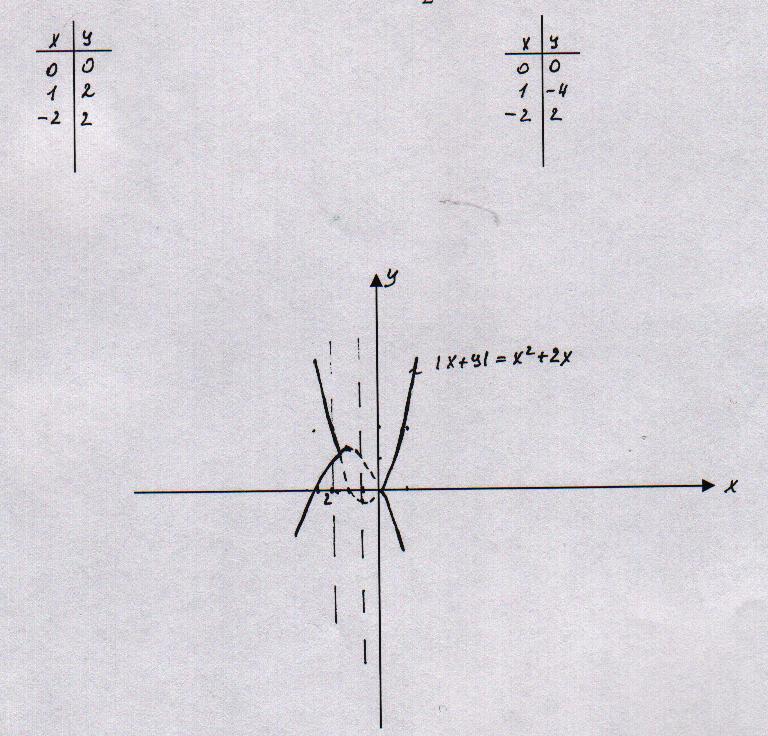
4. 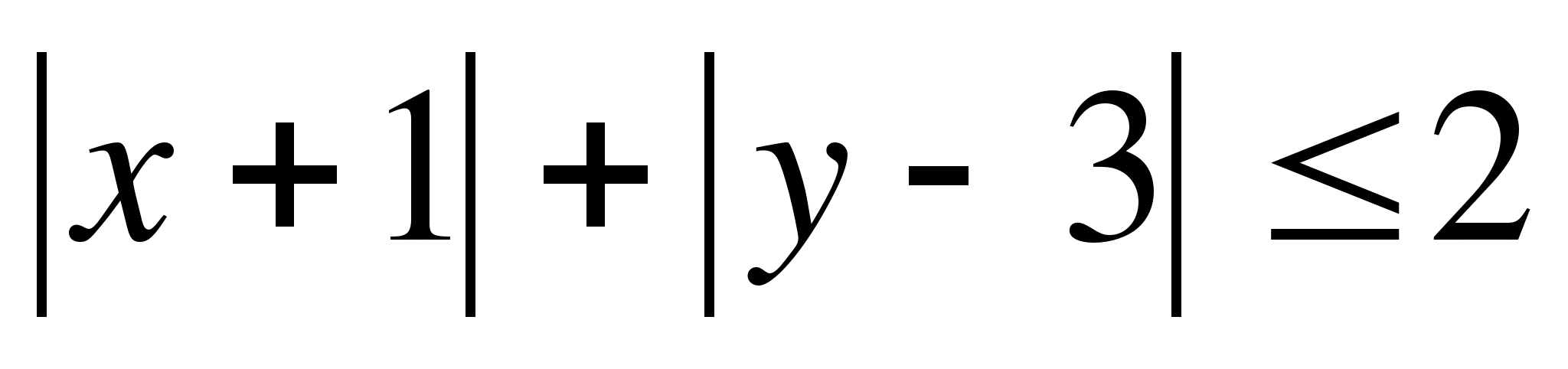
1. строим границу 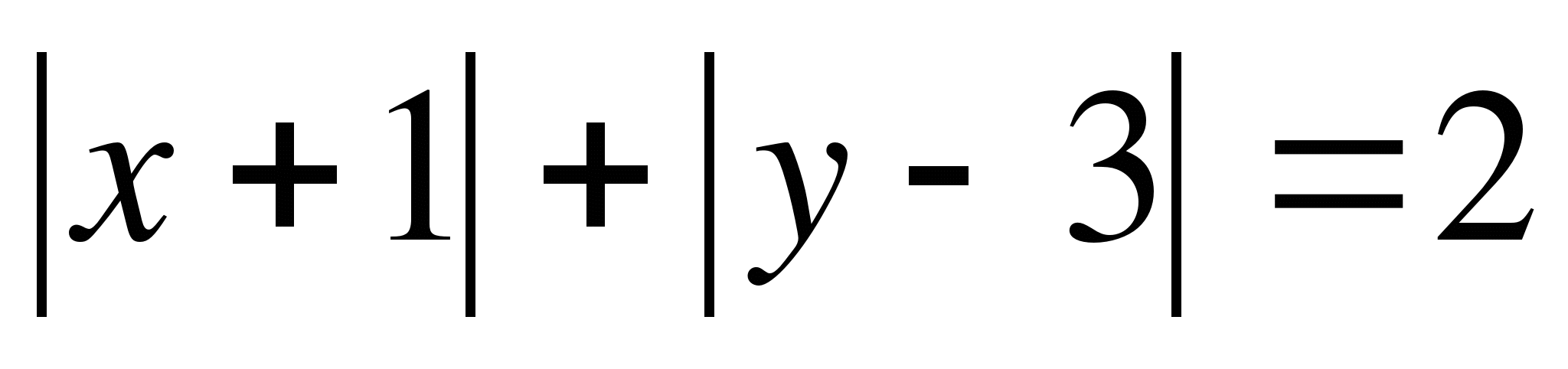
2. берём контрольную точку (0; 0) и подставляем в условие.
Если получим верное неравенство, то т.(0; 0) входит в заштрихованную область, если неравенство не будет верным, то точка (0; 0) не входит в заштрихованную область. Данный метод называется Методом областей. С помощью этого метода можно решать неравенства с параметром. В девятом классе такой метод надо рассматривать на простейшем примере.
Решить неравенство 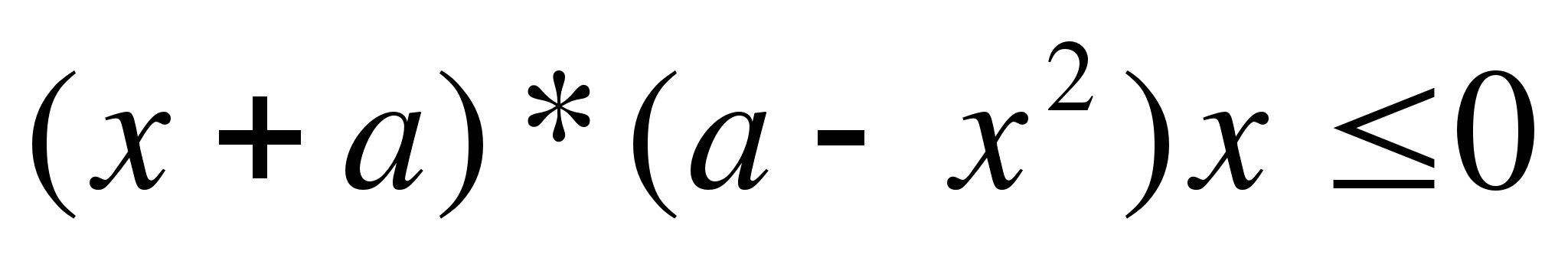 при всех значениях а
при всех значениях а
Построим график неравенства
 в системе ХОУ.
в системе ХОУ.
а) 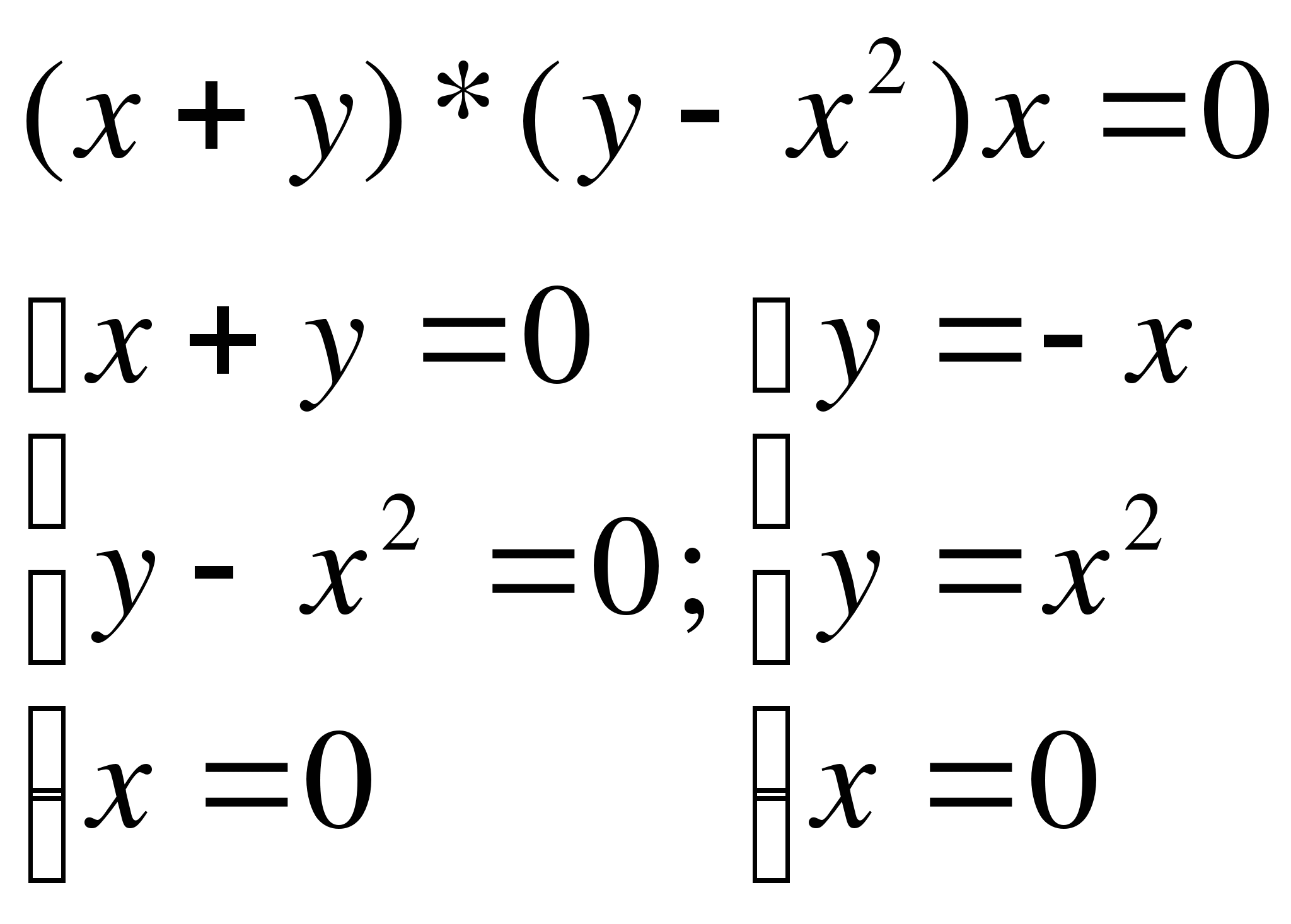
б) точка контрольная (100; 0) подходит. Далее следим за знаками скобок и заштриховываем области «через одну»
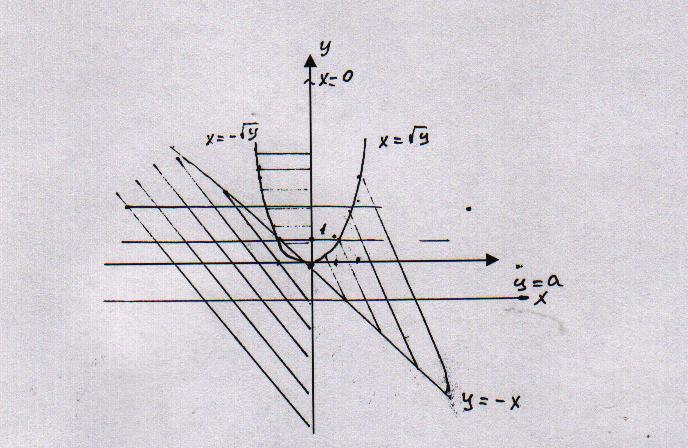
в) для решения неравенства описываем каждую кривую выразив х через у.
г) Мысленно перемещаем прямую у=а и прослеживаем, какая часть прямой попала в заштрихованную область
Ответ: 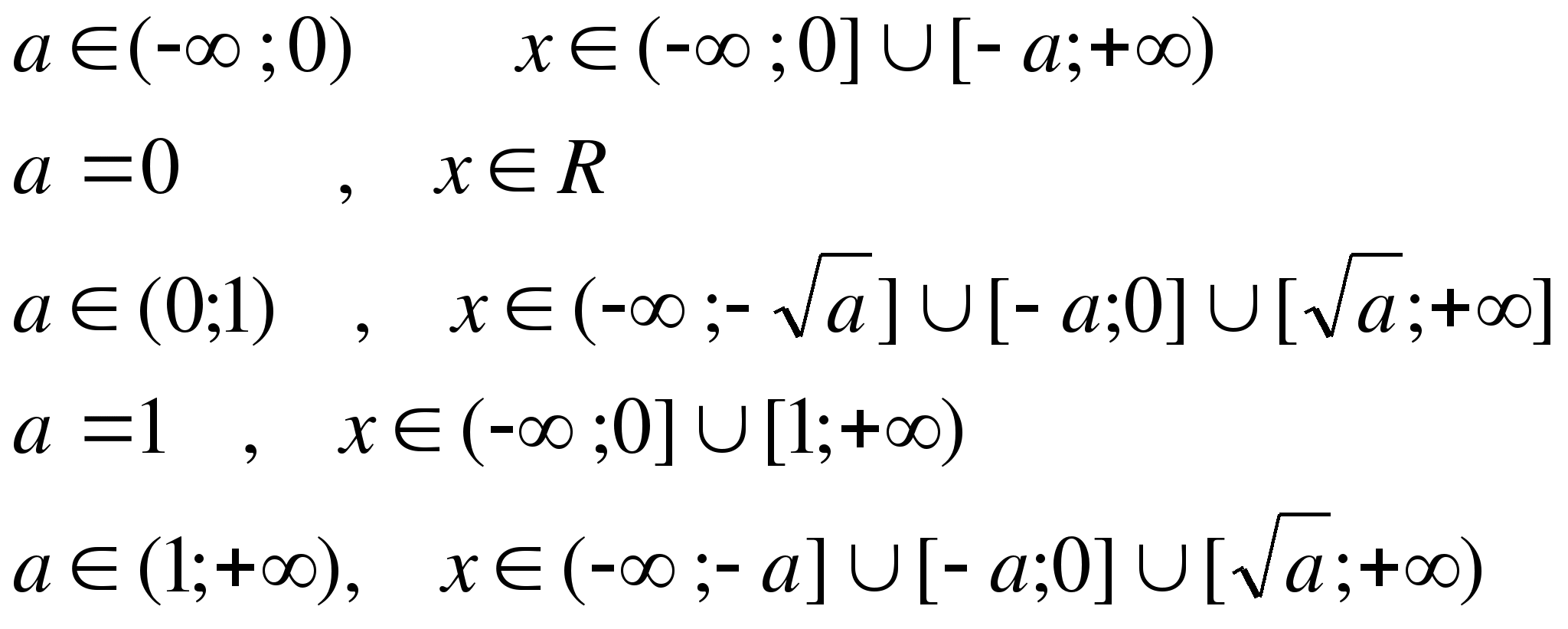
Найти число корней уравнения
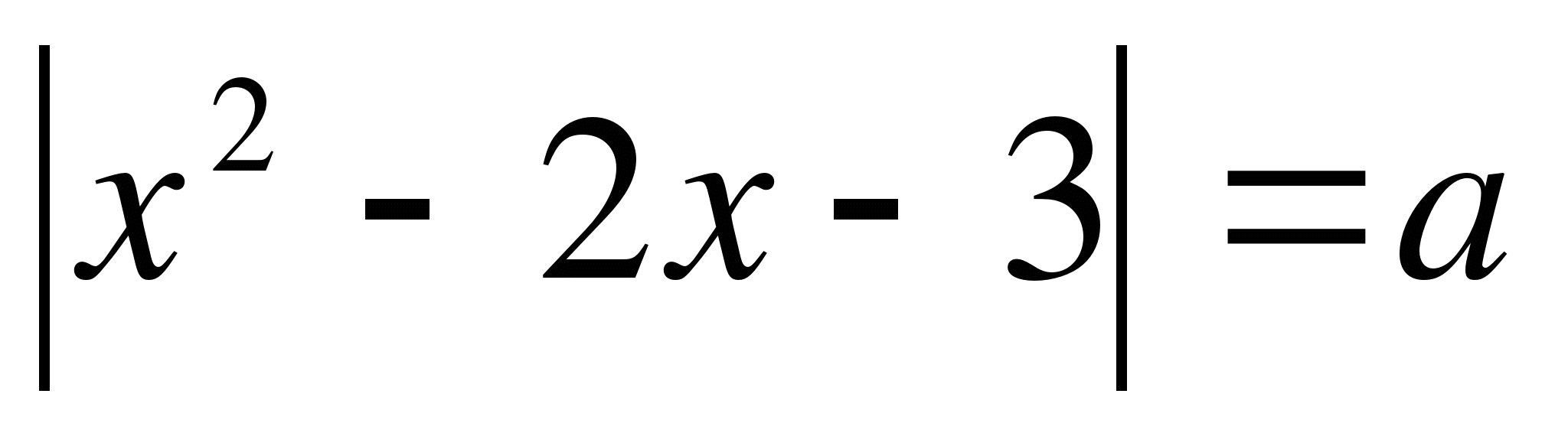 в зависимости от параметра а
в зависимости от параметра а
П остроим графики функций
остроим графики функций 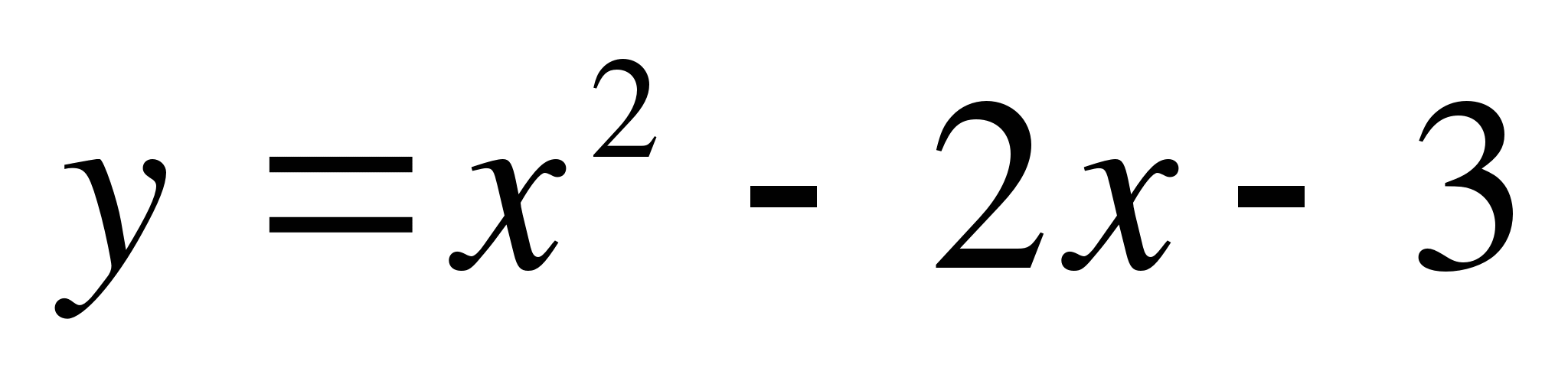
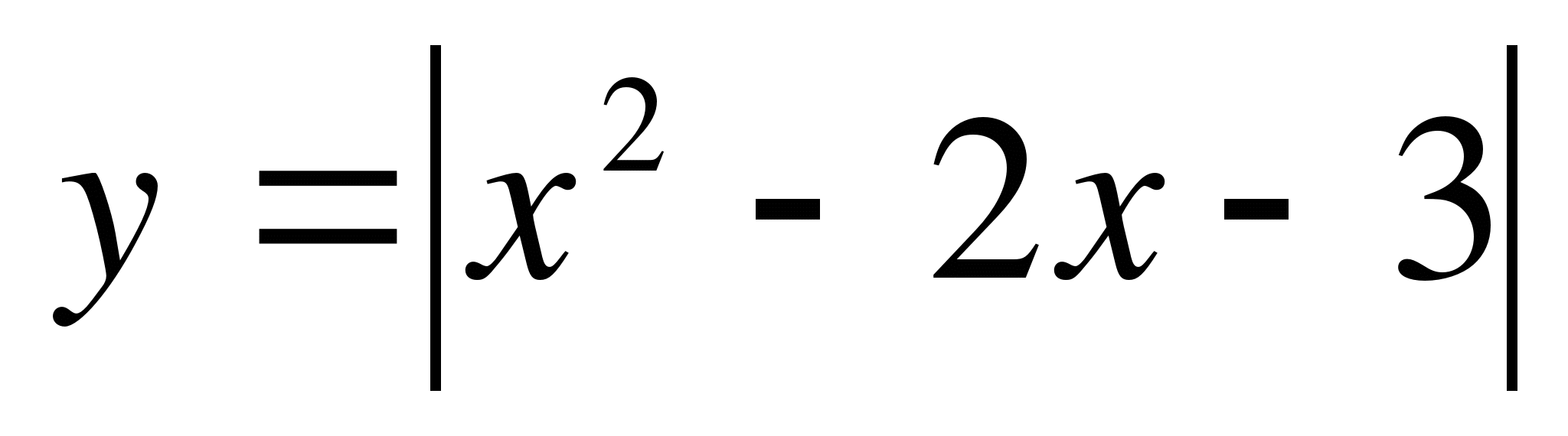
(можно было выделить полный квадрат. 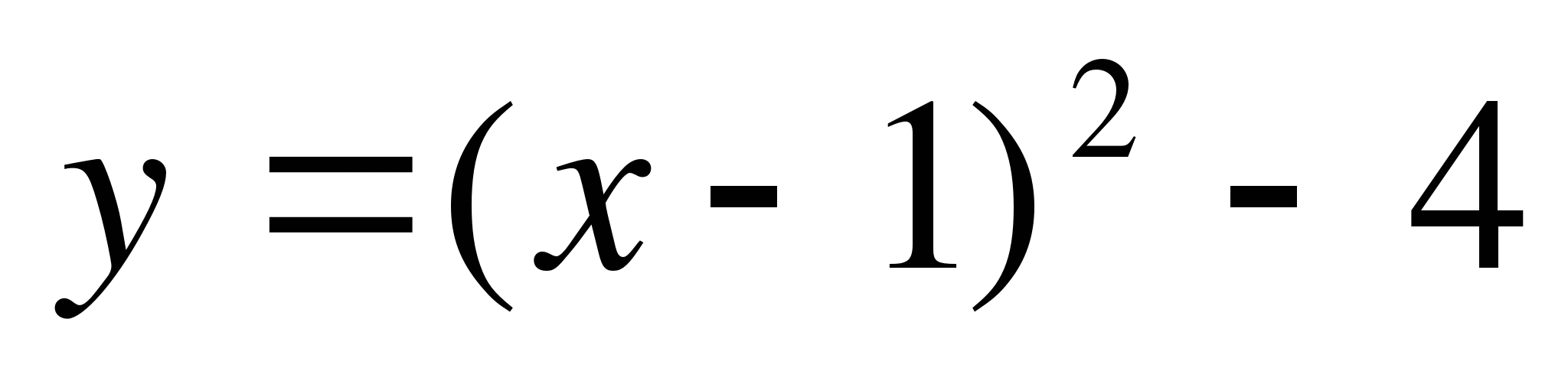
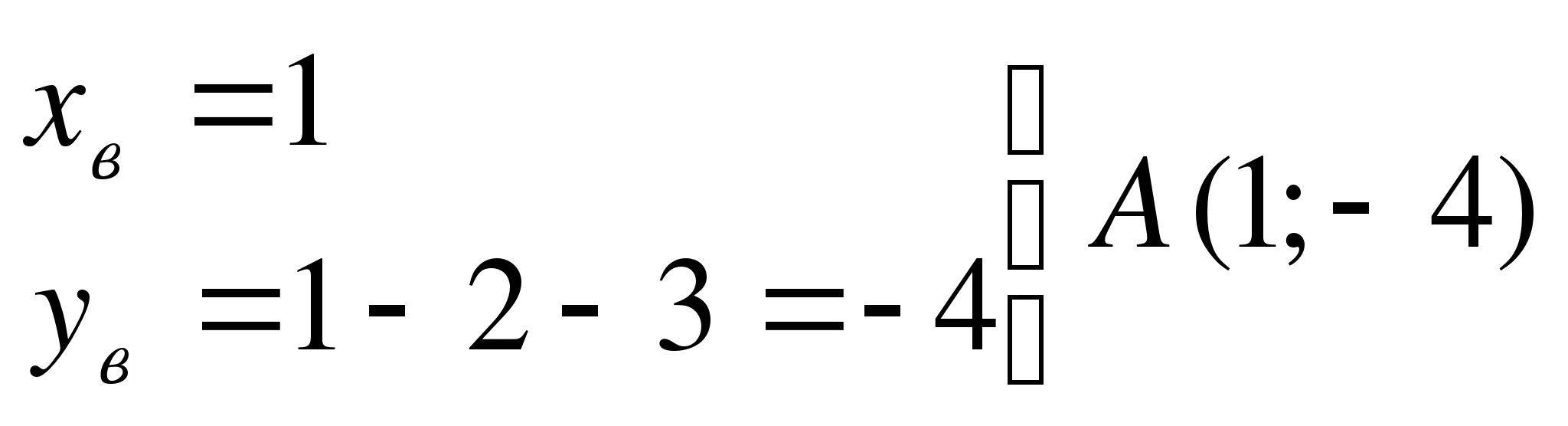
Ось симметрии задаётся уравнением х=1
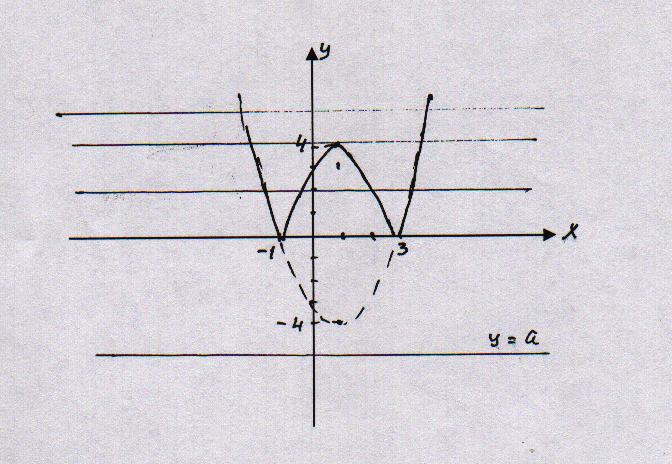
Ответ:

7. Уже в 9 классе можно познакомить с координатно – параметрическим методом.
Решить уравнение 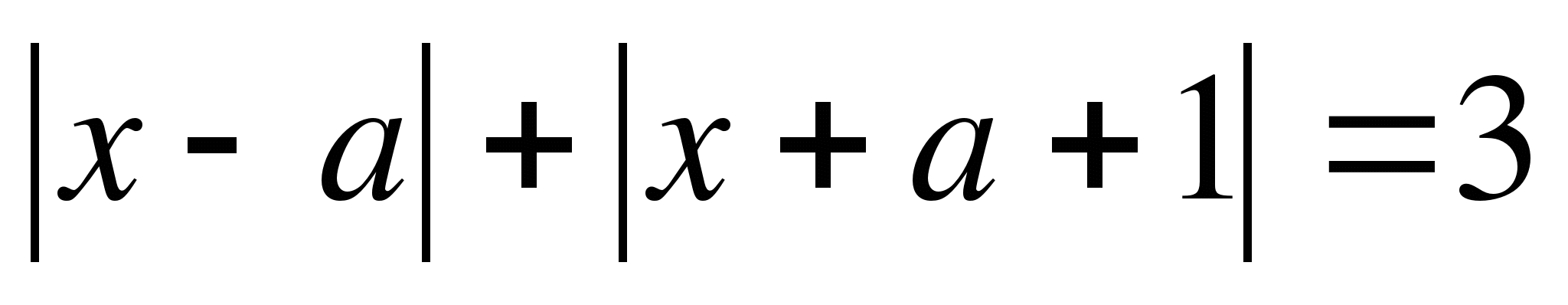 для каждого действительного а.
для каждого действительного а.
Решение: На плоскости аОУ с параметрической осью Оа и координатной плоскостью ОУ построим прямые х=а и х=-а-1
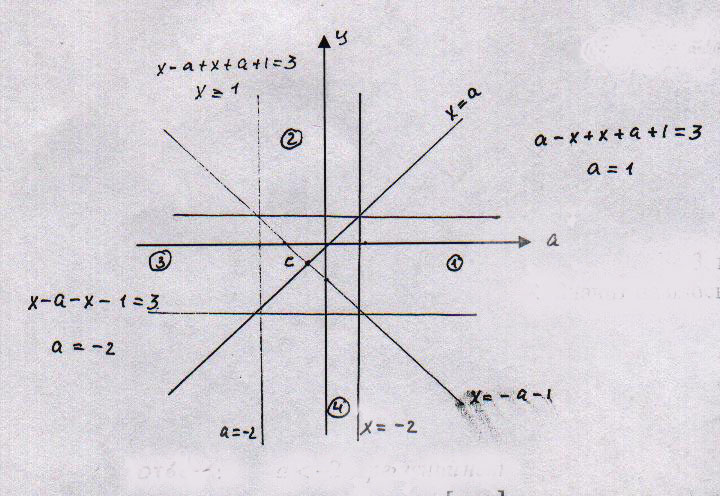
Прямые пересекаются в точке С (
 )
)Образовались 4 области
в 1 области 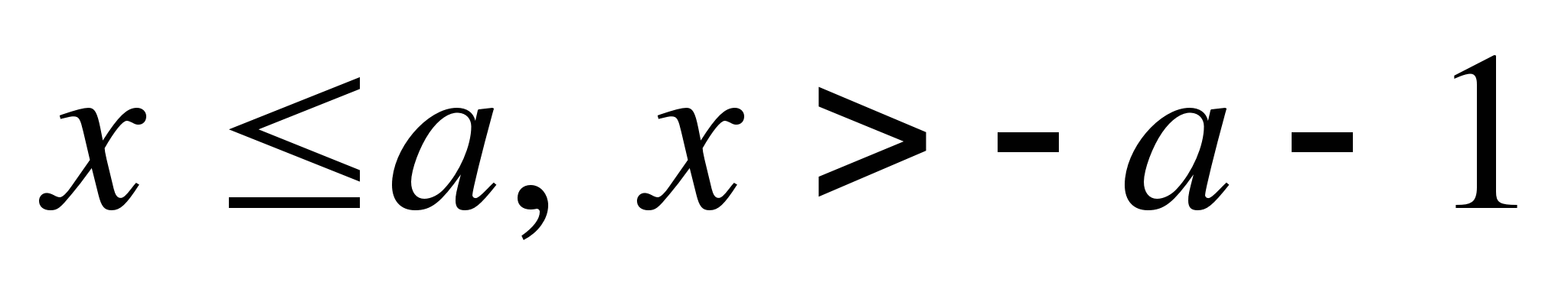
во 2 области 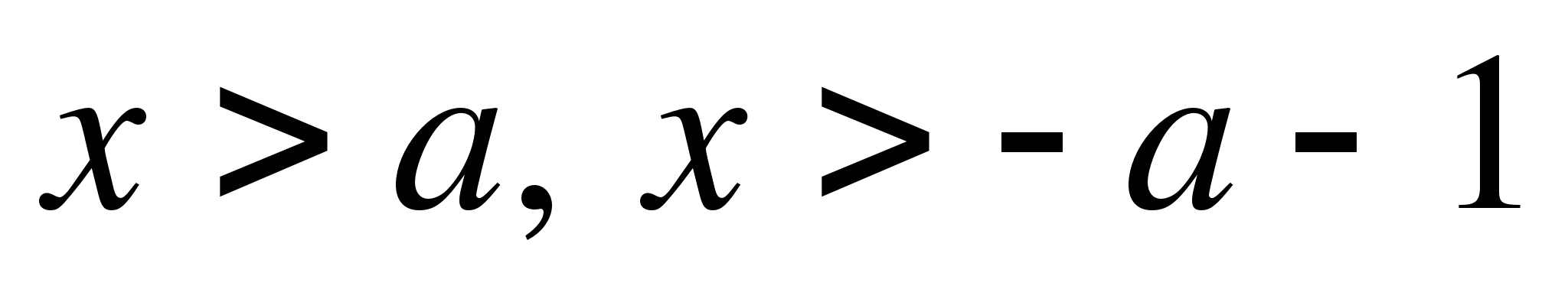
в 3 области 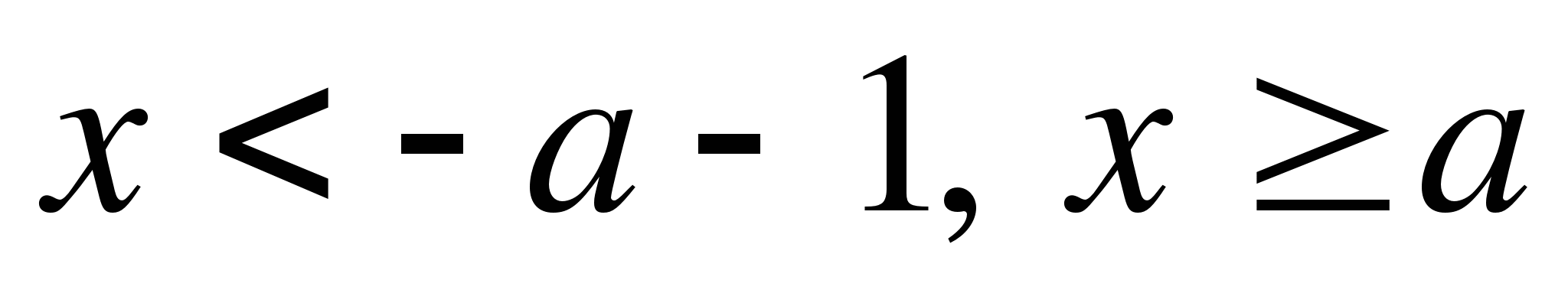
в 4 области 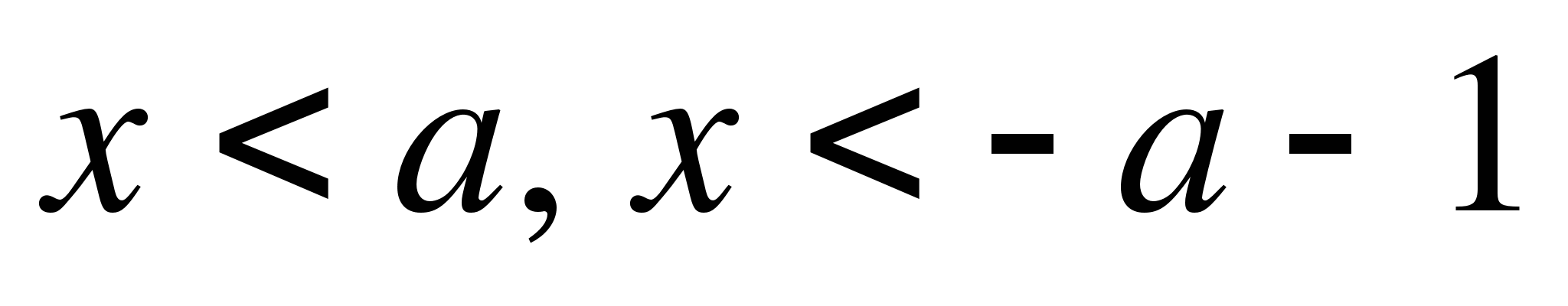
3. в каждой области раскроем модуль
4. Значит на плоскости аОХ все точки границы дают
решение уравнения
Ответ:
Ответ при

Литература, которую очень полезно использовать для проведения уроков.
учебники: В.П. Моденов «Математика»
Родионов Е.М., Синакова С.А. «Математика»
Б.Г.Зив; В.А.Гольдиг «Дидактические материалы».
infourok.ru
Неравенства с модулем
Решим несколько неравенств с модулем. Как правило, наличие модуля в неравенстве вызывает если не испуг, то напряжение (ну не любят обычно с модулем возиться), поэтому лишний раз потренируем решение такого вида неравенств.
Задача 1. Решите неравенство:
![Rendered by QuickLaTeX.com \[\frac{3\mid \upsilon+9 \mid}{1+\frac{20}{\mid \upsilon+9 \mid}}-3>0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-02a6cbed08e732d8941bf99f8d173f5f_l3.png)
Приведем к общему знаменателю … знаменатель.
![Rendered by QuickLaTeX.com \[\frac{3\mid \upsilon+9 \mid}{\frac{\mid \upsilon+9 \mid +20}{\mid \upsilon+9 \mid}}-3>0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b1223a200d0f49347f40b5609184f83f_l3.png)
![Rendered by QuickLaTeX.com \[\frac{3{\mid \upsilon+9 \mid}^2}{\mid \upsilon+9 \mid+20}-3>0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c81bd80a3e70f0765d14cd0f17988bfd_l3.png)
Теперь приводим к общему знаменателю первое и второе слагаемые:
![Rendered by QuickLaTeX.com \[\frac{3{\mid \upsilon+9 \mid}^2}{\mid \upsilon+9 \mid+20}-\frac{3(\mid \upsilon+9 \mid+20)}{\mid \upsilon+9 \mid+20}>0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0d584697c2d2e49359e939494b04ff50_l3.png)
При возведении модуля в квадрат можно снять модуль:
![Rendered by QuickLaTeX.com \[\frac{3(\upsilon+9)^2-3\mid \upsilon+9 \mid-60}{\mid \upsilon+9 \mid+20}>0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-16aff3c1c1473e195bbd232b2c796459_l3.png)
Теперь наша задача – снять модуль.
Тогда получим такую совокупность из систем:
![Rendered by QuickLaTeX.com \[\begin{bmatrix}{\begin{Bmatrix}{\frac{3(\upsilon+9)^2-3(\upsilon+9)-60}{\upsilon+9 +20}>0 }\\{}\\{\upsilon>-9}\\{}\\{\upsilon+29 \neq0}\end{matrix} }\\{{\begin{Bmatrix}{\frac{3(\upsilon+9)^2+3(\upsilon+9)-60}{-\upsilon-9+20}>0 }\\{\upsilon<9}\\{11- \upsilon \neq 0}\end{matrix}}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-95c4df2093c4d5986b81bd051b1073e4_l3.png)
Решаем по отдельности:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{\frac{3(\upsilon+9)^2-3(\upsilon+9)-60}{\upsilon+29}>0 }\\{\upsilon>-9}\\{\upsilon\neq-29}\end{matrix} }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0c7c8031169cce15b56452e31aefc039_l3.png)
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{\frac{3\upsilon^2+51\upsilon+156}{\upsilon+29}>0 }\\{\upsilon>-9}\\{\upsilon\neq-29}\end{matrix} }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3ecd5dd7e272f1f4fd8b0a872d28097f_l3.png)
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{\frac{\upsilon^2+17\upsilon+52}{\upsilon+29}>0 }\\{\upsilon>-9}\\{\upsilon\neq-29}\end{matrix} }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-43cd9b5b88121e14f7d96e80f8894517_l3.png)
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{\frac{(\upsilon+4)(\upsilon+13}{\upsilon+29}>0 }\\{\upsilon>-9}\\{\upsilon\neq-29}\end{matrix} }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6eba9d8d9077faa8519677b06e90a5f4_l3.png)

Рисунок 1.
Решением этой системы является интервал  – ведь корень
– ведь корень  не попадает в интервал, на котором мы раскрыли модуль!
не попадает в интервал, на котором мы раскрыли модуль!
Раскрываем модуль с минусом:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{\frac{3(\upsilon+9)^2+3(\upsilon+9)-60}{-\upsilon-9+20}>0 }\\{\upsilon<-9}\\{11- \upsilon \neq 0}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-422eb0077b4de8a0c390756a62aab15f_l3.png)
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{\frac{3\upsilon^2+57\upsilon+210}{11-\upsilon}>0 }\\{\upsilon<-9}\\{11- \upsilon \neq 0}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4dc5aa15cd5aecc6f26078d35de791dc_l3.png)
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{\frac{\upsilon^2+19\upsilon+70}{11-\upsilon}>0 }\\{\upsilon<-9}\\{11- \upsilon \neq 0}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b4f0752d5cc376ad762f05b5324b0ab9_l3.png)
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{\frac{(\upsilon+14)(\upsilon+5)}{11-\upsilon}>0 }\\{\upsilon<-9}\\{11- \upsilon \neq 0}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e88aaa8e99c74fd1b9db695a7018b9df_l3.png)

Рисунок 2.
Корень  и точка
и точка  не попадают в интервал раскрытия модуля, поэтому решение этой системы – интервал
не попадают в интервал раскрытия модуля, поэтому решение этой системы – интервал  .
.
Объединяем оба решения в ответ:

Задача 2. Решите неравенство:
![Rendered by QuickLaTeX.com \[\mid l^2-8l \mid+\mid -l+3 \mid+5l^2+8l+2 \leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7e2337389d3ec68aacd0170cf0951320_l3.png)
Чтобы решить такое неравенство, надо определить точки, где подмодульное выражение будет менять знак. Для этого приравняем к нулю подмодульные выражения. Первое будет менять знак в точках  и
и  , второе – в точке
, второе – в точке  :
:

Рисунок 3
Таким образом, получили 4 интервала, на рисунке указано, с какими знаками на каждом интервале будем раскрывать модуль.
На первом интервале оба модуля раскрываем с плюсом:
![Rendered by QuickLaTeX.com \[l^2-8l -l+3+5l^2+8l+2 \leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-949ccb250a51644978d8dc27951c6a6e_l3.png)
![Rendered by QuickLaTeX.com \[6l^2-l+5 \leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d55588312e673ce3389236e6d8722495_l3.png)
Так как дискриминант отрицателен, то, при положительном первом коэффициенте трехчлена, весь трехчлен имеет положительный знак. Поэтому неравенство решений на этом интервале не имеет.
Второй промежуток:
![Rendered by QuickLaTeX.com \[8l - l^2-l+3+5l^2+8l+2 \leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9117efc4c69123258cf29436d4b27ba9_l3.png)
![Rendered by QuickLaTeX.com \[4l^2+15l+5 \leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-11ed981deb347db3370b4e60dbe4cc46_l3.png)
В этом случае дискриминант положителен, но корни, увы, не принадлежат рассматриваемому интервалу, оба меньше 0:
![Rendered by QuickLaTeX.com \[l_{1,2}=\frac{-15 \pm \sqrt{225-4\cdot4\cdot5}}{8}=\frac{-15 \pm \sqrt{145}}{8}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-faca98c70b8d1a16208edf265be26836_l3.png)
Третий промежуток:
![Rendered by QuickLaTeX.com \[8l - l^2+l-3+5l^2+8l+2 \leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-553fc808e84bccdacbbe7af3cbfb6374_l3.png)
![Rendered by QuickLaTeX.com \[4l^2+17l-1 \leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-48bb8148feb2f38611b092bf5807bfc7_l3.png)
Корни:
![Rendered by QuickLaTeX.com \[l_{3,4}=\frac{-17 \pm \sqrt{289+4\cdot4\cdot1}}{8}=\frac{-17 \pm \sqrt{305}}{8}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8d4052b2178c75f93ba0cbe88e698bb4_l3.png)
Снова корни не попали в промежуток!
Наконец, последний, четвертый:
![Rendered by QuickLaTeX.com \[l^2 -8l +l-3+5l^2+8l+2 \leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-fe009aee85409a1af608bc4ef8f64820_l3.png)
![Rendered by QuickLaTeX.com \[6l^2+l-1 \leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8dbe79c8124411ad7e068feb1c01113d_l3.png)
Корни:
![Rendered by QuickLaTeX.com \[l_{5,6}=\frac{-1 \pm \sqrt{25}}{12}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b24ed851de3cac6de2119de5822cbf35_l3.png)
![Rendered by QuickLaTeX.com \[l_5=\frac{1}{3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7698b81210fde6a6653de5549d004e85_l3.png)
![Rendered by QuickLaTeX.com \[l_6=-\frac{1}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0c23ec354bca0cc8bab8953613c06939_l3.png)
И снова корни не попали в нужный промежуток! Увы, решений у данного неравенства нет. Так и запишем:
Ответ: {}
easy-physic.ru
Исследовательская работа на тему «Решение неравенств с модулем»
РАССМОТРЕНО
Педагогическим советом МОУ
«Зашижемская СОШ»
Протокол № 1
от « 14 » августа 2015г.
СОГЛАСОВАНО
Заместитель директора по УВР
_______ /Сидоркина Р.Л./
« 14 » августа 2015 г.
УТВЕРЖДАЮ
Директор школы:
________ А.П.Конаков
Приказ №63
от « 01» сентября 2015 г.
Решение уравнений и неравенств с модулем
Исследовательская работа
Программу составила:
учитель математики высшей
категории МОУ «Зашижемская СОШ»
Сидоркина Р.Л.
с.Зашижемье, 2014 г.
Оглавление
Введение…………………………………………………………………3
Простейшие уравнения и неравенства с модулем……………………5
Графическое решение уравнений и неравенств с модулем………….8
Иные способы решения уравнений и неравенств с модулем…………10
Заключение ……………………………………………………………..16
Список литературы………………………………………………………18
Понятие абсолютной величины (модуля) является одной из важнейших характеристик числа как в области действительных, так и в области комплексных чисел.
Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсах высшей математики, физики и технических наук, изучаемых в вузах. Например, в теории приближенных вычислений используются понятия абсолютной и относительной погрешностей приближенного числа. В механике и геометрии изучаются понятия вектора и его длины (модуля вектора). В математическом анализе понятие абсолютной величины числа содержится в определениях таких основных понятий, как предел, ограниченная функция и др. Задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах, вступительных экзаменах в вузы и на ЕГЭ. И поэтому для нас стало важно изучить некоторые аспекты этой темы.
Главной целью в нашей работе является изучение различных методов решения уравнений и неравенств с модулями.
Данная цель должна быть достигнута при решении следующих задач:
Изучить определение и некоторые свойства модуля.
Освоить решение простейших уравнений и неравенств с модулем через равносильные переходы
Рассмотреть различные методы решения уравнений и неравенств с модулем.
Объектом исследования являются некоторые типы уравнений и неравенств с модулем.
Предмет исследования – различные методы решения уравнений и неравенств с модулем, а именно: графический способ, метод геометрической интерпретации, использование тождества 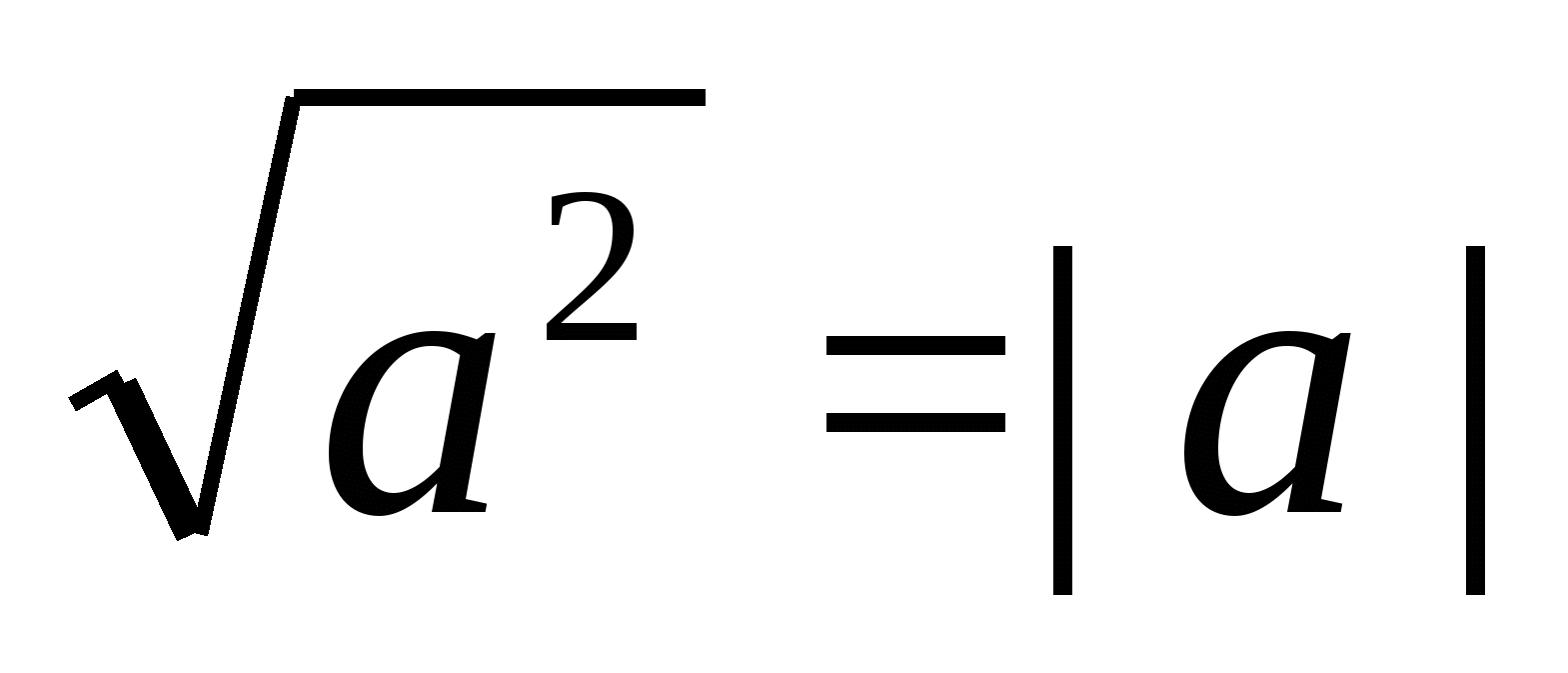 , применение теоремы о знаках, метод перехода к следствию, метод интервалов, метод домножения на положительный множитель ,метод раскрытия модулей.
, применение теоремы о знаках, метод перехода к следствию, метод интервалов, метод домножения на положительный множитель ,метод раскрытия модулей.
В ходе исследования применялись такие методы, как изучение литературы по данному вопросу и практический метод.
В ходе работы мы исследовал такие источники, как:
1. «Большая математическая энциклопедия» для школьников и студентов;
Математика. ЕГЭ – 2011-2012. Типовые экзаменационные варианты. / Под редакцией А.Л. Семенова, И.В. Ященко.
М.Я. Выгодский. Справочник по элементарной математике
«Новейший справочник школьника»;
Энциклопедия «Я познаю мир» Математика;
http://ru.wikipedia.org/wiki/Заглавная_страница;
К простейшим уравнениям мы будем относить уравнения, решаемые одним из нижеприведенных равносильных переходов: 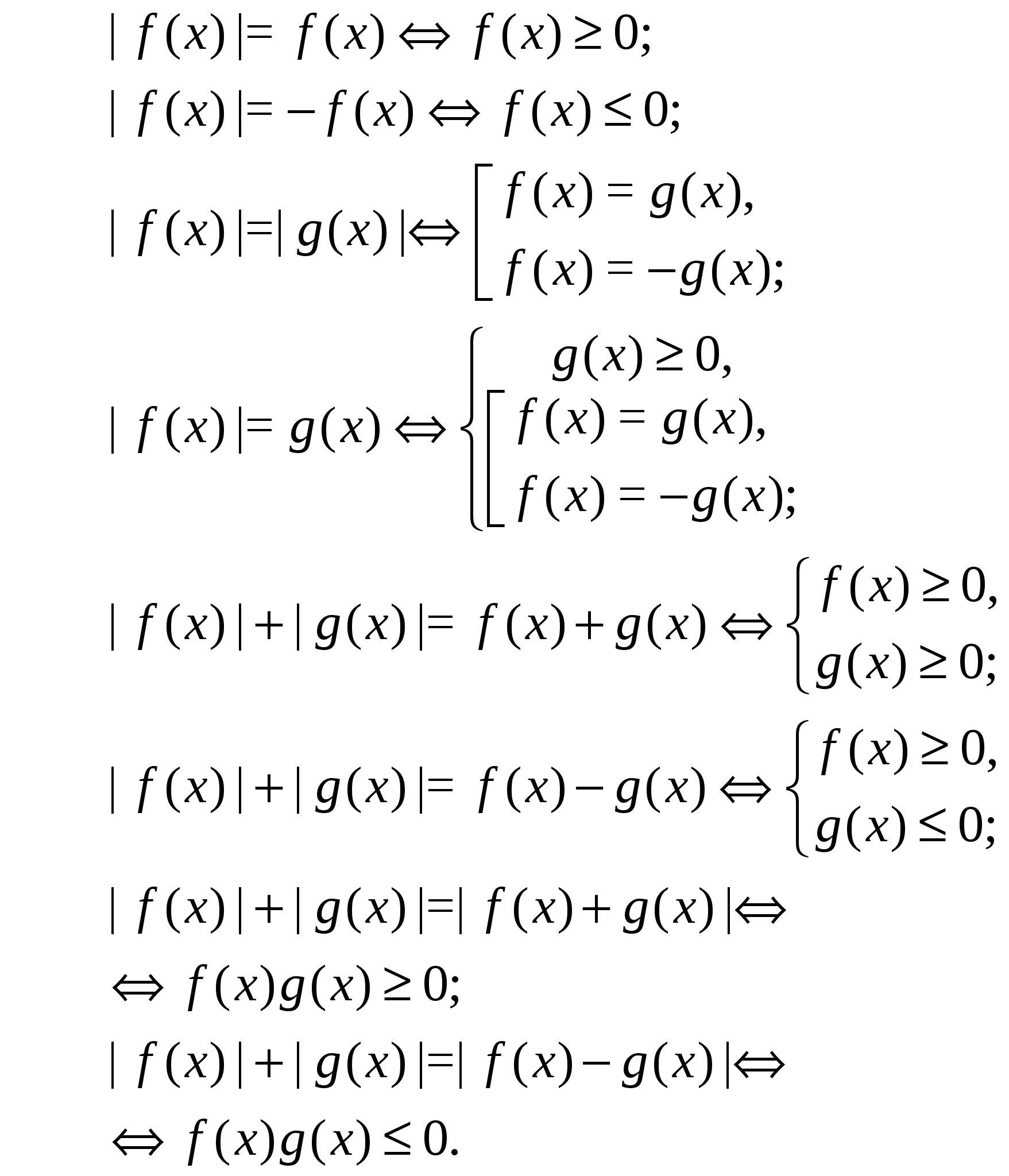
Примеры решения простейших уравнений.
Пример 1 Решим уравнение 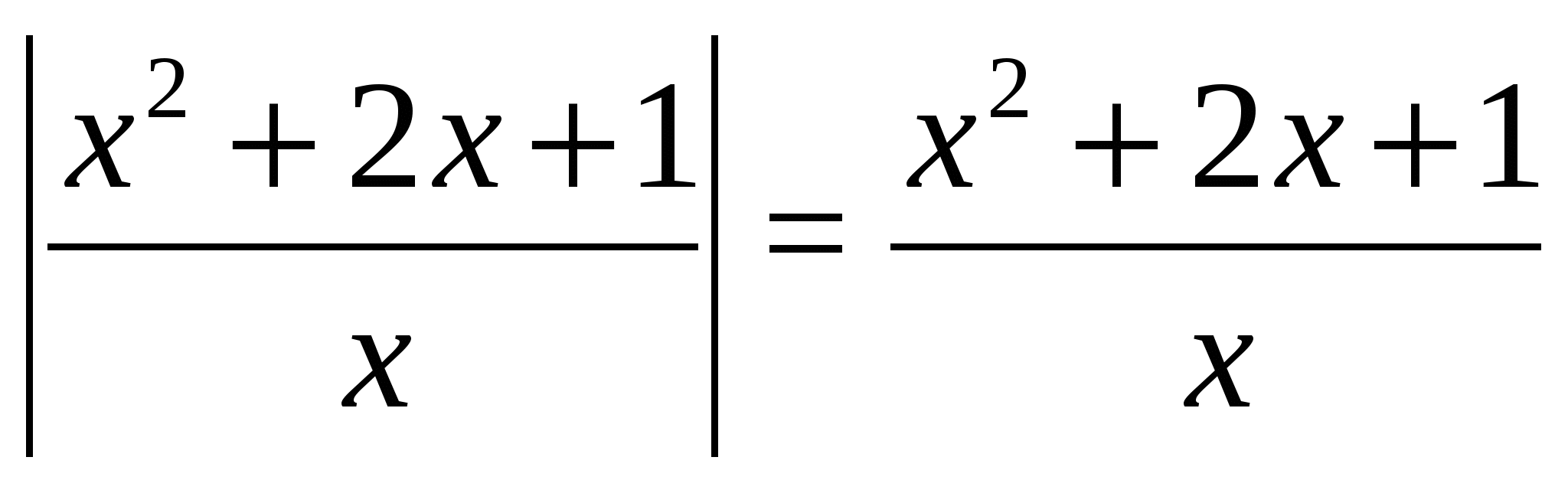 .
.
Решение.
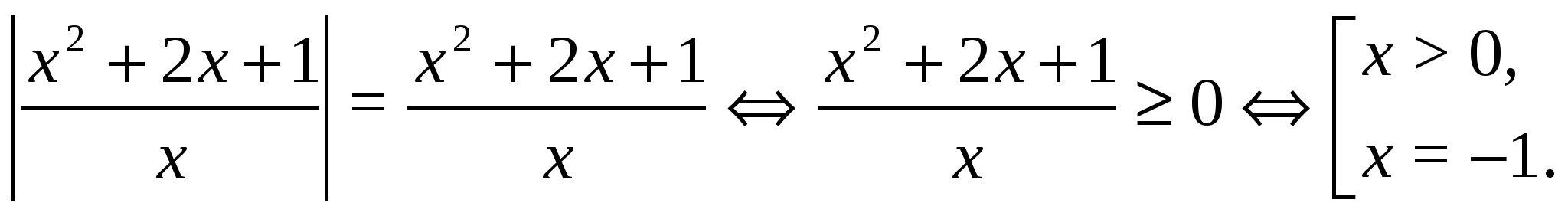
Ответ. 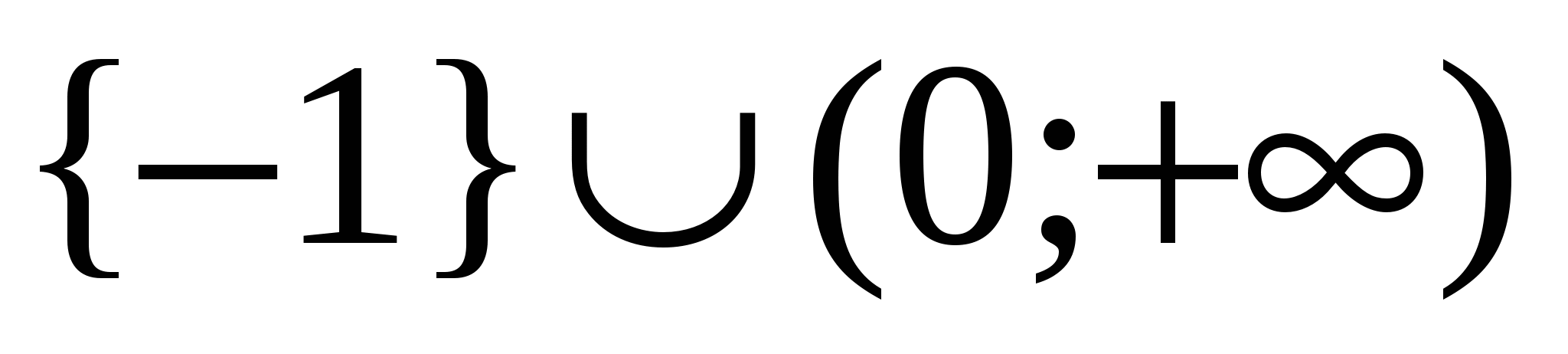 .
.
Пример 2 Решим уравнение 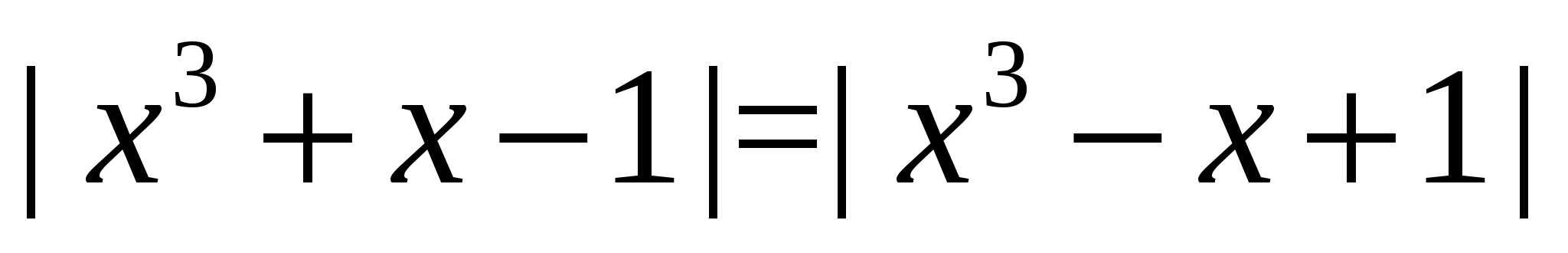 .
.
Решение.
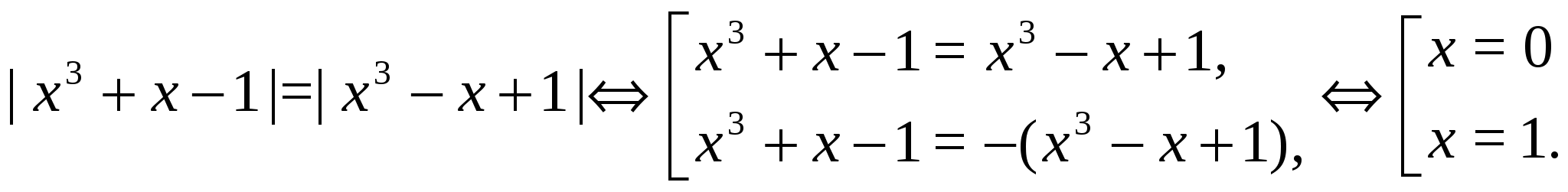
Ответ. 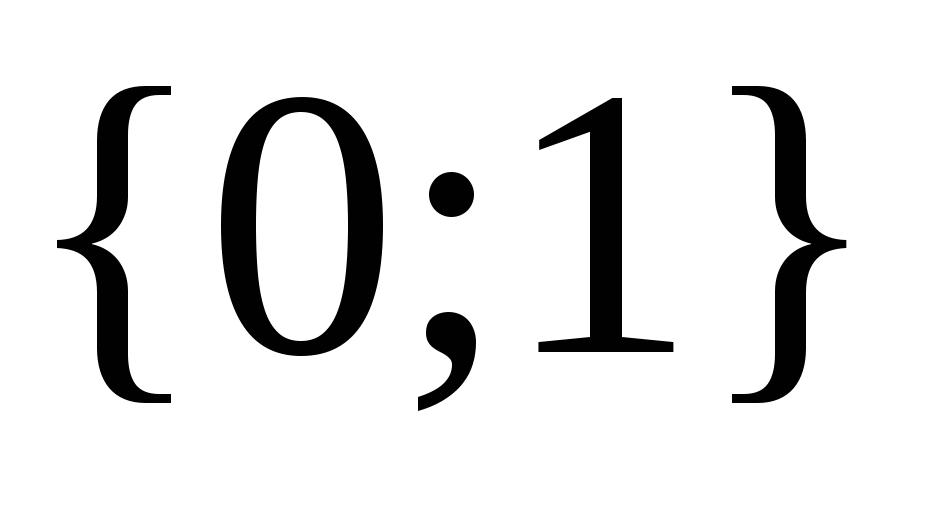 .
.
Пример 3 Решим уравнение 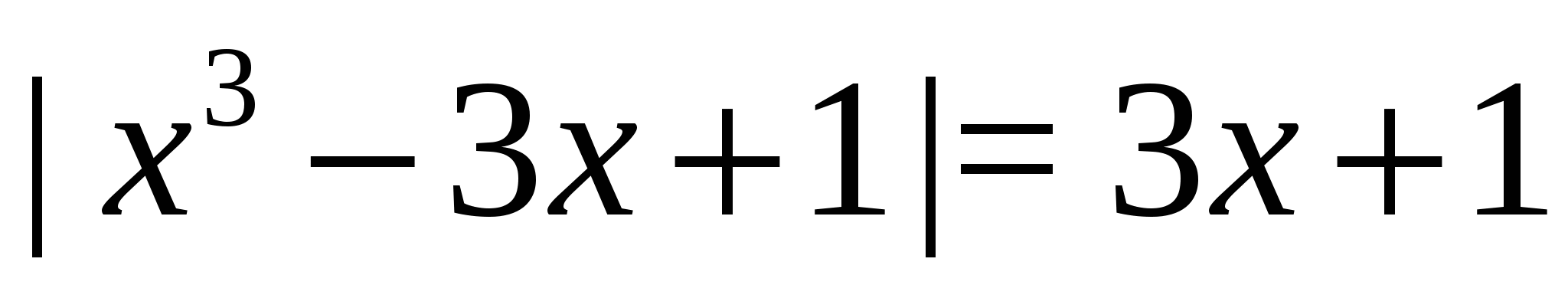 .
.
Решение.
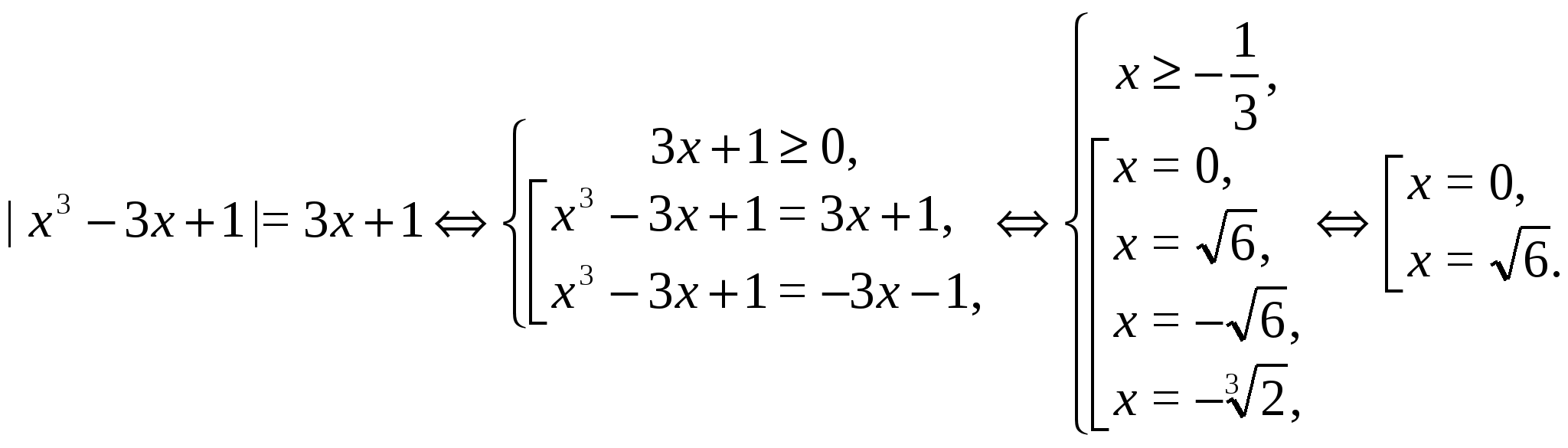
Ответ. 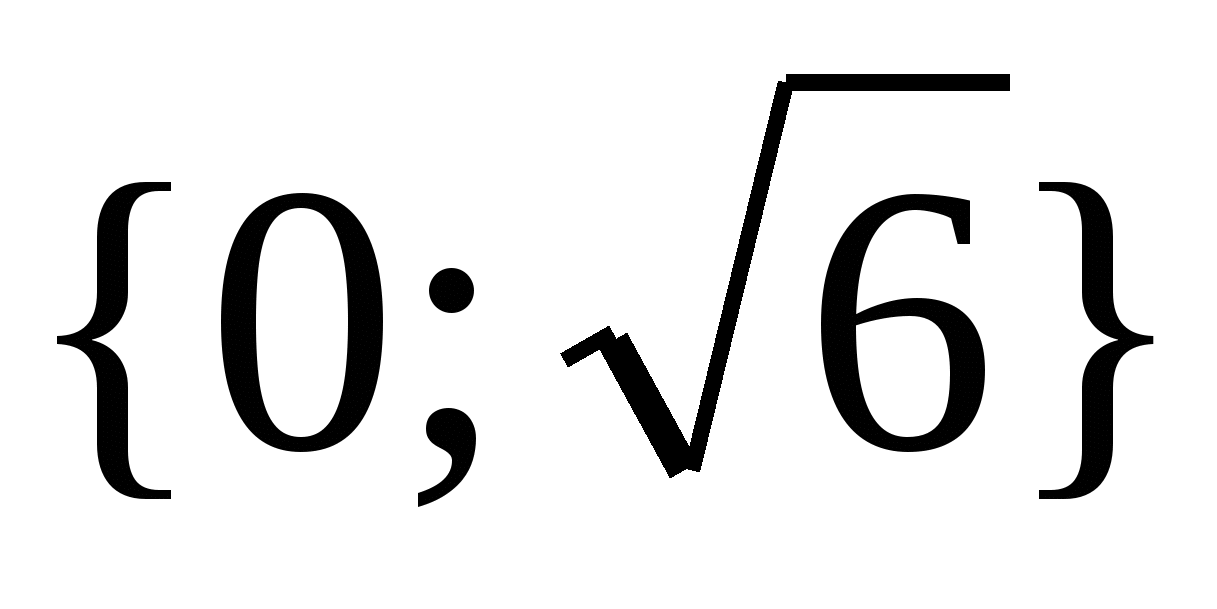 .
.
Ряд уравнений решается с использованием следующей теоремы.
Теорема.4 Сумма модулей равна алгебраической сумме подмодульнх величин тогда и только тогда, когда каждая величина имеет тот знак, с которым она входит в алгебраическую сумму.
Пример 5 Решить уравнение
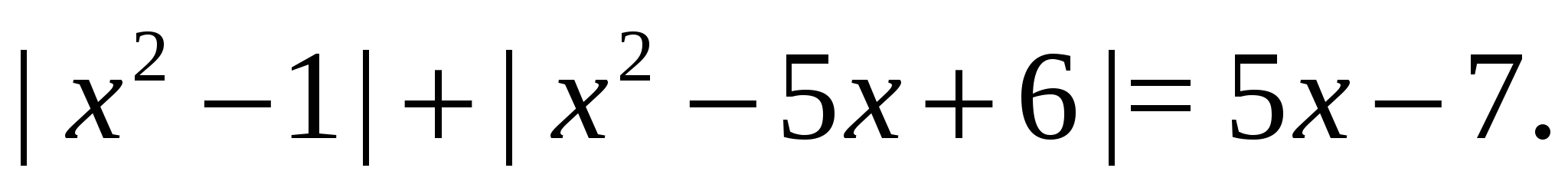
Решение. Так как 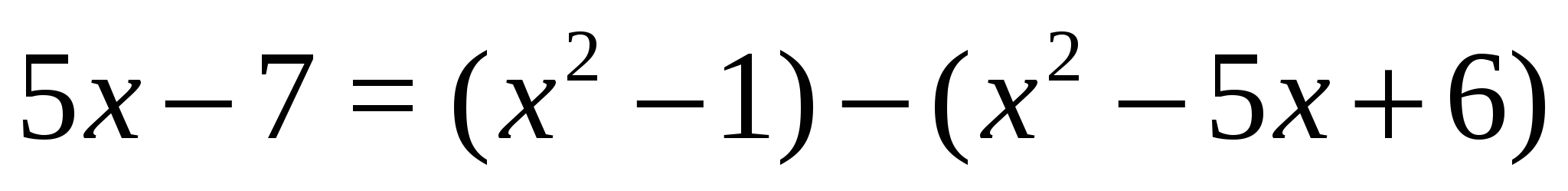 , то мы имеем равенство вида
, то мы имеем равенство вида 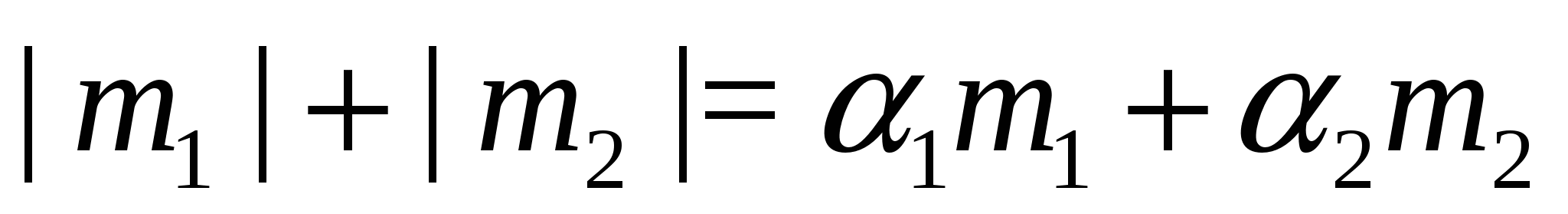 , где
, где 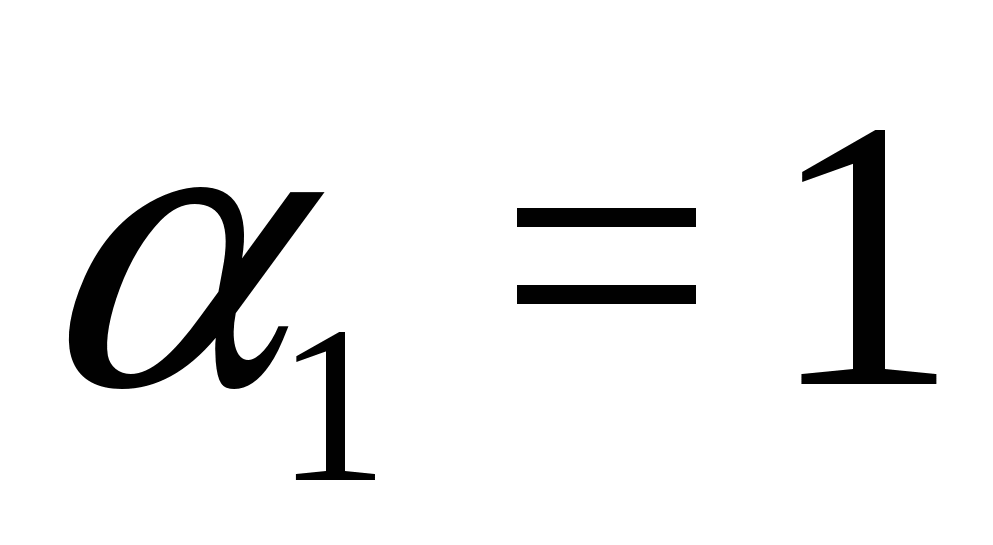 ,
, 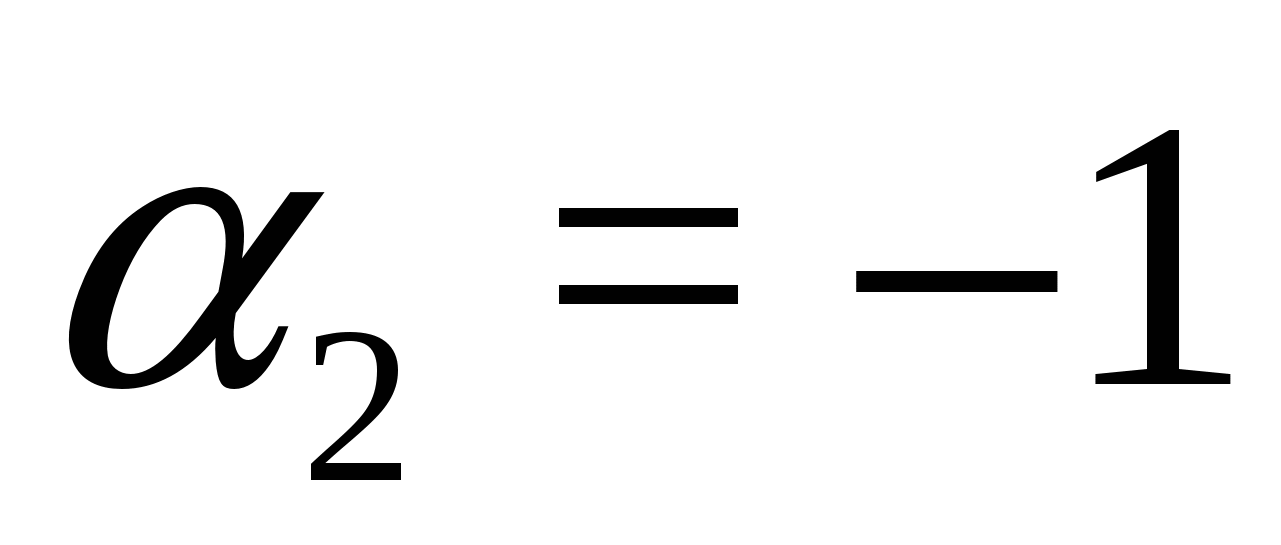 . Поэтому исходное уравнение равносильно системе:
. Поэтому исходное уравнение равносильно системе:
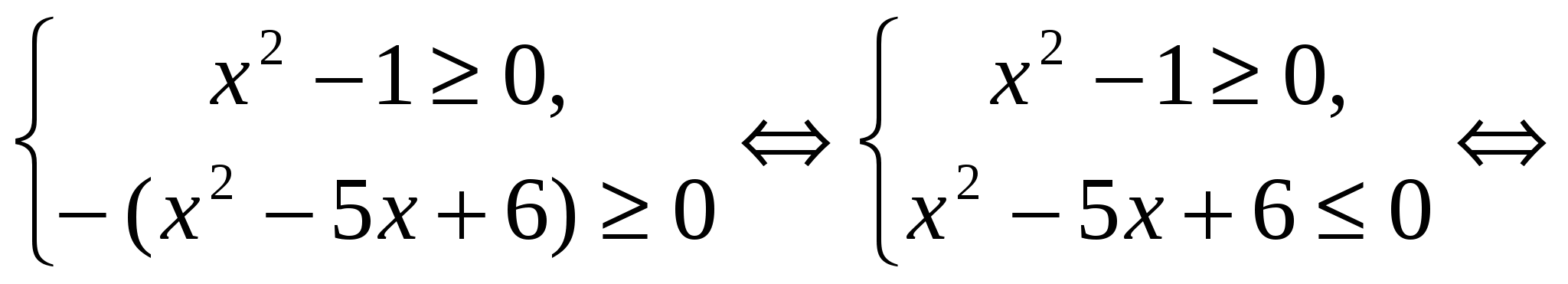
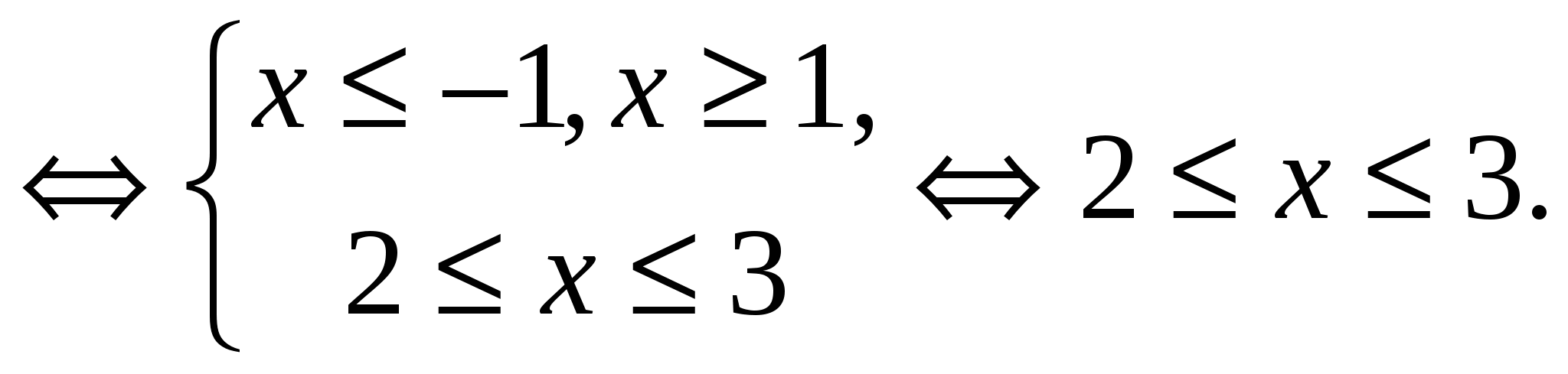
Ответ. 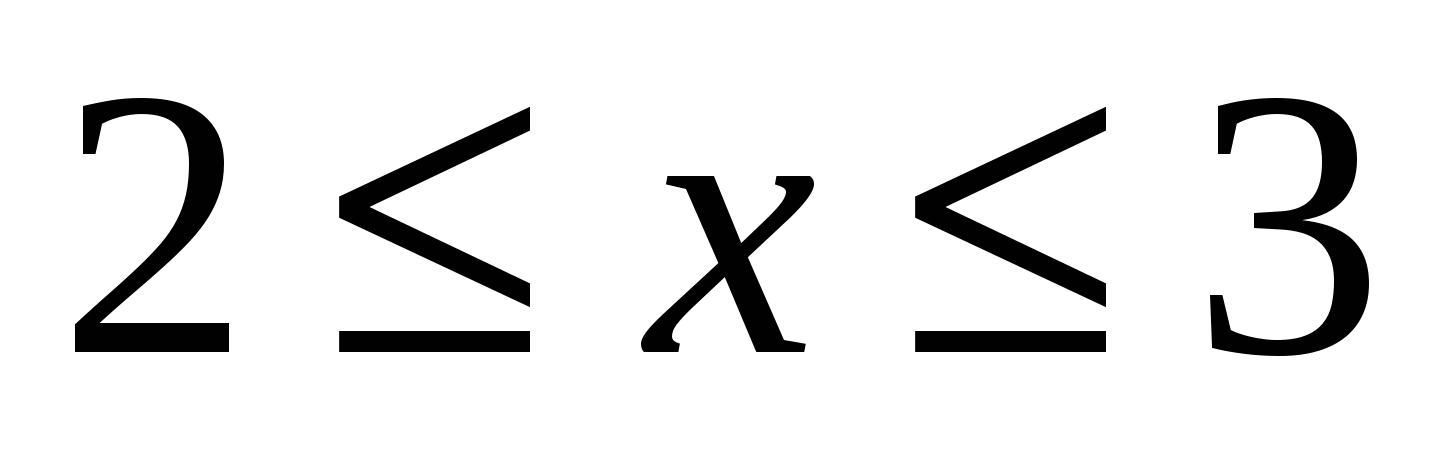 .
.
Примеры решения простейших неравенств.
Пример 6 Решим неравенство 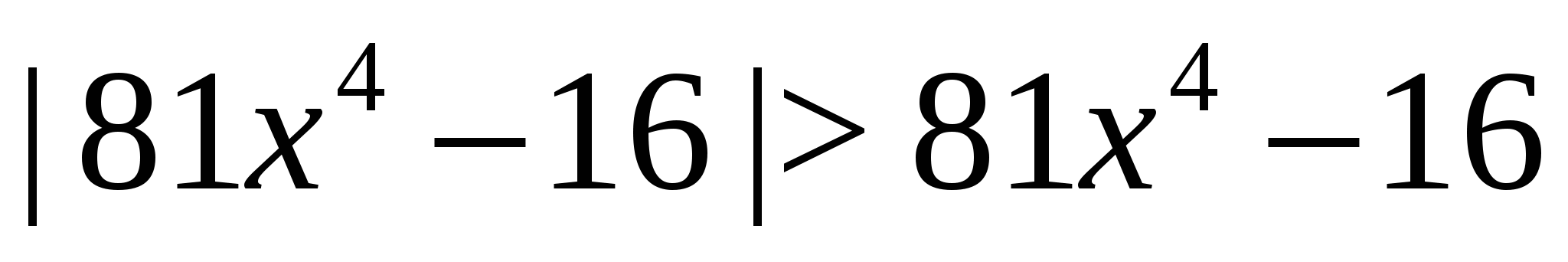 .
.
Решение.
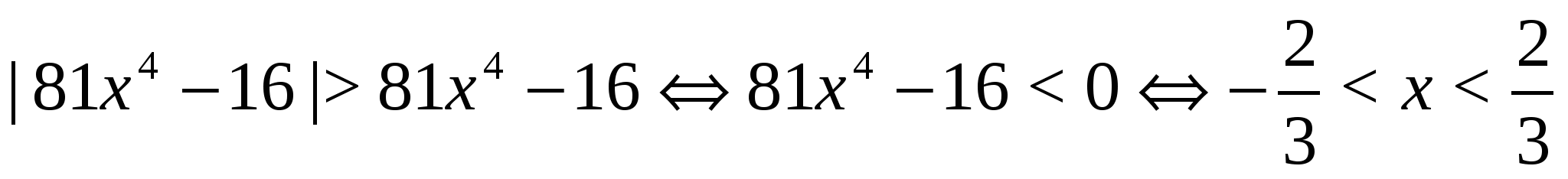 .
.
Ответ. 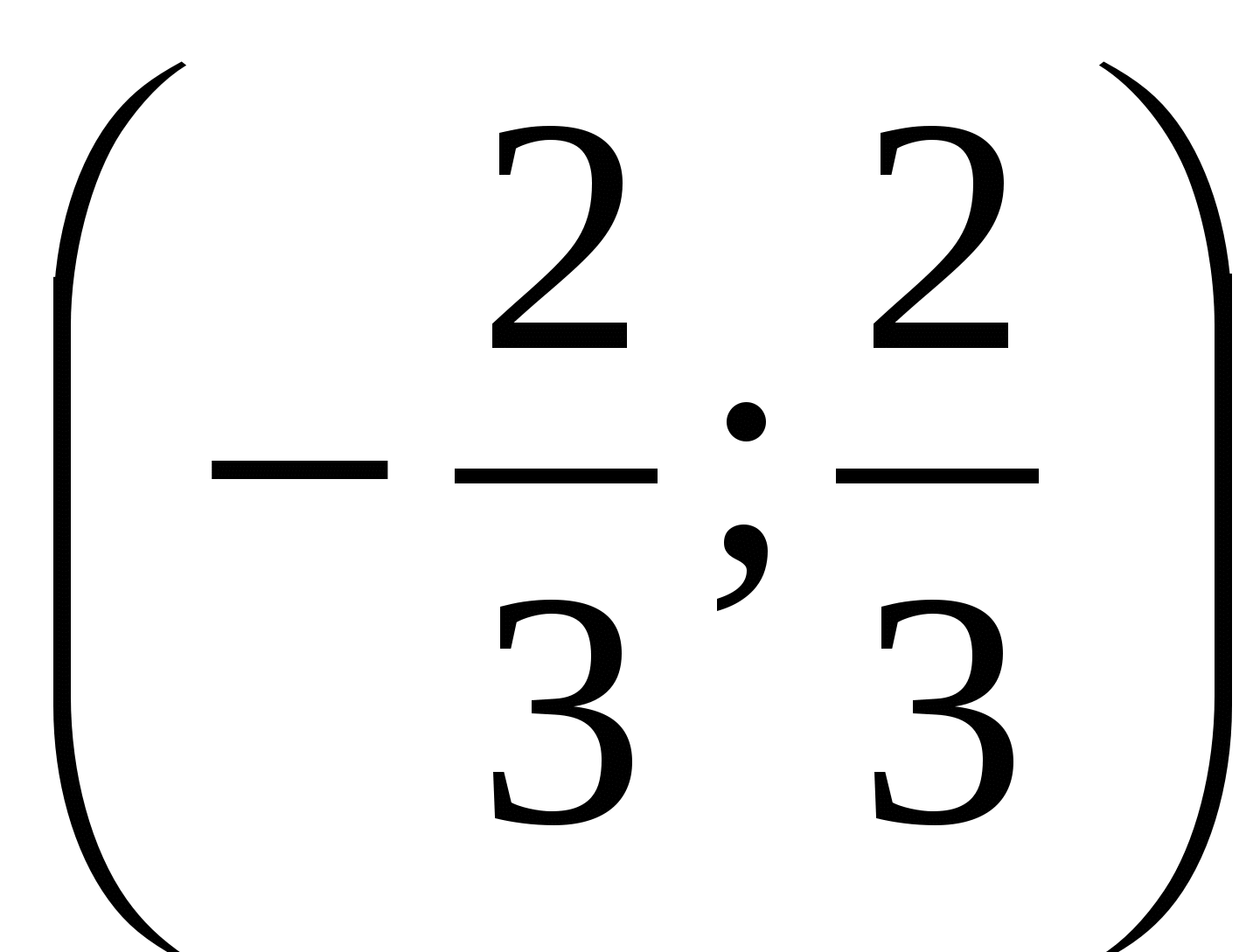 .
.
Пример 7 Решим неравенство 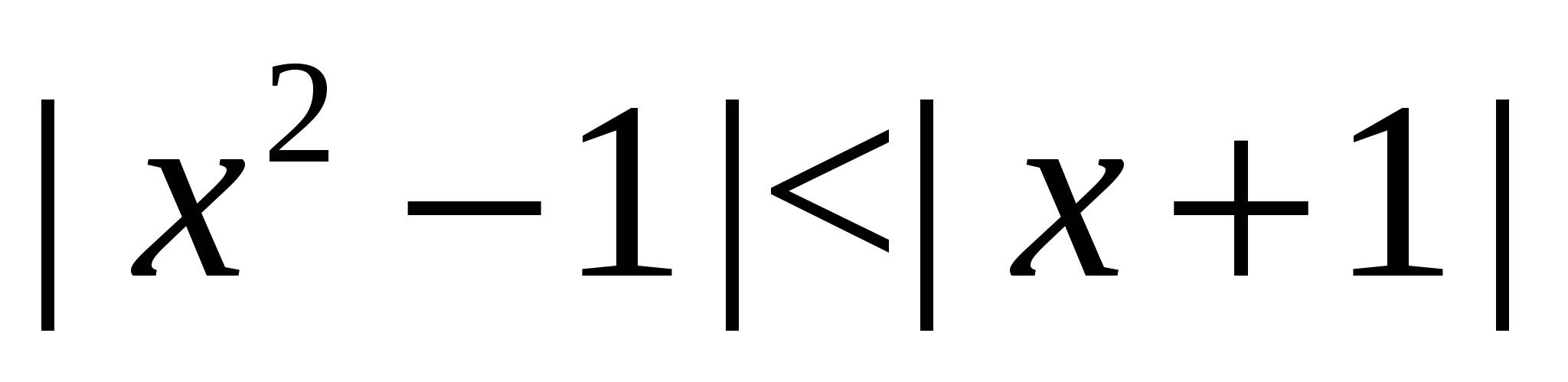 .
.
Решение.
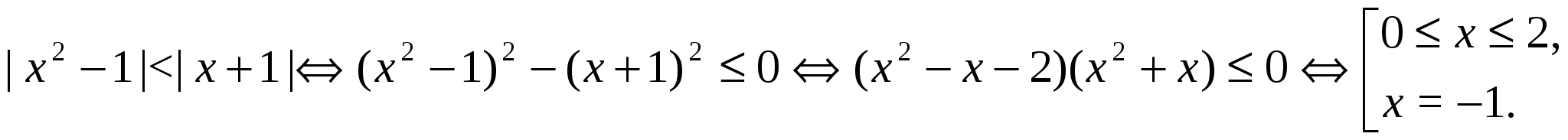
Ответ. 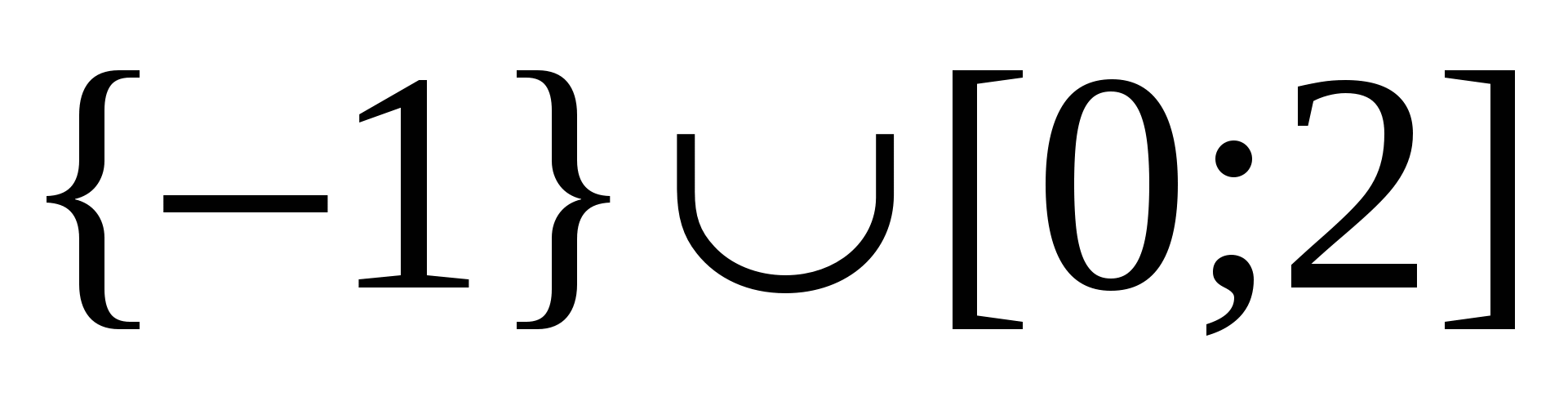 .
.
Как ни странно, но 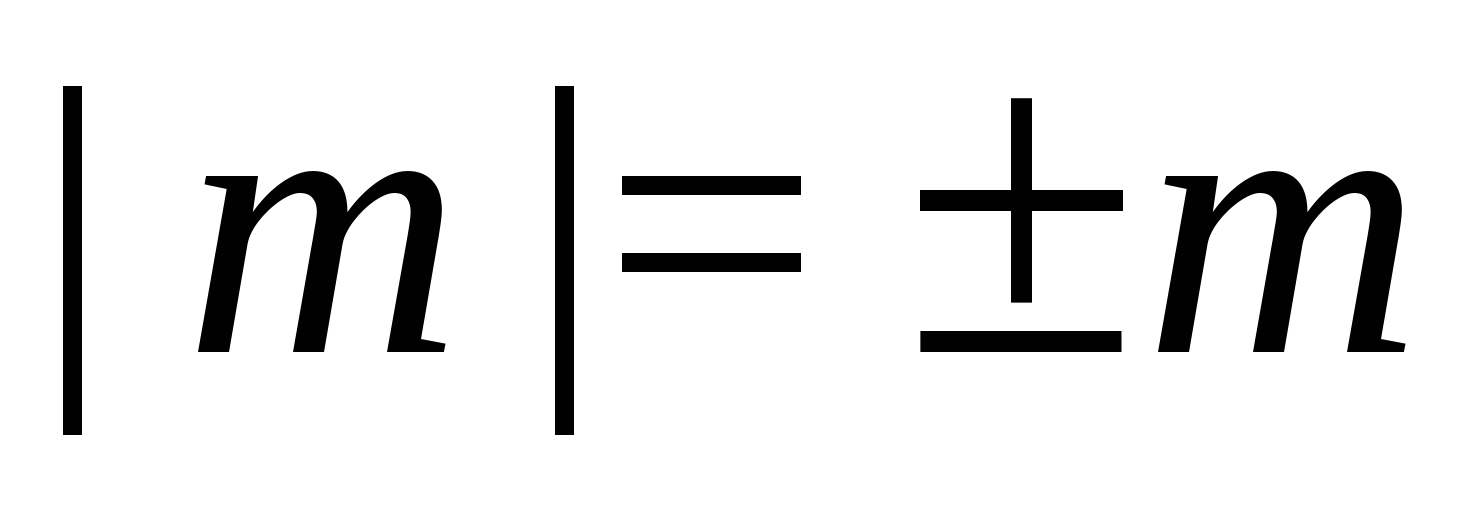 достаточно, чтобы избавиться от знака модуля в любых неравенствах.
достаточно, чтобы избавиться от знака модуля в любых неравенствах.
Пример 8 Решить неравенство
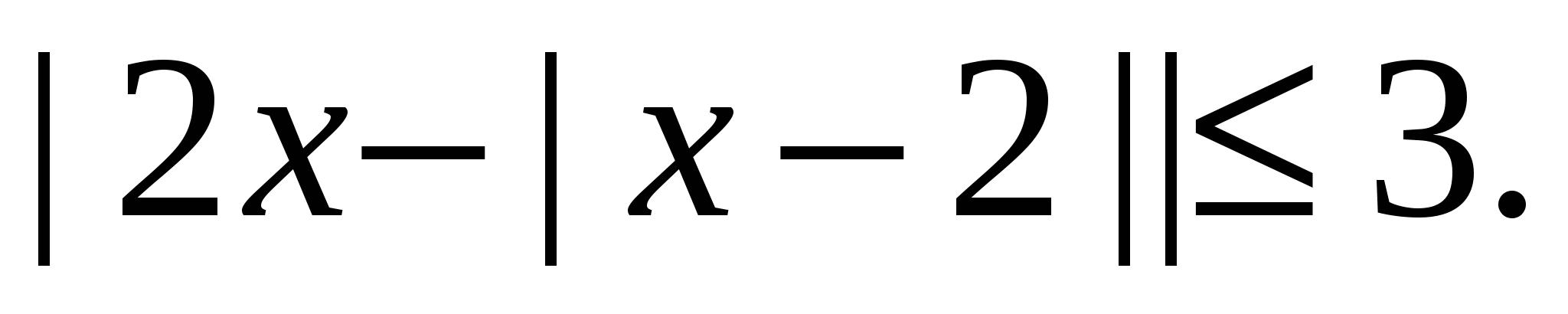
Решение.
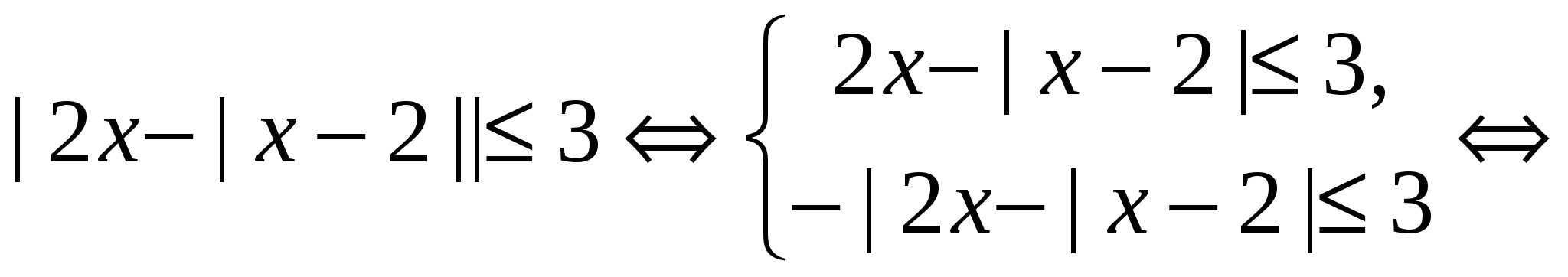
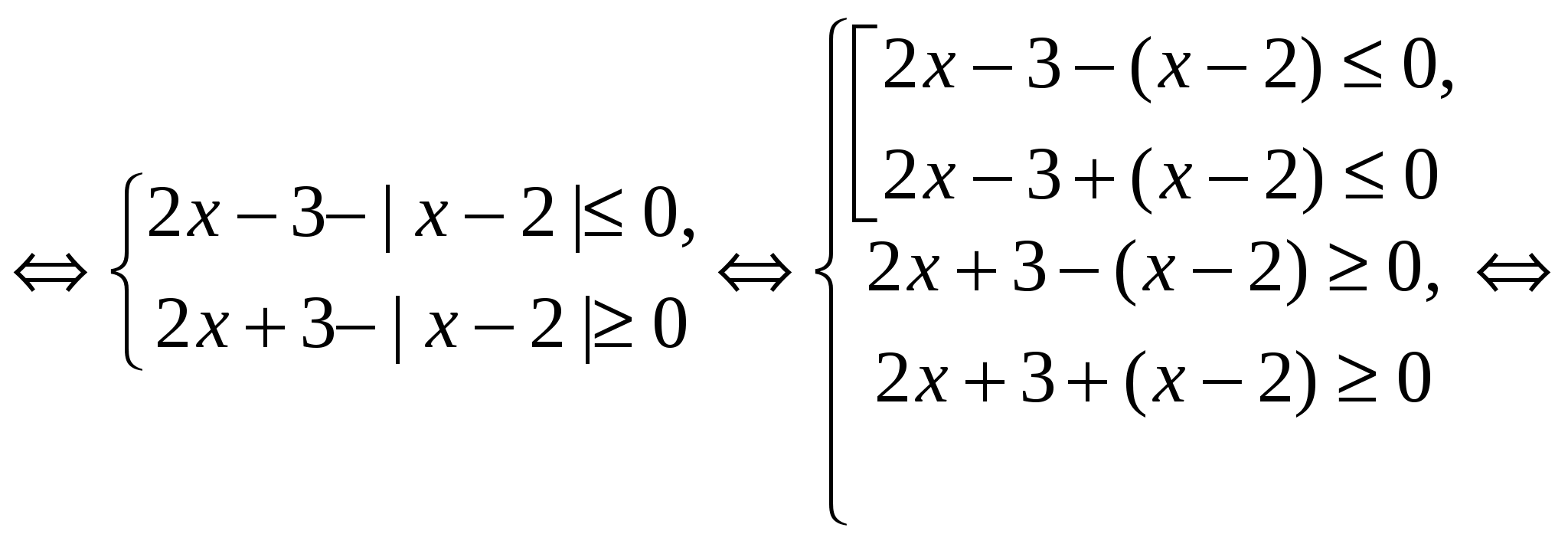
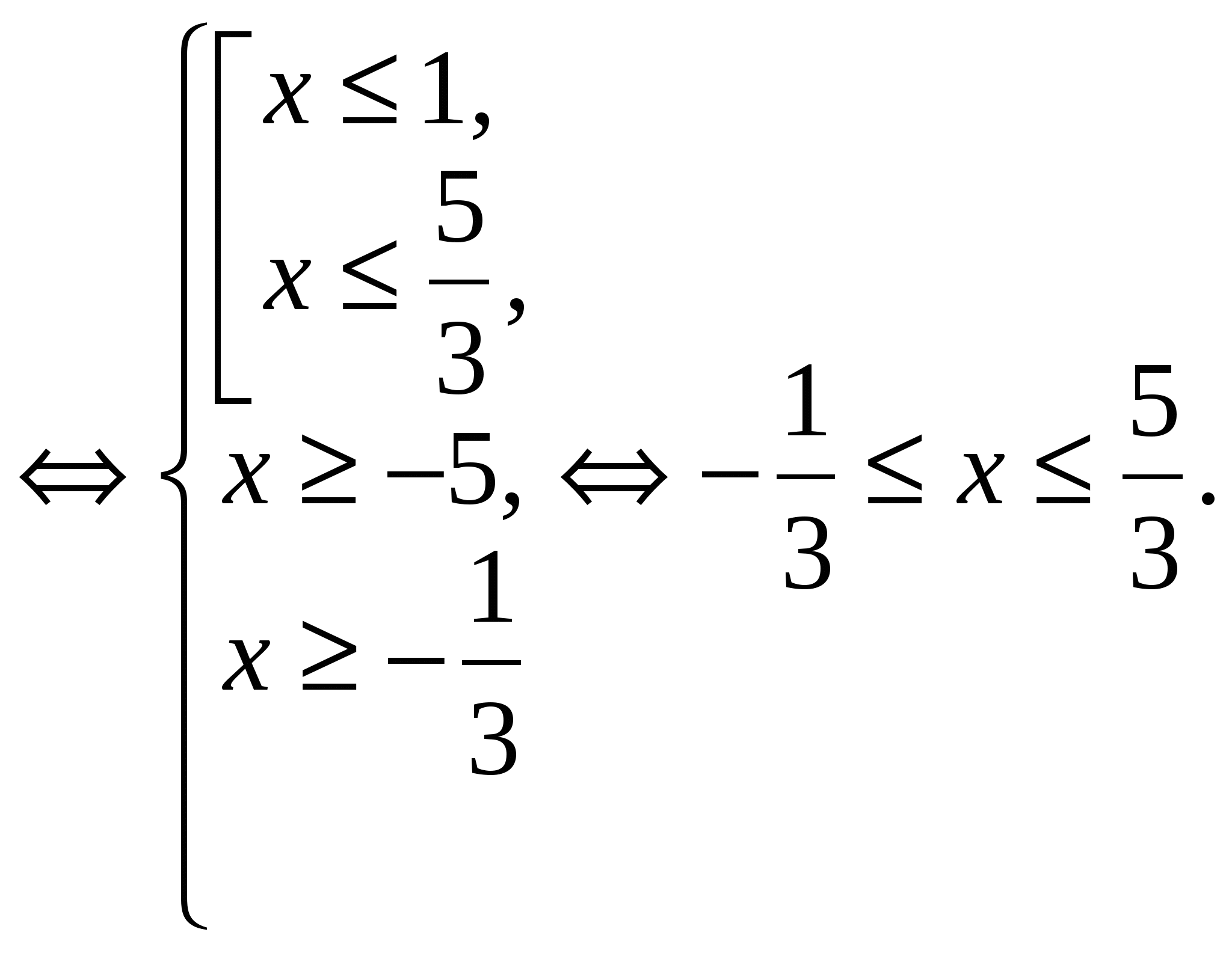
Ответ. 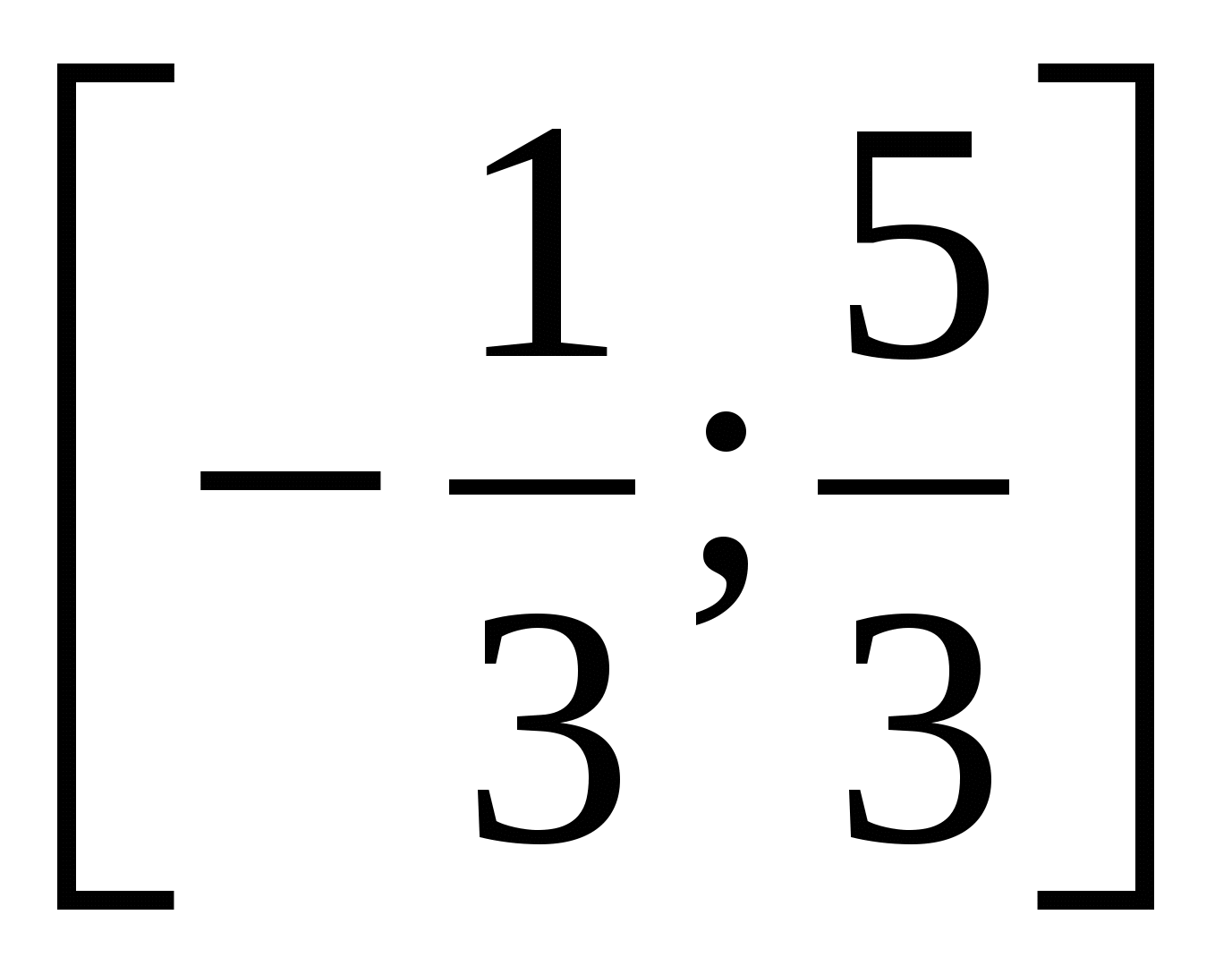 .
.
3. Графическое решение уравнений и неравенств с модулем
Решение уравнений, содержащих знак абсолютной величины часто гораздо удобнее решать не аналитически, а графически (особенно уравнения содержащие параметры).
Пример 9 (С5, ЕГЭ — 2010)
C5. Для каждого значения a укажите число решений уравнения 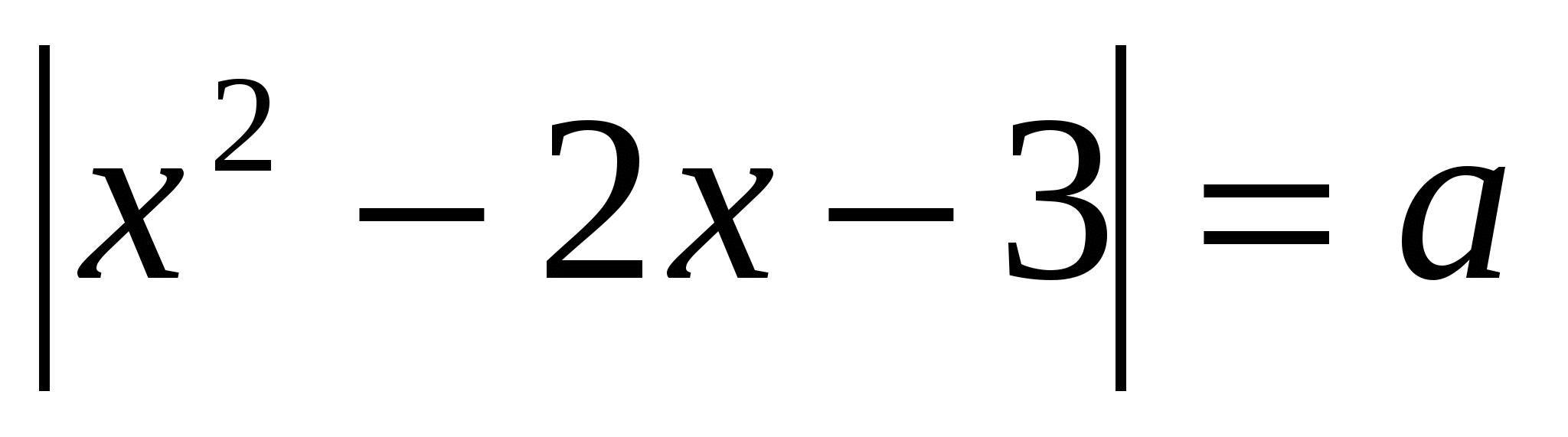
Решение. Построим график функции  . Для этого выделим полный квадрат :
. Для этого выделим полный квадрат : 
Число точек пересечения графика функции у = 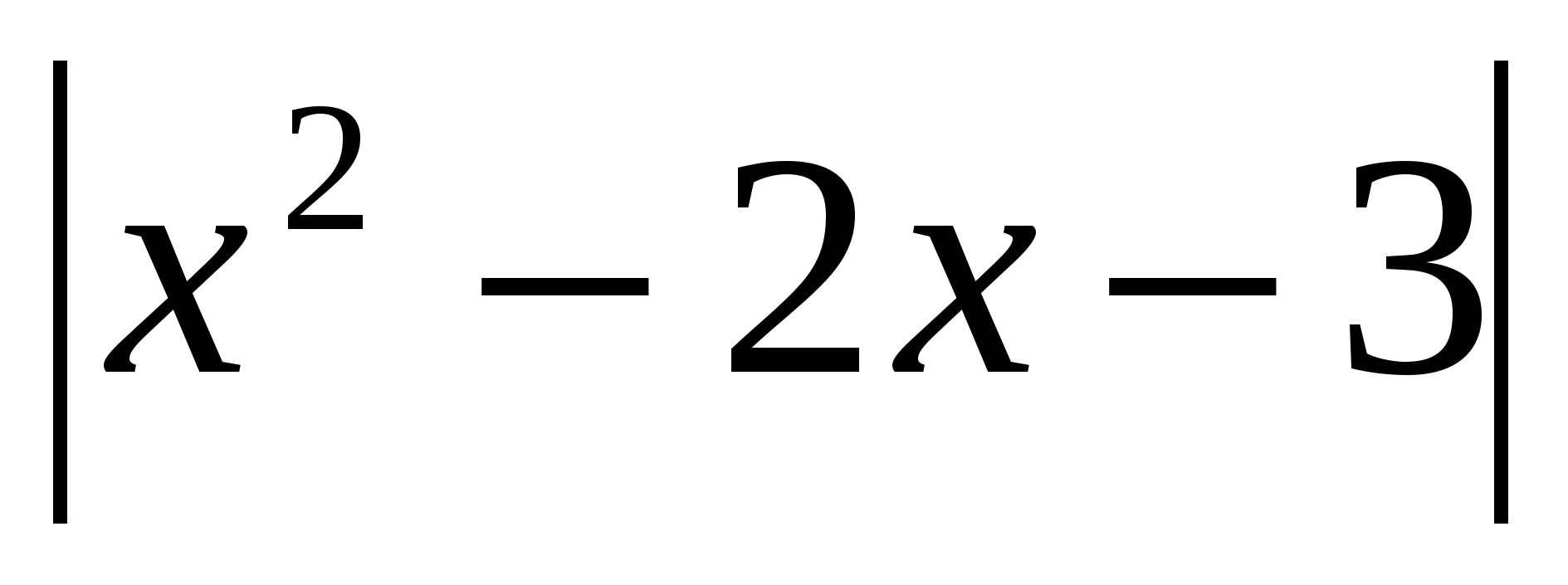 с горизонтальными прямыми у = а равно числу решений уравнения.
с горизонтальными прямыми у = а равно числу решений уравнения.
О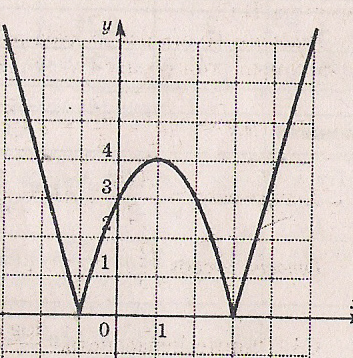 твет: если
твет: если  < 0, то решений нет; если а= 0, то два решения, если
< 0, то решений нет; если а= 0, то два решения, если  0 < а < 4, то четыре решения; если а=4, то три решения; если а > 4, то два решения.
0 < а < 4, то четыре решения; если а=4, то три решения; если а > 4, то два решения.
Метод раскрытия модулей
Метод раскрытия модулей рассмотрим на примере:
Пример 10 Решить уравнение
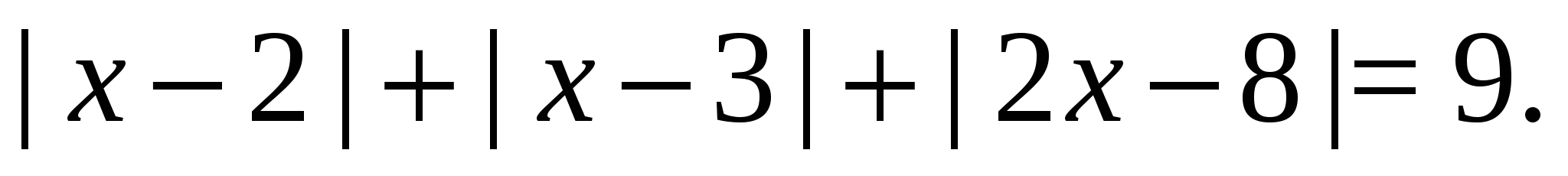
Решение. Это уравнение содержит более одного модуля.
Метод решения уравнений, содержащих переменные под знаком двух и более модулей, состоит в следующем.
1. Найти значения переменной, при которых каждый из модулей обращается в нуль: 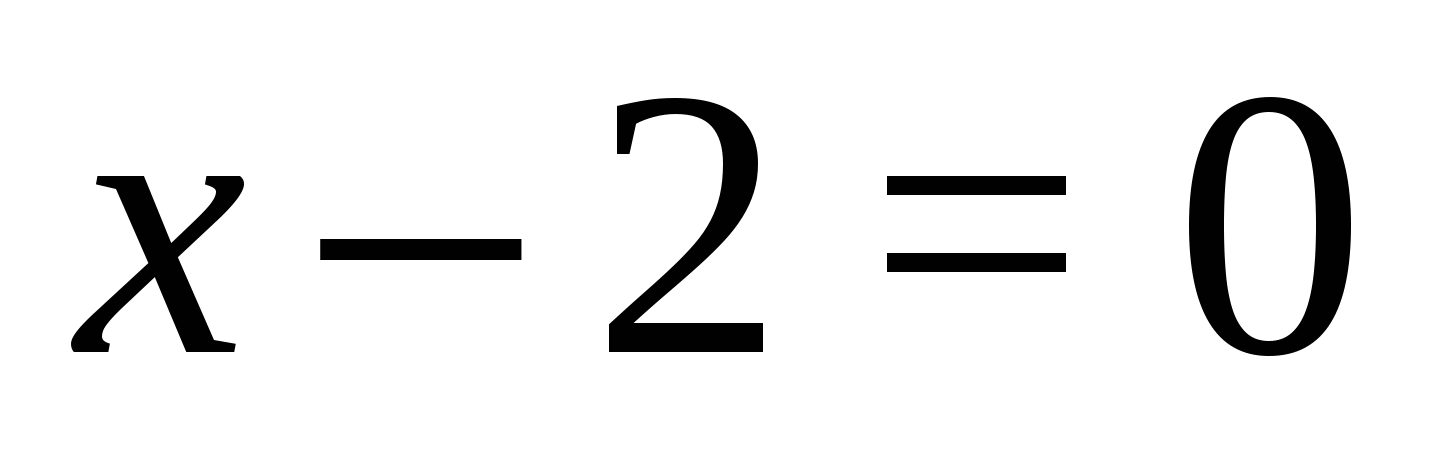 ,
, 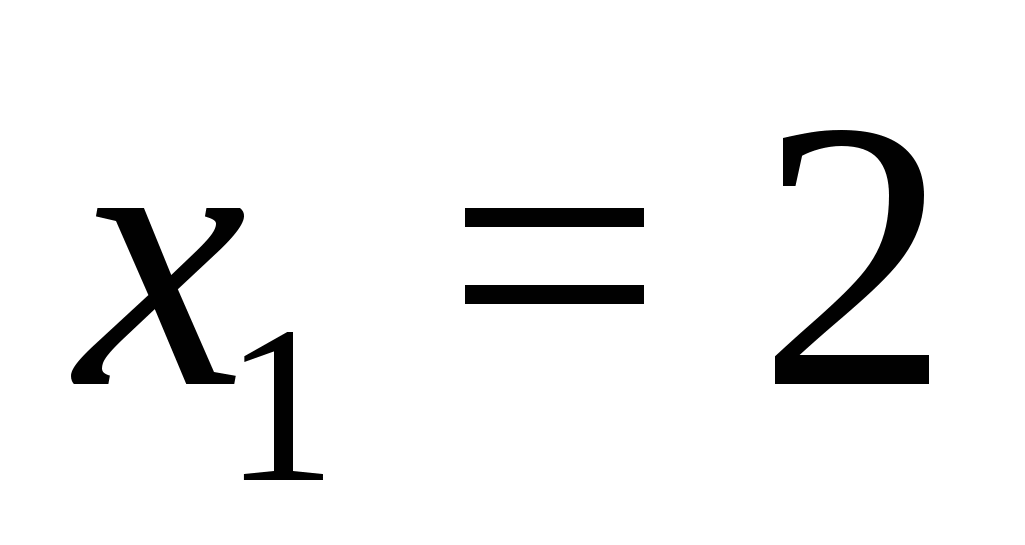 ;
; 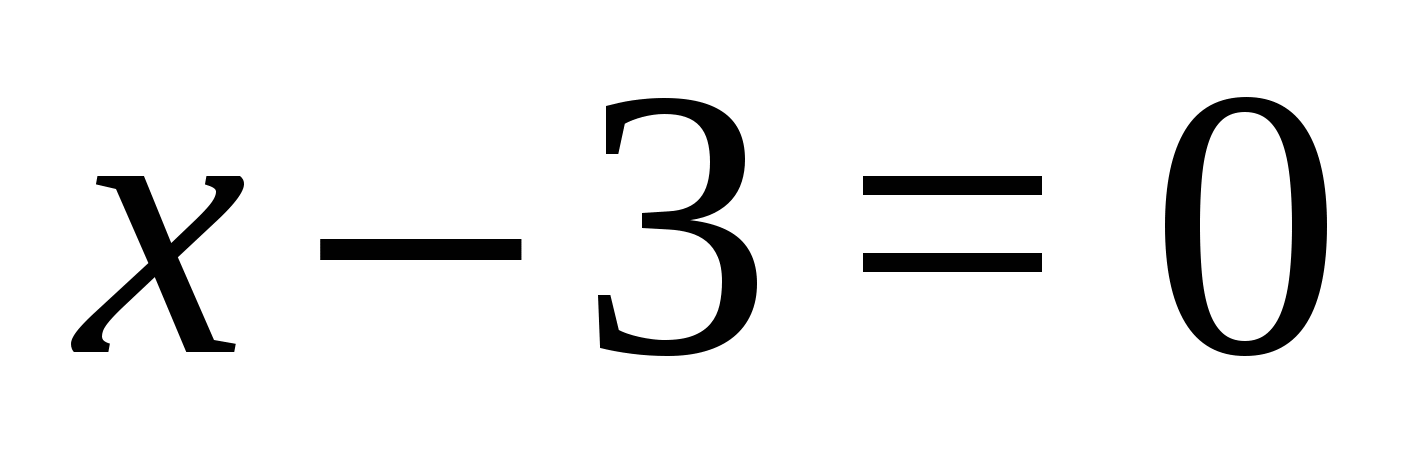 ,
, 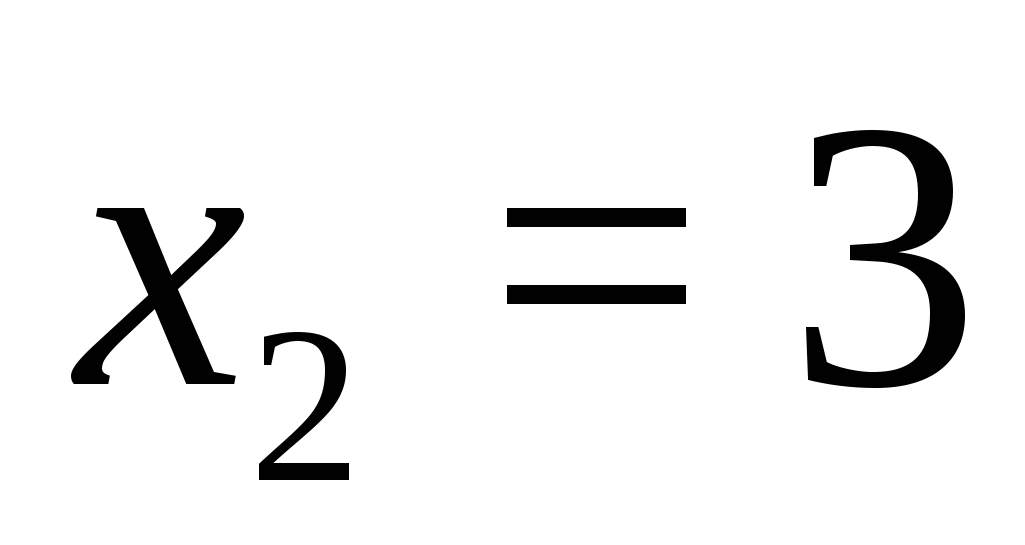 ;
; 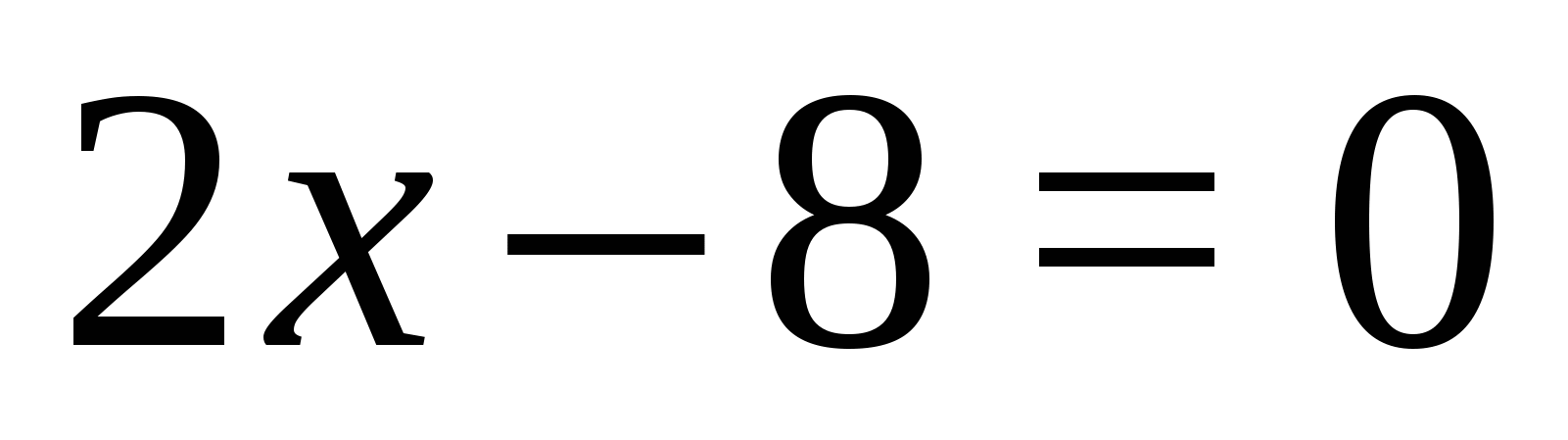 ,
, 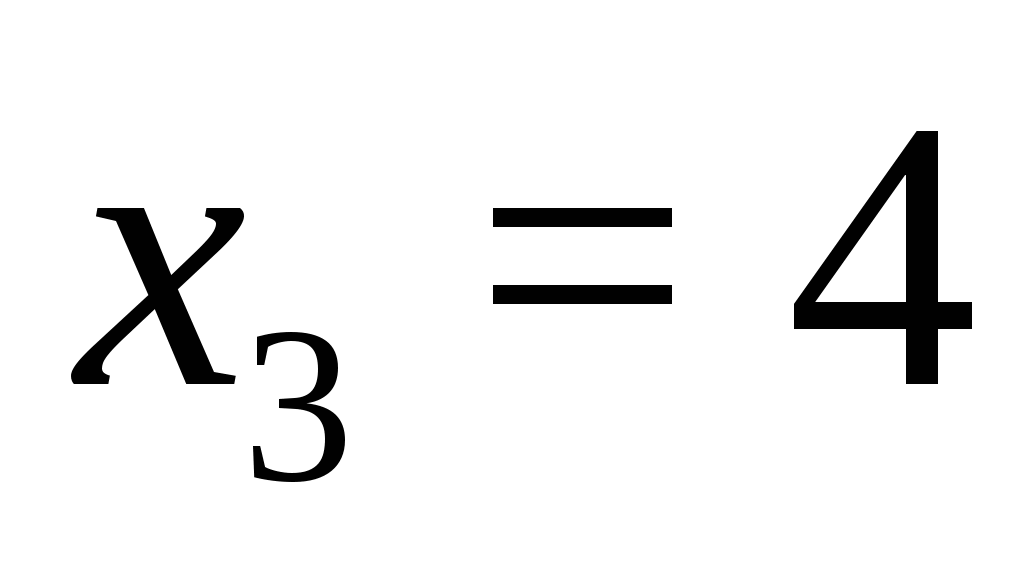 .
.
2. Отметить эти точки на числовой прямой.
3. Рассматриваем уравнение на каждом из промежутков и устанавливаем знак выражений, которые находятся под модулями.
1) При 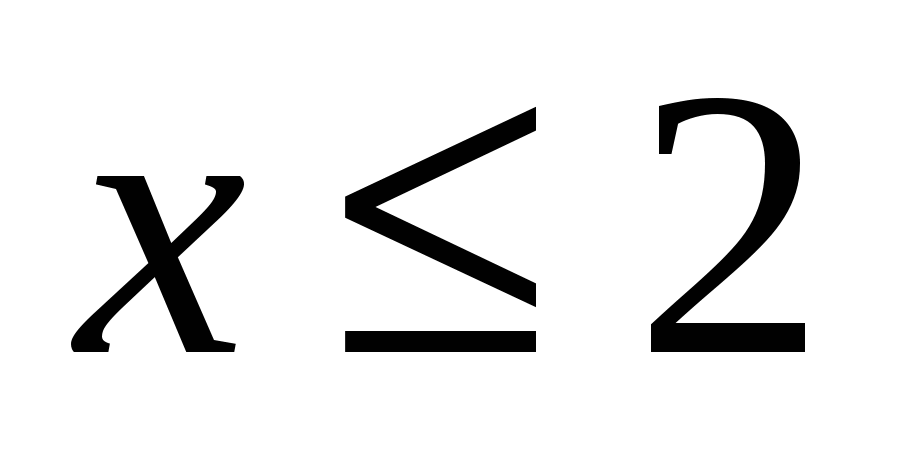 или
или 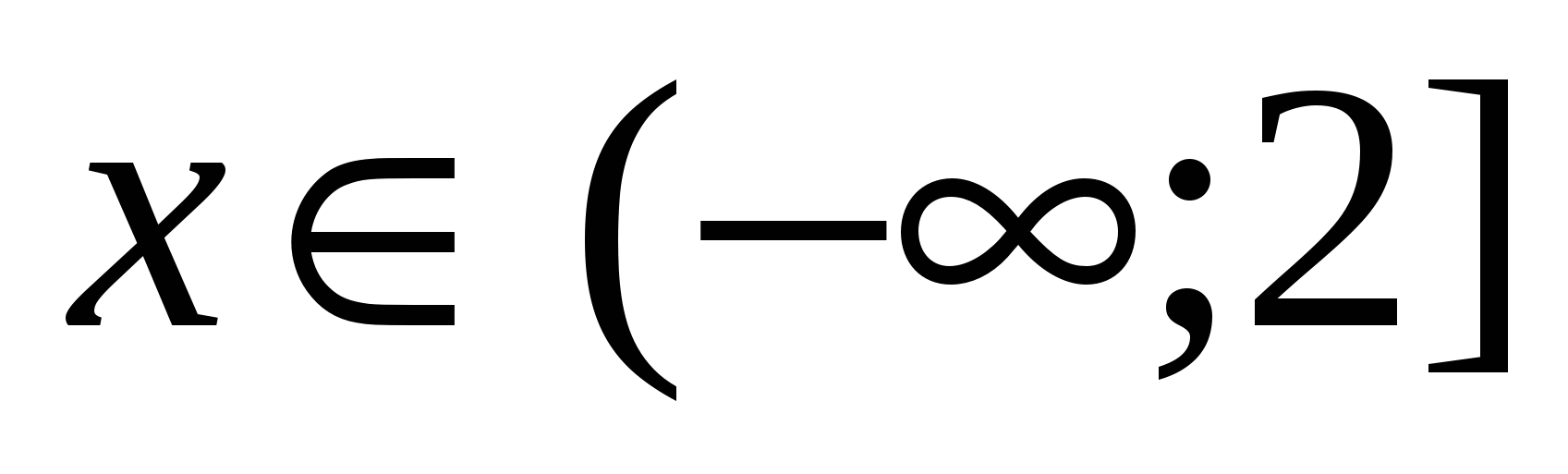 . Чтобы определить знак каждого из выражений под модулем на этом промежутке, достаточно взять любое значение
. Чтобы определить знак каждого из выражений под модулем на этом промежутке, достаточно взять любое значение 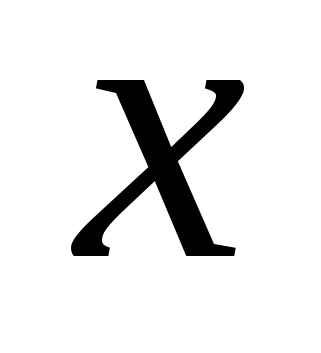 из этого промежутка и подставить в выражение. Если полученное значение отрицательно, значит, при всех
из этого промежутка и подставить в выражение. Если полученное значение отрицательно, значит, при всех 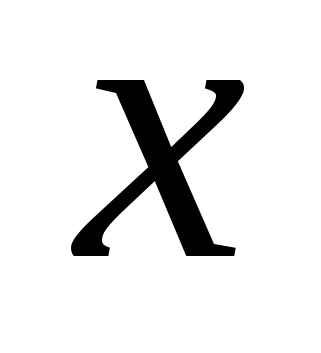 из этого промежутка выражение будет отрицательным; если полученное числовое значение положительно, значит, при всех значениях
из этого промежутка выражение будет отрицательным; если полученное числовое значение положительно, значит, при всех значениях 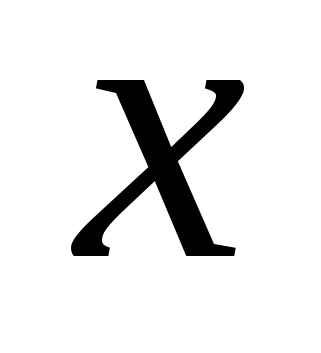 из этого промежутка выражение будет положительным.
из этого промежутка выражение будет положительным.
Возьмем значение 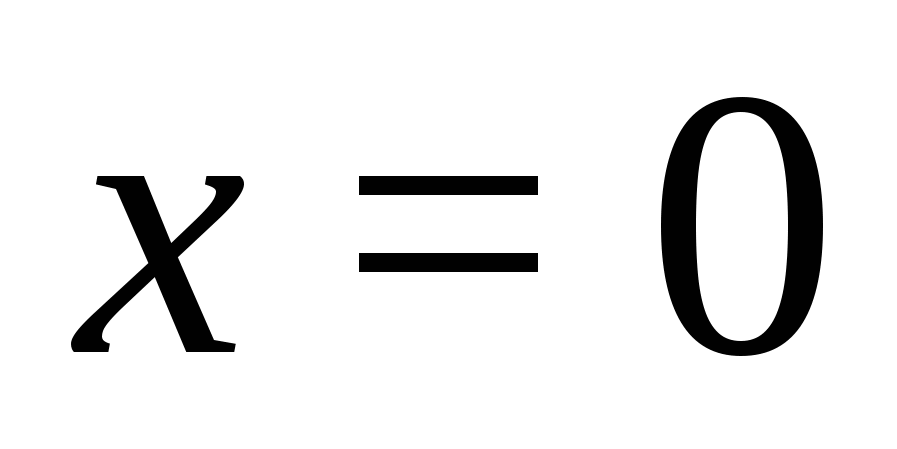 из промежутка
из промежутка 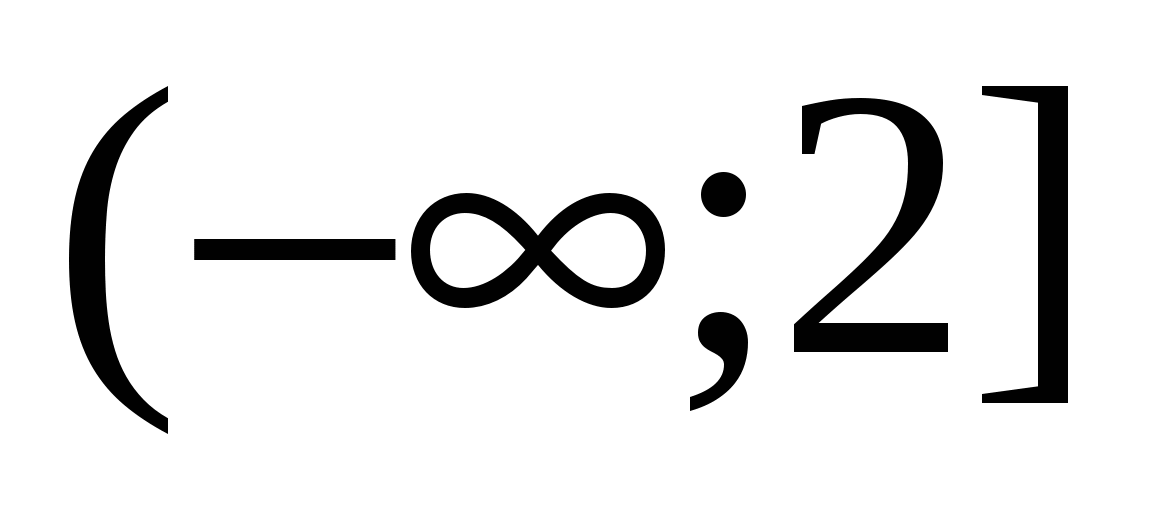 и подставим его значение в выражение
и подставим его значение в выражение 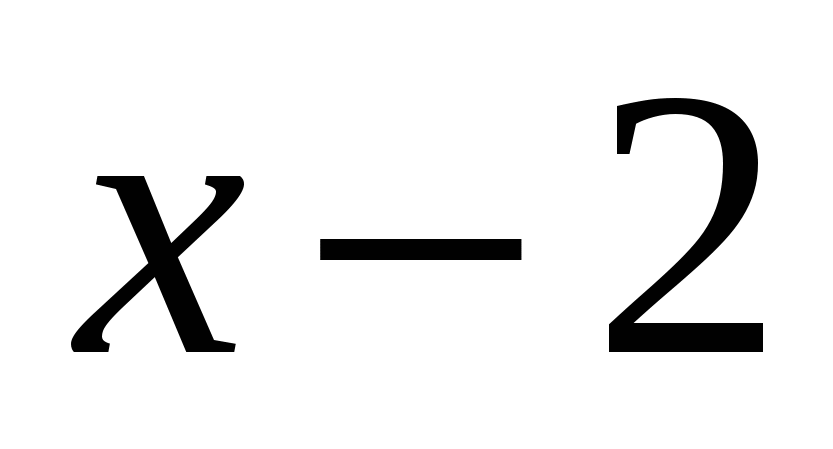 , получаем
, получаем 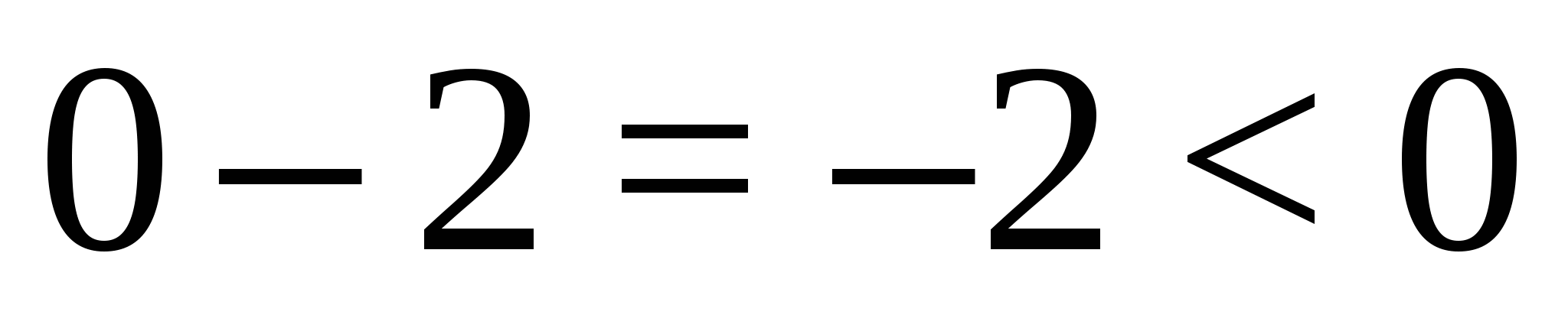 , значит на этом промежутке
, значит на этом промежутке 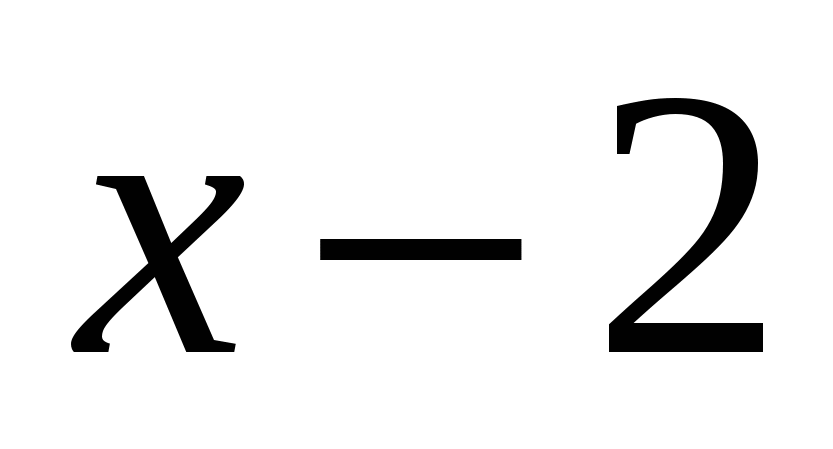 отрицательно, а следовательно «выйдет» из под модуля со знаком «минус», получим:
отрицательно, а следовательно «выйдет» из под модуля со знаком «минус», получим: 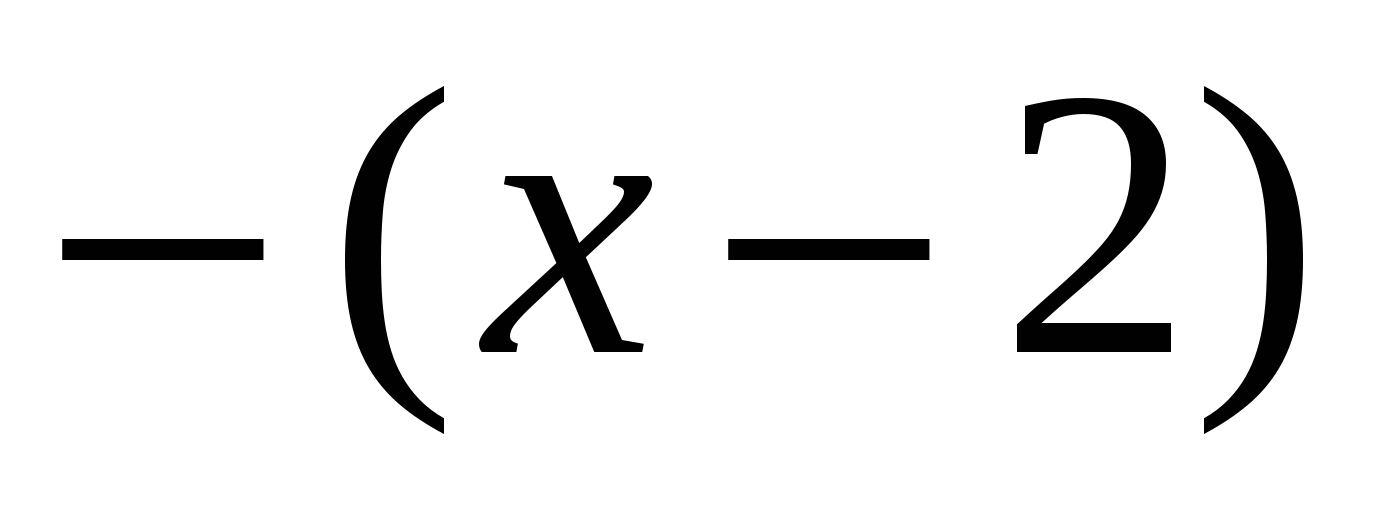 .
.
При этом значении 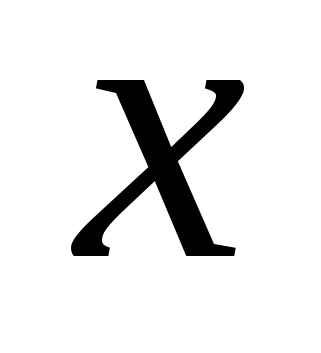 , выражение
, выражение 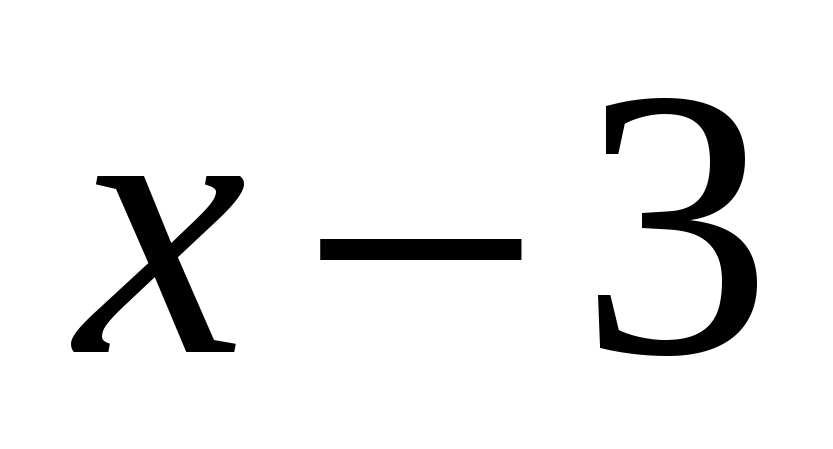 получит значение
получит значение 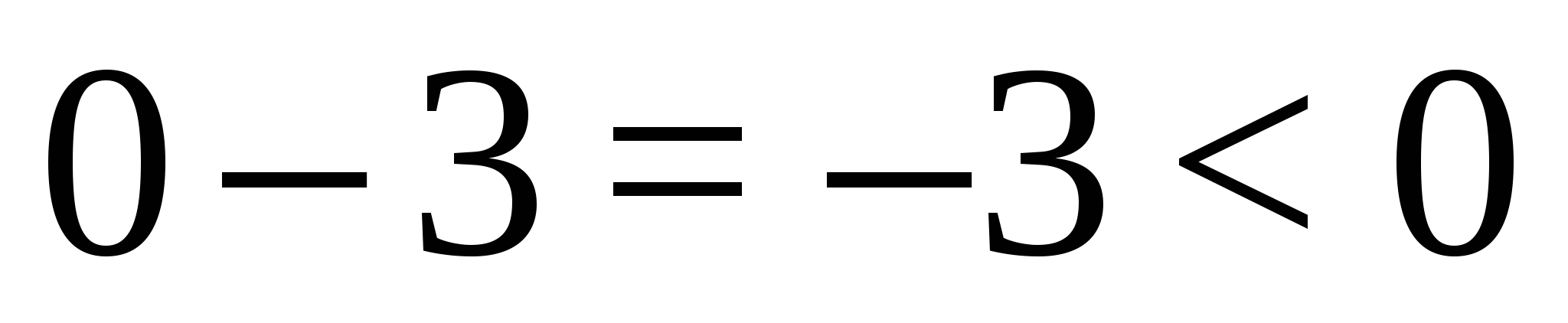 , значит, оно на промежутке
, значит, оно на промежутке 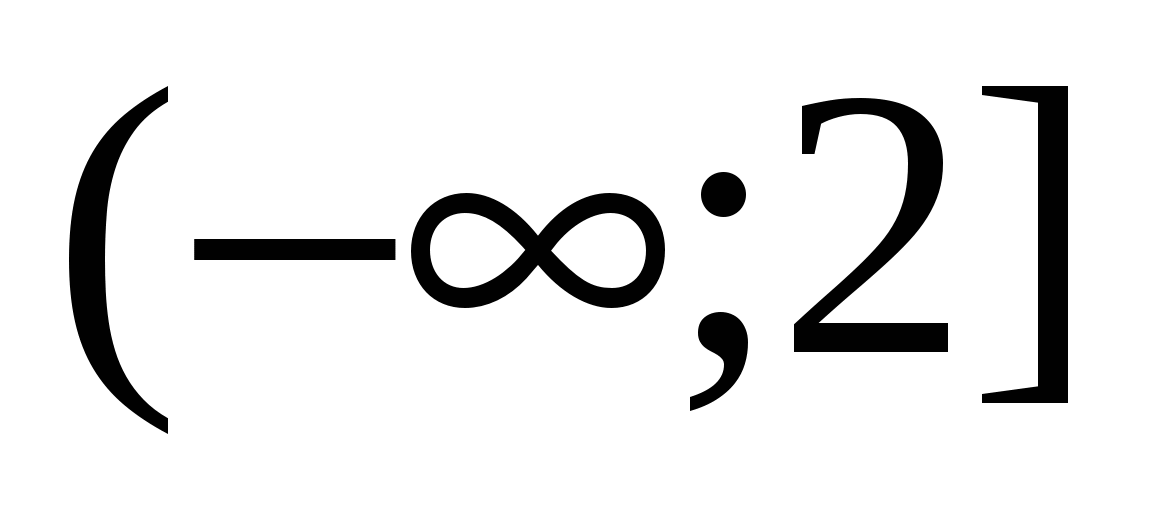 также принимает отрицательные значения и «выйдет» из модуля со знаком «минус», получим:
также принимает отрицательные значения и «выйдет» из модуля со знаком «минус», получим: 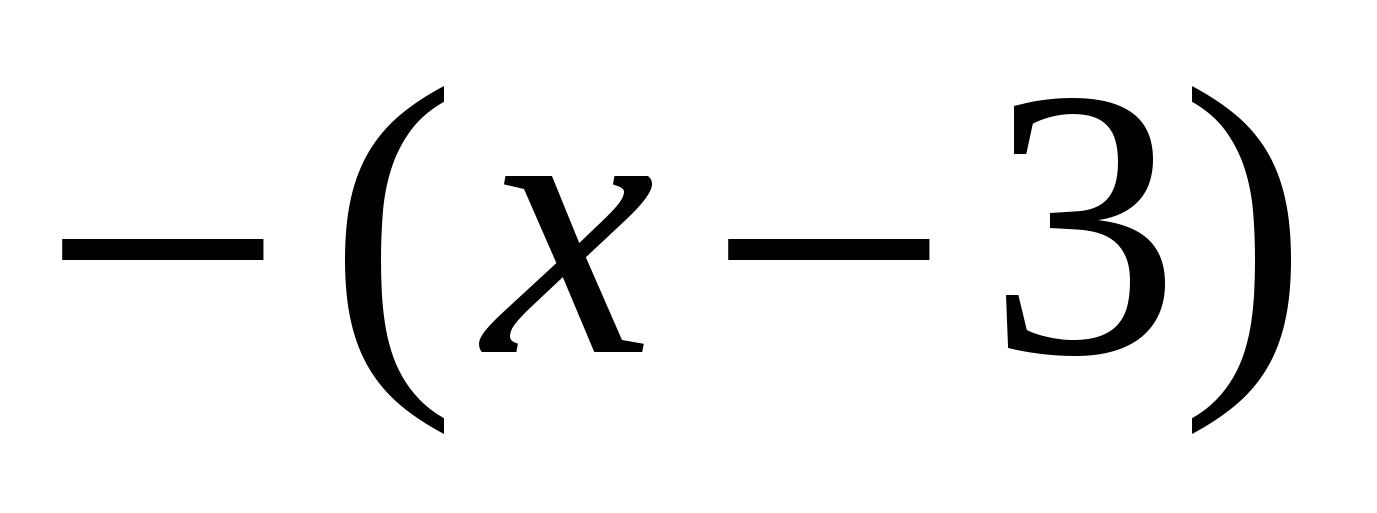 .
.
Выражение 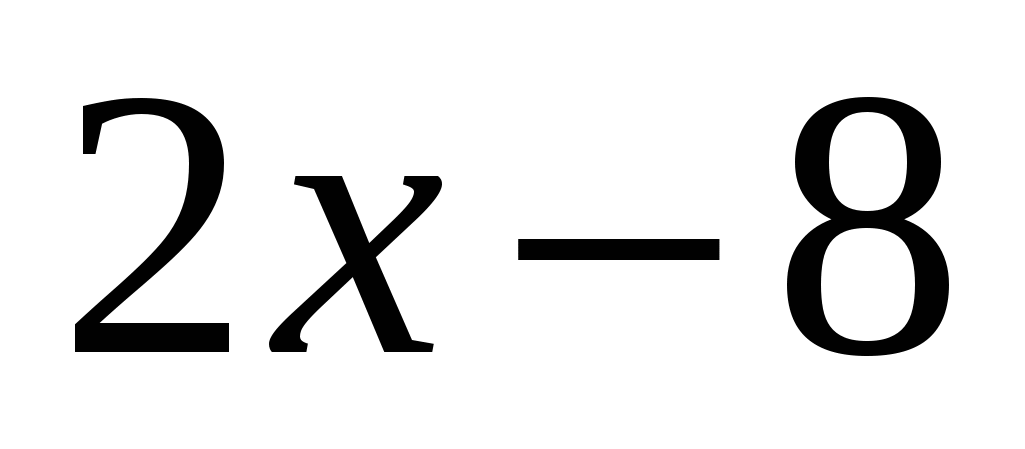 получит значение
получит значение 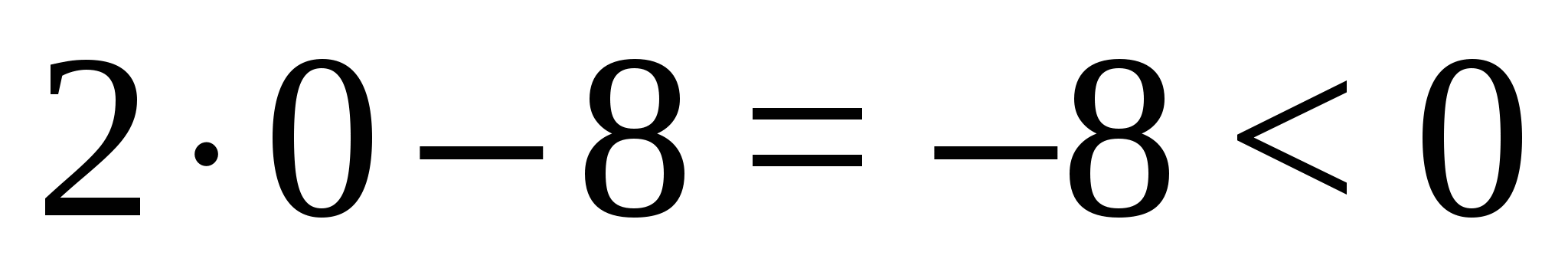 и «выйдет» из под модуля со знаком «минус»:
и «выйдет» из под модуля со знаком «минус»: 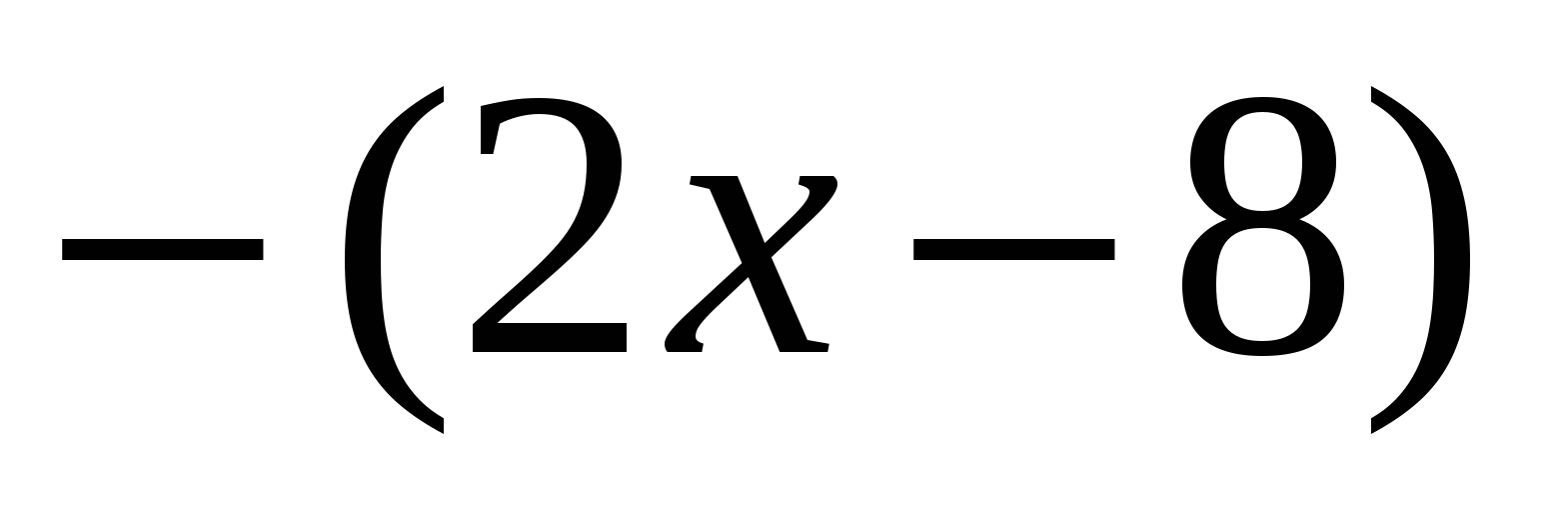 .
.
Уравнение на этом промежутке получится таким: 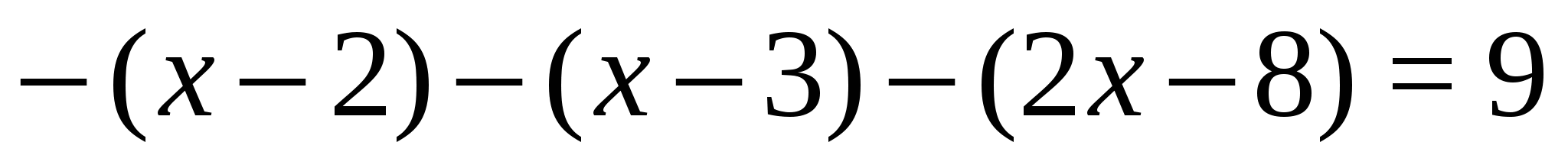 , решая его, находим:
, решая его, находим: 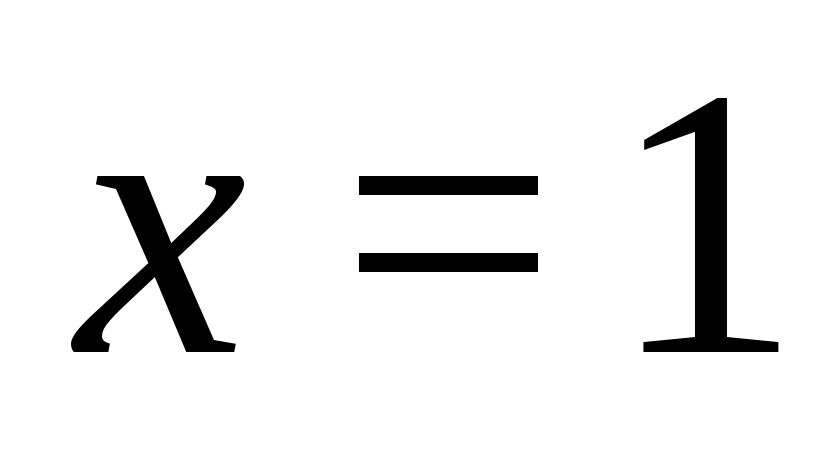 .
.
Выясняем, входит ли это значение в промежуток 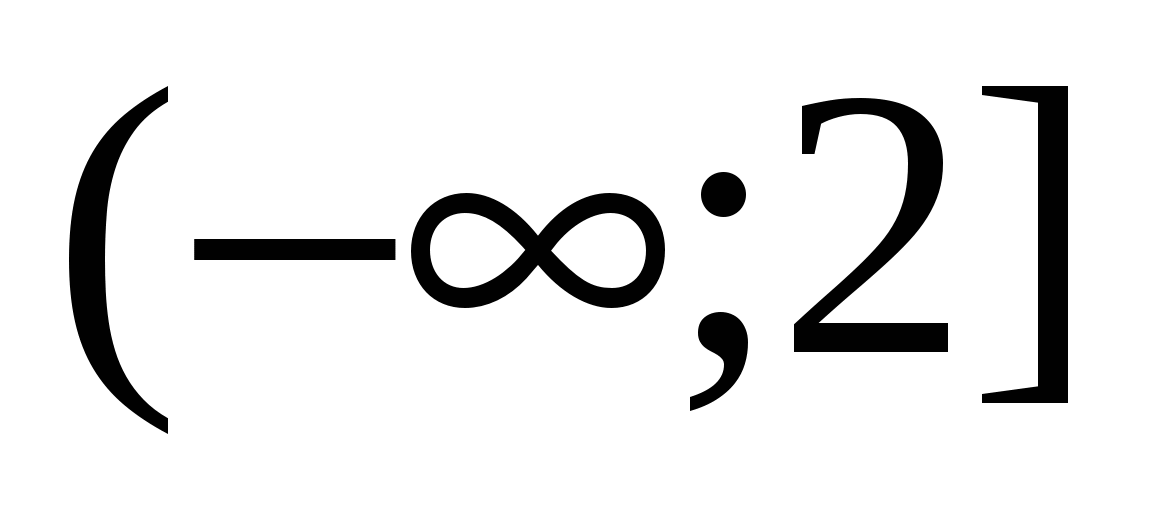 . Оказывается входит, значит
. Оказывается входит, значит 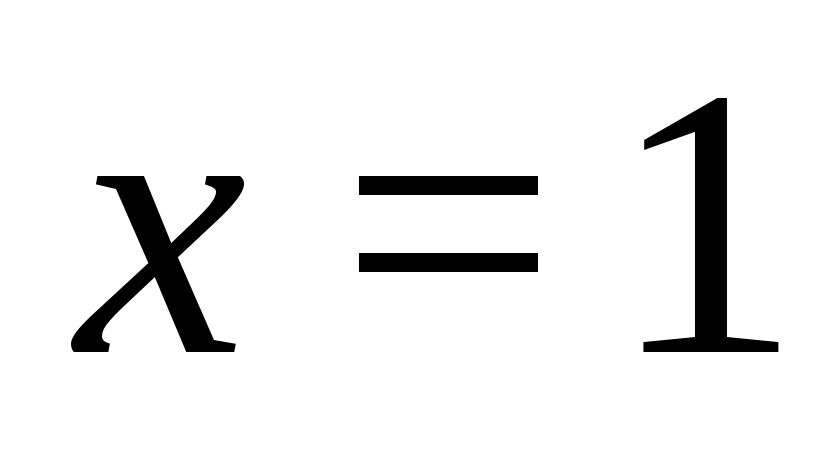 является корнем уравнения.
является корнем уравнения.
2) При 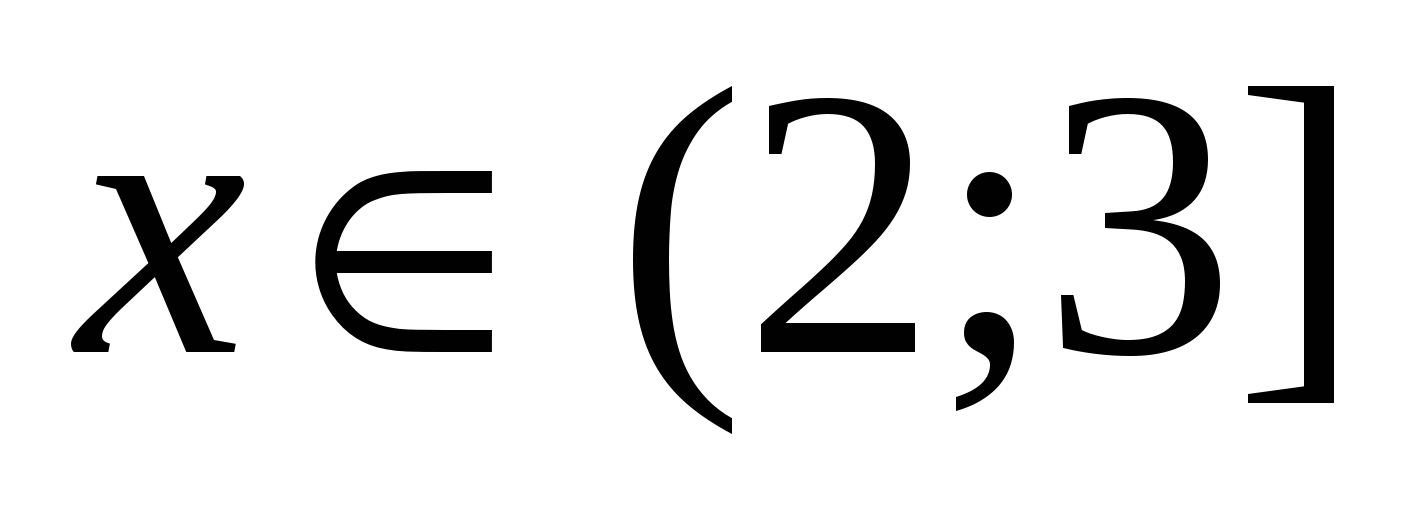 . Выбираем любое значение
. Выбираем любое значение 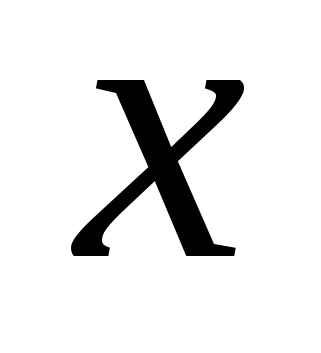 из этого промежутка. Пусть
из этого промежутка. Пусть 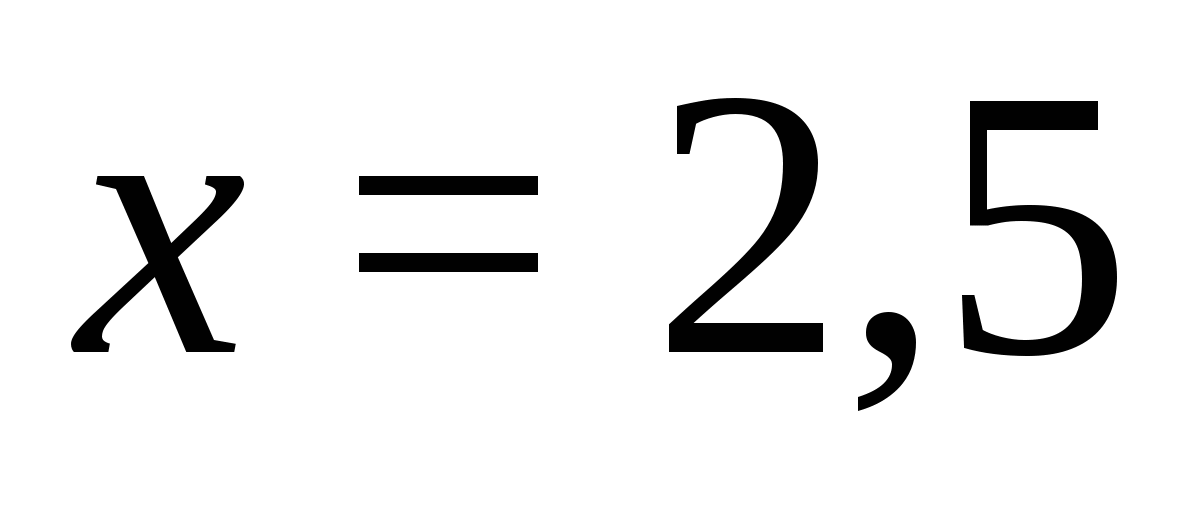 . Определяем знак каждого из выражений под модулем при этом значении
. Определяем знак каждого из выражений под модулем при этом значении 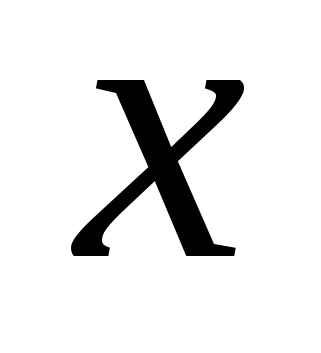 . Оказывается, что выражение
. Оказывается, что выражение 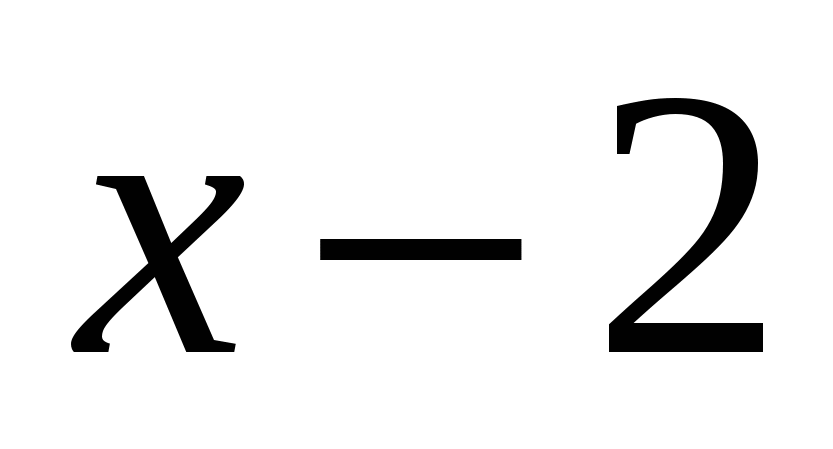 положительно, а два других отрицательны.
положительно, а два других отрицательны.
Уравнение на этом промежутке примет вид: 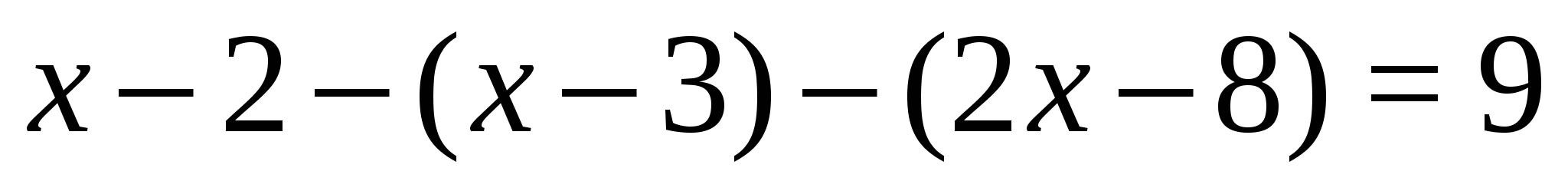 . Решая его, находим
. Решая его, находим 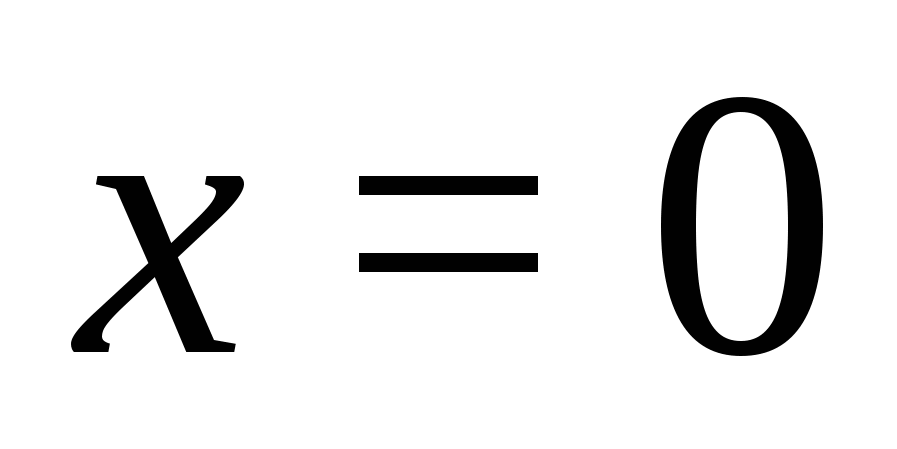 . Это значение не входит в промежуток
. Это значение не входит в промежуток 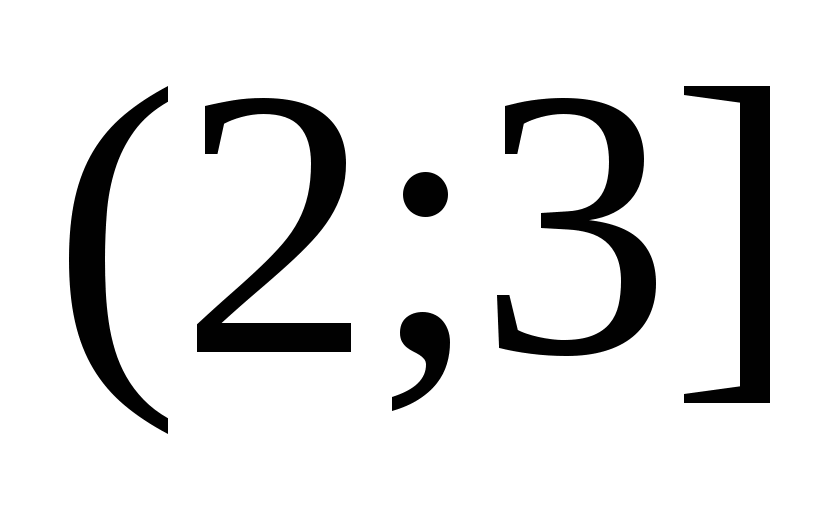 , а значит, не является корнем уравнения.
, а значит, не является корнем уравнения.
3) При 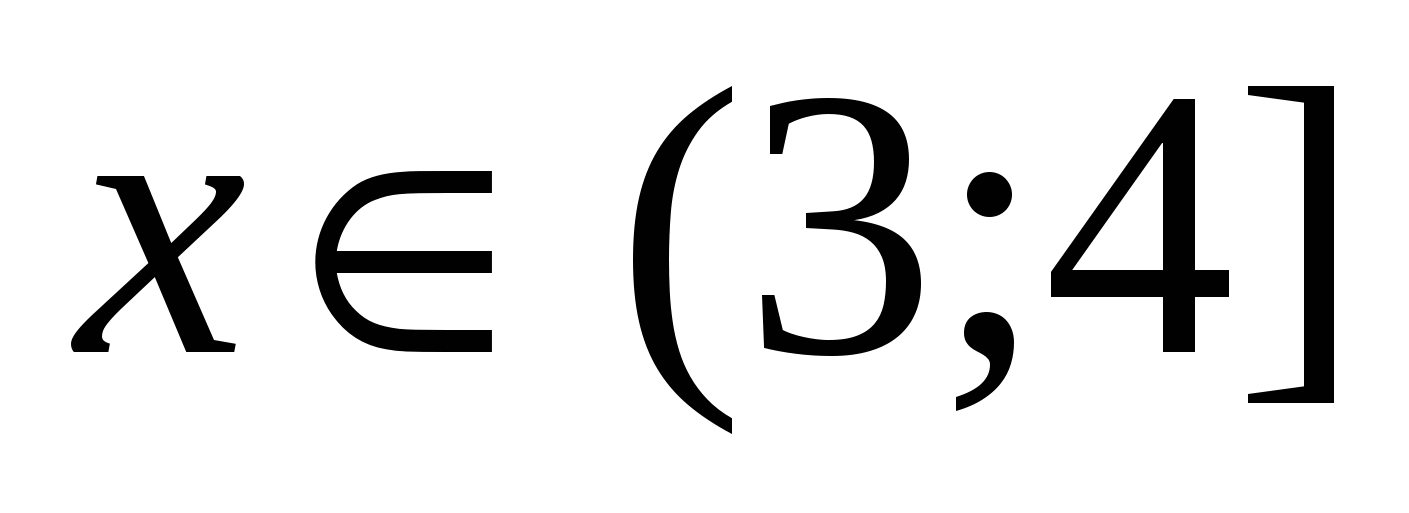 . Выбираем произвольное значение
. Выбираем произвольное значение 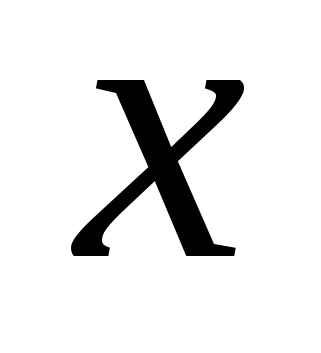 из этого промежутка, скажем,
из этого промежутка, скажем, 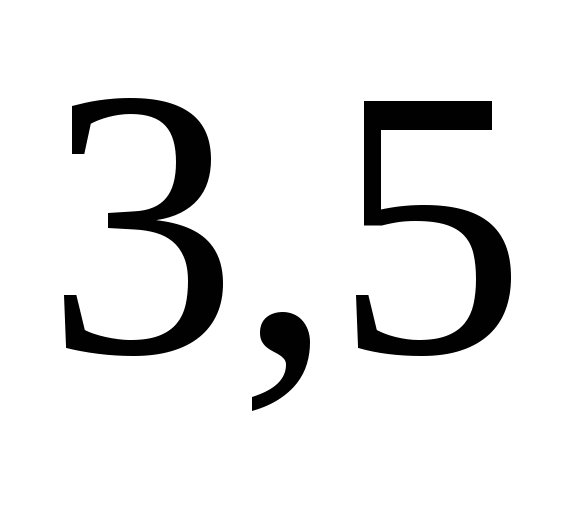 и подставляем в каждое из выражений. Находим, что выражения
и подставляем в каждое из выражений. Находим, что выражения 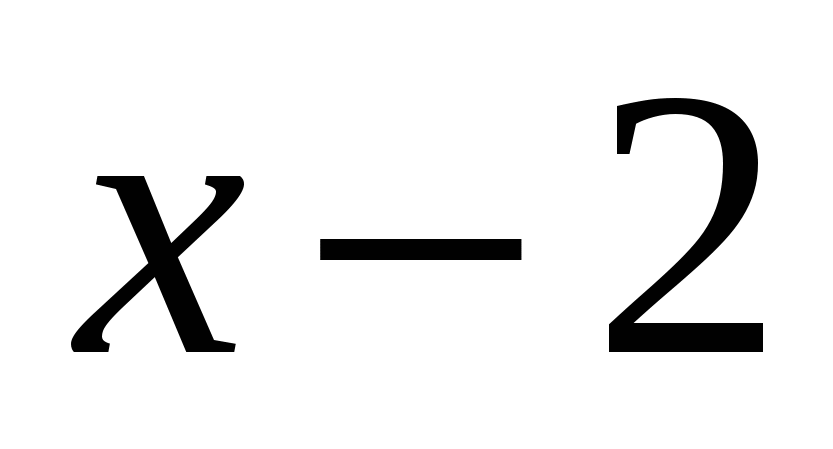 и
и 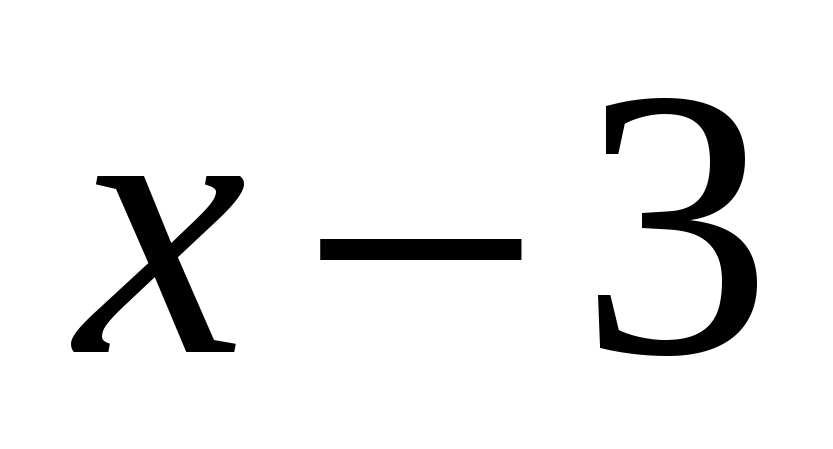 положительны, а
положительны, а 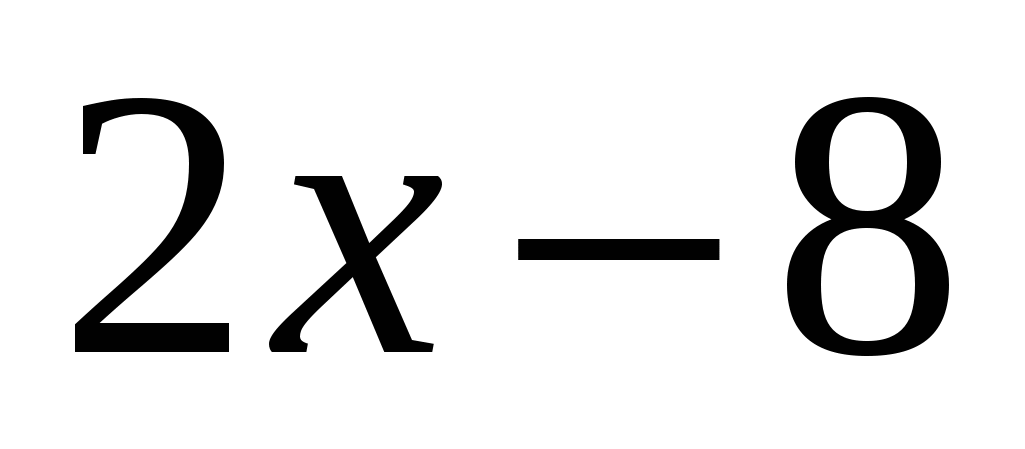 — отрицательно. Получим следующее уравнение:
— отрицательно. Получим следующее уравнение: 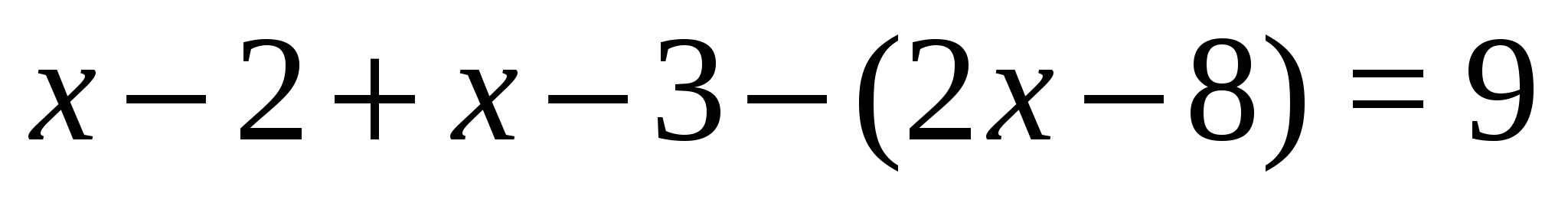 .
.
После преобразования, получим: 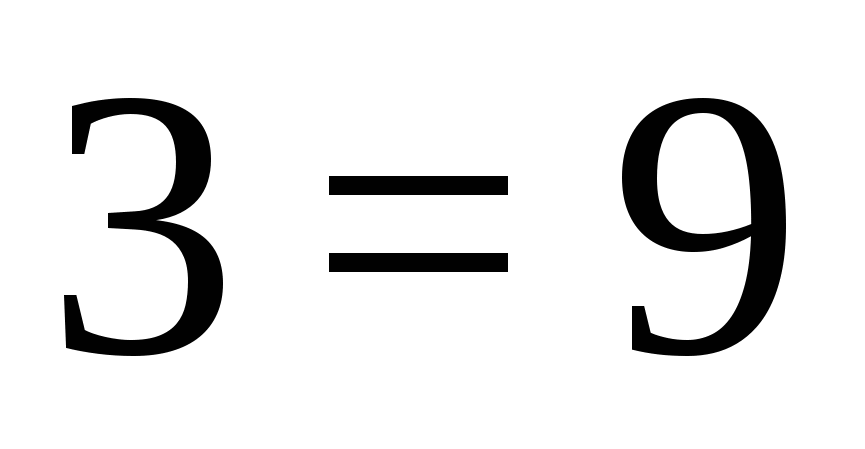 , а значит, уравнение не имеет корней на этом промежутке.
, а значит, уравнение не имеет корней на этом промежутке.
4) При 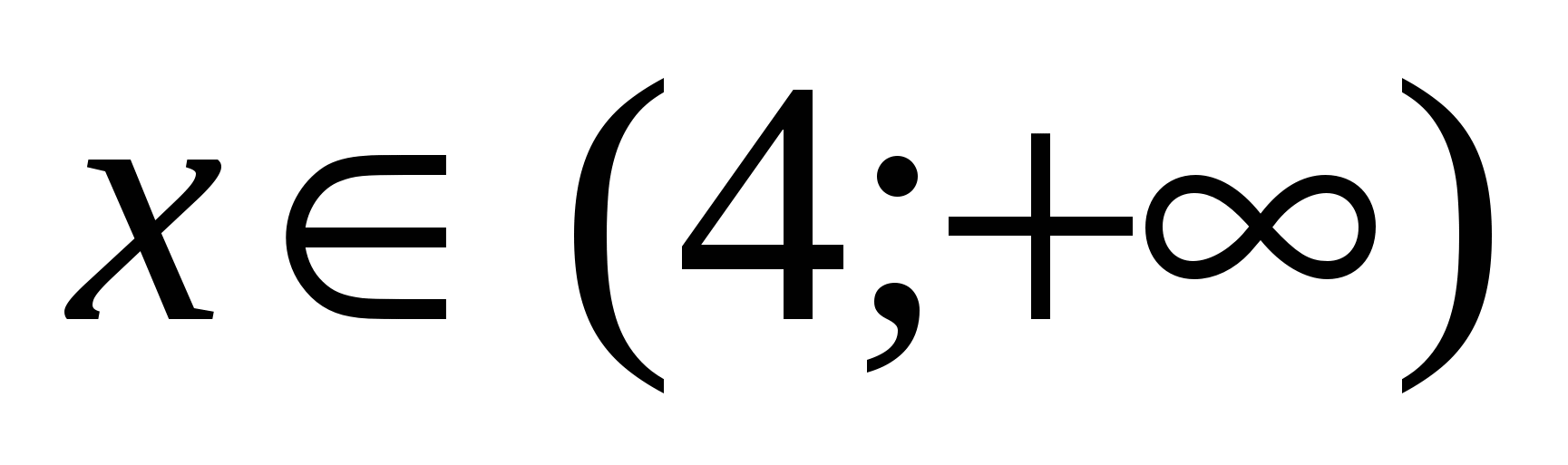 . Нетрудно установить, что все выражения на этом промежутке положительны, а значит получим уравнение:
. Нетрудно установить, что все выражения на этом промежутке положительны, а значит получим уравнение: 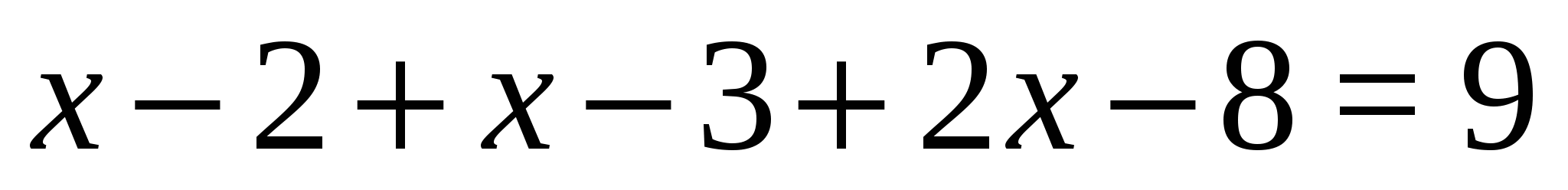 ,
, 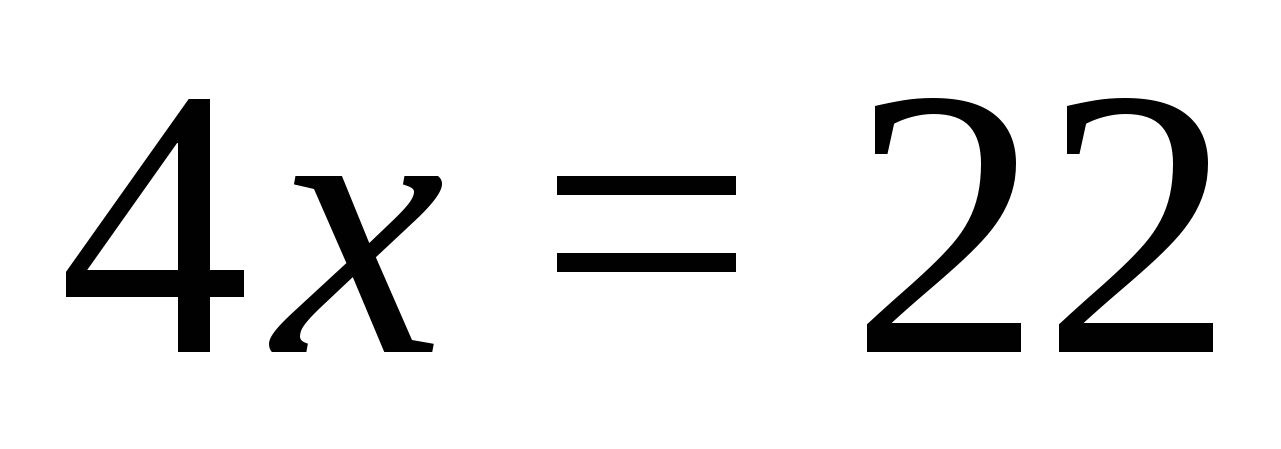 ,
, 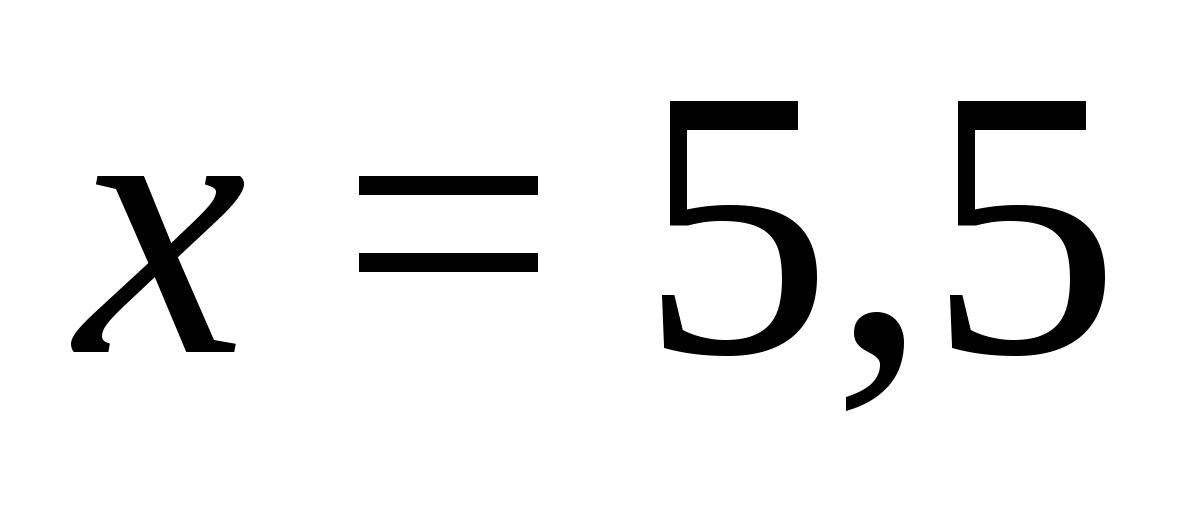 которое входит в промежуток и является корнем уравнения.
которое входит в промежуток и является корнем уравнения.
Ответ. 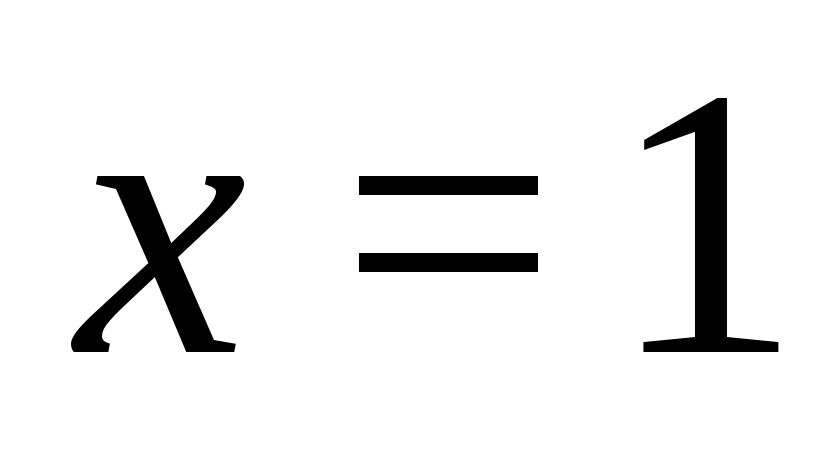 ,
, 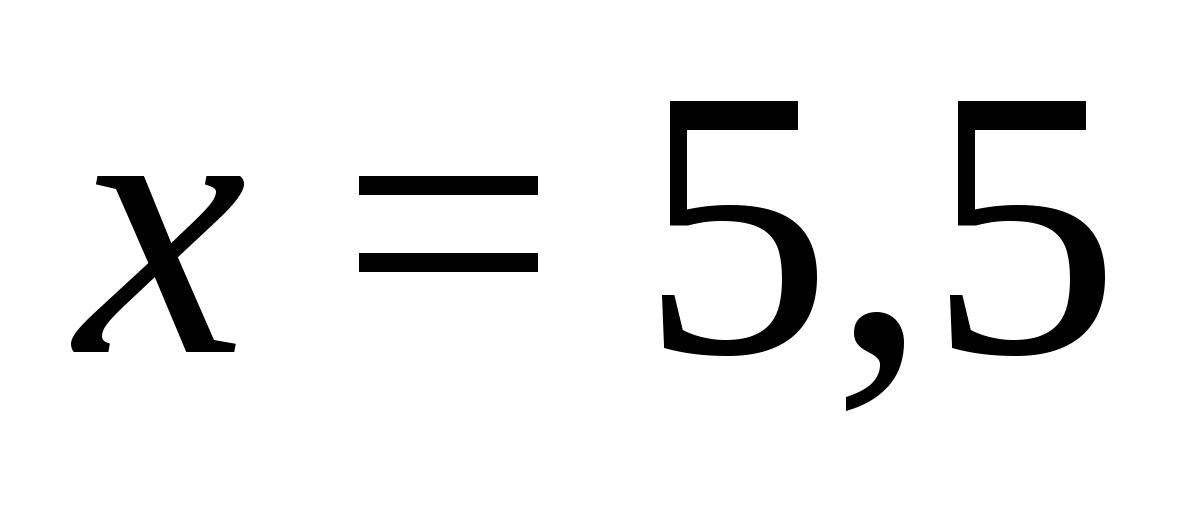 .
.
Решение уравнений содержащих модули неотрицательных выражений
Пример 11 Чему равна сумма корней уравнения (корень, если он один) уравнения
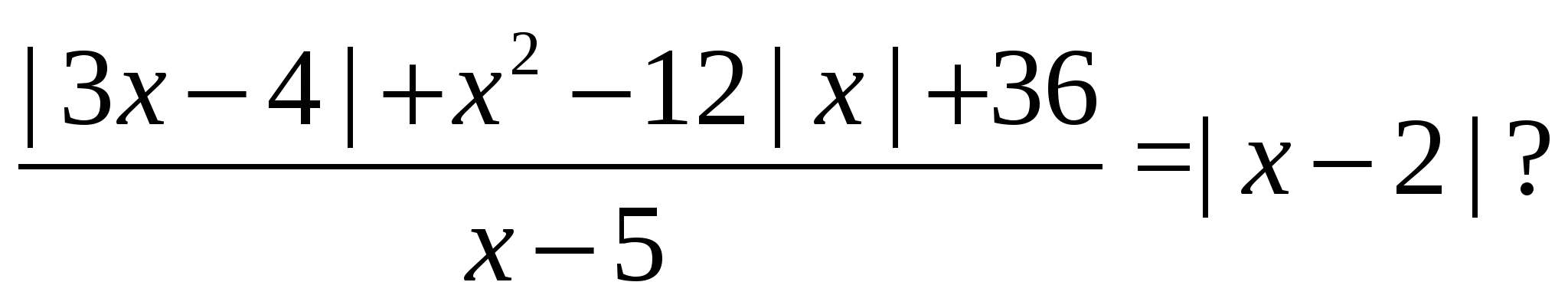
Решение. Рассмотрим выражение
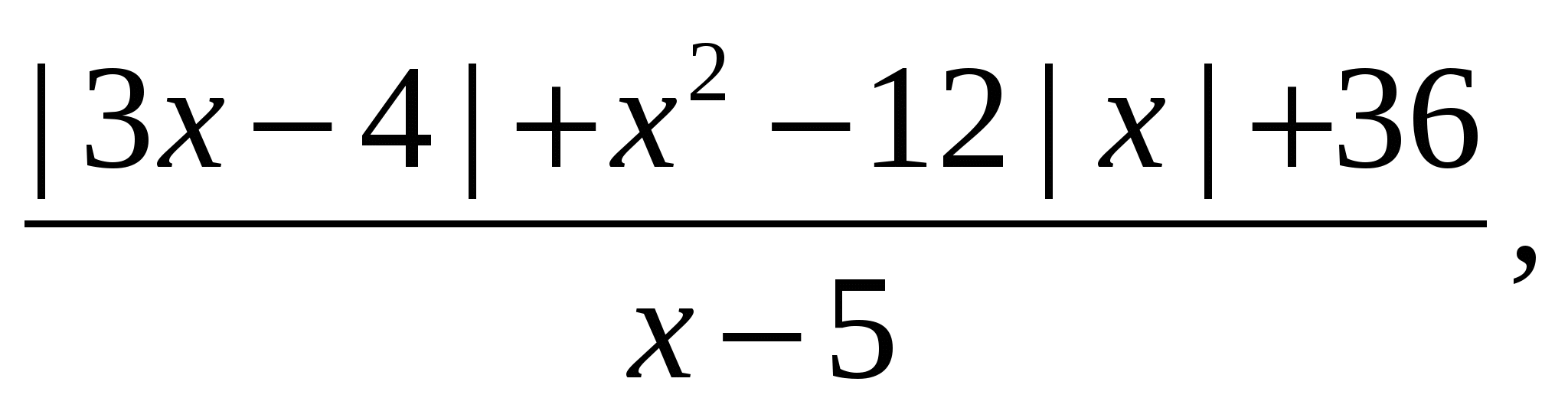 и преобразуем его к виду
и преобразуем его к виду 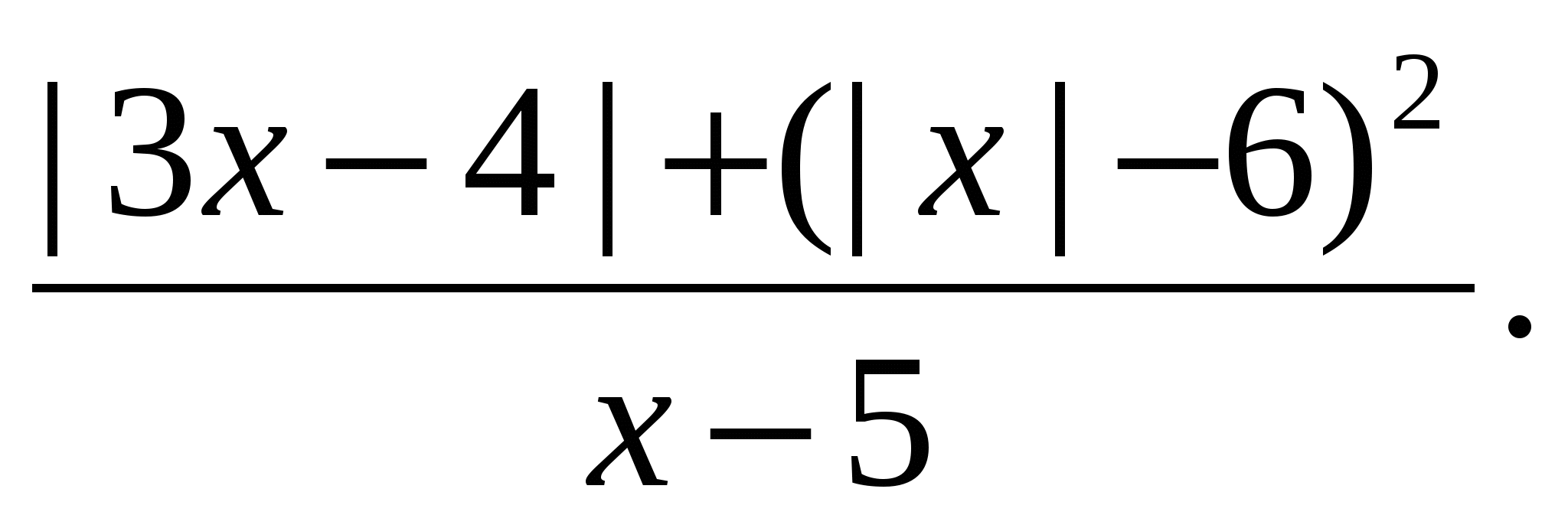
Очевидно, что числитель дроби при любых значениях переменной является положительным числом. Значит дробное выражение положительно, если 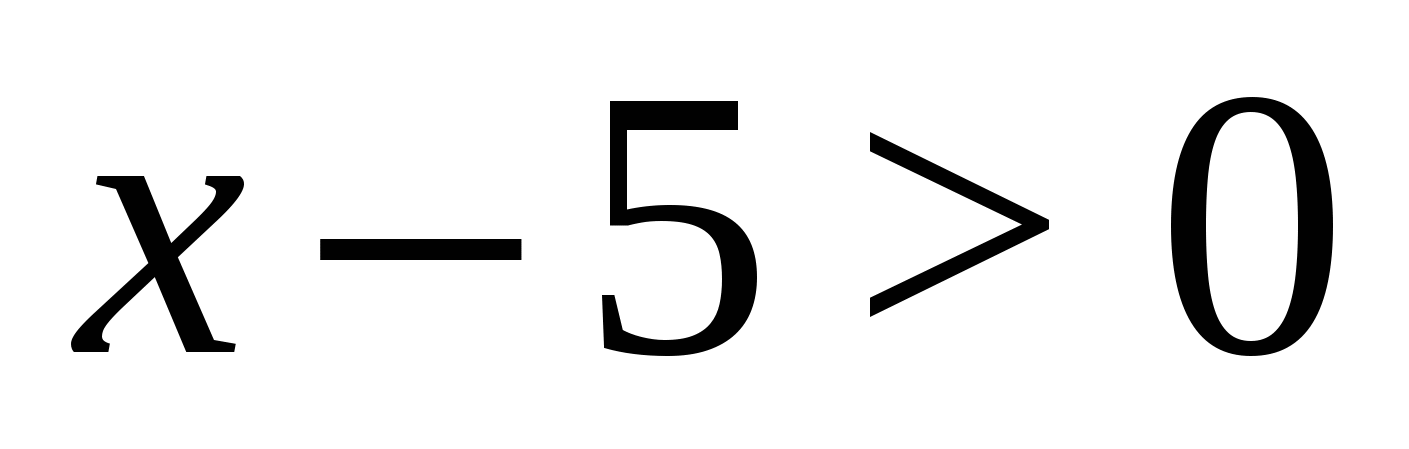 (т.к.
(т.к. 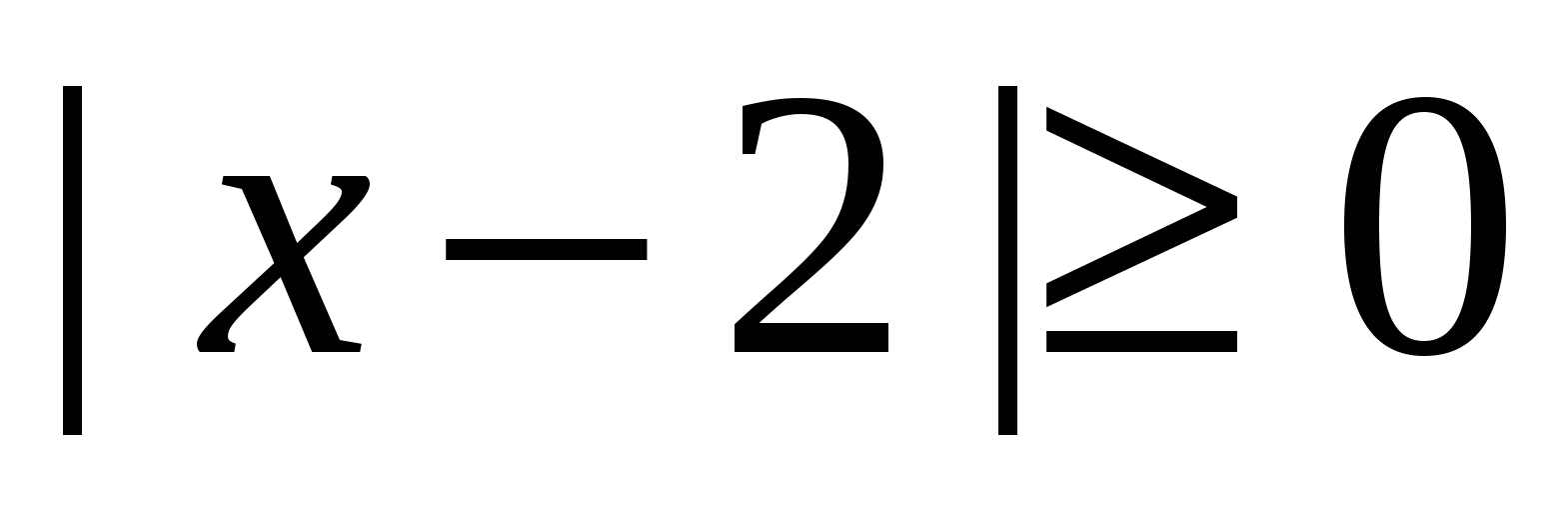 ). Преобразуем полученное выражение, при условии
). Преобразуем полученное выражение, при условии 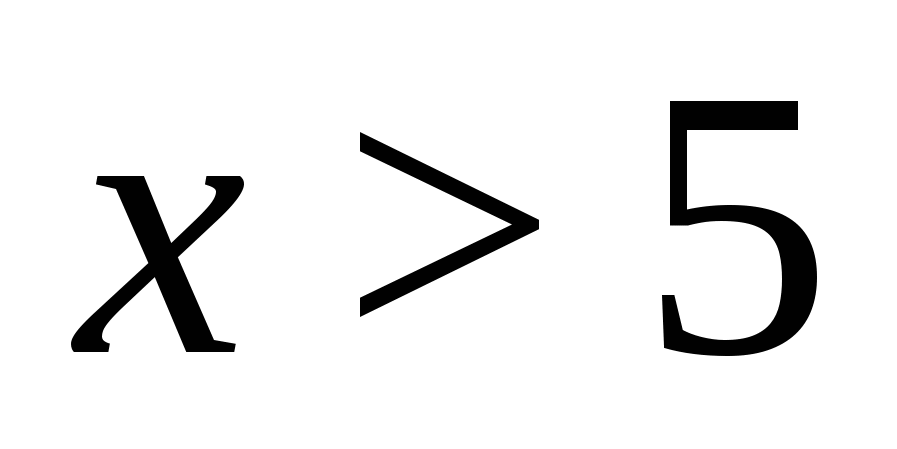 . Получим уравнение, равносильное исходному:
. Получим уравнение, равносильное исходному:
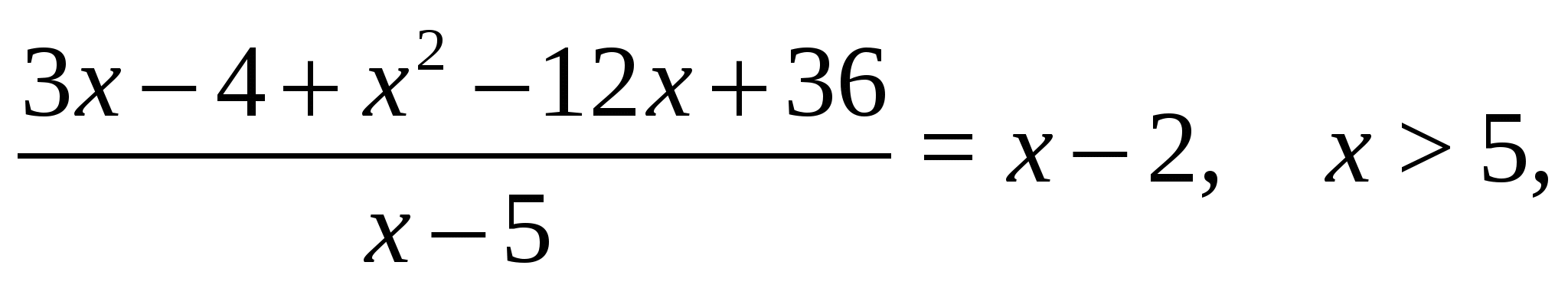
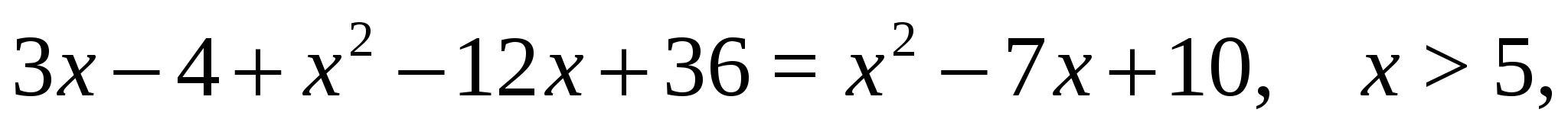
Ответ. 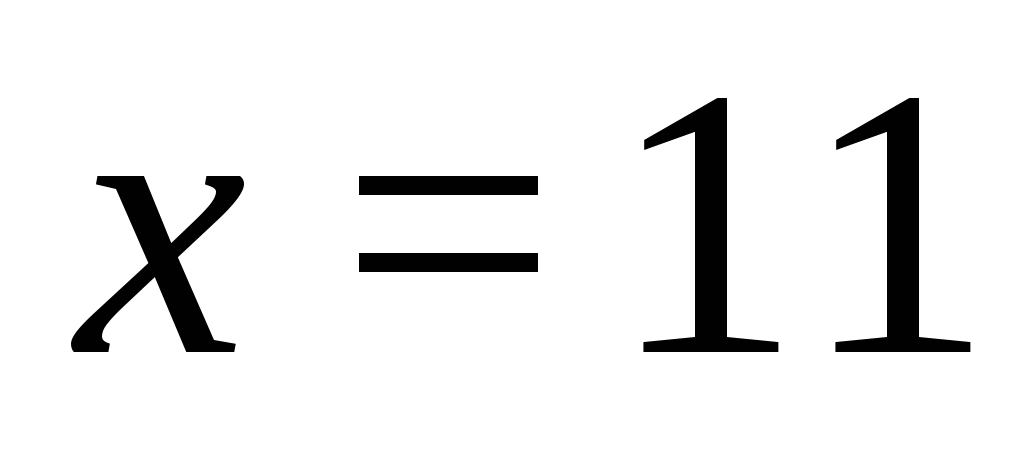 .
.
Пример 12 Решить уравнение
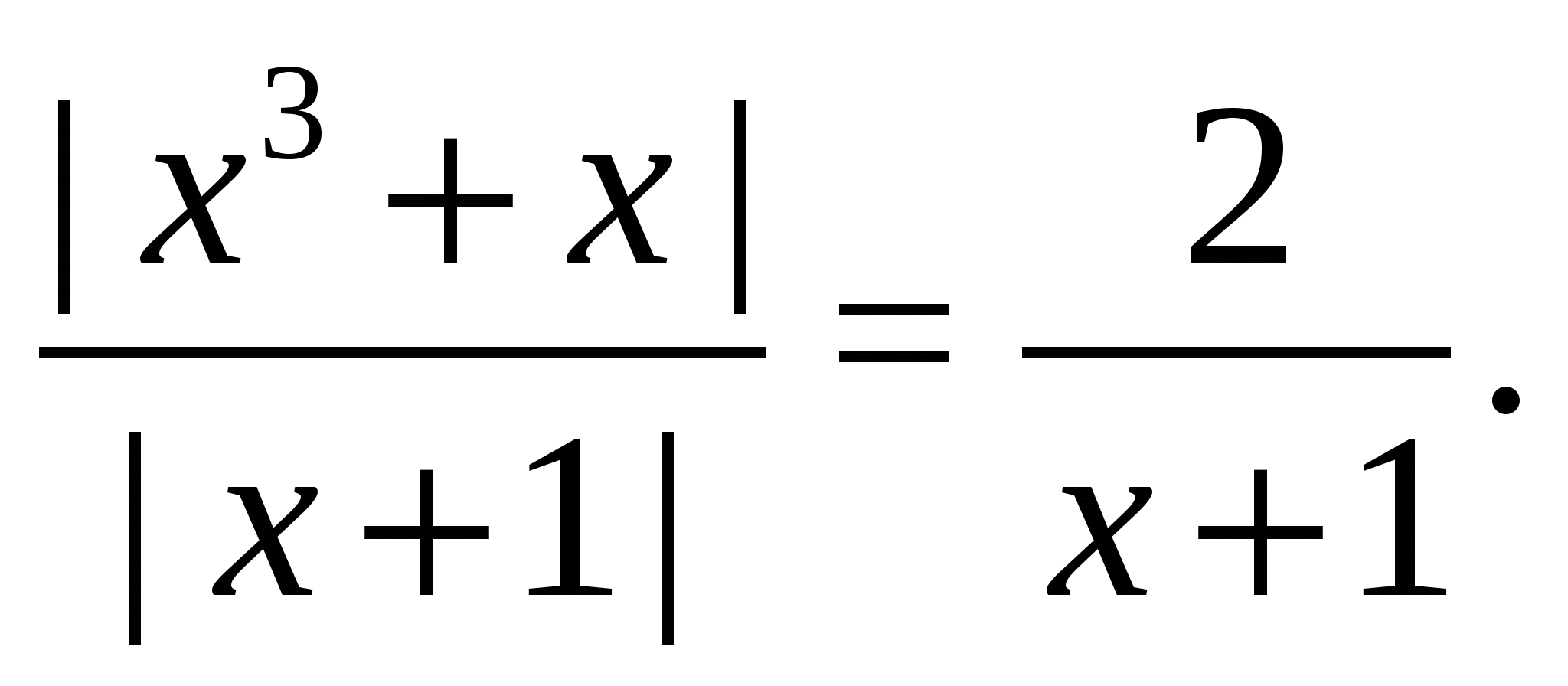
Решение. Поскольку левая часть уравнения неотрицательна, при всех допустимых значениях переменной, на множестве корней уравнения правая его часть тоже должна быть неотрицательной, отсюда условие 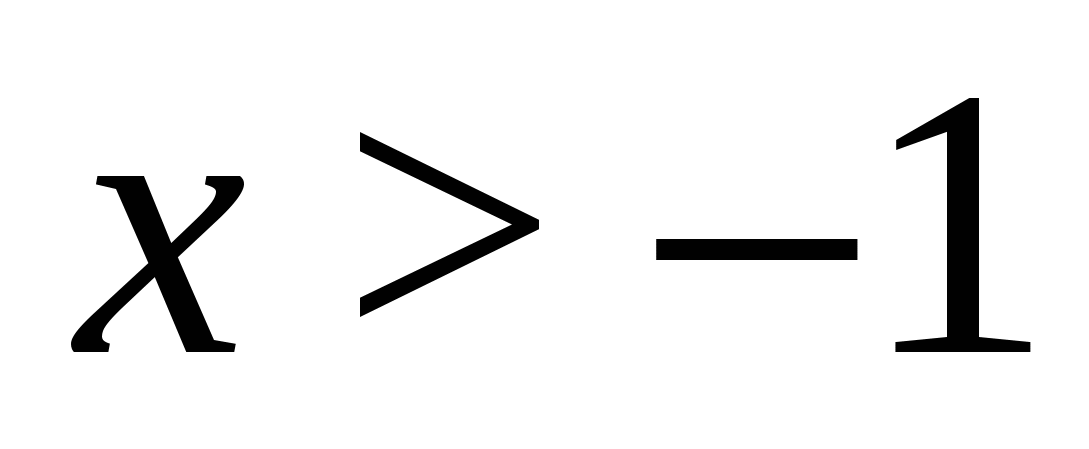 , на этом промежутке знаменатели обеих дробей равны, и остается решить уравнение
, на этом промежутке знаменатели обеих дробей равны, и остается решить уравнение 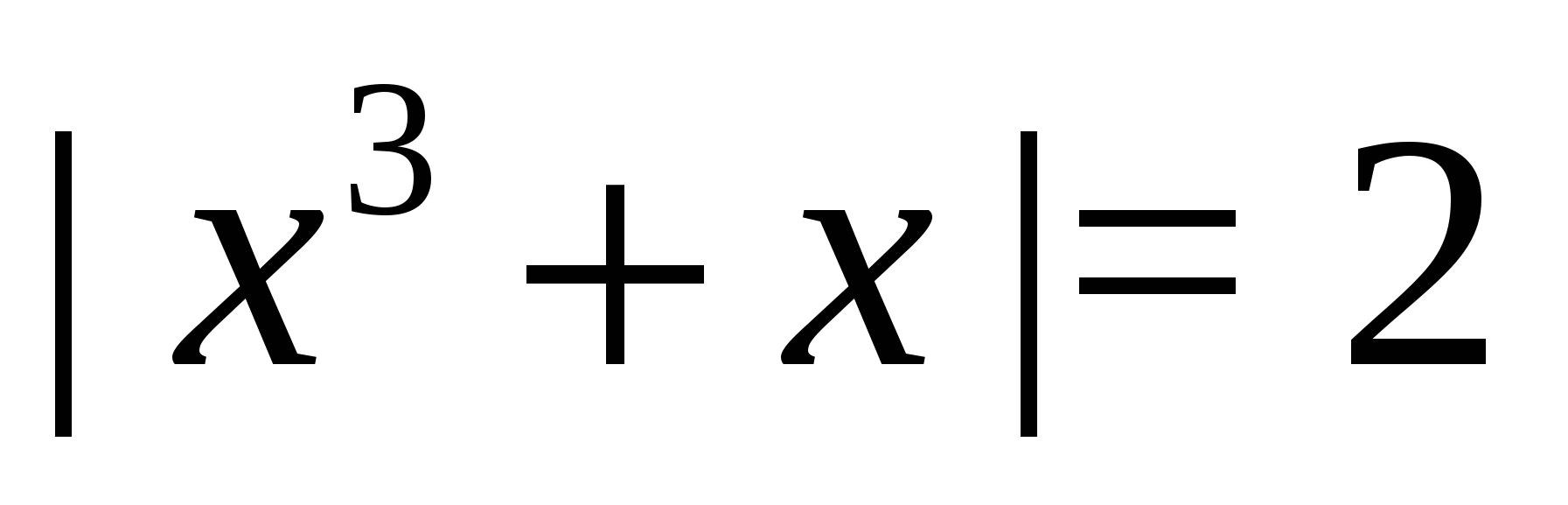 . Решая его и учитывая ограничение
. Решая его и учитывая ограничение 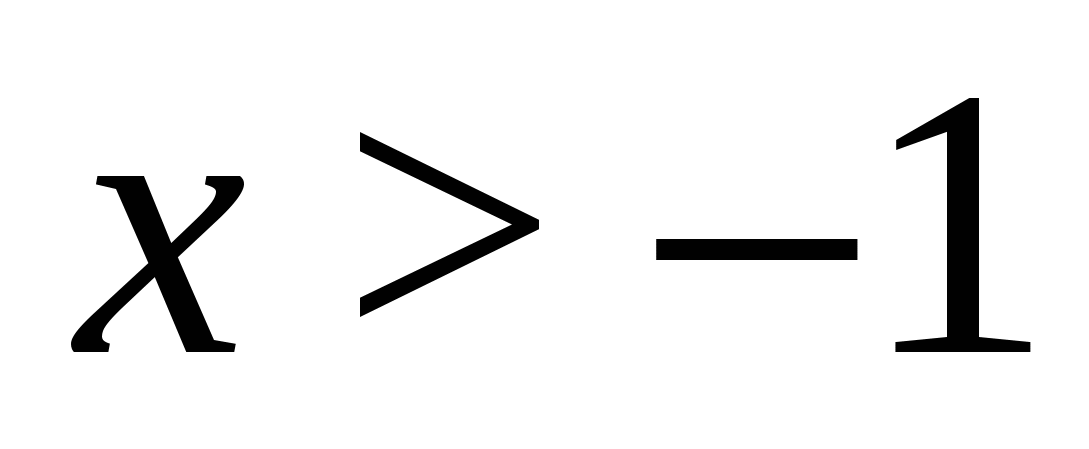 , получаем
, получаем
Ответ. 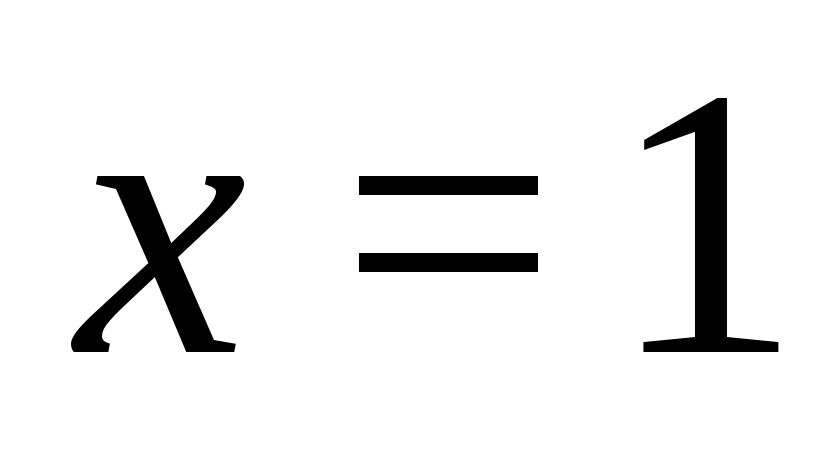 .
.
Решение уравнений с использованием геометрической интерпретации
Геометрический смысл выражения 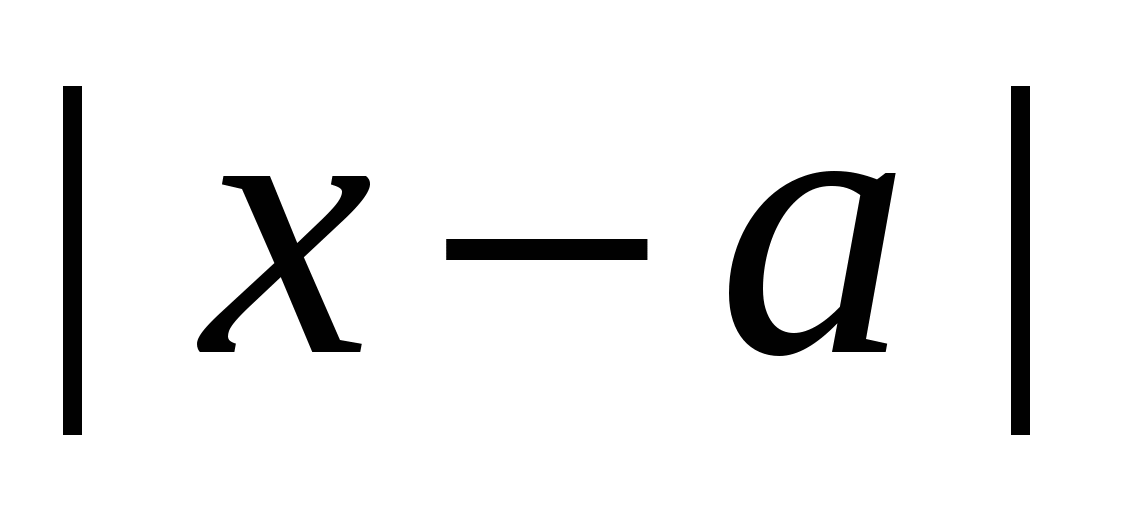 — длина отрезка координатной оси, соединяющего точки с абсциссами
— длина отрезка координатной оси, соединяющего точки с абсциссами 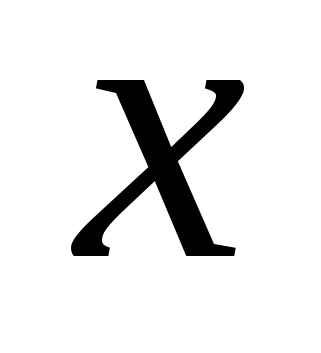 и
и  . Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок.
. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких выкладок.
Пример 13 Решим уравнение 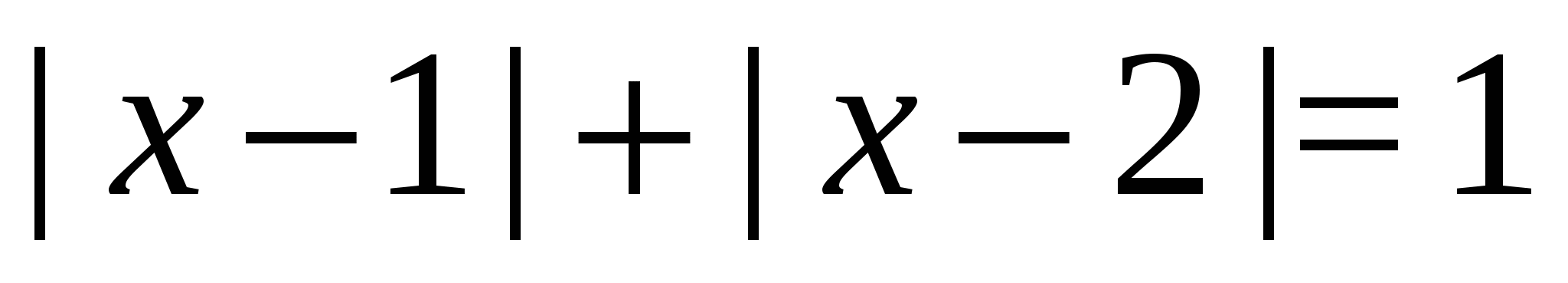 .
.
Решение. Будем рассуждать следующим образом: исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой 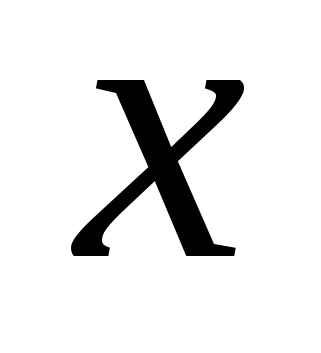 до двух фиксированных точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка
до двух фиксированных точек с абсциссами 1 и 2. Тогда все точки с абсциссами из отрезка 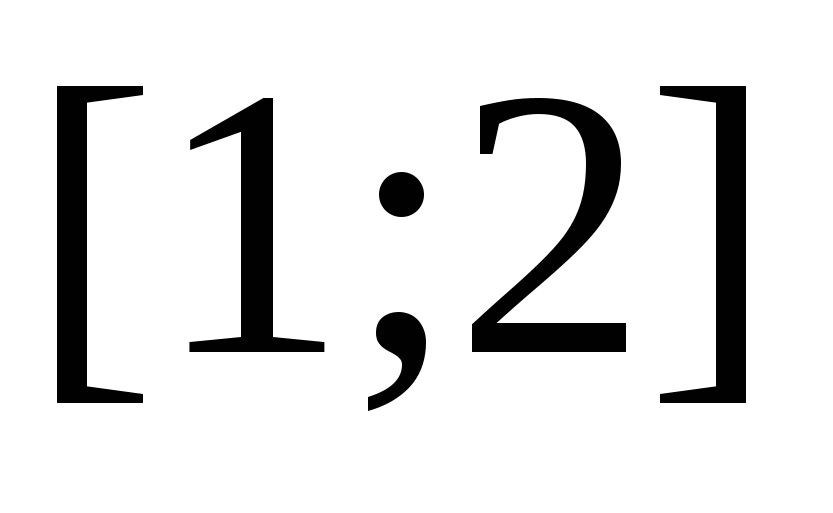 обладают требуемым свойством, а точки, расположенные вне этого отрезка, — нет.
обладают требуемым свойством, а точки, расположенные вне этого отрезка, — нет.
Ответ. 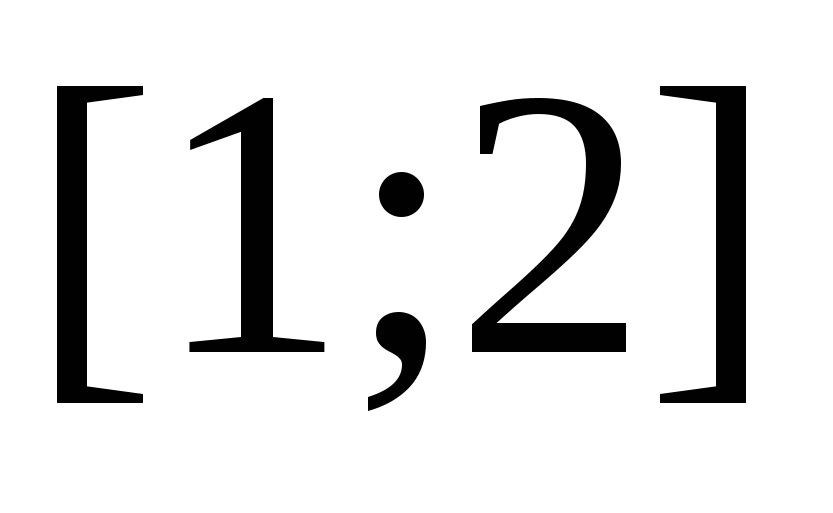 .
.
Пример 14 Решить неравенство 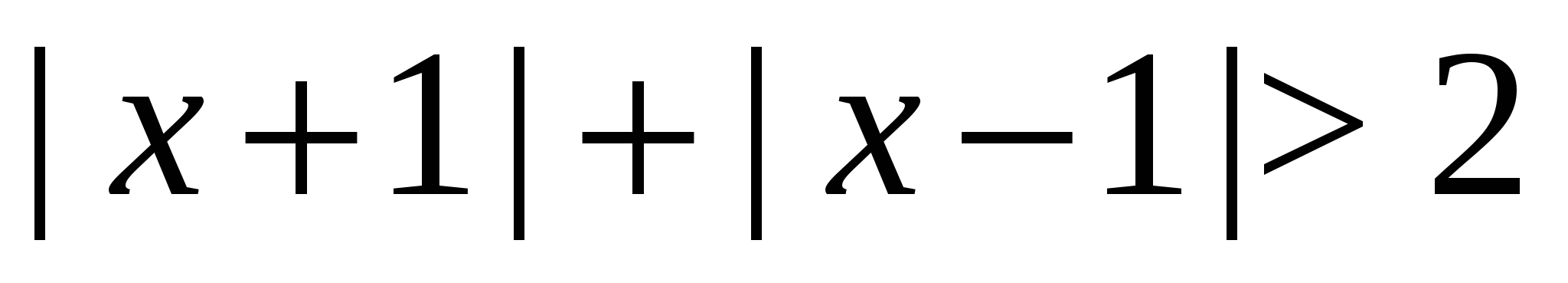 .
.
Решение. Изобразим на координатной прямой точки, сумма расстояний от которых до точек 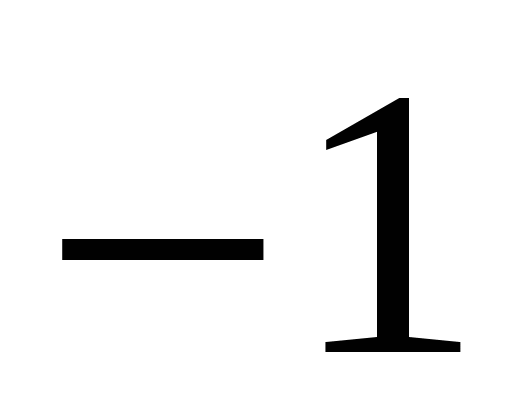 и
и 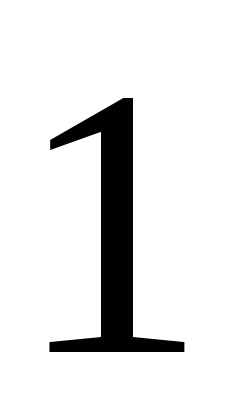 в точности равна
в точности равна 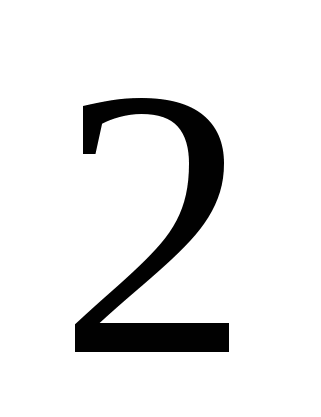 . Это все точки отрезка
. Это все точки отрезка 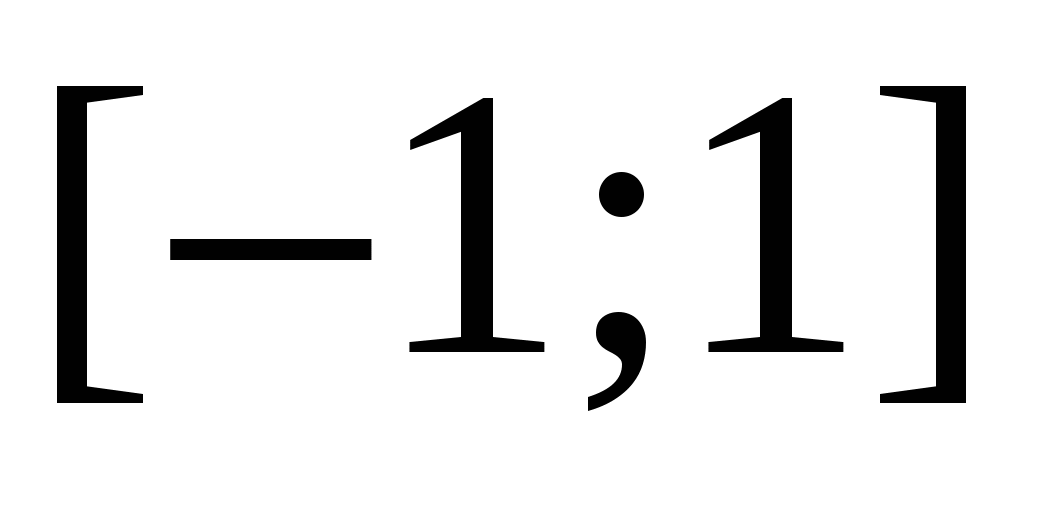 . Для всех чисел вне данного отрезка сумма расстояний будет больше двух.
. Для всех чисел вне данного отрезка сумма расстояний будет больше двух.
Ответ. 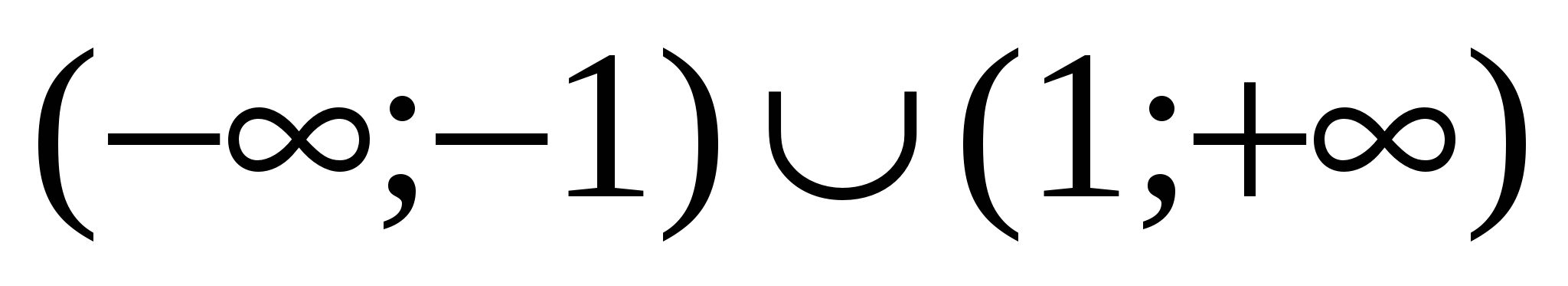 .
.
Пример (С3, ЕГЭ — 2010)15 Решить уравнение

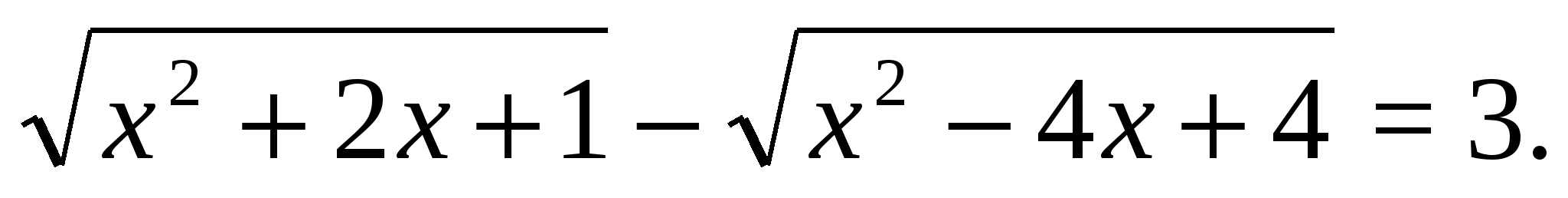
Решение. Дважды применяя тождество 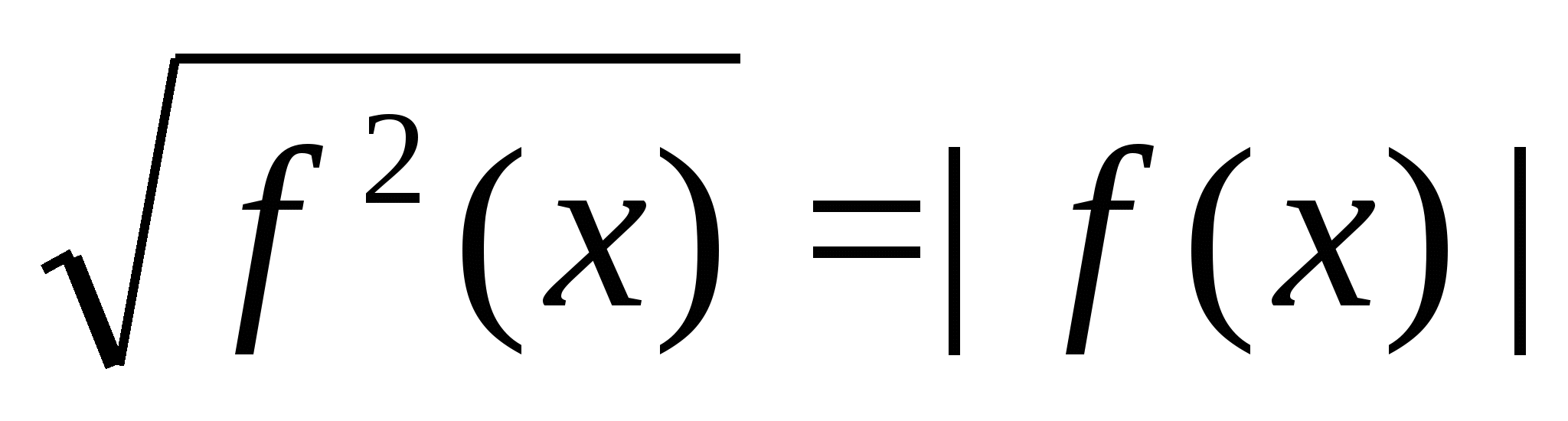 , получим уравнение
, получим уравнение
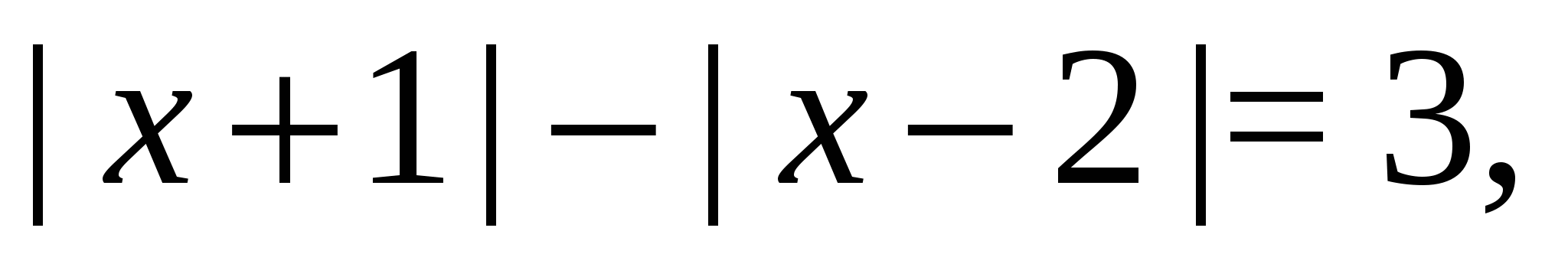
решением которого является интервал 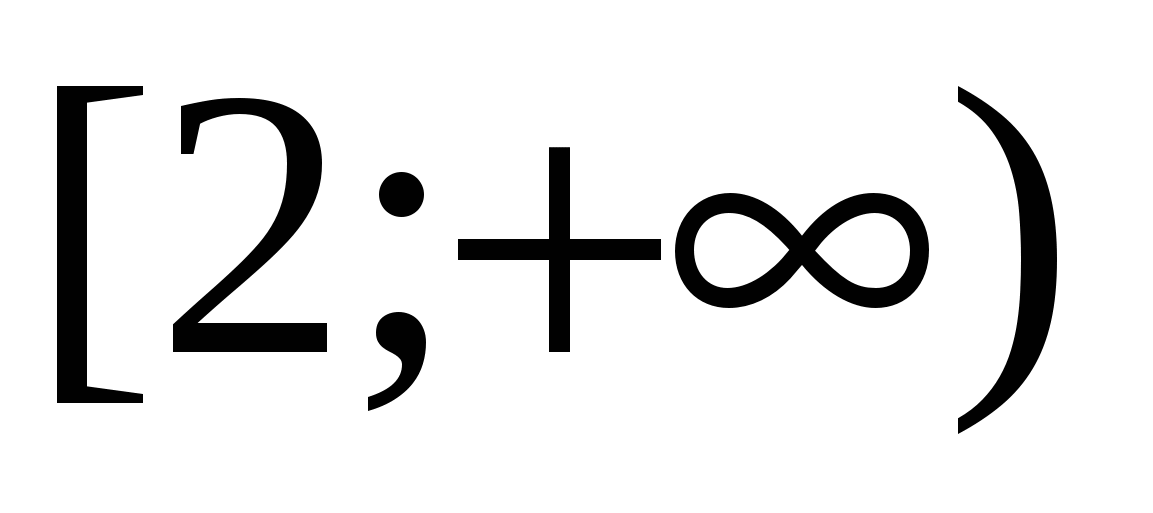 .
.
Ответ. 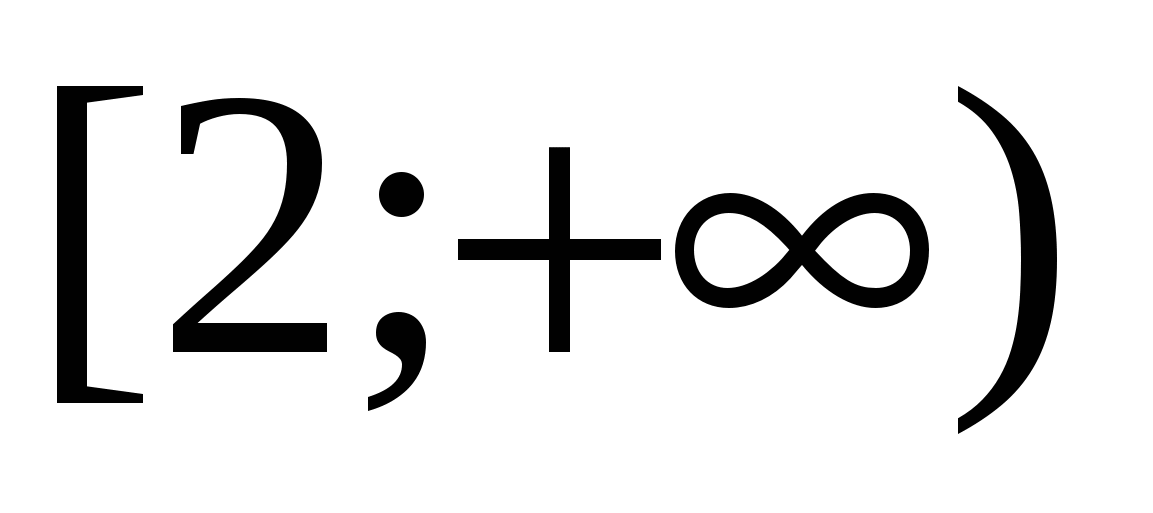 .
.
Пример (С3, ЕГЭ — 2011)16 17 Решить уравнение
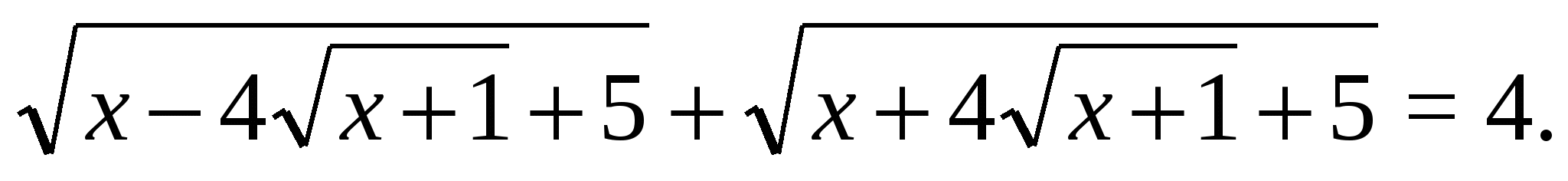
Решение. 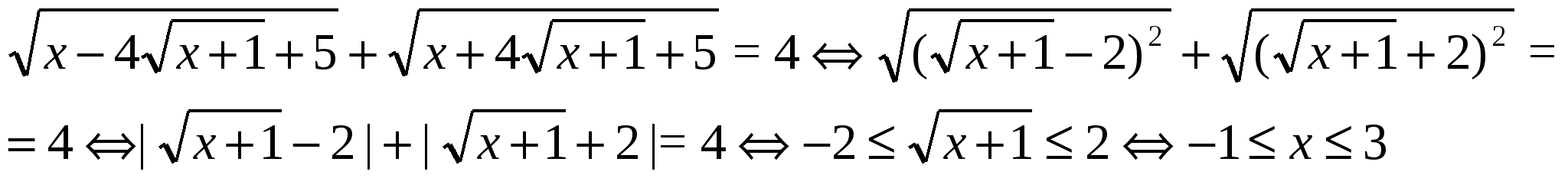 .
.
Ответ. 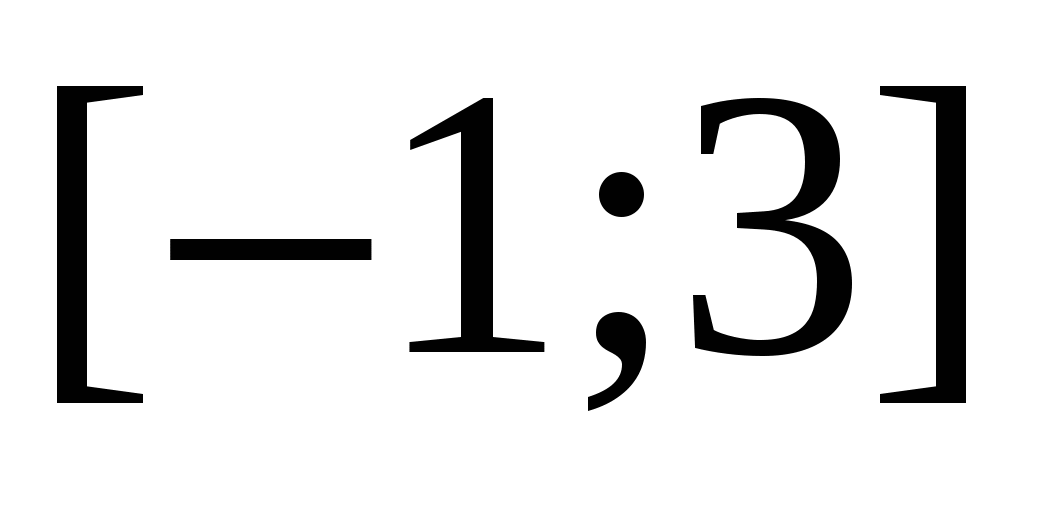 .
.
Применение теоремы о знаках при решении уравнений
Сформулируем теорему, удобную при решении неравенств, относительно произведений или частных разности модулей:
Теорема 18 Знак разности модулей двух выражений совпадает со знаком разности квадратов этих выражений.
Пример 19 Решить неравенство
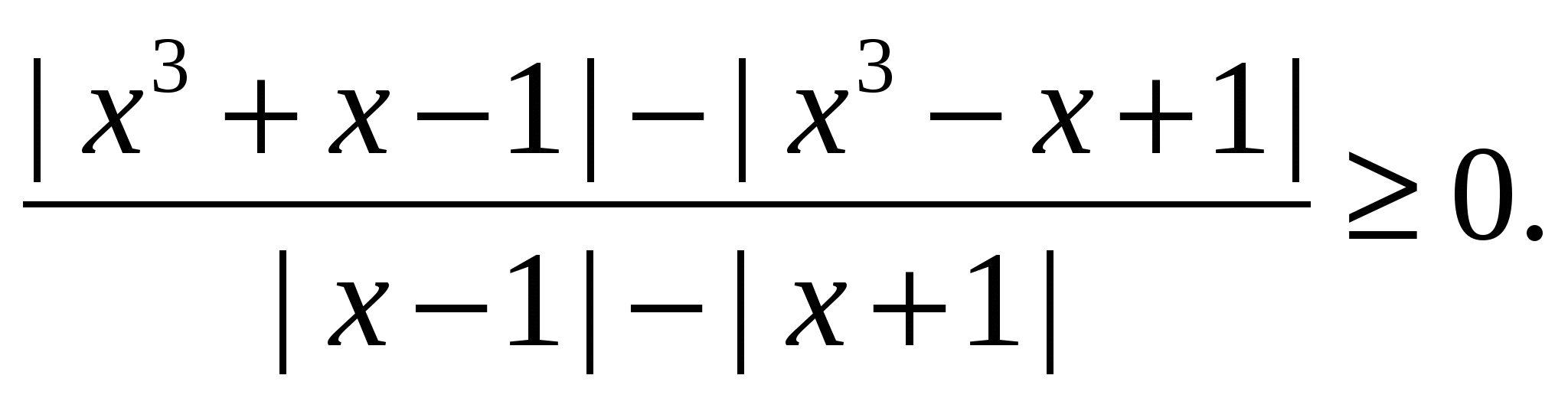
Решение. Воспользуемся теоремой:
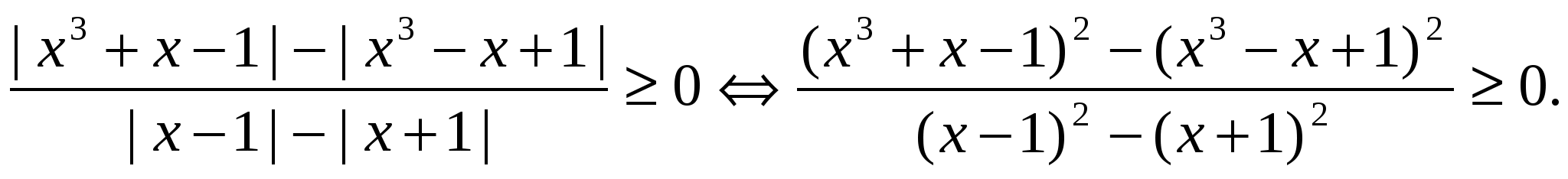
Используя формулу разности квадратов, разложим числитель и знаменатель на множители и решим полученное рациональное неравенство.
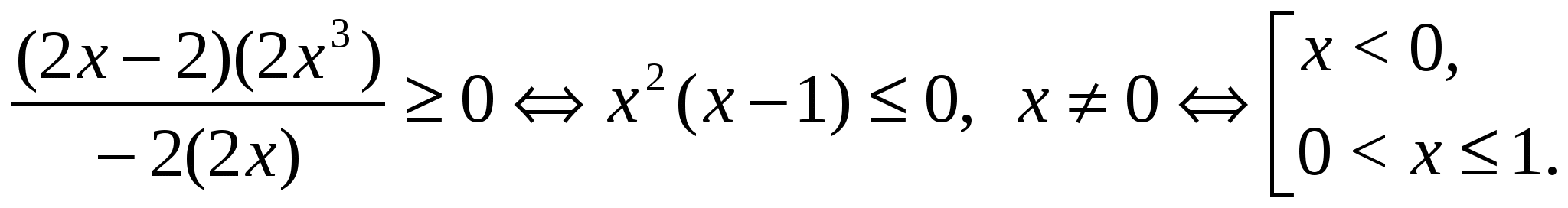
Ответ. 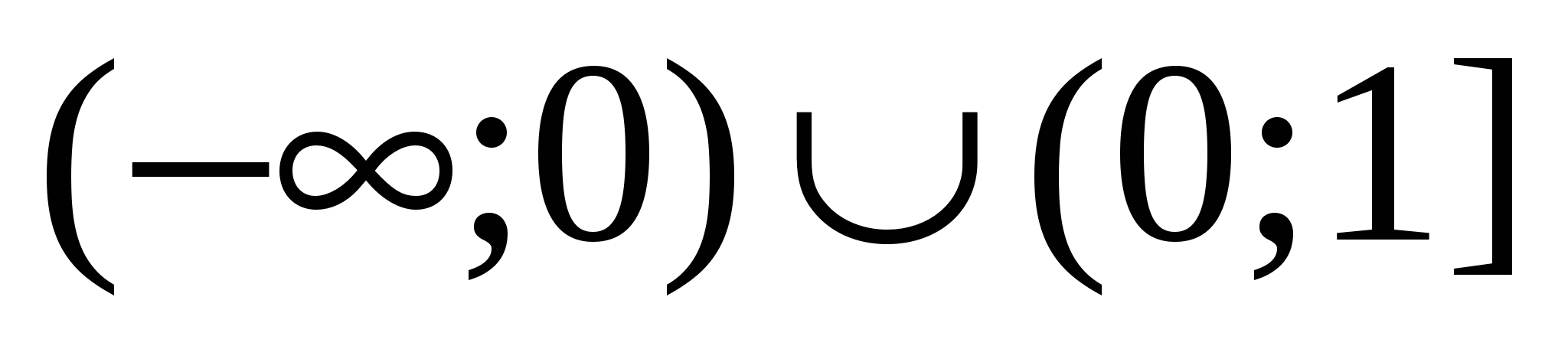
Решение уравнений переходом к следствию
Все уравнения с модулями могут быть решены следующим образом: рассмотрим весь набор уравнений, который может получится при раскрытии модулей, но не будем выписывать соответствующие промежутки. Решая каждое из полученных уравнений, получим следствия исходного уравнения. Остается только проверить не приобрели ли мы посторонних корней прямой их подстановкой в исходное уравнение.
Пример 20 Решим уравнение
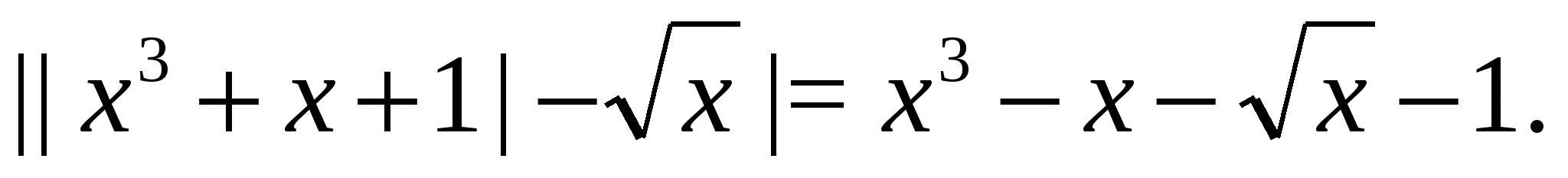
Решение. Последовательно переходя к следствиям, получаем:
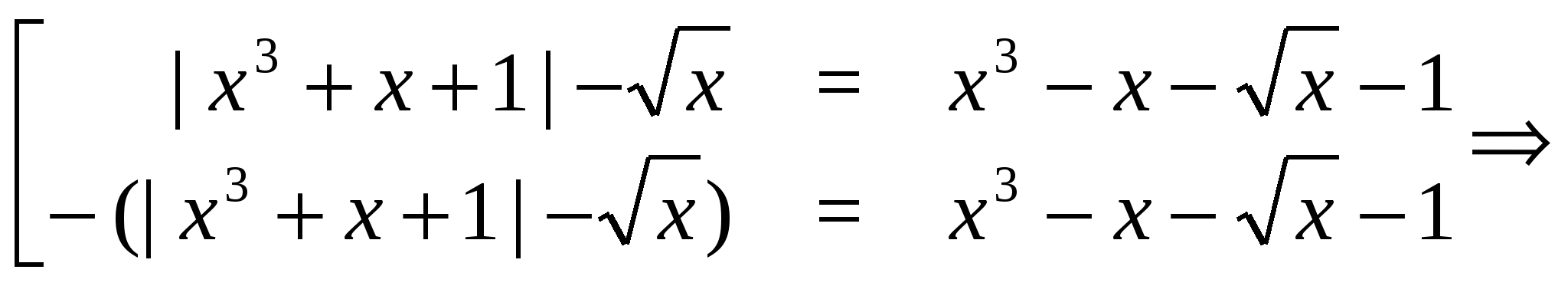
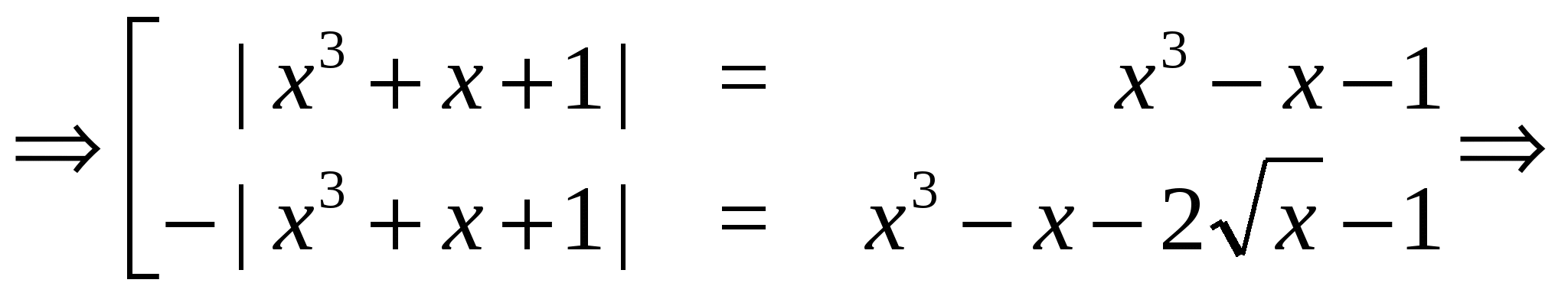
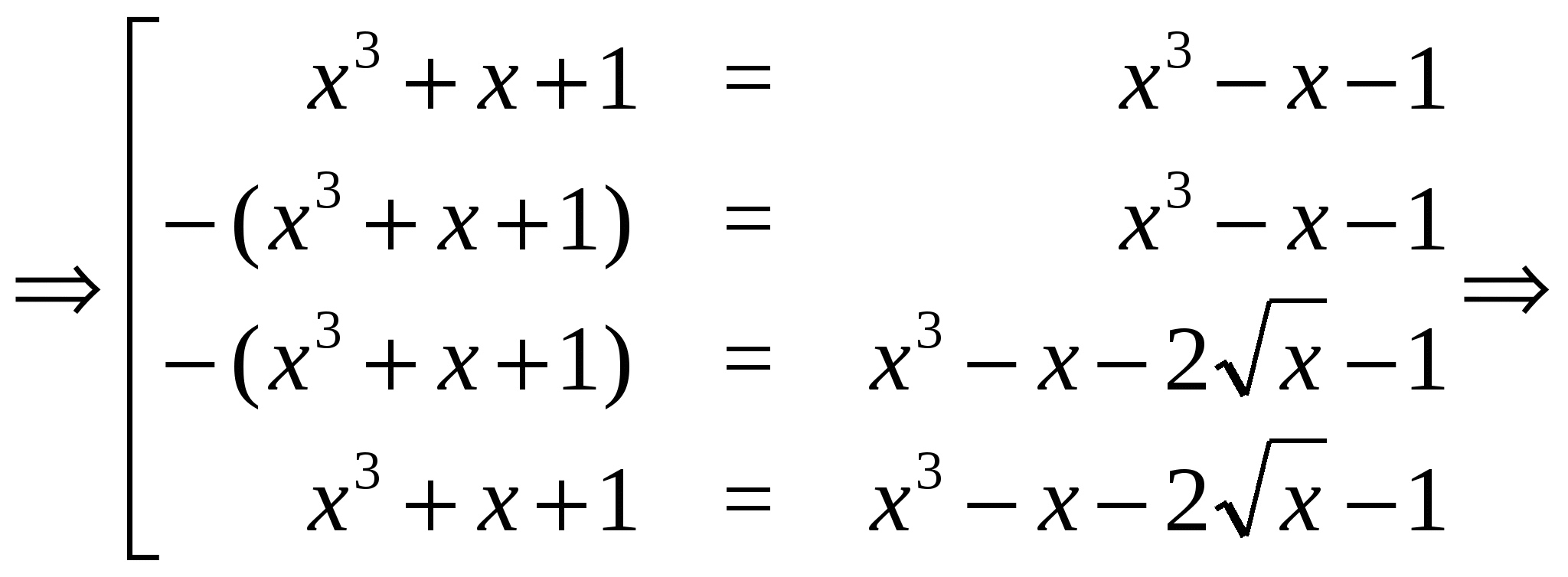
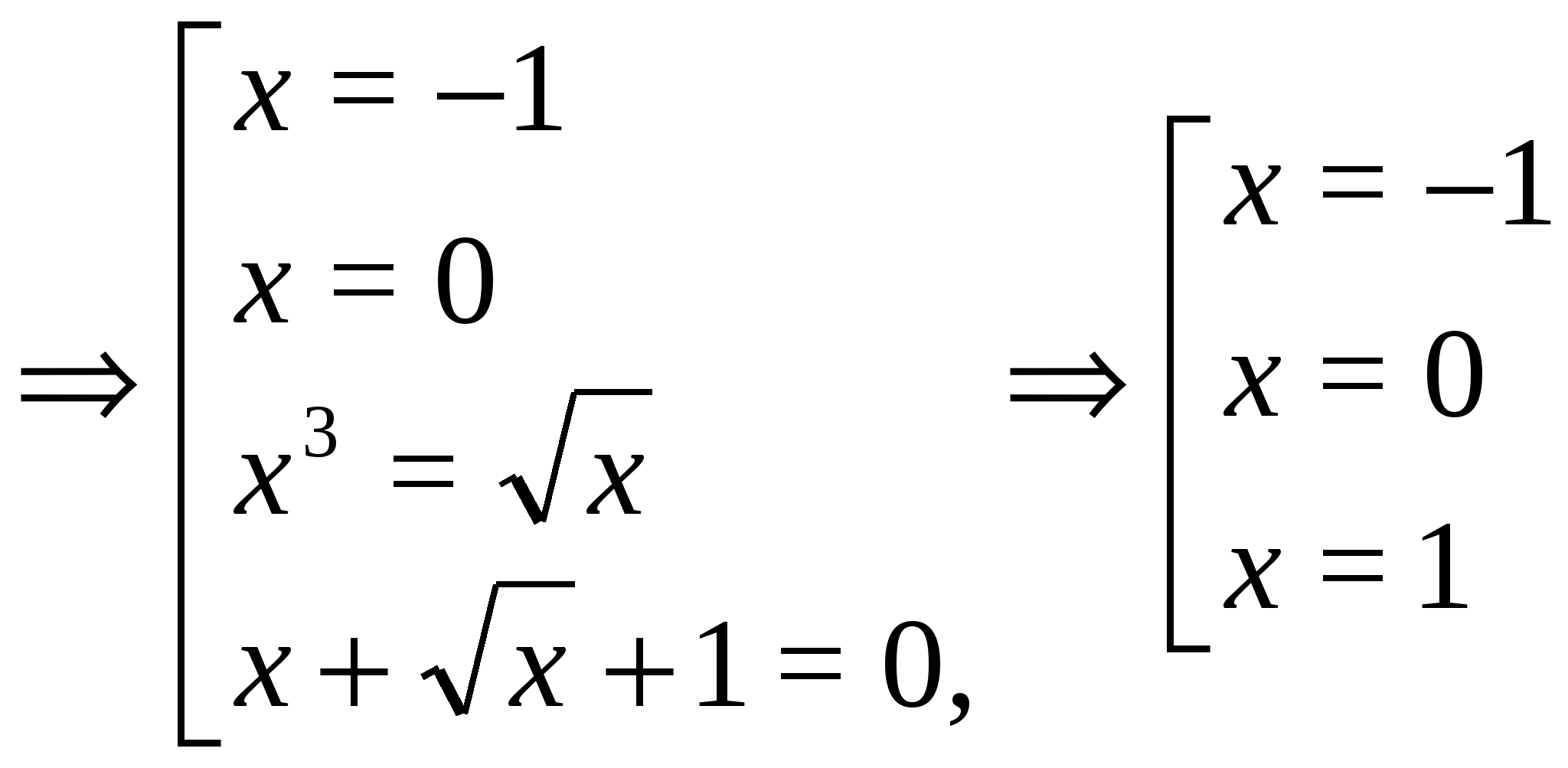
Нетрудно убедиться, что найденные числа не являются корнями исходного уравнения.
Ответ. нет решения.
Решение неравенств методом интервалов
Применение метода интервалов основано на следующей теореме.
Теорема 21 Функция, непрерывная на промежутке и необращающаяся на нем в нуль, сохраняет на этом промежутке свой знак.
Это означает, что нули функции и границы промежутков ее непрерывности разделяют область определения функции на участки, где она сохраняет постоянный знак. Применение метода поясним на примере.
Пример 22 Решим неравенство
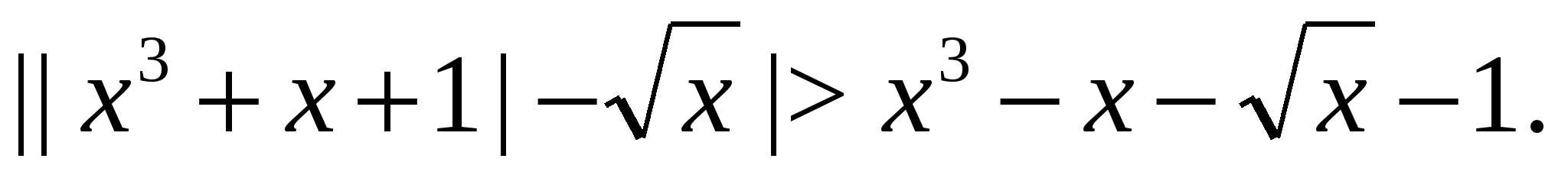
Пусть 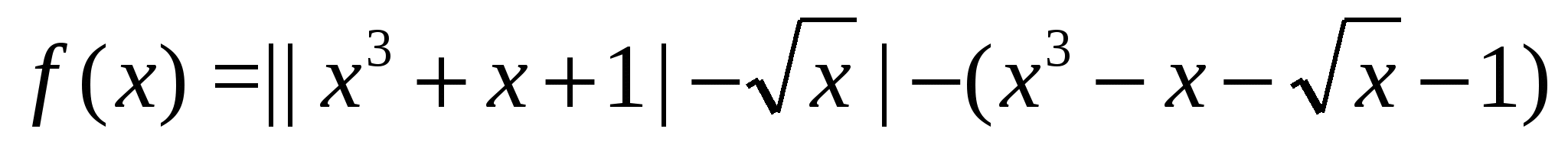 . Областью определения данной функции есть
. Областью определения данной функции есть 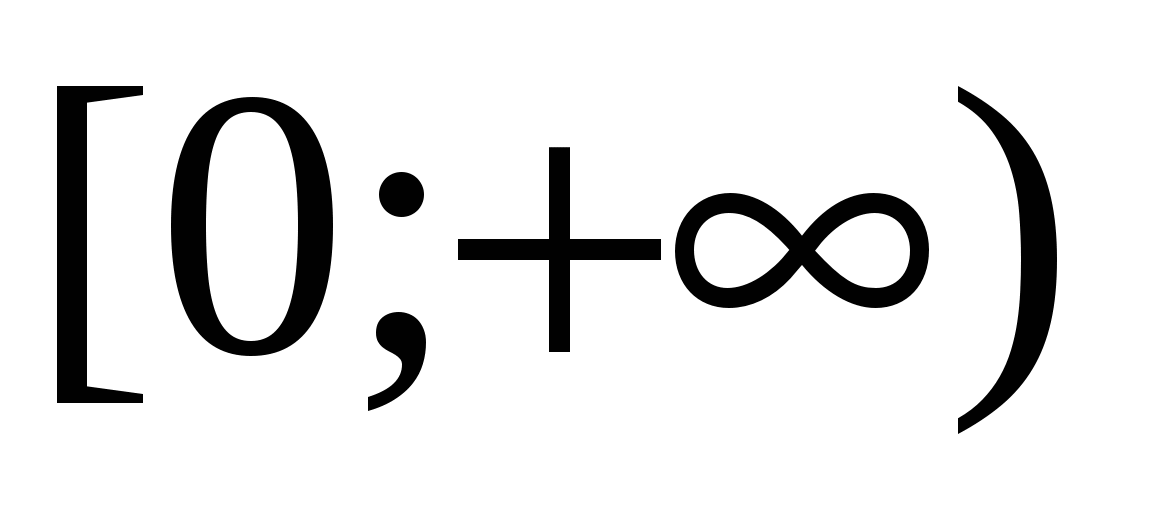 . Решая уравнение получим, что функция
. Решая уравнение получим, что функция 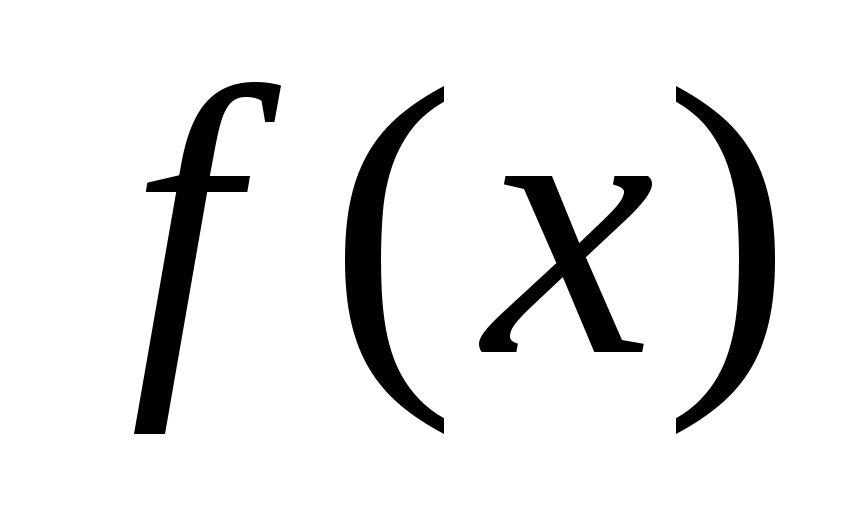 не обращается в нуль ни при каком значении переменной. Это означает, что на всей области определения функция является знакопостоянной. Вычисляя, например,
не обращается в нуль ни при каком значении переменной. Это означает, что на всей области определения функция является знакопостоянной. Вычисляя, например, 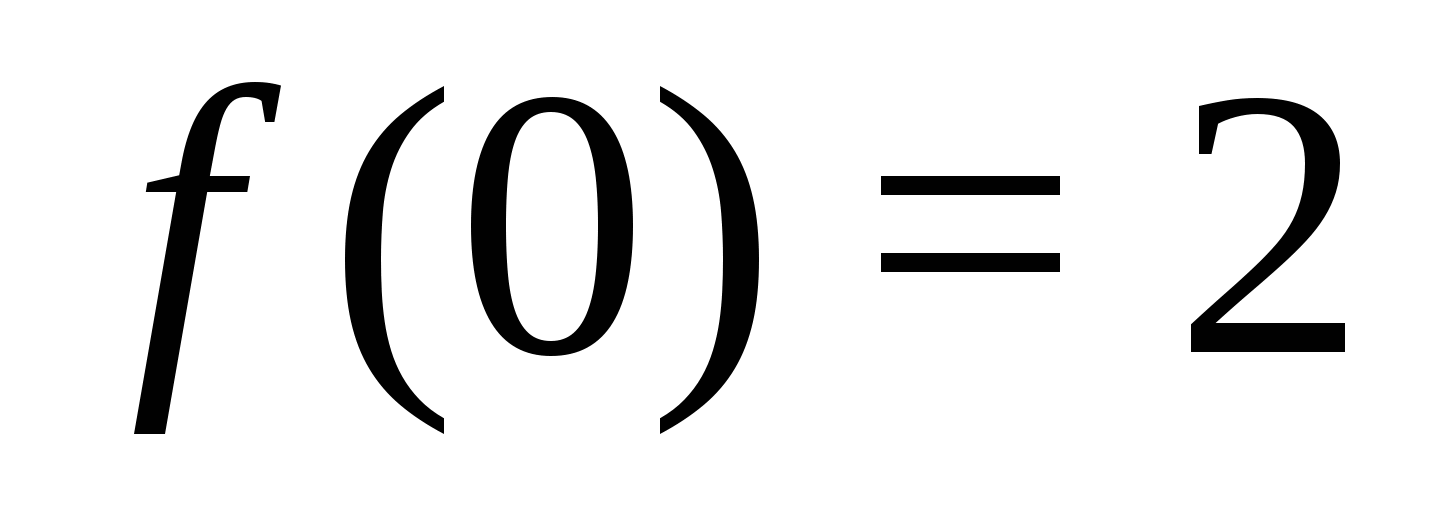 , получаем, что функция принимает только положительные значения.
, получаем, что функция принимает только положительные значения.
Ответ. 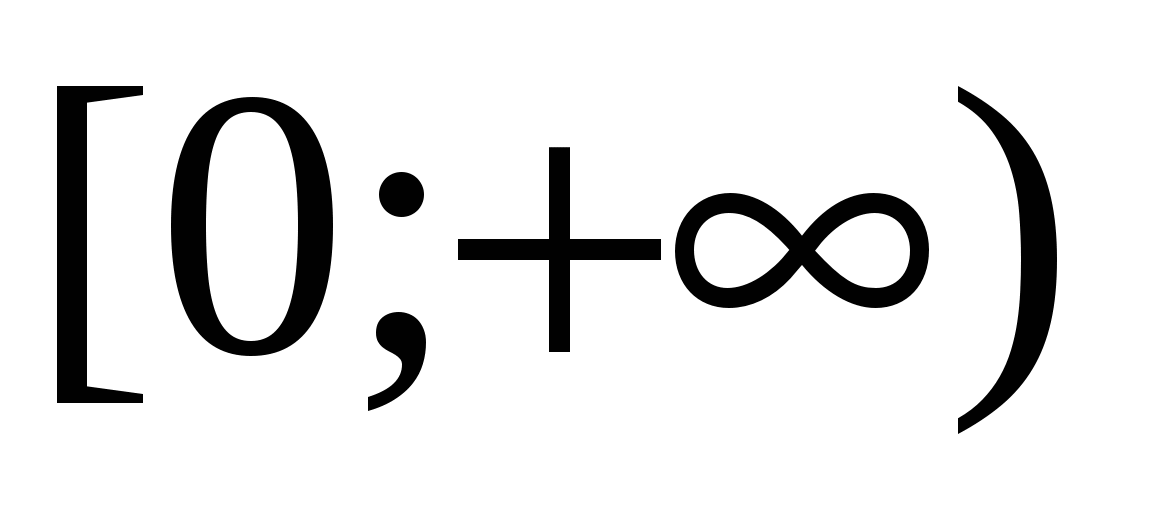 .
.
Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих выражений. Это позволяет, последовательно перебирая эти промежутки, одновременно избавляться от всех модулей и решать обычное уравнение или неравенство (проверяя при этом, что найденный ответ входит в данный промежуток).
Решение уравнений домножением на положительный множитель
Пример 23 Решить неравенство
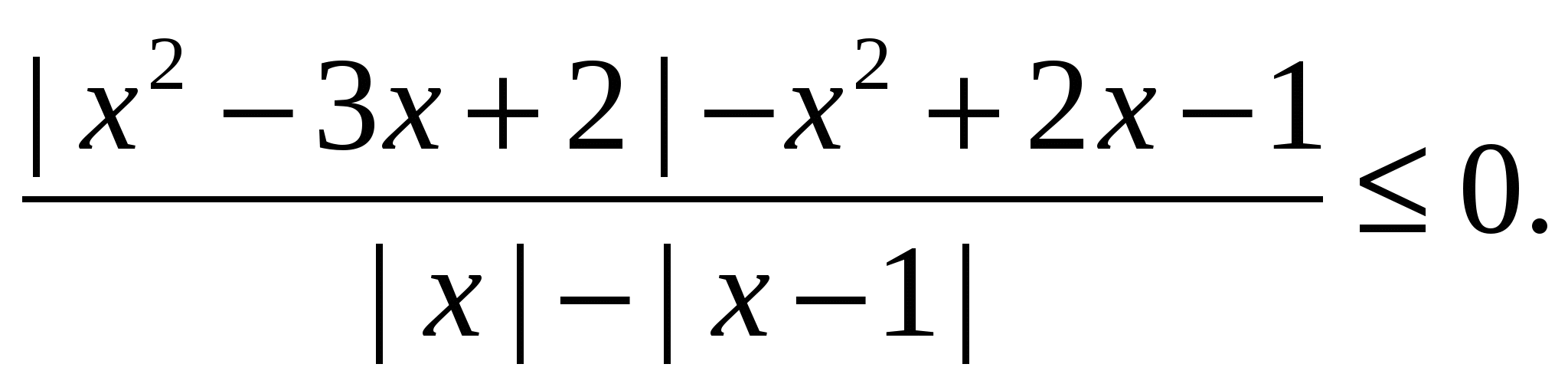
Решение. «Ловушка» заключается в том, что в задаче имеется несколько модулей, раскрывать которые — значит получить, громоздкое решение. Умножим дробь на некоторое выражение, принимающее лишь положительные значения и такое, чтобы упростить исходное неравенство:
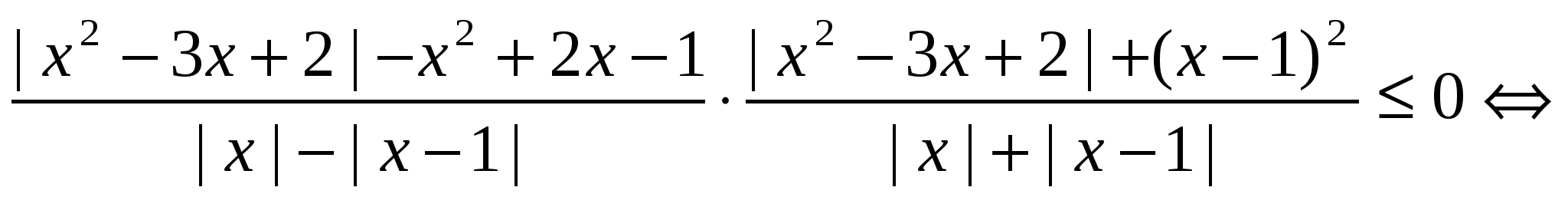
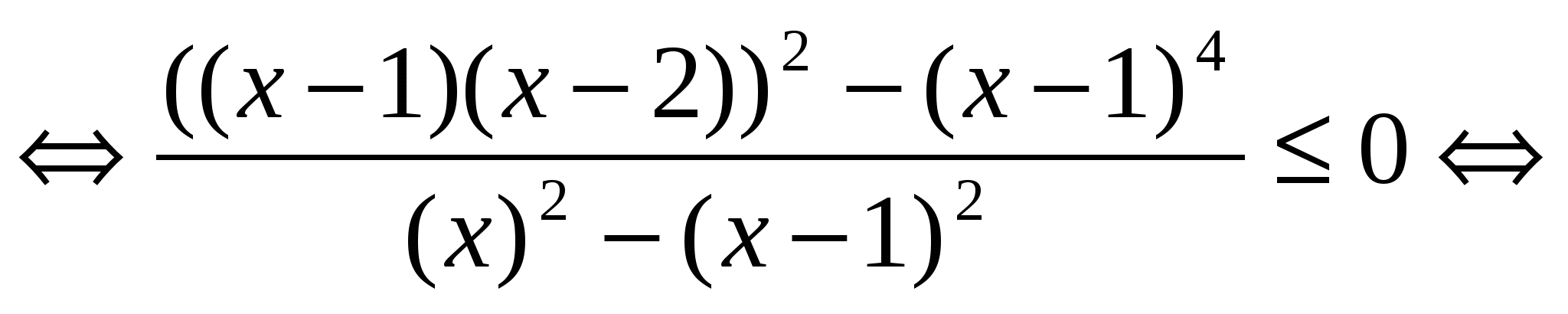
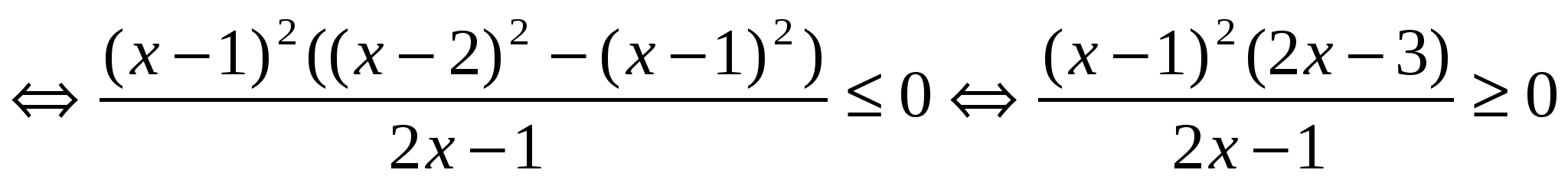
Ответ. 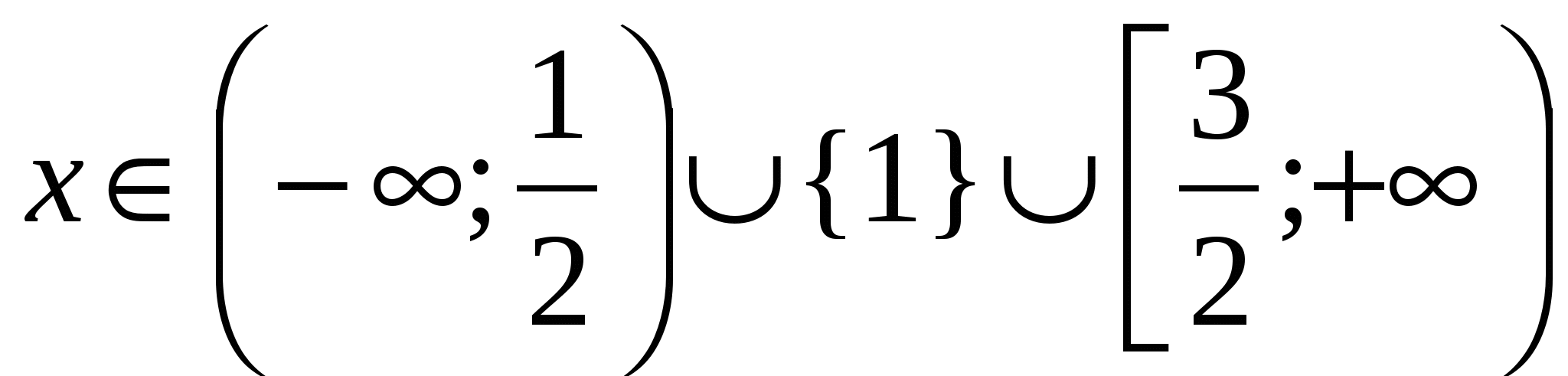 .
.
Заключение.
Подводя итог нашей работы, можно сказать следующее.
Целью работы было изучение различных методов решения уравнений и неравенств с модулями.
Рассмотрены некоторые разновидности простейших уравнений и неравенств с модулем, решаемых с помощью равносильных переходов,а также теоремы о сумме модулей; графический способ решения уравнений. Нужно сказать, что в школьном курсе математики именно эти методы решения наиболее часто используются. Графический метод особо актуален при решении задач C5 из контрольно-измерительных материалов ЕГЭ.
Далее мы изучили на нескольких примерах иные способы решения уравнений и неравенств с модулями, а именно: метод раскрытия модулей; решение уравнений, содержащих модули неотрицательных выражений; решение уравнений с использованием геометрической интерпретации; с использованием тождества 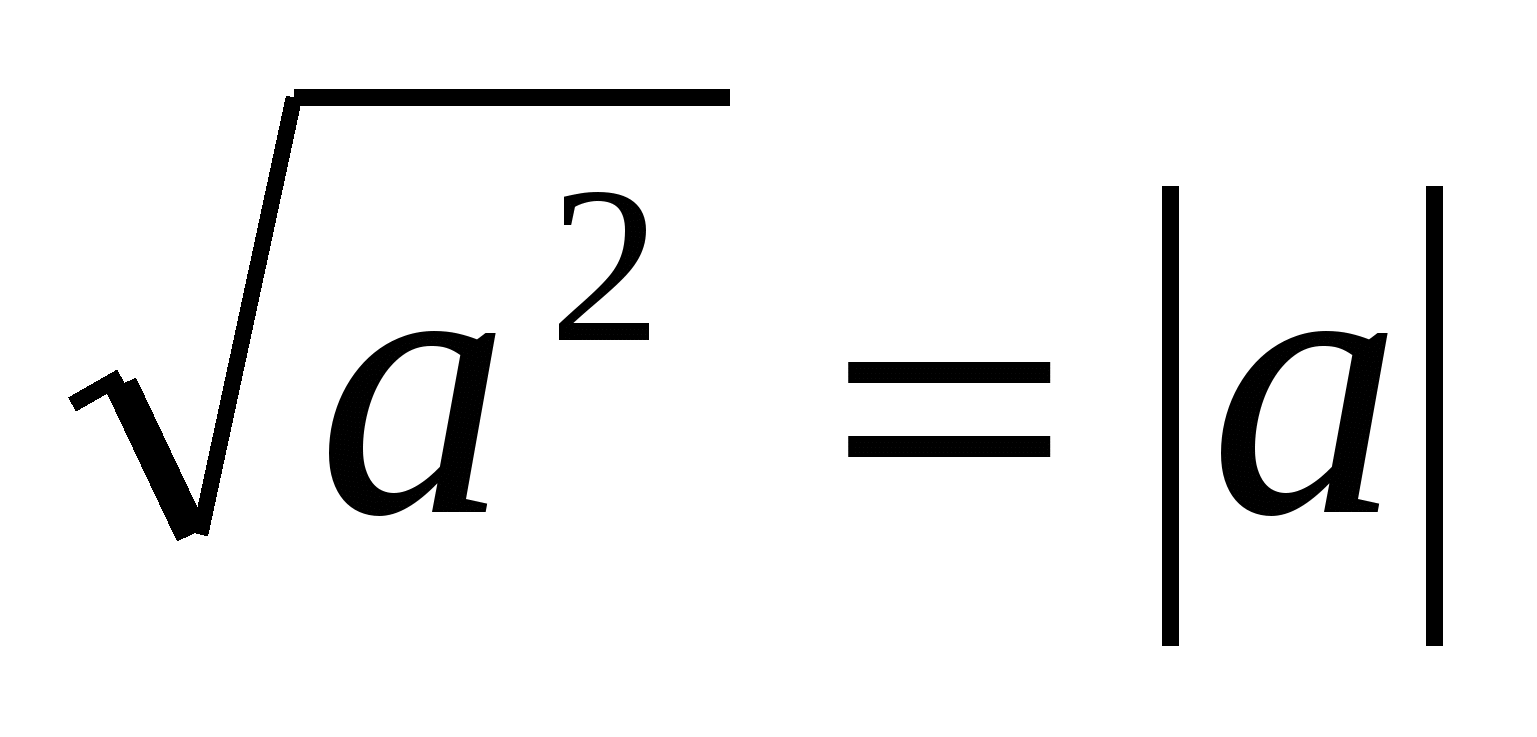 ; применение теоремы о знаках; решение уравнений переходом к следствию, домножением на положительный множитель,а также решение неравенств методом интервалов.
; применение теоремы о знаках; решение уравнений переходом к следствию, домножением на положительный множитель,а также решение неравенств методом интервалов.
Таким образом, в ходе исследования мы пришли к следующим выводам.
Наиболее универсальными и применимыми к наибольшему количеству задач мы считаем метод раскрытия модулей, графический метод и метод интервалов. Это убеждение возникло в результате решения большого числа задач из контрольно-измерительных материалов ЕГЭ, предметных чемпионатов, олимпиадных задач, а также изучение литературы по данному вопросу. Также очень важным мы считаем знание и применение тождества 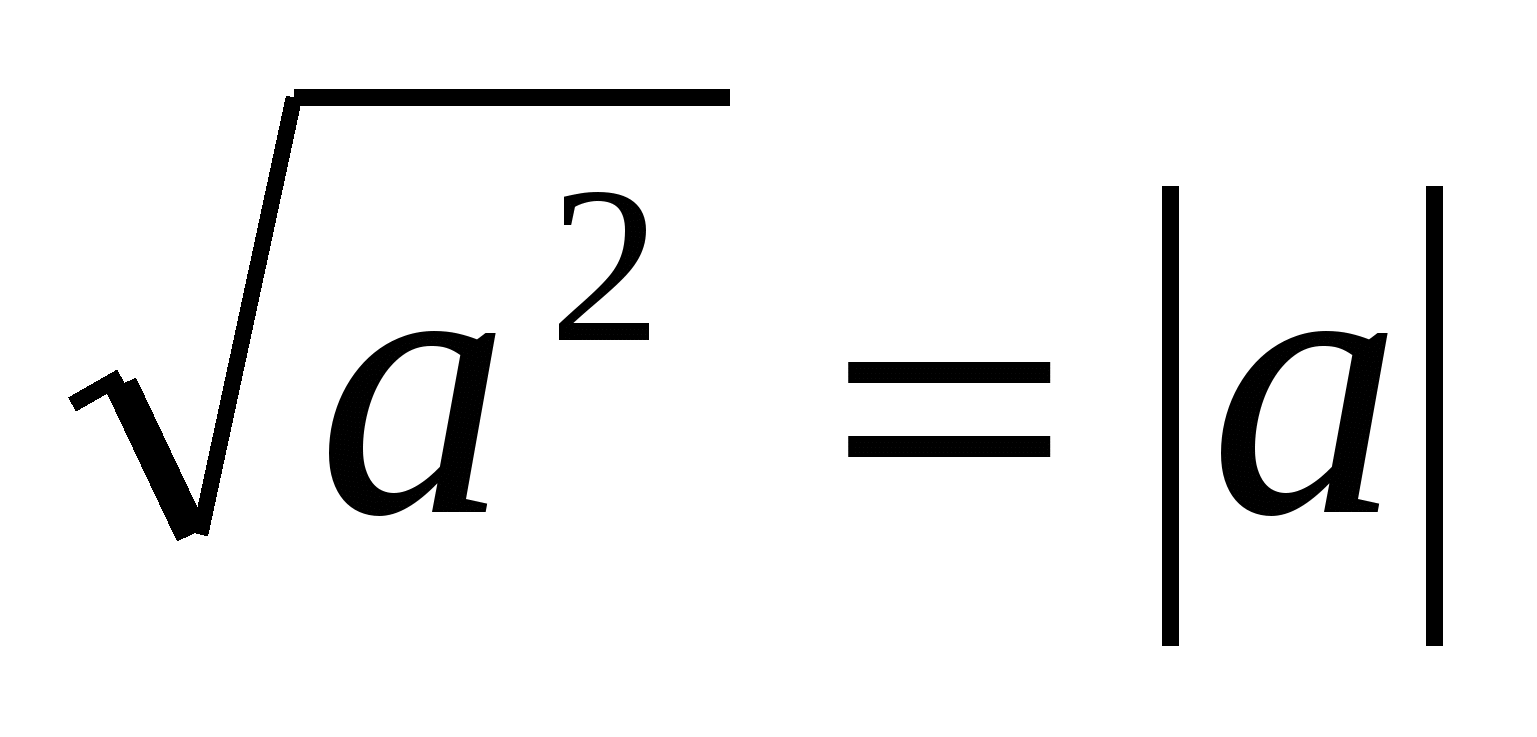 , так как оно используется не только при решении уравнений и неравенств, но и для преобразования многих выражений с радикалами. Остальные методы решения, которые мы рассмотрели, безусловно, представляют большой интерес в плане расширения математического кругозора и общего математического развития. Поэтому мы планируем использовать их для подготовки к государственной итоговой аттестации в форме ЕГЭ и подготовке к обучению в высшем учебном заведении.
, так как оно используется не только при решении уравнений и неравенств, но и для преобразования многих выражений с радикалами. Остальные методы решения, которые мы рассмотрели, безусловно, представляют большой интерес в плане расширения математического кругозора и общего математического развития. Поэтому мы планируем использовать их для подготовки к государственной итоговой аттестации в форме ЕГЭ и подготовке к обучению в высшем учебном заведении.
Список используемой литературы.
«Большая математическая энциклопедия» для школьников и студентов;
Математика. ЕГЭ – 2011, 2012. Типовые экзаменационные варианты. / Под редакцией А.Л. Семенова, И.В. Ященко.
М.Я. Выгодский. Справочник по элементарной математике
«Новейший справочник школьника»;
Энциклопедия «Я познаю мир. Математика»;
http://ru.wikipedia.org/wiki/Заглавная_страница;
infourok.ru
Программа элективного курса для учащихся 10-11 классов «Решение уравнений и неравенств с параметрами и модулем»
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №6 им. М.В. Ломоносова
с углубленным изучением отдельных предметов г.о. Самара
«РАССМОТРЕНО»на заседании МО
учителей математики и информатики
Руководитель МО
_________/Бессонова Н.С./
Протокол №____
«___» _________ 2015 г.
«СОГЛАСОВАНО»
Зам. директора по УВР
МБОУ СОШ №6
____________ /Золотовская М.А./
«___» _________ 2015 г.
«УТВЕРЖДАЮ»
Директор МБОУ СОШ №6
___________ /С.А.Кручинина/
Приказ №___
«___» _________ 2015 г.
«РАССМОТРЕНО»на заседании МО
учителей математики и информатики
Руководитель МО
_________/Бессонова Н.С./
Протокол №____
«___» _________ 2013 г.
«СОГЛАСОВАНО»
Зам. директора по УВР
МБОУ СОШ №6
____________ /Золотовская М.А./
«___» _________ 2013 г.
«УТВЕРЖДАЮ»
Директор МБОУ СОШ №6
___________ /С.А.Кручинина/
Приказ №___
«___» _________ 2013 г.
«РАССМОТРЕНО»на заседании МО
учителей математики и информатики
Руководитель МО
_________/Бессонова Н.С./
Протокол №____
«___» _________ 2013 г.
«СОГЛАСОВАНО»
Зам. директора по УВР
МБОУ СОШ №6
____________ /Золотовская М.А./
«___» _________ 2013 г.
«УТВЕРЖДАЮ»
Директор МБОУ СОШ №6
___________ /С.А.Кручинина/
Приказ №___
«___» _________ 2013 г.
Программа элективного курса для учащихся 10-11классов
«Решение уравнений и неравенств с параметрами и модулем»
Направленность элективного курса: расширение границ углубляемых учебных дисциплин из числа обучаемых предметов федерального компонента.
Автор программы:
Макарова Ирина Викторовна,
учитель математики
Самара , 2015
Пояснительная записка
Решению задач с параметрами и модулем в школе уделяется очень мало внимания. Поэтому трудно рассчитывать на то, что учащиеся, не получившие необходимых навыков в решении уравнений и неравенств с параметрами и модулем, смогут на ЕГЭ по математике получить высокий балл. Кроме того навыки в решении уравнений и неравенств с параметрами или модулем будут хорошим подспорьем для успешных выступлений на математических олимпиадах.
Подготовка к ЕГЭ по математике и успешность выступления на олимпиадах это лишь одна сторона вопроса. Другой, на мой взгляд, наиболее значимой, является математическое развитие учащихся. Задачи с параметрами или модулем играют важную роль в формировании логического мышления, математической культуры школьников, способствуют развитию интеллекта, умения анализировать, сравнивать, обобщать, делать выводы.
Практика показывает, что у большинства учащихся решение задач с параметрами и модулем вызывает значительные затруднения, которые обусловлены тем, что наличие параметра или модуля не позволяет решать уравнение или неравенство по шаблону, а требует рассматривать различные случаи, при которых методы решения, как правило, отличаются друг от друга.
Данный элективный курс позволяет глубже познакомиться с методами решения уравнений и неравенств с параметрами или модулем, способствует формированию устойчивого интереса к предмету, развитию познавательной активности учащихся.
Цели элективного курса:
углубление и расширение знаний учащихся о способах и методах решения уравнений и неравенств с параметрами;
систематизация полученных знаний, умений и навыков при решении заданий ЕГЭ, содержащих параметры;
развитие навыков исследовательской деятельности учащихся, их математических способностей, формирование интереса к предмету.
Задачи курса:
систематизировать основные приемы и методы решения уравнений и неравенств с параметрами и модулем;
способствовать формированию у учащихся умения выбирать наиболее рациональные методы решения уравнений и неравенств с параметрами и модулем;
сформировать у учащихся устойчивый интерес к предмету;
способствовать формированию навыков исследовательской деятельности школьников при решении задач с параметрами;
Программа курса рассчитана на 1 час в неделю. Всего 34 часа.
Планируемые образовательные результаты:
В результате изучения курса учащиеся должны:
усвоить основные методы решения уравнений и неравенств с параметрами;
осуществлять выбор методов решения уравнений, неравенств, содержащих параметр и проводить их полное обоснование;
повысить уровень логического мышления, овладеть навыками исследовательской деятельности.
Формы проведения
Основными формами проведения элективного курса являются лекции с элементами беседы, групповая работа, практикумы по решению задач, тестирование.
Календарно-тематическое планирование
Тема занятия
даты
Кол-во часов
Виды
деятельности
1 Блок
4.09-25.12.
17
1.
Понятие параметра и модуля, уравнения и неравенства с параметрами и модулем.
4.09- 11.09.
2
Лекция с элементами беседы.
Решение простейших задач.
2.
Линейные уравнения с одним или несколькими параметрами и модулем.
18.09-25.09
2
Лекция.
Практикум по решению задач.
3.
Уравнения с параметрами или модулем , приводимые к линейным.
2.10-9.10-16.10
3
Проверка усвоения ранее изученного материала (самостоятельная работа).
Лекция. Решение задач.
4.
Системы линейных уравнений с параметрами или модулем.
23.10-30.10
2
Лекция с элементами беседы.
Решение задач.
5.
Методы решения квадратных уравнений с параметрами или модулем.
13.11-20.11-27.11-4.12
4
Лекция.
Практикум по решению задач.
6.
Уравнения с параметрами или модулем, сводящиеся к квадратным.
11.12-18.12-25.12-15.01
4
Проверка усвоения ранее изученного материала (тест).
Лекция. Решение задач.
2 Блок
15.01-21.05.
17
7.
Линейные неравенства с параметром или модулем.
22.01-29.01
2
Лекция с элементами беседы.
Решение задач.
8.
Неравенства с параметром или модулем, приводимые к линейным.
5.02-12.02
2
Лекция с элементами беседы.
Решение задач.
9.
Решение квадратичных неравенств с параметром или модулем.
19.02-26.02
2
Лекция с элементами беседы.
Решение задач.
10.
Показательные уравнения и неравенства с параметрами или модулем.
5.03-12.03-19.03
3
Лекция с элементами беседы.
Практикум по решению задач, разбор заданий из сборников по подготовке к ЕГЭ (тест).
11.
Логарифмические уравнения и неравенства с параметрами или модулем.
2.04-9.04-16.04
3
Лекция с элементами беседы.
Практикум по решению задач, разбор заданий из сборников по подготовке к ЕГЭ (тест).
12.
Тригонометрические уравнения и неравенства с параметрами или модулем.
23.04-30.04-7.05
3
Лекция с элементами беседы.
Практикум по решению задач, разбор заданий из сборников по подготовке к ЕГЭ (тест).
13.
Повторение вопросов курса «Решение уравнений и неравенств с
параметрами и модулем». Проверочная работа по курсу.
14.05-21.05
2
Групповая работа по решению заданий всего курса. Проверочная работа с последующим анализом (тест).
Общее количество часов
34
Содержание элективного курса
Тема 1. Понятие параметра, уравнения и неравенства с параметрами и модулем.
На первом занятии учащимся сообщаются цель и значение элективного курса. Рассматриваются понятие параметра и способы решения простейших уравнений с параметрами и модулем.
Тема 2. Линейные уравнения с одним или несколькими параметрами и модулем.
Вводится понятие линейного уравнения с одним или несколькими параметрами. Используя это понятие, решаются уравнения данного типа.
Тема 3. Уравнения с параметрами, приводимые к линейным.
Решение уравнений с параметрами, приводимых к линейным: дробно-рациональных, уравнений, содержащих абсолютную величину.
Тема 4. Системы линейных уравнений с параметрами и модулем.
Решение систем линейных уравнений с параметрами, одно из уравнений которых содержит параметр или модуль.
Тема 5. Методы решения квадратных уравнений с параметрами или модуль.
Рассматривается понятие и методы решения квадратных уравнений с параметрами или модулем.
Тема 6. Уравнения с параметрами, сводящиеся к квадратным.
Рассматривается методы решения уравнений, сводящихся к квадратным уравнениям с параметрами или модулем.
Тема 7. Линейные неравенства с параметром или модулем.
Рассматривается понятие и методы решения линейных неравенств с параметрами или модулем.
Тема 8. Неравенства с параметром или модулем, приводимые к линейным.
Рассматривается методы решения неравенств с параметрами, сводящихся к линейным неравенствам с параметрами или модулем.
Тема 9. Решение квадратичных неравенств с параметром и модулем.
Рассматривается понятие и методы решения квадратных неравенств с параметрами и модулем.
Тема 10. Показательные уравнения и неравенства с параметрами или модулем.
Рассматривается методы решения показательных уравнений с параметрами и моделем и решения показательных уравнений с параметрами и модулем, встречающихся на ЕГЭ.
Тема 11. Логарифмические уравнения и неравенства с параметрами или модулем.
Рассматривается методы решения логарифмических уравнений с параметрами или модулем и решения логарифмических уравнений с параметрами или модулем, встречающихся на ЕГЭ.
Тема 12. Тригонометрические уравнения и неравенства с параметрами или модулем.
Рассматривается методы решения тригонометрических уравнений с параметрами или модулем и решения тригонометрических уравнений с параметрами или модулем , встречающихся на ЕГЭ.
Тема 13. Повторение вопросов курса «Решение уравнений и неравенств с
параметрами и модулем». Проверочная работа по курсу.
Список литературы
Высоцкий В.С. Задачи с параметрами при подготовке к ЕГЭ. — М.: Научный мир, 2011.- 316 с.
Д.Ф.Айвазян. Математика 10-11 классы Решение уравнений и неравенств с параметрами. В. Учитель.2009 г.
Иванов С.О., Войта Е.А., Ковалевская А.С., Ольховская Л.С.; под ред. Ф.Ф.Лысенко. Учимся решать задачи с параметром, Подготовка к ЕГЭ. – Ростов – на – Дону: Легион – М.: 2011. – 48с.
Локоть В.В.. Задачи с параметрами. Линейные и квадратные уравнения, неравенства, системы. – М.: АРКТИ, 2005. – 96 с.
Локоть В.В. Задачи с параметром. Иррациональные уравнения, неравенства, системы, задачи с модулем. – М.: АРКТИ, 2010. – 64 с.
Локоть В.В. Задачи с параметром и их решение: Тригонометрия: уравнения и неравенства. Системы. 10 класс. – М.: АРКТИ, 2008. – 64 с.
Локоть В.В. Задачи с параметрами. Показательные и логарифмические уравнения, неравенства, системы. – М.: АРКТИ, 2004. – 96 с.
Прокофьев А.А. Задачи с параметрами. – М.: МИЭТ, 2004. – 258 с.
Потапов М.К., Олехник С.Н., Нестеренко Ю.В. Уравнения и неравенства с параметрами. Издат МГУ, 1992 г.
Ястребинецкий Г.А. Уравнения и неравенства, содержащие параметры. Пособие для учителей. — М.: Просвещение, 1972.
infourok.ru
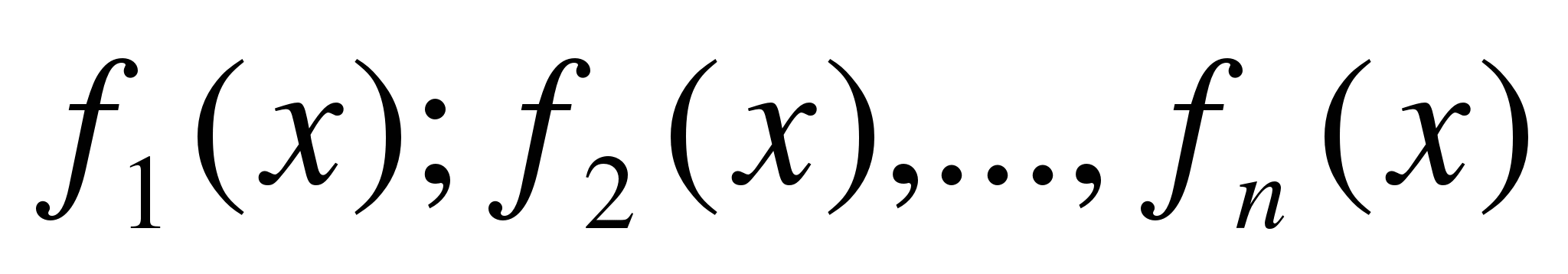
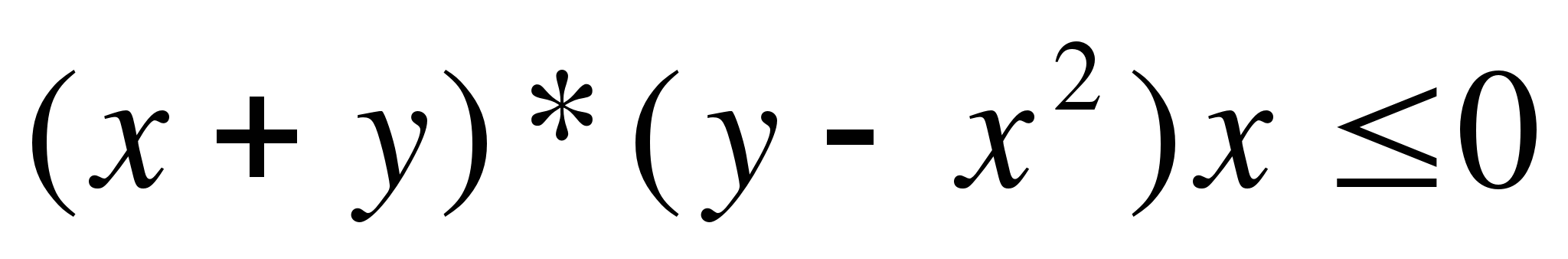 в системе ХОУ.
в системе ХОУ.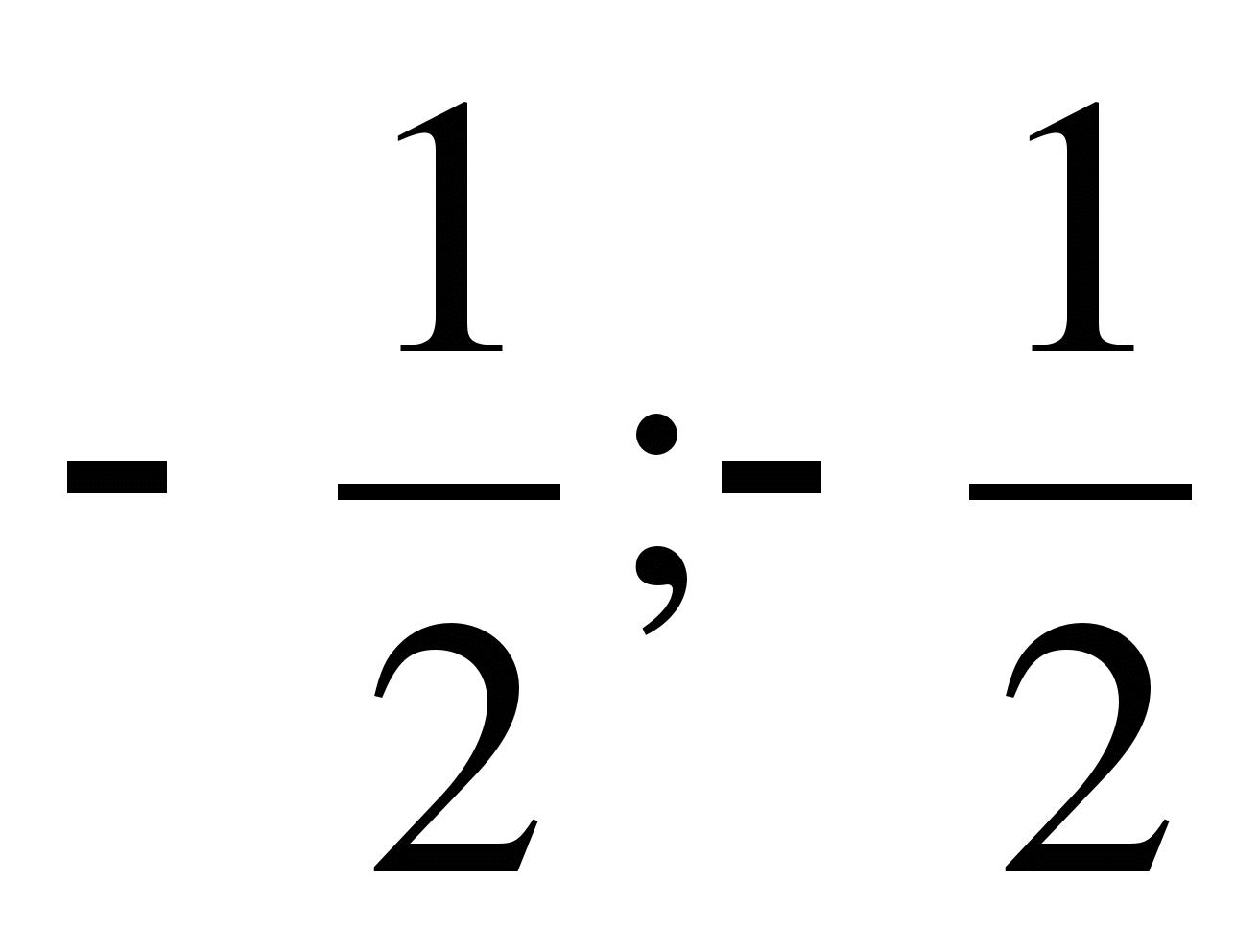 )
)