Решение систем неравенств с двумя переменными
Вопросы занятия:
· повторить алгоритм решения неравенств с двумя переменными;
· повторить алгоритм решения систем неравенств с двумя переменными.
Материал урока
Рассмотрим неравенство:
При х = -3 и у = 0 это неравенство обращается в верное числовое неравенство 19 > 8.
А при x = 2 и y = 10, это неравенство обращается в числовое неравенство -41 > 8. Очевидно, что это неверное числовое неравенство.
То есть мы можем сказать, что пара чисел (-3; 0) является решением данного неравенства, а пара чисел (2; 10) не является решением этого неравенства.
Повторим определение.
Определение.
Решением неравенства
с двумя переменными называется пара значений этих переменных, обращающая данное
неравенство в верное числовое неравенство.
Возвращаясь к нашему примеру, мы можем сказать, что пара чисел (-3; 0) является решением данного неравенства.
Очевидно, что это не единственное решение.
Теперь давайте вспомним алгоритм решения неравенств с двумя переменными:
1. Заменить знак неравенства на знак равенства.
2. Выразить переменную у через х.
3. Построить график полученного уравнения.
4. Выделить часть плоскости, соответствующую знаку неравенства.
Пример.
Пример.
Пример.
Пример.
Прежде чем перейти к решению систем неравенств с двумя переменными, давайте вспомним определения.
Определение.
Говорят, что задана система двух неравенств с двумя переменными
, если требуется найти все значения переменных, при которых оба неравенства системы обращаются в верные числовые неравенства.
Определение.
Решением системы неравенств называют такое значение переменной, при котором неравенства системы преобразуются в верные числовые неравенства.
Определение.
Решить систему неравенств это значит найти все её решения или доказать, что решений нет.
Алгоритм решения систем неравенств с двумя переменными практически такой же, как и алгоритм решения системы неравенств с одной переменной:
1. Решить каждое из неравенств системы отдельно.
2. Изобразить полученные решения в координатной плоскости.
3. Найти пересечение этих решений.
4. Общая часть этих решений и является решением данной системы неравенств.
Пример.
Рассмотрим ещё один пример.
Пример.
Решим ещё одну систему неравенств.
Пример.
Итоги урока
Сегодня на уроке мы повторили алгоритмы решения
неравенств и систем неравенств с двумя переменными. Решили несколько задач.
Решили несколько задач.
Системы неравенств онлайн с решением. Неравенства и системы неравенств с двумя переменными
Статья раскрывает тему неравенств, разбираются определения систем и их решения. Будут рассмотрены часто встречающиеся примеры решения систем уравнений в школе на алгебре.
Определение системы неравенств
Системы неравенств определяют по определениям систем уравнений, значит, что особое внимание уделяется записям и смыслу самого уравнения.
Определение 1
Системой неравенств называют запись уравнений, объединенных фигурной скобкой с множеством решений одновременно для всех неравенств, входящих в систему.
Ниже приведены примеры неравенств. Даны два неравенства 2 · x − 3 > 0 и 5 − x ≥ 4 · x − 11 . Необходимо записать одно уравнение под другим, после чего объединим при помощи фигурной скобки:
2 · x — 3 > 0 , 5 — x ≥ 4 · x — 11
Таким же образом определение систем неравенств представлены в школьных учебниках как для использования одной переменной, так и двух.
Основные виды системы неравенств
Имеет место составление бесконечного множества систем неравенств. Их классифицируют по группам, отличающихся по определенным признакам. Неравенства подразделяют по критериям:
- количество неравенств системы;
- количество переменных записи;
- вид неравенств.
Количество входящих неравенств может насчитывать от двух и более. В предыдущем пункте рассматривался пример решения системы с двумя неравенствами.
2 · x — 3 > 0 , 5 — x ≥ 4 · x — 11
Рассмотрим решение системы с четырьмя неравенствами.
x ≥ — 2 , y ≤ 5 , x + y + z ≥ 3 , z ≤ 1 — x 2 — 4 · y 2
Решение неравенства отдельно не говорит о решение системы в целом. Для решения системы необходимо задействовать все имеющиеся неравенства.
Такие системы неравенств могут иметь одну, две, три и более переменных. В последней изображенной системе это отчетливо видно, там имеем три переменные: x , y , z . Уравнения могут содержать по одной переменной, как в примере, либо по несколько.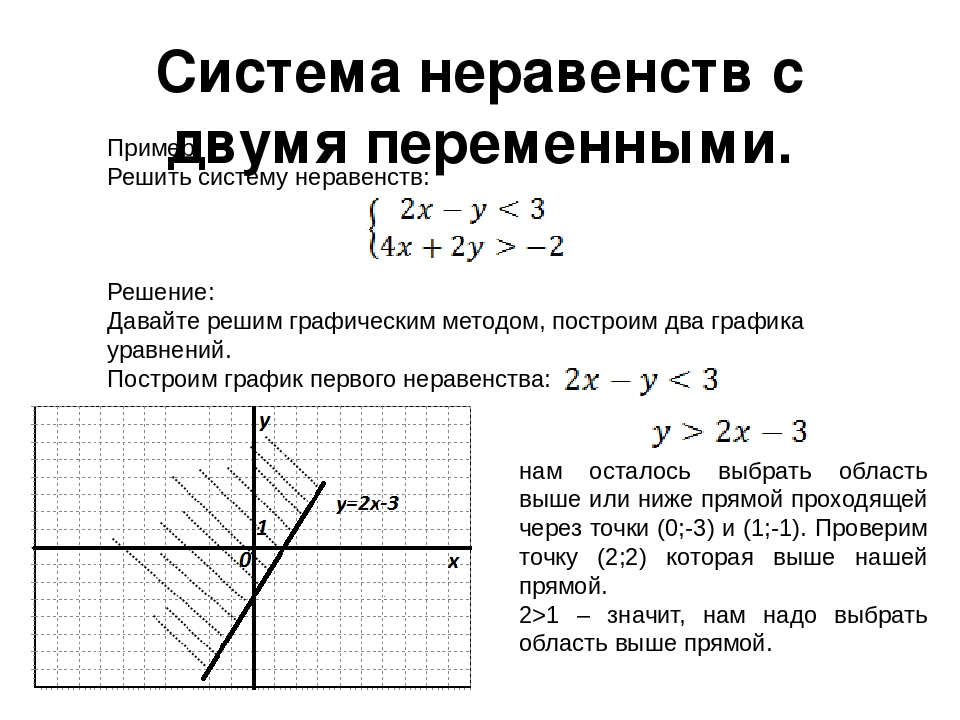 Исходя из примеров, неравенство x + 0 · y + 0 · z ≥ − 2 и 0 · x + y + 0 · z ≤ 5 не считают равнозначными. Школьным программам уделяют внимание решению неравенств с одной переменной.
Исходя из примеров, неравенство x + 0 · y + 0 · z ≥ − 2 и 0 · x + y + 0 · z ≤ 5 не считают равнозначными. Школьным программам уделяют внимание решению неравенств с одной переменной.
При записи системы могут быть задействованы уравнения разных видов и с разным количеством переменных. Чаще всего встречаются целые неравенства разных степеней. При подготовке к экзаменам могут встретиться системы с иррациональными, логарифмическими, показательными уравнениями вида:
544 — 4 — x 32 — 2 — x ≥ 17 , log x 2 16 x + 20 16 ≤ 1
Такая система включает в себя показательное и логарифмическое уравнение.
Решение системы неравенств
Определение 2Рассмотрим пример решения систем уравнений с одной переменной.
x > 7 , 2 — 3 · x ≤ 0
Если значение х = 8 , то решение системы очевидно, так как выполняется 8 > 7 и 2 − 3 · 8 ≤ 0 . При х = 1 система не решится, так как первое числовое неравенство во время подстановки имеет 1 > 7 . Таким же образом решается система с двумя и более переменными.
Определение 3
Решение системы неравенств с двумя и более переменными называют значения, которые являются решением всех неравенств при обращении каждого в верное числовое неравенство.
Если х = 1 и у = 2 будет решением неравенства x + y
При решении системы неравенств могут давать определенное количество ответов, а могут и бесконечное. Имеется ввиду множество решений такой системы. При отсутствии решений говорят о том, что она имеет пустое множество решений. Если решение имеет определенное число, тогда множества решений имеет конечное число элементов. Если решений много, тогда множество решений содержит бесконечное множество чисел.
Некоторые учебники дают определение частного решения системы неравенств, которое понимается как отдельно взятое решение. А общим решением системы неравенствсчитают все его частные решения. Такое определение используется редко, поэтому говорят «решение системы неравенств».
Данные определения систем неравенств и решения рассматриваются как пересечения множеств решений всех неравенств системы. Особое внимание стоит уделить разделу, посвященному равносильным неравенствам.
Особое внимание стоит уделить разделу, посвященному равносильным неравенствам.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Системой неравенств принято называть любую совокупность двух или более неравенств, содержащих неизвестную величину.
Наглядно данную формулировку иллюстрируют, к примеру, такие системы неравенств :
Решить систему неравенств — означает найти все значения неизвестной переменной, при которых реализуется каждое неравенство системы, либо обосновать, что таких не бывает.
Значит, для каждого отдельного неравенства системы вычисляем неизвестную переменную. Далее из получившихся значений выбирает только те, которые верны и для первого и для второго неравенства. Следовательно, при подстановке выбранного значения оба неравенства системы становятся правильными.
Разберем решение нескольких неравенств:
Разместим одну под другой пару числовых прямых; на верхнею нанесем величину x , при которых первое неравенств о (x > 1) становиться верным, а на нижней—величину х , которые являются решением второго неравенства (х
 2-1)≥0\\x
2-1)≥0\\xРешение системы неравенств
Чтобы
решить систему неравенств нужно найти значения иксов, которые подойдут всем неравенствам в системе – это и значит, что они выполняются одновременно.Пример. Решим систему \(\begin{cases}x>4\\x\leq7\end{cases}\)
Решение: Первое неравенство становится верным, если икс больше \(4\). То есть, решения первого неравенства – все значения иксов из \((4;\infty)\), или на числовой оси:
Второму неравенству подойдут значения иксов меньшие чем 7, то есть любой икс из интервала \((-\infty;7]\) или на числовой оси:
А какие значения подойдут обоим неравенствам? Те, которые принадлежат обоим промежуткам, то есть где промежутки пересекаются.
Ответ: \((4;7]\)
Как вы могли заметить для пересечения решений неравенств в системе удобно использовать числовые оси.
Общий принцип решения систем неравенств: нужно найти решение каждого неравенства, а потом пересечь эти решения с помощью числовой прямой.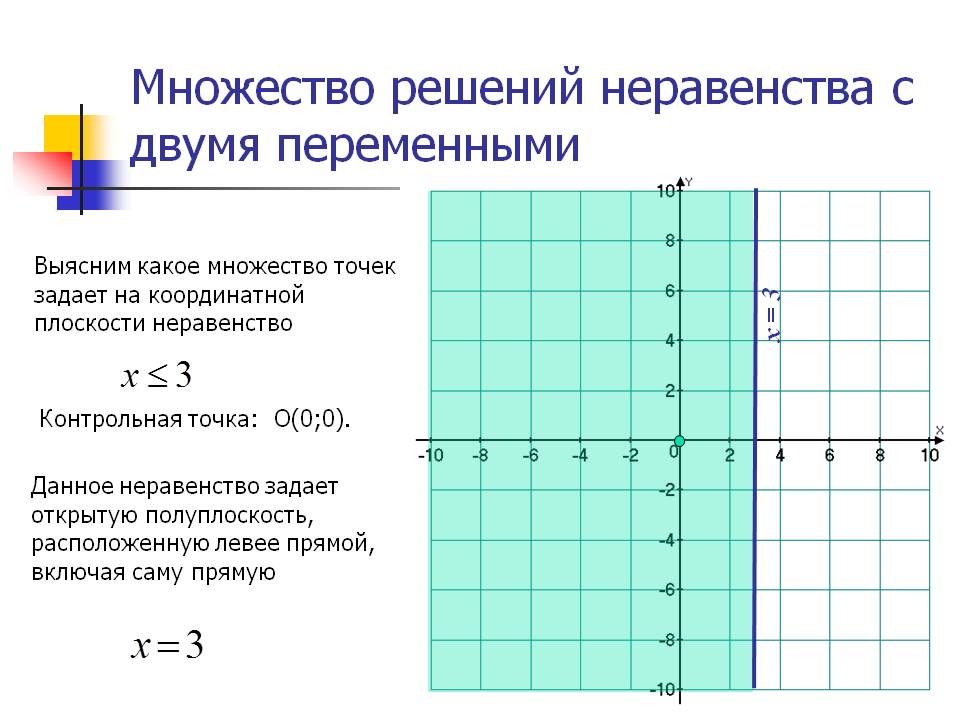
Пример: (Задание из ОГЭ) Решить систему \(\begin{cases} 7(3x+2)-3(7x+2)>2x\\(x-5)(x+8)
Решение:
\(\begin{cases} 7(3x+2)-3(7x+2)>2x\\(x-5)(x+8) | Давайте каждое неравенство решим отдельно от другого. |
Перевернем получившееся неравенство. | |
Поделим все неравенство на \(2\). | |
Запишем ответ для первого неравенства. | |
\(x∈(-∞;4)\) | Теперь решим второе неравенство. |
2) \((x-5)(x+8) | Неравенство уже в идеальном виде для применения . |
Запишем ответ для второго неравенства. | |
Объединим оба решения с помощью числовых осей. | |
Перед нами обычное – выразим \(x\). Для этого перенесем \(10\) в правую часть. | |
Поделим неравенство на \(-2\). Так как число отрицательное меняем знак неравенства. | |
Отметим решение на числовой прямой. | |
Запишем ответ к первому неравенству. | |
\(x∈(-∞;5]\) | На данном этапе главное не забыть, что есть второе неравенство. |
2) \(2-7x≤14-3x\) | Опять линейное неравенство – опять выражаем \(x\). |
\(-7x+3x≤14-2\) | Приводим подобные слагаемые. |
Делим все неравенство на \(-4\), перевернув при этом знак. | |
Изобразим решение на числовой оси и выпишем ответ для этого неравенства. | |
| \(x∈[-3;∞)\) | А теперь объединим решения. |
Решение неравенств онлайн
Перед тем как решать неравенства, необходимо хорошо усвоить как решаются уравнения .
Не важно каким является неравенство – строгим () или нестрогим (≤, ≥), первым делом приступают к решению уравнения, заменив знак неравенства на равенство (=).
Поясним что означает решить неравенство?
После изучения уравнений в голове у школьника складывается следующая картина: нужно найти такие значения переменной, при которых обе части уравнения принимают одинаковые значения. Другими словами, найти все точки, в которых выполняется равенство. Всё правильно!
Когда говорят о неравенствах, имеют в виду нахождение интервалов (отрезков), на которых выполняется неравенство. Если в неравенстве две переменные, то решением будут уже не интервалы, а какие-то площади на плоскости. Догадайтесь сами, что будет решением неравенства от трех переменных?
Как решать неравенства?
Универсальным способом решения неравенств считают метод интервалов (он же метод промежутков), который заключается в определении всех интервалов, в границах которых будет выполняться заданное неравенство.
Не вдаваясь в тип неравенства, в данном случае это не суть, требуется решить соответствующее уравнение и определить его корни с последующим обозначением этих решений на числовой оси.
Как правильно записывать решение неравенства?
Когда вы определили интервалы решений неравенства, нужно грамотно выписать само решение. Есть важный нюанс – входят ли границы интервалов в решение?
Тут всё просто. Если решение уравнения удовлетворяет ОДЗ и неравенство является нестрогим, то граница интервала входит в решение неравенства. В противном случае – нет.
Рассматривая каждый интервал, решением неравенства может оказаться сам интервал, либо полуинтервал (когда одна из его границ удовлетворяет неравенству), либо отрезок – интервал вместе с его границами.
Важный момент
Не думайте, что решением неравенства могут быть только интервалы, полуинтервалы и отрезки. Нет, в решение могут входить и отдельно взятые точки.
Например, у неравенства |x|≤0 всего одно решение – это точка 0.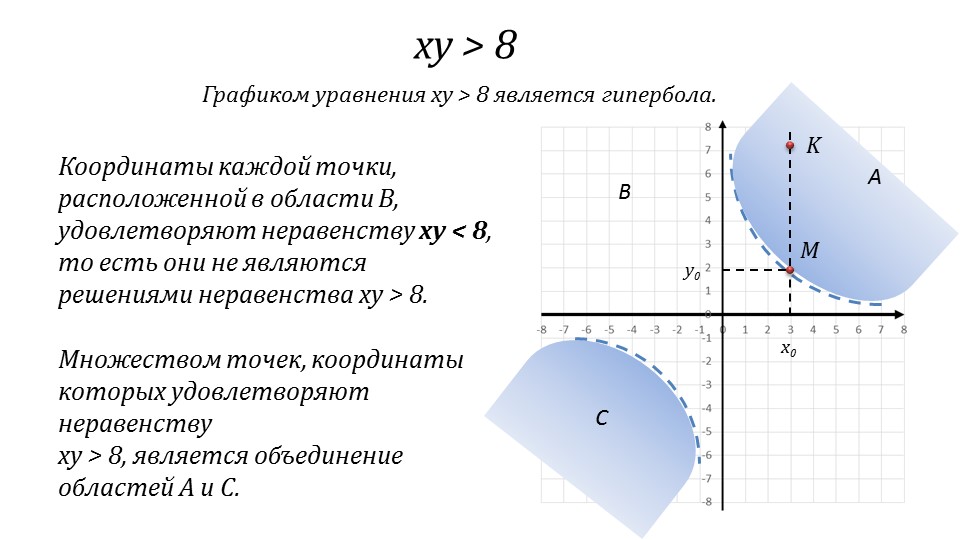
А у неравенства |x|
Для чего нужен калькулятор неравенств?
Калькулятор неравенств выдает правильный итоговый ответ. При этом в большинстве случаев приводится иллюстрация числовой оси или плоскости. Видно, входят ли границы интервалов в решение или нет – точки отображаются закрашенными или проколотыми.
Благодаря онлайн калькулятору неравенств можно проверить правильно ли вы нашли корни уравнения, отметили их на числовой оси и проверили на интервалах (и границах) выполнение условия неравенства?
Если ваш ответ расходится с ответом калькулятора, то однозначно нужно перепроверить свое решение и выявить допущенную ошибку.
В этой статье собрана начальная информация о системах неравенств. Здесь дано определение системы неравенств и определение решения системы неравенств. А также перечислены основные виды систем, с которыми наиболее часто приходится работать на уроках алгебры в школе, и приведены примеры.
Навигация по странице.
Что такое система неравенств?
Системы неравенств удобно определить аналогично тому, как мы вводили определение системы уравнений , то есть, по виду записи и смыслу, вложенному в нее.
Определение.
Система неравенств – это запись, представляющая собой некоторое число записанных друг под другом неравенств, объединенных слева фигурной скобкой, и обозначающая множество всех решений, являющихся одновременно решениями каждого неравенства системы.
Приведем пример системы неравенств. Возьмем два произвольных , например, 2·x−3>0
и 5−x≥4·x−11
, запишем их одно под другим
2·x−3>0
,
5−x≥4·x−11
и объединим знаком системы – фигурной скобкой, в результате получим систему неравенств такого вида:
Аналогично дается представление о системах неравенств в школьных учебниках. Стоит отметить, что в них определения даются более узко: для неравенств с одной переменной или с двумя переменными .
Основные виды систем неравенств
Понятно, что можно составить бесконечно много различных систем неравенств. Чтобы не заблудиться в этом многообразии, их целесообразно рассматривать по группам, имеющим свои отличительные признаки. Все системы неравенств можно разбить на группы по следующим критериям:
Все системы неравенств можно разбить на группы по следующим критериям:
- по числу неравенств в системе;
- по числу переменных, участвующих в записи;
- по виду самих неравенств.
По числу неравенств, входящих в запись, различают системы двух, трех, четырех и т.д. неравенств. В предыдущем пункте мы привели пример системы , которая является системой двух неравенств. Покажем еще пример системы четырех неравенств .
Отдельно скажем, что нет смысла говорить о системе одного неравенства, в этом случае по сути речь идет о самом неравенстве, а не о системе.
Если смотреть на число переменных, то имеют место системы неравенств с одной, двумя, тремя и т.д. переменными (или, как еще говорят, неизвестными). Посмотрите на последнюю систему неравенств, записанную двумя абзацами выше. Это система с тремя переменными x
, y
и z
. Обратите внимание, что ее два первых неравенства содержат не все три переменные, а лишь по одной из них. В контексте этой системы их стоит понимать как неравенства с тремя переменными вида x+0·y+0·z≥−2
и 0·x+y+0·z≤5
соответственно. Заметим, что в школе основное внимание уделяется неравенствам с одной переменной.
Заметим, что в школе основное внимание уделяется неравенствам с одной переменной.
Осталось обговорить, какие виды неравенств участвуют в записи систем. В школе в основном рассматривают системы двух неравенств (реже – трех, еще реже — четырех и более) с одной или двумя переменными, причем сами неравенства обычно являются целыми неравенствами первой или второй степени (реже – более высоких степеней или дробно рациональными). Но не удивляйтесь, если в материалах по подготовке к ОГЭ столкнетесь с системами неравенств, содержащими иррациональные, логарифмические, показательные и другие неравенства. В качестве примера приведем систему неравенств , она взята из .
Что называется решением системы неравенств?
Введем еще одно определение, связанное с системами неравенств, — определение решения системы неравенств :
Определение.
Решением системы неравенств с одной переменной называется такое значение переменной, обращающее каждое из неравенств системы в верное , другими словами, являющееся решением каждого неравенства системы.
Поясним на примере. Возьмем систему двух неравенств с одной переменной . Возьмем значение переменной x , равное 8 , оно является решением нашей системы неравенств по определению, так как его подстановка в неравенства системы дает два верных числовых неравенства 8>7 и 2−3·8≤0 . Напротив, единица не является решением системы, так как при ее подстановке вместо переменной x первое неравенство обратится в неверное числовое неравенство 1>7 .
Аналогично можно ввести определение решения системы неравенств с двумя, тремя и большим числом переменных:
Определение.
Решением системы неравенств с двумя, тремя и т.д. переменными называется пара, тройка и т.д. значений этих переменных, которая одновременно является решением каждого неравенства системы, то есть, обращает каждое неравенство системы в верное числовое неравенство.
К примеру, пара значений x=1 , y=2 или в другой записи (1, 2) является решением системы неравенств с двумя переменными , так как 1+2
Системы неравенств могут не иметь решений, могут иметь конечное число решений, а могут иметь и бесконечно много решений. Часто говорят о множестве решений системы неравенств. Когда система не имеет решений, то имеет место пустое множество ее решений. Когда решений конечное число, то множество решений содержит конечное число элементов, а когда решений бесконечно много, то и множество решений состоит из бесконечного числа элементов.
Часто говорят о множестве решений системы неравенств. Когда система не имеет решений, то имеет место пустое множество ее решений. Когда решений конечное число, то множество решений содержит конечное число элементов, а когда решений бесконечно много, то и множество решений состоит из бесконечного числа элементов.
В некоторых источниках вводятся определения частного и общего решения системы неравенств, как, например, в учебниках Мордковича . Под частным решением системы неравенств понимают ее одно отдельно взятое решение. В свою очередь общее решение системы неравенств — это все ее частные решения. Однако в этих терминах есть смысл лишь тогда, когда требуется особо подчеркнуть, о каком решении идет речь, но обычно это и так понятно из контекста, поэтому намного чаще говорят просто «решение системы неравенств».
Из введенных в этой статье определений системы неравенств и ее решений следует, что решение системы неравенств представляет собой пересечение множеств решений всех неравенств этой системы.
Список литературы.
- Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
- Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
- Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 13-е изд., стер. — М.: Мнемозина, 2011. — 222 с.: ил. ISBN 978-5-346-01752-3.
- Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. — 2-е изд., стер. — М.: Мнемозина, 2008. — 287 с.
 : ил. ISBN 978-5-346-01027-2.
: ил. ISBN 978-5-346-01027-2. - ЕГЭ -2013. Математика: типовые экзаменационные варианты: 30 вариантов / под ред. А. Л. Семенова, И. В. Ященко. – М.: Издательство «Национальное образование», 2012. – 192 с. – (ЕГЭ-2013. ФИПИ – школе).
Разработка урока «Решение систем неравенств с двумя переменными» в 9 классе
Тема: Решение систем неравенств с двумя переменными
9 класс.
Цель урока: Обобщить пройденный материал. Научиться решать системы неравенств с двумя переменными. Разобрать решение неравенств, содержащие знак модуля у двух переменных. Продолжить формирование умений классифицировать, строить графики, находить решения неравенств.
Формирование УУД:
Познавательные: определять способы решения и обосновывать свое мнение;
анализировать задачу, ситуацию.
Регулятивные: выполнять самопроверку и самооценку выполнения учебного задания; умение планировать и осуществлять деятельность, направленную на решение проблем различного характера.
Коммуникативные: предлагать и обосновывать своё мнение.
Личностные: определять личностный смысл деятельности; осуществлять выбор в соответствии с задачей деятельности
Оборудование: Карточки для практических работ, проектор, презентация.
Тип урока: урок комплексного применения знаний, умений и навыков.
Структура урока
Организационный этап.
Устная работа.
Актуализация опорных знаний (тестовая работа)
Изучение новых знаний, необходимых для формирования умений.
Мотивация обучения.
Творческое применение и добывание знаний в новой ситуации (проблемные задачи).
Домашнее задание.
Итоги урока. Рефлексия.
Эпиграф к уроку: «Дорогу осилит идущий, а математику – мыслящий!»
Ход урока
1. Организационный этап. Здравствуйте, ребята. Сегодня у нас на уроке гости. Улыбнёмся гостям, друг другу, мне и начнём урок с хорошим настроением.
Организационный этап. Здравствуйте, ребята. Сегодня у нас на уроке гости. Улыбнёмся гостям, друг другу, мне и начнём урок с хорошим настроением.
Сообщение темы и цели урока (читают учащиеся)
2.Устная работа.
Повторим основные приёмы и отличия.
Проанализируйте неравенства и скажите, в чём отличие первого неравенства от второго: х2 – 2х≥1; х2 – 2у≥ 1? ( В первом неравенстве одна переменная, во втором две).
Как изобразить решение таких неравенств? (на координатной прямой и координатной плоскости).
Какие особенности изображения решения строгого и нестрогого неравенства? (Строгое неравенство: ˃ , < пустые точки на прямой, пунктирная линия графика на плоскости
Нестрогое неравенство: ≥ , ≤ жирные точки на прямой, сплошная линия графика на плоскости)
Задание на повторение. Решить систему неравенств:
5х+1˃62х-4<3
0<4х+2≤6
х2-5х+4≤0
9-4х<0
y=kx+b, (x-х0)2+(y-у0)2=r2, y=a(x-m)2+n, у=a х2+bx+c, y=k/x, у = k х3 + b
соответствует: прямой, параболе, гиперболе, окружности, куб. параболе?
параболе?
Что является решением неравенства с двумя переменными? (Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство)
Определите, является ли пара чисел (4,0), (1; 2) решением неравенства х2 – 2у≥ 1?
Алгоритм решения неравенства с двумя переменными. Решите неравенство.
Как найти множество решений неравенства?(Для изображения множества решений неравенства на координатной плоскости поступают следующим образом:
1. Строим график функции y = f(x), который разбивает плоскость на две области.
2. Выбираем на графике любую точку с координатами (х0,у0). Проводим в данной точке перпендикуляр к оси х. Выбираем точку с координатой у больше или меньше у0 в зависимости от знака неравенства или пробная точка.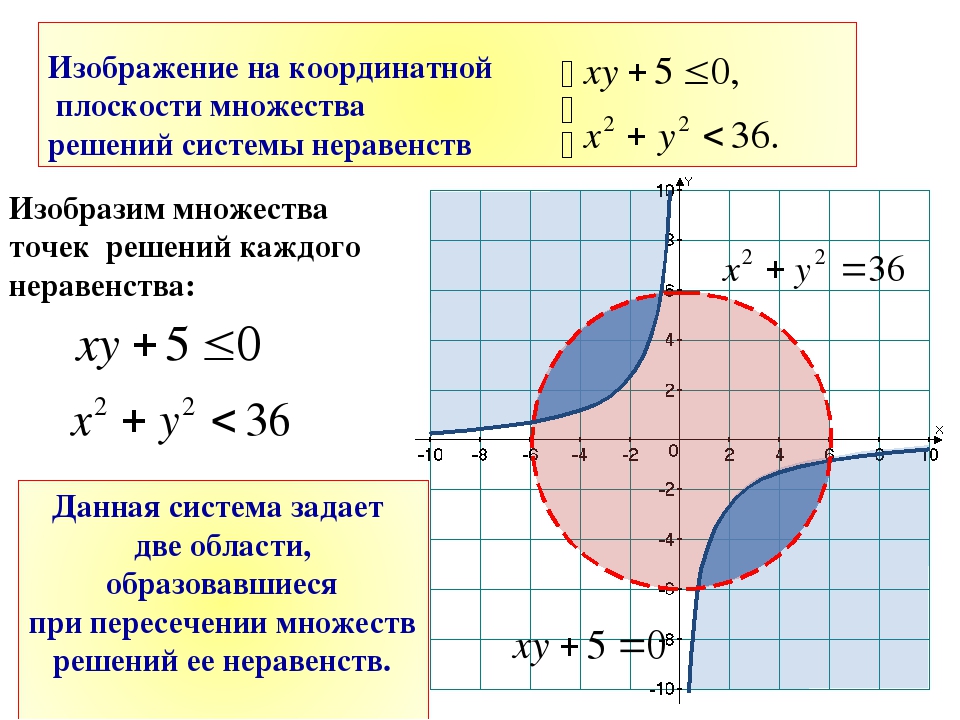 Проверяем выполнимость исходного неравенства для этой точки. Если в результате проверки получается верное числовое неравенство, то заключаем, что исходное неравенство выполняется во всей области, которой принадлежит выбранная точка. Таким образом, множеством решений неравенства – является область, которой принадлежит выбранная точка. Если в результате проверки получается неверное числовое неравенство, то множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.
Проверяем выполнимость исходного неравенства для этой точки. Если в результате проверки получается верное числовое неравенство, то заключаем, что исходное неравенство выполняется во всей области, которой принадлежит выбранная точка. Таким образом, множеством решений неравенства – является область, которой принадлежит выбранная точка. Если в результате проверки получается неверное числовое неравенство, то множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.
3. Если неравенство строгое, то границы области, то есть точки графика функции y = f(x), не включают в множество решений и границу изображают пунктиром. Если неравенство нестрогое, то границы области, то есть точки графика функции y = f(x), включают в множество решений данного неравенства и границу в таком случае изображают сплошной линией.)
Вывод:- решением неравенства f(x,y)˃0, f(x,y)<0, f(x,y)≤0 f(x,y)≥0 называется упорядоченная пара чисел, которая превращает его в правильное числовое неравенство.
-графиком неравенства с двумя переменными х и у называется множество всех точек координатной плоскости с координатами (х, у), где каждая пара (х,у) является решением данного неравенства. Решением неравенства с двумя переменными будет внутренняя или внешняя область фигуры.)
3. Актуализация знаний.
Тренировочный блок:
№ 492 (а).
Р е ш е н и е
ху ≥ 0.
Произведение двух чисел является неотрицательным в том случае, если эти числа имеют одинаковые знаки. Значит, когда
Первой системе соответствует первая координатная четверть, а другой системе – третья координатная четверть. Множеством решений неравенства-объединение первой и третьей координатных четвертей, включая оси координат.
Разминка
Задание 1.На готовых шаблонах координатных плоскостей А-3 изобразите множество решений неравенства
х2 +у2 ≥25у ≤ — х2+1
у≥(х-1) 2
(х-1)2 +(у-2)2 ≤ 9
у ≥0
х ≤ 0
у≤-2
х ≥3
Решение неравенств (по слайдам 1-5 презентации)
Тестовая работа.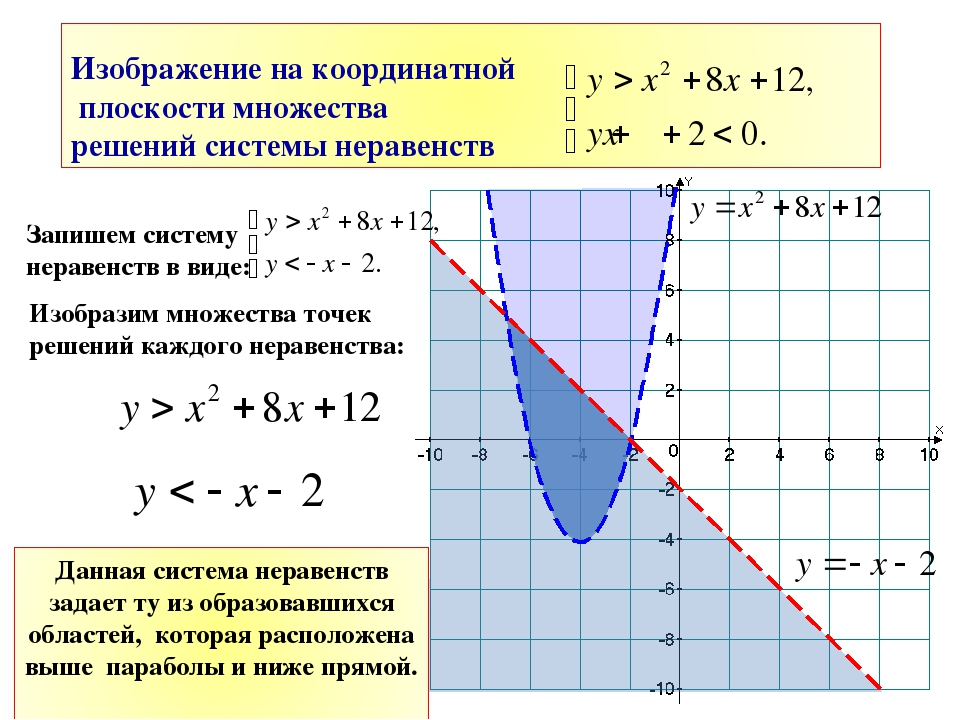
Определить неравенство по графику. (Задания на распознавание неравенств -3 мин)
Ответы:
1.22.3
3.2
4.3
5.1
Установить соответствие:
Предложенные ответыВаш ответ
ху-6˃0
ху-6 ≥0
ху-6<0
ху-6≤0
1)
х2 +у2˃16
х2 +у2<16
х2 +у2≤16
х2 +у2≥16
2)
у≤1-|х|
у< 1-|х|
у˃ 1-|х|
у≥ 1-|х|
3)
у≥ 2х-х2
у<2х-х2
у≤2х-х2
у˃2х-х2
4)
|у| ≤2
|х| ≤2
|у| ≥2
|х|≥2
5)
4. Изучение новых знаний, необходимых для формирования умений.
Изучение новых знаний, необходимых для формирования умений.
Подведение к новой теме:
1 задание (на листах А-4).
на предыдущем уроке вы нашли решение одного из неравенств с двумя переменными, в таком же формате решим ещё одно неравенство (задание в парах выполняют на файле, в который вложен чертёж координатной плоскости). А теперь найдём общее решение этих неравенств, т.е. решим систему неравенств.
Демонстрация работ
Алгоритм решения неравенств с двумя переменными:
1. Заменить знак неравенства на знак равенства.
2. Выразить переменную у через х.
3. Построить график полученного уравнения.
4. Выделить часть плоскости, соответствующую знаку неравенства.
Алгоритм решения систем неравенств с двумя переменными:
1. Решить каждое из неравенств системы отдельно.
2. Изобразить полученные решения на одной координатной плоскости.
3. Найти пересечение этих решений.
4. Общая часть этих решений и является решением данной системы неравенств.
№500(а,в)
1. Решение систем неравенств с использованием шаблонов (по слайдам презентации)
Разгрузочная пауза-лирическое отступление. Дания на протяжении почти 50 лет удерживает I место по показателям индекса благополучия и счастья. Датчане стараются во всём видеть хорошее и умеют получать радость от жизни и пользу. ХЮГГЕ! СЕКРЕТ ДАТСКОГО СЧАСТЬЯ! Мне бы хотелось чтобы РОССИЯ была на I месте всегда и во всём. Давайте поболеем за Россию: флаг (дети встают и садятся по очереди, получается волна, приветствуем Россию: хлопаем в ладоши (тук——тук——тук-тук-тук). В жизни всегда есть место подвигу. Вы его совершили. Надеюсь, что 40 минут урока дадут вам хороший позитив. Но России нужны хорошие инженеры и т.д. Знания собираются по капле — продолжаем работать.
5. Мотивация обучения. Формирование умений и навыков.
1задание. Решить систему неравенств используя шаблоны (на листах А-3):
х2+ у2<25х 2+ у2<9
y≥6/x
у≤х3
у≥ х2-4
х2+ (у+3)2<9
(х2+ у2—4)(х2+ у2-16) <0
у≤х+2
х≥ у2 -3
у≥х-3
х 2+у2 ≤16
Проверочная работа (задание по вариантам):
Дополнить неравенствами до систем по горизонтали:
I вариант: (у ≥ х2, у≤ 0, у ≥ 0, у ≤ — х2+3, х2+ у2≤ 9, х≤ 0)
II вариант: (у≤ — х2, у ≥0, у ≤ 0, у ≥ х2-3, х2+ у2≤ 4, х ≥ 0)
Решить систему неравенств (графики изобразить схематически с помощью шаблонов)
6. Творческое применение и добывание знаний в новой ситуации (проблемные задачи).
Творческое применение и добывание знаний в новой ситуации (проблемные задачи).
2. Решение неравенств с модулем
Мотивация обучения.
Мы изучили решение неравенств, когда под знаком модуля находится одна из переменных например: у≥|х|, у| ≤|x|-1. Эти же рассуждения проведём для решения неравенств, в которых модуль содержится у двух переменных. Например | х | + | у | ≤ 1;
а) Изучение новых знаний, необходимых для формирования умений.
б) Изобразим на координатной плоскости фигуру, которую задает неравенство . Если пара (x0,y0) является решением неравенства, то каждая из пар (x0,-y0), (-x0,y0) и (-x0,-y0) также является его решением. Значит, искомая фигура симметрична относительно оси x и оси y. Изобразим сначала ее часть, расположенную в первой координатной четверти.
x+y=1
используя свойства симметрии, изобразим три остальные части. Полученная фигура представляет собой квадрат.
Алгоритм решения неравенств с двумя переменными, содержащие знак модуля
Построить график функции у=f(x,y) в первой координатной плоскости
Использовать преобразования графиков уравнений, связанных с модулем.
Взяв из какой — либо области пробную точку установить, являются ли ее координаты решением неравенства
Сделать вывод о решении неравенства
№ 556.
Р е ш е н и е
| х | + | у | ≤ 1;
| у | ≤ 1 – | х |.
Построим график уравнения | у | = 1 – | х |. Для этого нужно раскрыть знаки модуля.
Получим четыре случая:
1) х ≥ 0, у ≥ 0;у = 1 – х.
2) х ≥ 0, у < 0; –у = 1 – х; у = х – 1.
3) х < 0, у ≥ 0;у = 1 + x.
4) x < 0, y < 0;–у = 1 + х;у = –х – 1.
Объединяя все эти случаи, получим фигуру:
Данному неравенству удовлетворяет множество точек внутренней области этой фигуры.
Творческое применение и добывание знаний в новой ситуации (проблемные задачи).
Изобразите на координатной плоскости множество решений неравенства:
х2 + у2-2|x|-2|y|+1≥0
Решение
Фигура симметрична относительно оси Х и оси Y.
1.Преобразуем неравенство к виду (|x|-1) 2+(|y|-1) 2≥1
2.Строим график уравнения , используя свойства модуля.
4. С помощью пробной точки устанавливаем решение неравенства.
7. Домашнее задание: Выучить теоретические факты, №498, 500 (б, г), инд. задание по карточкам
8. Рефлексия.
Вопросы:
– Что называется решением неравенства с двумя переменными?
– Чем отличается решение строгого неравенства от нестрогого? (линия функции пунктирная или сплошная)
– Как можно проверить правильно ли вы выбрали множество? (Правило пробной точки)
–Сколько решений может иметь система неравенств с двумя переменными?
– Как решить уравнение с модулем?
Давайте оценим себя, лист самооценки.
Заполнить таблицу, поставив в соответствующей графе «+».
ДА
Не очень хорошо
Не знаю
Уравнения графиков изученных функций
Как определить функцию, если она задана в нестандартном виде
Алгоритм преобразования графиков, связанных с модулем
Как выбирать пробную точку
Алгоритм решения неравенств с двумя переменными
Я умею:
Различать графики функций
Изображать график функции
Выполнять преобразование графиков, связанных с модулем
При помощи пробной точки устанавливать, являются ли ее координаты решением неравенства
Изображать решение неравенства с двумя неизвестными
Подсчитать в столбце «ДА» количество выставленных «+».
Критерии оценок:
9-10«5»
7-8
«4»
5-6
«3»
Меньше 5
«2»
Урок 28.
 системы неравенств с двумя переменными — Алгебра — 9 класс
системы неравенств с двумя переменными — Алгебра — 9 класс
Рассмотрим систему неравенств с двумя переменными.
y – x>5,
x2 – 1>y
Пара чисел 6 и 12 являются решением данной системы, так как при подстановке этих значений вместо переменных получаются верные числовые неравенства.
Сделаем вывод: пара чисел, которая является общим решением всех неравенств системы, называется решением системы неравенств с двумя переменными, а множеством решений системы неравенств с двумя переменными является пересечение множеств решений входящих в нее неравенств.
Рассмотрим пример. Выясним, какое множество точек задает на координатной плоскости данная система.
x2 + y2 ≤16
x – y ≤ 4
Для этого изобразим соответствующие графики функций на одной координатной плоскости. Графиком первой функции будет являться окружность с центром в точке начала отсчета и радиусом 4, а второй – прямая.
Множеством решений первого неравенства изначальной системы будет область внутри круга, включая точки окружности, а решением второго неравенства, полуплоскость, которая находится ниже прямой, включая все точки прямой.
Итак, множество точек, которые являются решением данной системы неравенств является часть плоскости, отмеченная на рисунке двойной штриховкой.
Рассмотрим еще один пример.
y>x2 + 3
x2 + y2<25
Множеством точек, задаваемым первым неравенством, является часть плоскость, расположенная выше параболы игрик равен икс в квадрате плюс три.
А второе неравенство задает множество точек, расположенных внутри круга с центром в точек нуль нуль и радусом 5.
Пересечение этих множеств является решением данной системы неравенств.
Двойные неравенства. 2 способа решения
Например:
\(5<11<17\)
\(-2\leq3x+5\leq2\)
\(2x-5\leq3x+7\leq8x\)
Двойное неравенство по своей сути – это система из двух неравенств, записанных в одну строку. Поэтому их всегда можно представить в виде системы.
Поэтому их всегда можно представить в виде системы.
Например:
\(-2\leq3x+5\leq2\Leftrightarrow\begin{cases}-2\leq3x+5\\3x+5\leq2\end{cases}\)
\(2x-5\leq3x+7\leq8x\Leftrightarrow\begin{cases}2x-5\leq3x+7\\3x+7\leq8x\end{cases}\)
Но делать это нужно не всегда.
2 способа решения двойного неравенства
1) Если в крайней левой и крайней правой частях двойного неравенства нет неизвестных, то удобнее оставить его как есть. При этом в процессе решения стремится равносильными преобразованиями привести неравенство к виду \([число]\)\(<\)\(x\)\(<\)\([число]\).
Пример: Решите двойное неравенство:
|
\(-2\leq3x+5\leq2\) \(|-5\) |
Здесь нет неизвестных по краям, поэтому к системе переходить не будем. |
|
|
\(-7≤3x≤-3\) \(|:3\) |
Теперь нам мешает \(3\). Поделим все три части неравенства на \(3\). |
|
|
\(-\)\(\frac{7}{3}\)\(\leq x \leq-1\) |
Готово, наш икс «голый». Можно записывать ответ. |
2) Если в крайних частях двойного неравенства есть неизвестные лучше перевести неравенство в систему и решать его как обычную систему неравенств.
Пример: Решите двойное неравенство:
|
\(2x-5<3x+7≤8x\) |
В крайней левой и крайней правой частях есть неизвестные –значит переходим к системе. |
|
\(\begin{cases}2x-5<3x+7\\3x+7\leq8x\end{cases}\) |
Решаем обычные линейные неравенства: все, что с иксами переносим в левую сторону, все что без иксов — в правую. |
|
\(\begin{cases}2x-3x<7+5\\3x-8x\leq-7\end{cases}\) |
Приводим подобные слагаемые |
|
\(\begin{cases}-x<12 \\-5x\leq-7 \end{cases}\) |
«Оголим» иксы, поделив верхнее неравенство на \((-1)\), нижнее на \((-5)\). Не забываем при этом перевернуть знаки сравнения, так как мы делим на отрицательное число. |
|
\(\begin{cases}x>-12 \\x\geq \frac{7}{5}\end{cases}\) |
Отметим на числовой оси оба решения |
|
Так как у нас система, то мы ищем значения иксов, которые подойдут обоим неравенствам, т. |
Ответ: \([\)\(\frac{7}{5}\)\(;\infty)\)
3.4 Графики линейных неравенств с двумя переменными — Алгебра среднего уровня 2e
Цели обучения
К концу этого раздела вы сможете:
- Проверять решения неравенства с двумя переменными.
- Распознать связь между решениями неравенства и его графиком.
- График линейных неравенств с двумя переменными
- Решение приложений с использованием линейных неравенств с двумя переменными
Приготовься 3.10
Прежде чем начать, пройдите этот тест на готовность.
График x>2x>2 на числовой прямой.
Если вы пропустили эту проблему, просмотрите пример 2.48.
Приготовься 3.11
Решите: 4x+3>234x+3>23.
Если вы пропустили эту проблему, просмотрите пример 2. 52.
52.
Приготовься 3.12
Перевести: 8
Если вы пропустили эту проблему, просмотрите пример 2.56.
Проверка решения неравенства двух переменных
Раньше мы учились решать неравенства только с одной переменной.Теперь мы узнаем о неравенствах, содержащих две переменные. В частности мы рассмотрим линейных неравенств с двумя переменными, которые очень похожи на линейные уравнения с двумя переменными.
Линейные неравенства с двумя переменными имеют множество применений. Например, если вы управляете бизнесом, вы хотели бы, чтобы ваши доходы превышали ваши расходы, чтобы ваш бизнес приносил прибыль.
Линейное неравенство
Линейное неравенство — это неравенство, которое может быть записано в одной из следующих форм:
Ax+By>CAx+By≥CAx+By
Напомним, что неравенство с одной переменной имело множество решений. Например, решением неравенства x>3x>3 является любое число больше 3. Мы показали это на числовой прямой, заштриховав числовую строку справа от 3 и поместив открытую скобку на 3. См. рис. 3.10. .
Фигура 3.10
Аналогично линейные неравенства с двумя переменными имеют множество решений. Любая упорядоченная пара (x,y)(x,y), которая делает неравенство верным при подстановке значений, является решением линейного неравенства.
Решение линейного неравенства
Упорядоченная пара (x,y)(x,y) является решением линейного неравенства , если неравенство верно, когда мы подставляем значения x и y .
Пример 3,34
Определить, является ли каждая упорядоченная пара решением неравенства y>x+4:y>x+4:
ⓐ (0,0)(0,0) ⓑ (1,6)(1,6) ⓒ (2,6)(2,6) ⓓ (−5,−15)(−5,−15) ⓔ (−8,12)(−8,12)
Решение
ⓐ
| (0,0)(0,0) | |
Упрощение. | |
| Итак, (0,0)(0,0) не является решением y>x+4.y>x+4. |
ⓑ
| (1,6)(1,6) | |
| Упрощение. | |
| Итак, (1,6)(1,6) является решением y>x+4.y>x+4. |
ⓒ
| (2,6)(2,6) | |
Упрощение. | |
| Итак, (2,6)(2,6) не является решением y>x+4.y>x+4. |
ⓓ
| (-5,-15)(-5,-15) | |
| Упрощение. | |
| Итак, (−5,−15)(−5,−15) не является решением y>x+4.y>x+4. |
ⓔ
| (−8,12)(−8,12) | |
Упрощение. | |
| Итак, (−8,12)(−8,12) является решением y>x+4.y>x+4. |
Попробуй 3,67
Определить, является ли каждая упорядоченная пара решением неравенства y>x−3:y>x−3:
ⓐ (0,0)(0,0) ⓑ (4,9)(4,9) ⓒ (−2,1)(−2,1) ⓓ (−5,−3)(−5,−3) ) ⓔ (5,1)(5,1)
Попробуй 3,68
Определить, является ли каждая упорядоченная пара решением неравенства y
ⓐ (0,0)(0,0) ⓑ (8,6)(8,6) ⓒ (−2,−1)(−2,−1) ⓓ (3,4)(3,4) ⓔ (−1,−4)(−1,−4)
Распознать связь между решениями неравенства и его графиком
Теперь посмотрим, как решения неравенства соотносятся с его графиком.
Давайте снова подумаем о числовой строке, показанной ранее. Точка x=3x=3 разделила эту числовую прямую на две части. С одной стороны от 3 все числа меньше 3. С другой стороны от 3 все числа больше 3. См. рис. 3.11.
С другой стороны от 3 все числа больше 3. См. рис. 3.11.
Точно так же линия y=x+4y=x+4 разделяет плоскость на две области. По одну сторону прямой находятся точки с y
Граничная линия
Линия с уравнением Ax+By=CAx+By=C является граничной линией , которая отделяет область, где Ax+By>CAx+By>C, от области, где Ax+By
Для неравенства в одной переменной конечная точка отображается в круглой скобке или квадратной скобке в зависимости от того, включено ли a в решение:
Аналогично, для неравенства двух переменных граничная линия отображается сплошной или пунктирной линией, чтобы показать, включена ли эта линия в решение.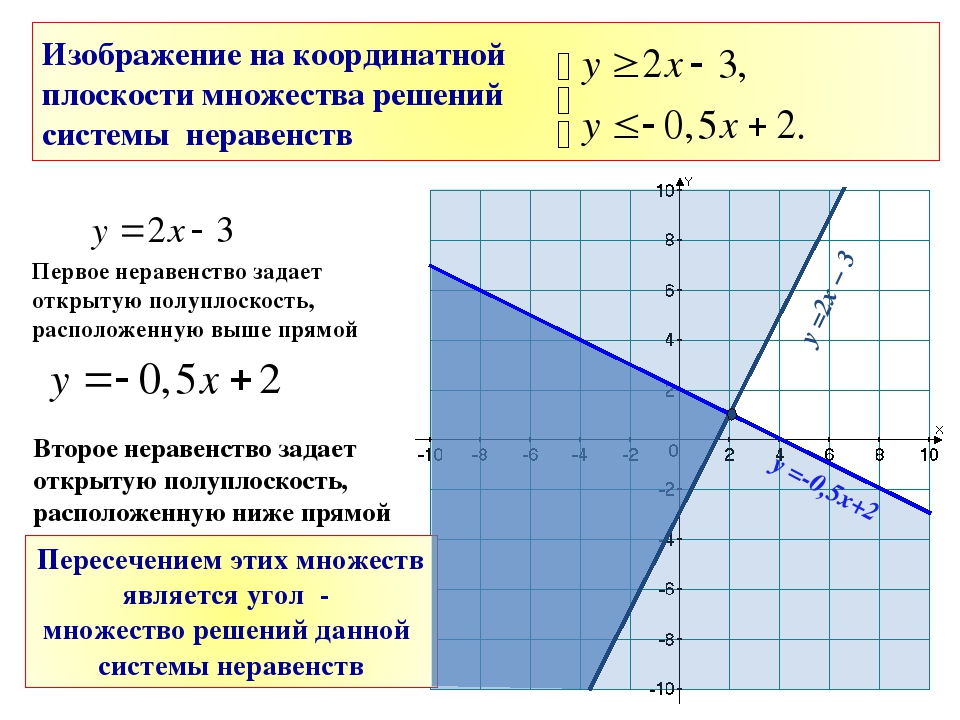
Теперь давайте посмотрим, что мы нашли в примере 3.34. Мы начнем с построения графика линии y=x+4,y=x+4, а затем нанесем пять проверенных точек, как показано на графике.См. Рисунок 3.12.
Фигура 3.12
В примере 3.34 мы обнаружили, что некоторые точки являются решениями неравенства y>x+4y>x+4, а некоторые — нет.
Какие из нанесенных нами точек являются решениями неравенства y>x+4?y>x+4?
Точки (1,6)(1,6) и (−8,12)(−8,12) являются решениями неравенства y>x+4.y>x+4. Обратите внимание, что они оба находятся по одну сторону от граничной линии y=x+4. y=x+4.
y=x+4.
Две точки (0,0)(0,0) и (−5,−15)(−5,−15) находятся по другую сторону от граничной линии y=x+4,y=x+4, и они не являются решениями неравенства y>x+4.у>х+4. Для этих двух точек y
А точка (2,6)?(2,6)? Поскольку 6=2+4,6=2+4, точка является решением уравнения y=x+4,y=x+4, но не решением неравенства y>x+4.y>x+ 4. Итак, точка (2,6)(2,6) находится на граничной линии.
Возьмем другую точку над граничной линией и проверим, является ли она решением неравенства y>x+4.y>x+4. Точка (0,10)(0,10) явно находится выше линии границы, не так ли? Это решение неравенства?
у>х+410>?0+410>4у>х+410>?0+410>4Итак, (0,10)(0,10) является решением уравнения y>x+4.у>х+4.
Любая выбранная вами точка выше граничной линии является решением неравенства y>x+4.y>x+4. Все точки над граничной линией являются решениями.
Аналогично, все точки ниже граничной линии, сторона с (0,0)(0,0) и (−5,−15),(−5,−15), не являются решениями y>x+4, y>x+4, как показано на рис. 3.13.
3.13.
Фигура 3.13
График неравенства y>x+4y>x+4 показан ниже.
Линия y=x+4y=x+4 делит плоскость на две области.Заштрихованная сторона показывает решения неравенства y>x+4.y>x+4.
Точки на граничной линии, где y=x+4,y=x+4, не являются решениями неравенства y>x+4,y>x+4, поэтому сама линия не является частью решения . Мы показываем это, делая линию пунктирной, а не сплошной.
Пример 3,35
Линия границы, показанная на этом графике, имеет вид y=2x−1.y=2x−1. Запишите неравенство, показанное на графике.
Решение
Линия y=2x−1y=2x−1 является границей.По одну сторону прямой находятся точки с y>2x−1y>2x−1, а по другую сторону — точки с y<2x−1.y<2x−1.
Протестируем точку (0,0)(0,0) и посмотрим, какое неравенство описывает ее положение относительно линии границы.
При (0,0),(0,0) какое неравенство верно: y>2x−1y>2x−1 или y<2x−1?y<2x−1?
y>2x−1y<2x−10>?2·0−10−1True0<−1Falsey>2x−1y<2x−10>?2·0−10−1Истина0<−1Ложь Поскольку y>2x−1y>2x−1 верно, сторона прямой с (0,0),(0,0) является решением. Заштрихованная область показывает решение неравенства y>2x−1.y>2x−1.
Заштрихованная область показывает решение неравенства y>2x−1.y>2x−1.
Поскольку линия границы изображена сплошной линией, в неравенстве стоит знак равенства.
На графике показано неравенство y≥2x−1.y≥2x−1.
В качестве контрольной точки можно использовать любую точку, если она не находится на прямой. Почему мы выбрали (0,0)?(0,0)? Потому что это проще всего оценить. Вы можете выбрать точку по другую сторону линии границы и проверить, что y<2x−1.y<2x−1.
Попробуй 3,69
Запишите неравенство, показанное на графике, с граничной линией y=−2x+3.y=−2x+3.
Попробуй 3,70
Запишите неравенство, показанное на графике, с граничной линией y=12x−4.y=12x−4.
Пример 3,36
Граничная линия, показанная на этом графике, имеет вид 2x+3y=6,2x+3y=6. Запишите неравенство, показанное на графике.
Решение
Линия 2x+3y=62x+3y=6 является границей. На одной стороне линии находятся точки с 2x+3y>62x+3y>6, а на другой стороне линии — точки с 2x+3y<6,2x+3y<6.
На одной стороне линии находятся точки с 2x+3y>62x+3y>6, а на другой стороне линии — точки с 2x+3y<6,2x+3y<6.
Проверим точку (0,0)(0,0) и посмотрим, какое неравенство описывает ее сторону от граничной линии.
При (0,0),(0,0) какое неравенство верно: 2x+3y>62x+3y>6 или 2x+3y<6?2x+3y<6?
2x+3y>62(0)+3(0)>?60>6False2x+3y<62(0)+3(0)62(0)+3(0)>?60 >6False2x+3y<62(0)+3(0) Таким образом, сторона с (0,0)(0,0) — это сторона, где 2x+3y<6.2х+3у<6.(Вы можете выбрать точку по другую сторону линии границы и проверить, что 2x+3y>6,2x+3y>6.)
Поскольку линия границы изображена пунктирной линией, в неравенстве нет знака равенства.
Заштрихованная область показывает решение неравенства 2x+3y<6,2x+3y<6.
Попробуй 3,71
Запишите неравенство, показанное заштрихованной областью на графике с граничной линией x−4y=8.x−4y=8.
Попробуй 3.72
Запишите неравенство, показанное заштрихованной областью на графике с граничной линией 3x−y=6,3x−y=6.
График линейных неравенств с двумя переменными
Теперь, когда мы знаем, как выглядит график линейного неравенства и как он соотносится с граничным уравнением, мы можем использовать эти знания для построения графика заданного линейного неравенства.
Пример 3,37
Как построить линейное уравнение с двумя переменными
Нарисуйте график линейного неравенства y≥34x−2.у≥34x−2.
Попробуй 3,73
Нарисуйте график линейного неравенства y≥52x−4.y≥52x−4.
Попробуй 3,74
Нарисуйте график линейного неравенства y<23x−5.y<23x−5.
Шаги, которые мы предпринимаем для построения графика линейного неравенства, суммированы здесь.
Как
Нарисуйте график линейного неравенства с двумя переменными.
- Шаг 1.
Определите и начертите линию границы.
- Если неравенство ≤или≥,≤или≥, граница сплошная.

- Если неравенство равно <или>,<или>, линия границы становится пунктирной.
- Если неравенство ≤или≥,≤или≥, граница сплошная.
- Шаг 2. Проверьте точку, которая не находится на линии границы. Это решение неравенства?
- Шаг 3.
Заштрихуйте одну сторону линии границы.
- Если тестовая точка является раствором, заштрихуйте ту сторону, которая включает точку.
- Если контрольная точка не является раствором, заштрихуйте противоположную сторону.
Пример 3,38
Нарисуйте график линейного неравенства x−2y<5.х-2у<5.
Решение
Сначала мы рисуем граничную линию x−2y=5.x−2y=5. Неравенство <<, поэтому мы рисуем пунктирную линию.
Затем мы проверяем точку. Мы снова будем использовать (0,0)(0,0), потому что его легко вычислить и он не находится на граничной линии.
Является ли (0,0)(0,0) решением x−2y<5?x−2y<5?
Точка (0,0)(0,0) является решением уравнения x−2y<5,x−2y<5, поэтому мы заштриховываем эту сторону граничной линии.
Все точки в заштрихованной области, кроме точек на граничной линии, представляют решения x−2y<5.х-2у<5.
Попробуй 3,75
Нарисуйте линейное неравенство: 2x−3y<6,2x−3y<6.
Попробуй 3,76
Нарисуйте линейное неравенство: 2x−y>3,2x−y>3.
Что делать, если линия границы проходит через начало координат? Тогда мы не сможем использовать (0,0)(0,0) в качестве контрольной точки. Нет проблем — мы просто выберем другую точку, не лежащую на граничной линии.
Пример 3,39
Нарисуйте график линейного неравенства: y≤−4x.у≤−4x.
Решение
Сначала мы рисуем граничную линию y=−4x.y=−4x. Он находится в форме пересечения наклона с m = −4m = −4 и b = 0,b = 0. Неравенство ≤≤, поэтому рисуем сплошную линию.
Теперь нам нужна контрольная точка. Мы видим, что точка (1,0)(1,0) не находится на граничной линии.
Является ли (1,0)(1,0) решением уравнения y≤−4x?y≤−4x?
Точка (1,0)(1,0) не является решением уравнения y≤−4x,y≤−4x, поэтому мы заштриховываем противоположную сторону граничной линии.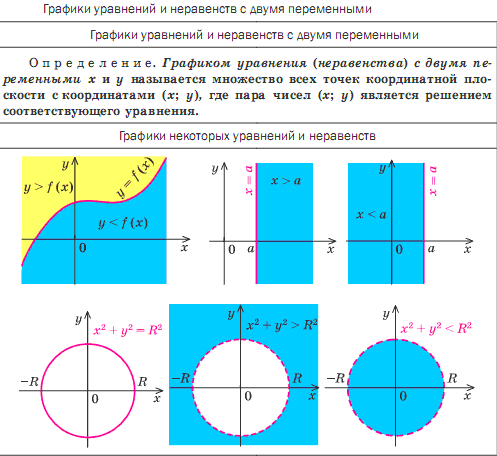
Все точки в заштрихованной области и на граничной линии представляют собой решения y≤−4x.y≤−4x.
Попробуй 3,77
Нарисуйте линейное неравенство: y>−3x.y>−3x.
Попробуй 3,78
Нарисуйте линейное неравенство: y≥−2x.y≥−2x.
Некоторые линейные неравенства имеют только одну переменную. У них может быть x , но не y , или y , но не x . В этих случаях линия границы будет либо вертикальной, либо горизонтальной линией.
Напомним, что:
x=вертикальная линия=bгоризонтальная линияx=вертикальная линия=bгоризонтальная линияПример 3,40
Нарисуйте линейное неравенство: y>3.y>3.
Решение
Сначала мы рисуем линию границы y=3.y=3. Это горизонтальная линия. Неравенство >> поэтому мы рисуем пунктирную линию.
Проверяем точку (0,0).(0,0).
Итак, (0,0)(0,0) не является решением y>3.y>3.
Итак, мы заштриховали сторону, которая не включает (0,0)(0,0), как показано на этом графике.
Все точки в заштрихованной области, кроме точек на граничной линии, представляют решения y>3.y>3.
Попробуй 3,79
Нарисуйте график линейного неравенства: y<5.y<5.
Попробуй 3,80
Нарисуйте линейное неравенство: y≤−1.y≤−1.
Решение приложений с использованием линейных неравенств с двумя переменными
Многие поля используют линейные неравенства для моделирования проблемы. Хотя наши примеры могут относиться к простым ситуациям, они дают нам возможность развить наши навыки и почувствовать, как их можно использовать.
Пример 3,41
Хилария работает на двух работах неполный рабочий день, чтобы заработать достаточно денег, чтобы выполнить свои обязательства, по крайней мере, 240 долларов в неделю. Ее работа в сфере общественного питания приносит 10 долларов в час, а репетиторство в кампусе — 15 долларов в час. Сколько часов Хиларии нужно работать на каждой работе, чтобы заработать не менее 240 долларов?
Ее работа в сфере общественного питания приносит 10 долларов в час, а репетиторство в кампусе — 15 долларов в час. Сколько часов Хиларии нужно работать на каждой работе, чтобы заработать не менее 240 долларов?
ⓐ Пусть xx будет количеством часов, которое она работает на работе в сфере общественного питания, и пусть y будет количеством часов, которые она работает репетитором. Напишите неравенство, моделирующее эту ситуацию.
ⓑ Нарисуйте неравенство.
ⓒ Найдите три упорядоченные пары (x,y)(x,y), которые были бы решениями неравенства. Затем объясните, что это значит для Хиларии.
Решение
ⓐ Пусть x будет количеством часов, которые она работает на работе в сфере общественного питания, и пусть y будет количеством часов, которые она работает репетитором.
Она зарабатывает 10 долларов в час на работе в сфере общественного питания и 15 долларов в час на репетиторстве. На каждой работе количество часов, умноженное на почасовую заработную плату, дает сумму, заработанную на этой работе.
На каждой работе количество часов, умноженное на почасовую заработную плату, дает сумму, заработанную на этой работе.
ⓑ Чтобы построить график неравенства, мы поместим его в виде наклона и пересечения.
10x+15y≥24015y≥−10x+240y≥−23x+1610x+15y≥24015y≥−10x+240y≥−23x+16ⓒ Из графика видно, что упорядоченные пары (15,10),(0,16),(24,0)(15,10),(0,16),(24,0) представляют три бесконечно много решений. Проверьте значения в неравенстве.
Для Хиларии это означает, что для того, чтобы заработать не менее 240 долларов, она может работать 15 часов репетиторством и 10 часов в фаст-фуде, зарабатывать все свои деньги репетиторством в течение 16 часов или зарабатывать все свои деньги, работая 24 часа на работе. в сфере общественного питания.
Попробуй 3,81
Хью работает на двух работах неполный рабочий день. Один работает в продуктовом магазине, где платит 10 долларов в час, а другой работает няней за 13 долларов в час. Между двумя работами Хью хочет зарабатывать не менее 260 долларов в неделю. Сколько часов Хью нужно отработать на каждой работе, чтобы заработать не менее 260 долларов?
Сколько часов Хью нужно отработать на каждой работе, чтобы заработать не менее 260 долларов?
ⓐ Пусть x будет количеством часов, которое он проработает в продуктовом магазине, а y будет количеством часов, которое он проработает няней. Напишите неравенство, моделирующее эту ситуацию.
ⓑ Нарисуйте неравенство.
ⓒ Найдите три упорядоченные пары ( x , y ), которые будут решениями неравенства. Затем объясните, что это значит для Хью.
Попробуй 3,82
Вероника работает на двух работах с частичной занятостью, чтобы заработать достаточно денег, чтобы выполнять свои обязательства в размере не менее 280 долларов в неделю. Ее работа в дневном спа-салоне оплачивается 10 долларов в час, а работа административного помощника в кампусе — 17,50 долларов в час. Сколько часов Веронике нужно отработать на каждой работе, чтобы заработать не менее 280 долларов?
ⓐ Пусть x будет количеством часов, которое она работает в дневном спа-салоне, и пусть y будет количеством часов, в течение которых она работает помощником по административным вопросам. Напишите неравенство, моделирующее эту ситуацию.
Напишите неравенство, моделирующее эту ситуацию.
ⓑ Нарисуйте неравенство.
ⓒ Найдите три упорядоченные пары ( x , y ), которые будут решениями неравенства. Затем объясните, что это значит для Вероники
.Раздел 3.4 Упражнения
Практика делает совершенным
Проверка решения неравенства двух переменных
В следующих упражнениях определите, является ли каждая упорядоченная пара решением данного неравенства.
237 .Определить, является ли каждая упорядоченная пара решением неравенства y>x−1:y>x−1:
ⓐ (0,1)(0,1)
ⓑ (−4,−1)(−4,−1)
ⓒ (4,2)(4,2)
ⓓ (3,0)(3 ,0)
ⓔ (−2,−3)(−2,−3)
Определить, является ли каждая упорядоченная пара решением неравенства y>x−3:y>x−3:
ⓐ (0,0)(0,0)
ⓑ (2,1)(2,1)
ⓒ (−1,−5)(−1,−5)
ⓓ (−6,−3) (−6,−3)
ⓔ (1,0)(1,0)

Определить, является ли каждая упорядоченная пара решением неравенства y<3x+2:y<3x+2:
ⓐ (0,3)(0,3)
ⓑ (−3,−2)(−3,−2)
ⓒ (−2,0)(−2,0)
ⓓ (0,0) (0,0)
ⓔ (−1,4)(−1,4)
Определить, является ли каждая упорядоченная пара решением неравенства y<−2x+5:y<−2x+5:
ⓐ (−3,0)(−3,0)
ⓑ (1,6)(1,6)
ⓒ (−6,−2)(−6,−2)
ⓓ (0,1) (0,1)
ⓔ (5,−4)(5,−4)
Определить, является ли каждая упорядоченная пара решением неравенства 3x−4y>4:3x−4y>4:
ⓐ (5,1)(5,1)
ⓑ (−2,6)(−2,6)
ⓒ (3,2)(3,2)
ⓓ (10,−5)(10, −5)
ⓔ (0,0)(0,0)
Определить, является ли каждая упорядоченная пара решением неравенства 2x+3y>2:2x+3y>2:
ⓐ (1,1)(1,1)
ⓑ (4,−3)(4,−3)
ⓒ (0,0)(0,0)
ⓓ (−8,12)(−8 ,12)
ⓔ (3,0)(3,0)
Распознать связь между решениями неравенства и его графиком
В следующих упражнениях запишите неравенство, показанное заштрихованной областью.
Запишите неравенство, показанное на графике, с граничной линией y=3x−4.y=3x−4.
244 .Запишите неравенство, показанное на графике, с граничной линией y=2x−4.y=2x−4.
245 .Запишите неравенство, показанное на графике, с граничной линией y=12x+1.y=12x+1.
246 .Запишите неравенство, показанное на графике, с граничной линией y=−13x−2.y=−13x−2.
247 .Запишите неравенство, показанное заштрихованной областью на графике с граничной линией x+y=5.х+у=5.
248 .Запишите неравенство, показанное заштрихованной областью на графике с граничной линией x+y=3.x+y=3.
249 .Запишите неравенство, показанное заштрихованной областью на графике с граничной линией 3x−y=6,3x−y=6.
250 .Запишите неравенство, показанное заштрихованной областью на графике с граничной линией 2x−y=4,2x−y=4.
График линейных неравенств с двумя переменными
В следующих упражнениях постройте график каждого линейного неравенства.
Нарисуйте линейное неравенство: y>23x−1.y>23x−1.
252 .Нарисуйте линейное неравенство: y<35x+2.y<35x+2.
253 .Нарисуйте линейное неравенство: y≤−12x+4.y≤−12x+4.
254 .Начертите линейное неравенство: y≥−13x−2.y≥−13x−2.
255 .Нарисуйте линейное неравенство: x−y≤3.x−y≤3.
256 .Нарисуйте график линейного неравенства: x−y≥−2.x−y≥−2.
257 .Нарисуйте линейное неравенство: 4x+y>−4.4х+у>−4.
258 .Нарисуйте линейное неравенство: x+5y<−5.x+5y<−5.
259 .Нарисуйте линейное неравенство: 3x+2y≥−6,3x+2y≥−6.
260 .Нарисуйте линейное неравенство: 4x+2y≥−8,4x+2y≥−8.
261 .Нарисуйте линейное неравенство: y>4x.y>4x.
262 .Нарисуйте линейное неравенство: y≤−3x.y≤−3x.
263 .Нарисуйте график линейного неравенства: y<−10.y<−10.
264 .Нарисуйте график линейного неравенства: y≥2.у≥2.
265 .
Нарисуйте линейное неравенство: x≤5.x≤5.
266 .Нарисуйте линейное неравенство: x≥0.x≥0.
267 .Нарисуйте линейное неравенство: x−y<4.x−y<4.
268 .Нарисуйте линейное неравенство: x−y<−3.x−y<−3.
269 .Нарисуйте линейное неравенство: y≥32x.y≥32x.
270 .Нарисуйте линейное неравенство: y≤54x.y≤54x.
271 .Нарисуйте линейное неравенство: y>−2x+1.y>−2x+1.
272 .Нарисуйте линейное неравенство: y<−3x−4.y<−3x−4.
273 .Нарисуйте линейное неравенство: 2x+y≥−4,2x+y≥−4.
274 .Нарисуйте линейное неравенство: x+2y≤−2.x+2y≤−2.
275 .Нарисуйте линейное неравенство: 2x−5y>10,2x−5y>10.
276 .Нарисуйте линейное неравенство: 4x−3y>12,4x−3y>12.
Решение приложений с использованием линейных неравенств с двумя переменными
277 . Харрисон работает на двух работах неполный рабочий день. Один на заправочной станции, где платят 11 долларов в час, а другой занимается устранением неполадок в сфере ИТ за 16,50 долларов в час. Между двумя работами Харрисон хочет зарабатывать не менее 330 долларов в неделю. Сколько часов Харрисону нужно отработать на каждой работе, чтобы заработать не менее 330 долларов?
Один на заправочной станции, где платят 11 долларов в час, а другой занимается устранением неполадок в сфере ИТ за 16,50 долларов в час. Между двумя работами Харрисон хочет зарабатывать не менее 330 долларов в неделю. Сколько часов Харрисону нужно отработать на каждой работе, чтобы заработать не менее 330 долларов?
ⓐ Пусть x будет количеством часов, в течение которых он работает на заправке, а y будет количеством (часов, в течение которых он работает над устранением неполадок. Напишите неравенство, моделирующее эту ситуацию.
ⓑ Нарисуйте неравенство.
ⓒ Найдите три упорядоченные пары (x,y)(x,y), которые были бы решениями неравенства. Затем объясните, что это значит для Харрисона.
278 . Елена должна зарабатывать не менее 450 долларов в неделю во время летних каникул, чтобы оплачивать обучение в колледже. Она работает на двух работах. Один работает инструктором по плаванию с оплатой 9 долларов в час, а другой стажером в лаборатории генетики за 22,50 доллара в час. Сколько часов Елене нужно работать на каждой работе, чтобы зарабатывать не менее 450 долларов в неделю?
Сколько часов Елене нужно работать на каждой работе, чтобы зарабатывать не менее 450 долларов в неделю?
ⓐ Пусть x будет количеством часов, в течение которых она обучает плаванию, и пусть y будет количеством часов, в течение которых она работает стажером.Напишите неравенство, моделирующее эту ситуацию.
ⓑ Нарисуйте неравенство.
ⓒ Найдите три упорядоченные пары (x,y)(x,y), которые были бы решениями неравенства. Затем объясните, что это значит для Елены.
279 .Врач говорит Лауре, что ей нужно достаточно тренироваться, чтобы сжигать 500 калорий каждый день. Она предпочитает бегать или ездить на велосипеде и сжигает 15 калорий в минуту во время бега и 10 калорий в минуту во время езды на велосипеде.
ⓐ Если x — это количество минут, в течение которых Лаура бежит, а y — это количество минут, в течение которых она едет на велосипеде, найдите неравенство, моделирующее ситуацию.
ⓑ Нарисуйте неравенство.
ⓒ Назовите три решения неравенства. Какие возможности предоставляют решения Laura?
280 . ТренировкиАрмандо состоят из кикбоксинга и плавания. Во время кикбоксинга он сжигает 10 калорий в минуту, а во время плавания – 7 калорий в минуту. Он хочет сжигать 600 калорий каждый день.
ⓐ Если x — это количество минут, в течение которых Армандо будет заниматься кикбоксингом, а y — это количество минут, в течение которых он будет плавать, найдите неравенство, которое поможет Армандо составить тренировку на сегодня.
ⓑ Нарисуйте неравенство.
ⓒ Назовите три решения неравенства. Какие возможности предоставляют решения Armando?
Письменные упражнения
281 . Лестер считает, что решением любого неравенства со знаком >> является область над чертой, а решением любого неравенства со знаком << является область под чертой. Лестер прав? Объясните, почему да или почему нет.
Лестер прав? Объясните, почему да или почему нет.
Объясните, почему на некоторых графиках линейных неравенств граничная линия сплошная, а на других — пунктирная.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ По шкале от 1 до 10, как бы вы оценили свое знание этого раздела в свете ваших ответов на контрольный список? Как вы можете улучшить это?
4.1: Графики линейных неравенств с двумя переменными
Проверка решения неравенства с двумя переменными
В разделе 1.1 мы научились решать неравенства только с одной переменной.Теперь мы узнаем о неравенствах, содержащих две переменные. В частности мы рассмотрим линейных неравенств с двумя переменными, которые очень похожи на линейные уравнения с двумя переменными.
Линейные неравенства с двумя переменными имеют множество применений. Например, если вы управляете бизнесом, вы хотели бы, чтобы ваши доходы превышали ваши расходы, чтобы ваш бизнес приносил прибыль.
Например, если вы управляете бизнесом, вы хотели бы, чтобы ваши доходы превышали ваши расходы, чтобы ваш бизнес приносил прибыль.
ЛИНЕЙНОЕ НЕРАВЕНСТВО
Линейное неравенство — это неравенство, которое может быть записано в одной из следующих форм:
\( \begin{array} {l} { }& {Ax+By>C} &{Ax+By\geq C} &{Ax+By
Где A и B не равны нулю.
Напомним, что неравенство с одной переменной имело множество решений. Например, решением неравенства \(x>3\) является любое число больше 3. Мы показали это на числовой строке, заштриховав числовую строку справа от 3 и поставив открытую скобку на 3.
Рисунок \(\PageIndex{1}\) Аналогично, линейные неравенства с двумя переменными имеют множество решений. Любая упорядоченная пара \((x,y)\), которая делает неравенство верным при подстановке значений, является решением линейного неравенства .
Решение ЛИНЕЙНОГО НЕРАВЕНСТВА
Упорядоченная пара \((x,y)\) является решением линейного неравенства , если неравенство верно, когда мы подставляем значения x и y .
Пример \(\PageIndex{1}\)
Определить, является ли каждая упорядоченная пара решением неравенства y>x+4:
а. (0,0) б. (1,6) в. (2,6) д. (−5,−15) e. (−8,12)
- Ответить
а.
\((0,0)\) Упрощение. 
Итак, \((0,0)\) не является решением \(y>x+4\).
б.
\((1,6)\) Упрощение. Итак, \((1,6)\) является решением \(y>x+4\). 
в.
\((2,6)\) Упрощение. Итак, \((2,6)\) не является решением \(y>x+4\). д.
Is negative 15 greater than negative 5 plus 4? Simplify. Negative 15 is not greater than negative 1 so (negative 5, negative 15) is not a solution to y is greater than x plus 4.»>\((−5,−15)\) Упрощение. Итак, \((−5,−15)\) не является решением задачи \(y>x+4\). эл.
12 is greater than negative 4 so (negative 8, 12) is a solution to y is greater than x plus 4.»>\((−8,12)\) Упрощение. Итак, \((−8,12)\) является решением \(y>x+4\).
Пример \(\PageIndex{2}\)
Определить, является ли каждая упорядоченная пара решением неравенства \(y>x−3\):
а. \((0,0)\) б. \((4,9)\) в. \((−2,1)\) d. \((−5,−3)\) e. \((5,1)\)
\((5,1)\)
- Ответить
а.да б. да в. да д. да е. №
Пример \(\PageIndex{3}\)
Определить, является ли каждая упорядоченная пара решением неравенства \(y
а. \((0,0)\) б. \((8,6)\) в. \((−2,−1)\) d. \((3,4)\) e. \((−1,−4)\)
- Ответить
а. да б. да в. кивать головой. нет е. да
Распознать связь между решениями неравенства и его графиком
Теперь посмотрим, как решения неравенства соотносятся с его графиком.Рассмотрим неравенство \(x>3\).
Давайте снова подумаем о числовой строке, показанной ранее. Точка \(x=3\) разделила эту числовую прямую на две части. По одну сторону от 3 находятся все числа, меньшие 3, что делает неравенство ложным. С другой стороны от 3 все числа больше 3, что делает неравенство верным.
Рисунок \(\PageIndex{2}\) : Решением задачи \(x>3\) является заштрихованная часть числовой прямой справа от \(x=3\).
Точно так же линия \(y=x+4\) разделяет плоскость на две области.На одной стороне линии находятся точки с \(y
ГРАНИЦА
Линия с уравнением \(Ax+By=C\) является граничной линией , которая отделяет область, где \(Ax+By>C\), от области, где \(Ax+By
Для неравенства в одной переменной конечная точка отображается в скобках или квадратных скобках в зависимости от того, включена ли конечная точка в решение:
Аналогично, для неравенства двух переменных граничная линия отображается сплошной или пунктирной линией, чтобы показать, включена ли эта линия в решение.
\[ \begin{array} {ll} {Ax+By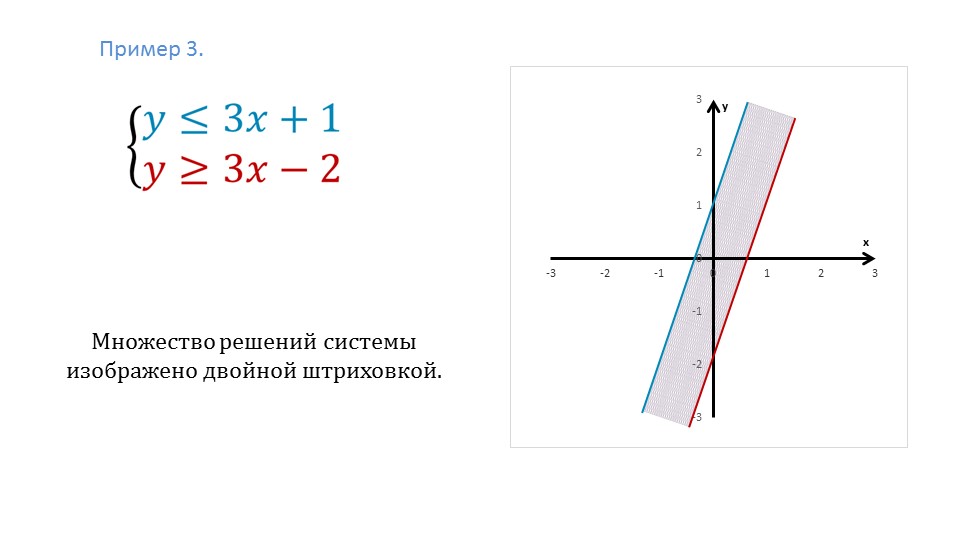 }} \\ {\textbf{Ограничительная линия пунктирная.}} &{\textbf{Ограничительная линия сплошная.}} \\ \nonumber \end{массив} \]
}} \\ {\textbf{Ограничительная линия пунктирная.}} &{\textbf{Ограничительная линия сплошная.}} \\ \nonumber \end{массив} \]
Теперь давайте посмотрим, что мы нашли в примере 4.1.1. Мы начнем с построения графика линии \(y=x+4\), а затем нанесем пять проверенных точек, как показано на графике.
Рисунок \(\PageIndex{3}\)В примере 4.1.1 мы обнаружили, что некоторые точки являются решениями неравенства \(y>x+4\), а некоторые нет.
Какие из нанесенных нами точек являются решениями неравенства \(y>x+4\)?
Точки \((1,6)\) и \((−8,12)\) являются решениями неравенства \(y>x+4\). Обратите внимание, что они оба находятся по одну сторону от граничной линии \(y=x+4\).
Две точки \((0,0)\) и \((−5,−15)\) находятся по другую сторону линии границы \(y=x+4\), и они не являются решениями задачи неравенство \(y>x+4\).Для этих двух точек \(y
А точка \((2,6)\)? Поскольку \(6=2+4\), точка является решением уравнения \(y=x+4\), но не решением неравенства \(y>x+4\). Итак, точка \((2,6)\) находится на граничной линии.
Итак, точка \((2,6)\) находится на граничной линии.
Возьмем другую точку над граничной линией и проверим, является ли она решением неравенства \(y>x+4\). Точка \((0,10)\) явно смотрит выше линии границы, не так ли? Это решение неравенства?
\[\begin{array} {lll} {y} &{>} &{x+4} \\ {10} &{\overset{?}{>}} &{0+4} \\ {10 } &{>} &{4} \\ \nonumber \end{массив}\]
Итак, \((0,10)\) является решением \(y>x+4\).
Любая выбранная вами точка над граничной линией является решением неравенства \(y>x+4\). Все точки над граничной линией являются решениями.
Точно так же все точки ниже граничной линии, стороны с \((0,0)\) и \((−5,−15)\), не являются решениями \(y>x+4\), поскольку показано на графике ниже.
Рисунок \(\PageIndex{4}\)График неравенства \(y>x+4\) показан ниже.
Линия \(y=x+4\) делит плоскость на две области. Заштрихованная сторона показывает решения неравенства \(y>x+4\).
Точки на граничной линии, где \(y=x+4\), не являются решениями неравенства \(y>x+4\), поэтому сама линия не является частью решения. Мы показываем это, делая линию пунктирной, а не сплошной.
Мы показываем это, делая линию пунктирной, а не сплошной.
Пример \(\PageIndex{4}\)
Граница, показанная на этом графике, равна \(y=2x−1\). Запишите неравенство, показанное на графике.
- Ответить
Линия \(y=2x−1\) является границей.На одной стороне линии находятся точки с \(y>2x−1\), а на другой стороне линии — точки с \(y<2x−1\).
Проверим точку \((0,0)\) и посмотрим, какое неравенство описывает ее положение относительно граничной линии.
При \((0,0)\) какое неравенство верно: \(y>2x−1\) или \(y<2x−1\)?
\[\begin{массив} {ll} {y>2x−1} &{y<2x−1} \\ {0\overset{?}{>}2·0−1} &{0\overset{ ?}{<}2·0−1} \\ {0>−1\text{ True}} &{0<−1\text{ False}} \\ \nonumber \end{массив}\]
Поскольку \(y>2x−1\) верно, сторона прямой с \((0,0)\) является решением.Заштрихованная область показывает решение неравенства \(y>2x−1\).
Поскольку линия границы изображена сплошной линией, в неравенстве стоит знак равенства.

На графике показано неравенство \(y\geq 2x−1\).
В качестве контрольной точки можно использовать любую точку, если она не находится на прямой. Почему мы выбрали \((0,0)\)? Потому что это проще всего оценить. Вы можете выбрать точку по другую сторону линии границы и проверить, что \(y<2x−1\).
Пример \(\PageIndex{5}\)
Запишите неравенство, показанное на графике, с граничной линией \(y=−2x+3\).
- Ответить
\(у\geq −2x+3\)
Пример \(\PageIndex{6}\)
Запишите неравенство, показанное на графике, с граничной линией \(y=\frac{1}{2}x−4\).
- Ответить
\(y\leq \frac{1}{2}x−4\)
Пример \(\PageIndex{7}\)
Граница, показанная на этом графике, равна \(2x+3y=6\).Запишите неравенство, показанное на графике.
- Ответить
Линия \(2x+3y=6\) является границей.
 На одной стороне линии находятся точки с \(2x+3y>6\), а на другой стороне линии — точки с \(2x+3y<6\).
На одной стороне линии находятся точки с \(2x+3y>6\), а на другой стороне линии — точки с \(2x+3y<6\).Проверим точку \((0,0)\) и посмотрим, какое неравенство описывает ее сторону от граничной линии.
При \((0,0)\) какое неравенство верно: \(2x+3y>6\) или \(2x+3y<6\)?
\[\begin{массив} {ll} {2x+3y>6} &{2x+3y<6} \\ {2(0)+3(0)\overset{?}{>}6} &{ 2(0)+3(0)\overset{?}{<}6} \\ {0>6\text{ False}} &{0<6\text{ True}} \\ \nonumber \end{array }\]
Таким образом, сторона с \((0,0)\) — это сторона, где \(2x+3y<6\).
(Вы можете выбрать точку по другую сторону линии границы и проверить, что \(2x+3y>6\).)
Поскольку линия границы изображена пунктирной линией, в неравенстве нет знака равенства.
Заштрихованная область показывает решение неравенства \(2x+3y<6\).
Пример \(\PageIndex{8}\)
Запишите неравенство, показанное заштрихованной областью на графике с граничной линией \(x−4y=8\).
- Ответить
\(x−4y\leq 8\)
Пример \(\PageIndex{9}\)
Запишите неравенство, показанное заштрихованной областью на графике с граничной линией \(3x−y=6\).
- Ответить
\(3x−y\geq 6\)
График линейных неравенств с двумя переменными
Теперь, когда мы знаем, как выглядит график линейного неравенства и как он соотносится с граничным уравнением, мы можем использовать эти знания для построения графика заданного линейного неравенства.
Шаги, которые мы предпринимаем для построения графика линейного неравенства, суммированы здесь.
ПОКАЗАТЬ ЛИНЕЙНОЕ НЕРАВЕНСТВО С ДВУМЯ ПЕРЕМЕННЫМИ.
- Определите и начертите линию границы.
- Если неравенство равно \(\leq\) или \(\geq\), линия границы сплошная.
- Если неравенство < или >, линия границы отображается пунктиром.

- Проверка точки, которая не находится на линии границы. (Если не на граничной линии, \((0, 0)\) обычно является удобной контрольной точкой.) Является ли оно решением неравенства?
- Затенение с одной стороны линии границы.
- Если тестовая точка является раствором, заштрихуйте ту сторону, которая включает точку.
- Если контрольная точка не является раствором, заштрихуйте противоположную сторону.
Пример \(\PageIndex{10}\): построение графика линейного уравнения с двумя переменными
Начертите линейное неравенство \(y\geq \frac{3}{4}x−2\).
Раствор
Пример \(\PageIndex{11}\)
Нарисуйте график линейного неравенства \(y>\frac{5}{2}x−4\).
- Ответить
Все точки в заштрихованной области и на граничной линии представляют решения \(y>\frac{5}{2}x−4\).

Пример \(\PageIndex{12}\)
Нарисуйте график линейного неравенства \(y<\frac{2}{3}x−5\).
- Ответить
Все точки в заштрихованной области, кроме точек на граничной линии, представляют решения \(y<\frac{2}{3}x−5\).
Пример \(\PageIndex{13}\)
Нарисуйте график линейного неравенства \(x−2y<5\).
- Ответить
Сначала мы рисуем граничную линию \(x−2y=5\). Неравенство \(<\), поэтому мы рисуем пунктирную линию.
Затем мы проверяем точку. Мы снова будем использовать \((0,0)\), потому что его легко вычислить, и он не находится на граничной линии.
Является ли \((0,0)\) решением \(x−2y<5\)?
Точка \((0,0)\) является решением \(x−2y<5\), поэтому мы заштриховываем эту сторону граничной линии.
Все точки в заштрихованной области, кроме точек на граничной линии, представляют решения \(x−2y<5\).

Пример \(\PageIndex{14}\)
Нарисуйте линейное неравенство: \(2x−3y<6\).
- Ответить
Все точки в заштрихованной области, кроме точек на граничной линии, представляют решения \(2x−3y<6\).
Пример \(\PageIndex{15}\)
Нарисуйте линейное неравенство: \(2x−y>3\).
- Ответить
Все точки в заштрихованной области, кроме точек на граничной линии, представляют решения \(2x−y>3\).
Что делать, если линия границы проходит через начало координат? Тогда мы не сможем использовать \((0,0)\) в качестве контрольной точки. Нет проблем — мы просто выберем другую точку, не лежащую на граничной линии.
Пример \(\PageIndex{16}\)
Нарисуйте график линейного неравенства: \(y\leq −4x\).
- Ответить
Сначала мы рисуем граничную линию \(y=−4x\).
 Он находится в форме пересечения наклона с \ (m = −4 \) и \ (b = 0 \). Неравенство \(\leq\), поэтому мы рисуем сплошную линию.
Он находится в форме пересечения наклона с \ (m = −4 \) и \ (b = 0 \). Неравенство \(\leq\), поэтому мы рисуем сплошную линию.Теперь нам нужна контрольная точка. Мы видим, что точка (1,0)(1,0) не находится на граничной линии.
Является ли \((1,0)\) решением \(y\leq −4x\)?
Точка \((1,0)\) не является решением \(y\leq −4x\), поэтому мы заштриховываем противоположную сторону граничной линии.
Все точки в заштрихованной области и на граничной линии представляют решения \(y\leq −4x\).
Пример \(\PageIndex{17}\)
Нарисуйте линейное неравенство: \(y>−3x\).
- Ответить
Все точки в заштрихованной области, кроме точек на граничной линии, представляют решения \(y>−3x\).
Пример \(\PageIndex{18}\)
Нарисуйте график линейного неравенства: \(y\geq −2x\).
- Ответить
Все точки в заштрихованной области и на граничной линии представляют решения \(y\geq −2x\).

Некоторые линейные неравенства имеют только одну переменную. У них может быть x , но не y , или y , но не x . В этих случаях линия границы будет либо вертикальной, либо горизонтальной линией.
Напомним, что:
\[\begin{array} {ll} {x=a} &{\text{вертикальная линия}} \\ {y=b} &{\text{горизонтальная линия}} \\ \nonumber \end{массив} \]
Пример \(\PageIndex{19}\)
Нарисуйте линейное неравенство: \(y>3\).
- Ответить
Сначала мы рисуем граничную линию \(y=3\). Это горизонтальная линия. Неравенство \(>\), поэтому мы рисуем пунктирную линию.
Проверяем точку \((0,0)\).
\[y>3\не число\]\[0\слеш{>}3\не число\]
Итак, \((0,0)\) не является решением \(y>3\).
Итак, мы заштриховали сторону, которая не включает \((0,0)\), как показано на этом графике.

Все точки в заштрихованной области, кроме точек на граничной линии, представляют решения \(y>3\).
Пример \(\PageIndex{20}\)
Нарисуйте линейное неравенство: \(y<5\).
- Ответить
Все точки в заштрихованной области, кроме точек на граничной линии, представляют решения \(y<5\).
Пример \(\PageIndex{21}\)
Нарисуйте график линейного неравенства: \(y\leq −1\).
- Ответить
Все точки в заштрихованной области и на граничной линии представляют собой решения \(y\leq −1\).
Решение приложений с использованием линейных неравенств с двумя переменными
Многие поля используют линейные неравенства для моделирования проблемы. Хотя наши примеры могут относиться к простым ситуациям, они дают нам возможность развить наши навыки и почувствовать, как их можно использовать.
Пример \(\PageIndex{22}\)
Хилария работает на двух работах неполный рабочий день, чтобы заработать достаточно денег, чтобы выполнить свои обязательства, по крайней мере, 240 долларов в неделю. Ее работа в сфере общественного питания приносит 10 долларов в час, а репетиторство в кампусе — 15 долларов в час.Сколько часов Хиларии нужно работать на каждой работе, чтобы заработать не менее 240 долларов?
а. Пусть x будет количеством часов, которое она работает в сфере общественного питания, а y будет количеством часов, которые она работает репетитором. Напишите неравенство, моделирующее эту ситуацию.
б. Нарисуйте неравенство.
с. Найдите три упорядоченные пары \((x,y)\), которые были бы решениями неравенства. Затем объясните, что это значит для Хиларии.
- Ответить
а.Пусть x будет количеством часов, которое она работает на работе в сфере общественного питания, и пусть y будет количеством часов, которые она работает репетитором.

Она зарабатывает 10 долларов в час на работе в сфере общественного питания и 15 долларов в час на репетиторстве. На каждой работе количество часов, умноженное на почасовую заработную плату, дает сумму, заработанную на этой работе.
б. Чтобы изобразить неравенство, мы представим его в виде наклона и пересечения.
\[\begin{align} {10x+15y} &\geq 240 \\ 15y &\geq -10x+240 \\ y &\geq {−\frac{2}{3}x+16} \\ \ неномер \end{align}\]
с.Из графика видно, что упорядоченные пары \((15,10)\), \(((0,16)\), \((24,0)\) представляют три из бесконечного множества решений. Проверьте значения в неравенстве.
Для Хиларии это означает, что для того, чтобы заработать не менее 240 долларов, она может работать 15 часов репетиторством и 10 часов в фаст-фуде, зарабатывать все свои деньги репетиторством в течение 16 часов или зарабатывать все свои деньги, работая 24 часа на работе. в сфере общественного питания.
Пример \(\PageIndex{23}\)
Хью работает на двух работах неполный рабочий день. Один работает в продуктовом магазине, где платит 10 долларов в час, а другой работает няней за 13 долларов в час. Между двумя работами Хью хочет зарабатывать не менее 260 долларов в неделю. Сколько часов Хью нужно отработать на каждой работе, чтобы заработать не менее 260 долларов?
Один работает в продуктовом магазине, где платит 10 долларов в час, а другой работает няней за 13 долларов в час. Между двумя работами Хью хочет зарабатывать не менее 260 долларов в неделю. Сколько часов Хью нужно отработать на каждой работе, чтобы заработать не менее 260 долларов?
а. Пусть х будет количеством часов, которое он работает в продуктовом магазине, и пусть y будет количеством часов, которое он работает няней. Напишите неравенство, моделирующее эту ситуацию.
б. Нарисуйте неравенство.
с. Найдите три упорядоченные пары ( x , y ), которые были бы решениями неравенства.Затем объясните, что это значит для Хью.
- Ответить
а. \(10x+13y\geq 260\)
б.с. Ответы будут различаться.
Пример \(\PageIndex{24}\)
Вероника работает на двух работах с частичной занятостью, чтобы заработать достаточно денег, чтобы выполнять свои обязательства в размере не менее 280 долларов в неделю. Ее работа в дневном спа-салоне оплачивается 10 долларов в час, а работа административного помощника в кампусе — 17,50 долларов в час. Сколько часов Веронике нужно отработать на каждой работе, чтобы заработать не менее 280 долларов?
Ее работа в дневном спа-салоне оплачивается 10 долларов в час, а работа административного помощника в кампусе — 17,50 долларов в час. Сколько часов Веронике нужно отработать на каждой работе, чтобы заработать не менее 280 долларов?
а.Пусть x будет количеством часов, которое она работает в дневном спа-салоне, и пусть y будет количеством часов, в течение которых она работает помощником по административным вопросам. Напишите неравенство, моделирующее эту ситуацию.
б. Нарисуйте неравенство.
с. Найдите три упорядоченные пары ( x , y ), которые были бы решениями неравенства. Затем объясните, что это значит для Вероники
.- Ответить
а. \(10x+17.5y\geq 280\)
б.с. Ответы будут различаться.
Получите доступ к этому онлайн-ресурсу, чтобы получить дополнительные инструкции и попрактиковаться в построении графиков линейных неравенств с двумя переменными.
Графическое решение неравенства с двумя переменными
СОДЕРЖАНИЕ
— Ревизия линейного уравнения с двумя переменными.
— Графическое представление неравенств с двумя переменными.
-Графическое решение одновременного неравенства с двумя переменными.
Оценка
9Решить графически для интегральных значений x и y
y ≥ 1, x — y ≥ 1 и 3x + 4y ≤ 12
Общая оценка / Ревизия Вопросы
Решите графически одновременные неравенства
1. Если (i) x + 3y≤ 12 (ii) y ≥-1 (iii) x > -2 для целых значений x и y
Если (i) x + 3y≤ 12 (ii) y ≥-1 (iii) x > -2 для целых значений x и y
2.y таков, что 4y – 7 ≤ 3y и 3y≤5y + 8
а) Какой диапазон значений y удовлетворяет обоим неравенствам?
b) Следовательно, представим 4y – 7 ≤ 5y + 8 в виде a ≤ y ≤ b, где a и b — целые числа
3.Если 65x 2 +x-10=0 найти значения x
4. Решить уравнения 2 x+y =1 и 25 xy = 125 одновременно SSS2, страницы 98-111, упражнение 10e.
Мы заинтересованы в продвижении БЕСПЛАТНОГО обучения. Расскажите своим друзьям о Stoplearn.com. Нажмите кнопку «Поделиться» ниже! Загрузите наше бесплатное мобильное приложение для Android : Сохраняйте свои данные при использовании нашего бесплатного приложения.Нажмите, чтобы загрузить приложение StopLearn. Скачать бесплатно редактируемые шаблоны резюме/CV : Нажмите здесь. Присоединяйтесь к дискуссионному форуму и выполняйте задание : Найдите вопросы в конце каждого урока. Обсудите свои ответы на этом форуме. Нажмите на картинку, чтобы следовать. Родственные
Обсудите свои ответы на этом форуме. Нажмите на картинку, чтобы следовать. Родственные | Начальная алгебра Урок 24. Графики линейных неравенств
Цели обучения
Введение
Учебник
Практические задачи
Нужна дополнительная помощь по этим темам?
|
Графики неравенств с двумя переменными — концепция
Как и в уравнениях, иногда в неравенстве есть две переменные. Графики неравенств с двумя переменными включают затенение области выше или ниже линии, чтобы указать все возможные решения неравенства. При графическом отображении неравенств с двумя переменными мы используем некоторые из тех же методов, что и при графическом построении линий, чтобы найти границу заштрихованной области.
Когда вы рисуете неравенства, в которых есть и x, и y, вы хотите использовать трехэтапный процесс.
Первое, что вы хотите сделать, это нарисовать линию, используя технику y=mx+b. Под этим я подразумеваю получить y сам по себе, поставить точку на ваших перехватах y, оттуда подсчитать наклон, а затем соединить линию.
Следующее, что вам нужно сделать, это скорректировать линию, основываясь на том, является ли она одним из этих символов неравенства или одним из этих, меньше или больше, чем просьба нарисовать пунктирную линию, потому что эти точки на самом деле не являются техническими решениями.Вы получите сплошную линию, если это один из этих символов неравенства.
Наконец, каждый раз, когда вы рисуете неравенство, у вас будет штриховка, например, помните, на числовой прямой, как вы должны были построить график, выходящий в направлениях, похожих на форму гантели или что-то еще, что вам нужно было нарисовать штриховку, то же самое верно и в плоскости xy, только вы будете затенять, как половина плоскости, подумайте о координатной плоскости xy с линией, пересекающей ее, вы будете затенять либо все по одну сторону от этой линии, либо Другая сторона.Способ выяснить, какой способ затенения, — это выбрать любую точку, которую вы хотите, которая не находится на этой линии, подставив ваши значения x и y в неравенство, и вы собираетесь затенять сторону линии, которая делает неравенство верным.
Итак, это действительно важный трехэтапный процесс, который вы, возможно, захотите записать на карточке для заметок или на чем-то, что вы можете иметь рядом с собой, когда будете решать домашние задания, и если вы сможете запомнить этот процесс и не усложнять его, вы’ У нас будет большой успех в решении этих проблем.
2. Решение линейных неравенств
Процедура решения линейных неравенств с одной переменной похоже на решение основных уравнений. (См. Решение уравнений.)
Нам нужно быть осторожными с смыслом равенства при умножении или делении на отрицательные числа.
Ниже приведены несколько примеров решения уравнений, содержащих неравенства.
Пример 1
Решить x + 2
Ответ
Нам нужно вычесть `2` из обеих частей неравенства.
`х+2<4`
`x<4-2`
`x<2`
График этого решения выглядит следующим образом:
Пример 2
Решите `x/2>4`
Ответ
Нам нужно умножить обе части неравенства на `2`.
`x/2>4`
`x>4xx2`
`х>8`
Вот график этого решения:
Пример 3
Решить 2 x ≤ 4
Ответ
Нам нужно разделить обе части неравенства на `2`.
`2x<=4`
`x<=4/2`
`х<=2`
Вот график этого решения:
Пример 4
Решите неравенство 3 − 2 x ≥ 15
Ответ
В этом примере нам нужно вычесть 3 с обеих сторон; затем разделите обе части на «-2» (не забывая изменить направление неравенства).
`3-2x>=15`
`-2x>=15-3`
`-2x>=12`
`x<=12/(-2)`
`х<=-6`
Вот график этого решения:
(Обратите внимание на изменение смысла из-за деления на отрицательный номер)
Проверить: Всегда проверяйте свое решение, и вы можете быть уверены, что ваш ответ правильный.
В этом случае любое число меньше `-6` должно «работать» в исходном уравнении, а любое число больше `-6` не должно работать.
Возьмем `x = -10` (удобное число меньше, чем `-6`)
LHS `= 3 − 2 (-10) = 3 + 20 = 23`. Это больше, чем «15», так что это правда.
Теперь возьмем `x = 0` (удобное число больше, чем `-6`)
LHS `= 3 − 2(0) = 3`. Это НЕ больше, чем «15», на что мы и надеялись.
Таким образом, мы можем быть уверены, что наш ответ правильный.
Пример 5
Решите неравенство `3/2(1-x)>1/4-x`
Ответ
`3/2(1-x)>1/4-x`
Умножение обеих сторон на 4 дает нам:
`6(1-x)>1-4x`
`6-6x>1-4x`
`-6x+4x>1-6`
`-2x> -5`
`x<5/2`
(Обратите внимание на изменение смысла в последней строке из-за деления на отрицательный
номер).
Вот график этого решения:
Проверка: Взятие x = 0 (что должно работать):
`»LHS» = 3/2(1 − 0) = 3/2`
`»RHS» = 1/4`
ВЕРНО, что `3/2 > 1/4`, так что это хорошо.
Теперь возьмем х = 3 (удобное число больше 5/2, которое не должно работать):
`»LHS» = 3/2(1 − 3) = -3`
`»RHS» = 1/4 − 3 = -2 3/4`
Это НЕ правда, что `-3 > -2 3/4` и поэтому `x=3` терпит неудачу, как мы надеялись.
Мы можем быть уверены, что наш ответ (`x<5/2`) правильный.
Неравенства с тремя членами
Пример 6
Решите −1 < 2 x + 3 < 6
Ответ
`- 1 < 2x + 3 < 6`
Вычесть «3» со всех трех сторон
`- 1 — 3 < 2x + 3 - 3 < 6 - 3`
`- 4 < 2x < 3`
Разделить все стороны на `2`
`-2 < x < 3/2`
Граф решения:
Пример 7
Решите 2 x < x − 4 ≤ 3 x + 8
Ответ
Другой способ решения более сложных неравенств с 3 членов (сторон) состоит в том, чтобы переписать неравенство в виде
`2x < x - 4` и `x — 4 ≤ 3x + 8`
Тогда, решив каждое из этих неравенств, получим:
Левое неравенство:
`х < - 4`
Правая сторона неравенства:
`x — 4 ≤ 3x + 8`
`- 4 ≤ 2x + 8`
`- 12 ≤ 2x`
`х ≥ -6`
Принимая во внимание, что окончательное решение должно удовлетворять неравенств, получаем:
`x < -4` и `x ≥ -6`
Эти две части отображаются как:
При рассмотрении области, где пересекаются две части, мы получаем
`-6 ≤ x < -4`
Это окончательный граф решения:
Упражнения
Решите следующие неравенства для x :
1. Решить 3 − 3 x < − 1
Решить 3 − 3 x < − 1
Ответ
`3 — 3x < -1`
`- 3x`x> 4/3 ~~ 1,333…`
Вот график решения:
2. Решите −2( x + 4) > 1 − 5 x
Ответ
`-2(x + 4) > 1 — 5x`
`-2x — 8 > 1 — 5x ``3x — 8 > 1`
`3x > 9`
`х > 3`
Граф решения:
3. Решите `x/5-2>2/3(x+3)`
Ответ
`х/5-2>2/3(х+3)`
Умножить на 5:
`x-10>10/3(x+3)`
Умножить на 3:
`3x-30>10(x+3)`
`3x-30>10x+30`
`3x>10x+60`
`-7x>60`
`x<(-60)/7~~-8.57`
Граф решения:
4. Решить х — 1 < 2 х + 2 < 3 х + 1
Ответ
Нам нужно найти пересечение «истинных» значений.
`x — 1 < 2x + 2` и `2x + 2 < 3x + 1`
`x < 2x + 3` и `2x < 3x - 1`
`x > -3` и `x > 1`
Эти 2 неравенства на одной оси выглядят следующим образом:
Пересечение этих двух областей `x > 1`.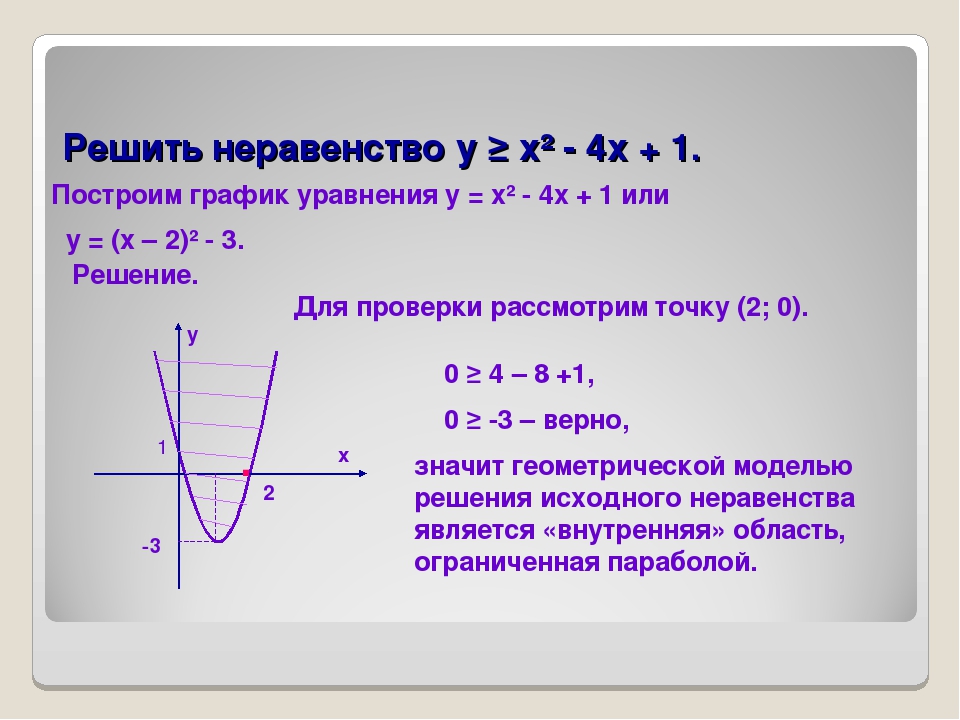
Всегда проверяйте свои ответы!
Вот окончательный график решения:
Занятия в классе: линейные неравенства с двумя переменными — Texas Instruments
Управляйте настройками файлов cookie
Вы можете контролировать свои предпочтения относительно того, как мы используем файлы cookie для сбора и использования информации, когда вы находитесь на веб-сайтах TI, настраивая статус этих категорий.
| Категория | Описание | Разрешить |
|---|---|---|
| Аналитические и эксплуатационные файлы cookie | Эти файлы cookie, в том числе файлы cookie из Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI, а также отслеживать, как посетители перемещаются по нашим сайтам.Это помогает нам улучшить работу сайтов TI (например, упрощая поиск информации на сайте). | |
| Рекламные и маркетинговые файлы cookie | Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах. Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламные объявления, чтобы они лучше соответствовали вашим интересам, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах. Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламные объявления, чтобы они лучше соответствовали вашим интересам, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы. | |
| Функциональные файлы cookie | Эти файлы cookie помогают определить, кто вы, и сохраняют информацию о вашей деятельности и учетной записи, чтобы обеспечить расширенные функциональные возможности, включая более персонализированный и актуальный опыт на наших сайтах.Если вы не разрешите использование этих файлов cookie, некоторые или все функции и службы сайта могут работать неправильно. Если вы не разрешите использование этих файлов cookie, некоторые или все функции и службы сайта могут работать неправильно. |
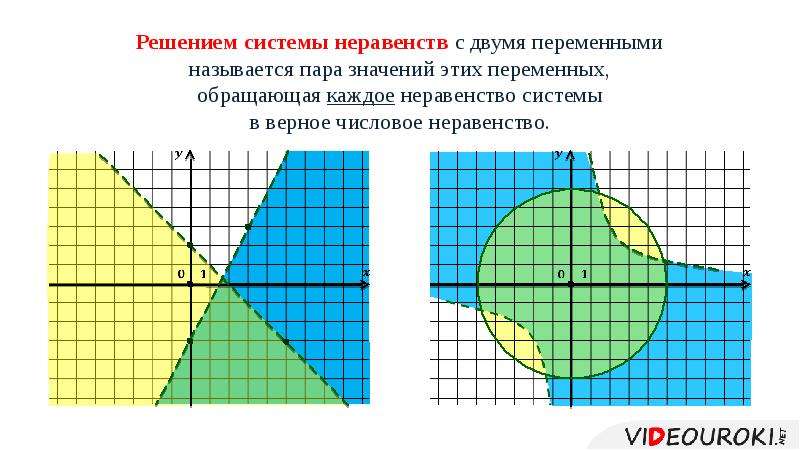 2\)
2\) 2-55x+2500\end{cases}\)
2-55x+2500\end{cases}\) : ил. ISBN 978-5-346-01027-2.
: ил. ISBN 978-5-346-01027-2.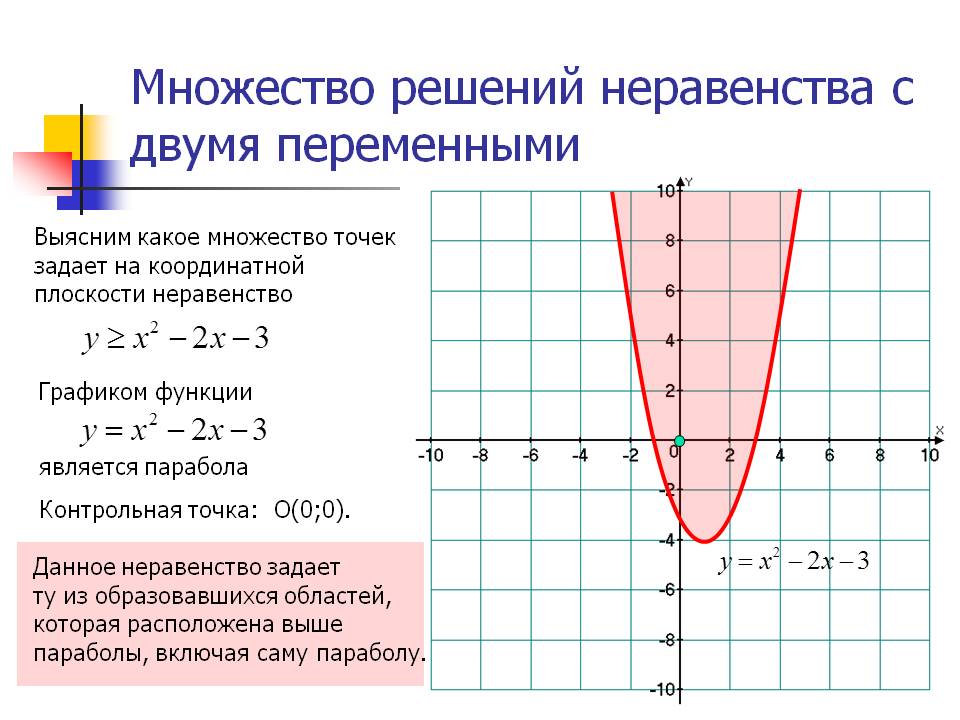 Вместо этого делаем такие преобразования, чтоб в центре остался голый икс, а по краям — числа.
Вместо этого делаем такие преобразования, чтоб в центре остался голый икс, а по краям — числа.
 е. интервал, где есть двойная штриховка: и сверху, и снизу. Его и запишем ответ.
е. интервал, где есть двойная штриховка: и сверху, и снизу. Его и запишем ответ.




 На одной стороне линии находятся точки с \(2x+3y>6\), а на другой стороне линии — точки с \(2x+3y<6\).
На одной стороне линии находятся точки с \(2x+3y>6\), а на другой стороне линии — точки с \(2x+3y<6\).

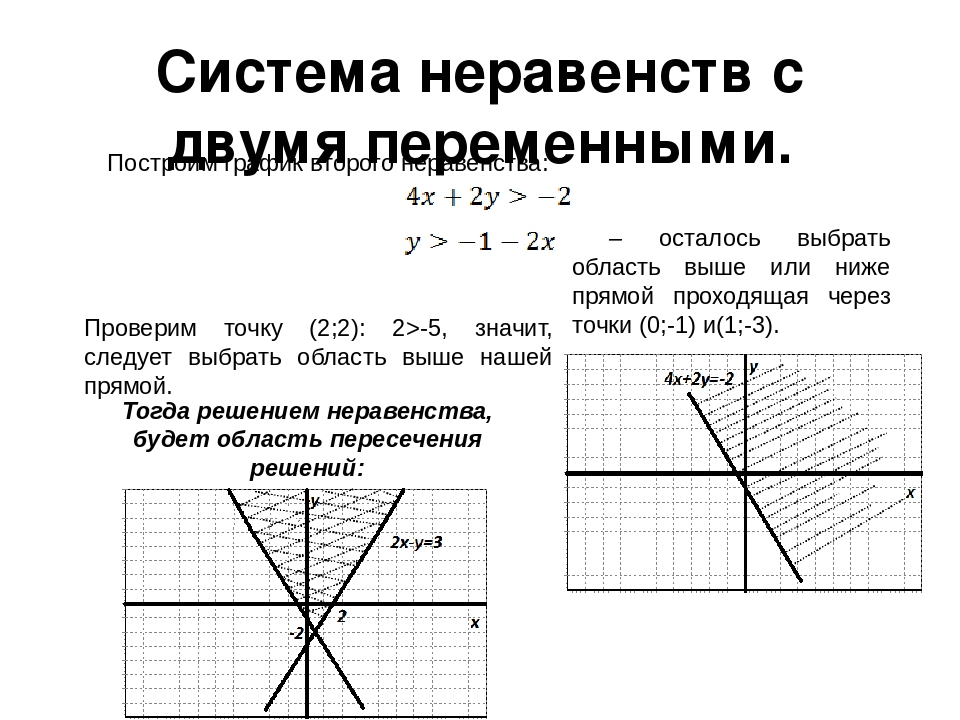
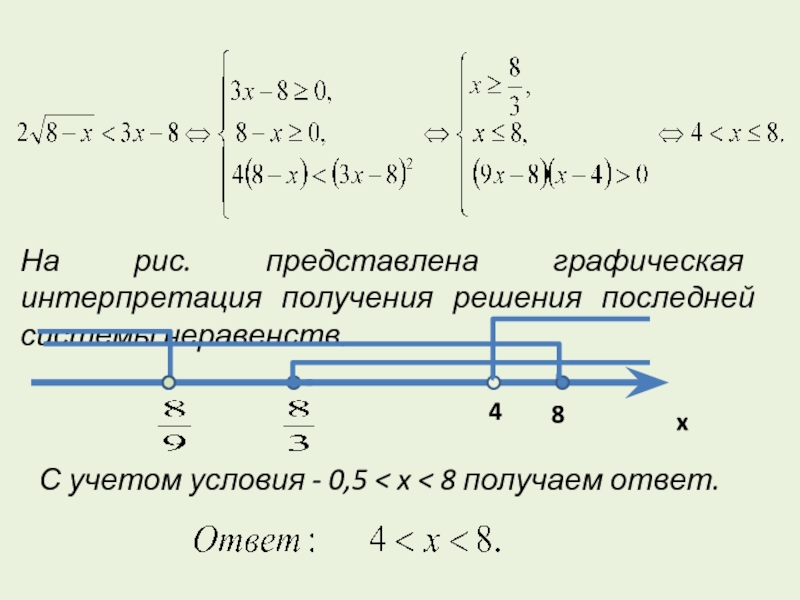 Он находится в форме пересечения наклона с \ (m = −4 \) и \ (b = 0 \). Неравенство \(\leq\), поэтому мы рисуем сплошную линию.
Он находится в форме пересечения наклона с \ (m = −4 \) и \ (b = 0 \). Неравенство \(\leq\), поэтому мы рисуем сплошную линию.


 Некоторые из этих проблем могут стать немного
длинная.
Не позволяйте этому обескуражить вас, вы можете это сделать. Держитесь, многие шаги — это концепции из прошлого, вещи, которые вы
должны были уже увидеть и сделать раньше. вставлю ссылки на
материал, который вам нужно вспомнить из прошлого, в случае, если вам нужно
Обзор. Во многих случаях математика работает таким образом, используйте то, что вы
знать, чтобы узнать новую концепцию. Давайте посмотрим, что вы можете сделать с
эти
неравенства.
Некоторые из этих проблем могут стать немного
длинная.
Не позволяйте этому обескуражить вас, вы можете это сделать. Держитесь, многие шаги — это концепции из прошлого, вещи, которые вы
должны были уже увидеть и сделать раньше. вставлю ссылки на
материал, который вам нужно вспомнить из прошлого, в случае, если вам нужно
Обзор. Во многих случаях математика работает таким образом, используйте то, что вы
знать, чтобы узнать новую концепцию. Давайте посмотрим, что вы можете сделать с
эти
неравенства.

 Ты только
нужно решить, нужна ли вам сплошная линия или пунктирная линия.
Ты только
нужно решить, нужна ли вам сплошная линия или пунктирная линия.  Заштрихуйте ответ на
неравенство.
Заштрихуйте ответ на
неравенство.

 1
1 


 на -3 дел.
по -3
на -3 дел.
по -3 





 На самом деле практики много не бывает.
На самом деле практики много не бывает.
