Методы решения уравнений
Уравнения, решение уравнений
В этой статье дан краткий обзор всех основных методов решения уравнений. Здесь также приведены ссылки на материалы с подробной информацией по каждому методу. Это дает возможность познакомиться со всеми методами решения уравнений, а в случае необходимости — изучить методы решения уравнений углубленно.
Метод введения новой переменной (замены переменной)
Метод введения новой переменной, он же метод замены переменной, позволяет решать уравнения f(g(x))=0 или f1(g(x))=f2(g(x)), где f, f1 и f2 – некоторые функции, а x – неизвестная переменная, а также уравнения, которые могут быть приведены к указанному виду. Состоит метод во введении новой переменной t=g(x). Введение переменной позволяет от исходного уравнения f(g(x))=0 или f1(g(x))=f2(g(x)) перейти к уравнению с новой переменной f(t)=0 или f1(t)=f2(t) соответственно.
Например, метод введения новой переменной позволяет решить уравнение . Здесь стоит принять . Это позволяет перейти от исходного уравнения к квадратному уравнению t2−3·t+2=0 с новой переменной t, которое имеет два корня t1=1 и t2=2. Обратная замена происходит путем составления совокупности двух уравнений и . Это рациональные уравнения. Решением первого является x=2, а решением второго является x=1,5. Так методом введения новой переменной получено решение исходного уравнения: 1,5, 2.
Подробное описание метода введения новой переменной, включающее обоснование метода, алгоритм решения уравнений этим методом и примеры решения характерных уравнений, дано в этой статье.
К началу страницы
Метод разложения на множители
Метод разложения на множители предназначен для решения уравнений f1(x)·f2(x)·…·fn(x)=0, где f1(x), f2(x),…, fn(x) – некоторые выражения, x – переменная. То есть, методом разложения на множители решаются уравнения, в левой части которых находится произведение нескольких выражений, а в правой – нуль. Суть метода состоит в замене решения уравнения f1(x)·f2(x)·…·fn(x)=0 решением совокупности уравнений f1(x)=0, f2(x)=0, …, fn(x)=0 на области допустимых значений (ОДЗ) для исходного уравнения.
Приведем простой пример. Уравнение может быть решено методом разложения на множители. Переходим от исходного уравнения к совокупности двух уравнений и . Иррациональное уравнение имеет единственное решение x
 Значит, совокупность уравнений имеет два решения x1=1, x2=4. Но области допустимых значений для исходного уравнения, которой является множество (3, +∞), принадлежит лишь одно из решений x1=1, x2=4, а именно, x2=4. Оно и является единственным корнем уравнения .
Значит, совокупность уравнений имеет два решения x1=1, x2=4. Но области допустимых значений для исходного уравнения, которой является множество (3, +∞), принадлежит лишь одно из решений x1=1, x2=4, а именно, x2=4. Оно и является единственным корнем уравнения .
Подробное описание этого метода и решения других характерных примеров смотрите в статье «метод разложения на множители».
К началу страницы
Метод решения уравнений «дробь равна нулю»
Из названия понятно, что этот метод используется при решении уравнений f(x)/g(x)=0. Например, он позволяет решить уравнение . Метод состоит в переходе от решения уравнения f(x)/g(x)=0 к решению уравнения f(x)=0 на ОДЗ для исходного уравнения. Следовательно, чтобы решить уравнение , надо решить уравнение (x−1)·(x
2−4)=0 на ОДЗ для исходного уравнения.
Обоснование метода и примеры с решениями смотрите здесь.
К началу страницы
Метод решения уравнений через преобразования
Метод базируется на преобразовании уравнений с целью выстраивания последовательностей равносильных уравнений и уравнений-следствий со сравнительно простыми последними уравнениями, по решениям которых находятся решения исходных уравнений.
Например, для решения уравнения 3·x4−48=0 последовательно проводятся два преобразования: переносится слагаемое −48 из левой части уравнения в правую с противоположным знаком, после чего проводится деление обеих частей уравнения на число 3. В результате получается равносильное уравнение x
Вот другой пример. Замена выражения в левой части уравнения тождественно равным выражением (x−1)·(x+2) дает уравнение-следствие (x−1)·(x+2)=0, имеющее два корня x1=1 и x2=−2. Проверка показывает, что только первый корень является корнем исходного уравнения, а второй корень – посторонний.
Проверка показывает, что только первый корень является корнем исходного уравнения, а второй корень – посторонний.
Какие преобразования используются при решении уравнений? Когда нужно делать проверку для отсеивания посторонних корней, а когда такую проверку делать необязательно? Ответы на эти и многие другие вопросы по теме есть в этом материале.
К началу страницы
Метод решения уравнений, сводящихся к числовым равенствам
Иногда в результате преобразования уравнений получаются числовые равенства. Например, уравнение сводится к верному числовому равенству 0=0, а уравнение сводится к неверному числовому равенству 0=5. Решением уравнений, сводящихся к верным числовым равенствам, является множество, совпадающее с ОДЗ для исходного уравнения. Так, решением уравнения является множество x≥0. А уравнения, сводящиеся к неверным числовым равенствам, не имеют решений. То есть, уравнение не имеет решений.
Здесь есть один нюанс. Если среди преобразований, приводящих уравнение к верному числовому равенству, есть возведение обеих частей уравнения в одну и ту же четную степень, то нельзя утверждать, что решением уравнения является любое число из ОДЗ. Этот нюанс разобран в статье «решение уравнений, сводящихся к числовым равенствам».
Если среди преобразований, приводящих уравнение к верному числовому равенству, есть возведение обеих частей уравнения в одну и ту же четную степень, то нельзя утверждать, что решением уравнения является любое число из ОДЗ. Этот нюанс разобран в статье «решение уравнений, сводящихся к числовым равенствам».
К началу страницы
Функционально-графический метод
Обзор методов решения уравнений продолжаем функционально-графическии методом. Этот метод предполагает использование функций, отвечающих частям решаемого уравнения, а точнее, их графиков и свойств. Можно выделить три основных направления функционально-графического метода:
- Графический метод
- Метод, базирующийся на возрастании-убывании функций
- Метод оценки
Давайте рассмотрим их.
Графический метод
Первое направление базируется на использовании графиков функций. Это так называемый графический метод решения уравнений. По этому методу, во-первых, выполняется построение в одной прямоугольной системе координат графиков функций, отвечающих частям уравнения. Во-вторых, по чертежу определяется количество точек пересечения графиков, сколько точек пересечения – столько и корней у решаемого уравнения. В-третьих, определяются абсциссы точек пересечения – это значения корней.
Это так называемый графический метод решения уравнений. По этому методу, во-первых, выполняется построение в одной прямоугольной системе координат графиков функций, отвечающих частям уравнения. Во-вторых, по чертежу определяется количество точек пересечения графиков, сколько точек пересечения – столько и корней у решаемого уравнения. В-третьих, определяются абсциссы точек пересечения – это значения корней.
Например, графически можно решить уравнение . Из чертежа, приведенного ниже, видно, что графики имеют единственную точку пересечения с абсциссой 2. Это единственный корень уравнения.
К началу страницы
Метод, базирующийся на возрастании-убывании функций
Второе направление в своей основе имеет использование свойств возрастающих и убывающих функций. Соответствующий метод используется тогда, когда есть возможность подобрать корень уравнения и доказать возрастание функции, отвечающей одной из частей уравнения, и убывание функции, отвечающей другой части уравнения. В этом случае подобранный корень является единственным.
В этом случае подобранный корень является единственным.
Приведем пример. Для уравнения 3(1−x)3+1=2x несложно подобрать корень, им является число 1. Также несложно обосновать убывание функции, соответствующей левой части уравнения, и возрастание функции, отвечающей правой части уравнения. Это доказывает единственность подобранного корня.
За более полной информацией следуйте сюда
К началу страницы
Метод оценки
Третье направление основано на использовании свойств ограниченности функций. Это так называемый метод оценки. Согласно этому методу, в первую очередь нужно оценить значения выражений, находящихся в левой и правой части уравнения. Если множества, соответствующие полученным оценкам, не пересекаются, то уравнение не имеет корней. Если множества имеют конечное число общих элементов t1, t2, …, tn, то решение уравнения f(x)=g(x) заменяется решением совокупности систем , , …, . Если же множества, соответствующие оценкам имеют бесконечно много общих элементов, то надо либо уточнять оценки, либо искать другой метод решения.
Если же множества, соответствующие оценкам имеют бесконечно много общих элементов, то надо либо уточнять оценки, либо искать другой метод решения.
Например, методом оценки можно решить уравнение . Значения левой части этого уравнения не превосходят нуля, а значения правой части не меньше нуля. Это позволяет перейти к системе , решение которой дает искомое решение уравнения.
К началу страницы
Метод освобождения от внешней функции
Метод освобождения от внешней функции используется для решения уравнений h(f(x))=h(g(x)), где f, g и h – функции, причем функция y=h(t) принимает каждое свое значение по одному разу, в частности, строго возрастает или строго убывает, а x – независимая переменная. Этот метод состоит в переходе от уравнения h(f(x))=h(g(x)) к уравнению f(x)=g(x) на ОДЗ для исходного уравнения.
Например, методом освобождения от внешней функции можно решить уравнение . Здесь в качестве внешней функции выступает y=h(t), где . Эта функция возрастающая как сумма двух возрастающих функций и , значит, каждое свое значение она принимает по одному разу. Это позволяет перейти от исходного уравнения к уравнению . Равносильные преобразования позволяют привести последнее уравнение к квадратному уравнению x
Эта функция возрастающая как сумма двух возрастающих функций и , значит, каждое свое значение она принимает по одному разу. Это позволяет перейти от исходного уравнения к уравнению . Равносильные преобразования позволяют привести последнее уравнение к квадратному уравнению x
Рекомендуем детально разобраться с этим методом решения уравнений, обратившись к материалу статьи «метод освобождения от внешней функции».
К началу страницы
Метод решения уравнений через ОДЗ
Через ОДЗ решаются уравнения, области допустимых значений которых являются либо пустыми множествами, либо состоят из конечного количества чисел. Когда ОДЗ есть пустое множество, уравнение не имеет решений. Когда ОДЗ состоит из конечного количества чисел, то следует по очереди проверить эти числа через подстановку. Те из них, которые удовлетворяют решаемому уравнению являются его корнями, остальные – не являются.
Те из них, которые удовлетворяют решаемому уравнению являются его корнями, остальные – не являются.
Например, уравнение не имеет решений, так как ОДЗ для него есть пустое множество. А для уравнения ОДЗ состоит из двух чисел −1 и 7. Проверка подстановкой показывает, что −1 является корнем уравнения, а 7 – не является.
Более полная информация по этому методу решения уравнений содержится в этой статье.
К началу страницы
Метод возведения обеих частей уравнения в одну и ту же степень
Этот метод, в основном, используется для решения иррациональных уравнений. Он заключается в возведении обеих частей уравнения в одну и ту же степень с целью избавления от корней. Например, возведение обеих частей уравнения в квадрат дает уравнение без корня 1−5·x=(x−3)2. Возведение в нечетную степень дает равносильное уравнение. Возведение в четную степень в общем случае дает уравнение-следствие, поэтому, при этом необходимо позаботиться об отсеивании посторонних корней. Причем отсеивание следует проводить способом, не связанным с ОДЗ, обычно, через проверку подстановкой, так как возведение частей уравнения в четную степень может приводить к появлению посторонних корней в рамках ОДЗ.
Причем отсеивание следует проводить способом, не связанным с ОДЗ, обычно, через проверку подстановкой, так как возведение частей уравнения в четную степень может приводить к появлению посторонних корней в рамках ОДЗ.
Аналогично разбираемый метод может использоваться и для решения уравнений, в которых фигурируют степени с рациональными и иррациональными показателями. Решения соответствующих примеров смотрите здесь.
К началу страницы
Метод решения уравнений по определению логарифма
По определению логарифма, как правило, решают уравнения следующего вида logh(x)f(x)=g(x), например, log2(x2+4·x+3)=3, log2(9−2x)=3−x, logx(3·xlgx+4)=2·lgx и т.п.
Согласно методу решения уравнений по определению логарифма, решение уравнения logh(x)f(x)=g(x)заменяется решением уравнения f(x)=(h(x))g(x) на ОДЗ переменной x для исходного уравнения. Например, от уравнения logx(3·xlgx+4)=2·lgx можно перейти к уравнению 3·xlgx+4=x2·lgx на ОДЗ для исходного уравнения.
Например, от уравнения logx(3·xlgx+4)=2·lgx можно перейти к уравнению 3·xlgx+4=x2·lgx на ОДЗ для исходного уравнения.
Более полная информация содержится в основной статье.
К началу страницы
Метод потенцирования
Методом потенцирования решаются логарифмические уравнения, обе части которых являются логарифмами по одному и тому же основанию, например, lgx=lg(3·x+5), и т.п. Метод заключается в замене решения уравнения logh(x)f(x)=logh(x)g(x) решением уравнения f(x)=g(x) на ОДЗ для исходного уравнения. По этому методу от уравнения lgx=lg(3·x+5) следует перейти к уравнению x=3·x+5 на ОДЗ для исходного уравнения, которая определяется двумя условиями: x>0, 3·x+5>0.
Обоснование метода и примеры с подробными решениями смотрите в этой статье.
К началу страницы
Метод логарифмирования
Метод подразумевает логарифмирование обеих частей уравнения по одному и тому же основанию. К нему следует прибегать тогда, когда логарифмирование позволяет избавиться от степеней с переменной в показателях. В частности, его можно использовать для решения показательных уравнений, обе части которых являются степенями с одинаковыми основаниями, например, 51−x=52·x+1. Почленное логарифмирование этого уравнения дает очень простое уравнение 1−x=2·x+1, решение которого дает решение исходного уравнения.
К нему следует прибегать тогда, когда логарифмирование позволяет избавиться от степеней с переменной в показателях. В частности, его можно использовать для решения показательных уравнений, обе части которых являются степенями с одинаковыми основаниями, например, 51−x=52·x+1. Почленное логарифмирование этого уравнения дает очень простое уравнение 1−x=2·x+1, решение которого дает решение исходного уравнения.
Также метод подходит для решения показательных уравнений, степени в которых имеют разные основания и отличающиеся показатели, например, . Более того, метод логарифмирования является чуть ли не основным методом решения показательно-степенных уравнений, вроде таких xlgx−1=100, .
Более детальная информация и примеры с решениями есть в этом материале.
К началу страницы
Квадратная формула I и II типов — Решение уравнений einfach erklärt
Квадратные уравнения — уравнения вида:
$ax^2+bx+c=0$
i
Подсказка
Вы можете использовать либо pq-формулу (Квадратная формула I), либо abc-формулу (Квадратная формула II). 2-5}$
2-5}$
$x_{1,2} = -3 \pm\sqrt{4}$
$x_{1,2} = -3 \pm2$
Вычиcлим
$x_{1} = -3+2=-1$$x_{2} = -3-2=-5$
Урок математики по теме: «Решение уравнений»
Тема: Решение уравнений.
Цель урока: обобщение и систематизация знаний обучающихся по теме “Решение уравнений”.
Форма работы: групповая.
Подготовка к уроку: класс разбит на три группы по 5 человек в каждой. У учеников в группе номера от 1 до 5. В группе выбирается консультант (“сильный” учащийся). Консультант оказывает помощь товарищам по группе, проверяет решения, выставляет оценки.
Оборудование: карточки с заданиями (см. Приложение 1), бланки для выставления оценок, схема решения уравнений.
Ход урока
Класс разбит на 3 группы по 5 человек в каждой. (Группы первого состава).
1. Организационный момент.
2. Подготовительный этап. Повторение.
Сегодня мы с вами должны повторить правила решения уравнений. Устранить все ошибки, которые вы допускаете при решении уравнений, и подготовиться к диагностике.
Давайте повторим этапы решения уравнений. (При повторении на доску вывешивается схема решения уравнения).
| Этапы решения уравнения. | Схема. | Дополнительные вопросы. |
| 1. Раскрыть скобки. ( Если они есть). | Каким правилом будем пользоваться? | |
| 2. Сгруппировать слагаемые с неизвестным в левой части, числа в правой части. | Какое правило нужно соблюдать? | |
3. Привести подобные слагаемые, и
прийти к линейному уравнению. Привести подобные слагаемые, и
прийти к линейному уравнению. |
Какой вид имеет линейное уравнение? | |
| 4. Решить линейное уравнения. | Как решается линейное уравнение? |
3. Устный счет.
Устно повторим все действия, про которые мы сейчас вспомнили.
| -10х = 15 | 12 (b – 3c) |
| 5c + 7a – 12c | 0.4c + 0.3b – 0.1c +2b |
| 6 (a -7) | 7x = -2.1 |
| -3(a – b + 2) | -3a = -3.3 |
4. Работа в группах первого состава.
Сейчас вы разбиты на три группы. У каждой группы
будет свое задание. Первая группа будет решать
уравнения, в которых нет никаких преобразований.
Вторая группа решает уравнения, в которых нужно
раскрыть скобки, и третья группа решает
уравнения с дробными коэффициентами.
У каждой группы
будет свое задание. Первая группа будет решать
уравнения, в которых нет никаких преобразований.
Вторая группа решает уравнения, в которых нужно
раскрыть скобки, и третья группа решает
уравнения с дробными коэффициентами.
Ваша задача в своих группах хорошо разобраться в решении уравнений данного типа, так, чтобы вы смогли объяснить решение другим.
Работа в группах. Задания см. Приложение 1.
5. Работа в группах второго состава.
После того, как в группах прорешены все уравнения, консультанты выставляют оценки за работу каждому в группе, класс разбивается на пять групп по три человека в каждой (по номерам), так, чтобы в каждой группе было по одному человеку из каждой группы первого состава. Каждой группе выдается новое задание, которое содержит все типы уравнений. (см. Приложение1.)
При работе групп второго состава проверку
осуществляет учитель и выставляет оценки. Некоторые ученики проверку могут сделать сами по
готовым ответам и выставить себе оценку.
Некоторые ученики проверку могут сделать сами по
готовым ответам и выставить себе оценку.
6. Подведение итогов. Выставление оценок.
Наглядная интерпретация. Графическое решение уравнений на компьютере
Мы приводим результаты решения уравнения, левой частью которого является логарифмическая функция, а правой – показательная, причем с одинаковыми основаниями. Так как уравнения решались с помощью компьютера, это позволило проанализировать количество решений в зависимости от значения оснований вышеуказанных функций, что было бы невозможно при построении графиков вручную. О возможности существования трех корней в уравнении такого вида упоминается в учебнике по «Алгебре и началам анализа» для 11-го класса, авторы Н.Я. Виленкин и другие, но ни в одном школьном учебнике математики не приводятся графики, показывающие наличие трех корней. Поэтому у учеников создается впечатление, что уравнение данного вида всегда имеет не более одного решения.
Полностью публикация приведена в формате PDF:Скачать/Просмотреть(Для просмотра необходима программа Adobe Reader или ее произвольный аналог).
Используемые в приведенном здесь уравнении функции относятся к тем немногочисленным функциям, которые основательно изучаются в школе, и на их свойства часто опираются при решении различного рода задач. А тем не менее и они могут преподнести сюрпризы, если использовать только их графическую иллюстрацию решения, пренебрегая правилами исследования функций.
Вопросу решения уравнений графическими методами в школьном курсе математики отводится далеко не последнее место, причем делается это в течение всего времени изучения курса алгебры и начал анализа. К графической иллюстрации решения уравнений, систем уравнений, задач с параметрами и во многих других случаях активно обращаются авторы всех школьных учебников и многочисленных методических пособий. Не обойден вниманием этот метод и в задачах для сдачи ЕГЭ – и это, конечно, оправдано, как говорится, лучше один раз увидеть.
Однако, несмотря на такое внимание к данному вопросу, полного понимания о границах применения данного метода у учеников все-таки нет. Об этом красноречиво свидетельствуют результаты экзаменационных работ как в традиционной форме, так и в форме ЕГЭ. Поэтому мы решили еще раз обратиться к этой теме, тем более что будут рассмотрены функции, тщательно изучаемые в школе. Этот факт интересен тем, что даже в случаях, когда мы имеем дело с графиками хорошо знакомых функций, очень легко ошибиться, если не провести исследование методами высшей математики, а строить графики по точкам.
Итак, рассмотрим уравнение , графическое решение которого приведено на рис. 1.
Функция монотонно возрастает на всей области определения, скорость ее роста больше скорости роста функции , а значит, уравнение решений не имеет. Для всех оснований показательной и логарифмической функций картина принципиально не изменится. Другое дело при . Возьмем уравнение . Его решение изображено на рис. 2.
Так как показательная и логарифмическая функции с одинаковыми основаниями являются взаимообратными, то их графики симметричны относительно прямой , а значит, одно решение лежит на биссектрисе первого координатного угла.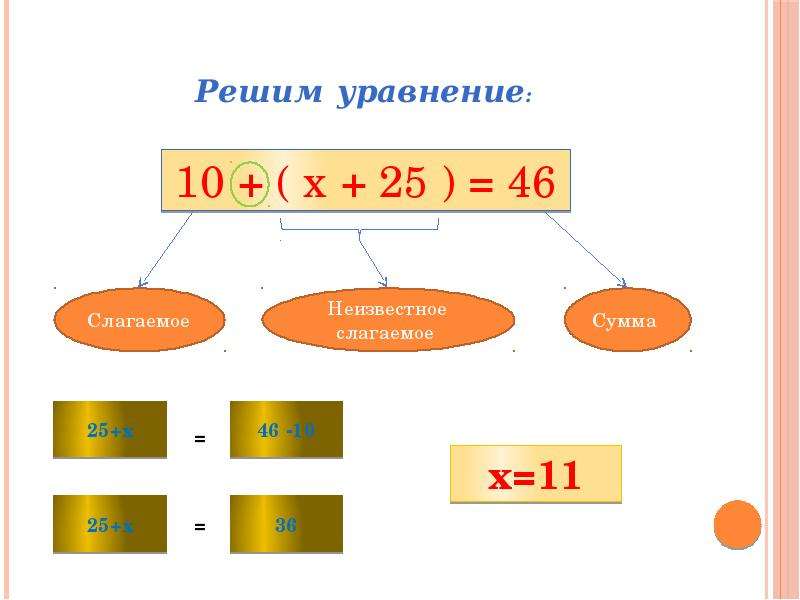 И вроде бы никаких других корней быть не должно, хотя утверждать это, конечно, мы не имеем права. Обе функции – логарифмическая и показательная – монотонно убывают на всей области определения, следовательно, решение может быть и не единственным.
И вроде бы никаких других корней быть не должно, хотя утверждать это, конечно, мы не имеем права. Обе функции – логарифмическая и показательная – монотонно убывают на всей области определения, следовательно, решение может быть и не единственным.
Действительно, утверждать, что имеется одно решение, можно только тогда, когда одна функция монотонно убывает, а вторая монотонно возрастает. К сожалению, об этой теореме ребята часто забывают, полагаясь только на визуальное восприятие картины, и делают ошибки. Ведь при сдаче ЕГЭ им приходится решать уравнения, в которых один корень надо угадать, а потом доказать, что других корней нет, опираясь на свойства монотонных функций. Тем не менее в рассматриваемом случае решение все-таки одно.
Рассмотрим другое уравнение
Оно очень похоже на предыдущее, у него есть решение, лежащее на биссектрисе угла первой четверти, но при этом присутствует достаточно большой кусок, на котором графики фактически сливаются, как говорится, картина «замазана» и визуально никакого заключения сделать нельзя (рис. 3). Возникает искушение провести аналогию с первым случаем и сделать вывод о единственном корне уравнения. Однако имеется еще два решения: и . Их легко проверить.
3). Возникает искушение провести аналогию с первым случаем и сделать вывод о единственном корне уравнения. Однако имеется еще два решения: и . Их легко проверить.
Возьмем еще одно аналогичное уравнение . Его графическое решение проиллюстрировано на рис. 4, на котором хорошо видно наличие трех корней. Вручную просчитать точки и построить графики второго и третьего уравнений просто нереально, именно по этой причине ученики не могут наглядно увидеть приведенную выше картину, построив графики самостоятельно. В данном случае все приведенные выше графические решения были получены с помощью компьютера.
Конечно же, возникает вопрос, при каком основании a в уравнении появляются три корня вместо одного? Используя численные методы решения уравнений, иными словами, опять же с помощью компьютера, мы получили приблизительный ответ. А несколько позже было получено и аналитическое решение: оказалось, что это происходит при .
Надо еще раз отметить, что получить правильные графические решения уравнений типа для малых оснований a без применения компьютера не представляется возможным. Поэтому у учеников, которые строят графики с гораздо большими основаниями, создается превратное впечатление о количестве корней, такого, казалось бы, хорошо знакомого им уравнения.
Поэтому у учеников, которые строят графики с гораздо большими основаниями, создается превратное впечатление о количестве корней, такого, казалось бы, хорошо знакомого им уравнения.
Итак, использование компьютера для построения некоторых трудоемких графиков разного вида функций в различных ситуациях, безусловно, помогает учителю полнее проиллюстрировать конкретную проблему, сведя затраты времени к минимуму, а школьникам легче в полном объеме разобраться в каждой конкретной задаче, требующей графической интерпретации.
Григорий АСТРАХАРЧИК, сотрудник политехнического университета Каталонии, Испания;
Нина АСТРАХАРЧИК, учитель математики Троицкого лицея, Московская область
Уравнения. Решение уравнений — МАТВОКС
Простейшие уравнения в Древнем Египте умели решать еще 4000 лет тому назад.
Математики древнего Вавилона простейшие уравнения решали с помощью особых таблиц.
Древние греки алгебраические уравнения решали при помощи отрезков. Они алгебраические выражения изображали с помощью чертежей и рисунков. Если нужно было решить уравнение с двумя неизвестными, то одно неизвестное называли «длиной», другое неизвестное называли «шириной», а произведение этих неизвестных называли «площадью». Если решали кубическое уравнение, то третью неизвестную величину они называли «глубина», следовательно, произведение «длины», «ширины» и «глубины» называли «объёмом».
Они алгебраические выражения изображали с помощью чертежей и рисунков. Если нужно было решить уравнение с двумя неизвестными, то одно неизвестное называли «длиной», другое неизвестное называли «шириной», а произведение этих неизвестных называли «площадью». Если решали кубическое уравнение, то третью неизвестную величину они называли «глубина», следовательно, произведение «длины», «ширины» и «глубины» называли «объёмом».
В III веке до новой эры древнегреческий математик Эвклид вторую книгу «Начала» посвятил решению квадратных уравнений.
В I веке до новой эры греческий математик и инженер Герон решение квадратных уравнений впервые описывает алгебраическим способом.
И уже в III веке новой эры греческий учёный Диофант решает квадратные уравнения только алгебраическим путем. Он применял буквенные обозначения для неизвестных и использовал сокращения слов.
В 499 году новой эры индийский математик и астроном Ариабхата в трактате по астрономии «Ариабхатия» решал задачи с квадратными уравнениями.
В VII веке новой эры индийский ученый Брахмагупта изложил правила решения квадратных уравнений, приведенных в виду ax2+bx=c, где a>0.
В 825 году арабский математик и астроном Мухаммед Аль-Хорезми написал трактат «Китаб аль-джебр валь-мукабала», что в переводе означает «Краткая книга о восполнении и противопоставлении».
Трактат аль-Хорезми — важная веха развития арифметики и классической алгебры, науки о решении уравнений. Он на столетия определил характер алгебры как практической науки без аксиоматической основы.
Буквенные обозначения для коэффициентов уравнения и неизвестных величин впервые ввел французский математик Франсуа Виет.
В 1544 г немецкий математик Михаэль Штифель сформулировал общие правила решения квадратных уравнений, приведенных к виду x2+bx=c.
В XVII веке французский математик Альбер Жирар (жил в Нидерландах) написал книгу «Новое открытие в алгебре». В своем труде А. Жирар сформулировал теорему о корнях уравнения.
Немецкий математик Иоганн Карл Фридрих Гаусс в 1798 г в книге «Арифметические исследования» дал строгое доказательство о корнях уравнения.
Благодаря трудам многих ученых-математиков способ решения квадратных уравнений принял современный вид в XVII веке.
Решение и интегрирование уравнений с помощью Графического калькулятора на Mac
В меню «Уравнения» Графического калькулятора имеются функции для поиска значений уравнений и интегрирования.
Открыть Графический калькулятор
Поиск решения уравнения в заданной точке
В приложении «Графический калькулятор» на Mac создайте график или откройте уже существующий график.
Выделите уравнение и затем выберите «Уравнение» > «Вычисление».

В окне «Вычисление» введите точку, для которой нужно найти значение, в поле «Ввод» (для трехмерных графиков предусмотрено два поля ввода) и нажмите клавишу Return.
В списке под полем «Ввод» появятся автоматически вычисленные значения.
Можно выполнить любое из следующих действий.
Просмотр связанных уравнений на графике. Выберите уравнения в разделе «Просмотр».
Изменение цвета связанных уравнений. Нажимайте цветные кнопки рядом с уравнениями.
Добавление выделенных связанных уравнений на график. Нажмите «Начертить».
Вычисление интегралов
В приложении «Графический калькулятор» на Mac создайте график или откройте уже существующий график.
Выделите уравнение и затем выберите «Уравнение» > «Интегрирование».
В окне «Интегрирование» выберите нужные варианты.
Выбор вычисляемых значений.
 Нажмите всплывающее меню «Интеграция» и выберите вариант.
Нажмите всплывающее меню «Интеграция» и выберите вариант.Ввод границ. Введите значения в поля над и под знаком интеграла.
Граница — бесконечность. Нажмите всплывающее меню рядом со знаком интеграла (у трехмерных графиков есть такое меню рядом с каждым знаком интеграла).
Изменение метода вычисления значения. Нажмите треугольник рядом с полем «Метод», нажмите всплывающее меню и выберите метод вычисления. Эти значения по умолчанию можно изменить для любого из методов.
Вычисление интеграла. Нажмите «Вычислить». Это действие выделит область или поверхность уравнения на графике.
Снятие выделения. Закройте диалоговое окно «Интегрирование» и выберите «Уравнение» > «Удалить интегрируемую область».
Урок 24. Решение уравнений в Mathcad – использование функций
Решение уравнений является важным для решения практических задач. Поэтому уделим уравнениям еще один урок.
Блок решения в функции
Если Вы хотите исследовать изобразить на графике поведение уравнения в зависимости от значения определенного параметра, Вам, возможно, придется решить систему уравнений много раз. Вы можете сделать это, используя блок решения в функции. Покажем на примере: предположим, мы хотим исследовать поведение решения следующего уравнения в зависимости от различных значения параметра A:
Блоку решения не нужно ни значение параметра, ни начальное приближение, поскольку решение есть функция этих двух значений. Эти значения мы будем задавать при вызове функции.
Функцию можно использовать сколько угодно раз:
Использовать функцию можно с диапазоном переменных:
Такая техника решения не самая надежная. Если хотя бы одно решение не может быть найдено, Вы не получите и решений для других параметров (это произойдет, если задать A<0.7). Поэтому лучше заранее проверить свою функцию.
Сообщения об ошибке можно избежать, написав маленькую программу:
Если блок решения выдает сообщение об ошибке, на выходе получим значение NaN (Not a Number – «Не Число»), которое просто не отображается на графике:
Построим две ветки уравнения с использованием этого приема:
Когда переменных много
Расчеты часто содержат несколько переменных, но Вам, возможно, придется использовать лишь некоторые из них. В качестве примера рассмотрим систему восьми уравнений, где нам нужно получить только значения X и Y. Начальные приближения следует задать для всех переменных:
Решение представляет собой вектор из восьми элементов, но нам нужны лишь элементы с индексами 0 и 1.
Минимизация ошибки
Find() – не единственный решатель в Mathcad. Еще один полезным решателем является Minnerr(), находящий решения, которые минимизируют ошибку в системе уравнений. Рассмотрим пример: есть набор данных, которые мы хотим аппроксимировать уравнением Бейтмена:
Рассмотрим пример: есть набор данных, которые мы хотим аппроксимировать уравнением Бейтмена:
Мы хотим подобрать три константы в уравнении Бейтмена таким образом, чтобы ошибка приближения была минимальна. У нас есть семь уравнений (по одной для каждого эксперимента) и три константы, так что в системе избыток данных. Minerr() может обработать эту проблему:
Замечания:
- Три константы являются переменными для этой системы.
- Переменные не могут иметь счетных индексов.
- У параметров (t и c) могут быть счетные индексы.
Возможно, Вам хотелось бы использовать цикл for для семи уравнений, но в блоке решений этого сделать нельзя.
Для полностью определенных систем (с одинаковым числом независимых уравнений и неизвестных) функция Minerr() дает тот же ответ, что и Find().
Резюме
В этом уроке мы определили способы расширенного использования блоков решения:
- Вы можете определить вывод блока решения как функцию.
 Таким образом в блок решения можно передавать параметры и начальные приближения.
Таким образом в блок решения можно передавать параметры и начальные приближения. - Если при вычислении точек для графика хотя бы одно решение не будет найдено, то график не будет построен. Этой ошибки можно избежать, написав небольшую программу с использованием “try/on error”, которая выводит NaN (Not a Number – Не Число), если результат отсутствует.
- Для двух и более неизвестных (и уравнений) вывод блока решения является вектором. Если нужен один или два элемента этого вектора, их можно вывести, используя подстрочные индексы.
- Вместо функции Find() можно использовать Minerr() – она минимизирует ошибку для заданного набора ограничений, в том числе, если данные избыточны. Minerr() часто может дать приближенный результат, когда Find() выдает ошибку.
Другие интересные материалы
9.8: Решение систем с помощью правила Крамера
Цели обучения
- Оценить 2 × 2 определителя.

- Используйте правило Крамера, чтобы решить систему уравнений с двумя переменными.
- Оценить 3 × 3 определителя.
- Используйте правило Крамера, чтобы решить систему из трех уравнений с тремя переменными.
- Знать свойства определителей.
Мы научились решать системы уравнений с двумя переменными и тремя переменными, а также несколькими методами: подстановкой, сложением, методом исключения Гаусса, использованием обратной матрицы и построением графика.Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.
Вычисление определителя матрицы 2 × 2
Определитель — это действительное число, которое может быть очень полезно в математике, поскольку имеет множество применений, например, для вычисления площади, объема и других величин. Здесь мы будем использовать определители, чтобы выяснить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются закодированными в матрице. Данные могут быть расшифрованы только с помощью обратимой матрицы и определителя. Для наших целей мы сосредоточимся на определителе как признаке обратимости матрицы. Вычисление определителя матрицы включает в себя следование определенным шаблонам, описанным в этом разделе.
НАЙТИ ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2 × 2
Определитель матрицы 2 × 2 при заданном
\(A=\begin{bmatrix}a&b\\c&d\end{bmatrix}\)
определяется как
Обратите внимание на изменение обозначений.Есть несколько способов указать определитель, в том числе \(\det(A)\) и замена скобок в матрице прямыми, \(| A |\).
Пример \(\PageIndex{1}\): нахождение определителя матрицы \(2 × 2\)
Найдите определитель данной матрицы.
\(A=\begin{bmatrix}5&2\\−6&3\end{bmatrix}\)
Раствор
\[\begin{align*} \det(A)&= \begin{vmatrix}5&2\\-6&3\end{vmatrix}\\ &= 5(3)-(-6)(2)\\ & = 27 \конец{выравнивание*}\]
Использование правила Крамера для решения системы двух уравнений с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители. Этот метод, известный как правило Крамера , восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году в году. Курб алгебры . Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных.
Этот метод, известный как правило Крамера , восходит к середине 18 века и назван в честь его новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году в году. Курб алгебры . Правило Крамера — жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, как и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если она существует.Однако, если система не имеет решения или имеет бесконечное число решений, на это будет указывать нулевой определитель. Чтобы выяснить, является ли система противоречивой или зависимой, придется использовать другой метод, такой как исключение.
Чтобы понять правило Крамера, давайте внимательно посмотрим, как мы решаем системы линейных уравнений, используя основные операции со строками. Рассмотрим систему двух уравнений с двумя переменными.
\[\begin{align} a_1x+b_1y&= c_1 (1) \label{eq1}\\ a_2x+b_2y&= c_2 (2) \label{eq2}\\ \end{align}\]
Мы исключаем одну переменную, используя операции со строками, и находим другую. Скажем, что мы хотим найти \(x\). Если уравнение \ref{eq2} умножается на коэффициент, противоположный коэффициенту \(y\) в уравнении \ref{eq1}, уравнение \ref{eq1} умножается на коэффициент \(y\) в уравнении \ref {eq2}, и мы добавим два уравнения, переменная \(y\) будет исключена.
Скажем, что мы хотим найти \(x\). Если уравнение \ref{eq2} умножается на коэффициент, противоположный коэффициенту \(y\) в уравнении \ref{eq1}, уравнение \ref{eq1} умножается на коэффициент \(y\) в уравнении \ref {eq2}, и мы добавим два уравнения, переменная \(y\) будет исключена.
\[\begin{align*} &b_2a_1x+b_2b_1y = b_2c_1 & \text{Умножить}R_1 \text{ на }b_2 \\ -&\underline{b_1a_2x-b_1b_2y=-b_1c_2} & \text{Умножить}R_2 \text { по }-b_1 \\ & b_2a_1x-b_1a_2x=b_2c_1-b_1c_2 \end{align*}\]
Теперь найдите \(x\).
\[\begin{align*} b_2a_1x−b_1a_2x &= b_2c_1−b_1c_2 \\ x(b_2a_1−b_1a_2) &= b_2c_1−b_1c_2 \\ x &= \dfrac{b_2c_1−b_1c_2}{b_2a_1−b_1a_2}=\dfrac {\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align*}\]
Аналогично, чтобы найти \(y\), мы исключим \(x\).
\[\begin{align*} & a_2a_1x+a_2b_1y = a_2c_1 & \text{Multiply}R_1 \text{ на }a_2 \\ -& \underline{a_1a_2x-a_1b_2y=-a_1c_2} & \text{Multiply}R_2 \ text{ by }-a_1 \\ & a_2b_1y-a_1b_2y =a_2c_1-a_1c_2 \end{align*}\]
Решение для \(y\) дает
\[ \begin{align*} a_2b_1y−a_1b_2y &= a_2c_1−a_1c_2 \\ y(a_2b_1−a_1b_2) &= a_2c_1−a_1c_2 \\ y &= \dfrac{a_2c_1−a_1c_2}{a_2b_1−a_1b_2}=\dfrac {a_1c_2−a_2c_1}{a_1b_2−a_2b_1}=\dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix}} \end{align* }\]
Обратите внимание, что знаменатель для \(x\) и \(y\) является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для решения \(x\) и \(y\), но правило Крамера также вводит новое обозначение:
- \(D\): определитель матрицы коэффициентов
- \(D_x\): определитель числителя в решении \(x\)
\[х=\dfrac{D_x}{D}\]
- \(D_y\): определитель числителя в решении \(y\)
\[y=\dfrac{D_y}{D}\]
Ключом к правилу Крамера является замена интересующего столбца переменных столбцом констант и вычисление определителей.Тогда мы можем выразить \(x\) и \(y\) как частное двух определителей.
ПРАВИЛО КРАМЕРА ДЛЯ \(2×2\) СИСТЕМ
Правило Крамера — это метод, использующий определители для решения систем уравнений, в которых число уравнений равно числу переменных.
Рассмотрим систему двух линейных уравнений с двумя переменными.
\[\begin{align*} a_1x+b_1y&= c_1\\ a_2x+b_2y&= c_2 \end{align*}\]
Решение с использованием правила Крамера дано как
\[\begin{align} x&= \dfrac{D_x}{D} = \dfrac{\begin{bmatrix}c_1&b_1\\c_2&b_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{ бматрица}}\; , D\neq 0\\ y&= \dfrac{D_y}{D} = \dfrac{\begin{bmatrix}a_1&c_1\\a_2&c_2\end{bmatrix}}{\begin{bmatrix}a_1&b_1\\a_2&b_2\end{bmatrix }}\; , D\neq 0 \end{align}\]
Если мы находим \(x\), столбец \(x\) заменяется столбцом констант. Если мы ищем \(y\), столбец \(y\) заменяется постоянным столбцом.
Если мы ищем \(y\), столбец \(y\) заменяется постоянным столбцом.
Пример \(\PageIndex{2}\): использование правила Крамера для решения системы \(2 × 2\)
Решите следующую систему \(2 × 2\), используя правило Крамера.
\[\begin{align*} 12x+3y&= 15\\ 2x-3y&= 13 \end{align*}\]
Раствор
Найдите \(x\).
\[\begin{align*} x&= \dfrac{D_x}{D}\\ &= \dfrac{\begin{bmatrix}15&3\\13&-3\end{bmatrix}}{\begin{bmatrix}12&3 \\2&-3\end{bmatrix}}\\ &= \dfrac{-45-39}{-36-6}\\ &= \dfrac{-84}{-42}\\ &= 2 \end {выравнивание*}\]
Найдите \(y\).
\[\begin{align*} y&= \dfrac{D_y}{D}\\ &= \dfrac{\begin{bmatrix}12&15\\2&13\end{bmatrix}}{\begin{bmatrix}12&3\\ 2&-3\end{bmatrix}}\\ &= \dfrac{156-30}{-36-6}\\ &= -\dfrac{126}{42}\\ &= -3 \end{align* }\]
Решение: \((2,−3)\).
Упражнение \(\PageIndex{1}\)
Используйте правило Крамера, чтобы решить систему \(2 × 2\) уравнений.
\[\begin{align*} x+2y&= -11\\ -2x+y&= -13 \end{align*}\]
- Ответить
\((3,−7)\)
Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2×2 несложно, но найти определитель матрицы 3×3 сложнее.Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (слева вверху справа внизу) и вычитаем произведения записей на по каждой из трех диагоналей (слева внизу на право вверху). Это легче понять с визуальным и пример.
Найдите определитель матрицы 3×3.
\(A=\begin{bmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{bmatrix}\)
- Дополнить \(A\) первыми двумя столбцами.
\(\det(A)=\left| \begin{array}{ccc|cc} a_1&b_1&c_1&a_1&b_1\\a_2&b_2&c_2&a_2&b_2\\a_3&b_3&c_3&a_3&b_3\end{array} \right|\)
- От верхнего левого угла к нижнему правому: умножьте числа по первой диагонали.
 Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали. - Из нижнего левого угла в верхний правый: вычтите произведение записей вверх по первой диагонали.Из этого результата вычтите произведение вхождений вверх по второй диагонали. Из этого результата вычтите произведение вхождений вверх по третьей диагонали.
Алгебра выглядит следующим образом:
\(| A |=a_1b_2c_3+b_1c_2a_3+c_1a_2b_3−a_3b_2c_1−b_3c_2a_1−c_3a_2b_1\)
Пример \(\PageIndex{3}\): нахождение определителя матрицы 3 × 3
Найдите определитель матрицы \(3 × 3\) по данному
\(A=\begin{bmatrix}0&2&1\\3&−1&1\\4&0&1\end{bmatrix}\)
Раствор
Дополните матрицу первыми двумя столбцами, а затем следуйте формуле.Таким образом,
\[\begin{align*} | А | &= \влево| \begin{массив}{ccc|cc}0&2&1&0&2\\3&-1&1&3&-1\\4&0&1&4&0\end{массив}\right| \\ &= 0(−1)(1)+2(1)(4)+1(3)(0)−4(−1)(1)−0(1)(0)−1(3) (2) \\ &=0+8+0+4−0−6 \\ &= 6 \end{align*}\]
Упражнение \(\PageIndex{2}\)
Найдите определитель матрицы 3 × 3.
\(\det(A)=\begin{vmatrix}1&−3&7\\1&1&1\\1&−2&3\end{vmatrix}\)
- Ответить
\(−10\)
Q&A: Можно ли использовать тот же метод для нахождения определителя большей матрицы?
Нет, этот метод работает только для матриц 2 × 2 и 3 × 3.Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы \(3 × 3\), мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными. Правило Крамера является простым и следует шаблону, согласующемуся с правилом Крамера для матриц \(2 × 2\). Однако по мере увеличения порядка матрицы до \(3 × 3\) требуется гораздо больше вычислений.
Когда мы вычисляем определитель равным нулю, правило Крамера не указывает, имеет ли система решение или бесконечное число решений. Чтобы выяснить это, мы должны выполнить исключение в системе.
Чтобы выяснить это, мы должны выполнить исключение в системе.
Рассмотрим систему уравнений \(3 × 3\).
\[\begin{align} a_1x+b_1y+c_1z &= \color{blue}d_1 \\ a_2x+b_2y+c_2z &= \color{blue}d_2 \\ a_3x+b_3y+c_3z &= \color{blue} d_3 \\ \end{выравнивание}\]
\(x=\dfrac{D_x}{D}\), \(y=\dfrac{D_y}{D}\), \(z=\dfrac{D_z}{D}\), \(D≠ 0\)
где
\[D = \begin{vmatrix} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_x = \begin{vmatrix} \color{blue}d_1 & b_1 & c_1\\ \color{blue}d_2 & b_2 & c_2\\ \color{blue}d_3 & b_3 & c_3 \end{vmatrix}\; ,\; D_y = \begin{vmatrix} a_1 & \color{blue}d_1 & c_1\\ a_2 & \color{blue}d_2 & c_2\\ a_3 & \color{blue}d_3 & c_3 \end{vmatrix}\; ,\; D_z = \begin{vmatrix} a_1 & b_1 & \color{blue}d_1\\ a_2 & b_2 & \color{blue}d_2\\ a_3 & b_3 & \color{blue}d_3 \end{vmatrix}\]
Если мы записываем определитель \(D_x\), мы заменяем столбец \(x\) столбцом констант.Если мы записываем определитель \(D_y\), мы заменяем их столбец y на постоянный столбец. Если мы записываем определитель \(D_z\), мы заменяем столбец \(z\) постоянным столбцом. Всегда проверяйте ответ.
Если мы записываем определитель \(D_z\), мы заменяем столбец \(z\) постоянным столбцом. Всегда проверяйте ответ.
Пример \(\PageIndex{4}\): решение системы \(3 × 3\) с использованием правила Крамера
Найдите решение данной системы \(3 × 3\), используя правило Крамера.
\[\begin{align*} x+y-z&= 6\\ 3x-2y+z&= -5\\ x+3y-2z&= 14 \end{align*}\]
Раствор
Используйте правило Крамера.
\(D=\begin{vmatrix}1&1&−1\\3&−2&1\\1&3&−2\end{vmatrix}\), \(D_x=\begin{vmatrix}6&1&−1\\−5&−2&1\ \14&3&−2\end{vmatrix}\), \(D_y=\begin{vmatrix}1&6&−1\\3&−5&1\\1&14&−2\end{vmatrix}\), \(D_z=\begin{vmatrix }1&1&6\\3&−2&−5\\1&3&14\end{vmatrix}\)
Затем,
\[\begin{align*} x&= \dfrac{D_x}{D}&= \dfrac{-3}{-3}&= 1\\ y&= \dfrac{D_y}{D}&= \dfrac {-9}{-3}&= 3\\ z&= \dfrac{D_z}{D}&= \dfrac{6}{-3}&= -2\\ \end{align*}\]
Решение: \((1,3,−2)\).
Упражнение \(\PageIndex{3}\)
Используйте правило Крамера, чтобы решить матрицу \(3 × 3\).
\[\begin{align*} x-3y+7z&= 13\\ x+y+z&= 1\\ x-2y+3z&= 4 \end{align*}\]
- Ответить
\(\влево(−2,\dfrac{3}{5},\dfrac{12}{5}\вправо)\)
Пример \(\PageIndex{5A}\): использование правила Крамера для решения несогласованной системы
Решите систему уравнений по правилу Крамера.
\[\begin{align} 3x-2y&= 4 \label{eq3}\\ 6x-4y&= 0 \label{eq4}\end{align}\]
Раствор
Начнем с нахождения определителей \(D\), \(D_x\) и \(D_y\).
\(D=\begin{vmatrix}3&-2\\6&-4\end{vmatrix}=3(-4)−6(-2)=0\)
Мы знаем, что определитель, равный нулю, означает, что либо система не имеет решений, либо имеет бесконечное число решений. Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.
- Умножить уравнение \ref{eq3} на \(−2\).
- Добавьте результат к уравнению \ref{eq4}.
\[\begin{align*} &−6x+4y=−8 \\ &\;\;\;\underline{6x−4y=0} \\ &\;\;\;\;\;\ ;\;\;\;\; 0=−8 \end{align*}\]
Получаем уравнение \(0=−8\), которое неверно. Следовательно, система не имеет решений. График системы показывает две параллельные линии. См. рисунок \(\PageIndex{1}\).
Следовательно, система не имеет решений. График системы показывает две параллельные линии. См. рисунок \(\PageIndex{1}\).
Пример \(\PageIndex{5B}\): использование правила Крамера для решения зависимой системы
Решите систему с бесконечным числом решений.
\[\begin{align} x-2y+3z&= 0 \label{eq5}\\ 3x+y-2z&= 0 \label{eq6}\\ 2x-4y+6z&= 0 \label{eq7} \end {выравнивание}\]
Раствор
Сначала найдем определитель. Настройте матрицу, дополненную первыми двумя столбцами.
\(\left| \begin{array}{ccc|cc}1&−2&3&1&-2\\3&1&−2&3&1\\2&−4&6&2&-4\end{массив}\right|\)
Затем,
\(1(1)(6)+(−2)(−2)(2)+3(3)(−4)−2(1)(3)−(−4)(−2)(1 )−6(3)(−2)=0\)
Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное число решений.Мы должны выполнить исключение, чтобы узнать.
1. Умножьте уравнение \ref{eq5} на \(−2\) и добавьте результат к уравнению \ref{eq7}:
\[\begin{align*} &−2x+4y−6x=0 \\ &\;\;\underline{2x−4y+6z=0} \\ &\;\;\;\;\;\ ;\;\;\;\;\;\;\;\;\;\;0=0 \end{align*}\]
2. Получение ответа \(0=0\), утверждение, которое всегда истинно, означает, что система имеет бесконечное число решений. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой.См. рисунок \(\PageIndex{2}\).
Получение ответа \(0=0\), утверждение, которое всегда истинно, означает, что система имеет бесконечное число решений. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой.См. рисунок \(\PageIndex{2}\).
Понимание свойств определителей
Есть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
- Если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
- При перестановке двух строк определитель меняет знак.{−1}\) — величина, обратная определителю матрицы \(A\).
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
Пример \(\PageIndex{6}\): Иллюстрация свойств определителей
Проиллюстрируйте каждое из свойств определителей.
Раствор
Свойство 1 гласит, что если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
\(A=\begin{bmatrix}1&2&3\\0&2&1\\0&0&−1\end{bmatrix}\)
Дополнить \(A\) первыми двумя столбцами.
\(A=\left[ \begin{array}{ccc|cc}1&2&3&1&2\\0&2&1&0&2\\0&0&-1&0&0\end{массив}\right]\)
Затем
\[\begin{align*} \det(A)&= 1(2)(-1)+2(1)(0)+3(0)(0)-0(2)(3)-0 (1)(1)+1(0)(2)\\ &= -2 \end{align*}\]
Свойство 2 указывает, что при перестановке строк меняется знак.Учитывая
\[\begin{align*} A&=\begin{bmatrix}-1&5\\4&-3\end{bmatrix}\\ \det(A)&= (-1)(-3)-(4)( 5)\\ &= 3-20\\ &= -17 \end{align*}\]
\[\begin{align*} B&= \begin{bmatrix}4&-3\\-1&5\end{bmatrix}\\ \det(B)&= (4)(5)-(-1)(- 3)\\ &= 20-3\\ &= 17 \end{align*}\]
Свойство 3 гласит, что если две строки или два столбца идентичны, определитель равен нулю.
\[\begin{align*} A&=\left[ \begin{array}{ccc|cc}1&2&2&1&2\\2&2&2&2&2\\-1&2&2&-1&2\end{массив}\right]\\ \det(A)& =1(2)(2)+2(2)(-1)+2(2)(2)+1(2)(2)-2(2)(1)-2(2)(2)\ \ &=4-4+8+4-4-8\\ &=0 \end{align*}\]
Свойство 4 гласит, что если строка или столбец равны нулю, определитель равен нулю. {-1})&=-2\left(-\dfrac{1}{2}\right)-\dfrac{3}{2}(1)\\ &=-\dfrac{1}{2} \ конец{выравнивание*}\]
{-1})&=-2\left(-\dfrac{1}{2}\right)-\dfrac{3}{2}(1)\\ &=-\dfrac{1}{2} \ конец{выравнивание*}\]
Свойство 6 гласит, что если любую строку или столбец матрицы умножить на константу, определитель умножается на тот же коэффициент. Таким образом,
\[\begin{align*} A&=\begin{bmatrix}1&2\\3&4\end{bmatrix}\\ \det(A)&=1(4)-2(3)\\ &=-2 \ конец{выравнивание*}\]
\[\begin{align*} B&=\begin{bmatrix}2(1)&2(2)\\3&4\end{bmatrix}\\ \det(B)&=2(4)-3(4) \\ &=-4 \end{выравнивание*}\]
Пример \(\PageIndex{7}\): использование правила Крамера и свойств определителя для решения системы
Найдите решение данной системы \(3 × 3\).
\[\begin{align} 2x+4y+4z&=2 \label{eq8}\\ 3x+7y+7z&=-5 \label{eq9}\\ x+2y+2z&=4 \label{eq10}\ конец{выравнивание}\]
Раствор
Используя правило Крамера, мы имеем
\(D=\begin{bmatrix}2&4&4\\3&7&7\\1&2&2\end{bmatrix}\)
Обратите внимание, что второй и третий столбцы идентичны.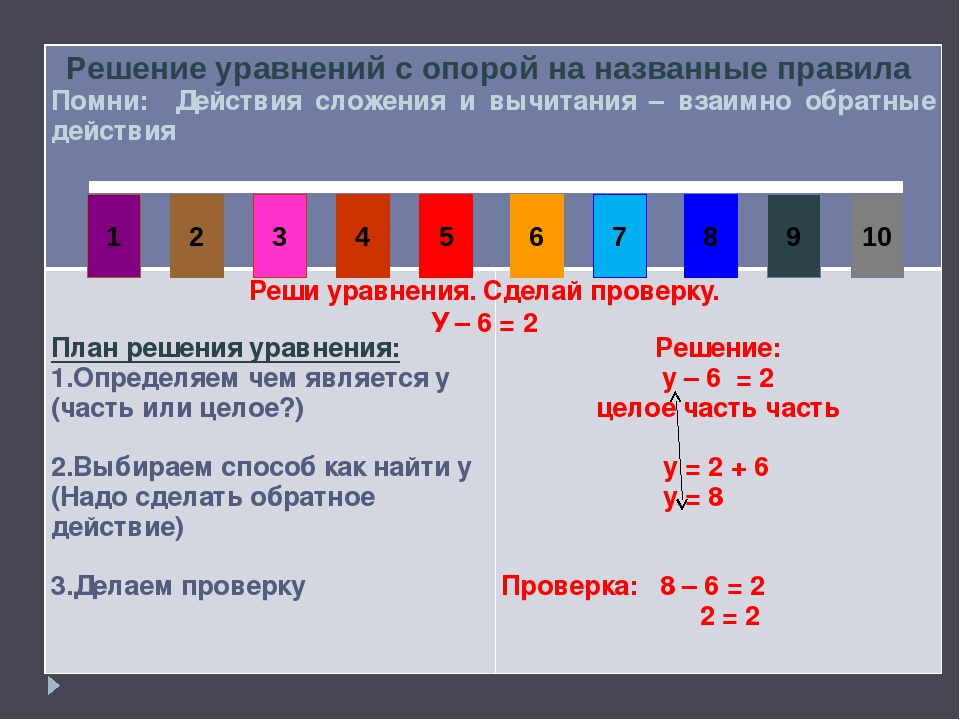 Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество.Мы должны выполнить исключение, чтобы узнать.
Согласно свойству 3 определитель будет равен нулю, поэтому решения либо нет, либо решений бесконечное множество.Мы должны выполнить исключение, чтобы узнать.
1. Умножьте уравнение \ref{eq10} на \(–2\) и добавьте результат к уравнению \ref{eq8}.
\[\begin{align*} -2x-4y-4x&=-8\\ 2x+4y+4z&=2\\ 0&=-6 \end{align*}\]
Получение утверждения, являющегося противоречием, означает, что система не имеет решения.
СМИ
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с правилом Крамера.
Ключевые понятия
- Определитель для \(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) равен \(ad-bc\).См. пример \(\PageIndex{1}\).
- Правило Крамера заменяет столбец переменной столбцом константы. Решения: \(x=\dfrac{D_x}{D}\), \(y=\dfrac{D_y}{D}\). См. пример \(\PageIndex{2}\).
- Чтобы найти определитель матрицы \(3×3\), увеличьте первые два столбца. Сложите три диагональных элемента (слева вверху справа внизу) и вычтите три элемента по диагонали (слева внизу справа вверху).
 См. пример \(\PageIndex{3}\).
См. пример \(\PageIndex{3}\). - Чтобы решить систему из трех уравнений с тремя переменными с помощью правила Крамера, замените столбец переменных столбцом констант для каждого требуемого решения: \(x=\dfrac{D_x}{D}\), \(y=\dfrac{ D_y}{D}\), \(z=\dfrac{D_z}{D}\).См. пример \(\PageIndex{4}\).
- Правило Крамера также полезно для нахождения решения системы уравнений без решения или с бесконечным числом решений. См. Пример \(\PageIndex{5}\) и Пример \(\PageIndex{6}\).
- Некоторые свойства определителей полезны при решении задач. Например:
- Если матрица имеет форму верхнего треугольника, определитель равен произведению элементов по главной диагонали.
- При перестановке двух строк определитель меняет знак.{−1}\) — величина, обратная определителю матрицы \(A\).
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент. См. Пример \(\PageIndex{7}\) и Пример \(\PageIndex{8}\).

Авторы и авторство
Решения с использованием определителей с тремя переменными
Линейные уравнения: решения с использованием определителей с тремя переменными
Определитель матрицы 2 × 2 определяется следующим образом:
Определитель матрицы 3 × 3 можно определить, как показано ниже.
Каждый младший определитель получается вычеркиванием первого столбца и одной строки.
Пример 1
Оцените следующий определитель.
Сначала найдите второстепенные определители.
Решение
Чтобы использовать определители для решения системы трех уравнений с тремя переменными (правило Крамера), скажем, x , y и z , четыре определителя должны быть сформированы следующим образом:
Запишите все уравнения в стандартной форме.
Создайте определитель знаменателя, D , используя коэффициенты x , y и z из уравнений и оцените его.

создать
5 x d Z D Y D Y 5 D D D Y , и Z -Neumerator, D Z заменив соответствующие коэффициенты x , y и z константами из уравнений в стандартной форме и оценив каждый определитель.
Ответы для x , y и z следующие:
Пример 2
Решите эту систему уравнений, используя правило Крамера.
Найдите второстепенные определители.
Используйте константы для замены x -коэффициентов.
Используйте константы для замены y ‐коэффициентов.
Используйте константы для замены z ‐коэффициентов.
Следовательно,
Чек оставлен вам. Решение: x = 1, y = -2, z = -3.
Если определитель знаменателя D равен нулю, то система либо несовместима, либо зависима. Система зависима, если все определители равны нулю. Система несовместна, если хотя бы один из определителей D x , D y или D z имеет значение, отличное от нуля, а определитель знаменателя имеет значение, не равное нулю. .
Система зависима, если все определители равны нулю. Система несовместна, если хотя бы один из определителей D x , D y или D z имеет значение, отличное от нуля, а определитель знаменателя имеет значение, не равное нулю. .
Решение системы уравнений – методы и примеры
Как решить систему уравнений?
Теперь у вас есть представление о том, как решать линейные уравнения, содержащие одну переменную. Что, если бы вам представили множественных линейных уравнений, содержащих более одной переменной ? Набор линейных уравнений с двумя или более переменными известен как система уравнений .
Существует несколько методов решения систем линейных уравнений.
Эта статья научит решать линейные уравнения с использованием широко используемых методов , а именно подстановки и исключения.
Метод подстановки
Подстановка — это метод решения линейных уравнений, при котором переменная в одном уравнении выделяется, а затем используется в другом уравнении для решения оставшейся переменной.
Общие шаги для замены:
- Составьте подлежащее формулы для переменной в одном из данных уравнений.
- Подставьте значение этой переменной во второе уравнение.’
- Решите уравнение, чтобы получить значение одной из переменных.
- Подставьте полученное значение в любое из уравнений, чтобы также получить значение другой переменной.
Решим пару примеров методом подстановки.
Пример 1
Решите приведенные ниже системы уравнений.
б = а + 2
а + б = 4.
Решение
Подставьте значение b во второе уравнение.
а + (а + 2) = 4
Теперь найдем
а + а + 2 = 4
2а + 2 = 4
2а = 4 – 2
а = 2/2 = 7 9001
Подставьте полученное значение a в первое уравнение.
b = a + 2
b = 1 + 2
b = 3
Следовательно, решение для двух уравнений: a = 1 и b = 3.
Пример 2
Решите следующие уравнения с помощью подстановки.
7x – 3y = 31 ——— (i)
9x – 5y = 41 ——— (ii)
Решение
Из уравнения (i),
7x – 3y = 31
Сделать 900 предмет формулы в уравнении:7x – 3y = 31
Вычтите 7x из обеих частей уравнения 7x – 3y = 31, чтобы получить;
– 3y = 31 – 7x
3y = 7x – 31
3y/3 = (7x – 31)/3
Следовательно, y = (7x – 31)/3
Теперь подставим уравнение y = ( 7x – 31)/3 во второе уравнение: 9x – 5y = 41
9x – 5 × (7x – 31)/3 = 41
Решение уравнения дает;
27x – 35x + 155 = 41 × 3
–8x + 155 – 155 = 123 – 155 x в уравнении y = (7x – 31)/3, получаем;
y = (7 × 4 – 31)/3
y = (28 – 31)/3
y = –3/3
y = –1
Следовательно, решением этих систем уравнений является x = 4 и y = –1
Пример 3
Решите следующие системы уравнений:
2x + 3y = 9 и x – y = 3
Решение 6 x0 90 формула во втором уравнении.
х = 3 + у.
Теперь подставьте это значение x в первое уравнение: 2x + 3y = 9.
⇒ 2(3 + y) + 3y = 9
⇒ 6 + 2y + 3y = 9
y = ⅗ = 0,6
Подставляем полученное значение y во второе уравнение – y =3.
⇒ x = 3 + 0,6
x = 3,6
Следовательно, решение x = 3,6 и y = 0,6
- Приравнять коэффициенты данных уравнений путем умножения на константу.
- Вычтите общие коэффициенты новых уравнений с одинаковыми знаками и сложите, если общие коэффициенты имеют противоположные знаки,
- Решите уравнение, полученное в результате сложения или вычитания
- Подставьте полученное значение в любое из уравнений, чтобы получить значение другого Переменная.
пример 4
4a+3a) +(5b – 5b) = 12 + 9
7a = 21
a = 21/ 7
a = 3
полученное значение a=3 подставляем в уравнение первое уравнение
4(3) + 5b = 12,
12 + 5b = 12
5b = 12-12
5b = 0
b = 0/5 = 0
Следовательно, решение a = 3 и b = 0.
Пример 5
Решить методом исключения.
2x + 3y = 9 ———–(i)
x – y = 3 ———–(ii)
Решение
Умножьте два уравнения на 2 и выполните вычитание.
2x + 3y = 9
(-)
2x – 2y = 6
-5y = -3
y = ⅗ = 0,6
Теперь подставим полученное значение x – y во второе уравнение: = 3
x – 0,6 = 3
x = 3,6
Следовательно, решение: x = 3,6 и y = 0,6
Типы систем уравнений
Непротиворечивые и непротиворечивые системы
Набор решений системы уравнений состоит из всех решений этой системы.Возможны три варианта набора решений для системы.
1.) Система имеет конечное число решений.
2.) Система имеет бесконечное число решений.
3.) Система не имеет решений.
Системы уравнений делятся на две категории: непротиворечивые системы и непротиворечивые системы. непротиворечивая система уравнений имеет по крайней мере одно решение. Несовместимая система не имеет решений. Из трех возможностей множества решений системы первые две представляют непротиворечивую систему, поскольку в обоих случаях система имеет по крайней мере одно решение.Третья возможность представляет собой несогласованную систему, потому что у системы нет решения.
непротиворечивая система уравнений имеет по крайней мере одно решение. Несовместимая система не имеет решений. Из трех возможностей множества решений системы первые две представляют непротиворечивую систему, поскольку в обоих случаях система имеет по крайней мере одно решение.Третья возможность представляет собой несогласованную систему, потому что у системы нет решения.
Например, рассмотрим наш пример с вечеринкой в честь открытия. Мы увидели, что система имеет решение. Таким образом, система является последовательной системой. Мы также можем видеть это на графике этой системы. Если система совместна, то она имеет хотя бы одно решение, а значит, графики уравнений системы хотя бы один раз пересекаются. Поскольку график нашей системы показывает точку пересечения, мы знаем, что система непротиворечива.2 = 1
y = x — 2
Заметим, что график этой системы не имеет точек пересечения. Отсюда следует, что система не имеет решений и является несовместной системой.
Независимые и зависимые системы
Теперь давайте сделаем еще один шаг в классификации наших типов систем. Как мы уже говорили, система непротиворечива, если она имеет хотя бы одно решение.Мы можем дополнительно классифицировать эти непротиворечивые системы. Когда система имеет ровно одно решение, мы говорим, что система независима . Наш первоначальный пример с вечеринкой подпадает под эту категорию, потому что система имеет ровно одно решение. Таким образом, эта система непротиворечива и независима.
Когда система имеет бесконечно много решений, мы называем систему зависимой . Вам может быть интересно, что означает для системы бесконечное множество решений. Чтобы продемонстрировать это явление, рассмотрим следующую систему:
3 x — 5 y = 12
6 x — 10 y = 24
Когда мы рисуем эту систему, как показано на изображении выше, мы видим, что два уравнения имеют один и тот же график. Из-за этого графики пересекаются везде. Поскольку множество решений состоит из всех точек пересечения графиков уравнений системы, мы видим, что существует бесконечное множество решений этой системы. Таким образом, мы бы сказали, что эта система непротиворечива и зависима.
Из-за этого графики пересекаются везде. Поскольку множество решений состоит из всех точек пересечения графиков уравнений системы, мы видим, что существует бесконечное множество решений этой системы. Таким образом, мы бы сказали, что эта система непротиворечива и зависима.
Резюме урока
Система уравнений представляет собой группу из двух или более уравнений с одинаковыми переменными. Решение системы уравнений — это значения переменных, которые делают все уравнения системы верными.Решение системы также является точкой пересечения графиков уравнений системы. Набор решений системы уравнений состоит из всех решений этой системы.
Существует три варианта набора решений системы. Может быть конечное число решений, бесконечное число решений или отсутствие решений. Когда система имеет хотя бы одно решение, мы называем ее согласованной , а когда система не имеет решения, мы называем ее несовместимой .2 + 20,25 Y &= 0\\
Y(Y-1)(Y-20,25)&=0.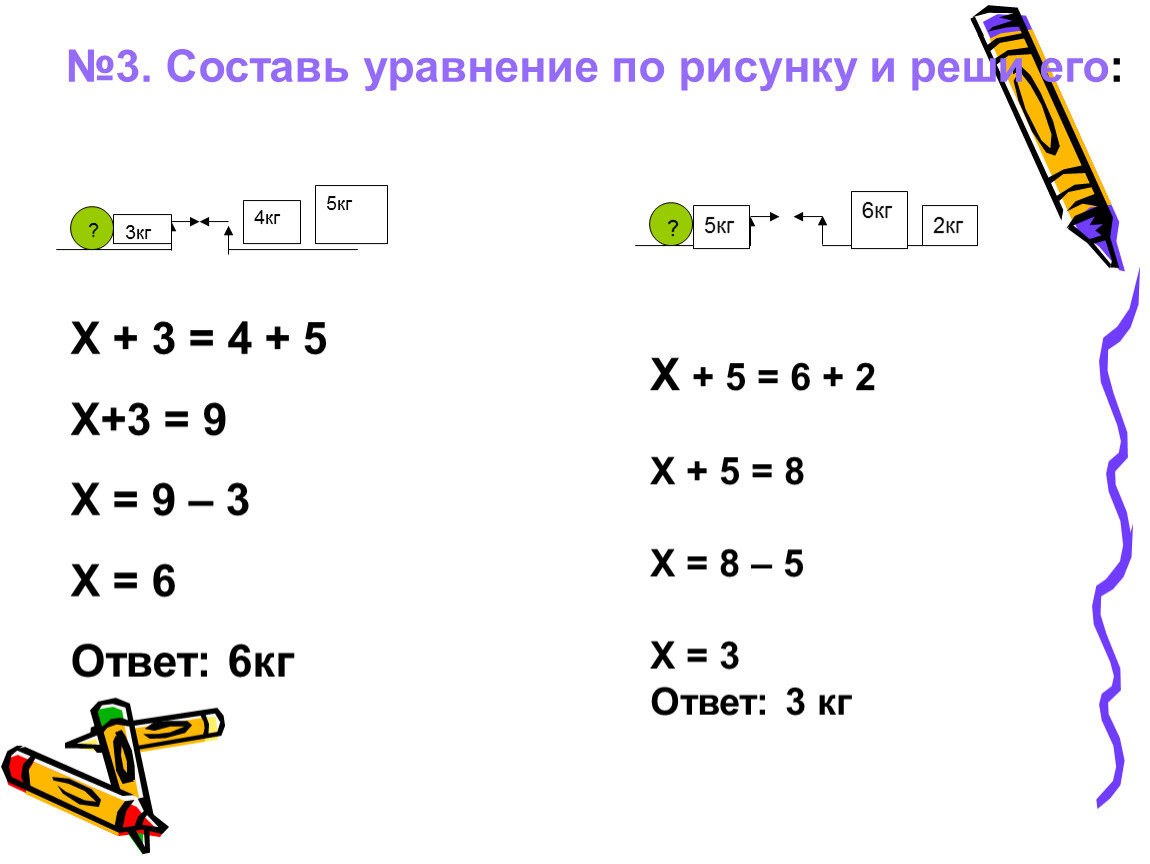 \end{выровнено}Y3 +2f×Y2 +16f2 −4h×Y-64g2Y3 –21,25Y2 +161806,25–(4×370,5625)×Y-6402Y3 -21,25Y2 +16(1806,25–1482,25) ×Y−0Y3 −21,25Y2 +20,25YY(Y−1)(Y−20,25)=0=0=0=0=0.
Тогда 3 корня уравнения равны
Y1=0, Y2=1,Y3= 20,25.Y_1= 0, \quad Y_2= 1, \quad Y_3= 20,25.Y1=0, Y2=1,Y3= 20,25.
Теперь пусть ppp и qqq будут квадратными корнями из любых двух ненулевых чисел Y1,Y2,Y_1, Y_2,Y1,Y2 или Y3:Y_3:Y3:
p=20,25=4,5,q=1=1.p=\sqrt{20,25} = 4,5, \quad q=\sqrt{1}= 1.р=20,25=4,5, q=1=1.
потом
r=-g8×pq=0,s=b4×a=64×3=0,5.r= \frac{-g}{8\times pq} = 0, \quad s=\frac{b}{4\ раз a}= \frac {6}{4×3} = 0,5.r=8×pq−g=0,s=4×ab=4×36=0,5.
Тогда четыре корня уравнения четвертой степени равны
X1=p+q+r-s=4,5+1+0-0,5=5X2=p-q-r-s=4,5-1-0-0,5=3X3=-p+q-r-s=-4,5+ 1-0-0,5=-4X4=-p-q+r-s=-4,5-1+0-0,5=-6. □\begin{выровнено}
X_1&= p + q + r -s = 4,5 + 1 + 0 — 0,5 = 5\\
X_2&= p — q — r -s = 4,5 — 1 — 0 — 0,5 = 3\\
X_3&= -p + q — r -s = -4,5 + 1 — 0 — 0,5 = -4\\
X_4&= -p — q + r -s = -4.5 — 1 + 0 — 0,5 = -6.
\end{выровнено}Y3 +2f×Y2 +16f2 −4h×Y-64g2Y3 –21,25Y2 +161806,25–(4×370,5625)×Y-6402Y3 -21,25Y2 +16(1806,25–1482,25) ×Y−0Y3 −21,25Y2 +20,25YY(Y−1)(Y−20,25)=0=0=0=0=0.
Тогда 3 корня уравнения равны
Y1=0, Y2=1,Y3= 20,25.Y_1= 0, \quad Y_2= 1, \quad Y_3= 20,25.Y1=0, Y2=1,Y3= 20,25.
Теперь пусть ppp и qqq будут квадратными корнями из любых двух ненулевых чисел Y1,Y2,Y_1, Y_2,Y1,Y2 или Y3:Y_3:Y3:
p=20,25=4,5,q=1=1.p=\sqrt{20,25} = 4,5, \quad q=\sqrt{1}= 1.р=20,25=4,5, q=1=1.
потом
r=-g8×pq=0,s=b4×a=64×3=0,5.r= \frac{-g}{8\times pq} = 0, \quad s=\frac{b}{4\ раз a}= \frac {6}{4×3} = 0,5.r=8×pq−g=0,s=4×ab=4×36=0,5.
Тогда четыре корня уравнения четвертой степени равны
X1=p+q+r-s=4,5+1+0-0,5=5X2=p-q-r-s=4,5-1-0-0,5=3X3=-p+q-r-s=-4,5+ 1-0-0,5=-4X4=-p-q+r-s=-4,5-1+0-0,5=-6. □\begin{выровнено}
X_1&= p + q + r -s = 4,5 + 1 + 0 — 0,5 = 5\\
X_2&= p — q — r -s = 4,5 — 1 — 0 — 0,5 = 3\\
X_3&= -p + q — r -s = -4,5 + 1 — 0 — 0,5 = -4\\
X_4&= -p — q + r -s = -4.5 — 1 + 0 — 0,5 = -6. \ _\квадрат
\end{выровнено} X1X2X3X4=p+q+r-s=4.5+1+0-0.5=5=p-q-r-s=4.5-1-0-0.5=3 =-p+q-r-s=-4,5+1-0-0,5=-4=-p-q+r-s=-4,5-1+0-0,5=-6. □
\ _\квадрат
\end{выровнено} X1X2X3X4=p+q+r-s=4.5+1+0-0.5=5=p-q-r-s=4.5-1-0-0.5=3 =-p+q-r-s=-4,5+1-0-0,5=-4=-p-q+r-s=-4,5-1+0-0,5=-6. □
Преобразование уравнений
Уравнения как важный геологический инструмент
Профессор, говорящий на «Математике», что может показаться другим языком! фото Дженнифер М. Веннер.
Иногда может показаться, что ваш инструктор по геофизике говорит на другом языке, когда говорит об уравнениях или формулах.Особенно, если он/она ожидает, что вы «манипулируете» ими или переставите их! Но уравнения могут предоставить мощные инструменты для описания мира природы. В науках о земле мы можем описать поведение многих природных явлений, написав уравнение для линии ( y = mx + b ) или с помощью экспоненциальных функций ( y = e xt ). И с помощью небольшой алгебры мы можем изменить эти уравнения, чтобы решить ЛЮБУЮ из переменных в них.
Хотя это может показаться волшебством, для этого не нужно быть «математиком».Эта страница предназначена для того, чтобы дать вам некоторые инструменты, которые помогут вам изучить некоторые простые шаги, которые помогут вам решить уравнение для любой из переменных (буквы, которые представляют интересующий элемент или количество).
Зачем мне манипулировать уравнениями?
Фотография жонглирования Кена Эндрюса (ученый из JPL). Изменено Джен Веннер.Хотите верьте, хотите нет, но есть много веских причин для развития вашей способности переставлять уравнения, важные для наук о Земле.Это может сэкономить время, помочь вам с единицами и сэкономить место в мозгу! Вот несколько причин развивать свои навыки работы с уравнениями (в произвольном порядке):
- Уравнения легче обрабатывать перед вставкой чисел! И если вы можете изолировать переменную на одной стороне уравнения, оно применимо к любой подобной задаче, которую вам нужно решить для этой переменной!
- Если вы знаете, как манипулировать уравнениями, вам нужно запомнить только одно уравнение, в котором есть все интересующие вас переменные — вы можете манипулировать им, чтобы решить любую другую переменную! Это означает меньше запоминания!
- Работа с уравнениями может помочь вам отслеживать (или вычислять) единицы измерения числа.
 Поскольку единицы определяются уравнениями, если вы манипулируете, подставляете числа и отменяете единицы измерения, вы получите в точности правильные единицы измерения (для данной переменной)!
Поскольку единицы определяются уравнениями, если вы манипулируете, подставляете числа и отменяете единицы измерения, вы получите в точности правильные единицы измерения (для данной переменной)!
Где это используется в науках о Земле?
Честно говоря, манипуляции с уравнениями происходят почти во всех аспектах наук о Земле. Каждый раз, когда вы видите P или T, ρ или x (или даже =), есть уравнение, которым вы можете манипулировать. Поскольку уравнения могут использоваться для описания многих важных природных явлений, возможность манипулировать ими дает вам мощный инструмент для понимания окружающего мира!
Несколько примеров см. на странице Практика манипулирования уравнениями.
Обзор важных правил преобразования уравнений
Решение для y Дженнифер М. Веннер.
Вероятно, вы выучили несколько правил работы с уравнениями на предыдущем курсе алгебры. Никогда не помешает напомнить себе о правилах. Итак, давайте рассмотрим:
Итак, давайте рассмотрим:
- ПРАВИЛО №1: вы можете складывать, вычитать, умножать и делить на что угодно, до тех пор, пока вы делаете то же самое с обеих сторон знака равенства. В уравнении знак равенства действует как точка опоры весов: если вы прибавляете 5 чего-то к одной чаше весов, вы должны прибавить такое же количество к другой стороне, чтобы равновесие оставалось стабильным.То же самое относится и к уравнению — выполнение одной и той же операции с обеими сторонами сохраняет значение уравнения от изменения.
Давайте используем уравнение для линии, чтобы проиллюстрировать пример того, как использовать Правило № 1. Общее уравнение для линии:
Если мы хотим найти b в этом уравнении, мы должны вычесть mx из обеих частей.
Если мы выполним математические действия с каждой стороны (то есть вычтем mx из mx справа), то получим следующее уравнение:
Это уравнение также можно записать в виде b = y — mx, если вы предпочитаете, чтобы решаемая переменная находилась слева.
- ПРАВИЛО №2: чтобы переместить или отменить величину или переменную в одной части уравнения, выполните с ней «противоположные» операции в обеих частях уравнения. Например, если у вас есть g-1=w и вы хотите изолировать g, добавьте 1 к обеим сторонам (g-1+1 = w+1). Упростите (потому что (-1+1)=0) и в итоге получите g = w+1.
Давайте воспользуемся более сложным уравнением, которое геологи могут использовать для выяснения отношения толщины к плотности плавающих веществ (т.г., кора в мантии, айсберги в воде):
, где H над = высота объекта над поверхностью жидкости, в которой он плавает,
H total = общая высота (или толщина) плавающего объекта
ρ объект = плотность объекта
и ρ жидкости = плотность жидкости
Давайте представим, что мы изучаем айсберг и хотим знать, какова плотность этого айсберга. Как нам изменить уравнение для решения этой переменной? Потребуется несколько шагов, чтобы изолировать объект ρ с одной стороны уравнения. С чего начать?
С чего начать?- Начнем с выделения той части уравнения, которая заключена в скобки. Для этого нам нужно разделить обе части на H итого :
Сущность, разделенная сама на себя, равна 1:
, и, поскольку 1, умноженное на что-то, равно этому чему-то, мы можем упростить, чтобы получить: - Мы еще не совсем там. Что еще нужно передвинуть, чтобы изолировать ρ объект ? Давайте выделим дробь, содержащую его, поэтому мы хотим вычесть 1 с обеих сторон:
и 1 минус 1 равно 0, поэтому мы можем избавиться от единиц в левой части. - Нам еще нужно сделать еще несколько операций, чтобы изолировать ρ объект . Сначала умножьте обе части на ρ жидкости , чтобы очистить дробь:
Мы можем сократить ρ жидкости с каждой стороны: - Затем нам нужно избавиться от отрицательного знака:
Умножьте обе части на -1, чтобы сделать -ρ флюид положительным:
Отрицательное число (или символ), умноженное на отрицательное число, является положительным числом. Поскольку мы умножаем на -1, мы просто меняем знак у всех чисел и символов с обеих сторон и в итоге получаем:
Поскольку мы умножаем на -1, мы просто меняем знак у всех чисел и символов с обеих сторон и в итоге получаем: - Немного изменив правую часть уравнения, мы получим уравнение, которое нужно решить для плотности айсберга!
Несколько простых шагов для работы с уравнениями
Вот несколько простых шагов для работы с уравнениями. Под каждым шагом вы найдете пример того, как это сделать, с примером, который использует геологический контекст плотности (мера массы на единицу объема).
- Оцените, что у вас есть (для каких переменных у вас есть значения?, какие единицы измерения присутствуют? и т. д.). Пока НЕ вставляйте номера! Например: у вас есть куб пирита размером 3 см х 3 см х 3 см. Вы знаете, что плотность пирита составляет 5,02 г/см 3 . Сможете ли вы вычислить, сколько весит этот куб пирита (без использования весов)?
Во-первых, вам нужно знать, что плотность (ρ) равна массе (m), деленной на объем (v).
. Мы можем записать это как математическое выражение (или уравнение, если хотите):
Мы можем записать это как математическое выражение (или уравнение, если хотите):
Какие из этих значений у вас есть в вопросе выше? У вас плотность (5,02 г/см 3 ). И с информацией вы можете определить объем (длина х ширина х высота). - Определите, какую из переменных вы хотите использовать в качестве ответа. (Какой вопрос вам нужно рассчитать? Что такое неизвестная переменная?)
В приведенном выше вопросе вам предлагается определить массу куба пирита (не взвешивая его/используя информацию, приведенную в задаче).Итак, в уравнении для плотности вы хотите определить «массу». Помните, пока ничего не подключайте.
- Перестройте уравнение так, чтобы неизвестная переменная находилась по одну сторону от знака равенства (=), а все остальные переменные — по другую. ПРАВИЛО № 1: вы можете складывать, вычитать, умножать и делить на что угодно, до тех пор, пока вы делаете то же самое с обеих сторон знака равенства.
 Возьмем уравнение плотности:
Возьмем уравнение плотности:
и переставить его.Мы хотим изолировать переменную для массы (m). Для этого мы сначала умножаем обе части уравнения на объем (v). Тогда мы можем отменить объем в правой части уравнения (объем х объем = 1).
Обратите внимание, что эти первые два шага аналогичны перекрестному умножению. Если вы более знакомы с этим методом, вы также можете сделать это. Так или иначе… Мы приходим к уравнению, в котором масса изолирована с одной стороны уравнения! - ТЕПЕРЬ подставьте числа! Замените известные переменные их значениями и не забывайте следить за единицами измерения! Наше уравнение такое.Самое приятное в этом уравнении то, что теперь, когда мы его переставили, все наши известные переменные находятся на одной стороне, а та, которую мы не знаем, — на другой.
 Начните с подстановки того, что мы знаем: ρ (плотность пирита) и V (объем (длина x ширина x высота) куба):
Начните с подстановки того, что мы знаем: ρ (плотность пирита) и V (объем (длина x ширина x высота) куба):
Упростите термин объема, умножив:
Отменить одинаковые единицы измерения сверху и снизу (где это возможно), чтобы в итоге мы получили нужные единицы (если вы не понимаете, как это сделать, см. модуль «Преобразование единиц измерения»): - Определите значение неизвестной переменной, выполнив математические функции.То есть сложите, вычтите, умножьте и разделите в соответствии с уравнением, которое вы написали для шага 2.
В данном случае это простое умножение:
И получаем массу: - Спросите себя, разумен ли ответ в контексте того, что вы знаете о науках о Земле и сколько должны весить вещи.
Это вещь, которая в основном требует опыта. Если вы не уверены, вы можете найти баланс и взвесить куб, чтобы убедиться, что вы находитесь на правильном уровне.Если вы держите его в руке, вы можете догадаться, кажется ли это правильным.
 .. Что еще более важно, если вы получите число вроде 135 000 г, считаете ли вы это разумным? Это 135 кг (около 300 фунтов!), и это, вероятно, неправильно. А что, если вы получите что-то вроде 0,00135 грамма? Важно уметь различать, находитесь ли вы в правильном диапазоне, а не то, что вы точно правы.
.. Что еще более важно, если вы получите число вроде 135 000 г, считаете ли вы это разумным? Это 135 кг (около 300 фунтов!), и это, вероятно, неправильно. А что, если вы получите что-то вроде 0,00135 грамма? Важно уметь различать, находитесь ли вы в правильном диапазоне, а не то, что вы точно правы.Еще один способ подумать о том, правы ли вы, — это найти что-то, что имеет такое же значение, исходя из вашего собственного опыта.На что похожи 135 г? Что ж, в фунте около 450 г, поэтому 135 г составляют от 1/4 фунта до 1/3 фунта. Что вы знаете, что имеет аналогичный вес? (Первое, что приходит мне на ум, это гамбургеры…). Есть ли смысл в том, что куб пирита (золотого металлического минерала) со стороной примерно один дюйм с каждой стороны будет весить столько? Используйте свой собственный опыт, чтобы разработать способ оценки весов и других мер.
Следующие шаги
Дополнительная помощь с уравнениями
На химическом факультете Texas A&M есть страница математического обзора об алгебраических манипуляциях.

На факультете экономики и бизнеса Университета Сиднея есть страница, на которой вы можете попрактиковаться в своих навыках работы с уравнениями! Возьмите алгебраические викторины манипуляции!
Эта страница была написана и составлена доктором Дженнифер М. Веннер, факультет геологии, Висконсинский университет Ошкош, и доктором Эриком М. Баером, программа геологии, Highline Community College
- Начнем с выделения той части уравнения, которая заключена в скобки. Для этого нам нужно разделить обе части на H итого :
Математический гений изобрел чрезвычайно простой новый способ решения квадратных уравнений
Если вы изучали алгебру в старшей школе (или изучаете ее прямо сейчас), велика вероятность, что вы знакомы с квадратичной формулой.Если нет, возможно, вы подавили его.
К этому моменту миллиардам из нас пришлось выучить, запомнить и реализовать этот громоздкий алгоритм для решения квадратных уравнений, но, по словам математика По-Шен Ло из Университета Карнеги-Меллона, на самом деле существовал более простой и лучший способ все время, хотя он оставался почти полностью скрытым в течение тысяч лет.
В новой исследовательской статье Ло прославляет квадратичную формулу как «выдающийся триумф ранних математиков», относящуюся к началу древневавилонского периода около 2000 г. до н.э., но также свободно признает некоторые из ее древних недостатков.
«К сожалению, для миллиардов людей во всем мире квадратичная формула является также их первым (и, возможно, единственным) опытом работы с довольно сложной формулой, которую они должны запомнить», — пишет Лох.
Эта трудоемкая задача, которую выполняли студенты-математики с возрастом около четырех тысячелетий, не меньше, возможно, была не совсем необходимой, как это бывает. Конечно, всегда существовали альтернативы квадратичной формуле, такие как разложение на множители, завершение квадрата или даже разбиение миллиметровки.
Но квадратичная формула обычно считается наиболее полным и надежным методом решения квадратичных задач, даже если она немного непостижима. Вот как это выглядит:
Вот как это выглядит:
Эту формулу можно использовать для решения квадратных уравнений стандартной формы, где x 2 + bx + c = 0.
В сентябре Лох провел мозговой штурм. математика, стоящая за квадратными уравнениями, когда он наткнулся на новый, упрощенный способ вывода той же формулы — альтернативный метод, который он описывает в своей статье как «эффективный в вычислительном отношении, естественный и легко запоминающийся алгоритм решения общих квадратных уравнений». .
«Я был ошеломлен, — говорит Ло об открытии. «Как это может быть, что я никогда не видел этого раньше, и я никогда не видел этого ни в одном учебнике?»
В новом методе Лох начинает со стандартного метода, пытаясь разложить квадратное число x² + bx + c на множители как (x − )(x − ), что сводится к поиску двух чисел, которые нужно поместить в пробелы с суммой −b и продукт c. Он использует метод усреднения, который концентрируется на сумме, в отличие от более распространенного метода, основанного на произведении двух чисел, составляющих c, который требует догадок для решения задач.
«Сумма двух чисел равна 2, когда их среднее значение равно 1.» Объясняет Ло на своем сайте.
«Итак, мы можем попытаться найти числа, которые равны 1 плюс некоторая сумма и 1 минус та же сумма. Все, что нам нужно сделать, это найти, существует ли au такое, что 1 + u и 1 — u работают как два числа, и u может быть 0».
Согласно Лоху, допустимое значение для u всегда можно определить с помощью альтернативного квадратичного метода Лоха интуитивно понятным способом, что позволяет решить любое квадратное уравнение.
В статье Лох он признает, что был бы «очень удивлен, если бы этот подход полностью ускользал от человеческих открытий до сегодняшнего дня, учитывая 4000-летнюю историю этой темы», но говорит об альтернативной технике, которая сочетает в себе шаги, впервые вавилонскими, греческими и французскими математиками — «конечно, широко не преподается и не известен (автор не смог найти доказательств этого в английских источниках)».
Однако с тех пор, как в октябре Лох впервые поделился предпечатной статьей, описывающей простое доказательство, в Интернете, Лох говорит, что его внимание привлекла исследовательская статья 1989 года, которая больше всего похожа на предыдущую работу, которую он нашел, и собирается каким-то образом оправдать свое недоверие. что этот альтернативный метод не был идентифицирован до сих пор.
что этот альтернативный метод не был идентифицирован до сих пор.
«Другая работа частично совпадала во всех расчетах, с очевидной логической разницей в предположении, что каждый квадратичный показатель может быть разложен на множители, и педагогической разницей в выборе знака», — объяснил Ло в ScienceAlert в электронном письме.
Остается только разгадать тайну того, почему этот метод не стал более широко известен до этого, поскольку он дает нам, по словам Лоха, «восхитительный альтернативный подход к решению квадратных уравнений, который практичен». для интеграции во все основные учебные программы».
(Не говоря уже о том, что это может просто означать, что никому больше не нужно запоминать квадратную формулу.)
Мы до сих пор не знаем, как это ускользнуло от более широкого внимания на протяжении тысячелетий, но если инстинкты Ло верны , учебники по математике могут оказаться на грани исторического переписывания, и мы не воспринимаем легкомысленно открытия, изменяющие учебники.

 Нажмите всплывающее меню «Интеграция» и выберите вариант.
Нажмите всплывающее меню «Интеграция» и выберите вариант. Таким образом в блок решения можно передавать параметры и начальные приближения.
Таким образом в блок решения можно передавать параметры и начальные приближения.
 Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.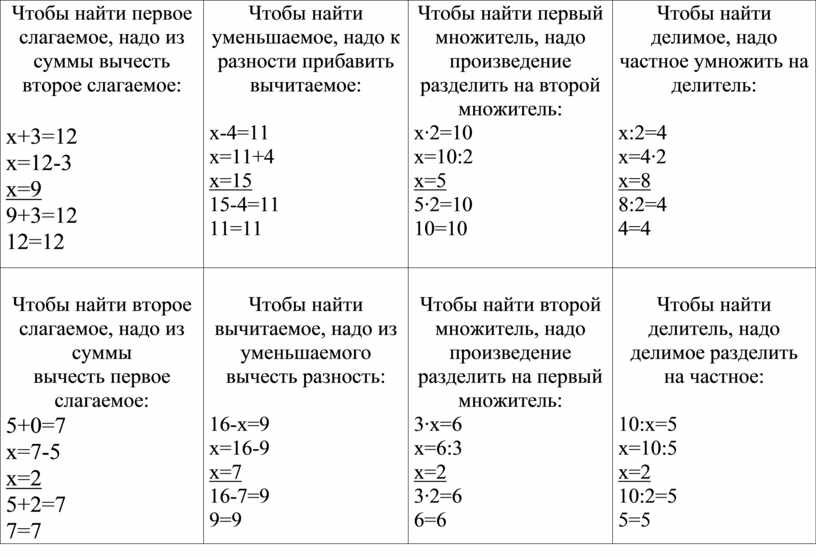 См. пример \(\PageIndex{3}\).
См. пример \(\PageIndex{3}\).

 Поскольку единицы определяются уравнениями, если вы манипулируете, подставляете числа и отменяете единицы измерения, вы получите в точности правильные единицы измерения (для данной переменной)!
Поскольку единицы определяются уравнениями, если вы манипулируете, подставляете числа и отменяете единицы измерения, вы получите в точности правильные единицы измерения (для данной переменной)!
 С чего начать?
С чего начать? Поскольку мы умножаем на -1, мы просто меняем знак у всех чисел и символов с обеих сторон и в итоге получаем:
Поскольку мы умножаем на -1, мы просто меняем знак у всех чисел и символов с обеих сторон и в итоге получаем: Мы можем записать это как математическое выражение (или уравнение, если хотите):
Мы можем записать это как математическое выражение (или уравнение, если хотите): Возьмем уравнение плотности:
Возьмем уравнение плотности:  Начните с подстановки того, что мы знаем: ρ (плотность пирита) и V (объем (длина x ширина x высота) куба):
Начните с подстановки того, что мы знаем: ρ (плотность пирита) и V (объем (длина x ширина x высота) куба):  .. Что еще более важно, если вы получите число вроде 135 000 г, считаете ли вы это разумным? Это 135 кг (около 300 фунтов!), и это, вероятно, неправильно. А что, если вы получите что-то вроде 0,00135 грамма? Важно уметь различать, находитесь ли вы в правильном диапазоне, а не то, что вы точно правы.
.. Что еще более важно, если вы получите число вроде 135 000 г, считаете ли вы это разумным? Это 135 кг (около 300 фунтов!), и это, вероятно, неправильно. А что, если вы получите что-то вроде 0,00135 грамма? Важно уметь различать, находитесь ли вы в правильном диапазоне, а не то, что вы точно правы.