Открытый урок математики по теме «Решение задач на движение»

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Вид урока: урок закрепления новых знаний.

Цель урока: научить учащихся решать задачи на движение.

Задачи:

Образовательные:

1. формировать умение решать задачи на движение;
2. вырабатывать и совершенствовать прочные вычислительные навыки;
3. учить применять на практике ЗУН, полученные в ходе изучения данной темы.
4. посредством наблюдения, сравнения и анализа прийти к выводу, что скорость сближения и удаления при одновременном движении навстречу друг другу и при одновременном движении друг от друга равна сумме скоростей, а скорость сближения и удаления при одновременном движении в одну сторону равна разности скоростей. Учить детей преобразованию величин.

Развивающие:

1. развивать внимание и оперативную память;
2. развивать логическое мышление;
3. развивать математическую речь учащихся.

Воспитательная:

1. формировать навыки работы в группе.

Оборудование – интерактивная доска (или мультимедиа проектор), компьютер, конверты с заданиями, чистые карточки для записи слов, фломастеры, цветовые жетоны для распределения по группам.

Ход урока

Ι. Постановка проблемы, формулировка темы урока.

Слайд 2. – V, автомобиль, см, км/ч, t, м/мин, S, пешеход, пловец.

– Какая тема объединяет эти понятия?

Слайд 3. – Движение.

2. Слайд 4. – Какие могут быть ситуации в задачах на движение?

1. Как вы понимаете, какие задачи вам предстоит продолжить учиться решать?
2. Встречались ли вы с такими задачами в жизни? Приведите примеры.
3. Сформулируйте цель своей работы на уроке.
4. Чему каждый должен научиться на уроке, что нужно понимать, что узнать?

ΙI. Устный счет.

Слайд 6-17.

ΙII. Актуализация знаний.

Слайд 18-24.

1. ИНТЕРВЬЮИРОВАНИЕ в группах.

Учащиеся берут интервью друг у друга на конкретную тему: «Решение задач на движение»

– Что общего в задачах на движение?

– В этих задачах соотношения между одними и теми же величинами: расстоянием, скоростью и временем.

– Что такое скорость?

– Как находится скорость?

– Какими единицами измеряется скорость?

– Скорость – это расстояние, пройденное за единицу времени.

– В каком случае речь идет о скорости сближения, а в каком – о скорости удаления?

– Когда две машины едут навстречу – скорость сближения, когда едут в противоположных направлениях – скорость удаления.

– Что такое время?

– Что такое расстояние?

– В каких случаях происходит изменение расстояния между движущимися объектами?

– Движение в противоположные стороны, движение вдогонку, с отставанием, встречное движение.

– В каких случаях расстояние между движущимися объектами уменьшается?

– Встречное движение, вдогонку.

Учитель – Как находим скорость сближения при встречном движении?

Дети – ν₁ + ν₂

Учитель – Как находим скорость при движении вдогонку?

Дети – ν₁ – ν₂

Учитель – Произойдет ли встреча?

Дети – Произойдет.

Учитель – В каких случаях расстояние между движущимися объектами увеличивается?

Дети – Движение в противоположные стороны, с отставанием.

Учитель – Какую скорость мы находим при движении в противоположные стороны, с отставанием?

Дети – ν_удал

IV. Самостоятельная работа в группах.

1.«Лови ошибку». Ученики группой ищут заранее приготовленные задачи с ошибкой, совещаются. Выбирают спикера, он оглашает результат.

1. Нерпа за 20с проплывает 160м. На сколько она должна увеличить скорость, чтобы проплыть это же расстояние за 16с?

Решение:

V	t	S
?	20c	160м
на ? больше	16с	такое же

1. 160 : 20 = 8(км/ч) – скорость нерпы в одну секунду.
2. 160 : 10 =16(км/ч) – скорость нерпы за 16 секунд.
3. 16 – 8 = 8(км/ч) – на 8 км/ч нерпа должна увеличить скорость.

Ответ: на 8 км/ч нерпа должна увеличить скорость, чтобы проплыть это же расстояние за 16с.

2. Налим за 7с проплывает 105 м. На сколько он должен увеличить скорость, чтобы проплыть это же расстояние за 5с?

Решение:

V	t	S
?	7c	105м
на ? больше	5с	такое же

1. 105 : 7 = 15(км/ч) – скорость налима в одну секунду.
2. 105 : 5 =21(км/ч) – скорость налима за 5 секунд.
3. 21 – 15 = 6 (км/ч) – на 6 км/ч налим должен увеличить скорость.

Ответ: на 6 км/ч налим должен увеличить скорость, чтобы проплыть это же расстояние за 5с.

3. Щука за 20 с проплывает 500 м. Сможет ли она проплыть 2 км за 1 минуту, если будет двигаться с той же скоростью?

Решение:

V	t	S
?	20c	500м
такая же	1 мин	?сможет ли проплыть 2км?

1. 500 : 20 = 25 (м/с) – скорость щуки в одну секунду.
2. 2км = 2000 (м)
3. 1мин = 60 (с)
4. 1 * 25 = 25 (км) – проплывет щука за 1 мин.

Ответ: сможет, если будет двигаться со скоростью 25м/с.

4. Омуль за 9с проплывает 36м. За какое время проплывет это расстояние таймень, если его скорость на 2 м/с больше, чем скорость омуля?

Решение:

	V	t	S
омуль	?	9c	36 м
таймень	? на 2 м/с больше	?	это же

1. 36 : 9 = 4 (м/с) – скорость омуля в одну секунду.
2. 4 + 2 = 6 (м/с) – скорость тайменя в одну секунду
3. 36 : 6 = 6 (с) – время тайменя за 36 м

Ответ: за 6 мин проплывет это расстояние таймень

5. Навстречу друг другу плывут хариус и ленок. Через 2 мин расстояние между ними стало 500м. На каком расстоянии они были друг от друга изначально, если скорость хариуса 200м/мин, а скорость ленка 300м/мин?

Решение:

	V	t	S
хариус	200м/мин	2мин	500м
ленок	300м/мин

1. 200 * 2 =400(м) – проплыл хариус
2. 300 * 2 =600 (м) – проплыл ленок
3. 400 + 600 = 1000(м) – на расстоянии 1км они были друг от друга изначально
4. 1000 + 500 = 1500 (м) – общее расстояние

Ответ: на расстоянии 1500км/мин они были друг от друга изначально.

6. Щука одновременно с сорогой поплыли навстречу друг другу. Щука со скоростью 25м/с, а сорога 5м/с.

На сколько они приблизятся друг к другу за 1 с? а за 2с?

Решение:

	V	t	S
щука	25м/с	1с, 2с	?
сорога	5м/с

1. (25 + 5) * 1 = 30 (м) – на 30м они приблизятся друг к другу за 1 секунду
2. 30 * 2 = 60 (м) – на 60м они приблизятся друг к другу за 2 секунды

Ответ: на 30м/с, на 60м они приблизятся друг к другу

V. Составление и решение задач по схемам. Работа в группах.

Слайд 25.

– Вам надо самостоятельно решить четыре задачи. Условие задач на карточках у каждой группы дано в виде схем. После того, как решите задачи, вы объясняете свое решение и оцениваете друг друга. Обратите внимание на правильное применение словосочетаний “скорость сближения” и “скорость удаления”.

3. Слайд 26. Определение для каждой схемы скорости сближения и скорости удаления. Работа в группах.

– Как находятся скорости сближения и удаления в решенных вами задачах?

– Скорость сближения и скорость удаления находятся действием сложения скоростей объектов.

U1+U2=U сближения при одновременном движении навстречу друг другу.

U1+U2=U удаления при одновременном движении друг от друга.

U1-U2=U сближения при одновременном движении в одну сторону, когда скорость первого больше скорости второго..

U1 – U2=U удаления при одновременном движении в одну сторону, когда скорость 1 меньше скорости 2.

VI. Решение задачи с использованием алгоритма и сравнение с эталоном.

Слайд 27–28.

Алгоритм:

1. Прочитайте задачу.
2. Что известно?
3. Что надо узнать?
4. Сможем ли мы сразу ответить на вопрос?
5. Что надо узнать сначала?

Что потом?

 

Учитель – Проверка выполненной работы.

VII. Рефлексия урока.

Учитель – Ребята, на закрепление каких знаний были направлены задания?

Дети – решали задачи на движение, отрабатывали вычислительные навыки, повторяли формулы, по которым рассчитываются скорость, время, расстояние движения.

Учитель – В каких заданиях были допущены ошибки?

Учитель – Достигли ли мы цели урока?

Учитель – Вы очень старались на уроке, преодолевая трудности, стремились к знаниям.

Учитель – Какая же главная задача стоит перед вами?

Дети – Учиться.

Учитель – И мне хочется закончить урок таким высказыванием:

“Ученье – везде найдет примененье”

VIII. Домашнее задание

– Используя данные, отраженные в таблице, составьте задачи на движение:

Скорости, с которыми летают птицы

Название птицы	Скорость
Орел Стриж Сокол Утка Лебедь Грач Голубь Сорока Чайка Ворон	160 км/ч 108 км/ч 99 км/ч 96 км/ч 88 км/ч 72 км/ч 62 км/ч 56 км/ч 49 км/ч 38 км/ч

Фотоальбом.

urok.1sept.ru

Задачи на движение с решениями

В задачах на движение  рассматриваются три взаимосвязанные величины:

S — расстояние (пройденный путь),

t — время движения и

V — скорость – расстояние, пройденное за единицу времени.

• Расстояние – это произведение скорости на время движения;

S = V t

• Скорость – это расстояние, которое тело проходит за единицу времени;
• Скорость  — это частное от деления расстояния на время движения;

V = S / t

• Время – это частное от деления расстояния на скорость движения

t = S / V

 

Какие могут быть ситуации?

 

Ситуация первая

Два объекта движение начинают одновременно навстречу друг другу.

Встречное  движение.

Ситуация вторая

Два объекта движение начинают одновременно в противоположных направлениях.

Движение в противоположных направлениях из одного пункта

Ситуация третья

Два объекта движение начинают одновременно в одном направлении.

При решении этих задач надо использовать понятия «скорость сближения» и « скорость удаления».

 

ЗАДАЧА 1

В данный момент расстояние между двумя таксистами 345 км. На каком расстоянии будут находиться таксисты через два часа, если скорость одного 72 км /ч., а другого  -68 км /ч., и они выезжают навстречу друг другу одновременно?

Первый способ решения
1) 72 + 68 =140 (км /ч.) – скорость сближения таксистов.
2) 140 * 2 = 280 (км) – на такое расстояние таксисты    приблизятся друг к другу за 2 часа.
3) 345 – 280 = 145 (км) – на таком расстоянии будут таксисты через 2 часа.
Ответ: 145 км.

Второй способ решения

1) 72 * 2 =144 (км) – такое расстояние проедет один таксист за 2 часа.

2)  68 * 2 = 136 (км) – такое расстояние проедет другой таксист за 2 часа.

3) 144+ 136 =280 (км) – на такое расстояние таксисты приблизятся друг к другу за 2 часа.

4) 345 – 280 = 145 (км) – на таком расстоянии будут таксисты через 2 часа.

Ответ: 145 км.

ЗАДАЧА 2

Расстояние между городами А и В 720км. Из А в В вышел скорый поезд со скоростью 80 км /ч. Через 2 часа навстречу ему  из В в А  вышел

пассажирский поезд  со  скоростью 60 км /ч. Через  сколько  часов после   выхода  пассажирского  поезда  эти  поезда встретятся?

Решение

1) 80*2=160(км) -прошёл скорый поезд за 2 часа.

2) 720-160=560(км) -осталось пройти поездам.

3) 80+60=140(км/ч) -скорость сближения 2 поездов.

4) 560:140=4(ч) -был в пути пассажирский поезд.

Ответ: 4часа.

ЗАДАЧА 3

Из двух пунктов навстречу друг другу одновременно выехали два автобуса.  Скорость  одного  автобуса  45 км /ч,  а скорость другого автобуса 72 км /ч. Первый автобус до встречи проехал 135км.
Найдите расстояние между пунктами.

Решение

Первый способ решения
1) 135 : 45 = 3 (часа) – ехали автобусы до встречи.
2) 72 * 3 = 216 (км) – проехал второй автобус до встречи.
3) 135 + 216 = 351 (км) – расстояние между пунктами.
Ответ: 351 км.

Второй способ решения

1) 135 : 45 = 3 (часа) – ехали автобусы до встречи.

2) 45 +72 = 117 (км/ ч.). – скорость сближения автобусов .

3) 117 * 3 = 351 (км) – расстояние между пунктами.

Ответ: 351 км.

Что такое скорость сближения?

ЗАДАЧА 4

Машина и автобус выехали из двух городов, находящихся на расстоянии 740 км навстречу друг другу со скоростями 70 км/ч и 50 км/ч.  Какое расстояние будет между машинами через 5 часов?

Решение

Первый способ решения

1) 50 * 5 = 250 (км) – проедет машина до встречи.

2) 70 * 5 = 350 (км) – проедет автобус до встречи.

3) 250 + 350 = 600 (км) — на такое расстояние они приблизятся друг к другу.

4) 740 -600 = 140 (км)  — такое расстояние будет между ними через 5 часов.

Ответ: 140 км.

Второй способ решения

1) 50 + 70 = 120 (км /ч.) – скорость сближения автобуса и машины.

2) 120 * 5 = 600 (км) – на такое расстояние они приблизятся друг к другу.

3) 740 – 600 = 140 (км) – такое расстояние будет между ними через 5 часов.

Ответ: 140 км.

ЗАДАЧА 5

Две гоночные машины выехали навстречу друг другу. Расстояние между ними было 660 км. Одна ехала со скоростью 100 км/ч, а другая 120 км/ч.  Через какое время они встретятся?

Решение

1) 100+120=220(км/ч)- скорость сближения машин .

2) 660:220=3(ч) -через такое время встретятся гоночные машины.

Ответ: через 3 часа.

ЗАДАЧА 6

Из одного логова одновременно в противоположных направлениях выбежало два тигра. Скорость одного тигра 48 км / ч.,  а  другого  – 54 км ч. Какое расстояние будет между тиграми через 3 часа?

Решение

Первый способ решения

1) 48 * 2 = 96 (км) – пробежит один тигр за 2 часа.

2) 54 * 2 = 108 (км) – пробежит другой тигр за 2 часа.

3) 96 + 108 = 204 (км) – будет между тиграми через 2 часа.

Ответ: 204 км.

Второй способ решения

1) 48 + 54 =102 (км /ч.) – скорость удаления тигров.

2) 102 * 2 =204 (км) – будет между тиграми через 2 часа.

Ответ: 204 км.

ЗАДАЧА 7

Максим и Саша вышли из школы со скоростью 50 м/мин. Рома вышел вслед за ними через 6 минут со скоростью 80 м/мин. Через сколько минут  Рома догонит Максима и Сашу?

Решение

1) 80 — 50 = 30 (км /ч.) –скорость сближения мальчиков.

2) 50 * 6 = 300 (км) – такое расстояние было между мальчиками перед выходом из школы Ромы.

3) 300 : 30 = 10 (мин.) – через такое время Рома догонит друзей.

Ответ: через 10 мин.

 

ИТОГИ

1) При решении задач на движении двух объектов применяются понятия «скорость сближения» и «скорость удаления».

2) При решении задач на встречное движение  и движение в противоположных направлениях скорость сближения и скорость удаления находятся сложением скоростей движущихся объектов.

3) При решении задач на движение в одном направлении скорость сближения и скорость удаления находятся вычитанием скоростей движущихся объектов.

iumka.ru

«Задачи на движение для учеников 10-11 классов для подготовки к ЕГЭ по математике».

Элективный курс 10 класс.

Задачи на движение

Для педагогов не секрет, что решение текстовых задач вызывало и вызывает затруднение у большей части учащихся. Умение анализировать условие и составлять математическую модель оказывается далеко не под силу каждому. Задачи на движение, совместную работу, смеси и сплавы рассматриваются в школьном курсе математики не один год. Но многие учащиеся из года в год при выполнении домашних работ, контрольных и диагностических работ выбирают задания повышенного уровня С, игнорируя текстовые задачи. Ограниченность во времени при контроле знаний, напряжение и насыщенный объем работ не позволяет полностью свободно поразмыслить над схемой решения задания. С другой стороны развитое логическое мышление, приемы моделирования позволяет остальным учащимся успешно справиться с задачами такого типа. Вашему вниманию предложены задания по теме, которые можно использовать при различных формах организации работы по подготовке к ЕГЭ.

1. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.

Решение. Скорость сближения поездов 65 + 35 = 100 (км/ч) = (м/с). Общий путь за 36 с составляет * 36 = 1000 (м). Тогда 1000 – 700 = 300 (м) — длина скорого поезда.

Ответ: 300 м

2. Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Комментарий. Не уставайте напоминать учащимся формулу:

Средняя скорость = .

Ответ: 72 км/ч

3. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.

Решение. Важно объяснить, что в отличие от задачи 1, придорожный столб зафиксирован. Поезд за 36 с проезжает расстояние, равное собственной длине, со скоростью 80 км/ч = 80 * (м/с) = (м/с). Длина поезда * 36 = 800 (м).

Ответ: 800 м

Комментарий. Учащиеся при переводе км/ч в м/с часто путают деление с умножением величины на 3,6. Не пытайтесь заставить их выучить нужное действие. Проще в соответствии с наименованием (км/ч) умножить величину на 1000 м и разделить на 3600с. Ошибок будет намного меньше.

4. Дальнобойщик, погрузив груз в фуру, отправился в путь со скоростью 60 км/ч. Через 1 ч он сделал остановку на заправке на 30 мин, а затем продолжил путь с первоначальной скоростью. Через 1 ч после отправки фуры диспетчер склада обнаружил, что он забыл отдать дальнобойщику сопроводительные документы на груз и выехал вдогонку на мотоцикле со скоростью 100 км/ч. Какое расстояние (в километрах) проедет мотоциклист до места встречи?

Решение. Задачи на движение вдогонку встречаются часто. Собака догоняет шляпу, унесенную ветром, ребенок проезжает на велосипеде путь, возвращаясь от конечной точки до равномерно движущихся вслед за ним родителей и т. д.

В данной задаче путь дальнобойщика равен пути мотоциклиста. Важно не забыть, что дальнобойщик двигался (1+х–0,5) часа, где х ч – время движения мотоциклиста. Решив уравнение 60(х + 0,5) = 100х, х = 0,75, найдем путь мотоциклиста, который равен 75 км.

Ответ: 75 км

5. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

Решение. Пусть х км/ч –скорость второго сухогруза, у км/ч -скорость первого сухогруза. Необходимо найти величину (х–у) км/ч. За 12 мин = 0,2 ч второй сухогруз прошел 0,2х км, что составляет (0,4 + 0,12 + 0,6 + 0,2у) км. (Необходимо помнить о длине второго сухогруза, как в задачах о поездах).

Из уравнения 0,2х = 0,4 + 0,12 + 0,6 + 0,2у находим х — у = 5,6.

Ответ: на 5,6 км/ч скорость первого сухогруза меньше скорости второго.

6. Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

7. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени — со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

8. Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого  — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч.

9. Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Решение. Трудность для учащихся — в круговой трассе. Пусть х км/ч – скорость второго автомобиля, его путь за 40 мин равен х км. Путь первого автомобиля составил 80* км, что на 1 круг больше. Уравнение 80* — х = 14. Часть учащихся обратят внимание на скорость удаления и составят более простое уравнение: (80 – х) = 14.

Ответ: скорость второго автомобиля 59 км/ч.

10. Теплоход, скорость которого в неподвижной воде равна 25 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 30 часов после отплытия из него. Сколько километров прошел теплоход за весь рейс?

11. Товарный поезд каждую минуту проезжает на 750 м меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч.

12. Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.

13. Из городов A и B, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города B. Найдите скорость автомобиля, выехавшего из города A. Ответ дайте в км/ч.

14. Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.

15. Пристани A и B расположены на озере, расстояние между ними 390 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день после прибытия она отправилась обратно со скоростью на 3 км/ч больше прежней, сделав по пути остановку на 9 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.

16. Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, баржа отправилась назад и вернулась в пункт А в 16:00. Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.

17. Катер проплывает 20 км против течения реки и еще 24 км по течению за то же время, за какое может проплыть по этой реке 9 км. Во сколько раз скорость катера больше скорости реки?

Решение. Как и в задаче 5, не нужно стремиться найти скорости катера и течения реки. Необходимо вычислить отношение , где х км/ч – собственная скорость катера, у км/ч – скорость течения реки. Уравнение + = после преобразований примет вид: 5у² + 44 ху – 9х² = 0. Разделив обе части уравнения на у² ≠ 0 и обозначив = m, имеем 9m² — 44m – 5 = 0. m₁ = 5, m₂ = — – не соответствует условию задачи. В 5 раз скорость катера больше скорости реки.

Ответ: в 5 раз

    Продолжаем рассматривать задачи на движение. Есть группа задач, которая отличается от обычных задач на движение – это задачи на круговое движение (круговая трасса, движение стрелок часов).  Принципы решения те же самые, формула используется та же (формула закона прямолинейного движения). Но есть небольшие нюансы в подходах к решению.

Рассмотрим задачи:

1. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 22 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 20 км/ч больше скорости другого?

На первый взгляд, кому-то задачи на круговое движение могут показаться сложными и какими-то запутанными в сравнении с обычными задачами на прямолинейное движение. Но это только на первый взгляд. Данная задача легко превращается в задачу на прямолинейное движение. Как?

Мысленно развернём круговую трассу в прямую. На ней стоят два мотоциклиста. Один из них отстаёт от другого  на 11 км, так как сказано в условии, что длина трассы 22 километра.

Скорость отстающего на 20 километров в час больше (он догоняет того, кто впереди). Вот вам и задача на прямолинейное движение.

Итак, искомую величину (время, через которое они поравняются) примем за х часов. Скорость первого (находящегося впереди) обозначим у км/ч, тогда скорость второго (догоняющего) будет  (у + 20)км/ч.

Занесем скорость и время в таблицу.

Заполняем графу «расстояние»:

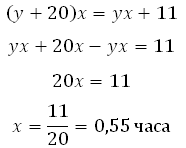
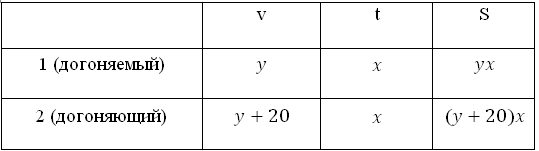
Второй проезжает расстояние (до встречи) на 11 км больше, значит

11/20 часа это то же, что и 33/60 часа. То есть, до их встречи прошло 33  минуты.

Как видим, сама скорость мотоциклистов в данном случае  не имеет значения.

Ответ: 33

2)Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?

3)Из одной точки круговой трассы, длина которой равна 25 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 25 минут после старта он опережал второй автомобиль на один круг.  Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Два автомобиля одновременно начинают движение в одном направлении. Скорость первого равна 112 км/ч. Через 25 минут он опережает второго на 25 км (т.к. сказано, что на один круг). Найти скорость второго.

Решение:

Очень важно в задачах на движение представить сам процесс этого движения.

Сравнение произведем по расстоянию, так как нам известно, что один опередил другого на 25 км.

За x принимаем искомую величину – скорость второго. Время движения 25 минут (25/60 часа) для обоих.  Заполним графу «расстояние»:

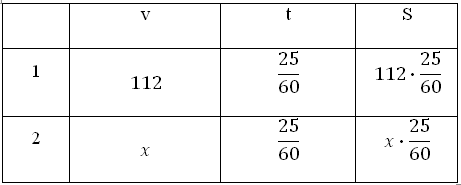
Расстояние, пройденное первым, больше расстояния, который прошёл второй на 25 км. То есть:

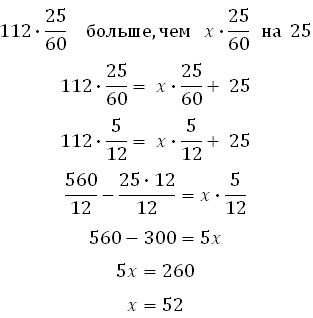
Скорость второго автомобиля 52  (км/ч).

Ответ: 52

3) Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг.  Найдите скорость второго автомобиля. Ответ дайте в км/ч.

4) Из пункта A круговой трассы выехал велосипедист, а через 40 минут следом за ним отправился мотоциклист. Через 8 минут после отправления он догнал велосипедиста в первый раз, а еще через 36 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.

Решение:

Данная задача представляет относительную сложность. Что сразу стоит отметить? Это то, что мотоциклист  проходит  с велосипедистом одинаковое расстояние, догоняя его первый раз. Затем он снова догоняет его второй раз, причём разница пройденных расстояний после первой встречи составляет 30 километров (длина круга). Таким образом, можно будет составить два уравнения и решить их систему. Нам не даны скорости участников движения, поэтому можно будет ввести две переменные. Система из двух уравнений с двумя переменными решается.

Итак, переведем минуты в часы, поскольку скорость надо найти в км/ч.

Сорок минут это 2/3 часа, 8 минут это 8/60 часа, 36 минут это 36/60 часа.

Скорости участников обозначим за х км/ч (у велосипедиста) и у км/ч (у мотоциклиста).

В первый раз мотоциклист обогнал велосипедиста через 8 минут, то есть через 8/60 часа после старта.

До этого момента велосипедист был в пути уже  40+8=48 минут, то есть  48/60 часа.

Запишем эти данные в таблицу:

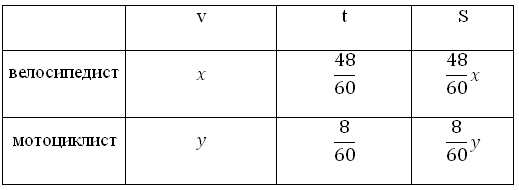
Оба проехали одинаковые расстояния, то есть

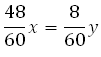
Затем мотоциклист второй раз догнал велосипедиста. Произошло это через 36 минут, то есть через 36/60 часа после первого обгона.

Составим вторую таблицу, заполним графу «расстояние»:

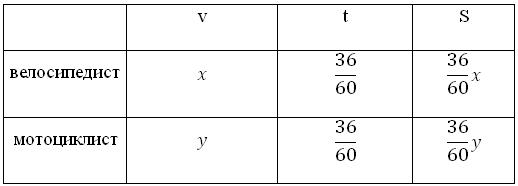
Так как сказано, что через 36 минут мотоциклист снова догнал велосипедиста. Значит, он (мотоциклист)  проехал расстояние равное 30 километрам (один круг) плюс расстояние, которое за это время проехал велосипедист. Это ключевой момент для составления второго уравнения.

Один круг — это длина трассы, она равна 30 км.

Получаем второе уравнение:

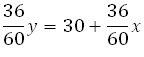
Решаем систему их двух уравнений:

Значит   у = 6 ∙10 = 60.

То есть скорость мотоциклиста равна 60 км/ч.

Ответ: 60

5) Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.

Следующий тип задач на круговое движение вообще «уникален». Есть задачи, которые решаются устно. И есть такие, которые без глубокого понимания и большой внимательности при рассуждениях решить крайне сложно. Речь идёт о задачах про стрелки часов.

Вот пример простейшей задачи:

1. Часы со стрелками показывают 11 часов 20 минут. Через сколько минут минутная стрелка в первый раз поравняется с часовой?

Ответ очевиден, через 40 минут, когда будет ровно двенадцать. Даже если сразу не смогли понять, то нарисовав  циферблат (сделав эскиз) на листке, вы без труда определите ответ.

Примеры других задач (непростых):

2. Часы со стрелками показывают 6 часов 35 минут. Через сколько минут минутная стрелка в пятый раз поравняется с часовой?

3. Часы со стрелками показывают 2 часа ровно. Через сколько минут минутная стрелка в десятый раз поравняется с часовой?

4. Часы со стрелками показывают 4 часа 45 минут. Через сколько минут минутная стрелка в седьмой раз поравняется с часовой? 

5. Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?

Вообще, можно дать совет, так как на ЕГЭ с такой задачей можно легко запутаться, вычислить неверно или просто потерять много времени на решение, можно взять с собой на ЕГЭ механические часы со стрелками… Догадались?

Если вам попадёт такая задач, то берёте часы, ставите исходное время оговоренное в условии  (например, 6:35) и прокручиваете заданное число раз. А затем смотрите: сколько «отмотали» минут от исходного времени. Вот и всё.

infourok.ru

Урок по математике «Задачи на движение»

Урок математики. 4 класс.

Тема: «Решение задач на движение».

Цель: научить учащихся решать задачи на движение.

Задачи:

Образовательная: установить зависимость между величинами скорость, время, расстояние;

формировать умение анализировать и решать задачи на движение;

вырабатывать и совершенствовать вычислительные навыки;

учить применять на практике знания, умения и навыки, полученные в ходе изучения данной темы.

Развивающая: развивать внимание и оперативную память; логическое мышление; математическую речь учащихся; познавательные способности учащихся; формировать коммуникативные умения и навыки

Воспитательная: воспитывать интерес к изучению математики;
чувство коллективизма, взаимопомощи, адекватной самооценки; воспитывать умение видеть математические задачи в окружающем мире.

Оборудование и оснащение урока: компьютер, проектор, экран(презентация) карточки, листы для самоанализа, смайлики.

Ход урока

1. Самоопределение к деятельности:

Ребята, у нас сегодня много гостей, поприветствуйте, пожалуйста, гостей и друг друга улыбкой.

Чтение стихотворения:

Друзья мои!

Сегодня мы откроем тайну,

Ведь в жизни нашей часты чудеса.

Секрет математических чудес необычайных,

Узнаем мы всего за полчаса.

Орешек знаний расколоть, помогут нам

Волшебные слова

«ХОЧУ ВСЕ ЗНАТЬ!» СЛАЙД 2

Эти слова будут девизом нашего урока. На нем мы закрепим знания по изученным темам, будем решать задачи и узнаем кое – что из истории создания транспорта. Поэтому я предлагаю вам совершить путешествие в прошлое.

Показ видеофильма (3-4мин)о преобразовании колеса в современные виды транспорта.

— Какие виды транспорта вы знаете и для чего они предназначены? На каком из них вы ездили, латали, может даже плавали.(связь с жизнью)

— Ребята, сегодня у нас необычный урок. А в чем заключается эта необычность, вы узнаете, если выполните это задание.

МАТЕМАТИЧЕСКАЯ РАЗМИНКА.

1. Расположите величины в порядке возрастания: СЛАЙД 3.

800 мм	4 дм	500см	67 дм	590 дм	900 м	6 км	8200м
Д	В	И	Ж	Е	Н	И	Е

Откройте, пожалуйста, тетради, запишите число, классная работа. Запишите ответы в нужном порядке.

— Причитай то, что у вас получилось?

— Движение. Самопроверка знаний – на слайде. СЛАЙД 4.

— Как вы думаете, что такое движение?

— Движение – это перемещение в пространстве.

Запомните это ключевое слово нашего урока.

— А математическая разминка – это движение мысли.

— Тема сегодняшнего урока «Решение задач на движение». Запишите, пожалуйста.

Актуализация знаний и фиксация затруднения в деятельности. СЛАЙД 4.

С какими из этих предметов, созданных человеком, мы чаще всего связываем слова: скорость, расстояние, время. СЛАЙД 5.

— Машины, поезда, самолет, велосипед, теплоход. СЛАЙД 6.

— Как назвать эти предметы одним словом?

-Транспорт. СЛАЙД 7.

— Какие правила нам пешеходам нужно соблюдать для того, чтобы перейти улицу?

Закрепление знаний связей между величинами в задачах на движение.

А мы с вами вспомним, как решаются задачи на движение: СЛАЙД 5

— Какие из этих формул понадобятся нам для решения задач на движение?

СЛАЙД 8.

S = V * t	P = a *4
V = S : t	S = a * b
t = S : V	P = 2 * (a + b)

-Как найти расстояние?

-Как найти скорость движения?

-Как найти время движения?

Работа с учебником стр. 12, №63. СЛАЙД 9 — 12.

— Прочитайте задачу и внимание на экран.

— Составьте по схемам взаимообратные задачи? В чем их особенность?

— Так как это взаимообратные задачи, у них одинаковый сюжет, данные. Меняется вопрос и искомое?

Фронтальная работа с проговариванием вопросов подводящего диалога вслух.

Запись решения в тетради:

1 задача:

– Что неизвестно?

— Расстояние.

Как нашли?

(4+5) * 3 = 27 (км), или

4 * 3 + 5 * 3 = 27 (км) – S

2 задача

— Что неизвестно?

— Скорости

Как нашли?

27 : 3 – 4 = 5 (км/ч) – 1 V

27 :3 – 5 = 4 (км/ч) – 2 V

3 задача

— Что неизвестно?

— Время.

Как нашли?

27 : (4 + 5) = 3 (ч) – t

Самопроверка знаний – на слайде. Запись в тетрадь. СЛАЙД 13.

— На какое направление движения эти задачи?

— Движение навстречу друг другу.

— Какие еще направления движения вы знаете?

— Движение в противоположных направлениях, в одном направлении или вдогонку.

— Сейчас мы с вами решим задачу на движение в одном направлении. Но перед этим заправимся энергией

Изучение нового материала. Решение задачи. СЛАЙД 14.

Работа над задачей:

-Что нам известно?

— Скорость первого поезда, скорость второго поезда и время, когда произошла встреча.

— У какого поезда скорость больше?

— У второго.

— Что будет происходить с расстоянием между поездами?

— Уменьшаться.

— Почему?

— Потому что они движутся друг за другом, а так как скорость второго поезда больше, то он догонит первый поезд.

— Через какое время второй поезд догонит первый?

— Он его догонит через 4 часа.

— Что нам надо найти?

— Расстояние между пунктами А и В.

-Сможем ли мы сразу узнать это расстояние?

— Нет. Как вы думаете, почему?

— Так как мы не знаем скорость сближения.

— Как мы можем узнать скорость сближения?

110 – 80 = 30 (км/ч)

Что показывает скорость сближения?

— Она показывает, что второй поезд за каждый час сближается с первым поездом на 30 км.

— Значит на каком расстоянии друг от друга находятся пункты А и В? Как узнать?

30 * 4 = 120 (км)

— Каким еще способом мы можем решить эту задачу?

2способ

1. 80 * 4 = 320 (км) – S 1 поезда

2. 110 * 4 = 440 (км) – S 2 поезда

3. 440 – 320 = 120 (км) – S друг от друга

3способ

110 * 4 – 80 * 4 = 120 (км)

— Какие затруднения возникли при решении задачи?

Показать алгоритм задачи. СЛАЙД 15.

Самостоятельная работа.

Проверь себя: работа у доски. Задание на внимание.

25068 22518|3___ 7600

15679 756(7506) 20_

10399(9389) 14200(152000)

— Найдите ошибки в решении примеров. Запишите и решите их правильно. Попытайтесь объяснить, в чем причина данных ошибок. Проверьте друг у друга

— У кого нет ошибок? Кто с ошибками написал, проводит работу над ошибками.

Самоанализ деятельности.

Перед вами листы самооценки. Проведите самоанализ вашей деятельности на уроке

	Зна Знаю ли я что такое скорость?
	Зна Знаю ли я как найти время ?
Знаю ли я как найти скорость?
	Зна Знаю ли я как найти расстояние ?
	Умею ли я решать простые задачи на движение? Смогу ли я самостоятельно решать задачи на движение в одном направлении или вдогонку?
		Обратите внимание на свои ответы. -У кого все «+»? Хорошо. Вы справились -У к -У кого есть «-»? Ничего страшного, если что то сегодня не получилось, значзначит нам есть еще над чем поработать. Выс тавление оценок . Домашнее задание. Придумать задачи на движение. СЛАЙД 19. Реф Рефлексия. ЗакЗакончите предложения: На у-Я на уроке я узнал(а)…… На у-Я на уроке я научился(ась)…… На -Для меня на уроке самое трудное было……. -Какое задание было для вас интересным? Нужно ли быть внимательными при движении на дорогах и почему? В результате нашего урока, мы закрепили наши знания, умения , навыки устного счёта. Закрепили свои знания по решению задач на движение. На На следующих уроках мы познакомимся с другими типами задач на Дви движение. Все На столах у вас лежат смайлики с разным настроением, выберите себе то настнастроение, которое вы ощущаете. СпаСпасибо. Молодцы. СЛАЙД 20.

СЛАЙД 16. Групповая работа (2 ряд) На карточках из разных видов транспорта детям предлагаются задания : каждый решает по 2 выражения, затем ребята расшифровывают слово, расположив в таблице ответов числа в порядке убывания.

53319 – 3580 =49739 П 721 : 7 =103 О

8009 + 705 = 8714 Х 6800 * 70 = 476000 Т

87953 – 9721 = 78232 Е 657 : 9 = 73 Д

3452 * 4 = 13808 О 25567 + 4562 = 30129Л

476000	78232	49739	30129	13808	8714	103	73
Т	Е	П	Л	О	Х	О	Д

Самопроверка знаний – на слайде. СЛАЙД 17.

Теплоход – вид водного транспорта. Какие еще виды водного транспорта вы знаете?

— Лодка, катер, баржа, корабль…

— В чем особенность движения теплохода по реке?

— Скорость этого транспорта зависит от течения реки. Мы с вами сегодня решали задачи на встречное движение, на движение в одном направлении, но есть еще другие задачи на движение. Вот одна из них. На какое движение эта задача? Мы ее решим на следующем уроке.

СЛАЙД 18.

multiurok.ru

Открытый урок по математике «Решение задач на движение»

Открытый урок математики 4 класс.

Тема урока «Решение задач на движение. Закрепление.»

Цель урока: Сформировать у обучающихся алгоритм решения задач на все виды движения.

Образовательные задачи:

-закрепить умение решать задачи на встречное движение, учить использовать рациональные способы устных вычислений.

Воспитательные задачи:

-воспитывать интерес к математическим знаниям;

-воспитывать ответственность за выполнение коллективной работы.

Развивающие задачи (УУД).

Регулятивные УУД:

— уметь организовывать свою деятельность;

-принимать и ставить учебно-познавательную задачу;

-строить логические рассуждения;

-планировать свои действия.

Познавательные УУД:

-учиться использовать схемы при решении задач.

Коммуникативные УУД:

-уметь использовать математическую речь при объяснении своих действий;

-осуществлять взаимный контроль и оказывать необходимую помощь товарищам.

Тип урока: закрепление.

Методы использованные на уроке: словесные, наглядные, практические, частично поисковые, сравнение, аналогия и обобщение.

Медиапродукт: презентация к уроку.

Средства обучения: компьютер, мультимедийный проектор, презентация Power Point, карточки –формулы , карточки – тренажёры.

Ход урока

1. Мотивационный этап.

— Я рада всех вас видеть на нашем уроке. Я желаю вам хорошего настроения и отличных ответов. Повернитесь к своему соседу, улыбнитесь. Пожелайте ему удачи.

2. Актуализация прежних знаний.

А сейчас небольшая разминка перед серьёзной работой.

— Правила игры следующие: я задаю вопросы, кто первым правильно поднимет руку и правильно ответит , тот перемещается на свободное место.

1. Чтобы узнать скорость надо…(S:t)

2. чтобы узнать время надо…(S:V)

3. Чтобы узнать расстояние надо…(V*t)

4. км\ч- это ед. измерения…(скорости)

5. час, мин- это ед. измерения…(времени)

6. м\мин- это ед. измерения… (скорости)

7. м, км- это ед. измерения …(расстояния)

8. S=12км, t=6 ч. Чему равна скорость?

9. V=5км/ч, t=5ч.Чему равно расстояние?

10. V=3км\ч, S=15км.Чему равно время?

11. Как найти скорость сближения или отдаления? (сумма скоростей)

12. За 5 секунд заяц пробегает 100 метров. Найти скорость зайца. (20 м/сек)

13. За какое время охотник , двигаясь на лыжах со скоростью 7 км/ч, пройдёт 14 км? (2 часа)

-Молодцы! Займите все свои места.

Встаньте те, кто переместился больше 3 раз, 2 раза, 1 раз.

-Оцените свою работу в графе «устный счёт» в баллах. Те кто переместился 1 и более раз ставят 5 баллов, не переместился- 0 баллов.

2.Постановка темы и цели урока.

—Как вы думаете, какая тема нашего урока. (Решение задач на движение)

—Какие виды задач на движение вы знаете? ( задачи на нахождение скорости , времени и расстояния, задачи на встречное движение, задачи на движение в противоположных направлениях)

—Каковы цели нашего урока? Что нам нужно знать , чтобы правильно решить эти задачи?(знать формулы для нахождения скорости, времени, расстояния, уметь правильно применять эти формулы при решении задач на движение)

— Назовите формулу нахождения скорости. ( путь : время)

— Как найти время движения? (путь : скорость)

— Как найти расстояние? (скорость * время)

-Мы повторили формулы для решения задач на движение.

Слайд №1(формулы)

2. Работа в парах.

—Примените данные формулы в выполнении задания по карточке № 1. Это задание выполняем в парах в карточке.

— Проверьте самостоятельно по карточке №2 и оцените свою работу в оценочных листах: если нет ошибок-5 баллов, 1 ошибка- 4 балла, 2 ошибки -3 балла.

3.Работа по учебнику.

-Откройте учебник стр.154-я № 15-й.

— Паша, прочитай задачу.

-Решите самостоятельно в тетради.

-Проверьте решение задачи по слайду. Слайд №2

— А кто-нибудь решил эту задачу другим способом? Каким?

-Оцените свою работу в графе «работа по учебнику».

4.Физминутка.

Встаньте.

-Если называю единицу измерения

расстояния-весело шагаем

скорости- плавные движения руками

времени- отдыхаем, присядем , склонив голову

км, м/мин, час, м, сутки, м/сек, см, км/ч, сек.

5.Работа в группах. (на доске правила)

—Прежде чем приступить к работе в группах, вспомним правила , которые необходимо соблюдать.

—Возьмите карточку №3. Дана краткая запись задачи, представленная в виде таблицы. Составьте задачу и запишите её решение. Распределите роли и приступайте к выполнению задания.

группы сформированы по рядам

-Проверьте решение задачи по слайду Слайд 3

— Оцените свою работу в оценочных листах в графе «работа в группах»

6. Дифференцированная работа.

— Ребята, каждый возьмите карточку №4.

Я предлагаю вам задачи разные по сложности.

Подумайте, какую задачу вы выберете, какая вам понравится и решение запишите в тетрадь.

—Проверьте правильность решения по карточке №5, оцените свой результат в графе «самостоятельная работа»

7. Физминутка для глаз. Слайд №4

-Посмотрите на слайд и проследите глазами за фигурой.

8.Решение задач по слайдам. Слайды № 8-18

-Ребята, мы с вами весь урок решали задачи, сейчас я предлагаю вам игру «Математическое лото».

— Возьмите карточку №6, где вы должны будете закрасить ответы , на предложенные вам задачи.

Какая цифра у вас получилась? Покажите.

-Оцените свою работу в графе «устное решение задач»

-Молодцы!

-Давайте ребята ещё раз назовём формулы нахождения времени, скорости и расстояния.

V=S : t

S=V* t

t=S :V

— Ребята, давайте вспомним, какую цель мы ставили перед собой в начале урока?

-Как вы думаете, мы достигли этой цели?

11. Подведение итогов.

А сейчас, ребята, подведите итог своей работы в целом в оценочных листах, подсчитайте баллы и поставьте соответствующую оценку.

12. Рефлексия.

-У вас на столе смайлы. Оцените свои достижения , по следующим критериям.

13. Домашнее задание. Слайд №18

— Вы сегодня хорошо потрудились. Решили много интересных задач . Предлагаю вам дома продолжить работу по выбору.

Спасибо за урок!

infourok.ru

Решение задач на движение.

Решение задач на движение

Велика роль учителя математики в коррекционной школе в формировании конкретных, осознанных представлений у детей о расстоя­нии, времени и скорости, зависимости меж­ду ними.

Обучаясь, ещё в начальных классах учащиеся знакомятся с временными понятиями год, месяц, сутки, час, минута. Таким образом, к моменту изучения в шестом классе темы «Скорость. Время. Расстояние. Решение задач на движение» при систематической серьёзной работе учителя, учащиеся имеют конкретные временные представления и осознанное понимание длины.

Без особых затруднений шестиклассники могут назвать скорость различных тел, скорость черепахи и птицы, лыжников, машины, самолета и ракеты.

При решении задач на движение особую трудность восприятия вызывают задачи на встречное движение, когда учащиеся должны мысленно понять момент сближения тел за 1ч, 2 ч, 3 ч и т. д. Здесь особое внимание обращается на усвоение выражения одновременно. Подчеркивается, что если тела вышли одновременно, то они от начала движения до момента встречи были в пути одинаковое время. Поэтому в устные упражнения включаются одни задачи с одновременным началом движения, другие — с неодновременным. Сравнивая условия таких задач и их решения учащиеся приходят к выводу, что при одновременном начале движения двух моменту их встречи каждое из них находилась в пути одинаковое время, а при неодновременном начале каждое тело в в пути разное время.

Например:

1. Из двух поселков навстречу друг другу выехали две машины в 9 ч утра. Встретились в 11 ч. Сколько часов в пути была каждая машина?

2.Из двух поселков навстречу друг другу выехали две машины. Одна выехала в 7 ч утра другая в 9 ч. Встретились они в 11 часов. Сколько часов в пути была каждая машина?

Приведу фрагменты уроков по ознакомлению учащихся с решением задач на встречное движение.

Урок 1.

Тема урока «Решение задач на встречное движение» проходил по следующему плану.

Повторение взаимосвязи величин скорость, расстояние.

Ответы на вопросы: с какими величинами вы встречаетесь в задачах на движение? Чтобы найти скорость, значение каких величин нужно знать? Если известны скорость, время, что можно определить? Значение каких двух величин нужно знать, чтобы найти время?

Составление по таблице задачи (устно), нахождение искомой величины:

Птицы

Скорость

Время

Расстояние

Скворец

15м

8с

?

Грач

?

10с

100м

Ворона

14м

7с

?

Орёл

?

4с

120м

После составления таблицы учащиеся отве­чали на следующие вопросы: у какой птицы наибольшая скорость? Почему расстоя­ния, которые пролетели скворец и орел, равны, а скорости разные?

Вызов к доске двух учеников

а) Два ученика становятся у доски спиной друг к другу. По команде учителя они идут в противоположных направлениях: один ученик идет к окну, другой — к двери.

Какой вид дви­жения изображают ученики у доски? (Учени­ки у доски идут в противоположном направлении). Пока ученики уходили друг от друга, прошло 5 с. Как изменялось расстояние между ребятами? (Расстояние между ребятами увеличивалось, так как они удаля­лись друг от друга).

б) По команде два ученика, один из которых стоит у окна, а другой — у двери, идут друг к другу, встречаются.

Учитель спрашивает: как двигались эти уче­ники? (Два ученика шли навстречу друг другу). Пока они шли навстречу друг другу, как изменялось расстояние между ними? (Рас­стояние между двумя учениками сокращалось).

4. Сообщение темы урока. Сегодня ученики бу­дут решать задачи на встречное движе­ние. Решение задачи №507.

Затем проводится анализ задачи по следую­щим вопросам: о чем говорится в задаче? Ка­кие величины в задаче известны? Какая величина является искомой? Покажите на чертеже начало движения каждого пешехода. Что озна­чает флажок? Почему флажок поставлен бли­же к началу пути первого пешехода? Что оз­начают стрелки и числа над ним? Если извест­ны время и скорость движения, что можно найти? Как?

После ответов на вопросы учителя составля­ется выражение

4*2+3*2=18(км)

Получив ответ на вопрос задачи, учитель спрашивает: можно ли решить задачу другим способом?

Этим вопросом я хочу довести до сознания учеников результат сближения пе­шеходов за 1 ч, 2 ч, 3 ч. Очень важно, что­бы шестиклассники поняли, что в выражении (4 + 3)*2 сначала узнается, на сколько кило­метров приблизились два пешехода друг к дру­гу за 1 ч, а затем за 2 ч. Аналогично с подробным объяснением решаются задачи № 508,509 и проводится срав­нение всех трех решенных задач. При сравне­нии выясняется, что в этих задачах общего. (Все три задачи на встречное движение, в каждой зада­че содержатся три величины: скорость, время, расстояние, в каждой задаче требовалось найти расстояние)

Урок 2.

Тема урока «Решение задач на встреч­ное движение».

Урок проходит по следующему плану.

1. Проведение устного счета.

В устный счет включается решение следую­щих задач.

1) За 1 мин лошадь пробегает 200 м, а поезд за это же время проходит расстояние в 4 ра­за больше. Какое расстояние пройдет поезд за это время?

2) Поезд прошел 459 км за 9 ч. Какова ско­рость поезда?

2. Решение задачи № 510 под руководством учителя.

После анализа задачи учащиеся выполняют в тетрадях чертеж к задаче и отвечают на во­прос: какое транспортное средство проедет больше расстояние? Почему?

Составляется план решения задачи. При со­ставлении плана еще раз обращается внимание на правильную постановку первого вопроса (На сколько километров приблизятся друг к другу два теплохода за 2ч?)

3. Составление обратных задач к задаче № 510

Решение записывается по вариантам. Первый вариант ставит вопрос: каково расстояние ме­жду городами. Второй вариант — с какой скоростью ехал автобус?

В помощь некоторым учащимся предлагают­ся карточки с чертежами вновь составленных задач. Проверка задач проводится фронтально или с использованием индивидуальных досок.

4. Самостоятельное решение задачи № 510 (2).

В помощь некоторым ученикам к задаче предлагается карточка с чертежом:

скорость первого лыжника 13 км в час, а второго 18 км в час?»

6. Задание на дом: № 4511 (сделать чертёж).

Урок 3.

Тема урока «Решение задач на движение.

Урок проходил по следующему плану.

1. Решение задач и под руководством учителя.

Ответы на вопросы учителя: кто из вас умеет плавать? Где вы плавали? После ответов на вопросы следует решение задачи о двух пловцах. «Два пловца плыли навстречу друг другу с противоположных берегов озера. Один пловец проплывает в минуту 70 м, а другой 60 м. Какова ширина озера, если пловцы встретились через 7 мин?» Решению задачи предшествует ее анализ по вопросам: какие величины известны в задаче? Какая величина является искомой? Затем составляется план решения задачи и запись решения

2. Устное составление и решение взаимообратных задач.

3. Самостоятельное составление и решение задачи по таблице.

Расстоя­ние

Скорость

Время

Теплоход

Пароход

216 км

72 км

?

24 км в час

Одинаковое

4. Решение задачи на смекалку.

Отец ехал в город на автобусе, а сын ехал из города на велосипеде. Кто из них дальше будет от города в момент их встречи, если скорость автобуса 50 км в час, а велосипедиста 18 км в час?

В план каждого урока математики до конца учебного года систематически включаю решение задач на движение. К концу учебного года учащиеся шестого класса должны:

1. Четко усвоить, что скорость — это расстояние, которое проходит тело за определённую единицу времени: час, минуту, секунду.

2. Знать взаимосвязь между скоростью, временем и расстоянием.

3. Конкретно представлять направления движения тел: в одном направлении, навстречу другу, в противоположном направлении.

4. Уметь решать задачи на движение.

infourok.ru

Конспект урока математики в 4 классе по теме «Решение задач на движение в противоположных направлениях»

Урок математики в 4-ом классе.

Ф. И. О. педагога: Сергеенкова Людмила Ивановна

Тема урока: Решение задач на движение в противоположных направлениях.

Тип урока: Урок формирования первоначальных предметных навыков, овладения предметными умениями.

Цели урока:

Образовательные: учить решать задачи на движение в противоположных направлениях; учить составлять обратные задачи на движение в противоположных направлениях; формировать вычислительные навыки; усвоить полученные знания, умения и навыки при выполнении проверки деления умножением, развивать умения переносить навыки в сходные и новые условия, закрепить вычислительные навыки, умения решать задачи изученных видов.

Развивающие: развивать наблюдательность и умение рассуждать, логическое мышление, внимание и интерес к предмету, умение сравнивать;

Воспитательные: воспитывать навыки самоконтроля и самопроверки; интерес к точным наукам
Задачи урока:

1.Формировать умение решать задачи на движение в противоположных направлениях; вычислительные навыки; навыки работы в малых группах; закреплять полученные знания, умения и навыки при делении и умножении многозначных чисел.

2.Развивать навыки устного счета.

3.Развивать логическое мышление.

Планируемые результаты:

Предметные:

• Овладение основами логического мышления, счётом многозначных чисел.

• Умение самостоятельно решать задачи изученных видов.

• Умение построения логической цепи рассуждения.

Личностные:

• Развитие мотивации учебной деятельности и личностного смысла учения.

• Умение анализировать свои действия и управлять ими.

Метапредметные:

• Умение планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её выполнения, определять наиболее эффективные способы достижения результата.

• Умение участвовать в диалоге при обсуждении прочитанного и прослушанного.

Оборудование: компьютер, мультимедиапроектор

Ход урока:

1.Организационный момент.

— Добрый день, ребята! Я рада приветствовать вас на уроке царицы наук – МАТЕМАТИКЕ. Я желаю, чтобы урок принес вам радость общения друг с другом, и чтобы каждый ушел с урока с весомым багажом знаний. А теперь улыбнитесь и пожелайте друг другу успешной работы.

Слайд № 2

Сегодня на уроке понадобятся все ваши знания и умения, чтобы справиться с возможными препятствиями, которые могут встретиться на нашем пути. Нам нужно будет их преодолеть всем вместе, поэтому я прошу быть внимательными, доброжелательными друг к другу. Только все вместе мы можем все преодолеть.

Нужно расшифровать ключевое слово урока, выполнив задания.

II Актуализация опорных знаний.

1. Интегративная разминка.

(Работа в парах).

Арифметический диктант (Учащиеся находят зашифрованное слово)

320 уменьшить в 8 раз. (40)

Найдите произведение чисел 250 и 10. (2500)

частное чисел 900 и 9? (100)

Первый множитель 800, второй множитель 3. Найдите произведение. (2400)

Делимое 450, делитель 5. Найдите частное. (90)

Найдите разность чисел 500 и 8. (492)

Уменьшаемое 940, вычитаемое 50. Чему равна разность? (890)

70 увеличить в 8 раз (560)

Слайд № 3

-Проверим ваши ответы. Поднимите руки, кто не совершил ни одной ошибки? 1 ошибку? 2 ошибки?

Слайд № 3

-Каждому числу соответствует буква. Распределите ответы по возрастанию

— Какое слово у вас получилось?

Слайд № 3

Д В И Ж Е Н И Е

-Что такое движение? (Это перемещение какого-либо объекта на определенное расстояние) (Вывешиваю слово «Движение»)

Слайд № 4

-У вас на партах лежат буквы. Выделите буквы, которыми обозначаются величины скорость, время, расстояние.

-Назовите единицы скорости, времени, длины.

Слайд №5 Игра «Найди лишнее»:

— На партах лежат карточки с величинами. Вам нужно выбрать те величины, которые не используются в задачах на движение.

Кг, км, т, с, км/ч, см, сут, м, ц, ч, мин, м/мин, км/c, м/с, дм

-Проверьте на экране: км, с, км/ч, м, ч, мин, м/мин, км/с, м/с

Слайд № 6 – На какие 3 группы можно разделить данные единицы измерения?

Единицы скорости, времени и расстояния.

— Для решения каких задач мы используем эти величины?

Для решения задач на движение.

— Умеете ли вы решать такие задачи?

— Сейчас проверим.

2.Устный счёт.

Задачи на движение:

Слайд №7 «Улитка ползет со скоростью 5 м/ч. Какое расстояние она преодолеет за 4 ч?»

Слайд № 8 «Черепаха за 10 мин проползет 40 м. С какой скоростью ползет черепаха?»

Слайд № 9

«Верблюд передвигается по пустыне со скоростью 9 км/ч. За какое время он пройдет 54 км?»

Слайд №10 «Заяц за 3 ч пробегает 72 км. С какой скоростью бежит заяц?»

Слайд №11 «Голубь летит со скоростью 50 км/ч. Какое расстояние пролетит голубь за 6 ч?»

Слайд №12 «Орел летит со скоростью 30 м/с.

За какое время он пролетит 270 м?»
Слайд №13- Повторим еще раз, как найти скорость, время, расстояние?

Слайд №14

Работа на доске –игра «Баскетбол»

— Какое умение мы сейчас отрабатывали?

— Отрабатывали знание зависимости между величинами скорость, время и расстояние

III Самоопределение к деятельности.

1. Определение темы и целей урока.

— Какое ключевое слово сегодня на уроке?

— Движение.

— С этим понятием мы встречались когда?

-Определите тему урока.

— Сегодня мы будем решать задачи на движение.

— О чём вам говорит эта схема?

Слайд №15

— Одновременное движение навстречу друг другу.

— А теперь что происходит с объектами?

Слайд №16

— Одновременное движение в разные стороны.

— Объедините эти две схемы. Определите более точно тему урока?

— Мы будем решать задачи на одновременное движение в противоположных направлениях. (Вывешиваю слова всей темы)

— Мы первый урок занимаемся по данной теме?

—Нет.

— Какую определим цель сегодня на уроке?

Слайд №17

— Закреплять умение решать задачи на одновременное движение в противоположных направлениях.

— Какие задачи мы поставим перед собой на уроке?

закрепление знаний между величинами S, t и v

закрепление знаний о скорости, расстоянии, времени и удаления

тренироваться составлять и решать задачи на одновременное движение в противоположных направлениях

Слайд № 18 Зарядка для глаз.

IV Изучение нового материала.

1.Сообщение темы и целей урока:

-Сегодня мы продолжаем работу с задачами на движение

и в том числе с новым видом задач «Движение в противоположных направлениях».

2.Объяснение нового материала.

— Откройте учебники на странице 27, найдите № 135 и прочитайте первую задачу.

Слайд №19

«Из поселка вышли одновременно два пешехода и пошли в противоположных направлениях. Средняя скорость одного пешехода 5 км/ч, другого – 4 км/ч. На каком расстоянии друг от друга будут пешеходы через 3 ч?»

5 км/ч 4 км/ч

? км

— Что известно? Что нужно найти? Как находим расстояние?

-Известны скорости и время. Найти надо расстояние. Чтобы найти расстояние, надо скорость умножить на время.

— Чтобы найти расстояние, что находим 1-ым действием?

-Скорость удаления.

— Записываем решение.

Слайд №20

5 + 4 = 9 ( км/ч) – скорость удаления

9 ∙ 3 = 27 (км) – расстояние

Ответ: расстояние – 27 километров.
— Прочитайте вторую задачу.

Слайд №21

«Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км?»

5 км/ч 4 км/ч

27 км

— Что известно? Что нужно найти? Как находим время?

-Известны скорости и расстояние. Найти надо время. Чтобы найти время, надо расстояние разделить на скорость.

— Чтобы найти время, что находим 1-ым действием?

-Скорость удаления.

— Записываем решение.

Слайд №22

5 + 4 = 9 ( км/ч) – скорость удаления

27 : 9 = 3 (ч)

Ответ: время – 3 часа.
— Прочитайте третью задачу.

Слайд №23

«Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 ч расстояние между ними было 27 км. Первый пешеход шел со средней скоростью 5 км/ч. С какой скоростью шел второй пешеход?

5 км/ч ? км/ч

27 км

— Что известно? Что нужно найти? Как находим скорость?

-Известны расстояние, одна из скоростей и время. Найти надо вторую скорость. Чтобы найти неизвестную скорость, надо от общей скорости отнять известную.

— Чтобы найти неизвестную скорость, что находим 1-ым действием?

-Скорость удаления.

— Записываем решение.

Слайд №24

27 : 3 = 9 ( км/ч) – скорость удаления

9 – 5 = 4 (км/ч)

Ответ: скорость – 4 километра в час.

— Похожи ли эти задачи?

-Это задачи на движение в противоположном направлении.

— Чем отличаются эти задачи?

— Если в задаче № 1 неизвестно расстояние, то в задаче № 2 оно дано. Но известное в задаче № 1, станет неизвестным в задаче

№ 2.

— Как называются такие задачи?

— Обратные.

V. Релаксационная пауза.

Руки в стороны – в полет (руки в стороны)

Отправляем самолет,

Правое крыло вперед (поворот вправо)

Левое крыло вперед (поворот влево)

Раз, два, три, четыре (прыжки на месте)

Полетел наш самолет.

VI. Первичное закрепление нового материала.

— Прочитайте задачу № 143 на стр. 28.

«Два лыжника вышли из поселка одновременно и пошли в противоположных направлениях. Один из них шел со средней скоростью 12 км/ч, а другой – 10 км/ч. Через сколько часов расстояние между ними будет 44 км? Какое расстояние пройдет за это время каждый лыжник?»

— Что в задаче известно?

-Направление, скорость и общее расстояние.

— Что нужно узнать?

-Время движения и расстояние, которое пройдет каждый лыжник.

— Выполним чертеж к этой задаче.

12 км/ч 10 км/ч

? км ? км

44 км ? ч

— Если расстояние и время у этих лыжников общее. Что нужно узнать первым действием?

-Общую скорость.

— Подумайте, как будет называться такая скорость, если при встречном движении мы говорим о скорости сближения?

-Скорость удаления.

— Верно. Находим скорость удаления, т. е. На сколько километров удалятся друг от друга лыжники за 1 час.

— Зная расстояние и скорость, как узнать время?

— Нужно расстояние разделить на скорость удаления.

— Зная время и скорость каждого лыжника, мы можем узнать расстояние, которое проехал каждый лыжник. Как это сделать?

— Нужно скорость умножить на время.

— Запишите решение этой задачи.

1) 12 + 10 = 22 (км/ч) – скорость удаления

2) 44 : 22 = 2 (ч) – время

3) 12 ˑ 2 = 24 (км) – 1 лыжник

4) 10 ˑ 2 = 20 (км) – 2 лыжник

Ответ: через 2 часа, 24 км и 20 км.

VII. Закрепление изученного материала.

Работа по учебнику:

№ 138 (самостоятельная работа).

VIII. Контроль.

Слайд №25

— Выберите задачи, где ход решения будет одинаков

— а) и г)

— Объясните свой выбор.

— И в первой, и во второй сначала необходимо найти скорость двух объектов, а затем умножить её на время.

— О каких скоростях идёт речь?

— в задаче а) – скорость сближения. В задаче г) – скорость удаления.

— Запишите самостоятельно решение этих задач выражением с ответом.

— Найдите схему решения этих задач.

ВЫБИРАЮТ СХЕМУ И ОБЪЯСНЯЮТ

-Сколько способов?

— Какой на данный момент более рациональный?

— Проговорите ответы.

— Какое умение мы сейчас отрабатывали?

— Формулировка задач

— Решение задач на нахождение расстояния сближения или удаления выражением

— У какой из оставшихся задач решение будет начинаться так же, как и у двух предыдущих?

— б)

— Объясните свой выбор.

— Сначала будем находит скорость сближения, потому что чтобы найти время одновременного движения двух объектов надо расстояние сближения поделить на скорость сближения.

— Запишите самостоятельно решение задачи выражением с ответом.

— Найдите схему решения этой задачи.

ВЫБИРАЮТ СХЕМУ И ОБЪЯСНЯЮТ

— Проговорите ответы.

IX. Рефлексия.

Слайд №26

— Что нового узнали на уроке? Чему научились?

— Научились решать задачи на движение в противоположных направлениях.

— С какой скоростью движутся объекты при движении в противоположных направлениях?

— Объекты движутся со скоростью удаления.

Самооценка.

— Как вы считаете хорошо ли вы усвоили материал сегодняшнего урока? Если да, то встаем, а если не очень – поднимаем правую руку.

— На последующих уроках мы с вами продолжим работу над задачами на движение.

(Выставление оценок.)

X. Домашнее задание.

стр. 27 № 136.
— Спасибо за урок. Урок окончен.

infourok.ru