Решение по задач тригонометрии: Задачи с решением — Тригонометрические уравнения — Детская игровая комната «Волшебный лес»

Posted on 03.04.197128.12.2021 by alexxlab

2(t)$.
8. $x=\frac{πn}{10}$; $x=\frac{πn}{2}$.
10. 0.
11. $x=\frac{π}{4}+2πn$; n∈Z.
12. $x=\frac{π}{20}+\frac{πn}{10}$; $x=±\frac{π}{9}+\frac{2πn}{3}$.

Содержание

Решение тригонометрических уравнений | Математика, которая мне нравится

Простейшие тригонометрические уравнения

Уравнение при решений не имеет,

при имеет решения ,

при всех остальных имеет решения .

Уравнение при решений не имеет,

при имеет решения ,

при имеет решения >,

при имеет решения ,

при всех остальных имеет решения .

Уравнение имеет решения .

Приемы решения тригонометрических уравнений

1. Сведение к одной функции

1. заменяем на , — на .

Пример 1.

Пример 2.

заменяем на , — на , — на .

Пример 1.

1) 2) ,
В первом случае решений нет, во втором .

Пример 2.

Пример 3.

3. Однородные уравнения относительно .

Если , то деля обе части уравнения на или на , получаем равносильные уравнения. Действительно, пусть — корень уравнения и . Подставляя в уравнение, получаем, что и , а это невозможно.

Пример.

4. Уравнения, приводящиеся к однородным

а) Домножение на

Пример.

б) Переход к половинному аргументу

Пример.

5. Использование формулы

Пример.

6. Замена .

Пример.

Разложение на множители

1. Формулы преобразования суммы в произведение

2. Формулы

Пример 1.

Ответ. .

Пример 2.

, решений нет,

Ответ. , .

Понижение степени

Использование формул

Сравнение левой и правой части

Пример 1.

что невозможно.

Ответ. .
Пример 2.

Ответ. .
Пример 3.

Пусть

Подставляем во второе уравнение:

Ответ. .

Пример 4.

или

Если , то . Если , то .

Ответ. .

Решение задач сферической тригонометрии Вариант 3

Скачать с Depositfiles

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра геоинформатики и геодезии

Отчет

по лабораторной работе №2:

Тема: «Решение задач сферической тригонометрии»

Вариант №3

Выполнил:

Ст. гр.

Проверил:

асс.каф.ГиГ

Ковалёв К. В.

г. Донецк 2013

Решение задач сферической тригонометрии

Решить сферический треугольник – значит найти все его элементы по заданным. Каждый сферический треугольник содержит 6 элементов – три стороны и три угла. Чтобы решить треугольник, нужно знать три его элемента (рис. 1.1).

Рис. 1.1

В практике применяется три общих случая решения сферических треугольников:

— по трем сторонам – а, b, c;

— двум сторонам и углу между ними, например, а, b и ;

— по углам и стороне и между ними, например, А, В и С.

Прежде чем приступить к решению сферического треугольника, нужно проверить, соответствуют ли заданные элементы условиям существования такого треугольника, учитывая свойства его углов и сторон. При получении решения, необходимо проверить, удовлетворяют ли найденные величины условиям существования треугольника; если не удовлетворяют, то такие результаты должны быть отброшены.

Это важно тогда, когда по значению функции может быть найдено два угла.

Решение сферических треугольников включает следующие операции:

— оценка исходных данных;

— выбор формул;

— составление схемы и вычисления;

— анализ полученных результатов;

— контрольные вычисления.

Основные формулы сферической тригонометрии:

Для других сторон и углов сферического треугольника аналогичные формулы могут быть получены соответствующей перестановкой элементов треугольника.

Кроме них применяют формулы полупериметра:

ЗАДАНИЕ

Вариант №3

1. В прямоугольном сферическом треугольнике даны:

гипотенуза ;
катет .

Решить треугольник.

2. В прямоугольном сферическом треугольнике даны:

Решить треугольник.

3. В сферическом треугольнике даны стороны:

Решить треугольник.

РЕШЕНИЕ.

1. В прямоугольном сферическом треугольнике даны:

гипотенуза ;
катет .

Найти: углы В, и катет с.

Рис. 1.2. Расположение элементов треугольника

Правило Непера:

Косинус каждого из элементов сферического треугольника равняется произведению или котангенсов соседних с ним элементов или синусов несмежных.

По правилу Непера для угла :

Для катета запишем:

Откуда:

Аналогично для катета с получим:

Контрольная формула получается, если соединить искомые величины В, и с по правилу Непера:

Решение треугольника приведено в таблице 1. 1.

Таблица 1.1. Решение прямоугольного сферического треугольника.

Вычисление			Вычисление В		Вычисление с
ctg a	0,4865928		sin b	0,6437379	cos a	0,4375430
tg b	0,8412168		sin a	0,8991975	cos b	0,7652461
cos	0,4093300		sin B	0,7159027	cos c	0,5717677
	65°50’14. 09»		B	45°43’02.02»	с	55°07’35.09»
Контроль			Ответ: 65°50’14» В = 45°43’02» с = 55°07’35»
cos		0,4093300
sin B		0,7159027
cos c		0,5717677
cos		0,4093300

2. В прямоугольном сферическом треугольнике даны:

Найти: a, b и .

По правилу Непера для угла :

Для катета b запишем:

Откуда:

Для угла В запишем:

Откуда:

Контрольная формула получается, если соединить искомые величины a, b и и по правилу Непера:

Решение треугольника приведено в таблице 1.2.

Таблица 1.2. Решение прямоугольного сферическоготреугольника.

Вычисление			Вычисление a		Вычисление b
sin B		0,7373363	cos B	0,6755259	sin c	0,6215694
cos c		0,7833591	tg c	0,7934668	ctg B	0,9161706
cos		0,5775991	ctg a	0,8513600	tg b	0,6784429
		54°43’05. 33»	a	49°35’24.92»	b	34°09’16.75»
Контроль			Ответ: 54°43’05» a = 49°35’25» b = 34°09’17»
cos	0,5775991
tg b	0,6784429
ctg a	0,8513600
cos	0,5775991

3. В сферическом треугольнике даны стороны:

Найти: А, В и .

Так как известны все три стороны треугольника, то удобно применить формулы полупериметра. Решение выполняется в таблице 1.3.

Промежуточным контролем здесь является формула:

Для окончательного контроля вычислений применяется соотношение между синусами сторон и противолежащих им углов. Контроль выполняется в таблице 1.4.

Таблица1.3. Решение треугольника по формулам полупериметра

Порядок действий	Формулы	Значения	Примечание
1	a
2	b
3	c
4	2p=a+b+c	110°36’34»
5	p	55°18’17»	Выписатьр
6	p-a	35°03’37»
7	p-b	15°51’05»
8	p-c	04°23’35»
9	p	55°18’17»	Контроль
10	sin (p-a)	0,5744379
11	sin (p-b)	0,2731432
12	sin (p-c)	0,0765982
13	sin p	0,8221910
14		0,0146177
15	M	0,1209037
16	M:sin p	0,1470506	Сравнитьс 20
17	tg (A/2)	0,2104731
18	tg (B/2)	0,4426385
19	tg (/2)	1,5784144
20	tg (A/2)tg (B/2)tg (/2)	0,1470506	Сравнитьс 16
21	A	23°46’17»
22	B	47°45’07»
23		115°17’15»

Контрольныевычисления

Таблица1. 4.

Формулы	Значения	Формулы	Значения	Формулы	Значения
sin a	0,3460261	sin b	0,6354495	sin c	0,7761748
sin A	0,4030884	sin B	0,7402409	sin	0,9041758
	0,8584373		0,8584361		0,8584335

Скачать с Depositfiles

Использование геометрии при решении тригонометрических задач

Геометрия является самым могущественным средством
для изощрения наших умственных способностей и
дает нам возможность правильно мыслить и рассуждать.

Г.Галлилей

Алгебра – не что иное, как записанная в символах геометрия,
а геометрия — это просто алгебра, воплощенная в фигурах

София Жермен

Многие тригонометрические задачи не решаются привычными для них методами или решаются очень сложно, а использование какого-нибудь геометрического приема дает короткое решение. Тригонометрические функции — это испытанный аппарат геометрии и их тоже нужно излагать, отправляясь от простых наглядных задач, как они практически и возникли — из решения треугольников

В школе мы начинаем изучать тригонометрию с вывода тригонометрических зависимостей из прямоугольного треугольника. Еще в 8-м классе, я начинаю работу по обучению детей тригонометрии, так как значительное число упражнений с аргументами из промежутка (0; ) выполняются геометрически. При таком подходе очевидны следующие плюсы.

Во-первых, раннее ознакомление учеников с тригонометрическими заданиями способствует раскрытию творческого потенциала учеников. Во-вторых, расширению математического кругозора. В-третьих, увеличению объема предметных умений. В-четвертых, использование свойств равнобедренного и прямоугольного треугольников, формул для нахождения площадей фигур, теорем синусов и косинусов приобретают устойчивость.

В 10-м классе геометрический метод дает порой более легкий способ решения тригонометрических заданий. Геометрически можно показать интересные решения тригонометрических задач и проявить при этом смекалку и эрудицию.

Несколько примеров с использованием равнобедренного треугольника.

При решении используются следующие утверждения:

1⁰ Высота равнобедренного треугольника, проведенная к основанию. Является медианой и биссектрисой.

2⁰ Основание равнобедренного треугольника равно удвоенному произведению боковой стороны на косинус угла при основании.

3⁰ Биссектриса угла делит противоположную сторону треугольника на части пропорциональные прилежащим сторонам.

Задача 1. Вычислите cos15°.
В 10-м классе используется формула cos (45° – 30°)
В 8-м классе можно решить, используя равнобедренный треугольник
Для нахождения sin.cos. tg угла 22°30’ используем равнобедренный треугольник с углом против основания 45° далее аналогичное решение.

Задача 2. Найти sin 18°
В 10-м классе можно решить следующим образом.
sin 36°= cos 54°= cos (18° + 36°)
2 sin18° cos18° = cos18° cos36° – sin18° sin36°;
2 sin18° cos18°= cos18°(1 – 2sin²18°) – 2sin²18°cos18°
2 sin18° = 1 – 4sin²18°, решаем квадратное уравнение и учтем, что sin18° > 0, получим
sin18° = .
Эту задачу можно решить геометрически
Строим равнобедренный треугольник АВС с АВ=ВС и АВС=36°, тогда ВАС — ВСА = 72° (см рис. 2)
Проведем AD биссектрису ВАС. Получим равнобедренные AВD и AСD. Обозначим AD=ВD=АС= а и АВ=b, тогда СD= а– b. Далее используем подобие треугольников или свойство биссектрисы угла и решим квадратное уравнение получим
Так как sin18° = cos72°. Рассмотрим AСD СD = 2АС·cos72° (свойство2⁰) <–> cos = =
sin18° = cos
Рис. 2
При решении многих тригонометрических задач удобно применять прямоугольный треугольник
Задачи, связанные с обратными тригонометрическими функциями, решаются геометрически быстрее и проще
Задача 3. Вычислите Переформулируем задачу “Вычислить косинус суммы углов ”
Рис. 3
Построим углы . Из рисунка видно, что ANB = DSC (по двум катетам), следовательно т. е.

Задача 4. Вычислите
В 10-м классе можно решить задачу с помощью формул, затратив на это немало усилий. Геометрически эта задача решается намного проще
Рис. 4
Обозначим . tg. Вычислим Построим прямоугольный АВС, где ВС=5n, АС=12n, тогда АВ=13n и ВАС = . Для угла строим ВСК, так, чтобы катет ВС был прилежащим к углу . В результате построения АВD равнобедренный, АВ=АD=13n . АВD= АDВ = , 2

0, т.е. = 0.
Задача 5. Решить уравнение: arcsin x + arcsin 2x =
Пусть arcsin x = , arcsin 2x = , где + = , тогда sin = x, sin = 2x.
Отметим, что x > 0 (иначе arcsin x < 0, arcsin 2x < 0, их сумма < 0).Построим прямоугольные треугольники, так чтобы + образовали прямой угол.
(рис. 5)
АВСD – прямоугольник.
Пусть АС = 1, тогда ВС = 1 · sin = sin = x, и CD = 1 · sin = sin = 2x.
По теореме Пифагора из треугольника АВС:
AB² + BC² = AC²,
(2x)² + x² = 1,
5x² = 1,
x² = ,
x = , x = – – не подходит по условию задачи.
Ответ: .
Задача 6. Решить уравнение: arcsin x + arcsin 2x = .
Пусть arcsin x = , arcsin 2x = , тогда + = .
x = sin , 2x = sin . Заметим, что x > 0.
РИС. 6
Построим АОМ = , АОВ = , МОВ = + = . АМОМ.
Пусть ОА = 1, тогда, из треугольника АОМ, АМ = 1 · sin = sin = 2x.
Проведём АКОВ. Из треугольника АОК АК = 1 · sin = sin = x.
Проведём КС ОМ. СКА = КОМ = – как углы с взаимно перпендикулярными сторонами.
Проведём АD КС. Из АDК KD = AK · cos 60° = x · = .
DC = AM = 2x. Значит, КС = KD + DC = + 2x = .
Из АОК по теореме Пифагора:
ОК = = .
Из ОКС: ОК · sin 60° = KC
Ответ: .
Примеры решения тригонометрических уравнений.

Задача 7. Решить уравнение cos x – sin x = 1.
cos x – sin x = 1
Разделим левую и правую часть уравнения на корень квадратный из суммы квадратов коэффициентов при cos x и sin x, т. е. на = :
Геометрическое решение:
Рис. 7
cos x – sin x = 1
ВС = 1 · sin x = sin x,
АС = 1 · cos x = cos x.
Следовательно, АС – ВС = 1. Но в АВС каждая сторона больше разности двух других сторон, т. е.
АВ > АС – ВС <=> АС – ВС < 1, т. к. АВ = 1. Но по условию задачи требуется, чтобы АС – ВС = 1. Это возможно только, если ABС превратится в отрезок, т.е.
если АС = 1, а ВС = 0, т.е. x₁ = 0 + 2k, x₁= 2k, kZ
если АС = 0, а ВС = 1, т. е. x₂ = –x₂ = – + 2l, lZ
Ответ: 2k; – + 2l, kZ.
Задача 8 Решить уравнение , если х – острый угол
Геометрическое решение. Проведем BDAC.
Сумма двух отрезков равна 4 .Отрезки найдены по теореме косинусов

Многие математические задачи допускают несколько вариантов решения. Часто первый избранный бывает далеко не самым удачным. Нахождение “наиболее простых”, оригинальных путей решения нередко является результатом длительной и кропотливой работы. Умение решать задачу различными способами является одним из признаков хорошей математической подготовки
Решение тригонометрических задач методом, основанным на наглядно-геометрической интерпретации развивает логическое мышление и пространственное воображение

Литература
А Г Мордкович. Алгебра и начала математического анализа. Учебник для 10 класса. Москва, “Мнемозина”, 2010.

А.Ф. Бермант, Л.А. Люстерник. Тригонометрия. Москва, 1957.

Савин А. Тригонометрия Квант, 1996. – №4.

Презентация
Тригонометрия

ТРИГОНОМЕТРИЯ – раздел математики, изучающий тригонометрические функции и их применение в решении задач, главным образом геометрических. Слово «тригонометрия» дословно с греческого языка переводится как «треугольник+измерение»..

Задачи тригонометрии
Основная задача тригонометрии – решение треугольников, то есть нахождение неизвестных величин треугольника через известные его величины. Любую геометрическую задача можно свести к решению с помощью треугольников, поэтому тригонометрия применима и в планиметрии (изучении плоских геометрических фигур), и в стереометрии (изучении пространственных геометрических фигур).
Любая тригонометрическая величина есть функция угла (изменяется с изменением угла), поэтому и появилось название «тригонометрические функции».
Тригонометрические функции – функции угла: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec) и косеканс (cosec).

Обратные тригонометрические функции, или круговые функции, — арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).

Прямые функции угла используют, когда по угла находят функцию, а обратные – когда по функции находят угол.

История тригонометрии
Решение треугольников было долгое время одним из разделов астрономии. Но зачатки науки можно найти в математических рукописях Древнего Египта, Китая и Вавилона. Считается, что измерение углов в градусах, минутах и секундах пришло к нам от вавилонских математиков.

Способы решения сферических треугольников впервые были письменно изложены греческим астрономом Гиппархом в середины II века до н.э.

Решения треугольников Гиппархом и Птолемеем (создателем геоцентрической системы мира, господствовавшей до Коперника) не знали синусов, косинусов и тангенсов. Линии синусов и косинусов начали использовать индийские астрономы (IV-V в.в.). В дальнейшем тригонометрия развивалась арабоязычными учеными (Муххамед из Буджана, Насир эд-Дина из Туса).

Европейцы познакомились с тригонометрией в XII в. Выдающийся немецкий астроном Региомонтан составил таблицы синусов с точностью до седьмой значащей цифры с интервалом 1´.

Термин «тригонометрия» впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613).

Буквенные обозначения появились в тригонометрии лишь в середине XVIII в., ввели х русский академик Эйлер, именно он придал тригонометрии такой вид, который присущ ей до сих пор. Он же ввел и обратные тригонометрические функция.

См. также полезные материалы по тригонометрии: Содержание главы:
Периметр и площадь прямоугольника | Описание курса | Синус

Решение задач по механике с использованием тригонометрии
1.
Решение задач по механике с использованием тригонометрии МОУ СОШ № 34
Решение задач по
механике с
использованием
тригонометрии
Для профильного физикоматематического 10 класса
Пихтовникова С.А., учитель математики,
Бурлаков А.Д., учитель физики.
2. Наука начинается тогда, когда начинают считать. Д.И.Менделеев
Наука начинается тогда,
когда начинают считать.
Д.И.Менделеев
3. Слеп физик без математики. М.В.Ломоносов
Слеп физик без математики.
М.В.Ломоносов
5. Устно:
Уравнение скорости:
vx (t ) vox ax t
Перемещение при равноускоренном
ax
движении:
S x vox t
t
2
Тело брошено под углом к горизонту.
Дальность полета, высота полета:
(дальность) l x(t ) v0 cos t
2
q
t
(высота)
h y (t ) v0 sin t
2
2
Формула для нахождения силы трения:
Закон сохранения импульса:
FТр N
/
/
m1 v1 m2v2 m1v1 m2v2
Закон сохранения механической энергии(без
учета трения)
Ek0 En0 Ek En
x
tg , x 2 tg
2
1 способ:
x
1
0
0
cos 60 , x 2 cos 60 2 1
2
2
x
ctg , x ctg
1
1 способ:
2
2
2
0
sin 30 , x
4
0
1
x
sin 30
2
y
1 группа
v
v0
h
l
x
2 группа
l
l
m1
v1
m2
l
h
v
3 группа
y
F
N
x
mg
FТр
а
в
l
l
m1
y
v1
l
h
m2
v
y
v
v0
F
h
x
l
x
N
mg
FТр
а
в
Историю с натягиванием
веревки продолжают еще
несколько древних терминов:
катет — значит «отвес»,
гипотенуза — «натянутая», а
другой катет прямоугольного
треугольника не назывался
катетом (т. е. отвесом), о нем
говорили как об основании
22. Задача 1. Определить расстояние от корабля, находящегося в море, до берега
23. Задача 2. Наблюдают недоступный морской остров
«Тригонометрия», которое буквально
означает «измерение треугольника».
Термин тригонометрия состоит из двух
греческих слов: тригоном, что означает
«треугольник» и метрейн, что означает
«измерять».
Греческое слово хорде, от которого происходит наш термин «хорда», буквально
означает «тетива лука», «струна». Индийские ученые впервые предложили
рассматривать величину полухорды (синуса), которую называли архаджива, что
буквально означает «половина тетивы лука», но потом стали называть джива,
что значит «тетива лука».
Как по примеру индийских математиков не увидеть на рис. 9 лук с натянутой
стрелой?
Арабские математики, которые позже (начиная с VIII в.) осваивали
накопленные математические знания, писали слово джива в арабской
транскрипции как джиба, что созвучно арабскому слову джайб, которое
дословно означает «пазуха».
Вместе с военными завоеваниями арабов слово «пазуха» для обозначения
полухорды в тригонометрии попало в Европу (X—XII вв.), где европейские
ученые перевели его на латынь как «синус».
Европейские математики XII—XVI вв.
часто называли синус sinus rectus (прямой
синус), а радиус тригонометрической
окружности sinus totus, т.е. весь (полный)
синус. Слово «косинус» — это сокращение
латинского выражения complementy sinus,
т.е. «дополнительный синус» или, иначе,
«синус дополнительной дуги»; вспомните:
cos a = sin (90° — а).
Начиная с XIV—XV вв. центр математических исследований
перемещается в Европу. В XIII— XIV вв. при переводе арабских
произведений на латинский язык новые тригонометрические
функции котангенс и тангенс были названы umbra recta -прямая
тень, и umbra versa — обратная тень. Известно, что линию
тангенсов уже использовал в своих работах английский
математик Томас Брадвар-дин (1290-1349).
Термин tangens (от лат. касающийся [отрезок касательной]) был
введен только в 1583 г. датским математиком Томасом Финком в
связи с ролью этой линии на тригонометрической окружности.
Термин «котангенс» образован по аналогии с термином
«косинус», и встречается впервые в 1620 г. у английского
ученого Эдмунта Гутера.
Если до этого главной целью тригонометрии считалось
решение треугольников, вычисление элементов
геометрических фигур, а учение о
тригонометрических функциях строилось на
геометрической основе, то развитие нового
(аналитического) направления привело к тому, что
тригонометрия постепенно стала одной из глав
математического анализа. Начало этого
преображения тригонометрии связано с именем
знаменитого ученого много лет работавшего в
Петербурге Леонарда Эйлера (1707—1783). Эйлер
усовершенствовал как символику, так и содержание
тригонометрии.
29. Практическая работа:
F
v
а
в
Задача на нахождение корней тригонометрического уравнения — «Шпаргалка ЕГЭ»
Решите уравнение: .
Решение задачи
Данный урок показывает, как правильно решить тригонометрическое уравнение, представленное в виде дроби, у которой числитель представлен квадратным тригонометрическим выражением, а знаменатель – иррациональной тригонометрической функцией. Для решения подобного необходимо представить решение в виде системы, в которой первое выражение – это числитель дроби приравненный к нулю, а второе выражение – неравенство, полученное из условия положительности подкоренного выражения. В данном случае первое выражение – квадратное тригонометрическое уравнение, для решения которого используется замена с помощью основной тригонометрической формулы: . Последующая замена тригонометрической функции на неизвестную, позволяет получить стандартное квадратное уравнение, решение которого можно получить через нахождение дискриминанта или по теореме Виета. После получения корней квадратного уравнения, выполняем обратную замену и находим решения уже двух тригонометрических уравнений. Следует помнить, что при работе с синусами и косинусами, значения функции должны находится в границах [-1; 1], в противном случае такое тригонометрическое уравнение корней не имеет. Полученные корни тригонометрических уравнений наносим на тригонометрическую окружность, с помощью которой легко выбрать корни, которые входят в область определения функции – это значение мы получаем, решив тригонометрическое неравенство. В данном случае это просто значение синуса, а следовательно, нас в решении будут интересовать только первая и вторая четверти. Исключив лишние корни, получаем итоговый ответ.
Решение данной задачи рекомендовано для учащихся 10-х классов при изучении тем «Тригонометрические функции» («Синус и косинус»), «Тригонометрические уравнения» («Арккосинус», «Арккосинус и решение уравнения cost=a», «Арксинус», «Арксинус и решение уравнения sint=a»). При подготовке к ЕГЭ урок рекомендован при повторении тем «Тригонометрические функции», «Тригонометрические уравнения».
Тригонометрических уравнений и их решений — Учебный материал для IIT JEE
Тригонометрическое уравнение
Уравнение, включающее одно или несколько тригонометрических отношений неизвестных углов, называется тригонометрическим уравнением. Тригонометрическое уравнение можно записать как Q ₁ (sin θ, cos θ, tan θ, cot θ, sec θ, cosec θ) = Q ₂ (sin θ, cos θ, tan θ, cot θ, sec θ , cosec θ), где Q ₁ и Q ₂ — рациональные функции.
Пример: Рассмотрим уравнение cos ² x — 4 sin x = 1.
Это тригонометрическое уравнение, а не тождество, поскольку оно не выполняется для всех значений x, например уравнение не выполняется при (2n + 1) π / 4.
Решение тригонометрического уравнения:
Все возможные значения неизвестного, которые удовлетворяют данному уравнению, называются решением данного уравнения.
Для полного решения должны быть получены «все возможные значения», удовлетворяющие уравнению.
Когда мы пытаемся решить тригонометрическое уравнение, мы пытаемся найти все наборы значений θ, которые удовлетворяют данному уравнению.Иногда в простых уравнениях и когда легко нарисовать график уравнения, можно найти решение, просто просмотрев график.
Период выполнения:
Функция f (x) называется периодической, если существует T> 0 такое, что f (x + T) = f (x) для всех x в области определения f (x). Если T — наименьшее положительное действительное число такое, что f (x + T) = f (x), то оно называется периодом f (x).
Тригонометрические функции, такие как sin, cos и tan, являются периодическими функциями.
Иллюстрация: Мы пытаемся найти решения уравнения sin θ = 0, отличные от θ = 0. Глядя на уравнение, можно сразу прийти к выводу, что θ = 0 — единственное решение. Но в случае тригонометрических уравнений важно исключить все возможности, чтобы найти правильное решение.
Пусть OX будет начальной строкой
Пусть ∠POX = θ и OP = r
от ΔPOL,
sin θ = PL / OP = y / r.
Теперь sin θ = 0
⇒ y / r = 0; ⇒ y = 0.
Это возможно только тогда, когда OP совпадает с OX или OX ’.
Когда OP совпадает с OX, θ = 0, ± 2π, ± 4π и ± 6π ……… (1)
И когда OP совпадает с OX ’, θ = ± π, ± 3π, ± 5π ……… (2)
Таким образом, из (1) и (2) следует, что при sin θ = 0
θ = nπ, где n = 0, ± 1, ± 2, ………
Мы называем θ = nπ общим решением тригонометрического уравнения sin θ = 0, потому что для всех значений n это решение удовлетворяет данному уравнению.
Иллюстрация: Общее решение cos θ = 0
cos θ = 0 ⇒ x = π / 2.
Это возможно только тогда, когда OP совпадает с OY или OY ’
Когда OP совпадает с OY,
θ = π / 2, 5π / 2, 9π / 2 или, -3π / 2, -7π / 2 .. ……… (1)
, когда OP совпадает с OY ’
θ = -3π / 2, -7π / 2 или, -π / 2, -5π / 2 ………… (2)
Таким образом, из (1) и (2) следует, что общее решение cos θ = 0 есть θ (2n + 1) π / 2, где n = 0, ± 1, ± 2 ………
Подробнее о тригонометрических уравнениях см. В видео ниже:
<noscript><img src='/800/600/https/ds04.infourok.ru/uploads/ex/02c7/00101bde-0d0316c9/hello_html_m6ab0a33e.jpg' /></noscript> youtube.com/embed/N6C8TP26K7E?feature=player_detailpage»/>
Общее решение уравнения sin θ = k.
Мы знаем, что когда sin θ = k, k должно быть таким, что –1 ≤ k ≤ 1
Всегда можно найти α ∈ [–π / 2, π / 2]
Так как sin (-π) / 2 = -1 & sin π / 2 = 1, так что sin θ = k, т.е. α = sin-1k
, т.е. sin θ = sin α, α ∈ [–π / 2, π / 2]
⇒ грех θ — грех α = 0
⇒ 2 sin {(θ — α) / 2} cos {θ + α) / 2} = 0
из приведенного выше уравнения, либо sin {(θ — α) / 2) = 0
и, следовательно, ((θ — α) / 2) = целое кратное π
∴ θ — α = 2nπ
и.е. θ = 2nπ + α
θ = 2nπ + (–1) 2n α, где n = 0, ± 1, ± 2… (1)
или, cos {(θ + α) / 2} = 0
, т.е. {(θ + α) / 2} = любое нечетное число, кратное π / 2
, т.е. {(θ + α) / 2} = (2n + 1) π / 2
, т.е. θ = (2n + 1) π — α
⇒ θ = (2n +1) π + (–1) 2n + 1 α… (2)
Из (1) и (2) заключаем, что
θ = nπ + (–1) n α, где n — целое кратное, является общим решением уравнения sin θ = k
Тригонометрические уравнения и их общие решения:
Тригонометрическое уравнение
Общее решение
грех θ = 0
Тогда θ = nπ
cos θ = 0
θ = (nπ + π / 2)
тангенс угла θ = 0
θ = nπ
грех θ = 1
θ = (2nπ + π / 2) = (4n + 1) π / 2
cos θ = 1
θ = 2nπ
грех θ = грех α
θ = nπ + (-1) nα, где α ∈ [-π / 2, π / 2]
cos θ = cos α
θ = 2nπ ± α, где α ∈ (0, π]
тангенс угла θ = тангенс угла α
θ = nπ + α, где α ∈ (-π / 2, π / 2]
sin2 θ = sin2 α
θ = nπ ± α
cos2 θ = cos2 α
θ = nπ ± α
tan2 θ = tan2 α
θ = nπ ± α
Если предполагается, что α является наименьшим положительным значением θ, которое удовлетворяет двум данным тригонометрическим уравнениям, то общее значение θ будет 2nπ + α.
Иллюстрация: Найдите общее решение уравнения sin θ = 1/2
Решение: Мы знаем, что sin θ = 1/2 = sin π / 6.
Итак, общее решение данного уравнения: θ = nπ + (–1) nπ / 6, n ∈ 0, ± 1, ± 2
Иллюстрация: Решите уравнение sin 6x + sin 4x = 0.
Решение: Применяя формулы для суммы синусов, т.е.
грех А + грех В = грех (А + В) / 2. cos (A-B) / 2, имеем
sin 5x cos x = 0 ……… (1)
Если «x» является решением уравнения, то верно хотя бы одно из следующих уравнений:
sin 5x = 0 или cos x = 0 ……… (2)
И наоборот, если x является решением одного из уравнений (2), то это также решение уравнения (1).Таким образом, уравнение (1) эквивалентно уравнению (2). Решения уравнения (2) даются формулой
x = nπ / 5, x = (2n + 1) π / 2, где n = 0, ± 1, ± 2 ……
Все эти значения x и только эти значения являются решениями исходного уравнения.
Иллюстрация: Найдите наиболее общее значение θ, где sin θ = — √3 / 2 и tan θ = √3.
Решение: Знаки имеют большое значение в случае тригонометрических функций. Студенты обычно склонны упоминать общие решения sin и tan θ, что неверно, поскольку это не дает нам полного решения.
sin θ отрицателен в 3-м и 4-м квадрантах, а tan θ положителен в 1-м и 3-м квадрантах.
Таким образом, обычным является 3-й квадрант, и при θ = 4π / 3 удовлетворяются оба.
∴ Общее решение — 2nπ + 4π / 3.
Это потому, что в интервале [0, 2π] оно выполняется только при 4π / 3. Снова в [2π, 4π] это выполняется при 2π + 4π / 3 и так далее.
Следовательно, общее решение уравнения равно 2nπ + 4π / 3.
Иллюстрация: Найдите общее решение для cos 3θ = sin 2θ.
Решение: Эту проблему можно решить двумя способами.
Метод 1: Мы можем записать данное уравнение как
cos 3θ = cos (π / 2 — 2θ)
⇒ 3θ = 2nπ + (π / 2 — 2θ), где n = 0, ± 1, ± 2 ……
или 5θ = 2nπ + π / 2, а также θ = 2nπ — π / 2
или θ = (4n + 1) π / 10 и
θ = (4n – 1) π / 2, где n ∈ I …… (A)
Метод 2: sin 2θ = sin (π / 2 — 3θ)
2θ = nπ + (–1) ⁿ (π / 2 — 3θ).
Случай I: Когда n четное, n = 2m, где m = 0, ± 1, ± 2 ……
2θ = 2mπ + π / 2 — 3θ
θ = (4m + 1) π / 10, где m ∈ I ……. (В)
Случай II: Если n нечетное, n = (2m + 1)
2θ = (2m + 1) π — (π / 2 — 3θ)
θ = — (4m + 1) π / 2, где m = 0, ± 1, ± 2 …… (B)
Примечание: Без сомнения, решения, полученные обоими методами для нечетных значений n, различны, но, как показано на диаграмме ниже, вы можете видеть, что все возможные значения θ могут быть получены обоими данными решениями:
из B
от A
для m = 0, θ = — π / 2,
для n = 0, θ = — π / 2
для m = 1, θ = — 5π / 2,
для n = 1, θ = + 3π / 2
для m = 2, θ = — 9π / 2,
для n = 2, θ = + 7π / 2
для m = –1, θ = — 3π / 2,
для m = –1, θ = — 5π / 2
для m = –2, θ = 7π / 2
для m = –2, θ = — 9π / 2
Общее решение sin ² θ = k, где k ∈ [0, 1]
Учитывая, что sin ² θ = k, k ∈ [0, 1]
Мы можем найти такое α, что
⇒ sin ² θ = sin ² α, где α = sin ^-1 √k
и. е. (грех θ — грех α) (грех θ + грех α) = 0
либо sin θ — sin α = 0
θ = nπ + (–1) ⁿ α, где n = 0, ± 1, ± 2 ……… (1)
или, sin θ + sin α = 0
sin θ = — sin α
θ = nπ — (–1) ⁿ α, где n = 0, ± 1, ± 2 …… .. (2)
Из (1) и (2) получаем общее решение уравнения для данного
θ = nπ ± α, где n = 0, ± 1, ± 2 …… и α = sin ^-1 √k
Иллюстрация: Решите уравнение 7tan ² θ — 9 = 3 секунды ² θ
Решение: Дано, 7tan ² θ — 9 = 3 секунды ² θ
или, 7tan ² θ — 9 = 3 (1 + tan ² θ)
или, 4tan ² θ = 12
или, tan ² θ = 3
или, tan ² θ = (tan π / 3) ²
⇒ θ = nπ + π / 3, где n = 0, ± 1, ± 2 …………
Примечание : Мы не можем определить уникальный метод решения тригонометрических уравнений. В каждом случае успех решения тригонометрического уравнения зависит, в частности, от знания и умения применять тригонометрические формулы, а также от практики решения задач. Многие тригонометрические формулы являются истинными равенствами для всех значений переменных, входящих в них.
Иллюстрация: Решите уравнение: cos θ = 0
Решение: Мы можем решить его, чтобы получить две формы
cos θ = 0 ⇒ θ = (2n + 1) π / 2
cos θ = cos π / 2 ⇒ θ = 2nπ + π / 2
или θ = (4n + 1) π / 2.
Важно: Следующие советы и шаги помогут вам систематически решать тригонометрические уравнения.
1. Попытайтесь сократить уравнение в терминах одного единственного тригонометрического отношения, предпочтительно sin θ или cos θ.
Если у нас есть выбор преобразовать задачу в синус или косинус, тогда форма косинуса удобнее по сравнению с формой синуса. Это связано с тем, что в общем решении синуса нам придется иметь дело с (–1) ⁿ, что неудобно по сравнению с рассмотрением +, полученного в форме косинуса.
2. Факторизуйте многочлен в терминах этих отношений.
3. Чтобы LHS был равен нулю, решите для каждого фактора. И запишите общее решение для каждого фактора на основе стандартных результатов, полученных ранее в этом разделе.
например sin θ — k ₁ = 0 ⇒ θ = nπ + (–1) ⁿ sin ^-1 k ₁
cos θ — k ₂ = 0 ⇒ θ = 2nπ + cos ^–1 k ₂.
Внимание: Вы должны проверить, что k ₁, k ₂ ∈ [–1, 1].Не пишите вслепую, как есть, иначе будет абсурдно, если они не принадлежат [–1, 1].
Иллюстрация: Решите уравнение 5sin θ — 2 cos ² θ — 1 = 0
Решение: Дано, 5 sin θ — 2 cos ² θ — 1 = 0
или, 5 sin θ — 2 (1 — sin ² θ) — 1 = 0
или, 2 sin ² θ + 5 sin θ — 3 = 0
или, (sin θ + 3) (2 sin θ — 1) = 0
∴ sin θ = -3 или sin θ = ½
Сначала рассмотрим случай, когда sin θ = -3.
Но этот случай невозможен, так как диапазон синуса составляет [-1, 1].
Когда sin θ = ½
Тогда sin θ = sin π / 6.
⇒ θ = nπ + (–1) ⁿ π / 6, где n = 0, ± 1, ± 2 ………
Примечание: Никогда не делите на любое нулевое выражение. например Если данное уравнение имеет вид (sin θ — cos θ) (A) = (B), где A и B обозначают тригонометрические уравнения, тогда вы можете разделить на (sin θ — cos θ) только тогда, когда θ ≠ nπ + π / 4
Иллюстрация: Решите уравнение tan θ + sec θ = √3
Решение: tan θ + сек θ = √3 …… (1)
Тогда (sin θ) / (cos θ) + 1 / (cos θ) = √3 …… (2)
или, cos (θ + π / 6) = cos π / 3
Общее решение θ + π / 6 = 2nπ ± π / 3, n ∈ I
Принимая положительный знак, θ + π / 6 = 2nπ + π / 3
⇒ θ = 2nπ + π / 6
Принимая отрицательный знак, θ + π / 6 = 2nπ — π / 3
⇒ θ = 2nπ — π / 2
и. е. θ = (4n — 1) π / 2.
Но полученное решение является правильным, только если, cos θ ≠ 0, иначе (2) не определено.
то есть θ ≠ нечетное кратное π / 2
⇒ θ ≠ (4n — 1) π / 2.
Следовательно, общее решение будет θ = 2nπ + π / 6 только тогда, когда n = 0, ± 1, ± 2 ……
Примечание: Домен уравнения не должен изменяться. В случае его изменения необходимо внести необходимые изменения в общее решение.
Иллюстрация: Решите уравнение tan 5θ = tan 3θ
Решение: Теперь tan 5θ = tan 3θ
⇒ 5θ = nπ + 3θ
или, 2θ = nπ
θ = nπ / 2, где n = 0, ± 1, ± 2 ……
положить n = 0 дает θ = 0, исходное уравнение выполнено
положив n = 1, получаем θ = π / 2, уравнение принимает вид tan 5π / 2 = tan 3π / 2.
Уравнение не определено для нечетного числа, кратного π / 2.
Отсюда заключаем, что θ = 2nπ, где n = 0, ± 1, ± 2 ………
Некоторые ключевые моменты, на которые следует обратить внимание:
1. Если в уравнении участвует tan θ или sec θ, θ нечетное число, кратное π / 2.
2. Если в уравнении участвует cot θ или cosec θ, θ ≠ кратно π или 0.
Тригонометрия полна формул, и студентам рекомендуется изучить все тригонометрические формулы, включая основы тригонометрии, чтобы оставаться конкурентоспособными на экзаменах JEE и других инженерных экзаменах.Студенты должны практиковать различные задачи тригонометрии, основанные на тригонометрических соотношениях и основах тригонометрии, чтобы познакомиться с темой.
Возможно, вы захотите сослаться на некоторые из связанных ресурсов, перечисленных ниже:
Чтобы узнать больше, купите учебные материалы по Тригонометрия , включая учебные заметки, заметки о пересмотре, видеолекции, решенные вопросы за предыдущий год и т. Д. Также дополнительные учебные материалы по математике можно найти здесь .
Как найти все решения тригонометрических уравнений?
Общее описание состоит из 3 шагов. Эти шаги могут быть очень сложными или даже невозможными, в зависимости от уравнения.
Шаг 1: Найдите тригонометрические значения, необходимые для решения уравнения.
Шаг 2: Найдите все «углы», которые дают нам эти значения из шага 1.
Шаг 3: Найдите значения неизвестного, которые приведут к углам, которые мы получили на шаге 2.
(Длинный) Пример
Решение: # 2sin (4x-pi / 3) = 1 #
Шаг 1: Единственная триггерная функция в этом уравнении — # sin #.
Иногда полезно упростить задачу, заменив, например, так:
Замените #sin (4x-pi / 3) # одной буквой # S #. Теперь нам нужно найти # S #, чтобы получилось # 2S = 1 #. Простой! Сделайте # S = 1/2 #
Итак, решение должно будет сделать #sin (4x- pi / 3) = 1/2 #
Шаг 2: «Угол» в этом уравнении равен # (4x-pi / 3) #. А пока назовем это # theta #. Нам нужен #sin theta = 1/2 #
Таких # theta # бесконечно много, нам нужно найти их все.
Каждый # theta #, составляющий #sin theta = 1/2 #, совпадает с # pi / 6 # или с # (5 pi) / 6 #.(Пройдите один период графика или один раз по единичному кругу.)
Итак, # theta # Что, помните, наш короткий способ написания # 4x-pi / 3 # должен иметь форму: #theta = pi / 6 +2 pi k # для некоторого целого числа # k # или вида #theta = (5 pi) / 6 +2 pi k # для некоторого целого числа # k #.
Шаг 3:
Заменяя # theta # в последнем бите шага 2, мы видим, что нам нужен один из: # 4x- pi / 3 = pi / 6 + 2 pi k # для целого числа # k #
или # 4x- pi / 3 = (5 pi) / 6 + 2 pi k # для целого числа # k #.
Добавление # pi / 3 # в форме # (2 pi) / 6 # к обеим сторонам этих уравнений дает нам:
# 4x = (3 pi) / 6 + 2 pi k = pi / 2 + 2 pi k # для целого числа # k # или
# 4x = (7 pi) / 6 + 2 pi k # для целого числа # k #.
Деление на # 4 # (умножение на # 1/4 #) дает:
# x = pi / 8 + (2pi k) / 4 # или
# x = (7 pi) / 24 + (2 pi k) / 4 # для целого числа # k #.
Мы можем записать это в более простой форме:
# x = pi / 8 + pi / 2 k # или
# x = (7 pi) / 24 + pi / 2 k # для целого числа # k #.
Заключительное примечание Целое число # k # может быть положительным или отрицательным целым числом или 0. Если # k # отрицательное, мы фактически вычитаем из основного решения.
7.5 Решение тригонометрических уравнений — Предварительное вычисление
Цели обучения
В этом разделе вы:
Решите линейные тригонометрические уравнения с синусом и косинусом.
Решите уравнения, содержащие одну тригонометрическую функцию.
Решите тригонометрические уравнения с помощью калькулятора.
Решите тригонометрические уравнения квадратичной формы.
Решите тригонометрические уравнения, используя фундаментальные тождества.
Решите тригонометрические уравнения с несколькими углами.
Решите задачи прямоугольного треугольника.
Рисунок 1 Египетские пирамиды, стоящие возле современного города. (кредит: Ойсин Малвихилл)
Фалес Милетский (около 625–547 гг. до н.э.) известен как основоположник геометрии.Легенда гласит, что он рассчитал высоту Великой пирамиды в Гизе в Египте, используя теорию подобных треугольников , которую он разработал, измерив тень своего посоха. Эта теория, основанная на пропорциях, имеет приложения в ряде областей, включая фрактальную геометрию, инженерию и архитектуру. Часто угол возвышения и угол депрессии находят с помощью одинаковых треугольников.
В предыдущих разделах этой главы мы рассматривали тригонометрические тождества.Тождества верны для всех значений в домене переменной. В этом разделе мы начинаем изучение тригонометрических уравнений для изучения реальных сценариев, таких как определение размеров пирамид.
Решение линейных тригонометрических уравнений с синусом и косинусом
Тригонометрические уравнения, как следует из названия, включают в себя тригонометрические функции. Во многом аналогично решению полиномиальных или рациональных уравнений, только определенные значения переменной будут решениями, если решения вообще есть.Часто мы решаем тригонометрическое уравнение на заданном интервале. Однако так же часто нас просят найти все возможные решения, и, поскольку тригонометрические функции являются периодическими, решения повторяются в течение каждого периода. Другими словами, тригонометрические уравнения могут иметь бесконечное количество решений. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предполагаем, что какое-либо решение является действительным. Период синусоидальной функции и косинусной функции равен 2π.2π. Другими словами, каждые 2π2π единицы повторяются значения y- . Если нам нужно найти все возможные решения, мы должны добавить 2πk, 2πk, где kk — целое число, к начальному решению. Вспомните правило, которое дает формат для определения всех возможных решений для функции с периодом 2π: 2π:
sinθ = sin (θ ± 2kπ) sinθ = sin (θ ± 2kπ)
Существуют аналогичные правила для указания всех возможных решений для других тригонометрических функций. Решение тригонометрических уравнений требует тех же методов, что и решение алгебраических уравнений.Мы читаем уравнение слева направо по горизонтали, как предложение. Мы ищем известные шаблоны, множители, находим общие знаменатели и заменяем определенные выражения на переменные, чтобы упростить процесс решения. Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.
Пример 1
Решение линейного тригонометрического уравнения с использованием функции косинуса
Найдите все возможные точные решения уравнения cosθ = 12.cosθ = 12.
Решение
Из единичного круга мы знаем, что
cosθ = 12 θ = π3,5π3cosθ = 12 θ = π3,5π3
Это решения в интервале [0,2π]. [0,2π]. Все возможные решения приведены в
π3 ± 2kπ и 5π3 ± 2kππ3 ± 2kπ и 5π3 ± 2kπ
, где kk — целое число.
Пример 2
Решение линейного уравнения с использованием функции синуса
Найдите все возможные точные решения уравнения sint = 12. sint = 12.
Решение
Решение для всех возможных значений t означает, что решения включают углы, превышающие период 2π.2π. Из рисунка 2 видно, что решениями являются π6π6 и 5π6,5π6. Но проблема в том, чтобы указать все возможные значения, которые решают уравнение. Следовательно, ответ
π6 ± 2πk и 5π6 ± 2πkπ6 ± 2πk и 5π6 ± 2πk
, где kk — целое число.
Как к
Для данного тригонометрического уравнения решите с помощью алгебры .
Найдите шаблон, который предлагает алгебраическое свойство, например разницу квадратов или возможность разложения на множители.
Замените тригонометрическое выражение одной переменной, например xx или u.u.
Решите уравнение так же, как и алгебраическое уравнение.
Подставьте тригонометрическое выражение обратно вместо переменной в результирующих выражениях.
Найдите угол.
Пример 3
Решите тригонометрическое уравнение в линейной форме
Точно решите уравнение: 2cosθ − 3 = −5,0≤θ <2π.2cosθ − 3 = −5,0≤θ <2π.
Решение
Используйте алгебраические методы для решения уравнения.
2cosθ − 3 = −5 2cosθ = −2 cosθ = −1 θ = π2cosθ − 3 = −5 2cosθ = −2 cosθ = −1 θ = π
Попробуй # 1
Решите в точности следующее линейное уравнение на интервале [0,2π): 2sinx + 1 = 0. [0,2π): 2sinx + 1 = 0.
Решение уравнений, содержащих одну тригонометрическую функцию
Когда нам задают уравнения, которые включают только одну из шести тригонометрических функций, их решения требуют использования алгебраических методов и единичного круга (см. Рисунок 2).Когда уравнение включает тригонометрические функции, отличные от синуса и косинуса, необходимо учитывать несколько факторов. Проблемы, связанные с величинами, обратными первичным тригонометрическим функциям, необходимо рассматривать с алгебраической точки зрения. Другими словами, мы напишем обратную функцию и найдем углы, используя эту функцию. Кроме того, уравнение, включающее функцию тангенса, немного отличается от уравнения, содержащего функцию синуса или косинуса. Во-первых, как мы знаем, период касательной равен π, π, а не 2π.2π. Кроме того, область касательной — это все действительные числа, за исключением нечетных целых кратных π2, π2, если, конечно, проблема не накладывает свои собственные ограничения на область.
Пример 4
Решение задачи, связанной с одной тригонометрической функцией
Точно решите задачу: 2sin2θ − 1 = 0,0≤θ <2π. 2sin2θ − 1 = 0,0≤θ <2π.
Решение
Поскольку эту проблему нелегко разложить на множители, мы решим ее, используя свойство квадратного корня. Во-первых, мы используем алгебру, чтобы выделить sinθ.sinθ. Потом найдем углы.
2sin2θ − 1 = 0 2sin2θ = 1 sin2θ = 12 sin2θ = ± 12 sinθ = ± 12 = ± 22 θ = π4,3π4,5π4,7π42sin2θ − 1 = 0 2sin2θ = 1 sin2θ = 12 sin2θ = ± 12 sinθ = ± 12 = ± 22 θ = π4,3π4,5π4,7π4
Пример 5
Решение тригонометрического уравнения с косекансом
Точно решите следующее уравнение: cscθ = −2,0≤θ <4π.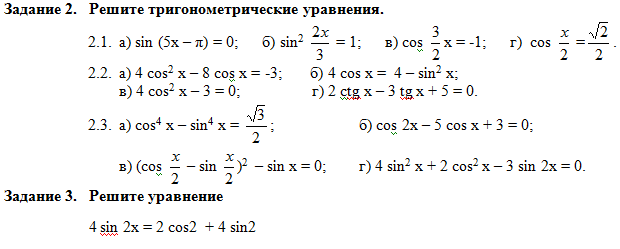 cscθ = −2,0≤θ <4π.
Решение
Нам нужны все значения θθ, для которых cscθ = −2cscθ = −2 в интервале 0≤θ <4π.0≤θ <4π.
cscθ = −21sinθ = −2sinθ = −12 θ = 7π6,11π6,19π6,23π6cscθ = −21sinθ = −2sinθ = −12 θ = 7π6,11π6,19π6,23π6
Анализ
Поскольку sinθ = −12, sinθ = −12, обратите внимание, что все четыре решения находятся в третьем и четвертом квадрантах.
Пример 6
Решение уравнения с касательной
Точно решите уравнение: tan (θ − π2) = 1,0≤θ <2π.tan (θ − π2) = 1,0≤θ <2π.
Решение
Напомним, что касательная функция имеет период π.π. На интервале [0, π), [0, π) и под углом π4, π4 касательная имеет значение 1. Однако нам нужен угол (θ − π2). (Θ − π2) . Таким образом, если tan (π4) = 1, tan (π4) = 1, то
θ − π2 = π4θ = 3π4 ± kπθ − π2 = π4θ = 3π4 ± kπ
На интервале [0,2π), [0,2π) имеем два решения:
3π4 и 3π4 + π = 7π43π4 и 3π4 + π = 7π4
Попробуй # 2
Найдите все решения для tanx = 3. tanx = 3.
Пример 7
Определите все решения уравнения, содержащего касательную
Определите все точные решения уравнения 2 (tanx + 3) = 5 + tanx, 0≤x <2π.2 (tanx + 3) = 5 + tanx, 0≤x <2π.
Решение
Мы можем решить это уравнение, используя только алгебру. Выделите выражение tanxtanx слева от знака равенства.
2 (tanx) +2 (3) = 5 + tanx2tanx + 6 = 5 + tanx2tanx − tanx = 5−6tanx = −12 (tanx) +2 (3) = 5 + tanx2tanx + 6 = 5 + tanx2tanx − tanx = 5 −6tanx = −1
На единичной окружности есть два угла, значение касательной которых равно −1: θ = 3π4−1: θ = 3π4 и θ = 7π4.θ = 7π4.
Решение тригонометрических уравнений с помощью калькулятора
Не все функции могут быть решены точно с использованием только единичной окружности.Когда мы должны решить уравнение, включающее угол, отличный от одного из специальных углов, нам понадобится калькулятор. Убедитесь, что установлен правильный режим, градусы или радианы, в зависимости от критериев данной проблемы.
Пример 8
Использование калькулятора для решения тригонометрического уравнения с синусом
Воспользуйтесь калькулятором, чтобы решить уравнение sinθ = 0,8, sinθ = 0,8, где θθ выражается в радианах.
Решение
Убедитесь, что установлен режим радианы.Чтобы найти θ, θ, используйте функцию обратного синуса. На большинстве калькуляторов вам нужно будет нажать кнопку 2 ^ND, а затем кнопку SIN, чтобы вызвать функцию sin − 1sin − 1. На экране отображается sin − 1 (.sin − 1 (. Калькулятор готов к вводу в скобках. Для этой задачи мы вводим sin − 1 (0,8), sin − 1 (0,8)) и нажимаем ENTER. Таким образом, с четырьмя десятичными знаками,
sin − 1 (0,8) ≈0,9273 sin − 1 (0,8) ≈0,9273
Решение
Угол в градусах
θ≈53.1∘θ≈180∘ − 53,1∘ ≈126,9∘θ≈53,1∘θ≈180∘ − 53,1∘ ≈126,9∘
Анализ
Обратите внимание, что калькулятор возвращает только угол в квадрантах I или IV для синусоидальной функции, поскольку это диапазон обратного синуса. Другой угол получается с помощью π − θ.π − θ.
Пример 9
Использование калькулятора для решения тригонометрического уравнения с секущей
Воспользуйтесь калькулятором, чтобы решить уравнение secθ = −4, secθ = −4, получив ответ в радианах.
Решение
Мы можем начать с некоторой алгебры.
secθ = −41cosθ = −4cosθ = −14secθ = −41cosθ = −4cosθ = −14
Убедитесь, что РЕЖИМ установлен в радианах. Теперь используйте функцию обратного косинуса.
cos − 1 (−14) ≈1,8235 θ≈1,8235 + 2πkcos − 1 (−14) ≈1,8235 θ≈1,8235 + 2πk
Поскольку π2≈1,57π2≈1,57 и π≈3,14, π≈3,14, 1,8235 находится между этими двумя числами, поэтому θ≈1,8235θ≈1,8235 находится во втором квадранте. Косинус также отрицателен в квадранте III. Обратите внимание, что калькулятор возвращает только угол в квадрантах I или II для функции косинуса, поскольку это диапазон обратного косинуса.См. Рисунок 2.
Рисунок 2
Итак, нам также нужно найти меру угла в квадранте III. В квадранте III опорный угол равен θ’≈π − 1,8235≈1,3181. Θ’≈π − 1,8235≈1,3181. Другое решение в квадранте III: π + 1,3181≈4,4597.π + 1,3181≈4,4597.
Решения: 1.8235 ± 2πk1.8235 ± 2πk и 4.4597 ± 2πk.4.4597 ± 2πk.
Попробуй # 3
Решить cosθ = −0.2.cosθ = −0.2.
Решение тригонометрических уравнений в квадратичной форме
Решение квадратного уравнения может быть более сложным, но, опять же, мы можем использовать алгебру, как и любое квадратное уравнение.Посмотрите на схему уравнения. Есть ли в уравнении более одной тригонометрической функции или только одна? Какая тригонометрическая функция возведена в квадрат? Если представлена только одна функция и один из членов возведен в квадрат, подумайте о стандартной форме квадратичной функции. Замените тригонометрическую функцию переменной, например xx или u.u. Если после подстановки уравнение выглядит как квадратное уравнение, то мы можем использовать те же методы решения квадратичных уравнений для решения тригонометрических уравнений.
Пример 10
Решение тригонометрического уравнения в квадратичной форме
Точно решите уравнение: cos2θ + 3cosθ − 1 = 0,0≤θ <2π.cos2θ + 3cosθ − 1 = 0,0≤θ <2π.
Решение
Начнем с подстановки и замены cos θθ на x.x. Нет необходимости использовать замену, но это может облегчить визуальное решение проблемы. Пусть cosθ = x.cosθ = x. У нас
Уравнение не может быть разложено на множители, поэтому мы будем использовать формулу корней квадратного уравнения x = −b ± b2−4ac2a.x = −b ± b2−4ac2a.
x = −3 ± (3) 2−4 (1) (- 1) 2 = −3 ± 132x = −3 ± (3) 2−4 (1) (- 1) 2 = −3 ± 132
Заменить xx с cosθ, cosθ и решить. Таким образом,
cosθ = −3 ± 132 θ = cos − 1 (−3 + 132) cosθ = −3 ± 132 θ = cos − 1 (−3 + 132)
Обратите внимание, что используется только знак +. Это связано с тем, что мы получаем ошибку, когда решаем θ = cos − 1 (−3−132) θ = cos − 1 (−3−132) на калькуляторе, поскольку область определения функции обратного косинуса равна [−1,1 ]. [- 1,1]. Однако есть и второе решение:
cos − 1 (−3 + 132) ≈1,26 cos − 1 (−3 + 132) ≈1,26
Эта конечная сторона угла лежит в квадранте I.Поскольку косинус также положителен в квадранте IV, второе решение —
2π − cos − 1 (−3 + 132) ≈5.022π − cos − 1 (−3 + 132) ≈5.02
Пример 11
Решение тригонометрического уравнения в квадратичной форме факторингом
Точно решите уравнение: 2sin2θ − 5sinθ + 3 = 0,0≤θ≤2π.2sin2θ − 5sinθ + 3 = 0,0≤θ≤2π.
Решение
Используя группировку, эту квадратичную величину можно разложить на множители. Либо сделайте настоящую замену, sinθ = u, sinθ = u, либо представьте ее, как мы множим:
2sin2θ − 5sinθ + 3 = 0 (2sinθ − 3) (sinθ − 1) = 0 2sin2θ − 5sinθ + 3 = 0 (2sinθ − 3) (sinθ − 1) = 0
Теперь установите каждый множитель равным нулю.
2sinθ − 3 = 0 2sinθ = 3 sinθ = 32 sinθ − 1 = 0 sinθ = 12sinθ − 3 = 0 2sinθ = 3 sinθ = 32 sinθ − 1 = 0 sinθ = 1
Затем найдите θ: sinθ ≠ 32, θ: sinθ ≠ 32, так как диапазон синусоидальной функции равен [−1,1]. [- 1,1]. Однако sinθ = 1, sinθ = 1, что дает решение π2.π2.
Анализ
Обязательно проверьте все решения в данном домене, так как некоторые факторы не имеют решения.
Попробуй # 4
Решить sin2θ = 2cosθ + 2,0≤θ≤2π.sin2θ = 2cosθ + 2,0≤θ≤2π.[Подсказка: сделайте замену, чтобы выразить уравнение только через косинус.]
Пример 12
Решение тригонометрического уравнения с помощью алгебры
Решите точно:
2sin2θ + sinθ = 0; 0≤θ <2π2sin2θ + sinθ = 0; 0≤θ <2π
Решение
Эта задача должна показаться вам знакомой, поскольку она похожа на квадратичную. Пусть sinθ = x.sinθ = x. Уравнение принимает вид 2×2 + x = 0,2×2 + x = 0. Начнем с факторинга:
2×2 + x = 0x (2x + 1) = 0 2×2 + x = 0x (2x + 1) = 0
Установите каждый коэффициент равным нулю.
x = 0 (2x + 1) = 0 x = −12 x = 0 (2x + 1) = 0 x = −12
Затем подставьте обратно в уравнение исходное выражение sinθsinθ вместо x. x. Таким образом,
sinθ = 0 θ = 0, πsinθ = −12 θ = 7π6,11π6sinθ = 0 θ = 0, πsinθ = −12 θ = 7π6,11π6
Решения в области 0≤θ <2π0≤θ <2π равны 0, π , 7π6,11π6. 0, π, 7π6,11π6.
Если мы предпочитаем не заменять, мы можем решить уравнение, следуя той же схеме факторизации и установив каждый коэффициент равным нулю.
2sin2θ + sinθ = 0sinθ (2sinθ + 1) = 0 sinθ = 0 θ = 0, π 2sinθ + 1 = 0 2sinθ = −1 sinθ = −12 θ = 7π6,11π6 2sin2θ + sinθ = 0sinθ (2sinθ + 1) = 0 sinθ = 0 θ = 0, π 2sinθ + 1 = 0 2sinθ = −1 sinθ = −12 θ = 7π6,11π6
Анализ
Мы можем видеть решения на графике на рисунке 3. На интервале 0≤θ <2π, 0≤θ <2π график пересекает ось x- четыре раза в отмеченных решениях.Обратите внимание, что тригонометрические уравнения в квадратичной форме могут дать до четырех решений вместо ожидаемых двух, которые можно найти с помощью квадратных уравнений. В этом примере каждое решение (угол), соответствующее положительному значению синуса, даст два угла, которые приведут к этому значению.
Рисунок 3
Мы также можем проверить решения на единичном круге на Рисунке 2.
Пример 13
Решение тригонометрического уравнения, квадратичного по форме
Решите квадратное по форме уравнение: 2sin2θ − 3sinθ + 1 = 0,0≤θ <2π.2sin2θ − 3sinθ + 1 = 0,0≤θ <2π.
Решение
Мы можем факторизовать, используя группировку. Значения решения θθ можно найти на единичной окружности:
(2sinθ − 1) (sinθ − 1) = 0 2sinθ − 1 = 0 sinθ = 12 θ = π6,5π6 sinθ = 1 θ = π2 (2sinθ − 1) (sinθ − 1) = 0 2sinθ − 1 = 0 sinθ = 12 θ = π6,5π6 sinθ = 1 θ = π2
Попробуй # 5
Решите квадратное уравнение 2cos2θ + cosθ = 0.2cos2θ + cosθ = 0.
Решение тригонометрических уравнений с использованием основных тождеств
Хотя алгебру можно использовать для решения ряда тригонометрических уравнений, мы также можем использовать фундаментальные тождества, потому что они упрощают решение уравнений. Помните, что методы, которые мы используем для решения проблем, не совпадают с методами проверки личности. Здесь применяются основные правила алгебры, а не переписывание одной стороны идентичности для соответствия другой стороне. В следующем примере мы используем два тождества, чтобы упростить уравнение.
Пример 14
Использование идентичностей для решения уравнения
Используйте тождества, чтобы точно решить тригонометрическое уравнение в интервале 0≤x <2π.0≤x <2π.
cosxcos (2x) + sinxsin (2x) = 32cosxcos (2x) + sinxsin (2x) = 32
Решение
Обратите внимание, что левая часть уравнения — это формула разности для косинуса.
cosxcos (2x) + sinxsin (2x) = 32 cos (x − 2x) = 32 Формула разности для косинуса cos (−x) = 32 Используйте тождество отрицательного угла.cosx = 32cosxcos (2x) + sinxsin (2x) = 32 cos (x − 2x) = 32 Формула разности для косинуса cos (−x) = 32 Используйте тождество отрицательного угла. cosx = 32
Из единичного круга на рисунке 2 мы видим, что cosx = 32cosx = 32, когда x = π6,11π6.x = π6,11π6.
Пример 15
Решение уравнения с использованием формулы двойного угла
Точно решите уравнение, используя формулу двойного угла: cos (2θ) = cosθ.cos (2θ) = cosθ.
Решение
У нас есть три варианта выражения для замены двойного угла косинуса. Поскольку проще решать одну тригонометрическую функцию за раз, мы выберем тождество с двойным углом, включающее только косинус:
cos (2θ) = cosθ 2cos2θ − 1 = cosθ 2cos2θ − cosθ − 1 = 0 (2cosθ + 1) (cosθ − 1) = 0 2cosθ + 1 = 0 cosθ = −12 cosθ − 1 = 0 cosθ = 1 cos (2θ ) = cosθ 2cos2θ − 1 = cosθ 2cos2θ − cosθ − 1 = 0 (2cosθ + 1) (cosθ − 1) = 0 2cosθ + 1 = 0 cosθ = −12 cosθ − 1 = 0 cosθ = 1
Итак, если cosθ = −12, cosθ = −12, тогда θ = 2π3 ± 2πkθ = 2π3 ± 2πk и θ = 4π3 ± 2πk; θ = 4π3 ± 2πk; если cosθ = 1, cosθ = 1, то θ = 0 ± 2πk. θ = 0 ± 2πk.
Пример 16
Решение уравнения с использованием идентификатора
Точно решите уравнение, используя тождество: 3cosθ + 3 = 2sin2θ, 0≤θ <2π. 3cosθ + 3 = 2sin2θ, 0≤θ <2π.
Решение
Если мы перепишем правую часть, мы можем записать уравнение через косинус:
3 cosθ + 3 = 2 sin2θ3 cosθ + 3 = 2 (1 − cos2θ) 3 cosθ + 3 = 2−2cos2θ2cos2θ + 3 cosθ + 1 = 0 (2 cosθ + 1) (cosθ + 1) = 02 cosθ + 1 = 0cosθ = −12θ = 2π3,4π3cosθ + 1 = 0cosθ = −1θ = π3 cosθ + 3 = 2 sin2θ3 cosθ + 3 = 2 (1 − cos2θ) 3 cosθ + 3 = 2−2cos2θ2cos2θ + 3 cosθ + 1 = 0 (2 cosθ +1) (cosθ + 1) = 02 cosθ + 1 = 0cosθ = −12θ = 2π3,4π3cosθ + 1 = 0cosθ = −1θ = π
Наши решения: 2π3,4π3, π.2π3,4π3, π.
Решение тригонометрических уравнений с несколькими углами
Иногда невозможно решить тригонометрическое уравнение с тождествами, имеющими кратный угол, например sin (2x) sin (2x) или cos (3x) . cos (3x). Столкнувшись с этими уравнениями, вспомните, что y = sin (2x) y = sin (2x) — это горизонтальное сжатие в 2 раза функции y = sinx.y = sinx. На интервале 2π, 2π мы можем изобразить два периода y = sin (2x), y = sin (2x), в отличие от одного цикла y = sinx.y = sinx.Такое сжатие графика приводит нас к мысли, что может быть в два раза больше перехватов или решений x для sin (2x) = 0sin (2x) = 0 по сравнению с sinx = 0. sinx = 0. Эта информация поможет нам решить уравнение.
Пример 17
Решение многоугольного тригонометрического уравнения
Решите точно: cos (2x) = 12cos (2x) = 12 на [0,2π). [0,2π).
Решение
Мы видим, что это уравнение является стандартным уравнением с углом, кратным углу.Если cos (α) = 12, cos (α) = 12, мы знаем, что αα находится в квадрантах I и IV. Хотя θ = cos − 112θ = cos − 112 даст решения только в квадрантах I и II, мы понимаем, что решения уравнения cosθ = 12cosθ = 12 будут в квадрантах I и IV.
Следовательно, возможные углы равны θ = π3θ = π3 и θ = 5π3.θ = 5π3. Итак, 2x = π32x = π3 или 2x = 5π3,2x = 5π3, что означает, что x = π6x = π6 или x = 5π6.x = 5π6. Имеет ли это смысл? Да, потому что cos (2 (π6)) = cos (π3) = 12. cos (2 (π6)) = cos (π3) = 12.
Есть еще возможные ответы? Вернемся к нашему первому шагу.
В квадранте I 2x = π3,2x = π3, поэтому x = π6x = π6, как указано. Давайте снова обратимся по кругу:
2x = π3 + 2π = π3 + 6π3 = 7π32x = π3 + 2π = π3 + 6π3 = 7π3
, поэтому x = 7π6.x = 7π6.
Еще один оборот дает
2x = π3 + 4π = π3 + 12π3 = 13π32x = π3 + 4π = π3 + 12π3 = 13π3
x = 13π6> 2π, x = 13π6> 2π, поэтому это значение для xx больше 2π, 2π, поэтому оно не решение на [0,2π). [0,2π).
В квадранте IV 2x = 5π3,2x = 5π3, поэтому x = 5π6x = 5π6, как указано. Давайте снова обратимся по кругу:
2x = 5π3 + 2π = 5π3 + 6π3 = 11π32x = 5π3 + 2π = 5π3 + 6π3 = 11π3
, поэтому x = 11π6.х = 11π6.
Еще один оборот дает
2x = 5π3 + 4π = 5π3 + 12π3 = 17π32x = 5π3 + 4π = 5π3 + 12π3 = 17π3
x = 17π6> 2π, x = 17π6> 2π, поэтому это значение для xx больше 2π, 2π, поэтому оно не решение на [0,2π). [0,2π).
Наши решения: π6,5π6,7π6, 11π6.π6,5π6,7π6 и 11π6. Обратите внимание, что всякий раз, когда мы решаем задачу в форме sin (nx) = c, sin (nx) = c, мы должны обойти единичный круг nn раз.
Решение задач прямоугольного треугольника
Теперь мы можем использовать все изученные нами методы для решения проблем, связанных с применением свойств прямоугольных треугольников и теоремы Пифагора.Мы начинаем с известной теоремы Пифагора, a2 + b2 = c2, a2 + b2 = c2, и моделируем уравнение в соответствии с ситуацией.
Пример 18
Использование теоремы Пифагора для моделирования уравнения
Используйте теорему Пифагора и свойства прямоугольных треугольников, чтобы смоделировать уравнение, которое соответствует задаче.
Один из тросов, прикрепляющих центр колеса обозрения «Лондонский глаз» к земле, необходимо заменить. Центр колеса обозрения находится на высоте 69,5 метров над землей, а второй якорь на земле находится в 23 метрах от основания колеса обозрения. Примерно какой длины кабель и каков угол подъема (от земли до центра колеса обозрения)? См. Рисунок 4.
Рисунок 4
Решение
Используя данную информацию, мы можем нарисовать прямоугольный треугольник. Мы можем найти длину кабеля с помощью теоремы Пифагора.
a2 + b2 = c2 (23) 2+ (69,5) 2≈5359 5359≈73,2 м a2 + b2 = c2 (23) 2+ (69,5) 2≈5359 5359≈73,2 м
Угол возвышения θ, θ, образованный вторым якорем на земле и тросом, идущим к центру колеса.Мы можем использовать касательную функцию, чтобы найти ее меру. Округлить до двух десятичных знаков.
tanθ = 69,523tan − 1 (69,523) ≈1,2522 ≈71,69∘ tanθ = 69,523tan − 1 (69,523) ≈1,2522 ≈71,69∘
Угол возвышения составляет примерно 71,7∘, 71,7∘, а длина кабеля составляет 73,2 метра. .
Пример 19
Использование теоремы Пифагора для моделирования абстрактной задачи
Правила безопасности OSHA требуют, чтобы основание лестницы располагалось на расстоянии 1 фута от стены на каждые 4 фута длины лестницы. Найдите угол, который образует лестница любой длины с землей, и высоту, на которой лестница касается стены.
Решение
Для лестницы любой длины расстояние от основания должно быть равным одной четвертой длины лестницы от стены. Эквивалентно, если основание лестницы находится на расстоянии футов от стены фут, длина лестницы будет 4 на фут. См. Рисунок 5.
Рис. 5
Сторона, примыкающая к θθ, равна a , а гипотенуза равна 4a.4а. Таким образом,
cosθ = a4a = 14cos − 1 (14) ≈75,5∘ cosθ = a4a = 14cos − 1 (14) ≈75,5∘
Высота лестницы составляет 75,5∘75,5∘ с землей. Высота, на которой лестница касается стены, может быть найдена с помощью теоремы Пифагора:
a2 + b2 = (4a) 2 b2 = (4a) 2 − a2 b2 = 16a2 − a2 b2 = 15a2 b = 15aa2 + b2 = (4a) 2 b2 = (4a) 2 − a2 b2 = 16a2 − a2 b2 = 15a2 b = 15a
Таким образом, лестница касается стены на высоте 15a15a футов от земли.
7.Упражнения из 5 частей
Устные
1.
Всегда ли будут решения уравнений тригонометрических функций? Если нет, опишите уравнение, у которого не было бы решения. Объясните, почему да или почему нет.
2.
При решении тригонометрического уравнения, включающего более одной тригонометрической функции, всегда ли мы хотим попытаться переписать уравнение так, чтобы оно выражалось в терминах одной тригонометрической функции? Почему или почему нет?
3.
При решении линейных тригонометрических уравнений только с помощью синуса или косинуса, как мы узнаем, будут ли решения?
Алгебраические
Для следующих упражнений найдите все решения точно на интервале 0≤θ <2π.0≤θ <2π.
Для следующих упражнений решите точно на [0,2π). [0,2π).
19.
2cos (3θ) = — 22cos (3θ) = — 2
20.
cos (2θ) = — 32cos (2θ) = — 32
22.
2cos (π5θ) = 32cos (π5θ) = 3
Для следующих упражнений найдите все точные решения на [0,2π). [0,2π).
23.
сек (x) sin (x) −2sin (x) = 0sec (x) sin (x) −2sin (x) = 0
24.
tan (x) −2sin (x) tan (x) = 0tan (x) −2sin (x) tan (x) = 0
25.
2cos2t + cos (t) = 12cos2t + cos (t) = 1
26.
2tan2 (t) = 3сек (t) 2tan2 (t) = 3сек (t)
27.
2sin (x) cos (x) −sin (x) + 2cos (x) −1 = 02sin (x) cos (x) −sin (x) + 2cos (x) −1 = 0
30.
tan2 (x) = — 1 + 2tan (−x) tan2 (x) = — 1 + 2tan (−x)
31.
8sin2 (x) + 6sin (x) + 1 = 08sin2 (x) + 6sin (x) + 1 = 0
32.
tan5 (x) = tan (x) tan5 (x) = tan (x)
Для следующих упражнений решайте методами, указанными в этом разделе, точно на интервале [0,2π). [0,2π).
33.
sin (3x) cos (6x) −cos (3x) sin (6x) = — 0.9sin (3x) cos (6x) −cos (3x) sin (6x) = — 0.9
34.
sin (6x) cos (11x) −cos (6x) sin (11x) = — 0,1 sin (6x) cos (11x) −cos (6x) sin (11x) = — 0,1
35.
cos (2x) cosx + sin (2x) sinx = 1cos (2x) cosx + sin (2x) sinx = 1
36.
6sin (2t) + 9sint = 06sin (2t) + 9sint = 0
37.
9cos (2θ) = 9cos2θ − 49cos (2θ) = 9cos2θ − 4
40.
cos (6x) −cos (3x) = 0cos (6x) −cos (3x) = 0
Для следующих упражнений решите точно на отрезке [0,2π). [0,2π). Если уравнения не учитываются, используйте формулу корней квадратного уравнения.
41.
tan2x − 3tanx = 0tan2x − 3tanx = 0
42.
sin2x + sinx − 2 = 0sin2x + sinx − 2 = 0
43.
sin2x − 2sinx − 4 = 0sin2x − 2sinx − 4 = 0
44.
5cos2x + 3cosx − 1 = 05cos2x + 3cosx − 1 = 0
45.
3cos2x − 2cosx − 2 = 03cos2x − 2cosx − 2 = 0.
46.
5sin2x + 2sinx − 1 = 05sin2x + 2sinx − 1 = 0
47.
tan2x + 5tanx − 1 = 0tan2x + 5tanx − 1 = 0
48.
cot2x = −cotxcot2x = −cotx
49.
−tan2x − tanx − 2 = 0 − tan2x − tanx − 2 = 0
Для следующих упражнений найдите точные решения на интервале [0,2π). [0,2π). Ищите возможности использовать тригонометрические тождества.
50.
sin2x − cos2x − sinx = 0sin2x − cos2x − sinx = 0
51.
sin2x + cos2x = 0sin2x + cos2x = 0
52.
sin (2x) −sinx = 0sin (2x) −sinx = 0
53.
cos (2x) −cosx = 0cos (2x) −cosx = 0.
54.
2tanx2 − sec2x − sin2x = cos2x2tanx2 − sec2x − sin2x = cos2x
55.
1 − cos (2x) = 1 + cos (2x) 1 − cos (2x) = 1 + cos (2x).
57.
10sinxcosx = 6cosx10sinxcosx = 6cosx
58.
−3sint = 15costsint − 3sint = 15costsint
59.
4cos2x − 4 = 15cosx4cos2x − 4 = 15cosx
60.
8sin2x + 6sinx + 1 = 08sin2x + 6sinx + 1 = 0
61.
8cos2θ = 3−2cosθ8cos2θ = 3−2cosθ
62.
6cos2x + 7sinx − 8 = 06cos2x + 7sinx − 8 = 0.
63.
12sin2t + cost − 6 = 012sin2t + cost − 6 = 0
Графический
Для следующих упражнений точно алгебраически определите все решения тригонометрического уравнения, затем проверьте результаты, построив уравнение на графике и найдя нули.
66.
6sin2x − 5sinx + 1 = 06sin2x − 5sinx + 1 = 0
67.
8cos2x − 2cosx − 1 = 08cos2x − 2cosx − 1 = 0.
68.
100tan2x + 20tanx − 3 = 0100tan2x + 20tanx − 3 = 0
69.
2cos2x − cosx + 15 = 02cos2x − cosx + 15 = 0.
70.
20sin2x − 27sinx + 7 = 020sin2x − 27sinx + 7 = 0
71.
2tan2x + 7tanx + 6 = 02tan2x + 7tanx + 6 = 0
72.
130tan2x + 69tanx − 130 = 0130tan2x + 69tanx − 130 = 0
Технологии
Для следующих упражнений используйте калькулятор, чтобы найти все решения до четырех знаков после запятой.
Для следующих упражнений решите уравнения алгебраически, а затем с помощью калькулятора найдите значения на интервале [0,2π).[0,2π). Округлить до четырех знаков после запятой.
77.
tan2x + 3tanx − 3 = 0tan2x + 3tanx − 3 = 0
78.
6tan2x + 13tanx = −66tan2x + 13tanx = −6
79.
tan2x − secx = 1tan2x − secx = 1
80.
sin2x − 2cos2x = 0sin2x − 2cos2x = 0
81.
2tan2x + 9tanx − 6 = 02tan2x + 9tanx − 6 = 0
82.
4sin2x + sin (2x) secx − 3 = 04sin2x + sin (2x) secx − 3 = 0
Расширения
Для следующих упражнений найдите все решения уравнений в точности на интервале [0,2π). [0,2π).
83.
csc2x − 3cscx − 4 = 0csc2x − 3cscx − 4 = 0
84.
sin2x − cos2x − 1 = 0sin2x − cos2x − 1 = 0
85.
sin2x (1 − sin2x) + cos2x (1 − sin2x) = 0sin2x (1 − sin2x) + cos2x (1 − sin2x) = 0
86.
3sec2x + 2 + sin2x − tan2x + cos2x = 03sec2x + 2 + sin2x − tan2x + cos2x = 0
87.
sin2x − 1 + 2cos (2x) −cos2x = 1sin2x − 1 + 2cos (2x) −cos2x = 1
88.
tan2x − 1 − sec3xcosx = 0tan2x − 1 − sec3xcosx = 0
89.
sin (2x) sec2x = 0sin (2x) sec2x = 0
90.
sin (2x) 2csc2x = 0sin (2x) 2csc2x = 0
91.
2cos2x − sin2x − cosx − 5 = 02cos2x − sin2x − cosx − 5 = 0
92.
1sec2x + 2 + sin2x + 4cos2x = 41sec2x + 2 + sin2x + 4cos2x = 4
Реальные приложения
93.
У самолета достаточно бензина, чтобы долететь до города в 200 милях к северо-востоку от его текущего местоположения. Если пилот знает, что город находится в 25 милях к северу, на сколько градусов к северу от востока должен лететь самолет?
94.
Если погрузочная рампа расположена рядом с грузовиком на высоте 4 фута, а ее длина составляет 15 футов, то какой угол образует аппарель с землей?
95.
Если погрузочная рампа расположена рядом с грузовиком на высоте 2 фута, а ее длина составляет 20 футов, какой угол будет иметь аппарель относительно земли?
96.
Женщина наблюдает за запущенной ракетой, которая сейчас находится на высоте 11 миль. Если она стоит в 4 милях от стартовой площадки, под каким углом она смотрит вверх из горизонтали?
97.
Астронавт находится в запущенной ракете, которая сейчас находится на высоте 15 миль. Если мужчина стоит в 2 милях от стартовой площадки, под каким углом она смотрит на него сверху вниз из горизонтали? (Подсказка: это называется углом депрессии.)
98.
Женщина стоит в 8 метрах от 10-метрового здания.Под каким углом она смотрит на крышу здания?
99.
Мужчина стоит в 10 метрах от 6-метрового дома. Кто-то наверху здания смотрит на него сверху вниз. Под каким углом смотрит на него человек?
100.
У здания высотой 20 футов есть тень длиной 55 футов. Какой угол подъема солнца?
101.
У здания высотой 90 футов есть тень длиной 2 фута. Какой угол подъема солнца?
102.
Прожектор на земле в 3 метрах от человека ростом 2 метра отбрасывает 6-метровую тень на стену в 6 метрах от человека.Под каким углом свет?
103.
Прожектор на земле в 3 футах от женщины 5 футов высотой отбрасывает тень 15 футов высотой на стену в 6 футах от женщины. Под каким углом свет?
Для следующих упражнений найдите решение задачи со словом алгебраически. Затем воспользуйтесь калькулятором, чтобы проверить результат. Ответ округлите до десятых долей градуса.
104.
Человек выполняет стойку на руках, когда его ноги касаются стены, а руки находятся на расстоянии 1,5 фута от стены.Если рост человека 6 футов, какой угол у его ступни со стеной?
105.
Человек выполняет стойку на руках, при этом ноги касаются стены, а руки находятся на расстоянии 3 футов от стены. Если рост человека 5 футов, какой угол у его ступни со стеной?
106.
Лестница высотой 23 фута стоит рядом с домом. Если лестница соскользнет на расстоянии 7 футов от дома при недостаточном сцеплении с дорогой, какой угол должна быть сделана по отношению к земле, чтобы избежать скольжения?
6.1: Решение тригонометрических уравнений — Математика LibreTexts
Уравнение, включающее тригонометрические функции, называется тригонометрическим уравнением .\ circ k \ quad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\]
Это является наиболее общим решением уравнения. Часто часть, в которой говорится «для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)», опускается, поскольку обычно понял, что \ (k \) изменяется для всех целых чисел. Общее решение в радианах будет:
\ [\ nonumber
A ~ = ~ 0.6435 \; + \; \ pi k \ quad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\]
Пример 6.1
Решите уравнение \ (\; 2 \, \ sin \; \ theta \; + \; 1 ~ = ~ 0 \). 2 \; \ theta ~ = ~ \ frac {1} {2} \ quad \ Rightarrow \ quad \ cos \; \ theta ~ = ~ \ pm \, \ frac {1} {\ sqrt {2}}
\ quad \ Rightarrow \ quad \ theta ~ = ~ \ frac {\ pi} {4} \ ;, ~ \ frac {3 \ pi} {4} \ ;, ~ \ frac {5 \ pi} {4} \ ;, ~
\ frac {7 \ pi} {4} ~,
\]
и поскольку период косинуса равен \ (2 \ pi \), мы бы добавили \ (2 \ pi k \) к каждому из этих углов, чтобы получить общее решение. Но обратите внимание, что указанные выше углы различаются кратно \ (\ frac {\ pi} {2} \). Итак, поскольку каждое кратное \ (2 \ pi \) также кратно \ (\ frac {\ pi} {2} \), мы можем объединить эти четыре отдельных ответа в один:
\ [\ nonumber
\ boxed { \ theta ~ = ~ \ frac {\ pi} {4} \; + \; \ frac {\ pi} {2} \, k}
\ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ ( … \)}
\]
Пример 6.3
Решите уравнение \ (\; 2 \, \ sec \; \ theta ~ = ~ 1 \).
Решение:
Изоляция \ (\; \ sec \; \ theta \) дает нам
\ [\ nonumber
\ sec \; \ theta ~ = ~ \ frac {1} {2} \ quad \ Rightarrow \ quad \ cos \; \ theta ~ = ~ \ frac {1} {\ sec \; \ theta} ~ = ~ 2 ~,
\]
, что невозможно. 2 \; + \; Икс \;-\; 1 ~ = ~ 0 \ quad \ Rightarrow \ quad x ~ = ~ \ frac {-1 \; \ pm \; \ sqrt {1 — (4) \, (- 1)}} {
2 \, (1)} ~ = ~ \ frac {-1 \; \ pm \; \ sqrt {5}} {2} ~ = ~ -1.618 \ ;, ~ 0.618
\]
по формуле корней квадратного уравнения из элементарной алгебры. Но \ (- 1.618 <-1 \), поэтому невозможно, чтобы \ (\; \ sin \ theta = x = -1.618 \). Таким образом, мы должны иметь \ (\; \ sin \; \ theta = x = 0,618 \). Следовательно, есть два возможных решения: \ (\ theta = 0,666 \) рад в QI и его отражение \ (\ pi - \ theta = 2,475 \) рад вокруг оси \ (y \) - в QII. Добавление к ним кратных \ (2 \ pi \) дает нам общее решение:
\ [\ nonumber
\ boxed {\ theta ~ = ~ 0.666 \; + \; 2 \ пи к \ квад \ текст {и} \ квад 2.475 \; + \; 2 \ pi k}
\ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\ ]
Пример 6.5
Решите уравнение \ (\; \ sin \; \ theta ~ = ~ \ tan \; \ theta \).
Решение:
Используя тот же метод, что и в предыдущем примере, мы получаем
\ [\ nonumber \ begin {align *}
\ sin \; \ theta ~ & = ~ \ tan \; \ theta \\ \ nonumber
\ sin \; \ theta ~ & = ~ \ frac {\ sin \; \ theta} {\ cos \; \ theta} \\ \ nonumber
\ sin \; \ theta ~ \ cos \; \ theta ~ & = ~ \ sin \; \ theta \\ \ nonumber
\ sin \; \ theta ~ \ cos \; \ theta \; — \; \ sin \; \ theta ~ & = ~ 0 \\ \ nonumber
\ sin \; \ theta ~ (\ cos \; \ theta \; — \; 1) ~ & = ~ 0 \\ \ nonumber
& \ Rightarrow \ quad \ sin \; \ theta ~ = ~ 0 \ quad \ text {или} \ quad \ cos \; \ theta ~ = ~ 1 \\ \ nonumber
& \ Rightarrow \ quad \ theta ~ = ~ 0 \ ;, ~ \ pi \ quad \ text {или} \ quad \ theta ~ = ~ 0 \\ \ nonumber
& \ Rightarrow \ quad \ theta ~ = ~ 0 \ ;, ~ \ pi ~,
\ end {align *} \ ]
плюс число, кратное \ (2 \ pi \). Итак, поскольку указанные выше углы кратны \ (\ pi \), а каждое кратное \ (2 \ pi \) кратно \ (\ pi \), мы можем объединить два ответа в один для общего решения:
\ [\ nonumber
\ boxed {\ theta ~ = ~ \ pi k} \ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \ ), \ (… \)}
\]
Пример 6.6
Решите уравнение \ (\; \ cos \; 3 \ theta ~ = ~ \ frac {1} {2} \).
Решение:
Идея состоит в том, чтобы сначала решить для \ (3 \ theta \), используя наиболее общее решение, а затем разделить это решение на \ (3 \).{-1} \ frac {1} {2} = \ frac {\ pi} {3} \), есть два возможных решения для \ (3 \ theta \): \ (3 \ theta = \ frac {\ pi } {3} \) в QI и его отражение \ (- 3 \ theta = — \ frac {\ pi} {3} \) вокруг оси \ (x \) — в QIV. Добавление к ним кратных \ (2 \ pi \) дает нам:
\ [\ nonumber
3 \ theta ~ = ~ \ pm \, \ frac {\ pi} {3} \; + \; 2 \ pi k \ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (. .. \)}
\]
Таким образом, разделив все на \ (3 \), мы получим общее решение для \ (\ theta \):
\ [\ nonumber
\ boxed {\ theta ~ = ~ \ pm \, \ frac {\ pi} {9} \ ; + \; \ frac {2 \ pi} {3} k}
\ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\]
Пример 6.7
Решите уравнение \ (\; \ sin \; 2 \ theta ~ = ~ \ sin \; \ theta \).
Решение:
Здесь мы используем формулу двойного угла для синуса:
\ [\ nonumber \ begin {align *}
\ sin \; 2 \ theta ~ & = ~ \ sin \; \ theta \\ \ nonumber
2 \, \ sin \ theta ~ \ cos \; \ theta ~ & = ~ \ sin \; \ theta \\ \ nonumber
\ sin \; \ theta ~ (2 \, \ cos \; \ theta \ ; — \; 1) ~ & = ~ 0 \\ \ nonumber
& \ Rightarrow \ quad \ sin \; \ theta ~ = ~ 0 \ quad \ text {или} \ quad \ cos \; \ theta ~ = ~ \ frac {1} {2} \\ \ nonumber
& \ Rightarrow \ quad \ theta ~ = ~ 0 \ ;, ~ \ pi \ quad \ text {или} \ quad \ theta ~ = ~ \ pm \, \ frac { \ pi} {3} \\ \ nonumber
& \ Rightarrow \ quad \ boxed {\ theta ~ = ~ \ pi k \ quad \ text {и} \ quad \ pm \, \ frac {\ pi} {3} \ ; + \; 2 \ pi k}
\ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (. .. \)}
\ end {align *}
\]
Рисунок 6.1.1
Решение:
Мы будем использовать технику, которую мы обсуждали в главе 5, для нахождения амплитуды комбинации синусоидальных и косинусных функций. Возьмите коэффициенты \ (2 \) и \ (3 \) при \ (\; \ sin \; \ theta \) и \ (\; — \ cos \; \ theta \), соответственно, в приведенном выше уравнении и сделайте им ноги прямоугольного треугольника, как на рисунке 6.1.1. Пусть \ (\ phi \) будет углом, показанным в прямоугольном треугольнике. Нога с длиной \ (3> 0 \) означает, что угол \ (\ phi \) находится выше оси \ (x \) -, а нога с длиной \ (2> 0 \) означает, что \ (\ phi \) находится справа от оси \ (y \).Следовательно, \ (\ phi \) должен находиться в QI. Гипотенуза имеет длину \ (\ sqrt {13} \) по теореме Пифагора, и, следовательно, \ (\; \ cos \; \ phi = \ frac {2} {\ sqrt {13}} \) и \ (\; \ sin \; \ theta = \ frac {3} {\ sqrt {13}} \). Мы можем использовать это, чтобы преобразовать уравнение для решения следующим образом:
\ [\ nonumber \ begin {align *}
2 \, \ sin \; \ theta \; — \; 3 \, \ cos \; \ theta ~ & = ~ 1 \\ \ nonumber
\ sqrt {13} \, \ left (\ tfrac {2} {\ sqrt {13}} \, \ sin \; \ theta \ ; — \; \ tfrac {3} {\ sqrt {13}} \, \ cos \; \ theta
\ right) ~ & = ~ 1 \\ \ nonumber
\ sqrt {13} \, (\ cos \; \ phi \; \ sin \; \ theta \; — \; \ sin \; \ phi \; \ cos \; \ theta) ~ & = ~ 1 \\ \ nonumber
\ sqrt {13} \, \ sin \ ; (\ theta — \ phi) ~ & = ~ 1 \ quad \ text {(по формуле вычитания синуса)} \\ \ nonumber
\ sin \; (\ theta — \ phi) ~ & = ~ \ tfrac {1 } {\ sqrt {13}} \\ \ nonumber
& \ Rightarrow \ quad \ theta — \ phi ~ = ~ 0. 281 \ quad \ text {или} \ quad \ theta — \ phi ~ = ~ \ pi — 0,281 = 2,861 \\ \ nonumber
& \ Rightarrow \ quad \ theta ~ = ~ \ phi \; + \; 0.281 \ quad \ text {или} \ quad \ theta ~ = ~ \ phi \; + \; 2.861
\ end {align *} \]
Теперь, поскольку \ (\; \ cos \; \ phi = \ frac {2} {\ sqrt {13}} \) и \ (\ phi \) находится в QI , наиболее общим решением для \ (\ phi \) является \ (\ phi = 0.983 + 2 \ pi k \) для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \ , 2 \), \ (… \). Итак, поскольку нам нужно было добавить кратные \ (2 \ pi \) к решениям \ (0.281 \) и \ (2.861 \) в любом случае, наиболее общее решение для \ (\ theta \):
\ [\ begin {align *}
\ theta ~ & = ~ 0.983 \; + \; 0,281 \; + \; 2 \ пи к \ квад \ текст {и} \ квад 0,983 \; + \; 2,861 \; + \; 2 \ pi k \\
& \ Rightarrow \ quad \ boxed {\ theta ~ = ~ 1.264 \; + \; 2 \ пи к \ квад \ текст {и} \ квад 3.844 \; + \; 2 \ pi k}
\ quad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\ конец {выравнивание *} \]
Примечание: в примере 6.8, если бы уравнение было \ (\; 2 \, \ sin \; \ theta \; + \; 3 \, \ cos \; \ theta ~ = ~ 1 \), то мы все равно использовали бы прямоугольный треугольник с катетами длины \ (2 \) и \ (3 \), но мы бы использовали формулу сложения синуса вместо формулы вычитания.
Авторы и авторство
Как найти общее решение тригонометрических уравнений?
Как найти общее решение тригонометрических уравнений?

Тригонометрические уравнения
Определение:
Уравнение, включающее одно или несколько тригонометрических соотношений неизвестного угла, называется тригонометрическим уравнением

Тригонометрическое уравнение отличается от тригонометрических тождеств. Идентичность выполняется для каждого значения неизвестного угла , например, ., Cos ² x = 1 — sin ² x истинно ∀ x ∈ R, в то время как тригонометрическое уравнение выполняется для некоторых конкретных значений неизвестного угла .
(1) Корни тригонометрического уравнения: Значение неизвестного угла (переменная величина), которое удовлетворяет данному уравнению, называется корнем уравнения, например, ., Cos θ = ½, корень равен θ = 60 ° или θ = 300 °, потому что уравнение будет выполнено, если мы положим θ = 60 ° или θ = 300 °.
(2) Решение тригонометрических уравнений: Значение неизвестного угла, удовлетворяющее тригонометрическому уравнению, называется его решением.
Поскольку все тригонометрические отношения периодичны по своей природе, обычно тригонометрическое уравнение имеет более одного решения или бесконечное количество решений. Существует три основных типа решений:
Частное решение: Определенное значение неизвестного угла, удовлетворяющее уравнению.
Главное решение: Наименьшее числовое значение неизвестного угла, удовлетворяющее уравнению (Наименьшее числовое частное решение).
Общее решение: Полный набор значений неизвестного угла, удовлетворяющий уравнению. Он содержит все частные решения, а также основные решения.
Тригонометрические уравнения с их общим решением
+ π / 2 901 63
Тригонометрическое уравнение Общее решение
sin θ = 0 θ = n15 θ15
tan θ = 0 θ = nπ
sin θ = 1 θ = 2nπ + π / 2
cos θ = 1 θ6 = 2n16π sin θ = sin α θ = nπ + (−1) ⁿ α
cos θ = cos α θ = 2nπ ± α
tan θ = tan α θ = nπ ± α
sin ² θ = sin ² α θ = nπ ± α
tan ² θ = tan ² α θ = nπ ± α
cos ² θ = cos ² α θ = nπ ± α
sin θ = sin α
cos θ = cos α θ = nπ + α
sin θ = sin α
tan θ = tan α θ = nπ + α
tan θ = tan α
cos θ = cos α θ = nπ + α
Общее решение формы a cos θ + b sin θ = c
Метод нахождения главного значения
Предположим, мы должны найти главное значение sin θ = −½, удовлетворяющее уравнению.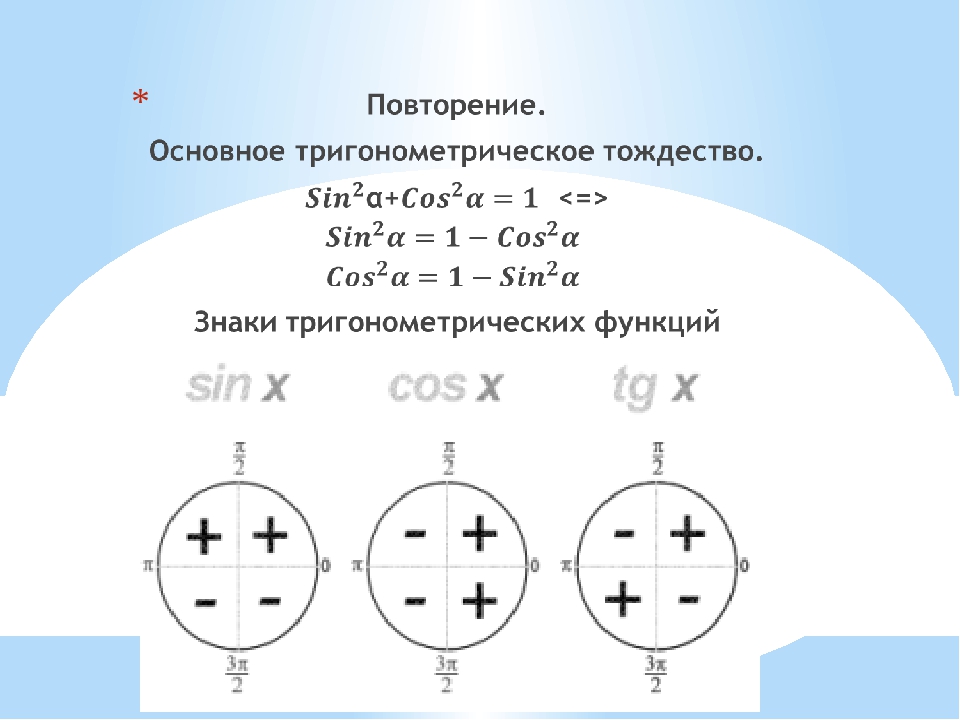
Поскольку sin θ отрицателен, θ будет в квадранте 3 ^rd или 4 ^th. Мы можем подойти к 3-му или 4-му квадранту с двух сторон. Если мы возьмем направление против часовой стрелки, числовое значение угла будет больше π. Если подойти к нему по часовой стрелке, угол будет численно меньше π. За главное значение мы должны взять численно наименьший угол. Итак, для главного значения.
(1) Если угол находится в 1-м или 2-м квадранте, мы должны выбрать направление против часовой стрелки, а если угол находится в квадранте 3 ^rd или 4 ^th, мы должны выбрать направление по часовой стрелке.
(2) Главное значение никогда не может быть численно больше π.
(3) Главное значение всегда находится в первом круге (то есть в первом повороте). По вышеуказанным критериям θ будет -π / 6 или -5π / 6. Между этими двумя -π / 6 имеет наименьшее числовое значение. Следовательно, −π / 6 — это главное значение θ, удовлетворяющее уравнению sin θ = −½.
Из приведенного выше обсуждения метод нахождения главного значения можно резюмировать следующим образом:
Сначала нарисуйте тригонометрический круг и отметьте квадрант, в котором может находиться угол.
Выберите направление против часовой стрелки для квадрантов 1 ^-й и 2 ^-й и выберите направление по часовой стрелке для квадрантов 3 ^-й и 4 ^-й.
Найдите угол при первом повороте.
Выберите численно наименьший угол. Найденный таким образом угол будет главной величиной.
В случае, если два угла, один с положительным знаком, а другой с отрицательным знаком, соответствуют численно наименьшему углу, тогда принято выбирать угол с положительным знаком в качестве главного значения.
Тригонометрические уравнения Задачи с решениями
1.

Решение:

2.

Решение:

3.

Решение

Решение:

5.

Решение:

6.

Решение:

7.

Решение: 9507 90.

Решение:

9.

Решение:
Базовые тригонометрические уравнения :
Когда просят решить 2x — 1 = 0, мы можем легко получить 2x = 1 и x = как ответ.
Когда просят решить 2 sin x — 1 = 0, мы действуем аналогичным образом. Сначала мы смотрим на sin x как на переменную уравнения и решаем, как мы это делали в первом примере.
2 sin x — 1 = 0
2 sin x = 1
sin x = 1/2
Знаки и квадранты :
Решения тригонометрических уравнений также можно найти, исследуя знак триггера значение и определение подходящего квадранта (ов) для этого значения.
Решение задач со словами с помощью тригонометрии
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
границ | Обучение решению задач тригонометрии, требующих навыков алгебраического преобразования, посредством обучения по аналогии и обучения по сравнению
Введение
Тема тригонометрии входит в программу средней математики. Тригонометрия является необходимым условием для изучения математического анализа в старших классах математики и необходима студентам, желающим изучать курсы естествознания, технологий, инженерии и математики (STEM). Изучение задач тригонометрии требует понимания множества взаимосвязанных математических понятий, таких как навыков алгебраического преобразования , знаний геометрии и рассуждений о графическом представлении концепций . Из-за необходимости изучать несколько взаимосвязанных понятий, студенты испытывают большие трудности при изучении задач тригонометрии (Blackett and Tall, 1991; Kendal and Stacey, 1998).Наша цель в этой статье концептуального анализа — подчеркнуть важность навыков алгебраических преобразований для облегчения начального этапа изучения задач тригонометрии. Основное внимание здесь уделяется вычислению неизвестной стороны прямоугольного треугольника по известной стороне и углу, что может стать проблемой для многих студентов. В частности, мы утверждаем, что у некоторых студентов могут возникнуть трудности при решении sin30 ° = x /5, скажем, несмотря на то, что они узнали, как решить аналогичную задачу, например, x /4 = 3. Для более сложных задач тригонометрии, таких как sin30 ° = 12/ x , где местоимение является знаменателем, студентов учили «заменять» x на sin30 °, а затем, исходя из этого, решать для x (Источник : личное общение).
Мы утверждаем, что такая детализированная стратегия обучения для задач тригонометрии не соответствует навыкам алгебраического преобразования, которые требуются для решения задач тригонометрии. Например, он не пытается связать предварительные знания учащегося о решении линейных уравнений с дробью с решением задач тригонометрии.Помимо этого, учащиеся могут столкнуться с большими трудностями, когда они попытаются различить два типа задач тригонометрии, которые выглядят одинаково, но концептуально отличаются друг от друга, следовательно, из-за относительного положения местоимения (т. Е. Числитель vs знаменатель) (Кендал и Стейси, 1998). Исходя из этого, преподавателям важно рассмотреть различные теоретические подходы, педагогические стратегии и / или образовательные программы, которые могут помочь учащимся приобрести соответствующие навыки для решения задач тригонометрии, различающихся расположением местоимения (т. е., числитель против знаменателя). Одна из возможностей, например, связана с использованием различных, но сопоставимых теорий обучения, которые могут способствовать эффективному обучению и способствовать осмысленному пониманию. Таким образом, цель этой статьи, расположенной в контексте актуальной темы тригонометрии, состоит в том, чтобы мы исследовали эффективность двух теорий обучения: обучения по аналогии, и обучения по сравнению . Мы утверждаем, что этот анализ может стать основой для дальнейшего развития исследований, теоретически, эмпирически, концептуально и / или методологически, в целях эффективного применения различных теорий обучения.
Концепция обучения по аналогии
Обучение по аналогии , подкрепленное теорией отображения структуры (Gentner, 1983), обеспечило теоретическую основу для развития исследований в области изучения словесных проблем (Reed et al., 1985, 2012; Reed, 1987; Ross and Кеннеди, 1990; Камминс, 1992). Теория структурных отображений подчеркивает построение «реляционных общностей» между исходным примером (изученная проблема) и целевой проблемой (новая проблема) с точки зрения структуры проблемы. Проблемы, состоящие из двух слов, могут иметь разные контексты, но разделять схожую структуру проблемы, например: (i) «Если 20% моей экономии составляет 300 долларов, какова моя экономия?» vs. (ii) «Джошуа платит 260 долларов в неделю за аренду, что составляет 25% его недельной заработной платы. Сколько зарабатывает Джошуа в неделю? » Используя подход Алгебры , мы можем составить два уравнения, например, 20% x = 300 долларов США и 25% x = 260 долларов США, соответственно, и решить для x . Поскольку эти два уравнения имеют общие реляционные элементы, они используют одну и ту же процедуру решения.Аналогичный перенос вероятен, если учащиеся смогут успешно сопоставить элементы отношений между исходным примером и целевой проблемой. Действительно, рассуждение по аналогии изученной проблемы и новой проблемы позволяет учащимся извлечь схему для изученной проблемы, которая применима для решения новой проблемы.
Holyoak (1984) и Holyoak and Koh (1987) выделили четыре задачи для облегчения обучения по аналогии: построить мысленное представление исходного примера и целевой проблемы (Задача 1), получить исходный пример как аналог целевой проблемы (Задача 2), сопоставьте реляционные элементы исходного примера и целевой проблемы (Задача 3) и расширьте сопоставление для решения целевой проблемы (Задача 4). Авторы не предложили определенную последовательность для реализации этих четырех задач и не указали, какие задачи или задачи являются критическими для стимулирования аналогичного обучения.
Research сообщило о преимуществах включения вспомогательных сигналов , таких как подсказка (Novick and Holyoak, 1991) или напоминание (Ross, 1984) для доступа к исходному примеру. Таким образом, подсказка обращается к Задаче 2. В исследовании, проведенном Cummins (1992), практика извлечения сходных понятий между исходным примером и целевой проблемой привела к аналогичному переносу.Мы можем приписать извлечение сходных концепций деятельности по картированию, которая обращается к Задаче 3. Другие исследователи также подчеркивали процесс картирования для достижения аналогичного переноса (Gentner et al., 2003). Участники, заполнившие диаграмму, выделяющую элементы взаимосвязи между двумя сценариями переговоров, превзошли тех участников, которые просто изучали эти два сценария переговоров. В отличие от этого, однако, Рид (1989) не смог найти доказательств аналогичного переноса для словесных задач, несмотря на то, что он обратился к Задачам 2 и 3: (1) предоставил студентам подсказку для доступа к исходному примеру, (2) потребовал, чтобы студенты построили концептуально- сопоставление задач между исходным примером и целевой проблемой.
Исследование, проведенное одним из нас несколько лет назад (Ngu and Yeung, 2012), показало, что наличие нескольких компонентов в исходном примере (например, символические уравнения, категоризация) или целевой проблеме (например, подсказка, категоризация) или и то, и другое фактически способствовало отображению символьных уравнений исходного примера на целевую задачу, что привело к эффективности аналогичного переноса. Полученные данные, как мы утверждаем, предоставили новое теоретическое понимание обучения по аналогии, подчеркнув важность наличия нескольких компонентов, а не одного компонента, для содействия аналоговой передаче для словесных задач.
В свете предшествующих исследований обучения по аналогии, использование подсказок для доступа к исходному примеру кажется критически важной задачей по аналогии для облегчения передачи. Тем не менее, использование подсказки для доступа к источнику станет излишним, если исходный пример остается видимым, в то время как учащиеся занимаются отображением исходного примера и целевой проблемы (Richland et al., 2007). Ряд исследователей (Gentner et al., 2003; Rittle-Johnson and Star, 2007; Richland and McDonough, 2010) отметили преимущество представления двух примеров одновременно, а не последовательно.В этом случае одновременное представление двух примеров устраняет необходимость подсказывать учащимся, как получить доступ к исходному примеру. Представление примеров в последовательной манере, напротив, требует возможной необходимости предоставить соответствующие подсказки, чтобы напомнить учащимся об исходном примере.
Действительно, сопоставление двух проработанных примеров не только делает ненужным поиск исходного примера, но также дает учащимся возможность участвовать в сложном сравнении. В своем исследовании Kurtz et al.(2001) выступали за реализацию взаимного согласования, чтобы способствовать абстракции лежащей в основе общей структуры в двух частично понятых сценариях. Участники, которые совместно интерпретировали два сценария в сочетании с перечислением конкретных соответствий, продемонстрировали большую взаимную согласованность, чем те участники, которые либо совместно, либо по отдельности интерпретировали два сценария. Более того, взаимное согласование двух частично понятых текстовых примеров способствовало аналогичной передаче сложной научной концепции (Orton et al., 2012).
Очевидно, что из предыдущих разделов исследование поддержало использование сопоставления двух примеров для продвижения обучения по аналогии. Тем не менее, эффективность выполнения однозначного сопоставления зависит от ориентации двух изображений (Kurtz and Gentner, 2013) или объектов в двух примерах (Matlen et al., 2020). Выравнивание двух примеров в одной ориентации вместо разных ориентаций в этом случае способствует прямому согласованию процесса сопоставления, что повышает эффективность рассуждений по аналогии.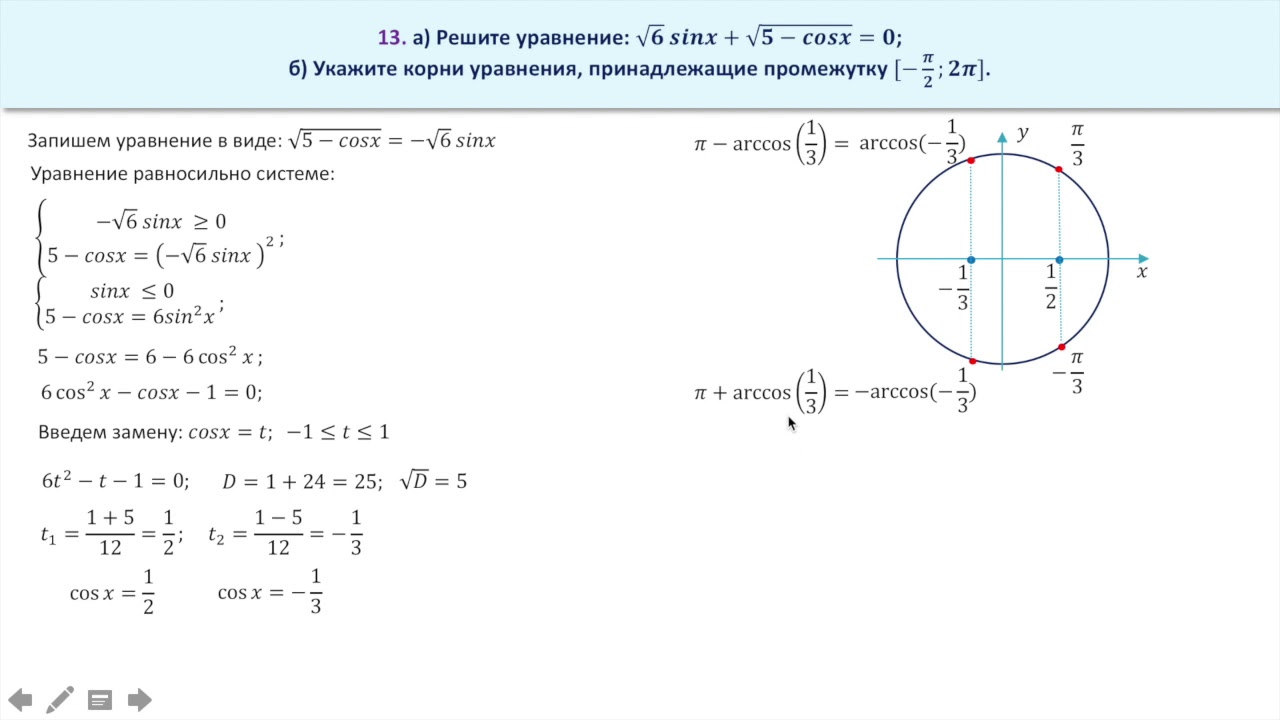
Концепция обучения путем сравнения
Основываясь на теории отображения структуры (Gentner, 1983), чтобы способствовать аналогичной передаче, ряд исследований недавно выявил положительные эффекты обучения по сравнению с (Alfieri et al., 2013; Ziegler and Stern, 2014; Rittle-Johnson et al. др., 2017). Например, Дуркин и Риттл-Джонсон (2012) исследовали эффект сравнения правильных и неправильных примеров для изучения десятичных чисел. Отображение правильных десятичных и неправильных десятичных понятий одновременно помогло учащимся исправить свои неправильные представления о величине десятичных чисел.Аналогичное направление исследований включало просьбу студентов обосновать, почему конкретный шаг решения был хорошим шагом (например, 1 = 2 x — 5, 6 = 2 x ) или неправильным шагом (например, 3 = 6 x — 2, 3 = 3 x ), помог студентам консолидировать и уточнить свое понимание концептуальных знаний, которые использовались при решении линейных уравнений (Booth et al. , 2013). Более того, Große и Renkl (2007) продемонстрировали положительный эффект от использования правильных и неправильных рабочих примеров в области проблем вероятности.Они утверждали, что обучение на правильных и неправильных примерах дает учащимся возможность различать сходства и различия между двумя типами проработанных примеров.
Вместо сравнения правильных и неправильных проработанных примеров для облегчения изучения математики, сравнение двух противоположных выражений алгебры (например, y ³ + y ³ = 2 y ³ vs. y ³ × y ³ = y ⁶) бок о бок также помогли учащимся различать внешне похожие (например,g., буква, число), но концептуально разные концепции (например, сложение или умножение) в двух противоположных рабочих примерах (Ziegler and Stern, 2014). Студенты, изучавшие противоположные выражения алгебры одновременно, превзошли тех студентов, которые изучали выражения алгебры последовательно. Таким образом, в целом развитие исследований на сегодняшний день подтвердило преимущество использования обучения в сравнении для повышения эффективности обучения математике.
Обучение по аналогии и обучение по сравнению в классе математики
Помимо проведения лабораторных тестов, исследователи также изучили межнациональные различия при использовании обучения по аналогии на уроках математики для восьмиклассников (Richland et al., 2007). Например, учителя в странах с высокими показателями по математике (например, Гонконг, Япония), как правило, используют гораздо больше визуально-пространственных опор и связывающих жестов, чтобы подчеркнуть аналогичные сравнения, чем их коллеги из США. Частое использование визуально-пространственных опор и связующих жестов, которые направляют внимание студентов на аналог источника, может помочь снизить требования к когнитивной обработке, поскольку устраняет необходимость поиска аналога источника (Richland et al., 2017).
Вместо того, чтобы проводить обучение путем сравнения в неповрежденных классах, которое длилось несколько дней, Star et al. (2015), напротив, реализовали одногодичное вмешательство между учебной программой «сравнения» и учебной программой «как обычно». Учебная программа сравнения была включена в обычную учебную программу в качестве дополнительных материалов. Более широкое использование сравнительных материалов коррелировало с более высоким ростом процедурных знаний. Тем не менее, было непросто побудить учителей постоянно использовать сравнительные материалы в течение года.
Действительно, исходя из вышесказанного, аналогичные рассуждения облегчаются использованием вспомогательных сигналов (например,g., подсказка), чтобы привлечь внимание учащихся к соответствующему исходному примеру, в котором описана процедура решения, аналогичная целевой задаче. Тем не менее, мы могли бы исключить подсказку для доступа к исходному примеру, если бы мы поместили исходный пример и целевую задачу рядом (например, Rittle-Johnson and Star, 2007). Сопоставление реляционных общностей между исходным примером и целевой проблемой — еще одна важная задача по аналогии, которая облегчает передачу по аналогии. Однако успешный аналогичный перенос зависит от активного процесса сравнения (например,g., совместная интерпретация плюс список конкретных соответствий) (например, Kurtz et al., 2001) и прямое согласование примеров (например, Matlen et al., 2020). Тем не менее, интересно отметить, что из нашего изучения литературы, построение мысленного представления исходного примера на начальном этапе обучения по аналогии (Holyoak and Koh, 1987) получило минимальное внимание с точки зрения исследований и / или преподавания. разработка.
Существенным моментом обучения путем сравнения, напротив, является одновременное отображение двух проработанных примеров бок о бок, что затем позволяет учащимся идентифицировать сходства и различия между двумя процедурами решения двух проработанных примеров (Rittle-Johnson et al. al., 2017). Следовательно, обучение путем сравнения может улучшить понимание учащимся математических концепций (или заблуждений), а также конкретных процедур, относящихся к двум проработанным примерам (например, Booth et al. , 2013).
Интересно отметить, что с методологической точки зрения обучение по аналогии и обучение по сравнению состояли из использования различных типов вмешательств. Что касается обучения по аналогии, исследователи внедрили меры вмешательства в лабораторных и учебных классах (Alfieri et al., 2013) и также включали использование визуально-пространственных опор и связывающих жестов (Richland et al., 2007). Аналогичным образом, для обучения путем сравнения, исследователи проводили как краткосрочные вмешательства (например, Rittle-Johnson and Star, 2007), так и долгосрочные вмешательства (например, один календарный год), чтобы улучшить изучение алгебры (Star и др., 2015). Таким образом, в целом мы утверждаем, что педагогические практики, которые включают использование обучения по аналогии и обучения по сравнению, являются эффективными, помогая облегчить изучение математики учащимися.Какой подход более уместен и / или эффективен? С нашей точки зрения, мы признаем, что два педагогических подхода дополняют друг друга — сила одного подхода может противостоять слабости другого подхода, и поэтому этот «дополнительный баланс» может отражать целостную позицию, когда человек узнает, как для решения задач тригонометрии.
Задачи тригонометрии
Наша цель для обсуждения — предложить эффективную инструкцию, которая могла бы облегчить изучение двух разных типов задач тригонометрии, которые различаются из-за относительного положения местоимения, например, cos60 ° = x /2, где местоимение числитель, а sin30 ° = 8/ x , где местоимение является знаменателем.Как отмечалось ранее, задачи тригонометрии аналогичны линейным уравнениям с дробью. В ходе нашего исследования мы обнаружили, что сложнее решать линейные уравнения с дробью, особенно если местоимение является знаменателем, а не числителем, поскольку первое включает больше шагов решения (Ngu and Phan, 2016).
Несмотря на важность задач тригонометрии в учебной программе средней школы по математике, исследования, касающиеся эффективного преподавания и обучения этому типу задач, относительно немногочисленны (Kendal and Stacey, 1998; Weber, 2005; Weber et al., 2008). Исследования показали, что студенты испытывают большие трудности, когда им нужно научиться решать оба типа задач тригонометрии (например, sin30 ° = 8/ x против cos60 ° = x /2) (Kendal and Stacey, 1998). . Чтобы решить эту проблему, Кендал и Стейси (1998) сравнили метод единичного круга и метод отношения с особым вниманием к трудностям студентов в применении навыков алгебраического преобразования для решения задач тригонометрии с местоимениями в качестве знаменателей.Для метода единичного круга авторы создали прямоугольный треугольник, который имеет те же свойства, что и данный прямоугольный треугольник. Требовалось несколько навыков для создания масштабного коэффициента, который позволил бы решать задачи тригонометрии с местоимениями в качестве знаменателей (например, выровнять два прямоугольных треугольника с точки зрения схожих свойств). Для метода отношения, напротив, на основе информации, представленной в прямоугольном треугольнике, студенты должны были выразить тригонометрическое соотношение в уравнении (например,g., cos60 ° = x /2), а затем решите относительно x . Результаты пост-теста показали, что метод единичного круга уступает методу отношения, независимо от типа задач тригонометрии (т. е. sin30 ° = 8/ x или cos60 ° = x /2).
Хорошо известно, что научиться решать тригонометрические задачи, требующие навыков алгебраического преобразования, является повсеместной проблемой, которая по-прежнему сохраняется для многих учащихся средних школ (Weber, 2005).Эта трудность, возможно, усугубляется существующими учебными материалами, которые описаны и рекомендованы в учебниках (например, Vincent et al., 2012). Например, Винсент и др. (2012) подробно описали процедуру решения задач тригонометрии, в которых числителями являются местоимения (например, cos50 ° = x /8): умножьте обе стороны на 8, что включает одну операцию. Напротив, когда местоимение является знаменателем (например, sin30 ° = 12/ x ), авторы рекомендовали две операции: (i) умножить обе стороны на x и (ii) разделить обе стороны на sin30 °.Мы утверждаем, что представление процедуры решения обоих типов задач тригонометрии логично. Сказав это, однако, отметим, что Винсент и др. (2012) не пытались связать два типа задач тригонометрии с предварительным знанием студентами линейных уравнений с дробью.
Мы утверждаем, что важно учитывать, в какой степени обучение по аналогии, которое может опираться на предварительные знания учащегося о решении линейных уравнений с дробью, может способствовать эффективному решению задач тригонометрии, требующих навыков алгебраических преобразований.В то же время мы также рассматриваем эффективность обучения путем сравнения, чтобы различать различные процедуры решения для задач тригонометрии, которые имеют местоимение в качестве знаменателя (например, sin30 ° = 8/ x ) или числителей (например, cos60 ° = x /2). Мы обсудим процедуру решения линейных уравнений с дробью в следующем разделе, учитывая, что они связаны с задачами тригонометрии.
Процедура решения линейных уравнений
В соответствии с предыдущими исследованиями (e.г., Нгу и др., 2015; Ngu and Phan, 2016), мы используем реляционных и рабочих строк для описания процедуры решения линейного уравнения. Линия отношения относится к «количественному отношению, в котором левая часть уравнения приравнивается к правой части уравнения». Операционная строка, напротив, относится к использованию «операции, которая изменяет состояние уравнения, и, следовательно, такой процедурный шаг сохранит равенство уравнения». Например, обращаясь к формуле.1 на рисунке 1, строки 1 и 3 являются линиями отношений, тогда как, напротив, линия 2 — это рабочая линия. Более того, в этом примере мы используем обратный метод , чтобы проиллюстрировать процедуру решения уравнений, содержащих дробь (рисунок 1). Наше предыдущее исследование подтвердило использование обратного метода, а не метода баланса для решения линейных уравнений, особенно тех уравнений, которые включают несколько шагов решения (Ngu et al., 2015, 2018). Основное различие между обратным методом и балансовым методом в этом смысле заключается в оперативной строке (т.е.g., × 4 с обеих сторон по сравнению с ÷ 2 становится × 2) (см. рисунок 1 для обратного метода). Центральное место в природе обратного метода занимает сама обратная операция. Концептуализация обратной операции деления в данном случае — умножение (т.е. ÷ 2 становится × 2). По словам Дина (2016), интересно, что понимание обратной операции в младшие школьные годы, вероятно, поможет при изучении математики в старших классах (например, дифференциация и интеграция в исчислении). Обратный метод, как мы выяснили из нашего существующего исследования, вероятно, вызовет меньшую когнитивную нагрузку, чем метод баланса, особенно для линейных уравнений, которые имеют несколько шагов решения.
Рисунок 1. Три варианта исходных примеров.
Задачи тригонометрии с местоимением в числителе
В этом разделе статьи подробно описывается наша основная посылка, которая «приравнивает» задачу тригонометрии, в которой числителем является местоимение (например, sin30 ° = x /6), с задачей линейного уравнения с дробью (например, х /4 = 3). Используя существующие исследования (Holyoak, 1984; Holyoak, Koh, 1987; Kurtz et al. , 2001; Нгу и Йунг, 2012; Альфиери и др., 2013; Риттл-Джонсон и др., 2017; Matlen et al., 2020), мы предлагаем два основных этапа, чтобы облегчить аналогичное обучение для задач тригонометрии, которые включают навыки алгебраического преобразования. Теперь мы подробно обсудим каждый из приведенных ниже этапов.
Первый этап: три варианта исходных примеров
В соответствии с разработкой учебной программы и расписанием мы предполагаем, что студенты выучили бы линейные уравнения с дробью до того, как изучат тему тригонометрии (Винсент и др., 2012). Такое упорядочение является преимуществом, поскольку оно позволяет преподавателям проводить параллель между изученной задачей, такой как линейное уравнение с дробью, x /4 = 3 (исходный пример), и новой задачей, такой как задача тригонометрии, sin30 ° = x /6 (целевая задача). Однако начинающие ученики не обязательно могут распознать сходство между исходным примером и целевой проблемой без поддержки учителя. Чтобы облегчить обучение по аналогии, первый этап включает мысленное представление трех вариантов исходных примеров в терминах процедуры решения (рис. 1).В данном случае цель состоит в том, чтобы помочь учащимся выбрать соответствующий исходный пример из трех различных вариантов исходных примеров, который затем может служить руководством для решения целевой проблемы.
Все три варианта исходных примеров представляют собой одношаговые уравнения с одной рабочей строкой и двумя реляционными строками (Ngu and Phan, 2016, 2017). Мы помещаем три уравнения рядом, чтобы облегчить процесс картирования (Курц и др., 2001; Риттл-Джонсон и Стар, 2009; Матлен и др., 2020).Кроме того, мы помечаем шаги решения, например, строки 1, 2 и 3 в уравнении. 1 (Ngu and Phan, 2016, 2017), чтобы дать четкую подсказку (Richland et al., 2017), которая будет поощрять и облегчать активное сравнение. По сути, уравнение. 1 является основным примером источника, тогда как уравнения. 2 и 3 являются производными уравнения. 1. Уровень сложности трех вариантов увеличивается по сравнению с уравнениями 1–3. Уравнение 1 отличается от уравнения. 2 с точки зрения относительного положения пронумерала (т. Е. Левая сторона по сравнению с правой). Различная ориентация пронумерала может препятствовать прямому выравниванию реляционных элементов (Kurtz, Gentner, 2013; Matlen et al., 2020), и, следовательно, это отрицательно скажется на эффективности аналогичного сравнения. Напротив, отображение уравнений. 2 и 3 в той же ориентации, при которой местоимение расположено в правой части уравнения, позволило бы прямое выравнивание реляционных элементов и, таким образом, облегчило бы процесс сопоставления (Kurtz and Gentner, 2013). Следует отметить, что уравнение. 2 (например, 2 = x /5) соответствует целевой задаче (например, sin30 ° = x /6), учитывая, что обе задачи имеют местоимения, расположенные в правой части уравнения.Уравнение 3, напротив, отличается от уравнения 2, поскольку первое имеет десятичное число. Расположение местоимения в правой части уравнения и наличие десятичного числа считаются особенностями одношаговых уравнений; Эти особенности, как мы утверждаем, создают серьезные проблемы для многих студентов (Ngu and Phan, 2017).
В соответствии с рекомендацией Kurtz et al. (2001), чтобы облегчить рассуждение по аналогии, наша концептуализация требует, чтобы учащиеся выполнили три задачи (см. Рисунок 1).Наша цель — побудить студентов к углубленной обработке трех исходных примеров. Для выполнения первого задания учащиеся должны сравнить и описать сходства и различия между тремя уравнениями по отношению к Строке 1. Цель состоит в том, чтобы помочь учащимся провести глубокие аналогичные рассуждения, ведущие к выявлению общей структуры отношений во всей системе. три уравнения. Сравнение формул. 1 и 2, например, раскрывают различное расположение местоимения (т. Е., левая сторона против правой). Сравнение формул. 2 и 3, напротив, показали бы, что эти уравнения не демонстрируют взаимно-однозначного соответствия с точки зрения атрибута элементов из-за присутствия десятичного числа в уравнении. 3. Следует отметить, что уравнение. 3 (1,2 = x /3) соответствует целевой задаче (sin30 ° = x /6), учитывая, что обе задачи имеют местоимения, расположенные в правой части уравнения, и что sin30 ° можно выразить в виде десятичной дроби. . Кроме того, как мы видим, математическая операция для строки 1 (например,g., ÷ 2 становится × 2 в уравнении. 1) одинаков во всех трех уравнениях. Таким образом, сравнив строку 1 трех уравнений, мы ожидаем, что учащиеся поймут, что эти три уравнения принадлежат к одной и той же категории линейных уравнений, что требует использования одной и той же математической операции для решения.
Что касается второй задачи, студенты должны генерировать параллельные шаги решения, такие как строки 2 и 3 уравнений. 2 и 3, которые совпадают со строками 2 и 3 в уравнении. 1 (Курц и др., 2001).Создание параллельных шагов решения для уравнений. 2 и 3 привлекут внимание студентов к взаимно однозначному соответствию со ссылкой на элементы взаимосвязи между тремя уравнениями. Третье задание, напротив, требует от студентов ответа на наводящий вопрос, например: «Почему может быть полезно сравнить уравнения. 1–3? » Мы ожидаем, что такая задача укрепит понимание учащимися сходства между тремя уравнениями с точки зрения схемы для процедуры совместного решения. Короче говоря, выполнив три задачи, мы ожидаем, что студенты сделают вывод и осознают, что три уравнения имеют схожую процедуру решения, несмотря на относительное положение местоимения (т.е., правая сторона против левой) и разница в формате числа (например, 2 против 1,2). После того, как учащиеся мысленно представили три варианта исходных примеров и вывели схему для общей процедуры решения, мы ожидаем, что они выберут соответствующий исходный пример (1,2 = x /3) и впоследствии будут использовать его для решения целевой задачи тригонометрии. (sin30 ° = x /6). Это будет вторым этапом в аналогичном процессе обучения.
Второй этап: сопоставьте соответствующий пример источника и целевую проблему
Мы предполагаем, что учащиеся выучили бы определение тригонометрических соотношений до того, как научились решать задачи тригонометрии, требующие навыков алгебраического преобразования.Каждое тригонометрическое соотношение представляет собой число (т.е. дробь или десятичное число), которое определяется как одна сторона над другой стороной в прямоугольном треугольнике.
Как показано на рисунке 2, поместив рядом соответствующий пример источника (1,2 = x /3) и целевую задачу (sin30 ° = x /6), нет необходимости предоставлять подсказку. для доступа к соответствующему примеру источника (Rittle-Johnson and Star, 2009; Matlen et al., 2020). И снова мы даем явную подсказку (Richland et al., 2017), в которых мы используем строки 1, 2, 3 и так далее для обозначения процедуры решения. Для первого задания студенты должны изучить шаги решения строк 1, 2 и 3 в соответствующем исходном примере, а затем сгенерировать параллельные шаги решения для целевой проблемы, которые обозначены строками 2, 3 и 4. Изучив целевую задачу, мы ожидаем, что студенты восстановят свои предварительные знания о выражении sin30 ° в десятичном числе, а затем заполнят Строку 2 целевой задачи. При этом студенты, вероятно, заметят сходство между строкой 1 соответствующего исходного примера (1.2 = x /3) и первый шаг решения целевой задачи (0,5 = x /6). Следовательно, посредством действий по сопоставлению мы утверждаем, что это будет направлять создание шагов решения для строк 3 и 4 целевых проблем, которые аналогичны шагам решения строк 2 и 3 соответствующего исходного примера. Соответственно, с нашей точки зрения, наилучшее согласование между соответствующим исходным примером и первым шагом решения целевой проблемы могло бы произойти, поскольку оба имеют схожие объекты и отношения (Richland et al., 2006).
Рисунок 2. Процедура решения соответствующего исходного примера и целевой проблемы.
Сгенерировав недостающие параллельные шаги решения целевой проблемы, учащиеся переходят ко второму заданию. Мы рекомендуем использовать открытые вопросы в качестве дополнительных вспомогательных сигналов для размышлений, консолидации и понимания — например, «Почему может быть полезно сравнить соответствующий исходный пример и целевую проблему?» Мы утверждаем, что вопросы для размышления могут помочь учащимся глубоко проанализировать соответствующий исходный пример и целевую проблему (Rittle-Johnson and Star, 2007).В конечном итоге, выполнив обе задачи на рисунке 2, мы ожидаем, что студенты сделают вывод со ссылкой на схему для общей процедуры решения линейного уравнения с дробью (например, 1,2 = x /3) и первый шаг решения Задача тригонометрии (например, 0,5 = x /6), при которой sin30 ° в цели заменен десятичным числом.
Сводка
Мы предлагаем мысленное представление трех вариантов исходных примеров, что приводит к выбору подходящего исходного примера для целевой задачи.Наше предложение отличается от предыдущих исследований (Holyoak and Koh, 1987; Ngu and Yeung, 2012), которые предполагают мысленное представление только одного примера источника. Существующие рекомендации подчеркивают взаимно однозначное сопоставление случаев или примеров для облегчения обучения по аналогии (Alfieri et al., 2013; Goldwater and Schalk, 2016). Однако, в отличие от существующих рекомендаций, мы подчеркиваем общую процедуру решения между соответствующим исходным примером и первым шагом решения целевой проблемы (т. Е., подмножество целевой задачи).
В соответствии с концепцией обучения путем сравнения (Rittle-Johnson et al., 2017) мы помещаем соответствующий исходный пример и целевую задачу рядом. Мы также помечаем процедуру решения соответствующего исходного примера, а также отсутствующую процедуру параллельного решения целевой проблемы. Наша цель здесь, в этом анализе, — привлечь внимание студентов к важнейшей особенности шагов решения, которая составляет общую структуру между релевантным источником и целевой проблемой.Активное аналогичное сравнение будет результатом, когда студенты генерируют недостающие параллельные шаги решения для целевых задач. Предоставление наводящего вопроса в сочетании с генерацией недостающих параллельных шагов решения для целевой проблемы, с нашей точки зрения, поможет студентам вывести схему общей процедуры решения между соответствующим исходным примером и первым шагом решения. целевой проблемы.
В целом, мы утверждаем, что предложенные нами два основных этапа обеспечивают важные идеи, которые могут способствовать аналогичному обучению: (i) мысленное представление трех вариантов исходных примеров с последующим выбором среди них подходящего исходного примера и (ii) выполнение картографических действий между соответствующим исходным примером и целевой проблемой.Мы утверждаем, что наше предложение, в отличие от существующих исследований, является информативным благодаря своей структурированной последовательности, позволяющей учащимся выстраивать свое понимание при решении задач тригонометрии, которые включают навыки алгебраического преобразования, посредством использования как обучения по аналогии, так и обучения через концепции сравнения.
Исследование эффекта реверсии опыта сделало акцент на конкретном взаимодействии между методом обучения и опытом учащегося в соответствующей области (Kalyuga et al., 2003). Вкратце, с акцентом на обратном эффекте опыта, следует отметить, что учащимся с разным уровнем знаний потребуются разные типы учебных методов. Соответственно, учащимся-экспертам не обязательно нужно мысленно представлять три варианта исходных примеров и выбирать соответствующий исходный пример и / или мысленно представлять целевую проблему плюс ее первый шаг решения. Обладая глубокими знаниями и пониманием линейных уравнений и тригонометрических соотношений, опытные ученики могут понять, что sin20 ° = x /6 аналогично 3 = x /8.Как только они поймут, что sin20 ° является десятичным числом, у них будет решение для sin20 ° = x /6. В самом деле, обнаружение сходства между sin20 ° = x /6 и 3 = x /8 привело бы к тому, что опытные ученики извлекли бы выученную процедуру решения для решения 3 = x /8, которую затем можно было бы использовать для решить sin20 ° = x /6.
Теоретическое обоснование, объясняющее процедуру решения задач тригонометрии с местоимением в качестве числителя, может быть применено к задачам тригонометрии, которые имеют местоимение в качестве знаменателя, при условии, что оба типа задач тригонометрии связаны с линейными уравнениями с дробью.В следующем разделе мы подробно исследуем решение задач тригонометрии, в знаменателе которых используются местоимения.
Задачи тригонометрии с местоимением в знаменателе
Как отмечалось ранее, относительное расположение местоимения (т. Е. Числитель против знаменателя) определяет сложность задачи тригонометрии. Шаги дифференциального решения отдают предпочтение задачам тригонометрии, в которых числитель является местоимением. В частности, задачи тригонометрии, в которых местоимение является знаменателем, более сложны, чем задачи тригонометрии, в которых местоимение используется в качестве числителя.В этом анализе у первого больше операционных линий (2 против 1) и линий отношений (3 против 2) по сравнению со вторым (см. Рисунки 2, 4). Обоснование для продвижения аналогичного обучения для двух типов задач тригонометрии, которые различаются расположением местоимения (то есть числитель против знаменателя), аналогично одинаково. Поэтому, как и в случае обучения тому, как решать задачи тригонометрии с местоимениями в качестве числителя (например, sin30 ° = x /6), мы утверждаем, что обучение решению cos60 ° = 4/ x потребует от учащихся вовлечения в следующем: (i) мысленно представить три варианта исходных примеров, а затем выбрать соответствующий исходный пример из этих исходных примеров (рисунок 3), (ii) сопоставить соответствующий исходный пример и целевую проблему (рисунок 4).
Рисунок 3. Три варианта исходных примеров.
Рисунок 4. Сопоставление релевантного исходного примера и целевой проблемы.
Три варианта исходных примеров представляют собой одношаговые линейные уравнения с двумя операционными линиями и тремя линиями отношения (рисунок 3). Уравнения 1, 2 аналогичны, за исключением расположения пронумерали (левая или правая сторона). Для уравнения. 2 расположение местоимения находится в правой части уравнения (4 = 32/ x ), что аналогично расположению местоимения для целевой задачи (Cos60 ° = 4/ x ) (Kurtz и Гентнер, 2013).Уравнения 2 и 3 аналогичны, за исключением десятичного числа для последнего. Как отмечалось ранее, наличие специальных функций (например, местоимение, расположенное в правой части уравнения, десятичное число и т. Д.) Усложняет одношаговые уравнения. Соответственно, три варианта линейных уравнений увеличивают сложность по сравнению с уравнениями. 1–3. Следует отметить, что обоснование выполнения задач на рисунках 3, 4 для изучения задач тригонометрии с местоимением в качестве знаменателя аналогично обоснованию выполнения задач на рисунках 1, 2 для изучения задач тригонометрии с местоимением в числителе. .Таким образом, мы не будем здесь отдельно обсуждать задачи на рисунках 3, 4.
Изучение процедуры решения для двух типов задач тригонометрии (то есть местоимение в числителе и местоимение в знаменателе) позволяет предположить, что есть несколько заметных различий. Как отмечалось ранее, например, разностное количество реляционных (3 против 4) и операционных (1 против 2) благоприятствует задачам тригонометрии, в которых местоимение используется в числителе (Ngu and Phan, 2016). Следовательно, исходя из этого несоответствия, мы утверждаем, что научиться решать Cos60 ° = 4/ x будет сложнее, чем научиться решать sin30 ° = x /6 (т.е.е., см. рисунок 2 в сравнении с рисунком 4). Однако, сказав это, мы утверждаем, что предварительные знания (например, знания алгебраических преобразований) помогли бы учащемуся сократить количество реляционных линий. Например, обращаясь к рисунку 4, обучающийся может пропустить Строку 2 соответствующего исходного примера (т. Е. 2,4 × x = 3) и соответствующую Строку 3 целевой задачи (т. Е. 0,5 × x = 4). . Следует отметить, что опытные ученики также могут распознать и понять, что cos40 ° = 5/ x и 3 = 12/ x подобны друг другу.Как только они поймут, что cos60 ° является десятичным числом (т. е. 0,5), они бы поняли, что для решения обеих задач можно использовать один и тот же метод.
Как мы можем помочь учащимся различать два типа задач тригонометрии: местоимение в качестве числителя (например, sin30 ° = x /6) и местоимение в качестве знаменателя (например, cos60 ° = 4/ x )? Предыдущие исследования показали, что учащиеся средней школы лучше учатся, когда местоимение является числителем, а не знаменателем (Kendal and Stacey, 1998; Weber, 2005).Количество операционных и реляционных линий, как мы утверждали, отражает сложность процедуры решения. Как отмечалось ранее, задачи тригонометрии, в которых местоимение является числителем, имеют меньше операционных (например, 1 против 2) и относительных (3 против 4) строк, чем задачи тригонометрии, в которых местоимение является знаменателем.
Различия двух типов задач тригонометрии
Концепция обучения путем сравнения, с нашей точки зрения, может помочь учащимся различать два типа задач тригонометрии. Мы предлагаем расположить два типа задач тригонометрии бок о бок и проинструктировать учащихся определять сходства и различия между ними (Rittle-Johnson et al., 2017). Например, со ссылкой на рисунок 5 мы могли бы попросить учащихся указать основные сходства и / или различия. На наш взгляд, существует ряд возможностей: (i) расположение местоимения (т. Е. Числитель против знаменателя), (ii) sin30 ° аналогичен cos50 °, оба из которых являются десятичными числами, (iii ) как только мы заменим sin30 ° или cos50 ° на десятичное число, оно превратится в линейное уравнение с дробью (например,g., рисунки 2, 4), (iv) различное количество реляционных линий (т. е. 2 против 3) и рабочих линий (т. е. 1 против 2) способствует решению задачи тригонометрии, в которой местоимение используется в качестве числителя, и ( v) обратный метод используется для решения обоих типов задач тригонометрии. После того, как учащиеся сравнили и определили сходства и различия между двумя типами задач тригонометрии, мы прогнозируем, что они заметили бы навыки дифференциально-алгебраического преобразования, используемые при решении этих двух типов задач тригонометрии.
Рисунок 5. Сравнение процедуры решения двух типов тригонометрических задач.
Для новичков, напротив, мы утверждаем, что в качестве основного шага для понимания было бы идеальным сравнить линейные уравнения с дробью бок о бок, чтобы определить их сходства и / или различия (см. Рисунок 6). Одна примечательная характеристика для идентификации в данном случае связана с расположением местоимения (т.е.как числитель vs.знаменатель), который влияет на навыки алгебраического преобразования, необходимые для решения этих двух типов линейных уравнений. Мы утверждаем, что изучение и освоение этого базового шага может облегчить понимание задач тригонометрии, в которых местоимения используются как в числителе, так и в знаменателе. Например, сравнение cos60 ° = 2/ x и cos60 ° = x /2 бок о бок указывает на то, что основное различие заключается в расположении местоимения, то есть 2/ x vs x /2.Эта идентификация, в свою очередь, подготовит новичков к решению обоих типов задач тригонометрии — в данном случае sin30 ° = 8/ x vs. cos60 ° = x /2.
Рисунок 6. Сравнение уравнения с местоимением в качестве числителя и уравнения с местоимением в качестве знаменателя.
Обсуждение
Тригонометрия действительно является сложной темой для многих учеников средней школы, особенно когда мы смешиваем проблемы тригонометрии с расположением местоимения (т.е., числитель против знаменателя) (Kendal and Stacey, 1998). Мы утверждаем, что можно противостоять этой распространенной проблеме, рассматривая использование теорий обучения — в данном случае обучения по аналогии и обучения по концепциям сравнения (Kurtz et al., 2001; Rittle-Johnson and Star, 2007; Alfieri et al. ., 2013). Наша концептуализация, подробно описанная в предыдущих разделах, предлагала мысленное представление трех вариантов исходных примеров. Из этих трех вариантов исходных примеров мы выбираем один релевантный исходный пример для целевой задачи.Мы выделяем сопоставление соответствующего исходного примера и первого шага решения целевой проблемы, чтобы достичь оптимального согласования между этими двумя проблемами. Наше предложение, в его совокупности, продвинуло изучение обучения по аналогии для его обсуждения на соответствующем исходном примере из трех вариантов исходных примеров. Это педагогическое утверждение отличается от предыдущего исследования (например, Holyoak and Koh, 1987), в котором акцент делается на использовании примера из одного источника. Более того, мы выделяем подмножество целевой проблемы, а не всю целевую проблему с целью реализации задачи однозначного сопоставления между соответствующим исходным примером и первым шагом решения целевой проблемы.Поэтому мы рекомендуем сравнение исходного примера и подмножества целевой задачи, чтобы облегчить обучение по аналогии.
В то же время, опираясь на важность обучения путем сравнения, мы рассматриваем возможность использования сравнения в контексте задач тригонометрии из-за их сходств и различий. Наша концептуализация, которую на сегодняшний день исследователи не изучили, является новаторской, поскольку в ней делается упор на одновременное сравнение различных типов задач тригонометрии. Это сравнение двух типов задач тригонометрии бок о бок, в частности, направлено на преодоление давних трудностей изучения задач тригонометрии, которые различаются из-за относительного положения местоимения (то есть числитель против знаменателя). Имея это в виду, мы призываем преподавателей рассмотреть возможность использования учебных практик, которые помогают учащимся распознавать и понимать два основных типа задач тригонометрии.
Как концепции обучения по аналогии и обучения по сравнению могут помочь нам в нашей педагогической практике в других областях математики? Рассмотрим в этом случае изучение задач выражения алгебры , которые представлены на рисунке 7.В данном случае фокус понимания связан с нашим предыдущим упоминанием сравнения, то есть параллельное сравнение проводится между «2 (3 + 5)» и « a (2 + b )». Наше постулирование состоит в том, что выравнивание реляционных элементов может помочь учащимся понять логику манипулирования переменными. Например, как показано, 2 a просто означает, что 2 умножается на a (переменная). Исходя из этого, в средней школе ученик может сравнить два уравнения бок о бок и сделать вывод, что 2 равно a , а 5 равно b .В том же ключе мы утверждаем, что полезно рассматривать обучение путем сравнения как учебный инструмент, который может облегчить изучение линейных уравнений . В качестве точки сравнения линейных уравнений, которые имеют дробную часть (например, рисунок 7), мы, например, отметим, что меньшее количество шагов решения (метод 1) более выгодно, поскольку это приведет к более низкой когнитивной нагрузке (Ngu et al., 2018 ).
Рис. 7. Примеры обучения математике через обучение по аналогии и обучение по сравнению.
В заключение, как преподаватели, мы признаем важную тему тригонометрии. Более того, исходя из нашего профессионального опыта, мы признаем, что существует распространенная проблема, когда в задачах тригонометрии есть местоимения, которые действуют как числитель, так и знаменатель.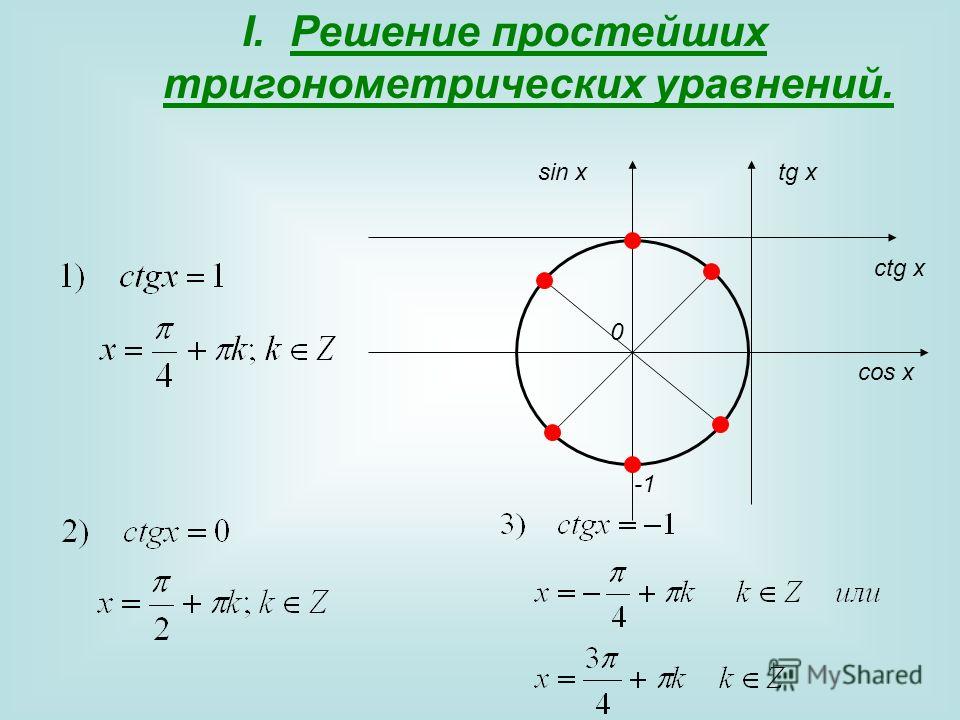 Это различие (т.е. местоимение в качестве числителя и местоимение в качестве знаменателя), как мы утверждаем, является относительно уникальным, затрудняя понимание учащимися того, как решать различные типы задач тригонометрии, требующие навыков алгебраического преобразования.На основе наших существующих эмпирических исследований и запросов и выводов других исследователей мы получили педагогическую концепцию, которая могла бы помочь студентам понять сложность задач тригонометрии. В этом анализе, рассматривая эффективность обучения по аналогии и обучения по сравнению, мы предложили ученикам альтернативную последовательность шагов. Мы рекомендуем преподавателям реализовать и изучить возможности нашего предложения при обучении двум типам задач тригонометрии, которые различаются относительным расположением местоимения (т.е., числитель против знаменателя).
Авторские взносы
BN и HP были ответственны за концептуализацию и редактирование этой рукописи. Оба автора внесли свой вклад в статью и одобрили представленную версию.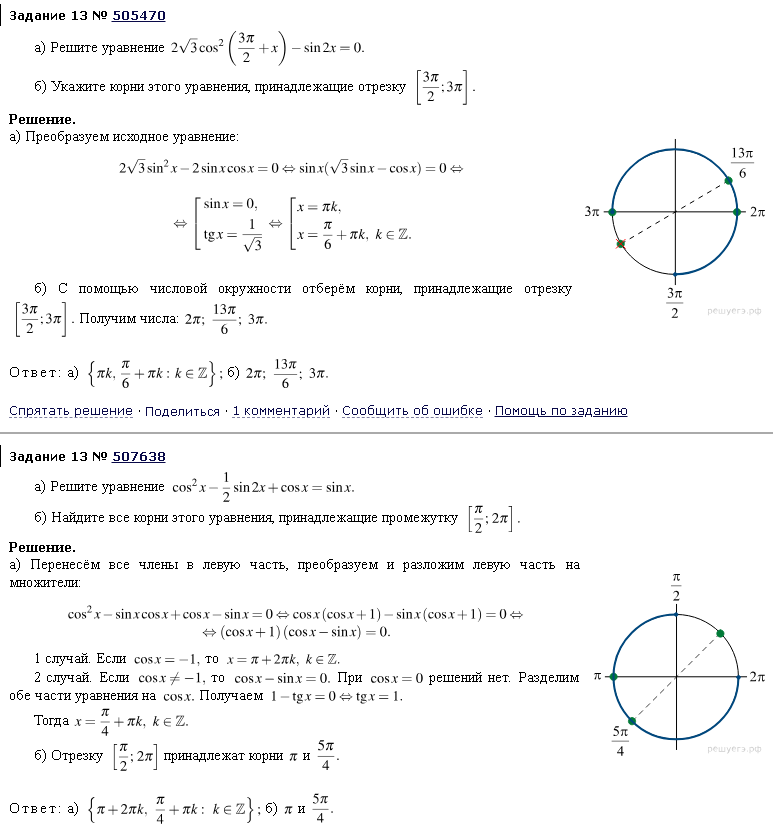
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.
Благодарности
Мы хотели бы выразить нашу признательность и благодарность двум рецензентам и редактору за их проницательные комментарии.
Список литературы
Альфиери, Л., Нокс-Малах, Т. Дж., И Шунн, К. Д. (2013). Обучение через сравнение случаев: метааналитический обзор. Educ. Psychol. 48, 87–113. DOI: 10.1080 / 00461520.2013.775712
CrossRef Полный текст | Google Scholar
Бехер Т. (1987). «Дисциплинарное формирование профессий», в Академическая профессия , изд. Б. Р. Кларк (Беркли, Калифорния: Калифорнийский университет Press), 271–303.
Google Scholar
Блэкетт, Н.и Толл Д. О. (1991). «Гендер и разностороннее изучение тригонометрии с помощью компьютерного программного обеспечения», Труды 15-го заседания Международной группы психологии математического образования , изд. Ф. Фурингетти (Италия: PME), 144–151.
Google Scholar
Бут, Дж. Л., Ланге, К. Э., Кёдингер, К. Р., Ньютон, К. Дж. (2013). Использование примеров задач для улучшения обучения студентов алгебре: различение правильных и неправильных примеров. ЖЖ. Instr. 25, 24–34. DOI: 10.1016 / j.learninstruc.2012.11.002
CrossRef Полный текст | Google Scholar
Камминс, Д. Д. (1992). Роль рассуждений по аналогии в индукции категорий проблем. J. Exp. Psychol. Учиться. Mem. Cogn. 18, 1103–1124. DOI: 10.1037 / 0278-7393.18.5.1103
CrossRef Полный текст | Google Scholar
Дин М. (2016). Возможности учиться: обратные отношения в учебниках США и Китая. Math.Считать. Учиться. 18, 45–68. DOI: 10.1080 / 10986065.2016.1107819
CrossRef Полный текст | Google Scholar
Дуркин, К., Риттл-Джонсон, Б. (2012). Эффективность использования неправильных примеров для поддержки изучения десятичной величины. ЖЖ. Instr. 22, 206–214. DOI: 10.1016 / j.learninstruc.2011.11.001
CrossRef Полный текст | Google Scholar
Гентнер Д. (1983). Структурное отображение: теоретическая основа для аналогии. Cogn.Sci. 7, 155–170. DOI: 10.1207 / s15516709cog0702_3
CrossRef Полный текст | Google Scholar
Гентнер Д., Лёвенштейн Дж. И Томпсон Л. (2003). Изучение и передача: общая роль аналогового кодирования. J. Educ. Psychol. 95, 393–405. DOI: 10.1037 / 0022-0663.95.2.393
CrossRef Полный текст | Google Scholar
Große, C. S., and Renkl, A. (2007). Обнаружение и исправление ошибок в отработанных примерах: может ли это способствовать результатам обучения? ЖЖ.Instr. 17, 612–634. DOI: 10.1016 / j.learninstruc.2007.09.008
CrossRef Полный текст | Google Scholar
Холиоук, К. Дж. (1984). «Аналогичное мышление и человеческий интеллект», в Успехах в психологии человеческого интеллекта , изд. Р. Дж. Стернберг (Хиллсдейл, Нью-Джерси: Эрлбаум), 199–230.
Google Scholar
Калюга С., Эйрес П., Чандлер П. и Свеллер Дж. (2003). Эффект отмены экспертизы. Educ. Psychol. 38, 23–31.DOI: 10.1207 / s15326985ep3801_4
CrossRef Полный текст | Google Scholar
Кендал М. и Стейси К. (1998). Обучение тригонометрии. Austral. Математика. Учат. 54, 34–39.
Google Scholar
Курц, К. Дж., И Гентнер, Д. (2013). Обнаружение аномальных свойств в сложных стимулах: роль структурированного сравнения. J. Exp. Psychol. Прил. 19, 219–232. DOI: 10.1037 / a0034395
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Курц, К.J., Miao, C.-H., и Gentner, D. (2001). Обучение с помощью аналогичного бутстрэппинга. J. Learn. Sci. 10, 417–446. DOI: 10.1207 / s15327809jls1004new_2
CrossRef Полный текст | Google Scholar
Нгу, Б. Х., Чунг, С. Ф., Юнг, А. С. (2015). Познавательная нагрузка в алгебре: интерактивность элементов при решении уравнений. Educ. Psychol. 35, 271–293. DOI: 10.1080 / 01443410.2013.878019
CrossRef Полный текст | Google Scholar
Нгу, Б. Х., и Фан, Х.П. (2016). Распаковка сложности линейных уравнений с точки зрения теории когнитивной нагрузки. Educ. Psychol. Ред. 28, 95–118. DOI: 10.1007 / s10648-015-9298-2
CrossRef Полный текст | Google Scholar
Нгу, Б. Х., и Фан, Х. П. (2017). Будет ли трудной задачей для учащихся 8-х классов научиться решать одношаговые уравнения? Внутр. J. Math. Educ. Sci. Technol. 48, 876–894. DOI: 10.1080 / 0020739x.2017.1293856
CrossRef Полный текст | Google Scholar
Нгу, Б.Х., Фан, Х. П., Йунг, А. С., Чунг, С. Ф. (2018). Управление интерактивностью элементов при решении уравнений. Educ. Psychol. Rev. 30, 255–272. DOI: 10.1007 / s10648-016-9397-8
CrossRef Полный текст | Google Scholar
Нгу, Б. Х., Юнг, А. С. (2012). Содействие передаче по аналогии: многокомпонентный подход к решению задач алгебры в контексте химии. Contemp. Educ. Psychol. 37, 14–32. DOI: 10.1016 / j.cedpsych.2011.09.001
CrossRef Полный текст | Google Scholar
Новик, Л.Р., и Холиоук, К. Дж. (1991). Решение математических задач по аналогии. J. Exp. Psychol. Учиться. Mem. Cogn. 17, 398–415.
Google Scholar
Ортон, Дж. М., Анггоро, Ф. К., и Джи, Б. Д. (2012). Взаимное сопоставление сравнения облегчает абстрагирование и передачу сложной научной концепции. Educ. Stud. 38, 473–477. DOI: 10.1080 / 03055698.2011.643104
CrossRef Полный текст | Google Scholar
Рид, С. К. (1987). Модель отображения структуры для текстовых задач. J. Exp. Psychol. Учиться. Mem. Cogn. 13, 124–139. DOI: 10.1037 / 0278-7393.13.1.124
CrossRef Полный текст | Google Scholar
Рид, С. К. (1989). Ограничения на абстракцию решений. J. Educ. Psychol. 81, 532–540. DOI: 10.1037 / 0022-0663.81.4.532
CrossRef Полный текст | Google Scholar
Рид, С.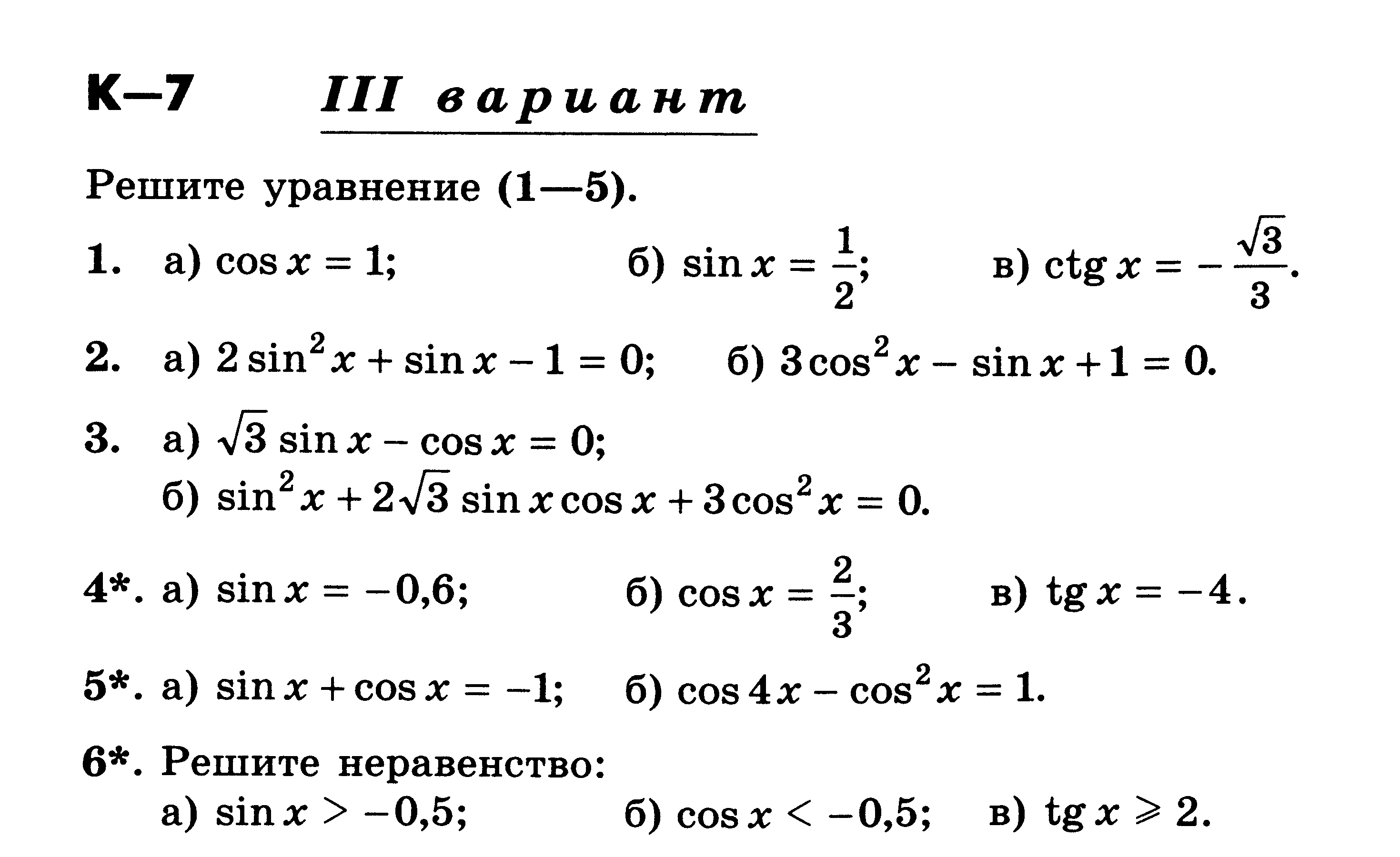 К., Демпстер, А., Эттингер, М. (1985). Полезность аналогичных решений для решения словесных задач алгебры. J. Exp.Psychol. Учиться. Mem. Cogn. 11, 106–125. DOI: 10.1037 / 0278-7393.11.1.106
CrossRef Полный текст | Google Scholar
Рид, С. К., Стебик, С., Коми, Б., и Кэрролл, Д. (2012). Обнаружение сходств и различий в решениях словесных задач. J. Educ. Psychol. 104, 636–646. DOI: 10.1037 / a0027181
CrossRef Полный текст | Google Scholar
Ричленд, Л. Э., Беголли, К. Н., Симмс, Н., Фраузель, Р. Р., Лайонс, Э. А. (2017). Поддерживающие математические дискуссии: роли сравнения и познавательная нагрузка. Educ. Psychol. Rev. 29, 41–53. DOI: 10.1007 / s10648-016-9382-2
CrossRef Полный текст | Google Scholar
Ричленд, Л. Э., и МакДонаф, И. М. (2010). Обучение по аналогии: различение потенциальных аналогов. Contemp. Educ. Psychol. 35, 28–43. DOI: 10.1016 / j.cedpsych.2009.09.001
CrossRef Полный текст | Google Scholar
Ричленд, Л. Э., и МакДонаф, И. М. (2010). Обучение по аналогии: различение потенциальных аналогов. Contemp. Educ. Psychol. 35, 28–43. DOI: 10.1016 / j.cedpsych.2009.09.001
CrossRef Полный текст | Google Scholar
Ричленд, Л. Э., Моррисон, Р. Г., и Холиоук, К. Дж. (2006). Развитие у детей рассуждений по аналогии: выводы из задач по аналогии со сценой. J. Exp. Детская психол. 94, 249. DOI: 10.1016 / j.jecp.2006.02.002
PubMed Аннотация | CrossRef Полный текст | Google Scholar
Риттл-Джонсон, Б., и Стар, Дж. Р. (2007).Облегчает ли сравнение методов решения концептуальные и процедурные знания? Экспериментальное исследование по обучению решению уравнений. J. Educ. Psychol. 99, 561–574. DOI: 10.1037 / 0022-0663.99.3.561
CrossRef Полный текст | Google Scholar
Риттл-Джонсон, Б., и Стар, Дж. Р. (2009). По сравнению с чем? Влияние различных сравнений на концептуальные знания и процедурную гибкость при решении уравнений. J. Educ. Psychol. 101, 529–544. DOI: 10.1037 / a0014224
CrossRef Полный текст | Google Scholar
Риттл-Джонсон, Б., Стар, Дж. Р., Дуркин, К. (2017). «Сила сравнения в обучении математике: экспериментальные данные из классных комнат», в «Математическое познание и обучение: приобретение сложных арифметических навыков и математических понятий высшего порядка» , ред. Д. К. Гири, Д. Б. Берч и К. М. Кёпке (Уолтем, Массачусетс: Эльзеви), 273–295. DOI: 10.1016 / b978-0-12-805086-6.00012-6
CrossRef Полный текст | Google Scholar
Росс, Б.Х. (1984). Напоминания и их влияние на обучение когнитивным навыкам. Cogn. Psychol. 16, 371–416. DOI: 10.1016 / 0010-0285 (84) -8
CrossRef Полный текст | Google Scholar
Росс, Б. Х., и Кеннеди, П. Т. (1990). Обобщение использования предыдущих примеров при решении проблем. J. Exp. Psychol. Учиться. Mem. Cogn. 16, 42–55. DOI: 10.1037 / 0278-7393.16.1.42
CrossRef Полный текст | Google Scholar
Стар, Дж. Р., Поллак, К., Дуркин, К., Риттл-Джонсон, Б., Линч, К., Ньютон, К. и др. (2015). Учимся на сравнении в алгебре. Contemp. Educ. Psychol. 40, 41–54. DOI: 10.1016 / j.cedpsych.2014.05.005
CrossRef Полный текст | Google Scholar
Винсент, Дж., Прайс, Б., Карузо, Н., Ромерил, Г., и Тайнан, Д. (2012). MathsWorld 9 Австралийский учебный план. Южная Ярра, Виктория: Макмиллан.
Google Scholar
Вебер, К. (2005). Понимание учащимися тригонометрических функций. Math. Educ. Res. J. 17, 91–112. DOI: 10.1007 / bf03217423
CrossRef Полный текст | Google Scholar
Вебер К., Нотт Л. и Эвиттс Т. А. (2008). Обучение тригонометрическим функциям: уроки, извлеченные из исследований. Math. Учат. 102, 144–150.
Google Scholar
Циглер, Э., Стерн, Э. (2014). Отложенные преимущества изучения элементарных алгебраических преобразований посредством контрастных сравнений. ЖЖ. Instr. 33, 131–146.