Удобные случаи простейших тригонометрических уравнений вида Sinx=a

by Колпаков А.Н. on 14 сентября 2010

Частные случаи:

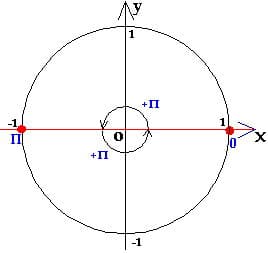1) Нули синуса: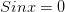

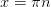
Уравнение можно решить
по общей формуле, однако наличие нуля в правой части делает ответ более удобным для дальнейшего отбора корней.

2) решение уравнения Sinx=1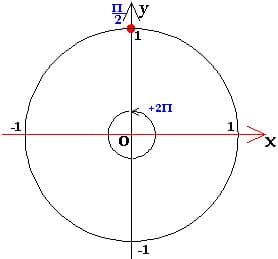

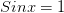
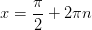
Уравнение можно решить
по общей формуле, однако наличие единицы в правой части делает ответ более удобным для дальнейшего отбора корней.

3)решение уравнения SinX=-1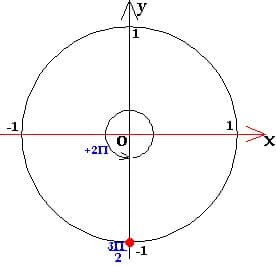

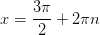
Уравнение можно решить
по общей формуле, однако наличие минус единицы в правой части делает ответ более удобным для дальнейшего отбора корней.

Посмотреть тригонометрические формулы.

Колпаков Александр Николаевич, репетитор по математике

Метки: Графики функций, Решение уравнений, Тригонометрия, Ученикам

ankolpakov.ru

sinx = 1/2 решение

Доброй ночи!
Уравнения вида, которое вы нам предоставили — очень часто вызывает различные затруднение. Но это, на самом деле, не так страшно и не так сложно. Прежде, чем разобраться с Вашей уравнением sinx = 1/2, нужно подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Вот так будет выглядеть Ваше условие на математическом языке: 

   

Да, я понимаю, что это Вам особо не помогло. Но для этого есть определённое правило решения подобных уравнений, которое примет такой общий вид: 

   

 

   

Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения: 

   

 

   

Значение  мы найдём при помощи таблицы. И исходя из этого получаем, что 
Так как с основным разобрались, то теперь можем и решить до конца Ваше уравнение: 

   

 

   

Ответ: 

ru.solverbook.com

sinx = 1/3 решение

Доброй Вам ночи!
Уравнения вида, которое вы нам предоставили — очень часто вызывает различные затруднение. Но это, на самом деле, не так страшно и не так сложно. Прежде, чем разобраться с Вашей уравнением sinx = 1/3 решение, нужно подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Вот так будет выглядеть Ваше условие на математическом языке:

   

Да, я понимаю, что это Вам особо не помогло. Но для этого есть определённое правило решения подобных уравнений, которое примет такой общий вид: 

   

 

   

Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения: 

   

 

   

Значение  мы не найдём при помощи таблицы, как делали это с другими уравнениями. По-\тому у нас ответ будет не такой красивый, как хотелось бы. Но ничего не поделаешь — это математика.
Так как с основным разобрались, то теперь можем и решить до конца Ваше уравнение: 

   

 

   

Ответ: 

ru.solverbook.com

sinx 1 2

Вы искали sinx 1 2? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и решение sinx 1 2, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «sinx 1 2».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как sinx 1 2,решение sinx 1 2,решите уравнение sin x 1 2. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и sinx 1 2. Просто введите задачу в окошко и нажмите «решить» здесь (например, решите уравнение sin x 1 2).

Где можно решить любую задачу по математике, а так же sinx 1 2 Онлайн?

Решить задачу sinx 1 2 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

www.pocketteacher.ru

sinx = 1/4 решение

Доброй ночи!
Уравнения вида, которое вы нам предоставили — очень часто вызывает различные затруднение. Но это, на самом деле, не так страшно и не так сложно. Прежде, чем разобраться с Вашей уравнением sinx = 1/4 решение, нужно подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Вот так будет выглядеть Ваше условие на математическом языке: 

   

Да, я понимаю, что это Вам особо не помогло. Но для этого есть определённое правило решения подобных уравнений, которое примет такой общий вид: 

   

 

   

Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения: 

   

 

   

Значение  мы не найдём с Вами при помощи таблицы.
Так как с основным разобрались, то теперь можем и решить до конца Ваше уравнение: 

   

 

   

Ответ:

ru.solverbook.com

Простейшие тригонометрические уравнения

Когда-то я стал свидетелем разговора двух абитуриентов:

– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!

– И у меня такая же проблема.

Так и хотелось им сказать: «Не запоминать надо, а понимать!»

Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:

1) sinx=a ,

2) cosx=a ,

3) tgx=a и

4) ctgx=a.

Числовая окружность

Наряду с понятием числовой прямой есть еще и понятие числовой окружности. Как мы знаем, в прямоугольной системе координат окружность ,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность : начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.

Свойства числовой окружности

• Каждое действительное число находится на одной точке числовой окружности.
• На каждой точке числовой окружности находятся бесконечно много действительных чисел. Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; … 

Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A.

• Так как длина полуокружности равна π, то разность между любыми двумя числами на диаметрально противоположных точках числовой окружности равна одному из чисел : ±π ; ±3π ; ±5π ; …

Проведем диаметр АС (рис. 2). Так как x_0 – одно из чисел точки А, то числа x_0±π ; x_0±3π; x_0±5π; … и только они будут числами точки C. Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).

Сделаем вывод: зная одно из чисел на одной из точек A или C диаметра АС, мы можем найти все числа на этих точках.

• Два противоположных числа находятся на симметричных относительно оси абсцисс точках окружности.

Проведем вертикальную хорду АВ (рис. 2). Так как точки A и B симметричны относительно оси Ox, то число -x_0 находится на точке B и, значит, все числа точки B задаются формулой: x_B=-x_0+2πk ,k∈Z. Числа на точках A и B запишем одной формулой: x_(A ; B)=±x_0+2πk ,k∈Z. Сделаем вывод: зная одно из чисел на одной из точек A или B вертикальной хорды АВ, мы можем найти все числа на этих точках. Рассмотрим горизонтальную хорду AD и найдем числа точки D (рис. 2). Так как BD – диаметр и число -x_0 принадлежит точке В, то -x_0 + π одно из чисел точки D и, значит, все числа этой точки задаются формулой x_D=-x_0+π+2πk ,k∈Z. Числа на точках A и D можно записать с помощью одной формулы: x_(A ; D)=(-1)^k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).

Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.

Шестнадцать основных точек числовой окружности

На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.

Теперь можем указать по одному числу на точках:

0 на A1 ,

π/6 на B1 ,

π/3 на С1 и

π/2 на A2 .

Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности. На рисунке отмечены также и координаты этих точек (опустим описание их получения).

Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a) простейших уравнений.

Решить уравнения

1) sinx=1⁄(2 ).

– Что от нас требуется?

– Найти все те числа x, синус которых равен 1/2.

Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x . На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».

2) sinx=-√3⁄2 .

Нам надо найти все числа на точках C4 и C3.

3) sinx=1. На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.

Ответ: x=π/2+2πk , k∈Z .

4) sinx=-1 .

Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.

Ответ: x=-π/2+2πk , k∈Z .

5) sinx=0 .

На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .

Ответ: x=πk ,k∈Z .

6) cosx=√2⁄2 .

Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x. На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.

Ответ: x=±π/4+2πk , k∈Z .

7) cosx=-1⁄2 .

Надо найти числа на точках C_2 и C_3 .

Ответ: x=±2π/3+2πk , k∈Z .

10) cosx=0 .

Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут  решениями уравнения. . 

Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosx<0 удовлетворяют только числа b_3
Ответ: x=-5π/6+2πk , k∈Z .

Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе

Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Решить уравнения :2 sin x

    Перед нами уравнение, где неизвестный член содержится под знаком тригонометрической функции sin.

Тригонометрические уравнения 

   Тригонометрическим уравнением называют уравнение, в котором переменная содержится под знаком тригонометрической функции. Выделяют три группы таких функций:

1. простые тригонометрические функции cosx и sinx ;
2. производные тригонометрические функции tgx и ctgx;
3. другие тригонометрические функции secx и cosecx.

  Решение любого тригонометрического уравнения сводится к двум этапам — приведению его к простейшему виду и решению полученного простейшего тригонометрического уравнения. Простейшее тригонометрическое уравнение имеет вид:

F(x) = a,

где F — любая из тригонометрических функций (sin, cos, tg, ctg, sec или cosec),

 a — числовой коэффициент.

   Для приведения к простейшему виду можно проводить алгебраические преобразования:

1. переносить члены уравнения с одной части в другую с противоположным знаком;
2. прибавлять/вычитать одно и то же число, при этом получим уравнение, равносильное первоначальному;
3. делить/умножить на одно и то же число.

  Попробуем преобразовать заданное уравнение и привести его к простейшему виду.

Решим заданное уравнение

   Дано уравнение вида 2sinx — 1 = 0. Первый этап решения начнём с его преобразования, а именно: прибавим к левой и правой части уравнения одно и то же число — единицу:

2sinx — 1 = 0,

2sinx — 1 + 1 = 0 + 1,

2sinx = 1.

   Далее, чтобы избавить от числового аргумента при тригонометрической функции sin, разделив обе части уравнения на одно и то же число два:

(2sinx)/2 = 1/2,

sinx = 1/2.

   В результате алгебраических преобразований привели уравнение к простейшему виду sinx = a, общим решением которого является решение вида:

Х = (-1)^k * arcsin(а) +- пk, k e Z, при этом |а| <=1.

   На втором этапе решим полученное равносильное уравнение простейшего вида. Числовой коэффициент а = 1/2, значит |1/2| <=1 и уравнение имеет решение:

sinx = 1/2,

x = (-1)^k * arcsin (1/2) + пk, k e Z;

x = (-1)^k * п/6 + пk, k e Z.

или 

х1 = п/6 + 2пk, k e Z,

x2 = 5п/6 + 2пk, k e Z.

Ответ:  х1 = п/6 + 2пk, k e Z; x2 = 5п/6 + 2пk, k e Z.

 

vashurok.ru