Матричный метод — Википедия
Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.
Пусть дана система линейных уравнений с n{\displaystyle n} неизвестными (над произвольным полем):
{a11x1+…+a1nxn=b1,⋯⋯⋯⋯⋯⋯⋯,an1x1+…+annxn=bn;{\displaystyle {\begin{cases}a_{11}x_{1}+\ldots +a_{1n}x_{n}=b_{1},\\\cdots \cdots \cdots \cdots \cdots \cdots \cdots ,\\a_{n1}x_{1}+\ldots +a_{nn}x_{n}=b_{n};\end{cases}}}
Тогда её можно переписать в матричной форме:
AX=B{\displaystyle AX=B}, где A{\displaystyle A} — основная матрица системы, B{\displaystyle B} и X{\displaystyle X} — столбцы свободных членов и решений системы соответственно:
A=(a11a12…a1na21a22…a2n⋮⋮⋱⋮an1an2…ann),B=(b1b2⋮bn),X=(x1x2⋮xn){\displaystyle A={\begin{pmatrix}a_{11}&a_{12}&\ldots &a_{1n}\\a_{21}&a_{22}&\ldots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&\ldots &a_{nn}\end{pmatrix}},B={\begin{pmatrix}b_{1}\\b_{2}\\\vdots \\b_{n}\end{pmatrix}},X={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}}
Умножим это матричное уравнение слева на A−1{\displaystyle A^{-1}} — матрицу, обратную к матрице A{\displaystyle A}: A−1(AX)=A−1B{\displaystyle A^{-1}\left(AX\right)=A^{-1}B}
Так как A−1A=E{\displaystyle A^{-1}A=E}, получаем X=A−1B{\displaystyle X=A^{-1}B}. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:
- detA≠0{\displaystyle \det A\neq 0}.
Для однородной системы линейных уравнений, то есть когда вектор B=0{\displaystyle B=0}, действительно обратное правило: система AX=0{\displaystyle AX=0} имеет нетривиальное (то есть ненулевое) решение только если detA=0{\displaystyle \det A=0}. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
{3x+2y−z=4,2x−y+5z=23,x+7y−z=5;{\displaystyle {\begin{cases}3x+2y-z=4,\\2x-y+5z=23,\\x+7y-z=5;\end{cases}}}
Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.
|32−12−1517−1|=3−14+10−1−105+4=−103;{\displaystyle {\begin{vmatrix}3&2&-1\\2&-1&5\\1&7&-1\end{vmatrix}}=3-14+10-1-105+4=-103;}
Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.
A11=(−1)1+1⋅|−157−1|=−34;{\displaystyle A_{11}=(-1)^{1+1}\cdot {\begin{vmatrix}-1&5\\7&-1\end{vmatrix}}=-34;}
A12=(−1)1+2⋅|251−1|=7;{\displaystyle A_{12}=(-1)^{1+2}\cdot {\begin{vmatrix}2&5\\1&-1\end{vmatrix}}=7;}
A13=(−1)1+3⋅|2−117|=15;{\displaystyle A_{13}=(-1)^{1+3}\cdot {\begin{vmatrix}2&-1\\1&7\end{vmatrix}}=15;}
A21=(−1)2+1⋅|2−17−1|=−5;{\displaystyle A_{21}=(-1)^{2+1}\cdot {\begin{vmatrix}2&-1\\7&-1\end{vmatrix}}=-5;}
A22=(−1)2+2⋅|3−11−1|=−2;{\displaystyle A_{22}=(-1)^{2+2}\cdot {\begin{vmatrix}3&-1\\1&-1\end{vmatrix}}=-2;}
A23=(−1)2+3⋅|3217|=−19;{\displaystyle A_{23}=(-1)^{2+3}\cdot {\begin{vmatrix}3&2\\1&7\end{vmatrix}}=-19;}
A31=(−1)3+1⋅|2−1−15|=9;{\displaystyle A_{31}=(-1)^{3+1}\cdot {\begin{vmatrix}2&-1\\-1&5\end{vmatrix}}=9;}
A32=(−1)3+2⋅|3−125|=−17;{\displaystyle A_{32}=(-1)^{3+2}\cdot {\begin{vmatrix}3&-1\\2&5\end{vmatrix}}=-17;}
A33=(−1)3+3⋅|322−1|=−7;{\displaystyle A_{33}=(-1)^{3+3}\cdot {\begin{vmatrix}3&2\\2&-1\end{vmatrix}}=-7;}
Далее найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы.
C∗=(−34715−5−2−199−17−7);{\displaystyle C^{*}={\begin{pmatrix}-34&7&15\\-5&-2&-19\\9&-17&-7\end{pmatrix}};}
(C∗)T=(−34−597−2−1715−19−7);{\displaystyle (C^{*})^{T}={\begin{pmatrix}-34&-5&9\\7&-2&-17\\15&-19&-7\end{pmatrix}};}
A−1=1detA⋅(C∗)T{\displaystyle A^{-1}={\frac {1}{\det A}}\cdot (C^{*})^{T}}
Подставляя переменные в формулу, получаем:
A−1=1−103⋅(−34−597−2−1715−19−7)=(341035103−9103−7103210317103−15103191037103);{\displaystyle A^{-1}={\frac {1}{-103}}\cdot {\begin{pmatrix}-34&-5&9\\7&-2&-17\\15&-19&-7\end{pmatrix}}={\begin{pmatrix}{\frac {34}{103}}&{\frac {5}{103}}&-{\frac {9}{103}}\\-{\frac {7}{103}}&{\frac {2}{103}}&{\frac {17}{103}}\\-{\frac {15}{103}}&{\frac {19}{103}}&{\frac {7}{103}}\end{pmatrix}};}
Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.
X=A−1⋅B;{\displaystyle X=A^{-1}\cdot B;}
X=(341035103−9103−7103210317103−15103191037103)⋅(4235)=(214){\displaystyle X={\begin{pmatrix}{\frac {34}{103}}&{\frac {5}{103}}&-{\frac {9}{103}}\\-{\frac {7}{103}}&{\frac {2}{103}}&{\frac {17}{103}}\\-{\frac {15}{103}}&{\frac {19}{103}}&{\frac {7}{103}}\end{pmatrix}}\cdot {\begin{pmatrix}4\\23\\5\end{pmatrix}}={\begin{pmatrix}2\\1\\4\end{pmatrix}}}
Итак, x = 2; y = 1; z = 4.
ru.wikipedia.org
Свойства обратной матрицы.
Понятие
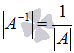
обратной матрицы, равенство  ,
определения операций над матрицами и
свойства определителя матрицы позволяют
обосновать следующие свойства
обратной матрицы:
,
определения операций над матрицами и
свойства определителя матрицы позволяют
обосновать следующие свойства
обратной матрицы:
Для невырожденной квадратной матрицы А справедливо равенство
 .
.Для обратимой матрицы А выполняется равенство
 .
.Для любого отличного от нуля числа k справедливо равенство
 .
.Для невырожденных квадратных матриц А и В одного порядка выполняется равенство
 .
.
Нахождение элементов обратной матрицы с помощью решения соответствующих систем линейных алгебраических уравнений.
Рассмотрим еще один способ нахождения обратной матрицы для квадратной матрицы Апорядка n на n.
Этот метод основан на решении n систем линейных неоднородных алгебраических уравнений с n неизвестными. Неизвестными переменными в этих системах уравнений являются элементы обратной матрицы.
Идея
очень проста. Обозначим обратную матрицу
как X,
то есть, 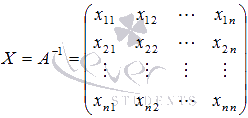 .
Так как по определению обратной матрицы
.
Так как по определению обратной матрицы 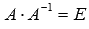 ,
то
,
то 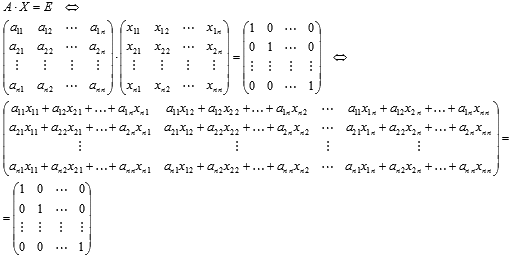
Приравнивая
соответствующие элементы по столбцам,
получим n систем
линейных уравнений 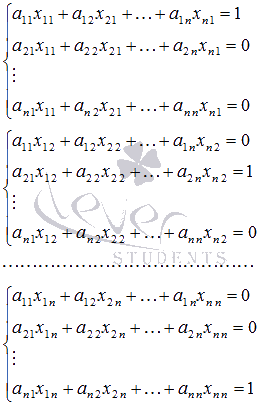
Решаем их любым способом и из найденных значений составляем обратную матрицу.
Разберем этот метод на примере.
Пример.
Дана
матрица 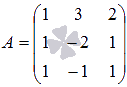 .
Найдите обратную матрицу.
.
Найдите обратную матрицу.
Решение.
Примем 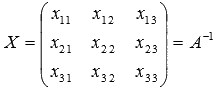 .
Равенство
.
Равенство 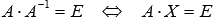 дает
нам три системы линейных неоднородных
алгебраических уравнений:
дает
нам три системы линейных неоднородных
алгебраических уравнений: 
Не будем расписывать решение этих систем, при необходимости обращайтесь к разделурешение систем линейных алгебраических уравнений.
Из первой системы уравнений имеем 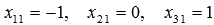 ,
из второй —
,
из второй — 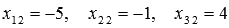 ,
из третьей —
,
из третьей —  .
Следовательно, искомая обратная матрица
имеет вид
.
Следовательно, искомая обратная матрица
имеет вид 
Подведем итог.
Мы рассмотрели понятие обратной матрицы, ее свойства и три метода ее нахождения.
Пример решений методом обратной матрицы
Задание 1. Решить СЛАУ методом обратной матрицы. 2 x 1 + 3x2 + 3x3+ x4= 1 3 x 1 + 5x2 + 3x3+ 2x4= 2 5 x 1 + 7x2 + 6x3+ 2x4= 3 4 x 1 + 4x2 + 3x3+ x4= 4
Начало формы

Конец формы
Решение. Запишем матрицу в виде: Вектор B: BT = (1,2,3,4) Главный определитель Минор для (1,1): = 5•(6•1-3•2)-7•(3•1-3•2)+4•(3•2-6•2) = -3 Минор для (2,1): = 3•(6•1-3•2)-7•(3•1-3•1)+4•(3•2-6•1) = 0 Минор для (3,1): = 3•(3•1-3•2)-5•(3•1-3•1)+4•(3•2-3•1) = 3 Минор для (4,1): = 3•(3•2-6•2)-5•(3•2-6•1)+7•(3•2-3•1) = 3 Определитель минора ∆ = 2•(-3)-3•0+5•3-4•3 = -3
Транспонированная матрица Алгебраические дополнения ∆1,1 = 5•(6•1-2•3)-3•(7•1-2•4)+2•(7•3-6•4) = -3 ∆1,2 = -3•(6•1-2•3)-3•(7•1-2•4)+1•(7•3-6•4) = 0 ∆1,3 = 3•(3•1-2•3)-3•(5•1-2•4)+1•(5•3-3•4) = 3 ∆1,4 = -3•(3•2-2•6)-3•(5•2-2•7)+1•(5•6-3•7) = -3 ∆2,1 = -3•(6•1-2•3)-3•(5•1-2•4)+2•(5•3-6•4) = 9 ∆2,2 = 2•(6•1-2•3)-3•(5•1-2•4)+1•(5•3-6•4) = 0 ∆2,3 = -2•(3•1-2•3)-3•(3•1-2•4)+1•(3•3-3•4) = -6 ∆2,4 = 2•(3•2-2•6)-3•(3•2-2•5)+1•(3•6-3•5) = 3 ∆3,1 = 3•(7•1-2•4)-5•(5•1-2•4)+2•(5•4-7•4) = -4 ∆3,2 = -2•(7•1-2•4)-3•(5•1-2•4)+1•(5•4-7•4) = 1 ∆3,3 = 2•(5•1-2•4)-3•(3•1-2•4)+1•(3•4-5•4) = 1 ∆3,4
= -2•(5•2-2•7)-3•(3•2-2•5)+1•(3•7-5•5) = 0 ∆4,1 = -3•(7•3-6•4)-5•(5•3-6•4)+3•(5•4-7•4) = -12 ∆4,2 = 2•(7•3-6•4)-3•(5•3-6•4)+3•(5•4-7•4) = -3 ∆4,3 = -2•(5•3-3•4)-3•(3•3-3•4)+3•(3•4-5•4) = 9 ∆4,4 = 2•(5•6-3•7)-3•(3•6-3•5)+3•(3•7-5•5) = -3 Обратная матрица Вектор результатов X X = A-1 ∙ B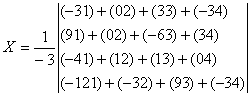 XT =
(2,-1,-0.33,1)
x1 =
2
x2 =
-1
x3 =
-0.33
x4 =
1
XT =
(2,-1,-0.33,1)
x1 =
2
x2 =
-1
x3 =
-0.33
x4 =
1см. также решений СЛАУ методом обратной матрицы online. Для этого введите свои данные и получите решение с подробными комментариями.
Задание 2. Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения. Решение:xml:xls
Пример
2.
Записать систему уравнений в матричной
форме и решить с помощью обратной
матрицы.
Пример. Дана система трех линейных уравнений с тремя неизвестными. Требуется: 1) найти ее решение с помощью формул Крамера; 2) записать систему в матричной форме и решить ее средствами матричного исчисления. Методические рекомендации. После решения методом Крамера, найдите кнопку «Решение методом обратной матрицы для исходных данных». Вы получите соответствующее решение. Таким образом, данные вновь заполнять не придется. Решение. Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B — матрицу-столбец свободных членов:
Вектор B: BT=(4,-3,-3) С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B. Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А-1. Умножив обе части уравнения на А-1, получим: А-1*А*Х = А -1*B, А-1*А=Е. Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1. Система будет иметь решение, если определитель матрицы A отличен от нуля. Найдем главный определитель. ∆=-1•(-2•(-1)-1•1)-3•(3•(-1)-1•0)+2•(3•1-(-2•0))=14 Итак, определитель 14 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения. Пусть имеем невырожденную матрицу А:
A= |
|
Тогда:
A=1/∆ |
|
где Aij — алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (—1)i+j на минор (определитель) n-1 порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А. Транспонированная матрица
Вычисляем алгебраические дополнения.
∆1,1=(-2•(-1)-1•1)=1
∆1,2=-(3•(-1)-0•1)=3
∆1,3=(3•1-0•(-2))=3
∆2,1=-(3•(-1)-1•2)=5
∆2,2=(-1•(-1)-0•2)=1
∆2,3=-(-1•1-0•3)=1
∆3,1=(3•1-(-2•2))=7
∆3,2=-(-1•1-3•2)=7
∆3,3=(-1•(-2)-3•3)=-7 Обратная матрица
Вектор результатов X X=A-1 • B
XT=(-1,1,2) x1=-14 / 14=-1 x2=14
studfile.net
Обратная матрица
Задача №6. Найти матрицу, обратную
к матрице .
.
Решение.
1) Найдем 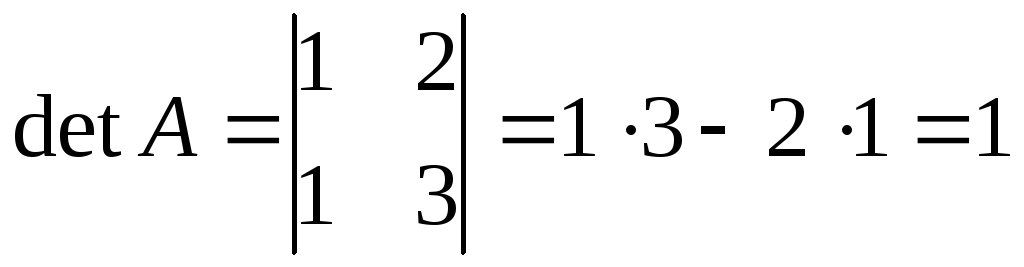
 ,
следовательно обратная матрица
существует.
,
следовательно обратная матрица
существует.
2) Найдем алгебраические дополнения к элементам матрицы А
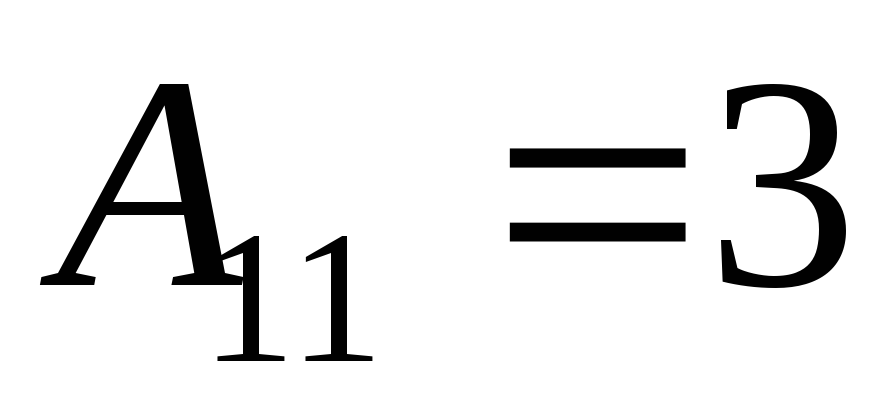

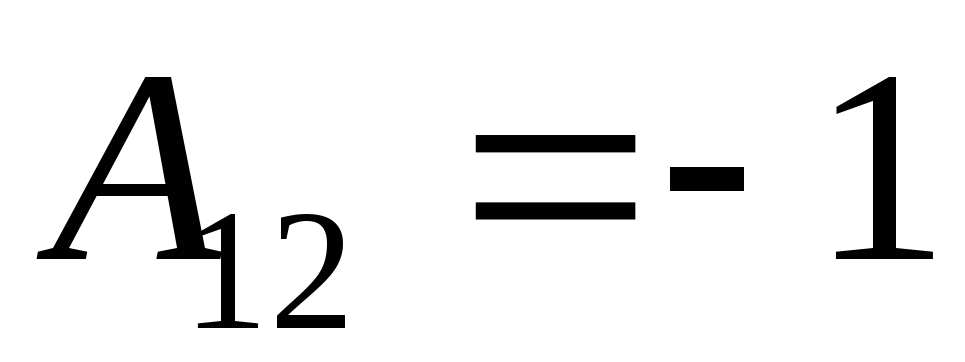
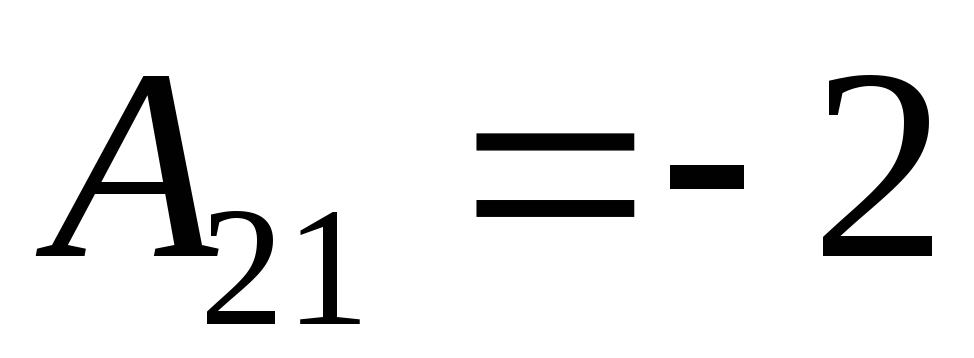
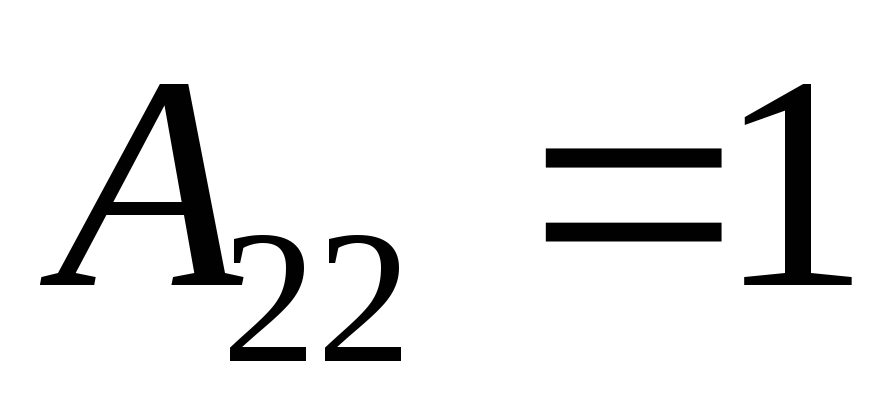
3) Запишем союзную матрицу
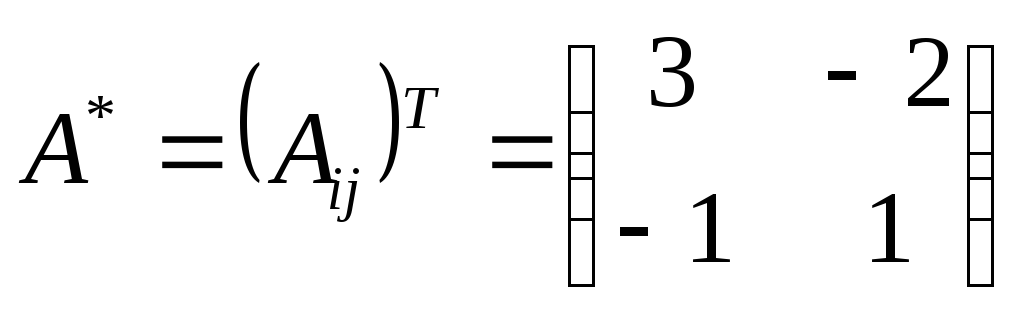
4) Найдем обратную матрицу

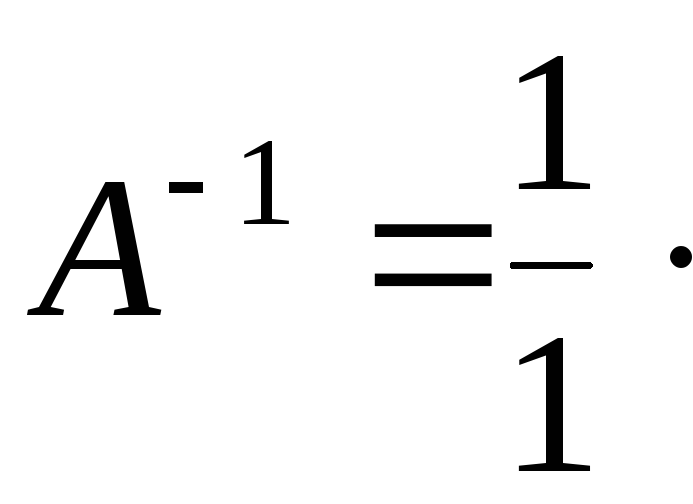
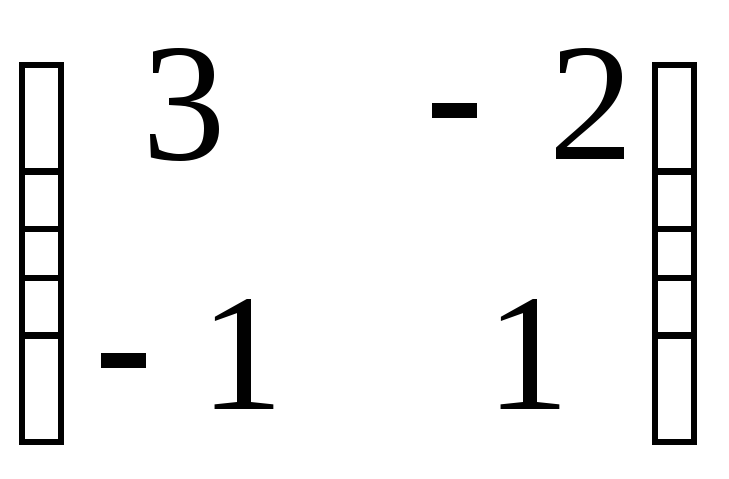
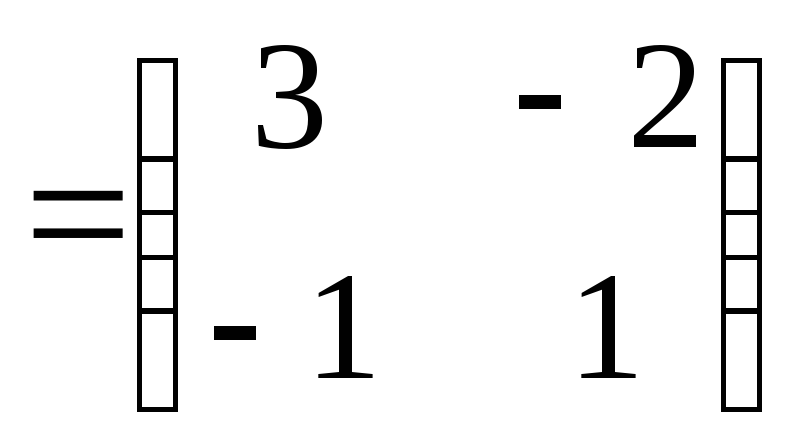
5) Сделаем проверку


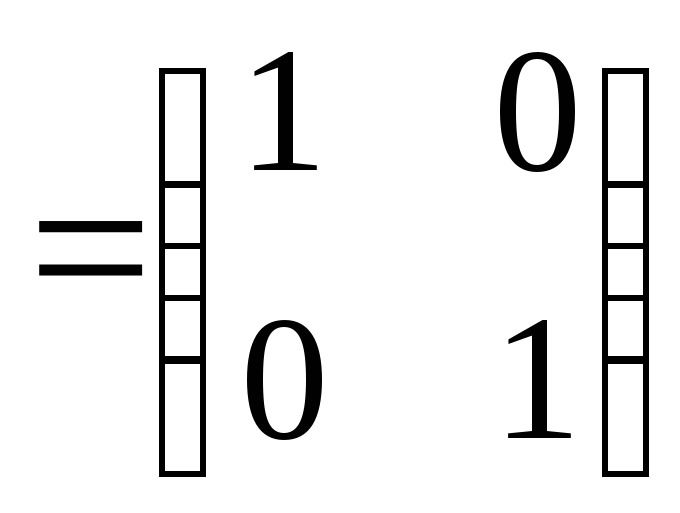
Задача №7. Найти матрицу, обратную
к матрице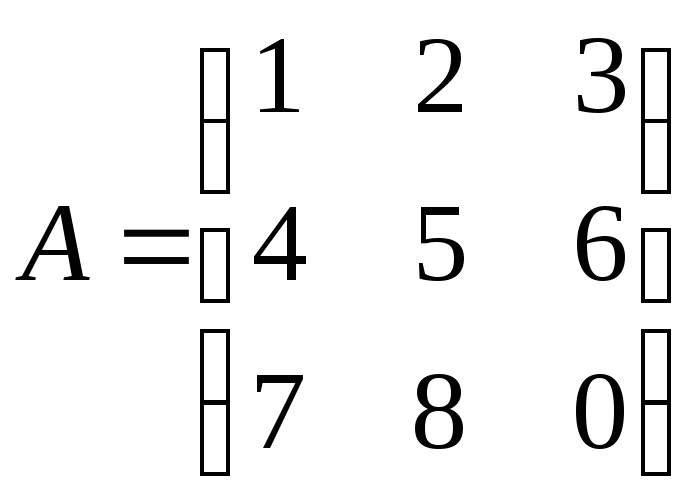 .
.
Решение.
1) Найдем 
 ,
следовательно обратная матрица
существует.
,
следовательно обратная матрица
существует.
2) Найдем алгебраические дополнения элементов матрицы А
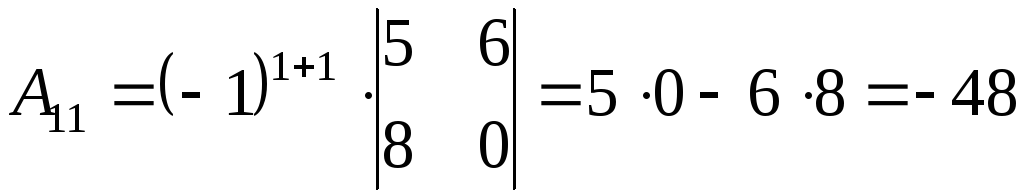
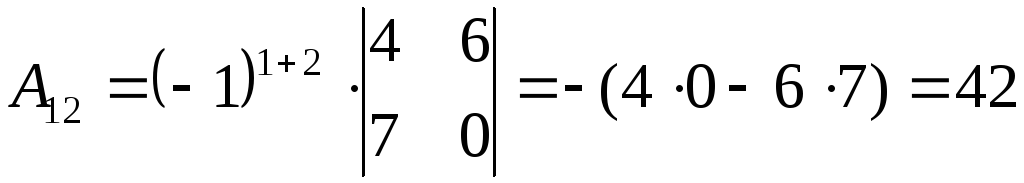

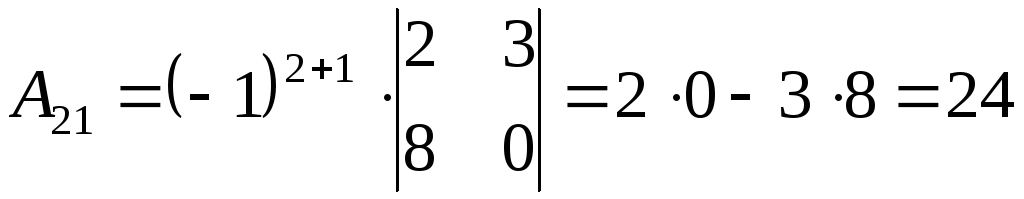
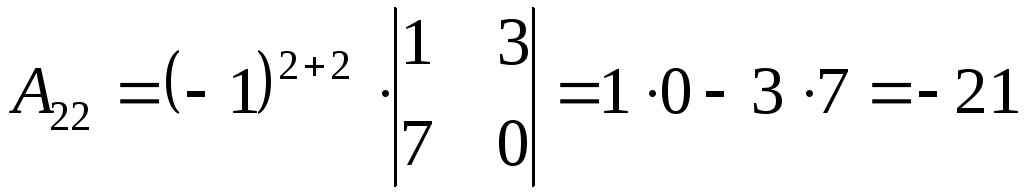

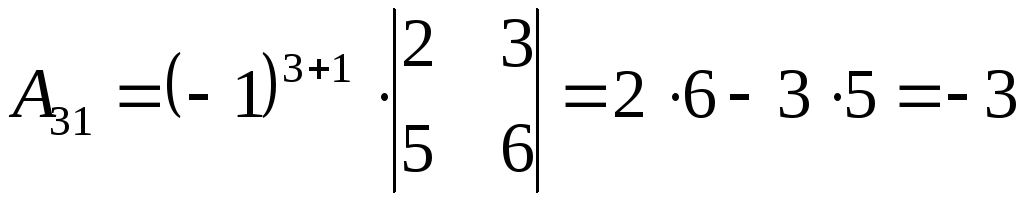

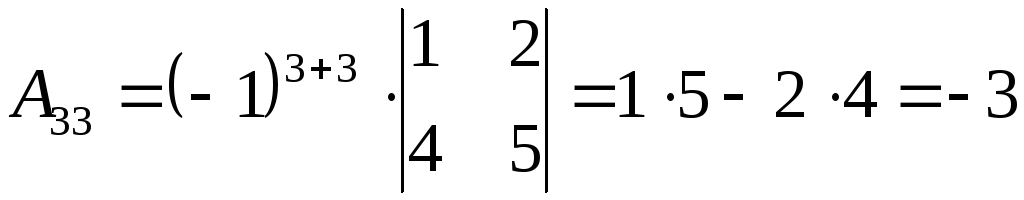
3) Запишем союзную матрицу
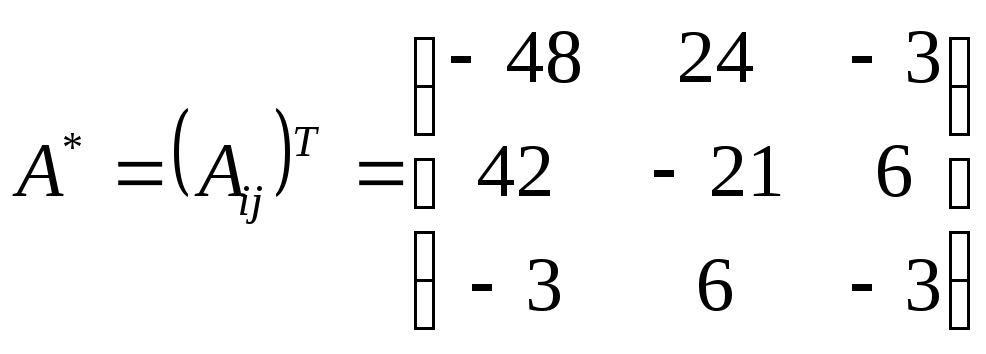
4) Найдем обратную матрицу
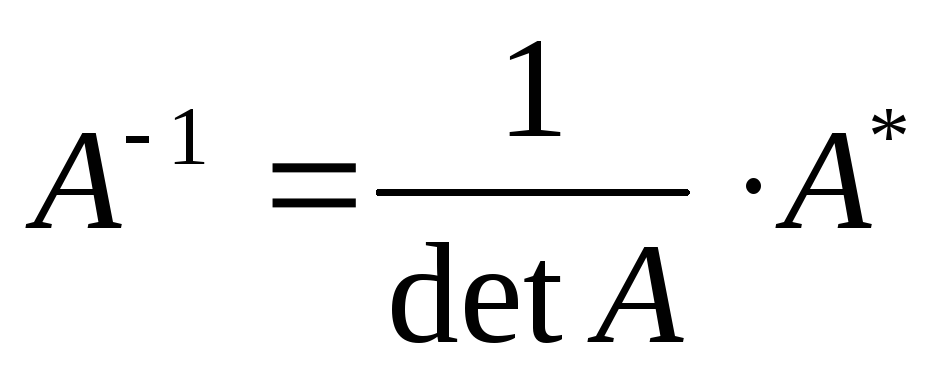
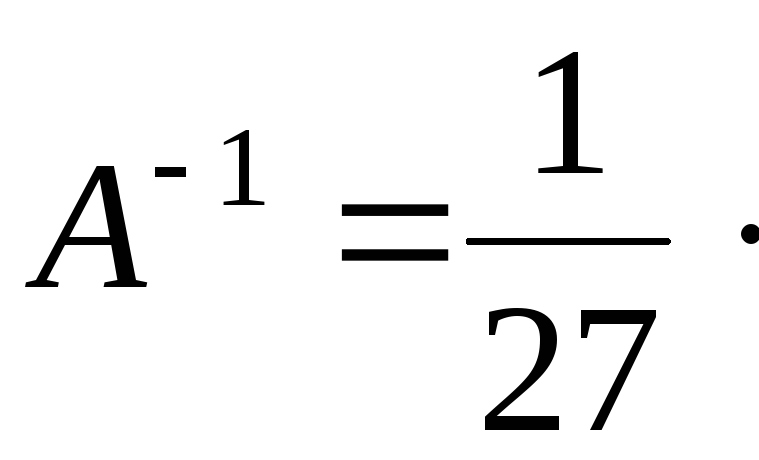

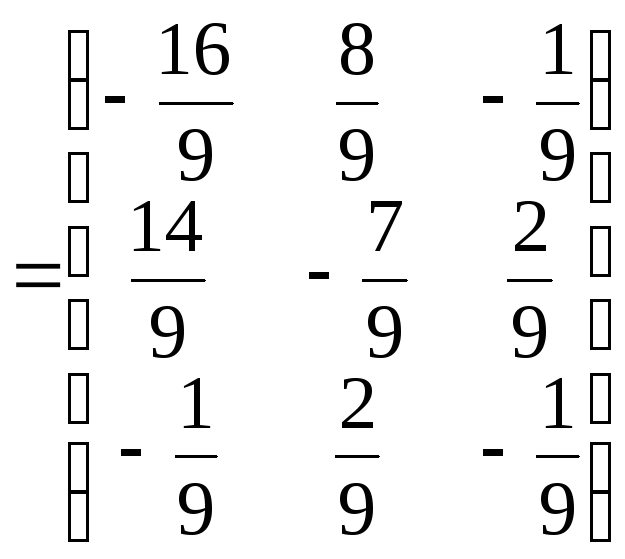
5) Сделаем проверку
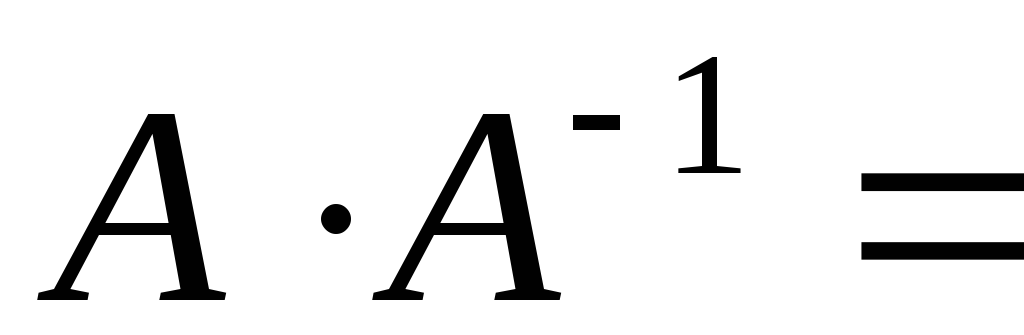

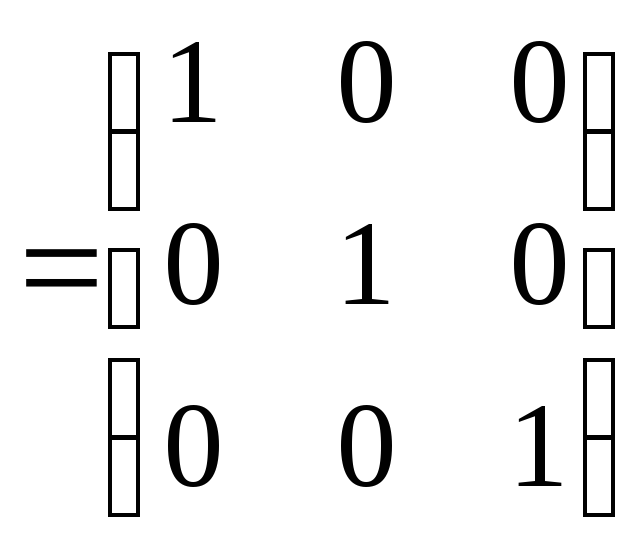
Задача №8. Найти матрицу, обратную
к матрице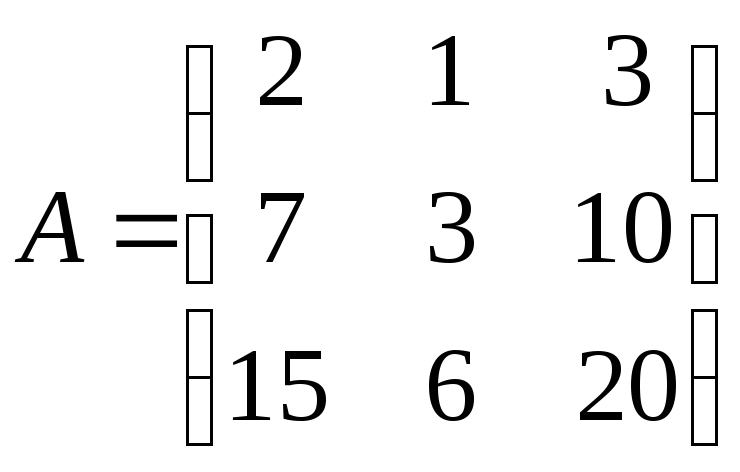 .
.
Решение.
1) Найдем 
 ,
следовательно обратная матрица
существует.
,
следовательно обратная матрица
существует.
2) Найдем алгебраические дополнения к элементам матрицы А
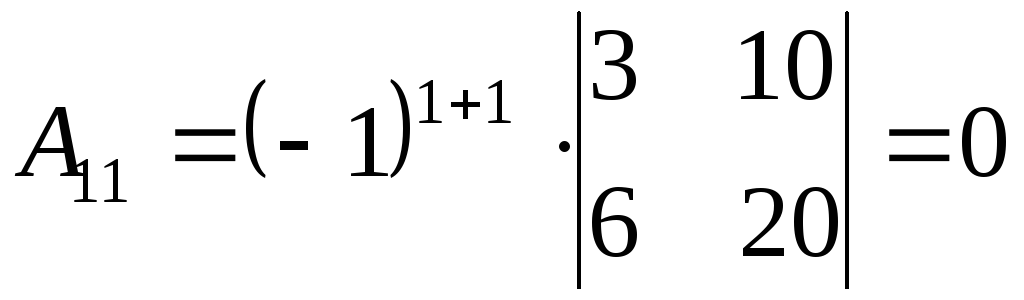

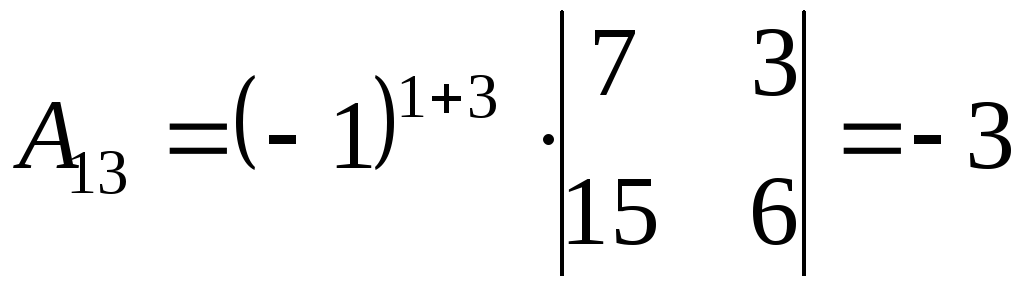
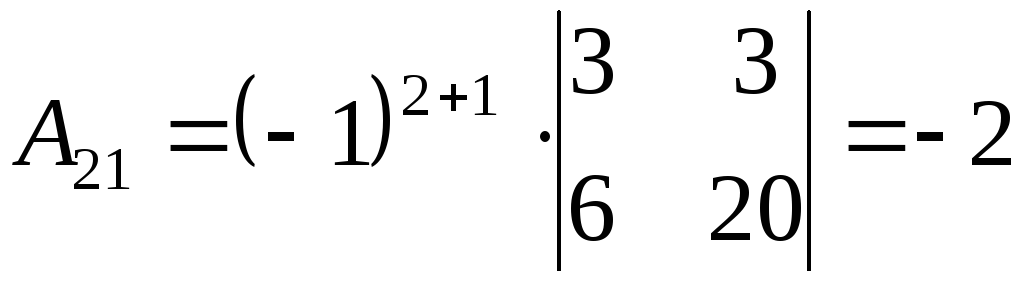
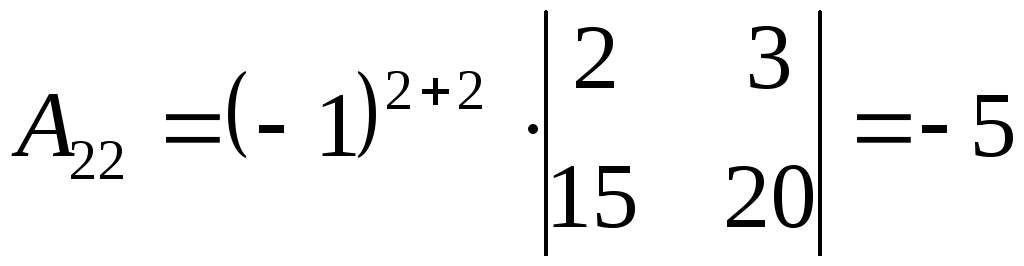

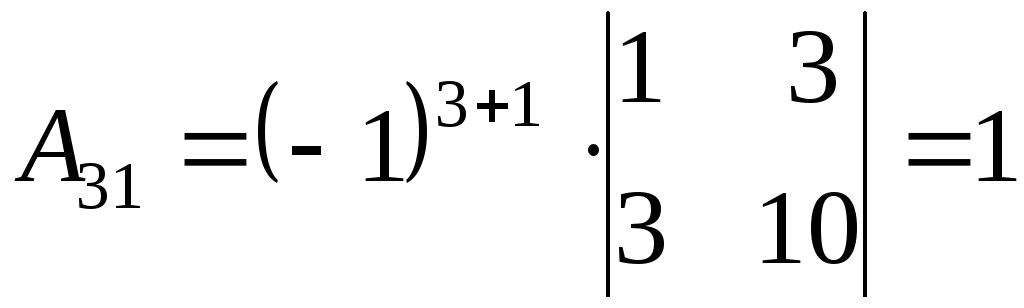
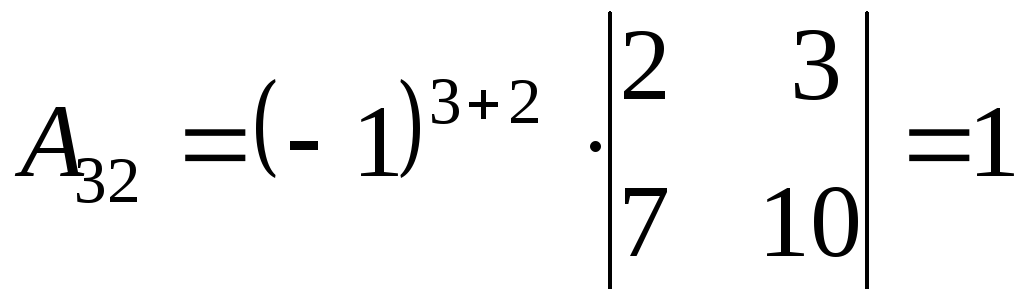
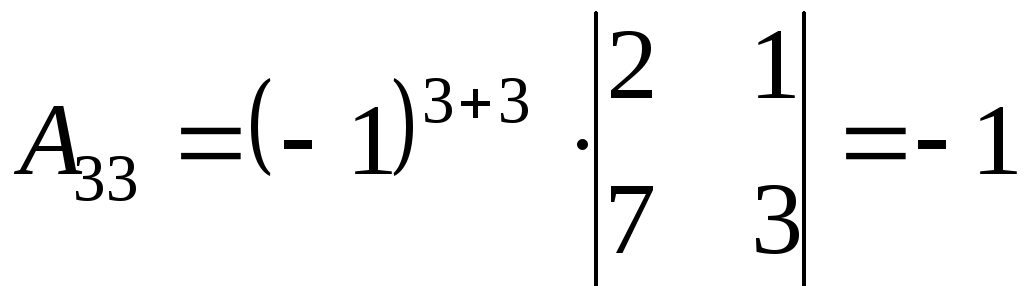
3) Запишем союзную матрицу
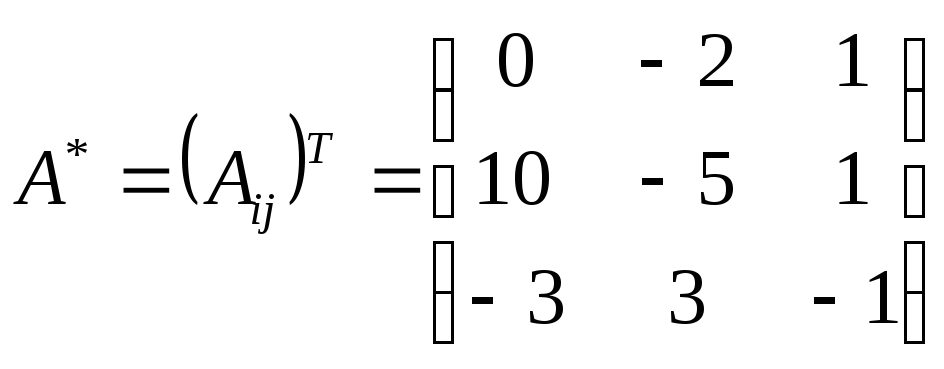
4) Найдем обратную матрицу
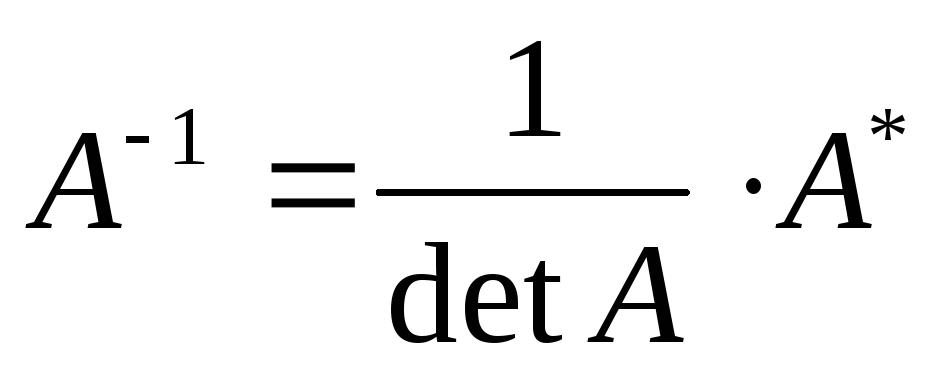


5) Сделаем проверку
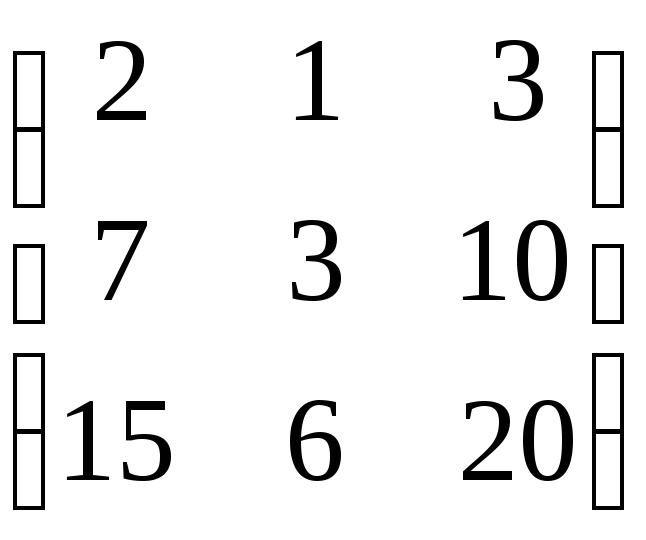

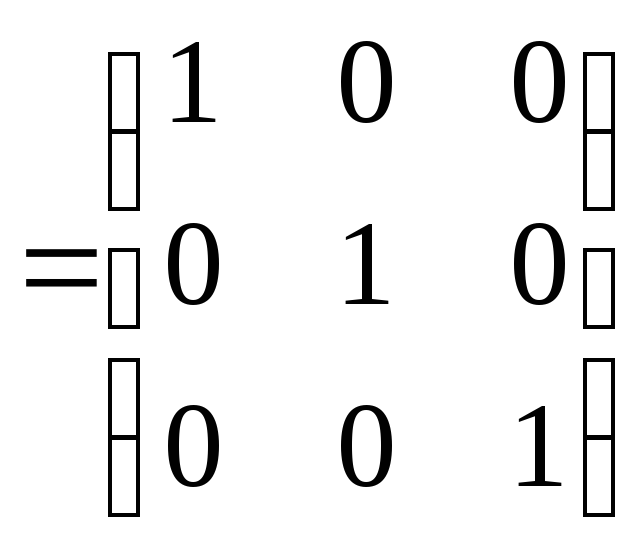
Задача №9. С помощью
элементарных преобразований строк
найти матрицу, обратную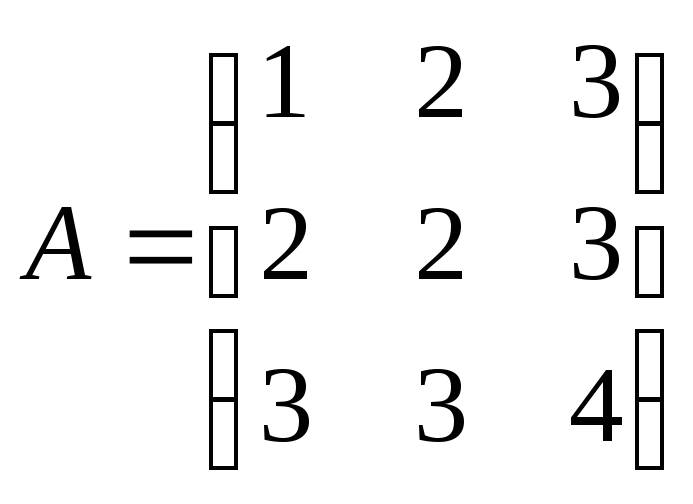 .
.
Решение.
Припишем к матрице  справа единичную матрицу и будем
выполнять элементарные преобразования
строк объединенной матрицы до тех пор
справа единичную матрицу и будем
выполнять элементарные преобразования
строк объединенной матрицы до тех пор
Задача №10. Найти ранг матрицы
Решение.

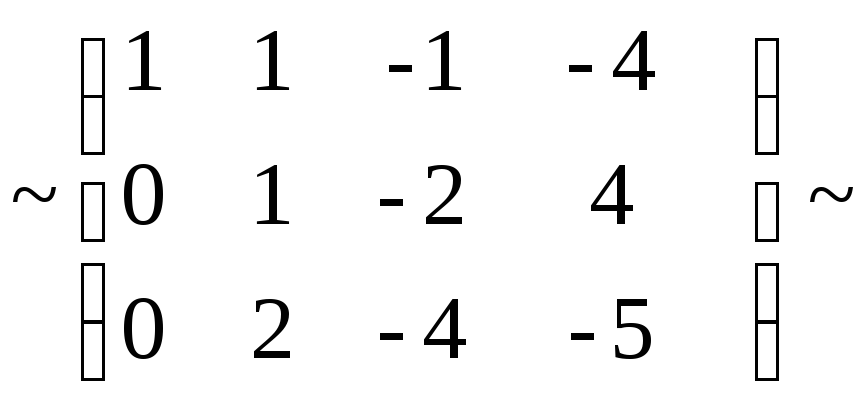
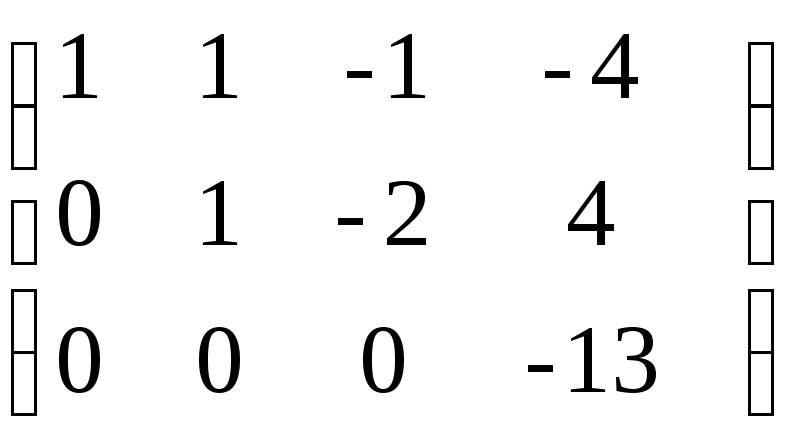
Ранг матрицы равен 3.
Задачи для самостоятельного решения:
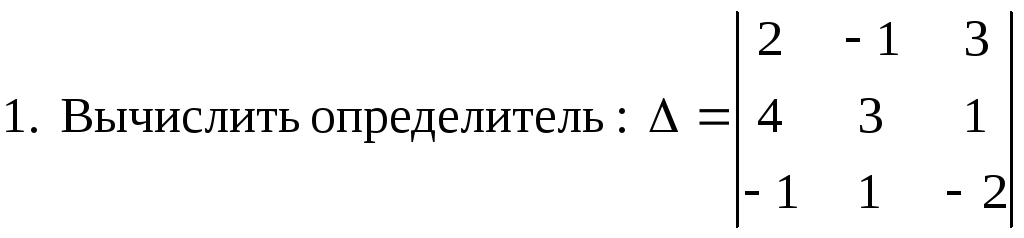
а) по правилу треугольника;
б) с помощью разложения по первой строке;
в) преобразованием, используя свойства определителей.
2. Найти
минор и алгебраическое дополнение
элемента a13 определителя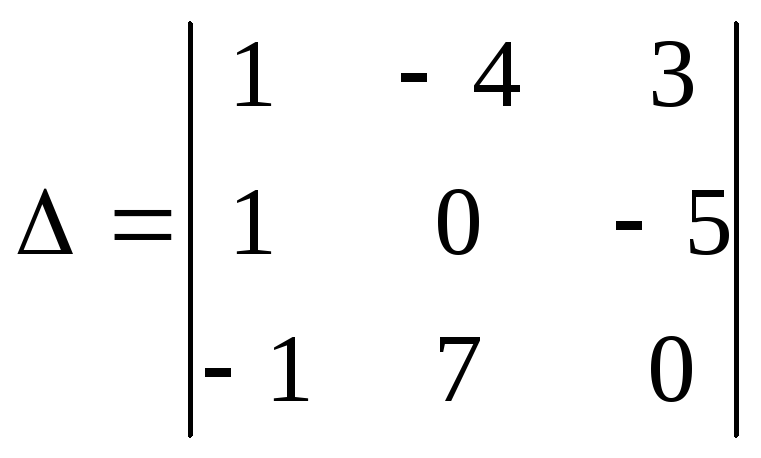 и вычислить его разложением по элементам
строки или столбца.
и вычислить его разложением по элементам
строки или столбца.
3. Решить уравнение 
4. Вычислить определитель 4-го порядка
разложением по элементам строки или
столбца: 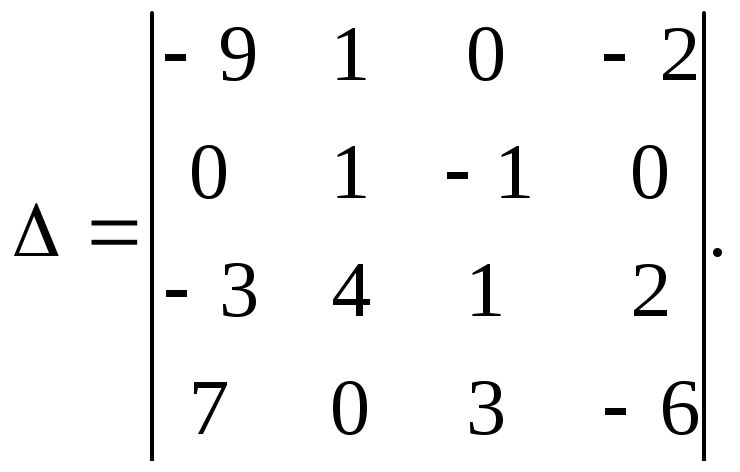
5. Найти обратную матрицу для следующих матриц:
 ;
2)
;
2) ;
3)
;
3) ;
4)
;
4) .
.
6. Решить матричные уравнения:
1) 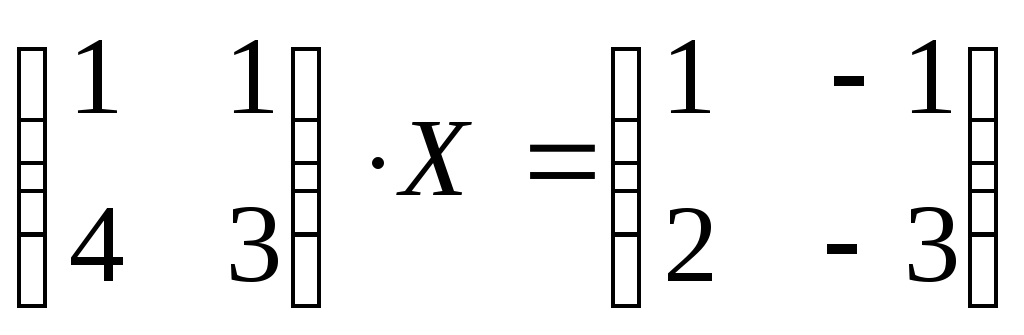 ;
;
2)  ;
;
3) 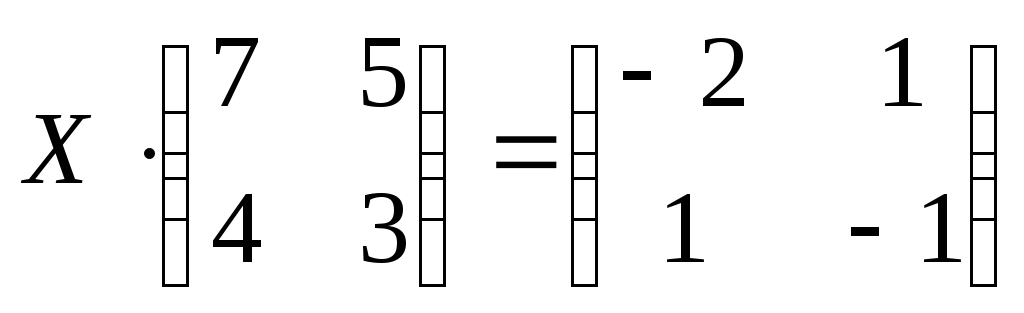 ;
;
4) 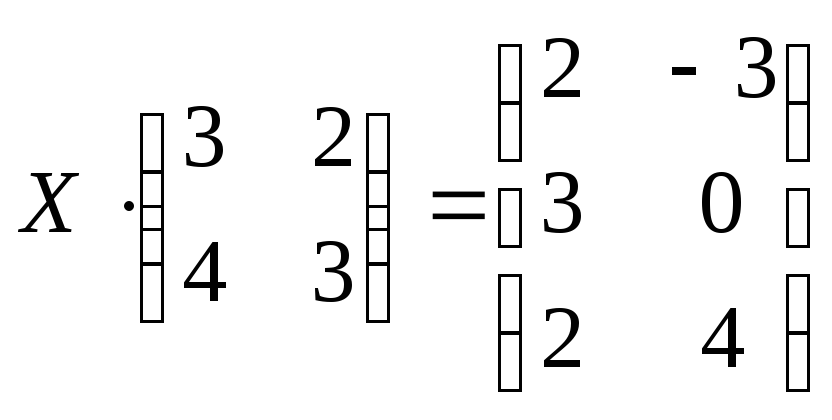 ;
;
5)  ;
;
6) 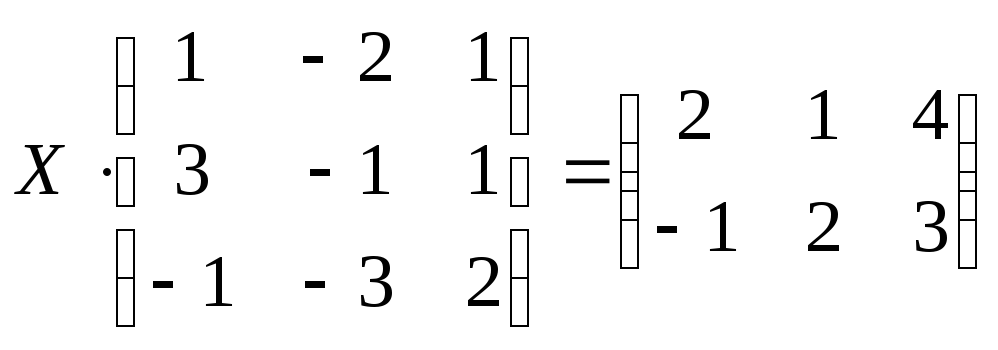 ;
;
7)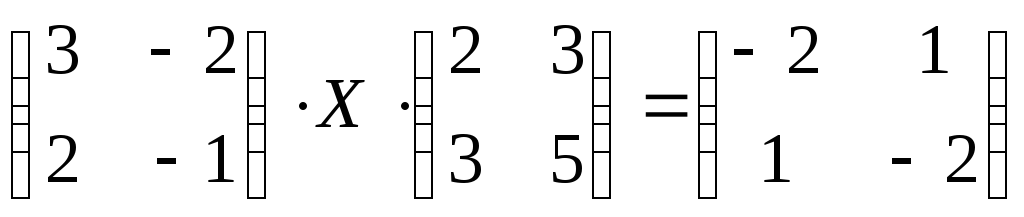 ;
;
8) .
.
7. Доказать, что если А – квадратная матрица и (А+Е)2=О, то матрица А имеет обратную. Найти обратную для А матрицу.
8. Найти все матрицы второго порядка, для которых А-1=А.
Занятие 3. Решение систем линейных уравнений методом Крамера и методом обратной матрицы.
Для усвоения практического материала нужно ответить на следующие теоретические вопросы:
Понятие системы линейных алгебраических уравнений.
Понятие решения системы линейных алгебраических уравнений.
Определение совместной и несовместной системы.
Достаточное условие совместной системы.
Определение однородной и неоднородной системы.
Формулы Крамера.
Алгоритм решения систем линейных уравнений с помощью обратной матрицы.
Типовые примеры Решение систем линейных уравнений методом Крамера
Задача №1. Решить систему:
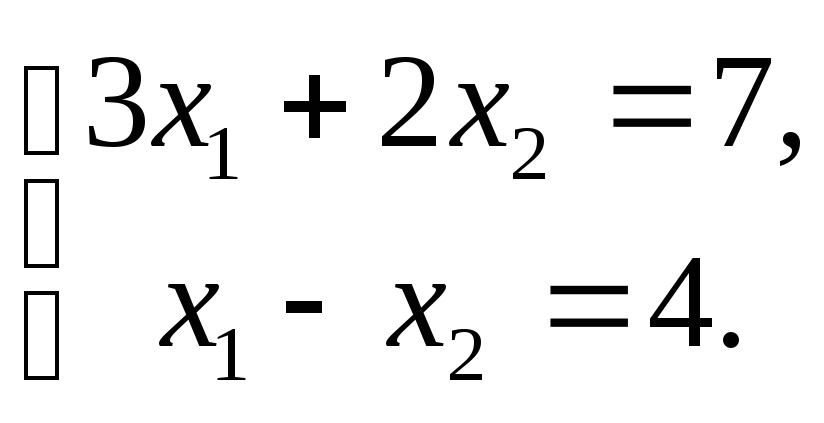
Решение.
Определитель системы:
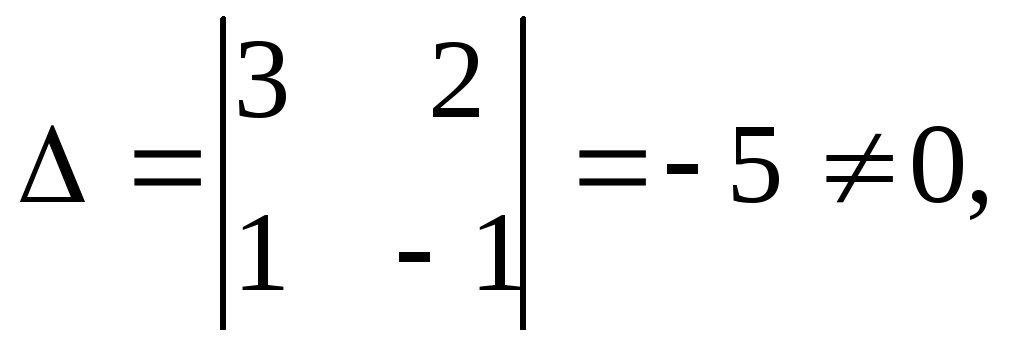
 поэтому
ее решение определяется по формулам
Крамера:
поэтому
ее решение определяется по формулам
Крамера:
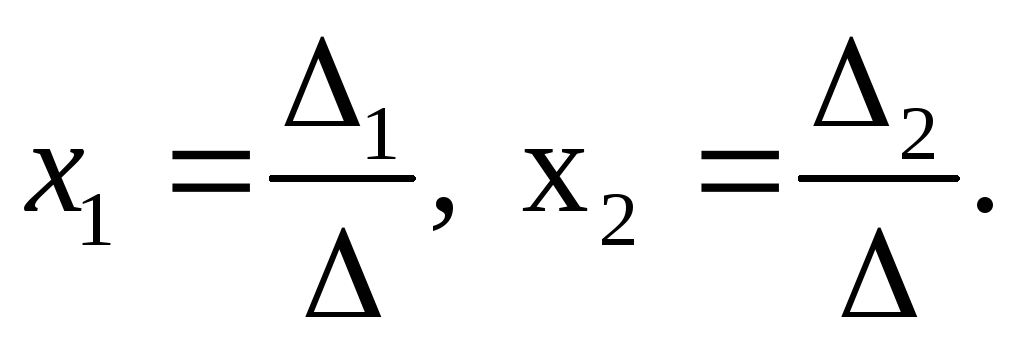
Но
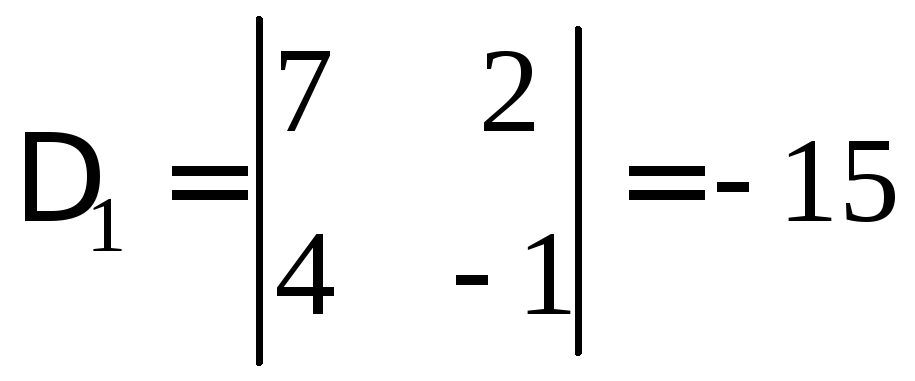 ,
,
Тогда 


Задача №2. Решить систему:
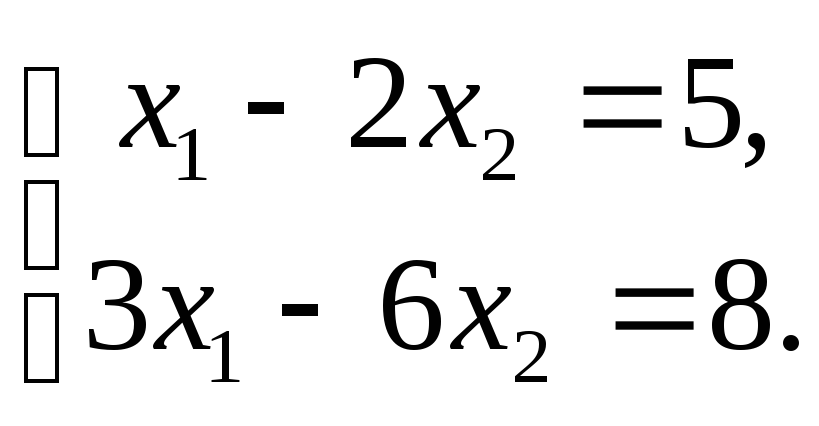
Решение.
Определитель данной системы 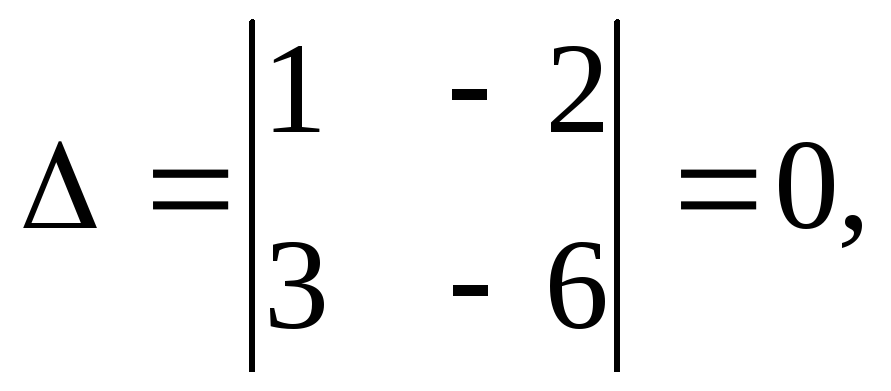 но
определитель
но
определитель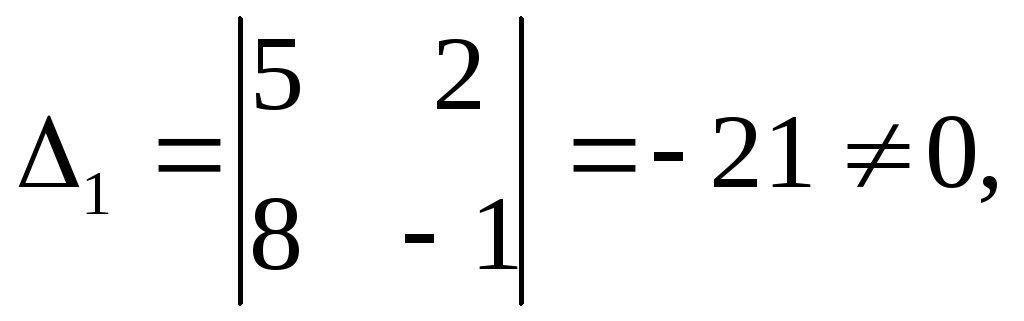 что говорит о несовместности системы.
Геометрически это означает, что данные
прямые не пересекаются, т.е. параллельны.
что говорит о несовместности системы.
Геометрически это означает, что данные
прямые не пересекаются, т.е. параллельны.
Задача №3. Решить систему:
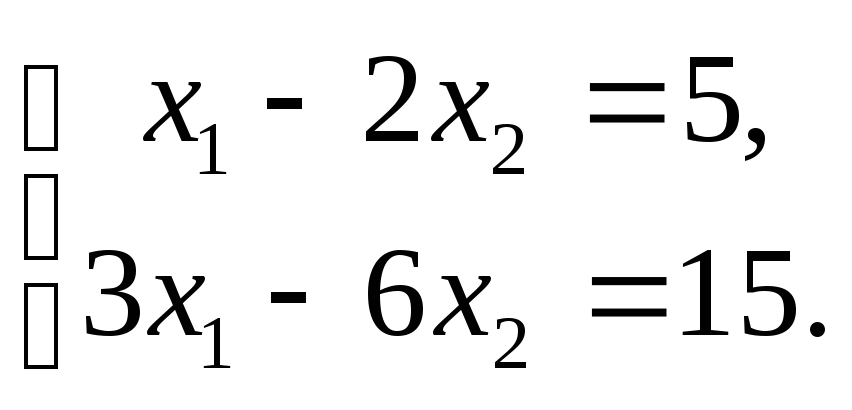
Решение.
Определители 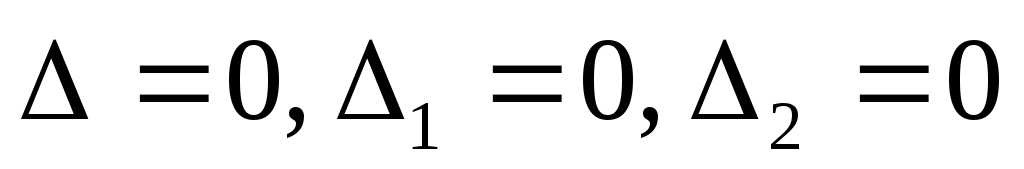 ,
так как у них строки пропорциональны.
Здесь оба уравнения системы определяют
одну и ту же прямую и решением системы
являются координаты любой точки этой
прямой. Отсюда следует, что система
имеет бесчисленное множество решений.
,
так как у них строки пропорциональны.
Здесь оба уравнения системы определяют
одну и ту же прямую и решением системы
являются координаты любой точки этой
прямой. Отсюда следует, что система
имеет бесчисленное множество решений.
Задача №4. Решить систему
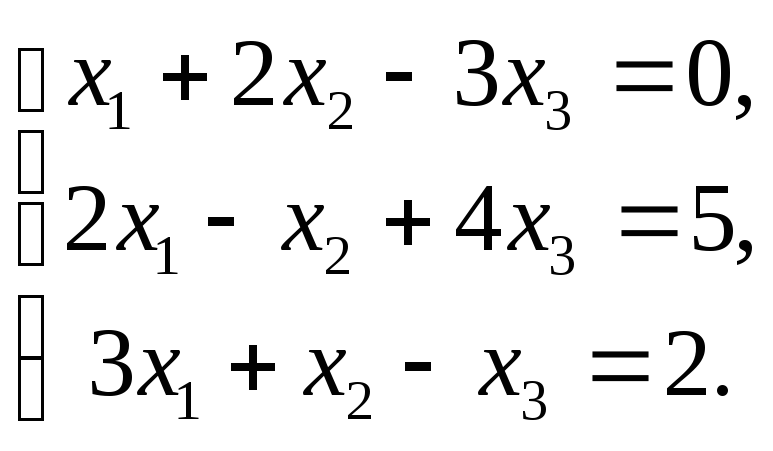
Решение.
Вычисляем определители:
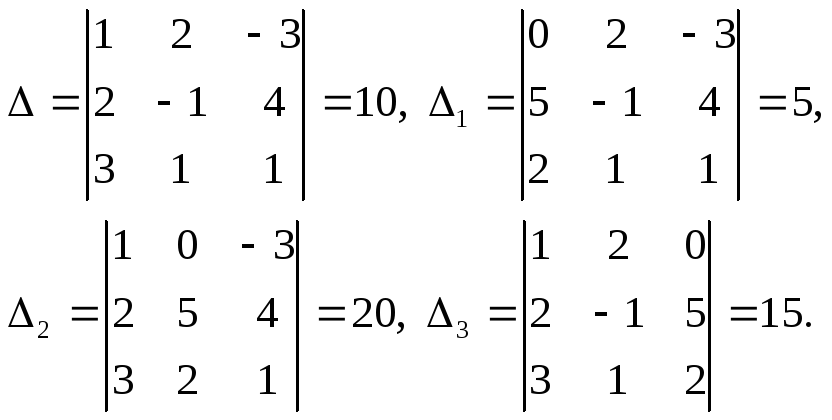
Так как 
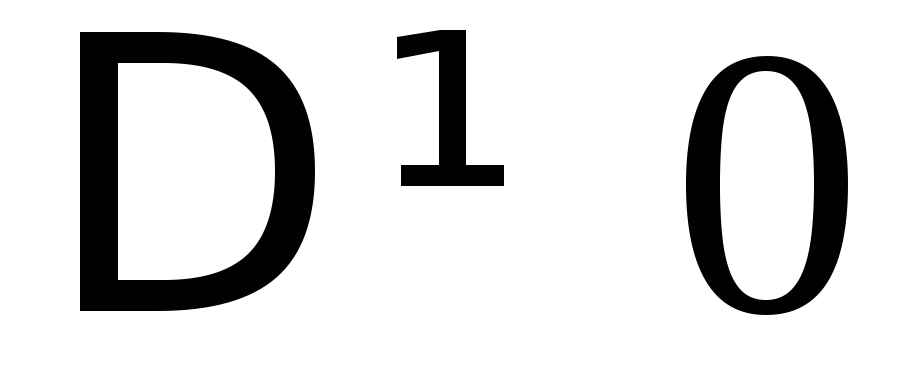 ,
то данная система имеет единственное
решение. Находим его по формулам Крамера:
,
то данная система имеет единственное
решение. Находим его по формулам Крамера:

studfile.net
Решение систем линейных алгебраических уравнений матричным способом (с помощью обратной матрицы)
Рассмотрим систему n-линейных алгебраических уравнений с n-неизвестными:
 (1)
(1)
Составим матрицу из коэффициентов при неизвестных:
A
=  .
.
Запишем матрицу-столбец из неизвестных членов:
Х
= 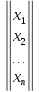 .
.
Запишем матрицу-столбец из свободных членов:
B
=  .
.
Запишем систему (1) в матричной форме:
A ∙ X = B. (2)
Умножим
обе части (2) на 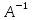 слева, тогда получим:
слева, тогда получим:
 или
или
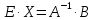 или
или

Пример.
Решить систему линейных алгебраических уравнений матричным способом:
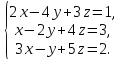
Составим матрицу из коэффициентов при неизвестных:
A
=  .
.
Запишем матрицу-столбец из неизвестных членов и матрицу-столбец из свободных членов:
X
= 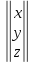 ,B
=
,B
=  .
.
Найдем обратную матрицу для матрицы А:
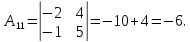

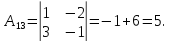

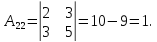
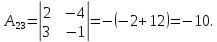
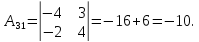
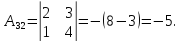
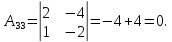
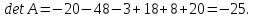
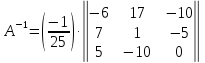
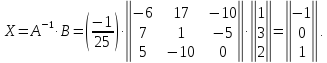


Метод Гаусса
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений . Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
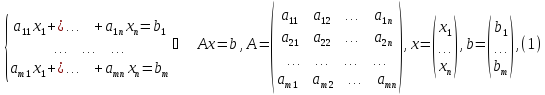 Матрица
Матрица  называется
основной матрицей системы,b — столбцом свободных членов.
называется
основной матрицей системы,b — столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):
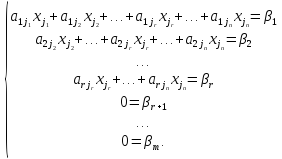
При
этом будем считать, что базисный минор
(ненулевой минор максимального порядка)
основной матрицы находится в верхнем
левом углу, то есть в него входят только
коэффициенты при переменных 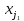 ,
… ,
,
… ,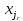 .
.
Тогда
переменные 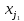 ,
… ,
,
… , называютсяглавными переменными. Все остальные называются свободными.
называютсяглавными переменными. Все остальные называются свободными.
Если
хотя бы одно число 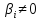 ,
где
,
где ,
то рассматриваемая система несовместна.
,
то рассматриваемая система несовместна.
Пусть 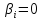 для любых
для любых .
.
Перенесём
свободные переменные за знаки равенств
и поделим каждое из уравнений системы
на свой коэффициент при самом левом 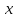 (
(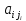 ,
,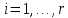 где
где — номер строки):
— номер строки):
 ,
(2)
,
(2)
где 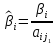 ,
, ,
,
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
Пример
Покажем, как методом Гаусса можно решить следующую систему:
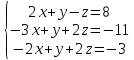
Обнулим
коэффициенты при  во второй и третьей строчках. Для этого
вычтем из них первую строчку, умноженную
на
во второй и третьей строчках. Для этого
вычтем из них первую строчку, умноженную
на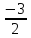 и
и ,
соответственно:
,
соответственно:

Теперь
обнулим коэффициент при 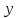 в
третьей строке, вычтя из неё вторую
строку, умноженную на 4:
в
третьей строке, вычтя из неё вторую
строку, умноженную на 4:

В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
 из
третьего;
из
третьего; из
второго, подставив полученное
из
второго, подставив полученное  ;
; из
первого, подставив полученные
из
первого, подставив полученные  и
и .
.
Таким образом исходная система решена.
studfile.net
 .
.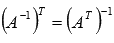 .
.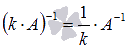 .
.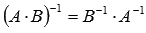 .
. ;
2)
;
2)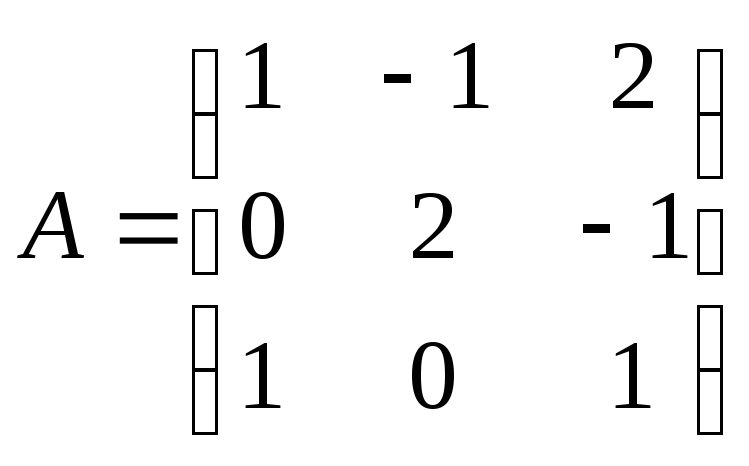 ;
3)
;
3)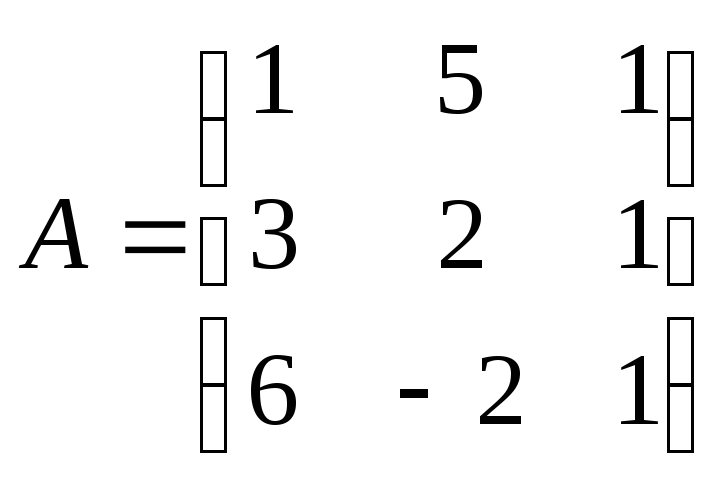 ;
4)
;
4) .
.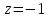 из
третьего;
из
третьего;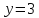 из
второго, подставив полученное
из
второго, подставив полученное 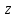 ;
;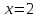 из
первого, подставив полученные
из
первого, подставив полученные  и
и .
.