Решение систем уравнений с параметром: Урок «Решение систем уравнений с параметром» (углубленный уровень) — Детская игровая комната «Волшебный лес»

Posted on 16.09.202002.06.2021 by alexxlab

Содержание

Урок «Решение систем уравнений с параметром» (углубленный уровень)

Конспект урока по теме: «Решение систем уравнений с параметром»

Часть 1.

Решение систем уравнений с параметром

УМК Никольский С.М. «Алгебра и начала анализа»

Место урока в системе уроков по теме (всего уроков на тему/номер урока по теме): 1/2

Тип урока: урок открытия нового знания

Дидактические единицы учебного материала, которыми ученик должен владеть для успешной работы на уроке

Дидактические единицы учебного материала, которые ученик изучит на уроке

Представлять, понимать

Знать

Уметь

Понятия: система уравнений с параметром

Утверждения (теоремы, аксиомы): что значит решить систему уравнений с параметром

Алгоритмы (правила): общие принципы решения систем уравнений с параметром

Методы (рассуждений, решения задач): дедуктивный

-основные виды графиков известных на данном этапе обучения функций,

-как выглядит уравнение с параметром,

-в чем заключается графический метод решения систем уравнений с параметром

-понятие параметра,

-понятие уравнения с параметром,

-система двух уравнений,

-что значит решить уравнение,

-в чем заключаются различные методы решений уравнений с параметром

-находить решение системы уравнений,

-находить решение уравнения с параметром

Планируемые предметные результаты урока

Ученик должен знать

Ученик должен уметь

Ученик научится представлять и понимать

На 3

На 4

На 5

На 3

На 4

На 5

-понятие уравнения,

-понятие системы уравнений,

-основные методы решения систем уравнений

-понятие уравнения,

-понятие системы уравнений,

-понятие параметра,

-основные методы решения систем уравнений

-понятие уравнения,

-понятие системы уравнений,

-понятие параметра,

-принцип решения уравнения с параметром,

-основные методы решения систем уравнений

-находить решение системы двух уравнений любым из известных ему способов

-находить решения уравнения с параметром,

-находить решение системы двух уравнений любым из известных ему способов

-находить решения уравнения с параметром,

-находить решение системы двух уравнений различными способами (аналитический, графический), определяя при этом наиболее предпочтительный

Научится находить решение системы уравнений с параметром, применяя различные методы решения

Метапредметная направленность урока заключается в —

посредством —

Личностная направленность урока заключается в —

посредством —

Технология обучения

Форма обучения

Метод обучения

проблемное обучение

лекция, беседа

объяснительно-иллюстративный

Дидактические средства обучения

компьютер, проектор, презентация Power Point

Источники информации:

для учителя

для обучающихся

Методические пособия для учителей по теме урока, справочники

Учебное пособие, презентация, конспект в тетради, справочные материалы

Цель урока:

(определяется планируемыми результатами и способами их достижения)

Задачи урока:

(конкретизация цели)

Овладение методами решения систем уравнений с параметрами

Повторить, закрепить и узнать приемы решения уравнений и их систем с параметрами из различных разделов элементарной математики: иррациональных, показательных, логарифмических и других трансцендентных уравнений, неравенств и их систем.

Отработать навыки решения различных уравнений и неравенств, содержащихся в примерных вариантах профильного уровня ЕГЭ.

воспитание чувства ответственности, формирование творческого подхода к решению поставленной задачи, интереса к познавательному поиску.

Часть 2.

1. Мотивирование на учебную деятельность

(1-2 мин)

Поприветствовать детей, создать благожелательную атмосферу урока, нацелить учащихся на работу

—

Личностные:

— сформированность позитивной моральной самооценки и моральных чувств.

Коммуникативные:

— умение слушать,

— интегрироваться в группу сверстников и строить продуктивное взаимодействие и сотрудничество со сверстниками и взрослыми,

— умение выражать свои мысли в соответствии с условиями коммуникации,

— планирование учебного сотрудничества с учителем и сверстниками.

Регулятивные:

— предвосхищение результата и уровня усвоения знаний.

—

2. Актуализация знаний

(5-7 мин)

Актуализировать ранее изученные понятия, алгоритмы и навыки

Вспомнить, в чем заключается понятие уравнения, что значит решить уравнение, что значит решить систему двух уравнений, основные виды графиков известных функций, в чем заключается понятие параметра, уравнения с параметром, как решить уравнение с параметром, какие применяются для этого методы

Коммуникативные:

— умение задавать вопросы,

— формулирование собственного мнения,

Познавательные:

— умение строить речевое высказывание,

— анализ объектов с целью выделения признаков,

— сравнение,

— выбор оснований и критериев для сравнения,

— классификация объектов.

Регулятивные:

— планирование своих действий

Презентация, учебник

3. Целеполагание, постановка проблемы

(2-5 мин)

Подведение детей к формулировке и постановке задач урока. Составление плана работы

Организовать анализ учащимися возникшей ситуации и на этой основе выявить места и причины затруднения, осознать то, в чем именно состоит недостаточность их знаний, умений или способностей.

—

Коммуникативные:

— умение выражать свои мысли в соответствии с условиями коммуникации,

— планирование учебного сотрудничества с учителем и сверстниками.

Познавательные:

— структурирование знаний,

— установление причинно-следственных связей,

— построение рассуждения в форме связи простых суждений об объекте,

— формулирование проблемы,

— создание способов решения проблемы.

Доска, презентация

4. Решение проблемы

(15 мин)

Предложить сформулировать цель урока.

Научить учащихся, применяя полученные знания, решать системы двух уравнений с параметром, использовать для этого различные известные методы

Сформировать умение применять на практике освоенные умения как при решении задачи, вызвавшей затруднение, так и при решении других задач такого типа.

Находить множество решений систем уравнений с параметром, отработать этот навык, рассмотрев задания, содержащиеся в примерных вариантах профильного уровня ЕГЭ.

Коммуникативные:

-учёт разных мнений и стремление к координации различных позиций в сотрудничестве,

Регулятивные:

— принятие и сохранение учебной задачи,

— планирование своих действий в соответствии с поставленной задачей и условиями её реализации,

Познавательные:

— выделение существенной информации,

— формулирование проблемы,

— поиск разнообразных способов решения задачи

Презентация, учебник

5. Систематизация знаний

(15 мин)

Усвоение учащимися навыка решения систем уравнений с параметром

Этап первичного закрепления и самостоятельного решения несколько типовых заданий на закрепление нового навыка

Личностные:

— формирование мотивов достижения целей,

Формирование границ «знания» и «незнания».

Регулятивные:

— принятие и сохранение учебной задачи,

— учёт правила в планировании и контроле способа решения,

— различение способа и результата действия.

Познавательные:

— структурирование знаний,

— построение речевого высказывания в письменной форме,

— установление причинно-следственных связей

Презентация

6. Подведение итогов

(1-2 мин)

Соотнесение поставленных задач с достигнутым результатом, фиксация нового знания, постановка дальнейших целей

—

Личностные:

— формирование самоидентификации, адекватной позитивной самооценки, самоуважения и самопринятия.

Регулятивные:

— восприятие оценки учителя,

— адекватная самооценка.

Познавательные:

— построение речевого высказывания в устной и письменной форме.

Презентация

Деятельность учителя

(с указанием конкретных методов и приемов, техник обучения, средств и форм контроля, учебно-познавательных и учебно-практических задач, решаемых на данном этапе)

Деятельность учащихся

Продукт деятельности учащихся

1. Мотивирование на учебную деятельность

(1-2 мин)

Организационный момент, приветствие, пожелание.

Приветствует учащихся, проверяет их готовность к уроку

Приветствуют учителя, проверяют свою готовность к уроку

—

2. Актуализация знаний

(5-7 мин)

Задает учащимся вопросы по пройденным темам, актуализируя знания, необходимые для формулирования темы урока, представляет вниманию учащихся задания для отработки освоенных ранее навыков

Отвечают на вопросы учителя, решают уравнения с параметром, вспоминают такие понятия, как параметр, уравнения с параметром, система двух уравнений, что значит решить уравнение, в чем заключаются различные методы решений уравнений с параметром

Конспект учащихся в тетради

Выявление места и причины затруднения

(2-5 мин)

Организует диалог с учащимися, в ходе которого конкретизирует понятия, формулирует некоторые задачи урока, помогает учащимся сформулировать возникшую проблему нахождения решений системы уравнений с параметром

На основе наводящих вопросов учителя самостоятельно формулируют проблему, с которой столкнулись

Конспект учащихся в тетради

Решение проблемы

(15 мин)

Дает определение системы уравнений с параметром и понятия, что значит решить систему уравнений с параметром, рассказывает об известных методах решения системы уравнений с параметром.

Выписывают выводы, определения. Учатся решать системы уравнений с параметром различными методами

Конспект в тетради

5. Систематизация знаний

(15 мин)

Возвращает учащихся к исходной системе уравнений, вызвавшей трудность, показывает, что теперь они могут самостоятельно справиться с данной проблемой.

Предлагает учащимся выполнить самостоятельно ряд заданий на закрепление приобретенных навыков

Применяют полученные знания в решении поставленной в ходе урока проблемы, выполняют самостоятельно ряд заданий на закрепление изученной темы

Выполненные в тетради самостоятельные задания

6. Подведение итогов

(1-2 мин)

Задает вопросы о задачах урока.

Рефлексия

Проговаривают по плану новые знания, высказывают свои впечатления от урока

Лист самооценки

Часть 3.

Ход урока.

Этап 1. Мотивирование на учебную деятельность (1-2 мин)

Добрый день, дорогие ученики! Рада приветствовать вас на уроке алгебры. Как ваше настроение? Сегодня нас ждёт новая, но интересная тема. Я уверена, что к концу урока каждый из вас научится применять новые знания на практике. Запишите, пожалуйста в ваших тетрадях сегодняшнее число и «Классная работа». Начнём!

Этап 2. Актуализация знаний (5-7 мин)

Для того, чтобы успешно усвоить новые знания сегодняшнего урока, давайте вспомним с вами ряд понятий и определений, изученные вами на сегодняшний день.

Вопрос. Кто скажет мне, что же такое уравнение? (Уравнение – это равенство, содержащее неизвестную, значение которой необходимо найти)

Вопрос. Хорошо! А что же тогда значит решить уравнение? (Решить уравнение – значит найти все его корни (значения неизвестной) или доказать, что корней нет)

Вопрос. Молодцы! Но уравнения бывают совершенно разные! На предыдущих уроках мы с вами изучали решение уравнений и неравенств с параметром. Напомните мне, что же это такое? (Параметр – это величина, значение которой является постоянным в пределах рассматриваемой задачи)

Вопрос. И как же найти решение уравнения с параметром? (Найти множество всех значений корней при заданных условиях, удовлетворяющих заданному параметру)

Отлично! Вижу, материал усвоили хорошо, поэтому мы можем смело переходить к следующей вехе в большой области знаний под названием «Уравнения с параметром» и, для начала, поговорим о системах двух уравнений.

Вопрос. Какие основные методы решения систем уравнений вам известны? (Аналитический и графический)

Аналитический метод не вызывает, как правило у вас сложностей, а по поводу графического – стоит вспомнить основные функции и их графики. Попробуем установить соответствие? (Учитель показывает на слайде функции и их графики, учащиеся устанавливают между ними соответствия)

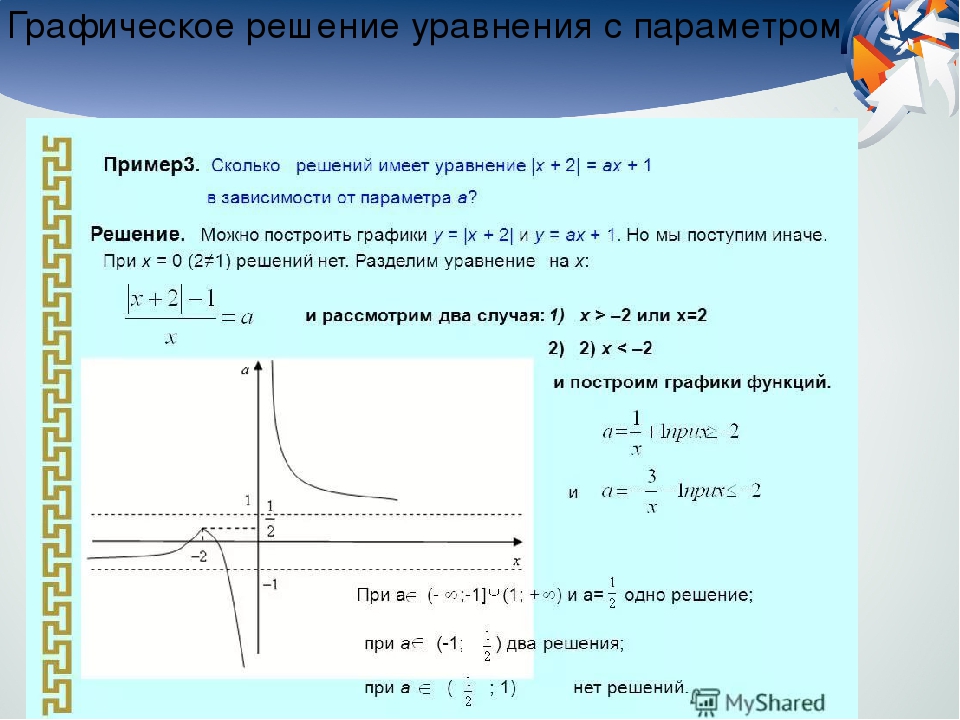
И с этой задачей справились на «ура»! Мы с вами вспомнили основные моменты, пришло время перейти от слов к делу. Давайте попробуем решить такую систему и определить, сколько же она имеет решений:

Анализируя данную систему, можно заметить, что первое уравнение представляет из себя уравнение окружности с неизвестным нам радиусом. Второе же – хорошо знакомая вам квадратичная функция, графиком которой является парабола с ветвями, направленными вверх. Так как же нам быть? Как определить, каков радиус нашей окружности? Как узнать количество решений такой системы? Именно об этом мы и будем говорить сегодня на уроке!

Этап 4. Решение проблемы (15 мин)

Решение уравнений с параметрами возможно аналитически и графически. Решение уравнений графически позволяет наглядно представить решение.

Научимся решать системы уравнений с параметром на примере:

Пример. Найдите все значения a, при каждом из которых система

имеет единственное решение.

Решение.

Решение системы может быть единственным в двух случаях.

Случай 1. Единственное решение является граничной точкой для множества решений каждого из двух неравенств. В этом случае это единственное решение должно удовлетворять системе уравнений

Вычитая из второго уравнения первое, получаем

откуда или

Если то а значит, При этом значении a система принимает вид

Единственное решение:

Если то откуда Получаем

При этом значении a система имеет бесконечно много решений.

Случай 2. Одно из неравенств имеет единственное решение, удовлетворяющее другому неравенству.

Первое неравенство имеет единственное решение при

откуда

Первое неравенство имеет единственное решение , которое удовлетворяет второму неравенству.

Второе неравенство имеет единственное решение при

откуда

Второе неравенство имеет единственное решение , которое не удовлетворяет первому неравенству.

Ответ:

В данном примере мы применили аналитический метод решения системы уравнений.

Рассмотрим другой пример

Пример. Найдите все значения a, при каждом из которых система уравнений

имеет более двух решений.

Решение Рассмотрим первое уравнение системы. Мы видим, что данное уравнение распадается в совокупность двух систем

Найдем значения параметра a, при которых система имеет более 2 решений.

2 решения система имеет в случае касания окружностей (точки А и D) и выполняется условие: (Слайд 7-8)

Получим уравнение:

Откуда

3 решения система имеет в случае, когда прямая проходит через точку пересечения двух окружностей. Точки В и С (Слайд 9-10)

Найдем их координаты, решив систему

, получим точки (3; -4) и (5;0).

Подставив эти координаты в уравнение прямой с параметром, получим:

Четыре решения система имеет между точками касания и полученными точками.

В остальных случаях либо нет решения, либо два решения.

Получим окончательный ответ

Ответ:

Этап 5. Систематизация знаний (15 мин)

Давайте теперь вернемся к нашей системе уравнений, решить которую мы сначала не смогли и найдем её корни.

Построим графики уравнений.

Из рисунка видно, при любом значении а, система будет иметь 2 решения.

А теперь закрепим полученные знания выполнением небольшой самостоятельной работы. (самостоятельно решают в тетрадях одну систему из учебника (№15.24-15.29)

Этап 6. Подведение итогов (1-2 мин)

Трудным ли для вас было покорение этой математической вершины? Я бы хотела узнать, где вы находитесь:

по-прежнему у подножия горы;
на середине пути;
на вершине;
изобразите себя на этой горе.

(Учащимся раздаются карточки с домашним заданием)

СПАСИБО ЗА УРОК!

Решение системы уравнений с параметром. Задание 18 (Из тренировочной работы СтатГрад 24 сентября 2015 года)

Найдите все целочисленные значения параметра , при каждом из которых система

имеет единственное решение.

Посмотрим внимательно на структуру первого уравнения. Если мы рассмотрим две точки и , то выражение — это расстояние между точками A и B. Аналогично расстояние между точками и равно

Точки и имеют разные абсциссы, но одинаковые ординаты. Следовательно, они лежат на прямой .

Равенство показывает, что сумма расстояний от точки до точек и равно 4. При этом расстояние между точками и также равно 4. Следовательно, точка принадлежит отрезку , лежащему на прямой .

Таким образом, решением первого уравнения являются все значения из отрезка при любом действительном значении .

Исходная система имеет единственное решение, если второе уравнение системы имеет единственное решение на отрезке [1;5].

Теперь мы имеем дело с задачей на расположение корней квадратного трехчлена: «при каком значении параметра уравнение имеет единственный корень на отрезке [1;5]?».

Заметим, что по теореме Виета для квадратного трехчлена, стоящего в левой части уравнения справедливо:

Мы видим, что произведение корней отрицательно (), следовательно, корни квадратного трехчлена имеют разные знаки.

Рассмотрим функцию

При условии, что квадратный трехчлен имеет единственный корень на отрезке [1;5], мы получаем такую картинку:

Данный квадратный трехчлен имеет единственный корень на отрезке [1;5], если

Получаем систему неравенств:

Решим каждое неравенство:

(1)

Так как , а , неравенство (1) выполняется при любом значении х.

(2)

Это неравенство с модулем равносильно системе:

Решим каждое неравенство.

(1)

(2)

(3)

Чтобы решить систему, мы должны все точки расположить на одной координатной прямой, а для этого оценить значения всех полученных выражений.

Оценим, в каких пределах лежит значение выражения :

Аналогично получим:

Получаем такую картинку:

Теперь легко видеть, что целые значения , удовлетворяющие данной системе неравенств (лежащие на голубом промежутке) — это числа -2, -1, 0, 1.

Ответ: -2, -1, 0, 1.

И.В. Фельдман, репетитор по математике.

Решение линейных уравнений и систем линейных уравнений, содержащих параметры (4 урока)

Цели урока: формировать умение решать системы линейных уравнений, содержащих параметры; осуществить оперативный контроль и самоконтроль учащихся; развивать исследовательскую и познавательную деятельность школьников.

Тип урока: введение нового материала.

Ход урока

1. Проверка домашнего задания.

2. Введение нового материала.

Говорят, что дана система двух уравнений первой степени с двумя неизвестными x и y, если требуется найти пары чисел (x₀; y₀), являющиеся решениями одновременно и первого, и второго уравнения.

Если то система имеет единственное решение.
Если то система не имеет решений.
Если то система имеет бесконечно много решений.

Пример 1. При каких значениях параметра a система

а) имеет бесконечное множество решений;
б) имеет единственное решение?

Решение.

Ответ: а) если a=4, то система имеет бесконечное множество решений; б) если то решение единственное.

Пример 2. Решите систему уравнений

Решение. система имеет единственное решение.

1–ym–y=n–2y , –ym+y=n–1;

исходная система решений не имеет.

система имеет бесконечно много решений.

Ответ: если m=1 и n1, то решений нет; если m = 1 и n = 1, то решений бесконечное множество, если m  1 и n – любое, то

Пример 3. (Предложите ученикам выполнить это задание самостоятельно с последующей проверкой.) Решите систему уравнений

Решение.

Пример 4. Определите, при каком условии уравнение

а) имеет единственное решение;
б) имеет бесконечно много корней;
в) не имеет корней.

Решение.

– при этом условии уравнение корней не имеет.

– при этом условии решение исходного уравнения есть любое число из R.

Ответ:
б) если a = 0 или b = 0, то x – любое число;
в) если 2b = a, a  0, b  0, то корней нет.

Самостоятельная работа

Вариант 1

1. При каком значении k система имеет бесконечное множество решений?

2. Решите систему уравнений

Вариант 2

1. При каком значении d система не имеет решений?

2. Решите систему уравнений

Ответы

В-1. 1. k = 2,5. 2. Если b = 0, c = 0, то решений нет; если b = c, d  0, a – любое число, то решений нет; если a = 0, b, c, d – любые числа, то решений нет; если c  0, b  0, a  0, b  c, d – любое число, то если b = c, d = 0, то

В-2. 1. d = – 20. 2. Если b = 0, c = 0, то решений нет; если c = – b, то решений нет; если b  0 и c  0, c  – b, то если c = – b и dbc = ac, то

Задание на дом

1. При каких значениях параметра b система уравнений

а) имеет бесконечное множество решений;
б) не имеет решений?

2. Графики функций y = ax + 3 и y = (2 – a)x + a пересекаются в точке с абсциссой – 1. Найдите ординату точки пересечения графиков.

3. Графики функций y = 4x + b и y = kx + 6 симметричны относительно оси ординат.

а) Найдите b и k.
б) найдите координаты точки пересечения этих графиков.

4. Решите систему уравнений

Ответы: 1. а) b = 10; б) b  10. 2. 3. а) b = 6, k = – 4; б) (0; 6). 4. Если mn = – 1 и m 1, n – 1, то решений нет; если m = 1 и n = – 1, то x – любое число, y = 1 + mx; если mn  1 и n  – 1, m  1, то

Правила решения систем уравнений с параметрами. Уравнения с параметром. Исследование квадратного трёхчлена

1. Системы линейных уравнений с параметром

Системы линейных уравнений с параметром решаются теми же основными методами, что и обычные системы уравнений: метод подстановки, метод сложения уравнений и графический метод. Знание графической интерпретации линейных систем позволяет легко ответить на вопрос о количестве корней и их существовании.

Пример 1.

Найти все значения для параметра а, при которых система уравнений не имеет решений.

{х + (а 2 – 3)у = а,
{х + у = 2.

Решение.

Рассмотрим несколько способов решения данного задания.

1 способ . Используем свойство: система не имеет решений, если отношение коэффициентов перед х равно отношению коэффициентов перед у, но не равно отношению свободных членов (а/а 1 = b/b 1 ≠ c/c 1). Тогда имеем:

1/1 = (а 2 – 3)/1 ≠ а/2 или систему

{а 2 – 3 = 1,
{а ≠ 2.

Из первого уравнения а 2 = 4, поэтому с учетом условия, что а ≠ 2, получаем ответ.

Ответ: а = -2.

2 способ . Решаем методом подстановки.

{2 – у + (а 2 – 3)у = а,
{х = 2 – у,

{(а 2 – 3)у – у = а – 2,
{х = 2 – у.

После вынесения в первом уравнении общего множителя у за скобки, получим:

{(а 2 – 4)у = а – 2,
{х = 2 – у.

Система не имеет решений, если первое уравнение не будет иметь решений, то есть

{а 2 – 4 = 0,
{а – 2 ≠ 0.

Очевидно, что а = ±2, но с учетом второго условия в ответ идет только ответ с минусом.

Ответ: а = -2.

Пример 2.

Найти все значения для параметра а, при которых система уравнений имеет бесконечное множество решений.

{8х + ау = 2,
{ах + 2у = 1.

Решение.

По свойству, если отношение коэффициентов при х и у одинаковое, и равно отношению свободных членов системы, то она имеет бесконечное множество решений (т. е. а/а 1 = b/b 1 = c/c 1). Следовательно 8/а = а/2 = 2/1. Решая каждое из полученных уравнений находим, что а = 4 – ответ в данном примере.

Ответ: а = 4.

2. Системы рациональных уравнений с параметром

Пример 3.

{3|х| + у = 2,
{|х| + 2у = a.

Решение.

Умножим первое уравнение системы на 2:

{6|х| + 2у = 4,
{|х| + 2у = a.

Вычтем из первого второе уравнение, получим 5|х| = 4 – а. Это уравнение будет иметь единственное решение при а = 4. В других случаях это уравнение будет иметь два решения (при а 4).

Ответ: а = 4.

Пример 4.

Найти все значения параметра а, при которых система уравнений имеет единственное решение.

{х + у = а,
{у – х 2 = 1.

Решение.

Данную систему решим с использованием графического метода. Так, графиком второго уравнения системы является парабола, поднятая по оси Оу вверх на один единичный отрезок. Первое уравнение задает множество прямых, параллельных прямой y = -x (рисунок 1) . Из рисунка хорошо видно, что система имеет решение, если прямая у = -х + а является касательной к параболе в точке с координатами (-0,5; 1,25). Подставив в уравнение прямой вместо х и у эти координаты, находим значение параметра а:

1,25 = 0,5 + а;

Ответ: а = 0,75.

Пример 5.

Используя метод подстановки, выясните, при каком значении параметра а, система имеет единственное решение.

{ах – у = а + 1,
{ах + (а + 2)у = 2.

Решение.

Из первого уравнения выразим у и подставим во второе:

{у = ах – а – 1,
{ах + (а + 2)(ах – а – 1) = 2.

Приведем второе уравнение к виду kx = b, которое будет иметь единственное решение при k ≠ 0. Имеем:

ах + а 2 х – а 2 – а + 2ах – 2а – 2 = 2;

а 2 х + 3ах = 2 + а 2 + 3а + 2.

Квадратный трехчлен а 2 + 3а + 2 представим в виде произведения скобок

(а + 2)(а + 1), а слева вынесем х за скобки:

(а 2 + 3а)х = 2 + (а + 2)(а + 1).

Очевидно, что а 2 + 3а не должно быть равным нулю, поэтому,

а 2 + 3а ≠ 0, а(а + 3) ≠ 0, а значит а ≠ 0 и ≠ -3.

Ответ: а ≠ 0; ≠ -3.

Пример 6.

Используя графический метод решения, определите, при каком значении параметра а, система имеет единственное решение.

{х 2 + у 2 = 9,
{у – |х| = а.

Решение.

Исходя из условия, строим окружность с центром в начале координат и радиусом 3 единичных отрезка, именно ее задает первое уравнение системы

х 2 + у 2 = 9. Второе уравнение системы (у = |х| + а) – ломаная. С помощью рисунка 2 рассматриваем все возможные случаи ее расположения относительно окружности. Легко видеть, что а = 3.

Ответ: а = 3.

Остались вопросы? Не знаете, как решать системы уравнений?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Внимание: мелкие насыщенные графики можно увеличить, щелкнув по ним мышью.

Исследование и решение уравнений с параметрами считается не самым простым разделом школьной математики. Однако, параметр, как понятие, часто воспринимается школьниками гораздо более сложным, чем есть в действительности. Здесь в первом пункте представлены очень простые вводные примеры использования параметров в уравнениях. Те, для кого это понятие не составляет большой трудности, могут сразу перейти к решению задач, которые представлены ниже.

Что такое уравнение с параметром?

Рассмотрим пример.

Допустим нам нужно решить уравнение 2х + 5 = 2 − x .
Решение: 2x + x = 2 − 5; 3x = −3; x = −3/3 = −1.

Теперь нужно решить уравнение 2x + 5 = 3 − x .
Решение: 2x + x = 3 − 5; 3x = −2; x = −2/3 ~ −0,67.

Затем нужно решить уравнение 2x + 5 = 0,5 − x .
Решение: 2x + x = 0,5 − 5; 3x = −4,5; x = −4,5/3 = −1,5.

А потом может потребоваться решить уравнение 2x + 5 = 10,7 − x или уравнение 2x + 5 = −0,19 − x .
Понятно, что уравнения похожи, а потому их решение будет сопровождаться теми же действиями, что выше. Возникает естественный вопрос — сколько можно делать одно и то же?

Уменьшим себе трудозатраты. Заметим, что все эти уравнения отличаются только одним числом в правой части. Обозначим это число символом a .
Получим уравнение 2х + 5 = a − х ,
где a — переменная величина, вместо которой можно подставить нужное числовое значение и получить нужное уравнение. Эта переменная и называется параметром.

Решим это уравнение так же, как и все предыдущие.
Решение: 2х + 5 = a − x ; 2x + x = a − 5; 3x = a − 5; x = (a − 5)/3.

Теперь для того, чтобы найти ответы для двух последних примеров, мы можем не повторять полностью всё решение каждого уравнения, а просто подставить в полученную формулу для х числовое значение параметра а :
x = (10,7 − 5)/3 = 5,7/3 = 1,9;
x = (−0,19 − 5)/3 = −5,19/3 = −1,73.

Таким образом, под термином «уравнение с параметром», фактически, скрывается целое семейство «почти одинаковых уравнений» , которые отличаются друг от друга только одним числом (одним слагаемым или одним коэффициентом) и одинаково решаются. Параметр — это число, которое меняется от уравнения к уравнению.
Полученную формулу для корня уравнения мы можем запрограммировать на компьютере. Достаточно будет только ввести значение параметра a , чтобы получить решение любого такого уравнения.

Рассмотрим еще один пример.

Нужно решить несколько уравнений:
2х + 5 = 2 − x ;
3х + 5 = 2 − x ;
−4х + 5 = 2 − x ;
17х + 5 = 2 − x ;
0,5х + 5 = 2 − x .

Замечаем, что они похожи друг на друга и отличаются только первым коэффициентом. Обозначим его, например, символом k .
Решим уравнение kх + 5 = 2 − x с параметром k .

Решение:
kх + 5 = 2 − x ;
kх + х = 2 − 5;
(k + 1)x = −3;
x = −3/(k + 1).

С помощью этой формулы вычислим все ответы для приведенных уравнений.
x = −3/(2 + 1) = −1
x = −3/(3 + 1) = −0,75
x = −3/(−4 + 1) = 1
x = −3/(17 + 1) = −1/6 ~ −0,167
x = −3/(0,5 + 1) = −2

Можем ли мы теперь запрограммировать эту формулу и сказать, что с её помощью можно решить любое аналогичное уравнение?
Запрограммировать можем. Компьютер справится как с очень большими значениями коэффициента, так и с очень маленькими.
Например, если введём k = 945739721, то для уравнения заданного вида будет получен корень примерно равный −0,0000000031721201195353831188, если k = 0,0000004, то получим корень ≈ −2,9999988000004799998080000768.
Но, если мы введем в программу, казалось бы, более простое значение k = −1, то компьютер зависнет.
Почему?

Посмотрим внимательнее на формулу x = −3/(−1 + 1) = −3/0. Деление на ноль?!!
Посмотрим на соответствующее уравнение −1·х + 5 = 2 − x .
Преобразуем его −х + x = 2 − 5.
Оказывается, оно равносильно уравнению 0 = −3 (?!! ) и не может иметь корней.
Таким образом, из общего подхода к решению «почти одинаковых уравнений» могут существовать исключения, о которых нужно позаботиться отдельно. Т.е. провести предварительное исследование всего семейства уравнений. Именно этому и учатся на уроках математики с помощью так называемых задач с параметрами.

Графические способы решения уравнений

Сначала вспомним, что представляет собой графический способ решения обычного уравнения (без параметра).
Пусть дано уравнение вида f(x) = g(x) . Построим графики функций y = f(x) и y = g(x) и найдём точки пересечения этих графиков. Абсциссы точек пересечения и есть корни уравнения.

Для быстрого построения эскизов графиков повторите еще раз которые изучаются в школьном курсе математики, и

Рассмотрим примеры.

1. Решить уравнение
2х + 5 = 2 − x

Ответ: x = −1 .

2. Решить уравнение
2х 2 + 4х − 1 = 2х + 3

Ответ: x 1 = -2; x 2 = 1 .

3. Решить уравнение
l og 2 х = −0,5х + 4

Ответ: x = 2 .

Первые два из приведенных уравнений вы можете решить и аналитически, так как это обычные линейное и квадратное уравнения. Второе уравнение содержит функции разных классов — степенную (здесь линейную) и трансцендентную (здесь логарифмическую). Для таких случаев выбор способов решения у школьников очень ограничен. Фактически, единственным доступным способом является именно графическое решение.

Внимание: Для корней, найденных графическим способом, обязательна проверка! Вы уверены, что на третьем рисунке пересечение именно в точке х = 4 , а не в точке 3,9 или 4,1? А если на реальном экзамене у вас нет возможности построить график достаточно точно? На чертеже «от руки» разброс может быть еще больше. Поэтому алгоритм действий должен быть следующим:

Предварительный вывод: х ≈ 4.
Проверка: l og 2 4 = −0,5·4 + 4; 2 = −2 + 4; 2 ≡ 2.
Окончательный вывод х = 4.

Чтобы графически решать уравнения с параметрами надо строить не отдельные графики, а их семейства.

Решение уравнений с параметрами с помощью графиков.

Задача 1.

q при которых уравнение |x + 1| − |x − 3| − x = q 2 − 8q + 13 имеет ровно 2 корня.

При каждом значении параметра q можно вычислить значение выражения q 2 − 8q + 13 . Результат обозначим переменной а .
Т.е. примем q 2 − 8q + 13 = a и решим уравнение с параметром |x + 1| − |x − 3| − x = a

Строим график функции y = |x + 1| − |x − 3| − x , расположенной в левой части уравнения.
Для этого разобьём числовую ось на отрезки точками, в которых каждый из встречающихся модулей принимает нулевое значение.

|x + 1| = 0; x = −1;
|x − 3| = 0; x = 3.

Для каждого из этих участков раскроем модули с учётом знаков.
Вспомним: по определению |x | = x , если х ≥ 0 , и |x | = −x , если х . Чтобы проверить знаки модулей на участке достаточно подставить любое промежуточное значение x из этого отрезка, например, −2, 0 и 4.

Таким образом на участке I , где −∞ х ≤ −1, имеем −(x + 1) + (x − 3) − x = − x − 4.
Следовательно, должны построить график функции y = − x − 4 .
Это линейная функция. Её график прямая линия, которую можно построить по двум точкам, например, x = 0, y = −4 и у = 0, x = −4. Cтроим всю прямую бледной линией, а затем выделяем часть графика, относящуюся только к рассматриваемому участку.

Аналогично, разбираемся с оставшимися двумя участками.

На участке II , где −1 х ≤ 3, имеем (x + 1) + (x − 3) − x = x − 2
y = x − 2 .

На участке III , где 3 х ≤ ∞ , имеем (x + 1) − (x − 3) − x = − x + 4
и должны построить соответствующую часть графика функции y = − x + 4 .

Последовательное построение итогового графика показано ниже. (Чтобы увеличить рисунок, нужно щелкнуть по нему левой кнопкой мыши.)

Замечание: если вы освоили тему , то с этой частью задачи сможете справиться быстрее, чем показано в примере.

Итак, построение графика функции, расположенной в левой части уравнения, мы завершили. Посмотрим, что находится в правой части.

График функции y = a представляет собой прямую линию, параллельную оси абсцисс (Ox ), и пересекающую ось ординат (Oy ) в точке а . Так как а — параметр, который может принимать разные значения, то нужно построить целое семейство таких параллельных линий, пересекающих ось ординат на разной высоте. Очевидно, что все графики семейства построить мы не сможем, поскольку их бесконечное множество. Изобразим для примера несколько штук в районе уже построенного графика функции. Ниже прямые семейства y = a показаны красным цветом.

Из рисунка видно, что количество точек пересечения каждой из красных прямых с ранее построенным (зелёным) графиком зависит от высоты, на которой расположена эта прямая, т.е. от параметра а . Прямые, расположенные ниже y = −3 , пересекают график в одной точке, а значит эти уравнения имеют только одно решение. Прямые, проходящие на уровне −3 y y = 1 , снова имеют только по одной точке пересечения.
Ровно две точки пересечения с зелёным графиком будут иметь только прямые y = 1 и y = −3 . Соответствующие уравнения будут иметь ровно два корня, что и требовалось определить в задании.

Однако мы нашли значения введённого нами параметра а , при котором заданное уравнение имеет 2 корня, а вопрос задачи состоял в том, чтобы найти все значения параметра q . Для этого придётся решить следующую совокупность уравнений:

Это обычные квадратные уравнения, которые решаются через дискриминант или по теореме Виета.

Таким образом, окончательный ответ: {2;4;6}.

Задача 2.

Найти все значения параметра a , при которых уравнение (2 − x )x (x − 4) = a имеет ровно 3 корня.

Рассмотрим функцию y = (2 − x )x (x − 4) . Видно, что если раскрыть скобки, то старший член будет −х 3 . Т.е. графиком функции должна быть кубическая парабола, причем на при x , стремящемcя к +∞, y → −∞, а при x , стремящемся к −∞, y → +∞.
Поскольку уравнение (2 − x )x (x − 4) = 0 имеет три корня 2, 0 и 4, то график функции будет пересекать ось абсцисс трижды.
Понятно, что при упомянутых условиях график непрерывной функции должен иметь участок с «волной». Строим от руки эскиз графика.

Правая часть уравнения y = a такая же, как в предыдущей задаче. Поэтому дальнейшие построения не требуют комментариев. Смотрите рисунки. Чтобы увеличить, используйте щелчок мышью.

Из рисунков видно, что прямые, отделяющие линии с тремя точками пересечения от других случаев, проходят через экстремумы кубической функции. Поэтому определяем значения y max и y min через производную. (Исследовать функцию полностью не нужно, так как примерное положение точек экстремума мы видим на эскизе графика.) Обратите внимание на то, что при вычислении значений функции используются точные значения x и формулы сокращенного умножения. Приближенные значения в промежуточных вычислениях не используют.

Ответ:

Задача для самостоятельного решения

Задача 3.

При каком наибольшем отрицательном значении параметра а уравнение имеет один корень?

Показать решение.

Чтобы увеличить рисунок, нужно щелкнуть по нему левой кнопкой мыши.
Переносим 2x в правую часть уравнения, в результате получим две элементарные функции, графики которых изучались в школе.
По рисунку видим, что условию задачи удовлетворяет линия, которая касается графика. 2 — 2y — 2a + 1 =0$. Дискриминант каждого из них равен $D = 16a-4$.

Заметим, что не может получиться так, что пара корней первого из квадратных уравнений совпадает с парой корней второго квадратного уравнения, так как сумма корней первого равна $-1$, а второго 1.

Значит, нужно, чтобы у каждого из этих уравнений было по одному корню, тогда у исходной системы их будет два решения. То есть $D = 16a — 4 = 0$.

Ответ. $a=\dfrac{1}{4}$

Найдите все значения параметра $a$, при каждом из которых уравнение $4x-|3x-|x+a||=9|x-3|$ имеет два корня.

Решение

Перепишем уравнение в виде:

$ 9|x-3|-4x+|3x-|x+a|| = 0. $

Рассмотрим функцию $f(x) = 9|x-3|-4x+|3x-|x+a||$.

При $x\geqslant 3$ первый модуль раскрывается со знаком плюс, и функция принимает вид: $f(x) = 5x-27+|3x-|x+a||$. Очевидно, что при любом раскрытии модулей в итоге будет получаться линейная функция с коэффициентом $k\geqslant 5-3-1=1>0$, то есть эта функция на данном промежутке неограниченно возрастает. {-1}}\right\}$

Уравнение вида f (x ; a ) = 0 называется уравнением с переменной х и параметром а .

Решить уравнение с параметром а – это значит, для каждого значения а найти значения х , удовлетворяющие этому уравнению.

Пример 1. ах = 0

Пример 2. ах = а

Пример 3.

х + 2 = ах
х – ах = -2
х(1 – а) = -2

Если 1 – а = 0, т.е. а = 1, то х 0 = -2 корней нет

Если 1 – а 0, т.е. а 1, то х =

Пример 4.

(а 2 – 1) х = 2а 2 + а – 3
(а – 1)(а + 1)х = 2(а – 1)(а – 1,5)
(а – 1)(а + 1)х = (1а – 3)(а – 1)

Если а = 1, то 0х = 0
х – любое действительное число

Если а = -1, то 0х = -2
Корней нет

Если а 1, а -1, то х = (единственное решение).

Это значит, что каждому допустимому значению а соответствует единственное значение х .

Например:

если а = 5, то х = = ;
если а = 0, то х = 3 и т. д.

Дидактический материал

1. ах = х + 3
2. 4 + ах = 3х – 1
3. а = +

при а = 1 корней нет.

при а = 3 корней нет.

при а = 1 х – любое действительное число, кроме х = 1
при а = -1, а = 0 решений нет.

при а = 0, а = 2 решений нет.

при а = -3, а = 0, 5, а = -2 решений нет

при а = —с , с = 0 решений нет.

Квадратные уравнения с параметром

Пример 1. Решить уравнение

(а – 1)х 2 = 2(2а + 1)х + 4а + 3 = 0

При а = 1 6х + 7 = 0

В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.

Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16

20а + 16 = 0

20а = -16

Если а Д

Если а > -4/5 и а 1, то Д > 0,

х =

Если а = 4/5, то Д = 0,

Пример 2. При каких значениях параметра а уравнение

х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?

Д = 4(а + 1) 2 – 4(9а – 5) = 4а 2 – 28а + 24 = 4(а – 1)(а – 6)

4(а – 1)(а – 6) > 0

по т. Виета: х 1 + х 2 = -2(а + 1)
х 1 х 2 = 9а – 5

По условию х 1 х 2 а + 1) а – 5 > 0

В итоге

4(а – 1)(а – 6) > 0
— 2(а + 1) 9а – 5 > 0

а 6
а > — 1
а > 5/9

(Рис. 1 )

a a > 6

Пример 3. Найдите значения а , при которых данное уравнение имеет решение.

х 2 – 2(а – 1)х + 2а + 1 = 0

Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а
4а 2 – 16 0
4а (а – 4) 0

а(а – 4)) 0

а(а – 4) = 0

а = 0 или а – 4 = 0
а = 4

(Рис. 2 )

Ответ: а 0 и а 4

Дидактический материал

1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?
2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?
3. При каких значениях а уравнение (а 2 – 6а + 8) х 2 + (а 2 – 4) х + (10 – 3а – а 2) = 0 имеет более двух корней?
4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?
5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?

1. При а = — 1/7, а = 0, а = 1
2. При а = 0
3. При а = 2
4. При а = 10
5. При а = — 2

Показательные уравнения с параметром

Пример 1 .Найти все значения а , при которых уравнение

9 х – (а + 2)*3 х-1/х +2а *3 -2/х = 0 (1) имеет ровно два корня.

Решение. Умножив обе части уравнения (1) на 3 2/х, получим равносильное уравнение

3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)

Пусть 3 х+1/х = у , тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или

(у – 2)(у – а ) = 0, откуда у 1 =2, у 2 = а .

Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log 3 2 , или х 2 – х log 3 2 + 1 = 0.

Это уравнение не имеет действительных корней, так как его Д = log 2 3 2 – 4

Если у = а , т.е. 3 х+1/х = а то х + 1/х = log 3 а , или х 2 – х log 3 а + 1 = 0. (3)

Уравнение (3) имеет ровно два корня тогда и только тогда, когда

Д = log 2 3 2 – 4 > 0, или |log 3 а| > 2.

Если log 3 а > 2, то а > 9, а если log 3 а а

Ответ: 0 а а > 9.

Пример 2 . При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?

Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х 1 = -3, х 2 = а = >

а – положительное число.

Ответ: при а > 0

Дидактический материал

1. Найти все значения а, при которых уравнение

25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.

2. При каких значениях а уравнение

2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?

3. При каких значениях параметра а уравнение

4 х — (5а -3)2 х +4а 2 – 3а = 0 имеет единственное решение?

Логарифмические уравнения с параметром

Пример 1. Найти все значения а , при которых уравнение

log 4x (1 + ах ) = 1/2 (1)

имеет единственное решение.

Решение. Уравнение (1) равносильно уравнению

1 + ах = 2х при х > 0, х 1/4 (3)

х = у

ау 2 –у + 1 = 0 (4)

Не выполняется (2) условие из (3).

Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.Чтобы решить неравенство (3), построим графики функций Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение курса алгебры и математического анализа. – М.: Просвещение, 1990

Крамор В. С . Повторяем и систематизируем школьный курс алгебры и начал анализа. – М.: Просвещение, 1990.

Галицкий М.Л., Гольдман А.М., Звавич Л.И . Сборник задач по алгебре. – М.: Просвещение, 1994.

Звавич Л.И., Шляпочник Л.Я. Алгебра и начала анализа. Решение экзаменационных задач. – М.: Дрофа, 1998.

Макарычев Ю.Н. и др. Дидактические материалы по алгебре 7, 8, 9 кл. – М.: Просвещение, 2001.

Саакян С.И., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа для 10–11-х классов. – М.: Просвещение, 1990.

Журналы “Математика в школе”.

Л.С. Лаппо и др. ЕГЭ. Учебное пособие. – М.: Экзамен, 2001–2008.

К задачам с параметром можно отнести, например, поиск решения линейных и квадратных уравнений в общем виде, исследование уравнения на количество имеющихся корней в зависимости от значения параметра.

Не приводя подробных определений, в качестве примеров рассмотрим следующие уравнения:

у = kx, где x, y – переменные, k – параметр;

у = kx + b, где x, y – переменные, k и b – параметр;

аx 2 + bх + с = 0, где x – переменные, а, b и с – параметр.

Решить уравнение (неравенство, систему) с параметром это значит, как правило, решить бесконечное множество уравнений (неравенств, систем).

Задачи с параметром можно условно разделить на два типа:

а) в условии сказано: решить уравнение (неравенство, систему) – это значит, для всех значений параметра найти все решения. Если хотя бы один случай остался неисследованным, признать такое решение удовлетворительным нельзя.

б) требуется указать возможные значения параметра, при которых уравнение (неравенство, система) обладает определенными свойствами. Например, имеет одно решение, не имеет решений, имеет решения, принадлежащие промежутку и т. д. В таких заданиях необходимо четко указать, при каком значении параметра требуемое условие выполняется.

Параметр, являясь неизвестным фиксированным числом, имеет как бы особую двойственность. В первую очередь, необходимо учитывать, что предполагаемая известность говорит о том, что параметр необходимо воспринимать как число. Во вторую очередь, свобода обращения с параметром ограничивается его неизвестностью. Так, например, операции деления на выражение, в котором присутствует параметр или извлечения корня четной степени из подобного выражения требуют предварительных исследований. Поэтому необходима аккуратность в обращении с параметром.

Например, чтобы сравнить два числа -6а и 3а, необходимо рассмотреть три случая:

1) -6a будет больше 3a, если а отрицательное число;

2) -6а = 3а в случае, когда а = 0;

3) -6а будет меньше, чем 3а, если а – число положительное 0.

Решение и будет являться ответом.

Пусть дано уравнение kx = b. Это уравнение – краткая запись бесконечного множества уравнений с одной переменной.

При решении таких уравнений могут быть случаи:

1. Пусть k – любое действительное число не равное нулю и b – любое число изR, тогда x = b/k.

2. Пусть k = 0 и b ≠ 0, исходное уравнение примет вид 0 · x = b. Очевидно, что у такого уравнения решений нет.

3. Пусть k и b числа, равные нулю, тогда имеем равенство 0 · x = 0. Его решение – любое действительное число.

Алгоритм решения такого типа уравнений:

1. Определить «контрольные» значения параметра.

2. Решить исходное уравнение относительно х при тех значениях параметра, которые были определены в первом пункте.

3. Решить исходное уравнение относительно х при значениях параметра, отличающихся от выбранных в первом пункте.

4. Записать ответ можно в следующем виде:

1) при … (значения параметра), уравнение имеет корни …;

2) при … (значения параметра), в уравнении корней нет.

Пример 1.

Решить уравнение с параметром |6 – x| = a.

Решение.

Легко видеть, что здесь a ≥ 0.

По правилу модуля 6 – x = ±a, выразим х:

Ответ: х = 6 ± a, где a ≥ 0.

Пример 2.

Решить уравнение a(х – 1) + 2(х – 1) = 0 относительно переменной х.

Решение.

Раскроем скобки: aх – а + 2х – 2 = 0

Запишем уравнение в стандартном виде: х(а + 2) = а + 2.

В случае, если выражение а + 2 не нуль, т. е. если а ≠ -2, имеем решение х = (а + 2) / (а + 2), т.е. х = 1.

В случае, если а + 2 равно нулю, т.е. а = -2, то имеем верное равенство 0 · x = 0, поэтому х – любое действительное число.

Ответ: х = 1 при а ≠ -2 и х € R при а = -2.

Пример 3.

Решить уравнение x/a + 1 = а + х относительно переменной х.

Решение.

Если а = 0, то преобразуем уравнение к виду а + х = а 2 + ах или (а – 1)х = -а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.

Если а ≠ 1, то последнее уравнение примет вид х = -а.

Данное решение можно проиллюстрировать на координатной прямой (рис. 1)

Ответ: нет решений при а = 0; х – любое число при а = 1; х = -а при а ≠ 0 и а ≠ 1.

Графический метод

Рассмотрим еще один способ решения уравнений с параметром – графический. Этот метод применяется достаточно часто.

Пример 4.

Сколько корней в зависимости от параметра a имеет уравнение ||x| – 2| = a?

Решение.

Для решения графическим методом строим графики функций y = ||x| – 2| и y = a (рис. 2) .

На чертеже наглядно видны возможные случаи расположения прямой y = a и количество корней в каждом из них.

Ответ: корней у уравнения не будет, если а 2 и а = 0; три корня уравнение будет иметь в случае а = 2; четыре корня – при 0

Пример 5.

При каком а уравнение 2|x| + |x – 1| = a имеет единственный корень?

Решение.

Изобразим графики функций y = 2|x| + |x – 1| и y = a. Для y = 2|x| + |x – 1|, раскрыв модули методом промежутков, получим:

{-3x + 1, при x

y = {x + 1, при 0 ≤ x ≤ 1,

{3x – 1, при x > 1.

На рисунке 3 хорошо видно, что единственный корень уравнение будет иметь только при а = 1.

Ответ: а = 1.

Пример 6.

Определить число решений уравнения |x + 1| + |x + 2| = a в зависимости от параметра а?

Решение.

График функции y = |x + 1| + |x + 2| будет представлять собой ломаную. Ее вершины будут располагаться в точках (-2; 1) и (-1; 1) (рисунок 4) .

Ответ: если параметр a будет меньше единицы, то корней у уравнения не будет; если а = 1, то решение уравнения является бесконечное множество чисел из отрезка [-2; -1]; если значения параметра а будут больше одного, то уравнение будет иметь два корня.

Остались вопросы? Не знаете, как решать уравнения с параметром?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Тема уравнения и неравенства с параметрами содержащие модуль

Тема: Уравнения и неравенства с параметрами, содержащие модуль

Цель: повторить решение уравнение и неравенств с модулем графическим методом; научить учащихся решать уравнения и неравенства с параметрами, содержащих модуль; развивать логическое мышление, умение сравнивать, анализировать.

Орг. момент.

Актуализация знаний.
1. Вспомнить в чем заключается графический метод решения уравнений и неравенств с модулем.

Решить графически уравнение ||x| — 3| = 3.

Строим графики функций у = ||x| — 3| и у = 3

По графику видим, что решением исходного уравнения являются три числа -6, 0, 6

Новая тема

Уравнения и неравенства, содержащие модуль иногда целесообразно решать графически. Для этого выражение, содержащее параметр, обособляют в одной части уравнения (или неравенства) и строят графики левой и правой частей уравнения (неравенства). После чего делается вывод о решении уравнения.

Графический метод решения уравнений наиболее удобен, когда встает вопрос о количестве корней уравнений в зависимости от параметра.

Пример 1. Решить уравнение |x – 1| + |x – 3| = a.

Строим графики функций у = |x – 1| + |x – 3| и у = a.

По графику видим

при a < 2, решений нет

при а > 2 два решения

при а = 2 решением является промежуток [1; 3].

Найдем решения при а > 2.

Раскроем модуль на интервалах

1) (-∞; 1), – (х – 1) – (х – 3) = а; -х + 1 – х + 3 = а;

-2х + 4 = а, откуда

2) (3; +∞), х – 1 + х – 3 = а; 2х — 4 = а, откуда

Ответ: при a < 2, решений нет; при а > 2 , ; при а = 2 х [1; 3].

Пример 2. Сколько корней имеет уравнение |x – 2| · (x – 2) = a в зависимости от параметра а.

Строим графики функций у = |x – 2| · (x – 2) и у = a.

Из графика видим, что

при a < 0 и a > 4, 1 корень

при a = 0 и a = 4, 2 корня

при 0 < a < 4, 3 корня

Решение задач.

Для подборки заданий по данной теме можно воспользоваться следующей литературой

Норин А.В. и др. Сборник задач по математике для поступающих в вузы: Учебное пособие. – СПб: Питер, 2003

стр. 209 – 210.

«Математика» приложение к газете «1 сентября», № 30 – 2003, № 27 – 28 – 2002, № 29 – 2003, № 22 – 2002, № 2 – 2003
Фальке Л.Я. и др. Изучение сложных тем курса алгебры в средней школе: Учебно-методические материалы по математике. – М.: Илекса, 2002

Для отработки решений уравнений и неравенств с параметрами, содержащими модуль, можно также воспользоваться сборником для проведения письменного экзамена по алгебре и началам анализа: стр. 145 № 6.211 – 6.218

Итог урока
Домашнее задание

Сборник для проведения письменного экзамена по алгебре и началам анализа: стр. 146 № 6.221 – 6.224

Примечание. Если на данном уроке вы не ставите целью урока отработку построения графиков функций, то эти уроки можно провести с помощью компьютера. Компьютеру отвести роль построения графика функции или с помощью электронных таблиц Excel, или с использованием ППП «Matematica 4.2».

Тема: Системы уравнений, содержащие параметр

Цель: сформировать у учащихся умение решать системы уравнений с параметрами, содержащими модуль, различными методами; развивать творческую и исследовательскую деятельность, развивать логическое мышление, внимание, сообразительность

Орг. момент
Мотивация

Изучение математики не бывает легким занятием, но те трудности, которые здесь появляются, необходимо преодолевать, не скрывая их. Это оттачивает математическую мысль и рождает новые идеи.

Древнекитайский мыслитель и философ Конфуций сказал: «Три пути ведут к знанию: путь размышления – самый благородный, путь подражания – самый легкий и путь опыта – это путь самый горький…» Мне хотелось бы, чтобы, изучая данную тему, вы размышляли над решениями систем уравнений, содержащих параметры, тем самым не подражали, а приобретали бы свой опыт в решении таких систем.

Объяснение нового материала

Вспомним известные факты из курса алгебры о решении систем линейных уравнений.

Пусть дана система линейных уравнений .

Данная система имеет единственное решение, если
Система имеет бесконечно много решений, если
Система не имеет решений, если

Задание 1. Определить число решений системы

а) б) в)

Решение.

а) Имеем , значит, система имеет единственное решение.

б) Для второй системы характерно , поэтому система имеет бесконечно много решений.

в) Для третьей системы имеем , поэтому система не имеет решений.

Эти же известные факты удобно применять и при решении систем уравнений, содержащих параметр, в которых необходимо выяснить вопрос о количестве решений системы уравнений.

Пример 1. Определить все значения параметра а, при которых система уравнений имеет единственное решение.

Данная система является линейной системой из двух уравнений. Если а ≠ 0, то система имеет единственное решение, если .

Составим данное отношение , то 3а² ≠ а + 2, тогда 3а² — а – 2 ≠ 0. Соответствующее квадратное уравнение 3а² — а – 2 = 0 имеет корни и . Значит, при и выполняется условие 3а² ≠ а + 2, а, следовательно, система имеет единственное решение.

На закрепление изученного факта предложить учащимся для самостоятельного решения:

Укажите все значения параметра а, при которых система уравнений имеет единственное решение.
Определить все значения параметра а, при которых система уравнений имеет бесконечно много решений.
При каком значении параметра а система уравнений не имеет решений?
При всех значениях параметра а решите систему уравнений .

Следующим этапом изучения данной темы – это графический метод решения систем уравнений, содержащих параметр.

Пример 2. При всех значениях параметра а решить систему уравнений .

Построим в одной системе координат график каждого уравнения.

у = 1 – х — это прямая, проходящая через точки (1; 0) и (0; 1).

— это квадрат, вершины которого лежат на координатных осях в точках (а; 0), (0; а), (-а; 0) и (0; -а).

По графикам видим, что количество решений данной системы зависит от параметра.

Если а = 1, то одна из сторон квадрата совпадает с частью прямой у = 1 – х, значит решением системы является промежуток [0; 1].

При а < 1 квадрат и прямая не имеют точек пересечения, а значит, система уравнений не имеет решений.

При а > 1 квадрат и прямая пересекаются в двух точках. Определим координаты точек пересечения.

Имеем . Раскрывая знак модуля получаем = ,

тогда -2х + 1 = а, отсюда ; 2х — 1 = а, отсюда .

Значит, и

Т.о. получаем при а = 1 х 0; 1; при а < 1 система решений не имеет; при a > 1 система имеет два решения и

Пример 3. В зависимости от параметра а найти число решений системы уравнений

На этот вопрос не сложно ответить используя графический метод.

В одной системе координат построим график каждого уравнения. Первое уравнение системы определяет квадрат с вершинами в точках (1; 0), (0; 1), (-1; 0), (0; -1). Второе уравнение системы задает окружность с центром в начале координат и радиуса при условии . Возможны следующие варианты взаимного расположения квадрата и окружности:

1) 2) 3)

4) 5) 6)

Теперь следует лишь аккуратно указать границы для значений параметра.

Если а < 0, то второе уравнение системы решений не имеет. Если а = 0, то второе уравнение системы имеет единственное решение (0; 0), которое не является решением первого уравнения системы.

Определим радиус окружности, когда окружность касается сторон квадрата. Радиус вписанной окружности в квадрат вычисляется по формуле , где а – сторона квадрата. Сторона исходного квадрата равна , значит

Окружность находится внутри квадрата, если её радиус меньше, чем , т.е. ,
Если , т.е. , то окружность касается четырех сторон квадрата.
Если , то окружность пересекает каждую сторону квадрата в двух точках, не являющихся вершинами.
Если а = 1, то окружность проходит через все вершины квадрата.
Если а > 1, то квадрат находится внутри круга.

Т.о. получаем, что система не имеет решений, если ; система имеет 4 решения при а = 0,5 и а = 1; система имеет 8 решений при

Решение задач

На закрепление изученного материала можно предложить следующие задания:

При каких значениях параметра а система уравнений имеет максимальное число решений?
При каких значениях параметра а система имеет единственное решение?
При каких значениях параметра а система имеет 2 решения?
При каких значениях параметра а система имеет 3 решения?

Итог урока

Домашнее задание

Семенов В. И. Некоторые методические и методологические аспекты углубленного изучении математики. 9 – 11 классы: Учебное пособие. – Кемерово: ОблИУУ, 1998. – стр. 58 – 71.

Кочагин В. Курс «Уравнения и неравенства с параметрами» / Математика. – 2002. — № 33. — стр. 27

Тема: Методы решения и исследования уравнений с параметрами

Цель: продолжить формирование умений и навыков при решении уравнений с параметрами различными методами; развивать исследовательскую и познавательную деятельность учащихся; обеспечить условия для самостоятельной творческой работы учащихся; развивать компьютерную грамотность учащихся.

Орг. момент
Вступительное слово учителя.

Великий математик Карл Фридрих Гаусс в своё время назвал математику «царицей всех наук», а академик Соболев С.Л. её называет «служанкой всех наук». «Математика скорее добрая фея, только получить у неё можно не волшебную палочку, а надежный и точный инструмент – математические методы» (Петровский И. Г.)

Мы на протяжении нескольких уроков изучаем математические методы решения уравнений с параметрами: аналитический, графический, решение относительно параметра, компьютерное решение. Овладение методикой решения уравнений с параметрами существенно повышает уровень логической подготовки учащихся, развивает мышление, внимание. О человеке, у которого хорошо развито логическое мышление, говорят, что он основательно мыслит, дисциплинировано рассуждает.

Тема нашего занятия «Методы решения и исследования уравнений с параметрами», цель которого продолжить формирование умений и навыков при решении уравнений с параметрами различными методами.

Решение задач

Решить уравнения относительно х (работа в двух группах).

а) (а² – 4) х = а² + а – 6 б) ах² – 6х + 1 = 0

(а – 2)(а + 2) = (а – 2)(а + 3) а = 0, -6х + 1 = 0,

а = 2, 0х = 0, х R а  0, D₁ = 9 – а,

а = -2, 0х = -4, решений нет 1) 9 – а > 0

а  + 2,

2) 9 – a = 0, a = 9,

, т. е.

3) 9 – а < 0, a > 9, решений нет

При каком значении параметра а корни уравнения х² + (а + 1) х + а + 4 = 0 существуют, различны и отрицательны? (совместное обсуждение и самостоятельное решение).

Обсуждение.

т.к. корни существуют и различны, то D > 0

т.к. корни отрицательны, то х₁ + х₂ < 0; х₁ · х₂ > 0

Имеем D = a² – 2a – 15, х₁ + х₂ = — (a + 1), х₁ · х₂ = a + 4.

Получаем систему , решением которой является а  (5; +)

Сколько корней имеет уравнение х² – 6х + 5 = а в зависимости от параметра?

(работа с таблицей)

Сколько корней имеет уравнение в зависимости от параметра?

Обдумать ход решения данного задания.

Совместное построение графика функции на доске.

Вывод самостоятельно.

Графический метод решения некоторых уравнений с параметром весьма эффективен, когда нужно установить, сколько корней имеет уравнений в зависимости от параметра.

Практическая работа с использованием ППП «Matematica 4.0»

1 вариант

Решить уравнение:

а) 4а – а²х = 2ах б)

Сколько корней имеет уравнение в зависимости от параметра а?

2 вариант

Решить уравнение:

а) (а²– 9)х = 9а² – 10 а – 51 б)

Сколько корней имеет уравнение в зависимости от параметра а?

3 вариант

Решить уравнение:

а) (а²— 5а + 6) х = а⁴ – 16 б)

Сколько корней имеет уравнение в зависимости от параметра а?

Ответы к практической работе.

при а ≠ 1 х = а; настойчивость

при а = 1 корней нет

при а = 3 х – любое число;

при а ≠ 3 и а ≠ — 3 математикой

при а = -3 корней нет

при а ≠ 0 х = 0 мозг

при а = 0 корней нет

при а = 2

при а = 3 Ø упорство

при а ≠ 3, а ≠ 2

при а < 0 Ø

при а = 0, а < 3 4 корня

при 0 < a < 1 8 корней занимается

при а = 1 6 корней

при а = 3 3 решения

при а > 3 2 решения

при а < 1 корней нет

при а = 1 х [-2; -1] развивает

при а > 1 два решения

при а ≠ -2, а ≠ 0

при а = 0 тренирует

при а = -2 Ø

при а = 1, а = -1,5, а = 3,5 Ø воспитывает

при других а

при а < 0 Ø

при а = 0, а > 4 два корня

при 0 < а < 3, а = 4 четыре корня внимание

при а = 3 пять корней

при 3 < а < 4 шесть корней

при а ≠ -2, а ≠ 0 достижении цели

при а = 0

при а < 0 Ø

при а = 0, 1 < а < 3 4 корня

при 0 < a < 1 8 корней волю

при а = 1 6 корней

при а = 3 3 решения

при а > 3 2 решения

В результате выполнения практической работы и соотнесение ответов со словами учащиеся совместно составляют высказывание Маркушевича А. И. «Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает в себе настойчивость и упорство в достижении цели».

Итог занятия

Домашнее задание.

При каких значениях параметра а уравнение х² – (2а + 1)х + а² + а – 6 = 0 имеет:

а) два положительных корня;

б) два отрицательных корня;

в) корни разных знаков?

Найдите наибольшее целое а, при котором уравнение имеет четыре корня.

УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КУРСА

А. Рекомендуемая литература

Алгебра и начала анализа. Сборник задач для подготовки и проведения итоговой аттестации за курс средней школы / под ред. Шестакова С.А. — М.: Внешсигма – М, 2003
Башмаков М.И. и др. Алгебра и начала анализа. 10 – 11 кл.: Учебно-методическое пособие. – М.: Дрофа, 2001
Галицкий М.Л. и др. Сборник задач по алгебре для 8 – 9 классов: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики. – М.: Просвещение, 1994
Гольдштейн З.М. и др. Сборник задач по математике для подготовительных курсов ТУСУР. – Томск, 1999
Горнштейн П.И. и др. Задачи с параметрами. – М.: Илекса, 2002
Горнштейн П.И. Решение конкурсных задач по математике из сборника под редакцией М.И. Сканави. Группа В. — Киев: РИА «Текст МП «ОКО», 1992
Гусак А.А. Пособие к решению задач по высшей математике. – Минск, 1967
Данко П.Е. и др. Высшая математика в упражнениях и задачах. В 2-х частях. Ч. 1. – М.: Высшая школа, 1999
Джумаева О.А. Математика: подготовка к государственному централизованному тестированию. – Саратов: Лицей, 2002
Дорофеев Г.В. и др. Сборник заданий для подготовки и проведения письменного экзамена по математике (курс А) и алгебре и началам анализа (курс В) за курс средней школы. 11 класс. – М.: Дрофа, 2004
Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по алгебре и началам анализа для 10 – 11 классов. – М.: Илекса, 2003
Избранные вопросы математики. 9 кл. Факультативный курс. / Сост. Боковнев О.А. и др. – М.: Просвещение, 1979
Казак В.В., Козак А.В. Тесты по математике. Тестирование и единый экзамен. — М., 2003
Клейменов В.А. Математика. Решение задач повышенной сложности. – М.: Интеллект-Центр, 2004
Капустина Т. В. Компьютерная система MATHEMATICA 3.0 // Математика в школе. — 2003, № 7
Карп А.П. «Сборник задач по алгебре и началам анализа. 10 – 11». — М.: Просвещение, 1995
Колмогоров А.Н. Алгебра и начала анализа. 10 — 11 кл. – М.: Просвещение, 2001
Кордемский Б.А. Увлечь школьников математикой. – М.: Просвещение, 1981
Лаппо Л.Д., Попов М.А. ЕГЭ. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ: Учебно-методическое пособие. – М.: Экзамен, 2005
Лаппо Л.Д., Попов М.А. Математика. Пособие для подготовки к ЕГЭ и централизованному тестированию: Учебно-методическое пособие. – М.: Экзамен, 2004
Лиман М.М. Школьникам о математике и математиках. – М.: Просвещение, 1981
Макарычев Ю.Н., Миндюк Н.Г. Алгебра: Доп. главы к шк. учеб. 8 кл. – М.: Просвещение, 1998
Макарычев Ю.Н., Миндюк Н.Г. Алгебра: Доп. главы к шк. учеб. 9 кл. – М.: Просвещение, 1997
Мочалин А.А. Сборник задач по математике с решениями. — Саратов: Издательство «Лицей», 1998 г.
Норин А.В. и др. Сборник задач по математике для поступающих в вузы: Учебное пособие. – СПб: Питер, 2003
Олехник С.Н. и др. Алгебра и начала анализа. Уравнения и неравенства. — Москва: «Экзамен», 1998 г.
Олехник С.Н. и др. Уравнения и неравенства. Нестандартные методы решения. 10 – 11 классы. – М.: Дрофа, 2001
Петраков И.С. Математические кружки в 8 – 10 классах. – М.: Просвещение, 1987
Письменный Д.Т. Готовимся к экзамену по математике. – М.: АЙРИС, 1996
Предметная неделя математики. / Сост. Н.П. Токарчук. – Волгоград, 2007
Сборник конкурсных задач по математике для поступающих во втузы / Под ред М.И. Сканави. — М., 1994
Семенов В.И. Некоторые методические и методологические аспекты углубленного изучения математики. 9 – 11 классы. – Кемерово: ОблИУУ, 1998
Семёнов В.И. По страницам учебника М.Л. Галицкого …. — Кемерово, 1999 г.
Симонов А.Я. и др. Система тренировочных задач и упражнений по математике. – М.: Просвещение, 1991
Тесты: Варианты и ответы централизованного тестирования. – М.: АСТ-ПРЕСС; Центр тестирования выпускников общеобразовательных учреждений РФ, 2000
Фальке Л.Я. и др. Изучение сложных тем курса алгебры в средней школе: Учебно-методические материалы по математике. – М.: Илекса, 2002
Черкасов О.Ю. и др. «Математика. Интенсивный курс подготовки к экзамену». — Москва, 1997
Шарыгин И.Ф. Математика для школьников старших классов. – М.: Дрофа, 1995
Шарыгин И.Ф. «Факультативный курс по математике 10 – 11 кл.»
Шевкин А.В. Задачи с параметром. Линейные уравнения и их системы. – М.: Русское слово, 2003
Шевкин А.В. Итоговый тест за курс алгебры и начала анализа. В 2-х частях. Часть 1. – М.: Русское слово, 2003
Шевкин А.В. Итоговый тест за курс алгебры и начала анализа. В 2-х частях. Часть 2. – М.: Русское слово, 2003
3000 конкурсных задач по математике. – М., 1997 год
«Математика» приложение к газете «1 сентября», № 30 – 2003, № 27 – 28 – 2002, № 29 – 2003, № 22 – 2002, № 2 – 2003
www. center. fio. ru
www. 1september. ru
www. profile-edu. ru

В. Мультимедийные обучающие пособия

Математика абитуриенту. Версия 2.0
1С: Репетитор. Математика. Часть 1.
Курс математики 2000. Версия 4.5
MATHEMATICA 4.2. Компьютерная математика
1С: Репетитор. Сдаем Единый экзамен
Выпускнику и абитуриенту
Математика для школьников и студентов. Теория и практика
Электронный учебник-справочник. Алгебра. 7 – 11 класс
1С: Математика 5 – 11 классы. Практикум.
Математика 5 – 11. Новые возможности для усвоения курса математики.
Вычислительная математика и программирование. 10 – 11 классы.
Готовимся к ЕГЭ. Математика. Решение экзаменационных задач в интерактивном режиме.

Решение систем линейных уравнений с параметрами

Решение систем линейных уравнений с параметрами — страница №1/1

Занятие 3.

Тема: Решение систем линейных уравнений с параметрами.
Объяснение теоретического материала.
Определение. Системой линейных уравнений с двумя переменными называется два линейных уравнения, рассматриваемых совместно:

Решениями системы линейных уравнений называются такие пары чисел , которые являются решениями одновременно и первого, и второго уравнения системы.

Пусть числа a,b,сотличны от нуля.

Если , то система имеет единственное решение.

Если , то система не имеет решений.

Если , то система имеет бесконечно много решений.

Если с_1,с₂равны нулю, то система называется однородной и всегда имеет решение (0 ; 0). Если однородная система имеет нулевое решение (x₀; y₀), значит, она имеет бесконечное множество решений (kx₀; ky₀).
Пример 1. При каких значениях параметра a система

_{а) имеет бесконечное множество решений;}

б) имеет единственное решение?
Решение. Данная система уравнений является линейной, причем коэффициенты первого уравнения отличны от нуля.

а) Система имеет бесконечное множество решений, если а = 4.

б) Система имеет единственное решение, если а4

Обратить внимание на то, что уравнения поменяли местами, так как число а неопределенно. В нашем случае а=0 является решением в случае б), чтобы не было недоумений с делением на нуль, лучше вторым считать то уравнение, в котором все коэффициенты определены и не равны нулю.
Ответ: а) если а = 4, то система имеет бесконечное множество решений; б) если а4, то решение единственное.
Пример 2. Решите систему уравнений:

Решение. Данная система уравнений является линейной.

а) Система имеет единственное решение, если , то есть m.

Решим систему при m:

1-(m+1) y = n-2y;

2y-(m+1) y = n-1;

y (1-m) = n-1;

, где m1.

Найдем х, воспользовавшись любым уравнением системы:

Итак, при m 1 решением системы является пара .

б) Система не имеет решений, если , то есть при m =1, n1.

в) Система имеет бесконечно много решений, если , то есть m =1, n =1.

Пары вида , где x₀– любое число, являются решением системы в этом случае.

Ответ: если m =1, n1 то решений нет; если m =1, n =1, то решений бесконечное множество ;

если mи n – любое число, то решение единственное: .

Решить самостоятельно.

При каких значениях параметра b система уравнений

а) имеет бесконечное множество решений

б) не имеет решений?

2.Графики функций y = ax+3 и y=(2-a)x+a пересекаются в точке с абсциссой -1. Найдите ординату точки пересечения графиков.

3. Решите систему уравнений:

Общие методы решения систем уравнений. Алгебра, 11 класс: уроки, тесты, задания.

1.	Система уравнений с применением теоремы Виета Сложность: лёгкое	3
2.	Определение числа решений в системе по графикам Сложность: лёгкое	1
3.	Взаимное расположение прямых — графиков линейных уравнений системы Сложность: лёгкое	1
4.	Система иррациональных уравнений Сложность: среднее	3
5.	Система, состоящая из иррациональных уравнений Сложность: среднее	4
6.	Система логарифмических уравнений Сложность: среднее	3
7.	Система уравнений (формула суммы кубов) Сложность: среднее	4
8.	Система, состоящая из логарифмического и квадратного уравнений Сложность: среднее	6
9.	Система, состоящая из иррационального и линейного уравнений Сложность: среднее	3
10.	Система уравнений с взаимнообратными величинами Сложность: среднее	4
11.	Система иррациональных уравнений Сложность: среднее	4
12.	Система логарифмических уравнений Сложность: среднее	4
13.	Система показательных уравнений с модулем Сложность: среднее	4
14.	Система линейных уравнений (количество решений) Сложность: среднее	1
15.	Система линейных уравнений с параметром, вычисление параметра, если система не имеет решения Сложность: среднее	1
16.	Система линейных уравнений с параметром, вычисление параметра, бесконечное множество решений Сложность: среднее	3
17.	Система уравнений Сложность: сложное	8
18.	Система иррациональных уравнений Сложность: сложное	1
19.	Составление уравнения параболы Сложность: сложное	3

Линейная система уравнений с параметрами

Решение нескольких линейных линий с помощью аналитических методов займет много времени. Не забывайте, что одна ошибка может дорого вам обойтись. Вот почему мы предпочитаем численные методы для предсказания решения. Когда дело доходит до решения, есть два метода, на которые вы можете положиться: один — это решение линейной системы по правилу Крамера, а второй — метод исключения Гаусса.

Решение линейной системы уравнений с параметрами по правилу Крамера

В этом методе мы будем использовать правило Крамера, чтобы найти ранг, а также спрогнозировать значение неизвестных переменных в системе.Ниже приведен пример линейной системы с одной неизвестной переменной.

Здесь k — неизвестная переменная. Первым шагом является преобразование системы в матрицу коэффициентов и расширенную матрицу.

A представляет матрицу коэффициентов, а A ‘представляет расширенную матрицу. Следующим шагом является поиск определителей обеих матриц.

С помощью рангов теперь можно определить тип системы.

Если

, значит, система будет Несогласованная система.

Если

, значит, система будет Согласованная независимая система.

Поскольку мы знаем, с каким типом системы имеем дело, теперь мы можем сосредоточиться на поиске решения для линейной системы. Это уравнение также может быть решено методом исключения Гаусса, но сейчас мы сосредотачиваемся на правиле Крамера.

000

000 рядом со мной выдающиеся репетиторы по математике.

Лучшие доступные репетиторы по математике

Первый урок бесплатно

2. Решение линейной системы уравнений с параметрами методом исключения Гаусса

Исключение Гаусса — это прямой метод численного анализа, который помогает найти определитель, а также ранг матрица. По сути, прямые методы дают точный ответ, но при условии, что они выполняются с бесконечной точностью. Метод исключения Гаусса предполагает, что с помощью операций со строками мы можем найти определитель и ранг матрицы. Иногда вам может потребоваться выполнить частичный поворот, но это не обязательно.

В методе исключения Гаусса нам нужно преобразовать расширенную матрицу в верхнюю треугольную матрицу. В случае, если вы не знаете верхнюю треугольную матрицу, тогда это матрица, в которой все элементы ниже диагонали равны нулю.Вот иллюстрация верхней треугольной матрицы.

В этой верхней треугольной матрице

— диагональные элементы, а остальные переменные — константы. Если вы умножите все элементы диагонали, вы получите определитель матрицы. Необходимо определить, существует ли какое-либо значение м для обеспечения согласованности системы. Если да, решите систему для этого значения м .

Преобразуйте его в расширенную матрицу:

Операции со строками:

Если вы посмотрите на левую часть операции со строкой, это означает, что вы применяете операцию со строкой к этой конкретной строке. Правая часть операции со строкой показывает операцию, которую вы хотите применить к этой конкретной строке. Обратите внимание, что эта строковая операция будет применена ко всей строке.

Кроме того, вы можете сместить столбец. Например, в приведенной выше матрице, если мы поменяем местами столбцы 2 и 3, мы можем легко получить верхнюю треугольную матрицу.

Если

, это означает, следовательно, система будет Несогласованная система .

Если

, это означает, что система будет Согласованной зависимой системой .

Примеры

Поскольку матрица уже имеет форму верхней треугольной матрицы, мы можем использовать обратную подстановку напрямую, чтобы найти значения x, y и z.

Следовательно, будет два решения:

или

Если система будет быть Несогласованная система

Если

, следовательно, система Согласованная зависимая система.

Если

, значит, система является согласованной независимой системой .

Если

Приведенная выше система будет несовместимой с .

Если

Вышеупомянутая система будет согласованной зависимой системой .

Посмотрите, на что вам следует обратить внимание в репетиторе математики рядом со мной.

Системы линейных уравнений

В первой половине этого учебника нас в первую очередь будет интересовать понимание решений систем линейных уравнений.

Определение

Уравнение с неизвестными x, y, z, … называется линейным , если обе части уравнения являются суммой (постоянных) кратных x, y, z, … плюс необязательная константа.

Например,

3x + 4y = 2z − x − z = 100

— линейные уравнения, но

3x + yz = 3sin (x) −cos (y) = 2

— нет.

Обычно мы перемещаем неизвестные в левую часть уравнения, а константы — вправо.

Система линейных уравнений представляет собой набор нескольких линейных уравнений, например

Ax + 2y + 3z = 62x − 3y + 2z = 143x + y − z = −2.(1.1.1)

Определение (наборы решений)

Решение системы уравнений — это список чисел x, y, z, …, которые делают все уравнения истинными одновременно.
Набор решений системы уравнений — это совокупность всех решений.
Решение система означает нахождение всех решений с формулами, включающими некоторое количество параметров.

Система линейных уравнений не требует решения.Например, не существует чисел x и y, при которых одновременно выполняются следующие два уравнения:

Сх + 2у = 3х + 2у = −3.

В данном случае набор решений — пустой . Поскольку это довольно важное свойство системы уравнений, оно имеет собственное название.

Определение

Система уравнений называется несогласованной , если она не имеет решений. В противном случае он называется согласованным .

Решение системы уравнений от n переменных — это список из n чисел.Например, (x, y, z) = (1, −2,3) является решением (1.1.1). Поскольку в этом тексте мы будем изучать решения систем уравнений, сейчас хорошее время, чтобы исправить наши представления о списках чисел.

Мы используем R для обозначения набора всех действительных чисел, то есть числовой прямой. Он содержит числа вроде 0,32, −π, 104, …

Определение

Пусть n — целое положительное число. Определяем

Rn = все упорядоченные наборы вещественных чисел (x1, x2, x3, …, xn).

Набор из n действительных чисел называется точкой числа Rn.

Другими словами, Rn — это просто набор всех (упорядоченных) списков n действительных чисел. Сейчас мы нарисуем Rn, но имейте в виду, что — это определение . Например, (0,32, −π) и (1, −2,3) являются точками R3.

Пример (числовая строка)

Когда n = 1, мы просто возвращаем R: R1 = R. Геометрически это числовая прямая.

Пример (Евклидова плоскость)

Когда n = 2, мы можем думать о R2 как о плоскости xy. Мы можем это сделать, потому что каждая точка на плоскости может быть представлена упорядоченной парой действительных чисел, а именно ее координатами x и y.

Пример (3-пробел)

Когда n = 3, мы можем думать о R3 как о пространстве , в котором мы (кажется) живем. Мы можем это сделать, потому что каждая точка в пространстве может быть представлена упорядоченной тройкой вещественных чисел, а именно ее x-, y- и z-координаты.

Так что же такое R4? или R5? или Rn? Их труднее визуализировать, поэтому вам нужно вернуться к определению: Rn — это набор всех упорядоченных наборов n действительных чисел (x1, x2, x3, …, xn).

Они по-прежнему являются «геометрическими» пространствами в том смысле, что наша интуиция относительно R2 и R3 часто распространяется на Rn.

Мы сделаем определения и теоремы, применимые к любому Rn, но мы будем рисовать только изображения для R2 и R3.

Сила использования этих пространств заключается в возможности пометить различных объектов интереса, таких как геометрические объекты и решения систем уравнений, точками Rn.

В приведенных выше примерах с психологической точки зрения было полезно заменить список из четырех чисел (представляющих поток трафика) или из 841 числа (представляющих QR-код) одним фрагментом данных: точкой в некотором Rn.Это мощная концепция; начиная с раздела 2.2, мы будем почти исключительно записывать решения систем линейных уравнений таким способом.

Прежде чем обсуждать, как решить систему линейных уравнений ниже, полезно увидеть несколько изображений того, как эти наборы решений выглядят геометрически.

Одно уравнение с двумя переменными

Рассмотрим линейное уравнение x + y = 1. Мы можем переписать это как y = 1 − x, что определяет прямую на плоскости: наклон равен −1, а точка пересечения по оси x равна 1.

Определение (линии)

Для наших целей линия — это луч, который представляет собой прямой и бесконечный в обоих направлениях.

Одно уравнение в трех переменных

Рассмотрим линейное уравнение x + y + z = 1. Это неявное уравнение для плоскости в пространстве.

Определение (самолеты)

Плоскость — это плоский лист, бесконечный во всех направлениях.

Уравнение x + y + z + w = 1 определяет «3-плоскость» в 4-м пространстве, и, в более общем смысле, одно линейное уравнение с n переменными определяет «(n − 1) -плоскость» в n-пространстве. .Мы уточним эти утверждения в разделе 2.7.

Два уравнения с двумя переменными

Теперь рассмотрим систему двух линейных уравнений

Cx − 3y = −32x + y = 8.

Каждое уравнение индивидуально определяет линию на плоскости, изображенную ниже.

Решение системы обоих уравнений — это пара чисел (x, y), которая делает оба уравнения одновременно истинными. Другими словами, это точка, лежащая одновременно на обеих линиях. На картинке выше видно, что есть только одна точка пересечения линий: следовательно, эта система имеет ровно одно решение.(Это решение (3,2), как может убедиться читатель.)

Обычно две прямые на плоскости пересекаются в одной точке, но, конечно, это не всегда так. Рассмотрим теперь систему уравнений

Cx − 3y = −3x − 3y = 3.

Они определяют параллельных прямых на плоскости.

Тот факт, что линии не пересекаются, означает, что система уравнений не имеет решения. Конечно, это легко увидеть алгебраически: если x − 3y = −3, то не может быть и x − 3y = 3.

Есть еще одна возможность. Рассмотрим систему уравнений

Cx − 3y = −32x − 6y = −6.

Второе уравнение кратно первому, поэтому эти уравнения определяют ту же линию на плоскости.

В этом случае решений системы уравнений бесконечно много.

Два уравнения с тремя переменными

Рассмотрим систему двух линейных уравнений

Bx + y + z = 1x − z = 0.

Каждое уравнение индивидуально определяет плоскость в пространстве.Решениями системы обоих уравнений являются точки, лежащие на обеих плоскостях. На картинке ниже мы видим, что плоскости пересекаются в линию. В частности, у этой системы бесконечно много решений.

Рисунок 21 Плоскости, определяемые уравнениями x + y + z = 1 и x − z = 0, пересекаются красной линией, которая является множеством решений системы обоих уравнений.

В общем случае решение системы уравнений от n переменных является пересечением «(n − 1) -плоскостей» в n-пространстве. Это всегда какое-то линейное пространство, о чем мы поговорим в разделе 2. 4.

Согласно этому определению, решение системы уравнений означает запись всех решений через некоторое количество параметров. Мы дадим систематический способ сделать это в Разделе 1.3; а пока дадим параметрические описания в примерах предыдущего раздела.

Строки

Рассмотрим линейное уравнение x + y = 1 этого примера. В этом контексте мы называем x + y = 1 неявным уравнением линии. Мы можем записать ту же строку в параметрической форме следующим образом:

(x, y) = (t, 1 − t) для любого t∈R.

Это означает, что каждая точка на прямой имеет вид (t, 1 − t) для некоторого действительного числа t. В этом случае мы называем t параметром , поскольку он параметризует точек на линии.

Теперь рассмотрим систему двух линейных уравнений

Bx + y + z = 1x − z = 0

этого примера. Все вместе они образуют неявных уравнения для линии в R3. (Для определения линии в пространстве необходимы как минимум два уравнения. ) Эта линия также имеет параметрическую форму с одним параметром t:

(х, у, z) = (t, 1-2t, t).

Рисунок 24 Плоскости, определяемые уравнениями x + y + z = 1 и x − z = 0, пересекаются желтой линией, которая параметризуется как (x, y, z) = (t, 1−2t, t). Переместите ползунок, чтобы изменить параметризованную точку.
Обратите внимание, что в каждом случае параметр t позволяет нам использовать R для , обозначая точек на линии. Однако ни одна из линий не совпадает с числовой прямой R: действительно, каждая точка в первой строке имеет две координаты, как точка (0,1), и каждая точка во второй строке имеет три координаты, например (0,1 , 0).
Самолеты
Рассмотрим линейное уравнение x + y + z = 1 этого примера. Это неявное уравнение плоскости в пространстве. У этой плоскости есть уравнение в параметрической форме : мы можем записать каждую точку на плоскости как
(x, y, z) = (1 − t − w, t, w) для любого, w∈R.
В этом случае нам нужны два параметра t и w для описания всех точек на плоскости.
Рисунок 26 — Плоскость в R3, определяемая уравнением x + y + z = 1. Эта плоскость параметризуется двумя числами t, w; переместите ползунки, чтобы изменить параметризованную точку.
Обратите внимание, что параметры t, w позволяют нам использовать от R2 до для обозначения точек на плоскости. Однако эта плоскость , а не , такая же, как плоскость R2: действительно, каждая точка на этой плоскости имеет три координаты, как и точка (0,0,1).
Когда существует уникальное решение, как в этом примере, нет необходимости использовать параметры для описания набора решений.
Как решить систему линейных уравнений с дополнительным параметром?
(Для получения дополнительной информации о матрицах, векторах, векторных произведениях и других связанных темах ознакомьтесь с нашей серией электронных книг по линейной алгебре.)
Сегодня Коннор задал следующий вопрос, связанный с системой линейных уравнений с дополнительным параметром:
Учитывая, что $ x_1 + hx_2 = 4 $ и $ 3x_1 + 6x_2 = 8 $, найдите все пары вида $ ( x_1, x_2) $, удовлетворяющие обоим уравнениям.
Хорошо … Что нам делать с этими дополнительными $ h $? Что ж, читайте дальше!
Нам дана эта система линейных уравнений с самого начала:
\ begin {cases} x_1 + hx_2 = 4 & (a) \\ 3x_1 + 6x_2 = 8 & (b) \ end {cases}
Что делать? Что ж, мы можем попытаться решить эту систему линейных уравнений, сначала рассматривая $ h $ как обычный коэффициент, и посмотреть, к чему это приведет нас, когда мы будем действовать разумно.Во-первых, разделив уравнение $ (b) $ на $ 3 $ с обеих сторон, получим следующую эквивалентную систему:
\ begin {cases} x_1 + hx_2 = 4 & (1) \\ x_1 + 2x_2 = \ frac {8} { 3} & (2) \ end {cases}
Превращая уравнение 2 ^и в $ (2) — (1) $, получаем:
\ begin {align *} \ begin {cases} x_1 + hx_2 = 4 \\ (2-h) x_2 = \ frac {8} {3} -4 \ end {cases} \ qquad & \ Leftrightarrow \ qquad \ begin {cases} x_1 + hx_2 = 4 & (3) \\ ( h-2) x_2 = 4- \ frac {8} {3} = \ frac {4} {3} & (4) \ end {cases} \ end {align *}
На данный момент наша последняя система по-прежнему эквивалент исходному (т.е., $ (a) $ и $ (b) \ iff (3) $ и $ (4) $). А с $ (4) $ мы определенно на один шаг ближе к решению для $ x_2 $. Но прежде чем мы это сделаем, обратите внимание, что мы не можем решить для $ x_2 $, переместив $ h-2 $ вправо, если $ h-2 = 0 $ (т.е. $ h = 2 $). Тогда откроются две банки с червями…
Замените $ h $ на 2 в уравнениях $ (3) $ и $ (4) $, появится следующая система:
\ begin {cases} x_1 + 2x_2 = 4 \\ 0 = \ frac {4} {3} \ end {cases}
Ой. Противоречие. Во всяком случае, этого не может быть, поэтому в данном случае нет решения.
На самом деле нам даже не нужно переходить к $ (3) $ и $ (4) $, чтобы увидеть это. Это потому, что если мы просто подключим 2 к $ h $ к тому времени, когда мы дойдем до $ (1) $ и $ (2) $, мы получим следующую систему:
\ begin {cases} x_1 + 2x_2 = 4 \\ x_1 + 2x_2 = \ frac {8} {3} \ end {ases}
который, как мы видим, уже является системой, уравнения которой противоречат друг другу. Здесь — картинка стоит тысячи слов:
Понимаете … это потому, что они параллельны друг другу. Значит, точки пересечения нет!
Как только вышеупомянутое тривиальное препятствие будет устранено, мы можем перейти к чему-то более серьезному.Для записи, вот последняя система, которая у нас есть:
\ begin {cases} x_1 + hx_2 = 4 & (3) \\ (h-2) x_2 = 4 — \ frac {8} {3} = \ frac {4} {3} & (4) \ end {ases}
Поскольку $ h \ ne 2 $ сейчас, $ h-2 \ ne 0 $. Таким образом, мы можем разделить уравнение $ (4) $ на $ h-2 $ с обеих сторон, и в этом случае мы получим:
\ begin {cases} x_1 + hx_2 = 4 & (5) \\ x_2 = \ frac {4} {3 (h-2)} & (6) \ end {ases}
Наконец, если мы превратим $ (5) $ в $ (5) -h (6) $, мы получим очень аккуратный система взамен:
\ begin {cases} x_1 = 4 — \ frac {4h} {3 (h-2)} = \ frac {8h-24} {3h-6} & (7) \\ x_2 = \ frac {4} {3 (h-2)} = \ frac {4} {3h-6} & (8) \ end {ases}
Итак, для каждого $ h \ ne 2 $ мы получаем уникальный пара решений вида $ \ left (\ dfrac {8h-24} {3h-6}, \ dfrac {4} {3h-6} \ right) $.
Некоторые иллюстрации
Например, если $ h = 0 $, то исходная система принимает вид:
\ begin {cases} x_1 = 4 \\ 3x_1 + 6x_2 = 8 \ end {ases}
В этом случае, единственное решение:
$$ \ left (\ frac {8h-24} {3h-6}, \ frac {4} {3h-6} \ right) _ {h = 0} = \ left (4 , — \ frac {2} {3} \ right) $$
Вот изображение:
Точка пересечения находится в $ (4, — \ frac {2} {3}) $.
И в случае, когда $ h = 10 $, исходная система принимает вид:
\ begin {cases} x_1 + 10x_2 = 4 \\ 3x_1 + 6x_2 = 8 \ end {ases}
В этом случае единственное решение будет:
$$ \ left (\ frac {8h-24} {3h-6}, \ frac {4} {3h-6} \ right) _ {h = 10} = \ left (\ frac {56 } {24}, \ frac {4} {24} \ right) = \ left (\ frac {7} {3}, \ frac {1} {6} \ right) $$
Еще раз изображение:
Обратите внимание, как уравнение 1 ^st (красная линия) повернулось против часовой стрелки примерно на $ (4,0) $ при увеличении h.Точка пересечения теперь находится в $ \ displaystyle \ left (\ frac {7} {3}, \ frac {1} {16} \ right) $.
И вот как мы можем решить одновременно бесконечно много систем линейных уравнений! Для последней проверки работоспособности вот анимация Desmos, которую мы собрали — просто для того, чтобы мы могли объединить все, что мы узнали до сих пор, на одном слайде.
Система линейных уравнений — линейная алгебра с приложениями
Практические задачи во многих областях науки, таких как биология, бизнес, химия, информатика, экономика, электроника, инженерия, физика и социальные науки, часто можно свести к решению системы линейных уравнений.Линейная алгебра возникла в результате попыток найти систематические методы решения этих систем, поэтому естественно начать эту книгу с изучения линейных уравнений.
Если, и — действительные числа, график уравнения вида
— прямая линия (если и не равны нулю), поэтому такое уравнение называется линейным уравнением в переменных и. Однако часто удобно записывать переменные как, особенно когда задействовано более двух переменных.Уравнение вида
называется линейным уравнением в переменных. Здесь обозначают действительные числа (называемые коэффициентами соответственно), а также число (называемое постоянным членом уравнения). Конечный набор линейных уравнений в переменных называется системой линейных уравнений в этих переменных. Следовательно,
— линейное уравнение; коэффициенты при, и равны, и, а постоянный член равен.Обратите внимание, что каждая переменная в линейном уравнении встречается только в первой степени.
Для линейного уравнения последовательность чисел называется решением уравнения, если
, то есть, если уравнение удовлетворяется при выполнении замен. Последовательность чисел называется решением системы уравнений, если она является решением каждого уравнения в системе.
Система может вообще не иметь решения, или она может иметь уникальное решение, или она может иметь бесконечное семейство решений.Например, система не имеет решения, потому что сумма двух чисел не может быть одновременно 2 и 3. Система, у которой нет решения, называется несогласованной ; система с хотя бы одним решением называется согласованная .
Покажите, что для произвольных значений и
— это решение системы
Просто подставьте эти значения,, и в каждое уравнение.
Поскольку оба уравнения удовлетворяются, это решение для любого выбора и.
Величины и в этом примере называются параметрами , а набор решений, описанный таким образом, считается заданным в параметрической форме и называется общим решением для системы. Оказывается, что решения каждой системы уравнений (если есть решения ) могут быть даны в параметрической форме (то есть, переменные, задаются в терминах новых независимых переменных и т. Д. .).

Когда задействованы только две переменные, решения систем линейных уравнений могут быть описаны геометрически, потому что график линейного уравнения представляет собой прямую линию, если и не оба равны нулю. Более того, точка с координатами и лежит на прямой тогда и только тогда, когда — то есть когда, является решением уравнения. Следовательно, решения системы линейных уравнений соответствуют точкам, которые лежат на всех рассматриваемых линиях.

В частности, если система состоит только из одного уравнения, должно быть бесконечно много решений, потому что на прямой бесконечно много точек. Если система имеет два уравнения, есть три возможности для соответствующих прямых:

Линии пересекаются в одной точке. Тогда в системе есть уникальное решение , соответствующее этой точке.
Прямые параллельны (и четкие) и не пересекаются. Тогда в системе нет решения .
Строки идентичны. Тогда в системе будет бесконечно много решений — по одному на каждую точку на (общей) прямой.

С тремя переменными график уравнения может быть показан как плоскость и, таким образом, снова дает «картину» множества решений. Однако у этого графического метода есть свои ограничения: когда задействовано более трех переменных, физическое изображение графов (называемых гиперплоскостями) невозможно. Необходимо обратиться к более «алгебраическому» методу решения.

Перед описанием метода мы вводим понятие, упрощающее вычисления. Рассмотрим следующую систему

трех уравнений с четырьмя переменными. Массив чисел

, встречающееся в системе, называется расширенной матрицей системы. Каждая строка матрицы состоит из коэффициентов переменных (по порядку) из соответствующего уравнения вместе с постоянным членом. Для наглядности константы разделены вертикальной линией.Расширенная матрица — это просто другой способ описания системы уравнений. Массив коэффициентов переменных

называется матрицей коэффициентов системы, а
называется постоянной матрицей системы.

Элементарные операции

Алгебраический метод решения систем линейных уравнений описывается следующим образом. Две такие системы называются эквивалентами , если они имеют одинаковый набор решений.Система решается путем написания серии систем, одна за другой, каждая из которых эквивалентна предыдущей системе. Каждая из этих систем имеет тот же набор решений, что и исходная; цель состоит в том, чтобы получить систему, которую легко решить. Каждая система в серии получается из предыдущей системы простой манипуляцией, выбранной так, чтобы она не меняла набор решений.

В качестве иллюстрации мы решаем систему таким образом. На каждом этапе отображается соответствующая расширенная матрица.Исходная система —

Сначала вычтите дважды первое уравнение из второго. В результате получается система

.
, что эквивалентно оригиналу. На этом этапе мы получаем, умножив второе уравнение на. В результате получается эквивалентная система
.
Наконец, мы дважды вычитаем второе уравнение из первого, чтобы получить другую эквивалентную систему.
Теперь эту систему легко решить! И поскольку он эквивалентен исходной системе, он обеспечивает решение этой системы.
Обратите внимание, что на каждом этапе в системе (и, следовательно, в расширенной матрице) выполняется определенная операция для создания эквивалентной системы.
Следующие операции, называемые элементарными операциями , могут в обычном порядке выполняться над системами линейных уравнений для получения эквивалентных систем.
Поменяйте местами два уравнения.
Умножьте одно уравнение на ненулевое число.
Добавьте одно уравнение, кратное одному, к другому уравнению.
Предположим, что последовательность элементарных операций выполняется над системой линейных уравнений. Тогда результирующая система имеет тот же набор решений, что и исходная, поэтому две системы эквивалентны.
Элементарные операции, выполняемые над системой уравнений, производят соответствующие манипуляции с строками расширенной матрицы. Таким образом, умножение строки матрицы на число означает умножение каждой записи строки на.Добавление одной строки к другой означает добавление каждой записи этой строки к соответствующей записи другой строки. Аналогично производится вычитание двух строк. Обратите внимание, что мы считаем две строки равными, если соответствующие записи совпадают.
В ручных вычислениях (и в компьютерных программах) мы манипулируем строками расширенной матрицы, а не уравнениями. По этой причине мы переформулируем эти элементарные операции для матриц.
Следующие операции называются операциями с элементарной строкой матрицы.
Поменять местами два ряда.
Умножить одну строку на ненулевое число.
Добавить в другую строку, кратное одной строке.
На иллюстрации выше серия таких операций привела к матрице вида
, где звездочки обозначают произвольные числа. В случае трех уравнений с тремя переменными цель состоит в том, чтобы получить матрицу вида
Это не всегда происходит, как мы увидим в следующем разделе.Вот пример, в котором это действительно происходит.
Решение:
Расширенная матрица исходной системы —
Чтобы создать в верхнем левом углу, мы можем умножить строку с 1 на. Однако можно получить без введения дробей, вычтя строку 2 из строки 1. Результат:
Верхний левый угол теперь используется для «очистки» первого столбца, то есть для создания нулей в других позициях в этом столбце.Сначала отнимите строку 1 от строки 2, чтобы получить
.
Затем вычтите строку 1 из строки 3. Результат:
.
Это завершает работу над столбцом 1. Теперь мы используем во второй позиции второй строки, чтобы очистить второй столбец, вычитая строку 2 из строки 1 и затем добавляя строку 2 к строке 3. Для удобства обе операции со строками сделано за один шаг. Результат
Обратите внимание, что две последние манипуляции не повлияли на первый столбец (во второй строке там стоит ноль), поэтому наши предыдущие усилия там не были подорваны.Наконец, мы очищаем третий столбец. Начните с умножения строки 3 на, чтобы получить
.
Теперь вычтите временную строку 3 из строки 1, а затем добавьте умноженную строку 3 к строке 2, чтобы получить
.
Соответствующие уравнения:, и, которые дают (единственное) решение.
Алгебраический метод, представленный в предыдущем разделе, можно резюмировать следующим образом: Для данной системы линейных уравнений используйте последовательность элементарных операций со строками, чтобы преобразовать расширенную матрицу в «красивую» матрицу (это означает, что соответствующие уравнения легко решить. ).В примере 1.1.3 эта красивая матрица приняла вид
.
Следующие определения идентифицируют хорошие матрицы, возникающие в этом процессе.
Матрица, как говорят, находится в форме эшелона строк (и будет называться матрицей эшелонов строк , если она удовлетворяет следующим трем условиям:
Все нулевые строки (полностью состоящие из нулей) находятся внизу.
Первая ненулевая запись слева в каждой ненулевой строке — это a, называемая ведущей для этой строки.
Каждый ведущий элемент находится справа от всех ведущих строк в строках над ним.
Матрица строка-эшелон называется сокращенной строкой-эшелонной формой (и будет называться сокращенной матрицей строка-эшелон , если, кроме того, она удовлетворяет следующему условию:
4. Каждый ведущий элемент — это единственная ненулевая запись в своем столбце.
Матрицы «строка-эшелон» имеют форму «ступеньки», как показано в следующем примере (звездочки указывают произвольные числа).
Ведущие идут «вниз и вправо» через матрицу. Записи выше и справа от ведущих s произвольны, но все записи ниже и слева от них равны нулю. Следовательно, матрица в виде эшелона строк находится в сокращенной форме, если, кроме того, все записи непосредственно над каждым ведущим равны нулю. Обратите внимание, что матрица в форме эшелона строк может с помощью нескольких дополнительных операций со строками быть приведена к сокращенной форме (используйте операции со строками, чтобы последовательно создавать нули над каждой ведущей единицей, начиная справа).
Важность матриц строка-эшелон вытекает из следующей теоремы.
Каждая матрица может быть приведена к (сокращенной) форме строки-эшелона последовательностью элементарных операций со строками.
Фактически, мы можем дать пошаговую процедуру для фактического нахождения матрицы ряда строк. Обратите внимание: несмотря на то, что существует множество последовательностей операций со строками, которые приведут матрицу к форме ряда строк, та, которую мы используем, является систематической и ее легко программировать на компьютере. Обратите внимание, что алгоритм имеет дело с матрицами в целом, возможно, со столбцами нулей.
Шаг 1. Если матрица полностью состоит из нулей, остановитесь — она уже в виде эшелона строк.
Шаг 2. В противном случае найдите первый столбец слева, содержащий ненулевую запись (назовите его), и переместите строку, содержащую эту запись, в верхнюю позицию.
Шаг 3. Теперь умножьте новую верхнюю строку на, чтобы создать интерлиньяж.
Шаг 4. Вычитая кратные числа этой строки из строк под ней, сделайте каждую запись ниже начального нуля. Это завершает первую строку, и все дальнейшие операции со строками выполняются с оставшимися строками.
Шаг 5. Повторите шаги 1–4 для матрицы, состоящей из оставшихся строк.
Процесс останавливается, когда либо на шаге 5 не остается строк, либо оставшиеся строки состоят полностью из нулей.
Обратите внимание на то, что гауссовский алгоритм является рекурсивным: когда получен первый ведущий, процедура повторяется для оставшихся строк матрицы. Это упрощает использование алгоритма на компьютере. Обратите внимание, что в решении примера 1.1.3 не использовался гауссовский алгоритм в том виде, в каком он был написан, потому что первый ведущий не был создан путем деления строки 1 на.Причина этого в том, что он избегает дробей. Однако общий шаблон ясен: создайте ведущие слева направо, используя каждый из них по очереди, чтобы создать нули под ним. Вот один пример.
Решение:
Соответствующая расширенная матрица —
Создайте первую ведущую, поменяв местами строки 1 и 2
Теперь вычтите умноженную строку 1 из строки 2 и вычтите умноженную строку 1 из строки 3.Результат
Теперь вычтите строку 2 из строки 3, чтобы получить
.
Это означает, что следующая сокращенная система уравнений
эквивалентен исходной системе. Другими словами, у них одинаковые решения. Но эта последняя система явно не имеет решения (последнее уравнение требует этого и удовлетворяет, а таких чисел не существует). Следовательно, исходная система не имеет решения.
Чтобы решить линейную систему, расширенная матрица приводится к сокращенной форме строки-эшелона, а переменные, соответствующие ведущим, называются ведущими переменными .Поскольку матрица представлена в сокращенной форме, каждая ведущая переменная встречается ровно в одном уравнении, поэтому это уравнение может быть решено для получения формулы для ведущей переменной в терминах не ведущих переменных. Принято называть нелидирующие переменные «свободными» переменными и маркировать их новыми переменными, называемыми параметрами . Каждый выбор этих параметров приводит к решению системы, и каждое решение возникает таким образом. Эта процедура в целом работает и получила название
.
Для решения системы линейных уравнений выполните следующие действия:
Перенести расширенную матрицу \ index {расширенная матрица} \ index {матрица! Расширенная матрица} в сокращенную матрицу-эшелон строк, используя элементарные операции со строками.
Если возникает строка, система несовместима.
В противном случае присвойте не ведущие переменные (если они есть) в качестве параметров и используйте уравнения, соответствующие сокращенной матрице строки-эшелон, чтобы найти ведущие переменные в терминах параметров.
Существует вариант этой процедуры, в котором расширенная матрица переносится только в строчно-эшелонированную форму. Не ведущие переменные назначаются как параметры, как и раньше. Затем последнее уравнение (соответствующее форме строки-эшелона) используется для решения последней ведущей переменной в терминах параметров.Эта последняя ведущая переменная затем подставляется во все предыдущие уравнения. Затем второе последнее уравнение дает вторую последнюю ведущую переменную, которая также подставляется обратно. Процесс продолжает давать общее решение. Эта процедура называется обратной заменой . Можно показать, что эта процедура численно более эффективна и поэтому важна при решении очень больших систем.
Рейтинг
Можно доказать, что уменьшенная строковая форма матрицы однозначно определяется.То есть, независимо от того, какая серия операций со строками используется для переноса в сокращенную матрицу эшелонов строк, результатом всегда будет одна и та же матрица. Напротив, это неверно для матриц ряда строк: разные серии операций со строками могут переносить одну и ту же матрицу в разные матрицы ряда строк. В самом деле, матрица может быть перенесена (с помощью одной строковой операции) в матрицу-эшелон строк, а затем с помощью другой строковой операции в (сокращенную) матрицу-эшелон. Тем не менее, — это , правда, что количество ведущих единиц должно быть одинаковым в каждой из этих матриц строки-эшелон (это будет доказано позже).Следовательно, количество зависит только от того, каким образом приведено в строй.
Ранг матрицы — это количество ведущих s в любой матрице строка-эшелон, которую можно перенести с помощью строковых операций.
Вычислить ранг.
Решение:
Приведение к строчной форме
Так как эта матрица эшелонов строк имеет два ведущих s, rank.
Предположим, что ранг, где — матрица со строками и столбцами.Тогда потому что ведущие s лежат в разных строках, и потому что ведущие s лежат в разных столбцах. Более того, у ранга есть полезное приложение к уравнениям. Напомним, что система линейных уравнений называется непротиворечивой, если она имеет хотя бы одно решение.
Проба:
Тот факт, что ранг расширенной матрицы равен, означает, что есть ровно ведущие переменные и, следовательно, точно не ведущие переменные. Все эти нелидирующие переменные назначаются как параметры в гауссовском алгоритме, поэтому набор решений включает в себя именно параметры.Следовательно, если существует хотя бы один параметр, а значит, и решений бесконечно много. Если, нет параметров и поэтому единственное решение.
Теорема 1.2.2 показывает, что для любой системы линейных уравнений существуют ровно три возможности:
Нет решения . Это происходит, когда ряд встречается в форме эшелона строк. Это тот случай, когда система несовместима.
Уникальное решение . Это происходит, когда каждая переменная является ведущей переменной.
Бесконечно много решений . Это происходит, когда система согласована и есть хотя бы одна не ведущая переменная, поэтому задействован хотя бы один параметр.
https://www.geogebra.org/m/cwQ9uYCZ
Пожалуйста, ответьте на эти вопросы после открытия веб-страницы:
1. Для данной линейной системы, что представляет каждая из них?
2. Исходя из графика, что можно сказать о решениях? Есть ли у системы одно решение, нет решения или бесконечно много решений? Почему
3.Измените постоянный член в каждом уравнении на 0, что изменилось на графике?
4. Для следующей линейной системы:
Можете ли вы решить это методом исключения Гаусса? Что вы наблюдаете, когда смотрите на график?
Многие важные проблемы связаны с линейными неравенствами , а не с линейными уравнениями Например, условие для переменных может принимать форму неравенства, а не равенства.Существует метод (называемый симплексным алгоритмом ) для поиска решений системы таких неравенств, который максимизирует функцию вида где и являются фиксированными константами.
Система уравнений с переменными называется однородной , если все постоянные члены равны нулю, то есть если каждое уравнение системы имеет вид
Очевидно, решение такой системы; это называется тривиальным решением .Любое решение, в котором хотя бы одна переменная имеет ненулевое значение, называется нетривиальным решением .
Наша главная цель в этом разделе — дать полезное условие, при котором однородная система имеет нетривиальные решения. Следующий пример поучителен.
Покажите, что следующая однородная система имеет нетривиальные решения.
Решение:
Приведение расширенной матрицы к сокращенной форме эшелона строк описано ниже.
Ведущими переменными являются,, и, например, назначается в качестве параметра.Тогда общее решение:,,,. Следовательно, взяв (скажем), мы получим нетривиальное решение:,,,.
Существование нетривиального решения в примере 1.3.1 обеспечивается наличием параметра в решении. Это связано с тем, что существует не ведущая переменная (в данном случае). Но здесь должно быть не ведущей переменной, потому что здесь четыре переменных и только три уравнения (и, следовательно, не более три ведущие переменные).Это обсуждение обобщает доказательство следующей основной теоремы.
Если однородная система линейных уравнений имеет больше переменных, чем уравнений, то она имеет нетривиальное решение (фактически бесконечно много).
Проба:
Предположим, что есть уравнения в переменных, где, и пусть обозначают сокращенную строчно-эшелонированную форму расширенной матрицы. Если есть ведущие переменные, есть не ведущие переменные и, следовательно, параметры. Следовательно, достаточно показать это.Но потому что имеет ведущие единицы и строки, и по гипотезе. Итак, что дает.
Обратите внимание, что обратное утверждение теоремы 1.3.1 неверно: если однородная система имеет нетривиальные решения, она не должна иметь больше переменных, чем уравнения (система имеет нетривиальные решения, но.)
Теорема 1.3.1 очень полезна в приложениях. В следующем примере представлена иллюстрация из геометрии.
Мы называем график уравнения конической , если числа, и не все равны нулю.Покажите, что есть хотя бы одна коника, проходящая через любые пять точек на плоскости, которые не все лежат на одной прямой.
Решение:
Пусть координаты пяти точек будут,,, и. График проходов if
Это дает пять уравнений, по одному для каждого, линейных по шести переменным,,,,, и. Следовательно, по теореме 1.1.3 существует нетривиальное решение. Если все пять точек лежат на линии с уравнением, вопреки предположению. Следовательно, один из « отличен от нуля.
Линейные комбинации и базовые решения
Что касается строк, два столбца рассматриваются как , равные , если они имеют одинаковое количество записей и соответствующие записи одинаковы. Позвольте и быть столбцами с одинаковым количеством записей. Что касается операций с элементарными строками, их сумма получается путем сложения соответствующих записей, и, если это число, скалярное произведение определяется путем умножения каждой записи на. Точнее:
Сумма скалярных кратных нескольких столбцов называется линейной комбинацией этих столбцов.Например, это линейная комбинация и для любого выбора чисел и.
Решение:
Для, мы должны определить, существуют ли числа, и такие, что, то есть
Приравнивание соответствующих элементов дает систему линейных уравнений,, и для,, и. Путем исключения Гаусса решение есть, и где — параметр. Взяв, мы видим, что это линейная комбинация, и.
Обращаясь к, снова ищем, и такие, что; то есть
, что приводит к уравнениям,, и для действительных чисел, и.Но на этот раз существует , нет решения , как может проверить читатель, а также , а не , линейная комбинация, и.
Наш интерес к линейным комбинациям проистекает из того факта, что они предоставляют один из лучших способов описания общего решения однородной системы линейных уравнений. Когда
решает такую систему с переменными, запишите переменные в виде матрицы столбцов:. Обозначено тривиальное решение. В качестве иллюстрации, общее решение в
Пример 1.3.1 — это,, и, где — параметр, и теперь мы могли бы выразить это как
, говоря, что общее решение -, где произвольно.
Теперь пусть и — два решения однородной системы с переменными. Тогда любая линейная комбинация этих решений снова оказывается решением системы. В более общем плане:
Фактически, предположим, что типичное уравнение в системе имеет вид, и предположим, что
, являются решениями. Потом и
.
Следовательно, это тоже решение, потому что
Аналогичный аргумент показывает, что Утверждение 1.1 верно для линейных комбинаций более двух решений.
Примечательно то, что каждое решение однородной системы представляет собой линейную комбинацию определенных частных решений, и, фактически, эти решения легко вычисляются с использованием гауссовского алгоритма. Вот пример.
Решить однородную систему с матрицей коэффициентов
Решение:
Приведение расширенной матрицы к уменьшенной форме —
, поэтому решениями являются,, и методом исключения Гаусса.Следовательно, мы можем записать общее решение в матричной форме
Вот и частные решения, определяемые гауссовским алгоритмом.
Решения и в примере 1.3.5 обозначены следующим образом:
Алгоритм Гаусса систематически выдает решения для любой однородной линейной системы, называемые базовыми решениями , по одному для каждого параметра.
Кроме того, алгоритм дает стандартный способ выразить каждое решение как линейную комбинацию базовых решений, как в Примере 1.3.5, где общее решение принимает вид
Следовательно, вводя новый параметр, мы можем умножить исходное базовое решение на 5 и таким образом исключить дроби.
По этой причине:
Любое ненулевое скалярное кратное базового решения будет по-прежнему называться базовым решением.
Точно так же алгоритм Гаусса выдает базовые решения для в каждой однородной системе, по одному для каждого параметра (есть нет базовых решений, если система имеет только тривиальное решение).Более того, каждое решение задается алгоритмом как линейная комбинация
этих базовых решений (как в Примере 1.3.5). Если имеет ранг, теорема 1.2.2 показывает, что есть ровно параметры, а значит, и базовые решения. Это доказывает:
Найдите основные решения однородной системы с матрицей коэффициентов и выразите каждое решение как линейную комбинацию основных решений, где
Решение:
Приведение расширенной матрицы к сокращенной строчно-эшелонированной форме —
, поэтому общее решение — это,,,, и где, и — параметры.В матричной форме это
Отсюда базовые решения —
Линейные системы с двумя переменными
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 7-1: Линейные системы с двумя переменными
Линейная система двух уравнений с двумя переменными — это любая система, которую можно записать в форме.
\ [\ begin {align *} ax + by & = p \\ cx + dy & = q \ end {align *} \]
, где любая из констант может быть равна нулю, за исключением того, что каждое уравнение должно содержать хотя бы одну переменную.
Также система называется линейной, если переменные указаны только в первой степени, присутствуют только в числителе и нет произведений переменных ни в одном из уравнений.
Вот пример системы с числами.
\ [\ begin {align *} 3x — y & = 7 \\ 2x + 3y & = 1 \ end {align *} \]
Прежде чем мы обсудим, как решать системы, мы должны сначала поговорить о том, что такое решение системы уравнений.Решение системы уравнений — это значение \ (x \) и значение \ (y \), которые при подстановке в уравнения удовлетворяют обоим уравнениям одновременно.
В приведенном выше примере \ (x = 2 \) и \ (y = — 1 \) является решением системы. Проверить это достаточно легко.
\ [\ begin {align *} 3 \ left (2 \ right) — \ left ({- 1} \ right) & = 7 \\ 2 \ left (2 \ right) + 3 \ left ({- 1} \ вправо) & = 1 \ end {выровнять *} \]
Итак, конечно, эта пара чисел является решением системы.Не беспокойтесь о том, как мы получили эти ценности. Это будет самая первая система, которую мы решим, когда перейдем к примерам.
Обратите внимание, что важно, чтобы пара чисел удовлетворяла обоим уравнениям. Например, \ (x = 1 \) и \ (y = — 4 \) удовлетворяют первому уравнению, но не второму, и поэтому не являются решением системы. Аналогично, \ (x = — 1 \) и \ (y = 1 \) будут удовлетворять второму уравнению, но не первому, и поэтому не могут быть решением системы.
Итак, что же представляет собой решение системы двух уравнений? Хорошо, если вы думаете об этом, оба уравнения в системе являются линиями.Итак, давайте построим их график и посмотрим, что мы получим.
Как видите, решение системы — это координаты точки пересечения двух линий. Итак, при решении линейных систем с двумя переменными мы действительно спрашиваем, где пересекаются две линии.
В этом разделе мы рассмотрим два метода решения систем.
Первый метод называется методом подстановки . В этом методе мы решим одно из уравнений для одной из переменных и подставим его в другое уравнение.Это даст одно уравнение с одной переменной, которую мы можем решить. Как только это решено, мы подставляем это значение обратно в одно из уравнений, чтобы найти значение оставшейся переменной.
На словах этот метод не всегда очень понятен. Давайте рассмотрим пару примеров, чтобы увидеть, как работает этот метод.
Пример 1 Решите каждую из следующих систем.
\ (\ begin {align *} 3x — y & = 7 \\ 2x + 3y & = 1 \ end {align *} \)
\ (\ begin {align *} 5x + 4y & = 1 \\ 3x — 6y & = 2 \ end {align *} \)
Показать все решения Скрыть все решения a \ (\ begin {align *} 3x — y & = 7 \\ 2x + 3y & = 1 \ end {align *} \) Показать решение
Итак, это была первая система, которую мы рассмотрели выше.Мы уже знаем решение, но это даст нам возможность проверить значения, которые мы записали для решения.
Теперь метод говорит, что нам нужно решить одно из уравнений для одной из переменных. Какое уравнение мы выберем и какую переменную выбрать, зависит от вас, но обычно лучше выбрать уравнение и переменную, с которыми будет легко иметь дело. Это означает, что мы должны стараться избегать дробей, если это вообще возможно.
В этом случае, похоже, будет действительно легко решить первое уравнение для \ (y \), так что давайте сделаем это.
\ [3x — 7 = y \]
Теперь подставьте это во второе уравнение.
\ [2x + 3 \ влево ({3x — 7} \ вправо) = 1 \]
Это уравнение в \ (x \), которое мы можем решить, так что давайте сделаем это.
\ [\ begin {align *} 2x + 9x — 21 & = 1 \\ 11x & = 22 \\ x & = 2 \ end {align *} \]
Итак, есть часть решения \ (x \).
Наконец, НЕ забудьте вернуться назад и найти часть решения \ (y \).Это одна из наиболее распространенных ошибок, которые студенты делают при решении систем. Для этого мы можем либо вставить значение \ (x \) в одно из исходных уравнений и решить для \ (y \), либо мы можем просто вставить его в нашу замену, которую мы нашли на первом шаге. Так будет проще, так что давайте.
\ [y = 3x — 7 = 3 \ left (2 \ right) — 7 = — 1 \]
Итак, решение — \ (x = 2 \) и \ (y = — 1 \), как мы отметили выше.

b \ (\ begin {align *} 5x + 4y & = 1 \\ 3x — 6y & = 2 \ end {align *} \) Показать решение
С этой системой мы не сможем полностью избежать дробей.Однако похоже, что если мы решим второе уравнение для \ (x \), мы сможем их минимизировать. Вот эта работа.
\ [\ begin {align *} 3x & = 6y + 2 \\ x & = 2y + \ frac {2} {3} \ end {align *} \]
Теперь подставьте это в первое уравнение и решите полученное уравнение относительно \ (y \).
\ [\ begin {align *} 5 \ left ({2y + \ frac {2} {3}} \ right) + 4y & = 1 \\ 10y + \ frac {{10}} {3} + 4y & = 1 \\ 14y & = 1 — \ frac {{10}} {3} = — \ frac {7} {3} \\ y & = — \ left ({\ frac {7} {3}} \ right) \ left ({\ frac {1} {{14}}} \ right) \\ y & = — \ frac {1} {6} \ end {align *} \]
Наконец, подставьте это в исходную замену, чтобы найти \ (x \).
\ [x = 2 \ left ({- \ frac {1} {6}} \ right) + \ frac {2} {3} = — \ frac {1} {3} + \ frac {2} {3} = \ frac {1} {3} \]
Итак, решение этой системы — \ (x = \ frac {1} {3} \) и \ (y = — \ frac {1} {6} \).
Как и в случае с отдельными уравнениями, мы всегда можем вернуться и проверить это решение, подключив его к обоим уравнениям и убедившись, что оно удовлетворяет обоим уравнениям. Также обратите внимание, что нам действительно нужно включить оба уравнения.Вполне возможно, что ошибка может привести к тому, что пара чисел будет удовлетворять одному из уравнений, но не другому.
Теперь перейдем к следующему методу решения систем уравнений. Как мы видели в последней части предыдущего примера, метод подстановки часто заставляет нас иметь дело с дробями, что увеличивает вероятность ошибок. У второго метода этой проблемы не будет. Что ж, это не совсем так. Если будут отображаться дроби, они будут отображаться только на последнем этапе, и они будут отображаться только в том случае, если решение содержит дроби.
Этот второй метод называется методом исключения . В этом методе мы умножаем одно или оба уравнения на соответствующие числа (, т.е. умножаем каждый член в уравнении на число), чтобы одна из переменных имела одинаковый коэффициент с противоположными знаками. Следующим шагом будет сложение двух уравнений. Поскольку одна из переменных имела одинаковый коэффициент с противоположными знаками, она будет удалена, когда мы сложим два уравнения.Результатом будет одно уравнение, которое мы можем решить для одной из переменных. Как только это будет сделано, замените этот ответ на одно из исходных уравнений.
Как и в случае с первым методом, гораздо легче увидеть, что здесь происходит, с помощью пары примеров.
Пример 2 Постановка задачи.
\ (\ begin {align *} 5x + 4y & = 1 \\ 3x — 6y & = 2 \ end {align *} \)
\ (\ begin {align *} 2x + 4y & = — 10 \\ 6x + 3y & = 6 \ end {align *} \)
Показать все решения Скрыть все решения a \ (\ begin {align *} 5x + 4y & = 1 \\ 3x — 6y & = 2 \ end {align *} \) Показать решение
Это система из предыдущего набора примеров, которая заставила нас работать с дробями.Работа с ним здесь покажет различия между двумя методами, а также покажет, что любой метод может использоваться для получения решения для системы.
Итак, нам нужно умножить одно или оба уравнения на константы, чтобы одна из переменных имела одинаковый коэффициент с противоположными знаками. Итак, поскольку члены \ (y \) уже имеют противоположные знаки, давайте работать с этими терминами. Похоже, что если мы умножим первое уравнение на 3, а второе уравнение на 2, члены \ (y \) будут иметь коэффициенты 12 и -12, что нам и нужно для этого метода.
Вот работа для этого шага.
\ [\ begin {align *} 5x + 4y & = 1 & \ underrightarrow {\ times \, \, 3} \ hspace {0.5in} & 15x + 12y = 3 \\ 3x-6y & = 2 & \ underrightarrow {\ times \, \, 2} \ hspace {0,5 дюйма} & \ underline {\, \, 6x-12y = 4} \\ & & & 21x \ hspace {0,5 дюйма} = 7 \\ \ конец {выравнивание *} \]
Итак, как и было обещано в описании метода, у нас есть уравнение, которое можно решить относительно \ (x \).Это дает \ (x = \ frac {1} {3} \), что мы и нашли в предыдущем примере. Обратите внимание, однако, что единственная дробь, с которой нам пришлось иметь дело до этого момента, — это сам ответ, который отличается от метода подстановки.
Теперь снова не забудьте найти \ (y \). В этом случае работы будет немного больше, чем метод подстановки. Чтобы найти \ (y \), нам нужно подставить значение \ (x \) в любое из исходных уравнений и решить относительно \ (y \).Поскольку \ (x \) является дробью, заметим, что в этом случае, если мы подставим это значение во второе уравнение, мы потеряем дроби, по крайней мере, временно. Обратите внимание, что часто этого не происходит, и нам придется иметь дело с дробями, хотим мы этого или нет.
\ [\ begin {align *} 3 \ left ({\ frac {1} {3}} \ right) — 6y & = 2 \\ 1 — 6y & = 2 \\ — 6y & = 1 \\ y & = — \ frac {1} {6} \ end {align *} \]
Опять же, это то же самое значение, которое мы нашли в предыдущем примере.

b \ (\ begin {align *} 2x + 4y & = — 10 \\ 6x + 3y & = 6 \ end {align *} \) Показать решение
В этой части все переменные положительны, поэтому нам придется принудительно установить противоположный знак, умножив где-нибудь на отрицательное число. Также заметим, что в этом случае, если мы просто умножим первое уравнение на -3, тогда коэффициенты \ (x \) будут -6 и 6.
Иногда нам нужно только умножить одно из уравнений, а другое можно оставить в покое.Вот эта работа по этой части.
\ [\ begin {align *} 2x + 4y & = -10 & \ underrightarrow {\ times \, \, — 3} \ hspace {0,5 дюйма} & -6x-12y = 30 \\ 6x + 3y & = 6 & \ underrightarrow {\ text {same}} \ hspace {0,5 дюйма} & \ underline {\ hspace {0,35 дюйма} 6x + 3y = 6} \\ & & & \ hspace {0,5 дюйма} -9y = 36 \\ & & & \ hspace {0,85 дюйма} y = -4 \\ \ конец {выравнивание *} \]
Наконец, подставьте это в любое из уравнений и решите относительно \ (x \).На этот раз мы воспользуемся первым уравнением.
\ [\ begin {align *} 2x + 4 \ left ({- 4} \ right) & = — 10 \\ 2x — 16 & = — 10 \\ 2x & = 6 \\ x & = 3 \ end {align *} \]
Итак, решение этой системы — \ (x = 3 \) и \ (y = — 4 \).
Существует третий метод, который мы рассмотрим для решения систем из двух уравнений, но он немного сложнее и, вероятно, более полезен для систем как минимум с тремя уравнениями, поэтому мы рассмотрим его в следующем разделе.
Перед тем, как покинуть этот раздел, мы должны рассмотреть несколько частных случаев решения систем.
Пример 3 Решите следующие системы уравнений. \ [\ begin {align *} x — y & = 6 \\ — 2x + 2y & = 1 \ end {align *} \] Показать решение
Здесь мы можем использовать любой метод, но похоже, что замена будет немного проще. Мы решим первое уравнение относительно \ (x \) и подставим его во второе уравнение.
\ [\ begin {align *} x & = 6 + y \\ & \\ — 2 \ left ({6 + y} \ right) + 2y & = 1 \\ — 12 — 2y + 2y & = 1 \\ — 12 & = 1 \, \, \, ?? \ end {align *} \]
Итак, это явно неправда, и, похоже, нигде в нашей работе нет ошибки. Так в чем проблема? Чтобы увидеть, давайте изобразим эти две линии и посмотрим, что мы получим.
Похоже, что эти две прямые параллельны (можете ли вы проверить это с помощью наклона?), И мы знаем, что две параллельные линии с разными пересечениями \ (y \) (что важно) никогда не пересекутся.
Как мы видели в начале обсуждения этого раздела, решения представляют собой точку пересечения двух линий. Если две линии не пересекаются, у нас не будет решения.
Итак, когда мы получаем такой бессмысленный ответ в результате нашей работы, у нас есть две параллельные линии, и не существует решения этой системы уравнений.
Система в предыдущем примере называется несовместимая .Также обратите внимание, что если бы мы использовали исключение в этой системе, мы бы получили аналогичный бессмысленный ответ.
Пример 4 Решите следующую систему уравнений. \ [\ begin {align *} 2x + 5y & = — 1 \\ — 10x — 25y & = 5 \ end {align *} \] Показать решение
В этом примере кажется, что устранение было бы самым простым методом.
\ [\ begin {align *} 2x + 5y & = -1 & \ underrightarrow {\ times \, \, 5} \ hspace {0.5in} & \, \, \, \, 10x + 25y = -5 \\ -10x-25y & = 5 & \ underrightarrow {\ text {same}} \ hspace {0,5 дюйма} & \ underline {-10x-25y = 5} \\ & & & \ hspace {0.9in} 0 = 0 \\ \ конец {выравнивание *} \]
На первый взгляд может показаться, что это та же проблема, что и в предыдущем примере. Однако в этом случае мы пришли к равенству, которое просто не соответствовало действительности. В этом случае мы имеем 0 = 0, и это истинное равенство, и в этом смысле в этом нет ничего плохого.
Однако это явно не тот ответ, который мы ожидали здесь, и поэтому нам нужно определить, что именно происходит.
Мы предоставим вам проверить это, но если вы найдете наклон и \ (y \) — точки пересечения для этих двух линий, вы обнаружите, что обе линии имеют точно такой же наклон, и обе линии имеют одинаковые \ ( y \) — перехват. Итак, что это значит для нас? Хорошо, если две линии имеют одинаковый наклон и одинаковые \ (y \) — точки пересечения, тогда графики этих двух линий являются одним и тем же графиком.Другими словами, графики этих двух линий — это один и тот же график. В этих случаях любой набор точек, удовлетворяющий одному из уравнений, также будет удовлетворять другому уравнению.
Также напомним, что график уравнения — это не что иное, как набор всех точек, удовлетворяющих уравнению. Другими словами, существует бесконечный набор точек, которые удовлетворяют этой системе уравнений.
В этих случаях мы действительно хотим записать что-нибудь для решения.Итак, что мы сделаем, так это решим одно из уравнений для одной из переменных (неважно, что вы выберете). Решим первый относительно \ (y \).
\ [\ begin {align *} 2x + 5y & = — 1 \\ 5y & = — 2x — 1 \\ y & = — \ frac {2} {5} x — \ frac {1} {5} \ end {выровнять*}\]
Затем для любого \ (x \) мы можем найти \ (y \), и эти два числа образуют решение системы уравнений. Обычно мы обозначаем это, записывая решение следующим образом:
\ [\ begin {array} {* {20} {c}} \ begin {align} x & = t \\ y & = — \ frac {2} {5} t — \ frac {1} {5} \ конец {выровнен} & {\ hspace {0.25in} {\ mbox {где}} \, t {\ mbox {- любое действительное число}}} \ end {array} \]
Чтобы показать, что они дают решения, давайте рассмотрим несколько значений \ (t \).
\ (t = 0 \)
\ [x = 0 \ hspace {0,25 дюйма} y = — \ frac {1} {5} \]
Чтобы показать, что это решение, нам нужно вставить его в оба уравнения системы.
\ [\ begin {align *} 2 \ left (0 \ right) + 5 \ left ({- \ frac {1} {5}} \ right) & \ mathop = \ limits ^? — 1 & \ hspace {0.? 5 \\ — 1 & = — 1 & \ hspace {0,25 дюйма} 5 & = 5 \ end {align *} \]
Итак, \ (x = 0 \) и \ (y = — \ frac {1} {5} \) является решением системы. Давай быстро сделаем еще один.
\ (t = — 3 \)
\ [x = — 3 \ hspace {0,25 дюйма} y = — \ frac {2} {5} \ left ({- 3} \ right) — \ frac {1} {5} = \ frac {6} {5 } — \ frac {1} {5} = 1 \]
И снова нам нужно вставить его в оба уравнения системы, чтобы показать, что это решение.? 5 \\ — 1 & = — 1 & \ hspace {0,25 дюйма} 5 & = 5 \ end {align *} \]
Конечно, \ (x = — 3 \) и \ (y = 1 \) — это решение.
Итак, поскольку существует бесконечное количество возможных \ (t \) ‘, должно быть бесконечное количество решений для этой системы, и они даются как,
\ [\ begin {array} {* {20} {c}} \ begin {align} x & = t \\ y & = — \ frac {2} {5} t — \ frac {1} {5} \ конец {выровнен} & {\ hspace {0.25in} {\ mbox {где}} \, t {\ mbox {- любое действительное число}}} \ end {array} \]
Системы, подобные тем, что в предыдущих примерах, называются зависимыми .
Теперь мы увидели все три возможности решения системы уравнений. Система уравнений не будет иметь решения, ровно одно решение или бесконечно много решений.
Систем уравнений с тремя переменными
Решение систем уравнений с тремя переменными
Система уравнений с тремя переменными включает два или более уравнений, каждое из которых содержит от одной до трех переменных.
Цели обучения
Решите систему уравнений с тремя переменными графически с помощью подстановки или исключения
Основные выводы
Ключевые моменты
В системе из уравнений с тремя переменными вы можете иметь одно или несколько уравнений, каждое из которых может содержать одну или несколько из трех переменных, обычно x , y и из . Введение переменной z означает, что функции на графике теперь представляют плоскости, а не линии.
Метод подстановки включает решение для одной из переменных в одном из уравнений и включение ее в остальные уравнения для сокращения системы. Повторяйте, пока не останется одно уравнение, а затем, используя это уравнение, вернитесь назад, чтобы решить предыдущие уравнения.
Графический метод включает построение системы в виде графика и нахождение единственной точки пересечения плоскостей.
Метод исключения включает добавление или вычитание кратных значений одного уравнения из других уравнений, удаление переменных из каждого уравнения до тех пор, пока в каждом уравнении не останется одна переменная.
Ключевые термины
Система уравнений с тремя переменными : Набор из одного или нескольких уравнений, каждое из которых может содержать одну или несколько из трех переменных, обычно x, y и z.
Система уравнений : Набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
Системы уравнений с тремя переменными
В математике одновременные уравнения — это система уравнений, содержащая несколько переменных.Этот набор часто называют системой уравнений . Решение системы уравнений — это конкретная спецификация значений всех переменных, которая одновременно удовлетворяет всем уравнениям. Графически решение находится там, где функции пересекаются.
В системе уравнений с тремя переменными вы можете иметь одно или несколько уравнений, каждое из которых может содержать одну или несколько из трех переменных, обычно x , y и z .Введение переменной z означает, что функции на графике теперь представляют плоскости, а не линии.
Простой пример
Это набор линейных уравнений, также известный как линейная система уравнений, с тремя переменными:
[латекс] \ left \ {\ begin {matrix} 3x + 2y-z = 6 \\ -2x + 2y + z = 3 \\ x + y + z = 4 \\ \ end {matrix} \ right. [ / латекс]
Решение этой системы уравнений:
[латекс] \ left \ {\ begin {matrix} x = 1 \\ y = 2 \\ z = 1 \\ \ end {matrix} \ right.[/ латекс]
Подставьте эти значения в каждое из уравнений, чтобы убедиться, что решение удовлетворяет всем трем уравнениям.
Решение систем уравнений с тремя переменными
Графический метод
Графический метод решения системы уравнений с тремя переменными включает построение плоскостей, которые образуются при построении графика каждого уравнения в системе, а затем нахождение точки пересечения всех трех плоскостей. Единственная точка пересечения всех трех плоскостей — это единственное решение системы.
Система линейных уравнений: На этом изображении показана система трех уравнений с тремя переменными. Точка пересечения (белая точка) — единственное решение этой системы.
Метод замещения
Метод подстановки для решения системы уравнений с тремя переменными включает определение уравнения, которое может быть легко записано с одной переменной в качестве предмета (путем решения уравнения для этой переменной). Затем замените это выражение, где эта переменная появляется в двух других уравнениях, тем самым получив меньшую систему с меньшим количеством переменных.После того, как эта меньшая система решена, будь то дальнейшее применение метода подстановки или другими методами, подставьте найденные решения для переменных обратно в первое выражение в правой части.
Например, рассмотрим эту систему уравнений:
[латекс] \ left \ {\ begin {matrix} 3x + 2y-z = 6 \\ -2x + 2y + z = 3 \\ x + y + z = 4 \\ \ end {matrix} \ right. [ / латекс]
Поскольку коэффициент z уже равен 1 в первом уравнении, решите относительно z , чтобы получить:
[латекс] z = 3x + 2y-6 [/ латекс]
Подставьте это выражение для z в два других уравнения:
[латекс] \ left \ {\ begin {matrix} -2x + 2y + (3x + 2y-6) = 3 \\ x + y + (3x + 2y-6) = 4 \\ \ end {matrix} \ right.[/ латекс]
Эта новая система упрощается до:
[латекс] \ left \ {\ begin {matrix} x + 4y = 9 \\ 4x + 3y = 10 \\ \ end {matrix} \ right. [/ Latex]
Теперь, решая относительно x в первом уравнении, получаем:
[латекс] x = 9-4y [/ латекс].
Подставьте это выражение для x в последнее уравнение системы и решите относительно y :
[латекс] \ displaystyle \ begin {align} 4 (9-4y) + 3y & = 10 \\ 36-16y + 3y & = 10 \\ 13y & = 26 \\ y & = 2 \ end {align} [/ latex]
Теперь, когда у вас есть значение y , восстановите уравнение.Подставьте [латекс] y = 2 [/ latex] в уравнение [latex] x = 9-4y [/ latex], чтобы получить [latex] x = 1 [/ latex].
Работая снова, подставьте [latex] (1,2) [/ latex] в первое подставленное уравнение и решите относительно z :
[латекс] \ begin {align} z & = 3x + 2y-6 \\ z & = (3 \ cdot 1) + (2 \ cdot 2) -6 \\ z & = 1 \ end {align} [/ latex]
Следовательно, решение системы уравнений — [латекс] (1,2,1) [/ латекс].
Метод исключения
Устранение путем разумного умножения — еще один широко используемый метод решения одновременных линейных уравнений.Он использует общие принципы, согласно которым каждая сторона уравнения по-прежнему равна другой, когда обе стороны умножаются (или делятся) на одну и ту же величину, или когда одна и та же величина добавляется (или вычитается) с обеих сторон.
По мере того, как уравнения становятся проще за счет исключения некоторых переменных, переменная в конечном итоге появляется в полностью решаемой форме, и это значение затем может быть «подставлено обратно» в ранее выведенные уравнения, подставив это значение в качестве переменной. Обычно каждая «обратная подстановка» может позволить решить другую переменную в системе.
Рассмотрим следующую систему:
[латекс] \ left \ {\ begin {matrix} x + y + z = 2 \\ x-y + 3z = 4 \\ 2x + 2y + z = 3 \\ \ end {matrix} \ right. [/ латекс]
Используя метод исключения, начните с вычитания первого уравнения из второго и упрощения:
[латекс] \ displaystyle \ begin {align} x-y + 3z- (x + y + z) & = 4-2 \\ — 2y + 2z & = 2 \ end {align} [/ latex]
Теперь у нас есть следующая система уравнений:
[латекс] \ left \ {\ begin {matrix} x + y + z = 2 \\ -2y + 2z = 2 \\ 2x + 2y + z = 3 \\ \ end {matrix} \ right.[/ латекс]
Теперь вычтите дважды первое уравнение из третьего, чтобы получить
.
[латекс] \ begin {align} 2x + 2y + z-2 (x + y + z) & = 3-2 (2) \\ 2x + 2y + z-2x-2y-2z & = — 1 \\ z & = 1 \ end {align} [/ latex]
При этом отображается новая система:
[латекс] \ left \ {\ begin {matrix} x + y + z = 2 \\ -2y + 2z = 2 \\ z = 1 \\ \ end {matrix} \ right. [/ Latex]
Затем вычтите дважды третье уравнение из второго уравнения и упростите:
[латекс] \ begin {align} -2y + 2z-2z & = 2-2 \\ y & = 0 \ end {align} [/ latex]
При этом отображается новая система:
[латекс] \ left \ {\ begin {matrix} x + y + z = 2 \\ y = 0 \\ z = 1 \\ \ end {matrix} \ right.[/ латекс]
Наконец, вычтите третье и второе уравнение из первого, чтобы получить
[латекс] \ begin {align} x + y + z-y-z & = 2-0-1 \\ x & = 1 \ end {align} [/ latex]
Таким образом, окончательная решенная система:
[латекс] \ left \ {\ begin {matrix} x = 1 \\ y = 0 \\ z = 1 \\ \ end {matrix} \ right. [/ Latex]
Несогласованные и зависимые системы с тремя переменными
Системы уравнений с тремя переменными могут быть независимыми, зависимыми или несовместимыми; каждый случай можно установить алгебраически и представить графически.
Цели обучения
Объясните графически, что это значит, что системы уравнений с тремя переменными непоследовательны или зависимы, а также как распознать алгебраически, когда это имеет место
Основные выводы
Ключевые моменты
Зависимые системы имеют бесконечное количество решений. Графически бесконечное количество решений находится на линии или плоскости, которая служит пересечением трех плоскостей в пространстве.
Решение зависимой системы путем исключения приводит к выражению, которое всегда истинно, например [latex] 0 = 0 [/ latex].
Несогласованные системы не имеют решения. Графически система без решения представлена тремя плоскостями, не имеющими общей точки.
Решение противоречивой системы путем исключения приводит к утверждению, которое является противоречием, например [латекс] 3 = 0 [/ латекс].
Ключевые термины
Независимая система : Система уравнений с одним решением. Для систем уравнений с тремя переменными это решение представляет собой упорядоченную тройку [латекс] (x, y, z) [/ latex], которая представляет собой единственную точку пересечения трех плоскостей.
Зависимая система : Система уравнений с бесконечным числом решений. Для систем уравнений с тремя переменными существует бесконечное количество решений на прямой или плоскости, которая является пересечением трех плоскостей в пространстве.
Несогласованная система : Система уравнений без решения. Система уравнений с тремя переменными без решений представлена тремя плоскостями, не имеющими общей точки.
Определение зависимых и несовместимых систем
Напомним, что решение линейной системы — это присвоение чисел переменным таким образом, чтобы все уравнения выполнялись одновременно.Решение системы уравнений с тремя переменными представляет собой упорядоченную тройку [латекс] (x, y, z) [/ latex] и описывает точку пересечения трех плоскостей в пространстве.
Существуют три возможных сценария решения системы трех уравнений с тремя переменными:
Независимые системы имеют единое решение. Решение системы путем исключения приводит к единственной упорядоченной тройке [латекс] (x, y, z) [/ latex]. Графически упорядоченная тройка определяет точку, являющуюся пересечением трех плоскостей в пространстве.
Зависимые системы имеют бесконечное количество решений. Графически решения попадают на линию или плоскость, которая является пересечением трех плоскостей в пространстве.
Несогласованные системы не имеют решения. Графически система без решения представлена тремя плоскостями, не имеющими общей точки.
Зависимые системы уравнений с тремя переменными
Из работы с системами уравнений с двумя переменными мы знаем, что зависимая система уравнений имеет бесконечное число решений.То же верно и для зависимых систем уравнений с тремя переменными. Бесконечное количество решений может возникнуть из нескольких ситуаций. Три плоскости могут быть одинаковыми, так что решение одного уравнения будет решением двух других уравнений. Все три уравнения могут быть разными, но они пересекаются на линии, имеющей бесконечное количество решений (см. Ниже графическое представление). Или два уравнения могут быть одинаковыми и пересекать третье по линии (см. Пример задачи для графического представления).
Зависимые системы: Пример трех различных уравнений, пересекающихся на линии.
Например, рассмотрим эту систему уравнений:
[латекс] \ left \ {\ begin {matrix} \ begin {align} 2x + y — 3z & = 0 \\ 4x + 2y — 6z & = 0 \\ x — y + z & = 0 \ end {выровняйте } \ end {matrix} \ right. [/ latex]
Сначала умножьте первое уравнение на [латекс] -2 [/ латекс] и добавьте его ко второму уравнению:
[латекс] \ begin {align} -2 (2x + y — 3z) + (4x + 2y — 6z) & = 0 + 0 \\ (-4x + 4x) + (-2y + 2y) + (6z — 6z) & = 0 \\ 0 & = 0 \ end {align} [/ latex]
Нам больше не нужно идти.В результате мы получаем тождество [latex] 0 = 0 [/ latex], которое говорит нам, что эта система имеет бесконечное количество решений. Есть и другие способы начать решать эту систему, например, умножив третье уравнение на [латекс] -2 [/ латекс] и добавив его к первому уравнению. Затем мы выполняем те же шаги, что и выше, и получаем тот же результат, [latex] 0 = 0 [/ latex].
Если бы мы изобразили график каждого из трех уравнений, у нас были бы три плоскости, изображенные ниже. Обратите внимание, что две плоскости одинаковы, и они пересекают третью плоскость по прямой.Множество решений бесконечно, так как все точки на линии пересечения будут удовлетворять всем трем уравнениям.
Зависимая система : два уравнения представляют одну и ту же плоскость, и они пересекают третью плоскость на прямой.
Несогласованные системы уравнений с тремя переменными
Как и в случае с системами уравнений с двумя переменными, мы можем встретить несовместимую систему уравнений с тремя переменными, что означает, что у нее нет решения, которое удовлетворяет всем трем уравнениям.Уравнения могут представлять три параллельные плоскости, две параллельные плоскости и одну пересекающуюся плоскость или три плоскости, которые пересекают две другие, но не в одном месте. Процесс исключения приведет к ложному утверждению, например [латекс] 3 = 7 [/ латекс], или другому противоречию.
Несогласованные системы : Все три цифры представляют системы три на три без решения. (а) Три плоскости пересекаются друг с другом по трем различным параллельным линиям, которые не пересекаются в общей точке.(b) Две плоскости параллельны и пересекаются с третьей плоскостью, но не друг с другом. (c) Все три плоскости параллельны, поэтому точки пересечения нет.
Например, рассмотрим систему уравнений
[латекс] \ left \ {\ begin {matrix} \ begin {align} x — 3y + z & = 4 \\ -x + 2y — 5z & = 3 \\ 5x — 13y + 13z & = 8 \ end { align} \ end {matrix} \ right. [/ latex]
Используя метод исключения для решения системы уравнений с тремя переменными, обратите внимание, что мы можем добавить первое и второе уравнения, чтобы сократить [latex] x [/ latex]:
[латекс] \ begin {align} (x — 3y + z) + (-x + 2y — 5z) & = 4 + 3 \\ (x — x) + (-3y + 2y) + (z-5z) & = 7 \\ -y — 4z & = 7 \ end {align} [/ latex]
Затем умножьте первое уравнение на [латекс] -5 [/ латекс] и добавьте его к третьему уравнению:
[латекс] \ begin {align} -5 (x — 3y + z) + (5x — 13y + 13z) & = -5 (4) + 8 \\ (-5x + 5x) + (15y — 13y) + (-5z + 13z) & = -20 + 8 \\ 2y + 8z & = -12 \ end {align} [/ latex]
Теперь обратите внимание, что у нас есть система уравнений с двумя переменными:
[латекс] \ left \ {\ begin {matrix} \ begin {align} -y — 4z & = 7 \\ 2y + 8z & = -12 \ end {align} \ end {matrix} \ right.[/ латекс]
Мы можем решить эту проблему, умножив верхнее уравнение на 2 и прибавив его к нижнему уравнению:
[латекс] \ begin {align} 2 (-y-4z) + (2y + 8z) & = 2 (7) -12 \\ (-2y + 2y) + (-8z + 8z) & = 14 — 12 \\ 0 & = 2 \ end {align} [/ latex]
Окончательное уравнение [латекс] 0 = 2 [/ латекс] является противоречием, поэтому мы заключаем, что система уравнений несовместима и, следовательно, не имеет решения.
Систем уравнений с двумя переменными
Введение в системы уравнений
Система уравнений состоит из двух или более уравнений с двумя или более переменными, где любое решение должно одновременно удовлетворять всем уравнениям в системе.
Цели обучения
Объясните, какие системы уравнений могут представлять
Основные выводы
Ключевые моменты
Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно.
Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно.
Чтобы линейная система имела единственное решение, должно быть по крайней мере столько же уравнений, сколько переменных.
Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара [латекс] (x, y) [/ latex], которая удовлетворяет каждому уравнению независимо. Графически решения — это точки пересечения линий.
Ключевые термины
система линейных уравнений : Набор из двух или более уравнений, состоящих из двух или более переменных, которые рассматриваются одновременно.
зависимая система : система линейных уравнений, в которой два уравнения представляют
одну и ту же линию; существует бесконечное количество решений зависимой системы.
несовместимая система : Система линейных уравнений без общего решения, потому что они
представляют собой параллельные линии, которые не имеют общих точек или прямых.
независимая система : Система линейных уравнений с ровно одной парой решений [latex] (x, y) [/ latex].
Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям системы одновременно. Некоторые линейные системы могут не иметь решения, в то время как другие могут иметь бесконечное количество решений. Чтобы линейная система имела единственное решение, должно быть по крайней мере столько же уравнений, сколько переменных.Даже в этом случае это не гарантирует уникального решения.
В этом разделе мы сосредоточимся в первую очередь на системах линейных уравнений, которые состоят из двух уравнений, содержащих две разные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными:
[латекс] 2x + y = 15 \ 3x — y = 5 [/ латекс]
Решение системы линейных уравнений с двумя переменными — это любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо. В этом примере упорядоченная пара (4, 7) является решением системы линейных уравнений.Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.
[латекс] 2 (4) + 7 = 15 \\ 3 (4) — 7 = 5 [/ латекс]
Оба эти утверждения верны, поэтому [latex] (4, 7) [/ latex] действительно является решением системы уравнений.
Обратите внимание, что система линейных уравнений может содержать более двух уравнений и более двух переменных. Например,
[латекс] 3x + 2y — z = 12 \\ x — 2y + 4z = -2 \\ -x + 12y -z = 0 [/ латекс]
— это система трех уравнений с тремя переменными [латекс] x, y, z [/ latex].Решение системы выше дается
[латекс] x = 1 \ y = -2 \ z = — 2 [/ латекс]
, поскольку он делает все три уравнения действительными.
Типы линейных систем и их решения
В общем, линейная система может вести себя одним из трех возможных способов:
Система имеет единственное уникальное решение.
В системе нет решения .
В системе бесконечно много решений .
Каждая из этих возможностей представляет собой определенный тип системы линейных уравнений с двумя переменными. Каждый из них может отображаться графически, как показано ниже. Обратите внимание, что решение системы линейных уравнений — это любая точка, в которой линии пересекаются.
Системы линейных уравнений: Графические представления трех типов систем.
Независимая система имеет ровно одну пару решений [latex] (x, y) [/ latex]. Точка пересечения двух линий — единственное решение.
Непоследовательная система не имеет решения. Обратите внимание, что две линии параллельны и никогда не пересекутся.
У зависимой системы бесконечно много решений. Линии точно такие же, поэтому каждая пара координат на линии является решением обоих уравнений.
Графическое решение систем
Простой способ решить систему уравнений — это найти точку или точки пересечения уравнений. Это графический метод.
Цели обучения
Графическое решение системы уравнений с двумя переменными
Основные выводы
Ключевые моменты
Чтобы решить систему уравнений графически, нарисуйте уравнения и укажите точки пересечения как решения.У системы уравнений может быть несколько решений.
Система линейных уравнений будет иметь одну точку пересечения или одно решение.
Чтобы построить график системы уравнений, записанных в стандартной форме, вы должны переписать уравнения в форме пересечения угла наклона.
Ключевые термины
система уравнений : набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
Графический метод : способ визуального поиска набора значений, который решает систему уравнений.
Система уравнений (также известная как одновременные уравнения) — это система уравнений с несколькими переменными, решаемая, когда значения всех переменных одновременно удовлетворяют всем уравнениям. Наиболее распространенные способы решения системы уравнений:
Графический метод
Метод замещения
Метод исключения
Здесь мы обратимся к графическому методу.
Графическое решение систем
Некоторые системы имеют только один набор правильных ответов, в то время как другие имеют несколько наборов, которые удовлетворяют всем уравнениям.Графически показано, что набор уравнений, решенных только с одним набором ответов, будет иметь только одну точку пересечения, как показано ниже. Эта точка считается решением системы уравнений. В наборе линейных уравнений (например, на изображении ниже) есть только одно решение.
Система линейных уравнений с двумя переменными : На этом графике показана система уравнений с двумя переменными и только один набор ответов, который удовлетворяет обоим уравнениям.
Система с двумя наборами ответов, которые удовлетворяют обоим уравнениям, имеет две точки пересечения (таким образом, два решения системы), как показано на изображении ниже.
Система уравнений с несколькими ответами: Это пример системы уравнений, показанной графически, которая имеет два набора ответов, которые удовлетворяют обоим уравнениям в системе.
Преобразование в форму пересечения уклона
Прежде чем успешно решить систему графически, необходимо понять, как графически отображать уравнения, записанные в стандартной форме, или [latex] Ax + By = C [/ latex]. Вы всегда можете использовать графический калькулятор для графического представления уравнений, но полезно знать, как самостоятельно формулировать такие уравнения.
Для этого необходимо преобразовать уравнения в форму пересечения наклона или [латекс] y = mx + b [/ latex], где м = наклон и b = пересечение по оси y.
Лучший способ преобразовать уравнение в форму с пересечением наклона — сначала выделить переменную y , а затем разделить правую часть на B , как показано ниже.
[латекс] \ begin {align} \ displaystyle Ax + By & = C \\ By & = — Ax + C \\ y & = \ frac {-Ax + C} {B} \\ y & = — \ frac {A} { B} x + \ frac {C} {B} \ end {align} [/ latex]
Теперь [latex] \ displaystyle — \ frac {A} {B} [/ latex] — это наклон м, и [latex] \ displaystyle \ frac {C} {B} [/ latex] — это точка пересечения по оси Y б .
Определение решений на графике
После того, как вы преобразовали уравнения в форму с пересечением наклона, вы можете нанести их на график. Чтобы определить решения системы уравнений, определите точки пересечения между графическими уравнениями. Упорядоченная пара, которая представляет собой пересечение (я), представляет собой решение (я) системы уравнений.
Метод замещения
Метод подстановки — это способ решения системы уравнений путем выражения уравнений только с помощью одной переменной.
Цели обучения
Решите системы уравнений с двумя переменными с помощью подстановки
Основные выводы
Ключевые моменты
Система уравнений — это система уравнений, которая может быть решена с использованием определенного набора значений.
Метод подстановки работает, выражая одну из переменных через другую, затем подставляя ее обратно в исходное уравнение и упрощая его.
Очень важно проверить свою работу после того, как вы нашли набор значений для переменных.Сделайте это, подставив найденные вами значения обратно в исходные уравнения.
Решение системы уравнений можно записать в виде упорядоченной пары ( x , y ).
Ключевые термины
метод подстановки : Метод решения системы уравнений путем выражения уравнения только одной переменной
Система уравнений : Набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
Метод замены для решения систем уравнений — это способ упростить систему уравнений, выразив одну переменную через другую, тем самым удалив одну переменную из уравнения. Когда полученное упрощенное уравнение имеет только одну переменную, с которой можно работать, уравнение становится разрешимым.
Метод замещения состоит из следующих шагов:
В первом уравнении решите одну из переменных через другие.
Подставьте это выражение в остальные уравнения.
Продолжайте, пока не сведете систему к одному линейному уравнению.
Решите это уравнение, а затем выполняйте обратную замену, пока решение не будет найдено.
Решение методом подстановки
Попрактикуемся в этом, решив следующую систему уравнений:
[латекс] x-y = -1 [/ латекс]
[латекс] x + 2y = -4 [/ латекс]
Начнем с решения первого уравнения, чтобы можно было выразить x через y .
[латекс] \ begin {align} \ displaystyle x-y & = — 1 \\ x & = y-1 \ end {align} [/ latex]
Затем мы заменим наше новое определение x во второе уравнение:
[латекс] \ displaystyle \ begin {align} x + 2y & = — 4 \\ (y-1) + 2y & = — 4 \ end {align} [/ latex]
Обратите внимание, что теперь это уравнение имеет только одну переменную (y). Затем мы можем упростить это уравнение и решить относительно y :
[латекс] \ displaystyle \ begin {align} (y-1) + 2y & = — 4 \\ 3y-1 & = — 4 \\ 3y & = — 3 \\ y & = — 1 \ end {align} [/ latex]
Теперь, когда мы знаем значение y , мы можем использовать его, чтобы найти значение другой переменной, x. Для этого подставьте значение y в первое уравнение и решите относительно x .
[латекс] \ displaystyle \ begin {align} x-y & = — 1 \\ x — (- 1) & = — 1 \\ x + 1 & = — 1 \\ x & = — 1-1 \\ x & = — 2 \ end {align} [/ latex]
Таким образом, решение системы: [latex] (- 2, -1) [/ latex], то есть точка, где две функции графически пересекаются. Проверьте решение, подставив значения в одно из уравнений.
[латекс] \ displaystyle \ begin {align} x-y & = — 1 \\ (- 2) — (- 1) & = — 1 \\ — 2 + 1 & = — 1 \\ — 1 & = — 1 \ end {align} [/ латекс]
Метод исключения
Метод исключения используется для исключения переменной, чтобы упростить поиск оставшейся переменной (переменных) в системе уравнений.
Цели обучения
Решите системы уравнений с двумя переменными методом исключения
Основные выводы
Ключевые моменты
Шаги метода исключения: (1) составить уравнения так, чтобы переменные выстроились в одну линию, (2) изменить одно уравнение, чтобы оба уравнения использовали согласованную переменную, которую можно исключить, (3) сложить уравнения, чтобы исключить переменную, (4) решить и (5) выполнить обратную замену для поиска другой переменной.
Всегда проверяйте ответ.Это делается путем включения обоих значений в одно или оба исходных уравнения.
Ключевые термины
метод исключения : Процесс решения системы уравнений путем исключения одной переменной для более простого решения оставшейся переменной.
Система уравнений : Набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
Метод исключения для решения систем уравнений, также известный как исключение добавлением , представляет собой способ исключения одной из переменных в системе, чтобы более просто оценить оставшуюся переменную.После успешного нахождения значений остальных переменных они подставляются в исходное уравнение, чтобы найти правильное значение для другой переменной.
Метод исключения состоит из следующих шагов:
Перепишите уравнения так, чтобы переменные выровнялись.
Измените одно уравнение так, чтобы оба уравнения имели переменную, которая компенсируется при сложении уравнений.
Добавьте уравнения и удалите переменную.
Найдите оставшуюся переменную.
Выполните обратную замену и решите для другой переменной.
Решение методом исключения
Метод исключения можно продемонстрировать на простом примере:
[латекс] \ displaystyle 4x + y = 8 \\ 2y + x = 9 [/ латекс]
Сначала выровняйте переменные, чтобы уравнения можно было легко сложить на более позднем этапе:
[латекс] \ displaystyle \ begin {align} 4x + y & = 8 \\ x + 2y & = 9 \ end {align} [/ latex]
Затем посмотрите, не настроены ли уже какие-либо переменные таким образом, что их сложение приведет к их исключению из системы.Если нет, умножьте одно уравнение на число, позволяющее компенсировать переменные. В этом примере переменную y можно исключить, если мы умножим верхнее уравнение на [латекс] -2 [/ латекс], а затем сложим уравнения.
Шаг умножения:
[латекс] \ displaystyle \ begin {align} -2 (4x + y & = 8) \\ x + 2y & = 9 \ end {align} [/ latex]
Результат:
[латекс] \ displaystyle \ begin {align} -8x-2y & = — 16 \\ x + 2y & = 9 \ end {align} [/ latex]
Теперь добавьте уравнения, чтобы исключить переменную y .
[латекс] \ displaystyle \ begin {align} -8x + x-2y + 2y & = — 16 + 9 \\ — 7x & = — 7 \ end {align} [/ latex]
Наконец, найдите переменную x .
[латекс] \ displaystyle \ begin {align} -7x & = — 7 \\ x & = \ frac {-7} {- 7} \\ x & = 1 \ end {align} [/ latex]
Затем вернитесь к одному из исходных уравнений и замените найденное нами значение на x . Проще всего выбрать простейшее уравнение, но подойдет любое уравнение.
[латекс] \ displaystyle \ begin {align} 4x + y & = 8 \\ 4 (1) + y & = 8 \\ 4 + y & = 8 \\ y & = 4 \ end {align} [/ latex]
Следовательно, решение уравнения (1,4).Всегда важно проверить ответ, подставив оба этих значения вместо соответствующих переменных в одно из уравнений.
[латекс] \ displaystyle \ begin {align} 4x + y & = 8 \\ 4 (1) + 4 & = 8 \\ 4 + 4 & = 8 \\ 8 & = 8 \ end {align} [/ latex]
Несогласованные и зависимые системы с двумя переменными
Для линейных уравнений с двумя переменными несовместные системы не имеют решений, а зависимые системы имеют бесконечно много решений.
Цели обучения
Объясните, когда системы уравнений с двумя переменными несовместимы или зависимы как графически, так и алгебраически.
Основные выводы
Ключевые моменты
Графически уравнения в зависимой системе представляют собой одну и ту же линию. Уравнения в противоречивой системе представляют собой параллельные линии, которые никогда не пересекаются.
Мы можем использовать методы решения систем уравнений для определения зависимых и несовместимых систем: Зависимые системы имеют бесконечное количество решений. Применение методов решения систем уравнений приведет к истинному тождеству, например [латекс] 0 = 0 [/ латекс].Несогласованные системы не имеют решений. Применение методов решения систем уравнений приведет к противоречию, например к утверждению [латекс] 0 = 1 [/ латекс].
Ключевые термины
несовместимая система : Система линейных уравнений без общего решения, потому что они
представляют собой параллельные линии, которые не имеют общих точек или прямых.
независимая система : Система линейных уравнений с ровно одной парой решений.
зависимая система : система линейных уравнений, в которой два уравнения представляют
одну и ту же линию; существует бесконечное количество решений зависимой системы.
Напомним, что линейная система может вести себя одним из трех возможных способов:
Система имеет единственное уникальное решение.
В системе нет решения.
В системе бесконечно много решений.
Также напомним, что каждая из этих возможностей соответствует типу системы линейных уравнений с двумя переменными. Независимая система уравнений имеет ровно одно решение [latex] (x, y) [/ latex]. Несогласованная система не имеет решения, а зависимая система имеет бесконечное количество решений.
В предыдущих модулях обсуждалось, как найти решение для независимой системы уравнений. Теперь мы сосредоточимся на выявлении зависимых и несовместимых систем линейных уравнений.
Зависимые системы
Уравнения линейной системы независимы, если ни одно из уравнений не может быть получено алгебраически из других. Когда уравнения независимы, каждое уравнение содержит новую информацию о переменных, и удаление любого из уравнений увеличивает размер набора решений.Системы, которые не являются независимыми, по определению являются зависимыми . Уравнения в зависимой системе могут выводиться друг из друга; они описывают одну и ту же линию. Они не добавляют новую информацию о переменных, и потеря уравнения из зависимой системы не изменяет размер набора решений.
Мы можем применять методы замены или исключения для решения систем уравнений, чтобы идентифицировать зависимые системы. Зависимые системы имеют бесконечное количество решений, потому что все точки на одной линии также находятся на другой линии.После использования замены или добавления результирующее уравнение будет идентичным, например [латекс] 0 = 0 [/ латекс].
Например, рассмотрим два уравнения
[латекс] 3x + 2y = 6 \ 6x + 4y = 12 [/ латекс]
Мы можем применить метод исключения для их оценки. Если бы мы умножили первое уравнение на коэффициент [латекс] -2 [/ латекс], мы получили бы:
[латекс] \ displaystyle \ begin {align} -2 (3x + 2y & = 6) \\ — 6x-4y & = — 12 \ end {align} [/ latex]
Добавление этого ко второму уравнению даст [латекс] 0 = 0 [/ латекс].Таким образом, две линии зависимы. Также обратите внимание, что это одно и то же уравнение, увеличенное в два раза; другими словами, второе уравнение может быть получено из первого.
На графике два уравнения дают идентичные линии, как показано ниже.
Зависимая система : Уравнения [латекс] 3x + 2y = 6 [/ latex] и [latex] 6x + 4y = 12 [/ latex] являются зависимыми, и при отображении на графике они образуют одну и ту же линию.
Обратите внимание, что существует бесконечное количество решений для зависимой системы, и эти решения относятся к общей линии.
Несогласованные системы
Линейная система непротиворечива, если у нее есть решение, и непоследовательна в противном случае. Напомним, что графическое представление несовместимой системы состоит из параллельных линий, которые имеют одинаковый наклон, но разные точки пересечения [latex] y [/ latex]. Они никогда не пересекутся.
Мы также можем применять методы решения систем уравнений для выявления несовместимых систем. Когда система несовместима, можно вывести противоречие из уравнений, например, утверждение [латекс] 0 = 1 [/ латекс].
Рассмотрим следующие два уравнения:
[латекс] 3x + 2y = 6 \ 3x + 2y = 12 [/ латекс]
Мы можем применить метод исключения, чтобы попытаться решить эту систему. Вычитая первое уравнение из второго, обе переменные удаляются, и мы получаем [латекс] 0 = 6 [/ латекс]. Это противоречие, и мы можем определить, что это несовместимая система. Графики этих уравнений на плоскости [latex] xy [/ latex] представляют собой пару параллельных линий.
Несогласованная система: Уравнения [латекс] 3x + 2y = 6 [/ латекс] и [латекс] 3x + 2y = 12 [/ латекс] несовместимы.
В общем случае несоответствия возникают, если левые части уравнений в системе линейно зависимы, а постоянные члены не удовлетворяют соотношению зависимости. Система уравнений, левые части которой линейно независимы, всегда непротиворечива.
Приложения систем уравнений
Системы уравнений могут использоваться для решения многих реальных задач, в которых для одних и тех же переменных используются несколько ограничений.
Цели обучения
Применение систем уравнений с двумя переменными к реальным примерам
Основные выводы
Ключевые моменты
Если у вас есть проблема, которая включает несколько переменных, вы можете решить ее, создав систему уравнений.
После определения переменных определите отношения между ними и запишите их в виде уравнений.
Ключевые термины
система уравнений : набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
Системы уравнений в реальном мире
Система уравнений, также известная как одновременные уравнения, представляет собой набор уравнений с несколькими переменными. Ответ на систему уравнений — это набор значений, который удовлетворяет всем уравнениям в системе, и таких ответов может быть много для любой данной системы.Ответы обычно записываются в виде упорядоченной пары: [латекс] \ left (x, y \ right) [/ latex]. Подходы к решению системы уравнений включают замену и исключение, а также графические методы.
Существует несколько практических приложений систем уравнений. Они подробно показаны ниже.
Планирование мероприятия
Система уравнений может использоваться для решения задачи планирования, где необходимо учитывать несколько ограничений:
Эмили устраивает большую вечеринку после школы.Принципал наложил два ограничения. Во-первых, общее количество людей (учителей и студентов, вместе взятых) должно быть [латексным] 56 [/ латексным]. Во-вторых, на каждые семь учеников должен приходиться один учитель. Итак, сколько учеников и сколько учителей приглашено на вечеринку?
Во-первых, нам нужно идентифицировать и назвать наши переменные. В данном случае нашими переменными являются учителя и ученики. Количество учителей будет [латекс] Т [/ латекс], а количество учеников — [латекс] S [/ латекс].
Теперь нам нужно составить наши уравнения.Существует ограничение, ограничивающее общее количество людей [латекс] 56 [/ латекс], поэтому:
[латекс] T + S = 56 [/ латекс]
На каждые семь учеников должен приходиться один учитель, поэтому:
[латекс] \ frac {S} {7} = T [/ латекс]
Теперь у нас есть система уравнений, которую можно решить с помощью подстановки, исключения или графически. Решение системы: [латекс] S = 49 [/ латекс] и [латекс] T = 7 [/ латекс].
Поиск неизвестных величин
Этот следующий пример показывает, как системы уравнений используются для нахождения величин.
Группа студентов и учителей [латекс] 75 [/ латекс] в поле собирает сладкий картофель для нуждающихся. Кейси собирает в три раза больше сладкого картофеля, чем Дэвис, а затем, возвращаясь к машине, берет еще пять! Глядя на ее недавно увеличившуюся кучу, Дэвис замечает: «Ух ты, у тебя [латекса] 29 [/ латекса] картофеля больше, чем у меня!» Сколько сладкого картофеля собрали Кейси и Дэвис каждый?
Чтобы решить, мы сначала определяем наши переменные. Количество сладкого картофеля, которое собирает Кейси, — [латекс] K [/ латекс], а количество сладкого картофеля, которое собирает Дэвис, — [латекс] D [/ латекс].
Теперь мы можем писать уравнения на основе ситуации:
[латекс] К-5 = 3D [/ латекс]
[латекс] D + 29 = K [/ латекс]
Отсюда замена, исключение или построение графика покажут, что [латекс] K = 41 [/ латекс] и [латекс] D = 12 [/ латекс].