Алгоритм решения линейных систем дифференциальных уравнений третьего порядка.

Алгоритм решения линейных систем дифференциальных уравнений третьего порядка.

Для более глубокого понимания происходящего в этой статье можно ознакомиться с краткой теоретической справкой.

Рассмотрим однородную систему дифференциальных уравнений третьего порядка

Здесь x(t), y(t), z(t) — искомые функции на промежутке (a, b), a_ij (i, j =1, 2, 3) — вещественные числа.

Запишем исходную систему в матричном виде
,
где

Решение исходной системы будем искать в виде
,
где , C₁, C₂, C₃ — произвольные постоянные.

Чтобы найти фундаментальную систему решений, нужно решить так называемое характеристическое уравнение

Это уравнение является алгебраическим уравнением третьего порядка, следовательно оно имеет 3 корня. При этом возможны следующие случаи:

1. Корни (собственные значения) действительны и различны.

2. Среди корней (собственных значений) есть комплексно-сопряженные, пусть

— действительный корень
=

3. Корни (собственные значения) действительны. Один из корней кратный.

Чтобы разобраться, как действовать в каждом из этих случаев, нам понадобятся:
Теорема 1.
Пусть — попарно различные собственные значения матрица А, а — соответствующие им собственные векторы. Тогда

образуют фундаментальную систему решений исходной системы.

Замечание.
Пусть

dpva.ru

I. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.

Федеральное агентство по образованию

­­­­­­­­­­­­­­­­­­­­­­

Государственное образовательное учреждение высшего

профессионального образования

«МАТИ» – Российский государственный технологический

университет им. К.Э. Циолковского

Кафедра «Высшая математика»

Решение систем линейных дифференциальных уравнений с постоянными коэффициентами

Устойчивость решений

Методические указания для студентов и преподавателей

Составитель: Заварзина И.Ф.

Кулакова Р.Д.

Москва 2008

Методические указания предназначены для студентов второго курса, изучающих в рамках курса высшей математики тему «Дифференциальные уравнения». В них рассматривается решение систем линейных дифференциальных уравнений с постоянными коэффициентами. Кроме того, рассматривается устойчивость по Ляпунову, исследуются точки покоя. Приводятся примеры решения задач. Для закрепления материала студентам предлагается выполнить самостоятельную работу.

1. Общие понятия.

Во многих задачах математики, физики и техники требуется определить сразу несколько функций, связанных между собой дифференциальными уравнениями. Совокупность таких уравнений называется системой дифференциальных уравнений.

Рассмотрим неоднородную систему линейных дифференциальных уравнений с постоянными коэффициентами, которую называют нормальной системой:

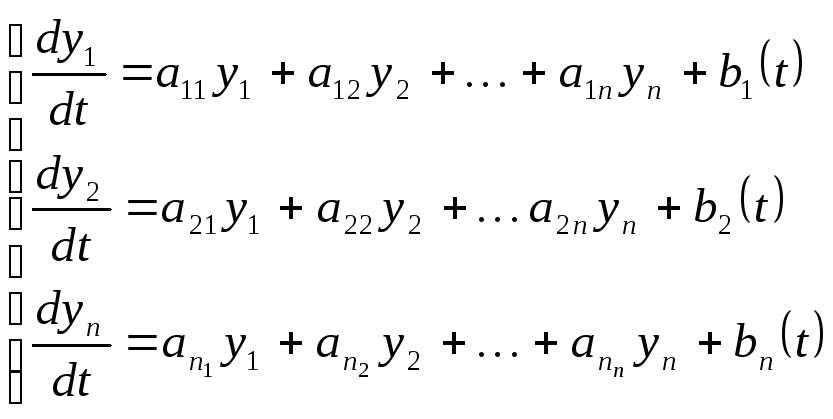(1.1),

где

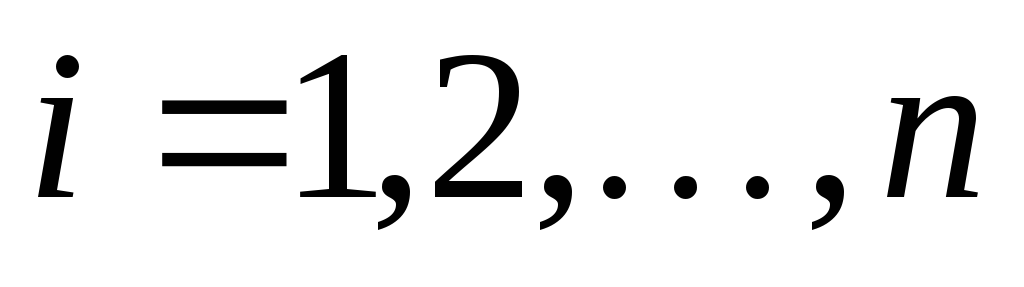, – искомые функции; , 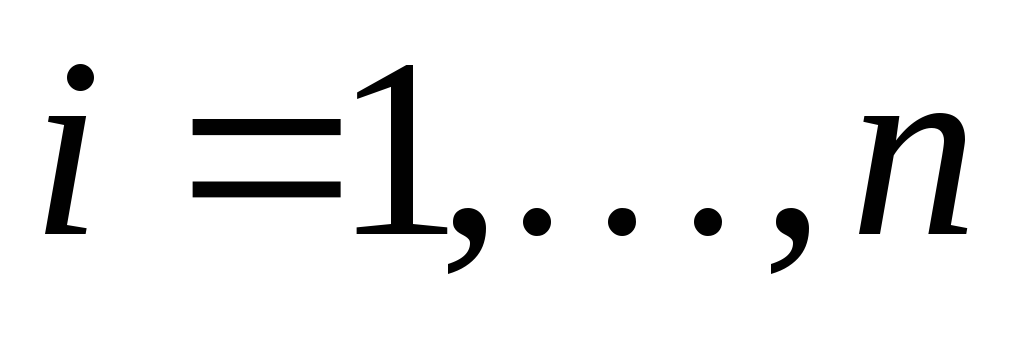; 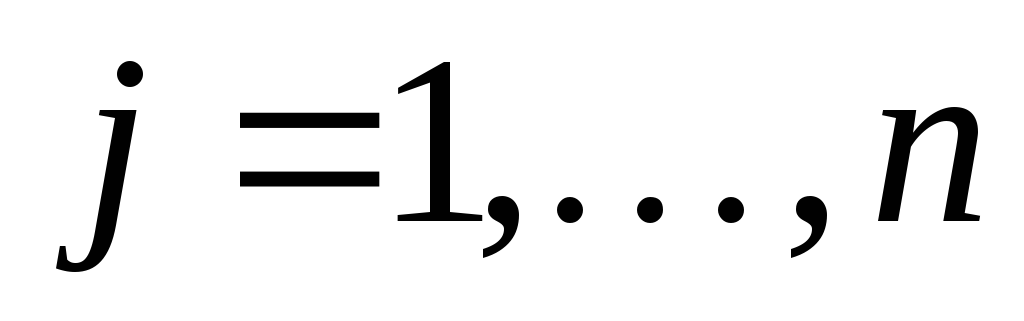– постоянные действительные коэффициенты, 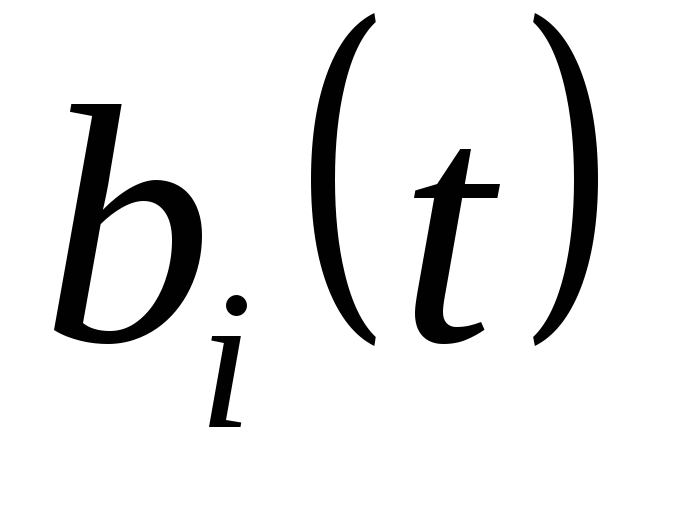, 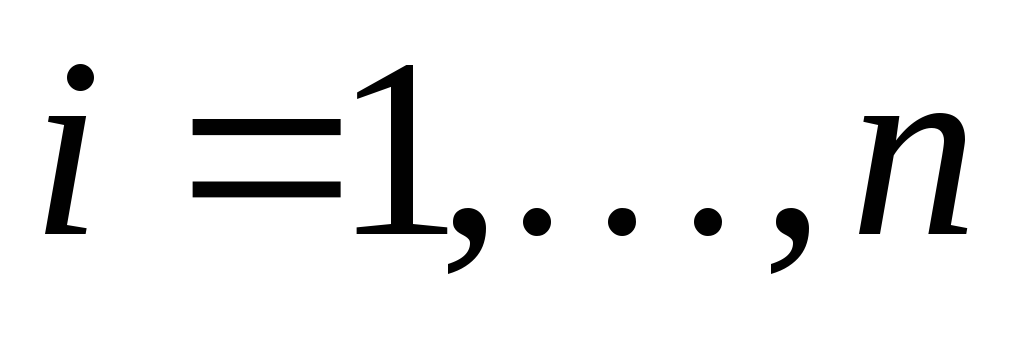– заданные непрерывные функции.

Если 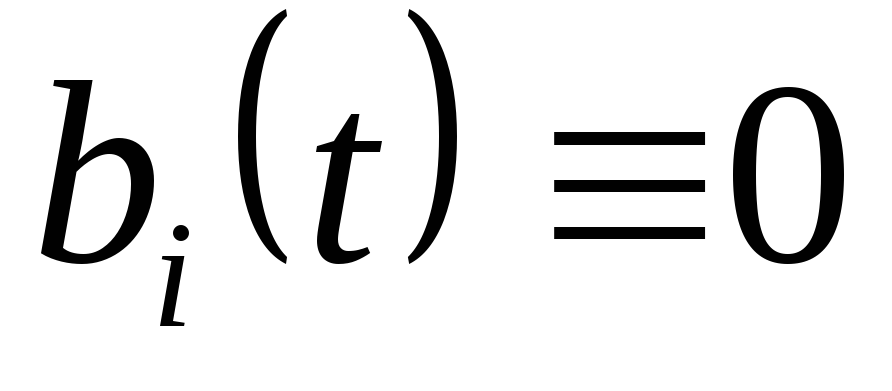, то система называется однородной.

Систему (1.1) можно зависать в векторной форме.

Введем обозначения:

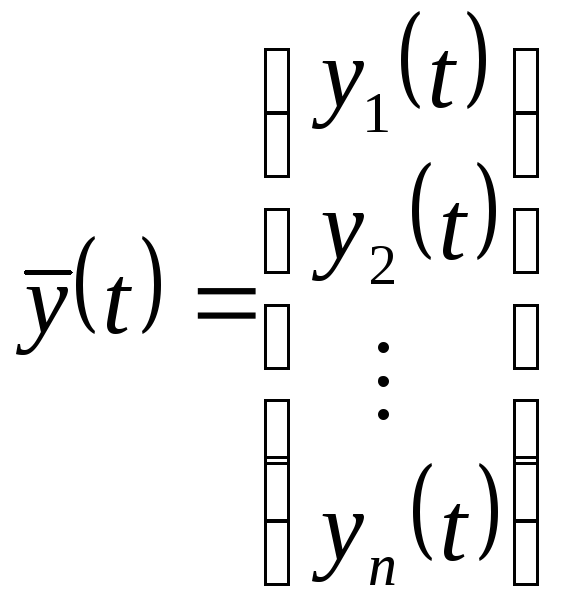
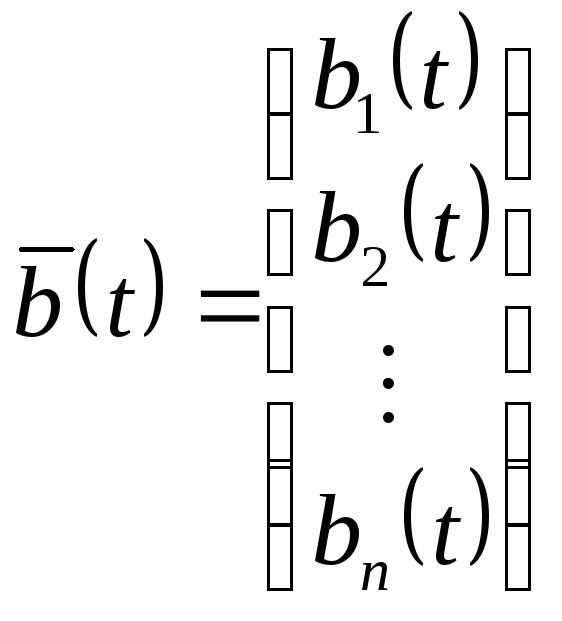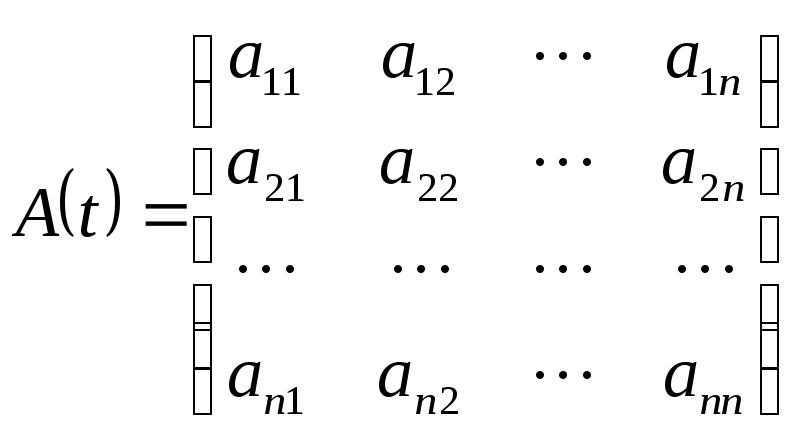; ; (1.2).

Система (1.1) принимает вид:

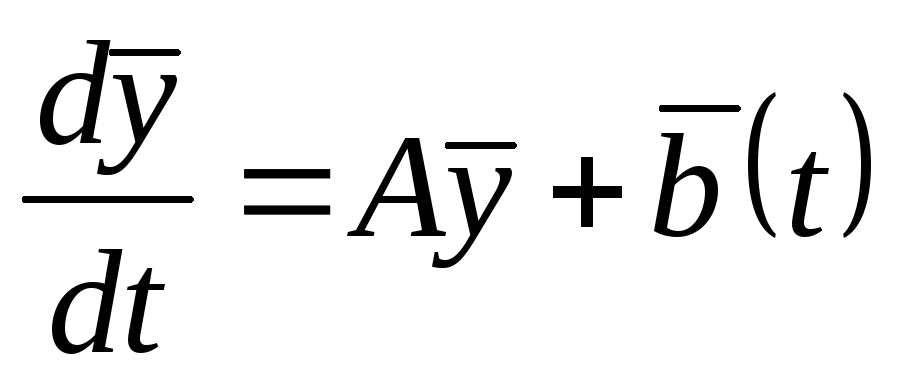(1.3).

Однородная система линейных уравнений в векторной форме имеет вид:

(1.4).

Решение системы линейных дифференциальных уравнений представляется совокупностью функций: (1.5).

Система функций (1.5) называется фундаментальной системой решений. Линейная комбинация фундаментальной системы решений позволяет записать общее решение системы (1.4) в виде:

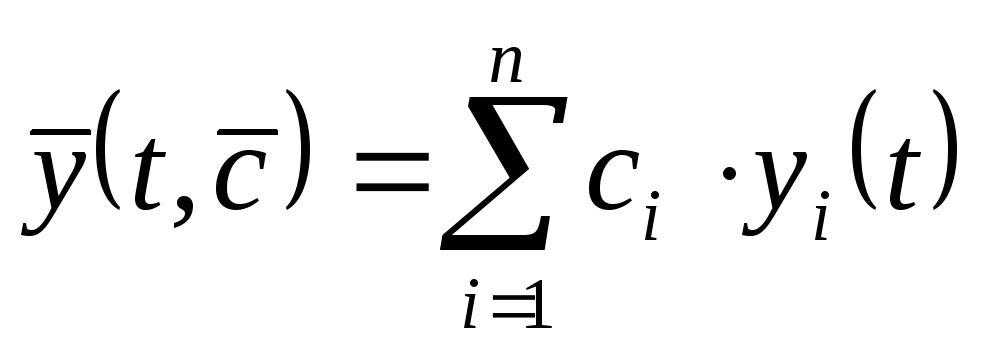(1.6).

Если при решении системы дифференциальных уравнений задаются начальные условия, которые в векторной форме имеют вид: (1.7), тогда определяется единственное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.

В курсе лекций доказывается, что общее решение системы (1.3) представляется в виде суммы общего решения однородной системы дифференциальных уравнений (1.4), записанного в виде (1.6) и какого-нибудь частного решения неоднородной системы.

Рассмотрим получение решения однородной системы (1.4).

Будем искать частное решение системы в следующем виде:

(1.8),

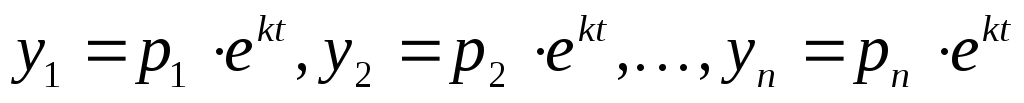
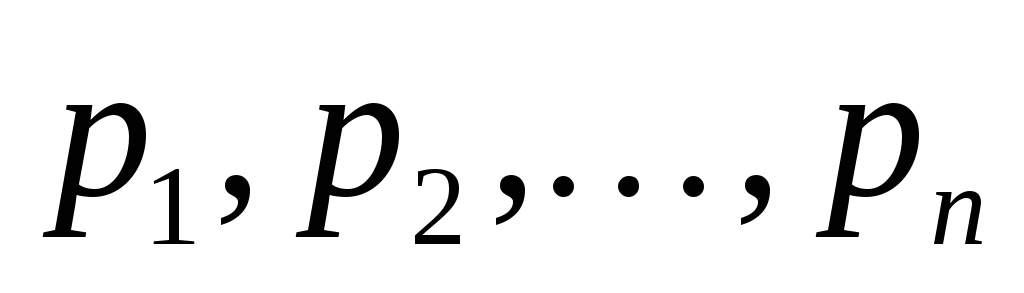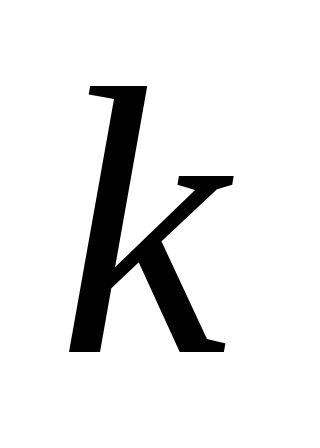, – константы, которые подлежат определению.

Подставим (1.8) в систему (1.4) и получим:

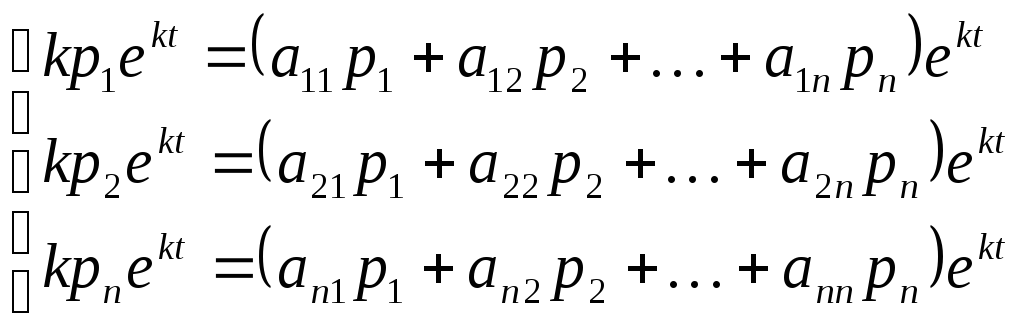(1.9)

Упростим систему (1.9):

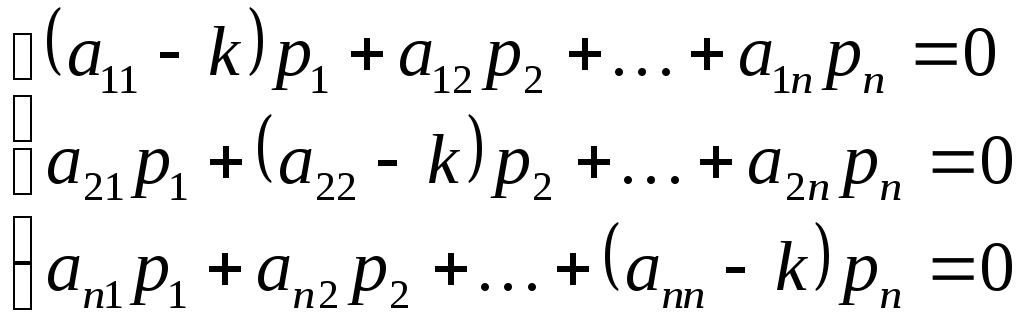(1.10)

Система (1.4) – однородная система дифференциальных уравнений. Эта система имеет тривиальное решение: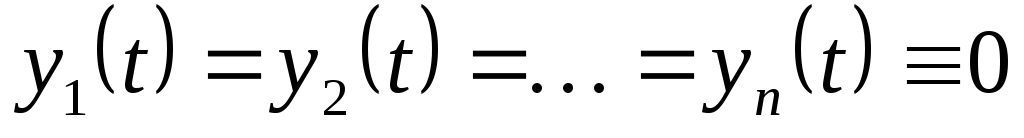, если определитель системы (1.10)

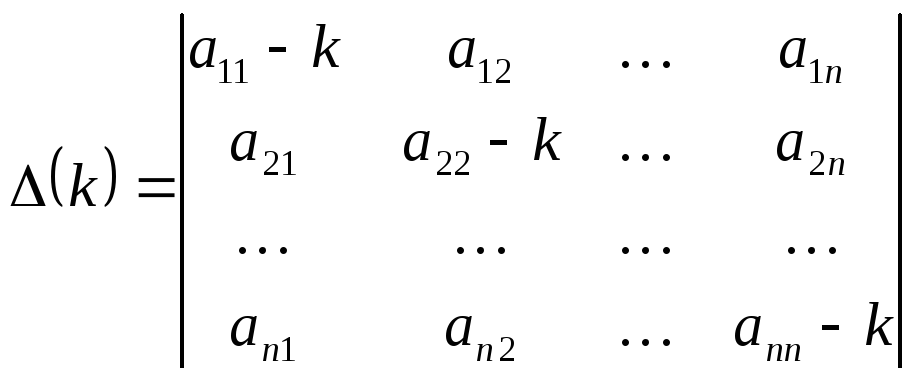(1.11)

отличен от нуля, а нас интересует частное решение системы (1.4), представленное в виде (1.8) и отличное от тривиального.

Нетривиальное решение (1.8) будет получено при условии равенства нулю определителя (1.11).

Приравнивая определитель (1.11) нулю, получим уравнение относительно , которое называется характеристическим уравнением:

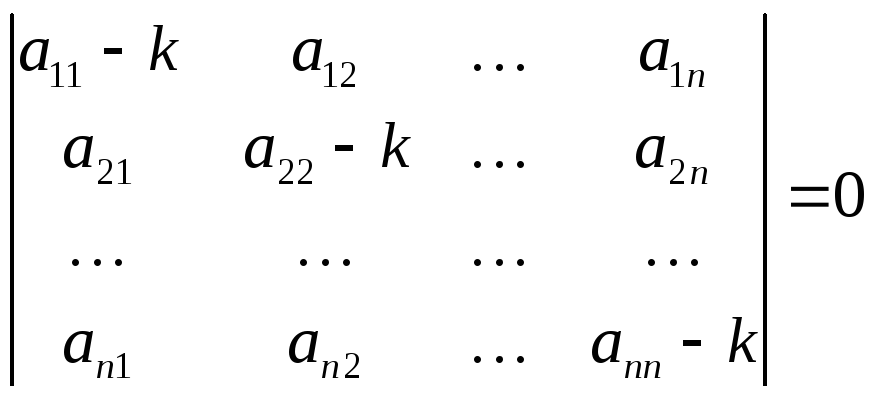(1.12)

корни характеристического уравнения (1.12) определяют вид решения (1.8).

2. Получение фундаментальной системы решений.

Характеристическое уравнение (1.12) системы (1.4) является уравнением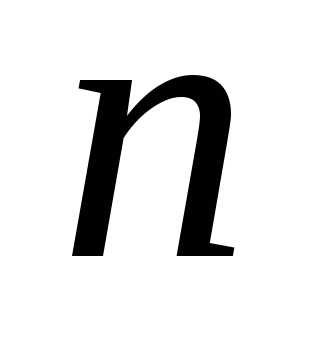

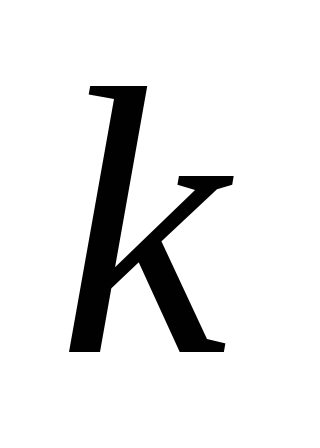-ой степени относительно.

Предположим, что характеристическое уравнение имеет различных корней, которые являются характеристическими числами матрицы. Каждому характеристическому числу соответствует свой собственный вектор. Для каждого характеристического числа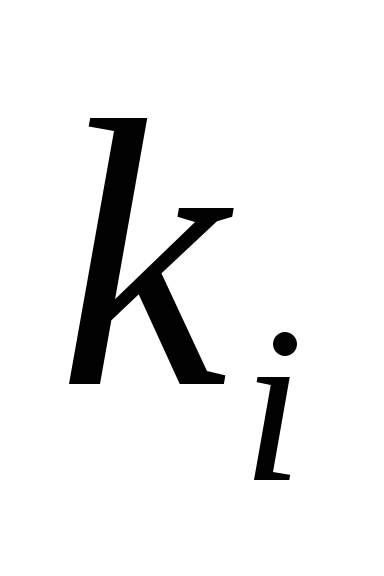напишем систему (1.10) и определим собственный вектор.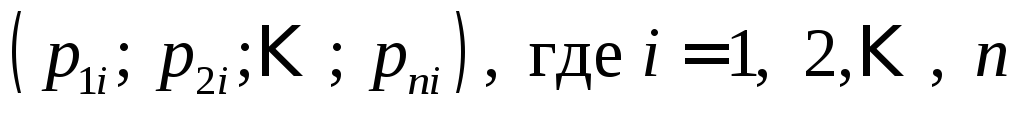

Тогда система дифференциальных уравнений имеет

решений:

1-е решение, соответствующее корню :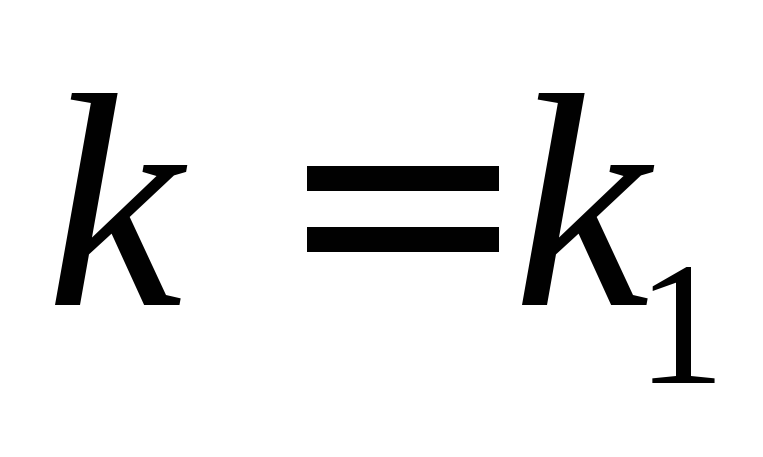

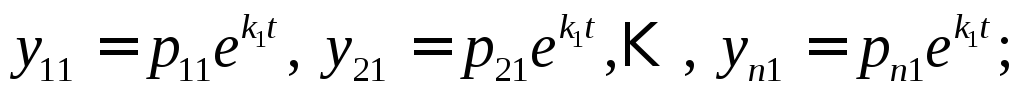
2-е решение, соответствующее корню :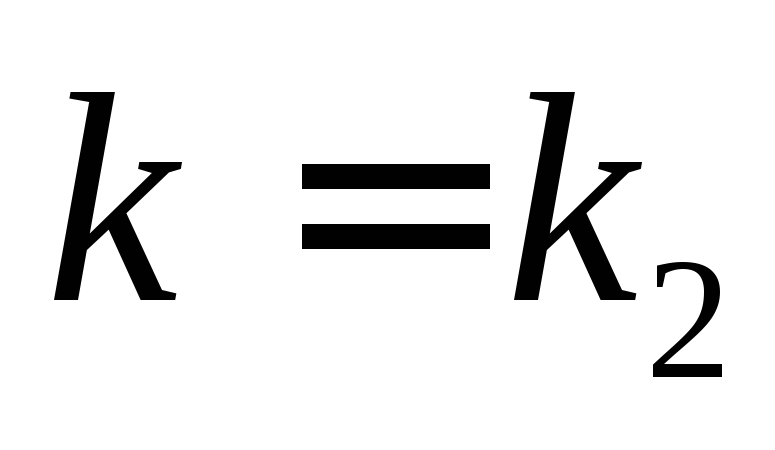

;

…………………………………………………

-е решение, соответствующее корню :

.

Мы получили фундаментальную систему решений. Общее решение системы (1.4) таково:

,

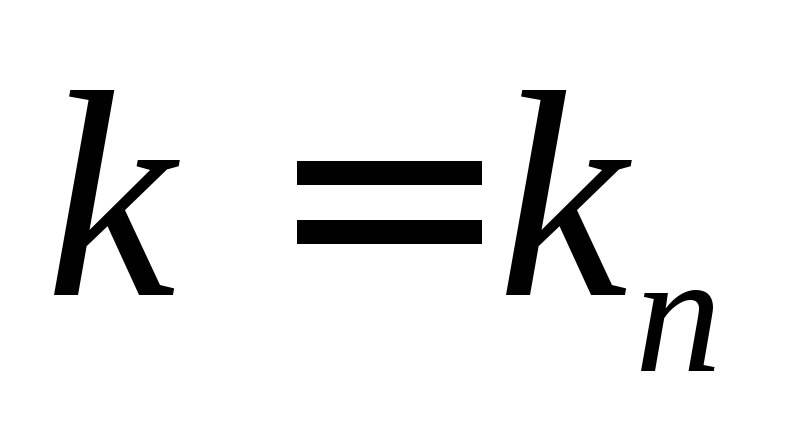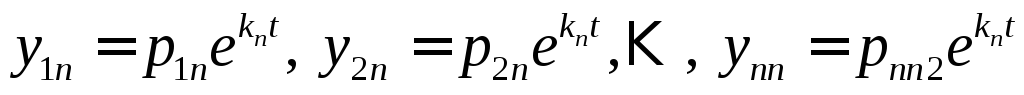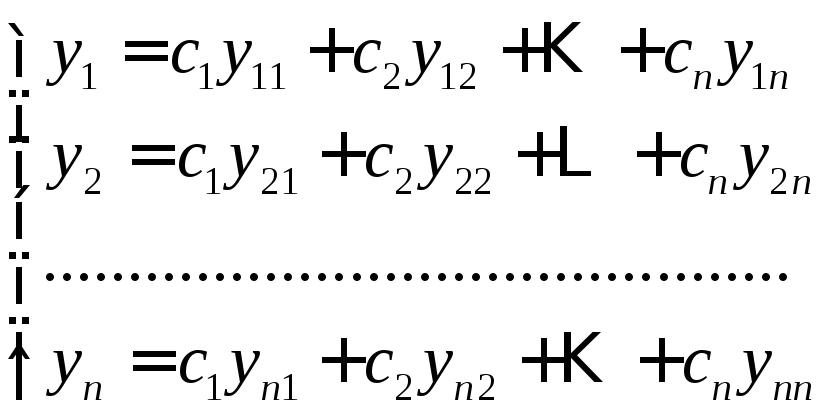где 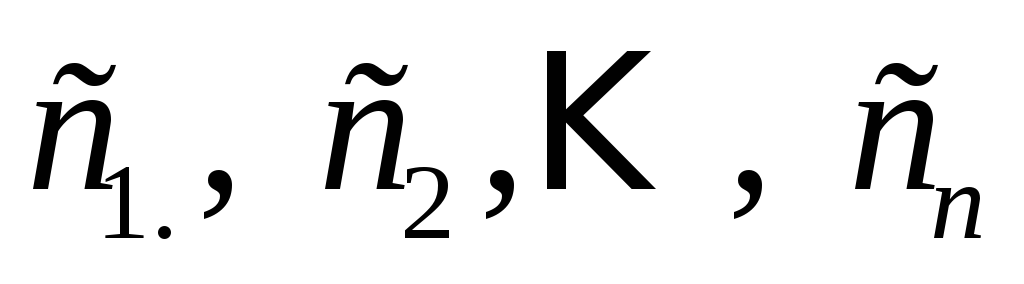– произвольные постоянные.

Случаи комплексных и кратных корней рассмотрим на примерах.

studfile.net

Системы дифференциальных уравнений, все формулы

Типы систем дифференциальных уравнений

Имеется два основных типа систем дифференциальных уравнений: линейные однородные и линейные неоднородные системы дифференциальных уравнений. Для решения таких систем применяется два основных способа: метод исключения (в ходе решения система сводится к одному дифференциальному уравнению) и метод Эйлера (с помощью характеристического уравнения матрицы этой системы).

Рассмотрим далее линейные однородные системы дифференциальных уравнений (СДУ), которые в общем случае имеют вид

   

где – некоторые действительные числа, – неизвестные искомые функции.

Решением системы дифференциальных уравнений называются такие функции и , которые удовлетворяют всем уравнениям рассматриваемой системы.

Задачей Коши для СДУ называется такая задача, при которой необходимо найти частное решение этой системы, удовлетворяющее заданным начальным условиям.

Метод исключения для решения систем дифференциальных уравнений

Указанный метод проиллюстрируем на следующем примере.

Рассмотрим теперь линейные неоднородные системы дифференциальных уравнений. Такая система имеет следующий вид:

   

то есть она отличается от однородной системы, описанной выше, лишь добавками-слагаемыми и .

Найдем решение неоднородной системы линейных дифференциальных уравнений методом исключения.

Метод Эйлера (метод характеристического уравнения)

Работу этого метода рассмотрим на примере.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Глава 90. Системы линейных дифференциальных уравнений с постоянными к

Определение

Совокупность уравнений Вида

(8.7.1)

Где X –независимая переменная, – искомые функции, – их производные, называется Системой дифференциальных уравнений первого порядка.

Система дифференциальных уравнений, разрешенных относительно производных от неизвестных функций, называется Нормальной системой дифференциальных уравнений и имеет следующий общий вид:

.

(8.7.2)

Совокупность n функций

(8.7.3)

Определенных в интервале , называется Решением нормальной системы (8.7.2), если эти функции при подстановке в уравнение системы (8.7.2) обращают их в тождество.

Теорема (Коши)

Пусть для системы дифференциальных уравнений первого порядка (8.7.2) выполняются следующие условия:

— функции определены и непрерывны по всем аргументам в замкнутой области ,

— частные производные непрерывны в области .

Тогда Существует одна и только Одна система решений уравнений (2):

,

(8.7.4)

Определенная в некоторой окрестности точки и Удовлетворяющая в этой точке заданным Начальным условиям:

.

(8.7.5)

Условия (8.7.5) называются Начальными условиями решения, а задача отыскания решения по заданным начальным условиям – Задачей Коши.

Совокупность n функций

(8.7.6)

Зависящих от x и n произвольных постоянных , будем называть Общим решением Системы (8.7.2) в некоторой области , если при любых значениях постоянных эти функции представляют решение системы и если любое решение этой системы может быть записано в виде (8.7.6) при некоторых значениях постоянных .

Совокупность n функций

(8.7.7)

Получающееся из общего решения (6) системы (8.7.2) при определенных значениях постоянных будем называть частным решением системы (8.7.2).

Если в области выполнены условия теоремы Коши, то для нахождения частного решения (8.7.7) достаточно разрешить уравнения

(8.7.8)

Относительно и подставить найденные значения постоянных в соотношения (8.7.6).

Одним из основных методов нахождения решения нормальных систем является метод исключения постоянных. С помощью этого метода данная система сводится к одному уравнению n–го порядка относительно одной неизвестной функции.

Пример

Найти общее решение системы уравнений

И выделить из него частное решение, удовлетворяющее начальным условиям при .

Решение

Продифференцировав первое из уравнений системы по x, получаем . Подставляя в это равенство выражение из второго уравнения системы и заменяя функцию z ее выражением из первого, приходим к линейному однородному уравнению второго порядка относительно одной неизвестной функции: . Решив это уравнение, находим его общее решение . Дифференцируя последнее равенство, имеем . Подставляя выражения для y и в первое уравнение системы и приводя подобные члены, получим .

Окончательно, общее решение системы имеет вид

, .

Решим теперь задачу Коши. Подставив в систему (*) вместо y, z и x их начальные значения 0, 1 и 0, получаем систему уравнений для определения постоянных и : , .

Отсюда . Следовательно, искомым частным решением являются функции , .

Если правые части нормальной системы (8.7.2) являются линейными функциями относительно неизвестных функций , то такая система называется Линейной и имеет вид

(8.7.9)

Если функции тождественно равны нулю, то линейная система называется Однородной, в противном случае – Неоднородной.

Системы линейных однородных диф. уравнений с постоянными коэффициентами

Рассмотрим систему трех уравнений с тремя неизвестными функциями x, e и z:

(8.7.10)

Где – вещественные числа, t – независимая переменная.

Будем искать частное решение системы (8.7.10) в следующем виде:

(8.7.11)

Где a, b, g и k некоторые числа (причем ), которые надо определить так, чтобы функции (8.7.11) были решением системы (8.7.10).

Подставляя функции (8.7.11) и их производные в уравнения системы (8.7.10) и сокращая на , получим

Перенося все члены в одну часть равенства и группируя коэффициенты при a, b, g, получим систему уравнений

(8.7.12)

Система (8.7.12) – это однородная система трех уравнений первой степени с тремя неизвестными a, b и g. Как известно, чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы определитель был равен нулю, т. е. число k было корнем уравнения

(8.7.13)

Уравнение (8.7.13) называют характеристическим уравнением для системы (8.7.10). Оно является уравнением третьей степени относительно k и имеет три корня: . Каждому корню соответствует ненулевое решение системы (8.7.12) ( ), а следовательно, и частное решение данной системы (8.7.10):

Если корни характеристического уравнения различны и вещественны, то общее решение системы (8.7.10) запишется в виде

или

(8.7.14)

Где – произвольные постоянные.

В случае, когда среди корней характеристического уравнения имеются кратные, корню k1кратности r соответствует частное решение системы (8.7.10), имеющее вид

(8.7.15)

Где – многочлены степени не выше .

Пример

Найти общее решение системы .

Решение

Ищем частное решение системы в виде . Подставляя эти функции в систему, получаем

(П.1)

Составляем характеристическое уравнение . Отсюда получаем уравнение . Корни характеристического уравнения различны и вещественны.

Найдем частное решение, соответствующее корню . Подставим его значение в систему (П.1). Полагая , находим . Решение имеет вид .

Аналогично для корня получаем . Решение имеет вид .

Третий корень дает . Решение .

Общее решение системы имеет вид

Пример

Найти общее решение системы

Решение

Ищем частное решение в виде . При этом получаем характеристическое уравнение: или . Корни этого уравнения комплексно сопряженные. Для первого корня имеем и, значит, – решение данной системы.

Аналогично для второго корня частное решение равно . Выделив из обоих частных решений вещественные части, получаем общее решение системы

Пример

Найти общее решение системы

(П.2)

Решение

Характеристическое уравнение , или имеет корни

Найдем частное решение вида , соответствующее корню . Из системы имеем . Искомым частным решением являются функции .

Теперь найдем два частных решения, соответствующих кратному корню Согласно (8.7.15), ему отвечает решение вида

(П.3)

Коэффициенты определяются подстановкой (П.3) в систему (П.2). Выбрав в качестве произвольных коэффициенты , найдем . Решения (П.3) принимают вид .

Полагая сначала , а затем , находим два частных решения, соответствующих кратному корню : .

И, наконец, общим решением данной системы являются функции

.

90.1. Упражнения

Проинтегрировать следующие уравнения различных типов:

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.

Проинтегрировать следующие системы. уравнений:

< Предыдущая		Следующая >

matica.org.ua

3. Системы дифференциальных уравнений

3.1. Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами сведением к одному дифференциальному уравнению

Многие системы дифференциальных уравнений, как однородные, так и неоднородные, могут быть сведены к одному уравнению относительно одной неизвестной функции. Покажем метод на примерах.

Пример 3.1. Решить систему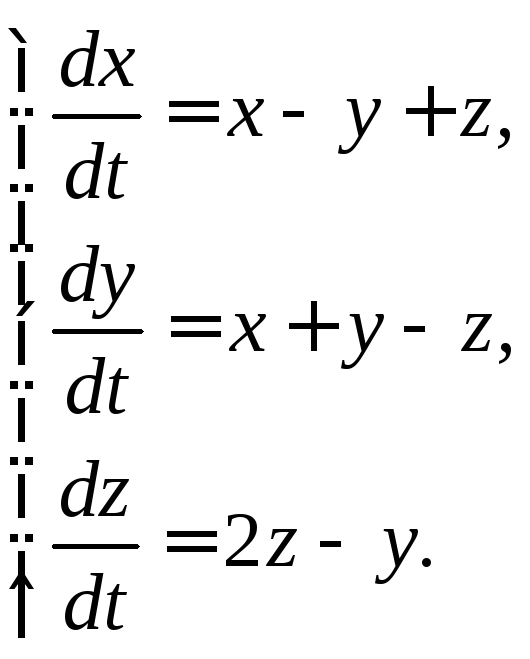

Решение. 1) Дифференцируя по t первое уравнение и используя второе и третье уравнения для замены и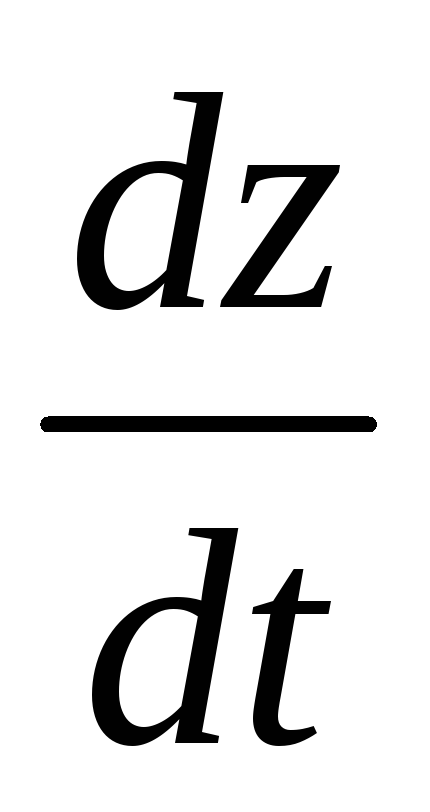, находим

.

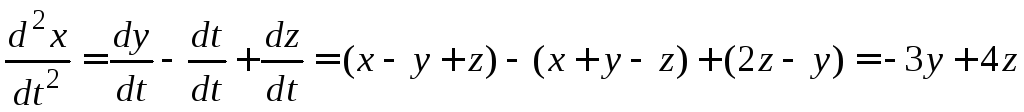Полученное уравнение дифференцируем по еще раз

.

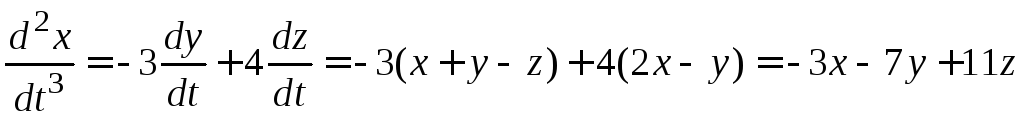1) Составляем систему

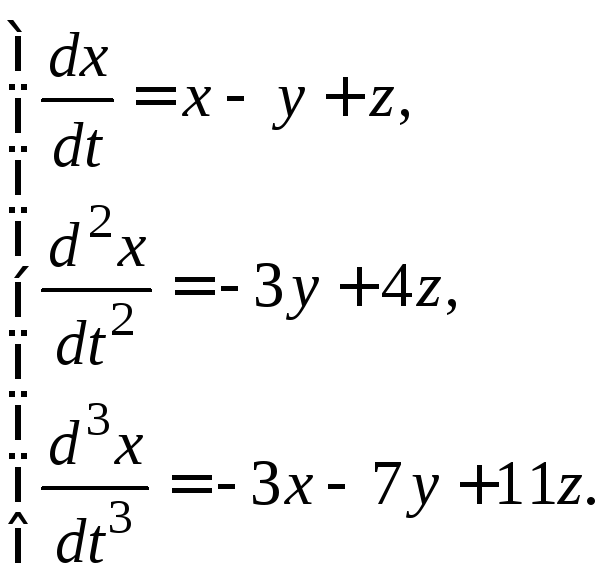
Из первых двух уравнений системы выразим переменные ичерез: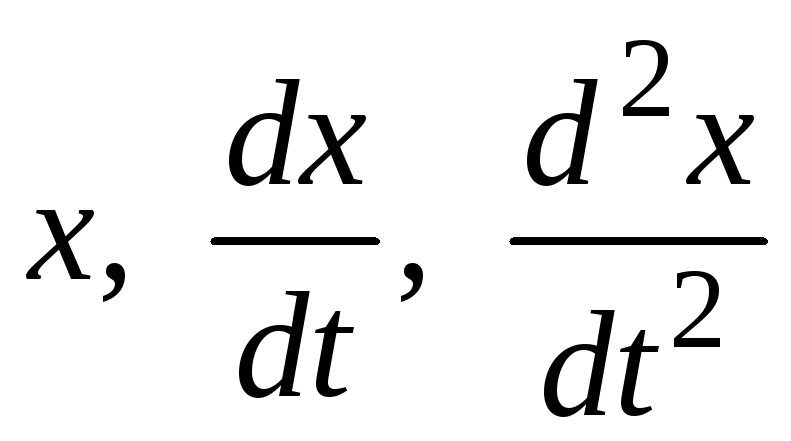

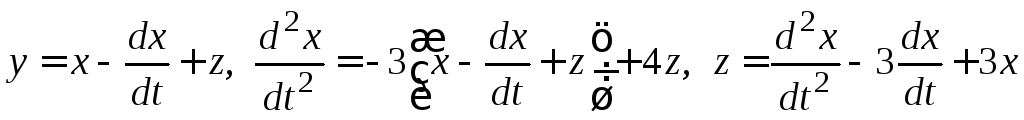. (3.1)

Подставим найденные выражения для ив третье уравнение системы

.

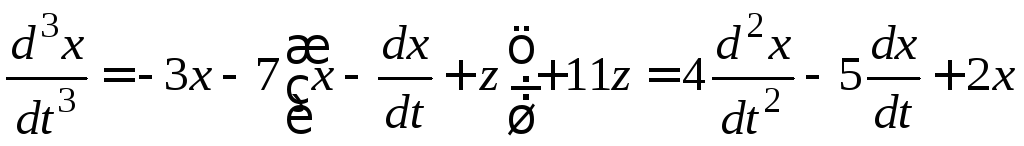Итак, для нахождения функции получили дифференциальное уравнение третьего порядка с постоянными коэффициентами

.

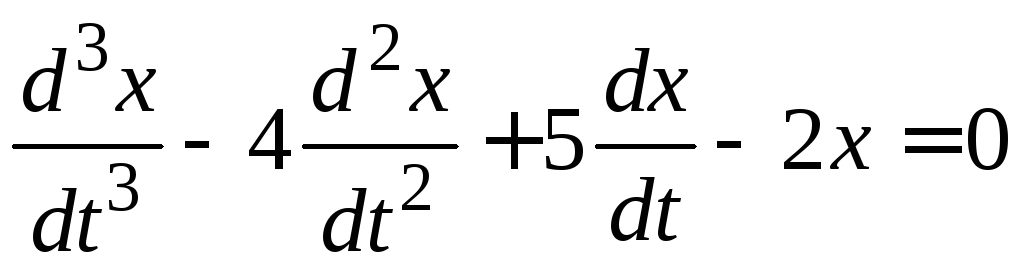2) Интегрируем последнее уравнение стандартным методом: составляем характеристическое уравнение 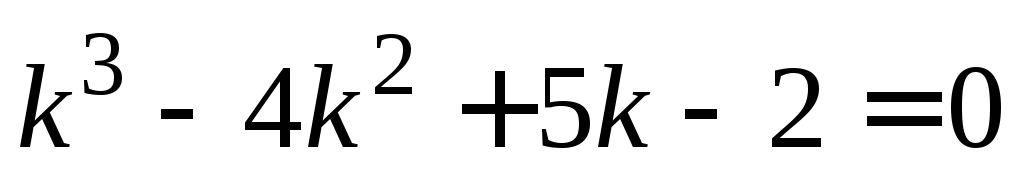, находим его корни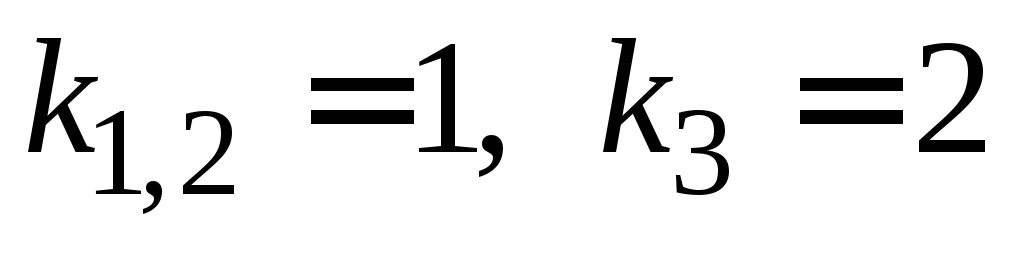и строим общее решение в виде линейной комбинации экспонент, учитывая кратность одного из корней:.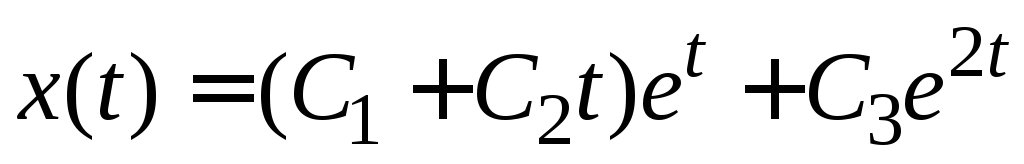

3) Далее, чтобы найти две оставшиеся функции и, дифференцируем дважды полученную функцию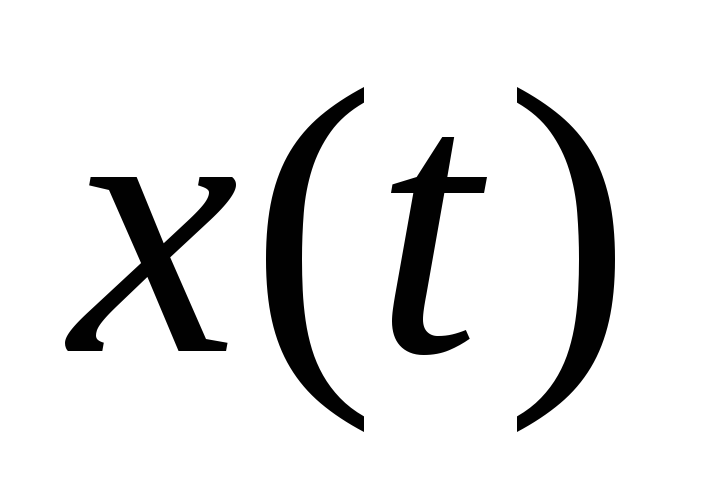

.

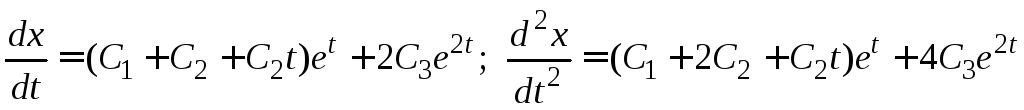Используя связи (3.1) между функциями системы, восстанавливаем оставшиеся неизвестные

.

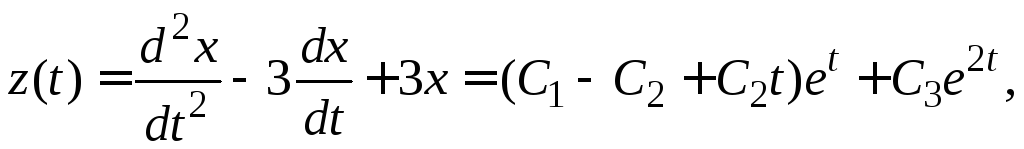
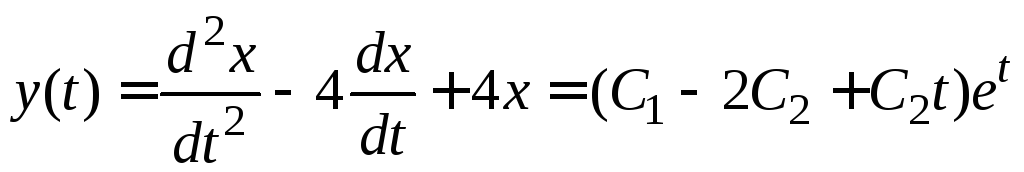Ответ. ,,.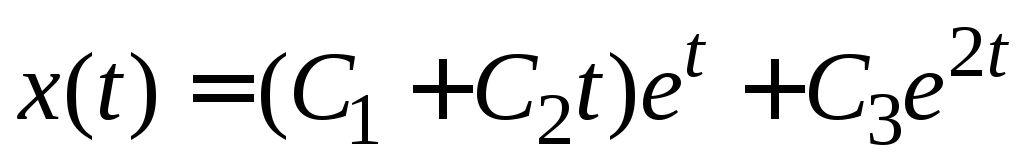

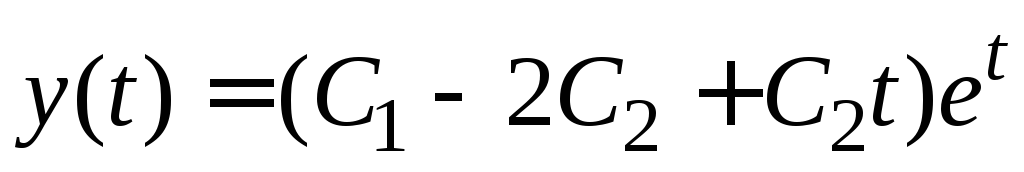Может оказаться, что все известные функции кроме одной исключаются из системы третьего порядка уже при однократном дифференцировании. В таком случае, порядок дифференциального уравнения для ее нахождения будет меньше, чем число неизвестных функций в исходной системе.

Пример 3.2. Проинтегрировать систему

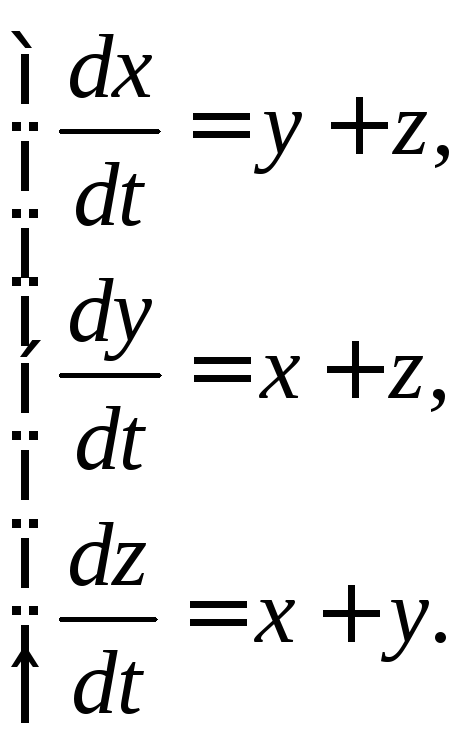(3.2)

Решение. 1) Дифференцируя по первое уравнение, находим

.

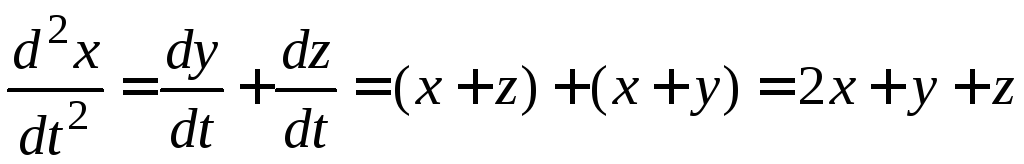Исключая переменные ииз уравнений

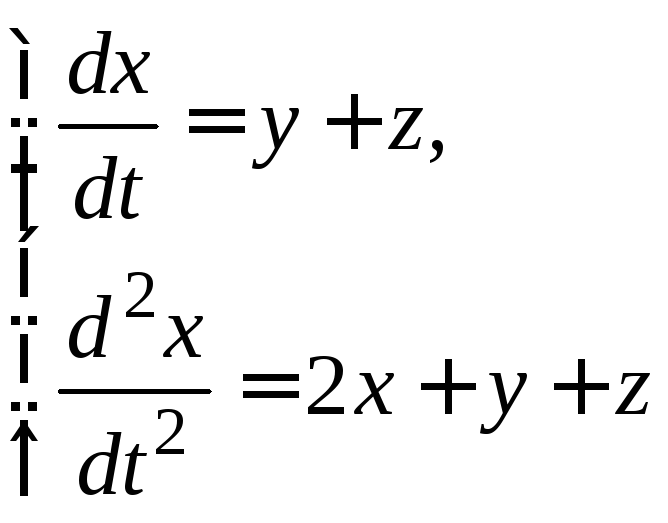
будем иметь уравнение второго порядка относительно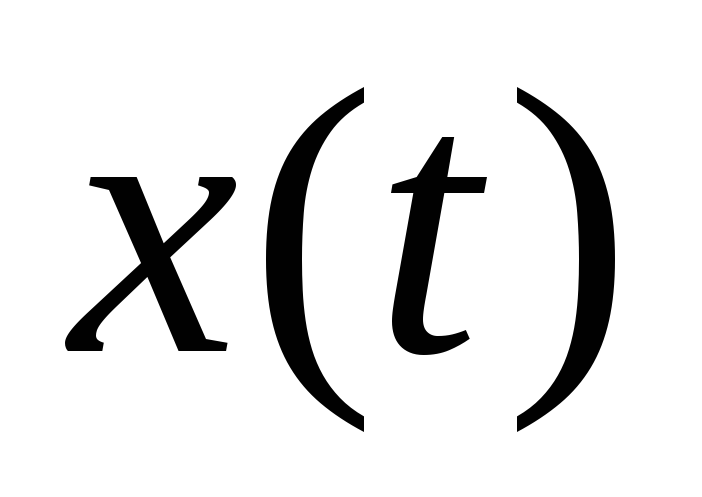

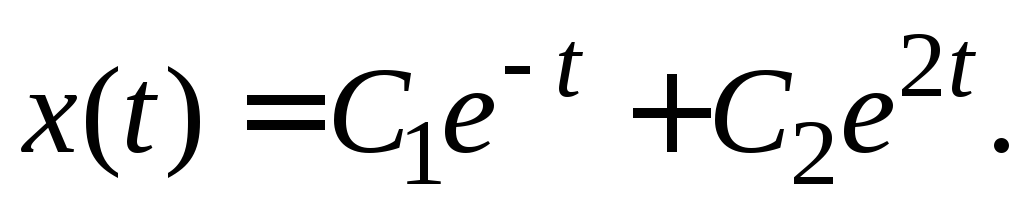(3.3)

2) Из первого уравнения системы (3.2) имеем

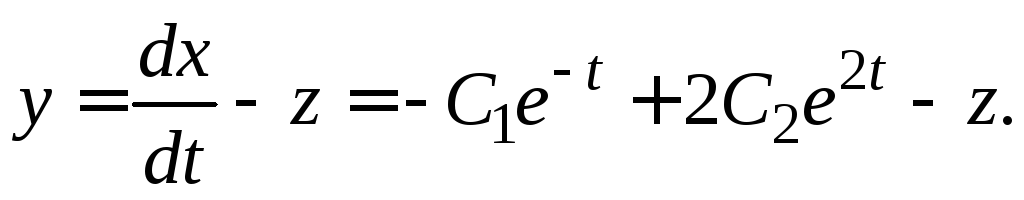(3.4)

Подставляя в третье уравнение системы (3.2) найденные выражения (3.3) и (3.4) для и, получим дифференциальное уравнение первого порядка для определения функции

Интегрируя это неоднородное уравнение с постоянными коэффициентами первого порядка, найдем Используя (3.4), находим функцию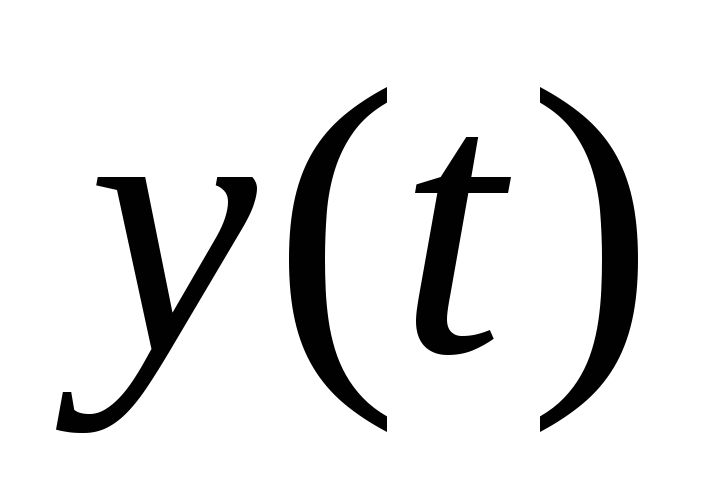

Ответ. ,,.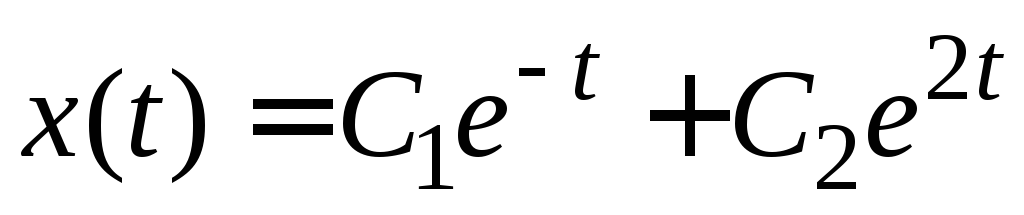

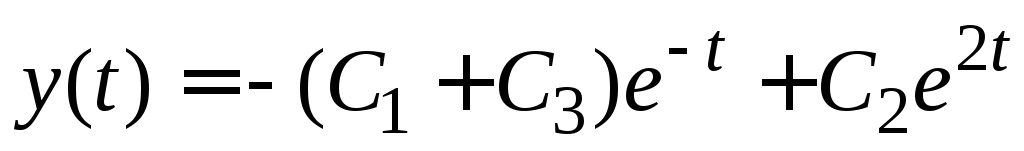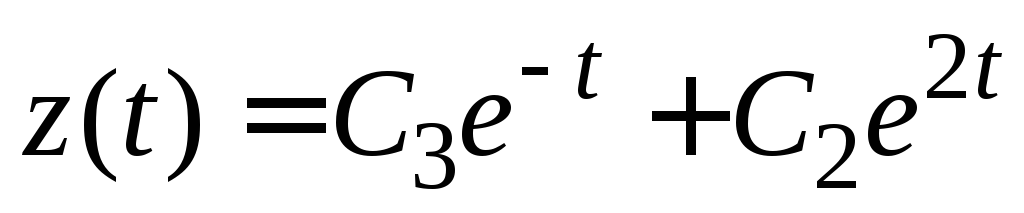Задание 3.1. Решить однородные системы сведением к одному дифференциальному уравнению.

3.1.1. 3.1.2.

3.1.3. 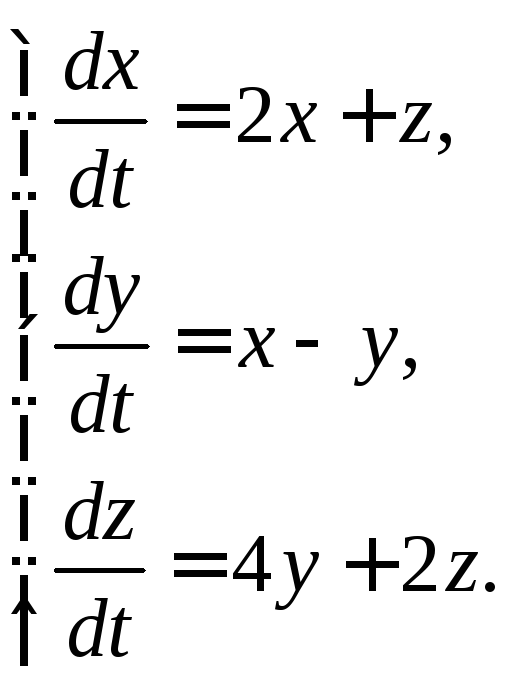3.1.4.

3.1.5. 3.1.6.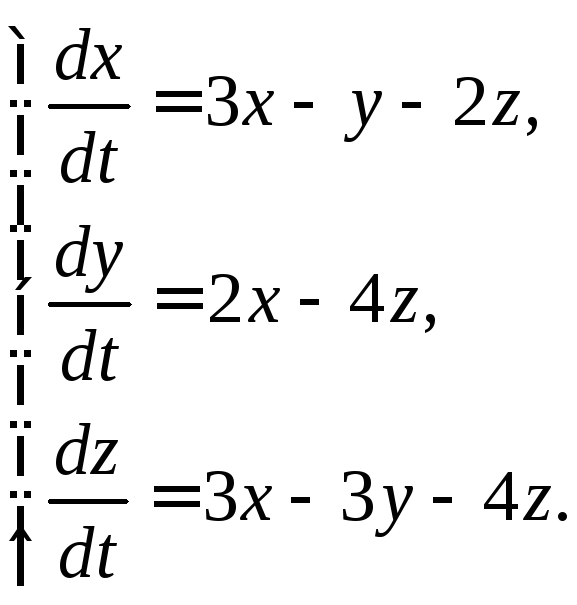

3.1.7. 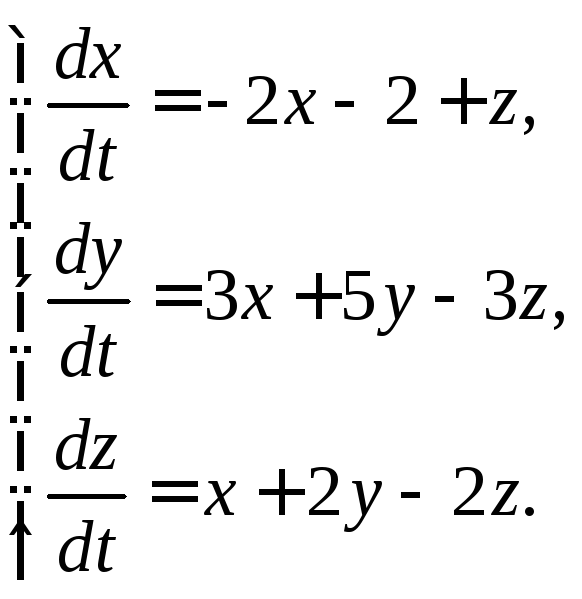3.1.8.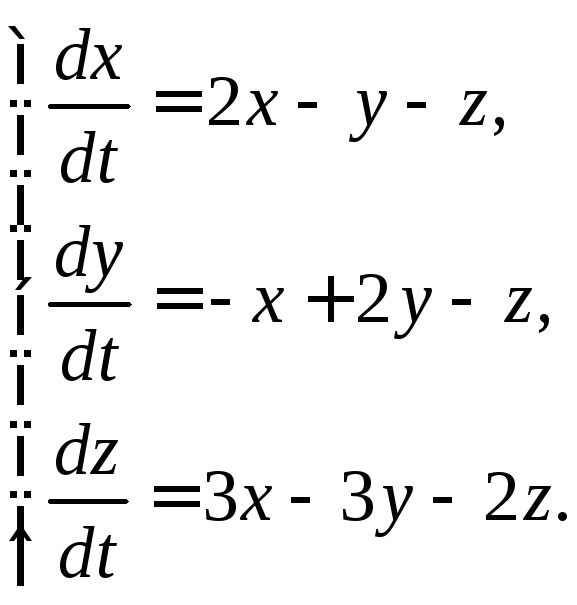

3.1.9. 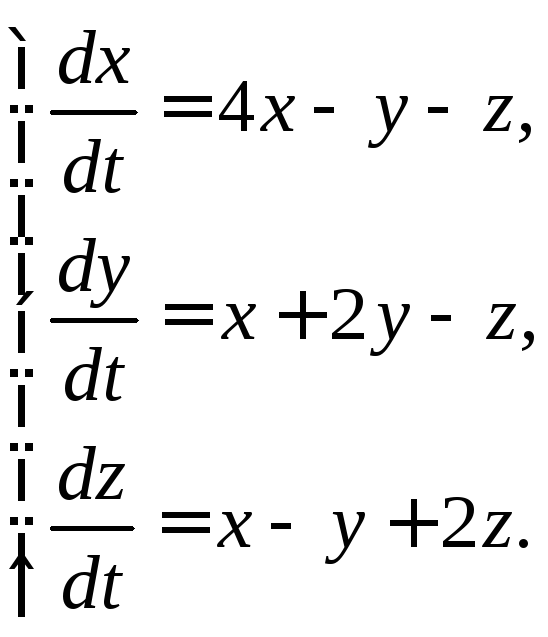3.1.10.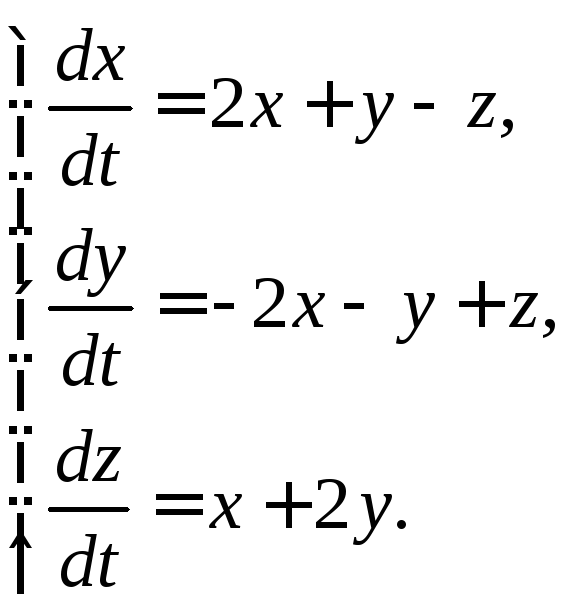

3.1.11. 3.1.12.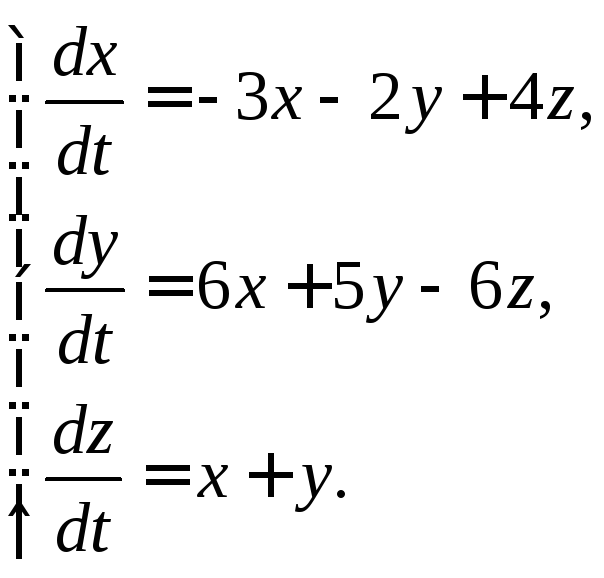

3.1.13. 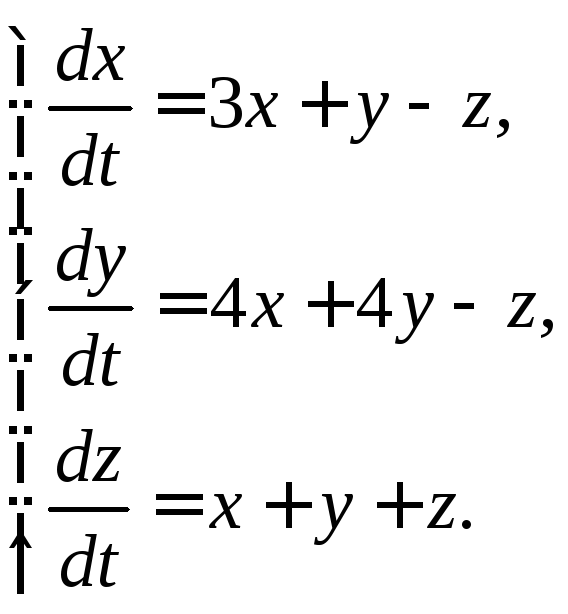3.1.14.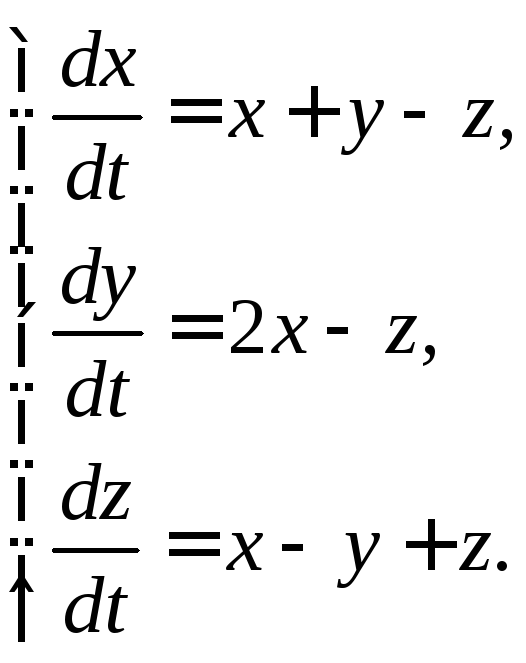

3.1.15. 3.1.16.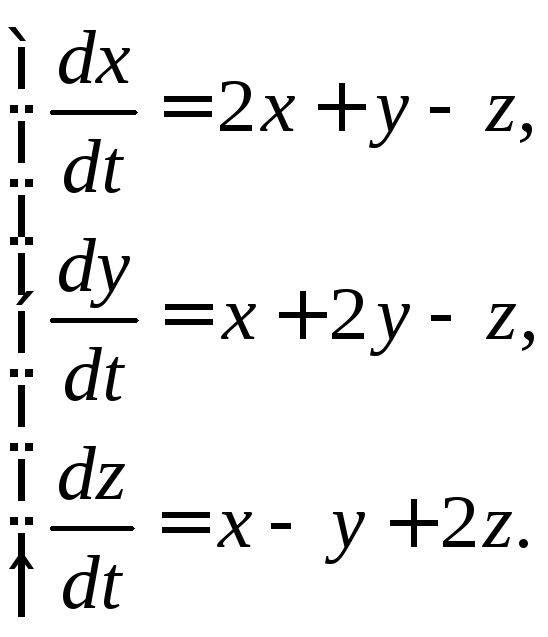

3.1.17. 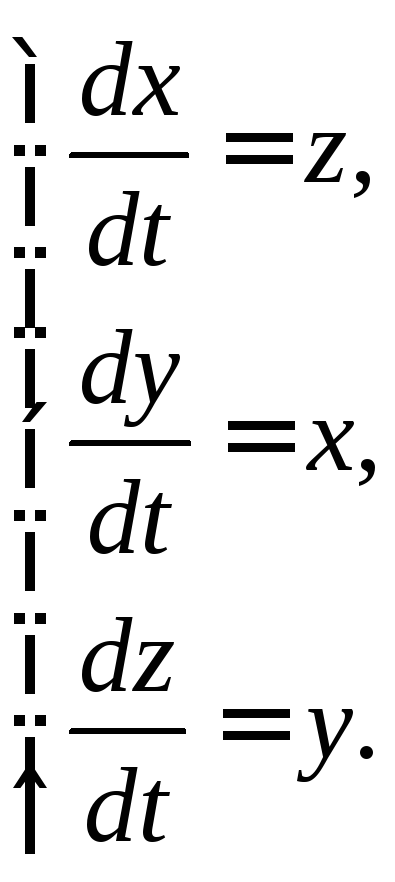3.1.18.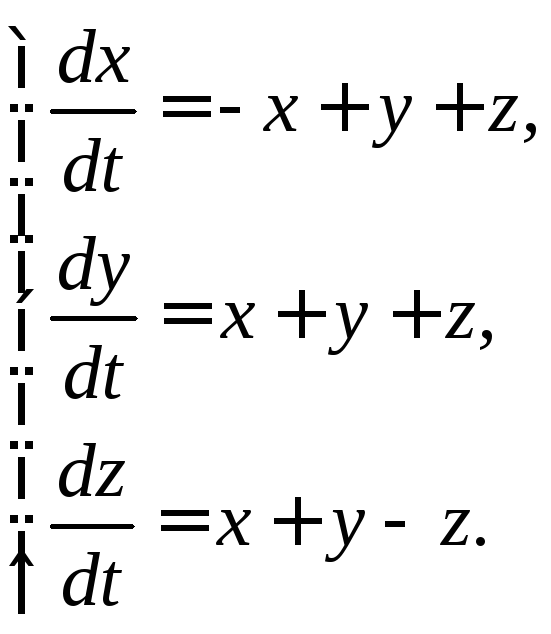

3.1.19. 3.1.20.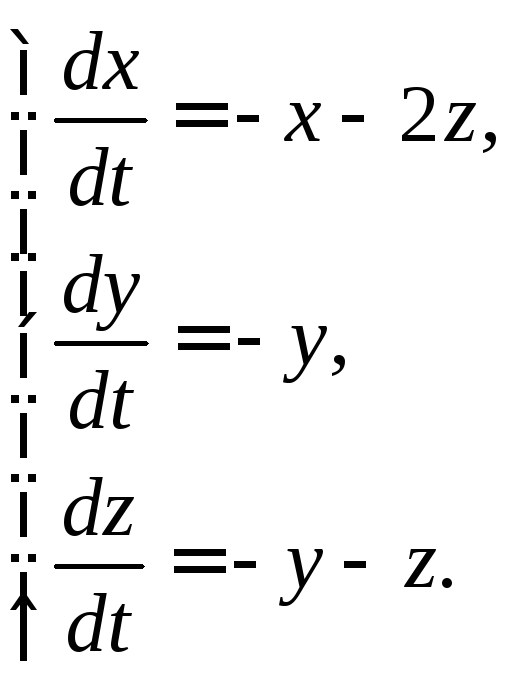

3.1.21. 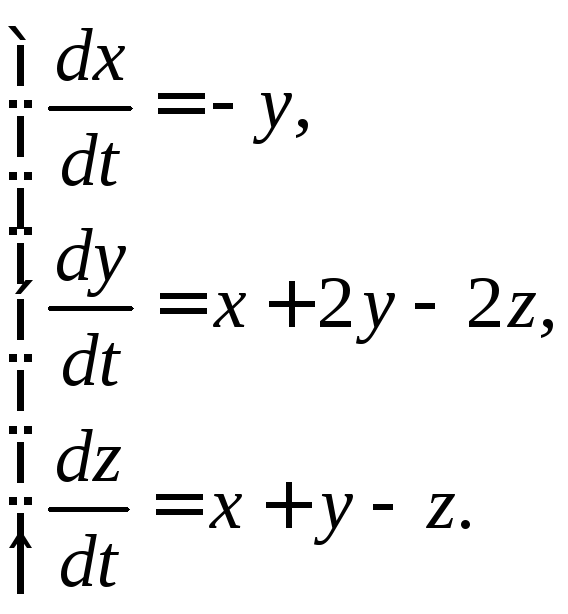3.1.22.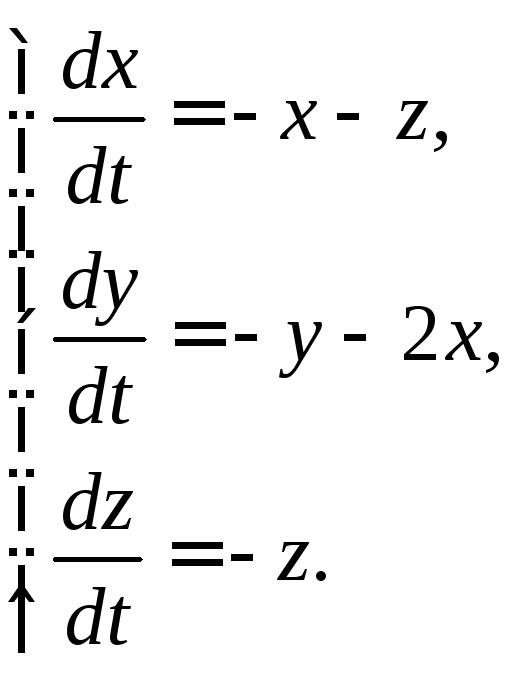

3.1.23. 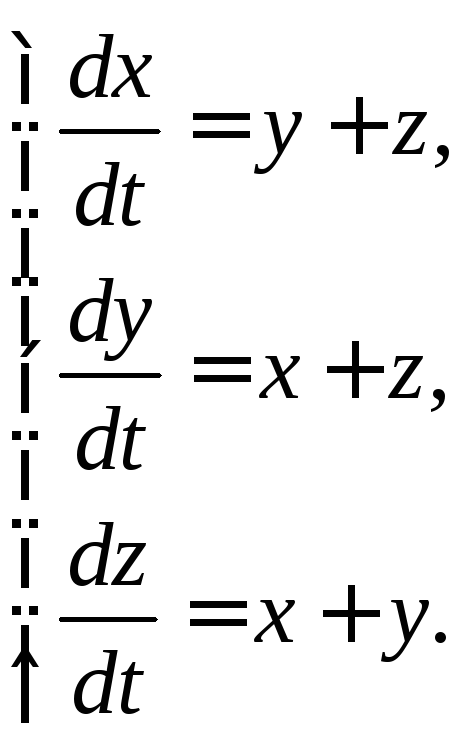3.1.24.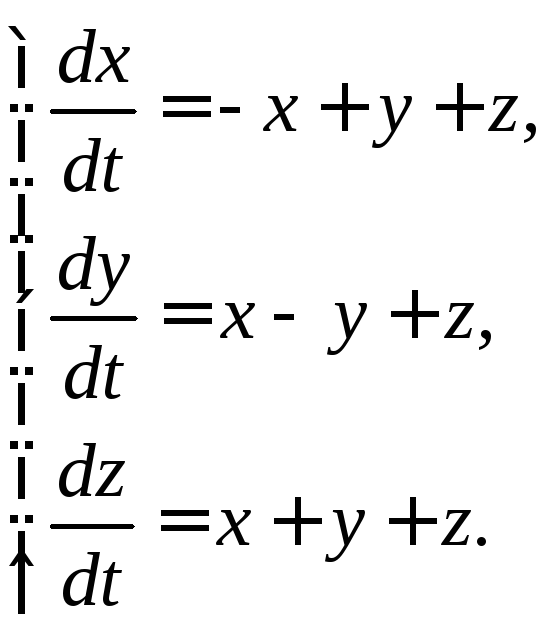

3.1.25. 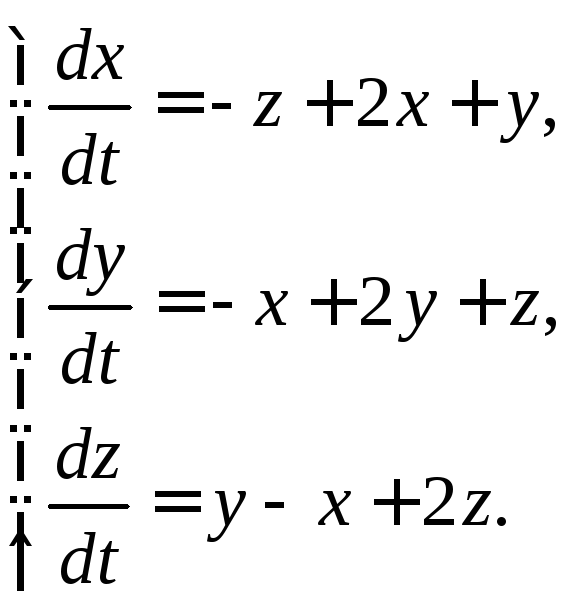3.1.26.

3.1.27. 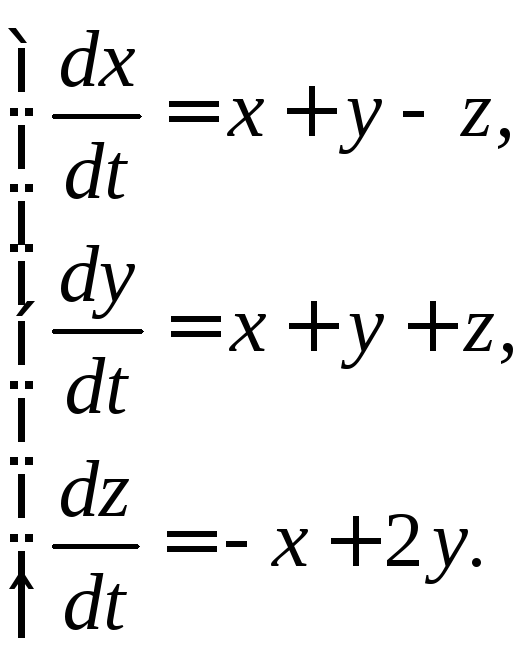3.1.28.

3.1.29. 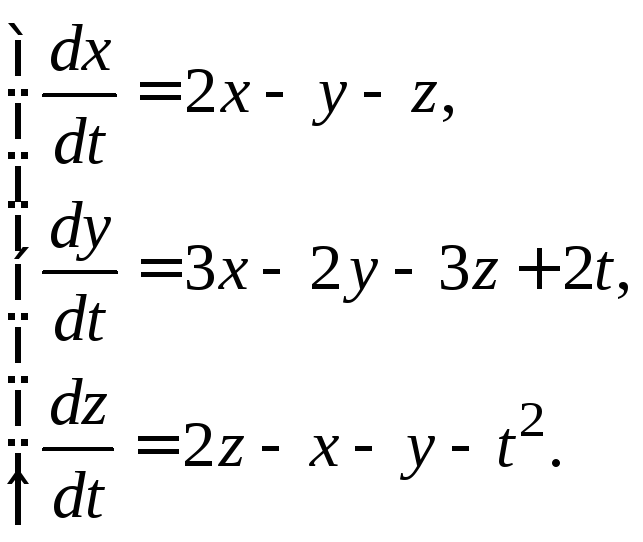3.1.30.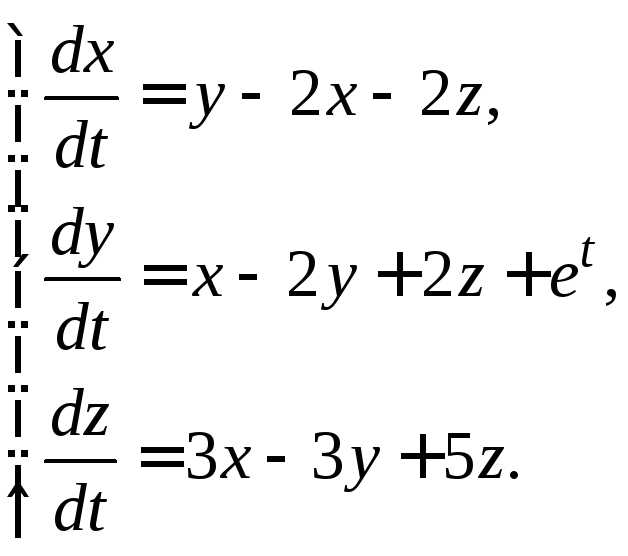

3.2. Решение систем линейных однородных дифференциальных уравнений с постоянными коэффициентами с помощью нахождения фундаментальной системы решений

Общее решение системы линейных однородных дифференциальных уравнений может быть найдено как линейная комбинация фундаментальных решений системы. В случае систем с постоянными коэффициентами для нахождения фундаментальных решений могут быть использованы методы линейной алгебры.

Пример 3.3. Решить систему

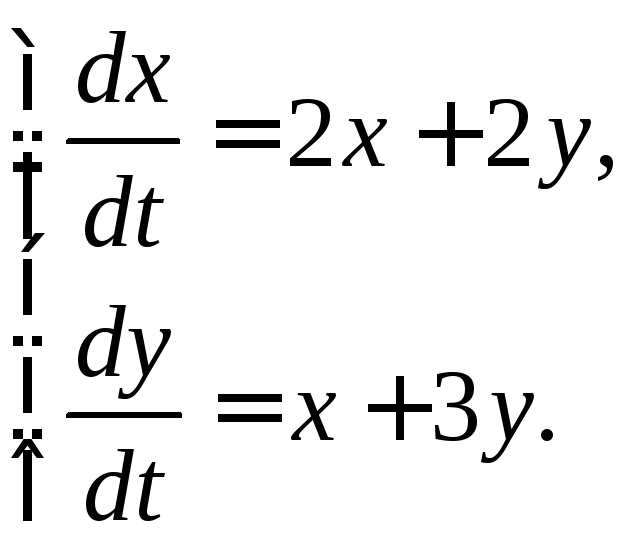(3.5)

Решение. 1) Перепишем систему в матричном виде

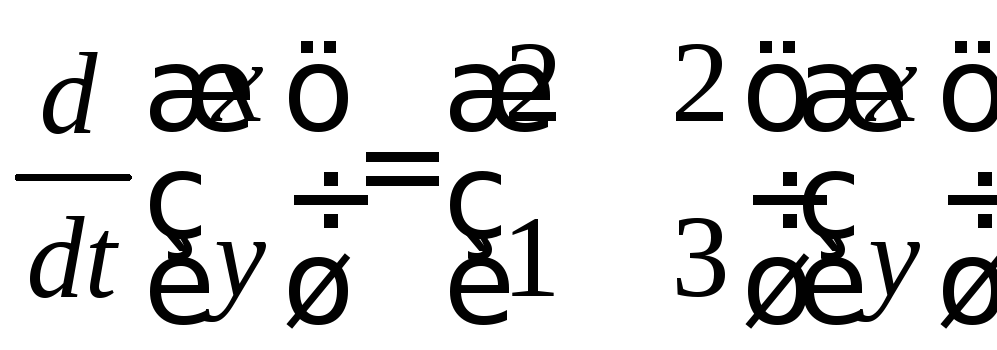. (3.6)

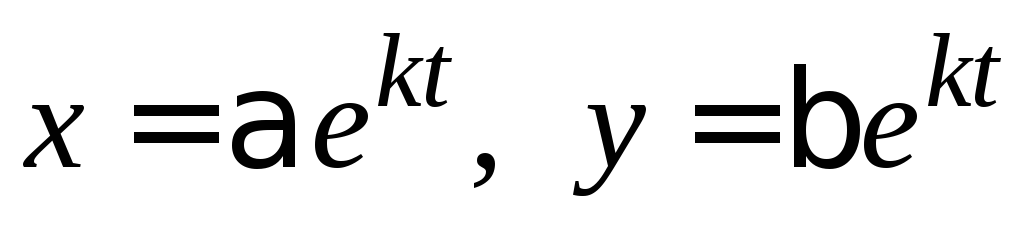2) Будем искать фундаментальное решение системы в виде вектора . Подставляя функциив (3.6) и сокращая на, получим

или

, (3.7)

то есть число 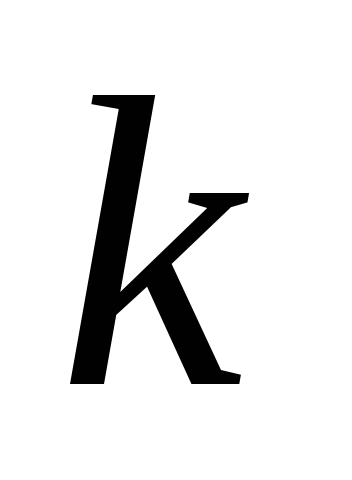должно быть собственным числом матрицы, а векторсоответствующим собственным вектором.

3) Из курса линейной алгебры известно, что система (3.7) имеет нетривиальное решение, если ее определитель равен нулю

,

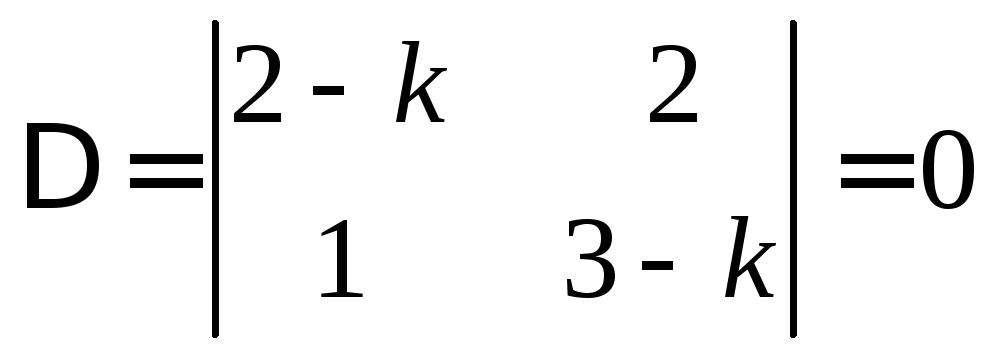то есть 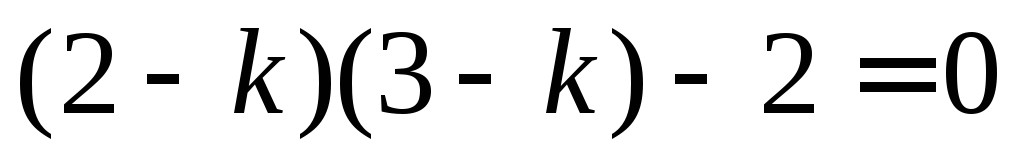. Отсюда находим собственные значения.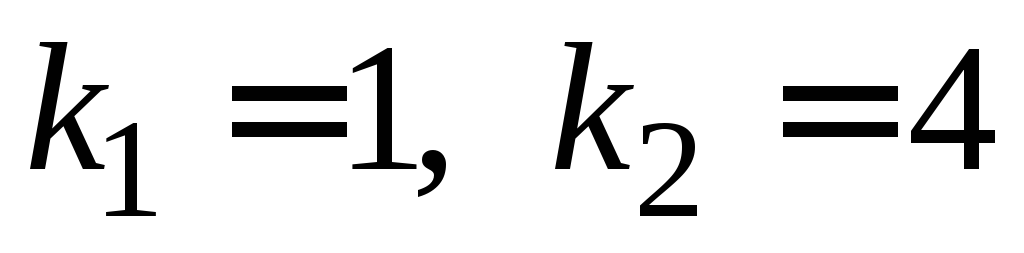

4) Найдем соответствующие собственные векторы. Подставляя в (3.7) первое значение 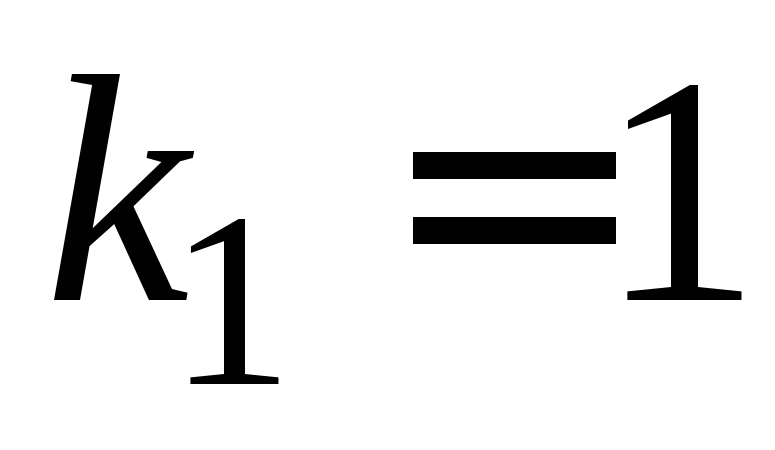, получим систему для нахождения первого собственного вектора

или

Отсюда получаем связь между неизвестными 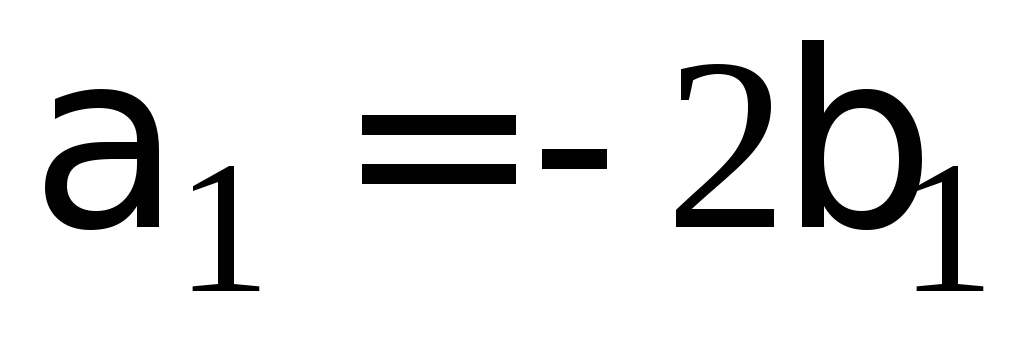. Нам достаточно выбрать одно нетривиальное решение. Полагая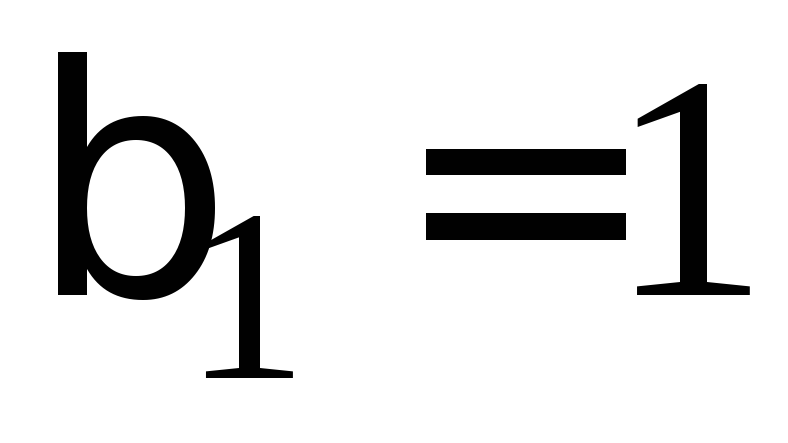, тогда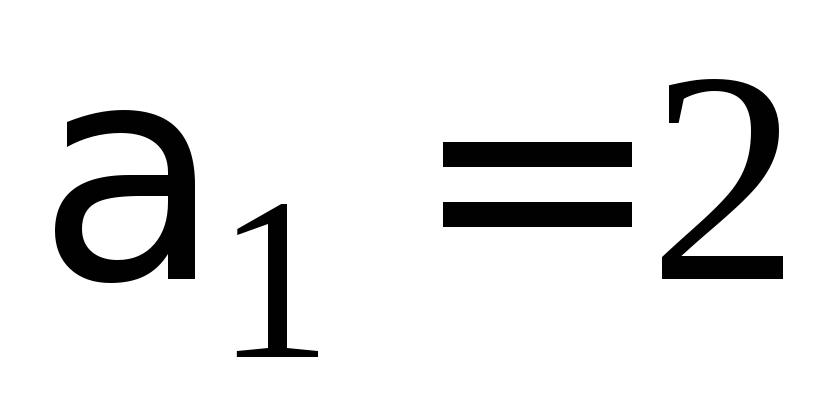, то есть векторявляется собственным для собственного значения, а вектор функциифундаментальным решением заданной системы дифференциальных уравнений (3.5). Аналогично, при подстановке второго корня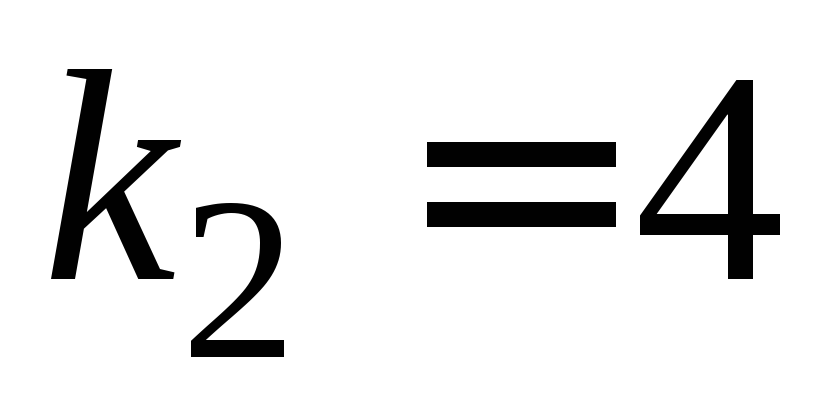в (3.7) имеем матричное уравнение для второго собственного вектора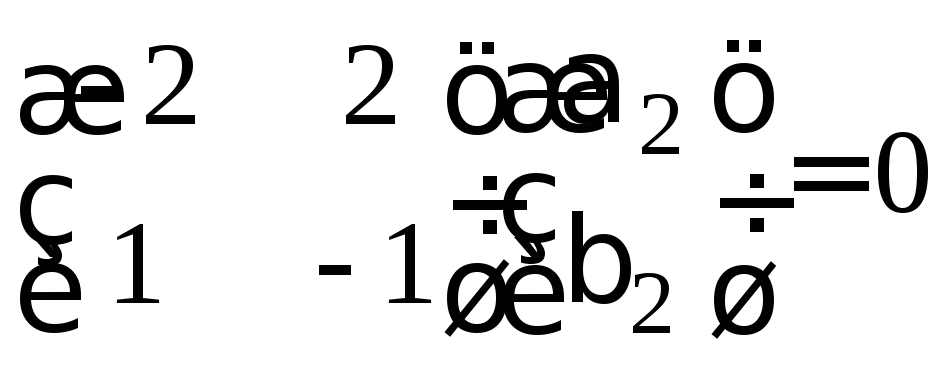. Откуда получаем связь между его компонентами. Таким образом, имеем второе фундаментальное решение

.

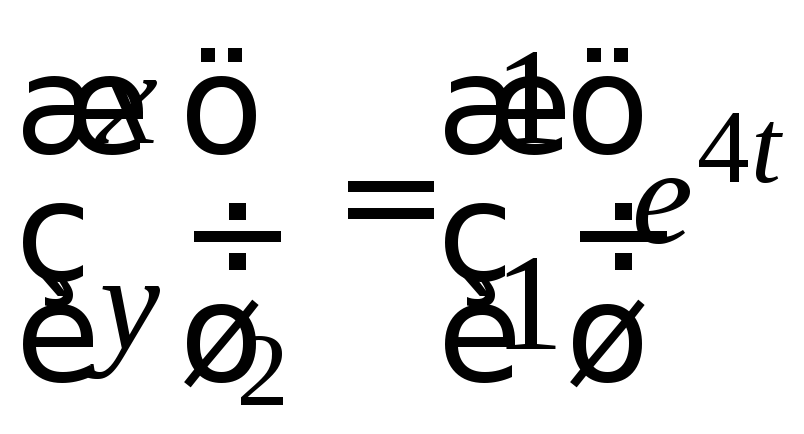5) Общее решение системы (3.5) строится как линейная комбинация двух полученных фундаментальных решений

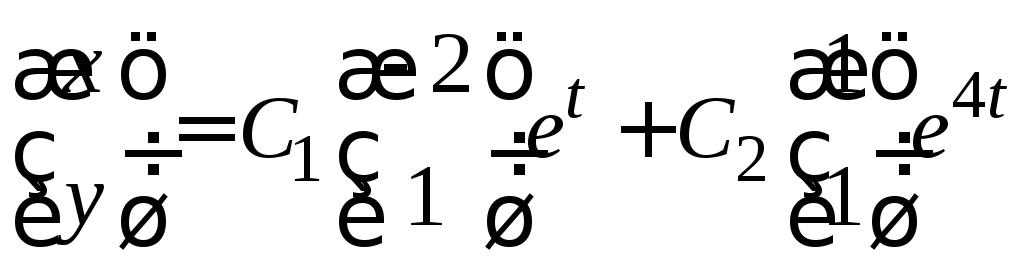
или в координатном виде

.

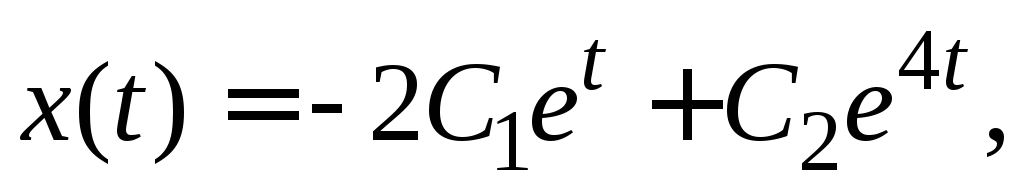
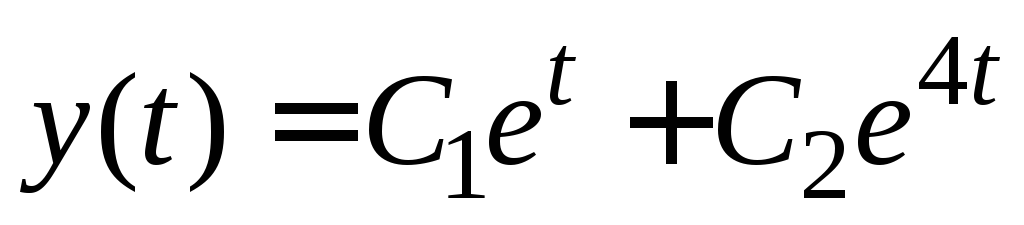Ответ. .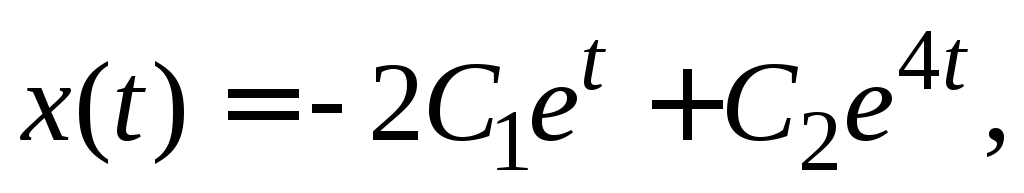

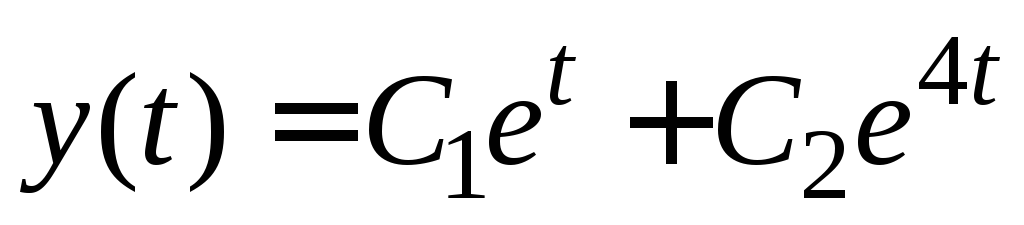Задание 3.2. Решить системы, находя фундаментальную систему решений.

studfile.net

Системы обыкновенных дифференциальных уравнений

Уважаемые читатели, сегодня в моей статье речь пойдет о системах дифференциальных уравнениях. Я покажу Вам примеры решения с пояснениями, но если у Вас возникнут вопросы, оставляйте их в комментариях или же записывайтесь на мои занятия в расписании на сайте.

Целый ряд явлений и процессов для адекватного описания требуют нескольких функций. Отыскание этих функций приводит к системе нескольких дифференциальных уравнений.

Рассматриваем следующую систему дифференциальных уравнений первого порядка:

Где y₁, y₂,…, y_n – функции от x, которые следует найти.

Систему, когда в левой части уравнений стоят производные первого порядка, а правая часть не содержит производных, называется нормальной системой дифференциальных уравнений. Ее решение составляет набор (или вектор) из функций, которые удовлетворяют все уравнения системы.

Начальные условия (задача Коши) для нормальной системы имеет вид:

y₁(x₀) = y₁₀; y₂(x₀) = y₂₀; …; y_n(x₀) = y_n0 (1.2)

где x₀,y₁₀,y₂₀,…, y_n0  – заданные числа.

Сведение нормальной системы дифференциальных уравнений к интегрированию одного уравнения высшего порядка является одним из основных методов интегрирования таких систем.

Пример 1.1. Решить систему уравнений

Решение.

Продифференцируем первое из уравнений по переменной x, получим

Заменим  его значением из второго уравнения:

Подставив вместо него выражение из первого уравнения, приходим к линейному неоднородному дифференциальному уравнению второго порядка:

Решаем это уравнение.

Из соотношения

Получим

Множество решений данной системы задается функциями:

         

где С₁ и C₂– произвольные постоянные.

Пример 1.2. Решить систему дифференциальных уравнений двумя способами:

а) сведением к дифференциальному уравнению второго порядка;

б) с помощью характеристического уравнения.

Решение:

а) продифференцируем одно из уравнений системы, например, первое. В полученном уравнении заменим его выражением из второго уравнения данной системы:

Из первого уравнения системы находим

и подставляем его в уравнения (1.4). В результате придем к дифференциальному уравнению 2-го порядка относительно неизвестной функции x₁(t):

Это линейное однородное дифференциальное уравнение с постоянными коэффициентами. Поскольку его характеристическое уравнение имеет корни k₁ = 2, k₂ = 7, следовательно

Подставив эту функцию в равенство (1.5), найдем x₂(t):

Следовательно, общим решением системы (1.3) являются функции:

б) составим для данной системы характеристическое уравнение:

или

k² – 9k + 14 = 0

Его корни:

k₁ = 2, k₂ = 7

Подставим корень k₁ = 2:

откуда находим . Полагая , получим . Таким образом, получаем первое частное решение системы (1.3):

Для корня k₂ = 7 получим систему

откуда  Если  Записываем второе частное решение системы

.

Согласно формуле (1.5) общее решение исходной системы имеет вид

Следовательно, полученные решения двумя способами одинаковы. 

Также системы дифференциальных уравнений можно решать операционным методом.

Пример 1.3. Найти решение системы

Решение:

 

Запишем систему исходя из предложенной замены

Решим систему методом Крамера

Используя таблицу изображений

Спасибо за внимание. До встречи на занятиях!

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

12.13. Системы линейных дифференциальных уравнений первого порядка с постоянными коэффициентами

а) Нормальной системой дифференциальных уравнений называется система уравнений вида:

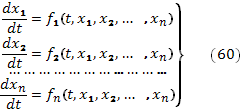
В этой системе уравнений неизвестными являются n функций 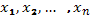, а независимой переменной – .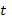

Особенности нормальной системы дифференциальных уравнений:

1) Все входящие в систему уравнения являются уравнениями первого порядка

2) Все уравнения системы разрешены относительно производных искомых функций

Если нормальная система уравнений (60) линейна, а коэффициенты при неизвестных функциях постоянны, то она имеет вид:

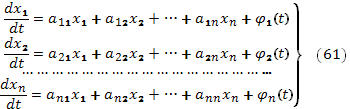
Все искомые функции входят в систему (61) в первой степени, а функции — функции независимой переменной 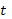, по которой вычислены производные.

Если все эти функции равны нулю, то система (61) называется однородной, а если хотя бы одна из них не равна нулю – неоднородной.

Число произвольных постоянных, входящих в общее решение нормальной системы уравнений, равно числу неизвестных функций, входящих в систему. Произвольные постоянные определяются из начальных или краевых условий.

Способ интегрирования нормальных систем линейных уравнений с постоянными коэффициентами покажем на примере однородной системы из трех уравнений.

Пример 19. Найти общее решение системы

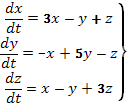(A)

Решение: Неизвестными функциями являются , а независимой переменной – .

Приведем решение этой системы к решению одного уравнения, порядок которого равен числу уравнений, входящих в систему.

Для этого любое из уравнений системы продифференцируем по 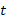и заменим в полученном уравнении производные и их выражениями из системы.

Поступая так, например, с первым уравнением, получим .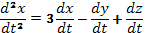

Заменим в этом уравнении производные 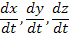, стоящие в правой части, их выражениями из второго и третьего уравнений заданной системы и получим уравнение

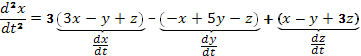, откуда после приведения подобных членов в правой части найдем 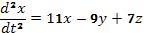(B)

Это уравнение опять дифференцируем по 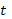и получим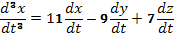

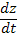Снова заменим в правой части производные и их выражениями из заданной системы и получим уравнение , которое после приведения подобных членов в правой части запишется так: 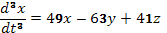(С).

Рассмотрим систему уравнений, состоящую из первого уравнения заданной системы, т.е. уравнения, обе части которого мы дифференцировали, и уравнений (B) и (С)

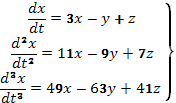(D)

Чтобы прийти к уравнению, содержащему только одну неизвестную функцию, из первых двух уравнений системы (D) определим функци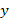и и 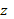. Из этих уравнений следует:

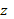Решая их относительно и , получим (E)

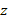Подставляя эти значения и в третье уравнение системы (D), найдем

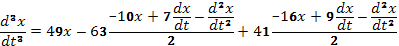
После упрощений в правой части получаем 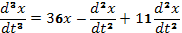(F)

Уравнение (F) – линейное однородное уравнение третьего порядка с постоянными коэффициентами. Перепишем его так 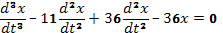(G) и найдем его общее решение по известным правилам.

Составляем характеристическое уравнение: .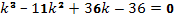

Корнями этого уравнения являются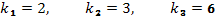

Частными решениями уравнения (G) будут функции: 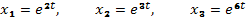, а его общим решением .

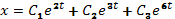Чтобы определить две остальные неизвестные функции и 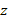, воспользуемся выражением (Е). После подстановки в (Е) выражени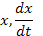й и получим:

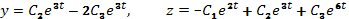
12.14. Системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами

С линейными системами дифференциальных уравнений второго порядка приходится встречаться часто в теоретической механике, сопротивлении материалов и в других приложениях математики.

Система дифференциальных уравнений, разрешенных относительно наивысших производных искомых функций, называется канонической.

В случае трех неизвестных функций 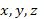и независимой переменной 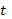эта система уравнений записывается так:

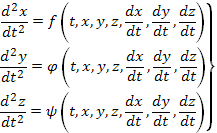(62)

Общее решение этой системы содержит шесть произвольных постоянных, для определения которых задается шесть начальных условий (в механике это начальное положение и скорость точки в некоторый момент времени ).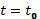

Для определения решения канонической системы (62) применяется такой же прием, как и при решении рассмотренных выше нормальных систем: последовательным дифференцированием одного уравнения системы (или нескольких ее уравнений) следует исключить все искомые функции, кроме одной.

Сущность этого приема подробно разберем на примере.

Пример 20. Найти общее решение системы уравнений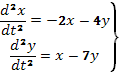

Решение: Продифференцируем первое уравнение два раза по и получим

(63)

Подставим в (63) вместо его выражение из второго уравнения системы.

Тогда 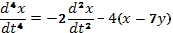, или (64)

Из первого уравнения системы определим 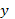и подставим его в уравнение (64) 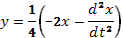(65)

C этим значением уравнение (64) перепишется так: 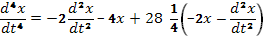, раскрывая скобки, получим 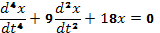. Характеристическое уравнение 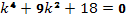имеет корни

Функция (66)

Теперь из (65) найдем у, из (66) находим

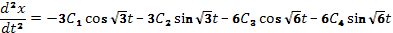
Подставляя х и 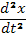в (65), получаем

.

studfile.net