Решение систем линейных уравнений в матричной форме.
Пусть для
матрицы А порядка n на n существует
обратная матрица 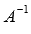 .
Умножим обе части матричного
уравнения
.
Умножим обе части матричного
уравнения 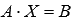 слева
на
слева
на  (порядки
матриц A ⋅ X и В позволяют
произвести такую операцию, смотрите
статью операции
над матрицами, свойства операций).
Имеем
(порядки
матриц A ⋅ X и В позволяют
произвести такую операцию, смотрите
статью операции
над матрицами, свойства операций).
Имеем  .
Так как для операции умножения матриц
подходящих порядков характерно свойство
ассоциативности, то последнее равенство
можно переписать как
.
Так как для операции умножения матриц
подходящих порядков характерно свойство
ассоциативности, то последнее равенство
можно переписать как 
 (E–
единичная матрица порядка n на n),
поэтому
(E–
единичная матрица порядка n на n),
поэтому  Таким
образом, решение
системы линейных алгебраических
уравнений по матричному методу
определяется равенством
Таким
образом, решение
системы линейных алгебраических
уравнений по матричному методу
определяется равенством  .
Другими словами, решение СЛАУ находится
с помощью обратной матрицы
.
Другими словами, решение СЛАУ находится
с помощью обратной матрицы  . Мы
знаем, что квадратная
матрица А порядка n на n имеет
обратную матрицу
. Мы
знаем, что квадратная
матрица А порядка n на n имеет
обратную матрицу  только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С nНЕИЗВЕСТНЫМИ
МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО
ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ
МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С nНЕИЗВЕСТНЫМИ
МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО
ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ
МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ. С помощью обратной
матрицы найдите решение системы линейных
уравнений  . Решение. В
матричной форме исходная система
запишется как
. Решение. В
матричной форме исходная система
запишется как 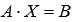 ,
где
,
где  .
Вычислим определитель основной матрицы
и убедимся, что он отличен от нуля. В
противном случае мы не сможем решить
систему матричным методом. Имеем
.
Вычислим определитель основной матрицы
и убедимся, что он отличен от нуля. В
противном случае мы не сможем решить
систему матричным методом. Имеем  ,
следовательно, для матрицы А может
быть найдена обратная матрица
,
следовательно, для матрицы А может
быть найдена обратная матрица  .
Таким образом, если мы отыщем обратную
матрицу, то искомое решение СЛАУ определим
как
.
Таким образом, если мы отыщем обратную
матрицу, то искомое решение СЛАУ определим
как 
 .
Найдем ее. Мы знаем, что для
матрицы
.
Найдем ее. Мы знаем, что для
матрицы  обратная
матрица может быть найдена как
обратная
матрица может быть найдена как  ,
где
,
где  —
алгебраические дополнения элементов
—
алгебраические дополнения элементов 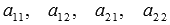 . В
нашем случае
. В
нашем случае 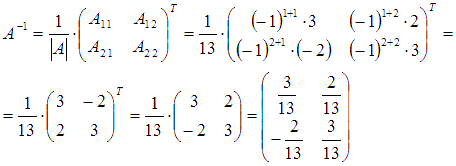 Тогда
Тогда  Выполним
проверку полученного решения
Выполним
проверку полученного решения  ,
подставив его в матричную форму исходной
системы уравнений
,
подставив его в матричную форму исходной
системы уравнений 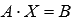 .
Это равенство должно обратиться в
тождество, в противном случае где-то
была допущена ошибка.
.
Это равенство должно обратиться в
тождество, в противном случае где-то
была допущена ошибка.  Следовательно,
решение найдено верно. Ответ:
Следовательно,
решение найдено верно. Ответ: 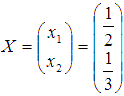 или
в другой записи
или
в другой записи  .
. Пример. Решите
СЛАУ  матричным
методом. Решение. Первое
уравнение системы не содержит неизвестной
переменной x2,
второе – x1
матричным
методом. Решение. Первое
уравнение системы не содержит неизвестной
переменной x2,
второе – x1
 .
От такого вида проще перейти к матричной
форме записи СЛАУ
.
От такого вида проще перейти к матричной
форме записи СЛАУ 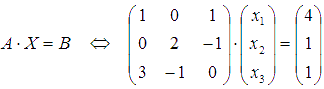 .
Убедимся в том, что эта система уравнений
может быть решена с помощью обратной
матрицы. Другими словами, покажем
что
.
Убедимся в том, что эта система уравнений
может быть решена с помощью обратной
матрицы. Другими словами, покажем
что  :
:  Построим
обратную матрицу
Построим
обратную матрицу 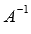 с
помощью матрицы из алгебраических
дополнений:
с
помощью матрицы из алгебраических
дополнений:  тогда,
тогда,  Осталось
найти решение СЛАУ:
Осталось
найти решение СЛАУ:  Рекомендуем
выполнить проверку. Ответ:
Рекомендуем
выполнить проверку. Ответ:  .
. При переходе от
обычного вида системы линейных
алгебраических уравнений к ее матричной
форме следует быть внимательным с
порядком следования неизвестных
переменных в уравнениях системы. К
примеру, СЛАУ  НЕЛЬЗЯ
записать как
НЕЛЬЗЯ
записать как  .
Нужно сначала упорядочить все неизвестные
переменные во всех уравнениях системы,
а потом переходить к матричной
записи:
.
Нужно сначала упорядочить все неизвестные
переменные во всех уравнениях системы,
а потом переходить к матричной
записи:  или
или 
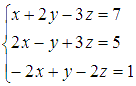 в
матричной форме запишется как
в
матричной форме запишется как  . Разберем
пример. Пример. Найдите
решение системы линейных алгебраических
уравнений с
помощью обратной матрицы. Решение. Упорядочив
неизвестные переменные в уравнениях
системы, запишем ее в матичной форме
. Разберем
пример. Пример. Найдите
решение системы линейных алгебраических
уравнений с
помощью обратной матрицы. Решение. Упорядочив
неизвестные переменные в уравнениях
системы, запишем ее в матичной форме  .
Вычислим определитель основной
матрицы:
.
Вычислим определитель основной
матрицы:  Он
отличен от нуля, поэтому решение системы
уравнений может быть найдено с помощью
обратной матрицы как
Он
отличен от нуля, поэтому решение системы
уравнений может быть найдено с помощью
обратной матрицы как  .
Найдем обратную матрицу по
формуле
.
Найдем обратную матрицу по
формуле 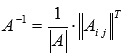 :
:  Получим
искомое решение:
Получим
искомое решение:  Ответ: x
= 0, y = -2, z = 3. Пример. Найдите
решение системы линейных алгебраических
уравнений
Ответ: x
= 0, y = -2, z = 3. Пример. Найдите
решение системы линейных алгебраических
уравнений 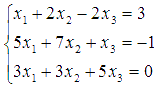 матричным
методом. Решение. Определитель
основной матрицы системы равен
нулю
матричным
методом. Решение. Определитель
основной матрицы системы равен
нулю  поэтому,
мы не можем применить матричный метод.
поэтому,
мы не можем применить матричный метод. Пример. Решите
СЛАУ 
 —
некоторое действительное
число. Решение. Система
уравнений в матричной форме имеет вид
—
некоторое действительное
число. Решение. Система
уравнений в матричной форме имеет вид 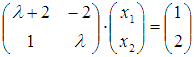 .
Вычислим определитель основной матрицы
системы и убедимся в том, что он отличен
от нуля:
.
Вычислим определитель основной матрицы
системы и убедимся в том, что он отличен
от нуля:  Квадратных
трехчлен
Квадратных
трехчлен  не
обращается в ноль ни при каких
действительных значениях
не
обращается в ноль ни при каких
действительных значениях  ,
так как его дискриминант отрицателен
,
так как его дискриминант отрицателен  ,
поэтому определитель основной матрицы
системы не равен нулю ни при каких
действительных
,
поэтому определитель основной матрицы
системы не равен нулю ни при каких
действительных  .
По матричному методу имеем
.
По матричному методу имеем  .
Построим обратную матрицу по
формуле
.
Построим обратную матрицу по
формуле 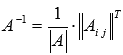 :
:  Тогда
Тогда  Ответ:
Ответ: 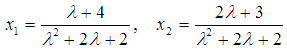 .
.Обратная матрица. Вычисление обратной матрицы методом присоединённой матрицы. Решение систем линейных уравнений методом обратной матрицы.
Определение. Матрица А-1называется обратной к матрице А, если
выполняется условие: АА-1= А-1А=Е,
где Е — единичная матрица того же порядка,
что и матрица А. Обратная А
Определение. Квадратная матрица
А= называется невырожденной, если её
определитель неравен нулю, в противном
случае матрица называется вырожденной.
называется невырожденной, если её
определитель неравен нулю, в противном
случае матрица называется вырожденной.
Теорема.Всякая невырожденная матрица имеет обратную.
Определение. Присоединенной матрицей к матрице А называется матрица вида:
к матрице А называется матрица вида:
 =
= ,
где Аij-алгебраическое
дополнение элемента аij.
,
где Аij-алгебраическое
дополнение элемента аij.
Находят обратную матрицу поформуле:
А-1=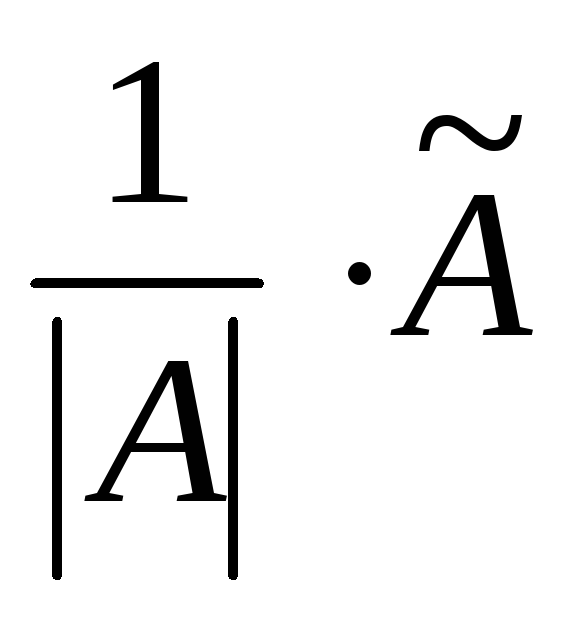 .
.
Пример 3.1
Найти обратную матрицу методом присоединенной матрицы.
А=
Решение.
Выясним, является ли данная матрица невырожденной. Для этого найдем определитель матрицы:
 =3(-1)1+1
=3(-1)1+1 +0(-1)2+1
+0(-1)2+1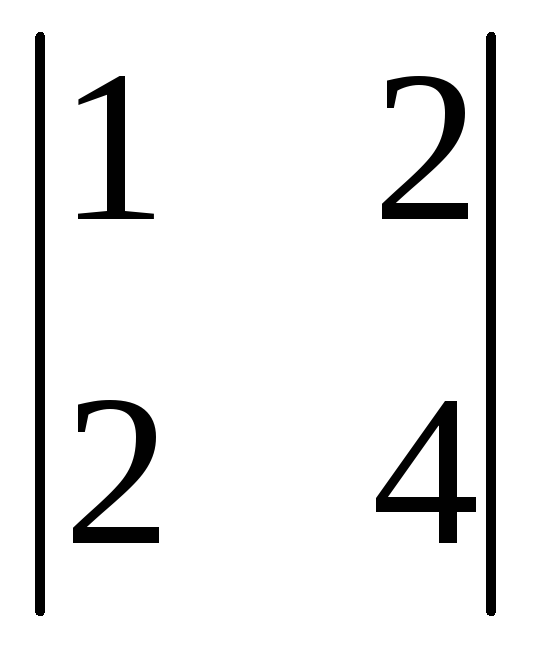 +1(-1)3+1=3(12-4)+0+(2-6)=24-4=20.
+1(-1)3+1=3(12-4)+0+(2-6)=24-4=20.
Т.к.  0,
следовательно, данная матрица имеет
обратную.
0,
следовательно, данная матрица имеет
обратную.
Найдем транспонированную матрицу.
АТ=
Вычислим присоединенную матрицу. Для этого найдем алгебраическое дополнение каждого элемента матрицы.
 =
(-1)1+1
=
(-1)1+1 =12-4=8
=12-4=8
 =
(-1)1+2
=
(-1)1+2 =
-(4-4)= 0
=
-(4-4)= 0
 =
(-1)1+3
=
(-1)1+3 =
2-6= -4
=
2-6= -4
 =
(-1)2+1
=
(-1)2+1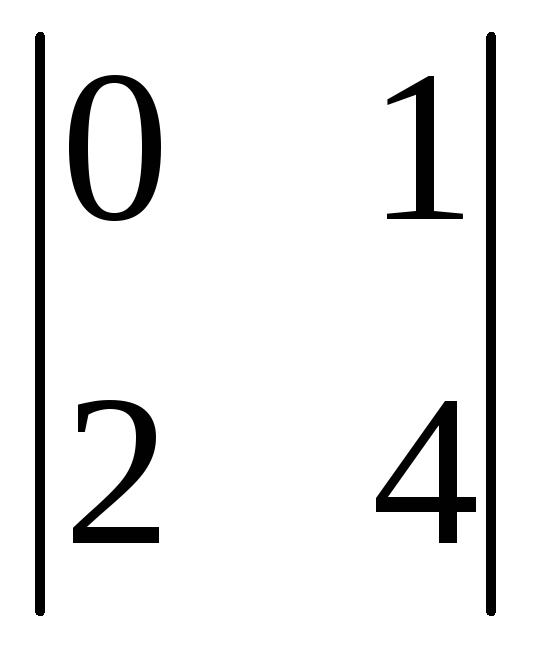 =
-(0-2)=2
=
-(0-2)=2
 =
(-1)2+2
=
(-1)2+2 =
12-2=10
=
12-2=10
 =
(-1)2+3
=
(-1)2+3 =
-(6-0)= -6
=
-(6-0)= -6
 =
(-1)3+1
=
(-1)3+1 =
0-3= -3
=
0-3= -3
 =
(-1)3+2
=
(-1)3+2 =
-(6-1)= -5
=
-(6-1)= -5
 =
(-1)3+3
=
(-1)3+3 =
9-0=9.
=
9-0=9.
 =
=
4. Воспользуемся формулой: А-1= .
.
А-1=
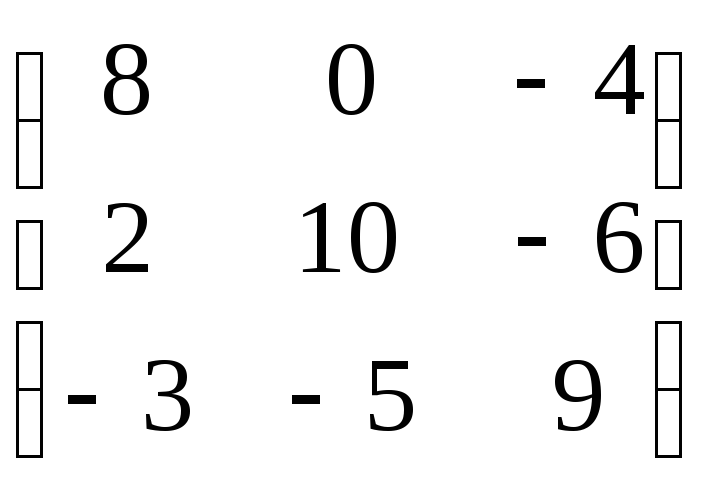 =
= .
.
Решение систем линейных уравнений методом обратной матрицы
Пусть дана система линейных уравнений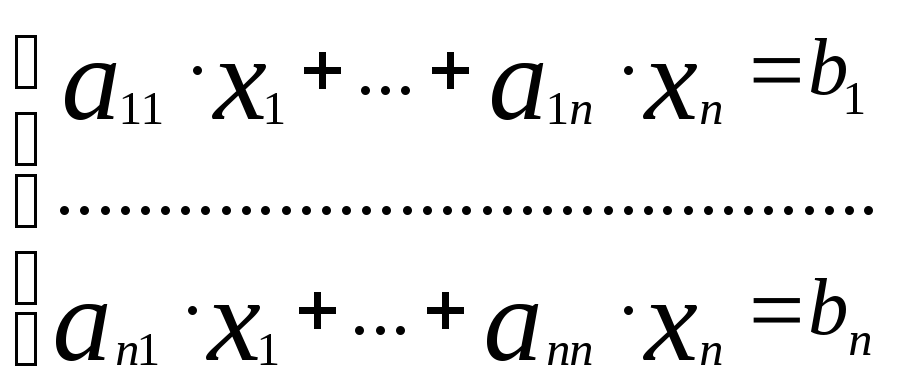 .
Обозначим её через (1). Выпишим основную
матрицу данной системы: А=
.
Обозначим её через (1). Выпишим основную
матрицу данной системы: А= ,
вектор-столбец неизвестных:X=
,
вектор-столбец неизвестных:X= и
вектор-столбец свободных членов:B=
и
вектор-столбец свободных членов:B= .
Теперь перепишем систему (1) в матричной
форме:AX=B
.
Теперь перепишем систему (1) в матричной
форме:AX=B X=A-1B-
решение системы (1).
X=A-1B-
решение системы (1).
Пример 3.2
Решить систему линейных уравнений:  методом обратной матрицы.
методом обратной матрицы.
Решение.
Формула, по которой будем находить решение системы: X=A-1B.
Основная матрица системы А= ,
вектор-столбец неизвестных:X=
,
вектор-столбец неизвестных:X=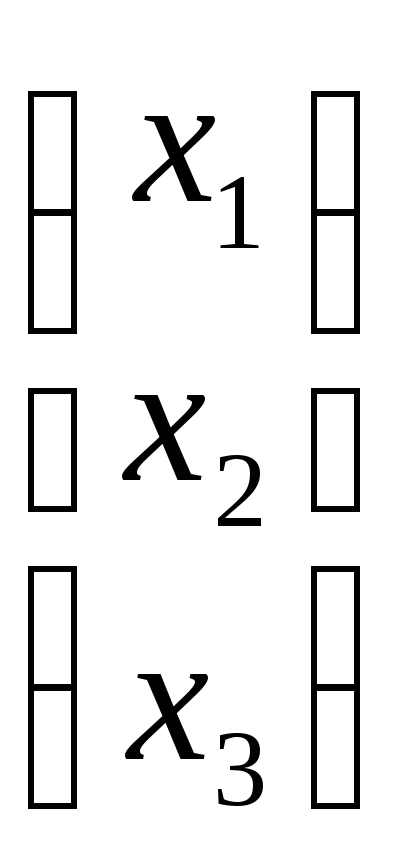
 и
вектор-столбец свободных членов:B=
и
вектор-столбец свободных членов:B= .
.
Найдем определитель  =3(-1)1+1
=3(-1)1+1 +0(-1)2+1
+0(-1)2+1 +1(-1)3+1
+1(-1)3+1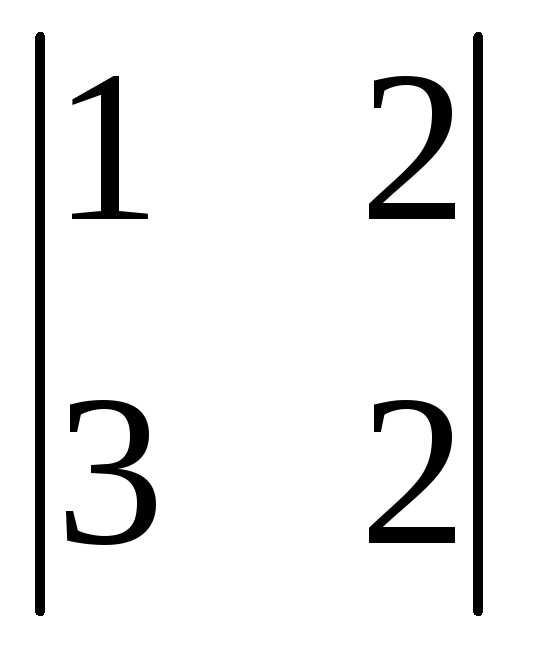 =3(12-4)+0+(2-6)=24-4=20.
=3(12-4)+0+(2-6)=24-4=20.
Т.к.  0,
следовательно, данная матрица имеет
обратную.
0,
следовательно, данная матрица имеет
обратную.
Найдем обратную матрицу с помощью присоединенной матрицы (см. пример 3.1):
А-1= .
.
Подставим в формулу X=A-1B,
получим:X=
 =
=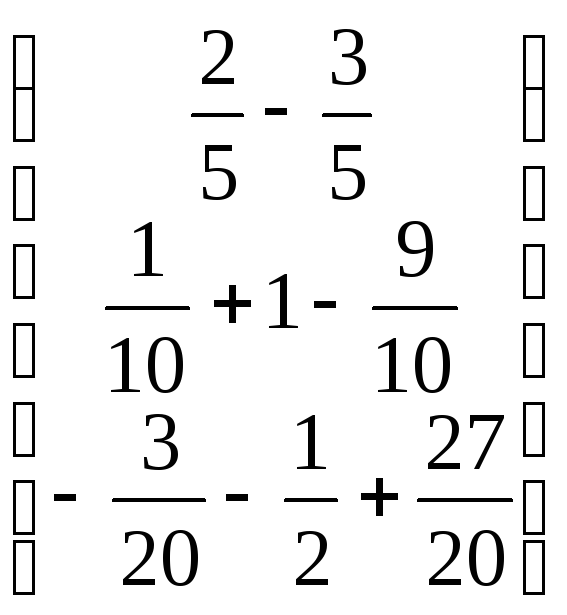 =
=
Ответ:  =
= ,
,  ,
, .
.
Правильность решения легко проверить,
подставив полученные результаты ,
, 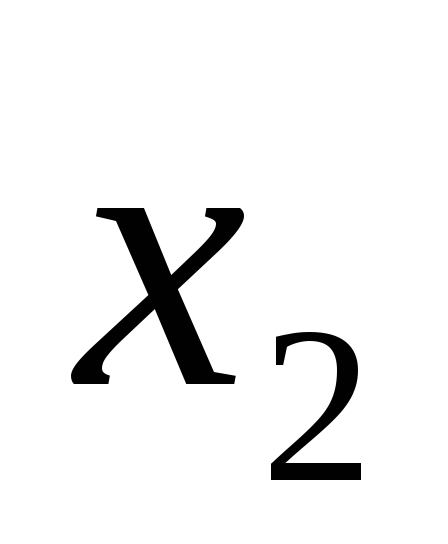 ,
,  в данную систему уравнения.
в данную систему уравнения.
Решение систем линейных уравнений методом Гаусса и Крамера
Пусть дана система линейных уравнений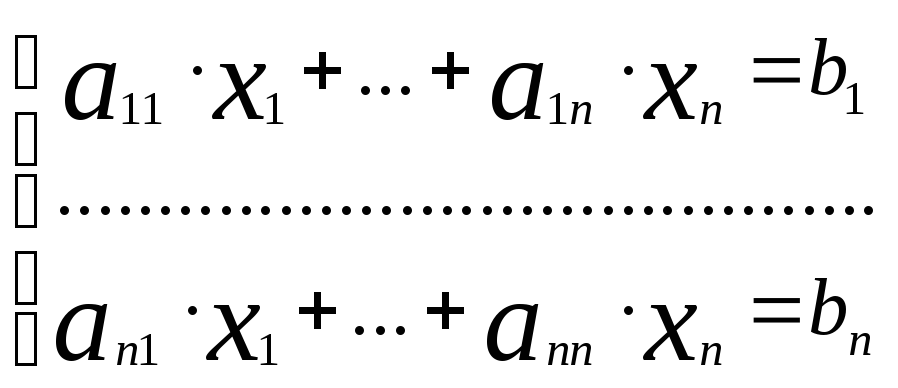 .
Обозначим её через (1). Основная матрица
данной системы: А=
.
Обозначим её через (1). Основная матрица
данной системы: А= ,
вектор-столбец неизвестных:X=
,
вектор-столбец неизвестных:X= и
вектор-столбец свободных членов:B=
и
вектор-столбец свободных членов:B= .
Теперь запишем систему (1) в матричной
форме:AX=B.
.
Теперь запишем систему (1) в матричной
форме:AX=B.
Теорема Крамера. Пусть  —определитель
матрицы А,
—определитель
матрицы А,  j—определитель матрицы, получаемой из А
заменойj-го столбца
столбцом свободных членов. Тогда, если
j—определитель матрицы, получаемой из А
заменойj-го столбца
столбцом свободных членов. Тогда, если
 0,
то система имеет единственное решение:
0,
то система имеет единственное решение: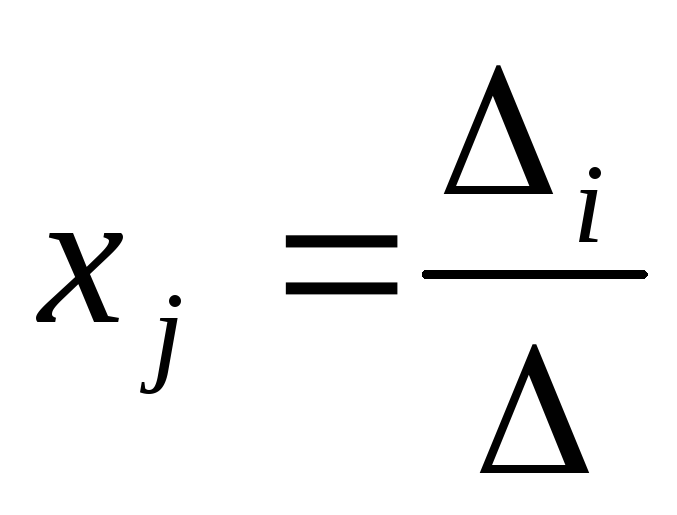 ,
(1jn).
,
(1jn).
Пример 4.1
Решить систему линейных уравнений:  методом Крамера.
методом Крамера.
Решение.
Основная матрица системы А= и вектор-столбец свободных членов:B=
и вектор-столбец свободных членов:B= .
.
Найдем определитель  =
= =3(-1)1+1
=3(-1)1+1 +0(-1)2+1
+0(-1)2+1 +1(-1)3+1
+1(-1)3+1 =3(12-4)+0+(2-6)=24-4=20. Т.к.
=3(12-4)+0+(2-6)=24-4=20. Т.к. 0,
следовательно, можно применить формулы
Крамера.
0,
следовательно, можно применить формулы
Крамера.
Найдем определители  ,
,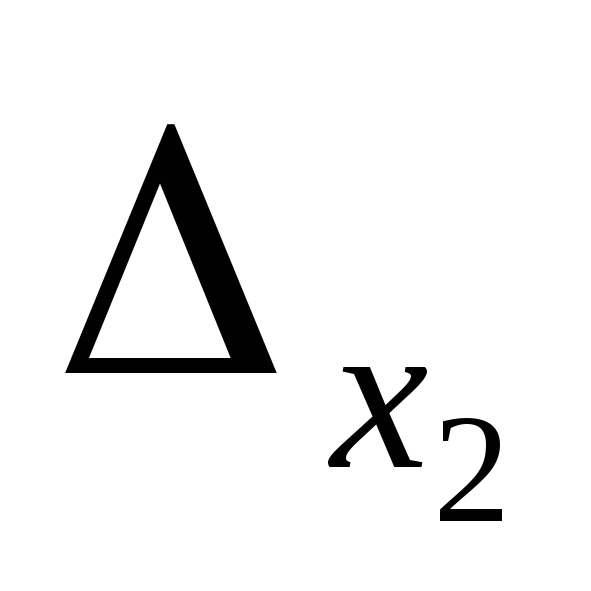 ,
, ,
полученные заменой соответствующих
столбцов столбцом свободных членов:
,
полученные заменой соответствующих
столбцов столбцом свободных членов:
 =
=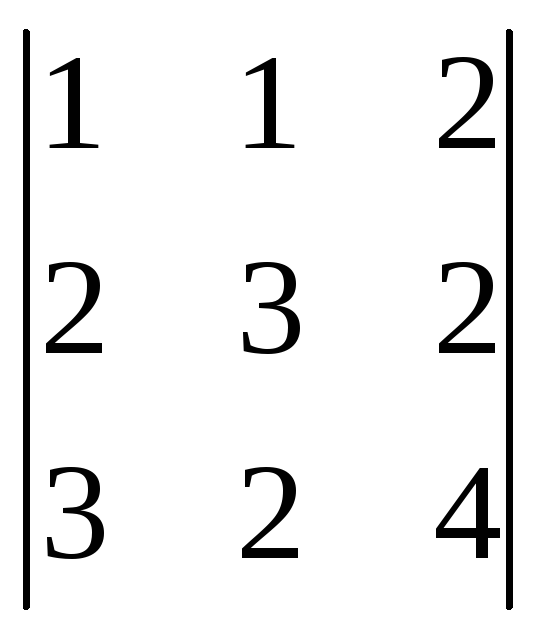 =1(12-4)-1(8-6)+2(4-9)=8-2-10=
-4;
=1(12-4)-1(8-6)+2(4-9)=8-2-10=
-4;
 =
= =3(8-6)-0+1(2-4)=6-2=4;
=3(8-6)-0+1(2-4)=6-2=4;
 =
=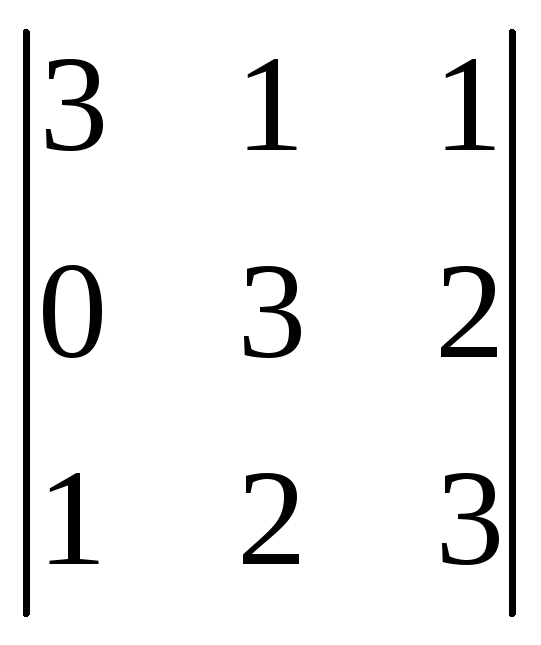 =3(9-4)-0+1(2-3)=15-1=14.
=3(9-4)-0+1(2-3)=15-1=14.
Тогда, по формуле Крамера:
 =
= =
—
=
—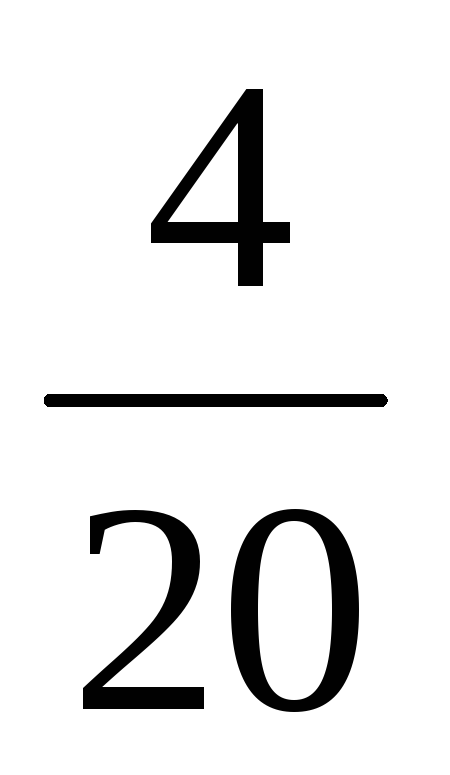 =
= ;
;
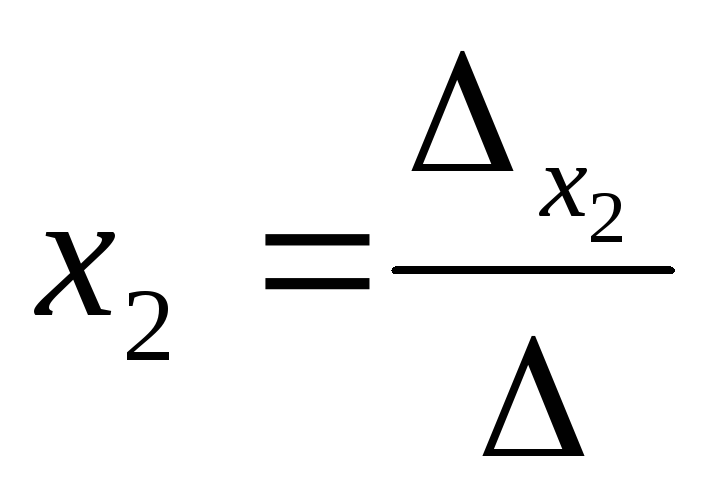 =
= ;
;
 =
= .
.
Ответ:  =
=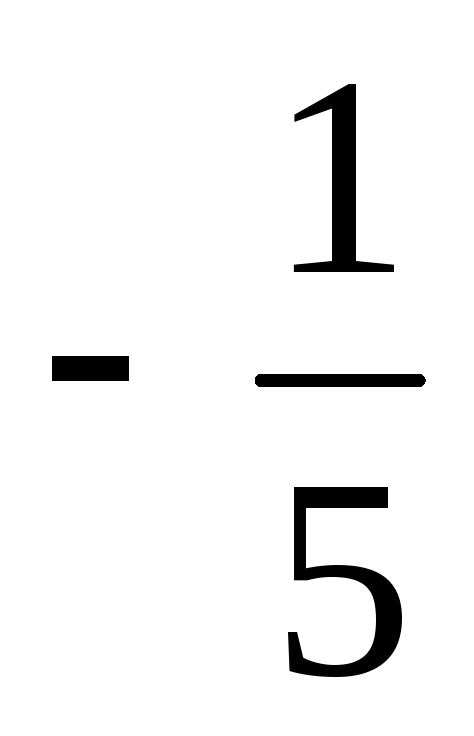 ,
, 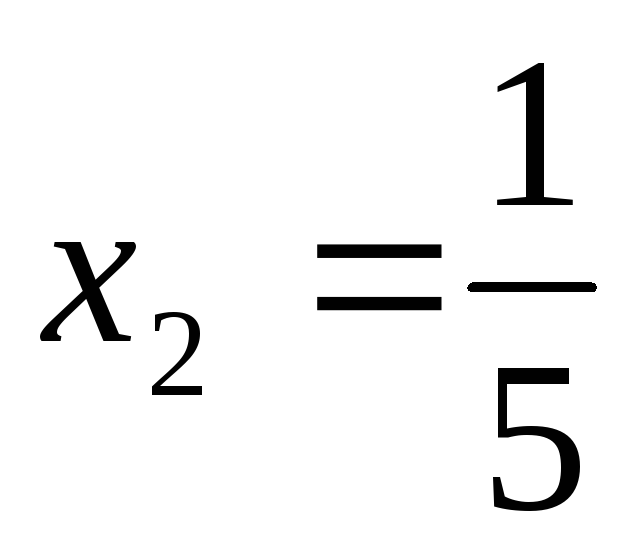 ,
, .
.
Решение систем линейных уравнений методом Гаусса
Пусть дана система линейных уравнений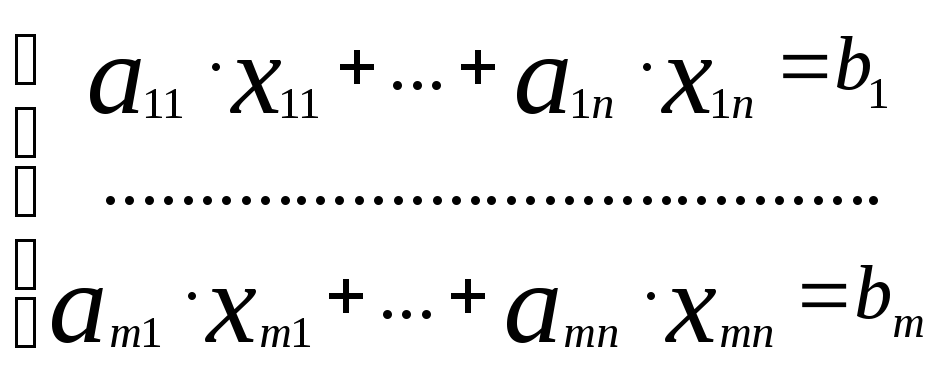 .
Рассмотрим расширенную матрицу (АВ)
данной системы и с помощью элементарных
преобразований приведем её к ступенчатому
виду, в результате получим расширенную
матрицу (АВ).
.
Рассмотрим расширенную матрицу (АВ)
данной системы и с помощью элементарных
преобразований приведем её к ступенчатому
виду, в результате получим расширенную
матрицу (АВ).
Если ранг основной матрицы системы меньше ранга расширенной матрицы r(A)<r(АВ), то система несовместна. Еслиr(A)=r(АВ)=n, гдеn-число неизвестных, то система совместна и определена. Еслиr(A)=r(АВ)<n, гдеn-число неизвестных, то система совместна и неопределенна.
Записываем систему линейных уравнений из полученной ступенчатой матрицы. Определяем базисные и свободные переменные, и выражая базисные переменные через свободные получаем решение системы.
Пример 4.2
Решить систему линейных уравнений:  методом Гаусса.
методом Гаусса.
Решение.


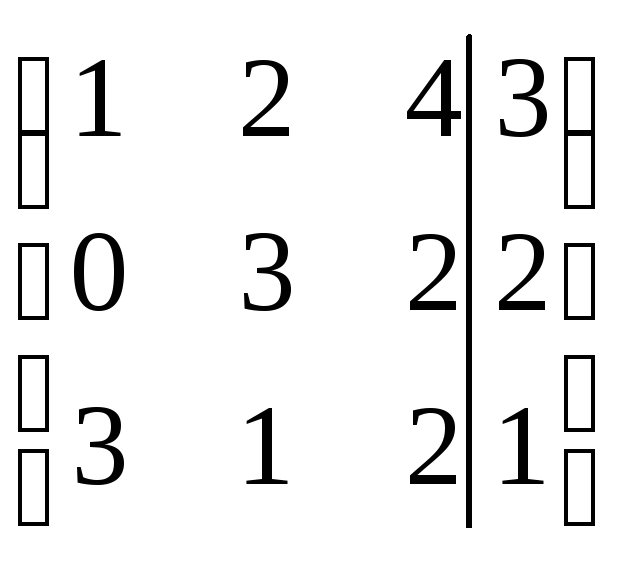
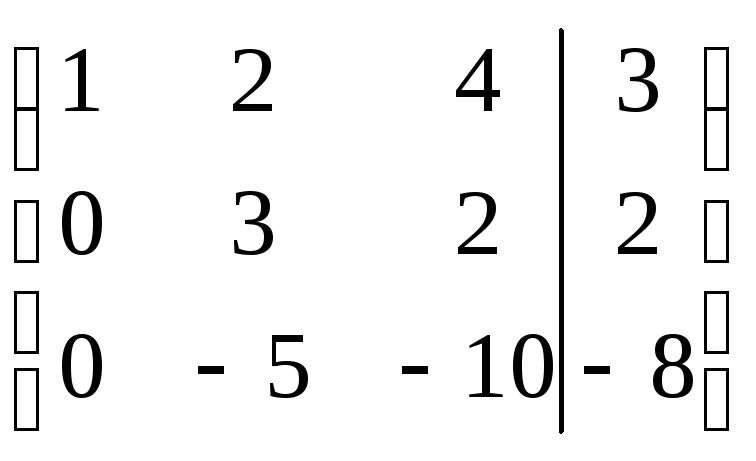

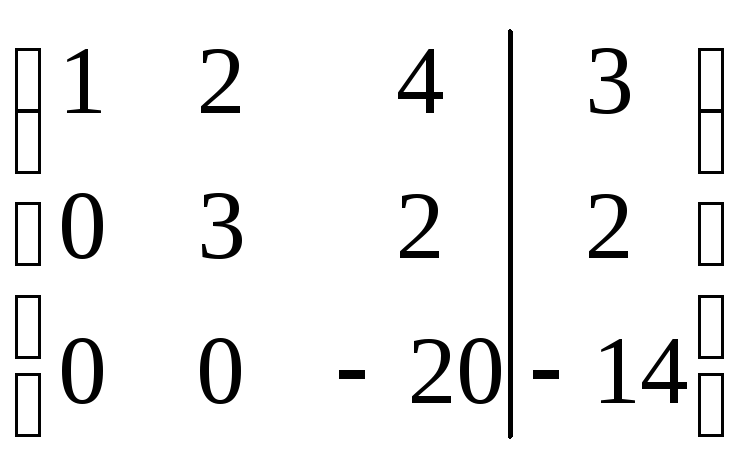
r(A)=r(АВ)=n система совместна и определена.
система совместна и определена.
Отсюда, запишем эквивалентную систему
уравнений, имеем:
Решая её, получаем: 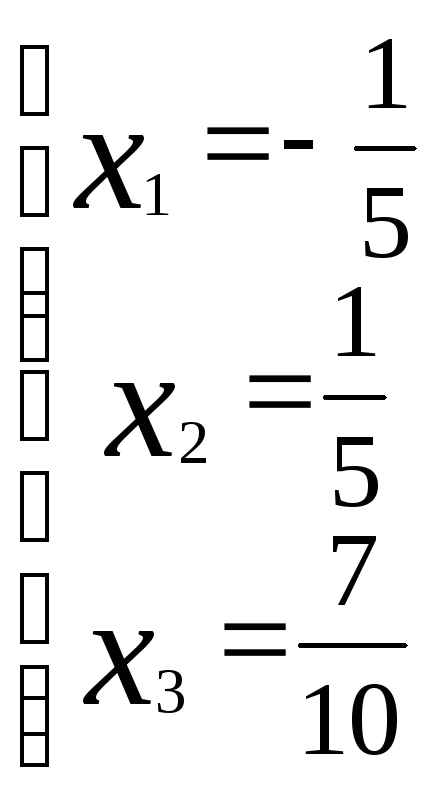
Ответ:  =
= ,
,  ,
, .
.
Пример 4.3
Найти общее решение системы:  .
.
Решение.
Составим матрицу системы: А=
Приведем её к треугольному виду:


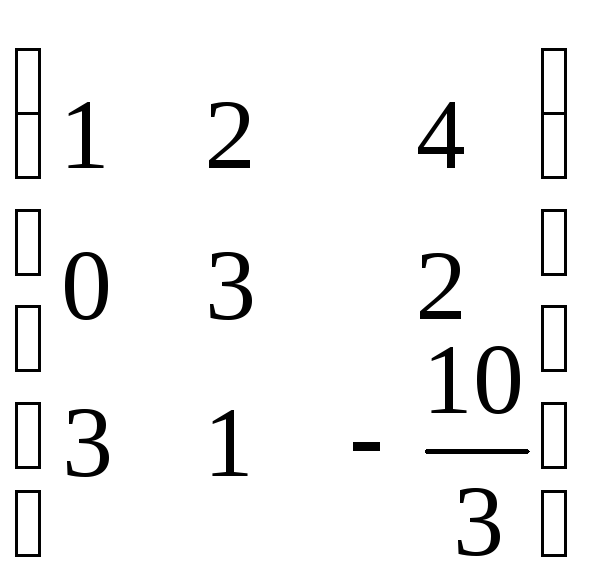


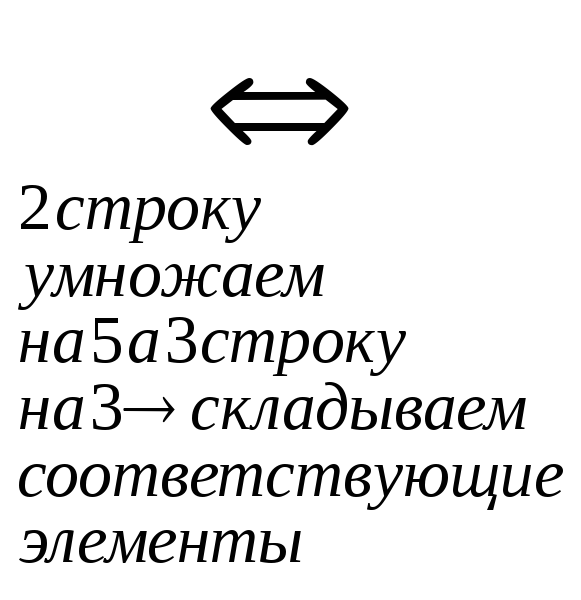

r(A)=2. Запишем
эквивалентную систему уравнений:
Примем за базисные переменные 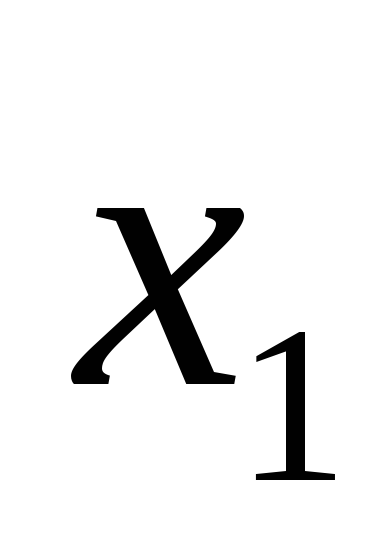 и
и ,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (3-2)=1, т. е. у нас одна свободная
переменная это
,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (3-2)=1, т. е. у нас одна свободная
переменная это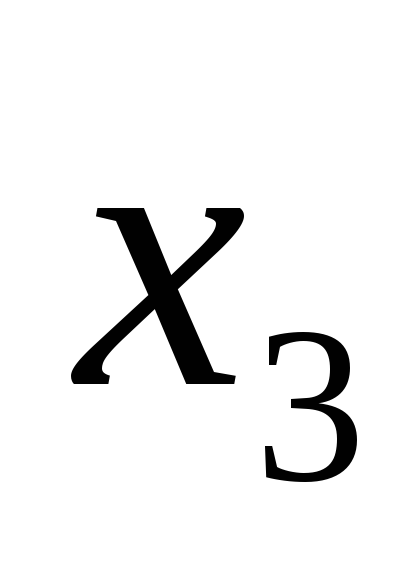 .
.
Выразим базисные переменные через
свободные: 

 .
Обозначая свободную переменную:
.
Обозначая свободную переменную: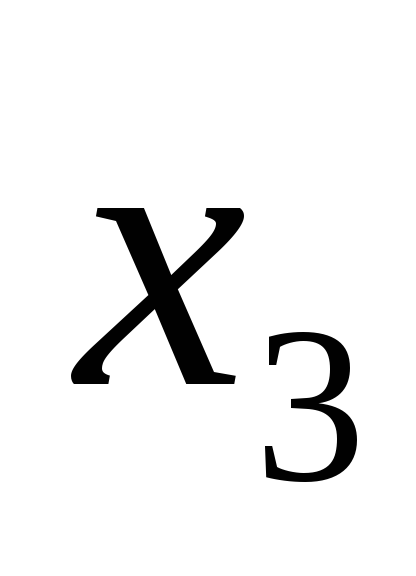 =
= ,
получаем общее решение в виде:
,
получаем общее решение в виде:
Пример 4.4
Найти общее решение системы: 
Решение.
Приведем расширенную матрицу системы к ступенчатому виду:
АВ= 


r(A)=r(AВ)=2<n,
гдеn-число неизвестных,
то система совместная и неопределенная.
Запишем эквивалентную систему уравнений: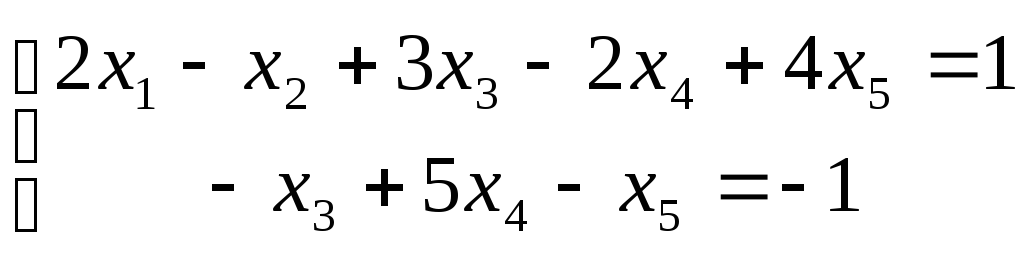
Примем за базисные переменные  и
и ,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (5-2)=3, значит
,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (5-2)=3, значит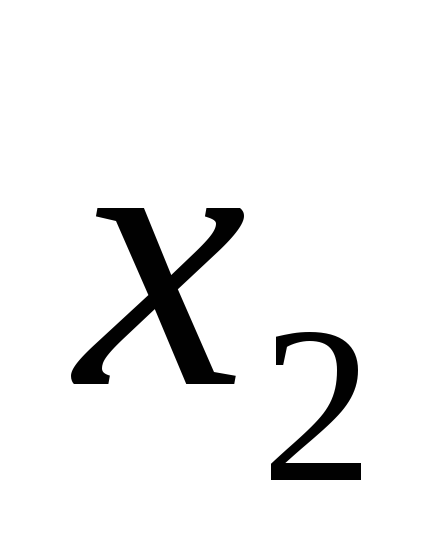 ,
,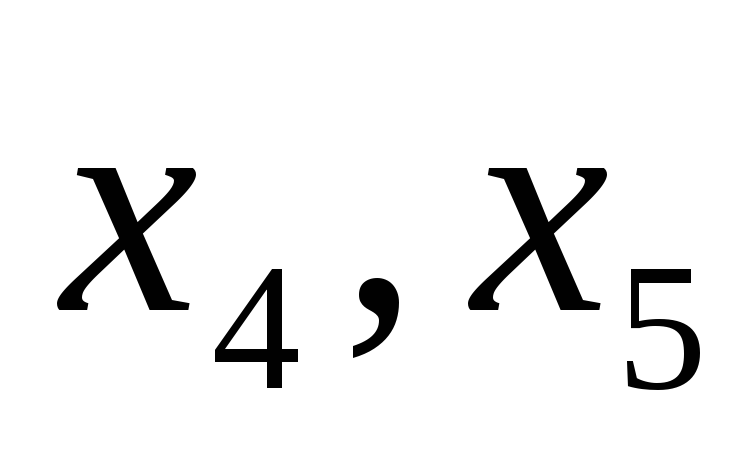 -свободные
переменные.
-свободные
переменные.
Выразим базисные переменные через
свободные:  Обозначая свободную переменную:
Обозначая свободную переменную: =
= ,
, ,
, получаем
общее решение в виде:
получаем
общее решение в виде: .
.
§3. Решение системы линейных уравнений с помощью обратной матрицы
Весьма удобно записывать систему линейных уравнений
 (1)
(1)
в матричной форме, а именно: если А=(аij) – основная матрица системы, а В и X – столбцы свободных членов и неизвестных, то (1) можно записать в виде
A·X=B. (2)
Как и в предыдущем параграфе, предположим, что определитель системы Δ≠0. Отсюда вытекает, что основная матрица системы имеет обратную А—1. Умножим обе части матричного равенства (2) на матрицу А—1. Используя ассоциативность умножения матриц и роль единичной матрицы, как единицы при умножении матриц, будем иметь:
A—1(AX)= A—1B,
(A—1A)X= A—1B,
EX= A—1B,
X= A—1B. (3)
Последнее равенство и дает выражение столбца неизвестных через обратную матрицу и столбец свободных членов. Вспомним вид обратной матрицы
A—1=(Аji/Δ) и приравняем j—е элементы столбцов, стоящих в левой и правой частях (3):
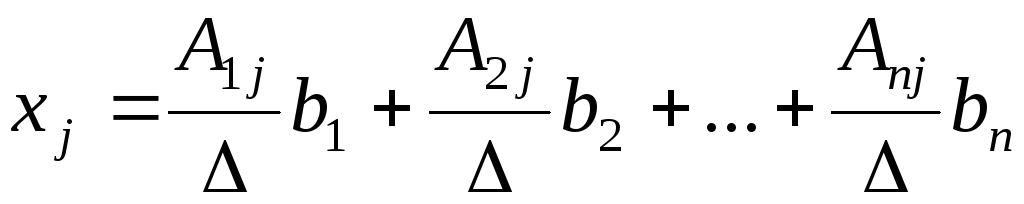
или
 .
.
Выражение, стоящее в скобках, есть не что иное, как разложение определителя Δj (из предыдущего параграфа) по j—му столбцу. Поэтому (3) равносильно
 ,
,
и мы снова пришли к формулам Крамера.
Итак, если определитель Δ основной матрицы А системы линейных уравнений отличен от нуля, то существует и притом единственное решение матричного уравнения
АХ=В,
определяемое соотношением
Х=А-1В,
которое эквивалентно формулам Крамера.
§4. Решение системы линейных уравнений методом Гаусса
Вначале одно предварительное замечание. Применяя метод Гаусса, приходится выполнять такие преобразования системы: 1) переставлять местами два уравнения; 2) умножать обе части какого-нибудь уравнения системы на одно и то же число, отличное от нуля; 3) обе части одного из уравнений системы, умноженные на одно и то же число, вычитать из соответствующих частей некоторого другого уравнения системы. Нетрудно показать, что система, полученная в результате этих преобразований, будет эквивалентна исходной.
Перейдем теперь к изложению методом Гаусса, который называется также методом последовательного исключения неизвестных.
Пусть дана произвольная система линейных уравнений
 (1)
(1)
Предположим, что а11≠0 (в противном случае пришлось бы переставить два уравнения: ведь какой-нибудь из коэффициентов при x1 отличен от 0). С помощью 1-го уравнения исключим неизвестное x1 из всех уравнений системы, начиная со второго. Для этого вычтем из i—го уравнения первое уравнение, умноженное на аі1/a11 , i=2,3,…,m. В результате придем к новой системе, эквивалентной исходной:
 (2)
(2)
Далее будем
преобразовывать систему (2), причем 1-е
уравнение мы не будем трогать совсем и
подлежащей преобразованиям будем
считать лишь часть этой системы, состоящую
из всех уравнений, кроме первого. При
этом мы считаем, что среди этих уравнений
нет таких, все коэффициенты левых частей
которых равны нулю: такие уравнения мы
выбросили бы, если бы и их свободные
члены были равны нулю, а в противном
случае мы уже доказали бы несовместимость
нашей системы. Таким образом, среди
коэффициентов  есть
отличные от нуля; для определенности
примем, что
есть
отличные от нуля; для определенности
примем, что (в противном случае пришлось бы
переставлять уравнения или неизвестные).
С помощью 2-го уравнения системы (2)
исключим неизвестноеx2 из всех уравнений системы (2), начиная с
третьего. Для этого вычтем из j—го
уравнения второе, умноженное на
(в противном случае пришлось бы
переставлять уравнения или неизвестные).
С помощью 2-го уравнения системы (2)
исключим неизвестноеx2 из всех уравнений системы (2), начиная с
третьего. Для этого вычтем из j—го
уравнения второе, умноженное на  .
Придем к следующей системе, эквивалентной
системе (2), а значит (1):
.
Придем к следующей системе, эквивалентной
системе (2), а значит (1):
 (3)
(3)
Наша система содержит теперь p уравнений, p≤m, так как некоторые уравнения оказались, возможно, отброшенными. В дальнейшем подлежит преобразованиям, аналогично уже поделанным, часть полученной системы, содержащей все уравнения, кроме двух первых.
Когда остановится этот процесс последовательного исключения неизвестных?
Если мы придем к такой системе, одно из уравнений которой имеет отличный от нуля свободный член, а все коэффициенты левой части равны нулю, то, как мы знаем, наша исходная система несовместна.
Если же таких уравнений не встретится, то процесс исключения закончится не позже чем на (m–1)—ом шаге. Обозначим через k – число уравнений, которые останутся в системе после завершения процесса исключения неизвестных. Возможны случаи: k=n, k<n, k>n.
В случае, когда k=n получим так называемую “треугольную” систему
 (4)
(4)
у которой в каждом последующем уравнении ровно на одно неизвестное меньше, чем в предыдущем. Из последнего уравнения мы получаем вполне определенное значение для неизвестного xn. Подставив его в предпоследнее уравнение, мы найдем однозначно определенное значение для неизвестного xn—1. Продолжая так далее, мы найдем, что система (4), а поэтому и система (1) обладают единственным решением, т.е. совместна и определена.
Пусть теперь k<n. Система, полученная после завершения процесса исключения, имеет так называемую “трапецеидальную” форму:
 (5)
(5)
Назовем неизвестные xk+1, xk+2,…,xn свободными, придадим им произвольные числовые значения и перенесем члены, содержащие их, в правые части уравнений. Мы получим систему “треугольной” формы (4), из которой однозначно определяется неизвестные x1, x2,…,xk. Так как значения для свободных неизвестных можно выбирать бесконечным числом различных способов, то наша система (5) и, следовательно, система (1) будут совместными, но неопределенными. Легко проверить, что указанным здесь методом будут найдены все решения системы (1).
Третий случай,
когда k>n кажется возможным лишь первый момент.
Система имеет вид, получающийся
приписыванием к системе (4) еще нескольких
уравнений, содержащих лишь неизвестное xn.
В действительности, однако, в этом случае
преобразования просто не доведены до
конца: так как  ,
то из всех уравнений, начиная с (n+1)—го,
неизвестное xn может быть исключено.
,
то из всех уравнений, начиная с (n+1)—го,
неизвестное xn может быть исключено.
Итак, подведем итоги. Метод Гаусса применим к любой системе линейных уравнений. При этом система будет несовместной, если в процессе исключения неизвестных мы получим уравнение, в котором коэффициенты при всех неизвестных равны нулю, а свободный член отличен от нуля; Если же такого уравнения мы не встретим, то система будет совместной. Совместная система будет определенной, если приводится к треугольному виду (4) (число оставшихся уравнений равно числу неизвестных), и неопределенной, если приводится к трапецеидальному виду (5) (число оставшихся уравнений меньше числа неизвестных).
Замечание. При практическом применении метода Гаусса следует выписать основную матрицу системы и, приписав к ней столбец свободных членов, получить так называемую расширенную матрицу системы. Все преобразования выполняют над строками этой матрицы. Для удобства столбец свободных членов можно отделить вертикальной чертой от остальных столбцов матрицы.
Пример. Решить систему
Решение. Подвергаем преобразованиям расширенную матрицу этой системы.






Краткие пояснения. 1-й шаг: первую строку вычитаем из третьей. 2-й шаг: вторую строку умножаем на 5 и вычитаем из третьей, а также умножаем на 7 и прибавляем к четвертой. 3-й шаг: третью строку умножаем на 2 и прибавляем к четвертой. 4-й шаг: отбрасываем четвертую строку, сплошь состоящую из нулей, и делим третью строку на 2. Мыприходим, следовательно, к системе:

В качестве свободного неизвестного можно принять любое из неизвестных х3 или х4. Пусть х4=α. Тогда из 3-го уравнения х3=6+2α, из 2-го получаем х2=3+α, а из первого х1= –8. Итак, общий вид решения заданной системы:
(–8; 3+α; 6+2α; α), где α – произвольное число.
Обратная матрица. Вычисление обратной матрицы методом присоединённой матрицы. Решение систем линейных уравнений методом обратной матрицы.
Определение. Матрица А-1называется обратной к матрице А, если выполняется условие: АА-1= А-1А=Е, где Е — единичная матрица того же порядка, что и матрица А. Обратная А-1матрица имеет ту же размерность, что и матрица А.
Определение. Квадратная матрица
А= называется невырожденной, если её
определитель неравен нулю, в противном
случае матрица называется вырожденной.
называется невырожденной, если её
определитель неравен нулю, в противном
случае матрица называется вырожденной.
Теорема.Всякая невырожденная матрица имеет обратную.
Определение. Присоединенной матрицей к матрице А называется матрица вида:
к матрице А называется матрица вида:
 =
=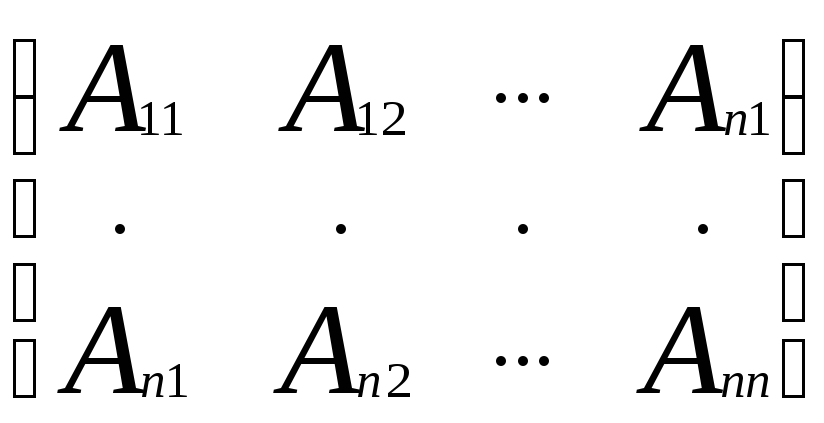 ,
где Аij-алгебраическое
дополнение элемента аij.
,
где Аij-алгебраическое
дополнение элемента аij.
Находят обратную матрицу поформуле:
А-1=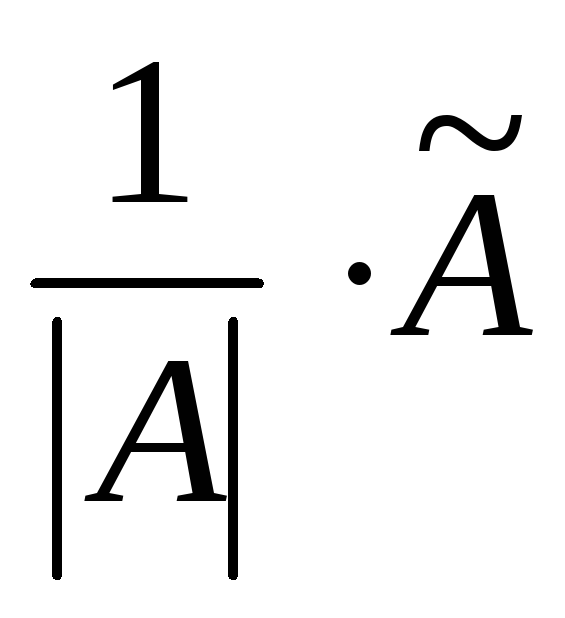 .
.
Пример 3.1
Найти обратную матрицу методом присоединенной матрицы.
А=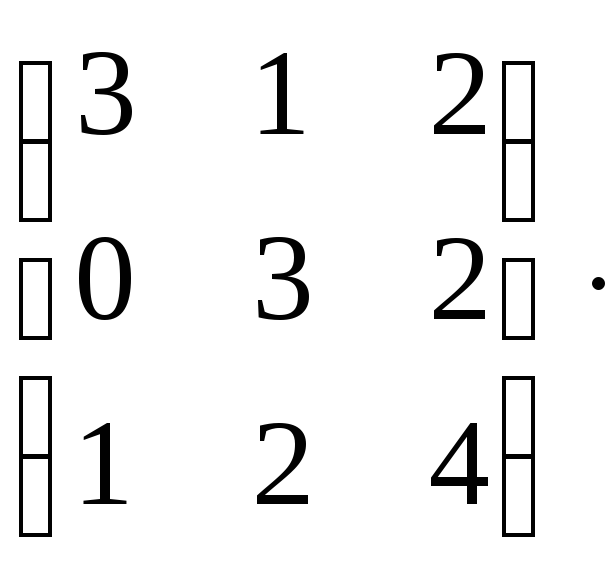
Решение.
Выясним, является ли данная матрица невырожденной. Для этого найдем определитель матрицы:
 =3(-1)1+1
=3(-1)1+1 +0(-1)2+1
+0(-1)2+1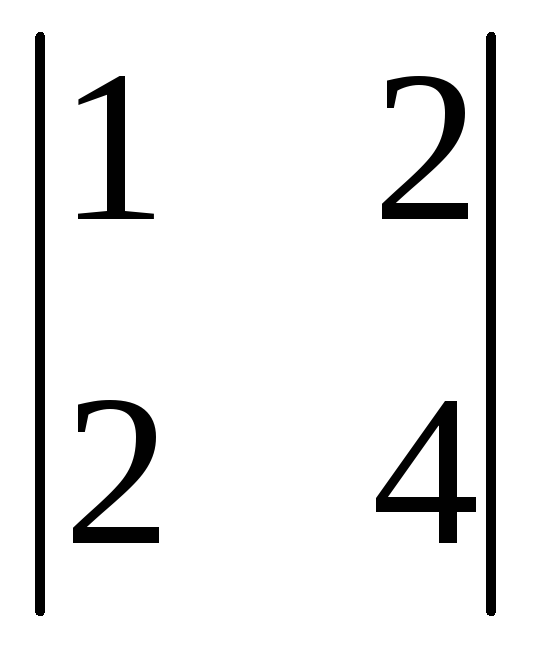 +1(-1)3+1
+1(-1)3+1 =3(12-4)+0+(2-6)=24-4=20.
=3(12-4)+0+(2-6)=24-4=20.
Т.к.  0,
следовательно, данная матрица имеет
обратную.
0,
следовательно, данная матрица имеет
обратную.
Найдем транспонированную матрицу.
АТ=
Вычислим присоединенную матрицу. Для этого найдем алгебраическое дополнение каждого элемента матрицы.
 =
(-1)1+1
=
(-1)1+1 =12-4=8
=12-4=8
 =
(-1)1+2
=
(-1)1+2 =
-(4-4)= 0
=
-(4-4)= 0
 =
(-1)1+3
=
(-1)1+3 =
2-6= -4
=
2-6= -4
 =
(-1)2+1
=
(-1)2+1 =
-(0-2)=2
=
-(0-2)=2
 =
(-1)2+2
=
(-1)2+2 =
12-2=10
=
12-2=10
 =
(-1)2+3
=
(-1)2+3 =
-(6-0)= -6
=
-(6-0)= -6
 =
(-1)3+1
=
(-1)3+1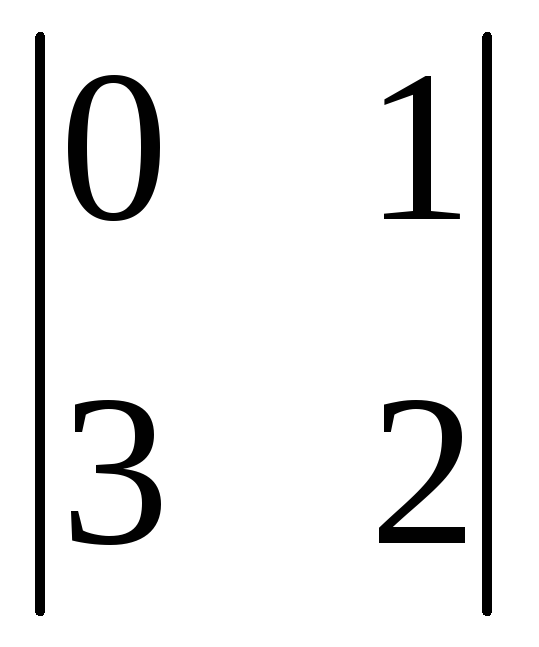 =
0-3= -3
=
0-3= -3
 =
(-1)3+2
=
(-1)3+2 =
-(6-1)= -5
=
-(6-1)= -5
 =
(-1)3+3=
9-0=9.
=
(-1)3+3=
9-0=9.
 =
=
4. Воспользуемся формулой: А-1= .
.
А-1=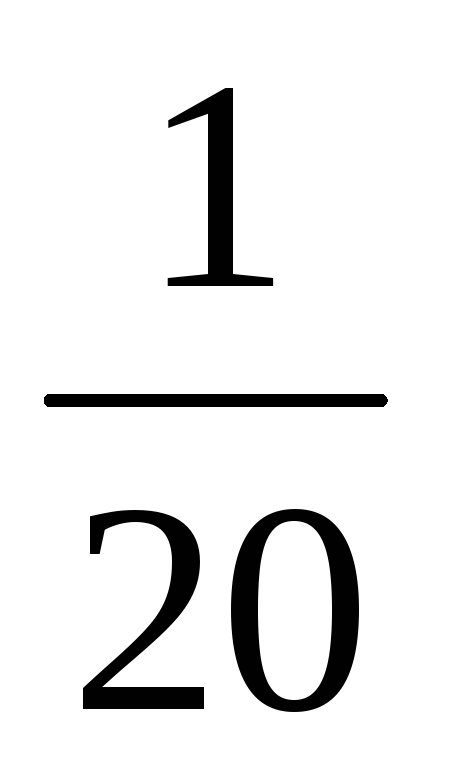
 =
= .
.
Решение систем линейных уравнений методом обратной матрицы
Пусть дана система линейных уравнений .
Обозначим её через (1). Выпишим основную
матрицу данной системы: А=
.
Обозначим её через (1). Выпишим основную
матрицу данной системы: А=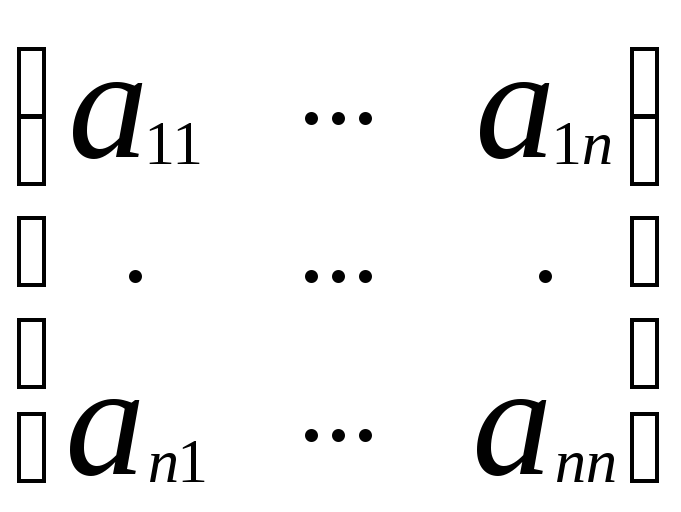 ,
вектор-столбец неизвестных:X=
,
вектор-столбец неизвестных:X= и
вектор-столбец свободных членов:B=
и
вектор-столбец свободных членов:B= .
Теперь перепишем систему (1) в матричной
форме:AX=B
.
Теперь перепишем систему (1) в матричной
форме:AX=B X=A-1B-
решение системы (1).
X=A-1B-
решение системы (1).
Пример 3.2
Решить систему линейных уравнений:  методом обратной матрицы.
методом обратной матрицы.
Решение.
Формула, по которой будем находить решение системы: X=A-1B.
Основная матрица системы А= ,
вектор-столбец неизвестных:X=
,
вектор-столбец неизвестных:X=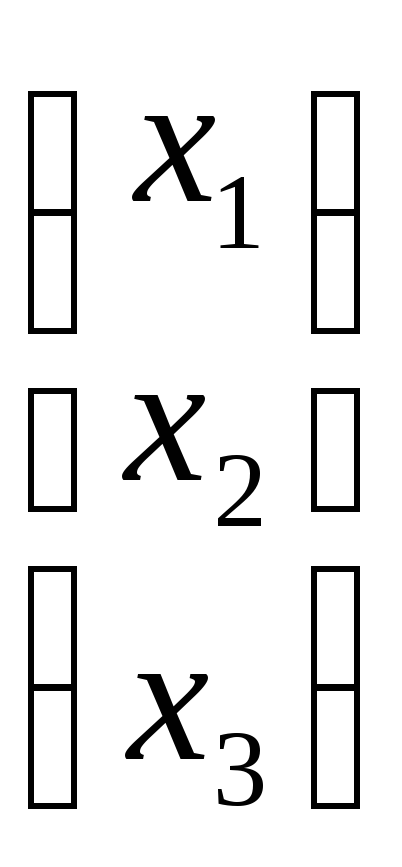
 и
вектор-столбец свободных членов:B=
и
вектор-столбец свободных членов:B= .
.
Найдем определитель  =3(-1)1+1
=3(-1)1+1 +0(-1)2+1
+0(-1)2+1 +1(-1)3+1
+1(-1)3+1 =3(12-4)+0+(2-6)=24-4=20.
=3(12-4)+0+(2-6)=24-4=20.
Т.к.  0,
следовательно, данная матрица имеет
обратную.
0,
следовательно, данная матрица имеет
обратную.
Найдем обратную матрицу с помощью присоединенной матрицы (см. пример 3.1):
А-1= .
.
Подставим в формулу X=A-1B,
получим:X=
 =
=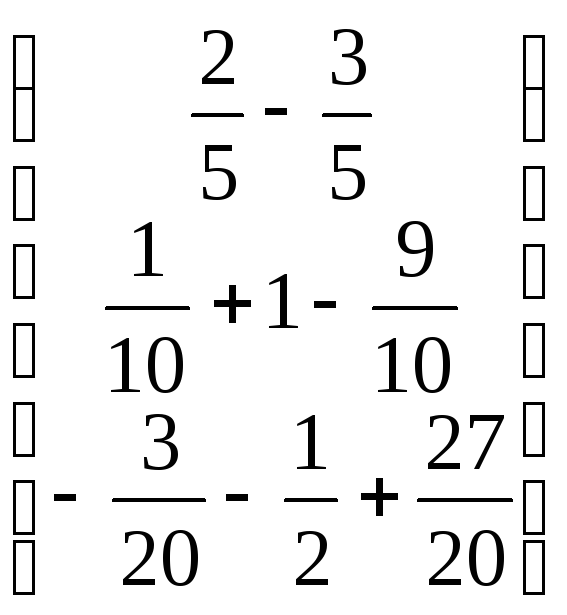 =
=
Ответ:  =
=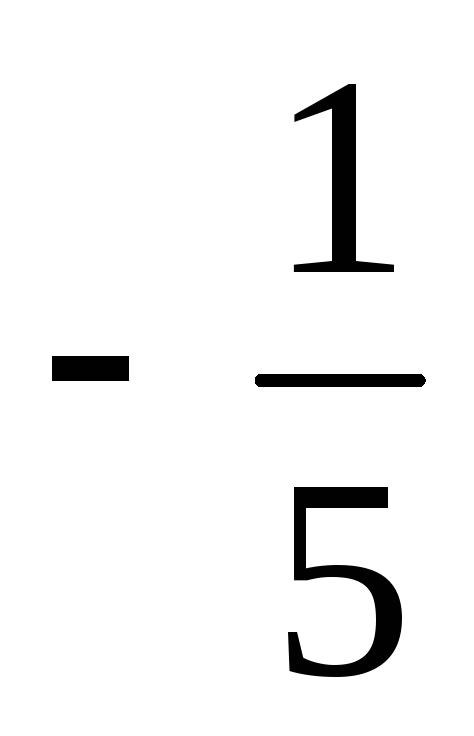 ,
,  ,
, .
.
Правильность решения легко проверить,
подставив полученные результаты ,
,  ,
,  в данную систему уравнения.
в данную систему уравнения.
Решение систем линейных уравнений методом Гаусса и Крамера
Пусть дана система линейных уравнений .
Обозначим её через (1). Основная матрица
данной системы: А=
.
Обозначим её через (1). Основная матрица
данной системы: А=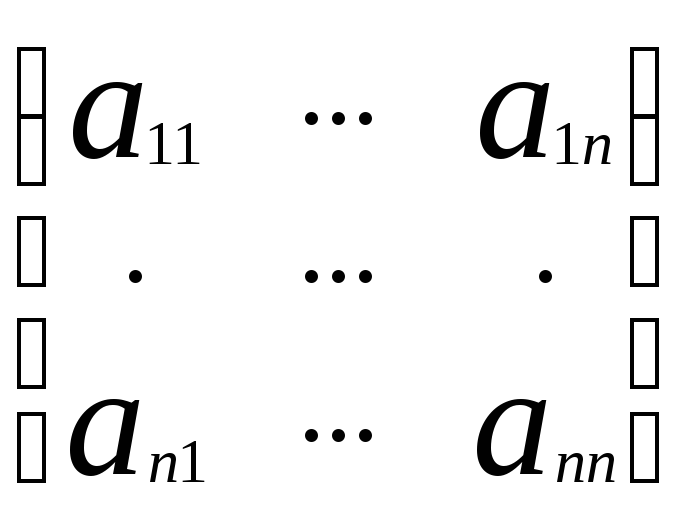 ,
вектор-столбец неизвестных:X=
,
вектор-столбец неизвестных:X= и
вектор-столбец свободных членов:B=
и
вектор-столбец свободных членов:B= .
Теперь запишем систему (1) в матричной
форме:AX=B.
.
Теперь запишем систему (1) в матричной
форме:AX=B.
Теорема Крамера. Пусть  —определитель
матрицы А,
—определитель
матрицы А,  j—определитель матрицы, получаемой из А
заменойj-го столбца
столбцом свободных членов. Тогда, если
j—определитель матрицы, получаемой из А
заменойj-го столбца
столбцом свободных членов. Тогда, если
 0,
то система имеет единственное решение:
0,
то система имеет единственное решение: ,
(1jn).
,
(1jn).
Пример 4.1
Решить систему линейных уравнений:  методом Крамера.
методом Крамера.
Решение.
Основная матрица системы А=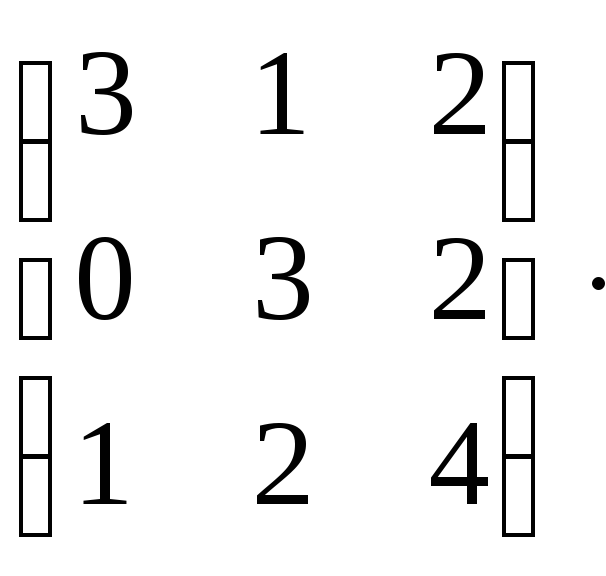 и вектор-столбец свободных членов:B=
и вектор-столбец свободных членов:B= .
.
Найдем определитель  =
= =3(-1)1+1
=3(-1)1+1 +0(-1)2+1
+0(-1)2+1 +1(-1)3+1
+1(-1)3+1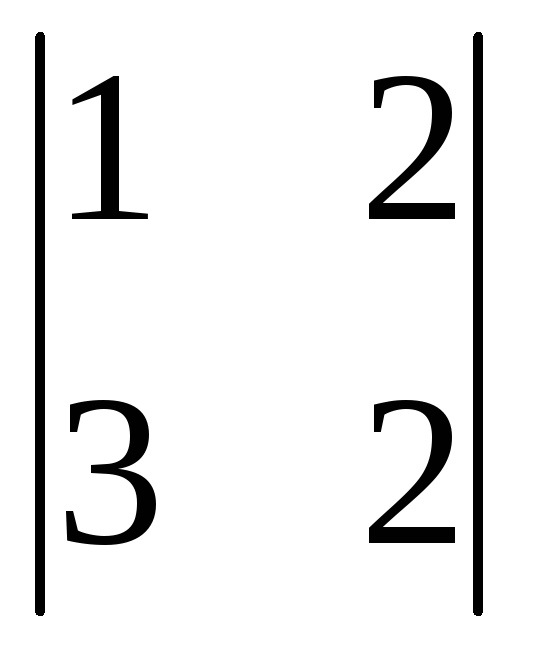 =3(12-4)+0+(2-6)=24-4=20. Т.к.
=3(12-4)+0+(2-6)=24-4=20. Т.к. 0,
следовательно, можно применить формулы
Крамера.
0,
следовательно, можно применить формулы
Крамера.
Найдем определители  ,
, ,
,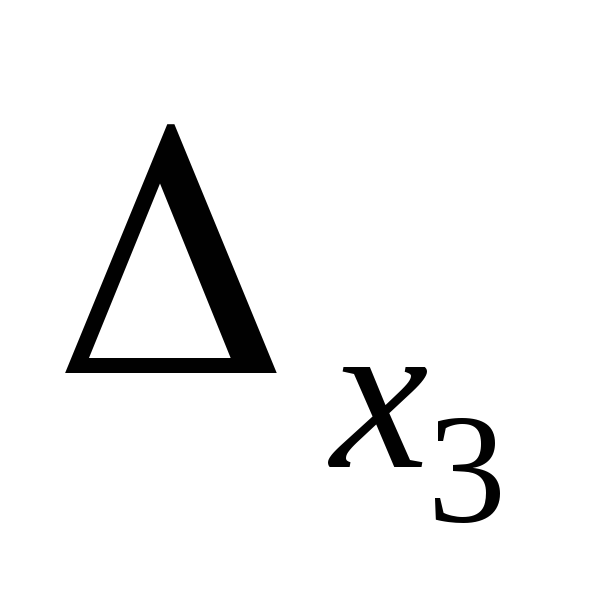 ,
полученные заменой соответствующих
столбцов столбцом свободных членов:
,
полученные заменой соответствующих
столбцов столбцом свободных членов:
 =
= =1(12-4)-1(8-6)+2(4-9)=8-2-10=
-4;
=1(12-4)-1(8-6)+2(4-9)=8-2-10=
-4;
 =
= =3(8-6)-0+1(2-4)=6-2=4;
=3(8-6)-0+1(2-4)=6-2=4;
 =
= =3(9-4)-0+1(2-3)=15-1=14.
=3(9-4)-0+1(2-3)=15-1=14.
Тогда, по формуле Крамера:
 =
= =
—
=
— =
= ;
;
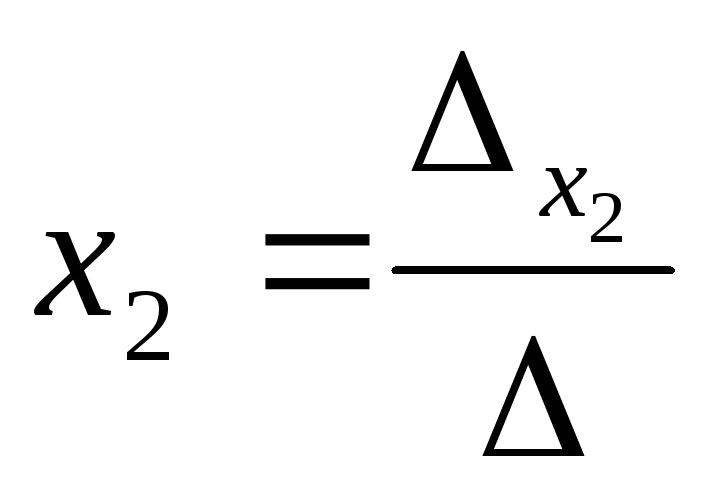 =
=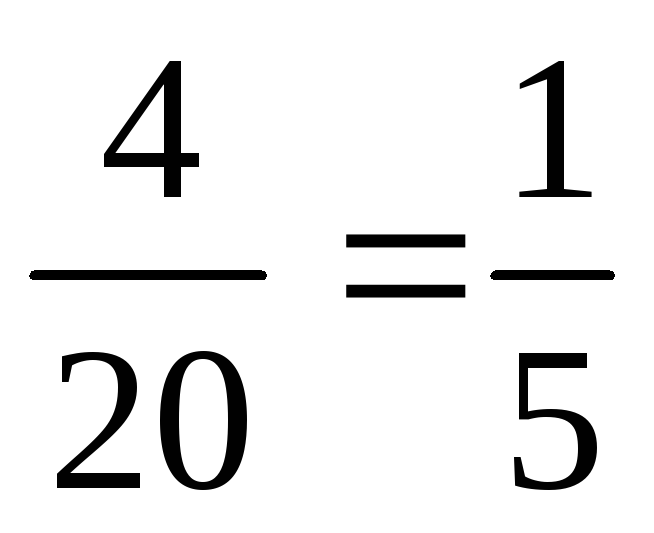 ;
;
 =
=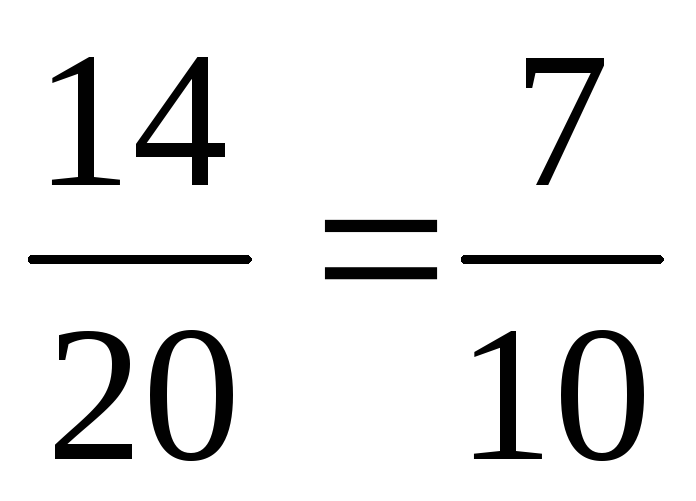 .
.
Ответ:  =
= ,
,  ,
, .
.
Решение систем линейных уравнений методом Гаусса
Пусть дана система линейных уравнений .
Рассмотрим расширенную матрицу (АВ)
данной системы и с помощью элементарных
преобразований приведем её к ступенчатому
виду, в результате получим расширенную
матрицу (АВ).
.
Рассмотрим расширенную матрицу (АВ)
данной системы и с помощью элементарных
преобразований приведем её к ступенчатому
виду, в результате получим расширенную
матрицу (АВ).
Если ранг основной матрицы системы меньше ранга расширенной матрицы r(A)<r(АВ), то система несовместна. Еслиr(A)=r(АВ)=n, гдеn-число неизвестных, то система совместна и определена. Еслиr(A)=r(АВ)<n, гдеn-число неизвестных, то система совместна и неопределенна.
Записываем систему линейных уравнений из полученной ступенчатой матрицы. Определяем базисные и свободные переменные, и выражая базисные переменные через свободные получаем решение системы.
Пример 4.2
Решить систему линейных уравнений:  методом Гаусса.
методом Гаусса.
Решение.



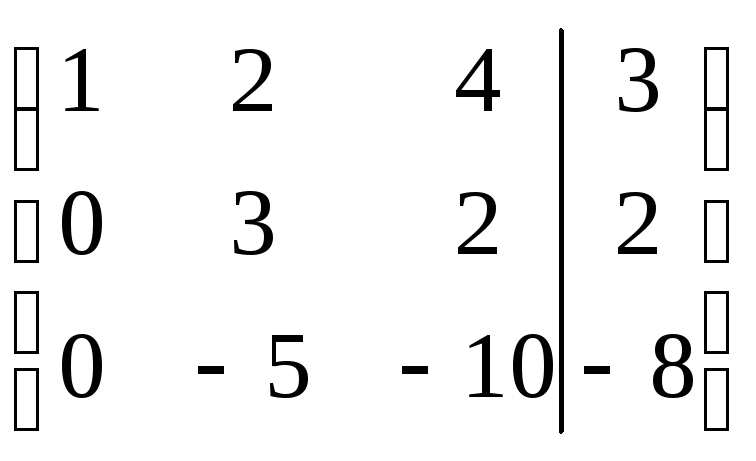


r(A)=r(АВ)=n система совместна и определена.
система совместна и определена.
Отсюда, запишем эквивалентную систему
уравнений, имеем: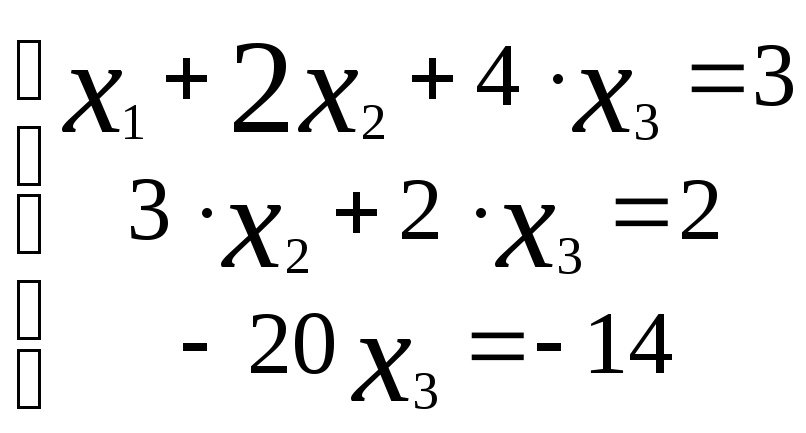
Решая её, получаем: 
Ответ:  =
= ,
, 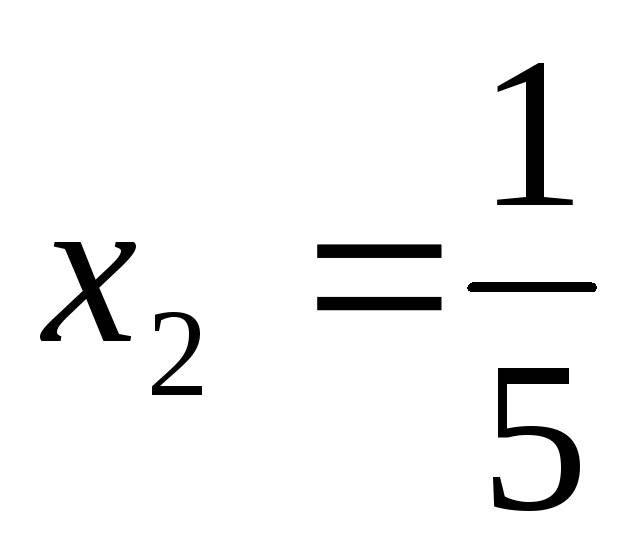 ,
, .
.
Пример 4.3
Найти общее решение системы:  .
.
Решение.
Составим матрицу системы: А=
Приведем её к треугольному виду:


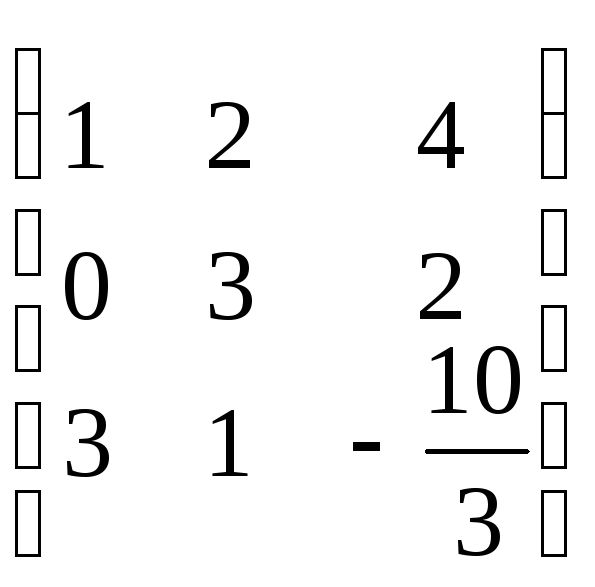


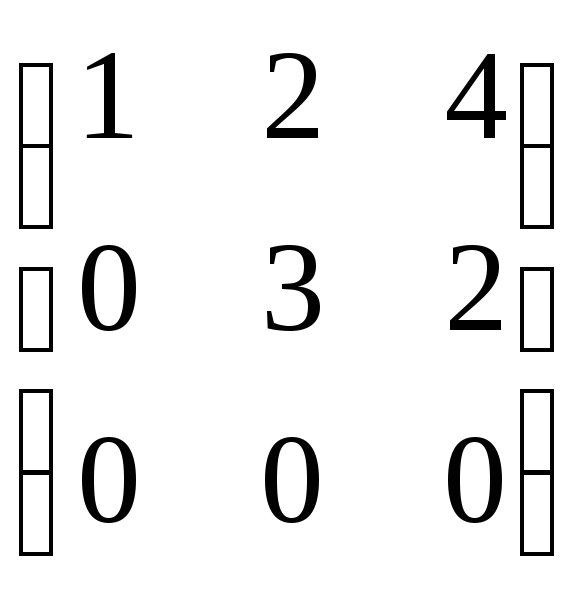
r(A)=2. Запишем
эквивалентную систему уравнений: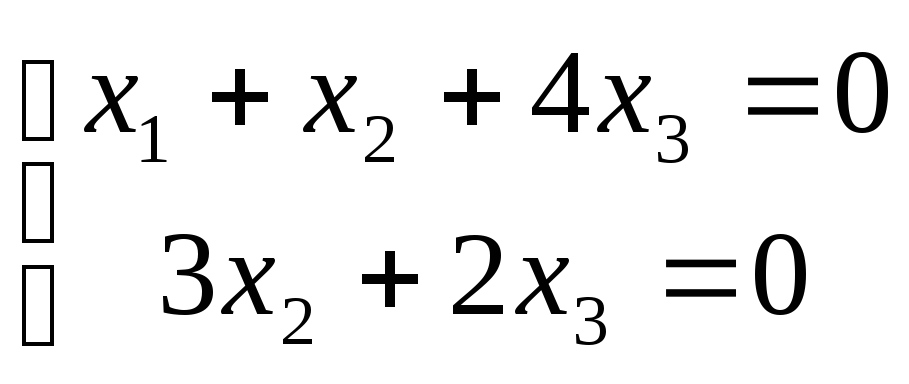
Примем за базисные переменные 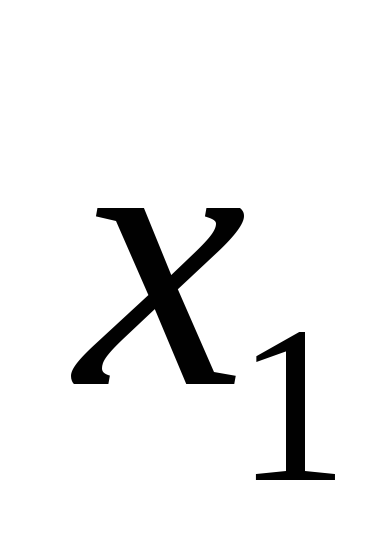 и
и ,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (3-2)=1, т. е. у нас одна свободная
переменная это
,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (3-2)=1, т. е. у нас одна свободная
переменная это .
.
Выразим базисные переменные через
свободные: 

 .
Обозначая свободную переменную:
.
Обозначая свободную переменную: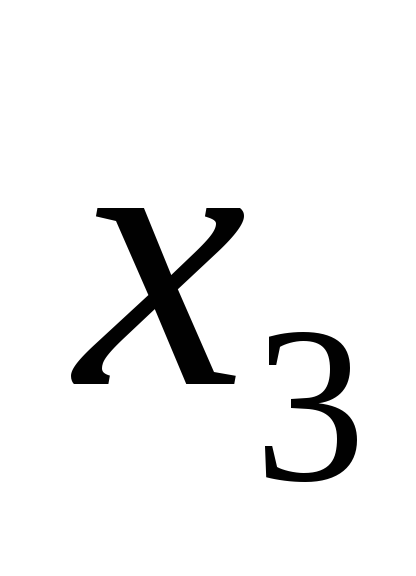 =
= ,
получаем общее решение в виде:
,
получаем общее решение в виде:
Пример 4.4
Найти общее решение системы: 
Решение.
Приведем расширенную матрицу системы к ступенчатому виду:
АВ= 


r(A)=r(AВ)=2<n,
гдеn-число неизвестных,
то система совместная и неопределенная.
Запишем эквивалентную систему уравнений:
Примем за базисные переменные  и
и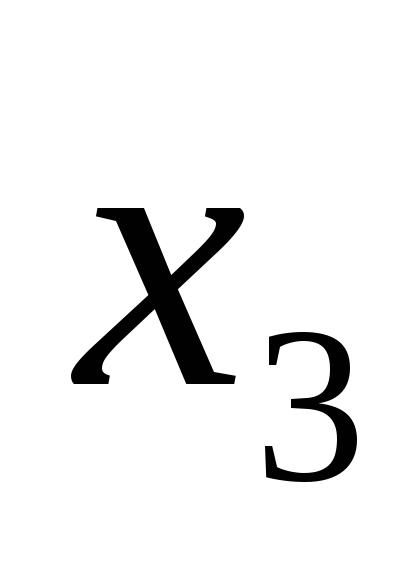 ,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (5-2)=3, значит
,
а свободные находим из условия (n-r),
гдеn-число неизвестных,
получаем (5-2)=3, значит ,
, -свободные
переменные.
-свободные
переменные.
Выразим базисные переменные через
свободные:  Обозначая свободную переменную:
Обозначая свободную переменную: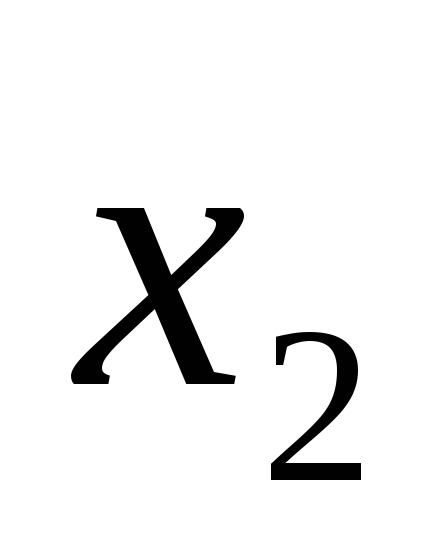 =
= ,
,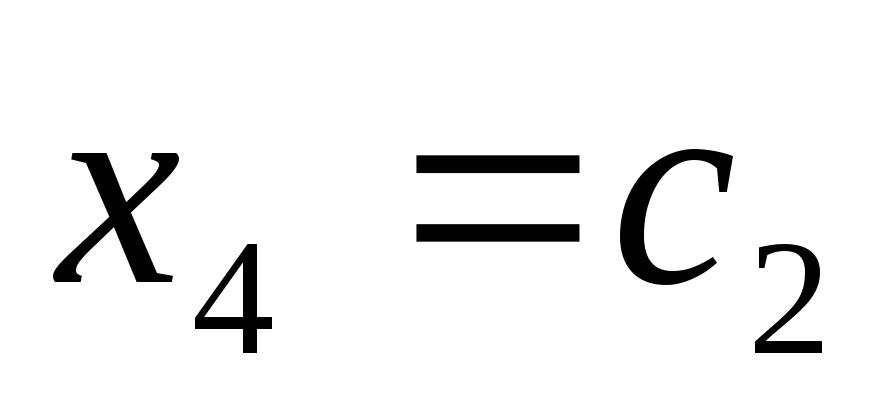 ,
, получаем
общее решение в виде:
получаем
общее решение в виде: .
.
§3. Решение системы линейных уравнений с помощью обратной матрицы
Весьма удобно записывать систему линейных уравнений
 (1)
(1)
в матричной форме, а именно: если А=(аij) – основная матрица системы, а В и X – столбцы свободных членов и неизвестных, то (1) можно записать в виде
A·X=B. (2)
Как и в предыдущем параграфе, предположим, что определитель системы Δ≠0. Отсюда вытекает, что основная матрица системы имеет обратную А—1. Умножим обе части матричного равенства (2) на матрицу А—1. Используя ассоциативность умножения матриц и роль единичной матрицы, как единицы при умножении матриц, будем иметь:
A—1(AX)= A—1B,
(A—1A)X= A—1B,
EX= A—1B,
X= A—1B. (3)
Последнее равенство и дает выражение столбца неизвестных через обратную матрицу и столбец свободных членов. Вспомним вид обратной матрицы
A—1=(Аji/Δ) и приравняем j—е элементы столбцов, стоящих в левой и правой частях (3):

или
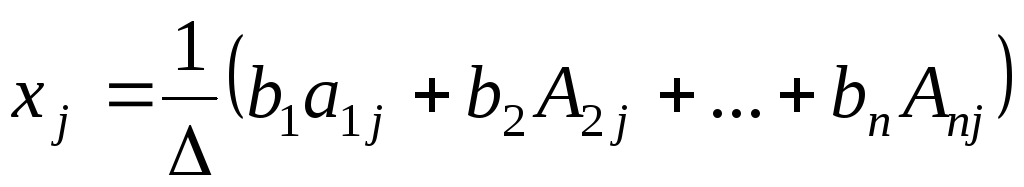 .
.
Выражение, стоящее в скобках, есть не что иное, как разложение определителя Δj (из предыдущего параграфа) по j—му столбцу. Поэтому (3) равносильно
 ,
,
и мы снова пришли к формулам Крамера.
Итак, если определитель Δ основной матрицы А системы линейных уравнений отличен от нуля, то существует и притом единственное решение матричного уравнения
АХ=В,
определяемое соотношением
Х=А-1В,
которое эквивалентно формулам Крамера.
§4. Решение системы линейных уравнений методом Гаусса
Вначале одно предварительное замечание. Применяя метод Гаусса, приходится выполнять такие преобразования системы: 1) переставлять местами два уравнения; 2) умножать обе части какого-нибудь уравнения системы на одно и то же число, отличное от нуля; 3) обе части одного из уравнений системы, умноженные на одно и то же число, вычитать из соответствующих частей некоторого другого уравнения системы. Нетрудно показать, что система, полученная в результате этих преобразований, будет эквивалентна исходной.
Перейдем теперь к изложению методом Гаусса, который называется также методом последовательного исключения неизвестных.
Пусть дана произвольная система линейных уравнений
 (1)
(1)
Предположим, что а11≠0 (в противном случае пришлось бы переставить два уравнения: ведь какой-нибудь из коэффициентов при x1 отличен от 0). С помощью 1-го уравнения исключим неизвестное x1 из всех уравнений системы, начиная со второго. Для этого вычтем из i—го уравнения первое уравнение, умноженное на аі1/a11 , i=2,3,…,m. В результате придем к новой системе, эквивалентной исходной:
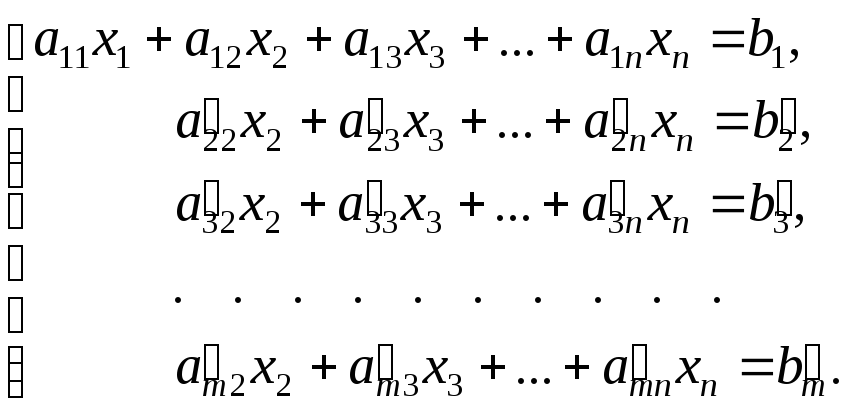 (2)
(2)
Далее будем
преобразовывать систему (2), причем 1-е
уравнение мы не будем трогать совсем и
подлежащей преобразованиям будем
считать лишь часть этой системы, состоящую
из всех уравнений, кроме первого. При
этом мы считаем, что среди этих уравнений
нет таких, все коэффициенты левых частей
которых равны нулю: такие уравнения мы
выбросили бы, если бы и их свободные
члены были равны нулю, а в противном
случае мы уже доказали бы несовместимость
нашей системы. Таким образом, среди
коэффициентов  есть
отличные от нуля; для определенности
примем, что
есть
отличные от нуля; для определенности
примем, что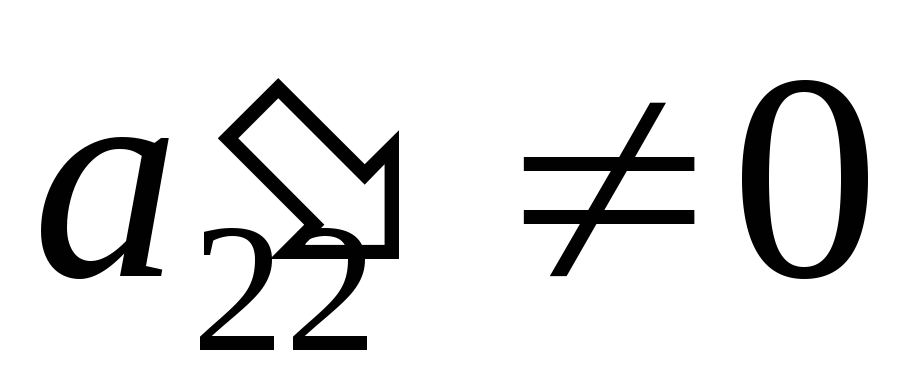 (в противном случае пришлось бы
переставлять уравнения или неизвестные).
С помощью 2-го уравнения системы (2)
исключим неизвестноеx2 из всех уравнений системы (2), начиная с
третьего. Для этого вычтем из j—го
уравнения второе, умноженное на
(в противном случае пришлось бы
переставлять уравнения или неизвестные).
С помощью 2-го уравнения системы (2)
исключим неизвестноеx2 из всех уравнений системы (2), начиная с
третьего. Для этого вычтем из j—го
уравнения второе, умноженное на 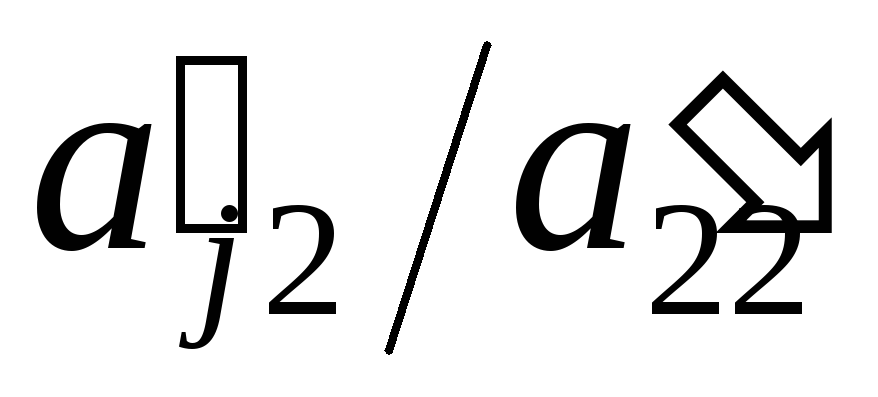 .
Придем к следующей системе, эквивалентной
системе (2), а значит (1):
.
Придем к следующей системе, эквивалентной
системе (2), а значит (1):
 (3)
(3)
Наша система содержит теперь p уравнений, p≤m, так как некоторые уравнения оказались, возможно, отброшенными. В дальнейшем подлежит преобразованиям, аналогично уже поделанным, часть полученной системы, содержащей все уравнения, кроме двух первых.
Когда остановится этот процесс последовательного исключения неизвестных?
Если мы придем к такой системе, одно из уравнений которой имеет отличный от нуля свободный член, а все коэффициенты левой части равны нулю, то, как мы знаем, наша исходная система несовместна.
Если же таких уравнений не встретится, то процесс исключения закончится не позже чем на (m–1)—ом шаге. Обозначим через k – число уравнений, которые останутся в системе после завершения процесса исключения неизвестных. Возможны случаи: k=n, k<n, k>n.
В случае, когда k=n получим так называемую “треугольную” систему
 (4)
(4)
у которой в каждом последующем уравнении ровно на одно неизвестное меньше, чем в предыдущем. Из последнего уравнения мы получаем вполне определенное значение для неизвестного xn. Подставив его в предпоследнее уравнение, мы найдем однозначно определенное значение для неизвестного xn—1. Продолжая так далее, мы найдем, что система (4), а поэтому и система (1) обладают единственным решением, т.е. совместна и определена.
Пусть теперь k<n. Система, полученная после завершения процесса исключения, имеет так называемую “трапецеидальную” форму:
 (5)
(5)
Назовем неизвестные xk+1, xk+2,…,xn свободными, придадим им произвольные числовые значения и перенесем члены, содержащие их, в правые части уравнений. Мы получим систему “треугольной” формы (4), из которой однозначно определяется неизвестные x1, x2,…,xk. Так как значения для свободных неизвестных можно выбирать бесконечным числом различных способов, то наша система (5) и, следовательно, система (1) будут совместными, но неопределенными. Легко проверить, что указанным здесь методом будут найдены все решения системы (1).
Третий случай,
когда k>n кажется возможным лишь первый момент.
Система имеет вид, получающийся
приписыванием к системе (4) еще нескольких
уравнений, содержащих лишь неизвестное xn.
В действительности, однако, в этом случае
преобразования просто не доведены до
конца: так как  ,
то из всех уравнений, начиная с (n+1)—го,
неизвестное xn может быть исключено.
,
то из всех уравнений, начиная с (n+1)—го,
неизвестное xn может быть исключено.
Итак, подведем итоги. Метод Гаусса применим к любой системе линейных уравнений. При этом система будет несовместной, если в процессе исключения неизвестных мы получим уравнение, в котором коэффициенты при всех неизвестных равны нулю, а свободный член отличен от нуля; Если же такого уравнения мы не встретим, то система будет совместной. Совместная система будет определенной, если приводится к треугольному виду (4) (число оставшихся уравнений равно числу неизвестных), и неопределенной, если приводится к трапецеидальному виду (5) (число оставшихся уравнений меньше числа неизвестных).
Замечание. При практическом применении метода Гаусса следует выписать основную матрицу системы и, приписав к ней столбец свободных членов, получить так называемую расширенную матрицу системы. Все преобразования выполняют над строками этой матрицы. Для удобства столбец свободных членов можно отделить вертикальной чертой от остальных столбцов матрицы.
Пример. Решить систему
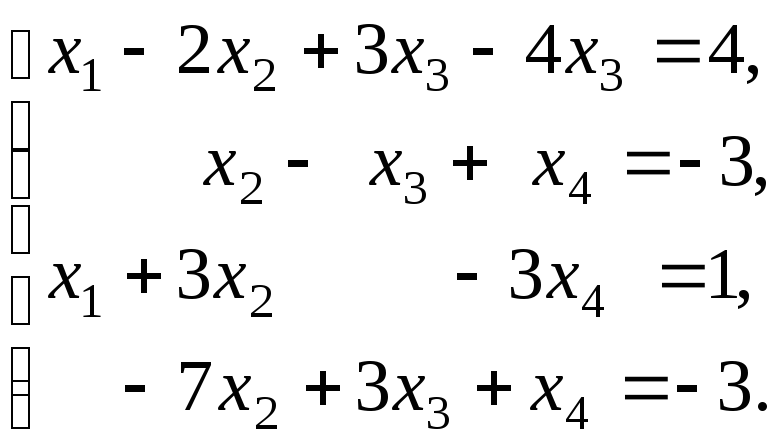
Решение. Подвергаем преобразованиям расширенную матрицу этой системы.






Краткие пояснения. 1-й шаг: первую строку вычитаем из третьей. 2-й шаг: вторую строку умножаем на 5 и вычитаем из третьей, а также умножаем на 7 и прибавляем к четвертой. 3-й шаг: третью строку умножаем на 2 и прибавляем к четвертой. 4-й шаг: отбрасываем четвертую строку, сплошь состоящую из нулей, и делим третью строку на 2. Мыприходим, следовательно, к системе:

В качестве свободного неизвестного можно принять любое из неизвестных х3 или х4. Пусть х4=α. Тогда из 3-го уравнения х3=6+2α, из 2-го получаем х2=3+α, а из первого х1= –8. Итак, общий вид решения заданной системы:
(–8; 3+α; 6+2α; α), где α – произвольное число.
2.4. Элементарные преобразования матрицы
Элементарные преобразования матрицы:
— умножение строки на число, отличное от нуля;
— прибавление к элементам одной строки элементов другой строки;
— перестановка строк;
— вычеркивание одной из одинаковых строк;
— транспонирование.
В
матрице порядка 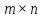 минор
порядка
минор
порядка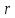 называетсябазисным, если
он не равен нулю, а все миноры порядка
называетсябазисным, если
он не равен нулю, а все миноры порядка 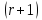 и выше равны нулю.
и выше равны нулю.
В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.
2.5. Ранг матрицы
Ранг матрицы – это наивысший из порядков миноров матрицы отличных от нуля.
Обозначение
ранга матрицы 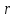 или
или
Матрицы, полученные в результате элементарного преобразования, называют эквивалентными матрицами.
Очень важным свойством элементарных преобразований матриц является то, что они не изменяют ранг матрицы.
Ранг матрицы равен числу ненулевых строк в матрице, приведенной с помощью элементарных преобразований к треугольному (ступенчатому) виду.
Рассмотрим пример. Определить ранг матрицы
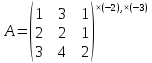

Тогда 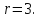
Или
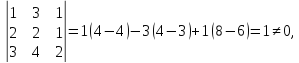
следовательно, ранг матрицы
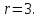
Контрольные вопросы
Какая матрица называется обратной?
Пояснить алгоритм вычисления обратной матрицы.
Дать определение системы линейных алгебраических уравнений. Что называется ее решением?
Для каких систем применимо правило Крамера?
Записать формулы Крамера.
Пояснить алгоритм решения систем методом обратной матрицы.
Дать определение ранга матрицы.
Лекция №3. Метод Гаусса решения систем линейных алгебраических уравнений. Однородные системы линейных алгебраических уравнений
3.1. Теорема Кронекера – Капелли.
3.2. Метод Гаусса решения систем m линейных уравнений с n неизвестными.
3.3 Общее, базисное и частное решение систем линейных алгебраических уравнений.
3.4. Однородные системы линейных алгебраических уравнений.
3.1. Теорема Кронекера-Капелли
Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы равен рангу расширенной матрицы этой системы.
Для совместных систем линейных уравнений верны следующие теоремы.
Если ранг матрицы совместной системы равен числу переменных, т.е.
 то
система имеет единственное решение.
то
система имеет единственное решение.Если ранг матрицы совместной системы меньше числа переменных, т.е.
 то
система неопределенная и имеет
бесконечное множество решений.
то
система неопределенная и имеет
бесконечное множество решений.
3.2. Метод Гаусса решения систем m линейных уравнений с n неизвестными
Метод Гаусса – метод последовательного исключения переменных, заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Шаг первый. Умножая первое уравнение на подходящие числа
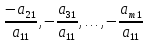
и
прибавляя полученные уравнения
соответственно ко второму, третьему,
…, 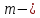 му
уравнению системы, исключим переменную
му
уравнению системы, исключим переменную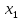 из всех последующих уравнений, начиная
со второго. Получим
из всех последующих уравнений, начиная
со второго. Получим
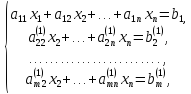
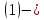 обозначены
новые коэффициенты, полученные после
первого шага.
обозначены
новые коэффициенты, полученные после
первого шага.
Шаг
2. Пусть 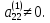 Умножая
второе уравнение на подходящие числа
Умножая
второе уравнение на подходящие числа

и
прибавляя полученные уравнения
соответственно к третьему, четвертому,  му
уравнению системы, исключим переменную
му
уравнению системы, исключим переменную из
всех последующих уравнений, начиная с
третьего.
из
всех последующих уравнений, начиная с
третьего.
Последующие шаги проводятся аналогично.
Процесс
последовательного исключения переменных
после  -го
шага приводит к системе
-го
шага приводит к системе
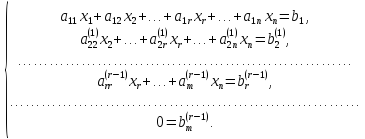
Если
хотя бы одно из чисел 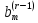 не равно нулю, то соответствующее
равенство противоречиво, и системанесовместна.
Для любой совместной системы числа
не равно нулю, то соответствующее
равенство противоречиво, и системанесовместна.
Для любой совместной системы числа 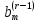 в системе равны нулю.
в системе равны нулю.
После отбрасывания «лишних» уравнений возможны два случая:
а)
число уравнений системы, приведенной
к ступенчатому виду равно числу
переменных, т.е. 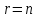 ;
;
б)
число уравнений системы, приведенной
к ступенчатому виду меньше числа
переменных 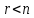 .
.
Переход системы к равносильной ей системе называется прямым ходом метода Гаусса, а нахождение переменных из равносильной системы – обратным ходом.
Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов.
Рассмотрим пример. Решить систему уравнений методом Гаусса

Составим по данной системе расширенную матрицу
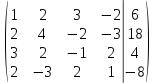
умножим
первую строку на 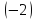 и сложим со второй строкой и с четвертой
строкой; умножим первую строку на
и сложим со второй строкой и с четвертой
строкой; умножим первую строку на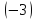 и
сложим с третьей строкой, получим
и
сложим с третьей строкой, получим
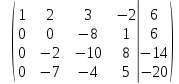
поменяем местами вторую и третью строки
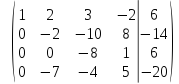
умножим вторую строку на 7 и сложим с четвертой строкой
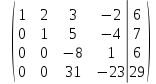
умножим третью строку на 31, а четвертую на 8 и сложим эти строки
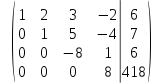
разделим последнюю строку на 2

От ступенчатого вида матрицы переходим к системе
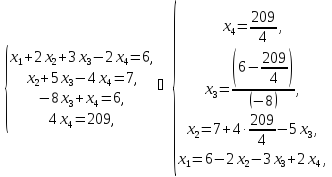
т.е. обратным ходом Гаусса находим все переменные.
Рассмотрим пример. Решить систему методом Гаусса
Составим по данной системе расширенную матрицу
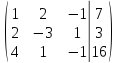
умножим
первую строку на 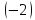 и сложим со второй строкой; умножим
первую строку на
и сложим со второй строкой; умножим
первую строку на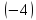 и сложим с третьей строкой, получим
и сложим с третьей строкой, получим
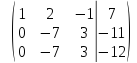
умножим
вторую строку на 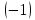 и сложим с третьей строкой
и сложим с третьей строкой
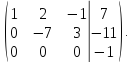
В
данном случае последняя строка
противоречива, так как 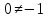 ,
следовательно, система несовместна.
,
следовательно, система несовместна.
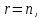 то
система имеет единственное решение.
то
система имеет единственное решение. то
система неопределенная и имеет
бесконечное множество решений.
то
система неопределенная и имеет
бесконечное множество решений.