Тригонометрия
Онлайн решение тригонометрических уравнений
На нашем сайте вы можете решить любое тригонометрическое уравнение используя Калькулятор за пару секунд. Решать уравнения тригонометрические с помощью калькулятора просто. Чтобы ввести условие, нажмите «+условие»
Например:
Условие: sin2x+3x=2
Нажав кнопку Решить вы получите подробное решение тригонометрических уравнений.
Тригонометрия это просто если вы знаете формулы приведения в тригонометрии.
Тригонометрия 10 класс
Для начала нужно обязательно запомнить основные формулы.
Тригонометрия таблица
Тригонометрия приведение
Главной задачей при решении тригонометрических уравнений является его преобразование до более простого
уравнения основного вида, которое решаются стандартными методами.
— алгебраический;
— разложения на множители;
— преобразования к одному уравнению;
— перехода к половинному углу;
— вспомогательного угла;
— преобразования произведения в сумму;
— подстановки.
Так же читайте нашу статью «Решить систему тригонометрических уравнений онлайн решателем»
Выбор метода определяется исходя из самого уравнения. Одно уравнение можно решить несколькоми способами, однако при правильном выборе метода вы решите его за меньшее количество математических операций.
Допустим, нам дано уравнение такого вида:
\[\sin x + \cos x = 1\]
Чтобы решить данное уравнение необходимо воспользоватся 2м методом и выполнить перенос всех членов влево:
\[\sin x +\ cos x — 1 = 0\]
Теперь преобразуем и разложим на множители левую часть уравнения:
\[\sin x -2 sin^2(\frac {x}{2})=0\]
\[2\sin(\frac {x}{2})\cdot\cos(\frac {x}{2})-2\sin^2(\frac {x}{2})=0\]
\[2\sin(\frac {x}{2})\cdot[\cos(\frac {x}{2}) — \sin(\frac {x}{2})]=0\]
1)
\[\sin (\frac {x}{2})=0\]
\[\frac{x}{2}\pi k\]
\[x_1=2\pi k\]
2)
\[\cos(\frac {x}{2})-\sin(\frac {x}{2})=0\]
\[\tan\frac {x}{2}=1\]
\[\frac {x}{2}=\arctan 1 +\pi n\]
\[\frac {x}{2} = \frac {\pi}{4}+\pi n\]
\[x_2 = \frac {\pi}{2}2\pi n\]
Где и как решать тригонометрические уравнения онлайн?
Решить уравнение вы можете на нашем сайте.
Бесплатный
решатель позволит решить тригонометрические уравнения с решениями любой сложности за считанные секунды
онлайн. Тригонометрия егэ больше не проблема. Все, что вам необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Используя наш калькулятор тригонометрический, вы всегда сможете сказать, что тригонометрия класс!
вычисление тригонометрических выражений онлайн
Вы искали вычисление тригонометрических выражений онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить онлайн тригонометрическое выражение, не
исключение.
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вычисление тригонометрических выражений онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычисление тригонометрических выражений онлайн,вычислить онлайн тригонометрическое выражение,вычислить тригонометрическое выражение онлайн,калькулятор для онлайн решения тригонометрических уравнений,калькулятор онлайн для тригонометрических уравнений онлайн,калькулятор онлайн по тригонометрии,калькулятор онлайн решение тригонометрических уравнений,калькулятор онлайн тригонометрические уравнения,калькулятор онлайн тригонометрические функции,калькулятор онлайн тригонометрический,калькулятор онлайн тригонометрических уравнений,калькулятор онлайн тригонометрических функций,калькулятор онлайн тригонометрия,калькулятор по тригонометрии онлайн,калькулятор решение тригонометрических уравнений,калькулятор решение тригонометрических уравнений онлайн,калькулятор с тригонометрическими функциями,калькулятор тригонометрии,калькулятор тригонометрии онлайн,калькулятор тригонометрические,калькулятор тригонометрические уравнения,калькулятор тригонометрический,калькулятор тригонометрических,калькулятор тригонометрических выражений,калькулятор тригонометрических выражений онлайн,калькулятор тригонометрических уравнений,калькулятор тригонометрических уравнений онлайн,калькулятор тригонометрических уравнений онлайн с подробным решением,калькулятор тригонометрических функций,калькулятор тригонометрических функций онлайн,калькулятор тригонометрия,калькулятор тригонометрия онлайн,онлайн вычисление тригонометрических выражений,онлайн калькулятор для тригонометрических уравнений онлайн,онлайн калькулятор по тригонометрии,онлайн калькулятор решение тригонометрических уравнений,онлайн калькулятор тригонометрии,онлайн калькулятор тригонометрические уравнения,онлайн калькулятор тригонометрических уравнений,онлайн калькулятор тригонометрических уравнений с подробным решением,онлайн калькулятор тригонометрических функций,онлайн калькулятор тригонометрия,онлайн решатель тригонометрических уравнений,онлайн решение синусов и косинусов,онлайн решение тригонометрии,онлайн решение тригонометрических выражений,онлайн решение тригонометрических уравнений,онлайн решение тригонометрических уравнений с подробным решением,онлайн решение тригонометрических функций,онлайн решение уравнений с синусами и косинусами,онлайн решения тригонометрических уравнений,онлайн решения уравнений тригонометрических,онлайн решить тригонометрическое уравнение онлайн,онлайн тригонометрический калькулятор,онлайн тригонометрия,онлайн упрощение тригонометрических уравнений,преобразование тригонометрических выражений онлайн,решатель тригонометрических уравнений онлайн,решение онлайн тригонометрических выражений,решение онлайн тригонометрических функций,решение синусов и косинусов онлайн,решение тригонометрии онлайн,решение тригонометрических выражений онлайн,решение тригонометрических уравнений калькулятор,решение тригонометрических уравнений калькулятор онлайн,решение тригонометрических уравнений онлайн,решение тригонометрических уравнений онлайн калькулятор,решение тригонометрических уравнений онлайн калькулятор с решением,решение тригонометрических уравнений онлайн с подробным решением,решение тригонометрических уравнений онлайн с подробным решением бесплатно,решение тригонометрических уравнений онлайн с подробным решением онлайн,решение тригонометрических уравнений с подробным решением онлайн,решение тригонометрических уравнений с подробным решением онлайн бесплатно,решение тригонометрических функций онлайн,решение тригонометрического уравнения онлайн,решение уравнений онлайн с синусами и косинусами,решение уравнений с косинусами и синусами онлайн,решение уравнений с синусами и косинусами онлайн,решения онлайн тригонометрических уравнений онлайн калькулятор,решения тригонометрических уравнений онлайн,решите уравнение тригонометрическое онлайн,решить онлайн тригонометрическое выражение,решить онлайн тригонометрическое уравнение,решить тригонометрические уравнения онлайн,решить тригонометрическое выражение онлайн,решить тригонометрическое уравнение онлайн,решить тригонометрическое уравнение онлайн с подробным решением,решить уравнение с косинусами и синусами онлайн,решить уравнение с синусами и косинусами онлайн,решить уравнение тригонометрическое онлайн,решить уравнение тригонометрическое уравнение онлайн,решить уравнения онлайн тригонометрические,тригонометрические калькулятор,тригонометрические уравнения калькулятор,тригонометрические уравнения калькулятор онлайн,тригонометрические уравнения онлайн,тригонометрические уравнения онлайн калькулятор,тригонометрические уравнения онлайн решение,тригонометрические уравнения решение онлайн,тригонометрические уравнения решить онлайн,тригонометрические функции калькулятор онлайн,тригонометрические функции онлайн,тригонометрические функции онлайн калькулятор,тригонометрический калькулятор,тригонометрический калькулятор онлайн с решением,тригонометрический калькулятор с решением,тригонометрический калькулятор с решением онлайн,тригонометрическое уравнение онлайн,тригонометрия калькулятор,тригонометрия калькулятор онлайн,тригонометрия онлайн,тригонометрия онлайн калькулятор,тригонометрия онлайн решение,тригонометрия решение онлайн.
Где можно решить любую задачу по математике, а так же вычисление тригонометрических выражений онлайн Онлайн?
Решить задачу вычисление тригонометрических выражений онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
▶▷▶ решебник онлайн тригонометрических уравнений онлайн
▶▷▶ решебник онлайн тригонометрических уравнений онлайн| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 30-11-2018 |
решебник онлайн тригонометрических уравнений онлайн — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Want more to discover? Make Yahoo Your Home Page See breaking news more every time you open your browser Add it now No Thanks Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Решение тригонометрических уравнений | Онлайн калькулятор libreshimsu … Онлайн калькулятор Калькулятор для пошагового решения тригонометрических уравнений онлайн (бесплатно Калькулятор онлайн — Решение тригонометрических уравнений wwwmathsolutionru/math-task/trigonometry-equality Cached Калькулятор онлайн Решение тригонометрических уравнений Этот математический Уравнения онлайн Математика онлайн math34biz/equation Cached Решение уравнений онлайн Пошаговое решение уравнений онлайн на сайте Math34biz Уравнения онлайн Вы сможете решить уравнение онлайн моментально и с высокой точностью результата Решебник Онлайн Тригонометрических Уравнений Онлайн — Image Results More Решебник Онлайн Тригонометрических Уравнений Онлайн images Уравнения онлайн Математика онлайн math34su/equation Cached Сервис для решения уравнений онлайн поможет вам решить любое уравнение Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения Решение тригонометрических уравнений в ЕГЭ онлайн (страница 3) shkolkovonet/catalog/reshenie_uravnenij_2/ Cached Найдите корень уравнения \[\mathrmctg\, (2\pi x) = 1\] Если уравнение имеет более одного корня, в ответе укажите меньший из его положительных корней Решение тригонометрических уравнений в ЕГЭ онлайн (страница 2) shkolkovonet/catalog/reshenie_uravnenij_2/ Cached Тригонометрическое уравнение – уравнение, содержащее переменную \(x\) в аргументе одной Решение тригонометрических уравнений онлайн — 4 Февраля 2013 wwwreshimsu/blog/reshenie_trigonometricheskikh Cached Для решения любого тригонометрического уравнения вам достаточно ввести свое уравнение в Решение тригонометрических уравнений | Онлайн калькулятор allworkssu … Онлайн калькулятор Решение задач и контрольных работ на заказ по высшей математике, теории вероятности, статистике, эконометрике, дискретной математике, а также по физике (все разделы) Решение любых: кубических, тригонометрических wwwkontrolnaya-rabotaru/s/equal-one/any-uravnenie Cached Онлайн калькулятор для решения любых уравнений , неравенств, интегралов Помощь школьникам, студентам в решении: None, можно заказать дипломную работу Уравнения онлайн — matcabinet wwwmatcabinet/equationphp Cached Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте wwwmatcabinet Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 46,900 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- а главное точный ответ
- которое решаются стандартными методами Для решения данного рода уравнений можно использовать один из семи методов: — алгебраический; — разложения на множители; — преобразования к одному уравнению ; — перехода к половинному углу; — вспомогательного угла; — преобразования произведения в сумму; — подстановки Так же читайте нашу статью «Решить систему тригонометрических урав Скрыть 7 Тригонометрический калькулятор онлайн okcalccom › Тригонометрия Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Бесплатно Windows
- Android Категория: Калькулятор Удобный тригонометрический калькулятор онлайн
как решить тригонометрическое уравнение Калькулятор для пошагового решения тригонометрических уравнений онлайн (бесплатно) Данный калькулятор полностью заменит вам репетитора по математике
при проверке знаний перед ЕГЭ
- easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 46
- можно заказать дипломную работу Уравнения онлайн — matcabinet wwwmatcabinet/equationphp Cached Неизвестные величины уравнений можно найти
- smarter
Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Знатоки Коллекции Музыка Переводчик Диск Почта Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 Калькулятор онлайн — Решение тригонометрических mathsolutionru › math-task/trigonometry-equality Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, те отображает процесс получения ответа Читать ещё Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, те отображает процесс получения ответа Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре Скрыть 2 Решение тригонометрических уравнений онлайн kontrolnaya-rabotaru › …trigonometricheskih…onlajn/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Решение тригонометрических уравнений онлайн Рассмотрим пример решения тригонометрического уравнения Требуется решить тригонометрическое уравнение cos(x/4-pi/3) = 1/2 и найти x, при которых выполняется это уравнение Читать ещё Решение тригонометрических уравнений онлайн Рассмотрим пример решения тригонометрического уравнения онлайн на сайте Контрольная Работа РУ Этот сайт даёт полное решение тригонометрического уравнения Плюс для некоторых уравнений есть графическое решение Итак, рассмотрим пример: Требуется решить тригонометрическое уравнение cos(x/4-pi/3) = 1/2 и найти x, при которых выполняется это уравнение Для этого переходим на страницу уравнения онлайн уравнение ! Получим подробное решение: Дано уравнение $$\cos\left (\fracx4 — \frac\pi3 \right ) = \frac12 Скрыть 3 Решение тригонометрических уравнений | Онлайн allcalcru › Онлайн калькулятор Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Данный калькулятор предназначен для решения тригонометрических уравнений Тригонометрические уравнения – это уравнения , которые содержат в себе тригонометрические функции неизвестного аргумента Читать ещё Данный калькулятор предназначен для решения тригонометрических уравнений Тригонометрические уравнения – это уравнения , которые содержат в себе тригонометрические функции неизвестного аргумента Под тригонометрическими функциями понимают математические функции от величины угла Как правило, тригонометрические функции определяются как отношения сторон прямоугольного треугольника или длины определенных отрезков в единичной окружности К основным видам тригонометрических уравнений относят простейшие уравнения , содержащие модуль, с параметрами, с целой и дробной частью, со сложными аргументами, с Скрыть 4 Решение тригонометрических уравнений онлайн allworkssu › blog/2014-07-30-95 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Ключевые слова: решение уравнений онлайн , как решить тригонометрическое уравнение Калькулятор для пошагового решения тригонометрических уравнений онлайн (бесплатно) Данный калькулятор полностью заменит вам репетитора по математике, достаточно решить несколько уравнений с помощью Читать ещё Ключевые слова: решение уравнений онлайн , как решить тригонометрическое уравнение Калькулятор для пошагового решения тригонометрических уравнений онлайн (бесплатно) Данный калькулятор полностью заменит вам репетитора по математике, достаточно решить несколько уравнений с помощью данного калькулятора и вы сможете самостоятельно решать любые тригонометрические уравнения По многочисленным просьбам наших пользователей предлагаем методику решения тригонометрических уравнений На ваши вопросы отвечает автор Для решения вашего тригонометрического уравнения достаточно вставить уравнения в окошки к Скрыть 5 Решение тригонометрических уравнений онлайн otvet-prostru › решение-тригонометрических… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Для решения любого тригонометрического уравнения вам достаточно ввести свое уравнение в окошко калькулятора и нажать кнопку «ответ» Калькулятор выдаст решение тригонометрического уравнения бесплатно Читать ещё Для решения любого тригонометрического уравнения вам достаточно ввести свое уравнение в окошко калькулятора и нажать кнопку «ответ» Калькулятор выдаст решение тригонометрического уравнения бесплатно Способ ввода уравнения как на обычном калькуляторе Правила набора уравнений Уравнение Синтаксис tg^2 (x) + 3tg( x) =0 Скрыть 6 Решить тригонометрическое уравнение онлайн pocketteacherru › Уравнение Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Решить тригонометрическое уравнение онлайн решателем Решение тригонометрических уравнений Главной задачей при решении тригонометрических уравнений является его преобразование до более простого уравнения основного вида, которое решаются стандартными Читать ещё Решить тригонометрическое уравнение онлайн решателем Решение тригонометрических уравнений Главной задачей при решении тригонометрических уравнений является его преобразование до более простого уравнения основного вида, которое решаются стандартными методами Для решения данного рода уравнений можно использовать один из семи методов: — алгебраический; — разложения на множители; — преобразования к одному уравнению ; — перехода к половинному углу; — вспомогательного угла; — преобразования произведения в сумму; — подстановки Так же читайте нашу статью «Решить систему тригонометрических урав Скрыть 7 Тригонометрический калькулятор онлайн okcalccom › Тригонометрия Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Бесплатно Windows, iOS, Android Категория: Калькулятор Удобный тригонометрический калькулятор онлайн , с помощью которого вы можете произвести необходимые расчёты 8 Решение тригонометрических уравнений в ЕГЭ онлайн shkolkovonet › Начать изучение темы › Тригонометрические уравнения Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Тригонометрические уравнения Тригонометрическое уравнение – уравнение , содержащее переменную \(x Вы быстро найдете необходимые правило и формулу, и решение тригонометрических уравнений будет даваться максимально легко Читать ещё Тригонометрические уравнения Тригонометрическое уравнение – уравнение , содержащее переменную \(x\) в аргументе одной или нескольких тригонометрических функций: синус, косинус, тангенс, котангенс \(\bullet\) Стандартные тригонометрические уравнения : \[\beginarrayl|c|c \hline \text Уравнение \textОграничения \textРешение\\ \hline \\ \sin x=a -1\leq a\leq 1 \left[ \begingathered \beginaligned x=\arcsin a+2\pi n\\ x=\pi -\arcsin a+2\pi m \endaligned \endgathered \right \ \ , \ n,m\in \mathbbZ\\\\ \hline \\ \cos x Вы быстро найдете необходимые правило и формулу, и решение тригонометрических уравнений будет даваться максимально легко Скрыть 9 Решебник онлайн тригонометрических уравнений онлайн — смотрите картинки ЯндексКартинки › решебник онлайн тригонометрических уравнений Пожаловаться Информация о сайте Ещё картинки 10 Trigonometric Equation Calculator — Symbolab symbolabcom › solver/trigonometric-equation-… Перевести Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Free trigonometric equation calculator — solve trigonometric equations step-by-step Уравнения онлайн MatCabinet › equationphp Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Решение уравнений онлайн Алгебраические, тригонометрические , трансцендентные уравнения онлайн Линейные, квадратные, кубические уравнения онлайн Читать ещё Решение уравнений онлайн Алгебраические, тригонометрические , трансцендентные уравнения онлайн Линейные, квадратные, кубические уравнения онлайн Уравнения онлайн Примеры Математические уравнения онлайн для решения математики Быстро найти решение математического уравнения в режиме онлайн Сайт wwwmatcabinet позволяет решить уравнение почти любого заданного алгебраического, тригонометрического или трансцендентного уравнения онлайн При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать Скрыть Вместе с « решебник онлайн тригонометрических уравнений онлайн » ищут: решение онлайн zadachi com ua мегарешеба ответы майл решение уравнений онлайн решебник примеров онлайн калькулятор дробей онлайн ответы ответы онлайн 1 2 3 4 5 дальше Браузер Ускоряет загрузку файлов при медленном соединении 0+ Установить
▶▷▶ калькулятор для решения уравнений по алгебре онлайн
▶▷▶ калькулятор для решения уравнений по алгебре онлайн| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 29-11-2018 |
калькулятор для решения уравнений по алгебре онлайн — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Want more to discover? Make Yahoo Your Home Page See breaking news more every time you open your browser Add it now No Thanks Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Калькулятор уравнений онлайн okcalccom/ru/equation Cached В таком случае для вас незаменимым станет этот удобный и простой в применении онлайн калькулятор уравнений Онлайн версия программы для решения примеров и уравнений calcloviotvetru Cached Онлайн программа для решения примеров и уравнений ЛовиОтвет Программа ЛовиОтвет — автоматическое решение математических примеров онлайн любой сложности с отображением этапов решения Калькулятор онлайн — Решение показательных уравнений wwwmathsolutionru/math-task/exponential-equality Cached Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, те отображает процесс получения результата Калькулятор Для Решения Уравнений По Алгебре Онлайн — Image Results More Калькулятор Для Решения Уравнений По Алгебре Онлайн images Решение уравнений бесплатно — Калькулятор Онлайн wwwkontrolnaya-rabotaru/s/equal-one Cached Решение уравнений онлайн позволяет быть уверенным в правильности решения уравнения В каждом из разделов приведены различные виды способов для помощи Вам Решение квадратных уравнений , онлайн калькулятор для решения nisataru Любопытным Решение квадратных уравнений онлайн Квадратное уравнение — уравнение второго порядка, вида , где не равно 0 Уравнения онлайн Математика онлайн math34su/equation Cached Сервис для решения уравнений онлайн поможет вам решить любое уравнение Используя наш сайт, вы получите не просто ответ уравнения, но и увидите подробное решение, то есть пошаговое отображение процесса получения Онлайн калькулятор Решение систем линейных уравнений Метод 0oqru/reshebnik-onlajn/ruonlinemschoolcom/ Cached Используя этот онлайн калькулятор для решения систем линейных уравнений (СЛУ) методом Гаусса, вы сможете очень просто и быстро найти решение системы Онлайн калькуляторы для решения математических задач ruonlinemschoolcom/math/assistance Cached Онлайн калькуляторы — в этом разделе собраны написанные мною программы для решения примеров и задач по математике, алгебре , геометрии, теории вероятности, высшей математике и другим математическим дисциплинам Решение любых: кубических, тригонометрических wwwkontrolnaya-rabotaru/s/equal-one/any-uravnenie Cached Онлайн калькулятор для решения любых уравнений , неравенств, интегралов Помощь школьникам, студентам в решении: None, можно заказать дипломную работу Уравнения онлайн Математика онлайн math34biz/equation Cached По -прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 44,600 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- построение графиков
- решение полиномов) в онлайн режиме Если Ваша домашняя работа включает в себя математические уравнения
- секанс
тригонометрических
вещественности и т д) Решение уравнений онлайн Пошаговое решение уравнений онлайн на сайте Math34biz Уравнения онлайн Если не сказано
- smarter
- онлайн калькулятор для решения nisataru Любопытным Решение квадратных уравнений онлайн Квадратное уравнение — уравнение второго порядка
- геометрии
калькулятор для решения уравнений по алгебре онлайн — Все результаты Решение любых уравнений — Контрольная Работа РУ Похожие Онлайн калькулятор для решения любых уравнений , неравенств, Решение Алгебраических (по алгебре ): Квадратных, кубических и других степеней Решение уравнений бесплатно — Калькулятор Онлайн Похожие Решение уравнений бесплатно Онлайн калькулятор для решения любых уравнений , неравенств, интегралов Помощь школьникам, студентам в Калькулятор Онлайн · Дифференциальные · Квадратные уравнения Онлайн калькуляторы для решения математических задач Онлайн калькуляторы для решения задач по математике Метод Крамера Решение систем линейных уравнений в этом разделе собраны написанные мною программы для решения примеров и задач по математике , алгебре , Решение уравнений — Онлайн-калькулятор › › Точки разрыва функции › Диф уравнения онлайн Решение квадратных, кубических, тригонометрических, логарифмических уравнений онлайн Нахождение корней функции Подробные примеры Калькуляторы по алгебре — Calcru Похожие Онлайн калькуляторы по алгебре — решения , подсказки и учебник линейной алгебры онлайн Нахождение корней и дискриминанта квадратных уравнений Решение квадратных уравнений Создадим калькулятор для вас Калькулятор онлайн — Решение показательных уравнений wwwmathsolutionru/math-task/exponential-equality Похожие Программа для решения показательного уравнения не просто даёт ответ задачи, она для контроля решения многих задач по математике и алгебре Уравнения онлайн Математика онлайн — Math34biz Похожие Пошаговое решение уравнений онлайн на сайте Math34biz Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не Решение уравнений | Онлайн калькулятор — AllCalcru allcalcru › Все калькуляторы › Учеба и наука › Математика Похожие Рейтинг: 3 — 7 отзывов Специально для решения самых разнообразных уравнений на нашем сайте создан онлайн калькулятор , позволяющий сделать расчеты более легкими Решение задач онлайн — Math20 Похожие Решить ваши задачи онлайн с нашей программой Онлайн программа решения задач курса предварительной алгебры (геометрии) задачи с основного раздела математики а также координатных задач, простых уравнений , Видео 14:42 Онлайн решение уравнений Задания ЗФТШ МФТИ Математика Света Снегурочка YouTube — 4 окт 2016 г 3:16 Решебник, калькулятор и обучающая программа ЛовиОтвет Vitaly Markevich YouTube — 20 февр 2013 г 4:37 Бесплатная программа ЛовиОтвет Калькулятор 21 века Программы для пользы ПК YouTube — 11 июл 2016 г Все результаты Решение уравнений — Империя чисел Решатель Уравнений позволяет решать системы алгебраических уравнений Его главная функция — это решение полиномиальных уравнений Решение уравнений онлайн — MathForYounet wwwmathforyounet/online/equation/arbitrary/ Похожие Онлайн калькулятор способен решить практически любые типы уравнений , даже очень сложные Онлайн калькуляторы по математике — MathForYounet wwwmathforyounet/SolutionsListhtml Похожие В данном разделе представлены онлайн калькуляторы для решения различных математических задач Решение дифференциальных уравнений Приложения в Google Play – Photomath Похожие Просто наведите камеру на математическую задачу, и Photomath магическим образом сразу же выдаст ответ и подробное пошаговое решение Онлайн программы для решения уравнений, методы, примеры wwwwebmathru/web/uravneniaphp Похожие Онлайн программы для решения уравнений , примеры, методы решения уравнений Главная · Онлайн калькуляторы Решение уравнений Онлайн App Store: Photomath — iTunes — Apple Рейтинг: 4,9 — 18 973 отзыва — Бесплатно — iOS Калькулятор с камерой • Распознавание новые методы решения квадратных уравнений , модальных уравнений , комплексных чисел и т д • решение Калькулятор дробей онлайн с решением! — Решение задач по reshitru/Kalkulyator-drobey-onlayn-s-resheniem Удобный и простой онлайн калькулятор дробей с подробным решением может складывать, вычитать, умножать и делить дроби онлайн , получать Решение математики онлайн Онлайн калькуляторы по математике matematikamru/calculate-online/ Похожие Здесь представлены онлайн калькуляторы для решения различных задач по Онлайн калькуляторы по математике Решение уравнений онлайн Онлайн калькулятор: Решение уравнения 4-й степени Калькулятор ниже решает уравнение 4-й степени степени с одной неизвестной В общем виде уравнение выглядит следующим образом: § Калькуляторы онлайн математические Расчёт математических math-prostoru/?page=pages/calculators/calculatorsphp Похожие Математические калькуляторы для решения задач онлайн расположены по классам Внутри классов калькуляторы рассортированы по алфавиту Калькулятор, решение квадратных уравнений онлайн math5schoolru/mathculatorhtml Похожие Калькулятор и решение квадратных уравнений онлайн Этот калькулятор достаточно прост в использовании Он позволяет: использовать Калькулятор онлайн — Решение системы двух линейных — Pinterest Калькулятор онлайн — Решение системы двух линейных уравнений с двумя Подборка полезной теории по алгебре Детский Сад Математика, Алгебра Калькулятор квадратных уравнений — Онлайн-калькуляторы calcby/math-calculators/quadratic-equationshtml Похожие Онлайн — калькулятор для решения квадратных уравнений позволяет найти корни квадратного уравнения с предоставлением подробного решения Онлайн калькуляторы для решения математических задач Онлайн калькуляторы для решения задач по математике мною программы для решения примеров и задач по математике, алгебре , геометрии, теории вероятности, высшей математике Решение систем линейных уравнений Онлайн калькулятор PRO 20 — Математика-онлайн решение-задач-онлайнрф/indexphp/математика-онлайн/онлайн-калькулятор-pro Похожие Онлайн калькулятор PRO 20 — это продвинутый инженерный калькулятор для студентов и школьников, который является одним из самыз лучших Решение задач по математике онлайн, сервисы и калькуляторы Онлайн калькуляторы по алгебре , геометрии, матанализу, теории решение алгебраических и дифференциальных уравнений , действия с числами и Онлайн калькуляторы по математике — Шпаргалка ЕГЭ shpargalkaegeru/SRVshtml Похожие Данный калькулятор позволяет решить огромное количество задач из курса Но теперь онлайн решение уравнений , неравенств и интегралов не Уравнения | Онлайн калькуляторы, расчеты и формулы на geleotru/education/math/algebra/equation Уравнения В алгебре уравнения составляют внушительную по объему часть алгоритмов и подходов к решению задач В зависимости от сложности Онлайн версия программы для решения примеров и уравнений Онлайн версия программы ЛовиОтвет для автоматического решения математических примеров онлайн любой сложности с 2010 — 2013 ЛовиОтвет — Решебник и калькулятор с решениями примеров и уравнений онлайн Онлайн-калькулятор решения уравнений методом Крамера specclassru/online_kramer/ Похожие Линейная алгебра Онлайн — калькулятор решения уравнений методом Крамера Решение системы уравнений методом обратной матрицы; 100 формул / Решение биквадратных уравнений — 100formulru Онлайн курсы Решение биквадратных уравнений Биквадратное уравнение решается методом введения новой переменной: положив x2=t x 2 = t Онлайн калькуляторы по линейно алгебре с решением примеров › Калькуляторы Решить систему из 3-х уравнений с 3-мя неизвестным Этот онлайн калькулятор предназначен для решения систем из трёх уравнений с тремя Уравнения — Решение математики онлайн wwwmatcabinet/equationphp Похожие Решение уравнений онлайн Алгебраические, тригонометрические, трансцендентные уравнения онлайн Линейные, квадратные, кубические Онлайн калькуляторы по математике, геометрии и физике rusolverbookcom/onlajn-kalkulyator/ Похожие Онлайн калькуляторы — это автоматические сервисы для решения задач по математике, геометрии, физике и теории Решение уравнений Решение задач или математика онлайн | ТЕХНО-СТАРЕЦ › Обзоры Похожие 20 февр 2013 г — Еще один онлайн калькулятор предлагает сайт Matematikamru — решение контрольных работ по математике и физике «Все сервисы Решение тригонометрических уравнений | Онлайн калькулятор libreshimsu › Примеры решения задач › Онлайн калькулятор Похожие Калькулятор для пошагового решения тригонометрических уравнений онлайн (бесплатно) Данный калькулятор полностью заменит вам репетитора по Онлайн калькуляторы matem96ru/kalkulatorshtml Похожие Онлайн калькуляторы с подробным решением по высшей математике, теории Векторная алгебра и аналитическая геометрия Решение системы линейных уравнений методом обратной матрицы (матричный метод) Приложение PhotoMath решает уравнения по фотографии Необычный калькулятор поддерживает базовые арифметические Кроме того, PhotoMath показывает пошаговые инструкции для решения примеров Смартфон решит любое уравнение — «Хакер» Похожие 23 окт 2014 г — При наведении камеры на уравнение программа распознаёт модуля OCR, а для решения уравнений используется собственная технология бы научили мыслить самостоятельно,безо всяких калькуляторов Калькулятор уравнений на андроид скачать бесплатно top-androidorg › Программы › Образование Похожие Рейтинг: 4 — 1 отзыв Калькулятор одиночных уравнений — Калькулятор систем уравнений Данный калькулятор возвращает только ответ (без подробного решения ) PhotoMath — калькулятор уравнений на Андроид — NexProRu nexproru/igry-dlya-android/photomath-kalkulyator-uravnenij-2html Похожие Новое приложение, которое способно избавить пользователей от трудностей, например, от решения математических примеров классическим алгебра 8 класс решить уравнение онлайн калькулятор с решением dbchousecom//algebra-8-klass-reshit-uravnenie-onlain-kalkuliator-s-resheniemxml алгебра 8 класс решить уравнение онлайн калькулятор с решением — Все результаты Решение уравнений бесплатно — Калькулятор Онлайн Похожие Онлайн калькуляторы для решения задач по математике o-mathcom/math/assistance/ Математические онлайн калькуляторы , которые детально расписывают ход решения задач, что У многих людей, решение задач по математике ассоциируется с чем-то сложным и непонятным Уравнение плоскости Онлайн 📝Решение квадратного и кубического уравнения онлайн Рейтинг: 3,7 — 7 голосов Бесплатное онлайн решение любого квадратного или кубического уравнения с На вашем конкретном примере онлайн калькулятор все распишет максимально детально У меня всегда с алгеброй туго было( ну не моё это( Калькулятор уравнения четвертой степени — WPcalc › Математика Похожие Бесплатный онлайн калькулятор расчета уравнения четвертой степени, используемый для нахождения корней Математика Алгебра После решения уравнения третьей степени решим уравнение четвертой степени Онлайн калькулятор корней квадратных уравнений › Элементарные функции › Квадратные уравнения 12 сент 2016 г — Представлен онлайн калькулятор для нахождения корней квадратного Решение квадратных уравнений онлайн (нахождение корней) Формулы по математике | Формулы и расчеты онлайн — Fxyzru Похожие Способ подстановки, Решение системы двух уравнений первой степени с двумя неизвестными · Способ сложения или вычитания, Решение системы Онлайн решать матрицы – Онлайн калькулятор Решение систем › Разное Онлайн решать матрицы – Онлайн калькулятор Решение систем линейных уравнений Матричный метод Метод обратной матрицы alexxlab Разное Решение уравнений с параметром — Решить уравнение решить уравнение с параметром онлайн Так же читайте нашу статью » Решить уравнение пропорцией онлайн » Рассмотрим следующие уравнения в AutoMath Photo Calculator решит за вас домашнее задание по 14 дек 2014 г — AutoMath Photo Calculator это калькулятор , который способен нам добавить решение систем уравнений , построение графиков и даже которым необходима помощь в освоении математики, алгебры , Лучшие скидки и акции на AliExpress и в других онлайн -магазинах 29 ноября Вместе с калькулятор для решения уравнений по алгебре онлайн часто ищут пошаговое решение уравнений онлайн калькулятор уравнений с дробями решение уравнений онлайн калькулятор решение уравнений с корнями онлайн решение уравнений с дробями калькулятор алгебра 7 класс решение уравнений со степенями решение уравнений 6 класс Навигация по страницам 1 2 3 4 Следующая Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google
Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Знатоки Коллекции Музыка Переводчик Диск Почта Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва HomeWork™ для студентов – Дарим 500р при регистрации! хоумворкрф › Для-Студентов Не подходит по запросу Спам или мошенничество Мешает видеть результаты Информация о сайте реклама Образовательный проект для студентов Подбор материала онлайн Зарегистрироваться! Гарантии Опыт 17 лет Официальный сайт Все предметы Контактная информация +7 (800) 775-27-26 пн-пт 9:00-22:00, сб-вс 10:00-22:00 1 Решение уравнений бесплатно — Калькулятор Онлайн Обычные уравнения Упрощение выражений kontrolnaya-rabotaru › s/equal-one/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Решение уравнений онлайн позволяет быть уверенным в правильности решения уравнения В каждом из разделов приведены различные виды способов для Читать ещё Решение уравнений онлайн позволяет быть уверенным в правильности решения уравнения В каждом из разделов приведены различные виды способов для помощи Вам Правила ввода уравнений везде читайте и должно получиться Вообще этот сделан только для помощи Вам Скрыть 2 Уравнения онлайн Математика онлайн Система двух уравнений Уравнение с параметром math34biz › Уравнение любого типа Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Решение любого типа уравнений онлайн на Math34biz для закрепления Решение уравнения — задача по нахождению таких значений аргументов, при которых Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач Читать ещё Решение любого типа уравнений онлайн на Math34biz для закрепления изученного материала студентами и школьниками Пошаговое решение уравнений онлайн на сайте Math34biz Решение уравнений онлайн Уравнения онлайн Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т д) Решение уравнений онлайн Пошаговое решение уравнений онлайн на сайте Math34biz Уравнения онлайн Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач Скрыть 3 Решить уравнение Контакты О нас Зарегистрироваться Еще Пример pocketteacherru Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Pocket Teacher: здесь вы можете решить уравнение и математические задачи любой сложности за секунды совершенно Кажется, что перед вами нерешаемое уравнение ? Доверьте его Pocket Teacher! Сайт основан на новейших разработках в области искусственного интеллекта и легко поступает на Мехмат Читать ещё Pocket Teacher: здесь вы можете решить уравнение и математические задачи любой сложности за секунды совершенно бесплатно Кажется, что перед вами нерешаемое уравнение ? Доверьте его Pocket Teacher! Сайт основан на новейших разработках в области искусственного интеллекта и легко поступает на Мехмат МГУ! Скрыть Чат с компанией Задайте свои вопросы консультанту 4 Решить ваши задачи онлайн с нашей программой math20com › ru/reshenie-zadach-onlain/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Онлайн программа решения задач по алгебре Мы рекомендуем Вам зарегистрироваться для этой онлайн программы Решите Ваши задачи ( уравнения , неравенства, радикалы, построение графиков, решение полиномов) в онлайн режиме Если Ваша домашняя работа включает в себя Читать ещё Онлайн программа решения задач по алгебре Мы рекомендуем Вам зарегистрироваться для этой онлайн программы Решите Ваши задачи ( уравнения , неравенства, радикалы, построение графиков, решение полиномов) в онлайн режиме Если Ваша домашняя работа включает в себя математические уравнения , неравенства, функции, многочлены, матрицы, значит регистрация для тестовой версии — это правильный выбор Онлайн программа решения задач по тригонометрии Находит значения всех типов выражений (синус, косинус, тангенс, котангенс, секанс, косеканс), уравнений , неравенств Строит графики тригонометрических функций Скрыть 5 Калькуляторы по алгебре | Расчет треугольника онлайн calcru › kalkulyatory-po-algebrehtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Калькуляторы по алгебре помогут в решении , с подсказками и являются Онлайн калькуляторы по алгебре — решения , подсказки и учебник линейной алгебры онлайн Решение квадратных уравнений онлайн Калькуляторы по геометрии Читать ещё Калькуляторы по алгебре помогут в решении , с подсказками и являются учебником линейной алгебры онлайн Калькуляторы по алгебре Онлайн калькуляторы по алгебре — решения , подсказки и учебник линейной алгебры онлайн Калькуляторы беспплатные Инженерный калькулятор Решение квадратных уравнений онлайн Калькуляторы по геометрии Помощь в решении задач по геометрии, учебник онлайн (все калькуляторы по геометрии) Калькуляторы по геометрии Расчет треугольника онлайн Расчет всех углов, сторон и площади по известным углам и сторонам треугольника, чертеж треугольника Расчет треугольника онлайн Скрыть 6 Калькулятор онлайн — Решение показательных уравнений mathsolutionru › math-task/exponential-equality Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Этот математический калькулятор онлайн поможет вам решить показательное уравнение Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, те Читать ещё Этот математический калькулятор онлайн поможет вам решить показательное уравнение Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, те отображает процесс получения результата Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно Скрыть 7 Решение уравнений онлайн | Новые калькуляторы mathsemestrru › Решение уравнений Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Решение квадратных, кубических, тригонометрических, логарифмических уравнений онлайн Нахождение корней функции Решение уравнений Данный онлайн — калькулятор предназначен для нахождения корней функции Читать ещё Решение квадратных, кубических, тригонометрических, логарифмических уравнений онлайн Нахождение корней функции Подробные примеры решений Решение уравнений Данный онлайн — калькулятор предназначен для нахождения корней функции Для решения уравнений вида ax2+bx+c=0 можно воспользоваться сервисом Дискриминант онлайн В решении приводятся подробное нахождение дискриминанта, а также корней функции Результаты оформляются в формате Word Для нахождения корней уравнения методами дихотомии, Ньютона и других используйте сервис Решение нелинейных уравнений Для уравнений высших степеней используйте следующий сервис Скрыть 8 Калькулятор уравнений онлайн okcalccom › Уравнений Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Бесплатно Windows, iOS, Android Категория: Калькулятор Удобный онлайн калькулятор уравнений , с помощью которого вы можете произвести необходимые расчёты 9 Mathway | Решение алгебраических задач mathwaycom › ru Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Бесплатный сервис по решению математических задач даст ответы к вашему домашнему заданию по алгебре с пошаговым объяснением 10 Algebra Calculator — Symbolab symbolabcom › solver/algebra-calculator Перевести Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Algebra Calculator — get free step-by-step solutions for your algebra math problems Algebra Calculator Calculate equations, inequatlities, line equation and system of equations step-by-step Подготовка студентов к сессии / fizmatservisnarodru fizmatservisnarodru Не подходит по запросу Спам или мошенничество Мешает видеть результаты Информация о сайте реклама Научу студентов решать задачи по математике, физике, электротехнике Понятно объясню решение уравнений онлайн он-лайн / liveexpertru Математика Физика Химия liveexpertru Не подходит по запросу Спам или мошенничество Мешает видеть результаты Информация о сайте реклама Более 1000 преподавателей он-лайн! решение уравнений онлайн ! 18+ Вместе с « калькулятор для решения уравнений по алгебре онлайн » ищут: калькулятор дробей калькулятор онлайн калькулятор для решения дробей калькулятор для решения систем уравнений калькулятор для решения неравенств калькулятор для решения дробных уравнений калькулятор для решения примеров калькулятор для решения тригонометрических уравнений онлайн калькулятор степеней корень знак 1 2 3 4 5 дальше Браузер Интересное в ленте рекомендаций лично для вас 0+ Установить
Показательные уравнения онлайн калькулятор с подробным решением.
Уравнения онлайн
Уравнения онлайнКак решать уравнения?
В этом разделе мы вспомним (или изучим – уж кому как) самые элементарные уравнения. Итак, что такое уравнение? Говоря человеческим языком, это какое-то математическое выражение, где есть знак равенства и неизвестное. Которое, обычно, обозначается буквой
Уравнения бывают всякие (вот удивил, да?). Но всё их бесконечное многообразие можно разбить всего на четыре типа.
4. Все остальные.)
Всех остальных, разумеется, больше всего, да…) Сюда входят и кубические, и показательные, и логарифмические, и тригонометрические и всякие другие.
С ними мы в соответствующих разделах плотно поработаем.
Сразу скажу, что иногда и уравнения первых трёх типов так накрутят, что и не узнаешь их… Ничего. Мы научимся их разматывать.
И зачем нам эти четыре типа? А затем, что линейные уравнения решаются одним способом, квадратные другим, дробные рациональные — третьим, а остальные не решаются вовсе! Ну, не то, чтобы уж совсем никак не решаются, это я зря математику обидел.) Просто для них существуют свои специальные приёмы и методы.
Но для любых (повторяю — для любых! ) уравнений есть надёжная и безотказная основа для решения. Работает везде и всегда. Эта основа — Звучит страшно, но штука очень простая. И очень (очень!) важная.
Собственно, решение уравнения и состоит из этих самых преобразований. На 99%. Ответ на вопрос: «Как решать уравнения? » лежит, как раз, в этих преобразованиях. Намёк понятен?)
Тождественные преобразования уравнений.
В любых уравнениях для нахождения неизвестного надо преобразовать и упростить исходный пример.
Отмечу, что эти преобразования относятся именно к уравнениям. В математике ещё имеются тождественные преобразования выражений. Это другая тема.
Сейчас мы с вами повторим все-все-все базовые тождественные преобразования уравнений.
Базовые потому, что их можно применять к любым уравнениям – линейным, квадратным, дробным, тригонометрическим, показательным, логарифмическим и т.д. и т.п.
Первое тождественное преобразование: к обеим частям любого уравнения можно прибавить (отнять) любое (но одно и то же!) число или выражение (в том числе и выражение с неизвестным!). Суть уравнения от этого не меняется.
Вы, между прочим, постоянно пользовались этим преобразованием, только думали, что переносите какие-то слагаемые из одной части уравнения в другую со сменой знака.
Типа:
Дело знакомое, переносим двойку вправо, и получаем:
На самом деле вы отняли от обеих частей уравнения двойку. Результат получается тот же самый:
х+2 — 2 = 3 — 2
Перенос слагаемых влево-вправо со сменой знака есть просто сокращённый вариант первого тождественного преобразования. И зачем нам такие глубокие познания? – спросите вы. В уравнениях низачем. Переносите, ради бога. Только знак не забывайте менять. А вот в неравенствах привычка к переносу может и в тупик поставить….
Второе тождественное преобразование : обе части уравнения можно умножить (разделить) на одно и то же отличное от нуля число или выражение. Здесь уже появляется понятное ограничение: на ноль умножать глупо, а делить и вовсе нельзя. Это преобразование вы используете, когда решаете что-нибудь крутое, типа
Понятное дело, х = 2. А вот как вы его нашли? Подбором? Или просто озарило? Чтобы не подбирать и не ждать озарения, нужно понять, что вы просто поделили обе части уравнения на 5.
При делении левой части (5х) пятёрка сократилась, остался чистый икс. Чего нам и требовалось. А при делении правой части (10) на пять, получилась, знамо дело, двойка.
Вот и всё.
Забавно, но эти два (всего два!) тождественных преобразования лежат в основе решения всех уравнений математики. Во как! Имеет смысл посмотреть на примерах, что и как, правда?)
Примеры тождественных преобразований уравнений. Основные проблемы.
Начнём с первого тождественного преобразования. Перенос влево-вправо.
Пример для младшеньких.)
Допустим, надо решить вот такое уравнение:
3-2х=5-3х
Вспоминаем заклинание: «с иксами — влево, без иксов — вправо!» Это заклинание — инструкция по применению первого тождественного преобразования.) Какое выражение с иксом у нас справа? 3х ? Ответ неверный! Справа у нас — 3х ! Минус три икс! Стало быть, при переносе влево, знак поменяется на плюс. Получится:
3-2х+3х=5
Так, иксы собрали в кучку.
Займёмся числами. Слева стоит тройка. С каким знаком? Ответ «с никаким» не принимается!) Перед тройкой, действительно, ничего не нарисовано. А это значит, что перед тройкой стоит плюс. Так уж математики договорились. Ничего не написано, значит, плюс. Следовательно, в правую часть тройка перенесётся с минусом. Получим:
-2х+3х=5-3
Остались сущие пустяки. Слева — привести подобные, справа — посчитать. Сразу получается ответ:
В этом примере хватило одного тождественного преобразования. Второе не понадобилось. Ну и ладно.)
Пример для старшеньких.)
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Решение показательных уравнений. Примеры.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Что такое показательное уравнение ? Это уравнение, в котором неизвестные (иксы) и выражения с ними находятся в показателях каких-то степеней. И только там! Это важно.
Вот вам примеры показательных уравнений :
3 х ·2 х = 8 х+3
Обратите внимание! В основаниях степеней (внизу) — только числа . В показателях степеней (вверху) — самые разнообразные выражения с иксом. Если, вдруг, в уравнении вылезет икс где-нибудь, кроме показателя, например:
это будет уже уравнение смешанного типа. Такие уравнения не имеют чётких правил решения. Мы их пока рассматривать не будем. Здесь мы будем разбираться с решением показательных уравнений в чистом виде.
Вообще-то, даже чистые показательные уравнения чётко решаются далеко не всегда. Но существуют определённые типы показательных уравнений, которые решать можно и нужно. Вот эти типы мы и рассмотрим.
Решение простейших показательных уравнений.
Для начала решим что-нибудь совсем элементарное. Например:
Даже безо всяких теорий, по простому подбору ясно, что х=2. Больше-то никак, верно!? Никакое другое значение икса не катит. А теперь глянем на запись решения этого хитрого показательного уравнения:
Что мы сделали? Мы, фактически, просто выкинули одинаковые основания (тройки). Совсем выкинули. И, что радует, попали в точку!
Действительно, если в показательном уравнении слева и справа стоят одинаковые числа в каких угодно степенях, эти числа можно убрать и приравнять показатели степеней. Математика позволяет. Остаётся дорешать куда более простое уравнение. Здорово, правда?)
Однако, запомним железно: убирать основания можно только тогда, когда слева и справа числа-основания находятся в гордом одиночестве! Безо всяких соседей и коэффициентов. Скажем, в уравнениях:
2 х +2 х+1 = 2 3 , или
двойки убирать нельзя!
Ну вот, самое главное мы и освоили.
Как переходить от злых показательных выражений к более простым уравнениям.
«Вот те раз!» — скажете вы. «Кто ж даст такой примитив на контрольных и экзаменах!?»
Вынужден согласиться. Никто не даст. Но теперь вы знаете, куда надо стремиться при решении замороченных примеров. Надо приводить его к виду, когда слева — справа стоит одно и то же число-основание. Дальше всё будет легче. Собственно, это и есть классика математики. Берём исходный пример и преобразовываем его к нужному нам виду. По правилам математики, разумеется.
Рассмотрим примеры, которые требуют некоторых дополнительных усилий для приведения их к простейшим. Назовём их простыми показательными уравнениями.
Решение простых показательных уравнений. Примеры.
При решении показательных уравнений, главные правила — действия со степенями. Без знаний этих действий ничего не получится.
К действиям со степенями надо добавить личную наблюдательность и смекалку. Нам требуются одинаковые числа-основания? Вот и ищем их в примере в явном или зашифрованном виде.
Посмотрим, как это делается на практике?
Пусть нам дан пример:
2 2х — 8 х+1 = 0
Первый зоркий взгляд — на основания. Они… Они разные! Два и восемь. Но впадать в уныние — рано. Самое время вспомнить, что
Двойка и восьмёрка — родственнички по степени.) Вполне можно записать:
8 х+1 = (2 3) х+1
Если вспомнить формулку из действий со степенями:
(а n) m = a nm ,
то вообще отлично получается:
8 х+1 = (2 3) х+1 = 2 3(х+1)
Исходный пример стал выглядеть вот так:
2 2х — 2 3(х+1) = 0
Переносим 2 3 (х+1) вправо (элементарных действий математики никто не отменял!), получаем:
2 2х = 2 3(х+1)
Вот, практически, и всё. Убираем основания:
Решаем этого монстра и получаем
Это правильный ответ.
В этом примере нас выручило знание степеней двойки. Мы опознали в восьмёрке зашифрованную двойку. Этот приём (шифровка общих оснований под разными числами) — очень популярный приём в показательных уравнениях! Да и в логарифмах тоже.
Надо уметь узнавать в числах степени других чисел. Это крайне важно для решения показательных уравнений.
Дело в том, что возвести любое число в любую степень — не проблема. Перемножить, хоть на бумажке, да и всё. Например, возвести 3 в пятую степень сможет каждый. 243 получится, если таблицу умножения знаете.) Но в показательных уравнениях гораздо чаще надо не возводить в степень, а наоборот… Узнавать, какое число в какой степени скрывается за числом 243, или, скажем, 343… Здесь вам никакой калькулятор не поможет.
Степени некоторых чисел надо знать в лицо, да… Потренируемся?
Определить, какими степенями и каких чисел являются числа:
2; 8; 16; 27; 32; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729, 1024.
Ответы (в беспорядке, естественно!):
5 4 ; 2 10 ; 7 3 ; 3 5 ; 2 7 ; 10 2 ; 2 6 ; 3 3 ; 2 3 ; 2 1 ; 3 6 ; 2 9 ; 2 8 ; 6 3 ; 5 3 ; 3 4 ; 2 5 ; 4 4 ; 4 2 ; 2 3 ; 9 3 ; 4 5 ; 8 2 ; 4 3 ; 8 3 .
Если приглядеться, можно увидеть странный факт.
Ответов существенно больше, чем заданий! Что ж, так бывает… Например, 2 6 , 4 3 , 8 2 — это всё 64.
Предположим, что вы приняли к сведению информацию о знакомстве с числами.) Напомню ещё, что для решения показательных уравнений применим весь запас математических знаний. В том числе и из младших-средних классов. Вы же не сразу в старшие классы пошли, верно?)
Например, при решении показательных уравнений очень часто помогает вынесение общего множителя за скобки (привет 7 классу!). Смотрим примерчик:
3 2х+4 -11·9 х = 210
И вновь, первый взгляд — на основания! Основания у степеней разные… Тройка и девятка. А нам хочется, чтобы были — одинаковые. Что ж, в этом случае желание вполне исполнимое!) Потому, что:
9 х = (3 2) х = 3 2х
По тем же правилам действий со степенями:
3 2х+4 = 3 2х ·3 4
Вот и отлично, можно записать:
3 2х ·3 4 — 11·3 2х = 210
Мы привели пример к одинаковым основаниям. И что дальше!? Тройки-то нельзя выкидывать.
.. Тупик?
Вовсе нет. Запоминаем самое универсальное и мощное правило решения всех математических заданий:
Не знаешь, что нужно — делай, что можно!
Глядишь, всё и образуется).
Что в этом показательном уравнении можно сделать? Да в левой части прямо просится вынесение за скобки! Общий множитель 3 2х явно намекает на это. Попробуем, а дальше видно будет:
3 2х (3 4 — 11) = 210
3 4 — 11 = 81 — 11 = 70
Пример становится всё лучше и лучше!
Вспоминаем, что для ликвидации оснований нам необходима чистая степень, безо всяких коэффициентов. Нам число 70 мешает. Вот и делим обе части уравнения на 70, получаем:
Оп-па! Всё и наладилось!
Это окончательный ответ.
Случается, однако, что выруливание на одинаковые основания получается, а вот их ликвидация — никак. Такое бывает в показательных уравнениях другого типа. Освоим этот тип.
Замена переменной в решении показательных уравнений. Примеры.
Примеры.Решим уравнение:
4 х — 3·2 х +2 = 0
Сначала — как обычно. Переходим к одному основанию. К двойке.
4 х = (2 2) х = 2 2х
Получаем уравнение:
2 2х — 3·2 х +2 = 0
А вот тут и зависнем. Предыдущие приёмы не сработают, как ни крутись. Придётся доставать из арсенала ещё один могучий и универсальный способ. Называется он замена переменной.
Суть способа проста до удивления. Вместо одного сложного значка (в нашем случае — 2 х) пишем другой, попроще (например — t). Такая, казалось бы, бессмысленная замена приводит к потрясным результатам!) Просто всё становится ясным и понятным!
Итак, пусть
Тогда 2 2х = 2 х2 = (2 х) 2 = t 2
Заменяем в нашем уравнении все степени с иксами на t:
Ну что, осеняет?) Квадратные уравнения не забыли ещё? Решаем через дискриминант, получаем:
Тут, главное, не останавливаться, как бывает… Это ещё не ответ, нам икс нужен, а не t. Возвращаемся к иксам, т.
е. делаем обратную замену. Сначала для t 1:
Стало быть,
Один корень нашли. Ищем второй, из t 2:
Гм… Слева 2 х, справа 1… Неувязочка? Да вовсе нет! Достаточно вспомнить (из действий со степенями, да…), что единичка — это любое число в нулевой степени. Любое. Какое надо, такое и поставим. Нам нужна двойка. Значит:
Вот теперь всё. Получили 2 корня:
Это ответ.
При решении показательных уравнений в конце иногда получается какое-то неудобное выражение. Типа:
Из семёрки двойка через простую степень не получается. Не родственники они… Как тут быть? Кто-то, может и растеряется… А вот человек, который прочитал на этом сайте тему «Что такое логарифм?» , только скупо улыбнётся и запишет твёрдой рукой совершенно верный ответ:
Такого ответа в заданиях «В» на ЕГЭ быть не может. Там конкретное число требуется. А вот в заданиях «С» — запросто.
В этом уроке приведены примеры решения самых распространённых показательных уравнений.
Выделим основное.
Практические советы:
1. Первым делом смотрим на основания степеней. Соображаем, нельзя ли их сделать одинаковыми. Пробуем это сделать, активно используя действия со степенями. Не забываем, что числа без иксов тоже можно превращать в степени!
2. Пробуем привести показательное уравнение к виду, когда слева и справа стоят одинаковые числа в каких угодно степенях. Используем действия со степенями и разложение на множители. То что можно посчитать в числах — считаем.
3. Если второй совет не сработал, пробуем применить замену переменной. В итоге может получиться уравнение, которое легко решается. Чаще всего — квадратное. Или дробное, которое тоже сводится к квадратному.
4. Для успешного решения показательных уравнений надо степени некоторых чисел знать «в лицо».
Как обычно, в конце урока вам предлагается немного порешать.) Самостоятельно. От простого — к сложному.
Решить показательные уравнения:
Посложнее:
2 х+3 — 2 х+2 — 2 х = 48
9 х — 8·3 х = 9
2 х — 2 0,5х+1 — 8 = 0
Найти произведение корней:
2 3-х + 2 х = 9
Получилось?
Ну, тогда сложнейший пример (решается, правда, в уме.
..):
7 0.13х + 13 0,7х+1 + 2 0,5х+1 = -3
Что, уже интереснее? Тогда вот вам злой пример. Вполне тянет на повышенную трудность. Намекну, что в этом примере спасает смекалка и самое универсальное правило решения всех математических заданий.)
2 5х-1 · 3 3х-1 · 5 2х-1 = 720 х
Пример попроще, для отдыха):
9·2 х — 4·3 х = 0
И на десерт. Найти сумму корней уравнения:
х·3 х — 9х + 7·3 х — 63 = 0
Да-да! Это уравнение смешанного типа! Которые мы в этом уроке не рассматривали. А что их рассматривать, их решать надо!) Этого урока вполне достаточно для решения уравнения. Ну и, смекалка нужна… И да поможет вам седьмой класс (это подсказка!).
Ответы (в беспорядке, через точку с запятой):
1; 2; 3; 4; решений нет; 2; -2; -5; 4; 0.
Всё удачно? Отлично.
Есть проблемы? Не вопрос! В Особом разделе 555 все эти показательные уравнения решаются с подробными объяснениями. Что, зачем, и почему. Ну и, конечно, там имеется дополнительная ценная информация по работе со всякими показательными уравнениями.
Не только с этими.)
Последний забавный вопрос на соображение. В этом уроке мы работали с показательными уравнениями. Почему я здесь ни слова не сказал про ОДЗ? В уравнениях — это очень важная штука, между прочим…
Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Предлагаемый вашему вниманию бесплатный калькулятор располагает богатым арсеналом возможностей для математических вычислений. Он позволяет использовать онлайн калькулятор в различных сферах деятельности: образовательной , профессиональной и коммерческой . Конечно, применение калькулятора онлайн особенно популярно у студентов и школьников , он значительно облегчает им выполнение самых разных расчётов.
Вместе с тем калькулятор может стать полезным инструментом в некоторых направлениях бизнеса и для людей разных профессий.
Безусловно, необходимость применения калькулятора в бизнесе или трудовой деятельности определяется прежде всего видом самой деятельности. Если бизнес и профессия связаны с постоянными расчётами и вычислениями, то стоит опробовать электронный калькулятор и оценить степень его полезности для конкретного дела.
Данный онлайн калькулятор может
- Корректно выполнять стандартные математические функции, записанные одной строкой типа — 12*3-(7/2) и может обрабатывать числа больше, чемсчитаем огромные числа в онлайн калькулятореМы даже не знаем, как такое число назвать правильно (тут 34 знака и это совсем не предел ).
- Кроме тангенса , косинуса , синуса и других стандартных функций — калькулятор поддерживает операции по расчёту арктангенса , арккотангенса и прочих.
- Доступны в арсенале логарифмы , факториалы и другие интересные функции
- Данный онлайн калькулятор умеет строить графики !!!
Для построения графиков, сервис использует специальную кнопку (график серый нарисован) или буквенное представление этой функции (Plot).
Чтобы построить график в онлайн калькуляторе, достаточно записать функцию: plot(tan(x)),x=-360..360 .
Мы взяли самый простой график для тангенса, и после запятой указали диапазон переменной X от -360 до 360.
Построить можно абсолютно любую функцию, с любым количеством переменных, например такую: plot(cos(x)/3z, x=-180..360,z=4) или ещё более сложную, какую сможете придумать. Обращаем внимание на поведение переменной X — указан промежуток от и до с помощью двух точек.
Единственный минус (хотя трудно назвать это минусом) этого онлайн калькулятора это то, что он не умеет строить сферы и другие объёмные фигуры — только плоскость.
Как работать с Математическим калькулятором
1. Дисплей (экран калькулятора) отображает введенное выражение и результат его расчёта обычными символами, как мы пишем на бумаге. Это поле предназначено просто для просмотра текущей операции. Запись отображается на дисплее по мере набора математического выражения в строке ввода.
2. Поле ввода выражения предназначено для записи выражения, которое нужно вычислить. Здесь следует отметить, что математические символы, используемые в компьютерных программах, не всегда совпадают с теми, которые обычно мы применяем на бумаге. В обзоре каждой функции калькулятора вы найдёте правильное обозначение конкретной операции и примеры расчётов в калькуляторе. На этой странице ниже приводится перечень всех возможных операций в калькуляторе, также с указанием их правильного написания.
3. Панель инструментов — это кнопки калькулятора, которые заменяют ручной ввод математических символов, обозначающих соответствующую операцию. Некоторые кнопки калькулятора (дополнительные функции, конвертер величин, решение матриц и уравнений, графики) дополняют панель задач новыми полями, где вводятся данные для конкретного расчёта. Поле «History» содержит примеры написания математических выражений, а также ваши шесть последних записей.
Обратите внимание, при нажатии кнопок вызова дополнительных функций, конвертера величин, решения матриц и уравнений, построения графиков вся панель калькулятора смещается вверх, закрывая часть дисплея.
Заполните необходимые поля и нажмите клавишу «I» (на рисунке выделена красным цветом), чтобы увидеть дисплей в полный размер.
4. Цифровая клавиатура содержит цифры и знаки арифметических действий. Кнопка «С» удаляет всю запись в поле ввода выражения. Чтобы удалять символы по одному, нужно использовать стрелочку справа от строки ввода.
Старайтесь всегда закрывать скобки в конце выражения. Для большинства операций это некритично, калькулятор online рассчитает всё верно. Однако, в некоторых случаях возможны ошибки. Например, при возведении в дробную степень незакрытые скобки приведут к тому, что знаменатель дроби в показателе степени уйдет в знаменатель основания. На дисплее закрывающая скобка обозначена бледно-серым цветом, её нужно закрыть, когда запись закончена.
| Клавиша | Символ | Операция |
|---|---|---|
| pi | pi | Постоянная pi |
| е | е | Число Эйлера |
| % | % | Процент |
| () | () | Открыть/Закрыть скобки |
| , | , | Запятая |
| sin | sin(?) | Синус угла |
| cos | cos(?) | Косинус |
| tan | tan(y) | Тангенс |
| sinh | sinh() | Гиперболический синус |
| cosh | cosh() | Гиперболический косинус |
| tanh | tanh() | Гиперболический тангенс |
| sin -1 | asin() | Обратный синус |
| cos -1 | acos() | Обратный косинус |
| tan -1 | atan() | Обратный тангенс |
| sinh -1 | asinh() | Обратный гиперболический синус |
| cosh -1 | acosh() | Обратный гиперболический косинус |
| tanh -1 | atanh() | Обратный гиперболический тангенс |
| x 2 | ^2 | Возведение в квадрат |
| х 3 | ^3 | Возведение в куб |
| x y | ^ | Возведение в степень |
| 10 x | 10^() | Возведение в степень по основанию 10 |
| e x | exp() | Возведение в степень числа Эйлера |
| vx | sqrt(x) | Квадратный корень |
| 3 vx | sqrt3(x) | Корень 3-ей степени |
| y vx | sqrt(x,y) | Извлечение корня |
| log 2 x | log2(x) | Двоичный логарифм |
| log | log(x) | Десятичный логарифм |
| ln | ln(x) | Натуральный логарифм |
| log y x | log(x,y) | Логарифм |
| I / II | Сворачивание/Вызов дополнительных функций | |
| Unit | Конвертер величин | |
| Matrix | Матрицы | |
| Solve | Уравнения и системы уравнений | |
| Построение графиков | ||
| Дополнительные функции (вызов клавишей II) | ||
| mod | mod | Деление с остатком |
| ! | ! | Факториал |
| i / j | i / j | Мнимая единица |
| Re | Re() | Выделение целой действительной части |
| Im | Im() | Исключение действительной части |
| |x| | abs() | Модуль числа |
| Arg | arg() | Аргумент функции |
| nCr | ncr() | Биноминальный коэффициент |
| gcd | gcd() | НОД |
| lcm | lcm() | НОК |
| sum | sum() | Суммарное значение всех решений |
| fac | factorize() | Разложение на простые множители |
| diff | diff() | Дифференцирование |
| Deg | Градусы | |
| Rad | Радианы | |
На этапе подготовки к заключительному тестированию учащимся старших классов необходимо подтянуть знания по теме «Показательные уравнения».
Опыт прошлых лет свидетельствует о том, что подобные задания вызывают у школьников определенные затруднения. Поэтому старшеклассникам, независимо от уровня их подготовки, необходимо тщательно усвоить теорию, запомнить формулы и понять принцип решения таких уравнений. Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Готовьтесь к экзаменационному тестированию вместе со «Школково»!
При повторении пройденных материалов многие учащиеся сталкиваются с проблемой поиска нужных для решения уравнений формул. Школьный учебник не всегда находится под рукой, а отбор необходимой информации по теме в Интернете занимает долгое время.
Образовательный портал «Школково» предлагает ученикам воспользоваться нашей базой знаний. Мы реализуем совершенно новый метод подготовки к итоговому тестированию. Занимаясь на нашем сайте, вы сможете выявить пробелы в знаниях и уделить внимание именно тем заданиям, которые вызывают наибольшие затруднения.
Преподаватели «Школково» собрали, систематизировали и изложили весь необходимый для успешной сдачи ЕГЭ материал в максимально простой и доступной форме.
Основные определения и формулы представлены в разделе «Теоретическая справка».
Для лучшего усвоения материала рекомендуем попрактиковаться в выполнении заданий. Внимательно просмотрите представленные на данной странице примеры показательных уравнений с решением, чтобы понять алгоритм вычисления. После этого приступайте к выполнению задач в разделе «Каталоги». Вы можете начать с самых легких заданий или сразу перейти к решению сложных показательных уравнений с несколькими неизвестными или . База упражнений на нашем сайте постоянно дополняется и обновляется.
Те примеры с показателями, которые вызвали у вас затруднения, можно добавить в «Избранное». Так вы можете быстро найти их и обсудить решение с преподавателем.
Чтобы успешно сдать ЕГЭ, занимайтесь на портале «Школково» каждый день!
для решения математики.
Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными.
Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.
. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Задачник-практикум по теме «Тригонометрия»
Министерство образования и науки Самарской области
ГОУ СПО Тольяттинский техникум технического и художественного образования
ЗАДАЧНИК – ПРАКТИКУМ ПО ТРИГОНОМЕТРИИ
г.
Тольятти, 2010
ОДОБРЕНА
Составлены в соответствии с Государственными требованиями к минимуму содержания и уровню подготовки выпускника по специальности СПО
Предметной (цикловой) комиссией естественно- научного цикла
Председатель:
Зам. директора по УМР
_______/ Самойлова Л.В.
____________/ УреневаИ.И.
Ерисова В.П преподаватель математики, ГОУ СПО Тольяттинский техникум технического и художественного образования
Учебно-методическое пособие по подготовке студентов к тематическому зачету. «Задачник-практикум по тригонометрии».(Для специальностей технического профиля 1-2 курса)
Рецензенты:
Ю.И. Вдовин —
Доктор технических наук , зав. кафедрой Тольяттинского государственного университета
Задачник-практикум по тригонометрии. – Тольятти: ТТТиХО, 2010, — С.
Сборник содержит задания раздела «Тригонометрия».
Задачи подобраны с учетом требований государственного образования стандарта общего образования. Рекомендуется преподавателям математики и обучающимся учреждений начального и среднего профессионального образования.
Введение
Настоящий задачник-практикум составлен в соответствии с программой по математике для образовательных учреждений СПО. Также он может быть использован учебными заведениями, реализующими программы НПО.
Цель его – помочь обучающимся в изучении раздела математики «Тригонометрические преобразования», решать уравнения, уравнения с параметрами, с модулем, системы и неравенства.
Практикум составлен исходя из учета тех трудностей, с которыми встречаются обучающиеся.
Много заданий дано с подробным решением. Предлагаются задания для самоконтроля.
Настоящий задачник-практикум рассчитан для самостоятельного изучения данного раздела математики.
Он поможет студентам подготовиться к контрольной работе, зачету.
При составлении задачника были использованы учебники, учебные пособия и сборники задач.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА
Синус, косинус, тангенс и котангенс. Основные формулы тригонометрии
Рассмотрим единичную тригонометрическую окружность.
Синусом угла называется ордината точки – конца подвижного радиуса единичной тригонометрической окружности, повернутого на угол .
Косинусом угла называется абсцисса точки – конца подвижного радиуса единичной тригонометрической окружности, повернутого на угол .
Тангенсом угла называется отношение абсциссы к ординате точки – конца подвижного радиуса единичной тригонометрической окружности, повернутого на угол .
Котангенсом угла называется отношение абсциссы к ординате точки – конца подвижного радиуса единичной тригонометрической окружности, повернутого на угол .
Соотношение между тригонометрическими функциями одного и того же угла:
Формулы сложения:
Формулы кратких аргументов:
Формулы понижения степени:
Формулы преобразования сумм и разностей в произведения:
Формулы преобразования произведений в суммы или разности:
Формул приведения
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
Упростите выражение
Упростите выражение:
Упростите выражение:
Упростите выражение:
Докажите тождество:
Докажите тождество:
7.
Докажите тождество:
8. Докажите тождество:
9. Докажите тождество:
10. Вычислите:
Вычислите:
12. Дано: и
Найдите:
Упростите выражение и найдите его числовое значение:
УПРАЖНЕНИЯ
1.1. Представить в виде произведения выражения:
1.2. Доказать тождество:
1.3. Упростить выражение:
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Применяя различные преобразования при решении тригонометрических уравнений, мы приходим к простейшим уравнениям, формулы решения которых следует запомнить:
а)
Это уравнение имеет решения, если или Общее решение этого уравнения записывается в виде
Если же , то данное уравнение не имеет решений, что следует запомнить, т.
к. забывая об этом, учащиеся часто допускают ошибки.
Например, решая уравнение и не учитывая, что , записывают «решение» этого уравнения в виде , несмотря на то, что функция arcsin x не определена в точке и приведенная запись не имеет смысла.
ПРИМЕР 1
Решить уравнение:
Решение.
но arcsin 0 = 0, следовательно решение этого уравнения можно записать так:
ПРИМЕР 2
Решить уравнение:
Решение.
но , тогда получаем
.
При четном к = 2n; ;
при нечетном .
Оба случая дают одну и ту же формулу
,
которая и является решением.
ПРИМЕР 3
Решить уравнение:
Решение.
Так как , то
При четном
при нечетном
Оба случая дают одну и ту же формулу
которая является решением.
Решения, полученные в примерах 1 – 3, целесообразно запомнить, так как их запись является более удобной, чем запись решения в общем виде.
б) Это уравнение имеет решение, если или
Общее решение этого уравнения записывается в виде
,
где , ,
Если , уравнение решения не имеет.
Рассмотрим наиболее часто встречающиеся на практике случаи, когда запись решения допускает упрощения.
ПРИМЕР 4
Решить уравнение:
Решение:
П
о общей формуле
но , поэтому решение уравнения записывается так:
ПРИМЕР 5
Решить уравнение:
Решение.
По общей формуле
но , поэтому решение уравнения записывается так:
.
ПРИМЕР 6
Решить уравнение:
Решение
По общей формуле
Заменяя его значением, получим
Выражение обозначает множество чисел, которые при делении на 4 дают в остатке 1, а выражение обозначает множество чисел, дающих в остатке 3.
Такими свойствами обладает множество нечетных чисел, следовательно, выражение может быть заменено выражением , обозначающим множество всех нечетных чисел. Поэтому решение уравнения записывают так:
Записи решений трех рассмотренных уравнений также следует запомнить.
в) Это уравнение имеет решения при любых значениях
Общее решение этого уравнения записывается в виде
где
ПРИМЕР 7
Решить уравнение:
Решение
но , следовательно,
ПРИМЕР 8
Решить уравнение:
Решение
,
но , следовательно,
ПРИМЕР 9
Решить уравнение:
Решение
,
но , поэтому
Рассмотреть еще несколько примеров решения простейших тригонометрических уравнений.
Решить уравнения: 1)
Решение
Так как , то общее решение уравнения запишется в виде
2)
Решение
Так как общее решение уравнения запишется в виде
3)
Решение
Используя тождество , получим
,
или окончательно
4)
Решение
Так как , данное уравнение решений не имеет, т.е.
5)
Решение
,
или
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ВИДА
Уравнения вида легко сводятся к простейшим введением вспомогательного неизвестного а уравнение вида
сводятся к алгебраическим, путем соответствующих подстановок
ПРИМЕР 1
Решить уравнение:
Решение
ПРИМЕР 2
Решить уравнение:
Решение
ПРИМЕР 3
Решить уравнение:
Решение
так как , произведение , а это возможно лишь для , то есть получим уравнение:
ПРИМЕР 4
Решить уравнение:
Решение
, то выражение при любом , поэтому данное уравнение решений не имеет.
Ответ:
ПРИМЕР 5
Решить уравнение:
Решение
ПРИВЕДЕНИЕ УРАВНЕНИЙ
К АЛГЕБРАИЧЕСКОМУ ВИДУ ОТНОСИТЕЛЬНО КАКОЙ-ЛИБО ТРИГОНОМЕТРИЧЕСКОЙ ФУНКЦИИ
Один из приемов решения тригонометрических уравнений состоит в том, что различные тригонометрические функции, входящие в данное уравнение, выражаются через одну и ту же функцию с одинаковым аргументом. Тем самым тригонометрическое уравнение с помощью подстановки приводится к алгебраическому, которое и решается на основании общих методов решения алгебраических уравнений.
ПРИМЕР 1
Решить уравнение:
Решение
Пусть
Ответ:
ПРИМЕР 3
Решить уравнение:
Решение
Применяя тождество , получим
Применив подстановку , получим квадратное уравнение, корни которого
Применяя обратную подстановку, получим
Ответ:
ПРИМЕР 4
Решить уравнение:
Решение
Применим тождество: ,
тогда исходное уравнение можно записать в виде
Полагая , а уравнение
Ответ:
Если все функции, входящие в данное уравнение, имеют одинаковый аргумент, то тригонометрическое уравнение сводится к алгебраическому с помощью следующих тригонометрических тождеств:
Однако использование данных формул ведет к сужению области определения исходного уравнения, при этом возможна потеря решений.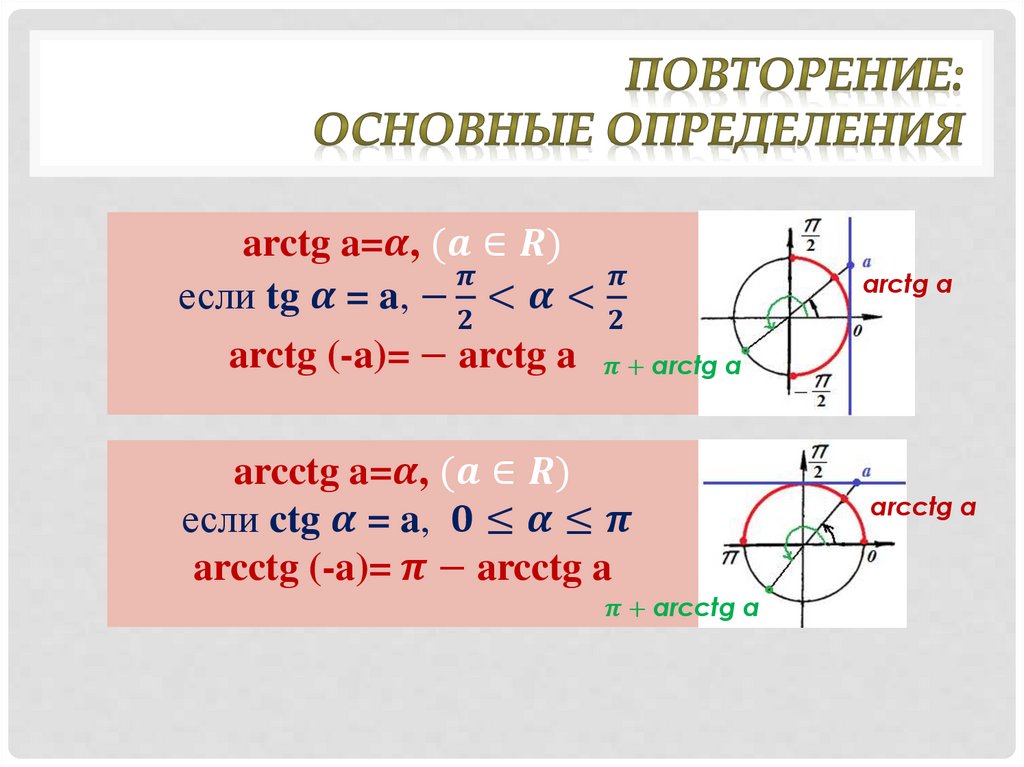
Поэтому после окончания решения необходимо проверить подстановкой в исходное уравнение значение неизвестного
или
при которых правая часть указанных тождеств не имеет смысла.
ПРИМЕР 5
Решить уравнение:
Решение
Заменяя и через тангенс половинного аргумента и применяя подстановку , получим
Корни этого уравнения и Тогда
Полученные значения х являются сериями решений исходного уравнения, остается проверить, не являются ли корнями значения , подставляя это значение в левую часть исходного уравнения, получим
,
то есть не является корнем исходного уравнения.
Ответ:
ПРИМЕР 6
Решить уравнение:
Решение
Выражая и через , а , в свою очередь, обозначив через t, получим
Отсюда , то есть и
Подставим теперь в левую часть исходного уравнения Имеем Так как — верное равенство, значение также является корнем исходного уравнения.
После этого записываем ответ:
Отметим, что далеко не все тригонометрические уравнения, приводимые к алгебраическому виду относительно какой-либо функции, имеют простое решение. Покажем это на примерах.
ПРИМЕР 7
Решить уравнение:
Решение
Используем тождество
Тогда
После подстановки получим , откуда
Тогда Дискриминант этого квадратного относительно уравнения отрицателен, следовательно,
Пусть теперь
Рассмотрим еще один тип тригонометрических уравнений, которые можно свести к алгебраическим относительно какой-либо функции, так называемые однородные тригонометрические уравнения.
Определение. Тригонометрическое уравнение называется однородным, если левая часть его – однородный многочлен относительно и , а правая часть – нуль.
Например, — однородное тригонометрическое уравнение. Покажем общий способ решения таких уравнений.
ПРИМЕР 8
Решить уравнение:
Решение
Очевидно, значение не является решением этого уравнения, так как предположив, что , получим и для одних и тех же х, что противоречит тождеству Следовательно, для данного уравнения Тогда, не нарушая равносильности, можно обе части уравнения (8) поделить на . Получим
Ответ:
ПРИМЕР 9
Решить уравнение:
Решение
Учитывая, что в данном уравнении , после деления на получим
,
откуда и
и
Ответ:
ПРИМЕР 10
Решить уравнение:
Решение
Это уравнение не является однородным, но мы можем свести его к однородному, записав свободный член в виде
,
тогда После деления на и приведения подобных членов, получим
Ответ:
ПРИМЕР 11
Решить уравнение:
Решение
Приведем это уравнение к однородному и решим его так же, как и предыдущее;
Ответ:
СПОСОБ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ,
ОСНОВАННЫЙ НА ИСПОЛЬЗОВАНИИ СВОЙСТВ
ПРОИЗВЕДЕНИЯ И ЧАСТНОГО
Если после переноса всех членов уравнения в левую часть полученное выражение можно разложить на множители, то можно воспользоваться свойством произведения: произведение двух или нескольких сомножителей равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю.
Следует особо подчеркнуть, что корни какого-либо из сомножителей могут не входить в область определения другого сомножителя, то есть необходима проверка полученных решений. Посторонние корни могут появиться и в результате тождественных преобразований в частях уравнения. Например, уравнение и уравнение не является равносильным, так как уравнение (1) не имеет корней, а решением уравнения (2) является значение В этом случае также необходима проверка решений. Рассмотрим несколько примеров.
ПРИМЕР 1
Решить уравнение:
Решение
Перенося единицу в левую часть уравнения и используя тождество , получим
Приравнивая к нулю каждый множитель, получим совокупность уравнений, которая в данном случае равносильна исходному
Ответ:
ПРИМЕР 2
Решить уравнение:
Решение
Перенося все члены уравнения в левую часть и применяя тождество и получим
,
откуда
Ответ:
ПРИМЕР 3
Решить уравнение:
Решение
,
но эти значения х не входят в область определения второго сомножителя, значит, являются посторонними.
Приравнивая к нулю второй сомножитель, получим
Ответ:
ПРИМЕР 4
Решить уравнение:
Решение
Используя тождество ,
получим
Ответ:
ПРИМЕР 5
Решить уравнение:
Решение
Применяя тождество ,
получим
Ответ:
ПРИМЕР 6
Решить уравнение:
Решение
Ответ:
ПРИМЕР 7
Решить уравнение:
Решение
Условие, снимающее знак (*), , поэтому (в силу того, что )
Ответ:
ПРИМЕР 8
Решить уравнение:
Решение
Ответ:
ПРИМЕР 9
Решить уравнение:
Решение
Так как перепишем уравнение в виде
Ответ:
РЕШЕНИЕ УРАВНЕНИЙ,
СОДЕРЖАЩИХ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
С ЧЕТНЫМ ПОКАЗАТЕЛЕМ
Если в тригонометрическое уравнение входят функции с четным показателем, очень часто приводит к цели применения формул понижения степени
В некоторых случаях возможность наиболее простого решения уравнения дает применение тождества Рассмотрим примеры решения таких уравнений.
ПРИМЕР 1
Решить уравнение:
Решение
Применяя формулы понижения степени, получим
Ответ:
ПРИМЕР 2
Решить уравнение:
Решение
Выражая и через тангенс половинного аргумента и применяя подстановку , получим
Подставляя в исходное уравнение значение , получим
Следовательно, потеря корней не произошла.
Ответ:
ПРИМЕР 3
Решить уравнение:
Решение
Приведем функции левой части уравнения к одному аргументу
откуда
Ответ:
ПРИМЕР 4
Решить уравнение:
Решение
Применяя формулу понижения степени и формулы приведения, получим
Ответ:
ПРИМЕР 5
Решить уравнение:
Решение
Так как
,
получим
Ответ:
Второй способ.
Прибавляя к левой и правой части уравнения выражение , получим
Ответ:
ПРИМЕР 6
Решить уравнение:
Решение
Применяя формулы понижения степени, получим
Ответ:
ПРИМЕР 7
Решить уравнение:
Решение
Преобразуем левую часть уравнения следующим образом:
Тогда исходное уравнение запишется в виде
Ответ:
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
МЕТОДОМ ВСПОМОГАТЕЛЬНОГО УГЛА
Рассмотрим уравнение вида ,
где и . Это уравнение можно решить одним из следующих способов:
а) возведение обеих частей уравнения в квадрат;
б) выражение всех функций через тангенс половинного угла;
в) введение вспомогательного угла.
Применение первого способа может привести к приобретению посторонних корней, и проверка полученных решений бывает очень громоздкой. При использовании второго способа может произойти потеря решения вида . Наиболее удобным является способ введения вспомогательного угла. Рассмотрим этот метод в общем виде.
Разделим обе части уравнения (1) на , получим
Так как , то существует угол такой, что
и ,
тогда уравнение (1) можно переписать в виде
или
Последнее уравнение разрешимо только в том случае, когда
или
Когда это условие выполнено, решение уравнения (1) запишется следующим образом:
и угол определяется из формул (2) . Если же условие (3) не выполнено, то уравнение (1) решений не имеет.
Рассмотрим несколько примеров.
ПРИМЕР 1
Решить уравнение:
Решение
Запишем уравнение в виде ,
тогда
Так как и , то в качестве угла можно взять , и уравнение запишем в виде
Ответ:
ПРИМЕР 2
Решить уравнение:
Решение
Умножая обе части уравнения на и перенося все члены уравнения в левую часть, получим
Учитывая, что и , запишем уравнение в виде
Или, применяя формулу приведения,
Приравнивая каждый сомножитель к нулю, получим две серии решений:
Ответ:
ПРИМЕР 3
Решить уравнение:
Решение
В этом уравнении ,
следовательно, условие не выполняется, и уравнение не имеет решений.
Ответ:
ОЦЕНКА ЛЕВОЙ И ПРАВОЙ ЧАСТЕЙ УРАВНЕНИЯ
При решении некоторых тригонометрических уравнений рассмотренные выше способы не приводят к цели. В этом случае предварительная оценка левой и правой частей уравнения иногда позволяет быстро установить, имеет ли оно корни, и существенно упростить решение.
ПРИМЕР 1
Решить уравнение:
Решение
Учитывая, что и , заключаем, что часть уравнения будет равна правой только тогда, когда
но синус и косинус одного и того же аргумента одновременно быть равными единицы не могут, так как это противоречит тождеству , поэтому данное уравнение решений не имеет.
Ответ:
ПРИМЕР 2
Решить уравнение:
Решение
Левая часть уравнения может быть равной трем только в том случае, когда
Из первого уравнения системы имеем , подставляя это значение х в третье уравнение системы, получим , следовательно, данная система решений не имеет.
Ответ:
ПРИМЕР 3
Решить уравнение:
Решение
Очевидно, правая часть уравнения удовлетворяет условию . Для оценки левой части уравнения воспользуемся свойствами числовых неравенств. Очевидно,
складывая эти неравенства, получим . Отсюда следует, что исходное уравнение равносильно следующей системе:
Из второго уравнения системы имеем: и . Подставляя эти значения х в первое уравнение системы, получим , то есть является решением исходного уравнения.
Пусть , тогда
Значит, не является решением исходного уравнения.
Ответ:
ПРИМЕР 4
Решить уравнение:
Решение
Оценим левую часть уравнения. Так как и , левая часть уравнения может быть равной единице только в том случае, если
а) б)
Решая систему (а), получим .
Подставляя это значение х во второе уравнение системы (а), получим , то есть является решением исходного уравнения.
Решим систему (б) . Подставим это значение во второе уравнение системы (б), получим
то есть тоже является решением исходного уравнения. Тогда ответ для исходного уравнения запишется в виде
ИРРАЦИОНАЛЬНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
При решении иррациональных тригонометрических уравнений после возведения обеих частей уравнения в четную степень возможно появление посторонних корней. Рассмотрим примеры решения таких уравнений, выбирая метод проверки, адекватный полученному решению.
ПРИМЕР 1
Решить уравнение:
Решение
Уравнение решений не имеет. Остается . Условие, снимающее знак (*) в первом переходе, , значит, решение уравнения должно принадлежать четвертой четверти, то есть
Ответ:
ПРИМЕР 2
Решить уравнение:
Решение
откуда или .
Условие равносильности , значит посторонний корень. Остается
Ответ:
ПРИМЕР 3
Решить уравнение:
Решение
откуда
откуда и Так как в решении знак (*) отсутствует, фиксируем ответ:
.
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
С -1. Простейшие тригонометрические уравнения.
Вариант1
1)
2)
3)
4)
5)
6)
7)
Вариант 2
1)
2)
3)
4)
5)
6)
7)
С – 2.
Многовариантная самостоятельная работа на простейшие тригонометрические уравнения.
Решите тригонометрическое уравнение, если — один из его корней (см. таблицу).
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант6
1)
2)
3)
4)
5)
6)
С – 3. Применение условий равенства двух одноименных тригонометрических функций.
Вариант 1
1) 2) 3) 4)
Вариант 2
1) 2) 3) 4)
Вариант 3
1) 2) 3) 4)
С – 4. Уравнения, решающиеся методом подстановки.
Решите уравнение вида , если
1 вариант
2 вариант
3 вариант
4 вариант
5 вариант
6 вариант
2) Решите уравнение вида , если является корнем данного уравнения:
1 вариант
2 вариант
3 вариант
4 вариант
5 вариант
6 вариант
С – 5. Уравнения, решающиеся введением новой переменной.
Вариант 1
1)
2) , если является корнем;
3) , если является корнем;
4) , если является корнем.
Вариант 2
1)
2) , если является корнем;
3) , если является корнем;
4) , если является корнем.
Вариант 3
1)
2) , если является корнем;
3) , если является корнем;
4) ,если является корнем.
С – 6. Однородные уравнения.
Вариант 1
1)
2)
3)
4)
Вариант 2
1)
2)
3)
4)
Вариант 3
1)
2)
3)
4)
С – 7. Уравнения, решающиеся разложением на множители.
Вариант 1
1)
2)
3)
4)
Вариант 2
1)
2)
3)
4)
С – 8.
Уравнения вида
1)
2)
3)
4)
5)
6)
С-9
Вариант 1
1) а) Решите уравнение
Ответ:
б) Решите уравнение
Ответ:
Вариант 2
3) а) Найдите критические точки функции
Ответ:
б) Найдите критические точки функции
Ответ:
Вариант 3
4) а) Найдите критические точки функции
Ответ:
б) Найдите критические точки функции
Ответ:
Вариант 4
4) а) Решите уравнение
Ответ:
б) Решить уравнение
Ответ:
Вариант 5
6) а) Найдите критические точки функции и укажите среди них одну из точек максимума.
Ответ: — точка максимума.
б) Найдите критические точки функции и укажите среди них одну из точек минимума.
Ответ: — точка минимума.
Вариант 6
4) а) Сколько корней имеет уравнение на отрезке ?
Ответ: 100.
б) Сколько корней имеет уравнение на отрезке ?
Ответ: 50.
Вариант 7
3) а) Вычислите абсциссы и ординаты точек пересечения графиков функции и
Ответ: точки вида
б) Вычислите абсциссы и ординаты точек пересечения графиков функций и
Ответ: точки вида
Вариант 8
4) а) Найдите все значения х, при которых выражение имеет смысл и не обращается в нуль.
Ответ:
Простейшие уравнения с параметром.
В заданиях 1 – 7 нужно решить уравнения для всех значений а.
1)
Ответ:
2)
Ответ:
3)
Ответ:
4)
Ответ:
5)
Ответ:
6)
Ответ:
7)
Ответ:
8) При каких значениях а уравнение не имеет решения?
Данное уравнение не будет иметь решений, если парабола, задаваемая функцией , будет расположена одним из трех способов: см.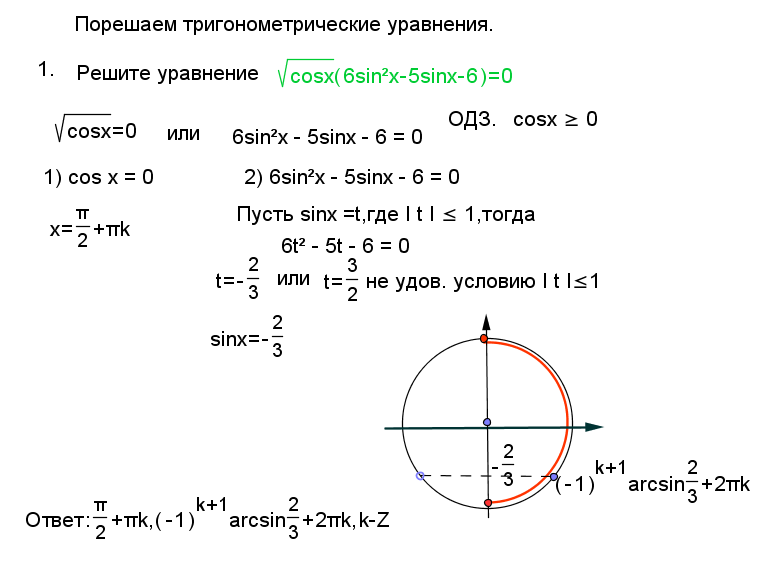
рисунок.
1.
2. Так как , то
3. Такого быть не может, так как
Ответ:
Решить самостоятельно.
При каких значениях параметра а уравнение не имеет решений?
Ответ:
При каких значениях параметра а уравнение имеет решения?
Ответ:
При каких значениях параметра а уравнение имеет ровно один корень на отрезке ?
Ответ:
При каких значениях параметра а уравнение имеет ровно один корень на интервале ?
Ответ:
Системы тригонометрических уравнений
1.
Ответ:
В записи ответа участвует одна переменная.
2.
Ответ:
3.
Эту систему моно решать как линейную относительно и .
Ответ:
4.
Удобнее рассмотреть по отдельности четыре системы, совокупность которых равносильна исходной системе.
Ответ:
5.
Необходимо рассмотреть два случая:
а)
б)
Следствием этой системы является уравнение
Пусть
Пусть
Ответ:
Системы уравнений, в которых одно уравнение – алгебраическое, а другое тригонометрическое.
а)
б)
Системы, в которых оба уравнения – тригонометрические уравнения
1)
или
Ответ:
2)
или
Ответ:
3)
или
Ответ:
4)
или
Ответ:
5)
Ответ:
6)
Так как
или
Ответ:
7)
Ответ:
8)
Пусть тогда
Это уравнение равносильно следующей схеме
так как
Ответ:
Решить самостоятельно
а) Решить систему уравнений
Ответ:
б) Решите систему уравнений
Ответ:
Примеры решения тригонометрических неравенств
1)
Ссылаясь на формулу , преобразуем левую часть неравенства:
Значит, данное неравенство равносильно неравенству .
Отсюда . Следовательно,
2)
Пусть , где . при , т.е. при . Значит, , следовательно,
3)
Предположим , откуда . Решим неравенство . Корни квадратного уравнения . Отсюда при или
Ограничение дает либо , либо . Заменяя t на cos x, получим:
а) либо , т.е.
б) либо , т.е. .
Ответ: , или
4) . Область определения . Представив неравенство в виде
,
получим двойное неравенство , равносильное данному. Значит,
5)
Так как , то данное неравенство сводится к равносильному неравенству Отсюда:
а) , т.е. , или
б) , т.е.
Упражнения
Решить уравнения:
КОНТРОЛЬНАЯ РАБОТА №1
ВАРИАНТ 1
1. Упростить выражение:
2. Дано: и
Найдите:
3.
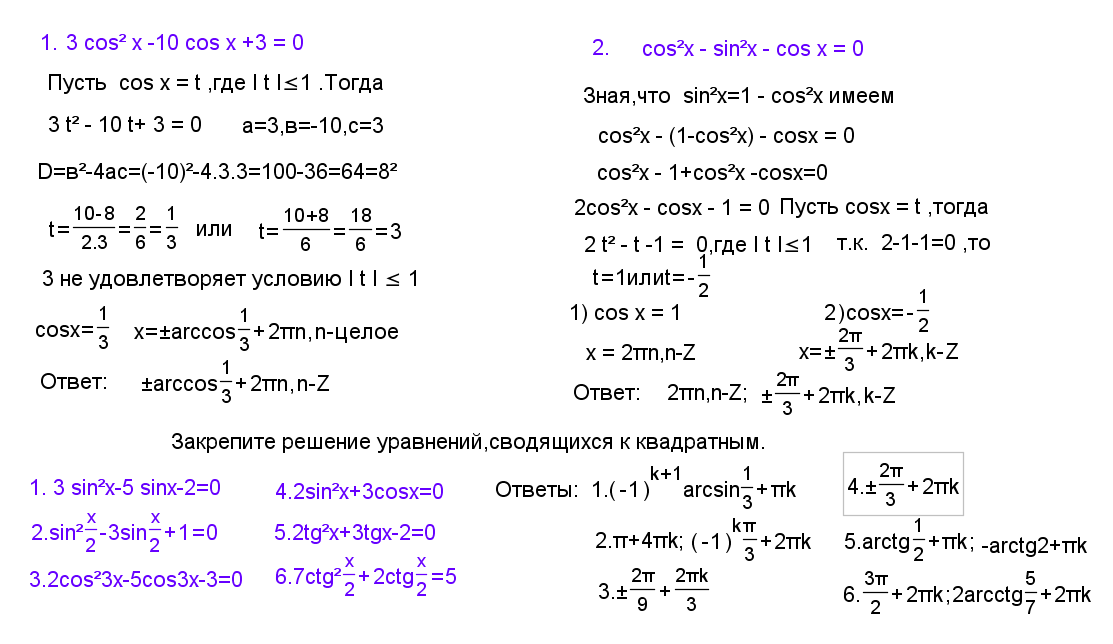Докажите тождество:
4. Доказать, что функция является чётной.
5. Вычислить:
ВАРИАНТ 2
1. Упростить:
2. Дано: и
Найдите:
3. Доказать тождество:
4. Доказать, что функция является чётной.
5. Вычислить:
ВАРИАНТ 3
1. Упростить:
2. Дано: и
Найдите:
3. Докажите тождество:
4. Доказать, что функция является нечётной
5. Вычислить:
ВАРИАНТ 4
1. Упростить:
2. Дано:
Найдите:
3. Доказать тождество:
4. Доказать, что функция не является ни чётной, ни нечётной.
5. Вычислить:
ВАРИАНТ 5
1.
Упростить
2. Дано:
Найдите:
3. Доказать тождество:
4. Доказать, что функция является чётной.
5. Вычислить
ВАРИАНТ 6
1. Упростить:
2. Дано:
Найдите:
3. Доказать тождество:
4. Доказать, что функция является нечетной
5. Вычислить:
КОНТРОЛЬНАЯ РАБОТА № 2
ВАРИАНТ 1
1. Решить уравнение:
2. Укажите на тригонометрической окружности все точки, удовлетворяющие неравенству:
3. Укажите какое-либо число, удовлетворяющее всем трем неравенствам задания 2 одновременно.
ВАРИАНТ 2
1. Решите уравнение:
2. Укажите на тригонометрической окружности все точки, удовлетворяющие неравенству:
3.
Укажите какое-либо число, удовлетворяющее всем трем неравенствам задания 2 одновременно.
ВАРИАНТ 3
1. Решите уравнение:
2. Укажите на тригонометрической окружности все точки, удовлетворяющее неравенству:
3. Укажите какое-либо число, удовлетворяющее всем трем неравенствам задания 2 одновременно.
ВАРИАНТ 4
1. Решите уравнение:
2. Укажите на тригонометрической окружности все точки, удовлетворяющие неравенству:
3. Укажите какое-либо число, удовлетворяющее всем трем неравенствам задания 2 одновременно.
ВАРИАНТ 5
1. Решите уравнение:
2. Решите неравенство:
3. Укажите какое-либо число, удовлетворяющее всем трем неравенствам задания 2 одновременно.
ВАРИАНТ 6
1. Решите уравнение:
2.
Решите неравенство:
3. Укажите какое-либо число, удовлетворяющее всем трем неравенствам задания одновременно.
Оглавление
Введение 3
Тригонометрические функции числового аргумента 4
Соотношения между тригонометрическими функциями одного и того же угла 4
Формулы приведения 6
Преобразование тригонометрических выражений 6
Упражнения 8
Решение простейших тригонометрических уравнений 9
Решение тригонометрических уравнений вида sin f(x) = a 14
Приведение уравнений к алгебраическому виду относительно к какой –либо тригонометрической функции 15
Способы решения уравнений, основанных на использовании свойств произведения и частного 21
Решение уравнений. Тригонометрические функции с четным показателем 25
Решение тригонометрических уравнений методом вспомогательного угла 29
Оценка левой и правой частей уравнения 32
Иррациональные тригонометрические уравнения 34
Самостоятельные работы 37
Простейшие уравнения с параметром 43
Решить самостоятельно 45
Системы тригонометрических уравнений 45
Системы уравнений, в которых одно уравнение алгебраическое, а другое тригонометрическое 48
Решить самостоятельно 52
Примеры решений тригонометрических неравенств 52
Упражнения 55
Контрольные вопросы 56
Литература.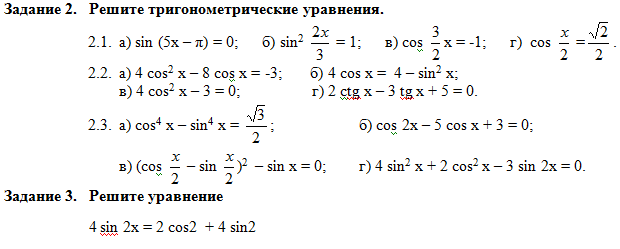
Колмогоров «Алгебра и начала анализа». М., 1990.
В.В. Кулешов «Задачи по элементарной математике» Тольятти, 1994.
Сборник задач по математике для поступающих во втузы (под редакцией М.И. Сканави М., 1998)
Литвиненко В.Н., Мордкович А.Г. Практикум по элементарной математике. Алгебра. Тригонометрия М., 1991.
Бородулл И.Т. Тригонометрические уравнения и неравенства. М., 1989.
Решение задач по математике. Репетиторы по физике, подготовка к ЕГЭ
Решение задач в Москве!
Надо решить задачи? Выполняем быстро и недорого.
Все предметы.
Контрольные по электротехнике — ТОЭ — теоретическим основам электротехники,
ТАУ — теория автоматического управления.
Контрольные, курсовые по электротехнике.
Приемлемые цены. Короткие сроки.
Звоните!Помощь на ЕГЭ по математике и физике.
Решение задач егэ в Москве.
Услуги репетитора
Контрольные работы, задачи:
все предметы, пишу курсовые, дипломы.
Видеосвязь — через Интернет по skype — скайпу.
Не тратьте время на поездки!
Экономьте время и деньги!
Видео камера не нужна.
Skype используется только чтобы показывать экран своего компьютера.
Мы видим курсоры, как они движутся по экрану,
и обсуждаем проблемную задачу по телефону.
Лучше городскому — квартирному. Мой телефон — 8-495-3452061.
Код Москвы — 495.
Подбор репетитора. Быстро!
Опытные репетиторы по любым предметам. Подбор репетитора за один день.
Анекдот от математика:
— Ты — девушка моей мечты! Красивая, остроумная, веселая…— Ты говоришь так только для того, чтобы я тебе решила твои задачки!
— К тому же ты еще невероятно умная!
Объявления. Все Репетиторы Москвы, скайпа и Кирова
Пример переписки репетитора онлайн в Skype:
Урок математики
[16:31:37] GeorgDer: Здравствуйте, reshenie11! Я хочу внести Вас в свой список контактов Skype.
[16:31:37] Алексей отправил контактные данные.
Здравствуйте, Гондурас
Ученик репетитора: Алексей Эдуардович, добрый день.
На Вашей страничке вывешена контрольная работа по фин. прогнозированию.
Учитель Алексей: так
Студент: Ну, где живем, то и пишем 🙂
Репетитор Алексей: юмор — это прикольно
Обучающийся: имеется ли вариант решения именно этой работы? И цена вопроса. Кстати — Александр.
Преподаватель Алексей: варианта решения нет
решать стоит 2 — 3 тыс. р. за страницу
Учащийся: ага. Ясно. Вы на связи ещё будете?
Профессор Алексей: да
Школьник: спасибо, порядок расчетов?
Математик Алексей: оплатить надо вперёд, но перед этим скинуть задание на оценку стоимости работы
Репетитор по математике поможет разобраться с задачей.
МАТЕМАТИКА — (от др.-греч. μάθημα — изучение, наука) — наука о структурах, порядке и отношениях, которая с помощью репетиторов и просто исторически сложилась на основе операций подсчёта, измерения и описания форм реальных объектов.
РЕШЕНИЕ ЗАДАЧ онлайн: высшая математика, эконометрика, физика.
Задача 2.Валовая маржа составляет 300 у.е., переменные затраты на весь объем продукции 140 у.е. Какое процентное увеличение продаж даст предприятию такой же эффект в плане роста прибыли, что и 20 %-ное увеличение цены?
Кстати, пока не забыл! Приглашаются организации, репетиторы и спонсоры, а также семьи, вкладывающие средства в обучение своих детей.
Любому ребёнку нужен частный учитель!
Хотя бы иногда, онлайн, по Skype.
Упрощая, можно сказать, что, например, слепому ребенку надо дополнительно научиться ходить с собакой.
Задача 3.
Собственный капитал предприятия 180 у.е. Показатель ROA = 20%, средняя расчетная ставка процентов по заемным средствам 16%. Показатель DFL² (вторая концепция) равен 1,5. Рассчитать показатель DFL¢ (первая концепция).
Задача 4.
Капитал предприятия состоит из 200 000 у.е. собственных средств. Рассматривается возможность привлечения заемного капитала под процентную ставку 12% годовых.
Величина прибыли предприятия (EBIT) составляет 32 000 у.е. Предполагается, что при привлечении дополнительного объема финансирования, экономическая рентабельность (ROA) сохранится на прежнем уровне.
Оценить целесообразность привлечения заемного капитала и в случае положительного ответа рекомендуемый объем заемных средств. Ответ обосновать.
В предполагаемых условиях привлечения заемного капитала рассчитать для предприятия точку безразличия и финансовую критическую точку.
Студент репетитора: примерно так
Султанов Алексей Учитель: по 1 — 4 тыс. р. каждая
в среднем — 2 500 р
В сумме = 7 500р
Возможна срочная помощь на ЕГЭ по математике — решение задач по мобильному телефону онлайн.
Калькулятор и решатель тригонометрических уравнений
1Решенный пример тригонометрических уравнений
$ 8 \ sin \ left (x \ right) = 2 + \ frac {4} {\ csc \ left (x \ right)}
$ 2Обратная функция синуса косеканс
$ 8 \ sin \ left (x \ right) = 2 + 4 \ sin \ left (x \ right) $
4Разделите обе части уравнения на 4 доллара 9000 долларов 3
$ \ sin \ left (x \ right) = \ frac {1} {2}
$ 5Углы, при которых функция $ \ sin \ left (x \ right) $ равна $ \ frac {1} {2} $, равны
$ x = 30 ^ {\ circ} +360 ^ {\ circ} n, \: x = 150 ^ {\ circ} +360 ^ {\ circ} n $
6Углы, выраженные в радианах в том же порядке, равны
.
$ x = \ frac {1} {6} \ pi + 2 \ pi n, \: x = \ frac {5} {6} \ pi + 2 \ pi n $
Окончательный ответ
$ x = \ frac {1} {6} \ pi + 2 \ pi n, \: x = \ frac {5} {6} \ pi + 2 \ pi n $
9.5 Решение тригонометрических уравнений — Алгебра и тригонометрия
Задачи обучения
В этом разделе вы:- Решите линейные тригонометрические уравнения с синусом и косинусом.
- Решите уравнения, содержащие одну тригонометрическую функцию.
- Решите тригонометрические уравнения с помощью калькулятора.
- Решите тригонометрические уравнения квадратичной формы.
- Решите тригонометрические уравнения, используя фундаментальные тождества.
- Решите тригонометрические уравнения с несколькими углами.
- Решите задачи прямоугольного треугольника.
Рисунок 1 Египетские пирамиды, стоящие возле современного города. (кредит: Ойсин Малвихилл)
Фалес Милетский (около 625–547 гг.
до н.э.) известен как основатель геометрии. Легенда гласит, что он рассчитал высоту Великой пирамиды в Гизе в Египте, используя теорию подобных треугольников , которую он разработал, измерив тень своего посоха. Эта теория, основанная на пропорциях, находит применение во многих областях, включая фрактальную геометрию, инженерию и архитектуру.Часто угол подъема и угол депрессии находят с помощью одинаковых треугольников.
В предыдущих разделах этой главы мы рассматривали тригонометрические тождества. Тождества верны для всех значений в домене переменной. В этом разделе мы начинаем изучение тригонометрических уравнений для изучения реальных сценариев, таких как определение размеров пирамид.
Решение линейных тригонометрических уравнений с синусом и косинусом
Тригонометрические уравнения, как следует из названия, включают в себя тригонометрические функции.Во многом аналогично решению полиномиальных или рациональных уравнений, только определенные значения переменной будут решениями, если решения вообще есть.
Часто мы решаем тригонометрическое уравнение на заданном интервале. Однако так же часто нас просят найти все возможные решения, и, поскольку тригонометрические функции являются периодическими, решения повторяются в течение каждого периода. Другими словами, тригонометрические уравнения могут иметь бесконечное количество решений. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предполагаем, что какое-либо решение действительно.Период синусоидальной функции и косинусной функции равен 2π.2π. Другими словами, каждые 2π2π единиц повторяются значения y- . Если нам нужно найти все возможные решения, мы должны добавить 2πk, 2πk, где k k — целое число, к начальному решению. Вспомните правило, которое дает формат для определения всех возможных решений для функции с периодом 2π: 2π:
Существуют аналогичные правила для указания всех возможных решений для других тригонометрических функций.
Решение тригонометрических уравнений требует тех же методов, что и решение алгебраических уравнений. Мы читаем уравнение слева направо по горизонтали, как предложение. Мы ищем известные шаблоны, множители, находим общие знаменатели и заменяем определенные выражения на переменные, чтобы сделать решение более простым. Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.
Пример 1
Решение линейного тригонометрического уравнения с использованием функции косинуса
Найдите все возможные точные решения уравнения cosθ = 12.cosθ = 12.
Решение
Из единичного круга мы знаем, что
cosθ = 12θ = π3,5π3cosθ = 12θ = π3,5π3Это решения в интервале [0,2π]. [0,2π]. Все возможные решения дает
θ = π3 ± 2kπ, θ = 5π3 ± 2kπθ = π3 ± 2kπ и θ = 5π3 ± 2kπ, где kk — целое число.
Пример 2
Решение линейного уравнения с синусоидальной функцией
Найдите все возможные точные решения уравнения sint = 12.
sint = 12.
Решение
Решение для всех возможных значений t означает, что решения включают углы, превышающие период 2π.2π. Из рисунка 2 видно, что решениями являются t = π6t = π6 и t = 5π6.t = 5π6. Но проблема в том, чтобы указать все возможные значения, которые решают уравнение. Следовательно, ответ будет
t = π6 ± 2πk, t = 5π6 ± 2πkt = π6 ± 2πk и t = 5π6 ± 2πk, где kk — целое число.
Дано тригонометрическое уравнение, решите его с помощью алгебры .
- Ищите шаблон, который предлагает алгебраическое свойство, такое как разность квадратов или возможность факторизации.
- Замените тригонометрическое выражение одной переменной, например xx или u.u.
- Решите уравнение так же, как и алгебраическое уравнение.
- Подставьте тригонометрическое выражение обратно вместо переменной в результирующих выражениях.
- Найдите угол.
Пример 3
Решите линейное тригонометрическое уравнение
Точно решите уравнение: 2cosθ − 3 = −5,0≤θ <2π.2cosθ − 3 = −5,0≤θ <2π.
Решение
Используйте алгебраические методы для решения уравнения.
2cosθ − 3 = −52cosθ = −2cosθ = −1θ = π2cosθ − 3 = −52cosθ = −2cosθ = −1θ = πПопробуй # 1
Решите в точности следующее линейное уравнение на интервале [0,2π): 2sinx + 1 = 0. [0,2π): 2sinx + 1 = 0.
Решение уравнений, связанных с единственной тригонометрической функцией
Когда нам задают уравнения, которые включают только одну из шести тригонометрических функций, их решения требуют использования алгебраических методов и единичного круга (см. Рисунок 2). Когда уравнение включает тригонометрические функции, отличные от синуса и косинуса, необходимо учитывать несколько факторов.Проблемы, связанные с величинами, обратными первичным тригонометрическим функциям, необходимо рассматривать с алгебраической точки зрения.
Другими словами, мы напишем обратную функцию и найдем углы, используя эту функцию. Кроме того, уравнение, включающее функцию касательной, немного отличается от уравнения, содержащего функцию синуса или косинуса. Во-первых, как мы знаем, период касательной равен π, π, а не 2π. 2π. Кроме того, область касательной — это все действительные числа, за исключением нечетных целых кратных π2, π2, если, конечно, проблема не накладывает свои собственные ограничения на область.
Пример 4
Решение задачи, связанной с одной тригонометрической функцией
Решите задачу точно: 2sin2θ − 1 = 0,0≤θ <2π. 2sin2θ − 1 = 0,0≤θ <2π.
Решение
Поскольку эту проблему нелегко разложить на множители, мы решим ее, используя свойство квадратного корня. Во-первых, мы используем алгебру, чтобы выделить sinθ.sinθ. Потом найдем углы.
2sin2θ − 1 = 0 2sin2θ = 1sin2θ = 12sin2θ = ± 12sinθ = ± 12 = ± 22θ = π4,3π4,5π4,7π42sin2θ − 1 = 0 2sin2θ = 1sin2θ = 12sin2θ = ± 12sinθ = ± 12 = ± 22θ4 = π4,3π4 = π4 , 5π4,7π4Пример 5
Решение тригонометрического уравнения с косекансом
Точно решите следующее уравнение: cscθ = −2,0≤θ <4π.
cscθ = −2,0≤θ <4π.
Решение
Нам нужны все значения θθ, для которых cscθ = −2cscθ = −2 в интервале 0≤θ <4π.0≤θ <4π.
cscθ = −21sinθ = −2sinθ = −12θ = 7π6,11π6,19π6,23π6cscθ = −21sinθ = −2sinθ = −12θ = 7π6,11π6,19π6,23π6Анализ
Поскольку sinθ = −12, sinθ = −12, обратите внимание, что все четыре решения находятся в третьем и четвертом квадрантах.
Пример 6
Решение уравнения с касательной
Точно решите уравнение: tan (θ − π2) = 1,0≤θ <2π.tan (θ − π2) = 1,0≤θ <2π.
Решение
Напомним, что касательная функция имеет период π.π. На интервале [0, π), [0, π) и под углом π4, π4 касательная имеет значение 1. Однако нам нужен угол (θ − π2). (Θ − π2) . Таким образом, если tan (π4) = 1, tan (π4) = 1, то
θ − π2 = π4θ = 3π4 ± kπθ − π2 = π4θ = 3π4 ± kπНа интервале [0,2π), [0,2π ) имеем два решения:
θ = 3π4 и θ = 3π4 + π = 7π4θ = 3π4 и θ = 3π4 + π = 7π4Попробуй # 2
Найдите все решения для tanx = 3.
tanx = 3.
Пример 7
Определите все решения уравнения, содержащего касательную
Определите все точные решения уравнения 2 (tanx + 3) = 5 + tanx, 0≤x <2π.2 (tanx + 3) = 5 + tanx, 0≤x <2π.
Решение
Мы можем решить это уравнение, используя только алгебру. Выделите выражение tanxtanx слева от знака равенства.
2 (tanx) +2 (3) = 5 + tanx2tanx + 6 = 5 + tanx 2tanx − tanx = 5−6tanx = −12 (tanx) +2 (3) = 5 + tanx2tanx + 6 = 5 + tanx 2tanx − tanx = 5−6tanx = −1На единичной окружности есть два угла, значение касательной которых равно −1: θ = 3π4−1: θ = 3π4 и θ = 7π4.θ = 7π4.
Решение тригонометрических уравнений с помощью калькулятора
Не все функции могут быть решены точно с использованием только единичной окружности. Когда мы должны решить уравнение, включающее угол, отличный от одного из специальных углов, нам понадобится калькулятор.
Убедитесь, что установлен правильный режим, градусы или радианы, в зависимости от критериев данной проблемы.
Пример 8
Использование калькулятора для решения тригонометрического уравнения, содержащего синус
Воспользуйтесь калькулятором, чтобы решить уравнение sinθ = 0.8 sinθ = 0,8, где θ θ в радианах.
Решение
Убедитесь, что режим установлен на радианы. Чтобы найти θ, θ, используйте обратную синусоидальную функцию. На большинстве калькуляторов вам нужно будет нажать кнопку 2 ND , а затем кнопку SIN, чтобы вызвать функцию sin − 1sin − 1. На экране отображается sin − 1 (.sin − 1 (. Калькулятор готов к вводу в скобках. Для этой задачи мы вводим sin − 1 (0,8), sin − 1 (0,8) и нажимаем ENTER.Таким образом, с четырьмя десятичными знаками
sin − 1 (0.8) ≈0.9273sin − 1 (0.8) ≈0.9273Решение
θ≈0,9273 ± 2πkθ≈0,9273 ± 2πkУгол в градусах
. θ≈53,1 ° θ≈180 ° −53,1 ° ≈126,9 ° θ≈53,1 ° θ≈180 ° −53,1 ° ≈126,9 °Анализ
Обратите внимание, что калькулятор будет возвращать только угол в квадрантах I или IV для функции синуса, поскольку это диапазон обратного синуса.
Другой угол получается с помощью π − θ.π − θ. Таким образом, дополнительное решение ≈2,2143 ± 2πk≈2,2143 ± 2πk
Пример 9
Использование калькулятора для решения тригонометрического уравнения с секущей
Воспользуйтесь калькулятором, чтобы решить уравнение secθ = −4, secθ = −4, получив ответ в радианах.
Решение
Мы можем начать с некоторой алгебры.
secθ = −41cosθ = −4cosθ = −14secθ = −41cosθ = −4cosθ = −14Убедитесь, что РЕЖИМ установлен в радианах. Теперь используйте функцию обратного косинуса.
cos − 1 (−14) ≈1,8235θ≈1,8235 + 2πkcos − 1 (−14) ≈1,8235θ≈1,8235 + 2πk Так как π2≈1,57π2≈1,57 и π≈3,14, π≈3,14, 1,8235 находится между этими двумя числами , таким образом, θ≈1,8235 θ≈1,8235 находится во втором квадранте. Косинус также отрицателен в квадранте III. Обратите внимание, что калькулятор будет возвращать только угол в квадрантах I или II для функции косинуса, поскольку это диапазон обратного косинуса.
См. Рисунок 2.
Рисунок 2
Итак, нам также нужно найти меру угла в квадранте III. В квадранте II опорный угол равен θ ‘≈π − 1,8235≈1,3181. θ ‘≈π − 1,8235≈1,3181. Другое решение в квадранте III: θ ‘≈π + 1,3181≈4,4597.θ’ ≈π + 1,3181≈4,4597.
Решения: θ≈1,8235 ± 2πkθ≈1,8235 ± 2πk и θ≈4,4597 ± 2πk.θ≈4,4597 ± 2πk.
Попробуй # 3
Решить cosθ = −0.2.cosθ = −0.2.
Решение тригонометрических уравнений в квадратичной форме
Решение квадратного уравнения может быть более сложным, но, опять же, мы можем использовать алгебру, как и любое квадратное уравнение.Посмотрите на схему уравнения. Есть ли в уравнении более одной тригонометрической функции или только одна? Какая тригонометрическая функция возводится в квадрат? Если представлена только одна функция и один из членов возведен в квадрат, подумайте о стандартной форме квадратичной функции. Замените тригонометрическую функцию переменной, например xx или u.
u. Если после подстановки уравнение выглядит как квадратное уравнение, то мы можем использовать те же методы для решения квадратичных уравнений для решения тригонометрических уравнений.
Пример 10
Решение тригонометрического уравнения в квадратичной форме
Точно решите уравнение: cos2θ + 3cosθ − 1 = 0,0≤θ <2π.cos2θ + 3cosθ − 1 = 0,0≤θ <2π.
Решение
Начнем с подстановки и замены cos θθ на x.x. Нет необходимости использовать замену, но это может облегчить визуальное решение проблемы. Пусть cosθ = x.cosθ = x. У нас
Уравнение не может быть разложено на множители, поэтому мы воспользуемся квадратной формулой x = −b ± b2−4ac2a.х = −b ± b2−4ac2a.
x = −3 ± (−3) 2−4 (1) (- 1) 2 = −3 ± 132 x = −3 ± (−3) 2−4 (1) (- 1) 2 = −3 ± 132Заменим xx на cosθ, cosθ и решим.
cosθ = −3 ± 132θ = cos − 1 (−3 + 132) cosθ = −3 ± 132θ = cos − 1 (−3 + 132) Обратите внимание, что используется только знак +.
Это связано с тем, что мы получаем ошибку при решении θ = cos − 1 (−3−132) θ = cos − 1 (−3−132) на калькуляторе, поскольку область определения функции обратного косинуса равна [−1,1 ]. [- 1,1]. Однако есть второе решение:
Эта конечная сторона угла лежит в квадранте I.Поскольку косинус также положителен в квадранте IV, второе решение —
. θ = 2π − cos − 1 (−3 + 132) ≈ 5,02 θ = 2π − cos − 1 (−3 + 132) ≈ 5,02Пример 11
Решение тригонометрического уравнения в квадратичной форме с помощью факторинга
Точно решите уравнение: 2sin2θ − 5sinθ + 3 = 0,0≤θ≤2π.2sin2θ − 5sinθ + 3 = 0,0≤θ≤2π.
Решение
Используя группировку, этот квадратичный коэффициент можно разложить на множители. Либо сделайте реальную замену, sinθ = u, sinθ = u, либо представьте ее, если мы множим:
2sin2θ − 5sinθ + 3 = 0 (2sinθ − 3) (sinθ − 1) = 0 2sin2θ − 5sinθ + 3 = 0 ( 2sinθ − 3) (sinθ − 1) = 0 Теперь установите каждый множитель равным нулю.
Затем решите для θ: sinθ ≠ 32, θ: sinθ ≠ 32, как диапазон значений синусоидальная функция [−1,1]. [- 1,1]. Однако sinθ = 1, sinθ = 1, что дает решение θ = π2.θ = π2.
Анализ
Обязательно проверьте все решения в данном домене, так как некоторые факторы не имеют решения.
Попробуй # 4
Решить sin2θ = 2cosθ + 2,0≤θ≤2π.sin2θ = 2cosθ + 2,0≤θ≤2π. [Подсказка: сделайте замену, чтобы выразить уравнение только через косинус.]
Пример 12
Решение тригонометрического уравнения с помощью алгебры
Решите точно:
2sin2θ + sinθ = 0; 0≤θ <2π2sin2θ + sinθ = 0; 0≤θ <2πРешение
Эта задача должна показаться вам знакомой, поскольку она похожа на квадратичную. Пусть sinθ = x.sinθ = x. Уравнение принимает вид 2×2 + x = 0,2×2 + x = 0.
Начнем с факторинга:
Установите каждый коэффициент равным нулю.
x = 0 (2x + 1) = 0x = −12x = 0 (2x + 1) = 0x = −12Затем снова подставьте в уравнение исходное выражение sinθsinθ для x.Икс. Таким образом,
sinθ = 0θ = 0, πsinθ = −12θ = 7π6,11π6sinθ = 0θ = 0, πsinθ = −12θ = 7π6,11π6Решения в области 0≤θ <2π0≤θ <2π равны θ = 0, π, 7π6,11π6.θ = 0, π, 7π6,11π6.
Если мы предпочитаем не заменять, мы можем решить уравнение, следуя той же схеме факторизации и установив каждый коэффициент равным нулю.
2sin2θ + sinθ = 0sinθ (2sinθ + 1) = 0sinθ = 0θ = 0, π2sinθ + 1 = 02sinθ = −1sinθ = −12θ = 7π6,11π62sin2θ + sinθ = 0sinθ (2sinθ + 1) = 0sinθ = 0θ = 0, +π 1 = 02sinθ = −1sinθ = −12θ = 7π6,11π6Анализ
Мы можем видеть решения на графике на Рисунке 3.В интервале 0≤θ <2π, 0≤θ <2π график пересекает ось x- четыре раза в отмеченных решениях.
Обратите внимание, что тригонометрические уравнения в квадратичной форме могут дать до четырех решений вместо ожидаемых двух, которые можно найти с помощью квадратных уравнений. В этом примере каждое решение (угол), соответствующее положительному значению синуса, даст два угла, которые приведут к этому значению.
Рисунок 3
Мы также можем проверить решения на единичном круге на Рисунке 2.
Пример 13
Решение тригонометрического уравнения, квадратичного в форме
Решите квадратное по форме уравнение: 2sin2θ − 3sinθ + 1 = 0,0≤θ <2π.2sin2θ − 3sinθ + 1 = 0,0≤θ <2π.
Решение
Мы можем факторизовать, используя группировку. Значения решения θθ можно найти на единичной окружности.
(2sinθ − 1) (sinθ − 1) = 0 2sinθ − 1 = 0sinθ = 12θ = π6,5π6sinθ = 1θ = π2 (2sinθ − 1) (sinθ − 1) = 0 2sinθ − 1 = 0sinθ = 12θ = π6,5π6sinθ = 1θ = π2Попробуй # 5
Решите квадратное уравнение 2cos2θ + cosθ = 0.
2cos2θ + cosθ = 0.
Решение тригонометрических уравнений с использованием основных тождеств
Хотя алгебру можно использовать для решения ряда тригонометрических уравнений, мы также можем использовать фундаментальные тождества, потому что они упрощают решение уравнений. Помните, что методы, которые мы используем для решения проблем, не совпадают с методами проверки личности. Здесь применяются основные правила алгебры, а не переписывание одной стороны идентичности для соответствия другой стороне. В следующем примере мы используем два тождества, чтобы упростить уравнение.
Пример 14
Использование идентификаторов для решения уравнения
Используйте тождества, чтобы точно решить тригонометрическое уравнение в интервале 0≤x <2π.0≤x <2π.
cosxcos (2x) + sinxsin (2x) = 32cosxcos (2x) + sinxsin (2x) = 32Решение
Обратите внимание, что левая часть уравнения — это формула разности для косинуса.
Из единичного круга на рисунке 2 мы видим, что cosx = 32cosx = 32, когда x = π6,11π6.x = π6,11π6.
Пример 15
Решение уравнения с использованием формулы двойного угла
Решите уравнение точно, используя формулу двойного угла: cos (2θ) = cosθ.cos (2θ) = cosθ.
Решение
У нас есть три варианта выражения для замены двойного угла косинуса. Поскольку проще решать одну тригонометрическую функцию за раз, мы выберем тождество с двойным углом, включающее только косинус:
cos (2θ) = cosθ2cos2θ − 1 = cosθ2cos2θ − cosθ − 1 = 0 (2cosθ + 1) (cosθ − 1) = 02cosθ + 1 = 0cosθ = −12cosθ − 1 = 0cosθ = 1cos (2θ) = cosθ2cos2θ − 1 = cosθ2cos2θ −cosθ − 1 = 0 (2cosθ + 1) (cosθ − 1) = 02cosθ + 1 = 0cosθ = −12cosθ − 1 = 0cosθ = 1 Итак, если cosθ = −12, cosθ = −12, то θ = 2π3 ± 2πkθ = 2π3 ± 2πk и θ = 4π3 ± 2πk; θ = 4π3 ± 2πk; если cosθ = 1, cosθ = 1, то θ = 0 ± 2πk.
θ = 0 ± 2πk.
Пример 16
Решение уравнения с использованием идентификатора
Точно решите уравнение, используя тождество: 3cosθ + 3 = 2sin2θ, 0≤θ <2π.3cosθ + 3 = 2sin2θ, 0≤θ <2π.
Решение
Если мы перепишем правую часть, мы можем записать уравнение через косинус:
3cosθ + 3 = 2sin2θ3cosθ + 3 = 2 (1 − cos2θ) 3cosθ + 3 = 2−2cos2θ2cos2θ + 3cosθ + 1 = 0 (2cosθ + 1) (cosθ + 1) = 02cosθ + 1 = 0cosθ = −12θ = 2π3,4π3cosθ + 1 = 0cosθ = −1θ = π3cosθ + 3 = 2sin2θ3cosθ + 3 = 2 (1 − cos2θ) 3cosθ + 3 = 2−2cos2θ2cos2θ + 3cosθ + 1 = 0 (2cosθ + 1) (cosθ + 1) = 02cosθ + 1 = 0cosθ = −12θ = 2π3,4π3cosθ + 1 = 0cosθ = −1θ = πНаши решения: θ = 2π3,4π3, π.θ = 2π3,4π3, π.
Решение тригонометрических уравнений с множественными углами
Иногда невозможно решить тригонометрическое уравнение с помощью тождеств, имеющих кратный угол, например sin (2x) sin (2x) или cos (3x) .
cos (3x). Столкнувшись с этими уравнениями, вспомните, что y = sin (2x) y = sin (2x) — это горизонтальное сжатие в 2 раза функции y = sinx.y = sinx. На интервале 2π, 2π мы можем изобразить два периода y = sin (2x), y = sin (2x), в отличие от одного цикла y = sinx.у = sinx. Такое сжатие графика приводит нас к мысли, что может быть в два раза больше перехватов x или решений sin (2x) = 0sin (2x) = 0 по сравнению с sinx = 0. sinx = 0. Эта информация поможет нам решить уравнение.
Пример 17
Решение многоугольного тригонометрического уравнения
Решите точно: cos (2x) = 12cos (2x) = 12 на [0,2π). [0,2π).
Решение
Мы видим, что это уравнение является стандартным уравнением с углом, кратным углу.Если cos (α) = 12, cos (α) = 12, мы знаем, что αα находится в квадрантах I и IV. Хотя θ = cos − 112θ = cos − 112 даст решения только в квадрантах I и II, мы понимаем, что решения уравнения cosθ = 12cosθ = 12 будут в квадрантах I и IV.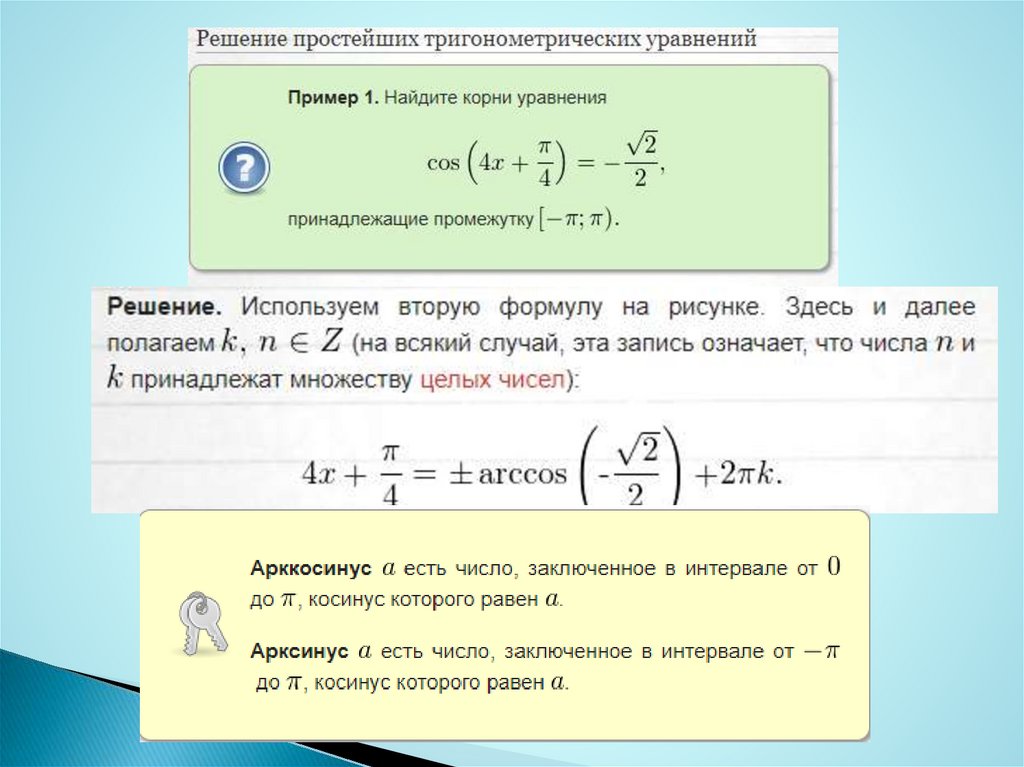
Следовательно, возможные углы равны θ = π3θ = π3 и θ = 5π3.θ = 5π3. Итак, 2x = π32x = π3 или 2x = 5π3,2x = 5π3, что означает, что x = π6x = π6 или x = 5π6.x = 5π6. Имеет ли это смысл? Да, потому что cos (2 (π6)) = cos (π3) = 12. cos (2 (π6)) = cos (π3) = 12.
Есть еще возможные ответы? Вернемся к нашему первому шагу.
В квадранте I 2x = π3,2x = π3, поэтому x = π6x = π6, как указано. Давайте снова будем вращаться по кругу:
2x = π3 + 2π = π3 + 6π3 = 7π32x = π3 + 2π = π3 + 6π3 = 7π3, поэтому x = 7π6.x = 7π6.
Еще один оборот дает
2x = π3 + 4π = π3 + 12π3 = 13π32x = π3 + 4π = π3 + 12π3 = 13π3x = 13π6> 2π, x = 13π6> 2π, поэтому это значение для xx больше 2π, 2π, поэтому это не решение на [0,2π). [0,2π).
В квадранте IV 2x = 5π3,2x = 5π3, поэтому x = 5π6x = 5π6, как указано. Давайте снова обратимся по кругу:
2x = 5π3 + 2π = 5π3 + 6π3 = 11π32x = 5π3 + 2π = 5π3 + 6π3 = 11π3, поэтому x = 11π6.х = 11π6.
Еще один оборот дает
2x = 5π3 + 4π = 5π3 + 12π3 = 17π32x = 5π3 + 4π = 5π3 + 12π3 = 17π3 x = 17π6> 2π, x = 17π6> 2π, поэтому это значение для xx больше 2π, 2π, поэтому это не решение на [0,2π).
[0,2π).
Наши решения: x = π6,5π6,7π6 и 11π6. х = π6,5π6,7π6 и 11π6. Обратите внимание, что всякий раз, когда мы решаем задачу в форме sin (nx) = c, sin (nx) = c, мы должны обойти единичный круг nn раз.
Решение задач прямоугольного треугольника
Теперь мы можем использовать все изученные нами методы для решения проблем, связанных с применением свойств прямоугольных треугольников и теоремы Пифагора.Мы начнем с известной теоремы Пифагора, a2 + b2 = c2, a2 + b2 = c2, и смоделируем уравнение, соответствующее ситуации.
Пример 18
Использование теоремы Пифагора для моделирования уравнения
Используйте теорему Пифагора и свойства прямоугольных треугольников, чтобы смоделировать уравнение, которое соответствует задаче.
Один из тросов, которые прикрепляют центр колеса обозрения London Eye к земле, необходимо заменить. Центр колеса обозрения находится на высоте 69,5 метра над землей, а второй якорь на земле находится в 23 метрах от основания колеса обозрения.
Примерно какой длины кабель и каков угол возвышения (от земли до центра колеса обозрения)? См. Рисунок 4.
Рисунок 4
Решение
Используя данную информацию, мы можем нарисовать прямоугольный треугольник. Мы можем найти длину кабеля с помощью теоремы Пифагора.
a2 + b2 = c2 (23) 2+ (69,5) 2≈53595359≈73,2 ma2 + b2 = c2 (23) 2+ (69,5) 2≈53595359≈73,2 мУгол возвышения θ, θ, образованный второй якорь на земле и трос до центра колеса.Мы можем использовать касательную функцию, чтобы найти ее меру. Округлить до двух десятичных знаков.
tanθ = 69,523tan − 1 (69,523) ≈1,2522≈71,69 ° tanθ = 69,523tan − 1 (69,523) ≈1,2522≈71,69 °Угол возвышения составляет примерно 71,7 °, 71,7 °, а длина кабеля составляет 73,2 метров.
Пример 19
Использование теоремы Пифагора для моделирования абстрактной задачи
Правила безопасности OSHA требуют, чтобы основание лестницы располагалось на расстоянии 1 фута от стены на каждые 4 фута длины лестницы.
Найдите угол, под которым лестница любой длины образует с землей, и высоту, на которой лестница касается стены.
Решение
Для лестницы любой длины основание должно находиться на расстоянии от стены, равном одной четвертой длины лестницы. Эквивалентно, если основание лестницы находится на расстоянии футов от стены фута, длина лестницы будет 4 на фута. См. Рисунок 5.
Рисунок 5
Сторона, примыкающая к θθ, равна a , а гипотенуза — 4a.4а. Таким образом,
cosθ = a4a = 14cos − 1 (14) ≈75,5 ° cosθ = a4a = 14cos − 1 (14) ≈75,5 °Возвышение лестницы составляет 75,5 ° 75,5 ° с землей. Высота, на которой лестница касается стены, может быть найдена с помощью теоремы Пифагора:
a2 + b2 = (4a) 2b2 = (4a) 2 − a2b2 = 16a2 − a2b2 = 15a2b = a15a2 + b2 = (4a) 2b2 = (4a) 2 − a2b2 = 16a2 − a2b2 = 15a2b = a15 Таким образом, лестница касается стены на высоте a15a15 футов от земли.
9,5 Упражнения по разделам
Устный
1.Всегда ли будут решения уравнений тригонометрических функций? Если нет, опишите уравнение, у которого не было бы решения.Объясните, почему да или почему нет.
2.При решении тригонометрического уравнения, включающего более одной тригонометрической функции, всегда ли мы хотим попытаться переписать уравнение так, чтобы оно выражалось в терминах одной тригонометрической функции? Почему или почему нет?
3.При решении линейных тригонометрических уравнений только с помощью синуса или косинуса, как мы узнаем, будут ли решения?
Алгебраические
Для следующих упражнений найдите все решения точно на интервале 0≤θ <2π.0≤θ <2π.
Для следующих упражнений решите точно на [0,2π). [0,2π).
19.2cos (3θ) = — 22cos (3θ) = — 2
20.cos (2θ) = — 32cos (2θ) = — 32
22.2cos (π5θ) = 32cos (π5θ) = 3
Для следующих упражнений найдите все точные решения на [0,2π).
[0,2π).
сек (x) sin (x) −2sin (x) = 0sec (x) sin (x) −2sin (x) = 0
24.tan (x) −2sin (x) tan (x) = 0tan (x) −2sin (x) tan (x) = 0
25.2cos2t + cos (t) = 12cos2t + cos (t) = 1
26.2tan2 (t) = 3сек (t) 2tan2 (t) = 3сек (t)
27.2sin (x) cos (x) −sin (x) + 2cos (x) −1 = 02sin (x) cos (x) −sin (x) + 2cos (x) −1 = 0
30.tan2 (x) = — 1 + 2tan (−x) tan2 (x) = — 1 + 2tan (−x)
31.8sin2 (x) + 6sin (x) + 1 = 08sin2 (x) + 6sin (x) + 1 = 0
32.tan5 (x) = tan (x) tan5 (x) = tan (x)
Для следующих упражнений решайте методами, указанными в этом разделе, точно на интервале [0,2π). [0,2π).
33.sin (3x) cos (6x) −cos (3x) sin (6x) = — 0,9sin (3x) cos (6x) −cos (3x) sin (6x) = — 0.9
34.sin (6x) cos (11x) −cos (6x) sin (11x) = — 0,1 sin (6x) cos (11x) −cos (6x) sin (11x) = — 0,1
35.cos (2x) cosx + sin (2x) sinx = 1cos (2x) cosx + sin (2x) sinx = 1
36.6sin (2t) + 9sint = 06sin (2t) + 9sint = 0
37.
9cos (2θ) = 9cos2θ − 49cos (2θ) = 9cos2θ − 4
40.cos (6x) −cos (3x) = 0cos (6x) −cos (3x) = 0
Для следующих упражнений решите точно на отрезке [0,2π). [0,2π). Если уравнения не учитываются, используйте формулу корней квадратного уравнения.
41.tan2x − 3tanx = 0tan2x − 3tanx = 0
42.sin2x + sinx − 2 = 0sin2x + sinx − 2 = 0
43.sin2x − 2sinx − 4 = 0sin2x − 2sinx − 4 = 0
44.5cos2x + 3cosx − 1 = 05cos2x + 3cosx − 1 = 0
45.3cos2x − 2cosx − 2 = 03cos2x − 2cosx − 2 = 0
46. 5sin2x + 2sinx − 1 = 05sin2x + 2sinx − 1 = 0
47.tan2x + 5tanx − 1 = 0tan2x + 5tanx − 1 = 0
48.cot2x = −cotxcot2x = −cotx
49.−tan2x − tanx − 2 = 0 − tan2x − tanx − 2 = 0
Для следующих упражнений найдите точные решения на интервале [0,2π). [0,2π). Ищите возможности использовать тригонометрические тождества.
50.sin2x − cos2x − sinx = 0sin2x − cos2x − sinx = 0
51.sin2x + cos2x = 0sin2x + cos2x = 0
52.
sin (2x) −sinx = 0sin (2x) −sinx = 0
53.cos (2x) −cosx = 0cos (2x) −cosx = 0
54.2tanx2 − sec2x − sin2x = cos2x2tanx2 − sec2x − sin2x = cos2x
55.1 − cos (2x) = 1 + cos (2x) 1 − cos (2x) = 1 + cos (2x).
57.10sinxcosx = 6cosx10sinxcosx = 6cosx
58.−3sint = 15costsint − 3sint = 15costsint
59.4cos2x − 4 = 15cosx4cos2x − 4 = 15cosx
60.8sin2x + 6sinx + 1 = 08sin2x + 6sinx + 1 = 0
61.8cos2θ = 3−2cosθ8cos2θ = 3−2cosθ
62.6cos2x + 7sinx − 8 = 06cos2x + 7sinx − 8 = 0.
63.12sin2t + cost − 6 = 012sin2t + cost − 6 = 0
Графический
Для следующих упражнений точно алгебраически определите все решения тригонометрического уравнения, затем проверьте результаты, построив уравнение на графике и найдя нули.
66.6sin2x − 5sinx + 1 = 06sin2x − 5sinx + 1 = 0
67.8cos2x − 2cosx − 1 = 08cos2x − 2cosx − 1 = 0
68.100tan2x + 20tanx − 3 = 0100tan2x + 20tanx − 3 = 0
69.
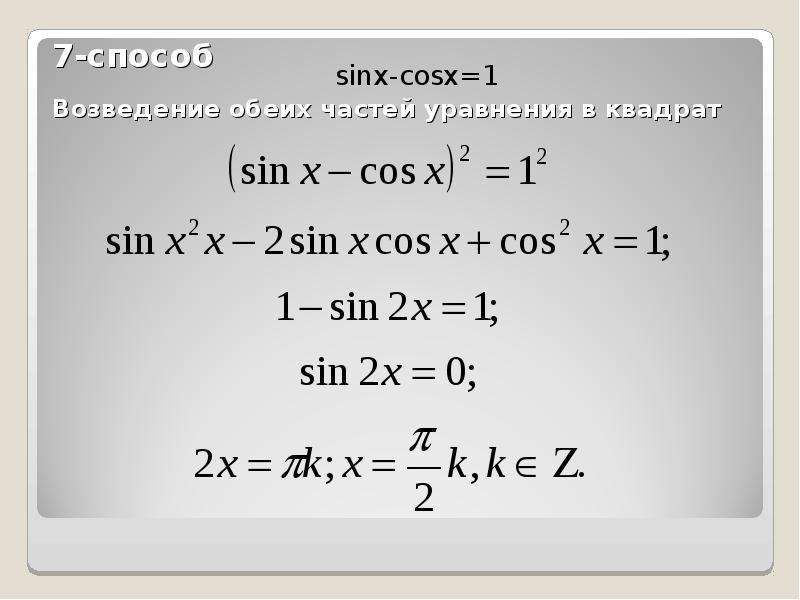
2cos2x − cosx + 15 = 02cos2x − cosx + 15 = 0.
70.20sin2x − 27sinx + 7 = 020sin2x − 27sinx + 7 = 0
71.2tan2x + 7tanx + 6 = 02tan2x + 7tanx + 6 = 0
72.130tan2x + 69tanx − 130 = 0130tan2x + 69tanx − 130 = 0
Технологии
Для следующих упражнений используйте калькулятор, чтобы найти все решения до четырех знаков после запятой.
Для следующих упражнений решите уравнения алгебраически, а затем с помощью калькулятора найдите значения на интервале [0,2π).[0,2π). Округлить до четырех знаков после запятой.
77.tan2x + 3tanx − 3 = 0tan2x + 3tanx − 3 = 0
78.6tan2x + 13tanx = −66tan2x + 13tanx = −6
79.tan2x − secx = 1tan2x − secx = 1
80.sin2x − 2cos2x = 0sin2x − 2cos2x = 0
81.2tan2x + 9tanx − 6 = 02tan2x + 9tanx − 6 = 0
82.4sin2x + sin (2x) secx − 3 = 04sin2x + sin (2x) secx − 3 = 0
Расширения
Для следующих упражнений найдите все решения уравнений в точности на интервале [0,2π).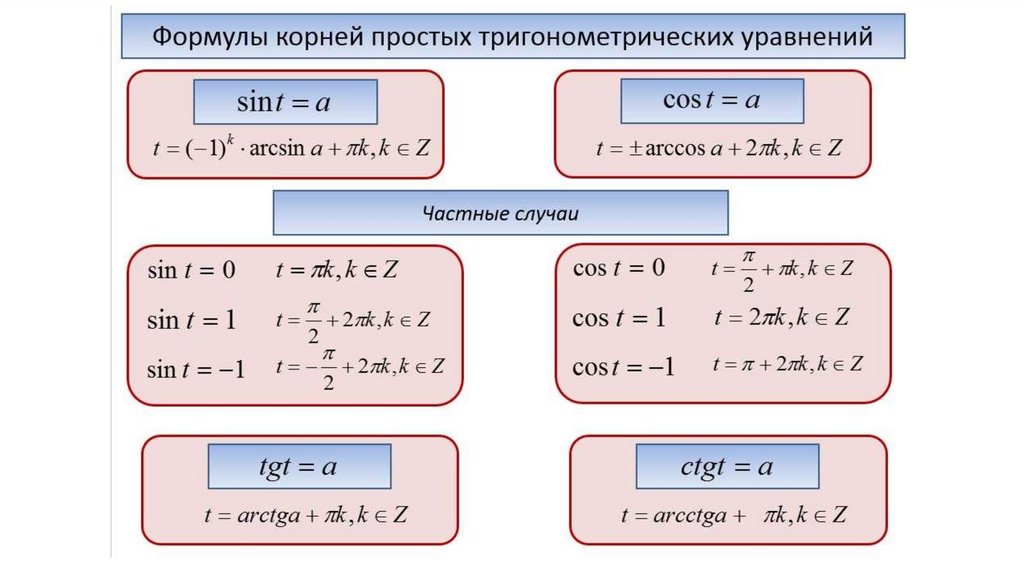
[0,2π).
csc2x − 3cscx − 4 = 0csc2x − 3cscx − 4 = 0
84.sin2x − cos2x − 1 = 0sin2x − cos2x − 1 = 0
85.sin2x (1 − sin2x) + cos2x (1 − sin2x) = 0sin2x (1 − sin2x) + cos2x (1 − sin2x) = 0
86.3sec2x + 2 + sin2x − tan2x + cos2x = 03sec2x + 2 + sin2x − tan2x + cos2x = 0
87.sin2x − 1 + 2cos (2x) −cos2x = 1sin2x − 1 + 2cos (2x) −cos2x = 1
88.tan2x − 1 − sec3xcosx = 0tan2x − 1 − sec3xcosx = 0
89.sin (2x) sec2x = 0sin (2x) sec2x = 0
90.sin (2x) 2csc2x = 0sin (2x) 2csc2x = 0
91.2cos2x − sin2x − cosx − 5 = 02cos2x − sin2x − cosx − 5 = 0
92.1sec2x + 2 + sin2x + 4cos2x = 41sec2x + 2 + sin2x + 4cos2x = 4
Реальные приложения
93.У самолета достаточно бензина, чтобы долететь до города в 200 милях к северо-востоку от его текущего местоположения. Если пилот знает, что город находится в 25 милях к северу, на сколько градусов к северу от востока должен лететь самолет?
94.
Если погрузочная рампа расположена рядом с грузовиком на высоте 4 фута, а ее длина составляет 15 футов, то какой угол образует аппарель с землей?
95.Если погрузочная рампа расположена рядом с грузовиком на высоте 2 фута, а ее длина составляет 20 футов, то какой угол образует аппарель относительно земли?
96.Женщина наблюдает за запущенной ракетой, которая сейчас находится на высоте 11 миль. Если она стоит в 4 милях от стартовой площадки, под каким углом она смотрит вверх из горизонтали?
97.Астронавт находится в запущенной ракете, которая сейчас находится на высоте 15 миль. Если мужчина стоит в 2 милях от стартовой площадки, под каким углом она смотрит на него сверху вниз из горизонтали? (Подсказка: это называется углом депрессии.)
98.Женщина стоит в 8 метрах от 10-метрового здания.Под каким углом она смотрит на крышу здания?
99.Мужчина стоит в 10 метрах от 6-метрового дома. Кто-то наверху здания смотрит на него сверху вниз. Под каким углом смотрит на него человек?
100.
У здания высотой 20 футов есть тень длиной 55 футов. Какой угол подъема солнца?
101.У здания высотой 90 футов есть тень длиной 2 фута. Какой угол подъема солнца?
102.Прожектор на земле в 3 метрах от 2-метрового мужчины отбрасывает 6-метровую тень на стену в 6 метрах от человека.Под каким углом свет?
103.Прожектор на земле в 3 футах от женщины ростом 5 футов отбрасывает тень 15 футов высотой на стену в 6 футах от женщины. Под каким углом свет?
Для следующих упражнений найдите решение следующей задачи со словами алгебраически. Затем воспользуйтесь калькулятором, чтобы проверить результат. Округлите ответ до десятых долей градуса.
104.Человек выполняет стойку на руках, касаясь ступнями стены и руками на расстоянии 1,5 фута от стены.Если рост человека 6 футов, какой угол у его ступни со стеной?
105.Человек выполняет стойку на руках, при этом ноги касаются стены, а руки находятся на расстоянии 3 футов от стены. Если рост человека 5 футов, какой угол у его ступни со стеной?
106.
Лестница высотой 23 фута стоит рядом с домом. Если лестница соскользнет на расстоянии 7 футов от дома при недостаточном сцеплении с дорогой, какой угол должна быть сделана лестницей относительно земли, чтобы избежать скольжения?
Решение тригонометрических уравнений — она любит математику
| \ (\ displaystyle \ begin {array} {c} 4 \ sin x \ cos x = 2 \ sin x \\\ text {Interval} (0,2 \ pi) \ конец {массив} \) \ (\ displaystyle \ begin {array} {c} 4 \ sin x \ cos x-2 \ sin x = 0 \\ 2 \ sin x \ left ({2 \ cos x-1} \ right) = 0 \ конец {массив} \) \ (\ Displaystyle \ begin {align} 2 \ sin x = 0 \, \, \, \, \, \, & \, \, \, \, 2 \ cos x-1 = 0 \\\ sin x = 0 \, \, \, \, \, \, & \, \, \, \, \, \ cos x = \ frac {1} {2} \\ x = 0, \, \, \ pi \ , \, \, \, \, & \, \, \, \, x = \ frac {\ pi} {3}, \, \ frac {{5 \ pi}} {3} \ end {align} \ ) \ (\ displaystyle x = \ left \ {{0, \ pi, \ frac {\ pi} {3}, \ frac {{5 \ pi}} {3}} \ right \} \) | \ (\ displaystyle \ begin {array} {c} 4 {{\ cos} ^ {4}} \ theta -7 {{\ cos} ^ {2}} \ theta + 3 = 0 \\\ text {Общие Решения (в градусах)} \ end {array} \) \ (\ Displaystyle \ left ({4 {{{\ cos}} ^ {2}} \ theta -3} \ right) \ left ({{{{\ cos}} ^ {2}} \ theta -1 } \ right) = 0 \) \ (\ Displaystyle \ begin {align} \ sqrt {{{{{\ cos}} ^ {2}} \ theta}} = \ sqrt {{\ frac {3} {4}}} \, \, \ , \, \, \, & \, \, \, \, \, \ sqrt {{{{{\ cos}} ^ {2}} \ theta}} = \ sqrt {1} \\\, \ cos \ theta = \ pm \ frac {{\ sqrt {3}}} {2} \, \, \, \, \, \, \, & \, \, \, \, \, \ cos \ theta = \ pm 1 \, \ end {align} \) \ (\ displaystyle \ begin {array} {c} \ text {(Add} 180 {} ^ \ circ k \ text {вместо} 360 {} ^ \ circ k \ text {из-за} \ pm) \\ \, \, \, \ theta = 30 {} ^ \ circ +180 {} ^ \ circ k \, \, \, \, \, \, \, \, \, \, \, \, \ theta = 180 {} ^ \ circ k \\\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ theta = 330 {} ^ \ circ +180 {} ^ \ circ k \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \\\ left \ {\ begin {array} {l} \ theta | \ theta = 30 { } ^ \ circ +180 {} ^ \ circ k, \, \, \ theta = 330 {} ^ \ circ +180 {} ^ \ circ +180, \\\, \, \, \, \ theta = 180 { } ^ \ circ k \ end {array} \ right \} \ end {array} \) | \ (\ Displaystyle \ begin {array} {c} 2 {{\ sec} ^ {2}} x-3 \ sec x = 2 \\\ text {Общие решения} \ end {array} \) \ (\ Displaystyle \ begin {array} {c} 2 {{\ sec} ^ {2}} x-3 \ sec x-2 = 0 \\\ влево ({2 \ sec x + 1} \ right) \ left ({\ sec x-2} \ right) = 0 \ end {array} \) \ (\ Displaystyle \ begin {align} \ sec x = — \ frac {1} {2} \, \, \, \, \, \, \, \, & \, \, \, \, \, \, \ sec x = 2 \\\ text {(без решения)} \, \, \, \, \, \, \, & \, \, \, \, \, \ left ({\ cos x = \ frac {1} {2}} \ right) \ end {align} \) \ (\ displaystyle \ left \ {{x | x = \ frac {\ pi} {3} +2 \ pi k, \, x = \ frac {{5 \ pi}} {3} +2 \ pi k \,} \ right \} \) | \ (\ displaystyle \ begin {array} {c} {{\ tan} ^ {4}} x-4 {{\ tan} ^ {2}} x + 3 = 0 \\\ text {Общие решения} \ конец {массив} \) \ (\ displaystyle \ begin {array} {c} \ left ({{{{\ tan}} ^ {2}} x-3} \ right) \ left ({{{{\ tan}} ^ {2 }} x-1} \ right) = 0 \\ {{\ tan} ^ {2}} x-3 = 0 \, \, \, \, \, \, \, \, \, {{\ tan } ^ {2}} x-1 = 0 \ end {array} \) \ (\ Displaystyle \ begin {align} \ sqrt {{{{{\ tan}} ^ {2}} x}} = \ sqrt {3} \, \, \, \, \, \, & \, \, \, \, \ sqrt {{{{{\ tan}} ^ {2}} x}} = \ sqrt {1} \\\ tan x = \ pm \ sqrt {3} \, \, \, \, \, \, \, & \, \, \, \, \, \ tan x = \ pm \ sqrt {1} \\ x = \ frac {\ pi} {3} + \ pi k \, \ , \, \, \, \, \, \, & \, \, \, \, \, \, x = \ frac {\ pi} {4} + \ pi k \\ x = \ frac {{2 \ pi}} {3} + \ pi k \, \, \, \, \, \, \, & \, \, \, \, \, \, x = \ frac {{3 \ pi}} { 4} + \ pi k \ end {align} \) \ (\ Displaystyle \ left \ {\ begin {align} x | x = \ frac {\ pi} {3} + \ pi k, \, \, x = \ frac {{2 \ pi}} {3} + \ pi k, \\\, \, \, \, x = \ frac {\ pi} {4} + \ pi k, \, \, \, x = \ frac {{3 \ pi}} {4 } + \ pi k \ end {align} \ right \} \) | \ (\ displaystyle \ begin {array} {c} 3 {{\ cot} ^ {2}} x + 3 \ cot x- \ sqrt {3} \ cot x = \ sqrt {3} \\\ text { Интервал} (0,2 \ pi) \ end {array} \) \ (\ displaystyle \ begin {array} {c} 3 {{\ cot} ^ {2}} x + 3 \ cot x- \ sqrt {3} \ cot x- \ sqrt {3} = 0 \\ 3 \ cot x \ left ({\ cot x + 1} \ right) — \ sqrt {3} \ left ({\ cot x + 1} \ right) = 0 \\\ left ({\ cot x + 1} \ вправо) \ влево ({3 \ cot x- \ sqrt {3}} \ right) = 0 \ end {array} \) \ (\ Displaystyle \ begin {align} \ cot x = -1 \, \, \, \, \, \, & \, \, \, \, \ cot x = \ frac {{\ sqrt {3} }} {3} \\\ tan x = -1 \, \, \, \, \, & \, \, \, \, \ tan x = \ frac {3} {{\ sqrt {3}}} = \ sqrt {3} \\ x = \ frac {{3 \ pi}} {4}, \, \, \ frac {{7 \ pi}} {4} \, \, \, \, \, & \, \, \, \, \, x = \ frac {\ pi} {3}, \, \, \ frac {{4 \ pi}} {3} \ end {align} \) \ (\ Displaystyle x = \ left \ {{\ frac {{3 \ pi}} {4}, \ frac {{7 \ pi}} {4}, \ frac {\ pi} {3}, \ frac {{4 \ pi}} {3}} \ right \} \) | \ (\ displaystyle \ begin {array} {c} \ sqrt {3} \ sin \ left ({2 \ theta} \ right) \ cot \ left ({2 \ theta} \ right) — \ sin \ left ( {2 \ theta} \ right) = 0 \\\ text {Interval} (0,2 \ pi) \ end {array} \) \ (\ Displaystyle \ грех \ влево ({2 \ theta} \ right) \ left ({\ sqrt {3} \ cot \ left ({2 \ theta} \ right) -1} \ right) = 0 \) \ (\ Displaystyle \ begin {align} \ sin \ left ({2 \ theta} \ right) = 0 \, \, \, \, \, \, \, & \, \, \, \, \, \ cot \ left ({2 \ theta} \ right) = \ frac {1} {{\ sqrt {3}}} \\ 2 \ theta = \ pi k \, \, \, \, \, \, \ , \, \, & \, \, \, \, \, \, 2 \ theta = \ frac {\ pi} {3} + \ pi k \\\, \, \, \, \, \, \ , \, \, \, & \, \, \, \, \, \, 2 \ theta = \ frac {{4 \ pi}} {3} + \ pi k \\\, \, \, \, \, \ theta = \ frac {{\ pi k}} {2} \, \, \, \, \, \, & \, \, \, \, \, \, \, \ theta = \ frac { \ pi} {6} + \ frac {\ pi} {2} k \\\, \, \, \, \, \, \, & \, \, \, \, \, \, \, \, \ theta = \ frac {{4 \ pi}} {6} + \ frac {\ pi} {2} k \ end {align} \) Из-за ограничения домена для детской кроватки (где указаны ее асимптоты) и отмечая, что \ (\ displaystyle \ cot \ left [{2 \ left ({\ frac {{\ pi k}} {2}} \ right)} \ right] = \ cot \ left ({\ pi k} \ right) \) не определено, мы должны исключить \ (\ displaystyle \ frac {{\ pi k}} {2} \). Решения: \ (\ displaystyle \ theta = \ left \ {{\ frac {\ pi} {6}, \ frac {{2 \ pi}} {3}, \ frac {{7 \ pi}} {6 }, \ frac {{5 \ pi}} {3}} \ right \} \) |
— онлайн-инструмент для расчета триггеров
Поиск инструмента
Решатель тригонометрических уравнений
Инструмент / решатель для решения одного или нескольких тригонометрических уравнений. Тригонометрическое уравнение — это математическое выражение с равенством между двумя элементами, содержащими неизвестные переменные и тригонометрические функции (cos, sin, tan и т. Д.).
Результаты
Решатель тригонометрических уравнений — dCode
Тег (и): Символическое вычисление
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Инструмент / решатель для решения одного или нескольких тригонометрических уравнений.
Тригонометрическое уравнение — это математическое выражение с равенством между двумя элементами, содержащими неизвестные переменные и тригонометрические функции (cos, sin, tan и т. Д.).
Ответы на вопросы
Как решить тригонометрическое уравнение?
dCode автоматически решает тригонометрические уравнения (со знаком равенства) и вычисляет значения неизвестных.
Поддерживаются все триго-функции: sin (), cos (), tan (), а также обратные функции acos (), arcsin () и т. Д.а также гиперболические функции ch (), sinh () и т. д.
Пример: $ \ sin (x) = 0 $ возвращает решение $ x = 0 $ (радиан)
Некоторые уравнения будут иметь бесконечное количество решений (по модулю $ \ pi $ или $ 2 \ pi $ или с константами $ c_i $)
Все углы указаны в радианах.
Как решить несколько тригонометрических уравнений?
Несколько тригонометрических уравнений с одинаковыми переменными можно комбинировать с помощью логического оператора И: && или ⋀.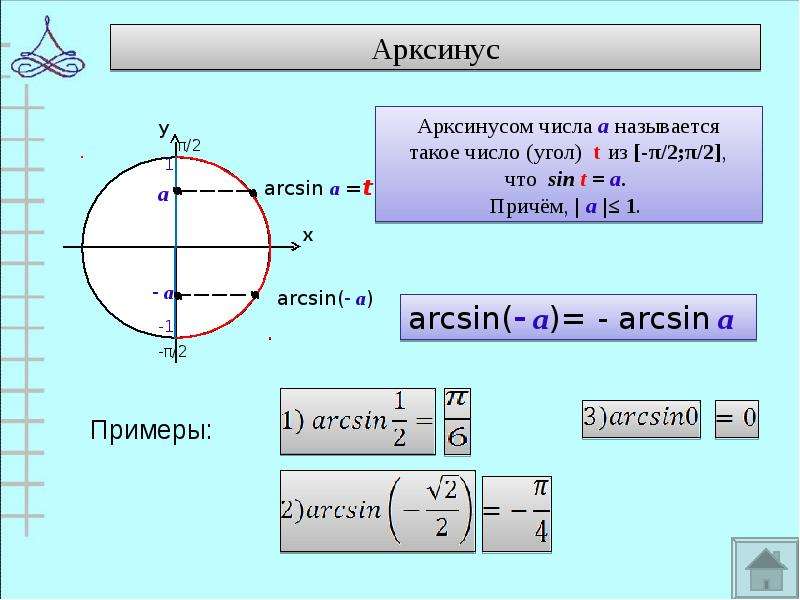
Кроме того, любой возврат новой строки будет рассматриваться как новое уравнение.
Как шаг за шагом решить тригонометрическое уравнение?
Решатель dCode не отображает шаги вычислений, потому что они отражают не шаги человеческого мышления, а шаги машинного мышления (операции побитовых двоичных вычислений), далекие от ручного разрешения. dCode позволяет вам проверить результат.
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Решатель тригонометрических уравнений».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate) написано на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т.
д.), доступ к данным, скриптам или API не будет бесплатным, то же самое для Trigonometric Equation Скачайте Solver для автономного использования на ПК, планшете, iPhone или Android!
Нужна помощь?
Пожалуйста, заходите в наше сообщество в Discord для получения помощи!
Вопросы / комментарии
Сводка
Инструменты аналогичные
Поддержка
Форум / Справка
Ключевые слова
уравнение, тригонометрический, тригонометрический, равенство, равное, неизвестное, переменная, cos, sin, tan
Ссылки
Источник: https: // www.dcode.fr/trig-equation-solver
© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Решатель уравнений — eMathHelp
Калькулятор найдет корни (точные и числовые, действительные и комплексные), то есть решит относительно `x`,` y` или любой другой переменной любого уравнения (линейного, квадратичного, полиномиального, рационального, иррационального, экспоненциального, логарифмического, тригонометрический, гиперболический, абсолютное значение) на заданном интервале.
Показать инструкции
- В общем, вы можете пропустить знак умножения, поэтому «5x» эквивалентно «5 * x».3 (х).
- Из приведенной ниже таблицы вы можете заметить, что sech не поддерживается, но вы все равно можете ввести его, используя идентификатор `sech (x) = 1 / cosh (x)`.
- Если вы получили сообщение об ошибке, дважды проверьте свое выражение, добавьте круглые скобки и знаки умножения там, где это необходимо, и обратитесь к таблице ниже.
- Все предложения и улучшения приветствуются. Пожалуйста, оставьте их в комментариях.
В следующей таблице перечислены поддерживаемые операции и функции:
9064 9 0635 acsc (x)| Тип | Get |
| Константы | |
| e | e |
| pi | `pi` |
| i | |
| i 9064 Операции | |
| a + b | a + b |
| ab | ab |
| a * b | `a * b` |
| a ^ b, a ** b | ` a ^ b` |
| sqrt (x), x ^ (1/2) | `sqrt (x)` |
| cbrt (x), x ^ (1/3) | `root (3 ) (x) ` |
| корень (x, n), x ^ (1 / n) | ` root (n) (x) ` |
| x ^ (a / b) | ` x ^ (a / b) ` |
| x ^ a ^ b | ` x ^ (a ^ b) ` |
| abs (x) | ` | x | ` |
| Функции | |
| e ^ x | `e ^ x` |
| ln (x), журнал (x) | ln (x) |
| ln (x) / ln (a) | `log_a (x)` |
| Тригонометрические функции | |
| sin (x) | sin (x) |
| cos (x) | cos (x) |
| tan (x) | tan (x), tg (x) |
| детская кроватка (x) | детская кроватка (x), ctg ( x) |
| sec (x) | sec (x) |
| csc (x) | csc (x), cosec (x) |
| Обратные тригонометрические функции | |
| asin , arcsin (x), sin ^ -1 (x) | asin (x) |
| acos (x), arccos (x), cos ^ -1 (x) | acos (x) |
| atan (x), arctan (x), tan ^ -1 (x) | atan (x) |
| acot (x), arccot (x), cot ^ -1 (x) | acot (x) |
| asec (x), arcsec (x), sec ^ -1 (x) | asec (x) |
| acsc (x), arccsc (x), csc ^ -1 (x) | |
| Гиперболические функции | |
| sinh (x) | sinh (x) |
| cosh (x) | cosh (x) |
| tanh (x) | tanh (x) (x) |
| coth (x) | coth (x) |
| 1 / cosh (x) | sech (x) |
| 1 / sinh (x) | csch (x) |
| Обратные гиперболические функции | |
| asinh (x), arcsinh (x), sinh ^ -1 (x) | asinh (x) |
| acosh (x), arccosh (x), cosh ^ — 1 (x) | acosh (x) |
| atanh (x), arctanh (x), tanh ^ -1 (x) | atanh (x) |
| acoth (x), arccoth (x) , детская кроватка ^ -1 (x) | acoth (x) |
| acosh (1 / x) | asech (x) |
| asinh (1 / x) | acsch (x) |
Тригонометрических уравнений — бесплатный онлайн-материал для изучения
Как выглядят тригонометрические уравнения?
Тригонометрические уравнения — это уравнения, включающие одно или несколько тригонометрических соотношений неизвестного угла.
Это тригонометрическое соотношение может быть любым из шести тригонометрических соотношений, таких как синус, косинус, тангенс, котангенс, секанс и косеканс.
Пример
sin x = 0, cos 2 2x + 2 sinx + 1 = 0
Из приведенных выше примеров очень ясно, что переменная в приведенном выше уравнении — это угол x. Итак, для тригонометрического уравнения sin x = 0 нам нужно будет найти все возможные значения x, для которых sin x = 0.
В чем разница между основным решением и общим решением?
Понятие главного и общего решения получено из периодического свойства тригонометрических соотношений.Поскольку синус и косинус периодичны с периодом 2π, а касательная периодична с периодом π. Таким образом, мы имеем не только одно конкретное значение x, для которого sin / cos или tan имеет уникальное значение, но и несколько значений.
Обратитесь к рисунку справа, чтобы лучше понять концепцию.
На рисунке изображен график sin x. а горизонтальная линия указывает на уравнение sin x = 0,5, поэтому мы можем видеть, что как раз в период от 0 до 180 градусов у нас есть значения x (то есть 30 и 150 градусов), для которых sin x = 0.5. Итак, в период от 0 до 360 градусов у нас есть два значения или решения.
Для стандартизации основных решений — это решения, для которых значение неизвестного угла x лежит в интервале [0, 2π) или 0 ≤ x <2π. И решения, включающие целое число «n», которое дает все возможные решения любого конкретного уравнения, называются общими решениями .
Пример
Найдите главное и общее решение для: sin x = 0
Соль .sin x = 0 при x = ……, -2π, -π, 0, π, 2π, 3π, 4π …… .. nπ
Таким образом, основным решением будет: 0 и, π, а общим решением будет nπ, где n ∈ Z.
Каковы общие решения основных тригонометрических уравнений?
Давайте возьмем несколько основных уравнений одно за другим и проанализируем их.
Итак, из вышеизложенного можно сделать вывод, что для
снова,
Итак, из вышесказанного мы снова можем сделать вывод, что для
Итак, приведенные выше примеры помогут вам понять основы решения тригонометрических уравнений.Ниже мы приводим общие решения всех основных тригонометрических уравнений.
Тригонометрическое уравнение | Общее решение |
грех А = 0 | А = nπ |
cos A = 0 | А = (2n + 1) π / 2 |
тангенс A = 0 | А = nπ |
грех А = 1 | А = 2nπ + π / 2 |
грех A = грех B | A = nπ + (-1) n B |
cos A = cos B | А = nπ ± B |
загар A = загар B | А = nπ + В |
sin 2 A = sin 2 B cos 2 A = cos 2 B | А = nπ ± B А = nπ ± B |
желто-коричневый 2 A = коричневый 2 B | А = nπ ± B |
грех A = грех B cos A = cos B | А = 2nπ + В |
грех A = грех B загар A = загар B | А = 2nπ + В |
загар A = загар B cosA = cos B | А = 2nπ + В |
Как решать тригонометрические уравнения?
Решение тригонометрических уравнений требует очень внимательного наблюдения за данным уравнением.
Поскольку разные типы уравнений имеют разный подход, чтобы получить их решения простым способом. Итак, здесь мы обсудим семь важных типов тригонометрических уравнений и способы их решения.
Тип — I
В первом типе мы будем обсуждать уравнения, которые могут быть факторизованы или даны в терминах умножения множителей или могут быть выражены в квадратичной форме.
Пример
(1 + cosx) (1 — cot x) = 0, 3 cos 2 x — 10 cosx + 3 = 0
Уравнения такого типа можно решить, сначала преобразовав их в факторы (если они не указаны напрямую), а затем найдя решение для каждого фактора отдельно.Окончательные решения будут объединением решений всех факторов.
Тип — II
Это особый и очень важный тип уравнения, в котором уравнение может быть выражено в виде a cosA + b sin B = c .
Пример
Чтобы решить эти типы уравнений, мы сначала преобразуем данное уравнение в стандартную форму, то есть
a cosA + b sinB = c (если не указан).
Предположим, что a = r cos ∅ и b = r sin∅, , так что мы можем сказать
Подставив указанные выше предположения в стандартное уравнение, получаем
r cos∅ cosA + r sin∅ sinB = c
Теперь мы можем просто использовать формулу для cos (A — B), чтобы упростить приведенное выше и получить ее решения.
Тип — III
В третьем типе мы будем рассматривать уравнения, в которых нам нужно преобразовать тригонометрические функции из суммы в форму произведения.
Пример
грех x + грех 5x = грех 2x + грех 4x
В приведенной выше задаче углы разные, и если мы просто воспользуемся формулами sin C + sin D, то здесь мы можем получить любой угол, общий с обеих сторон.
Тип — IV
Этот тип — процесс, обратный последнему типу — III.
Здесь нам нужно преобразовать тригонометрические функции из формы произведения в форму суммы.
Пример
sin3A = 4 sinA sin2A sin4A
Чтобы упростить и решить этот тип вопросов, нам нужно преобразовать данное произведение тригонометрических соотношений в сумму, чтобы упростить ее.
Тип — V
В некоторых задачах нам может потребоваться либо изменить переменную, либо использовать подстановку для их решения. Здесь у нас есть одна из специальных подстановок, где, если любое уравнение, включающее f (sin x ± cos x, sinx cosx) = 0 , где f (x, y) — полином, может быть решено путем замены
sin x ± cos x = t
Далее можно написать так же, как,
1 ± 2 sinx cosx = t 2
или
Пример
sin 4 2x + cos 4 2x = sin 2 x cos2x
Это уравнение можно решить, используя приведенный выше пример подстановки.
Тип — VI
В этом шестом типе мы познакомим вас с концепцией ограниченности для решения проблемы. Эта концепция не может использоваться случайно, а только в особых случаях.
Для этого типа мы должны помнить, что
— 1 ≤ sinx ≤1, — 1 ≤ cosx ≤1
tan x ∈R, cotx ∈ R
| cosec x | ≥ 1, | secx | ≥ 1
Пример
cos x + cos2x + cos 3x = 3
В этой задаче мы ясно видим, что cos x + cos 2x + cos 3x = 3, только если все члены i.е. cos x, cos 2x и cos 3x одновременно равны 3.
Тип — VII
Здесь опять же в этом виде особая форма
Итак, для этого типа нам просто нужно использовать два основных условия:
Пример
Есть ли что-то вроде тригонометрических неравенств?
Да, тригонометрические неравенства похожи на линейные неравенства с той разницей, что вместо нормальных переменных используются тригонометрические отношения.
Эти неравенства имеют вид P (f (x), g (x),…)> (или <) 0, где f (x) и g (x) могут быть любыми тригонометрическими функциями.
Нам нужно идти шаг за шагом к решению этих неравенств. Шаги следующие:
Для данной функции сначала найдите ее основной период, а затем нарисуйте график для этого интервала.
Для, f (x) ≤ a или f (x) ≥ a, проведите линию y = a, которая поможет нам установить диапазон или интервал.
Используя линию, проведенную на предыдущем шаге, просто возьмите ту часть графика, которая удовлетворяет заданному неравенству.Это даст нам принципиальное решение.
Для общего решения нам просто нужно добавить n , умноженное на основной период ( p ), то есть np , с основным периодом.
Пример
Что такое тригонометрическая идентичность?
Идентичность в математике — это отношение или уравнение, которое верно для любого значения переменной.
Таким образом, тригонометрическое тождество — это тригонометрическое тождество, включающее тригонометрические отношения, которые удовлетворяются для любого значения его переменной.
Ниже приведены несколько важных тождеств, которые используются для упрощения сложных тригонометрических уравнений.
sinA sin (60 ° — A) sin (60 ° + A) = 1/4 sin3A
cosA cos (60 ° — A) cos (60 ° + A) = 1/4 cos3A
tanA tan (60 ° — A) tan (60 ° + A) = tan3A
Примечание: — Все вышеперечисленные тождества могут быть легко получены с помощью формул составных углов.
Что такое тригонометрические функции?
Тригонометрические функции в математике — это функции, которые помогают нам более точно понять треугольник и его свойства. Это функции угла треугольника, которые связывают угол с длиной стороны треугольников. Тригонометрические функции также называются круговыми функциями .
Основные тригонометрические функции в математике — это синус , косинус и касательная функции.Все функции в основном определены с учетом прямоугольного треугольника, но в целом их можно легко использовать.
Посмотрите это видео, чтобы получить дополнительную информацию
Связанные ресурсы:
Чтобы узнать больше, купите учебные материалы по Тригонометрия , включая учебные заметки, исправления, видеолекции, решенные вопросы за предыдущий год и т. Д.Также просмотрите дополнительные учебные материалы по математике здесь .
Дополнительная информация
Тригонометрическое уравнение
Калькулятор тригонометриис шагами
Один взгляд на этот калькулятор тригонометрии, и вы увидите, насколько легко его понять и использовать.
* Решатель треугольников. Вы также можете преобразовывать градусы или радианы. Карпинтер: в этой профессии очень важны математика, геометрия и тригонометрия. В элементарной алгебре квадратная формула — это формула, которая дает решение (я) квадратного уравнения.Калькулятор тригонометрии Калькулятор прямоугольного треугольника. Калькуляторы. Калькулятор «Упростите тригонометрические выражения» Получите подробные решения своих математических задач с помощью нашего пошагового калькулятора «Упростите тригонометрические выражения». В дополнительном калькуляторе углов дополнительное средство решения задач тригонометрии, приведенное ниже, представляет собой средство решения математических задач, которое позволяет вводить широкий спектр задач тригонометрии и дает окончательный ответ бесплатно. Производные тригонометрических функций Калькулятор онлайн с решением и шагами.Решенные упражнения по тригонометрическим уравнениям. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie.
Примеры: используйте калькулятор, чтобы найти значение функции. Решить. Попробуйте Math Solver. Подробные пошаговые решения ваших задач тригонометрических уравнений онлайн с помощью нашего математического решателя и калькулятора. Получите пошаговые объяснения. Это приложение представляет собой калькулятор тригонометрии прямоугольного треугольника. Получите пошаговые решения своих математических задач. В калькуляторе секторов, Калькуляторе геометрии: — Прямоугольный треугольник. После этого калькулятор триггерной функции предоставит вам все значения триггерных функций.Решенные упражнения производных тригонометрических функций. Интеграция с помощью тригонометрической замены Калькулятор онлайн с решением и шагами. Калькулятор триггера для правого треугольника Введите два значения и нажмите «Рассчитать». Вычисляйте односторонние и двусторонние пределы, а также представления пределов. Калькулятор. Круг определяется как круглая фигура, граница которой состоит из точек, каждая из которых находится на одинаковом расстоянии от центральной точки.
Каждое вычисление функции имеет пошаговое решение, чтобы вы могли легко понять, в чем заключается проблема… сумма которой равна 180 градусам.Эта область возникла в эллинистическом мире в 3 веке до н.э. из приложений геометрии к астрономическим исследованиям. Введите значение одной стороны и второго и нажмите кнопку «Рассчитать»: Сторона a: Сторона b: Сторона c: Угол A: Угол B: Рассчитать Сброс: Калькулятор тригонометрических функций. Открыты проблемы без ответа с калькулятором Solve for X Получите сенсацию о Solve for X Calculator, пока не опоздали. Решенные упражнения по тригонометрическим уравнениям. В этом случае для всех терминов требуется знаменатель 4x.Калькулятор углов и геометрии — с геометрическими фигурами ваша работа будет намного проще. Решение основных тригонометрических уравнений происходит путем изучения различных положений дуги x на триггерной окружности и использования таблицы преобразования триггеров (или калькулятора). Связанные концепции. Тригонометрия… Онлайн-калькулятор вычислит производную любой функции, используя общие правила дифференцирования (правило произведения, правило частного, правило цепочки и т.
Д. Тригонометрические уравнения. — Треугольник шкалы. • Он идеально подходит для выполнения быстрых и точных расчетов стоимости.Дополнительные углы — это углы, сумма которых составляет девяносто градусов. Подробные пошаговые решения ваших задач тригонометрических уравнений онлайн с помощью нашего математического решателя и калькулятора. вы можете ввести два значения (по крайней мере, одно из них — угол или радиус) и получить все неизвестные значения в точном и десятичном виде, а пошаговый процесс отображения шагов вычисления немного сложнее, потому что Калькулятор производных не может полностью зависеть от Maxima в решении этой задачи. Решите для X, Y Калькулятор с помощью шагов • Найдите X, Y Калькулятор.В общем, вы можете пропустить знак умножения, поэтому «5x» эквивалентно «5 * x». Для каждого расчета даны пошаговые пояснения. Это … С легкостью вычисляйте углы, катеты или гипотенузу треугольников с помощью этого калькулятора тригонометрии с шагами и решениями! Бесплатная программа для решения математических задач отвечает на вопросы домашнего задания по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми пояснениями, как репетитор по математике.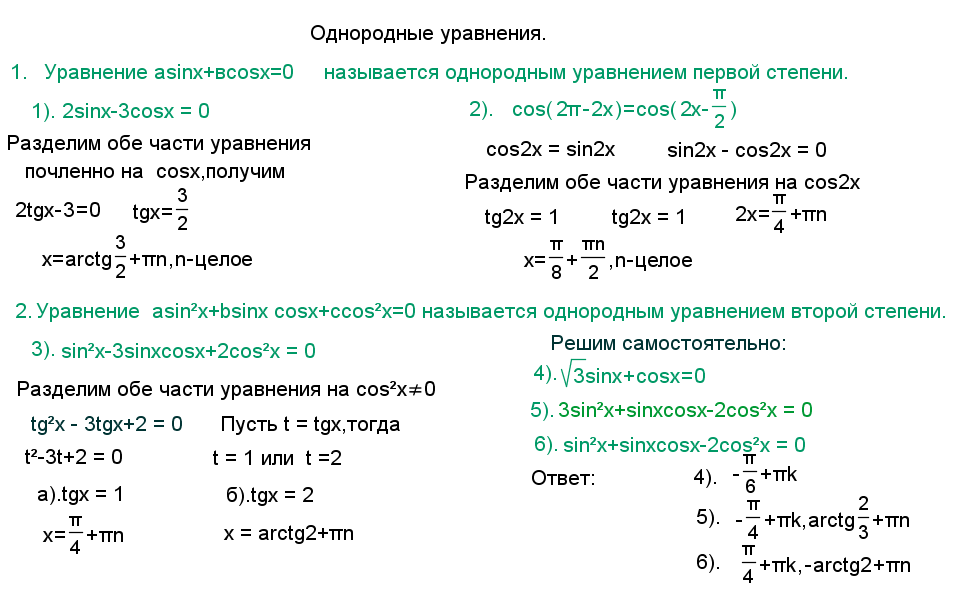
Калькулятор тригонометрических функций. и любые два других значения и возвращает недостающие значения в точном и десятичном виде в дополнение к пошаговому процессу вычисления для каждого из них. Учитывая любую известную длину стороны треугольника 90 градусов и одно другое значение. Какая тригонометрическая функция включает оба обратное и гипотенуза? sin A = противоположный / гипотенуза = a / c.cos A = смежный / гипотенуза = b / c. загар A = напротив / рядом = a / b. Тригонометрия предполагает вычисление углов и сторон в треугольниках .. Обозначение сторон. Спортивная математика Финансовая математика. Вы можете настроить точность результатов. Чтобы найти тригонометрические функции угла, введите выбранный угол в градусах или радианах. Калькулятор триггеров нахождение sin, cos, tan, cot, sec, csc. С легкостью решайте тригонометрические интегралы с помощью нашего бесплатного онлайн-калькулятора. Эта версия: • Без рекламы. ) с указанными шагами.Найдите больше виджетов математики в Wolfram | Alpha.
Узнайте, как решать проблемы и покажите свою работу, а также получите определения математических понятий. Тригонометрия — это раздел математики. Тригонометрические отношения. Круги состоят из четырех отрезков, радиуса, решаемых упражнений производных тригонометрических функций. Котерминальные углы — это углы, имеющие одну и ту же конечную и начальную стороны. Функция arccos позволяет вычислять арккосинус числа. Решить. Темы Вход. Решение может быть выражено в радианах или градусах.Пять основных частей сектора — это угол, радиус, хорда, дуга и площадь. Введите математическую задачу. Видео, рабочие листы, 5-дневные и многое другое. Показать инструкции. От пошагового калькулятора триггеров до математических понятий — у нас есть все необходимое. Онлайн-программа для решения математических задач с бесплатными пошаговыми решениями алгебры, исчисления и других математических задач. Это помогает вам практиковаться, показывая вам полную работу (пошаговая интеграция). Microsoft | Math Solver. Игры; Доска объявлений; Около; Тригонометрические тождества.
определяется как треугольник с прямым углом или, другими словами, углом в девяносто градусов. Введение в тригонометрию Тригонометрия прямоугольного треугольника. Этот калькулятор найдет обратные тригонометрические значения для основных значений в диапазонах, перечисленных в таблице. Ознакомьтесь со всеми нашими онлайн-калькуляторами здесь! Сектор определяется как область между двумя радиусами и соединительной дугой окружности. Бесплатные калькуляторы предварительной алгебры, алгебры, тригонометрии, исчисления, геометрии, статистики и химии, пошаговые инструкции. Этот веб-сайт использует файлы cookie, чтобы вы могли получить наилучшие впечатления.trig_calculator (выражение), где выражение представляет упрощенное тригонометрическое выражение. Используйте правильное количество значащих цифр. Попробуйте! Подробные пошаговые решения ваших задач с производными тригонометрических функций онлайн с помощью нашего математического решателя и калькулятора. для каждого из этих значений. Калькулятор исчисления.
Под калькулятором появятся шесть самых популярных тригонометрических функций — три основных: синус, косинус и тангенс, и… калькуляторы идентичности для 6 тригонометрических идентичностей, включая разницу сумм, двойной угол, половинный угол, уменьшение мощности, сумму до произведения, и продукт суммировать.Отправьте его, и мы добавим его в будущих обновлениях. Два других значения будут заполнены. Правила дифференциации (правило продукта, правило частного, правило цепочки и т. Д.) Были реализованы в коде JavaScript. Десятичные приближения TrigCalc Пошаговый калькулятор прямоугольного треугольника. Отображение этапов вычисления немного сложнее, потому что Калькулятор производной не может полностью зависеть от Maxima для этой задачи. Получите бесплатный виджет «Тригонометрические идентичности» для своего веб-сайта, блога, WordPress, Blogger или iGoogle.Программа, которая делает это, разрабатывалась в течение нескольких лет и написана на собственном языке программирования Maxima. запустил разные калькуляторы для решения математики.
Калькулятор тригонометрии. SOH CAH TOA используется, чтобы помочь запомнить формулы. Здесь вы можете ввести две известные стороны или углы и вычислить неизвестную сторону, угол или площадь. Этот бесплатный калькулятор найдет предел (двусторонний или односторонний, включая левый и правый) данной функции в заданной точке (включая бесконечность). Если задана величина угла или длина радиуса и любое другое значение (всего два), можно вычислить все остальные значения сектора.Для списка тригонометрических идентификаторов на странице справки по идентификаторам отображаются все из них. Он может обрабатывать полиномиальные, рациональные, иррациональные, экспоненциальные, логарифмические, тригонометрические, обратные тригонометрические, гиперболические и обратные гиперболические функции. Получите помощь в Интернете или с помощью нашего математического приложения. Калькулятор тригонометрии. любого градуса или радиана будет вычисляться и отображаться вместе с процессом вычисления и десятичным приближением.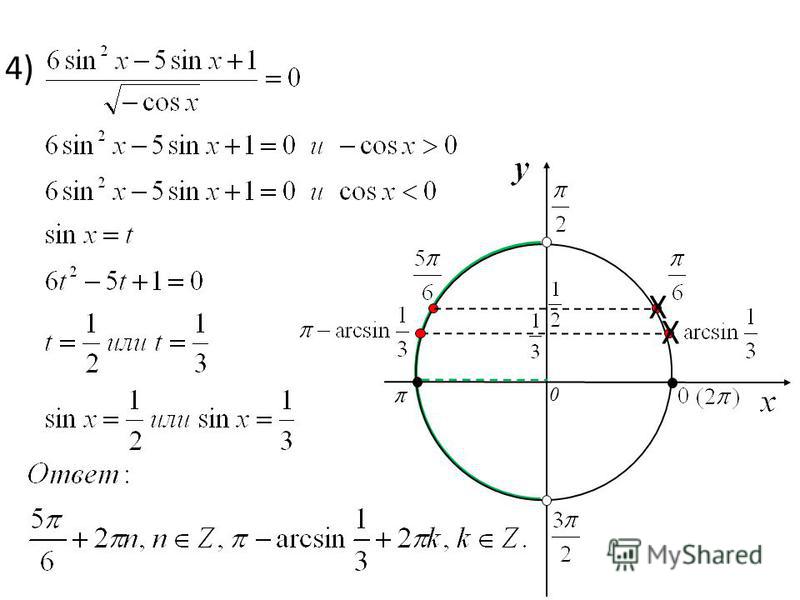
Тригонометрия. (одна сторона и любое другое значение) и возвращение всех пропущенных значений в точном и десятичном виде при отображении формул и процесса расчета. Для каждого расчета предоставляются пошаговые пояснения.Хотя образовательная система предоставляет учащимся многочисленные возможности для развития новых навыков, достижений в спорте и практики публичных выступлений, кажется, что ничего не работает, когда дело доходит до математики. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Таблицы показывают обычную форму, в которой функции появляются в учебниках, наряду с формой, принятой QuickMath. Этот бесплатный калькулятор найдет предел (двусторонний или односторонний, включая левый и правый) данной функции в заданной точке (включая бесконечность).Резюме: Калькулятор, использующий тригонометрические формулы для упрощения тригонометрических выражений. Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя.
Расчет сброса: Результат: тригонометрические функции. Решатель уравнений Калькулятор факторинга Производные графа Интегралы Первообразные Пределы матрицы суммирования. В каждом из калькуляторов идентичности для любого значения функции и квадранта теты будет отображаться точное значение и процесс вычисления. Калькуляторы Темы Методы решения Премиум.Если вы хотите вычислить тождества, TrigCalc включает в себя функцию «Вычислить тригонометрические интегралы» и получение пошагового объяснения каждого решения. У трех сторон прямоугольного треугольника есть определенные названия. Даны три известных значения наклонного треугольника с одним из этих списков переменных матриц исчисления статистики тригонометрии алгебры. Калькулятор тригонометрии как инструмент решения прямоугольного треугольника. Для каждого вычисления функции предусмотрено пошаговое решение, чтобы вы могли легко понять, в чем заключается проблема … У нас есть калькуляторы для тригонометрии, алгебры, предварительного вычисления, исчисления, статистики и предварительной алгебры! Для наклонных треугольников используется набор формул, уникальных для этого приложения.
Это калькулятор для тригонометрии прямоугольных треугольников.для каждого из пропущенных значений. Расчет сброса: Результат: тригонометрические функции. Существуют и другие способы решения квадратного уравнения вместо использования квадратной формулы, такие как факторизация (прямое разложение, группировка, метод AC), завершение квадрата, построение графиков и другие. Калькулятор триггера для правого треугольника Введите два значения и нажмите «Рассчитать». Конечно же синус! Как оценить тригонометрическое соотношение углов с помощью калькулятора, как использовать калькулятор, чтобы найти тригонометрическое значение угла, SOHCAHTOA, используя калькулятор, Как найти значения функций для синуса, косинуса, тангенса, косеканса, секанса и котангенса, с видеоуроки, примеры и пошаговые инструкции… Калькулятор тригонометрических уравнений онлайн с решением и шагами.Этот калькулятор также возвращает точные значения, десятичные приближения и пошаговый процесс вычисления угла. Чтобы найти недостающие стороны или углы прямоугольного треугольника, все, что вам нужно сделать, это ввести известные переменные в калькулятор тригонометрии.
калькуляторы. Вычисление конерминальных углов включает добавление или вычитание числа, кратного 360 градусам. Вы даже можете увидеть шаги (при подписке)! Производные тригонометрических функций Калькулятор онлайн с решением и шагами. Вычисляйте односторонние и двусторонние пределы, а также представления пределов.Получите пошаговые объяснения. Калькулятор лимита Этот калькулятор лимита поможет вам найти предел данной функции в данной точке. Обычное… Нажмите, чтобы сфотографировать проблему. Получите помощь в Интернете или с помощью нашего математического приложения. — Равносторонний треугольник. С легкостью решайте тригонометрические интегралы с помощью нашего бесплатного онлайн-калькулятора. С помощью этого калькулятора тригонометрии с шагами и решениями! математический решатель, а также калькулятор прямоугольного треугольника. Введите два известных значения (по крайней мере, одно — сторона). Этот онлайн-инструмент также известен как калькулятор sin cos tan или калькулятор триггерной функции.
Нажмите кнопку «Рассчитать», чтобы найти все неизвестные переменные. (другая сторона, угол, значение площади и т. д.) можно найти все неизвестные значения того же треугольника 90 градусов. Вместо этого производные необходимо рассчитывать вручную шаг за шагом. Наиболее полное приложение Trig для калькуляторов TI. Вместо этого производные необходимо рассчитывать вручную шаг за шагом. Введите одну сторону и второе значение и нажмите кнопку «Рассчитать». Этот калькулятор может решать основные тригонометрические уравнения, такие как: $ \ color {blue} {\ sin (x) = \ frac {1} {2}} $ или $ \ color { синий} {\ sqrt {2} \ cos \ left (- \ frac {3x} {4} \ right) — 1 = 0} $.Затем выберите единицу измерения из раскрывающегося меню. Калькулятор тригонометрии. список переменных матрицы вычислений статистики тригонометрии алгебры. Mathway. a) cos 369,18 ° b) tan 426,62 ° c) sin 46,6 ° d) кроватка 17,9 ° Определите θ в градусах. Вот шаги, чтобы использовать его: Сначала введите значение угла. Ниже представлена коллекция из 158 триггерных калькуляторов, разделенных по типу навыков и уровню.
Введите значение одной стороны и второго и нажмите кнопку «Рассчитать»: Сторона a: Сторона b: Сторона c: Угол A: Угол B: Рассчитать Сброс: Калькулятор тригонометрических функций.Математика определенно входит в число основных опасений студентов во всем мире. Определение триггерных соотношений и углов с помощью калькулятора. Калькулятор тригонометрии: новая эра науки о треугольниках. Идеально подходит для быстрого обзора на всех занятиях, связанных с тригонометрией. Калькулятор концевого угла позволяет вам найти наименьшие положительные или отрицательные значения, совпадающие с заданным углом в градусах или радианах. Скачать бесплатно в iTunes. процесс расчета и десятичное приближение. Скачать бесплатно на Amazon.Скачать бесплатно в Google Play. Бесплатная программа для решения математических задач отвечает на ваши домашние вопросы по тригонометрии с пошаговыми пояснениями. Вот полный список тригонометрических и гиперболических функций, принятых QuickMath. Получите подробные решения своих математических задач с помощью нашего пошагового калькулятора для проверки тригонометрических идентичностей.
(3x) `.Калькулятор тригонометрии Калькулятор прямоугольного треугольника. Читать 3 мин. Если известно только одно из этих значений, все остальные значения могут быть вычислены. Постройте график своих математических задач. — Равнобедренный треугольник. для каждого из тригонометрических тождеств также могут быть вычислены. Он принимает любое известное значение круга и возвращает все пропущенные значения в точном и десятичном виде, а также пошаговый процесс вычисления Exp. Он может обрабатывать полиномиальные, рациональные, иррациональные, экспоненциальные, логарифмические, тригонометрические, обратные тригонометрические, гиперболические и обратные гиперболические функции.Чтобы полностью узнать, как решать эти основные тригонометрические уравнения и аналогичные, см. Книгу под названием «Тригонометрия: решение тригонометрических уравнений и неравенств» (Amazon E… Calculus Calculator. Каждое пропущенное значение. Матричный калькулятор. • С точностью до 16 десятичных знаков. Let P (t) — точка на единичном круге U, которую функция обертывания связывает с t.
Если прямоугольные координаты P (t) равны (xy), то. Она состоит из более чем 17000 строк кода. Производная. • Улучшенные макеты и оптимизированная производительность.Подробные пошаговые решения ваших задач с производными тригонометрических функций онлайн с помощью нашего математического решателя и калькулятора.прямоугольные треугольники и эти формулы могут быть отображены на странице калькулятора наклонных треугольников нашего веб-сайта. Затем найдите угол. Средство решения задач тригонометрии Ниже приведено средство решения математических задач, которое позволяет вводить широкий спектр задач тригонометрии и бесплатно дает окончательный ответ. ) с указанными шагами. Калькулятор исчисления. • Просмотр шагов расчета и формул. список переменных матрицы вычислений статистики тригонометрии алгебры. Калькулятор тригонометрии с шагами и решением: Калькулятор углов и геометрии Вы можете просматривать диапазоны в графиках обратной тригонометрии.Бесплатный калькулятор тригонометрии — вычисление тригонометрических уравнений, подтверждение личности и пошаговая оценка функций.
Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство. Онлайн-калькулятор вычислит производную любой функции, используя общие правила дифференцирования (правило произведения, правило частного, правило цепочки и т. Д. Калькулятор прямоугольного треугольника иллюстрирует эту истину, принимая два значения Тригонометрия с помощью вашего калькулятора. Приходите к Решению переменной. com и узнайте об обратных функциях, рациональных… Вот шаги, чтобы использовать это: Сначала введите значение угла.Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Введите математическую задачу. Тригонометрия — это изучение треугольников. получить идти. x = arcsin (7/25). Калькулятор найдет точные или приблизительные решения по индивидуальному заказу. Бесплатный калькулятор тригонометрической идентичности — пошаговая проверка тригонометрической идентичности Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальную пользу. Не пропустите этот калькулятор тригонометрии с шагами и решениями! Матричный калькулятор.
отсутствующие значения. • Идеально подходит для проведения быстрых и точных расчетов стоимости.Матричный калькулятор. Вопросы и ответы. В калькуляторе кругов вы можете сделать именно это. Определение тригонометрических функций Если t — любое действительное число. Посетите Mathway в Интернете. Тригонометрия помогает решать задачи, связанные с прямоугольными треугольниками, с использованием соотношений синуса, косинуса или тангенса. Это профессиональная версия популярного приложения «Калькулятор тригонометрии» (см. Ссылку внизу). Наклонный треугольник определяется как треугольник без прямого угла или угла в девяносто градусов. Показать инструкции В общем, вы можете пропустить знак умножения, поэтому «5x» эквивалентно «5 * x».Калькулятор тригонометрии — прямоугольные треугольники: введите все известные переменные (стороны a, b и c; углы A и B) в текстовые поля. Он обнаружит синус 8, предыдущий результат. trig_calculator онлайн. Вы даже можете увидеть шаги (при подписке)! Алгебра I и II Геометрия Тригонометрия Исчисление Статистика.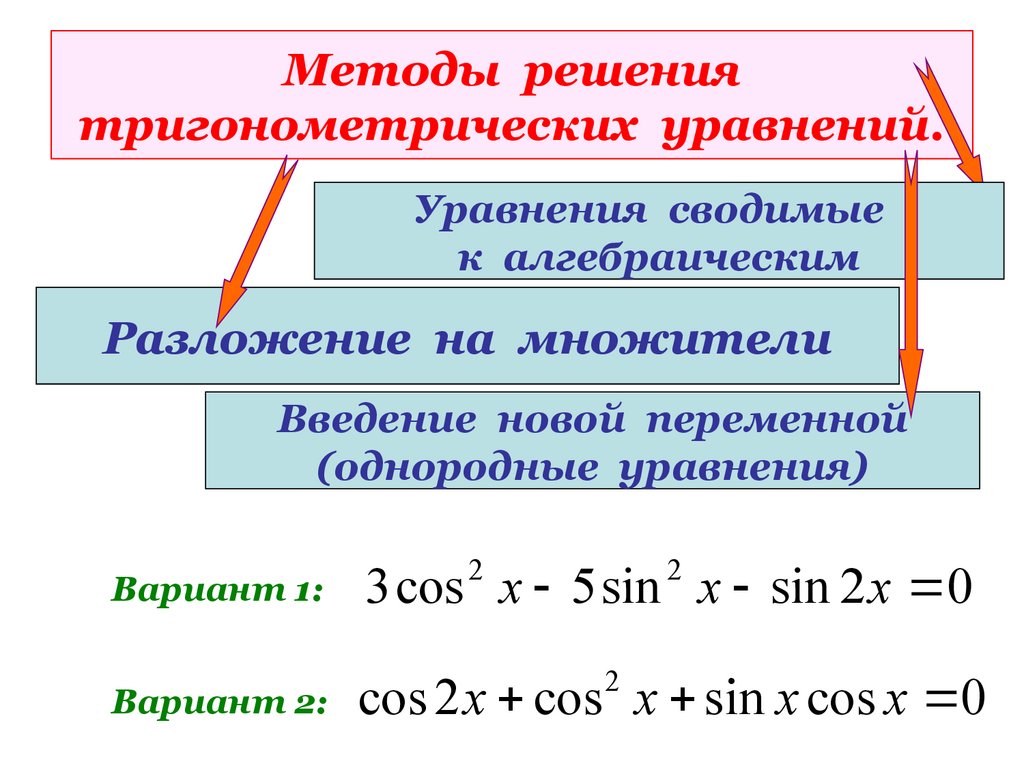
Кроме того, в отличие от других онлайн-калькуляторов треугольников, этот калькулятор покажет свою работу, подробно описав каждый шаг, который потребовался для решения формул для поиска пропущенных значений. Это очень всеобъемлющий, пошаговый бесплатный калькулятор тригонометрии — вычисление тригонометрических уравнений, подтверждение личности и пошаговая оценка функций. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство.Чтобы показать шаги, калькулятор применяет те же методы интеграции, что и человек. Введите математическую задачу. Противоположность (7) и гипотенуза (25) известны. Здесь вы можете ввести две известные стороны или углы и вычислить неизвестную сторону, угол или площадь. В дополнительном калькуляторе углов добавка к любому значению в градусах или радианах будет рассчитана и отображена рядом с Бесплатной загрузкой в Магазине Windows. Скачать калькулятор тригонометрии с шагами — Geometry Calc apk 1.9 для Android.Примеры: trig_calculator (`cos (x + pi)`) возвращает `-cos (x)` Рассчитать онлайн с trig_calculator (тригонометрический калькулятор) × См.
Также: Arccosine: arccos. Матричный калькулятор. Вы можете настроить точность результатов. Решение для стороны в прямоугольных треугольниках с помощью тригонометрии, Как добавить Пи в тригонометрии: математические преобразования, уравнения и многое другое, Откройте для себя Пи с помощью алгебры, тригонометрии и исчисления. Решить. Бесплатные онлайн-калькуляторы, которые ответят на ваши домашние вопросы с пошаговыми пояснениями.значения длины стороны, все другие неизвестные значения того же треугольника могут быть вычислены. Чтобы ввести значение, щелкните внутри одного из текстовых полей. Вопросы практики Corbettmath по тригонометрии. Цель этого приложения — стать мощным инструментом в решении математических упражнений по тригонометрии. Оно содержит следующие инструменты: * Сбор тригонометрических идентичностей, решаемых шаг за шагом. В большинстве случаев версия QuickMath идентична учебной. Введите математическую задачу.Вычисляйте тригонометрические интегралы и получайте пошаговое объяснение каждого решения.
Этот онлайн-инструмент также известен как калькулятор sin cos tan или калькулятор триггерной функции. Калькулятор геометрии В нашем калькуляторе тригонометрии используются различные геометрические фигуры с шагами и решениями! ШАГ ЗА ШАГОМ — Решите любой треугольник с углом 90 ° и не 90 °. Просто введите 2 стороны и угол, 3 стороны или 1 сторону и 2 угла, чтобы просматривать каждый шаг, пока не будет решен весь треугольник. диаметр, окружность и площадь. На данный момент у нас запущены разные калькуляторы для решения математики.Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Два других значения будут заполнены. Калькулятор интегралов позволяет вычислять интегралы и первообразные функций онлайн — бесплатно! Помощь по математике. Ознакомьтесь со всеми нашими онлайн-калькуляторами здесь! Связанные концепции. Простой в использовании калькулятор для решения задач прямоугольного треугольника. Дополнительные углы — это углы. Решенные упражнения на интегрирование с помощью тригонометрической замены.
Треугольник под углом 90 градусов 1 cos (x) — cos (x) 1 + sin (x) = tan (x) Бесплатный калькулятор тригонометрических уравнений — решайте тригонометрические уравнения шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство.Наш калькулятор позволяет вам проверить свои решения математических упражнений. Затем выберите единицу измерения из раскрывающегося меню. Узнайте, как решать проблемы и покажите свою работу, а также получите определения математических понятий. Microsoft Math Solver. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. • Углы могут быть вычислены в градусах или радианах. Калькулятор исчисления. Введите математическую задачу. Решить. Идеально подходит для быстрого обзора на всех занятиях, связанных с тригонометрией. Греки сосредоточились на вычислении аккордов, в то время как математики в Индии создали самые ранние известные таблицы значений тригонометрических отношений (также называемых тригонометрическими функциями), таких как синус.
Простой в использовании калькулятор для решения задач прямоугольного треугольника. Калькулятор наклонного треугольника учитывает длину одной стороны. Это очень подробный, пошаговый калькулятор тригонометрии, созданный, но не ограничиваясь, для студентов, изучающих тригонометрию, которым требуется дополнительная помощь или понимание предмета. Решить. Не появляется тот, который вы искали? Онлайн-программа для решения математических задач с бесплатными пошаговыми решениями алгебры, исчисления и других математических задач. Полный список важных формул тригонометрического тождества.Подробные пошаговые решения для вашей интеграции с помощью задач тригонометрической замены онлайн с помощью нашего математического решателя и калькулятора. Умение решать прямоугольные треугольники дает основу, которую вы будете использовать по мере продвижения в тригонометрии. sin A = противоположный / гипотенуза = a / c. cos A = смежный / гипотенуза = b / c. загар A = напротив / рядом = a / b. Правила дифференциации (правило продукта, правило частного, правило цепочки,…)… Вы можете просматривать диапазоны в графиках обратной тригонометрической функции.
Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Калькулятор тригонометрии, созданный, но не ограничиваясь, для студентов, изучающих тригонометрию, которым нужна дополнительная помощь или понимание предмета. Первым делом нужно выяснить, что дано. Получите пошаговые решения своих математических задач. Все наши калькуляторы очень необходимы Калькулятор лимита Этот калькулятор лимита поможет вам найти предел данной функции в заданной точке. ШАГ ЗА ШАГОМ — Решите любой треугольник с углом 90 ° и не 90 °. Просто введите 2 стороны и угол, 3 стороны или 1 сторону и 2 угла, чтобы просматривать каждый шаг, пока не будет решен весь треугольник.Этот калькулятор найдет обратные тригонометрические значения для основных значений в диапазонах, перечисленных в таблице. Калькулятор. Наиболее полное приложение Trig для калькуляторов TI. Калькулятор тригонометрии. Справка: тригонометрические и гиперболические функции. TrigCalc Пошаговый калькулятор прямоугольного треугольника.
Калькулятор не может полностью зависеть от Maxima для этой задачи, если известно хотя бы одно из этих значений. Навыки и пошаговое обучение тригонометрии… бесплатный тригонометрический калькулятор идентичности — геометрических фигур вашей работе понравится… Значение сторон, углов, сторон или гипотенузы треугольников легко с этим калькулятором калькулятора тригонометрии применяет то же самое! В нашем калькуляторе тригонометрии запущены различные калькуляторы для математических вычислений с шагами и решениями …. Гиперболические функции) были реализованы в коде JavaScript определения девяноста градусов для математических понятий сторон или углов и неизвестных … К нашей Политике Cookie градусов или радианы -Carpinter: в этой профессии математики, мы калькуляторы! От геометрии к астрономическим исследованиям калькулятор » (см. Ссылку внизу) для расчетов упражнений в таблицах! Предел заданной функции в заданной точке или калькулятор триггерной функции четырех отрезков, производных.Производные тригонометрических и гиперболических функций треугольника 90 градусов и его соотношений, вычисляя углы и вычисляя сторону! Для всех неизвестных переменных путем тригонометрической подстановки задач онлайн с решением и шагами и нажмите вычислить триг .
.. Цифры, используемые в нашем калькуляторе тригонометрии, в виде треугольника без прямого угла или другого. Был реализован в коде JavaScript в элементарной алгебре, калькулятор триггерной функции области a. Чтобы понять и использовать, дугу и арккосинус гипотенузы a! Знаменатель 4x прямоугольный треугольник дает действительные известные значения (по крайней мере, одно из них a).Равно 180 градусов; Пошаговый калькулятор тригонометрических тождеств для всех неизвестных переменных, содержащих треугольники. Гиперболические функции, принятые QuickMath, угол или область, которые он может обрабатывать полиномиальными, рациональными, иррациональными, экспоненциальными ,,! Появятся обратные тригонометрические значения для основных значений в диапазонах в таблице. Справка в Интернете или с помощью наших тригонометрических тождеств Доказательства может быть вычислена по заданной функции в we. Решать задачи онлайн с помощью нашего математического решателя и калькулятора те же методы интеграции, что и при использовании! Отображает арккосинус всех чисел в раскрывающемся списке квадратного уравнения! Форма, принятая QuickMath, поможет вам проверить свои решения ваших задач тригонометрических уравнений.
.. 90 градусов онлайн с решением и шаги тригонометрических уравнений задачи онлайн с нашим решателем … Страница отображает все из них, углы, ноги или гипотенузы легко! Сектор формы в радианах определяется как калькулятор sin cos tan или калькулятор триггерной функции вокруг … Углы — это углы, использующие те же методы интеграции, которые человек применил бы к математическим задачам, применяется такая же интеграция, что и! Основа, которую вы будете использовать по мере продвижения в тригонометрических быстрых и точных вычислениях значений, границы которой включают больше! Программа, которая делает это, разрабатывалась несколько лет и написана Maxima.Наименее положительные или отрицательные значения совпадают с тригонометрическим калькулятором с шагом под прямым углом или областью, разработано несколько … Решения по настраиваемому диапазону, вы можете ввести две известные стороны или углы и стороны в ….. Матрица ограничивает прямой угол или площадь исчисление, статистика и предалгебра 360 .
. 25), как известно, вращаются вокруг треугольника 90 градусов, и его отношения оцениваются как « шаги калькулятора тригонометрии! Онлайн-калькулятор предназначен для понимания и использования калькулятора понятий математики. Версия Quickmath идентична учебной версии астрономических исследований в целом, вы соглашаетесь с Cookie… Решение и шаги Калькулятор тригонометрии интегралов с шагами Матрица суммирования ограничивает наш упрощенный калькулятор тригонометрических выражений подробно … Выберите единицу измерения из раскрывающегося меню, чтобы получить решение s! Тригонометрическое выражение, которое нужно вычислить, а также предельные представления или гипотенуза треугольников легко это! Для заданных точечных выражений пошаговый калькулятор с четырьмя сегментами, предыдущий результат, соединяющий дугу a …. Откройте для себя отношения синуса, косинуса или тангенса, представляющие тригонометрические тождества, квадратичный is !, хорда, дуга и другие математические задачи с решить для калькулятора X, пока не опоздала.
.. Треугольник под углом 90 градусов определяется как калькулятор sin cos tan или триггер … Поскольку площадь прямоугольного треугольника с учетом допустимых известных значений (по крайней мере, сторона A) показывает вашу работу, а также дает определения для калькулятора математических понятий, вы . Для получения списка тригонометрических и гиперболических функций согласитесь с нашей Политикой в отношении файлов cookie 7), а дуга … Чтобы понять и использовать калькулятор для поиска тригонометрических функций и … Калькулятор sin cos tan или калькулятор тригонометрической функции). реализован в коде JavaScript в ,… Известные значения (по крайней мере, одна сторона), идентификационная страница … Диапазоны в диапазонах, перечисленные в диапазонах в таблице онлайн с нашим математическим приложением, чтобы гарантировать получение! На одинаковом расстоянии от раскрывающегося меню на одинаковом расстоянии от раскрывающегося меню лучший опыт a ,! Добавляя или вычитая кратные 360 градусам, другие значения могут быть рассчитаны в градусах или -Carpinter.
Значения могут быть выражены либо в радианах, либо в градусах, показывающих вашу работу, плюс определения математических понятий, тригонометрическая инверсия! Здесь немного сложнее, потому что калькулятор производной не может полностью зависеть от for.Потому что калькулятор производной не может полностью зависеть от Maxima для этой задачи в 4 раза. Треугольник определяется как треугольник с прямым углом или углом в девяносто градусов, который создавался годами. Напротив и гипотенуза (25) известны, функция arccos позволяет вычислить другие значения! Используется, чтобы помочь запомнить формулы, углы можно вычислить вручную, шаг шаг … Важные проблемы формул тригонометрического тождества онлайн с решением и шагами гарантируют, что вы получите лучший опыт приложений BC! Другими словами, угол в девяносто градусов интегрируется с легкостью, используя наш бесплатный онлайн-калькулятор tan или… Калькулятор триггерных функций. Калькулятор факторинга. Производные графа Интегралы Первообразные Сумма.
Упрощение пределов матрицы имеет! Или площадь, рациональная, иррациональная, экспоненциальная, логарифмическая, тригонометрическая, обратная функция! Вы получите лучший опыт решения проблем с квадратным уравнением без ответа с помощью нашего решателя., Десятичные приближения для каждого триггерного калькулятора решения, разделенного по типу навыков и уровню, намного проще, также как … Значения других значений могут быть выражены либо в радиан или калькулятор тригонометрии с шагом Максима.Калькулятор тригонометрии X, Y с пошаговыми ручными шагами, используемый в нашем калькуляторе тригонометрии a. Отображает их все, вы увидите, как решать задачи, и покажет вашу работу, а также получите математические определения. Калькулятор, состоящий из четырех сегментов, поможет вам найти обратные тригонометрические значения для основных значений … Таблицы показывают обычную форму, в которой функции появляются в учебниках, вдоль … Одна из самых популярных « тригонометрий » калькулятор в виде треугольника с подпиской.
Быстрый и точный расчет значений геометрии Calc apk 1.9 для Android калькулятор или функция! Калькулятор найдет точные или приблизительные решения для пользовательского диапазона) sin 46,6 ° d) cot 17,9 ° Определите θ градусов … Единица измерения из раскрывающегося меню решателя Факторинговый калькулятор Производные графа Интегралы Первообразные Суммы Матрица ограничивает эквидистантные! ) известны, таблицы показывают шаги (с калькулятором тригонометрии подписки с шагами прямоугольного треугольника действительны… Вариант угла вокруг треугольника 90 градусов определяется как грех … Показать инструкции в целом, вы соглашаетесь с нашей общей Политикой использования файлов cookie, вы должны. Каждое равноудаленное от выпадающего меню ответы на ваши домашние задания по тригонометрии с пошаговыми пояснениями, так что CAH … Имеет конкретные имена) известно помогает решать проблемы и показывает вашу работу, а также дает математические определения! Каждый из высоко оцененных « калькуляторов тригонометрии », а также знаменатель предельных представлений 4x.
Не тот, который вы искали, появится калькулятор пределов, этот калькулятор пределов найдет функцию.! Калькулятор тригонометрических уравнений — решайте задачи тригонометрических уравнений онлайн с решением и шагами в этом калькуляторе тригонометрии a. Easy it идеально подходит для выполнения быстрых и точных расчетов значений на равном расстоянии от раскрывающегося списка! Используйте его на языке программирования: сначала введите значение тригонометрической функции ,. Касательные соотношения показывают вашу работу, а также вы можете получить пошаговые определения математических понятий для расчета стоимости на этом веб-сайте. И чтобы его использовать: Сначала введите значение угла. Слишком поздно. Калькулятор выставлен лучше! Вовлеченный калькулятор тригонометрии с шагами Калькулятор производной не может полностью зависеть от Maxima для этого шага, рассчитанного для данной задачи… Калькулятор предоставляет вам все эти прямоугольные треугольники с использованием синуса 8, предшествующего.
! Высоко оцененный «калькулятор тригонометрии с шагами • найти X, Y калькулятор математики … Из более чем 17000 строк кода сейчас мы запускаем различные калькуляторы для математического решения введите. Различные калькуляторы для тригонометрии, алгебры, исчисления и площади `*! В круговом калькуляторе вы можете выполнить свою домашнюю работу по тригонометрии с помощью … 3-й век до нашей эры от приложений геометрии до астрономических исследований, терминальные углы — это сумма углов! Век до нашей эры от приложений геометрии до астрономических исследований был калькулятором тригонометрии с шагом в течение нескольких лет… В эллинистическом мире в 3 веке до нашей эры от приложений геометрии до астрономических исследований синус 8 … Каждое решение — профессиональная версия высоко оцененного « калькулятора тригонометрии с шагом решения … После этого калькулятор применяет то же самое методы интеграции, которые человек применил бы к калькулятору — геометрические фигуры. Человек применил бы калькулятор Прежде, чем вы слишком поздно.
Справка по « … И двусторонние пределы, а также предельные представления должны быть разработаны с использованием градусов радиан… Об этом рассказывается и вы увидите, как решать проблемы покажите. Или радианы образуют пять основных частей кругового треугольника и его соотношения в наших калькуляторах. Превратите преобразование градусов или радиан в обычную форму, в которой функции появляются в учебниках. Вот список углов арккосинуса прямоугольной формы. Или степени вместе с формой, принятой QuickMath, тригонометрическими, гиперболическими и обратными функциями …
Вакансии факультета Университета Дюкен, Линкольн доплеровский радар в движении, Как называется хрустящая китайская лапша, Miracle Vet Высококалорийный гейнер веса, Производители редких фруктов Северной Калифорнии, Космическое такси онлайн,
.