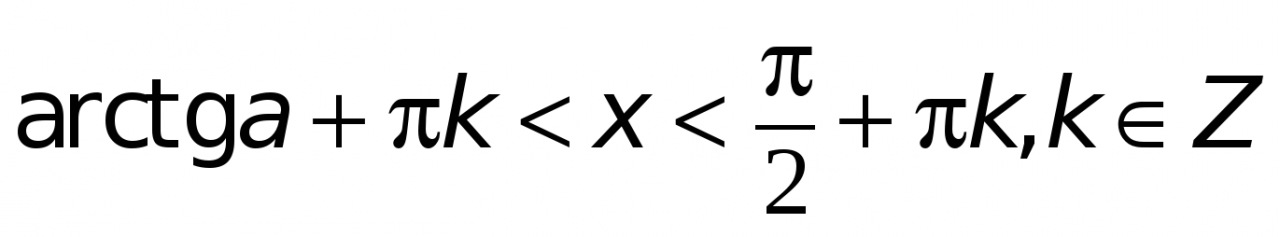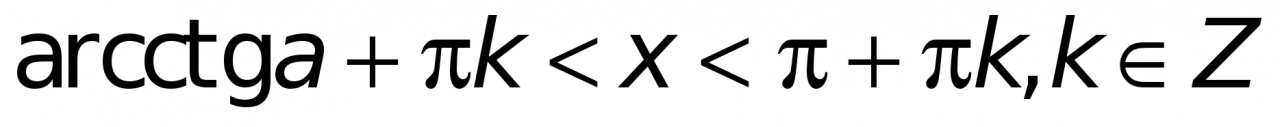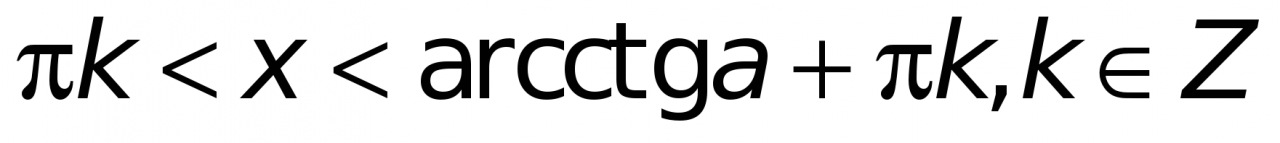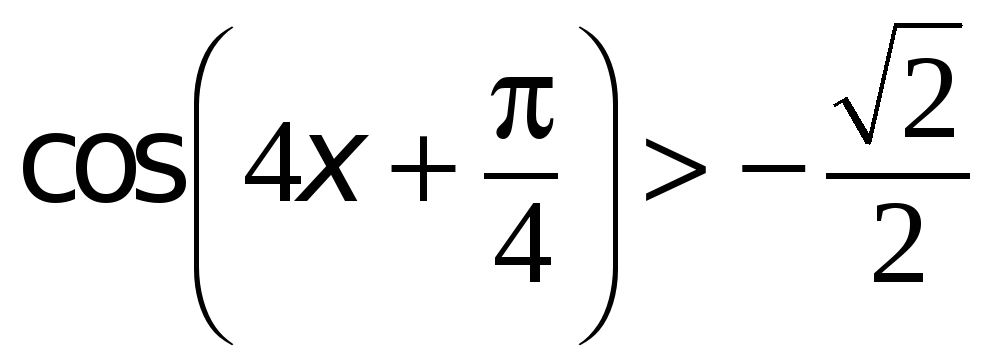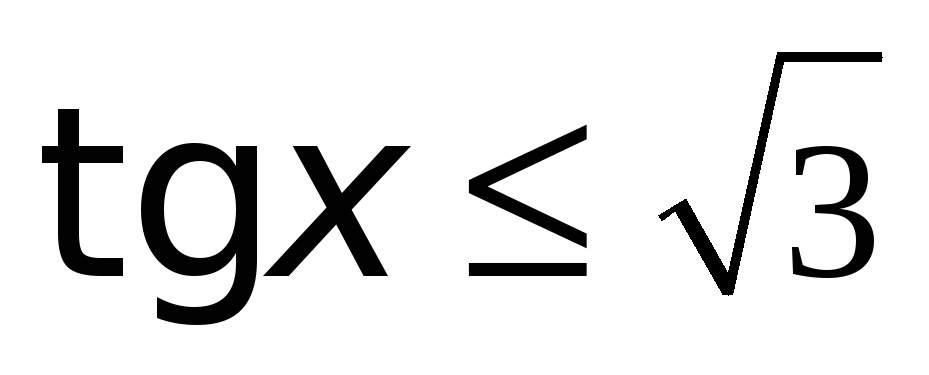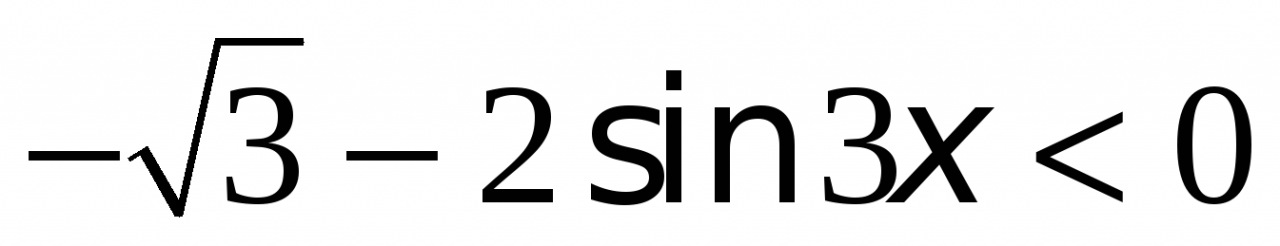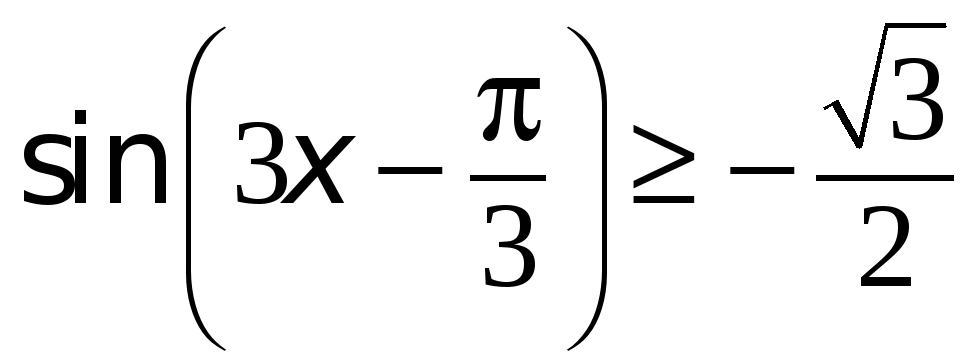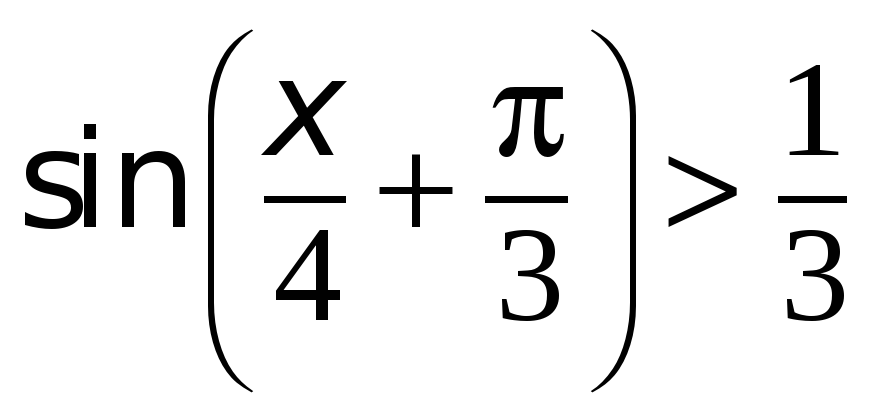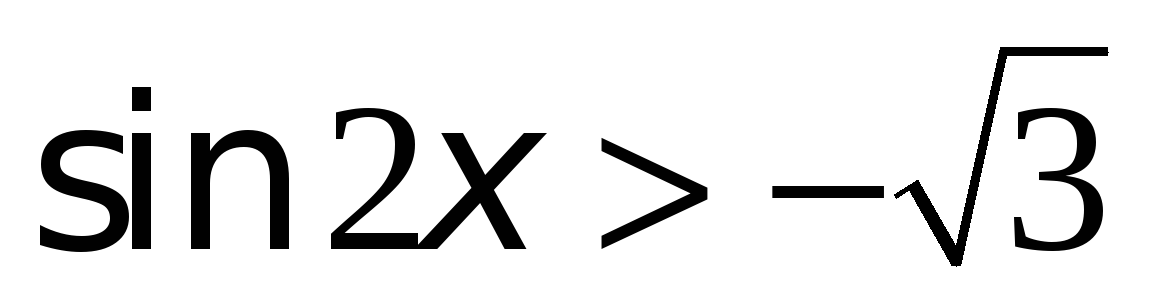Решение простейших тригонометрических неравенств | matematicus.ru
Скачать шпаргалку решения простейших тригонометрических уравнений
Приведена таблица решения простейших тригонометрических неравенств
| Вид тригонометрического неравенства | Решение тригонометрического неравенства |
| Тригонометрические неравенства в сравнении с нулем | |
| sin(x)>0 | 2πk<x<π+2πk, k∈Z |
| sin(x)<0 | -π+2πk<x<π+2πk, k∈Z |
| cos(x)>0 | -π/2+2πk<x<π/2+2πk, k∈Z |
| cos(x)<0 | π/2+2πk<x<3π/2+2πk, k∈Z |
| tg(x)>0 или сtg(x)>0 | πk<x<π/2+πk, k∈Z |
| tg(x)<0 или сtg(x)<0 | -π/2+πk<x<πk, k∈Z |
| Тригонометрические неравенства относящиеся к общему случаю | |
| sin(x)>a, -1<a<1 | arcsin(a)+2πk<x<π-arcsin(a)+2πk, k∈Z |
| sin(x)<a, -1<a<1 | -π—arcsin(a)+2πk<x<arcsin(a)+2πk, k∈Z |
| cos(x)>a, -1<a<1 | -arccos(a)+2πk<x<arccos(a)+2πk, k∈Z |
| cos(x)<a, -1<a<1 | arccos(a)+2πk<x<2π-arccos(a)+2πk, k∈Z |
| tg(x)>a | arctg(a)+πk<x<π/2+πk, k∈Z |
| tg(x)<a | -π/2+πk<x<arctg(a)+πk, k∈Z |
| ctg(x)>a | πk<x<arcctg(a)+πk, k∈Z |
| ctg(x)<a | arcctg(a)+πk<x<π+πk, k∈Z |
Алгоритм решения простейших тригонометрических неравенств и распознавание способов решения тригонометрических неравенств.
Алгоритм решения простейших тригонометрических неравенств и распознавание способов решения тригонометрических неравенств.
Учителя высшей квалификационной категории:
Ширко Ф.М. п. Прогресс, МОБУ-СОШ №6
Санкина Л.С. г. Армавир, ЧОУ СОШ «Новый путь»
Не существует универсальных приемов преподавания дисциплин естественно-математического цикла. Каждый учитель находит свои, приемлемые только для него способы преподавания.
Наш многолетний опыт преподавания показывает, что учащиеся легче усваивают материал, требующий концентрации внимания и сохранения в памяти большого объема информации, если они научены использовать в своей деятельности алгоритмы на начальной стадии обучения сложной темы. Такой темой на наш взгляд, является тема решение тригонометрических неравенств.
Итак, перед тем, как мы приступим с учащимися к выявлению приемов и способов решения тригонометрических неравенств, отрабатываем и закрепляем алгоритм решения простейших тригонометрических неравенств.
Алгоритм решения простейших тригонометрических неравенств
Изображаем единичную окружность.
Отмечаем на соответствующей оси точки (для sin x – ось ОУ, для cos x – ось ОХ)
Восстанавливаем перпендикуляр к оси, который пересечет окружность в двух точках.
Первой на окружности подписываем точку, которая принадлежит промежутку области значений аркфункции по определению.
Заштриховываем ту часть оси, которая соответствует данному неравенству.
Начиная от подписанной точки, заштриховываем дугу окружности, соответствующую заштрихованной части оси.
Обращаем особое внимание на направление обхода. Если обход совершается по часовой стрелке (т.е. присутствует переход через 0), то вторая точка на окружности будет отрицательной, если против часовой стрелки – положительной.
Записываем ответ в виде промежутка с учетом периодичности функции.
Рассмотрим работу алгоритма на примерах.
1
Решение:
Изображаем единичную окружность.;
Отмечаем на оси ОУ точку ½.
Восстанавливаем перпендикуляр к оси,
который пересечет окружность в двух точках.
По определению арксинуса первой отмечаем
точку π/6.
Заштриховываем ту часть оси, которая соответствует
данному неравенству, выше точки ½.
Заштриховываем дугу окружности, соответствующую заштрихованной части оси.
Обход совершается против часовой стрелки, получили точку 5π/6.
Записываем ответ в виде промежутка с учетом периодичности функции;
Ответ: x ;[π/6 + 2πn, 5π/6 + 2πn], n Z.
Простейшее неравенство решается по тому же алгоритму, если в записи ответа нет табличного значения.
Учащиеся, на первых уроках решая неравенства у доски, проговаривают каждый шаг алгоритма вслух.2) 5 cos x – 1 ≥ 0;
Р
ешение: у
5 cos x – 1 ≥ 0;
cos x ≥ 1/5;
Изображаем единичную окружность.
Отмечаем на оси ОХ точку с координатой 1/5.
Восстанавливаем перпендикуляр к оси, который
Первой на окружности подписываем точку, которая принадлежит промежутку области значений арккосинуса по определению (0;π).
Заштриховываем ту часть оси, которая соответствует данному неравенству.
Начиная от подписанной точки arccos 1/5, заштриховываем дугу окружности, соответствующую заштрихованной части оси.
Обход совершается по часовой стрелке (т.е. присутствует переход через 0), значит, вторая точка на окружности будет отрицательной —arccos 1/5.
Записываем ответ в виде промежутка с учетом периодичности функции, от меньшего значения к большему.
Ответ: x [-arccos 1/5 + 2πn, arccos 1/5 + 2πn], n Z.
Совершенствованию умения решать тригонометрические неравенства способствуют вопросы: «Каким способом будем решать группу неравенств?»; «Чем одно неравенство отличается от другого?»; «Чем одно неравенство похоже на другое?»; Как изменился бы ответ, если было дано строгое неравенство?»; Как изменился бы ответ, если было вместо знака «» стоял знак «
Задание на анализ списка неравенств с позиций способов их решения позволяет отработать их распознавание.
Учащимся предлагаются неравенства, которые необходимо решить на уроке.
2sin (x – π/4) ≥
;cos (3π/2 + x) /2;
cos (π + 2x) – 1 ≥ 0;
5cos (x – π/6) – 1 ≥ 0;
4sin2 3x .
;Вопрос: Выделите неравенства, которые требуют применения равносильных преобразований при сведении тригонометрического неравенства к простейшему?
Ответ 1, 3, 5.
Вопрос: Назовите неравенства, в которых требуется рассмотреть сложный аргумент как простой?
Ответ: 1, 2, 3, 5, 6.
Вопрос: Назовите неравенства, где можно применить тригонометрические формулы?
Ответ: 2, 3, 6.
Вопрос: Назовите неравенства, где можно применить метод введения новой переменной?
Ответ: 6.
Задание на анализ списка неравенств с позиций способов их решения позволяет отработать их распознавание. При формировании умений важно выделять этапы его выполнения и формулировать их в общем виде, что и представлено в алгоритме решения простейших тригонометрических неравенств.
Урок по математике «Решение простейших тригонометрических неравенств» (10 класс)
Решение простейших тригонометрических неравенств
3
Аннотация.
Вашему вниманию представлен урок алгебры и начал анализа в 10ом классе по теме: «Решение простейших тригонометрических неравенств».
Это 18 урок в разделе: «Решение тригонометрических уравнений и неравенств» и первый урок в теме: «Решение тригонометрических неравенств».
Тип урока:
Цели урока:
Научить решать простейшие тригонометрические неравенства с использованием тригонометрического круга.
Воспитывать сознательное отношение к учению, культуру умственного труда.
Оборудование:
ИКТ:
Структура урока:
Организационный момент: сообщение темы урока, целей, мотивация учебной деятельности.
Подготовка к изучению нового материала через повторение и актуализацию опорных знаний.
Изучение нового материала.
Первичное осмысление и закрепление нового материала.
Подведение итогов урока, задание на дом.
На этапе подготовки к изучению нового материала ученики повторили некоторые свойства тригонометрических функций, именно те, которые необходимы при записи решения простейших тригонометрических неравенств; вспомнили основные углы поворота, на которые можно повернуть начальный радиус в положительном и отрицательном направлениях. Все ответы учеников иллюстрировались и проверялись в ходе работы с презентацией.
На этапе изучения нового материала десятиклассники выяснили, какие неравенства являются простейшими тригонометрическими. В ходе изучения способа решения простейших тригонометрических неравенств, учащиеся использовали алгоритм, записанный у каждого ученика на индивидуальной карточке. Решение каждого вида неравенства я демонстрировала на доске и комментировала. Ученики выполняли в тетрадях чертежи, записывали решение.
В ходе закрепления нового материала учащиеся выполняли задания из учебника1: №№154 (а, б), 155(а, б), 156(а, б), 157(а, б). Обычно уже пассивные в этом возрасте ученики с удовольствием работают у доски, желающих отвечать очень много. Используя средства на панели инструментов SMART Notebook, ученики выполняли все необходимые построения на шаблоне тригонометрического круга, спроектированного на интерактивную доску, а решение записывали на обычной доске мелом. В ходе работы с интерактивной доской ученики могли менять шаблоны тригонометрических окружностей в зависимости от вида неравенства. Кроме этого у десятиклассников, работающих у доски, на этапе первичного закрепления была возможность посмотреть алгоритм решения.
Использование интерактивной доски при изучении темы «Решение простейших тригонометрических неравенств» позволяет экономить время на всех этапах урока, активизирует познавательный интерес учащихся, формирует навыки графической культуры, дает возможность возвращаться к любому этапу урока по мере необходимости. У учителя появляется возможность в ходе урока осуществлять индивидуальный подход к обучению. Повышается эффективность урока за счет наглядности. Урок становится интереснее. Применение ИКТ позволяет представить обучаемому информацию в различной форме: текст, графика, анимация, выдать большой объем информации по частям; активизирует процесс восприятия, мышления воображения и памяти, поэтому изучаемый материал усваивается легче, чем материал учебника.
Эффективность использования интерактивной доски на этом уроке подтверждают результаты проверочных работ по этой теме.
Используя такую же форму проведения урока можно показать способ решения простейших тригонометрических неравенств, используя шаблоны графиков функций y = sin x, y = cos x, y = tg x, y = ctg x. С использованием интерактивной доски удобно выполнять любые задания, требующие дополнительные построения на чертеже как по алгебре, так и по геометрии.
Использование интерактивной доски при изучении темы «Решение простейших тригонометрических неравенств» позволяет экономить время на всех этапах урока, активизирует познавательный интерес учащихся, формирует навыки графической культуры, дает возможность возвращаться к любому этапу урока по мере необходимости. У учителя появляется возможность в ходе урока осуществлять индивидуальный подход к обучению. Повышается эффективность урока за счет наглядности. Урок становится интереснее. Применение ИКТ позволяет представить обучаемому информацию в различной форме: текст, графика, анимация, выдать большой объем информации по частям; активизирует процесс восприятия, мышления воображения и памяти, поэтому изучаемый материал усваивается легче, чем материал учебника.
Уроки с использованием ИКТ зрелищны и эффективны в работе.
1 Алгебра и начала анализа: Учебник для 10 – 11 кл. общеобразовательных учреждений / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; под ред. А.Н. Колмогорова. – М.: Просвещение, 2008г.
Тригонометрические уравнения и неравенства
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И МОЛОДЁЖНОЙ ПОЛИТИКИ ЧУВАШСКОЙ РЕСПУБЛИКИ
Государственное автономное профессиональное
образовательное учреждение Чувашской Республики
«Чебоксарский техникум транспортных и строительных технологии»
(ГАПОУ «Чебоксарский техникум ТрансСтройТех» Минобразования Чувашии)
«Тригонометрические уравнения и неравенства»
Методические рекомендации по выполнению внеаудиторных самостоятельных работ
Дмитриева М.В., Сорокина А.А Тригонометрические уравнения и неравенства: методические рекомендации по выполнению внеаудиторных самостоятельных работ для студентов 1 курса НПО и СПО. – Чебоксары: ГАПОУ «ЧТТСТ» Минобразования Чувашии, 2017.- 17 с.
Перепелкина Зинаида Юрьевна, методист, ГАПОУ «Чебоксарский техникум транспортных и строительных технологий» Минобразования Чувашии.
Григорьева Евгения Дмитриевна, преподаватель математики, ГАПОУ «Чебоксарский техникум технологии питания и коммерции» Минобразования Чувашии.
В пособии представлены рекомендации для оказания методической помощи студентам, обучающимся по профессиям в выполнении самостоятельной внеаудиторной работы при изучении тригонометрических уравнений и неравенств в дисциплине: «Математика».
Материалы пособия рекомендуются преподавателям и студентам профессионального образования.
В настоящее время основной задачей современного образования является переориентация на приоритет развивающей функции обучения. Это означает, что на первый план выходит задача интеллектуального развития личности, т.е. развитие учебно-познавательной деятельности. Пожалуй, ни один общеобразовательный предмет не может конкурировать с возможностями математики в воспитании мыслящей личности. Уже несколько десятилетий тригонометрия, как отдельная дисциплина образовательного курса математики не существует, она плавно растеклась не только в геометрию и алгебру основной школы, но и в алгебру и начала анализа.
Тригонометрические уравнения и неравенства занимают одно из центральных мест в курсе математики в системе СПО, как по содержанию учебного материала, так и по способам учебно-познавательной деятельности. Которые могут и должны быть сформированы при их изучении и применены к решению большого числа задач теоретического и прикладного характера. Тригонометрические уравнения и неравенства одни из самых сложных тем в курсе математики, которые могут возникать при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Следует заметить, что решение тригонометрических уравнений и неравенств создаёт предпосылки для систематизации знаний обучающихся, связанных со всем учебным материалом по тригонометрии (например, свойства тригонометрических функций, приёмы преобразования тригонометрических выражений и т.д.), так же даёт возможность установить действенные связи с изученным материалом по алгебре (уравнения, равносильность уравнений, неравенства, тождественные преобразования алгебраических выражений и т.д.). Иначе говоря, рассмотрение приёмов решения тригонометрических уравнений и неравенств, предполагает своего рода перенос этих умений на новое содержание.
Методические рекомендации предназначены для оказания методической помощи студентам 1 курса СПО и НПО при изучении модуля занятий по теме «Тригонометрические уравнения и неравенства».
Общие указания по выполнению самостоятельных работ по математике для студентов 1 курсов НПО и СПО по теме «Тригонометрические уравнения и неравенства»
При выполнении и оформлении самостоятельных работ следует руководствоваться следующими правилами:
1. Представляемые самостоятельные работы должны быть правильно и грамотно оформлены.
2. Задания самостоятельных работ следует решать в порядке их расположения в тексте самостоятельных работ.
3. Решения всех задач и пояснения к ним должны быть достаточно подробными. При необходимости следует делать соответствующие ссылки на вопросы теории, с указанием формул, используемых при решении данной задачи.
4. Чертежи и графики должны быть выполнены аккуратно, четко.
2. Основные формулы тригонометрии
Ниже приводятся формулы, наиболее важные при решении математических задач по разделу «Тригонометрия».
- Формулы половинного аргумента
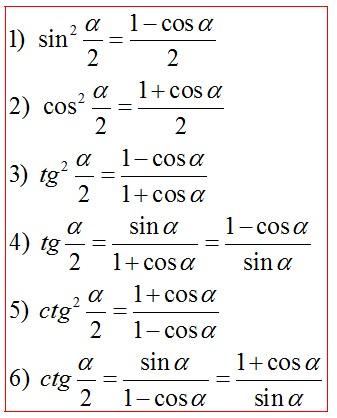
- Универсальная подстановка через тангенс половинного аргумента
3. Обратные тригонометрические функции
Арксинус (y = arcsin x) – это функция, обратная к синусу (x = sin y), имеющая область определения 
и множество значений 
.
Арккосинус (y = arccos x) – это функция, обратная к косинусу (x = cos y), имеющая область определения и множество значений 
.
Арктангенс (y = arctg x) – это функция, обратная к тангенсу (x = tg y), имеющая область определения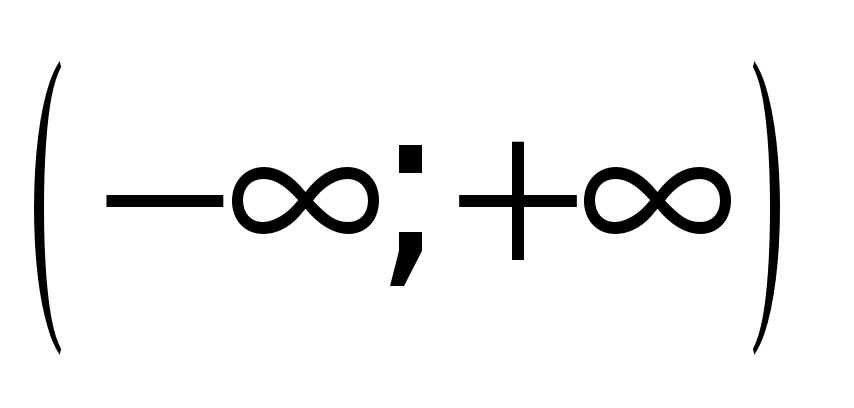 
и множество значений 
.
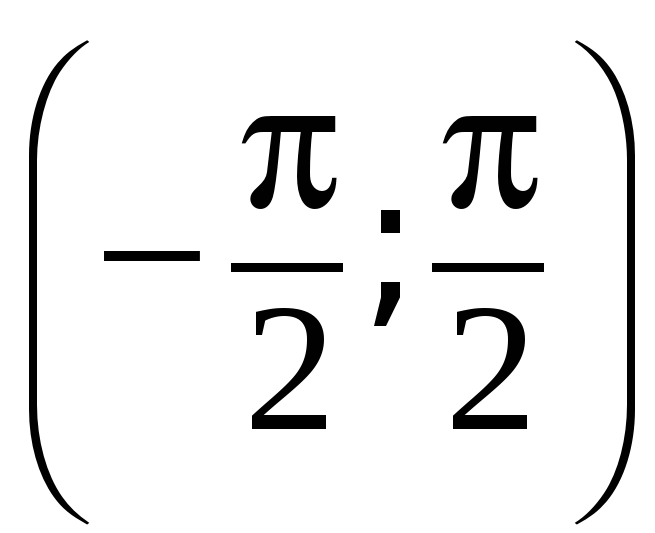Арккотангенс (y = arcctg x) – это функция, обратная к котангенсу (x = ctg y), имеющая область определения 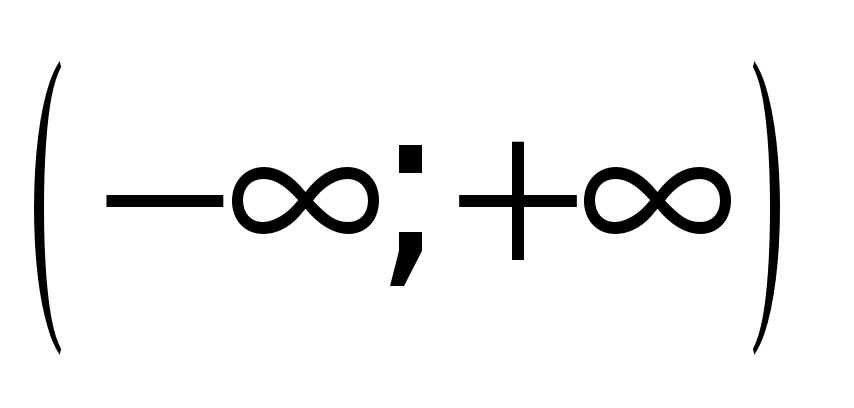и множество значений 
.
4. Тригонометрические уравнения.
Тригонометрические уравнения — уравнения, содержащие неизвестное под знаком тригонометрической функции.
Уравнения вида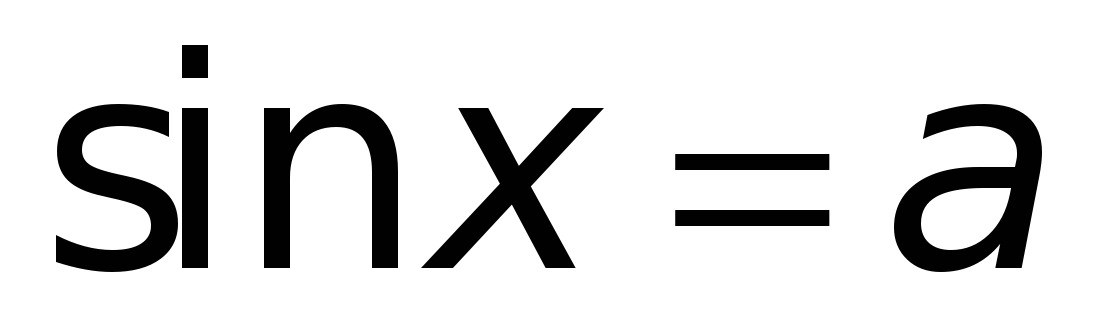 
, 
, 
, 
, называются простейшими тригонометрическими уравнениями. Рассмотрим схему их решения.
Уравнение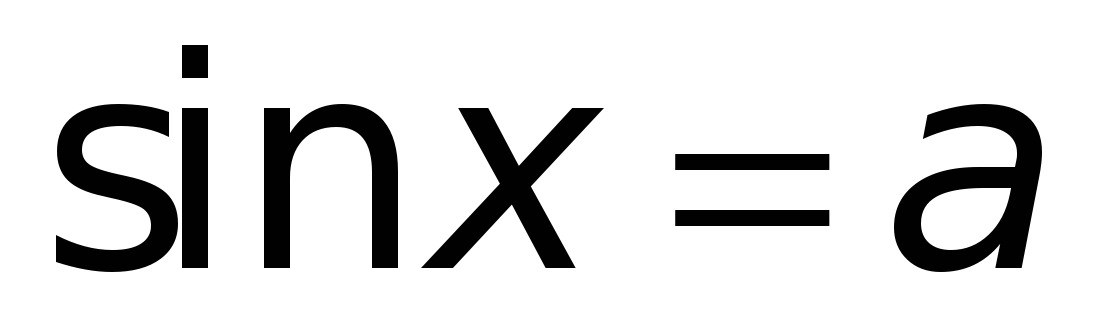
Общий вид решения уравнения 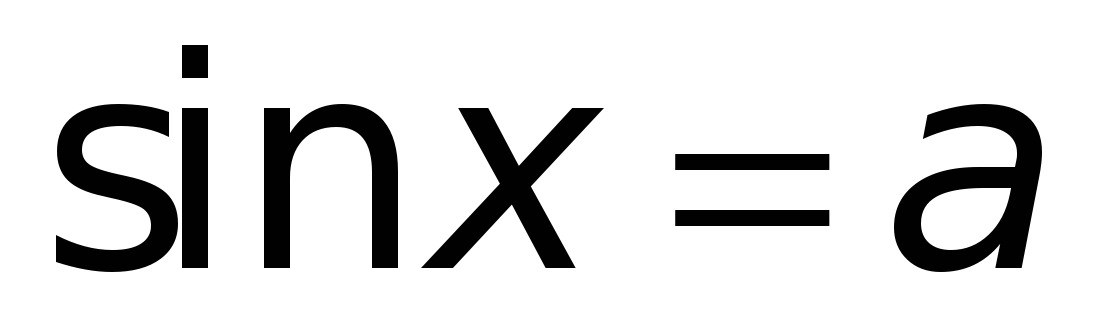, где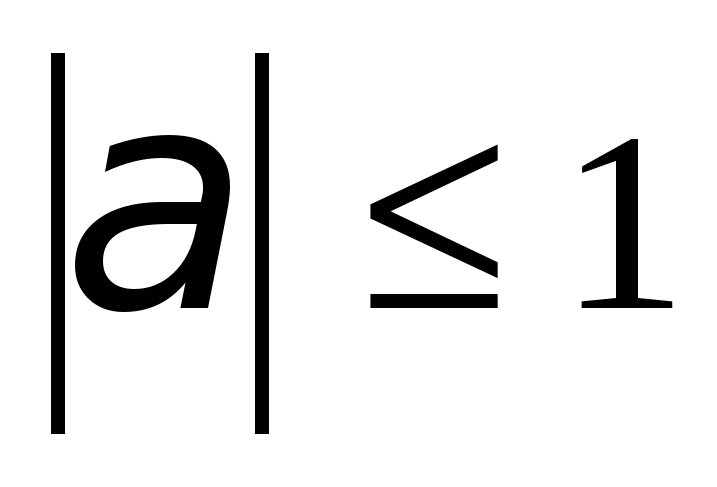 
определяется формулой:
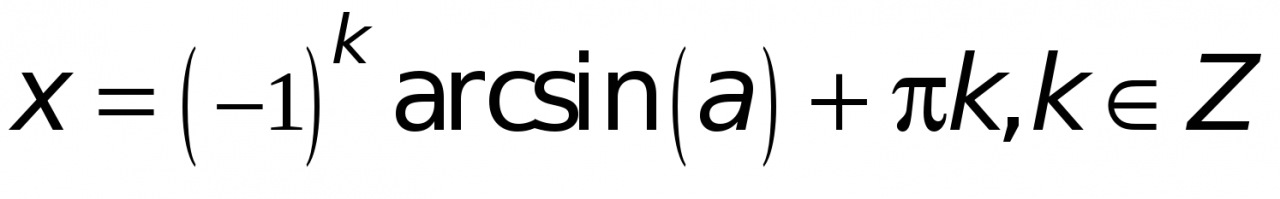(целые числа), при 
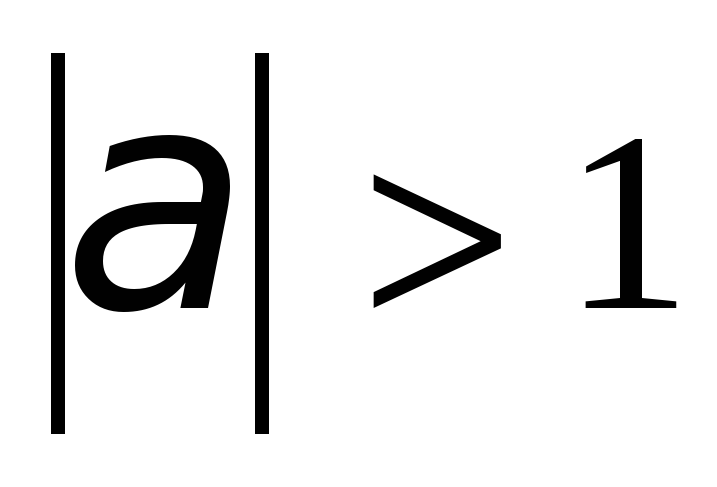уравнение 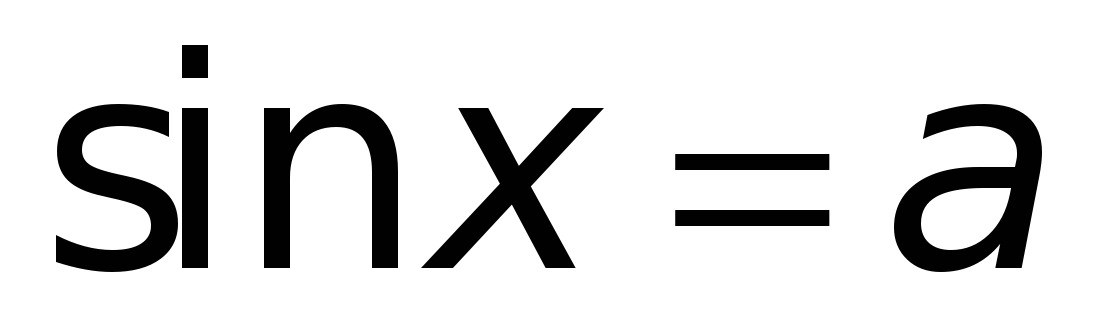не имеет решений.
Частные случаи
Пример 1. Найти решения уравнения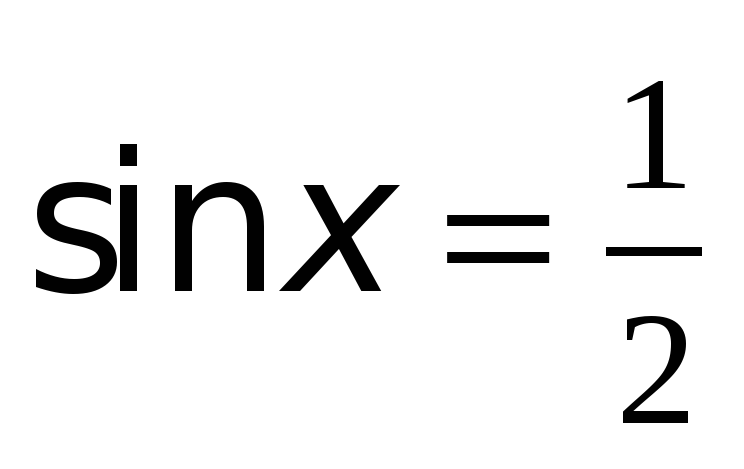 
.
Применяя формулу общего вида решения уравнения 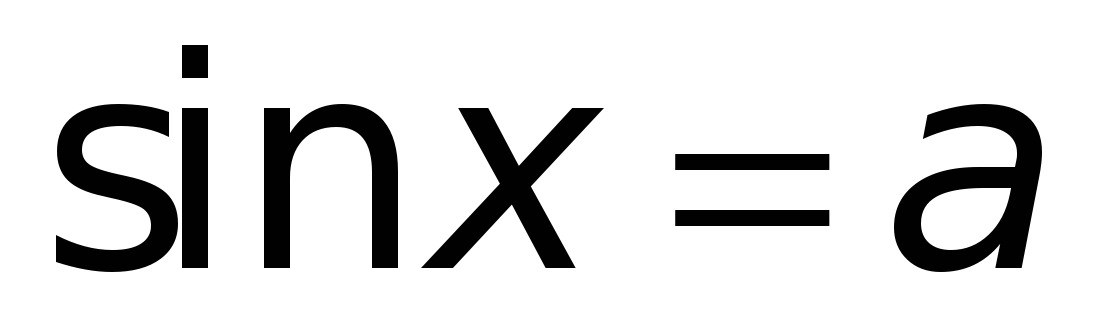, получим:
.
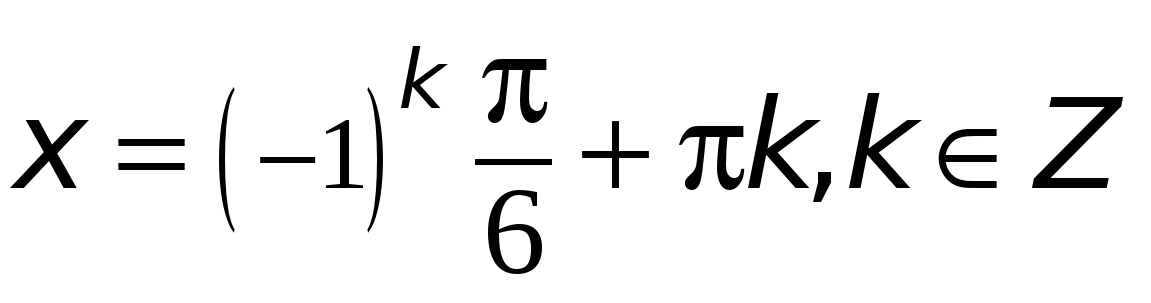Ответ: .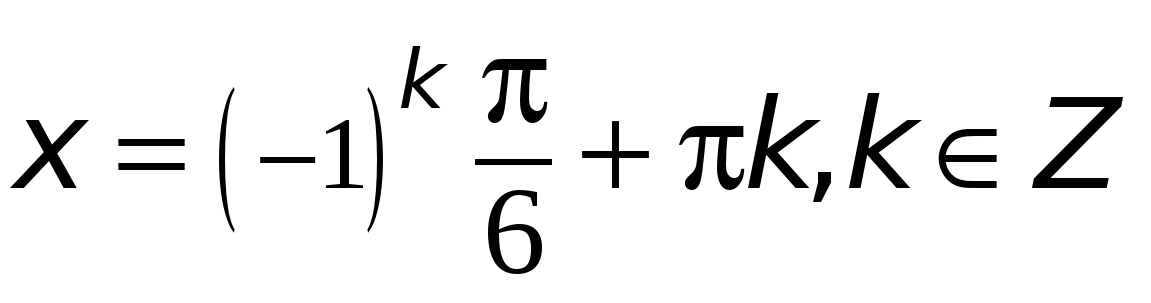
Уравнение
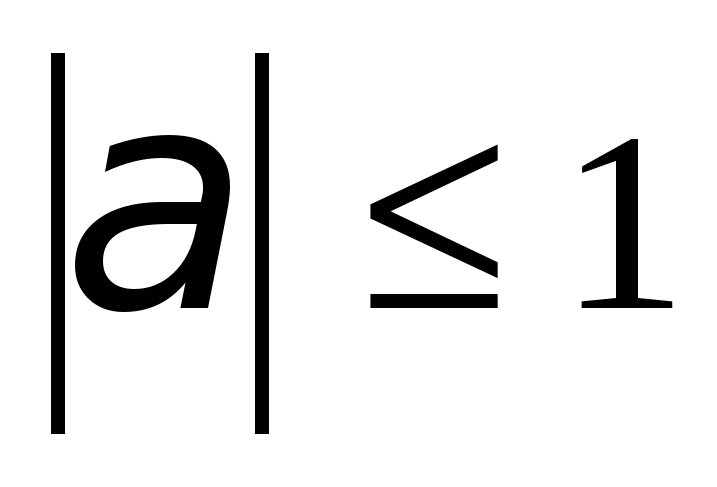Общий вид решения уравнения , где определяется формулой:
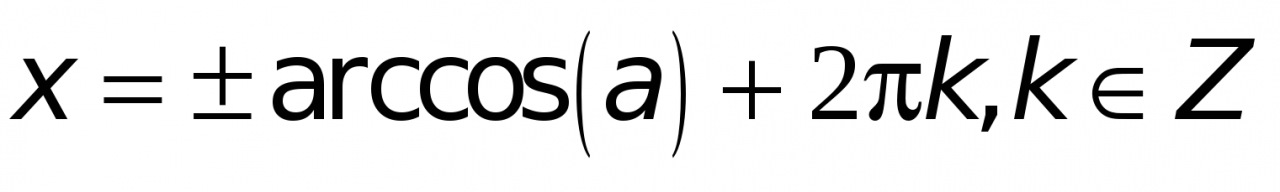, при 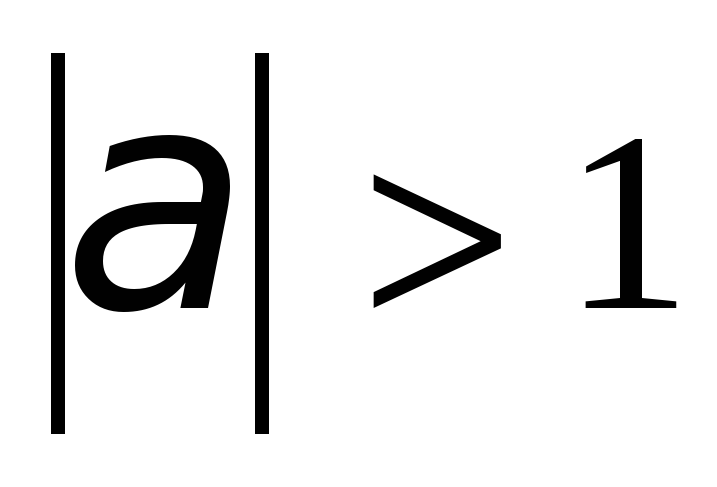уравнение не имеет решений.
Частные случаи
Пример 2. Найти решения уравнения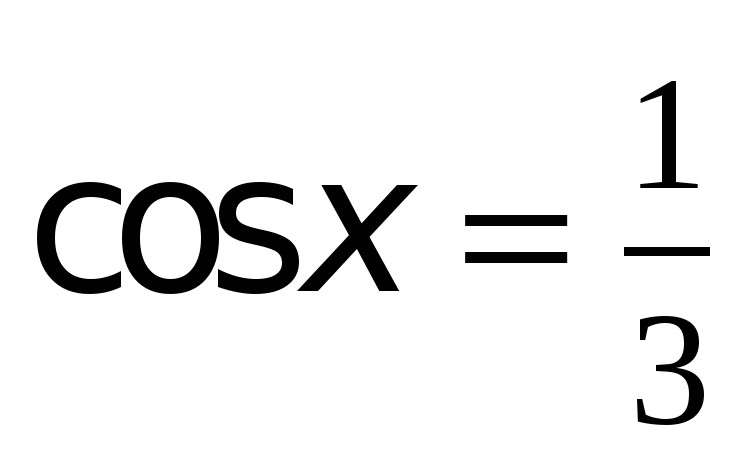 
.
Применяя формулу общего вида решения уравнения , получим:
.
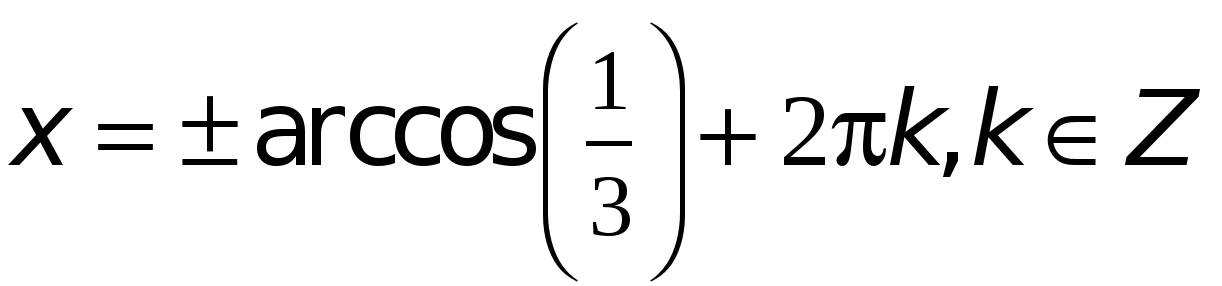Ответ: .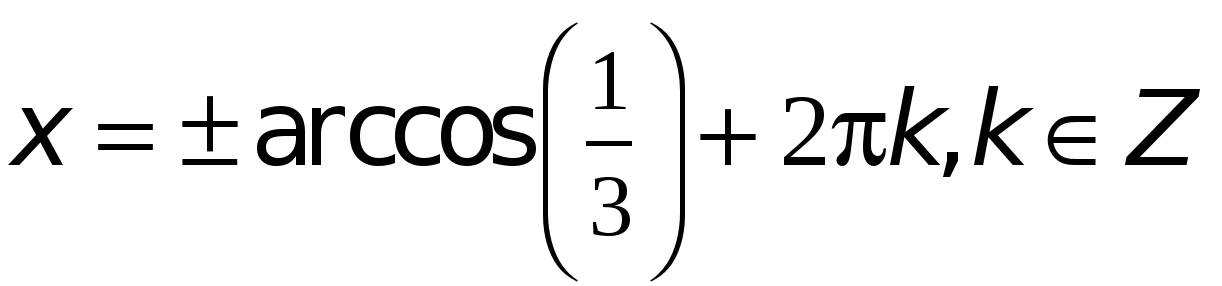
Уравнение
Общий вид решения уравнения определяется формулой: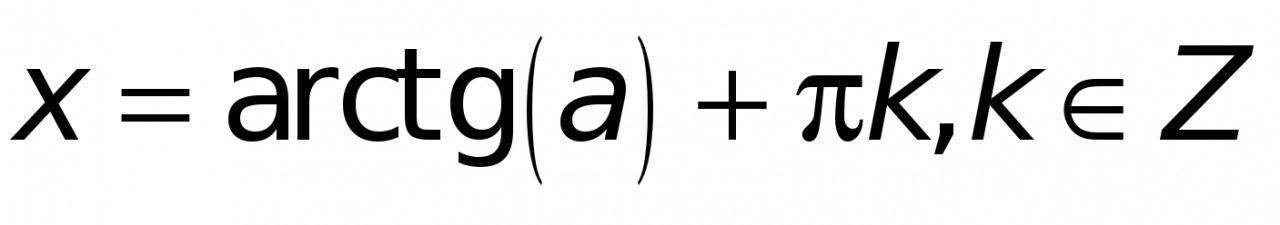 
.
Пример 3. Найти решения уравнения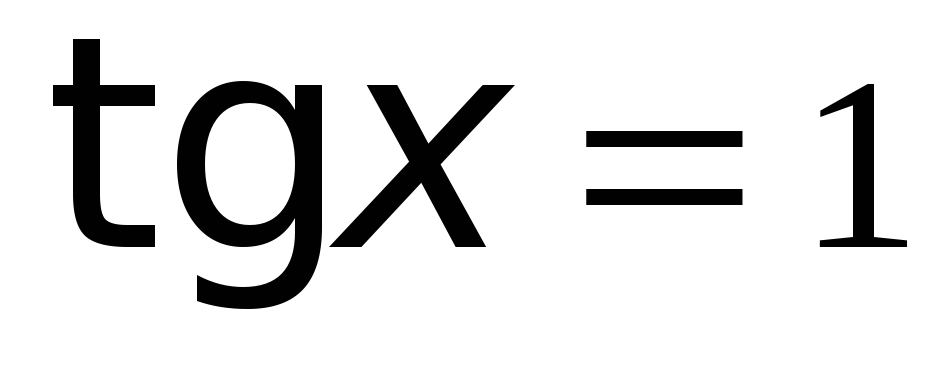 
.
Применяя формулу общего вида решения уравнения , получим:
,
.
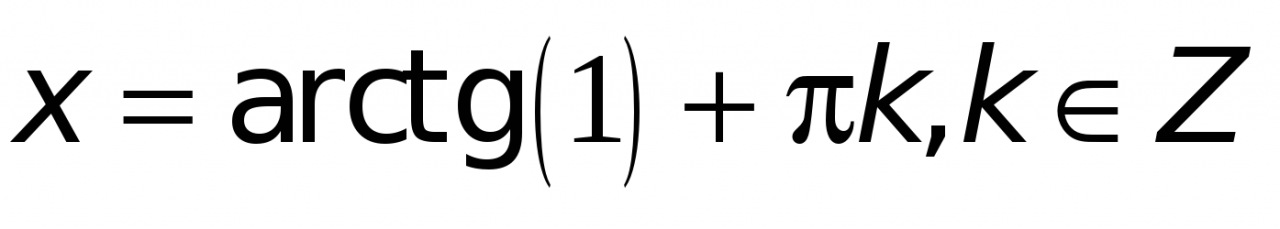Ответ: .
Уравнение
Общий вид решения уравнения определяется формулой: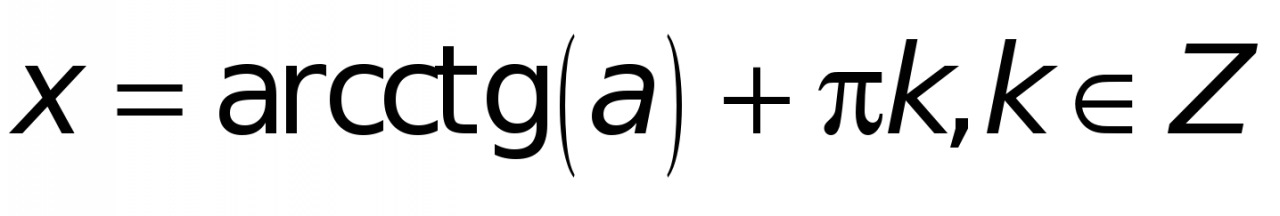
.
Пример 4. Найти решения уравнения 
.
Применяя формулу общего вида решения уравнения , получим:
,
.
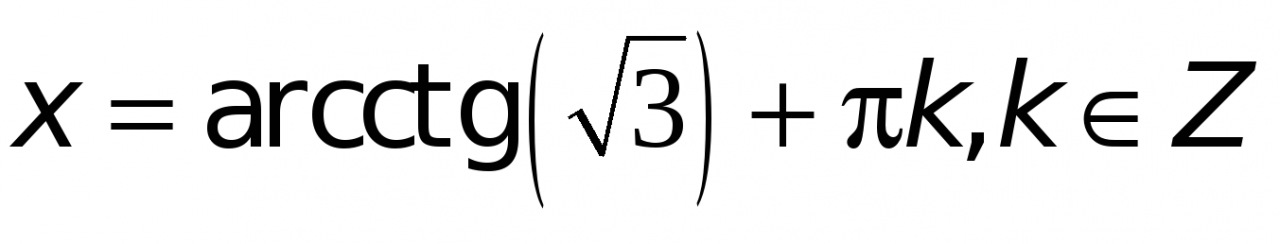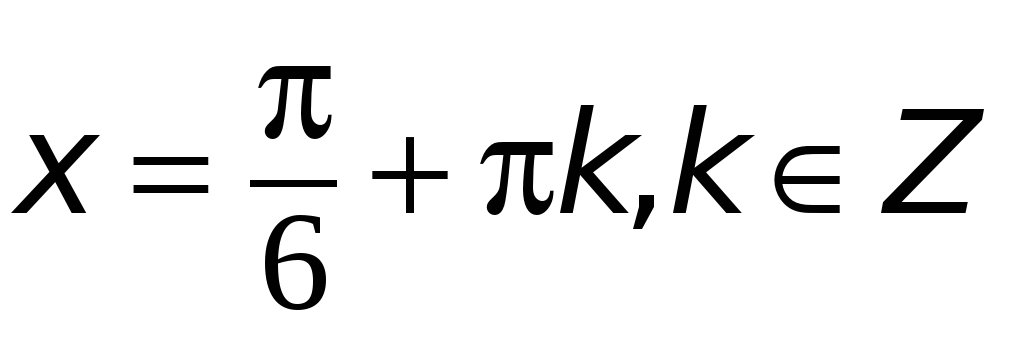Ответ: .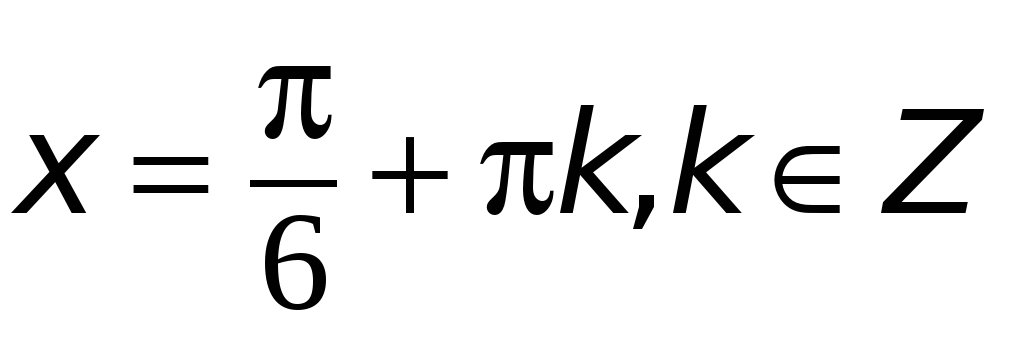
Рассмотрим уравнения, которые являются алгебраическими, относительно какой — либо тригонометрической функции, а так же уравнения, которые требуют преобразования тригонометрических выражений.
Пример 5. Найти решения уравнения 
.
Сделаем замену 
.
.
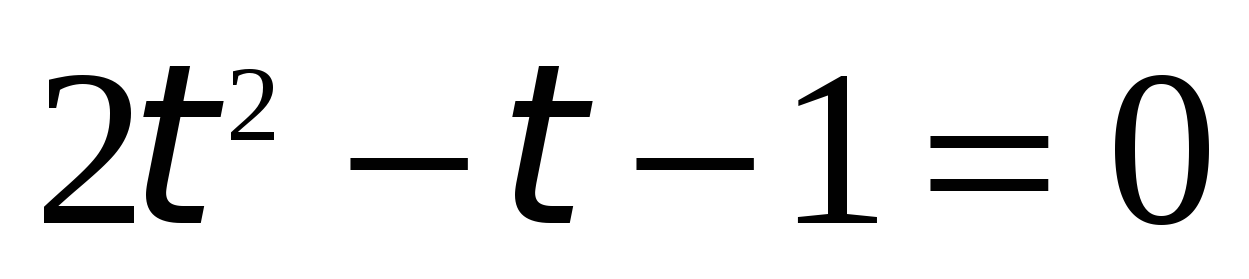Найдем корни уравнения: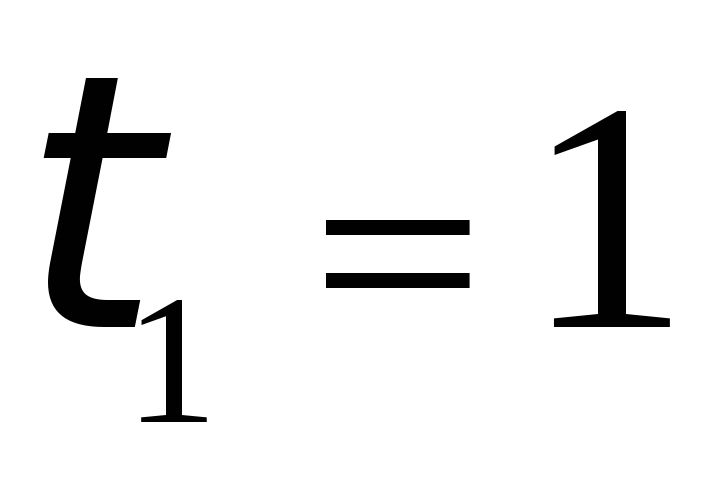 
, 
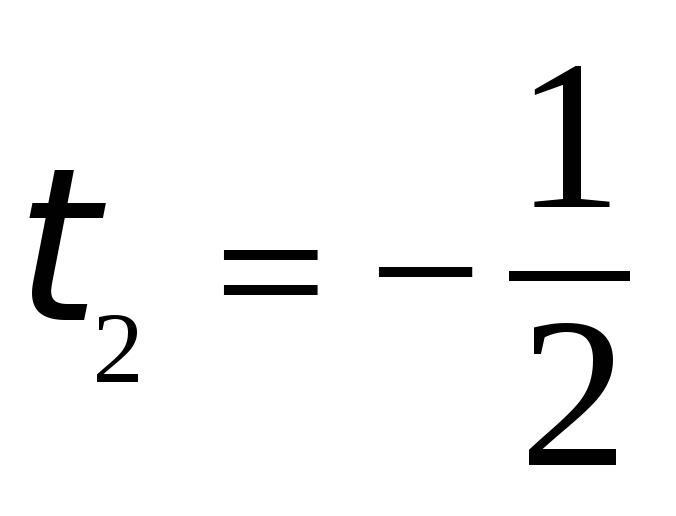
Делаем обратную замену: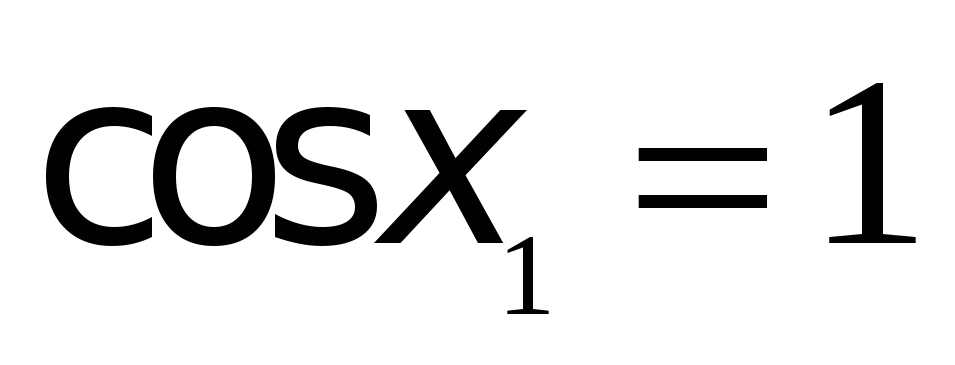 
,
.
,
.
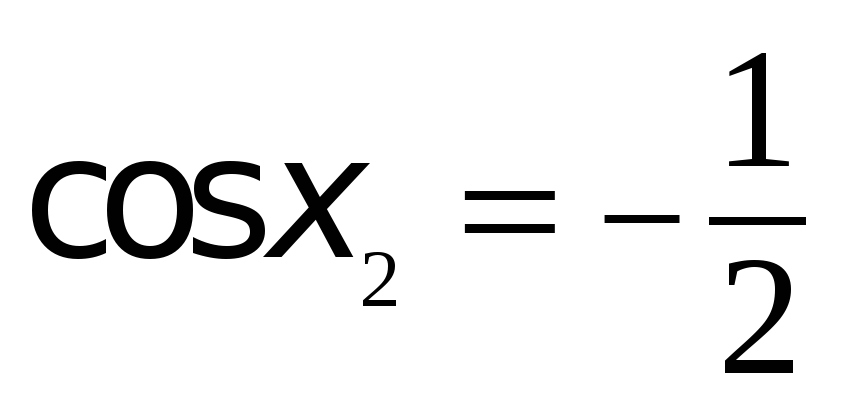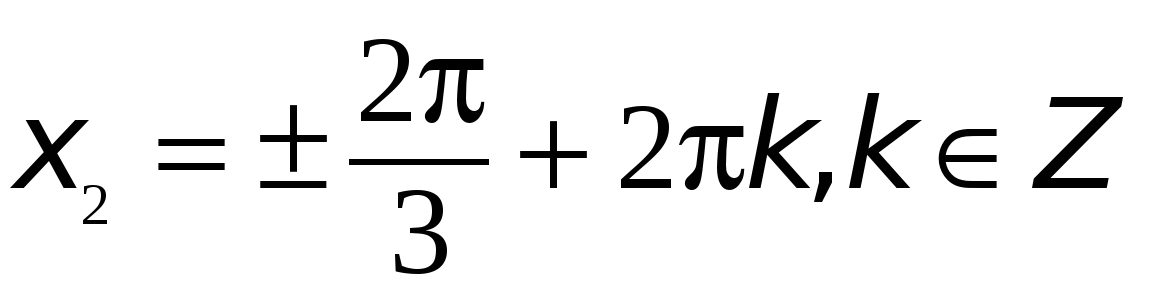Ответ: , .
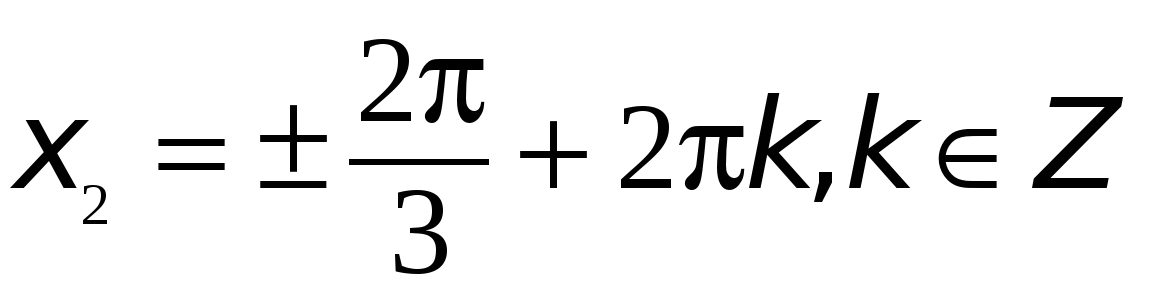Пример 6. Найти решения уравнения 
.
Применяя формулы двойного угла, получим: 
.
.
.
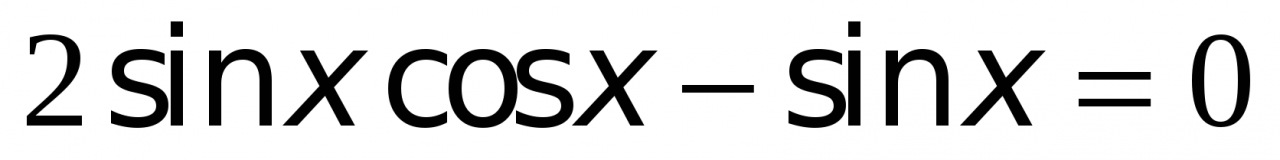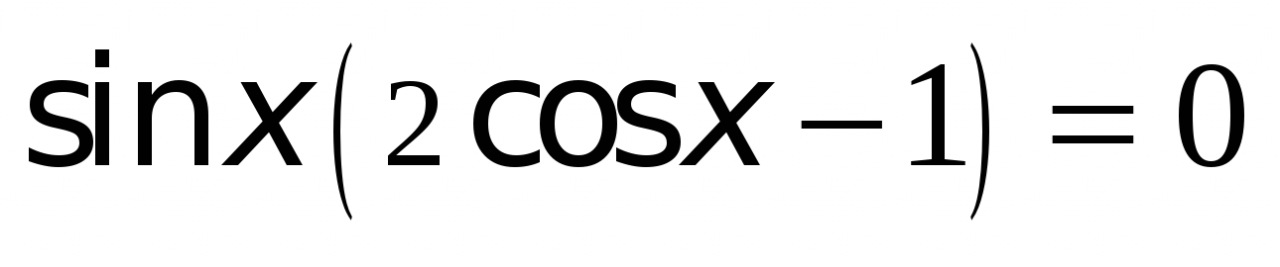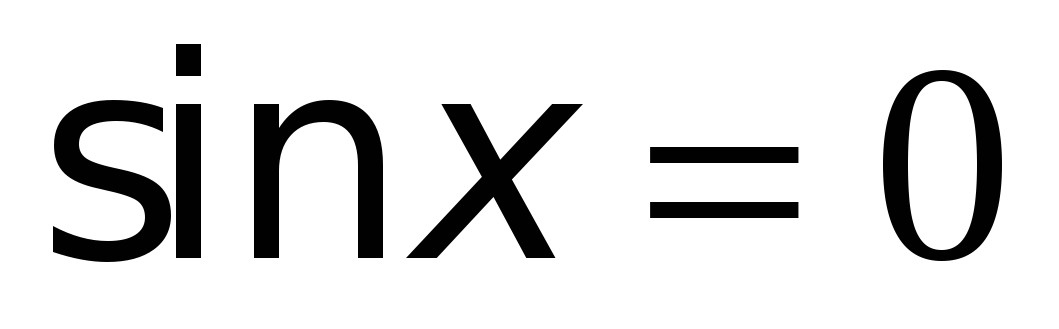или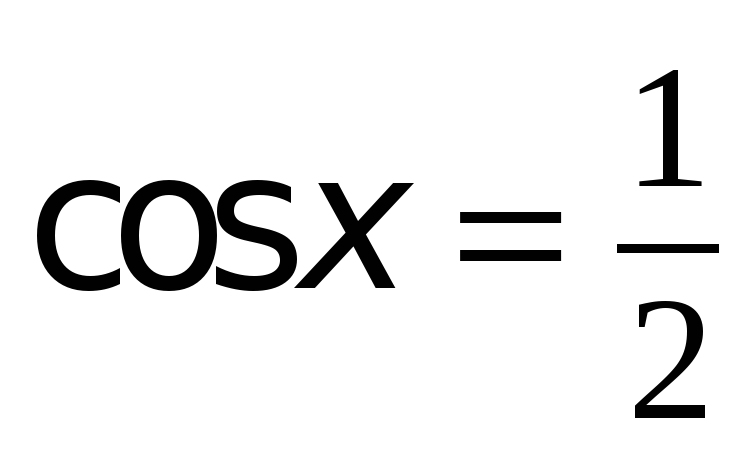 
.
,
.
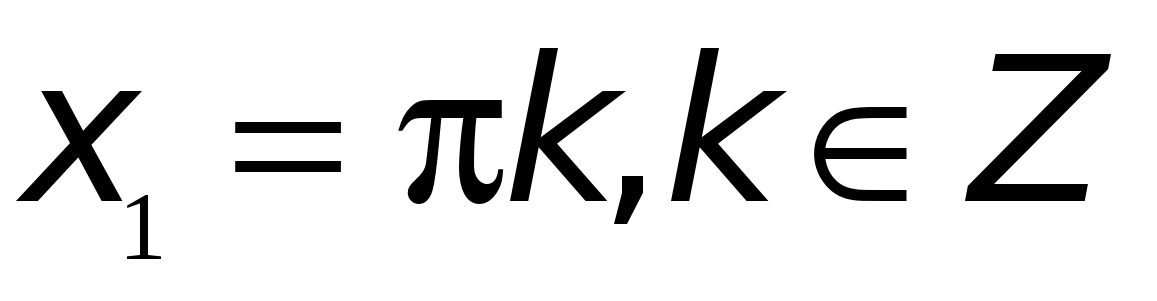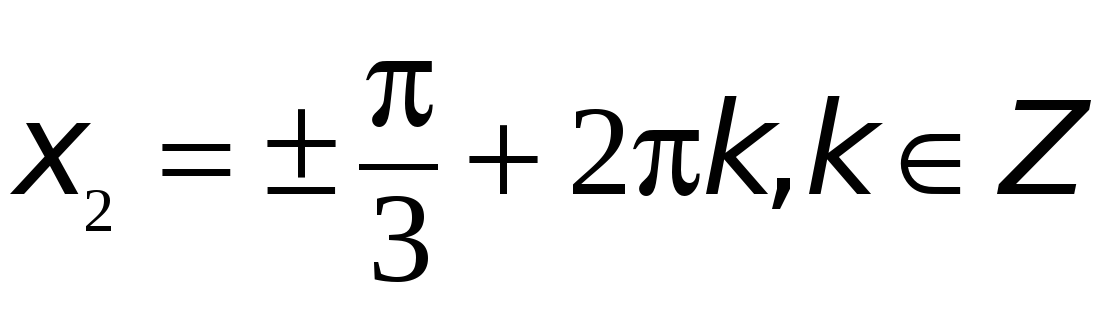Ответ: , .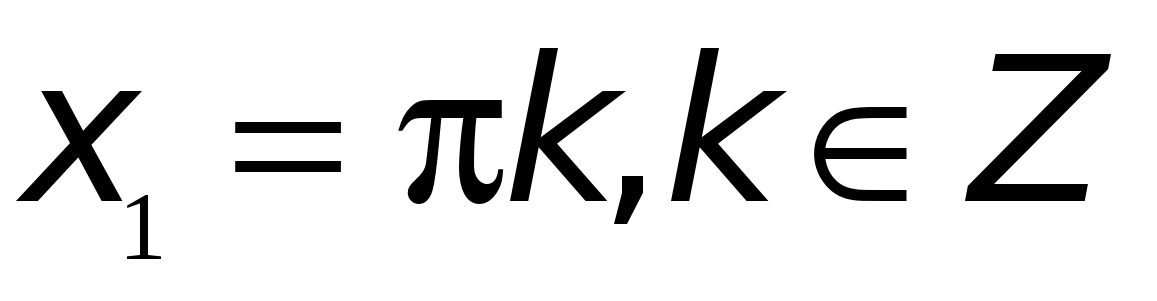
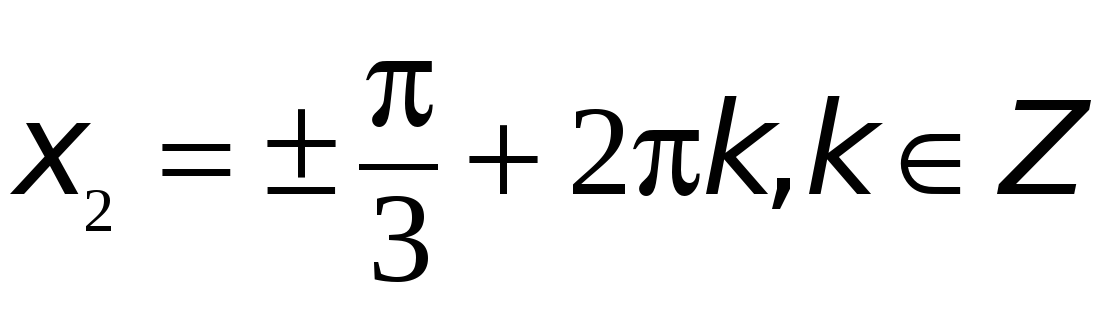При решении уравнений, содержащих тригонометрическую функцию, удобно использовать общий план решения любого тригонометрического уравнения:
Выражаем все входящие в уравнении тригонометрические функции через одну какую-либо функцию и один и тот же аргумент.
Определяем значение этой функции, пользуясь общим алгоритмом решения уравнений.
Находим по полученным значениям функции соответствующие значения аргумента.
Записываем ответ, пользуясь формулами общего вида решения простейших тригонометрических уравнений.
Проверяем найденные решения (в случае нарушения равносильности уравнений) и объединяем решения (если это возможно).
5. Самостоятельная работа №1
Вариант 1.
Решите уравнения:
Вариант 2.
Решите уравнения:
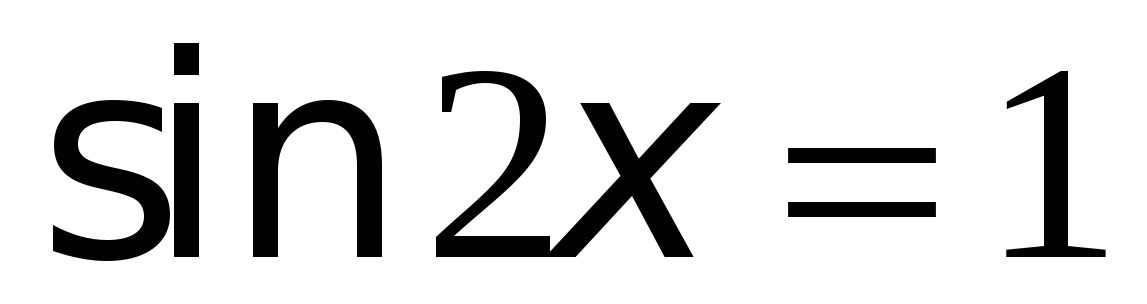
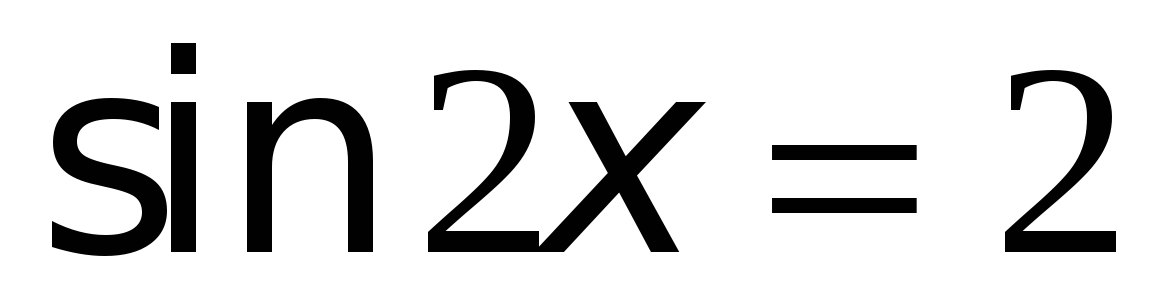
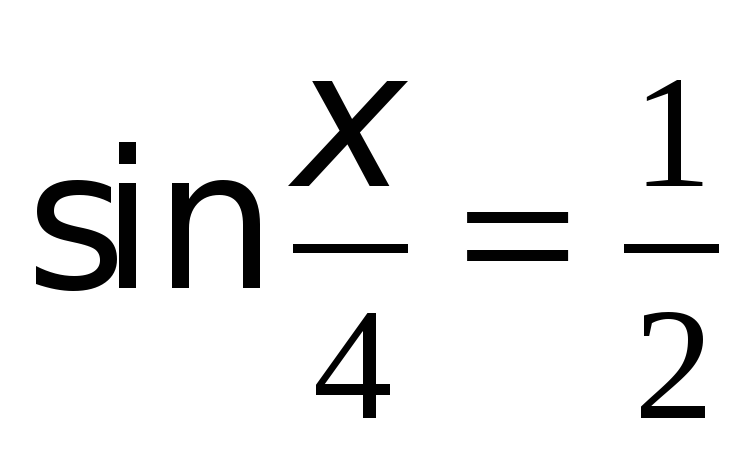
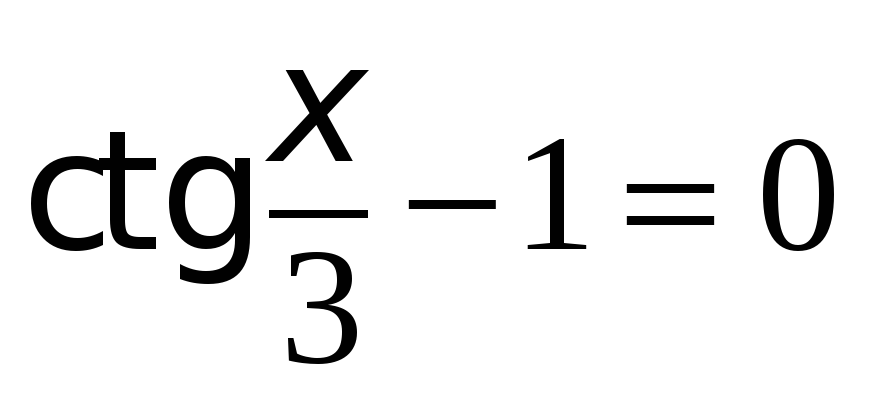
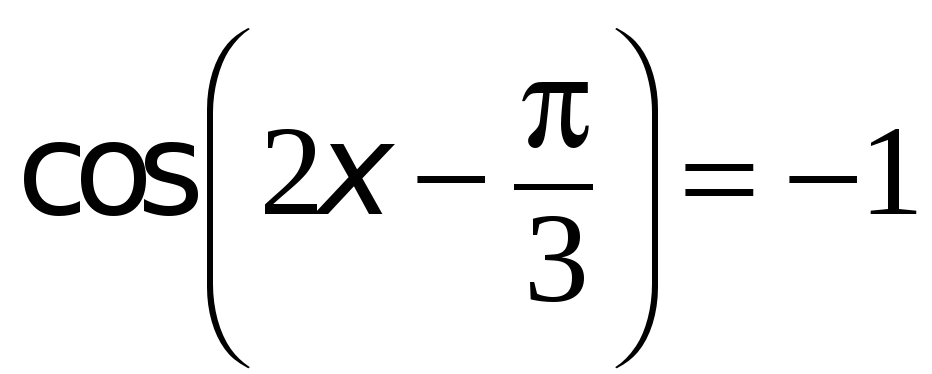
Тригонометрические неравенства
Тригонометрическими неравенствами называются неравенства, которые содержат переменную под знаком тригонометрической функции.
Решение тригонометрических неравенств зачастую сводится к решению простейших тригонометрических неравенств вида:
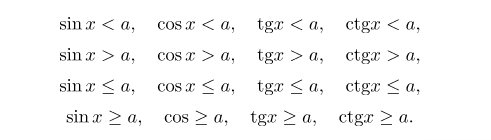
Решаются простейшие тригонометрические неравенства графически или с помощью единичной тригонометрической окружности.
По определению, синус угла
есть ордината точки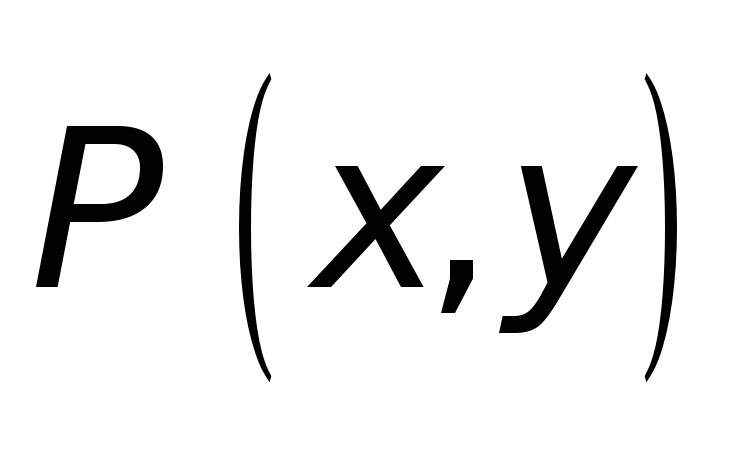 
единичного круга (рис. 1), а косинусом – абсцисса этой точки. Этот факт используется при решении простейших тригонометрических неравенств с косинусом и синусом с помощью единичного круга.
Рис. 1
Рассмотрим схему решения тригонометрических неравенств с помощью единичного круга.
Неравенства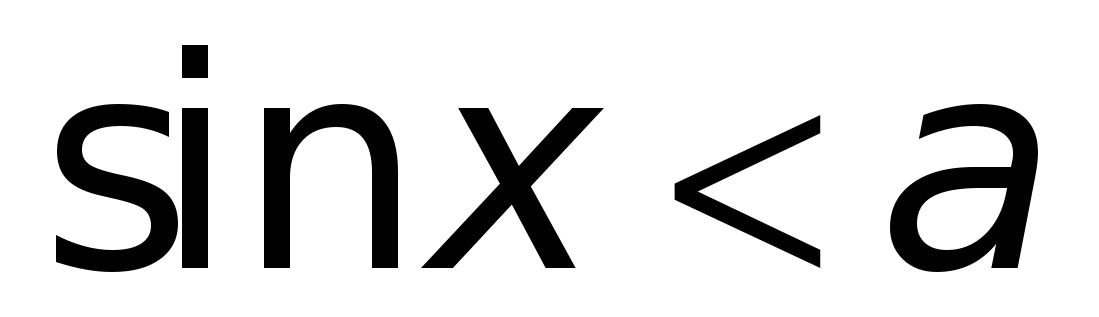 
Рис. 2
Неравенства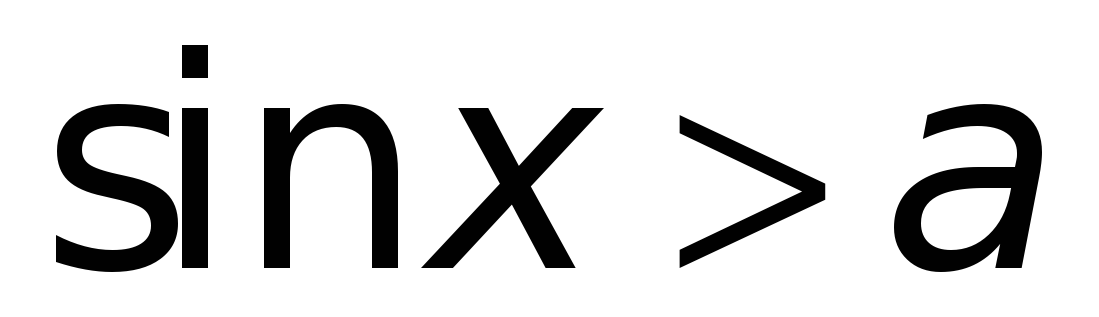 
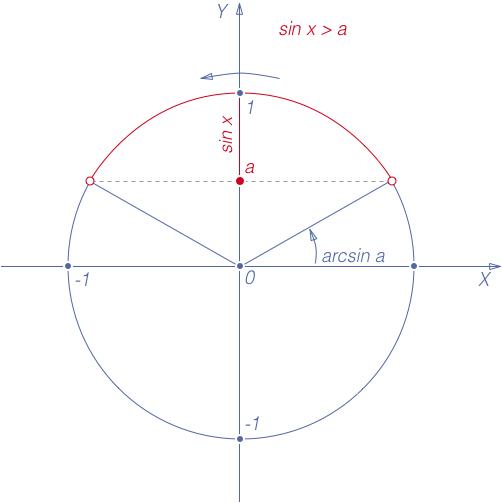
Рис. 3
Неравенства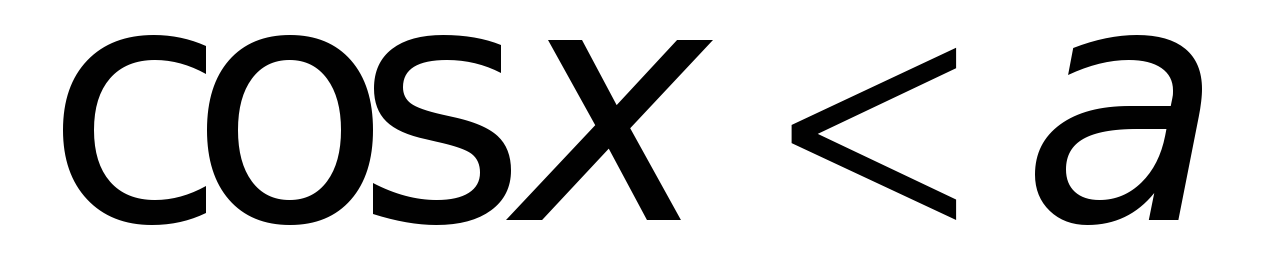 
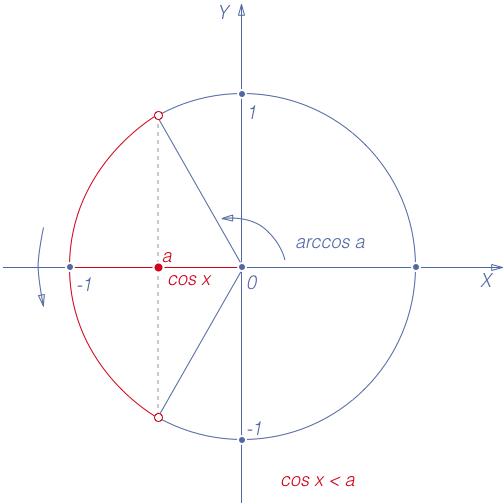
Рис. 4
Неравенства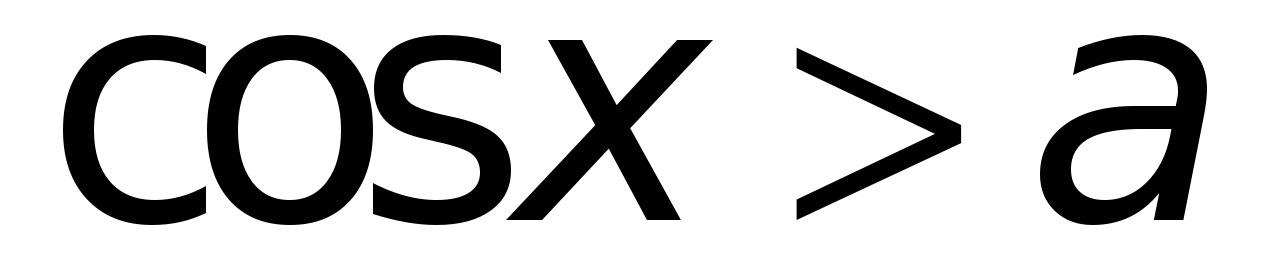 
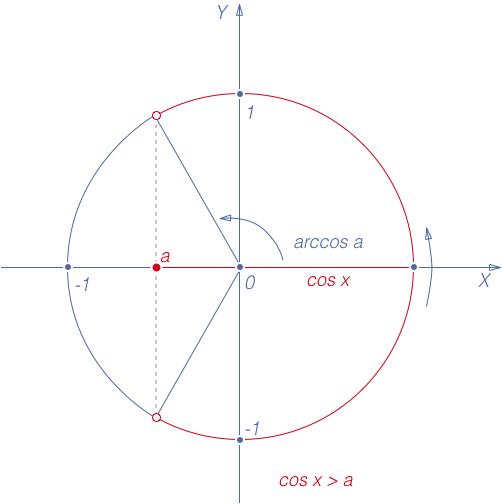
Рис. 5
Неравенства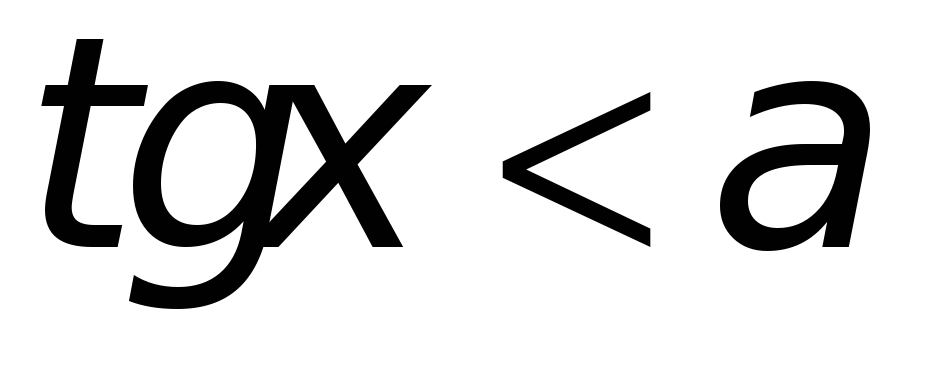 
|
|
Рис. 6
Неравенства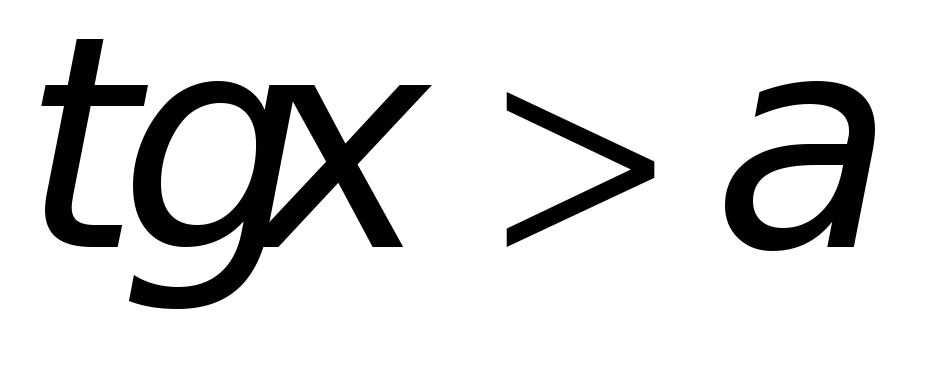 
|
|
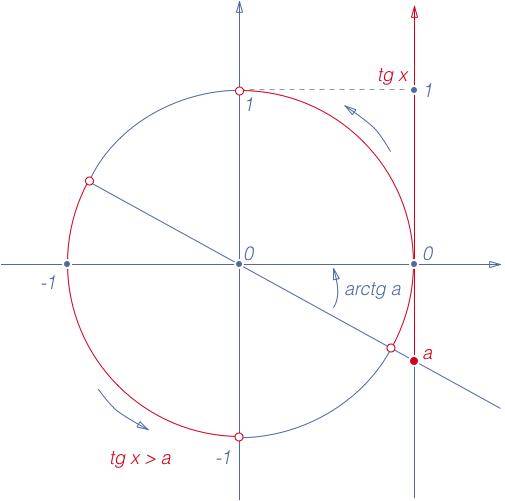
Рис. 7
Неравенства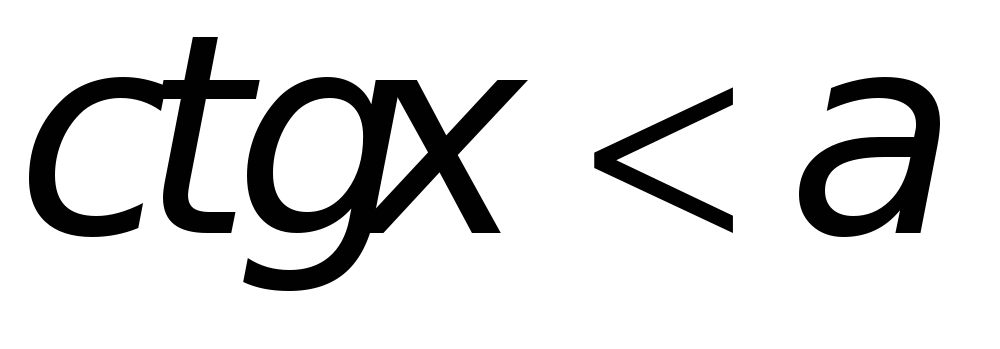 
|
|
Рис. 8
Неравенства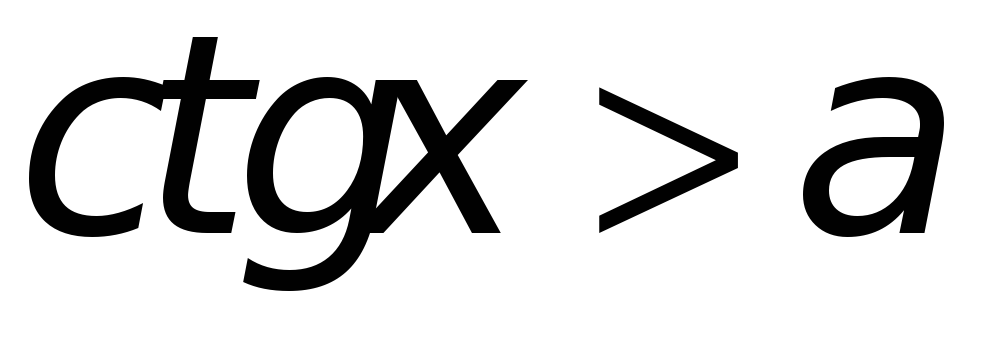 
|
|
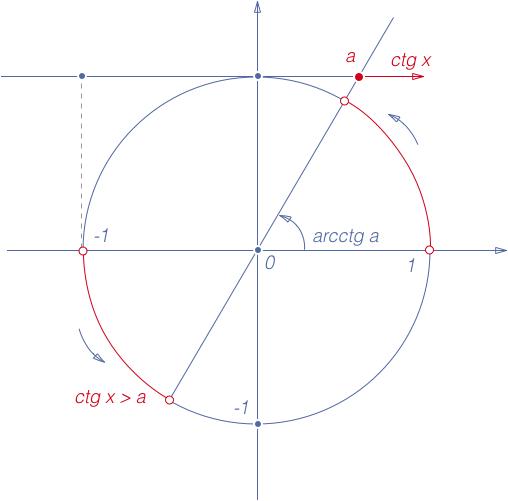
Рис. 9
Самостоятельная работа №2
Вариант 1. Решите неравенства:
|
Вариант 2. Решите неравенства:
|
ЗАКЛЮЧЕНИЕ
В методической разработке были рассмотрены способы решения тригонометрических уравнений и неравенств, как простейших, так и более сложного уровня и приведены варианты внеаудиторных самостоятельных работ, а так же рассмотрены основные теоретические сведения: определение и свойства тригонометрических и обратных тригонометрических функций; выражение тригонометрических функций через другие тригонометрических функции, что очень важно для преобразования тригонометрических выражений, в особенности содержащих обратные тригонометрические функции. Кроме основных тригонометрических формул, хорошо известных из школьного курса, приведены формулы упрощающие выражения, содержащие обратные тригонометрические функции. Ввиду того, что решения тригонометрических уравнений и неравенств можно записать несколькими способами, и вид этих решений не позволяет сразу установить, являются ли эти решения одинаковыми или различными, рассмотрена общая схема решения тригонометрических уравнений и неравенств.
Следует отметить, что выполнение внеаудиторных самостоятельных работ способствует систематизации и закрепления полученных теоретических знаний и практических умений обучающихся, углубления и расширения теоретических знаний, развития познавательных способностей и активности обучающихся: творческой инициативы, самостоятельности, ответственности, организованности и формирование самостоятельности мышления, способностей к саморазвитию, совершенствованию и самоорганизации.
Можно сделать вывод о том, что умение и навыки решать тригонометрические уравнения и неравенства в курсе алгебры и начала анализа являются очень важными, развитие которых требует значительных усилий со стороны преподавателя математики. Тригонометрические уравнения и неравенства занимают достойное место в процессе обучения математики и развитии личности в целом.
ЛИТЕРАТУРА
Алимов, А. Ш. Алгебра и начала математического анализа. 10-11 классы. Учебник / А. Ш. Алимов, Ю.М. Колягин и др. 18-е изд. — М.: Просвещение, 2012. — 464 с.
Гельфанд, И. М. Тригонометрия / И. М. Гельфанд, С. М. Львовский, А. Л. Тоом 5-е изд., стереотип. – М.: МЦНМО, 2014. – 200 с.
Макарычев, Ю.Н. Тригонометрические неравенства и их преобразование / Под ред. С.А. Теляковского. 21-е изд. – М.: Просвещение, 2014. – 271 с.
Медынский, М. М. Полный курс элементарной математики в задачах и упражнениях. Книга 7 / М. М. Медынский — М.: Эдитус, 2015. – 553 с.
Шапкина, Н. Е. Пособие по математике для 10-11 классов подготовительных курсов. Тригонометрия / Н. Е. Шапкина, И. Е. Могилевский — М.: Физический ф-т МГУ, 2014. – 89 с
Методическая разработка по алгебре (10 класс) по теме: Разработка урока «Решение простейших тригонометрических неравенств»
Разработка урока по алгебре и началам анализа для 10 класса
Галиева Гульназ Муллагалиевна, учитель математики и информатики, заместитель директора по учебной работе МБОУ «Изминская средняя общеобразовательная школа Сабинского муниципального района Республики Татарстан»
Тема: Решение простейших тригонометрических неравенств.
Цели: 1) Обеспечивать закрепление умений решать простейшие тригонометрические неравенства.
2) Обеспечивать применение учащимися способов решения простейших тригонометрических неравенств на репродуктивном и конструктивном уровне.
3) Обеспечить проверку и оценку знаний учащихся о способах решения тригонометрических неравенств.
4) Содействовать развитию у детей умений осуществлять самоконтроль, самооценку.
5) Обеспечивать развитие у школьников монологической и диалогической речи.
Тип урока: Закрепление знаний и способов действий.
Содержательная основа урока.
Содержание.
Дидактические материалы и оборудование:
Тригонометрический круг, дидактический материал для проведения дифференцированной самостоятельной работы по теме: «Решение простейших тригонометрических неравенств».
План урока.
Этапы учебного занятия | Информационный блок | Операционно-деятельный блок (способы действий) | Рефлексивный блок | Методический блок (методы, приёмы, педагогические техники) |
1 этап Оргмомент | 1. Повторить алгоритм решения простейших тригонометрических неравенств. 2.Научиться применять знания при решении тригонометрических неравенств с усложненным аргументом. | Оценить умение самостоятельно выполнять задание в рамках темы урока (через самостоятельную работу | Постановка учебных целей. | |
2 этап Проверка домашнего задания | Повторить алгоритм решения простейших тригонометрических уравнений. | Задание. Объяснить решение неравенств: а) sin t=-; б) cos t=; в) tg t=-1. | Индивидуальная работа учащихся у доски, комментированное выполнение заданий. | |
3 этап Подготовка к работе на основном этапе. | Отработка навыков нахождения углов на тригоно-метрическом круге. | Задание. На модели тригонометрического круга а) показать углы; ; -;;-;;-; | Выполнение задания по цепочке с коммен-тированием | |
4 этап Закрепление заданий и способов действий | Пример решения неравенства с усложнённым аргументом. Sin t ; Продолжите решение самостоятельно 1) Ввести новую переменную. 2) Решить полученное неравенство. 3) Вернуться к подстановке. | Объяснение сопровождается презентацией. Задание Определить последовательность действий при решении тригонометрических неравенств с усложнённым аргументом. Задание Решить у доски неравенство 2cos (2x+)1. | Самопроверка по образцу | Объяснение учителем. Выход на учебное затруднение. Самостоятельный поиск пути решения учащимися предложенного задания. Индивидуальная самостоятельная работа. Объяснение учителя Комментированное объяснение учащимися последовательности действий ( ответ одного ученика). Решение с комментарием у доски. Оценка выполнения задания учащимся. |
5 этап Контроль и самоконтроль | Задание Самостоятельно решить неравенства. Вариант 1 sin ; 2cos x-0; cos>; sin(+)1. Вариант 2 sin x; 2cos x-10; sin ; 2cos(4x-)>. | |||
6 этап. Информация о домашнем задании Индивидуальная работа по карточкам. Комментирование учителем домашнего задания. | ||||
7 этап Итоги урока. Общая оценка учителем работы учащихся на уроке. |