Решение тригонометрических уравнений онлайн
В общем виде, тригонометрическое уравнение можно записать следующим образом:
f(trig(x)) = 0
где f — некоторая произвольная функция, trig(x) — некоторая тригонометрическая функция.
Как правило, метод решения тригонометрических уравнений заключается в преобразовании исходного уравнения к более простому, решение которого известно. Преобразования осуществляются при помощи различных тригонометрических формул.
Например, рассмотрим решение тригонометрического уравнения:
Используя формулу косинуса двойного угла, преобразуем данное уравнение:
Полученное уравнение является простейшим и легко решается. Наш онлайн калькулятор, построенный на системе Wolfram Alpha способен решить более сложные тригонометрические уравнения с описанием подробного хода решения.
mathforyou.net
Тригонометрия
Онлайн решение тригонометрических уравнений
На нашем сайте вы можете решить любое тригонометрическое уравнение используя Калькулятор за пару секунд. Решать уравнения тригонометрические с помощью калькулятора просто. Чтобы ввести условие, нажмите «+условие»
Например:
Условие: sin2x+3x=2
Нажав кнопку Решить вы получите подробное решение тригонометрических уравнений.
Тригонометрия это просто если вы знаете формулы приведения в тригонометрии.
Тригонометрия 10 класс
Для начала нужно обязательно запомнить основные формулы.
Тригонометрия таблица
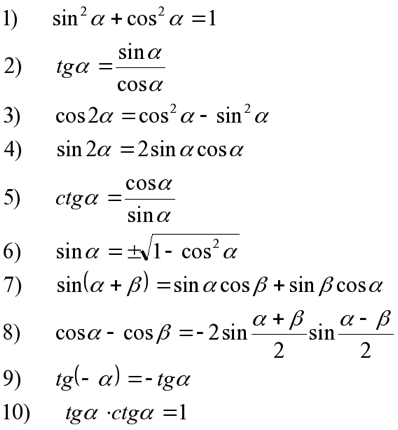
Тригонометрия приведение
Главной задачей при решении тригонометрических уравнений является его преобразование до более простого уравнения основного вида, которое решаются стандартными методами. Для решения данного рода уравнений можно использовать один из семи методов:
— алгебраический;
— разложения на множители;
— преобразования к одному уравнению;
— перехода к половинному углу;
— вспомогательного угла;
— преобразования произведения в сумму;
— подстановки.

Выбор метода определяется исходя из самого уравнения. Одно уравнение можно решить несколькоми способами, однако при правильном выборе метода вы решите его за меньшее количество математических операций.
Допустим, нам дано уравнение такого вида:
\[\sin x + \cos x = 1\]
Чтобы решить данное уравнение необходимо воспользоватся 2м методом и выполнить перенос всех членов влево:
\[\sin x +\ cos x — 1 = 0\]
Теперь преобразуем и разложим на множители левую часть уравнения:
\[\sin x -2 sin^2(\frac {x}{2})=0\]
\[2\sin(\frac {x}{2})\cdot\cos(\frac {x}{2})-2\sin^2(\frac {x}{2})=0\]
\[2\sin(\frac {x}{2})\cdot[\cos(\frac {x}{2}) — \sin(\frac {x}{2})]=0\]
1)
\[\sin (\frac {x}{2})=0\]
\[\frac{x}{2}\pi k\]
\[x_1=2\pi k\]
2)
\[\cos(\frac {x}{2})-\sin(\frac {x}{2})=0\]
\[\tan\frac {x}{2}=1\]
\[\frac {x}{2}=\arctan 1 +\pi n\]
\[\frac {x}{2} = \frac {\pi}{4}+\pi n\]
\[x_2 = \frac {\pi}{2}2\pi n\]
Где и как решать тригонометрические уравнения онлайн?
Решить уравнение вы можете на нашем сайте. Бесплатный решатель позволит решить тригонометрические уравнения с решениями любой сложности за считанные секунды онлайн. Тригонометрия егэ больше не проблема. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Используя наш калькулятор тригонометрический, вы всегда сможете сказать, что тригонометрия класс!
www.pocketteacher.ru
Решение тригонометрических уравнений онлайн — Ответ Прост!
Решение тригонометрических уравнений онлайн
Предлагаем вашему вниманию калькулятор нового поколения
для пошагового решения любых тригонометрических уравнений.
Для решения любого тригонометрического уравнения вам достаточно ввести свое уравнение в окошко калькулятора и нажать кнопку «ответ». Калькулятор выдаст решение тригонометрического уравнения бесплатно.
Способ ввода уравнения как на обычном калькуляторе.
Правила набора уравнений | |
Уравнение | Синтаксис |
tg^2 (x) + 3tg( x) =0 | |
4sin^4 (x) + cos (4x) = 1 + 12cos^4 (x) | |
6cos^2( x) + cos (3x )= cos(x) | |
2cos (x)cos(2x)= cos(x ) | |
sin(2x)/(1-cos(2x))=(1+cos(2x))/(2cos(x)) | |
3sin ^2( x) + sin( x )cos (x) = 2cos^ 2( x) | |
29,853 просмотров всего, 12 просмотров сегодня
otvet-prost.ru
Решение тригонометрических уравнений | Онлайн калькулятор
Калькулятор для пошагового решения тригонометрических уравнений онлайн (бесплатно). Данный калькулятор полностью заменит вам репетитора по математике, достаточно решить несколько уравнений с помощью данного калькулятора и вы сможете самостоятельно решать любые тригонометрические уравнения.
Для решения вашего тригонометрического уравнения достаточно вставить уравнение в окошко калькулятора и нажать кнопку «ответ(submit)«.
По многочисленным просьбам наших пользователей предлагаем методику решения всех типов тригонометрических уравнений. На ваши вопросы отвечает автор.
Способ ввода уравнения как на обычном калькуляторе.
Например: надо решить уравнение
Набираете: 6*cos^2(x)+5*sin(x)-7=0, нажимаете кнопку «ответ», получаете пошаговое решение тригонометрического уравнения
Правила ввода уравнения:
Основные константы
- Число : Pi
- Число : E
- Бесконечность : Infinity или inf
Основные функции
: x^a
модуль x: abs(x)
lib.reshim.su
| Функция | Описание | Пример ввода | Результат ввода |
|---|---|---|---|
| pi | Число \(\pi\) | pi | $$ \pi $$ |
| e | Число \(e\) | e | $$ e $$ |
| e^x | Степень числа \(e\) | e^(2x) | $$ e^{2x} $$ |
| exp(x) | Степень числа \(e\) | exp(1/3) | $$ \sqrt[3]{e} $$ |
| |x| abs(x) |
Модуль (абсолютное значение) числа \(x\) | |x-1| abs(cos(x)) |
\( |x-1| \) \( |\cos(x)| \) |
| sin(x) | Синус | sin(x-1) | $$ sin(x-1) $$ |
| cos(x) | Косинус | 1/(cos(x))^2 | $$ \frac{1}{cos^2(x)} $$ |
| tg(x) | Тангенс | x*tg(x) | $$ x \cdot tg(x) $$ |
| ctg(x) | Котангенс | 3ctg(1/x) | $$ 3 ctg \left( \frac{1}{x} \right) $$ |
| arcsin(x) | Арксинус | arcsin(x) | $$ arcsin(x) $$ |
| arccos(x) | Арккосинус | arccos(x) | $$ arccos(x) $$ |
| arctg(x) | Арктангенс | arctg(x) | $$ arctg(x) $$ |
| arcctg(x) | Арккотангенс | arcctg(x) | $$ arcctg(x) $$ |
| sqrt(x) | Квадратный корень | sqrt(1/x) | $$ \sqrt{\frac{1}{x}} $$ |
| x^(1/n) | Корень произвольной числовой целой степени >= 2 x^(1/2) эквивалентно sqrt(x) |
(cos(x))^(1/3) | $$ \sqrt[\Large 3 \normalsize]{cos(x)} $$ |
| ln(x) | Натуральный логарифм (основание — число e) |
1/ln(3-x) | $$ \frac{1}{ln(3-x)} $$ |
| log(a,x) | Логарифм x по основанию a | log(3,cos(x)) | $$ log_3(cos(x)) $$ |
| sh(x) | Гиперболический синус | sh(x-1) | $$ sh(x-1) $$ |
| ch(x) | Гиперболический косинус | ch(x) | $$ ch(x) $$ |
| th(x) | Гиперболический тангенс | th(x) | $$ th(x) $$ |
| cth(x) | Гиперболический котангенс | cth(x) | $$ cth(x) $$ |
| Вывод | Перевод, пояснение | ||
| Solve for x over the real numbers | Решить относительно х в действительных числах (бывают ещё комплексные) | ||
| Multiply both sides by … | Умножаем обе части на … | ||
| Simplify and substitute … | Упрощаем и делаем подстановку … | ||
| Simplify trigonometric functions | Упрощаем тригонометрические функции | ||
| Bring … together using the commom denominator … | Приводим … к общему знаменателю … | ||
| The left hand side factors into a product with two terms | Левая часть разбивается на множители как два многочлена | ||
| Split into two equations | Разделяем на два уравнения | ||
| Take the square root of both sides | Извлекаем квадратный корень из обоих частей | ||
| Subtract … from both sides | Вычитаем … из обеих частей уравнения | ||
| Add … to both sides | Прибавляем … к обоим частям уравнения | ||
| Multiply both sides by … | Умножаем обе части уравнения на … | ||
| Divide both sides by … | Делим обе части уравнения на … | ||
| Substitute … Then … | Делаем подстановку … Тогда … | ||
| Substitute back for … | Обратная подстановка для … | ||
| … has no solution since for all … | … не имеет решения для всех … | ||
| Take the inverse sine of both sides | Извлекаем обратный синус (арксинус) из обоих частей | ||
| Simplify the expression | Упрощаем выражение | ||
| Answer | Ответ | ||
| \(log(x)\) | Натуральный логарифм, основание — число e. У нас пишут \(ln(x)\) | ||
| \(arccos(x)\) или \(cos^{-1}(x)\) | Арккосинус. У нас пишут \( arccos(x) \) | ||
| \(arcsin(x)\) или \(sin^{-1}(x)\) | Арксинус. У нас пишут \( arcsin(x) \) | ||
| \(tan(x)\) | Тангенс. У нас пишут \(tg(x) = \frac{sin(x)}{cos(x)}\) | ||
| \(arctan(x)\) или \(tan^{-1}(x)\) | Арктангенс. У нас пишут \(arctg(x)\) | ||
| \(cot(x)\) | Котангенс. У нас пишут \(ctg(x) = \frac{cos(x)}{sin(x)}\) | ||
| \(arccot(x)\) или \(cot^{-1}(x)\) | Арккотангенс. У нас пишут \(arcctg(x)\) | ||
| \(sec(x)\) | Секанс. У нас пишут также \(sec(x) = \frac{1}{cos(x)}\) | ||
| \(csc(x)\) | Косеканс. У нас пишут \(cosec(x) = \frac{1}{sin(x)}\) | ||
| \(cosh(x)\) | Гиперболический косинус. У нас пишут \(ch(x) = \frac{e^x+e^{-x}}{2} \) | ||
| \(sinh(x)\) | Гиперболический синус. У нас пишут \(sh(x) = \frac{e^x-e^{-x}}{2} \) | ||
| \(tanh(x)\) | Гиперболический тангенс. У нас пишут \(th(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} \) | ||
| \(coth(x)\) | Гиперболический котангенс. У нас пишут \(cth(x) = \frac{1}{th(x)} \) |
www.math-solution.ru
Уравнения онлайн
Математические уравнения онлайн для решения математики. Быстро найти решение математического уравнения в режиме онлайн. Сайт www.matcabi.net позволяет решить уравнение почти любого заданного алгебраического, тригонометрического или трансцендентного уравнения онлайн. При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн. Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.matcabi.net решение уравнений онлайн займет несколько минут. Основное преимущество www.matcabi.net при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн, тригонометрические уравнения онлайн, трансцендентные уравнения онлайн, а также уравнения с неизвестными параметрами в режиме онлайн. Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.matcabi.net. Любое алгебраическое уравнение, тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений. При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн. Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.matcabi.net, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн, тригонометрических уравнений онлайн, а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.matcabi.net вполне достаточно. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.matcabi.net. Необходимо правильно записать уравнение и моментально получите онлайн решение, после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое, тригонометрическое, трансцендентное или уравнение с неизвестными параметрами.
www.matcabi.net
Решение тригонометрических неравенств онлайн · Как пользоваться Контрольная Работа РУ
Рассмотрим пример решения тригонометрического неравенства онлайн на сайте Контрольная Работа РУ.
Этот сайт даёт полное решение тригонометрического неравенства.

Плюс для некоторых неравенств есть решение, изображённое на графике.
Итак, рассмотрим пример:
Требуется решить тригонометрическое неравенство cos(x/4-pi/3) > 1/2 и найти x, при которых выполняется это неравенство.
Для этого переходим на страницу
>>неравенства онлайн<<и нажимаем Решить неравенство!
.
Получаем ответ 8*pi*n<x<1/3*(24*pi*n+8*pi), где n принадлежит N.
А также следующее подробное решение:
Дано неравенство: $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} > \frac{1}{2}$$ Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние: $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} = \frac{1}{2}$$ Решаем:
Дано уравнение $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} = \frac{1}{2}$$ — это простейшее тригонометрическое ур-ние.
Это ур-ние преобразуется в $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n + \operatorname{asin}{\left (\frac{1}{2} \right )}$$ $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n — \operatorname{asin}{\left (\frac{1}{2} \right )} + \pi$$ Или $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n + \frac{\pi}{6}$$ $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n + \frac{5 \pi}{6}$$ , где n — любое целое число.
Перенесём $$\frac{\pi}{6}$$ в правую часть ур-ния с противоположным знаком, итого: $$\frac{x}{4} = 2 \pi n$$ $$\frac{x}{4} = 2 \pi n + \frac{2 \pi}{3}$$ Разделим обе части полученного ур-ния на $$\frac{1}{4}$$ $$x_{1} = 8 \pi n$$ $$x_{2} = 8 \pi n + \frac{8 \pi}{3}$$ $$x_{1} = 8 \pi n$$ $$x_{2} = 8 \pi n + \frac{8 \pi}{3}$$ Данные корни $$x_{1} = 8 \pi n$$ $$x_{2} = 8 \pi n + \frac{8 \pi}{3}$$ являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки: $$x_{0} < x_{1}$$ Возьмём например точку $$x_{0} = x_{1} — \frac{1}{10}$$ = $$8 \pi n + — \frac{1}{10}$$ = $$8 \pi n — \frac{1}{10}$$ подставляем в выражение $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} > \frac{1}{2}$$
/8*pi*n - 1/10 pi\ cos|------------- - --| > 1/2 | 1 1| \ 4 3 / /1 pi \ cos|-- + -- - 2*pi*n| > 1/2 \40 3 /
Тогда $$x < 8 \pi n$$ не выполняется, значит одно из решений нашего неравенства будет при: $$x > 8 \pi n \wedge x < 8 \pi n + \frac{8 \pi}{3}$$
_____
/ \
-------ο-------ο-------
x1 x2
www.kontrolnaya-rabota.ru