Решение тригонометрических уравнений

В данной статье остановимся кратко на решении задач C1 из ЕГЭ по математике. Эти задания представляют собой уравнения, которые требуется, во-первых, решить (то есть найти их решения, причем все), во-вторых, осуществить отбор решений по тому или иному ограничению. В последние годы на ЕГЭ по математике в заданиях C1 школьникам предлагаются для решения тригонометрические уравнения, поэтому в данной статье разобраны только они. Примеры структурированы по методам решения уравнений, от самых элементарных, до достаточно сложных.
Прежде чем перейти к разбору конкретных тригонометрических уравнений, вспомним основные формулы тригонометрии. Приведем их здесь в справочном виде.

Основные тригонометрические формулы

Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений
Пример 1. Найдите корни уравнения ![Rendered by QuickLaTeX.com \[ \cos\left(4x+\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}, \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-7cea1f5663bb6ad8fdbc9fea4f463c6b_l3.png)
принадлежащие промежутку 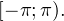
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем 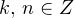
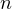 и
и 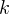 принадлежат множеству целых чисел):
принадлежат множеству целых чисел): ![Rendered by QuickLaTeX.com \[ 4x+\frac{\pi}{4}=\pm\operatorname{arccos \left(-\frac{\sqrt{2}}{2}\right)}+2\pi k. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-600bd6daa90af5fa4124c683eb7663ac_l3.png)
Другими словами, нам нужно подобрать такое число из промежутка ![Rendered by QuickLaTeX.com [0;2\pi],](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-6516ce3e8a2a72f3c1e75c74df6dcab5_l3.png)
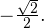 Это число
Это число  Используя это, получаем:
Используя это, получаем: ![Rendered by QuickLaTeX.com \[ 4x+\frac{\pi}{4} = \pm\frac{3\pi}{4}+2\pi k\Leftrightarrow \left[\begin{array}{l}x = \frac{\pi}{8}+\frac{\pi k}{2}, \\ x = -\frac{\pi}{4}+\frac{\pi n}{2}.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4e1b7dcb8f1bb9b0ff44ee1900d0e206_l3.png)
Вообще, значения тригонометрических функций от основных аргументов нужно знать. Их совсем чуть-чуть:
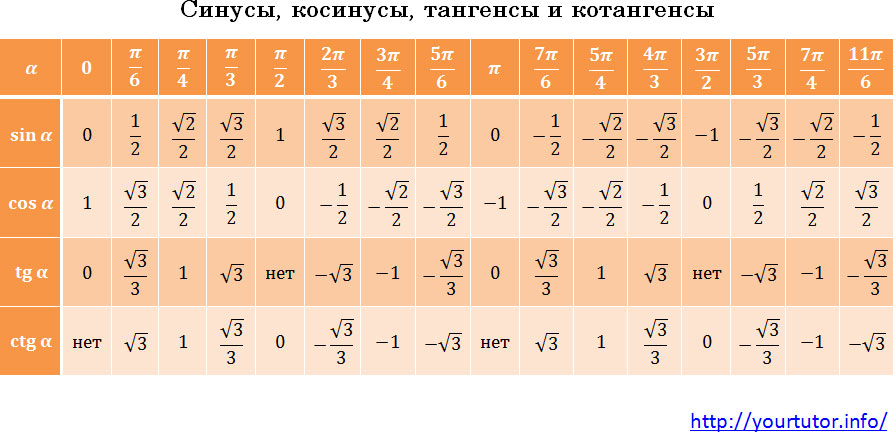
Таблица значений тригонометрических функций
Хотя на самом деле запоминать их вовсе не обязательно. Существует очень простой алгоритм, используя который, можно в уме легко вычислять значения тригонометрических функций всех основных аргументов. Просто у каждого он свой. Придумайте его и для себя. Просто посмотрите на эту таблицу. Числа в ней расположены не случайным образом, определенная закономерность есть, постарайтесь ее найти.
Итак, вернемся к нашему заданию. Из полученных серий выбираем только те ответы, которые принадлежат промежутку 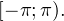 Воспользуемся для этого методом двойных неравенств. Вы помните, что
Воспользуемся для этого методом двойных неравенств. Вы помните, что 
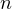 — целые числа:
— целые числа:1) 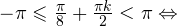
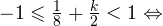
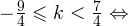
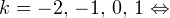

2) 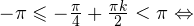
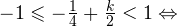

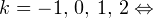
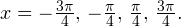
Задача для самостоятельного решения №1. Найдите корни уравнения  принадлежащие промежутку
принадлежащие промежутку 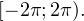
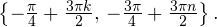
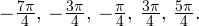
Решение линейных тригонометрических уравнений
Пример 2. Найдите корни уравнения ![Rendered by QuickLaTeX.com \[ \sin x+\sqrt{3}\cos x=1, \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c8549fd428fc2b8f8612668c1bcafa38_l3.png)
принадлежащие промежутку ![Rendered by QuickLaTeX.com [-2\pi;4\pi].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e5ab0d4ddd997ad7264282447126bc7c_l3.png)
Решение. Подобные уравнения решаются один весьма интересным, на мой взгляд, способом. Разделим обе части на 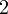 , уравнение тогда примет вид:
, уравнение тогда примет вид:
![Rendered by QuickLaTeX.com \[ \frac{1}{2}\sin x+\frac{\sqrt{3}}{2}\cos x = 1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-65ffb48c7a579b1bbdee9fbba7af59f4_l3.png)
Подберем такое число, синус которого равен 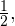 а косинус равен
а косинус равен 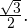 Например, пусть это будет число
Например, пусть это будет число 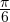
![Rendered by QuickLaTeX.com \[ \sin\frac{\pi}{6}\sin x+\cos\frac{\pi}{6}\cos x=\frac{1}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4c7a1d290000c0bba4b160c010d5f32f_l3.png)
Присмотревшись, слева от знака равенства усматриваем разложение косинуса разности 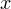 и
и  Это и есть ключ к решению. Имеем:
Это и есть ключ к решению. Имеем:
![Rendered by QuickLaTeX.com \[ \cos\left(x-\frac{\pi}{6}\right)=\frac{1}{2}\Leftrightarrow x-\frac{\pi}{6}=\pm\frac{\pi}{3}+2\pi k\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-99933eb31e68aa68196b01149d3cf7e7_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}x-\frac{\pi}{6}=\frac{\pi}{3}+2\pi k, \\ x-\frac{\pi}{6}=-\frac{\pi}{3}+2\pi n\end{array}\right.\Leftrightarrow\left[\begin{array}{l}x=\frac{\pi}{2}+2\pi k, \\ x=-\frac{\pi}{6}+2\pi n.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-a7f7798906bca8730370d50380d0b2c5_l3.png)
Осуществляем отбор решений, входящих в промежуток 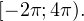 :
:
1) 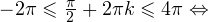

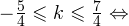

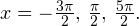
2) 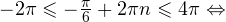
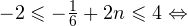
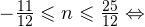
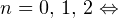
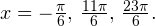
Задача для самостоятельного решения №2. Найдите корни уравнения 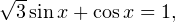 принадлежащие промежутку
принадлежащие промежутку ![Rendered by QuickLaTeX.com [-3\pi;3\pi].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-979d4671d337b296584d0c825376e1e8_l3.png)
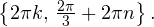
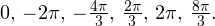
Решение тригонометрических уравнений методом замены переменной
Пример 3. Дано уравнение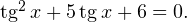
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезке ![Rendered by QuickLaTeX.com \left[-2\pi;-\frac{\pi}{2}\right].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2e56a5618e53c514d925c4318432710e_l3.png)
Решение. Сразу оговорим ограничения, накладываемые на переменную 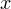 в этом уравнении:
в этом уравнении:  Откуда взялось это ограничение? Правильно, функция
Откуда взялось это ограничение? Правильно, функция 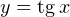 не существует при этих значениях
не существует при этих значениях 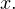 Используем замену переменной:
Используем замену переменной: 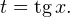 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ t^2+5t+6=0\Leftrightarrow\left[\begin{array}{l}t=-3, \\t=-2.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c8cb0eceec5f7707e25585504f135ed9_l3.png)
Переходим к обратной замене:
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\operatorname{tg}x = -3,\\ \operatorname{tg}x = -2\end{array}\right.\Leftrightarrow \left[\begin{array}{l}x = -\operatorname{arctg} 3+\pi k, \\ x=-\operatorname{arctg} 2+\pi n.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-184ca285f5fe0c4b521f49f2c1fef113_l3.png)
Осуществляем отбор решений. Проведем его на этот раз с использованием единичной окружности.
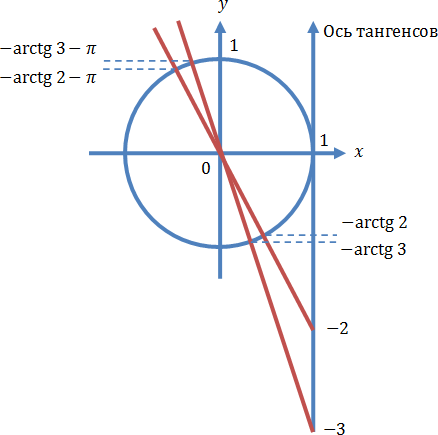
Отбор корней с помощью единичной окружности
Из рисунка видно, что в интересующий нас промежуток входят только два значения из этих серий:  Обратите внимание на один существенный момент. На рисунке точки
Обратите внимание на один существенный момент. На рисунке точки 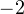 и
и 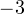 принадлежат оси тангенсов, а точки
принадлежат оси тангенсов, а точки 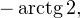
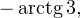
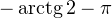 и
и 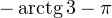 — единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
— единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
Ответ: 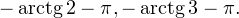
Задача для самостоятельного решения №3. Дано уравнение 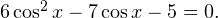
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![Rendered by QuickLaTeX.com [-\pi;2\pi].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-7619bf74ede16b0f138212b37cf78df2_l3.png)
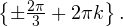
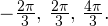
Решение тригонометрических уравнений методом разложения на множители
Пример 4. Дано уравнение ![Rendered by QuickLaTeX.com \[ \sin 2x=2\sin x-\cos x+1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-314ae6ec8084938924dcb1b7a0324414_l3.png)
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![Rendered by QuickLaTeX.com \left[-2\pi; -\frac{\pi}{2}\right].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-092d4dc81779071955ee1bdf99bce52e_l3.png)
Решение. Равносильными преобразования приводим уравнение к виду:
![Rendered by QuickLaTeX.com \[ \sin 2x=2\sin x-\cos x+1\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-26079fe9cc286a9b505cebcad4b20a54_l3.png)
![Rendered by QuickLaTeX.com \[ 2\sin x\cos x-2\sin x+\cos x-1=0\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-16b853ad0976a5741efaebe9dbf734a3_l3.png)
![Rendered by QuickLaTeX.com \[ 2\sin x(\cos x-1)+\cos x-1 =0\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-cb5e2726eaee2ea2b3d7aef7d4811e45_l3.png)
![Rendered by QuickLaTeX.com \[ (\cos x-1)(2\sin x+1) = 0\Lefrightarrow \left[\begin{array}{l}\cos x-1=0, \\ 2\sin x+1=0\end{array}\right.\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-1e2e696cbfce62ef0d378fc226247d45_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\cos x=1, \\ \sin x=-\frac{1}{2} \end{array}\right.\Leftrightarrow\left[\begin{array}{l}x=2\pi k, \\ x=-\frac{\pi}{6}+2\pi n, \\ x=-\frac{5\pi}{6}+2\pi z.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c0ac3379edc46ce1bf97df0f46a830ac_l3.png)
Осуществляем отбор решений с помощью единичной окружности.
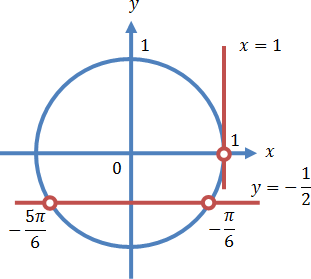
Отбор решений с помощью единичной окружности
Из рисунка видно, что в интересующий нас промежуток входят только два значения из всех этих серий: 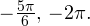
Задача для самостоятельного решения №4. Дано уравнение
![Rendered by QuickLaTeX.com \[ 3\sin 2x-4\cos x+3\sin x-2=0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-28a0aa4a8809041869a0dd165374f983_l3.png)
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![Rendered by QuickLaTeX.com \left[\frac{\pi}{2};\frac{3\pi}{2}\right].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0afd161af4c492ee4549edea05061c7b_l3.png)
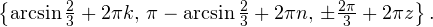
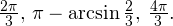
Комбинированные уравнения
При решении уравнений этого типа важно обращать внимание на область допустимых значений входящих в него переменных. Именно поэтому составители вариантов ЕГЭ не просят учеников осуществлять отбор решений из полученных серий ответов. Решение этих уравнений само собой подразумевает выполнение данной математической операции.
Пример 5. Решите уравнение: ![Rendered by QuickLaTeX.com \[ \sqrt{1-2\sin 3x\sin 7x}=\sqrt{\cos 10x}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0676b2ec24b14219e132ecfeffe1beff_l3.png)
Решение. Данное уравнение эквивалентно следующей системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}1-2\sin 3x\sin 7x=\cos 10x, \\ \cos 10x\geqslant 0.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-5e7804c5a3444eda3706d8c6a9cc8bc0_l3.png)
Обратите внимание! Писать, что 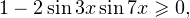 нет никакой необходимости, поскольку по условию это выражение равно выражению
нет никакой необходимости, поскольку по условию это выражение равно выражению 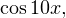 которое, в свою очередь, больше или равно нулю.
которое, в свою очередь, больше или равно нулю.
Решаем первое уравнение системы:
![Rendered by QuickLaTeX.com \[ 1-2\sin 3x\sin 7x=\cos (7x+10x)\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-85f99b88ebecfe2323a0bc59bac8e027_l3.png)
![Rendered by QuickLaTeX.com \[ 1-2\sin 3x\sin 7x=\cos 3x\cos 7x-\sin 3x\sin 7x\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-30cfd48e7e1658096abdeb1390486c83_l3.png)
![Rendered by QuickLaTeX.com \[ 1=\cos 3x\cos 7x+\sin 3x\sin 7x\Leftrightarrow \cos 4x=1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e7341e12fbea6fe289a80d2965e67b8b_l3.png)
![Rendered by QuickLaTeX.com \[ \cos 10x = 1\Leftrightarrow 4x=2\pi k\Leftrightarrow x = \frac{\pi k}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-69acc2d98a3a49c3c563dbcb9e3f3976_l3.png)
Нужно, чтобы 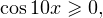 поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только
поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только 
Ответ: 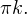
Задача для самостоятельного решения №5. Решите уравнение: 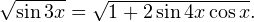
 Пример 6. Решите уравнение:
Пример 6. Решите уравнение: ![Rendered by QuickLaTeX.com \[ \frac{2\sin^2 x-\sin\left(\frac{3\pi}{2}+x\right)-1}{\sqrt{\sin x}}=0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-b29f83ad79819cdf0623a3f50f53cbf1_l3.png)
Решение. Данное уравение равносильно системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}2\sin^2 x-\sin\left(\frac{3\pi}{2}+x\right)-1=0, \\ \sin x>0\end{cases}\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-9796d3e88520ad252eea21fb51f21987_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}2\cos^2 x-\cos x-1=0,\\ \sin x>0\end{cases}\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-dbab64445b6b27423f4c9a5b3a45e710_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}\left[\begin{array}{l}\cos x = 1, \\ \cos x =-\frac{1}{2},\end{array} \\ \sin x >0\right.\end{cases}\Leftrightarrow \begin{cases}\left[\begin{array}{l}x=2\pi k, \\ x=\pm\frac{2\pi}{3}+2\pi n,\end{array} \\ \sin x >0\right.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-20bc473770ab6419cd1a45ba72b7178f_l3.png)
Тригонометрическая функция синус положительна в первой и второй координатной четвертях, поэтому из полученных серий выбираем только эту: 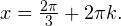
Раз уж мы с этим столкнулись, не лишним будет повторить, какие знаки принимают тригонометрические функций в различных координатных четвертях:
Знаки функций, входящих в тригонометрические уравнения, по координатным четвертям
Ответ: 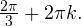
Задача для самостоятельного решения №6. Решите уравнение: 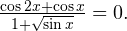
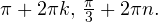 Пример 7. Решите уравнение:
Пример 7. Решите уравнение: 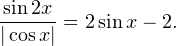
Решение. Область допустимых значения уравнения определяется условием: 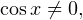 то есть
то есть  Разобьем решение на два случая:
Разобьем решение на два случая:
1) Пусть 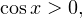 тогда уравнение принимает вид:
тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ \frac{2\sin x\cos x}{\cos x} = 2\sin x-2\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-fe301b6a371887b4ca249562d051d06c_l3.png)
![Rendered by QuickLaTeX.com \[ 2\sin x=2\sin x-2\Leftrightarrow 0=-2. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-89fc402230aca1d5d103f2eba93d497e_l3.png)
Последнее равенство неверно, поэтому в данном случае решений у уравнения не будет.
2) Пусть 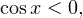 тогда уравнение принимает вид:
тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ -\frac{2\sin x\cos x}{\cos x} = 2\sin x-2\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-8bd35cba0d719a8226b8f9034ef98024_l3.png)
![Rendered by QuickLaTeX.com \[ \sin x = \frac{1}{2}\Leftrightarrow \left[\begin{array}{l}x = \frac{\pi}{6}+2\pi k, \\ x=\frac{5\pi}{6}+2\pi n.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-217ffb2b7eeca2a312b56ee28296fa3a_l3.png)
Условию 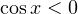 удовлетворяет только последняя серия.
удовлетворяет только последняя серия.
Ответ: 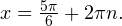
Задача для самостоятельного решения №7. Решите уравнение: 
ЕГЭ по математике 2012 позади, все в ожидании результатов, которые обещали объявить во вторник 19 июня. Сейчас уже поздно желать высоких баллов на экзаменах нынешним выпускникам. Но вот пожелать успехов сегодняшним десятиклассникам я возможности не упущу. Удачи вам в подготовке и помните, что чем раньше она начнется, тем лучше будут результаты на экзамене.

Репетитор математики
Сергей Валерьевич
P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.
yourtutor.info
Тригонометрические уравнения 1
В этой статье будут рассмотрены тригонометрические уравнения с корнями. Прежде чем приступить к решению, вспомним, когда появляется опасность потерять корни или приобрести посторонние. Итак:
При решении тригонометрических уравнений могут появиться посторонние корни, если:
1) Уравнение содержит тангенс или котангенс;
2) Обе части уравнения умножаются или делятся на выражение, содержащее неизвестное;
3) Обе части уравнения возводятся в квадрат.
При решении тригонометрических уравнений могут быть потеряны корни, если:
1) Обе части уравнения умножаются или делятся на выражение, содержащее неизвестное;
2) Используются тригонометрические формулы, которые справедливы не при всех значениях неизвестного;
3) При решении системы тригонометрических уравнений для обозначения целого числа в найденных значениях x и y используется только одна буква.
Теперь можно начать решение.
Задача 1. Решить уравнение: 
Возводим обе части уравнения в квадрат:

Разложим формулу  , и представим единицу как сумму квадрата синуса и квадрата косинуса:
, и представим единицу как сумму квадрата синуса и квадрата косинуса:

Сгруппируем слагаемые:

Видим, что в первой скобке – квадрат суммы:


Приравниваем к нулю каждый множитель и решаем два получившихся уравнения:
Первое: 


При возведении в квадрат:




Заметим, что по решению синус и косинус равны по модулю, но разные по знаку. В этом варианте решения в исходном уравнении слева под корнем окажется величина отрицательная, значит, это – посторонние корни, поэтому мы даже не будем их записывать. Приобрели мы посторонние корни в результате возведения уравнения квадрат.
Второе: 


Возводим в квадрат:




Снова уравнение распалось на два:
 – это посторонний корень, который приведет к появлению в исходном уравнении корня из отрицательного числа в правой части.
– это посторонний корень, который приведет к появлению в исходном уравнении корня из отрицательного числа в правой части.
 или
или  – данный корень тоже содержит посторонние корни, которые также приобретены в результате возведения уравнения в квадрат. При синусе, равном нулю, косинус может быть равен как 1, так и (-1). Второе – недопустимо: в этом случае в правой части исходного уравнения – отрицательное число под корнем. Поэтому решение у уравнения всего одно:
– данный корень тоже содержит посторонние корни, которые также приобретены в результате возведения уравнения в квадрат. При синусе, равном нулю, косинус может быть равен как 1, так и (-1). Второе – недопустимо: в этом случае в правой части исходного уравнения – отрицательное число под корнем. Поэтому решение у уравнения всего одно:  .
.
Задача 2. Решить уравнение: 
Возводим обе части уравнения в квадрат:

Косинус двойного аргумента заменяем, также от синуса переходим к косинусу с помощью основного тригонометрического тождества:



Вводим замену:


Корни: 
Обратная замена:
 или
или 
Решения: 
Проверка показывает, что все корни удовлетворяют исходному уравнению.
Задача 3. Решить уравнение: 
Чтобы избавиться от корня, возведем в квадрат:


Домножим на 2 для удобства:


Произведем перегруппировку:



 или
или 
Первое:


При возведении в квадрат:




Так как правая часть уравнения должна быть неотрицательной, и, кроме того, синус и косинус – разных знаков, то решение одно:

Второе:

Так как решения уравнения  не являются решениями исходного уравнения, то деление на
не являются решениями исходного уравнения, то деление на  не приведет к потере корней, тогда разделим на
не приведет к потере корней, тогда разделим на  :
:


Решением этого уравнения является угол, синус и косинус которого имеют разные знаки. При этом угол в четвертом квадранте нам не подойдет: у такого угла отрицательный синус и положительный косинус, а это противоречит исходному уравнению: приведет к отрицательному значению операции извлечения корня. Угол во втором квадранте нас устроит.

Ответ:  ,
, 
Задача 4. Решить уравнение: 
Сразу делаем вывод, что полученный нами далее в ходе решения  должен быть неположительным , иначе результат извлечения корня не будет положительным.
должен быть неположительным , иначе результат извлечения корня не будет положительным.
Возводим все уравнение в квадрат, чтобы избавиться от корня:

Раскрываем формулу двойного аргумента и заменяем синусы на косинусы:

Получили квадратное уравнение относительно косинусов:

 или
или  – очевидно, что решение второго – пустое множество.
– очевидно, что решение второго – пустое множество.
С учетом того, что синус должен быть отрицателен (или равен нулю), решение единственное:
Ответ:  .
.
Задача 5. Решить уравнение: 
Полученный в ходе решения косинус может быть или отрицательным числом, или нулем.
Возводим уравнение в квадрат:

Формулу тройного аргумента раскроем:



 или
или  – сумма коэффициентов уравнения равна 0, поэтому первый корень – 1, а второй – с/a – (-1/2)
– сумма коэффициентов уравнения равна 0, поэтому первый корень – 1, а второй – с/a – (-1/2)
Итак, имеем:  , или
, или  , или
, или
Решения первого уравнения:

Решения второго уравнения:
 – не являются решениями исходного уравнения, так как косинус должен быть отрицателен.
– не являются решениями исходного уравнения, так как косинус должен быть отрицателен.
Решения третьего:

Ответ:  ,
, 
Задача 6. Решить уравнение: 
Замечаем, что синус должен быть неотрицательным числом, так как слева – корень.
Возводим в квадрат:

Раскроем формулу тройного аргумента:

Домножим на 3 для удобства:


Приравняем к нулю оба множителя:
 или
или 

Решаем теперь второе, квадратное, уравнение:


Корни получаются такие: 2/3 и (-3/4) – последний корень не подходит по ОДЗ, так как результат извлечения корня не может быть отрицательным.
Второму корню будет соответствовать решение:
 и
и  , эти два решения можно объединить в одно и записать:
, эти два решения можно объединить в одно и записать: 
Ответ:  ,
,  .
.
easy-physic.ru
Формулы для решения простейших тригонометрических уравнений
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Содержание статьи:
Простейшие тригонометрические уравнения
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| \leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + \pi n, n \in Z`

Таблица арксинусов
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`

Таблица арккосинусов
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`

Таблица арктангенсов
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`

Таблица арккотангенсов
Формулы корней тригонометрических уравнений в таблице
Для синуса: Для косинуса:
Для косинуса: Для тангенса и котангенса:
Для тангенса и котангенса: Формулы решения уравнений, содержащих обратные тригонометрические функции:
Формулы решения уравнений, содержащих обратные тригонометрические функции:

Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью тригонометрических формул преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 — x)+1=0`
Решение. Используя формулы приведения, имеем:
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
делаем замену: `cos(x+\frac \pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Ответ: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n`, `x_2=\pi/2+ 2\pi n`.
Ответ: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x \ne 0` — для первого случая, и на `cos^2 x \ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x \ne 0`, получим:
`\frac {sin^2 x}{cos^2 x}+\frac{sin x cos x}{cos^2 x} — \frac{2 cos^2 x}{cos^2 x}=0`
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.
Ответ. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Ответ. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt {a^2+b^2}`:
`\frac a{sqrt {a^2+b^2}} sin x +` `\frac b{sqrt {a^2+b^2}} cos x =` `\frac c{sqrt {a^2+b^2}}`.
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `\frac a{sqrt {a^2+b^2}}=cos \varphi`, ` \frac b{sqrt {a^2+b^2}} =sin \varphi`, `\frac c{sqrt {a^2+b^2}}=C`, тогда:
`cos \varphi sin x + sin \varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt {3^2+4^2}`, получим:
`\frac {3 sin x} {sqrt {3^2+4^2}}+` `\frac{4 cos x}{sqrt {3^2+4^2}}=` `\frac 2{sqrt {3^2+4^2}}`
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos \varphi` , `4/5=sin \varphi`. Так как `sin \varphi>0`, `cos \varphi>0`, то в качестве вспомогательного угла возьмем `\varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos \varphi sin x+sin \varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`sin (x+\varphi)=2/5`,
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `\frac {sin x}{1+cos x}=1-cos x`.
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
`\frac {sin x}{1+cos x}=` `\frac {(1-cos x)(1+cos x)}{1+cos x}`
`\frac {sin x}{1+cos x}=` `\frac {1-cos^2 x}{1+cos x}`
`\frac {sin x}{1+cos x}=` `\frac {sin^2 x}{1+cos x}`
`\frac {sin x}{1+cos x}-` `\frac {sin^2 x}{1+cos x}=0`
`\frac {sin x-sin^2 x}{1+cos x}=0`
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Материалы по теме:
Поделиться с друзьями:
 Загрузка…
Загрузка…matemonline.com
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Тригонометрия

Простейшими тригонометрическими уравнениями называют уравнения вида:
sin x = a , cos x = a ,
tg x = a , ctgx = a .
где a – произвольное число.
Решение уравнения sin x = a
| Обычная форма записи решения |  |
| Более удобная форма записи решения | 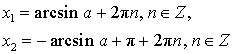 |
| Ограничения на число a | В случае, когда  , ,уравнение решений не имеет |
Обычная форма записи решения:

Более удобная форма записи решения:
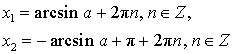
Ограничения на число a:
В случае, когда  , уравнение решений не имеет.
, уравнение решений не имеет.
Графическое обоснование решения уравнения sin x = a представлено на рисунке 1
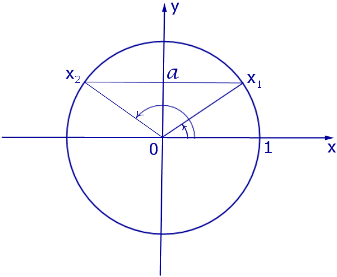

Рис. 1
Частные случаи решения уравнений sin x = a
Уравнение: sin x = – 1 Решение: 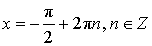 |
Уравнение: 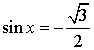 Решение:  |
Уравнение:  Решение:  |
Уравнение: 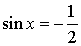 Решение: >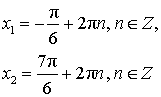 |
Уравнение: sin x = 0 Решение: 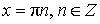 |
Уравнение: 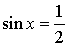 Решение: 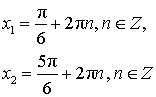 |
Уравнение: 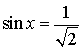 Решение: 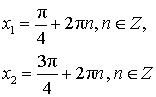 |
Уравнение: 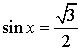 Решение: 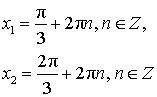 |
Уравнение: sin x = 1 Решение:  |
Решение уравнения cos x = a
| Обычная форма записи решения | 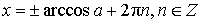 |
| Более удобная форма записи решения | 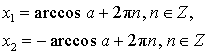 |
| Ограничения на число a | В случае, когда  , ,уравнение решений не имеет |
Обычная форма записи решения:
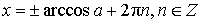
Более удобная форма записи решения:
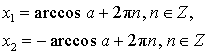
Ограничения на число a
В случае, когда  , уравнение решений не имеет.
, уравнение решений не имеет.
Графическое обоснование решения уравнения cos x = a представлено на рисунке 2

Рис. 2
Частные случаи решения уравнений cos x = a
Уравнение: cos x = – 1 Решение:  |
Уравнение:  Решение:  |
Уравнение: 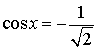 Решение: 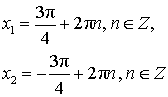 |
Уравнение: 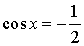 Решение:  |
Уравнение: cos x = 0 Решение: 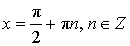 |
Уравнение:  Решение:  |
Уравнение: 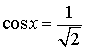 Решение:  |
Уравнение:  Решение: 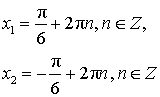 |
Уравнение: cos x = 1 Решение: 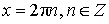 |
Решение уравнения tg x = a
| Обычная форма записи решения: | 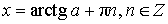 |
| Более удобная форма записи решения |  |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:
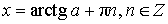
Более удобная форма записи решения:

Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.

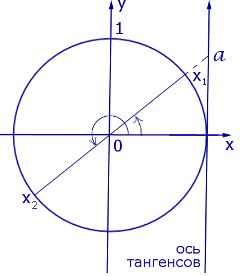
Рис. 3
Частные случаи решения уравнений tg x = a
Уравнение: 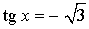 Решение: 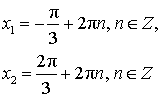 |
Уравнение: tg x = – 1 Решение: 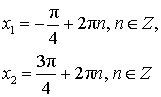 |
Уравнение: 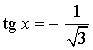 Решение:  |
Уравнение: tg x = 0 Решение: 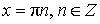 |
Уравнение: 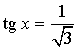 Решение:  |
Уравнение: tg x = 1 Решение: 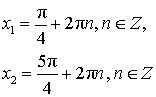 |
Уравнение: 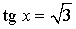 Решение: 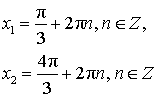 |
Решение уравнения ctg x = a
| Обычная форма записи решения |  |
| Более удобная форма записи решения | 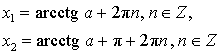 |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:

Более удобная форма записи решения:
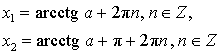
Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения ctg x = a представлено на рисунке 4.
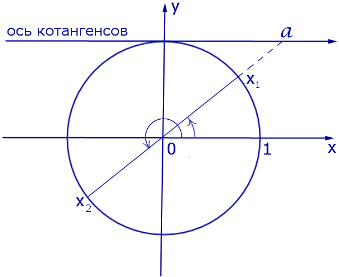
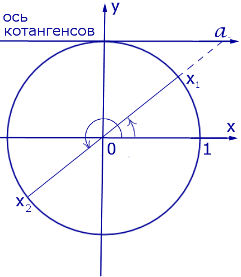
Рис. 4
Частные случаи решения уравнений ctg x = a
Уравнение:  Решение:  |
Уравнение: ctg x = – 1 Решение: 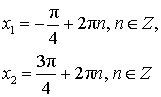 |
Уравнение:  Решение: 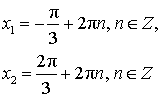 |
Уравнение: ctg x = 0 Решение: 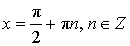 |
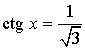 Решение: 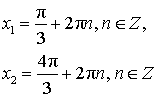 |
Уравнение: ctg x = 1 Решение: 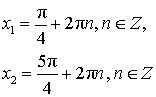 |
Уравнение: 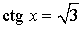 Решение:  |

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
www.resolventa.ru
Основные виды тригонометрических уравнений
Рассмотрим некоторые наиболее часто встречающиеся виды тригонометрических уравнений и способы их решения.
\(\blacktriangleright\) Квадратные тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: \[{\Large{af^2(x)+bf(x)+c=0}}\] где \(a\ne 0, \ f(x)\) — одна из функций \(\sin x, \cos
x, \mathrm{tg}\,x, \mathrm{ctg}\, x\),
то такое уравнение с помощью замены \(f(x)=t\) сводится к квадратному уравнению.
Часто при решении таких уравнений используются
основные тождества: \[\begin{array}{|ccc|}
\hline \sin^2 \alpha+\cos^2 \alpha =1&& \mathrm{tg}\, \alpha \cdot
\mathrm{ctg}\, \alpha
=1\\ &&\\
\mathrm{tg}\, \alpha=\dfrac{\sin \alpha}{\cos
\alpha}&&\mathrm{ctg}\, \alpha
=\dfrac{\cos \alpha}{\sin \alpha}\\&&\\
1+\mathrm{tg}^2\, \alpha =\dfrac1{\cos^2 \alpha} && 1+\mathrm{ctg}^2\, \alpha=\dfrac1{\sin^2 \alpha}\\&&\\
\hline
\end{array}\]
формулы двойного угла: \[\begin{array}{|lc|cr|}
\hline \sin {2\alpha}=2\sin \alpha\cos \alpha & \qquad &\qquad & \cos{2\alpha}=\cos^2\alpha -\sin^2\alpha\\
\sin \alpha\cos \alpha =\dfrac12\sin {2\alpha} && & \cos{2\alpha}=2\cos^2\alpha -1\\
& & & \cos{2\alpha}=1-2\sin^2 \alpha\\
\hline &&&\\
\mathrm{tg}\, 2\alpha = \dfrac{2\mathrm{tg}\,
\alpha}{1-\mathrm{tg}^2\, \alpha} && & \mathrm{ctg}\, 2\alpha
= \dfrac{\mathrm{ctg}^2\, \alpha-1}{2\mathrm{ctg}\, \alpha}\\&&&\\
\hline
\end{array}\]
Пример 1. Решить уравнение \(6\cos^2x-13\sin x-13=0\)
С помощью формулы \(\cos^2\alpha=1-\sin^2\alpha\) уравнение сводится к виду:
\(6\sin^2x+13\sin x+7=0\). Сделаем замену \(t=\sin x\). Т.к. область значений синуса \(\sin x\in [-1;1]\), то \(t\in[-1;1]\). Получим уравнение:
\(6t^2+13t+7=0\). Корни данного уравнения \(t_1=-\dfrac76, \ t_2=-1\).
Таким образом, корень \(t_1\) не подходит. Сделаем обратную замену:
\(\sin x=-1 \Rightarrow x=-\dfrac{\pi}2+2\pi n, n\in\mathbb{Z}\).
Пример 2. Решить уравнение \(5\sin 2x=\cos 4x-3\)
С помощью формулы двойного угла для косинуса \(\cos
2\alpha=1-2\sin^2\alpha\) имеем:
\(\cos4x=1-2\sin^22x\). Сделаем эту подстановку и получим:
\(2\sin^22x+5\sin 2x+2=0\). Сделаем замену \(t=\sin 2x\). Т.к. область значений синуса \(\sin 2x\in [-1;1]\), то \(t\in[-1;1]\). Получим уравнение:
\(2t^2+5t+2=0\). Корни данного уравнения \(t_1=-2, \ t_2=-\dfrac12\).
Таким образом, корень \(t_1\) не подходит. Сделаем обратную замену: \(\sin 2x=-\dfrac12 \Rightarrow x_1=-\dfrac{\pi}{12}+\pi n, \ x_2=-\dfrac{5\pi}{12}+\pi n, n\in\mathbb{Z}\).
Пример 3. Решить уравнение \(\mathrm{tg}\, x+3\mathrm{ctg}\,x+4=0\)
Т.к. \(\mathrm{tg}\,x\cdot \mathrm{ctg}\,x=1\), то \(\mathrm{ctg}\,x=\dfrac1{\mathrm{tg}\,x}\). Сделаем замену \(\mathrm{tg}\,x=t\). Т.к. область значений тангенса \(\mathrm{tg}\,x\in\mathbb{R}\), то \(t\in\mathbb{R}\). Получим уравнение:
\(t+\dfrac3t+4=0 \Rightarrow \dfrac{t^2+4t+3}{t}=0\). Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. Таким образом:
\(\begin{cases} t^2+4t+3=0\\t\ne 0 \end{cases} \Rightarrow \left[\begin{gathered} \begin{aligned} &t_1=-3\\&t_2=-1 \end{aligned}\end{gathered}\right.\)
Сделаем обратную замену:
\(\left[\begin{gathered} \begin{aligned} &\mathrm{tg}\,x=-3\\ &\mathrm{tg}\,x=-1 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=-\mathrm{arctg}\,3+\pi n\\ &x=-\dfrac{\pi}4+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)
\(\blacktriangleright\) Кубические тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: \[{\Large{af^3(x)+bf^2(x)+cf(x)+d=0}}\] где \(a\ne 0, \ f(x)\) — одна из функций \(\sin x, \cos
x, \mathrm{tg}\,x, \mathrm{ctg}\, x\),
то такое уравнение с помощью замены \(f(x)=t\) сводится к кубическому уравнению.
Часто при решении таких уравнений в дополнение к предыдущим формулам используются
формулы тройного угла: \[\begin{array}{|lc|cr|}
\hline &&&\\
\sin {3\alpha}=3\sin \alpha -4\sin^3\alpha &&&
\cos{3\alpha}=4\cos^3\alpha -3\cos \alpha\\&&&\\ \hline
\end{array}\]
Пример 4. Решить уравнение \(11\cos 2x-3=3\sin 3x-11\sin x\)
При помощи формул \(\sin 3x=3\sin x-4\sin^3x\) и \(\cos2x=1-2\sin^2x\) можно свести уравнение к уравнению только с \(\sin x\):
\(12\sin^3x-9\sin x+11\sin x-3+11-22\sin^2 x=0\). Сделаем замену \(\sin x=t, \ t\in[-1;1]\):
\(6t^3-11t^2+t+4=0\). Подбором находим, что один из корней равен \(t_1=1\). Выполнив деление в столбик многочлена \(6t^3-11t^2+t+4\) на \(t-1\), получим:
\((t-1)(2t+1)(3t-4)=0 \Rightarrow\) корнями являются \(t_1=1, \ t_2=-\dfrac12, \ t_3=\dfrac43\).
Таким образом, корень \(t_3\) не подходит. Сделаем обратную замену:
\(\left[\begin{gathered} \begin{aligned} &\sin x=1\\&\sin x=-\dfrac12 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=\dfrac{\pi}2+2\pi n\\[1ex]&x=-\dfrac{\pi}6+2\pi n\\[1ex] &x=-\dfrac{5\pi}6+2\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)
\(\blacktriangleright\) Однородные тригонометрические уравнения второй степени: \[I. \quad {\Large{a\sin^2x+b\sin x\cos x+c\cos^2x=0}}, \quad a\ne 0,c\ne 0\]
Заметим, что в данном уравнении никогда не являются решениями те значения \(x\), при которых \(\cos x=0\) или \(\sin x=0\). Действительно, если \(\cos x=0\), то, подставив вместо косинуса ноль в уравнение, получим: \(a\sin^2 x=0\), откуда следует, что и \(\sin x=0\). Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если \(\cos x=0\), то \(\sin x=\pm 1\).
Аналогично и \(\sin x=0\) не является решением такого уравнения.
Значит, данное уравнение можно делить на \(\cos^2 x\) или на \(\sin^2 x\). Разделим, например, на \(\cos^2 x\):
\(a \ \dfrac{\sin^2x}{\cos^2x}+b \ \dfrac{\sin x\cos x}{\cos^2x}+c \ \dfrac{\cos^2x}{\cos^2x}=0 \Leftrightarrow a\mathrm{tg}^2\,x+b\mathrm{tg}\,x+c=0\)
Таким образом, данное уравнение при помощи деления на \(\cos^2x\) и замены \(t=\mathrm{tg}\,x\) сводится к квадратному уравнению:
\(at^2+bt+c=0\), способ решения которого вам известен.
Уравнения вида \[I’. \quad {\Large{a\sin^2x+b\sin x\cos x+c\cos^2x=d}}, \quad a\ne0,c\ne 0\] с легкостью сводятся к уравнению вида \(I\) с помощью использования основного тригонометрического тождества: \[d=d\cdot 1=d\cdot (\sin^2x+\cos^2x)\]
Заметим, что благодаря формуле \(\sin2x=2\sin x\cos x\) однородное уравнение можно записать в виде
\(a\sin^2 x+b\sin 2x+c\cos^2x=0\)
Пример 5. Решить уравнение \(2\sin^2x+3\sin x\cos x=3\cos^2x+1\)
Подставим вместо \(1=\sin^2x+\cos^2x\) и получим:
\(\sin^2x+3\sin x\cos x-4\cos^2x=0\). Разделим данное уравнение на \(\cos^2x\):
\(\mathrm{tg}^2\,x+3\mathrm{tg}\,x-4=0\) и сделаем замену \(t=\mathrm{tg}\,x, \ t\in\mathbb{R}\). Уравнение примет вид:
\(t^2+3t-4=0\). Корнями являются \(t_1=-4, \ t_2=1\). Сделаем обратную замену:
\(\left[\begin{gathered} \begin{aligned} &\mathrm{tg}\,x=1\\&\mathrm{tg}\,x=-4 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=\dfrac{\pi}4+\pi n\\[1ex]&x=-\mathrm{arctg}\,4+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)
\(\blacktriangleright\) Однородные тригонометрические уравнения первой степени: \[II.\quad {\Large{a\sin x+b\cos x=0}}, a\ne0, b\ne 0\]
Заметим, что в данном уравнении никогда не являются решениями те значения \(x\), при которых \(\cos x=0\) или \(\sin x=0\). Действительно, если \(\cos x=0\), то, подставив вместо косинуса ноль в уравнение, получим: \(a\sin x=0\), откуда следует, что и \(\sin x=0\). Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если \(\cos x=0\), то \(\sin x=\pm 1\).
Аналогично и \(\sin x=0\) не является решением такого уравнения.
Значит, данное уравнение можно делить на \(\cos x\) или на \(\sin x\). Разделим, например, на \(\cos x\):
\(a \ \dfrac{\sin x}{\cos x}+b \ \dfrac{\cos x}{\cos x}=0\), откуда имеем \(a\mathrm{tg}\, x+b=0 \Rightarrow \mathrm{tg}\, x=-\dfrac ba\)
Пример 6. Решить уравнение \(\sin x+\cos x=0\)
Разделим правую и левую части уравнения на \(\sin x\):
\(1+\mathrm{ctg}\, x=0 \Rightarrow \mathrm{ctg}\, x=-1 \Rightarrow x=-\dfrac{\pi}4+\pi n, n\in\mathbb{Z}\)
\(\blacktriangleright\) Неоднородные тригонометрические уравнения первой степени: \[II.\quad {\Large{a\sin x+b\cos x=c}}, a\ne0, b\ne 0, c\ne 0\]
Существует несколько способов решения подобных уравнений. Рассмотрим те из них, которые можно использовать для любого такого уравнения:
1 СПОСОБ: при помощи формул двойного угла для синуса и косинуса и основного тригонометрического тождества: \({\large{\sin x=2\sin{\dfrac x2}\cos{\dfrac x2}, \qquad \cos x=\cos^2 {\dfrac x2}-\sin^2 {\dfrac x2},\qquad c=c\cdot \Big(\sin^2 {\dfrac x2}+\cos^2 {\dfrac x2}\Big)}}\) данное уравнение сведется к уравнению \(I\):
Пример 7. Решить уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)
Распишем \(\sin 2x=2\sin x\cos x, \ \cos 2x=\cos^2x-\sin^2 x, \ -1=-\sin^2 x-\cos^2x\). Тогда уравнение примет вид:
\((1+\sqrt3)\sin^2x+2\sin x\cos x+(1-\sqrt3)\cos^2x=0\). Данное уравнение с помощью деления на \(\cos^2x\) и замены \(\mathrm{tg}\,x=t\) сводится к:
\((1+\sqrt3)t^2+2t+1-\sqrt3=0\). Корнями этого уравнения являются \(t_1=-1, \ t_2=\dfrac{\sqrt3-1}{\sqrt3+1}=2-\sqrt3\). Сделаем обратную замену:
\(\left[ \begin{gathered} \begin{aligned}&\mathrm{tg}\,x=-1\\ &\mathrm{tg}\,x=2-\sqrt3 \end{aligned}\end{gathered}\right. \Rightarrow \left[ \begin{gathered} \begin{aligned} &x=-\dfrac{\pi}4+\pi n\\[1ex] &x=\mathrm{arctg}\,(2-\sqrt3)+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)
2 СПОСОБ: при помощи формул выражения функций через тангенс половинного угла: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin{\alpha}=\dfrac{2\mathrm{tg}\, \dfrac{\alpha}2}{1+\mathrm{tg}^2\, \dfrac{\alpha}2} &&& \cos{\alpha}=\dfrac{1-\mathrm{tg}^2\, \dfrac{\alpha}2}{1+\mathrm{tg}^2\, \dfrac{\alpha}2}\\&&&\\ \hline \end{array}\] уравнение сведется к квадратному уравнению относительно \(\mathrm{tg}\, \dfrac x2\)
Пример 8. Решить то же уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)
Сделаем подстановку \(\sin 2x=\dfrac{2\mathrm{tg}\,x}{1+\mathrm{tg}^2\,x}, \ \cos2x=\dfrac{1-\mathrm{tg}^2\,x}{1+\mathrm{tg}^2\,x}\) и замену \(\mathrm{tg}\,x=t\):
\(\dfrac{(\sqrt3+1)t^2+2t+1-\sqrt3}{1+t^2}=0 \Rightarrow (\sqrt3+1)t^2+2t+1-\sqrt3=0\) (т.к. \(1+t^2\geqslant 1\) при всех \(t\), то есть всегда \(\ne 0\))
Таким образом, мы получили то же уравнение, что и, решая первым способом.
3 СПОСОБ: при помощи формулы вспомогательного угла.
\[{\large{a\sin x+b\cos x=\sqrt{a^2+b^2}\,\sin (x+\phi),}} \quad \text{где } \cos \phi=\dfrac
a{\sqrt{a^2+b^2}}\]
Для использования данной формулы нам понадобятся формулы сложения углов: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin{(\alpha\pm \beta)}=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha &&& \cos{(\alpha\pm \beta)}=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &&&\\ \hline \end{array}\]
Пример 9. Решить то же уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)
Т.к. мы решаем уравнение, то можно не преобразовывать левую часть, а просто разделить обе части уравнения на \(\sqrt{1^2+(-\sqrt3)^2}=2\):
\(\dfrac12\sin 2x-\dfrac{\sqrt3}2\cos 2x=-\dfrac12\)
Заметим, что числа \(\dfrac12\) и \(\dfrac{\sqrt3}2\) получились табличные. Можно, например, взять за \(\dfrac12=\cos \dfrac{\pi}3, \ \dfrac{\sqrt3}2=\sin \dfrac{\pi}3\). Тогда уравнение примет вид:
\(\sin 2x\cos \dfrac{\pi}3-\sin \dfrac{\pi}3\cos 2x=-\dfrac12 \Rightarrow \sin\left(2x-\dfrac{\pi}3\right)=-\dfrac12\)
Решениями данного уравнения являются:
\(\left[ \begin{gathered} \begin{aligned} &2x-\dfrac{\pi}3=-\dfrac{\pi}6+2\pi n\\[1.5ex] &2x-\dfrac{\pi}3=-\dfrac{5\pi}6+2\pi n \end{aligned} \end{gathered} \right. \Rightarrow \left[ \begin{gathered} \begin{aligned} &x=\dfrac{\pi}{12}+\pi n\\[1.5ex] &x=-\dfrac{\pi}4+\pi n \end{aligned} \end{gathered} \right. \ \ n\in\mathbb{Z}\)
Заметим, что при решении уравнения третьим способом мы добились “более красивого” ответа (хотя ответы, естественно, одинаковы), чем при решении первым или вторым способом (которые, по сути, приводят уравнение к одному и тому же виду).
Таким образом, не стоит пренебрегать третьим способом решения данного уравнения.
\(\blacktriangleright\) Если тригонометрическое уравнение можно свести к виду \[{\Large{a(\sin x\pm \cos x)+b\sin x\cos x+c=0}}, \text{где } a\ne 0, b\ne 0,\] то с помощью формулы \[{\large{(\sin x\pm\cos x)^2=1\pm2\sin x\cos x}} \ \ (*)\] данное уравнение можно свести к квадратному.
Для этого необходимо сделать замену \(t=\sin x\pm \cos x\), тогда \(\sin x\cos x=\pm \dfrac{t^2-1}2\).
Заметим, что формула \((*)\) есть не что иное, как формула сокращенного умножения \((A\pm B)^2=A^2\pm 2AB+B^2\) при подстановке в нее \(A=\sin x, B=\cos x\).
Пример 10. Решить уравнение \(3\sin 2x+3\cos 2x=16\sin x\cos^3x-8\sin x\cos x\).
Вынесем общий множитель за скобки в правой части: \(3\sin 2x+3\cos
2x=8\sin x\cos x(2\cos^2 x-1)\).
По формулам двойного угла \(2\sin x\cos x=\sin 2x, 2\cos^2x-1=\cos
2x\) имеем: \[3(\sin 2x+\cos 2x)=4\sin 2x\cos 2x\] Заметим, что полученное уравнение как раз записано в необходимом нам виде. Сделаем замену \(t=\sin 2x+\cos 2x\), тогда \(\sin 2x\cos
2x=\dfrac{t^2-1}2\). Тогда уравнение примет вид: \[3t=2t^2-2 \Rightarrow 2t^2-3t-2=0\] Корнями данного уравнения являются \(t_1=2, t_2=-\dfrac12\).
По формулам вспомогательного аргумента \(\sin2x+\cos
2x=\sqrt2\sin\left(2x+\dfrac{\pi}4\right)\), следовательно, сделав обратную замену: \[\left[ \begin{gathered} \begin{aligned}
&\sqrt2\sin\left(2x+\dfrac{\pi}4\right)=2\\[1ex]
&\sqrt2\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac12 \end{aligned}
\end{gathered} \right. \Rightarrow
\left[ \begin{gathered} \begin{aligned}
&\sin\left(2x+\dfrac{\pi}4\right)=\sqrt2\\[1ex]
&\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac1{2\sqrt2} \end{aligned}
\end{gathered} \right.\] Первое уравнение корней не имеет, т.к. область значений синуса находится в пределах от \(-1\) до \(1\). Значит: \(\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac1{2\sqrt2} \Rightarrow
\left[ \begin{gathered} \begin{aligned}
&2x+\dfrac{\pi}4=-\arcsin {\dfrac1{2\sqrt2}}+2\pi n\\[1ex]
&2x+\dfrac{\pi}4=\pi+\arcsin {\dfrac1{2\sqrt2}}+2\pi n
\end{aligned}
\end{gathered} \right. \Rightarrow \)
\(\Rightarrow \left[ \begin{gathered} \begin{aligned}
&x=-\dfrac12\arcsin {\dfrac1{2\sqrt2}}-\dfrac{\pi}8+\pi n\\[1ex]
&x=\dfrac{3\pi}8+\dfrac12\arcsin {\dfrac1{2\sqrt2}}+\pi n
\end{aligned}
\end{gathered} \right. \ \ n\in\mathbb{Z}\)
\(\blacktriangleright\) Формулы сокращенного умножения в тригонометрическом варианте:
\(I\) Квадрат суммы или разности \((A\pm B)^2=A^2\pm 2AB+B^2\):
\((\sin x\pm \cos x)^2=\sin^2 x\pm 2\sin x\cos x+\cos^2x=(\sin^2 x+\cos^2 x)\pm 2\sin x\cos x=1\pm \sin 2x\)
\(II\) Разность квадратов \(A^2-B^2=(A-B)(A+B)\):
\((\cos x-\sin x)(\cos x+\sin x)=\cos^2x-\sin^2x=\cos 2x\)
\(\sin^2x-\cos^2x=-\cos2x\)
\(III\) Сумма или разность кубов \(A^3\pm B^3=(A\pm B)(A^2\mp AB+B^2)\):
\(\sin^3x\pm \cos^3x=(\sin x\pm \cos x)(\sin^2x\mp \sin x\cos x+\cos^2x)=(\sin x\pm \cos x)(1\mp \sin x\cos x)=\)
\(=(\sin x\pm \cos x)(1\mp \frac12\sin 2x)\)
\(IV\) Куб суммы или разности \((A\pm B)^3=A^3\pm B^3\pm 3AB(A\pm B)\):
\((\sin x\pm \cos x)^3=(\sin x\pm \cos x)(\sin x\pm \cos x)^2=(\sin x\pm \cos x)(1\pm \sin 2x)\) (по первой формуле)
shkolkovo.net
Тригонометрические уравнения и их решение
Простейшие тригонометрические уравнения
К простейшим тригонометрическим уравнениям относятся уравнения вида
Рассмотрим подробнее каждое из этих уравнений и их решение.
Уравнение вида . При и уравнение корней не имеет. При , корни этого уравнения находятся по формуле
Особые случаи:
Уравнение вида . При и уравнение корней не имеет. При , корни этого уравнения находятся по формуле
Особые случаи:
Замечание. .
Уравнение вида . Корни этого уравнения находятся по формуле
Уравнение вида . Корни этого уравнения находятся по формуле
Тригонометрические уравнения, приводящиеся к квадратным уравнениям
Это тригонометрические уравнения, которые после замены тригонометрической функции, которая входит в уравнение, становится квадратным.
Уравнение вида, где . Такие уравнения решают с помощью введения дополнительного угла. Считая, что , поделим обе части исходного уравнения на , получим
Для полученных коэффициентов при синусе и косинусе справедливы следующие соотношения
Тогда можно утверждать, что существует угол , такой что, например
Таким образом, последнее уравнение примет вид
По формуле суммы для тригонометрических функций, последнее уравнение сводится к простейшему тригонометрическому уравнению
откуда достаточно легко найти x.
Однородные тригонометрические уравнения
Однородные тригонометрические уравнения – это уравнения вида
где – действительные числа, . Такое уравнение легко приводится к уравнению относительно , если все его члены поделить на . При этом, если , то деление не приведет к потере корней. Действительно, если , то первоначальное уравнение примет вид , откуда , что не возможно, так как и одновременно не могут быть равны нулю.
Дробно-рациональные тригонометрические уравнения
Основной сложностью решения таких уравнений является отбор корней уравнения для формирования ответа.
ru.solverbook.com
Отбор корней в тригонометрических уравнениях
Отбор корней в тригонометрических уравненияхПрактика приемных экзаменов в вузы показывает, что при решении тригонометрических уравнений абитуриенты нередко затрудняются как в выборе способа решения уравнения, так и при отборе его корней.
Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений специфична. Лишние корни могут появиться вследствие того, что в процессе решения произошло расширение области определения уравнения. Запись ответа тригонометрического уравнения часто связана с понятиями объединения и пересечения множеств. Обычно при решении таких уравнений получают серии корней, и в окончательном варианте ответ записывают в виде объединения этих серий. Но как быть, если эти серии пересекаются? Надо ли исключать повторяющиеся корни решения или этого можно не делать?
С понятием пересечения множеств связан и еще один важный вопрос: в ответе не должно быть значений переменной, при которых выражения в левой или правой частях уравнения не определены. Такие значения надо исключить. Для этого надо уметь находить пересечение различных серий.
В предлагаемой работе на конкретных примерах рассматриваются различные способы и приемы при выборе ответа. Надеемся, что данная работа поможет учителям старших классов и самим учащимся при подготовке к вступительным экзаменам в вузы.
1. Отбор чисел на тригонометрическом круге
Проблему отбора корней, отсеивания лишних корней при решении тригонометрических уравнений часто можно решить с помощью изображения чисел на тригонометрическом круге. В ряде случаев этот прием, на наш взгляд, более наглядный и убедительный.
Пример 1. cos x + cos 2x – cos 3x = 1.
Решение.
cos x – cos 3x – (1 – cos 2x) = 0,
2sin x sin 2x – 2sin2 x = 0,
2sin x (sin 2x – sin x) = 0,
.
Из рис. 1 видно, что серия x3(*) включает в себя один из корней серии x1(·).
Ответ:
Пример 2. tg x + tg 2x – tg 3x = 0.
Решение.
Серия x2(*) не удовлетворяет ОДЗ (рис. 2). Серия x1(o) входит в серию x3(·), поэтому ответ можно записать одной формулой:
Пример 3.
Решение.
sin 4x cos x + sin 2x cos 7x = 0,
sin 2x (2cos 2x cos x + cos 7x) = 0,
sin 2x (cos 3x + cos x + cos 7x) = 0,
sin 2x (cos 3x + 2cos 4x cos 3x) = 0,
sin 2x cos 3x (1 + 2cos 4x) = 0,
Объединяя все три серии корней, ответ можно записать так:
Пример 4. sin2 x + sin2 2x = sin2 3x.
Решение.
– (cos 2x + cos 4x) + 1 + cos 6x = 0,
– 2cos 3x cos x + 2cos2 3x = 0,
cos 3x (cos 3x – cos x) = 0,
cos 3x sin 2x sin x = 0,
Серия корней x2 содержится в серии x1 и x3, в чем легко убедиться, изобразив их различными точками на круге, поэтому
ответ:
Пример 5. sin x + sin 7x – cos 5x + cos (3x – 2p) = 0.
Решение.
sin x + sin 7x – cos 5x + cos 3x = 0,
2sin 4x cos 3x + 2sin 4x sin x = 0,
sin 4x (cos 3x + sin x) = 0,
Серия x2 содержится в серии корней x1, а на круге (рис. 4) изобразим точками серии x1(·) и x3(О), которые не совпадают.
Пример 6. ctg 2x + 2ctg x – tg 2x = sin 5x.
Решение.
ОДЗ
Учитывая ОДЗ, получим
Пример 7.
Решение.
Иногда случается, что часть
серии входит в ответ, а часть нет.
Нанесем на тригонометрический круг (рис. 6) все
числа серии
и выбросим корни, удовлетворяющие условию
Оставшиеся решения из серии x1 можно объединить в формулу
2. Отбор корней в тригонометрическом уравнении алгебраическим способом
Изображение корней на тригонометрическом круге не всегда удобно, когда период меньше 2p.
Пример 8. sin2 2x + sin2 3x + sin2 4x + sin2 5x = 2.
Решение.
cos 4x + cos 6x + cos 8x + cos 10x = 0,
2cos 5x cos x + 2cos 9x cos x = 0,
cos x cos 2x cos 7x = 0.
«Период» серий равен p. Рассмотрим те корни из серий x1, x2, x3, которые попадают в промежуток [0; p]. Это будут:
Сразу видно, что серия x1 содержится в серии x3, а серии x2 и x3 не пересекаются. Значит, ответ можно записать в виде .
Способ алгебраический. Общим знаменателем в сериях x1 и x2 будет 4:
Если x1 = x2, то 2 + 4k = 1 + 2l, но слева – четное число, а справа – нечетное. Равенство невозможно, серии x1 и x2 не пересекаются. Аналогично получаем, что серии х3 и х2 тоже не пересекаются, а вот для серий x1 и x3 получаются формулы
Из равенства 7 + 14k = 1 + 2m получаем m = 7k + 3. Это означает, что для всякого k найдется целое m такое, что будет выполняться равенство 7 + 14k = 1 + 2m, т. е. всякий корень из серии x1 встретится и в серии x3, поэтому серия x1 содержится в серии x3, и в ответе писать ее не надо.
При решении некоторых тригонометрических уравнений их заменяют эквивалентной системой уравнений, а затем находят пересечение множеств решений. Эти пересечения часто найти легко. Но иногда для нахождения решений необходимо решать диафантово уравнение (ax + by = c).
Пример 9.
Решение.
В данном случае сделать отбор решений на тригонометрическом круге неудобно, так как периоды серий разные. Найдем такие целые k, при которых x = p + 2pk имеет посторонние корни, удовлетворяющие условию x № 3pn, n О Z. Пусть p + 2pk = 3pn; 1 + 2k = 3n. Отсюда n = 2m + 1 Ю k = 3m + 1. Итак, посторонние корни в серии x = p + 2pk будет при k = 3m + 1, m О Z.
Ответ: {x = p + 2pk, где k № 3m + 1, m О Z} = {x = p + 6pm, x = 3p + 6pm, m О Z}.
Пример 10. cos 7x (sin 5x – 1) = 0.
Решение.
Пересекаются ли эти серии? Из равенства
следует 5k = 14n + 1. Выразим ту неизвестную, коэффициент при которой меньше по абсолютной величине:
– целое число.
Пусть
Ответ можно записать в виде
.
Пример 11.
Решение.
Поскольку наибольшее значение функции y = cos t равно 1, уравнение равносильно системе
Решением уравнения является пересечение серий x1 и x2, т. е. нам надо решить уравнение
Из него получаем уравнение, имеющее решение k = 8t, n = 3t.
Ответ: {8pt, t О Z}.
Пример 12.
Решение.
Решением уравнения является пересечение серий x1 и x2;
,
где – целое число;
Ответ: x = 2p + 8pm, m О Z.
Пример 13.
Решение.
sin 2x sin 4x = sin x (sin 2x + sin 4x),
sin 2x sin 4x = 2sin x sin 3x cos x,
sin 2x sin 4x = sin 2x sin 3x,
sin 2x (sin 4x – sin 3x) = 0,
Остается проверить, лежат ли они в области x О R,
Серию x1 проверить легко: поскольку ,
а при n, кратных 8, n = 8l (l О Z), получается как раз x № 2pl, вся серия x1 исключается. Сложнее обстоит дело с серией x2. Здесь надо выяснить, при каких целых k найдется такое n, что выполняется равенство ,
и исключить такие k. Последнее уравнение приводится к виду 8k + 4 = 7n, причем решать это уравнение надо в целых числах. Из него следует, что n = 4l, поскольку левая часть уравнения делится на 4. Подставляя n = 4l в уравнение, получаем 8k + 4 = 28l, откуда 2k + 1 = 7l. Далее, l должно быть нечетно, l = 2t + 1; поэтому 2k + 1 = 14t + 7, k = 7t + 3. Вот решение и получилось:
k = 7t + 3, n = 4l = 4(2t + 1) = 8t + 4.
Ответ:
3. Отбор корней в тригонометрическом уравнении с некоторыми условиями
Изложенные выше способы отбора корней в тригонометрических уравнениях не всегда применяются в чистом виде: выбор способа зависит от конкретных условий, но иногда эти способы комбинируются.
Пример 14. Найти корни уравнения sin 2x = cos x | cos x |,
удовлетворяющие условию x О [0; 2p].
Решение.
Условию cos x і 0 удовлетворяют
из серии
из серии
Наконец,
Пример 15. Найти все решения уравнения
удовлетворяющие условию
так как то
Ответ: x = 2p + 4pk, k О Z.
Пример 16. Найти все решения уравнения
принадлежащие отрезку .
Решение.
Отметим ОДЗ на тригонометрическом круге (рис. 9):
Отрезку принадлежит только один промежуток из ОДЗ, а именно .
Решим уравнение и выберем корни, принадлежащие этому промежутку:
1 + sin 2x = 2cos2 3x Ю sin 2x = cos 6x,
Из серии при n = 2 имеем
Из серии при n = 5 имеем
Пример 17.
Решение.
а) cos x і 0;
б) cos x < 0;
Ответ:
Пример 18. Найти все корни уравнения
которые удовлетворяют условию .
Решение.
10sin2 x = – cos 2x + 3 Ю 10sin2x = 2sin2 x – 1 + 3,
Выберем корни, удовлетворяющие условию задачи. Из серии
При
при .
Аналогично выберем корни, удовлетворяющие условию задачи, из второй серии. Это будут .
Пример 19.
Решение.
sin x и cos x должны быть одинакового знака, а, учитывая первое неравенство, только при sin x > 0 и cos x > 0 система совместна. Значит, x оканчивается в первой четверти. Имеем
1 + 2sin x cos x = 4sin x cos x Ю sin 2x = 1,
Ответ:
Пример 20.
Решение.
Ответ:
Пример 21.
Решение.
а)
Но ctg x < 0. Это противоречит условию tg x > 0. Решений нет.
б)
Ответ:
.
Примеры для самостоятельного решения
7. Найти все решения уравнения, принадлежащие указанным промежуткам:
ОТВЕТЫ
Л. Максименко,
Р. Зинченко,
г. Ангарск
mat.1sept.ru