Решение уравнений и неравенств методом оценок

Примеры решения задач

 

Пример 1.   Решить уравнение  

 

                               .                               (1)

 

 

Решение.  Так как    и  

,

то левая часть уравнения (1) больше или равна . Отсюда и из уравнения (1) следует, что    

    Система уравнений имеет единственный корень  .

    Ответ:   .

 

Пример 2.  Решить неравенство  

 

                                         .                                       (2)

 

Решение. Областью допустимых значений переменной в  неравенстве (2) являются  .

Так как  , то   . Если при этом учесть, что  , то неравенство (2) выполняется для любых    из области допустимых значений.

Ответ:  .

 

Пример 3.   Решить уравнение  

 

                     .                              (3)

 

Решение. Так как     и   , то  

.

    Отсюда получаем квадратное неравенство  , которое противоречиво, поскольку  . Следовательно, уравнение (3) корней не имеет.

    Ответ:  нет корней.

 

Пример 4.  Решить уравнение  

 

              .                            (4)

 

 

Решение.  Областью допустимых значения переменной в уравнении (4) являются . Если воспользоваться неравенством Коши  , где    и  , то получим верхние оценки каждого из слагаемых левой части уравнения (4), т.е.

,

,

,

.

    Таким образом, для левой части уравнения (4) имеем неравенство

.

    Отсюда и из уравнения (4) следует , , или . Поскольку областью допустимых значений уравнения (4) являются  , то уравнение корней не имеет.

Ответ: нет корней.

 

Пример 5.  Решить уравнение  

 

                   .                              (5)

 

 

Решение. Если возвести в квадрат обе части уравнения (5), то

,

,

               .            (6)

Левая часть уравнения (6) меньше или равна 0, а правая часть является неотрицательной. Поэтому равенство в уравнении (6) может быть только в том случае, когда обе его части одновременно равны 0. А это возможно только в том случае, если  ,  и  .

Ответ:  , , .

 

Пример 6.  Решить систему уравнений  

 

                                                                           (7)

 

Решение. Так как и , то из первого уравнения системы (7) вытекает . Отсюда, используя неравенство Коши , где    и  ,  получаем неравенство  

.

Из второго уравнения системы (7) следует, что , т.е. . Ранее было установлено, что . Поэтому  или  ,  . Если найденные значения    подставить во второе уравнение системы (7), то получим    и  .

Ответ:  , , , .

 

Пример 7.  Решить уравнение  

 

                          .                              (8)

 

Решение. Поскольку , то уравнение (8) можно переписать в виде   

                                      .                                    (9)

Так как и , то из уравнения (9) следует, что   или  . В таком случае , ,  и  из уравнения (9) получаем

  или   .

Ответ:  .

 

Пример 8.  Решить систему

 

                                                              (10)

 

Решение. Если уравнение системы (10) прологарифмировать по основанию 5, то получим    или

                                        .                               (11)

    Так как    и  , то из уравнения (11)  вытекает неравенство . В таком случае , и из  неравенства системы (10) следует , или .  Однако ,  поэтому  .

    Если значение подставить в уравнение (11),  то  получим квадратное уравнение  , корнями которого    и   .

    Ответ:  , , , .

 

Пример 9.  Решить неравенство  

 

                          .                            (12)

 

Решение. Так как и , то    и  , т.е. имеет место неравенство

.

Отсюда и из неравенства (12) вытекает уравнение

,

равенство в котором имеет место только в том случае, когда оба сомножителя в левой его части одновременно равны 1, т.е.

Из первого уравнения системы получим и подставим его во второе уравнение. Так как  , то  найденное значение   является решением неравенства (12).

Ответ:  .

 

Пример 10.  Решить уравнение  

 

                          .                         (13)

 

Решение. Первоначально оценим снизу левую часть уравнения (13). Так как  , то  и  .  

С другой стороны, для правой части уравнения (13) справедлива верхняя оценка    .

    Отсюда можно сделать вывод о том, что равенство в уравнении (13) имеет место лишь в том случае, когда обе его части одновременно равны 4, т.е.

    или   

Отсюда получаем единственный корень уравнения (13).

    Ответ:  .

 

Пример 11.  Решить уравнение  

 

                                  .                                         (14)

 

Решение. Так как и , то равенство в уравнении (14) достигается только в том случае, когда   и , т.е. имеет место совокупность двух систем уравнений

        и         

Поскольку   , то нетрудно видеть, что первая система уравнений равносильна уравнению  , а вторая система уравнений является несовместной.  Корнями уравнения     являются ,  где  целое число.

Ответ:  , где  целое число.

 

Пример 12.  Решить неравенство  

 

                              .                                    (15)

 

Решение. Поскольку  , то . Однако ,  поэтому   .

Отсюда и из неравенства (15) получаем уравнение

                                           ,                                 (16)

равенство в котором имеет место только в том случае, когда обе его части равны 1, т.е. имеет место система уравнений

                      или        

    Корнями каждого из уравнений последней системы являются

                                                                                          (17)

где   целые числа.

    Для получения корней уравнения (16) необходимо построить пересечение двух серий корней (17).

    Имеет место    или   .  Поскольку левая часть равенства нечетная, то  , где  целое число. Тогда  или   . Так как левая часть последнего равенства является четной, то  , где  целое число. В таком случае получаем    или   . Если подставить выражение в первую серию корней (17), то

.

Следовательно, корнями заданного неравенства (15) являются , где    целое число.

Ответ:  , где  целое число.

 

Пример 13.  Решить уравнение  

 

                       .                      (18)

 

blog.tutoronline.ru

2. Методы решения уравнений и неравенств

1. Решение уравнений и неравенств с использованием определения абсолютной величины (модуля)

Определение 2.1.1: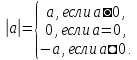

Из определения следует, что

1)

;

2)

3)

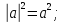
4) = ;

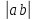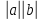5);

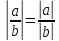6)= а, при а≥0;

7) =.

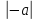Например, докажем четвертое равенство. Если

а и b — числа одинаковых знаков, то, аb = аb — верное равенство. Если а и b — числа разных знаков, например то (-аb) = (-аb) — также верное равенство.

Рассмотрим решение упражнений, связанных только с

определением модуля числа.

Пример 2.1.1: Записать выражение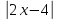 без знака модуля.

Решение. =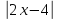

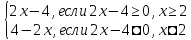
Пример 2.1.2: Решить неравенство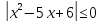

Решение. Поскольку 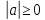, то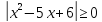 при всех , а

поэтому данное неравенство выполняется только при тех значениях x,при которых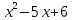 =0, откуда х=2 и x = 3.

Пример 2.1.3: Решить уравнение:

.

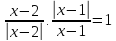Решение. Заметим, что и 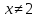. При выполнении этих условий исходное уравнение равносильно уравнению 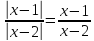. И так как 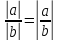, то 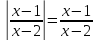. По определению модуля все корни данного уравнения находятся среди решений неравенства 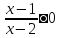. Ясно, что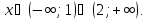

Ответ:.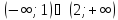

Пример 2.1. 4: Решить неравенство: .

Решение: Так как 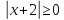при , то в нашем случае 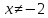. Исходное неравенство равносильно системе 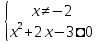. Решение может быть показано на координатной прямой.

Ответ: .

Пример 2.1.5: Решить уравнение .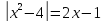

Решение. Пусть 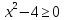, тогда , 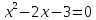; корни последнего уравнения 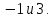Первый из них не удовлетворяет неравенству 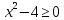и является посторонним для данного уравнения. Пусть 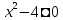, тогда 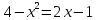, 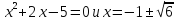. Неравенству удовлетворяет корень .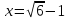

Ответ: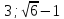. [3]

2. Метод решения при помощи зависимостей между числами а и в, их модулями и квадратами этих чисел

Помимо приведенных мною выше способов существует определенная равносильность, между числами и модулями данных чисел, а также между квадратами и модулями данных чисел:

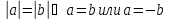
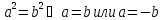(1).

Отсюда в свою очередь получим, что

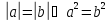(2).

Опорная информация:

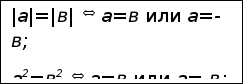
Пример 2.2.1: Решим уравнение | двумя различными способами.

1. Учитывая соотношение (1), получим:

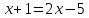или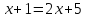

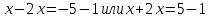
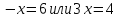
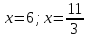
Корень первого урав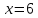нения , корень второго уравнения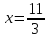

Таким образом корни исходного уравнения.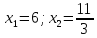

2. В силу соотношения (2), получим

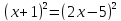, или

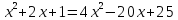
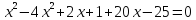
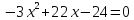
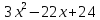=0

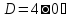уравнение имеет 2 различных корня.

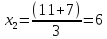
Как показывает решение, корнями данного уравнения также являются числа 11/3 и 6

Ответ: х1=6, х2=11/3

Пример 2.2.2: Решим уравнение .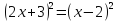

Учитывая соотношение (2), получим, что откуда по образцу предыдущего примера(и по соотношению (1)):

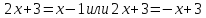
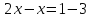
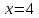
Таким образом корнями уравнения являются х1=-4, и х2=-0,(6)

Ответ: х1=-4, х2=0,(6)

Пример 2.2.3: Решим уравнение .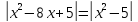

Учитывая соотношение (1), получим:

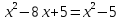или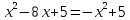

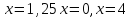
Таким образом, корни исходного уравнения: х₁=1,25; х₂=0; х₃=4.

Ответ: 1,25; 0; 4.

Пример 2.2.4: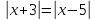

В силу соотношения (2) получаем: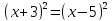

.

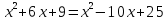
Ответ:1.

Пример 2.2.5: (1-3х)²=(х-2)².

Учитывая соотношение (2), получаем: |1-3х|=|х-2|, откуда из соотношения (1), имеем:

1-3х=х-2 или 1-3х= -х+2

х=0,75 х= -0,5.

Ответ: 0,75; -0,5. [4]

3. Метод интервалов

Применение метода интервалов основано на следующей теореме:

Теорема 2.3.1: Функция, непрерывная на промежутке и необращающаяся на нем в нуль, соxраняет на этом промежутке свой знак.

Это означает, что нули функции и границы промежутков ее непрерывности разделяют область определения функции на участки, где она сохраняет постоянный знак. Применение метода поясним на примере.

Метод интервалов позволяет решать более сложные уравнения и неравенства с модулями, но в этом случае он имеет несколько иное назначение. Суть состоит в слудующем. Находим корни всех подмодульных выражений и разбиваем числовую ось на промежутки знакопостоянства этих выражений. Это позволяет, последовательно перебирая эти промежутки, одновременно избавляться от всех модулей и решать обычное уравнение или неравенство (проверяя при этом, что найденный ответ входит в данный промежуток).

Метод интервалов – это метод разбиения числовой прямой на промежутки, в которых по определению модуля знак абсолютной величины можно будет снять. Для каждого из промежутков необходимо решить уравнение и сделать вывод относительно получившихся корней. Корни, удовлетворяющие промежуткам, и дадут окончательный ответ.

Поэтому алгоритм решения задачи методом интервалов (промежутков) выглядит следующим образом:

1. На числовой прямой отметить все нули подмодульных выражений.

2. Определить знак каждого из этих выражений на каждом из промежутков, например, по знаку этого выражения при каком-нибудь значении x з промежутка (кроме концевых точек).

3. Раскрыть модули на каждом из промежутков и решать полученное уравнение (неравенство).

4. Из полученных решений выбрать только те, которые этому промежутку принадлежат.

5. Объединить решения из всех промежутков.

Покажем на примерах как работает этот метод.

Пример 2.3.1: Решим неравенство

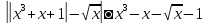
Решение: Пусть 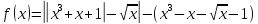. Областью определения данной функции есть 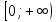. Решая уравнение получим, что функция не обращается в нуль ни при каком значении переменной. Это означает, что на всей области определения функция является знакопостоянной. Вычисляя, например, , получаем, что функция принимает только положительные значения.

Ответ. .

Пример 2.3.2: Решим уравнение . Найдем корни (нули) каждого выражения, содержащегося под знаком модуля: 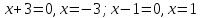. Эти значения 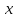разбивают числовую прямую на три промежутка:

Рис.6

Решим уравнение отдельно в каждом из получившихся промежутков. В первом промежутке оба выражения, стоящие под знаком модуля отрицательны, поэтому при записи уравнения без абсолютной величины знаки этих выражений меняем на противоположные. Получим уравнение:

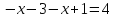. Откуда х=-4. Число -4 является решением данного уравнения, так как оно принадлежит рассматриваемому промежутку. Во втором промежутке (-3 ≤ х < 1) первое выражение положительно, а второе отрицательно. Рассуждая аналогично, получим уравнение: 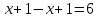, откуда получаем неверное числовое равенство, то есть в рассматриваемом промежутке уравнение корней не имеет. В последнем промежутке (х ≥ 1) оба выражения положительны, поэтому уравнение записывается так: . Откуда х=2. Это значение удовлетворяет неравенству х ≥ 1.

Ответ: -4; 2.

Пример 2.3.3: .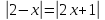

Прежде всего, следует установить область допустимых значений. Возникает естественный вопрос, почему в предыдущих примерах не было необходимости этого делать. В этом уравнении в правой части стоит выражение с переменной, которое может быть отрицательным. Таким образом, область допустимых значений – это промежуток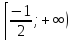. Найдем нуль выражения, стоящего под знаком модуля: .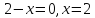

Рис.7

В первом промежутке:.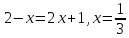

Это значение принадлежит ОДЗ, значит, является корнем уравнения.

Во втором промежутке: 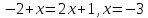.-3 не принадлежит ОДЗ, а следовательно не является корнем уравнения.

Ответ: ⅓. [5]

studfile.net

Показательные уравнения и неравенства

Показательными уравнениями и неравенствами считают такие уравнения и неравенства, в которых неизвестное содержится в показателе степени.

Решение показательных уравнений часто сводится к решению уравнения а^х = а^b, где а > 0, а ≠ 1, х – неизвестное. Это уравнение имеет единственный корень х = b, так как справедлива следующая теорема:

Теорема. Если а > 0, а ≠ 1 и а^х1 = а^х2, то х₁ = х₂.

Обоснуем рассмотренное утверждение.

Предположим, что равенство х₁ = х₂ не выполняется, т.е. х₁ < х₂ или х₁ = х₂. Пусть, например, х₁ < х₂. Тогда если а > 1, то показательная функция у = а^х возрастает и поэтому должно выполняться неравенство а^х1 < а^х2; если 0 < а < 1, то функция убывает и должно выполняться неравенство а^х1 > а^х2. В обоих случаях мы получили противоречие условию а^х1 = а^х2.

Рассмотрим несколько задач.

Задача 1.

Решить уравнение 4 ∙ 2^х = 1.

Решение.

Запишем уравнение в виде 2² ∙ 2^х = 2⁰ – 2^х+2 = 2⁰, откуда получаем х + 2 = 0, т.е. х = -2.

Ответ. х = -2.

Задача 2.

Решить уравнение 2^3х ∙ 3^х = 576.

Решение.

Так как 2^3х = (2³)^х = 8^х, 576 = 24², то уравнение можно записать в виде 8^х ∙ 3^х = 24² или в виде 24^х = 24².

Отсюда получаем х = 2.

Ответ. х = 2.

Задача 3.

Решить уравнение 3^х+1 – 2∙3^{х — 2} = 25.

Решение.

Вынося в левой части за скобки общий множитель 3^{х — 2}, получаем 3^{х — 2} ∙ (3³ – 2) = 25 – 3^{х — 2}∙ 25 = 25,

откуда 3^{х — 2} = 1, т.е. х – 2 = 0, х = 2.

Ответ. х = 2.

Задача 4.

Решить уравнение 3^х = 7^х.

Решение.

Так как 7^х ≠ 0, то уравнение можно записать в виде 3^х/7^х = 1, откуда (3/7)^х = 1, х = 0.

Ответ. х = 0.

Задача 5.

Решить уравнение 9^х – 4 ∙ 3^х – 45 = 0.

Решение.

Заменой 3^х = а данное уравнение сводится к квадратному уравнению а² – 4а – 45 = 0.

Решая это уравнение, находим его корни: а₁ = 9, а₂ = -5, откуда 3^х = 9, 3^х = -5.

Уравнение 3^х = 9 имеет корень 2, а уравнение 3^х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.

Ответ. х = 2.

Решение показательных неравенств часто сводится к решению неравенств а^х > а^b или а^х < а^b. Эти неравенства решаются с помощью свойства возрастания или убывания показательной функции.

Рассмотрим некоторые задачи.

Задача 1.

Решить неравенство 3^х < 81.

Решение.

Запишем неравенство в виде 3^х < 3⁴. Так как 3 > 1, то функция у = 3^х является возрастающей.

Следовательно, при х < 4 выполняется неравенство 3^х < 3⁴, а при х ≥ 4 выполняется неравенство 3^х ≥ 3⁴.

Таким образом, при х < 4 неравенство 3^х < 3⁴ является верным, а при х ≥ 4 – неверным, т.е. неравенство
3^х < 81 выполняется тогда и только тогда, когда х < 4.

Ответ. х < 4.

Задача 2.

Решить неравенство 16^х +4^х – 2 > 0.

Решение.

Обозначим 4^х = t, тогда получим квадратное неравенство t2 + t – 2 > 0.

Это неравенство выполняется при t < -2 и при t > 1.

Так как t = 4^х, то получим два неравенства 4^х < -2, 4^х > 1.

Первое неравенство не имеет решений, так как 4^х > 0 при всех х € R.

Второе неравенство запишем в виде 4^х > 4⁰, откуда х > 0.

Ответ. х > 0.

Задача 3.

Графически решить уравнение (1/3)^х = х – 2/3.

Решение.

1) Построим графики функций у = (1/3)^х и у = х – 2/3.

2) Опираясь на наш рисунок, можно сделать вывод, что графики рассмотренных функций пересекаются в точке с абсциссой х ≈ 1. Проверка доказывает, что

х = 1 – корень данного уравнения:

(1/3)¹ = 1/3 и 1 – 2/3 = 1/3.

Иными словами, мы нашли один из корней уравнения.

3) Найдем другие корни или докажем, что таковых нет. Функция (1/3)^х убывающая, а функция у = х – 2/3 возрастающая. Следовательно, при х > 1 значения первой функции меньше 1/3, а второй – больше 1/3; при х < 1, наоборот, значения первой функции больше 1/3, а второй – меньше 1/3. Геометрически это означает, что графики этих функций при х > 1 и х < 1 «расходятся» и потому не могут иметь точек пересечения при х ≠ 1.

Ответ. х = 1.

!!! Заметим, что из решения этой задачи, в частности, следует, что неравенство (1/3)^х > х – 2/3 выполняется при х < 1, а неравенство (1/3)^х < х – 2/3 – при х > 1.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Решение неравенств, все формулы и примеры

Определение и формулы неравенств

Знаки > называются знаками строгого неравенства, а знаки — знаками нестрогого неравенства.

Если в неравенство входят только числовые величины, то такое неравенство называется числовым неравенством.

Неравенства называют равносильными, если они имеют одно и тоже множество решений.

Основные правила, применяемые при решении неравенств

1. Если какое-либо слагаемое перенести из одной части неравенства в другую, изменив при этом его знак на противоположный, то получим неравенство, равносильное данному.
2. Если обе части неравенства умножить (разделить) на одно и то же положительное число, то получим неравенство, равносильное данному.
3. Если обе части неравенства умножить (разделить) на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получим неравенство, равносильное данному.

В зависимости от того, какие функции входят в неравенство, различают линейные, квадратные, дробно-рациональные, иррациональные, логарифмические, показательные неравенства, неравенства с параметром.

Если требуется все общие решения двух или нескольких неравенств, то решают систему неравенств. Как и систему уравнений, систему неравенств записывают с помощью фигурной скобки. Решение системы неравенств есть пересечение решений всех входящих в нее неравенств.

Одним из основных методов решения неравенств является метод интервалов.

Примеры решения неравенств

Понравился сайт? Расскажи друзьям!

ru.solverbook.com