Уравнения с дробями 8 класса онлайн

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Алгебра в 8 классе охватывает изучение множества видов уравнений с дробями, степенями, рациональными числами, иррациональными и многими другими видами. В данной статье вы познакомитесь с тем, как решать уравнения с дробями.

Так же читайте нашу статью «Решить уравнение с дробями онлайн решателем»

Алгебраические дроби представляют собой выражения следующего вида:

\[\frac{R}{A}\]

В данном выражении \[R\] и \[A\] являются многочленами, \[R\] — числитель, \[A\] — знаменатель. Основываясь на том, что \[R\] и \[А\] являются многочленами, то с ними можно производить определенные действия:

* сокращения числителя;

* сокращения знаменателя;

* разложение на множители;

* и другие.

Например, у нас есть такое уравнение:

\[\frac{a^2+2ab +b^2}{a^2- b^2}\]

Чтобы сократить дробь данного вида воспользуемся формулами сокращённого умножения для квадрата суммы и разности квадратов. Получим следующий результат:

\[\frac{ a^2+2ab + b^2}{ a^2- b^2}=\frac{(a+b)^2}{(a-b)(a+b)} =\frac{a+b}{a- b}\]

Сначала мы выполнили разложение дроби на множители, а далее знаменатель и числитель разделили на многочлен \[(a+b).\] Чтобы закрепить свои знания решайте уравнения онлайн 8 класса, поскольку так вы сможете на практике изучить все особенности дробных уравнений.

Где можно решить уравнение с дрбями 8 класса онлайн?

Решить дробное уравнение онлайн с подробным решением вы можете на сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

Калькулятор дробей

Дроби

Что такое дроби и как их решать

Дробь в математике – это число, являющееся частью единицы или несколькими её частями. То есть если мы хотим указать на половину части целого, то мы пишем обыкновенную дробь ½.

Дробью необязательно мы можем указать часть целого. С помощью дроби мы можем обозначить вообще любое число. Например, дробь 4/2 будет равняться двум, то есть целому числу.

Обыкновенная дробь представляет собой два числа, разделенных горизонтальной чертой – знаком деления. Число, которое располагается над чертой, – числитель, а число под чертой – знаменатель. Знаменатель обозначает количество равных частей, на которое делится целое, а числитель дроби – количество взятых частей данного целого для дальнейшего деления на знаменатель.

Дробь может иметь десятичную форму. Например, обыкновенная дробь 1/10 может обозначаться как 0,1 в десятичной форме. Десятичная форма – это рациональное или иррациональное число, обозначающее дробь. Десятичная форма, может иметь бесконечный вид, например, дробь 1/3 имеет в десятично виде бесконечную форму 0,333333333…

Дроби могут быть правильными и неправильными. Правильной называют такую дробь, у которой числитель меньше знаменателя. В случае если числитель дроби больше знаменателя, она называется неправильной. Дробь, записанная в виде целого числа и правильной дроби называется смешанной. А дробь, которая не имеет целую часть, называется простой дробью. Любую смешанную дробь можно преобразовать в неправильную простую дробь.

Так же читайте нашу статью «Калькулятор факториалов онлайн»

Как пользоваться калькулятором дробей?

Воспользоваться калькулятором дробей вы всегда сможете на сайте pocketteacher.ru. Бесплатный онлайн решатель позволит решить дробное выражение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

Решение рациональных уравнений. Видеоурок. Алгебра 8 Класс

Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями

Урок: Решение рациональных уравнений

Как вы уже успели заметить на предыдущем уроке, основа решения рациональных уравнений – техника преобразования рациональных выражений. Рассмотрим пример решения рационального уравнения.

Пример 1

Решить уравнение: .

Решение:

В первую очередь обратим внимание на то, что в числителях обеих дробей, а также в правой части уравнения стоят чётные числа. То есть, можно упростить уравнение, поделив обе его части на . Этот шаг не является обязательным, но, чем проще уравнение, тем легче его решать, а чем меньше числа, фигурирующие в уравнении, тем легче арифметические вычисления при его решении.

В результате сокращения получаем:

Теперь перенесём все члены уравнения в левую часть, чтобы получить справа

, а затем приведём полученные в левой части дроби к общему знаменателю:

Напомним, что дробь равна  тогда и только тогда, когда её числитель равен , а знаменатель не равен

. Поэтому наше уравнение превращается в следующую систему:

 

Теперь вспомним ещё один важный факт: произведение равно  тогда и только тогда, когда хотя бы один из его множителей равен , а остальные множители при этом существуют. И наша система превращается в следующую:

.

Оба полученных корня являются решениями данного уравнения, так как при них знаменатель определён.

Ответ:

.

Рассмотренное нами уравнение является моделью для такой задачи:

Задача 1

Лодка прошла  по течению реки и  против течения реки, затратив на весь путь . Чему равна собственная скорость лодки, если скорость течения реки равна ?

Решение:

Решение данной задачи осуществим с помощью метода математического моделирования и выделим 3 этапа данного метода.

Этап 1. Составление математической модели

Обозначим через  собственную скорость лодки (это стандартный приём при решении текстовых задач – обозначить с помощью неизвестной ту величину, которая спрашивается в условии задачи). Тогда:

 – скорость движения лодки по течению реки;

 – скорость движения лодки против течения реки.

В этом случае, воспользовавшись формулой: , получаем, что время движения лодки по течению реки выражается как 

, а время движения лодки против течения реки – . Тогда общее время движения лодки равно , откуда получаем уравнение:

 – это и есть математическая модель данной задачи.

Этап 2. Работа с математической моделью

В данном случае работа с математической моделью сводится к решению данного рационального уравнения, что мы уже сделали в примере 1. При этом получили корни уравнения:

.

Этап 3. Ответ на вопрос задачи

Дело в том, что математическая модель потому и является математической, что абстрагирована от реальной жизни. Если брать конкретно данную задачу, то математическая модель – это уравнение, которое может иметь любые корни. Однако неизвестная величина обозначает скорость лодки, поэтому не может быть, к примеру, отрицательной. Или: не может быть меньше скорости течения реки, иначе бы лодка не смогла бы плыть против течения. И такие ограничения могут быть в самых разных задачах. Поэтому, прежде чем записать ответ, необходимо оценить, является ли он правдоподобным.

В данном случае очевидно, что  не подходит, так как лодка не смогла бы с такой скоростью плыть против течения. Поэтому в ответ пойдёт только одна величина:

.

Ответ:

Рассмотрим несколько примеров на решение непосредственно рациональных уравнений.

Пример 2

Решить уравнение: .

Решение:

Перенесём все слагаемые в левую часть, а затем приведём дроби к общему знаменателю.

Снова воспользуемся тем фактом, что дробь равна  тогда и только тогда, когда её числитель равен , а знаменатель не равен . Из этого следует, что данное уравнение эквивалентно системе:

Ответ:.

Пример 3

Решить уравнение: .

Решение:

В данном уравнении в правой части уже стоит , поэтому ничего переносить левую часть не нужно. Сразу приведём дроби в левой части к общему знаменателю:

.

Снова воспользуемся тем фактом, что дробь равна  тогда и только тогда, когда её числитель равен , а знаменатель не равен . Из этого следует, что данное уравнение эквивалентно системе:

. Подставив данное значение в знаменатель, убеждаемся, что он не равен . Значит, это значение переменной является ответом.

Ответ:.

Пример 4

Решить уравнение: .

Решение:

Схема решения данного уравнения абсолютно такая же, как и у предыдущих:

Ответ:.

К решению рациональных уравнений часто сводятся различные задачи. Рассмотрим один из таких примеров.

Задача 2

Существует ли такое значение , при котором разность дробей  и  равна ?

Решение:

Запишем уравнение, соответствующее условию данной задачи: .

Решим данное рациональное уравнение точно так же, как и в предыдущих примерах.

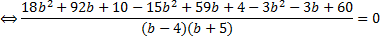
Приведём подобные слагаемые в числителе (они отмечены одинаковым цветом):

То есть, такое значение  существует.

Ответ: существует:.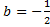

Итак, мы рассмотрели примеры решения рациональных уравнений, а также их использование при решении различных задач. На следующих уроках мы перейдём к изучению новой темы, посвящённой различным функциям.

 

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.

2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интерн

interneturok.ru

Онлайн калькулятор дробей с решением со степенями со скобками с буквами

Данный онлайн калькулятор дробей предназначен для сложения, вычитания, деления и умножения между собой обыкновенных дробей. А так же дробей с целой частью и  десятичных дробей.
Основные возможности:

1. Сложение, вычитание, деление и умножение дробей.
2. Расчет дробей с подробнейшим решением.
3. Расчет дробей со степенями, скобками и буквами.
4. Сокращение дробей.
5. Поддержка до трех дробей онлайн.

На данном калькуляторе можно посчитать сложение вычитание деление или умножение дробей.
Калькулятор умеет:

1. Вносить целую часть дроби в числитель для смешанных дробей.
2. Расчет дробей со скобками- поддержка до двух уровней вложенности скобок.
3. Расчет дробей со степенями — степенью может быть только число.
4. Расчет дробей с буквами — любые анг. буквы или символы.
5. Сокращение дробей — только для дробей без букв.

Основные символы:

1. * символ звездочки интерпретируется как умножение.
2. / слеш интерпретируется как деление.
3. + и — интерпретируются как сложение и вычитание.
4. ^ символ интерпретируется как степень.
5. ( ) символы интерпретируются как открывающаяся и закрывающаяся скобки.

Подробности:

1. Между двумя буквами необязательно ставить знак умножения (если они умножаются). Пример вместо x*x можно написать xx.
2. После знака степени ^ должно стоять число степени. Если оно отрицательно необходимо заключить его в скобки. Пример x^2+1 или x^(-2) +1.
3. При сложении дробей состоящих только из чисел калькулятор вычисляет НОД и НОК.
4. При расчете сразу трех дробей сначала выполняется операция умножение(деления), затем сложения(вычитания). Для изменения этого порядка поставьте галочку в поле «Большие скобки» и выберите нужный порядок расчета. В этом случае первой будет выполняться операция в больших скобках.

calculatori.ru

Решить дробное уравнение онлайн решателем

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Все уравнения, которые можно свести к дроби \[f(x) \div g(x) = 0\] именуются рациональными уравнениями с дробями. Найти пути решения данного рода уравнений — это не самое сложное, что можно встретить в математике. Однако для этого необходимо знать алгоритм их решения, который будет разобран на уравнении такого вида:

\[\frac{(x^2 — x — 56)(x — 3)}{x^2 + 5x + 6} = 0 \]

Уравнение выше и есть ярким примером дробного рационального уравнения. Решение таких уравнений начинается с поиска корня числителя. Для этого решим уравнение квадратного вида:

\[ (x^2 — x — 56)(x — 3) = 0 \to x = 3; x^2 — x — 56 = 0\]

Определим дискриминант по уже известной нам формуле \[D = b^2 — 4ac:\]

\[D = (-1)^2 — 4 \cdot 1(-56) = 225 +25^2\]

Определим корни:

\[x = \frac{1 \pm 15}{2} \to x_1 = 8; x_2 = -7\]

Получим 3 нуля числителя:

\[x = 8; x = -7; x = 3.\]

Так же читайте нашу статью «Решить систему уравнений 9 класса онлайн решателем»

Теперь решим квадратное уравнение. Для этого применим теорему Виета:

\[\begin{Bmatrix} x_1 + x_2 & = & -5 \\ x_1 \cdot x_2 & = & 6 \end{Bmatrix}\]

\[\begin{Bmatrix} x_1 & = & -2 \\ x_2 & = & -3 \end{Bmatrix}\]

Из полученного выше результата делаем вывод, что числитель и знаменатель не имеют общих корней. Следовательно, все найденные нами значения \[x = 8, x = -7, x = 3\] и будут решением данного несложного уравнения.

Где можно решить дробные рациональные уравнения онлайн?

Решить уравнение онлайн вы можете на нашем сайте pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

Калькулятор дробей ОНЛАЙН с решением уравнений в столбик

Онлайн калькулятор дробей позволяет производить простейшие арифметические операции с дробями: сложение дробей, вычитание дробей, умножение дробей, деление дробей. Чтобы произвести вычисления, заполните поля соответствующие числителям и знаменателям двух дробей.

Онлайн калькулятор уравнений с дробями

Дробью в математике называется число, представляющее часть единицы или несколько её частей.

Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.

Дроби бывают правильными и неправильными.

• Правильной называется дробь, у которой числитель меньше знаменателя.
• Неправильная дробь – если у дроби числитель больше знаменателя.

Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть, называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь.

---

Как перевести смешанную дробь в обыкновенную

Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: 

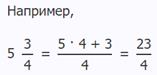
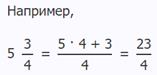
Как перевести обыкновенную дробь в смешанную

Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:

1. Поделить числитель дроби на её знаменатель
2. Результат от деления будет являться целой частью
3. Остаток отделения будет являться числителем

Как перевести обыкновенную дробь в десятичную

Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.

Как перевести десятичную дробь в обыкновенную

Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:

1. Записать дробь в виде десятичная 
2. Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
3. Найти наибольший общий делитель и сократить дробь.

Как перевести дробь в проценты

Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.

Как перевести проценты в дробь

Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.

Сложение дробей

Алгоритм действий при сложении двух дробей такой:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Выполнить сложение дробей путем сложения их числителей.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Вычитание дробей

Алгоритм действий при вычитании двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
3. Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Умножение дробей

Алгоритм действий при умножении двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
3. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
4. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Деление дробей

Алгоритм действий при делении двух дробей:

1. Перевести смешанные дроби в обыкновенные (избавиться от целой части).
2. Чтобы произвести деление дробей, нужно преобразовать вторую дробь, поменяв местами её числитель и знаменатель, а затем произвести умножение дробей.
3. Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй.
4. Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
5. Если числитель итоговой дроби больше знаменателя, то выделить целую часть.

Понравилось? Поделись с друзьями ⇊

calconline.pro

Онлайн калькулятор дробей. Вычисления с дробями. Сложение, вычитание, умножение и деление дробей.

Инструкция использования калькулятора дробей

Для решения вашей задачи выполните следующие действия:

• введите ваш пример в калькулятор;
• нажмите кнопку  для выполнения вычислений.

Ввод данных в калькулятор дробей

В калькулятор дробей можно вводить: целые числа, десятичные дроби, обыкновенные дроби и смешанные числа.

Целые числа. Для ввода целых чисел используйте цифровые клавиши калькулятора или цифровые клавиши вашего компьютера. 1 2 3 4 5 6 7 8 9 0

Десятичные дроби. Десятичные дроби вводятся также как и целые числа, в качестве десятичного разделителя рекомендуется использовать точку .

Обыкновенные дроби: Для ввода обыкновенной дроби нажмите клавишу на клавиатуре калькулятора — после чего введите значения числителя и знаменателя дроби используя числовые клавиши.

Смешанные числа: Используя числовые клавиши введите целую часть смешанной дроби, нажмите клавишу дроби на клавиатуре калькулятора — после чего введите значения числителя и знаменателя дроби используя числовые клавиши.

Отрицательные числа: Перед числом поставьте знак минус -, не забывайте брать отрицательные числа в скобки ( ).

Возведение в степень: Для возведения числа в степень введите число нажмите клавишу a^b, затем введите значение степени. (На компьютере степень можно ввести нажав клавишу «^». Например, для ввода 4³ нужно набрать 4^3)

N.B. Калькулятор поддерживает только целые степени!

N.B. Буквенные выражения, операции извлечения корня калькулятор не поддерживает!

Дополнительные возможности калькулятора дробей — старая версия

• С — полностью очистить поле ввода.
•  — удалить один символ.
•   для перемещения между полями калькулятора.

ru.onlinemschool.com