Числовая последовательность и способы ее задания. Видеоурок. Алгебра 9 Класс
Пусть 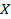 – числовое множество.
– числовое множество.
Числовой функцией
называется закон, по которому каждому элементу из
сопоставляется единственное число.
Множество 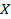 – это область определения.
– это область определения.
Числовая последовательность – это числовая функция (
), которая определена на множестве натуральных чисел ( ).
Областью определения является множество натуральных чисел (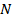 ).
).
Обозначают члены последовательности так:
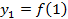 ;
; 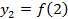 ;
; 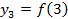 ;…;
;…; 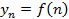
Числовая последовательность – это частный случай функции. Как и любая функция, последовательность может задаваться различными способами.
Способы задания числовой последовательности:
1. Аналитический (при помощи формулы)
2. Словесный
3. Рекуррентный
Последовательность задана аналитически, если указана формула для вычисления ее -го члена.
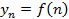 , где
, где 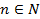
Рассмотрим примеры:
1. 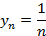 ,
,
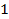 ;
;  ;
;  ;…;
;…;  ;… Указав конкретное значение
;… Указав конкретное значение 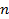 , нетрудно найти член последовательности с соответствующим номером.
, нетрудно найти член последовательности с соответствующим номером.Построим график данной последовательности. Согласно определению графика функции, графиком данной последовательности является множество всех точек 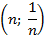
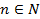 (см. Рис. 1). Все эти точки лежат на правой ветви гиперболы
(см. Рис. 1). Все эти точки лежат на правой ветви гиперболы 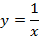 .
.
Рис. 1. График числовой последовательности 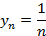
Функция 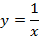 при
при 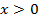
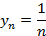 также убывает.
также убывает.2. 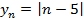
Выпишем несколько членов данной числовой последовательности:
 ;
; 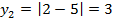 ;
; 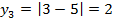 ;…
;…
График данной последовательности – это множество точек с координатами 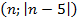
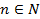 (см. Рис. 2). Все эти точки лежат на ломаной
(см. Рис. 2). Все эти точки лежат на ломаной 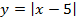 .
.
Рис. 2. График числовой последовательности 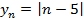
Числовая последовательность 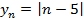
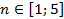 , возрастает при
, возрастает при 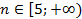 .
.Словесный способ задания числовой последовательности используется, когда правило задания последовательности описано словами, не указывая формулы.
Пример
Дано: 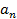 – это -я цифра после запятой в десятичной записи числа
– это -я цифра после запятой в десятичной записи числа 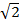 .
.

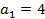 ;
; 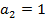 ;
; 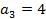 ;
;  ;
; 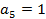 ;…
;…
Последовательность задана рекуррентно, если указано правило, по которому -й член вычисляется по предыдущим членам.
Пример

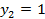 ;
; 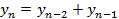 , где
, где 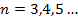
В данном примере задана возможность получения любого -го члена последовательности:
 ;
; 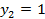 ;
; 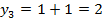 ;
; 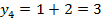
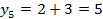 ;…
;…В числовой последовательности  ;
; 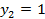 ;
; 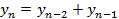 , где
, где 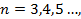 найти 7 член.
найти 7 член.
Решение
Для того чтобы найти 7 член данной последовательности, необходимо знать 5 и 6 член. В предыдущем примере мы нашли 3, 4 и 5 член, следовательно, можно найти 6, а далее и 7 член.
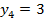 ;
; 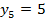 ;
; 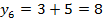 ;
; 
Ответ: 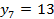 .
.
Дано:

Найти: 
Решение
Подставляем 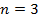 в формулу для -го члена последовательности
в формулу для -го члена последовательности 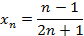 :
:
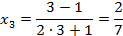
Ответ: 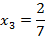 .
.
Дано:

Найти: является ли число 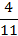 некоторым членом заданной последовательности?
некоторым членом заданной последовательности?
Решение
Приравниваем формулу для -го члена последовательности 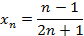 к числу
к числу 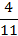 , получим уравнение относительно
, получим уравнение относительно 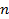 . Если
. Если 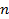 будет натуральным числом, то число
будет натуральным числом, то число 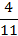 является членом заданной последовательности.
является членом заданной последовательности.
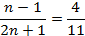


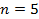
Следовательно: 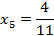
Ответ: число 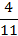 является 5 членом заданной последовательности.
является 5 членом заданной последовательности.
Укажите формулу общего члена последовательности, которая задана несколькими членами: 1; 4; 9; 16; 25.
Решение
Запишем каждый член последовательности в следующем виде:




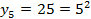
Видно, что члены последовательности представляют собой квадраты последовательных натуральных чисел. Таким образом, делаем вывод, что:
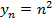 , где
, где 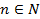
Ответ: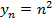 , где
, где 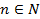 .
.
Список литературы
1. Виленкин Н.Я., Сурвило Г.С. Алгебра 9 кл. С углубленным изучением математики. – М.: Просвещение, 2006.
2. Макарычев Ю.Н., Миндюк Н.Г., Нешков, К.И. Алгебра для 9 класса с углубл. изуч. математики. – М.: Мнемозина, 2003.
3. Мордкович А.Г. Алгебра 9 класс, учебник для общеобразовательных учреждений. – М.: Мнемозина, 2002.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт «ЯКласс» (Источник)
2. Интернет-сайт hijos.ru (Источник)
3. Интернет-сайт Hellper.ru (Источник)
4. Интернет-сайт YouTube (Источник)
Домашнее задание
1. Упражнения 1, 7 (в-е), 8, (глава 11,§1 стр. 219) – Виленкин Н.Я., Сурвило Г.С. Алгебра 9 кл. (Источник)
2. Найти 15 член последовательности, заданной формулой -го члена: 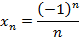 ,
, 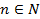
3. Последовательность задана при помощи рекуррентного соотношения 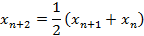 ,
,  ,
, 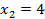 . Выписать несколько первых членов этой последовательности.
. Выписать несколько первых членов этой последовательности.
4. Проверить, являются ли числа 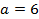 и
и 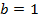 членами последовательности
членами последовательности 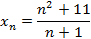
Определение числовой последовательности — урок. Алгебра, 9 класс.
Функцию y=f(x), x∈ℕ, называют функцией натурального аргумента, или числовой последовательностью, и обозначают \(y=f(n)\), или y1,y2,y3…yn…
Значения y1,y2,y3…yn (и т. д.) называют соответственно первым, вторым, третьим (и т. д.) членами последовательности.
В символе yn число \(n\) называют индексом, который задаёт порядковый номер того или иного члена последовательности. Иногда для обозначения последовательности используется запись yn.
Как известно, функция может быть задана различными способами, например, аналитически, графически, словесно и т. д. Последовательности тоже можно задавать различными способами, среди которых особенно важны три: аналитический, словесный и рекуррентный.
1. Аналитическое задание последовательности.
Говорят, что последовательность задана аналитически, если указана формула её \(n\)-го члена yn=f(n).
Пример:
1. yn=n2.
Это аналитическое задание последовательности \(1, 4, 9, 16…\) n2\(…\), о которой шла речь выше.
Пример:
2. yn=C. Это значит, что речь идёт о последовательности \(C, C, C… C…\), которую называют стационарной.
2. Словесное задание последовательности.
Пример:
последовательность простых чисел: \(2, 3, 5, 7, 11, 13, 17, 19, 23, 29…\)
Последовательность задана словесно.
Нахождение аналитического задания последовательности по её словесному описанию часто бывает сложной (а иногда и неразрешимой) задачей.
3. Рекуррентное задание последовательности.
Этот способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить \(n\)-й член последовательности, если известны её предыдущие члены.
При вычислении членов последовательности по этому правилу мы как бы всё время возвращаемся назад, выясняем, чему равны предыдущие члены. Такой способ задания последовательности называют рекуррентным (от лат. recurrere — возвращаться).
Чаще всего в таких случаях указывают формулу, позволяющую выразить \(n\)-й член последовательности через предыдущие, и задают один-два начальных члена последовательности.
Пример:
y1=3;yn=yn−1+4, если n=2,3,4…
Имеем
y1=3;y2=y1+4=3+4=7;y3=y2+4=7+4=11;y4=y3+4=11+4=15и т. д.
Тем самым получаем последовательность \(3, 7, 11, 15…\)
Возрастающие и убывающие последовательности объединяют общим термином — монотонные последовательности.
Последовательность yn называют возрастающей, если каждый её член (кроме первого) больше предыдущего.
Последовательность yn называют убывающей, если каждый её член (кроме первого) меньше предыдущего.
Методическая разработка (алгебра, 9 класс) по теме: «Числовые последовательности»
Государственное бюджетное образовательное учреждение
Средняя общеобразовательная школа № 466
Курортного района Санкт-Петербурга
Урок алгебры в 9 классе по теме
«Числовые последовательности»
Учитель математики
Хамина Ирина Анатольевна
Санкт-Петербург
2013
Цели уроков:
- Формирование представления о числовой последовательности как функции с натуральным аргументом.
- Формирование знаний о способах задания числовых последовательностей, умений находить члены последовательности по предложенной формуле, а также умений находить саму формулу, задающую последовательность.
- Развитие умений применять ранее изученный материал.
- Развитие умений анализировать, сравнивать, обобщать.
- Привитие санитарно-гигиенических навыков, пропаганда здорового образа жизни.
Ход уроков
- Организационный момент.
- Повторение видов функций.
- Подготовка к восприятию новых знаний.
- Изучение нового материала.
- Закрепление.
- Знаменитые последовательности.
- Дополнительные задачи.
- Домашнее задание.
- Подведение итогов урока.
Оборудование и материалы.
- Рабочий лист для учащихся с планом уроков и упражнениями. Приложение 1.
- Лист с домашней работой. Приложение 2.
- Мультимедийный проектор.
- Экран.
- Презентация.
Урок 1.
1. Организационный момент.
Последовательность — одно из самых основных понятий математики. Последовательность может быть составлена из чисел, точек, функций, векторов и т.д.
Сегодня на уроке мы познакомимся с понятием » числовая последовательность», узнаем, какие могут быть последовательности, познакомимся со знаменитыми последовательностями.
2. Повторение видов функций.
Вам известны функции, определённые на всей числовой прямой или на её непрерывных промежутках:
- линейная функция у = кх+в,
- квадратичная функция у = ах2+вх+с,
- функция у =,
- прямая пропорциональность у = кх,
- обратная пропорциональность у = ,
- кубическая функция у = х3,
- функция у =|х|.
(Графики функций показываются на слайдах презентации).
Для каждой функции указать область определения и способы задания функции.
3. Подготовка к восприятию новых знаний.
Но бывают функции, заданные на других множествах.
Пример. Во многих семьях есть обычай, своего рода ритуал: в день рождения ребёнка родители подводят его к дверному косяку и торжественно отмечают на нём рост именинника. Ребёнок растёт, и на косяке с годами возникает целая лесенка отметок. Три, пять, два: Такова последовательность приростов от года к году. Но есть и другая последовательность, и именно её члены аккуратно выписывают рядом с засечками. Это — последовательность значений роста. Слайд презентации.
Две последовательности связаны друг с другом.
Вторая получается из первой сложением.
Рост — это сумма приростов за все предыдущие годы.
Рассмотрим ещё несколько задач.
Задача 1. На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе в 1 день? 2 день? 3 день? 4 день? 5 день?
(Ответы учащихся записываются на доске: 500, 530, 560, 590, 620).
Задача 2. В период интенсивного роста человек растёт в среднем на 5 см в год. Сейчас рост у ученика С. — 180 см. Какого роста он будет в 2018 году? (2м 30 см). Но этого быть не может. Почему?
Задача 3. Ежедневно каждый болеющий гриппом человек может заразить 4 окружающих. Через сколько дней заболеют все ученики нашей школы (300 человек)? (Через 4 дня).
Это примеры функций, заданных на множестве натуральных чисел-числовые последовательности.
Ставится цель урока: Найти способы нахождения любого члена последовательности.
Задачи урока: Выяснить, что такое числовая последовательность и как задаются последовательности.
Изучение нового материала.
Определение: Числовая последовательность- это функция, заданная на множестве натуральных чисел (слайд: последовательности составляют такие элементы природы, которые можно пронумеровать).
Понятие числовой последовательности возникло и развилось задолго до создания учения о функции. Вот примеры бесконечных числовых последовательностей, известных еще в древности:
1, 2, 3, 4, 5, : — последовательность натуральных чисел;
2, 4, 6, 8, 10, :- последовательность четных чисел;
1, 3, 5, 7, 9, : — последовательность нечетных чисел;
1, 4, 9, 16, 25, : — последовательность квадратов натуральных чисел;
2, 3, 5, 7, 11, : — последовательность простых чисел;
1, , , , :- последовательность чисел, обратных натуральным.
Число членов каждого из этих рядов бесконечно; первые пять последовательностей — монотонно возрастающие, последняя — монотонно убывающая.
Обозначение: у1, у2, у3, у4, у5,:
1, 2, 3, 4, 5, :п,:-порядковый номер члена последовательности.
(уп)- последовательность, уп- п-ый член последовательности.
(ап)- последовательность, ап — п-ый член последовательности.
ап-1 -предыдущий член последовательности,
ап+1 — последующий член последовательности.
№ 332.
Последовательности бывают конечными и бесконечными, возрастающие и убывающие.
Задание. Записать первые 5 членов последовательности:
От первого натурального числа увеличение на 3.
От 10 увеличение в 2 раза и уменьшение на 1.
От числа 6 чередовать увеличение на 2 и увеличение в 2 раза.
Эти числовые ряды тоже называются числовыми последовательностями.
5. Знаменитые последовательности:
Числа Фибоначчи. Приложение 3.
Треугольник Паскаля. Приложение 3.
Урок 2.
Числовая последовательность считается заданной, если указан способ, позволяющий найти член последовательности любого номера.
1. Способы задания последовательностей:
Словесный.
(уп)- последовательность натуральных чисел, кратных трём.
(уп): 3, 6, 9, 12, 15, :
Табличный.
Слайд презентации.
Графический.
Слайд презентации.
Аналитический.
Указать формулу п-ого члена последовательности.
(уп = 3п)
Рекуррентный (от латинского — возвращаться).
Это формула, выражающая любой член последовательности, начиная с некоторого, через предыдущие.
(уп = уп-1 + 3).
2. Закрепление.
сп = . Запишите первые 5 членов последовательности.
(По одному человеку решают у доски, остальные — в тетради).
: 74, 81, 88, 95, 102, : Задайте формулу п-ого члена.
(уп = уп-1 + 7).
Рабочая тетрадь: с. 46, № 38.
3. Дополнительные задачи.
Запишите первые пять членов последовательности, заданной таким описанием: каждый член последовательности на 1 больше соответствующего члена ряда Фибоначчи.
Запишите первые пять членов последовательности, заданной формулой ап = (-3)п-1.
Запишите первые пять членов последовательности, заданной рекуррентно:
а1 = 4, ап+1 = ап + 2.
Запишите первые пять членов последовательности, заданной графиком:
Домашнее задание. Приложение 2.
Подведение итогов урока.
Итак, мы разобрали понятие последовательности и способы её задания. Ответьте на вопросы:
- Что такое последовательность?
- Какие виды последовательностей вы узнали?
- Какие способы задания вы узнали?
- О каких ученых и их трудах вы узнали?
Литература.
- О.В. Занина , И.Н. Данкова. Поурочные разработки по алгебре. 9 класс.
- Л.А. Тапилина, Т.Л. Афанасьева. Алгебра. 9 класс. Поурочные планы.
- Энциклопедический словарь юного математика.
- Материалы Фестиваля педагогических идей «Открытый урок»:
- А.А.Болбас. Урок алгебры по теме «Числовые последовательности». 9 класс.
- А.В. Худякова. Урок по алгебре для 9 класса по теме «Последовательности и способы их задания».
- Е.Е. Журавлёва. Урок-лекция в 9 классе на тему «Последовательности, понятие, определение. Возрастающие и убывающие последовательности. Способы задания последовательности».
- Г.А. Бархатова. Интегрированный урок математики и валеологии на тему «Прогрессия». Решение прикладных задач.
- К. Кноп. «Трактат о кроликах, рождающих великие открытия».
- Г.И. Глейзер. История математики в средней школе.
- Ю.В. Пухначев, Ю.П. Попов. Математика без формул.
Приложение 1. Лист для учащихся.
Тема уроков «ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ».
План 1 урока.
- Повторение видов функций, определение функций, область определения функций.
2. Устное решение задач.
Задача 1. На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля будет на складе в 1 день? 2 день? 3 день? 4 день? 5 день?
Задача 2. В период интенсивного роста человек растёт в среднем на 5 см в год. Сейчас рост у ученика С. – 180 см. Какого роста он будет в 2018 году?
Задача 3. Ежедневно каждый болеющий гриппом человек может заразить 4 окружающих.
Через сколько дней могут заболеть все ученики нашей школы?
3. Определение числовой последовательности.
4. Обозначение.
5. Виды последовательностей.
Задание 1. Записать первые пять членов последовательностей:
- От первого натурального числа увеличение на 3.
2. От 10 увеличение в 2 раза и уменьшение на 1.
3. От числа 6 чередовать увеличение на 2 и увеличение в 2 раза.
6. Знаменитые последовательности:
- Числа Фибоначчи.
- Треугольник Паскаля.
План 2 урока.
1. Способы задания последовательностей:
(уп) – последовательность натуральных чисел, кратных трём.
- Графический.
- Аналитический.
- Рекуррентный (от латинского — возвращаться).
2. Решение упражнений.
1) сп = . Запишите первые 5 членов последовательности.
2) …74, 81, 88, 95, 102,… Задайте формулу п- ого члена последовательности.
3) Рабочая тетрадь: с. 46, № 38.
Приложение 2
Приложение 3.
ЧИСЛА ФИБОНАЧЧИ.
Леонардо Фибоначчи (1180-1240).
Слайд презентации.
Крупный итальянский математик, автор «Книги абака».
Эта книга несколько веков оставалась основным хранилищем сведений по арифметике и алгебре. Именно по трудам Л. Фибоначчи вся Европа осваивала арабские цифры, систему счета, а также практическую геометрию. Они оставались настольными учебниками, чуть ли не до эпохи Декарта (а это уже 17 век!). Но по иронии судьбы до нашего времени сохранилась память только об одной задаче из этой книги.
Некто поместил пару кроликов в некоем месте, огражденном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производила на свет другую пару, а рождают кролики со второго месяца после своего рождения. (Слайд презентации).
Именно в этой задаче появляется последовательность, обессмертившая имя Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
В этой последовательности сумма любых двух предыдущих чисел равна следующему числу: 1+2=3, 3+5=8, 5+8=13,… .Отношение любого числа последовательности к предыдущему колеблется вокруг значения, которое ещё в древности под названием золотого сечения: 1,61803398…
«Золотое сечение» определяется как такое положительное число, которое на единицу больше обратного к нему числа: t — = 1. «Золотое сечение», как идеальная и приятная глазу пропорция человеческого тела и его элементов, широко использовалось многими художниками, начиная с другого великого Леонардо – Леонардо да Винчи. Слайд презентации.
Много интересного в арифметики чисел Фибоначчи. Каждое третье число Фибоначчи чётно, каждое четвёртое делится на три, каждое пятнадцатое оканчивается нулём, два соседних числа взаимно просты. Число ап делится на число ак тогда и только тогда, когда п делится на к.
ТРЕУГОЛЬНИК ПАСКАЛЯ.
Это бесконечная числовая таблица треугольной формы, в которой на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ними слева и справа в предыдущей строке.
Блез Паскаль (1623-1662) один из самых знаменитых людей в истории человечества.
В такой форме треугольник Паскаля приведён в «Трактате
об арифметическом треугольнике», опубликованном в 1665 г.,
уже после смерти автора. Слайд презентации
Популярность чисел, составляющих треугольник Паскаля,
не удивительна: они возникают в самых естественных задачах
алгебры, комбинаторики, теории вероятностей,
математического анализа, теории чисел. Этот треугольник можно записать в прямоугольной форме.
Слайд презентации.
Суммы чисел по диагоналям равны последовательным
числам Фибоначчи.
Приложение 4
09.2. Числовые последовательности | Решение задач по математике и други
Числовые последовательности
Чтобы определить место числовых последовательностей в системе основных понятий математического анализа, рассмотрим некоторые примеры. Мы встречаемся с нумерацией дней недели. Первый день – понедельник, второй – вторник и так далее, седьмой день – воскресенье. Каждому натуральному числу от 1 до 7 поставлен в соответствие день недели. Другой пример – знаменитая таблица Менделеева, в которой раскрывается связь между натуральными числами и соответствующими им химическими элементами. В настоящий момент такая связь установлена между числами от 1 до 114 соответствующими элементами.
В этих двух примерах соответствием охвачено конечное число элементов. С конечными числовыми последовательностями вы уже встречались, изучая арифметическую и геометрическую прогрессии. Рассмотрим теперь вписанные в круг правильные n–Угольники. Каждый из них имеет
свою площадь. Соответствие между натуральными числами и площадями правильных n–Угольников, вписанных в круг, связано с бесконечным числом элементов. Можно также рассмотреть соответствие между натуральными числами и их синусами. Во всех случаях, если изучаемое соответствие является отображением множества натуральных чисел на какое-либо другое, то говорят, что такое соответствие задает числовую последовательность.
Конечная числовая последовательность может быть задана непосредственным перечислением ее членов, для бесконечной последовательности такое перечисление принципиально невозможно. Мы будем в дальнейшем рассматривать свойства бесконечных последовательностей.
Таким образом, ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ – это функция натурального аргумента:
|
Рис. 9.20. График числовой последовательности. |
Графически числовая последовательность представляет собой совокупность изолированных точек плоскости (рис. 9.20). Такое изображение не всегда бывает удобно.
Все числовые последовательности определены на множестве натуральных чисел, поэтому в их задании используется упрощенная запись, или просто – ,. Например,
Вместо графического представления числовой последовательности, приведенного на рис. 9.20, может быть использовано изображение членов числовой последовательности точками на числовой оси. Так, например, на рис. 9.21 представлена последовательность
.
|
Рис. 9.21. Изображение числовой |
Часто хn и yn называют общими членами последовательностей.
Арифметическая и геометрическая прогрессии задаются формулами общего члена, соответственно:
Где а1 – первый член арифметической прогрессии, d – ее разность, b1 – первый член геометрической прогрессии, q – ее знаменатель.
Достаточно часто используется рекуррентный способ задания числовых последовательностей, состоящий в том, что n–Й член последовательности выражается через предыдущие.
Например,
А уже привычные формулы:
Являются рекуррентной формой задания соответственно арифметической и геометрической прогрессий.
Более двух тысяч лет известен алгоритм Евклида для определения наибольшего общего делителя двух целых положительных чисел A и B:
Где – положительные остатки, получающиеся в результате делений, а – неполные частные. Эти остатки тоже являются функциями натурального аргумента, а значит, числовыми последовательностями. (Напомним, что последний отличный от нуля остаток и является наибольшим общим делителем чисел A и B.)
Рекуррентный способ задания числовых последовательностей позволяет более эффективно организовать вычисления на ЭВМ, снижая погрешность результата и ускоряя сходимость вычислительных процессов.
Оправдан ли автоматический перенос всех известных свойств функций на числовые последовательности? Нет, не всегда. Оказывается, что числовые последовательности могут быть монотонными, ограниченными, неограниченными.
Но они не могут быть периодическими, четными или же нечетными.
Они могут при определенных условиях достигать наибольшего и наименьшего значения, но нет смысла говорить о выпуклости и вогнутости по отношению к последовательностям.
Распространим понятие предела функции на числовые последовательности. Учитывая, что в любой сколь угодно малой окрестности предельной точки, за исключением, быть может, самой предельной точки, функция должна быть определена, мы обнаруживаем, что неразумно рассматривать предел числовой последовательности, когда n конечно, например, при . Для всех числовых последовательностей можно говорить о пределе при .
Число A называется ПРЕДЕЛОМ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ при , если для любого положительного числа найдется такой номер n0, что для всех номеров будет справедливо неравенство
Иначе говоря,
|
Сходится ли произведение двух расходящихся числовых последовательностей? |
Числовая последовательность, имеющая конечный предел, называется СХОДЯЩЕЙСЯ, в противном случае – РАСХОДЯЩЕЙСЯ.
Докажем, например, что
|
Расходится ли произведение двух сходящихся числовых последовательностей? |
Пользуясь определением предела.
Действительно,
Рассмотрим неравенство
Но
Поэтому, если будут найдены n, удовлетворяющие неравенству
То эти n тем более удовлетворят неравенству
Получаем:
В качестве числа n0 можно выбрать натуральное число, превосходящее целую часть действительного числа .
Существует даже специальная функция
Обозначающая наибольшее целое число, не превосходящее x.
Например,
Возвращаясь к доказательству рассматриваемого утверждения, получим, что для будет справедливо неравенство
Что и требовалось доказать.
Конечно, не всегда достаточно легко можно решить соответствующее неравенство, сделать упрощающую оценку. В частности, при доказательстве существования предела
Будем иметь
.
Полученное неравенство не может быть оценено так же, как в предыдущем примере, однако сравнительно просто методом подбора на ЭВМ по конкретному E обнаруживается номер n0, начиная с которого неравенство будет выполняться. Возможно, это не достаточно строгий путь доказательства существования предела, так как целью рассуждений является определение возможности отыскания по Любому E > 0 номера n0, того “порога”, начиная с которого неравенство
Будет выполняться. Мы, однако, уже догадываемся, что при числовые последовательности
и
Не будут отличаться существенно в своем поведении. Это обстоятельство найдет у нас в дальнейшем строгое подтверждение при рассмотрении асимптотических равенств и позволит найти способ упрощения некоторых функциональных зависимостей в окрестностях предельных точек.
Рассмотренные примеры можно решить значительно легче, если применить теоремы о пределах, которые мы уже доказали для функций.
Так,
Для числовых последовательностей удалось найти достаточный признак их сходимости, который мы приведем без доказательства.
ТЕОРЕМА ВЕЙЕРШТРАССА. Если числовая последовательность монотонно возрастает (убывает) и ограничена сверху (снизу), то она является сходящейся.
|
Справедливо ли утверждение: если числовая последовательность сходится, то она монотонно возрастает (убывает) и ограничена сверху (снизу)? |
|
Приведите другие примеры числовых последовательностей, для которых хотя бы одно из условий теоремы Вейерштрасса не выполняется, но они имеют все-таки предел. |
Достаточность этих условий состоит в том, что их вполне хватает, чтобы гарантировать сходимость числовой последовательности. Могут быть, однако, и другие сходящиеся числовые последовательности, поэтому условия теоремы не являются необходимыми.
Например, числовая последовательность
Не является монотонной, но, как легко убедиться, она сходится к нулю.
|
Справедлива ли теорема Вейерштрасса для функций действительного аргумента? Если да, то дайте ее формулировку для случаев, когда предельная точка конечна и бесконечна. |
Семидесятилетний старец, сидя в кресле, читал лекцию, в которой было отточено каждое слово. Ему помогал студент, записывавший под диктовку необходимые формулы на доске. Зал с трудом понимал ход мысли лектора, но сосредоточенно слушал, боясь пропустить хоть одно слово. Присутствовала тысяча человек: профессора университетов и преподаватели лицеев, учащиеся и студенты, дипломаты и политики.
|
В цветном разноголосом Хороводе, В мелькании различий и Примет Есть люди, от которых Свет исходит, И люди, поглощающие свет. И. Губерман |
|
Всякая ли сходящаяся числовая последовательность ограничена? Приведите примеры. |
Они прибыли из десятков стран. Это была вводная лекция по математическому анализу. Ее читал в 1885 году Карл Вейерштрасс – великий ученый и добрый учитель. Он щедро делился своими идеями с теми, кому посчастливилось работать с ним. Спустя годы, сами ученики опубликовали книги об его научных достижениях, а его любимая ученица – Софья Ковалевская – вспоминала позже, что основными своими достижениями в математике и механике она обязана именно ему.
| < Предыдущая | Следующая > |
|---|
Числовые последовательности
Класс 9
Урок № __61__
Тема: Числовые последовательности
Цели и задачи урока:
Образовательная: Организовать деятельность учащихся по повторению понятий числовой последовательности, арифметической и геометрической прогрессии, содействовать в закреплении навыков словесного, аналитического и рекуррентного задания числовой последовательности, применение полученных знаний на практике.
Развивающая: Содействовать формированию научного мировоззрения, развитию исследовательских навыков, умение подмечать закономерности, аргументировать и классифицировать.
Воспитательная: Содействовать развитию внимательности, умению общаться, инициативности, трудолюбия, творческих способностей, сознательного восприятия учебного материала.
Тип урока: урок обобщающего повторения и систематизации знаний.
Методы обучения: частично – поисковый, системные обобщения
Формы деятельности обучающихся на уроке: фронтальная работа, групповая работа, парная работа, самостоятельная работа, самопроверка, взаимопроверка.
Оборудование: доска, компьютер, мультимедийный проектор, презентация по теме урока, таблички с формулами, магниты
Раздаточный материал: карточки на установление соответствия, карточки с текстом заданий самостоятельной работы, сборники ЕНТ.
ПЛАН УРОКА
№ | Этап урока | Деятельность учителя | Деятельность ученика | Время |
Орг. момент | Приветствие, сообщение темы урока, постановка цели урока. | Формирование задач на урок | ||
Активизация опорных знаний | Проведение математического диктанта в форме разноуровневого теста с взаимопроверкой, оглашение критериев оценивания, раздача оценочных листов | Выполнение задания, взаимопроверка, занесение результатов в оценочные листы | ||
Повторение теоретического материала | Деление на группы, постановка проблемы в рамках одной группы | Решение поставленной проблемы, составление кластера по теме «Числовая последовательность», 1 представитель группы ищет определение понятия «Прогрессия» её историю, составляет кластер. Взаимооценивание | ||
Решение задач | Постановка проблемы. Озвучивание задания упражнения и комментарий задания. | Решение задания. Составление заданий по аналогии. | ||
Постановка проблемы. Раздача ресурса | Решение задания. Формулирование вопроса. Обсуждение в парах | |||
Озвучивание вопроса, вызов к обдумыванию и обсуждению | Обдумывание, обсуждение, формирование общей идеи | |||
Рефлексия и постановка Д/з | Раздача листов с вопросами и домашним заданием | Обсуждение вопросов и формирование ответов на них | ||
Итог урока | Выставление оценок с комментарием, | Участие в обсуждении и выставлении оценок |
Ход урока:
Организационный этап:
Здравствуйте! Тема нашего урока: «Числовые последовательности».
– Сегодня на уроке мы обобщим и систематизируем те знания, которые получили во время изучения темы «Числовые последовательности».
Эпиграф урока.
Закончился XX век.
Куда стремится человек?
Изучен космос и моря,
Строенье звёзд и вся Земля.
Но математиков зовёт
Известный лозунг:
«Прогрессио – движение вперёд»
(На доске спроецированы цели урока) Ваша задача поставить перед собой Учебные задачи на урок. (Ученики записывают поставленные задачи на стикеры ).
Активизация опорных знаний
Ученикам предлагаются задания, выдаются оценочные листы с критериями оценивания.
Ф. И. обучающегося | Этапы урока | |||||||||||||
Установи соответствие | Работа в группе по составлению кластера | Решение разноуровневых задач в парах | Решение задач двумя способами. | Обсуждение вопросов в группе | ||||||||||
7 | 5 | 5 | 3 | 5 | ||||||||||
Итог урока | Общее кол-во баллов _____ | Оценка за урок _____ | ||||||||||||
Уровень А
Составить определение:
Числовой последовательностью называется множество чисел, элементы которого можно пронумеровать. (1 балл)
Если каждый член последовательности начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом, то эта последовательность называется арифметической прогрессией. (3 балла)
Если каждый член последовательности начиная со второго, равен произведению предыдущего члена на некоторое постоянное число, не равное нулю, то эта последовательность называется геометрической прогрессией. (3 балла)
Уровень В
№ п\п | Вопрос | Формула |
1 | Сумма бесконечно убывающей геометрической прогрессии |
|
2 | Формула n-го члена арифметической прогрессии. |
|
3 | Сумма n-первых членов арифметической прогрессии. |
|
4 | Сумма n-первых членов геометрической прогрессии. |
|
5 | Формула n-го члена геометрической прогрессии. |
|
6 | Знаменатель геометрической прогрессии. |
|
7 | Разность арифметической прогрессии. |
|
Код ответа:5834291 | ||
Обучающиеся в течение 5 минут решают предложенные задания, обмениваются тетрадями для взаимопроверки, проводят комментарий допущенных ошибок.
Повторение теоретического материала
Класс делиться на группы. Каждой группе раздается ресурс. Каждой группые необходимо составить кластер на тему «Последовательность. Прогрессия. История возникновения понятий последовательность и прогрессия».
Время работы 7 мин.
Последовательности (ресурс)
Фундаментальную роль числа в природе определил еще Пифагор своим утверждением «Все есть число». Поэтому математика являлась одной из основ религии последователей Пифагора (пифагорейского союза). Пифагорейцы считали, что бог Дионис положил число в основу мировой организации, в основу порядка; оно отражало единство мира, его начало, а мир представлял собой множество, состоящее из противоположностей. То, что приводит противоположности к единству, и есть гармония. Гармония является божественной и заключается в числовых соотношениях.
Слово «прогрессия» латинского происхождения (progressio), буквально означает «движение вперед» ( как и слово «прогресс») и встречается впервые у римского автора Боэция (V-VI вв.).
Прогрессии известны издавна, а потому нельзя сказать, кто их открыл. Ведь и натуральный ряд – это арифметическая прогрессия. Во время раскопок в Египте был найден папирус, который датируется 2000 г. до н.э., но и его было переписано из другого, еще более раннего, отнесенного к ІІІ тысячелетию до н.э. Ученые расшифровали текст папируса, содержание некоторых задач дает возможность отнести их к задачам на прогрессии.
В вавилонских текстах рассказывается о том, что увеличение освещенной части лунного диска на протяжении первых пяти дней происходит по закону геометрической прогрессии со знаменателем 2, а в следующие десять дней – по закону арифметической прогрессии с разностью 16.
Задачи на прогрессии встречаются в одной из древнейших памяток права – «Русской правде», составленной при Киевском князе Ярославе Мудром (ХІ ст.). В этом документе есть статья, посвященная вычислению приплода от 22 овец за 12 лет при условии, что каждая овца ежегодно приносит одну овцу и два барана. Так же содержатся сведения о приплоде от пчел за определенный промежуток времени, о количестве зерна, собранного на определенном участкае земли и др. Эти задачи не имели хозяйственного значения, а были результатом развития интереса к математике и математическому содержанию данных задач.
О том, как давно была известная геометрическая прогрессия, свидетельствует и легенда об истории изобретения шахмат. Изобретатель шахмат, ученый Сета, попросил в награду у индийского царя Сирама за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клеточку шахматной доски положить одно зерно, на вторую – два, на третью- четыре, т.е. чтобы число зерен все время удваивалось. Рассказывают, что индийский царь Сирам рассмеялся, услышав, какую награду попросил у него изобретатель шахмат.
Сколько зёрен должен был получить изобретатель шахмат? (Учащиеся должны подсчитать дома)
S64 = 264 – 1 = 18 446 744 073 709 551 615.
Современники сказали бы так:
S64 = 1, 84• 1019 – стандартный вид данного числа.
Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая и моря , и океаны, и пустыни, и Арктику с Антарктикой, то получить удовлетворительный урожай, то за пять лет он смог бы рассчитаться с просителем. Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности Земли. Это превосходит количество пшеницы, собранной человечеством до нашего времени.
Чтобы разместить это зерно в амбаре, то его размеры будут: высота 4 м, ширина 10м, длина будет 30 000 000км- вдвое больше, чем расстояние от Земли до Солнца
Решение задач
— В группах решить задачи, обсудить решение внутри группы.
1. Дана арифметическая прогрессия: -8, -16, … Найдите разность арифметической прогрессии.
2. Найдите знаменатель геометрической прогрессии, если  12,
12,  4.
4.
———————————————————————————————
3. Найдите пятый член геометрической прогрессии 4, 1, …
4. Найти седьмой член арифметической прогрессии, если  15,
15,  — 4.
— 4.
———————————————————————————————-
— В розданных сборниках ЕНТ найти задания на прогрессию, числовую последовательность и решить с обсуждением в парах.
— подумайте, что дает нам знание формул n-го члена арифметической и геометрической прогрессии
Составить задачи по аналогии с дальнейшим взаимообменом для решения.
Взаимооценивание.
Физ.минутка
Задача из папируса Райнда звучит так:
«У семи лиц по семи кошек; каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа этого ряда и их сумма?»
Решение задачи выполняется в тетрадях и на доске.
Людей всего 7, кошек 72=49, они съедают 73=343 мыши, которые съедают всего 74=2401 колосьев, из них вырастает 75=16807 мер ячменя. В сумме эти числа дают 19 607.
Парам предлагается решить задачи двумя способами:
1) Не используя формул прогрессий;
2) Используя изученные формулы арифметической и геометрической прогрессии.
Задача первой группе (решают самостоятельно)
Как известно из медицинской статистики, одна выкуренная сигарета сокращает жизнь человека на 10 минут. Вычислите, сколько сигарет в среднем сократят жизнь человека на 1 день. (144 сигареты).
Задача второй группе (решают самостоятельно)
Курс воздушных ванн начинает с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 мин. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45 мин? Ответ: 10 дней
Рефлексия. Постановка Д/з.
Ответить на поставленные вопросы:
Из области, каких наук данные задачи?
Какой способ позволяет быстрее решить задачи?
Что было бы, если бы вы не знали формул прогрессий?
Для чего необходимо изучать арифметическую и геометрическую прогрессии?
Приведите ещё примеры наук или специальностей, которые могут использовать знания по арифметической и геометрической прогрессии.
Д/з :
А)Задача
В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две. Указать количество бактерий, рожденных одной бактерией за 7 минут.
Б) Придумать и составить задачу на применение знаний по прогрессии в вашей будущей специальности.
Прошу вас взять ваши стикеры и сделать анализ, достигли ли вы поставленных перед собой задач?
А теперь выберите смайлик, характеризующий ваше настроение на конец урока и поставьте его на той ступеньке лестницы-успеха, которой вы достигли к концу урока по вашему мнению.



Обсуждение и выставление оценок.
Урок сегодня завершён,
Но каждый должен знать:
Познание, упорство, труд
К прогрессу в жизни приведут.
Ф. И. обучающегося | Этапы урока | |||||||||||||
Установи соответствие | Работа в группе по составлению кластера | Решение разноуровневых задач в парах | Решение задач двумя способами. | Обсуждение вопросов в группе | ||||||||||
7 | 5 | 5 | 3 | 5 | ||||||||||
Итог урока | Общее кол-во баллов _____ | Оценка за урок _____ | ||||||||||||
Ф. И. обучающегося | Этапы урока | |||||||||||||
Установи соответствие | Работа в группе по составлению кластера | Решение разноуровневых задач в парах | Решение задач двумя способами. | Обсуждение вопросов в группе | ||||||||||
7 | 5 | 5 | 3 | 5 | ||||||||||
Итог урока | Общее кол-во баллов _____ | Оценка за урок _____ | ||||||||||||
Ф. И. обучающегося | Этапы урока | |||||||||||||
Установи соответствие | Работа в группе по составлению кластера | Решение разноуровневых задач в парах | Решение задач двумя способами. | Обсуждение вопросов в группе | ||||||||||
7 | 5 | 5 | 3 | 5 | ||||||||||
Итог урока | Общее кол-во баллов _____ | Оценка за урок _____ | ||||||||||||
Ф. И. обучающегося | Этапы урока | |||||||||||||
Установи соответствие | Работа в группе по составлению кластера | Решение разноуровневых задач в парах | Решение задач двумя способами. | Обсуждение вопросов в группе | ||||||||||
7 | 5 | 5 | 3 | 5 | ||||||||||
Итог урока | Общее кол-во баллов _____ | Оценка за урок _____ | ||||||||||||
Ф. И. обучающегося | Этапы урока | |||||||||||||
Установи соответствие | Работа в группе по составлению кластера | Решение разноуровневых задач в парах | Решение задач двумя способами. | Обсуждение вопросов в группе | ||||||||||
7 | 5 | 5 | 3 | 5 | ||||||||||
Итог урока | Общее кол-во баллов _____ | Оценка за урок _____ | ||||||||||||
Задача первой группе (решают самостоятельно)
Как известно из медицинской статистики, одна выкуренная сигарета сокращает жизнь человека на 10 минут. Вычислите, сколько сигарет в среднем сократят жизнь человека на 1 день.
Задача первой группе (решают самостоятельно)
Как известно из медицинской статистики, одна выкуренная сигарета сокращает жизнь человека на 10 минут. Вычислите, сколько сигарет в среднем сократят жизнь человека на 1 день.
Задача второй группе (решают самостоятельно)
Курс воздушных ванн начинает с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 мин. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45 мин?
Задача второй группе (решают самостоятельно)
Курс воздушных ванн начинает с 15 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 мин. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы достичь их максимальной продолжительности 1ч 45 мин?
Вопросы для обсуждения:
Из области, каких наук данные задачи?
Какой способ позволяет быстрее решить задачи?
Что было бы, если бы вы не знали формул прогрессий?
Для чего необходимо изучать арифметическую и геометрическую прогрессии?
Приведите ещё примеры наук или специальностей, которые могут использовать знания по арифметической и геометрической прогрессии.
Вопросы для обсуждения:
Из области, каких наук данные задачи?
Какой способ позволяет быстрее решить задачи?
Что было бы, если бы вы не знали формул прогрессий?
Для чего необходимо изучать арифметическую и геометрическую прогрессии?
Приведите ещё примеры наук или специальностей, которые могут использовать знания по арифметической и геометрической прогрессии.
1. Дана арифметическая прогрессия: -8, -16, … Найдите разность арифметической прогрессии.
2. Найдите знаменатель геометрической прогрессии, если  12,
12,  4.
4.
———————————————————————————————
3. Найдите пятый член геометрической прогрессии 4, 1, …
4. Найти седьмой член арифметической прогрессии, если  15,
15,  — 4.
— 4.
———————————————————————————————-
1. Дана арифметическая прогрессия: -8, -16, … Найдите разность арифметической прогрессии.
2. Найдите знаменатель геометрической прогрессии, если  12,
12,  4.
4.
———————————————————————————————
3. Найдите пятый член геометрической прогрессии 4, 1, …
4. Найти седьмой член арифметической прогрессии, если  15,
15,  — 4.
— 4.
———————————————————————————————-
1. Дана арифметическая прогрессия: -8, -16, … Найдите разность арифметической прогрессии.
2. Найдите знаменатель геометрической прогрессии, если  12,
12,  4.
4.
———————————————————————————————
3. Найдите пятый член геометрической прогрессии 4, 1, …
4. Найти седьмой член арифметической прогрессии, если  15,
15,  — 4.
— 4.
———————————————————————————————-
1. Дана арифметическая прогрессия: -8, -16, … Найдите разность арифметической прогрессии.
2. Найдите знаменатель геометрической прогрессии, если  12,
12,  4.
4.
———————————————————————————————
3. Найдите пятый член геометрической прогрессии 4, 1, …
4. Найти седьмой член арифметической прогрессии, если  15,
15,  — 4.
— 4.
———————————————————————————————-
1. Дана арифметическая прогрессия: -8, -16, … Найдите разность арифметической прогрессии.
2. Найдите знаменатель геометрической прогрессии, если  12,
12,  4.
4.
———————————————————————————————
3. Найдите пятый член геометрической прогрессии 4, 1, …
4. Найти седьмой член арифметической прогрессии, если  15,
15,  — 4.
— 4.
———————————————————————————————-
Последовательности (ресурс)
Фундаментальную роль числа в природе определил еще Пифагор своим утверждением «Все есть число». Поэтому математика являлась одной из основ религии последователей Пифагора (пифагорейского союза). Пифагорейцы считали, что бог Дионис положил число в основу мировой организации, в основу порядка; оно отражало единство мира, его начало, а мир представлял собой множество, состоящее из противоположностей. То, что приводит противоположности к единству, и есть гармония. Гармония является божественной и заключается в числовых соотношениях.
Слово «прогрессия» латинского происхождения (progressio), буквально означает «движение вперед» ( как и слово «прогресс») и встречается впервые у римского автора Боэция (V-VI вв.).
Прогрессии известны издавна, а потому нельзя сказать, кто их открыл. Ведь и натуральный ряд – это арифметическая прогрессия. Во время раскопок в Египте был найден папирус, который датируется 2000 г. до н.э., но и его было переписано из другого, еще более раннего, отнесенного к ІІІ тысячелетию до н.э. Ученые расшифровали текст папируса, содержание некоторых задач дает возможность отнести их к задачам на прогрессии.
В вавилонских текстах рассказывается о том, что увеличение освещенной части лунного диска на протяжении первых пяти дней происходит по закону геометрической прогрессии со знаменателем 2, а в следующие десять дней – по закону арифметической прогрессии с разностью 16.
Задачи на прогрессии встречаются в одной из древнейших памяток права – «Русской правде», составленной при Киевском князе Ярославе Мудром (ХІ ст.). В этом документе есть статья, посвященная вычислению приплода от 22 овец за 12 лет при условии, что каждая овца ежегодно приносит одну овцу и два барана. Так же содержатся сведения о приплоде от пчел за определенный промежуток времени, о количестве зерна, собранного на определенном участкае земли и др. Эти задачи не имели хозяйственного значения, а были результатом развития интереса к математике и математическому содержанию данных задач.
О том, как давно была известная геометрическая прогрессия, свидетельствует и легенда об истории изобретения шахмат. Изобретатель шахмат, ученый Сета, попросил в награду у индийского царя Сирама за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клеточку шахматной доски положить одно зерно, на вторую – два, на третью- четыре, т.е. чтобы число зерен все время удваивалось. Рассказывают, что индийский царь Сирам рассмеялся, услышав, какую награду попросил у него изобретатель шахмат.
Сколько зёрен должен был получить изобретатель шахмат? (Учащиеся должны подсчитать дома)
S64 = 264 – 1 = 18 446 744 073 709 551 615.
Современники сказали бы так:
S64 = 1, 84• 1019 – стандартный вид данного числа.
Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая и моря , и океаны, и пустыни, и Арктику с Антарктикой, то получить удовлетворительный урожай, то за пять лет он смог бы рассчитаться с просителем. Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности Земли. Это превосходит количество пшеницы, собранной человечеством до нашего времени.
Чтобы разместить это зерно в амбаре, то его размеры будут: высота 4 м, ширина 10м, длина будет 30 000 000км- вдвое больше, чем расстояние от Земли до Солнца
Установи соответствие:
№ п\п | Вопрос | Формула |
1 | Сумма бесконечно убывающей геометрической прогрессии |
|
2 | Формула n-го члена арифметической прогрессии. |
|
3 | Сумма n-первых членов арифметической прогрессии. |
|
4 | Сумма n-первых членов геометрической прогрессии. |
|
5 | Формула n-го члена геометрической прогрессии. |
|
6 | Знаменатель геометрической прогрессии. |
|
7 | Разность арифметической прогрессии. |
|
Код ответа: | ||
Установи соответствие:
№ п\п | Вопрос | Формула |
1 | Сумма бесконечно убывающей геометрической прогрессии |
|
2 | Формула n-го члена арифметической прогрессии. |
|
3 | Сумма n-первых членов арифметической прогрессии. |
|
4 | Сумма n-первых членов геометрической прогрессии. |
|
5 | Формула n-го члена геометрической прогрессии. |
|
6 | Знаменатель геометрической прогрессии. |
|
7 | Разность арифметической прогрессии. |
|
Код ответа: | ||
Числовой последовательностью называется множество чисел, элементы которого можно пронумеровать.
Если каждый член последовательности начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом, то эта последовательность называется арифметической прогрессией.
Если каждый член последовательности начиная со второго, равен произведению предыдущего члена на некоторое постоянное число, не равное нулю, то эта последовательность называется геометрической прогрессией.
«Числовая последовательность. Решение задач. Выбор схемы»
Календарно — тематическое планирование по математике 1 класс (4 часа в неделю)
п/п | Тема урока (содержание урока) | Кол-во ча сов | материал учебника | материал рабочей тетради | сам. работы | Характеристика деятельности обучающихся | Дата план | Дата факт |
Сравнение и счёт предметов | 12ч. | |||||||
1 | Знакомство с учебником математики. Форма предметов. | 1 | 1 часть стр. 4-5 | 1 часть стр. 4-5 | Выделять в окружающей обстановке объекты по указанным признакам. Называть признаки различия, сходства предметов, числа в порядке их следования при счете. Исследовать предметы окружающей обстановки и сопоставлять их с геометрическими формами: круглая, прямоугольная, квадратная, треугольная, овальная. Сравнивать предметы по форме, размерам и другим признакам. Распознавать фигуры: треугольник, квадрат, круг, прямоугольник. Описывать признаки предметов с использованием слов: большой-маленький, высокий – низкий, широкий – узкий, шире – уже, толстый – тонкий, длинный – короткий. Наблюдать, анализировать и описывать расположение объектов с использованием слов: наверху – внизу, выше – ниже, верхний – нижний, слева – справа, левее – правее, рядом, около, посередине, под, у, над, перед, за, между, близко – далеко, ближе – дальше, впереди – позади. Отсчитывать из множества предметов заданное количество отдельных предметов. Оценивать количество предметов и проверять сделанные оценки подсчётом. Вести счёт как в прямом, так и в обратном порядке в пределах 10, порядковый счет предметов. Устанавливать и называть порядковый номер каждого предмета в ряду, используя числительные: первый, второй… Упорядочивать события, располагая их в порядке следования (раньше, позже, ещё позднее). Читать и описывать маршруты движения, используя слова: вверх – вниз, вправо – влево. | 4.09 | ||
2 | Разговор о величине. Сравнение предметов по форме, размерам и другим признакам. | 1 | стр. 6-7 | стр. 6-7 | 5.09. | |||
3. | Расположение предметов. Описание расположения объектов с использованием слов: наверху – внизу, выше – ниже, верхний – нижний, | 1 | Стр.8-9 | Стр.8-9 | 6.08 | |||
4. | Количественный счёт предметов в пределах 10 | 1 | стр.10-11 | стр.10-11 | 7.09 | |||
5. | Порядковый счёт предметов, используя числительные: первый, второй… | 1 | стр. 12-13 | стр. 12-13 | 11.09 | |||
6. | Сравнение предметов. Признаки отличия, сходства двух-трех предметов. | 1 | стр. 14-15 | стр. 14-15 | тест 2 | 12.09 | ||
7. | Расположение предметов по размеру. Порядок расположения предметов по величине. | 1 | стр. 16-17 | стр. 16-17 | 13.09 | |||
8. | Сравнение групп предметов. Отношения «столько же, «больше, «меньше». | 1 | стр. 18-19 | стр. 18-19 | тест3 | 14.09 | ||
9. | Расположение по времени. Порядок следования событий: Что сначала? Что потом? | 1 | стр. 20-21 | стр. 20-21 | 18.09 | |||
10. | Сравнение предметов. Отношения «на сколько больше? на сколько меньше?» | 1 | стр. 22-24 | стр. 22 | 19.09 | |||
11. | Сравнение предметов. Отношение «поровну». | 1 | стр.25-26 | стр. 23 | тест 4 | 20.09 | ||
12. | Проверочная работа №1 по теме «Сравнение и счет предметов» | 1 | стр.27 | 21.09 | ||||
Множества и действия с ними | 9 ч. | |||||||
13 | Множество. Элементы множества. Характерные свойства элементов множества. | 1 | стр. 28-29 | стр. 24-25 | Называть элементы множества, характеристическое свойство элементов множества. Группировать элементы множества в зависимости от указанного или самостоятельно выявленного свойства. Задавать множество наглядно или перечислением его элементов. Устанавливать равные множества Распознавать точки и линии на чертеже. Называть обозначение точки. Располагать точки на прямой и плоскости в указанном порядке. Описывать порядок расположения точек, используя слова: внутри, вне, между. Моделировать на прямой и на плоскости отношения: внутри, вне, между. Рисовать орнаменты и бордюры. | 25.09 | ||
14. | Части множества. Способы задания множеств. | 1 | стр. 30-31 | стр. 26 | тест 5 | 26.09 | ||
15 | Части множества. Способы задания множеств путем перечисления его элементов. | 1 | стр. 32-33 | стр. 27 | 27.09 | |||
16 | Знакомство с понятием «равные множества». Объединение предметов в группы по сходным признакам. | 1 | стр. 34-35 | стр. 28 | тест 6 | 28. 09 | ||
17 | Сравнение равных и неравных множеств. | 1 | стр. 36-37 | стр, 29 | 2.10 | |||
18 | Точки и линии. Обозначение точек на чертеже. | 1 | стр. 38-39 | стр. 30-31 | 3.10 | |||
19 | Расположение множеств. Расположение точек на прямой и плоскости в указанном порядке. | 1 | стр.40-43 | Стр. 32-33 | 4.10 | |||
20 | Повторение изученного по теме «Множества и действия с ними» | 1 | стр. 44-45 | 5.10 | ||||
21 | Проверочная работа № 2 по теме «Множества и действия с ними». | 1 | 9.10 | |||||
Числа от 1 до 10. Число 0. Нумерация. | 25ч. | |||||||
22 | Знакомство с числом 1 и цифрой 1. | 1 | стр. 46-47 | стр. 34-35 | Записывать числа от 1 до 10. Воспроизводить последовательность чисел от 1 до 10 как в прямом, так и в обратном порядке, начиная с любого числа. Определять место каждого числа в этой последовательности. Образовывать следующее число прибавлением 1 к предыдущему числу или вычитанием 1 из следующего за ним в ряду чисел. Считать различные объекты (предметы, группы предметов, звуки, слова и т.п.) и устанавливать порядковый номер того или иного объекта при заданном порядке счета. Различать и называть прямую линию. Обозначать прямую двумя точками. Различать, изображать и называть отрезок, треугольник, линии замкнутые и незамкнутые на чертеже. Упорядочивать объекты по длине (на глаз, наложением, с использованием мерок). Сравнивать длины отрезков на глаз, с помощью полоски бумаги, нити, общей мерки. Соотносить реальные предметы и их элементы с изученными геометрическими линиями. Изображать на чертеже прямую линию с помощью линейки. Составлять рассказ по парным картинкам или схематическим рисункам, на которых представлены ситуации, иллюстрирующие действие сложения (вычитания). Читать, записывать и составлять числовые выражения с использованием знаков + (плюс), — (минус), = (равно) Моделировать ситуации, иллюстрирующие действие сложения (вычитания). Составлять числовые выражения на нахождение суммы (разности). Вычислять сумму (разность) чисел в пределах 10. Читать числовые выражения на сложение с использованием термина «сумма» различными способами. | 10.10 | ||
23 | Знакомство с числом 2 и цифрой 2. | 1 | стр. 48-49 | стр. 36-37 | тест 7 | 11.10 | ||
24 | Прямая. Обозначение и изображение прямой на чертеже. | 1 | стр.50-51 | стр. 38-39 | 12.10 | |||
25. | Составление математических рассказов. Подготовка к введению понятия «задача» | 1 | Стр.52-53 | Стр.40-41 | тест 8 | 16.10 | ||
26. | Знаки математических действий. Составление рассказа по картинкам и числовым выражениям | 1 | Стр.54-55 | Стр. 42-43 | 17.10 | |||
27. | Отрезок. Обозначение отрезка на чертеже. | 1 | стр. 56-57 | стр. 44-45 | 18.10 | |||
28. | Знакомство с числом 3 и цифрой 3. | 1 | стр.58-59 | стр. 46-47 | 19.10 | |||
29. | Треугольник. Обозначение треугольника. | 1 | Стр.60-61 | Стр. 48-49 | 23.10 | |||
30. | Знакомство с числом 4 и цифрой 4. | 1 | стр.62-63 | стр. 50-51 | 24.10 | |||
31. | Четырёхугольник. Изображение четырехугольника на чертеже. | 1 | Стр.64-65 | Стр. 52-53 | 25.10 | |||
32. | Сравнение чисел. Запись результатов сравнения с помощью знаков (больше), | 1 | стр.66-67 | стр. 54-55 | 26.10 | |||
33. | Знакомство с числом 5 и цифрой 5. | 1 | стр.68-69 | стр. 56-57 | 6.11 | |||
34. | Знакомство с числом 6 и цифрой 6. | 1 | стр.70-71 | стр. 58-59 | 7.11 | |||
35 | Замкнутые и незамкнутые линии. Распознавание линий на чертеже. | 1 | Стр.72-73 | Стр. 60-61 | 8.11 | |||
36. | Проверочная работа № 3 по теме «Нумерация» | 1 | 9.11 | |||||
37. | Введение понятия «суммы». Составление числовых выражений на нахождение суммы. | 1 | стр.74-75 | стр. 62-63 | 13.11 | |||
38 | Введение понятия «разность». Действие «вычитание». | 1 | стр.76-77 | стр. 64-64 | 14.11 | |||
39 | Знакомство с числом 7 и цифрой 7. | 1 | стр.78-79 | стр. 66-67 | 15.11 | |||
40. | Отрезок. Длина отрезка. Сравнение длины отрезков. | 1 | Стр.80-81 | Стр. 68-69 | 16.11 | |||
41 | Знакомство с числом 0 и цифрой 0. | 1 | стр.82-83 | стр. 70-71 | 20.11 | |||
42 | Знакомство с числом 8 и цифрой 8. | 1 | стр.84-85 | стр. 72-73 | 21.11 | |||
43 | Знакомство с числом 9 и цифрой 9. | 1 | стр.86-87 | стр.74-75 | 22.11 | |||
44 | Знакомство с числом 10. Работа над составом чисел от 2 до 10. | 1 | стр.88-89 | стр. 76 | 23.11 | |||
45 | Проверочная работа № 4 по теме «Числа от 1 до 10» | 1 | 27.11 | |||||
46 | Работа над ошибками. Повторение по теме «Числа от 1 до 20» | 1 | Стр.90-91 | стр. 77 | 28.11 | |||
Сложение и вычитание | 59 ч. | |||||||
47 | Понятие «числового отрезка». Действия сложения и вычитания с помощью числового отрезка | 1 | стр. 92-93 | стр. 78-79 | Моделировать действия сложения и вычитания с помощью числового отрезка; составлять по рисункам схемы арифметических действий сложения и вычитания, записывать по ним числовые равенства Выполнять сложение и вычитание. Присчитывать и отсчитывать по 1,2….с помощью числового отрезка. Выполнять вычисления вида — 6, — 7, — 8, — 9, применяя знания состава чисел 6, 7, 8, 9 или способа дополнения до 10. Сравнивать разные способы вычислений, выбирать наиболее удобный. Выполнять сложение с использованием таблицы сложения чисел в пределах 10, 20 с переходом и без перехода через разряд. Решать задачи, раскрывающие смысл действий сложения и вычитания. Составлять задачи на сложение и вычитание по одному и тому же рисунку, схематическому чертежу, решению. Выделять задачи из предложенных текстов. Дополнять условие задачи недостающим данным или вопросом. Решать задачи, раскрывающие смысл отношений «столько», «столько же и еще…» «столько же, но без …», задачи в одно действие на увеличение (уменьшение) числа на несколько единиц. Объяснять и обосновывать действие, выбранное для решения задачи. Моделировать условие задачи в два действия. Анализировать условие задачи в два действия, составлять план её решения. Измерять отрезки и выражать их длину в сантиметрах. Чертить отрезки заданной длины ( в сантиметрах). Сравнивать предметы по массе. Упорядочивать предметы, располагая их в порядке увеличения (уменьшения) массы Использовать математические термины (слагаемые, сумма) при составлении и чтении математических записей. Применять переместительное свойство сложения для случаев вида: + 5, + 6, + 7, + 8, + 9. Проверять правильность выполнения сложения, используя другой прием сложения. Образовывать числа второго десятка из одного десятка и несколько единиц. Сравнивать числа, опираясь на порядок следования чисел второго десятка при счете. Читать и записывать числа второго десятка, объясняя, что означает каждая цифра в их записи. | 29.11 | ||
48 | Сложение и вычитание числа 1. | 1 | стр. 94-95 | стр. 80-81 | 30.11 | |||
49 | Сложение и вычитание вида □ + 1; □ – 1. | 1 | Стр.96-97 | Стр.82- 83 | 4.12 | |||
50 | Нахождение значения числового выражения в несколько действий с помощью числового отрезка. | 1 | стр. 98-99 | Стр. 84-85 | 5.12 | |||
51 | Сложение и вычитание числа 2. | 1 | стр.100-101 | стр. 86-87 | 6.12 | |||
52 | Сложение и вычитание вида □ + 2; □ – 2. | 1 | стр.102-103 | Стр. 88-89 | 7.12 | |||
53 | Введение понятия «задача». Составление задачи на сложение и вычитание. | 1 | стр.104-105 | стр. 90-91 | 11.12 | |||
54 | Сложение и вычитание числа 3. | 1 | стр. 106-107 | стр. 92-93 | 12.12 | |||
55 | Сложение и вычитание вида □ + 3; □ – 3. | 1 | Стр.108-109 | Стр.94-95 | 13.12 | |||
56 | Сантиметр. Измерение отрезков. Чертеж отрезков заданной длины. | 1 | стр.110-111 | 2 часть стр. 4-5 | 14.12 | |||
57 | Сложение и вычитание числа 4. | 1 | стр.112-113 | стр. 6-7 | 18.12 | |||
58 | Освоение приёма вида □ + 4; □ – 4. | 1 | стр.114-115 | стр. 8-9 | 19.12 | |||
59 | Контрольная работа №1 по теме: Сложение и вычитание в пределах 4» | 1 | 20.12 | |||||
60 | Практическое освоение понятия «столько же…». | 1 | стр.116-117 | стр. 10-11 | 21.12 | |||
61 | Практическое освоение понятия «столько же и ещё…; столько же.., но без…». | 1 | стр.118-119 | стр. 12-13 | 25.12 | |||
62 | Задачи на увеличение числа на несколько единиц. | 1 | стр.120-121 | стр. 14-15 | 26.12 | |||
63 | Проверочная работа № 5 по теме «Столько же, но без..» | 1 | 27.12 | |||||
64 | Задачи на уменьшение числа на несколько единиц. | 1 | стр.122-123 | Стр. 16-17 | 28.12 | |||
65 | Повторение изученного по теме: «Столько же, но ез…» | 1 | стр.124-125 | тест 9 | 15.01 | |||
66 | Закрепление по теме: «Задачи на увеличение (уменьшение) числа на несколько единиц». | 1 | стр. 126-128 | 16.01 |
Разработка урока на тему «Способы задания и свойства числовых последовательностей
Урок по теме «Способы задания и свойства числовых последовательностей»
Основные цели:
1 формирование представления о числовой последовательности как функции с натуральным аргументом;
2 формирование знаний о способах задания числовых последовательностей, 3 умений находить члены последовательности по предложенной формуле, а также 4 умений находить саму формулу, задающую последовательность;
5 развитие умений анализировать, сравнивать, обобщать.
План урока
1 Изучение нового материала
2 устная работа
3 способы задания числовых последовательностей
4закрепление материала
5 Свойства числовых последовательностей
6 Решение примеров на свойста
7самостоятельная работа
8Домашнее задание.
9Подведение итогов урока
.
Ход урока
1 Изучение нового материала
Функции, область определения которых является множеством натуральных чисел или его частью, называются числовыми последовательностями.
числовой последовательностью является 1,3,5,7,9…
Числа, записанные в последовательности, называются членами последовательности. Обычно их обозначают маленькими буквами, например, a1,a2,a3…an…, где индекс 1,2,3,4…n… после буквы a указывает на порядковый номер каждого члена последовательности.
Общий вид последовательности — это (an), или a1,a2,a3…an…
an называется общим членом последовательности, или n-м членом, где n — порядковый номер члена последовательности.
У натуральных чисел, считая от 1, десятый член последовательности — это a10=10.
Последовательность возможно задать, указав все её члены или указав общую формулу. Формула показывает, как найти любой член последовательности, если известен порядковый номер n.
Пример:
в последовательности, где общая формула an=3n, написать a) первые четыре члена; b) двадцатый член.
a) Если n=1, то вместо n в формулу подставляется 1: a1=3⋅1=3;
a2=3⋅2=6;
a3=3⋅3=9;
a4=3⋅4=12.
b) Если n=20, то вместо n в формулу подставляется 20: a20=3⋅20=60.
Числовая последовательность бесконечна, если вместо n можно подставлять любые другие натуральные числа (бесконечное множество).
2 устная работа
1 Назвать первые несколько членов последовательности натуральных чисел, кратных 3, взятых в порядке возрастания. Укажите ее первый, пятый, десятый, сотый и n-й члены.
Решение: 3; 6; 9; 12; … а1 = 3, а5 = 15, а10 = 30, а100 = 300, аn = 3n
2 Перечислите члены последовательности (хn), которые расположены между: а) х31 и х35, б) хn-2 и xn+2.
Решение: а) х32, х33, х34; б) xn-1, xn, xn+1.
3 Найдите первые шесть членов последовательности, заданной формулой n- го члена: хn = 2n – 1.
Решение: х1 = 1, х2 = 3, х3 = 5, х4 = 7, х5 = 9, х6 = 11.
3 способы задания числовых последовательностей:
. словесный
когда правило последовательности описано словами, без указания формулы.
Пример:
последовательность простых чисел: 2,3,5,7,11,13,17,19,23,29,31…
. аналитический
— когда указана формула её n-го члена.
Пример:
1. yn=n2;
последовательность 1,4,9,16…n2…
Шаги решения: n=1,2,3…
y1=12=1;y2=22=4;y3=32=9;y4=42=16;y5=…
2. yn=5(yn=C);
последовательность
5,5,5…5…(C,C,C…C…).
Шаги решения:
y1=5;y2=5;y3=5;y4=…
Последовательность yn=C называют постоянной, или стационарной;
. рекуррентный
— когда указывают правило, позволяющее вычислить n-й член последовательности, если известны её предыдущие члены.
— Арифметическая прогрессия — (an), заданная рекуррентно соотношениями: a1=a,an+1=an+d.
— Последовательность Фибоначчи — в которой каждое последующее число равно сумме двух предыдущих чисел.
an+1=an+an−11,1,2,3,5,8,13,21,34,55…
. графический
— график последовательности состоит из точек с абсциссами 1,2,3,4…
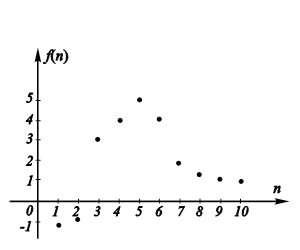
4 закрепление материала
Решение примеров
1 Запиши первые пять членов последовательности, если общая формула последовательности: an=0,8n.
Вход
2 Найди три первые члена последовательности an=(−1)13n+13n и вычисли их сумму.
3 Дана последовательность, у которой a1=9, a2=6 и an=3⋅an−2−an−1. Вычисли четвёртый член последовательности.
4Укажи номер члена последовательности yn=12−n5n+5, равного 825.
:
5 Свойства числовых последовательностей
1 Последовательность называется возрастающей, если для любого n∈N выполняется неравенство an<an+1.
2 Последовательность называется убывающей, если для любого n∈N выполняется неравенство an>an+1.
3 Возрастающие и убывающие последовательности называются монотонными.
1. Последовательность, заданная формулой an=nn+1, является монотонной, возрастающей, т. к. разница an+1−an=n+1n+2−nn+1=1(n+1)⋅(n+2)>0.
то есть an<an+1.
2. Последовательность с общим членом an=1+(−1)n не является монотонной, т. к. a1<a2,a2>a3.
Последовательность называется ограниченной сверху, если существует такое число M∈R, что an≤M. При этом число M называется верхней границей последовательности.
Последовательность называется ограниченной снизу, если существует такое число m∈R, что an≥m. Число m называется нижней границей последовательности.
1. последовательность, заданная формулой an=n (1,2,3…n…), ограничена снизу, но не ограничена сверху.
2. Последовательность, заданная формулой an=(−1)nn;(−1,2,−3,4…(−1)nn…), не ограничена ни сверху, ни снизу.
Последовательность называется ограниченной, если она одновременно ограничена и сверху, и снизу.
6 Решение примеров на свойства
Вход
1Начиная с какого номера все члены последовательности (xn) будут не меньше заданного числа A?
xn=5n−4; A=24.
Ответ:
2 Использование свойств функции в вычислении членов последовательности
Найди наименьший член последовательности и укажи его номер:
yn=4n2−19n+9.
3 Вычисление значения параметра р в ограниченной последовательности
При каких значениях параметра p последовательность yn=31n+p32n−1 ограничена сверху числом 1?
(В ответе первым выбери знак неравенства, потом введи число.
Самостоятельная работа с выбором ответа
1 Дана последовательность: 2,3,5,8,13…
Найти Четырнадцатый член этой последовательности
Ответы А-25- Б 48 В-69 Г 81
2 Вычисли три последующих члена последовательности, если a1=3 и an=2⋅an−1+2.
Ответы А-6- Б 8 В-13 Г 7
3 По заданной формуле n-го члена вычисли первые три члена последовательности (yn). yn=3n2−7n
Ответы А [-7. -2 . 6 ] Б [ -5. -1 . 8 ] В [2. -3. 5 ] Г [-1.5. 3 ]
4 Является ли последовательность ограниченной?
1;−1;1;−2;1;−3…
Ответы А –да Б- нет
5 Выясни, какой является последовательность: возрастающей или убывающей?
xn=n29n.
В своих рассуждениях используй доказательство. Запиши, чему равна разность данных членов последовательности (сначала упрости выражение):
yn+1−yn= n+−n2n+1.
Запиши в виде формулы неравенство, подтверждающее или опровергающее характер монотонности:
y<y.
Ответ А разность 54 убыв Б разность 72 возр
В разность64 возр Г разность95 убыв
Проверка ответов 1-Г 2- Б 3-, А 4-Б 5 В
8Домашнее задание
1 Выясни, является ли заданная функция числовой последовательностью:
y=3x−3, x∈(0;+
2 Найди несколько начальных членов возрастающей последовательности всех натуральных чисел, кратных пяти. Вычисли её шестой, девятый, двадцать первый, n-й члены
3 Докажи, что последовательность возрастает:
xn=10nn+1
4Последовательность задана рекуррентным способом. Вычисли формулу её n-го члена:
а) x1=3,xn=xn−1+5, если n=2,3,4…
9 Итог урока
 называется закон, по которому каждому элементу из
называется закон, по которому каждому элементу из 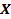 сопоставляется единственное число.
сопоставляется единственное число.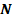 ).
).






