Решение задач на круговое движение

Задача1

Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 22 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 20 км/ч больше скорости другого?

Заполняем графу «расстояние»:

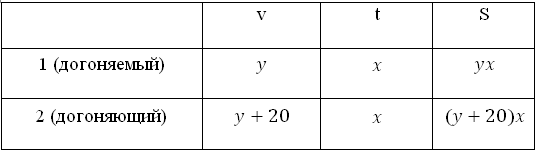
Второй проезжает расстояние (до встречи) на 11 км больше, значит

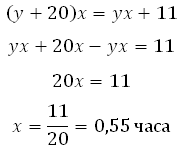
11/20 часа это то же, что и 33/60 часа. То есть, до их встречи прошло 33  минуты. Как переводить часы в минуты, и наоборот, можете посмотреть в статье «Пропорция спасает».

Как видим, сама скорость мотоциклистов в данном случае  не имеет значения.

Ответ: 33

Решите самостоятельно:

Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?

Посмотреть решение

Задача4

Из пункта A круговой трассы выехал велосипедист, а через 40 минут следом за ним отправился мотоциклист. Через 8 минут после отправления он догнал велосипедиста в первый раз, а еще через 36 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.

Данная задача представляет относительную сложность. Что сразу ст

так, переведем минуты в часы, поскольку скорость надо найти в км/ч.

Сорок минут это 2/3 часа, 8 минут это 8/60 часа, 36 минут это 36/60 часа.

Скорости участников обозначим за х км/ч (у велосипедиста) и у км/ч (у мотоциклиста).

В первый раз мотоциклист обогнал велосипедиста через 8 минут, то есть через 8/60 часа после старта.

До этого момента велосипедист был в пути уже  40+8=48 минут, то есть  48/60 часа.

Запишем эти данные в таблицу:

Оба проехали одинаковые расстояния, то есть

Затем мотоциклист второй раз догнал велосипедиста. Произошло это через 36 минут, то есть через 36/60 часа после первого обгона.

Составим вторую таблицу, заполним графу «расстояние»:

Так как сказано, что через 36 минут мотоциклист снова догнал велосипедиста. Значит, он (мотоциклист)  проехал расстояние равное 30 километрам (один круг) плюс расстояние, которое за это время проехал велосипедист. Это ключевой момент для составления второго уравнения.

Один круг — это длина трассы, она равна 30 км.

Получаем второе уравнение:

Решаем систему их двух уравнений:

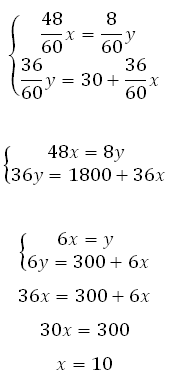
Значит   у = 6 ∙10 = 60.

То есть скорость мотоциклиста равна 60 км/ч.

Задача 5

Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.

видеолекция «Решение текстовых задач на движение по кругу и воде»

В видеолекции «Решение текстовых задач на движение по кругу и воде» рассмотрены все типы задач на движение по кругу и воде из Открытого банка заданий ЕГЭ по математике.

Вы можете познакомиться с содержанием видеолекции и посмотреть ее фрагмент.

Задачи на движение по кругу:

1. Два мо­то­цик­ли­ста стар­ту­ют од­но­вре­мен­но в одном на­прав­ле­нии из двух диа­мет­раль­но про­ти­во­по­лож­ных точек кру­го­вой трас­сы, длина ко­то­рой равна 7 км. Через сколь­ко минут мо­то­цик­ли­сты по­рав­ня­ют­ся в пер­вый раз, если ско­рость од­но­го из них на 5 км/ч боль­ше ско­ро­сти дру­го­го?

2. Из пунк­та A кру­го­вой трас­сы вы­ехал ве­ло­си­пе­дист, а через 20 минут сле­дом за ним от­пра­вил­ся мо­то­цик­лист. Через 5 минут после от­прав­ле­ния он до­гнал ве­ло­си­пе­ди­ста в пер­вый раз, а еще через 46 минут после этого до­гнал его во вто­рой раз. Най­ди­те ско­рость мо­то­цик­ли­ста, если длина трас­сы равна 46 км. Ответ дайте в км/ч.

3. Часы со стрел­ка­ми по­ка­зы­ва­ют 6 часов 45 минут. Через сколь­ко минут ми­нут­ная стрел­ка в пятый раз по­рав­ня­ет­ся с ча­со­вой?

4. Два гон­щи­ка участ­ву­ют в гон­ках. Им пред­сто­ит про­ехать 22 круга по коль­це­вой трас­се про­тяжённо­стью 3 км. Оба гон­щи­ка стар­то­ва­ли од­но­вре­мен­но, а на финиш пер­вый пришёл рань­ше вто­ро­го на 11 минут. Чему рав­ня­лась сред­няя ско­рость вто­ро­го гон­щи­ка, если из­вест­но, что пер­вый гон­щик в пер­вый раз обо­гнал вто­ро­го на круг через 10 минут?

 

Задачи на движение по воде:

5. Мо­тор­ная лодка про­шла про­тив те­че­ния реки 72 км и вер­ну­лась в пункт от­прав­ле­ния, за­тра­тив на об­рат­ный путь на 6 часов мень­ше. Най­ди­те ско­рость лодки в не­по­движ­ной воде, если ско­рость те­че­ния равна 3 км/ч. Ответ дайте в км/ч.

6. Рас­сто­я­ние между при­ста­ня­ми A и B равно 72 км. Из A в B по те­че­нию реки от­пра­вил­ся плот, а через 3 часа вслед за ним от­пра­ви­лась яхта, ко­то­рая, при­быв в пункт B, тот­час по­вер­ну­ла об­рат­но и воз­вра­ти­лась в A. К этому вре­ме­ни плот про­шел 39 км. Най­ди­те ско­рость яхты в не­по­движ­ной воде, если ско­рость те­че­ния реки равна 3 км/ч. Ответ дайте в км/ч.

7. Рас­сто­я­ние от пристани M до пристани N по течению реки катер проходит за  6 ч. Однажды, не дойдя 40 км до пристани N, катер повернул назад и возвратился к пристани M, затратив на весь путь 9 ч. Найдите скорость катера в стоячей воде, если скорость течения 2 км/ч.

8. Из пункта  A одновременно отплыли вниз по течению реки катер и плот. Пройдя 40/3 км катер повернул обратно и, пройдя 28/3 км, встретился с плотом. Требуется найти собственную скорость катера, если известно, что скорость течения   4 км/ч.

9. Моторная лодка проплыла по озеру, а потом спустилась вниз по реке, вытекающей из озера. Путь по озеру на 15% меньше пути по реке. Время движения лодки по озеру на 2% больше, чем по реке. На сколько процентов скорость течения меньше собственной скорости лодки?

10. Весной катер идет против течения реки в 1 2/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее, поэтому летом катер идет против течения реки в 1 1/2  раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

Фрагмент видеолекции:

 

КУПИТЬ ВИДЕОЛЕКЦИЮ

И.В. Фельдман, репетитор по математике

Задачи на движение по воде, по замкнутой трассе и движение протяженных тел (обучающие модули для дистанционной самоподготовки).

Представленные в комплекте презентационные материалы могут быть использованы на уроках или факультативных занятиях в среднем звене, т.к. данные задачи в учебниках не представлены.

 

 

Главы 1-5 статьи, в том числе  Ресурс «Задачи на движение по реке»,  опубликованы в №29 «Учительской газеты» от 17 июля 2012 года.

 

5. Ресурс «Задачи на движение по окружности (кольцевой трассе)». Краткая аннотация.

В ресурсе представлено 7 задач.

Понять суть движения по окружности несложно. Динамическая модель на втором слайде поможет детям в осмыслении таких задач. Запускать модель можно многократно. Не важно, сколько кругов «намотают» участники забега по кольцевой трассе. Чтобы произошла встреча, количество кругов одного должно быть ровно на один круг больше, чем у другого.

Примеры. Один проехал 3 круга, значит, второй, чтобы догнать соперника должен проехать за то же время 4 круга. Один проехал 10 кругов, значит, второй, чтобы догнать соперника, должен проехать за то же время 11 кругов. И т.д.

Если два велосипедиста одновременно начинают движение по окружности в одну сторону со скоростями v₁ и v₂ соответственно (v₁ > v₂ соответственно), то первый велосипедист приближается ко второму со скоростью v₁ – v₂ (скорость вдогонку). В момент, когда 1-й велосипедист в первый раз догоняет 2-го, он проходит расстояние на один круг больше. В момент, когда 1-й велосипедист во второй раз догоняет 2-го, он проходит расстояние на два круга больше и т.д. Данные задачи ничем не отличаются от задач на движение вдогонку. Многие можно решить арифметическим способом. Второй способ решения оформлен в заметках к слайдам.

 

Задача 3. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?

Второй способ в заметках к слайду.

Скорость одного на 21 км/ч больше скорости второго – это означает, что скорость в вдогонку 21 км/ч.

Узнаем, за какое время он ликвидирует разницу в 7 км (именно такое расстояние между ними изначально – это половина круга от всей трассы 14 км).

7 : 21 = 1/3 (ч)

Осталось перевести 1/3 ч в минуты – это 20 мин. 

Акцентируем внимание на тонкостях: надо понимать, что за 20 минут мотоциклист проедет не 7 км, а может больше круга. Мотоциклист преодолеет разницу в 7 км.

 

Задача 4. Лыжные соревнования проходят на круговой лыжне. Первый лыжник проходит один круг на 2 минуты быстрее второго и через час опережает второго ровно на один круг. За сколько минут второй лыжник проходит один круг?

Если расстояние между пунктами, из которых начинают движение два тела, не задано, иногда бывает удобно положить его равным единице. Это правило применимо и в задачах на движение по окружности. Расстояние не задано, поэтому удобно считать, что длина всей трассы 1 часть. Если время в задаче дано в минутах, то скорость будет выражаться в особых единицах: часть/мин. 

«Первый лыжник проходит один круг на 2 минуты быстрее второго». Эта фраза поможет выразить скорость каждого лыжника.

В первой таблице выводятся скорости лыжников. Во второй таблице выводятся расстояния, которые пройдут лыжники через 1 час (60 мин). На выходе стрелкой показано условие, которое приведет к составлению уравнения: первый лыжник опережает соперника на один круг (1 часть).

 

Скриншот динамической модели к задаче 4.

Запустив модель, можно посчитать количество кругов, которое прошел каждый лыжник. Первый лыжник догнал второго и прошел при этом на 1 круг больше.

 

Задачи 1, 2, 5 и 7 во вложенном файле.

 

Задача 6. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.

На одном слайде подробно разбирается ситуация из условия задачи, когда произошла первая встреча. Велосипедист был в пути до первой встречи 40 мин (2/3 ч), а мотоциклист –  10 мин (1/6 ч). Расстояние за это время они проехали равное. Время движения различно, но равны расстояния, пройденные каждым участником. Это условие нам поможет составить уравнение.

В полученном уравнении две неизвестных величины, поэтому необходимо еще одно уравнение, связывающее неизвестные величины.

На другом слайде разбирается ситуация со второй встречей. Велосипедист и мотоциклист были в пути на трассе 30 мин (1/2 ч) от точки первой встречи до точки второй встречи, ведь они начали движение одновременно от места 1-й встречи. Время движения равно, но мотоциклист за это время проехал на 1 круг больше.

 

Скриншот к задаче №6.

 

6. Ресурс «Задачи на движение протяженных тел». Краткая аннотация.

В ресурсе представлено 7 задач.

В задачах на движение протяженных тел требуется, как правило, определить длину одного из них. Наиболее типичная ситуация: определение длины поезда, проезжающего мимо столба или протяженной платформы. В первом случае поезд проходит мимо столба расстояние, равное длине поезда, во втором случае — расстояние, равное сумме длин поезда и платформы.

 

Задача 1. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.

Пройденное расстояние равно длине поезда – это первый и главный шаг в рассуждениях. Далее остается выразить заданные величины в задаче в сходственных единицах измерения и найти расстояние, которое пройдет поезд за 36 секунд со скоростью 80 км/ч – это и будет искомая длина поезда.

На слайде есть помощь: повторение взаимосвязи между единицами времени. Удобная схема напомнит, как перевести время, заданное в секундах, в минуты и в часы.

 

Задача 2. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.

 

Скриншот к задаче №2.

 

На динамической модели хорошо видно, что мимо лесополосы недостаточно проехать первому вагону. Необходимо проехать вперед на расстояние, равное всей длине состава, т.е. надо прокатить вперед все вагоны до последнего! Тогда пройденное расстояние равно длине поезда плюс длине лесополосы – это первый и главный шаг в рассуждениях. Далее остается выразить заданные величины в задаче в сходственных единицах измерения и найти расстояние, которое пройдет поезд за 1 минуту со скоростью 60 км/ч – это будет длина поезда вместе с лесополосой.

Можно решить задачу, составив уравнение. На следующем слайде показан второй способ. Для составления уравнений используется формула связи расстояния, скорости и времени.

 

Задача 3. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй – длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?

При решении задач на движение двух тел часто очень удобно считать одно тело неподвижным, а другое – приближающимся к нему со скоростью, равной сумме скоростей этих тел (при движении навстречу) или разности скоростей (при движении вдогонку). Такая модель помогает разобраться с условием задачи, получить нужные уравнения.

Будем считать, что первый сухогруз неподвижен, а второй приближается к нему со скоростью v (м/мин), равной разности скоростей второго и первого сухогрузов. Прекрасное дополнение к задаче динамическая модель движения. Начинается показ с момента, когда второй сухогруз отстает от первого. На носу второго сухогруза закреплен флажок, он поможет сообразить, на какое расстояние он должен обогнать баржу.

Конечно, важно, чтобы ученик понял, что второй сухогруз пройдет не 1200 м, а значительно больше! 1200 м – это расстояние, на которое он должен обогнать баржу. А пройти он за это время может 4000 или 5000 м. Но я думаю, даже если ученик не совсем понимает суть, он может довести задачу до правильного ответа.

 

Задача 4. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.

Будем считать, что один поезд неподвижен, а второй приближается к нему со скоростью v (м/мин), равной разности скоростей поездов. Тогда за 1 минуту второй поезд обгонит первый на расстояние, равное сумме длин этих составов.

Удобно решать такие задачи с помощью уравнения. Если на уроке учителю не хватает времени рассматривать различные способы решения задач, то дистанционно он может предложить познакомиться с различными способами. Ученик определится, что ему подходит, что более понятно. А также ребенок может предложить свой способ решения на сайте.

 

Задача 5. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.

 

Задача 6. Поезд, двигаясь равномерно со скоростью 54 км/ч, проезжает мимо идущего параллельно путям со скоростью 6 км/ч навстречу ему пешехода за 30 секунд. Найдите длину поезда в метрах.

Будем считать, что пешеход неподвижен, а поезд двигается со скоростью v (м/мин), равной сумме скоростей поезда и пешехода. Пешеход не имеет «протяженной» длины (если бы это была колонна солдат, то мы бы учли это).

За 30 секунд со скоростью, равной разности скоростей поезда и пешехода, поезд пройдет расстояние, равное своей длине.  

 

Задача 7. Поезд, двигаясь равномерно со скоростью 65 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 5 км/ч пешехода за 30 секунд. Найдите длину поезда в метрах.

Будем считать, что пешеход неподвижен, а поезд двигается со скоростью v (м/мин), равной разности скоростей поезда и пешехода. Пешеход не имеет «протяженной» длины.

За 30 секунд со скоростью, равной разности скоростей поезда и пешехода, поезд пройдет расстояние, равное своей длине.

 

Использованные источники и литература

1)      Открытый банк заданий ЕГЭ по математике. ЕГЭ 2011. http://mathege.ru/or/ege/Main.html

2)      Рымкевич А.П. Физика. Задачник. 10-11 кл. Пособие для общеобразоват. учеб. заведений. – 5-е изд. Перераб. – М.: дроф, 2001. – 192с.: ил. – (задачники «Дрофы».)

3)      ВикипедиЯ. http://ru.wikipedia.org/wiki/%D0%94%D0%B8%D1%81%D1%82%D0%B0%D0%BD%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%BE%D0%B5_%D0%BE%D0%B1%D1%83%D1%87%D0%B5%D0%BD%D0%B8%D0%B5

4)      ЕГЭ 2010. Математика. Задача В12. С.А. Шестаков, Д.Д. Гущин. Под редакцией А. Л. Семенова и И. В. Ященко. Разработано МИОО. Электронная версия сборника http://www.2x2abc.com/forum/users/2010/B12.pdf

5)      Дидактические основы компьютерных технологий. http://xa.ucoz.com/news/2010-04-04-2

 

Елена Савченко, учитель математики гимназии №1 города Полярные Зори Мурманской области, победитель XIV Всероссийского конкурса «Сто друзей»

Во вложенных файлах — три презентации.

Решение текстовых задач на движение. Задачи 10

Решение текстовых задач на движение

Задачи 10 — 13

Весь список текстовых задач на движение здесь.

10. Условие задачи: Пункт В находится по реке ниже пункта А. В одно и то же время из пункта А отплыли плот и первая моторная лодка, а из пункта В — вторая моторная лодка. Через некоторое время лодки встретились в пункте С, а плот за это время проплыл третью часть пути от А до С. Если бы первая лодка без остановки доплыла до пункта В, то плот за это время прибыл бы в пункт С. Если бы из пункта А в пункт В отплыла вторая лодка, а из пункта В в пункт А — первая лодка, то они встретились бы в 40 км от пункта А. Какова скорость обеих лодок в стоячей воде, а также расстояние между пунктами А и В, если скорость течения реки равна 3 км/ч?
    Решение: Пусть — расстояние между A и B, и — скорости первой и второй лодок в стоячей воде соответственно.  За время, которое понадобится первой лодке, чтобы доплыть до С (скорость лодки по течению равна , где — скорость течения реки), плот проплывает только третью часть, то есть скорость лодки в 3 раза больше скорости реки. Отсюда и .
    Если первая и вторая лодки отправляются одновременно из А и В (безразлично, какая откуда начинает движение), то время встречи равно . Значит, . Время, за которое плот доберется до С, равно . За это же время первая лодка проплывет до В, то есть или , откуда км/ч.
    Если вторая лодка начинает движение из А, а первая — из В, то их встреча произойдет в 40 км от пункта А. Поэтому или , то есть км
    Ответ: 6 км/ч; 21 км/ч; 45 км
11. Условие задачи: Два тела, двигаясь по окружности в одном направлении, встречаются через каждые 112 мин, а двигаясь в противоположных направлениях — через каждые 16 мин. Во втором случае расстояние между телами уменьшилось с 40 м до 26 м за 12 с. Сколько метров в минуту проходит каждое тело и какова длина окружности?
    Решение: Обратим внимание, что необходимо привести размерности величин к одному виду, например, к минутам. Пусть — длина окружности, , — скорости тел. Тогда и . Так как за 12 с = 1/5 мин тела сблизились на 40 — 26 = 14 м, то , откуда . Из первых двух уравнений получаем, что , откуда . Далее легко находятся все неизвестные величины.
    Ответ: 1120 м; 40 м/мин, 30 м/мин
12. Условие задачи: Две точки, двигаясь по окружности в одном направлении, встречаются каждые 12 мин, причем первая обходит окружность на 10 с быстрее, чем вторая. Какую часть окружности проходит за 1 с каждая точка?
    Решение: Пусть длина окружности равна , , — скорости точек. Тогда , откуда . Так как первая точка обходит окружность за , а вторая за , то . Обозначим за , . Тогда и . Подставив во второе уравнение, получим квадратное уравнение , откуда (второй корень отрицателен). Тогда .
    Ответ: 1/80 и 1/90 части окружности
13. Условие задачи: Два тела движутся навстречу друг другу из двух точек, расстояние между которыми 390 м. Первое тело прошло в первую секунду 6 м, а в каждую последующую секунду проходило на 6 м больше, чем в предыдущую. Второе тело двигалось равномерно со скоростью 12 м/c и начало движение спустя 5 с после первого. Через сколько секунд после того, как начало двигаться первое тело, они встретятся?
    Решение: Первое тело двигалось равноускоренно. Поэтому для имеем , для имеем , то есть . Здесь мы воспользовались формулами для равноускоренного движения. Из этих уравнений находим, что м/c, м/c². Поэтому тело движется по закону . Пусть — момент времени, в который две точки встретятся. Первая пройдет за это время расстояние , а вторая — , так как она движется равномерно и начала движение через 5 с после первой. Из условия получим, что , откуда и c.
    Ответ: 10 с

 

Метки решение, текстовые задачи. Смотреть запись.