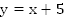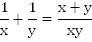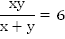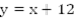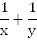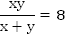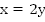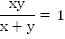Системы уравнений в задачах на работу. Видеоурок. Алгебра 9 Класс

Тема: Системы уравнений

Урок: Системы уравнений в задачах на работу 

В данном уроке будут рассмотрены задачи на работу. Как и в задачах на движение, здесь потребуется техника перевода из словесной модели в математическую, получение системы уравнений и её решение.

Задача 1.

Два комбайна, работая вместе, могут выполнить задание за 6 часов. Первый комбайн, работая один, может выполнить задание на 5 часов быстрее, чем второй комбайн. За сколько времени может выполнить задание первый комбайн, работая один?

Решение:

Вспомним основное уравнение для работы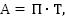  

А – объем работы,

П – производительность,

Т – время.

	А	П
Первый комбайн	1		x
Второй комбайн	1
Два комбайна вместе	1

Пусть всю работу первый комбайн может выполнить за x часов, с производительностью 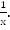 Второй комбайн может выполнить всю работу за y часов, причем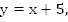

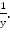 с производительностью  Оба комбайна, работая вместе, имеют производительность  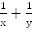  и выполняют всю работу за 6 часов, т.е. . Составим и решим систему.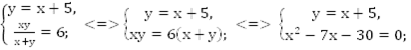

 

 

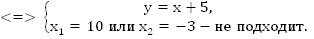
Ответ: 10 часов.

Задача 2.

Две бригады, работая вместе, могут выполнить работу за 8 часов. Первая бригада, работая одна, могла бы выполнить эту работу на 12 часов быстрее, чем вторая бригада. За сколько часов могла бы выполнить всю работу первая бригада, если бы она работала одна?

Решение:

Опишем каждого участника работы на каждом участке работы, и выявим связи между ними.

	А	П
Первая бригада	1
Вторая бригада	1
Обе бригады вместе	1

Первая бригада может выполнить всю работу за x часов с производительностью 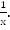 Вторая бригада может выполнить всю работу за y часов,  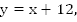с производительностью  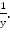Обе бригады вместе имеют производительность 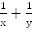. Всю работу они выполнят за время

Составим и решим систему уравнений.

 

 

 

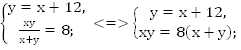
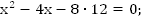
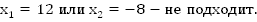
Ответ: 12 часов.

Задача 3.

Чан наполняется двумя кранами при совместной работе за 1 час. Наполнение чана только через первый кран длится вдвое больше, чем только через второй кран. За какой промежуток времени каждый кран может наполнить чан?

Решение:

	А	П
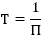
Первый кран	1
Второй кран	1		y
Оба крана вместе	1

Пусть первый кран наполняет чан за x часов, с производительностью 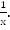 Второй кран наполняет чан за y часов,  с производительностью

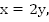 Оба крана выполняют работу с производительностью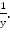 за время 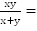1 часу Составим и решим систему.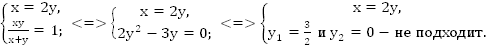

 

 

Ответ: 3 часа и 1,5 часа.

Задача 4.

Два тракториста, работая вместе, вспахали поле за 48 часов. Если бы половину поля вспахал один из них, а затем оставшуюся половину другой, то работа была бы выполнена за 100 часов. За сколько часов мог бы вспахать поле каждый тракторист, работая отдельно?

Решение:

	А	П
Первый трактор всю работу	1		x
Второй трактор всю работу	1		y
Два трактора вместе	1
Первый трактор половину работы
Второй трактор половину работы

Пусть первый трактор делает всю работу за x часов с производительностью 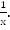 Пусть второй трактор делает всю работу за y часов с производительностью  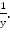Если они работают вместе, их производительность равна  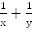и они будут работать 48 часов,  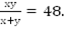Если всё поле первый тракторист вспашет за x часов, то половину поля – за   часов. Аналогично, второй тракторист вспашет половину поля за   часов. По условию задачи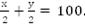 

Cоставим и решим систему.

 

 

 

 

 

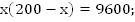
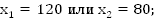
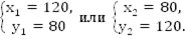
Ответ: 120 часов и 80 часов.

Мы решили серию текстовых задач на работу, используя стандартную методику для составления математической модели.

 

Список рекомендованной литературы

1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.

2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.

3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.

4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.

5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.

6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.

 

Рекомендованные ссылки на интернет-ресурсы

1. Раздел College.ru по математике (Источник).

2. Интернет-проект «Задачи» (Источник).

3. Образовательный портал «РЕШУ ЕГЭ» (Источник).

 

Рекомендованное домашнее задание

1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 165, 170, 189, 190.

Решение задач с помощью систем уравнений (задачи на совместную работу)

Урок №122

Тема: Решение задач с помощью систем уравнений (задачи на совместную работу)

Цель:

 — личностные:

• проявление воли и настойчивости для достижения конечных результатов;

• умение выдвигать гипотезы, отыскивать доказательства и рассуждать логично;

• выработка уверенности во взаимоотношениях с людьми;

• умения уверенно и легко выполнять математические операции;

• формировать навыки самостоятельной работы и самооценки знаний.

 — метапредметные:

• творческого решения  практических задач; умения самостоятельно выполнять творческую работу;

• способность вступать в речевое общение, участие в диалоге;

• формировать умения оценивать свои учебные достижения, своё эмоциональное состояние.

— предметные:

• осмысление ранее изученных понятий «выражение переменных из формул» и «способы решения систем уравнений различными способами», умения составлять уравнения по тексту задачи в разнообразных интерпретациях; применять правила выражения переменных; овладения навыкам составления и решения уравнений , систем  для решения несложных задач.

Тип урока: урок применения знаний

Оборудование:

Содержание урока

1. Организационный момент……………………………………..2мин

2. Постановка темы и целей урока……………………………….1мин

3. Проверка домашнего задания…………………………………2мин

4. Актуализация опорных знаний………………………………..7мин

5. Мотивация необходимости изучения материала……………2мин

6. Изучение нового материала……………………………………5мин

7. Физкультминутка……………………………………………….1мин

8. Первичное осмысление материала……………………………6мин

9. Закрепление знаний, отработка умений и навыков…………15мин

10. Постановка домашнего задания……………………………….1мин

11. Итог урока……………………………………………………….3мин

Ход урока

1. Организационный момент (2мин)

1. Постановка темы и целей урока (1мин)

Беседа

• Какую тему мы изучали на прошлом уроке?

• С какими типами задач мы уже познакомились?

• Какой следующий типа задач мы изучим?

• Кто сможет назвать тему сегодняшнего урока?

• Какова цель нашего урока?

1. Проверка домашнего задания (3мин)

Самопроверка и самооценивание

1. Актуализация опорных знаний (7мин)

Взаимоопрос «Лото»

Вопросы на экране, учащиеся достают бочонок с номером вопроса и спрашивают любого учащегося класса

1. Что такое линейное уравнение с двумя переменными?

2. Сколько решений может иметь линейное уравнение с двумя переменными?

3. Какая линия является графиком линейного уравнения с двумя переменными?

4. Как называются числа a, b и с в линейном уравнении с двумя переменными?

5. Что такое система линейных уравнений с двумя переменными?

6. Сколько решений может иметь система линейных уравнений с двумя переменными?

7. Что означает фигурная скобка в системе уравнений?

8. Сколько уравнений в себя может включать система уравнений?

9. Как зависит количество решений системы уравнений от расположения графиков уравнений системы?

10. Какие существуют способы решения систем уравнений?

11. В чем заключается графический способ решения систем уравнений?

12. В чем заключается способ подстановки?

13. В чем заключается способ сложения?

14. На какие типы подразделяют задачи?

15. Алгоритм решения задач

м

а

т

р

и

ч

н

ы

й

м

е

т

о

д

На экране открылся еще один метод решения систем уравнений, который вы изучите, поступив после 11 класса в высшие учебные заведения. Метод решения с помощью матриц. Матрица – это прямоугольная таблица из нескольких строк и столбцов

1. Мотивация необходимости изучения материала (2мин)

Одна из задач экзамена 9 класса – решение текстовых задач. Я подобрала для вас задачи именно на совместную работу, которые можно решить с помощью систем линейных уравнений. Эти задачи попадаются ребятам на экзамене в 9 классе. Ознакомьтесь с ними!

За­да­ние 1. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

За­да­ние 2. Игорь и Паша кра­сят забор за 20 часов. Паша и Во­ло­дя кра­сят этот же забор за 24 часа, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

За­да­ние 3. Чтобы на­ка­чать в бак 117 л воды, тре­бу­ет­ся на 5 минут боль­ше вре­ме­ни, чем на то, чтобы вы­ка­чать из него 96 л воды. За одну ми­ну­ту можно вы­ка­чать на 3 л воды боль­ше, чем на­ка­чать. Сколь­ко лит­ров воды на­ка­чи­ва­ет­ся в бак за ми­ну­ту?

• Что общего у этих задач?

• А хотим ли мы на экзамене решить такую задачу и сдать экзамен на «отлично»?

• Тогда давайте работать для этого и у нас всё получится!

1. Изучение нового материала (5мин)

Задачи, которые перед вами сейчас, достаточно сложные и на экзамене они входят в раздел задач повышенной сложности.

Пользуясь алгоритмом, попробуем решить эту задачу.

1 человек – 1 действие

За­да­ние 1. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

Составим краткое условие:

Ученик – 231 дет — ?ч, на 11ч ? дет – 1 ч, на 4 дет

Мастер – 462 дет — ?ч ? дет – 1 ч

Математическая модель задачи:

Пусть в час ученик делает х деталей, а мастер у. Т.к. ученик в час делает на 4 детали , тогда у-х=4

Если ученик делает х деталей в час, то 231 деталей за ч, а мастер . Причем на 11 больше чем . Тогда . Составим систему уравнений.

К сожалению, такие системы мы научимся решать только в 8 классе. Но саму систему вы уже с легкостью составите, если правильно определите тип задачи. В 8 классе вы узнаете, что . Значит ученик в час делает 3 детали.

Ответ: 3

1. Физкультминутка (1мин)

Видеоролик «Космос»

1. Первичное осмысление материала (7мин)

Рассмотрим задачу №2 (самостоятельно с помощью учителя)

За­да­ние 2. Игорь и Паша кра­сят забор за 20 часов. Паша и Во­ло­дя кра­сят этот же забор за 24 часа, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

И – ?часть в час

20ч

П – ?часть в час ?ч

24ч

В – ?часть в час

В+И=30ч

Решение

Пусть Игорь красит x в час, Паша – y, Володя – z.

Тогда за 20 часов Игорь покрасит 20х забора, Паша 20yА вместе они покрасят весь забор, выполнят всю работу, которую принимают за единицу.

То есть: 20х + 20у = 1

За 24 часа: Паша 24у, Володя – 24z, а вместе весь забор – 1.

То есть: 24y + 24z = 1

За 30 часов: Игорь – 30х, Володя – 30z, а вместе – весь забор

То есть: 30х + 30z = 1

Составим и решим систему уравнений:

Тогда Игорь в час красит забора, Владимир — , а Павел — . А вместе за час — . А весь забор за 16 часов.

1. Закрепление знаний, отработка умений и навыков (15мин)

Работа у доски + на опережение

№

1. Постановка домашнего задания (1мин)

1.№

2.* Решить №2, №3 на карточке

1. Итог урока. Оценки (2мин)

Подводя итог урок, хочу выслушать ваше мнение. Какие трудности возникают при решении систем различными способами? Что наиболее сложное при решении задач?

Спасибо за урок! Вы отлично потрудились!

Лист самооценивания

Фамилия, Имя_________________________

Класс_______

№ п/п	Моя деятельность	Моя оценка
1	Домашнее задание
2	Устный опрос
3	Работа у доски
4	Кроссворд
5	Дополнительный ответ
6	Дополнительный ответ
7	Дополнительный ответ

Экзаменационные задачи

За­да­ние 1. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

За­да­ние 2. Игорь и Паша кра­сят забор за 20 часов. Паша и Во­ло­дя кра­сят этот же забор за 24 часа, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

За­да­ние 3. Чтобы на­ка­чать в бак 117 л воды, тре­бу­ет­ся на 5 минут боль­ше вре­ме­ни, чем на то, чтобы вы­ка­чать из него 96 л воды. За одну ми­ну­ту можно вы­ка­чать на 3 л воды боль­ше, чем на­ка­чать. Сколь­ко лит­ров воды на­ка­чи­ва­ет­ся в бак за ми­ну­ту?

Экзаменационные задачи

За­да­ние 1. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

За­да­ние 2. Игорь и Паша кра­сят забор за 20 часов. Паша и Во­ло­дя кра­сят этот же забор за 24 часа, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

За­да­ние 3. Чтобы на­ка­чать в бак 117 л воды, тре­бу­ет­ся на 5 минут боль­ше вре­ме­ни, чем на то, чтобы вы­ка­чать из него 96 л воды. За одну ми­ну­ту можно вы­ка­чать на 3 л воды боль­ше, чем на­ка­чать. Сколь­ко лит­ров воды на­ка­чи­ва­ет­ся в бак за ми­ну­ту?

Экзаменационные задачи

За­да­ние 1. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

За­да­ние 2. Игорь и Паша кра­сят забор за 20 часов. Паша и Во­ло­дя кра­сят этот же забор за 24 часа, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

За­да­ние 3. Чтобы на­ка­чать в бак 117 л воды, тре­бу­ет­ся на 5 минут боль­ше вре­ме­ни, чем на то, чтобы вы­ка­чать из него 96 л воды. За одну ми­ну­ту можно вы­ка­чать на 3 л воды боль­ше, чем на­ка­чать. Сколь­ко лит­ров воды на­ка­чи­ва­ет­ся в бак за ми­ну­ту?

Экзаменационные задачи

За­да­ние 1. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

За­да­ние 2. Игорь и Паша кра­сят забор за 20 часов. Паша и Во­ло­дя кра­сят этот же забор за 24 часа, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

За­да­ние 3. Чтобы на­ка­чать в бак 117 л воды, тре­бу­ет­ся на 5 минут боль­ше вре­ме­ни, чем на то, чтобы вы­ка­чать из него 96 л воды. За одну ми­ну­ту можно вы­ка­чать на 3 л воды боль­ше, чем на­ка­чать. Сколь­ко лит­ров воды на­ка­чи­ва­ет­ся в бак за ми­ну­ту?

Взаимоопрос «Лото»

Вопросы на экране, учащиеся достают бочонок с номером вопроса и спрашивают любого учащегося класса

1. Что такое линейное уравнение с двумя переменными?

2. Сколько решений может иметь линейное уравнение с двумя переменными?

3. Какая линия является графиком линейного уравнения с двумя переменными?

4. Как называются числа a, b и с в линейном уравнении с двумя переменными?

5. Что такое система линейных уравнений с двумя переменными?

6. Сколько решений может иметь система линейных уравнений с двумя переменными?

7. Что означает фигурная скобка в системе уравнений?

8. Сколько уравнений в себя может включать система уравнений?

9. Как зависит количество решений системы уравнений от расположения графиков уравнений системы?

10. Какие существуют способы решения систем уравнений?

11. В чем заключается графический способ решения систем уравнений?

12. В чем заключается способ подстановки?

13. В чем заключается способ сложения?

14. На какие типы подразделяют задачи?

15. Алгоритм решения задач

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

«Системы уравнений как математические модели реальных ситуаций. Решение задач на работу» (9 класс)

Урок по теме :

«Системы уравнений как математические модели реальных ситуаций» (9 класс).

Решение задач на работу.

Цель урока: показать способ решения задач с помощью составления систем уравнений; способствовать развитию навыков и умений при решении систем уравнений; развивать навыки само и взаимоконтроля.

Учебник: 1.А.Г.Мордкович, Н.П.Николаев «Алгебра-9». Учебник. Изд. Мнемозина, М. 2009. 2.Л.И.Звавич, А.Р.Рязановский, В.П.Семенов «Алгебра-9». Задачник. Изд. Мнемозина, М. 2009.

Ход урока.

1. Повторение ранее изученного.

На примере задачи 8 класса вспоминаем понятия: работа, производительность

Задача.

Токарь должен был обработать 120 деталей к определенному сроку. Применив новый резец, он стал обтачивать в час на 20 деталей больше и поэтому закончил работу на 1 ч раньше срока. Сколько деталей он должен был обрабатывать по плану?

Ответ: 40 деталей.

2. Решение задач на совместную работу с помощью системы уравнений.

Объяснение учителя.

Задача №1.

Два экскаватора, работая одновременно, выполняют некоторый объем земляных работ за 3 ч 45 мин. Один экскаватор, работая отдельно, может выполнить этот объем работ на 4 ч быстрее, чем другой. Сколько времени требуется каждому экскаватору в отдельности для выполнения того же объема земляных работ?

I.Составление математической модели

Примем объем всей работы за 1. Пусть первый экскаватор один работает x ч, второй в одиночку выполнит всю работу за y ч, тогда ; часть работы, выполненная первым экскаватором за 1 ч, производительность второго за 1 ч; производительность обоих экскаваторов за 1 ч. Составим систему уравнений:

;

II.Работа с составленной моделью

15()+=()

60++=+

—60=0

III.Ответ на вопрос задачи.

не удовлетворяет условию задачи

Если , то .

Ответ: 6 ч, 10 ч.

Задача №2.(№14.39)

Один учащийся решает у доски, остальные в тетрадях.

Двое рабочих, работая вместе, выполняют некоторую работу за 8 ч. Один из них, работая отдельно, может выполнить всю работу на 12 ч быстрее, чем другой рабочий, если последний будет работать один. За сколько часов, работая отдельно, каждый из них может выполнить работу?

I.Составление математической модели

Примем объем работы за 1. ч работает первый рабочий, y ч в одиночку выполнит все задание второй рабочий.

Получим систему уравнений:

II.Работа с составленной моделью

8()+=()

96++=+

—96=0

III.Ответ на вопрос задачи.

не удовлетворяет условию задачи

Если , то .

Ответ: 12 ч, 24 ч.

Задача №3.(№14.34)

Решение задачи объясняет учитель, привлекая к обсуждению учащихся.

При одновременном действии двух труб бассейн наполняется водой за 40 ч. Если бы бассейна наполнила первая труба, а потом остальную часть вторая труба, то потребовалось бы 78 ч. Сколько времени требуется для наполнения бассейна каждой трубой в отдельности?

I.Составление математической модели

Примем объем работы за 1. Пусть ч наполняет бассейн первая труба, а y ч – вторая труба.

Получим систему уравнений:

II.Работа с составленной моделью

-+4680=0

III.Ответ на вопрос задачи.

удовлетворяет условию задачи, тогда

удовлетворяет условию задачи, тогда

Ответ: 65 ч и 104 ч или 72 ч и 90 ч.

Задача №3.(№14.36)

Решение задачи объясняет учитель, привлекая к обсуждению учащихся.

Совхоз располагает тракторами четырех марок: А, Б, В и Г. Бригада из четырех тракторов (двух тракторов марки Б и по одному марок В и Г) производит вспашку поля за два дня. Бригада из двух тракторов марки А и одного трактора марки В тратит на эту работу три дня, а три трактора марок А, Б, В – четыре дня. За какое время выполнит работу бригада, составленная из четырех тракторов разных марок?

I.Составление математической модели

Примем объем работы за 1. Пусть за дн. вспашет поле трактор марки А, за y дн. – марки Б, за z дн. – марки В и за v дн. – марки Г.

Получим систему уравнений:

Из (2) получим:

Подставим в (3):

Подставим в (1) и получим:

Тогда можно ответить на вопрос задачи

Ответ: дня.

4.Итоги урока.

5.Домашнее задание: разобрать пример 3, 4 из параграфа 14 на с.103-108; решить №14.33, №14.32, №14.37.

Разработка урока «Решение задач на работу»

Название предмета	Алгебра
Класс	9
УМК (название учебника, автор, год издания)	Алгебра 9 класс Авт.: А.Г. Мордкович, М.: Мнемозина -2010
Уровень обучения	базовый
Тема урока	Системы уравнений как математические модели реальных ситуаций. Задачи на совместную работу.
Общее количество часов, отведенное на изучение темы	5
Место урока в системе уроков по теме	4 урок по теме. Урок закрепления и применений знаний в новых условиях.
Цель урока	Научить учащихся решать задачи на работу с помощью систем уравнений как математических моделей реальных ситуаций.
Задачи урока	Общеобразовательные: познакомить учащихся с применением систем уравнений при решении задач на работу; обеспечить овладение основными алгоритмическими приемами применения систем уравнений при решении задач на работу; формировать умения переносить знания в новую ситуацию, закрепить знания и умения учащихся в решении систем уравнений различными методами Развивающие: развитие аналитического мышления; познавательной активности мышления, умения работать с текстовой, графической информацией через использование задач моделирующих жизненные ситуации Воспитательные: формирование умения работать в группе.
Планируемые результаты	Учащийся должен знать: алгоритм решения задач на работу с помощью систем уравнений. Учащийся должен уметь: составлять систему уравнений к условию задач на работу; использовать таблицы при интерпретации задач на работу; исследовать построенную модель; работать в группах, индивидуально.
Техническое обеспечение урока	интерактивная доска, мультимедиапроектор, презентация по теме урока
Дополнительное методическое и дидактическое обеспечение урока (возможны ссылки на интернет-ресурсы)	А.Г. Мордкович Алгебра . 9 класс.: В двух частях: Учеб. для общеобразовательных учреждений.-5-е изд. – М.: Мнемозина, 2013, http://interneturok.ru/algebra/9-klass/algebra-9-klass-a-g-mordkovich; http://problems.ru/; https://math-oge.sdamgia.ru/

Содержание урока

Урок №4. Тема: Системы уравнений как математические модели реальных ситуаций. Задачи на совместную работу.

Ход урока.

1. Организационный момент.

Здравствуйте, друзья! Рада приветствовать Вас на нашем уроке.

2. Мотивация урока.

Ещё Платон говорил: «Человек, способный к математике, изощрён во всех науках». (Слайд 2)

Как вы понимаете это высказывание?

Таким образом, мы сегодня будем размышлять, искать простые и красивые решения, развивать логическое мышление, правильно и последовательно рассуждать, тренировать память, внимание.

3. Актуализация опорных знаний. Проверка д/з.

Вспомним что мы изучали на предыдущем уроке	Решение задач на движение с помощью системы уравнений как математической модели реальных ситуаций
Давайте вспомним алгоритм составление математической модели	Составление математической модели. Работа с составленной моделью. Ответ на вопрос задачи.
Каков алгоритм решения задач на движение с помощью системы уравнений?	Обозначить неизвестные величины буквами. Выразить оставшиеся неизвестные величины. Найти в задаче условия для составления уравнений. Решить получившуюся систему. Найденное решение использовать для ответа на вопрос задачи
Назовите основные методы решения системы уравнений	Алгебраического сложения, подстановки, введение новых переменных.

Эти алгоритмы и способы решения систем уравнений Вы должны были применить при выполнении домашнего задания.

Давайте откроем рабочие тетради и начнём проверку домашнего задания с №7.2.

Я его тоже решала, и вот что у меня получилось. Всё ли у меня получилось верно? (Слайд 5) (Фронтальная проверка) №7.19 (Слайд 6).

Спасибо!

4. Фиксация затруднений в индивидуальной деятельности.

Самостоятельная работа. Задания для самостоятельной работы. Приложение1.

Учащиеся проверяют результаты выполнения самостоятельной работы по эталону и проговаривают вместе с учителем вслух те понятия, алгоритмы из теоретической базы, на которые они допустили ошибки. (Слайды 7-9). При проверке задания 1 остановиться на анализе неверного ответа на слайде 4, обосновать свой ответ.

Сегодня на уроке мы начнем рассматривать решение еще одного вида задач с помощью систем уравнений второй степени с двумя переменными.

5. Изучение нового материала.

Дорогие ребята! Область применения математике очень широка. Рассмотрим старинную задачу из математической рукописи XYII века. (Слайд 10).

Задача.

Два плотника рядились двор ставить. И говорит первый:

— Только бы мне одному двор ставить, то я бы поставил на 3 года быстрее.

А другой молвил:

— А если бы мы работали ладно, управились и за 2 года.

Сколько долго они ставили двор по одиночке? Кому отдал предпочтение хозяин?

Откройте тетради, запишите число, сформулируйте тему урока (Слайд 11).

Давайте проанализируем ситуации задачи и оформим анализ условия в виде таблицы, аналогичной таблицам задач на движение.

1. О каких ситуациях (процессах) идет речь в задаче?- о работе

2. Сколько ситуаций (процессов) описано в задаче?- работа 1 плотника, работа 2 плотника, совместная работа

3. Какими величинами характеризуется каждый процесс, описанный в задаче?- производительность, время, работа

4. Как будем решать задачу? – составим систему

5. С чего начнем? – обозначим неизвестные величины буквами

6. Как обозначим эти неизвестные величины? — обозначим за х лет время выполнения работ первого плотника, а у лет время выполнения работ второго

7. Занесите все известные данные в таблицу самостоятельно. Что у вас получилось? (заполняют таблицу на доске самостоятельно)

8. Что делаем дальше? – выразим оставшиеся величины.

9. Можем ли мы сейчас это сделать? – нет, не хватает данных

10. Что можно сказать об объеме выполняемой работы? (Объем работы один и тот же, но не выражен числом) Если объем выполненной работы неизвестен, т.е. нет никаких данных, позволяющих его найти — работа принимается за единицу

11. Что делаем дальше? – выразим оставшиеся величины (Слайд 13)

12. Если работая вместе, всю работу плотники выполняют за 2 года, то какую часть работы выполнят они вместе, работая 1 год? – 1/2

13. Что дальше? – найдем условия для составления уравнений

14. Выделим эти условия.

– Первый плотник, работая один, мог бы выполнить работу на 3 года быстрее, чем второй. (Слайд 13)

— Работая вместе, могут выполнить работу за 2 года.

	Производительность N	Время t	Объем работы А
1 плотник		х	1
2 плотник		у	1
1 и 2 вместе		2	1

Составим пояснительный текст задачи.

Пусть х лет время работы первого плотника, а у лет время работы второго плотника. Известно, что время выполнения всей работы первым плотником меньше на 3 года, чем время работы второго плотника. Составим первое уравнение системы у-х=3.

Используя третью строку таблицы, получим второе уравнение системы .

Составим и решим систему уравнений:

не удовлетворяет условию задачи

Ответ: 3 года и 6 лет.

Подведем итоги

Что необходимо знать? (Слайд 14)

1. Объём, выполняемой работы! (A)

2. Время работы! (t)

3. Производительность! (N)

Что необходимо делать? (Слайд 15)

• Задачу прочти

• Немного помолчи

• Про себя повтори

• Ещё раз прочти

• Нет объёма работы, за 1 прими

• Данные в таблицу занеси

• Уравнение запиши

• Уравнение реши!

1. Включение с систему знаний и повторения. Приложение 2

А теперь поработаем в группах. На столах у каждой группы в конвертах лежит задание. Каждое задание состоит из двух частей. Вам предстоит решить задачу и в бланк ответа вписать составленную систему, которая позволит решить задачу, а далее необходимо решить данную систему и выбрать правильный вариант ответа предложенный ниже. После чего один представитель от каждой группы должен внести эти результаты в компьютер, тем самым проверить правильность выполнения задания. Каждый учащийся в группе получит отметку, зависящую от того, насколько удачно сработает его группа.

(Контроль учителя за работой групп)

Первая группа:

Задача 1. Мастер, работая самостоятельно, может изготовить партию из 200 деталей за некоторое время. Ученик за это же время может изготовить только половину всех деталей. Работая вместе, они могут изготовить всю партию деталей за 4 ч. За какое время мастер может изготовить все детали, работая самостоятельно? Заполняется карточка (рис 1).

	Объем работы (А)	Производительность (N)	Время (t)
Мастер
Ученик
вместе

1. Составьте систему уравнений для решения задачи, обозначив переменными x и y производительность мастера и ученика.

2. Выберите правильный вариант ответ из ниже приведённых.

6 ч. 7 ч. 9 ч. 12ч.

Вторая группа:

Бассейн на­пол­ня­ет­ся двумя кра­на­ми при сов­мест­ной ра­бо­те за 1 час. На­пол­не­ние бассейна толь­ко через пер­вый кран длит­ся вдвое боль­ше, чем толь­ко через вто­рой кран. За какой про­ме­жу­ток вре­ме­ни каж­дый кран может на­пол­нить бассейн?

	Объем работы (А)	Производительность (N)	Время (t)
1 кран
2 кран
вместе

1. Составьте систему уравнений для решения задачи, обозначив переменными x и y время наполнения бассейна каждым краном.

2. Выберите правильный вариант ответ из ниже приведённых.

3 часа и 1,5 часа 2часа и 2,5 часа 3часа и 1 час 2часа и 2,5 часа

Третья группа:

Два трак­то­ри­ста, ра­бо­тая вме­сте, вспа­ха­ли поле за 48 часов. Если бы по­ло­ви­ну поля вспа­хал один из них, а затем остав­шу­ю­ся по­ло­ви­ну дру­гой, то ра­бо­та была бы вы­пол­не­на за 100 часов. За сколь­ко часов мог бы вспа­хать поле каж­дый трак­то­рист, ра­бо­тая от­дель­но?

	Объем работы (А)	Производительность (N)	Время (t)
1 тракторист
2 тракторист
вместе

1. Составьте систему уравнений для решения задачи, обозначив переменными x и y время работы каждого трактора.

2. Выберите правильный вариант ответа из ниже приведённых.

60 часов и 90 часов 120 часов и 80 часов 110 часов и 70 часов 82 часа и 98 часов

7. Результаты самостоятельной работы (Учащиеся группы и учитель)

8. Домашнее задание.(Слайд 16)

Выучить параграф 7. Решить № 7.23, 7.26.

9. Подведение итогов урока. Рефлексия. (Слайд 17)

1. Комфортно ли Вам было сегодня на уроке?

Мне тоже, потому что я рада была работать вместе с Вами!

Давайте вместе с Вами подведём итоги нашего урока.

а) Сегодня на уроке мы повторили…

б) Сегодня на уроке мы изучили…

И в качественного беспристрастного помощника у нас сегодня выступал компьютер.

На листе бумаги обведите свою ладошку.

Каждый палец – это какая то позиция, по которой необходимо высказать свое мнение.

• большой –я решу задачу на работу

• указательный — я получил конкретные рекомендации…

• средний — мне было трудно ( не понравилось)…

• безымянный – моя оценка психологической атмосферы…

• мизинец — для меня было недостаточно

Дорогие друзья, это был еще один урок по теме «Система уравнений как математическая модель реальных ситуаций». На следующих уроках Вы продолжите работу по этой теме. Я надеюсь, что мы с Вами ощутили радость! Спасибо за урок!

Решение задач с помощью систем уравнений (задачи на совместную работу)

Урок №122

Тема: Решение задач с помощью систем уравнений (задачи на совместную работу)

Цель:

 — личностные:

• проявление воли и настойчивости для достижения конечных результатов;

• умение выдвигать гипотезы, отыскивать доказательства и рассуждать логично;

• выработка уверенности во взаимоотношениях с людьми;

• умения уверенно и легко выполнять математические операции;

• формировать навыки самостоятельной работы и самооценки знаний.

 — метапредметные:

• творческого решения  практических задач; умения самостоятельно выполнять творческую работу;

• способность вступать в речевое общение, участие в диалоге;

• формировать умения оценивать свои учебные достижения, своё эмоциональное состояние.

— предметные:

• осмысление ранее изученных понятий «выражение переменных из формул» и «способы решения систем уравнений различными способами», умения составлять уравнения по тексту задачи в разнообразных интерпретациях; применять правила выражения переменных; овладения навыкам составления и решения уравнений , систем  для решения несложных задач.

Тип урока: урок применения знаний

Оборудование:

Содержание урока

1. Организационный момент……………………………………..2мин

2. Постановка темы и целей урока……………………………….1мин

3. Проверка домашнего задания…………………………………2мин

4. Актуализация опорных знаний………………………………..7мин

5. Мотивация необходимости изучения материала……………2мин

6. Изучение нового материала……………………………………5мин

7. Физкультминутка……………………………………………….1мин

8. Первичное осмысление материала……………………………6мин

9. Закрепление знаний, отработка умений и навыков…………15мин

10. Постановка домашнего задания……………………………….1мин

11. Итог урока……………………………………………………….3мин

Ход урока

1. Организационный момент (2мин)

1. Постановка темы и целей урока (1мин)

Беседа

• Какую тему мы изучали на прошлом уроке?

• С какими типами задач мы уже познакомились?

• Какой следующий типа задач мы изучим?

• Кто сможет назвать тему сегодняшнего урока?

• Какова цель нашего урока?

1. Проверка домашнего задания (3мин)

Самопроверка и самооценивание

1. Актуализация опорных знаний (7мин)

Взаимоопрос «Лото»

Вопросы на экране, учащиеся достают бочонок с номером вопроса и спрашивают любого учащегося класса

1. Что такое линейное уравнение с двумя переменными?

2. Сколько решений может иметь линейное уравнение с двумя переменными?

3. Какая линия является графиком линейного уравнения с двумя переменными?

4. Как называются числа a, b и с в линейном уравнении с двумя переменными?

5. Что такое система линейных уравнений с двумя переменными?

6. Сколько решений может иметь система линейных уравнений с двумя переменными?

7. Что означает фигурная скобка в системе уравнений?

8. Сколько уравнений в себя может включать система уравнений?

9. Как зависит количество решений системы уравнений от расположения графиков уравнений системы?

10. Какие существуют способы решения систем уравнений?

11. В чем заключается графический способ решения систем уравнений?

12. В чем заключается способ подстановки?

13. В чем заключается способ сложения?

14. На какие типы подразделяют задачи?

15. Алгоритм решения задач

м

а

т

р

и

ч

н

ы

й

м

е

т

о

д

На экране открылся еще один метод решения систем уравнений, который вы изучите, поступив после 11 класса в высшие учебные заведения. Метод решения с помощью матриц. Матрица – это прямоугольная таблица из нескольких строк и столбцов

1. Мотивация необходимости изучения материала (2мин)

Одна из задач экзамена 9 класса – решение текстовых задач. Я подобрала для вас задачи именно на совместную работу, которые можно решить с помощью систем линейных уравнений. Эти задачи попадаются ребятам на экзамене в 9 классе. Ознакомьтесь с ними!

За­да­ние 1. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

За­да­ние 2. Игорь и Паша кра­сят забор за 20 часов. Паша и Во­ло­дя кра­сят этот же забор за 24 часа, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

За­да­ние 3. Чтобы на­ка­чать в бак 117 л воды, тре­бу­ет­ся на 5 минут боль­ше вре­ме­ни, чем на то, чтобы вы­ка­чать из него 96 л воды. За одну ми­ну­ту можно вы­ка­чать на 3 л воды боль­ше, чем на­ка­чать. Сколь­ко лит­ров воды на­ка­чи­ва­ет­ся в бак за ми­ну­ту?

• Что общего у этих задач?

• А хотим ли мы на экзамене решить такую задачу и сдать экзамен на «отлично»?

• Тогда давайте работать для этого и у нас всё получится!

1. Изучение нового материала (5мин)

Задачи, которые перед вами сейчас, достаточно сложные и на экзамене они входят в раздел задач повышенной сложности.

Пользуясь алгоритмом, попробуем решить эту задачу.

1 человек – 1 действие

За­да­ние 1. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

Составим краткое условие:

Ученик – 231 дет — ?ч, на 11ч ? дет – 1 ч, на 4 дет

Мастер – 462 дет — ?ч ? дет – 1 ч

Математическая модель задачи:

Пусть в час ученик делает х деталей, а мастер у. Т.к. ученик в час делает на 4 детали , тогда у-х=4

Если ученик делает х деталей в час, то 231 деталей за ч, а мастер . Причем на 11 больше чем . Тогда . Составим систему уравнений.

К сожалению, такие системы мы научимся решать только в 8 классе. Но саму систему вы уже с легкостью составите, если правильно определите тип задачи. В 8 классе вы узнаете, что . Значит ученик в час делает 3 детали.

Ответ: 3

1. Физкультминутка (1мин)

Видеоролик «Космос»

1. Первичное осмысление материала (7мин)

Рассмотрим задачу №2 (самостоятельно с помощью учителя)

За­да­ние 2. Игорь и Паша кра­сят забор за 20 часов. Паша и Во­ло­дя кра­сят этот же забор за 24 часа, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

И – ?часть в час

20ч

П – ?часть в час ?ч

24ч

В – ?часть в час

В+И=30ч

Решение

Пусть Игорь красит x в час, Паша – y, Володя – z.

Тогда за 20 часов Игорь покрасит 20х забора, Паша 20yА вместе они покрасят весь забор, выполнят всю работу, которую принимают за единицу.

То есть: 20х + 20у = 1

За 24 часа: Паша 24у, Володя – 24z, а вместе весь забор – 1.

То есть: 24y + 24z = 1

За 30 часов: Игорь – 30х, Володя – 30z, а вместе – весь забор

То есть: 30х + 30z = 1

Составим и решим систему уравнений:

Тогда Игорь в час красит забора, Владимир — , а Павел — . А вместе за час — . А весь забор за 16 часов.

1. Закрепление знаний, отработка умений и навыков (15мин)

Работа у доски + на опережение

№

1. Постановка домашнего задания (1мин)

1.№

2.* Решить №2, №3 на карточке

1. Итог урока. Оценки (2мин)

Подводя итог урок, хочу выслушать ваше мнение. Какие трудности возникают при решении систем различными способами? Что наиболее сложное при решении задач?

Спасибо за урок! Вы отлично потрудились!

Лист самооценивания

Фамилия, Имя_________________________

Класс_______

№ п/п	Моя деятельность	Моя оценка
1	Домашнее задание
2	Устный опрос
3	Работа у доски
4	Кроссворд
5	Дополнительный ответ
6	Дополнительный ответ
7	Дополнительный ответ

Экзаменационные задачи

За­да­ние 1. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

За­да­ние 2. Игорь и Паша кра­сят забор за 20 часов. Паша и Во­ло­дя кра­сят этот же забор за 24 часа, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

За­да­ние 3. Чтобы на­ка­чать в бак 117 л воды, тре­бу­ет­ся на 5 минут боль­ше вре­ме­ни, чем на то, чтобы вы­ка­чать из него 96 л воды. За одну ми­ну­ту можно вы­ка­чать на 3 л воды боль­ше, чем на­ка­чать. Сколь­ко лит­ров воды на­ка­чи­ва­ет­ся в бак за ми­ну­ту?

Экзаменационные задачи

За­да­ние 1. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

За­да­ние 2. Игорь и Паша кра­сят забор за 20 часов. Паша и Во­ло­дя кра­сят этот же забор за 24 часа, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

За­да­ние 3. Чтобы на­ка­чать в бак 117 л воды, тре­бу­ет­ся на 5 минут боль­ше вре­ме­ни, чем на то, чтобы вы­ка­чать из него 96 л воды. За одну ми­ну­ту можно вы­ка­чать на 3 л воды боль­ше, чем на­ка­чать. Сколь­ко лит­ров воды на­ка­чи­ва­ет­ся в бак за ми­ну­ту?

Экзаменационные задачи

За­да­ние 1. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

За­да­ние 2. Игорь и Паша кра­сят забор за 20 часов. Паша и Во­ло­дя кра­сят этот же забор за 24 часа, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

За­да­ние 3. Чтобы на­ка­чать в бак 117 л воды, тре­бу­ет­ся на 5 минут боль­ше вре­ме­ни, чем на то, чтобы вы­ка­чать из него 96 л воды. За одну ми­ну­ту можно вы­ка­чать на 3 л воды боль­ше, чем на­ка­чать. Сколь­ко лит­ров воды на­ка­чи­ва­ет­ся в бак за ми­ну­ту?

Экзаменационные задачи

За­да­ние 1. На из­го­тов­ле­ние 231 де­та­ли уче­ник тра­тит на 11 часов боль­ше, чем ма­стер на из­го­тов­ле­ние 462 таких же де­та­лей. Из­вест­но, что уче­ник за час де­ла­ет на 4 де­та­ли мень­ше, чем ма­стер. Сколь­ко де­та­лей в час де­ла­ет уче­ник?

За­да­ние 2. Игорь и Паша кра­сят забор за 20 часов. Паша и Во­ло­дя кра­сят этот же забор за 24 часа, а Во­ло­дя и Игорь — за 30 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втроём?

За­да­ние 3. Чтобы на­ка­чать в бак 117 л воды, тре­бу­ет­ся на 5 минут боль­ше вре­ме­ни, чем на то, чтобы вы­ка­чать из него 96 л воды. За одну ми­ну­ту можно вы­ка­чать на 3 л воды боль­ше, чем на­ка­чать. Сколь­ко лит­ров воды на­ка­чи­ва­ет­ся в бак за ми­ну­ту?

Взаимоопрос «Лото»

Вопросы на экране, учащиеся достают бочонок с номером вопроса и спрашивают любого учащегося класса

1. Что такое линейное уравнение с двумя переменными?

2. Сколько решений может иметь линейное уравнение с двумя переменными?

3. Какая линия является графиком линейного уравнения с двумя переменными?

4. Как называются числа a, b и с в линейном уравнении с двумя переменными?

5. Что такое система линейных уравнений с двумя переменными?

6. Сколько решений может иметь система линейных уравнений с двумя переменными?

7. Что означает фигурная скобка в системе уравнений?

8. Сколько уравнений в себя может включать система уравнений?

9. Как зависит количество решений системы уравнений от расположения графиков уравнений системы?

10. Какие существуют способы решения систем уравнений?

11. В чем заключается графический способ решения систем уравнений?

12. В чем заключается способ подстановки?

13. В чем заключается способ сложения?

14. На какие типы подразделяют задачи?

15. Алгоритм решения задач

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

Решение задач с помощью с-м ур-ний 2-ой степени

Алгоритм решения задач с помощью систем уравнений второй степени:

·        обозначить неизвестные величины буквами и составить систему уравнений;

·        решить полученную систему;

·        записать ответ в соответствии с условием задачи.

Пример.

Найти два положительных числа, произведение которых равно 300, а разность — 13.

Пусть x - большее число, а y - меньшее число. Получим:

Решим полученную систему способом подстановки:

Уравнение имеет два корня: 25 и -12. Корень x= -12 не подходит нам по условию, так как в задаче идёт речь о положительных числах. Значит, положительные числа будут 25 и 12.

Пример.

Периметр прямоугольника равен 170 сантиметров, а сумма длин его диагоналей — 130 сантиметров. Нужно найти длины сторон прямоугольника.

Пусть а — ширина прямоугольника, b - длина прямоугольника.

Периметр прямоугольника равен 170 см. Сумма диагоналей равна 130 см. Диагонали прямоугольника равны, и их можно найти из прямоугольного треугольника с помощью теоремы Пифагора:

Получаем систему уравнений:

Полученную систему будем решать способом подстановки:

Решив уравнение с одной переменной, получим:

Получили два решения. Выбираем первую пару решений, так как по условию а — ширина прямоугольника, b - длина прямоугольника. Запишем, а=25 см. и b=60 см.

Пример.

Двое рабочих выполнили некоторую работу за 12 часов. Если бы сначала первый сделал половину этой работы, а затем второй — остальную её часть, то вся работа была бы выполнена за 25 часов. За какое время мог бы выполнить всю работу каждый рабочий в отдельности?

При решении задач на совместную работу важно помнить формулу:

А — объём работы

P - производительность труда

t - время работы.

Чтобы было проще составить систему уравнений, заполним таблицу, в которой отобразим работу, производительность труда и время для каждого из рабочих, а так же для их совместной работы:

Работу обозначим за 1. Первый рабочий выполняет всю работу за х часов, а второй — за у часов. Вместе они выполняют работу за 12 часов. По формуле выразим производительность труда. Для первого рабочего — , для второго — .

Из условия задачи известно, что работая вместе, рабочие выполнили всю работу за 12 часов. И далее сказано, если бы сначала первый сделал половину этой работы, а затем второй — остальную её часть, то вся работа была бы выполнена за 25 часов.

Cоставим систему уравнений:

Решим систему:

 

Применим способ подстановки, преобразовав уравнение с одной переменной, получаем квадратное уравнение:

Его корнями будут числа 20 и 30.

В условии задачи не сказано, какой рабочий работал быстрее, а какой медленнее. Поэтому в данном случае в ответ можно записать любую пару. Ведь они отличаются только порядком следования значений.

Получили, что каждому рабочему в отдельности потребуется 20 и 30 часов.

План-конспект урока по алгебре (9 класс) по теме: Разработка урока «Решение задач на работу»

                                                                                                                               Приложение 1.

 Задания для самостоятельной работы

1.         Два автомобиля выехали одновременно из одного города в другой. Расстояние между городами 200 км. Скорость первого автомобиля на 10 км/ч больше скорости второго. Найти скорость каждого автомобиля, если первый автомобиль прибыл в другой город на 1 час раньше второго.

         Выберите систему уравнений, соответствующую  условию задачи.

А)                                                                                                                                        Б)      

 В)             Г)    

2.         Фермер отправился на машине в город, находящийся на расстоянии 110 км от фермы. Через 20 мин из города на ферму выехал его сын, который проезжал в час на 5 км больше. Встреча произошла в 50 км от города. С какой скоростью ехал фермер?

                   

Введите переменные и заполнить таблицу для решения задачи

	V  скорость	t   время	S путь

                                   

 3. Составьте уравнение для решения задачи

4. Определите метод решения системы уравнений.