Конспект урока геометрии «Решение задач «Параллелограмм» (8 класс)
Параллелограмм и трапеция (§ 2)
Решение задач по теме «Параллелограмм» (п. 42,43)
Цели:
Развивающая: Развитие правильной устной и письменной математической речи; внимания, памяти, сообразительности.
Воспитательная: Воспитание интереса к предмету.
Ход урока
2. ПодготовительныйФронтальная работа с классом
1. Проверка домашнего задания: № (вынести на доску).
2. Теоретический опрос:
1. Дайте определение параллелограмма. Является ли параллелограмм выпуклым четырёхугольником?
2. Докажите, что в параллелограмме противоположные стороны равны и противоположные углы равны.
3. Докажите, что диагонали параллелограмма точкой пересечения делятся пополам.
4. Сформулируйте признаки параллелограмма.
3. Решение задач
I. Решение задач на готовых чертежах:
1) Рис. 114. 3) Рис. 116. 5) Рис. 118.
2) Рис. 115. 4) Рис. 117. 6) Рис. 119.
II. Работа по учебнику:
№ 376 (г, д)
Для сильных учащихся: № 383.
4. Итоги урока.
1. Что нового вы сегодня узнали на уроке?
2. Что повторили из ранее изученного материала?
5. Домашнее задание
Пп. 42 – 43. Вопросы № 6 – 9. № 377; № 382.
infourok.ruКонспект урока на тему «Решение задач на тему «Параллелограмм»»
Урок по геометрии в 8 классе « Решение задач на тему параллелограмм и его свойства»
Цель урока: Обобщение и закрепление полученных знаний и умений по теме «Параллелограмм и его свойства», развитие интереса к предмету.
Ожидаемые результаты: а) Уметь различать признаки параллелограмма от его свойств.
б) Научиться применять прямую и обратную теорему о признаках параллелограмма.
с) Решение задач с применением свойств биссектрисы угла в параллелограмме.
Ключевые понятия: Обсудить и перечислить, где можно применить свойства параллелограмма на практике.
Ресурсы: интерактивная доска, слайды, раздаточные материалы, постеры, стикеры, маркеры.
Задания:кроссворд,задачи
Осмысление.
Решение задач.
Рефлексия.
Оценивание.
ЭТАПЫ УРОКА
ЗАДАЧИ ЭТАПА
ДЕЯТЕЛЬНОСТЬ УЧИТЕЛЯ
ДЕЯТЕЛЬНОСТЬ УЧЕНИКА
1. Организационный этап.
2 мин
Подготовить учащихся к уроку.
Приветствие.
2.Подготовка к повторению пройденного материала.
5 мин
Организация проверки знаний учащихся.
Деление на группы с помощью смайликов.
Сообщить тему урока. Повторение и обобщение темы «Параллелограмм и его свойства».
Цель урока, обобщить знания и умения по теме « Параллелограмм и его свойства».
Разделились на пары.
Записали в тетради дату и тему урока.
Повторение пройденной темы.
3.Проверка усвоение пройденного материала.
10 мин
Проверить знания учащихся путем решения кроссворда.
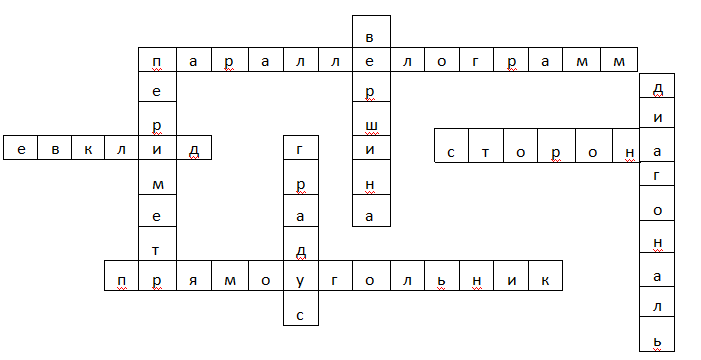
1.Решить кроссворд По горизонтали
1.Четырехугольник, у которого противоположные стороны параллельны. 2.Отрезок,соединяющий соседние вершины. 3.Параллелограмм, у которого все углы прямые.
4.Древнегреческий ученый.
По вертикали 1.Сумма длин всех сторон. 2.Единица измерения углов. 3.Точка, из которой выходят две стороны четырехугольника 4.Отрезок, соединяющий противоположные вершины четырехугольника.
Работают на раздаточных материалах.
Взаимооценивание в парах. Посчитать правильные ответы.
4.Закрепление пройденного материала . 22 мин.
1.Решение задач.
2.Расположить рисунок и решить задачу.
Консультирует и контролирует слабых. Корректирует и организует проверку заданий.
Задачи. 1.У параллелограмма сумма двух углов равна 80°. Найдите углы параллелограмма? 2.Один из углов параллелограмма равен 35°. Найти остальные углы. 3.Найдите стороны параллелограмма, если одна сторона АВ равна 16 дм, а сторона ВС в 2 раза больше стороны АВ 4.У параллелограмма периметр равен 60 см. Найдите стороны, если они относятся как 2:3. 5.У параллелограмма один угол 90°. Чему равны остальные углы?
Слайд № 9,10. 1.Диоганаль квадрата равна стороне другого квадрата (расположить рисунок) 2.Диоганаль квадрата равна 4м, сторона его равна диагонали другого квадрата. Найдите сторону последнего.
рис.1
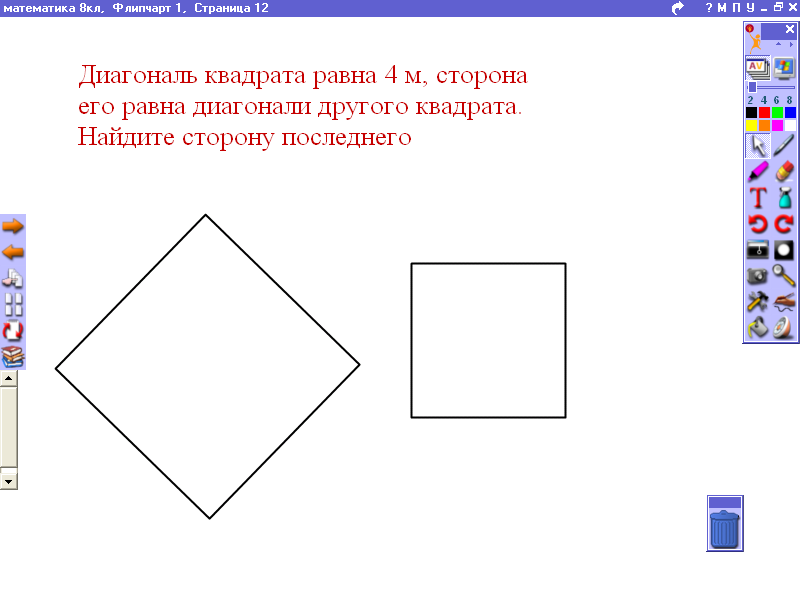
рис.2
В тетради делают записи, чертеж. Обсуждают в группе, анализируют при решении задач Один член группы выходит к доске и защищает работу, остальные проверяют и исправляют ошибки.
Из другой группы выходит ученик и защищает работу.
5.Подведение итогов, домашнее задание.
6. Рефлексия.
5 мин
Д\З Чтение следующей темы «Прямоугольник и его свойства»
Учебник Геометрия 8 класс. И. Бекбоев. Изд-во «Мектеп» 2012 г Алматы
Учебник Геометрия 7-11класс А.В.Погорелов №12,13,14 Изд-во «Просвящение» 1990 Москва.
Проводит рефлексию.
1. Какие трудности возникали в ходе работы?
2. Какие моменты урока вам больше всего понравились?
3. Как вы себя чувствовали на уроке?
Комментируют домашнее задание.
Записывают рефлексию.
1.Четырехугольник, у которого противоположные стороны параллельны. 2.Отрезок,соединяющий соседние вершины. 3.Параллелограмм, у которого все углы прямые. 4.Древнегреческий ученый.
Задачи. 1.У параллелограмма сумма двух углов равна 80°. Найдите углы параллелограмма? 2.Один из углов параллелограмма равен 35°. Найти остальные углы. 3.Найдите стороны параллелограмма, если одна сторона АВ равна 16 дм, а сторона ВС в 2 раза больше стороны АВ 4.У параллелограмма периметр равен 60 см. Найдите стороны, если они относятся как 2:3. 5.У параллелограмма один угол 90°. Чему равны остальные углы?
Ф.И. ученика
infourok.ru
«Параллелограмм. Решение задач.». — Математика
Муниципальное бюджетное образовательное учреждение
Билярская средняя общеобразовательная школа
Алексеевского муниципального района Республики Татарстан
Открытый урок по теме: «Параллелограмм. Решение задач.».
8 класс
Учитель: Гатауллина Фания Хамитовна
2014-2015 уч. год
Тема: Параллелограмм. Решение задач.
Цели урока: обучающие- закрепить знания о свойствах и признаках параллелограмма в процессе решения задач, совершенствовать навыки решения задач;
метапредметные –формировать умения анализировать, строить логическое рассуждение делать выводы, составлять алгоритм решения, схему, коммуникативную и проблемную компетентности;
воспитательные – воспитывать самостоятельность, внимательное отношение друг – другу.
Ход урока.
Орг. часть.
-Здравствуйте, ребята. Сегодня урок необычный, необычный он тем, что у нас сегодня присутствуют гости. День солнечный, светит нам солнце. Надеюсь урок будет плодотворным.
Сообщить тему урока, сформировать цели урока.
Актуализация знаний.
Проверка д/з.
2 ученика отвечают у доски.
№376
Дано: АВСД-параллелограмм, 
А=84
Найти: В,
Д -? Решение. Т.к. противоположные углы равны, то С=А=84
В=Д=(360-84*2):2=96
или В=
Вопросы отвечающему:
-Свойство противоположных углов
— Свойство односторонних углов
Дополнительная задача:
Дано: АВСД- четырехугольник, АС
ВД=О, АС=2 дм, АО=10см, ВД=1,5 см, ВО=7см.
Выяснить: АВСД – параллелограмм?
Решение:
В С По признаку параллелограмма АО= 
А Д 1=*2, ВО=ВД, 0,7=*1,5. Значит АВСД не
является параллелограммом.
Вопросы отвечающему:
-Что такое параллелограмм?
-Свойство диагоналей параллелограмма.
Вопросы к классу (пока около доски ученики готовятся)
-Как найти периметр параллелограмма?
-Каким свойством обладает катет, лежащий против угла в 30 в прямоугольном треугольнике?
-Свойства параллельных прямых?
Работа над новым материалом.
а) Работа в тетрадях.
Выяснить, являются ли следующие фигуры параллелограммами.
К
В С N P
A D Д M Q E
КВС=
СДЕNPQ=PQE1 ) параллелограмм 2) недостаточно данных
Ответы учащихся:
1)А=КВС – как соответственные углы при параллельных прямых ВС и АД и секущей АК АД IIВССДЕ — как соответственные углы при параллельных прямых АВ и СД и секущей АЕВАIIСДАВСД – параллелограмм
2) Недостаточно данных
б) Проверка умений учащихся применять знания в нестандартных ситуациях.
-Сейчас мы переходим к решению задач, в которых нельзя получить результат, выполнив 1-2 шага.
Задача. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
-Перед нами какая проблема возникла?
-Доказать, что полученный треугольник равнобедренный.
-Решать эту задачу поможет нам Таблица Фила. На столах лежат таблицы, заполняем.
Дети заполняют, обсуждаем , 1 ученик доказывает на доске.
Таблица Фила
Факты | Идеи |
Дано: АВСД- параллелограмм, АН- биссектриса Доказать: АВН- равнобедренный | 1.Параллелограмм 2.Равнобедренный треугольник 3.Биссектриса угла 4.Параллельные прямые 5. Накрест лежащие углы |
Обучающие вопросы | План действия |
1.Что такое параллелограмм 2.Какой треугольник называется равнобедренным? 3.Свойство углов равнобедренного треугольника? 4. Какой отрезок называется биссектрисой? 5. Свойство параллельных прямых? 6. Свойство накрест лежащих углов при параллельных прямых и секущей? | 1.Найти накрест лежащие углы. 2. Найти углы при основании треугольника. 3.Вспомнить свойство биссектрисы. 4.Спросить у учителя. 5.Искать в интернете |
Н
Дано: АВСД- параллелограмм, АН- биссектриса В С
Доказать: АВН- равнобедренный
А Д
Доказательство:
ВАН = НАД так как АН – биссектриса,ВНА = НАД – как накрест лежащие углы при параллельных прямых ВС и АД И секущей АН. Значит НАВ =ВНА – углы при основании равнобедренного треугольника АВН. Отсюда следует, что АВН- равнобедренный треугольник.
IV.Рефлексия.
1 вариант
Дано: АВСД – параллелограмм, К принадлежит ВС, АК биссектриса, ВК = 15 см, КС = 9 см
Найти: Периметр параллелограмма АВСД.
2 вариант
Дано: АВСД – параллелограмм, Е принадлежит АД, ВЕ – биссектриса, АЕ =12 см, ЕД = 4 см
Найти: Периметр параллелограмма АВСД.
Подведем итоги урока, выполнив следующее задание. Мы попробуем обобщить нашу информацию, но не только её, но и наши чувства, идеи, в очень короткой записи.
У вас на столах лежат таблицы, надо их заполнить.
1.Пишем одно существительное | параллелограмм |
2. Пишем два прилагательных, описывающих данный предмет | (параллельный, равный, острый, кривой) |
3. Пишем три глагола, характеризуем предмет | (строить, вычислять, находить, определять) |
4. Пишем фразу из четырех значимых слов. | (противоположные углы, стороны равны) |
Домашнее задание: пункт 42,43, №375,401
multiurok.ru
«Параллелограмм. Решение задач.». — Математика
Муниципальное бюджетное образовательное учреждение
Билярская средняя общеобразовательная школа
Алексеевского муниципального района Республики Татарстан
Открытый урок по теме: «Параллелограмм. Решение задач.».
8 класс
Учитель: Гатауллина Фания Хамитовна
2014-2015 уч. год
Тема: Параллелограмм. Решение задач.
Цели урока: обучающие- закрепить знания о свойствах и признаках параллелограмма в процессе решения задач, совершенствовать навыки решения задач;
метапредметные –формировать умения анализировать, строить логическое рассуждение делать выводы, составлять алгоритм решения, схему, коммуникативную и проблемную компетентности;
воспитательные – воспитывать самостоятельность, внимательное отношение друг – другу.
Ход урока.
Орг. часть.
-Здравствуйте, ребята. Сегодня урок необычный, необычный он тем, что у нас сегодня присутствуют гости. День солнечный, светит нам солнце. Надеюсь урок будет плодотворным.
Сообщить тему урока, сформировать цели урока.
Актуализация знаний.
Проверка д/з.
2 ученика отвечают у доски.
№376
Дано: АВСД-параллелограмм, А=84
Найти: В, С, Д -?
Решение. Т.к. противоположные углы равны, то С=А=84
В=Д=(360-84*2):2=96
или В=Д=180-84=96
Вопросы отвечающему:
-Свойство противоположных углов
— Свойство односторонних углов
Дополнительная задача:
Дано: АВСД- четырехугольник, АСВД=О, АС=2 дм, АО=10см, ВД=1,5 см, ВО=7см.
Выяснить: АВСД – параллелограмм?
Решение:
В С По признаку параллелограмма АО= АС,
А Д 1=*2, ВО=ВД, 0,7=*1,5. Значит АВСД не
является параллелограммом.
Вопросы отвечающему:
-Что такое параллелограмм?
-Свойство диагоналей параллелограмма.
Вопросы к классу (пока около доски ученики готовятся)
-Как найти периметр параллелограмма?
-Каким свойством обладает катет, лежащий против угла в 30 в прямоугольном треугольнике?
-Свойства параллельных прямых?
Работа над новым материалом.
а) Работа в тетрадях.
Выяснить, являются ли следующие фигуры параллелограммами.
К
В С N P
A D Д M Q E
КВС=КАД= СДЕNPQ=PQE
1 ) параллелограмм 2) недостаточно данных
Ответы учащихся:
1)А=КВС – как соответственные углы при параллельных прямых ВС и АД и секущей АК АД IIВСА=СДЕ — как соответственные углы при параллельных прямых АВ и СД и секущей АЕВАIIСДАВСД – параллелограмм
2) Недостаточно данных
б) Проверка умений учащихся применять знания в нестандартных ситуациях.
-Сейчас мы переходим к решению задач, в которых нельзя получить результат, выполнив 1-2 шага.
Задача. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
-Перед нами какая проблема возникла?
-Доказать, что полученный треугольник равнобедренный.
-Решать эту задачу поможет нам Таблица Фила. На столах лежат таблицы, заполняем.
Дети заполняют, обсуждаем , 1 ученик доказывает на доске.
Таблица Фила
Факты | Идеи |
Дано: АВСД- параллелограмм, АН- биссектриса Доказать: АВН- равнобедренный | 1.Параллелограмм 2.Равнобедренный треугольник 3.Биссектриса угла 4.Параллельные прямые 5. Накрест лежащие углы |
Обучающие вопросы | План действия |
1.Что такое параллелограмм 2.Какой треугольник называется равнобедренным? 3.Свойство углов равнобедренного треугольника? 4. Какой отрезок называется биссектрисой? 5. Свойство параллельных прямых? 6. Свойство накрест лежащих углов при параллельных прямых и секущей? | 1.Найти накрест лежащие углы. 2. Найти углы при основании треугольника. 3.Вспомнить свойство биссектрисы. 4.Спросить у учителя. 5.Искать в интернете |
Н
Дано: АВСД- параллелограмм, АН- биссектриса В С
Доказать: АВН- равнобедренный
А Д
Доказательство:
ВАН = НАД так как АН – биссектриса,ВНА = НАД – как накрест лежащие углы при параллельных прямых ВС и АД И секущей АН. Значит НАВ =ВНА – углы при основании равнобедренного треугольника АВН. Отсюда следует, что АВН- равнобедренный треугольник.
IV.Рефлексия.
1 вариант
Дано: АВСД – параллелограмм, К принадлежит ВС, АК биссектриса, ВК = 15 см, КС = 9 см
Найти: Периметр параллелограмма АВСД.
2 вариант
Дано: АВСД – параллелограмм, Е принадлежит АД, ВЕ – биссектриса, АЕ =12 см, ЕД = 4 см
Найти: Периметр параллелограмма АВСД.
Подведем итоги урока, выполнив следующее задание. Мы попробуем обобщить нашу информацию, но не только её, но и наши чувства, идеи, в очень короткой записи.
У вас на столах лежат таблицы, надо их заполнить.
1.Пишем одно существительное | параллелограмм |
2. Пишем два прилагательных, описывающих данный предмет | (параллельный, равный, острый, кривой) |
3. Пишем три глагола, характеризуем предмет | (строить, вычислять, находить, определять) |
4. Пишем фразу из четырех значимых слов. | (противоположные углы, стороны равны) |
Домашнее задание: пункт 42,43, №375,401
multiurok.ru
Обобщающий урок-игра по теме «Параллелограмм и трапеция» в 8-м классе
Цели:
- В занимательной форме повторить тему “Параллелограмм и трапеция”.
- Совершенствовать практические навыки в решении задач с применением теоретического материала.
- Развивать умение обобщать и конкретизировать свойства изучаемых фигур.
Оборудование:
- компьютерное обеспечение учительского стола с экраном,
- карточки с готовыми чертежами задач,
- карточки с домашней работой.
Ход урока
I. ВСТУПЛЕНИЕ.
Здравствуйте, ребята!
Прошу занять свои места
Который будет посвящен
Двум четырехугольникам.
Слушайте меня внимательно
На вопросы отвечайте,
Все ребята подмечайте,
Ничего не забывайте!
Итак, м ы н а ч и н а е м!
II. “ПОВТОРЕНИЕ- МАТЬ УЧЕНЬЯ”.
Так говорил … (кто?). а). В ходе повторения заполним кроссворд. За каждый правильный ответ вы получаете жетон.
Жетоны разного цвета:
- красный — правильный ответ,
- синий — неполный ответ,
- желтый — неправильный ответ.
- Как называется фигура, состоящая из 4-х точек и 4-х последовательно соединяющих их отрезков?
- Как называется четырехугольник, у которого противоположные стороны параллельны?
- Как называется отрезок, соединяющий не соседние вершины?
- Четырехугольник, у которого только две противоположные стороны параллельны, а две другие не параллельны?
- Четырехугольник, который лежит в одной полуплоскости от прямой, содержащей любую его сторону? (Приложение 1).
На экране заполняется кроссворд и по окончании выделяется слово “ГРИПП”. Учитель задает вопросы о гриппе: почему вдруг заговорили об этой болезни; чем сопровождается эта болезнь; какие народные средства помог
urok.1sept.ru
Урок геометрии в 8 классе на тему «Решение задач по теме «Четырехугольники»
8 класс
Тема. Решение задач по теме «Четырехугольники».
М-М А-П
Задачи:
— обучающие:
Усвоение всеми учащимися стандартного минимума и расширение фактических сведений о параллелограмме, прямоугольнике, ромбе, квадрате и их свойствах;
совершенствование навыков решения задач по теме «Четырехугольники».
— развивающие:
Развитие психологических характеристик учащихся, таких как умение сопоставлять факты и делать выводы с научных и эстетических позиций;
развитие логического мышления, познавательного интереса, развитие устной и письменной математической речи; формирование навыков обобщения и систематизации.
— воспитательные:
Воспитание сознательного, творческого отношения к учебному труду;
обеспечение гуманистического характера обучения.
здоровьесберегающие:
Планируемые результаты:
учащиеся научатся применять свойства изученных четырехугольников к решению задач базового уровня, увидят возможность применения этих знаний в измененной, более сложной ситуации.
Смогут грамотно и логично излагать свои мысли; решать задачи; применять правила работы в парах и группах, оценивать свою работу на уроке.
Формы работы учащихся: фронтальная, индивидуальная, групповая.
Оборудование: мультимедийный проектор, компьютер, раздаточный материал.
Алгоритм М-М
1.Организационный момент. Постановка цели урока.
Начинаем урок, на котором вы должны продемонстрировать не только стандартный минимум фактических сведений об изученных четырехугольниках, но и расширить свои знания, математический кругозор, интуицию, логику.
Сегодня мы посетим интерактивную выставку: «Мир четырехугольников».
2.Первичная актуализация знаний:
Мы попадаем в первый зал, который открывают картины известных художников – кубистов
Хуана Гриса «Кружка пива», «Портрет Пикассо», «Жалюзи»,»Курильщик»,»Натюрморт»,Ферена Леже «Дама в красном»,»Композиция: диск».
Справка. Кубизм — направление в изобразительном искусстве характеризующееся использованием геометрических форм, стремлением «раздробить» объекты на геометрические фигуры.
Центральная фигура выставки параллелограмм
Можно сказать, что параллелограмм — одна из значимых фигур в планиметрии. Он обладает интересными свойствами и достоинствами. А вот какими, вы сейчас мне напомните.
Прямоугольник несёт красоту, чёткость, стройность.
Оглянитесь вокруг: стены, пол, потолок, поверхность стола, футбольное поле, грани карандашей, даже сотовый телефон – все это прямоугольники.
Попробуйте построить дом или сделать раму для картины, не зная свойств прямоугольника.
Одна из них – картина Казимира Малевича «Черный квадрат» выполнена в технике плоскостных фигур у многих вызывает противоречивые чувства. А какие чувства она вызывает у вас?А какими свойствами обладает квадрат, как геометрическая фигура?
Квадрат. Ни наука, ни техника, не обходятся без квадрата.
В основании мраморных колонн лежит квадрат.
Играя в шахматы, фигуры по квадратам передвигают.
В хирургическом отделении для пересадки кожи применяют специальную машинку, которая вырезает кожу в виде квадратов. Их располагают на обожжённом участке в шахматном порядке.
В сельском хозяйстве применяют квадратно- гнездовой способ посадки и т.д
Полюбуйтесь на затейливые узоры витражей, паркета, колоритные рисунки украинских вышивок. Какая фигура здесь наиболее заметна?
Ромб. Плиточники укладывают плитки в виде ромба,– из них получаются красивые узоры.
Реечный домкрат для легковых автомобилей также имеет форму ромба.
Математический диктант. «Кодированный ответ»
1). Любой ромб является: 1.квадратом 2.прямоугольником 3. параллелограммом
2). Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм: 1. ромб 2. прямоугольник 3. нет правильного ответа
3). Любой прямоугольник является: 1. ромбом 2. квадратом 3. параллелограммом
4). Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник: 1. ромб 2. квадрат 3. прямоугольник 4. нет правильного ответа
5). Диагонали четырёхугольника в точке пересечения делятся пополам. Одна из его сторон равна 4 см. Чему равна противолежащая сторона?
1. 2 см 2. 8 см 3. 4 см 4. 6 см
6). Сумма двух углов параллелограмма равна 100 градусов, найдите углы параллелограмма.
1. 40, 140 2. 80, 100 3. 50, 130 4. 40, 60
7). Квадрат — это… 1. параллелограмм с равными сторонами 2. параллелограмм с равными углами
3.прямоугольник, у которого все стороны равны
8). У этого четырёхугольника диагонали равны
1. прямоугольник 2. ромб 3. параллелограмм
9). Какое из утверждений неверное?
1. у прямоугольника углы – прямые 2. у ромба все стороны равны 3. у квадрата диагонали взаимно перпендикулярны 4. у параллелограмма диагонали равны
10). Какое утверждение неверно:
1. квадрат — одновременно параллелограмм и прямоугольник
2. . угол между стороной и диагональю квадрата равен 45 град.
3. диагонали квадрата взаимно перпендикулярны 4. существует квадрат, который не является ромбом
Ответ 3 134 333 144
Тестовые задания
3. Решение задач.
1. А мы проявляем фантазию и находчивость, решая задачи устно по готовым чертежам .
Задачи практического содержания.(устно)
1. Противоположные стороны четырехугольной плитки паркета параллельны и равны. Как, пользуясь линейкой, выяснить, имеет ли плитка форму прямоугольника?
Решение. Измерить диагонали.
2. Как швея убеждается в том, что кусок материи имеет форму квадрата?
Проверить, будет ли данный кусок материи квадратом?
Решение. Сложить кусок по диагонали и пополам. Если получаются равные четыре треугольника, то этот кусок – квадрат.
Работа в группах.
I группа
1. Угол ромба равен 32°. Найдите углы, которые образует его сторона с диагоналями
2. ВМ — медиана треугольника АВС. На ее продолжении за точку М отложен отрезок MD, равный ВМ. Докажите, что четырехугольник АВCD — параллелограмм.
II группа
1. ABCD — параллелограмм, диагонали АС и BD которого пересекаются в точке О. Докажите, что ВО — медиана треугольника АВС.
2.Угол между диагоналями прямоугольника равен 80°. Найдите углы между диагональю прямоугольника и его сторонами.
III группа
1. В параллелограмме AВCD диагональ BD равна 9 см, сторона DC — 11 см, сторона ВС — 4 см. Найдите периметр треугольника AВD.
2. Сторона ромба равна 18 см, а один из углов — 150. Найдите высоту ромба
IV группа
Сторона АВ параллелограмма ABCD равна 7 см, а его диагонали АС и ВD равны 6 см и 10 см соответственно. О — точка пересечения диагоналей. Определите периметр треугольника АОВ.
Докажите, что ромб является квадратом, если его стороны образуют с диагоналями равные углы.
IV группа
Задача. На сторонах АВ и CD прямоугольника АВСD взяты точки К и М так, что АКСМ – ромб. Диагональ АС составляет со стороной АВ угол 30°. Найдите сторону ромба, если наибольшая сторона прямоугольника равна 3.
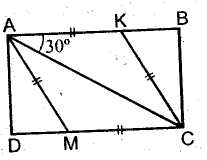
Дано: АВСD – прямоугольник, АВ = 3, КАВ, МСD,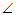
КАС = 30°, АКСМ – ромб.
АВА Найти: АК.
Решение:1)АКСМ – ромб, тогда АК = КС, АКС – равнобедренный, значит 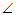КСА = 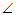КАС = 30°,
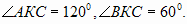
2)
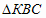— прямоугольный, в нем 
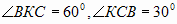, тогда КВ = КС/2 = AK/2.
3) Т.к. КВ=АК/2,АВ = АК + КВ = АК + АК/2 =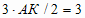 
, то АК = 2.
Подведение итогов (рефлексия):
Наша экскурсия подходит к концу и наступает момент творчества. Мы создадим картину «Радуга настроения». И пусть она соединит в себе ваше настроение, ваши чувства и эмоции от урока.«Радуга настроения»
Урок понравился и было интересно (красный цвет)
Урок заставил задуматься (зеленый цвет)
Ты изменил свой взгляд на геометрию (синий цвет)
Урок оставил тебя равнодушным (серый цвет)
Пожалуйста, выберите деталь любого цвета — значения цветов записаны на доске, подойдите к доске и наклейте её. Что же у нас получилось? Очень яркая радуга говорит о том, что вы с интересом работали на уроке, узнали много нового, что заставило вас задуматься и изменить свое отношение к геометрии. — А те знания, что вы приобрели, сегодня пусть останутся с вами навсегда.
infourok.ru
Разработка урока по геометрии 8 класс на тему: «Четырёхугольники. Решение задач»
Тема урока
«Четырехугольники. Решение задач«
Тип урока: комплексное применение знаний и умений.
Цель: создать условия для систематизации и закрепления знаний обучающихся при решении задач.
Планируемые результаты:
личностные:
формирование ответственного отношения к учению на основе мотивации к обучению и познанию,
формирование осознанного, уважительного и доброжелательного отношения к другому человеку, его мнению,
формирование коммуникативной компетенции в общении и сотрудничестве со сверстниками и взрослыми в процессе учебной деятельности.
метапредметные:
умение определять понятия, создавать обобщения, классифицировать, строить рассуждение, умозаключение и делать выводы,
умение оценивать правильность выполнения учебной задачи, собственные возможности ее решения,
умение применять теоретические знания на практике,
развитие памяти, внимания, наблюдательности,
развитие мотивации учения через эмоциональное удовлетворение от открытий,
предметные:
обобщить знания обучающихся о четырехугольниках,
формировать умения решать задачи, с использованием признаков и свойств четырехугольников.
Оборудование и учебно-методическое обеспечение: компьютер, проектор, задания для самостоятельной работы, задания для домашней работы.
ХОД УРОКА
I. Организационный момент.
Сообщить тему урока, сформулировать цели урока.
Мотивация урока.
Мы изучили материал главы «Четырёхугольники», работая с каждым видом отдельно. В ходе работы научились применять полученные знания на практике. Сегодня на уроке мы обобщим и закрепим пройденный материал в устной работе и в процессе решения упражнений. В ходе выполнения самостоятельной работы и проверочного тестирования выявим уровень овладения знаниями, умениями, навыками и устраним пробелы.
Уметь определять вид четырёхугольника и применять его свойства необходимо будет и в дальнейшем, как при введении новых тем, так и в практике. Даже в 10,11 классах, при работе с объёмными фигурами эти знания часто применяются при решении задач. Поэтому очень важно усвоить весь материал и научиться его применять на практике.
Актуализация опорных знаний. Проверка д/з.
Повторим определения и свойства четырехугольников
Фронтальный опрос /устно/. Cоставляем cхему изображающую четырехугольники и его виды.
1 — что называется четырехугольником?
2 – назовите виды четырехугольников;
3 – что называется параллелограммом?
4 – назовите свойства параллелограмма;
5 – что называется прямоугольником?
6 – назовите свойства прямоугольника;
7 – что называется ромбом?
8 – назовите свойства ромба;
9 – что называется квадратом?
10- назовите свойства квадрата;
11- что такое трапеция?
12- назовите виды и свойства трапеции.
Теоретическая самостоятельная работа
(заполнение «семантической карты)
Заполните таблицу, отметив знаки «+»-да, «-» -нет (7 баллов)
и проверочный тест (3 балла)
1 вариант2 вариант
1. Любой прямоугольник является:
а) ромбом;
б) квадратом;
в) параллелограммом;
г) нет правильного ответа.
1. Любой ромб является:
а) квадратом;
б) прямоугольником;
в) параллелограммом;
г) нет правильного ответа.
2. Если в четырехугольнике диагонали перпендикулярны, то этот четырехугольник-
а) ромб;
б) квадрат;
в) прямоугольник;
г) нет правильного ответа.
2. Если в параллелограмме диагонали перпендикулярны, то этот параллелограмм:
а) ромб;
б) квадрат;
в) прямоугольник;
г) нет правильного ответа.
Ромб – это четырехугольник, в котором…
а) диагонали точкой пересечения делятся пополам и равны;
б) диагонали взаимно перпендикулярны и точкой пересечения делятся пополам;
в) противолежащие углы равны, а противолежащие стороны параллельны;
г) нет правильного ответа.
Прямоугольник – это четырехугольник, в котором:
а) диагонали точкой пересечения делятся пополам и являются биссектрисами углов;
б) противолежащие стороны параллельны, а диагонали равны;
в) два угла прямые и две стороны равны;
г) нет правильного ответа.
Взаимопроверка работ по готовым ответам
10 – 9 баллов – отметка 5
8 – 7 баллов – отметка 4
6 – 5 баллов – отметка 3
менее 5 баллов – отметка 2
Решение задач по готовым чертежам (устно)
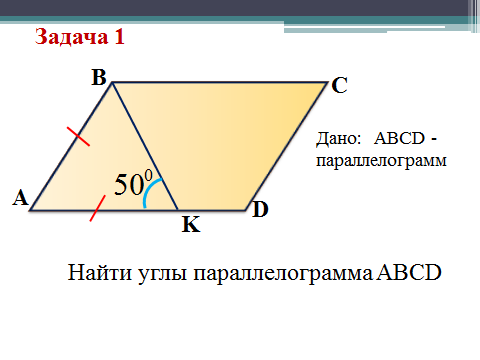
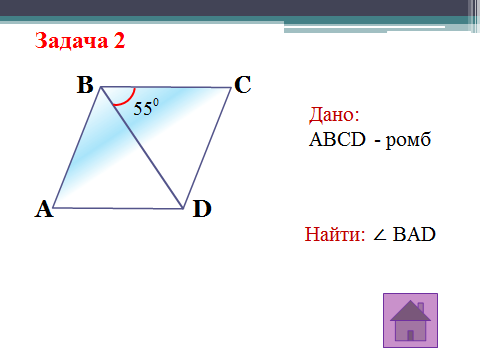
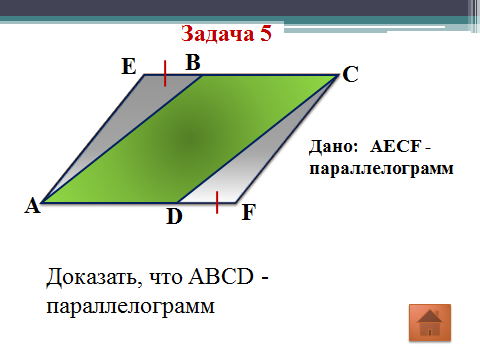
Физкультминутка
упражнения для глаз
«истинно — ложно» Я скажу несколько предложений. Если предложение ложное, то вы топаете ногами, если верное, то хлопаете в ладоши.
Диагонали прямоугольника равны.
Все углы квадрата прямые.
Диагонали ромба равны.
Диагонали параллелограмма равны.
В ромбе все стороны равны.
Диагонали прямоугольника перпендикулярны.
В параллелограмме противоположные стороны равны.
Текстовые задачи (письменно)
1. В равнобедренной трапеции большее основание равно 25 см, боковая сторона равна 10 см, угол между ними 60º. Найдите меньшее основание
2. Периметр параллелограмма равен 48. Одна сторона параллелограмма на 3 больше другой найдите меньшую сторону параллелограмма.
3. В трапеции АВСD, ВС – меньшее основание. На отрезке АD взята точка Е так, что ВЕ ║СD; угол АВЕ = 70º, угол ВЕА = 50º. Найдите углы трапеции.
4. MNKP – параллелограмм. МТ – биссектриса угла NМР, NТ = 6 см, ТК = 4 см. Найдите периметр параллелограмма.
5. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
Рефлексия. Подведение итогов урока.
В начале урока мы поставили цели. Выполнили ли мы свою задачу?
Выставление отметок.
Домашнее задание.
Составить буклет, можно компьютерный вариант, или закладку, в которых вы рассмотрите и укажете все свойства изученных вами четырехугольников.
А так же задачи на листках.
infourok.ru