Разбор и решение задания №1 ОГЭ по математике
Числа и вычисления
Описание задания
Первое задание проверяет наши умения проведения вычислений. Это самое простое задание из всего модуля и требует от нас только знания арифметики. В первом задании арифметические действия будут самыми простыми. В демонстрационном варианте ОГЭ предлагается сложить две дроби: обыкновенную и десятичную. Тем не менее, в соответствии с документами о проведении ОГЭ, учащиеся должны быть готовы и к выполнению некоторых других несложных заданий. Ответом в первом задании является целое число или конечная десятичная дробь.
Тематика заданий: числа и вычисления
Первичный бал: 1
Сложность задания: ♦◊◊
Примерное время выполнения: 3 мин.
Теория к заданию №1
Итак, для успешного выполнения необходимо помнить:
- порядок проведения арифметических операций — сначала производятся действия в скобках, затем возведение в степень или извлечение корня, затем умножения и деления, а затем вычитания и сложения
- правила умножения и деления в столбик
- правила вычисления обыкновенных дробей
Напоминаем правила операций с обыкновенными дробями:
Рекомендуем вычислить отдельно числитель и знаменатель, а затем разделить числитель на знаменатель. Остальные рекомендации смотрите ниже при разборе типовых вариантов первого задания ОГЭ по математике. 🙂
Разбор типовых вариантов задания №1 ОГЭ по математике
Первый вариант задания
Найдите значение выражения:
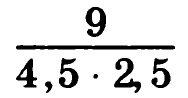
или:
9 / (4,5 • 2,5)
Решение:
Задачу можно решать разными путями, а именно менять последовательность действий
, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.Вычислим значение знаменателя:
4,5 • 2,5
Можно произвести вычисления в столбик, тогда получим:
4,5 • 2,5 = 11,25
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции — деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
Получаем ответ: 0,8
Подводя итог, сделаем выводы:
Удобней сразу переходить к дробям простого вида. Надежней производить вычисления последовательно в числителе и знаменателе.
Второй вариант задания
Найдите значение выражения:
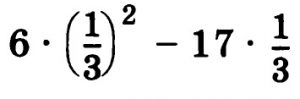
или:
6 • (1/3)² — 17 • 1/3
Решение:
Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.
1/3 • (6 • (1/3) — 17 )
Проведя вычисления в скобках, получим:
1/3 • ( 6 • (1/3) — 17 ) = 1/3 • (6 /3 — 17 ) = 1/3 • ( 2 — 17 ) = 1/3 • ( -15 )
Теперь умножим полученное значение -15 на 1/3:
1/3 • ( -15 ) = -5
Ответ: -5
Какие выводы можно сделать: не всегда стоит стараться решить задачу «в лоб», даже в ОГЭ.
Третий вариант задания
Найдите значение выражения:
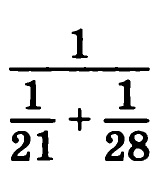
Решение:
Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:
1/21 + 1/28 = 4/84 + 3/84
Затем складываем:
4/84 + 3/84 = 7/84
Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:
1 / ( 7 / 84 ) = 1 •84/7 = 84/7
Далее остается поделить 84 на 7:
84 / 7 = 12
Ответ: 12
Демонстрационный вариант ОГЭ 2019
Найдите значение выражения: ¼ + 0,07
Решение:
К данному заданию, как и к большинству заданий 1 модуля Алгебры, подход к решению заключается в переводе дроби от одного вида к другому. В нашем случае это переход от обыкновенной дроби к десятичной.
Переводим ¼ из обыкновенной дроби в десятичную. Делим 1 на 4, получаем 0,25. Затем переписываем выражение с использованием только десятичных дробей и вычисляем:
0,25 + 0,07 = 0,32
Ответ: 0,32
Четвертый вариант задания
Найдите значение выражения:
–0,3·(–10)4+4·(–10)2–59
Решение:
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
–0,3·(–10)4+4·(–10)2–59 =
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
= –0,3·10000+4·100–59 =
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
= –3000+400–59 =
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
= –2600–59 =
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
= –(2600+59) = –2659
Ответ: –2659
Пятый вариант задания
Найдите значение выражения:
–13·(–9,3)–7,8
Решение:
Это задание требует простого умения выполнять арифметические действия с десятичными дробями.
–13·(–9,3)–7,8 =
Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:
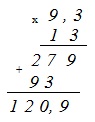
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:
= 120,9–7,8 =
Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:
= 113,1
Ответ: 113,1
Скачать PDF
Распечататьspadilo.ru
Разбор и решение задания №9 ОГЭ по математике
Статистика и вероятности
Рассмотрим типовые задания 9 ОГЭ по математике. Тематика 9 задания — статистика и вероятности. Задание не является трудным даже для человека, не знакомого с теорией вероятностей или статистикой.
Обычно нам предлагается набор вещей — яблок, конфет, чашек или чего угодно различающихся цветом или другим качеством. Нам необходимо оценить вероятность попадания одного из класса вещей одному человеку. Задача сводится к вычислению общего количества вещей, а затем делению числа вещей необходимого класса на общее количество.
Итак, перейдем к рассмотрению типовых вариантов.
Разбор типовых вариантов задания №9 ОГЭ по математике
Первый вариант задания
У бабушки 20 чашек: 6 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Решение:
Как было сказано выше, найдем общее число чашек — в данном случае это известно по условию — 20 чашек. Нам необходимо найти число синих чашек:
20 — 6 = 14
Теперь мы можем найти вероятность:
14 / 20 = 7 / 10 = 0,7
Ответ: 0,7
Второй вариант задания
Решение:
Найдем вначале число черных ручек, для этого из общего числа вычитаем все известные цвета и делим на два, так как синих и чёрных ручек поровну:
(138 — 34 — 23 — 11) / 2 = 35
После этого можем найти вероятность, сложив количество чёрных и красных, разделив на общее количество:
(35 + 34) / 138 = 0,5
Ответ: 0,5
Третий вариант задания
В фирме такси в данный момент свободно 12 машин: 1 чёрная, 3 жёлтых и 8,зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
Решение:
Найдем общее число машин:
1 + 3 + 8 = 12
Теперь оценим вероятность, разделив количество желтых на общее число:
3 / 12 = 0,25Ответ: 0,25
Демонстрационный вариант ОГЭ 2019
На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.
Решение:
Классическая задача по теории вероятностей. В нашем случае удачный исход — это пирожок с яблоком. Пирожков с яблоками 3, а всего пирожков:
4 + 8 + 3 = 15
Вероятность того, что попадется пирожок с яблоками — это количество пирожков с яблоками, деленное на общее количество:
3 / 15 = 0,2 или 20%
Ответ: 0,2
Четвертый вариант задания
Вероятность того, что новый принтер прослужит больше года, равна 0,95. Вероятность того, что он прослужит два года или больше, равна 0,88. Найдите вероятность того, что он прослужит меньше двух лет, но не меньше года.
Решение:
Введем обозначения событий:
X – принтер прослужит «больше 1 года»;
Y – принтер прослужит «2 года или больше»;
Z – принтер прослужит «не менее 1 года, но меньше 2-х лет».
Анализируем. События Y и Z независимы, т.к. исключают друг друга. Событие X произойдет в любом случае, т.е. и при наступлении события Y, и наступлении события Z. Действительно, «больше 1 года» означает и «2 года», и «больше 2-х лет», и «меньше 2-х лет, но не менее 1 года».
Если так, то событие X можно считать суммой событий, и тогда на основании теоремы о сложении вероятностей запишем:
Р(X)=Р(Y)+Р(Z).
По условию вероятность события Х (т.е. «больше года») равно 0,95, события Y (т.е. «2 года и больше») – 0,88.
Подставим в формулу числовые данные:
0,95=0,88+Р(Z)
Получаем:
Р(Z)=0,95–0,88=0,07
Р(Z) – искомое событие.
Ответ: 0,07
Пятый вариант задания
За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что девочки окажутся на соседних местах.
Решение:
Для расчета вероятности используем классическую ее формулу:
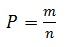где m – кол-во благоприятных исходов для искомого события, n – общее кол-во всех возможных исходов.
Одна из девочек (которая села первой) занимает стул произвольно. Значит, для другой имеется 9-1=8 стульев, чтобы сесть. Т.е. кол-во всех возможных вариантов событий равно n=8.
Другая девочка должна занять один из 2-х стульев, соседствующих со стулом первой. Только такая ситуация может считаться благоприятным исходом события. Значит, кол-во благоприятных исходов составляет m=2.
Подставляем данные в формулу для расчета вероятности:
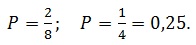
Ответ: 0,25
spadilo.ru
Разбор и решение задания №2 ОГЭ по математике
Описание задания
Второе задание, которое раньше было 14, относится к «реальной математике», где нам предстоит решать задачи из жизненных ситуаций и окружающего мира. В нашей практике учащиеся решают эти задачи гораздо лучше, так как они сформулированы понятнее, нежели абстрактные задания из алгебры. Тем не менее при решении задач необходимо быть внимательными и проверять решение, так как легко можно что-то упустить или понять не правильно. Во втором задании необходимо отнести значение к группе. Это может быть спортивный результат или любое свойство предмета, по которому его необходимо распределить в ту или иную группу. Для полного понимаю лучше сразу приступить к рассмотрению типовых вариантов.
Тематика заданий: анализ диаграмм, таблиц и графиков
Первичный бал: 1
Сложность задания: ♦◊◊
Примерное время выполнения: 2 мин.
Разбор типовых вариантов задания №2 ОГЭ по математике
Первый вариант задания
Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья. Используя данные, представленные в таблице, определите, к какой категории относится яйцо массой 51,8 г.
- Высшая
- Первая
- Вторая
- Третья
Решение:
Смотрим на таблицу и замечаем, что наше яйцо весом 51,8 грамма попадает во вторую категорию, так как оно весит меньше 55, но более 45. Чтобы оно попало в первую категорию, необходим вес более 55, например 56, поэтому все, что меньше 55 и больше 45 попадает во вторую категорию.
Ответ: 3
Второй вариант задания
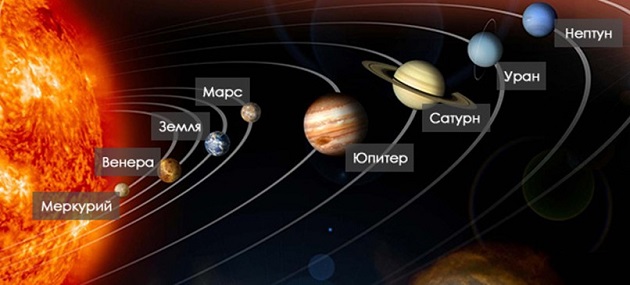
В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы. Какая из этих планет ближе всех к Солнцу?
- Нептун
- Юпитер
- Уран
- Венера
Решение:
Ближе всего к Солнцу та планета, чье расстояние до него меньше. Сначала смотрим на степени числа 10. У Нептуна и Урана степени числа 10 — 9, значит они дальше в 10 раз чем Юпитер и Венера, у которых степени 8. Далее сравниваем значения — у Юпитера это 7,7 — у Венеры — 1,0 — значит, Венера ближе.
Ответ можно сказать сразу, если знаешь расположения планет, что, конечно, должен знать каждый:
Третий вариант задания
Учёный Куликов выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 8:30. В таблице дано расписание ночных поездов Москва—Санкт-Петербург.
Путь от вокзала до университета занимает полчаса. Укажите номер самого позднего (по времени отправления) поезда, который подходит учёному Куликову.
Решение:
Если необходимо прибыть в университет в 8:30, а дорога занимает 30 минут, то в Санкт-Петербурге Куликову необходимо быть в 8:00.
Смотрим поезд, который прибывают раньше 8:00 — это 002А — он прибывает в 7:55 — самое близкое значение к 8 часам. Значит, ответ 002А.
Ответ: 002А
Демонстрационный вариант ОГЭ 2019
В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.
Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?
- Отлично
- Хорошо
- Удовлетворительно
- Норматив не выполнен
Решение:
Так как вопрос про девочку, соответственно ищем цифры в столбцах для девочек.
Что означает отлично? Это значит, что 5 получает та, которая пробегает 30 метров за 5 секунд или быстрее, то есть за 3 секунды или за 4,5.
Что означает хорошо? Это значит, что 4 получает та девочка, которая пробегает 30 метров за 5,5 секунд или быстрее, то есть за 5,2 секунды или за 5,3.
Что означает удовлетворительно? Это значит, что 3 получает та, которая пробегает 30 метров за 5,9 секунд или быстрее, то есть за 5,6 секунды или за 5,8.
У нас спрашивают про девочку, пробегающую за 5,36 секунд. Очевидно, это второй вариант.
Четвертый вариант задания
В таблице дано соответствие размеров женских платьев в Белоруссии, России, Англии и Европейском Союзе.
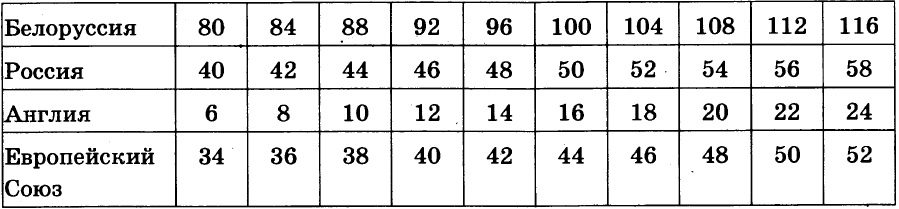
Какому английскому размеру соответствует 46-й размер платья в Европейском Союзе?
1) 12 2) 18 3) 40 4) 52
Решение:
Поиск нужного значения выполняем по принципу использования таблицы Пифагора. Т.е. определяем строку и столбец с исходными данными, и на их пересечении находим результат.
Находим в таблице «Европейский союз». Это последняя строка. Двигаясь по ней вправо, находим число 46 (дано в условии). Оно зафиксировано в 7-м столбце таблицы (считая от начала числовых данных).
В этом же – седьмом – столбце поднимаемся вверх до строки под названием «Англия». Записанное в найденной ячейке число и есть ответ. Это – 18. Соответственно, прав.вариант ответа – 2.
Ответ: 2
Пятый вариант задания
На рулоне обоев написано, что длина полотна равна 10 м ± 4 %. Какую длину не может иметь полотно?
1) 10 м 30 см 3) 10 м 6 см
2) 10 м 44 см 4) 9 м 95 см
Решение:
4% от 10 м составляет 10·0,04=0,4 м=40 см. Это означает, что допустимое искажение точной длины в 10 м равно 40 см. Тогда минимальная и длина обоев в рулоне равна 10 м–40 см=9 м 60 см, а максимальная равна 10 м+40 см=10 м 40 см. Т.е. получаем диапазон допустимых значений: 9 м 60 см ÷ 10 м 40 см.
В этот диапазон входят все значения (из вариантов ответов), кроме 2-го, равного 10 м 44 см. Эту длину рулон обоев иметь не может.
Ответ: 2
spadilo.ru
Разбор и решение задания №23 ОГЭ по математике
Анализ графика функции
Разбор типовых вариантов заданий №23 ОГЭ по математике
Первый вариант задания
Постройте график функции
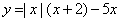
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем функцию в зависимости от знака переменной х.
Если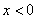 
. 
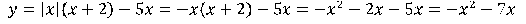
Если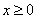 
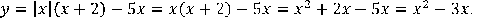
2. График функции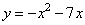 
заданных значениях х — часть параболы, ветви которой направлены вниз.
Вершина расположена в точке с координатами: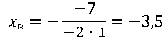 
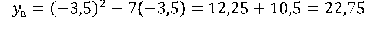
Найдем нули функции: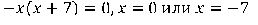 
График проходит через начало координат и точку (-2;-7).
Графиком второй функции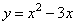 
является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
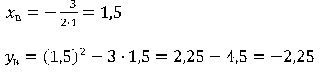
Определим нули параболы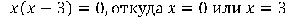 
3. Изображаем график функции на координатной плоскости:
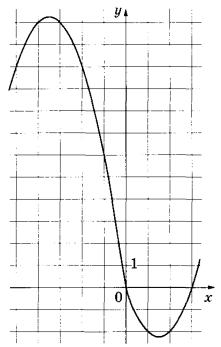
4. Из построения легко видно, что прямая y = m имеет с графиком ровно две точки, когда проходит через вершину одной из парабол, образующих график данной функции.
Значит, две общие точки функция и прямая имеют при m = -2,25 или m = 12,25.
Ответ: -2,25; 12,25.
Второй вариант задания
Постройте график функции
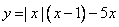
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу в зависимости от знака переменной х:
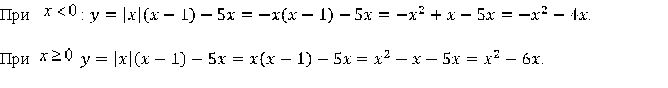
2. Графиком функции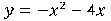 
является парабола, ветви которой направлены вниз.
Вершина ее находится в точке :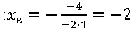 
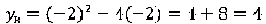
Найдем нули функции: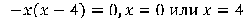 
График проходит через начало координат и точку (0;4).
Графиком второй функции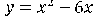 
является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
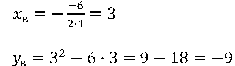
Определим нули параболы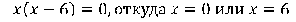 
3. Изображаем график на координатной плоскости:
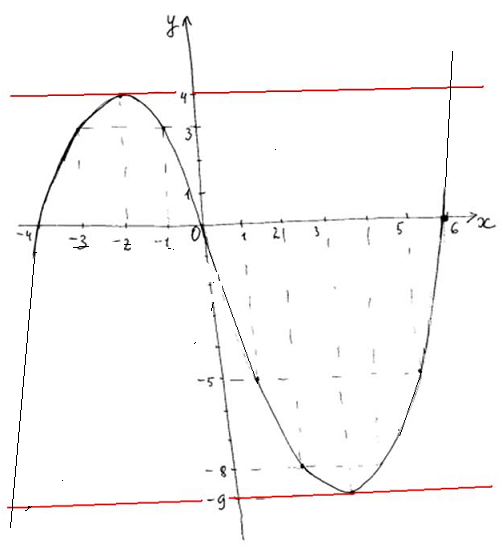
Из изображения видно, что прямая y= m имеет с графиком только две общих точки, когда m=-9 или m=4. На графике прямая изображена красной линией при каждом значении m.
Ответ: -9; 4.
Третий вариант задания
Постройте график функции
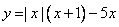
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу функции в зависимости от знака переменной
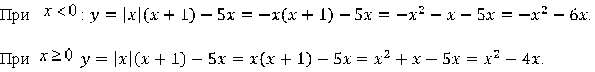
2. Определяем вид функции и находим дополнительные точки для каждого участка графика.
График при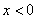 
— часть парабола, ветви которой направлены вниз. Потому как коэффициент а=-1 – отрицательный.
Определим вершину параболы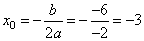 
и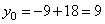 
.
Вершина находится в точке (-3; 9).
Парабола проходит еще через точки (0;0) и (0;6).
Если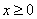 
, ветви параболы направлены вверх. Найдем вершину:
, 
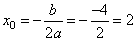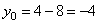(2; -4).
График проходит также через точки (0;0) и (0;4).
3. Строим искомый график:
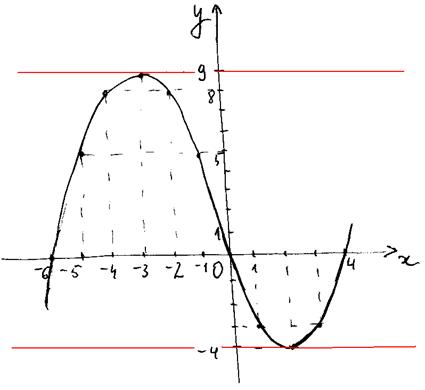
Из построения видно, что прямая y=m имеет только 2 общие точки с графиком функции в случаях, когда m=-4 или m=9. На рисунке прямые изображены красным цветом.
Ответ: -4; 9.
Четвертый вариант задания
Постройте график функции
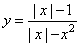
Определите, при каких значениях k прямая у = kx не имеет с графиком общих точек.
Алгоритм решения:
- Раскрываем модуль и преобразовываем формул функции.
- Определяем вид функции на каждом промежутке и находим дополнительные точки графика.
- Строим график.
- Определяем искомые значения k.
- Записываем ответ.
Решение:
1. Если x < 0, то
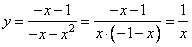
Дробь, получившаяся в результате, определена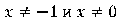 
. График представляет собой часть гиперболы.
Точки для построения графика:
| x | -5 | -4 | -3 | -2 |
| y | -1/5 | -1/4 | -1/3 | -1/2 |
2. Если x > 0, то
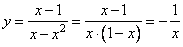
Функция определена при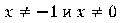 
График представляет собой часть гиперболы.
Точки для построения графика:
| x | 2 | 3 | 4 | 5 |
| y | -1/2 | -1/3 | -1/4 | -1/5 |
3. Построим график заданной функции:
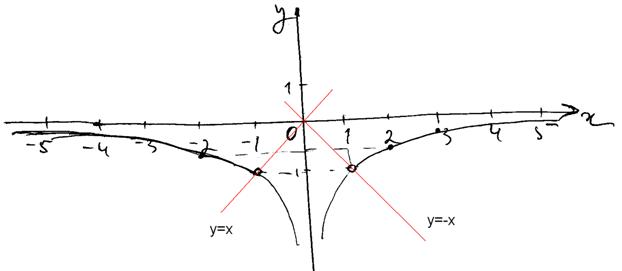
4. Прямая y=kx не имеет общих точек с графиком, при k=-1; 0 и 1, потому как тогда прямая проходит через точки, не входящие в область определения заданной функции.
На графике прямые для k=-1; 1изображены красным.
При k = 0 прямая совпадает с осью абсцисс и тоже не имеет общих точек с графиком функции.
Ответ: -1; 0; 1.
Пятый вариант задания
Постройте график функции
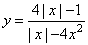
Определите, при каких значениях k прямая y = kx не имеет с графиком общих точек.
Алгоритм решения:
- Раскрываем модуль и преобразовываем формул функции.
- Определяем вид функции на каждом промежутке и находим дополнительные точки графика.
- Строим график.
- Определяем искомые значения k.
- Записываем ответ.
Решение:
1. Раскрываем модуль и для каждого случая.
Если x < 0, то
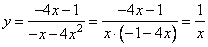
определена при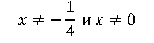 
и представляет собой часть гиперболы. Дополнительные точки для построения:
| x | -5 | -4 | -3 | -2 | -1 |
| y | -1/5 | -1/4 | -1/3 | -1/2 | -1 |
2. Если x > 0, то
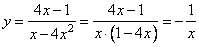
определена при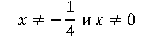 
и представляет собой часть гиперболы.
Точки для построения графика:
| x | 1 | 2 | 3 | 4 | 5 |
| y | -1 | -1/2 | -1/3 | -1/4 | -1/5 |
3. Изображаем график:
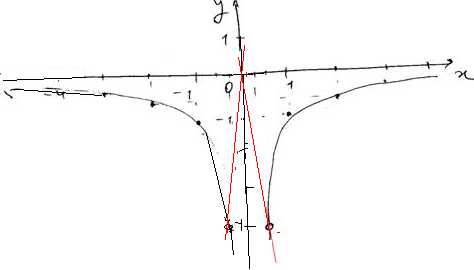
Прямая y=kx не имеет общих точек с графиком данной функции, когда k=-16; 0 и 16. Тогда прямые проходят черед точки с абсциссами ¼ и — ¼ . На рисунке эти прямые изображены красным.
При k = 0 прямая совпадает с осью абсцисс. Она тоже не имеет общих точек с графиком.
Ответ: -16; 0; 16.
Демонстрационный вариант ОГЭ 2019
Постройте график функции
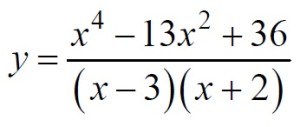
и определите, при каких значениях с прямая y = c имеет с графиком ровно одну общую точку.
Разложим числитель дроби на множители:
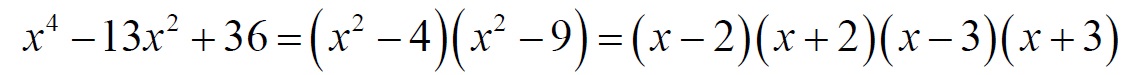
При x ≠2 и x ≠ 3 функция принимает вид:
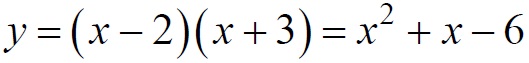
её график — парабола, из которой выколоты точки ( -2; -4) и ( 3; 6).
Прямая y = c имеет с графиком ровно одну общую точку либо тогда, когда проходит через вершину параболы, либо тогда, когда пересекает параболу в двух точках, одна из которых — выколотая.
Вершина параболы имеет координаты ( -0,5; -6,25 ).
Поэтому c = — 6,25, c = — 4 или c = 6.
Ответ: c = — 6,25, c = — 4 или c = 6.
spadilo.ru
Разбор и решение задания №21 ОГЭ по математике
x2 +7x+12.
Составим квадратное уравнение для вычисления оставшихся двух корней:
x2 +7x+12=0
6. Решим его с помощью формул корней и дискриминанта
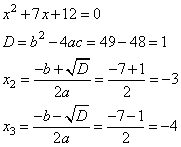
7. Получили три корня 3; -3; -4.
Ответ: 3;-3;-4.
Второй вариант задания
Решите уравнение
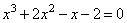
Алгоритм решения:
- Определить тип уравнения.
- Найти делители свободного члена уравнения.
- Определить среди делителей один из корней.
- Выполнить деление кубического многочлена на выражение х-а, где а – найденный корень.
- Записать получившийся в результате деления квадратный трехчлен и составим уравнение.
- Решить уравнение.
- Записать ответ.
1. Перед нами кубическое уравнение общего вида.
2. Найдем делители свободного члена уравнения. Это числа: 1; -1 и 2; -2.
3. Определим один из корней кубического уравнения среди делителей свободного члена .Для этого подставим каждый из этих делителей вместо x и проверим, какой их них является корнем:
— для x=1: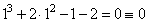 
— подходит это и есть один из корней.
4. Теперь выполним деление кубического многочлена на x-1, воспользовавшись схемой Горнера, имеем:
Искать квадратный трехчлен можно другим способом, выполнив деление многочлена столбиком:
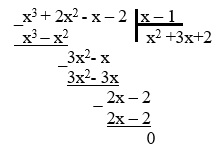
5. Получаем квадратный трехчлен
x2 +3x+2.
6. Составим и решим квадратное уравнение для вычисления оставшихся двух корней. Для этого воспользуемся формулами корней квадратного уравнения и дискриминантом.
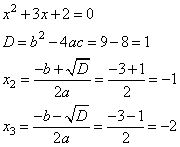
7. Получили три корня -2; -1; 1.
Ответ: -2; -1; 1.
Третий вариант задания
Решите уравнение
(х–2)4+3(х–2)2–10=0.
Алгоритм решения:
- Выполняем замену выражения с х на альтернативную переменную. Это позволит упростить уравнение и привести его к форме обычного квадратного.
- Решаем полученное квадратное уравнения.
- Переходим обратно к выражению с х, для которого была выполнена замена.
- Находим искомые корни уравнения.
Решение:
(х–2)4+3(х–2)2–10=0
Выполняем замену: (х–2)2=а.
Получаем:
а2+3а–10=0
Это уравнение можно решить с помощью т.Виета. Согласно теореме, имеем:
а1+а2=–b, a1·a2=c.
Здесь а1, а2 – корни этого уравнения, b=3, c=–10.
Отсюда получаем: а1=2, а2=–5.
Возвращаемся к переменной х. Поскольку (х–2)2=а, то получим:
1) (х–2)2=2
2) (х–2)2=–5
это уравнение корней не имеет, т.к. нельзя извлечь корень из отрицат.числа
Ответ: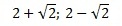 
Четвертый вариант задания
Решите неравенство
(3х–7)2≥(7х–3)2.
Алгоритм решения:
- Используя ф-лу сокращенного умножения для квадрата разности, раскрываем скобки в левой и правой части нер-ва.
- Группируем элементы (слагаемые) неравенства: слагаемые с «х» должны оказаться в левой части, свободные члены – в правой. Приводим подобные.
- Решаем полученное нер-во.
Решение:
9х2–42х+49≥49х2–42х+9
9х2–42х–49х2+42х≥9–49
–40х2≥–40
х2≤1
х≤|1| → –1≤x≤1 → xϵ[–1; 1]
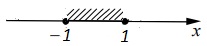
Ответ: [–1; 1]
Пятый вариант задания
Решите систему уравнений
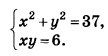
Алгоритм решения:
- Из 2-го уравнения выражаем у через х.
- Подставляем полученное выражение для у в 1-е уравнение.
- В полученном ур-нии с одной переменной (х) выполняем тождественные преобразования. Приводим его к квадратичному виду.
- Выполняем замену х2 на а. Решаем полученное квадратное ур-ние.
- Возвращаемся от а к х. Находим все значения (корни) для х.
- Определяем соответствующие им значения для у.
- Фиксируем в ответе пары соответствующих корней.
Решение:
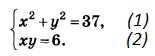
Из (2) выражаем у через х:
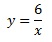
Полученное выражение для у подставляем в (1):
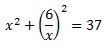
Выполним преобразования:
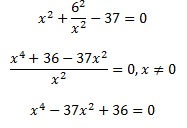
Выполним замену: х2= , а≠0 .
Получим:
а2–37а+36=0
По т.Виета а1=1, а2=36
Отсюда имеем:
х2=1 → х=±1 → х1=–1, х2=1
х2=36 → х=±6 → х3=–6, х4=6
Теперь возвращаемся к уравнению, в котором у выражено через х. И вычисляем соответствующие значения для у:
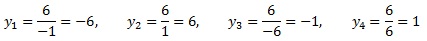
Ответ: (–1; –6), (1; 6), (–6; –1), (6; 1)
spadilo.ru
Разбор и решение задания №16 ОГЭ по математике
Треугольники, четырёхугольники, многоугольники и их элементы
Перейдем к разбору модуля «Геометрия». В задании 16 проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами. По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.
Проверьте, что вы не ошибаетесь в определениях тригонометрических функций острого угла в прямоугольном треугольнике.
Кроме того, убедитесь, что все данные задачи отражены на вашем чертеже. При необходимости применяйте теорему Пифагора. Если сюжет задачи развивается в равнобедренном треугольнике, то учтите, что высота, опущенная из вершины такого треугольника, делит его на два равных прямоугольных треугольника и далее задача решается в прямоугольном треугольнике. Если события происходят в окружности, то, помимо всего прочего, надо учесть, что вписанный угол равен половине центрального угла, который опирается на ту же дугу. Пусть треугольник вписан в окружность. Если этот треугольник остроугольный, то центр окружности лежит внутри треугольника. Если этот треугольник тупоугольный, то центр окружности лежит вне треугольника. А если это прямоугольный треугольник, то центр окружности лежит на середине гипотенузы.
В 16 задании нам предстоит продемонстрировать свои знания в нахождении неизвестных элементов треугольника. Это могут быть углы, стороны, высоты, медианы или биссектрисы. Могут встретится задания на нахождение площади.
Теория к заданию №16
Так как задания №16 основаны на теории по теме «треугольники», рассмотрим базовые понятия, определения и формулы.
Вначале предлагаю рассмотреть углы на плоскости:
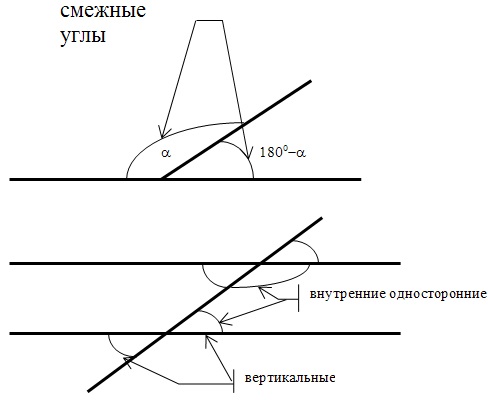
Многие задачи построены на нахождении медиан и биссектрис треугольника:
Биссектриса – отрезок, выходящий из вершины треугольника и делящий угол пополам.
- Биссектриса делит противолежащую сторону на части , пропорциональные прилежащим сторонам: ab : ac = b : c
- Биссектриса делит площадь треугольника, пропорционально прилежащим сторонам.
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
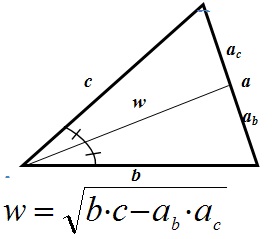
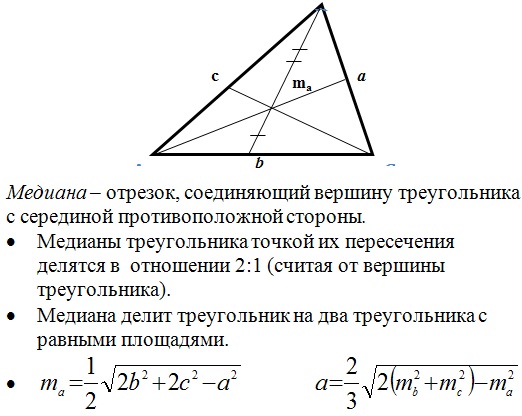
Медиана:
Теперь вспомним основные формулы нахождения площади треугольника:
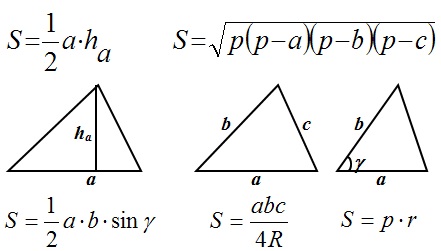
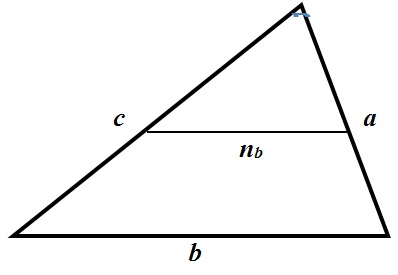
Во многих задачах встречается понятие средняя линия:
Средняя линия – отрезок, соединяющий середины двух сторон треугольника.
- Средняя линия параллельна третьей стороне и равна её половине.
- Средняя линия отсекает подобный треугольник, площадь которого равна одной четверти от исходного.
Теперь рассмотрим частные случаи треугольников — равнобедренный, равносторонний, прямоугольный.
Перейдем к рассмотрению равнобедренного треугольника:
Равнобедренный треугольник — треугольник, у которого две стороны равны.
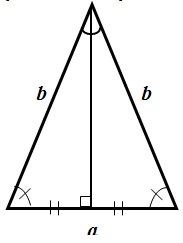
Свойства равнобедренного треугольника:
- Углы, при основании треугольника, равны.
- Высота, проведенная из вершины, является биссектрисой и медианой.
Рассмотрим равносторонний треугольник:
Равносторонний треугольник — треугольник, у которого все стороны равны.
- Все углы равны 60°.
- Каждая из высот является одновременно биссектрисой и медианой.
- Центры описанной и вписанной окружностей совпадают.
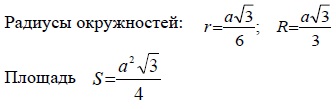
Прямоугольный треугольник:
Разбор типовых вариантов заданий №16 ОГЭ по математике
Первый вариант задания
В треугольнике два угла равны 73° и 48°. Найдите его третий угол. Ответ дайте в градусах.
Решение:
Для решения этого задания достаточно знать правило — сумма углов в треугольнике равна 180°.
Нам известны два угла, значит можем найти третий:
180 — 73 — 48 = 59
Ответ: 59°
Второй вариант задания
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 20, сторона BC равна 58, сторона AC равна 64. Найдите MN.
Решение:
Для решения этой задачи не нужно пользоваться всеми данными в условии. Для успешного решения необходимо знать, что такое средняя линия треугольника.
Средняя линия — это линия соединяющая середины сторон и параллельная основанию.
Средняя линия равна половине основания, которому она параллельна.
Таким образом, если точки M и N являются серединами сторон AB и BC, значит эта линия параллельна AC — третьей стороне. А это в свою очередь означает, что она равна половине AC:
MN =½ • AC = 64 / 2 = 32
Ответ: 32
Третий вариант задания
В треугольнике ABC известно, что AB = BC, ∠ABC = 122°. Найдите угол BCA. Ответ дайте в градусах.
Решение:
Если в треугольнике две стороны равны — значит он равнобедренный. А в равнобедренном треугольнике углы при основании равны. Так как сумма углов в треугольнике равна 180°, угол в вершине равен 122°, значит сумма углов при основании равна:
180 — 122 = 58°
Так как углы при основании равны, значит угол BCA равен углу BAC:
∠BCA = ∠BAC
58° = ∠BCA + ∠BAC = 2 ∠BCA
∠BCA = 58 / 2 = 29°
Ответ: 29°
Четвертый вариант задания
Сторона равностороннего треугольника равна 10√3. Найдите его медиану.
Решение:
Для решения этой задачи необходимо знать формулу медианы в равностороннем треугольнике, или уметь выводить её из теоремы Пифагора. В данном случае мы воспользуемся готовой формулой, и я советую вам её запомнить, чтобы не тратить время на вывод в каждом случае:
m = ( a • √3 )/ 2
Где m — медиана в равностороннем треугольнике, а a — сторона. Таким образом, для решения данной задачи подставим значение в формулу:
m = ( 10√3 • √3 )/ 2 = ( 10 • 3 )/ 2 = 30 / 2 = 15
Ответ: 15
Пятый вариант задания
Один из острых углов прямоугольного треугольника равен 23°. Найдите второй острый угол. Ответ дайте в градусах.
Решение:
Так как сумма углов в треугольнике равна 180°, а в прямоугольном треугольнике один из углов прямой, то сумма двух острых углов равна 90°. Отсюда можно вывести следующее правило:
Сумма острых углов в прямоугольном треугольнике равна 90°.
Следовательно, второй острый угол равен:
90 — 23 = 67°
Ответ: 67°.
Шестой вариант задания
В треугольнике ABC известно, что AC = 56, BM — медиана, BM = 48. Найдите AM.
Решение:
Для решения необходимо вспомнить определение медианы.
Медиана — отрезок, проведенный из вершины и делящий противоположную сторону на два равных отрезка.
Таким образом, медиана BM делит сторону AC (противоположную вершине B) пополам, следовательно^
AM = ½ AC = ½ 56 = 28
Ответ: 28.
Седьмой вариант задания
Два катета прямоугольного треугольника равны 15 и 4. Найдите его площадь.
Решение:
Формула площади для прямоугольного треугольника выглядит следующим образом:
Площадь прямоугольного треугольника равна половине произведения его катетов.
Это следует из того, что один из катетов является высотой к основанию, которым является второй катет.
Исходя из вышесказанного, можем решить задачу:
S = ½ • 15 • 4 = 30
Ответ: 30.
Восьмой вариант задания
Сторона равностороннего треугольника равна 12√3. Найдите его высоту.
Решение:
Вспоминаем, что в равностороннем треугольнике высота является и медианой и биссектрисой.
Для медианы, а значит и для высоты, формулу я приводил чуть выше:
m = ( a • √3 )/ 2
Подставим значение:
m = ( 12√3 • √3 )/ 2 = ( 12 • 3 )/ 2 = 36 / 2 = 18
Ответ: 18.
Девятый вариант задания
Катеты прямоугольного треугольника равны 12 и 16. Найдите гипотенузу этого треугольника.
Решение:
Воспользуемся теоремой Пифагора:
c² = 12² + 16² = 144 + 256 = 400
c = √400 = 20
Ответ: 20.
Десятый вариант задания
Биссектриса равностороннего треугольника равна 11√3. Найдите его сторону.
Решение:
До этого мы искали медиану, биссектрису или высоту равностороннего треугольника по формуле:
m = ( a • √3 )/ 2
Здесь же нам необходимо решить обратную задачу, найти a, если известно m.
Выразим a:
a = ( 2 • m ) / √3
Подставим значение:
a = ( 2 • m ) / √3 = ( 2 • 11 • √3 ) / √3 = 22
Ответ: 22
Демонстрационный вариант ОГЭ 2019
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123° . Найдите величину угла ВАС. Ответ дайте в градусах.
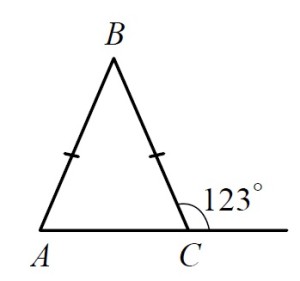
Решение:
Для решения этого задания нужно помнить два факта:
- Внутренний угол с внешним углом дают в сумме 180°
- Углы при основании равнобедренного треугольника равны.
Из первого пункта следует, что угол BCA = 180 — 123 = 57°
Из второго — что ∠BCA = ∠BAC = 57°
Ответ: 57°
spadilo.ru
Разбор и решение задания №24 ОГЭ по математике
Решение:
1. Выполняем соответствующий чертеж: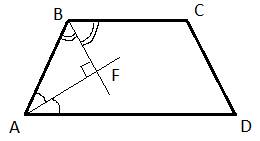
2. Трапеция ABCD имеет основаниями стороны ВС и AD, значит, они параллельны. Тогда в ней внутренние односторонние при пересечении прямых, которые содержат эти основания, секущей АВ. Следовательно, они удовлетворяют равенству: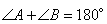 
.
3. По построению, заданному условием задачи AF и BF являются биссектрисы данных углов. Тогда в треугольнике ABF
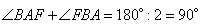
Отсюда получаем:
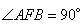
Таким образом, треугольник AFB прямоугольный, а сторона AB – его гипотенуза.
4. Используем теорему Пифагора: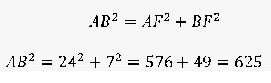 
Отсюда АВ=25.
Ответ 25.
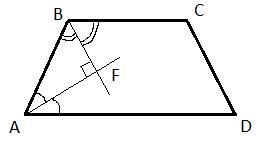
Шестой вариант задания
Биссектрисы углов А и В при боковой стороне АВ трапеции ABCD пересекаются в точке F. Найдите АВ, если AF = 20, BF = 15.
Алгоритм решения:
- Делаем чертеж.
- Рассматриваем углы трапеции и проведенные биссектрисы.
- Определяем вид треугольника AFB.
- Находим длину АВ.
- Записываем ответ.
Решение:
1. Выполняем рисунок, соответствующий данному условию.
2. Рассмотрим трапецию ABCD. В ней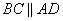 
как основания. Углы А и В составляют в сумме 1800, как углы при основаниях. Отсюда следует, что 
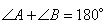как соседние при двух основаниях. По условию лучи AF и BF – биссектрисы этих углов, тогда их сумма
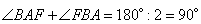
3. Рассматриваем треугольник ABF. В нем угол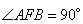 
по свойству углов треугольника, т.е. построенный треугольник AFB – прямоугольный. И гипотенузой в нем является сторона AB.
4. Вычислим сторону по теореме Пифагора: АВ2 = AF2 + BF2
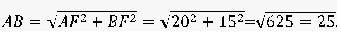
Следовательно, АВ=25.
Ответ: 25.
Демонстрационный вариант ОГЭ 2019
В прямоугольном треугольнике ABC с прямым углом C известны катеты: AC = 6 , BC = 8 . Найдите медиану CK этого треугольника.
Алгоритм решения:
- Используя св-во медианы в прямоуг.треугольнике, показываем, что искомый отрезок СК равен половине АВ.
- Используя т.Пифагора, находим АВ.
- Зная АВ, вычисляем СК.
Решение:
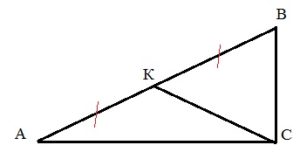
У прямоуг.треугольника есть свойство: его медиана, опущенная из вершины прямого угла на гипотенузу, равна ее половине. Поскольку ∆АВС прямоугольный, то СК=АВ/2. Это означает, что СК=АК=КВ:
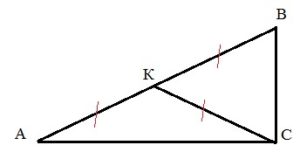
Гипотенузу АВ найдет по т.Пифагора:
АВ2=АС2+ВС2
Отсюда:
Тогда получаем:
СК=10/2=5.
Ответ: 5
spadilo.ru