Проект «Решение уравнений с параметром»
В процессе проведения индивидуальной исследовательской работы на тему «Решение уравнений с параметром» авторка рассмотрела способы решения различных примеров с параметром, создала справочный материал для изучения способов решения примеров с параметром.
Подробнее о работе:
В готовом исследовательском проекте по математике «Решение уравнений с параметром» авторка проанализировала представленный материал по решению примеров с параметром, нашла оптимальный способ их решения, для дальнейшего предоставления его учащимся старших классов, а также составила информационный продукт, понятный для восприятия. Подготовила учащихся к решению заданий с параметрами из ЕГЭ.
Оглавление
Введение
Противоречие в том, что для успешной сдачи ЕГЭ учащимся 10-11 классов необходимо знать, как решать различные уравнения с параметром, но школьный курс не подразумевает глубокого изучения данной темы
Проблема: как подготовиться к решению заданий с параметрами из ЕГЭ
Цель проекта: Рассмотреть способы решения различных примеров с параметром. Создать удобный и полный справочный материал для изучения способов решения примеров с параметром, который поможет выпускникам школ успешно аттестоваться по математике. Также справочный формат в формате презентации может помочь учителям в ознакомлении учеников в данной теме.
Создать удобный и полный справочный материал для изучения способов решения примеров с параметром, который поможет выпускникам школ успешно аттестоваться по математике. Также справочный формат в формате презентации может помочь учителям в ознакомлении учеников в данной теме.
Задачи проекта:
- Проанализировать представленный материал по решению примеров с параметром.
- Найти оптимальный способ их решения, для дальнейшего предоставления его учащимся 10-11 классов.
- Составить грамотный информационный продукт, который будет прост и понятен для восприятия.
Геометрические фигуры окружают нас повсюду, алгебра помогает в повседневной жизни, к примеру: совершать банковские расчеты или составлять списки покупок с подробным расчетом продуктов по их средней цене. Веками люди совершенствовали знания в точных науках. Многие алгебраические задачи содействовали появлению новых научных направлений, и наоборот, решение многих научных проблем было получено с использованием алгебраических методов.
В общеобразовательных школах геометрию и алгебру школьники начинают углубленно изучать в 7 классе. Простейшую алгебру преподают с первого класса, и это делается не просто так. Внедрение арифметики помогает детям развивать критическое мышление и способствует развитию умения составления логических цепочек, высказываний. Математическое мышление необходимо для структурирования и лучшего усваивания всей поступающей информации. Таким образом, математическое образование является важнейшим элементом общей культуры. Этот факт является неоспоримым.
Этот неоспоримый факт находит отражение в изменении содержания и структуры КИМов единого государственного экзамена по математике в сторону увеличения количества и повышения сложности алгебраических заданий.
В целях качественного отбора выпускников для продолжения образования в высших учебных заведениях, часто с высокими требованиями к уровню математической подготовки выпускников. Задания 2 части ЕГЭ предназначены для проверки знаний на том уровне требований, которые традиционно предъявляются вузами с профильным экзаменом по математике. Задачи с параметром вызывают наибольшие затруднения (справляются порядка 10-17%), т.к. эти задания показывают насколько обширны знания учащихся в алгебре, как школьном предмете, так и науке. Данные задачи также предназначены для конкурсного отбора в наиболее престижные ВУЗы с наиболее высоким конкурсом на специальности и повышенными требованиями к математической подготовке абитуриентов.
Задания 2 части ЕГЭ предназначены для проверки знаний на том уровне требований, которые традиционно предъявляются вузами с профильным экзаменом по математике. Задачи с параметром вызывают наибольшие затруднения (справляются порядка 10-17%), т.к. эти задания показывают насколько обширны знания учащихся в алгебре, как школьном предмете, так и науке. Данные задачи также предназначены для конкурсного отбора в наиболее престижные ВУЗы с наиболее высоким конкурсом на специальности и повышенными требованиями к математической подготовке абитуриентов.
Также это связано с обилием различных типов алгебраических задач и с многообразием приемов и методов их решения. Чаще всего, трудности при решении этих задач возникают по следующим причинам:
- материал по теме либо был плохо усвоен в основной школе, либо уже забылся выпускниками;
- для решения задачи нужно знать некоторые методы и приемы решения, которые либо не рассматриваются при изучении основного курса алгебры, либо не отрабатываются.

Чтобы изменить сложившиеся ситуацию, необходимо провести систематизацию знаний, полученных учениками в основной школе, также проанализировать доступные источники с более узконаправленным материалом. Продуктом данной исследовательской деятельности станет информационный буклет, где будут собраны наиболее удобные и понятный методы и приемы по данной теме: «Решение примеров с параметром». В нем также будет сделан акцент и на грамотное оформление решения.
Актуальность: Данный навык необходим для успешной сдачи ЕГЭ
Обоснование актуальности: ЕГЭ — экзамен, через который проходит любой ученик, поступающий в Вузы в России. Многие направления в институтах требуют сдачи профильной математики. Примеры с параметром — задание, за которое выпускник может получить весомое кол-во баллов. В моем проекте я рассматриваю самые оптимальные способы решения данного задания.
Продукт проекта: информационный урок для учащихся 10-11 классов
Дорожная карта
| Этапы работы над проектом | Содержание работы | Деятельность обучающегося | Временные рамки |
| Подготовительный | Определение темы. Анализ проблемы. Формулировка цели, задач и гипотезы Анализ проблемы. Формулировка цели, задач и гипотезы | Согласовала тему проекта с куратором и начала составление возможных противоречий, проблем, целей, задач и гипотез | Октябрь-Ноябрь 2020 года |
| Организационный | А) Определение источников необходимой информации. Б) Определение способов сбора и анализа информации. В) Определение типа проекта, способа представления результатов, продукта проектной деятельности | Формулирую задачи проекта, вырабатывают план дальнейших действий. Делаю предположения по поводу итогового продукта проекта. Анализирую различные источники информации (методические материалы, уже существующие проекты на эту тему, статистику от сайта ФИПИ, Решу ЕГЭ Д.Гущина) | Ноябрь-Декабрь 2020 года |
| Практический | Сбор и уточнение информации (интервью, опросы, наблюдения, и т.д.). Выявление и обсуждение альтернатив, возникших в ходе выполнения проекта. | Поэтапное выполнение задач проекта. Оформление исследовательской части проекта. | Январь-Февраль 2021 года |
| Презинтационный | Сдача имеющийся исследовательской части проекта | Сдаю исследовательскую часть в ГБОУ лицее №150 | Конец февраля 2021 года |
| Аналитический | Анализ выполнения проекта, достигнутых результатов. | Провожу самоанализ проектной деятельности, результатов проекта. Оформляю описание проекта и дорабатываю продукт проекта | Февраль- Апрель 2021 года |
| Презентационный | Поиск подходящих конференций и публичный показ своего проекта | Защита проекта на конференции не ниже района. Получение сертификата об участии/победе в конференции | Март-Апрель 2021 года |
| Аналитический | Анализ публичной защиты проекта. Вносятся необходимые поправки Вносятся необходимые поправки | Анализирую собственное выступление, делаю выводы и вношу необходимые поправки в проект | Апрель 2021 года |
SWOT-анализ
| Сильные стороны: 1. востребованность качественного обучающего материала для учеников 10-11 классов 2.самообразование в части углубленного изучения данного раздела математики | Слабые стороны: 2. возможное недоверие к качеству предоставляемого материала 2.большое количество аналогичных пособий, следовательно, высокая конкуренция |
| Угрозы: 1. возможность появления фактический ошибки в составленном учебном материале | Возможности: 2. создание качественного продукта, который помочь выпускникам сдать ЕГЭ на высокие баллы 2.укрепление знаний обучающихся в выбранной теме с помощью развернутого и понятного раскрытия материала |
На ЕГЭ встречается два типа задач с параметрами.
Первый «для каждого значения параметра найти все решения некоторого уравнения или неравенства».
Второй «найти все значения параметра, при каждом из которых решения уравнения или неравенства удовлетворяют заданным условиям».
Ответы в данных задачах имеют разную структуру и требования. В задачах первого типа ответ выглядит так: перечисляются все возможные значения параметра и для каждого из этих значений записываются решения уравнения.
В ответах второго типа задач с параметром перечисляются все значения параметра, при которых выполнены условия задачи.
Что необходимо ученикам?
Учащиеся должны знать:
- применение равносильных преобразований уравнений, неравенств и их систем;
- свойства квадратичной функции, ее графики, формула.
Учащиеся должны уметь:
- правильно анализировать условие задачи;
- выбирать наиболее рациональный метод решения и обосновывать его;
- логически обосновывать собственное мнение;
- использовать символический язык для записи решений алгебраических задач;
- применять имеющиеся теоретические знания при решении задач.

Исследовательская часть
В параллели 10 классов моей школы я провела простой социальный опрос, который должен был выявить уровень подготовленности учеников по 18 заданию ЕГЭ. Опрос показал, что 87% учеников не имеют представление о том, какую структуру имеют задания с параметром Это связано с особенностями составления программы по изучению алгебры и обучению математическому анализу в старшей школе. Примеры с параметрами в ней или не рассматриваются, или данная тема затрагивается поверхностно.

Теоретическая часть.
Примеры с параметром – 18 задание в ЕГЭ, то есть оно относится ко второй части экзамена. Задания второй части имеют формат развернутого ответа. Тем самым ответом будет подробное решение задачи/примера, с описанием всех этапов рассуждения.
Ответ оценивается по определенным критериям. Всего за данное задание можно получить 4 первичных балла, что является довольно высоким максимальным баллом, если сравнивать его с остальными шестью заданиями второй части.
Критерии к оцениванию таковы
| Критерии оценивания выполнения задания | Баллы |
| Обоснованно получен правильный ответ. | 4 |
| Получен верный ответ. Решение в целом верное. Обосновано найдены оба промежутка значений параметра из ответа к задаче, при этом возможны неточности с (не)включением концов и(или) вычислительная погрешность. | 3 |
Обосновано найден хотя бы один промежуток значений параметра из ответа к задаче, при этом возможны неточности с (не)включением концов и(или) вычислительная погрешность. | 2 |
| Решение содержит: − или верное описание расположения двух лучей и прямой из условия задачи; − или верное получение квадратного уравнения с параметром a относительно одной из переменных. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 4 |
Представленные выше критерии необходимо соблюдать, чтобы получить максимальный балл. Нельзя не обратить внимание на необходимость «красивого» оформления: аккуратный и разборчивый почерк важная составляющая получения высшего балла. Неразборчиво написанные слова и буквы могут быть неправильно поняты экспертом. Даже во время экзамена, имея правильную логику решения, ученик может сам запутаться в записях и дать неверный ответ в итоге.
В проекте представлены методические материалы в формате урока, который может помочь учителям в объяснении темы «примеры с параметром». В урок включены следующие аспекты: методы решения уравнений, виды уравнений с параметром, особенности уравнений с параметром в ЕГЭ(18 задание), примеры для более подробного разбора решения (применение способов решения).
В урок включены следующие аспекты: методы решения уравнений, виды уравнений с параметром, особенности уравнений с параметром в ЕГЭ(18 задание), примеры для более подробного разбора решения (применение способов решения).
Цель урока: ознакомление с видами уравнений с параметром, встречающихся на ЕГЭ. Способами их решения.
К информационному уроку прикреплена презентация с методическими материалами. Данной презентацией может воспользоваться не только учитель, но и ученик, готовящийся к 18 заданию профильной математики
Урок рассчитан на 40 мин. 5 минут отводится на дополнительные вопросы учеников.
Информационный урок по теме «Параметры»
1 слайд
Презентация: «Уравнения с параметром»
Подготовила: Шиндина Полина, ученица 10 класса «А» ГБОУ лицея №150
Что же такое параметр?
Если в уравнении некоторые коэффициенты заданы не конкретными значениями, а обозначены буквами, то они называются параметрами, а уравнение параметрическим.
Решить уравнение с параметром – значит указать, при каких значениях параметров существуют решения и каковы они.
Где может пригодиться умение решать уравнения с параметром?
■ Уравнения с параметром включены в школьную программу 10 или 11 класса, следовательно, ученики, заранее ознакомленные с материалом, лучше его усваивают, следовательно, показывают лучшие результаты на экзамене
■ Данный тип уравнений включен в 18 задание ЕГЭ по профильной математике, следовательно, данный навык понадобится выпускникам Российских школ, которые планируют сдавать данный экзамен
Какие типы задач с параметром включены в ЕГЭ?
В 18 задании ЕГЭ встречается 2 формулировки заданий:
«для каждого значения параметра найти все решения некоторого уравнения или неравенства»
«найти все значения параметра, при каждом из которых решения уравнения или неравенства удовлетворяют заданным условиям»
Заключение
В течении всего времени создания данного проекта: от задумки до реализации продукта – я узнавала все больше нюансов решения примеров с параметром и совершенствовала свои знания в данной теме. Я считаю, что данную тему, хотя бы косвенно, но должен затронуть каждый учащийся 10-11классов во время подготовки к Единому Государственному Экзамену. Ведь параметры встречаются в жизни гораздо чаще, чем мы можем себе представить.
Я считаю, что данную тему, хотя бы косвенно, но должен затронуть каждый учащийся 10-11классов во время подготовки к Единому Государственному Экзамену. Ведь параметры встречаются в жизни гораздо чаще, чем мы можем себе представить.
Во время более детального рассмотрения данной темы я выделила для себя наиболее удобный подход к решению уравнений с параметром: алгебраический. Я склоняюсь к использованию данного способа и во время сдачи профильного ЕГЭ по математике, так как он занимает меньшего всего времени. Экономия времени поможет мне лучше сконцентрироваться на заданиях второй части.
Если страница Вам понравилась, поделитесь в социальных сетях:
Способы решения уравнений и неравенств с параметрами
Задачи с параметрами являются самыми сложными из всех заданий школьного курса математики. Для их решения требуется умение мыслить логически: необходимо в каждый момент проведения решения достаточно отчётливо представлять себе, что уже сделано, что ещё надо сделать, что означают уже полученные результаты. В заданиях ЕГЭ по математике проверяется умение выпускника мыслить сжато, логично и аргументировано.
В заданиях ЕГЭ по математике проверяется умение выпускника мыслить сжато, логично и аргументировано.
Имеется несколько способов решения параметрических уравнений и неравенств׃ алгебраический, аналитический, функционально-графический. А в некоторых задачах применяются методы математического анализа.
Суть каждого способа рассмотрена на примерах. (Приложение)
1. Алгебраический способ решения иррациональных уравнений с параметрами
Задача 1. При каких уравнение имеет единственное решение?
Решение: 1 способ. Обеспечим неотрицательность обеих частей, возведем в квадрат обе части уравнения:
Найдем дискриминант квадратного уравнения:
1) По условию уравнение должно иметь один корень, значит,
но надо проверить, удовлетворяет ли это значение ОДЗ уравнения:
.
2) Если , то только один корень уравнения должен удовлетворять условию .
а)
б) Ø
Ответ:
2 способ. Решим это задание аналитическим способом.
Проведем графический анализ менее трудоемкий, чем построение графика — полупараболы с вершиной х=-3; – множество параллельных прямых, с угловым коэффициентом 2.
Рассмотрим схему расположения графиков при различных значениях а, причем с ростом a прямая у=2х – a перемещается вправо.
Когда прямая является касательной к полупараболе и, начиная с положения, когда прямая проходит через вершину параболы (- 3; 0),мы имеем одну точку пересечения, т. е одно решение исходного уравнения. Напишем уравнение касательной в точке
Угловой коэффициент равен 2, т. е. =2 , — абсцисса точки касания
Тогда уравнение касательной , a =
При х=-3, у=0 графики пересекаются в двух точках. При этом .
А при имеем одну точку пересечения.
Ответ:
2. Аналитический способ решения тригонометрического уравнения с параметром
Задача 2. При каких значениях параметра a уравнение
имеет на промежутке не меньше 3 корней?
Решение:
1 способ. Заменим , причем |t| ≤ 1
при любом a.
Рассмотрим 2 случая:
1) , тогда уравнения будут иметь не больше 2 корней, но по условию должно быть не меньше 3 корней. Следовательно, этот случай не надо рассматривать.
2) ,
Рассмотрим расположение корней уравнения на тригонометрической окружности.
Видим, что при уравнение имеет два решения. Чтобы оно имело не меньше трех решений и .
Ответ:
2 способ. Пусть , , тогда . Рассмотрим график .
В промежутке при t= — 1 уравнение имеет один корень
При — два корня, при — один корень.
Поэтому чтобы исходное уравнение имело не меньше 3 корней необходимо выполнение условия:
| Первая система имеет 4 решения. | |
| Вторая система имеет 3 решения. |
Расположим корни квадратного трехчлена по этим двум условиям:
1)
2)
Объединяя 1) и 2) получаем
3. Два способа решения одного тригонометрического неравенства с параметром
Задача 3. При каких а неравенство верно для всех х?
Решение: 1 способ. Преобразуем неравенство и приведем его к виду
Пусть. Получим неравенство
Это значит, что парабола при 0≤t≤1 находится ниже оси ох
Рассмотрим 3 случая:
1)
Получаем условия для
2)
Но если .
Ø
3)
Полученное неравенство верно при любых 0≤t≤1; объединяем 3 случая и получаем ответ: .
2 способ. Уединяем параметр
,
Минимум f(x) достигается при ; т.к — минимум числителя, — максимум знаменателя. Значит,
Максимум f(x) достигается при ; т.е .
Схема:
Заметим, что минимум числителя и максимум знаменателя достигается при одном и том же х.
для всех х при
Ответ: .
4. Графически и аналитический способы решения неравенства с параметром, содержащего знак модуля
Задача 5. При каких a неравенство выполняется для всех ?
Решение: . Рассмотрим две функции
Построим эскизы графиков функций:
Найдем уравнение касательной в точке функции y= |x2-4x+3|
Тогда . Так как
Так как
Подставим значение точки х0 в производную рассматриваемой функции и получаем, что — —a=-2-4, a=4+2.
Следовательно, при a =4+2 y=1-ax – касательная к y=|x2-4x+3|. Значит, чтобы неравенство выполнялось, нужно, чтобы
II способ.
1 случай.
Это значит, что
2 случай.
А это значит, что
Чтобы неравенство выполнялось при всех x:
Ответ: .
Решение уравнений и неравенств с параметрами алгебраическим, аналитическим и графическим способами заключается в том, что при одном способе решение может быть громоздким, а при другом — более простым и наглядным. А это говорит о том, что нужно перед началом решения задания оценить его и выбрать тот путь, который проще.
Литература
- Сборник задач по математике для подготовки к вступительным экзаменам УГНТУ, Уфа-2003 г.

- Факультативный курс по математике, 10 класс. Шарыгин.И.Ф. Москва «Просвещение» 1989 г.
- Уравнение с параметрами на факультативных занятиях. С.Я.Постникова. «Математика в школе», №8, 2002 г.
- Математика абитуриенту. В.В.Ткачук, Москва, 2002 г.
Решение уравнений с параметрами (Реферат)
Городская открытая научно – практическая конференция
Тема: Решение уравнений с параметрами, связанных со свойствами показательной, логарифмической и тригонометрической функциями
Автор:
Научный руководитель:
2007 г.
Содержание
1. Введение
2. Решение уравнений с параметрами
3. Решение уравнений с параметрами, связанных со свойствами показательной, логарифмической и тригонометрической функциями
4. Заключение
5. Используемая литература
Используемая литература
Введение
Актуальность данной темы определяется необходимостью уметь решать такие уравнения с параметрами при сдачи Единого Государственного экзамена и на вступительных экзаменах в высшие учебные заведения.
Цель данной работы рассказать о решении уравнений с параметрами, связанных со свойствами показательной, логарифмической и тригонометрической функциями.
Для достижения поставленной цели необходимо решить следующие задачи:
дать определения понятиям уравнение с параметрами;
показать принцип решения данных уравнений на общих случаях;
показать решение уравнений с параметрами, связанных со свойствами показательной, логарифмической и тригонометрической функциями.
Для выполнения поставленной
цели были использованы следующие методы:
использование литературы разного типа,
работа в группах на уроках алгебры и
занятиях элективного курса по математике,
участие проектной группы в городской
конференции по данной теме в 2006 году.
Объектом исследовательской работы было решение уравнений с параметрами, связанных со свойствами выше представленных функций.
Структура данной работы включает в себя теорию, практическую часть, заключение, библиографический список.
Решение уравнений с параметрами
Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры у школьников, но их решение вызывает у них значительные затруднения. Это связано с тем, что каждое уравнение с параметрами представляет собой целый класс обычных уравнений, для каждого из которых должно быть получено решение. Такие задачи предлагаются на едином государственном экзамене и на вступительных экзаменах в вузы.
Большинство пособий адресовано
абитуриентам, однако начинать знакомиться
с подобными задачами нужно намного
раньше – параллельно с соответствующими
разделами школьной программы по
математике.
Если в уравнении некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а уравнение параметрическим.
Естественно, такой небольшой класс задач многим не позволяет усвоить главное: параметр, будучи фиксированным, но неизвестным числом, имеет как бы двойственную природу. Во-первых, предполагаемая известность позволяет «общаться» с параметром как с числом, а во-вторых, — степень свободы общения ограничивается его неизвестностью. Так, деление на выражение, содержащее параметр, извлечение корня четной степени из подобных выражений требуют предварительных исследований. Как правило, результаты этих исследований влияют и на решение, и на ответ.
Основное, что нужно усвоить при
первом знакомстве с параметром, — это
необходимость осторожного, даже, если
хотите, деликатного обращения с
фиксированным, но неизвестным числом.
Этому, по нашему мнению, во многом будут
способствовать наши примеры.
Необходимость аккуратного обращения с параметром хорошо видна на тех примерах, где замена параметра числом делает задачу банальной. К таким задачам, например, относятся: сравнить два числа, решить линейное или квадратное уравнение, неравенство и т.д.
Обычно в уравнение буквами обозначают неизвестные.
Решить уравнение — значит:
найти множество значений неизвестных, удовлетворяющих этому уравнению. Иногда уравнения, кроме букв, обозначающих неизвестное(X, Y,Z), содержат другие буквы, называемые параметрами(a, b, c). Тогда мы имеем дело не с одним, а с бесконечным множеством уравнений.
При одних значениях параметров уравнение не имеет корней, при других – имеет только один корень, при третьих – два корня.
При решении таких уравнений надо:
1) найти множество всех доступных значений параметров;
2) перенести все члены, содержащие неизвестное, в левую часть уравнения, а все члены, не содержащие неизвестного в правую;
3) привести подобные слагаемые;
4) решать уравнение ax
= b.
Возможно три случая.
1. а 0, b – любое действительное число. Уравнение имеет единственное решение х = .
2. а = 0, b = 0. Уравнение принимает вид: 0х = 0, решениями являются все хR.
3. а = 0, b 0. Уравнение 0х = b
решений не имеет.
Сделаем одно замечание. Существенным этапом решения уравнений с параметрами является запись ответа. Особенно это относится к тем примерам, где решение как бы «ветвится» в зависимости от значений параметра. В подобных случаях составление ответа – это сбор ранее полученных результатов. И здесь очень важно не забыть отразить в ответе все этапы решения.
В только что разобранном примере запись ответа практически повторяет решение. Тем не менее, я считаю целесообразным привести ответ.
Ответ:
х = при а 0, b – любое действительное число;
х – любое число при а = 0, b = 0;
решений нет при а = 0, b
≠ 0.
Уравнение (неравенство) с параметрами — это… Что такое Уравнение (неравенство) с параметрами?
[[Участник:Уравнение (неравенство) с параметрами — математическое уравнение (неравенство), внешний вид и решение которого зависит от значений одного или нескольких параметров.
Решить уравнение с параметром означает:
- Найти все системы значений параметров, при которых данное уравнение имеет решение.
- Найти все решения для каждой найденной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.
Уравнения с параметром могут быть как линейными, так и нелинейными.
Пример линейного уравнения с параметром:
Пример нелинейного уравнения с параметром:
где — независимая переменная — параметр.
Аналогично подразделяются и неравенства. Ниже будут представлены примеры решений уравнений и неравенств с параметрами.
Примеры
- Пример 1.При каком квадратное уравнение имеет ровно один корень?
Решение. Любое квадратное уравнение имеет одно решение, когда его дискриминант равен нулю. Итак, дискриминант нашего уравнения: . Далее имеем: , откуда .
- Ответ:.
- Пример 2. При каком система уравнений :
.
имеет ровно два решения?
Решение. Сначала надо преобразовать два уравнения системы, выделив в них полные квадраты:
Нетрудно догадаться, что эти два равенства системы есть не что иное как уравнения окружностей. Первая окружность имеет центр в точке , радиус , а вторая центр в точке и радиус . Если построить схематично эти окружности в одной системе координат, то можно заметить, что их общих точек пересечения будет две втом случае, если . И задачу можно считать решённой.
- Ответ:.
- Пример 3. При всех решить неравенство .
Решение. Рассмотрим три случая:
Рассмотрим три случая:
- Если , то неравенство приобретает вид ;
- Если , то все коэффициенты квадратного трехчлена будут положительны, значит, решение неравенства можно представить в виде , где , — корни многочлена и . Далее находим:
Следовательно, , если и , если .
- 3. Если , то ветви параболы направлены вниз, естественно решение в общем виде будет выглядеть вот так: .
Нам остается лишь записать ответ.
- Ответ: если , то ; если , то ; если , то ; если , то .
См. также
]]
Электронный научный журнал // Информационно-коммуникационные технологии в педагогическом образовании
Научный руководитель: Алдакишкина Валентина Владимировна
Изучение многих физических и геометрических закономерностей нередко приводит к решению задач с параметрами.
В настоящее время на выпускных экзаменах школьники часто встречаются с уравнениями, неравенствами и системами с параметрами, которые часто бывают весьма сложными и требующими нестандартного подхода к решению. Решение задач с параметрами вызывает большие трудности, так как их изучение не является отдельной составляющей школьного курса математики, и рассматривается только на немногочисленных факультативных занятиях, а их решение требует не только знания свойств функций и уравнений, умения выполнять алгебраические преобразования, но также высокой логической культуры и хорошей техники исследования.
Решение задач с параметрами вызывает большие трудности, так как их изучение не является отдельной составляющей школьного курса математики, и рассматривается только на немногочисленных факультативных занятиях, а их решение требует не только знания свойств функций и уравнений, умения выполнять алгебраические преобразования, но также высокой логической культуры и хорошей техники исследования.
Трудности при изучении данного вида уравнений связаны со следующими их особенностями: обилие формул и методов, используемых при решении уравнений данного вида; возможность решения одного и того же уравнения, содержащего параметр, различными методами.
Уравнение вида называется уравнением, содержащим параметры, где a, b, c, …, k – параметры, x — неизвестное.
Параметром называется независимая переменная, значение которой в задаче считается заданным, фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Выделяют несколько типов задач с параметрами.
-
Задачи, которые необходимо решить для всех значений параметра или для значений параметра из заданного промежутка.
Например. Решите уравнение в зависимости от параметра a.
-
Задачи, где требуется найти количество решений в зависимости от значения параметра.
Например. Определить количество решений уравнения .
-
Задачи, где необходимо найти значения параметра, при которых задача имеет заданное количество решений.
Например. Дано уравнение . Определить значения параметра a, при которых оно имеет единственное решение.
-
Задачи, в которых необходимо найти значения параметра, при которых множество решений удовлетворяет заданным условиям.

Например. При каком значении параметра a решением уравнения является множество .
К основным методам решения задач с параметрами относятся:
-
метод «ветвления»;
-
использование свойств функций в задачах с параметрами;
-
графический метод.
Метод «ветвления»
Поскольку уравнение с параметром это целый класс уравнений, то решать надо сразу весь этот класс, что влечет за собой необходимость разбора различных случаев в зависимости от определенных значений параметра.
Именно этот факт и позволяет нам решать уравнения с параметром таким методом («ветвления»).
Пример 1. Решить уравнение
В зависимости от значений параметра m.
Решение. .
.
ОДЗ:
Достаточно рассмотреть три случая, т. к. число m стоит под знаком модуля, следовательно, может принимать как положительные, так и отрицательные значения, и отдельно следует рассмотреть случай, когда m=0.
к. число m стоит под знаком модуля, следовательно, может принимать как положительные, так и отрицательные значения, и отдельно следует рассмотреть случай, когда m=0.
-
m=0.
Уравнение будет выполняться при любых значениях x, удовлетворяющих ОДЗ. Следовательно, при m=0
-
.
.
Замена: , .
Проверим, являются ли данные корни корнями исходного уравнения.
.
— посторонние корни.
Выполняя аналогичные действия для , заключаем, что — корни исходного уравнения.
-
Аналогично пункту 2 рассматриваем случай и заключаем, что — корни исходного уравнения.
Ответ: при ; при ; при
Свойства функций в задачах с параметром
Для успешного решения уравнений с параметрами нужно не только владеть основными приемами их решения, но и знать и уметь применять некоторые преобразования, основанные на свойствах функций. Сформулируем некоторые из них в виде теорем.
Сформулируем некоторые из них в виде теорем.
Теорема 1. Если функция f(x) возрастает (убывает) на промежутке I и функция g(x) возрастает (убывает) на промежутке I, то функция h(x)=f(x)+g(x)+C также возрастает (убывает) на промежутке I (C – произвольная постоянная).
Теорема 2. Если функция f(x) неотрицательна и возрастает на промежутке I, функция g(x) неотрицательна и возрастает на промежутке I, , то функция также возрастает на промежутке I.
Аналогичное свойство имеет место и для убывающих функций, а также для .
Теорема 3. Если функция f(t) монотонна на промежутке I, то уравнение f(g(x))=f(h(x)) равносильно на промежутке I уравнению g(x)=h(x).
Теорема 4. Если функция f(x) монотонна на промежутке I, то уравнение f(x)=C имеет на промежутке I не более одного корня.
Теорема 5. Если функция f(x) возрастает на промежутке I, а функция g(x) убывает на промежутке I, то уравнение f(x)=g(x) имеет на промежутке I не более одного корня.
Теорема 6. Если функция f(x) возрастает на промежутке I, то уравнение f(f(x))=x равносильно на промежутке I уравнению f(x)=x.
Теорема 7. Если для функций f(x) и g(x) , то
Пример 2. Найдите все значения параметра a, при которых уравнение имеет ровно один корень.
Найдите все значения параметра a, при которых уравнение имеет ровно один корень.
Решение.
Рассмотрим функцию . По теореме 1 она является возрастающей на множестве всех действительных чисел.
Тогда исходное уравнение можно записать в виде .
По теореме 3 оно равносильно уравнению .
Т. к. по условию задачи нужно найти те значения параметра, при которых уравнение имеет ровно один корень, а это возможно, когда дискриминант полученного равносильными преобразованиями квадратного уравнения равен нулю, то .
Ответ: при уравнение имеет ровно один корень.
Графические методы
Координатная плоскость (x;y)
Задачи, содержащие параметр, требуют к себе своеобразный подход, здесь необходимо грамотное и тщательное исследование. Для применения графических методов требуется умение выполнять дополнительное построение различных графиков, вести графические исследования, соответствующие данным значениям параметра.
Пример 3. Для каждого значения параметра определить число решений уравнения .
Решение. Построим график функции .
Пусть , тогда
— окружность с центром в точке (1;0) и радиусом 1.
Пусть , тогда
— окружность с центром в точке (-1;0) и радиусом 1.
Рассмотрим функцию . Это прямая параллельна оси Оx. Построим следующие случаи этой прямой: .
Из полученного графика хорошо видно, что при уравнение решений не имеет, при уравнение имеет два решения, при – три решения, при — четыре решения.
Ответ: при уравнение решений не имеет, при уравнение имеет два решения, при – три решения, при — четыре решения.
Координатная плоскость (x;a)
Рассмотрим метод, упрощающий работу по решению уравнений с параметром. Метод состоит в следующем:
Метод состоит в следующем:
-
из уравнения с переменной x и параметра a выразим параметр как функцию от x: ;
-
в координатной плоскости xOa строим график функции ;
-
Рассмотрим прямые и выделим те промежутки оси Oa, на которых эти прямые удовлетворяют следующим условиям: a) не пересекает график функции ,
б) пересекает график функции в одной точке,
в) в двух точках,
г) в трех точках и так далее.
-
Если поставлена задача найти значения x, то выражаем x через a для каждого из найденных промежутков значения a в отдельности.
Взгляд на параметр как на равноправную переменную находит свое отражение в графических методах. Таким образом, возникает координатная плоскость . Казалось бы, такая незначительная деталь, как отказ от традиционного обозначения координатной плоскости буквами x и y определяет один из эффективнейших методов решения задач с параметрами.
Казалось бы, такая незначительная деталь, как отказ от традиционного обозначения координатной плоскости буквами x и y определяет один из эффективнейших методов решения задач с параметрами.
Описанный метод очень нагляден. Кроме того, в нем находят применение почти все основные понятия курса алгебры и начал анализа. Задействуется весь набор знаний, связанных с исследованием функции: применение производной к определению точек экстремума, нахождение предела функции, асимптот и т. д.
Пример 4. При каких значениях параметра уравнение имеет два корня?
Решение. Переходим к равносильной системе
Найдем координаты вершины параболы: (0,5; -0,25).Построим график функции.
Из графика видно, что при уравнение имеет 2 корня.
Ответ: при уравнение имеет два корня.
Трансцендентное уравнение – уравнение, содержащее трансцендентные функции (иррациональные, логарифмические, показательные, тригонометрические и обратные тригонометрические) от неизвестного (переменного), например уравнения: .
Решить уравнение с параметром означает:
-
Найти все системы значений параметров, при которых данное уравнение имеет решение.
-
Найти все решения для каждой найденной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.
Трансцендентные уравнения с параметрами включают в себя ряд различных трансцендентных функций, именно поэтому решения этих уравнений в большей степени зависят от свойств функций. Рассмотрим каждый вид трансцендентных уравнений с параметрами и попробуем заметить эти особенности при решении задач.
Иррациональные уравнения с параметромУравнение называется иррациональным с одним неизвестным x, если одна или обе его части содержат выражения, иррациональные относительно x.
При решении иррациональных уравнений с параметрами следует помнить, что уравнение вида равносильно системе
Неравенство следует из уравнения .
Пример 5. Решить уравнение в зависимости от значений параметра a.
Решение. Преобразуем данное уравнение к виду
Возведем в квадрат обе части уравнения, получим:
Получили квадратное уравнение относительно x. Оно, как известно, имеет решение при , значит для дальнейшего решения необходимо найти дискриминант квадратного уравнения.
1)
.
Подставим полученное значение параметра a в уравнение (2) и найдем значение x.
,
,
,
.
Итак, при .
2)
.
При .
3)Исходя из того, что при уравнение не имеет решений, определим значения параметра a, при которых данное условие выполняется.
.
При уравнение решений не имеет.
Теперь необходимо выполнить проверку.
При подстановке в уравнение (2), имеем: . Получили неверное равенство, так как корень есть число положительное. Значит не является корнем исходного уравнения.
Подставим в уравнение (2), имеем:
,
.
Получили, что правая часть – число отрицательно, следовательно не является решением исходного уравнения.
Подставим в уравнение (2), имеем:
,
. (3) Если , то можем возвести обе части уравнения (3) в квадрат.
.
.
.
Имеем истинное равенство при условии, что . Это условие выполняется при , а может быть корнем уравнения (1) при , следовательно, — корень уравнения (1) при .
Ответ: при ; при уравнение решений не имеет.
Логарифмические уравнения с параметрамиУравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением.
 Простейшим логарифмическим уравнением является уравнение вида , где .
Простейшим логарифмическим уравнением является уравнение вида , где .При решении логарифмических уравнений удобно использовать следующие утверждения:
Утверждение 1. Если , уравнение при любом действительном b имеет единственное решение .
Утверждение 2. Уравнение равносильно одной из систем:
Утверждение 3. Уравнение равносильно одной из систем:
Пример 6. Найдите все значения параметра а, при которых уравнение
loga + loga=1 не имеет решения.
Решение.
ОДЗ:
Воспользовавшись основным свойством логарифма, запишем: 1=logaa. Преобразуя наше уравнение, получим равносильное уравнение:
=а,
Проделав равносильные преобразования, и заметив, что знаменатель дробей 1+ всегда положителен, получим уравнение:
(3+2)(4+)=а(1+)2,
(6-а)х+(17-2а)+12-а=0.
Замена: =y, y0.
(6-а)y2+(17-2а)y+12-а=0. (1)
D=(17-2а2)-4(6-а)(12-а)=4а+1.
Так как а>0, то D>0 и квадратное уравнение (1) имеет 2 корня. Учитывая условие y0, имеем y1<0 и y2<0, то есть y1y2>0, y1+y2<0.
y1y2=, y1+y2=.
Значит,
С учетом условия а>0 и а≠1, имеем а(0;1)(1;6)(12;+∞).
Рассмотрим отдельно случай а=6. Тогда квадратное уравнение становится линейным 5y+6=0, то есть y=-6/5, что не удовлетворяет условию y0.
Ответ: при а(0;1)(1;6)(12;+∞) уравнение не имеет решений.[4, № 58]
Показательные уравнения с параметрами
Уравнение, содержащее переменную в показателе степени, называется показательным.
Большинство показательных уравнений с параметрами сводятся к показательным уравнениям вида
где .
Область допустимых значений такого уравнения находится как пересечение областей допустимых значений функций и . Для решения уравнения (1) следует рассмотреть следующие случаи:
Для решения уравнения (1) следует рассмотреть следующие случаи:
-
при a=b=1 решением уравнения (1) является его ОДЗ;
-
при решением уравнения (1) служит решение уравнения на ОДЗ;
-
при решением уравнения (1) служит решение уравнения на ОДЗ;
-
при уравнение (1) равносильно уравнению на ОДЗ;
-
при уравнение (1) тождественно уравнению
(2)
на ОДЗ.
Тождественное преобразование (2) называют логарифмированием. Такое преобразование может привести к потере корней.
Следует отметить, что, исходя из определения показательной функции, случай, когда основание a отрицательно, рассматривать не следует.
Пример 7. Найдите все значения параметра a, при которых уравнение
Найдите все значения параметра a, при которых уравнение
имеет ровно три корня.
Решение.
Данное уравнение можно записать в виде ,где функция на основании теоремы 2 является возрастающей.
В самом деле, так как , то , следовательно, . Таким образом, исходное уравнение равносильно (по теореме 3) следующему .
Дальнейшее решение проведем графическим способом. Для этого определим, при каких значениях параметра a графики функций
и имеют ровно три общих точки на координатной плоскости yOx.
По графику видим, что требованию задачи отвечает случай . Решая полученное уравнение, находим или .
Ответ: при уравнение имеет ровно три решения.
Тригонометрические уравнения с параметрами
Тригонометрическое уравнение — уравнение, содержащее тригонометрические функции неизвестного аргумента. Формулы решений простейших тригонометрических уравнений:
Формулы решений простейших тригонометрических уравнений:
.
.
.
При решении тригонометрических уравнений удобно использовать следующие принципы:
-
При решении простейшего тригонометрического уравнения удобно понизить его степень за счет изменения его аргумента.
-
В случае необходимости проверки удобно подставлять в уравнение не значение найденного аргумента, а значения используемых в решении тригонометрических функций.
Пример 8. Найдите все значения параметра a, при которых число 2 является корнем уравнения
Решение.
Поставим в уравнение Получим уравнение относительно параметра a:
Ответ: при корнем уравнения является .
Помимо тригонометрических уравнений среди задач с параметрами встречаются и задачи с параметрами, содержащие обратные тригонометрические функции.
Напомним определения обратных тригонометрических функций:
-
— это функция, определенная на отрезке [-1;1], обратная функции
. Таким образом,
Для любого x из отрезка [-1;1] имеем:
-
— это функция, определенная на отрезке [-1;1], обратная функции
. Таким образом,
Для любого x из отрезка [-1;1] имеем:
-
— это функция, определенная на интервале , обратная функции
. Таким образом,
Для любого x имеем:
-
— это функция, определенная на интервале , обратная функции
. Таким образом,
Таким образом,
Для любого x имеем:
Функции называются обратными тригонометрическими функциями или аркфункциями.
Отметим некоторые важные тождества:
Пример 9. Найдите все значения параметра a, при каждом из которых уравнение
имеет ровно три решения.
Решение.
Перепишем исходное уравнение в виде
.
Поскольку равенство равносильно тому, что и , исходное уравнение равносильно тригонометрическому уравнению
Решим уравнение (1).
Если , то
При совокупность, а значит и уравнение (1), имеет бесконечно много корней вида: , которые удовлетворяют условию (2). Т. е. не удовлетворяет требованию задачи.
Т. е. не удовлетворяет требованию задачи.
При уравнение (1) имеет бесконечно много корней вида: .
Для них условие (2) превращается в неравенство
Параметр a включается в ответ тогда и только тогда, когда это неравенство имеет ровно три целочисленных решения. Используя геометрическую интерпретацию модуля разности двух чисел, видно, что это равносильно неравенству
Учитывая условие , получаем
Если решением уравнения (1) являются все действительные числа, условие же (2) принимает вид: , так что множество решений исходного уравнение – это интервал . Поскольку это множество бесконечно, значение не входит в ответ.
Ответ: при уравнение имеет ровно три решения.
Исходя из всех рассмотренных задач, можно сделать вывод, что решать трансцендентные уравнения с параметрами первого и четвертого типов лучше всего методом «ветвления», т. к. требуется найти все значения переменной при каждом возможном значении параметра (или при значениях параметра из заданного промежутка) или же при которых множество решений удовлетворяет заданным условиям. Однако такой метод не всегда надежен, поскольку ход решения достаточно длителен и сложен, поэтому изначально целесообразно определить, возможно ли применить к заданному уравнению функциональный подход, который значительно упрощает решение.
к. требуется найти все значения переменной при каждом возможном значении параметра (или при значениях параметра из заданного промежутка) или же при которых множество решений удовлетворяет заданным условиям. Однако такой метод не всегда надежен, поскольку ход решения достаточно длителен и сложен, поэтому изначально целесообразно определить, возможно ли применить к заданному уравнению функциональный подход, который значительно упрощает решение.
А вот решать трансцендентные уравнения с параметрами второго и третьего типов значительно проще, используя графический метод, поскольку в условии всего лишь требуется определить либо количество решений в зависимости от значения параметра, либо, наоборот, значения параметра, при которых задача имеет заданное количество решений. Из построенных графиков наглядно видно, когда выполняются заданные условия.
Однако не всегда возможно применение того или иного метода, иногда встречаются и такие задачи, для решения которых нужно применить не один, а несколько методов решения.
Задачи с параметрами представляют собой весьма широкое поле для полноценной математической деятельности. Решение такого рода задач открывает перед учащимися значительное число эвристических приемов общего характера, ценных для математического развития личности, применимых в исследованиях и на любом другом математическом материале.
Спецификой задач с параметрами является то, что наряду с неизвестными величинами в них фигурируют параметры, численные значения которых не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом значения параметров существенно влияют на логический и технический ход решения задачи и форму ответа.
Квадратные уравнения с параметром: определение, пример решения
Понятие уравнения с параметром и его решения
Часто на практике создаётся такая математическая модель, в которой приходится решать не одно, а целое «семейство» похожих уравнений. 2 = 0, $$
2 = 0, $$
один корень $x_0 = -2$
$$ D(a) \gt 0 при -3 \lt a \lt 1 $$
Уравнение имеет два корня:
$$ x_{1,2} = \frac{a-1 \pm \sqrt{-3(a-1)(a+3)}}{2} $$
$$ D(a) \lt 0 при a \lt -3 \cap a \gt 1 $$
Решений нет.
Ответ:
При a = -3 один корень $x_0 = -2$
При a = 1 один корень $x_0 = 0$
При $-3 \lt a \lt 1$ два корня $x_{1,2} = \frac{a-1 \pm \sqrt{-3(a-1)(a+3)}}{2}$
При других a решений нет.
Система линейных уравнений — линейная алгебра с приложениями
Практические задачи во многих областях науки, таких как биология, бизнес, химия, информатика, экономика, электроника, инженерия, физика и социальные науки, часто можно свести к решению системы линейных уравнений. Линейная алгебра возникла в результате попыток найти систематические методы решения этих систем, поэтому естественно начать эту книгу с изучения линейных уравнений.
Если, и — действительные числа, график уравнения вида
— прямая линия (если и не равны нулю), поэтому такое уравнение называется линейным уравнением в переменных и. Однако часто удобно записывать переменные как, особенно когда задействовано более двух переменных. Уравнение вида
Однако часто удобно записывать переменные как, особенно когда задействовано более двух переменных. Уравнение вида
называется линейным уравнением в переменных. Здесь обозначают действительные числа (называемые коэффициентами соответственно), а также число (называемое постоянным членом уравнения). Конечный набор линейных уравнений в переменных называется системой линейных уравнений в этих переменных.Следовательно,
— линейное уравнение; коэффициенты при, и равны, и, а постоянный член равен. Обратите внимание, что каждая переменная в линейном уравнении встречается только в первой степени.
Для линейного уравнения последовательность чисел называется решением уравнения, если
, то есть, если уравнение удовлетворяется при выполнении замен. Последовательность чисел называется решением системы уравнений, если она является решением каждого уравнения в системе.
Система может вообще не иметь решения, или она может иметь уникальное решение, или она может иметь бесконечное семейство решений. Например, система не имеет решения, потому что сумма двух чисел не может быть одновременно 2 и 3. Система, у которой нет решения, называется несогласованной ; система с хотя бы одним решением называется согласованная .
Покажите, что для произвольных значений и
— решение системы
Просто подставьте эти значения,, и в каждое уравнение.
Поскольку оба уравнения удовлетворяются, это решение для любого выбора и.
Величины и в этом примере называются параметрами , а набор решений, описанный таким образом, считается заданным в параметрической форме и называется общим решением для системы. Оказывается, что решения каждой системы уравнений (если есть — это решений) могут быть даны в параметрической форме (то есть, переменные, задаются в терминах новых независимых переменных и т. Д. .).
Д. .).
Когда задействованы только две переменные, решения систем линейных уравнений могут быть описаны геометрически, потому что график линейного уравнения представляет собой прямую линию, если оба они не равны нулю. Более того, точка с координатами и лежит на прямой тогда и только тогда, когда — то есть когда, является решением уравнения. Следовательно, решения системы линейных уравнений соответствуют точкам, которые лежат на всех рассматриваемых линиях.
В частности, если система состоит только из одного уравнения, должно быть бесконечно много решений, потому что на прямой бесконечно много точек. Если система имеет два уравнения, есть три возможности для соответствующих прямых:
- Линии пересекаются в одной точке. Тогда в системе есть уникальное решение , соответствующее этой точке.
- Линии параллельны (и четкие) и не пересекаются. Тогда в системе нет решения .

- Строки идентичны. Тогда в системе будет бесконечно много решений — по одному для каждой точки на (общей) прямой.
С тремя переменными график уравнения может быть показан как плоскость и, таким образом, снова дает «картину» множества решений. Однако у этого графического метода есть свои ограничения: когда задействовано более трех переменных, физическое изображение графов (называемых гиперплоскостями) невозможно. Необходимо обратиться к более «алгебраическому» методу решения.
Перед описанием метода мы вводим понятие, упрощающее вычисления. Рассмотрим следующую систему
трех уравнений с четырьмя переменными. Массив чисел
, встречающееся в системе, называется расширенной матрицей системы. Каждая строка матрицы состоит из коэффициентов переменных (по порядку) из соответствующего уравнения вместе с постоянным членом. Для наглядности константы разделены вертикальной линией. Расширенная матрица — это просто другой способ описания системы уравнений. Массив коэффициентов при переменных
Расширенная матрица — это просто другой способ описания системы уравнений. Массив коэффициентов при переменных
называется матрицей коэффициентов системы, а
называется постоянной матрицей системы.
Элементарные операции
Алгебраический метод решения систем линейных уравнений описывается следующим образом. Две такие системы называются эквивалентами , если они имеют одинаковый набор решений.Система решается путем написания серии систем, одна за другой, каждая из которых эквивалентна предыдущей системе. Каждая из этих систем имеет тот же набор решений, что и исходная; цель состоит в том, чтобы получить систему, которую легко решить. Каждая система в серии получается из предыдущей системы простой манипуляцией, выбранной так, чтобы она не меняла набор решений.
В качестве иллюстрации мы решаем систему таким образом. На каждом этапе отображается соответствующая расширенная матрица. Исходная система —
Исходная система —
Сначала вычтите дважды первое уравнение из второго. В результате получается система
., что эквивалентно оригиналу. На этом этапе мы получаем, умножив второе уравнение на. В результате получается эквивалентная система
.Наконец, мы дважды вычитаем второе уравнение из первого, чтобы получить другую эквивалентную систему.
Теперь эту систему легко решить! И поскольку он эквивалентен исходной системе, он обеспечивает решение этой системы.
Обратите внимание, что на каждом этапе в системе (и, следовательно, в расширенной матрице) выполняется определенная операция для создания эквивалентной системы.
Следующие операции, называемые элементарными операциями , могут в обычном порядке выполняться над системами линейных уравнений для получения эквивалентных систем.
- Поменяйте местами два уравнения.
- Умножьте одно уравнение на ненулевое число.

- Добавьте одно уравнение, кратное одному, к другому уравнению.
Предположим, что последовательность элементарных операций выполняется над системой линейных уравнений. Тогда результирующая система имеет тот же набор решений, что и исходная, поэтому две системы эквивалентны.
Элементарные операции, выполняемые над системой уравнений, производят соответствующие манипуляции с строками расширенной матрицы. Таким образом, умножение строки матрицы на число означает умножение каждой записи строки на.Добавление одной строки в другую означает добавление каждой записи этой строки к соответствующей записи другой строки. Аналогично производится вычитание двух строк. Обратите внимание, что мы считаем две строки равными, если соответствующие записи совпадают.
В ручных вычислениях (и в компьютерных программах) мы манипулируем строками расширенной матрицы, а не уравнениями. По этой причине мы переформулируем эти элементарные операции для матриц.
По этой причине мы переформулируем эти элементарные операции для матриц.
Следующие операции называются операциями с элементарной строкой матрицы.
- Поменять местами два ряда.
- Умножьте одну строку на ненулевое число.
- Добавьте одну строку, кратную одной, в другую строку.
На иллюстрации выше серия таких операций привела к матрице вида
, где звездочки обозначают произвольные числа. В случае трех уравнений с тремя переменными цель состоит в том, чтобы получить матрицу вида
Это не всегда происходит, как мы увидим в следующем разделе.Вот пример, в котором это действительно происходит.
Решение:
Расширенная матрица исходной системы —
Чтобы создать в верхнем левом углу, мы можем умножить строку с 1 на. Однако можно получить без введения дробей, вычтя строку 2 из строки 1. Результат:
Верхний левый угол теперь используется для «очистки» первого столбца, то есть для создания нулей в других позициях в этом столбце. Сначала отнимите строку 1 от строки 2, чтобы получить
Сначала отнимите строку 1 от строки 2, чтобы получить
Далее вычтите строку 1 из строки 3. Результат:
.Это завершает работу над столбцом 1. Теперь мы используем во второй позиции второй строки, чтобы очистить второй столбец, вычитая строку 2 из строки 1 и затем добавляя строку 2 к строке 3. Для удобства обе операции со строками являются сделано за один шаг. Результат
Обратите внимание, что две последние манипуляции не повлияли на первый столбец (во второй строке там стоит ноль), поэтому наши предыдущие усилия там не были подорваны.Наконец, мы очищаем третий столбец. Начните с умножения строки 3 на, чтобы получить
.Теперь вычтите умножение строки 3 из строки 1, а затем прибавьте умножение строки 3 к строке 2, чтобы получить
Соответствующие уравнения:, и, которые дают (единственное) решение.
Алгебраический метод, представленный в предыдущем разделе, можно резюмировать следующим образом: Для данной системы линейных уравнений используйте последовательность элементарных операций со строками, чтобы преобразовать расширенную матрицу в «красивую» матрицу (что означает, что соответствующие уравнения легко решить. ).В примере 1.1.3 эта красивая матрица приняла вид
).В примере 1.1.3 эта красивая матрица приняла вид
Следующие определения идентифицируют хорошие матрицы, возникающие в этом процессе.
Матрица, как говорят, находится в форме ряда строк (и будет называться матрицей ряда , если она удовлетворяет следующим трем условиям:
- Все нулевые строки (полностью состоящие из нулей) находятся внизу.
- Первая ненулевая запись слева в каждой ненулевой строке — это a, называемая ведущей для этой строки.
- Каждый ведущий находится справа от всех ведущих в строках над ним.
Матрица-эшелон строка называется сокращенной строкой-эшелоном (и будет называться сокращенной матрицей-строкой , если, кроме того, она удовлетворяет следующему условию:
4. Каждый ведущий элемент — это единственная ненулевая запись в своем столбце.
Матрицы «строка-эшелон» имеют форму «ступеньки», как показано в следующем примере (звездочки указывают произвольные числа).
Ведущие идут «вниз и вправо» через матрицу. Записи выше и справа от ведущих s произвольны, но все записи ниже и слева от них равны нулю. Следовательно, матрица в виде эшелона строк находится в сокращенной форме, если, кроме того, все элементы непосредственно над каждым ведущим равны нулю. Обратите внимание, что матрица в форме эшелона строк может с помощью нескольких дополнительных операций со строками быть приведена к сокращенной форме (используйте операции со строками, чтобы последовательно создавать нули над каждой ведущей единицей, начиная справа).
Важность матриц строка-эшелон вытекает из следующей теоремы.
Каждая матрица может быть приведена к (сокращенной) форме строки-эшелона последовательностью элементарных операций со строками.
Фактически, мы можем дать пошаговую процедуру для фактического нахождения матрицы ряда строк. Обратите внимание: несмотря на то, что существует множество последовательностей операций со строками, которые приведут матрицу к форме ряда строк, та, которую мы используем, является систематической и ее легко программировать на компьютере. Обратите внимание, что алгоритм имеет дело с матрицами в целом, возможно, со столбцами нулей.
Обратите внимание, что алгоритм имеет дело с матрицами в целом, возможно, со столбцами нулей.
Шаг 1. Если матрица полностью состоит из нулей, остановитесь — она уже в виде эшелона строк.
Шаг 2. В противном случае найдите первый столбец слева, содержащий ненулевую запись (назовите его), и переместите строку, содержащую эту запись, в верхнюю позицию.
Шаг 3. Теперь умножьте новую верхнюю строку на, чтобы создать интерлиньяж.
Шаг 4. Вычитая числа, кратные этой строке, из строк под ней, сделайте каждую запись ниже начального нуля. Это завершает первую строку, и все дальнейшие операции со строками выполняются с оставшимися строками.
Шаг 5. Повторите шаги 1–4 для матрицы, состоящей из оставшихся строк.
Процесс останавливается, когда либо на шаге 5 не остается строк, либо оставшиеся строки состоят полностью из нулей.
Обратите внимание на то, что гауссовский алгоритм является рекурсивным: когда получен первый ведущий, процедура повторяется для оставшихся строк матрицы. Это упрощает использование алгоритма на компьютере. Обратите внимание, что решение примера 1.1.3 не использовало гауссовский алгоритм в том виде, в каком он был написан, потому что первый ведущий не был создан путем деления строки 1 на.Причина этого в том, что он избегает дробей. Однако общий шаблон ясен: создайте ведущие слева направо, используя каждый из них по очереди, чтобы создать нули под ним. Вот один пример.
Это упрощает использование алгоритма на компьютере. Обратите внимание, что решение примера 1.1.3 не использовало гауссовский алгоритм в том виде, в каком он был написан, потому что первый ведущий не был создан путем деления строки 1 на.Причина этого в том, что он избегает дробей. Однако общий шаблон ясен: создайте ведущие слева направо, используя каждый из них по очереди, чтобы создать нули под ним. Вот один пример.
Решение:
Соответствующая расширенная матрица —
Создайте первую ведущую, поменяв местами строки 1 и 2
Теперь вычтите умноженную строку 1 из строки 2 и вычтите умноженную строку 1 из строки 3.Результат
Теперь вычтите строку 2 из строки 3, чтобы получить
.Это означает, что следующая сокращенная система уравнений
эквивалентен исходной системе. Другими словами, у них одинаковые решения. Но эта последняя система явно не имеет решения (последнее уравнение требует этого и удовлетворяет, а таких чисел не существует). Следовательно, исходная система не имеет решения.
Следовательно, исходная система не имеет решения.
Для решения линейной системы расширенная матрица преобразуется в сокращенную форму строки-эшелон, а переменные, соответствующие ведущим, называются ведущими переменными .Поскольку матрица представлена в сокращенной форме, каждая ведущая переменная встречается ровно в одном уравнении, поэтому это уравнение может быть решено для получения формулы для ведущей переменной в терминах не ведущих переменных. Принято называть нелидирующие переменные «свободными» переменными и маркировать их новыми переменными, называемыми параметрами . Каждый выбор этих параметров приводит к решению системы, и каждое решение возникает таким образом. Эта процедура в целом работает и получила название
.Для решения системы линейных уравнений выполните следующие действия:
- Перенести расширенную матрицу \ index {расширенная матрица} \ index {матрица! Расширенная матрица} в сокращенную матрицу-эшелон строк, используя элементарные операции со строками.

- Если возникает строка, система несовместима.
- В противном случае назначьте не ведущие переменные (если они есть) в качестве параметров и используйте уравнения, соответствующие сокращенной матрице строки-эшелон, чтобы найти ведущие переменные в терминах параметров.
Существует вариант этой процедуры, в котором расширенная матрица переносится только в строчно-эшелонированную форму. Не ведущие переменные, как и раньше, назначаются как параметры. Затем последнее уравнение (соответствующее форме строки-эшелона) используется для решения последней ведущей переменной в терминах параметров.Эта последняя ведущая переменная затем подставляется во все предыдущие уравнения. Затем второе последнее уравнение дает вторую последнюю ведущую переменную, которая также подставляется обратно. Процесс продолжает давать общее решение. Эта процедура называется обратной заменой . Можно показать, что эта процедура численно более эффективна и поэтому важна при решении очень больших систем.
Рейтинг
Можно доказать, что уменьшенная строка-эшелонированная форма матрицы однозначно определяется.То есть, независимо от того, какая серия операций со строками используется для переноса в сокращенную матрицу эшелонов строк, результатом всегда будет одна и та же матрица. Напротив, это неверно для матриц ряда строк: разные последовательности операций со строками могут переносить одну и ту же матрицу в разные матрицы эшелонов строк. В самом деле, матрица может быть перенесена (с помощью одной строковой операции) в матрицу-эшелон строк, а затем с помощью другой строковой операции в (сокращенную) матрицу-эшелон. Однако — это , правда, что количество ведущих единиц должно быть одинаковым в каждой из этих матриц строка-эшелон (это будет доказано позже).Следовательно, количество зависит только от того, каким образом приведено в строй.
Ранг матрицы — это количество ведущих s в любой матрице строка-эшелон, к которой могут быть перенесены операции со строками. Вычислить ранг.
Вычислить ранг.Решение:
Приведение к строчной форме
Так как эта матрица эшелонов строк имеет два ведущих s, rank.
Предположим, что ранг, где — матрица со строками и столбцами.Тогда потому что ведущие s лежат в разных строках, и потому что ведущие s лежат в разных столбцах. Более того, у ранга есть полезное приложение к уравнениям. Напомним, что система линейных уравнений называется непротиворечивой, если она имеет хотя бы одно решение.
Проба:
Тот факт, что ранг расширенной матрицы равен, означает, что есть ровно ведущие переменные и, следовательно, точно не ведущие переменные. Все эти нелидирующие переменные назначаются как параметры в гауссовском алгоритме, поэтому набор решений включает в себя именно параметры.Следовательно, если существует хотя бы один параметр, а значит, бесконечно много решений. Если, нет параметров и поэтому единственное решение.
Теорема 1.2.2 показывает, что для любой системы линейных уравнений существуют ровно три возможности:
- Нет решения .
 Это происходит, когда ряд встречается в форме эшелона строк. Это тот случай, когда система несовместима.
Это происходит, когда ряд встречается в форме эшелона строк. Это тот случай, когда система несовместима. - Уникальное решение . Это происходит, когда каждая переменная является ведущей переменной.
- Бесконечно много решений . Это происходит, когда система согласована и есть хотя бы одна не ведущая переменная, поэтому задействован хотя бы один параметр.
https://www.geogebra.org/m/cwQ9uYCZ
Пожалуйста, ответьте на эти вопросы после открытия веб-страницы:
1. Для данной линейной системы, что представляет каждая из них?
2. Исходя из графика, что можно сказать о решениях? Есть ли у системы одно решение, нет решения или бесконечно много решений? Почему
3.Измените постоянный член в каждом уравнении на 0, что изменилось на графике?
4. Для следующей линейной системы:
Можете ли вы решить это методом исключения Гаусса? Что вы наблюдаете, глядя на график?
Многие важные проблемы связаны с линейными неравенствами , а не с линейными уравнениями Например, условие для переменных может принимать форму неравенства, а не равенства. Существует метод (называемый симплексным алгоритмом ) для поиска решений системы таких неравенств, который максимизирует функцию вида где и являются фиксированными константами.
Существует метод (называемый симплексным алгоритмом ) для поиска решений системы таких неравенств, который максимизирует функцию вида где и являются фиксированными константами.
Система уравнений с переменными называется однородной , если все постоянные члены равны нулю, то есть если каждое уравнение системы имеет вид
Очевидно, решение такой системы; это называется тривиальным решением .Любое решение, в котором хотя бы одна переменная имеет ненулевое значение, называется нетривиальным решением .
Наша главная цель в этом разделе — дать полезное условие, при котором однородная система имеет нетривиальные решения. Следующий пример поучителен.
Решение:
Приведение расширенной матрицы к сокращенной форме эшелона строк описано ниже.
Ведущими переменными являются,, и, например, назначается в качестве параметра. Тогда общее решение:,,,. Отсюда, взяв (скажем), получим нетривиальное решение:,,,.
Тогда общее решение:,,,. Отсюда, взяв (скажем), получим нетривиальное решение:,,,.
Существование нетривиального решения в примере 1.3.1 обеспечивается наличием параметра в решении. Это связано с тем, что существует не ведущая переменная (в данном случае). Но здесь должно быть не ведущей переменной, потому что есть четыре переменных и только три уравнения (и, следовательно, не более три ведущие переменные).Это обсуждение обобщает доказательство следующей основной теоремы.
Если однородная система линейных уравнений имеет больше переменных, чем уравнений, то она имеет нетривиальное решение (фактически бесконечно много).
Проба:
Предположим, что есть уравнения в переменных, где, и пусть обозначают приведенную строчно-эшелонированную форму расширенной матрицы. Если есть ведущие переменные, есть не ведущие переменные и, следовательно, параметры. Следовательно, достаточно показать это. Но потому что имеет ведущие единицы и строки, и по гипотезе. Итак, что дает.
Но потому что имеет ведущие единицы и строки, и по гипотезе. Итак, что дает.
Обратите внимание, что обратное утверждение теоремы 1.3.1 неверно: если однородная система имеет нетривиальные решения, у нее не должно быть больше переменных, чем у уравнений (система имеет нетривиальные решения, но.)
Теорема 1.3.1 очень полезна в приложениях. В следующем примере представлена иллюстрация из геометрии.
Мы называем график уравнения коникой , если не все числа, и равны нулю.Покажите, что есть хотя бы одна коника, проходящая через любые пять точек на плоскости, которые не все лежат на одной прямой.Решение:
Пусть координаты пяти точек будут,,, и. График проходов if
Это дает пять уравнений, по одному для каждого, линейных по шести переменным,,,,, и. Следовательно, по теореме 1.1.3 существует нетривиальное решение. Если все пять точек лежат на линии с уравнением, вопреки предположению. Следовательно, один из « отличен от нуля.
Линейные комбинации и базовые решения
Что касается строк, два столбца считаются равными , если они имеют одинаковое количество записей и соответствующие записи одинаковы. Позвольте и быть столбцами с одинаковым количеством записей. Что касается операций с элементарными строками, их сумма получается путем сложения соответствующих записей, и, если это число, скалярное произведение определяется путем умножения каждой записи на. Точнее:
Сумма скалярных кратных нескольких столбцов называется линейной комбинацией этих столбцов.Например, это линейная комбинация и для любого выбора чисел и.
Решение:
Для, мы должны определить, существуют ли числа, и такие, что, то есть
Приравнивание соответствующих элементов дает систему линейных уравнений,, и для,, и. Путем исключения Гаусса решение есть, и где — параметр. Взяв, мы видим, что это линейная комбинация, и.
Обращаясь к, снова ищем, и такие, что; то есть
приводит к уравнениям,, и для действительных чисел, и.Но на этот раз, как может проверить читатель, нет решения , равно как и , а не , линейная комбинация, и.
Наш интерес к линейным комбинациям проистекает из того факта, что они предоставляют один из лучших способов описания общего решения однородной системы линейных уравнений. Когда
решает такую систему с переменными, запишите переменные в виде матрицы столбцов:. Обозначается тривиальное решение. В качестве иллюстрации, общее решение в примере 1
.3.1 — это,, и, где — параметр, и теперь мы могли бы выразить это как
, говоря, что общее решение -, где произвольно.
Теперь позвольте и — два решения однородной системы с переменными. Тогда любая линейная комбинация этих решений снова оказывается решением системы. В более общем плане:
Фактически, предположим, что типичное уравнение в системе имеет вид, и предположим, что
, являются решениями. Потом и
Потом и
.
Следовательно, это тоже решение, потому что
Аналогичный аргумент показывает, что Утверждение 1.1 верно для линейных комбинаций более двух решений.
Примечательно то, что каждое решение однородной системы представляет собой линейную комбинацию определенных частных решений, и, фактически, эти решения легко вычисляются с использованием гауссовского алгоритма. Вот пример.
Решить однородную систему с матрицей коэффициентовРешение:
Приведение дополненной матрицы к уменьшенной форме —
, поэтому решения являются,,, и методом исключения Гаусса.Следовательно, мы можем записать общее решение в матричной форме
Вот и частные решения, определяемые гауссовским алгоритмом.
Решения и в примере 1.3.5 обозначены следующим образом:
Алгоритм Гаусса систематически выдает решения для любой однородной линейной системы, называемые базовыми решениями , по одному для каждого параметра.
Кроме того, алгоритм дает стандартный способ выразить каждое решение как линейную комбинацию базовых решений, как в Примере 1.3.5, где общее решение принимает вид
Следовательно, вводя новый параметр, мы можем умножить исходное базовое решение на 5 и, таким образом, исключить дроби.
По этой причине:
Любое ненулевое скалярное кратное базового решения будет по-прежнему называться базовым решением.
Таким же образом алгоритм Гаусса выдает базовые решения для в каждой однородной системе, по одному для каждого параметра (есть нет базовых решений, если система имеет только тривиальное решение).Более того, каждое решение задается алгоритмом как линейная комбинация
этих базовых решений (как в Примере 1.3.5). Если имеет ранг, теорема 1.2.2 показывает, что есть ровно параметры, а значит, и базовые решения. Это доказывает:
Решение:
Приведение расширенной матрицы к сокращенной строчно-эшелонированной форме составляет
, поэтому общее решение — это,,,, и где, и — параметры. В матричной форме это
В матричной форме это
Отсюда базовые решения —
Параметрическая форма
Существует одна возможность для строковой сокращенной формы матрицы, которую мы не видели в разделе 1.2.
Пример (система со свободной переменной)
Рассмотрим линейную систему
E2x + y + 12z = 1x + 2y + 9z = −1.
Решаем с помощью сокращения строк:
C21121129−1DR1 ← → R2 −−−− → C129−121121D (Необязательно) R2 = R2−2R1 −−−−−− → C129−10−3−63D (Step1c) R2 = R2 ÷ −3 −−−−− → C129−1012−1D (Шаг2b) R1 = R1−2R2 −−−−−− → C1051012−1D (Шаг2c)Эта сокращенная по строкам матрица соответствует линейной системе
Ex + 5z = 1y + 2z = -1.
В каком смысле решена система? Перепишем как
Ex = 1−5zy = −1−2z.
Для любого значения z существует ровно одно значение x и y, при котором уравнения верны. Но мы можем выбрать для любого значения z.
Мы нашли все решения: это набор всех значений x, y, z, где
Fx = 1−5zy = −1−2zz = zzanyrealnumber.
Это называется параметрической формой для решения линейной системы. Переменная z называется свободной переменной .
Рисунок 2 — Изображение набора решений (желтая линия) линейной системы в этом примере. Для каждого значения z существует уникальное решение; переместите ползунок, чтобы изменить z.Учитывая параметрическую форму решения линейной системы, мы можем получить конкретные решения, заменив свободные переменные любыми конкретными действительными числами. Например, установка z = 0 в последнем примере дает решение (x, y, z) = (1, −1,0), а установка z = 1 дает решение (x, y, z) = (- 4 , −3,1).
Определение
Рассмотрим непротиворечивую систему уравнений относительно переменных x1, x2 ,…, хн. Пусть A — строчная форма расширенной матрицы для этой системы.
Мы говорим, что xi — это свободная переменная , если ее соответствующий столбец в A равен , а не — сводный столбец.
В приведенном выше примере переменная z была свободной, потому что матрица сокращенной формы эшелона строк была
В матрице
свободными переменными являются x2 и x4. (Расширенный столбец не является бесплатным, потому что он не соответствует переменной.)
(Расширенный столбец не является бесплатным, потому что он не соответствует переменной.)
Рецепт: Параметрическая форма
Параметрическая форма множества решений согласованной системы линейных уравнений получается следующим образом.
- Запишите систему как расширенную матрицу.
- Ряд сокращается до ступенчатой формы пониженного ряда.
- Напишите соответствующую (решенную) систему линейных уравнений.
- Переместите все свободные переменные в правую часть уравнений.
Перемещение свободных переменных в правую часть уравнений сводится к решению для несвободных переменных (тех, которые идут в сводные столбцы) в терминах свободных переменных. Можно думать о свободных переменных как о независимых переменных , а о несвободных переменных как о зависимых .
Вы можете выбрать любое значение для свободных переменных в (согласованной) линейной системе.
Свободные переменные берутся из столбцов без точек поворота в матрице в виде эшелона строк.
Имеется трех возможностей для сокращенной формы эшелона строк расширенной матрицы линейной системы.
- Последний столбец — это сводный столбец. В данном случае система несовместима . Есть нулевые решения, т.е.е., набор решений пуст. Например, матрица исходит из линейной системы без решений.
- Каждый столбец, кроме последнего, является сводным столбцом. В данном случае в системе имеется уникальных решений. Например, матрица говорит нам, что единственное решение (x, y, z) = (a, b, c).
- Последний столбец не является сводным столбцом, и какой-либо другой столбец также не является сводным столбцом. В этом случае система имеет бесконечно много решений, соответствующих бесконечному числу возможных значений свободной переменной (переменных).Например, в системе, соответствующей матрице любые значения x2 и x4 дают решение системы уравнений.
(PDF) Решение уравнений с параметрами
Б. -С. Илани, Д. Хасидов
-С. Илани, Д. Хасидов
Скемп (1987) утверждает, что правила обучения без причины позволяют ученику функционировать только в узких рамках
и иметь дело только со стандартными задачами. Однако такой подход ограничивает понимание учащимися, и они не смогут справиться с более сложными задачами.Понимание позволяет ученику решать
нестандартных задач, которые не могут быть решены механическим применением формул. Fischbein и Muzicant
(2002) указывают, что ученики обучались преимущественно процедурным образом и, следовательно, они часто не различают
концептуального и процедурного знания. Многие ученики затрудняются распознать, что буква представляет собой
числа, и не знают, как работать с символическими значениями (Kieran, 1992, 2014).
Широко признано, что учителям важно осознавать, как их ученики воспринимают математические темы
, в частности, конкретные причины совершения ошибок (Almog & Ilany, 2012).
На начальных курсах студенты привыкают к тому, что x (а позже y и z) являются переменными, а буквы, такие как a, b, c
, являются константами или параметрами.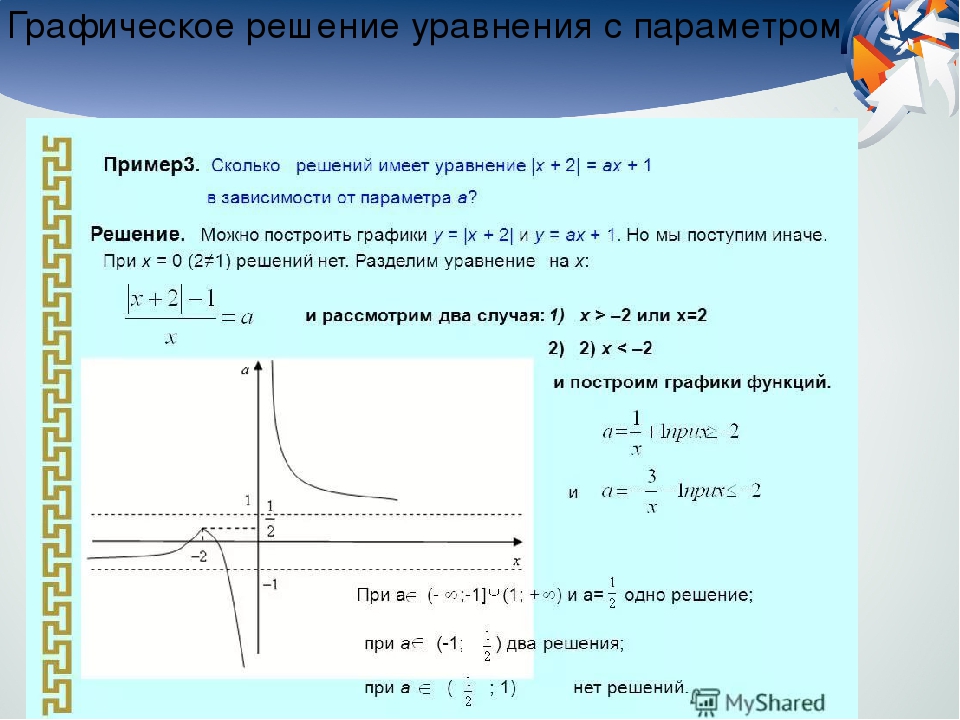 Однако на более продвинутых курсах они сталкиваются с вопросами, в которых буквы
Однако на более продвинутых курсах они сталкиваются с вопросами, в которых буквы
используются по-другому, и они находят это очень запутанным.Например, задачи интеграции, где x фиксировано, а y равно
переменной. Или объемные вопросы, где a, b, c используются в качестве переменных.
Ученики решают в школе бесчисленные упражнения с уравнениями, в которых буква x представляет собой переменную, которая должна быть выражена
буквами a, b, c и т. Д. В этом исследовании испытуемым предлагалось множество уравнений с
нестандартная подача, о чем говорилось выше.
2. Цель
Цели исследования — изучить и выявить трудности старшеклассников и старшеклассников
учителей при решении уравнений с параметрами.Кроме того, выяснить, есть ли существенные различия между
учениками и студентами-учителями в отношении решения таких уравнений. Какие процедуры используются и какие трудности возникают при решении уравнений с параметрами.
3. Вопросы для исследования
Вопросы для исследования
1) Как испытуемые решают уравнения с параметрами, в которых они должны выражать различные буквы через
других букв и параметров? В частности, когда уравнения не построены стандартным образом.
2) Есть ли различия между учениками и студентами-учителями в том, как они решают такие уравнения.
И если да, то в чем отличия.
Примеры уравнений, исследованных в статье (нумерация вопросов соответствует нумерации вопросов
анкеты):
• Вопрос 16: Найдите x (через a) в
(довольно стандартное уравнение с переменной x и
параметр a).
• Вопрос 1. Найдите c (в терминах x) в
(менее стандартно, поскольку требуется выразить c в терминах
x).
• Вопрос 9: Найдите b (через x) в
(менее стандартно, так как требуется, чтобы «правильно» переставить уравнение
, а затем выразить b через x).
• Вопрос 21: Следующее уравнение линейно по x, хотя может ошибочно показаться квадратичным уравнением:
в терминах a:
()
2
11 2a xx ax− + = −−
.
Мы называем знания, необходимые для решения простых уравнений, процедурными.Уравнение
с нестандартными презентациями требует более гибкого подхода.
4. Метод
Исследуемая выборка состояла из 115 студентов-учителей математики на третьем и четвертом году обучения и
133 учеников двенадцатых классов с высшим уровнем математики (5-элементный поток математики) в четырех средних школах.
Инструменты. Для исследования был разработан вопросник, который был разослан обеим группам. Часть анкеты
состоит из шести вопросов, которые включают уравнения с параметрами.В этом исследовании сообщается о результатах
двух вопросов уравнений первой степени (вопросы (5) и (21)) и трех вопросов уравнений второй степени
(вопросы 16, 1 и 9). Вопросы перечислены в Таблице 1 и Таблице 3.
Процедура: Чтобы понять процесс решения предметов, были просмотрены пять учеников и шесть студентов-учителей. Вопросы для интервью были разработаны после заполнения и анализа анкеты. Целью
Целью
было разъяснение и дальнейшее продвижение результатов анкеты.Кроме того, были проведены открытые наблюдения в
, чтобы внимательно изучить ответы испытуемых.
Метод изменения параметров
Эта страница посвящена дифференциальным уравнениям второго порядка этого типа:
d 2 y dx 2 + P (x) dy dx + Q (x) y = f (x)
где P (x), Q (x) и f (x) — функции от x.
Два метода
Существует два основных метода решения уравнений, например
.d 2 y dx 2 + P (x) dy dx + Q (x) y = f (x)
Undetermined Coefficients, который работает только тогда, когда f (x) является полиномом, экспонентой, синусом, косинусом или их линейной комбинацией.
Варианты параметров (которые мы узнаем здесь), который работает с широким спектром функций, но немного беспорядочный в использовании.
Изменение параметров
Для простоты рассмотрим только корпус:
d 2 y dx 2 + p dy dx + qy = f (x)
где p и q — константы, а f (x) — ненулевая функция от x.Полное решение такого уравнения можно найти сочетая два типа решения:
- Общее решение однородное уравнение d 2 y dx 2 + p dy dx + qy = 0
- Частные решения неоднородное уравнение d 2 y dx 2 + p dy dx + qy = f (x)
Обратите внимание, что f (x) может быть одной функцией или суммой двух или более функции.
Как только мы нашли общее решение и все частные
решений, то окончательное полное решение находится путем добавления всех
решения вместе.
Этот метод основан на интеграции.
Проблема с этим методом заключается в том, что, хотя он может дать решение, в некоторых случаях решение нужно оставить в виде интеграла.
Начните с общего решения
При введении в дифференциальные уравнения второго порядка мы узнаем, как найти общее решение.
В основном мы берем уравнение
d 2 y dx 2 + p dy dx + qy = 0
и свести его к «характеристическому уравнению»:
р 2 + пр + д = 0
Это квадратное уравнение, которое имеет три возможных типа решения в зависимости от дискриминанта p 2 — 4q . Когда p 2 — 4q равно
положительный получаем два действительных корня, и решение равно
y = Ae r 1 x + Be r 2 x
ноль получаем один действительный корень, а решение —
y = Ae rx + Bxe rx
отрицательный получаем два комплексных корня r 1 = v + wi и r 2 = v — wi , и решение равно
y = e vx (Ccos (wx) + iDsin (wx))
Фундаментальные решения уравнения
Во всех трех случаях «y» состоит из двух частей:
- y = Ae r 1 x + Be r 2 x состоит из y 1 = Ae r 1 x и y 52 = r 2 x
- y = Ae rx + Bxe rx состоит из y 1 = Ae rx и y 2 = Bxe rx
- y = e vx (Ccos (wx) + iDsin (wx)) состоит из y 1 = e vx Ccos (wx) и y 2 = e vx iDsin (шх)
y 1 и y 2 известны как фундаментальные решения уравнения
И y 1 и y 2 называются линейно независимый , потому что ни одна из функций не является постоянным кратным
разное.
Вронскианец
Когда y 1 и y 2 являются двумя фундаментальными решениями однородного уравнения
d 2 y dx 2 + p dy dx + qy = 0
, то вронскиан W (y 1 , y 2 ) является определяющим матрицы
Так
W (y 1 , y 2 ) = y 1 y 2 ‘ — y 2 y 1 ‘
Вронскиан назван в честь польского математика и философ Юзеф Хене-Вронский (1776–1853).
Поскольку y 1 и y 2 линейно независимы, значение вронскиана не может равняться нулю.
Особое решение
Используя вронскиан, мы можем теперь найти частное решение дифференциального уравнения
d 2 y dx 2 + p dy dx + qy = f (x)
по формуле:
y p (x) = −y 1 (x) ∫ y 2 (x) f (x) W (y 1 , y 2 ) dx + y 2 (x) ∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
Пример 1: Решить
d 2 y dx 2 — 3 dy dx + 2y = e 3x 1. Найдите общее решение для d 2 y dx 2 — 3 dy dx + 2y = 0
Найдите общее решение для d 2 y dx 2 — 3 dy dx + 2y = 0
Характеристическое уравнение: r 2 — 3r + 2 = 0
Фактор: (r — 1) (r — 2) = 0
r = 1 или 2
Итак, общее решение дифференциального уравнения: y = Ae x + Be 2x
Итак, в этом случае фундаментальные решения и их производные:
y 1 (x) = e x
y 1 ‘(x) = e x
y 2 (x) = e 2x
y 2 ‘(x) = 2e 2x
2.Найдите вронскианца:
W (y 1 , y 2 ) = y 1 y 2 ‘ — y 2 y 1 ‘= 2e 3x — e 3x = e 3x
3. Найдите частное решение по формуле:
y p (x) = −y 1 (x) ∫ y 2 (x) f (x) W (y 1 , y 2 ) dx + y 2 (x) ∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
4. Сначала решаем интегралы:
Сначала решаем интегралы:
∫ y 2 (x) f (x) W (y 1 , y 2 ) dx
= ∫ e 2x e 3x e 3x dx
= ∫e 2x dx
= 1 2e 2x
Итак:
−y 1 (x) ∫ y 2 (x) f (x) W (y 1 , y 2 ) dx = — (e x ) ( 1 2e 2x ) = — 1 2e 3x
А также:
∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
= ∫ e x e 3x e 3x dx
= ∫e x dx
= e x
Итак:
y 2 (x) ∫ y 1 (x) f (x) W (y 1 , y 2 ) dx = (e 2x ) (e x ) = e 3x
Наконец:
y p (x) = −y 1 (x) ∫ y 2 (x) f (x) W (y 1 , y 2 ) dx + y 2 (x) ∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
= — 1 2e 3x + e 3x
= 1 2e 3x
и полное решение дифференциального уравнения d 2 y dx 2 — 3 dy dx + 2y = e 3x is
y = Ae x + Be 2x + 1 2e 3x
Что выглядит следующим образом (примеры значений A и B):
Пример 2: Решить
d 2 y dx 2 — y = 2x 2 — x — 31.
 Найдите общее решение для d 2 y dx 2 — y = 0
Найдите общее решение для d 2 y dx 2 — y = 0Характеристическое уравнение: r 2 — 1 = 0
Фактор: (r — 1) (r + 1) = 0
r = 1 или −1
Итак, общее решение дифференциального уравнения: y = Ae x + Be −x
Итак, в этом случае фундаментальные решения и их производные:
y 1 (x) = e x
y 1 ‘(x) = e x
y 2 (x) = e −x
y 2 ‘(x) = −e −x
2.Найдите вронскианца:
W (y 1 , y 2 ) = y 1 y 2 ‘ — y 2 y 1 ‘= −e x e −x — e x e −x = −2
3. Найдите частное решение по формуле:
y p (x) = −y 1 (x) ∫ y 2 (x) f (x) W (y 1 , y 2 ) dx + y 2 (x) ∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
4. Решите интегралы:
Решите интегралы:
∫ y 2 (x) f (x) W (y 1 , y 2 ) dx
= ∫ e −x (2x 2 −x − 3) −2 dx
= — 1 2 ∫ (2x 2 −x − 3) e −x dx
= — 1 2 [- (2x 2 −x − 3) e −x + ∫ (4x − 1) e −x dx]
= — 1 2 [- (2x 2 −x − 3) e −x — (4x — 1) e −x + ∫4e −x dx ]
= — 1 2 [- (2x 2 −x − 3) e −x — (4x — 1) e −x — 4e −x ]
= e −x 2 [2x 2 — x — 3 + 4x −1 + 4]
= e −x 2 [2x 2 + 3x]
Итак:
−y 1 (x) ∫ y 2 (x) f (x) W (y 1 , y 2 ) dx = (−e x ) [ e −x 2 ( 2x 2 + 3x)] = — 1 2 (2x 2 + 3x)
А этот:
∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
= ∫ e x (2x 2 −x − 3) −2 dx
= — 1 2 ∫ (2x 2 −x − 3) e x dx
= — 1 2 [(2x 2 −x − 3) e x — ∫ (4x − 1) e x dx]
= — 1 2 [(2x 2 −x − 3) e x — (4x — 1) e x + ∫4e x dx ]
= — 1 2 [(2x 2 −x − 3) e x — (4x — 1) e x + 4e x ]
= −e x 2 [2x 2 — x — 3 — 4x + 1 + 4]
= −e x 2 [2x 2 — 5x + 2]
Итак:
y 2 (x) ∫ y 1 (x) f (x) W (y 1 , y 2 ) dx = (e −x ) [ −e x 2 ( 2x 2 — 5x + 2)] = — 1 2 ( 2x 2 — 5x + 2)
Наконец:
y p (x) = −y 1 (x) ∫ y 2 (x) f (x) W (y 1 , y 2 ) dx + y 2 (x) ∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
= — 1 2 (2x 2 + 3x) — 1 2 (2x 2 — 5x + 2)
= — 1 2 (4x 2 — 2x + 2)
= −2x 2 + x — 1
и полное решение дифференциального уравнения d 2 y dx 2 — y = 2x 2 — x — 3 is
y = Ae x + Be −x — 2x 2 + x — 1
(Это тот же ответ, который мы получили в Примере 1 на странице Метод неопределенных коэффициентов. )
)
Пример 3: Решить
d 2 y dx 2 — 6 dy dx + 9y = 1 x1. Найдите общее решение для d 2 y dx 2 — 6 dy dx + 9y = 0
Характеристическое уравнение: r 2 — 6r + 9 = 0
Фактор: (r — 3) (r — 3) = 0
г = 3
Итак, общее решение дифференциального уравнения: y = Ae 3x + Bxe 3x
Итак, в этом случае фундаментальные решения и их производные:
y 1 (x) = e 3x
y 1 ‘(x) = 3e 3x
y 2 (x) = xe 3x
y 2 ‘(x) = (3x + 1) e 3x
2.Найдите вронскианца:
W (y 1 , y 2 ) = y 1 y 2 ‘ — y 2 y 1 ‘= (3x + 1) e 3x e 3x — 3xe 3x e 3x = e 6x
3. Найдите частное решение по формуле:
Найдите частное решение по формуле:
y p (x) = −y 1 (x) ∫ y 2 (x) f (x) W (y 1 , y 2 ) dx + y 2 (x) ∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
4.Решите интегралы:
∫ y 2 (x) f (x) W (y 1 , y 2 ) dx
= ∫ (xe 3x ) x −1 e 6x dx (Примечание: 1 x = x −1 )
= ∫e −3x dx
= — 1 3e −3x
Итак:
−y 1 (x) ∫ y 2 (x) f (x) W (y 1 , y 2 ) dx = — (e 3x ) (- 1 3e −3x ) = 1 3
А этот:
∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
= ∫ e 3x x −1 e 6x dx
= ∫e −3x x −1 dx
Это не может быть интегрировано, поэтому это пример, когда ответ
оставить как интеграл.
Итак:
y 2 (x) ∫ y 1 (x) f (x) W (y 1 , y 2 ) dx = (xe 3x ) (∫e −3x x −1 dx ) = xe 3x ∫e −3x x −1 dx
Наконец:
y p (x) = −y 1 (x) ∫ y 2 (x) f (x) W (y 1 , y 2 ) dx + y 2 (x) ∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
= 1 3 + xe 3x ∫e −3x x −1 dx
Итак, полное решение дифференциального уравнения d 2 y dx 2 — 6 dy dx + 9y = 1 x равно
y = Ae 3x + Bxe 3x + 1 3 + xe 3x ∫e −3x x −1 dx
Пример 4 (более сложный пример): Решить
d 2 y dx 2 — 6 dy dx + 13y = 195cos (4x)В этом примере используются следующие тригонометрические удостоверения
sin 2 (θ) + cos 2 (θ) = 1
sin (θ ± φ) = sin (θ) cos (φ) ± cos (θ) sin (φ)
cos (θ ± φ) = cos (θ) cos (φ) sin (θ) sin (φ)
sin (θ) cos (φ) = 1 2 [sin (θ
+ φ) + sin (θ — φ)]
cos (θ) cos (φ) = 1 2 [cos (θ
— φ) + cos (θ + φ)]
1.
 Найдите общее решение для d 2 y dx 2 -6 dy dx + 13y = 0
Найдите общее решение для d 2 y dx 2 -6 dy dx + 13y = 0Характеристическое уравнение: r 2 — 6r + 13 = 0
Используйте квадратное уравнение формула
x = −b ± √ (b 2 — 4ac) 2a
с a = 1, b = −6 и c = 13
Итак:
r = — (- 6) ± √ [(- 6) 2 — 4 (1) (13)] 2 (1)
= 6 ± √ [36−52] 2
= 6 ± √ [−16] 2
= 6 ± 4i 2
= 3 ± 2i
Итак, α = 3 и β = 2
⇒ y = e 3x [Acos (2x) + iBsin (2x)]
Итак, в данном случае имеем:
y 1 (x) = e 3x cos (2x)
y 1 ‘(x) = e 3x [3cos (2x) — 2sin (2x)]
y 2 (x) = e 3x sin (2x)
y 2 ‘(x) = e 3x [3sin (2x) + 2cos (2x)]
2. Найдите вронскианца:
Найдите вронскианца:
W (y 1 , y 2 ) = y 1 y 2 ‘- y 2 y 1 ‘
= e 6x cos (2x) [3sin (2x) + 2cos (2x)] — e 6x sin (2x) [3cos (2x) — 2син (2х)]
= e 6x [3cos (2x) sin (2x) + 2cos 2 (2x) — 3sin (2x) cos (2x) + 2sin 2 (2x)]
= 2e 6x
3. Найдите частное решение по формуле:
y p (x) = −y 1 (x) ∫ y 2 (x) f (x) W (y 1 , y 2 ) dx + y 2 (x) ∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
4.Решите интегралы:
∫ y 2 (x) f (x) W (y 1 , y 2 ) dx
= ∫ e 3x sin (2x) [195cos (4x)] 2e 6x dx
= 195 2 ∫e −3x sin (2x) cos (4x) dx
= 195 4 ∫e −3x [sin (6x)
— грех (2x)] dx . .. (1)
.. (1)
В этом случае мы еще не выполняем интеграцию по причинам, которые проясняется в мгновение ока.
Другой интеграл:
∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
= ∫ e 3x cos (2x) [195cos (4x)] 2e 6x dx
= 195 2 ∫e −3x cos (2x) cos (4x) dx
= 195 4 ∫e −3x [cos (6x) + cos (2x)] dx … (2)
Из уравнений (1) и (2) мы видим, что есть четыре очень похожих
интеграций, которые нам необходимо выполнить:
I 1 = ∫e −3x sin (6x) dx
I 2 = ∫e −3x sin (2x) dx
I 3 = ∫e — 3x cos (6x) dx
I 4 = ∫e −3x cos (2x) dx
Каждый из них может быть получен путем двукратного использования интеграции по частям, но есть более простой способ:
I 1 = ∫e −3x sin (6x) dx = — 1 6 e −3x cos (6x) — 3 6 ∫e −3x cos (6x) dx = — 1 6 e −3x cos (6x) — 1 2 I 3
⇒ 2 I 1 + I 3 = — 1 3e −3x cos (6x)
. .. (3)
.. (3)
I 2 = ∫e −3x sin (2x) dx = — 1 2 e −3x cos (2x) — 3 2∫e −3x cos (2x) dx = — 1 2e −3x cos (2x) — 3 2 I 4
⇒ 2 I 2 + 3 I 4 = — e −3x cos (2x) … (4)
I 3 = ∫e −3x cos (6x) dx
= 1 6 e −3x sin (6x)
+ 3 6 ∫e −3x sin (6x) dx
= 1 6 e −3x sin (6x)
+ 1 2 I 1
⇒ 2 I 3 — I 1 = 1 3e −3x sin (6x)
… (5)
I 4 = ∫e −3x cos (2x) dx
= 1 2 e −3x sin (2x)
+ 3 2∫e −3x sin (2x) dx
= 1 2e −3x sin (2x) + 3 2 I 2
⇒ 2 I 4 —
3 I 2 = e −3x sin (2x)
. .. (6)
.. (6)
Решите уравнения (3) и (5) одновременно:
2 I 1 + I 3 = — 1 3e −3x cos (6x) … (3)
2 I 3 — I 1 = 1 3e −3x sin (6x) … (5)
Умножьте уравнение (5) на 2 и сложите их (член I 1 нейтрализует):
⇒ 5 I 3 = — 1 3e −3x cos (6x) + 2 3e −3x sin (6x)
= 1 3e −3x [2sin (6x) — cos (6x)]
⇒ I 3 = 1 15e −3x [2sin (6x) — cos (6x)]
Умножьте уравнение (3) на 2 и вычтите (член I 3 нейтрализует):
⇒ 5 I 1 = — 2 3e −3x cos (6x) — 1 3e −3x sin (6x)
= — 1 3e −3x [2cos (6x) + грех (6x)]
⇒ I 1 = — 1 15e −3x [2cos (6x) + грех (6x)]
Решите уравнения (4) и (6) одновременно:
2 I 2 + 3 I 4 = — e −3x cos (2x). .. (4)
.. (4)
2 I 4 — 3 I 2 = e −3x sin (2x) … (6)
Умножьте уравнение (4) на 3 и уравнение (6) на 2 и сложите (член I 2 нейтрализует):
⇒ 13 I 4 = — 3e −3x cos (2x) + 2e −3x sin (2x)
= e −3x [2sin (2x) — 3 cos (2x)]
⇒ I 4 = 1 13e −3x [2sin (2x) — 3cos (2x)]
Умножьте уравнение (4) на 2 и уравнение (6) на 3 и вычтите (член I 4 нейтрализует):
⇒ 13 I 2 = — 2e −3x cos (2x) — 3e −3x sin (2x)
= — e −3x [2cos (2x) + 3 sin (2x)]
⇒ I 2 = — 1 13e −3x [2cos (2x) + 3sin (2x)]
Заменить в (1) и (2):
∫ y 2 (x) f (x) W (y 1 , y 2 ) dx
= 195 4∫e −3x [sin (6x)
— sin (2x)] dx. .. (1)
.. (1)
= 195 4 [– 1 15e −3x [2cos (6x) + sin (6x)] — [- 1 13e −3x [2cos (2x) + 3sin (2x)]]]
= e −3x 4 [−13 (2cos (6x) + sin (6x)) + 15 (2 cos (2x) + 3sin (2x))]
∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
= 195 4 ∫e −3x [cos (6x) + cos (2x)] dx… (2)
= 195 4 [ 1 15e −3x [2sin (6x) — cos (6x)] + 1 13e −3x [2sin (2x) — 3cos (2x)]]
= e −3x 4 [13 (2sin (6x) — cos (6x)) + 15 (2sin (2x) — 3cos (2x))]
Итак, y p (x) = −y 1 (x) ∫ y 2 (x) f (x) W (y 1 , y 2 ) dx + y 2 (x) ∫ y 1 (x) f (x) W (y 1 , y 2 ) dx
= — e 3x cos (2x) e −3x 4 [−13 (2cos (6x) + sin (6x)) + 15 (2 cos (2x) + 3sin (2x))] + e 3x sin (2x) e −3x 4 [13 (2sin (6x) — cos (6x)) + 15 (2sin (2x) — 3cos (2x))]
= — 1 4cos (2x) [−13 (2cos (6x) — sin (6x)) + 15 (2 cos (2x) + 3sin (2x))] + 1 4 sin (2x) [13 (2sin (6x) — cos (6x)) + 15 (2 sin (2x) — 3cos (2x))]
= 1 4 [26cos (2x) cos (6x) + 13cos (2x) sin (6x) — 30cos 2 (2x) — 45cos (2x) sin (2x) + 26sin (2x) sin (6x) — 13sin (2x) cos (6x) + 30sin 2 (2x) — 45sin (2x) cos (2x)]
= 1 4 [26 [cos (2x) cos (6x) + sin (2x) sin (6x)] + 13 [cos (2x) sin (6x) — sin (2x) cos (6x)] — 30 [cos 2 (2x) — sin 2 (2x)] — 45 [cos (2x) sin (2x) + sin (2x) cos (2x)]]
= 1 4 [26cos (4x) + 13sin (4x) — 30cos (4x) — 45sin (4x)]
= 1 4 [−4cos (4x) — 32sin (4x)]
= −cos (4x) — 8 sin (4x)
Итак, полное решение дифференциального уравнения d 2 y dx 2 — 6 dy dx + 13y = 195cos (4x) равно
y = e 3x (Acos (2x) + iBsin (2x)) —
cos (4x) — 8sin (4x)
9529, 9530, 9531, 9532, 9533, 9534, 9535, 9536, 9537, 9538
Параметрических уравнений
Прямоугольное уравнение или уравнение в прямоугольной форме — это уравнение, состоящее из таких переменных, как
Икс
и
у
которое можно изобразить на регулярной декартовой плоскости. Например
у
знак равно
4
Икс
+
3
— прямоугольное уравнение.
Например
у
знак равно
4
Икс
+
3
— прямоугольное уравнение.
Кривая на плоскости называется параметризованной, если набор координат на кривой ( Икс , у ) , представлены как функции переменной т .
Икс знак равно ж ( т ) у знак равно г ( т )
Эти уравнения могут быть изображены или не изображены на декартовой плоскости.
Пример 1:
Найдите систему параметрических уравнений для уравнения у знак равно Икс 2 + 5 .
Решение:
Присвойте любой из переменных значение
т
. (сказать
Икс
знак равно
т
).
Тогда данное уравнение можно переписать в виде у знак равно т 2 + 5 .
Следовательно, система параметрических уравнений имеет вид Икс знак равно т и у знак равно т 2 + 5 .
Пример 2:
Удалите параметр и найдите соответствующее прямоугольное уравнение.
Икс знак равно т + 5 у знак равно т 2
Решение:
Перепишите уравнение Икс знак равно т + 5 в виде т с точки зрения Икс .
т + 5 знак равно Икс т знак равно Икс — 5
Теперь замените
т
от (
Икс
—
5
) в уравнении
у
знак равно
т
2
.
у знак равно ( Икс — 5 ) 2
Следовательно, соответствующее прямоугольное уравнение имеет вид у знак равно ( Икс — 5 ) 2 .{(n-1)} + \ cdots + P_n (x) y. \ nonumber \]
Когда мы говорим о решениях этого уравнения и дополнительного уравнения \ (Ly = 0 \), мы имеем в виду решения на \ ((a, b) \). Мы покажем, как использовать метод вариации параметров, чтобы найти частное решение \ (Ly = F \), при условии, что мы знаем фундаментальный набор решений \ (\ {y_1, y_2, \ dots, y_n \} \) из \ (Ly = 0 \).
Мы ищем частное решение \ (Ly = F \) в виде
\ [\ label {eq: 9.4.2} y_p = u_1y_1 + u_2y_2 + \ cdots + u_ny_n \]
, где \ (\ {y_1, y_2, \ dots, y_n \} \) — известный фундаментальный набор решений дополнительного уравнения
\ [P_0 (x) y ^ {(n)} + P_1 (x) y ^ {(n-1)} + \ cdots + P_n (x) y = 0 \ nonumber \]
и \ (u_1 \), \ (u_2 \),…, \ (u_n \) — функции, которые необходимо определить. {(r)} _ n, \ 0 \ le r \ le n-1. \]
{(r)} _ n, \ 0 \ le r \ le n-1. \]
Эти формулы легко запомнить, поскольку они выглядят так, как будто мы получили их, дифференцируя уравнение \ ref {eq: 9.4.2} \ (n-1 \) раз при обработке \ (u_1 \), \ (u_2 \), …, \ (U_n \) как константы. Чтобы увидеть, что уравнение \ ref {eq: 9.4.3} подразумевает уравнение \ ref {eq: 9.4.4}, мы сначала дифференцируем уравнение \ ref {eq: 9.4.2}, чтобы получить
\ [y_p ‘= u_1y_1’ + u_2y_2 ‘+ \ cdots + u_ny_n’ + u_1’y_1 + u_2’y_2 + \ cdots + u_n’y_n, \ nonumber \]
, что сокращается до
\ [y_p ‘= u_1y_1’ + u_2y_2 ‘+ \ cdots + u_ny_n’ \ nonumber \]
из-за первого уравнения в уравнении \ ref {eq: 9.{n-j} {FW_j \ over P_0W}, \ quad 1 \ le j \ le n, \]
, где \ (W_j \) — вронскиан набора функций, полученных удалением \ (y_j \) из \ (\ {y_1, y_2, \ dots, y_n \} \) и сохранением остальных функций в том же порядке. Эквивалентно, \ (W_j \) — это определитель, полученный путем удаления последней строки и \ (j \) — го столбца \ (W \).
Получив \ (u_1 ‘\), \ (u_2’ \) \ (, \ dots, \) \ (u_n ‘\), мы можем проинтегрировать, чтобы получить \ (u_1, \, u_2, \ dots, u_n \) . Как и в разделе 5.7, мы принимаем постоянные интегрирования равными нулю и отбрасываем любую линейную комбинацию \ (\ {y_1, y_2, \ dots, y_n \} \), которая может появиться в \ (y_p \).{(n-1)} W_ {j}. \ nonumber \]
Уравнения третьего порядка
Если \ (n = 3 \), то
\ [W = \ left | \ begin {array} {ccc} y_1 & y_2 & y_3 \\ [4pt] y’_1 & y’_2 & y’_3 \\ [4pt] y » _ 1 & y » _ 2 & y » _ 3 \ end {array} \ right |. \ nonumber \]
Следовательно,
\ [W_1 = \ left | \ begin {array} {cc} y_2 & y_3 \\ [4pt] y’_2 & y’_3 \ end {array} \ right |, \ quad W_2 = \ left | \ begin {array} {cc} y_1 & y_3 \\ [4pt] y’_1 & y’_3 \ end {array} \ right |, \ quad W_3 = \ left | \ begin {array} {cc} y_1 & y_2 \\ [4pt] y’_1 & y’_2 \ end {array} \ right |, \ nonumber \]
и уравнение \ ref {eq: 9.{-x}. \ nonumber \]
Уравнения четвертого порядка
Если \ (n = 4 \), то
\ [W = \ left | \ begin {array} {cccc} y_1 & y_2 & y_3 & y_4 \\ [4pt] y’_1 & y’_2 & y’_3 & y_4 ‘\\ [4pt] y’ ‘_ 1 & y’ ‘_ 2 & y’ ‘_ 3 & y_4’ ‘\\ [4pt] y’ » _ 1 & y ‘ » _2 & y » ‘_ 3 & y_4’ » \ end {array} \ right |, \ nonumber \]
Следовательно,
\ [W_1 = \ left | \ begin {array} {ccc} y_2 & y_3 & y_4 \\ [4pt] y’_2 & y’_3 & y_4 ‘\\ [4pt] y’ ‘_ 2 & y’ ‘_ 3 & y_4’ ‘\ end {array} \ right |, \ quad W_2 = \ left | \ begin {array} {ccc} y_1 & y_3 & y_4 \\ [4pt] y’_1 & y’_3 & y_4 ‘\\ [4pt] y’ ‘_ 1 & y’ ‘_ 3 & y_4’ ‘\ end {array} \ right |, \ nonumber \]
\ [W_3 = \ left | \ begin {array} {ccc} y_1 & y_2 & y_4 \\ [4pt] y’_1 & y’_2 & y_4 ‘\\ [4pt] y’ ‘_ 1 & y’ ‘_ 2 & y_4’ ‘\ end {array} \ right |, \ quad W_4 = \ left | \ begin {array} {ccc} y_1 & y_2 & y_3 \\ [4pt] y_1 ‘& y’_2 & y_3’ \\ [4pt] y_1 » & y » _ 2 & y_3 » \ end {array} \ right |, \ nonumber \]
и уравнение \ ref {eq: 9. 2} \ nonumber \]
2} \ nonumber \]
— это общее решение уравнения \ ref {eq: 9.4.10} на \ ((- \ infty, 0) \) и \ ((0, \ infty) \).
Изменение параметров
Изменение параметровЭтот метод интересен всякий раз, когда предыдущий метод не применяется (когда г ( x ) не нужной формы). Общая идея похожа на то, что мы сделали для линейных уравнений второго порядка, за исключением того, что В случае, мы имели дело с небольшой системой, и здесь мы можем иметь дело с большим (в зависимости от порядка дифференциала уравнение).Опишем общий случай (постоянные коэффициенты или нет). Рассмотрим уравнение
Предположим, что набор независимых решений связанного однородного уравнения. Затем конкретный решение можно найти как
где функции могут быть получены из следующей системы:
.
Определитель этой системы — вронскиан , что не равно нулю. Формулы Крамера дадут
,
где W ( x ) — вронскиан, а —
определитель, полученный из вронскиана W заменой
-столбец в векторном столбце (0,0 ,. ., 0,1). Следовательно,
частное решение уравнения ( NH ) дается формулой
., 0,1). Следовательно,
частное решение уравнения ( NH ) дается формулой
Обратите внимание, что если порядок уравнения невысокий, вы можете захотеть
решить систему, используя методы, отличные от формул Крамера.
Пример: Найдите частное решение
Решение: Выполним следующие шаги:
- (1)
- Характеристическое уравнение
Поскольку корни характеристического уравнения являются .Следовательно, набор независимых решений есть ;
- (2)
- Частное решение задается выражением, где — решения системы
;
- (3)
- Разрешение системы дает
После интеграция мы получаем
;
- (4)
- Частное решение дается
Обратите внимание, что константа 1 in может быть опущена, поскольку это решение связанного однородного уравнения.

Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Автор: Мохамед Амин ХамсиАвторские права 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователей онлайн за последний час .








 Это происходит, когда ряд встречается в форме эшелона строк. Это тот случай, когда система несовместима.
Это происходит, когда ряд встречается в форме эшелона строк. Это тот случай, когда система несовместима.