Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)
Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)
Видеоурок: Метод Жордана-Гаусса (метод прямоугольников)
Пример из видеоурока в рукописном виде:
Пример 2.
Запишем систему в виде:
1 | -2 | 2 | -1 | -1 | 2 | 4 |
0 | -1 | 1 | 3 | -1 | 2 | -2 |
-2 | 4 | -4 | -2 | -2 | 1 | 1 |
-1 | 1 | 0 | -1 | 1 | 1 | -2 |
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника: НЭ = СЭ — (А*В)/РЭ, где РЭ — разрешающий элемент (1), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
1 | -2 | 2 | -1 | -1 | 2 | 4 |
0 | -1 | 1 | 3 | -1 | 2 | -2 |
0 | 0 | 0 | -4 | -4 | 5 | 9 |
0 | -1 | 2 | -2 | 0 | 3 | 2 |
Разрешающий элемент равен (-1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 | 0 | 0 | -7 | 1 | -2 | 8 |
0 | 1 | -1 | -3 | 1 | -2 | 2 |
0 | 0 | 0 | -4 | -4 | 5 | 9 |
0 | 0 | 1 | -5 | 1 | 1 | 4 |
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 | 0 | 0 | -7 | 1 | -2 | 8 |
0 | 1 | 0 | -8 | 2 | -1 | 6 |
0 | 0 | 1 | -5 | 1 | 1 | 4 |
0 | 0 | 0 | -4 | -4 | 5 | 9 |
Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 | 0 | 0 | 0 | 8 | -10.75 | -7.75 |
0 | 1 | 0 | 0 | 10 | -11 | -12 |
0 | 0 | 1 | 0 | 6 | -5.25 | -7.25 |
0 | 0 | 0 | 1 | 1 | -1.25 | -2.25 |
Теперь исходную систему можно записать как:
x1 = -7.75 — 8×5 — 10.75×6
x2 = -12 — 10×5 — 11×6
x3 = -7.25 — 6×5 — 5.25×6
x4 = -2.25 — x5 — 1.25×6
Необходимо переменные x5,x6 принять в качестве свободных переменных и через них выразить остальные переменные.
Приравняем переменные x5,x6 к 0
x1 = -7.75
x2 = -12
x3 = -7.25
x4 = -2.25
Среди базисных переменных есть отрицательные значения. Следовательно, данное решение не опорное.
Тема 3. Решение систем линейных уравнений методом Жордана – Гаусса.
Общим решением системы m линейных уравнений с n неизвестными называется
решение, в котором свободные неизвестные произвольны
!решение, в котором базисные неизвестные линейно выражаются через свободные неизвестные
сумма частных решений этой системы
сумма частных и базисных решений этой системы
Частным решением системы m линейных уравнений с n неизвестными называется
!решение, полученное из общего решения, если свободным неизвестным придать произвольные значения
решение, состоящее только из свободных неизвестных
решение, в котором все компоненты – дробные
частное от деления общего решения на базисное
При отыскании общего решения системы m линейных уравнений с n неизвестными методом Жордана – Гаусса в качестве разрешающего элемента выбирается
элемент
таблицы, удовлетворяющий условию 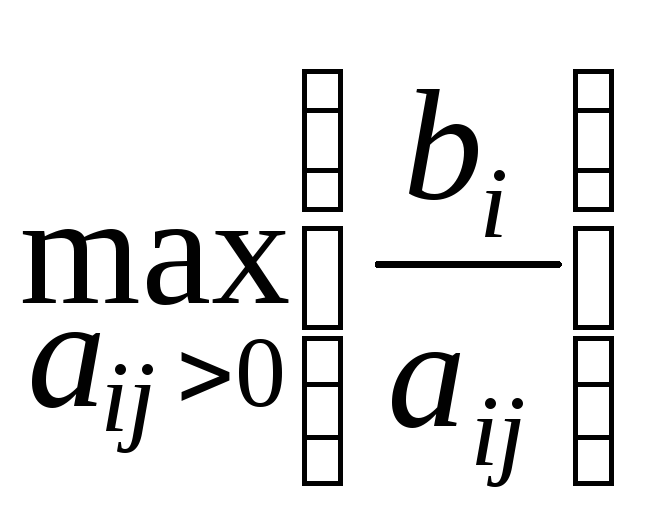
элемент
таблицы, удовлетворяющий условию 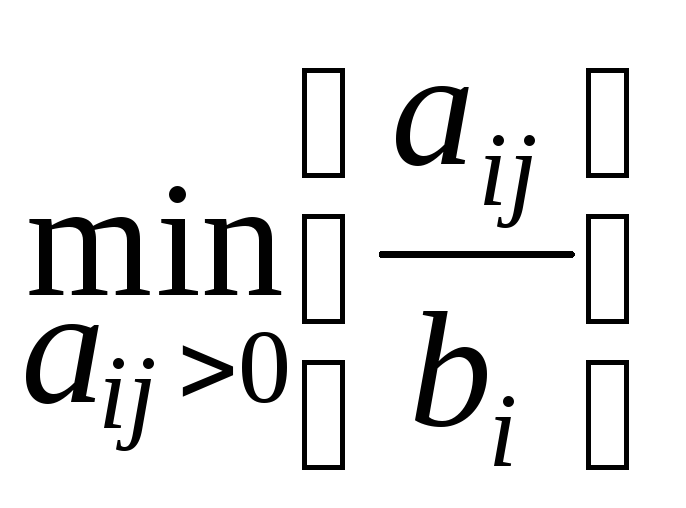
!любой отличный от нуля элемент таблицы, кроме элементов столбца свободных членов и контрольного столбца
любой элемент таблицы
Система m линейных уравнений с n неизвестными не имеет решений, если на некоторой итерации
все элементы какой либо строки таблицы Жордана – Гаусса равны нулю
две какие – либо строки таблицы Жордана – Гаусса одинаковы
какой
– либо из свободных членов 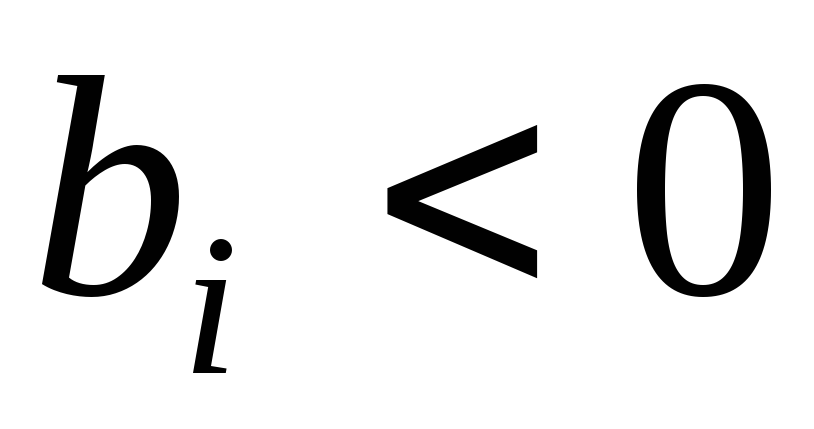
!все элементы какой – либо строки таблицы Жордана – Гаусса, кроме свободного члена, равны нулю
Базисным решением системы m линейных уравнений с n неизвестными называется
!решение, полученное из общего решения системы, в котором свободные неизвестные равны 0
решение, в котором базисные неизвестные произвольны
решение, в котором свободные неизвестные произвольны
система, приведенная к единичному базису
Если r – число базисных неизвестных, а n – общее число неизвестных в произвольной системе m линейных уравнений, то система имеет бесконечное множество решений при
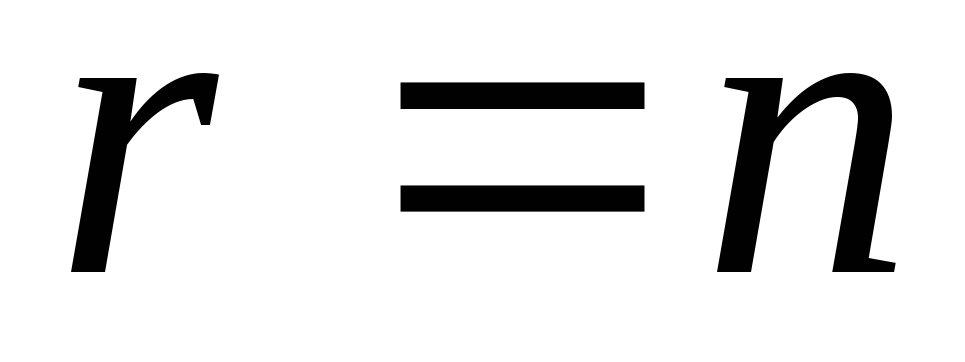
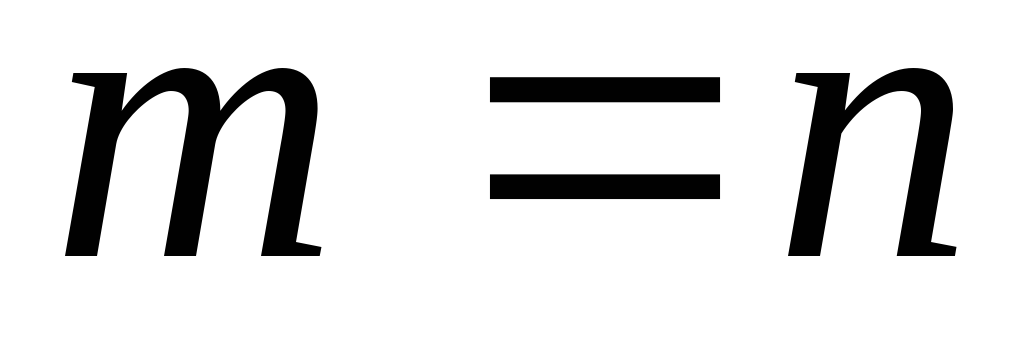
!
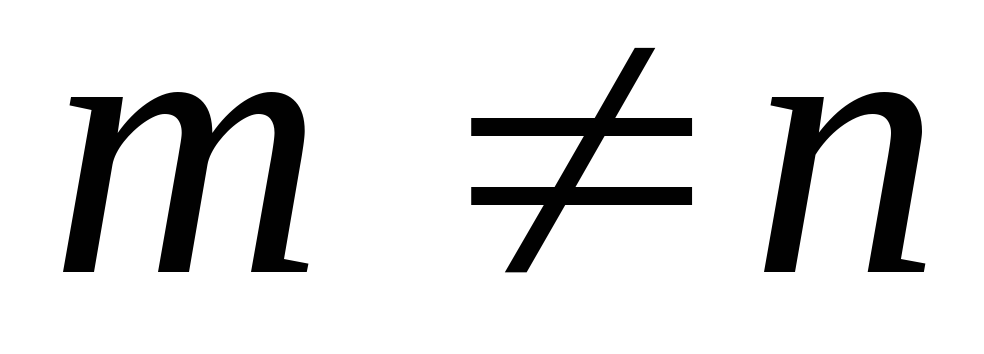
Если
дано матричное уравнение 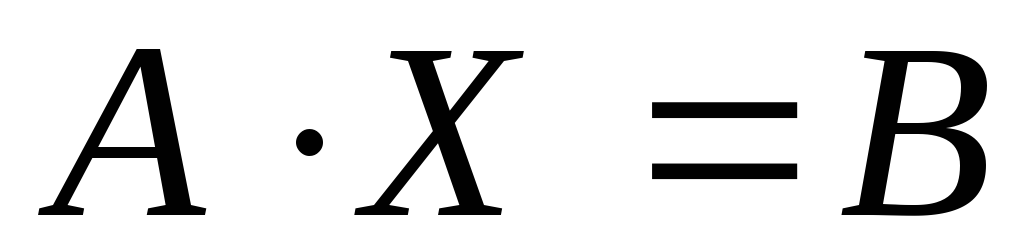 ,
то его решение определяется по формуле
,
то его решение определяется по формуле
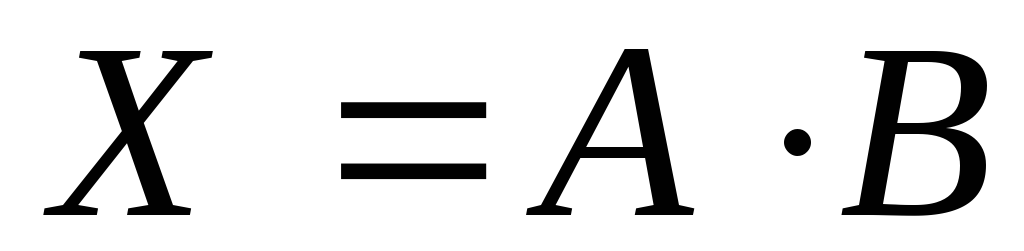
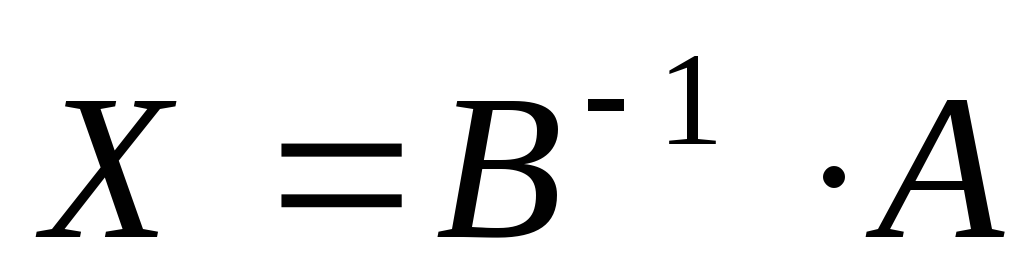

!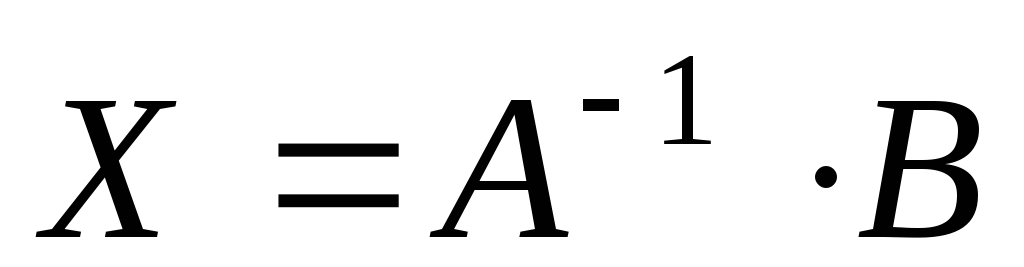
Если
в таблице Жордана – Гаусса 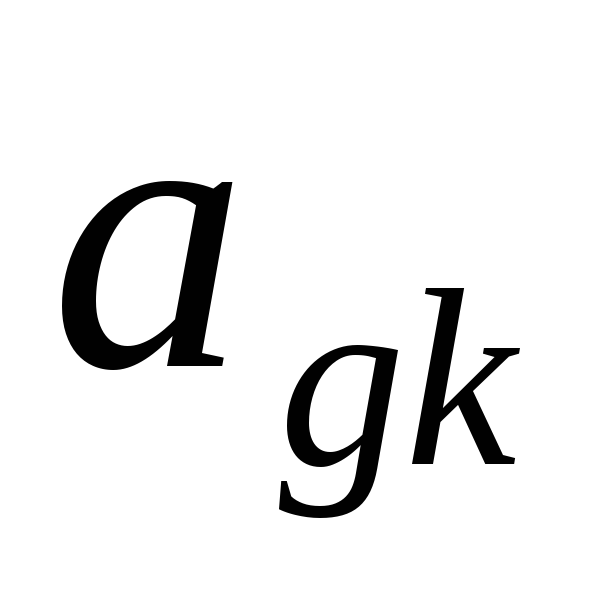 — разрешающий элемент, то элемент
— разрешающий элемент, то элемент  находится по формуле (правило
прямоугольника)
находится по формуле (правило
прямоугольника)
!
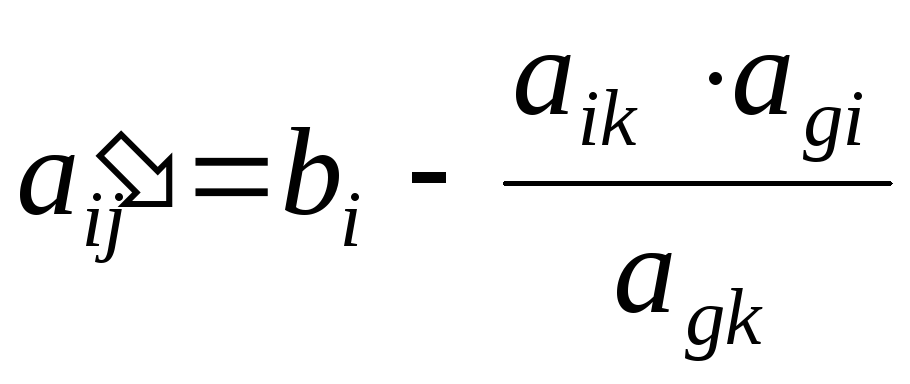
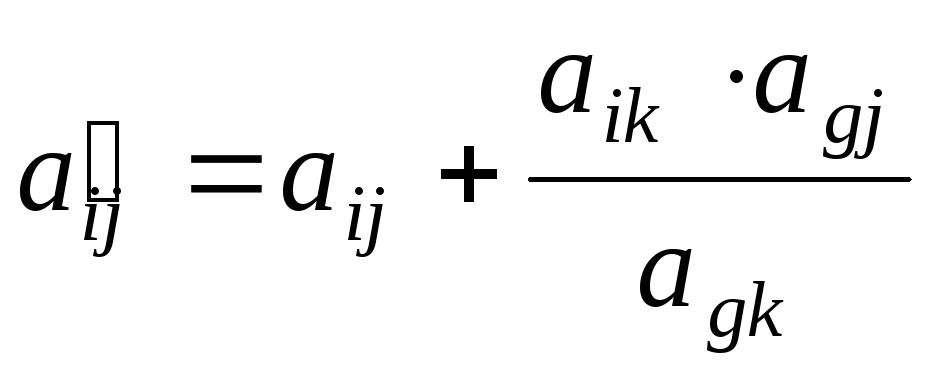
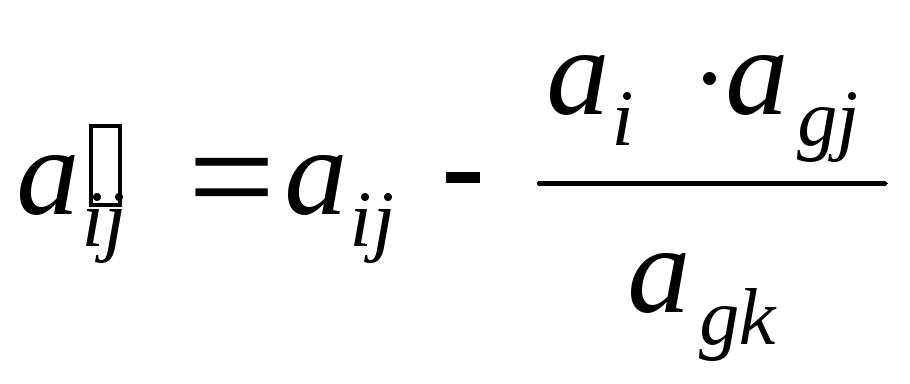
Итерацией в методе Жордана — Гаусса называется
расчет одной строки в таблице Жордана – Гаусса
!расчет элементов одной таблицы Жордана – Гаусса
вычисление элементов одного столбца в таблице Жордана – Гаусса
вычисление элементов вводимой строки
Метод Жордана – Гаусса это
нахождение производной
нахождение разрешающего уравнения
!последовательное исключение неизвестных
нахождение разрешающего элемента
Если в таблице Жордана – Гаусса имеются две одинаковые строки, то
их нужно сложить
их нужно перемножить
одну из них сложить со строкой, элементы которой отличаются
!одну из них можно вычеркнуть
Единичным называется столбец таблицы Жордана – Гаусса, который состоит из
единиц
!одной единицы и остальных 0
двух единиц и нулей
нулей
Переменная называется базисной, если в таблице Жордана – Гаусса столбец коэффициентов перед ней является
нулевым
отрицательным
!единичным
положительным
Если в таблице Жордана – Гаусса имеются две пропорциональные строки, то
одну можно вычесть из другой
их нужно сложить
их нужно перемножить
!одну из них нужно вычеркнуть
Переменная называется свободной, если в таблице Жордана – Гаусса
столбец коэффициентов при ней нулевой
!она не входит в столбец — базис
столбец коэффициентов при ней состоит из единиц
она входит в столбец — базис
Система
m линейных уравнений с n
неизвестными называется однородной,
если свободные члены 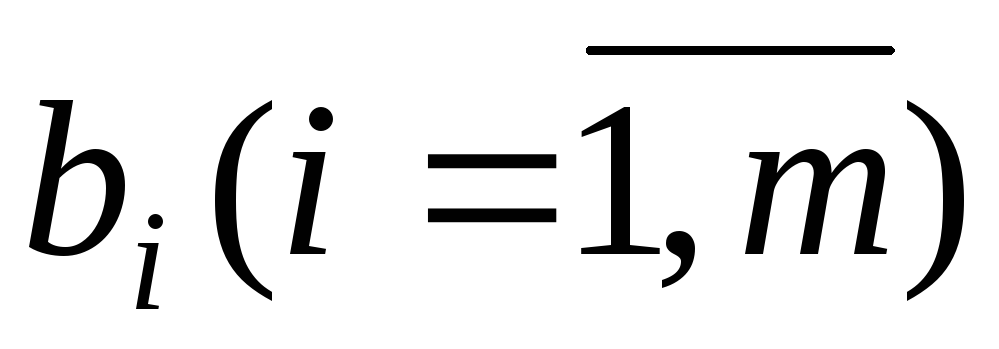
!равны 0
положительны
отрицательны
принимают любые значения
Матрица
коэффициентов при неизвестных системы
m линейных уравнений с n
неизвестными 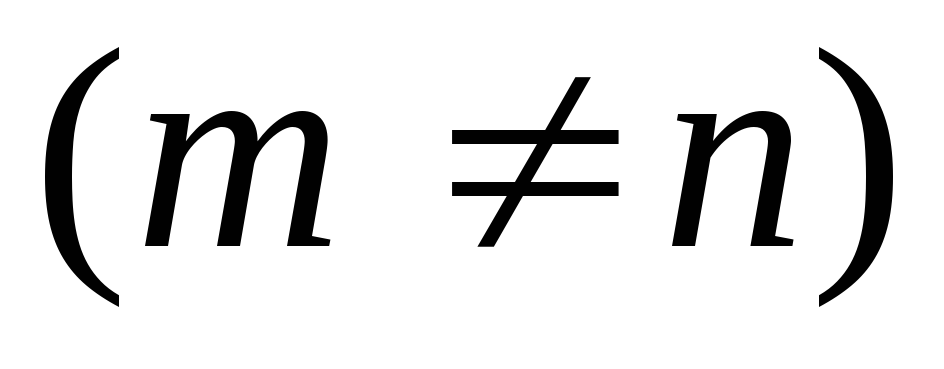 является
является
квадратной
диагональной
!прямоугольной
матрицей столбцом
Число частных решений равно
числу базисных решений
числу опорных решений
числу допустимых решений
!бесчисленному множеству решений
Переход от одного базисного решения к другому осуществляется путем
!проведения еще одной итерации метода Жордана – Гаусса
выбора разрешающей строки
выбора разрешающего столбца
проведения симплексных преобразований
Элементы вводимой строки в таблице Жордана – Гаусса находятся
умножением элементов разрешающей строки предыдущей таблицы на (-1)
делением элементов разрешающей строки предыдущей таблицы на (-1)
!делением элементов разрешающей строки предыдущей таблицы на разрешающей элемент
умножением элементов разрешающей строки предыдущей таблицы на разрешающий элемент
Число базисных решений произвольной системы m линейных уравнений с n неизвестными определяется
!формулой 
числом уравнений
числом неизвестных
размерностью матрицы системы
Решение системы m линейных уравнений с n неизвестными, в котором базисные неизвестные линейно выражаются через свободные, называется
частным
допустимым
!общим
единственным
Систему можно решить матричным способом, если
число уравнений не равно числу неизвестных
!число уравнений равно числу неизвестных
число уравнений меньше числа неизвестных
число уравнений больше числа неизвестных
Решение, полученное из общего решения, если свободным неизвестным придать произвольные значения, называется
допустимым
опорным
!частным
единственным
Значение базисных переменных в таблице Жордана – Гаусса находится в
вводимой строке
!столбце 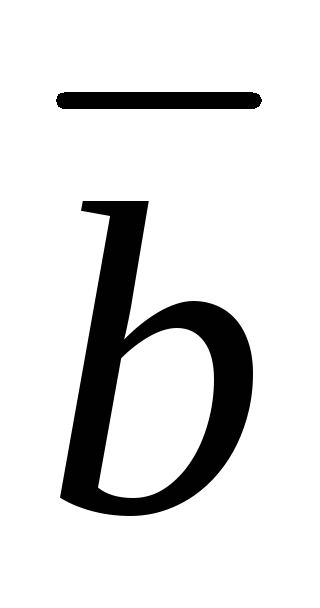
контрольном столбце
в разрешающей строке
В контрольный столбец 1-й таблицы Жордана – Гаусса записывается
сумма элементов по каждой строке, включая свободные члены
!сумма коэффициентов при неизвестных по каждой строке
разность
коэффициентов при неизвестных 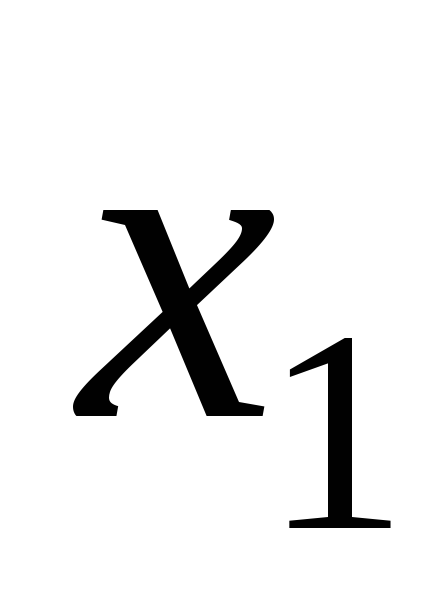 и
и 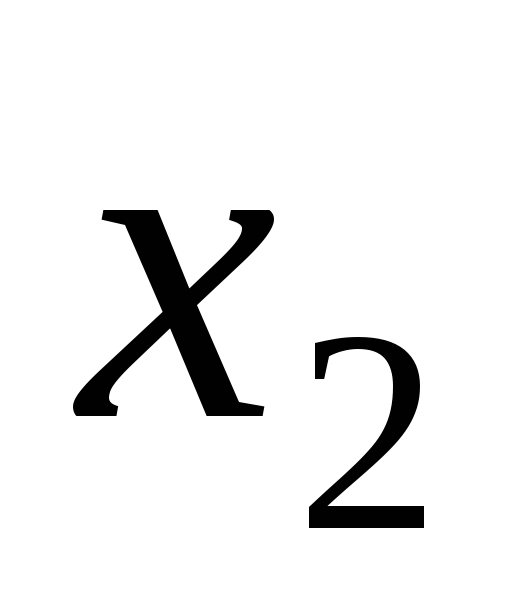
произведение коэффициентов при неизвестных по каждой строке
Матрица коэффициентов при неизвестных при решении системы n линейных уравнений с n неизвестными матричным способом является
прямоугольной
!невырожденной
диагональной
вырожденной
При решении системы m линейных уравнений с n неизвестными методом Жордана – Гаусса контроль вычислений в таблицах Гаусса, начиная со 2 –ой, проводится путем
сравнения
элементов столбца 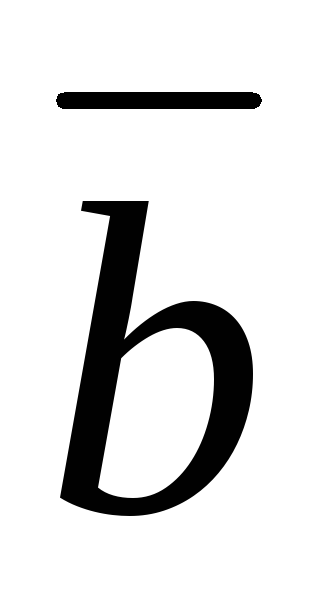 с элементами контрольного столбца
с элементами контрольного столбца
сравнения сумм коэффициентов при неизвестных с элементами контрольного столбца
нахождение
разности элементов столбца 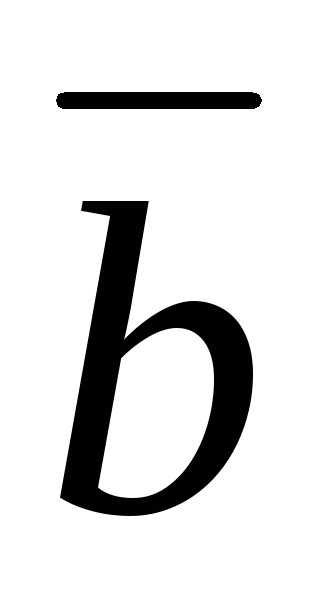 и контрольного столбца
и контрольного столбца
!сравнения суммы элементов по каждой строке, включая свободные члены, с элементами контрольного столбца
В
столбце 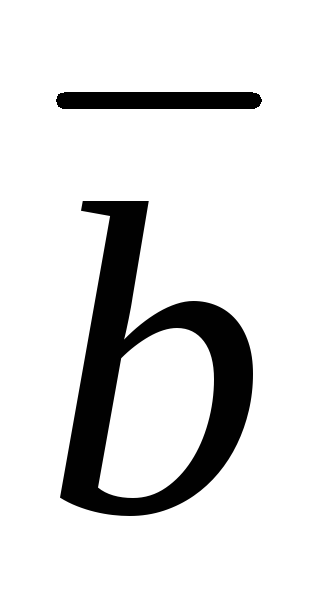 таблицы Жордана – Гаусса находятся
значения неизвестных
таблицы Жордана – Гаусса находятся
значения неизвестных
свободных
искусственных
!базисных
отрицательных
Решение системы линейных уравнений с n неизвестными находится с применением обратной матрицы, если число уравнений равно
!n
m
n+m
n-m
Решение,
матричного уравнения находится по
формуле 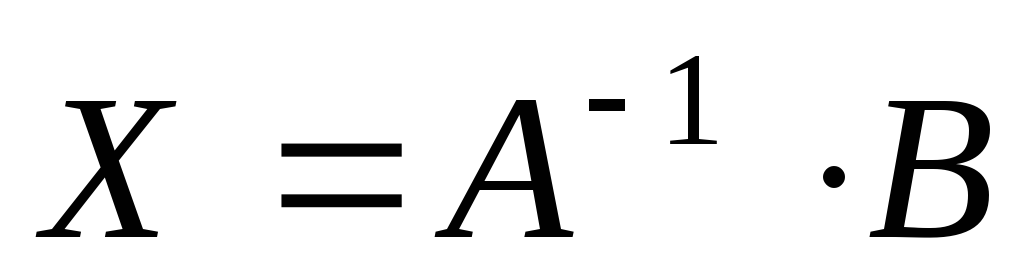 ,
если оно имеет вид
,
если оно имеет вид
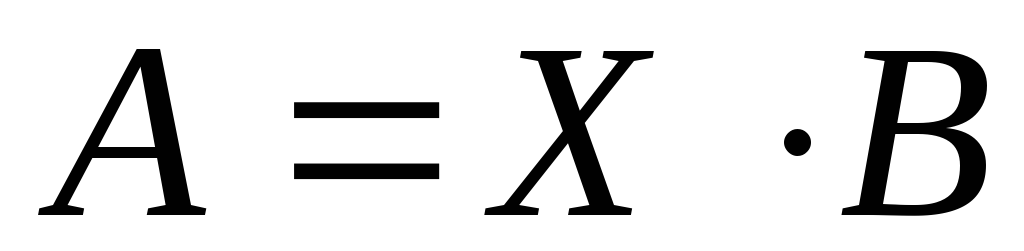
!

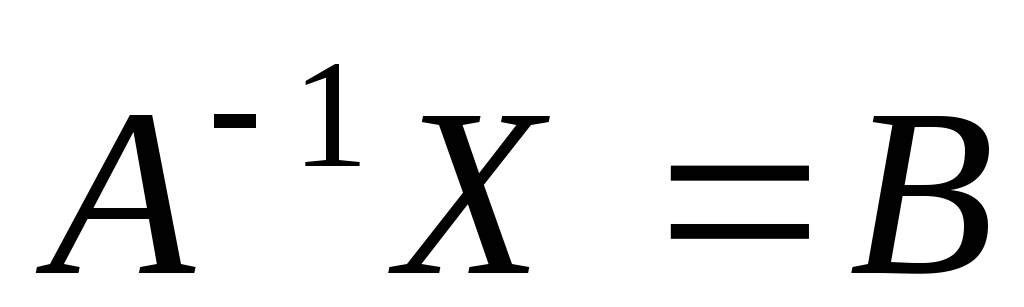
Решение, полученное из общего решения, если свободным неизвестным придать нулевые значения называется
частным
единственным
опорным
!базисным
Если в таблице Жордана – Гаусса все элементы какой – либо строки, кроме свободного члена, равны нулю, то система m линейных уравнений с n неизвестными
имеет единственное решение
!не имеет решений
имеет бесчисленное множество решений
имеет m решений
Если
в системе m линейных
уравнений с n неизвестными
r — число базисных неизвестных
и при этом  ,
то система имеет
,
то система имеет
единственное решение
r решений
m решений
!бесчисленное множество решений
Если при решении системы m линейных уравнений c n неизвестными в разрешающей строке таблицы Жордана – Гаусса находится нуль, то столбец, содержащий этот нуль
!переносится в следующую таблицу без изменения
рассчитывается по правилу прямоугольника
становится единичным
становится нулевым
Если при решении системы m линейных уравнений c n неизвестными в разрешающем столбце таблицы Жордана – Гаусса имеется нуль, то строка, содержащая этот нуль
в следующей таблице состоит из нулей
!переносится в следующую таблицу без изменения
рассчитывается по правилу прямоугольника
в следующую таблицу переносится с обратными знаками
Если
в базисном решении системы линейных
уравнений 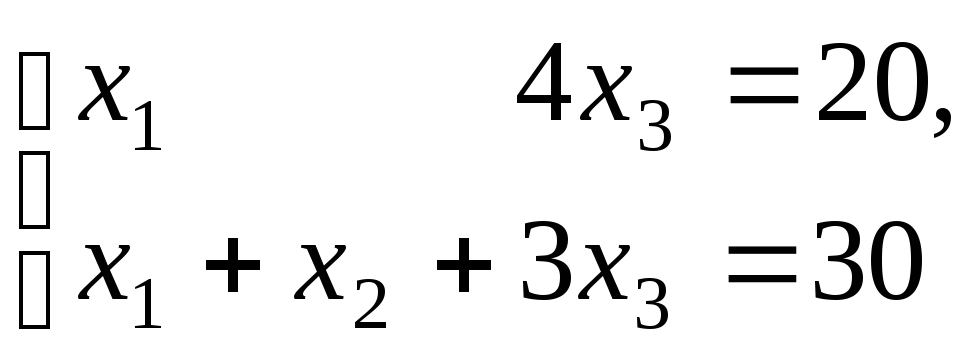
 ,
, 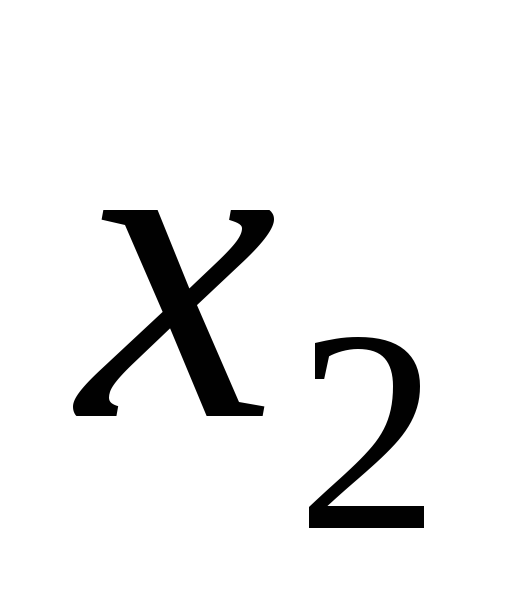 − базисные переменные, то
− базисные переменные, то  равно
равно
35
3
!30
20
Если
в базисном решении системы линейных
уравнений 
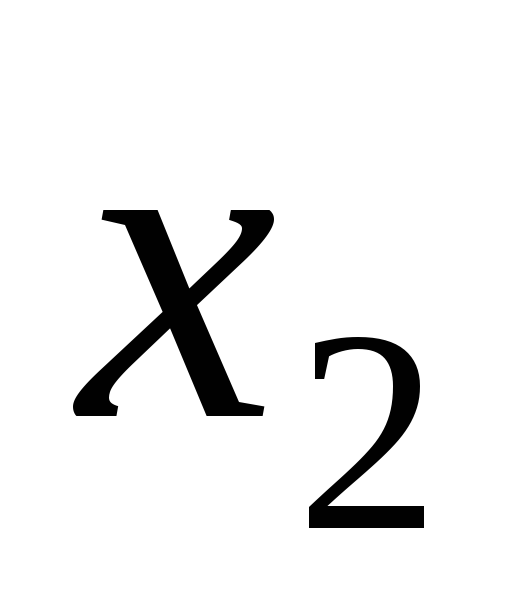 ,
, 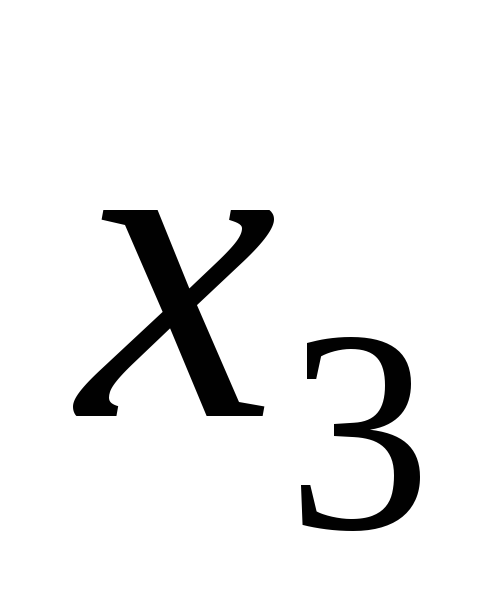 − базисные переменные, то
− базисные переменные, то 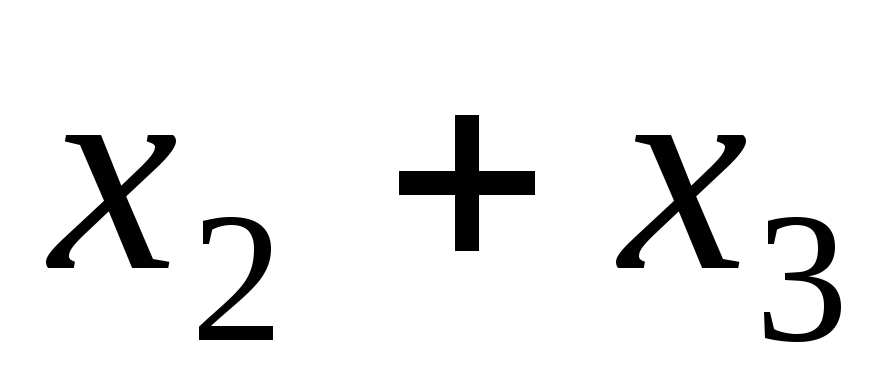 равно
равно
!16
20
2
4
Если
в системе m линейных
уравнений с n неизвестными 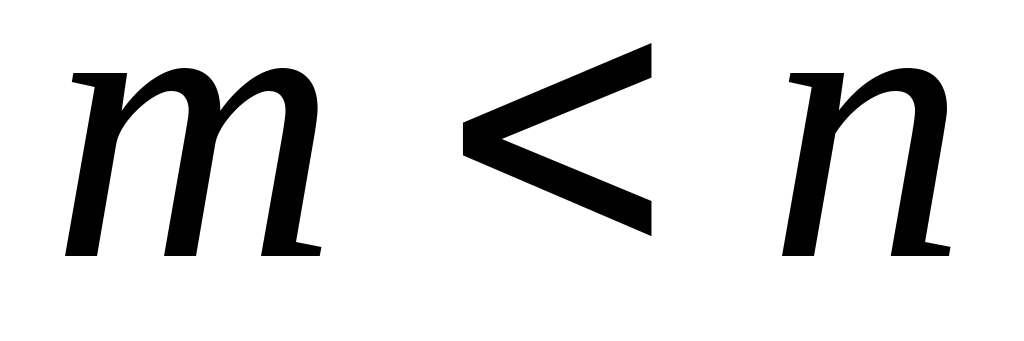 ,
то система называется
,
то система называется
переопределенной
однородной
несовместной
!неопределенной
Если
в системе m линейных
уравнений с n неизвестными 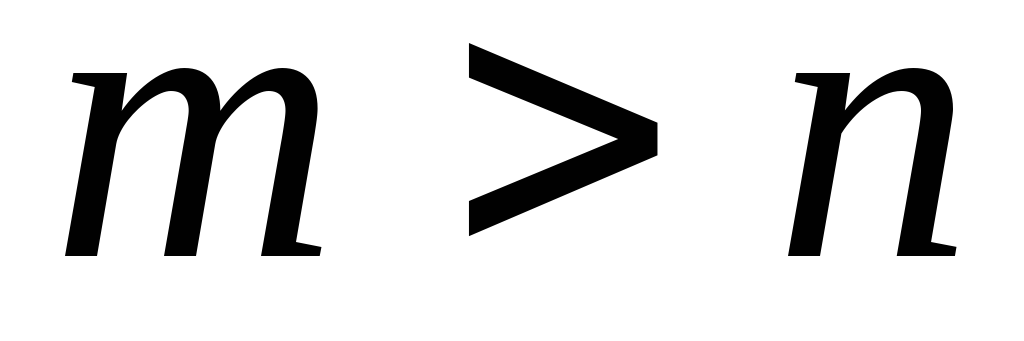 ,
то система называется
,
то система называется
!переопределенной
несовместной
однородной
неопределенной
В системе m линейных уравнений с n неизвестными число базисных решений равно
только m
только n
n—m
!
Если
в базисном решении системы линейных
уравнений 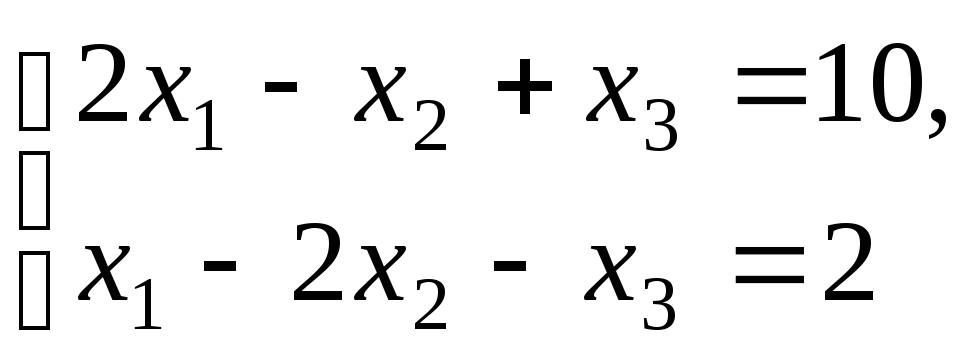
 ,
, 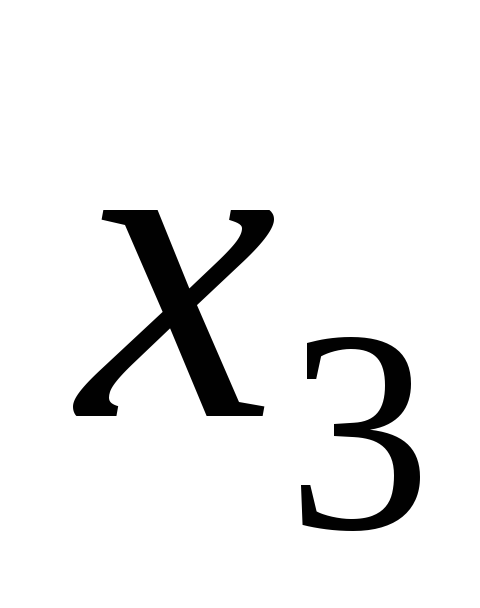 − базисные переменные, то
− базисные переменные, то  равно
равно
8
1
!6
0
Если
в базисном решении системы линейных
уравнений 
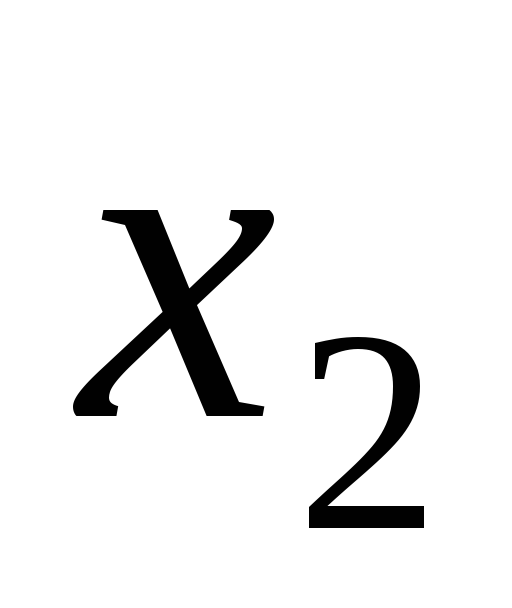 ,
, 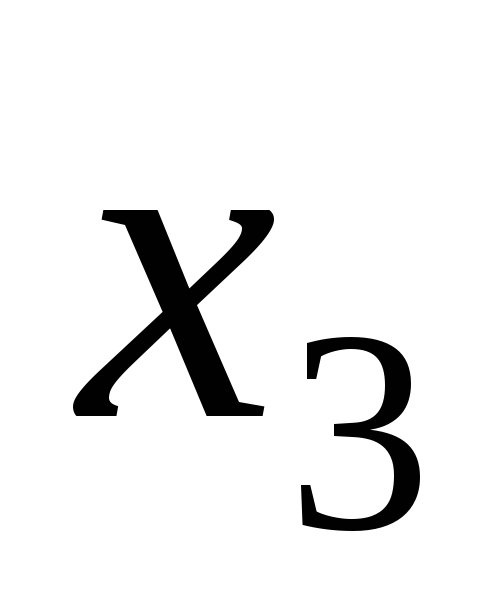 − базисные переменные, то
− базисные переменные, то 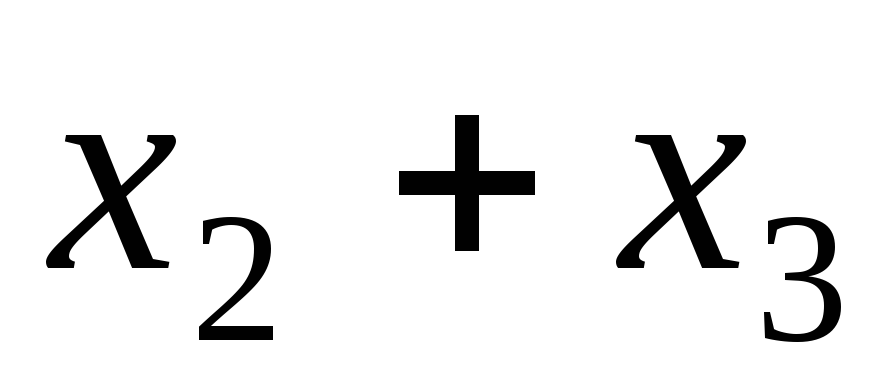 равно
равно
!6
8
0
2
Метод Жордана — Гаусса — Студопедия
Метод Жордана-Гаусса опирается на следующее свойство систем уравнений: если к какому-либо уравнению системы прибавить любое другое уравнение системы, умноженное на некоторое число, то получится система, равносильная исходной системе уравнений. Если такое преобразование применить к системе несколько раз, то вновь полученная система уравнений также будет равносильна исходной системе.
С помощью элементарных преобразований исключим переменную 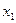 из всех уравнений, начиная со второго; затем исключим переменную
из всех уравнений, начиная со второго; затем исключим переменную 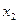 из всех уравнений, начиная с третьего, и т.д. Этот процесс называется прямым ходом и продолжается до тех пор, пока система уравнений не приобретет ступенчатого или треугольного вида. Если система совместна, то выполняется обратный ход − нахождение решений.
из всех уравнений, начиная с третьего, и т.д. Этот процесс называется прямым ходом и продолжается до тех пор, пока система уравнений не приобретет ступенчатого или треугольного вида. Если система совместна, то выполняется обратный ход − нахождение решений.
Алгоритм метода рассмотрим на конкретных примерах.
Случай 1.Решить систему уравнений:
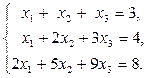
Решение. Запишем расширенную матрицу системы
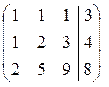
и выполним элементарные преобразования ее строк. Для этого умножим первую строку на (−1) и прибавим ко второй строке; затем умножим первую строку на (−2) и прибавим к третьей строке. В результате мы исключим переменную  из всех уравнений, кроме первого. Получим
из всех уравнений, кроме первого. Получим

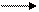

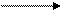
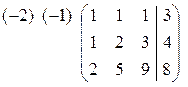 ~
~ 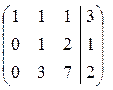 .
.
Исключим переменную  из третьего уравнения. Умножим вторую строку полученной матрицы на (−3) и прибавим к третьей строке:
из третьего уравнения. Умножим вторую строку полученной матрицы на (−3) и прибавим к третьей строке:

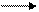
 ~
~ 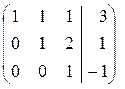
Прямой ход закончен. 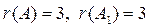 . Так как
. Так как 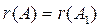 , то система уравнений совместна. Ранг матрицы системы
, то система уравнений совместна. Ранг матрицы системы 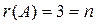 , поэтому система имеет единственное решение.
, поэтому система имеет единственное решение.
Выполним обратный ход:






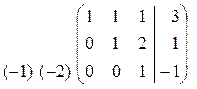 ~
~ 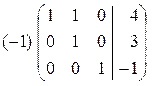 ~
~ 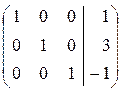 .
.
Последней матрице соответствует система уравнений 
Таким образом, (1; 3;−1) − единственное решение системы уравнений.
Случай 2. Решить систему уравнений:
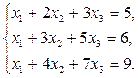
Решение. Запишем расширенную матрицу системы и выполним элементарные преобразования строк как в примере 1.





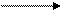
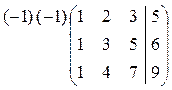 ~
~ 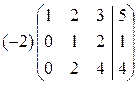 ~
~ 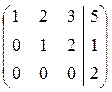









 A ~
A ~ 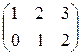 , A1 ~
, A1 ~  .
.
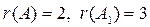 . Итак,
. Итак, 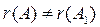 , значит, данная система уравнений несовместна.
, значит, данная система уравнений несовместна.
Случай 3. Решить систему уравнений:
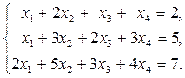
Решение. Запишем расширенную матрицу системы и выполним элементарные преобразования строк как в примере 1.






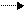



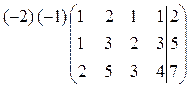 ~
~ 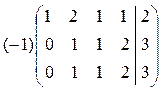 ~
~ 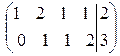 .
.
Система уравнений совместна, так как 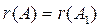 =2. Так как
=2. Так как 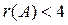 , то система неопределенная. Определитель, составленный из коэффициентов при переменных
, то система неопределенная. Определитель, составленный из коэффициентов при переменных 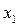 и
и 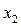 ,
,
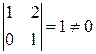 .
.
Поэтому переменные х1 и х2 будем считать основными, или базисными, а х3 и х4 − свободными.
Выполним обратный ход:


 ~
~ 
Запишем систему уравнений, соответствующую последней матрице:
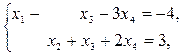 или
или 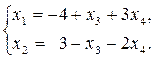
Выражение основных переменных через свободные называется общим решением системы уравнений. Придавая свободным переменным произвольные числовые значения, получим частное решение системы уравнений.
Система имеет бесконечное множество решений
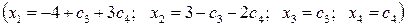 .
.
 Выводы:
Выводы:
Если 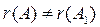 , то система уравнений несовместна.
, то система уравнений несовместна.
Если 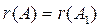 , то система уравнений совместна.
, то система уравнений совместна.
Если 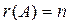 , то система уравнений имеет единственное решение.
, то система уравнений имеет единственное решение.
Если 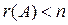 , тосистема уравнений имеет бесконечное множество
, тосистема уравнений имеет бесконечное множество
решений.
1.Решение систем линейных уравнений методом гаусса – жордана
1.1. Основные понятия
Система m линейных уравнений с n неизвестными имеет следующий вид:

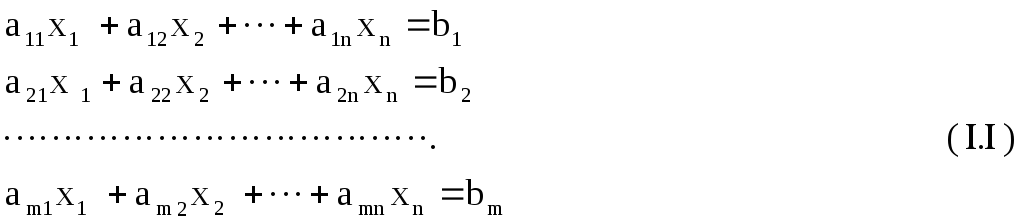
Здесь хj ( j=1, n ) – переменные ( или неизвестные) системы, аij ( i =1,m; j = 1,n ) – коэффициенты при переменных, вi ( i =1,m ) – свободные члены.
Решением системы ( І.І) называется всякий набор значений переменных х1, х2, …, хn, при котором все уравнения превращаются в тождества. Система называется совместной, если она имеет хотя бы одно решение, и несовместной – в противном случае.
Например, система

совместна, так как она имеет, в частности, такое решение:
х1 =
1; х2 =
2; х3 = 0 .
Система же 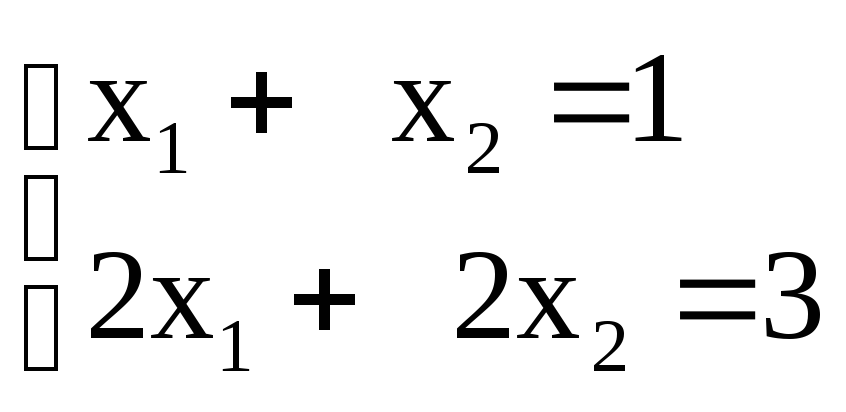
несовместна.
Две системы линейных уравнений называются равносильными, если каждое решение одной из них является решением другой, и наоборот. Если какое-либо уравнение системы умножить на постоянный множитель λ ≠ 0 , то получится система уравнений, равносильная исходной. Аналогично, если к какому-либо уравнению системы прибавить другое уравнение системы, то получится система, равносильная исходной.
Наконец если, в системе есть уравнение вида
0∙х1 + 0∙х2 + … + 0∙ хn = 0, то такое уравнение можно убрать, получив систему, равносильную исходной.
1.2. Приведение системы линейных уравнений к жордановой форме
Процесс отыскания решения системы линейных уравнений начинается с того, что система приводится к жордановой форме.
Определение. Жордановой формой системы (I.I) называется система линейных уравнений, обладающая следующими свойствами:
а) она равносильна системе (I.I)
б) в каждом уравнении жордановой формы есть такая переменная, которая входит в это уравнение с коэффициентом 1, а в остальные уравнения — с коэффициентом 0.
Так, если системе (I.I) равносильна следующая система линейных уравнений:
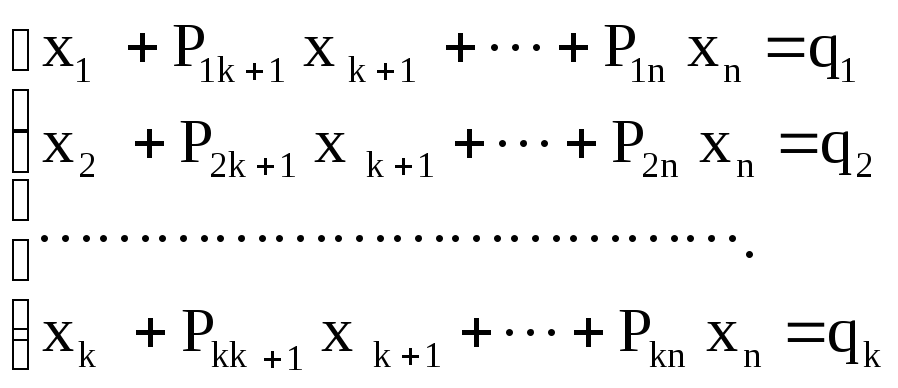 (1.2)
(1.2)
то (І.2) есть жорданова форма для (I.I). При этом переменные х1, х2,… ,хк называются базисными, остальные переменные хк+1,…, хn называются свободными. Жорданова форма всегда является совместной системой линейных уравнений. Действительно, система (І.2) имеет следующее решение:
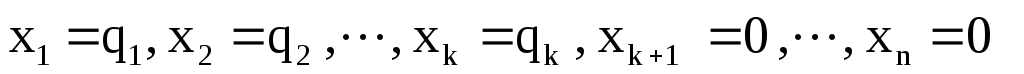 (І.3)
(І.3)
Так как система (І.2) равносильна системе ( І.І ) , то (І.3) является решением системы (І.І).
Таким образом, если для системы линейных уравнений ( І.І ) существует жорданова форма, то ( І.І ) – совместная система. Несовместная система жордановой формы не имеет.
Покажем, что любую совместную систему можно привести к жордановой форме. Это достигается методом Гаусса-Жордана, который состоит в следующем.
Рассмотрим первое уравнение системы (І.І). Выберем в нем переменную, коэффициент при которой отличен от нуля. Предположим, что а11 ≠ 0. Поделим уравнение на а11.
Получим уравнение
х1+ а12х2 + … + а1nхn = в1 (І.4)
Будем переменную х1 делать базисной в жордановой форме. Для этого ее нужно исключить из остальных уравнений системы. Чтобы исключить х1 из второго уравнения, умножим уравнение (І.4) на -а21 и сложим со вторым уравнением. Затем исключим х1 из третьего уравнения, для чего уравнение (І.4) умножим на –а31 и сложим с третьим уравнением. Аналогично переменная х1 исключается из остальных уравнений. Таким образом, взяв в качестве «ведущего» первое уравнение и проведя серию «жордановых исключений», мы получим равносильную (I.I) систему уравнений, в которой x1 входит в первое уравнение с коэффициентом 1 , а в остальные уравнения — с коэффициентом 0.
После этого выбираем в качестве ведущего второе уравнение полученной системы. В этом уравнении берем коэффициент, отличный от нуля (пусть это коэффициент при х2), делим уравнение на этот коэффициент и затем исключаем х2 из всех остальных уравнений (в том числе и из первого). Затем в качестве ведущего выбираем третье уравнение и т.д.
Если на некотором шаге возникнет уравнение вида
0∙х1 + 0∙х2 + … + 0∙ хn = 0 (І.5)
то удаляем его из системы. Если же возникнет уравнение вида
0∙х1 + 0∙х2 + … + 0∙ хn = b ≠ 0, то это свидетельствует о несовместности исходной системы ( І.І), а несовместная система к жордановой форме не приводится.
Таким образом, метод Гаусса-Жордана совместную систему линейных уравнений приводит к жордановой форме, а в случае несовместности системы обнаруживает несовместность.
Ясно,
что в жордановой
форме число уравнений не может быть
больше числа уравнений в исходной
системе. Так, если система (1.2) является
жордановой формой для системы (I.I),
то 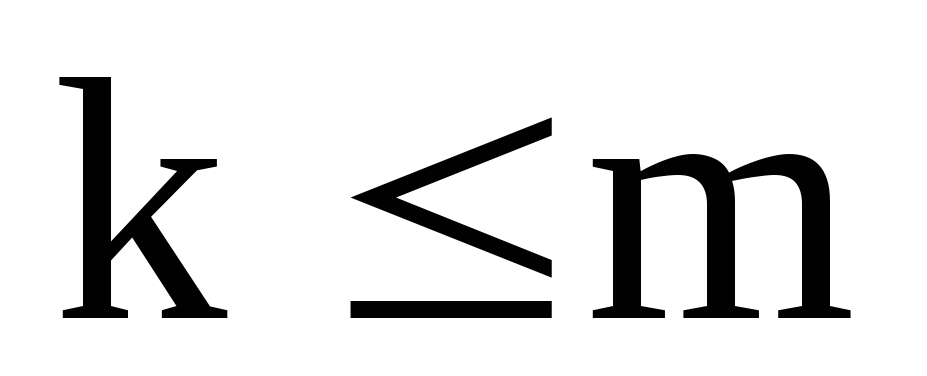 ,
причем строгое неравенство имеет место
тогда, когда на некоторых шагах жордановой
процедуры удалялись уравнения вида
(1.5).
,
причем строгое неравенство имеет место
тогда, когда на некоторых шагах жордановой
процедуры удалялись уравнения вида
(1.5).
Очевидно, одна и та же система может иметь много различных жордановых форм.
Пример. Привести к жордановой форме
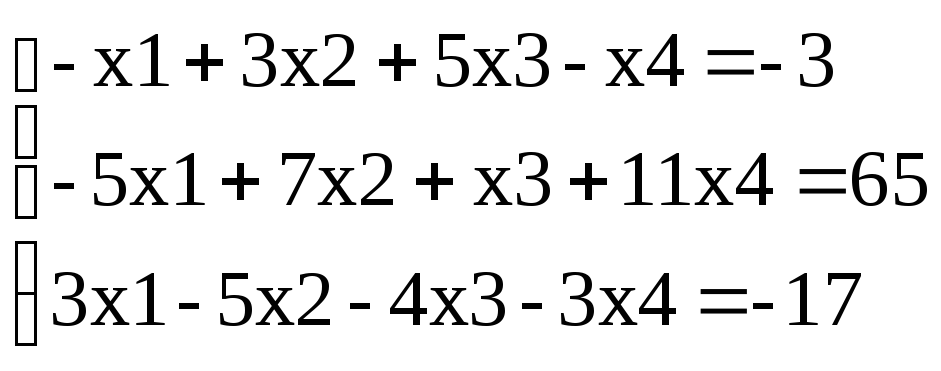
Выберем в качестве ведущего первое уравнение, а в качестве базисной переменной — переменную х1. Поделим первое уравнение на (-1) (коэффициент при х1), получим:
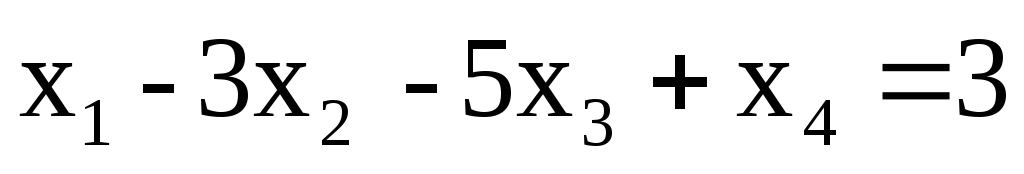

Умножим это уравнение на (+5) и прибавим ко второму уравнению, затем умножим его на (-3) и прибавим к третьему уравнению.
Получим систему:
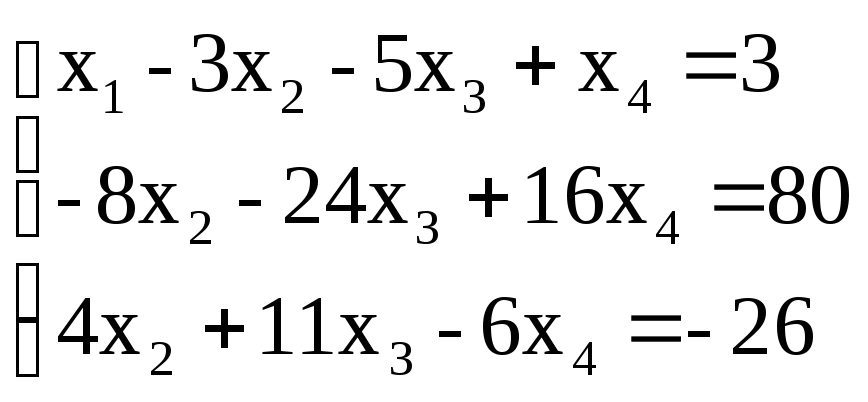
Теперь
сделаем ведущим второе уравнение, а
базисной переменной — переменную 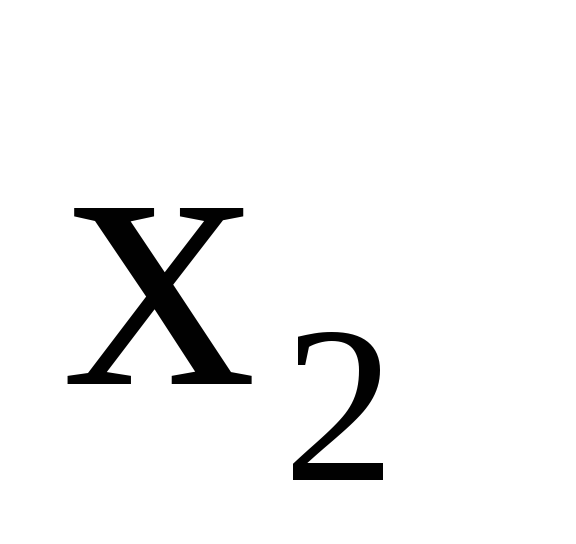 .
Поделив второе уравнение на (-8) и исключив
.
Поделив второе уравнение на (-8) и исключив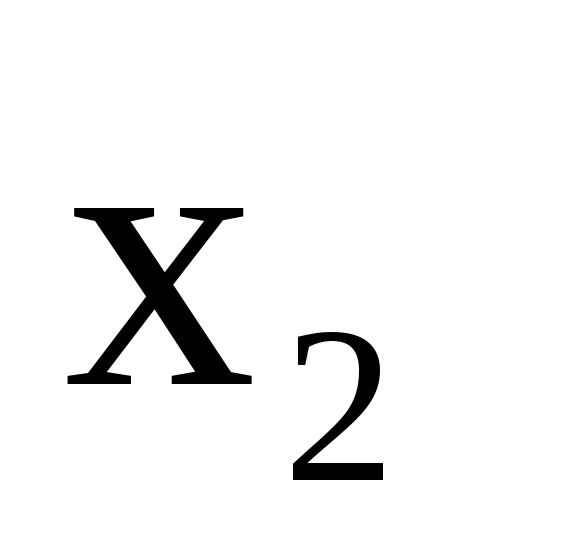 из
первого и третьего уравнений, получим
систему:
из
первого и третьего уравнений, получим
систему:
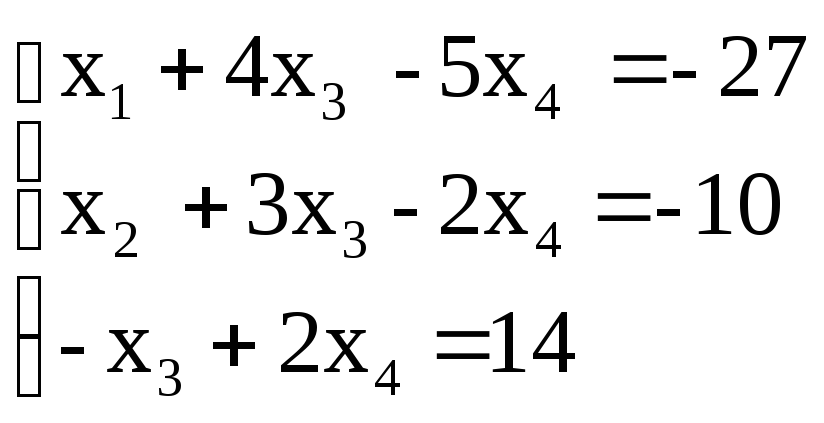
Наконец,
в третьем уравнении выбираем в качестве
базисной переменную .
Поделим это уравнение на (-1) и исключим
.
Поделим это уравнение на (-1) и исключим из остальных уравнений. Получим жорданову
форму:
из остальных уравнений. Получим жорданову
форму:
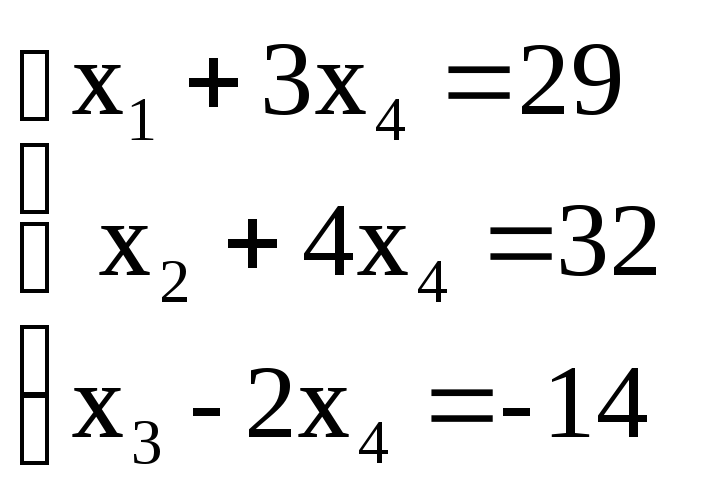
Переменные 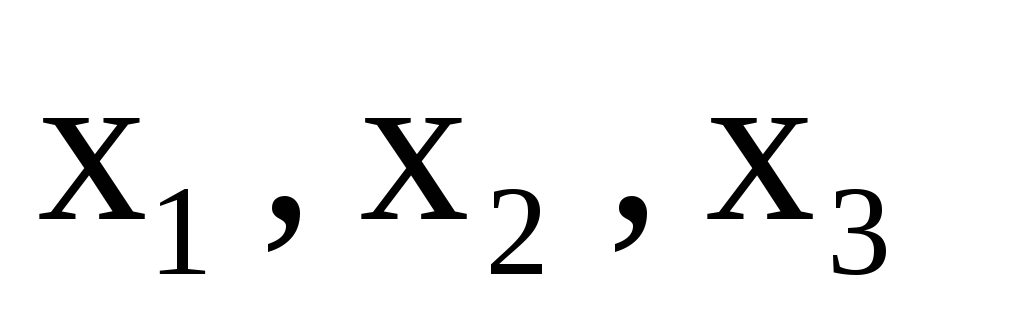 являются
базисными, переменная
являются
базисными, переменная —
свободной.
—
свободной.
Метод Гаусса-Жордана_методичка
Березнёва Т. Д.
Тема 7
«СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
МЕТОД ГАУССА – ЖОРДАНА.»
(Учебная дисциплина “Введение в линейную алгебру и аналитическую геометрию”)
СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
МЕТОД ГАУССА – ЖОРДАНА.
Основные понятия
Уравнение с n переменными называется линейным, если все переменные (x1,x2, …xn) входят в него в степени 1. Общий вид такого уравнения формально записывается следующим образом:
a1x1 + a2x2 + … ajxj + … anxn = b, (*)
или

 = b.
= b.
Величины aj, j = 1,…,n, и b являются известными (заданными). Величины aj называются коэффициентами при переменных (при неизвестных), а b — свободным членом.
Решением линейного
уравнения (*) называется упорядоченный набор ( ,
,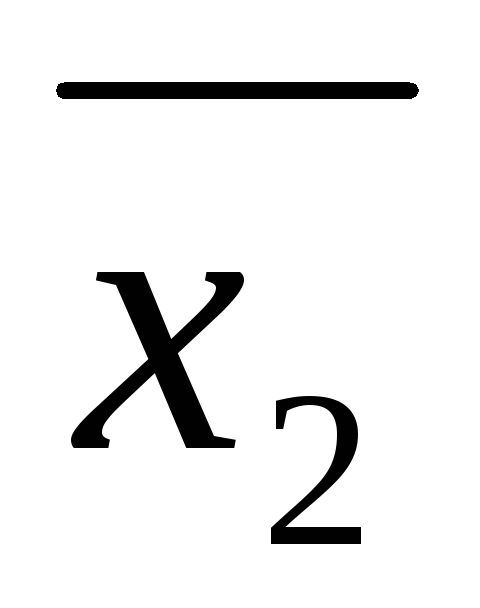 ,…,
,…,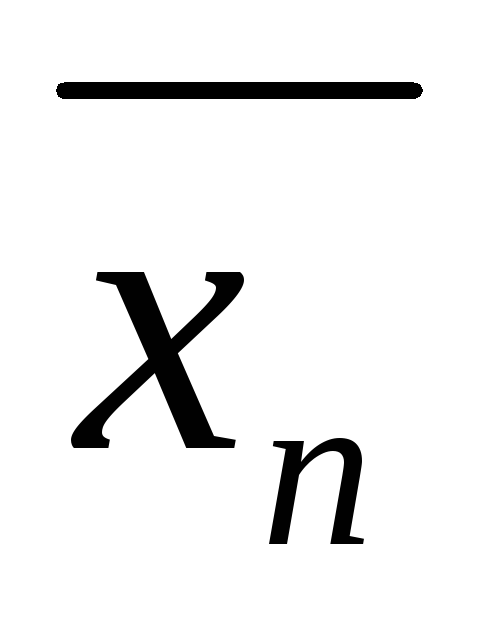 )
значений переменных, который при
подстановке в уравнение (т.е. при замене xj на
)
значений переменных, который при
подстановке в уравнение (т.е. при замене xj на 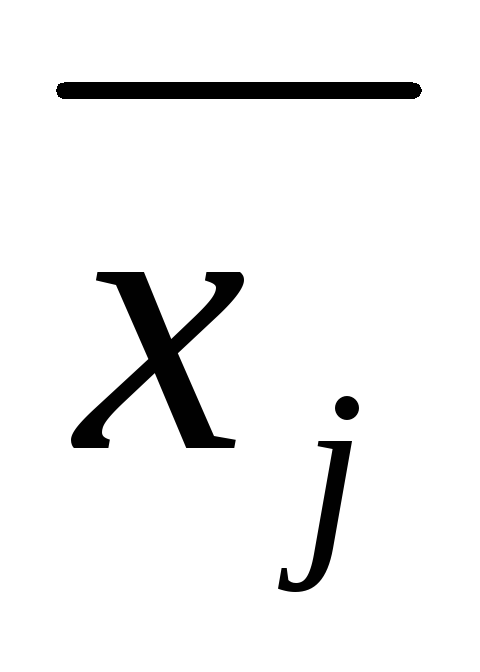 при всех j от 1до n обращает его в тождество. Подчеркнем,
что решение уравнения с n
переменными всегда есть набор из n
чисел и каждый такой набор из n
чисел представляет собой одно решение. Очевидно, что если хотя бы один
коэффициент при переменных не равен 0,
то уравнение (*) имеет решение. В противном
случае решение существует только при
b
= 0, и это все произвольные наборы из n
чисел.
при всех j от 1до n обращает его в тождество. Подчеркнем,
что решение уравнения с n
переменными всегда есть набор из n
чисел и каждый такой набор из n
чисел представляет собой одно решение. Очевидно, что если хотя бы один
коэффициент при переменных не равен 0,
то уравнение (*) имеет решение. В противном
случае решение существует только при
b
= 0, и это все произвольные наборы из n
чисел.
Рассмотрим одновременно m уравнений вида (*), т.е. систему m линейных алгебраических уравнений с n переменными. Пусть каждое i — е уравнение, i = 1,2,…,m, задается коэффициентами при переменных ai1, ai2, …, ain и свободным членом bi, т.е. имеет вид
ai1x1 + ai2 x2 + … + aij xj + … + ain xn = bi.
Тогда в общем виде система m линейных алгебраических уравнений с n переменными может быть записана в виде:
a11x1 + a12 x2 + … + a1j xj + … + a1n xn = b1
a21x1 + a22 x2 + … + a2j xj + … + a2n xn = b2
………………………………………………………………………………
ai1x1 + ai2 x2 + … + aij xj + … + ain xn = bi (1)
…………………………………………………
am1x1 + am2 x2 + … + amj xj + … + amn xn = bm
или, что то же самое,
 = bi, i = 1,…,m.
= bi, i = 1,…,m.
Если все свободные члены равны нулю, то система (1) называется однородной, т.е. имеет вид
 =
0, i = 1,…,m, (10)
=
0, i = 1,…,m, (10)
в противном случае — неоднородной. Система (10) является частным случает общей системы (1).
Решением системы
уравнений (1) называется упорядоченный набор ( ,
,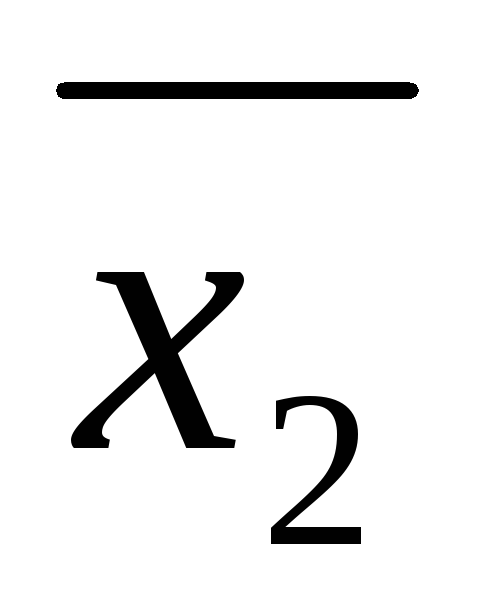 ,…,
,…,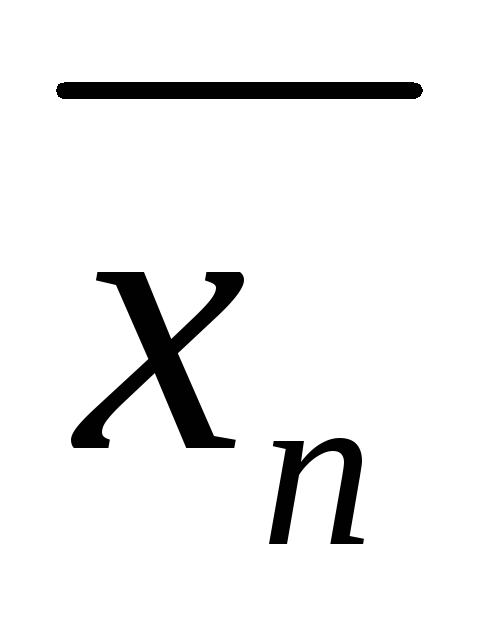 )
значений переменных, который при
подстановке в уравнения системы (1)
(т.е. при замене xj на
)
значений переменных, который при
подстановке в уравнения системы (1)
(т.е. при замене xj на 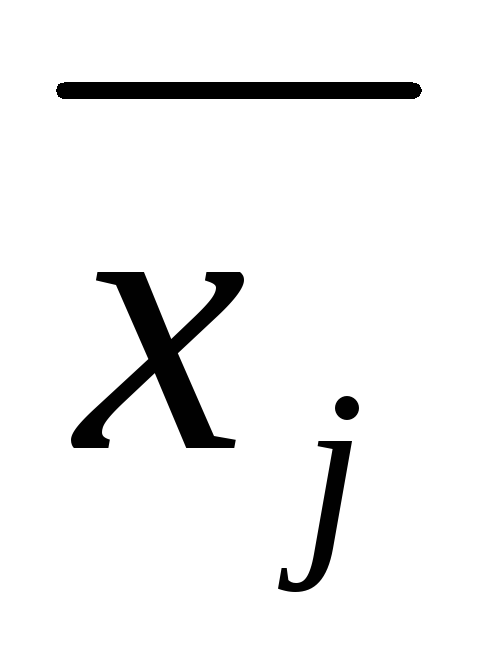 , j
= 1,…,n) все эти уравнения обращает в тождества,
т.е.
, j
= 1,…,n) все эти уравнения обращает в тождества,
т.е. 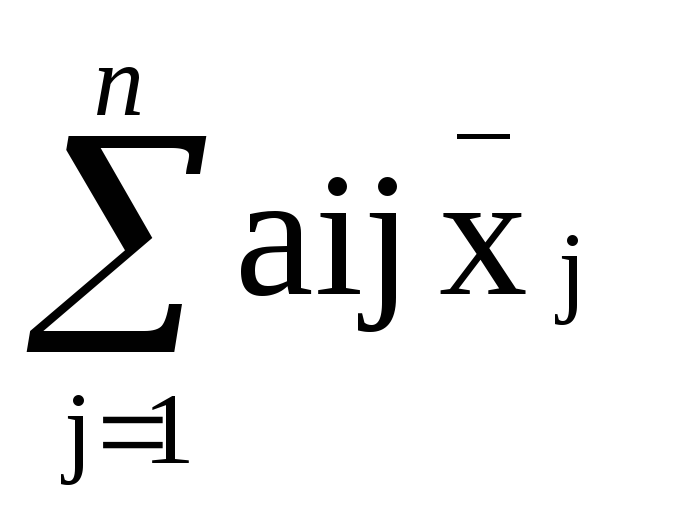 =
bi при всех i
= 1,…,m.
=
bi при всех i
= 1,…,m.
Система уравнений (1) называется совместной, если у нее существует хотя бы одно решение. В противном случае система называется несовместной.
Совокупность всех
решений системы уравнений (1) мы будем
называть множеством
ее решений и обозначать Xb (X0,
если система однородная). Если система
несовместна, то Xb =  .
.
Основная задача теории систем линейных алгебраических уравнений состоит в том, чтобы выяснить, совместна ли система (1), и, если совместна, то описать множество всех её решений. Существуют методы анализа таких систем, которые позволяют описывать множество всех решений в случае совместных систем или убеждаться в несовместности в противном случае. Одним из таких универсальных методов является метод последовательного полного исключения неизвестных, или метод Гаусса — Жордана, который мы будем подробно изучать.
Прежде, чем переходить к описанию метода Гаусса — Жордана, приведем ряд полезных для дальнейшего определений и утверждений.
Две системы уравнений называются эквивалентными, если они имеют одно и то же множество решений. Другими словами, каждое решение одной системы является решением другой, и наоборот. Все несовместные системы считаются эквивалентными между собой.
Из определений эквивалентности и множества решений систем вида (1) сразу же вытекает справедливость следующих утверждений, которые мы сформулируем в виде теоремы.
Теорема 1. Если в системе
(1) имеется уравнение с номером k,
1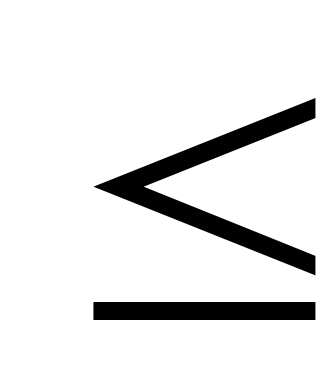 k
k 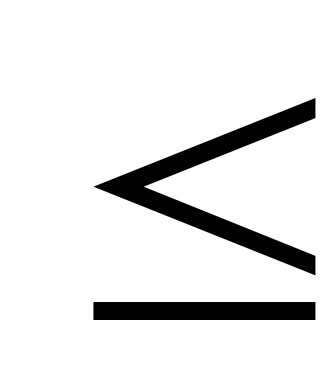 m,
такое, что akj = 0
m,
такое, что akj = 0  j,
то
j,
то
если соответствующий свободный член bk
 0,
то система (1) несовместна;
0,
то система (1) несовместна;если соответствующий свободный член bk = 0, то k — е уравнение можно отбросить и получить систему из (m – 1) — го уравнения с n переменными, эквивалентную исходной.
Справедливость утверждений теоремы становится очевидной, если заметить, что k – е уравнение имеет вид
0x1 + 0 x2 + … + 0 xj + … + 0 xn = bk.
Теорема 2. Если к одному уравнению системы (1) прибавить другое уравнение этой же системы, умноженное на любое число, то получится система уравнений, эквивалентная исходной системе.
Доказательство. Умножим, например, второе уравнение
системы (1) на некоторое число  и
прибавим его к первому уравнению. В
результате этого преобразования получим
систему (1’), в которой все уравнения,
начиная со второго, не изменились, а
первое имеет следующий вид
и
прибавим его к первому уравнению. В
результате этого преобразования получим
систему (1’), в которой все уравнения,
начиная со второго, не изменились, а
первое имеет следующий вид
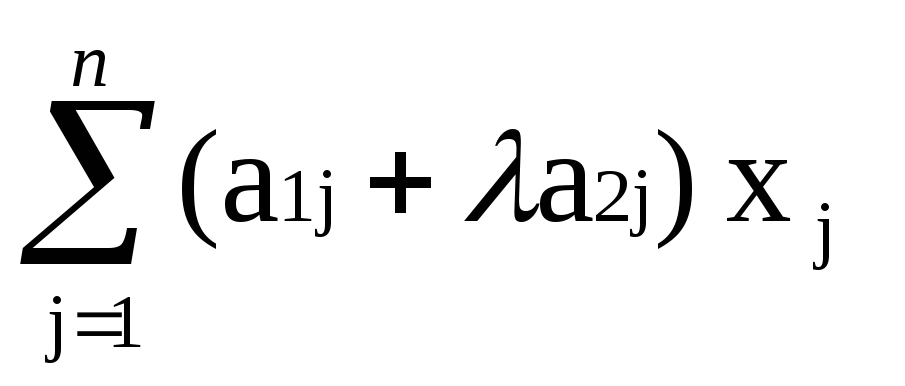 = b1 +
= b1 +  b2.
b2.
Очевидно, если
какой-нибудь набор (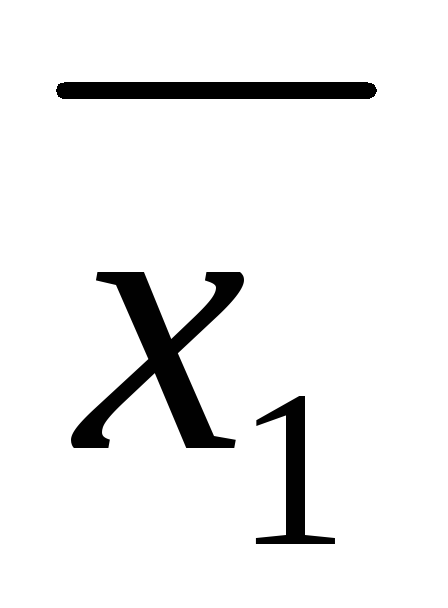 ,
,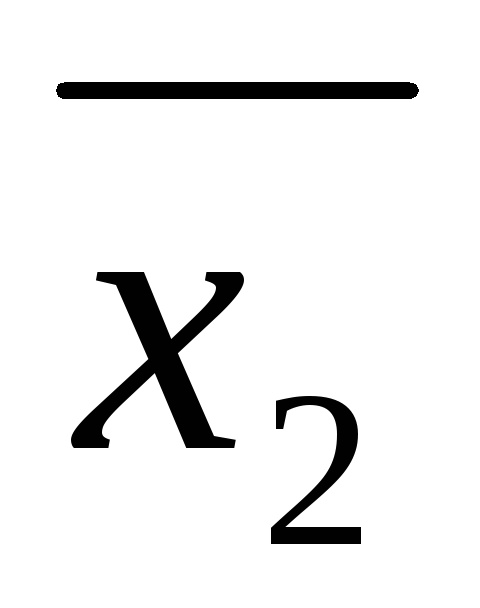 ,…,
,…,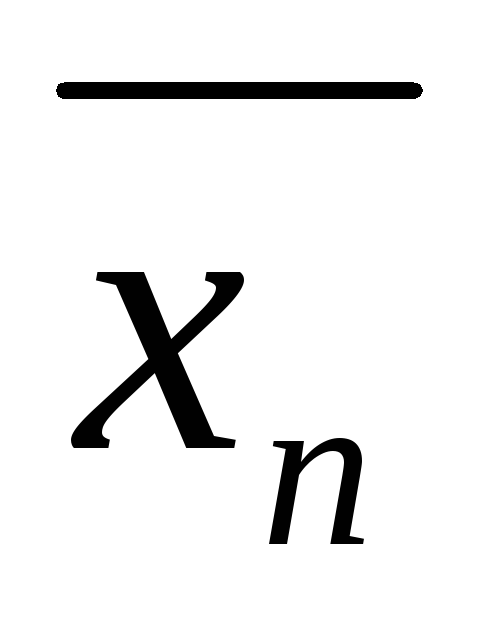 )
значений переменных обращает в тождества
все уравнения системы (1), то он обращает
в тождества и все уравнения системы
(1’). Наоборот, решение (x’1 ,x’2 ,…,x’j , … ,x’n)
системы (1’) является также решением
системы (1), так как система (1) получается
из системы (1’) с помощью аналогичного
преобразования, когда к первому уравнению
системы (1’) прибавляется второе уравнение
системы (1’), умноженное на число (-
)
значений переменных обращает в тождества
все уравнения системы (1), то он обращает
в тождества и все уравнения системы
(1’). Наоборот, решение (x’1 ,x’2 ,…,x’j , … ,x’n)
системы (1’) является также решением
системы (1), так как система (1) получается
из системы (1’) с помощью аналогичного
преобразования, когда к первому уравнению
системы (1’) прибавляется второе уравнение
системы (1’), умноженное на число (- ) .
) .
Точно также доказывается и следующее утверждение.
Теорема 2’. Умножение произвольного уравнения системы (1) на любое число, отличное от нуля, переводит систему (1) в эквивалентную ей систему уравнений.
Теоремы 2 и 2’ дают два вида преобразований, которым подвергалась система (1), оставаясь эквивалентной:
а) умножение (или деление) произвольного уравнения системы (1) на любое число, отличное от нуля;
б) прибавление (или вычитание) к одному уравнению другого, умноженного на некоторое число.
Такие преобразования а) и б) называются элементарными преобразованиями системы уравнений (1).
Если к системе уравнений (1) несколько раз применить элементарные преобразования, то полученная в результате система, очевидно, также будет эквивалентна первоначальной.
Систему уравнений (1) можно записать в табличной форме:
x1 | x2 | xj | xn | b | ||
a11 | a12 | … | a1j | … | a1n | b1 |
a21 | a22 | … | a2j | … | a2n | b2 |
… | … | … | … | … | … | … |
ai1 | ai2 | … | aij | … | ain | bi |
… | … | … | … | … | … | … |
am1 | am2 | … | amj | … | amn | bm |
(2)
Прямоугольная
таблица чисел, составленная из
коэффициентов aij при неизвестных системы (1), называется матрицей системы (1) и обозначается A
(в ней m
строк и n
столбцов), столбец свободных членов
обозначается b.
Прямоугольная таблица, составленная
из коэффициентов aij при неизвестных и из столбца свободных
членов b
системы (1), называется расширенной
матрицей системы
(1) и обозначается  (в ней m
строк и (n+1)
столбцов), т.е
(в ней m
строк и (n+1)
столбцов), т.е  = (A,
b).
В i
– ой строке матрицы
= (A,
b).
В i
– ой строке матрицы  содержатся все известные параметры, характеризующие i
— ое уравнение системы (1), i
= 1,…, m.
В j
– м столбце матрицы A
содержатся все коэффициенты при
неизвестном xj,
встречающиеся в системе (1).
содержатся все известные параметры, характеризующие i
— ое уравнение системы (1), i
= 1,…, m.
В j
– м столбце матрицы A
содержатся все коэффициенты при
неизвестном xj,
встречающиеся в системе (1).
Числа aij называются элементами матрицы А. Элемент aij находится в i — ой строке и в j — м столбце матрицы А. Принято говорить, что элемент aij находится на пересечении i — ой строки и j — го столбца матрицы А. Если все элементы строки (столбца) матрицы А (кроме одного) равны нулю, а ненулевой элемент равен единице, то такая строка (столбец) называется единичной (единичным).
Элементарным преобразованиям системы (1) соответствуют следующие элементарные преобразования таблицы (2):
а) умножение (или деление) всех элементов произвольной строки таблицы (2) на любое число, отличное от нуля,
б) прибавление (или вычитание) к одной строке (поэлементно) другой строки, умноженной на некоторое число.
В результате любого элементарного преобразования получается новая таблица, в которой вместо той строки, к которой прибавляли (или умножали на любое число, отличное от нуля), пишется новая строка, а остальные строки (в том числе и та, которую прибавляли) пишутся без изменения. Новая таблица соответствует системе уравнений, эквивалентной исходной системе.
Применяя элементарные преобразования можно таблицу (2) и соответственно систему (1) упростить так, что решить исходную систему становится просто. На этом и основан предлагаемый метод.
Метод последовательного полного исключения неизвестных
(Метод Гаусса — Жордана)
Метод последовательного полного исключения неизвестных, или метод Гаусса – Жордана, является универсальным методом анализа любых (заранее неизвестно, каких — совместных или несовместных) систем линейных алгебраических уравнений. Он позволяет решать совместные системы или убеждаться в несовместности несовместных систем.
Отметим принципиальное отличие предлагаемого метода решения систем линейных алгебраических уравнений от метода решения, скажем, стандартного квадратного уравнения. Оно решается с помощью хорошо известных формул, в которых неизвестные выражаются через коэффициенты уравнения. В случае общих систем линейных алгебраических уравнений мы таких формул не имеем и используем для отыскания решения метод итераций, или итеративный метод, или итерационный метод. Такие методы задают не формулы, а последовательность действий.
Метод Гаусса — Жордана представляет собой последовательную реализацию ряда однотипных больших шагов (или итераций). Это конкретный итерационный метод — один из многих методов итераций, предложенных для решения систем линейных алгебраических уравнений вида (1). Он состоит из начального этапа, основного этапа и заключительного этапа. Основной этап содержит повторяющиеся итерации – наборы однотипных действий.
Пусть задана конкретная система линейных алгебраических уравнений (1). Это значит, что известны n, m, aij, bi, i = 1,…,m; j = 1,…,n. Опишем предлагаемый метод решения этой системы.
Начальный этап включает в себя построение таблицы I(0) вида (2) и выбор в ней ведущего элемента – любого ненулевого коэффициента при переменных из таблицы (2). Столбец и строка, на пересечении которых стоит ведущий элемент, называются ведущими. (Пусть выбран элемент ai0j0. Тогда i0 – ая строка ведущая, j0— й столбец ведущий.) Переходим к основному этапу. Заметим, что часто ведущий элемент называют разрешающим.
Основной этап состоит из повторяющихся однотипных итераций с номерами k = 1, 2,…. Опишем подробно итерации метода Гаусса — Жордана.
К началу каждой итерации известна некоторая таблица I вида (2), в ней выбран ведущий (разрешающий) элемент и, соответственно, ведущий столбец и ведущая строка. Кроме того, имеется информация о том, какие строки и столбцы уже были ведущими. (Так, например, после начального этапа, т.е. на итерации 1 известны I(0), ведущий (разрешающий) элемент ai0j0 и i0 – ая строка ведущая, j0— ой столбец ведущий.)
Итерация(с номером k) состоит из следующих действий.
Преобразование ведущего столбца (т.е. столбца, содержащего ведущий элемент) в единичный с 1 на месте ведущего элемента путем последовательного поэлементного вычитания ведущей строки (т.е. строки, содержащей ведущий элемент), умноженной на некоторые числа, из остальных строк таблицы. Сама ведущая строка преобразуется путем поэлементного деления ее на ведущий элемент.
Выписывается новая таблица I(k), (k — номер итерации), в которой все столбцы, которые были когда-либо ведущими, – единичные.
Проверяется, можно ли в таблице I(k) выбрать новый ведущий (разрешающий) элемент. По определению это любой ненулевой элемент, который стоит на пересечении строки и столбца, которые еще не были ведущими.
Если такой выбор возможен, то столбец и строка, на пересечении которых стоит ведущий (разрешающий) элемент, называются ведущими. Затем итерация повторяется с новой таблицей I(k), т.е. действия 1 – 3 повторяются с новой таблицей I(k). При этом строится новая таблица I(k+1).
Если нельзя выбрать новый ведущий элемент, то переходим к заключительному этапу.
Заключительный этап. Пусть проделано r итераций, получена таблица I(r), состоящая из матрицы коэффициентов при переменных A(r) и столбца свободных членов b(r) , и в ней нельзя выбрать новый ведущий элемент, т.е. метод остановился. Заметим, что метод обязательно остановится за конечное число шагов, т.к. r не может быть больше min{m,n}.
Каковы варианты остановки метода? Что значит «нельзя выбрать новый ведущий элемент»? Это значит, что после r – ой итерации в матрице A(r) новой системы, эквивалентной системе (1), либо
а) все строки A(r) были ведущими, т.е. в каждой строке стоит одна и ровно одна единица, которая не стоит больше не в какой другой строке,
либо
б) остались строки в A(r) , состоящие только из нулей.
Рассмотрим эти варианты.
а) В этом случае r
= m,
m 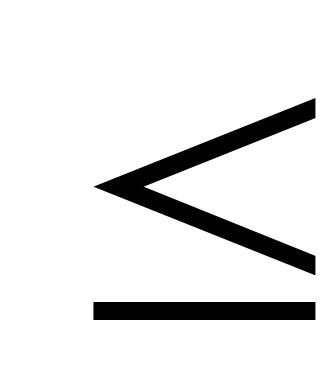 n.
Переставив строки и перенумеровав
переменные (т.е. переставив столбцы),
можно таблицу I(r) представить в виде
n.
Переставив строки и перенумеровав
переменные (т.е. переставив столбцы),
можно таблицу I(r) представить в виде
x1 | x2 | xr | xr+1 | xn | b | ||
1 | 0 | … | 0 | a(r)1,r+1 | … | a(r)1n | b(r)1 |
0 | 1 | … | 0 | a(r)2,r+1 | … | a(r)2n | b(r)2 |
… | … | … | … | … | … | … | … |
0 | 0 | … | 0 | a(r)i,r+1 | … | a(r)in | b(r)i |
… | … | … | … | … | … | … | … |
0 | 0 | … | 1 | a(r)m,r+1 | … | a(r)mn | b(r)m |
(3)
Подчеркнем, что в таблице (3) каждая переменная с номером i, не превосходящим r, встречается только в одной строке. Таблица (3) соответствует системе линейных уравнений вида
x1 + 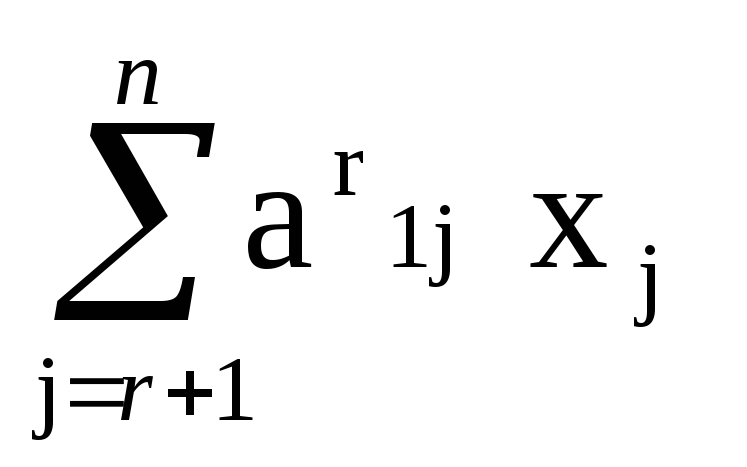 =
b(r)1 ,
=
b(r)1 ,
x2 + 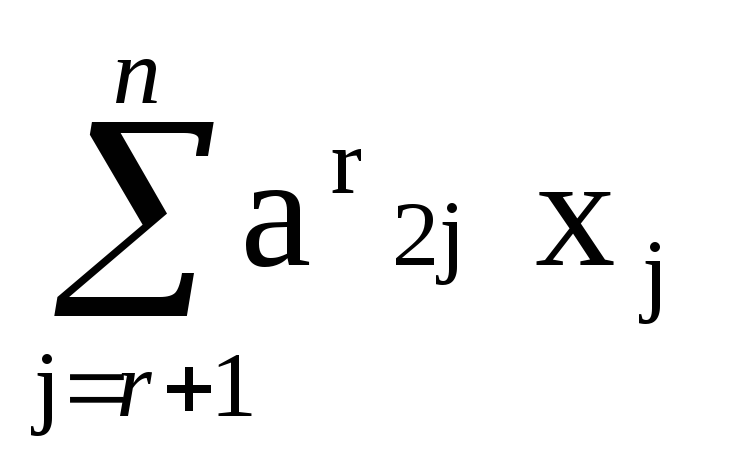 =
b(r)2 ,
=
b(r)2 ,
………………………, (4)
xr +  =
b(r)r ,
=
b(r)r ,
в которой каждая переменная с номером i, не превосходящим r, однозначно выражается через переменные xr+1 , … ,xn, коэффициенты матрицы a(r)ij , j = r+1,…,n, и свободный член b(r)i, представленные в таблице (3). На переменные xr+1 , … ,xn не накладываются никакие ограничения, т.е. они могут принимать любые значения. Отсюда произвольное решение системы, описываемой таблицей (3), или, что то же самое, произвольное решение системы (4), или, что то же самое, произвольное решение системы (1) имеет вид
xi = b(r)i — 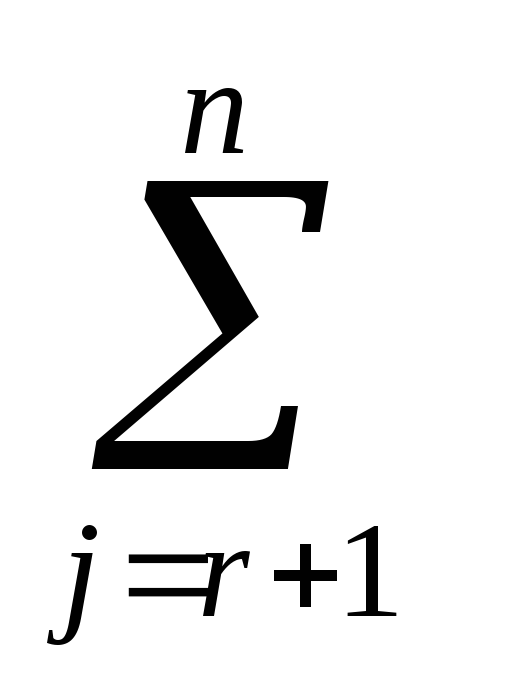 a(r)ijxj,
i = 1,…,r = m; xj – любое
при
j = (r+1),…,n. (5)
a(r)ijxj,
i = 1,…,r = m; xj – любое
при
j = (r+1),…,n. (5)
Тогда множество решений системы (1) можно записать как
Xb = {x=(x1 , … ,xn)
: xi = b(r)i — 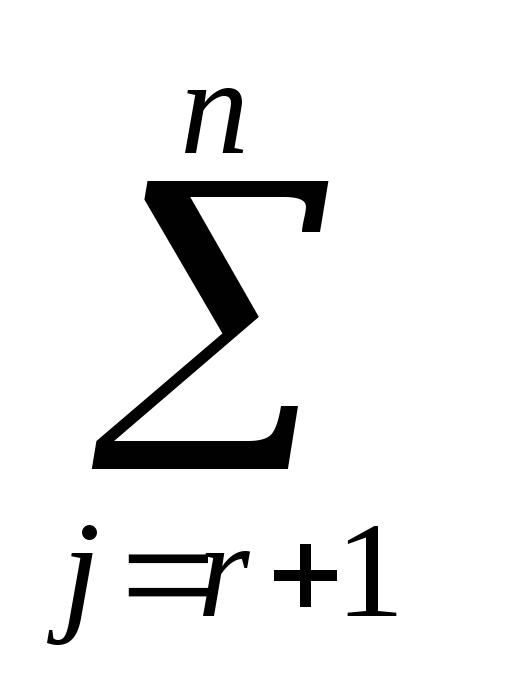 a(r)ijxj при i
= 1,…, r
= m;
xj – любое при j
=(r+1),…,n.}.
a(r)ijxj при i
= 1,…, r
= m;
xj – любое при j
=(r+1),…,n.}.
б) В этом случае r < m, и существует хотя бы одна строка k, k > r, (предполагаем, что сделана перестановка строк и столбцов такая же, как в пункте а)) такая, что a(r)kj = 0 при всех j. Тогда, если соответствующий свободный член b(r)k не равен 0, то k — е уравнение не имеет решения, и, следовательно, вся система не имеет решения, т.е. система (1) несовместна.
Если же соответствующий b(r)k равен 0, то k — ое уравнение является лишним и его можно отбросить. Отбросив все такие уравнения, получим, что система (1) эквивалентна системе из r уравнений с n переменными, которая через r шагов записывается с помощью таблицы вида (3), в которой все строки были ведущими. Таким образом, мы пришли к рассмотренному выше случаю а) и можем выписать решение вида (5).
Метод Гаусса – Жордана описан полностью. За конечное число итераций система линейных алгебраических уравнений будет решена (если она совместна) или будет очевидно, что она несовместна (если она действительно несовместна).
Переменные, соответствующие ведущим (разрешающим) элементам, или стоящие в ведущих столбцах, принято называть базисными, а остальные переменные — свободными.
Обратим внимание на следующее.
1) Когда мы начинаем решать систему методом Гаусса — Жордана, мы можем не знать, совместна эта система или нет. Метод Гаусса — Жордана за конечное число итераций r даст ответ на этот вопрос. В случае совместной системы на основании последней таблицы выписывается общее решение исходной системы. В этом случае число базисных переменных обязательно равно номеру r последней итерации, т.е. числу выполненных итераций. Число r всегда не превосходит min{m,n}, где m — число уравнений системы, а n — число переменных системы. Если r < n, то (n – r) равно числу свободных переменных.
2) При записи общего решения не нужно перенумеровывать переменные, как это делалось для простоты понимания при описании Заключительного этапа. Это сделано для более ясного понимания.
3) При решении системы (1) методом Гаусса — Жордана базисными переменными будут только переменные, соответствующие столбцам, которые на каких-то итерациях выступали в роли ведущих, и наоборот, если на какой-то итерации столбец выступал в качестве ведущего, соответствующая ему переменная обязательно будет в числе базисных.
4) Если общее решение системы (1) содержит хотя бы одну свободную переменную, то эта система имеет бесконечно много частных решений, если же свободных переменных нет, то система имеет единственное решение, которое совпадает с общим решением.
5) Ведущие элементы могут быть выбраны на каждой итерации различным способом. Важно только то, что это ненулевые коэффициенты, стоящие на пересечении строки и столбца, которые до этого не были ведущими. Различный выбор ведущих элементов может дать различные записи множества решений. Однако, само множество решений при любой записи одно и то же.
Поясним работу метода на примерах.
Пример I. Решить следующую систему линейных алгебраических уравнений
2 x1 – 3 x2 + 3 x3 + 5 x4 = -1,
3 x1 + 4 x2 — 2 x3 + 6 x4 = 2, (6)
5 x1 – 4 x2 + 6 x3 + 10 x4 = 2
8. Решение систем линейных уравнений методом Гаусса и с использованием преобразований Жордана-Гаусса:
Определение матрицы. Перечислите основные виды матриц:
Матрицей называется прямоугольная таблица размерностью m на n, где m – число строк, n – число столбцов. Числа, из которых состоит матрица, называются элементами матрицы. Обозначается матрица всегда заглавными (прописными) латинскими буквами. Элементы матрицы заключаются в круглые и квадратные скобки, обозначаются они строчными буквами с индексом ij, где i – строка, j – столбец. Элемент матрицы находится на пересечении i-строки и j-столбца.
Основные виды матриц:
Прямоугольная – состоит из m строк и n столбцов.
Строчная (матрица строка, вектор строка) – матрица, состоящая из одной строки.
Столбцовая (матрица столбец, вектор столбец) – матрица, состоящая из одного столбца.
Квадратная – матрица, у которой число строк и столбцов одинаковое.
Диагональная – квадратная матрица, у которой все элементы, не принадлежащие главной диагонали равны нулю (главную диагональ образую элементы, у которых i=j).
Единичная – диагональная матрица, у которой все элементы, находящиеся на главной диагонали равны единице.
Симметричная – матрица, у которой все элементы симметричны относительно главной диагонали.
Нулевая – матрица любой размерности, все элементы которой равны нулю.
Квадратная матрица называется верхней треугольной (нижней треугольной), если все ее элементы, стоящие ниже (выше) главной диагонали, равны нулю. Верхняя треугольная матрица иногда называется правой треугольной, а нижняя треугольная — левой треугольной.
Если матрица прямоугольная, то мы можем преобразовать её в квази-треугольную, ступенчатую или трапециевидную матрицу
Операции над матрицами:
Произведением матрицы А на число λ называется матрица B, у которой каждый элемент равен произведению соответствующего элемента матрицы А на число λ.
Делить матрицы нельзя.
Суммой двух матриц А и В, с одинаковым количеством строк и столбцов, называется матрица С, элементы которой равны суммам соответствующих элементов матриц слагаемых.
Умножение матриц определяется только для согласованных матриц. Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. Если матрица А и В квадратные, то они всегда взаимно-согласованы.
Произведением матрицы Аmxk на матрицу Вkxn, называется матрица Сmxn, каждый элемент которой равен сумме произведений элементов i-строки матрицы А на соответствующие элементы j-столбца матрицы В.
Свойства умножения матриц:
1.(А*В)*λ = (А*λ)*В = А*(В*λ), где λ – любое число
2.(А + В)*С = А*С + В*С
3.(А*В*С) = (В*С*А) – если матрицы согласованы между собой.
4.А*Е = Е*А = А, где Е – единичная матрица
5.А*О = О*А = О, где О – нулевая матрица.
Транспонирование матрицы осуществляется путём замены каждой её строки столбцом с тем же номером.
Свойства транспонирования матриц:
1.(Ат)т = А
2.(А + В)т = Ат + Вт
3.( λ*А)т = λ*Ат
4.(А*В)т = Ат*Вт, если матрицы согласованы между собой.
Расчёт определителей второго и третьего порядка:
Определителем второго порядка называется число:
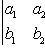
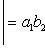

Определителем третьего порядка называется число, полученное при расчёте определителя по формуле Сарруса:
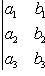


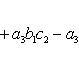
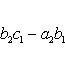

Свойства определителей:
1.Определитель не изменится, при замене всех его строк соответствующими столбцами (при транспонировании).
2.При перестановке двух столбцов (строк) местами определитель меняет знак на противоположный.
3.Определители с двумя одинаковыми столбцами (строками) всегда равен нулю.
4.Множитель, общий для элементов некоторого столбца (строки) можно выносить за знак определителя. За знак определителя можно выносить общий множитель любой строки (столбца) любой матрицы, за знак которой можно выносить общий множитель всех элементов.
5.Определитель равен нулю, если все элементы некоторого столбца (строки) равны нулю.
6.Определитель с двумя пропорциональными столбцами (строками) всегда равен нулю.
7.Если в определителе все элементы некоторого столбца (строки) равны суммам двух слагаемых, то такой определитель равен сумме двух соответствующих определителей.
8.Определитель не изменится, если к элементам некоторого столбца (строки) прибавить соответствующие элементы другого столбца (строки), предварительно умножив их на один и тот же коэффициент.
9.Минором Мij элемента аij матрицы n-ного порядка называется определитель матрицы (n-1)-го порядка, получаемой из матрицы n-ного порядка путём вычёркивания i-строки и j-столбца.
Каждая матрица n-ного порядка имеет n2 миноров n-первого порядка.
10.Алгебраическим дополнением Аij элемента аij называется минор элемента aij умноженный на (-1)i+j
Дополнение всегда обозначают той же буквой, что и матрица, но всегда с индексами.
11.Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
12. Определитель произведения двух квадратных матриц равен произведению их определителей.
13. Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения другой строки (столбца) всегда равна нулю.
Обратная матрица. Теорема (необходимое и достаточное условие существования обратной матрицы). Алгоритм вычисления обратной матрицы методом Гаусса.
Обратной для квадратной матрицы А называется матрица А-1, для которой выполняется: А-1*А=А*А-1=Е
Из определения следует, что обратную матрицу можно построить только для квадратной, обе матрицы прямая и обратная имеют один и тот же порядок.
Необходимое и достаточное условие существования обратной матрицы:
Определитель прямой матрицы должен быть отличен от нуля. Тогда матрица А называется не вырожденной или не особенной. В противном случае, если определитель равен нулю, матрица называется вырожденной или особенной.
Теорема:
Обратная матрица А-1 существует и единственна тогда и только тогда, когда исходная матрица не вырождена.
Необходимость.
Пусть для матрицы А существует обратная А-1, т.е. А* А-1 = А-1*А = Е. Тогда, |А* А-1|=|А|*|А-1|=|Е|=1,т.е.|А| ≠ 0 и |А-1| ≠ 0; А – невырожденная.
Достаточность.
Пусть дана невырожденная матрица порядка n
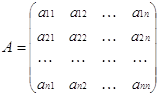 ,
,
так что ее определитель 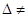 0.
Рассмотри матрицу, составленную из
алгебраических дополнений к элементам
матрицы А:
0.
Рассмотри матрицу, составленную из
алгебраических дополнений к элементам
матрицы А:
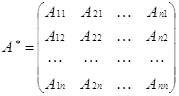 ,
,
ее называют присоединенной к матрице А.
Следует обратить
внимание на то, что алгебраические
дополнения к элементам i-той строки
матрицы А стоят в i-том столбце матрицы
А*,
для 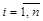 .
.
Найдем произведения матриц АА* и А*А. Обозначим АА* через С, тогда по определению произведения матриц имеем: Сij = аi1А 1j + аi2А 2j + … + аinАnj ;
При i = j получим
сумму произведений элементов i — той
строки на алгебраические дополнения
этой же строки, такая сумма равняется
значению определителя. Таким образом
Сij =
|А| = D — это элементы главной диагонали
матрицы С. При i 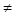 j,
т.е. для элементов Сij вне главной
диагонали матрицы С, имеем сумму
произведений всех элементов некоторой
строки на алгебраические дополнения
другой строки, такая сумма равняется
нулю. Итак,
j,
т.е. для элементов Сij вне главной
диагонали матрицы С, имеем сумму
произведений всех элементов некоторой
строки на алгебраические дополнения
другой строки, такая сумма равняется
нулю. Итак, 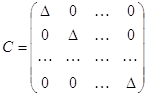 =
АА*
=
АА*
Аналогично доказывается, что произведение А на А* равно той же матрице С. Таким образом, имеем А*А = АА* = С. Отсюда следует, что
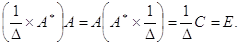
Поэтому, если в
качестве обратной матрицы взять 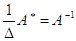 ,
то
,
то Итак,
обратная матрица существует и имеет
вид:
Итак,
обратная матрица существует и имеет
вид:
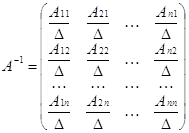 .
.
Вычисление обратной матрицы методом Гаусса:
Алгоритм вычисления обратной матрицы методом Гаусса состоит в следующем действии: (А|E) = (E|A-1), которое проводится посредством тех же операций, что и при вычислении определителя или посредством преобразований Гаусса.
Системы линейных уравнений. Основные понятия и определения.
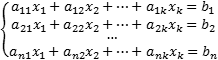
aij – коэффициенты при неизвестном
bi – свободные члены.
i/j от 1 до n
Решением данной системы называется упорядоченная совокупность n чисел: c1, c2, c3…cn, подстановка которых в каждое уравнение системы обращает его в истинное тождество.
Система, имеющая хотя бы одно решение, называется совместной.
Система, не имеющая ни одного решения, называется не совместной.
Совместная система называется определённой, если она имеет только одно решение и не определённой, если она имеет более одного решения.
Линейная система называется не определённой, если существуют свободные члены, отличные от нуля.
Если все свободные члены равны нулю, то такая система называется однородной.
Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и то же множество решений.
Любые две не совместные системы всегда эквивалентны (нет решений).
Решение систем линейных уравнений методом обратной матрицы и методом Крамера:
Формула решения системы методом обратной матрицы:
X = A-1*B, применяется если определитель прямой матрицы отличен от нуля.
Где Х – матрица столбец, содержащая решения системы x1, x2…xn, а В – матрица столбец, в которой содержатся свободные члены системы b1, b2…bn.
Рассмотрим квадратную матрицу
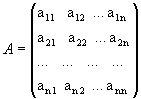 .
.
Обозначим =det A. – определитель.
Обратная матрица вычисляется по формуле
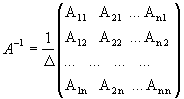
где А i j — алгебраические дополнения элементов a i j.
Аij = (-1)i+j * Мij
Рассмотрим систему уравнений, решив её методом Крамера:
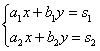
Вычислим определитель:
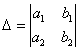 ,
,
Если 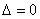 ,
то система имеет бесконечно много
решений или несовместна (не имеет
решений).
,
то система имеет бесконечно много
решений или несовместна (не имеет
решений).
В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.
Если 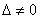 ,
то система имеет единственное решение,
и для нахождения корней мы должны
вычислить еще два определителя:
,
то система имеет единственное решение,
и для нахождения корней мы должны
вычислить еще два определителя: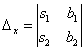 и
и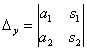
Корни
уравнения находим по формулам:  ,
,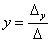

Для решения данной системы применяется метод последовательного исключения неизвестных (метод Гаусса) с использованием жордановских преобразований. Такой совокупный метод носит название метода Жордана-Гаусса. Для этого метода удобно записывать систему таблицей.
Выбираем любой не нулевой элемент таблицы (в качестве выбранного элемента должен быть коэффициент при переменной) aij. Свободные члены никогда не выбираются. Выбранный коэффициент заключается в прямоугольную рамочку (этот элемент называется разрешающим). Строка и столбец, содержащие данный элемент также называются разрешающими или разрешёнными
Система уравнений называется разрешённой, если каждое уравнение системы содержит разрешённую неизвестную. Разрешённые неизвестные взятые по одной из каждых уравнений, образует полный набор разрешённых неизвестных систем. Разрешённые неизвестные, входящие в полный набор также называются базисными, а все остальные свободными.
Для того, чтобы провести Жордана-Гауссовские преобразования, нужно разрешающую строку умножить на подходящий коэффициент и сложить полученную строку с другой (желательно, чтобы коэффициент был противоположным разрешающему элементу, либо любым другим числом, при сложении с которым получался бы нуль).
Таким образом проделываем вышесказанное с каждой строкой и получаем упрощённый вариант нашей системы, из которой уже можно получить решения заданной системы уравнений.
Ранг матрицы. Основные свойства ранга матрицы.
Рангом матрицы называется наибольший из порядков её миноров, отличных от нуля. Обозначается ранг матрицы как: r, rang (A), Rang (A), Rg.
При вычислении ранга матрицы следует переходить от миноров меньших порядков к минорам больших порядков.
Ранг матрицы равен нулю, если все элементы данной матрицы равны нулю.
Для квадратной матрицы n-ного порядка, ранг матрицы равен n тогда и только тогда, если заданная матрица будет не вырожденная (определитель не равен нулю).
Основные свойства для вычисления ранга матрицы:
1). Ранг транспонированной матрицы всегда равен рангу исходной матрицы.
2). Ранг матрицы не изменится, если вычеркнуть или приписать нулевую строку или столбец.
3). Ранг матрицы не изменится при элементарных преобразованиях матрицы:
— отбрасывание нулевой строки или столбца
— умножение всех элементов строки или столбца на число, отличное от нуля.
— перестановка местами двух строк или столбцов.
— транспонирование матрицы
— прибавление к каждому элементу строки или столбца элемента другой строки или столбца, умноженного на const.
*замечание*
Для вычисления ранга матрицы можно не использовать метод окаймляющих миноров, а свести исходную матрицу к треугольному, диагональному или трапециевидному виду.
Модель межотраслевого баланса Леонтьева:
Цель балансового анализа — ответить на вопрос, возникающий в макроэкономике, связанный с эффективностью сведения многоотраслевого хозяйства.
Каким должен быть объём производства каждой n-отрасли, чтобы удовлетворить все потребности в продукции данной отрасли, при этом каждая отрасль выступает как производителем некоторой продукции, так и как потребитель своей продукции и произведённой другими отраслями.
Связь между отраслями отражается в таблицах межотраслевого баланса.
Математическая модель, позволяющая её анализировать, разработана в 1936 году американским экономистом Леонтьевым.
Рассмотрим процесс производства за некоторый период времени (например: за год).
xij – объём продукции i-отрасли, потребляемой j-отрасли в процессе производства.
yi – объём конечного продукта i-отрасли.
xi – общий объём продукции i-отрасли (валовой объём).
n
Хi = Σ Хij + Уi – валовой объём
j=1 i-отрасли равен суммарному объёму продукции, потребляемой n отраслями, и конечному продукту.
aij = хij/xj
xij = aij*xj (линейная модель)
aij – коэффициент прямых затрат, показывает затраты продукции i-отрасли
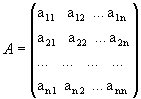
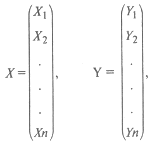
, где A – матрица прямых затрат, X – вектор валового выпуска, Y – вектор конечного продукта.
Основная задача межотраслевого баланса состоит в нахождении такого вектора валового выпуска X, который, при заданной матрице А, обеспечит вектор конечного продукта Y.
Х = АХ + Y
Х – АХ = Y
(Е – А)*Х = Y
Х = (Е – А)-1* Y
(Е – А)-1 = S – матрица полных затрат
|E – A| ≠ 0
Каждый элемент данной матрицы есть величина валового выпуска продукции i-отрасли, необходимого для обеспечения выпуска единицы конечного продукта.
Оценка продуктивности матрицы А:
1). Матрица А называется продуктивной, если все её элементы
≥ 0, если для любого элемента Y ≥ 0, существует матрица Х, все элементы которой ≥ 0.
2). Матрица А продуктивна, если максимум сумм элементов её столбцов не превосходит единицы, причём хотя бы для одного из столбцов строго меньше единицы. Это является проверкой рентабельности производства.
3). Матрица А продуктивна тогда и только тогда, когда существует матрица S и все её элементы ≥ 0.
12. N-мерным
вектором называется упорядоченная совокупность
n
действительных чисел. N-мерным
вектором называется
последовательность 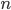 чисел.
Эти числа называются координатами вектора.
Число координат вектора n
называется размерностью вектора.
чисел.
Эти числа называются координатами вектора.
Число координат вектора n
называется размерностью вектора.
Линейные опреации:
a+b=b+a
(a+b)+c=a+(b+c)
c,b=const c(ba)=(cb)a
(c+b)a=ca+ba
a+0=a
a+(-a)=0
a*1=a
Систем линейных уравнений: исключение Гаусса
Системы
линейных уравнений:
Решение методом исключения Гаусса (стр.
6 из 7)
Разделы: Определения, Решение по графику, Подстановка, Исключение / добавление, исключение по Гауссу.

Решение трех переменных, линейных систем с тремя уравнениями сложнее, по крайней мере на начальном этапе, чем решение систем с двумя переменными, потому что требуемые вычисления более грязный.Вам нужно будет очень аккуратно работать, и вы должны планируйте использовать много бумаги для заметок. Метод решения этих систем является расширением метода сложения двух переменных, поэтому сделайте конечно ты знаешь это метод хорошо и можно использовать его последовательно правильно.
Хотя метод решения основан на добавлении / исключении, попытка выполнить фактическое добавление имеет тенденцию становится очень запутанным, поэтому существует систематизированный метод решения трех или более переменных системы.Этот метод называется «исключением по Гауссу» (с уравнения заканчиваются тем, что называется «строковой формой»).
Начнем с простого, и работаем над более сложными примерами.
- Решите следующие проблемы система уравнений.
Достаточно легко увидеть как действовать в этом случае. Я просто обратно заменю значение z -value из третьего уравнения во второе уравнение, решите результат для л , г. а затем подключите z и y в первое уравнение и решите результат для x .
10 л 3 (3) = 11
10 y 9 = 11
10 y = 20
y = 2
5x +
4 (2) (3) = 0
5 x + 8 3 = 0
5 x + 5 = 0
5 x = 5
x = 1
Тогда решение ( х , y , z ) = (1, 2, 3).
Причина, по которой эта система была легко решить, что система была «треугольной»; это относится к уравнениям, имеющим форму треугольника, из-за нижних уравнений содержащий только более поздние переменные.
Дело в том, что в этом формат, система проста в решении. А гауссовское исключение — это метод, который мы будем использовать для преобразования систем в эту верхнетреугольную форму, используя операции со строками, которые мы изучили, когда применили метод сложения.
- Решите следующие проблемы система уравнений с использованием исключения Гаусса.
Уравнение не решается для переменной, поэтому мне нужно будет выполнить умножение и сложение чтобы упростить эту систему. Чтобы отслеживать свою работу, напишу вниз на каждом шагу, когда я иду. Но я сделаю свои вычисления на бумаге для заметок. Вот как я это сделал:
Первое, что нужно сделать избавиться от первых x -термов в два ряда.А пока я просто посмотрю, какие строки будут легко расчистить; Я могу поменять строки позже, чтобы перевести систему в «верхний треугольной формы. Нет правила, согласно которому я должен использовать x — срок из первой строки, и в этом случае, думаю, будет проще используйте термин x из третьей строки, так как его коэффициент просто «1». Я умножу третью строку на 3, и добавьте его в первую строку.Я делаю вычисления на бумаге для заметок:
… а потом записываю результатов:
(Когда мы решали системы с двумя переменными, мы могли умножить строку, переписав систему в сторону, а затем добавить. Для этого нет места в трехвариантная система, поэтому нам и нужна бумажка.)
Предупреждение: поскольку я не на самом деле ничего не делаю с третьей строкой, я скопировал ее без изменений, в новую матрицу уравнений. Я б / у третий ряд, но я на самом деле не менял Это. Не путайте «использование» с «изменением».
Чтобы получить меньшие числа для коэффициентов умножу первую строку на половину:
Теперь умножу третий ряд на 5 и добавьте это ко второму строка.Работаю на бумаге для заметок:
… а потом записываю результаты: Авторские права Элизабет Стапель 2003-2011 Все права защищены
Я ничего не делал с первым рядом, поэтому я скопировал его без изменений. Я работал с третий ряд, но я работал только на вторая строка, поэтому вторая строка обновляется, а третья строка копируется более без изменений.
Хорошо, теперь x — столбец удаляется, за исключением ведущего члена в третьей строке. Так что дальше Приходится работать над колонкой y .
Предупреждение: Начиная с третьего уравнение имеет член x , Я больше не могу использовать его ни в одном из двух других уравнений (или я отменить мой прогресс). Я могу работать на уравнении, но не с Это.
Если я добавлю дважды первое во вторую строку, это даст мне ведущую 1 во втором ряду. Я не буду избавились от ведущего y -терм во втором ряду, но я его преобразовал (не вмешиваясь дробями) в более простую форму. (Вы должны сохранить обратите внимание на такого рода упрощения.) Сначала я делаю царапину работа:
… а потом записываю результатов:
Теперь могу использовать второй ряд, чтобы убрать и -семестр в первом ряду. Вторую строку умножу на 7 и добавить. Сначала я царапаю работа:
… а потом записываю результатов:
я могу сказать что z сейчас, но для большей точности я разделю первую строку на 43.Затем я переставляю ряды, чтобы придать им верхнетреугольную форму:
Теперь я могу начать процесс обратного решения:
Тогда решение ( х , y , z ) = ( 2, 3, 1 ) .
Примечание: нет ничего священного о шагах, которые я использовал при решении указанной выше системы; там ничего не было особенно о том, как я решил эту систему. Вы могли бы работать в другом упорядочивайте или упрощайте разные строки, и все равно получите правильный ответ. Эти системы достаточно сложны, поэтому вряд ли один правильный способ вычисления ответа. Так что не беспокойтесь о том, «как она знала, что делать дальше? », потому что здесь нет правила.я просто делал все, что пришло мне в голову; Я делал то, что казалось самым простым или что-то еще пришла в голову первая. Не волнуйтесь, если бы вы использовали совершенно другой шаги. Если каждый шаг на пути верен, вы придумаете тот же ответ.
В приведенном выше примере я мог пошли дальше в своих вычислениях и более тщательно изучали строковые операции, очищая все термины и кроме этого во второй строке и во всех терминах z кроме того, что в первой строке.Вот что будет тогда процесс посмотрели так:
Так я могу просто читать от значений x , л , г. и z , и мне не нужно возиться с обратной заменой. Это более полное метод решения называется «методом исключения Гаусса-Жордана» (с уравнения, попадающие в так называемый «пониженный ряд-эшелон» образуют «).Многие тексты доходят только до исключения Гаусса, но я всегда было легче продолжать и делать Гаусс-Джордан.
Обратите внимание, что я выполнил две строковые операции сразу на этом последнем шаге перед переключением строк. Пока я не работая с и работая на в том же ряду на том же шаге, это хорошо. В этом случае я работал с первой строкой и рабочая по второй и третий ряды.
<< Предыдущая Вверх | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Вернуться к указателю Далее >>
Цитируйте эту статью как: | Стапель, Елизавета.
«Системы линейных уравнений, решаемые методом исключения Гаусса». Purplemath |
УСТРАНЕНИЕ Гаусса: РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ: ПРИМЕРЫ И РЕШАЕМЫЕ ЗАДАЧИ: ВЫСШАЯ ШКОЛА
Содержимое этой страницы:
Введение
Система уравнений (линейная) — это группа (линейных) уравнений с различные неизвестные факторы. Вообще говоря, неизвестные факторы входят в различные уравнения.
Уравнение с различными неизвестными факторами связывает их друг с другом.
Решение системы состоит в нахождении значения неизвестных факторов таким образом, чтобы все уравнений, составляющих систему.
Если существует одно решение (одно значение для каждого неизвестного фактора), мы будем говорить, что система Согласованная независимая система (СНГ) .
Если есть различные решения (система имеет бесконечно много решений), мы говорим, что система является Согласованная зависимая система (CDS). .
Если решения нет, а это произойдет, если есть два или несколько уравнений, которые нельзя проверить одновременно, мы говорим, что это несогласованная система (IS) .Например, следующая система уравнений
$$ \ begin {case} \ begin {array} {lcl} y & = & 0 \\ 2x + y & = & 0 \\ 2x + y & = & 2 \ end {array} \ end {cases} $ $
несовместимо, потому что мы получаем решение x = 0 из второго уравнения и, из третьего, x = 1 .
В этом разделе мы собираемся решать системы с использованием метода исключения Гаусса , который заключается в простом выполнении элементарных операций в строке или столбце расширенной матрицы, чтобы получить свой эшелон из или его пониженный эшелон форма (Гаусс-Иордан).
Метод разрешения
Применяем метод исключения Гаусса-Джордана : получаем сокращенного эшелона строки формы из расширенной матрицы систему уравнений, выполняя элементарные операции в строках (или столбцах).
Получив матрицу, мы применяем теорему Руше-Капелли , чтобы определить тип системы и получить решение (я), а именно:
Пусть A · X = B будет системой m линейных уравнений с n неизвестным факторы, m и n натуральные числа (не ноль):
AX = B соответствует тогда и только тогда, когда
$$ ранг (A) = ранг (A | B) $$
AX = B — непротиворечивый независимый тогда и только тогда, когда,
$$ ранг (A) = n = ранг (A | B) $$
Примечание: Элементарные операции в строках или столбцах позволяют нам получить системы, эквивалентные исходной, но с формой, упрощающей получение решений (если они есть).Также есть более быстрые инструменты для разработки решений в СНГ, такие как правило Крамера.
Система 1
Показать решение
Расширенная матрица системы
того же размера, что и система (2×3). Вертикальная линия, отделяющая коэффициенты матрицы от вектора независимых членов.
Выполняем элементарные операции в строках для получения сокращенной формы эшелона строк:Умножаем первую строку на 1/5 а вторую на 1/3
Добавляем вторую строку с первой
Вторую строку умножаем на 5/7
Складываем первую строку со второй, умноженной на -2/5
Эта последняя эквивалентная матрица представлена в сокращенной форме эшелона строк. и это позволяет нам быстро увидеть рейтинг матрица коэффициентов и расширенная.
Считаем ранги:
По теореме Руше-Капелли система непротиворечива Независимая. Полученная матрица представляет собой систему
, который является решением исходной системы.
Система 2
Показать решение
Расширенная матрица системы
Проводим элементарные операции в строках для получения приведенных форма эшелона строки:
Вторую строку умножаем на 1/2
Добавляем первую строку со второй
Умножаем первую строку на 1/3
Эта последняя эквивалентная матрица имеет вид сокращенного эшелона строк и имеет пустую строку, что означает, что строки в исходной системе линейно зависимы. (любой из них может быть получен путем умножения другого на скаляр, не равный нулю).
Рассчитываем ранги
По теореме Руше-Капелли система непротиворечива. Кроме того, это зависит, потому что ранг (1) ниже, чем количество неизвестных факторов (2).
Полученная матрица представляет систему
Решения
Система 3
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить приведенную форму строкиИзменяем порядок строк (таким образом, у нас уже будет 1 в первой строке без необходимости умножать)
Складываем вторую строку с первой, умноженной на 5 :
Вторую строку умножаем на -1/15
Эта последняя матрица имеет эшелонированную форму (не сокращена).
Мы можем непосредственно заметить, что система несовместима, потому что у нас следующее равенство (вторая строка):
$$ 0x + 0y = 1 $$, это невозможное равенство.
Рассчитываем ранги матрицы коэффициентов и дополненной:
По теореме Руше-Капелли система несовместна (решения нет). Полученная матрица представляет собой систему
Система непоследовательна, потому что мы имеем невозможное равенство
$$ 0 = 1 $$
Система 4
Показать решение
Расширенная матрица системы
(размер 3х4).
Выполняем элементарные операции в строках, чтобы получить приведенную форму строкиУмножаем первую строку на 1/5
Складываем вторую и третью строки, умножив первую на -2
Вторую и третью строки умножаем на 5
Вторую строку складываем с третьей, умноженной на -1
Умножаем вторую строку на -1/10 и третью на 1/11
К первой строке добавляем вторую, умноженную на -2/5 , а третью — со второй, умноженной на -1
Третью строку умножаем на -11/5
Эта последняя эквивалентная матрица находится в сокращенной форме эшелона строк (мы знаем ее, потому что это единичная матрица).Имея единичную матрицу, мы знаем, что это согласованная независимая система, и можем получить единственное решение.
Рассчитываем ранги
По теореме Руше-Капелли система непротиворечива Независимая. Полученная матрица представляет собой систему
, который является решением системы.
Система 5
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить приведенную форму строкиМы вычитаем первую строку из второй и добавляем третью строку с первой.
Умножаем первую строку на 1/2 , а вторую на 1/3
Мы складываем первую строку со второй, умноженной на 1/2 , и третью строку со второй, умноженной на -2
Третью строку умножаем на 1/3
Складываем первую строку с третьей, умноженной на -3/2
Эта последняя матрица является эшелонированной матрицей с сокращенной строкой (мы знаем это, потому что у нас есть единичная матрица).
Рассчитываем ранги
По теореме Руше-Капелли система непротиворечива Независимая. Полученная матрица представляет собой систему
Система 6
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить приведенную форму строкиУмножаем вторую строку на -1/3 и третью на 1/4
Складываем вторую и третью строки, умножив первую на -1
Умножаем вторую строку на -3/4 и третью на -1
Третью строку складываем со второй, умноженной на -1
Эта последняя матрица имеет эшелонированную форму (но не сокращена) и мы не продолжаем выполнять операции по строкам, потому что можем видим, что последняя строка делает систему непоследовательной.Эта строка сообщает нам:
$$ 0x + 0y + 0z = -1 $$И все это невозможное равенство.
Фактически у нас есть ранги
По теореме Руше-Капелли система несовместна.
Система 7
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить приведенную форму строкиУмножаем первую и вторую строки на 1/3 и на 1/6 соответственно
Вторую строку вычитаем из третьей
Добавляем первую строку со второй
Третью строку умножаем на 3
Эта последняя матрица находится в сокращенном эшелоне строк формы , поэтому мы можем легко вычислить ранги:
Рассчитываем ранги
По теореме Руше-Капелли система непротиворечива.Но он не является независимым, потому что количество неизвестных факторов (3) отличается от ранга. Полученная матрица представляет собой систему
Решения
Система 8
Показать решение
Расширенная матрица системы
Примечание: , прежде чем мы начнем, мы должны прокомментировать, что процедура будет таким же, как и до сих пор.Но у нас есть корни в матрице, а значит, операции над строками будут длинными и утомительно. Эта задача не очень интересна в дидактическом смысле, помимо расчетов.
Проводим элементарные операции в строках, чтобы получить пониженный рядный эшелон формы
Мы складываем вторую строку с первой, умноженной на -√5 и, с третий, умноженный на -2/5
Умножаем вторую строку на 1 / √5 и третью на 5/17
Складываем первую строку с третьей и со второй вычитаем третью
Переписываем матрицу
Вторую строку умножаем на (√5 / 5-5) -1
Складываем первую строку со второй, умноженной на -5
В этой последней матрице (почти) в строке уменьшено форма эшелона (надо поменять второй и третий ряды так что это правда).Из последней матрицы получаем решения:
Система 9
Показать решение
Расширенная матрица системы
Выполняем элементарные операции в строках, чтобы получить приведенную форму строкиМы складываем третью и четвертую строки, умножая первую на 3 и -2 соответственно
Складываем первую, вторую и третью строки с четвертой, умноженной на 2 , -3 и 5 соответственно
Четвертую строку умножаем на -1 и меняем на вторую
Умножаем третью и четвертую строки на 1/34 и -1/22 соответственно
Вычитаем третью строку из четвертой
Четвертую умножаем на -187/42
Добавляем в первую строку третью умноженную на -13 и вторую на 8
К первой строке прибавляем четвертую умноженную на 5/34 , ко второй прибавляем первую, умноженную на 5/17 и к третьему добавляем первое, умноженное на -3/34
По теореме Руше-Капелли, система является непротиворечивой Независимой, и решение равно
Система 10
Показать решение
Расширенная матрица системы
Примечание: Эта система была включена в цель отметить, что теория матрицы применима к комплексным числам.Единственное отличие от предыдущих систем в том, что теперь нам нужно действовать путем умножения и деления комплексные числа.
Выполняем элементарные операции в строках для получения приведенной формы эшелона строк
Умножаем вторую строку на 1/2 и меняем ее на первую
Добавляем вторую строку, первую, умноженную на — (1 + i)
Вторую строку умножаем на
Добавляем первую строку ко второй умноженной на -i / 2
Эта последняя матрица имеет сокращенную форму, потому что это единичная матрица.
По теореме Руше-Капелли, система является непротиворечивой Независимой, и решение равно
Matesfacil.com
компании J. Llopis под лицензией
творческий
Международная лицензия Commons Attribution-NonCommercial 4.0.
,
Исключение Гаусса
Тип 2. Умножьте строку на ненулевую константу.
Тип 3. Добавьте одну строку, кратную одной, в другую.
Цель этих операций — преобразовать — или уменьшить — исходную расширенную матрицу в одну из форм  , где A ′ — верхний треугольник ( a ij ′ = 0 для i> j ) , любые нулевые строки появляются внизу матрицы, а первая ненулевая запись в любой строке находится справа от первой ненулевой записи в любой более высокой строке; такая матрица называется эшелон .Решения системы, представленной более простой расширенной матрицей, [ A ′ | b ′], можно найти путем осмотра нижних рядов и обратной подстановки в более высокие ряды. Поскольку операции с элементарными строками не меняют решений системы, векторы x , которые удовлетворяют более простой системе A ′ x = b ′, являются в точности теми, которые удовлетворяют исходной системе, A x = b .
, где A ′ — верхний треугольник ( a ij ′ = 0 для i> j ) , любые нулевые строки появляются внизу матрицы, а первая ненулевая запись в любой строке находится справа от первой ненулевой записи в любой более высокой строке; такая матрица называется эшелон .Решения системы, представленной более простой расширенной матрицей, [ A ′ | b ′], можно найти путем осмотра нижних рядов и обратной подстановки в более высокие ряды. Поскольку операции с элементарными строками не меняют решений системы, векторы x , которые удовлетворяют более простой системе A ′ x = b ′, являются в точности теми, которые удовлетворяют исходной системе, A x = b .
Пример 3 : Решите следующую систему с помощью исключения Гаусса:

Расширенная матрица, которая представляет эту систему:

Первая цель состоит в том, чтобы получить нули под первой записью в первом столбце , что означает исключение первой переменной x из второго и третьего уравнений.Для этого выполняются следующие операции со строками:

Вторая цель — получить ноль под второй записью во втором столбце, что означает исключение второй переменной y из третьего уравнения. Один из способов добиться этого — добавить -1/5 второй строки к третьей строке. Однако, чтобы избежать дробей, есть еще один вариант: сначала поменять местами второй и третий ряды. Замена двух строк просто меняет местами уравнения, что явно не изменит решения системы:

Теперь прибавьте −5 раз вторую строку к третьей строке:

Поскольку матрица коэффициентов была преобразована в эшелонированную форму, «прямая» часть исключения Гаусса завершена.Теперь остается использовать третью строку для оценки третьего неизвестного, затем выполнить обратную подстановку во вторую строку для оценки второго неизвестного и, наконец, выполнить обратную замену в первой строке для оценки первого неизвестного.
Третья строка окончательной матрицы переводится в 10 z = 10, что дает z = 1. Обратная подстановка этого значения во вторую строку, которая представляет уравнение y — 3 z = — 1, дает y = 2.Обратная подстановка обоих этих значений в первую строку, которая представляет уравнение x — 2 y + z = 0, дает x = 3. Следовательно, решение этой системы: ( x, y, z ) = (3, 2, 1).
Пример 4 : Решите следующую систему с помощью исключения Гаусса:

Для этой системы расширенная матрица (вертикальная линия опущена) составляет

Сначала умножьте строку 1 на 1/2:

Теперь добавление −1 первой строки ко второй строке дает нули под первой записью в первом столбце:

Перестановка второй и третьей строк дает желаемую матрицу коэффициентов верхней треугольной формы:

В третьей строке теперь указано z = 4.Обратная подстановка этого значения во вторую строку дает y = 1, а обратная подстановка обоих этих значений в первую строку дает x = −2. Решение этой системы, следовательно, ( x, y, z ) = (−2, 1, 4).
Исключение Гаусса-Джордана . Исключение по Гауссу осуществляется путем выполнения элементарных операций со строками для получения нулей ниже диагонали матрицы коэффициентов, чтобы привести ее к эшелонированной форме. (Напомним, что матрица A ′ = [ a ij ′] имеет эшелонированную форму, когда a ij ′ = 0 для i> j , любые нулевые строки появляются в нижней части матрицы , а первая ненулевая запись в любой строке находится справа от первой ненулевой записи в любой более высокой строке.Как только это будет сделано, проверка нижних строк и обратная подстановка в верхние строки определяют значения неизвестных.
Однако можно сократить (или полностью исключить) вычисления, связанные с обратной подстановкой, путем выполнения дополнительных операций со строками для преобразования матрицы из эшелонированной формы в сокращенную форму . Матрица находится в форме сокращенного эшелона, когда, помимо того, что она находится в форме эшелона, каждый столбец, содержащий ненулевую запись (обычно равную 1), имеет нули не только под этой записью, но и над этой записью.Грубо говоря, гауссовское исключение работает сверху вниз, чтобы создать матрицу в форме эшелона, тогда как Гаусс-Джордан исключение продолжается с того места, где остановился гауссов, затем работая снизу вверх, чтобы создать матрицу в форме сокращенного эшелона. Техника будет проиллюстрирована на следующем примере.
Пример 5 : Известно, что высота, y , брошенного в воздух объекта задается квадратичной функцией от t (время) в форме y = at 2 + bt + c .Если объект находится на высоте y = 23/4 в момент времени t = 1/2, при y = 7 в момент времени t = 1 и при y = 2 при t = 2 , определите коэффициенты a, b и c .
Так как t = 1/2 дает y = 23/4

, а два других условия: y ( t = 1) = 7 и y ( t = 2) = 2, дают следующие уравнения для a, b и c :

Следовательно, цель — решить систему

Расширенная матрица для этой системы сокращается следующим образом:

На этом прямая часть исключения по Гауссу завершена, так как матрица коэффициентов приведена к эшелонированной форме.Однако для иллюстрации исключения Гаусса-Жордана выполняются следующие дополнительные элементарные операции со строками:

Эта окончательная матрица сразу дает решение: a = −5, b = 10 и c = 2.
Пример 6 : Решите следующую систему с помощью исключения Гаусса:

Расширенная матрица для этой системы —

Кратные значения первой строки добавляются к другим строкам, чтобы получить нули под первой записью в первом столбце:

Затем −1 раз вторая строка добавляется к третьей строке:

В третьей строке теперь указано 0 x + 0 y + 0 z = 1, уравнение, которому не могут соответствовать никакие значения x, y и z .Процесс останавливается: у этой системы нет решений.
Предыдущий пример показывает, как исключение Гаусса выявляет несовместимую систему. Небольшое изменение этой системы (например, изменение постоянного члена «7» в третьем уравнении на «6») проиллюстрирует систему с бесконечно большим числом решений.
Пример 7 : Решите следующую систему с помощью исключения Гаусса:

Те же операции, которые применялись к матрице дополнений системы в примере 6, применяются к матрице дополнений для данной системы:

Здесь третья строка переводится в 0 x + 0 y + 0 z = 0, уравнение, которому удовлетворяют любые x, y и z .Поскольку это не накладывает ограничений на неизвестные, на неизвестные нет трех условий, а только два (представленных двумя ненулевыми строками в окончательной расширенной матрице). Поскольку имеется 3 неизвестных, но только 2 константы, 3–2 = 1 неизвестных, скажем, z , произвольно; это называется свободной переменной . Пусть z = t , где t — любое действительное число. Обратная подстановка z = t во вторую строку (- y + 5 z = −6) дает

Обратная подстановка z = t и y = 6 + 5 t в первую строку ( x + y -3 z = 4) определяет x :

Следовательно, каждое решение системы имеет вид

, где t — любое действительное число.Существует бесконечно много решений, поскольку каждое действительное значение т дает отдельное конкретное решение. Например, выбор t = 1 дает ( x, y, z ) = (−4, 11, 1), а t = 3 дает ( x, y, z ) = (4, — 9, −3) и так далее. Геометрически эта система представляет собой три плоскости в R 3 , которые пересекаются по линии, и (*) — параметрическое уравнение для этой линии.
Пример 7 дает иллюстрацию системы с бесконечным числом решений, как возникает этот случай и как записывается решение.Каждая линейная система, имеющая бесконечно много решений, должна содержать хотя бы один произвольный параметр (свободная переменная). После того, как расширенная матрица была приведена к эшелонированной форме, количество свободных переменных равно общему количеству неизвестных минус количество ненулевых строк:

Это согласуется с теоремой B выше, которая утверждает, что линейная система с меньшим количеством уравнений, чем неизвестных, если согласована, имеет бесконечно много решений. Условие «меньше уравнений, чем неизвестных» означает, что количество строк в матрице коэффициентов меньше количества неизвестных.Следовательно, приведенное выше уравнение в рамке подразумевает, что должна быть хотя бы одна свободная переменная. Поскольку такая переменная по определению может принимать бесконечно много значений, система будет иметь бесконечно много решений.
Пример 8 : Найти все решения для системы

Во-первых, обратите внимание, что есть четыре неизвестных, но только три уравнения. Следовательно, если система непротиворечива, гарантировано, что она будет иметь бесконечно много решений, а это состояние характеризуется по крайней мере одним параметром в общем решении.После построения соответствующей расширенной матрицы исключение Гаусса дает

Тот факт, что в эшелонированной форме расширенной матрицы остались только две ненулевые строки, означает, что 4-2 = 2 переменных свободны:

Следовательно, выбирая y и z в качестве свободных переменных, пусть y = t 1 и z = t 2 . Во второй строке сокращенной расширенной матрицы следует

, а первая строка дает

Таким образом, решения системы имеют вид

, где т 1 т 2 могут принимать любые реальные значения.
Пример 9 : Пусть b = ( b 1 , b 2 , b 3 ) T и пусть A будет матрицей

Для каких значений b 1 , b 2 и b 3 будет ли система A x = b согласованной?
Расширенная матрица для системы A x = b читает

, который гауссовский элиминатин сокращает следующим образом:

Нижняя строка теперь подразумевает, что b 1 + 3 b 2 + b 3 должно быть равно нулю, чтобы эта система была согласованной.Следовательно, в данной системе есть решения (фактически бесконечно много) только для тех векторов-столбцов b = ( b 1 , b 2 , b 3 ) T , для которых b 1 + 3 b 2 + b 3 = 0.
Пример 10 : Решите следующую систему (сравните с Примером 12):

Такая система, как эта, где постоянный член в правой части каждого уравнения равен 0, называется гомогенной системой .В матричной форме он читается как A x = 0 . Поскольку каждая гомогенная система согласована — поскольку x = 0 всегда является решением, — однородная система имеет либо ровно одно решение ( тривиальное решение , x = 0 ), либо бесконечно много. Сокращение строки матрицы коэффициентов для этой системы уже было выполнено в примере 12. Нет необходимости явно дополнять матрицу коэффициентов столбцом b = 0 , поскольку никакая элементарная операция со строкой не может повлиять на эти нули.То есть, если A ‘является эшелонированной формой A , то операции элементарной строки преобразуют [ A | 0 ] в [ A ′ | 0 ]. По результатам Примера 12,

Поскольку последняя строка снова подразумевает, что z можно принять как свободную переменную, пусть z = t , где t — любое действительное число. Обратная подстановка z = t во вторую строку (- y + 5 z = 0) дает

и обратная подстановка z = t и y = 5 t в первую строку ( x + y — 3 z = 0) определяет x :

Следовательно, каждое решение этой системы имеет вид ( x, y, z ) = (−2 t , 5 t, t ), где t — любое действительное число.Существует бесконечно много растворяющих веществ, поскольку каждое действительное значение т дает уникальное частное решение.
Обратите внимание на разницу между набором решений для системы в Примере 12 и здесь. Хотя у обеих была одна и та же матрица коэффициентов A, , система в примере 12 была неоднородной ( A x = b , где b ≠ 0 ), а здесь — соответствующая однородная система, A x = 0 .Помещая свои решения рядом,
общее решение для Ax = 0 : ( x, y, z ) = (−2 t , 5 t , t )
общее решение для Ax = b : ( x, y, z ) = (−2 t , 5 t , t ) + (−2, 6, 0)
иллюстрирует важный факт:Теорема C . Общие решения для согласованной неоднородной лиенарной системы, A, x = b , равны общему решению соответствующей однородной системы, A x = 0 , плюс частное решение неоднородная система.То есть, если x = x h представляет собой общее решение A x = 0 , то x = x h + x представляет общее решение A x + b , где x — любое конкретное решение (согласованной) неоднородной системы A x = b .
[Техническое примечание: Теорема C, которая касается линейной системы , имеет аналог в теории линейных дифференциальных уравнений .Пусть L — линейный дифференциальный оператор; то общее решение разрешимого неоднородного линейного дифференциального уравнения, L (y) = d (где d ≢ 0), равно общему решению соответствующего однородного уравнения, L (y) = 0 плюс частное решение неоднородного уравнения. То есть, если y = y h повторно отображает общее решение L (y) = 0, то y = y h + y представляет собой общее решение L (y ) = d , где y — любое частное решение (решаемого) неоднородного линейного уравнения L (y) = d .]
Пример 11 : Определить все решения системы

Запишите расширенную матрицу и выполните следующую последовательность операций:

Поскольку в этой конечной (эшелонированной) матрице остаются только 2 ненулевые строки, есть только 2 ограничения, и, следовательно, 4-2 = 2 из неизвестных, например y и z , являются свободными переменными. Пусть y = t 1 и z = t 2 .Обратная подстановка y = t 1 и z = t 2 во вторую строку ( x — 3 y + 4 z = 1) дает

Наконец, обратная замена x = 1 + 3 t 1 -4 2 , y = t 1 и z = t 2 в первую строка (2 w -2 x + y = −1) определяет w :

Следовательно, каждое решение этой системы имеет вид

, где т 1 и т 2 — любые действительные числа.Другой способ написать решение:

где т 1 , т 2 ∈ R .
Пример 12 : Определите общее решение

, которая является однородной системой, соответствующей неоднородной в примере 11 выше.
Так как решение неоднородной системы в примере 11 —

Теорема C означает, что решение соответствующей однородной системы равно  (где t 1 , t 2 ∈ R ), которое получается из (*), просто отбрасывая конкретное решение, x = (1 / 2,1,0,0) неоднородной системы.
(где t 1 , t 2 ∈ R ), которое получается из (*), просто отбрасывая конкретное решение, x = (1 / 2,1,0,0) неоднородной системы.
Пример 13 : Докажите теорему A: независимо от ее размера или количества неизвестных, содержащихся в ее уравнениях, линейная система не будет иметь решений, ровно одно решение или бесконечно много решений.
Доказательство . Пусть данная линейная система записана в матричной форме A x = b . Теорема действительно сводится к следующему: если A x = b имеет более одного решения, то на самом деле их бесконечно много.Чтобы установить это, пусть x 1 и x 2 будут двумя разными решениями A x = b . Теперь будет показано, что для любого реального значения t вектор x 1 + t ( x 1 — x 2 ) также является решением A x = b ; Поскольку t может принимать бесконечно много различных значений, из этого следует желаемый вывод.Начиная с A x 1 = b и A x 2 ,

Следовательно, x 1 + t ( x 1 — x 2 ) действительно является решением A x = b , и теорема доказана.
,2 = 1 у = х[по одному в строке]
х Y
[по одному в строке]
Решить
ГРАФИЧЕСКИЕ РЕШЕНИЯ
Часто мы хотим найти одну упорядоченную пару, которая является решением двух различных линейных уравнения.Один из способов получить такую упорядоченную пару — построить график двух уравнений на одном наборе осей и определение координат точки, где они пересекаются.
Пример 1
Постройте уравнения
х + у = 5
х — у = 1
на том же наборе осей и определите упорядоченную пару, которая является решением для каждого уравнение.
Решение
Используя метод построения графика с перехватом, мы обнаруживаем, что две упорядоченные пары, которые решения x + y = 5 равны
(0, 5) и (5, 0)
И две упорядоченные пары, которые являются решениями
x — y = 1
(0, -1) и (1,0)
Показаны графики уравнений.
Точка пересечения — (3, 2). Таким образом, (3, 2) должны удовлетворять каждому уравнению.
Фактически, 3 + 2 = 5 и 3 — 2 = 1

В целом, графические решения являются приблизительными. Разработаем методы для точных решений в следующих разделах.
Считается, что линейные уравнения, рассматриваемые вместе таким образом, образуют систему уравнения. Как и в приведенном выше примере, решение системы линейных уравнений может быть одной упорядоченной парой. Компоненты этой упорядоченной пары удовлетворяют каждому из два уравнения.
Некоторые системы не имеют решений, в то время как другие имеют бесконечное количество решений. ЦИИ. Если графики уравнений в системе не пересекаются, то есть если линии параллельны (см. рис. 8.1а) — уравнения считаются несовместимыми , и не является упорядоченной парой, которая удовлетворяла бы обоим уравнениям. Если графики уравнений имеют вид на той же линии (см. рис. 8.1b), уравнения считаются зависимыми от , и каждое упорядоченная пара, которая удовлетворяет одному уравнению, будет удовлетворять обоим уравнениям.Заметь когда система несовместима, наклон линий тот же, но y-перехваты разные. Когда система зависима, наклоны и пересечения по оси Y одинаковые.
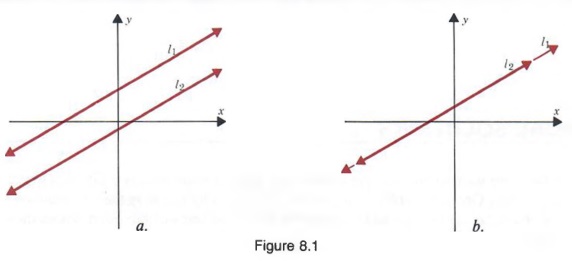
В нашей работе нас в первую очередь будут интересовать системы, имеющие один-единственный решение, которые считаются непротиворечивыми и независимыми. График такой система показана в решении Примера 1.
РЕШЕНИЕ СИСТЕМ ДОПОЛНЕНИЕМ I
Мы можем решать системы уравнений алгебраически.Более того, решения, которые мы получить алгебраическими методами точны.
Система в следующем примере — это система, которую мы рассматривали в разделе 8.1. на странице 335.
Пример 1
Решить
х + у = 5 (1)
х — у = 1 (2)
Решение
Мы можем получить уравнение с одной переменной, сложив уравнения (1) и (2)

Решение полученного уравнения относительно x дает
2х = 6, х = 3
Теперь мы можем заменить x на 3 либо в уравнении (1), либо в уравнении (2), чтобы получить соответствующее значение y.В этом случае мы выбрали уравнение (1) и получили
(3) + у = 5
г = 2
Таким образом, решение x = 3, y = 2; или (3, 2).
Обратите внимание, что мы просто применяем свойство сложения равенства, чтобы мы могли получить уравнение, содержащее единственную переменную. Уравнение с одной переменной, вместе с любым из исходных уравнений, то образует эквивалентную систему решение которого легко получить.
В приведенном выше примере мы смогли получить уравнение с одной переменной с помощью сложение уравнений (1) и (2), поскольку члены + y и -y являются отрицательными значениями каждого Другой.Иногда необходимо умножить каждый член одного из уравнений на -1, чтобы члены одной переменной имели противоположные знаки.
Пример 2
Решить
2a + b = 4 (3)
а + Ь = 3 (4)
Решение
Мы начинаем с умножения каждого члена уравнения (4) на -1, чтобы получить
2a + b = 4 (3)
-a — b = — 3 (4 ‘)
, где + b и -b отрицательны друг другу.
Символ ‘, называемый «простым», указывает на эквивалентное уравнение; то есть уравнение, которое имеет те же решения, что и исходное уравнение.Таким образом, уравнение (4 ‘) эквивалентно уравнению (4). Теперь складывая уравнения (3) и (4 ‘), получаем

Подставляя 1 вместо a в уравнении (3) или уравнении (4) [скажем, в уравнении (4)], мы получаем
1 + b = 3
б = 2
и наше решение — a = 1, b = 2 или (1, 2). Когда переменные a и b, упорядоченная пара задается в виде (a, b).
РЕШЕНИЕ СИСТЕМ ДОПОЛНЕНИЕМ II
Как мы видели в разделе 8.2, решение системы уравнений сложением зависит от одна из переменных в обоих уравнениях с коэффициентами, отрицательными друг друга.Если это не так, мы можем найти эквивалентные уравнения, которые действительно имеют переменные с такими коэффициентами.
Пример 1
Решите систему
-5x + 3y = -11
-7x — 2y = -3
Решение
Если мы умножим каждый член уравнения (1) на 2 и каждый член уравнения
(2) на 3, получаем эквивалентную систему
(2) (-5x) + (2) (3y) = (2) (- ll)
(3) (-7x) — (3) (2y) = (3) (- 3)
или
-10x + 6y = -22 (1 ‘)
-21x — 6y = -9 (2 ‘)
Теперь, сложив уравнения (1 ‘) и (2’), мы получим
-31x = -31
х = 1
Подстановка 1 вместо x в уравнении (1) дает
-5 (1) + 3у = -11
3y = -6
у = -2
Решение: x = 1, y = -2 или (1, -2).
Обратите внимание, что в уравнениях (1) и (2) члены, включающие переменные, находятся в левый член, а постоянный член находится в правом члене. Мы будем ссылаться таким договоренностям, как стандартный бланк для систем. Удобно расположить системы в стандартной форме, прежде чем приступить к их решению. Например, если мы хочу решить систему
3у = 5х — 11
-7x = 2 года — 3
мы сначала напишем систему в стандартной форме, добавив -5x к каждому члену уравнения (3) и добавлением -2y к каждому члену уравнения (4).Таким образом, получаем
-5x + 3y = -11
-lx — 2y = -3
, и теперь мы можем продолжить, как показано выше.
РЕШЕНИЕ СИСТЕМ ЗАМЕНЫ
В разделах 8.2 и 8.3 мы решали системы уравнений первой степени с двумя вариациями. способностей методом сложения. Другой метод, называемый методом подстановки, также могут быть использованы для решения таких систем.
Пример 1
Решите систему
-2x + y = 1 (1)
х + 2у = 17 (2)
Решение
Решая уравнение (1) относительно y через x, получаем
y = 2x + 1 (1 ‘)
Теперь мы можем заменить y 2x + 1 в уравнении (2), чтобы получить
х + 2 (2x + 1) = 17
х + 4х + 2 = 17
5x = 15
x = 3 (продолжение)
Подставляя 3 вместо x в уравнение (1 ‘), мы получаем
у = 2 (3) + 1 = 7
Таким образом, решение системы: x = 3, y = 7; или (3, 7).
В приведенном выше примере было легко выразить y явно через x, используя Уравнение (1). Но мы также могли бы использовать уравнение (2) для явной записи x в терминах из
х = -2у + 17 (2 ‘)
Теперь подставляя — 2y + 17 вместо x в уравнении (1), мы получаем

Подставляя 7 вместо y в уравнение (2 ‘), мы получаем
х = -2 (7) + 17 = 3
Решение системы снова (3, 7).
Обратите внимание, что метод подстановки полезен, если мы можем легко выразить одну переменную с точки зрения другой переменной.
ПРИЛОЖЕНИЯ, ИСПОЛЬЗУЮЩИЕ ДВЕ ПЕРЕМЕННЫЕ
Если две переменные связаны одним уравнением первой степени, существует бесконечно много упорядоченных пар, которые являются решениями уравнения. Но если две переменные связанных двумя независимыми уравнениями первой степени, может быть только одна упорядоченная пара, которая является решением обоих уравнений. Поэтому для решения задач с помощью двух переменных, мы должны представить два независимых отношения с помощью двух уравнений . Часто мы можем легче решать проблемы с помощью системы уравнений, чем с помощью используя одно уравнение с одной переменной.Мы будем следовать указанным шести шагам на стр. 115, с небольшими изменениями, как показано в следующем примере.
Пример 1
Сумма двух чисел равна 26. Чем больше число, тем больше 2 больше, чем в три раза меньшее количество. Найдите числа.
Решение
Шаги 1-2
Мы представляем то, что хотим найти, в виде двух словесных фраз. Тогда мы
представляют словосочетания в терминах двух переменных.
Меньшее число: x
Большее число: y
Шаг 3 Эскиз не применим.
Шаг 4 Теперь мы должны написать два уравнения, представляющих указанные условия.
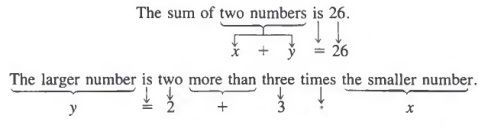
Сумма двух чисел равна 26.
Шаг 5 Чтобы найти числа, решаем систему
х + у = 26 (1)
у = 2 + 3х (2)
Поскольку уравнение (2) явно показывает y через x, мы решим систему следующим образом: метод подстановки. Подставляя 2 + 3x вместо y в уравнение (1), мы получаем
х + (2 + 3х) = 26
4x = 24
х = 6
Подставляя 6 вместо x в уравнении (2), мы получаем
у = 2 + 3 (6) = 20
Шаг 6 Меньшее число — 6, большее — 20.
РЕЗЮМЕ ГЛАВЫ
Два уравнения, рассматриваемые вместе, образуют систему уравнений . Решение обычно одна упорядоченная пара. Если графики уравнений представляют собой параллельных линий , уравнения считаются несогласованными ; если графики представляют собой ту же линию , уравнения считаются зависимыми .
Мы можем решить систему уравнений методом сложения , если сначала напишем системы в стандартной форме , в которой термины, включающие переменные, находятся в левый член, а постоянный член находится в правом члене.
Мы можем решить систему уравнений методом подстановки , если одна переменная в по крайней мере одно уравнение в системе сначала явно выражается через другое переменная.
Мы можем решать текстовые задачи, используя две переменные, представляя два независимых отношения двумя уравнениями.
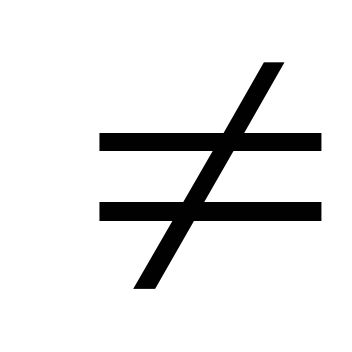 0,
то система (1) несовместна;
0,
то система (1) несовместна;