Решение СЛАУ методами подстановки и сложения

Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.

Например, уравнение

—

линейное, а уравнения и не являются линейными.

В общем виде система m линейных уравнений с n переменными записывается так:

. (1)

Числа
 
называются коэффициентами при переменных, а
 —
свободными членами.

Совокупность чисел

называется решением системы (1) линейных уравнений, если при подстановке их вместо переменных во все уравнения они обращаются в верные равенства.

Изучение систем линейных уравнений начинается в средней школе. В школьном курсе рассматриваются в основном системы двух линейных уравнений с двумя переменными и два метода их решения —

метод подстановки и метод сложения. Эти методы являются основой изучаемого в курсе высшей математике метода Гаусса. (Принципиально иной метод — метод Крамера — основан на использовании определителей).

Чтобы последовательно двигаться от простому к ещё более простому (сложному), повторим два школьных метода.

Решение. При решении системы линейный уравнений методом подстановки сначала из какого-нибудь уравнения выражают одну переменную через другую (другие, если неизвестных больше двух). Полученное выражение подставляют в другие уравнения, в результате чего приходят к уравнению с одной переменной. Затем находят соответствующее значение второй (и третьей, если она есть) переменной.

Начнём со вполне школьного примера системы двух линейных уравнений с двумя переменными.

Пример 1. Решить систему линейных уравнений методом подстановки:

Выразим из первого уравнения данной системы y через x (можно и наоборот) и получим:

Подставив во второе уравнение данной системы вместо y выражение , получим систему

Данная и полученная системы равносильны. В последней системе второе уравнение содержит только одну переменную. Решим это уравнение:

Соответствующее значение y найдём, подставив вместо x число -5 в выражение , откуда

Пара (-5; 2) является решением системы линейных уравнений.

Методом подстановки можно решать и системы трёх линейных уравнений с тремя переменными.

Пример 2. Решить систему линейных уравнений методом подстановки:

Из третьего уравнения системы выразим :

.

Подставим это выражение во второе уравнение данной системы:

.

Произведём преобразования и выразим из этого уравнения :

Полученные выражения для и подставим в первое уравнение системы и получим

.

Вместо можно вновь подставить его выражение, тогда получим уравнение с одним неизвестным:

откуда

.

Теперь из ранее полученных выражений для остальных переменных найдём и эти переменные:

Итак, решение данной системы линейных уравнений:

.

Пример 3. Решить систему линейных уравнений методом подстановки:

Из первого уравнения системы выразим :

.

Подставим это выражение во второе уравнение данной системы, после чего выполним преобразования и получим:

Из третьего уравнения выразим :

Полученное выражение для подставим в преобразованное второе уравнение системы и получим уравнение с одним неизвестным:

.

Произведём преобразования и найдём :

Теперь из ранее полученных выражений для остальных переменных найдём и эти переменные:

Итак, решение данной системы линейных уравнений:

.

При решении систем линейных уравнений методом сложения уравнения системы почленно складывают, причём одно или оба (несколько) уравнений могут быть умножены на различные числа. В результате приходят к эквивалентной (равносильной) системе линейных уравнений, в которой одно из уравнений содержит только одну переменную.

Пример 4. Решить систему линейных уравнений методом сложения:

Решение. В уравнениях данной системы в этом примере системы коэффициенты при y — противоположные числа. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной:

, или , .

Заменим одно из уравнений исходной системы, например, первое, уравнением . Получим систему

Решим полученную систему. Подставив значение в уравнение , получим уравнение с одной переменной y:

Пара (2; 1) является решением полученной системы линейных уравнений. Она является также решением исходной системы, так как эти две системы линейных уравнений равносильны.

Пример 5. Решить систему линейных уравнений методом сложения

Почленное сложение уравнений системы не приводит к исключению одной из переменных. Но если умножить все члены первого уравнения на -3, а второго уравнения на 2, то коэффициенты при x в полученных уравнениях будут противоположными числами:

Почленное сложение уравнений полученной в результате преобразований системы приводит к уравнению с одной переменной: . Из этого уравнения находим, что . Получили

Решением полученной системы, а следовательно и исходной системы линейных уравнений является пара чисел (-3; 0).

Пример 6. Решить систему линейных уравнений методом сложения:

Решение. Для упрощения решения произведём замену переменных:

, .

Приходим к системе линейных уравнений:

или

Умножим второе уравнение полученной системы на -2 и сложим с первым уравнением, получим , . Тогда .

Следовательно, имеем систему уравнений

или

Умножим второе уравнение полученной системы на 3 и сложим с первым уравнением. Получим

.

Решив задачи из примеров на решение систем линейных уравнений методом подстановки и методом сложения, мы научились производить элементарные преобразования, необходимые для решениях систем линейных уравнений в курсе высшей математики.

Продолжение темы «Системы уравнений и неравенств»

Начало темы «Линейная алгебра»

Поделиться с друзьями

Решение системы линейных уравнений.

Метод подстановки, сложения, графический. Особые случаи, тесты

Тестирование онлайн

• Система линейных уравнений

Система линейных уравнений

Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой

Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.

При решении системы уравнений используют свойства, справедливые для решения уравнений.

Решение системы линейных уравнений способом подстановки

Рассмотрим пример

1) Выразить в одном из уравнений переменную. Например, выразим

y в первом уравнении, получим систему:

2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.

Решение системы линейных уравнений способом сложения

Решим систему уравнений из предыдущего примера методом сложения.

1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».

2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:

Решение системы линейных уравнений графическим способом

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Графическое решение системы

Метод введения новых переменных

Замена переменных может привести к решению более простой системы уравнений, чем исходная.

Рассмотрим решение системы

Введем замену , тогда

Переходим к первоначальным переменным

Особые случаи

Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

Пусть дана система

1) Если , то система имеет единственное решение.

2) Если , то система решений не имеет. В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.

3) Если , то система имеет бесконечное множество решений. В этом случае прямые совпадают друг с другом.

Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.

Решение систем уравнений с примерами решения

Содержание:

1. Графический метод решения систем уравнений
2. Начнём с графического метода
3. Решение систем уравнений методом подстановки
4. Симметричные системы уравнений с двумя неизвестными

Графический метод решения систем уравнений

Вспоминаем то, что знаем

Что такое график уравнения с двумя неизвестными?

Что представляет собой график линейного уравнения с двумя неизвестными?

Решите графическим методом систему линейных уравнений:

Открываем новые знания

Решите графическим методом систему уравнений:

Как можно решить систему двух уравнений с двумя неизвестными с помощью графиков уравнений этой системы? Отвечаем, проверяем себя по тексту

В курсе алгебры 7-го класса вы изучали системы линейных уравнений.

Для их решения вы применяли три метода: графический, метод подстановки и метод алгебраического сложения. Эти же методы служат и для решения других систем двух уравнений с двумя неизвестными, в которых могут содержаться уравнения второй степени или другие рациональные уравнения — как целые, так и дробные.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Начнём с графического метода

Этот метод основан на том, что каждому уравнению с двумя неизвестными соответствует некоторое множество точек координатной плоскости (график этого уравнения). Построив графики уравнений, мы найдём точки пересечения этих графиков (если они есть), и пары чисел — координаты точек пересечения — будут представлять собой решения системы уравнений.

Найденные решения будут, вообще говоря, приближёнными, в зависимости от точности построений соответствующих графиков.

Таким образом, решить графически систему уравнений — значит найти общие точки графиков уравнений, входящих в систему.

Возможно вам будут полезны данные страницы:

Примеры с решением

Пример 1:

Решим систему уравнений:

Построим графики уравнений

Графиком первого уравнения является парабола, с вершиной в точке (0; 1) и ветвями, направленными вверх, графиком второго — прямая, проходящая через точки (0; 3) и (-3; 0).

Парабола и прямая пересекаются в точках А(2; 5) и В(— 1; 2).

Проверкой убеждаемся, что найденные пары чисел действительно являются решениями системы.

Ответ: (2; 5) и (-1; 2).

Пример 2:

Выясним количество решений системы уравнений:

Построим графики уравнений

Графики этих уравнений — окружности. Центр первой окружности — начало координат, а её радиус равен 2; центр второй окружности — точка Р(1; — 1), её радиус равен 3.

Окружности пересекаются в двух точках М и N, координаты которых можно найти приближённо. Поскольку нам нужно определить только количество решений, мы делать этого не будем.

Ответ: Два решения.

Решение систем уравнений методом подстановки

Вспоминаем то, что знаем

Расскажите, как решить систему двух линейных уравнений с двумя неизвестными методом подстановки.

Решите систему линейных уравнений методом подстановки:

Открываем новые знания

Как вы думаете, можно ли применять метод подстановки при решении систем, где не все уравнения являются линейными? При каком условии это удастся сделать?

Решите систему уравнений методом подстановки:

Как решить систему двух уравнений с двумя неизвестными методом подстановки?

Всякую ли систему двух уравнений с двумя неизвестными можно решить методом подстановки?

Ранее вы решали системы уравнений первой степени.

Теперь познакомимся с системами, в которых хотя бы одно уравнение не является линейным. Как и прежде, распространённым методом решения систем является метод подстановки.

Пример 3:

Решим систему:

Пусть (х; у) — решение системы.

Выразим х из уравнения

Подставим найденное выражение в первое уравнение:

Решим полученное уравнение:

Найдём х:

Убедиться, что найденные пары чисел действительно являются решениями системы, можно подстановкой.

Ответ: (5; 1), (-2;-2,5).

Чуть сложнее дело обстоит в следующем примере.

Пример 4:

Решим систему уравнений:

Пусть (х; у) — решение системы.

Выразим у из линейного уравнения:

Подставим найденное выражение в первое уравнение системы:

После преобразований получим:

Найдём у:

Ответ: (-0,5; 0,5), (4; 5).

Если это целесообразно, то можно осуществлять подстановку некоторого выражения «в целом».

Пример 5:

Решим систему:

Подставим во второе уравнение тогда его можно переписать в виде:

Теперь выразим х через у из первого уравнения системы:

Подставим в полученное ранее уравнение ху = 2:

Корни этого уравнения:

Найдём х:

.

Ответ: (2; 1), (-1;-2).

Иногда решить систему можно, используя метод алгебраического сложения.

Пример 6:

Решим систему:

Сложим уравнения, предварительно умножив первое уравнение на —1. В результате получим:

.

Корни этого уравнения:

Подставим найденные значения в первое уравнение. Рассмотрим два случая:

1)

2) , получим уравнение корней нет.

Ответ: (0; 1), (1; 1).

Иногда упростить решение удаётся, используя различные варианты замены неизвестных.

Пример 7:

Решим систему уравнений:

Обозначим

Второе уравнение системы примет вид:

Решим полученное уравнение. Получим, умножая обе части на 2а:

Таким образом:

Осталось решить методом подстановки линейные системы:

Ответ: (2; 1), (1; 2). Решение задач с помощью систем уравнений Знакомимся с новыми знаниями

Напомним, что при решении задач обычно действуют следующим образом:

1) обозначают буквами какие-нибудь неизвестные величины, выражают через них другие величины, составляют систему уравнений;

2) решают полученную систему;

3) отвечают на вопрос задачи.

Пример 8:

Периметр прямоугольника равен 34 см, а его диагональ 13 см. Найдите стороны прямоугольника.

Пусть х см — длина, у см — ширина (х у), тогда периметр прямоугольника — см.

Воспользуемся теоремой Пифагора:

Получим систему:

Решим систему. Выразим из первого уравнения у:

Подставим во второе уравнение:

Корни уравнения:

Найдём

С учётом условия получим ответ: длина — 12 см, ширина — 5 см.

Пример 9:

Если произведение двух положительных чисел увеличить на первое из них, то получится 128. Если это же произведение увеличить на второе из них то получится 135. Найдите эти числа.

Введём обозначения.

Пусть х — первое число, у — второе число.

Тогда: — произведение, увеличенное на первое число, ху 4-у — произведение, увеличенное на второе число.

Получим систему:

Вычтем из второго уравнения первое. Получим:

Дальше будем решать методом подстановки:

Подставим в первое уравнение выражение для у:

Корни уравнения: (не подходит по смыслу задачи).

Найдём у из уравнения:

Получим ответ: 16 и 7.

Симметричные системы уравнений с двумя неизвестными

Уравнение с двумя неизвестными называется симметричным, если при перестановке этих неизвестных местами уравнение не меняется. Например, уравнение симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид , то есть не меняется. А вот уравнение не симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид , то есть меняется.

Система двух уравнений с двумя неизвестными называется симметричной, если каждое уравнение этой системы симметричное.

ПРЕДУПРЕЖДЕНИЕ. В определении симметричной системы уравнений требуется, чтобы каждое уравнение в отдельности не менялось.

Например, если в системе уравнений

переставить местами неизвестные х и у, то получим систему:

Видно, что система в целом не изменилась (уравнения поменялись местами по сравнению с первоначальной системой). Но такая система не является симметричной, так как каждое из уравнений в отдельности изменилось.

Убедитесь, что симметричные системы с двумя неизвестными х и у можно решать с помощью замены неизвестных:

Сначала научитесь выражать через неизвестные выражения:

Решение системы линейных уравнений методом подстановки: алгоритм, правило, примеры

Алгоритм решения системы линейных уравнений методом подстановки

1. Из любого уравнения системы выразить одну переменную через другую.
2. Подставить во второе уравнение системы вместо переменной выражение, полученное на первом шаге.
3. Решить второе уравнение относительно выраженной переменной.
4. Подставить найденное значение переменной в выражение, полученное на первом шаге.
5. Найти значение второй переменой.
6. Записать ответ в виде упорядоченной пары найденных значений переменных.

Например: ${\left\{ \begin{array}{c} 3x+y = 5 \\ y-x = 1 \end{array} \right.}$

Шаг 1

Из второго уравнения выражаем y:

y = x+1

Шаг 2

Подставляем выражение для y в первое уравнение:

3x+(x+1) = 5

Шаг 3 Решаем первое уравнение:

4x = 5-1

x = 1

Шаг 4

Подставляем значение x в выражение для y:

y = 1+1

Шаг 5

Находим y:

y = 2

Шаг 6

Записываем ответ:

(1;2)

В последовательной записи:

$$ {\left\{ \begin{array}{c} 3x+y = 5 \\ y-x = 1 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 3x+y = 5 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 3x+(x+1) = 5 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 4x = 5-1 \\ y = x+1 \end{array} \right.} \Rightarrow $$ $$ \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 2\end{array} \right.} $$

Ответ: (1;2)

Примеры

Пример 1. Решите систему уравнений методом подстановки:

$ а) {\left\{ \begin{array}{c} 5x-4y = 3 \\ 2x-3y = 4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5x-4y = 3 \\ x = \frac{3y+4}{2} = 1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5(1,5y+2)-4y = 3 \\ x = 1,5y+2 \end{array} \right.} \Rightarrow $

$ \Rightarrow {\left\{ \begin{array}{c} 7,5y+10-4y = 3 \\ x=1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 3,5y = -7 \\ x = 1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y = -2 \\ x = 1,5y+2 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} x = -1 \\ y = -2\end{array} \right.} $

Ответ: (-1;-2)

$ б) {\left\{ \begin{array}{c} 4x-3y = 7 \\ 3x-4y = 0 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 4x-3y = 7 \\ y = \frac{3}{4} x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 4x-3\cdot \frac{3}{4} x = 7 \\ y = \frac{3}{4} x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} (4- \frac{9}{4})x = 7 \\ y = \frac{3}{4} x \end{array} \right.} \Rightarrow $

$\Rightarrow {\left\{ \begin{array}{c} x = 7 \cdot \frac{4}{7} = 4 \\ y = \frac{3}{4} x = \frac{3}{4} \cdot 4 = 3 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}x = 4 \\ y = 3 \end{array} \right.} $

Ответ: (4;3)

$ в) {\left\{ \begin{array}{c} 5a-4b = 9 \\ 2a+3b = -1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5a-4b = 9 \\ a = \frac{-3b-1}{2} = -1,5b-0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5(-1,5b-0,5)-4b = 9 \\ a = -1,5b-0,5 \end{array} \right. } \Rightarrow $

$ \Rightarrow {\left\{ \begin{array}{c} -7,5b-2,5-4b = 9 \\ a = -1,5b-0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}-11,5b = 11,5 \\ a = -1,5b-0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 1 \\ b = -1 \end{array} \right.} $

Ответ: (1;-1)

$ г) {\left\{ \begin{array}{c} 7a+4b = 5 \\ 3a+2b = 1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7a+4b = 5 \\ b = \frac{-3a+1}{2} = -1,5a+0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7a+4(-1,5a+0,5) = 5 \\ b = -1,5a+0,5 \end{array} \right.} \Rightarrow $

$ \Rightarrow {\left\{ \begin{array}{c} 7a-6a+2 = 5 \\ b = -1,5a+0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 3 \\ b = -1,5\cdot3+0,5 = -4 \end{array} \right.} $

Ответ: (3;-4)

Пример 2. Найдите решение системы уравнений:

$а) {\left\{ \begin{array}{c} \frac{x}{4}-y = 7 | \times 4 \\ 3x+ \frac{y}{2} = 9 | \times 2\end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x-4y = 28 \\ 6x+y = 18 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} x = 4y+28 = 4(y+7) \\ 6 \cdot 4(y+7)+y = 18 \end{array} \right.} \Rightarrow $

$\Rightarrow {\left\{ \begin{array}{c} x = 4(y+7) \\ 24y+168+y = 18 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 4(y+7) \\ 25y = -150 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}x = 4(-6+7) = 4 \\ y = -6 \end{array} \right.}$

Ответ: (4;-6)

$б) {\left\{ \begin{array}{c} \frac{x}{2}+ \frac{y}{3} = \frac{1}{6} |\times 6 \\ \frac{x}{3}+ \frac{y}{2} = -\frac{1}{6}| \times 6 \end{array} \right.}\Rightarrow {\left\{ \begin{array}{c} 3x+2y = 1 \\ 2x+3y = -1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y = \frac{-3x+1}{2} = -1,5x+0,5 \\ 2x+3(-1,5x+0,5) = -1\end{array} \right.} \Rightarrow$

$ \Rightarrow {\left\{ \begin{array}{c} y = -1,5x+0,5 \\ 2x-4,5x+1,5 = -1\end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y = -1,5x+0,5 \\ -2,5x = -2,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = -1 \end{array} \right. } $

Ответ: (1;-1)

$ в) {\left\{ \begin{array}{c} 3(5x-y)+14 = 5(x+y) \\ 2(x-y)+9 = 3(x+2y)-16 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 15x-3y+14 = 5x+5y \\ 2x-2y+9 = 3x+6y-16 \end{array} \right.} \Rightarrow $

$ \Rightarrow {\left\{ \begin{array}{c} 10x-8y = -14 |:2 \\ x+8y = 25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5x-4y = -7 \\ x = -8y+25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5(-8y+25)-4y = -7 \\ x = -8y+25 \end{array} \right.} \Rightarrow $

$ \Rightarrow {\left\{ \begin{array}{c} -40y+125-4y = -7 \\ x = -8y+25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} -44y = -132 \\ x = -8y+25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 3 \end{array} \right.} $

Ответ: (1;3)

$ г) {\left\{ \begin{array}{c} 5-3(2x+7y) = x+y-52 \\ 4+3(7x+2y) = 23x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5-6x-21y = x+y-52 \\ 4+21x+6y = 23x \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ 2x-6y = 4 |:2 \end{array} \right.}$

$$ \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ x-3y = 2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7(3y+2)+22y = 57 \\ x = 3y+2 \end{array} \right.} \Rightarrow $$

$$ \Rightarrow {\left\{ \begin{array}{c} 21y+14+22y = 57 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 43y = 43 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 5 \\ y = 1 \end{array} \right.}$$

Ответ: (5;1)

Пример 3*. Найдите решение системы уравнений:

$ {\left\{ \begin{array}{c} \frac{3}{2x-5y} + \frac{8}{x+y} = 5 \\ \frac{12}{x+y} — \frac{1}{2x-5y} = 2 \end{array} \right.} $

Введём новые переменные: $ {\left\{ \begin{array}{c} a = \frac{1}{2x-5y} \\ b = \frac{1}{x+y} \end{array} \right.} $

Перепишем систему и найдём решение для новых переменных:

$$ {\left\{ \begin{array}{c} 3a+8b = 5 \\ 12b-a = 2 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 3(12b-2)+8b = 5 \\ a = 12b-2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 36b-6+8b = 5 \\ a = 12b-2 \end{array} \right.} \Rightarrow $$

$$ \Rightarrow {\left\{ \begin{array}{c} 44b = 11 \\ a = 12b-2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 1 \\ b = \frac{1}{4} \end{array} \right.} $$

Получаем:

$$ {\left\{ \begin{array}{c} 2x-5y = \frac{1}{a} = 1 \\ x+y = \frac{1}{b} = 4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 2x-5(4-x) = 1 \\ y = 4-x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 2x-20+5x = 1 \\ y = 4-x \end{array} \right.} \Rightarrow $$

$$ \Rightarrow {\left\{ \begin{array}{c} 7x = 21 \\ y = 4-x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 3 \\ y = 1 \end{array} \right.} $$

Ответ: (3;1)

Внеклассный урок — Система уравнений второй степени. Способы решения. Системы уравнений второй степени.

Система уравнений второй степени. Способы решения

Система уравнений второй степени – это система уравнений, в которой есть хотя бы одно уравнение второй степени.

 

Систему из двух уравнений, в которой одно уравнение второй степени, а второе уравнение первой степени, решают следующим образом:

1) в уравнении первой степени одну переменную выражают через другую; 2) подставляют полученное выражение в уравнение второй степени, благодаря чему получается уравнение с одной переменной; 3) решают получившееся уравнение с одной переменной; 4) находят соответствующие значения второй переменной.

 

Пример: Решим систему уравнений

│x² – 3xy – 2y² = 2

│x + 2y = 1

 

Решение:

Следуем правилу:

1) Второе уравнение является уравнением первой степени. В  ней выражаем переменную x через y:

x = 1 – 2y

2) в первом уравнении вместо x подставляем полученное выражение 1 – 2y:

(1 – 2y)² – 3(1 – 2y)y – 2y² = 2.

Раскрываем скобки и упрощаем:

8y² – 7y + 1 = 2.

Приравниваем уравнение к нулю и решаем получившееся квадратное уравнение:

8y² – 7y + 1 – 2 = 0

8y² – 7y – 1 = 0.

3) Решив квадратное уравнение, найдем его корни:

y₁ = – 0,125

y₂ = 1.

4) Осталось найти значения x. Для этого в одно из двух уравнений системы просто подставляем значение y. Второе уравнение проще, поэтому выберем его.
Итак, подставляем значения y в уравнение x + 2y = 1 и получаем:
1) х + 2(-0,125) = 1
    х – 0,25 = 1
    х = 1 + 0,25
    х₁ = 1,25.

2) х + 2 · 1 = 1
    х + 2 =1
    х = 1 – 2
    х₂ = –1.

Ответ:

x₁ = 1,25,   y₁ = – 0,125
x₂ = –1,      y₂ = 1.

 

Способы решения системы уравнений с двумя уравнениями второй степени.

1. Замена системы уравнений равносильной совокупностью двух систем.

Пример: Решим систему уравнений

│x² – 9y² – x + 3y = 0
│x² – xy + y = 7

Здесь нет уравнений первой степени, поэтому решать их вроде бы сложнее. Но в первом уравнении многочлен можно разложить на линейные множители и применить метод группировки:

x² – 9y² – x + 3y = (x – 3y)(x + 3y) – (x – 3y) = (x – 3y)(x + 3y) – 1(x – 3y) = (x – 3y)(x + 3y – 1).

(Пояснение-напоминание: x – 3y встречается в выражении дважды и является общим множителем в многочлене (x – 3y)(x + 3y) – 1(x – 3y). По правилу группировки, мы умножили его на сумму вторых множителей и получили равносильное уравнение).

В результате наша система уравнений обретает иной вид:

│(x – 3y)(x + 3y – 1) = 0
│x² – xy + y = 7

Первое уравнение равно нулю только в том случае, если x – 3y = 0 или x + 3y – 1 = 0.

Значит, нашу систему уравнений мы можем записать в виде двух систем следующего вида:

│x – 3y = 0
│x² – xy + y = 7

и

│x + 3y – 1 = 0
│x² – xy + y = 7

Мы получили две системы, где первые уравнения являются уравнениями первой степени. Мы уже можем легко решить их. Понятно, что решив их и объединив затем множество решений этих двух систем, мы получим множество решений исходной системы. Говоря иначе, данная система равносильна совокупности двух систем уравнений.

Итак, решаем эти две системы уравнений. Очевидно, что здесь мы применим метод подстановки, подробно изложенный в предыдущем разделе.

Обратимся сначала к первой системе.
В уравнении первой степени выразим х через у:

х = 3у.

Подставим это значение во второе уравнение и преобразим его в квадратное уравнение:

(3у)² – 3у · у + у = 7,

9у² – 3у² + у = 7,

6у² + у = 7,

6у² + у – 7 = 0

Как решается квадратное – см.раздел «Квадратное уравнение». Здесь мы сразу напишем ответ:

                            7
у₁ = 1,    у₂ = – ——.
                           6

Теперь подставим полученные значения у в первое уравнение первой системы и решим его:

1) х – 3 · 1 = 0,

    х₁ = 3.

                      7
2) х – 3 · (– ——) = 0,
                      6

             7
    х + —— = 0,
             2

                 7
    х₂ = – ——
                 2

Итак, у нас есть первые ответы:

х₁ = 3,    у₁ = 1;

              7                     7
х₂ = – ——,   у₂ = – ——.
             2                     6

Переходим ко второй системе. Не будем производить вычисления – их порядок точно такой же, что и в случае с уравнениями первой системы. Поэтому сразу напишем результаты вычислений:

х₃ = –2,   у₃ = 1.

х₄ = –2,5,   у₄ = – 0,5.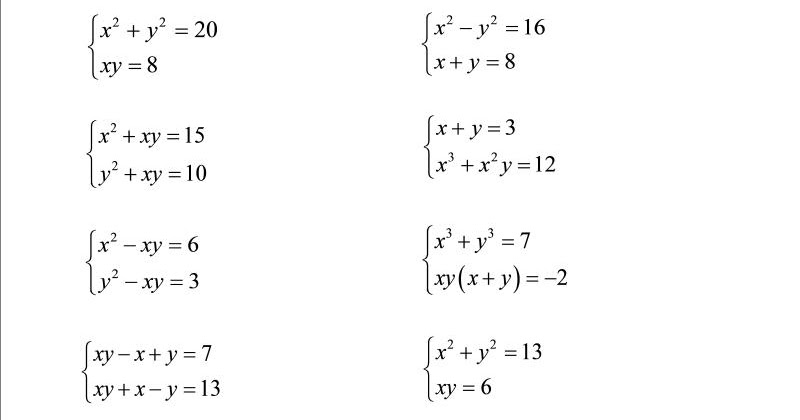

Таким образом, исходная система уравнений решена.

Ответ:

       1          1
(–3 — ; –1 — ),  (3; 1),  (2,5; –0,5),  (–2; 1).
       2          6

 

2. Решение способом сложения.

Пример 2: Решим систему уравнений

│2x² + 3y = xy
│x² – y = 3xy

Решение.

Второе уравнение умножим на 3:

3x² – 3y = 9xy

Зачем мы умножили уравнение на 3? Благодаря этому мы получили равносильное уравнение с числом -3y, которое встречается и в первом уравнении, но с противоположным знаком. Это поможет нам буквально при следующем шаге получить упрощенное уравнение (они будут взаимно сокращены).

Сложим почленно левые и правые части первого уравнения системы и нашего нового уравнения:

2x² + 3y + 3x² – 3y = xy + 9xy

Сводим подобные члены и получаем уравнение следующего вида:

5x² = 10xy

Упростим уравнение еще, для этого сокращаем обе части уравнения на 5 и получаем:

x² = 2xy

Приравняем уравнение к нулю:

x² – 2xy = 0

Это уравнение можно представить в виде x(x – 2y) = 0.

Здесь мы получаем ситуацию, с которой уже сталкивались в предыдущем примере: уравнение верно только в том случае, если x = 0 или x – 2y = 0.

Значит, исходную систему опять-таки можно заменить равносильной ей совокупностью двух систем:

│x = 0
│x² – y = 3xy

и

│x = 2y
│x² – y = 3xy

Обратите внимание: во второй системе уравнение x – 2y = 0 мы преобразовали в x = 2y.

Итак, в первой системе мы уже знаем значение x. Это ноль. То есть x₁ = 0. Легко вычислить и значение y: это тоже ноль. Таким образом, первая система имеет единственное решение: (0; 0).

Решив вторую систему, мы увидим, что она имеет два решения: (0; 0) и (–1; –0,5).

Таким образом, исходная система имеет следующие решения: (0; 0) и (–1; –0,5).

Пример решен.

 

3. Решение методом подстановки.

Этот метод был применен в начале раздела. Здесь мы выделяем его в качестве одного из способов решения. Приведем еще один пример.

Пример. Решить систему уравнений

│х + у = 9
│у² + х = 29

Решение.

Первое уравнение проще, поэтому выразим в нем х через у:

х = 9 – у.

Теперь произведем подстановку. Подставим это значение х во второе уравнение, получим квадратное уравнение и решим его:

у² + 9 – у = 29
у² – у – 20 = 0

D = b² – 4ас = 1 – 4 · 1 · (–20) = 81

√D = 9

         –b + √D          1 + 9
у₁ = ————  =  ——— = 5
             2a                  2

         –b – √D          1 – 9
у₂ = ————  =  ——— = –4
             2a                  2

Осталось найти значения х. Первое уравнение проще, поэтому им и воспользуемся:

1) х + 5 = 9
    х = 9 – 5
    х₁ = 4

2) х – 4 = 9
    х = 9 + 4
    х₂ = 13

Ответ: (4; 5), (13; –4).

 

Система линейных уравнений с двумя переменными. Методы решения систем уравнений.

Решением системы линейных уравнений двух переменных является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.

Как можно решить систему уравнений с двумя переменными?

Системы уравнений с двумя переменными можно решить методом подстановки:

 

 

---

 

Системы уравнений с двумя переменными можно решить методом сложения:

Пример. Решить систему методом сложения: \(\begin{equation*} \begin{cases} x-y-4=0 \\ 3x+y-8=0 \end{cases} \end{equation*}\).

Решение:

 

---

Система уравнений состоящее из двух переменных должно удовлетворять всем решениям одновременно. Система линейных уравнений из двух переменных рассматривается одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям системы одновременно. Некоторые линейные системы могут не иметь решения, и это  будет их решением, другие системы могут иметь бесконечное число решений. Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальное решение.

Выводы:

• Система линейных уравнений из двух переменных решается совместно методом подстановки или методом сложения.
• Чтобы найти решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям в системе одновременно.
• Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных.
• Решить систему уравнений это значит найти численное значение для каждой переменной в системе либо доказать что решений нет.

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Решить систему уравнений методом алгебраического сложения

☰

Суть данного метода заключается в том, чтобы сложить друг с другом левые части уравнений системы, приравняв к ним сумму правых частей тех же уравнений. Сложение может быть заменено вычитанием. Основная цель подобных действий – это избавиться от одной из переменных, после чего решить полученное уравнение с одной переменной легко.

Рассмотрим пример:
| 3x – y + 2 = 0
| –x + y + 4 = 0

Сложим уравнения системы:
(3x – y + 2) + (–x + y + 4) = 0 + 0
3x – y + 2 – x + y + 4 = 0
2x + 6 = 0

В результате мы получили уравнение с одной переменной, которое просто решить:
x = –6 / 2
x = –3

Подставляя x в любое линейное уравнение системы, получаем y:
–(–3) + y + 4 = 0
y = –7

Таким образом решением предложенной системы линейных уравнений с двумя переменными является точка с координатами (–3; –7).

Рассмотрим другой пример:
| 2x + 6y = 120
| 2x – 2y = 20

Здесь уже надо не складывать левые и правые части уравнений, а вычитать:
(2x + 6y) – (2x – 2y) = 120 – 20
2x + 6y – 2x + 2y = 100
8y = 100
y = 12.5

Находим x:
2x – 2 * 12.5 = 20
2x = 20 + 25
x = 45 / 2
x = 22.5
Ответ: (22.5; 12.5)

Теперь рассмотрим более сложный третий пример, когда ни при сложении, ни при вычитании ни одна из переменных не уничтожается:
| –4.5x – 2y + 12 = 0
| 10x + 3y – 7.5 = 0

Умножим первое уравнение на 3, а второе на 2:
| 3 * (–4.5x – 2y + 12) = 0 * 2
| 2 * (10x + 3y – 5) = 0 * 2

Тогда получим такую систему линейных уравнений с двумя переменными:
| –13.5x – 6y + 36 = 0
| 20x + 6y – 10 = 0

Как видим, при сложении уравнений переменная y уничтожается и в итоге получается уравнение с одной переменной:
20x – 10 – 13.5x + 36 = 0
6.5x = –26
x = –26 / 6.5
x = –4

Находим y:
–4. 5 * (–4) – 2y + 12 = 0
18 – 2y + 12 = 0
–2y = –30
y = 15

Ответ: x = –4, y = 15

Решение системы уравнений — методы и примеры

Как решить систему уравнений?

К настоящему времени у вас есть представление о том, как решать линейные уравнения, содержащие единственную переменную. Что, если бы вам представили множественных линейных уравнений, содержащих более одной переменной ? Набор линейных уравнений с двумя или более переменными известен как система уравнений .

Существует несколько методов решения систем линейных уравнений.

Эта статья научит решать линейные уравнения, используя обычно используемые методы , а именно замену и исключение.

Метод замещения

Замена — это метод решения линейных уравнений, в котором переменная в одном уравнении выделяется, а затем используется в другом уравнении для определения оставшейся переменной.

Общие шаги для замены:

• Сделайте предмет формулы для переменной в одном из данных уравнений.
• Подставьте значение этой переменной во второе уравнение. ‘
• Решите уравнение, чтобы получить значение одной из переменных.
• Подставьте полученное значение в любое из уравнений, чтобы также получить значение другой переменной.

Давайте решим пару примеров, используя метод подстановки.

Пример 1

Решите указанные ниже системы уравнений.

б = а + 2

а + Ь = 4.

Решение

Подставляем значение b во второе уравнение.

а + (а + 2) = 4

Теперь решите

а + а + 2 = 4

2a + 2 = 4

2a = 4–2

а = 2/2 = 1

Подставьте полученное значение a в первое уравнение.

б = а + 2

б = 1 + 2

б = 3

Следовательно, решение двойного уравнения: a = 1 и b = 3.

Пример 2

Решите следующие уравнения с помощью замены.
7x — 3y = 31 ——— (i)

9x — 5y = 41 ——— (ii)

Решение

Из уравнения (i),

7x — 3y = 31

Сделайте y предметом формулы в уравнении:

7x — 3y = 31

Вычтем 7x из обеих частей уравнения 7x — 3y = 31, чтобы получить;

— 3 года = 31 — 7x

3y = 7x — 31

3 года / 3 = (7x — 31) / 3

Следовательно, y = (7x — 31) / 3

Теперь подставьте уравнение y = (7x — 31) / 3 во второе уравнение: 9x — 5y = 41

9x — 5 × (7x — 31) / 3 = 41

Решение уравнения дает;

27x — 35x + 155 = 41 × 3

–8x + 155 — 155 = 123 — 155

–8x = –32

8x / 8 = 32/8

х = 4

Подставляя значение x в уравнение y = (7x — 31) / 3, получаем;

y = (7 × 4 — 31) / 3

г = (28 — 31) / 3

г = –3/3

г = –1

Следовательно, решение этих систем уравнений: x = 4 и y = –1

Пример 3

Решите следующие системы уравнений:

2x + 3y = 9 и x — y = 3

Решение

Сделайте x предметом формулы во втором уравнении.

х = 3 + у.

Теперь подставьте это значение x в первое уравнение: 2x + 3y = 9.

⇒ 2 (3 + y) + 3y = 9

⇒ 6 + 2y + 3y = 9

г = ⅗ = 0,6

Подставляем полученное значение y во второе уравнение — y = 3.

⇒ х = 3 + 0,6

х = 3,6

Следовательно, решение x = 3,6 и y = 0,6

Метод исключения

При решении систем уравнений методом исключения выполняются следующие шаги:

• Приравняйте коэффициенты данных уравнений, умножив их на константу.
• Вычтите из новых уравнений общие коэффициенты с одинаковыми знаками и добавьте, если общие коэффициенты имеют противоположные знаки,
• Решите уравнение, полученное в результате сложения или вычитания
• Подставьте полученное значение в любое из уравнений, чтобы получить значение другой переменной.

Пример 4

4a + 5b = 12,

3a — 5b = 9

Решение

Поскольку коэффициенты b в двух уравнениях одинаковы, мы складываем члены по вертикали.

4a + 3a) + (5b — 5b) = 12 + 9

7a = 21

а = 21/7

а = 3

подставляем полученное значение a = 3 в уравнение первое уравнение

4 (3) + 5b = 12,

12 + 5b = 12

5b = 12-12

5b = 0

б = 0/5 = 0

Следовательно, решение a = 3 и b = 0.

Пример 5

Решите методом исключения.

2x + 3y = 9 ———– (i)

x — y = 3 ———– (ii)

Решение

Умножьте два уравнения на 2 и выполните вычитание.

2x + 3y = 9

(-)

2x — 2y = 6

-5лет = -3

г = ⅗ = 0,6

Теперь подставим полученное значение y во второе уравнение: x — y = 3

х — 0,6 = 3

х = 3,6

Следовательно, решение: x = 3,6 и y = 0,6

Практические вопросы

1. Решите данную систему уравнений:

2 года + 3x = 38

г — 2x = 12

2. Решите x — y = 12 и 2x + y = 22

3. Решить x / 2 + 2/3 y = -1 и x — 1 / 3y = 3

4. Решите 2a — 3 / b = 12 и 5a — 7 / b = 1

5. Решите систему уравнений x + 2y = 7 и 2x + 3y = 11

6. Решите систему уравнений 5x — 3y = 1 и 2x + y = -4

7. Решите 2x — 3y = 1 и 3x — 4y = 1

8. Решите систему уравнений 3x — 5y = -23 и 5x + 3y = 7

Предыдущий урок | Главная страница | Следующий урок

Линейные системы с двумя переменными

Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 7-1: Линейные системы с двумя переменными

Линейная система двух уравнений с двумя переменными — это любая система, которую можно записать в форме.

\ [\ begin {align *} ax + by & = p \\ cx + dy & = q \ end {align *} \]

, где любая из констант может быть равна нулю, за исключением того, что каждое уравнение должно содержать хотя бы одну переменную.

Также система называется линейной, если переменные указаны только в первой степени, присутствуют только в числителе и нет произведений переменных ни в одном из уравнений.

Вот пример системы с числами.

\ [\ begin {align *} 3x — y & = 7 \\ 2x + 3y & = 1 \ end {align *} \]

Прежде чем мы обсудим, как решать системы, мы должны сначала поговорить о том, что такое решение системы уравнений.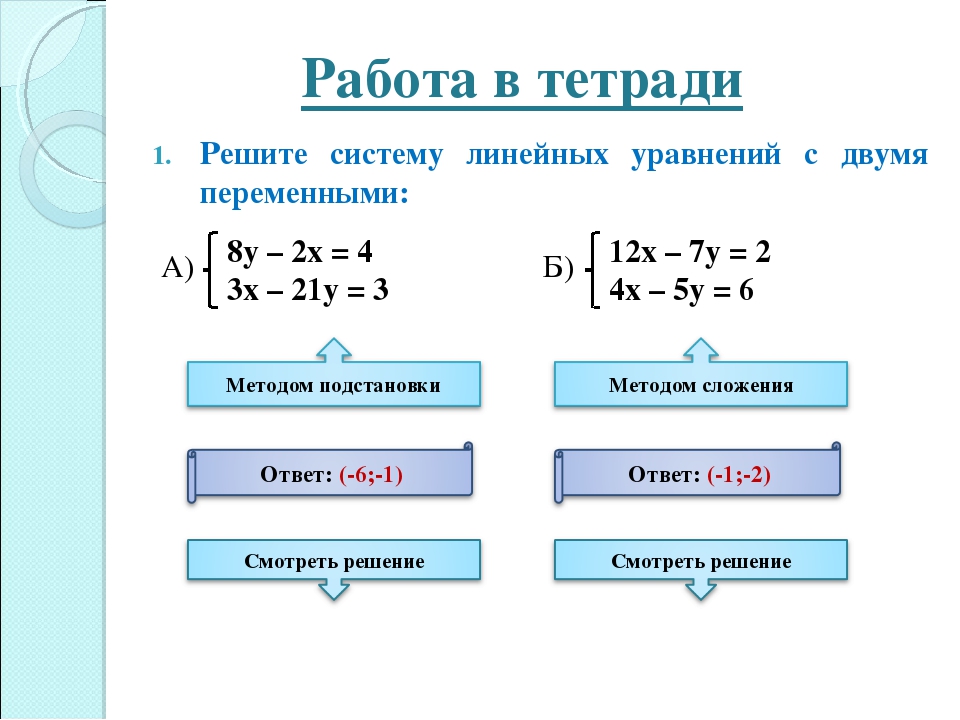 Решение системы уравнений — это значение \ (x \) и значение \ (y \), которые при подстановке в уравнения удовлетворяют обоим уравнениям одновременно.

В приведенном выше примере \ (x = 2 \) и \ (y = — 1 \) является решением системы. Проверить это достаточно легко.

\ [\ begin {align *} 3 \ left (2 \ right) — \ left ({- 1} \ right) & = 7 \\ 2 \ left (2 \ right) + 3 \ left ({- 1} \ вправо) & = 1 \ end {выровнять *} \]

Итак, конечно, эта пара чисел является решением системы.Не беспокойтесь о том, как мы получили эти ценности. Это будет самая первая система, которую мы решим, когда перейдем к примерам.

Обратите внимание, что важно, чтобы пара чисел удовлетворяла обоим уравнениям. Например, \ (x = 1 \) и \ (y = — 4 \) удовлетворяют первому уравнению, но не второму, и поэтому не являются решением системы. Точно так же \ (x = — 1 \) и \ (y = 1 \) будут удовлетворять второму уравнению, но не первому, и поэтому не могут быть решением системы.

Итак, что же представляет собой решение системы двух уравнений? Хорошо, если вы думаете об этом, оба уравнения в системе являются линиями.Итак, давайте построим их график и посмотрим, что мы получим.

Как видите, решение системы — это координаты точки пересечения двух линий. Итак, при решении линейных систем с двумя переменными мы действительно спрашиваем, где пересекаются две линии.

В этом разделе мы рассмотрим два метода решения систем.

Первый метод называется методом замены . В этом методе мы решим одно из уравнений для одной из переменных и подставим его в другое уравнение.Это даст одно уравнение с одной переменной, которую мы можем решить. Как только это решено, мы подставляем это значение обратно в одно из уравнений, чтобы найти значение оставшейся переменной.

На словах этот метод не всегда очень понятен. Давайте рассмотрим пару примеров, чтобы увидеть, как работает этот метод.

Пример 1 Решите каждую из следующих систем.

1. \ (\ begin {align *} 3x — y & = 7 \\ 2x + 3y & = 1 \ end {align *} \)
2. \ (\ begin {align *} 5x + 4y & = 1 \\ 3x — 6y & = 2 \ end {align *} \)

Показать все решения Скрыть все решения a \ (\ begin {align *} 3x — y & = 7 \\ 2x + 3y & = 1 \ end {align *} \) Показать решение

Итак, это была первая система, которую мы рассмотрели выше.Мы уже знаем решение, но это даст нам возможность проверить значения, которые мы записали для решения.

Теперь метод говорит, что нам нужно решить одно из уравнений для одной из переменных. Какое уравнение мы выберем и какую переменную выбрать, зависит от вас, но обычно лучше выбрать уравнение и переменную, с которыми будет легко иметь дело. Это означает, что мы должны стараться избегать дробей, если это вообще возможно.

В этом случае, похоже, будет действительно легко решить первое уравнение для \ (y \), так что давайте сделаем это.

\ [3x — 7 = y \]

Теперь подставьте это во второе уравнение.

\ [2x + 3 \ влево ({3x — 7} \ вправо) = 1 \]

Это уравнение в \ (x \), которое мы можем решить, так что давайте сделаем это.

\ [\ begin {align *} 2x + 9x — 21 & = 1 \\ 11x & = 22 \\ x & = 2 \ end {align *} \]

Итак, есть часть решения \ (x \).

Наконец, НЕ забудьте вернуться и найти часть решения \ (y \).Это одна из наиболее распространенных ошибок, которые студенты делают при решении систем. Для этого мы можем либо подставить значение \ (x \) в одно из исходных уравнений и решить для \ (y \), либо просто вставить его в нашу подстановку, которую мы нашли на первом шаге. Так будет проще, так что давайте.

\ [y = 3x — 7 = 3 \ left (2 \ right) — 7 = — 1 \]

Итак, решение — \ (x = 2 \) и \ (y = — 1 \), как мы отметили выше.

b \ (\ begin {align *} 5x + 4y & = 1 \\ 3x — 6y & = 2 \ end {align *} \) Показать решение

С этой системой мы не сможем полностью избежать дробей.Однако похоже, что если мы решим второе уравнение для \ (x \), мы сможем их минимизировать. Вот эта работа.

\ [\ begin {align *} 3x & = 6y + 2 \\ x & = 2y + \ frac {2} {3} \ end {align *} \]

Теперь подставьте это в первое уравнение и решите полученное уравнение относительно \ (y \).

\ [\ begin {align *} 5 \ left ({2y + \ frac {2} {3}} \ right) + 4y & = 1 \\ 10y + \ frac {{10}} {3} + 4y & = 1 \\ 14y & = 1 — \ frac {{10}} {3} = — \ frac {7} {3} \\ y & = — \ left ({\ frac {7} {3}} \ right) \ left ({\ frac {1} {{14}}} \ right) \\ y & = — \ frac {1} {6} \ end {align *} \]

Наконец, подставьте это в исходную замену, чтобы найти \ (x \).

\ [x = 2 \ left ({- \ frac {1} {6}} \ right) + \ frac {2} {3} = — \ frac {1} {3} + \ frac {2} {3} = \ frac {1} {3} \]

Итак, решение этой системы — \ (x = \ frac {1} {3} \) и \ (y = — \ frac {1} {6} \).

Как и в случае с отдельными уравнениями, мы всегда можем вернуться и проверить это решение, подключив его к обоим уравнениям и убедившись, что оно удовлетворяет обоим уравнениям. Также обратите внимание, что нам действительно нужно включить оба уравнения.Вполне возможно, что ошибка может привести к тому, что пара чисел будет удовлетворять одному из уравнений, но не другому.

Теперь перейдем к следующему методу решения систем уравнений. Как мы видели в последней части предыдущего примера, метод подстановки часто заставляет нас иметь дело с дробями, что увеличивает вероятность ошибок. У второго метода такой проблемы не будет. Что ж, это не совсем так. Если будут отображаться дроби, они будут отображаться только на последнем этапе, и они будут отображаться только в том случае, если решение содержит дроби.

Этот второй метод называется методом исключения . В этом методе мы умножаем одно или оба уравнения на соответствующие числа (, т.е. умножаем каждый член в уравнении на число), чтобы одна из переменных имела одинаковый коэффициент с противоположными знаками. Следующим шагом будет сложение двух уравнений. Поскольку одна из переменных имела одинаковый коэффициент с противоположными знаками, она будет удалена, когда мы сложим два уравнения.Результатом будет одно уравнение, которое мы можем решить для одной из переменных. Как только это будет сделано, замените этот ответ на одно из исходных уравнений.

Как и в случае с первым методом, гораздо легче увидеть, что здесь происходит, с помощью пары примеров.

Пример 2 Постановка задачи.

1. \ (\ begin {align *} 5x + 4y & = 1 \\ 3x — 6y & = 2 \ end {align *} \)
2. \ (\ begin {align *} 2x + 4y & = — 10 \\ 6x + 3y & = 6 \ end {align *} \)

Показать все решения Скрыть все решения a \ (\ begin {align *} 5x + 4y & = 1 \\ 3x — 6y & = 2 \ end {align *} \) Показать решение

Это система из предыдущего набора примеров, которая заставила нас работать с дробями.Работа с ним здесь покажет различия между двумя методами, а также покажет, что любой метод может использоваться для получения решения для системы.

Итак, нам нужно умножить одно или оба уравнения на константы, чтобы одна из переменных имела одинаковый коэффициент с противоположными знаками. Итак, поскольку члены \ (y \) уже имеют противоположные знаки, давайте работать с этими терминами. Похоже, что если мы умножим первое уравнение на 3, а второе уравнение на 2, члены \ (y \) будут иметь коэффициенты 12 и -12, что нам и нужно для этого метода.

Вот работа для этого шага.

\ [\ begin {align *} 5x + 4y & = 1 & \ underrightarrow {\ times \, \, 3} \ hspace {0.5in} & 15x + 12y = 3 \\ 3x-6y & = 2 & \ underrightarrow {\ times \, \, 2} \ hspace {0,5 дюйма} & \ underline {\, \, 6x-12y = 4} \\ & & & 21x \ hspace {0,5 дюйма} = 7 \\ \ конец {выравнивание *} \]

Итак, как и было обещано в описании метода, у нас есть уравнение, которое можно решить относительно \ (x \).Это дает \ (x = \ frac {1} {3} \), что мы и нашли в предыдущем примере. Однако обратите внимание, что единственная дробь, с которой нам пришлось иметь дело до этого момента, — это сам ответ, который отличается от метода подстановки.

Теперь снова не забудьте найти \ (y \). В этом случае работы будет немного больше, чем метод подстановки. Чтобы найти \ (y \), нам нужно подставить значение \ (x \) в любое из исходных уравнений и решить относительно \ (y \).Поскольку \ (x \) является дробью, заметим, что в этом случае, если мы подставим это значение во второе уравнение, мы потеряем дроби, по крайней мере, временно. Обратите внимание, что часто этого не происходит, и нам придется иметь дело с дробями, хотим мы этого или нет.

\ [\ begin {align *} 3 \ left ({\ frac {1} {3}} \ right) — 6y & = 2 \\ 1 — 6y & = 2 \\ — 6y & = 1 \\ y & = — \ frac {1} {6} \ end {align *} \]

Опять же, это то же значение, которое мы нашли в предыдущем примере.

b \ (\ begin {align *} 2x + 4y & = — 10 \\ 6x + 3y & = 6 \ end {align *} \) Показать решение

В этой части все переменные положительны, поэтому нам придется принудительно установить противоположный знак, умножив где-нибудь на отрицательное число. Также заметим, что в этом случае, если мы просто умножим первое уравнение на -3, то коэффициенты при \ (x \) будут -6 и 6.

Иногда нам нужно только умножить одно из уравнений, а другое можно оставить в покое.Вот эта работа по этой части.

\ [\ begin {align *} 2x + 4y & = -10 & \ underrightarrow {\ times \, \, — 3} \ hspace {0,5 дюйма} & -6x-12y = 30 \\ 6x + 3y & = 6 & \ underrightarrow {\ text {same}} \ hspace {0,5 дюйма} & \ underline {\ hspace {0,35 дюйма} 6x + 3y = 6} \\ & & & \ hspace {0,5 дюйма} -9y = 36 \\ & & & \ hspace {0,85 дюйма} y = -4 \\ \ конец {выравнивание *} \]

Наконец, подставьте это в любое из уравнений и решите относительно \ (x \).На этот раз мы воспользуемся первым уравнением.

\ [\ begin {align *} 2x + 4 \ left ({- 4} \ right) & = — 10 \\ 2x — 16 & = — 10 \\ 2x & = 6 \\ x & = 3 \ end {align *} \]

Итак, решение этой системы — \ (x = 3 \) и \ (y = — 4 \).

Существует третий метод, который мы рассмотрим для решения систем из двух уравнений, но он немного сложнее и, вероятно, более полезен для систем как минимум с тремя уравнениями, поэтому мы рассмотрим его в следующем разделе.

Перед тем, как покинуть этот раздел, мы должны рассмотреть несколько частных случаев решения систем.

Пример 3 Решите следующие системы уравнений. \ [\ begin {align *} x — y & = 6 \\ — 2x + 2y & = 1 \ end {align *} \] Показать решение

Здесь мы можем использовать любой метод, но похоже, что замена будет немного проще. Мы решим первое уравнение относительно \ (x \) и подставим его во второе уравнение.

\ [\ begin {align *} x & = 6 + y \\ & \\ — 2 \ left ({6 + y} \ right) + 2y & = 1 \\ — 12 — 2y + 2y & = 1 \\ — 12 & = 1 \, \, \, ?? \ end {align *} \]

Итак, это явно неправда, и, похоже, нигде в нашей работе нет ошибки. Так в чем проблема? Чтобы увидеть, давайте изобразим эти две линии и посмотрим, что мы получим.

Похоже, что эти две линии параллельны (вы можете проверить это с помощью наклона?), И мы знаем, что две параллельные линии с разными пересечениями \ (y \) (что важно) никогда не пересекутся.

Как мы видели в начале обсуждения этого раздела, решения представляют собой точку пересечения двух линий. Если две линии не пересекаются, у нас не будет решения.

Итак, когда мы получаем такой бессмысленный ответ в результате нашей работы, у нас есть две параллельные линии и нет решения этой системы уравнений.

Система в предыдущем примере называется несовместимая .Также обратите внимание, что если бы мы использовали исключение в этой системе, мы бы получили аналогичный бессмысленный ответ.

Пример 4 Решите следующую систему уравнений. \ [\ begin {align *} 2x + 5y & = — 1 \\ — 10x — 25y & = 5 \ end {align *} \] Показать решение

В этом примере кажется, что устранение было бы самым простым методом.

\ [\ begin {align *} 2x + 5y & = -1 & \ underrightarrow {\ times \, \, 5} \ hspace {0.5in} & \, \, \, \, 10x + 25y = -5 \\ -10x-25y & = 5 & \ underrightarrow {\ text {same}} \ hspace {0,5 дюйма} & \ underline {-10x-25y = 5} \\ & & & \ hspace {0.9in} 0 = 0 \\ \ конец {выравнивание *} \]

На первый взгляд может показаться, что это та же проблема, что и в предыдущем примере. Однако в этом случае мы пришли к равенству, которое просто не соответствовало действительности. В этом случае мы имеем 0 = 0, и это истинное равенство, и в этом смысле в этом нет ничего плохого.

Однако это явно не тот ответ, который мы ожидали здесь, и поэтому нам нужно определить, что именно происходит.

Мы предоставим вам возможность проверить это, но если вы найдете наклон и \ (y \) — точки пересечения для этих двух линий, вы обнаружите, что обе линии имеют точно такой же наклон, и обе линии имеют точно такие же \ ( y \) — перехват. Итак, что это значит для нас? Хорошо, если две линии имеют одинаковый наклон и одинаковые \ (y \) — точки пересечения, тогда графики этих двух линий являются одним и тем же графиком.Другими словами, графики этих двух линий — это один и тот же график. В этих случаях любой набор точек, удовлетворяющий одному из уравнений, также будет удовлетворять другому уравнению.

Также напомним, что график уравнения — это не что иное, как набор всех точек, удовлетворяющих уравнению. Другими словами, существует бесконечный набор точек, которые будут удовлетворять этой системе уравнений.

В этих случаях мы действительно хотим записать что-нибудь для решения.Итак, что мы сделаем, так это решим одно из уравнений для одной из переменных (неважно, что вы выберете). Решим первый относительно \ (y \).

\ [\ begin {align *} 2x + 5y & = — 1 \\ 5y & = — 2x — 1 \\ y & = — \ frac {2} {5} x — \ frac {1} {5} \ end {выровнять*}\]

Затем для любого \ (x \) мы можем найти \ (y \), и эти два числа образуют решение системы уравнений. Обычно мы обозначаем это, записывая решение следующим образом:

\ [\ begin {array} {* {20} {c}} \ begin {align} x & = t \\ y & = — \ frac {2} {5} t — \ frac {1} {5} \ конец {выровнен} & {\ hspace {0.25in} {\ mbox {где}} \, t {\ mbox {- любое действительное число}}} \ end {array} \]

Чтобы показать, что они дают решения, давайте рассмотрим несколько значений \ (t \).? — 1 & \ hspace {0.? 5 \\ — 1 & = — 1 & \ hspace {0,25 дюйма} 5 & = 5 \ end {align *} \]

Итак, \ (x = 0 \) и \ (y = — \ frac {1} {5} \) является решением системы. Давай быстро сделаем еще один.

\ (t = — 3 \)

\ [x = — 3 \ hspace {0,25 дюйма} y = — \ frac {2} {5} \ left ({- 3} \ right) — \ frac {1} {5} = \ frac {6} {5 } — \ frac {1} {5} = 1 \]

И снова нам нужно вставить его в оба уравнения системы, чтобы показать, что это решение.? 5 \\ — 1 & = — 1 & \ hspace {0,25 дюйма} 5 & = 5 \ end {align *} \]

Конечно, \ (x = — 3 \) и \ (y = 1 \) — это решение.

Итак, поскольку существует бесконечное количество возможных \ (t \), должно быть бесконечное количество решений для этой системы, и они даются как,

\ [\ begin {array} {* {20} {c}} \ begin {align} x & = t \\ y & = — \ frac {2} {5} t — \ frac {1} {5} \ конец {выровнен} & {\ hspace {0.25in} {\ mbox {где}} \, t {\ mbox {- любое действительное число}}} \ end {array} \]

Системы, подобные тем, что в предыдущих примерах, называются зависимыми .

Теперь мы увидели все три возможности решения системы уравнений. Система уравнений не будет иметь решения, ровно одно решение или бесконечно много решений.

Решение систем линейных уравнений

А система линейные уравнения представляет собой просто набор из двух или более линейных уравнений.

В двух переменных ( Икс а также у ) , график системы двух уравнений представляет собой пару прямых на плоскости.

Есть три возможности:

• Линии пересекаются в нулевых точках. (Линии параллельны.)
• Линии пересекаются ровно в одной точке. (Большинство случаев.)
• Прямые пересекаются в бесконечном множестве точек.(Два уравнения представляют собой одну и ту же линию.)

Нулевые решения: у знак равно — 2 Икс + 4 у знак равно — 2 Икс — 3
Одно решение: у знак равно 0.5 Икс + 2 у знак равно — 2 Икс — 3
Бесконечно много решений: у знак равно — 2 Икс — 4 у + 4 знак равно — 2 Икс	Существует несколько различных методов решения систем линейных уравнений: Графический метод . Это полезно, когда вам просто нужен приблизительный ответ или вы уверены, что пересечение происходит в целочисленных координатах. Просто нарисуйте две линии и посмотрите, где они пересекаются! См. Второй график выше. Решение — это место пересечения двух линий, точка ( — 2 , 1 ) . Метод замены . Сначала решите одно линейное уравнение для у с точки зрения Икс . Затем замените это выражение на у в другом линейном уравнении. Вы получите уравнение в Икс . Решите это, и у вас будет Икс -координата перекрестка. Затем подключите Икс к любому уравнению, чтобы найти соответствующее у -координат.(Если проще, вы можете начать с решения уравнения для Икс с точки зрения у , тоже — такая же разница!) Пример 1: Решите систему { 3 Икс + 2 у знак равно 16 7 Икс + у знак равно 19 Решите второе уравнение относительно у . у знак равно 19 — 7 Икс Заменять 19 — 7 Икс для у в первом уравнении и решите относительно Икс . 3 Икс + 2 ( 19 — 7 Икс ) знак равно 16 3 Икс + 38 — 14 Икс знак равно 16 — 11 Икс знак равно — 22 Икс знак равно 2 Заменять 2 для Икс в у знак равно 19 — 7 Икс и решить для у . у знак равно 19 — 7 ( 2 ) у знак равно 5 Решение ( 2 , 5 ) . Метод линейной комбинации , иначе Метод сложения , иначе Метод исключения. Сложить (или вычесть) одно уравнение, кратное другому уравнению (или из него), таким образом, чтобы либо Икс -термы или у -условия аннулируются.Затем решите для Икс (или же у , в зависимости от того, что осталось) и подставьте обратно, чтобы получить другую координату. Пример 2: Решите систему { 4 Икс + 3 у знак равно — 2 8 Икс — 2 у знак равно 12 Умножьте первое уравнение на — 2 и добавьте результат ко второму уравнению. — 8 Икс — 6 у знак равно 4 8 Икс — 2 у знак равно 12 _ — 8 у знак равно 16 Решить для у . у знак равно — 2 Замена для у в любом из исходных уравнений и решите относительно Икс . 4 Икс + 3 ( — 2 ) знак равно — 2 4 Икс — 6 знак равно — 2 4 Икс знак равно 4 Икс знак равно 1 Решение ( 1 , — 2 ) . Матричный метод . На самом деле это просто метод линейной комбинации, упрощенный за счет сокращения записи.

4.1: Решение систем линейных уравнений с двумя переменными

Определить, является ли упорядоченная пара решением системы уравнений

В разделе Решение линейных уравнений мы узнали, как решать линейные уравнения с одной переменной.Теперь мы будем работать с двумя или более линейными уравнениями, сгруппированными вместе, что известно как система линейных уравнений .

СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ

Когда два или более линейных уравнения сгруппированы вместе, они образуют систему линейных уравнений .

В этом разделе мы сосредоточим нашу работу на системах двух линейных уравнений с двумя неизвестными. Позже в этой главе мы решим более крупные системы уравнений.

Ниже показан пример системы двух линейных уравнений.Мы используем скобку, чтобы показать, что два уравнения сгруппированы вместе и образуют систему уравнений.

\ [\ left \ {\ begin {выровнено} 2x + y & = 7 \\ x − 2y & = 6 \ end {выровнено} \ right. \ nonumber \]

Линейное уравнение с двумя переменными, например \ (2x + y = 7 \), имеет бесконечное число решений. Его график представляет собой линию. Помните, что каждая точка на линии — это решение уравнения, а каждое решение уравнения — это точка на линии.

Чтобы решить систему двух линейных уравнений, мы хотим найти значения переменных, которые являются решениями обоих уравнений.Другими словами, мы ищем упорядоченные пары \ ((x, y) \), которые делают оба уравнения истинными. Они называются решениями системы уравнений .

РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ

решений системы уравнений — это значения переменных, которые делают все уравнения истинными. Решение системы двух линейных уравнений представляется упорядоченной парой \ ((x, y) \).

Чтобы определить, является ли упорядоченная пара решением системы двух уравнений, мы подставляем значения переменных в каждое уравнение.Если упорядоченная пара делает оба уравнения истинными, это решение системы.

Пример \ (\ PageIndex {1} \)

Определите, является ли упорядоченная пара решением системы \ (\ left \ {\ begin {array} {l} x − y = −1 \\ 2x − y = −5 \ end {array} \ right. \) .

ⓐ \ ((- 2, −1) \) ⓑ \ ((- 4, −3) \)

Ответ

ⓐ

ⓑ

Пример \ (\ PageIndex {2} \)

Определите, является ли упорядоченная пара решением системы \ (\ left \ {\ begin {array} 3x + y = 0 \\ x + 2y = −5 \ end {array} \ right.\).

ⓐ \ ((1, −3) \) ⓑ \ ((0,0) \)

Ответ

ⓐ да ⓑ нет

Пример \ (\ PageIndex {3} \)

Определите, является ли упорядоченная пара решением системы \ (\ left \ {\ begin {array} x − 3y = −8 \\ −3x − y = 4 \ end {array} \ right. \).

ⓐ \ ((2, −2) \) ⓑ \ ((- 2,2) \)

Ответ

ⓐ нет ⓑ да

Решите систему линейных уравнений с помощью построения графиков

В этом разделе мы будем использовать три метода для решения системы линейных уравнений.Первый метод, который мы будем использовать, — это построение графиков.

График линейного уравнения представляет собой линию. Каждая точка на линии — это решение уравнения. Для системы из двух уравнений мы построим график двумя линиями. Затем мы можем увидеть все точки, которые являются решениями каждого уравнения. И, обнаружив, что общего у линий, мы найдем решение системы.

Большинство линейных уравнений с одной переменной имеют одно решение, но мы видели, что некоторые уравнения, называемые противоречиями, не имеют решений, а для других уравнений, называемых тождествами, все числа являются решениями.

Точно так же, когда мы решаем систему двух линейных уравнений, представленную графиком из двух линий в одной плоскости, есть три возможных случая, как показано.

Рисунок \ (\ PageIndex {1} \)

Каждый раз, когда мы демонстрируем новый метод, мы будем использовать его в той же системе линейных уравнений. В конце раздела вы решите, какой метод был наиболее удобным для решения этой системы.

Пример \ (\ PageIndex {4} \): как решить систему уравнений с помощью построения графиков

Решите систему, построив график \ (\ left \ {\ begin {array} {l} 2x + y = 7 \\ x − 2y = 6 \ end {array} \ right.\).

Ответ

Пример \ (\ PageIndex {5} \)

Решите систему, построив график: \ (\ left \ {\ begin {array} {l} x − 3y = −3 \\ x + y = 5 \ end {array} \ right. \).

Ответ

\ ((3,2) \)

Пример \ (\ PageIndex {6} \)

Решите систему, построив график: \ (\ left \ {\ begin {array} {l} −x + y = 1 \\ 3x + 2y = 12 \ end {array} \ right.\)

Ответ

\ ((2,3) \)

Здесь показаны шаги, которые необходимо использовать для решения системы линейных уравнений с помощью построения графиков.

РЕШИТЕ ​​СИСТЕМУ ЛИНЕЙНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ ГРАФИКОВ.

1. Изобразите первое уравнение.
2. Постройте второе уравнение в той же прямоугольной системе координат.
3. Определите, пересекаются ли линии, параллельны или совпадают.
4. Определите решение системы.
   • Если линии пересекаются, укажите точку пересечения. Это решение системы.
   • Если линии параллельны, у системы нет решения.
   • Если линии совпадают, система имеет бесконечное количество решений.
5. Проверьте решение в обоих уравнениях.

В следующем примере мы сначала перепишем уравнения в форме углового пересечения, так как это упростит нам быстрое построение графиков линий.

Пример \ (\ PageIndex {7} \)

Решите систему, построив график: \ (\ left \ {\ begin {array} {l} 3x + y = −1 \\ 2x + y = 0 \ end {array} \ right. \)

Ответ

Мы решим оба этих уравнения относительно \ (y \), чтобы мы могли легко построить их график, используя их наклоны и \ (y \) — точки пересечения.

Пример \ (\ PageIndex {8} \)

Решите систему, построив график: \ (\ left \ {\ begin {array} {l} −x + y = 1 \\ 2x + y = 10 \ end {array} \ right.\).

Ответ

\ ((3,4) \)

Пример \ (\ PageIndex {9} \)

Решите систему, построив график: \ (\ left \ {\ begin {array} {l} 2x + y = 6 \\ x + y = 1 \ end {array} \ right. \).

Ответ

\ ((5, −4) \)

До сих пор во всех системах линейных уравнений линии пересекались, и решение было одной точкой. В следующих двух примерах мы рассмотрим систему уравнений, не имеющую решения, и систему уравнений, которая имеет бесконечное число решений.

Пример \ (\ PageIndex {10} \)

Решите систему, построив график: \ (\ left \ {\ begin {array} {l} y = \ tfrac {1} {2} x-3 \\ x-2y = 4 \ end {array} \ right. \ ).

Ответ

Пример \ (\ PageIndex {11} \)

Решите систему, построив график: \ (\ left \ {\ begin {array} {l} y = — \ tfrac {1} {4} x + 2 \\ x + 4y = 4 \ end {array} \ right. \).

Ответ

нет решения

Пример \ (\ PageIndex {12} \)

Решите систему, построив график: \ (\ left \ {\ begin {array} {l} y = 3x-1 \\ 6x-2y = 6 \ end {array} \ right.\).

Ответ

нет решения

Иногда уравнения в системе представляют собой одну и ту же линию. Поскольку каждая точка на прямой делает оба уравнения истинными, существует бесконечно много упорядоченных пар, которые делают оба уравнения истинными. У системы бесконечно много решений.

Пример \ (\ PageIndex {13} \)

Решите систему, построив график: \ (\ left \ {\ begin {array} {l} y = 2x-3 \\ -6x + 3y = 9 \ end {array} \ right.\).

Ответ

Если вы напишете второе уравнение в форме пересечения наклона, вы можете заметить, что уравнения имеют одинаковый наклон и одинаковую точку пересечения y .

Пример \ (\ PageIndex {14} \)

Решите систему, построив график: \ (\ left \ {\ begin {array} {l} y = -3x-6 \\ 6x + 2y = -12 \ end {array} \ right. \).

Ответ

бесконечно много решений

Пример \ (\ PageIndex {15} \)

Решите систему, построив график: \ (\ left \ {\ begin {array} {l} y = \ tfrac {1} {2} x-4 \\ 2x-4y = 16 \ end {array} \ right.\).

Ответ

бесконечно много решений

Когда мы нарисовали вторую линию в последнем примере, мы нарисовали ее прямо над первой линией. Мы говорим, что две строки совпадают с . Совпадающие линии имеют одинаковый наклон и точку пересечения y- .

СОВПАДАЮЩИЕ ЛИНИИ

Совпадающие линии имеют одинаковый наклон и одинаковую точку пересечения y- .

Каждая система уравнений в примере и примере имела две пересекающиеся линии.У каждой системы было одно решение.

В примере уравнения давали совпадающие линии, поэтому система имела бесконечно много решений.

Системы в этих трех примерах имели по крайней мере одно решение. Система уравнений, имеющая хотя бы одно решение, называется согласованной системой .

Система с параллельными линиями, такая как Пример , не имеет решения. Мы называем такую ​​систему уравнений несогласованной. Нет решения.

СОГЛАСОВАННЫЕ И НЕПОСРЕДСТВЕННЫЕ СИСТЕМЫ

Согласованная система уравнений — это система уравнений, имеющая по крайней мере одно решение.

Непоследовательная система уравнений — это система уравнений, не имеющая решения.

Мы также классифицируем уравнения в системе уравнений, называя уравнения независимыми или зависимыми . Если два уравнения независимы, каждое из них имеет собственный набор решений.Пересекающиеся линии и параллельные линии независимы.

Если два уравнения являются зависимыми, все решения одного уравнения также являются решениями другого уравнения. Когда мы строим график двух зависимых уравнений, мы получаем совпадающие линии.

Давайте подведем итог, посмотрев на графики трех типов систем. См. Ниже и таблицу .

Строки	Пересечение	Параллельный	Совпадение
Количество решений	1 балл	Нет решения	Бесконечно много
Согласованный / непоследовательный	Согласованный	Несоответствие	Согласованный
Зависимые / независимые	Независимый	Независимая	Зависимые

Пример \ (\ PageIndex {16} \)

Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.

ⓐ \ (\ left \ {\ begin {array} {l} y = 3x − 1 \\ 6x − 2y = 12 \ end {array} \ right. \) Ⓑ \ (\ left \ {\ begin {array} {l} 2x + y = −3 \\ x − 5y = 5 \ end {array} \ right. \)

Ответ

ⓐ Сравним наклоны и пересечения двух линий.

\ (\ begin {array} {lll} {} & {} & {\ left \ {\ begin {array} {l} {y = 3x-1} \\ {6x − 2y = 12} \ end {массив } \ right.} \\ {} & {} & {y = 3x-1} \\ {\ text {Первое уравнение уже находится в форме пересечения наклона.}} & {} & {} \\ {\ text {Запишите второе уравнение в форме пересечения наклона.}} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \\ {} & {} & {6x-2y = 12} \\ {} & {} & {- 2y = -6x + 12} \\ {} & { } & {\ frac {-2y} {- 2} = \ frac {-6x + 12} {- 2}} \\ {} & {} & {y = 3x-6} \\ {} & {y = 3x-1} & {y = 3x-6} \\ {} & {m = 3} & {m = 3} \\ {} & {b = -1} & {b = -6} \\ {\ text {Найдите наклон и точку пересечения каждой линии.}} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \ \ {} & {} & {} \\ {} & {\ text {Поскольку наклоны одинаковые, а точки пересечения y}} & {} \\ {} & {\ text {разные, линии параллельны.}} & {} \\ \ end {array} \)

ⓑ Мы сравним наклон и пересечения двух линий.

\ (\ begin {array} {lll} {} & {} & {} \\ {} & {\ left \ {\ begin {array} {l} 2x + y = -3 \\ x-5y = 5 \\ \ end {array} \ right.} & {} \\ {\ text {Запишите оба уравнения в форме углового пересечения.}} & {} & {} \\ {} & {} & {} \\ { } & {} & {} \\ {} & {} & {} \\ {} & {2x + y = -3} & {x-5y = 5} \\ {} & {y = -2x-3 } & {- 5y = -x + 5} \\ {} & {} & {\ frac {-5y} {- 5} = \ frac {-x + 5} {- 5}} \\ {} & { } & {y = \ frac {1} {5} -1} \\ {} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \\ {\ text {Найдите наклон и точку пересечения каждой линии.}} & {} & {} \\ {} & {} & {} \\ {} & {y = -2x-3} & {y = \ frac {1} {5} -1} \\ {} & {m = -2} & {m = \ frac {1} {5}} \\ {} & {b = -3} & {b = -1} \\ {} & {} & {} \\ {} & {\ text {Поскольку уклоны разные, линии пересекаются.}} & {} \\ \ end {array} \)

Система уравнений, графики которой пересекаются, имеет одно решение, непротиворечива и независима.

Пример \ (\ PageIndex {17} \)

Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.

ⓐ \ (\ left \ {\ begin {array} {l} y = −2x − 4 \\ 4x + 2y = 9 \ end {array} \ right. \) Ⓑ \ (\ left \ {\ begin {array } {l} 3x + 2y = 2 \\ 2x + y = 1 \ end {array} \ right. \)

Ответ

ⓐ нет решения, непоследовательное, независимое ⓑ одно решение, последовательное, независимое

Пример \ (\ PageIndex {18} \)

Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.

ⓐ \ (\ left \ {\ begin {array} {l} y = \ frac {1} {3} x − 5 \\ x − 3y = 6 \ end {array} \ right.\) Ⓑ \ (\ left \ {\ begin {array} {l} x + 4y = 12 \\ −x + y = 3 \ end {array} \ right. \)

Ответ

ⓐ нет решения, непоследовательное, независимое ⓑ одно решение, последовательное, независимое

Решение систем линейных уравнений с помощью графиков — хороший способ визуализировать типы решений, которые могут возникнуть. Однако во многих случаях решение системы с помощью построения графиков неудобно или неточно. Если графики выходят за пределы маленькой сетки с x и y как между \ (- 10 \), так и 10, построение линий может быть громоздким.И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения с графика.

Решите систему уравнений подстановкой

Теперь решим системы линейных уравнений методом подстановки.

Мы будем использовать ту же систему, которую мы использовали вначале для построения графиков.

\ [\ left \ {\ begin {array} {l} 2x + y = 7 \\ x − 2y = 6 \ end {array} \ right. \ nonumber \]

Сначала мы решим одно из уравнений относительно x или y .Мы можем выбрать любое уравнение и решить любую переменную, но мы постараемся сделать выбор, который упростит работу.

Затем мы подставляем это выражение в другое уравнение. В результате получается уравнение с одной переменной — и мы знаем, как его решить!

После того, как мы найдем значение одной переменной, мы подставим это значение в одно из исходных уравнений и решим для другой переменной. Наконец, мы проверяем наше решение и убеждаемся, что оно соответствует обоим уравнениям.

Пример \ (\ PageIndex {20} \)

Решите систему заменой: \ (\ left \ {\ begin {array} {l} −2x + y = −11 \\ x + 3y = 9 \ end {array} \ right. \)

Ответ

\ ((6,1) \)

Пример \ (\ PageIndex {21} \)

Решите систему заменой: \ (\ left \ {\ begin {array} {l} 2x + y = −1 \\ 4x + 3y = 3 \ end {array} \ right. \)

Ответ

\ ((- 3,5) \)

РЕШИТЕ ​​СИСТЕМУ УРАВНЕНИЙ ПОДСТАВКОЙ.

1. Решите одно из уравнений для любой переменной.
2. Подставьте выражение из шага 1 в другое уравнение.
3. Решите полученное уравнение.
4. Подставьте решение шага 3 в любое из исходных уравнений, чтобы найти другую переменную.
5. Запишите решение в виде упорядоченной пары.
6. Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.

Будьте очень осторожны со знаками в следующем примере.

Пример \ (\ PageIndex {22} \)

Решите систему заменой: \ (\ left \ {\ begin {array} {l} 4x + 2y = 4 \\ 6x − y = 8 \ end {array} \ right. \)

Ответ

Нам нужно решить одно уравнение для одной переменной. Решим первое уравнение относительно y .

Пример \ (\ PageIndex {23} \)

Решите систему заменой: \ (\ left \ {\ begin {array} {l} x − 4y = −4 \\ −3x + 4y = 0 \ end {array} \ right.\)

Ответ

\ ((2,32) \)

Пример \ (\ PageIndex {24} \)

Решите систему заменой: \ (\ left \ {\ begin {array} {l} 4x − y = 0 \\ 2x − 3y = 5 \ end {array} \ right. \)

Ответ

\ ((- 12, −2) \)

Решите систему уравнений методом исключения

Мы решили системы линейных уравнений с помощью построения графиков и подстановки.Построение графиков хорошо работает, когда переменные коэффициенты малы, а решение имеет целочисленные значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.

Третий метод решения систем линейных уравнений называется методом исключения. Когда мы решали систему с помощью подстановки, мы начинали с двух уравнений и двух переменных и сводили ее к одному уравнению с одной переменной. То же самое мы сделаем и с методом исключения, но у нас будет другой способ добиться этого.

Метод исключения основан на добавочном свойстве равенства. Свойство сложения равенства говорит, что когда вы добавляете одинаковую величину к обеим сторонам уравнения, вы все равно получаете равенство. Мы расширим свойство сложения равенства, чтобы сказать, что когда вы добавляете равные количества к обеим сторонам уравнения, результаты равны.

Для любых выражений a, b, c, и d .

\ [\ begin {array} {ll} {\ text {if}} & {a = b} \\ {\ text {and}} & {c = d} \\ {\ text {then}} & { а + с = б + г.} \\ \ nonumber \ end {array} \]

Чтобы решить систему уравнений методом исключения, мы начнем с обоих уравнений в стандартной форме. Затем мы решаем, какую переменную будет легче всего устранить. Как мы решаем? Мы хотим, чтобы коэффициенты одной переменной были противоположными, чтобы мы могли сложить уравнения и исключить эту переменную.

Обратите внимание, как это работает, когда мы складываем эти два уравнения вместе:

\ [\ left \ {\ begin {array} {l} 3x + y = 5 \\ \ underline {2x − y = 0} \ end {array} \ right.\ nonumber \]

\ [5x = 5 \ nonumber \]

и прибавляют к нулю, и мы получаем одно уравнение с одной переменной.

Давайте попробуем еще один:

\ [\ left \ {\ begin {array} x + 4y = 2 \\ 2x + 5y = −2 \ end {array} \ right. \ nonumber \]

На этот раз мы не видим переменную, которую можно было бы немедленно исключить, если мы добавим уравнения.

Но если мы умножим первое уравнение на \ (- 2 \), мы сделаем коэффициенты при x противоположными.Мы должны умножить каждый член в обеих частях уравнения на \ (- 2 \).

Затем перепишите систему уравнений.

Теперь мы видим, что коэффициенты членов x противоположны, поэтому x будут исключены, когда мы сложим эти два уравнения.

Как только мы получаем уравнение с одной переменной, мы его решаем. Затем мы подставляем это значение в одно из исходных уравнений, чтобы найти оставшуюся переменную.И, как всегда, мы проверяем наш ответ, чтобы убедиться, что он является решением обоих исходных уравнений.

Теперь мы увидим, как использовать исключение для решения той же системы уравнений, которую мы решили с помощью построения графиков и подстановки.

Упражнение \ (\ PageIndex {26} \)

Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} 3x + y = 5 \\ 2x − 3y = 7 \ end {array} \ right. \)

Ответ

\ ((2, −1) \)

Упражнение \ (\ PageIndex {27} \)

Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} 4x + y = −5 \\ ​​−2x − 2y = −2 \ end {array} \ right.\)

Ответ

\ ((- 2,3) \)

Шаги перечислены здесь для удобства.

РЕШИТЕ ​​СИСТЕМУ УРАВНЕНИЙ ПУТЕМ ИСКЛЮЧЕНИЯ.

1. Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробными, очистите их.
2. Сделайте коэффициенты одной переменной противоположными.
   • Решите, какую переменную исключить.
   • Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположными.
3. Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
4. Найдите оставшуюся переменную.
5. Подставьте решение из шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
6. Запишите решение в виде упорядоченной пары.
7. Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.

Теперь мы рассмотрим пример, в котором нам нужно умножить оба уравнения на константы, чтобы сделать коэффициенты одной переменной противоположными.

Упражнение \ (\ PageIndex {28} \)

Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} 4x − 3y = 9 \\ 7x + 2y = −6 \ end {array} \ right. \)

Ответ

В этом примере мы не можем умножить одно уравнение на любую константу, чтобы получить противоположные коэффициенты. Поэтому мы стратегически умножим оба уравнения на разные константы, чтобы получить противоположности.

Упражнение \ (\ PageIndex {29} \)

Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} 3x − 4y = −9 \\ 5x + 3y = 14 \ end {array} \ right.\)

Ответ

\ ((1,3) \)

Упражнение \ (\ PageIndex {30} \)

Решите каждую систему методом исключения: \ (\ left \ {\ begin {array} {l} 7x + 8y = 4 \\ 3x − 5y = 27 \ end {array} \ right. \)

Ответ

\ ((4, −3) \)

Когда система уравнений содержит дроби, мы сначала очистим дроби, умножив каждое уравнение на ЖК-дисплей всех дробей в уравнении.

Упражнение \ (\ PageIndex {31} \)

Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} x + \ tfrac {1} {2} y = 6 \\ \ tfrac {3} {2} x + \ tfrac {2} { 3} y = \ tfrac {17} {2} \ end {array} \ right. \)

Ответ

В этом примере в обоих уравнениях есть дроби. Нашим первым шагом будет умножение каждого уравнения на ЖК-дисплей всех дробей в уравнении, чтобы очистить дроби.

Упражнение \ (\ PageIndex {32} \)

Решите каждую систему методом исключения: \ (\ left \ {\ begin {array} {l} \ tfrac {1} {3} x− \ tfrac {1} {2} y = 1 \\ \ tfrac {3} { 4} x − y = \ tfrac {5} {2} \ end {array} \ right.\)

Ответ

\ ((6,2) \)

Упражнение \ (\ PageIndex {33} \)

Решите каждую систему методом исключения: \ (\ left \ {\ begin {array} {l} x + \ tfrac {3} {5} y = — \ tfrac {1} {5} \\ — \ tfrac {1} { 2} x− \ tfrac {2} {3} y = \ tfrac {5} {6} \ end {array} \ right. \)

Ответ

\ ((1, −2) \)

Когда мы решили систему с помощью построения графиков, мы увидели, что не все системы линейных уравнений имеют единственную упорядоченную пару в качестве решения.Когда два уравнения действительно представляли собой одну и ту же линию, решений было бесконечно много. Мы назвали это последовательной системой. Когда два уравнения описывали параллельные линии, решения не было. Мы назвали это несовместимой системой.

То же самое и с заменой или исключением. Если уравнение в конце замены или исключения является истинным утверждением, у нас есть непротиворечивая, но зависимая система, а система уравнений имеет бесконечно много решений. Если уравнение в конце замены или исключения является ложным утверждением, мы имеем несовместимую систему и система уравнений не имеет решения.

Упражнение \ (\ PageIndex {34} \)

Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} 3x + 4y = 12 \\ y = 3− \ tfrac {3} {4} x \ end {array} \ right. \ )

Ответ

\ (\ begin {array} {ll} {} & {\ left \ {\ begin {array} {l} 3x + 4y = 12 \\ y = 3− \ frac {3} {4} x \ end { array} \ right.} \\ {} & {} \\ {\ text {Запишите второе уравнение в стандартной форме.}} & {\ left \ {\ begin {array} {l} 3x + 4y = 12 \\ \ frac {3} {4} x + y = 3 \ end {array} \ right.} \\ {} & {} \\ {\ text {Очистите дроби, умножив} \\ \ text {второе уравнение на 4.}} & {\ left \ {\ begin {array} {l} 3x + 4y = 12 \\ 4 (\ frac {3} {4} x + y) = 4 (3) \ end {array} \ right. } \\ {} & {} \\ {\ text {Упростить.}} & {\ left \ {\ begin {array} {l} 3x + 4y = 12 \\ 3x + 4y = 12 \ end {array} \ верно. } \\ {} & {} \\ {\ text {Чтобы исключить переменную, мы умножаем второе уравнение} \\ \ text {на −1. Упростите и добавьте.}} & {\ Begin {array} {l} {\ left \ {\ begin {array} {l} 3x + 4y = 12 \\ \ underline {-3x-4y = -12} \ end { массив} \ право.} \\ {\ hspace {16mm} 0 = 0} \ end {array}} \\ \ end {array} \)

Это верное заявление. Уравнения непротиворечивы, но зависимы. Их графики будут одной линией. У системы бесконечно много решений.

Заметили ли вы, что после того, как мы очистили дроби во втором уравнении, эти два уравнения совпадают? Это означает, что у нас есть совпадающие линии.

Упражнение \ (\ PageIndex {35} \)

Решите систему путем исключения: \ (\ left \ {\ begin {array} {l} 5x − 3y = 15 \\ 5y = −5 + \ tfrac {5} {3} x \ end {array} \ right.\)

Ответ

бесконечно много решений

Упражнение \ (\ PageIndex {36} \)

Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} x + 2y = 6 \\ y = — \ tfrac {1} {2} x + 3 \ end {array} \ right. \)

Ответ

бесконечно много решений

Выберите наиболее удобный метод решения системы линейных уравнений

Когда вы решаете систему линейных уравнений в приложении, вам не скажут, какой метод использовать.Вам нужно будет принять это решение самостоятельно. Так что вы захотите выбрать самый простой метод, который сводит к минимуму ваши шансы на ошибку.

\ [\ textbf {Выберите наиболее удобный метод для решения системы линейных уравнений} \\ \ begin {array} {lll} {\ underline {\ textbf {Graphing}}} & {\ underline {\ textbf {Substitution} }} & {\ underline {\ textbf {Исключение}}} \\ {\ text {Используется, когда вам нужно}} & {\ text {Используется, когда одно уравнение равно}} & {\ text {Используется, когда уравнения a} } \\ {\ text {картина ситуации.}} & {\ text {уже решено или может быть}} & {\ text {переустановить стандартную форму.}} \\ {\ text {}} & {\ text {легко решено для одного}} & {\ text {} } \\ {\ text {}} & {\ text {переменная.}} & {\ text {}} \\ \ end {array} \ nonumber \]

Пример \ (\ PageIndex {37} \)

Решите для каждой системы линейных уравнений, что удобнее решить: заменой или исключением. Поясните свой ответ.

ⓐ \ (\ left \ {\ begin {array} {l} 3x + 8y = 40 \\ 7x − 4y = −32 \ end {array} \ right.\) Ⓑ \ (\ left \ {\ begin {array} {l} 5x + 6y = 12 \\ y = \ tfrac {2} {3} x − 1 \ end {array} \ right. \)

Ответ

ⓐ

\ [\ left \ {\ begin {array} {l} 3x + 8y = 40 \\ 7x − 4y = −32 \ end {array} \ right. \ Nonumber \]

Поскольку оба уравнения имеют стандартную форму, использование исключения будет наиболее удобным.

ⓑ

\ [\ left \ {\ begin {array} {l} 5x + 6y = 12 \\ y = \ tfrac {2} {3} x − 1 \ end {array} \ right. \ Nonumber \]

Поскольку одно уравнение уже решено относительно y , использование подстановки будет наиболее удобным.

Пример \ (\ PageIndex {38} \)

Для каждой системы линейных уравнений решите, что удобнее будет решить заменой или исключением. Поясните свой ответ.

ⓐ \ (\ left \ {\ begin {array} {l} 4x − 5y = −32 \\ 3x + 2y = −1 \ end {array} \ right. \) Ⓑ \ (\ left \ {\ begin { массив} {l} x = 2y − 1 \\ 3x − 5y = −7 \ end {array} \ right. \)

Ответ

ⓐ Поскольку оба уравнения имеют стандартную форму, использование исключения будет наиболее удобным.Ⓑ Поскольку одно уравнение уже решено для x , использование подстановки будет наиболее удобным.

Пример \ (\ PageIndex {39} \)

Для каждой системы линейных уравнений решите, что удобнее будет решить заменой или исключением. Поясните свой ответ.

ⓐ \ (\ left \ {\ begin {array} {l} y = 2x − 1 \\ 3x − 4y = −6 \ end {array} \ right. \) Ⓑ \ (\ left \ {\ begin {array } {l} 6x − 2y = 12 \\ 3x + 7y = −13 \ end {array} \ right. \)

Ответ

ⓐ Поскольку одно уравнение уже решено относительно y , использование подстановки будет наиболее удобным.Ⓑ Поскольку оба уравнения имеют стандартную форму, использование исключения будет наиболее удобным.

Как найти решение системы уравнений

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

систем линейных уравнений, примеры решений, рисунки и практические задачи. Система просто ..

Что такое система уравнений?

Отвечать

Система уравнений означает «более одного уравнения».’. Система линейных уравнений — это не более 1 строки, см. Рисунок:

Хорошо, а что такое

решение системы уравнений? Отвечать

Решение — это место, где уравнения «встречаются» или пересекаются. Красная точка — это решение системы.

Сколько решений могут иметь системы линейных уравнений?

Отвечать

Может быть нулевое решение, одно решение или бесконечное количество решений — каждый случай подробно описан ниже. Примечание. Хотя системы линейных уравнений могут иметь 3 или более уравнений, мы собираемся обратиться к наиболее распространенному случаю — стержню с ровно 2 линиями.

Вариант I: 1 Решение

Это наиболее распространенная ситуация, когда линии пересекаются ровно в одной точке.

---

Дело 2: Нет решений

Это происходит только тогда, когда линии параллельны.Как видите, параллельные линии никогда не встретятся.

Пример стержня, у которого нет решения:

• Строка 1: $$ y = 5x + 13 $$
• Строка 2: $$ y = 5x + 12 $$

---

Случай III: Бесконечные решения

Это самый редкий случай, и он возникает только тогда, когда у вас есть такая же строка
Рассмотрим, например, две строки ниже (y = 2x + 1 и 2y = 4x + 2).Эти два уравнения — одна и та же линия.

Пример системы с бесконечным числом решений:

• Строка 1: y = 2x + 1
• Строка 2: 2y = 4x + 2

Как найти решения систем уравнений?

Найти решение систем линейных уравнений можно любым из следующих способов:

Промежуточная алгебра Урок 19: Решение систем линейных уравнений в двух переменных WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня Цели обучения После изучения этого руководства вы сможете: Узнайте, является ли упорядоченная пара решением системы линейных уравнений в две переменные или нет. Решите систему линейных уравнений от двух переменных с помощью построения графиков. Решите систему линейных уравнений с двумя переменными заменой метод. Решите систему линейных уравнений с двумя переменными методом исключения метод. Введение В этом уроке мы будем специально рассматривать системы, которые имеют два уравнения и две неизвестные. Урок 20: Решение систем Линейный Уравнения в трех переменных будут охватывать системы, которые имеют три уравнения и три неизвестных. Мы рассмотрим их решение трех разных способы: построение графиков, метод подстановки и метод исключения. Это приведет нас к решению проблем со словами с системами, которые быть показано в Урок 21: Системы линейных уравнений и задачи Решение . Вот где мы можем ответить на печально известный вопрос, когда мы будем использовать это? Но сначала мы должны научиться работать с системами в Генеральная. Вот почему на этом этапе мы используем общие переменные, такие как x и y . Если вы знаете, как это решить в целом, тогда, когда у вас есть конкретный проблема что вы решаете, где переменные принимают значение, такое как время или Деньги (две вещи, которых нам, кажется, никогда не бывает достаточно), вы будете готовы к идти. Итак, давайте посмотрим на системы в целом, чтобы подготовить нас к решению предстоящих проблем из нас. Учебник Система линейных уравнений Система линейных уравнений состоит из двух или более линейных уравнения, которые решаются одновременно. В этом руководстве мы рассмотрим системы, которые имеют только два линейных уравнения и две неизвестные. В общем, решение системы двух переменных заказанный пара, которая делает ОБЕИХ уравнениями истинными. Другими словами, здесь пересекаются два графика, что у них есть в общем. Итак, если упорядоченная пара является решением одного уравнения, но не другой, то это НЕ решение системы. Согласованная система — это система, в которой хотя бы одно решение. Несогласованная система — это система, имеющая нет решения . Уравнения системы зависимы если ВСЕ решения одного уравнения являются решениями другого уравнения. В Другие словами, они заканчиваются той же строкой . Уравнения системы независимы , если они не разделяют ВСЕ решения . У них может быть одна общая черта, только не все их. Одно решение Если система с двумя переменными имеет одно решение, это заказанный пара, которая является решением ОБЕИХ уравнений. Другими словами, когда вы вставляете значения упорядоченной пары, она делает ОБА уравнения ПРАВДА. Если у вас есть одно решение для окончательного ответа, — это эта система непротиворечива или непоследовательна? Если вы сказали «последовательный», похлопайте себя по плечу! Если вы получите одно решение для окончательного ответа, будет уравнения быть зависимыми или независимыми? Если вы сказали независимый, вы правы! На приведенном ниже графике показана система двух уравнений. и два неизвестных у которого есть одно решение: Нет решения Если две линии параллельны друг другу, они будут никогда не пересекаются. Значит, у них нет ничего общего. В этом ситуация у вас не будет решения. Если вы не получили решения для окончательного ответа, — это эта система непротиворечива или непоследовательна? Если вы сказали «непоследовательно», вы правы! Если вы не получите окончательного ответа, будет уравнения быть зависимыми или независимыми? Если вы сказали независимый, вы правы! На приведенном ниже графике показана система двух уравнений. и два неизвестных без решения: Бесконечный Решения Если две линии в конечном итоге лежат друг на друге, то Там есть бесконечное количество решений. В этой ситуации они было бы в конечном итоге будут одной строкой, поэтому любое решение, которое будет работать в одном уравнение будет работать в другом. Если вы получите бесконечное количество решений для Ваш окончательный ответ, я сек эта система непротиворечива или непоследовательна? Если вы сказали «последовательный», вы правы! Если вы получите бесконечное количество решений для ваш окончательный ответ, будет уравнения быть зависимыми или независимыми? Если вы сказали иждивенец, вы правы! На приведенном ниже графике показана система двух уравнений. и два неизвестных имеющий бесконечное количество решений: Пример 1 : Определите, является ли каждая упорядоченная пара решением из система. (3, -1) и (0, 2) Давайте проверим упорядоченную пару (3, -1) в первом уравнение: * Вставка 3 для x и -1 для y * Истинное утверждение Пока все хорошо, (3, -1) является решением первое уравнение x + y = 2. Теперь давайте проверим (3, -1) во втором уравнении: * Вставка 3 для x и -1 для y * Истинное утверждение Эй, мы закончили с другим верным утверждением, которое означает, что (3, -1) является также решение второго уравнения x — y = 4. Вот большой вопрос, является ли (3, -1) решением данная система ????? Поскольку это было решение ОБЕИХ уравнений в системе, Затем это это решение для всей системы. Теперь давайте подставим (0, 2) в первое уравнение: * Вставьте 0 для x и 2 для y * Истинное заявление Это истинное утверждение, поэтому (0, 2) является решением первое уравнение x + y = 2. Наконец, поместим (0,2) во второе уравнение: * Вставьте 0 для x и 2 для y * Ложное заявление На этот раз мы получили ложное заявление, вы знаете, что это средства. (0, 2) НЕ является решением второго уравнения x — y = 4. Вот большой вопрос, является ли (0, 2) решением данная система ????? Поскольку это не было решением ОБОИХ уравнений в система, то это не решение всей системы. Три способа Решение систем линейных Уравнений с двумя переменными Шаг 1. Постройте первое уравнение. Шаг 2: Изобразите второе уравнение на та же координата система как первая. Вы изобразите второе уравнение так же, как и любое другое. уравнение. Обратитесь к первому шагу, если вам нужно рассмотреть различные способы график линия. Отличие в том, что на такой же ставишь система координат как первый. Это как две задачи с графиком в одной. Шаг 3. Найдите решение. Если две линии пересекаются в одном месте , то точка перекресток — решение системы. Если две линии параллельны , то они никогда не пересекаются, так что нет решения. Если у две линии лежат друг над другом , то они та же строка , и у вас есть бесконечное количество решений. . В этом случае вы можете записать любое уравнение как решение указывать это одна и та же линия. Шаг 4: Проверьте предложенный заказ парное решение в ОБА уравнения. Предлагаемое решение можно подключить к ОБА уравнения. Если это делает ОБЕИХ уравнения истинными, тогда у вас есть решение система. Если хотя бы один из них окажется ложным, вам нужно перейти назад и повторить проблема. Пример 2 : Решите систему уравнений, построив график. * Вставка 0 для y для x -int * x -intercept Перехват x — (3, 0). y — перехват * Вставка 0 для x для y -int * y -intercept Перехват y — (0, 3). Найти другого решение, положив x = 1. * Вставка 1 для x Другое решение (1, 2). Решения: х y (х, у) 3 0 (3, 0) 0 3 (0, 3) 1 2 (1, 2) Построение упорядоченных парных решений и построение линия: * Вставка 0 для y для x -int * x -intercept Перехват x — (1, 0). Y-перехват * Вставка 0 для x для y -int * инверсия мульт. на -1 — это div. по -1 * y -перехват Перехват y равен (0, -1). Найти другого решение, положив x = 2. * Вставьте 2 для x * Сумма, обратная сумме 2, является вспомогательной. 2 * инверсия мульт. на -1 это div по -1 Другое решение — (2, 1). Решения: х y (х, у) 1 0 (1, 0) 0 -1 (0, -1) 2 1 (2, 1) Построение упорядоченных парных решений и построение линия: Мы должны спросить себя, есть ли место, где две линии пересекаются, и если да, то где? Ответ — да, они пересекаются в (2, 1). Вы обнаружите, что если вы подключите заказанную пару (2, 1) в ОБЕИХ уравнения исходной системы, что это решение ОБЕИХ из них. Решение этой системы — (2, 1). Пример 3 : Решите систему уравнений, построив график. * Вставка 0 для y для x -int * x -intercept Перехват x — (5, 0). y — перехват * Вставка 0 для x для y -int * y -перехват Перехват y равен (0, 5). Найти другого решение, положив x = 1. * Вставить 1 для x * Сумма, обратная сумме 1, является вспомогательной. 1 Другое решение — (1, 4). Решения: х y (х, у) 5 0 (5, 0) 0 5 (0, 5) 1 4 (1, 4) Построение упорядоченных парных решений и построение линия: * Вставить 0 для y для x -int * Значение, обратное сложению 3, является sub.3 * инверсия мульт. на -1 — это div. по -1 * x -перехват Перехват x — (3, 0). y — перехват * Вставка 0 для x для y -int * y -intercept Перехват y — (0, 3). Найти другого решение, положив x = 1. * Вставка 1 для x Другое решение (1, 2). Решения: х y (х, у) 3 0 (3, 0) 0 3 (0, 3) 1 2 (1, 2) Построение упорядоченных парных решений и построение линия: Мы должны спросить себя, есть ли место, где две линии пересекаются, и если да, то где? Ответ — нет, они не пересекаются.Мы иметь два параллельных линий. Нет заказанных пар для проверки. Ответ — нет решения. Решить методом подстановки Шаг 1. При необходимости упростите. Это может включать в себя такие вещи, как удаление () и удаление фракций. Чтобы удалить (): просто используйте свойство distributive. Чтобы удалить дроби: поскольку дроби — это еще один способ написать деление, а обратное деление — умножение, дробь удаляется на умножение обе стороны ЖК-дисплеем всех ваших фракций. Шаг 2: Решите одно уравнение для любая переменная. Неважно, какое уравнение вы используете или какое переменная, которую вы выбираете решить для. Вы хотите сделать это как можно проще.Если один уравнений уже решено для одной из переменных, это быстро и легко способ идти. Если вам нужно найти переменную, попробуйте выбрать тот, у которого есть 1 как коэффициент. Таким образом, когда вы идете решать это, вы не будет делить на число и рисковать работать с доля (фу !!). Шаг 3. Замените то, что вы получаете, на шаг 2 в другое уравнение. Вот почему он называется методом замещения. Убедись в том, что вы подставляете выражение в ДРУГОЕ уравнение, то, которое вы не сделал использовать на шаге 2. Это даст вам одно уравнение с одним неизвестным. Шаг 4. Решите для оставшаяся переменная. Шаг 5: Решите для секунды Переменная. Если вы нашли значение переменной на шаге 4, что означает два уравнения имеют одно решение. Вставьте найденное значение в шаг 4 в любое из уравнений задачи и решить для другого Переменная. Если ваша переменная выпадает и вы получаете ЛОЖЬ заявление, что означает ваш ответ не решение. Если ваша переменная выпадает и у вас есть ИСТИНА заявление, что означает ваш ответ — бесконечные решения, которые были бы уравнением линия. Шаг 6: Проверьте предложенный заказанный парное решение в ОБЕ исходные уравнения. Предлагаемое решение можно подключить к ОБА уравнения. Если это делает ОБЕИЕ уравнения истинными, тогда у вас есть решение система. Если хотя бы один из них окажется ложным, вам нужно перейти назад и повторить проблема. Пример 4 : Решите систему уравнений заменой метод. Оба эти уравнения уже упрощены. Нет необходимости в работе делать здесь. Обратите внимание, что второе уравнение уже решено для y . Мы можем использовать его на этом этапе. Неважно, какое уравнение или какую переменную вы выбрать решение для. Но в ваших интересах, чтобы это было так просто, как возможный. Второе уравнение, решенное относительно y : * Решено для y Подставьте выражение 2 x + 4 вместо y в первое уравнение и решите относительно x : (когда вы вставляете подобное выражение, это похоже на то, как вы подключаете в номере вашей переменной) * Под.2 x + 4 дюйма для y * Расст. -5 через () * Объединить похожие термины * Обратное от sub. 20 добавлено 20 * Обратно div. by -7 есть мульт. по -7 Вставить -5 для x в уравнение в шаг 2, чтобы найти значение y . * Вставка -5 для x Вы обнаружите, что если вы подключите заказанную пару (-5, -6) в ОБЕИХ уравнения исходной системы, что это решение ОБЕИХ из их. (-5, -6) — это решение для нашей системы. Пример 5 : Решите систему уравнений заменой метод. Оба эти уравнения уже упрощены. Нет необходимости в работе делать здесь. На этот раз проблема была не так хороша для нас, мы придется проделайте небольшую работу, чтобы решить одно уравнение для одной из наших переменных. Неважно, какое уравнение или какую переменную вы выбрать решение для.Просто будь простым. Так как x в первом уравнение имеет коэффициент 1, это означало бы, что нам не нужно было бы делить на номер решить эту проблему и рискнуть работать с дробями (УРА !!) Самый простой способ — решить первое уравнение для x , и мы определенно хотим выбрать легкий путь. Ты бы не был неправильный чтобы выбрать другое уравнение и / или решить для y, снова вы хотите чтобы сделать его максимально простым. Решая первое уравнение для x , получаем: * Обратное от sub. 2 л прибавлено 2 л * Решено для x Подставьте выражение 5 + 2 y вместо x во второе уравнение и решите относительно y : (когда вы вставляете подобное выражение, это похоже на то, как вы подключаете в номере вашей переменной) * Под.5 + 2 y для x * Переменная выпала И ложь Погодите, а где наш переменная go ???? Как упоминалось выше, если ваша переменная выпадает и вы иметь оператор FALSE, тогда решения нет. Если бы мы изобразили эти два графика, они будут параллельны друг другу. Поскольку мы не получили значение для y , там здесь нечего подключать. Нет заказанных пар для проверки. Ответ — нет решения. Решить методом исключения Этот метод также известен как добавление или исключение добавлением метод. Шаг 1. Упростите и поместите оба уравнения в виде A x + B y = C, если необходимо. Это может включать в себя такие вещи, как удаление () и удаление фракций. Чтобы удалить (): просто используйте свойство distributive. Чтобы удалить дроби: поскольку дроби — это еще один способ написать деление, а обратное деление — умножение, дробь удаляется на умножение обе стороны ЖК-дисплеем всех ваших фракций. Шаг 2: Умножьте один или оба уравнения по числу который при необходимости создаст противоположные коэффициенты для x или y . Забегая вперед, мы добавим эти два уравнения вместе . В этом процессе нам нужно убедиться, что одна из переменных падает вне, оставив нам одно уравнение и одно неизвестное. Единственный способ, которым мы можем гарантия, что если мы добавляем противоположностей . Сумма противоположности равно 0. Если ни одна из переменных не выпадает, то мы застреваем с уравнение с две неизвестные, которые неразрешимы. Неважно, какую переменную вы выберете вне. Вы хотите, чтобы это было как можно проще. Если переменная уже имеет противоположные коэффициенты, чем при добавлении двух уравнений все вместе. В противном случае вам нужно умножить одно или оба уравнения на число. что создаст противоположные коэффициенты в одной из ваших переменных.Ты может думайте об этом как о ЖК-дисплее. Подумайте, какой номер оригинал коэффициенты оба входят и соответственно умножают каждое отдельное уравнение. Делать убедитесь, что одна переменная положительна, а другая отрицательна, прежде чем вы Добавлять. Например, если у вас есть 2 x в одном уравнении и 3 x в другом уравнении, мы могли бы умножать первое уравнение на 3 и получаем 6 x и в второе уравнение на -2, чтобы получить -6 x . Так когда вы собираетесь сложить эти два вместе, они выпадут. Сложите два уравнения. Переменная с противоположными коэффициентами будет выпадать из этого шаг, и у вас останется одно уравнение с одним неизвестным. Шаг 4: Найдите оставшуюся переменную. Решите уравнение, найденное на шаге 3, для переменной что осталось. Если вам нужен обзор по этому поводу, перейдите к Tutorial 7: Линейные уравнения с одной переменной. Если выпадают обе переменные и вы получаете ЛОЖЬ заявление, что означает ваш ответ не решение. Если выпадают обе переменные и у вас есть ИСТИНА заявление, что означает ваш ответ — бесконечные решения, которые были бы уравнением линия. Шаг 5: Найдите вторую переменную. Если вы нашли значение переменной на шаге 4, что означает два уравнения имеют одно решение. Вставьте найденное значение в шаг 4 в любое из уравнений задачи и решить для другого Переменная. Шаг 6: Проверьте предложенный заказанный парное решение в ОБЕ исходные уравнения. Предлагаемое решение можно подключить к ОБА уравнения.Если это делает ОБЕИХ уравнения истинными, тогда у вас есть решение система. Если хотя бы один из них окажется ложным, вам нужно перейти назад и повторить проблема. Пример 6 : Решите систему уравнений методом исключения метод. В этом уравнении полно неприятных дробей. Мы можем упростить оба уравнения, умножив каждое в отдельности на его ЖК-дисплей, как вы можете сделать это, когда работаете с одним уравнением. До тех пор, как вы проделайте то же самое с обеими сторонами уравнения, оставив обе стороны равны друг другу. Умножая каждое уравнение на соответствующий ЖК-дисплей, мы получить: * Мног. по ЖК из 15 * Мног. по ЖК из 6 Опять же, вы хотите сделать это так просто, как возможный.Обратите внимание, как коэффициенты для и равны 3. Мы должны иметь противоположности, поэтому, если один из них равен 3, а другой -3, Они будут взаимно отменять друг друга, когда мы перейдем к их добавлению. Если бы мы сложили их вместе, как сейчас, мы бы закончить с одно уравнение и две переменные, ничего бы не выпало. И мы было бы не смогу ее решить. Предлагаю умножить второе уравнение на -1, это будет создайте -3 перед x , и мы будем имеют наши противоположности. Обратите внимание, что мы могли бы так же легко умножить первое уравнение на -1 а не второй. В любом случае работа будет выполнена. Умножая второе уравнение на -1, получаем: * Мног.обе стороны 2-го ур. по -1 * y ‘а иметь противоположное коэффициенты * Обратите внимание, что y s выпал * Инверсная по отношению к мульт.на 3 — div. по 3 Вы можете выбрать любое уравнение, используемое в этой задаче, чтобы вставьте найденное значение x . Я выбираю подключить 11 для x в первое упрощенное уравнение (найдено на шаге 1), чтобы найти y ’s значение. * Вставка 11 для x * Сумма, обратная сумме 55, является sub.55 * инверсия мульт. на 3 — div. по 3 Вы обнаружите, что если вы подключите заказанную пару (11, -25/3) в ОБЕИХ уравнения исходной системы, что это решение ОБЕИХ из их. (11, -25/3) — это решение для нашей системы. Пример 7 : Решите систему уравнений методом исключения метод. Эта задача уже упрощена.Однако второй уравнение не записывается в виде Ax + By = C. Другими словами, нам нужно написать это в этой форме, поэтому все будет готово к работе, когда мы добавим два уравнения вместе. Переписывая второе уравнение, получаем: * Инверсия сложения 6 x — sub.6 х * Все в порядке Обратите внимание, что если мы умножим первое уравнение на 2, то Мы будем иметь -6 x , что является противоположностью 6 x , найденным во втором уравнении. Умножая первое уравнение на 2, получаем: * Мног.1-й экв. по 2 * x имеют противоположные коэффициенты * Переменные выпали И истинно Эй, откуда у нас переменные идти?? Как упоминалось выше, если переменная выпадает И мы иметь ИСТИННОЕ заявление, тогда когда есть бесконечное количество решений.Они в конечном итоге та же линия. Здесь нет никакой ценности для подключения. Здесь нет никакой ценности для подключения. Когда они оказываются в одном уравнении, у вас есть бесконечное число решений.Вы можете написать свой ответ, написав либо уравнение, чтобы указать, что это одно и то же уравнение. Два способа написать ответ: {( x , y ) | 3 x — 2 y = 1} OR {( x , y ) | 4 y = 6 x — 2}. Практические задачи Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Math работает так же, как что-нибудь иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться Это. Даже лучшим спортсменам и музыкантам помогали на протяжении всего пути. практиковаться, практиковаться, практиковаться, чтобы хорошо освоить свой вид спорта или инструмент. На самом деле не бывает слишком много практики. Чтобы получить от них максимальную отдачу, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, щелкнув ссылку для ответ / обсуждение для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа. Практика Задача 1a: Решите систему, построив график. Практика Задача 2а: Решите систему подстановкой метод. Практика Проблема 3a: Решите систему метод устранения. Нужна дополнительная помощь по этим темам? Последняя редакция 10 июля 2011 г. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт