Что это — ромб. Признаки и свойства ромба
Что такое ромб? Известно, что это равносторонний четырехугольник, который также является параллелограммом. А если у ромба все углы равны, то эту фигуру уже можно назвать квадратом. А все противолежащие стороны ромба являются параллельными.
Что такое ромб
Ромб — это равносторонний параллелограмм. Само слово греческого происхождения, и означает «бубен». Это сегодня бубны круглой формы, раньше же их изготавливали в форме квадрата. Именно поэтому ромб имеет такое название. Также имеет наименование как геральдическая фигура. Обратимся к словарю Ушакова. Что же такое ромб? По сравнению с квадратом, это косоугольник с равными углами. А также квадрат — это частный случай ромба. Иногда даже говорят, что эти фигуры можно сравнить.
Также с ромбом связано изображение масти «бубна» на картах, которые используют в азартных играх. Также эту фигуру применяли для изображения на знаменах, флагах и различных гербах, но она встречается намного реже, чем другие геометрические конструкции. А сегодня ромб также используется для изображения баскетбольного поля. Что такое ромб, нам известно, но давайте рассмотрим свойства и признаки этой фигуры.
А сегодня ромб также используется для изображения баскетбольного поля. Что такое ромб, нам известно, но давайте рассмотрим свойства и признаки этой фигуры.
Свойства ромба
- Ромб представляется параллелограммом, все стороны которого лежат противоположно, являются равными и параллельными.
- Диагонали этой математической конструкции пересекаются лишь под прямым углом и делятся пополам в точке пересечения. То есть эти диагонали делят ромб на четыре абсолютно равных треугольника.
- Биссектрисами углов являются именно диагонали.
- Совокупность квадратов диагоналей равняется квадрату стороны, которая умножена на четыре.
- Вершинами прямоугольника являются середины четырех сторон этой конструкции под названием ромб.
- Диагонали фигуры перпендикулярны осями своей симметрии.
- Окружность с лежащим на пересечении центром можно вписать в любую фигуру под названием ромб.
- Что такое диагональ ромба? Это линия, которая соединяет его углы.

Признаки ромба
Мы узнали, что такое ромб, но помимо свойств у этой фигуры существуют еще и признаки. Любой параллелограмм будет являться ромбом, если будет выполнять хоть одно из приведенных ниже условий:
- Две смежные стороны ромба являются равными по отношению друг к другу.
- Диагонали этой математической конструкции могут пересекаться лишь под прямым углом и никак иначе.
- Одна из диагоналей обязательно делит пополам все ее углы, которые в ней содержаться.
- А если предположить, что нам не известно, что четырехугольник является параллелограммом, но известно, что стороны фигуры равны, тогда уверенно можно сказать: четырехугольник — это ромб.
- Это часть прямой, которая образует угол равный 90 градусам при пересечении противолежащей стороны.
- Что такое высота ромба? Это часть прямой, которая образует угол 90 градусов, пересекая противолежащую сторону.
Площадь ромба
Нам известно, что такое ромб, каковы его свойства и признаки, но как же найти его площадь? Для того чтобы найти площадь ромба, следует поделить пополам произведения диагоналей этой фигуры. Так как ромб — это тот же параллелограмм, площадь такой математической конструкции равна произведению высоты на длину его сторон. Помимо этого, площадь фигуры можно найти при вычислении по формулам со смежными сторонами или же с радиусом вписанной окружности. Радиус вписанной окружности выражается через диагонали. Для того чтобы вычислить периметр ромба, следует умножить длину одной из четырех сторон на четыре.
Так как ромб — это тот же параллелограмм, площадь такой математической конструкции равна произведению высоты на длину его сторон. Помимо этого, площадь фигуры можно найти при вычислении по формулам со смежными сторонами или же с радиусом вписанной окружности. Радиус вписанной окружности выражается через диагонали. Для того чтобы вычислить периметр ромба, следует умножить длину одной из четырех сторон на четыре.
А для того, чтобы изобразить эту фигуру в виде рисунка, нужно соблюдать нижеприведенные наставления. Ведь при построении этой фигуры у многих появляются трудности. Так вот, для того чтобы аккуратно изобразить ромб, следует для начала нарисовать первую диагональ, следом перпендикулярно вторую, в конце соединить края отрезков. Нужно очень внимательно и аккуратно рисовать эту фигуру, для того чтобы вместо ромба вы не нарисовали квадрат.
Ромб. Формулы, признаки и свойства ромба
Определение.
Ромб — это параллелограмм, который имеет равные стороны.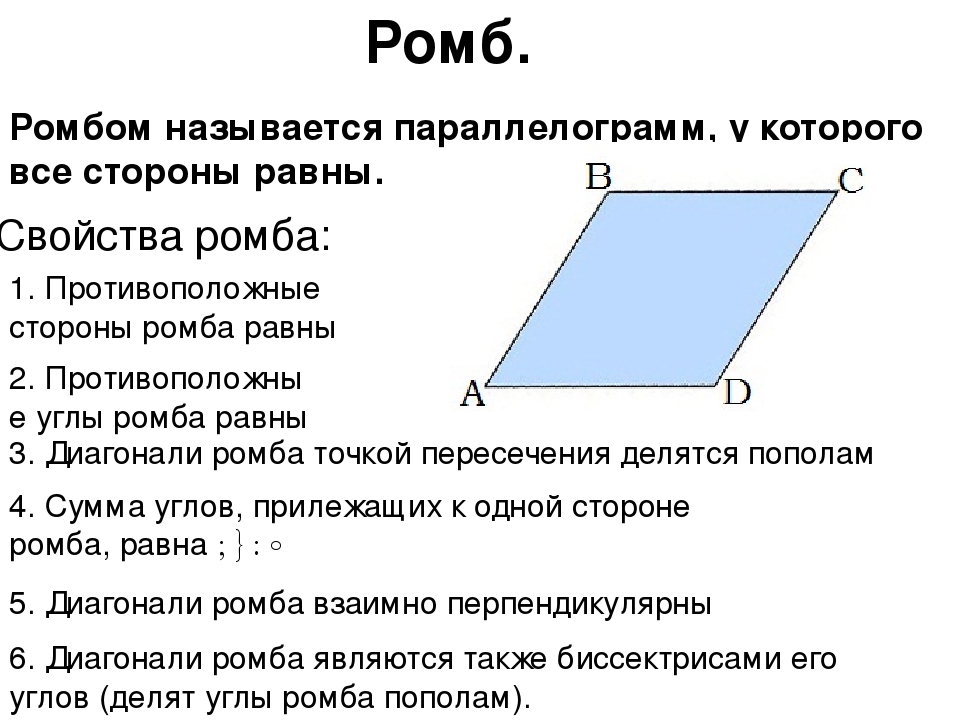 Если у ромба все углы прямые, тогда он называется квадратом.
Если у ромба все углы прямые, тогда он называется квадратом.Ромбы отличаются между собой размером стороны и размером углов.
| Рис.1 | Рис.2 |
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:AC┴BD
3. Одна из диагоналей (бисектрисса) делит содержащие её углы пополам:∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
Основные свойства ромба
2. Диагонали перпендикулярны:AC┴BD
3. Диагонали являются биссектрисами его углов:∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Определение.
Ромб имеет две диагонали — длинную d1, и короткую — d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)d1 = a√2 + 2 · cosα
d1 = a√2 — 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)d2 = a√2 + 2 · cosβ
d2 = a√2 — 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:d1
d1 = 2a · sin(β/2)
4. Формулы малой диагонали ромба через сторону и половинный угол:d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:d1 = √4a2 — d22
d2 = √4a2 — d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ: 8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.Длину стороны ромба можна найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба: P = 4aПлощадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:S = a · ha
2. Формула площади ромба через сторону и синус любого угла:S = a2 · sinα
3. Формула площади ромба через сторону и радиус:S = 2a · r
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ): Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба: 2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба: 3. Формула радиуса круга вписанного в ромб через площадь и синус угла: 4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла: 5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла: 6. Формула радиуса круга вписанного в ромб через две диагонали:| r = | d1 · d2 |
| 2√d12 + d22 |
 Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Формула радиуса круга вписанного в ромб через две диагонали и сторону:Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Ромб — что это такое, его свойства и признаки
Обновлено 21 июля 2021 Просмотров: 58 284 Автор: Дмитрий Петров- Ромб — это…
- Признаки
- Свойства ромба
- Периметр
- Площадь ромба
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем о такой геометрической фигуре, как РОМБ. Многие наверняка знают, как он выглядит.
Особенно спортивные болельщики, так как эмблемы многих команд связаны именно с ромбом. Тут достаточно вспомнить одну из главных российских команд – Спартак. Вот так она выглядит.
Ромб — это…
А вот как звучит официальное определение ромба:
Ромб – это геометрическая фигура, которая представляет собой особый вид параллелограмма (это как ?). И у него все стороны равны.
История возникновения самого слова весьма примечательна. На древнегреческом оно звучит как «ῥόμβος», а на латыни «rombus». И переводятся оба слова как «бубен».
На древнегреческом оно звучит как «ῥόμβος», а на латыни «rombus». И переводятся оба слова как «бубен».
Дело в том, что в Древней Греции делали барабаны и прочие ударные инструменты чаще именно такой формы. Просто натягивать ткань на параллелограмм было гораздо проще. А вот круглые, более привычные нам сегодня барабаны появились позже.
И еще один интересный факт – карточная масть «бубны» называется так точно по той же причине.
Говоря об определении РОМБА, не лишним будет тогда сказать и что такое параллелограмм, раз он там фигурирует.
Параллелограмм – это геометрическая фигура, которая представляет собой четырехугольник, у которого противоположные стороны равны между собой и параллельны друг другу.
Выглядит классический параллелограмм вот так:
Впервые его описал знаменитый древнегреческий математик Евклид в своей книге «Начала». Это произведение вышло в 300 году до нашей эры. И было посвящено основам математики, которые были известны на то время.
В частности, Евклид в своей книге разделил все четырехугольники на две большие категории – параллелограмм и трапеция (так как у нее две стороны не параллельны друг другу). Также в «Началах» Евклид указал, что ромб является частным случаем параллелограмма, так как у него противоположные стороны равны.
И наконец, частным случаем самого ромба является квадрат. У него противоположные стороны не только равны, но еще и пересекаются под прямым углом.
Признаки ромба
Чтобы понять, что перед нами ромб, должно выполняться всего лишь одно из трех простых условий:
- Все четыре стороны параллелограмма равны;
- Диагонали параллелограмма пересекаются под углом 90 градусов;
- Диагонали параллелограмма являются еще и биссектрисами.
И тут будет не лишним подтянуть теоретическую базу и напомнить, что такое диагональ, и уж тем более что такое биссектриса.
Диагональ – это отрезок, который соединяет две любые вершины в многоугольнике, которые не находятся рядом друг с другом.
Если говорить конкретно о четырехугольнике, которым является и ромб, то диагональ соединяет две противоположные вершины и никак иначе. И таких диагоналей в ромбе две:
На этом рисунке диагоналями являются отрезки AC и BD. И как показано, они пересекаются под прямым углом, о чем и говорится во втором признаке ромба.
Биссектриса – это линия, которая выходит из угла и делит его ровно на две части.
Кстати, само слово «биссектриса» имеет латинские корни. Оно состоит из двух половин – «bi» (двойное) и sectio (разрезание).
Свойства ромба
А можно все и перевернуть таким образом. Если вы точно определи, что перед вами ромб, то тогда для этой фигуры будут характерны вот такие свойства:
- Диагонали ромба пересекаются между собой под прямым углом.

- Диагонали ромба также представляют собой и биссектрисы его углов.
И есть еще одно свойство, которое помогает решать различные задачки на уроках геометрии. Оно звучит так:
Сумма квадратов обеих диагоналей ромба равна квадрату его сторону, умноженному на четыре.
Периметр ромба
Чтобы определить периметр любого четырехугольника, надо просто сложить между собой длины всех его сторон.
В случае с ромбом это совсем просто, так как они все равны между собой. И тогда формула для вычисления периметра получается такой:
Как несложно догадаться, буква «а» здесь – это длина стороны ромба.
Есть еще одна формула для вычисления периметра ромба – через диагонали. Она более сложная, но при решении различных задач вполне может и пригодиться.
Площадь ромба
Площадь любой геометрической фигуры – это размер пространства, заключенного в границы этой самой фигуры.
Классическая формула для расчета площади ромба – через длины стороны и высоты.
Главное, надо напомнить, что такое высота. Это отрезок, проведенный из вершины геометрической фигуры под прямым углом к противоположной стороне.
Она обозначается буквой «h» или «H» и выглядит вот так:
И наконец, формула для расчета площади ромба через сторону и высоту:
Есть и другие формулы для расчета площади ромба:
- Если известны диагонали:
- Если известны сторона и угол:
- Если известны угол и радиус вписанной окружности:
- Если известны сторона и радиус вписанной окружности:
Вот и все, что мы хотели рассказать о ромбе.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Свойства высоты ромба: Ромб. Формулы, признаки и свойства ромба — ЭкоДом: Дом своими руками
Ромб. Формулы, признаки и свойства ромба
Определение.
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
Ромбы отличаются между собой размером стороны и размером углов.
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:
AC┴BD
3. Одна из диагоналей (бисектрисса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4.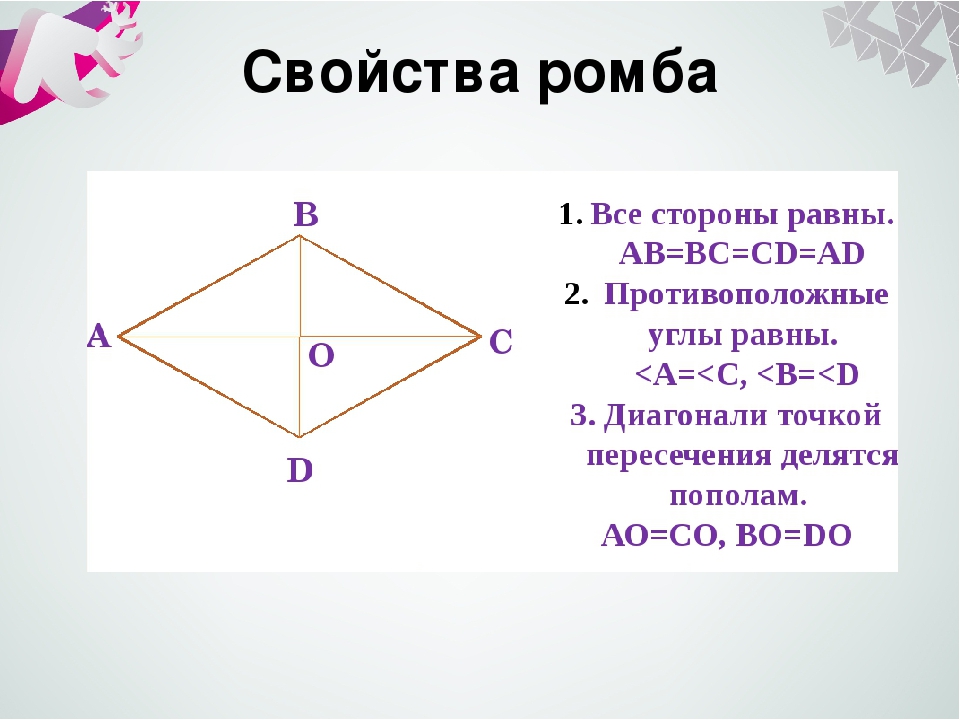 Если все высоты равны:
Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
Основные свойства ромба
2. Диагонали перпендикулярны:
AC┴BD
3. Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4.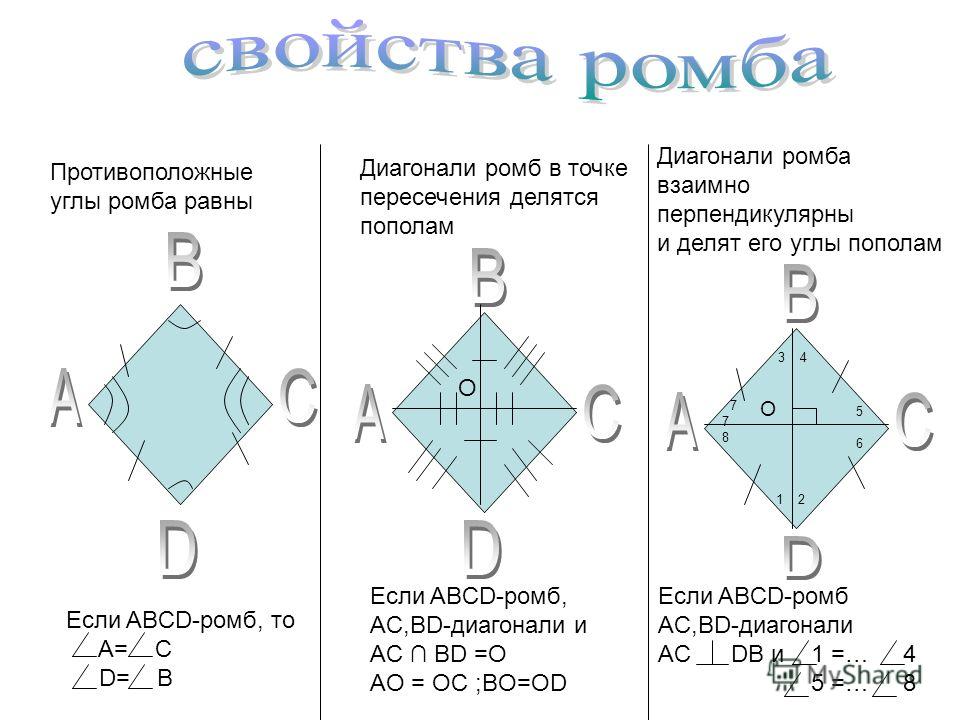 Формула стороны ромба через две диагонали:
Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Определение.
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Ромб имеет две диагонали — длинную d1, и короткую — d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 — 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 — 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
4. Формулы малой диагонали ромба через сторону и половинный угол:
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 — d22
d2 = √4a2 — d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можна найти за формулами указанными выше.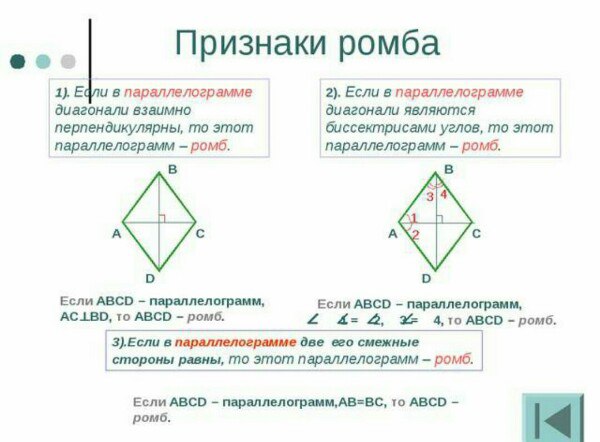
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.
Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d1 · d2 |
| 2√d12 + d22 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Ромб — Формулы | Свойства
Для расчёта всех основных параметров ромба воспользуйтесь калькулятором.
Свойства ромба
- Противолежащие стороны ромба параллельны и равны.

- Диагонали ромба перпендикулярны.
- Точка пересечения диагоналей делит их пополам.
- Диагонали ромба являются биссектрисами его углов.
- Диагонали образуют из ромба 4 прямоугольных треугольника.
- Любой ромб может содержать окружность с центром в точке пересечения его диагоналей.
- Сумма квадратов диагоналей равна квадрату одной из сторон ромба умноженному на четыре
Признаки ромба
- Параллелограмм с перпендикулярными диагоналями является ромбом.
- Когда в параллелограмме хотя бы одна из диагоналей разделяет оба угла (через которые она проходит) пополам, то эта фигурой будет ромб.
Примечание: Не каждая фигура (четырехугольник) с перпендикулярными диагоналями будет ромбом, так как прежде всего ромб это частный случай параллелограмма, а следовательно должен иметь все его признаки - Если в параллелограмм можно вписать круг, то он является ромбом
Формулы стороны ромба
Длина стороны ромба через площадь (S) и высоту (AE)
$$
AB = {S \over AE}
$$
Длина стороны ромба через площадь (S) и синус угла
$$
AB = {\sqrt{S} \over \sqrt{sin(∠CDA)}} = {\sqrt{S} \over \sqrt{sin(∠DAB)}}
$$
Длина стороны ромба через диагонали
$$
AB = {\sqrt{AC^2 + DB^2} \over 2}
$$
Длина стороны ромба через диагональ и угол
$$
AB = {BD \over 2 * cos(∠CDA)} = {AC \over 2 * cos(∠DAB)}
$$
Длина стороны ромба через периметр
$$
AB = {P \over 4}
$$
Формулы диагоналей ромба
Длина большой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
$$
BD = AB * \sqrt{2 + 2 * cos(∠CDA)}
$$
$$
BD = AB * \sqrt{2 — 2 * cos(∠DAB)}
$$
Длина малой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
$$
AC = AB * \sqrt{2 — 2 * cos(∠CDA)}
$$
$$
AC = AB * \sqrt{2 + 2 * cos(∠DAB)}
$$
Длина диагонали ромба через сторону и другую диагональ
$$
BD = \sqrt{4 * AB^2 + AC^2}
$$
$$
AC = \sqrt{4 * AB^2 + BD^2}
$$
Длина диагонали ромба через площадь и другую диагональ
$$
BD = {2 * S \over AC}
$$
$$
AC = {2 * S \over BD}
$$
Длина диагонали ромба через тангенс острого tg(∠CDA) или тупого tg(∠DAB) угла и другую диагональ
$$
BD = AC * tg({∠DAB \over 2 })
$$
$$
AC = BD * tg({∠CDA \over 2 })
$$
Формулы площади ромба
Площадь ромба через высоту (AE) и сторону
$$
S = AB * AE
$$
Площадь ромба через сторону и синус любого угла
$$
S = AB^2 * sin(∠CDA) = AB^2 * sin(∠DAB)
$$
Площадь ромба через две диагонали
$$
S = {1 \over 2} * AC * BD
$$
Площадь ромба через большую диагональ и тангенс острого угла(∠CDA) или малую диагональ и тангенс тупого угла(∠DAB)
$$
S = {1 \over 2} * BD^2 * tg({∠CDA \over 2})
$$
$$
S = {1 \over 2} * AC^2 * tg({∠DAB \over 2})
$$
Формулы радиуса круга вписанного в ромб
Радиус вписанного круга в ромб через высоту ромба (AE)
$$
R = {AE \over 2}
$$
Радиус вписанного круга в ромб через площадь и сторону ромба
$$
R = {S \over 2 * AB}
$$
Радиус вписанного круга в ромб через сторону и синус любого угла
$$
R = {AB * sin(∠CDA) \over 2} = {AB * sin(∠DAB) \over 2}
$$
Радиус вписанного круга в ромб через диагональ и синус угла
$$
R = {BD * sin(∠CDA / 2) \over 2}
$$
$$
R = {AC * sin(∠DAB / 2) \over 2}
$$
Радиус вписанного круга в ромб через две диагонали
$$
R = {BD * AC \over 2 * \sqrt{BD^2 + AC^2}}
$$
Формулы высоты ромба
Высота ромба через сторону и угол
$$
AE = AB * sin(∠CDA) = AB * sin(∠DAB)
$$
Высота ромба через диагональ и угол
$$
AE = BD * sin({∠CDA \over 2})
$$
$$
AE = AC * sin({∠DAB \over 2})
$$
Высота ромба через диагонали
$$
AE = {BD * AC \over \sqrt{BD^2 + AC^2}}
$$
Высота ромба через диагонали и сторону
$$
AE = {BD * AC \over 2 * AB}
$$
Формулы углов ромба
Косинус углов через диагональ и сторону
$$
cos(∠CDA) = {BD \over 2 * AB^2} — 1 = 1 — {AC \over 2 * AB^2}
$$
$$
cos(∠DAB) = {AC \over 2 * AB^2} — 1 = 1 — {BD \over 2 * AB^2}
$$
Синусы углов через диагонали
$$
sin(∠CDA) = sin(∠DAB) = {2 * BD * AC \over BD^2 + AC^2}
$$
Синусы углов через площадь и сторону
$$
sin(∠CDA) = sin(∠DAB) = {S \over AB^2}
$$
Тангенс половинных углов через диагонали
$$
tg(∠CDA) = {AC \over BD}
$$
$$
tg(∠DAB) = {BD \over AC}
$$
Ромб.

Площадь, периметр, радиус
В школьном курсе в геометрии среди основных задач значительное внимание уделено примерам вычисления площади и периметра ромба. Вспомним что ромб принадлежит к отдельному классу четырехугольников и выделяется среди них равными сторонами. Ромб также является частным случаем параллелограмма если у последнего все стороны равны AB=BC=CD=AD. Ниже приведен рисунок на котором изображен ромб.
Свойства ромба
Поскольку ромб занимает некоторую часть параллелограммов то свойства в них будут похожими.
- Противоположные углы ромба как и параллелограмма равны.
- Сумма углов ромба прилегающих к одной стороне равна 180°.
- Диагонали ромба пересекаются под углом 90 градусов.
- Диагонали ромба являются одновременно биссектрисами его углов.
- Диагонали ромба в точке пересечения делятся пополам.
Признаки ромба
Все признаки ромба вытекают из его свойств и помогают различать его среди четырехугольников, прямоугольников, параллелограммов.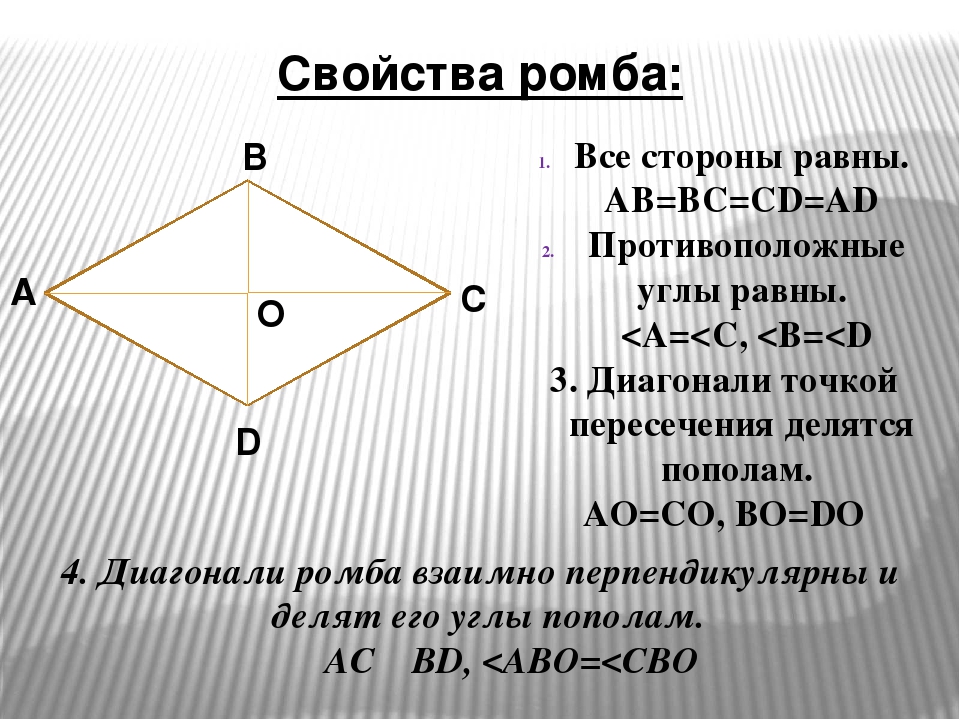
- Параллелограмм у которого диагонали пересекаются под прямым углом является ромбом.
- Параллелограмм у которого диагонали является биссектрисами является ромбом.
- Параллелограмм с равными сторонами является ромбом.
- Четырехугольник у которого все стороны равны является ромбом.
- Четырехугольник у которого диагонали является биссектрисами углов и пересекаются под прямым углом является ромбом.
- Параллелограмм с одинаковыми высотами является ромбом.
Формула периметра ромба
Периметр по определению равен сумме всех сторон. Поскольку в ромба все стороны равны то его периметр вычисляем по формуле
P=4a.
Периметр вычисляется в единицах длины.
Радиус окружности вписанной в ромб
Одними из распространенных задач при изучении ромба является нахождение радиуса или диаметра вписанной окружности. На рисунке изображенном ниже приведены одни из распространенных формул радиуса вписанной окружности в ромб.
Первая формула показывает что радиус окружности вписанной в ромб равен произведению диагоналей разделенному на сумму всех сторон (4а).
Другая формула показывает что радиус окружности вписанной в ромб равен половине высоты ромба
r=h/2.
Вторая формула на рисунке является модификацией первой и применяется при исчислении радиуса окружности вписанной в ромб когда известны диагонали ромба, то есть неизвестные стороны.
Третья формула радиуса вписанной окружности фактически находит половину высоты малого треугольника, который образуется пересечением диагоналей.
Среди менее популярных формул для вычисления радиуса окружности вписанной в ромб можно еще привести такие
здесь D – диагональ ромба, alpha – угол который рассекает диагональ.
Если известна площадь (S) ромба и величина острого угла (alpha) то для вычисления радиуса вписанной окружности нужно найти квадратный корень из четверти произведения площади на синус острого угла:
Из приведенных формул Вы без проблем найдете радиус вписанной в ромб окружности, если в условиях примера будут необходимый набор данных.
Формула площади ромба
Формул для вычисления площади приведены на рисунке.
Простейшая выводится как сумма площадей двух треугольников на которые разделяет ромб его диагональ.
Вторая формула площади применяется к задачам в которых известны диагонали ромба. Тогда площадь ромба равна половине произведению диагоналей
Она достаточно проста для того чтобы запомнить, а также — для вычислений.
Третья формула площади имеет смысл когда известен угол между сторонами. Согласно ей площадь ромба равна произведению квадрата стороны на синус угла. Острый он или нет значения не имеет поскольку синус обоих углов принимает одинаковое значение.
Периметр ромба
Периметр ромба равен сумме всех его сторон. Учитывая то что они все равны периметр принимает значение
P=4a.
И в завершение запомните что периметр измеряется в единицах длины, а площадь в квадратных единицах. Теперь Вы знаете как найти площадь и периметр ромба, поэтому пользуйтесь приведенным формулам при решении задач.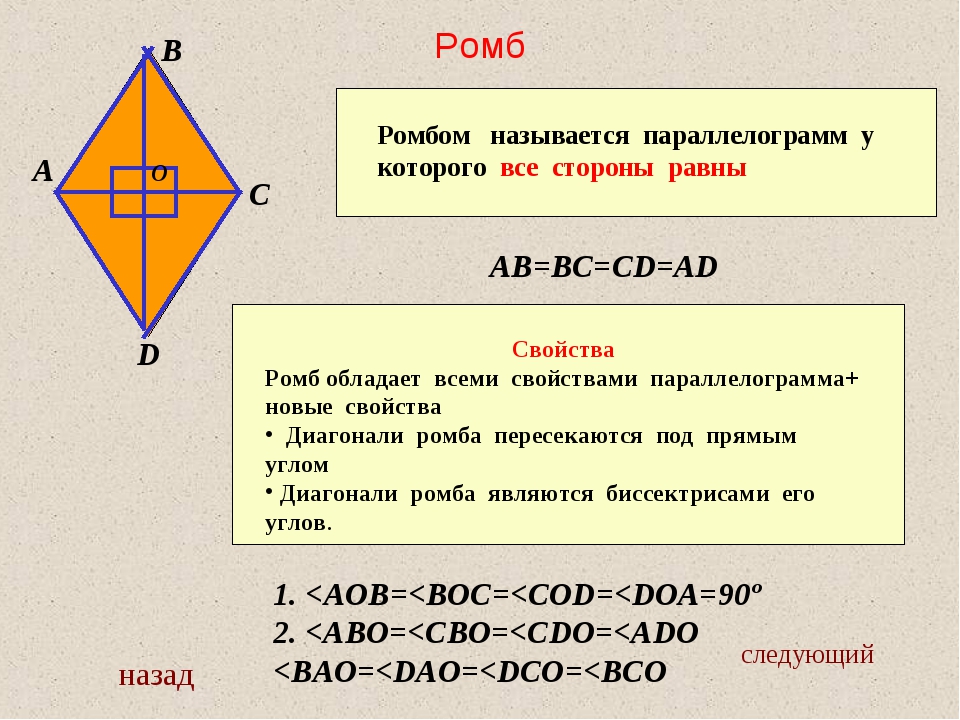
Посмотреть материалы:
Радиус вписанной окружности в ромб
Ромб – это параллелограмм, у которого все стороны равны. Следовательно, он наследует все свойства параллелограмма. А именно:
- Диагонали ромба взаимно перпендикулярны.
- Диагонали ромба являются биссектрисами его внутренних углов.
Окружность можно вписать в четырехугольник тогда и только тогда, когда суммы противоположных сторон равны.
Следовательно, в любой ромб можно вписать окружность. Центр вписанной окружности совпадает с центром пересечения диагоналей ромба.
Радиус вписанной окружности в ромб можно выразить несколькими способами
1 способ. Радиуса вписанной окружности в ромб через высоту
Высота ромба равна диаметру вписанной окружности. Это следует из свойства прямоугольника, который образуют диаметр вписанной окружности и высота ромба – у прямоугольника противолежащие стороны равны.
Следовательно формула радиуса вписанной окружности в ромб через высоту:
2 способ.

Радиус вписанной окружности в ромб через диагонали
Площадь ромба можно выразить через радиус вписанной окружности
, где Р– периметр ромба. Зная, что периметр это сумма всех сторон четырехугольника имеем P=4×а. Тогда
Но площадь ромба также равна половине произведения его диагоналей
Прировняв правые части формул площади, имеем следующее равенство
В результате получаем формулу, позволяющую вычислить радиус вписанной окружности в ромб чрез диагонали
Пример расчета радиуса окружности вписанной в ромб, если известны диагонали
Найти радиус окружности вписанной в ромб, если известно, что длина диагоналей 30 см и 40 см
Пусть ABCD-ромб, тогда AC и BD его диагонали. AC=30 см, BD=40 см
Пусть точка О – это центр вписанной в ромб ABCD окружности, тогда она будет также являться и точкой пересечения его диагоналей, делящих их пополам.
т.к диагонали ромба пересекаются под прямым углом, то треугольник AOB прямоугольный.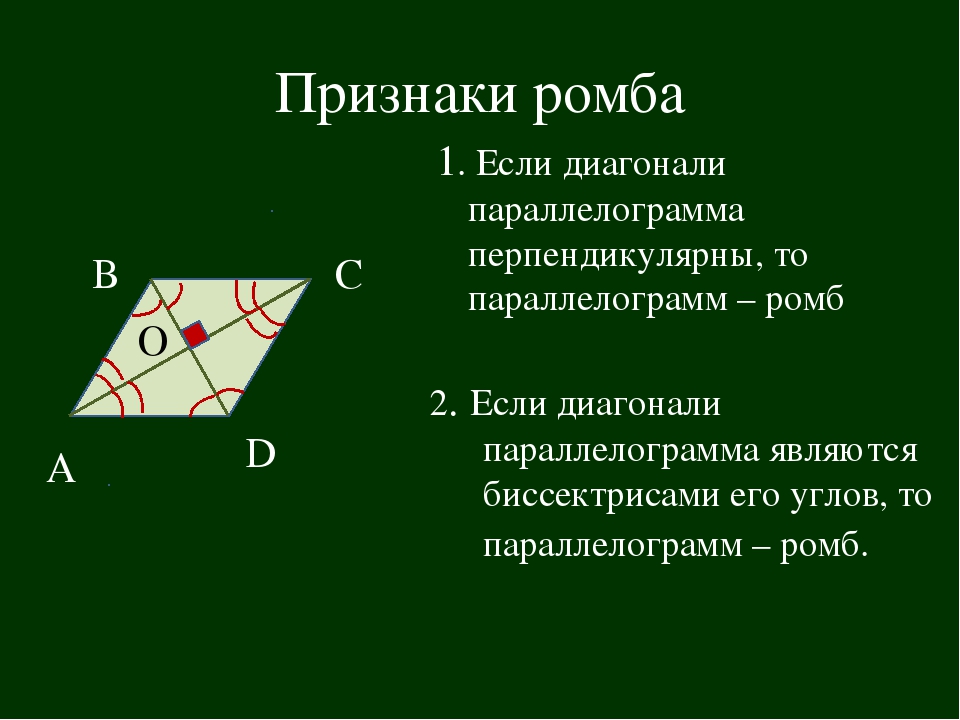 Тогда по теореме Пифагора
Тогда по теореме Пифагора
, подставляем в формулу ранее полученные значения
AB = 25 см
Применив ранее выведенную формулу для радиуса описанной окружности в ромб, получаем
3 способ. Радиус вписанной окружности в ромб через отрезки m и n
Точка F – точка касания окружности со стороной ромба, которая делит ее на отрезки AF и BF. Пусть AF=m, BF=n.
Точка O – центр пересечения диагоналей ромба и центр вписанной в него окружности.
Треугольник AOB – прямоугольный, так как диагонали ромба пересекаются под прямым углом.
, т.к. является радиусом, проведенным в точку касания окружности . Следовательно OF – высота треугольника AOB к гипотенузе. Тогда AF и BF – проекции катетов на гипотенузу.
Высота в прямоугольном треугольнике, опущенная на гипотенузу есть среднее пропорциональное между проекциями катетов на гипотенузу.
Формула радиуса вписанной окружности в ромб через отрезки равна корню квадратному из произведения этих отрезков, на которые делит сторону ромба точка касания окружности
Пример расчета радиуса окружности вписанной в ромб, если известны отрезки m и n
Найдите радиус описанной окружности в ромб, если точка касания делит сторону ромба на 9 и 4
Пусть ABCD-ромб, тогда AC и BD его диагонали..jpg)
Пусть точка O – это центр вписанной в ромб ABCD окружности.
Пусть точка F – точка касания окружности со стороной ромбаAB. Тогда. AF=9, BF=4
Применив ранее полученную формулу, получаем
Все Признаки и Свойства Ромба
Обновлено
Ромб — это параллелограмм, у которого
все стороны одинаковы.
С помощью свойств и признаков ромба можно определить является фигура
ромбом, или нет. Так, как ромб отчасти является параллелограммом,
то для него истинны все свойства параллелограмма.
Квадратом является ромб, у которого все углы прямые.
Все свойства ромба
- Ромб имеет две диагонали.
- Все стороны ромба одинаковы.
- Сумма всех углов ромба равна 360 градусам.
- В ромбе диагонали перпендикулярны
- биссектрисами углов ромба являются диагонали.

- Сумма всех квадратов диагоналей равна квадрату одной из
сторон ромба умноженной на четыре. - Центром симметрии у ромба является точка, где пересекаются
все диагонали. - Вне зависимости от длины сторон и градусных мер углов ромба,
в него можно вписать окружность. - Точка пересечения диагоналей ромба, также является центром
вписанной окружности. - Для ромба истинны все свойства параллелограмма.
Все признаки ромба
- Параллелограмм является ромбом, если в нем биссектрисы
углов являются диагоналями . - Параллелограмм является ромбом, если у него все диагонали
пересекаются только под углом в 90 градусов. - Параллелограмм является ромбом, если у него
все стороны одинаковы. - Параллелограмм является ромбом, если в него
может быть вписана окружность. - Параллелограмм является ромбом, если у него
все высоты одинаковы. - Четырехугольник является ромбом, если в нем диагонали
перпендикулярны и в точке их пересечения делятся пополам.
- Четырехугольник является ромбом, если для него истинны все
свойства параллелограмма и диагонали перпендикулярны,
и они же являются биссектрисами.
Ромб. Стороны ромба через его диагонали. Стороны ромба через площадь и высота. Сторона ромба через радиус вписанной окружности.
Ромб-это равносторонний четырехугольник то есть у него есть четыре стороны, которые равны по длине, но углы могут быть не равны. Противоположные стороны ромба перпендикулярны биссектрисам ромба, и разрезают друг друга ровно пополам под прямым углом. Ромб является частным случаем параллелограмма в том, что все четыре стороны равны по длине, а не только противоположные стороны. Квадрат-это частный случай ромба, в котором все углы равны \(90°\). 2}}2\)
- Формула стороны ромба через периметр:
\(a=\frac{P}{4}\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Как найти высоту ромба — Наука
Наука 2021
Параллелограмм — это плоская форма с противоположными сторонами, которые параллельны и равны по длине. Ромб — это параллелограмм с четырьмя равными (конгруэнтными) сторонами, например, ромб. Квадраты
Ромб — это параллелограмм с четырьмя равными (конгруэнтными) сторонами, например, ромб. Квадраты
Содержание:
Параллелограмм — это плоская форма с противоположными сторонами, которые параллельны и равны по длине. Ромб — это параллелограмм с четырьмя равными (конгруэнтными) сторонами, например, ромб. Квадраты и прямоугольники также являются типами параллелограммов. Вы можете определить высоту ромба, если знаете другие значения, такие как площадь, основание или диагонали.
TL; DR (слишком долго; не читал)
Чтобы найти высоту ромба, используйте формулу высота = площадь ÷ базы. Если вы знаете диагонали ромба, но не его площадь, используйте формулу area = (d1 x d2) ÷ 2, затем примените площадь к первой формуле.
Свойства ромба
Независимо от размера ромба, всегда применяются определенные правила. Все его стороны равны, его противоположные углы равны, а две его диагонали перпендикулярны (это означает, что они делят пополам друг друга под углом 90 градусов).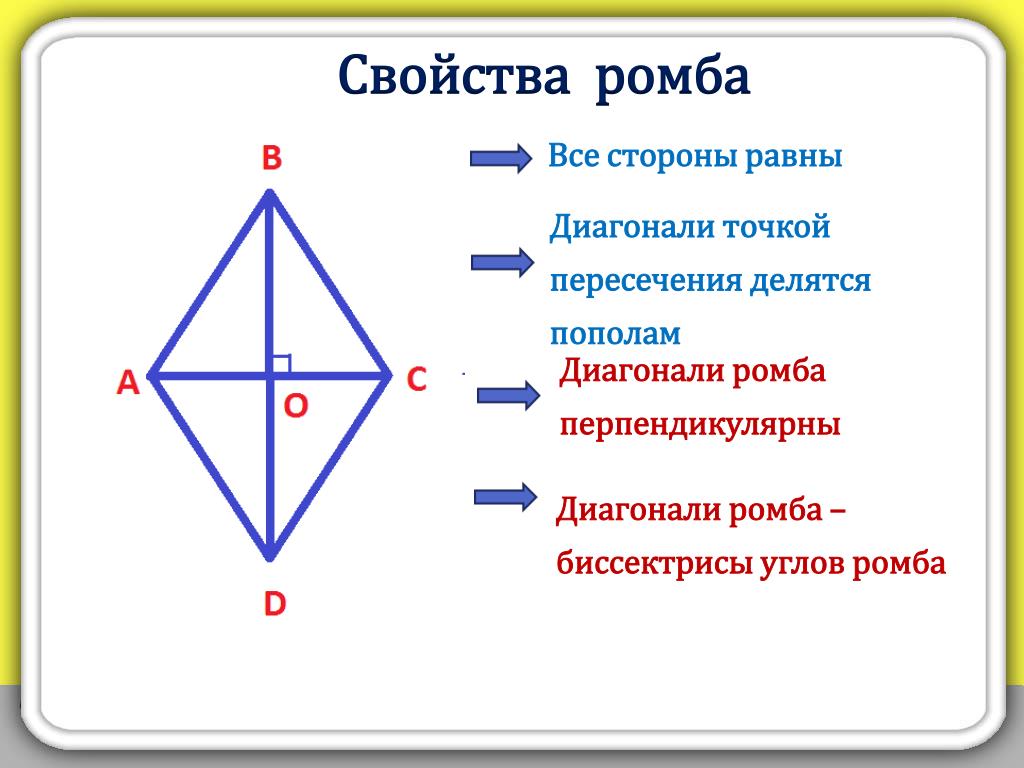 Высота ромба (также называемая его высотой) является кратчайшим перпендикулярным расстоянием от его основания до его противоположной стороны. Основание ромба может быть любым из четырех его сторон, в зависимости от того, как оно расположено.
Высота ромба (также называемая его высотой) является кратчайшим перпендикулярным расстоянием от его основания до его противоположной стороны. Основание ромба может быть любым из четырех его сторон, в зависимости от того, как оно расположено.
Нахождение высоты от области и базы
Формула для высоты ромба есть высота = площадь ÷ базы. Например, если вы знаете, что площадь ромба составляет 64 см2, а основание составляет 8 см, вы получите 64 ÷ 8 = 8. Высота ромба составляет 8 см. Помните, что основание — это одна из сторон, и они равны по длине, поэтому, если вы знаете длину одной из сторон, вы знаете длину их всех.
Та же формула применяется независимо от размера ромба или единиц измерения. Например, скажем, у вас есть ромб с площадью 1000 дюймов и основанием 20 дюймов. Отработать 1000 ÷ 20 = 50. Высота ромба составляет 50 дюймов.
Нахождение высоты от диагоналей
Если вам известны диагонали и основание ромба, но нет области, используйте формулу area = (d1 x d2) ÷ 2.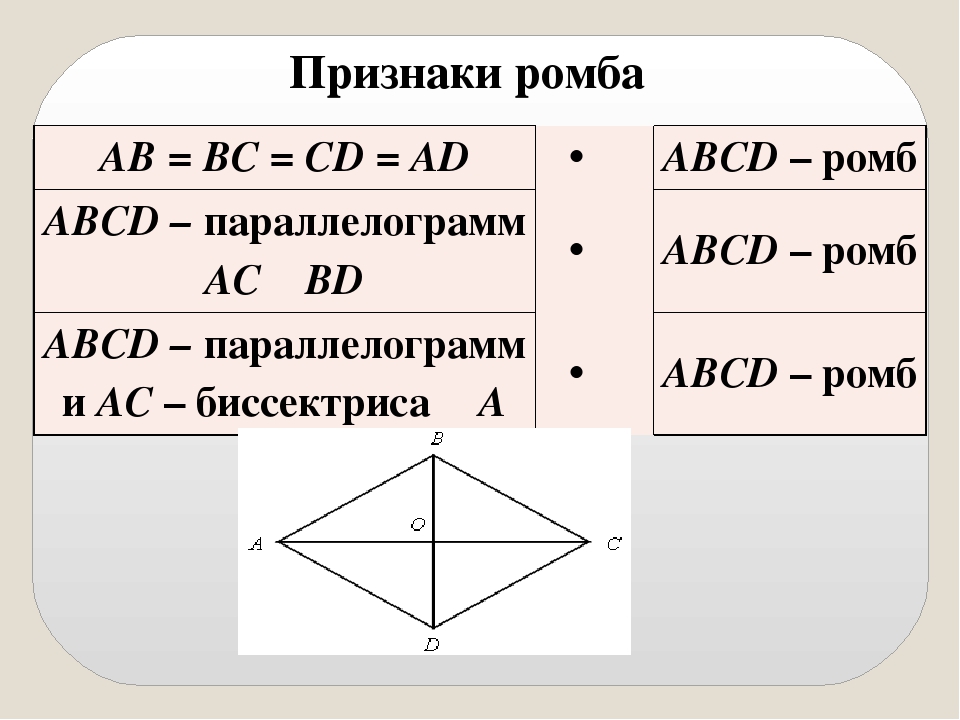 Например, если вы знаете, что d1 составляет 4 см, а d2 составляет 6 см, вы работаете (4 x 6) ÷ 2 = 12. Знаете, площадь 12 см2. Если основание составляет 2 см, отработайте 12 ÷ 2 = 6. Высота ромба составляет 6 см.
Например, если вы знаете, что d1 составляет 4 см, а d2 составляет 6 см, вы работаете (4 x 6) ÷ 2 = 12. Знаете, площадь 12 см2. Если основание составляет 2 см, отработайте 12 ÷ 2 = 6. Высота ромба составляет 6 см.
Rhombus — определение математического слова
Rhombus — определение математического слова — Math Open Reference
Попробуйте это Перетащите оранжевые точки на каждую вершину
изменить форму ромба. Обратите внимание, что четыре стороны остаются одинаковой длины, а противоположные стороны остаются параллельными.
На самом деле ромб — это просто особый тип параллелограмма.
Напомним, что в параллелограмме все пары противоположных сторон равны по длине.
У ромба все четыре стороны имеют одинаковую длину.Следовательно, он обладает всеми свойствами параллелограмма.
См. Определение параллелограмма
Это немного похоже на квадрат, который может « наклониться »
и внутренние углы должны быть , а не 90 °.
Иногда называется ромбовидной или ромбовидной формой.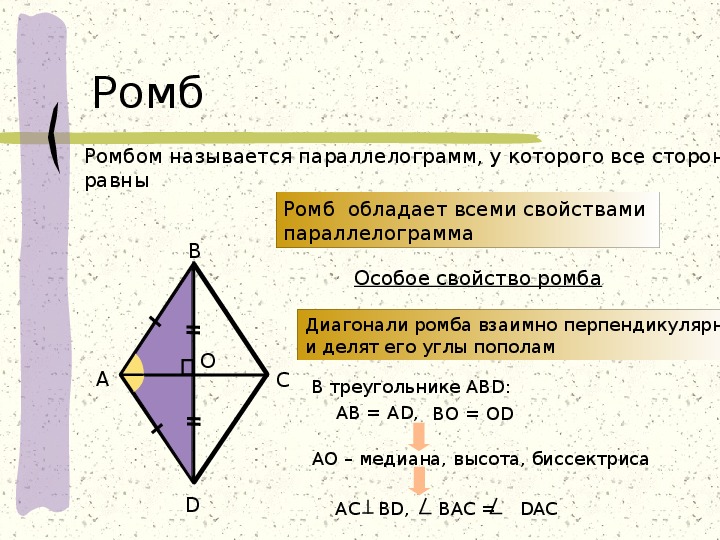
Свойства ромба
| База | Базой можно считать любую сторону. Выбирайте любой понравившийся. Если используется для расчета площади (см. Ниже), необходимо использовать соответствующую высоту. На рисунке выше была выбрана одна из четырех возможных баз. |
| Высота | Высота ромба — это расстояние по перпендикуляру. от основания на противоположную сторону (которую, возможно, придется удлинить). На рисунке выше показана высота, соответствующая базовому CD. |
| Площадь | Есть несколько способов найти площадь ромба. Самый распространенный — (база × высота). Каждый описан в Области ромба |
| Периметр | Расстояние вокруг ромба.Сумма длин сторон. См. Периметр ромба |
| Диагонали | Каждая из двух диагоналей — это серединный перпендикуляр другого. См. Диагонали ромба |
Другие полигоны
Общие
Типы многоугольника
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные полигоны
(C) Открытый справочник по математике, 2011 г.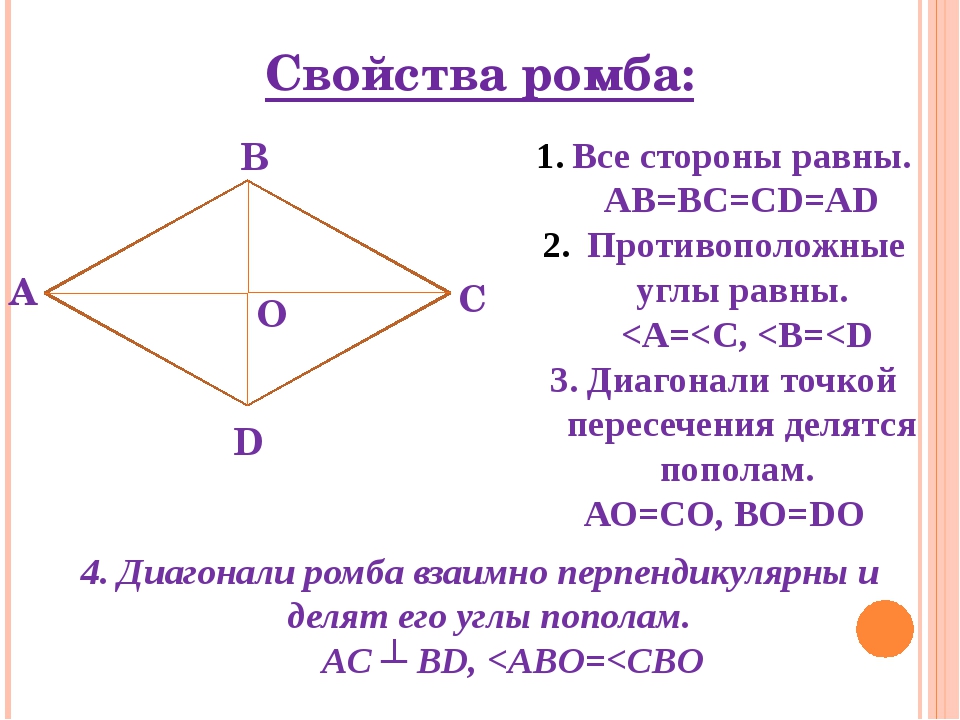
Все права защищены.
Как найти площадь ромба (формула и видео) // Tutors.
com
Содержание
- Что такое ромб?
- Площадь Формулы ромба
- Как найти площадь ромба
Ромб — плоская фигура, поэтому она двумерна. Это замкнутая фигура с прямыми (линейными) сторонами, один из множества четырехугольников (четырехугольников). Это частный случай параллелограмма.Все четыре стороны имеют одинаковую длину, и обе пары противоположных сторон параллельны. Противоположные углы тоже равны. Это оно!
Ромб можно также назвать ромбом, ромбом или ромбом. Квадрат — это ромб с четырьмя равными (прямыми) углами.
Иногда вы видите ромб с двумя горизонтальными сторонами, как если бы квадрат врезался автобусом и перевернулся (это удобная мнемоника, чтобы запомнить его название: беги, автобус; ромб). На этой презентации можно очень легко увидеть высоту (высоту) ромба.
Иногда ромб рисуется так, чтобы одна из двух его диагоналей (линий, соединяющих противоположные вершины) была горизонтальной, что делает форму ромба более очевидной.
Необычным качеством ромба является то, что его диагонали всегда перпендикулярны друг другу, независимо от углов четырех вершин ромба.
Эти диагонали также делят друг друга пополам, что означает, что они делят ромб на четыре прямоугольных треугольника. Квадраты длин двух диагоналей всегда в четыре раза больше квадрата стороны.
Ромб такой простой формы имеет множество частей и размеров. Знание того, как использовать эти измерения, может помочь вам найти площадь, периметр и другие сведения о ромбе.
Площадь Формулы ромба
Есть три разные формулы для определения площади ромба. Один использует высоту и сторону, другой — сторону и угол, а третий — диагонали. Три формулы для определения площади зависят от информации, которую вы знаете о ромбе.
- Если вы знаете высоту (высоту) и сторону s, формула будет следующей:
площадь = высота × s - Если вам известна длина одной стороны s и размер одного угла, формула будет следующей:
площадь = s2 sin∠A = s2 sin∠B - Если вам известны длины диагоналей, формула будет следующей:
площадь = (d1 × d2) 2
Как найти площадь ромба
Построим ромб со сторонами s и четырьмя вершинами с внутренними углами A, B, C и D.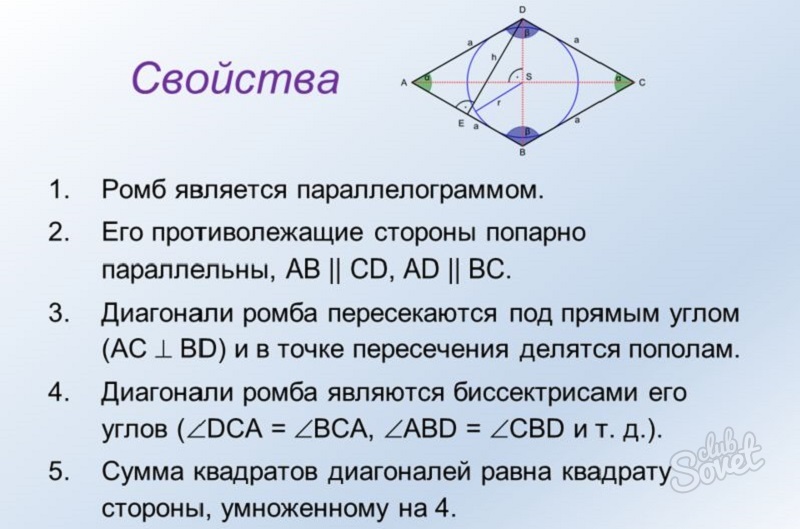 Мы можем соединить противоположные углы диагоналями d1 и d2. Соединение одной стороны с другой перпендикулярной линией дает высоту или высоту. В нашем ромбе:
Мы можем соединить противоположные углы диагоналями d1 и d2. Соединение одной стороны с другой перпендикулярной линией дает высоту или высоту. В нашем ромбе:
- Четыре стороны одинаковой длины: AB, BC, CD и DA
- Четыре внутренних угла с равными противоположными углами: ∠a = ∠c и ∠b = ∠d
- Две диагонали: d1 и d2; только в квадрате это будут диагонали одинаковой длины
- Высота или высота — Когда ромб сидит с двумя сторонами горизонтально (плоско), высота h — это расстояние от одной стороны до противоположной стороны; отрезок прямой, перпендикулярный одной стороне, соединяющийся с противоположной стороной
Поскольку четыре стороны равны, если вы знаете длину любой стороны s, вы знаете длину всех четырех сторон.
Поскольку противоположные углы равны, а четыре угла складываются в 360 °, если вы знаете один угол, вы можете найти все углы. Поскольку противоположные стороны параллельны, смежные углы в ромбе складываются в 180 °.
Для определения площади необходимо знать высоту или высоту h ромба.
Помните, что высота не равна длине стороны.
Формула
с использованием высоты и боковой поверхности
Если у вас есть мысленное представление о ромбе как о наклонном квадрате, этот первый метод будет иметь большой смысл.
Если бы ромб был квадратом, его площадь в квадратных единицах была бы сторона x сторона, верно? Что ж, когда ромб наклонен, вы можете представить, как отрезать треугольную часть на одной стороне ромба и сдвинуть ее к соответствующей другой стороне, восстанавливая форму до ее прямоугольности.
На самом деле вы не можете разрезать каждый встреченный ромб, поэтому подумайте, что это за построенная перпендикулярная сторона на самом деле: высота или высота ромба.
Итак, первый и, возможно, самый простой способ определить площадь ромба — это определить длину одной стороны и высоту ромба.Умножьте их, и вы получите площадь в квадратных единицах:
.
площадь = высота × сторона
Пример:
Итак, если у вас есть ромб высотой 3 дюйма со сторонами 5 дюймов, то площадь этого ромба составляет:
3 дюйма × 5 дюймов = 15 дюймов2
Другой пример: сторона s составляет 15 футов, а высота — 11 футов. Площадь этого ромба:
Площадь этого ромба:
15 × 11 = 165 квадратных футов
Формула с использованием стороны и угла
Второй способ найти площадь ромба — это знать длину стороны s и величину одного угла (∠A или ∠B).Здесь вам нужно найти синус угла, но формула все еще проста:
площадь = s2 sin∠A
площадь = s2 sin∠B
Как видите, эти две формулы дают одинаковый результат, поэтому
площадь = s2 sin∠A = s2 sin∠B
Пример:
В ромбе со стороной 10 ярдов и внутренними прилегающими углами 60 ° и 120 °, чтобы найти площадь этого ромба, мы должны включить это в нашу формулу для площади, используя сторону и угол.
площадь = 102 sin60 °
, что также совпадает с
площадь = 102 sin120 °
Затем мы умножаем эти два числа вместе:
площадь = 100 × 0,866
Тогда получаем ответ:
площадь = 86,6 квадратных ярда
Помните, что для этого метода угол, который вы выбираете, не имеет значения. Формула одинакова для обоих углов; вам просто нужно выбрать один.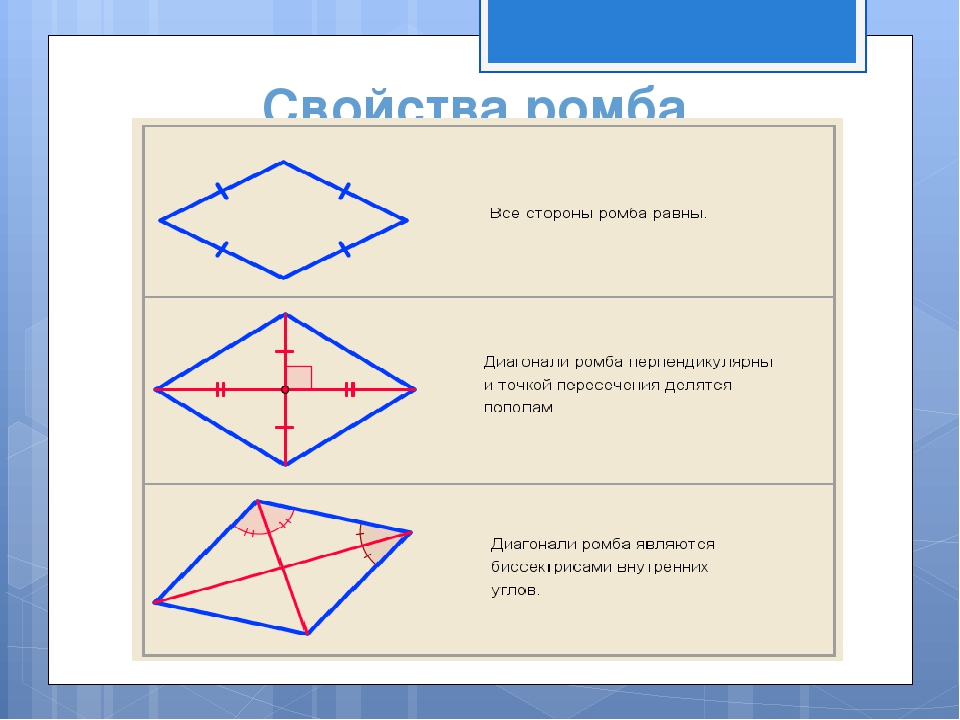
Синус 60 ° и 120 ° одинаков, 0,866
Формула с использованием диагоналей
Помните, что диагонали ромба всегда пересекаются под прямым углом и делят друг друга пополам.Это означает, что две диагонали образуют две стороны квадрата, который в два раза больше ромба.
Вы можете найти площадь ромба в квадратных единицах, умножив длины двух диагоналей (d1 и d2) и разделив на два.
Если у нашего ромба есть только размеры диагоналей, мы бы использовали эту формулу.
Пример:
Если бы наш ромб имел диагонали 24 и 18 метров в длину, то, чтобы найти площадь этого ромба, мы бы подставили числа в нашу формулу.
площадь = (24 × 18) 2
Умножаем две диагонали:
площадь = (432) 2
Тогда получаем ответ:
площадь = 216 квадратных метров
Краткое содержание урока
Вы рассмотрели, что такое ромб, как он вписывается в семейство четырехугольников, каковы его различные части и как найти его площадь.
Следующий урок:
Воздушные змеи в геометрии
5 Свойства ромба для математического класса
Кредит: Pixabay CC0 1.0
В геометрии ромб — это особый вид четырехугольника, в котором все 4 стороны имеют одинаковую длину. Ромб обладает некоторыми уникальными свойствами, которые являются следствием его определения. Некоторые ключевые свойства ромба включают:
- Противоположный угол конгруэнтен
- Соседние углы являются дополнительными
- Диагонали делят пополам противоположные углы
- Диагонали делят пополам друг друга
- Диагонали перпендикулярны друг другу
Определение ромба
9 В простейшем случае ромб определяется как любой простой (непересекающийся) четырехугольник с 4 сторонами равной длины.Согласно этому определению, квадрат также является ромбом, в котором все углы прямые. Другие названия ромба включают «равносторонний четырехугольник» и «ромб», хотя последний термин обычно используется для обозначения особого ромба, который имеет углы 2 45 ° и 2 135 °.
Можно доказать, что ромб — это частный случай параллелограмма, у которого все 4 стороны равны по длине. Это означает, что все ромбы являются параллелограммами, хотя обратное не обязательно, поскольку есть параллелограммы, которые не являются ромбами.Каждый ромб — это воздушный змей — четырехугольник с совпадающими смежными сторонами.
Слово «ромб» происходит от древнегреческого слова, означающего «вращать». Евклид использовал термин «ромб», чтобы описать эту двумерную форму, которая возникает из поперечного сечения двух круглых конусов, которые примыкают к основанию.
Существенные свойства ромба
1. Противоположные углы конгруэнтны
Первое ключевое свойство ромба — это отношение между парами противоположных углов.Пара противоположных углов в ромбе конгруэнтны, что означает, что они равны. Мы можем доказать это следующим:
Кредит: Автор
| Заявление | Причина | |||||||
| 1 | Ромб ABCD | 1 | Дано | 2 | Провести линию AC | 2 | 2 точки составляют линию | |
| 3 | AB || DC & BC || DA | 3 | По умолчанию. ромба ромба | |||||
| 4 | ∠ACD ≅ ∠BAC & ∠DAC ≅ ∠ACB | 4 | Альтернативные внутренние углы | |||||
| 5 | AB = BC = CD = DA | 5 | По умолчанию. ромба | |||||
| 6 | ΔACD = ΔABC | 6 | SAS | |||||
| 7 | ∠D ≅ ∠B | 7 | CPCTC.Q.E.D |
Это свойство ромба также показывает, что он является параллелограммом, поскольку существенным свойством параллелограмма является то, что его противоположные углы совпадают. То есть, если четырехугольник имеет равные противоположные углы, этого достаточно, чтобы гарантировать, что это параллелограмм.
(Примечание: «Q.E.D» в конце каждого доказательства является сокращением латинской фразы «quod erat manifestradum», что примерно переводится как «таким образом, это было продемонстрировано»).
2.Смежные углы являются дополнительными
Смежные углы ромба являются дополнительными, то есть в сумме они составляют 180 °. Мы можем доказать, что смежные углы в ромбе являются дополнительными:
Кредит: Автор
| Заявление | Причина | ||
| 1 | Ромб ABCD | Дано | |
| 2 | AB || DC & DA || BC | 2 | По умолчанию.ромба |
| 3 | AC | 3 | Две точки образуют линию |
| 4 | ∠A supp ∠B, ∠B supp C, ∠C supp ∠D , ∠D supp ∠A | 4 | Оно два || линии обрезаются пер., внутренние углы на той же стороне пер. являются дополнительными. Q.E.D |
Итак, мы можем доказать, что смежные углы в ромбе являются дополнительными.
3.Диагонали, разделенные пополам, противоположные углы
Третье важное свойство ромба связано с его диагоналями. Диагональ многоугольника — это любая линия, проведенная между двумя несмежными вершинами. У параллелограмма 4 точки, то есть всего 2 диагонали. Характерным свойством диагоналей ромба является то, что они делят пополам угол, из которого они начерчены. Мы можем доказать это следующим образом:
| Заявление | Причина | ||
| 1 | Rhombus ABCD | 1 | Дано |
| AB = BC = CD = DA | 2 | Отрезок ромба | |
| 3 | AC & BD | 3 | Две точки составляют линию |
| 4 | AC = AC | 4 | Отражающее свойство |
| 5 | ΔABC = ΔADC | 5 | SSS |
6 0 | AC 9 = BAC2 = BAC2 DAC = ∠ACD | 6 | Базовые s isos. треугольники совпадают треугольники совпадают |
| 7 | ∠DAC = ∠BAC ∠DCA = ∠BCA | 7 | CPCTC |
| 8 | AC ADC bisects D | 8 | Биссектриса угла делит угол на две равные части. Q.E.D |
Итак, мы только что доказали, что диагонали ромба делят пополам противоположные углы.Это уникальное свойство ромбов, которого нет у других четырехугольников.
4. Диагонали делят пополам
Четвертое главное свойство ромба также связано с его диагоналями. Это факт, что диагонали ромба пересекают друг друга пополам; то есть каждый из них разрезает друг друга на два равных отрезка. Точка их пересечения — середина обеих диагоналей.
| Заявление | Причина | ||
| 1 | Ромб ABCD | 1 | Дано |
| 2 DA | 2 | По умолчанию. ромба ромба | |
| 3 | AB || CD и DA || CB | 3 | По умолчанию. ромба |
| 4 | ∠AEB = ∠DEC | 4 | Пары вертикальных углов |
| 5 | ∠BAC = ∠ACD | 16 5 902ate внутренние углы | |
| 6 | ΔAEB ≅ ΔDEC | 6 | Теорема SAA |
| 7 | AE = EC DE = EB | ||
| 8 | AC и DB делят друг друга пополам | 8 | Две линии делят друг друга пополам, если точка, в которой они пересекаются, является средней точкой обеих линий.Q.E.D |
5. Диагонали перпендикулярны друг другу
Последней определяющей чертой ромба, которую мы докажем, является тот факт, что диагональные линии перпендикулярны друг другу.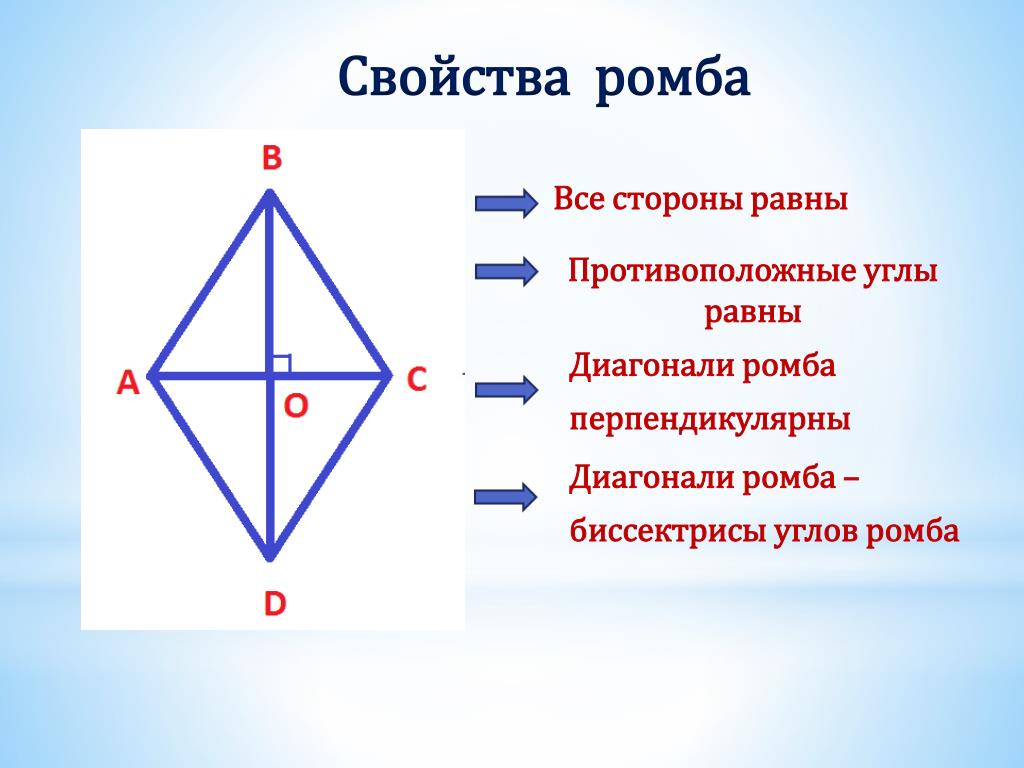 В ромбе две диагонали всегда пересекаются под прямым углом 90 °. Мы можем доказать это следующим образом:
В ромбе две диагонали всегда пересекаются под прямым углом 90 °. Мы можем доказать это следующим образом:
| Заявление | Причина | ||||||||||||||||||||||||||||||||||||||||||||||
| 1 | Ромб ABCD | 1
Другие свойства ромбаПлощадь Площадь ромба можно вычислить точно так же, как и любой другой четырехугольник, умножьте основание на высота. A = b x h Высота ромба — это мера линии, проведенной перпендикулярно от одной стороны к противоположной. Причина, по которой формула площади для ромба такая же, как для прямоугольника, проста; каждый ромб (и параллелограмм) можно разрезать на части и преобразовать в прямоугольник с тем же основанием и высотой (на следующем рисунке показан не ромбовидный параллелограмм, но тот же принцип справедлив и для ромбов). Кредит: WikiCommons CC0 1.0 Если вы проведете линию, перпендикулярную от одного основания к концу другого основания, вы получите трапецию и прямоугольный треугольник, которые можно преобразовать в прямоугольник с той же площадью, что и исходный ромб. Вы также можете вычислить площадь ромба, если вам известна только длина его диагоналей. Площадь ромба равна половине произведения его диагоналей. Итак, для ромба с диагоналями p и q математическая формула: A = pq / 2 Помните, что мы ранее доказали две вещи о диагоналях ромба: они делят друг друга пополам и перпендикулярны друг другу. Мы знаем, что AE = EC и DE = EB. Мы также знаем, что диагонали делят пополам пары противоположных углов.Итак, мы получаем два больших равнобедренных треугольника справа и слева, каждый из которых разделен на два меньших правых треугольника. Площадь всего ромба равна удвоенной площади одного из равнобедренных треугольников. Начиная с правого ΔABC, мы знаем, что его общая площадь составляет Площадь ΔABC = ½ (AC) (EB) Однако мы также знаем, что EB составляет половину DB (потому что линия делится пополам в точке E), поэтому мы можем заменить: Площадь ΔABC = ½ (AC) (½DB) , что упрощается до Площадь ΔABC = ¼ (AC) (DB) Поскольку мы знаем, что вся площадь ромба в два раза больше площади ΔABC , мы можем переписать Площадь ABCD = 2 × Площадь ΔABC = ½ (AC) (BD) Следовательно, площадь ромба можно вычислить как половину произведения его диагональных линий. Свойства тесселяции Ромб также может образовывать мозаику, то есть вы можете расположить ромб в виде правильных узоров, чтобы полностью заполнить двумерное лицо. Одно из трех возможных периодических ромбовидных мозаик. Предоставлено: Public Domain . Вы также можете сформировать мозаику ромбов из правильной мозаики шестиугольников.Просто разделите каждый шестиугольник на три, проведя линии из каждой другой вершины, которые встречаются в центре шестиугольника. Из шестиугольной плитки можно сформировать ромбовидную плитку. Предоставлено: WikiCommons CC BY-SA 3.0 Ромби можно расположить в виде мозаики, поскольку их можно расположить таким образом, чтобы сумма углов, окружающих каждую точку, составляла ровно 360 градусов. Это необходимое свойство фигур, которые можно мозаизировать; если вы не можете расположить фигуру таким образом, чтобы сумма всех углов, которые встречаются в вершине, составляла 360, вы не можете сделать из нее обычную мозаику. Итак, ромб — это название четырехугольника, в котором все 4 стороны имеют одинаковую длину. Все ромбы — это параллелограммы, а квадрат — это особый случай ромба, в котором все 4 внутренних угла являются прямыми углами. Ключевые свойства ромба: его противоположные углы совпадают, его смежные углы являются дополнительными, его диагонали делят пополам противоположные углы, его диагонали делят пополам друг друга, а его диагонали перпендикулярны друг другу. Была ли эта статья полезной? 😊 ☹️ Приятно слышать! Хотите больше научных тенденций? Подпишитесь на нашу рассылку новостей науки! Нам очень жаль это слышать! Мы любим отзывы 🙂 и хотим, чтобы вы внесли свой вклад в то, как сделать Science Trends еще лучше. Площадь ромба — формула, определение, решаемые примеры Площадь ромба определяется как объем пространства, заключенного или охваченного ромбом в двухмерной плоскости. Ромб — это особый тип параллелограмма, у которого все стороны равны друг другу. Что такое площадь ромба?Площадь ромба можно определить как объем пространства, заключенного ромбом в двухмерном пространстве. Он отображает общее количество единичных квадратов, которые могут уместиться в нем, и измеряется в квадратных единицах (например, в см 2 , в метрах 2 , в 2 и т. Д.). Ромб — это параллелограмм, у которого противоположные стороны параллельны, противоположные углы равны, а соседние углы дополняют друг друга. Следующие свойства используются для определения ромба.
Площадь Формулы ромбаДля вычисления площади ромба можно использовать разные формулы в зависимости от известных нам параметров.Для расчета площади ромба используются различные формулы:
Формула площади ромба, когда известны основание и высота Ромб — параллелограмм. Мы знаем, что площадь параллелограмма определяется умножением основания и высоты на квадратные единицы. То же самое и с ромбом. Пример: Найдите площадь ромба, длина стороны которого составляет 7 дюймов, а высота ромба — 10 дюймов. Формула площади ромба при известных диагоналях Площадь ромба равна половине произведения длин диагоналей. . Площадь = (\ (d_1 \) × \ (d_2 \)) / 2 кв. Единицы, где \ (d_1 \) и \ (d_2 \) — диагонали ромба. Рассмотрим ромб ABCD. Пусть E — точка пересечения двух диагоналей. Сделаем следующие наблюдения:
Площадь ромба ABCD = Площадь ∆ ADC + Площадь ∆ ABC Площадь ромба = 2 × Площадь ∆ ABC — (1) (∵ ∆ ABC, конгруэнтная ∆ ADC) Площадь ∆ ABC = 1/2 × Основание × Высота Площадь ромба ABCD Площадь = 2 × 1/4 × AC × BD = 1/2 × AC × BD (Из (1) и (2)) ∴ Площадь ромба = 1/2 × диагональ 1 × диагональ 2 шт. Формула площади ромба при известных сторонах и углахМы применяем концепцию тригонометрии при вычислении площади, когда известны стороны и углы.Мы можем использовать любой угол, потому что либо углы равны, либо они являются дополнительными, а дополнительные углы имеют одинаковый синус. Площадь ромба с учетом стороны и угла задается как . Площадь ромба = сторона 2 × sin (A) квадратных единиц, где A — внутренний угол. Пример: Какова площадь ромба, если длина его стороны составляет 4 ярда, а угол A равен 30º. Как рассчитать площадь ромбаРазличные методы вычисления площади ромба описаны ниже.Есть три метода вычисления площади ромба, которая задается как:
Площадь ромба по основанию и высоте
Полученное значение даст площадь ромба. Площадь ромба по диагоналям Рассмотрим ромб ABCD, имеющий две диагонали, то есть AC и BD.
Полученное значение даст площадь ромба ABCD. Площадь ромба по тригонометрии
Полученное значение даст площадь ромба. Пример: Рассмотрим ромб ABCD. AB, BC, CD, DA — равные (равные) стороны. AC и BD — диагонали, и они встречаются в E. Теперь мы знаем диагональ 1, AC = 16 футов. Далее нам нужно рассчитать BD. У нас все еще есть неизвестный, BE. BC 2 = BE 2 + EC 2 ∴ BE = 15 футов и BD = 30 футов Пора подставить все значения в области формулы ромба. Площадь ромба = 1/2 × \ (d_1 \) × \ (d_2 \) кв. Единиц Советы и хитрости:
Часто задаваемые вопросы о Area of RhombusЧто такое площадь ромба?Площадь ромба — это общий объем пространства, заключенного или охваченного ромбом в двухмерной плоскости. Он выражается в квадратных единицах (например, в см 2 , в метрах 2 , в 2 и т. Д.). Какова формула определения площади ромба? Для вычисления площади ромба можно использовать разные формулы в зависимости от известных нам параметров. Используя базу и высоту, формула задается следующим образом: Площадь ромба = основание × квадратные единицы высоты. Площадь ромба с использованием диагоналей равна: Площадь = (\ (d_1 \) × \ (d_2 \)) / 2 кв. Единицы, где \ (d_1 \) и \ (d_2 \) — диагонали ромба. Применяя концепцию тригонометрии с использованием стороны и угла, мы можем следовать формуле: Площадь ромба = сторона 2 × sin (A) квадратных единиц, где ‘a’ — это внутренний угол. Как найти сторону ромба с диагоналями?Площадь ромба можно рассчитать, используя длину диагоналей.Формула для определения площади в этом случае задается следующим образом: Площадь = (\ (d_1 \) × \ (d_2 \)) / 2 кв. Единицы, где \ (d_1 \) и \ (d_2 \) — диагонали ромб. Равны ли площади ромба и квадрата?Нет, площади ромба и квадрата не равны. Однако их площадь можно рассчитать таким же образом, учитывая их размеры. Площадь ромба или любого параллелограмма = основание × высота. У ромба сторона и высота не совпадают. Однако площадь квадрата = сторона × сторона, причем сторона также может быть высотой квадрата.Квадрат — это ромб, потому что у него четыре стороны, и каждая сторона имеет одинаковую длину. Однако квадрат далее определяется как форма, имеющая четыре равных угла по 90 градусов. Следовательно, квадрат — это ромб. Однако ромб — это не обязательно квадрат. Так что их области не могут быть одинаковыми. Как найти площадь ромба, если заданы сторона и высота? Площадь ромба может быть вычислена, если задана длина основания или стороны и высота. Какова высота ромба на данной территории?Чтобы вычислить высоту или высоту по заданной площади, нам нужна длина основания. Формула, которую можно применить для расчета высоты, выражается в единицах площади / базовых единиц. Площадь ромба: формула, вывод, определение, площадьПлощадь ромба: Ромб представляет собой четырехугольник с формой, напоминающей ромб.Это четырехугольник, у которого есть два набора параллельных сторон, равные противоположные стороны и равные противоположные углы. Его также называют равносторонним четырехугольником, потому что все его четыре стороны равны. Ромб встречается в нескольких вещах вокруг нас, таких как воздушный змей, окна автомобиля, ромбовидные серьги, конструкции зданий, бриллианты, зеркала и даже часть бейсбольного поля. Площадь ромба: содержание
Что такое ромб? Слово Rhombus происходит от греческого слова «ромбос», которое означает кусок дерева, вращающийся на веревке для создания ревущего шума, и это слово в конечном итоге произошло от греческого глагола «rhembo», означающего вращаться и вращаться. Ромб — параллелограмм равных возможностей. Нет стороны больше или меньше другой. Все стороны равны, а противоположные стороны параллельны. Ромб — это подмножество параллелограмма. Разница между квадратом и ромбом в том, что все углы квадрата прямые, но углы ромба не обязательно должны быть прямыми углами. Итак, ромб с прямыми углами становится квадратом. Следовательно, каждый квадрат — это ромб, но не все ромбы — это квадрат. Свойства ромба1.\ circ. \) Что такое площадь ромба?Площадь ромба можно интерпретировать как количество пространства, заключенного ромбом в пространстве \ (2D \). Площадь ромба можно рассчитать тремя разными способами.
Площадь Формулы ромбаПлощадь ромба в разных случаях имеет разные формулы, и наиболее часто используемые даны ниже:
Где, Площадь ромба с диагоналямиПоловина произведения диагоналей дает нам площадь ромба. Итак, площадь ромба \ (ABCD = 4 \) умножена на площадь \ (\ Delta AOB \) Площадь ромба со стороной (если известны его основание и высота) Если заданы длина основания (стороны) и высота ромба, площадь ромба со стороной легко найти. Площадь ромба с использованием концепции тригонометрииВ некоторых случаях, когда высота неизвестна, но известны основание и один из углов, площадь может быть вычислена путем умножения квадрата основания на синус этого угла.2} \ times \ sin \ left (a \ right) \) Площадь ромба в векторной формеКонцепция вектора также используется для вычисления площади ромба. Поскольку все ромбы являются параллелограммами, площадь ромба в векторной форме равна Решенных примеров — Площадь ромба Вопрос 1: Оцените площадь ромба, если его основание \ (8 \, {\ rm {cm}} \), а высота \ ({\ rm {5}} \, { \ rm {см}} {\ rm {. СводкаРомб — это четырехугольник, все стороны которого равны, а противоположные стороны параллельны. Ромб — это подмножество параллелограмма, и в частном случае он может быть квадратным.Свойства ромба и формула площади ромба широко используются для решения реальных задач. Каждая формула выводится из основных геометрических понятий. Часто задаваемые вопросы (FAQ) Q.1. Какова формула для определения площади ромба ? Q .2. Какова формула периметра и площади ромба? Q.7. Равны ли диагонали ромба? Q. Q.9. Как найти площадь ромба, если заданы основание и высота? Теперь, когда вам предоставлена вся информация о площади ромба, мы надеемся, что эта подробная статья будет вам полезна. Следите за Embibe, чтобы получать больше обновлений по математике и другим предметам. Также у нас есть статьи о конкурсных экзаменах. Проверь их! 71 Просмотры Скачать PDF-файлы формул факторизации на официальном сайте Embibe Формулы факторизации : Факторизация, также известная как факторинг, представляет собой процесс разбиения большого числа на несколько небольших. Факторизация — один из важных методов, который используется для разбивки алгебраического или квадратного уравнения в простую форму. Таким образом, чтобы разобрать сложное уравнение, нужно знать формулы факторизации. В этой статье мы предоставим вам всю необходимую информацию о важных формулах факторизации для многочленов, тригнометрии, алгебры и квадратных уравнений.В конце статьи студенты также могут скачать PDF-файл с формулами факторизации. ПРОЙДИТЕ БЕСПЛАТНЫЙ ИСПЫТАНИЕ НА ФАКТОРИЗАЦИЮ ЗДЕСЬ Формулы факторизации: значение факторизации Когда алгебраическое уравнение или квадратное уравнение сводится к более простому уравнению с помощью метода факторизации, более простое уравнение рассматривается как произведение факторов. Произведение факторов уравнения может быть целым числом, переменной или выражением. Основной подход метода факторизации заключается в том, что мы не будем расширять скобки дальше. Также, чек: Формулы факторизации для алгебраических и квадратных уравненийЧисла можно разложить на различные комбинации, и применить методы факторизации к числам очень просто. Найти факторы уравнения немного сложно. Числа 1, 3, 5 и 15 равны , делящимся на 15, , так как оно может делиться на само число 15.
Тот же метод факторизации применяется также для многочленов, алгебраических и квадратных уравнений. Важные формулы факторизации полиномов, алгебры и квадратного уравнения приведены ниже. Формулы факторизации для алгебры и квадратных уравнений(a + b) 2 = a 2 + 2ab + b 2 (a — b) 2 = a 2 — 2ab + b 2 (a + b) 3 = a 3 + b 3 + 3ab (a + b) (а — б) 3 = а 3 — б 3 — 3ab (а — б) (a + b) 4 = a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4 (a — b) 4 = a 4 — 4a 3 b + 6a 2 b 2 — 4ab 3 + b 4 (a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2ac + 2bc (a + b + c +…) 2 = a 2 + b 2 + c 2 +… + 2 (ab + ac + bc +…) Формулы факторизации для определенных чисел и многочленова 2 — б 2 = (а + б) (а — б) a 2 + b 2 = 1/2 [(a + b) 2 + (a — b) 2 ] a 3 — b 3 = (a — b) (a 2 + ab + b 2 ) a 3 + b 3 = (a + b) (a 2 — ab + b 2 ) a 4 — b 4 = (a — b) (a + b) (a 2 — ab + b 2 ) a 5 — b 5 = (a — b) (a 4 + a 3 b + a 2 b 2 + ab 3 + b 4 ) За исключением первых двух формул из приведенного выше списка, все остальные также относятся к разделу «Формулы факторизации кубических многочленов». Формулы факторизации для nth степениa n b n = (a — b) (b 0 a n-1 + b 1 a n-2 + …… + b n-2 a 1 + b n-1 a 0 ) a n + b n = (a — b) (b 0 a n-1 — b 1 a n-2 + …… b n-2 a 1 + b n-1 a 0 ) Формулы факторизации для уравнений тригнометрииФакторизация или тригонометрия по факторной формуле приведена ниже
Основная факторизация Факторизация — это процесс нахождения множителей данного числа, будь то простое или составное число. НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ УЗНАТЬ О PRIME FACTORISATION Решенные вопросы по факторизацииНесколько решенных примеров с использованием факторизации приведены ниже:
С помощью решенных выше примеров вы получите представление о том, как разложить на множители Квадратные уравнения. СКАЧАТЬ ФАКТОРИЗАЦИЮ NCERT SOLUTIONS PDF ЗДЕСЬ Часто задаваемые вопросы о формулах факторизацииЧасто задаваемые вопросы о формулах факторизации приведены ниже: В. A. Факторизация — это обратное умножению. Сложные алгебраические, полиномиальные или квадратные уравнения разбиваются на более простые уравнения. Более простое уравнение при обратном умножении дает фактическое уравнение.Этот процесс известен как факторизация. Q. Определение факторизации состояния. A. Факторизация может быть определена как разделение объекта на факторы, которые при умножении дают исходный объект. В. Каков первый метод решения квадратного уравнения? A. Первый метод решения квадратного уравнения — это факторинг. После факторинга нам нужно будет применить квадратичную формулу и заполнить квадрат. Q.Как вы находите HCF? A. Наивысший общий множитель в сокращении HCF находится путем умножения всех множителей этого конкретного числа. Теперь вам предоставлена вся необходимая информация о формулах факторизации. СКАЧАТЬ ФОРМУЛЫ ФАКТОРИЗАЦИИ PDF ЗДЕСЬ Мы надеемся, что эта подробная статья о формулах факторизации вам поможет. Если у вас есть какие-либо вопросы относительно этой статьи о формулах факторинга, напишите нам через поле для комментариев ниже, и мы свяжемся с вами как можно скорее. 920 Просмотры Таблица логарифмов с примерами и вопросамиТаблица журналов: В математике логарифм — это операция, обратная возведению в степень. Это означает, что логарифм числа — это показатель степени, до которого должно быть увеличено другое фиксированное значение, основание, чтобы получить это число.В простых случаях логарифм учитывает повторное умножение. Чтобы найти значение логарифмической функции, вы должны использовать таблицу журнала . Многие студенты затрудняются пользоваться таблицей логарифмов . Журнальная таблица: понятие и определениеПрежде чем мы предоставим вам таблицу логарифмов, из которой вы получите все значения, давайте разберемся с концепцией логарифмической функции.Логарифмические функции — это обратные экспоненты. Функция журнала определяется следующим образом:
Здесь f (x) — функция логарифма по основанию ‘b’. Наиболее распространенными основаниями, используемыми в функциях журнала, являются основание e и основание 10. Десятичный логарифм [f (x) = log 10 x] : Логарифм с основанием 10 (то есть b = 10) называется десятичным логарифмом и имеет множество применений в науке и технике. Натуральный логарифм [f (x) = log e x] : Основанием натурального логарифма является число e ( ≈ 2,718 ). Его использование широко распространено в математике и физике из-за его более простой производной. Двоичный логарифм [f (x) = log 2 x] : двоичный логарифм использует основание 2 (то есть b = 2) и обычно используется в компьютерных науках. Что такое характеристика и мантисса в логарифмической функции? Целая часть десятичного логарифма называется характеристикой , а дробная часть — мантиссой . Примечание: Мантисса логарифма числа всегда остается положительной. Таким образом, журнал любого номера N будет иметь вид:
важные статьи |
:
База журналов 10: полная таблица журналов
Здесь мы предоставили таблицу значений журнала для базы 10.
Как использовать таблицу журнала?: Пошаговый процесс с примером
Чтобы найти значение числа в журнале с помощью таблицы журнала, вы должны понимать процесс чтения таблицы журнала. Мы предоставили пошаговый процесс поиска значений на примере:
- Шаг 1: Найдите таблицу. Для разных баз используется разная таблица журналов. Приведенная выше таблица предназначена для базы 10. Таким образом, вы можете найти логарифмическое значение числа только с основанием 10.Чтобы найти натуральные или двоичные логарифмы, вам придется использовать другую таблицу.
- Шаг 2: Найдите целую и десятичную часть данного числа. Предположим, мы хотим найти логарифмическое значение n = 18,25. Итак, прежде всего, мы разделяем целое и десятичное число.
Целочисленная часть: 18
Десятичная часть: 25 - Шаг 3: Зайдите в таблицу общего журнала и найдите значение ячейки на следующих пересечениях:
Строка с первыми двумя цифрами n
Заголовок столбца с третьей цифрой of n
⇒ В этом примере log10 (18. 25) → строка 18, столбец 2 → значение ячейки 2601. Таким образом, получено значение 2601.
25) → строка 18, столбец 2 → значение ячейки 2601. Таким образом, получено значение 2601.
- Шаг 4: Всегда используйте таблицу десятичного логарифма со средней разностью. Теперь снова перейдите к строке 18 и столбцу 5 (четвертая цифра n) в таблице средних значений.
⇒ В этом примере журнал 10 (18,25) → строка 18, столбец средней разницы 5 → значение ячейки 12. Запишите соответствующее значение, равное 12.
- Шаг 5: Добавьте оба значения, полученные в шаг 3 и шаг 4.
То есть 2601 + 12 = 2613. - Шаг 6: Найдите характеристическую часть. Методом проб и ошибок найдите целое число p , такое, что p p + 1 > n. Здесь a — база, p — характерная часть. Для обычных журналов (с основанием 10) просто подсчитайте количество цифр слева от десятичной дроби и вычтите единицу.
Итак, Характеристическая часть = (количество цифр слева от десятичной дроби — 1).
В этом примере характеристика = 2 — 1
= 1 - Шаг 7: Объедините как характеристику, так и часть мантиссы, и вы получите окончательное значение, равное 1.
 2613.
2613.
Итак, лог 10 (18,25) = 1,2613
Свойства логарифмов
Здесь мы представили все важные законы и свойства, связанные с логарифмами.
Теорема 1 : Логарифм произведения двух чисел, скажем a и b, равен сумме логарифма двух чисел. База должна быть одинаковой для обоих чисел.
Эта теорема также известна как «правило произведения для логарифмов ».
Теорема 2 : Деление двух чисел является антилогарифмом разности логарифмов двух чисел.
Другими словами, логарифм деления двух чисел, скажем, a и b, равен разности логарифма двух чисел. База должна быть одинаковой для обоих чисел.
Эта теорема также называется «правилом частного для логарифмов ».
Теорема 3 : Логарифм числа по любому другому основанию может быть определен логарифмом того же числа по любому заданному основанию.
Теорема 4 : Логарифм числа, возведенного в степень, равен индексу степени, умноженному на логарифм числа. База у обоих одинакова.
База у обоих одинакова.
Эта теорема также известна как «правило мощности для логарифмов ».
Итак, это 4 логарифмических свойства. Вы сможете переписать логарифмическое выражение, используя правило мощности, правило продукта или правило частного для логарифмов.
Таблица десятичного логарифма
от 1 до 10
Получите таблицу общего журнала с 1 по 10 из приведенной ниже таблицы:
| Десятичный логарифм числа ( log 10 x) | Значения журнала |
| Log 1 | 0 |
| Log 2 | 0.3010 |
| Лог 3 | 0,4771 |
| Лог 4 | 0.6020 |
| Лог 5 | 0,6989 |
| Лог 6 | 0,7781 |
| Лог 7 | 0,8450 |
| Лог 8 | 0,9030 |
| Лог 9 | 0,9542 |
| Лог 10 | 1 |
Таблица натурального логарифма от 1 до 10
Здесь мы предоставили таблицу натуральных логарифмических значений от 1 до 10:
| Натуральный логарифм к числу (log e x) | Значения журнала |
| ln (1) | 0 |
| ln (2) | 0.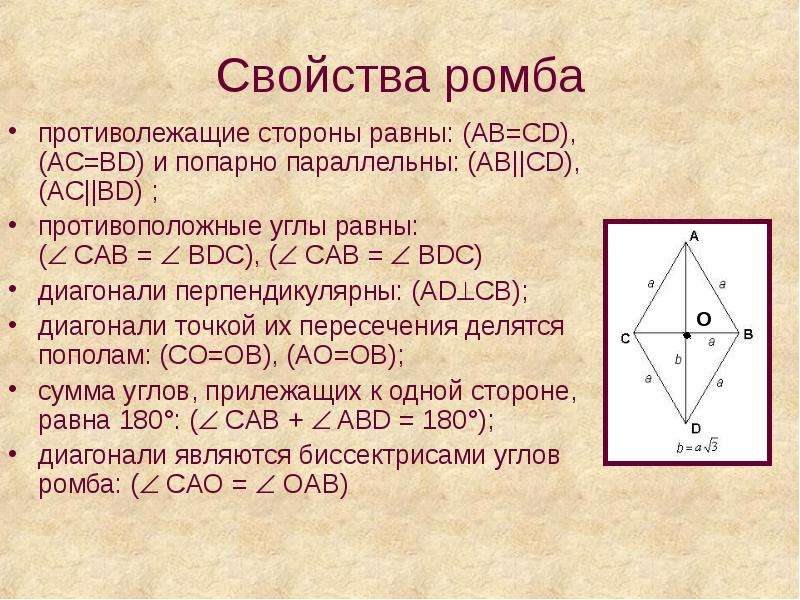 693147 693147 |
| лн (3) | 1.098612 |
| лн (4) | 1,386294 |
| лн (5) | 1.609438 |
| лн (6) | 1.7 |
| (7) | 1.94591 |
| ln (8) | 2.079442 |
| ln (9) | 2.197225 |
| ln (10) | 2.302585 |
Получить формулы Algebra Класс с 8 по 11 ниже:
Решенные примеры в таблице логарифмических формул
Здесь мы предоставили несколько примеров вопросов и ответов в таблицах журналов с 1 по 100:
| Вопрос 1. Найдите значение журнала 10 8.675 |
| Решение: Значение можно получить, выполнив следующие шаги: Шаг 1: Целое число = 8 и Десятичное число = 675 Шаг 2: Проверьте номер строки 86 (первый две цифры заданного числа) и столбец номер 7 (третья цифра заданного числа).  Таким образом, получено значение 9380. Таким образом, получено значение 9380. Шаг 3: Проверьте значение средней разницы для строки номер 86 и столбца средней разности 5. Значение, соответствующее строке и столбцу, равно 3. Шаг 4: Складываем значения, полученные на шагах 2 и 3, получаем 9383. Это часть мантиссы. Шаг 5: Поскольку количество цифр слева от десятичной части равно 1. Таким образом, характеристическая часть = (Количество цифр слева от десятичной части — 1) = 0 Шаг 6: Объединить характеристика и часть мантиссы. Таким образом, оно становится равным 0,9383. Следовательно, значение log 10 8,675 равно 0.9383. |
| Вопрос 2: Найдите значение журнала (45,67) с помощью таблицы журнала. |
| Решение: 45,67 = 4,567 × 10 1 Итак, log (45,67) = log (4,567 x 10) = log (4,567) + log (10) [Использование логарифма свойство: log (ab) = log a + log b] = log (4.  567) + 1 [∵ log (10) = 1, для общего журнала] 567) + 1 [∵ log (10) = 1, для общего журнала] Теперь давайте найдем значение log (4.567). Посмотрите на стандартную таблицу журнала.Перейдите к строке номер 45 (первые две цифры числа n) и столбцу номер 6 (третья цифра числа n). Запишите соответствующее значение, которое составляет 0,6590. Теперь снова перейдите к строке 45 и столбцу 7 (четвертая цифра n) в таблице средних значений. Запишите соответствующее значение, равное 7. Теперь сложите два значения. Получаем: 0,6590 + 7 = 0,6597 Это часть мантиссы. Поскольку мы используем общую таблицу журнала, характеристика = (Количество цифр слева от десятичной дроби — 1) = (1 — 1) = 0 ∴ Характеристика = 0 Теперь объедините обе части, мы получим журнал (4.567) = 0,6597 log (45,67) = log (4,567) + 1 = 0,6597 + 1 1,6597 Следовательно, значение log (45,67) равно 1,6597 |
| Вопрос 3: Использование таблица журнала для оценки следующей логарифмической функции: |
| Решение: Мы можем решить значение N за 4 шага: Шаг 1 : Преобразуйте выражение для N в простые журналы.  Шаг 2 : Оцените эти журналы с помощью таблицы журналов. Шаг 3 : Определите значение журнала N. Шаг 4 : Вычислите значение N, используя антилогарифмический журнал N. Итак, logN = log (647⋅32 × 0,00000147 / 8,473 × 64) = log (647⋅32) + log (0,00000147) — log (8,473) — log (64) [Используя правило произведения для логарифмов] Используя таблицу журнала, мы находим следующие значения: 647,32 = 6,4732 × 10 2 ⇒ log (647,32) = 2 + log (6,4732) = 2 + 0,8111 = 2,8111 0,00000147 = 1,47 × 10 -6 ⇒ log (0.00000147) = −6 + log (1,47) = -6 + 0,1673 8,473 = 8,473 × 10 0 ⇒ log (8,473) = 0,9280 64 = 6,4 × 10 1 ⇒ log (64) = 1 + log (6,4) = 1,8062 ∴ logN = 2,8111 + (-6 + 0,1673) — 0,9280 — 1,8062 = –5,7558 = –5 — 0,7558 = (–5 — 1) + 1 — 0,7558 [∵ мантисса не может быть отрицательным, мы добавили и вычли 1, чтобы сделать его положительным] = –6 + 0,2442 Теперь у нас есть характеристика = -6 и мантисса = 0,2442.  Чтобы найти значение N, мы используем формулу: N = antilog (Мантисса) × 10 Характеристика = antilog (0.2442) x 10 -6 = 1,7547 x 10 -6 [Использование таблицы антилогарифма] ⇒ N = 1,7547 × 10 -6 = 0,0000017547 Следовательно, значение N равно 0,0000017547. Вы можете проверить значение с помощью калькулятора. |
Практические вопросы по стандартной таблице логарифмов
Здесь мы предоставили некоторые практические вопросы в таблице математического журнала, чтобы вы могли практиковаться:
| Q1: Найдите значения логарифма следующих чисел по основанию 10, используя таблицу журналов: (i) 7.653 (ii) 14,25 (iii) 9,281 Q2: Если 3 + log 10 x = 2 log 10 y, найдите x через y. Q3: Докажите, что 7 log (10/9) + 3 log (81/80) = 2log (25/24) + log 2. Q4: Если log 10 2 = 0,30103, log 10 3 = 0,47712 и log 10 7 = 0,84510, найдите значения : Q5: Если log 9 = b и log 5 = c, оцените log 75 с точки зрения b и c. |
Часто задаваемые вопросы по Log Table Math
Здесь мы предоставили некоторые из часто задаваемых вопросов, связанных с таблицами онлайн-журнала, которые мы предоставили в этой статье.
| Q1: Как вы читаете таблицу журнала? A: Возьмите первые 2 цифры числа независимо от десятичной дроби и найдите строку с этим числом. Затем найдите номер столбца, соответствующий третьей цифре числа.Вам также может потребоваться изучить таблицу средних разностей, чтобы получить окончательное значение. 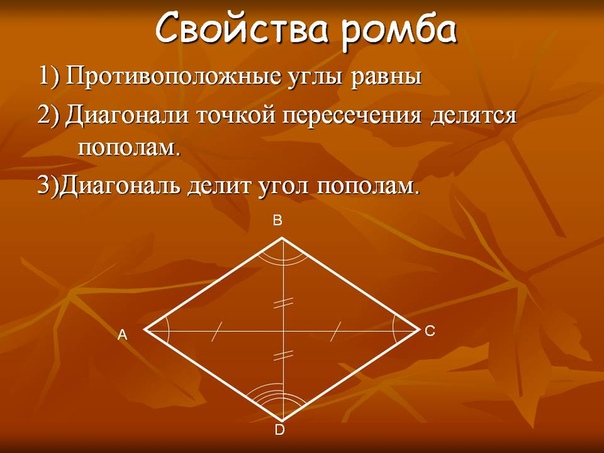 Пошаговый процесс чтения таблицы журнала представлен на этой странице. Пошаговый процесс чтения таблицы журнала представлен на этой странице. |
| Q2: Каково значение log от 1 до 10? A: Логарифм 1 по основанию 10 равен 0. |
| Q3: Какое значение e в натуральном логарифме? A: e — иррациональное и трансцендентное число, примерно равное 2.7182. |
| Q4: Как вы рассчитываете журналы? A: Степень, до которой необходимо возвести основание 10 для получения числа, называется десятичным логарифмом (логарифмом) числа. Для вычисления значений журнала мы используем математическую таблицу логарифмов. |
Прямоугольник. Ромб. Квадрат 8 класс онлайн-подготовка на Ростелеком Лицей
Прямоугольник. Ромб. Квадрат.
Прямоугольник – это четырехугольник, у которого все углы прямые.
Прямоугольник является параллелограммом, поэтому для него выполняются все свойства параллелограмма.
Особенное свойство прямоугольника: его диагонали равны ( AC = BD ). Это следует из равенства прямоугольных треугольников ACD и DBA.
Признаки:
- Если у параллелограмма все углы равны, то это прямоугольник.
- Если в параллелограмме хотя бы один угол прямой, то это прямоугольник.
- Если в параллелограмме диагонали равны, то это прямоугольник.
Ромб – это четырехугольник, у которого все стороны равны.
Ромб – это частный случай параллелограмма, поэтому он обладает всеми свойствами параллелограмма.
Особенное свойство ромба: диагонали ромба перпендикулярны и делят углы ромба пополам (являются биссектрисами углов). Это следует из равенства треугольников ABO = CBO = ADO = CDO.
Признаки:
- Если в параллелограмме диагональ является биссектрисой, то это ромб.
- Если в параллелограмме диагонали перпендикулярны, то это ромб.
Квадрат – это прямоугольник, у которого все стороны равны.
Квадрат является параллелограммом, прямоугольником и ромбом, а значит, обладает всеми их свойствами.
Признаки:
- Если диагонали прямоугольника пересекаются под прямым углом, то это квадрат.
- Если в ромбе все углы равны, то это квадрат.
- Если в ромбе диагонали равны, то это квадрат.
Урок 6. прямоугольник. ромб. квадрат — Геометрия — 8 класс
Понятие прямоугольника всем знакомо с начальной школы. Прямоугольник – это параллелограмм, у которого все углы прямые. Прямоугольник обладает всеми свойствами параллелограмма:
— противоположные стороны равны и параллельны;
— противоположные углы равны, углы, прилежащие к одной стороне составляют в сумме 180°;
— особо можно выделить, что все углы равны;
— диагонали пересекаются и точкой пересечения делятся пополам.
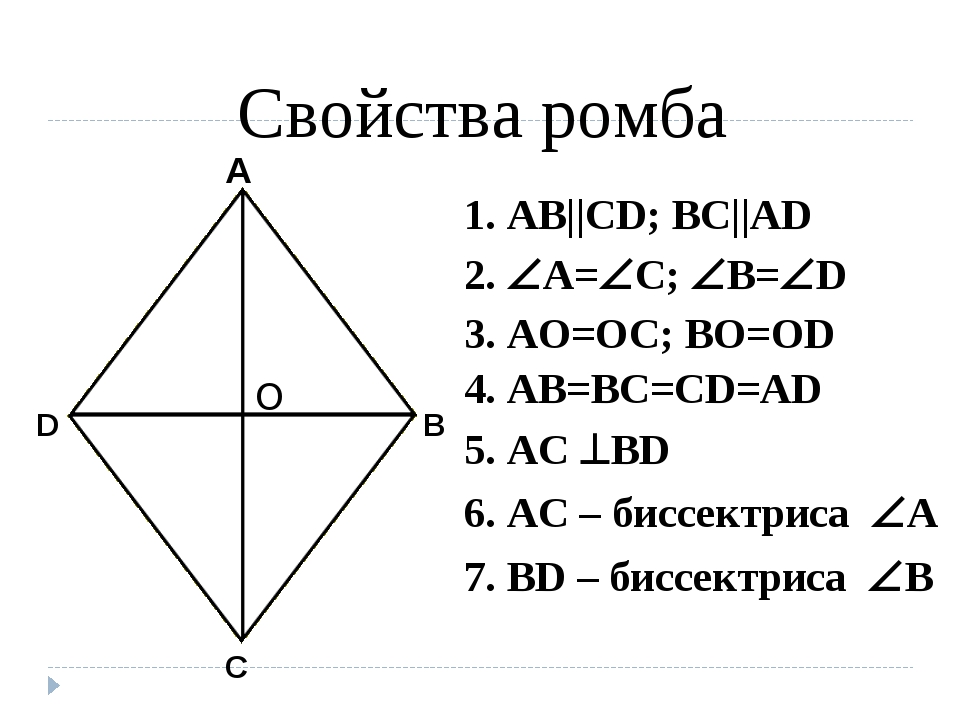
У прямоугольника есть особое свойство: диагонали прямоугольника равны.
| Элементы | Свойства от параллелограмма | Особое свойство |
|---|---|---|
| Стороны | Противоположные стороны равны и параллельны | |
| Углы | Противоположные углы равны, углы, прилежащие к одной стороне составляют в сумме 180° | Все углы равны |
| Диагонали | Диагонали пересекаются и точкой пересечения делятся пополам | Диагонали равны |
Для доказательства рассмотрим прямоугольник ABCD с диагоналями AC и BD.
Прямоугольные треугольники ABD и DCA равны по двум катетам, т.к. AD – общий катет, AB = CD. Следовательно, AC = BD.
Для того, чтобы определить, является ли данный параллелограмм прямоугольником нужен признак прямоугольника. Он вытекает из особого свойства прямоугольника: если в паралеллограмме диагонали равны, то этот паралеллограмм – прямоугольник.
Рассмотрим параллелограмм ABCD с равными диагоналями AC и BD.
ABD и DCA равны по трем сторонам: AC = BD (по условию), AB = CD (свойство параллелограмма). AD – общая сторона. Следовательно, ∠BAD = ∠CDA, но ∠BAD + ∠CDA = 180° и ∠BAD = ∠BCD, ∠CDA = ∠CDA, поэтому ∠BAD = ∠BCD = ∠CDA = ∠CDA = 90° значит, ABCD – прямоугольник.
Параллелограмм, у которого все стороны равны, называется ромбом, он обладает всеми его свойствами, а из определения ромба следует, что все стороны равны.
Ромб обладает и особым свойством: диагонали ромба взаимно перпендикулярны и делят его углы пополам.
| Элементы | Свойства от параллелограмма | Особое свойство |
|---|---|---|
| Стороны | Противоположные стороны равны и параллельны | Все стороны равны |
| Углы | Противоположные углы равны, углы, прилежащие к одной стороне составляют в сумме 180° | |
| Диагонали | Диагонали пересекаются и точкой пересечения делятся пополам | Диагонали взаимно перпендикулярны и делят углы пополам |
Для доказательства особого свойства рассмотрим ромб ABCD с диагоналями AC и BD.

AB = AD (ромб). Треугольник ABD – равнобедренный, AO – медиана, а значит высота и биссектриса этого треугольника. Следовательно, AC ⊥ BD, AC – биссектриса ∠BAD.
Признаки ромба получаются из особого свойства ромба:
— если диагонали параллелограмма взаимно перпендикулярны, то он является ромбом
— если диагональ параллелограмма является биссектрисой его угла, то он является ромбом.
Еще один знакомый с начальной школы четырёхугольник – это квадрат. Квадрат – это прямоугольник с равными сторонами или ромб с прямыми углами.
Ромб и его свойства, определение и примеры с решением
Ромбом называют параллелограмм, у которого все стороны равны (рис. 48).
Так как ромб является параллелограммом, то он имеет все свойства параллелограмма.
1. Сумма любых двух соседних углов ромба равна 180°.
2. У ромба противолежащие углы равны.
3. Диагонали ромба точкой пересечения делятся пополам.
4. Периметр ромба
Кроме того, ромб имеет еще и такое свойство.
5. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Доказательство:
Пусть и — диагонали ромба (рис. 49), — точка их пересечения. Поскольку и то — медиана равнобедренного треугольника проведенная к основанию Поэтому является также высотой и биссектрисой треугольника
Следовательно, и
Аналогично можно доказать, что диагональ АС делит пополам угол а диагональ делит пополам углы и
Пример:
Угол между высотой и диагональю ромба проведенными из одной вершины, равен 28°. Найдите углы ромба.
Решение:
Пусть — диагональ ромба а — его высота (рис. 50), = 28°.
1) В
2) Так как делит угол пополам, то
3) Тогда
Ответ. 124°, 56°, 124°, 56°.
124°, 56°, 124°, 56°.
Рассмотрим признаки ромба.
Теорема (признаки ромба). Если в параллелограмме: 1) две соседние стороны равны, или 2) диагонали пересекаются под прямым углом, или 3) диагональ делит пополам углы параллелограмма, — то параллелограмм является ромбом.
Доказательство:
1) Пусть — параллелограмм (рис. 48). Так как (по условию) и (по свойству параллелограмма), то Следовательно, — ромб.
2) Пусть (рис. 49). Поскольку (по свойству параллелограмма), то (по двум катетам). Следовательно, По п. 1 этой теоремы — ромб.
3) Диагональ делит пополам угол параллелограмма (рис. 49), то есть Так как — секущая, то (как внутренние накрест лежащие). Следовательно, Поэтому по признаку равнобедренного треугольника — равнобедренный и По п. 1 этой теоремы — ромб.
Пример:
Докажите, что если в четырехугольнике все стороны равны, то этот четырехугольник — ромб.
Доказательство:
Пусть (рис. 48).
48).
1) Так как противолежащие стороны четырехугольника попарно равны, то — параллелограмм по признаку параллелограмма.
2) У параллелограмма соседние стороны равны. Поэтому — ромб (по признаку ромба).
А еще раньше…
Слово «ромб» греческого происхождения, которое в древние времена означало вращающееся тело, веретено, волчок. Ромб тогда связывали с сечением веретена, на которое намотаны нити.
В «Началах» Евклида термин «ромб» встречается единожды, а свойства ромба Евклид вообще не рассматривал.
Форма и свойства ромба | Что такое ромб? — Видео и стенограмма урока
Что означает ромб?
Слово ромб происходит непосредственно от латинского ромб . Это, в свою очередь, происходит от греческого rhombos , что означает «вращающееся движение» или «волчка». Кроме того, rhombos происходит от греческого rhembesthai , что означает «крутиться или кружиться».Множественное число слова ромб может быть как ромбом, так и ромбом, а формы, родственные ромбу, можно назвать ромбовидным. Ромбами чаще называют ромбы, а иногда и ромбы. Квадрат — это особый тип ромба, который имеет четыре угла в девяносто градусов.
Кроме того, rhombos происходит от греческого rhembesthai , что означает «крутиться или кружиться».Множественное число слова ромб может быть как ромбом, так и ромбом, а формы, родственные ромбу, можно назвать ромбовидным. Ромбами чаще называют ромбы, а иногда и ромбы. Квадрат — это особый тип ромба, который имеет четыре угла в девяносто градусов.
Свойства ромба
Форма ромба
Ромб является четырехугольником, а это значит, что он имеет:
Кроме того, ромб имеет свои особые свойства.В ромбе:
- все четыре стороны имеют одинаковую длину
- противоположных углов равны
Обратите особое внимание на диагонали ромба, потому что они:
- делят противоположные углы пополам
- встречаются в центре ромба
- перпендикулярны друг другу
Ромб по сравнению с другими четырехугольниками
Все четырехугольники имеют четыре стороны, и это единственное, что их объединяет. После этого они классифицируются по тому, как их стороны и углы соответствуют друг другу. Ромб имеет сходство с большинством других типов четырехугольников.
После этого они классифицируются по тому, как их стороны и углы соответствуют друг другу. Ромб имеет сходство с большинством других типов четырехугольников.
Является ли ромб параллелограммом? да. В ромбе противоположные стороны параллельны друг другу, что делает его параллелограммом.
- Прямоугольник имеет две пары параллельных сторон и четыре равных угла, но не все стороны имеют одинаковую длину. Это параллелограмм.
- Трапеция имеет только две параллельные стороны, и ни одна из сторон или углов не должны быть одинаковыми.
- Воздушный змей имеет две пары сторон одинаковой длины. Стороны одинаковой длины примыкают друг к другу, но ни одна из них не параллельна.
Случай квадрата
В квадрате :
- все четыре стороны имеют одинаковую длину
- противоположные стороны параллельны
- все четыре ангела на девяносто градусов
Квадрат — это особый тип ромба, но также и особый тип прямоугольника.
Измерение ромба
В следующих нескольких разделах мы будем ссылаться на изображение ромба со следующими помеченными частями.Длина одной стороны . Длинная диагональ d1 — это красная линия, а более короткая диагональ d2 — синяя линия.
Периметр ромба
Периметр ( P ) — это расстояние вокруг внешнего края фигуры или сумма длин всех сторон. Поскольку все четыре стороны имеют длину a , периметр равен:
$$P = 4a $$
Площадь ромба
Площадь ( A ) ромба находится с помощью диагоналей.2 $$
Примеры
1. Чему равен периметр ромба со стороной 8?
$$P = 4(8) $$
$$P = 32 $$
2. Какова длина стороны ромба с длинами диагоналей 6 и 8?
Помните, что диагонали делят ромб на прямоугольные треугольники, а они делят друг друга пополам.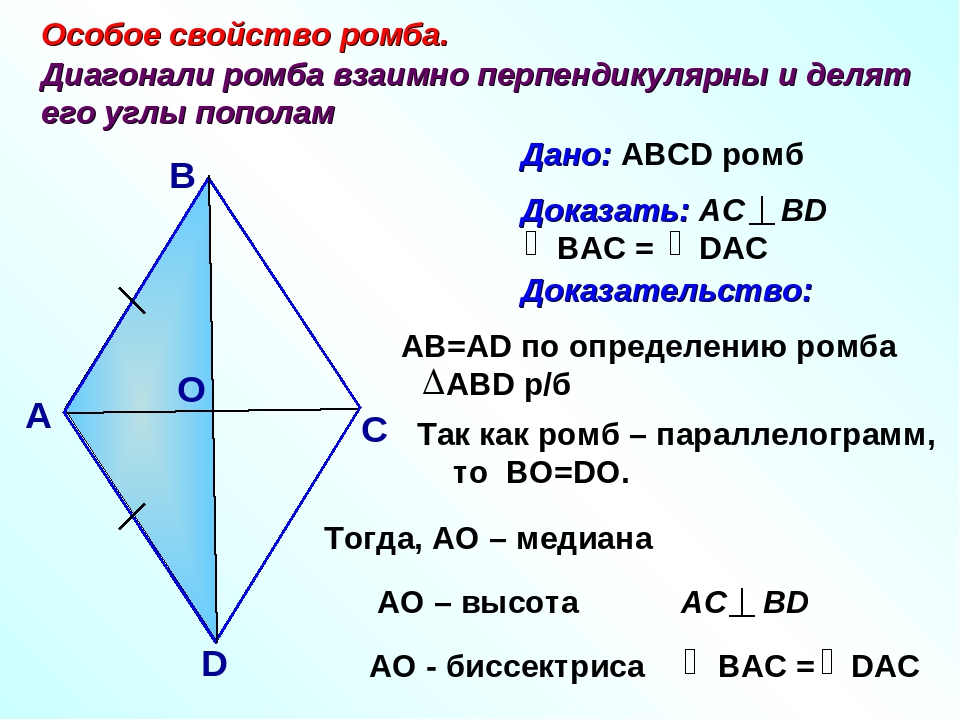 Это дает длину стороны треугольника d1 /2, d2 /2, с гипотенузой a . В этом случае мы можем использовать теорему Пифагора, чтобы найти a .2 = 25 $$
Это дает длину стороны треугольника d1 /2, d2 /2, с гипотенузой a . В этом случае мы можем использовать теорему Пифагора, чтобы найти a .2 = 25 $$
25 это квадрат a , поэтому:
$$a = 5 $$
3. Найдите периметр и площадь ромба.
Сначала найдем периметр. Поскольку одна сторона ромба равна 24, периметр равен:
$$P = 4(24) $$
$$P = 96 $$
Теперь найдем площадь. Однако для этого нам нужна другая диагональ.2 = 252 $$
$$d2 = 31,75 $$
Теперь мы можем найти площадь.
$$A = \frac{(36)(31,75)}{2} $$
$$A = 571,5 $$
Итоги урока
Ромб – это четырехугольник , параллелограмм . Это означает, что у него четыре стороны, и что противоположные стороны будут параллельны друг другу. Кроме того, у ромба все четыре стороны имеют одинаковую длину, а противоположные углы равны.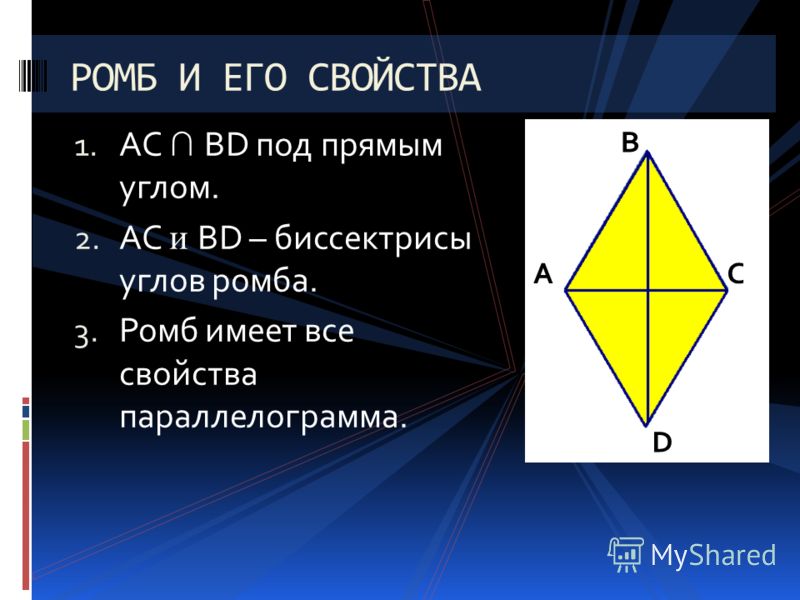
Помните, что диагонали также важны.Диагонали:
- делят пополам противоположные углы
- встречаются в центре ромба
- перпендикулярны друг другу
Ромб регулярно называют ромбом. Квадрат — это особый тип ромба, который имеет четыре угла по девяносто градусов.
Помните, что периметр ромба со стороной a равен:
$$P = 4a $$
Площадь ромба со стороной a и диагоналями d1 и 1 d2 равна:
$$A = \frac{(d1)(d2)}{2} $$
5 Свойства ромба для математического класса
Кредит: Pixabay CC0 1.0Ромб в геометрии — это особый вид четырехугольника, у которого все 4 стороны имеют одинаковую длину. Ромб обладает некоторыми уникальными свойствами, которые являются следствием его определения. Некоторые ключевые свойства ромба включают в себя:
- Противоположный угол Connoguent
- соседние углы Дополнительные
- диагонали бислект противоположные углы
- диагонали бислекта друг друга
- диагонали перпендикулярны друг другу
определение ромба
В самом простом случае ромб определяется как любой простой (непересекающийся) четырехугольник, у которого 4 стороны равны по длине. Согласно этому определению, квадрат также является ромбом, у которого все углы прямые. Другие названия ромба включают «равносторонний четырехугольник» и «ромб», хотя последний термин обычно используется для специального ромба, имеющего 2 угла по 45° и 2 угла по 135°.
Согласно этому определению, квадрат также является ромбом, у которого все углы прямые. Другие названия ромба включают «равносторонний четырехугольник» и «ромб», хотя последний термин обычно используется для специального ромба, имеющего 2 угла по 45° и 2 угла по 135°.
Можно доказать, что ромб является частным случаем параллелограмма, у которого все 4 стороны имеют одинаковую длину. Это означает, что все ромбы являются параллелограммами, хотя обратное не обязательно верно, поскольку существуют параллелограммы, не являющиеся ромбами.Каждый ромб — это воздушный змей — четырехугольник с конгруэнтными смежными сторонами.
Слово «ромб» происходит от древнегреческого слова, означающего «прясть». Евклид использовал термин «ромб» для описания двумерной формы, возникающей в результате взятия поперечного сечения двух круглых конусов, примыкающих к основанию.
Существенные свойства ромба
1. Противоположные углы конгруэнтны
Первое ключевое свойство ромба — отношение между парами противоположных углов. Пара противоположных углов в ромбе конгруэнтны, а это означает, что они имеют одинаковую меру. Мы можем доказать это со следующими:
Пара противоположных углов в ромбе конгруэнтны, а это означает, что они имеют одинаковую меру. Мы можем доказать это со следующими:
| | ||||
| ROMBUS ABCD | 1 | 1 | ||
| 2 | Линия розыгрыша AC | 2 | 2 очка Создать линию | |
| 9 3 | AB || DC & BC || DA | 3 | Def.Rhombus | |
| 4 | ∠Acd ≅ ≅bac & ∠dac ≅ ∠Acb | 4 | 4 | Альтернативные углы интерьера |
| AB = BC = CD = DA | 5 | По умолчанию Rhombus | ||
| 9 6 | ΔAcd = Δabc | 6 | SAS | |
| 7 | ∠d ≅ ≅b | 7 | CPCTC. QED QED |
Это свойство ромба также показывает, что он является параллелограммом, поскольку существенное свойство параллелограмма состоит в том, что его противоположные углы равны. То есть, если четырехугольник имеет конгруэнтные противоположные углы, этого достаточно, чтобы гарантировать, что это параллелограмм.
(Примечание: «Q.E.D» в конце каждого доказательства является аббревиатурой латинской фразы «quod Erat Demostradum», что примерно переводится как «таким образом было продемонстрировано».)
2.Смежные углы являются дополнительными
Смежные углы ромба являются дополнительными, то есть их сумма составляет 180°. Мы можем доказать, что соседние углы в ромбе дополнены следующим:
кредит: автор| | |||||
| 1 | Roombus ABCD | 1 | Дано | ||
| 2 | AB || округ Колумбия и округ Колумбия || BC | 2 | По умолчаниюRhombus | ||
| 3 | AC | 3 | 3 | Два балла Сделать линию | |
| 4 | ∠A supp ∠b, ∠b supp c, ∠c supp ∠d , ∠D supp ∠A | 4 | Это два || линии разрезаны пер. , внутренние углы по ту же сторону пер. являются дополнительными. Q.E.D , внутренние углы по ту же сторону пер. являются дополнительными. Q.E.D |
Таким образом, мы можем доказать, что смежные углы в ромбе являются дополнительными.
3.Диагонали делят пополам противоположные углы
Третье важное свойство ромба связано с его диагоналями. Диагональ многоугольника — это любая линия, проведенная между двумя несмежными вершинами. Параллелограмм имеет 4 вершины, значит, у него всего 2 диагонали. Характерным свойством диагоналей ромба является то, что они делят угол, из которого проведены, пополам. Мы можем доказать это со следующим:
| 0 | Причина | ||||||
| 1 | ROMBUS ABCD | 1 | |||||
| 2 | ab = bc = cd = da | 2 | 2 | ||||
| 3 | AC & BD | 3 | Два очка Создать линию | ||||
| 4 | AC = AC | 4 | Reflexive House | 1||||
| 9 5 | 5 | 5 | SSS | ||||
| 6 | ∠bac = ∠acb ∠ DAC = ∠ACD | 6 | Основание ∠s изос.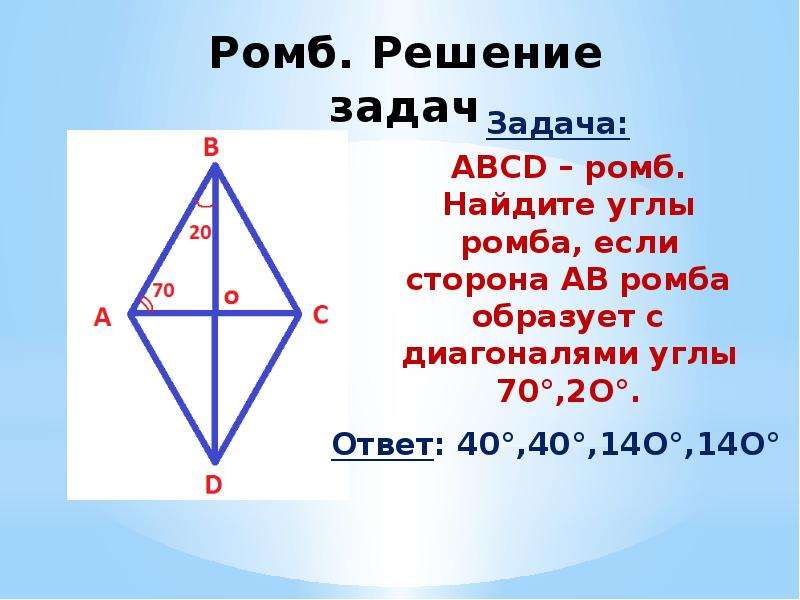 Треугольники конгруэнтны Треугольники конгруэнтны | ||||
| 9 7 | ∠dac = ∠BCA | 7 | CPCTC | ||||
| 8 | AC Bisects ∠dab BC BC | 8 | Биссектриса делит угол на две равные части. Q.E.D |
Итак, мы только что доказали, что диагонали ромба делят противоположные углы пополам.Это уникальное свойство ромбов, которого нет у других видов четырехугольников.
4. Диагонали делят друг друга пополам
Четвертое основное свойство ромба также связано с его диагоналями. Это факт, что диагонали ромба делят друг друга пополам; то есть каждый из них разрезает друг друга на два равных отрезка. Точка их пересечения есть середина обеих диагоналей.
| 0 | 9 | ||||||
| ROMBUS ABCD | 1 | ||||||
| 2 | ab = BC = CD = DA | 2 | По умолчаниюромба | ||||
| 3 | AB || компакт-диск и DA || CB | 3 | По умолчанию Rhombus | ||||
| 4 | ∠aeb = ∠dec | 4 | Пары вертикальных углов | ||||
| 5 | ∠bac = ∠ACD | 5 | Углы интерьера | ||||
| 6 | 6 | SAA Theorem | |||||
| 7 | AE = EC | De = Eb | 7 | CPCTC | |||
| 8 | AC и DB делят друг друга пополам | 8 | Две прямые делят друг друга пополам, если точка их пересечения является серединой обеих прямых. Q.E.D Q.E.D |
5. Диагонали перпендикулярны друг другу
Последнее определяющее свойство ромба, которое мы докажем, это тот факт, что диагональные линии перпендикулярны друг другу. В ромбе две диагонали всегда пересекаются под прямым углом 90°. Мы можем доказать это как показатели:
| 1 | ROMBUS ABCD | 1 | |||||
| 2 | AB = BC = CD = DA | 2 | По умолчаниюof Rhombus | ||||
| 3 | AE = EC de = Eb | 3 0 | Теорема: Диагонали ромба бислекта друг друга (от доказательства № 4) | ||||
| 9 4 | Δaeb = ΔBEC = ΔEC = Δaed | 4 | SSS | ||||
| 9 5 | 5 | 5 | 5 | 5 | CPCTC | ||
| 6 | ∠AEB + ∠BEC + ∠UCED + ∠DEA = 360 ° | 6 | Сумма углов, окружающих точку и совместное использование вершины 360 ° | ||||
| 7 | 4∠aeb = 360 ° | 7 9 7 | Упрощение | ||||
| ∠aeb = 90 ° | 8 | ||||||
| 9 | AC ⊥ BD | 9 | Две прямые перпендикулярны, если они пересекаются под прямым углом |
Другие свойства ромба
Площадь
Площадь ромба можно вычислить точно так же, как и любого другого четырехугольника, умножив основание на площадь высота.
A = b x h
Высота ромба – это мера линии, проведенной перпендикулярно с одной стороны на противоположную. Причина, по которой формула площади ромба такая же, как у прямоугольника, проста; каждый ромб (и параллелограмм) можно разрезать на части и перестроить в прямоугольник с тем же основанием и высотой (на следующем рисунке изображен параллелограмм, не являющийся ромбом, но тот же принцип справедлив и для ромбов).
Предоставлено: WikiCommons CC0 1.0Если вы проведете линию, перпендикулярную от одного основания к концу другого основания, вы получите трапецию и прямоугольный треугольник, которые можно превратить в прямоугольник с той же площадью, что и исходный ромб.
Вы также можете вычислить площадь ромба, если знаете только длины его диагоналей. Площадь ромба равна половине произведения его диагоналей. Итак, для ромба с диагоналями p и q математическая формула такова:
A = pq/2
Помните, что ранее мы доказали две вещи о диагоналях ромба: они делят друг друга пополам и перпендикулярны друг другу. Рассмотрим следующий ромб:
Рассмотрим следующий ромб:
Мы знаем, что AE = EC и DE = EB. Мы также знаем, что диагонали делят пары противоположных углов пополам.Таким образом, мы получаем два больших равнобедренных треугольника справа и слева, каждый из которых делится на два меньших прямоугольных треугольника. Площадь всего ромба в два раза больше площади одного из равнобедренных треугольников. Начиная с правой ΔABC, мы знаем, что ее общая площадь равна
Площадь ΔABC = ½(AC)(EB)
Однако мы также знаем, что EB составляет половину DB (поскольку линия делится пополам в точке E), поэтому мы можем заменить:
Площадь ΔABC = ½(AC)(½DB)
, что упрощается до
Площадь ΔABC = ¼(AC)(DB)
Поскольку мы знаем, что вся площадь ромба в два раза больше площади ΔABC , мы можем переписать
Площадь ABCD = 2 × Площадь ΔABC = ½(AC)(BD)
Следовательно, площадь ромба можно вычислить как половину произведения его диагональных линий.
Свойства мозаики
Ромб также может образовывать мозаику, что означает, что вы можете расположить ромбы в виде правильных узоров, чтобы полностью заполнить 2-мерную грань. Мозаика, состоящая из ромбов, называется мозаикой из ромбов. Плитки одинаковых ромбов могут заполнять плоскость тремя разными способами; в виде последовательной стопки ромбов, чередующейся стопки ромбов или групп из 3 ромбов, расположенных на грани куба.
Мозаика, состоящая из ромбов, называется мозаикой из ромбов. Плитки одинаковых ромбов могут заполнять плоскость тремя разными способами; в виде последовательной стопки ромбов, чередующейся стопки ромбов или групп из 3 ромбов, расположенных на грани куба.
. Вы также можете сформировать ромбовидную мозаику из обычной мозаики из шестиугольников.Просто разделите каждый шестиугольник на три, нарисовав линии от каждой другой вершины, которые встречаются в центре шестиугольника.
Из шестиугольной мозаики можно составить ромбическую мозаику. Предоставлено: WikiCommons CC BY-SA 3.0 Ромбы могут быть объединены в мозаику, потому что они могут быть расположены таким образом, что сумма углов, окружающих каждую точку, составляет ровно 360 градусов. Это необходимое свойство фигур, которые можно тесселировать; если вы не можете расположить фигуру так, чтобы сумма всех углов, сходящихся в вершине, равнялась 360, то из нее нельзя сделать правильную мозаику.
Итак, ромбом называется четырехугольник, у которого все 4 стороны имеют одинаковую длину. Все ромбы — параллелограммы, а квадрат — частный случай ромба, у которого все 4 внутренних угла — прямые. Основные свойства ромба: его противоположные углы конгруэнтны, его смежные углы являются дополнительными, его диагонали делят противоположные углы пополам, его диагонали делят друг друга пополам, а его диагонали перпендикулярны друг другу.
Была ли эта статья полезной?
😊 ☹️ Приятно слышать! Хотите узнать больше о научных тенденциях? Подпишитесь на нашу научную рассылку! Нам жаль это слышать! Мы любим отзывы 🙂 и хотим, чтобы вы внесли свой вклад в то, как сделать Science Trends еще лучше.Определение, формула, свойства и примеры
Почти каждый из нас знает, что ромб является четырехугольником, а значит, так же, как и другие четырехугольники, такие как квадрат, прямоугольник и т. д., имеет четыре вершины и четыре ребра, заключающие четыре угла. Тем не менее, это еще не все. Нам еще многое предстоит узнать об этой удивительной 2D-форме, которая играет важную роль в математике, одном из основных предметов, которые сопровождают нас от школы до высшего образования. Итак, давайте познакомимся со всеми ключевыми аспектами Rhombus.
Нам еще многое предстоит узнать об этой удивительной 2D-форме, которая играет важную роль в математике, одном из основных предметов, которые сопровождают нас от школы до высшего образования. Итак, давайте познакомимся со всеми ключевыми аспектами Rhombus.
Ромб Определение
В евклидовой геометрии ромб — это особый тип четырехугольника, который выглядит как параллелограмм, диагонали которого пересекают друг друга под прямым углом, т. е. под углом 90 градусов. Поскольку форма ромба такая же, как у алмаза, он также известен как алмаз. Фигура в форме ромба на игральных картах — один из лучших примеров ромба. Более того, возможно, все ромбы — воздушные змеи и параллелограммы, но если все углы ромба равны 90°, то он — квадрат.
Другими словами, ромб — это особый вид параллелограмма, у которого противоположные стороны параллельны, а противоположные углы равны. Помимо четырех сторон одинаковой длины, ромб содержит диагонали, которые делят друг друга пополам под углом 90 градусов, то есть под прямым углом.
На рисунке ниже показан ромб ABCD с четырьмя равными сторонами — AB, BC, CD и AD, и двумя диагоналями AC и BD, пересекающимися под прямым углом.
Теперь, увидев приведенный выше рисунок и прочитав информацию, упомянутую выше, вы можете немного запутаться, является ли ромб квадратным и наоборот или нет.Если да, то не беспокойтесь, так как здесь есть подходящее решение для вас.
Является ли квадрат ромбом?
Квадрат — это четырехугольник, все стороны которого равны по длине, то же самое относится и к ромбу. Кроме того, две диагонали квадрата перпендикулярны друг другу и делят противоположные углы пополам, как и ромб. Отсюда ясно, что квадрат — это ромб. С другой стороны, поскольку основное свойство квадрата гласит, что все его внутренние углы прямые, ромб не считается квадратом, если все внутренние углы не равны 90°.
Углы ромба
Любой ромб состоит из четырех углов, из которых противоположные равны друг другу.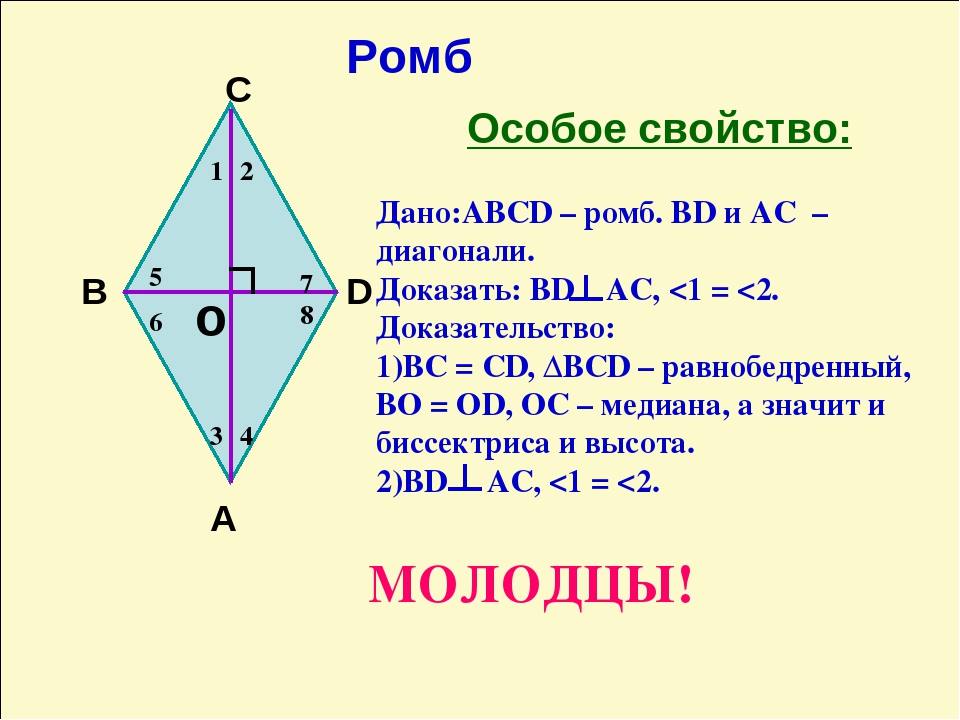 Кроме того, ромб состоит из диагоналей, которые делят друг друга пополам под прямым углом. Другими словами, можно сказать, что каждая диагональ ромба делит другую на две равные части, а угол, образованный в точках их пересечения, равен 90°. Диагонали также делят пополам противоположные углы ромба.
Кроме того, ромб состоит из диагоналей, которые делят друг друга пополам под прямым углом. Другими словами, можно сказать, что каждая диагональ ромба делит другую на две равные части, а угол, образованный в точках их пересечения, равен 90°. Диагонали также делят пополам противоположные углы ромба.
Формулы ромба
Формулы для любого ромба определяются с учетом двух основных атрибутов, таких как площадь и периметр.
Площадь ромба
Площадь ромба относится к области, покрываемой им в двумерной плоскости. Основываясь на этом определении, формула площади ромба равна произведению его диагоналей, деленному на 2, и может быть представлена в виде:
Площадь ромба (A) = (d1 x d2)/2 квадратных единиц, где d1 и d2 — диагонали ромба
Периметр ромба
Периметр ромба определяется либо как общая длина его границ, либо как сумма всех четырех его сторон.Следовательно, формула для периметра ромба может быть представлена как:
Периметр ромба (P) = 4a единиц, где а — сторона ромба.
Свойства ромба
Теперь взглянем на некоторые важные свойства ромба.
Все четыре стороны равны по длине
Противоположные стороны параллельны
Противоположные углы равны
Диагонали делятся пополам, i.е., 90 градусов
Диагонали ромба делят его противоположные углы пополам
Сумма двух смежных углов является дополнительной, т. е. 180°
В прямоугольном треугольнике две диагонали образуют четыре конгруэнтны друг другу
Соединив середины сторон ромба, получится прямоугольник
Соединив середины половин диагоналей, получится еще один ромб
Внутри ромба не может быть описанной окружности
Если меньшая диагональ ромба равна одной из его сторон, то получится два равных равносторонних треугольника
- При вращении ромба вокруг линии, соединяющей середины противоположных сторон в качестве осей вращения, образуется цилиндрическая поверхность с вогнутыми конусами на оба конца сформированы.

При вращении ромба вокруг любой из его сторон как осей вращения образуется цилиндрическая поверхность с вогнутым конусом на одном конце и выпуклым конусом на другом конце.
Если ромб вращать вокруг своей большей диагонали, являющейся осью вращения, то образуется твердое тело, к основаниям которого прикреплены два конуса. В этом случае максимальный диаметр фигуры (тела) будет равен меньшей диагонали ромба.
Когда ромб вращается вокруг его более короткой диагонали, являющейся осью вращения, вы получите твердое тело с двумя конусами, прикрепленными к его основаниям.Максимальный диаметр тела, полученного в этом случае, будет равен большей диагонали ромба.
Если соединить середины всех четырех сторон ромба, то получится прямоугольник, длина и ширина которого будут равны половине значения простой диагонали.
 При этом площадь образованного в этом случае прямоугольника будет равна половине ромба.
При этом площадь образованного в этом случае прямоугольника будет равна половине ромба.
Ромб — свойства, определение, формулы, примеры
Ромб — замкнутая двумерная плоская фигура.Он считается особым параллелограммом, и благодаря своим уникальным свойствам он приобретает индивидуальную идентичность четырехугольника. Ромб также называют равносторонним четырехугольником, так как все его стороны равны по длине. Термин «ромб» произошел от древнегреческого слова «ромбос», что на самом деле означает что-то вращающееся. Давайте узнаем больше о ромбе и его свойствах в этой статье.
Что такое ромб?
Ромб можно определить как особый параллелограмм , поскольку он удовлетворяет требованиям параллелограмма, т.е.е. четырехугольник с двумя парами параллельных сторон. Кроме того, у ромба все четыре стороны равны, как у квадрата. Вот почему он также известен как наклонный квадрат. Посмотрите на изображение ниже, чтобы понять взаимосвязь формы ромба с параллелограммом и квадратом.
На приведенном выше рисунке мы можем заметить, что каждый ромб, который мы видим, также будет параллелограммом, но не каждый параллелограмм является ромбом. Квадрат можно рассматривать как частный случай ромба, поскольку он имеет четыре равные стороны.Все углы квадрата прямые, но углы ромба не обязательно должны быть прямыми . И, следовательно, ромб с прямыми углами можно считать квадратом. Отсюда можно сделать вывод, что:
- Все ромбы или ромбы являются параллелограммами, но не все параллелограммы являются ромбами.
- Все ромбы или ромбы не являются квадратами, но все квадраты являются ромбами.
Ромб может иметь три дополнительных имени:
Свойства ромба
Ромб считается одним из особых параллелограммов, так как обладает всеми свойствами параллелограмма.Две диагонали ромба являются его двумя линиями симметрии. Ось симметрии можно рассматривать как линию, которая делит объект на две равные половины. Он создает зеркальное отражение обеих сторон объекта. Говорят, что ромб обладает симметрией отражения по обеим диагоналям. Общие свойства параллелограмма следующие:
Он создает зеркальное отражение обеих сторон объекта. Говорят, что ромб обладает симметрией отражения по обеим диагоналям. Общие свойства параллелограмма следующие:
Ромб, как и все геометрические фигуры, обладает уникальными свойствами. В таблице ниже описаны свойства ромба.
| Свойства ромба | Артикул |
|---|---|
Все стороны ромба конгруэнтны (равны). | Здесь AB = CD = DA = BC |
| Диагонали делят друг друга пополам под углом 90°, или мы также можем сказать, что каждая из двух диагоналей ромба является серединным перпендикуляром к другой. | Здесь диагонали DB и CA делят друг друга пополам под углом 90° |
Противоположные углы равны, а противоположные стороны параллельны. | Здесь, компакт-диск || АВ и ВС || ОБЪЯВЛЕНИЕ. ∠А = ∠С и ∠D = ∠В |
| Смежные углы в сумме дают 180° | ∠А + ∠В = 180° ∠В + ∠С = 180° ∠C + ∠D = 180° ∠А + ∠D = 180° |
Одна вещь, которую мы должны помнить о диагонали ромба, заключается в том, что в дополнение к разделению пополам под углом 90 ° две диагонали, разделенные пополам, будут иметь одинаковую длину. Например: если длина диагонали равна 10 см, а другая диагональ делит ее пополам, то она делится на два отрезка по 5 см. Если знать сторону ромба и величину некоторых углов, то можно определить длину диагонали.
Например: если длина диагонали равна 10 см, а другая диагональ делит ее пополам, то она делится на два отрезка по 5 см. Если знать сторону ромба и величину некоторых углов, то можно определить длину диагонали.
Как выглядит ромб?
Ромб – это четырехугольник в форме ромба, у которого все четыре стороны равны. Мы можем видеть фигуры в форме ромба в нашей повседневной жизни. Некоторые из реальных примеров ромба показаны на приведенном ниже рисунке: бриллиант, воздушный змей, серьга и т. д.
Формулы ромба
Формулы ромбов определены для двух атрибутов:
- Площадь ромба, A = 1/2 × d 1 × d 2 , где d 1 и d 2 — диагонали ромба.
- Периметр ромба, P = 4 × a, где a — сторона.
Площадь и периметр ромба
Площадь ромба можно определить как количество пространства, заключенного или охваченного ромбом в двухмерной плоскости. Это половина произведения длин диагоналей. Итак, A = 1/2 × d 1 × d 2 , где d 1 и d 2 — длины диагоналей.
Это половина произведения длин диагоналей. Итак, A = 1/2 × d 1 × d 2 , где d 1 и d 2 — длины диагоналей.
Так же, как и у квадрата, у ромба все четыре стороны равны, значит, формула периметра ромба есть произведение длины одной стороны на 4. Получаем P = (4×a) единиц, где а — сторона ромба.
☛ Важные примечания о ромбе
Вот список нескольких моментов, которые следует помнить при изучении ромба:- Смежные углы в ромбе смежные, в сумме они составляют 180°.
- Диагонали делят друг друга пополам под прямым углом.
- Все квадраты — ромбы, но не все ромбы — квадраты.
☛ Похожие темы:
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о ромбе и связанных с ним темах.
Часто задаваемые вопросы о Rhombus
Что такое ромб в геометрии?
Ромб — это двумерная фигура с четырьмя сторонами, поэтому ее называют четырехугольником.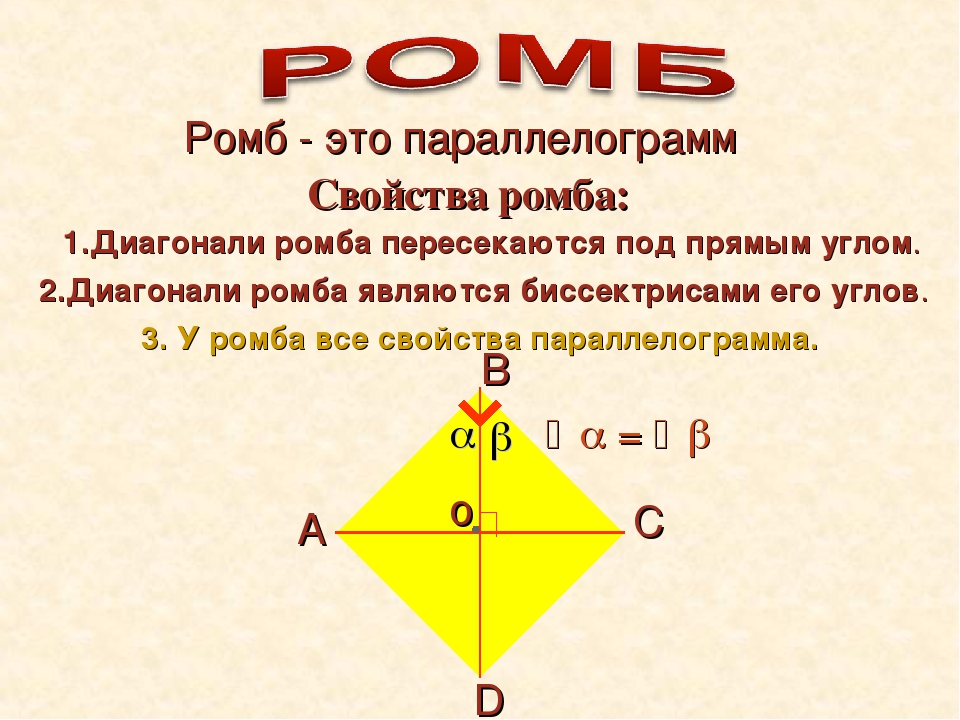 Он имеет две диагонали, которые делят друг друга пополам под прямым углом. У него также параллельны противоположные стороны, а сумма всех четырех внутренних углов равна 360 градусам.
Он имеет две диагонали, которые делят друг друга пополам под прямым углом. У него также параллельны противоположные стороны, а сумма всех четырех внутренних углов равна 360 градусам.
Все ли квадраты ромбы?
Да, все квадраты — ромбы. Квадрат можно рассматривать как частный случай ромба, поскольку он имеет четыре стороны одинаковой длины. Все углы квадрата прямые, но углы ромба не обязательно должны быть прямыми. Следовательно, ромб с прямыми углами можно считать квадратом.
Какой формы ромб?
Ромб – четырехугольник в форме ромба. Если вы посмотрите на колоду карт и вытащите 13 ромбовидных карт, вы обнаружите, что геометрическая форма ромба — это ромб. У него все четыре стороны равны, а противоположные стороны параллельны друг другу. Он выглядит как наклонный квадрат.
Является ли ромб правильным многоугольником?
Нет, ромб не является правильным многоугольником. Правильный многоугольник должен быть равноугольным (все его углы имеют одинаковую меру) и конгруэнтным или равносторонним (все его стороны имеют одинаковую длину). Но ромб только равносторонний: все его стороны имеют одинаковую длину и только противоположные углы равны. Ромб никогда нельзя считать правильным многоугольником, так как это всего лишь равносторонний многоугольник, а не равноугольный многоугольник.
Но ромб только равносторонний: все его стороны имеют одинаковую длину и только противоположные углы равны. Ромб никогда нельзя считать правильным многоугольником, так как это всего лишь равносторонний многоугольник, а не равноугольный многоугольник.
Какова площадь ромба?
Площадь ромба рассчитывается путем деления произведения диагоналей на 2. Математически это можно определить как: \(A = \frac{{d_1 d_2 }}{2}\), где d 1 и d 2 — диагонали ромба.
Каковы четыре свойства ромба?
Ромб — это четырехугольник, обладающий следующими четырьмя свойствами:
- Противоположные углы всегда равны.
- Все стороны равны, а противоположные стороны параллельны друг другу.
- Диагонали делят друг друга пополам под углом 90 градусов и имеют одинаковую длину.
- Сумма любых двух смежных углов всегда будет равна 180°.
В чем разница между ромбом и квадратом?
Основное отличие ромба от квадрата в том, что углы ромба не равны 90°, тогда как все углы квадрата равны 90°.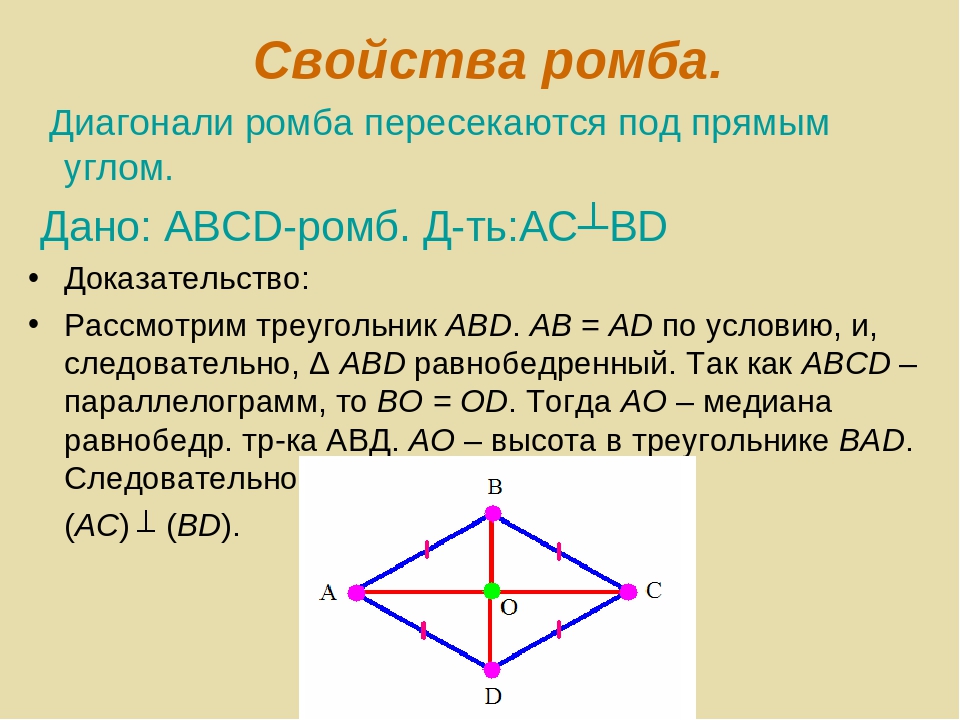 Часто говорят, что квадрат — это ромб, но ромб — это не всегда квадрат.
Часто говорят, что квадрат — это ромб, но ромб — это не всегда квадрат.
В чем разница между параллелограммом и ромбом?
Отличие параллелограмма от ромба в том, что у ромба все четыре стороны равны по размеру, тогда как у параллелограмма противоположные стороны равны.
Каковы основные формулы ромба?
Несколько основных формул ромба перечислены ниже:
- Площадь ромба = 1/2 × d 1 × d 2 квадратных единиц.
- Периметр ромба = (4 × стороны) единиц.
Чему равна сумма внутренних углов ромба?
Сумма внутренних углов ромба равна 360°.
Все ли углы ромба равны 90°?
Нет, углы ромба не обязательно должны быть прямыми. Ромб, у которого все четыре внутренних угла равны 90 градусам, считается квадратом.
Искусство решения проблем
Ромб — геометрическая фигура, лежащая на плоскости.Он определяется как четырехугольник, у которого все стороны равны. Это особый тип параллелограмма, и его свойства (помимо свойств параллелограмма) включают:
Это особый тип параллелограмма, и его свойства (помимо свойств параллелограмма) включают:
Доказательства
Доказательство того, что ромб является параллелограммом
Все стороны ромба равны, поэтому противоположные стороны равны, что является одним из свойств параллелограмма.
Или всегда есть более длинный путь:
В ромбе все 4 стороны равны (определение ромба).
, и .
Согласно постулату SSS, .
Соответствующие части конгруэнтных треугольников конгруэнтны, поэтому и . То же самое можно сделать и для двух других углов, поэтому .
Преобразуйте сравнения в меры, чтобы получить и . Сложение этих двух уравнений дает .
Внутренние углы четырехугольника составляют в сумме 360 градусов, поэтому , или .
Замена дает . При упрощении .
Если две прямые пересекаются секущей и внутренние углы с одной стороны в сумме составляют 180 градусов, то прямые параллельны.Это означает . То же самое можно сделать для двух других сторон, и мы знаем, что противоположные стороны параллельны.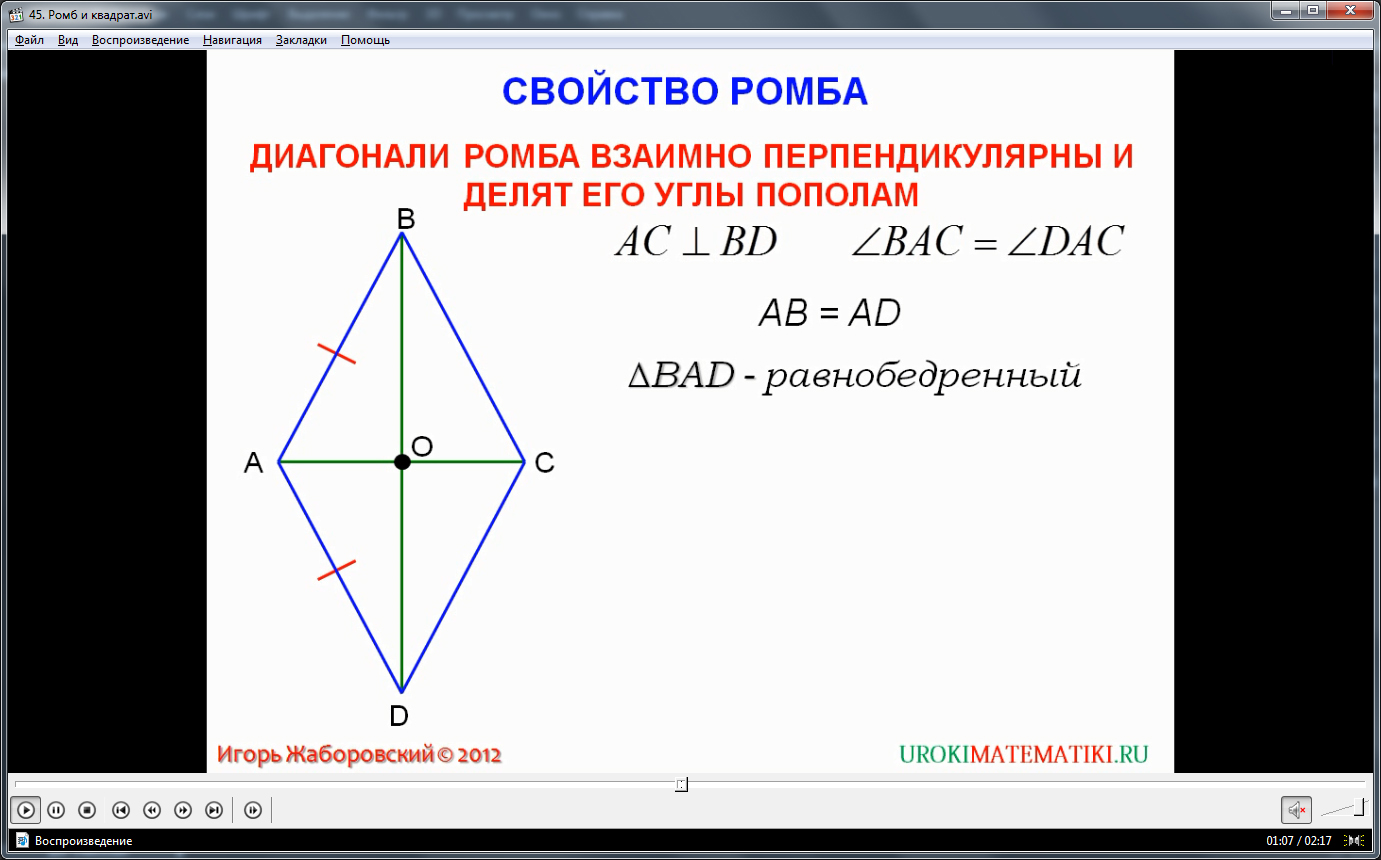 Следовательно, ромб является параллелограммом.
Следовательно, ромб является параллелограммом.
Доказательство того, что диагонали ромба делят его на 4 равных треугольника
В ромбе точка пересечения диагоналей.
Поскольку диагонали ромба являются биссектрисами друг друга, и .
Кроме того, все стороны конгруэнтны.
Согласно постулату SSS, 4 треугольника, образованные диагоналями ромба, конгруэнтны.
Доказательство перпендикулярности диагоналей ромба
Продолжение приведенного выше доказательства:
Соответствующие части конгруэнтных треугольников конгруэнтны, поэтому все 4 угла (те, что в середине) конгруэнтны.
Это приводит к тому, что все они равны 90 градусам, а диагонали перпендикулярны друг другу.
Примеры проблем
Вводный
Четырехугольники: Классификация
А четырехугольник это многоугольник с четырех сторон.
Существует много специальных типов четырехугольников.
А параллелограмм четырехугольник, у которого обе пары противоположных сторон параллельно .
Параллелограмм также обладает следующими свойствами:
- Противоположные углы равны;
- Противоположные стороны конгруэнтны;
- Смежные углы являются дополнительными;
- То диагонали делят друг друга пополам.
А прямоугольник является параллелограммом с четырьмя прямыми углами, поэтому все прямоугольники также являются параллелограммами и четырехугольниками. С другой стороны, не все четырехугольники и параллелограммы являются прямоугольниками.
Прямоугольник обладает всеми свойствами параллелограмма, а также следующими:
- Диагонали равны.
А ромб представляет собой параллелограмм с четырьмя
конгруэнтный
стороны. Множественное число слова ромб ромбы . (Я люблю это слово.)
Множественное число слова ромб ромбы . (Я люблю это слово.)
Ромб обладает всеми свойствами параллелограмма, а также следующими:
- Диагонали пересекаются под прямым углом.
А квадратный можно определить как ромб, который также является прямоугольником, другими словами, параллелограммом с четырьмя конгруэнтными сторонами и четырьмя прямыми углами.
А трапеция четырехугольник, у которого ровно одна пара параллельных сторон.(С этим словом может возникнуть некоторая путаница в зависимости от того, в какой стране вы находитесь. В Индии и Великобритании говорят трапеция ; в Америке трапеция обычно означает четырехугольник без параллельных сторон.)
Ан равнобедренная трапеция трапеция, у которой непараллельные стороны равны.
А летающий змей четырехугольник, у которого ровно две пары смежных равных сторон.(Это определение не включает ромбы. В некоторых учебниках говорится, что у воздушного змея есть по крайней мере две пары смежных конгруэнтных сторон, поэтому ромб является частным случаем воздушного змея.)
А неравносторонний четырехугольник – это четырехугольник, у которого нет конгруэнтных сторон. Ниже показаны три примера.
Диаграмма Венна классификации четырехугольников
На следующей диаграмме Венна показаны включения и пересечения четырехугольников различных типов.
Определение, формулы для площади и периметра
В евклидовой двумерной геометрии ромб — это четырехугольник, все четыре стороны которого равны, поэтому мы можем сказать, что это равносторонний четырехугольник. (множественное число от ромба — ромбы и ромбы) Ромб в математике также известен как как ромб , мы можем видеть эту форму ромба на игральных картах.
Что такое ромб?
Ромб — это тип четырехугольника, у которого противоположные стороны параллельны, а все четыре стороны равны по длине.Кроме того, ромб также известен как алмаз. Ромб в математике — это частный случай параллелограмма и воздушного змея . Если углы ромба прямые, то ромб известен 90 279 как квадрат 90 280 .
Здесь мы видим, что AB, BC, CD и AD — стороны ромба, а d 1 и d 2 — диагонали ромба. Свойства углов ромбаНекоторые важные свойства углов ромба в математике приведены ниже:
- Ромб имеет 4 внутренних угла.
- Сумма всех внутренних углов ромба равна 360 градусов.
- Диагональ ромба делит угол ромба пополам
- Противолежащие углы ромба равны.
- Смежные углы ромба являются дополнительными парами.
Узнайте больше о линиях здесь.
Является ли квадрат ромбом? Да, мы можем сказать, что квадрат — это ромб, но все ромбы не могут быть квадратами.
Мы говорим, что из-за некоторого сходства между квадратом и ромбом, которые приведены ниже:
| площадь | ROMBUS |
| Длина всех сторон квадрата равна | все стороны ромба равны по длине |
| диагональ квадратной бислекта друг друга | диагональ ромба бислекта друг друга |
| соседний угол квадрата добавляют дополнительную пару | соседний угол ромба дополнительная пара |
| противоположный угол квадрата равны | Противоположные углы ромба равны |
Площадь ромба: Мы можем определить площадь ромба в математике как количество пространства, покрытого всеми четырьмя сторонами ромб в двумерной плоскости.
Площадь ромба по диагоналям
Площадь ромба равна половине произведения длины диагонали ромба.
площадь Rhombus = D 1 D 2 ) / 2
Где D 1 и D 2 длина диагонали ромба.
Площадь ромба в математике с использованием высоты и основания ромба
Площадь ромба равна произведению длины основания и высоты (расстояния по перпендикуляру от основания до противоположной стороны ромба) ромба.
Площадь ромба по высоте и основанию ромбаПлощадь ромба = (b h)
Где b и h — длина основания и длина высоты ромба соответственно.
Площадь ромба с использованием стороны и тригонометрической функции
Площадь ромба равна произведению квадрата длины одной стороны ромба в математике и синуса любого внутреннего угла ромба.
Мы знаем, что вертикально противоположный угол треугольника равен
Итак, ∠A = ∠C и ∠d = ∠b
площадь Rhombus = A 2 Sina или a 2 sinB
Где a — длина стороны треугольника, а A и B — внутренние углы треугольника.
Периметр ромба: Суммарная длина границ ромба в мат.
Все стороны ромба равны AD = DC = CB = BA = a
Периметр ромба = 4a
Также откройте для себя концепции окружностей здесь.
Свойства ромбаНиже приведены важные свойства ромба в математике:
- Все стороны ромба равны.
- Противоположные стороны ромба параллельны друг другу.
- Диагонали ромба пересекаются под прямым углом пополам.
- Диагонали ромба делят ромб на четыре равных треугольника.
- Мы не можем вписать ромб в окружность.
- Мы не можем описать окружность вокруг ромба.
- Прямоугольник получится, если соединить все 4 середины сторон ромба и площадь прямоугольника будет равна половине площади ромба.
Также узнайте о треугольниках здесь.
Ромб Вопросы для конкурсных экзаменов
Вопрос 1 : Длины двух диагоналей ромба d 1 и d 2 2 см, соответственно, 1 8 см. {2}\)
{2}\)
⇒d2 = (350 x 2)/28 = 25 см
Длина другой диагонали 25 см.
Привет! Надеюсь, статья о ромбе в математике окажется для вас информативной и полезной. следите за обновлениями в приложении Testbook или посетите веб-сайт Testbook, чтобы узнать больше о похожих темах по математике и многим другим предметам, и даже можете проверить серию тестов, доступных для проверки ваших знаний о различных экзаменах.
Часто задаваемые вопросы о ромбеQ.1 Является ли квадрат ромбом?
Ответ.1Ромб можно рассматривать как четырехугольник с четырьмя сторонами одинаковой длины и противоположными сторонами, параллельными друг другу. Можно сказать, что все квадраты — ромбы, но не все ромбы — квадраты.
Q.2 Какова форма ромба?
Ans.2 Ромб — это двумерная плоская фигура с замкнутой формой, все четыре стороны которой равны, поэтому он также известен как равносторонний четырехугольник.
Q.3 Как выглядит четырехугольник?
Ответ.3Четырехугольник — это четырехсторонняя двумерная фигура. Все следующие двумерные фигуры являются четырехугольниками: квадрат, ромб, параллелограмм, прямоугольник, трапеция и воздушный змей.
Q.4 Каковы формулы для периметра ромба?
Анс.4Периметр ромба = 4а.
Q.5 Чему равна сумма внутренних углов четырехугольника?
Ans.5Сумма внутренних углов четырехугольника равна 360 градусов.
Создайте бесплатную учетную запись, чтобы продолжить чтение
Получайте мгновенные оповещения о вакансиях бесплатно!
Получите Daily GK и текущие события Capsule и PDF-файлы
Получите более 100 бесплатных пробных тестов и викторин
Подпишитесь бесплатно У вас уже есть аккаунт? Войти
Следующий пост
.




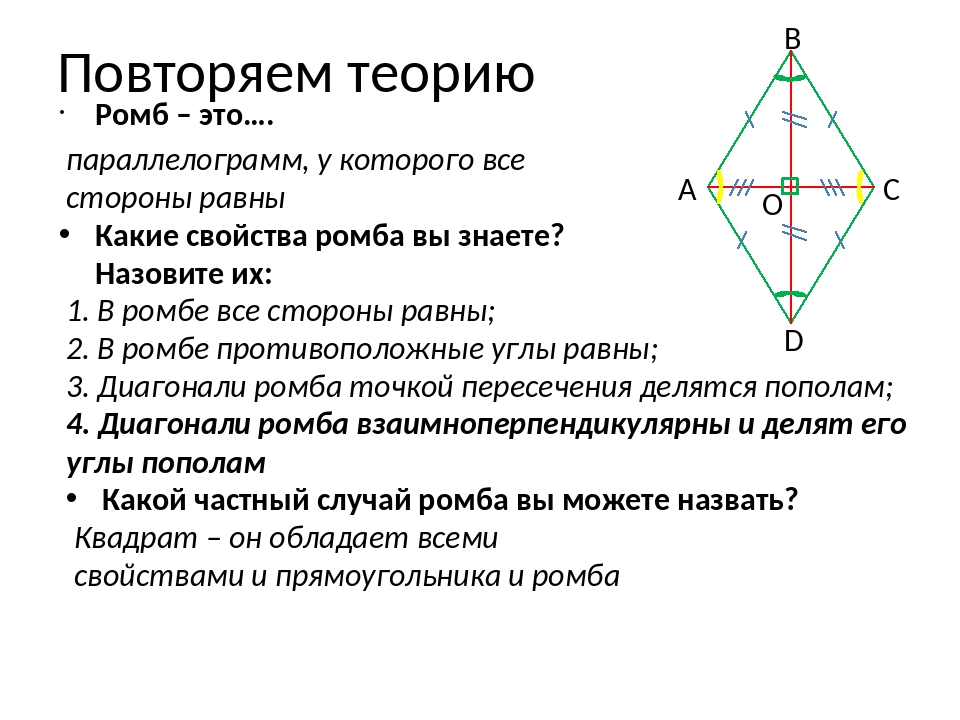

 Рассмотрим следующий ромб:
Рассмотрим следующий ромб: Мозаика из ромбов называется мозаикой ромбовидной формы. Плитки из одинаковых ромбов могут заполнять плоскость тремя разными способами; в виде последовательной стопки бриллиантов, чередующейся стопки бриллиантов или групп из 3 ромбов, расположенных на грани куба.
Мозаика из ромбов называется мозаикой ромбовидной формы. Плитки из одинаковых ромбов могут заполнять плоскость тремя разными способами; в виде последовательной стопки бриллиантов, чередующейся стопки бриллиантов или групп из 3 ромбов, расположенных на грани куба.
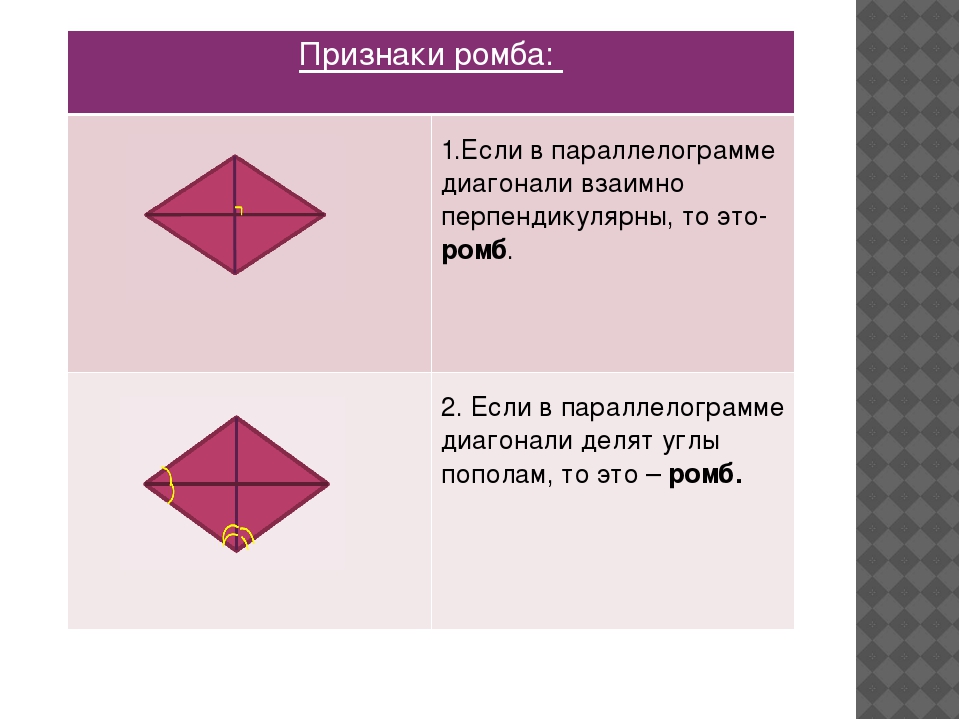 Ромб можно отличить от квадрата по величине его внутреннего угла. Внутренний угол ромба не обязательно должен быть прямым углом. Площадь ромба можно рассчитать по-разному, в зависимости от известных нам параметров.
Ромб можно отличить от квадрата по величине его внутреннего угла. Внутренний угол ромба не обязательно должен быть прямым углом. Площадь ромба можно рассчитать по-разному, в зависимости от известных нам параметров.
 Формула для вычисления площади ромба с использованием диагоналей имеет вид
Формула для вычисления площади ромба с использованием диагоналей имеет вид 2
2  Основание — это одна из его сторон ромба, а высота — это перпендикулярное расстояние от выбранного основания до противоположной стороны.
Основание — это одна из его сторон ромба, а высота — это перпендикулярное расстояние от выбранного основания до противоположной стороны.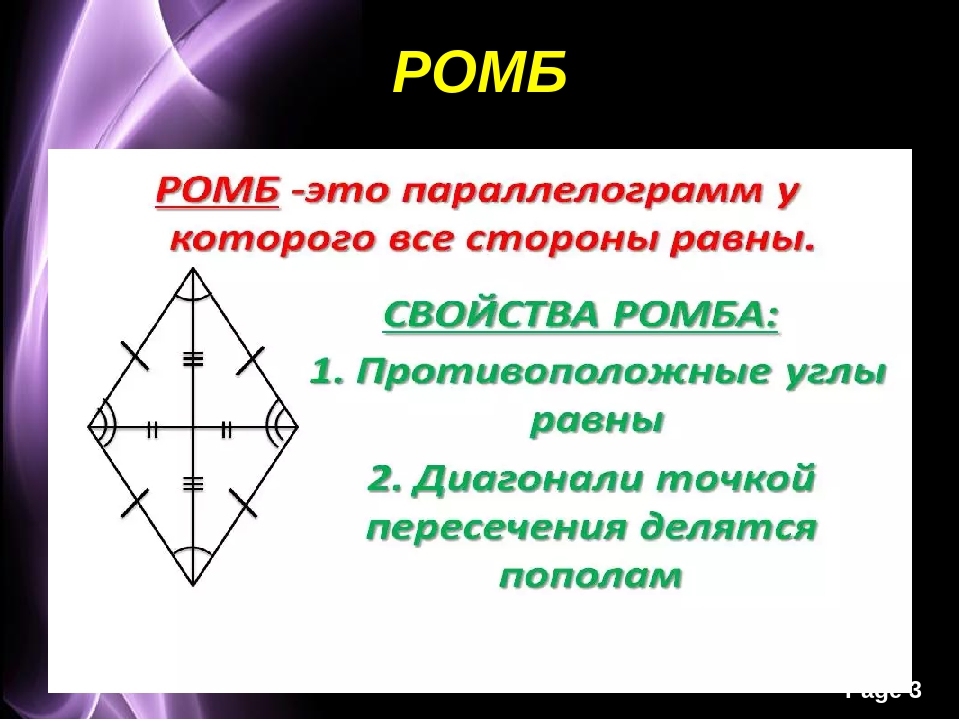 Учитывая CD = 17 футов и AE = 8 футов.
Учитывая CD = 17 футов и AE = 8 футов.

 Здесь под высотой понимается расстояние по перпендикуляру между параллельными сторонами, одну из которых мы взяли за основу.Формула для определения площади в данном случае задается как площадь ромба = основание × квадратные единицы высоты.
Здесь под высотой понимается расстояние по перпендикуляру между параллельными сторонами, одну из которых мы взяли за основу.Формула для определения площади в данном случае задается как площадь ромба = основание × квадратные единицы высоты. Свойства ромба и его формула площади широко используются для решения различных задач.Давайте обсудим их по очереди.
Свойства ромба и его формула площади широко используются для решения различных задач.Давайте обсудим их по очереди.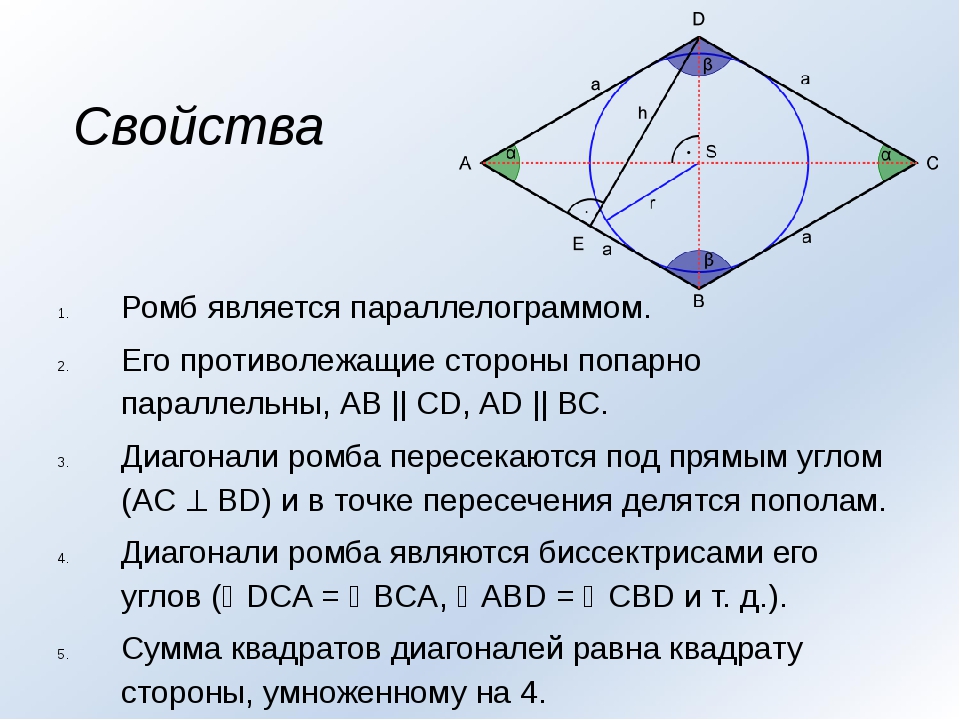 .
. \ ({d_1} = \) Длина диагонали \ (1. \)
\ ({d_1} = \) Длина диагонали \ (1. \)  Можно применить простую формулу, и вычислить площадь ромба со стороной. Если основание (сторона) ромба названо \ (b \), высота — как \ (h \), то произведение основания и высоты составляет площадь ромба.
Можно применить простую формулу, и вычислить площадь ромба со стороной. Если основание (сторона) ромба названо \ (b \), высота — как \ (h \), то произведение основания и высоты составляет площадь ромба.  2} \)
2} \)  \)
\) 8. Все ли ромбы параллелограммы?
8. Все ли ромбы параллелограммы? 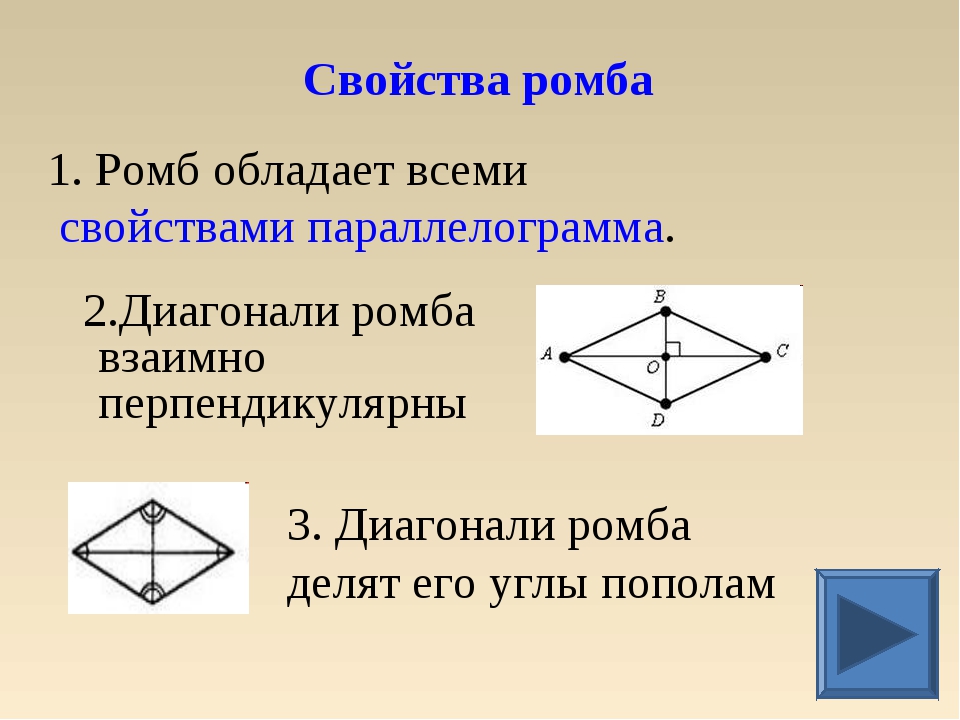 Когда эти маленькие числа умножаются, мы получим фактическое или исходное число. Обычно учащиеся знакомятся с концепциями факторизации в 6 классе.
Когда эти маленькие числа умножаются, мы получим фактическое или исходное число. Обычно учащиеся знакомятся с концепциями факторизации в 6 классе.

 В то время как Prime Factorization — это процесс нахождения простых факторов данного составного числа. То есть метод простой факторизации может применяться только для составного числа. Есть 2 метода найти основные факторы числа. Чтобы узнать все о том, как найти основные факторы данного числа, щелкните ссылку ниже.
В то время как Prime Factorization — это процесс нахождения простых факторов данного составного числа. То есть метод простой факторизации может применяться только для составного числа. Есть 2 метода найти основные факторы числа. Чтобы узнать все о том, как найти основные факторы данного числа, щелкните ссылку ниже.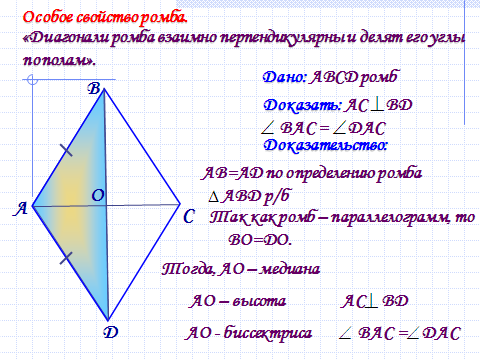 Решите квадратное уравнение методом факторизации (x + y) 2 — 4xy
Решите квадратное уравнение методом факторизации (x + y) 2 — 4xy 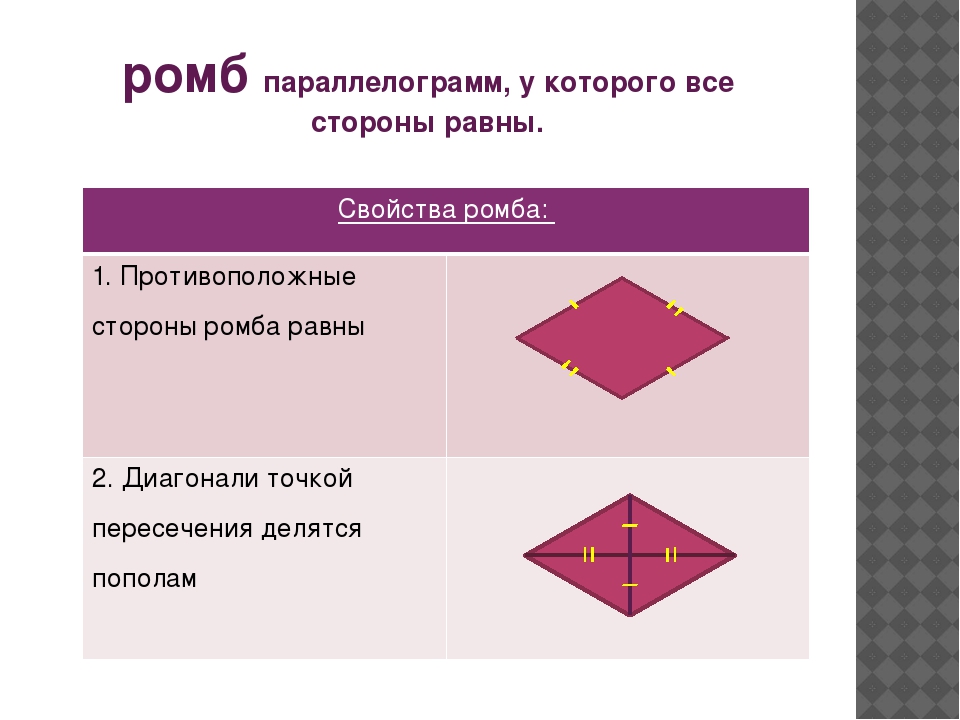 Что такое метод факторизации в математике?
Что такое метод факторизации в математике?  Студенты могут использовать NCERT Solutions , предоставленные Embibe, для подготовки к экзаменам.
Студенты могут использовать NCERT Solutions , предоставленные Embibe, для подготовки к экзаменам. Мы, в Embibe, предоставили на этой странице таблицу журналов в формате PDF вместе с определением таблицы. Кроме того, мы подробно объяснили, как пользоваться таблицей логарифмов.
Мы, в Embibe, предоставили на этой странице таблицу журналов в формате PDF вместе с определением таблицы. Кроме того, мы подробно объяснили, как пользоваться таблицей логарифмов.
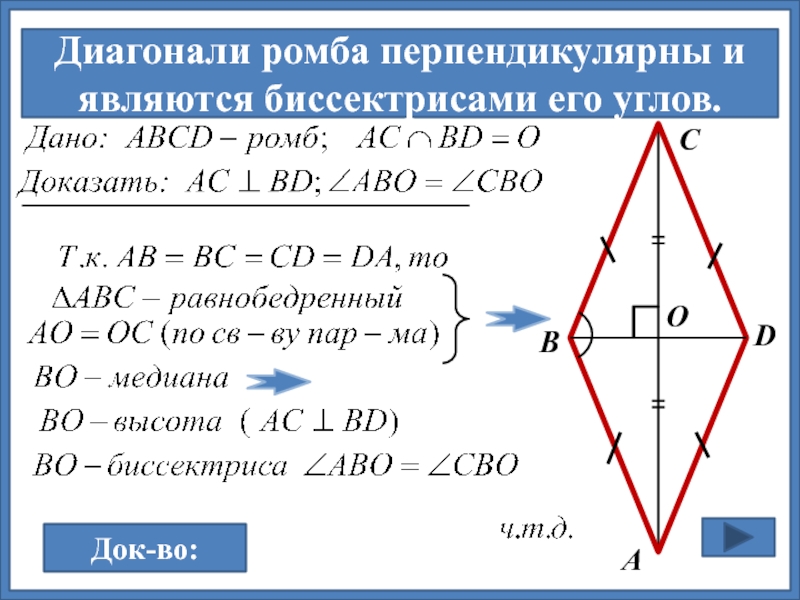 25) → строка 18, столбец 2 → значение ячейки 2601. Таким образом, получено значение 2601.
25) → строка 18, столбец 2 → значение ячейки 2601. Таким образом, получено значение 2601. 2613.
2613.

 При этом площадь образованного в этом случае прямоугольника будет равна половине ромба.
При этом площадь образованного в этом случае прямоугольника будет равна половине ромба.