Приклади розв’язання типових задач
Задача-приклад1. Визначте тривалість технологічного циклу оброблення партії деталей із 20 штук за послідовного, паралельного та послідовно-паралельного поєднання операцій, якщо тривалість виконання операційtiмає такі значення за часом, у хвилинах:t1 = 8;t2 = 4;t3 = 3;t4 = 10;t5 = 5;t6 = 4. У розрахунках узяти до уваги, що кількість робочих місць по операціях: першій і четвертій — по два; решті — по одному. У паралельному та послідовно-паралельному поєднанні операцій деталі обробляються транспортною партією по 5 штук.
Розв’язок
1. Тривалість
технологічного циклу за послідовного
поєднання операцій: 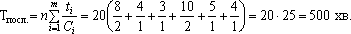 2. Тривалість
технологічного циклу за паралельного
поєднання операцій:
2. Тривалість
технологічного циклу за паралельного
поєднання операцій: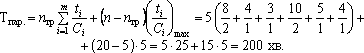
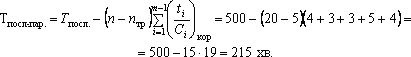 Задача-приклад2.На одній із
виробничих дільниць механічного цеху
виготовляються деталі партіями по 30
штук кожна. Застосовуваний спосіб
поєднання технологічних операцій —
послідовний. Час на підготовку виробництва
становить 1,5 год, а середній
міжопераційний час — 10 хв. Норма часу
на виконання окремих операцій становить:
1-ї — 2 хв; 2-ї — 5 хв; 3-ї — 12 хв; 4-ї — 8
хв. При цьому третя й четверта операції
виконуються на двох верстатах кожна.
Установлений режим роботи підприємства —
дві зміни по 8 год кожна. Коефіцієнт
календарності часу — 1,4.
Визначити
тривалість технологічного й виробничого
циклів оброблення деталей.Розв’язок
Задача-приклад2.На одній із
виробничих дільниць механічного цеху
виготовляються деталі партіями по 30
штук кожна. Застосовуваний спосіб
поєднання технологічних операцій —
послідовний. Час на підготовку виробництва
становить 1,5 год, а середній
міжопераційний час — 10 хв. Норма часу
на виконання окремих операцій становить:
1-ї — 2 хв; 2-ї — 5 хв; 3-ї — 12 хв; 4-ї — 8
хв. При цьому третя й четверта операції
виконуються на двох верстатах кожна.
Установлений режим роботи підприємства —
дві зміни по 8 год кожна. Коефіцієнт
календарності часу — 1,4.
Визначити
тривалість технологічного й виробничого
циклів оброблення деталей.Розв’язокТривалість технологічного циклу за послідовного поєднання операцій:
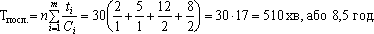
Тривалість виробничого циклу:

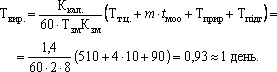 Задачі
для самостійного розв’язанняЗадача
1. У механічному цеху оброблення деталей
здійснюється партіями з використанням
послідовного, паралельного,
паралельно-послідовного видів їх руху.
Обсяг оброблюваної партії деталей
становить 45 шт., а величина транспортної
партії — 5 деталей. Нормативна
тривалість окремих технологічних
операцій (відповідно першої, другої та
третьої) дорівнює дві, три та чотири з
половиною хвилини. Середній міжопераційний
час перерв становить 2 хв. На першій
і другій операціях задіяно по одному
верстату, а на третій — два верстати.
Природні процеси за обраною технологією
здійснюються протягом 30 хв. Роботу
механічного цеху організовано у дві
зміни по 8 год кожна. Коефіцієнт
використання двозмінного фонду робочого
часу — 0,706.
Розрахувати тривалість
технологічного й виробничого циклів
механічної обробки деталей за різних
способів поєднання операцій.
Задачі
для самостійного розв’язанняЗадача
1. У механічному цеху оброблення деталей
здійснюється партіями з використанням
послідовного, паралельного,
паралельно-послідовного видів їх руху.
Обсяг оброблюваної партії деталей
становить 45 шт., а величина транспортної
партії — 5 деталей. Нормативна
тривалість окремих технологічних
операцій (відповідно першої, другої та
третьої) дорівнює дві, три та чотири з
половиною хвилини. Середній міжопераційний
час перерв становить 2 хв. На першій
і другій операціях задіяно по одному
верстату, а на третій — два верстати.
Природні процеси за обраною технологією
здійснюються протягом 30 хв. Роботу
механічного цеху організовано у дві
зміни по 8 год кожна. Коефіцієнт
використання двозмінного фонду робочого
часу — 0,706.
Розрахувати тривалість
технологічного й виробничого циклів
механічної обробки деталей за різних
способів поєднання операцій.
Номер операції | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Норма часу, хв | 3 | 7 | 9 | 6 | 2 | 3 | 6 |
Кількість верстатів | 1 | 2 | 3 | 2 | 1 | 1 | 2 |
Визначити зміну тривалості цих циклів, якщо другу операцію розділити на дві операції з нормами часу 3 та 4 хв, кожну з яких виконують на одному верстаті.
Задача 4. Визначити максимальну додаткову кількість верстатів для організації виготовлення деталей без перерв у роботі устаткування, якщо деталі обробляються паралельно, порівняно з варіантом використання по одному верстату на кожній операції. У скільки разів збільшиться при цьому випуск виробів протягом зміни?
Норми часу по операціях при цьому: 5,0; 2,0 та 0,5 хв. Тривалість зміни — 8 год. Задача 5. На предметно-замкненій дільниці обробляється ведуча шестерня. Величина виробничої партії — 400 шт., передаточної партії — 20 шт. Процес здійснюється у дві зміни по 8 год. Міжопераційний час після кожної операції — 0,5 год. Технологічний процес та його параметри характеризуються даними, поданими в таблиці.
№ операції | Найменування операції | Кількість верстатів | Норма штучного часу, хв |
1 | Фрезерування торців | 1 | 2,2 |
2 | Попереднє обточування | 2 | 4,6 |
3 | Обточування конуса | 1 | 1,8 |
4 | Остаточне обточування | 1 | 3,0 |
5 | Нарізання зубів шестерні | 3 | 11,4 |
6 | Попереднє шліфування шийки | 1 | 2,4 |
7 | Фрезерування різі | 1 | 0,6 |
Визначити:
виробничий цикл простого процесу виготовлення шестерень (у календарних днях) за паралельного руху;
зміни тривалості циклу за умови, що п’ята операція виконується на одному верстаті;
зміни тривалості виробничого циклу за збільшення розміру партії в 1,5 раза та розміру передаточної партії до 40 шт.
Задача 6. Визначити, який вид руху деталей у процесі виробництва треба прийняти для обробки партії деталей у 500 шт., щоб одержати мінімальну тривалість технологічного циклу, якщо передачу деталей з операції на операцію транспортними партіями замінити поштучною передачею. П’ята партія виконується на трьох верстатах, кожна з решти — на одному верстаті. Технологічний процес обробки складається з таких операцій:
№ з/п | Найменування операції | Норма часу на операцію, хв |
1 | Свердління | 12 |
2 | Розточування | 3 |
3 | Протягування | 2 |
4 | Обточування | 15 |
5 | Зубонарізання | 30 |
6 | Протягування | 3 |
7 | Зняття задирок | 6 |
8 | Свердління | 3 |
рактичне заняття № 9
studfile.net
Урок «Структура задачі. Поняття «умова задачі», «запитання», «розв’язання», «відповідь». Складання і розв’язування задач»
Урок математики у 1 класі
Структура задачі. Поняття «умова задачі», «запитання», «розв’язання», «відповідь». Складання і розв
’язування задачМета: Сформувати поняття «умова задачі», «запитання», «розв’язання», «відповідь». Формувати вміння застосовувати нові знання при розв’язуванні задач. Продовжувати роботу над розумінням зв’язку дій додавання та віднімання, поняттями «збільшити», «зменшити». Закріплення вмінь вимірювати відрізки. Повторення геометричних фігур.
Очікувані результати:
Предметні компетентності: розвиток умінь виділяти головне, суттєве, порівнювати; закріплення знань взаємозв’язку дій додавання і віднімання, тренування обчислювальних навичок.
особистісні: уміння працювати самостійно, в парах, групах, слухати співрозмовника, вести діалог, аргументувати свою точку зору, оцінювати об’єктивно свої знання та вміння та виконання завдань однокласниками.
міжпредметні: вміти обробляти інформацію; формувати комунікативну компетенцію учнів; контролювати і оцінювати процес та результати своєї діяльності.
Задачі:
навчальні: забезпечити свідоме сприйняття та засвоєння нових знань; створення умов для систематизації та засвоєння нових знань учнів;
виховні: уміння слухати та вступати в діалог, формувати уважність та охайність в обчисленнях, виховувати почуття взаємодопомоги, шанобливе ставлення до думки інших, культури навчальної праці;
розвивальні: сприяти розвитку творчої активності учнів; підвищити пізнавальний інтерес до предмета; розвиток навичок та здібностей критичного мислення ,образного мислення, фантазії дітей та їх здібності міркувати.
Використані технології:
Технологія формування критичного мислення.
ІКТ.
Технологія співпраці.
Гуманно-особистісна (створення ситуації успіху).
Форми роботи: робота в парах, групах, самостійна, фронтальна.
І. Мотивація. Привітання.
—Всі почули ви дзвінок—
Він покликав на урок.
Кожен з вас приготувався—
На перерві постарався.
Тож тепер часу не гаймо,
І урок розпочинаймо.
Стали, дітки,підтягнулись,
Одне одному всміхнулись,
І до гостей повернулись,
Та шановним посміхнулись.
—Діти, посмішка – це наш вірний друг у будь- якій справі. Тільки у гарному настрої ми розвиваємось, досягаємо мети, мріємо, радіємо успіхам товаришів та ловимо такого птаха, який називається «УСПІХ». Отже, я бажаю успіху 1 класу!
 Анімаційні слайди до орг. моменту:
Анімаційні слайди до орг. моменту:




—Діти, у народі говорять, що добрий гість—дому радість. До нас сьогодні завітали шановні гості подивитися на першокласників. Обіцяла завітати ще одна гостя—Білосніжка, але чомусь її досі немає. Ось лише якийсь лист лежить. Він адресований нам: «Учням 1 класу від Змія триголового». Прочитаємо?
Білосніжку взяв в полон

 Я, Змій триголовий.
Я, Змій триголовий.
А за звільнення таку
Ставлю я умову:
Якщо учні всі завдання
Зможуть розв’язати,
В себе в класі Білосніжку
Зможуть привітати.
А якщо мої завдання
Хтось зробить не вміє,
То назавжди Білосніжка
Лишиться у Змія.
А завдання ці я Гномам
Вже роздав й чекаю,
Чи віддати Білосніжку,
Чи залишити? Не знаю!
ІІ. Постановка загального завдання.
—Отже,діти, яке наше завдання на уроці? (Врятувати Білосніжку, виконавши всі його завдання).
 Завдання уроку:
Завдання уроку:
ІІІ. Повторення вивченого. Актуалізація знань.
 Пальчикова гімнастика
Пальчикова гімнастика
- Каліграфічна хвилинка. «Впізнай цифри».
Цвьохнув Змій своїм довгим хвостом і поламав наші цифри. Засмутився Дрімунчик : «Чи впізнають діти цифри?»
Нам треба їх полагодити .(Записати полагоджені цифри в зошит.)
1 4 7 2 3 8 6 9 0 5
Назвіть ці цифри у порядку зростання чисел, які вони позначають.
Назвіть у порядку спадання.
Які цифри позначають чарівні числа? (3,7) Чому? (Казкові, незвичайні: 3 голови у Змія, 3 сини у казках, 3 дороги, 3 богатирі, 7 днів тижня, 7 гномів і т. п.)
—Запишіть каліграфічно числа 3 і 7 у зошит, щоб Змію сподобалось.
Робота на картках(диференційована). Перевірка умінь додавати та віднімати 1.
Молодці! Виконали перше завдання.
2. Робота з підручником( №1, с.50).
 Розсердився Змій, що ми правильно виконали його перше завдання, і дає нам складніше: скласти і розв’язати приклади на додавання та віднімання.
Розсердився Змій, що ми правильно виконали його перше завдання, і дає нам складніше: скласти і розв’язати приклади на додавання та віднімання.
« Чи впораємось ми з ним?»—задумався
Чихунчик.
БЕСІДА. –Що означає додати, відняти? (Знайти суму,остачу).
— Що ми робимо при додаванні, відніманні? (При додаванні –об’єднуємо, при відніманні—вилучаємо).
—Що треба зробити, щоб зменшити (збільшити) кількість предметів?
4 качани було, та зайчик зменшив їх число :
1 качан він з грядки зняв, від чотирьох один відняв.
Щоб зменшити, треба відняти.
3 капустини в нас було, а зайчик збільшив їх число:
Ще 2 на возику примчав, зайчисько два до трьох додав.
Щоб збільшити, треба додати..

 3.Робота на планшетах для зворотнього зв’язку. Складання і розв’язання прикладів із самоперевіркою за анімаційними слайдами (10 прикладів), наприклад:
3.Робота на планшетах для зворотнього зв’язку. Складання і розв’язання прикладів із самоперевіркою за анімаційними слайдами (10 прикладів), наприклад:
4.Повторення зв’язку дій додавання і віднімання.
— Чи можемо ми останні два приклади назвати взаємооберненими? Чому? (Від суми 9 відняли один з доданків і отримали другий.)
4+5=9 9-5=4
— Складіть ще один приклад на віднімання. (9-4=5)
Впорались ми і з цим завданням. Ми—молодці!
Фізкультхвилинка .
Щоб нам Змія подолати,
Важливо всі завдання розв’язати.
Але ще, на всяк випадок,
Треба м’язи розім’яти.
Раз,два! Всі присіли,
Потім вгору полетіли.
Три,чотири! Нахилились,
Із струмочка гарно вмились.
П’ять,шість! Всі веселі
Крутимось на каруселі.
5. Поняття і термін «задача», види задач.
—Діти, чим приклад відрізняється від задачі?
—Що таке ЗАДАЧА? (Це такий вид математичної вправи, коли самому треба вказати дію до даних чисел, щоб відповісти на запитання.)
— Які види задач ми вже знаємо? (На знаходження суми та остачі).
ІV. Проблемна ситуація (робота в групах).
— Розв’яжемо задачі.
1.У Сергійка 5 кроликів, а у Толі 4. Скільки всього зошитів купили? (Не можемо розв’язати, тому що запитання не відповідає змісту умови).
2. На гілці сиділо 8 сорок, 2 перелетіло на інше дерево. (Немає питання, немає завдання.)
3. Скільки всього кущів посадили учні? (Немає даних задачі, немає умови.)
V. Визначення теми і мети уроку учнями за допомогою вчителя.
—Отже,що треба знати, щоб правильно, зрозуміло скласти задачу, щоб ми змогли її розв’язати, щоб будь-хто зміг її розв’язати? (Треба знати, з яких частин складається задача. )
—Звернемось до завдань уроку:

«Якщо ми не вивчимо
 будову задачі,
будову задачі,
не бачити нам Білосніжки,
а це таке важке завдання,
мабуть, прийдеться битися
зі Змієм!»,—нервується третій гном Буркунчик.
—Як думаєте, дітки, вивчимо? А допоможуть
нам в цьому наші вірні друзі: Равлик і Сонечко.
VІ. Вивчення нового матеріалу. Урок № 18 педагогічного програмного засобу освітньої галузі «Математика»
(фрагмент). Під час перегляду фрагмента ведуться записи на дошці та в зошитах розв’язання задач, повторення структурних елементів задачі.
 —Доведемо Змію, що ми запам’ятали назви частин задачі (повторення хором та індивідуально.)
—Доведемо Змію, що ми запам’ятали назви частин задачі (повторення хором та індивідуально.)
—Чи пригодяться нам ці знання? А для чого? (Ми тепер вміємо складати і розв’язувати задачі). І це дуже добре, адже Змій ще дужче розлютився, що 1-А такий розумний, і хоче перевірити, чи вміємо ми працювати парами та в групах, чи дружні діти, чи вмієте ви допомагати товаришеві та доводити свою думку.
Фізкультхвилинка під музику пісні «Усмішка».
VІ. Первинне закріплення знань.
- Робота в парах у зошитах з друкованою основою О.Черевко,
В. Федієнка «Математичні прописи» на сторінках 46, 47.
 Стидунчик : «Розв’яжіть задачі і дайте відповідь на запитання.»
Стидунчик : «Розв’яжіть задачі і дайте відповідь на запитання.»
Молодці!
2. Робота в групах.
 Мудрунчик плескає в долоні, бо впевнений, що наші учні ,
Мудрунчик плескає в долоні, бо впевнений, що наші учні ,
хоч іще тільки в 1 класі, але вже вміють працювати в групах.
 А от Змій вважає, що це завдання ми ніколи не виконаємо, бо він і сам не знає, як скласти задачу. Завдання: за малюнком скласти 1 групі умову задачі, 2 групі запитання, 3 групі розв’язання, 4 – відповідь, а 5 групі визначити вид задачі.
А от Змій вважає, що це завдання ми ніколи не виконаємо, бо він і сам не знає, як скласти задачу. Завдання: за малюнком скласти 1 групі умову задачі, 2 групі запитання, 3 групі розв’язання, 4 – відповідь, а 5 групі визначити вид задачі.
Презентація відповідей.
 VІІ.Самостійна робота у зошиті з друкованою основою з перевіркою за еталоном на дошці. Допоможемо Задумчику розв’язати задачу,щоб довести Змієві, що всі вміють це робити.
VІІ.Самостійна робота у зошиті з друкованою основою з перевіркою за еталоном на дошці. Допоможемо Задумчику розв’язати задачу,щоб довести Змієві, що всі вміють це робити.
VІІІ. Повторення геометричного матеріалу за слайдами.
 —А з Веселунчиком ми помандруємо в країну Геометрію до геометричних фігур, адже саме там тримає Змій нашу Білосніжку – на безлюдному острові серед фігур. І завдання наше – пригадати назви всіх фігур та виміряти відрізки.
—А з Веселунчиком ми помандруємо в країну Геометрію до геометричних фігур, адже саме там тримає Змій нашу Білосніжку – на безлюдному острові серед фігур. І завдання наше – пригадати назви всіх фігур та виміряти відрізки.
Самостійна практична робота. Вимірювання відрізків на картках. Після виконання – фронтальна перевірка.
ІХ. Підсумки уроку. Рефлексія. Обличчя настрою.
—Чи виконали ми завдання уроку? Які були труднощі?
—Що нового дізнались? Чого навчились?
—Допомагаючи Гномам, ми виконали багато роботи, і не тільки врятували Білосніжку, а й стали набагато розумнішими, навчилися складати задачі, вивчивши їх будову, закріпили вміння складати і розв’язувати приклади, вимірювати відрізки, а найголовніше: ми вчилися співпрацювати та бути дружними, адже тільки в дружному класі можна подолати будь-які труднощі. Ми – молодці!
Підніміть ті обличчя настрою, який ви відчуваєте зараз.





naurok.com.ua
Типові задачі і їх розв’язуваня
1. У результаті
аналізу рахунків 200 інвесторів на
фондовій біржі отримали таку інформацію
про кількість угод, укладених протягом
місяця (див. табл. 3, у якій 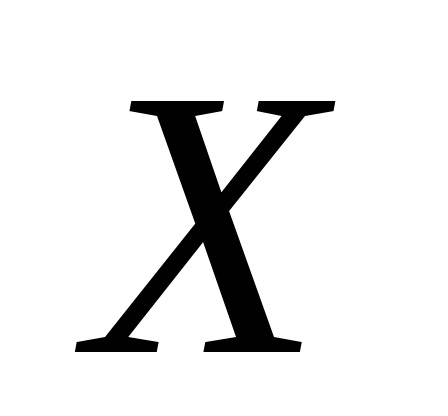 – кількість укладених угод, а
– кількість укладених угод, а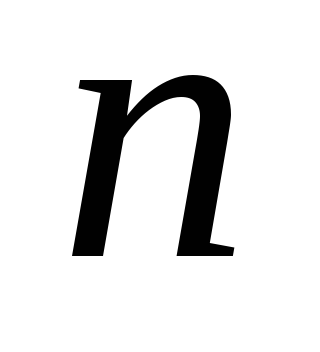 – кількість інвесторів).
– кількість інвесторів).
Таблиця 3

0
1
2
3
4
5
6
8

68
43
37
25
14
4
7
2
Знайти функцію
розподілу кількості укладених угод та
обчислити 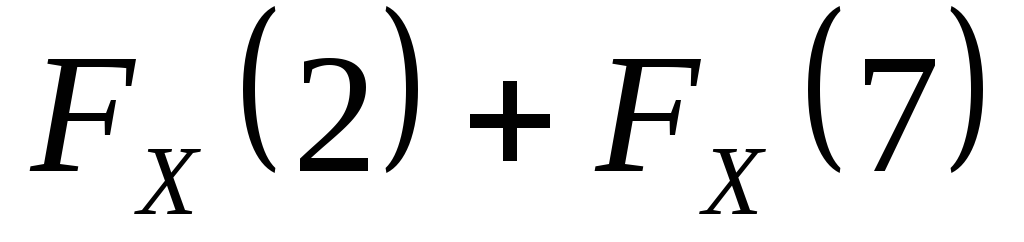 .
.
Розв’язування.
На підставі формули (2), функцію розподілу
випадкової величини 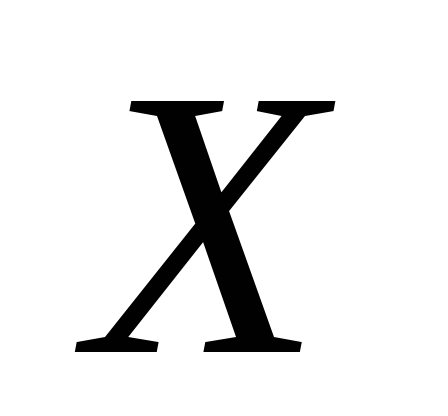 – кількості укладених угод можна подати
такою формулою:
– кількості укладених угод можна подати
такою формулою:
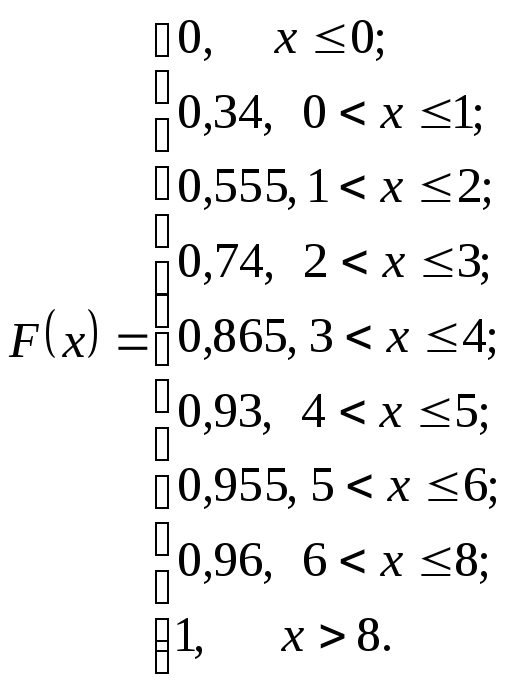
Оскільки 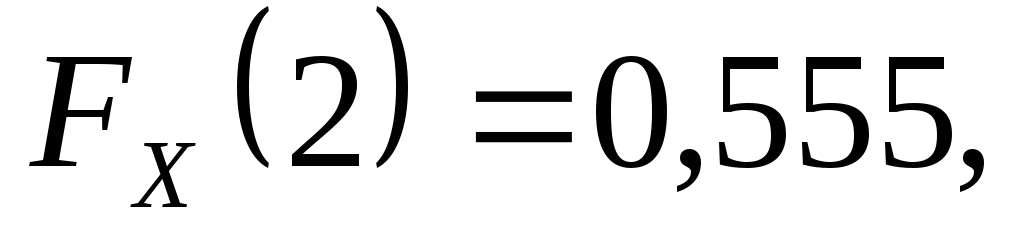 а
а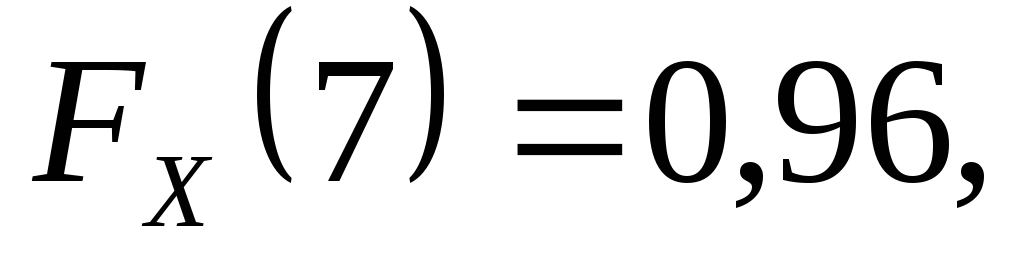 то
то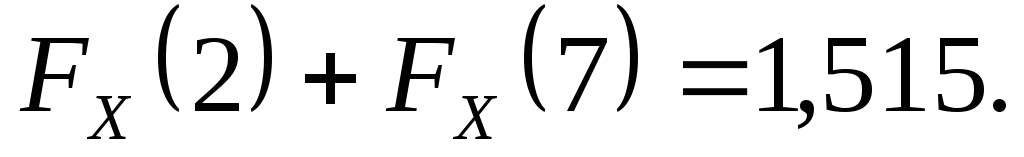
2. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення дискретної випадкової величини, заданої законом розподілу
Таблиця 4

-1
1
2
4

0,3
?
0,2
0,1
Розв’язування.
Для розв’язування задачі використаємо
формули (7), (18) і (23). Обчислимо спочатку
невідому ймовірність 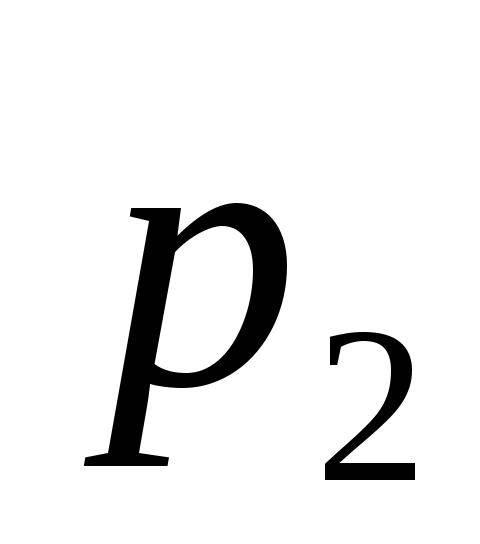 .
Оскільки сума ймовірностей всіх
значень випадкової величини (сума чисел
у другому рядку таблиці) дорівнює
одиниці, то
.
Оскільки сума ймовірностей всіх
значень випадкової величини (сума чисел
у другому рядку таблиці) дорівнює
одиниці, то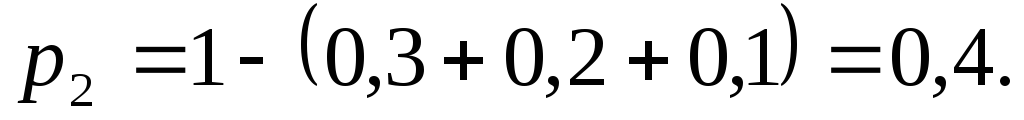 Математичне сподівання заданої випадкової
величини дорівнює
Математичне сподівання заданої випадкової
величини дорівнює
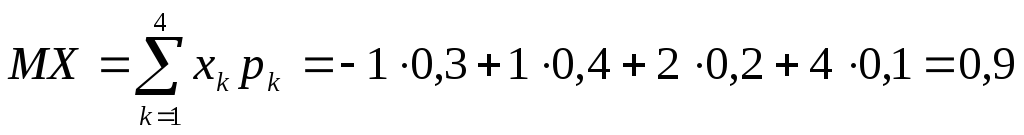 .
.
Перед тим як знайти
дисперсію, обчислимо 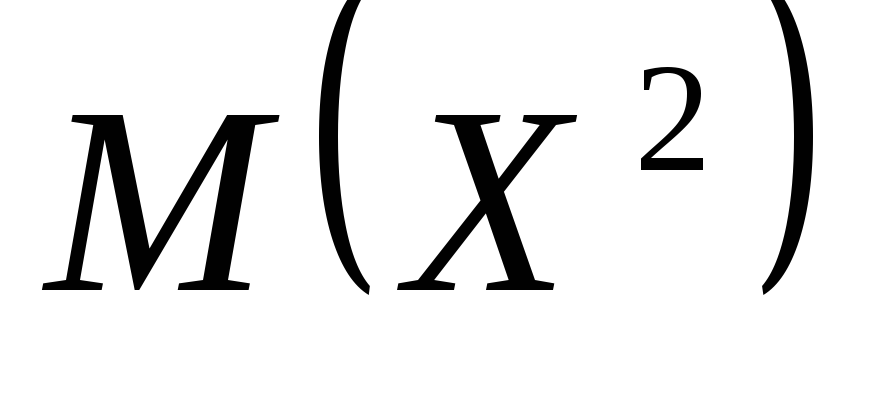 за формулою (19).
за формулою (19).
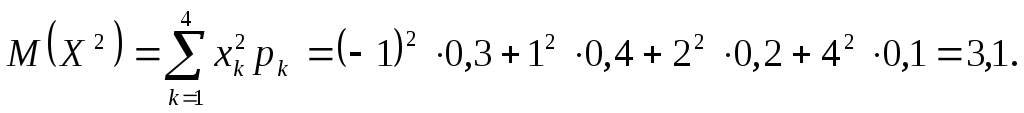
Тепер знайдемо дисперсію
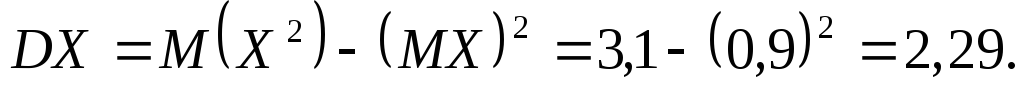
Середнє квадратичне відхилення заданої випадкової величини буде рівне
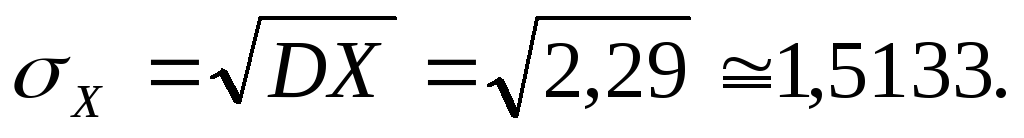
3. Випадкова
величина 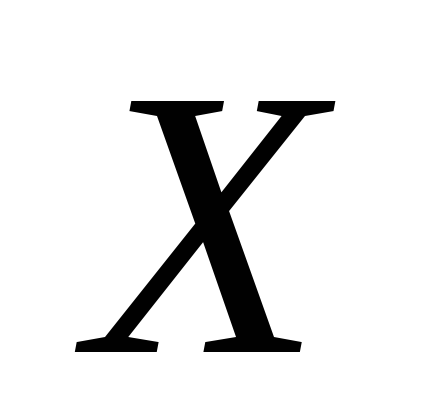 приймає лише два можливі значення
приймає лише два можливі значення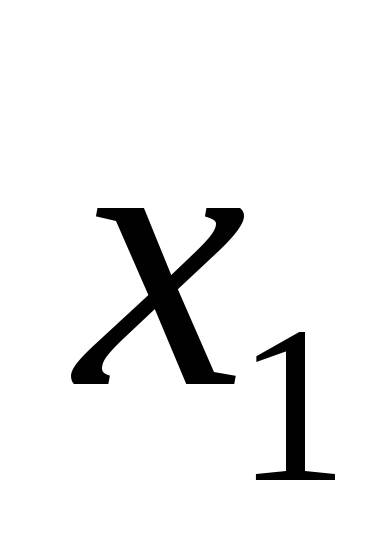 та
та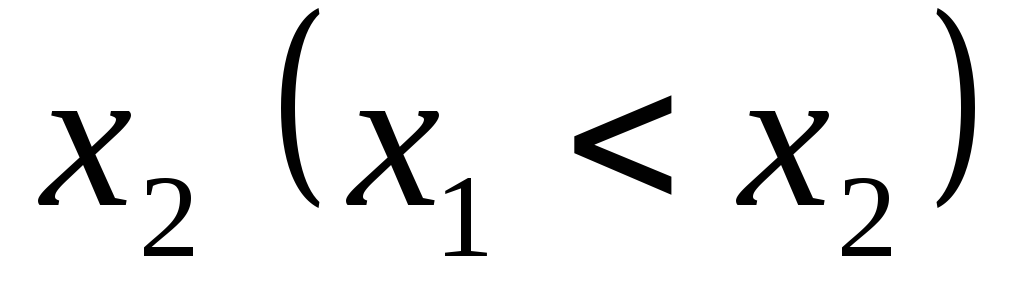 з ймовірностями
з ймовірностями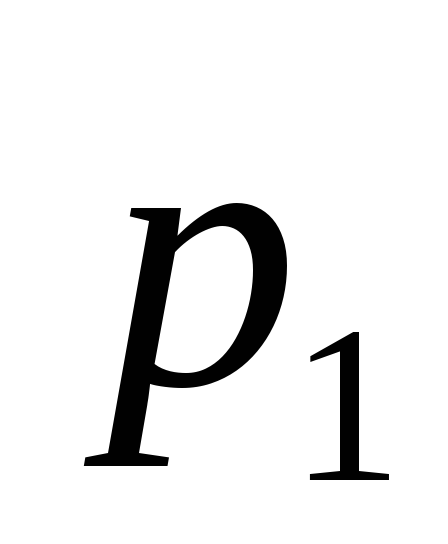 і
і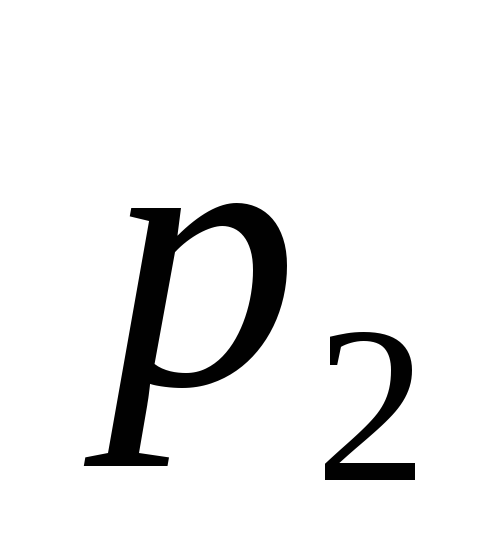 .
Знайти
.
Знайти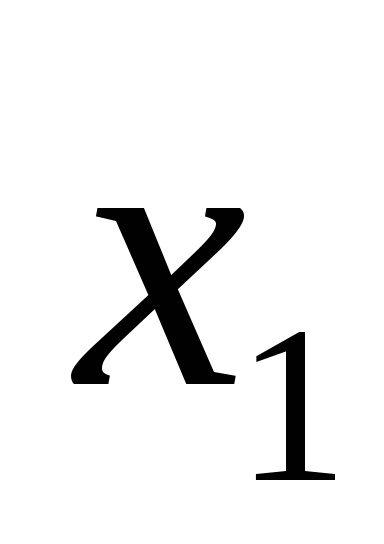 та
та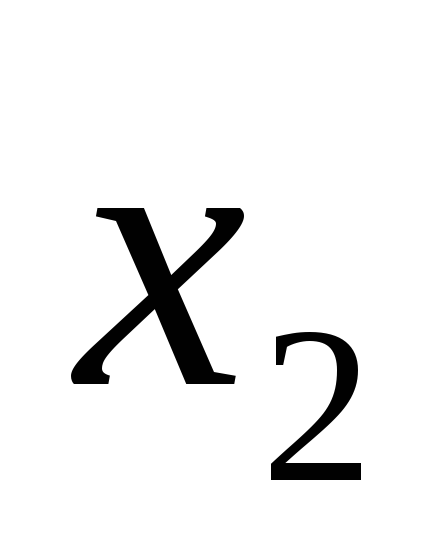 ,
якщо
,
якщо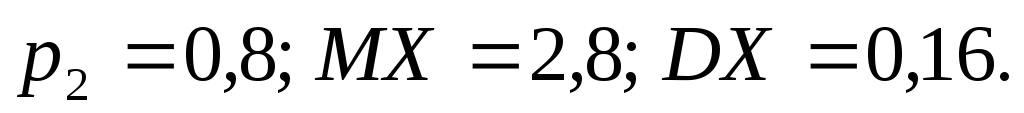
Розв’язування.
Оскільки випадкова величина 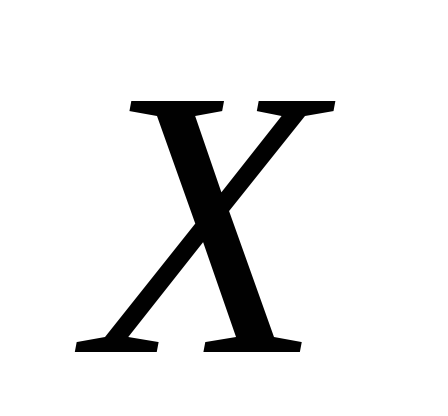 приймає лише два можливі значення, то
приймає лише два можливі значення, то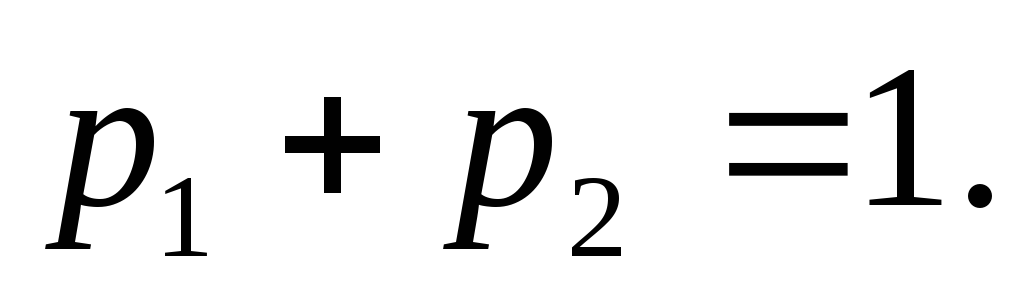 Звідси, врахувавши, що за умовою
Звідси, врахувавши, що за умовою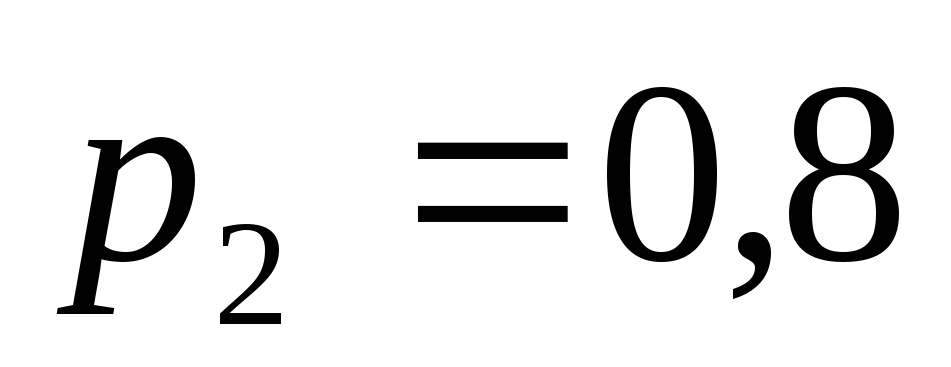 ,
знаходимо
,
знаходимо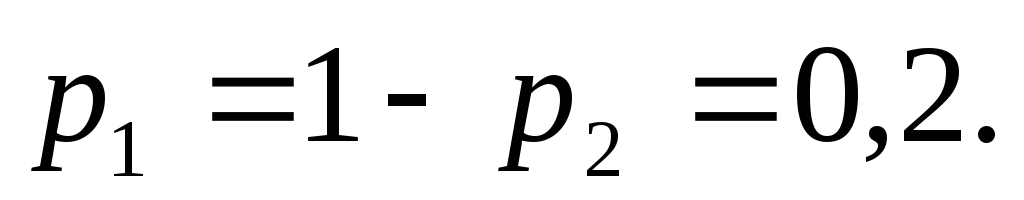 За умовою
За умовою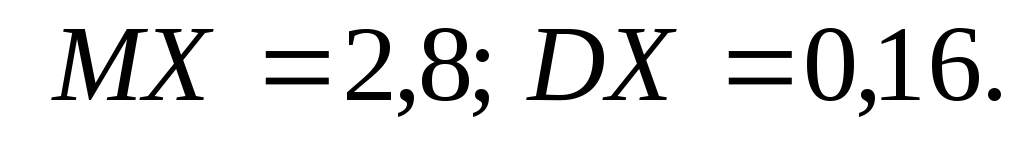 Використавши формулу (18), одержимо
Використавши формулу (18), одержимо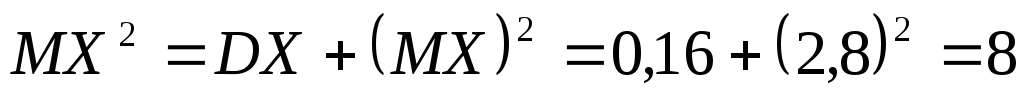 .
Тому для знаходження
.
Тому для знаходження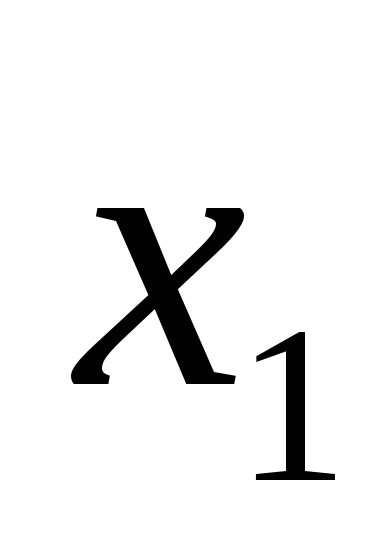 та
та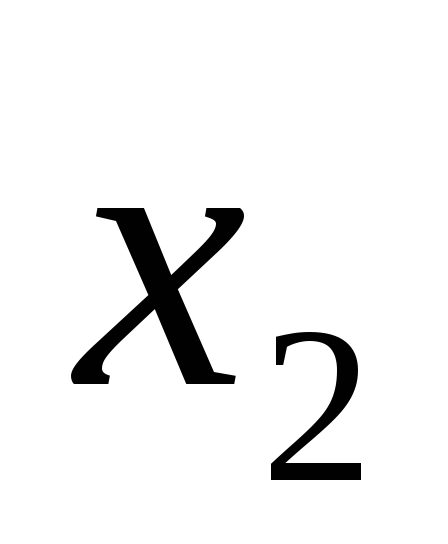 отримаємо систему двох рівнянь
отримаємо систему двох рівнянь
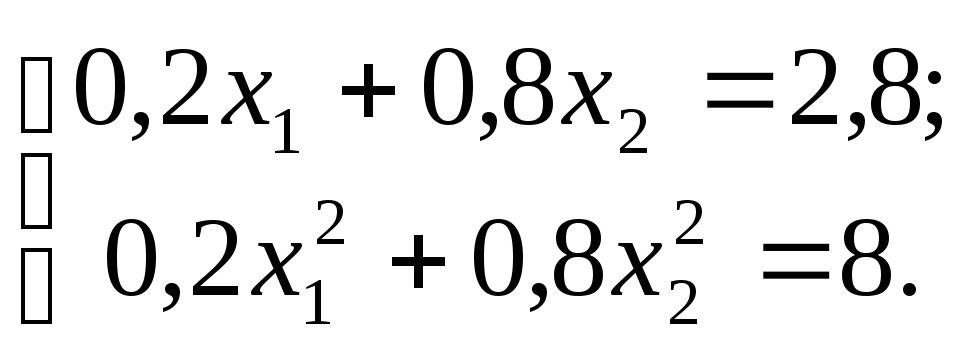
розв’язавши цю
систему рівнянь при умові 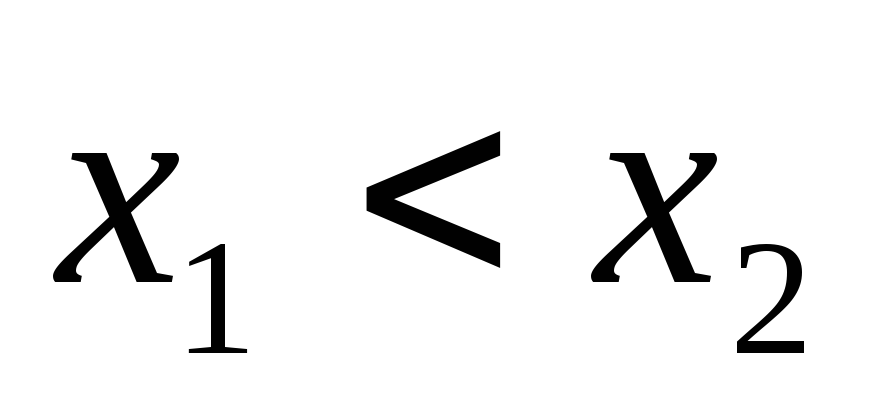 ,
одержимо
,
одержимо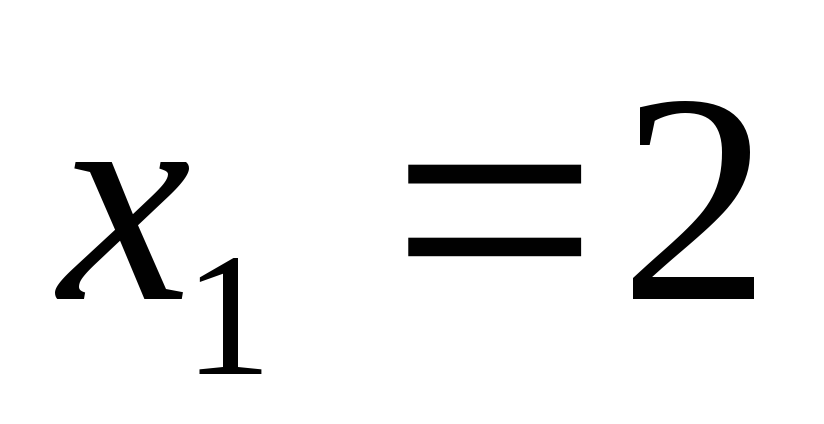 і
і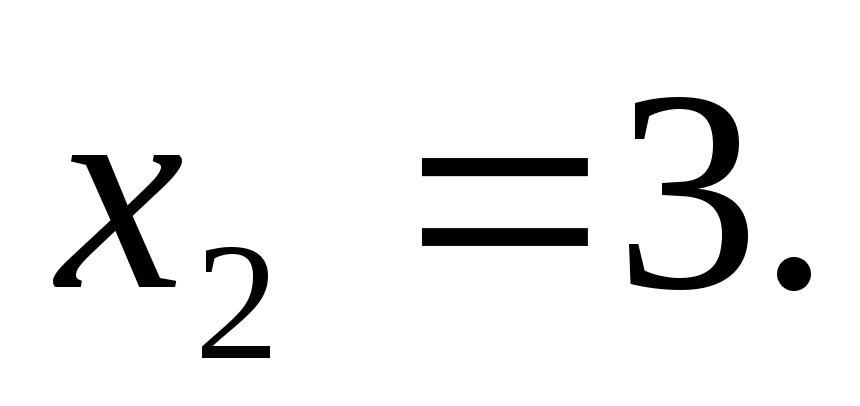
4. Математичне
сподівання дискретної випадкової
величини 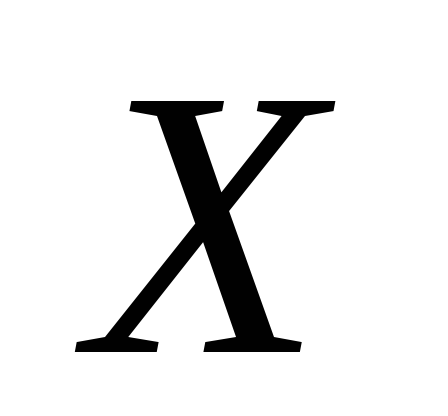 ,
яка набуває три можливі значення,
дорівнює 1,8. Задано два з цих значень
,
яка набуває три можливі значення,
дорівнює 1,8. Задано два з цих значень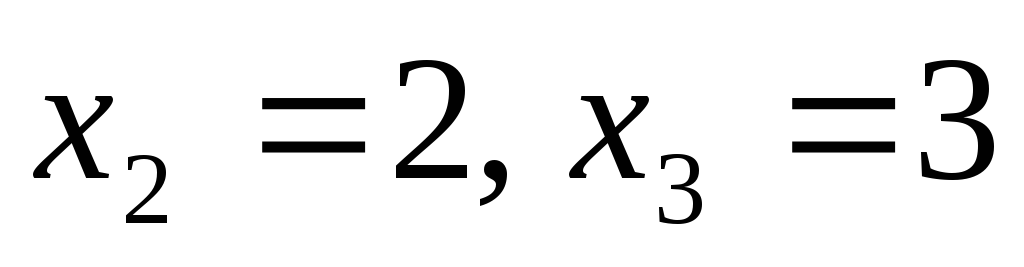 та їхні ймовірності
та їхні ймовірності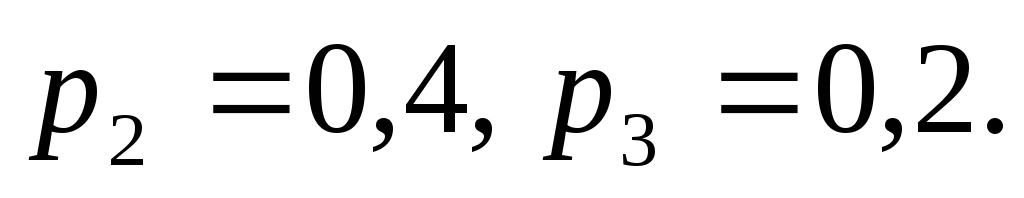 Знайти невідоме значення величини
Знайти невідоме значення величини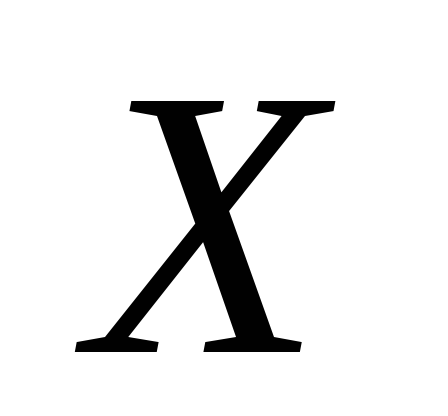 ,
а також середнє квадратичне відхилення,
коефіцієнт асиметрії та ексцес.
,
а також середнє квадратичне відхилення,
коефіцієнт асиметрії та ексцес.
Розв’язування.
Спочатку знайдемо невідому ймовірність 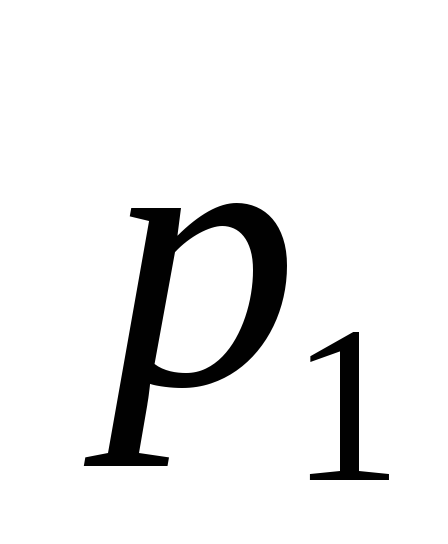 .
Оскільки випадкова величина
.
Оскільки випадкова величина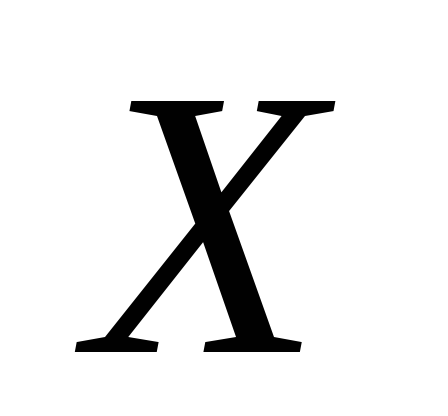 приймає лише три можливі значення, то
приймає лише три можливі значення, то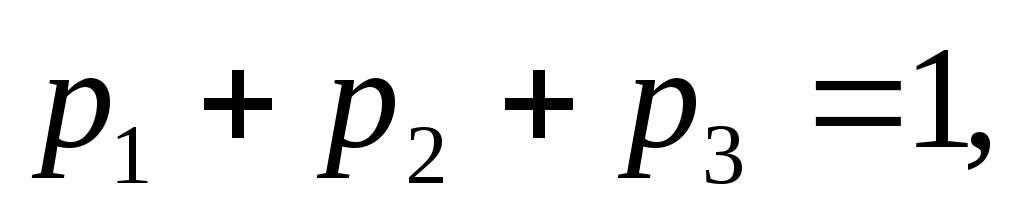 то
то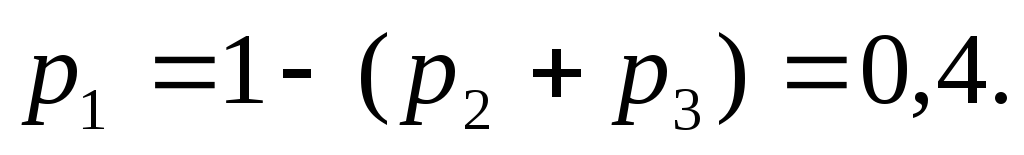
Математичне сподівання дискретної випадкової величини дорівнює сумі попарних добутків значень цієї величини на їхні ймовірності. Тому за умовою
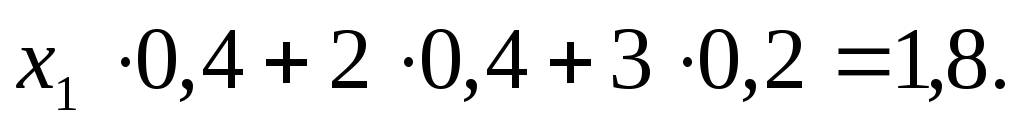
Звідси 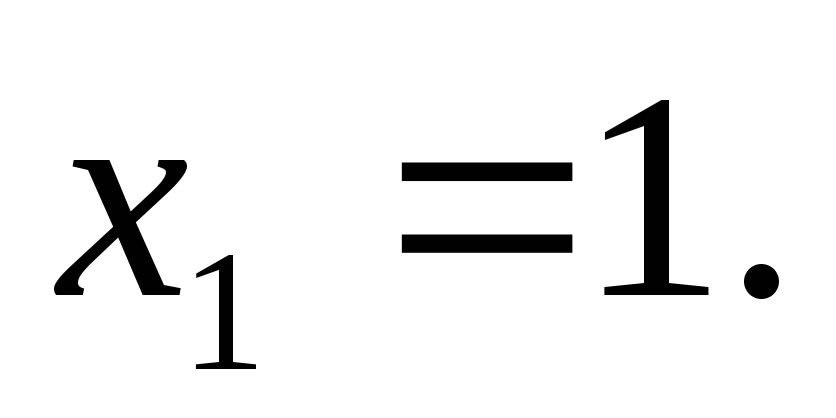
Обчислимо початкові
моменти 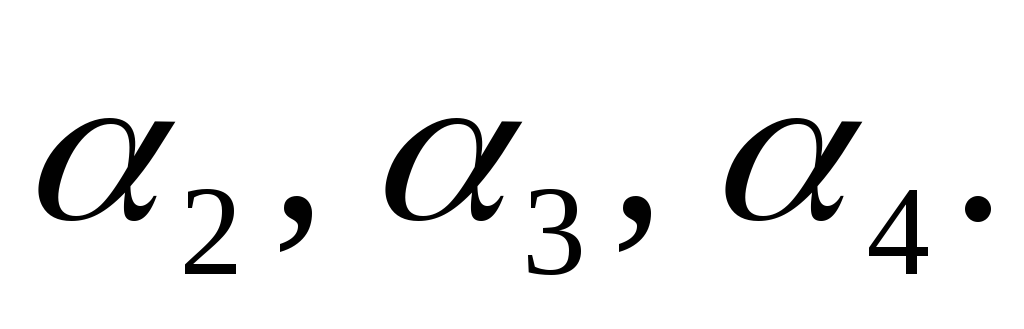
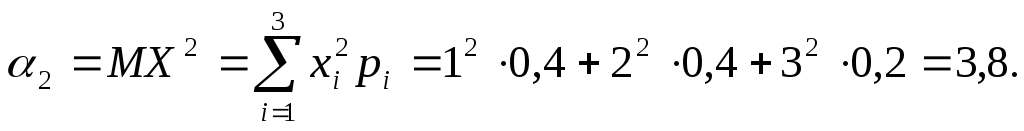
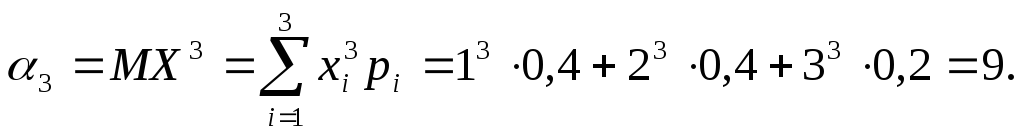
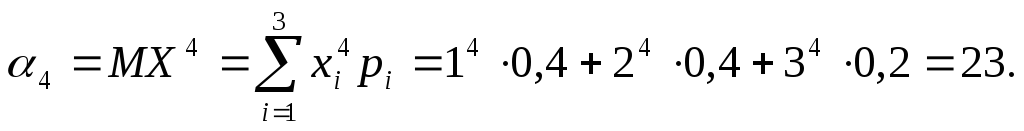
Тепер можна знайти дисперсію і середнє квадратичне відхилення
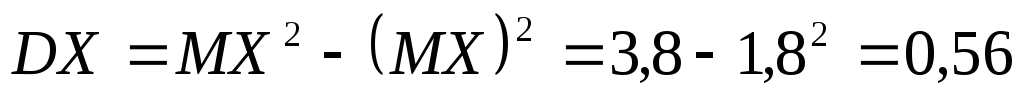 ,
, 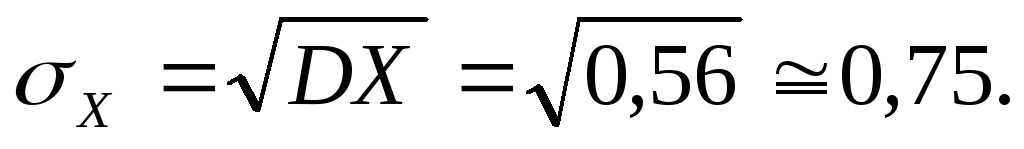
Для знаходження
коефіцієнта асиметрії та ексцесу
обчислимо центральні моменти третього
та четвертого порядку. При цьому урахуємо
те, що 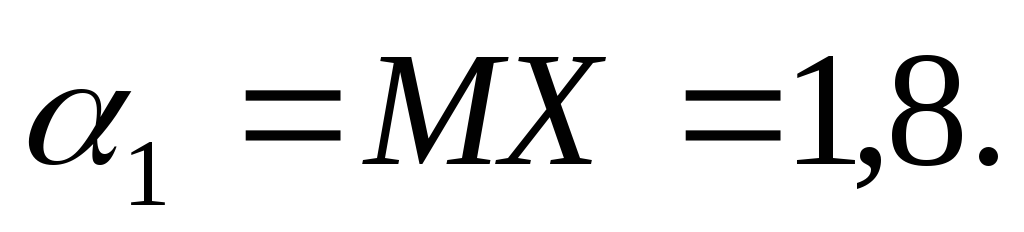 Отже
Отже
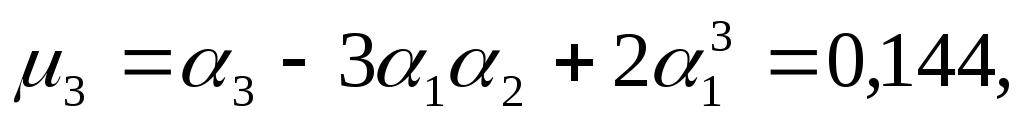
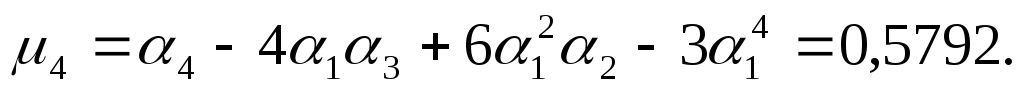
Звідси за формулами (30) і (31) одержимо
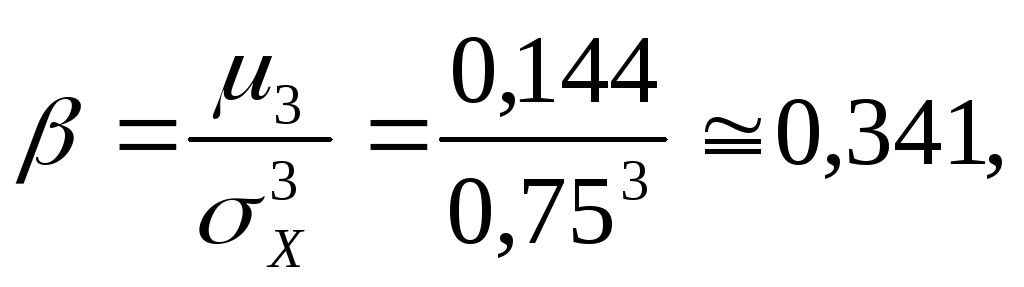
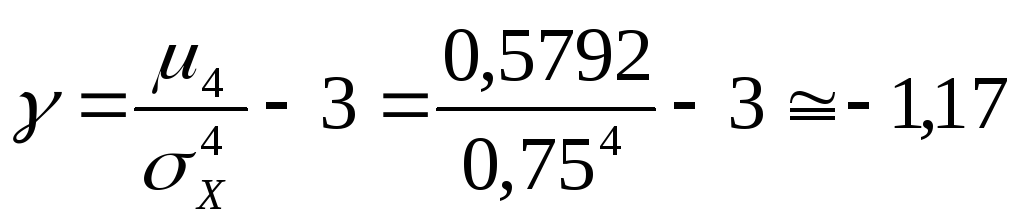 .
.
5. В містечку
тільки три великих підприємства.
Ймовірність невчасної сплати податку
першим підприємством дорівнює 0,05, другим
– 0,07 і третім – 0,09. Записати закон
розподілу дискретної випадкової величини 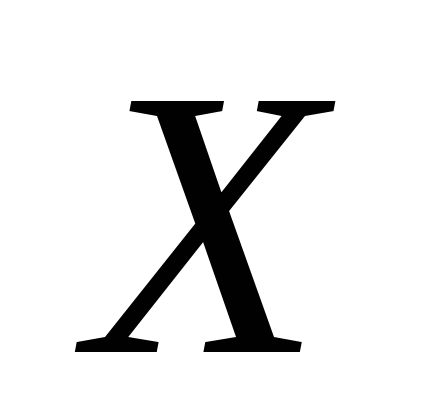 – кількість підприємств, що вчасно
сплатять податок. Обчислити математичне
сподівання величини
– кількість підприємств, що вчасно
сплатять податок. Обчислити математичне
сподівання величини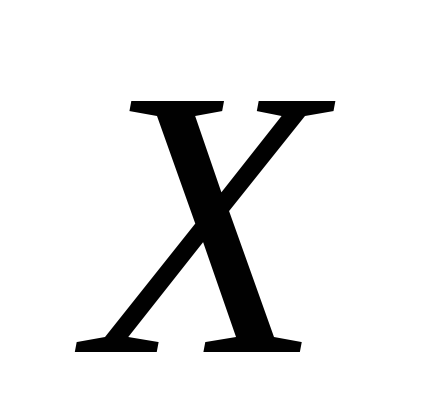 .
.
Розв’язування.
Випадкова величина 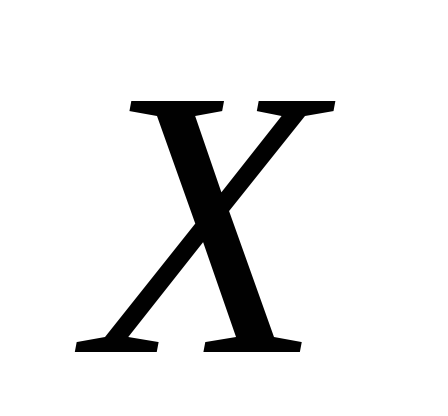 може приймати чотири значення: 0, 1, 2, або
3. Для кращого розуміння розглянемо ще
чотири події. Нехай подія
може приймати чотири значення: 0, 1, 2, або
3. Для кращого розуміння розглянемо ще
чотири події. Нехай подія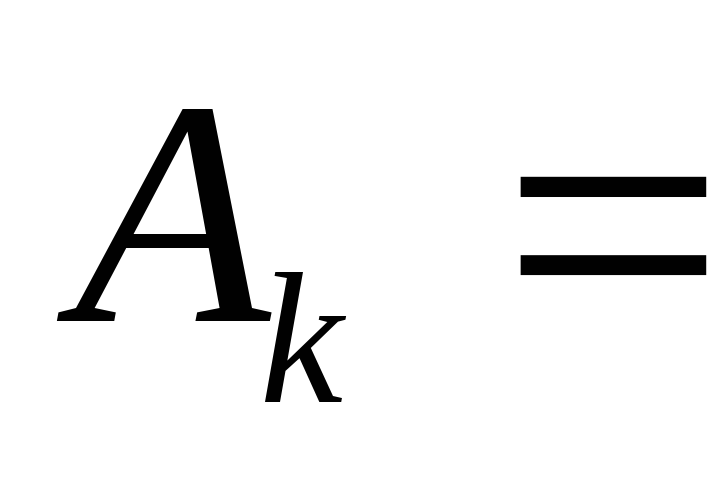 {вчасно
сплатять податок
{вчасно
сплатять податок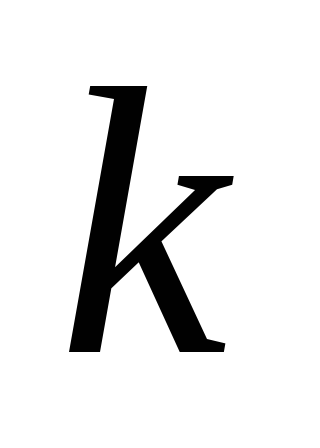 підприємств}
підприємств}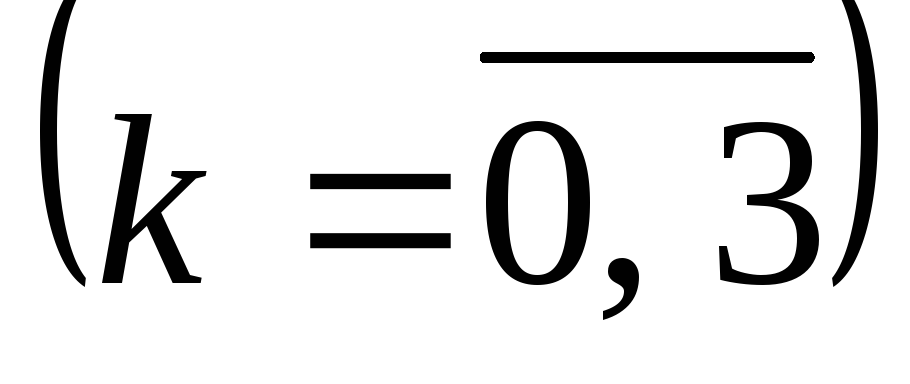 .
Знайдемо ймовірності цих подій, тобто
ймовірності того, що величина
.
Знайдемо ймовірності цих подій, тобто
ймовірності того, що величина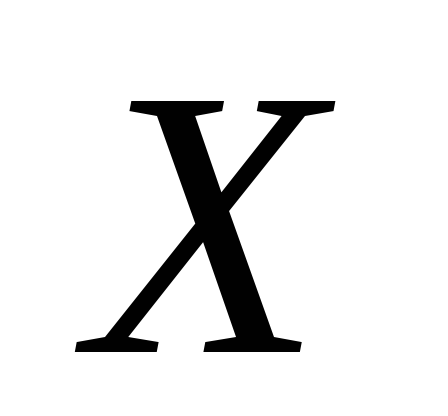 прийме кожне з розглянутих значень.
прийме кожне з розглянутих значень.
Позначимо ймовірність
вчасної сплати податку 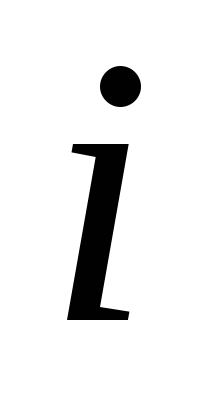 -им
підприємством через
-им
підприємством через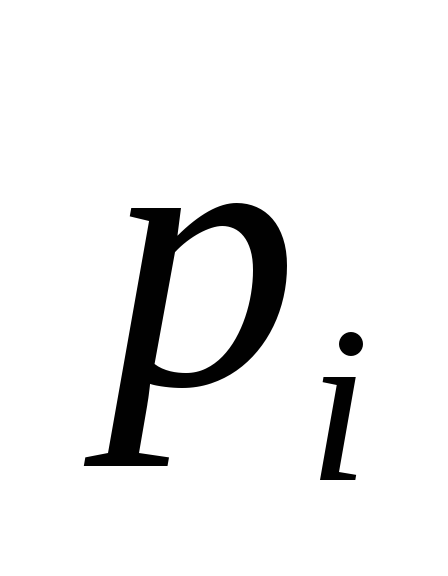 ,
а невчасної –
,
а невчасної –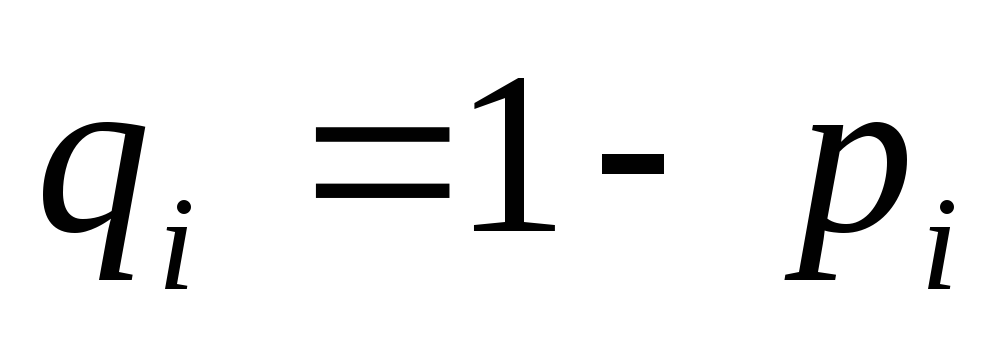 .
За умовою задачі
.
За умовою задачі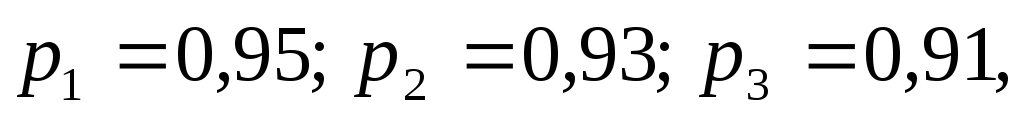 а
а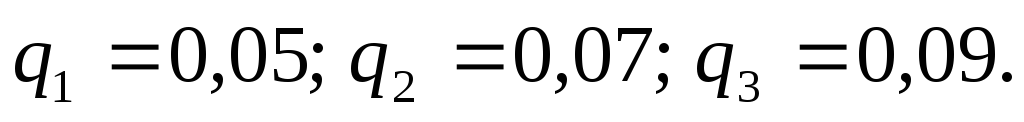 Тоді
Тоді
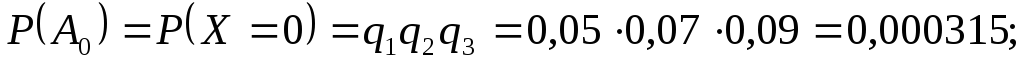
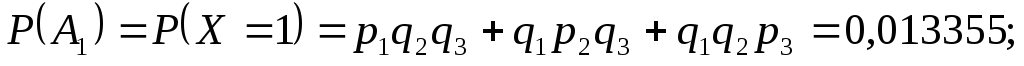
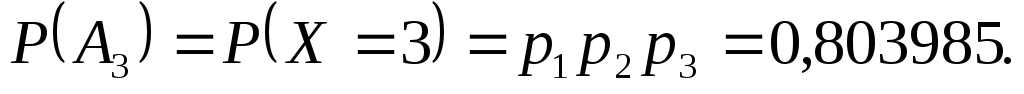
Отже, закон розподілу
дискретної випадкової величини 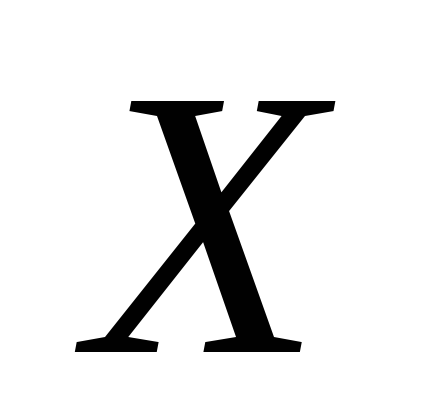 у табличній формі запишеться таким
чином
у табличній формі запишеться таким
чином
Таблиця 5

0
1
2
3

0,000315
0,013355
0,182345
0,803985
Математичне сподівання цієї величини буде
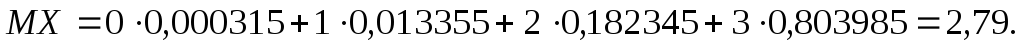
6. За заданою функцією розподілу
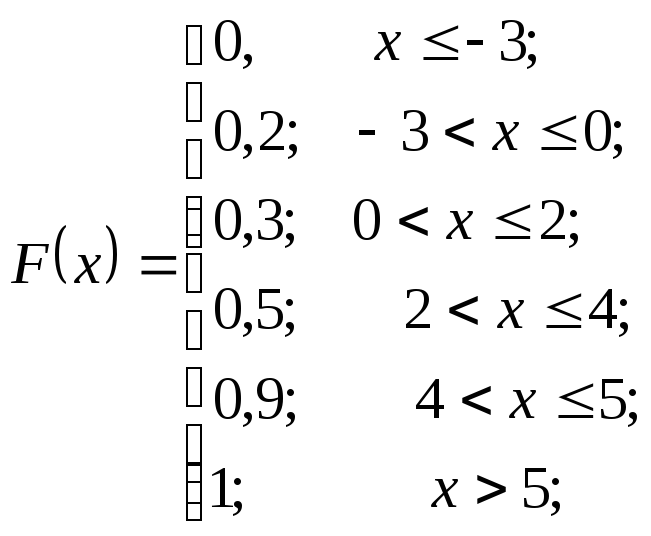
дискретної
випадкової величини 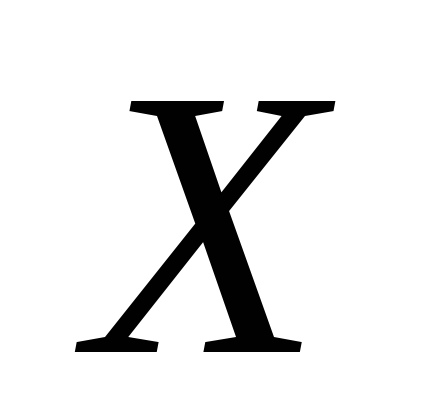 обчислити середнє квадратичне відхилення.
обчислити середнє квадратичне відхилення.
Розв’язування.
З умови задачі (з аналітичного запису
функції розподілу) зрозуміло, що
випадкова величина 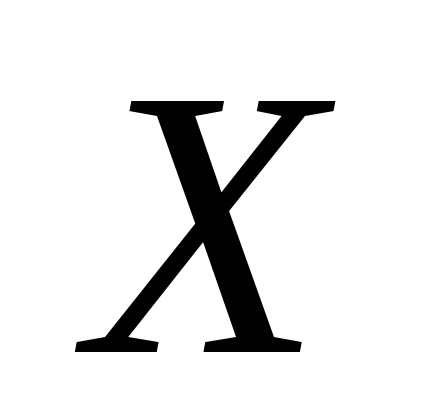 може приймати п’ять значень: -3, 0, 2, 4 і
5. Оскільки значення
може приймати п’ять значень: -3, 0, 2, 4 і
5. Оскільки значення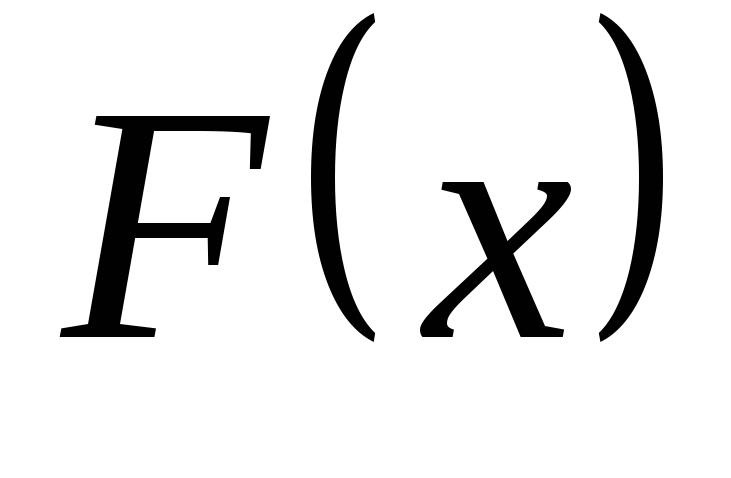 для
для 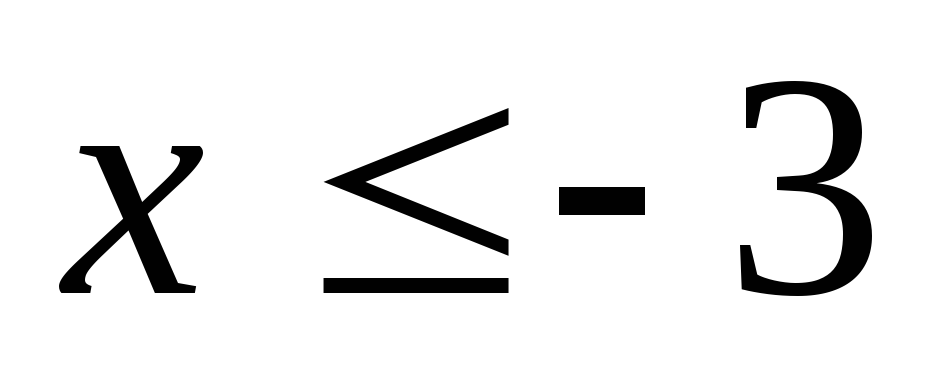 дорівнює нулю, а для
дорівнює нулю, а для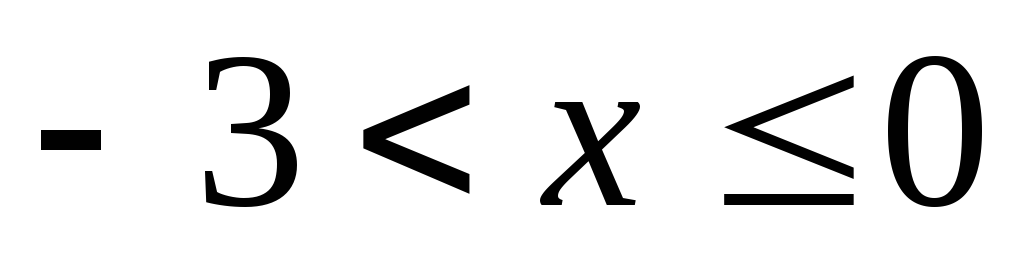 – дорівнює 0,2, то ймовірність того, що
випадкова величина
– дорівнює 0,2, то ймовірність того, що
випадкова величина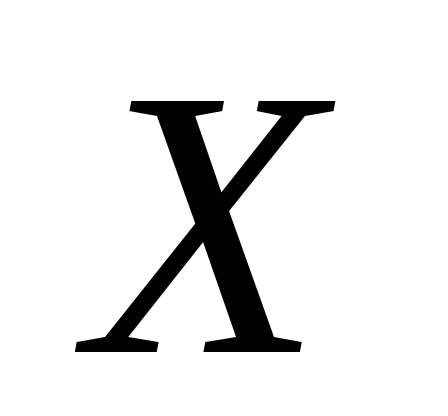 прийме значення (-3) буде дорівнювати
прийме значення (-3) буде дорівнювати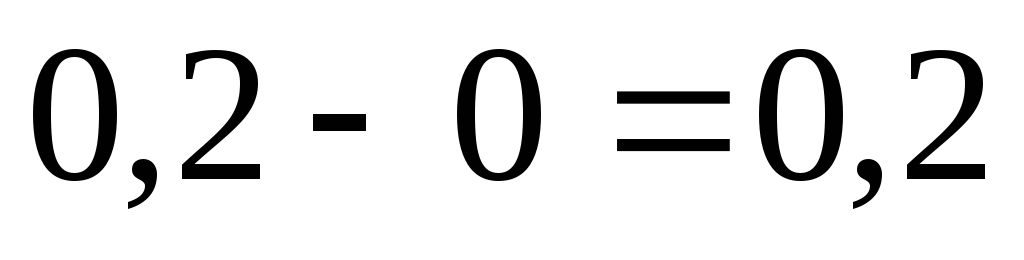 .
Тобто
.
Тобто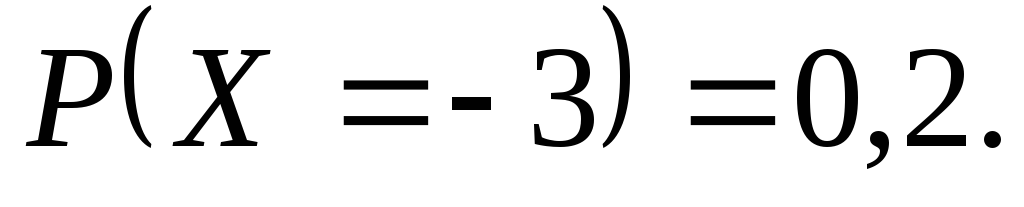 Аналогічно знаходимо інші ймовірності
Аналогічно знаходимо інші ймовірності
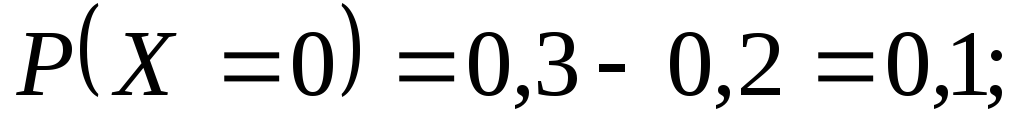
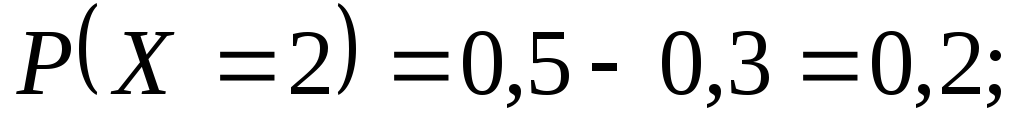
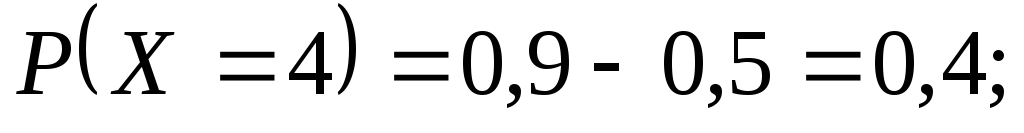
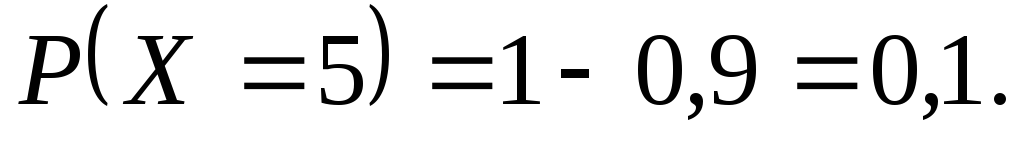
Таким чином, закон
розподілу дискретної випадкової величини 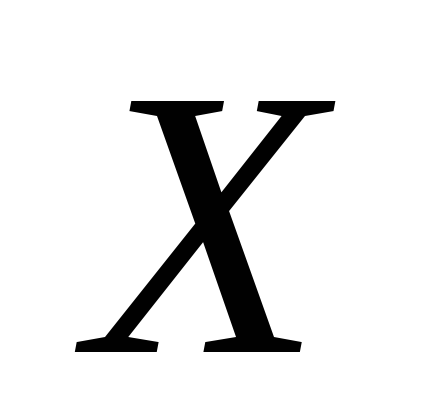
у табличній формі запишеться так
Таблиця 6

-3
0
2
4
5

0,2
0,1
0,2
0,4
0,1
Звідси
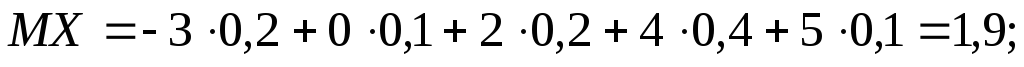
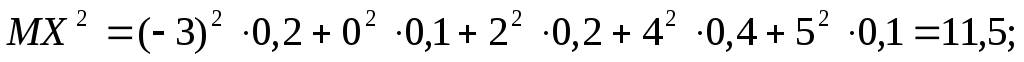
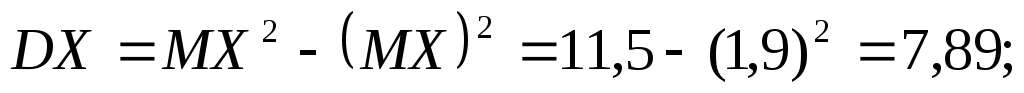
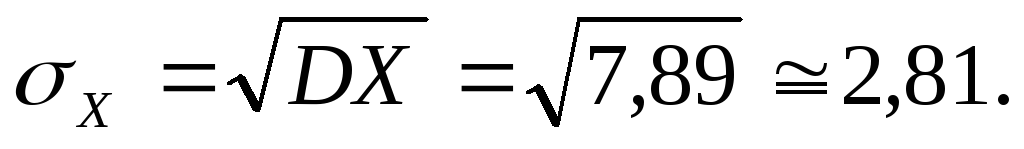
Отже, середнє
квадратичне відхилення дискретної
випадкової величини 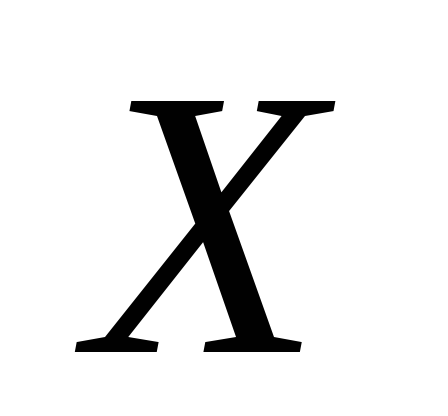 ,
яка задана функцією розподілу
,
яка задана функцією розподілу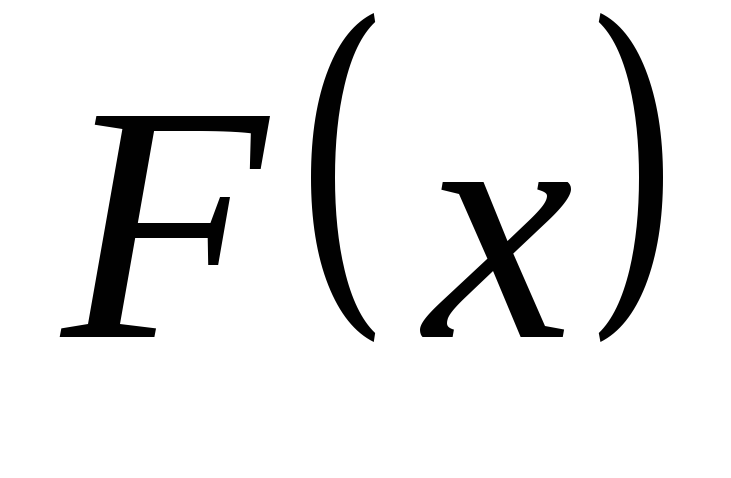 приблизно дорівнює 2,81.
приблизно дорівнює 2,81.
7. Знайти при
якому значенні параметра  задана функція
задана функція
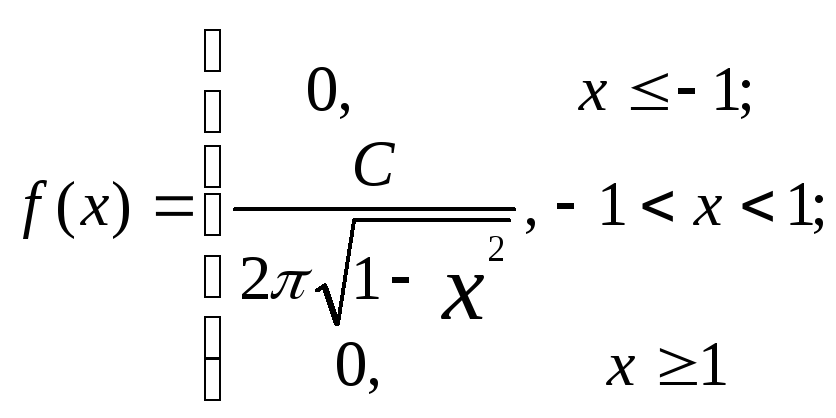
буде щільністю
розподілу неперервної випадкової
величини 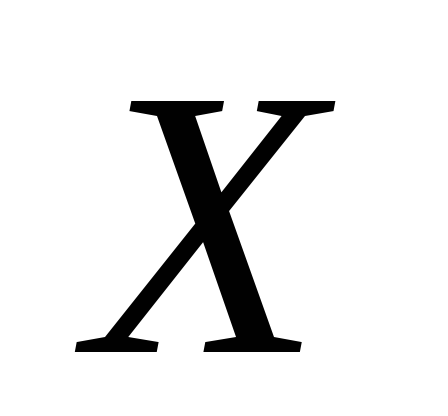 та записати її функцію розподілу.
Визначити ймовірність того, що випадкова
величина
та записати її функцію розподілу.
Визначити ймовірність того, що випадкова
величина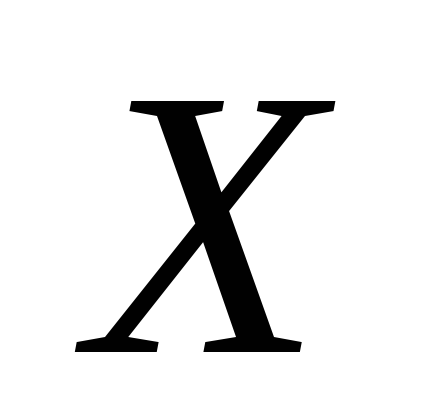 прийме значення з інтервалу
прийме значення з інтервалу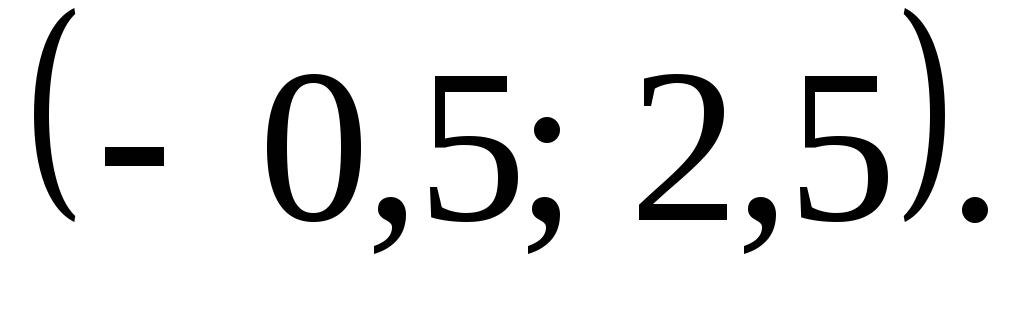
Розв’язування.
Для визначення  скористаємось четвертою властивістю
щільності розподілу, тобто тим, що
скористаємось четвертою властивістю
щільності розподілу, тобто тим, що
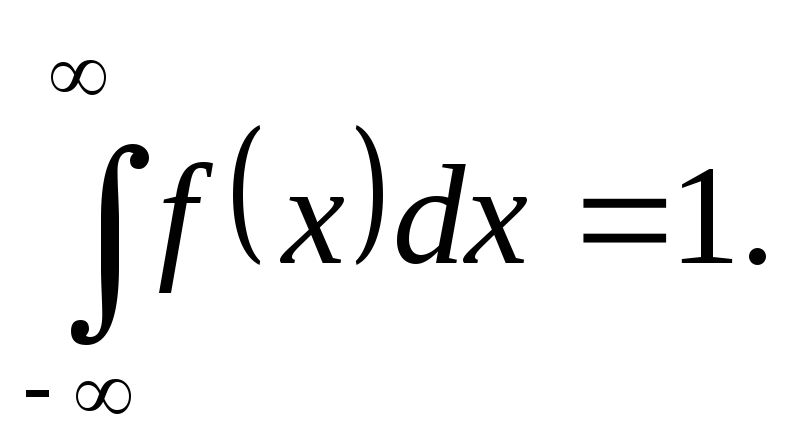
Оскільки
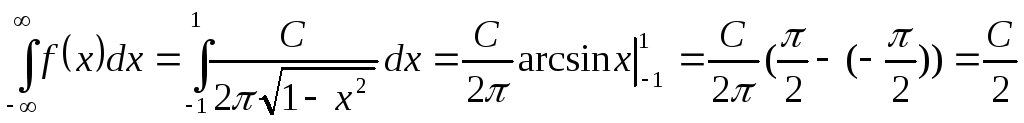 ,
,
то 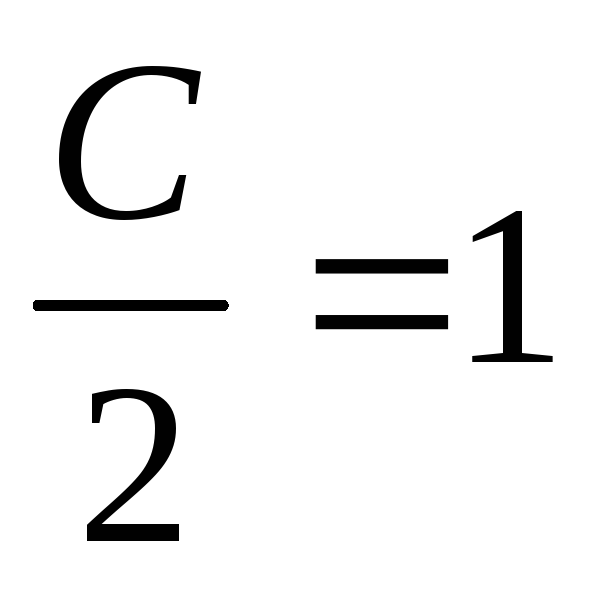 і
і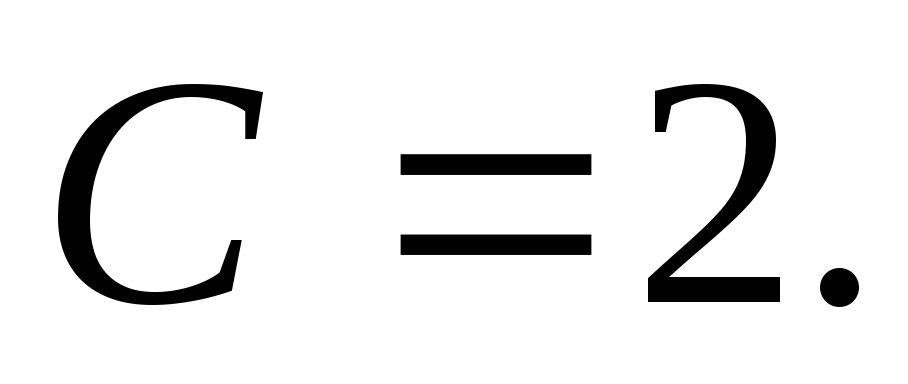
Функцію розподілу знайдемо за формулою (4)
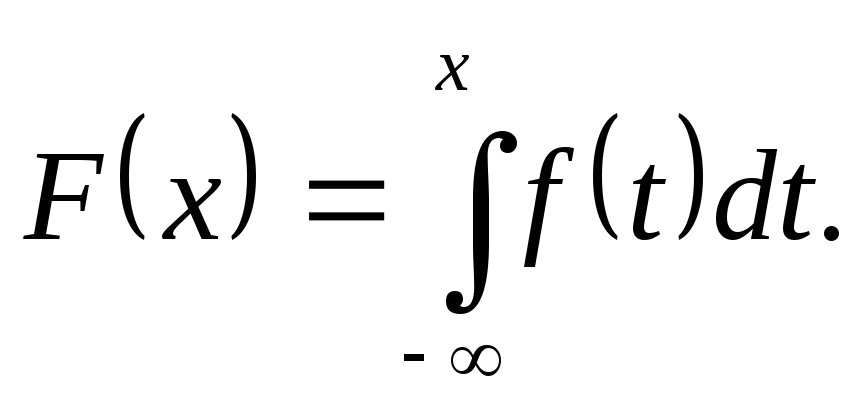
На підставі цієї формули одержимо
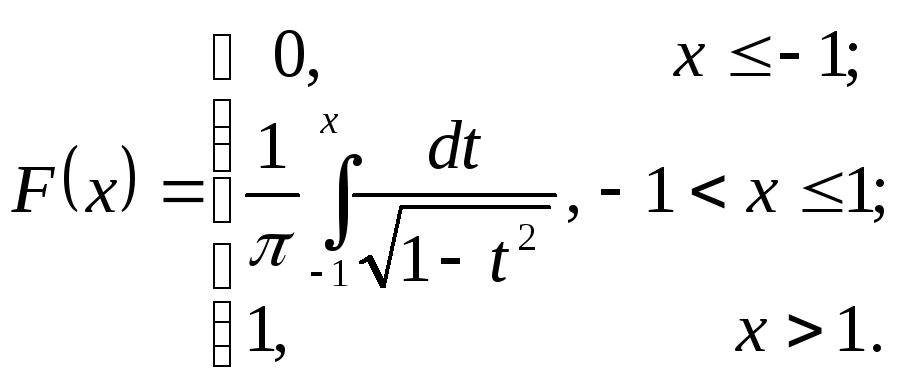
Знайдемо інтеграл
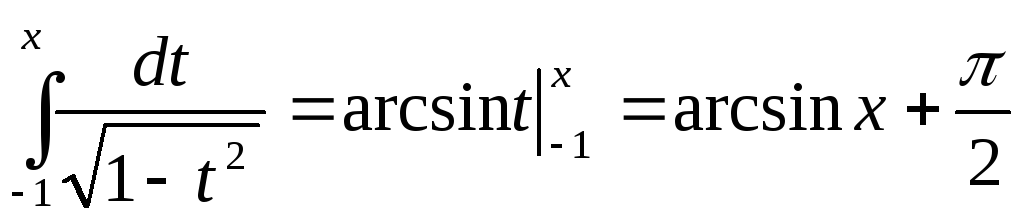 ,
,
В результаті будемо мати
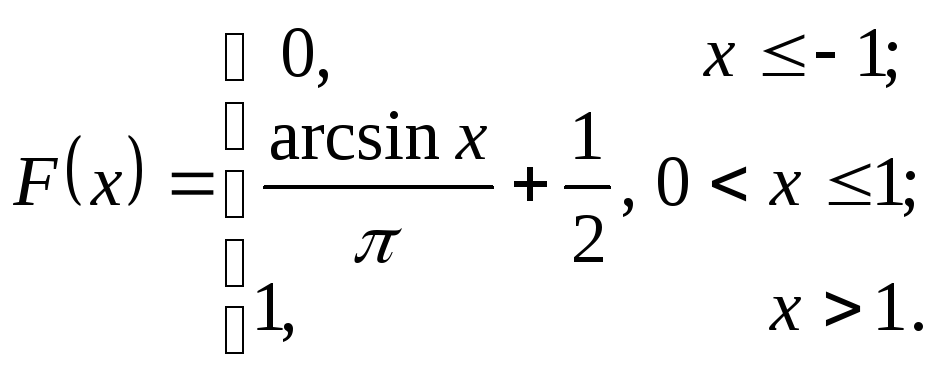
Ймовірність того,
що випадкова величина 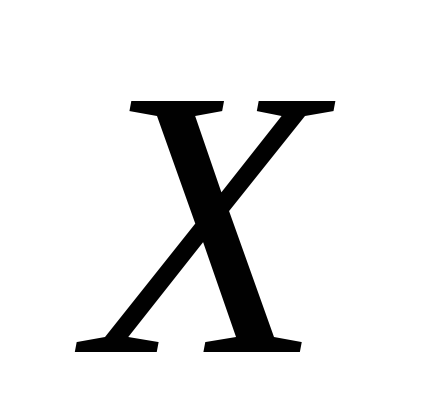 прийме значення з інтервалу
прийме значення з інтервалу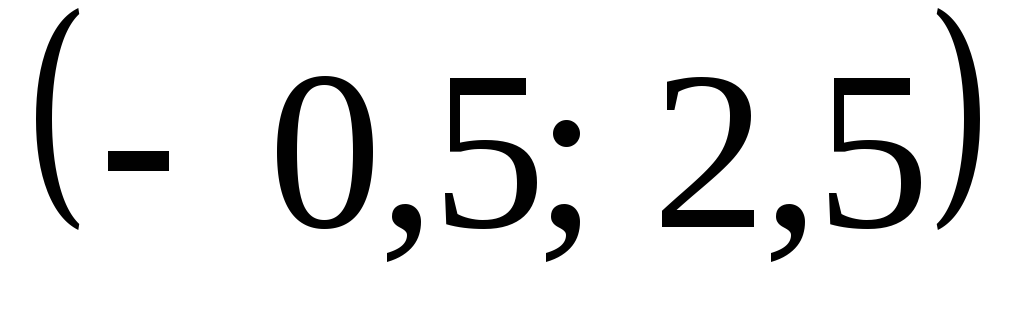 знайдемо на підставі третьої властивості
щільності розподілу. Тобто
знайдемо на підставі третьої властивості
щільності розподілу. Тобто
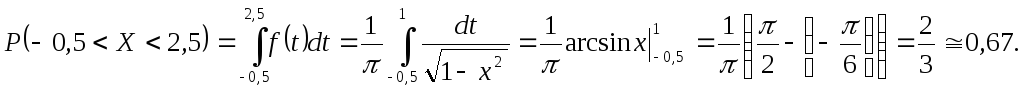
8. Порівняти
роботу двох дилерів 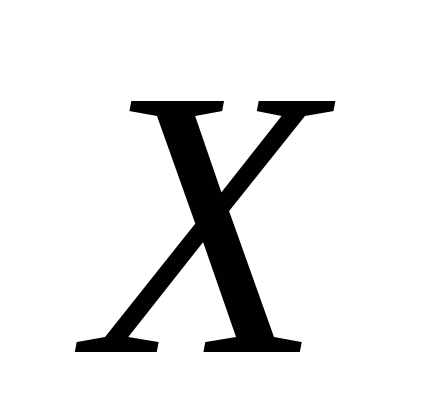 та
та з продажі нерухомого майна, якщо закони
розподілу кількості проданих за тиждень
об’єктів для кожного дилера мають такий
вигляд (див. табл. 7 і 8).
з продажі нерухомого майна, якщо закони
розподілу кількості проданих за тиждень
об’єктів для кожного дилера мають такий
вигляд (див. табл. 7 і 8).
Таблиця 7

1
2
3
4

0,3
0,2
0,2
0,3
Таблиця 8

1
2
3
4

0,2
0,3
0,3
0,2
Розв’язування. Знайдемо
для кожної випадкової величини 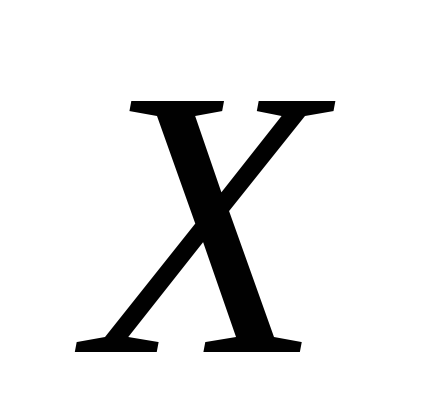 та
та математичне сподівання:
математичне сподівання:
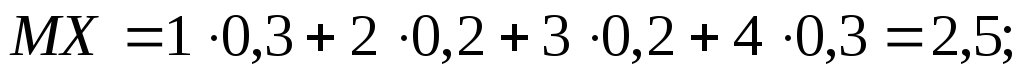
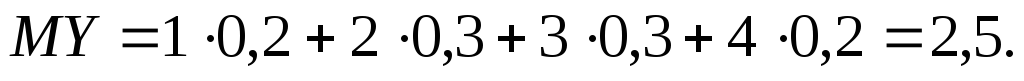
Оскільки 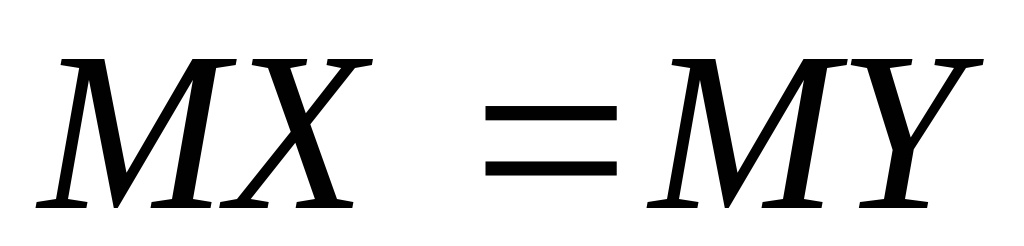 (середні значення для обох дилерів
співпадають), то для порівняння їх роботи
ми змушені шукати дисперсії.
(середні значення для обох дилерів
співпадають), то для порівняння їх роботи
ми змушені шукати дисперсії.
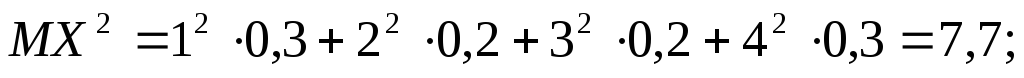
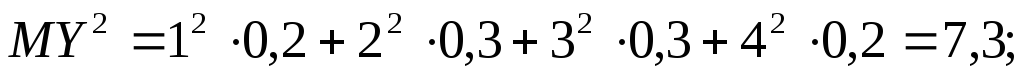
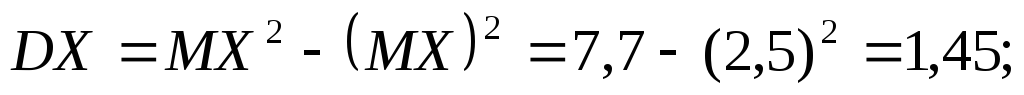
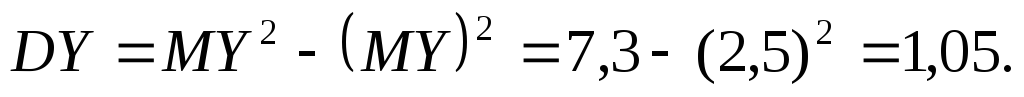
Отже, при однакових математичних сподіваннях кількості об’єктів проданих кожним дилером розсіювання в першого є більшим, ніж у другого, тобто результати другого є стійкішими.
9. Неперервна
випадкова величина 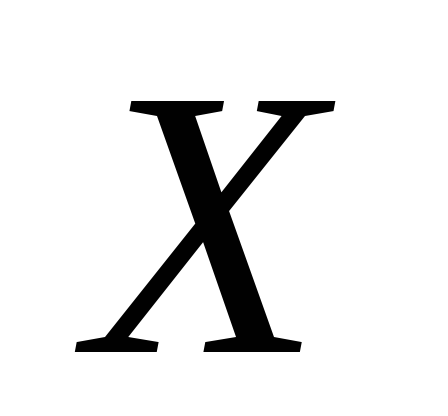 задана своєю щільністю розподілу
задана своєю щільністю розподілу
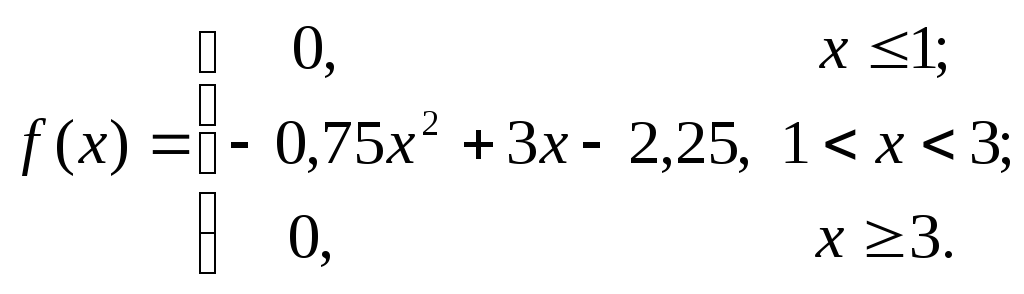
Знайти моду,
математичне сподівання і медіану
величини 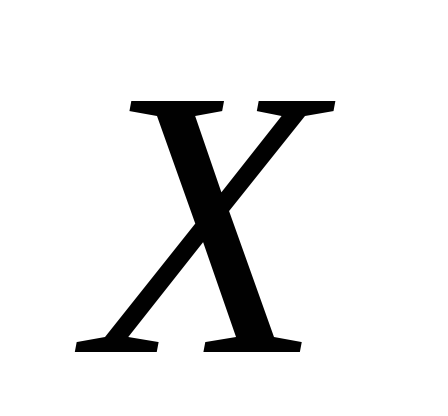 .
.
Розв’язування.
Перевірити функцію щільності розподілу
на існування максимуму можна методами
диференційного числення. Однак в даному
випадку можна поступити простіше.
Щільність розподілу випадкової величини 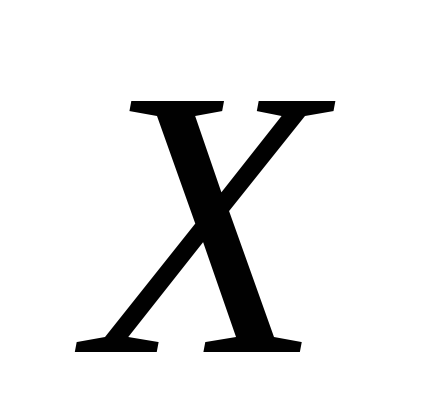 в інтервалі (1, 3) задана параболою, вітки
якої напрямлені вниз. На кінцях цього
проміжку (в точках
в інтервалі (1, 3) задана параболою, вітки
якої напрямлені вниз. На кінцях цього
проміжку (в точках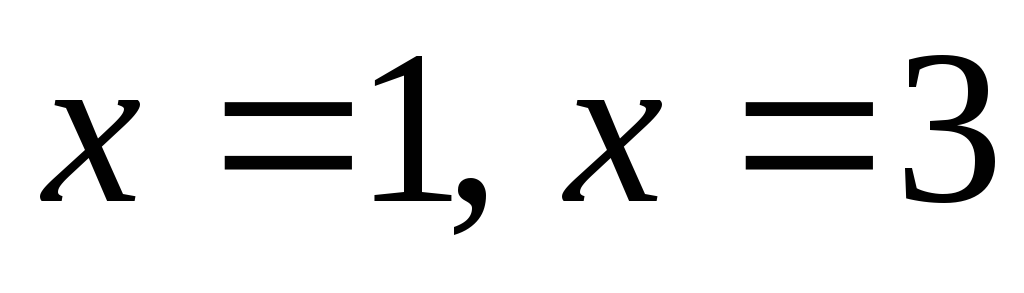 )
і поза ним задана щільність дорівнює
нулю. Абсциса вершини цієї параболи
)
і поза ним задана щільність дорівнює
нулю. Абсциса вершини цієї параболи
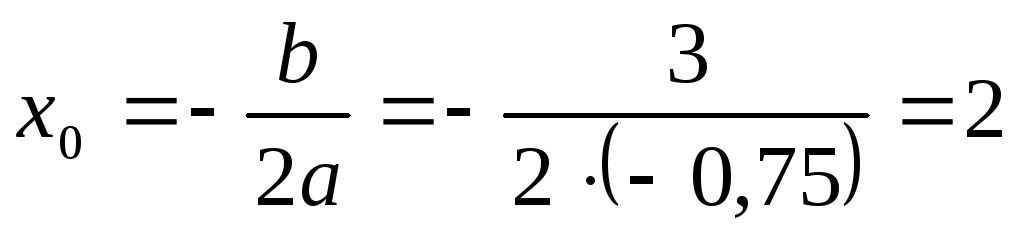
належить вказаному
проміжку, тому щільність розподілу
досягає максимуму у цій точці. Тобто, 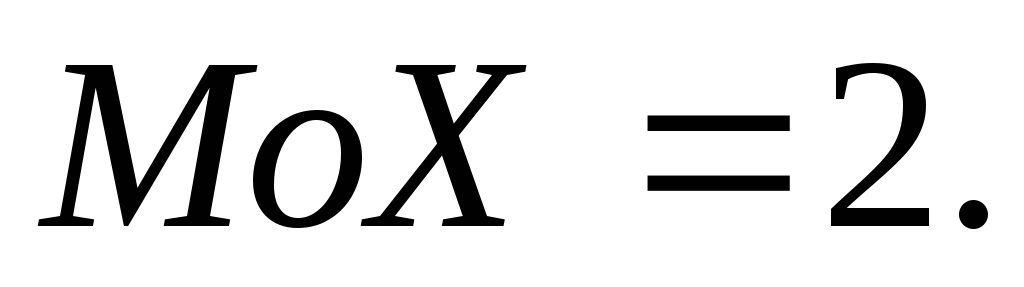
Цей самий результат ми отримаємо якщо виділимо у заданому квадратичному тричлені повний квадрат:
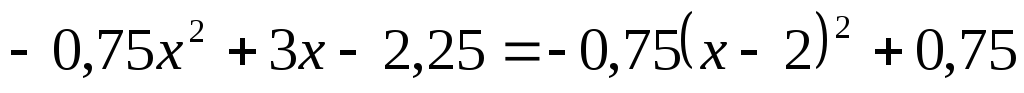 .
.
Звідси видно, що
абсциса вершини цієї параболи 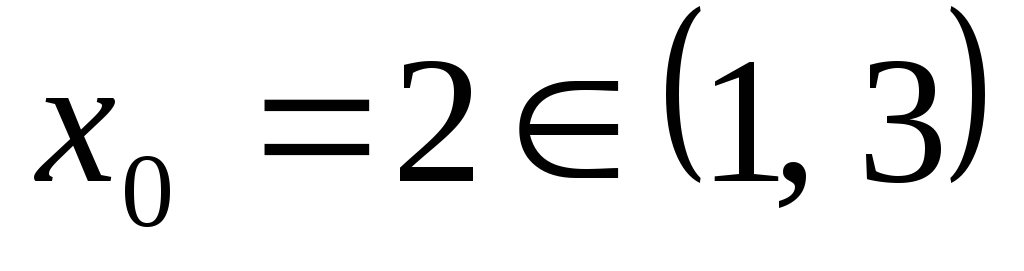 і
і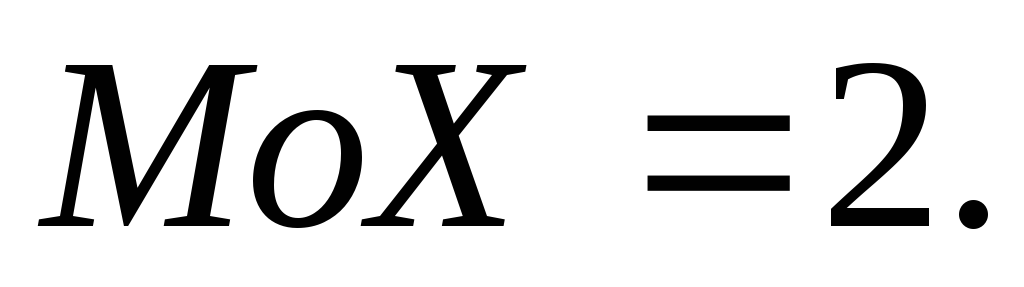
З розглянутих
міркувань очевидно, що крива розподілу
симетрична відносно прямої 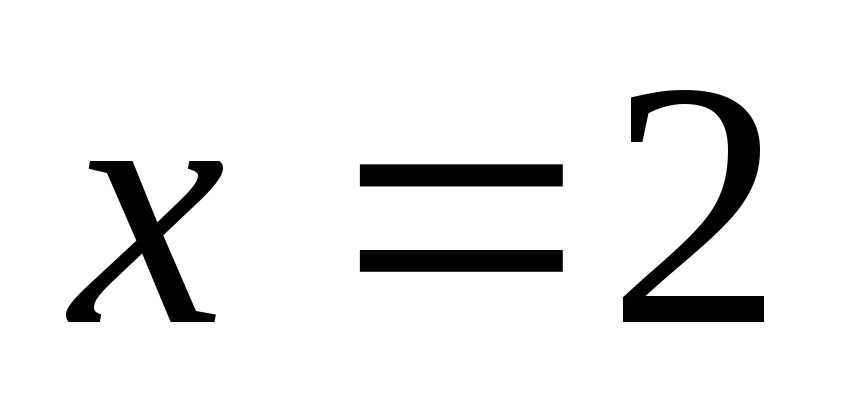 тому математичне сподівання
тому математичне сподівання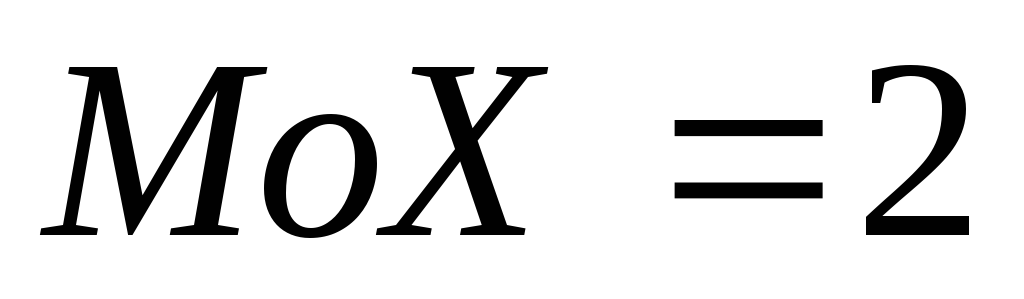 і медіана
і медіана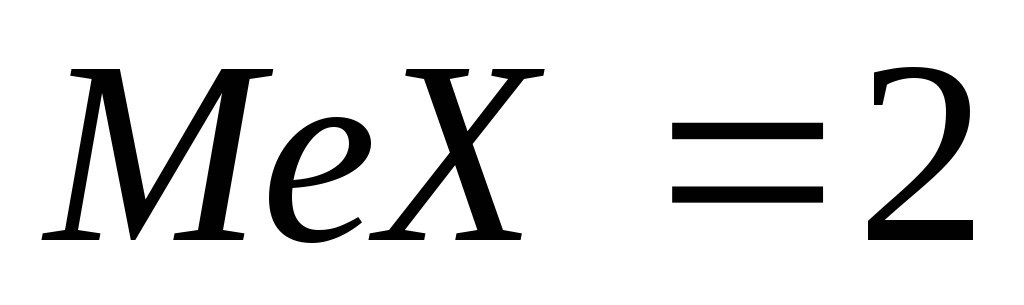 .
.
10. Знайти
дисперсію неперервної випадкова величина 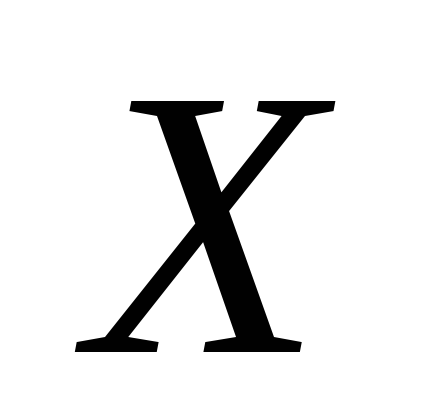 ,
заданої своєю функцією розподілу
,
заданої своєю функцією розподілу
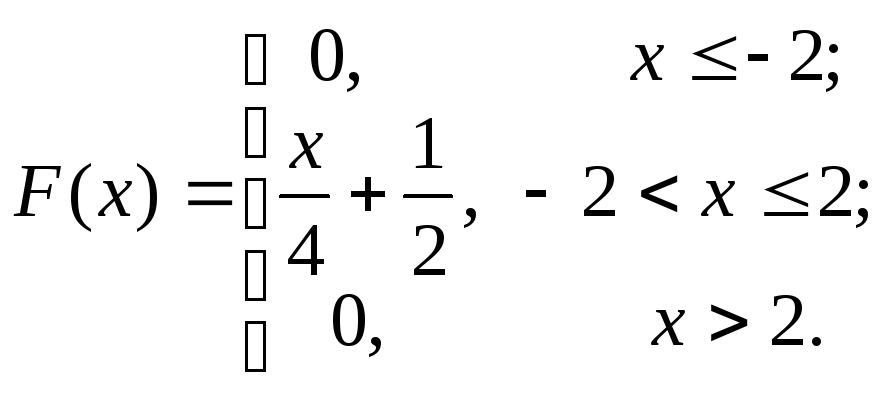
Розв’язування.
Спочатку знайдемо щільністю розподілу
випадкової величини 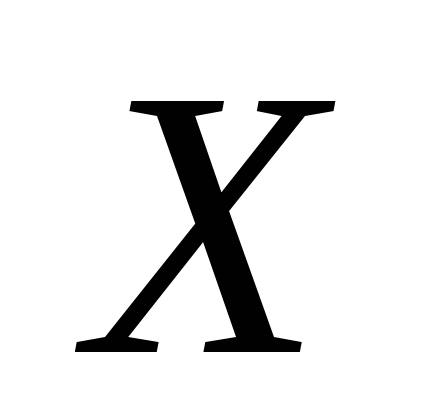 .
Для цього скористаємось другою властивістю
щільності розподілу, тобто тим, що в
точках неперервності щільності
.
Для цього скористаємось другою властивістю
щільності розподілу, тобто тим, що в
точках неперервності щільності 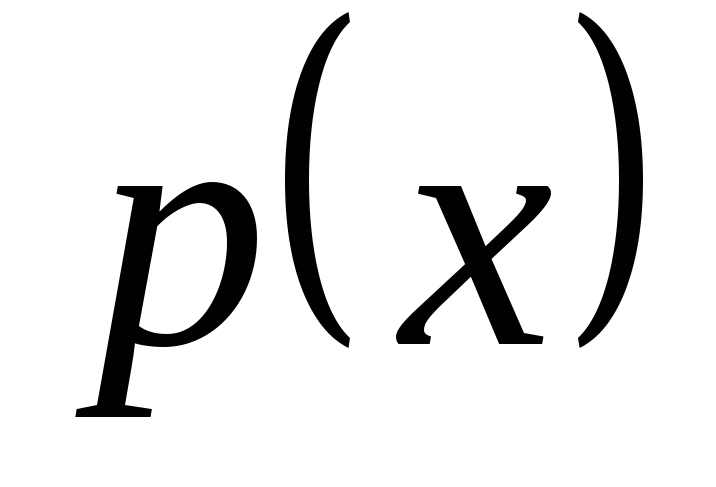 вона дорівнює
першій похідній від функції розподілу
вона дорівнює
першій похідній від функції розподілу 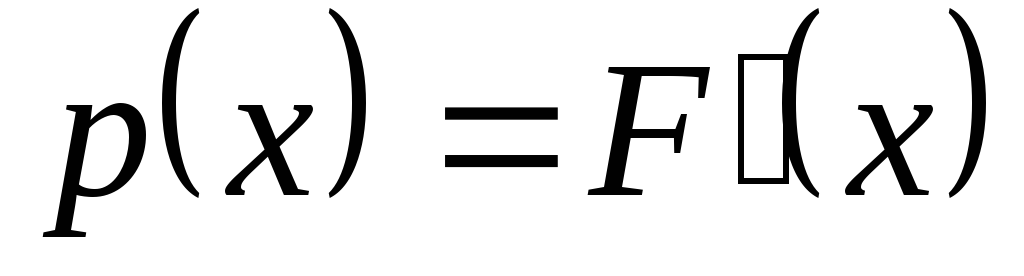 .
Отже
.
Отже
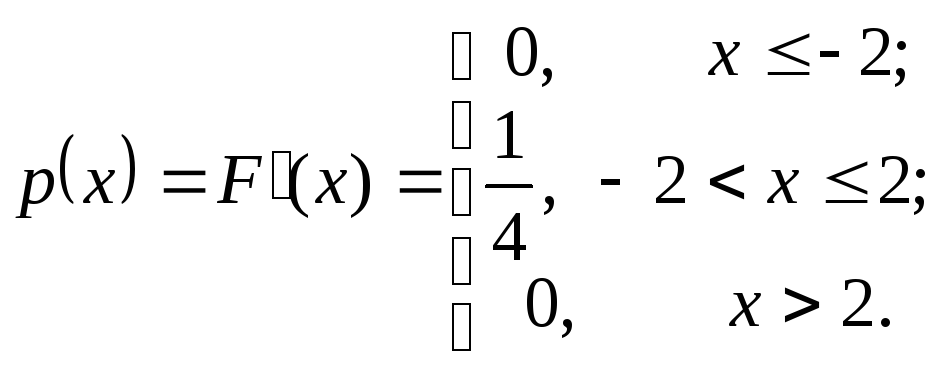
Тепер обчислимо математичне сподівання за формулою (8)
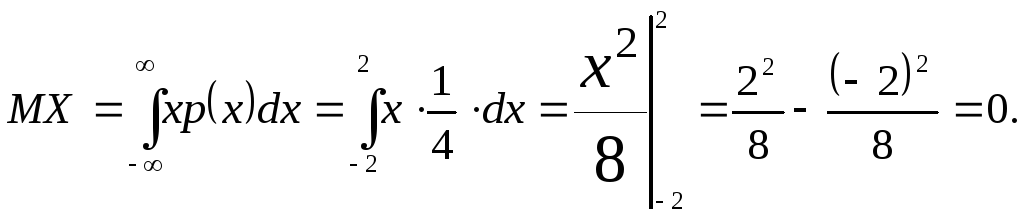
Факт рівності математичного сподівання нулю випливає також з того, що підінтегральна функція непарна, а межі інтегрування симетричні відносно початку координат.
Для знаходження дисперсії, спочатку за формулою (20) знайдемо
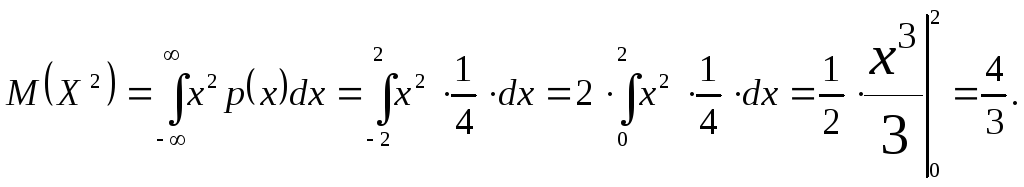
Тут ми врахували те, що підінтегральна функція парна, а межі інтегрування симетричні відносно початку координат. Тепер за формулою (18) одержимо
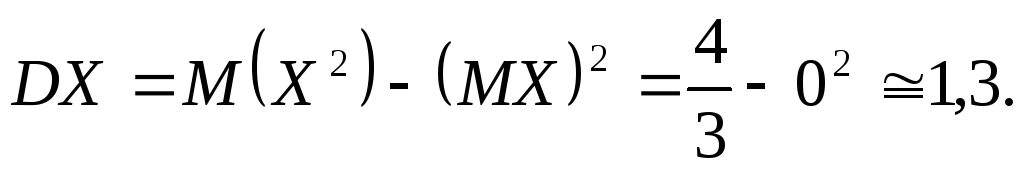
Таким чином, дисперсія заданої випадкова величина приблизно дорівнює 1,3.
Зауваження: У більшості випадків обчислювати дисперсію простіше (як ми і поступили) за формулою (18). Однак в даному прикладі, враховуючи те, що математичне сподівання дорівнює нулю, можна було обійтись формулою (17)
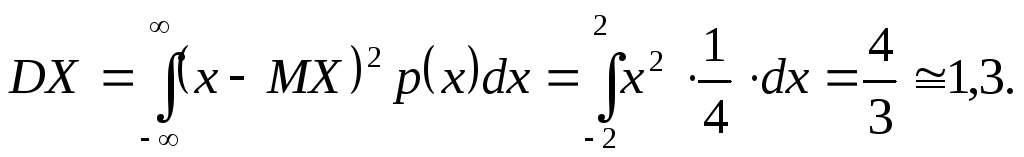
11. Обчислити
математичне сподівання та дисперсію
випадкової величини 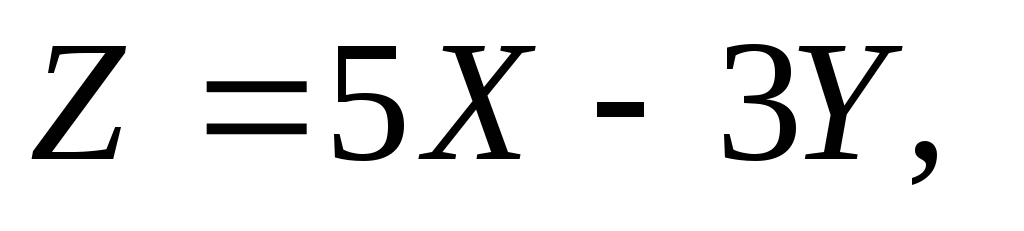 якщо відомі математичні сподівання
якщо відомі математичні сподівання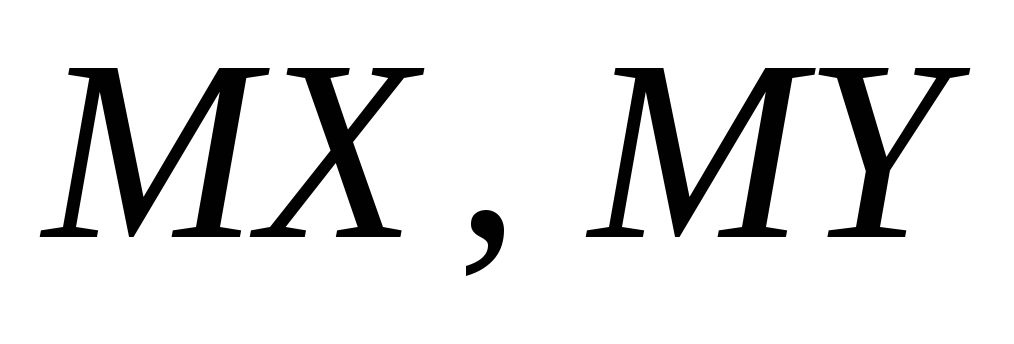 та дисперсії
та дисперсії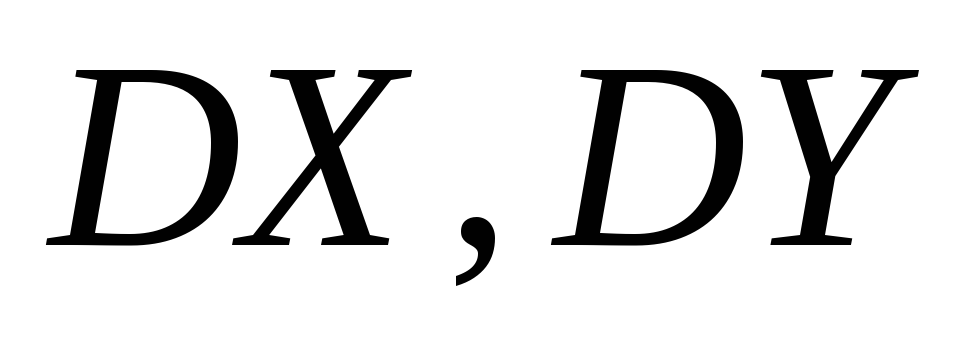 незалежних випадкових величин
незалежних випадкових величин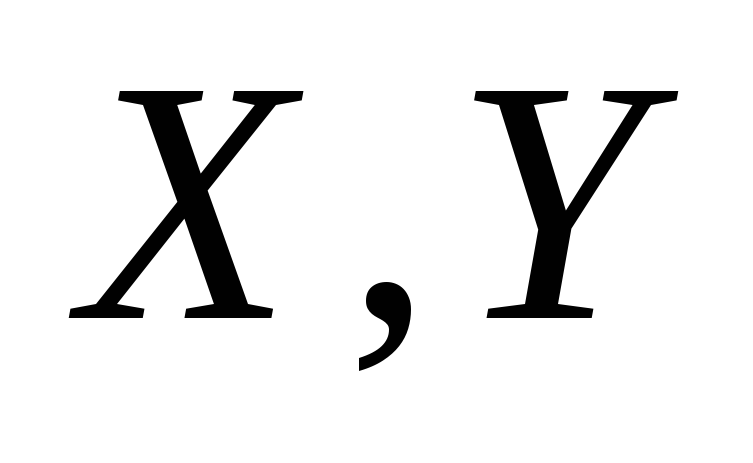 :
: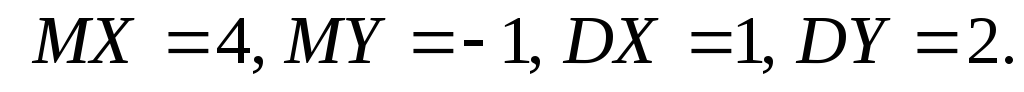
Розв’язування. Для обчислення шуканих величин, скористаємось властивостями математичного сподівання та дисперсії. В результаті одержимо
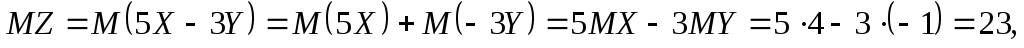
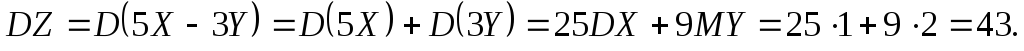
studfile.net
Розвязання типових задач
Задача 1. Напишіть формулу міцели гідрозолю кремнезему.
Розвязання. Поверхня агрегату міцели кремнезему, що складається з m молекул SiO2, реагуючи з оточуючою його водою, утворює метакремнійову кислоту H2SiO3. Метакремнійова кислота – слабкий електроліт, що дисоціює на іони за схемою H2SiO3 = 2H+ + SiO32- і виконує роль стабілізатора. Формула міцели такого золю має вигляд
{[m SiO2].n SiO23-.2(n – x) H+}.2x H+,
де m – кількість молекул в агрегаті міцели; n – кількість потенціалвизначаючих іонів стабілізатора, адсорбованих поверхнею агрегату; (n – x) – кількість протиіонів, що входять в адсорбційний шар; x – кількість протиіонів, які утворюють дифузійний шар.
Задача 2. Напишіть формулу міцели золю йодиду срібла, якщо стабілізатором є розчин азотнокислого срібла. Вкажіть заряд колоїдної частинки, агрегат, ядро, колоїдну частинку і міцелу.
Розвязання. Основу міцели складає m молекул AgI. Стабілізатор дисоціює на іони за схемою AgNO3 = Ag+ + NO3—. На поверхні агрегату з розчину AgNO3 адсорбується n іонів Ag+, які називаються потенціалвизначаючими. Протиіонами будуть іони NO3—. Міцела золю AgI буде мати наступну формулу:
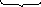 {[m AgI].n Ag+.(n—x)
NO3—}+.x NO3—.
{[m AgI].n Ag+.(n—x)
NO3—}+.x NO3—.
 агрегат
агрегат
 ядро
ядро
 колоїдна
частинка
колоїдна
частинка
міцела
Знак заряду колоїдної частинки визначається знаком заряду потенціалвизначаючих іонів. Таким чином, колоїдна частинка буде мати позитивний заряд. Критерієм правильності написання міцели є її електронейтральність: n (позитивних зарядів) = [(n – x) + x] (негативних зарядів), тобто число позитивних зарядів повинно дорівнювати числу негативних зарядів.
Задача 3. При отриманні золю CdS змішали 5 мл 0,03н. розчину CdCl2 з 30 мл 0,01н. розчину H2S. Напишіть формулу міцели отриманого золю та вкажіть заряд колоїдної частинки.
Розвязання. При змішуванні речовини прореагують між собою за рівнянням
CdCl2 + H2S = CdS + 2HCl.
Агрегатом міцели буде важкорозчинна сполука CdS. Будова міцели і заряд колоїдної частинки залежать від того, який з реагентів буде у надлишку. Розрахуємо кількість моль-еквівалентів кожного реагенту за рівнянням
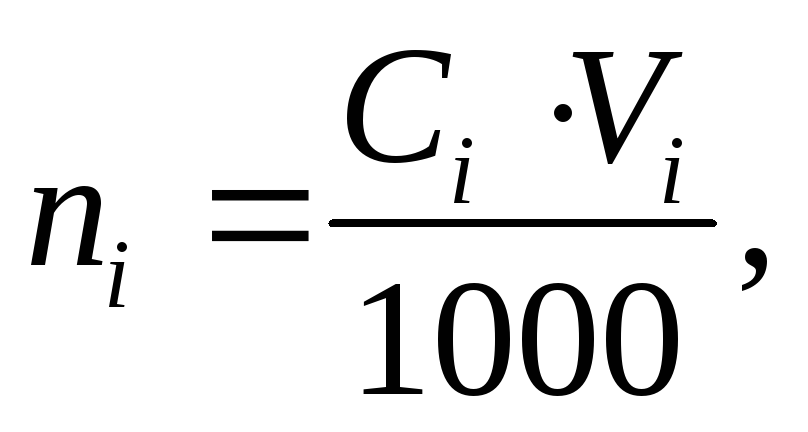
де Ci — молярна концентрація еквівалентів, моль-екв/л; Vi — обєм розчину,мл.
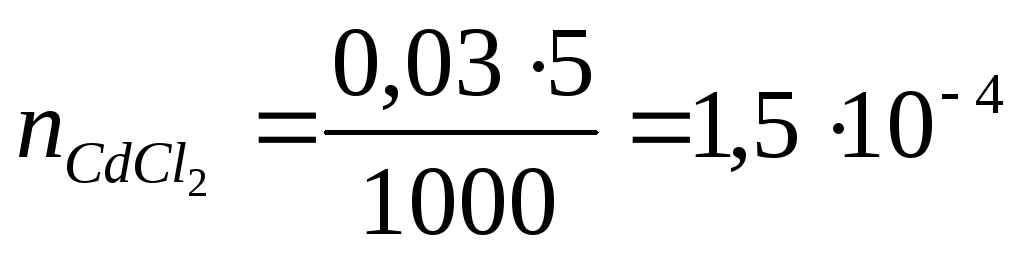 моль-екв.
моль-екв.
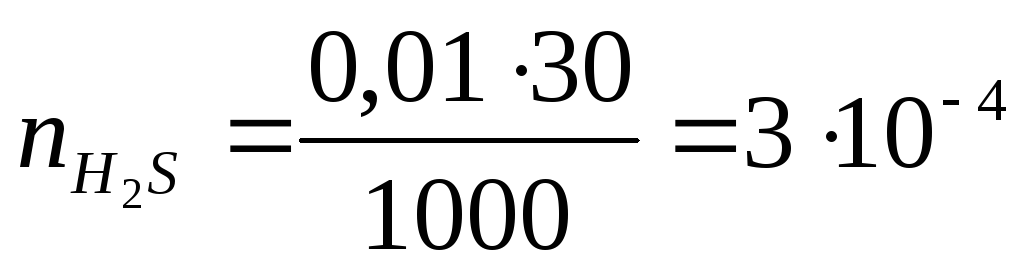 моль-екв.
моль-екв.
Так
як 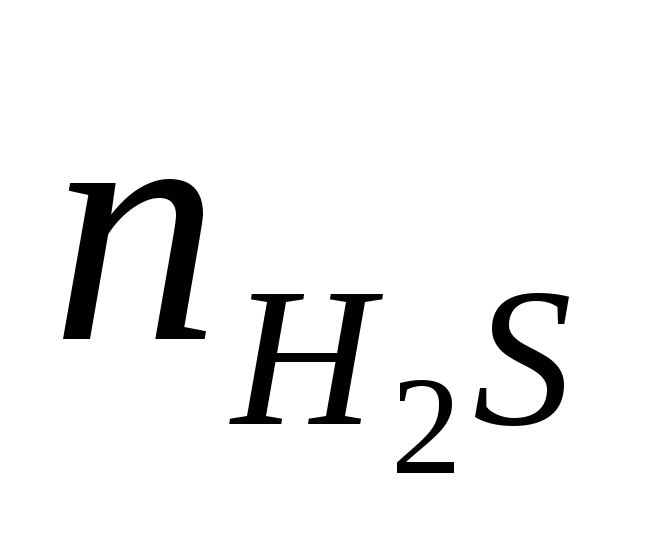 >
>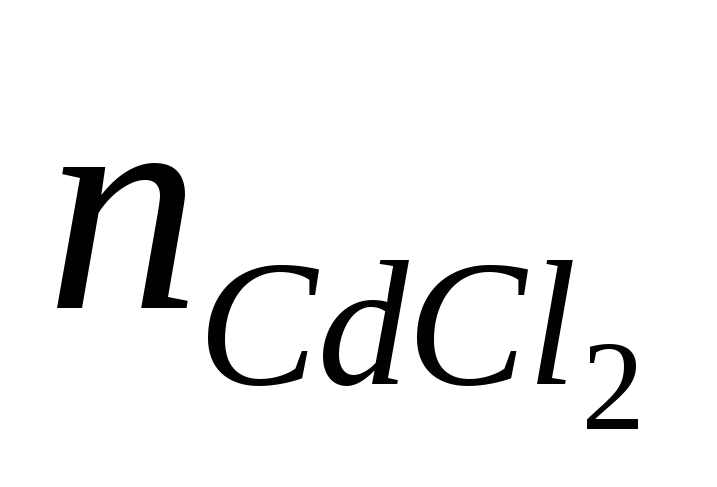 ,
то у надлишку знаходиться реагент H2S,
який і буде
виконувати
роль стабілізатора. Припустимо, що H2S
дисоціює на іони за наступною схемою:
H2S
= 2H+ + S2-.
За цих
умов формула міцели буде мати вигляд
,
то у надлишку знаходиться реагент H2S,
який і буде
виконувати
роль стабілізатора. Припустимо, що H2S
дисоціює на іони за наступною схемою:
H2S
= 2H+ + S2-.
За цих
умов формула міцели буде мати вигляд
{[m CdS] n S2-.2(n—x) H+}-.2x H+.
Колоїдна частинка матиме негативний заряд, так як потенціалвизначаючими іонами в даному випадку будуть іони S2-.
Задача 4. Який обєм 0,01н. розчину KBr треба додати до 10 мл 0,25н. розчину AgNO3, щоб колоїдні частинки золю AgBr мали позитивний заряд? Напишіть формулу міцели цього золю.
Розвязання. Між реагентами протікає реакція
KBr + AgNO3 = AgBr + KNO3.
Щоб отримати золь з позитивно зарядженими частинками, необхідно мати у надлишку розчин AgNO3. У відповідності до закону моль-еквівалентів С1.V1 = C2.V2.З цього рівняння визначимо обємKBr, який прореагує з 10мл0,25н. розчинуAgNO3.
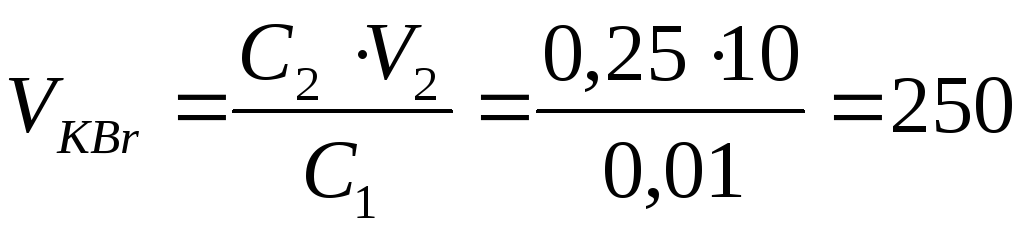 мл розчину KBr.
мл розчину KBr.
Щоб розчин AgNO3 був у надлишку, необхідно додати до нього обєм KBr менший за 250 мл. В цьому випадку отриманий золь буде мати негативно заряджені частинки. Будова золю AgBr відповідатиме наступній формулі
{[m AgBr] .n Ag+.(n-x) NO3—}.x NO3—.
studfile.net
Приклади розв`язання задач
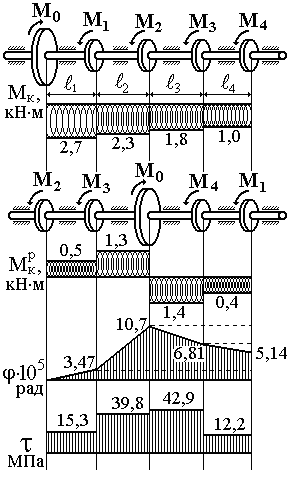
Зразок виконання задачі 1
| Потужність, що передається шківами, дорівнює:
при частоті обертання:
Довжини ділянок валу:
Допустимі дотичні навантаження:
Допустимий
відносний кут закручування:
Модуль зсуву – |
Рисунок 3.14 |
Порядок розв`язання задачі:
1. Накреслимо схему вала.
2.
Визначимо значення зовнішних крутних
моментів згідно відомої з теоретичної
механіки залежності 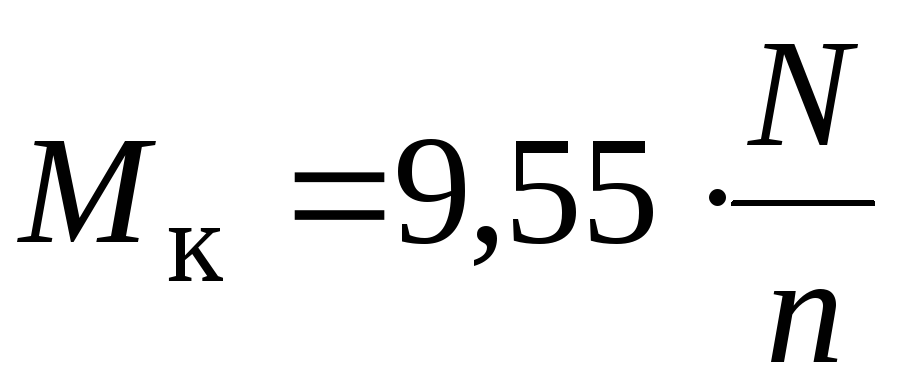 :
:
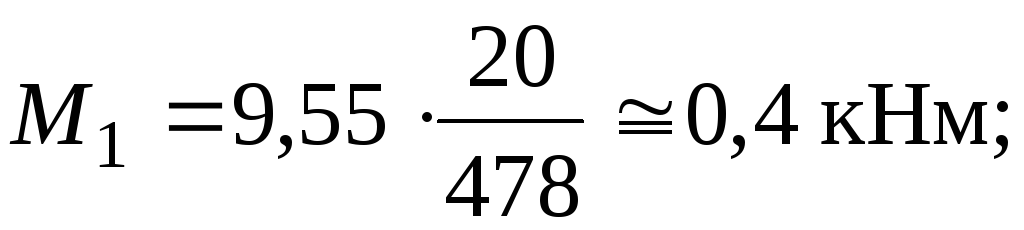

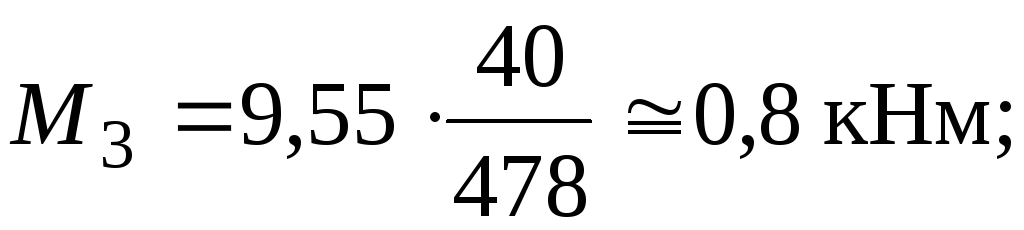
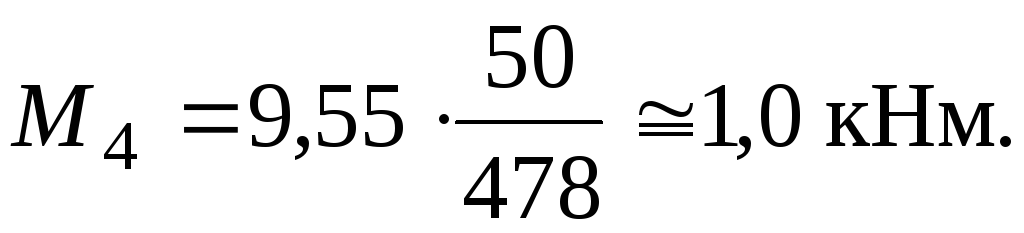
З умови статики:
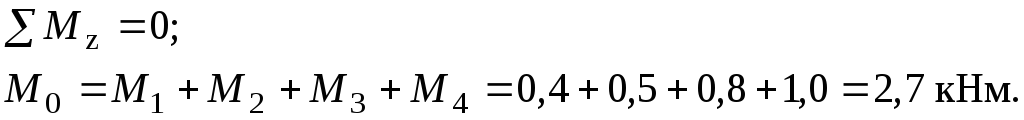 3.
Згідно з методом перерізів будуємо
епюру крутних моментів
3.
Згідно з методом перерізів будуємо
епюру крутних моментів 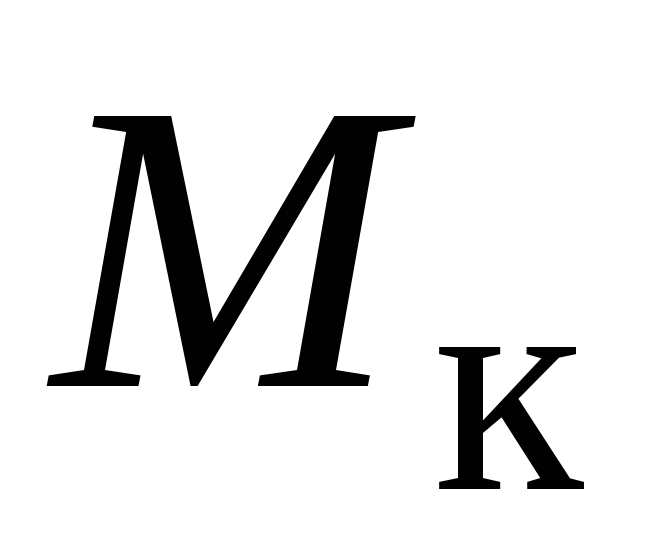 .
.
4.
Визначаємо діаметр  валу круглого перерізу з умови міцності
на найнебезпечнішій ділянці
валу круглого перерізу з умови міцності
на найнебезпечнішій ділянці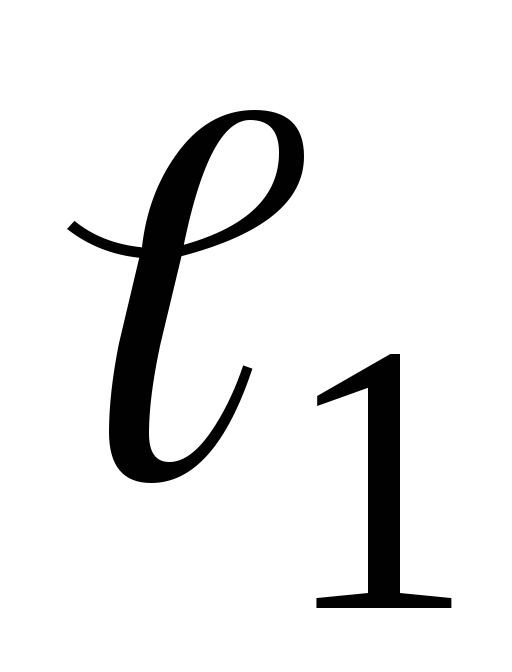 :
:
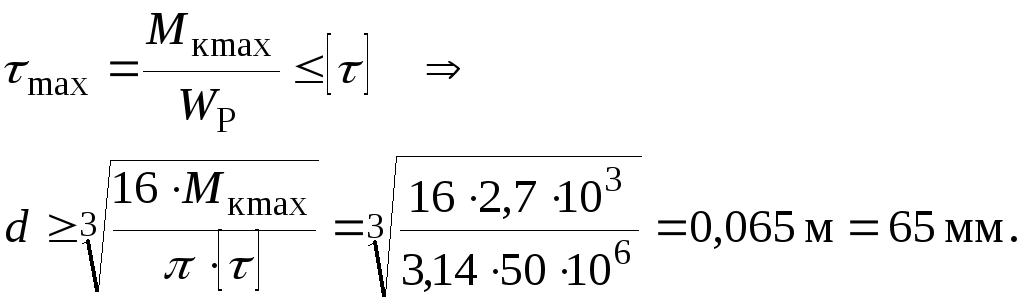
5.
З метою зменшення максимального крутного
моменту розташуємо шківи раціонально
і побудуємо епюру 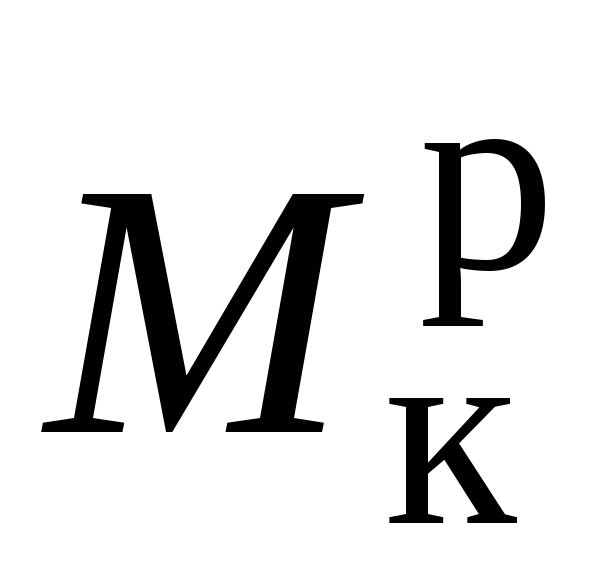 .
.
6. Визначаємо розміри поперечного перерізу при раціональному розташуванні шківів:
з умови міцності:

з умови жорсткості:

Значення
діаметра для суцільного валу обирається
найбільше з двох значень з урахуванням
стандарту на діаметри валів: 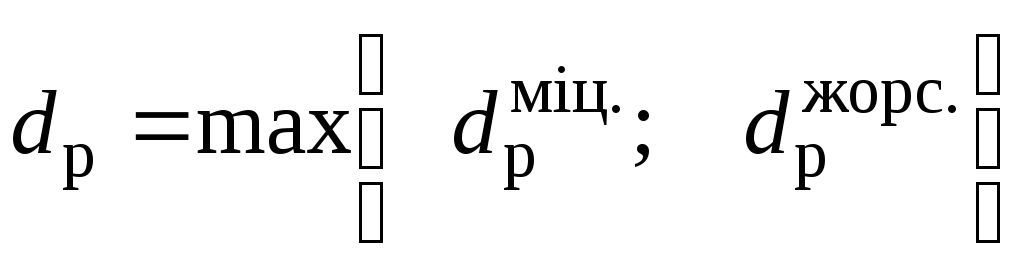 ,
тому
,
тому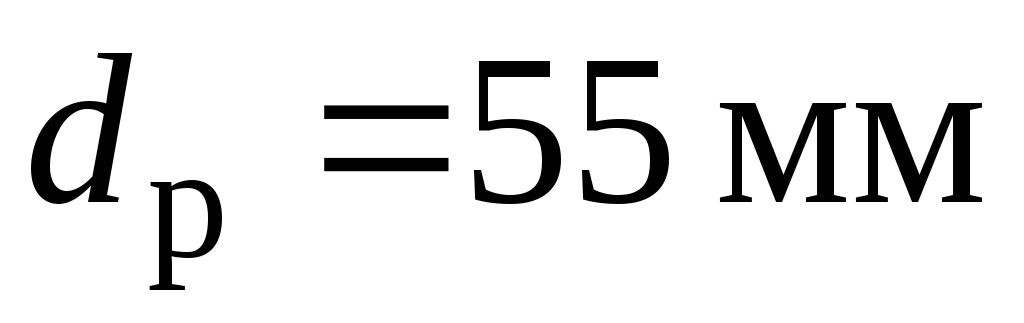 .
.
В
даному прикладі умова міцності виявилась
більш строгою, тому діаметр трубчастого
валу для раціонального розташування
шківів обчислюється при 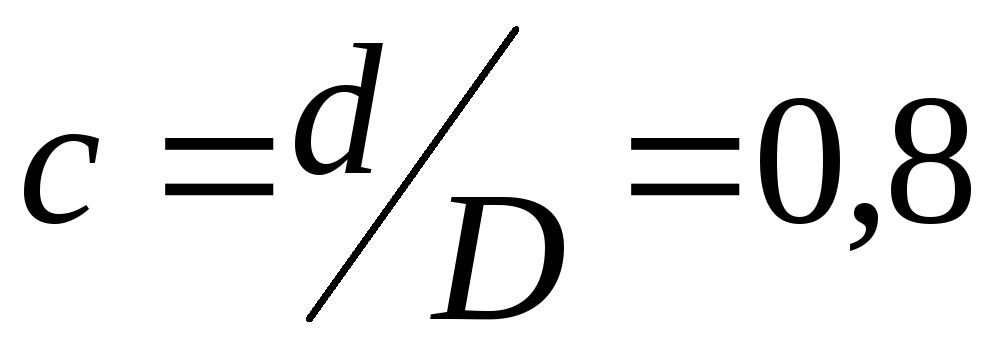 також з умови міцності:
також з умови міцності:
Обираємо 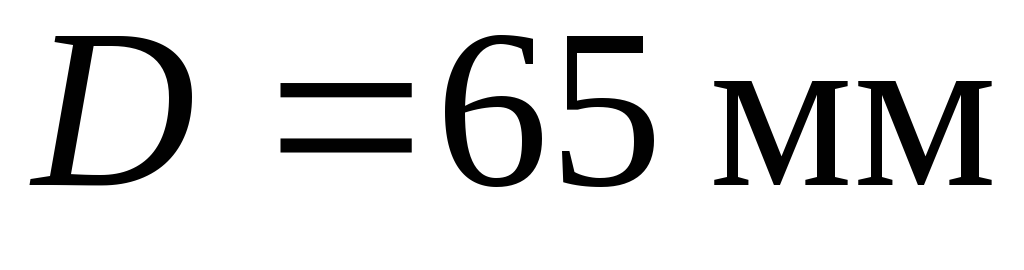 і обчислюємо максимальні дотичні
напруження для трубчастого валу:
і обчислюємо максимальні дотичні
напруження для трубчастого валу:
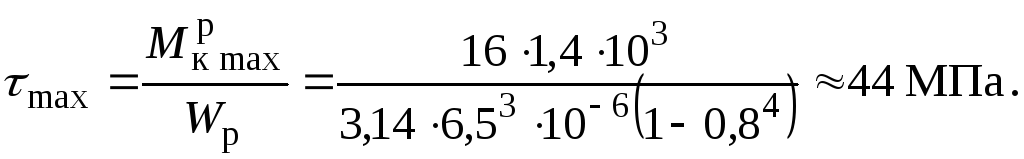
7. Будуємо епюру максимальних в перерізі дотичних напружень на ділянках валу круглого перерізу, для якого момент опору дорівнює:
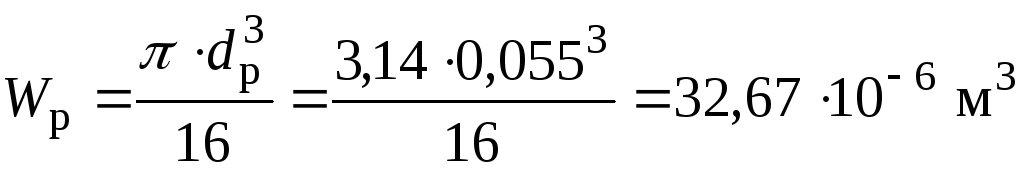 ,
тоді
,
тоді
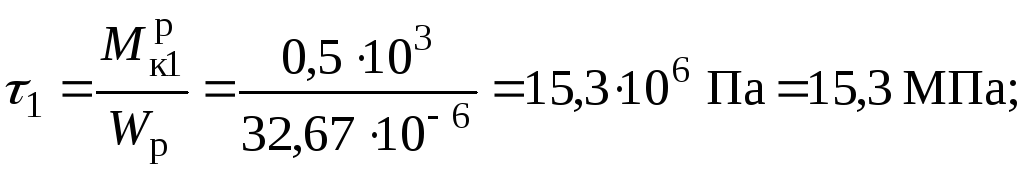
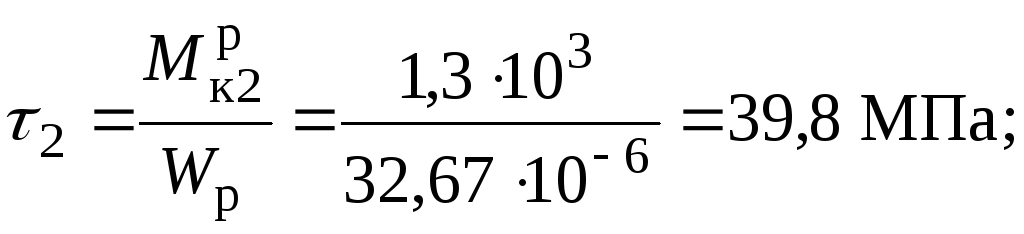
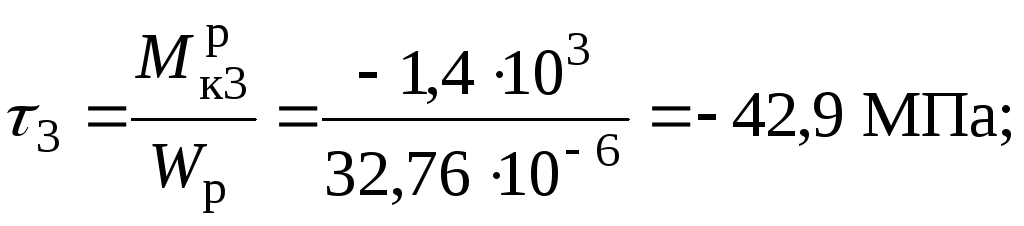
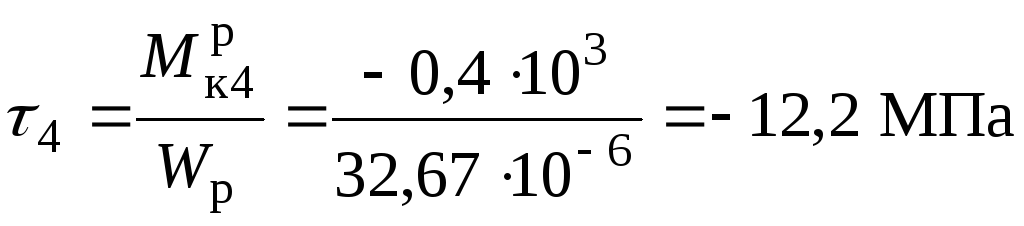 ,
,
Знак
дотичних напружень особливого значення
не має, тому при побудові епюри  можливо відкладання ординат по одну
сторону осі вала.
можливо відкладання ординат по одну
сторону осі вала.
Співвідношення ваги суцільного валу для заданої системи і ваги суцільного валу при раціональному розташуванні шківів дорівнюється чисельному співвідношенню площин поперечних перерізів:
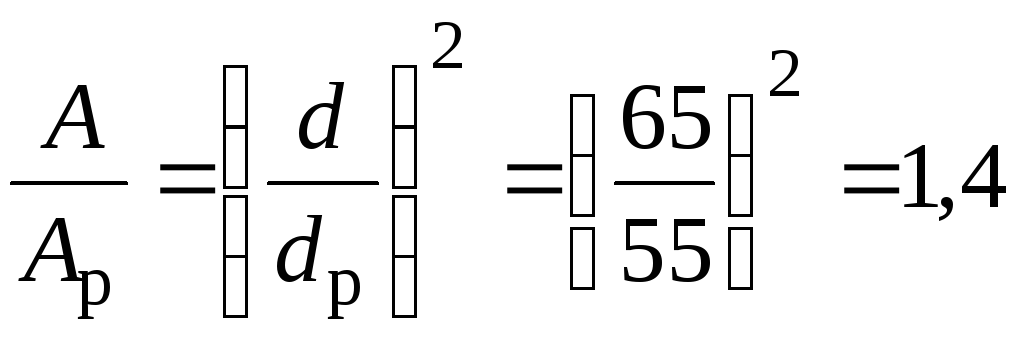 .
.
Співвідношення ваг суцільного і трубчастого валів дає:
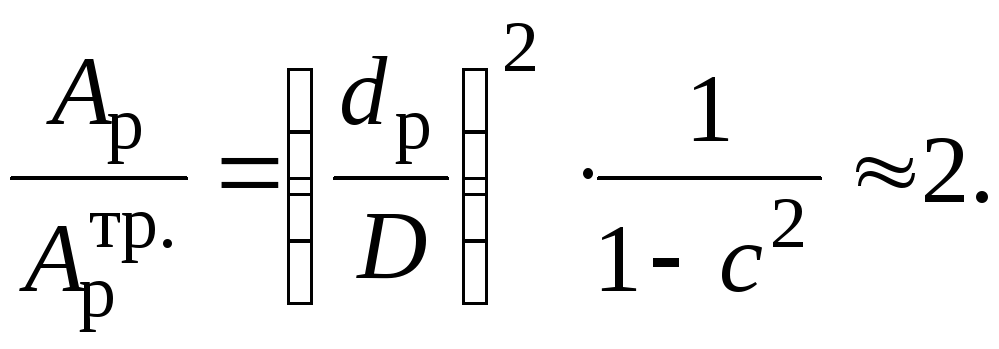
Будуємо епюру кутів закручування по ділянках валу:
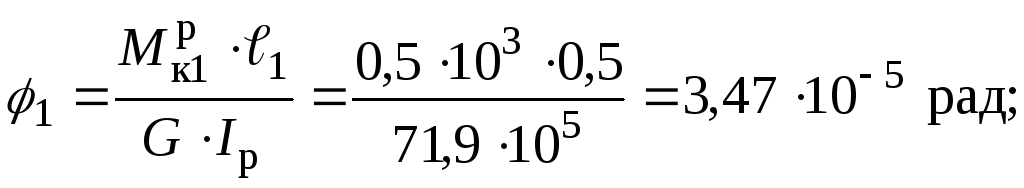
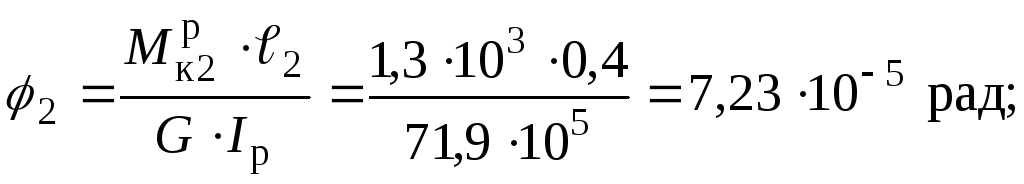
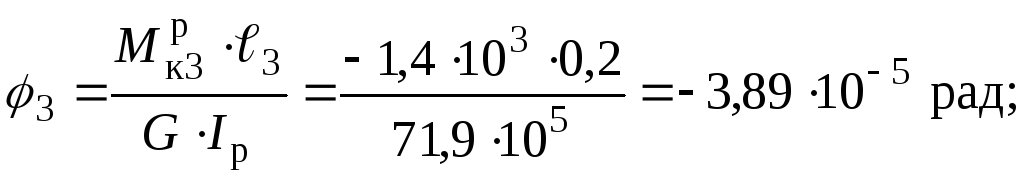
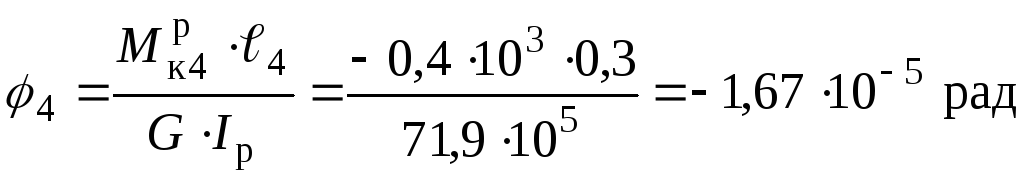 ,
,
де жорсткість при крученні суцільного валу:
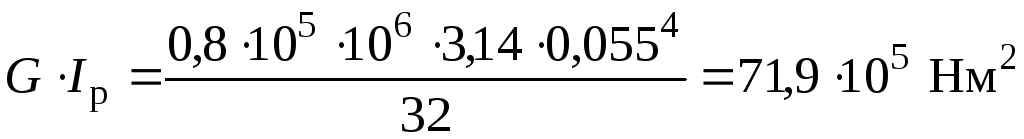 ,
,
а 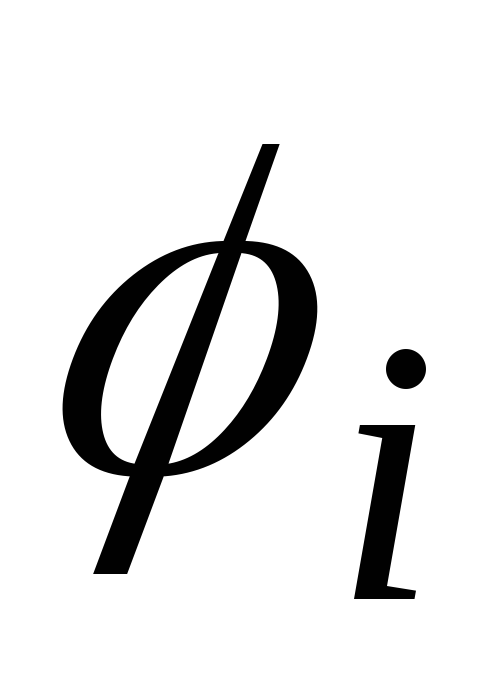 (i − номер ділянки) − це кут закручування
правого краю ділянки відносно лівого.
Обираємо початок координат в лівому
перерізі валу. Відкладаємо значення
(i − номер ділянки) − це кут закручування
правого краю ділянки відносно лівого.
Обираємо початок координат в лівому
перерізі валу. Відкладаємо значення 
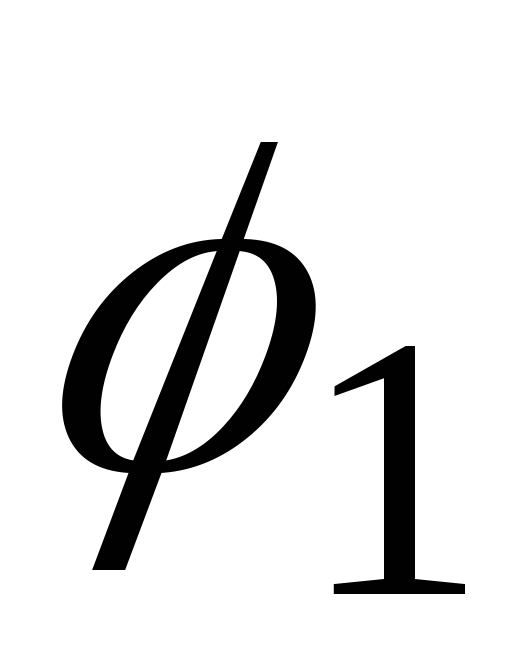 в правому перерізі першої ділянки. Кут
закручування правого перерізу другої
ділянки відносно початку координат
дорівнює сумі кутів
в правому перерізі першої ділянки. Кут
закручування правого перерізу другої
ділянки відносно початку координат
дорівнює сумі кутів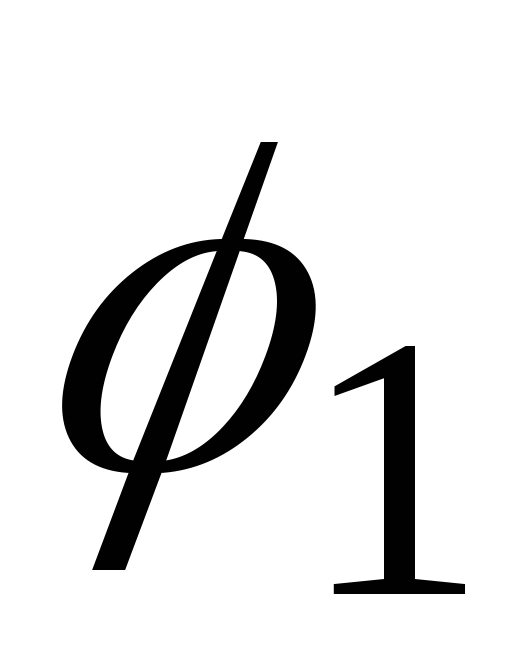 та
та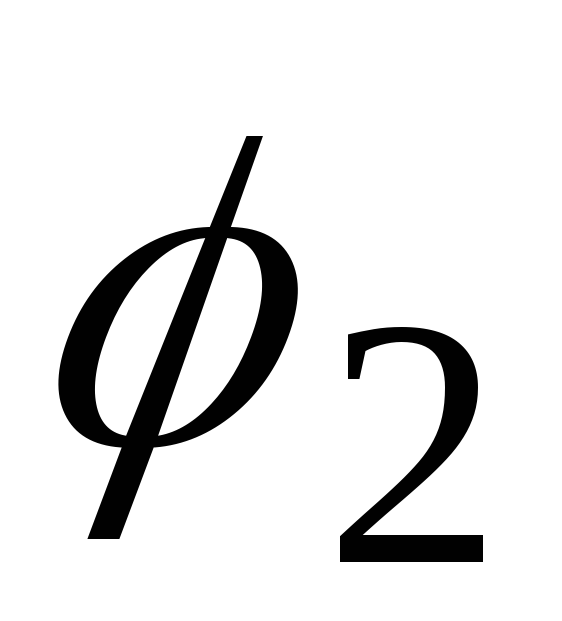 .
Кут закручування правого перерізу
третьої ділянки відносно початку
координат дорівнює сумі кутів
.
Кут закручування правого перерізу
третьої ділянки відносно початку
координат дорівнює сумі кутів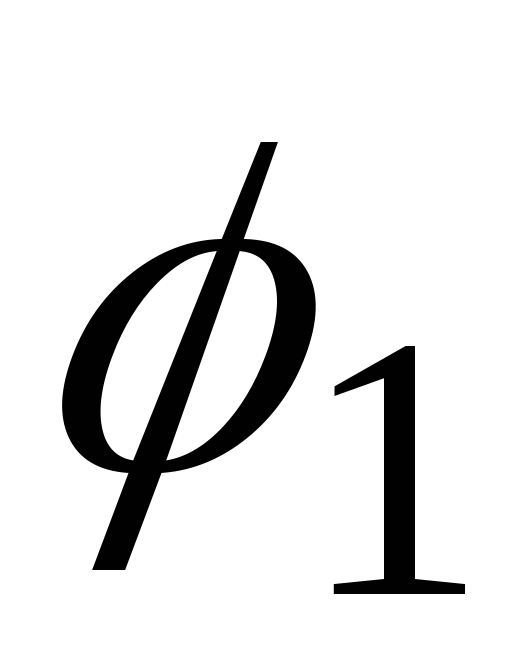 ,
,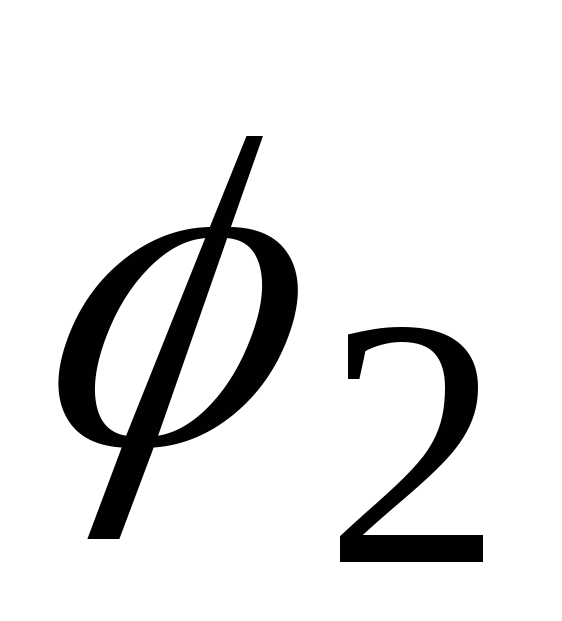 та
та . І, нарешті, кут закручування правого
перерізу четвертої ділянки відносно
початку координат дорівнює сумі кутів
. І, нарешті, кут закручування правого
перерізу четвертої ділянки відносно
початку координат дорівнює сумі кутів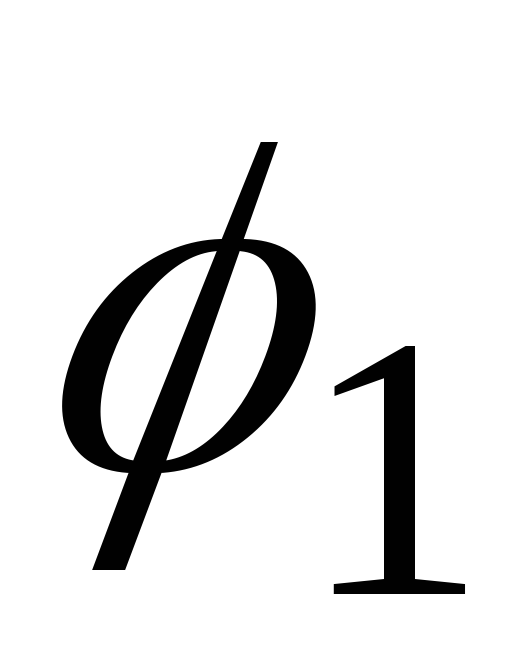 ,
,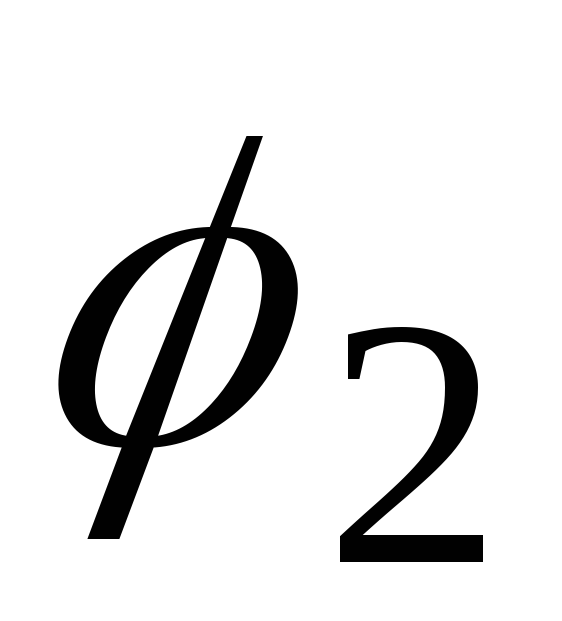 ,
, та
та .
.
Повний кут закручування правого краю валу відносно лівого дорівнює:
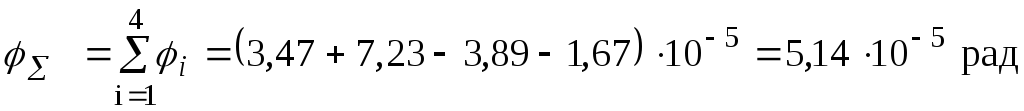 .
.
Найбільший відносний кут закручування:
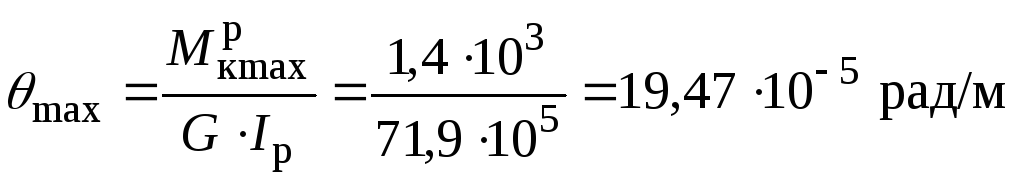 <<
<<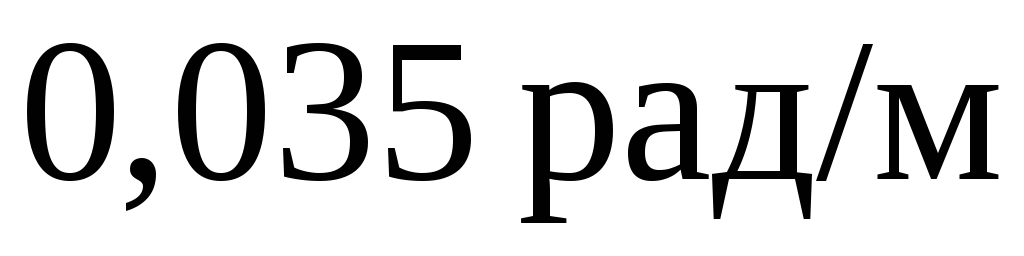 . Умова жорсткості
. Умова жорсткості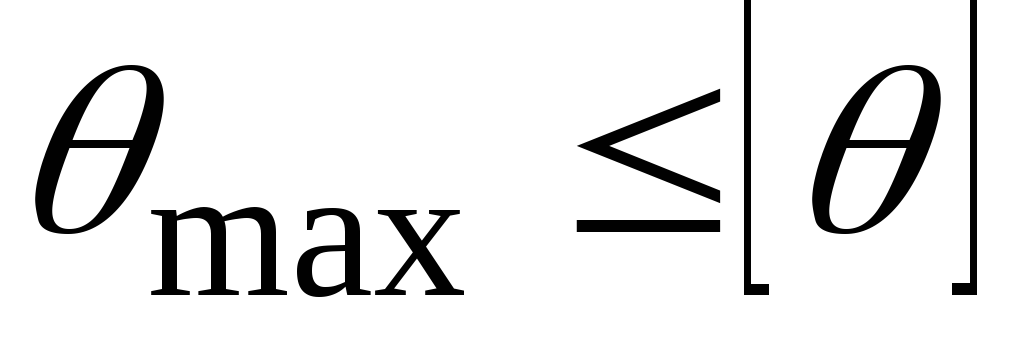 виконується з великим запасом.
виконується з великим запасом.
Побудуємо епюри дотичних напружень в поперечних перерізах суцільного і трубчастого валів:

Рисунок 3.15
Зразок виконання задачі 2
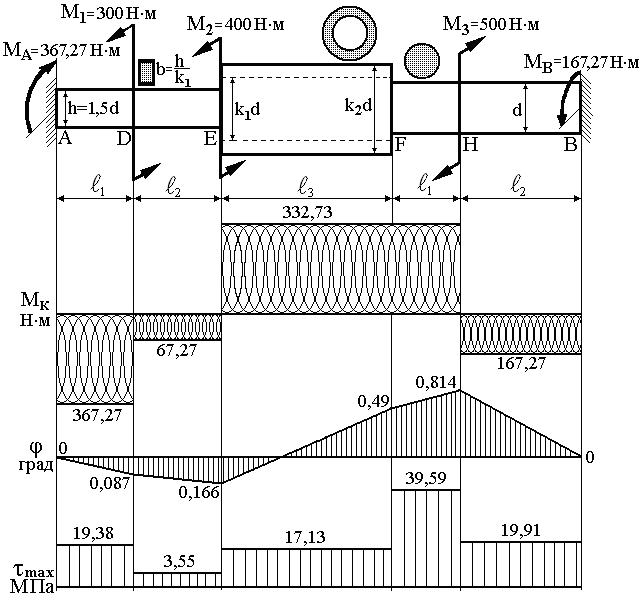
З умов міцності та жорсткості визначити розміри поперечних перерізів статично невизначуваного стержня з послідовним розташуванням ділянок прямокутного, кільцевого та круглого перерізів (рис. 3.16).
Дано:
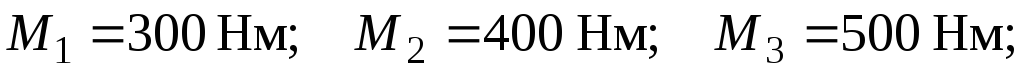
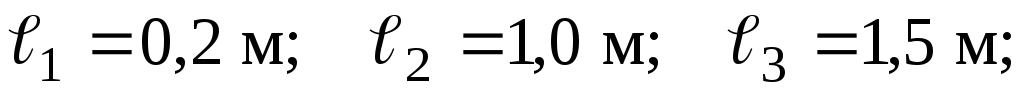
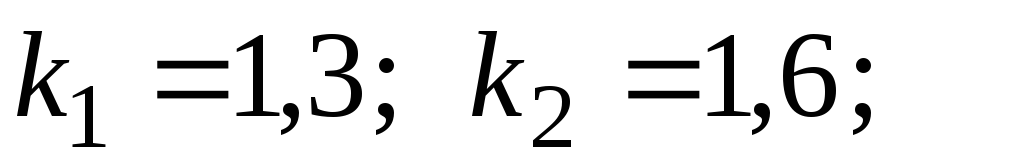
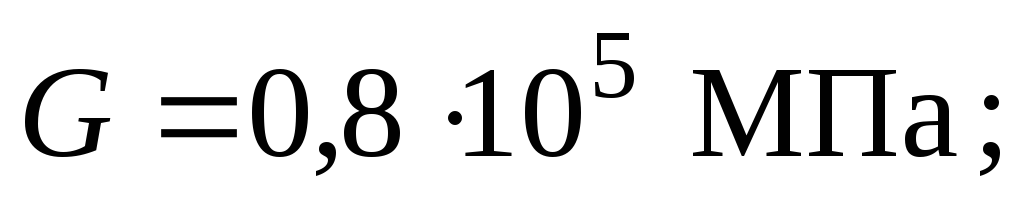
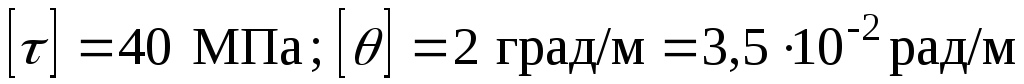 .
.
Визначимо геометричні характеристики поперечних перерізів ділянок стержня:
| Полярний момент інерції:
|
Полярний момент опору:
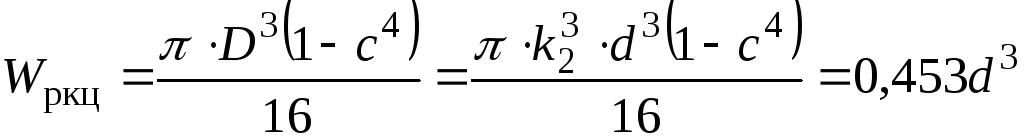 .
.
| Полярний момент інерції: Полярний момент опору: |
| Момент
інерції при крученні: |
Момент
опору при крученні ( 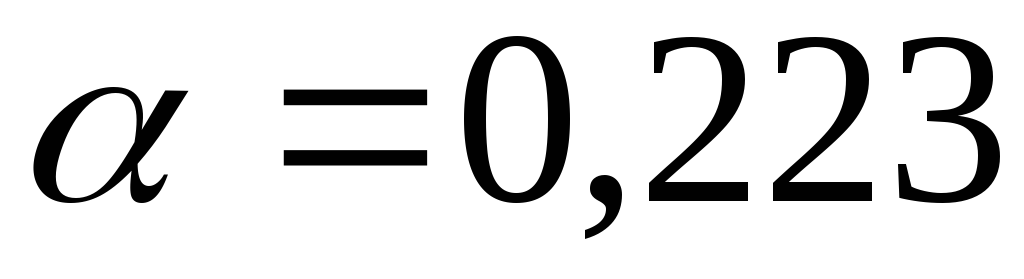 ,
див. табл. 3.1)
,
див. табл. 3.1)
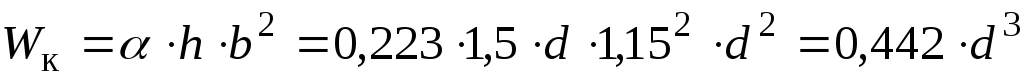 .
.
|
Рисунок 3.16 |
Розкриємо статичну невизначуваність задачі.
При
даному типі навантаження в місцях
закріплення вала виникають два реактивні
моменти 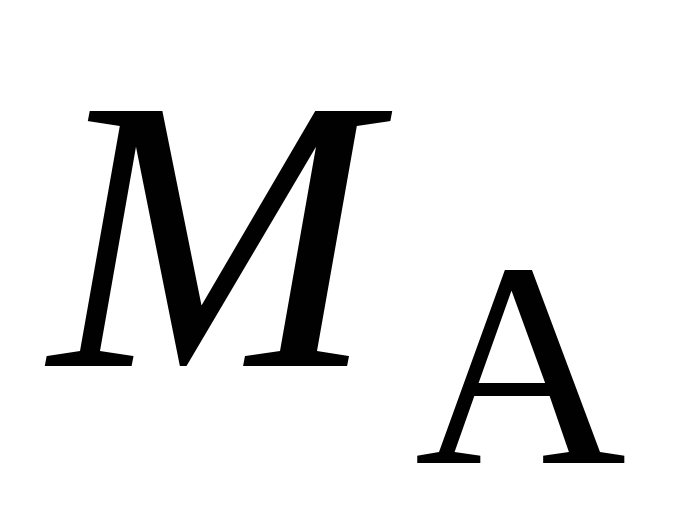 та
та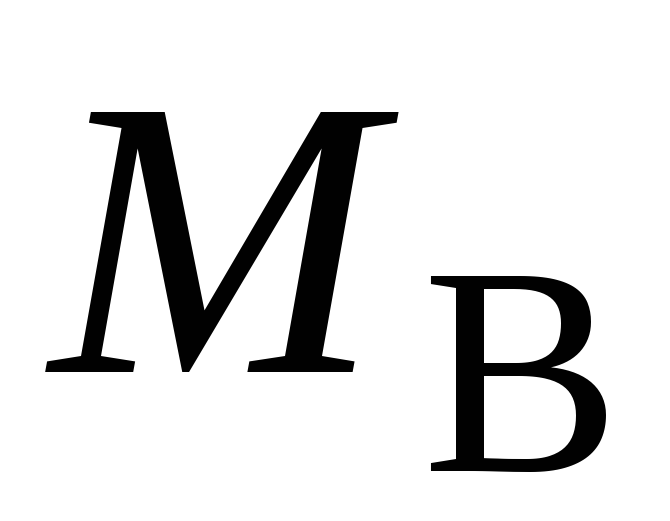 в площинах, перпендикулярних до осі
стержня. Ступінь статичної невизначуваності
в площинах, перпендикулярних до осі
стержня. Ступінь статичної невизначуваності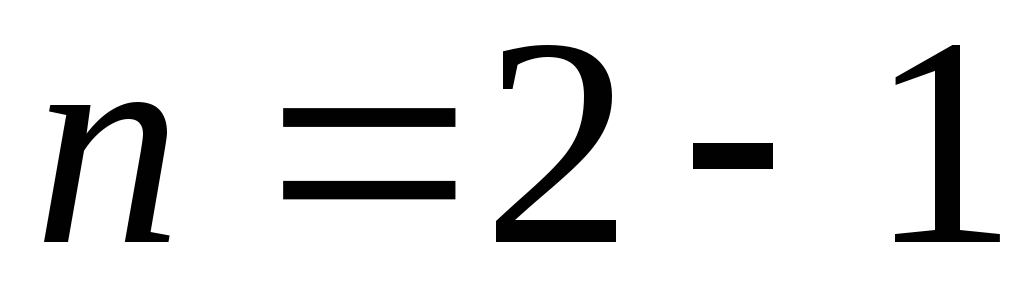 дорівнює одиниці, тому задача є один
раз статично невизначувана.
дорівнює одиниці, тому задача є один
раз статично невизначувана.
Статичний аспект задачі:
З умови рівноваги вала:
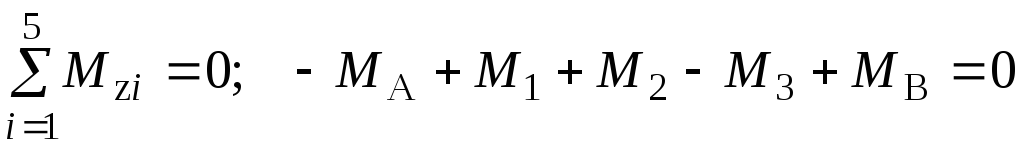 .
(3.17)
.
(3.17)
Геометричний аспект задачі:
Заміняємо початкову статично невизначувану задачу на статично визначувану, умовно відкидая ліву опору. На підставі принципу незалежності дії сил абсолютний кут закручування лівого краю стержня відносно нерухомого правого дорівнює алгебраїчній сумі кутів закручування від кожного зовнішнього моменту:
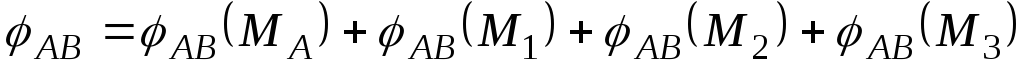
Оскільки обидва кінці валу жорстко закріплені, то кут повороту переріза А відносно В дорівнює нулю (рівняння сумісності кутів закручування):
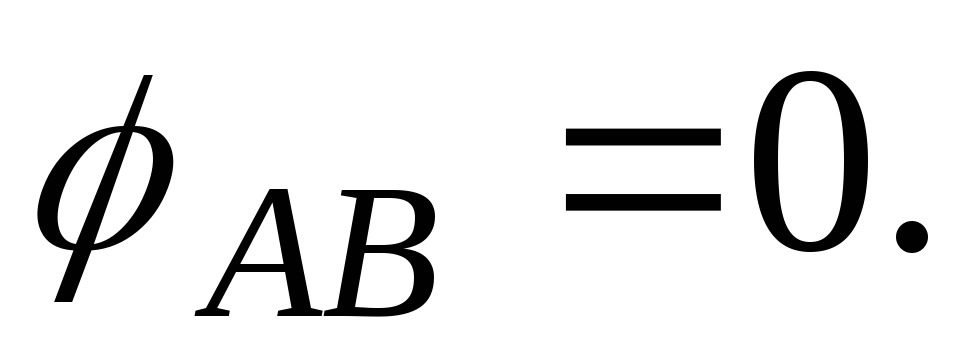 (3.18)
(3.18)
Фізичний аспект задачі:
Використовуючи формулу закону Гука, запишемо вирази для кутів закручування:
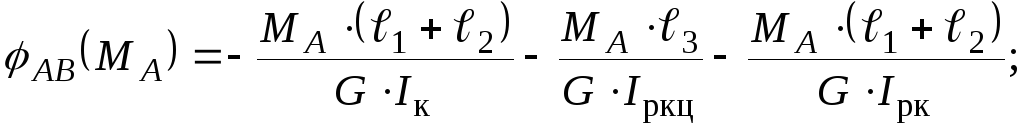
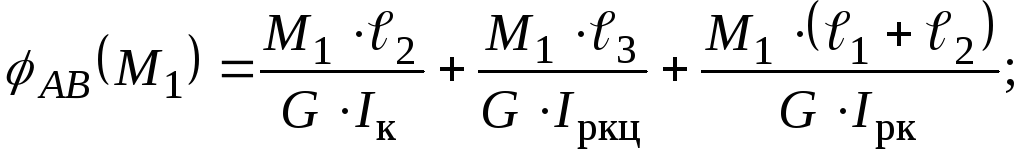
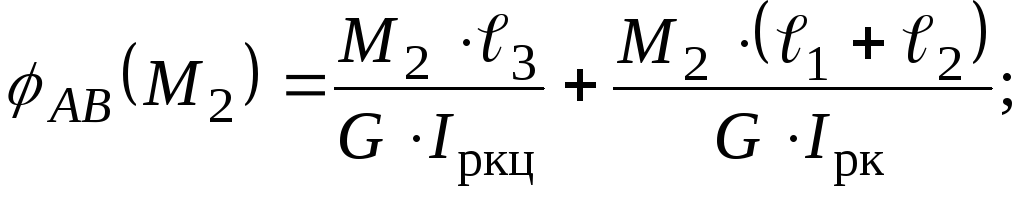 (3.19)
(3.19)
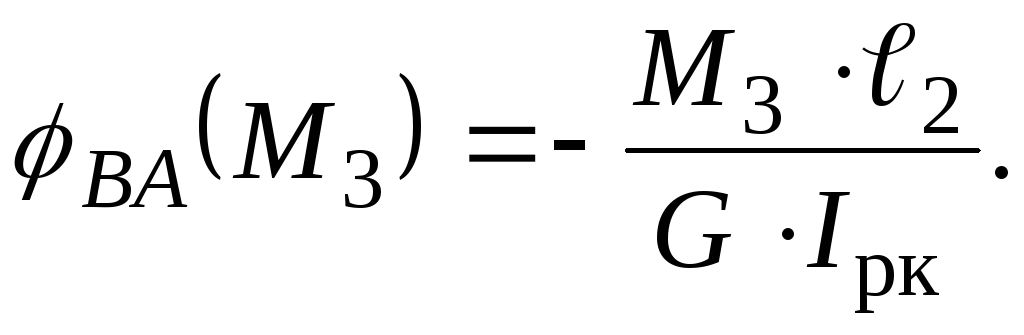
Якщо підставити вирази (3.19) у вираз (3.18), то матимемо:
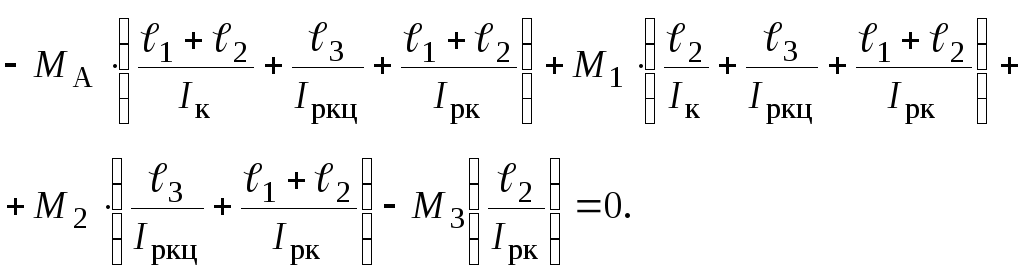 (3.20)
(3.20)
Із
рівняння (3.20) знаходимо значення 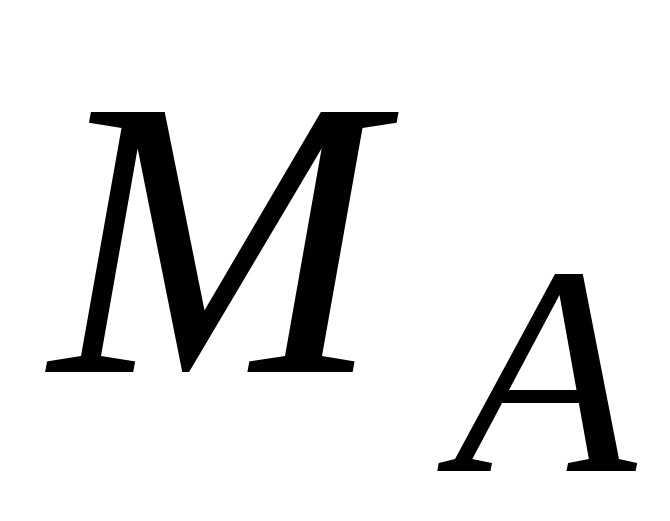 .
.
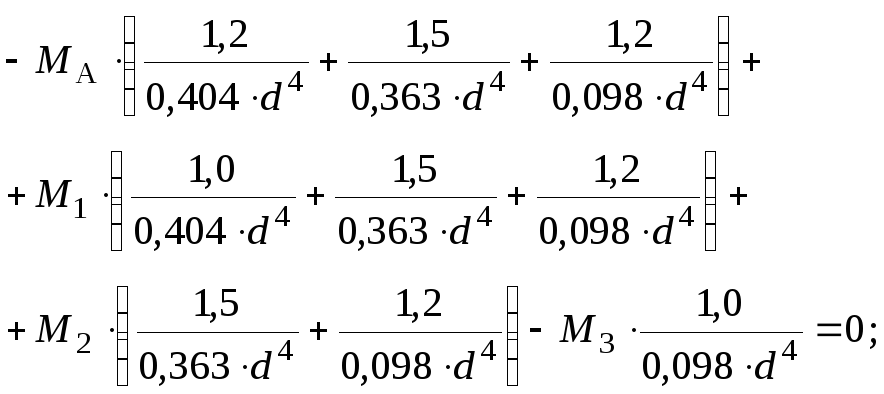
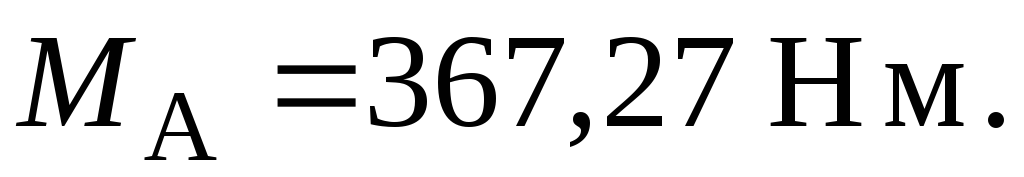
З
рівняння рівноваги (3.17) знаходимо
значення реактивного моменту 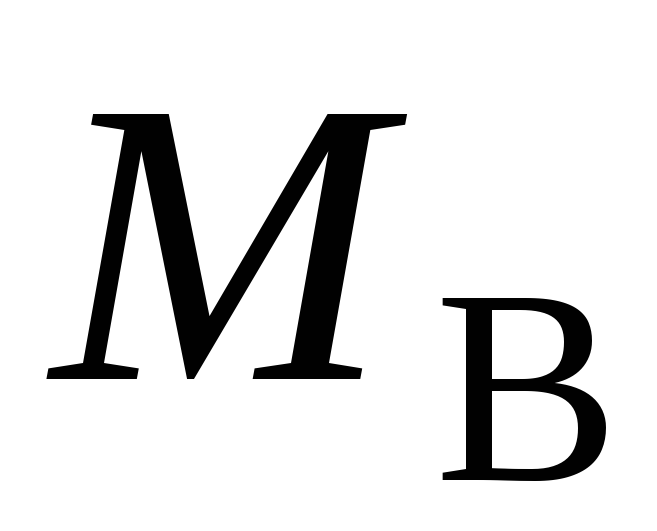 :
:
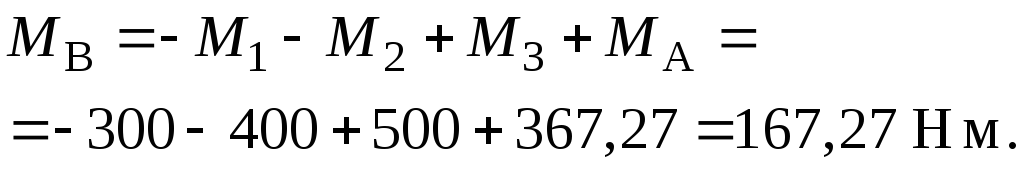
Будуємо епюру крутних моментів (рис. 3.16).
Визначаємо значення параметру
 для заданих форм поперечних перерізів
стержня з умови міцності:
для заданих форм поперечних перерізів
стержня з умови міцності:
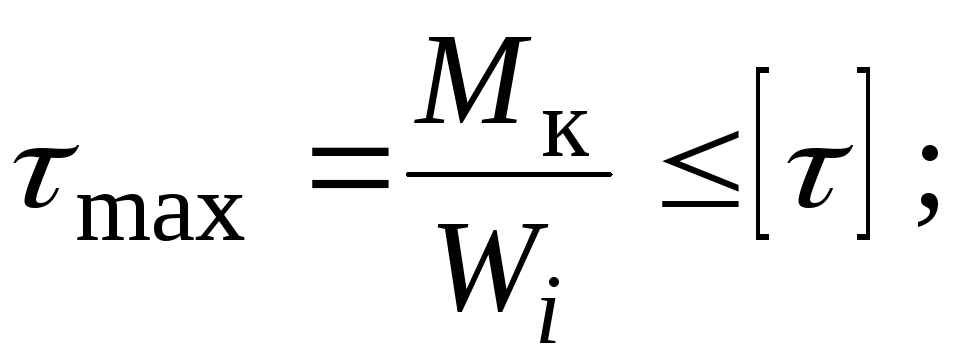
для
кільцевого перерізу з епюри крутного
моменту (рис. 3.16) 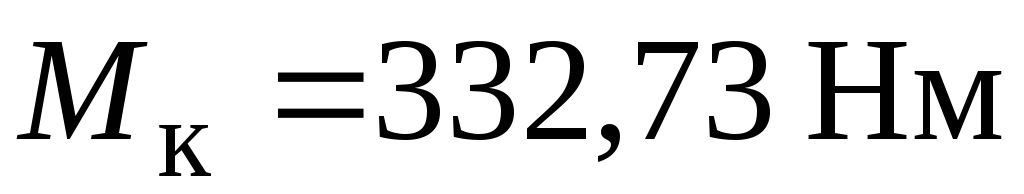 ,
тоді
,
тоді
 м;
м;
для
круглого перерізу (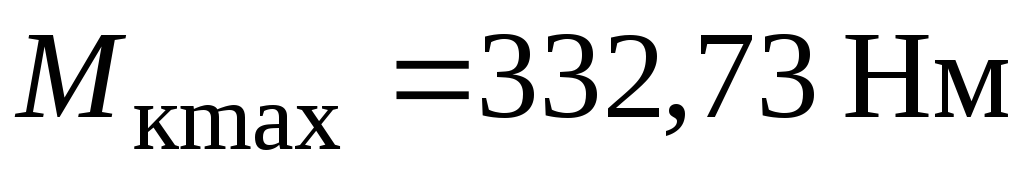 )
)
 м;
м;
для
прямокутного перерізу (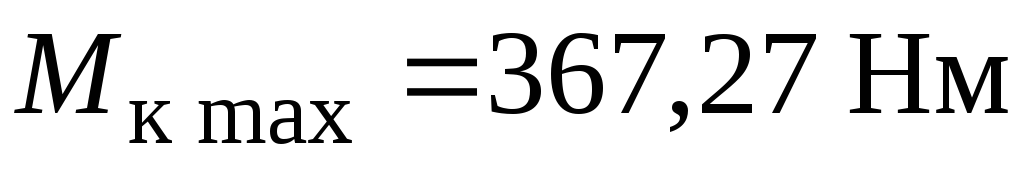 )
)
 м.
м.
З
трьох отриманих результатів слід
вибирати більший: 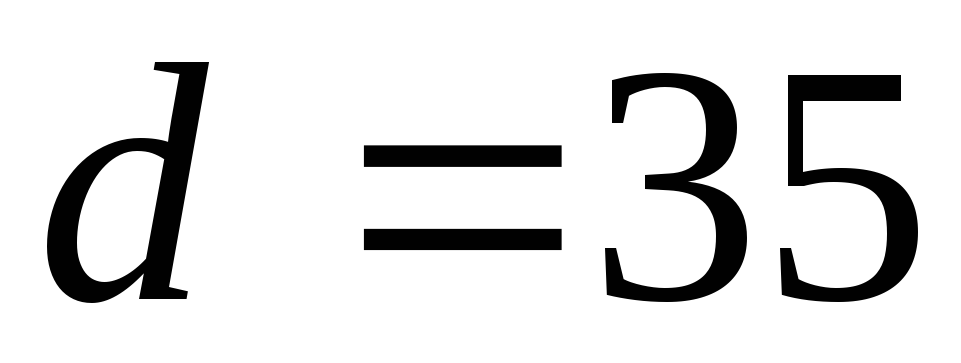 мм,
який знайдено з умови міцності для
круглого перерізу.
мм,
який знайдено з умови міцності для
круглого перерізу.
5.
Будуємо епюру розподілу максимальних
дотичних напружень по довжині стержня:
для круглого перерізу 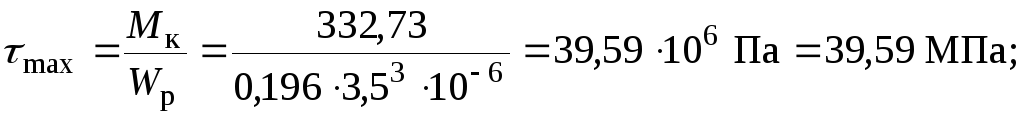
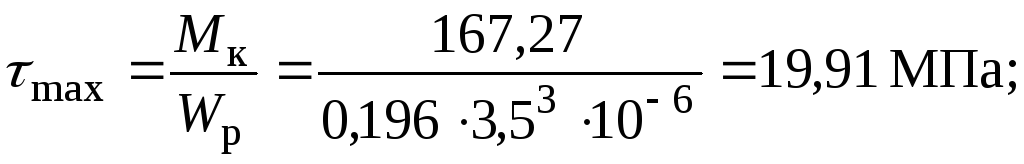
для кільцевого перерізу
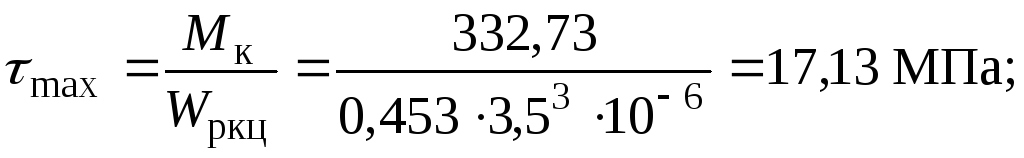
для прямокутного перерізу
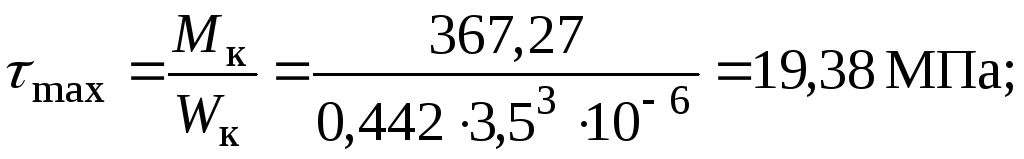
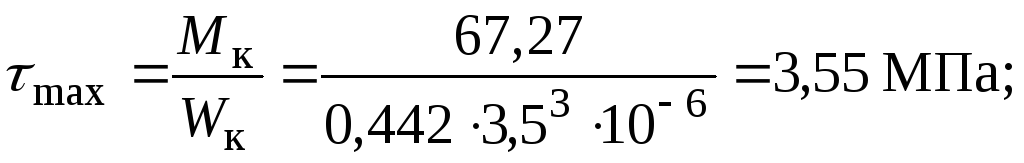
Побудуємо епюру кутів закручування.
Послідовно для частин стержня знаходимо значення кутів закручування.
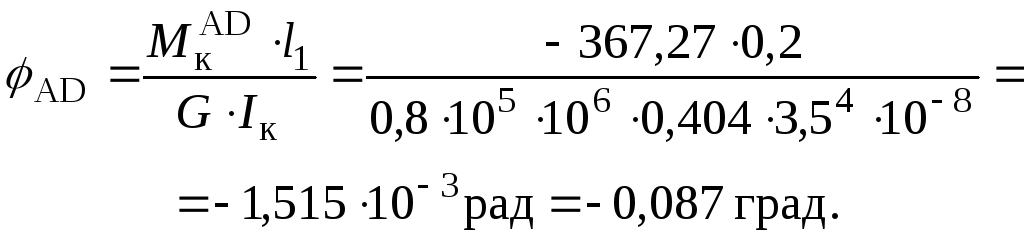
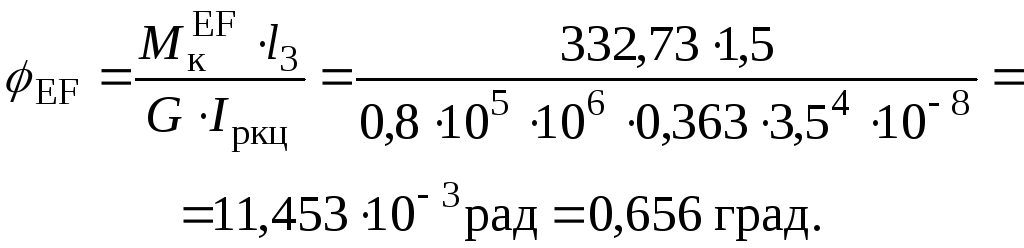
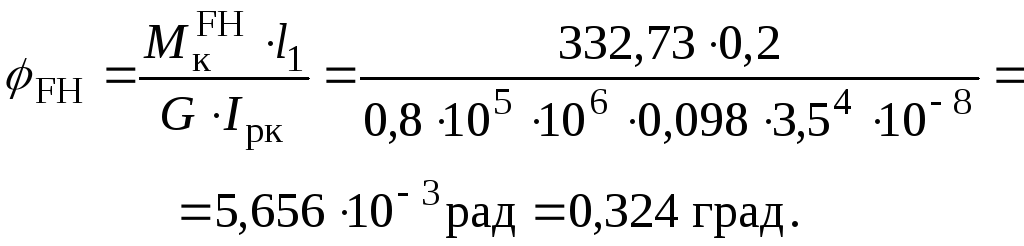
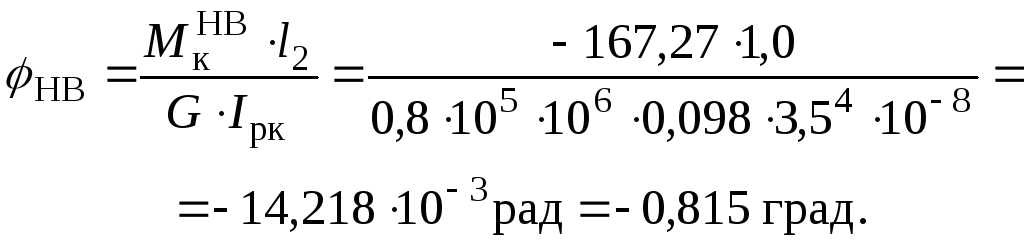
Перевіримо виконання умови жорсткості для найнебезпечнішої ділянки FH круглого перерізу, де відносний кут закручування дорівнює:
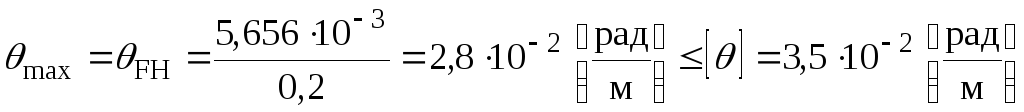 .
.
Умова жорсткості виконана.
Встановимо
початок координат у перерізі A
та будуємо епюру кутів закручування
для
деформаційної перевірки: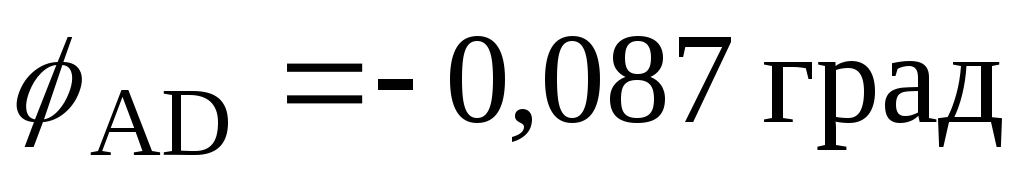 ;
;
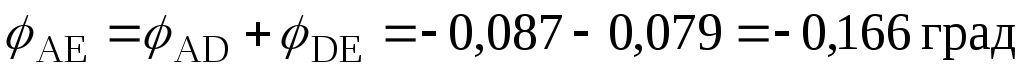 ;
;
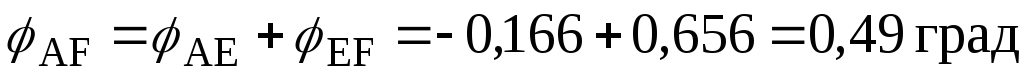 ;
;
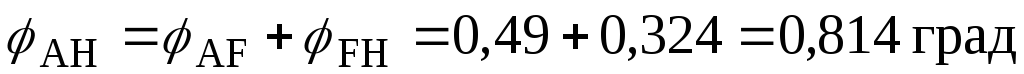 ;
;
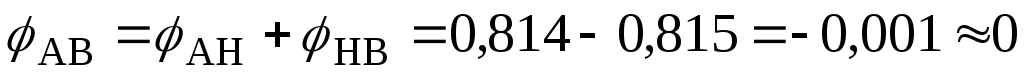 .
.
Абсолютний
кут закручування перерізу А відносно перерізу В повинен дорівнювати
нулю. Але отримана абсолютна похибка
(0,001) є результатом накопичення округлення
на кожному етапі рішення задачі. Тому
визначимо
відносну похибку обчислень 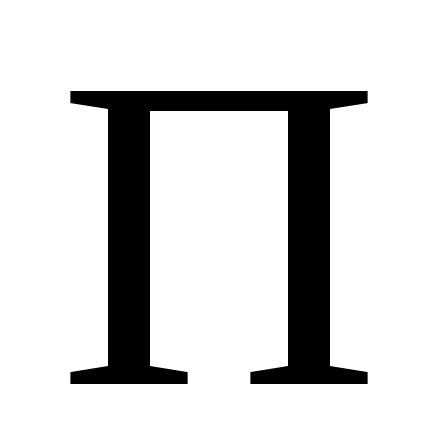 та порівняємо з її допустимим значенням:
та порівняємо з її допустимим значенням:
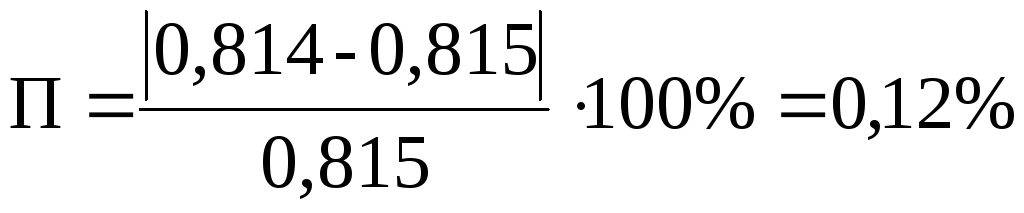 <<
5%,
<<
5%,
що свідчить про точність отриманих результатів та правильність рішення статично невизначуваної задачі.
studfile.net
Графічний метод розв язання задачі лінійного програмування Основи аналізу моделі на чутливість (стр. 1 из 2)
Пошукова робота на тему:
Графічний методрозв’язання задачі лінійного програмування. Основи аналізу моделі на чутливість
1.Знаходження оптимального розв’язку ЗЛП графічним методом.
Оскільки розглянута в темі 1 модель містить тільки дві змінні, задачу можна розв’язати графічно. У випадку трьох змінних графічний розв’язок стає менш наочним, а при більшому числі змвнних — взагалі неможливим. Незважаючи на це, розгляд графічного методу дасть змогу зробити висновки, що послужать основою для розробки загального методу розв’язання задач ЛП .
Перший крок при використанні графічного методу полягає в поданні області допустимих розв’язків, у якій водночас задовольняються всі обмеження моделі. Шукана область (простір) розв’язків задачі прикладу 1.1. показана на рис. 2.1. Умови невід’ємності змінних обмежують область їх допустимих значень першим квадрантом координатної площини (частина площини над віссю x1 і справа від осі x2).Інші межі простору розв’язків зображені прямими лініями, побудованими по рівняннях, що отримані заміною знака “£” знаком “=» в обмеженнях. Області, в яких відповідні обмеження виконуються як нерівності ( в нашому випадку — нерівності із знаком “<”), указуються стрілками, спрямованими вбік допустимих значень змінних. Отриманий простір розв’язків задачі про фарби — багатокутник АВСDЕF (рис. 2.1). У кожній точці, що належить внутрішній області або межам багатокутникарозв’язків АВСDЕF, всі обмеження виконуються, тому розв’язки, що відповідають цим точкам, є допустимими. Серед безкінечногочисла таких точок можна знайтиточку оптимальнного розв’язку, якщо з’ясувати, в якому напрямку зростає цільова функція.
Рис. 2.1. Простір допустимих розв’язків задачі “про фарби”.
На рис. 2.2 показано, як здійснюється така операція.
Рис. 2.2. Знаходження оптимального розв’язку ЗЛП графічним методом.
На графік наносять лінію рівня цільової функції c1×x1+c2×x2=z0, де z0 — довільне значення z. Будують вектор N (c1, c2), що є нормальним до ліній рівня цільової функції й визначає напрямок оптимізації z. Лінію рівня зрушують паралельно самій собі вздовж вектора N доти, поки вона не вийде за межі області допустимих розв’язків. Остання точка цієї області й буде точкою оптимуму. Очевидно, що оптимальному розв’язку відповідає точка С- точка перетину прямих (1) і (2). Значення x1та x2 в точці С визначаються шляхом розв’язання системи рівнянь:
Розв’язком цієї системи є x1=3 ; x2 =1 . Отриманий у цьому випадку прибуток складе: z=3x1+2x2 =3×3 +2×1 =12 (тис. г.о.)
Зазначимо, що у випадку, коли лінії рівня z мають такий самий нахил, як пряма зв’язуючого обмеження (тобто такого, що проходить через оптимальну точку), матимемо безліч оптимумів на відрізку.
2. Аналіз моделей ЗЛП на чутливість: мета і задачі.
Після одержання оптимального розв’язку задачі ЛП часто виникає потреба виявити чутливість цього розв’язку до певних змін параметрів вихідної моделі. Наприклад, в задачі про фарби може становити інтерес питання про те, як вплине на оптимальний розв’язок збільшення або зменшення попиту, зміна запасів ресурсів, а також ринкових цін на товари. При такому аналізі завжди розглядається деяка сукупність лінійних оптимізаційних моделей, що надає моделі динамічність, властиву реальним процесам. Відсутність методів, що дозволяють виявити вплив можливих змін параметрів моделі на оптимальний розв’язок, може призвести до того, що отриманий (статичний) розв’язок застаріє ще до своєї реалізації.
В рамках аналізу на чутливість розв’язку, отриманого графічним методом, розв’язуються такі три задачі:
1) аналіз на чутливість до зміни правих частин обмежень;
2) аналіз ступеня дефіцитності ресурсів;
3) аналіз розв’язку ЗЛП на чутливість до зміни коефіцієнтів цільової функції.
3. Перша задача аналізу на чутливість: аналіз на чутливість до зміни правих частин обмежень.
Дана задача дозволяє дати відповідь на питання:на скільки доцільно збільшити або скоротити запаси ресурсів?
Особливо важливо проаналізувати такі два аспекти.
1. На яку величину можна збільшити запас деякого ресурсу для поліпшення отриманого оптимального значення цільової функції?
2. На яку величину можна зменшити запас деякого ресурсу при збереженні отриманого оптимального значення цільової функції?
Оскільки величина запасу кожного з ресурсів фіксується в правих частинах обмежень, цей вид аналізу часто називають аналізом начутливістьдо правих частин(обмежень).
Перед тим , як відповісти на поставлені запитання, класифікуємо обмеження лінійної моделі на зв’язуючі (активні) та незв’язуючі (неактивні). Пряма, що відповідає зв’язуючому обмеженню, повинна проходити через оптимальну точку. На рис. 2.1 зв’язуючими є тільки обмеження (1) і (2), тобто ті, що лімітують запаси ресурсів А і В.
Якщо деяке обмеження є зв’язуючим, то ресурс, що йому відповідає, слід віднести до розрядудефіцитних ресурсів, оскільки він витрачається повністю. Ресурс, з яким асоційоване незв’язуюче обмеження, варто віднести до розряду недефіцитних ресурсів (тобто наявних у деякому надлишку). Таким чином, у ході аналізу моделі на чутливість до правих частин обмежень визначаються такі величини:
1) гранично допустиме збільшення запасу дефіцитного ресурсу, що дозволяє поліпшити знайдений раніше оптимальний розв’язок;
2) гранично допустиме зниження запасу недефіцитного ресурсу, що не змінює знайденого раніше значення цільової функції. Інформація, отримана в останньому випадку, особливо корисна в тих ситуаціях, коли надлишки недефіцитного ресурсу можуть бути використані для інших цілей.
Може виникнути питання: чи не варто проаналізувати, як вплине на оптимум збільшення обсягу ресурсів, які є в надлишку, і скорочення обсягу дефіцитних ресурсів. Відповідь на першу частину запитання є очевидною, тому що в цьому випадку ми спробували б зробити й без того надлишковий ресурс ще більш надлишковим, що ніяк не вплине на отриманий раніше розв’язок. Друга частина питання заслуговує особливої уваги, оскільки при можливих недопоставках дефіцитного ресурсу важливо знати, як це позначиться на результатах розв’язання задачі.
Звернемося знову до конкретного прикладу. В задачі «про фарби» продукти А и В (обмеження (1) і (2)) є дефіцитними ресурсами. Розглянемо спочатку ресурс А. На рис. 2.3 видно, що при збільшенні запасу цього ресурсу пряма (1) (або відрізок СD) переміщується вгору паралельно самій собі, поступово «стягуючи» у точку трикутник СD. Сторони CK і DK цього трикутника являють собою продовження прямих, що відповідають обмеженням (2) і (4). У точці К обмеження (2) і (4) стають зв’язуючими; оптимальному розв’язку при цьому відповідає точка К, а простором (допустимих) розв’язків стає багатокутник АВKЕF. У точці К обмеження (1) (для ресурсу А) стає надлишковим, оскільки будь-яке подальше зростання запасу відповідного ресурсу не вплине ні на простір розв’язків,ні на оптимальний розв’язок. Таким чином, обсяг ресурсу А не варто збільшувати зверх тієї межі, що відповідає точці, в якій обмеження (1) стає надлишковим.
Рис. 2.3. Визначення максимально допустимого збільшення запасу ресурсу А.
Цей граничний рівень визначається наступним чином. По-перше, встановлюються координати точки, в якій перетинаються прямі (2) і (4), тобто знаходиться розв’язок системи рівнянь:
В результаті одержимо x1=3 і x2=2. Підставляючи координати точки К в ліву частину обмеження (1), визначаємо максимально допустимий запас ресурсу А: x1+2 x2=2=3+2× 2=7 т.
Рис. 2.4 ілюструє ситуацію, коли розглядається питання про доцільність збільшення запасу дефіцитного ресурсу (2) (вихідного продукту В). Новою оптимальною точкою стає точка J, де перетинаються прямі (6) і (1), тобто x2=0, x1+2x2=6. Звідси випливає, що x1=6, x2=0, причому запас продукту В можна збільшити до значення, рівного 2x1+x2=2×6+1×0=12 т.
Рис. 2.4. Визначення максимально допустимого збільшення запасу ресурсу В.
Розглянемо тепер питання про зменшення правої частини незв’язуючих обмежень. Обмеження (4), x2 2 фіксує граничний рівень попиту на фарбу другого виду. На рис. 2.2. видно, що, не змінюючи оптимального розв’язку, пряму (4) (ЕD) можна опускати донизу до перетину з оптимальною точкою С. Оскільки точка С має координати x1 = і x2=то, зниження попиту на фарбу 2 до величини x2= ніяк не вплине на оптимальність раніше отриманого розв’язку.
Розглянемо обмеження (3), -x1+ x2 1, що описує співвідношення між попитом на фарбу 2 і попитом на фарбу 1. У цьому випадку праву частину обмеження можна зменшувати доти, поки пряма (3) (ЕF) не досягне точки С, При цьому права частина обмеження (3) стане рівною -x1+ x2=(-)+( )= -2, що дозволяє записати це обмеження у вигляді: -x1+ x2 -2, або в еквівалентній формі: x1— x2. Цей результат показує, що раніше отриманий оптимальний розв’язок не зміниться, якщо попит на фарбу 1 перевищить попит на фарбу 2 не більше, ніж на 2 т.
Результати проведеного аналізу можна звести в таку таблицю.
Таблиця 2.1
4. Друга задача аналізу на чутливість: оцінка дефіцитності ресурсів.
mirznanii.com
Диференціальні рівняння вищих порядків
ВІННИЦЬКИЙ ФІНАНСОВО-ЕКОНОМІЧНИЙ УНІВЕРСИТЕТКафедра економічної кібернетики
ЗВІТ
з навчальної практики на тему:
«Диференціальні рівняння вищих порядків»
Вінниця 2009
Зміст
Вступ
Диференціальне рівняння вищого порядку
Геометричне тлумачення задачі Коші
Зниження порядку диференціальних рівнянь другого порядку
Диференціальні рівняння є однорідними відносно функції у та її похідних і
Лінійні диференціальні рівняння другого порядку
Питання для перевірки
Тестові завдання
Задачі
Відповіді на тестові завдання
Розв’язок до задач
Охорона праці
Висновки
Література
Вступ
Для успішної участі у сучасному суспільному житті особистість повинна володіти певними прийомами математичної діяльності та навичками їх застосувань до розв’язання практичних задач. Певної математичної підготовки і готовності її застосовувати вимагає і вивчення багатьох навчальних предметів. Значні вимоги до володіння математикою у розв’язанні практичних задач ставлять сучасний ринок праці, отримання якісної професійної освіти, продовження освіти на наступних етапах. Тому одним з головних завдань цього тренінгу є забезпечення умов для досягнення кожним студентом практичної компетентності.
Прикладна спрямованість математичної освіти суттєво підвищується завдяки впровадженню комп’ютерів у навчання математики, повноцінному введенню ймовірносно-статистичної змістової лінії.
Мета: придбання знань, вмiнь та навичок, необхiдних для розв’язання та обчислення диференціальних рівнянь вищих порядків.
Завдання:
§ вивчення класичних і сучасних наближених методів розв’язання диференціальних рівнянь та їх систем;
§ придбання умінь використання методів розв’язання задач з початковими умовами та крайових задач для звичайних диференціальних рівнянь та диференціальних рівнянь з частинними похідними при моделюванні систем.
Студент повинен знати:
§ класифікацію наближених методів розв’язування диференціальних рівнянь та їх систем;
§ методи розв’язування трансцендентних, алгебраїчних і диференціальних рівнянь та їх систем;
§ методи чисельного інтегрування і диференціювання.
Студент повинен вміти: самостійно вибирати і обґрунтовувати раціональний метод розв’язування поставленої задачі.
Диференціальне рівняння вищого порядку
Диференційні рівняння вищого порядку стосовно функції у(х) має вигляд:
(1)
яке називають диференційованим рівнянням першого порядку, якщо рівняння (1) подано у вигляді:
(2)
та його називають диференційованим рівнянням першого порядку, яке є розв’язком відносно найстаршої похідної, або явним диференціальним рівнянням, або нормальним диференційованим рівнянням першого порядку.
Оскільки теоретичні поняття і методи інтегрування диференціальних рівнянь вищого порядку є споріднені для рівнянь різних порядків, то надалі ми обмежемось розглядом диференціальних рівнянь другого порядку:
(3)
(4).
Функція називається розв’язком диференціального рівняння (3)чи (4) проміжну (a,b), якщо вона двічі не перервно диференційованa на цьому проміжку і будучи підставлена у рівняння, перетворює його у тотожність, тобто
x є (a,b)
або
Графік функції називається при цьому інтегральною кривою диференціального рівняння (3) чи (4).
Зрозуміло, що інтегральна крива повинна міститися в області визначення функції F.
Наприклад, розв’язком диференційованого рівняння є функція на проміжку , бо ця функція є двічі диференційована на цьому проміжутку і Крім того, функція де C1,C2— довільні сталі, є також розв’язком цього рівняння.
Аналогічно переконаємось, що функція і є розвязками диференціального рівняння на проміжку , бо вони двічі диференційовані на цьому проміжку
Розвязком цього рівняння є також функції де — довільні сталі.
Далі будемо розглядпти основні поняття та означення для диференціального рівняння (4).
Функція де і довільні сталі називається загальним розв’язком диференційованого рівняння другого порядку, якщо вона є розв’язком цього рівняння для розв’язком функції і і з якої за рахунок вибору значень цих сталих можна отримати будь-який розв’язок цього рівняння (за винятком може окремих).
Розвязок який отримуємо із загального диференціального рівняння 2-го порядку, мадаючи і певних числових значень, називається числовим розвязком цього рівняння.
Задача Коші. Практичних задач, які зводяться до диференціального рівняння другого порядку, потрібно відшукати розвязок цього рівняння, що задовольняє певні додаткові умови.
Найчастіше ними є умови Коші:
(5)
Задача знаходження розвязку диференціального рівняння (4), який задовольняє умови (5), називається задачею Коші для цього рівняння. Цю задачу Коші записуватимемо коротко:
Геометрично, задача Коші для диференціального рівняння (4) полягає у знаходженні інтегральної кривої цього рівняння. Яке проходить через точку і яка дотикається у цій точці до вектора, що утворює кут y, з додатним напрямком осі
Геометричне тлумачення задачі Коші
Зрозуміло, що точки повинні лежати області визначення функції , тобто області визначення диференціального рівняння (4).
Можна показати, що правильне таке твердження: якщо функція та її частинні похідні і є неперервні в деякому околі точки , то існує єдиний розв’язок задачі Коші (4) – (5), який визначений у певному околі точки .
Геометрично це означає, що при виконанні умов сформульованої теореми, через точну проходить єдина інтегральна крива диференціального рівняння (4), яка замикається у цій точці до вектора, який утворює з додатним напрямом осі кут .
З теореми існування та розв’язку задачі Коші для рівняння (4) випливає, що при виконанні умов теореми в деякому околі точки існує загальний розв’язок цього рівняння, з розв’язком якого отримати розв’язок задачі Коші, визначивши значення сталих і із системи рівнянь:
(6)
Відзначемо, що система рівняння (6) завжди є розв’язком, бо існує розв’язок задачі Коші (4) – (5)
На практиці для диференціального рівняння другого порятку можуть бути задані інші умови замість умов Коші. Ними можуть бути крайові умови: і геометрична задача полягає у знаходженні інтигральної кривої диференціального рівняння (4), яка проходить через дві точки ,.
Примітка. Якщо диференціального рівняння (3) має один розвязок відносно , то воно рівносильне диференційномурівняню , де
Якщо ж диференціальне рівняння (3) має декілька розв’язком відносно , то воно рівносильне сукупності диференціальних рівнянь.
де
Зниження порядку диференціальних другого порядку
Основним методом інтегрування (знаходження загального розвязку або загального інтеграла) диференціальних рівнянь вищого порядку є зниження їх порядку і зведення до інтегрування диференціальних рівнянь першого порятку. Розглянемо деякі можливі видатки зниження порядку диференціальних рівнянь другого порядку.
1. Диференціальне рівняння не містить невідомої функції у, тобто має вигляд:
(7).
У цьому випадку робимо заміну і отримуємо диференціальне рівняння першого порядку стосовно невідомої функції Z:
Якщо знайдемо загальний розв’язок , рівнянь (8) то далі інтегруємо рівняння ; якщо ж знайдемо загальний інтеграл то для знаходження розв’язків диференціального рівняння (7) отримуємо наявне диференціальних рівнянь першого порятку
2. Диференціальне рівняння не містить явно аргументах х, тобто має вигляд
(9)
У розв’язаному випадку приймаємо за невідому функцію а й аргументи вважаємо у. Тоді маємо:
Підставимо вирази для у’,y” у рівняння (9), отримаємо відносно функцію диференціальних рівнянь першого порядку:
(10)
Якщо знайдемо загальний розв’язок рівняння (10), то дані інтнгруєм явне диференціальне рівняння першого порядку яке є з розв’язком функції змінними; якщо ж знайдено загальний інтеграл рівняння (17.10), то дані інтегруємо наявне диференційне рівняння першого порядку.
Диференціальне рівняння (3) є однорідним відносно функції у та її похідних і
тобто
У цьому випадку виконуємо заміну де z = z (x). Знаходимо Підготовимо вирази для та у рівняння (3) і використовуємо його однорідність:
У результаті приходимо до диференціальних рівнянь першого порятку стосовно функції
(11)
яке з точністюдо розвязку рівносильне рівняню (3)
Якщо знайдемо загальний розвязок рівняння (11), то речі інтегруємо розв’язане дифененційне рівняння першого порядку , яке є з відокремлюваними змінними; якщо ж знайдемо загальний інтеграл то приходимо до інтегрування наявного диференціального рівняння першого порядку:
При зниженні порядку вихідного рівняння міг бути втрачений його розв’язок у=0. Але він не втрачений, отримуємо із загального розв’язку при
Лінійні диференціальні рівняння другого порядку
Диференціальні рівняння розв’язку порядку (3) називається лінійним, якщо функція,є лінійно відносно тобто якщо воно має вигляд
(12)
Будемо вважати, що розв’язком і вільний член q(x) x є(a,b) i .
Якщо то маємо відповідне лінійне однорідне рівняння
(13)
Якщо ,то рівняння (12) називають лінійним не однорідним диференціальним рівняння другого порядку.
Питання для перевірки
1. Що називається диференціальним рівнянням вищого порядку ?
2. Задача Коші.
3. Основні методи інтегрування.
4. Лінійні диференціальні рівняння другого порядку.
Тестові завдання
1. Диференційні рівняння вищого порядку стосовно функції у(х) має вигляд:
1.
2.
3.
2. Функція (вписати відповідь) де і довільні сталі називається загальним розв’язком диференційованого рівняння другого порядку, якщо вона є розв’язком цього рівняння для розв’язком функції і і з якої за рахунок вибору значень цих сталих можна отримати будь-який розв’язок цього рівняння (за винятком може окремих).
3. Співвідношення яким певно додається загальний розв’язок диференціального рівняння 2-го порядку, називається (вписати відповідь) цього рівняння.
4. Диференціальне рівняння не містить невідомої функції у, тобто має вигляд:
1.
2.
3.
5. Розв’язок який отримуємо із загального диференціального рівняння 2-го порядку, падаючи і певних числових значень, називається числовим (вписати відповідь) цього рівняння.
6. Графік функції називається при цьому (вписати відповідь) диференціального рівняння (3) чи (4).
7. Диференціальні рівняння розв’язку порядку (3) називається лінійним, якщо функція,є лінійно відносно тобто якщо воно має вигляд
1.
2.
3.
8. Співвідношення … яким певно додається загальний розв’язок диференціального рівняння 2-го порядку, називається загальним інтегралом цього рівняння:
1.
2.
3.
9. З теореми існування та розв’язку задачі Коші для рівняння (4) випливає, що при виконанні умов теореми в деякому околі точки існує загальний розв’язок цього рівняння, з розв’язком якого отримати розв’язок задачі Коші, визначивши значення сталих і із системи рівнянь:
1.
2.
3.
Задачі
Задача 1. Знайти розв’язок диференційoваного рівняння що задовольняє умови
Розв’язання. Загальний розв’язок цього рівняння легко знайти шляхом інтегрування заданої рівності, бо тоді розв’язком функції , друга похідна яких дорівнює 6х:
загальний розв’язок рівняння.
Задача 2. Знайти розв’язок рівняння , який звдовольняє умови: .
Розв’язання. Оскільки у рівнянні явно не входить аргумент х, то знижуємо його порядок підстановкою з якої випливає, що
Підставити вирази для і , у дане рівняння, отримаємо диференціальне рівняння першого порядку
яке рівносильне сукупності рівнянь:
Інтегруємо друге рівняння, яке є з відокремлюваними змінними:
.
При відокремлені зміних втраченими могли бути розвязки і . Ці розв’язки не є втраченими, бо перший з них співпадає з першим рівнянням сукупності, а другий отримуємо з сімї
при
Отже, множина всіх розв’язкв дискретного рівняння у змінних y i z записується сукупністю розв’язком:
Враховуючи, що з одержаних розв’язків з яких отримуємо дві сукупності диференційних рівнянь:
Одже множина розв’язків вихідного диференціального рівняння складається з двох цілей інтегральних кривих і .
Розв’язок, який задовольняє початкові умови у(1)=1, у’(1)= -1 входить у другу сімю, яка виражається загальним інтегралом . З цього загального інтеграла вилучаємо розвязок, що задовольняє задані початкові умови. Для цього маємо систему рівнянь для визначенняі :
Таким чином, шуканий розв’язок задачі Коші має вигляд:
Задача 3. Проінтегрувати рівняння знаючи, що є розв’язком відповідного однорідного рівняння.
Розв’язання. Приймемо і обчислемо похожі Підставимо вирази для у рівняння:
Після елементарних перетворень отримуємо рівняння:
або
Виконуємо заміну z’=u і маємо лінійне диференціальне рівняння першого порядку
Інтегруємо відповідне однорідне рівняння:
Загальний розв’язок лінійного неоднорідного рівняння стосовно функції u шукаємо у вигляді
Підготовимо цю функцію в неоднорідне рівняння і знайдемоС(х):
Отже, загальний розв’язок лінійного неоднорідного рівняння стосовно функції u записується у вигляді
Врахувавши, що , одержуємо загальний розв’язок
вихідного рівняння.
Задача 4. Розв’яжіть рівняння
Задача 5. Розв’язати рівняння
Відповіді на тестові завдання
1.
2.
3. загальним інтегралом
4.
5. числовим розв’язком
6. інтегральною кривою
7.
8.
9.
Розв’язок до задач
Розв’язання до задачі 4. Дане рівняння не містить невідомої функції, тому приймаємо, що і отримуємо диференціальних рівнянь першого порятку
Інтнгруємо одержане рівняння з відокремлюваними змінними:
Далі інтегруємо рівняння
Прийнявши отримаємо загальний розв’язок рівняння у вигляді
Розв’язання до задачі 5. Дане рівняння є однорідне відносно у,у’,у”, бо
Приймемо, що одержуємо:
Вихідне рівняння з точністю до зводити до рівняння
Одержали для знаходження z лінійне неоднорідне диференційне рівняння першого порядку
Спочатку інтегруємо відповідне однорідне рівняння
Загальний розв’язок неоднорідного рівняння шукаємо методом варіації сталої, тобто у вигляді
Підготовимо цю функцію в неоднорідне рівняння і знайдемо функцію С(х):
Загальний розв’язок лінійного неоднорідного рівняння розв’язком функції z має вигляд
Оскільки , то далі інтегруємо диференціюємо рівняння
Після потенціювання отримуємо загальний розв’язок вихідного рівняння:
Охорона праці. Вентиляція виробничих приміщень
Одним з ефективних засобів нормалізації повітря у приміщенні є вентиляція.
Вентиляція — повітрообмін, завдяки якому забруднене повітря виводиться з приміщення, а замість нього вводиться свіже зовнішнє або очищене повітря.
Задачі вентиляції — забезпечення чистоти повітря та заданих мікрокліматич-них умов.
Вентиляція класифiкується:
1) по засособу переміщення повітря розрізнюють системи природньої, штучної (механічної) та змішаної вентиляції.
2) по напрямку руху повітря — підрозділяються на приточну (повітря подається у приміщення), витяжну (забруднений повітря удаляється з приміщення) та приточно — витяжну.
В залежності від місця дії вентиляція може бути загальнообмінною (використовується коли шкідливі речовини рівномірно розміщуються у робочої зоні), місцевою (- шкідливі речовин виділяються на декількох робочих місцях), локалізованою (- шкідливі речовин виділяються на робочих місцях, розташованих одне біля іншого) та комбiнованою.
Загальнообмінна вентиляція забезпечує створення необхідного мікроклімату та чистоти повітряного середовища у всьому об’ємі робочої зони. При місце-вій вентиляції шкідливі речовини виводяться (або розстворюються шляхом подачі чистого повітря) безпосередньо від місць їх створення.
По призначенню вентиляція може бути робочою (використовується при нормальному режимі роботи технологічних процесів) та аварійною (викорис-товується у випадку, якщо стався викид шкідливих речовин у наслідку аварії).
Вимоги до вентиляції:
1) кiлькiсть приточного повітря у одиницю часу повинне відповідати кiлькості витяжного повітря.
2) правильне розташування приточних та витяжних завіс. Свіже повітря подається, де концентрація шкідливих речовин менше, а удаляється, де концентрація більше.
3) вентиляція не повинна створювати перегрівання або охолодження працюю-чих.
4) вентиляція має бути пожежовибухонебезпечною.
Висновки
Ознайомившись з матеріалом ми можемо навчитися володіти певними прийомами математичної діяльності та навичками їх застосування до розв’язання практичних задач.
Виконавши головні завдання цього трейнінгу ми можемо досягти компетентності в практичні діяльності.
Ми оволоділи уміннями та навичками, необхідними для розв’язання та обчислення диференціальних рівнянь вищих порядків.
Ми вивчили класичні і сучасні методи розв’язання алгебраїчних, трансцендентних, диференціальних рівнянь та їх систем.
Ми навчились використовувати методи розв’язання задач з початковими умовами та крайових задач для звичайних диференціальних рівнянь та диференціальних рівнянь з частинними похідними при моделюванні систем.
Література
1. Ильин В.А., Позняк Э.Г., Аналитическая геометрия. Наука. М. 1978.-302 с.
2. Панков О.А., Панкова Т.Е. Вища математика.ВІРЕУ. 1998.-120с.
3. Булига К.Б., Барановська Л.В. Практикум з теорії ймовірностей та
математичної статистики. – К.: Видавництво Європейського університету, 2000
4. Чубатюк В.М. Вища математика. Навчальний посібник для студентів економічних спеціальностей навчальних закладів III та IV рівнів акредитації.- К.: ВД «Професіонал», 2006.-432 с.
5. Барковський В.В., Барковська Н.В., Математика для економістів. Вища математика.- К.: Н.А.У., 1999.- 428с.
ua-referat.com
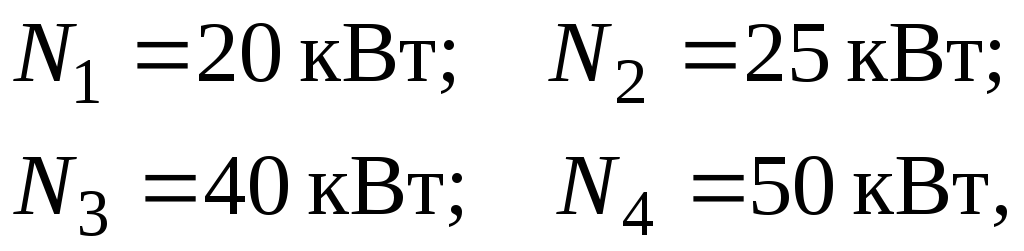
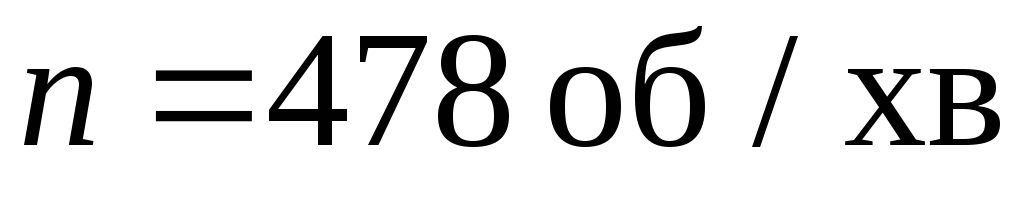 .
.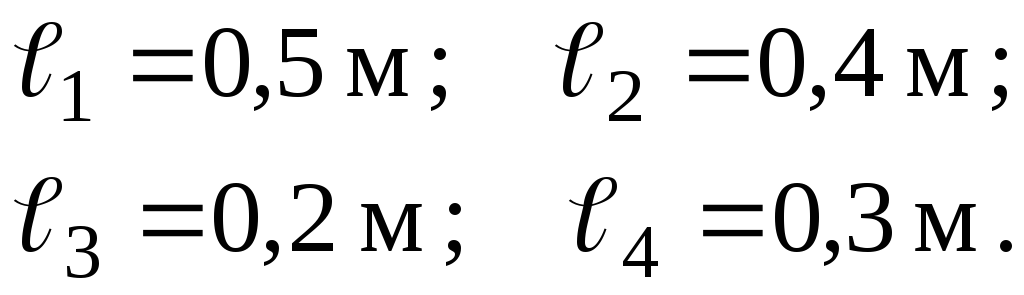
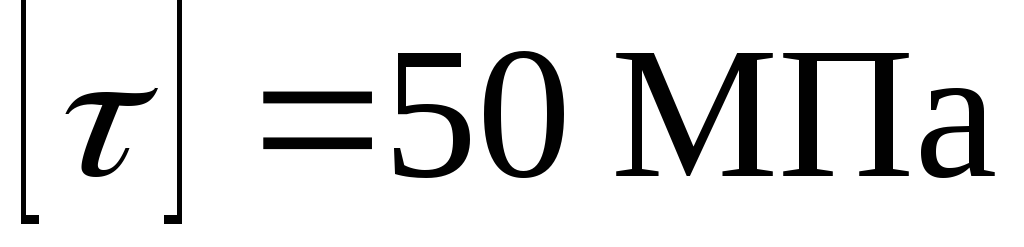 .
.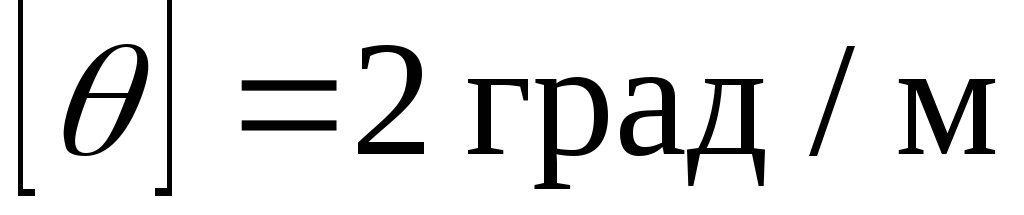 .
.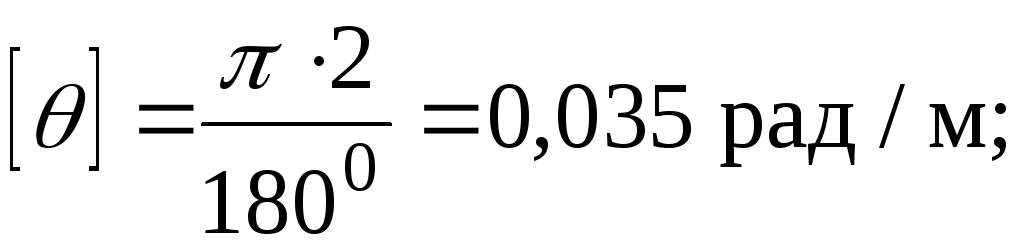
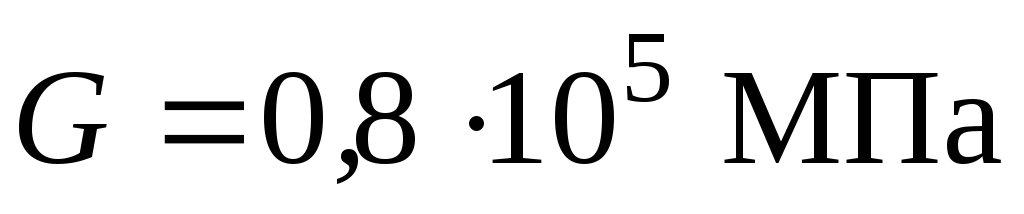 .
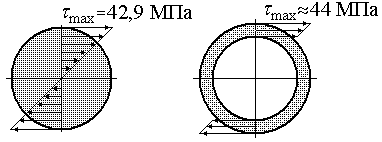
.
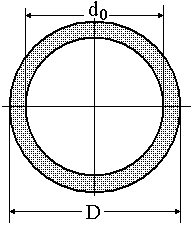
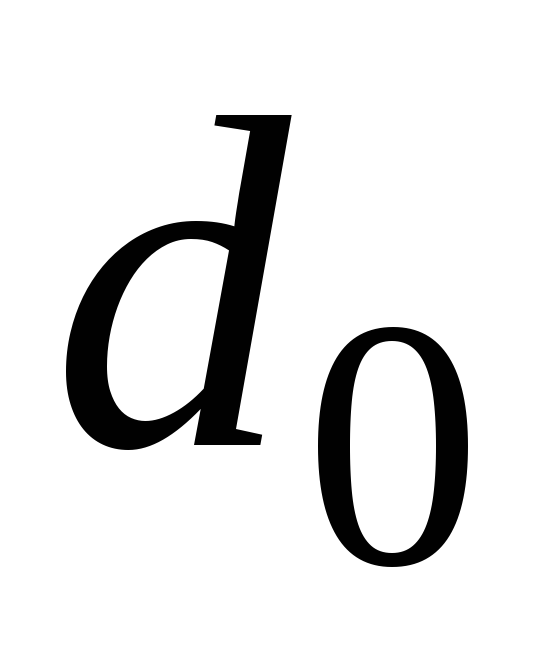 –внутрішній
діаметр;
–внутрішній
діаметр; 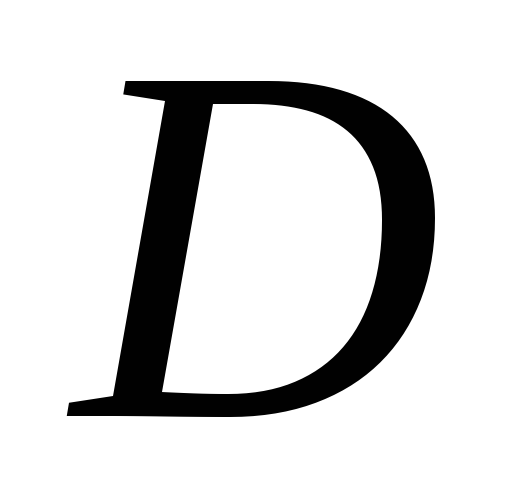 – зовнішній діаметр;
– зовнішній діаметр;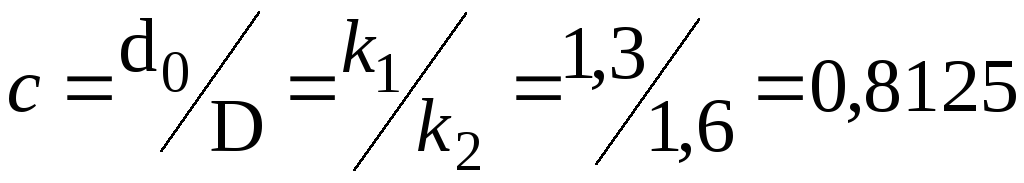 .
.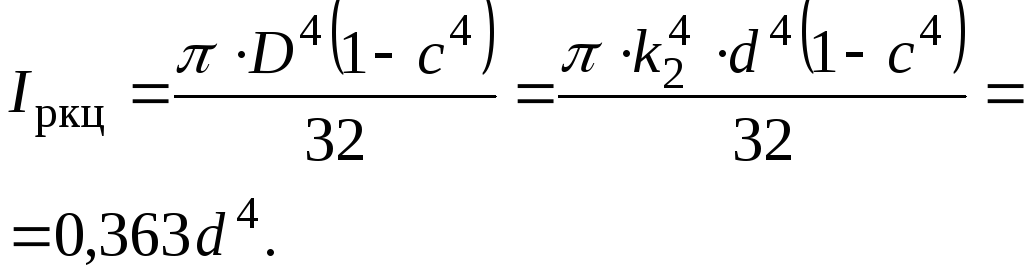
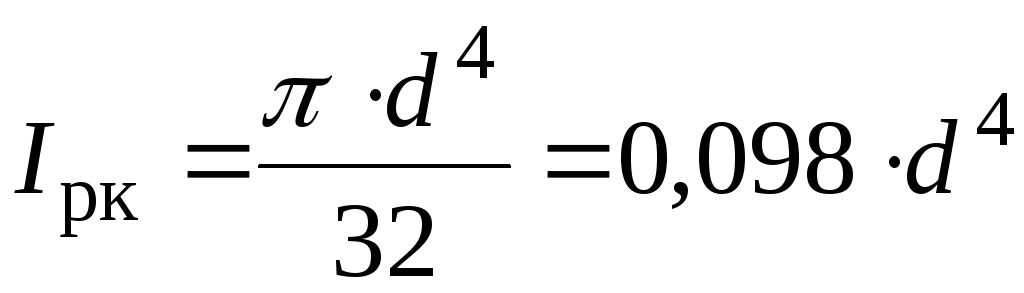 .
.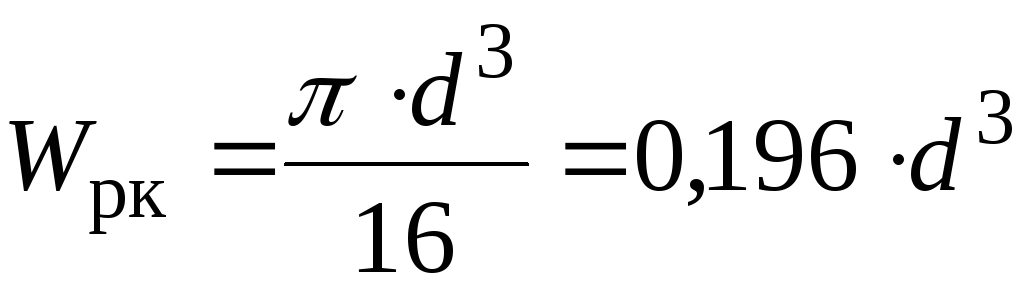 .
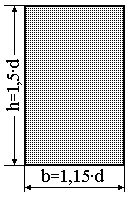
.
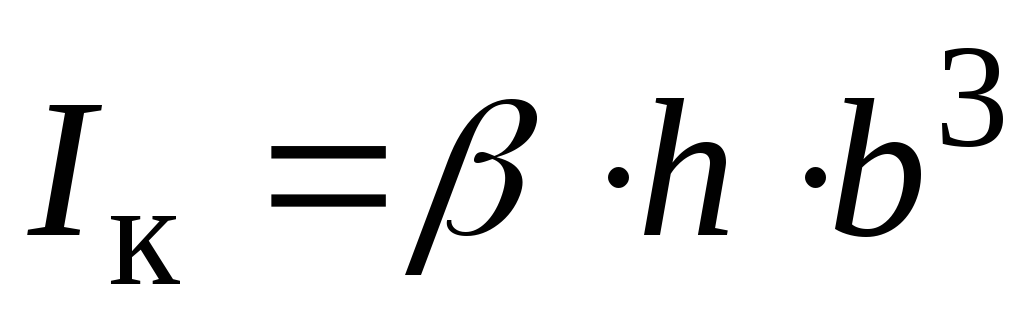 ,
,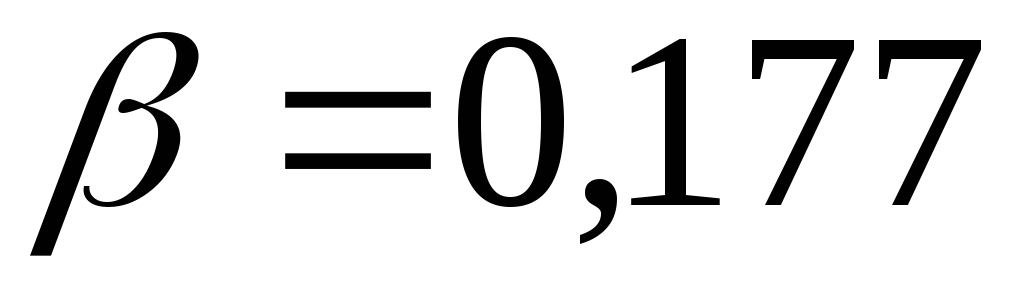 залежить
від співвідношення сторін прямокутника
залежить
від співвідношення сторін прямокутника 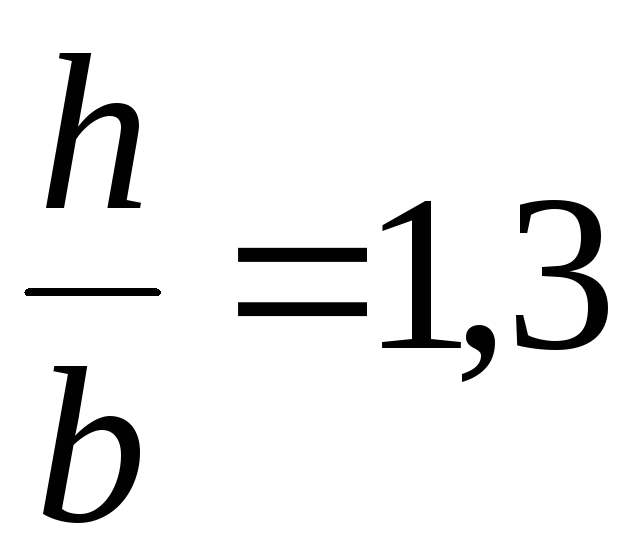 ;
(див. табл. 3.1).
;
(див. табл. 3.1).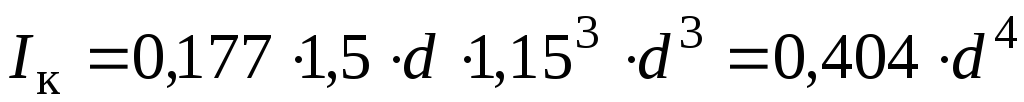 .
.
 для заданих форм поперечних перерізів
стержня з умови міцності:
для заданих форм поперечних перерізів
стержня з умови міцності: