Тетраэдр. Задачи на построение сечений в тетраэдре. Видеоурок. Геометрия 10 Класс
Тема: Параллельность прямых и плоскостей
Урок: Тетраэдр. Задачи на построение сечений в тетраэдре
Как построить тетраэдр? Возьмем произвольный треугольник АВС. Произвольную точку D, не лежащую в плоскости этого треугольника. Получим 4 треугольника. Поверхность, образованная этими 4 треугольниками, и называется тетраэдром (Рис. 1.). Внутренние точки, ограниченные этой поверхностью, также входят в состав тетраэдра.

Рис. 1. Тетраэдр АВСD
Элементы тетраэдра
А, B, C, D – вершины тетраэдра.
AB, AC, AD, BC, BD, CD — ребра тетраэдра
ABC, ABD, BDC, ADC — грани тетраэдра.
Замечание: можно принять плоскость АВС за основание тетраэдра, и тогда точка D является вершиной тетраэдра. Каждое ребро тетраэдра является пересечением двух плоскостей. Например, ребро АВ – это пересечение плоскостей АВD и АВС. Каждая вершина тетраэдра – это пересечение трех плоскостей. Вершина А лежит в плоскостях АВС, АВD, АDС. Точка А – это пересечение трех означенных плоскостей. Этот факт записывается следующим образом: А = АВС ∩ АВD ∩ АСD.
Тетраэдр определение
Итак, тетраэдр — это поверхность, образованная четырмя треугольниками.
Ребро тетраэдра — линия перечесения двух плоскостей тетраэдра.
Составьте из 6 спичек 4 равных треугольника. На плоскости решить задачу не получается. А в пространстве это сделать легко. Возьмем тетраэдр. 6 спичек – это его ребра, четыре грани тетраэдра и будут четырьмя равными треугольниками. Задача решена.
Дан тетраэдр АВСD. Точка M принадлежит ребру тетраэдра АВ, точка N принадлежит ребру тетраэдра ВD и точка Р принадлежит ребру DС (Рис. 2.). Постройте сечение тетраэдра плоскостью MNP.

Рис. 2. Рисунок к задаче 2 — Построить сечение тетраэдра плоскостью
Решение:
Рассмотрим грань тетраэдра DВС. В этой грани точки N и P принадлежат грани DВС, а значит, и тетраэдру. Но по условию точки N, P принадлежат секущей плоскости. Значит,

Рис. 3. Рисунок к задаче 2. Нахождение точки Е
Точка Е принадлежит плоскости сечения MNP, так как она лежит на прямой NР, а прямая NР целиком лежит в плоскости сечения MNP.
Также точка Е лежит в плоскости АВС, потому что она лежит на прямой ВС из плоскости АВС.
Получаем, что ЕМ – линия пересечения плоскостей АВС и MNP, так как точки Е и М лежат одновременно в двух плоскостях — АВС и MNP. Соединим точки М и Е, и продолжим прямую ЕМ до пересечения с прямой АС. Точку пересечения прямых ЕМ и АС обозначим Q.
Итак, в этом случае NPQМ — искомое сечение.

Рис. 4. Рисунок к задаче 2.Решение задачи 2
Рассмотрим теперь случай, когда NP параллельна BC. Если прямая NP параллельна какой-нибудь прямой, например, прямой ВС из плоскости АВС, то прямая NP параллельна всей плоскости АВС.
Искомая плоскость сечения проходит через прямую NP, параллельную плоскости АВС, и пересекает плоскость по прямой МQ. Значит, линия пересечения МQ параллельна прямой NP. Получаем, NPQМ — искомое сечение.
Точка М лежит на боковой грани АDВ тетраэдра АВСD. Постройте сечение тетраэдра плоскостью, которое проходит через точку М параллельно основанию АВС.

Рис. 5. Рисунок к задаче 3 Построить сечение тетраэдра плоскостью
Решение:
Секущая плоскость φ параллельна плоскости АВС по условию, значит, эта плоскость φ параллельна прямым АВ, АС, ВС.
В плоскости АВD через точку М проведем прямую PQ параллельно АВ (рис. 5). Прямая PQ лежит в плоскости АВD. Аналогично в плоскости АСD через точку Р проведем прямую РR параллельно АС. Получили точку R. Две пересекающиеся прямые PQ и РR плоскости РQR соответственно параллельны двум пересекающимся прямым АВ и АС плоскости АВС, значит, плоскости АВС и РQR параллельны. РQR – искомое сечение. Задача решена.
Дан тетраэдр АВСD. Точка М – точка внутренняя, точка грани тетраэдра АВD. N – внутренняя точка отрезка DС (Рис. 6.). Построить точку пересечения прямой NM и плоскости АВС.

Рис. 6. Рисунок к задаче 4
Решение:
Для решения построим вспомогательную плоскость DМN. Пусть прямая DМ пересекает прямую АВ в точке К (Рис. 7.). Тогда, СКD – это сечение плоскости DМN и тетраэдра. В плоскости DМN

Рис. 7. Рисунок к задаче 4. Решение задачи 4
Дан тетраэдр АВСD. М – внутренняя точка грани АВD. Р – внутренняя точка грани АВС. N – внутренняя точка ребра DС (Рис. 8.). Построить сечение тетраэдра плоскостью, проходящей через точки М, N и Р.

Рис. 8. Рисунок к задаче 5 Построить сечение тетраэдра плоскостью
Решение:
Рассмотрим первый случай, когда прямая MN не параллельна плоскости АВС. В прошлой задаче мы нашли точку пересечения прямой MN и плоскости АВС. Это точка К, она получена с помощью вспомогательной плоскости DМN, т.е. мы проводим DМ и получаем точку F. Проводим СF и на пересечении MN получаем точку К.

Рис. 9. Рисунок к задаче 5. Нахождение точки К
Проведем прямую КР. Прямая КР лежит и в плоскости сечения, и в плоскости АВС. Получаем точки Р1 и Р2. Соединяем Р1 и М и на продолжении получаем точку М1. Соединяем точку Р2 и N. В результате получаем искомое сечение
Рассмотрим второй случай, когда прямая MN параллельна плоскости АВС. Плоскость МNР проходит через прямую МN параллельную плоскости АВС и пересекает плоскость АВС по некоторой прямой Р1Р2, тогда прямая Р1Р2 параллельна данной прямой MN (Рис. 10.).

Рис. 10. Рисунок к задаче 5. Искомое сечение
Теперь проведем прямую Р1М и получим точку М1. Р1Р2NМ1 – искомое сечение.
Итак, мы рассмотрели тетраэдр, решили некоторые типовые задачи на тетраэдр. На следующем уроке мы рассмотрим параллелепипед.
Список рекомендованной литературы по теме «Тетраэдр»
1. И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М. : Мнемозина, 2008. – 288 с. : ил. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни)
2. Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений
3. Е. В. Потоскуев, Л. И. Звалич. – 6-е издание, стереотип. – М. : Дрофа, 008. – 233 с. :ил. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики
Дополнительные веб-ресурсы
1. Сечения тетраэдра (Источник).
2. Как построить сечение тетраэдра. Математика (Источник).
3. Фестиваль педагогических идей (Источник).
Сделай дома задачи по теме «Тетраэдр», как находить ребро тетраэдра, грани тетраэдра, вершины и поверхность тетраэдра
1. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М.: Мнемозина, 2008. – 288 с.: ил. Задания 18, 19, 20 стр. 50
2. Точка Е середина ребра МА тетраэдра МАВС. Постройте сечение тетраэдра плоскостью, проходящей через точки В, С и Е.
3. В тетраэдре МАВС точка М принадлежит грани АМВ, точка Р – грани ВМС, точка К – ребру АС. Постройте сечение тетраэдра плоскостью, проходящей через точки М, Р, К.
4. Какие фигуры могут получиться в результате пересечения плоскостью тетраэдра?
План-конспект урока по геометрии (10 класс) на тему: Урок геометрии в 10 классе «Построение сечений»
Урок «Построение сечений»
Сигодина Лариса Владимировна,
учитель математики
ОУ «Благовещенская муниципальная средняя образовательная школа №1»,
Благовещенского района
Цели и задачи:
Образовательные:
- организовать работу учащихся по выработке умения строить сечения тетраэдра и параллелепипеда;
- обеспечить закрепление указанного умения;
- организовать деятельность учащихся по самостоятельному применению знаний и умений;
Развивающие:
- создать условия для развития познавательной активности учащихся;
- создать условия для развития интеллектуальной, коммуникативной, рефлексивной культуры;
- создать условия для развития познавательного интереса к предмету;
Воспитательные:
- воспитывать культуру умственного труда;
- воспитывать умение работать в паре;
- воспитывать умение работы на компьютерах;
Оборудование: 10 персональных компьютеров, мультимедийный проектор, доска, мел. Урок сопровождается показом слайдов презентации «Построение сечений» ( Приложение1)
Ход урока:
- Организационный момент.
Сообщить тему урока и цели урока.
- Проверка домашнего задания.
— Давайте повторим, что называется секущей плоскостью?
— Секущая плоскость пересекает параллелепипед или тетраэдр по отрезкам или ломанной?
— Что является сечением многогранника?
— Какие могут получиться многоугольники в сечении параллелепипеда?
— Где расположены вершины многоугольника?
— Как проверить правильность построения сечения?
Слайд 2,3
Рассказать как построено сечение. Какой фигурой является (параллелограмм), доказать. Как доказать, что плоскости параллельны?
- Устная работа
1) На каком рисунке изображено сечение куба? Слайд 4
2) На каком рисунке изображено сечение тетраэдра? Слайд 5
3)Выполнить №75 по готовому чертежу.
Строим AKL,
Докажем, что OFE|| AKL (FE- средняя линия треугольника KLM,
FE|| KL, OE – средняя линия треугольника ALM, OE|| AL, две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости)
Треугольники подобны, так как их стороны пропорциональны, OE=2AL, FE=2RK, OF=2AK, k=2, S1 : S2=k2, SFOE= 24: 4=6 (см2)
- Тренировочные упражнения.
1) Построить сечение, проходящее через точки M, N, P.
2) Выполнить №87(б) у доски один ученик (не описывать ход построения)
- Самостоятельная работа.
Сейчас вам предстоит работать парами. Самостоятельно распределите роли: генератор идей, ответственный за техническое исполнение, ролями желательно меняться. До конца урока нужно выполнить 4-5 задач, для тех кто с ними справиться есть дополнительные.
Учащихся выполняют задания на компьютерах Приложение 2.
Учитель контролирует работу, дает необходимые консультации.
- Самопроверка.
Слайды 9-15
Обсудить возникшие вопросы.
- Подведение итогов
- Домашнее задание: №84, 85
.
Конспект урока на тему «Сечения» (10 класс)
Тема 2. Параллельность прямых и плоскостей в пространстве (21 час).
УРОК № 4. Аксиомы стереометрии. Взаимное расположение пр-х в простр-ве (10 ч).
Тема. Сечения.
Цели урока: формирование у учащихся умений построения сечений тетраэдра и параллелепипеда различными плоскостями; закрепление алгоритма построения сечений и отработка навыков построения сечений многогранников.
Ход урока.
Организационный момент. Проверка домашнего задания.
Актуализация опорных знаний.
1. Опрос по теории и решение задач устно.
Сформулировать аксиомы стереометрии.
Сформулировать следствия из аксиом стереометрии.
Объяснение нового материала.
Построить сечение означает начертить многоугольник в плоскости сечения, по которому эта плоскость пересекает грани многогранника.
Используем метод следов.
Следом сечения на указанной плоскости называется прямая пересечения этой плоскости с плоскостью сечения.
Основные правила построения сечений
1. Если даны (или уже построены) две точки плоскости сечения на одной грани многогранника, то след сечения в этой плоскости – прямая, проходящая через эти точки.
2. Если дана (или уже построена) прямая пересечения плоскости сечения с основанием многогранника (след на основании) и есть точка, принадлежащая определенной боковой грани, то нужно определить точку пересечения данного следа с этой боковой гранью.
3. Точку пересечения плоскости сечения с основанием можно определить как точку пересечения какой-либо прямой в плоскости сечения с ее проекцией на плоскость основания.
Алгоритм построения сечений многогранников:
а) определить грани, с которыми секущая плоскость имеет две общие точки, и провести через данные точки прямые;
б) определить грани, с которыми секущая плоскость имеет одну общую точку, построить вторую общую точку и провести через них прямую;
в) определить грани, с которыми секущая плоскость не имеет общих точек, построить две общие точки, и провести через них прямую;
г) выделить отрезки прямых, по которым секущая плоскость пересекает ребра многогранника, заштриховать полученный многоугольник.
Задача 1. Построить сечение тетраэдра плоскостью, проходящей через данные точки D, Е, K.
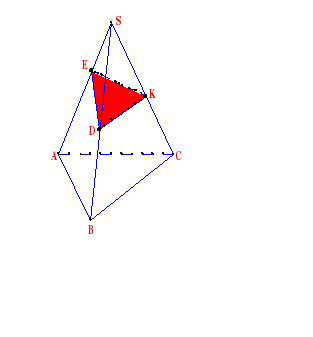
Построение:
1. DE
2. ЕК
3. DК
DЕK – искомое сечение
Задача 2. Построить сечение плоскостью, проходящей через данные точки D, Е, K.
П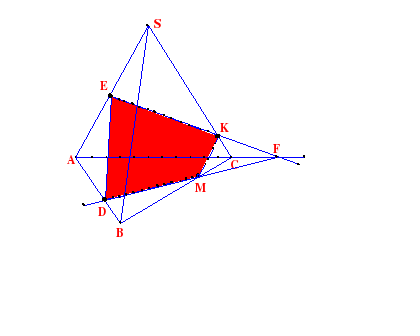 остроение:
остроение:
1. DE
2. ЕК
DК — нельзя
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
DЕKМ – искомое сечение
Задача 3. Построить сечение плоскостью, проходящей через точки
Т, Н, М, М Є АВ.
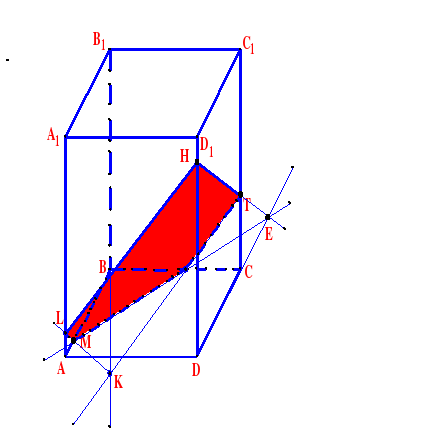
Построение:
1. НТ
2. НТ ∩ DС = E
3. ME ∩ ВС = F
4. ТF
5. ТF ∩ В1В = K
6. МK ∩ АА1= L
7. LН
НТFМL – искомое сечение
Задача 4. Построить сечение плоскостью, проходящей через данные точки Е, F, K.
П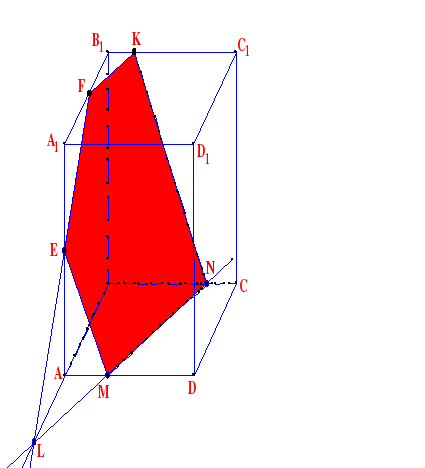 остроение:
остроение:
1. KF
2. FE
3. FE ∩ АB = L
4. LN ║ FK
5. LN ∩ AD = M
6. EM
7. KN
EFKNM – искомое сечение
Задача 5. Построить сечение плоскостью, проходящей через данные точки К, М, Р, Р Є (АВС)
П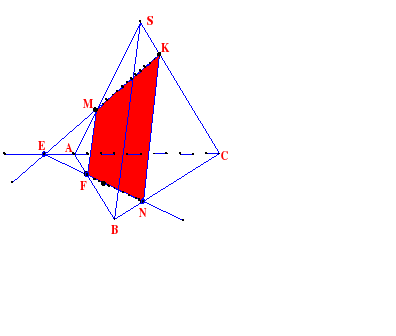 остроение:
остроение:
1. КМ
2. КМ ∩ СА = Е
3. EР
4. ЕР ∩ АВ = F
ЕР ∩ ВC = N
5. МF
6. NК
КМFN – искомое сечение
Подведение итогов урока.
Домашнее задание.
§ 21 (выучить теорию) (Уч. Бевз Математика 10).
Уч. Билянина с. 68
Задачи 1, 3, 5, 6, 7 (они с решением).
Постройте сечения на листе формата А4 (каждая задача на отдельном). Оформление как в классной работе:
Записать условие.
Выполнить чертеж (в цвете, оптимального размера).
Построение (кратко, каждый этап, на обратной стороне листа.)
Конспект урока по геометрии в 10 классе «Вычисление площади сечений многогранников»

 Лаврентьева Нина Семеновна, учитель математики
Лаврентьева Нина Семеновна, учитель математики
МБОУ «Гимназия»
г. Протвино Московской области
03.12.2013 г.
Тема урока « Вычисление площади сечений многогранников»
Цель урока: углубление, обобщение, систематизация, закрепление полученных знаний и развитие их в перспективе (нахождение площади сечений) (слайд 2)
Задачи урока:
Образовательная:
обобщить, систематизировать и закрепить полученные знания на предыдущих уроках;
проверить свои знания с помощью теста.
Развивающая:
развитие геометрической интуиции на образы, свойства, методы построения.
развитие пространственного мышления, пространственной абстракции, их общности, анализа и синтеза геометрических образов, пространственного воображения.
развитие логического мышления (владение правилами логического вывода и построения, владение разными методами геометрии).
Воспитательная:
воспитывать активность и самостоятельность, аккуратность учащихся, интерес к предмету
Знания, умения, навыки и качества, которые закрепят ученики в ходе урока:
умение пользоваться опорными знаниями, для получения новых знаний;
умение выделять существенные признаки и делать обобщения;
навыки творческого подхода к решению задач на построение сечений.
Тип урока: урок совершенствования знаний, умений и навыков.
Форма организации урока: урок-практикум.
Структура урока: (слайд 2)
1.Формирование у школьников мотивации к изучению данной темы (4 мин.)
2 Фронтальная устная работа по содержанию учебного материала всей главы (7 мин.)
3. Применение знаний в стандартной ситуации (тест с последующей проверкой) (4 мин.)
4. Решение задачи (15 мин.)
5. Самостоятельная работа (работа в парах) (10 мин.)
6.Подведение итогов урока, предварительная отметка, рефлексия (4 мин.)
7.Информация по домашнему заданию (1мин.)
Техническое оборудование урока:
компьютер,
мультимедийный проектор,
раздаточный материал.
Ход урока
Вступительная беседа. (слайды 4-5)
Учитель: Здравствуйте, ребята! Тема нашего урока «Вычисление площади сечений многогранников». Наши последние уроки были посвящены теме «Сечение многогранника». Мы изучили основные определения, познакомились с различными методами построения сечений, решали задачи на построение и конечно же анализировали свои решения и результаты. Сегодня на уроке мы будем не просто строить сечения многогранников, но и находить площади этих сечений, а также повторим, обобщим, закрепим полученные знания при решении задач.
Главная цель нашего урока в углублении, систематизации, закреплении полученных знаний и развитии их в перспективе.
Учитель: Когда то очень давно гениальный итальянский художник и выдающейся ученый Леонардо да Винчи сказал: «Те, кто влюбляются в практику без теории, уподобляются мореплавателю, садящемуся на корабль без руля и компаса и потому никогда не знающему, куда он плывет».
(слайд 5)
Это высказывание определяет первый этап нашего урока: повторение теоретического материала. Прежде чем перейти к проверке теории познакомьтесь с таблицей самоконтроля, в которой вы будете выставлять себе баллы.
Фронтальная устная работа по содержанию учебного материала всей главы (Соревнование между группами учащихся.) (Слайды 6-12)
Вопросы для фронтального опроса:
Определение многогранника и сечения многогранника.
Многогранником называется — тело, поверхность которого состоит из конечного числа плоских многоугольников.
Сечением поверхности геометрических тел называется — плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости.
Способы задания плоскости
Через три точки, по аксиоме: «Через три точки можно провести плоскость и только одну».
Через прямую и не лежащую на ней плоскость, по следствию из аксиомы: «Через прямую и не лежащую на ней точку можно провести плоскость и только одну»
Через две пересекающиеся прямые, по аксиоме: «Если две различные прямые имеют общую точку, то через них можно провести плоскость и только одну».
Через две параллельные прямые, по определению параллельных прямых: «Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются». Учитель: И так чтобы построить сечение многогранника нужно знать:
Что нужно знать для построения сечений?
Аксиомы стереометрии
Следствия из аксиом
Взаимное расположение в пространстве прямых и плоскостей.
Признак параллельности прямой и плоскости.
Признак параллельности плоскостей.
Свойство параллельных плоскостей
Методы построения сечений
грани многогранника. Прямую, по которой секущая плоскость пересекает какую-либо грань называют следом секущей плоскости)
случаях, когда почему-либо неудобно находить след секущей плоскости, например, след получается очень далеко от заданной фигуры. Используется метод параллельного проецирования).
приемы, изложенные в методе следов или методе внутреннего проектирования, а на других этапах применяются теоремы, изученные в разделе «Параллельность прямых и плоскостей»).
Виды сечений (диагональное сечение, сечение параллельное ребру или грани многогранника и другие)
Применение знаний в стандартной ситуации.
Учитель: А сейчас вы должны выполнить тест. (Слайды 14-17). Оцените свою работу.
Решение задач. (слайды 18 -21).
Учитель: Ну, а сейчас решаем задачи. А что значит решить задачу? Как научиться решать задачи? Рекомендации по этому вопросу дает Математик и педагог Дьёрдь Пойа, или Джордж Полиа (1887-1985), в своей книге «Как решать задачу». Название книги говорит само за себя — великолепная книга о решение математических задач. Стоит заметить, что не только математических. Я приведу слова из этой книги : «Умение решать задачи – практическое искусство, подобное плаванию, или катанию на лыжах … : научиться этому можно лишь подражая избранным образцам и постоянно тренируясь…» .
Вам нужно решить задачу: ( один ученик на доске строит сечение, другой ученик – решает задачу.)
Постройте сечение куба A…D1 ребро которого равно 2, проходящее через середины ребер А1В1, В1С1 и СС1. Найдите его площадь.
Решение: Сечение – правильный шестиугольник MNKPQR.Проведем RK, этот отрезок делит шестиугольник на две равнобедренные трапеции. Значит площадь сечения равна 2∙ S трапеции RМNK. Основания трапеции равны  и
и  . Высота трапеции равна
. Высота трапеции равна . Тогда площадь трапеции равна
. Тогда площадь трапеции равна  ∙
∙ = 3
= 3 . Ответ: 3
. Ответ: 3 .
.
Самостоятельная работа. (слайды 22-23).
Учитель: А сейчас ребята настало время для самостоятельной работы. Вы должны решить одну из двух задач (выбираете сами). Эти задачи были представлены в диагностических работах ЕГЭ в 2012 – 2013 учебном году. (Работа в парах).
Задача. (ЕГЭ 2012г.) Постройте сечение пирамиды SABCD, все ребра которой равны 4, проходящее через вершины B, D и середину ребра SC.
Найдите его площадь. (4 балла)
Задача. (ЕГЭ 2013г.) Постройте сечение правильной треугольной призмы ABCA1B1C1, сторона основания которой равны 6, а боковые ребра равны 4, проходящее через вершины A, B и середину ребра A1C1.
Найдите его площадь. (5 баллов)
Подведение итогов урока, предварительная отметка, рефлексия. (слайды 24-25).
Рефлексия.
Что мы делали на уроке?
Что запомнилось?
Где пригодятся вам эти знания?
Чему научились? Что повторили?
Какой этап урока вам понравился больше всего?
Какой вызвал наибольшее затруднение?
Чем вы можете оказать помощь?
В чем чувствуешь затруднение?
Оцените свою работу.
Предварительная отметка за урок ( из оценочного контрольного листа).
Оценка «3» — 58%-75%
Оценка «4» — 76%-88%
Оценка «5» — 94%-100%
Информация по домашнему заданию. (слайд 26).
Составить две задачи на вычисление площади сечений многогранников с использованием полученных знаний.
Учитель: Вы поставили себе оценку за урок. Окончательная оценка будет выставлена с учетом самостоятельной работы. Закончить урок я хочу опять словами Д. Пойа «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их».Спасибо за урок. (слайд 27).
Конспект урока математики. Раздел: геометрия. 10 класс. Тема: Построение сечений

Геометрия. 10 класс.
«Построение сечений».
Автор: учитель математики
МКОУ Брединской СОШ №2
Смирнова Галина Александровна.
Бреды. 2013.

ЦЕЛИ УРОКА:
- Повторить теоретический материал: секущая плоскость, пересечение плоскостей, пересечение плоскости и многоугольника, пересечение двух параллельных плоскостей третьей плоскостью, тетраэдр, параллелепипед. Формирование и закрепление навыков решения задач на построение сечений тетраэдра и параллелепипеда.
- Развитие логического мышления, пространственного воображения, умения применять изученный материал в нестандартных ситуациях. Развитие грамотной математической речи через теоретическое обоснование своих выводов. Повышение интереса к изучаемому предмету.
- Воспитание ответственного отношения к выполнению заданий, подготовке к уроку. Воспитание уважения к своим одноклассникам через умение слушать и слышать отвечающих, оказание помощи в трудных ситуациях.

Устно. Как пересекаются две плоскости?
(по прямой)

Построение:
Выбрать верный ход
МЕ
MF
EF

ВЕРНЫЙ ХОД!
Прямая EF – линия пересечения
плоскостей (EMF) и ,
пересекает плоскость в точке А.
А
А и М лежат в одной плоскости,
прямая АМ — линия пересечения плоскостей (EMF) и .

Как пересекаются плоскость и грань многогранника?
Помни!
Отрезок (концы которого лежат на одной грани) – линия пересечения плоскости с гранью многогранника.

Решение задач.
Постройте:
№ 1
P
С 1
А 1
а) MN (ABC).
б) MN (A 1 B 1 C 1 ).
в) KN (ABC).
г) (АВС) (MNK).
д) (АA 1 B 1 ) (MNK).
N
В 1
М
S
F
А
С
K
В

Сечения тетраэдра – треугольники или четырехугольники.

Сечения параллелепипеда – треугольники, четырехугольники, пятиугольники, шестиугольники.

Наши действия при построении сечения многогранника плоскостью.
- Соединим точки, принадлежащие одной грани.
- Дополним до прямых те ребра многогранника , которые при продолжении пересекутся с секущей плоскостью.
- Соединим точки, принадлежащие одной плоскости.
- Получим точки пересечения секущей плоскости и рёбер многогранника.
- Эти точки и будут вершинами многоугольника, являющегося искомым сечением.
Помним!
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

А
Искомое сечение!

Решение задач.
№ 2
На ребрах АВ, ВД, СД тетраэдра АВСД даны точки L, M, N такие, что MN и ВС не параллельны. Постройте сечение тетраэдра плоскостью LMN.
N
М
В
L
А

Решение задач.
№ 3
Построить сечение тетраэдра плоскостью, проходящей через данные точки M, N, K.
N
К
М

Решение задач.
№ 4
Построить сечение параллелепипеда плоскостью, проходящей через точки Р, К, М, где М∈ВС.
В 1
C 1
- ХКРТМ – искомое сечение
P
К
А 1
D 1
Т
М
S
С
В
D
А
Х

Решение задач.
№ 5
С 1
В 1
D 1
А 1
P
E
C
В
F
А
D

Решение задач.
Построить сечение куба плоскостью, проходящей через три данные точки F, K, P, являющиеся серединами его ребер.
№ 6
К
KP
Выбери:
FK
или
N
F и К принадлежат разным граням. Назад.
FM KP
Подсказка!
FM…
P
АВ КР = Е
Прямая МЕ
F
ВС = S
Е
В
А
Соединим
Р и S
Подсказка!
KN SM
К…
S
N и F.
Соединим
C
М
MFNKPS – искомое сечение.

Решение задач.
№ 7
C 1
В 1
А 1
D 1
N
В
С
М
А
D

Решение задач.
№ 8

Самостоятельная работа.
Постройте сечение многогранников плоскостью, проходящей через указанные точки.

Точки M и E принадлежат разным плоскостям,
соединять нельзя.
НАЗАД

Точки M и F принадлежат разным плоскостям,
соединять нельзя.
НАЗАД

Назад.
Есть параллельные грани.
Домашнее задание.
- Повторить теоретический материал п. 12 – 14.
Итоги урока.
- Секущая плоскость – это…
- Пересечением плоскостей является …
- Плоскость пересекает грань многогранника по …
- Сечением тетраэдра являются …
- Сечением параллелепипеда могут быть …
- Секущая плоскость пересекает параллельные грани по …
Что понравилось на уроке? Что осталось непонятым? На какие моменты выделить время на следующем уроке?
Литература:
- Геометрия 10 – 11. учебник для общеобразовательных учреждений. Авторы: Л.С.Атанасян и др. Москва, Просвещение, 2009г.
- Геометрия 10класс. Поурочные планы. Автор – составитель Г.И.Ковалева. Волгоград, изд. «Учитель» 2003г.
- Поурочные разработки по геометрии 10 класс. дифференцированный подход. Автор: В.А.Яровенко. Москва, «Вако», 2010г.
- Геометрия. 10класс. Дидактические материалы. Автор: Б.Г.Зив. Москва, Просвещение, 2009г.
- Изучение геометрии в 10 – 11 классах. Авторы: С.М. Саакян и В.Ф.Бутузов. Москва, Просвещение, 2010г.
- Геометрия 10. рабочая тетрадь. Авторы: Ю.А.Глазков, В.Ф.Бутузов. Москва, Просвещение, 2010г.
План-конспект урока по геометрии (10 класс) на тему: Задачи на построение сечений. 10-й класс
Задачи на построение сечений. 10-й класс
Цели урока:
- Образовательные:дальнейшее формирование у учащихся умений построения сечений тетраэдра и параллелепипеда различными плоскостями; закрепление алгоритма построения сечений и отработка навыков построения сечений многогранников;
- Воспитательные: воспитание чувства взаимопомощи, умения работать индивидуально над поставленными задачами, воспитание интереса к предмету и потребности в приобретении знаний;
- Развивающие: развитие у учащихся пространственного воображения, развитие графической культуры и математической речи.
Задачи урока: научиться строить сечения тетраэдра и параллелепипеда различными плоскостями.
Тип урока: урок формирования и совершенствования знаний.
Формы организации учебной деятельности: фронтальная, работа в парах, индивидуальная.
Техническое обеспечение урока: мультимедийный проектор, модели многогранников.
План урока:
1. Организационный момент.
2. Актуализация опорных знаний.
3. Изучение нового материала.
4. Закрепление изученного материала.
5. Подведение итогов урока.
6. Домашнее задание.
ХОД ЗАНЯТИЯ
1. Организационный момент
Сообщение темы, цели и задач урока учащимся. Выяснить были ли трудности с выполнением домашней работы.
2. Актуализация опорных знаний
Устная фронтальная работа по вопросам теории данной темы, с целью актуализации знаний учащихся. Повторение изученного материала: аксиом стереометрии, следствий из аксиом, способов задания плоскостей, терминов и определений, связанных с тетраэдром и параллелепипедом.
Вопросы:
1) Какие многогранники вы знаете? Назовите, покажите их модели.
2) Дайте определение тетраэдра.
3) Назовите элементы тетраэдра, показывая их на модели.
4) Дайте определение параллелепипеда.
5) Назовите элементы параллелепипеда, показывая их на модели.
6) Сформулируйте свойства, которыми обладает параллелепипед.
7) Сколько необходимо точек, чтобы провести прямую на плоскости?
8) Какая фигура получается при пересечении двух плоскостей?
8) Сформулируйте аксиомы стереометрии о взаимном расположении точек, прямых и плоскостей в пространстве.
9) Сформулируйте свойство параллельных плоскостей.
Демонстрация иллюстраций аксиом стереометрии и свойств параллельных плоскостей в презентации к уроку. (Слайды 2, 3, 4)
3. Изучение нового материала
1) Определение секущей плоскости
Секущей плоскостью многогранника называют такую плоскость, по обе стороны от которой имеются точки данного многогранника.
2) Сечения тетраэдра и параллелепипеда
Так как тетраэдр имеет четыре грани, то его сечениями могут быть треугольники и четырехугольники. Параллелепипед имеет шесть граней, поэтому его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники.
Демонстрация сечений тетраэдра и параллелепипеда. (Слайд 5)
3) Свойство параллельных плоскостей: если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны, сформулировать следующим образом: если секущая плоскость пересекает две противоположные грани по каким-то отрезкам, то эти отрезки параллельны.
4) Алгоритм построения сечений многогранников:
а) определить грани, с которыми секущая плоскость имеет две общие точки, и провести через данные точки прямые;
б) определить грани, с которыми секущая плоскость имеет одну общую точку, построить вторую общую точку и провести через них прямую;
в) определить грани, с которыми секущая плоскость не имеет общих точек, построить две общие точки, и провести через них прямую;
г) выделить отрезки прямых, по которым секущая плоскость пересекает ребра многогранника, заштриховать полученный многоугольник.
5) Примеры построения сечений тетраэдра и параллелепипеда
Демонстрация презентации с решениями задач №1 и №2, где учитель подробно объясняет каждый пункт построения сечений. (Слайд 6. Слайд 7)
Задача №1. Построить сечение тетраэдра SABC плоскостью, проходящей через точки D, E, К, где DAB, ESA, KSС.
Задача №2. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки Р, К, М, где PD1C1, KA1D1, МВС.
4. Закрепление изученного материала
1) Устная работа
Учащимся предлагается фронтально решить задачу №3, представленную в презентации. На экране в каждом пункте построения сечения появляется несколько вариантов действий, только один из них правильный, если выбран неверный вариант – с помощью гиперссылки возврат назад. (Слайды 8-27).
Задача №3. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки Т, Н, М, где ТСС1, НDD1, МАВ.
2) Решение задач на построение сечений
Для решения задач №4, №5, №6 и №7 чертежи тетраэдра и параллелепипеда подготовлены заранее на отдельных листах.
Один учащийся решает задачу №4 с помощью мультимедийного проектора, комментируя и объясняя последовательность построения сечения, а все остальные вместе с ним строят сечение на готовых чертежах.(Слайд 28)
Задача №4. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через данные точки Е, F, K, где ЕАА1, FА1B1, KB1C1.
Задачи №5 и №6 учащиеся выполняют самостоятельно в парах на готовых чертежах, проверка построения сечений и обсуждение действий осуществляется с помощью мультимедийного проектора. (Слайды 29, 30)
Задача №5.Построить сечение тетраэдра SABC плоскостью, проходящей через данные точки К, М, Р, где КSС, МSА, РАВС.
Задача №6. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки К, L, М, где КB1C1, L АА1, МAD .
3) Самостоятельная работа на построение сечения
Учащиеся самостоятельно выполняют задачу №7, верно выполнившие задания получают оценки.
Задача №7. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через данные точки F, K, L, где FAD, K D1C1, L СС1. (Слайд 31)
Правильность построения сечения в задаче №7 осуществляется с помощью мультимедийного проектора. (Слайд 32)
5. Подведение итогов урока
Повторение алгоритма построения сечений. Оценивание работы учащихся.
Выставить и прокомментировать оценки учащихся. Отметить, с чем учащиеся справились, успешно, а на что нужно еще обратить внимание.
6. Домашнее задание
п.14. №71(а, б), №72 (а), № 81(а, б)
Зачет по геометрии на тему «Сечения» 10 класс
Зачет по теме: Построение сечений. 10 класс Ф.И.______________________________________
Вариант-1
Задание 1. Построить сечение тетраэдра плоскостью, проходящей через данные точки


Задание 2. Построить сечение параллелепипеда плоскостью, проходящей через заданные точки.

Зачет по теме: Построение сечений. 10 класс Ф.И.______________________________________
Вариант-2
Задание 1. Построить сечение тетраэдра плоскостью, проходящей через данные точки

Задание 2. Построить сечение параллелепипеда плоскостью, проходящей через заданные точки.

Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построить сечение, проходящее через точки M, N, L.

Задание3.
Построить сечение плоскостью MNP. (Подсказка: вспомните решение домашних задач и примените их для построения).

3. Тетраэдр.
Вариант 2
Задание1 .
Построить сечение плоскостью, проходящей через точку М, параллельно основанию АВС.

Задание 2. Построить сечение по заданным точкам

3. Параллелепипед и его свойства
Контрольная работа по теме: Тетраэдр и параллелепипед. Построение сечений. 10 класс
вариант
Дан параллелепипед АВСDA1B1C1D1 Постройте сечение этого параллелепипеда плоскостью, проходящей через середину ребра АВ и параллельной плоскости АСС1.
Построить сечение по заданным точкам

М
Дано: МА1=4см, В1 В2 =9см, А1 А2 =МВ1 Найти: МА2, МВ2
2-вариант
Дан тетраэдр АВСD. Точка М — середина ребра СD, точка К – середина ребра АD. Постройте сечение тетраэдра плоскостью, содержащей точку К и параллельной плоскости АМВ.
Построить сечение по заданным точкам.

О
Дано: А1А2=2ОА1=10см, ОВ1 =7см, А1 А2 =МВ1 Найти: ОА2, ОВ2
Зачет ик р
Ответы в-1













Ответы к листу № 1


















Ответы к листу № 2














